【全国市级联考word】河南省新乡市2017届高三第三次模拟测试理数试题
2017年5月2017届高三第三次全国大联考(新课标Ⅲ卷)理数卷(参考答案及评分标准)

12017年第三次全国大联考【新课标III 卷】理科数学·参考答案13.3 14.590490 15.12 16.2sin 26x ⎛⎫- ⎪⎝⎭17.【解析】(Ⅰ)由cos cos 2a B b A +=,根据余弦定理,得222222222a c b b c a a b ac bc+-+-⋅+⋅=,整理,得2c =.………………2分由()cos 1cos cA b C =-,根据正弦定理,得()sin cos sin 1cos C A B C =-,即sin sin cos sin cos B C A B C =+,又sin B =()sin sin cos cos sin A C A C A C +=+,………4分sin cos sin cos B C A C =,故cos 0C =或sin sin A B =.………………5分当cos 0C =时,2C π=,故ABC △为直角三角形; 当sin sin A B =时,A B =,故ABC △为等腰三角形.………………7分(Ⅱ)因为13sin cos 226x x x x x ⎫π⎛⎫-=-=-⎪ ⎪⎪⎝⎭⎭,所以6C π=.………………8分 由(Ⅰ)知2c =,A B =,则a b =,………………9分 所以由余弦定理,得22242cos 6a a a π=+-,解得28a =+,………………10分 所以ABC ∆的面积21sin 226S a π==………………12分18.【解析】(Ⅰ)由题意,得参加跑步类的有778042013⨯=人,………………1分 所以420180240m =-=,78042018012060n =---=.………………3分 根据分层抽样法知,抽取的13人中参加200米的学生人数有180133780⨯=人.………………5分2(Ⅱ)由题意,得抽取的13人中参加400米的学生人数有240134780⨯=,参加跳绳的学生人数有3人,所以X 的所有可能取值为1、2、3、4,………………6分()134347C C 41C 35P X ===,()224347C C 182C 35P X ===,()314347C C 123C 35P X ===,()4447C 14C 35P X ===,………………9分所以离散型随机变量X 的分布列为:X 1 2 3 4P435 1835 1235 135所以41812116()1234353535357E X =⨯+⨯+⨯+⨯=.………………12分 19.【解析】(Ⅰ)如图,连接AC 交BD 于点M ,连接MH .∵AFBG DE ,BG DE =,AF ⊥平面ABCD ,∴四边形BDEG 为矩形,………………1分又∵H 为EG 中点,∴MHBGAF ,MH BG =,………………2分又∵AF ⊥平面ABCD ,∴MH ⊥平面ABCD ,∴MH ⊥BD .………………3分 在正方形ABCD 中,BD AC ⊥,且ACMH M =,∴BD ⊥平面CMH ,………………4分又CH ⊂平面CMH ,∴BD CH ⊥.………………5分(Ⅱ)由题意,以D 为坐标原点,以,,DA DC DE 分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,且设1AB AF BG DE ====,………………6分则()0,0,1E ,()1,0,1F ,()1,1,1G ,()0,1,0C ,()1,0,0EF =,()0,1,1EC =-,()1,1,0EG =. …………………………………………………………………7分 设()1111,,x y z =n 为平面FCE 的一个法向量,则由110EF EC ⎧=⎪⎨=⎪⎩n n ,得11100x y z =⎧⎨-=⎩,取11y =,得()10,1,1=n .………………9分3设()2222,,x y z =n 为平面GCE 的一个法向量,则由2200EG EC ⎧=⎪⎨=⎪⎩n n ,得222200x y y z +=⎧⎨-=⎩,取21y =,得()21,1,1=-n ,………………11分∴1212126cos ,||||323⋅===⋅⨯n n n n n n , ∴二面角F CE G --的余弦值为6.………………12分20.【解析】(Ⅰ)由题意,得63c a = ①,且12||2F F c =,21||b PF a=,则212146||||2b F F PF c a ⋅=⋅= ②.………………2分由①②联立,并结合222a b c =+,解得26a =,22b =,所以椭圆C 的方程为22162x y +=.………………4分 (Ⅱ)当直线m 与x 轴不垂直时,设直线m 的方程为()()20y k x k =-≠,代入椭圆C 的方程22162x y +=,得()222213121260k x k x k +-+-=.………………5分 设()11,A x y 、()22,B x y ,所以21221213k x x k+=+,212212613k x x k -=+.………………6分 根据题意,假设在x 轴上存在一个定点()0,0M x ,使得MA MB ⋅的值为定值, 则()()()()101202102012,,MA MB x x y x x y x x x x y y ⋅=-⋅-=--+()()()()()()222002222120120231210612413x x k x k x x k x x x k x k-++-=+-++++=+.…………7分要使上式为定值,即与k 无关,则()220003121036x x x -+=-,解得073x =,4此时,20569MA MB x ⋅=-=-,………………8分 所以在x 轴上存在定点7,03M ⎛⎫⎪⎝⎭,使得MA MB ⋅为定值,且073x =,定值为59-.……………9分当直线m 与x 轴垂直时,将2x =代入椭圆方程可求得出,A B 的坐标,不妨设,2,A B ⎛⎛ ⎝⎭⎝⎭,则161,,,33MA MB ⎛⎫⎛=-=- ⎪ ⎪ ⎝⎭⎝⎭∴115()()339MA MB ⋅=-⨯--=-.…………11分 综上可知,在x 轴上存在定点7,03M ⎛⎫⎪⎝⎭,使得MA MB ⋅为定值,且073x =,定值为59-.……12分21.【解析】(Ⅰ)函数()f x 的定义域为()1+∞-,,()()()()2331212111x a af x x x x +-'=+++-=,………………2分 当0a ≤时,()0f x '≥,函数()f x 在()1+∞-,上单调递增;……………3分 当0a >时,若1x ≥,则()0f x '≥,函数()f x 在1,)+∞上单调递增;若11x -<<,则()0f x '<,函数()f x 在(1)-上单调递减.……………4分综上所述,当0a ≤时,函数()f x 在()1+∞-,上单调递增;当0a >时,函数()f x 在区间()1-上单调递减,在)1,+∞上单调递增.………………5分(Ⅱ)22()323()3g x x x x x '=-=-,1,23x ⎡⎤∈⎢⎥⎣⎦,可见,当2,23x ⎡⎤∈⎢⎥⎣⎦时,()0g x '≥,()g x 在2,23⎡⎤⎢⎥⎣⎦上单调递增,当12,33x ⎡⎤∈⎢⎥⎣⎦时,()0g x '≤,()g x 在12,33⎡⎤⎢⎥⎣⎦上单调递减,………………7分而()1224327g g ⎛⎫=-<= ⎪⎝⎭,所以,()g x 在1,23⎡⎤⎢⎥⎣⎦上的最大值为4,………………8分 依题意,只需当12,13x ⎡⎤∈-⎢⎥⎣⎦时,()()11134x f x ++≥恒成立, 即()()1111x f x +≥,即()()1ln 111a x x x +++≥+在2,13⎡⎤-⎢⎥⎣⎦上恒成立,5亦即()()()211ln 1a x x x ≥+-++在2,13⎡⎤-⎢⎥⎣⎦上恒成立.………………9分 令()()()2()11ln 1h x x x x =+-++2,13x ⎛⎫⎡⎤∈- ⎪⎢⎥⎣⎦⎝⎭,则()()()21ln 1h x x x x '=--++,………9分显然(0)0h '=, 当2,03x ⎡⎫∈-⎪⎢⎣⎭时, 0x ->,()()21ln 10x x ++<,()0h x '>,即()h x 在2,03⎡⎫-⎪⎢⎣⎭上单调递增;………………10分当(]0,1x ∈时,0x -<,()()21ln 10x x ++>,()0h x '<,即()h x 在区间(]0,1上单调递减; 所以,当0x =时,函数()h x 取得最大值(0)1h =,………………112分 故1a ≥,即实数a 的取值范围是[)1,+∞.………………12分请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-4:坐标系与参数方程【解析】(Ⅰ)消去参数t ,得直线l 的普通方程为10x y -+=,斜率为1, 所以直线l '的斜率为1-.………………1分因为圆C 的极坐标方程可化为24cos 2sin 0m ρρθρθ--+=,所以将222,cos ,sin x y x y ρρθρθ=+==代入上述方程得圆C 的直角坐标方程为22420x y x y m +--+=,则配方,得()()22215x y m -+-=-,其圆心为()2,1C ,半径为)5m <.………………3分由题意,知直线l '经过圆心()2,1C ,所以直线l '的方程为()12y x -=--,即30x y +-=,所以由cos ,sin x y ρθρθ==,得直线l '的极坐标方程为()cos sin 3ρθθ+=.………………5分(Ⅱ)因为||AB =C 到直线l)5m =<.)5m =<,解得1m =.………………7分 (Ⅲ)当所求切线的斜率存在时,设切线方程为4(4)y k x -=-,即440kx y k --+=.2=,解得512k=,所以所求切线的方程为512280x y-+=;当所求切线的斜率不存在时,切线方程为4x=.………………9分综上,所求切线的方程为4x=或512280x y-+=.………………10分23.(本小题满分10分)选修4-5:不等式选讲【解析】(Ⅰ)设()222f x x x=+--,则()4,13,124,2x xf x x xx x--<-⎧⎪=-≤<⎨⎪+≥⎩,………………1分当1x<-时,由42x-->,得6x<-,6x<-∴;………………2分当12x-≤<时,由32x>,得23x>,223x<<∴;………………3分当2x≥时,由42x+>,得2x>-,2x≥∴.………………4分综上所述,集合M为2|63x x x⎧⎫><-⎨⎬⎩⎭或.………………5分(Ⅱ)由(Ⅰ)知1t=,则()()()1111a b c t---==.因为1,1,1a b c>>>,所以10,10,10a b c->->->,………………6分则()110a a=-+≥>,(当且仅当2a=时等号成立)……………7分()110b b=-+≥>,(当且仅当2b=时等号成立)………………8分()110c c=-+≥>,(当且仅当2c=时等号成立)………………9分则8abc≥≥(当且仅当2a b c===时等号成立),即8abc≥.………………10分67。
2020届河南省新乡市2017级高三三模考试数学(理)试卷参考答案

*$!$%5&!!&'5*'!1}~*+HnQ6* 槡!,5# * 槡!$!
!#!.!5678,9K.ex.;yD[\,9gze{g;./|l!
<($$%7$$%+h$''!1!1( e'*$ +0!!7$$%*1$!"$*=5'!>=5$*$#
%&$
$'
'! 1
!1(
gh$%
#-*%-*#*#-%*!#$:&'+#%-
+ij%
! #
8#8#8槡#'*槡'!
W+#%- +klm+mn%0ol,0#,0,bi#%-!pm0 +qr-1ol
)1!$%,0 ]a%)--1 +[0&')1-,0&')1,bi #%-&'st
u)%#%-
+vj2)%#%-
@
!L &*$%=5$$$'
'!1!1(
@
!
8$$%*$%=5$$!#
89$$%*
$#,=$5#$%!!
<*$$%*$#,=5$%!$''!1!1(!*$!%*$!
>9$''!1!!(:!89$$%%$!8$$%&9$''!!1(:!89$$%&$!8$$%!
!"#$%&'(%)*+,-
./0,1234
!!)!5678,9:.;<=>?,9>?@5AB! !"*!!%,++&""*!!,%++*%+#"*+!
【河南省新乡市】2017届高三第三次模拟测试数学(理科)试卷-答案

答案
一、选择题
1~5.ADBBC6~10.CDDAA11~12.CB
二、填空题
13.
14.18
15.
16.
三、解答题
17.解:(Ⅰ)由 得 , .
, .
由正弦定理得, ,则 .
(Ⅱ) , , .
由 得 .取 中点D,在 中, ,
,即BC边上的中线长为 .
18.(Ⅰ)证明:在矩形 中,连接 和 交于点 ,连接 ,则 是 的中点,由于 是 的中点,所以 是 的中位线,则
又 平面 , 平面 ,
所以 平面 .
又 ,同理得 平面 .
因为 ,所以平面 平面 .
(Ⅱ)分别以 , , 所在的直线为 轴, 轴, 轴建立如图所示的空间直角坐标系.
设 ,则 , ,故 , , , ,
故曲线M的参数方程为 .(k为参数,且 ).
(Ⅱ)由 ,得 , .
将 代入 整理得 ,
故直线OA与直线OB的斜率之和为4.
23.解:(Ⅰ)由 得 ,即 ,
而不等式 的解集为 ,
则 是方程 的解,解得 ( 舍去).
(Ⅱ) , 不等式 对 恒成立等价于
不等式 对 恒成立.
设 ,
则 .
, , .
所以 , , , ,
设平面 的一个法向量为 ,则有 ,即
令 ,则 , ,故 .
同理,可得平面 的一个法向量 .
所以 ,即二面角 的余弦值的绝对值为 .
19.解:(Ⅰ)
甲班
乙班
总计
成绩优良
9
16
25
成绩不优良Βιβλιοθήκη 11415总计
20
20
河南省新乡市2017-2018届高考第三次模拟测试数学(理)试题含答案

新乡市高三第三次模拟测试数学(理科) 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集{}{}{}6,5,5,4,3,8122==-≤∈=B C A x x Z x U u ,则B A =( ) A .{}6,5 B .{}4,3 C .{}3,2 D .{}6,5,4 2.已知复数21,z z 在复平面内对应的点分别为)1,0(),1,2(--,则=+221z z z ( ) A .i 22+ B .i 22- C .i +-2 D .i --23.已知R 上的奇函数)(x f 满足:当0 x 时,)1(log )(2x x f -=,则=))1((f f ( ) A .-1 B .-2 C .1 D .24.某中学有高中生3000人,初中生2000人,男、女生所占的比例如下图所示.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n 的样本,已知从高中生中抽取女生21人,则从初中生中抽取的男生人数是( )A .12B .15 C.20 D .215.已知等差数列{}n a 中,2017,320171010==S a ,则=2018S ( ) A .2018 B .-2018 C.-4036 D .40366.已知实数y x ,满足⎪⎩⎪⎨⎧≥+-≤-+≥++02074024y x y x y x ,则y x z +-=3的最大值与最小值之和为( )A .-7B .-2 C. -1 D .6 7.将函数21sin )(2-=x x f 的图像向右平移6π个单位长度后,再将图像上各点的纵坐标伸长到原来的2倍,得到函数)(x g y =的图像,则=⎪⎭⎫⎝⎛65πgA .21-B .21C.23- D .238.我国古代数学著作《九章算术》有如下问题:“今有三人共车,二车空;二人共车,九人步.问人与车各几何?”意思是:今有3人坐一辆车,有2辆车是空的;2人坐一辆车,有9个人需要步行.问人与车各多少?下图是该问题中求人数的程序框图,执行该程序框图,则输出S 的值为( )A .31B .33 C.35 D .399.下图是某几何体的三视图,则此几何体的表面积为( )A .23224++B .434+ C.23422++ D .428+10.已知三棱锥ABC P -中,侧面⊥PAC 底面ABC ,2,10,4,90=====∠PC PA AC AB BAC,则三棱锥ABC P -外接球的体积为( )A .π28B .π36 C.π48 D .π7211.已知双曲线()0,01:2222 b a by a x C =-的离心率332=e ,对称中心为O ,右焦点为F ,点A 是双曲线C的一条渐近线上位于第一象限内的点,OAF OAF AOF ∆∠=∠,的面积为33,则双曲线C 的方程为( )A .1123622=-y x B .1322=-y x C.13922=-y x D .141222=-y x12.设实数0 m ,若对任意的e x ≥,不等式0ln 2≥-xm me x x 恒成立,则m 的最大值是( ) A .e 1 B .3eC.e 2 D .e 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知非零向量)3,1(),0,(-==b t a,若b a 2+与a 的夹角等于b a 2+与b 的夹角,则=t .14.73)2(xx -的展开式中不含常数项的所有项的系数之和是 . 15.已知等比数列{}n a 的前n 项和为n S ,且9863=S S ,则=--+11n n n a a a (,2≥n 且N n ∈). 16.已知抛物线)0(2:2p py x C =的焦点为O F ,为坐标原点,点)2,1(),2,4(pN p M ---,射线NO MO ,分别交抛物线C 于异于点O 的点B A ,,若F B A ,,三点共线,则p 的值为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.在ABC ∆中,c b a 、、分别是内角C B A 、、的对边,已知C c a B b A a sin )(sin sin -=-. (1)求B 的大小; (2)若6,31cos ==a A ,求ABC ∆的面积S . 18.2018年2月22日,在韩国平昌冬奥会短道速滑男子500米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子500米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要经过4个直道与弯道的交接口)4,3,2,1(=k A k .已知某男子速滑运动员顺利通过每个交接口的概率均为43,摔倒的概率均为41.假定运动员只有在摔倒或达到终点时才停止滑行,现在用X 表示该运动员在滑行最后一圈时在这一圈后已经顺利通过的交接口数.(1)求该运动员停止滑行时恰好已顺利通过3个交接口的概率; (2)求X 的分布列及数学期望)(X E .19.在如图所示的几何体中,⊥AC AC DE ,∥平面60,1,2,42,=∠====BCD DC BC DE AC BCD .(1)证明:⊥BD 平面ACDE ;(2)求平面BCD 与平面BAE 所成二面角的正弦值.20.已知椭圆()01:2222 b a b y a x E =+的焦距为c 2,且c b 3=,圆)0(:222 r r y x O =+与x 轴交于点P N M ,,为椭圆E 上的动点,PMN a PN PM ∆=+,2面积最大值为3.(1)求圆O 与椭圆E 的方程;(2)圆O 的切线l 交椭圆E 于点B A ,,求AB 的取值范围. 21.已知函数)(ln 21)(2R a x ax x x f ∈+-=. (1)若)(x f 在定义域上不单调,求a 的取值范围;(2)设n m ee a ,,1+ 分别是)(xf 的极大值和极小值,且n m S -=,求S 的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系.已知直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+==t y t x 552552(t 为参数),曲线C 的极坐标方程为θθρsin 8cos 2=. (1)求曲线C 的直角坐标方程,并指出该曲线是什么曲线; (2)若直线l 与曲线C 的交点分别为N M ,,求MN . 23. 选修4-5:不等式选讲 已知函数35)(+--=x x x f . (1)解关于x 的不等式1)(+≥x x f ;(2)记函数)(x f 的最大值为m ,若m ab bae ee b a -=⋅24,0,0 ,求ab 的最小值.新乡市高三第三次模拟测试 数学参考答案(理科)一、选择题1-5:BACAD 6-10:CBDAB 11、12:CD 二、填空题13.4或-4 14.-449 15.21- 16.2 三、解答题17.解:(1)因为C c a B b A a sin )(sin sin -=-. 所以222c ac b a -=-,即ac b c a =-+222.又212cos 222=-+=ac b c a B , 所以3π=B .(2)因为()π,0,31cos ∈=A A , 所以322sin =A . 由B b A a sin sin =,可得469322236sin sin =⨯==A B a b . 又6322233121322)sin(sin +=⨯+⨯=+=B A C . 所以82273366322469621sin 21+=+⨯⨯⨯==C ab S . 18.解:(1)由题意可知:2562741433=⨯⎪⎭⎫ ⎝⎛=P .(2)X 的所有可能只为0,1,2,3,4.则)4,3,2,1(43)(==k A P k ,且4321,,,A A A A 相互独立. 故41)()0(1===A P X P ,1634143)()1(21=⨯=⋅==A A P X P ,6494143)()2(2321=⨯⎪⎭⎫ ⎝⎛=⋅⋅==A A A P X P , 256274143)()3(34321=⨯⎪⎭⎫ ⎝⎛=⋅⋅⋅==A A A A P X P , 2568143)()4(44321=⎪⎭⎫⎝⎛=⋅⋅⋅==A A A A P X P . 从而X 的分布列为所以2562564256364216140)(=⨯+⨯+⨯+⨯+⨯=X E . 19.解:(1)在BCD ∆中,360cos 2121222=⨯⨯-+= BD . 所以222DC BD BC +=,所以BCD ∆为直角三角形,CD BD ⊥. 又因为⊥AC 平面BCD ,所以BD AC ⊥. 而C CD AC = ,所以⊥BD 平面ACDE .(2)(方法一)如图延长AE ,CD 相交于G ,连接BG , 则平面 AEB 平面BG BCD =.二面角C BG A --就是平面BCD 与平面BAE 所成二面角. 因为DE AC AC DE 2,=∥,所以DE 是AGC ∆的中位线.1==DC GD ,这样BGC BCD BC GC ∆=⊥==,60,2 是等边三角形.取BG 的中点为H ,连接CH AH ,,因为⊥AC 平面BCD . 所以AHC ∠就是二面角C BG A --的平面角. 在3,4,==∆CH AC AHC Rt ,所以19194194sin ==∠AHC .(方法二)建立如图所示的空间直角坐标系xyz D -,可得)4,1,0(),2,0,0(),0,1,0(),0,0,3(),0,0,0(A E C B D .)2,1,0(),4,1,3(=-=EA BA .设),,(z y x n = 是平面BAE 的法向量,则⎪⎩⎪⎨⎧=+=⋅=++-=⋅02043z y n z y x BA n令3=z 得)3,32,2(-=n.取平面BCD 的法向量为)1,0,0(=m.设平面BCD 与平面BAE 所成二面角的平面角为θ,则193cos =⋅=m n m n θ,从而19194sin =θ.20.解:(1)因为c b 3=,所以c a 2=.①因为a PN PM 2=+,所以点N M ,为椭圆的焦点,所以22241a c r ==. 设),(00y x P ,则b y b ≤≤-0,所以0021y a y r S PMN =⋅=∆. 当b y =0时,()321max ==∆ab S PMN ,② 由①,②解得2=a ,所以3=b ,1=c .所以圆O 的方程为122=+y x ,椭圆E 的方程为13422=+y x . (2)①当直线l 的斜率不存在时,不妨取直线l 的方程为1=x ,解得3),23,1(),23,1(=-AB B A . ②当直线l 的斜率存在时,设直线l 的方程为),(),,(,2211m kx x B m kx x A m kx y +++=. 因为直线l 与圆相切,所以112=+k m ,即221k m +=,联立⎪⎩⎪⎨⎧+==+m kx y y x 13422,消去y 可得01248)34(222=-+++m kmx x k ,34124,348,0)23(48)34(482221221222+-=+-=++=-+=∆k m x x k km x x k m k . ()3434134412222212212+-+⋅+⋅=-+⋅+=k m k k x x x x k AB =()()3441433414333423134222222+⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⋅=+++k k k k k k =3431214311613222++⋅+⎪⎭⎫ ⎝⎛+⋅-⋅k k . 令4312+=k t ,则4343102≤+=k t ,所以AB =340,32116132≤++-⋅t t t , 所以AB =4)4(16132+--⋅t ,所以3643≤AB . 综上,AB 的取值范围是⎥⎦⎤⎢⎣⎡364,3. 21.解:由已知),0(1)(R a x a xx x f ∈-+=' , (1)①若)(x f 在定义域上单调递增,则0)(≥'x f ,即xx a 1+≤在(0,+∞)上恒成立, 而[)+∞∈+,21xx ,所以2≤a ; ②若)(x f 在定义域上单调递减,则0)(≤'x f ,即xx a 1+≥在(0,+∞)上恒成立, 而[)+∞∈+,21xx ,所以∅∈a . 因为)(x f 在定义域上不单调,所以2 a ,即()+∞∈,2a .(2)由(1)知,欲使)(x f 在(0,+∞)有极大值和极小值,必须2 a . 又e e a 1+,所以ee a 12+ . 令011)(2=+-=-+='xax x a x x x f 的两根分别为21,x x , 即012=+-ax x 的两根分别为21,x x ,于是⎩⎨⎧==+12121x x ax x .不妨设2110x x ,则)(x f 在()1,0x 上单调递增,在[]21,x x 上单调递减,在()+∞,2x 上单调递增, 所以)(),(21x f n x f m ==,所以)ln 21()ln 21()()(2222112121x ax x x ax x x f x f x m S ++-++=-=-=)ln (ln )()(2121212221x x x x a x x -+---=21122121212221212221ln 21ln 21ln )(21x x x x x x x x x x x x x x x x +⎪⎪⎭⎫ ⎝⎛-⨯-=+-⨯-=+--= 令)1,0(21∈=x x t ,于是t tt S ln )1(21+--=. )1,2(22)(12222121221212221e e a x x x x x x x x x x t t +∈-=-+=+=+, 由2211e e tt ++ ,得112 t e . 因为0)11(211)11(2122 --=++-='tt t S ,所以t t t S ln )1(21+--=在⎪⎭⎫⎝⎛1,12e 上为减函数. 所以⎪⎪⎭⎫⎝⎛--∈224214,0e e e S . 22.解:(1)因为θθρsin 8cos 2=所以θρθρsin 8cos 22=, 即y x 82=,所以曲线C 表示焦点坐标为(0,2),对称轴为y 轴的抛物线.(2)直线l 过抛物线焦点坐标(0,2),且参数方程为⎪⎪⎩⎪⎪⎨⎧+==t y t x 552552(t 为参数), 代入曲线C 的直角坐标方程,得020522=--t t , 所以20,522121-==+t t t t . 所以()1042122121=-+=-=t t t t t t MN .23.解:(1)当3-≤x 时,由135+≥++-x x x ,得7≤x , 所以3-≤x ;当53 x -时,由135+≥---x x x ,得31≤x , 所以313≤-x ; 当5≥x 时,由135+≥---x x x ,得9-≤x ,无解. 综上可知,31≤x ,即不等式1)(+≥x x f 的解集为⎥⎦⎤ ⎝⎛∞-31,.(2)因为83535=---≤+--x x x x , 所以函数)(x f 的最大值8=m .应为844-=⋅ab b a e e e ,所以844+=+ab b a . 又0,0 b a ,所以ab ab b a 4424=≥+,所以0484≥--ab ab ,即02≥--ab ab . 所以有.()0)2(1≥-+ab ab .又0 ab ,所以2≥ab ,4≥ab ,即ab 的最小值为4.。
(word完整版)2017全国三卷理科数学高考真题及答案,推荐文档
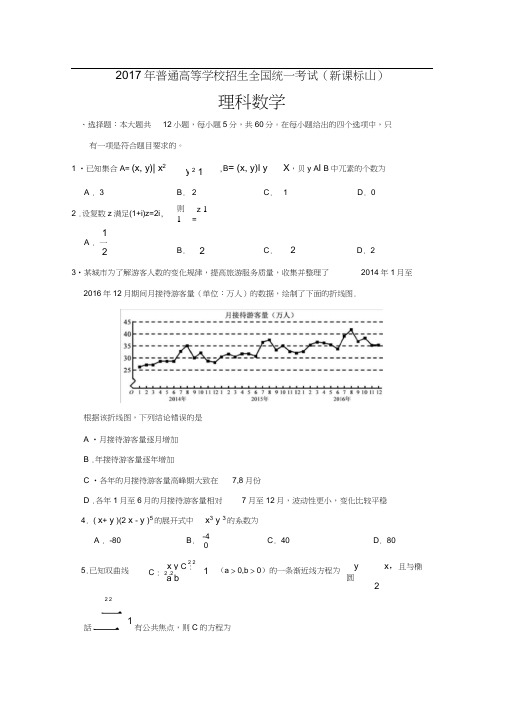
2017年普通高等学校招生全国统一考试(新课标山)理科数学、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1 •已知集合A= (x, y)| x2y21,B= (x, y)l y X,贝y A l B中兀素的个数为A . 3B. 2C. 1 D. 02 .设复数z满足(1+i)z=2i, 则1z 1=1A . 一2B. 2C. 2 D. 23•某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A •月接待游客量逐月增加B .年接待游客量逐年增加C •各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4. ( x+ y )(2 x - y )5的展开式中x3 y 3的系数为A . -80B. -4C. 40D. 805.已知双曲线2 2x y C :C : 2 .2a b1(a > 0,b > 0)的一条渐近线方程为y x,且与椭圆22 2話二1有公共焦点,则C的方程为体积为3 nnnA . nB .C .D .—4 2 49.等差数列a n 的首项为1,公差不为0 .若a 2, a 3, a 6成等比数列,则a n 前6项的和A . -24B . -3C . 3D . 82 2x y10 .已知椭圆 C :二 2 1 , ( a>b>0)的左、右顶点分别为 A 1, A 2,且以线段 A 1A 2为a b直径的圆与直线 bx ay 2ab 0相切,则C 的离心率为.3-1A .BC .D .33 3 32 2xy ’A .12 2x y ’ B .12x C.—52 x D.— 42y- i 36.设函数则下列结论错A • f(x)的一个周期为-2 B . y=f(x)的图像关于直线 8x=- 3对称C . f(x+n 的一个零点为x=—6D . f(x)在(一,n 单调递减22的同一个球的球面上,则该圆柱的N 的最小值为11 .已知函数f(x)2x 2x a(ex1e % 1)有唯一零点,则 a=11 1A .B.-C.-D . 1232uur12.在矩形ABC D中,AB=1 ,AD=2,动点P 在以点 C 为圆心且与 BD 相切的圆上.若APuuu uuurAB +AD , 则 +的最大值为A . 3B . 2 2C . 5D . 2二、 填空题:本题共 4小题,每小题5分,共20分。
河南省新乡市高三第三次模拟测试理数试题

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设复数错误!未找到引用源。
,则复数错误!未找到引用源。
的虚部为()A. 错误!未找到引用源。
B. 错误!未找到引用源。
C. 错误!未找到引用源。
D. 错误!未找到引用源。
【答案】A【解析】由题意错误!未找到引用源。
,故复数错误!未找到引用源。
的虚部为错误!未找到引用源。
,选A2. 若集合错误!未找到引用源。
,错误!未找到引用源。
,且错误!未找到引用源。
,则错误!未找到引用源。
的取值范围为()A. 错误!未找到引用源。
B. 错误!未找到引用源。
C. 错误!未找到引用源。
D. 错误!未找到引用源。
【答案】D3. 在错误!未找到引用源。
的展开式中,系数为有理数的项为()A. 第二项B. 第三项C. 第四项D. 第五项【答案】B【解析】解:由二项式展开式的通项公式有:错误!未找到引用源。
,系数为有理数的项时,错误!未找到引用源。
,即系数为有理数的项为第三项.本题选择B选项.4. 某程序框图如图所示,若输入的错误!未找到引用源。
,则输出的错误!未找到引用源。
等于()A. 2B. 3C. 4D. 5【答案】B点睛:本题考查了程序框图中的循环结构的应用,解题的关键是由框图的结构判断出框图的计算功能.5. 若函数错误!未找到引用源。
与错误!未找到引用源。
错误!未找到引用源。
存在相同的零点,则错误!未找到引用源。
的值为()A. 4或错误!未找到引用源。
B. 4或错误!未找到引用源。
C. 5或错误!未找到引用源。
D. 6或错误!未找到引用源。
【答案】C【解析】将函数错误!未找到引用源。
的零点错误!未找到引用源。
代入错误!未找到引用源。
得到错误!未找到引用源。
,解得错误!未找到引用源。
或错误!未找到引用源。
,故选C6. 记集合错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
(word完整版)2017全国三卷理科数学高考真题及答案,推荐文档

2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A I B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .2 C .2 D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6πD .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP u u u r=λAB u u u r +μAD u u u r,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。
2017年河南省新乡市高考数学三模试卷(理科)

2017年河南省新乡市高考数学三模试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)设复数z=3+4i,则复数z+的虚部为()A.B.i C.D.i2.(5分)若集合M={x|x2+5x﹣14<0},N={x|m<x<m+3},且M∩N=∅,则m 的取值范围为()A.(﹣10,2)B.(﹣∞,﹣10)∪(2,+∞)C.[﹣10,2]D.(﹣∞,﹣10]∪[2,+∞)3.(5分)在(x2)4的展开式中,系数为有理数的项为()A.第二项B.第三项C.第四项D.第五项4.(5分)某程序框图如图所示,若输入的t=4,则输出的k等于()A.2 B.3 C.4 D.55.(5分)若函数f(x)=log2(x+a)与g(x)=x2﹣(a+1)x﹣4(a+5)存在相同的零点,则a的值为()A.4或﹣B.4或﹣2 C.5或﹣2 D.6或﹣6.(5分)设集合A1={a1},A2={a2,a3},A3={a4,a5,a6},A4={a7,a8,a9,a10},…,其中{a n}为公差大于0的等差数列,若A2={3,5},则199属于()A.A12B.A13C.A14D.A157.(5分)已知向量,满足||=||=2,•=2,若=λ+μ,且λ+μ=1(λ,μ∈R),则||的最小值为()A.1 B.C.D.8.(5分)已知且,则等于()A. B.C.D.9.(5分)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为()A.5000立方尺 B.5500立方尺 C.6000立方尺 D.6500立方尺10.(5分)已知椭圆=1(a>b>0)的右顶点和上顶点分别为A,B,左焦点为F,以原点O为圆心的圆与直线BF相切,且该圆与y轴的正半轴交于点C,过点C的直线交椭圆于M,N两点,若四边形FAMN是平行四边形,则该椭圆的离心率为()A.B.C.D.11.(5分)设x.y满足约束条件,若的最大值为2,则a的值为()A.B.C.D.12.(5分)定义在(0,+∞)上的函数f(x)满足f(x)>2(x+)f′(x),其中f′(x)为f(x)的导函数,则下列不等式中,一定成立的是()A.f(1)>>B.>>C.f(1)<<D.<<二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)若函数f(x)=sin(ωx+)(0<ω<1)的图象关于点(﹣2,0)对称,则ω=.14.(5分)P为双曲线x2=1右支上一点,F1,F2为左、右焦点,若|PF1|+|PF2|=10,则=.15.(5分)若数列{a n+1﹣a n}是等比数列,且a1=1,a2=2,a3=5,则a n=.16.(5分)已知四面体ABCD的每个顶点都在球O的表面上,AB=AC=5,BC=8,AD⊥底面ABC,G为△ABC的重心,且直线DG与底面ABC所成角的正切值为,则球O的表面积为.三、解答题(本大题共5小题,共70分)17.(12分)设△ABC的内角A,B,C的对边分别为a,b,c,已知b2+c2﹣a2=bc.(1)若tanB=,求;(2)若B=,b=2,求BC边上的中线长.18.(12分)如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为矩形,且PD=AD=AB,E为PC的中点.(1)过点A作一条射线AG,使得AG∥BD,求证:平面PAG∥平面BDE;(2)求二面角D﹣BE﹣C得余弦值的绝对值.19.(12分)为推行“新课堂”教学法,某化学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.(1)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“成绩优良与教学方式有关”?附:.(n=a+b+c+d)独立性检验临界表(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法来抽取8人进行考核,在这8 人中,记成绩不优良的乙班人数为X,求X的分布列及数学期望.20.(12分)已知抛物线C:x2=2py(p>0)的焦点为F,直线2x﹣y+2=0交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.(Ⅰ)D是抛物线C上的动点,点E(﹣1,3),若直线AB过焦点F,求|DF|+|DE|的最小值;(Ⅱ)是否存在实数p,使|2+|=|2﹣|?若存在,求出p的值;若不存在,说明理由.21.(12分)已知函数f(x)=mlnx﹣x2+2(m≤8).(1)当曲线y=f(x)在点(1,f(1))处的切线的斜率大于﹣2时,求函数f(x)的单调区间.(2)若f(x)﹣f′(x)≤4x﹣3对x∈[1,+∞)恒成立,求m的取值范围.(提示:ln2≈0.7)四、选修4-4:坐标系与参数方程22.(10分)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4cosθ,曲线M的直角坐标方程为x﹣2y+2=0(x>0)(1)以曲线M上的点与点O连线的斜率k为参数,写出曲线M的参数方程;(2)设曲线C与曲线M的两个交点为A,B,求直线OA与直线OB的斜率之和.五、选修4-5:不等式选讲23.已知不等式|x﹣m|<|x|的解集为(1,+∞).(1)求实数m的值;(2)若不等式对x∈(0,+∞)恒成立,求实数a 的取值范围.2017年河南省新乡市高考数学三模试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)(2017•新乡三模)设复数z=3+4i,则复数z+的虚部为()A.B.i C.D.i【解答】解:∵z=3+4i,∴,∴z+==,∴复数z+的虚部为.故选:A.2.(5分)(2017•新乡三模)若集合M={x|x2+5x﹣14<0},N={x|m<x<m+3},且M∩N=∅,则m的取值范围为()A.(﹣10,2)B.(﹣∞,﹣10)∪(2,+∞)C.[﹣10,2]D.(﹣∞,﹣10]∪[2,+∞)【解答】解:M={x|x2+5x﹣14<0}={x|﹣7<x<2},N={x|m<x<m+3},且M∩N=∅,则m≥2或m+3≤﹣7,故m∈(﹣∞,﹣10]∪[2,+∞),故选:D.3.(5分)(2017•新乡三模)在(x2)4的展开式中,系数为有理数的项为()A.第二项B.第三项C.第四项D.第五项【解答】解:(x2)4的展开式中,通项公式为T r+1=••=•(﹣1)r••x8﹣3r,r=0,1,2,3,4;∴r=2时,=0,∴展开式中系数为有理数的项是第三项.故选:B.4.(5分)(2017•新乡三模)某程序框图如图所示,若输入的t=4,则输出的k 等于()A.2 B.3 C.4 D.5【解答】解:模拟程序的运行,可得t=4,S=0,k=8不满足条件S=4,执行循环体,S=8,k=7不满足条件S=4,执行循环体,S=1,k=6不满足条件S=4,执行循环体,S=5,k=5不满足条件S=4,执行循环体,S=0,k=4不满足条件S=4,执行循环体,S=4,k=3满足条件S=4,退出循环,输出k的值为3.故选:B.5.(5分)(2017•新乡三模)若函数f(x)=log2(x+a)与g(x)=x2﹣(a+1)x ﹣4(a+5)存在相同的零点,则a的值为()A.4或﹣B.4或﹣2 C.5或﹣2 D.6或﹣【解答】解:由x2﹣(a+1)x﹣4(a+5)=0,解得x=﹣4或x=a+5.∵函数f(x)=log2(x+a)与g(x)=x2﹣(a+1)x﹣4(a+5)存在相同的零点,∴x=﹣4,x=a+5也是方程log2(x+a)=0的根.即log2(﹣4+a)=0或log2(a+5+a)=0,解得a=5或a=﹣2.故选:C.6.(5分)(2017•新乡三模)设集合A1={a1},A2={a2,a3},A3={a4,a5,a6},A4={a7,a8,a9,a10},…,其中{a n}为公差大于0的等差数列,若A2={3,5},则199属于()A.A12B.A13C.A14D.A15【解答】解:∵{a n}为公差大于0的等差数列,A2═{a2,a3}={3,5},∴,解得a1=1,d=2,∴a n=1+(n﹣1)×2=2n﹣1,由a n=2n﹣1=199,解得n=100,∵1+2+3+4+5+6+7+8+9+10+11+12+13=91,1+2+3+4+5+6+7+8+9+10+11+12+13+14=105,∴199∈A14.故选:C.7.(5分)(2017•新乡三模)已知向量,满足||=||=2,•=2,若=λ+μ,且λ+μ=1(λ,μ∈R),则||的最小值为()A.1 B.C.D.【解答】解:cos<>==,∴∠AOB=60°,又OA=OB=2,∴O到直线AB的距离h=,∵=λ+μ,且λ+μ=1,∴==(λ﹣1)+μ=﹣μ+μ=μ()=μ,∴C在直线AB上,∴的最小距离为.故选D.8.(5分)(2017•新乡三模)已知且,则等于()A. B.C.D.【解答】解:∵,,∴<<,可得:cos()=﹣=﹣,∴=cos[()﹣]=cos()cos+sin()sin=(﹣)×+=.故选:D.9.(5分)(2017•新乡三模)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为()A.5000立方尺 B.5500立方尺 C.6000立方尺 D.6500立方尺【解答】解:由题意,将楔体分割为三棱柱与两个四棱锥的组合体,体积为+×2=5000立方尺,故选A.10.(5分)(2017•新乡三模)已知椭圆=1(a>b>0)的右顶点和上顶点分别为A,B,左焦点为F,以原点O为圆心的圆与直线BF相切,且该圆与y 轴的正半轴交于点C,过点C的直线交椭圆于M,N两点,若四边形FAMN是平行四边形,则该椭圆的离心率为()A.B.C.D.【解答】解:由O与BF相切,根据三角形的面积相等,即bc=ar,则r=,则圆O的半径为,即丨OC丨=,四边形FAMN是平行四边形,则M(,),代入圆的方程:,由e=,整理得:5e2+2e﹣3=0,由0<e<1,解得:e=,故选A.11.(5分)(2017•新乡三模)设x.y满足约束条件,若的最大值为2,则a的值为()A.B.C.D.【解答】解:分别作出直线2x+y﹣3=0和直线2x﹣2y﹣1=0,可得不等式2x+y﹣3≤0和2x﹣2y﹣1≤0的公共区域,求得交点为(,),由题意可得a<,作出不等式组的可行域,如右图.求得A(a,3﹣2a),B(a,),则表示可行域内的点与原点的斜率,可得范围为[k OB,k OA],即为[,].由的最大值为2,又==﹣1+,由图象可得k OB<0,k OA>0,由﹣1+=2,解得a=<,成立;由﹣1+=2,解得a=>,不成立.综上可得a=.故选:C.12.(5分)(2017•新乡三模)定义在(0,+∞)上的函数f(x)满足f(x)>2(x+)f′(x),其中f′(x)为f(x)的导函数,则下列不等式中,一定成立的是()A.f(1)>>B.>>C.f(1)<<D.<<【解答】解:构造函数g(x)=,则g′(x)==,∵在(0,+∞)上的函数f(x)满足f(x)>2(x+)f′(x),∴g′(x)<0,∴g(x)=在(0,+∞)上单调递减,∴g(1)>g(4)>g(9),∴>>,∴>>,故选:B二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)(2017•新乡三模)若函数f(x)=sin(ωx+)(0<ω<1)的图象关于点(﹣2,0)对称,则ω=.【解答】解:∵函数f(x)=sin(ωx+)(0<ω<1)的图象关于点(﹣2,0)对称,∴﹣2•ω+=kπ,即ω=﹣+,k∈Z,∴ω=,故答案为:.14.(5分)(2017•新乡三模)P为双曲线x2=1右支上一点,F1,F2为左、右焦点,若|PF1|+|PF2|=10,则=18.【解答】解:设P(x,y),由F1,F2分别为左、右焦点,即F1(﹣2,0),F2(2,0),∴=(﹣2﹣x,y)(2﹣x,y)=﹣(4﹣x2)+y2=﹣4+x2+y2,由P在双曲线x2=1,即3x2﹣y2=3,∴=﹣4+x2+y2=4x2﹣7,设丨丨=,丨丨=,则丨丨+丨丨=+==10,将3x2﹣y2=3,代入上式,解得x=,故=﹣4+x2+y2=4x2﹣7=25﹣7=18,故答案为:18,15.(5分)(2017•新乡三模)若数列{a n+1﹣a n}是等比数列,且a1=1,a2=2,a3=5,则a n=.﹣a n}是等比数列,且a1=1,a2=2,a3=5,【解答】解:∵数列{a n+1∴数列{a n﹣a n}的公比q===3,+1﹣a n=3n﹣1,∴a n+1a n=a1+(a2﹣a1)+(a3﹣a2)+…+(a n﹣a n﹣1)=1+1+3+32+…+3n﹣2=1+=.故答案为:.16.(5分)(2017•新乡三模)已知四面体ABCD的每个顶点都在球O的表面上,AB=AC=5,BC=8,AD⊥底面ABC,G为△ABC的重心,且直线DG与底面ABC所成角的正切值为,则球O的表面积为.【解答】解:由题意,AG=2,AD=1,cos∠BAC==﹣,∴sin∠BAC=,∴△ABC外接圆的直径为2r==,设球O的半径为R,∴R==∴球O的表面积为,故答案为.三、解答题(本大题共5小题,共70分)17.(12分)(2017•新乡三模)设△ABC的内角A,B,C的对边分别为a,b,c,已知b2+c2﹣a2=bc.(1)若tanB=,求;(2)若B=,b=2,求BC边上的中线长.【解答】解:(1)由余弦定理可得cosA==,∴sinA=,∵tanB=,∴sinB=,∴==;(2)B=,b=2,A=,∴BC=2,∴BC边上的中线长==.18.(12分)(2017•新乡三模)如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为矩形,且PD=AD=AB,E为PC的中点.(1)过点A作一条射线AG,使得AG∥BD,求证:平面PAG∥平面BDE;(2)求二面角D﹣BE﹣C得余弦值的绝对值.【解答】(1)证明:如图,连接AC交BD于F,连接FE,∵底面ABCD为矩形,∴F为AC的中点,又E为PC的中点,∴EF∥PA,则PA∥平面BDE,∵AG∥BD,BD⊂平面BDE,AG⊄平面PDE,∴AG∥平面BDE,又PA∩AG=A,∴平面PAG∥平面BDE;(2)∵PD⊥底面ABCD,底面ABCD为矩形,∴分别以DA、DC、DP所在直线为x、y、z轴建立空间直角坐标系,设PD=AD=AB=a,则D(0,0,0),B(a,2a,0),C(0,2a,0),E(0,a,),∴,=(0,a,),,.设平面DBE的一个法向量为,则,取z 1=2,得;设平面BCE的一个法向量为,则,取z 2=2,得.∴二面角D﹣BE﹣C得余弦值的绝对值为|cos<>|=||=||=.19.(12分)(2017•新乡三模)为推行“新课堂”教学法,某化学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.(1)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“成绩优良与教学方式有关”?附:.(n=a+b+c+d)独立性检验临界表(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法来抽取8人进行考核,在这8 人中,记成绩不优良的乙班人数为X,求X的分布列及数学期望.【解答】解:(1)根据2×2列联中的数据可得K2=≈5.227>5.024,∴在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”;(2)由表可知在8人中成绩不优良的人数为×8=3,X的可能取值为:0,1,2,3,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,∴X的分布列为:∴E(X)=0×+1×+2×+3×=.20.(12分)(2017•新乡三模)已知抛物线C:x2=2py(p>0)的焦点为F,直线2x﹣y+2=0交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.(Ⅰ)D是抛物线C上的动点,点E(﹣1,3),若直线AB过焦点F,求|DF|+|DE|的最小值;(Ⅱ)是否存在实数p,使|2+|=|2﹣|?若存在,求出p的值;若不存在,说明理由.【解答】解:(Ⅰ)∵F(0,2),p=4,∴抛物线方程为x2=8y,准线l:y=﹣2.设过D作DG⊥l于G,则|DF|+|DE|=|DG|+|DE|.当E,D,G三点共线时,|DF|+|DE|取最小值2+3=5;(Ⅱ)假设存在,由抛物线x2=2py与直线y=2x+2联立消去y得:x2﹣4px﹣4p=0.设A(x1,y1),B(x2,y2),△>0,则x1+x2=4p,x1x2=﹣4p,∴Q(2p,2p).∵|2+|=|2﹣|,∴QA⊥QB,∴•=0,∴(x1﹣2p)(x2﹣2p)+(y1﹣2p)(y2﹣2p)=0,即(x1﹣2p)(x2﹣2p)+(2x1+2﹣2p)(x2+2﹣2p)=0,∴5x1x2+(4﹣6p)(x1+x2)+8p2﹣8p+4=0,代入得4p2+3p﹣1=0,p=或p=﹣1(舍).故存在p=且满足△>0,∴p=.21.(12分)(2017•新乡三模)已知函数f(x)=mlnx﹣x2+2(m≤8).(1)当曲线y=f(x)在点(1,f(1))处的切线的斜率大于﹣2时,求函数f(x)的单调区间.(2)若f(x)﹣f′(x)≤4x﹣3对x∈[1,+∞)恒成立,求m的取值范围.(提示:ln2≈0.7)【解答】解:(1)函数f(x)的定义域是(0,+∞),f′(x)=﹣2x,f′(1)=m﹣2>﹣2,解得:m>0,故m∈(0,8],f′(x)=,令f′(x)>0,解得:0<x<,令f′(x)<0,解得:x>,故f(x)在(0,)递增,在(,+∞)递减;(2)令g(x)=mlnx﹣x2+2﹣+2x﹣4x+3=mlnx﹣x2﹣2x﹣+5,则g′(x)=﹣2x﹣2+=①,当m≤2时,g′(x)<0,所以g(x)在(1,+∞)上单调递减,所以当x≥1,g(x)≤g(1),故只需g(1)≤0,即﹣1﹣2﹣m+5≤0,即m≥2,所以m=2,②当2<m≤8时,解g′(x)=0,得x=±当1<x<时,g′(x)>0,g(x)单调递增;当x>时,g′(x)<0,g(x)单调递减.所以当x=时,g(x)取得最大值.故只需g()≤0,即mln﹣﹣2﹣+5≤0,令h(x)=xlnx﹣x﹣4+5,则h′(x)=1+lnx﹣1﹣=lnx﹣,h″(x)=+>0,所以h′(x)在(1,+∞)上单调递增,又h′(1)=﹣2<0,h′(4)=ln4﹣1>0,以∃x0∈(1,4),h′(x0)=0,所以h(x)在(1,x0)上单调递减,在(x0,4)上递增,而h(1)=﹣1﹣4+5=0,h(4)=4ln4﹣4﹣8+5=8ln2﹣7<0,所以x∈[1,4]上恒有h(x)≤0,所以当2<m≤8时,mln﹣﹣2﹣+5≤0,综上所述,2≤m≤8.四、选修4-4:坐标系与参数方程22.(10分)(2017•新乡三模)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4cosθ,曲线M的直角坐标方程为x﹣2y+2=0(x>0)(1)以曲线M上的点与点O连线的斜率k为参数,写出曲线M的参数方程;(2)设曲线C与曲线M的两个交点为A,B,求直线OA与直线OB的斜率之和.【解答】解:(1)联立,得到曲线M的参数方程为,(k为参数).(2)∵曲线C的极坐标方程为ρ=4cosθ,∴曲线C的直角坐标方程为(x﹣2)2+y2=4,联立,得或,∴直线OA与直线OB的斜率之和:k OA+k OB==4.五、选修4-5:不等式选讲23.(2017•新乡三模)已知不等式|x﹣m|<|x|的解集为(1,+∞).(1)求实数m的值;(2)若不等式对x∈(0,+∞)恒成立,求实数a 的取值范围.【解答】解:(1)由|x﹣m|<|x|得|x﹣m|2<|x|2,即2mx>m2,而不等式|x ﹣m|<|x|的解集为(1,+∞),∴1是方程2mx=m2的解,解得m=2(m=0舍去).(2)∵m=2,∴不等式对x∈(0,+∞)恒成立,等价于不等式a﹣5<|x+1|﹣|x﹣2|<a+2对x∈(0,+∞)恒成立.设,则f(x)∈(﹣1,3].∴a+2>3,且a﹣5≤﹣1,∴1<a≤4.参与本试卷答题和审题的老师有:sxs123;刘老师;742048;w3239003;zlzhan;zhczcb;lcb001;铭灏2016;双曲线;whgcn;caoqz(排名不分先后)菁优网2017年5月18日。
(完整word版)2017全国三卷理科数学高考真题及答案,推荐文档

2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A I B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣= A .12B .2 C .2 D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6πD .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP u u u r=λAB u u u r +μAD u u u r,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。
【河南省新乡】2017届高三第三次模拟测试数学年(理科)试题

河南省新乡一中2017届高三(上)第一次月考数学(理科)试卷答案2AC BD=0,连接是正方形,所以O是,BP BC λ=,0≤)-,1,(FP λ-2的法向量=n (1,0,0的法向量=n x y (,,()m FD z m FP λ⎧=--=⎪⎨=--⎪⎩20222∵二面角--B FD P π|m n =+2y k x -+=-20123又∵x y +=2200(k --=-1243∴过圆O :x 2=14242. kk k k +-+2343≤23133431)(k k k k k k +-+⇔-+⇔22231≥334313433≥03,,...,n 12,各式相加,得(()k k =∑<----2121313131t a =-2122()t t +-2124河南省新乡一中2017届高三(上)第一次月考数学(文科)试卷解析一、选择题1.【考点】交集及其运算。
【分析】求出A中不等式的解集确定出A,表示出B中不等式的解集,根据A与B的交集为空集,分两种情况考虑:B为空集与B不为空集,求出满足题意a的范围即可。
【解答】解:由A中不等式变形得:(x﹣4)(x+1)≤0,且x+1≠0,解得:﹣1<x≤4,即A=(﹣1,4],由B中不等式解得:2a<x<a2+1,即B=(2a,a2+1),∵A∩B=∅,∴分两种情况考虑:当B=∅时,2a=a2+1,即a=1;当B≠∅时,则有2a≥4或a2+1≤﹣1,即a≥2,综上,实数a的范围为{1}∪[2,+∞)。
故选:C.2.【考点】任意角的三角函数的定义。
【分析】由条件利用任意角的三角函数的定义转化求解sinα的值。
【解答】解:角α的终边上一点的坐标为(sin,cos)即(,),则由任意角的三角函数的定义,可得sinα=,故选:A.3.【考点】平面向量坐标表示的应用。
【分析】平面向量基本定理:若平面内两个向量、不共线,则平面内的任一向量都可以用向量、来线性表示,即存在唯一的实数对λ、μ,使=λ+μ成立。
2017年5月2017届高三第三次全国大联考(新课标Ⅲ卷)理数卷(解析版)

2017年第三次全国大联考【新课标III 卷】理科数学·全解全析(考试时间:120分钟 试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.已知集合{}2|20M x x x =--<,21{|1,}2N y y x x ==-+∈R ,则MN =( )A .{}|21x x -≤<B .{}|12x x <<C .{}|11x x -<≤D .{}|12x x ≤< 1.C 【命题意图】本题考查集合的运算、不等式的解法、二次函数的值域,意在考查运算求解能力.【解析】{}|12M x x =-<<,{}|1N y y =≤,则{}|11M N x x =-<≤,故选C .2.已知i 是虚数单位,若复数z 满足211i 122z =-+,则||z =( ) A .1 B .2 C 5 D 62.C 【命题意图】本题考查复数的运算、共轭复数与模的计算,意在考查运算求解能力.【解析】由211i 122z =-+,得()()()41i 41112i 1i 1i 1i z +=-=-=+--+,则||||5z z ==C .3.在长为4的线段PQ 上随机取一点R (R 不取端点值),以PR 为棱长的正方体体积大于27的概率为( ) A .12 B .14 C .3764D .2764 3.B 【命题意图】本题考查几何概型,意在考查运算求解能力.【解析】由题意,知327PR >,即43PR >>,则所求概率为43144-=,故选B. 4.设焦点为F 的抛物线C :22(0)y px p =>的准线与x 轴交于K 点,P 是抛物线C 上纵坐标为22的点,若22PKF S =△,则p =( ) A .12B .2C .4D .8 4.B 【命题意图】本题主要考查抛物线的几何性质,意在考查运算求解能力.【解析】由条件知11||222222PKF P S FK y p =⋅=⨯⨯=△,解得2p =,故选B . 5.已知函数()3122xxf x x ⎛⎫=-⋅ ⎪⎝⎭,且()20f x ->,则实数x 的取值范围是( ) A .()(),22,-∞+∞ B .(),2-∞ C .()2,+∞ D .(),-∞+∞5.A 【命题意图】本题主要考查函数的奇偶性与单调性的应用,意在考查运算求解能力、等价变换的能力.【解析】由题意易知()f x 为偶函数,且在[)0,+∞为增函数,()00f =,所以原不等式等价于()()|2|0f x f ->,所以|2|0x ->,所以2x ≠,故选A .6.已知变量 x y ,满足约束条件2204x y x y x -≥-⎧⎪-≤⎨⎪≥-⎩,若2m x y ≥-+恒成立时,则实数m 的取值范围为( ) A .[)0,+∞ B .[)4,+∞ C .[)2,-+∞ D .[)7,+∞ 6.D 【命题意图】本题主要考查线性规划问题,意在考查作图与识图能力.【解析】作出约束条件2204x y x y x -≥-⎧⎪-≤⎨⎪≥-⎩所对应的可行域(如图中阴影部分),令2z x y =-+,当直线经过点()4,1A --时,z 取得最大值,即()max 2417z =-⨯--=,所以7m ≥,故选D .7.如图,网格上小正方形的边长为1,粗实线与粗虚线画出的是正方体中挖去了两个半圆锥得到的一个几何体的三视图,则该几何体的体积为( )A .32643-π B .16643-π C .8643-π D .4643-π 7.B 【命题意图】本题主要考查三视图与正方体、圆锥的体积,意在考查空间想象能力、转换能力、运算求解能力.【解析】根据三视图还原出来的几何体如下图所示,其体积为3211422423V =-⨯⨯π⨯⨯=16643-π,故选B .8.函数()22exx xf x +=的大致图象是( )8.B 【命题意图】本题考查函数图象、导数与极值的关系,意在考查识图能力.【解析】由()f x 的解析式知有两个零点2x =-与0x =,排除A ,又()22e xx f x -'=,由()0f x '=知函数有两个极值点,排除C ,D ,故选B .9.执行下列程序框图,如果输出i 的值为3,那么输入的x 取值范围是( )A .16x <B .416x <<C .416x ≤<D .1664x ≤< 9.C 【命题意图】本题主要考查程序框图,意在考查辨识框图的能力、运算求解能力.【解析】执行下列程序:20,log i x x==→()221,log log i x x ==→()()2222,log log log i x x ==,()()()22223,log log log log i x x ==,则由()()()()()2222222log log log log 0log log log 0x x ⎧<⎪⎨≥⎪⎩,解得416x ≤<,故选C .10.已知过半径为2的球的球心的截面α圆内有一个内接正ABC △,点P 是过AB 且与平面α垂直的球的截面圆上任意一点,则点P 到平面ABC 的最大距离为( ) A .32B .3C .3D .23 10.B 【命题意图】本题主要考查球的性质、面面垂直的应用,意在考查空间想象能力、运算求解能力.【解析】如图所示,由题意,知平面PAB ⊥平面ABC ,所以点P 在平面ABC 上的射影D 落在AB 上,所以PD ⊥平面ABC ,所以当D 为AB 的中点时,点P 到平面ABC 的距离最大,即为PD .因为ABC △是正三角形,则31CD OD ==,,223PD OP OD =-=,故选B .11.已知双曲线C :22221(0,0)x y a b a b -=>>5C 的右顶点A 作倾斜角为34π的直线l 与两条渐近线12,l l 分别相交于,P Q 两点,且满足AP PQ λ=,则实数λ的值是( ) A .12 B .13C .2D .3 11.A 【命题意图】本题主要考查双曲线的几何性质、向量的线性关系,意在考查逻辑思维能力、运算求解开始x输入0i =2log x x=0?x <1i i =+i输出结束是否能力及方程思想的应用.【解析】由题意,得()0A a ,,直线l 的方程为y x a =-+,则由0y x a bx ay =-+⎧⎨-=⎩,得2,a ab P a b a b ⎛⎫⎪++⎝⎭.由0y x a bx ay =-+⎧⎨+=⎩,得2,a ab Q a b a b ⎛⎫- ⎪--⎝⎭,所以,abab AP a b a b ⎛⎫=- ⎪++⎝⎭,22222222,a b a b PQ a b a b ⎛⎫=- ⎪--⎝⎭.因为AP PQ λ=,所以2222ab a b a b a b λ-=⋅+-,即()21b a λ=+,又由5ce a==,结合222c a b =+,得2b a =,则212λ+=,即12λ=,故选A . 12.已知各项均为正数的递增数列{}n a 的前n 项和为n S 满足21n n S a =+,nn n a b a t=+(*t ∈N ),若12,,m b b b 成等差数列,则t m +=( )A .8B .9C .7或8D .8或912.D 【命题意图】本题考查数列通项n a 与前n 项和n S 间的关系、等差数列,意在考查运算求解能力、逻辑推理能力、估算能力.【解析】当1n =时,1121a a =+,解得11a =;当2n ≥时,由21n n S a =+,得212nn a S +⎛⎫= ⎪⎝⎭,则22111122nn n n n a a a S S --++⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,整理,得2211220n n n n a a a a -----=,配方,得()()22111n n a a --=+.由题意知,数列{}n a 为单调递增数列,且0n a >,则111n n a a --=+,即12n n a a --=,所以数列{}n a 为等差数列,则21n a n =-,所以2121n n b n t-=-+,则由12,,m b b b 成等差数列,得312123121m t t m t -⨯=+++-+,所以431m t =+-.因为,*m t ∈N ,故t 只能取2,3,5.当2t =时,7m =;当3t =时,5m =;当5t =时,4m =,所以8m t +=或9,故选D .第Ⅱ卷本试卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分)13.已知,AB DC 为梯形ABCD 的两腰,若()1,3AD =-,()1,2BC x x =-,则x =____________. 13.3【命题意图】本题主要考查平面向量的平行条件,意在考查运算求解能力与转化能力.【解析】由梯形的性质知ADBC ,且同向,则()12310x x -⋅--=,解得3x =.14.《孙子算经》是中国古代重要的数学专著,其中记载了一道有趣的数学问题:“今有出门,望见九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色.”则这个数学问题中动物有_____只.(数字作答)14.590490【命题意图】本题考查数学文化、等比数列,意在考查运算求解能力、审读能力.【解析】由题意,知“堤、木、枝、巢、禽、雏、毛”的数量构成一个首项19a =,公比9q =的等比数列{}n a ,其通项公式为1999n nn a -=⋅=,则动物的数量为()5655699919590490a a +=+=+=(只).15.某同学要用红、黄两种颜色给如下图中并排的七个矩形图形涂色,要求每一块矩形只涂一种颜色,要求任意两相邻的两块矩形至多有1块涂红色,且任意相邻三块矩形至少有一块矩形涂红色,则涂色方案有___________种.15.12【命题意图】本题主要考查计数原理的应用,意在考查运算求解能力、分类讨论思想的应用.【解析】分三类:(1)选2块矩形涂红色:第2块和第5块、第3块和第5块、第3块和第6块涂红色3种可能情况;(2)选3块矩形涂红色:考虑为插空问题,即涂红色的3块插入涂黄色的4块形成的5个空位中,有35C 种插入法,但须减去第1、5、2空涂红或第1、5、4空涂红色,所以有35C 28-=种涂法;(3)选4块矩形涂红色:只有第1、3、5、7块涂红色1种情况.根据分类加法计数原理知涂色方案共有38112++=种.16.将函数()()2sin 0,||2f x x ωϕωϕπ⎛⎫=+><⎪⎝⎭的图象上所有点的横坐标伸长到原来的4倍,再向右平移3π个单位得到得到函数()g x 的图象,若不等式()1g x ≥的解集为()74,43k k k π⎡⎤π+ππ+∈⎢⎥⎣⎦Z ,则()f x =___________.16.2sin 26x π⎛⎫-⎪⎝⎭【命题意图】本题主要考查三角函数的图象变换、三角函数性质,意在考查运算求解能力、逻辑推理能力.【解析】由题意,得()2sin 43g x x ωϕ⎡π⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦,则由()1g x ≥,即1sin 432x ωϕ⎡π⎤⎛⎫-+≥ ⎪⎢⎥⎝⎭⎣⎦,所以()5226436k x k k ωϕπππ⎛⎫π+≤-+≤π+∈ ⎪⎝⎭Z ,解得848612k k x ωϕωωωππππ⎛⎫++-≤≤ ⎪⎝⎭+()45612k ωϕωππ⎛⎫+-∈ ⎪⎝⎭Z ,则与()1g x ≥的解集区间比较得844612k k ωωϕωπ⎧=π⎪⎪⎨ππ⎛⎫⎪+-=π ⎪⎪⎝⎭⎩,解得2ω=,6ϕπ=-,检验知不等式()1g x ≥解集右端也成立,故()2sin 26f x x π⎛⎫=- ⎪⎝⎭.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12)在ABC △中,内角,,A B C 所对的边分别为,,a b c ,满足cos cos 2a B b A +=,且()cos 1cos c A b C =-.(Ⅰ)求c 的值及判断ABC △的形状;(Ⅱ)若()3sin 323sin()x x x C x =-∈R ,求ABC △的面积.17.【命题意图】本题考查正弦定理、余弦定理、三角形面积与三角恒等变换,意在考查运算求解能力、逻辑推理能力,以及方程思想、转化思想的应用.【解析】(Ⅰ)由cos cos 2a B b A +=,根据余弦定理,得222222222a c b b c a a b ac bc+-+-⋅+⋅=,整理,得2c =.………………2分由()cos 1cos c A b C =-,根据正弦定理,得()sin cos sin 1cos C A B C =-,即sin sin cos sin cos B C A B C =+,又sin B =()sin sin cos cos sin A C A C A C +=+,………4分sin cos sin cos B C A C =,故cos 0C =或sin sin A B =.………………5分当cos 0C =时,2C π=,故ABC △为直角三角形; 当sin sin A B =时,A B =,故ABC △为等腰三角形.………………7分(Ⅱ)因为313sin 323cos 23226x x x x x ⎫π⎛⎫-=-=-⎪ ⎪⎪⎝⎭⎭,所以6C π=.………………8分 由(Ⅰ)知2c =,A B =,则a b =,………………9分 所以由余弦定理,得22242cos 6a a a π=+-,解得2843a =+,………………10分 所以ABC ∆的面积21sin 2326S a π==………………12分 18.(本小题满分12分)某初级中学根据运动场地的影响,但为尽大可能让学生都参与到运动会中来,在2016冬季运动会中设置了五个项目,其中属于跑步类的两项,分别是200米和400米,另外三项分别为跳绳、跳远、跳高.学校要求每位学生必须参加,且只参加其中一项,该校780名学生参加各运动项目人数统计如下条形图:其中参加跑步类的人数所占频率为713,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.(Ⅰ)求条形图中m 和n 的值以及抽取的13人中参加200米的学生人数;(Ⅱ)现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X ,求离散型随机变量X 的分布列与数学期望.18.【命题意图】本题考查分层抽样、条形图、离散型随机变量的分布列与数学期望,意在考查学生的数据获取与处理能力、逻辑思维能力、运算求解能力. 【解析】(Ⅰ)由题意,得参加跑步类的有778042013⨯=人,………………1分 所以420180240m =-=,78042018012060n =---=.………………3分 根据分层抽样法知,抽取的13人中参加200米的学生人数有180133780⨯=人.………………5分 (Ⅱ)由题意,得抽取的13人中参加400米的学生人数有240134780⨯=,参加跳绳的学生人数有3人,所以X 的所有可能取值为1、2、3、4,………………6分()134347C C 41C 35P X ===,()224347C C 182C 35P X ===,()314347C C 123C 35P X ===,()4447C 14C 35P X ===,………………9分所以离散型随机变量X 的分布列为:X 1 2 3 4P435 1835 1235 135所以41812116()1234353535357E X =⨯+⨯+⨯+⨯=.………………12分 19.如图,在多面体ABCDEFG 中,ABCD 为正方形,AF ⊥平面ABCD ,AFBGDE ,且AB AF BG DE ===,H 为EG 中点.(Ⅰ)求证:BD CH ⊥;(Ⅱ)求二面角F CE G --的余弦值.19.【命题意图】本题考查空间直线与平面间平行和垂直的判断与证明、二面角、空间向量的应用,意在考查空间想象能力、逻辑推证能力、运算求解能力.【解析】(Ⅰ)如图,连接AC 交BD 于点M ,连接MH . ∵AFBG DE ,BG DE =,AF ⊥平面ABCD ,∴四边形BDEG 为矩形,………………1分又∵H 为EG 中点,∴MHBGAF,MH BG =,………………2分又∵AF ⊥平面ABCD ,∴MH ⊥平面ABCD ,∴MH ⊥BD .………………3分 在正方形ABCD 中,BD AC ⊥,且ACMH M =,∴BD ⊥平面CMH ,………………4分又CH ⊂平面CMH ,∴BD CH ⊥.………………5分(Ⅱ)由题意,以D 为坐标原点,以,,DA DC DE 分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,且设1AB AF BG DE ====,………………6分则()0,0,1E ,()1,0,1F ,()1,1,1G ,()0,1,0C ,()1,0,0EF =,()0,1,1EC =-,()1,1,0EG =. …………………………………………………………………7分 设()1111,,x y z =n 为平面FCE 的一个法向量,则由110EF EC ⎧=⎪⎨=⎪⎩n n ,得11100x y z =⎧⎨-=⎩,取11y =,得()10,1,1=n .………………9分设()2222,,x y z =n 为平面GCE 的一个法向量,则由2200EG EC ⎧=⎪⎨=⎪⎩n n ,得222200x y y z +=⎧⎨-=⎩,取21y =,得()21,1,1=-n ,………………11分∴1212126cos ,||||323⋅===⋅⨯n n n n n n , ∴二面角F CE G --的余弦值为6.………………12分20.(本小题满分12分)已知左、右焦点分别为12,F F 的椭圆C :22221(0)x y a b a b+=>>的离心率为63直线l 与椭圆C 交于,P Q 两个不同的点,当四边形12PF F Q 为矩形时,其面积为63. (Ⅰ)求椭圆C 的方程;(Ⅱ)若与x 轴不平行且过定点()2,0的直线m 与椭圆C 交于不同的两点,A B ,问:在x 轴上是否存在一个定点()0,0M x ,使得MA MB ⋅的值为定值?若存在,试求出0x 的值及定值;若不存在,请说明理由.20.【命题意图】本题主要考查椭圆的方程、直线与椭圆的位置关系,意在考查运算求解能力、逻辑推证能力、探究能力,以及分类讨论的思想、转化思想、设而不求法的应用.【解析】(Ⅰ)由题意,得6c a = ①,且12||2F F c =,21||b PF a =,则212146||||2b F F PF c a ⋅=⋅= ②.………………2分由①②联立,并结合222a b c =+,解得26a =,22b =,所以椭圆C 的方程为22162x y +=.………………4分 (Ⅱ)当直线m 与x 轴不垂直时,设直线m 的方程为()()20y k x k =-≠,代入椭圆C 的方程22162x y +=,得()222213121260k x k x k +-+-=.………………5分设()11,A x y 、()22,B x y ,所以21221213k x x k +=+,212212613k x x k -=+.………………6分根据题意,假设在x 轴上存在一个定点()0,0M x ,使得MA MB ⋅的值为定值, 则()()()()101202102012,,MA MB x x y x x y x x x x y y ⋅=-⋅-=--+()()()()()()222002222120120231210612413x x k x k x x k x x x k x k -++-=+-++++=+.…………7分要使上式为定值,即与k 无关,则()220003121036x x x -+=-,解得073x =, 此时,20569MA MB x ⋅=-=-,………………8分 所以在x 轴上存在定点7,03M ⎛⎫⎪⎝⎭,使得MA MB ⋅为定值,且073x =,定值为59-.……………9分当直线m 与x 轴垂直时,将2x =代入椭圆方程可求得出,A B 的坐标,不妨设662,,2,33A B ⎛⎛- ⎝⎭⎝⎭,则1616,,,3333MA MB ⎛⎫⎛=-=-- ⎪ ⎪ ⎝⎭⎝⎭ ∴11665()()339MA MB ⋅=-⨯--=-.…………11分 综上可知,在x 轴上存在定点7,03M ⎛⎫⎪⎝⎭,使得MA MB ⋅为定值,且073x =,定值为59-.……12分21.(本小题满分12分)已知函数()()()()2ln 11af x x a x =++∈+R .(Ⅰ)讨论函数()f x 的单调性;(Ⅱ)已知()32g x x x =-,若对于12,13x ⎡⎤∀∈-⎢⎥⎣⎦,21,23x ⎡⎤∀∈⎢⎥⎣⎦,不等式()()()11213x f x g x ++≥恒成立,求实数a 的取值范围.21.【命题意图】本题主要考查导数与函数单调性间的关系、不等式恒成立问题,意在考查运算求解能力、逻辑推理能力,以及分类讨论的思想、等价转化的思想、构造法的应用. 【解析】(Ⅰ)函数()f x 的定义域为()1+∞-,,()()()()2331212111x a af x x x x +-'=+++-=,………………2分 当0a ≤时,()0f x '≥,函数()f x 在()1+∞-,上单调递增;……………3分 当0a >时,若21x a ≥,则()0f x '≥,函数()f x 在(21,)a +∞上单调递增;若121x a -<<,则()0f x '<,函数()f x 在(21)a -上单调递减.……………4分综上所述,当0a ≤时,函数()f x 在()1+∞-,上单调递增;当0a >时,函数()f x 在区间()21a -上单调递减,在)21,a +∞上单调递增.………………5分(Ⅱ)22()323()3g x x x x x '=-=-,1,23x ⎡⎤∈⎢⎥⎣⎦,可见,当2,23x ⎡⎤∈⎢⎥⎣⎦时,()0g x '≥,()g x 在2,23⎡⎤⎢⎥⎣⎦上单调递增,当12,33x ⎡⎤∈⎢⎥⎣⎦时,()0g x '≤,()g x 在12,33⎡⎤⎢⎥⎣⎦上单调递减,………………7分而()1224327g g ⎛⎫=-<= ⎪⎝⎭,所以,()g x 在1,23⎡⎤⎢⎥⎣⎦上的最大值为4,………………8分 依题意,只需当12,13x ⎡⎤∈-⎢⎥⎣⎦时,()()11134x f x ++≥恒成立, 即()()1111x f x +≥,即()()1ln 111a x x x +++≥+在2,13⎡⎤-⎢⎥⎣⎦上恒成立, 亦即()()()211ln 1a x x x ≥+-++在2,13⎡⎤-⎢⎥⎣⎦上恒成立.………………9分 令()()()2()11ln 1h x x x x =+-++2,13x ⎛⎫⎡⎤∈- ⎪⎢⎥⎣⎦⎝⎭,则()()()21ln 1h x x x x '=--++,………9分显然(0)0h '=, 当2,03x ⎡⎫∈-⎪⎢⎣⎭时, 0x ->,()()21ln 10x x ++<,()0h x '>,即()h x 在2,03⎡⎫-⎪⎢⎣⎭上单调递增;………………10分当(]0,1x ∈时,0x -<,()()21ln 10x x ++>,()0h x '<,即()h x 在区间(]0,1上单调递减; 所以,当0x =时,函数()h x 取得最大值(0)1h =,………………112分 故1a ≥,即实数a 的取值范围是[)1,+∞.………………12分请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知直线l 的参数方程为21222x y ⎧=⎪⎪⎨⎪=+⎪⎩(t为参数),以原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为()4cos 2sin m ρρθθ--=-,且直线l 与圆C 相交于不同的,A B 两点.(Ⅰ)求线段AB 垂直平分线l '的极坐标方程; (Ⅱ)若||2AB =m 的值.(Ⅲ)若1m =,求过点()4,4N 与圆C 相切的切线方程.22.【命题意图】本题考查直线的极坐标与圆的参数方程、直线与圆的位置关系,意在考查运算求解能力、等价转化能力.【解析】(Ⅰ)消去参数t ,得直线l 的普通方程为10x y -+=,斜率为1, 所以直线l '的斜率为1-.………………1分因为圆C 的极坐标方程可化为24cos 2sin 0m ρρθρθ--+=,所以将222,cos ,sin x y x y ρρθρθ=+==代入上述方程得圆C 的直角坐标方程为22420x y x y m +--+=,则配方,得()()22215x y m -+-=-,其圆心为()2,1C ,半径为)55m m -<.………………3分由题意,知直线l '经过圆心()2,1C ,所以直线l '的方程为()12y x -=--,即30x y +-=,所以由cos ,sin x y ρθρθ==,得直线l '的极坐标方程为()cos sin 3ρθθ+=.………………5分(Ⅱ)因为||2AB =C 到直线l )22||5252AB r m m ⎛⎫-=--< ⎪⎝⎭.)5252m m =--<,解得1m =.………………7分 (Ⅲ)当所求切线的斜率存在时,设切线方程为4(4)y k x -=-,即440kx y k --+=. 221k =+,解得512k =,所以所求切线的方程为512280x y -+=; 当所求切线的斜率不存在时,切线方程为4x =.………………9分 综上,所求切线的方程为4x =或512280x y -+=.………………10分23.(本小题满分10分)选修4-5:不等式选讲已知不等式2222x x +-->的解集为M . (Ⅰ)求集合M ;(Ⅱ)已知t 为集合M 中的最小正整数,若1,1,1a b c >>>,且()()()111a b c t ---=,求证:8abc ≥.23.【命题意图】本题主要考查绝对值不等式的解法、不等式的证明,意在考查运算求解能力、逻辑推理能力、分类讨论与等价转化的思想.【解析】(Ⅰ)设()222f x x x =+--,则()4,13,124,2x x f x x x x x --<-⎧⎪=-≤<⎨⎪+≥⎩,………………1分当1x <-时,由42x -->,得6x <-,6x <-∴;………………2分 当12x -≤<时,由32x >,得23x >,223x <<∴;………………3分 当2x ≥时,由42x +>,得2x >-,2x ≥∴.………………4分 综上所述,集合M 为2|63x x x ⎧⎫><-⎨⎬⎩⎭或.………………5分 (Ⅱ)由(Ⅰ)知1t =,则()()()1111a b c t ---==.因为1,1,1a b c >>>,所以10,10,10a b c ->->->, ………………6分 则()11210a a a =-+≥->,(当且仅当2a =时等号成立)……………7分 ()11210b b b =-+≥->,(当且仅当2b =时等号成立)………………8分 ()11210c c c =-+≥->,(当且仅当2c =时等号成立)………………9分 则()()()81118abc a b c ≥---≥(当且仅当2a b c ===时等号成立), 即8abc ≥.………………10分。
【河南省新乡市】2017届高三第三次模拟测试理科综合物理试卷 (附答案)

河南省新乡市2017届高三第三次模拟测试理科综合物理试卷的电阻等效替代,则下列关系式正确的是().甲、乙两车在一平直公路上同向行驶,其速度时间图像如图所示,下列说法正确的是()n n (t t ==-.高频交流电源的变化周期随粒子速度的增大而减小(1)粗测小灯泡的电阻,应选择多用电表_________(填“×1”、“×10”或“×100”)倍率的电阻档,调零后,将表笔分别与小灯泡的两极连接,示数如图甲所示,结果为_________Ω。
(2)请在图乙所示的虚线框内补画出满足实验要求的电路图。
23.某同学为了测量木质材料与金属材料间的动摩擦因数,设计了一个实验方案:实验装置如图甲所示,金属板放在水平桌面上,且始终静止,他先用打点计时器测出木块运动的加速度,再利用牛顿第二定律计算出动摩擦因数。
(1)实验时_________(填“需要”或“不需要”)使砝码和砝码盘的质量m 远小于木块的质量M ;_________(填“需要”或“不需要”)把金属板的一端适当垫高来平衡摩擦力。
(2)图乙是某次实验时打点计时器所打出的纸带的一部分,纸带上计数点间的距离如图所示,则打点计时器打A 点时木块的速度为_________m /s ,木块运动的加速度为_________2m /s 。
(打点计时器所用电源的频率为50 Hz ,结果均保留两位小数)(3)若打图乙纸带时砝码和砝码盘的总质量为50 g ,木块的质量为200 g ,则测得木质材料与金属材料间的动摩擦因数为_________(重力加速度29.8/g m s =,结果保留两位有效数字)24.空间存在电场强度方向竖直向上的匀强电场,水平地面上有一根短管,与水平面之间的夹角为37°,如图所示,一略小于细短管直径、质量为m 、电荷量为q 的带正电小球,从水平地面上方一定高度处水平抛出,经时间t 小球恰好无碰撞地落入细短管,已知细短管到抛出点的水平距离为d ,重力加速度大小为g ,取sin370.6︒=,cos370.8︒=,空气阻力不计,求:①求气体在状态A 、B 时的热力学温度;②请通过计算判断气体从状态A 变化到状态C 的过程是吸热还是放热,同时求出传递的热量。
【联考】2017届河南省新乡市高三第三次模拟测试理科综合生物试卷(带解析)

绝密★启用前【联考】2017届河南省新乡市高三第三次模拟测试理科综合生物试卷(带解析)试卷副标题考试范围:xxx ;考试时间:35分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、植物激素甲、乙、丙和生长素类似物NAA 的作用模式如图所示,图中“+”表示促进作用,“—”表示抑制作用。
下列叙述错误的是A .激素甲最可能代表乙烯B .激素丙最可能代表生长素C .激素乙具有微量、高效的特点D .激素丙具有极性运输的特点2、黑腹果蝇的复眼缩小和眼睛正常是一对相对性状,由两对独立遗传的等位基因A 、a 和B 、b 控制,只有双显性才表现为复眼缩小,且基因型为Aa 的个体只有75%为显性性状。
现将一对基因型为AaBb 的果蝇杂交,假设后代数量足够多,下列分析错误的是 A. 后代中基因型相同的个体的表现型不一定相同B. 杂交后代眼睛正常个体中纯合子占6/17C. F 1性状分离比为复眼缩小:眼睛正常=15:17D. 两个眼睛正常的纯合亲本杂交,子代数量足够多时也可以全为复眼缩小3、某地草场中有如下食物链:牧草→野兔→鹰。
下图表示该食物链中各生物的个体数量的相对值。
下列有关分析错误的是A .甲的个体数量、总能量都是最多的B .乙的数量突增,短时间内物种丙的数量也会增加C .丙表示鹰,该种群营养极高,所含能量较少D .甲在不同地段、不同层次上的个体数量不同,主要是食物的原因4、下列实验的改变对其结果影响最大的是 A .用大蒜根尖代替洋葱根尖观察植物细胞有丝分裂 B .用有机溶剂丙酮代替无水酒精进行叶绿体色素的提取C .用纤维素酶处理过的植物细胞代替未处理的植物细胞做质壁分离实验D .用低温代替秋水仙素处理萌发的种子以诱导染色体数目加倍5、下列有关物质运输方式的叙述中,正确的是 A .神经递质通过胞吐作用释放到突触间隙 B .无机盐离子进出细胞的方式均为主动运输C .被动运输都是顺浓度梯度进行的,不需要载体和能量D .分泌蛋白分泌到细胞外的过程主要体现细胞膜的选择透过性6、下列有关细胞结构与功能的叙述,正确的是A .细胞核可以完成基因的复制和表达,是生命活动的控制中心B .细胞凋亡过程中有新蛋白质合成,体现了基因的选择性表达C .生物膜系统在细胞的生命活动中具有重要作用,细胞都具有生物膜系统D .洋葱根尖细胞中无叶绿体,所以用根尖细胞不能培育出含叶绿体的植物体第II 卷(非选择题)二、综合题(题型注释)7、[生物一选修3:现代生物科技专题] 请回答下列有关基因工程和胚胎工程的问题:(1)在基因工程中,获取目的基因的方法包括:①从基因文库中获取目的基因,②利用________扩增目的基因,③_____________________。
河南省新乡市2017届高三第三次模拟数学试题理含答案

新乡市高三第三次模拟测试数学试卷(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数34i =+z ,则复数+z z z 的虚部为( ) A .165 B .16i 5 C .185 D .18i 52.若集合{}25140=+-<M x x x ,{}3=<<+N x m x m ,且=∅MN ,则m 的取值范围为( )A .()10,2-B .()(),102,-∞-+∞ C .[]10,2- D .(][),102,-∞-+∞ 3.在423322⎛- ⎪⎝⎭x x 的展开式中,系数为有理数的项为( ) A .第二项 B .第三项 C .第四项 D .第五项4.某程序框图如图所示,若输入的4=t ,则输出的k 等于( )A .2B .3C .4D .55.若函数()()2log =+f x x a 与()()21=-+g x x a x ()45-+a 存在相同的零点,则a 的值为( )A .4或52-B .4或2-C .5或2-D .6或52- 6.记集合{}11=A a ,{}223,=A a a ,{}3456,,=A a a a ,{}478910,,,=A a a a a …,其中{}n a 为公差大于0的等差数列,若{}23,5=A ,则199属于( )A .12AB .13AC .14AD .15A7.已知向量OA ,OB 满足2==OA OB ,λμ=+OC OA OB ,若λμ=+OC OA OB 且1λμ+=(λ,R μ∈),则OC 的最小值为( )A .1B .5C .2D .3 8.已知2παπ<<,且3sin 65πα⎛⎫+= ⎪⎝⎭,则cos 6πα⎛⎫- ⎪⎝⎭等于( ) A .43310-- B .43310+ C .43310- D .33410- 9.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈;上袤二丈,无广;高一丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知1丈为10尺,现将该楔体的三视图给出如下图所示,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )A .5000立方尺B .5500立方尺C .6000立方尺D .6500立方尺10.已知椭圆22221x y a b+=(0a b >>)的右顶点和上顶点分别为A 、B ,左焦点为F .以原点O 为圆心的圆与直线BF 相切,且该圆与y 轴的正半轴交于点C ,过点C 的直线交椭圆于M 、N 两点.若四边形FAMN 是平行四边形,则该椭圆的离心率为( )A .35B .12C .23D .3411.设x ,y 满足约束条件230,2210,0,+-≤⎧⎪--≤⎨⎪-≥⎩x y x y x a 若-+x y x y 的最大值为2,则a 的值为( ) A .12 B .14 C .38 D .5912.定义在()0,+∞上的函数()f x 满足()(()2'>f x x f x ,其中()'f x 为()f x 的导函数,则下列不等式中,一定成立的是( )A .()()()23123>>f f fB .()()()149234>>f f f C .()()()23123<<f f f D .()()()149234<<f f f 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若函数()sin 3πω⎛⎫=+ ⎪⎝⎭f x x (01ω<<)的图象关于点()2,0-对称,则ω= .14.P 为双曲线2213-=y x 右支上一点,1F 、2F 为左、右焦点,若1210+=PF PF ,则12⋅=PF PF .15.若数列{}1--n n a a 是等比数列,且11=a ,22=a ,35=a ,则=n a .16.已知四面体ABCD 的每个顶点都在球O 的表面上,5==AB AC ,8=BC ,⊥AD 底面ABC ,G 为ABC 的重心,且直线DG 与底面ABC 所成角的正切值为12,则球O 的表面积为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设ABC 的内角A ,B ,C 的对边分别为a ,b ,c,已知222+-=b c a .(1)若tan =B b a;(2)若23π=B ,23=b ,求BC 边上的中线长.18.如图,在四棱锥-P ABCD 中,⊥PD 底面ABCD ,底面ABCD 为矩形,且12==PD AD AB ,E 为PC 的中点.(1)过点A 作一条射线AG ,使得∥AG BD ,求证:平面∥PAG 平面BDE ;(2)求二面角--D BE C 的余弦值的绝对值.19.为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.分数 [)50,59 [)60,69 [)70,79 [)80,89[]90,100甲班频数 5 6 4 41 一般频数 1 3 6 55 (1)由以下统计数据填写下面22⨯列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?甲班 乙班 总计成绩优良成绩不优良总计附:()()()()()22-=++++n ad bc K a b c d a c b d ,其中=+++n a b c d .临界值表()2≥P K k 0.10 0.05 0.025 0.010k 2.706 3.841 5.024 6.635(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为X ,求X 的分布列及数学期望.20.已知抛物线C :22=x py (0>p )的焦点为F ,直线220-+=x y 交抛物线C 于A 、B 两点,P 是线段AB 的中点,过P 作x 轴的垂线交抛物线C 于点Q .(1)D 是抛物线C 上的动点,点()1,3-E ,若直线AB 过焦点F ,求+DF DE 的最小值;(2)是否存在实数p ,使2+=QA QB 2-QA QB ?若存在,求出p 的值;若不存在,说明理由.21.已知函数()2ln 2=-+f x m x x (8≤m ). (1)当曲线()=y f x 在点()()1,1f 处的切线的斜率大于2-时,求函数()f x 的单调区间;(2)若()()'-f x f x 43≤-x 对[)1,∈+∞x 恒成立,求m 的取值范围.(提示:ln 20.7≈) 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为4cos ρθ=,曲线M 的直角坐标方程为220-+=x y (0>x ).(1)以曲线M 上的点与点O 连线的斜率k 为参数,写出曲线M 的参数方程;(2)设曲线C 与曲线M 的两个交点为A ,B ,求直线OA 与直线OB 的斜率之和.23.选修4-5:不等式选讲 已知不等式-<x m x 的解集为()1,+∞.(1)求实数m 的值;(2)若不等式511-<+-a x x 21+-<m a x x对()0,∈+∞x 恒成立,求实数a 的取值范围.新乡市高三第三次模拟测试数学试卷参考答案(理科)一、选择题1-5: ADBBC 6-10:CDDAA 11、12:CB二、填空题13.6π 14.18 15.1312-+n 16.6349π 三、解答题17.解:(1)由222+-=b c a得cos =A 6π∴=A. tan =B 1sin 5∴=B . 由正弦定理得,sin sin =a b A B ,则sin sin ==b B a A 125152=. (2)6π=A ,6ππ=--=C A B ,∴=AB BC .由sin sin =c b C B得2=c .取BC 中点D ,在ABD 中,2222=+-AD AB BD cos 7⨯⨯⨯=AB BD B,∴=AD ,即BC 边.18.(1)证明:在矩形ABCD 中,连接AC 和BD 交于点O ,连接OE ,则O 是AC 的中点,由于E 是PC 的中点,所以OE 是PAC 的中位线,则∥OE PA又⊂OE 平面BDE ,⊄PA 平面BDE ,所以∥PA 平面BDE .又∥AG BD ,同理得∥AG 平面BDE .因为=PA AG A ,所以平面∥PAG 平面BDE .(2)分别以DA ,DC ,DP 所在的直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系.设=AD a ,则=PD a ,2=AB a ,故(),2,0B a a ,()0,0,P a ,()0,2,0C a ,0,,2⎛⎫ ⎪⎝⎭a Ea , 所以(),2,0=DB a a ,0,,2⎛⎫= ⎪⎝⎭a DE a ,(),0,0=CB a ,0,,2⎛⎫=- ⎪⎝⎭a EC a ,设平面BDE 的一个法向量为()1111,,=n x y z ,则有110,0,⎧⋅=⎪⎨⋅=⎪⎩n DB n DE ,即20,0,2+=⎧⎪⎨+=⎪⎩ax ay aay z 令2=x ,则1=-y,2=z ,故()12,1,2=-n .同理,可得平面BEC 的一个法向量()20,1,2=n .所以121212cos ,⋅==n n n n n n 5,即二面角--D BE C 的余弦值的绝对值为5.19.解:(1)甲班 乙班 总计成绩优良 9 16 25成绩不优良 11 4 15总计 20 20 40根据22⨯列联表中的数据,得2K 的观测值为()24094161125152020⨯-⨯=⨯⨯⨯k 5.227 5.024≈>, ∴能在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”.(2)由表可知在8人中成绩不优良的人数为158340⨯=,则X 的可能取值为0,1,2,3. ()31131533091===C P X C ;()2111431544191===C C P X C ; ()12114315662455===C C P X C ;()3431543455===C P X C . ∴X 的分布列为:X0 1 2 3 P 3391 4491 66455 4455()3344019191∴=⨯+⨯E X 66423455455+⨯+⨯364455=. 20.解:(1)直线220-+=x y 与y 轴的交点为()0,2,()0,2∴F ,则抛物线C 的方程为28=x y ,准线l :2=-y .设过D 作⊥DG l 于G ,则+=DF DE +DG DE ,当E 、D 、G 三点共线时,+DF DE 取最小值235+=.(2)假设存在,抛物线22=x py 与直线22=+y x 联立方程组得: 2440--=x px p ,设()11,A x y ,()22,B x y ,则124+=x x p ,124=-x x p ,()2,2∴Q p p . 2+QA QB 2=-QA QB ,∴⊥QA QB .则0⋅=QA QB 得:()()1222--+x p x p ()()12220--=y p y p ,()()1222--+x p x p ()()122222220+-+-=x p x p ,()()1212546+-++x x p x x 28840-+=p p ,代入得24310+-=p p ,解得14=p 或1=-p (舍去).21.解:(1)的定义域为()0,+∞,()2'=-=m f x x x 22-+x m x ,()122'=->-f m ,0∴>m .由()0'=f x ,得2=m x .当02<<m x ()0'>f x ,()∴f x 的单调递增区间为2⎛ ⎝m ;当2>m x 时,()0'<f x ,()∴f x 的单调递减区间为,2⎫+∞⎪⎪⎭m . (2)令()2ln 2=-+g x m x x 243-+-+=m x x x 2ln 25---+m m x x x x,1≥x , 则()222'=--+=m m g x x x x 32222--++x x mx m x ()()2212+-=x m x x ,1≥x , ①当2≤m 时,()0'≤g x ,所以()g x 在()1,+∞上单调递减,所以当1≥x ,()()1≤g x g ,故只需()10≤g ,即1250---+≤m ,即2≥m ,所以2=m .②当28<≤m 时,令()0'=g x ,得2=m x . 当12≤<m x ()0'>g x ,()g x 单调递增; 当2>m x 时,()0'<g x ,()g x 单调递减. 所以当2=m x 时,()g x 取得最大值.故只需0≤g,即2-mm 50≤, 化简得ln 222--m mm 50+≤, 令2=m t,得ln 50--≤t t t (14<≤t ). 令()ln =--h x x xx 5(14<≤t ),则()1ln 1'=+-h x xln =x , 令()ln =-H x x ,()10'=+>H x x , 所以()'h x 在()1,+∞上单调递增,又()120'=-<h ,()4ln 410'=->h ,所以()01,4∃∈x ,()00'=h x ,所以()h x 在()01,x 上单调递减,在(]0,4x 上递增,而()11450=--+=h ,()44ln 4485=--+=h 8ln 270-<,所以(]1,4∈x 上恒有()0≤h x ,即当28<≤m时,ln 2-mm 50≤. 综上所述,28≤≤m .22.解:(1)由()2200-+=>⎧⎪⎨=⎪⎩x y x y kx 得221221⎧=⎪⎪-⎨⎪=⎪-⎩x k k y k . 故曲线M 的参数方程为221221⎧=⎪⎪-⎨⎪=⎪-⎩x k ky k .(k 为参数,且12>k ). (2)由4cos ρθ=,得24cos ρρθ=,224∴+=x y x . 将221221⎧=⎪⎪-⎨⎪=⎪-⎩x k ky k 代入224+=x y x 整理得2430-+=k k ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新乡市高三第三次模拟测试数学试卷(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数34i =+z ,则复数+zz z的虚部为( ) A .165 B .16i 5 C .185 D .18i 52.若集合{}25140=+-<M x x x ,{}3=<<+N x m x m ,且=∅I M N ,则m 的取值范围为( )A .()10,2-B .()(),102,-∞-+∞UC .[]10,2-D .(][),102,-∞-+∞U3.在42的展开式中,系数为有理数的项为( ) A .第二项 B .第三项 C .第四项 D .第五项 4.某程序框图如图所示,若输入的4=t ,则输出的k 等于( )A .2B .3C .4D .55.若函数()()2log =+f x x a 与()()21=-+g x x a x ()45-+a 存在相同的零点,则a 的值为( )A .4或52-B .4或2-C .5或2-D .6或52- 6.记集合{}11=A a ,{}223,=A a a ,{}3456,,=A a a a ,{}478910,,,=A a a a a …,其中{}n a 为公差大于0的等差数列,若{}23,5=A ,则199属于( ) A .12A B .13A C .14A D .15A7.已知向量uu r OA ,uu u r OB 满足2==uu r uu u r OA OB ,λμ=+u u u r u u r u u u r OC OA OB ,若λμ=+u u u r u u r u u u rOC OA OB 且1λμ+=(λ,R μ∈),则uuu rOC 的最小值为( )A .1B 8.已知2παπ<<,且3sin 65πα⎛⎫+= ⎪⎝⎭,则cos 6πα⎛⎫- ⎪⎝⎭等于( )A .410-- B .410+ C .410- D .4109.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈;上袤二丈,无广;高一丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知1丈为10尺,现将该楔体的三视图给出如下图所示,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )A .5000立方尺B .5500立方尺C .6000立方尺D .6500立方尺10.已知椭圆22221x y a b+=(0a b >>)的右顶点和上顶点分别为A 、B ,左焦点为F .以原点O 为圆心的圆与直线BF 相切,且该圆与y 轴的正半轴交于点C ,过点C 的直线交椭圆于M 、N 两点.若四边形FAMN 是平行四边形,则该椭圆的离心率为( )A .35B .12C .23D .3411.设x ,y 满足约束条件230,2210,0,+-≤⎧⎪--≤⎨⎪-≥⎩x y x y x a 若-+x y x y 的最大值为2,则a 的值为( )A .12 B .14 C .38 D .5912.定义在()0,+∞上的函数()f x 满足()(()2'>+f x x f x ,其中()'f x 为()f x 的导函数,则下列不等式中,一定成立的是( ) A .()()()23123>>f f f B .()()()149234>>f f f C .()()()23123<<f f f D .()()()149234<<f f f 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若函数()sin 3πω⎛⎫=+⎪⎝⎭f x x (01ω<<)的图象关于点()2,0-对称,则ω= . 14.P 为双曲线2213-=y x 右支上一点,1F 、2F 为左、右焦点,若1210+=PF PF ,则12⋅=uuu r uuu rPF PF .15.若数列{}1--n n a a 是等比数列,且11=a ,22=a ,35=a ,则=n a .16.已知四面体ABCD 的每个顶点都在球O 的表面上,5==AB AC ,8=BC ,⊥AD 底面ABC ,G 为V ABC 的重心,且直线DG 与底面ABC 所成角的正切值为12,则球O 的表面积为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设V ABC 的内角A ,B ,C 的对边分别为a ,b ,c,已知222+-=b c a . (1)若tan 12=B ,求b a ;(2)若23π=B,=b BC 边上的中线长. 18.如图,在四棱锥-P ABCD 中,⊥PD 底面ABCD ,底面ABCD 为矩形,且12==PD AD AB ,E 为PC 的中点.(1)过点A 作一条射线AG ,使得∥AG BD ,求证:平面∥PAG 平面BDE ; (2)求二面角--D BE C 的余弦值的绝对值.19.为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.(1)由以下统计数据填写下面22⨯列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?附:()()()()()22-=++++n ad bc K a b c d a c b d ,其中=+++n a b c d .临界值表(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为X ,求X 的分布列及数学期望.20.已知抛物线C :22=x py (0>p )的焦点为F ,直线220-+=x y 交抛物线C 于A 、B 两点,P是线段AB 的中点,过P 作x 轴的垂线交抛物线C 于点Q .(1)D 是抛物线C 上的动点,点()1,3-E ,若直线AB 过焦点F ,求+DF DE 的最小值;(2)是否存在实数p ,使2+=uu r uu u r QA QB 2-uu r uu u rQA QB ?若存在,求出p 的值;若不存在,说明理由.21.已知函数()2ln 2=-+f x m x x (8≤m ).(1)当曲线()=y f x 在点()()1,1f 处的切线的斜率大于2-时,求函数()f x 的单调区间; (2)若()()'-f x f x 43≤-x 对[)1,∈+∞x 恒成立,求m 的取值范围.(提示:ln 20.7≈)请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为4cos ρθ=,曲线M 的直角坐标方程为220-+=x y (0>x ).(1)以曲线M 上的点与点O 连线的斜率k 为参数,写出曲线M 的参数方程; (2)设曲线C 与曲线M 的两个交点为A ,B ,求直线OA 与直线OB 的斜率之和. 23.选修4-5:不等式选讲已知不等式-<x m x 的解集为()1,+∞. (1)求实数m 的值; (2)若不等式511-<+-a x x 21+-<m a x x对()0,∈+∞x 恒成立,求实数a 的取值范围.新乡市高三第三次模拟测试 数学试卷参考答案(理科)一、选择题1-5: ADBBC 6-10:CDDAA 11、12:CB二、填空题13.6π 14.18 15.1312-+n 16.6349π三、解答题17.解:(1)由222+-=b c a得cos 2=A ,6π∴=A.tan 12=Q B ,1sin 5∴=B .由正弦定理得,sin sin =a b A B ,则sin sin ==b B a A 125152=. (2)6π=Q A ,6ππ=--=C A B ,∴=AB BC .由sin sin =c bC B得2=c .取BC 中点D ,在V ABD中,2222=+-AD AB BD cos 7⨯⨯⨯=AB BD B,∴=AD BC18.(1)证明:在矩形ABCD 中,连接AC 和BD 交于点O ,连接OE ,则O 是AC 的中点,由于E 是PC 的中点,所以OE 是V PAC 的中位线,则∥OE PA 又⊂OE 平面BDE ,⊄PA 平面BDE , 所以∥PA 平面BDE .又∥AG BD ,同理得∥AG 平面BDE .因为=I PA AG A ,所以平面∥PAG 平面BDE .(2)分别以DA ,DC ,DP 所在的直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系. 设=AD a ,则=PD a ,2=AB a ,故(),2,0B a a ,()0,0,P a ,()0,2,0C a ,0,,2⎛⎫ ⎪⎝⎭a E a , 所以(),2,0=uu u r DB a a ,0,,2⎛⎫= ⎪⎝⎭uuu r a DE a ,(),0,0=uu r CB a ,0,,2⎛⎫=- ⎪⎝⎭uu u r a EC a ,设平面BDE 的一个法向量为()1111,,=u r n x y z ,则有110,0,⎧⋅=⎪⎨⋅=⎪⎩u r uu u r u r uuu rn DB n DE ,即20,0,2+=⎧⎪⎨+=⎪⎩ax ay aay z 令2=x ,则1=-y ,2=z ,故()12,1,2=-u r n . 同理,可得平面BEC 的一个法向量()20,1,2=u u rn .所以121212cos ,⋅==u r u u ru r u u r u r u u rn n n n nn 5--D BE C的余弦值的绝对值为5.19.解:(1)根据22⨯列联表中的数据,得2K 的观测值为()24094161125152020⨯-⨯=⨯⨯⨯k 5.227 5.024≈>, ∴能在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”.(2)由表可知在8人中成绩不优良的人数为158340⨯=,则X 的可能取值为0,1,2,3. ()31131533091===C P X C ;()2111431544191===C C P X C ; ()12114315662455===C C P X C ;()3431543455===C P X C . ∴X 的分布列为:()3344019191∴=⨯+⨯E X 66423455455+⨯+⨯364455=. 20.解:(1)Q 直线220-+=x y 与y 轴的交点为()0,2,()0,2∴F ,则抛物线C 的方程为28=x y ,准线l :2=-y .设过D 作⊥DG l 于G ,则+=DF DE +DG DE , 当E 、D 、G 三点共线时,+DF DE 取最小值235+=. (2)假设存在,抛物线22=x py 与直线22=+y x 联立方程组得:2440--=x px p ,设()11,A x y ,()22,B x y ,则124+=x x p ,124=-x x p ,()2,2∴Q p p .2+uu r uu u r Q QA QB 2=-uu r uu u rQA QB ,∴⊥QA QB .则0⋅=u u r u u u rQA QB 得:()()1222--+x p x p ()()12220--=y p y p ,()()1222--+x p x p ()()122222220+-+-=x p x p ,()()1212546+-++x x p x x 28840-+=p p ,代入得24310+-=p p , 解得14=p 或1=-p (舍去).21.解:(1)的定义域为()0,+∞,()2'=-=m f x x x 22-+x mx,()122'=->-Q f m ,0∴>m .由()0'=f x,得=x当0<<x ()0'>f x ,()∴f x的单调递增区间为⎛ ⎝;当>x 时,()0'<f x ,()∴f x的单调递减区间为⎫+∞⎪⎪⎭.(2)令()2ln 2=-+g x m x x 243-+-+=m x x x 2ln 25---+mm x x x x,1≥x , 则()222'=--+=m m g x x x x 32222--++x x mx m x ()()2212+-=x m xx ,1≥x , ①当2≤m 时,()0'≤g x ,所以()g x 在()1,+∞上单调递减,所以当1≥x ,()()1≤g x g ,故只需()10≤g ,即1250---+≤m ,即2≥m ,所以2=m . ②当28<≤m 时,令()0'=g x,得=x当1≤<x ()0'>g x ,()g x 单调递增;当>x 时,()0'<g x ,()g x 单调递减.所以当=x ()g x 取得最大值.故只需0≤g,即2-mm 50+≤, 化简得ln 222--m mm50≤, 令2=mt,得ln 50--≤t t t (14<≤t ). 令()ln =--h x x xx 5(14<≤t ),则()1ln 1'=+-h x xln =x , 令()ln =-H x x ()10'=+>H x x , 所以()'h x 在()1,+∞上单调递增,又()120'=-<h ,()4ln410'=->h ,所以()01,4∃∈x ,()00'=h x ,所以()h x 在()01,x 上单调递减,在(]0,4x 上递增,而()11450=--+=h ,()44ln 4485=--+=h 8ln 270-<, 所以(]1,4∈x 上恒有()0≤h x ,即当28<≤m时,ln2-mm 50≤. 综上所述,28≤≤m .22.解:(1)由()2200-+=>⎧⎪⎨=⎪⎩x y x y kx 得221221⎧=⎪⎪-⎨⎪=⎪-⎩x k k y k .故曲线M 的参数方程为221221⎧=⎪⎪-⎨⎪=⎪-⎩x k ky k .(k 为参数,且12>k ).(2)由4cos ρθ=,得24cos ρρθ=,224∴+=x y x .将221221⎧=⎪⎪-⎨⎪=⎪-⎩x k k y k 代入224+=x y x 整理得2430-+=k k , 故直线OA 与直线OB 的斜率之和为4.23.解:(1)由-<x m x 得22-<x m x ,即22>mx m ,而不等式-<x m x 的解集为()1,+∞,则1是方程22=mx m 的解,解得2=m (0=m 舍去). (2)2=Q m ,∴不等式511-<+-a x x 21+-<m a x x对()0,∈+∞x 恒成立等价于 不等式51-<+-a x 22-<+x a 对()0,∈+∞x 恒成立.设()12=+--=f x x x 21,023,2-<<⎧⎨≥⎩x x x ,则()(]1,3∈-f x .23∴+>a ,51-≤-a ,14∴<≤a .。
