北京市中考数学总复习第五单元三角形课时训练19等腰三角形试题
初三中考数学复习 等腰三角形 专项基础训练题 含答案

初三中考数学复习等腰三角形专项基础训练题含答案2019 初三中考数学复习等腰三角形专项基础训练题1.若等腰三角形的顶角为40°,则它的底角度数为( )A.40° B.50° C.60° D.70°2.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( ) A.30° B.40° C.45° D.60°3. 在△ABC中,∠B=∠C,AB=5,则AC的长为( )A.2 B.3 C.4 D.54. 下列条件中,不能判定△ABC是等腰三角形的是( )A.a=3,b=3,c=4B.a∶b∶c=2∶3∶4C.∠B=50°,∠C=80°D.∠A∶∠B∶∠C=1∶1∶25.如图,在△ABC 中,∠A=36°,AB=AC,BD 是∠ABC 的平分线.若在边 AB 上截取BE=BC,连接 DE,则图中等腰三角形共有()A.2 个B.3 个 C.4 个 D.5 个6. 如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形有( )A.2个 B.3个 C.4个 D.5个7. 有两个角等于60°的三角形是三角形;有一个角等于60°_______的三角形是等边三角形.8. 在△ABC中,∠A=30°,当∠B=_____________时,△ABC是等腰三角形.9. 如图,△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且AE=CD=BF,则△DEF为_______三角形.12. 2013. 45°14. 1315. 解:∵CE=CA,∴∠CAE=∠E=65°,∴∠ACE=180°-∠CAE-∠E=50°,∵AB∥EF,∴∠CAB=∠ACE=50°.16. 解:∠ADC的大小不变.理由:∵△ABC是等边三角形,∴AB=AC=BC,∠ABC=60°.∵BD=AB=BC,∴∠BAD=∠BDA,∠BDC=∠BCD.∵∠BDA+∠BAD+∠BDC+∠BCD+∠ABC=360°,∴2∠BDA+2∠BDC+60°=360°,∴∠BDA+∠BDC =150°,即∠ADC=150°.。
第19 讲 等腰三角形 (测)(解析版)

2021年中考数学一轮复习讲练测专题19等腰三角形达标检测1.(2020·河北九年级其他模拟)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2等于( )A.90°B.100°C.130°D.180°【答案】B【解析】试题分析:如图,∠1=90°-∠BAC;∠2=120°-∠ACB;∠3=120°-∠ABC;∴∠1+∠2+∠3=90°-∠BAC+120°-∠ACB+120°-∠ABC=150°∵∠3=50°∴∠1+∠2=100°故选B考点:1.特殊角的度数;2.三角形内角和2.(2020·河南濮阳市·油田十中八年级期中)等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为()A.12 B.15 C.12或15 D.18【答案】B试题分析:根据题意,要分情况讨论:①、3是腰;②、3是底.必须符合三角形三边的关系,任意两边之和大于第三边.解:①若3是腰,则另一腰也是3,底是6,但是3+3=6,∴不构成三角形,舍去.②若3是底,则腰是6,6.3+6>6,符合条件.成立.∴C=3+6+6=15.故选B.考点:等腰三角形的性质.3.(2020·四川广安市·九年级其他模拟)在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有A.5个B.4个C.3个D.2个【答案】B【解析】如图:满足条件的点Q共有(0,2)(0,22)(0,-22)(0,4).故选B.4.(2020·河北邢台市·九年级零模)在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?()A.1 B.2 C.3 D.4【详解】解:根据题意可得有以下三种情况:故选:C.【点睛】本题考查等腰三角形的性质.5.(2020·德昌县民族初级中学八年级期中)如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为()A.30°B.40°C.45°D.60°【答案】B【分析】先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.【详解】解:∵△ABD中,AB=AD,∠B=80°,∴∠B=∠ADB=80°,∴∠ADC=180°﹣∠ADB=100°,∵AD=CD,∴∠C=18018010040.22ADC-︒︒-=︒=︒∠故选B.考点:等腰三角形的性质.6.(2020·柳州市柳林中学中考真题)通过如下尺规作图,能确定点D是BC边中点的是()A.B.C.D.【答案】A【分析】作线段BC的垂直平分线可得线段BC的中点.【详解】作线段BC的垂直平分线可得线段BC的中点.由此可知:选项A符合条件,故选A.【点睛】本题考查作图﹣复杂作图,解题的关键是熟练掌握五种基本作图.7.(2020·浙江台州市·中考真题)如图,已知线段AB,分别以A,B为圆心,大于12AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是()A.AB平分∠CAD B.CD平分∠ACB C.AB⊥CD D.AB=CD【答案】D【分析】根据作图判断出四边形ACBD是菱形,再根据菱形的性质:菱形的对角线平分一组对角、菱形的对角线互相垂直平分可得出答案【详解】解:由作图知AC=AD=BC=BD,∴四边形ACBD是菱形,∴AB平分∠CAD、CD平分∠ACB、AB⊥CD,不能判断AB=CD,故选:D.【点睛】本题主要考查线段垂直平分线的尺规作图、菱形的判定方法等,解题的关键是掌握菱形的判定与性质.8.(2020·广东汕头市·九年级其他模拟)如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是()A.△DEF是等边三角形B.△ADF≌△BED≌△CFEC.DE=12ABD.S△ABC=3S△DEF【答案】C【分析】求出∠BDE=∠FEC=∠AFD=30°,求出∠DEF=∠DFE=∠EDF=60°,推出DF=DE=EF,即可得出等边三角形DEF,根据全等三角形性质推出三个三角形全等即可.求出AB=3BE,3,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.【详解】∵△ABC是等边三角形,∴AB=AC=BC,∠B=∠C=∠A=60°,∵DE ⊥BC 、EF ⊥AC 、FD ⊥AB ,∴∠DEB=∠EFC=∠FDA=90°,∴∠BDE=∠FEC=∠AFD=30°,∴∠DEF=∠DFE=∠EDF=180°﹣90°﹣30°=60°,∴DF=DE=EF ,∴△DEF 是等边三角形,在△ADF 、△BED 、△CFE 中ADF=BED=CFE{A=B=CDF=DE=EF∠∠∠∠∠∠ ∴△ADF ≌△BED ≌△CFE ,∴AD=BE=CF ,∵∠DEB=90°,∠BDE=30°,∴BD=2BE ,DE=3BE,∴AB=3BE ,即3DE=AB ,即DE=12AB 错误; ∵△ABC 和△DEF 是等边三角形,∴△ABC ∽△DEF ,∴S △ABC :S △DEF =(AB )2:(DE )2=(3DE )2:DE 2=3,即只有选项C 错误;选项A 、B 、D 正确.故选C .【点睛】本题主要考查等边三角形的判定及性质、全等三角形的判定及性质、相似三角形的判定及性质,熟练掌握判定定理和性质是关键.9.(2020·青海中考真题)如图所示ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC 于D,ΔDBC的周长是24cm,则BC=___________cm.【答案】10【分析】由MN是AB的垂直平分线可得AD=BD,于是将△BCD的周长转化为BC与边长AC的和来解答.【详解】C ,∵24cmDBC∴BD+DC+BC=24cm,∵MN垂直平分AB,∴AD=BD,∴AD+DC+BC=24cm,即AC+BC=24cm,又∵AC=14cm,∴BC=24-14=10cm.故答案为:10点睛:解答本题的关键是熟练掌握垂直平分线的性质:垂直平分线上的点到线段两端的距离相等.此题将垂直平分线的性质与三角形的周长问题相结合,体现了转化思想在解题时的巨大作用.10.(2020·浙江绍兴市·八年级其他模拟)做如下操作:在等腰三角形ABC中,AB= AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的象与△ACD 重合对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线和高互相重合由上述操作可得出的是_________(将正确结论的序号都填上)【答案】②③【分析】认真读题,由已知条件沿直线AD对折,重合,说明∠B与∠C相等,AD⊥BC,BD=CD,根据结论对号入座即可.【详解】解:从操作过程没有体现角相等,边就相等,故①不符合;因为AB=AC,操作之后得到∠B与∠C重合,即等边对等角,故②符合;根据所得的图象与△ACD重合,所以AD⊥BC,BD=CD,又AD平分∠BAC,所以③符合.故操作可以得出的是②③两结论.故答案为:②③.【点睛】本题考查了等腰三角形的性质及轴对称的性质;做题时,要认真读题,紧靠题目的已知条件和操作的结论进行判断.11.(2020·浙江绍兴市·八年级其他模拟)如图,△ABC为正三角形,BD是角平分线,点F 在线段BD上移动,直线CF与AB交于点E,连结AF,当AE=AF时,∠BCE=_____度.【答案】20.【分析】根据题意易得△ABF≌△CBF(SAS),设∠BAF=∠BCF=α,得到∠AEF=60°+α,在△AFE 中,得到α=20°,即可求解.【详解】解:∵△ABC为正三角形,BD是角平分线,∴∠ABC=60°,BD⊥AC,∴∠ABD=∠CBD=30°,AB=BC,∵BF=BF,∴△ABF≌△CBF(SAS),∴∠BAF=∠BCF,设∠BAF=∠BCF=α,∴∠AEF=60°+α,∵AE=AF,∴∠AEF=∠AFE=60°+α,∴60°+α+60°+α+α=180°,∴α=20°,∴∠BCE=20°,故答案为:20.【点睛】此题主要考查三角形全等的判定与性质、三角形的外角等于与其不相邻的两个内角和,熟练进行逻辑推理是解题关键.12.(2020·河北九年级其他模拟)如图,在等边三角形ABC中,点D是边BC的中点,则∠BAD=_________.【答案】30°【解析】【分析】根据等腰三角形的三线合一的性质和等边三角形三个内角相等的性质填空.【详解】∵△ABC 是等边三角形,∴60BAC AB AC ∠=︒=,.又点D 是边BC 的中点, ∴1302BAD BAC ∠=∠=︒. 故答案是:30°.【点睛】考查了等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.13.(2020·湖南永州市·九年级二模)如图,在ΔABC 中,∠A=36°,AB=AC,BD 平分∠ABC ,则图中等腰三角形的个数是__________【答案】3【解析】分析:由已知条件,利用三角形的内角和定理及角平分线的性质得到各角的度数,根据等腰三角形的定义及等角对等边得出答案.详解:∵AB=AC ,∴△ABC 是等腰三角形.∵∠A=36°,∴∠C=∠ABC=72°.∵BD 平分∠ABC 交AC 于D ,∴∠ABD=∠DBC=36°,∵∠A=∠ABD=36°,∴△ABD 是等腰三角形.∠BDC=∠A+∠ABD=36°+36°=72°=∠C , ∴△BDC 是等腰三角形.∴共有3个等腰三角形.故答案为3.点睛:本题考查了等腰三角形的判定与性质及三角形内角和定理;求得角的度数是正确解答本题的关键.14.(2020·浙江八年级其他模拟)如图,a ∥b ,∠ABC=50°,若△ABC 是等腰三角形,则∠α=__°(填一个即可)【答案】130【解析】分类讨论:(1)AB AC =则50∠=°ACB a ∥b130α∴=︒(2)AB BC =则65ACB ∠=︒ a ∥b115α∴=︒(3)AC BC =则80ACB ∠=︒a ∥b100α∴=︒综上述,=α 130或100或11515.(2020·黑龙江绥化市·九年级一模)等腰三角形一腰上的高与另一腰的夹角为48,则该等腰三角形的底角的度数为______.【答案】69°或21°【解析】分两种情况讨论:①若∠A<90°,如图1所示:∵BD ⊥AC ,∴∠A+∠ABD=90°,∵∠ABD=48°,∴∠A=90°−48°=42°,∵AB=AC ,∴∠ABC=∠C=12(180°−42°)=69°; ②若∠A>90°,如图2所示:同①可得:∠DAB=90°−48°=42°,∴∠BAC=180°−42°=138°,∵AB=AC ,∴∠ABC=∠C=12(180°−138°)=21°;综上所述:等腰三角形底角的度数为69°或21°.故答案为69°或21°.16.(2020·江苏镇江市·九年级其他模拟)如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD=___.【答案】44°【分析】根据等腰三角形两底角相等求出∠BAC,再根据两直线平行,内错角相等解答.【详解】∵AB=AC,∠ABC=68°,∴∠BAC=180°﹣2×68°=44°,∵AB∥CD,∴∠ACD=∠BAC=44°.故答案为44°.【点睛】本题考查了等腰三角形两底角相等的性质,平行线的性质,是基础题,熟记各性质是解题的关键.17.(2020·福建省福州第一中学九年级一模)根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).如图,已知△ABC中,AB=AC,BD是BA边的延长线.(1)作∠DAC的平分线AM;(2)作AC边的垂直平分线,与AM交于点E,与BC边交于点F;(3)联接AF,则线段AE与AF的数量关系为.【答案】答案见解析【分析】(1)直接利用角平分线的作法得出答案;(2)直接利用线段垂直平分线的作法得出答案;(3)根据线段中垂线的性质得出答案.【详解】(1) 如图所示:(2)如图所示:(3)AE=AF.【点睛】此题主要考查了复杂作图以及全等三角形的判定与性质等知识,属于基础题型.正确掌握基本作图方法是解题关键.18.(2020·广东清远市·九年级二模)作图题:(要求保留作图痕迹,不写作法)(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);(2)连结BE,若AC=10,AB=6,求△ABE的周长.【答案】(1)答案见解析;(2)16.【分析】(1)分别以点B、C为圆心,以大于12BC长为半径画弧,在BC的两侧两弧分别相交于一点,作这两点作直线即可;(2)根据线段垂直平分线上的点到线段两端点的距离相等可得BE=CE,从而得到△ABE的周长等于AB与AC的和,代入数据进行计算即可.【详解】解:(1)如图所示,(2)∵EF垂直平分BC,∴BE=EC,∴△ABE的周长=AB+BE+AE=AB+BE+EC=AB+BC,∵AB=6,BC=10,∴△ABE的周长=6+10=16.【点睛】此题主要考查了基本作图,正确线段垂直平分线的性质与画法是解题关键.19.(2020·贵州铜仁市·九年级零模)△ABC中,AB=AC,∠BAC=120°,点D、F分别为AB、AC中点,ED⊥AB,GF⊥AC,若BC=15cm,求EG的长.【答案】EG=5cm.【分析】连接AE、AG,根据线段垂直平分线上的点到线段两端点的距离相等可得EB=EA,再根据等腰三角形两底角相等求出∠B ,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEG=60°,同理求出∠AGE=60°,从而判断出,△AEG 为等边三角形,再根据等边三角形三边都相等列式求解即可.【详解】解:如图,连接AE 、AG ,∵D 为AB 中点,ED ⊥AB ,∴EB =EA ,∴△ABE 为等腰三角形,又∵∠B =1801202︒︒-=30°, ∴∠BAE =30°,∴∠AEG =60°,同理可证:∠AGE =60°,∴△AEG 为等边三角形,∴AE =EG =AG ,又∵AE =BE ,AG =GC ,∴BE =EG =GC ,又BE +EG +GC =BC =15(cm ),∴EG =5(cm ).【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线构造出等腰三角形与等边三角形是解题的关键.20.(2020·山东济南市·九年级一模)如图,点C 是线段AB 上任意一点,分别以AC BC 、为边在AB 的同侧作等边ACD ∆和等边BCE ∆,分别连接AE BD 、.求证:AE BD =.【答案】见解析【解析】【分析】根据等边三角形的性质,证ACE DCB ∆≅∆,得.AE BD =【详解】解:ACD ∆和BCE ∆是等边三角形,,,AC DC EC BC ∴== 60ACD BCE ∠=∠=ACD DCE BCE DCE ∴∠+∠=∠+∠ACE BCD ∴∠=∠ACE DCB ∴∆≅∆AE BD ∴=【点睛】考核知识点:等边三角形的性质,全等三角形判定和性质.理解性质是关键.21.(2020·河北九年级其他模拟)如图1,菱形ABCD 中,120ABC ∠=︒,P 是对角线BD 上的一点,点E 在AD 的延长线上,且PA PE =,PE 交CD 于F ,连接CE .(1)证明:ADP CDP △≌△;(2)判断CEP △的形状,并说明理由.(3)如图2,把菱形ABCD 改为正方形ABCD ,其他条件不变,直接..写出线段AP 与线段CE 的数量关系.【答案】(1)证明见解析;(2)CEP ∆是等边三角形,理由见解析;(3)2CE =.【分析】(1)由菱形ABCD 性质可知,AD CD =,ADP CDP ∠=∠,即可证明;(2)由△PDA ≌△PDC ,推出PA=PC ,由PA=PE ,推出DCP DEP ∠=∠,可知60CPF EDF ∠=∠=︒,由PA═PE=PC ,即可证明△PEC 是等边三角形;(3)由△PDA ≌△PDC ,推出PA=PC ,∠3=∠1,由PA=PE ,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC ,推出∠FPC=EDF=90°,推出△PEC 是等腰直角三角形即可解答;【详解】(1)证明:在菱形ABCD 中,AD CD =,ADP CDP ∠=∠,在ADP ∆和CDP ∆AD CD ADP CDP DP DP =⎧⎪∠=∠⎨⎪=⎩,∴()ADP CDP SAS ∆≅∆.(2)CEP ∆是等边三角形,由(1)知,ADP CDP ∆≅∆,∴DAP DCP ∠=∠,AP CP =,∵PA PE =,∴DAP DEP ∠=∠,∴DCP DEP ∠=∠,∵CFP EFD ∠=∠(对顶角相等),∴180180PFC PCF DFE DEP ︒-∠-∠=︒-∠-∠,即60CPF EDF ∠=∠=︒,又∵PA PE =,AP CP =;∴PE PC =,∴CEP ∆是等边三角形.(3)CE =.过程如下:证明:如图1中,∵四边形ABCD 是正方形,∴AD=DC ,∠ADB=∠CDB=45°,∠ADC=90°,在△PDA 和△PDC 中,PD PD PDA PDC DA DC ⎧⎪∠∠⎨⎪⎩===,, ∴△PDA ≌△PDC ,∴PA=PC ,∠3=∠1,∵PA=PE ,∴∠2=∠3,∴∠1=∠2,∵∠EDF=90°,∠DFE=∠PFC ,∴∠FPC=EDF=90°,∴△PEC 是等腰直角三角形.∴CE=2PC =2AP .【点睛】本题考查正方形的性质、菱形的性质、全等三角形的判定和性质、等边三角形判定、等腰直角三角形性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型. 22.(2020·通辽市科尔沁区第七中学八年级月考)问题探究:如图1,△ACB 和△DCE 均为等边三角形,点A 、D 、E 在同一直线上,连接BE .(1)证明:AD=BE;(2)求∠AEB的度数.问题变式:(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.【答案】(1)见详解;(2)60°;(3)(Ⅰ)90°;(Ⅱ)AE=BE+2CM,理由见详解.【分析】(1)由条件△ACB和△DCE均为等边三角形,易证△ACD≌△BCE,从而得到对应边相等,即AD=BE;(2)根据△ACD≌△BCE,可得∠ADC=∠BEC,由点A,D,E在同一直线上,可求出∠ADC=120°,从而可以求出∠AEB的度数;(3)(Ⅰ)首先根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD ≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°;(Ⅱ)根据DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM.【详解】解:(1)如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE.在△ACD和△BCE中,AC BCACD BCE CD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE(SAS),∴AD=BE;(2)如图1,∵△ACD≌△BCE,∴∠ADC=∠BEC,∵△DCE为等边三角形,∴∠CDE=∠CED=60°,∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC-∠CED=60°;(3)(Ⅰ)如图2,∵△ACB和△DCE均为等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE,在△ACD和△BCE中,AC BCACD BCE CD CE=⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE(SAS),∴BE=AD,∠BEC=∠ADC,∵点A,D,E在同一直线上,∴∠ADC=180-45=135°,∴∠BEC=135°,∴∠AEB=∠BEC-∠CED=135°-45°=90°,故答案为90°;(Ⅱ)如图2,∵∠DCE=90°,CD=CE,CM⊥DE,∴CM=DM=EM,∴DE=DM+EM=2CM,∵△ACD≌△BCE(已证),∴BE=AD,∴AE=AD+DE=BE+2CM,故答案为AE=BE+2CM.【点睛】本题属于三角形综合题,主要考查了全等三角形的判定方法和性质,等边三角形的性质以及等腰直角三角形的性质的综合应用.在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.。
中考数学复习《等腰三角形》专项测试卷(带答案)

中考数学复习《等腰三角形》专项测试卷(带答案)学校:___________班级:___________姓名:___________考号:___________一.选择题1. 如图,边长为4的等边△ABC 中,DE 为中位线,则四边形BCED 的面积为( ) (A )32(B )33(C )34(D )362. 如图,⊿ABC 和⊿CDE 均为等腰直角三角形,点B,C,D 在一条直线上,点M 是AE 的中点,下列结论:①tan ∠AEC=CDBC;②S ⊿ABC +S ⊿CDE ≧S ⊿ACE ;③BM ⊥DM;④BM=DM.正确结论的个数是( )(A )1个 (B )2个 (C )3个(D )4个MECA3. 如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°, 四边形ACDE 是平行四边形,连结CE 交AD 于点F ,连结BD 交CE 于点G ,连结BE . 下列结论中:① CE =BD ; ② △ADC 是等腰直角三角形; ③ ∠ADB =∠AEB ; ④ CD ·AE =EF ·CG ; 一定正确的结论有(第1题)A BCD EA.1个 B.2个 C.3个 D.4个4. 如图,ΔABC中,以B 为圆心,BC长为半径画弧,分别交AC和AB于D、E两点,并连接BD、DE若∠A=30∘,AB=AC,则∠BDE的度数为何?A. 45 B. 52.5 C. 67.5 D. 755. 如图(1),有两全等的正三角形ABC、DEF,且D、A分别为△ABC、△DEF的重心.固定D点,将△DEF逆时针旋转,使得A落在DE上,如图(2)所示.求图(1)与图(2)中,两个三角形重迭区域的面积比为何?图1 图2A.2:1 B. 3:2 C. 4:3 D. 5:46. 如果一个等腰三角形的两边长分别是5cm和6cm,那么此三角形的周长是A.15cm B.16cmC.17cm D.16cm或17cm7. 如图,在ABC△中13AB AC==,10BC=点D为BC的中点DE DE AB⊥垂足为点E,则DE等于()A.1013B.1513C.6013D.7513 ABCDE FG8.等腰三角形两边长分别为4和8,则这个等腰三角形的周长为 A .16 B .18 C .20 D .16或209.等腰三角形的顶角为80°,则它的底角是( ) A . 20° B . 50° C . 60° D . 80°10.把等腰△ABC 沿底边BC 翻折,得到△DBC ,那么四边形ABDC ( )11.如图,△ABC 是等边三角形,P 是∠ABC 的平分线BD 上一点,PE ⊥AB 于点E ,线段BP 的垂直平分线交BC 于点F ,垂足为点Q .若BF =2,则PE 的长为( )A . 2B .23C .3D .312.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点E ,过点E 作MN ∥BC 交AB 于M ,交AC 于N ,若BM+CN=9,则线段MN 的长为( )A .6B .7C .8D .9第11题图AD E F PQC13.已知实数x ,y 满足,则以x ,y 的值为两边长的等腰三角形的周长是( )A . 20或16B . 20C . 16D .以上答案均不对14.如图,在△ABC 中,AB =AC ,∠A =36°,BD 平分∠ABC 交AC 于点D ,若AC =2,则AD 的长是( )A .512- B .512+ C .51- D .51+15.如图,△ABC 为等边三角形,点E 在BA 的延长线上,点D 在BC 边上,且ED=EC .若△ABC 的边长为4,AE=2,则BD 的长为( )A . 2B . 3C .D . +116.如图,在菱形ABCD 中,∠A =60°,E ,F 分别是AB ,AD 的中点,DE ,BF 相交于点G ,连接BD ,CG ,有下列结论:①∠BGD =120° ;②BG +DG =CG ;③△BDF ≌△CGB ;④234ABD S AB =△.其中正确的结论有( )A .1个B .2个C .3个D .4个 二.填空题1. 边长为6cm 的等边三角形中,其一边上高的长度为________.2. 等腰三角形的周长为14,其一边长为4,那么,它的底边为 .3. 在等腰Rt △ABC 中,∠C =90°,AC =1,过点C 作直线l ∥AB ,F 是l 上的一点,且AB =AF ,则点F 到直线BC 的距离为 .4. 已知等边△ABC 中,点D,E 分别在边AB,BC 上,把△BDE 沿直线DE 翻折,使点B 落在点B ˊ处,DB ˊEB ˊ分别交边AC 于点F ,G ,若∠ADF=80º ,则∠EGC 的度数为5. 如图,在△ABC 中,AB =AC ,︒=∠40A 则△ABC 的外角∠BCD = °.6. 如图(四)所示,在△ABC 中,AB=AC ,∠B=50°,则∠A=_______。
2019年中考数学专题《等腰三角形》复习试卷含答案解析

2019年中考数学总复习等腰三角形专题综合训练题1.在△ABC中,∠ABC=30°,∠BAC=70°.在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )A.7条 B.8条C.9条D.10条2. 如图,在△ABC中,AB=AC,∠A=30°,DE垂直平分AC,则∠BCD的度数为( )A.80° B.75° C.65° D.45°3. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )A.3 B.4 C.5 D.64. 如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )A.6 B.3 C.2.5 D.25. 如图,在△ABC中,AB=AC,AD是∠B AC的平分线.已知AB=5,AD=3,则BC的长为( )A.5 B.6 C.8 D.106. 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于____.7. 如图钢架中,焊上等长的13根钢条来加固钢架.若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是____.8. 在△ABC中,∠C是最小内角.若过顶点B的一条直线把这个三角形分成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC的关于点B的伴侣分割线.例如:如图1,△ABC 中,∠A=90°,∠C=20°,若过顶点B的一条直线BD交AC于点D,且∠DBC=20°,则直线BD是△ABC 的关于点B的伴侣分割线.(1)如图2,△ABC中,∠C=20°,∠ABC=110°.请在图中画出△ABC关于点B的伴侣分割线,并注明角度;(2)△ABC中,设∠B的度数为y,最小内角∠C的度数为x.试探索y与x应满足什么要求时,△ABC存在关于点B的伴侣分割线.9. 如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C,B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.解析:第(2)题分别以点C,M,N为直角顶点分三类进行讨论,利用全等三角形和勾股定理求CM或CN的长,利用面积公式进行计算.10. 如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)11. 在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线l∥AB,F是l上的一点,且AB=AF,求点F 到直线BC的距离.12. 如图,已知抛物线y =ax 2+bx +c(a ≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)点M 是直线l 上的动点,且△MAC 为等腰三角形,求出所有符合条件的点M 的坐标.13. 如图,在△ABC 中,AB =AC ,∠BAC =90°,BD 是∠ABC 的平分线,CE ⊥BD ,垂足是E ,BA 和CE 的延长线交于点F.(1) 在图中找出与△ABD 全等的三角形,并证明你的结论; (2) 证明:BD =2EC.参考答案: 1. C2. D 【解析】∠BCA=12(180°-∠A)=75°,∠BCD =∠BCA-∠DCA=∠BCA-∠A=75°-30°=45°.3. C【解析】作PQ⊥MN 于Q ,由PM =PN 知PQ 垂直平分MN∴MQ=1.∠AOB=60°,OP =12,∴OQ =12OP =6,OM=OQ -MQ =6-1=5. 4. C【解析】 如图,以BC 为边作等腰直角三角形△EBC,延长BE 交AD 于F ,得△ABF 是等腰直角三角形,作EG⊥CD 于G ,得△EGC 是等腰直角三角形,在矩形ABCD 中剪去△ABF,△BCE ,△ECG 得到四边形EFDG ,此时剩余部分的面积最小,最小值为4×6-12×4×4-12×3×6-12×3×3=2.5,故选C.5. C 【解析】∵AB=AC ,AD 是∠BAC 的平分线,∴AD ⊥BC ,BD =CD ,∴BD =AB 2-AD 2=4,∴BC =2BD =8,故选C. 6. 20° 【解析】过点A 作AD∥l 1,根据平行线的性质可得∠BAD=∠β.AD∥l 2,从而得到∠DAC=∠α=40°.再根据等边△ABC 可得到∠BAC=60°,∴∠β=∠BAD=∠BAC-∠DAC=60°-40°=20°.7. 12° 【解析】设∠A=x ,∵AP 1=P 1P 2=P 2P 3=…=P 13P 14=P 14A ,∴∠A =∠AP 2P 1=∠AP 13P 14=x ,∴∠P 2P 1P 3=∠P 13P 14P 12=2x ,∴∠P 3P 2P 4=∠P 12P 13P 11=3x ,……,∠P 7P 6P 8=∠P 8P 9P 7=7x ,∴∠AP 7P 8=7x ,∠AP 8P 7=7x.在△AP 7P 8中,∠A +∠AP 7P 8+∠AP 8P 7=180°,即x +7x +7x =180°,解得x =12°.8. 解:(1)画图正确,角度标注正确,如图① (2)考虑直角顶点,只有点A ,B ,D 三种情况.当点A 为直角顶点时,如图②,此时y =90°-x.当点B 为直角顶点时,再分两种情况:若∠DBC=90°,如图③,此时y =90°+12(90°-x)=135°-12x.若∠ABD=90°,如图④,此时y =90°+x.当点D 为直角顶点时,又分两种情况:若△ABD 是等腰三角形,如图⑤,此时y =45°+(90°-x)=135°-x.若△DBC 是等腰三角形,如图⑥,此时x =45°,45°<y <90°9. 解:(1)把点A(4,0),B(1,3)代入抛物线y =ax 2+bx 中,得⎩⎪⎨⎪⎧0=16a +4b ,3=a +b ,解得⎩⎪⎨⎪⎧a =-1,b =4,∴抛物线表达式为:y =-x 2+4x (2)点C 的坐标为(3,3),点B 的坐标为(1,3),以点C ,M ,N 为顶点的三角形为等腰直角三角形时,分三类情况讨论:①以点M 为直角顶点且M 在x 轴上方时,如图2,CM =MN ,∠CMN=90°,则△CBM≌△MHN,∴BC =MH =2,BM =HN =3-2=1,∴M(1,2),N(2,0),由勾股定理得MC =22+12=5,∴S △CMN =12×5×5=52;②以点M 为直角顶点且M 在x 轴下方时,如图3,作辅助线,构建如图所示的两直角三角形:Rt △NEM 和Rt △MDC ,得Rt △NEM ≌Rt △MDC ,∴MD =ME =2,EM =CD =5,由勾股定理得CM =22+52=29,∴S △CMN=12×29×29=292;③以点N 为直角顶点且N 在y 轴左侧时,如图4,CN =MN ,∠MNC =90°,作辅助线,同理得CN =32+52=34,∴S △CMN =12×34×34=17;④以点N 为直角顶点且N 在y 轴右侧时,作辅助线,如图5,同理得CN =32+12=10,∴S △CMN =12×10×10=5;⑤以C 为直角顶点时,不能构成满足条件的等腰直角三角形.综上所述,△CMN 的面积为52或292或17或510. 解:满足条件的所有等腰三角形如下图所示:解析:利用等腰三角形的性质,分别以长度为3的边为等腰三角形的底边和腰长进行分类.11. 解:①如图a ,延长AC ,作FD⊥BC 于点D ,FE ⊥AC 于点E ,易得四边形CDFE 是正方形,则CD =DF=FE =EC.∵在等腰直角△ABC 中,AC =BC =1,AB =AF ,∴AB =AC 2+BC 2=12+12=2,∴AF = 2.在Rt △AEF 中,(1+EC)2+EF 2=AF 2,即 (1+DF)2+DF 2=(2)2,解得DF =3-12;②如图b ,延长BC ,作FD⊥BC 于点D ,延长CA ,作FE⊥CA 于点E ,易得四边形CDFE 是正方形,则CD =DF =FE =EC.在Rt △AEF 中,(EC -1)2+EF 2=AF 2,即(FD -1)2+FD 2=(2)2,解得FD =3+12.综上可知,点F 到BC 的距离为3+12或3-1212. 解:(1)将A(-1,0),B(3,0),C(0,-3)代入抛物线y =ax 2+bx +c 中,得⎩⎪⎨⎪⎧a -b +c =0,9a +3b +c =0,c =-3,解得⎩⎪⎨⎪⎧a =1,b =-2,c =-3,故抛物线的解析式为y =x 2-2x -3 (2)如图,抛物线的对称轴为x =-b 2a=1,设M(1,m),已知A(-1,0),C(0,-3),则MA 2=m 2+4,MC 2=(3+m)2+1=m 2+6m +10,AC 2=10.①若MA =MC ,则MA 2=MC 2,得m 2+4=m 2+6m +10,解得m =-1;②若MA =AC ,则MA 2=AC 2,得m 2+4=10,得m =±6;③若MC =AC ,则MC 2=AC 2,得m 2+6m +10=10,得m 1=0,m 2=-6,当m =-6时,M ,A ,C 三点共线,不构成三角形,不合题意,故舍去.综上可知,符合条件的M 点的坐标为 (1,6)(1,-6)(1,-1)(1,0)13. 解:(1)△ABD≌△ACF,证明:∵AB =AC ,∠BAC =90°,∴∠FAC =∠BAC=90°,∵BD ⊥CE ,∠BAC =90°,∠ADB =∠EDC,∴∠ABD =∠ACF,∴△ABD ≌△ACF(ASA)(2)∵△ABD≌△ACF,∴BD =CF ,∵BD ⊥CE ,∴∠BEF =∠BEC,∵BD 是∠ABC 的平分线,∴∠FBE =∠CBE,∵BE =BE ,∴△FBE ≌△CBE(ASA),∴CF =2CE ,∴BD =2CE2019-2020学年数学中考模拟试卷一、选择题1.如图,以边长为a 的等边三角形各定点为圆心,以a 为半径在对边之外作弧,由这三段圆弧组成的曲线是一种常宽曲线.此曲线的周长与直径为a 的圆的周长之比是( )A .1:1B .1:3C .3:1D .1:22.昆明市有关负责人表示,预计年昆明市的地铁修建资金将达到亿元,将亿用科学记数法表示为( )A.B.C. D.3.如图,在直角三角形ABC 中,∠ACB =90°,AC =3,BC =4,点P 在边AB 上,∠CPB 的平分线交边BC 于点D ,DE ⊥CP 于点E ,DF ⊥AB 于点F .当△PED 与△BFD 的面积相等时,BP 的值为( )A. B. C. D.4.下列计算的结果是a 6的为( ) A .a 12÷a 2B .a 7﹣aC .a 2•a 4D .(﹣a 2)35.如图,是一个几何体的三视图,根据图中标注的数据可求得这个几何体的体积为( )A .12πB .24πC .36πD .48π6.如图,抛物线()()142L y x t x t =---+:(常数0t >),双曲线6(0)y x x=>.设L 与双曲线有个交点的横坐标为0x ,且满足034x <<,在L 位置随t 变化的过程中,t 的取值范围是( )A .322t << B .34t << C .45t << D .57t <<7.如图所示的几何体的俯视图为( )A .B .C .D .8.如图,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,若∠BAC =20°,则∠ADC 的度数是( )A .90°B .100°C .110°D .130°9.如图,一次函数y =kx+b 与y =x+2的图象相交于点P (m ,4),则关于x ,y 的二元一次方程组2kx y by x -=-⎧⎨-=⎩的解是( )A .34x y =⎧⎨=⎩B . 1.84x y =⎧⎨=⎩C .24x y =⎧⎨=⎩D . 2.44x y =⎧⎨=⎩10.如图1,△ABC 中,∠A =30°,点P 从点A 出发以2cm/s 的速度沿折线A→C→B 运动,点Q 从点A 出发以vcm/s 的速度沿AB 运动,P ,Q 两点同时出发,当某一点运动到点B 时,两点同时停止运动.设运动时间为x (s ),△APQ 的面积为y (cm 2),y 关于x 的函数图象由C 1,C 2两段组成,如图2所示,有下列结论:①v =1;②sinB =13;③图象C 2段的函数表达式为y =﹣13x 2+103x ;④△APQ 面积的最大值为8,其中正确有( )A .①②B .①②④C .①③④D .①②③④11.已知函数6y x -= 与y =﹣x+1的图象的交点坐标是(m ,n ),则11m n+的值为( ) A .﹣16B .16C .﹣6D .612.整数a 满足下列两个条件,使不等式﹣2≤352x +<12a+1恰好只有3个整数解,使得分式方程135-22ax x x x----=1的解为整数,则所有满足条件的a 的和为( )A .2B .3C .5D .6二、填空题13.任意写出一个3的倍数(例如:111),首先把这个数各数位上的数字都立方,再相加,得到一个新数,然后把这个新数重复上述运算,运算结果最终会得到一个固定不变的数M ,它会掉入一个数字“黑洞”.那么最终掉入“黑洞”的那个数M 是______.14.如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是_______.15.如图,已知在△ABC 中,AB=AC ,BC=8,D 、E 两点分别在边BC 、AB 上,将△ABC 沿着直线DE 翻折,点B 正好落在边AC 上的点M 处,并且AC=4AM ,设BD=m ,那么∠ACD 的正切值是______(用含m 的代数式表示)16.如图,在平面直角坐标系中,直线l:y=x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在3x轴的正半轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A6B7A7的周长是______.17 ______.18.如图,AB是圆O的弦,AB=,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN的最大值是_____.三、解答题19.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于点A,B(3,0),交y轴于点C(0,3).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.20.如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB,⊙O及CB延长线交于点F、G、M.(1)求证:四边形ABCD为矩形;(2)若N为MF中点,求证:NB是⊙O的切线;(3)若F为GE中点,且DE=6,求⊙O的半径.21.某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)求该种水果每次降价的百分率;(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数解析式,并求出第几天时销售利润最大.22.已知二次函数y=ax2+4x+c,当x=﹣2时,y=﹣5;当x=1时,y=4(1)求这个二次函数表达式.(2)此函数图象与x轴交于点A,B(A在B的左边),与y轴交于点C,求点A,B,C点的坐标及△ABC的面积.(3)该函数值y能否取到﹣6?为什么?23.某高速铁路位于某省南部,是国家“八纵八横”高速铁路网的重要连接通道,也是某省“三横五纵”高速铁路网的重要组成部分.东起日照,向西贯穿临沂、曲阜、济宁、菏泽,与郑徐客运专线兰考南站接轨.工程有一段在一条河边,且刚好为东西走向.B处是一个高铁维护站,如图①,现在想过B处在河上修一座桥,需要知道河宽,一测量员在河对岸的A处测得B在它的东北方向,测量员从A点开始沿岸边向正东方向前进300米到达点C处,测得B在C的北偏西30度方向上.(1)求所测之处河的宽度;(结果保留的十分位)(2)除(1)的测量方案外,请你再设计一种测量河宽的方案,并在图②中画出图形.24.如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD(1)求证:△ABC≌△ADC;(2)若∠BAC =30°,∠BCA =45°,BC =2; ①求∠BAD 所对的弧BD 的长;②直接写出AC 的长.25.解不等式组1531x x x +≤⎧⎨->⎩①②请结合题意填空,完成本题的解答. (Ⅰ)解不等式①,得_________; (Ⅱ)解不等式②,得_________;(Ⅲ)把不等式①和②的解集在数轴上表示出来:(Ⅳ)原不等式组的解集为________.【参考答案】*** 一、选择题二、填空题 13.153 14.1215.316. 17.18.20 三、解答题19.(1)y =﹣x 2+2x+3;(2)点P 的坐标为(97,127);(3)当Q 的坐标为(0,0)或(9,0)时,以A ,C ,Q 为顶点的三角形与△BCD 相似. 【解析】 【分析】(1)根据点B ,C 的坐标,利用待定系数法可求出抛物线的解析式;(2)利用二次函数图象上点的坐标特征可得出点A 的坐标,由点B ,C 的坐标可得出直线BC 的解析式,作O关于BC的对称点O′,则点O′的坐标为(3,3),由两地之间线段最短可得出当A,P,O′共线时,PO+PA取最小值,由点O′,A的坐标可求出该最小值,由点A,O′的坐标,利用待定系数法可求出直线AO′的解析式,联立直线AO′和直线BC的解析式成方程组,通过解方程组可求出点P的坐标;(3)由点B,C,D的坐标可得出BC,BD,CD的长,由CD2+BC2=BD2可得出∠BCD=90°,由点A,C的坐标可得出OA,OC的长度,进而可得出OA OCCD CB=,结合∠AOC=∠DCB=90°可得出△AOC∽△DCB,进而可得出点Q与点O重合时△AQC∽△DCB;连接AC,过点C作CQ⊥AC,交x轴与点Q,则△ACQ∽△AOC∽△DCB,由相似三角形的性质可求出AQ的长度,进而可得出点Q的坐标.综上,此题得解.【详解】(1)将B(3,0),C(0,3)代入y=﹣x2+bx+c,得:9303b cc-++=⎧⎨=⎩,解得:23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3.(2)当y=0时,﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴点A的坐标为(﹣1,0).∵点B的坐标为(3,0),点C的坐标为(0,3),∴直线BC的解析式为y=﹣x+3.如图1,作O关于BC的对称点O′,则点O′的坐标为(3,3).∵O与O′关于直线BC对称,∴PO=PO′,∴PO+PA=5.设直线AO′的解析式为y=kx+m,将A(﹣1,0),Q′(3,3)代入y=kx+m,得:-k0 33mk m+=⎧⎨+=⎩,解得:3k434m⎧=⎪⎪⎨⎪=⎪⎩,∴直线AO′的解析式为y =34x+34. 联立直线AO′和直线BC 的解析式成方程组,得:33y 443x y x ⎧=+⎪⎨⎪=-+⎩,解得:9x 7127y ⎧=⎪⎪⎨⎪=⎪⎩,∴点P 的坐标为(97,127). (3)∵y =﹣x 2+2x+3=﹣(x ﹣1)2+4, ∴点D 的坐标为(1,4).又∵点C 的坐标为(0,3),点B 的坐标为(3,0), ∴CD,BC,BD∴CD 2+BC 2=BD 2, ∴∠BCD =90°.∵点A 的坐标(﹣1,0),点C 的坐标为(0,3), ∴OA =1,OC =3, ∴OA OC CD CB ==. 又∵∠AOC =∠DCB =90°, ∴△AOC ∽△DCB ,∴当Q 的坐标为(0,0)时,△AQC ∽△DCB . 如图2,连接AC ,过点C 作CQ ⊥AC ,交x 轴与点Q . ∵△ACQ 为直角三角形,CO ⊥AQ , ∴△ACQ ∽△AOC . 又∵△AOC ∽△DCB , ∴△ACQ ∽DCB ,∴AC AQDC DB =AQ=, ∴AQ =10,∴点Q 的坐标为(9,0).综上所述:当Q 的坐标为(0,0)或(9,0)时,以A ,C ,Q 为顶点的三角形与△BCD 相似. 【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及相似三角形的判定与性质,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用两点之间线段最短确定点P 的位置;(3)分两种情况,利用相似三角形的性质求出点Q 的坐标.20.(1)详见解析;(2)详见解析;(3)⊙O 的半径是2. 【解析】 【分析】(1)根据AC 为⊙O 直径,得到∠ADC =∠CBA =90°,通过全等三角形得到CD =AB ,推出四边形ABCD 是平行四边形,根据矩形的判定定理得到结论; (2)根据直角三角形的性质得到NB =12MF =NF ,根据等腰三角形的性质和余角的性质即可得到NB 是⊙O 的切线;(3)根据垂径定理得到DE =GE =6,根据四边形ABCD 是矩形,得到∠BAD =90°,根据余角的性质得到∠FAE =∠ADE ,推出△AEF ∽△DEA ,根据相似三角形的性质列比例式得到AE =,连接OD ,设⊙O 的半径为r ,根据勾股定理列方程即可得到结论. 【详解】解:(1)∵AC 为⊙O 直径, ∴∠ADC =∠CBA =90°,在Rt △ADC 与Rt △CBA 中,AC ACAD BC =⎧⎨=⎩,∴Rt △ADC ≌Rt △CBA , ∴CD =AB , ∵AD =BC ,∴四边形ABCD 是平行四边形, ∵∠CBA =90°, ∴四边形ABCD 是矩形; (2)连接OB ,∵∠MBF =∠ABC =90°, ∴NB =12MF =NF , ∴∠1=∠2,∵∠2=∠3,∴∠1=∠3,∵OB=OA,∴∠5=∠4,∵DG⊥AC,∴∠AEF=90°,∴∠3+∠4=90°,∴∠1+∠5=90°,∴OB⊥NB,∴NB是⊙O的切线;(3)∵AC为⊙O直径,AC⊥DG,∴DE=GE=6,∵F为GE中点,∴EF=GF=3,∵四边形ABCD是矩形,∴∠BAD=90°,∴∠FAE+∠DAE=90°,∵∠ADE+∠DAE=90°,∴∠FAE=∠ADE,∵∠AEF=∠DEA=90°,∴△AEF∽△DEA,∴AE EF DE AE,∴AE=,连接OD,设⊙O的半径为r,∴OA=OD=r,OE=r﹣,∵OE2+DE2=OD2,∴(r﹣)2+62=r2,∴r,∴⊙O的半径是2.【点睛】本题考查了圆周角定理,矩形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质,勾股定理,证得AEF∽△DEA是解决(3)的关键.21.(1)该种水果每次降价的百分率是10%;(2)第10天时销售利润最大;【解析】【分析】(1)设这个百分率是x,根据某商品原价为10元,由于各种原因连续两次降价,降价后的价格为8.1元,可列方程求解;(2)根据两个取值先计算:当1≤x<9时和9≤x<15时销售单价,由利润=(售价-进价)×销量-费用列函数关系式,并根据增减性求最大值,作对比;【详解】(1)设该种水果每次降价的百分率是x,10(1﹣x)2=8.1,x=10%或x=190%(舍去),答:该种水果每次降价的百分率是10%;(2)当1≤x<9时,第1次降价后的价格:10×(1﹣10%)=9,∴y=(9﹣4.1)(80﹣3x)﹣(40+3x)=﹣17.7x+352,∵﹣17.7<0,∴y随x的增大而减小,∴当x=1时,y有最大值,y大=﹣17.7×1+352=334.3(元),当9≤x<15时,第2次降价后的价格:8.1元,∴y=(8.1﹣4.1)﹣(3x2﹣64x+400)=﹣3x2+60x+80=﹣3(x﹣10)2+380,∵﹣3<0,∴当9≤x≤10时,y随x的增大而增大,当10<x<15时,y随x的增大而减小,∴当x=10时,y有最大值,y大=380(元),综上所述,第10天时销售利润最大.【点睛】本题考查了一元二次方程的应用及二次函数的有关知识,解题的关键是正确的找到题目中的等量关系且利用其列出方程,注意第2问中x 的取值,两个取值中的最大值才是最大利润.22.(1)y =x 2+4x ﹣1;(3)函数值y 不能取到﹣6;理由见解析. 【解析】 【分析】(1)把x =﹣2时,y =﹣5;x =1时,y =4代入y =ax 2+4x+c ,求得a 、c 的值即可求得;(2)令y =0,解方程求得A 、B 点的坐标,令x =0,求得y =﹣1,得到C 点的坐标,然后根据三角形面积公式即可求得△ABC 的面积;(3)把(1)中求得的解析式化成顶点式,求得函数y 的最小值为﹣5,故函数值y 不能取到﹣6. 【详解】解:(1)把x =﹣2时,y =﹣5;x =1时,y =4代入y =ax 2+4x+c 得48544a c a c -+=-⎧⎨++=⎩,解得11a c =⎧⎨=-⎩,∴这个二次函数表达式为y =x 2+4x ﹣1; (2)令y =0,则x 2+4x ﹣1=0,解得x∴A(﹣20),B(﹣0), 令x =0,则y =﹣1, ∴C(0,﹣1),∴△ABC 的面积:12AB•OC=12(﹣ (3)∵y =x 2+4x ﹣1=(x+2)2﹣5, ∴函数y 的最小值为﹣5, ∴函数值y 不能取到﹣6. 【点睛】本题考查了抛物线和x 轴的交点,待定系数法求二次函数的解析式,二次函数图象上点的坐标特征,以及二次函数的性质,二次函数图象上点的坐标适合解析式是解题的关键. 23.(1)所测之处江的宽度为190.5m ;(2)见解析. 【解析】 【分析】解:(1)过点B 作BF ⊥AC 于F ,根据题意得到∠EAB =45°,∠GCB =30°,AC =300m ,求得∠FBA =45°,∠CBF =30°,得到BF =AF ,解直角三角形即可得到结论;(2)构造相似三角形,根据相似三角形的性质得到方程即可得到结论.. 【详解】(1)过点B 作BF ⊥AC 于F ,由题意得:∠EAB =45°,∠GCB =30°,AC =300m , ∴∠FBA =45°,∠CBF =30°,∴FC =300﹣AF =300﹣BF (m ), 在Rt △BFC 中,tan ∠CBF =FCFB, ∴tan30°=300BFBF-,300BFBF-=,解得:BF ﹣150(3m ), 答:所测之处江的宽度为190.5m ;(2)①在河岸取点A ,使B 垂直于河岸,延长BA 至C ,测得AC 做记录, ②从C 沿平行于河岸的方向走到D ,测得CD ,做记录, ③B0与河岸交于E ,测AE ,做记录.根据△BAE ~△BCD , 得到比例线段,从而求出河宽AB .【点睛】此题考查了方向角问题.此题难度适中,注意能构造直角三角形,并能借助于解直角三角形的知识求解是关键,注意数形结合思想与方程思想的应用.24.(1)见解析;(2)①BD ;②AC =【解析】 【分析】(1)由“SSS”可证△ABC ≌△ADC ;(2)①由题意可得AC 垂直平分BD ,可得BE=DE ,AC ⊥BD ,由直角三角形的性质可得,,由等腰三角形的性质可得∠BAD=2∠BAC=60°,由弧长公式可求弧BD 的长;②由AC=AE+CE 可求解. 【详解】证明:(1)由题意可得AB =AD ,BC =CD ,∴△ABC ≌△ADC (SSS ); (2)①∵AB =AD ,BC =CD ∴AC 垂直平分BD ∴BE =DE ,AC ⊥BD ∵∠BCA =45°,BC =2;∴BE =CE ,且∠BAC =30°,AC ⊥BD∴AB =2BE =,AE ∵AB =AD ,AC ⊥BD ∴∠BAD =2∠BAC =60°∴60BD 1803π︒︒⨯⨯==②∵AC =AE+CE∴AC +【点睛】本题考查了全等三角形的判定和性质,直角三角形的性质,等腰三角形的性质,弧长公式,灵活运用这些性质解决问题是本题的关键. 25.(Ⅰ)4x ≤;(Ⅱ)12x >;(Ⅲ)见解析;(Ⅳ)142x <≤. 【解析】 【分析】(Ⅰ)直接移项即可得出答案;(Ⅱ)移项,两边同时除以2,即可得答案;(Ⅲ)根据解集在数轴上的表示方法表示出①②的解集即可;(Ⅳ)根据数轴找出两个解集的公共部分即可. 【详解】 (Ⅰ)15x +≤ 移项得:x≤4, 故答案为:x≤4 (Ⅱ) 31x x -> 移项得:2x>1,解得:x>12, 故答案为:x>12(Ⅲ)不等式①和②的解集在数轴上表示如图所示:(Ⅳ) 由数轴可得①和②的解集的公共解集为142x<≤,故原不等式的解集为:142x<≤,故答案为:14 2x<≤【点睛】本题考查的是一元一次不等式组的整数解,会求一元一次不等式组的解集是解决此类问题的关键.求不等式组的解集,借助数轴找公共部分或遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.2019-2020学年数学中考模拟试卷一、选择题1.某商品价格为a 元,降价10%后,又降价10%,因销售量猛增,商店决定再提价20%,提价后这种商品的价格为( )A.0.96a 元B.0.972a 元C.1.08a 元D.a 元 2.如图,一次函数y=-x 与二次函数y=ax 2+bx+c 的图象相交于点M 、N ,则关于x 的一元二次方程ax 2+(b+1)x+c=0的根的情况是( )A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根D.以上结论都正确 3.把抛物线y =ax 2+bx+c 图象先向左平移2个单位长度,再向下平移3个单位长度,所得的图象的解析式是y =x 2+5x+6,则a ﹣b+c 的值为( )A.2B.3C.5D.12 4.如图所示,小兰用尺规作图作△ABC 边AC 上的高BH ,作法如下:①分别以点DE 为圆心,大于DE 的长为半径作弧两弧交于F ;②作射线BF ,交边AC 于点H ;③以B 为圆心,BK 长为半径作弧,交直线AC 于点D 和E ;④取一点K 使K 和B 在AC 的两侧;所以BH 就是所求作的高.其中顺序正确的作图步骤是( )A.①②③④B.④③①②C.②④③①D.④③②①5.在平面直角坐标系中,点P(3,-5)关于原点对称的点的坐标是( )A .(3,5)B .(3,-5)C .(-3,-5)D .(-3,5)6.使用家用燃气灶烧开同一壶水所需的燃气量y (单位:3m )与旋钮的旋转角度x (单位:度)(090x <≤)近似满足函数关系y=ax 2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x 与燃气量y 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )A .18B .36C .41D .58o7.港珠澳大桥东起香港国际机场附近的香港口岸人工导,向西横跨伶仃洋海域后连接珠海和澳门人工岛,止于珠海港湾,全长55千米,设计时速100千米/小时,工程项目总投资额1269亿元,用科学记数法表示1269亿元为( )A .1269×108B .1.269×108C .1.269×1010D .1.269×10118.如图,在△ABC 中,AC =BC ,∠C =90°,AD 是∠BAC 的平分线且交BC 于点D ,DE ⊥AB ,垂足为点E ,若AB =8cm ,则△DBE 的周长( )A .B .cmC .8cmD .cm9.如图,在锐角ABC 中,延长BC 到点D ,点O 是AC 边上的一个动点,过点O 作直线MN BC ,MN 分别交ACB ∠、ACD ∠的平分线于E ,F 两点,连接AE 、AF .在下列结论中.①OE OF =;②CE CF =;③若12CE =,5CF =,则OC 的长为6;④当AO CO =时,四边形AECF 是矩形.其中正确的是( )A .①④B .①②C .①②③D .②③④ 10.如图,在菱形中,,,点是这个菱形内部或边上的一点,若以点,,为顶点的三角形是等腰三角形,则,(,两点不重合)两点间的最短距离为( )A. B. C. D.11.如图,在Rt ABC ∆中,90,6,8ACB AC BC ∠=︒==,则Rt ABC ∆的中线CD 的长为( )A.5B.6C.8D.1012.如果方程x 2﹣8x+15=0的两个根分别是Rt △ABC 的两条边,△ABC 最小的角为A ,那么tanA 的值为( ) A.34 B.35 C.45 D.34或35二、填空题13.据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为_______。
专题19 等腰三角形(解析版)-备战2024年中考数学一轮复习之必考点题型全归纳与分层精练

专题19等腰三角形【专题目录】技巧1:等腰三角形中四种常用作辅助线的方法技巧2:巧用特殊角构造含30°角的直角三角形技巧3:分类讨论思想在等腰三角形中的应用【题型】一、等腰三角形的定义【题型】二、根据等边对等角求角度【题型】三、根据三线合一求解【题型】四、根据等角对等边证明等腰三角形【题型】五、根据等角对等边求边长【题型】六、等腰三角形性质与判定的综合【题型】七、等边三角形的性质【题型】八、含30°角的直角三角形【考纲要求】1.了解等腰三角形的有关概念,掌握其性质及判定.2.了解等边三角形的有关概念,掌握其性质及判定.3.掌握线段中垂线的性质及判定.【考点总结】一、等腰三角形等腰三角形等腰三角形概念有两边相等的三角形角等腰三角形。
等腰三角形性质1:等腰三角形的两个底角相等(简写成“等边对等角”)2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。
(三线合一)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).【考点总结】二、等边三角形【考点总结】三、直角三角形【技巧归纳】技巧1:等腰三角形中四种常用作辅助线的方法【类型】一、作“三线”中的“一线”1.如图,在△ABC 中,AB =AC ,D 是BC 的中点,过点A 作EF ∥BC ,且AE =AF.求证:DE =DF.等边三角形等边三角形概念三条边都相等的三角形,叫等边三角形。
它是特殊的等腰三角形。
等边三角形性质和判定(1)等边三角形的三个内角都相等,并且每一个角都等于60º。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是60º的等腰三角形是等边三角形。
(4)在直角三角形中,如果一个锐角等于30º,那么它所对的直角边等于斜边的一半。
(补充:(1)三角形三个内角的平分线交于一点,并且这一点到三边的距离等。
(2)三角形三个边的中垂线交于一点,并且这一点到三个顶点的距离相等。
中考数学复习之等腰三角形的性质与判定,考点过关与基础练习题

22.等腰三角形➢知识过关1.等腰三角形的定义、性质和判定(1)等腰三角形的定义:有____相等的三角形是等腰三角形;(2)等腰三角形的性质①等腰三角形的两个底角相等(等边对等角)①等腰三角形的顶角平分线、_________底边上的中线互相重合(简称“三线合一”)(3)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)2.等边三角形的定义、性质和判定(1)等边三角形的的定义:三条边_____的三角形是等边三角形.(2)等边三角形的性质:等边三角形的_____都相等,并且每个角都等于_____(3)等边三角形的判定:有一个角等于_____的等腰三角形是等边三角形.3垂直平分线的性质定理和逆定理线段垂直平分线上的点到线段____的距离相等;到一条线段两端点的_____相等的点在线段的垂直平分线上.➢考点分类考点1等腰三角形的性质与判定例1如图所示,①ABC中,AB=AC,E为AB边上一点,D为①ABC外一点,DE=DC,(1)若AD||BC,求证:①EDC=①BAC;(2)若①EDC=①BAC,求证:AD||BC.考点2等边三角形的性质与判定例2 在等边①ABC中,(1)如图1,P、Q是BC边上的两点,AP=AQ,①BAP=20°,求①AQB的度数;(2)如图2,P、Q是BC边上的两个动点(不与点B、C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM、PM,求证:PA=PM考点3 线段垂直平分线的性质例3(1)如图所示,底边BC为23,顶角A为120°的等腰ABC中,DE垂直平分AB于D,则①ACE的周长为( )A.2+23B.2+3C.4D.3(2)如图所示,在①ABC中,AB=BC,①ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则①ABD=________➢真题演练1.如图,在△ABC中,AB=AC,∠BAC=24°,延长BC到点D,使CD=AC,连接AD,则∠D的度数为()A.39°B.40°C.49°D.51°2.如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,BE平分∠ABC交AC于点E.交AD于点F.则∠EFD的度数为()A.80°B.100°C.110°D.120°3.在△ABC中,∠A=80°,若△ABC为等腰三角形,则∠B的度数为()A.80°或50°B.80°或20°C.50°或20°D.80°或50°或20°4.如图所示,在△ABC中,AC=BC,边AC的垂直平分线交AB于点D,垂足为E,∠A =50°,则∠BCD=()A.30°B.40°C.50°D.60°5.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD 于点G,交BE于点H.①△ABE的面积=△BCE的面积;②AF=FB;③∠F AG=2∠ACF.以上说法正确的是()A.①③B.①②C.②③D.①②③6.如图,已知S△ABC=24m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC m2.7.如图,在△ABC中,BD平分∠ABC交AC于点D,E是BC上一点,且BE=AB,连结DE,若∠A=80°,∠CDE=50°,∠C的度数为.8.如图,在△ABC中,AB=AC,∠1=40°,∠2=∠3,则∠CDE=度.9.等腰△ABC中,AB=AC,点E为底边BC上一点,以点E为圆心,EA长为半径画弧,交AB于点D,测得∠CAE=80°,∠EAD=54°,则∠DEB=°.10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD 于点G,交BE于点H,下面说法正确的有(填写序号).①S△ABE=S△BCE;②∠AFG=∠AGF;③∠F AG=2∠ACF;④AF=FB.11.在△ABC中,AD是高,AE,BF是角平分线,AE交BF于点O,∠BAC=80°,∠C =70°.(1)求∠BOE的大小;(2)求证:DE=DC.12.已知:如图,在四边形ABCD 中,BC =DC ,点E 在边AB 上,∠EBC =∠EDC .(1)求证:EB =ED .(2)当∠A =90°,求证:∠BED =2∠BDA .13.如图,在△ABC 中,∠BAC 是钝角,∠B =2∠ACB .延长BA 至D ,使得AD =BA .过D 作DE ⊥BC 于E ,连结AC 交DE 于F ,连结AE ,CD .(1)求证:△EAC 为等腰三角形.(2)若:S △BAE =56S △DCE ,求BE AE 的值.14.如图,△ABC 的两条外角平分线CD 、BD 相交于点D ,MN 过点D ,且MN ∥BC ,分别交AB 、AC 于点M 、N .(1)求证:MN =CN +BM ;(2)若C △AMN +BC =2C △ABC ,求C △ABC MN 的值.➢课后练习1.用一条长为18cm的细绳围成一个腰与底边不等的等腰三角形,各边的长可能是()A.4,4,10B.3.6,7.2,7.2C.4,6,8D.6,6,62.如图,△ABC中,AB=AC,∠ABC与∠ACB的平分线交于点P,过P作BC的平行线,分别交AB,AC于点M,N,则图中等腰三角形的总个数是()A.2B.3C.4D.53.如图,在四边形ABCD中,AB∥DC,∠DAB的平分线交BC于点E,DE⊥AE,若AD =12,BC=8,则四边形ABCD的周长为()A.32B.20C.16D.284.如图,在△ABC中,AB=AC,点E、F分别在BA、BC的延长线上,∠EAC、∠ABC、∠ACF的平分线相交于点D.对于以下结论:①AD∥BC;②AD=AC;③∠ADC=∠ACB;④∠ADB与∠ADC互余.其中正确结论的个数为()A.4B.3C.2D.15.如图,在四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E,F分别是AC,BD的中点,连接EF.(1)求证:EF⊥BD;(2)若EF=3,BD=8,求AC的长.(简述过程)6.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且AE=AB.(1)求证:∠B=2∠C;(2)若AC=10,AD=6,求△ABC的周长.7.已知△ABC中,D为边BC上一点,AB=AD=CD.(1)试说明∠ABC=2∠C;(2)过点B作AD的平行线交CA的延长线于点E,若AD平分∠BAC,求证:AE=AB.8.如图,在△ABC中,∠ABC=3∠C,AD平分∠BAC,BE⊥AD于E,求证:BE=12(AC﹣AB).(提示:延长BE交AC于点F).9.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD =CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数.➢冲击A+综合与实践【问题情境】数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点,AE ⊥EP,EP与正方形的外角∠DCG的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;【思考尝试】(1)同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.【实践探究】(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形,∠AEP =90°,连接CP,可以求出∠DCP的大小,请你思考并解答这个问题.【拓展迁移】(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接DP.知道正方形的边长时,可以求出△ADP周长的最小值.当AB =4时,请你求出△ADP周长的最小值.。
中考数学总复习《等腰三角形》专项提升练习题(附答案)

中考数学总复习《等腰三角形》专项提升练习题(附答案) 学校:___________班级:___________姓名:___________考号:___________1.如图已知ABC △中AB=3,AC=5,BC=7,若过点A 的一条直线将ABC △分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )A.1条B.2条C.3条D.4条2.如图在ABC △中AB=AC ,D 是BC 边上的中点30B ∠=︒,则DAC ∠等于( )A.30°B.40°C.50°D.60°3.等腰三角形的一个内角是40︒,则它的顶角度数为( )A.100︒B.40︒或100︒C.70︒D.40︒4.如图,a//b,AB=AC,若162∠=︒,则A ∠的度数为( )A.56︒B.59︒C.62︒D.76︒5.已知等腰三角形的周长为19,其中一边长为3,则该等腰三角形的底边是( )A.3B.8C.3或8D.136.如图在ABC △中AC DC DB ==,100ACD ∠=︒则B ∠等于( )A.50°B.40°C.25°D.20°7.如图在Rt ABC △中90ACB ∠=︒,35ABC ∠=︒将ABC △绕点C 顺时针旋转至A B C '''△,使点A '恰好落在AB 上,则旋转角度为( )A.35︒B.55︒C.70︒D.90︒8.如图在ABC △中点D 在AC 上,点E 在AB 上,且AB AC =,BC BD =,AD DE EB ==,则A ∠等于( )A.45°B.30°C.60°D.75°9.如图点A 、B 、C 三点在O 上40OCB ∠=︒,则A ∠=_____________10.已知等腰三角形的一个外角是80︒,则它顶角的度数为________.11.等腰三角形的周长为20cm ,一边长为6cm ,则底边长为__________cm .12.如图52ABC ∠=︒,AD 是线段BC 的垂直平分线,垂足为点D ,ABC ∠的平分线BE 交AD 于点E ,连接EC ,则AEC ∠的度数是__________.13.如图将ABC △绕点A 逆时针旋转140︒得到ADE △,B ,C ,D 三点恰好在同一直线上.(1)判断ACE △的形状;(2)连接CE ,若CE BD ⊥,求BAC ∠的度数.14.如图在ABC △中AC 边的垂直平分线分别交BC 、AC 于点E 、F ,连接AE ,作AD BC ⊥于点D ,且D 为BE 的中点.(1)试说明:AB CE =;(2)若32C ∠=︒,求BAC ∠的度数.参考答案及解析1.答案:C解析:如图所示,当3AB AF ==,3BA BD ==与BG AG =时,都能得到符合题意的等腰三角形.综上,这样的直线最多可画3条.2.答案:D解析:在ABC △中已知AB AC =,D 是BC 边上的中点AD BC ∴⊥90ADC ∴∠=︒30B C ∠=∠=︒ 60DAC ∴∠=︒ 故选:D.3.答案:B解析:当40︒为等腰三角形的底角时,顶角为1804040100︒-︒-︒=︒;当40︒为等腰三角形的顶角时,则顶角为40︒.所以该等腰三角形的顶角度数为40︒或100︒.4.答案:A解析:AB AC =如图A B ABC C ∴=∠∠如图//a b 如图162ABC ∴∠=∠=︒如图180A ABC ACB ∠+∠+∠=︒如图18026256A ∠=⨯∴︒-︒=︒如图故选:A.5.答案:A解析:当3是腰长时,底边为193213-⨯=此时33613+=<,不能组成三角形;当3是底边时,腰长为()119382-=此时3,8,8三边能够组成三角形. 所以等腰三角形的底边是3.故选:A.6.答案:D解析:AC DC DB == 100ACD ∠=︒180100402CAD -∴︒︒∠==︒ CDB ∠是ACD △的外角10040100140CDB A ACD ︒∴∠=∠+∠=︒=+=︒︒DC DB =180140202B ︒︒-∴∠==︒.7.答案:C 解析:90ACB ∠=︒ 35ABC ∠=︒∴180903555A ∠=︒-︒-︒=︒将ABC △绕点C 顺时针旋转至A B C '''△,即其中一个旋转角为ACA '∠A C AC '∴=∴CAA '△是等腰三角形∴55CA A CAA ''∠=∠=︒∴180555570ACA '∠=︒-︒-︒=︒故选:C.8.答案:A解析:设EBD x ∠=DE EB =EBD EDB x ∴∠=∠=2AED EBD EDB x ∴∠=∠+∠=AD DE =2A AED x ∴∠=∠=3BDC A EBD x ∴∠=∠+∠=BC BD =3BDC C x ∴∠=∠=AB AC =3ABC C x ∴∠=∠=在ABC △中有180A ABC C ∠+∠+∠=︒,则233180x x x ++=︒22.5x ∴=︒245A x ∴∠==︒故选:A.9.答案:50︒解析:OB OC = 40OCB ∠=︒40OBC OCB ∴∠=∠=︒1804040100BOC ∴∠=︒-︒-︒=︒1502A BOC ∴∠=∠=︒.故答案为:50︒.10.答案:100︒.解析:等腰三角形一个外角为80︒,那相邻的内角为100︒如图三角形内角和为180︒,如果这个内角为底角,内角和将超过180︒如图所以100︒︒只可能是顶角.故答案为:100︒.11.答案:6或8. 解析:①6cm 是底边时,腰长()12067cm 2=-=此时三角形的三边分别为7cm 7cm 6cm 、、能组成三角形②6cm 是腰长时,底边20628cm =-⨯=此时三角形的三边分别为6cm 6cm 8cm 、、能组成三角形综上所述,底边长为6或8cm .故答案为:6或8.12.答案:116︒解析:52ABC ∠=︒,ABC ∠的平分线BE 交AD 于点E 11522622EBD ABC ∴∠=∠=⨯︒=︒点E 在BC 的垂直平分线上BE CE ∴= 90EDC ∠=︒26C EBD ∴∠=∠=︒2690116AEC C EDC ∴∠=∠+∠=︒+︒=︒.故答案为:116︒.13.答案:(1)顶角为140︒的等腰三角形(2)90︒解析:(1)ABC △绕点A 逆时针旋转140︒得到ADE △ AC AE ∴= 140CAE ∠=︒ ACE ∴△是以顶角为140︒的等腰三角形;(2)ABC △绕点A 逆时针旋转140︒得到ADE △ 140BAD CAE ∴∠=∠=︒ AB AD = AC AE = ∴在ABD △中180140202ABC ADB ︒-︒∠=∠==︒ 在ACE △中180140202ACE AEC ︒-︒∠=∠==︒ CE BD ⊥90ECB ∴∠=︒902070ACB ECB ACE ∴∠=∠-∠=︒-︒=︒在ABC △中180180207090BAC ABC ACB ∠=︒-∠-∠=︒-︒-︒=︒ BAC ∴∠的度数为90︒.14.答案:(1)见解析(2)84︒解析:(1)D 为BE 的中点BD DE ∴=AD BC ⊥ AB AE ∴=EF 是AC 的垂直平分线AE CE ∴=AB CE ∴=; (2)32C ∠=︒ AE CE =32C EAC ∴∠=∠=︒64AEB C EAC ∴∠=∠+∠=︒AB AE =64B AEB ∴∠=∠=︒180180646452BAE B AEB ∴∠=︒-∠-∠=︒-︒-︒=︒ 523284BAC BAE EAC ∴∠=∠+∠=︒+︒=︒.。
北京市中考数学复习三角形课时训练十九等腰三角形24含答案

课时训练(十九) 等腰三角形(限时:40分钟)|夯实基础|1.若等腰三角形的顶角为40°,则它的底角度数为()A.40°B.50°C.60°D.70°2.如图K19-1,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()图K19-1A.AE=ECB.AE=BEC.∠EBC=∠BACD.∠EBC=∠ABE3.[2017·昌平二模]如图K19-2,△ABC中,∠ACB=90°,∠B=55°,点D是斜边AB的中点,那么∠ACD的度数为()图K19-2A.15°B.25°C.35°D.45°4.如图K19-3,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF.若∠BAF=80°,则∠CAF的度数为()图K19-3A.40°B.50°C.60°D.80°5.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边长的取值范围是()A.1 cm<AB<4 cmB.5 cm<AB<10 cmC.4 cm<AB<8 cmD.4 cm<AB<10 cm6.[2017·门头沟二模]如图K19-4,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,则∠BAD=()图K19-4A.23°B.24°C.25°D.26°7.[2018·凉山州]如图K19-5,在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于AB长为半径作弧,两弧相交于M,N两点;②作直线MN交BC于D,连接AD.若AD=AC,∠B=25°,则∠C=()图K19-5A.70°B.60°C.50°D.40°8.[2018·师达中学月考]已知△ABC是等边三角形,边长为4,则BC边上的高是()A.4B.2C.2D.9.等腰三角形的一个内角为100°,则顶角的度数是.10.等腰三角形的周长为16,其一边长为6,则另两边长为.11.等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为.12.[2018·房山一模]一个正方形和两个等边三角形的位置如图K19-6所示,则∠1+∠2+∠3的度数为.图K19-613.在边长为4的等边三角形ABC中,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF= .14.[2018·义乌]等腰三角形ABC中,顶角∠A为40°,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为.15.[2018·丰台一模]如图K19-7,在△ABC中,AB=AC,D是BC边的中点,DE⊥AB于点E,DF⊥AC于点F.求证:DE=DF.图K19-716.[2018·通州一模]已知:如图K19-8,在△ABC中,∠B=45°,点D是BC边的中点,DE⊥BC于点D,交AB于点E,连接CE.(1)求∠AEC的度数;(2)请你判断AE,BE,AC三条线段之间的等量关系,并证明你的结论.图K19-8|拓展提升|17.[2018·延庆期末]如图K19-9,等边三角形ABC的边长为6,AD是BC边的中线,点E是AC边的中点.如果点P是AD 上的动点,那么EP+CP的最小值为.18.[2018·东城二模]如图K19-10所示,点P位于等边三角形ABC的内部,且∠ACP=∠CBP.图K19-10(1)∠BPC的度数为°;(2)延长BP至点D,使得PD=PC,连接AD,CD.①依题意补全图形;②证明:AD+CD=BD;(3)在(2)的条件下,若BD的长为2,求四边形ABCD的面积.1.D2.C [解析] ∵△ABC 是等腰三角形,AB=AC ,∴∠ABC=∠ACB.又∵BC=BE ,∴∠ACB=∠BEC ,∴∠BAC=∠EBC ,因此选C .3.C4.B5. B [解析] ∵在等腰三角形ABC 中,AB=AC ,其周长为20 cm,∴设AB=AC=x cm,则BC=(20-2x )cm,∴解得5<x<10.故选B .6.C7.C8.B9.100° [解析] 根据三角形的内角和等于180°,又等腰三角形的一个内角为100°,所以这个100°的内角只能是顶角,故填100°. 10.5,5或6,411.63°或27° [解析] 在三角形ABC 中,设AB=AC ,BD ⊥AC 于点D.①如图①,若三角形是锐角三角形,∠A=90°-36°=54°,此时底角=(180°-54°)÷2=63°;②如图②,若三角形是钝角三角形,∠BAC=36°+90°=126°,此时底角=(180°-126°)÷2=27°.所以等腰三角形底角的度数是63°或27°. 12.150°13.2[解析] 如图,过点C作CG⊥AB,垂足为G,连接AD,则AG=BG=2.∴CG===2.∵S△ABD+S△ACD=S△ABC,∴AB×DE+AC×DF=AB×CG.∴×4×DE+×4×DF=×4×CG.∴DE+DF=CG=2.14.30°或110°[解析] 根据题意作出图形(如图),当点P在AB右侧时,连接AP.∵AB=AC,∠BAC=40°,∴∠ABC=∠C=70°,∵AB=AB,AC=PB,BC=PA,∴△ABC≌△BAP,∴∠ABP=∠BAC=40°,∴∠PBC=∠ABC-∠ABP=30°.当点P'在AB左侧时,同理可得∠ABP'=40°,∴∠P'BC=40°+70°=110°.故答案为30°或110°.高效复习15.证明:连接AD.∵AB=AC,D是BC边上的中点,∴∠BAD=∠CAD.∵DE⊥AB于点E,DF⊥AC于点F,∴DE=DF.16.解:(1)∵点D是BC边的中点,DE⊥BC,∴DE是BC的垂直平分线.∴EB=EC.∴∠B=∠BCE.∵∠B=45°,∴∠AEC=90°.(2)AE2+BE2=AC2.证明:∵∠AEC=90°,∴△AEC是直角三角形.∴由勾股定理,得AE2+EC2=AC2.∵ED垂直平分BC,∴EB=EC.∴AE2+BE2=AC2.17.318.解:(1)120(2)①如图所示.②证明:在等边三角形ABC中,∠ACB=60°,∴∠ACP+∠BCP=60°.∵∠ACP=∠CBP,∴∠CBP+∠BCP=60°.∴∠BPC=180°-(∠CBP+∠BCP)=120°.∴∠CPD=180°-∠BPC=60°.∵PD=PC,∴△CDP为等边三角形.∵∠ACD+∠ACP=∠ACP+∠BCP=60°,∴∠ACD=∠BCP.在△ACD和△BCP中,∴△ACD≌△BCP(SAS).∴AD=BP.∴AD+CD=BP+PD=BD.(3)如图,作BM⊥AD于点M,BN⊥DC交DC的延长线于点N.∵∠ADB=∠ADC-∠PDC=60°,∴∠ADB=∠CDB=60°.∴BM=BN=BD=.又由(2)得AD+CD=BD=2,∴S四边形ABCD=S△ABD+S△BCD=AD·BM+CD·BN=(AD+CD)=×2=.用心工作,快乐生活!(工作好,才有好的生活!)此文档可编辑,欢迎使用!~~~专业文档,VIP专享。
北京市西城区普通中学2018届初三数学中考复习 等腰三角形 专项复习训练题 含答案

北京市西城区普通中学2018届初三数学中考复习等腰三角形专项复习训练题1.已知等腰三角形ABC中,腰AB=8,底BC=5,则这个三角形的周长为( ) A.21 B.20 C.19 D.182.如图,点D在AB上,AB=AC,AD=DC=BC,则图中的等腰三角形共有( )A.1个 B.2个 C.3个 D.无法确定3. 已知实数x,y满足|x-4|+(y-8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )A.20或16 B.20 C.16 D.以上答案均不对4. 下列关于等边三角形的说法错误的是( )A.三条边都相等的三角形是等边三角形B.等边三角形的三条边相等C.等边三角形不是等腰三角形D.等边三角形是等腰三角形的特殊情形5. 等腰三角形是轴对称图形,它的对称轴是( )A.过顶点的直线 B.底角的角平分线所在直线C.顶角平分线所在的直线 D.腰上的高所在的直线6.等腰三角形的对称轴( )A.只有1条 B.最多有2条 C.最多有3条D.不能确定7. 等腰三角形的周长为13,其中两边之差为1,则它的腰长为( )A.4 B.4或113 C.143D.4或1438. 等腰三角形的腰长与底边长之比为2∶3,其周长为28 cm,则底边长等于_______cm.9.如图,在△ABC中,AB=AC=10,DE垂直平分AB,△BDC周长为17,则BC 等于____.10. 如图,在△ABC中,AB=AC,AD是BC边上的高线,点E,F是AD的三等分点.若△ABC的面积为12 cm2,则图中阴影部分的面积是____ cm2.11. 如图,在△ABC中,AB=AC.(1)若∠1=∠2,BD=3 cm,则BC=_____cm;(2)若BD=CD,∠1=30°,则∠BAC=______.12. 如图,AP是等腰三角形ABC(AB=AC)的角平分线,在AB上任取一点D(不与A,B重合),作点D关于直线AP的对称点E,连结DE,DP,EP.则下列结论中正确的是___________.(填序号)①直线AP是等腰三角形ABC的对称轴;②点E在AC上;③DE∥BC;④△PDE是等腰三角形.13. 如图所示,用火柴棒首尾顺次相接,搭成等腰三角形,第一个三角形用了5根火柴棒,第二个三角形用了8根火柴棒,第三个三角形用了11根火柴棒,…,第n个三角形用了_______根火柴棒(用含n的代数式表示).14. 等腰三角形的周长为40 cm,以一边为边作等边三角形,这个等边三角形的周长为45 cm,那么这个等腰三角形的底边长为________________.15. 如图,已知C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC =ED.问:△ADC是等腰三角形吗?请说明理由.16. 如图,AD垂直平分BC,BE垂直平分AC,求证:△ABC是等边三角形.17. 一个等腰三角形的三边长分别是3x-2,4x-3,6-2x,求等腰三角形的周长.答案: 1---7 ACBCC CD 8. 12 9. 7 10. 611. (1) 6 (2) 60°12. ①②③④13. 3n +214. 10 cm 或15 cm15. 解:△ADC 是等腰三角形,理由如下:∵AB∥ED,∴∠B =∠E.在△ABC 和△CED 中,∵⎩⎪⎨⎪⎧AB =CE ,∠B =∠E,BC =ED ,∴△ABC ≌△CED(SAS).∴AC=CD.∴△ADC是等腰三角形.16. 证明:∵AD 垂直平分BC ,BE 垂直平分AC ,∴AB =AC ,BC =AB.∴AB =AC =BC.∴△ABC 是等边三角形.17. 解:①若3x -2=4x -3,得x =1,但1,1,4不能组成三角形;②若3x-2=6-2x ,得x =85,且145,145,175能组成三角形,这时周长为9;③若4x -3=6-2x ,得x =1.5,且2.5,3,3能组成三角形,这时周长为8.5.综上可知,等腰三角形的周长为9或8.5.。
中考数学复习《等腰、等边及直角三角形》经典题型(含答案)

中考数学复习《等腰、等边及直角三角形》经典题型(含答案)知识点一:等腰和等边三角形1.等腰三角形定义:有两条边相等的三角形叫等腰三角形(1)性质①等边对等角:两腰相等,底角相等,即AB=AC ∠B=∠C;②三线合一:顶角的平分线、底边上的中线和底边上的高互相重合;③对称性:等腰三角形是轴对称图形,直线AD是对称轴.(2)判定①定义:有两边相等的三角形是等腰三角形;注意:1.实际解题中的一个常用技巧是,构造等腰三角形,进而利用等腰三角形的性质为解题服务,常用的构造方法有:1)、“角平分线+平行线”构造等腰三角形。
2)、“角平分线+垂线”构造等腰三角形。
3)、用“垂直平分线”构造等腰三角形;4)、用“三角形中角的2倍关系”构造等腰三角形。
2.当等腰三角形的腰和底不明确时,需分类讨论.变式练习1:如若等腰三角形ABC的一个内角为30°,则另外两个角的度数为30°、120°或75°、75°.3.三角形中“垂线、角平分线、中线、等腰”四个条件中,只要满足其中两个,其余均成立.变式练习2:如右图,已知AD⊥BC,D为BC的中点,则三角形的形状是等腰三角形.②等角对等边:即若∠B=∠C,则△ABC是等腰三角形.变式练习3:一个等腰三角形的两边长分别为3和7,则它的周长为( ) A. 17 B. 15 C. 13 D. 13或17【解析】A ①当等腰三角形的腰为3,底为7时,3+3<7不能构成三角形;②当等腰三角形的腰为7,底为3时,周长为3+7+7=17,故这个等腰三角形的周长是17.变式练习4:如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为 __7__.变式练习5:一个等腰三角形的两边长分别为4,8,则它的周长为( C )A.12 B.16 C.20 D.16或202.等边三角形(1)性质①边角关系:三边相等,三角都相等且都等于60°.即AB=BC=AC,∠BAC=∠B=∠C=60°;②对称性:等边三角形是轴对称图形,三条高线(或角平分线或中线)所在的直线是对称轴.(2)判定①定义:三边都相等的三角形是等边三角形;②三个角都相等(均为60°)的三角形是等边三角形;③任一内角为60°的等腰三角形是等边三角形.即若AB=AC,且∠B=60°,则△ABC是等边三角形.变式练习1:△ABC中,∠B=60°,AB=A C,BC=3,则△ABC的周长为9.变式练习2:在等边△ABC中,点D,E分别在边BC,AC上,若CD=2,过点D 作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.解:∵△ABC是等边三角形,∴∠B=∠ACB=60°,∵DE∥AB,∴∠EDC=∠B=60°,∴△EDC是等边三角形,∴DE=DC=2,在Rt△DEF,∵∠DEF=90°,DE=2,∴DF=2DE=4,∴EF=DF2-DE2=42-22=2 3.变式练习3:如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC=__2__.知识点二:角平分线和垂直平分线1.角平分线(1)性质:角平分线上的点到角的两边的距离相等.即若∠1 =∠2,PA⊥OA,PB⊥OB,则PA=PB.(2)判定:角的内部到角的两边的距离相等的点在角的角平分线上.4.垂直平分线图形(1)性质:线段的垂直平分线上的点到这条线段的两端点距离相等.即若OP垂直且平分AB,则PA=PB.(2)判定:到一条线段两端点距离相等的点在这条线段的垂直平分线上.21P C OBAPCO B A注意:(1)等边三角形是特殊的等腰三角形,所以等边三角形也满足“三线合一”的性质.(2)等边三角形有一个特殊的角60°,所以当等边三角形出现高时,会结合直角三角形30°角的性质,即BD=1/2AB.变式练习:如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AC=6.知识点三:直角三角形的判定与性质1.直角三角形的性质(1)两锐角互余.即∠A+∠B=90°;(2) 30°角所对的直角边等于斜边的一半.即若∠B=30°则AC=12AB;(3)斜边上的中线长等于斜边长的一半.即若CD是中线,则CD=12AB.(4)勾股定理:两直角边a、b的平方和等于斜边c的平方.即a2+b2=c2 .2.直角三角形的判定(1) 有一个角是直角的三角形是直角三角形.即若∠C=90°,则△ABC是Rt△;(2) 如果三角形一条边的中线等于这条边的一半,那么这个三角形是直角三角形.即若AD=BD=CD,则△ ABC是Rt△(3) 勾股定理的逆定理:若a2+b2=c2,则△ABC是Rt△.3.直角三角形相似判定定理1).斜边与一条直角边对应成比例的两直角三角形相似。
中考数学专题复习等腰三角形练习(含答案)

中考数学专题复习等腰三角形练习一、选择题1. 如图所示,线段AC 的垂直平分线交线段AB 于点D ,∠A=50°,则∠BDC=( )A .50°B .100°C .120°D .130°2. 已知等腰三角形的一个角等于42°,则它的底角为( )A .42°B .69°C .69°或84°D .42°或69°3. 如图,等边三角形OAB 的边长为2,则点B 的坐标为( )A .(1,1)B .(1,) 3C .(,1)D .()33,34.如图,在△ABC 中,AB =AC ,∠C =65°,点D 是BC 边上任意一点,过点D 作DF ∥AB 交AC 于点E ,则∠FEC 的度数是( )A .120°B .130°C .145°D .150°CEF5.如图,在△ABC 中,AB =BC ∠BAC =30°,分别以点A ,C 为圆心,AC 的长为半径作弧,两弧交于点D ,连接DA ,DC ,则四边形ABCD 的面积为( )A.B.9C.6D.6.如图,等腰直角三角形ABC 中,∠ABC =90°,BA =BC ,将BC 绕点B 顺时针旋转θ(0°<θ<90°),得到BP ,连结CP ,过点A 作AH ⊥CP 交CP 的延长线于点H ,连结AP ,则∠PAH 的度数( )A .随着θ的增大而增大B .随着θ的增大而减小C .不变D .随着θ的增大,先增大后减小7.如图,在中,,观察图中尺规作图的痕迹,可知ABC ∆,40AC BC A =∠=︒的度数为BCG ∠A .B .C .D .40︒45︒50︒60︒8.七巧板是我们祖先的一项创造,被誉为“东方魔板”.在一次数学活动课上,小明用边长为4cm 的正方形纸片制作了如图所示的七巧板,并设计了下列四幅作品﹣﹣“奔跑者”,其中阴影部分的面积为5cm 2的是( )A.B.C.D.二、填空题9. 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是 .10.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .11.如图,在△ABC中,BC的垂直平分线分别交BC、AB于点E、F.若△AFC 是等边三角形,则∠B=________°.12.如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB 的中点.若BC=12,AD=8,则DE的长为.ECB A13.若等腰三角形的一个底角为,则这个等腰三角形的顶角为__________.72 14. 如图,等边三角形ABC 内有一点P ,分别连接AP ,BP ,CP ,若AP=6,BP=8,CP=10,则S △ABP +S △BPC = .15.如图,四边形ABCD 中,AB ∥CD ,∠ABC =60°,AD =BC =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则点M 到直线BC 的距离的最小值为 .MDC BA 16.如图,在直角坐标系中,点A (1,1),B (3,3)是第一象限角平分线上的两点,点C 的纵坐标为1,且CA =CB ,在y 轴上取一点D ,连接AC ,BC ,AD ,BD ,使得四边形ACBD 的周长最小,这个最小周长的值为.三、解答题17. 如图,在△ABC中,AB=AC,AD⊥BC于点D.(1)若∠C=42°,求∠BAD的度数;(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.18. 如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.19.如图,△ABC中,AB=AC,∠B的平分线交AC于D,AE∥BC交BD的延长线于点E,AF⊥AB交BE于点F.(1)若∠BAC=40°,求∠AFE的度数;(2)若AD=DC=2,求AF的长.FDEC AB 20. (12分)如图,在等边三角形ABC 中,点E 是边AC 上一定点,点D 是直线BC 上一动点,以DE 为一边作等边三角形DEF ,连接CF .【问题解决】如图1,若点D 在边BC 上,求证:CE +CF =CD ;【类比探究】如图2,若点D 在边BC 的延长线上,请探究线段CE ,CF 与CD 之间存在怎样的数量关系?并说明理由.21. 如图,在△ABC 中,AB =AC =5 cm ,BC =6 cm ,AD 是BC 边上的高.点P 由C 出发沿CA 方向匀速运动.速度为1 cm/s.同时,直线EF 由BC 出发沿DA 方向匀速运动,速度为1 cm/s ,EF //BC ,并且EF 分别交AB 、AD 、AC 于点E ,Q ,F ,连接PQ .若设运动时间为t (s)(0<t <4),解答下列问题:(1)当t为何值时,四边形BDFE是平行四边形?(2)设四边形QDCP的面积为y(cm2),求出y与t之间的函数关系式;(3)是否存在某一时刻t,使点Q在线段AP的垂直平分线上?若存在,求出此时点F到直线PQ的距离h;若不存在,请说明理由.答案一、选择题1. 【答案】B2. 【答案】D [解析] 在等腰三角形中,当一个锐角在未指明为顶角还是底角时,一定要分类讨论.①42°的角为等腰三角形的底角;②42°的角为等腰三角形的顶角,则底角为(180°-42°)÷2=69°.所以底角为42°或69°.3. 【答案】B [解析]过点B作BH⊥AO于点H,∵△OAB是等边三角形,33∴OH=1,BH=,∴点B的坐标为(1,).4. 【答案】B【解析】可利用三角形的外角性质求∠FEC的度数,结合等腰三角形与平行线的性质,可得∠EDC、∠B均与∠C相等.即:∵AB=AC,∴∠B=∠C=65°.∵DF∥AB,∴∠EDC=∠B=65°.∴∠FEC=∠EDC+∠C=65°+65°=130°.5. 【答案】D【解析】∵分别以点A、C为圆心,AC的长为半径作弧,两弧交于点D,∴AD=AC=CD,∴△ACD是等边三角形,∴∠DAC=60°.∵AB=BC ,AD=CD ,连接BD 交AC 于点E ,∴BD 垂直平分AC ,∴∠AEB=90°.∵∠BAC=30°, AB= ∴,AE=,∴AC=3.32在R t △ADE 中,∵∠DAC=60°,∠AED=90°,AE=,∴∴BD=32=∴四边形ABCD 的面积为:.3333221=⨯⨯6. 【答案】C【解析】本题考查了等腰三角形的性质,三角形的内角和,旋转的性质.由旋转得BC=BP=BA ,∴△BCP 和△ABP 均是等腰三角形.在△BCP 中,∠CBP=θ,BC=BP ,∴∠BPC=90°-θ.在△ABP 中,∠ABP=90°-θ,同理得∠12APB=45°+θ,∴∠APC=∠BPC +∠APB =135°,又∵∠AHC=90°,∴∠12PAH=45°,即其度数是个定值,不变.因此本题选C .7. 【答案】C【解析】由作法得,∵,∴平分,,CG AB ⊥AB AC =CG ACB ∠A B ∠=∠∵,∴.故选C .1804040100ACB ∠=︒-︒-︒=︒1502BCG ACB ∠=∠=︒8. 【答案】最小的等腰直角三角形的面积42=1(cm 2),平行四边形面=18×12×积为2cm 2,中等的等腰直角三角形的面积为2cm 2,最大的等腰直角三角形的面积为4cm 2,则A 、阴影部分的面积为2+2=4(cm 2),不符合题意;B 、阴影部分的面积为1+2=3(cm 2),不符合题意;C 、阴影部分的面积为4+2=6(cm 2),不符合题意;D 、阴影部分的面积为4+1=5(cm 2),符合题意.故选:D .二、填空题9. 【答案】1 [解析]由勾股定理可得,a 2+b 2=13,直角三角形面积=(13-1)÷4=3,即ab=3,所以ab=6,所以(a -b )2=a 2+b 2-2ab=13-12=1. 1210. 【答案】10或11.【解析】分3是腰长与底边长两种情况讨论求解即可.①3是腰长时,三角形的三边分别为3、3、4,∵此时能组成三角形,∴周长=3+3+4=10;②3是底边长时,三角形的三边分别为3、4、4,此时能组成三角形,所以周长=3+4+4=11.综上所述,这个等腰三角形的周长是10或11.故答案为:10或11.11. 【答案】30°【解析】本题考查了等边三角形和等腰三角形以及垂直平分线的性质.因为FE 垂直平分BC ,∴ FC =FB ∴∠B =∠BCF ∵△ACF 是等边三角形,∴∠AFC =60° ,∴ ∠B =30°12. 【答案】5【解析】∵AB =AC ,∠BAC 的平分线AD 交BC 于点D ,∴AD ⊥BC ,BD =CD =BC =6.在R t △ABD 中,由勾股定理,得AB =10.又∵E 12为AB 的中点,∴DE =AB =5.故答案为5.1213. 【答案】36°【解析】∵等腰三角形的一个底角为,∴等腰三角形的顶角72︒,180727236=︒-︒-︒=︒故答案为:.36︒14. 【答案】16+24 [解析]将△ABP 绕点B 顺时针旋转60°到△CBP',连接3PP',所以P'C=PA=6,BP=BP',∠PBP'=60°,所以△BPP'是等边三角形,其边长BP 为8,所以PP'=8,S △BPP'=16,3因为PC=10,所以PP'2+P'C 2=PC 2,所以△PP'C 是直角三角形,S △PP'C =24,所以S △ABP +S △BPC =S △BPP'+S △PP'C =163+24.15. 【答案】-2【解析】延长AD 、BC 交于点P , 作MH ⊥PB 于H .∵AB ∥CD ,∴=,∠ABC =∠DCP =60°.∵AD =BC =CD =4,∴PD =PD AD PC BCPC ,∴△PDC 为等边三角形,∴PD =PC =CD =4,∠P =60°. 由∠AMD =90°,可知点M 在以AD 为直径的⊙E 上,且在四边形ABCD 内的一个动点,根据垂线段最短可知E 、M 、H 三点共线时MH 最小.在R t △PEH 中,EP =6,∠P=60°,∴EH =EP ·sin 60°=∴MH 的最小值=EH -EM =2.16. 【答案】4+25【解析】先求点C 的坐标,再利用最短路径知识确定D 点位置,最后求四边形ACBD 的最小周长即可.由点A 与点C 的纵坐标均为1,可知AC ∥x 轴,又点A ,B 是第一象限角平分线上的两点,∴∠BAC =45°,又∵CA =CB ,∴∠CBA =45°,∴AC ⊥BC ,∴C(3,1),则AC =BC =2.如图,作点A 关于y 轴的对称点E ,连接BE 交y 轴于点D ,此时AD +BD 的值最小,为线段BE 的长.由轴对称性可知AE=2,则EC=4.在R t △BCE 中,根据勾股定理,得BE ===2.∴四边形ACBD 的最小周长为2+2+222EC BC +2242+5=4+2.55三、解答题17. 【答案】解:(1)(方法一):∵AB=AC ,∠C=42°,∴∠B=∠C=42°,∴∠BAC=180°-∠B -∠C=180°-42°-42°=96°.∵AD ⊥BC ,∴∠BAD=∠BAC=×96°=48°.1212(方法二):∵AB=AC ,∠C=42°,∴∠B=∠C=42°.∵AD ⊥BC 于点D ,∴∠ADB=90°,∴∠BAD=180°-90°-42°=48°.(2)证明:∵EF ∥AC ,∴∠CAF=∠F ,∵AB=AC ,AD ⊥BC ,∴∠CAF=∠BAF ,∴∠F=∠BAF ,∴AE=FE.18. 【答案】证明:∵AB =AC ,∴∠ABC =∠C ,∵AD 是BC 边上的中线,∴AD ⊥BC ,∴∠BAD +∠ABC =90°,(3分)∵BE ⊥AC,∴∠CBE +∠C =90°,∴∠CBE =∠BAD.(5分)19. 【答案】解:(1)∵AB =AC ,∠BAC =40°,∴∠ABC =×(180°-40°)=70°.12∵BD 平分∠ABC ,∴∠ABD =∠DBC =×70°=35°.12∵AF ⊥AB ,∴∠BAF =90°.∴∠AFE =∠BAF +∠ABD =90°+35°=125°.(2)∵BD 平分∠ABC ,BD =BD ,AD =CD ,∴△BDA ≌△BDC .∴AB =BC .又AB =AC ,∴AB =BC =AC .∴△ABC 为等边三角形.∴∠ABC =60°,∠ABD =30°.∵AD =DC =2,∴AB =4.在R t △ABF 中,AF =AB ·tan 30°=说明:此题中的条件AE ∥BC 是多余的.【解析】(1)由“等边对等角”求出∠ABC ,由角平分线的定义求出∠ABD ,∠AFE 是△ABF 的外角,因此∠AFE =∠BAF +∠ABD ;(2)由BD 既是△ABC 的角平分线又是中线可知AB =BC ,从而推出△ABC 是边长为2的等边三角形.在R t △ABF 中可解出AF .20. 【答案】【问题解决】在CD 上截取CH =CE ,易证△CEH 是等边三角形,得出EH =EC =CH ,证明△DEH ≌△FEC (SAS ),得出DH =CF ,即可得出结论;【类比探究】过D 作DG ∥AB ,交AC 的延长线于点G ,由平行线的性质易证∠GDC =∠DGC =60°,得出△GCD 为等边三角形,则DG =CD =CG ,证明△EGD ≌△FCD (SAS ),得出EG =FC ,即可得出FC =CD +CE .【问题解决】证明:在CD 上截取CH =CE ,如图1所示:∵△ABC 是等边三角形,∴∠ECH =60°,∴△CEH 是等边三角形,∴EH =EC =CH ,∠CEH =60°,∵△DEF 是等边三角形,∴DE=FE,∠DEF=60°,∴∠DEH+∠HEF=∠FEC+∠HEF=60°,∴∠DEH=∠FEC,在△DEH和△FEC中,,∴△DEH≌△FEC(SAS),∴DH=CF,∴CD=CH+DH=CE+CF,∴CE+CF=CD;【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:∵△ABC是等边三角形,∴∠A=∠B=60°,过D作DG∥AB,交AC的延长线于点G,如图2所示:∵GD∥AB,∴∠GDC=∠B=60°,∠DGC=∠A=60°,∴∠GDC=∠DGC=60°,∴△GCD为等边三角形,∴DG=CD=CG,∠GDC=60°,∵△EDF为等边三角形,∴ED=DF,∠EDF=∠GDC=60°,∴∠EDG=∠FDC,在△EGD和△FCD中,,∴△EGD≌△FCD(SAS),∴EG =FC ,∴FC =EG =CG +CE =CD +CE .21. 【答案】(1)如解图①,连接DF ,解图①∵AB =AC =5,BC =6,AD ⊥BC ,∴BD =CD =3,在Rt △ABD 中AD ==4,52-32∵EF //BC ,∴△AEF ∽△ABC ,∴=,EF BC AQ AD ∴=,∴EF =(4-t ),EF 64-t 432∵EF //BD ,∴当EF =BD 时,四边形EFDB 是平行四边形,∴(4-t )=3,32∴t =2,∴当t =2s 时,四边形EFDB 是平行四边形;(2)如解图②,作PN ⊥AD 于N ,解图②∵PN //DC ,∴=,PN DC AP AC ∴=,PN 35-t 5∴PN =(5-t ),35∴y =DC ·AD -AQ ·PN 1212=6-(4-t ) ·(5-t )1235=6-(t 2-t +6)3102710=-t 2+t (0<t <4);3102710(3)存在.理由如下:如解图③,作QN ⊥AC 于N ,作FH ⊥PQ 于H .解图③∵当QN 为AP 的垂直平分线时QA =QP ,QN ⊥AP ,∴AN =NP =AP =(5-t ),1212由题意cos ∠CAD ==,AD AC AN AQ∴=,∴t =,12(5-t )4-t 4573∴当t =s 时,点Q 在线段AP 的垂直平分线上.73∵sin ∠FPH ==sin ∠CAD =,∵PA =5-=,AF =AQ ÷=,FH PF 357383452512∴PF =,∴FH =.712720∴点F 到直线PQ 的距离h =(cm). 720。
北师大版中考数学复习《等腰三角形》专项测试卷-带答案

北师大版中考数学复习《等腰三角形》专项测试卷-带答案学校:___________班级:___________姓名:___________考号:___________一.选择题1.如图,在3×3的正方形网格中格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出()A.6个B.5个C.4个D.3个2.如图,已知△ABC的三条内角平分线相交于点I,三边的垂直平分线相交于点O.若∠BOC=148°,则∠BIC=()A.120°B.125°C.127°D.132°3.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=35°,则∠A+∠C=()A.30°B.40°C.17.5°D.35°4.如图,点C、D在线段AB的同侧,CA=4,AB=12,BD=9,M是AB的中点,∠CMD=120°,则CD 长的最大值是()A.16B.19C.20D.215.如图,在△ABC中AB=AD=DC,∠BAD=26°,则∠C的度数是()A.36°B.38.5°C.64°D.77°6.如图,已知每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有()A.4个B.5个C.6个D.7个7.如图,△ABC是等腰三角形,点O是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC 的腰长为5,面积为12,则OE+OF的值为()A.4B.C.15D.88.在Rt△ABC中∠ACB=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个?()A.9个B.7个C.6个D.5个9.如图,在△ABC中AB=AC,AB的垂直平分线交AB于点E,交BC于点F,连接AF,若∠F AC=∠B,则∠F AB的度数为()A.25°B.30°C.35°D.50°10.如图,B是直线l上的一点,线段AB与l的夹角为α(0°<α<180°),点C在l上,若以A、B、C 为顶点的三角形是等腰三角形,则满足条件的点C共有()A.2个B.3个C.2个或4个D.3个或4个二.填空题11.如图,在△ABC中DE是AC的垂直平分线,△ABD的周长为13,△ABC的周长为19,则AE =.12.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=.13.如图,在△ABC中点D、E在直线AB上,且点D、E分别是线段AC、BC的垂直平分线上的点.若∠ACB=30°,则∠DCE=14.若点A(a,2)与B(3,b)关于x轴对称,则a﹣b=.15.已知点A(2a+3b,﹣2)和点B(8,3a+1)关于y轴对称,那么a+b=.16.如图,在△ABC中D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE=.17.等腰三角形一腰上的高与另一腰的夹角为40°,则顶角的度数可能为.18.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=.19.如图,在△ABC中AB=AC,D、E是△ABC内两点.AD平分∠BAC,∠EBC=∠E=60°,若BE=7cm,DE=3cm,则BC=cm.20.如图,AD是△ABC的高,且AB+BD=DC,∠BAD=40°,则∠C的度数为.21.如图,在△ABC中AE=DE=BD,AD=EC,∠1=18°,则∠EBC的度数是.22.如图,在△ABC中点D、E分别在BC和AB上,若AD=BD=AE,BE=DE=DC,则∠CAD的度数是°.三、解答题23.在平面直角坐标系中横坐标和纵坐标都是整数的点称为整点.如图,A(﹣1,3),B(﹣3.﹣1),C (﹣1,﹣1)都是整点.请仅用无制度的直尺画图并回答下列问题.(1)在图1中画出△ABC关于y轴对称的△A1B1C1;(2)在图1中取整点D,画CD⊥AB.垂足为E,直接写出点D的坐标是;(3)在图2的AC边上画点F.使∠ABF=45°,并直接写出线段AF的长为.24.如图,平面直角坐标系中A(﹣2,1),B(﹣3,4),C(﹣1,3),过点(1,0)作x轴的垂线l.(1)作出△ABC关于直线l的轴对称图形△A1B1C1;(2)直接写出A1(,),B1(,),C1(,);(3)在△ABC内有一点P(m,n),则点P关于直线l的对称点P1的坐标为(,)(结果用含m,n的式子表示).25.在10×10的网格中建立如图的平面直角坐标系,每个小正方形的顶点称为格点,例如图中点A(0,4),B(4,2).仅用无刻度的直尺在给定网格中完成画图,并回答问题:(1)作出线段AB关于y轴对称的线段AD,并写点B的对应点D的坐标;(2)作直线l,使得点A和点B关于直线l对称(保留画图过程的痕迹);(3)在x轴上找一点P,使得∠APB=2∠OAP(保留画图过程的痕迹).26.在6×6的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点坐标分别为A(1,3),B(﹣3,2),C(﹣1,1).△DEF与△ABC关于x轴成轴对称(其中D,E,F分别是A,B,C的对应点).(1)请画出△DEF,并写出F点的坐标;(2)仅用无刻度的直尺完成画图,画图过程用虚线,画图结果用实线表示,请按步骤完成下列问题,不要求说明理由.①在格点上取点P,连接FP,使FP⊥AB,并写出点P的坐标;②设①中直线FP交AB于点M,在AB关于x轴的对称线段DE上找点N,使M,N关于x轴成轴对称.27.如图,在7×6的网格中横、纵坐标均为整数的点叫做格点,如A(4,0)、B(1,1)、C(6,2)都是格点,请用无刻度直尺画出下列图形,并保留作图痕迹.(1)直接写出点C关于x轴的对称点C的坐标:;(2)画出线段BD,使BD⊥AC于点D;(3)①画出线段CE,使CE⊥AB于点E;②画出线段AF,使AF⊥BC于点F.28.△ABC中D、E是BC边上的两点,且BA=BD,CA=CE,连接AD、AE.(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)如图2,若∠BAC=α(0°<α<180°),求证:∠DAE=90°﹣α;(3)若∠DAE=45°,直接写出∠BAC=.29.如图,在△ABC中AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.(1)若∠A=50°,∠D=30°,求∠GEF的度数;(2)若BD=CE,求证:FG=BF+CG.参考答案一.选择题1.如图,在3×3的正方形网格中格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出()A.6个B.5个C.4个D.3个解:如图,最多能画出6个格点三角形与△ABC成轴对称.故选:A.2.如图,已知△ABC的三条内角平分线相交于点I,三边的垂直平分线相交于点O.若∠BOC=148°,则∠BIC=()A.120°B.125°C.127°D.132°解:连接OA∵∠BOC=148°∴∠OBC+∠OCB=180°﹣∠BOC=32°∵O是三边的垂直平分线的交点∴OA=OB=OC∴∠OAB=∠OBA,∠OAC=∠OCA∴∠OBA+∠OCA=(180°﹣32°)÷2=74°∴∠ABC+∠ACB=74°+32°=106°∵△ABC的三条内角平分线相交于点I∴∠IBC=∠ABC,∠ICB=∠ACB∴∠BIC=180°﹣∠IBC﹣∠ICB=180°﹣(∠ABC+∠ACB)=127°故选:C.3.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=35°,则∠A+∠C=()A.30°B.40°C.17.5°D.35°解:连接OB∵线段AB、BC的垂直平分线l1、l2相交于点O∴AO=OB=OC∴∠AOD=∠BOD,∠BOE=∠COE,∠A=∠ABO,∠C=∠CBO∴∠A+∠C=∠ABC∵∠DOE+∠1=180°,∠1=35°∴∠DOE=145°∴∠ABC=360°﹣∠DOE﹣∠BDO﹣∠BEO=35°;故选:D.4.如图,点C、D在线段AB的同侧,CA=4,AB=12,BD=9,M是AB的中点,∠CMD=120°,则CD 长的最大值是()A.16B.19C.20D.21解:如图,作点A关于CM的对称点A′,点B关于DM的对称点B′.∵∠CMD=120°∴∠AMC+∠DMB=60°∴∠CMA′+∠DMB′=60°∴∠A′MB′=60°∵MA′=MB′∴△A′MB′为等边三角形∵CD≤CA′+A′B′+B′D=CA+AM+BD=4+6+9=19∴CD的最大值为19故选:B.5.如图,在△ABC中AB=AD=DC,∠BAD=26°,则∠C的度数是()A.36°B.38.5°C.64°D.77°解:∵在三角形ABD中AB=AD,∠BAD=26°∴∠B=∠ADB=(180°﹣26°)×=77°又∵AD=DC,在三角形ADC中∴∠C=∠ADB=77°×=38.5°.故选:B.6.如图,已知每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有()A.4个B.5个C.6个D.7个解:当AB为腰时,分别以A、B点为顶点,以AB为半径作圆,可找出格点点C的个数有6个;使△ABC是以AB为腰的等腰三角形,这样的格点C有6个.故选:C.7.如图,△ABC是等腰三角形,点O是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC 的腰长为5,面积为12,则OE+OF的值为()A.4B.C.15D.8解:连接AO,如图∵AB=AC=5∴S△ABC=S△ABO+S△AOC=AB•OE+AC•OF=12∵AB=AC∴AB(OE+OF)=12∴OE+OF=.故选:B.8.在Rt△ABC中∠ACB=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个?()A.9个B.7个C.6个D.5个解:如图:故选:B.9.如图,在△ABC中AB=AC,AB的垂直平分线交AB于点E,交BC于点F,连接AF,若∠F AC=∠B,则∠F AB的度数为()A.25°B.30°C.35°D.50°解:∵AB=AC∴∠B=∠C∵EF垂直平分AB∴BF=AF∴∠BAF=∠B=∠C∵∠F AC=∠B∴∠B+3∠B=180°∴∠B=25°∴∠F AB的度数为25°故选:A.10.如图,B是直线l上的一点,线段AB与l的夹角为α(0°<α<180°),点C在l上,若以A、B、C 为顶点的三角形是等腰三角形,则满足条件的点C共有()A.2个B.3个C.2个或4个D.3个或4个解;如图1,当α=90°,只有两个点符合要求同法当α为60°或120°时,只有两个点符合要求如图2,当α为锐角与钝角(除60°或120°)时符合条件的点有4个分别是AC3=AB,AB=BC2,AC1=BC,AB=BC.∴满足条件的点C共有:2或4个.故选:C.二.填空题11.如图,在△ABC中DE是AC的垂直平分线,△ABD的周长为13,△ABC的周长为19,则AE=3.解:∵DE是AC的垂直平分线.∴AD=DC∴△ABD的周长为13,即:AB+AD+BD=AB+BD+DC=AB+BC=13.∵△ABC的周长为19,即AB+BC+AC=19.∴AC=6.∴AE=AC=3故答案是:3.12.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE= 1.5.解:连接CD,BD∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE∴AE=AF∵DG是BC的垂直平分线∴CD=BD在Rt△CDF和Rt△BDE中∴Rt△CDF≌Rt△BDE(HL)∴BE=CF∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE∵AB=6,AC=3∴BE=1.5.故答案为:1.5.13.如图,在△ABC中点D、E在直线AB上,且点D、E分别是线段AC、BC的垂直平分线上的点.若∠ACB=30°,则∠DCE=120°解:∵∠ACB=30°∴△ABC中∠ABC+∠BAC=150°∵点D、E分别是线段AC、BC的垂直平分线上的点∴EB=EC,DC=DA∴∠E=180°﹣2∠ABC,∠D=180°﹣2∠BAC∴△DCE中∠DCE=180°﹣(∠E+∠D)=180°﹣(180°﹣2∠ABC+180°﹣2∠BAC)=180°﹣180°+2∠ABC﹣180°+2∠BAC=2(∠ABC+∠BAC)﹣180°=2×150°﹣180°=120°.故答案为:120°.14.若点A(a,2)与B(3,b)关于x轴对称,则a﹣b=5.解:∵点A(a,2)与点B(3,b)关于x轴对称∴a=3,b=﹣2∴a﹣b=3﹣(﹣2)=3+2=5故答案为:5.15.已知点A(2a+3b,﹣2)和点B(8,3a+1)关于y轴对称,那么a+b=﹣3.解:∵点A(2a+3b,﹣2)和点B(8,3a+1)关于y轴对称∴2a+3b=﹣8,3a+1=﹣2解得a=﹣1,b=﹣2∴a+b=﹣3故答案为:﹣3.16.如图,在△ABC中D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE=115°.解:∵AB=BD,AC=CE∴∠BAD=∠BDA,∠E=∠CAE设∠BAD=∠BDA=x,∠E=∠CAE=y∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y∵∠ABC+∠ACB+∠BAC=180°∴2x+2y+50°=180°∴x+y=65°∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.故答案为:115°.17.等腰三角形一腰上的高与另一腰的夹角为40°,则顶角的度数可能为50°或130°.解:①当为锐角三角形时,如图高与右边腰成40°夹角,由三角形内角和为180°可得,顶角为50°;②当为钝角三角形时,如图,此时垂足落到三角形外面因为三角形内角和为180°由图可以看出等腰三角形的顶角的补角为50°所以三角形的顶角为130°.故答案为50°或130°.18.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=5.解:过P作PD⊥OB,交OB于点D在Rt△OPD中cos60°==,OP=12∴OD=6∵PM=PN,PD⊥MN,MN=2∴MD=ND=MN=1∴OM=OD﹣MD=6﹣1=5.故答案为:5.19.如图,在△ABC中AB=AC,D、E是△ABC内两点.AD平分∠BAC,∠EBC=∠E=60°,若BE=7cm,DE=3cm,则BC=10cm.解;过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.∵EF⊥BC,∠EBF=60°∴∠BEF=30°∴BF=BE=×7=3.5∵∠BED=60°,∠BEF=30°∴∠DEG=30°.又∵DG⊥EF∴GD=ED=×3=1.5∵AB=AC,AD平分∠BAC∴AH⊥BC,且BH=CH.∵AH⊥BC,EF⊥BC,DG⊥EF∴四边形DGFH是矩形.∴FH=GD=1.5.∴BC=2BH=2×(3.5+1.5)=10.故答案为:10.20.如图,AD是△ABC的高,且AB+BD=DC,∠BAD=40°,则∠C的度数为25°.解:在线段DC上取一点E,使DE=DB,连接AE∵AD是△ABC的高∴AD⊥BC∴AD垂直平分BE∴AB=AE∴∠EAD=∠BAD=40°,∠AEB=∠B=90°﹣∠BAD=50°∵AB+BD=DC,DE+CE=DC∴AB=CE∴AE=CE∴∠EAC=∠C∵∠AEB=∠EAC+∠C=2∠C∴∠C=∠AEB=25°故答案为:25°.21.如图,在△ABC中AE=DE=BD,AD=EC,∠1=18°,则∠EBC的度数是54°.解:∵BD=DE∴∠DEB=∠1=18°∴∠ADE=∠1+∠DEB=36°∵AE=DE∴∠A=∠ADE=36°∵BD=AE,AD=CE∴AD+BD=CE+AE即AB=AC∴∠ABC=∠C=72°∴∠CBE=∠ABC﹣∠1=54°故答案为:54°.22.如图,在△ABC中点D、E分别在BC和AB上,若AD=BD=AE,BE=DE=DC,则∠CAD的度数是36°.解:∵AD=BD=AE∴∠B=∠BAD,∠ADE=∠AED∵BE=DE∴∠B=∠EDB设∠B=∠BAD=∠EDB=α∴∠AED=∠ADE=2α∴∠ADB=3α∵∠B+∠BAD+∠ADB=180°∴α+α+3α=180°∴α=36°∴∠ADB=108°,∠ADE=2α=72°,∠ADC=180°﹣∠ADB=72°∴∠ADE=∠ADC在△AED与△ACD中∴△AED≌△ACD(SAS)∴∠C=∠AED=72°∴∠DAC=180°﹣72°﹣72°=36°故答案为:36.三、解答题23.在平面直角坐标系中横坐标和纵坐标都是整数的点称为整点.如图,A(﹣1,3),B(﹣3.﹣1),C (﹣1,﹣1)都是整点.请仅用无制度的直尺画图并回答下列问题.(1)在图1中画出△ABC关于y轴对称的△A1B1C1;(2)在图1中取整点D,画CD⊥AB.垂足为E,直接写出点D的坐标是(3,﹣3)或(1,﹣2)或(﹣3,0);(3)在图2的AC边上画点F.使∠ABF=45°,并直接写出线段AF的长为.解:(1)如图1中△A1B1C1即为所求作.(2)如图1中直线CD,点E即为所求作,D(3,﹣3)或(1,﹣2)或(﹣3,0).故答案为(3,﹣3)或(1,﹣2)或(﹣3,0).(3)取格点E,连接AE,BE,BE交AC于点F,点F即为所求作.观察图象可知CF=∴AF=4﹣=.故答案为:24.如图,平面直角坐标系中A(﹣2,1),B(﹣3,4),C(﹣1,3),过点(1,0)作x轴的垂线l.(1)作出△ABC关于直线l的轴对称图形△A1B1C1;(2)直接写出A1(4,1),B1(5,4),C1(3,3);(3)在△ABC内有一点P(m,n),则点P关于直线l的对称点P1的坐标为(﹣m+2,n)(结果用含m,n的式子表示).解:(1)如图,△A1B1C1为所作;(2)A(4,1),B,(5,4),G(3,3);(3)点P关于直线l的对称点P1的坐标为(2﹣m,n).故答案为4,1;5,4;3,3;﹣m+2,n.25.在10×10的网格中建立如图的平面直角坐标系,每个小正方形的顶点称为格点,例如图中点A(0,4),B(4,2).仅用无刻度的直尺在给定网格中完成画图,并回答问题:(1)作出线段AB关于y轴对称的线段AD,并写点B的对应点D的坐标(﹣4,2);(2)作直线l,使得点A和点B关于直线l对称(保留画图过程的痕迹);(3)在x轴上找一点P,使得∠APB=2∠OAP(保留画图过程的痕迹).解:(1)如图,线段AD即为所求,D的坐标为(﹣4,2)故答案为(﹣4,2);(2)如图,直线EF即为所求;(3)如图,点P即为所求.26.在6×6的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点坐标分别为A(1,3),B(﹣3,2),C(﹣1,1).△DEF与△ABC关于x轴成轴对称(其中D,E,F分别是A,B,C的对应点).(1)请画出△DEF,并写出F点的坐标;(2)仅用无刻度的直尺完成画图,画图过程用虚线,画图结果用实线表示,请按步骤完成下列问题,不要求说明理由.①在格点上取点P,连接FP,使FP⊥AB,并写出点P的坐标;②设①中直线FP交AB于点M,在AB关于x轴的对称线段DE上找点N,使M,N关于x轴成轴对称.解:(1)如图,△DEF为所作,F点的坐标为(﹣1,﹣1);(2)①如图,线段FP即为所求,P点的坐标为(﹣2,3);②如图,点M、N即为所求.27.如图,在7×6的网格中横、纵坐标均为整数的点叫做格点,如A(4,0)、B(1,1)、C(6,2)都是格点,请用无刻度直尺画出下列图形,并保留作图痕迹.(1)直接写出点C关于x轴的对称点C的坐标:(6,﹣2);(2)画出线段BD,使BD⊥AC于点D;(3)①画出线段CE,使CE⊥AB于点E;②画出线段AF,使AF⊥BC于点F.解:(1)点C关于x轴的对称点C的坐标(6,﹣2).故答案为(6,﹣2).(2)如图,线段BD即为所求.(3)①如图,线段CE即为所求.②如图,线段AF即为所求.28.△ABC中D、E是BC边上的两点,且BA=BD,CA=CE,连接AD、AE.(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)如图2,若∠BAC=α(0°<α<180°),求证:∠DAE=90°﹣α;(3)若∠DAE=45°,直接写出∠BAC=90°.解:(1)如图1,∵BA=BD,∠B=40°∴∠BAD=∠BDA==70°∵CA=CE,∠C=60°∴∠AEC=∠EAC=60°∵∠AEC=∠B+∠BAE=60°∴∠BAE=20°∴∠DAE=∠BAD﹣∠DAE=70°﹣20°=50°;(2)如图2,∵BA=BD,CA=CE∴∠BAD=∠BDA=,∠AEC=∠EAC=∵∠BAD+∠CAE=∠BAC+∠DAE∴∠DAE=∠BAD+∠CAE﹣∠BAC=180°﹣(∠B+∠C)﹣∠BAC=180°﹣(180°﹣∠BAC)﹣∠BAC=90°﹣∠BAC=90°﹣α;(3)由(2)可知,∠DAE=90°﹣∠BAC∴∠BAC=180°﹣2∠DAE=180°﹣2×45°=90°.故答案为90°.29.如图,在△ABC中AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.(1)若∠A=50°,∠D=30°,求∠GEF的度数;(2)若BD=CE,求证:FG=BF+CG.(1)解:∵∠A=50°∴∠C=(180°﹣∠A)=(180°﹣50°)=65°∵EG⊥BC∴∠CEG=90°﹣∠C=90°﹣65°=25°∵∠A=50°,∠D=30°∴∠CEF=∠A+∠D=50°+30°=80°∴∠GEF=∠CEF﹣∠CEG=80°﹣25°=55°;(2)证明:过点E作EH∥AB交BC于H则∠ABC=∠EHC,∠D=∠FEH∵AB=AC∴∠ABC=∠C∴∠EHC=∠C∴EC=EH∵BD=CE∴BD=EH在△BDF和△HEF中∴△BDF≌△HEF(AAS)∴BF=FH又∵EC=EH,EG⊥BC∴CG=HG∴FG=FH+HG=BF+CG.。
2023北京初三一模数学汇编:等腰三角形
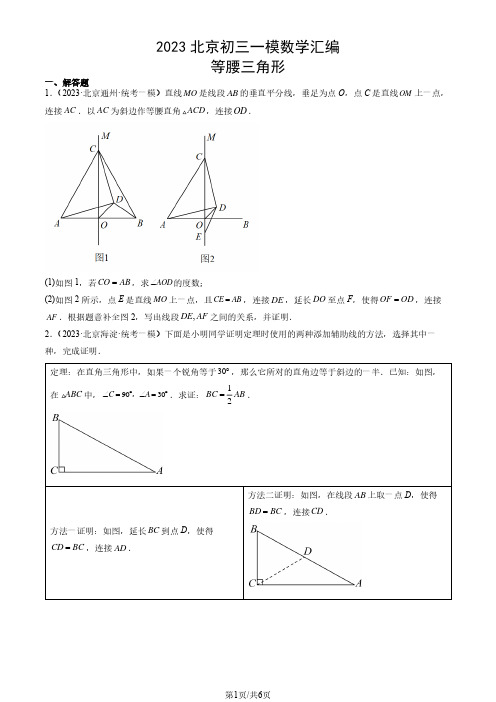
2023北京初三一模数学汇编等腰三角形 为斜边作等腰直角ACD ,连接(1)如图1,若CO AB =,求AOD ∠的度数;(2)如图2所示,点E 是直线MO 上一点,且CE AB =,连接AF .根据题意补全图2,写出线段,DE AF 之间的关系,并证明.2.(2023·北京海淀·统考一模)下面是小明同学证明定理时使用的两种添加辅助线的方法,选择其中一种,完成证明.定理:在直角三角形中,如果一个锐角等于30︒,那么它所对的直角边等于斜边的一半.已知:如图,在ABC 中,方法一证明:如图,延长BC 到点二、填空题 .(2023·北京平谷·统考一模)如图,在ABC 中,则ABD S =△______.统考一模)如图,在ABC 中,,则ABD △的周长是5.(2023·北京海淀·统考一模)如图,点件的x 的值_________.参考答案1.(1)135︒(2)见解析;DE AF ⊥,DE AF =【分析】(1)先证明全等三角形,得到等角,然后直接计算角度即可;(2)先按要求画图,然后证明两组全等三角形,即可得到边相等且平行的关系.【详解】(1)∵直线MO 是线段AB 的垂直平分线,垂足为点O ,∴MO AB ⊥,∵ACD 是等腰直角三角形,∴90ADC ∠=︒,CD AD =,∵ADC DAB O O D M A C ∠=∠+∠∠+,∴B OCD DA =∠∠,∵在CDO 和ADB 中,CD ADOCD DABCO AB=⎧⎪∠=∠⎨⎪=⎩∴(SAS)CDO ADB ≌,∴,OD BD DBO DOC =∠=∠,∴DOB DBO ∠=∠,∴DOB DOC ∠=∠,∵MO AB ⊥,∴45DOB DOC ∠=∠=︒,∴135AOD ∠=︒;(2)如图,连接BD ,与(1)同理可得:(SAS)CDE ADB ≌,∴DE DB =,EDC BDA ∠=∠,∴90CDA BDE ∠=∠=︒,∴DE DB ⊥,和OFA 中,∴(SAS)ODB OFA ≌AF DB =,B ∠=∠DB AF ∥,DE AF =DE AF ⊥.【点睛】此题考查全等三角形的判定与性质、三角形的外角性质、等腰直角三角形的性质,解题关键是通过已知条件判定全等三角形,得到边和角的关系.,先证明ACB ACD ≌,得到12AB =; =60B ︒,进而证明△,得到CD AD =,即可证明和ACD 中,90ACD =︒(SAS ACD △,BCD S=ABD S =ABD S =故答案为:【点睛】本题主要考查了含的关键是掌握同高的三角形,面积比等于底的比.,求出ABC 的周长【详解】解:DE 是AC ,AC 于点,2AB AC =,ABD ∴的周长为2AB BC ++=+故答案为:.【点睛】本题考查了等腰三角形性质和线段的垂直平分线性质,根据垂直平分线的性质求出答本题的关键.5.31︒(答案不唯一)180120302,当点M 在点E 处时,延长EF 交∵120AFE FAB ∠∠==︒,AFE ∠∴60AFH FAH ∠∠==︒,∴AH HF =,∴AHF 是正三角形,∴60H ∠=︒,∵AH HF =,AB EF =,AH AB +∴HBE 是正三角形,60ABE ∠=3060x ︒≤≤故答案为31︒【点睛】本题主要考查了正多边形的性质,等边三角形的判定及性质,三角形的内角和定理,熟练掌握正多边形的性质,等边三角形的判定及性质是解题的关键.。
中考数学一轮复习:课时训练19 等腰三角形(含答案)

课时训练(十九)等腰三角形(限时:30分钟)|夯实基础|1.若等腰三角形的顶角为50°,则它的底角度数为 ()A.40°B.50°C.60°D.65°2.等腰三角形的两边长分别为4 cm和8 cm,则它的周长为()A.16 cmB.17 cmC.20 cmD.16 cm或20 cm3.[最新·福建A卷]如图K19-1,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于()图K19-1A.15°B.30°C.45°D.60°4.[最新·雅安]已知:如图K19-2,在△ABC中,AB=AC,∠C=72°,BC=错误!未找到引用源。
,以点B为圆心,BC 为半径画弧,交AC于点D,则线段AD的长为 ()图K19-2A.2错误!未找到引用源。
B.2错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
5.[最新·凉山州]如图K19-3,在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于错误!未找到引用源。
AB长为半径作弧,两弧相交于M,N两点;②作直线MN交BC于D,连接AD.若AD=AC,∠B=25°,则∠C= ()图K19-3A.70°B.60°C.50°D.40°6.如图K19-4,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为()图K19-4A.6B.7C.8D.97.[最新·绥化]已知等腰三角形的一个外角为130°,则它的顶角的度数为.8.[最新·张家界]如图K19-5,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为.图K19-59.[最新·宁波]如图K19-6,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.图K19-6|拓展提升|10.[最新·淄博]在边长为4的等边三角形ABC中,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=.参考答案1.D2.C3.A[解析] ∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵AD⊥BC,∴BD=CD,AD是BC的垂直平分线,∴BE=CE,∴∠EBC=∠ECB=45°,∴∠ECA=60°-45°=15°.4.C[解析] 在△ABC中,AB=AC,∠C=72°,所以∠ABC=72°,∠A=36°,因为BC=BD,所以∠BDC=72°,所以∠ABD=36°,所以AD=BD=BC=错误!未找到引用源。
北京市2019年中考数学总复习 第五单元 三角形 第19课时 等腰三角形课件

第五单元 三角形
第 19 课时 等腰三角形
课前双基巩固
考点聚焦
考点一 等腰三角形的概念与性质
定义 有① 两边 相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一边叫做底
轴对称性 等腰三角形(底边和腰不相等)是轴对称图形,有② 1 条对称轴
性质
定理 1 定理 2
等腰三角形的两个底角相等(简称:③ 等边对等角 ) 等腰三角形顶角的平分线、底边上的④ 中线 、底边上的高互相重 合,简称“三线合一”
课前双基巩固
考点二 等腰三角形的判定
定义 有① 两边 相等的三角形是等腰三角形 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成:
定理 ② 等角对等边 ) (1)一边上的高与这边上的中线重合的三角形是等腰三角形
拓展 (2)一边上的高与这边所对的角的平分线重合的三角形是等腰三角形 (3)一边上的中线与这边所对的角的平分线重合的三角形是等腰三角形
高频考向探究
探究一 等腰三角形的性质与判定
例 1 如图 19-5,等腰三角形 ABC 中,AB=AC,∠DBC=15°,AB
的垂直平分线 MN 交 AC 于点 D,则∠A 的度数是
.
图 19-5 [方法模型] 等腰三角形的两条腰相等,两个底角相等;反之, 有两条边相等的三角形是等腰三角形;特别地,线段垂直平
定义 性质 判定 实质构成
经过线段的中点且与这条线段垂直的直线叫做这条线段的垂直平分线 线段垂直平分线上的点与这条线段两个端点的距离① 相等 与一条线段两个端点距离相等的点,在这条线段的② 垂直平分线 上 线段的垂直平分线可以看作到线段两个端点③ 距离相等 的所有点的集合
课前双基巩固
对点演练 题组一 必会题 1.[2018·福建 A 卷] 如图 19-1,等边三角形 ABC 中,AD⊥ BC,垂足为 D,点 E 在线段 AD 上,∠EBC=45°,则∠ACE 等 于( )
(北京专版)中考数学 第5单元 三角形 第19课时 等腰三角形作业-人教版初中九年级全册数学试题

等腰三角形1.[2015·] 阅读下面材料:在数学课上,老师提出如下问题:尺规作图:作一条线段的垂直平分线.已知:线段AB .图J19-1小芸的作法如下:如图J19-2,图J19-2(1)分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于C ,D 两点; (2)作直线C D.直线CD 就是所求作的垂直平分线.老师说:“小芸的作法正确.”请回答:小芸的作图依据是__________________________________________.2.[2015·] 如图J19-3,在△ABC 中,AB =AC ,AD 是BC 边上的中线,BE ⊥AC 于点E . 求证:∠CBE =∠BA D.图J19-31.[2014·东城一模] 如图J19-4,AB ∥CD ,点E 在BC 上,且CD =CE ,∠D =74°,则∠B 的度数为( )图J19-4A .68°B .32°C .22°D .16°2.[2015·东城二模] 如图J19-5,在已知的△ABC 中,按以下步骤作图:①分别以B ,C为圆心,大于12BC 的长为半径画弧,两弧相交于点M ,N ;②作直线MN 交AB 于点D ,连接CCD =AC ,∠B =25°,则∠ACB 的度数为( )图J19-5A .90°B .95°C .100°D .105°3.[2012·燕山一模]如图J19-6,点F 在线段AB 上,AD ∥BC ,AC 交DF 于点E ,∠BAC =∠ADF ,AE =B C.求证:△ACD 是等腰三角形.图J19-64.[2010·宣武一模] 请在所给网格中按下列要求操作:(1) 请在图J19-7中的网格中建立平面直角坐标系, 使A 点坐标为(0,2),B 点坐标为(-2,0);(2)在(1)的条件下,在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.图J19-75.[2014·某某二模] 已知∠ABC=90°,D是直线AB上的点,AD=B C.(1)如图J19-8①,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;(2)如图J19-8②,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.图J19-8一、选择题1.若等腰三角形的顶角为40°,则它的底角度数为( )A.40° B.50° C.60° D.70°2.[2014·顺义一模] 如图J19-9,AB=AC,AD∥BC,∠BAC=100°,则∠CAD的度数是( )图J19-9A.30° B.35° C.40° D.50°3.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边的取值X围是( )A.1 cm<AB<4 cmB.5 cm<AB<10 cmC.4 cm<AB<8 cm D.4 cm<AB<10 cm4.[2015·石景山二模] 如图J19-10,AB∥CD,AC的垂直平分线交CF于点F,交AC于点E,连接AF.若∠BAF=80°,则∠CAF的度数为( )图J19-10A.40° B.50° C.60° D.80°5.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )A.6条 B.7条 C.8条 D.9条二、填空题6.如图J19-11,在等腰三角形ABC中,AB=AC,∠A=36°,BD⊥AC于点D,则∠CBD=________°.图J19-117.等腰三角形的周长为16,其一边长为6,则另两边长为________.8.等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为________.9.[2015·某某二模] 如图J19-12,在△ABC 中,AB =AC ,AD 是BC 边上的中线,分别以点A ,C 为圆心,大于12AC 长为半径画弧,两弧的交点分别为点E ,F ,直线EF 与AD 相交于点O .若OA =2,则△ABC 外接圆的面积为________.图J19-12三、解答题10.如图J19-13,在△ABC 中,AB =AC ,M 是BC 的中点,D ,E 分别是AB ,AC 边上的点,且BD =CE .求证:MD =ME .图J19-1311.如图J19-14,在△ABC 中,点D ,E 分别在边AC ,AB 上,BD 与CE 交于点O ,给出下列三个条件:①∠EBO =∠DCO ;②BE =CD ;③OB =OC .(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形(用序号写出所有成立的情形)?(2)请选择(1)中的一种情形,写出证明过程.图J19-1412.如图J19-15,在△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题中所指的等腰三角形个数均不包括△ABC)(1)在图①中画一条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角的度数分别是________度和________度;(2)在图②中画两条线段,使图中有4个等腰三角形;(3)继续以上操作发现:在△ABC中画n条线段,则图中有________个等腰三角形,其中有________个黄金等腰三角形.图J19-1513.[2015·怀柔一模] 阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图J19-16,在△ABC中,∠A=2∠B,CD平分∠ACB,AD,ACBC的长.图J19-16小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图②).请回答:(1)△BDE是________三角形;(2)BC的长为________.参考小聪思考问题的方法,解决问题:如图J19-17,已知△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BD,BCAD的长.图J19-17参考答案真题演练1.到线段两个端点距离相等的点在这条线段的垂直平分线上以及两点确定一条直线2.证明:∵AB=AC,∴∠ABC=∠C.又∵AD是BC边上的中线,∴AD⊥BC,∴∠BAD+∠ABC=90°.∵BE⊥AC,∴∠CBE+∠C=90°,∴∠CBE=∠BA D.模拟训练1.B 2.D3.证明:∵AD∥BC,∴∠CAD=∠BCA,即∠EAD=∠BC A.又∵在△ADE和△CAB中,∠ADE=∠BAC,AE=BC,∴△ADE≌△CAB,∴AD=AC,∴△ACD是等腰三角形.4.解:(1)根据A点坐标为(0,2),B点坐标为(-2,0),则点A所在的纵线一定是y轴,点B所在的横线一定是x轴.在网格中建立平面直角坐标系如图所示:(2)分AB是底边和腰两种情况进行讨论.满足条件的点有4个:C1(2,0);C2(22-2,0);C3(0,0);C4(-2 2-2,0).如图所示.5.解:(1)△CDF是等腰直角三角形.证明:∵∠ABC=90°,AF⊥AB,∴∠FAD=∠DBC=90°.又∵AD=BC,AF=BD,∴△FAD≌△DBC,∴FD=DC,∠1=∠2.∵∠1+∠3=90°,∴∠2+∠3=90°,即∠CDF=90°.∴△CDF 是等腰直角三角形.(2)证明:过点A 作AF ⊥AB ,并截取AF =BD ,连接DF ,CF .∵∠ABC =90°,AF ⊥AB ,∴∠FAD =∠DB C.又∵AD =BC ,AF =BD ,∴△FAD ≌△DBC ,∴FD =DC ,∠1=∠2.∵∠1+∠3=90°,∴∠2+∠3=90°,即∠CDF =90°.∴△CDF 是等腰直角三角形,∴∠FCD =∠APD =45°,∴FC ∥AE .∵∠ABC =90°,AF ⊥AB ,∴AF ∥CE .∴四边形AFCE 是平行四边形,∴AF =CE ,∴BD =CE .自测训练1.D 2.C3.B [解析] ∵在等腰三角形ABC 中,AB =AC ,其周长为20 cm ,∴设AB =AC =xcm ,则BC =(20-2x )cm ,∴⎩⎪⎨⎪⎧2x>20-2x ,20-2x>0.解得5<x B. 4.B5.B [解析] 如图所示,当BC 1=AC 1,AC =CC 2,AB =BC 3,AC 4=CC 4,AB =AC 5,AB =AC 6,BC 7=CC 7时,都能得到符合题意的等腰三角形.故选B.6.18,5或6,48.63°或27° [解析] 在三角形ABC 中,设AB =AC ,BD ⊥AC 于点D. ①若三角形是锐角三角形,∠A =90°-36°=54°,此时底角=(180°-54°)÷2=63°;②若三角形是钝角三角形,∠BAC =36°+90°=126°,此时底角=(180°-126°)÷2=27°.所以等腰三角形底角的度数是63°或27°.9.4π10.证明:∵AB =AC ,∴∠B =∠C.∵M 是BC 的中点,∴BM =CM .在△BDM 和△CEM 中,⎩⎪⎨⎪⎧BD =CE ,∠B =∠C,BM =CM ,∴△BDM ≌△CEM ,∴MD =ME .11.解:(1)①②或①③(2)选择①②证明如下:在△BOE和△COD中,∵∠EBO=∠DCO,∠EOB=∠DOC,BE=CD,∴△BOE≌△COD,∴BO=CO,即∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形.12.解:(1)在图①中画线段如图所示(图中BD):这2个等腰三角形的顶角的度数分别是36度和108度.(2)在图②中画两条线段如图所示.四个等腰三角形分别是△ABD,△BCD,△BEC,△CE D.(3)2nn13.解:(1)△BDE是等腰三角形.(2)BC的长为5.8.解决问题:在△ABC中,AB=AC,∠A=20°,∴∠ABC=∠C=80°.∵BD平分∠AB C.∴∠1=∠2=40°,∠BDC=60°.在BA边上取一点E,使BE=BC=2,连接DE,则△DEB≌△DCB,∴∠BED=∠C=80°,∴∠4=60°,∴∠3=60°.在DA边上取一点F,使DF=DB,连接FE,则△BDE≌△FDE,∴∠5=∠1=40°,BE=EF=2.∵∠A=20°,∴∠6=20°,∴AF=EF=2.∵BD=DF,∴AD=2+2.3=4.3.。
北京市重点中学中考专项-等腰三角形(经典含答案)

等腰三角形(中考专项)1、等腰三角形的顶角等于︒40,则底角的度数为2、等边三角形的每个内角都等于 度3、等腰三角形腰长为cm 5,底边长为cm 4,则它的周长为 cm4、等边三角形的边长为6,则它的周长为5、等腰三角形是轴对称图形,它的对称轴是6、等腰三角形的一个角︒70,则其他两个角分别是7、等腰三角形的两边分别是cm 5和cm 10,则它的周长是 cm8、若等腰三角形底边上的高等于腰的一半,则它的顶角等于 度9、等边三角形边长为a ,则它的高为 ,面积为10、等腰三角形的底边长是4,它的周长不大于16,那么它的腰长m 的取值范围是11、已知:如图,D 是ABC ∆的边BC 上一点, 连结AD 使得ACD CAD ∠=∠,若ABD ∆和 ABC ∆周长分别是cm 24和cm 37,求AC 的长12、已知:如图,ABC ∆中,B ∠、C ∠的平分线交 于点O ,过点O 作BC DE //交AB 于D , 求证:EC BD DE +=13、求证:等腰三角形两腰上的高相等14、已知:如图,ABD ∆和BCE ∆是等边三角形, 且A 、B 、C 共线,AE 与BD 交于M , BE 与CD 交于N ,求证:AC MN //15、等腰三角形底边为a ,顶角是底角的4倍,则腰上的高是( ) A.a 21B. a 33C. a 63D. 6316、等腰三角形周长是cm 32,一边长为cm 10,则底边上高为( ) A. cm 8 B. cm 64 C. cm 8或cm 64 D. 不能确定17、等腰三角形两边长为3和6,则它的周长是( )A. 9B. 12C. 15D. 1818、等腰三角形一腰上的高等于腰长的一半,则顶角的度数为( ) A. ︒30 B. ︒150 C. ︒30或︒150 D. 不能确定19、如图,BC AD C B ⊥∠=∠,于D ,E 为AC 中点,6=AB ,则=DE20、如图,ABC ∆中,C D B ,15,90︒=∠︒=∠是BD 上一点且cm CD AC 8==, 则=AB cm ,=BC cm21、如图,ABC ∆中,DE 垂直平分AB , 交AC 于E ,若C ABC ∠=∠,20=AB , 8=BC ,则BEC ∆的周长是22、等腰三角形中的一个角是另一个角的2倍,则它的顶角是 度23、ABC ∆中,B ∠、C ∠的平分线交于点O ,若︒=∠108A ,则=∠BOC 度24、如果等腰三角形的两边长为cm 8、cm 10,那么连结这个三角形各边的中点所形成的三角形的周长为 cm25、等腰三角形一腰上的中线分三角形的周长为cm 6和cm 15两部分,则它的腰长是 cm ,底边长为 cm26、ABC ∆中,D AC AB ,=是BC 上一点,E 是AC 上一点,且AE AD =,若︒=∠︒=∠30,20C BAD ,则=∠ADE 度27、已知:如图,ABC ∆中,AE BC AC C ,,90=︒=∠是CAB ∠的平分线,求证:AB CE AC =+28、已知:如图,BDE ∆是等边三角形,A 在BE 延长线上,C 在BD 延长线上,且AC AD =, 求证:AE DC DE =+29、如图,ADC ABC AD AB ∠=∠=,, 求证:DC BC =30、如图,ABC ∆中,ACB ABC ∠=∠, 21∠=∠,求证:AO 平分BAC ∠31、如左图,ABC ∆中,AB DE BC FD C B ⊥⊥∠=∠,,,︒=∠158AFD ,求EDF ∠的度数32、ABC ∆中,AD 是角平分线,AB DE ⊥, AC DF ⊥,E 、F 为垂足,求证:EF AD ⊥33、ABC ∆中,︒=∠90C ,︒=∠45B , AE 平分CAB ∠,求证:CE AC AB +=34、如图,AD 为ABC ∆的角平分线,直线AD MN ⊥于A ,E 为MN 上一点,ABC ∆周长记为A P , EBC ∆周长记为E P ,比较A P 、E P 的大小35、草原上两个居民点在河流的同旁,汽车从A 点出发到B ,途中需要道河边加水,汽车到哪一点加水,可是行驶路程最短,在图中画出该点.等腰三角形(中考专项)答案:1、︒702、︒603、144、185、底边上的高所在的直线(或底边上的中线所在的直线、或顶角的平分线所在的直线)6、︒70和︒40或︒55和︒557、258、1209、243,23a a 10、62≤<m 11、cm 1312、提示:证DBO ∆、ECO ∆为等腰三角形13、提示:可通过全等证或通过面积证14、提示:先证ABE ∆≌DBC ∆,再证MAB ∆≌NDB ∆,判断BMN ∆为等边三角形,利用角的关系证明平行 15、A16、C17、C18、C19、320、34,421、28 22、36或90 23、144 24、13或14 25、10,1 26、40 27、提示:过E 作AB 的垂线28、提示:过C 点作DE CF //, 证AED ∆≌CFA ∆,进而得到AC BC BC CF AE CF ===,, 33、过E 作AB EF ⊥交AB 于F ,在EFB ∆中,Θ︒=∠45B ,∴FB EF =ΘAE 平分CAB ∠,︒=∠90C ,AB EF ⊥,∴CE EF = 易证AEC ∆≌AEB ∆,∴AF AC = ∴CE AC FB AF AB +=+=34、延长BA 至'C ,使AC AC =',ΘMAB AE C ∠=∠'而MAN 为一条直线,AD 为ABC ∆的角平分线,∴MAB CAN ∠=∠AE C CAN '∠=∠∴,连结E C ',AE C '∆≌CAE ∆在BE C '∆中,两边之和大于第三边,''BC E C BE >+, 即AC AB EC CB +>+,同时加上BC ,就得到了E A P P <。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时训练(十九) 等腰三角形
(限时:40分钟)
|夯实基础|
1.若等腰三角形的顶角为40°,则它的底角度数为()
A.40°
B.50°
C.60°
D.70°
2.如图K19-1,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是
()
图K19-1
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
3.[2017·昌平二模]如图K19-2,△ABC中,∠ACB=90°,∠B=55°,点D是斜边AB的中点,那么∠ACD的度数为()
图K19-2
A.15°
B.25°
C.35°
D.45°
4.如图K19-3,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF.若∠BAF=80°,则∠CAF的度数为()
图K19-3
A.40°
B.50°
C.60°
D.80°
5.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边长的取值范围是()
A.1 cm<AB<4 cm
B.5 cm<AB<10 cm
C.4 cm<AB<8 cm
D.4 cm<AB<10 cm
6.[2017·门头沟二模]如图K19-4,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,则∠BAD=()
图K19-4
A.23°
B.24°
C.25°
D.26°
AB长为半径作弧,两弧相交于7.[2018·凉山州]如图K19-5,在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于1
2
M,N两点;②作直线MN交BC于D,连接AD.若AD=AC,∠B=25°,则∠C=()
图K19-5
A.70°
B.60°
C.50°
D.40°
8.[2018·师达中学月考]已知△ABC是等边三角形,边长为4,则BC边上的高是()
A.4
B.2 3
C.2
D. 3
9.等腰三角形的一个内角为100°,则顶角的度数是.
10.等腰三角形的周长为16,其一边长为6,则另两边长为.
11.等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为.
12.[2018·房山一模]一个正方形和两个等边三角形的位置如图K19-6所示,则∠1+∠2+∠3的度数为.
图K19-6
13.在边长为4的等边三角形ABC中,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF= .
14.[2018·义乌]等腰三角形ABC中,顶角∠A为40°,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为.
15.[2018·丰台一模]如图K19-7,在△ABC中,AB=AC,D是BC边的中点,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
图K19-7
16.[2018·通州一模]已知:如图K19-8,在△ABC中,∠B=45°,点D是BC边的中点,DE⊥BC于点D,交AB于点E,连接CE.
(1)求∠AEC的度数;
(2)请你判断AE,BE,AC三条线段之间的等量关系,并证明你的结论.
图K19-8
|拓展提升|
17.[2018·延庆期末]如图K19-9,等边三角形ABC的边长为6,AD是BC边的中线,点E是AC边的中点.如果点P是AD 上的动点,那么EP+CP的最小值为.
图K19-9
18.[2018·东城二模]如图K19-10所示,点P位于等边三角形ABC的内部,且∠ACP=∠CBP.
图K19-10
(1)∠BPC的度数为°;
(2)延长BP至点D,使得PD=PC,连接AD,CD.
①依题意补全图形;
②证明:AD+CD=BD;
(3)在(2)的条件下,若BD的长为2,求四边形ABCD的面积.
参考答案
1.D
2.C[解析] ∵△ABC是等腰三角形,AB=AC,∴∠ABC=∠ACB.又∵BC=BE,∴∠ACB=∠BEC,∴∠BAC=∠EBC,因此选C.
3.C
4.B
5.B[解析] ∵在等腰三角形ABC中,AB=AC,其周长为20 cm,∴设AB=AC=x cm,则BC=(20-2x)cm,
∴2x>20-2x,
20-2x>0,
解得5<x<10.故选B.
6.C
7.C
8.B
9.100°[解析] 根据三角形的内角和等于180°,又等腰三角形的一个内角为100°,所以这个100°的内角只能是顶角,故填100°.
10.5,5或6,4
11.63°或27°[解析] 在三角形ABC中,设AB=AC,BD⊥AC于点D.
①如图①,若三角形是锐角三角形,∠A=90°-36°=54°,
此时底角=(180°-54°)÷2=63°;
②如图②,若三角形是钝角三角形,∠BAC=36°+90°=126°,
此时底角=(180°-126°)÷2=27°.
所以等腰三角形底角的度数是63°或27°.
12.150°
13.2 [解析] 如图,过点C 作CG ⊥AB ,垂足为G ,连接AD ,则AG=BG=2.
∴CG= A C 2-A G 2= 42-22=2 . ∵S △ABD +S △ACD =S △ABC ,
∴1
2AB×DE+1
2AC×DF=1
2AB×CG. ∴1
2×4×DE+1
2×4×DF=1
2×4×CG. ∴DE+DF=CG=2 3.
14.30°或110° [解析] 根据题意作出图形(如图),当点P 在AB 右侧时,连接AP.
∵AB=AC ,∠BAC=40°,∴∠ABC=∠C=70°, ∵AB=AB ,AC=PB ,BC=PA ,
∴△ABC ≌△BAP ,∴∠ABP=∠BAC=40°, ∴∠PBC=∠ABC-∠ABP=30°.
当点P'在AB 左侧时,同理可得∠ABP'=40°,
∴∠P'BC=40°+70°=110°.
故答案为30°或110°.
15.证明:连接AD.
∵AB=AC ,D 是BC 边上的中点,
∴∠BAD=∠CAD.
∵DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
16.解:(1)∵点D是BC边的中点,DE⊥BC, ∴DE是BC的垂直平分线.
∴EB=EC.∴∠B=∠BCE.∵∠B=45°,
∴∠AEC=90°.
(2)AE2+BE2=AC2.
证明:∵∠AEC=90°,
∴△AEC是直角三角形.
∴由勾股定理,得AE2+EC2=AC2.
∵ED垂直平分BC,∴EB=EC.
∴AE2+BE2=AC2.
17.3 3
18.解:(1)120
(2)①如图所示.
②证明:在等边三角形ABC中,∠ACB=60°,∴∠ACP+∠BCP=60°.
∵∠ACP=∠CBP,
∴∠CBP+∠BCP=60°.
∴∠BPC=180°-(∠CBP+∠BCP )=120°. ∴∠CPD=180°-∠BPC=60°. ∵PD=PC ,
∴△CDP 为等边三角形.
∵∠ACD+∠ACP=∠ACP+∠BCP=60°, ∴∠ACD=∠BCP.
在△ACD 和△BCP 中,
A C =
B C
,∠A
C D =∠B C P ,C D =C P
, ∴△ACD ≌△BCP (SAS). ∴AD=BP.
∴AD+CD=BP+PD=BD.
(3)如图,作BM ⊥AD 于点M ,BN ⊥DC 交DC 的延长线于点N.
∵∠ADB=∠ADC-∠PDC=60°, ∴∠ADB=∠CDB=60°. ∴BM=BN= 3
2BD= 3.
又由(2)得AD+CD=BD=2,
∴S 四边形ABCD =S △ABD +S △BCD
=12AD ·BM+1
2CD ·BN
=3
(AD+CD)
2
×2
=3
2
=3.。
