第一章小结与思考

合集下载

第一章4--7(定稿)

结晶的方法（两种）
（12嘉舟)如图是a、b两种固体物质的溶解度曲线，据图可以得到的正确信息是（） A．a的溶解度大于b的溶解度 B．b物质宜用冷却热饱和溶液的方法获取晶体 C．t1℃时，a、b两种物质的饱和溶液中，溶质的质量分数相等 D．t2℃时，100克水中最多能溶解的物质，b比a多
近年来，天气和气候的剧烈变化对人类生活、生产带来许多不良影响。 (1)今年年初，西南五省区发生严重旱情。缺水严重影响农作物的生长，原因之一是土壤中的无机盐必须溶于水后才能被植物的根吸收。 (2)旱区村民以天然水作为饮用水，天然水中含有许多杂质，饮用前需净化处理。请列举一种净化水的方法：如过滤（或沉淀）法。 (3)5月18日，温州龙湾下了一场冰雹，下落的冰雹“ 砸伤”了停在机场的飞机。由于地面气温较高，落地熔化的冰雹不久就成水（填物态变化）。
祝同学们：
学业进步，身体健康！
溶液
悬浊液
乳浊液
小液滴颗粒分散在液体中
形成过程
特征
固、液、气体固体颗粒分溶解在液体中散在液体中均一、稳定
不均一、不稳定、久置分层
不均一、不稳定、久置分层
相同点
都是混合物
知识回顾
浓溶液粗盐精制一定温度、溶解度 100克水、（单位:克）饱和状态溶液溶液中溶质的多少稀溶液无绝对关系饱和溶液溶质的质量溶液的质量＝溶质的质量分数此温度下该溶液是否还能继续溶解该溶质不饱和溶液
滤纸边缘比漏斗口稍低滤液液面低于滤纸的边缘
滤纸紧贴漏斗
漏斗末端靠烧杯内壁
不均一、不稳定、久置分层
不均一、不稳定、久置分层
相同点
都是混合物

小结与思考1

O
B
C
A
B
5.如图在梯形ABCD中 5.如图在梯形ABCD中, ∠DCB=900; 如图在梯形ABCD AB∥CD,AB=25,BC=24.将该梯形折叠将该梯形折叠, AB∥CD,AB=25,BC=24.将该梯形折叠,点A恰好与点D重合,BE为折痕,那么CD的长度为好与点D重合,BE为折痕,那么CD的长度为 ,BE为折痕 CD 7 _________.
(1)成轴对称的个图形全等成轴对称的2个图形全等成轴对称的个图形全等.
(2)如果个图形成轴对称那么对称轴是对如果2 个图形成轴对称,那么对称轴是对
称点连线的垂直平分线. 称点连线的垂边三角形、等腰梯形的对称性；
1.线段的轴对称性 1.线段的轴对称性
3.如图，AD是△ABC的角平分线，DE和DF 如图，是的角平分线，和如图的角平分线分别是△ 的高，分别是△ABD 和△ACD的高，问AD垂直平分的高垂直平分 EF吗？请说明理由吗请说明理由. A E 1 2 F D C
B
操作题 1.如图，找一点P，使点到AB、BC两边的距离如图，找一点，使点P到、两边的距离如图相等，且到B、两点的距离也相等两点的距离也相等，相等，且到、A两点的距离也相等，试用直尺和圆规作图，并保留作图痕迹）（试用直尺和圆规作图，并保留作图痕迹） A 如图点P就是要作的点如图点就是要作的点. 就是要作的点 B
小结与思考
轴对称与轴对称图形的特征、一.轴对称与轴对称图形的特征、区别轴对称与轴对称图形的特征和联系
1.轴对称 1.轴对称
沿某直线折叠与另一个图形重合与另一个图形重合一个图形
2.轴对称图形 2.轴对称图形

七年级上册第一章

巩固练习
主视图
左视图
俯视图
第一章丰富的图形世界
3、请说出下面三幅图分
巩固练习
别是从哪个方向看到的？
左视图
俯视图
主视图
第一章丰富的图形世界
4、请说出下面三幅图
巩固练习
分别是从哪个方向看到
的？
第一章丰富的图形世界
5、一个小立方块的六面分别标有字母A，B，C，
巩固练习
D，E，F.如图是从三个不同方向看到的情形.你
第一章丰富的图形世界归纳小结
谈谈你的收获.
第一章丰富的图形世界作业课本第4页，习题1.1，知识技能布置，1；数学理解，3.
第一章丰富的图形世界复习导入 1. 生活中常见的几何体有哪些？你
能将它们按一定的标准分类吗？
2.棱柱有些什么性质？
第一章丰富的图形世界探索新从以上问题中，你能得到什么结论吗？知
不识庐山真面目，只缘身在此山中.
我们从不同的方向观察同一物体时，可能
看到不同的图形.
第一章丰富的图形世界
4. 从三个方向看物体的形状
第一章丰富的图形世界请从不同方向观察下图. 探索新知
下面的五幅图形，分别是在哪个方向看到的？
第一章丰富的图形世界探索新知
第一章丰富的图形世界探索新知
能说出A，B，E对面分别是什么字母吗？你是怎么判断的？
第一章丰富的图形世界
一个几何体由几个大小相同的小立方
探块搭成，从上面看和从左面看所看到的平索面图形如图所示.请搭出满足条件的几何新体，你搭的几何体由几个小立方块搭成？知
第一章丰富的图形世界

物理化学第一章学习小结

绪论 1 学时基本要求：1、了解物理化学学科、阐明物理化学课程的基本内容和任务。

2、掌握物理化学的学习方法。

P V T 关系 3 学时气体的第一章基本要求：1、掌握理想气体性质、状态方程及基本定律。

2、了解实际气体的性质及范德华方程。

3、掌握临界状态概念、对应状态原理。

4、了解pVT 关系的普遍化计算方法。

重点：理想气体定义、分压力、分体积的概念；理想气体状态方程、范德华方程的应用，对应状态原理及其应用。

难点：分压力、分体积的概念，使用范德华方程及用压缩因子图对真实气体进行有关计算。

第一章气体的pVT关系主要公式及使用条件1.理想气体状态方程式nRTRT?(m/M)pV?pV?p(V/n)?RT 或m3V?V/n称为气体的摩尔体。

mol PaTp式中，V，及n单位分别为，m，K及m3 -1-1 -1，称为摩尔气体常数。

mol·K=8.314510 J ·m积，其单位为·mol。

R此式适用于理想气体，近似地适用于低压的真实气体。

气体混合物2.（1）组成? ) = y (或x 摩尔分数nn/BB ABA???yV/??体积分数Vy Bm,BBAm,AA?V?表示在一定T，p式中下纯气体为混合气体总的物质的量。

A的摩n Am,AA??为在一定T，p尔体积。

下混合之前各纯组分体积的总和。

Vy A,mAA（2）摩尔质量???n/M?m/nM??yM BmixBBB BBB??为混合气体总的物质的量。

上为混合气体的总质量，式中nm?nm?BBBB述各式适用于任意的气体混合物。

?y?n/n?p/p?V/V（3）BBBB式中p为气体B，在混合的T，V条件下，单独存在时所产生的压力，称为B B?V下，单独存在时所占的体积。

，p的分压力。

为B气体在混合气体的T B道尔顿定律3.?，p= yp pp?BB BB上式适用于任意气体。

对于理想气体p?nRT/V BB4.阿马加分体积定律?V?nRT/V BB此式只适用于理想气体。

小结与思考(1)

例3.已知方程组与
5x+y=3 ax+5y=4
x-2y=5 5x+by=1
有相同的
解，求a、b的值.
巩固提高：
1. 已知 x y x y 3 0 ，求x,y的值.
2
ax+y=2 2. 甲、乙两人都解方程组 2x-by=1
，
甲看错a得解解
x=1 y=2
x=1 y=1
,乙看错b得
3x 4 y 2.9 (2) 5x 2 y 0.5
例题讲解：
例1.写出一个二元一次方程，使得 x 1 x 2 都是它的解，并且
y 1 y 2
求出x=3时的方程的解.
例2.对于等式y=kx+b,当x=3时，y=5；当x=-4时，y=-9,求当x=-1时y的值.
初中数学七年级下册（苏科版）
小结与思考1
基础练习：
1.下列各组x,y的值是不是二元一次方
3x 4 y 2 程组 2 x y 5 的解？
x 3 x 2 x 2 （1）（2）（3） y 1 y 1 y 2
2 x y a 2.已知二元一次方程组 x 2 y b
x 3 的解 y 5
求a,b的值.
3.根据下表中所给的x值以及x与y的关系式，求出相应的y值，然后填入表内：
x Y=4x Y=10-x
y 4x 的解. ห้องสมุดไป่ตู้ y 10 x
1
2 3 4
5
6
7
8
9
10
根据上表找出二元一次方程组
4.解二元一次方程
x 2 y 5 (1) 3x y 1

小结与思考(2)

第一章小结与思考学习目标：通过对本章知识的小结与梳理，进一步掌握等腰三角形的性质和判定、直角三角形全等的判定、角平分线的性质定理与判定定理、特殊四边形（平行四边形、矩形、菱形、正方形）的定义、性质和判定；等腰梯形的性质和判定；中位线定理，并会灵活运用．学习难点：性质定理和判定定理的应用学习过程：一．知识点：1．根据“等腰三角形，等腰梯形的性质定理与判定定理，直角三角形全等的判定定理，角平分线的性质定理与判定定理，三角形中位线定理等。

”填表：直角三角形全等的判定方法有：。

二、例题学习1、我们学习了四边形和一些特殊的四边形，右图表示了在某种条件下它们之间的关系。

如果①，②两个条件分别是：①两组对边分别平行；②有且只有一组对边平行。

那么请你对标上的其他6个数字序号写出相对应的条件。

2、如图，已知四边形ABCD 中，R 、P 分别是BC 、CD 上的点，E 、F 分别是AP 、RP 的中点，当点P 在CD 上从C 向D 移动而点R 不动时，那么下列结论成立的是（） A 、线段EF 的长逐渐增大 B 、线段EF 的长逐渐减小C 、线段EF 的长不变D 、线段EF 的长与点P 的位置有关3、如图，在△ABC 中，D 是BC 边上的一点，E 是AD 的中点，过A 点作BC 的平行线交CE 的延长线于点F ，且AF =BD ，连结BF 。

（1）求证：BD =CD ；⑵如果AB =AC ，试判断四边形AFBD 的形状，并证明你的结论。

RP D CB AEFD图1A BCE【课后作业】1．平行四边形ABCD 中，如果∠A=55°，那么∠C 的度数是(A)45°(B)55° (C)125°(D)145°2．如图1，在△ABC 中，D 、E 分别是AB 、AC 的中点，BC=12，则DE 的长是(A)4(B)5(C)6(D)73、已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,E F ⊥ED. 求证:AE 平分∠BAD.4、如图11，已知A B C ∆中，D 是AB 中点，E 是AC 上的点，且A B E B A C ∠=∠，EF ∥AB ，DF ∥BE ，⑴猜想DF 与AE 有怎样的特殊关系？ ⑵证明你的猜想．5、如图，在□ABCD 中，∠DAB=60°，点E 、F 分别在CD 、AB 的延长线上，且AE=AD ，CF=CB ．（1）求证：四边形AFCE 是平行四边形；（2）若去掉已知条件的“∠DAB=60°，上述的结论还成立吗?若成立，请写出证明过程；若不成立，请说明理由．ON MF ECBA 6、在等腰△ABC 中，AB ＝AC ，点D 是直线BC 上一点，DE ∥AC 交直线AB 于E ，DF ∥AB 交直线AC 于点F ，解答下列各问：（1）如图1，当点D 在线段BC 上时，有DE ＋DF ＝AB ，请你说明理由；（2）如图2，当点D 在线段BC 的延长线上时，请你参考（1）画出正确的图形，并写出线段DE 、DF 、AB 之间的关系（不要求证明）．7、如图，△ABC 中，点O 是AC 边上的一个动点，过点O 作直线MN ∥BC ，设MN 交∠BCA 的平分线于点E ，交∠BCA 相邻的外角平分线CF 于是点F. （1）点O 运动到何处时，四边形AECF 是矩形？证明你的结论；（2）若AC 边上存在点O ，使四边形AECF 是正方形，试判别△ABC 的形状，并证明理由.8、操作：在△ABC 中，AC ＝BC ＝2，∠C＝90°，将一块等腰直角三角板的直角顶点放在斜边AB 的中点P 处，将三角板绕点P 旋转，三角板的两直角边分别交射线AC 、CB 于D 、E 两点.如图1，2，3是旋转三角板得到的图形中的3种情况.研究：（1）三角板绕点P 旋转，观察线段PD 和PE 之间有什么数量关系？并结合如图2加以证明.（2）三角板绕点P 旋转，△PBE 是否能成为等腰三角形？若能，指出所有情况（即写出△PBE 为等腰三角形时CE 的长；若不能，请说明理由. （3）若将三角板的直角顶点放在斜边AB 上的M 处，且AM∶MB＝1∶3，和前面一样操作，试问线段MD 和ME 之间有什么数量关系？并结合如图4加以证明.DABCF ED CBA 图1CD E PA B图3DECPAB图2 DCPEBAE图4。

第一章全等三角形(一)小结与思考(定稿)

课题：第一章小结与思考课型：复习主备：丁虎平备课组长：教研组长：班级姓名学号【学习目标】1.回顾、思考本章所学知识及所体现的数学思想方法，使所学知识系统化。

2.进一步丰富对全等三角形的认识，能有条理地、清晰地阐述自己的观点。

3.通过“小结与思考”的学习，学会归纳、反思的意识。

【重点难点】重点：回顾、思考本章所学知识及所体现的数学思想方法，使所学知识系统化。

难点：进一步丰富对全等三角形的认识，能有条理地、清晰地阐述自己的观点。

【尝试练习】1.已知：如图，AC=BD，∠1=∠2.求证：ΔADB≌ΔBCA.2.如图，点D，E分别在AB,AC上，BE，CD相交于点F.（1）如果AB=AC，∠B=∠C，试找出一对全等三角形，并证明；（2）如果BD=CE，∠B=∠C，试找出一对全等三角形，并证明.3.已知：如图，点A,B,C,D在一条直线上，AC=DB,AE=DF，BE=CF.求证：AE∥DF，BE∥CF.4.如图，∠A=∠D=90°，AB=DC,AC,BD相交于点E，证明：∠ABE=∠DCE.5.已知：如图，在ΔABC中，AB=AC，AD是高，DE⊥AB,DF⊥AC,垂足分别为E,F.求证：DE=DF.【典型例题】切记：“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等例 1. 如图，,,,A F E B四点共线，AC CE=。

求证：^，AE BF^，BD DF=，AC BDD@D。

ACF BDE例2.如图，在ABC???。

^，垂足为D。

求证：21C D中，BE是∠ABC的平分线，AD BE例 3. 如图，在ABC D 中，AB BC =，90ABC ? 。

F 为AB 延长线上一点，点E 在BC 上，BE BF ，连接,AE EF 和CF 。

求证：AE CF =。

【课堂巩固】一、选择题：1.如图，已知AE=CF ，∠AFD=∠CEB ，那么添加下列一个条件后，仍无法判定△ADF ≌△CBE 的是（）A ．∠A=∠CB ．AD=CBC ．BE=DFD ．AD ∥BC 2．如图所示，DE ⊥AB ，DF ⊥AC ，AE ＝AF ，则下列结论成立的是（） A. BD ＝CD B. DE ＝DF C. ∠B ＝∠C D. AB ＝AC 3.如图所示，AB ∥EF ∥CD ，∠ABC ＝90°，AB ＝DC ，那么图中的全等三角形有（） A. 1对 B. 2对 C. 3对 D. 4对4.如图所示，点E 在△ABC 外部，点D 在BC 边上，DE 交AC 于F ，若∠1＝∠2，∠E ＝∠C ，AE ＝AC ，则（） A. △ABC ≌△AFE B. △AFE ≌△ADCC. △AFE ≌△DFC D. △ABC ≌△ADE 5．如图所示，已知AB ∥CD ，AD ∥BC ，那么图中共有全等三角形（） A. 1对 B. 2对 C. 4对 D. 8对二、填空题：1．如图，在△ABC 和△DEF 中，点B 、F 、C 、E 在同一直线上，BF = CE ，AC ∥DF ，请添加一个条件，使△ABC ≌△DEF ，这个添加的条件可以是．（只需写一个，不添加辅助线） 2．如图，AB=AC ，要使△ABE ≌△ACD ，应添加的条件是（添加一个条件即可）． 3.如图，点B 、E 、C 、F 在一条直线上，AB ∥DE ，BE=CF ，请添加一个条件，使△ABC ≌△DEF ． 4.如图，△ABC ≌△DEF ，请根据图中提供的信息，写出x= ．A B C D EF第9题A B C DEF 第7题A B C DO 第3题图1 图2 图3 图4 图 55．△ABC ≌△DEF ，且△ABC 的周长为12，若AB =3，EF =4，AC = ．6. 将一张正方形纸片按如图的方式折叠，,BC BD 为折痕，则CBD ∠的大小为_________；7. 如图，在等腰Rt ABC D 中，90C ? ，AC BC =，AD 平分BAC Ð交BC 于D ，DE AB^于E ，若10AB =，则BDE D的周长等于____________； 8 如图，点,,,D E F B 在同一条直线上，AB //CD ，AE //CF ，且AE CF =，若10BD =，2BF =，则EF =___________；三、解答题：11. 如图，ABC ∆为等边三角形，点,M N 分别在,BC AC 上，且BM CN =，AM 与BN 交于Q 点。

苏科版八年级数学上册第一章第11课时小结与思考预习案

第11课时小结与思考预习目标1．通过对全等三角形的概念、性质和判定条件的回顾，构建知识结构框架图，形成一定的知识系统．2．熟练掌握全等三角形的性质以及判定三角形全等的条件，灵活运用它们解决与线段、角有关的问题．3．通过对一些作图过程的回顾，能较熟练地进行文字语言、符号语言和图形语言之间的表达和相互转化．4．逐步学会“分析”，并在此基础上有条理、清晰地表述自己的推理过程．知识梳理你能掌握这些知识要点吗？例题精讲例1 如图，在△ABC中，AB＝8，AC＝4，过BC的中点M作DM⊥BC，交∠BAC的平分线于点D，DE⊥AB于点E，DF⊥AC，交AC的延长线于点F．求AE的长．提示：根据条件可得△ADE≌△ADF，则有AE＝AF，而AE＝AB－BE，AF＝AC＋CF，因此只要能说明BE＝CF，就可以求出AE的长．点评：本题一共证明了三对全等的直角三角形，分别运用了“AAS”、“SAS”、“HL”三种不同的判别方法．解此类题的关键是灵活运用三角形全等的判定方法．例2在△ABC中，AC＝BC，∠ACB＝90°，点D是AB的中点，点E是AB边上一点．(1)直线BF垂直于直线CE于点F，交CD于点G（如图①）．求证：AE＝CG．(2)直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M(如图②)，找出图中与BE相等的线段，并给予证明．提示：(1)首先根据点D是AB的中点，∠ACB＝90°，可得出∠ACD＝∠BCD＝45°，证明△AEC≌△CGB，即可得出AE＝CG．(2)根据垂直的定义得出∠CMA＋∠MCH＝90°，∠BEC＋∠MCH＝90°，再根据AC＝BC，∠ACM＝∠CBE＝45°，得出△CAM ≌△BCE，进而证明出CM＝BE．点评：本题着重考查全等三角形的判定方法以及全等三角形的性质的应用．热身练习1．下列说法中，正确的是( )A．全等三角形的面积相等B．面积相等的三角形都是全等的三角形C．等边三角形的面积都相等D．面积相等的直角三角形都是全等的直角三角形2．下列条件中，不能判定两个三角形全等的是( )A．有两边和它们的夹角对应相等 B．有两边和其中一边的对角对应相等C．有两角和它们的夹边对应相等 D．有两角和其中一角的对边对应相等3．如图，AD平分∠BAC，AB＝AC，BD交AC于点F，CD交AB于点E，则图中全等三角形有( )A．2对B．3对C．4对D．5对4．如图所示的4×4正方形网格中，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7等于( ) A．330°B．315°C．310°D．320°5．如图，∠E＝∠F＝90°，∠B＝∠C，AE＝AF．给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN．其中正确的是_______（填序号）．6．如图，△ABC≌△DEF，BE＝4，AE＝1，则DE的长是_______．7．如图，把一张长方形纸片ABCD沿BD折叠，使点C落在点E处，BE与AD相交于点O，写出一组相等的线段_______(不包括AB＝CD和AD＝BC)．8．如图，D、E是BC上的两点，且AB＝AC，∠B＝∠C．要使△ABE≌△ACD，根据“SAS”的判定方法，还需要给出的条件是_______或_______．9．如图，小明把一块三角板放在纸上，用笔画出它的轮廓△ABC，然后把三角板绕着点C 旋转一个角度，又画出一个△EFC，他用量角器检查，发现∠ACE＝∠BCF，但不知道是什么原因．你能说明其中的理由吗？10．同学们都知道：有两边和一角对应相等的两个三角形不一定全等，你如何处理和安排这三个条件，使两个三角形全等？请你仿照方案(1)写出方案(2)、(3)、(4)……（至少写三种）．方案(1)：设有两边和一角对应相等的两个三角形，若这个角的对边恰好是这两条边中的较长的一条边，则这两个三角形全等．11．如图，点C是AB上的一点，△ACM、△CBN都是等边三角形．(1)求证：AN＝MB．(2)将△ACM绕点C按逆时针方向旋转180°，使点A落在CB上，请画出符合要求的图形．(3)在(2)所得到的图形中，结论“AN＝MB”是否成立？请说明理由．（注：等边三角形的三条边相等，三个角均为60°）参考答案1．A 2．B 3．C 4．B 5．①②③ 6．5 7．答案不唯一，如BO ＝DO 8．BD ＝CE BE ＝CD 9．略 10．略 11．(1)略 (2)略 (3)成立1、Be honest rather clever 20.7.177.17.202021:3921:39:28Jul-2021:392、By reading we enrich the mind; by conversation we polish it.二〇二〇年七月十七日2020年7月17日星期五3、All things are difficult before they areeasy.21:397.17.202021:397.17.202021:3921:39:287.17.202021:397.17.20204、By other's faults, wise men correct theirown.7.17.20207.17.202021:3921:3921:39:2821:39:285、Our destiny offers not the cup of despair, but the chalice of opportunity. So let us seize it, not in fear, but in gladness. Friday, July 17, 2020July 20Friday, July 17, 20207/17/20206、I have no trouble being taken seriously as a woman and a diplomat [in Ghana].。

第1章小结与思考苏科版八年级数学上册

∠DEB=∠ACB=90°.
∴∠BEF=180°-∠DEB=90°.
在Rt△BEF和Rt△BCF中,
旋转变换作为全等变换，在图形变换前后，对应线段、对应角保持相等关系.类似的还有平移变换、
翻折变换.
二、典型例题
例3：如图，在△ABC中, AD为BC边的中线. 求证：AB+AC >2AD.
[分析]要确定线段间的不等关系，通常在三角形中利用“两边之和大于
A
举反例是说明命题是假命题的重要方法.
①②④组合不能判定两个
[分析]画出草图,对照判定定理三角形全等，可以通过如
B
C 可知：
下图形举反例说明.
D
①②③组合满足“边角边”条件;
A(D)
①③④组合满足“角角边”条件；
E
F ②③④组合满足“角边角”条件. B
E
C(F)
变式训练
已知下列4个条件：①AB=m, ②AC=n,③∠A=α，④∠C=β，从中选择三个作为条件，能运用尺规作图作出唯一的△ABC 的组合有：_①__②_③__、__①__③_④__、__②_③__④__.
变式训练
如图，已知△ABC中，∠ACB=90°，将△ABC绕点B逆时针旋转得△DBE，在旋转过程中，直线DE与AC边交于点F. 当点E落在△ABC内部时，猜测线
段AF、EF、DE间的数量关系，并证明你的结论.
B C FE
[分析]在△ABC旋转的过程中DE=AC=AF+CF，只要将EF转化为CF即
边之间的关系，列出不等式：AC－CE<AE<AC+CE，从而得到：
BD
2cm<2AD<14cm，即AD的取值范围为1cm<AD<7cm. C

北师大版九年级数学下册：第一章《直角三角形的边角关系——回顾与思考》教案

北师大版九年级数学下册：第一章《直角三角形的边角关系——回顾与思考》教案一. 教材分析北师大版九年级数学下册第一章《直角三角形的边角关系——回顾与思考》主要介绍了直角三角形的性质，包括锐角三角函数的概念、直角三角形的边角关系等。

本章内容是初中数学的重要知识点，为后续学习三角形相似、解直角三角形等知识打下基础。

二. 学情分析九年级的学生已经掌握了三角形的基本概念和性质，具备了一定的逻辑思维能力和空间想象能力。

但学生在学习过程中，可能对锐角三角函数的理解和应用存在困难，因此需要通过本章内容的学习，帮助学生巩固直角三角形的性质，提高解题能力。

三. 教学目标1.理解直角三角形的性质，掌握锐角三角函数的概念。

2.学会运用直角三角形的性质解决实际问题。

3.培养学生的空间想象能力和逻辑思维能力。

四. 教学重难点1.重点：直角三角形的性质，锐角三角函数的概念。

2.难点：锐角三角函数的应用，解直角三角形。

五. 教学方法采用问题驱动法、案例分析法、合作学习法等，引导学生主动探究、积极思考，提高学生的学习兴趣和参与度。

六. 教学准备1.教学课件：制作直角三角形性质、锐角三角函数的课件。

2.教学素材：提供相关案例，如实际问题、例题等。

3.学习工具：准备好直角三角形、锐角三角函数的相关资料。

七. 教学过程1.导入（5分钟）利用生活中的实例，如测量身高、测距等，引出直角三角形的性质和锐角三角函数的概念。

激发学生的学习兴趣，引导学生思考直角三角形在实际生活中的应用。

2.呈现（15分钟）呈现直角三角形的性质和锐角三角函数的定义，通过动画、图片等形式展示，帮助学生直观地理解。

同时，给出相关案例，让学生体会直角三角形性质和锐角三角函数在实际问题中的作用。

3.操练（15分钟）针对直角三角形的性质和锐角三角函数，设计一系列练习题。

让学生独立完成，巩固所学知识。

教师及时批改、讲解，解答学生的疑问。

4.巩固（10分钟）通过小组合作学习，让学生运用直角三角形的性质和锐角三角函数解决实际问题。

第一章小结与思考(1)

如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连结BF. (1)求证：BD=CD； (2)如果AB=AC，试判断四边形AFBD的形状，并证明你的结论.
如图，在梯形ABCD中,AD∥BC,AB∥DE, AF∥CD,E、F两点在边BC上，且四边形AEFD 是平行四边形．（1）AD与BC有何等量关系？请说明理由；（2）当AB=DC时，求证：□AEFD是矩形
2、等腰三角形的两边长分别为4和9，则第三边长为
3、下列命题为真命题的是（） A：三角形的中位线把三角形的面积分成相等的两部分; B：对角线相等且相互平分的四边形是正方形; C：关于某直线对称的两个三角形是全等三角形; D：一组对边平行，另一组对边相等的四边形一定是等腰梯形
4、下列命题是假命题的是( ) A、四个角相等的四边形是矩形; B、对角线互相平分的四边形是平行四边形; C、四条边相等的四边形是菱形; D、对角线互相垂直且相等的四边形是正方形 5、在□ ABCD中，∠ABC的平分线交AD于E，且AE＝2， DE＝1，则□ ABCD的周长等于．
2、已知：如图，矩形ABCD的对角线AC与BD 相交于点O，点O关于直线AD的对称点是E，连结 AE、DE． (1)试判断四边形AODE的形状,说明理由； (2)请你连结EB、EC，并证明EB=EC．
3、已知：平行四边形ABCD中，对角线AC和BD 相交于点O，M，N分别是OA，OC的中点，求证：BM=DN ，BM∥DN.
回忆
• • • • 4. 等边三角形的判定: ______个角都相等的三角形是等边三角形; 有_____个角是600的三角形是等边三角形; 有一个角是600的_____三角线段垂直平分线上的点 • 到线段_______的距离相等;

苏科版八年级上册数学第一章小结与思考导学案

N MA BC第一章轴对称图形—小结与思考【学习目标】1、能够认识轴对称和轴对称图形，并能找出对称轴；2、会画已知点、线段、三角形关于已知直线l 的对称图形；3、知道线段、角、等腰三角形、等腰梯形的轴对称性及其相关性质。

【自主学习】1、下列图形是常见的安全标记，其中是轴对称图形．．．．．的是（ )2．如图所示，画出△ABC 关于直线MN 的轴对称图形.3.垂直并且平分一条线段的，叫做这条线段的垂直平分线。

．．．．．4.线段是图形，有条对称轴，分别为；线段的垂直平分线上的点到线段两端的距离；到线段两端距离相等的点，在这条线段的。

5.角是图形，它的对称轴是；角平分线上的点到角的两边距离；角的内部到角的两边距离相等的点，在这个角的上。

6.等腰三角形是图形，它的对称轴是；等边三角形是图形，有条对称轴。

7.等腰三角形的、、互相重合。

8．等腰梯形是图形，它的对称轴是【检测反馈】1．如图，求作点P，使点P同时满足：①PA=PB；②到直线m，n的距离相等．(尺规作图，保留作图痕迹) 的是( )2．下列说法中正确．．A．两个全等三角形成轴对称B．两个三角形关于某直线对称，不一定全等C．线段AB的对称轴垂直平分ABD．直线MN垂直平分线段AB，则直线MN是线段AB的对称轴3、如果两个图形关于某直线对称，那么连结的线段被垂直平分.4、成轴对称的两个图形的对应线段___ ___、对应角__ __.5、如图，在△ABC中，AB的垂直平分线DE交BC于点E，交AB于点D，△ACE的周长为11cm，AB＝4cm，则△ABC的周长为__________cm.【课后学习】6. 如图，在△ABC中，CD与CF，分别是△ABC的内角、外角平分线，DF//BC交AC于点E．试说明(1) △DCF为直角三角形；(2)DE=EF．7. 已知直线l及其两侧两点A、B，如图.（1）在直线l上求一点P，使PA=PB；（2）在直线l上求一点Q，使l平分∠AQB.(以上两小题保留作图痕迹，标出必要的字母，不要求写作法)专项训练二概率初步一、选择题1．(徐州中考)下列事件中的不可能事件是( )A．通常加热到100℃时，水沸腾B．抛掷2枚正方体骰子，都是6点朝上C．经过有交通信号灯的路口，遇到红灯D．任意画一个三角形，其内角和是360°2．小张抛一枚质地均匀的硬币，出现正面朝上的可能性是( )A．25% B．50% C．75% D．85%3．(2016·贵阳中考)2016年5月，为保证“中国大数据产业峰会及中国电子商务创新发展峰会”在贵阳顺利召开，组委会决定从“神州专车”中抽调200辆车作为服务用车，其中帕萨特60辆、狮跑40辆、君越80辆、迈腾20辆，现随机从这200辆车中抽取1辆作为开幕式用车，则抽中帕萨特的概率是( )A.110B.15C.310D.254．(金华中考)小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为( )A.14B.13C.12D.345．在一个不透明的袋中装着3个红球和1个黄球，它们只有颜色上的区别，随机从袋中摸出2个小球，两球恰好是一个黄球和一个红球的概率为( )A.12B.13C.14D.166．现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是( )A.13B.16C.19D.1127．分别转动图中两个转盘一次，当转盘停止转动时，两个指针分别落在某个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于( )A.316B.38C.58D.1316第7题图第8题图 8．(2016·呼和浩特中考)如图，△ABC 是一块绿化带，将阴影部分修建为花圃，已知AB ＝15，AC ＝9，BC ＝12，阴影部分是△ABC 的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为( )A.16B.π6C.π8D.π5二、填空题9．已知四个点的坐标分别是(－1，1)，(2，2)，⎝ ⎛⎭⎪⎫23，32，⎝⎛⎭⎪⎫－5，－15，从中随机选取一个点，在反比例函数y＝1x图象上的概率是________．10．(黄石中考)如图所示，一只蚂蚁从A点出发到D，E，F处寻觅食物．假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A，B，C都是岔路口)．那么，蚂蚁从A出发到达E处的概率是________．11．(贵阳中考)现有50张大小、质地及背面图案均相同的《西游记》任务卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回，洗匀后再抽．通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________．12．(荆门中考)荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况，随机选取了3名女生和2名男生，则从这5名学生中，选取2名同时跳绳，恰好选中一男一女的概率是________．13．(重庆中考)点P的坐标是(a，b)，从－2，－1，0，1，2这五个数中任取一个数作为a的值，再从余下的四个数中任取一个数作为b的值，则点P(a，b)在平面直角坐标系中第二象限内的概率是________．14．★从－1，1，2这三个数字中，随机抽取一个数记为a，那么，使关于x的一次函数y＝2x＋a的图象与x轴、y轴围成的三角形的面积为14，且使关于x的不等式组⎩⎪⎨⎪⎧x＋2≤a，1－x≤2a有解的概率为________．三、解答题15．(南昌中考)在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个．(1)先从袋子中取出m(m＞1)个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A，请完成下列表格：(2)先从袋子中取出m个红球，再放入m个一样的黑球并摇匀，随机摸出1个黑球的概率等于45，求m的值．16．(菏泽中考)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项)．(1)如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是________；(2)如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是________；(3)如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．17．(丹东中考)甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5.将三张牌背面朝上，洗匀后放在桌子上．(1)甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；(2)若两人抽取的数字之和为2的倍数，则甲获胜；若抽取的数字之和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．18．一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，3，5，x，甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个球上数字之和，记录后将小球放回袋中搅匀，进行重复实验．实验数据如下表：(1)如果实验继续进行下去，根据上表数据，出现“和为8”的频率稳定在它的概率附近，估计出现“和为8”的概率是________；(2)如果摸出的这两个小球上数字之和为9的概率是13，那么x的值可以取4吗？请用列表法或画树状图法说明理由；如果x的值不可以取4，请写出一个符合要求的x的值．参考答案与解析1．D 2.B 3.C 4.A 5.A 6.C 7.C8．B 解析：∵AB ＝15，BC ＝12，AC ＝9，∴AB 2＝BC 2＋AC 2，∴△ABC 为直角三角形，∴△ABC 的内切圆半径为12＋9－152＝3，∴S △ABC ＝12AC ·BC ＝12×12×9＝54，S 圆＝9π，∴小鸟落在花圃上的概率为9π54＝π6. 9.12 10.12 11.15 12.35 13.15 14.13 15．解：(1)4 2或3(2)根据题意得6＋m 10＝45，解得m ＝2，所以m 的值为2.16．解：(1)14 解析：第一道肯定能对，第二道对的概率为14，所以锐锐通关的概率为14；(2)16 解析：锐锐两次“求助”都在第二道题中使用，则第一道题对的概率为13，第二道题对的概率为12，所以锐锐能通关的概率为12×13＝16；(3)锐锐将每道题各用一次“求助”，分别用A ，B 表示剩下的第一道单选题的2个选项，a ，b ，c 表示剩下的第二道单选题的3个选项，树状图如图所示．共有6种等可能的结果，锐锐顺利通关的只有1种情况，∴锐锐顺利通关的概率为16.17．解：(1)所有可能出现的结果如下表，从表格可以看出，总共有9种结果，每种结果出现的可能性相同，其中两人抽取相同数字的结果有3种，所以两人抽取相同数字的概率为13；(2)不公平．从表格可以看出，两人抽取数字之和为2的倍数有5种，两人抽取数字之和为5的倍数有3种，所以甲获胜的概率为59，乙获胜的概率为13.∵59＞13，∴甲获胜的概率大，游戏不公平．18．解：(1)0.33(2)当x 为4时，数字和为9的概率为212＝16≠13，所以x 不能取4；当x ＝6时，摸出的两个小球上数字之和为9的概率是13.。

浙教版科学九年级上册第一章知识点总结

、第一章笔记内容大全§1-1物质的变化一、物质是在不断变化着的物理变化：变化中没有新物质产生，只有形态、状态的改变。

化学变化：变化中会产生新的物质。

【思考】物理变化和化学变化在本质上有什么不同？化学变化的实质是：构成物质的分子的原子重新组合，形成了新的分子。

而物理变化的实质：分子间的距离发生改变。

物理性质：不需要发生化学变化就能表现出来的性质化学性质：只在化学变化中表现出来的性质物质的性质物理性质: 颜色、气味、软硬、物质的溶解性、液体的沸点、熔点金属的延展性、光泽化学性质：可燃性、氧化性、还原性、酸碱性。

二、探究物质变化的方法通过观察和实验等来寻找物质变化的证据。

物质变化的证据：生成沉淀、颜色改变、气体产生、温度变化、性质变化、发光发热、PH变化、状态变化等。

演示实验：硫酸铜晶体的变化1、取1块硫酸铜晶体，观察形状、颜色。

___蓝色固体2、向盛有硫酸铜晶体的试管中加水，观察晶体能否溶解，水溶液颜色有什么变化。

能溶解，形成蓝色溶液。

3、在硫酸铜溶液中滴加氢氧化钠溶液，观察溶液有什么变化。

（写出化学方程式）形成蓝色絮状沉淀2NaOH＋CuSO4＝ Na2SO4+Cu(OH)2↓4、另取1块硫酸铜晶体，将它放在大试管中加热，观察硫酸铜晶体有什么变化。

（写出化学方程式）蓝色固体逐渐变白CuSO4·5H2O = CuSO4+ 5H2O5、实验完成后，熄灭酒精灯，冷却大试管，再在冷却后的硫酸铜白色粉末中逐滴加水，观察有什么现象产生（写出化学方程式）白色固体逐渐变蓝CuSO4 + 5H2O = CuSO4·5H2O根据现象，进行分析：有颜色变化的实验是2、3、 4 、5，原因是发生物理变化和化学变化有沉淀产生的实验是3,原因是发生化学变化；有状态变化的实验是2、3、4、5,原因是发生物理变化或化学变化;并总结出硫酸铜晶体的性质（包括物理性质和化学性质）蓝色晶体、易溶于水、受热易分解、能与氢氧化钠反应生成蓝色絮状沉淀小结：根据物质变化中所获得的信息对物质的性质进行分析推测的方法,是认识物质、探索物质变化规律的基本方法。

第一章+一元二次方程(小结思考)(课件)-2023-2024学年九年级数学上册同步精品课件(苏科版)

向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向终点
C以2cm/s的速度移动．如果P，Q两点分别从A，B两点同时出发，当点
Q运动到点C时，两点都停止运动．设运动时间为t s.
(1)填空：BQ＝____cm，PB＝________cm(用含t的代数式表示)．
(5－t)
2t
解：(1)∵点P从点A开始沿边AB向终点B以1 cm/s的速度移动，
9月份营业额的月增长率．
解：(1)450＋450×12％＝504（万元），
答：该商店“十一黄金周”这七天的总营业额为504万元．
(2)设该商店8、9月份营业额的月增长率为x，
由题意，得350(1＋x)2＝504，
解得x1＝0.2=20％，x2=－2.2（舍去），
答：该商店8、9月份营业额的月增长率为20％．
+ ( + ) + ( + ) =∴ ( − )( + ) = ，
∴ = . = %或 = −. (不合题意，舍去)，
答：进馆人次的月平均增长率为%．
增长率类
例2 ()因条件限制，学校图书馆每月接纳能力不超过人次，在进馆
一个无盖的盒子，已知盒子的容积为300cm3，则原铁皮的边长为( D )
A.10 cm
B.13 cm
C.14 cm
D.16 cm
解：设正方形铁皮的边长是xcm ，
则没有盖的长方体盒子的长、宽为(x-3×2) cm，高为3cm，
根据题意列方程得 (x-3×2)(x-3×2)×3=300，
解得 x1=16，x2=-4(不合题意，舍去)；
A
D
B
C
图1
解：()根据题意得， =

初二数学上学期备课组工作计

樊新玲
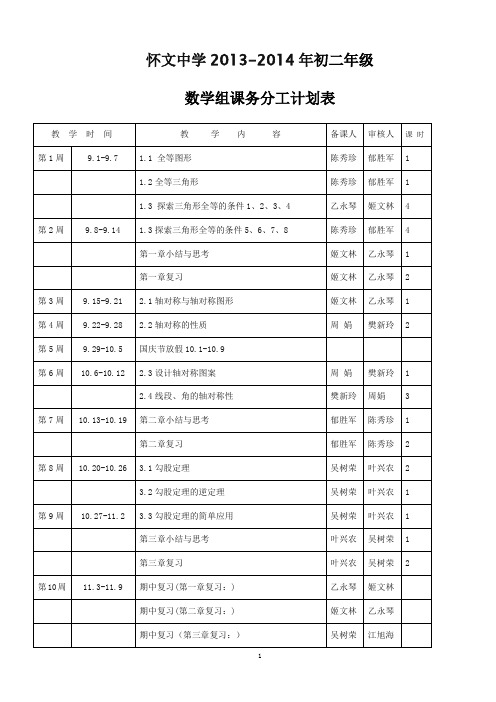
周娟
1
第五章复习1
江旭海
魏敏
1
第16周
12.156.1函数
陈秀珍
郁胜军
2
6.2一次函数
乙永琴
姬文林
2
6.3一次函数的图象
姬文林
乙永琴
2
第17周
12.22-12.28
6.4用一次函数解决问题
樊新玲
周娟
2
第18周
12.29-1.4
元旦放假3天
6.5一次函数与二元一次方程
毛云峰
王大勇
1
第19周
1.5-1.11
6.6一次函数、一元一次方程、一元一次不等式
王大勇
毛云峰
1
第六章小结与思考
周娟
樊新玲
1
第六章复习1、2
魏敏
毛云峰
2
期末复习(第一、二章复习:)
魏敏
毛云峰
期末复习(第三复习：)
王大勇
叶兴农
期末复习(第四章复习：)
姬文林
乙永琴
期末复习(第五章复习：)
江旭海
吴树荣
期末复习(第六章复习：)
第7周
10.13-10.19
第二章小结与思考
郁胜军
陈秀珍
1
第二章复习
郁胜军
陈秀珍
2
第8周
10.20-10.26
3.1勾股定理
吴树荣
叶兴农
2
3.2勾股定理的逆定理
吴树荣
叶兴农
1
第9周
10.27-11.2
3.3勾股定理的简单应用
吴树荣
叶兴农
1
第三章小结与思考
叶兴农
吴树荣

高等数学第一章的总结

则称函数 f ( x )在X上有界 .否则称无界 .
y M y=f(x) o -M x 有界 X M y
x0
o -M X 无界
x
数列的有界性：
定义: 使得一切正定义对数列 x n , 若存在正数 M , 使得一切正成立, 有界, 整数 n , 恒有 x n ≤ M 成立则称数列 x n 有界否则, 称为无界. 否则称为无界
lim f ( x ) =
P ( x0 ) = lim Q ( x ) Q ( x 0 ) = f ( x 0 ). x→ x
x → x0
0
lim P ( x )
x → x0
若Q ( x 0 ) = 0, 则商的法则不能应用 .
例
4x − 1 . 求 lim 2 x →1 x + 2 x − 3
x →1
-x o 偶函数 x
f ( x)
x
设D关于原点对称 , 对于∀x ∈ D, 有
f (− x ) = − f ( x )
称 f ( x )为奇函数 ;
y
y = f ( x)
f ( x)
-x o
f (− x )
x
x
奇函数
函数的周期性: 函数的周期性
设函数 f ( x )的定义域为 D, 如果存在一个不为零的数l , 使得对于任一 x ∈ D, ( x ± l ) ∈ D.且 f ( x + l ) = f ( x )
3 2+ + 3 2 2x + 3x + 5 x lim 3 = lim x →∞ 7 x + 4 x 2 − 1 x→∞ 4 7+ − x
(无穷小因子分出法无穷小因子分出法) 无穷小因子分出法

我就是创造与毁灭女神_随笔

《我就是创造与毁灭女神》读书随笔目录1. 内容概要 (2)1.1 书籍概述 (2)1.2 我的阅读动机 (3)1.3 导读笔记 (4)2. 第一章世界初开 (5)2.1 创造力的本源 (6)2.2 混沌之中的秩序 (7)2.3 第一章小结与思考 (8)3. 第二章女神创世实验 (9)3.1 天地的形成 (10)3.2 生命的诞生 (11)3.3 第二章阅读体会与感悟 (12)4. 第三章文明的曙光 (13)4.1 古代神话的解析 (15)4.2 科技进步与文明的碰撞 (16)4.3 第三章印象与反思 (17)5. 第四章毁灭与重生的周期 (19)5.1 灾害与战争 (19)5.2 人文精神的复苏 (20)5.3 第四章思考启示 (22)6. 第五章个人层面的创造与毁灭 (22)6.1 个性中的双刃剑 (23)6.2 自我更新的必要性 (24)6.3 第五章阅读心得 (25)7. 第六章未来世界的展望 (26)7.1 科技革新的影响 (27)7.2 应对未来的转换与适应 (28)7.3 第六章寄语与畅想 (30)1. 内容概要《我就是创造与毁灭女神》读书随笔的正文将首先概述书籍的主旨和内容，按照小说的时间线逐步展开。

这一部分将包括对书中的主要角色进行的初步介绍，并对他们所面临的挑战和冲突进行简短的描述。

文章将继续深入探讨小说中提到的创世和毁灭的概念，结合哲学和神话学的视角来分析作者的主题表达。

读书随笔还将讨论小说中的象征性和隐喻，以及它们如何为读者提供关于生命、存在和宇宙意义的深刻见解。

这部分将对书籍的文学技巧，如叙述风格、象征运用、比喻选择等进行评论，以此来揭示作者如何通过文字将创造与毁灭的主题展现得生动而有力。

读书随笔的这一章节不仅仅是内容的简要总结，更重要的是，它为读者提供了进入文本的一扇窗，帮助他们更加深入地探索故事背后的深层含义和作者的创作意图。

通过这一章节，读者可以更好地理解小说如何成为一个跨越文化和时代的哲学对话，以及在今天的世界中，创造与毁灭这一对双生概念如何继续影响着人类的发展和社会的进步。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章小结与思考
1如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动，行走2008厘米后停下，则这只蚂蚁停在点． 2．如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，AD ＝4， BC ＝8，则AE ＋EF 等于．
3如图，菱形ABCD 的两条对角线分别长6和8，点P 是对角线AC 上的一个动点，点M 、N 分别是边AB 、BC 的中点，则PM +PN 的最小值是_____________
4．如图，△ABC 中，AB +AC =6, BC 的垂直平分线l 与AC 相交于点D ，则△ABD 的周长为 A 、4 B 、8 C 、6 D 、10 （） 5.如图，在正方形ABCD 中，点E 、F 分别在CD 、BC 上，且BF=CE ，连结BE 、AF 相交于点G ，则下列结论：①BE=AF ；②∠DAF=∠BEC ；③∠AFB+∠BEC=900；④AF ⊥BE 中正确的有 A 、①②③ B 、②③④ C 、①②③④ D 、①②④ 6．如图，在平行四边形ABCD 中，AB =6，AD =9，∠BAD 的平分线交BC 于点E ，交DC
的延长线于点F ，BG ⊥AE ，垂足为G ，BG
=EF ＋CF 的长为（） A 、5 B 、4 C 、6 D
、
7、如图，在等腰R t △ABC 中，∠ACB =90°，D 为BC 的中点，
DE ⊥AB ，垂足为E ，过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF ．(1)求证：AD ⊥CF ；
(2)连接AF ，试判断△ACF 的形状，并说明理由．
C
A
D
B
G A B C
D
E F O
D A B C
P
M N （第
3题图）
8已知：如图，ΔABC 中，AD 平分∠BAC,BD ⊥AD 于D, 点E 的BC 边
的中点，AB=8,AC=12, 求DE 的长
9、如图，在直角梯形纸片ABCD 中，AB DC ∥，90A ∠=
，CD AD >，将纸片沿过点
D 的直线折叠，使点A 落在边CD 上的点
E 处，折痕为D
F ．连接EF 并展开纸片．（1）求证：四边形ADEF 是正方形；
（2）取线段AF 的中点G ，连接EG ，如果BG CD =，试说明四边形GBCE 是等腰梯形．
10、如图，在□ABCD 中，E 、F 分别为边ABCD 的中点，BD 是对角线，过A 点作AGDB
交CB 的延长线于点G ．（1）求证：DE ∥BF ；
（2）若∠G ＝90，求证四边形DEBF 是菱形．
E
C
B
D
A
G F
（第2题图）
E
D
B
C
A
11如图，在Rt △ABC 中，∠ACB =90°, ∠B =60°，BC =2．点0是AC 的中点，过点0的直线l 从与AC 重合的位置开始，绕点0作逆时针旋转，交AB 边于点D .过点C 作CE ∥AB 交直线l 于点E ，设直线l 的旋转角为α.
(1)①当α=________度时，四边形EDBC 是等腰梯形，此时AD 的长为_________； ②当α=________度时，四边形EDBC 是直角梯形，此时AD 的长为_________； (2)当α=90°时,判断四边形EDBC 是否为菱形，并说明理由．
12如图，四边形ABCD 是正方形，△ABE 是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60°得到BN ，连接EN 、AM 、CM. ⑴ 求证：△AMB ≌△ENB ；
⑵ ①当M 点在何处时，AM ＋CM 的值最小；
②当M 点在何处时，AM ＋BM ＋CM 的值最小，并说明理由；
⑶ 当AM ＋BM ＋CM 的最小值为13 时，求正方形的边长.
A D
B C
13、如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以
CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α，
得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否
仍然成立,并选取图2证明你的判断．
（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka，CG=kb(a≠b，k>0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．
（3）在第(2)题图5中，连结DG、BE，且a=3，b=2，k=1
2
，求22
BE DG
+的值．
14如图，在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10．点E•在下底边BC上，点F 在腰AB上．
（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF 的面积；
（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此BE 的长；若不存在，请说明理由；
（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1︰2的两部分？•若存在，求此时BE的长；若不存在，请说明理由．。