第5章 三元相图
合集下载
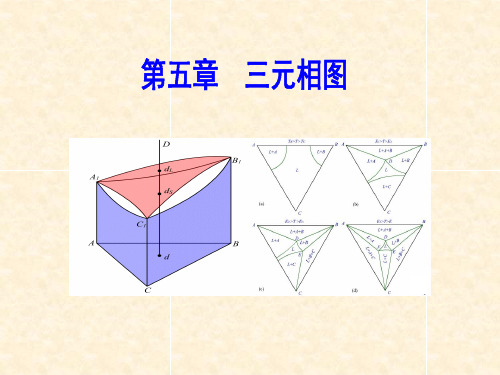
第五章 三元相图
B
B%
C%
A
← A% C% →
C
b c
a
图 部分浓度三角形
§5.1.2 浓度三角形中具有特定意义的线
1)与某一边平行的直线
C
含对角组元浓度相等
A% d C% c
Bc C% 100% BC
A
B B% 图 平行于浓度三角形某一条边的直线
确定O点的成分 1)过O作A角对边的平行线 2)求平行线与A坐标的截距 得组元A的含量 3)同理求组元B、C的含量
三元系中如果任意两个组 元都可以无限互溶,那么它们 所组成的三元合金也可以形 成无限固溶体,这样的三元合 金相图,叫三元匀晶相图。
相图概况
[1] 特征点: ta, tb, tc- 三个纯组 元的熔点; [2]特征面:液相面、固相面; [3]相区:L, α, L+α。
图 三元匀晶相图
§5.3.1 相图分析
( A B )
Ax nE nA Ee
( A B C )
Ax ne nA Ee
§5.4.2 组元在固态下有限溶解,具有共晶转变的三 元相图
1.相图分析
从占有空间的角度看,固态有限互溶三元共晶相图比固态 完全不互溶三元共晶相图要多三个单相区(α、 β、 γ)和三个 固态两相区(α+β、 β+ γ、 α+ γ)。
图 过成分三角形顶点的变温截面图
图 平行于成分三角形一边的变温截面图
用垂直截面图可以分析合金的平衡结晶过程,了解合金在 平衡冷却过程中发生相变的临界温度,以及可以了解合金在 一定温度下所处的平衡状态。 但是,用垂直截面图不能了解合金在一定温度下的平衡相 成分和平衡相的重量。
图 变温截面图的应用
三元合金相图
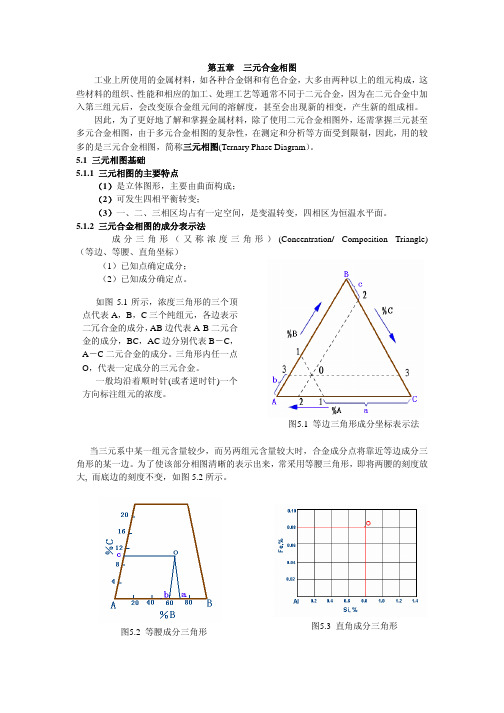
图5.3 直角成分三角形
如图 5.3 所示,当三元系成分以某一组元为主,其他两个组元含量很少时,合金成分点 将靠近等边三角形某一顶点。若采用直角坐标表示成分,则可使该部分相图更为清楚的表示 出来,一般用坐标原点代表高含量组元,而两个互相垂直的坐标轴代表其他两个组元的成分。 5.1.3 成分三角形中特殊的点和线
接。
三相平衡区的特点:直边三角形;两相区与之线接;单相区与之点接。
图 5.24 组元在固态有限互溶的三元相图的等温截面示意图 (3)变温截面
图 5.25 是组元在固态有限互溶的三元相图的变等温截面示意图。
图 5.8 三元相图中的重心定律
如图 5.8 所示,R 合金的重量与三个相的重量有如下关系
WR ⋅ Rd = Wα ⋅αd
Wα
= S∆Rβγ S ∆αβγ
= Rd αd
WR ⋅ Re = Wβ ⋅ βe
Wβ
= S∆Rαγ S ∆αβγ
= Re βe
WR ⋅ Rf = Wγ ⋅ γd
Wγ
= S∆Rαβ S ∆αβγ
以图 5.19 中合金 O 为例,可定量 计算其室温平衡组织的各组织组成物 的相对含量。
WA
=
oq Aq
×100%
WL
=
Ao Aq
×100%
W( A+C) = Eq × Ao ×100% W0 Ef Aq
W( A+B+C) = qf × Ao ×100%
W0
Ef Aq
图 5.20 是合金 o 的室温组织示意
(A+B+C)
5.3.2 固态有限互溶的三元共晶相图 固态下有限互溶的三元相图是由三对在液态无限互溶,而在固态有限互溶的二元共晶相
第5章三元共晶相图

A+B+C
A+B+C A+B+C A+B+C A+B+C
A初+( A+B+C ) B初+( A+B+C ) C初+( A+B+C )
( A+B+C )
e1
三元 简单共晶相图 平衡结晶产物 小结
A e
e3
B
e2
C
课堂练习
如图所示,已知A,B,C三组元固态完全不互溶,A,B,C的质量分数 分别为80%,10%,10%的O合金在冷却过程中将进行二元共晶反应和三 元共晶反应,在二元共晶反应开始时,该合金液相的质量分数成分(a点) A为60%,B为20%,C为20%,而三元共晶反应开始时的液相成分(E点) A为50%,B为10%,C为40%。 (1)试计算A(初)%,(A+B)%和 (A+B+C)%为多少? (2)写出图中Ⅰ和P合金的室温平衡组织。
投影图
A-e-B B-e-C
相变类型
L A+B L B+C L C+A L A+B+C
E1
相 区 L+C+A 四 相 L+A+B+C 区
A+B+C
C-e-A A-B-C A-B-C
A1-B1-C1
A3 A2 A1
TB B3 B2
E3
TC E
E2
B1
A e
BA
C3 C2 C1
B
C
A
e1
A
B
C1
C
液 相 面
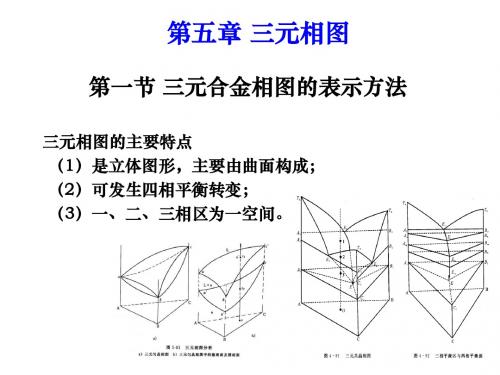
第五章 三元相图
B1
AБайду номын сангаас
B
C
(二)等温截面及其投影
L+C L
L+C L
L+A
L+A+C L+A L+C L
L+A+C L L+B
L+B
L+A+C L+A+B+C
C B
A+B+C
A
L+A+C L+A+B+C L+A+C L L+B
1.等温截面上的三相平衡区都是直边三角形,与 三角形相邻接的是两相平衡区 2.三角形的顶点与单相区相接,分别表示该温度 下三个平衡相的成分
LA+ C
TA C1 A3 A2 A1
E
L B + C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束
——
TB E1 B3 B2 E2 E B1
A
E3
TC
B
C3 C2 C1
C
中 转平 间 变衡 开 共 三面
始晶相
A3
A2 A1
E1
B2
B1
LA+ B
——
TA
A3 A2 A1
E TB E1 E3 TC E2 B3 B2 B1 B3 E2 B1 E C2 C1
B 10 20 30 40
50
C% 60 70 80 90
50 40 ← A%
30
20 10
C
课堂练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
第五章 三元合金相图

二元共晶
三元共晶
第四节三元共晶相图
通过成分三角形 顶点的变温截面
第四节三元共晶相图
(四) 投影图 1. 投影图分析
2. 合金O结晶过程 L----L+A------------L+A+(A+B)---------------A+(A+B)+(A+B+C)
二元共晶 三元共晶
第四节三元共晶相图
3.合金O在室温下的相和 组织含量
第一节三元合金相图的表示方法
B (1)确定O点的成分 1)过O作A角对边的平行线 B% C% 2)求平行线与A坐标的截距 得组元A的含量 3)同理求组元B、C的含量 O A C
← A%
第一节三元合金相图的表示方法
C B
A
Oa+Ob+Oc=AB=AC=BC=100% A浓度:Oa=Of=Cb B浓度:Ob=Od=Ac C浓度:Oc=Ba A浓度:55% B浓度:20% C浓度:25%
90 • 标出 50%A+20%B+30%C 的合金 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
80
70
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
第一节三元合金相图的表示方法
二、在成分三角形中具有特定意义的直线 B 成分三角形中特殊的点和线
第五章 三元合金相图
三元系相图简介
相图基本知识
三元相图的主要特点——立体图形,主要由曲面构成
三元系相图简介
垂直轴表示温度。 成分表示在棱柱底,通常是 一等边三角形。 棱柱的每个侧面表示三个二 元系统,如AB,BC,AC。
第5章-三元相图PPT课件

•20
2、结晶过程分析 O 自液态缓冷至于液互
相相交时,开始从液相中结晶出 α 固溶体,此时液相的成分l1即为合金成分, 而固相的成分为固相面某一点 s。
α 相越来 越多,固相的成分由s1点沿固相面移至s2 点,液相成分自l1点移至 l2点,由直线法则可知,合金的成分点必落 在l2和s2的连线上。
Ca=WA=30% Ac=WC=60% Ab=WB=10%。
中都有应用,但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金,它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律: a、 当温度一定时,若已知两平衡相的 成分,则合金的成分必位于两平衡相成分 的连线上; b、 当温度一定时,若已知一相的成分 及合金的成分,则另一平衡相的成分必位 于两已知成分点的连线的延长线上; c、 当温度变化时,两平衡相的成分变 化时,其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较,组元数增加 了1个,即成分变量是两个,故表示成分的坐 标轴应为2个,需要用一个平面表示,再加上 垂直于该平面的温度轴,这样三元相图就 演变成一个在三维空间的立体图形,分隔 相区的是一系列空间曲面,而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金
2、结晶过程分析 O 自液态缓冷至于液互
相相交时,开始从液相中结晶出 α 固溶体,此时液相的成分l1即为合金成分, 而固相的成分为固相面某一点 s。
α 相越来 越多,固相的成分由s1点沿固相面移至s2 点,液相成分自l1点移至 l2点,由直线法则可知,合金的成分点必落 在l2和s2的连线上。
Ca=WA=30% Ac=WC=60% Ab=WB=10%。
中都有应用,但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金,它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律: a、 当温度一定时,若已知两平衡相的 成分,则合金的成分必位于两平衡相成分 的连线上; b、 当温度一定时,若已知一相的成分 及合金的成分,则另一平衡相的成分必位 于两已知成分点的连线的延长线上; c、 当温度变化时,两平衡相的成分变 化时,其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较,组元数增加 了1个,即成分变量是两个,故表示成分的坐 标轴应为2个,需要用一个平面表示,再加上 垂直于该平面的温度轴,这样三元相图就 演变成一个在三维空间的立体图形,分隔 相区的是一系列空间曲面,而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金
第5章 三元合金相图

相对应成分点的连接直线称为连接线, 或称共轭连线;
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时,三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定,三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2, α相的成分变到mp线上的α2 , α2在 L2和 x 两点连线的延长线上,根据杠杆定律可 算出此时两相相对量为:
L2 %
x 2 L2 2
100 %
2%
L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中,就得到三元相图的投影图, 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中,并在每一条投影上标注 相应的温度,就得到等温线投影图;类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分, 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴,构成外形是一个三 棱柱体的三元相图;
● 三棱柱体的三个侧面是三组二元相图, 三棱柱体内部,有一系列空间曲面分隔 出若干相区。
● 三元相图复杂,不易描述相变过程和确 定相变温度。因此,实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上,包晶反应结束而进入α+β两相区。反应结束 时α和β两相的相对量为
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时,三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定,三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2, α相的成分变到mp线上的α2 , α2在 L2和 x 两点连线的延长线上,根据杠杆定律可 算出此时两相相对量为:
L2 %
x 2 L2 2
100 %
2%
L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中,就得到三元相图的投影图, 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中,并在每一条投影上标注 相应的温度,就得到等温线投影图;类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分, 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴,构成外形是一个三 棱柱体的三元相图;
● 三棱柱体的三个侧面是三组二元相图, 三棱柱体内部,有一系列空间曲面分隔 出若干相区。
● 三元相图复杂,不易描述相变过程和确 定相变温度。因此,实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上,包晶反应结束而进入α+β两相区。反应结束 时α和β两相的相对量为
第五章 三元相图

5.1
三元相图的成分表示法
C
二元系的成分可用一条 直线上的点来表示;三元 系合金有两个独立的成分 参数,所以必须用一个平 面三角形来表示,这个三 角形叫做成分三角形或浓 度三角形。常用的成分三 角形是等边三角形,有时 也用直角三角形或等腰三 角形。 A
A%
C%
B%
B
浓度三角形
5.1.1 浓度三角形 1. 等边三角形 三角形的三个顶点A,B, C分别表示3个纯组元, 三角形的边AB,BC, CA分别表示3个二元系 的成分坐标,三角形内 的任一点都代表一定成 分的三元合金. A 一般按顺时针(或逆时针) 标注组元浓度。
L(三元) ΔT α(三元)
自由度:f=c-P+1=3-2+1=2 故三元匀晶转变区可有两个自由度: 温度和相成分。
5.3.1 相图分析
1 画图 (1) 先画一成份三角形 (应为正三角形) (2) 画温度轴 (3) 画二元匀晶相图(每 两个合金上存在一个二 元相图) ---三元系立体图可视为三 个二元系在空间的延伸 液相面----三个二元系的液相线 所围成的面. 固相面----三个二元系的固相线 所围成的面.
5.4
三元共晶相图
TA A2 A3 A1 E3 E C2 C3 C1 C TB
5.4.1 组元在固态互不溶,具有共晶转变的相图
一、相图分析
1. 画图 (1) 先画一成份三角形
(2) 画温度轴
(3) 画二元共晶相图
E1 TC E2
B2 B3
B1 B
三个二元共晶相图向空间 A 延伸 (4) 画出四相平衡共晶转变平 面A1B1C1 (5) 三个二元系共晶点向空间 延伸为三条共晶沟线,交 A1B1C1面于E点,称为共晶点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)3个液相面以上:L; 2)3个液相面与6个二元空间曲面间:L+A,L+B,L+C; 3)6个二元共晶曲面和1个三元共晶面之间构成的3个空间三 棱曲面柱体:L+A+B, L+A+C,L+B+C; 4)1个三元共晶面(固相面): L+A+B+C; 5)三元共晶面(固相面)以下:A+B+C。 成分变化线:随温度降低,空间三棱曲面柱体中三个相 的成分变化的轨迹。 等温三角形:固定温度下三个平衡相的成分点连线(直 线)f=0
五、三元相图分析法总结
1.两相平衡
等温截面
成分变化:蝶形规则 共轭线:可杠杆定律
变温截面
判定转变温度范围, 不能用杠杆定律。 2.三相平衡 等温截面:直边 三角形,三顶点为 相成分点,可用重 心法则
变温截面: 曲边三角形或多边形 三相反应的判定: 1) 变温截面上
2)投影图判断三相反应 液相单变量线穿 过两旁固相成分点连 线的为二元共晶型, 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应,且靠近单变线 的为生成相
3.浓度三角形中特殊线: 平行浓度三角形任一边的直线 从浓度三角形的一个顶点到 对边的任意直线 4. 其它成分三角形的形式:
二、杠杆定律及重心法则
单相平衡勿须计算,四相平衡无从计算 两相平衡:杠杆定律 1.三元相图中杠杆定律 共线法则:三元合金中两相平衡时合金 成分点与两平衡相成分点在浓度三角形 的同一直线上 杠杆定律表达式:α%=EO/DE×100%,β=OD/DE×100% 注意:当一个合金O在液相的凝固过程中,析出α相成分不变时, 液相成分一定沿α相成分点与O点连线延长线变化。 2.三相平衡重心法则(重量三角形重心) x,y,z分别为α,β,γ成分点,则 α%=oa/ax×100%, β=ob/by×100%, γ%=oc/cz×100% 为什么三角形是直线而不是曲线连接?
三、匀晶三元相图
1. 立体模型 液相区,固相区,液、固两相区
2. 合金凝固过程及组织 a.平衡凝固 b.蝶形法则:如图 匀晶合金凝固中相成分变化 凝固中固、液相成分沿固相面、液相面呈曲线变化,每一个 温度下的固、液相成分连线在浓度三角形中投影呈蝴蝶状
3.等温截面 匀晶三元系的等温截面(实验方法测定,而非立体截取) 两相区内, f=3-2+1=2, T一定时,f=1, 只有一个平 衡相的成分 可以独立改 变。对于一 定的合金, 连接线唯一。 等温截面作用: 1. 该温度下三元系中各合金的相态 2.杠杆定律计算平衡相的相对量 3.反映液相面、固相面走向和坡度,确定熔点、凝固点
4、变温截面(实验测试而得)
变温截面的能与不能: 能分析某合金不同温度下状态分析合金的相变过程; 变温截面上的液相线和固相线不能表示平衡相的成分, 不能根据这些线应用杠杆元共晶相图模型(教材图5-12)
3个初晶液相面; 3条二元共晶线(共晶转变,三相平衡,f=1); 1个三元共晶点(四相平衡,f=0);1个三元共晶面(固相面) 6个二元共晶曲面 每3条成分变化线(单变量线)构成1个空间三棱曲面柱体 9个相区如下:
2. 简单三元共晶中合金的凝固过程和组织
投影图
如图x合金 L→A,L→A+B,L→A+B+C
4. 简单三元共晶的等温截面 二相区: 三相区:三角形,三个顶点代表成分点
5.变温截面: 平行于浓度三角形一边的变温截面cd 分析合金x的结晶过程:L→B,L→A+B,L→A+B+C 分析合金O的结晶过程 通过顶点的变温截面 注意:不能用杠杆定律,
第五章
三元相图
必要性:工业材料为多元合金 本章主要内容: 1. 三元相图的表达方式,使用方法 2.几种基本的三元相图立体模型 3.各种等温截面,变温截面及各相区在浓 度三角形上的投影图 4.典型合金的凝固过程及组织,各种相变 过程及相平衡关系。
一、三元相图的成分表示法
1.浓度等边三角形:
三个顶点为纯组元, 三条边为二元合金, 三角形内任一点为三元合金 2.三元合金成分确定 浓度等边三角形
3.四相平衡
反应类型判断 液相面投影图: 指向结点单变量线数为产物数 变温截面:根据水平线上、下方三相区判断
4.三元相图截面图上相区接触法则
相数差为1的两相邻相区线段为界 差大小1或等于零的为点接触
等温截面上 单相区边界线走向
