2015年广东省东莞市中考数学模拟试卷(七)
广东省东莞市2015年中考数学试卷(解析版)

最大最全最精的教育资源网2015 年广东省东莞市中考数学试卷一、选择题:本大题 10 小题,每题 3 分,共 30 分。
在每题给出的四个选项中,只有 一个是正确的,请把答题卡上对应题目所选的选项涂黑。
21·世纪 *教育网1.( 3 分)( 2015?东莞) |﹣ 2|=()A . 2B .﹣2C .D .2.(3 分)( 2015?东莞)据国家统计局网站 2014 年 12 月 4 日公布的信息, 2014 年广东省粮 食总产量约为 13 573 000 吨,将 13 573 000 用科学记数法表示为( ) 21*cnjy*comA . 1.3573×106B . 1.3573×107C . 1.3573×108D . 1.3573×1093.( 3 分)( 2015?东莞)一组数据 2, 6, 5, 2, 4,则这组数据的中位数是()A . 2B . 4C . 5D . 64.( 3 分)( 2015?东莞)如图,直线 a ∥b , ∠1=75°, ∠2=35°,则 ∠3 的度数是( )A . 75°B . 55°C . 40°D . 35°5.(3 分)( 2015?东莞)以下所述图形中,既是中心对称图形,又是轴对称图形的是()A . 矩形B . 平行四边形C . 正五边形D . 正三角形2( )6.( 3 分)( 2015?东莞)(﹣ 4x ) =2222A . ﹣ 8xB . 8xC . ﹣ 16xD . 16x7.( 3 分)( 2015?东莞)在 0,2,(﹣ 3) 0,﹣ 5 这四个数中,最大的数是( )A . 0B . 2C . (﹣3)0D .﹣58.( 3 分)( 2015?东莞)若对于 2=0 有两个不相等的实数根,则实数ax 的方程 x +x ﹣ a+ 的取值范围是( )教育名师】【出处: 21A . a ≥2B . a ≤2C . a > 2D . a < 29.(3 分)( 2015?东莞)如图, 某数学兴趣小组将边长为 3 的正方形铁丝框 ABCD 变形为以 A 为圆心, AB 为半径的扇形(忽视铁丝的粗细),则所得扇形 DAB 的面积为()A. 6B. 7C. 8D. 910.( 3 分)( 2015?东莞)如图,已知正△ABC 的边长为 2, E、 F、 G 分别是 AB 、 BC 、CA上的点,且 AE=BF=CG ,设△EFG 的面积为 y, AE 的长为 x,则 y 对于 x 的函数图象大概是()A.B.C.D.二、填空题:本大题 6 小题,每题 4 分,共 24 分。
【2015中考真题】广东省东莞市中考数学试题及解析

2015年广东省东莞市中考数学试卷一、选择题:本大题10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑。
2.(3分)(2015•东莞)据国家统计局网站2014年12月4日发布的消息,2014年广东省粮食总产量约为4.(3分)(2015•东莞)如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是()28.(3分)(2015•东莞)若关于x的方程x2+x﹣a+=0有两个不相等的实数根,则实数a的取值范围是()9.(3分)(2015•东莞)如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为()10.(3分)(2015•东莞)如图,已知正△ABC的边长为2,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是()A.B.C.D.二、填空题:本大题6小题,每小题4分,共24分。
请将下列各题的正确答案填写在答题卡相应的位置上。
11.(4分)(2015•东莞)正五边形的外角和等于(度).12.(4分)(2015•东莞)如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是.13.(4分)(2015•东莞)分式方程=的解是.14.(4分)(2015•东莞)若两个相似三角形的周长比为2:3,则它们的面积比是.15.(4分)(2015•东莞)观察下列一组数:,…,根据该组数的排列规律,可推出第10个数是.16.(4分)(2015•东莞)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是.三、解答题(一):本大题3小题,每小题6分,共18分。
17.(6分)(2015•东莞)解方程:x2﹣3x+2=0.18.(6分)(2015•东莞)先化简,再求值:,其中.19.(6分)(2015•东莞)如图,已知锐角△ABC.(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,若BC=5,AD=4,tan∠BAD=,求DC的长.四、解答题(二):本大题3小题,每小题7分,共21分。
2015年东莞市中考二模数学试卷

2015年东莞市中考二模数学试卷一、选择题(共10小题;共50分)1. 的倒数是A. B. C. D.2. 国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为度,若将数据用科学记数法表示为A. B. C. D.3. 气候宜人的省级度假胜地吴川吉兆,测得一至五月份的平均气温分别为,,,,(单位:),这组数据的中位数是.A. B. C. D.4. 如图,所给图形中是中心对称图形但不是轴对称图形的是A. B.C. D.5. 已知一个正多边形一个外角是,则这个正多边形是A. 四边形B. 五边形C. 六边形D. 七边形6. 下列各式中,是最简二次根式的是A. B. C. D.7. 下列运算正确的是A. B.C. D.8. 函数中,自变量的取值范围是A. B. C. D.9. 若关于的一元二次方程有实根,则的取值范围是A. B. 且C. D. 且10. 二次函数的大致图象如图,关于该二次函数,下列说法错误的是A. 函数有最小值B. 对称轴是直线C. 当,随的增大而减小D. 当时,二、填空题(共6小题;共30分)11. 化简:.12. 不等式组的解集是.13. 如图是一副三角板叠放的示意图,则.14. 已知,则.15. 如图,,,以为直径作半圆,圆心为.以点为圆心,为半径作弧,过点作的平行线交两弧于点,,则阴影部分的面积是.16. 第一个图形为矩形,依次连矩形各边的中点得到第二个图形(菱形),按照此方法继续下去.已知第一个图形的面积为,则第个图形的面积为.三、解答题(共9小题;共117分)17. 计算:.18. 某市为治理污水,需要铺设一条全长为米的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天的工效比原计划增加,结果提前天完成这一任务,求原计划每天铺设多少米管道?19. 如图,点在的边上,且.(1)作的平分线,交于点(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,判断直线与直线的位置关系(不要求证明).20. 如图,某船由西向东航行,在点测得小岛在北偏东,船航行了海里后到达点,这时测得小岛在北偏东,船继续航行到点时,测得小岛恰好在船的正北方,求此时船到小岛的距离.21. 甲、乙两组数据(单位:厘米)如下表:甲组乙组(1)根据以上数据填表(参考公式:)众数单位厘米平均数单位厘米方差单位厘米甲组乙组(2)哪一组数据比较稳定?22. 在菱形中,对角线与相交于点,,.过点作交的延长线于点.(1)求的周长;(2)点为线段上的点,连接并延长交于点.求证:.23. 如图,在平面直角坐标系中,函数的图象与一次函数的图象交点为.(1)求一次函数的解析式;(2)写出反比例函数值大于一次函数值时的取值范围;(3)设一次函数的图象与轴交于点,若是轴上一点,且满足的面积是,求的坐标.24. 已知抛物线与轴相交于,两点,与轴相交于点,且顶点为.(1)求和的值;(2)如图,连接,与抛物线的对称轴相交于点,点是线段上一动点,过点作,交抛物线于点,设点的横坐标为;①用含的代数式表示线段的长,并求当四边形为平行四边形时的值;②设的面积为,求与的函数关系式,并求出的最大值.25. 如图,已知为正方形的中心,分别延长到点,到点,使,,连接,将绕点逆时针旋转角得到.连接,.(1)如图,探究与的数量关系,并给予证明;(2)如图,当,时,求:①的度数;②的长度.答案第一部分1. C2. C3. C4. C5. B6. C7. C8. B9. B 10. D第二部分11.12.13.14.15.【解析】连接..阴影扇形扇形16.【解析】连接第二个图形的对角线,设第一个图形的长和宽分别为,,因为,第一个图形,所以,第二个图形,第三个图形,第四个图形,,所以,第个图形.第三部分17. 原式18. 设原计划每天铺设米管道,由题意得:解得:经检验: 是原方程的解. 答:原计划每天铺设 米管道. 19. (1) 如图所示, 即为所求.(2) 平行.20. 设 海里,依题意得, , , ,即 ,海里,答:船与小岛的距离是 海里. 21. (1) 填表如下:众数 单位 厘米 平均数 单位 厘米 方差 单位 厘米甲组 乙组(2) , 乙组数据比较稳定.22. (1) 四边形 菱形,, , , , , , , , 四边形 是平行四边形, , ,的周长是: . (2) 四边形 是菱形, , ,在 和 中, .23. (1) 将 代入得,,则点坐标为,将代入得,,解得,则一次函数解析式为;(2),根据图象可知:反比例函数值大于一次函数值时的取值范围;(3)一次函数与轴的交点为,与轴的交点为,,,解得.则点坐标为,.24. (1)设,顶点为,,,.(2)令,则,解得,或,则,.令,则,则.综上所述,,,,抛物线的对称轴是;①设直线的函数关系式为:.把,分别代入得:解得:,.所以直线的函数关系式为:.当时,,.当时,,.在中,当时,..当时,,.线段,线段.,当时,四边形为平行四边形.由,解得:,(不合题意,舍去).因此,当时,四边形为平行四边形.②设直线与轴交于点,由,,可得:.的最大值为.25. (1)正方形中,,又,,,则,在和中,,.(2)①当时,,,是等腰直角三角形,为中点,,②,,,,,,四边形是正方形,.。
2015广东省中考数学模拟卷(1)含答案

(图1)数学试题说明:全卷共 4 页,考试时间为 100 分钟,满分 120 分.答案写在答题卡上.一、选择题(本大题共 10 小题,每小题3分,共30 分.在每小题给出的4个选项中,有且只有一项是符合题目要求的.)1. 4-的绝对值是A. 4B. 4- C.14D.14-2. 下列四个几何体中,俯视图为四边形的是A. B. C. D.3. “送人玫瑰,手留余香”,广东有一批无私奉献的志愿者,目前注册志愿者已达274万人,274万用科学记数法表示为A. 42.7410⨯ B. 52.7410⨯ C. 62.7410⨯ D. 72.7410⨯4. 下列图形中既是中心对称图形,又是轴对称图形的是A . B. C. D.5.若3-=ba,则ab-的值是A.3- B.3 C.0 D.66.如图1,AB∥CD,∠CDE=140︒,则∠A的度数为A.40︒ B.60︒C.50︒ D.140︒7.肇庆市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如下表,则该周PM2.5指数的众数和中位数分别是A.150,150B.150,155C.155,150 D.150,152.58.下列式子中正确的是A.21()93-=- B.()326-=-C2=- D.()031-=9.如图2,AB是⊙O的直径,∠AOC =130°,则∠D的度数是(图3)D(图4)ECBA OA .65°B .25°C .15°D .35° 10.二次函教225y x x =+-有A .最大值5-B .最小值5-C .最大值6-D .最小值6-二、填空题(本大题共6 小题,每小题 4 分,共24分.) 11.计算:=⨯2731▲ . 12.一个正五边形绕它的中心至少要旋转 ▲ 度,才能和原来五边形重合.13.已知错误!未找到引用源。
是一元二次方程错误!未找到引用源。
2015年广东省初中毕业生学业考试数学模拟试卷(一)和答案

2015年石家庄第四十二中学第一次模拟考试数 学 试 卷本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.本试卷满分为120分,考试时间为120分钟.一、选择题(本大题共16个小题,1~6小题,每小题2分;7~16小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1. ﹣3的绝对值是( )A . -3B .3C . 1D .02. 未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( ) A .0.845×104亿元 B .8.45×103亿元 C .8.45×104亿元 D .84.5×102亿元3. 如图,直线a 、b 与直线c 相交,且a ∥b ,∠α=55°,则∠β的度数为( ) A . 125° B .115° C .105° D .35°4.下列计算中,正确的是( )A .123=-a aB .2229)3(y x y x +=+ C .725)(x x = D .91)3(2=-- 5. 如图是正三棱柱,它的主视图正确的是( )6. 若关于x ,y 的二元一次方程组 的解也是二元一次方程2x +3y =6的解,则k 的值为( )7. 小明用20元钱去买钢笔和铅笔,一支钢笔5元钱,一支铅笔1元钱,如果将这20元都买成铅笔或钢笔,购买方案共有( )A.3 种B.4种C.5种D.6种8. 某班分成甲、乙两组去距离学校4km 的烈士陵园扫墓.甲组步行,乙组骑自行车,他们同时从学校出发,结果乙组比甲组早20min 到达目的地.已知骑自行车的速度是步行速度的2倍,设步行的速度为x km/h ,则x 满足的方程为( )A .x 4-x 24=20 B .x 24-x 4=20 C .x 4-x 24=31 D .x 24-x 4=31 9. 若32=-b a ,则b a 249+-的值为( )A .12 B.6 C.3D.043.-A 43.B 34.-C 34.D11题图10.圆锥的母线长为6,底面半径为2,则此圆锥的侧面积是( )A .6π B.8π C.12π D.16π11.如图,在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于点D 、E ,若AD =4, DB =2, 则BDEBCES S ∆∆的值为( ) A .12 B .23 C .34D .3512. 如图,将△ABC 沿BC 方向平移2cm 得到△DEF ,若△ABC 的周长为16cm , 则四边形ABFD 的周长为( )A .16cmB .18cmC .20cmD .22cm13.如图,已知△ABC 面积为12cm 2,BP 为∠ABC 的角平分线,AP 垂直BP 于点P ,则△PBC 的面积为( ) A . 6cm 2 B .5cm 2 C . 4cm 2 D .3cm 214.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,且关于x 的一元二次方程20ax bx c m ++-=没有实数根,有下列结论:①240b ac ->;②0abc <;③2m >.其中,正确结论的个数是( ) A .0 B .1 C .2 D .314题图 15题图15、如图,双曲线 xm=y 与直线y=kx+b 交于点M 、N ,并且点M 的坐标 为(1,3),点N 的纵坐标为﹣1.根据图象信息可得关于x 的方程b kx +=x m 的解为( )A .﹣3,1B .﹣3,3C .﹣1,1D .﹣1,3 16.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a 岁,中位数为b 岁,则下列结论中正确的是( ) A.a <13,b =13 B.a <13,b <13 C.a >13,b <13 D.a >13,b =13卷Ⅱ(非选择题,共78分)13题图x二、填空题(本大题共4个小题,每小题3分,共12分.把答案写在题中横线上) 17.已知a +b =4,a ﹣b =3,则a 2﹣b 2= ________ . 18.计算:=+-++12112m m m m ______ .19.如图,在平面直角坐标系中,以O 为圆心,适当长为半径画弧,交x 轴于点M , 交y 轴于点N ,再分别以点M 、N 为圆心,大于 的长为半径画弧,两弧在第二 象限交于点P .若点P 的坐标为(2a ,b+1),则a 与b 的数量关系为 _____________ 20. 下面是一个某种规律排列的数阵:19题图 根据数阵的规律,第n (n 是整数,且n ≥3)行从左到右数第(n ﹣2)个数是_____________ (用含n 的代数式表示).三、解答题(本大题共6个小题,共66分.解答应写出文字说明、证明过程或演算步骤) 21.(9分) 我们已经知道:①1的任何次幂都为1;②-1的偶数次幂也为1; ③-1的奇数次幂为-1;④任何不等于零的数的零次幂都为1.请问当x 为何值时,代数式2014)32(++x x 的值为1.22. (10分)如图,在R t △ABC 中,∠ACB =90°,∠B =30°,.将△ABC 绕点C 按顺时针方向旋转n 度后,得到△DEC ,点D 刚好落在AB 边上.MN21(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.23.(10分)学习完统计知识后,小兵就本班同学的上学方式进行调查统计.如图是他通过收集数据后绘制的两幅不完整的统计图.请你根据图中提供的信息解答下列问题:(1)该班共有__________名学生;(2)将表示“步行”部分的条形统计图补充完整;(3)在扇形统计图中,“骑车”部分扇形所对应的圆心角是___________度;(4)若全年级共1000名学生,估计全年级步行上学的学生有_________名;(5)在全班同学中随机选出一名学生来宣读交通安全法规,选出的恰好是骑车上学的学生的概率是_______.24.(12分)如图,平面直角坐标系中,反比例函数)0(>=x xk y 的图象和矩形ABCD ,AD 平行于x 轴,且AB =2,AD =4,点A 的坐标为(2,6).(1)直接写出B 、C 、D 三点的坐标;(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的关系式.25.(12分)如图,扇形OBD 中∠BOD=60 o ,∠BOE =45o ,DA ⊥OB ,EB ⊥OB .(1)求BEDA的值;(2)若OE 与BD ⌒交于点M ,OC 平分∠BOE ,连接CM .说明CM 为⊙O 的切线;(3)在(2)的条件下,若BC =1,求tan ∠BCO 的值.N MMN NM题26图3题26图426. (13分)类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到,如下是一个案例,请补充完整。
2015年广东省东莞市东华中学中考一模数学试卷(解析版)

16.解方程:2x2+1=4x﹣1.
17.已知:
是方程
的一个根,求:方程的另一个根及 k
的值. 18.已知:三角形的一边比它边上的高大 4cm,若设三角形的一边长为 x(cm),
它的面积为 y(cm2). 写出:y 与 x 之间的函数关系式以及自变量 x 的取值范围. 四、解答题 19.某企业 2012 年盈利 1500 万元,2014 年克服不利影响,仍实现盈利 2160 万
A.x=1
B.x=﹣4
C.x1=﹣4,x2=1 D.x1=4,x2=﹣1
3.抛物线 y=2(x﹣3)2+1 的顶点坐标是( )A Nhomakorabea(3,1)
B.(﹣3,1)
C.(1,﹣3) D.(1,3)
4.抛物线 y=x2+2 的对称轴是( )
A.直线 x=0 B.直线 x=1
C.直线 x=1 D.直线 x=2
5.已知一元二次方程 x2+bx﹣6=0 有一个根为 2,则另一根为( )
.
13.已知点 A(3,y1),B(2,y2)在二次函数 y=(x﹣1)2+1 的图象上,则 y1 y2.
14.关于 x 的一元二次方程 x2﹣2x+m=0 有两个实数根,则 m 的取值范围
是
.
15.三角形两边长是 4 和 5,第三条边是方程 x2﹣3x+2=0 的解,则三角形的周
长是
.
三、解答题(解答应写出文字说明、证明过程或推演步骤.)
的值;
(3)按照这个规定,若
=1,求 x 的值.
23.已知 x1,x2 是关于 x 的方程 x2﹣(2m+1)x+m2=0 的两个根. (1)求 m 的取值范围; (2)若两根满足 x12+x22=7,求 m 的值. 24.如图 1,有长为 22 米的篱笆,一面利用墙(墙的最大可用长度为 14 米),
2015年广东省东莞市五校联考中考一模数学试卷(解析版)

3. (3 分)下列运算正确的是( A.2a2+a=3a3 C. (﹣a)2÷a=a
4. (3 分)下列图形中既是轴对称图形又是中心对称图形的是(
A.
B.
C.
D. )
5. (3 分) 下图的几何体是由三个同样大小的立方体搭成的, 其左视图为 (
A.
B.
C.
D.
6. (3 分)如图,在△ABC 中,点 D 在 BC 上,AB=AD=DC,∠B=80°,则 ∠C 的度数为( )
四、解答题(二) (每小题 7 分,共 21 分) 20. (7 分)如图,海中有一灯塔 C,它的周围 11 海里内有暗礁.一渔船以 18 海里/时的速度由西向东航行,在 A 点测得灯塔 C 位于北偏东 60°的方向上, 航行 40 分钟到达 B 点,此时测得灯塔 C 位于北偏东 30°的方向上,如果渔 船不改变航线继续向东航行,有没有触礁的危险?
22. (7 分)甲口袋中装有 2 个相同的小球,它们分别写有数值﹣1,5;乙口袋 中装有 3 个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取 一球,记它上面的数值为 m,再从乙口袋中随机取一球,记它上面的数值为 n.设点 A 的坐标为(m,n) . (1)请用树状图或列表法,列出(m,n)所有可能的结果; (2)求点 A 落在第一象限的概率. 五、解答题(三) (每小题 9 分,共 27 分) 23. (9 分)如图,二次函数 y= x2+bx+c 的图象交 x 轴于 A、D 两点,并经过 B 点,已知 A 点坐标是(2,0) ,B 点坐标是(8,6) . (1)求二次函数的解析式; (2)求函数图象的顶点坐标及 D 点的坐标; (3)二次函数的对称轴上是否存在一点 C,使得△CBD 的周长最小?若 C 点存 在,求出 C 点的坐标;若 C 点不存在,请说明理由.
人教版中考模拟考试数学试卷及答案(共七套)

19.(1) ;
(2)如下表:
小辰
A
A
A
B
B
B
C
C
C
小安
A
B
C
A
B
C
A
B
C
同一型号
√
√ቤተ መጻሕፍቲ ባይዱ
√
由表知:他们选择同一型号的概率为 。
20.(1)由两张图知:A有32人,占40%,所以样本容量是80人;
(2)求出B的人数是16人,补全条形图如图;
(3)D等占10%,扇形圆心角是36°;
(4)在被抽到的80人中,C等级24人,占30%,
以此估计全校2000人中评为C的可能有
2000×30%=600,即可能有600人。
21. 解:设增加了 行,则共有( )行,( )列,
根据题意: , ,
∵ ,∴ ,
答:增加了3列。
22. 提示(1)AB是直径,∠ACB=90°,∠B+∠2=90°;
DC=AC,那么∠D=∠1,而∠D=∠B,
(1)小辰随机选择一种型号是凝胶型免洗洗手液的概率是________;
(2)请你用列表法或画树状图法,求小辰和小安选择同一型号免洗洗手液的概率。
20.(本题8分)
学史明理,学史增信,学史崇德,学史力行。在建党100周年之际,某校对全校学生进行了一次党史知识测试,成绩评定共分为A,B,C,D四个等级,随机抽取了部分学生的成绩进行调查,将获得的数据整理绘制成如下两幅不完整的统计图:
则D(8,6),CD=5,
而A(5,0),OA=5,∴CD=OA,
∵CD∥OA,且CD=OA,∴四边形OADC是平行四边形;
(3)点C纵坐标为6,则CD与OA之间的距离为 ,
东莞市中考数学模拟试卷
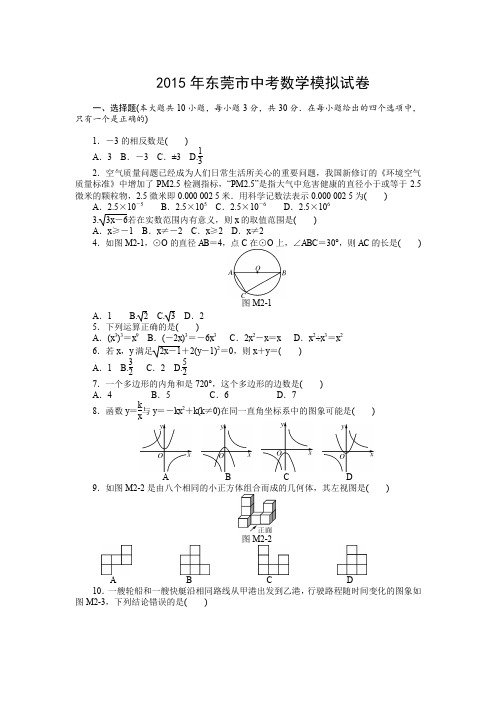
2015年东莞市中考数学模拟试卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)1.-3的相反数是( )A .3B .-3C .±3 D.132.空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.000 002 5米.用科学记数法表示0.000 002 5为( ) A .2.5×10-5 B .2.5×105 C .2.5×10-6 D .2.5×1063.3x -6若在实数范围内有意义,则x 的取值范围是( )A .x ≥-1B .x ≠-2C .x ≥2D .x ≠24.如图M2-1,⊙O 的直径AB =4,点C 在⊙O 上,∠ABC =30°,则AC 的长是( )图M2-1 A .1 B. 2 C. 3 D .25.下列运算正确的是( )A .(x 3)3=x 9B .(-2x )3=-6x 3C .2x 2-x =xD .x 2÷x 3=x 26.若x ,y 满足2x -1+2(y -1)2=0,则x +y =( )A .1 B.32 C .2 D.527.一个多边形的内角和是720°,这个多边形的边数是( )A .4B .5C .6D .78.函数y =k x与y =-kx 2+k (k ≠0)在同一直角坐标系中的图象可能是( )A B C D9.如图M2-2是由八个相同的小正方体组合而成的几何体,其左视图是( )图M2-2A B C D10.一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶路程随时间变化的图象如图M2-3,下列结论错误的是( )图M2-3A .轮船的速度为20 km/hB .快艇的速度为803km/h C .轮船比快艇先出发2 h D .快艇比轮船早到2 h二、填空题(本大题共6小题,每小题4分,共24分)11.二次函数y =ax 2+bx -1(a ≠0)的图象经过点(1,1).则代数式1-a -b 的值为________12.若△ABC ∽△DEF , △ABC 与△DEF 的相似比为1∶2,则△ABC 与△DEF 的周长比为________.13.分解因式:x 3-xy 2=________.14.如图M2-4,直线MN 与⊙O 相切于点M ,ME =EF ,且EF ∥MN ,则cos E =________.图M2-4 图M2-515.若将抛物线y =x 2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为________.16.如图M2-5,正方形ABCD 的边长为2,点E 为边BC 的中点,点P 在对角线BD 上移动,则PE +PC 的最小值是__________.三、解答题(一)(本大题共3小题,每小题6分,共18分)17.计算:|-3|+2sin45°+tan60°-⎝⎛⎭⎫-13-1-12+(π-3)0.18.证明平行四边形的判定定理:对角线互相平分的四边形是平行四边形.19.如图M2-6,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC (顶点是网格线的交点).(1)将△ABC 向上平移3个单位得到△A 1B 1C 1,请画出△A 1B 1C 1;(2)请画一个△A 2B 2C 2,使△A 2B 2C 2∽△ABC ,且相似比为2∶1.图M2-6四、解答题(二)(本大题共3小题,每小题7分,共21分)20.如图M2-7,小明想测山高和索道的长度.他在B 处仰望山顶A ,测得仰角∠B =31°,再往山的方向(水平方向)前进80 m 至索道口C 处,沿索道方向仰望山顶,测得仰角∠ACE =39°.(1)求这座山的高度(小明的身高忽略不计);(2)求索道AC 的长(结果精确到0.1 m).⎝⎛⎭⎫参考数据:tan31°≈35,sin31°≈12,tan39°≈911,sin39°≈711图M2-721.几个小伙伴打算去音乐厅观看演出,他们准备用360元购买门票.下面是两个小伙伴的对话:根据对话的内容,请你求出小伙伴们的人数.22.九年级(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:25<x ≤302 0.04图M2-8请解答以下问题:(1)把上面的频数分布表和频数分布直方图M2-8补充完整;(2)求该小区用水量不超过15 t 的家庭占被调查家庭总数的百分比;(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过20 t 的家庭大约有多少户?五、解答题(三)(本大题共3小题,每小题9分,共27分)23.如图M2-9,四边形ABCD 为正方形,点A 的坐标为(0,2),点B 的坐标为(0,-3),反比例函数y =k x(k ≠0)的图象经过点C . (1)求反比例函数的解析式;(2)若点P 是反比例函数图象上的一点,△P AD 的面积恰好等于正方形ABCD 的面积,求点P 的坐标.图M2-924.如图M2-10,AD是圆O的切线,切点为A,AB是圆O的弦.过点B作BC∥AD,交圆O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与圆O的位置关系,并说明理由;(2)若AB=9,BC=6,求PC的长.图M2-1025.如图M2-11,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C的圆与y轴的另一个交点为D.已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4).(1)求此抛物线的表达式与点D的坐标;(2)若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值.图M2-11。
往年广东省东莞市中考数学试题及答案

往年广东省东莞市中考数学试题及答案说明:1.全卷共4页,考试用时100分钟,满分为120分.2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、试室号、座位号.用2B 铅笔把对应该号码的标号涂黑. 3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑, 如需改动,用像皮檫干净后,再选涂其他答案,答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交回. 一、选择题(本大题10小题,每小题3分,共30分) 1. 2的相反数是A.21-B. 21C.-2D.2 2.下列几何体中,俯视图为四边形的是3.据报道,往年第一季度,广东省实现地区生产总值约1 260 000 000 000元,用科学记数法表示为A. 0.126×1012元 B. 1.26×1012元 C. 1.26×1011元 D. 12.6×1011元 4.已知实数a 、b ,若a >b ,则下列结论正确的是A.55-<-b aB.b a +<+22C.33ba < D.b a 33> 5.数据1、2、5、3、5、3、3的中位数是A.1B.2C.3D.56.如题6图,AC ∥DF,AB ∥EF,点D 、E 分别在AB 、AC 上,若∠2=50°,则∠1的大小是 A.30° B.40° C.50° D.60°7.下列等式正确的是A.1)1(3=-- B. 1)4(0=- C. 6322)2()2(-=-⨯- D.2245)5()5(-=-÷-8.不等式5215+>-x x 的解集在数轴上表示正确的是9.下列图形中,不是..轴对称图形的是10.已知210k k <<,则是函数11-=x k y 和xk y 2=的图象大致是二、填空题(本大题6小题,每小题4分,共24分) 11.分解因式:92-x =________________.12.若实数a 、b 满足042=-++b a ,则2a b=________.13.一个六边形的内角和是__________.14.在Rt △ABC 中,∠ABC=90°,AB=3,BC=4,则sinA=________.15.如题15图,将一张直角三角板纸片ABC 沿中位线DE 剪开后,在平面上将△BDE 绕着CB的中点D 逆时针旋转180°,点E 到了点E ′位置,则四边形ACE ′E 的形状是________. 16.如题16图,三个小正方形的边长都为1,则图中阴影部分面积的和是_____(结果保留π).三、解答题(一)(本大题3小题,每小题5分,共15分) 17.解方程组128x y x y =+⎧⎨+=⎩18.从三个代数式:①222b ab a +-,②b a 33-,③22b a -中任意选择两个代数式构造成分式,然后进行化简,并求当3,6==b a 时该分式的值.19.如题19图,已知□ABCD .(1)作图:延长BC,并在BC 的延长线上截取线段CE,使得CE=BC (用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,不连结AE,交CD 于点F,求证:△AFD ≌△EFC. 四、解答题(二)(本大题3小题,每小题8分,共24分)20.某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能选择最喜爱的一项运动项目),进行了随机抽样调查,并将调查结果统计后绘制成了如【表1】和题20图所示的不完整统计图表. (1)请你补全下列样本人数分布表(【表1】)和条形统计图(题20图); (2)若七年级学生总人数为920人,请你估计七年级学生喜爱羽毛球运动项目的人数.① ②21.雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?22.如题22图,矩形ABCD 中,以对角线BD 为一边构造一个矩形BDEF,使得另一边EF 过原矩形的顶点C.(1)设Rt △CBD 的面积为S 1, Rt △BFC 的面积为S 2, Rt △DCE 的 面积为S 3 , 则S 1______ S 2+ S 3(用“>”、“=”、“<”填空); (2)写出题22图中的三对相似三角形,并选择其中一对进行证明. 五、解答题(三)(本大题3小题,每小题9分,共27分) 23. 已知二次函数1222-+-=m mx x y .(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式; (2)如图,当2=m 时,该抛物线与y 轴交于点C,顶点为D,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P,使得PC+PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.24.如题24图,⊙O 是Rt △ABC 的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE ⊥DC 交DC的延长线于点E.(1)求证:∠BCA=∠BAD; (2)求DE 的长;(3)求证:BE 是⊙O 的切线.25.有一副直角三角板,在三角板ABC 中,∠BAC=90°,AB=AC=6,在三角板DEF 中,∠FDE=90°,DF=4,DE=34.将这副直角三角板按如题25图(1)所示位置摆放,点B 与点F 重合,直角边BA 与FD 在同一条直线上.现固定三角板ABC,将三角板DEF 沿射线BA 方向平行移动,当点F 运动到点A 时停止运动. (1)如题25图(2),当三角板DEF 运动到点D 与点A 重合时,设EF 与BC 交于点M,则∠EMC=______度;(2)如图(3),在三角板DEF 运动过程中,当EF 经过点C 时,求FC 的长; (3)在三角板DEF 运动过程中,设BF=x ,两块三角板重叠部分面积为y ,求y 与x 的函数解析式,并求出对应的x 取值范围.FED CBA参考答案一、C D B D C C B A C A二、11.)3)(3(-+x x ;12. 1;13. 720°;14.54;15.平行四边形;16.83π 三、17.⎩⎨⎧==23y x ;18.选取①、②得3)(3)(332222b a b a b a b a b ab a -=--=-+-,当3,6==b a 时,原式=1336=-(有6种情况).19. (1)如图所示,线段CE 为所求;(2)证明:在□ABCD 中,AD ∥BC,AD=BC.∴∠CEF=∠DAF ∵CE=BC,∴AD=CE,又∵∠CFE=∠DFA,∴△AFD ≌△EFC.20.(1)30%、10、50;图略;(2)276(人).21.(1)10%;(2)12100×(1+0.1)=13310(元). 22.(1) S 1= S 2+ S 3;(2)△BCF ∽△DBC ∽△CDE; 选△BCF ∽△CDE证明:在矩形ABCD 中,∠BCD=90°且点C 在边EF 上,∴∠BCF+∠DCE=90° 在矩形BDEF 中,∠F=∠E=90°,∴在Rt △BCF 中,∠CBF+∠BCF=90° ∴∠CBF=∠DCE,∴△BCF ∽△CDE.23.(1)m=±1,二次函数关系式为x x y x x y 2222-=+=或;(2)当m=2时,1)2(3422--=+-=x x x y ,∴D(2,-1);当0=x 时,3=y ,∴C(0,3). (3)存在.连结C 、D 交x 轴于点P,则点P 为所求,由C(0,3)、D(2,-1)求得直线CD 为32+-=x y当0=y 时,23=x ,∴P(23,0). 24.(1)∵AB=DB,∴∠BDA=∠BAD,又∵∠BDA=∠BCA,∴∠BCA=∠BAD.FNMEDC BAGFN MEDCB AFEA(2)在Rt △ABC 中,AC=135122222=+=+BC AB ,易证△ACB ∽△DBE,得ACBDAB DE =, ∴DE=13144131212=⨯ (3)连结OB,则OB=OC,∴∠OBC=∠OCB,∵四边形ABCD 内接于⊙O,∴∠BAC+∠BCD=180°,又∵∠BCE+∠BCD=180°,∴∠BCE=∠BAC,由(1)知∠BCA=∠BAD,∴∠BCE=∠OBC,∴OB ∥DE ∵BE ⊥DE,∴OB ⊥BE,∴BE 是⊙O 的切线.25. 解:(1)15;(2)在Rt △CFA 中,AC=6,∠ACF=∠E=30°,∴FC=30cos AC=6÷3423=(3)如图(4),设过点M 作MN ⊥AB 于点N,则MN ∥DE,∠NMB=∠B=45°,∴NB=NM,NF=NB-FB=MN-x∵MN ∥DE ∴△FMN ∽FED,∴FD FNDE MN =,即434x MN MN -=,∴x MN 233+= ①当20≤≤x 时,如图(4) ,设DE 与BC 相交于点G ,则DG=DB=4+x ∴x x x MN BF DG DB S S y BMF BGD 23321)4(2121212+⋅⋅-+=⋅⋅-⋅⋅=-=∆ 即844312+++-=x x y ; ②当3262-≤<x 时,如图(5),x x MN BF AC S S y BMFBCA 23321362121212+⋅-⨯=⋅⋅-⋅=-=∆ 即184332++-=x y ; ③当4326≤<-x 时, 如图(6) 设AC 与EF 交于点H, ∵AF=6-x ,∠AHF=∠E=30° ∴AH=)6(33x AF -=2)6(23)6(3)6(21x x x S y FHA -=-⋅-==∆综上所述,当20≤≤x 时,844312+++-=x x y 题25图(4)题25图(5)当3262-≤<x ,184332++-=x y 当4326≤<-x 时,2)6(23x y -=。
东莞市中考数学二模考试试卷有答案

东莞市2015届中考数学二模考试试卷(有答案)东莞市2015届中考数学二模考试试卷(有答案)一、选择题:(每题3分,共30分)1.-2的绝对值是()A.2B.-2C.0D.2.下列计算正确的是().A.B.C.D.3.人体中红细胞的直径约为0.0000077m,用科学记数法表示为()A.7.7B.7.7C.7.7D.4.如图所示支架(支架的两个台阶的高度和宽度都是同一长度)的主视图是()5.已知三角形两边的长分别是4和10,则此三角形的第三边长可能是().A.5B.6C.11D.166.要了解某市九年级学生的视力状况,从中抽查了500名学生的视力状况,那么样本是指()A.某市所有的九年级学生B.被抽查的500名九年级学生C.某市所有的九年级学生的视力状况D.被抽查的500名学生的视力状况7、如图,已知⊙0的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于()A.B.C.D.8.一元二次方程的根的情况是()A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.无实数根9.如图菱形中,,则菱形的周长为()A.20B.24C.28D.4010、在同一坐标系中,正比例函数y=—x与反比例函数y=的图象大致是()ABCD二.填空题(每题4分,共24分)11.函数中自变量x的取值范围。
12.一元二次方程的解是。
13.数组3、4、5的方差是14.因式分解:x3﹣2x2+x=.15.如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3则CE的长为。
16.如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为。
三、解答题:(每题6分,共18分)17.计算:18.解不等式组把解集在数轴上表示出来,并写出解集中的整数解.19.先化简,再求值:,再任选一个你喜欢的数代入求值. 四.解答题:(每题7分,共21分)20.某漆器厂接到制作480件漆器的订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多50%,结果提前10天完成任务.原来每天制作多少件?21.某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为.测得A,B之间的距离为4米,,,试求建筑物CD的高度.22.2014年5月,我市某中学举行了“中国梦校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:(1)参加演讲比赛的学生共有人,并把条形图补充完整;(2)扇形统计图中,m=,n=;C等级对应扇形的圆心角为度;(3)学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求获A等级的小明参加市比赛的概率.五、解答题:(每题9分,共27分)23.如图,已知⊙O上依次有A、B、C、D四个点,=,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.(1)若⊙O的半径为3,∠DAB=120°,求劣弧的长;(2)求证:BF=BD;(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.24.如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△DEC≌△EDA;(2)求DF的值;(3)如图2,若P为线段EC上一动点,过点P作△AEC 的内接矩形,使其定点Q落在线段AE上,定点M、N落在线段AC上,求当线段PE的长为何值时,矩形PQMN的面积最大?25.如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A 点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.(1)求该二次函数的解析式及点C的坐标;(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请写出E点坐标;.(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.2015届第二次模拟考试初三数学试卷一、选择题:(每题3分,共30分)1-5ACBCC6-10DBDAB二、填空题:(每题4分,共24分)11.x≠-112.x=0,x=213.14.15.616.36°三、解答题:(每题6分,共18分)17、解:原式=-1-27+41--4分=-24--618、不等式①,得:x<1,解不等式②,得:x≥……………2分所以不等式组的解集为:≤x<1.……4分解集中的整数解有.…………………………5分6 (6)19.解=÷(+)……………2分=÷……………3分=×=,……………4分把x=2代入原式==.……………6分四.解答题:(每题7分,共21分)20、解:设原来每天制作x件,根据题意得:……………1分﹣=10,……………4分解得:x=16,……………5分经检验x=16是原方程的解,……………6分答:原来每天制作16件……………7分21、解:设建筑物CD与EF的延长线交于点G,DG=x 米.…………1分在△中,,即.…………2分在△中,,即.…………3分∴,.∴∴.………5分解方程得:=19.2.………6分∴.答:建筑物高为20.4米.………7分五、解答题:(每题9分,共27分)22.解:(1)40,(2)10%40%144°(3)设A等级的小明用a表示,其他的几个学生用b、c、d表示.共有12种情况,其中小明参加的情况有6种,则P(小明参加比赛)==.23.(1)解:连接OB,OD,∵∠DAB=120°,∴所对圆心角的度数为240°,∴∠BOD=120°,∵⊙O的半径为3,∴劣弧的长为:×π×3=2π;……………3分(2)证明:连接AC,∵AB=BE,∴点B为AE的中点,∵F是EC的中点,∴BF为△EAC的中位线,∴BF=AC,∵=,∴+=+,∴=,∴BD=AC,∴BF=BD;……………6分(3)解:过点B作AE的垂线,与⊙O的交点即为所求的点P,……………7分∵BF为△EAC的中位线,∴BF∥AC,∴∠FBE=∠CAE,∵=,∴∠CAB=∠DBA,∵由作法可知BP⊥AE,∴∠GBP=∠FBP,∵G为BD的中点,∴BG=BD,∴BG=BF,在△PBG和△PBF中,,∴△PBG≌△PBF(SAS),∴PG=PF.……………9分24.(1)证明:由矩形的性质可知△ADC≌△CEA,∴AD=CE,DC=EA,∠ACD=∠CAE在△DEC与△EDA中∴△DEC≌△EDA(SSS);……………3分解:如图1,∵∠ACD=∠CAE,∴AF=CF,设DF=x,则AF=CF=4﹣x,在RT△ADF中,32+x2=(4﹣x)2,解得;x=,即DF=.……………6分(3)如图2,由矩形PQMN的性质得PQ∥CA∴又∵CE=3,AC==5设PE=x(0<x<3),则,即PQ=过E作EG⊥AC于G,则PN∥EG,∴=又∵在Rt△AEC中,EGAC=AECE,解得EG=∴=,即PN=(3﹣x)设矩形PQMN的面积为S则S=PQPN=﹣x2+4x=﹣+3(0<x<3)所以当x=,即PE=时,矩形PQMN的面积最大。
广东省2015年初中毕业生学业考试数学试卷(含答案)(WORD版)

机密★启用前2015年广东省初中毕业生学业考试数 学一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1. —5的相反数是( A )A. 5B. —5C.51D. 51-2. 地球半径约为6 400 000米,用科学记数法表示为( B )A. 0.64×107B. 6.4×106C. 64×105D. 640×1043. 数据8、8、6、5、6、1、6的众数是( C )A. 1B. 5C. 6D. 84. 如左图所示几何体的主视图是( B )5. 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( C )A. 5B. 6C. 11D. 16 二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上.6. 分解因式:2x 2 —10x = 2x (x —5) .7. 不等式3x —9>0的解集是 x>3 。
8. 如图,A 、B 、C 是⊙O 上的三个点,∠ABC = 250, 则∠AOC 的度数是 500 。
9. 若x 、y 为实数,且满足033=++-y x ,则2012⎪⎪⎭⎫⎝⎛y x 的值是 1 。
10. 如图,在□ABCD 中,AD =2,AB =4,∠A =300,以点A 为圆心,AD 的长为半径画弧交AB 于点E ,连结CE ,则阴影部分的面积是 π313- (结果保留π)。
A. B. C.D题4图ABCO题8图250300D CA E B三、解答题(一)(本大题5小题,每小题6分,共30分)11. 计算:()1028145sin 22-++--。
解:原式2112222+-⨯-= 21-= 12. 先化简,再求值:)2()3)(3(---+x x x x ,其中x = 4. 解:原式x x x 2922+--=92-=x当x = 4时,原式194292-=-⨯=-=x13. 解方程组:解:① + ②,得:4x = 20,∴ x = 5,把x = 5代入①,得:5—y = 4,∴ y = 1, ∴ 原方程组的解是⎩⎨⎧==15y x 。
广东东莞市东城旗峰学校2015届中考模拟测试题及答案

广东东莞市东城旗峰学校2015届中考模拟测试题(一)一、选择题(本大题5小题,每小题3分,共15分) 1、4的平方根是( ) A .2±B .2C .2±D .22、某校在“校园十佳歌手”比赛上,六位评委给1号选手的评分如下:90,96,91,96,95,94.那么,这组数据的众数和中位数分别是( )A .96,94.5B .96,95C .95,94.5D .95,95 3、图2是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )4、如图,已知AB∥CD,直线EF 分别交AB ,CD 于点E ,F , EG 平分∠BEF ,若∠1=5O°,则∠2的度数为( ).A.50°B.60°C.65°D.70°5、横跨深圳及香港之间的深圳湾大桥是中国唯一倾斜的独塔单索面桥,大桥全长4770米,这个数字用科学计数法表示为(保留两个有效数字)( )A .24710⨯B .34.710⨯C .34.810⨯D .35.010⨯一、填空题:(本大题5小题,每小题4分,共20分) 6、分解因式2233x y x y --- .7、如图,AB 是⊙O 的直径,点C 在⊙O 上 ,OD ∥BC ,若OD=1,则BC 的长为 . 8、关于的一元二次方程有两个实数根,则的取值范围是 .9、函数函数12-+=x x y 中自变量x 的取值范围是 . 10、如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是________三、解答题(一)(本大题5小题,每小题6分,共30分) ⒒计算:2202(3)( 3.14)8sin45π----+--︒.⒓解不等式组并写出该不等式组的最大整数解.⒔如图所示,ABC △是等边三角形, D 点是AC 的中点,延长BC 到E ,使CE CD =,(1)用尺规作图的方法,过D 点作DM BE ⊥,垂足是M (不写作法,保留作图痕迹); (2)求证:BM EM =.⒕如图,一次函数y kx b =+的图象与反比例函数my x=的图象相交于A 、B 两点 (1)根据图象,分别写出A 、B 的坐标; (2)求出两函数解析式;(3)根据图象回答:当x 为何值时,一次函数的函数值大于反比例函数的函数值.⒖如图,已知AB 是⊙O 的直径,锐角∠DAB 的平分线AC 交⊙O 于点C ,作CD ⊥AD ,垂足为D ,直线CD 与AB 的延长线交于点E . (1)求证:直线CD 为⊙O 的切线;(2)当AB =2BE ,且CE =3时,求AD 的长.四、解答题(二)(本大题4小题,每小题7分,共28分) ⒗如图10,利用一面墙,用80米长的篱笆围成一个矩形场地 (1)怎样围才能使矩形场地的面积为750平方米?(2)能否使所围的矩形场地面积为810平方米,为什么?ACB DEDABC O · E⒘有一个均匀的正六面体,六个面上分别标有数字1、2、3、4、5、6,随机地抛掷一次,把朝上一面的数字记为x ;另有三张背面完全相同,正面分别写有数字-2、-1、1的卡片,将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y ;然后计算出S =x +y 的值. (1)用树状图或列表法表示出S 的所有可能情况; (2)求当S <3时的概率.⒙如图,某电信公司计划修建一条连接B 、C 两地的电缆。
东莞2015届九年级上学期期末模拟考试数学试卷

广东省东莞市2015届九年级上学期期末数学模拟试卷一.选择题(每题3分,共30分,下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的,请把你认为正确结论的代号填入下面表格中)1.(3分)下列图形中,既是中心对称又是轴对称的图形是()A.B.C.D.2.(3分)下列事件中,必然发生的为()A.我市冬季比秋季的平均气温低B.走到车站公共汽车正好开过来C.打开电视机正转播奥运会实况D.掷一枚均匀硬币正面一定朝上3.(3分)在平面直角坐标系中,点P(2,﹣3)关于原点对称的点的坐标是()A.(2,3)B.(﹣2,3)C.(﹣2,﹣3)D.(﹣3,2)4.(3分)下列各式正确的是()A.B.C.D.5.(3分)一元二次方程x2﹣2x+3=0的根的情况是()A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.有两个实数根6.(3分)若⊙O1的半径为3cm,⊙O2的半径为4cm,且圆心距O1O1=1cm,则⊙O1与⊙O2的位置关系是()A.外离B.内切C.相交D.内含7.(3分)将二次函数化成y=a(x+m)2+n的形式是()A.B. C.D.8.(3分)某种商品零售价经过两次降价后,每件的价格由原来的800元降为现在的578元,则平均每次降价的百分率为()A.10% B.12% C.15% D.17%9.(3分)如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为()A.5﹕3 B.4﹕1 C.3﹕1 D.2﹕110.(3分)如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为()A.B.C.D.二.填空题(每题3分,共18分,直接填写结果)11.(3分)若式子在实数范围内有意义,则x的取值范围是.12.(3分)口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是.13.(3分)已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB=.14.(3分)将抛物线向左平移5个单位,再向上平移3个单位后得到的抛物线的解析式为.15.(3分)已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(﹣3,0),(2,0),则方程ax2+bx+c=0(a≠0)的解是.16.(3分)如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是元(结果保留整数).三.解答题(学好数学要有坚固的基础知识!本大题有4个小题,共34分)17.(8分)计算:18.(8分)解方程x(x﹣1)=2.有学生给出如下解法:∵x(x﹣1)=2=1×2=(﹣1)×(﹣2),∴,或,或,或.解上面第一、四方程组,无解;解第二、三方程组,得x=2或x=﹣1.∴x=2或x=﹣1.请问:这个解法对吗?试说明你的理由.如果你觉得这个解法不对,请你求出方程的解.19.(6分)如图,P为等边△ABC的中心.(1)画出将△ABP绕A逆时针旋转60°的图形;(不写画法,保留作图痕迹)(2)经过什么样的图形变换,可以把△ABP变换到右边的△CMN,请写出简要的文字说明.20.(12分)如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:(1)求线段AB的长及⊙C的半径;(2)求B点坐标及圆心C的坐标.四.解答题(学会用数学知识解决身边的实际问题!本大题有2个小题,共20分)21.(10分)在数学活动课上,同学们用一根长为1米的细绳围矩形.(1)小芳围出了一个面积为600cm2的矩形,请你算一算,她围成的矩形的边长是多少?(2)小华想用这根细绳围成一个面积尽可能大的矩形,请你用所学过的知识帮他分析应该怎么围,并求出最大面积?22.(10分)宝宝和贝贝是一对双胞胎,他们参加奥运志愿者选拔并与甲、乙、丙三人都进入了前5名.现从这5名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出:(1)宝宝和贝贝同时入选的概率;(2)宝宝和贝贝至少有一人入选的概率.五.解答题(学数学要善于观察思考,勇于探索!本大题有2个小题,共18分)23.(6分)先阅读,再回答问题:如果x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2,x1x2与系数a,b,c的关系是:x1+x2=﹣,x1x2=.例如:若x1,x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣=﹣=,x1x2===﹣.(1)若x1,x2是方程2x2+x﹣3=0的两个根,则x1+x2=,x1x2=;(2)若x1,x2是方程x2+x﹣3=0的两个根,求+的值.解:(1)x1+x2=,x1x2=.24.(12分)已知一条抛物线与y轴的交点为C,顶点为D,直线CD的解析式为y=x+3,并且线段CD的长为.(1)求这条抛物线的解析式;(2)设(1)中的抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在点B的左侧,求线段AB的长;(3)若以AB为直径作⊙M,请你判断直线CD与⊙M的位置关系,并说明理由.广东省东莞市2015届九年级上学期期末数学模拟试卷参考答案与试题解析一.选择题(每题3分,共30分,下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的,请把你认为正确结论的代号填入下面表格中)1.(3分)下列图形中,既是中心对称又是轴对称的图形是()A.B.C.D.考点:中心对称图形;轴对称图形;生活中的旋转现象.分析:根据轴对称图形与中心对称图形的概念求解.解答:解:A、不是轴对称图形,也不是中心对称图形;B、是轴对称图形,不是中心对称图形;C、是轴对称图形,也是中心对称图形;D、是轴对称图形,不是中心对称图形.故选C.点评:掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2.(3分)下列事件中,必然发生的为()A.我市冬季比秋季的平均气温低B.走到车站公共汽车正好开过来C.打开电视机正转播奥运会实况D.掷一枚均匀硬币正面一定朝上考点:随机事件.分析:必然事件就是一定发生的事件,即发生的概率是1的事件.解答:解:A、一定正确,为必然事件,故符合题意;B、C、D、可能发生,也可能不发生,为不确定事件,即随机事件,故不符合题意.故选A.点评:该题考查的是对必然事件的概念的理解.解决此类问题,要学会关注身边的事物,并用数学的思想和方法去分析、看待、解决问题,提高自身的数学素养.3.(3分)在平面直角坐标系中,点P(2,﹣3)关于原点对称的点的坐标是()A.(2,3)B.(﹣2,3)C.(﹣2,﹣3)D.(﹣3,2)考点:关于原点对称的点的坐标.分析:根据“平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y)”解答.解答:解:根据中心对称的性质,得点P(2,﹣3)关于原点对称的点的坐标是(﹣2,3).故选B.点评:关于原点对称的点坐标的关系,是需要识记的基本问题.记忆方法是结合平面直角坐标系的图形记忆.4.(3分)下列各式正确的是()A.B.C.D.考点:二次根式的乘除法;分母有理化;二次根式的加减法.分析:根据二次根式的相关运算法则分析判断各个选项.解答:解:A、结果应有,故错误;B、不是同类二次根式,不能合并,故错误;C、==×,正确D、结果应为,故错误.故选C.点评:熟练化简二次根式后,在加减的过程中,有同类二次根式的要合并;相乘的时候,被开方数简单的直接让被开方数相乘,再化简;较大的也可先化简,再相乘,灵活对待.5.(3分)一元二次方程x2﹣2x+3=0的根的情况是()A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.有两个实数根考点:根的判别式.专题:计算题.分析:根据根的判别式△=b2﹣4ac的符号来判定一元二次方程x2﹣2x+3=0的根的情况.解答:解:∵一元二次方程x2﹣2x+3=0的二次项系数a=1,一次项系数b=﹣2,常数项c=3,∴△=b2﹣4ac=4﹣12=﹣8<0,∴原方程无实数根.故选A.点评:本题考查了根的判别式,解题的关键是根据根的判别式的情况决定一元二次方程根的情况.6.(3分)若⊙O1的半径为3cm,⊙O2的半径为4cm,且圆心距O1O1=1cm,则⊙O1与⊙O2的位置关系是()A.外离B.内切C.相交D.内含考点:圆与圆的位置关系.专题:压轴题.分析:根据数量关系判断两圆的位置关系.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R﹣r<d<R+r;内切,则d=R﹣r;内含,则d<R﹣r.解答:解:依题意,得:r1﹣r2=4﹣3=1=O1O2,∴两圆内切.故选B.点评:本题主要考查根据数量关系来判断两圆的位置关系.7.(3分)将二次函数化成y=a(x+m)2+n的形式是()A.B. C.D.考点:二次函数的三种形式.分析:利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.解答:解:原式=(x2+4x﹣4)=(x2+4x+4﹣8)=(x+2)2﹣2故选A.点评:此题考查了二次函数一般式与顶点式的转换,解答此类问题时只要把函数式直接配方即可求解.8.(3分)某种商品零售价经过两次降价后,每件的价格由原来的800元降为现在的578元,则平均每次降价的百分率为()A.10% B.12% C.15% D.17%考点:一元二次方程的应用.专题:增长率问题.分析:设平均每次降价的百分率为x,那么第一次降价后为800(1﹣x),第二次降价后为800(1﹣x)(1﹣x),然后根据每件的价格由原来的800元降为现在的578元即可列出方程,解方程即可.解答:解:设平均每次降价的百分率为x,依题意得800(1﹣x)2=578,∴(1﹣x)2=∴1﹣x=±0.85,∴x=0.15=15%或x=1.85(舍去).答:平均每次降价的百分率为15%.故选C.点评:此题主要考查了增长率的问题,一般公式为原来的量×(1±x)2=后来的量,增长用+,减少用﹣.9.(3分)如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为()A.5﹕3 B.4﹕1 C.3﹕1 D.2﹕1考点:正多边形和圆.分析:连接OA、OP、OB,根据正六边形及等腰三角形的性质解答即可.解答:解:连接OA、OP、OB;∵向日葵图案是用等分圆周画出的,∴此圆内接多边形是正六边形,∴∠AOB=60°;∵△AOB是等腰三角形,P为AB边的中点,∴∠AOP=∠AOB=30°,△AOP是直角三角形,∴AP=OA,即⊙O与半圆P的半径的比为2:1.故选D.点评:此题比较简单,考查的是正六边形的性质及等腰三角形的性质;解答此题的关键是作出辅助线,构造出等腰三角形及直角三角形.10.(3分)如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为()A.B.C.D.考点:二次函数图象与系数的关系.分析:由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.解答:解:∵a<0,∴抛物线的开口方向向下,故第三个选项错误;∵c<0,∴抛物线与y轴的交点为在y轴的负半轴上,故第一个选项错误;∵a<0、b>0,对称轴为x=>0,∴对称轴在y轴右侧,故第四个选项错误.故选B.点评:考查二次函数y=ax2+bx+c系数符号的确定.二.填空题(每题3分,共18分,直接填写结果)11.(3分)若式子在实数范围内有意义,则x的取值范围是x≥﹣5.考点:二次根式有意义的条件.分析:根据二次根式的定义可知被开方数必须为非负数,列不等式求解.解答:解:根据题意得:x+5≥0,解得x≥﹣5.点评:主要考查了二次根式的意义和性质.概念:式子(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.12.(3分)口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是0.3.考点:概率公式.专题:压轴题.分析:让1减去摸出红球和白球的概率即为所求的概率.解答:解:根据概率公式摸出黑球的概率是1﹣0.2﹣0.5=0.3.点评:用到的知识点为:各个部分的概率之和为1.13.(3分)已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB=6.考点:切线长定理.分析:根据切线长定理知:PA=PB,由此可求出PB的长.解答:解:∵PA、PB都是⊙O的切线,且A、B是切点;∴PA=PB,即PB=6.点评:此题考查的是切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.14.(3分)将抛物线向左平移5个单位,再向上平移3个单位后得到的抛物线的解析式为.考点:二次函数图象与几何变换.分析:根据二次函数图象左加右减,上加下减的平移规律进行求解.解答:解:抛物线向左平移5个单位,得:y=﹣(x﹣5+5)2+3=﹣x2+3;再向上平移3个单位,得:y=﹣x2+3+3=﹣x2+6.点评:主要考查的是函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.15.(3分)已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(﹣3,0),(2,0),则方程ax2+bx+c=0(a≠0)的解是x1=﹣3,x2=2.考点:抛物线与x轴的交点.专题:计算题.分析:根据抛物线与x轴的交点的意义得到当x=﹣3或x=2时,y=0,即可得到方程ax2+bx+c=0的解.解答:解:∵抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(﹣3,0),(2,0),∴当x=﹣3或x=2时,y=0,即方程ax2+bx+c=0的解为x1=﹣3,x2=2.故答案为x1=﹣3,x2=2.点评:本题考查了抛物线y=ax2+bx+c(a≠0)与x轴的交点:抛物线与x轴的交点的意义就是当x取交点的横坐标时,函数值y等于0,即方程ax2+bx+c=0的解为交点的横坐标.16.(3分)如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是566元(结果保留整数).考点:圆锥的计算.专题:应用题.分析:购买油毡所需要的费用=圆锥的侧面积×10.解答:解:购买油毡所需要的费用=2π×3×6÷2×10≈566元.点评:本题主要考查圆锥侧面积的求法,圆锥的侧面积=底面周长×母线长÷2.三.解答题(学好数学要有坚固的基础知识!本大题有4个小题,共34分)17.(8分)计算:考点:二次根式的混合运算.专题:计算题.分析:先把各二次根式化为最简二次根式,再进行计算.解答:解:原式=3+2﹣+﹣=5﹣.点评:本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.18.(8分)解方程x(x﹣1)=2.有学生给出如下解法:∵x(x﹣1)=2=1×2=(﹣1)×(﹣2),∴,或,或,或.解上面第一、四方程组,无解;解第二、三方程组,得x=2或x=﹣1.∴x=2或x=﹣1.请问:这个解法对吗?试说明你的理由.如果你觉得这个解法不对,请你求出方程的解.考点:解一元二次方程-因式分解法.专题:压轴题;阅读型.分析:用因式分解法解方程,必须将方程左边化为两个一次因式的乘积,而方程右边必须是0;显然题目所给出的做法不符合这样的要求,因此解法是错误的.正确的解法应该是先移项,然后用十字相乘法进行求解.解答:答:解法不对(1分);理由:用因式分解法解一元二次方程,方程左边必须为两个一次因式的乘积,而方程右边必须为0,显然这位同学的做法不符合这样的要求,故解法错误.(4分)解:原方程可化为:x2﹣x﹣2=0,(x﹣2)(x+1)=0,则x﹣2=0或x+1=0,解得x1=2或x2=﹣1.(8分)点评:只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程.分解因式时,要根据情况灵活运用学过的因式分解的几种方法.19.(6分)如图,P为等边△ABC的中心.(1)画出将△ABP绕A逆时针旋转60°的图形;(不写画法,保留作图痕迹)(2)经过什么样的图形变换,可以把△ABP变换到右边的△CMN,请写出简要的文字说明.考点:作图-旋转变换.专题:作图题.分析:(1)易得AB边将旋转到AC,那么向右做∠PAP′=60°,且AP′=AP,连接P′C,△AP′C就是将△ABP绕A逆时针旋转60°的图形;(2)易得转到(1)后再顺时针旋转90°后即可得到△CMN.解答:解:(1)(3分);(2)先将△ABP绕A逆时针旋转60°,然后再将△ACP绕C顺时针旋转90°(6分);本题也可以先旋转,后平移,方法略.点评:本题考查旋转作图,掌握画图的方法和图形的特点是解题的关键.20.(12分)如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:(1)求线段AB的长及⊙C的半径;(2)求B点坐标及圆心C的坐标.考点:垂径定理;坐标与图形性质;勾股定理.分析:(1)连接AB;由圆周角定理可知,AB必为⊙C的直径;Rt△ABO中,易知OA 的长,而∠OAB=∠ODB=60°,通过解直角三角形,即可求得斜边AB的长,也就求得了⊙C 的半径;(2)在Rt△ABO中,由勾股定理即可求得OB的长,进而可得到B点的坐标;过C分别作弦OA、OB的垂线,设垂足为E、F;根据垂径定理即可求出OE、OF的长,也就得到了圆心C的坐标.解答:解:(1)连接AB;∵∠ODB=∠OAB,∠ODB=60°∴∠OAB=60°,∵∠AOB是直角,∴AB是⊙C的直径,∠OBA=30°;∴AB=2OA=4,∴⊙C的半径r=2;(5分)(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,∴OB=,∴B的坐标为:(,0)(8分)过C点作CE⊥OA于E,CF⊥OB于F,由垂径定理得:OE=AE=1,OF=BF=,∴CE=,CF=1,∴C的坐标为(,1).(12分)点评:此题主要考查了圆周角定理、垂径定理、点的坐标意义、勾股定理等知识的综合应用能力,综合性较强,难度适中.四.解答题(学会用数学知识解决身边的实际问题!本大题有2个小题,共20分)21.(10分)在数学活动课上,同学们用一根长为1米的细绳围矩形.(1)小芳围出了一个面积为600cm2的矩形,请你算一算,她围成的矩形的边长是多少?(2)小华想用这根细绳围成一个面积尽可能大的矩形,请你用所学过的知识帮他分析应该怎么围,并求出最大面积?考点:二次函数的应用;二次函数的最值.分析:(1)已知细绳长是1米,则已知围成的矩形的周长是1米,设她围成的矩形的一边长为xcm,则相邻的边长是50﹣xcm.根据矩形的面积公式,即可列出方程,求解;(2)设围成矩形的一边长为xcm,面积为ycm2,根据矩形面积公式就可以表示成边长x的函数,根据函数的性质即可求解.解答:解:(1)设她围成的矩形的一边长为xcm,得:x(50﹣x)=600(2分),解得x1=20,x2=30,当x=20时,50﹣x=30cm;当x=30时,50﹣x=20cm,(4分)所以小芳围成的矩形的两邻边分别是20cm,30cm(5分)(2)设围成矩形的一边长为xcm,面积为ycm2,则有:y=x(50﹣x),即y=﹣x2+50x,y=﹣(x﹣25)2+625(8分)当x=25时,y最大值=625;此时,50﹣x=25,矩形成为正方形.即用这根细绳围成一个边长为25cm的正方形时,其面积最大,最大面积是625cm2(10分)点评:本题考查的是二次函数在实际生活中的应用,比较简单.并且通过本题要理解,最值问题的解决方法一般是转化为函数问题.22.(10分)宝宝和贝贝是一对双胞胎,他们参加奥运志愿者选拔并与甲、乙、丙三人都进入了前5名.现从这5名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出:(1)宝宝和贝贝同时入选的概率;(2)宝宝和贝贝至少有一人入选的概率.考点:列表法与树状图法.分析:因为此题需要两步完成,所以采用列表法或者采用树状图法都比较简单;列举出符合题意的各种情况的个数,再根据概率公式解答即可.解答:解:树形图如下:或列表如下:共20种情况(6分)(1)宝宝和贝贝同时入选的概率为(9分)(2)宝宝和贝贝至少有一人入选的概率为(12分)点评:考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.五.解答题(学数学要善于观察思考,勇于探索!本大题有2个小题,共18分)23.(6分)先阅读,再回答问题:如果x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2,x1x2与系数a,b,c的关系是:x1+x2=﹣,x1x2=.例如:若x1,x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣=﹣=,x1x2===﹣.(1)若x1,x2是方程2x2+x﹣3=0的两个根,则x1+x2=﹣,x1x2=﹣;(2)若x1,x2是方程x2+x﹣3=0的两个根,求+的值.解:(1)x1+x2=﹣1,x1x2=﹣3.考点:根与系数的关系.专题:阅读型.分析:(1)利用根与系数的关系可求出x1+x2,x1x2的值;(2)先求出x1+x2,x1x2的值,然后把+通分,再把x1+x2,x1x2的值代入计算即可.解答:解:(1)根据题意得x1+x2=﹣,x1x2=﹣.(2)∵x1+x2=﹣1,x1x2=﹣3,∴+===﹣.点评:如果x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2,x1x2与系数a,b,c的关系是:x1+x2=﹣,x1x2=.24.(12分)已知一条抛物线与y轴的交点为C,顶点为D,直线CD的解析式为y=x+3,并且线段CD的长为.(1)求这条抛物线的解析式;(2)设(1)中的抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在点B的左侧,求线段AB的长;(3)若以AB为直径作⊙M,请你判断直线CD与⊙M的位置关系,并说明理由.考点:二次函数综合题.专题:代数几何综合题.分析:(1)分类讨论:①抛物线过C(0,3),D1(﹣3,0)时;②抛物线过C(0,3),D2(3,6)时,利用待定系数法求二次函数的解析式;(2)利用(1)中的抛物线的图象知:抛物线与x轴有两个交点只有②;然后求得该抛物线与x轴的两个顶点坐标A(,0)、B(,0);最后由两点间的距离公式来求线段AB的长;(3)直线CD与⊙M相切.过M作MG⊥CD于G.由已知和(2)推知M(3,0),然后根据勾股定理的逆定理证得此结论.解答:解:(1)由已知可得:C(0,3),D1(﹣3,0),D2(3,6)…2分①抛物线过C(0,3),D1(﹣3,0)时,设y1=a(x+3)2过(0,3)∴a=…3分∴…4分②抛物线过C(0,3),D2(3,6)时设y2=a(x﹣3)2+6过(0,3)∴a=…5分∴…6分(2)(1)中的抛物线与x轴有两个交点只有②…7分即令得∴A(,0)、B(,0)…8分∴|AB|=…9分(或者不解方程,直接计算|AB|=)(3)直线CD与⊙M相切.…10分图象及图形如图所示.过M作MG⊥CD于G,由已知和(2)知M(3,0)∴MG=CD==…11分∴直线CD与⊙M相切.…12分(答案仅参考,若有不同解法,过程和解法都正确,可相应给分)点评:本题考查了二次函数的综合题.解答(1)时,注意要分类讨论,以防漏解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年广东省东莞市中考数学模拟试卷(七)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.(3分)(2012•安徽)下面的数中,与﹣3的和为0的是()
A.3B.﹣3 C.D.
2.(3分)(2012•安徽)计算(﹣2x2)3的结果是()
A.﹣2x5B.﹣8x6C.﹣2x6D.﹣8x5
3.(3分)(2012•安徽)给甲乙丙三人打电话,若打电话的顺序是任意的,则第一个打电话给甲的概率为()
A.B.C.D.
4.(3分)(2006•临安市)某青年排球队12名队员的年龄情况如表:
年龄18 19 20 21 22
人数 1 4 3 2 2
则这个队队员年龄的众数和中位数是()
A.19,20 B.19,19 C.19,20.5 D.20,19
5.(3分)(2015•广东模拟)地球与月球的距离约为384000千米,这个数据可用科学记数法表示为()
A.3.84×104千米B.3.84×105千米C.3.84×106千米D.38.4×104千米
6.(3分)(2011•内江)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是()
A.32°B.58°C.68°D.60°
7.(3分)(2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为()
A . 2a 2
B . 3a 2
C . 4a 2
D . 5a 2 8.(3分)(2014•南通)化简
的结果是( A . x +1 B . x ﹣1 C . ﹣x D . x
9.(3分)(2012•安徽)如图,A 点在半径为2的⊙O 上,过线段OA 上的一点P 作直线l ,与⊙O 过A 点的切线交于点B ,且∠APB=60°,设OP=x ,则△PAB 的面积y 关于x 的函数图象大致是( )
A .
B .
C .
D .
10.(3分)(2012•包头)如图,过▱ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH ,那么图中的▱AEMG 的面积S 1与▱HCFM 的面积S 2的大小关系是( )
A . S 1>S 2
B . S 1<S 2
C . S 1=S 2
D . 2S 1=S 2
二、填空题(本大题共6小题,每小题4分,满分24分)
11.(4分)(2015•东莞模拟)到原点距离等于
的实数为
.
12.(4分)(2011•东营)分解因式:x 2y ﹣2xy+y= .
13.(4分)(2015•东莞模拟)一个角的余角比这个角的补角的一半小40°,则这个角为 度.
14.(4分)(2015•东莞模拟)将正方形与直角三角形纸片按如图所示方式叠放在一起,已知正方形的边长为20cm ,点O 为正方形的中心,AB=5cm ,则CD 的长为 cm .
15.(4分)(2005•四川)如果记y==f(x),并且f(1)表示当x=1时y的值,即f (1)==;f()表示当x=时y的值,即f()==,那么f(1)
+f(2)+f()+f(3)+f()+…+f(n)+f()=.(结果用含n的代数式表示,n为正整数).
16.(4分)(2015•东莞模拟)如图是圆心角为30°,半径分别是1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为S1、S2、S3、…,则S n=.(结果保留π)
三、解答题(本大题共3小题,每小题6分,满分18分)
17.(6分)(2015•东莞模拟)﹣2cos45°﹣(2014﹣π)0﹣()﹣1.
18.(6分)(2012•珠海)如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE 的平分线.
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)
19.(6分)(2015•东莞模拟)一个工程队修一条3000米的公路,由于施工中途增加了人员,实际每天修路比原来多50%,结果提前2天完成,求实际每天修路多少?
四、解答题(本大题共3小题,每小题7分,满分21分)
20.(7分)(2012•安徽)在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f,
(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:
m n m+n f
1 2 3 2
1 3 4 3
2 3 5 4
2 5 7
3 4 7
猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n的关系式是(不需要证明);
(2)当m、n不互质时,请画图验证你猜想的关系式是否依然成立.
21.(7分)(2009•宝安区二模)如图,AB是△ABC外接圆⊙O的直径,D是AB延长线上一点,且BD=AB,∠A=30°,CE⊥AB于E,过C的直径交⊙O于点F,连接CD、BF、
EF.
(1)求证:CD是⊙O的切线;
(2)求:tan∠BFE的值.
22.(7分)(2015•东莞模拟)如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.
(1)求∠COD度数;
(2)求证:四边形ODAC是菱形.
五、解答题(本大题共3小题,每小题9分,满分27分)
23.(9分)(2014•从化市一模)为促进资源节约型和环境友好型社会建设,根据国家发改委实施“阶梯电价”的有关文件要求,广州市决定从2012年7月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准(非夏季标准)见下表:
一户居民一个月用电量的范围电费价格(单位:元/千瓦时)
不超过200千瓦时的部分0.61
超过200千瓦时,但不超过400千瓦时的部分0.66
超过400千瓦时的部分0.91
(1)如果小明家3月用电120度,则需交电费多少元?
(2)求“超过200千瓦时,但不超过400千瓦时的部分”每月电费y(元)与用电量x(千瓦时)之间的函数关系式;
(3)试行“阶梯电价”收费以后,小明家用电量多少千瓦时,其当月的平均电价每千瓦时不超过0.71元?
24.(9分)(2011•岳阳)如图1,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一
起.
(1)操作:如图2,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F 在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BH•GD=BF2
(2)操作:如图3,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG=.请予证明.
25.(9分)(2007•金华)如图1,在平面直角坐标系中,已知点A(0,4),点B在x 正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
(1)求直线AB的解析式;
(2)求等边△PMN的边长(用t的代数式表示),并求出当等边△PMN的顶点M运动到与原点O重合时t的值;
(3)如果取OB的中点D,以OD为边在Rt△AOB内部作如图2所示的矩形ODCE,点C 在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S 与t的函数关系式,并求出S的最大值.。
