最新高中数学易错易混易忘题分类汇编

高考数学易错易误易忘题分类汇总及解析(61页)

f
1
x
1
1 x 1 2 1
2x 1 x
再求
y f 1 x 1 的反函数得 g x 2 x 。正确答案：B
1 x
【知识点分类点拔】函数 y f 1 x 1 与函数 y f x 1 并不互为反函数，他只是表示
f 1 x 中 x 用 x-1 替代后的反函数值。这是因为由求反函数的过程来看：设 y f x 1 则
答案：B 【易错点 4】求反函数与反函数值错位
例 4、已知函数 f x 1 2x ，函数 y g x的图像与 y f 1 x 1 的图象关于直线
1 x
y x 对称，则 y g x的解析式为（）
A、 g x 3 2x B、 g x 2 x C、 g x 1 x D、 g x 3
4
4
28
8
28
+ 因此当 x=-1 时 x2+y2 有最小值 1, 当 x=- 时，x2+y2 有最大值。故 x2+y2 的取值范围是[1,
3
3
3
28
]
3
【知识点归类点拔】事实上我们可以从解析几何的角度来理解条件 x 2 2 y2 1对 x、y 的限制，
4
显然方程表示以（-2，0）为中心的椭圆，则易知-3≤x≤-1， 2 y 2 。此外本题还可通过三角换元
x 的取值范围为（）A、 ( a2 1, ) 2a
(a, )
B、 (, a2 1) 2a
a2 1
C、 (
, a)
D、
2a
答案：A （ a 1 时， f x单调增函数，所以 f 1 x 1 f f 1 x f 1 x f 1 a2 1 .） 2a
【易错点 7】证明或判断函数的单调性要从定义出发，注意步骤的规范性及树立定义域优先的原则。

高中高考数学易错易混易忘题分类汇总及解析

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设{}2|8150A x x x =-+=，{}|10B x ax =-=，若A B B =I ，求实数a 组成的集合的子集有多少个？【易错点分析】此题由条件A B B =I 易知B A ⊆，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。

解析：集合A 化简得{}3,5A =，由A B B =I知B A ⊆故（Ⅰ）当B φ=时，即方程10ax -=无解，此时a=0符合已知条件（Ⅱ）当B φ≠时，即方程10ax -=的解为3或5，代入得13a =或15。

综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭，故其子集共有328=个。

【知识点归类点拔】（1）在应用条件A ∪B ＝Ｂ⇔A ∩B ＝Ａ⇔ＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：(){}22,|4A x y x y =+=，()()(){}222,|34B x y x y r =-+-=，其中0r >,若A B φ=I 求r 的取值范围。

高中数学高频错题总结 (含例题答案)

高一上学期易错陷阱总结1、对数型函数中，（易忽略真数位置大于0）5．已知y ＝log a (2－ax )在[0,1]上为减函数，则a 的取值范围为( ) A ．(0,1) B ．(1,2) C ．(0,2) D ．[2，＋∞) 2、集合中，空集的特殊性（易忘记讨论空集）13．已知集合A ＝{x |2a ＋1≤x ≤3a －5}，B ＝{x |x ＜－1，或x ＞16}，分别根据下列条件求实数a 的取值范围． (1)A ∩B ＝∅； (2)A ⊆(A ∩B )． 3、集合中，元素的互异性（易忽略导致取值错误）[例2] 已知集合⎩⎨⎧⎭⎬⎫1，a ，b a ＝{0，a 2，a ＋b }，求a 2 019＋b 2 020的值．跟踪探究 2.已知集合A ＝{2，x ，y }，B ＝{2x,2，y 2}且A ＝B ，求x ，y 的值．4、集合中，元素的特殊要求（比如：易忽略x等条件）跟踪探究 1.若集合A ＝{x |1≤x ≤3，x ∈N }，B ＝{x |x ≤2，x ∈N }，则A ∩B ＝( )A.{x |1≤x ≤2} B ．{x |x ≥1} C ．{2,3}D ．{1,2}5、抽象函数的定义域问题（定义域仅代表x ，括号内取值范围一致）14、函数的定义域为,则的定义域是___;函数的定义域为___.6、区间中默认a<b14.已知函数f （x ）=, x是偶函数，则a+b=7、换元法求值域类问题（易忽略换元后，t 的取值范围）(1)f (x ＋1)＝x ＋2x ，求f (x )的值域；8、动轴定区间类问题（分类讨论不重不漏）典型案例：求函数y ＝x 2－2ax －1在[0,2]上的最值．9同增异减求单调区间问题（对数型时不能忽略真数位置大于0）（多个区间，隔开）跟踪探究 2.求函数y ＝log 2(x 2－5x ＋6)的单调区间．10、分段函数单调性问题。

（易忽略结点处）13．已知函数f (x )＝⎩⎪⎨⎪⎧x 2－ax ＋4，(x ≤1)，－ax ＋3a －4，(x ＞1)且f (x )在R 上递减，则实数a 的取值范围________．11.解分式不等式。

高中高考数学易错易混易忘题分类汇总及解析

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设{}2|8150A x x x =-+=，{}|10B x ax =-=，若A B B =I ，求实数a 组成的集合的子集有多少个？【易错点分析】此题由条件A B B =I 易知B A ⊆，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。

解析：集合A 化简得{}3,5A =，由A B B =I知B A ⊆故（Ⅰ）当B φ=时，即方程10ax -=无解，此时a=0符合已知条件（Ⅱ）当Bφ≠时，即方程10ax -=的解为3或5，代入得13a =或15。

综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭，故其子集共有328=个。

【知识点归类点拔】（1）在应用条件A ∪B ＝Ｂ⇔A ∩B ＝Ａ⇔ＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：(){}22,|4A x y xy =+=，()()(){}222,|34B x y x y r =-+-=，其中0r >,若A B φ=I 求r的取值范围。

高中高考数学易错易混易忘题分类汇总及解析【精华版】

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设{}2|8150A x x x =-+=，{}|10B x ax =-=，若A B B =，求实数a 组成的集合的子集有多少个？【易错点分析】此题由条件A B B =易知B A ⊆，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。

解析：集合A 化简得{}3,5A =，由A B B =知B A ⊆故（Ⅰ）当B φ=时，即方程10ax -=无解，此时a=0符合已知条件（Ⅱ）当Bφ≠时，即方程10ax -=的解为3或5，代入得13a =或15。

综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭，故其子集共有328=个。

【知识点归类点拔】（1）在应用条件A ∪B ＝Ｂ⇔A ∩B ＝Ａ⇔ＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：(){}22,|4A x y x y =+=，()()(){}222,|34B x y x y r =-+-=，其中0r >,若A B φ=求r 的取值范围。

高中数学易错、易混、易忘题分类汇编二

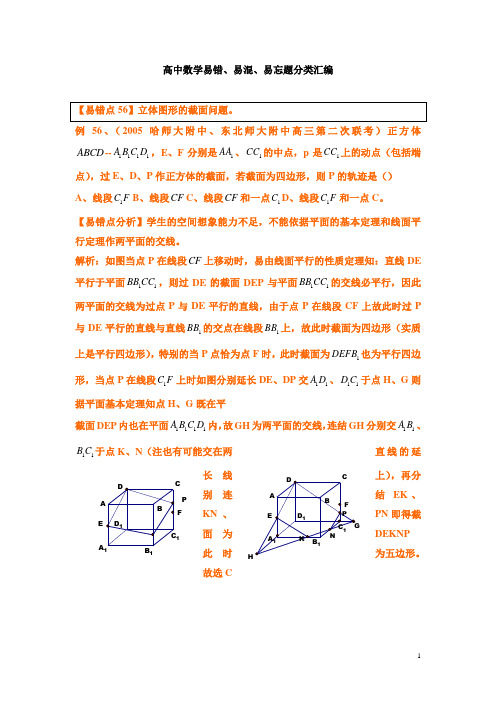
高中数学易错、易混、易忘题分类汇编【易错点56】立体图形的截面问题。

例56、（2005哈师大附中、东北师大附中高三第二次联考）正方体ABCD --1111A B C D ，E 、F 分别是1AA 、1CC 的中点，p 是1CC 上的动点（包括端点），过E 、D 、P 作正方体的截面，若截面为四边形，则P 的轨迹是（） A 、线段1C F B 、线段CF C 、线段CF 和一点1C D 、线段1C F 和一点C 。

【易错点分析】学生的空间想象能力不足，不能依据平面的基本定理和线面平行定理作两平面的交线。

解析：如图当点P 在线段CF 上移动时，易由线面平行的性质定理知：直线DE 平行于平面11BB CC ，则过DE 的截面DEP 与平面11BB CC 的交线必平行，因此两平面的交线为过点P 与DE 平行的直线，由于点P 在线段CF 上故此时过P 与DE 平行的直线与直线1BB 的交点在线段1BB 上，故此时截面为四边形（实质上是平行四边形），特别的当P 点恰为点F 时，此时截面为1DEFB 也为平行四边形，当点P 在线段1C F 上时如图分别延长DE 、DP 交11A D 、11D C 于点H 、G 则据平面基本定理知点H 、G 既在平截面DEP 内也在平面1111A B C D 内，故GH 为两平面的交线，连结GH 分别交11A B 、11B C 于点K 、N （注也有可能交在两直线的延长线上），再分别连结EK 、KN 、PN 即得截面为DEKNP 此时为五边形。

故选CP FE D 1C 11A 1BD KN HGP FE D 1C 1B 1A 1BD A【知识点归类点拔】高考对用一平面去截一立体图形所得平面图形的考查实质上对学生空间想象能力及对平面基本定理及线面平行与面面平行的性质定理的考查。

考生往往对这一类型的题感到吃力，实质上高中阶段对作截面的方法无非有如下两种：一种是利有平面的基本定理：一个就是一条直线上有两点在一平面内则这条直线上所在的点都在这平面内和两平面相交有且仅有一条通过该公共点的直线（即交线）（注意该定理地应用如证明诸线共点的方法：先证明其中两线相交，再证明此交点在第三条直线上即转化为此点为两平面的公共点而第三条直线是两平的交线则依据定理知交点在第三条直线；诸点共线：即证明此诸点都是某两平面的共公点即这此点转化为在两平的交线上）据这两种定理要做两平面的交线可在两平面内通过空间想象分别取两组直线分别相交，则其交点必为两平面的公共点，并且两交点的连线即为两平的交线。

高中高考数学易错易混易忘题分类汇总及解析

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设，，若，求实数a组成的集合的子集有多少个？【易错点分析】此题由条件易知，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a值产生漏解现象。

解析：集合A化简得，由知故（Ⅰ）当时，即方程无解，此时a=0符合已知条件（Ⅱ）当时，即方程的解为3或5，代入得或。

综上满足条件的a组成的集合为，故其子集共有个。

【知识点归类点拔】（1）在应用条件A∪B＝ＢA∩B＝ＡＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：，，其中 ,若求r的取值范围。

将集合所表达的数学语言向自然语言进行转化就是：集合A表示以原点为圆心以2的半径的圆，集合B表示以（3，4）为圆心，以r为半径的圆，当两圆无公共点即两圆相离或内含时，求半径r的取值范围。

思维马上就可利用两圆的位置关系来解答。

此外如不等式的解集等也要注意集合语言的应用。

【练1】已知集合、，若，则实数a的取值范围是。

答案：或。

【易错点2】求解函数值域或单调区间易忽视定义域优先的原则。

高考数学易错题型全归纳

高考数学易错题型全归纳
高考数学易错题型有很多，这里列出了一些常见的类型：
1. 集合问题：这类问题通常涉及对集合的理解，如交集、并集、补集等。

学生容易混淆这些概念，导致错误。

2. 函数性质理解：对于函数的单调性、奇偶性、周期性等性质，学生可能理解不透彻，导致在判断或应用时出错。

3. 等差数列和等比数列的性质理解：等差数列和等比数列是高中数学的重点内容，但学生容易在理解其性质和应用上出错。

4. 三角函数的性质：三角函数具有多种性质，如周期性、单调性、奇偶性等，学生可能对其中某些性质掌握不够，导致解题出错。

5. 立体几何中的空间想象：立体几何需要学生有一定的空间想象能力，对于空间中点、线、面的关系能够准确判断。

但学生往往由于缺乏这种能力而出错。

6. 解析几何中的问题：解析几何涉及直线、圆、椭圆等图形，学生可能在理解这些图形的性质和应用上出错。

7. 概率和统计问题：概率和统计是高考数学的必考内容，学生需要掌握各种概率和统计的基本概念和方法，一旦混淆就可能导致错误。

8. 不等式的性质和应用：不等式是高中数学的重要内容，但学生可能对不等式的性质和应用掌握不够，导致解题出错。

9. 数列的通项和求和公式：数列的通项和求和公式是高考数学的常见考点，学生需要准确理解和掌握这些公式，否则在解题时容易出现错误。

以上只是高考数学中可能出现的一些易错题型，实际上还有很多其他的问题，学生在备考时应全面复习，熟练掌握各种知识点，以应对各种题型。

高考数学66个易混易错点汇总

一、集合与函数1.进行集合的交、并、补运算时，不要忘了全集和空集的特殊情况，不要忘记了借助数轴和文氏图进行求解。

2.在应用条件时，易忽略是空集的情况3.你会用补集的思想解决有关问题吗?4.简单命题与复合命题有什么区别?四种命题之间的相互关系是什么?如何判断充分与必要条件?5.你知道“否命题”与“命题的否定形式”的区别。

6.求解与函数有关的问题易忽略定义域优先的原则。

7.判断函数奇偶性时，易忽略检验函数定义域是否关于原点对称。

8.求一个函数的解析式和一个函数的反函数时，易忽略标注该函数的定义域。

9.原函数在区间[-a，a]上单调递增，则一定存在反函数，且反函数也单调递增;但一个函数存在反函数，此函数不一定单调。

10.你熟练地掌握了函数单调性的证明方法吗?定义法(取值，作差，判正负)和导数法。

11.求函数单调性时，易错误地在多个单调区间之间添加符号“∪”和“或”;单调区间不能用集合或不等式表示。

12.求函数的值域必须先求函数的定义域。

13.如何应用函数的单调性与奇偶性解题?①比较函数值的大小;②解抽象函数不等式;③求参数的范围(恒成立问题)。

这几种基本应用你掌握了吗?14.解对数函数问题时，你注意到真数与底数的限制条件了吗?(真数大于零，底数大于零且不等于1)字母底数还需讨论15.三个二次(哪三个二次?)的关系及应用掌握了吗?如何利用二次函数求最值?16.用换元法解题时易忽略换元前后的等价性，易忽略参数的范围。

17.“实系数一元二次方程有实数解”转化时，你是否注意到：当时，“方程有解”不能转化为。

若原题中没有指出是二次方程，二次函数或二次不等式，你是否考虑到二次项系数可能为的零的情形?二、不等式18.利用均值不等式求最值时，你是否注意到：“一正;二定;三等”。

19.绝对值不等式的解法及其几何意义是什么?20.解分式不等式应注意什么问题?用“根轴法”解整式(分式)不等式的注意事项是什么?21.解含参数不等式的通法是“定义域为前提，函数的单调性为基础，分类讨论是关键”，注意解完之后要写上：“综上，原不等式的解集是……”。

高考数学易错易混易忘题分类汇总

高考易错易混易忘题分类汇总例1、设{}2|8150A x x x =-+=，{}|10B xa x =-=，若A B B = ，求实数a 组成的集合的子集个数？例2、已知()22214y x ++=,求22x y +的取值范围。

例3、 ()2112x xa f x ⋅-=+是R 上的奇函数，（1）求a 的值（2）求的反函数()1f x -。

例4、已知函数()121x f x x-=+，函数()y g x =的图像与()11y f x -=-的图象关于直线y x =对称，则()y g x =的解析式为（）A 、()32x g x x -=B 、()21x g x x -=+C 、()12xg x x-=+ D 、()32g x x =+例5、判断函数()2lg 1()22x f x x -=--的奇偶性。

例6、函数()2221211l o g 22x x f x x x -+⎛⎫=<-> ⎪⎝⎭或的反函数为()1f x -，证明()1f x -是奇函数且在定义域上是增函数。

例7、试判断函数()()0,0bf x a x a b x=+>>的单调性并给出证明。

例8、已知函数()3231f x a x x x =+-+上是减函数，求a 的取值范围。

例9、已知：a>0 , b>0 , a+b=1,求(a+a1)2+(b+b1)2的最小值。

例10、是否存在实数a 使函数()2l o g a x xaf x -=在[]2,4上是增函数？若存在求出a 的值，若不存在，说明理由。

例11、已知1sin sin 3x y +=求2s in c o s y x -的最大值。

例12、数列{}n a 前n 项和s 且1111,3n n a a s +==。

（1）求234,,a a a 的值及数列{}n a 的通项公式。

例13、等差数列{}n a 的首项10a >，前n 项和s，当lm ≠时，m l s s =。

高中高考数学易错易混易忘题分类汇总及解析

1 x
称，则 y g x 的解析式为（）
A、 g x 3 2x B、 g x 2 x C、 g x 1 x D、 g x 3
x
1 x
2 x
2 x
【易错点分析】解答本题时易由 y g x 与 y f 1 x 1 互为反函数，而认为 y f 1 x 1 的
反函数是
函数 f
x
2x2
log2 2x1
x
1 或x 2
1 2
的反函数为
f
1
x
，证明 f 1
x
是奇函数且在
其定义域上是增函数。
【思维分析】可求 f 1 x 的表达式，再证明。若注意到 f 1 x 与 f x 具有相同的单调性和奇偶性，
只需研究原函数 f x 的单调性和奇偶性即可。
2 x 1
f 1(b) a f (a) b 。
【练 6】（1）（99 全国高考题）已知 f (x) ex ex ，则如下结论正确的是（） 2
4
A、 f x 是奇函数且为增函数
B、 f x 是奇函数且为减函数
C、 f x 是偶函数且为增函数
D、 f x 是偶函数且为减函数
答案：A
（2）（2005 天津卷）设 f 1 x 是函数 f x 1 ax ax a 1 的反函数，则使 f 1 x 1 成立的 x 的 2
b a
和
b a
,
0
上分别为减函数.
【知识归类点拔】（1）函数的单调性广泛应用于比较大小、解不等式、求参数的范围、最值等问题中，应引起足够重视。
（2）单调性的定义等价于如下形式： f x 在a,b 上是增函数 f x1 f x2 0 ， f x 在
x1 x2
f a,b 上是减函数

高中高考数学易错易混易忘题分类汇总及解析

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设{}2|8150A x x x =-+=，{}|10B x ax =-=，若A B B =I ，求实数a 组成的集合的子集有多少个【易错点分析】此题由条件A B B =I 易知B A ⊆，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。

解析：集合A 化简得{}3,5A =，由A B B =I 知B A ⊆故（Ⅰ）当B φ=时，即方程10ax -=无解，此时a=0符合已知条件（Ⅱ）当Bφ≠时，即方程10ax -=的解为3或5，代入得13a =或15。

综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭，故其子集共有328=个。

【知识点归类点拔】（1）在应用条件A ∪B ＝Ｂ⇔A ∩B ＝Ａ⇔ＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：(){}22,|4A x y x y =+=，()()(){}222,|34B x y x y r =-+-=，其中0r >,若A B φ=I 求r 的取值范围。

高中数学易错易混易忘题分类汇编

【练 1】已知集合 A x | x2 4x 0 、 B x | x2 2a 1 x a2 1 0 ，若 B A，
则实数 a 的取值范围是
。答案： a 1 或 a 1。
【易错点 2】求解函数值域或单调区间易忽视定义域优先的原则。
例 2、已知 x 2 2 y2 1,求 x2 y2 的取值范围
言）和自然语言之间的转化如： A x, y | x2 y2 4 ，
B x, y | x 32 y 42 r2 ，其中 r 0 ,若 A B 求 r 的取值范围。将集合所表达
的数学语言向自然语言进行转化就是：集合 A 表示以原点为圆心以 2 的半径的圆，集合 B 表示以（3，4）为圆心，以 r 为半径的圆，当两圆无公共点即两圆相离或内含时，求半径 r 的取值范围。思维马上就可利用两圆的位置关系来解答。此外如不等式的解集等也要注意集合语言的应用。
b a
和
b a
,
0
上分别为减函数.
【知识归类点拔】（1）函数的单调性广泛应用于比较大小、解不等式、求参数的范围、最值等问题中，应引起足够重视。
（2）单调性的定义等价于如下形式： f x 在a,b 上是增函数 f x1 f x2 0 ， f x 在
x1 x2
f a,b 上是减函数
转化为三角最值求解。
【练
2】（05
高考重庆卷）若动点（x,y）在曲线
x2 4
y2 b2
1
b0
上变化，则 x2 2 y 的最大值为
（）
b2
40
（A） 4
2b b 4
b
4 （B）
b2
40
4
2b b 2
b
2 （C）
b2 4

汇总高中数学80个易错题大全

汇总高中数学80个易错点、易错题大全高中数学易错点梳理毀学中的粘警眾仲律茬般容品被您觇”这些陰斡羅件通常艘称为趣中的“附阱m解JS过秤巾一不小吧、at会押述去.車文列举出『岛屮课聿屮堕常葩陶關借点*井望同学fi在今匚的学习中引旦为贱.-、集合与简易邊辑易错点1对集合我示方法顼解存衽偏差【汨理】I: i21iM = |-il.r>0|^ = l v|y>ll T求川门用。

锚解I沖仃/<二e訓析：概念榄詡.未陡恵1E理狀坦會的♦:MLAA/J = fi2: ={} Lv = x + 2|^ = ((.v,y)lr+y:= 4). 4t-4Clfi.WM：AnB = K<\2)J~2t0)|正确普宪：冲仃J?手血刖析！荊题不慎*忽视优我兀劭*洪认対A为点集・反腿討集合班示注都分学生只風形说卜“胃賞，村瓜本展的理圳仃庄翅诊幕上的磧谡足不理悄生合曲注不i丛忽视坐合的代农兀橐.易钳点2在解含聲鯉锲合问题时惣机空擾【何壮】；L2^M=(A I 2^ < A <ci J t tf = [.V]-2<.V< l| T」丄a. a的取川范HL错駢’ [-L 0)剖析理视心0的怙况正他哄[-K 2]反恿；由F空集址_个箝蛛的集咋•它是任何集命的-fSr闕此对于集舍A匚ffffifr可旎理观fA=0."融解趣蜻卑钳谟〜尤共翠祀解舍参数的樂合诃题时・更应注意到叫塞数在臬*池同内奴值时，所鬻附騙會可貶是空坯时悄况。

考生巾于JHtt定式的康因.往注会在解題呻遗濫了这个集合，对致袴窠鹉段或碧案不住MiL易常点3庄解含穆嫂间题时忽视元養的互异性【讪醫】：己知隹5 + 2・仪7厂a2+ 3^+ 3人求实敌观的值*WW：«= -L-IJJ剂析=忽祝冗雀的”舁th 衣塑飞。

二—2时・+ = ?川"3引i '牛口― 一I时*d + 2 - ti-+ 3ZJ斗3二1辛均4、符合逓盘匸正临答系：£1=0反思t集合中的无裁尿有确宦性“巫异性*无序性.築會元索曲三性中的?L>f性对解屈杓齡响JS A-特别雄律参数的樂佥.实除上就18會？1附字埠参St的…些娶求®解题时可ifc求出字母参数的他再代人旳讣错点4命题的否定与否命懸美系不明【问幽】:马出“ K a童W理谊征P・回（1世M「|Fi的書命起、诩斛匸仰侖題为“卄中底M或ci底P「则存「切仃卩”制析=妣念機辎.片错阿类命盪他关累「鶴朋：仟命鬆为” n a G网阪e P•則a G M n H M剖脈知识不徒籃・gM或左住尸的書足也式应为册wAfLL/w尸E训吟絵科F E MH ME巴列。

2024年高考数学数列易错知识点总结

2024年高考数学数列易错知识点总结在2024年高考中，数学数列是一个常见的考点，也是一道容易出错的题型。

为了帮助考生顺利应对数列相关的考试题目，下面总结了一些常见的易错知识点。

一、等差数列的通项公式：等差数列是指数列中任意两项之间的差相等的数列。

它的通项公式为：$a_n = a_1 + (n-1)d$。

对于等差数列来说，考生容易犯的错误有：1. 弄混公差和公比。

公差指的是等差数列中任意两项之间的差，公比指的是等比数列中任意两项之间的比值。

考生在计算等差数列的时候，应该注意区分这两个概念。

2. 弄混首项和通项。

首项指的是数列中的第一项，通项指的是数列中第n项的表达式。

在计算等差数列的时候，考生应该注意首项和通项的区别。

3. 对于计算等差数列的题目，考生有时会直接套用公式，而忽略对问题的分析和推理。

在解题过程中，不应只关注于公式的使用，还应注重思考问题的本质，并结合实际情况进行合理的推理和分析。

二、等差数列的前n项和公式：等差数列的前n项和公式为：$S_n = \\frac{n}{2}(a_1 +a_n)$。

在计算等差数列前n项和的过程中，考生容易犯的错误有：1. 弄混首项和末项。

求前n项和的公式中，首项$a_1$和末项$a_n$都是需要用到的。

考生容易弄混这两个项，在计算过程中应该注意清楚。

2. 计算公式时漏写除以2。

前n项和的公式是$\\frac{n}{2}(a_1 + a_n)$，但考生在计算的时候经常漏写除以2的操作，导致结果错误。

3. 求前n项和时，考生有时对问题的理解不准确。

在一些应用题中，需要根据题目给出的条件和要求来求解前n项和。

考生如果对问题的理解不准确，很容易在计算过程中出错。

三、等比数列的通项公式：等比数列是指数列中任意两项之间的比值相等的数列。

它的通项公式为：$a_n = a_1 \\times q^{(n-1)}$。

对于等比数列来说，考生容易犯的错误有：1. 弄混公比和公差。

高中高考数学易错易混易忘题分类汇总及解析

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设{}2|8150A x xx =-+=，{}|10B x ax =-=，若A B B =I ，求实数a 组成的集合的子集有多少个？【易错点分析】此题由条件A B B =I 易知B A ⊆，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。

解析：集合A 化简得{}3,5A =，由A B B =I知B A ⊆故（Ⅰ）当B φ=时，即方程10ax -=无解，此时a=0符合已知条件（Ⅱ）当B φ≠时，即方程10ax -=的解为3或5，代入得13a =或15。

综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭，故其子集共有328=个。

【知识点归类点拔】（1）在应用条件A ∪B ＝Ｂ⇔A ∩B ＝Ａ⇔ＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：(){}22,|4A x y x y =+=，()()(){}222,|34B x y x y r =-+-=，其中0r >,若A B φ=I 求r 的取值范围。

高考数学易错易混易忘题分类汇总及解析(精华版)

高中高考数学易错易混易忘题分类汇总及解析“会而不对，对而不全”一直以来成为制约学生数学成绩提高的重要因素，成为学生挥之不去的痛，如何解决这个问题对决定学生的高考成败起着至关重要的作用。

本文结合笔者的多年高三教学经验精心挑选学生在考试中常见的66个易错、易混、易忘典型题目，这些问题也是高考中的热点和重点，做到力避偏、怪、难，进行精彩剖析并配以近几年的高考试题作为相应练习，一方面让你明确这样的问题在高考中确实存在，另一方面通过作针对性练习帮你识破命题者精心设计的陷阱，以达到授人以渔的目的，助你在高考中乘风破浪，实现自已的理想报负。

【易错点1】忽视空集是任何非空集合的子集导致思维不全面。

例1、设{}2|8150A x x x =-+=，{}|10B x ax =-=，若A B B =I ，求实数a 组成的集合的子集有多少个？【易错点分析】此题由条件A B B =I 易知B A ⊆，由于空集是任何非空集合的子集，但在解题中极易忽略这种特殊情况而造成求解满足条件的a 值产生漏解现象。

解析：集合A 化简得{}3,5A =，由A B B =I 知B A ⊆故（Ⅰ）当B φ=时，即方程10ax -=无解，此时a=0符合已知条件（Ⅱ）当Bφ≠时，即方程10ax -=的解为3或5，代入得13a =或15。

综上满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭，故其子集共有328=个。

【知识点归类点拔】（1）在应用条件A ∪B ＝Ｂ⇔A ∩B ＝Ａ⇔ＡＢ时，要树立起分类讨论的数学思想，将集合Ａ是空集Φ的情况优先进行讨论．（2）在解答集合问题时，要注意集合的性质“确定性、无序性、互异性”特别是互异性对集合元素的限制。

有时需要进行检验求解的结果是满足集合中元素的这个性质，此外，解题过程中要注意集合语言（数学语言）和自然语言之间的转化如：(){}22,|4A x y x y =+=，()()(){}222,|34B x y x y r =-+-=，其中0r >,若A B φ=I 求r 的取值范围。

高中数学易错、易混、易忘题分类汇编一

高中数学易错、易混、易忘题分类汇编【易错点42】向量与解析几何的交汇例42、（03年新课程高考）已知常数a>0，向量c=（0，a ），i=（1，0），经过原点O 以c+λi 为方向向量的直线与经过定点A （0，a ）以i －2λc 为方向向量的直线相交于点P ，其中λ∈R.试问：是否存在两个定点E 、F ，使得|PE|+|PF|为定值.若存在，求出E 、F 的坐标；若不存在，说明理由.【易错点分析】此题综合程度较高，一方面学生对题意的理解如对方向向量的概念的理解有误，另一面在向量的问题情景下不能很好的结合圆锥曲线的定义来解答，使思维陷入僵局。

解析：根据题设条件，首先求出点P 坐标满足的方程，据此再判断是否存在两定点，使得点P 到两定点距离的和为定值.∵i=（1，0），c=（0，a ）， ∴c+λi=（λ，a ），i －2λc=（1，－2λa ）因此，直线OP 和AP 的方程分别为 ax y =λ 和 ax a y λ2-=-.消去参数λ，得点),(y x P 的坐标满足方程222)(x a a y y -=-.整理得 .1)2()2(81222=-+aay x ……① 因为,0>a 所以得：（i ）当22=a 时，方程①是圆方程，故不存在合乎题意的定点E 和F ；（ii ）当220<<a 时，方程①表示椭圆，焦点)2,2121(2a a E -和)2,2121(2a a F --为合乎题意的两个定点；（iii ）当22>a 时，方程①也表示椭圆，焦点))21(21,0(2-+a a E 和))21(21,0(2--a a F 为合乎题意的两个定点.【知识点归类点拔】本小题主要考查平面向量的概念和计算,求轨迹的方法，椭圆的方程和性质，利用方程判定曲线的性质，曲线与方程的关系等解析几何的基本思想和综合解题能力。

在高考中向量与圆锥曲线的结合是成为高考命题的主旋律，在解题过程中一方面要注意在给出的向量问题情景中转化出来另一方面也要注意应用向量的坐标运算来解决解析几何问题如：线段的比值、长度、夹角特别是垂直、点共线等问题，提高自已应用向量知识解决解析几何问题的意识。