牛顿第二定律及其微分形式(精)
牛顿第二定律与动量定理的专题详解

牛顿第二定律与动量定理刍议广东省佛冈中学周长春在高中《物理》教材中,动量定理F·t=mv2-mv1,是由牛顿第二定律F=ma推导出来的,那么应如何准确地理解动量定理与牛顿第二定律呢?本文做一初浅的探讨。
一、动量定理是牛顿第二定律原来采用的形式在牛顿提出运动第二定律之前,伽利略在批判亚里士多德的力与速度的依赖关系的基础上,提出了力与加速度的依赖关系,但是他没有也不可能在当时的条件下发现作用力与加速度之间的定量关系。
在1684年8月之后,牛顿用几何法和极限概念论证了引力平方反比律,在为解决万有引力是否跟质量成正比的问题时,他发现了运动第二定律,具体的记载有两处,一处是在“论物体的运动”一文手稿中写道:“…动力与加速度的力之比等于运动与速度之比。
因为运动的量是由速度乘以物质的量导出的…”。
另一处是在《自然哲学的数学原理》的定义Ⅷ中给出的:“因为运动的量是由速度乘以物质的量求出来的,并且动力是由加速度的力乘以同一物质之量求出来的,物体的几个粒子上的加速的力的作用总和就是整个物体的动力”。
上面两段话中,“加速的力”指的是加速度,“运动”“运动的量”指的是动量,“动力”指的是与加速度对应的作用力,“物体”“物质的量”就是质量。
由此可知,牛顿在《自然哲学的数学原理》一书中已明确提出动量的定义:“运动量是用它的速度和质量一起来量度的”,“并把动量的变化率称之为力”,“他又用动量来表述运动第二定律”。
综上所述,牛顿其实已经提出了运动第二定律的文字表述:作用力与加速度成正比。
但当时牛顿并没有明确地用公式(F=ma)表述出来,牛顿第二定律原来采用的形式是力F、质量m、速度v和时间t这四个物理量,选择适当的单位,可使比例系数k=1,这时,牛顿第二定律可表示为①因此,牛顿第二运动定律的真实表述应该是物体所受外力等于其动量对时间的变化率。
①式也叫做牛顿第二定律的微分形式。
《自然哲学的数学原理》已经提出了作用力与加速度成正比,但当时牛顿并没有将公式①直接用F=ma表述出来,这是为什么呢?我国研究牛顿的资深学者阎康年先生在他的专著《牛顿的科学发现与科学思想》中专门研究了牛顿的质量观:“牛顿对质量概念的认识分静质量和动质量两个方面。
物理学第二章牛顿运动定律

l m
l
l
a2
m
a1
m
解:(1)以小球为研究对象,当小车沿水平方向作匀加速运
动时,分析受力:
在竖直方向小球加速度为零,水平方向的
T1
加速度为a。建立图示坐标系:
利用牛顿第二定律,列方程:
m
x方向: T1sinm1a
y方向: T 1co m s 0 g
解方程组,得到:
mg
直角坐标系中的分量形式
Fx mddvtx mdd2t2x
Fy mddvty
d2y mdt2
Fz mddvtz mdd2t2z
自然坐标系中的分量形式
Ft mat mddvt
Fn
man
mv2
2、牛顿第二定律的微分形式
牛顿第二定律原文意思:运动的变化与所加的动力成正 比,并且发生在这力所沿直线的方向上。
§2-1 牛顿第一定律和第三定律
1、牛顿第一定律
任何物体都保持静止或匀速直线运动的状态,直到其它物 体对它作用的力迫使它改变这种状态为止。
几点说明和注意
1、第一定律说明任何物体都具有惯性,牛顿第一定律又叫惯性 定律。
2、当物体受到其他物体作用时才会改变其运动状态,即其他物 体的作用是物体改变运动状态的原因。
大小:取决于绳的收紧程度。
T
方向:沿着绳指向绳收紧的方向。
(3)弹簧的弹力;
弹性限度内,弹性 力满足胡克定律:
Fkx
方向:指向要恢复 弹簧原长的方向。
O
x
F
F
3、 摩擦力
摩擦力:两个相互接触的物体在沿接触面相对运动
时,或者有相对运动趋势时,在它们的接触面间所 产生的一对阻碍相对运动或相对运动趋势的力。
牛二定律所有公式

牛顿第二定律所有公式牛顿第二定律是经典力学中的一个基本定律,它描述了力和加速度之间的关系。
牛顿第二定律可以用数学公式表达为:F=ma其中,F是作用在物体上的合外力,m是物体的质量,a是物体的加速度。
这个公式说明,物体的加速度与合外力成正比,与物体的质量成反比。
牛顿第二定律可以推导出许多其他的公式,用于解决不同情况下的力学问题。
下面我们介绍一些常见的牛顿第二定律的公式。
匀变速直线运动如果物体在直线上做匀变速运动,那么它的速度、位移和时间之间有如下关系:v=v0+ats=v0t+12at2v2=v20+2as其中,v是物体的末速度,v0是物体的初速度,s是物体在时间t内的位移,a是物体的加速度。
这些公式可以用牛顿第二定律和微积分推导出来。
圆周运动如果物体在圆周上做匀速运动,那么它的线速度、角速度和半径之间有如下关系:v=ωr其中,v是物体的线速度,ω是物体的角速度,r是圆周的半径。
这个公式可以用几何关系推导出来。
如果物体在圆周上做非匀速运动,那么它受到两个方向的加速度:向心加速度和切向加速度。
向心加速度指向圆心,切向加速度沿着切线方向。
这两个加速度和线速度、角速度和半径之间有如下关系:a c=v2r=ω2ra t=dvdt=rdωdt其中,a c是向心加速度,a t是切向加速度。
这些公式可以用牛顿第二定律和微积分推导出来。
受力平衡如果物体处于静止状态或匀速运动状态,那么它受到的合外力为零,即:∑F=0这个条件称为受力平衡条件,它可以用于求解静力学问题。
例如,如果一个物体悬挂在两根绳子上,那么它受到三个力:重力、绳子1的拉力、绳子2的拉力。
如果物体不动,那么这三个力必须平衡,即:F g+F1+F2=0其中,F g是重力,F1是绳子1的拉力,F2是绳子2的拉力。
这个方程可以用矢量相加或分解为水平和垂直分量来求解。
动量定理如果物体受到一个变化的力,在一段时间内从初速度变为末速度,那么它的动量也发生了变化。
牛顿定律积分形式(精)
单位:J/s W(瓦)
a , dA 0; 2 a , dA 0
2
②、功是过程量,只有物体的位置发生变化的过程 中才存在功。 ③、功的计算与参考系选择有关:同一个力对同一 质点在同一过程中作的功因参考系的不同而异。
2
, dA 0;
b dv A m d r m v d v a dt a a 1 1 1 2 v dv (v dv dv v ) d (v v ) d (v ) 2 2 2 b1 1 1 2 2 2 A md (v ) mv b mv a a 2 2 2 b
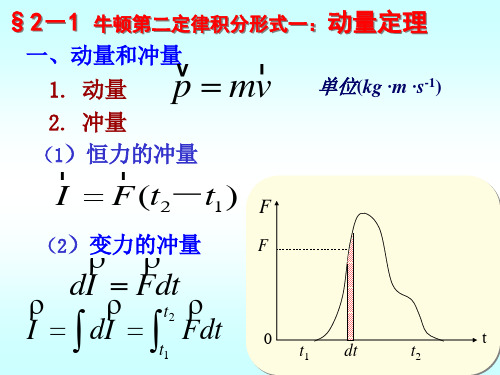
§2-1
牛顿第二定律积分形式一:动量定理
一、动量和冲量
1. 动量 2. 冲量 (1)恒力的冲量
p mv
单位(kg · m· s-1)
I F (t2-t1 )
(2)变力的冲量
F
F
t2 I dI Fdt
t1
dI Fdt
0
t1
dt
t2
t
二、 质点动量定理 由牛顿第二定 律微分形式
l l 2
1 2 1 2 1 2 l g l g mv lv 2 2 2 (2 l l ) v g
即:
s
v f v0
2 2
2
2
4 g sin
4g 4.1(m)
h s sin
v f vo
练习1、利用动能定理重做例题2-4。 解:如图所示,细棒下落过程中,合外力对它作的功为
应用动能定理,因初速 度为0,末速度v可求得如下
2
1 2 A (G B)dx ( l x) gdx l g l g 0 0 2
质点运动微分方程

质点运动微分方程
质点运动微分方程是描述质点在运动中位置、速度和加速度之间关系的微分方程。
根据牛顿第二定律,质点的加速度与作用在质点上的合力成正比,与质点的质量成反比。
因此,可以得到质点的运动微分方程为 F = ma,即 F(x(t), v(t), t) = m * v'(t),其中 F表示作用在质点上的合力,m表示质点的质量,v(t)表示质点的速度,x(t)表示质点的位移。
解决质点运动微分方程可以得到质点的速度和位移的函数表达式,从而可以进一步分析质点的运动规律和特性。
质点运动微分方程在物理学、工程学等领域中有广泛应用,例如在运动学、力学、电学、热学等方面,都需要使用微分方程来研究质点的运动。
- 1 -。
牛顿第二定律详解

牛顿第二定律详解实验:用控制变量法研究:a与F的关系,a与m的关系知识简析一、牛顿第二定律1.内容:物体的加速度跟物体所受合外力成正比,跟物体的质量成反比;a的方向与F合的方向总是相同。
2.表达式:F=ma揭示了:①力与a的因果关系,力是产生a的原因和改变物体运动状态的原因;②力与a的定量关系3、对牛顿第二定律理解:(1)F=ma中的F为物体所受到的合外力.(2)F=ma中的m,当对哪个物体受力分析,就是哪个物体的质量,当对一个系统(几个物体组成一个系统)做受力分析时,如果F是系统受到的合外力,则m是系统的合质量.(3)F=ma中的F与a有瞬时对应关系,F变a则变,F大小变,a则大小变,F方向变a也方向变.(4)F=ma中的F与a有矢量对应关系,a的方向一定与F的方向相同。
(5)F=ma中,可根据力的独立性原理求某个力产生的加速度,也可以求某一个方向合外力的加速度.(6)F=ma中,F的单位是牛顿,m的单位是kg,a的单位是米/秒2.(7)F=ma的适用范围:宏观、低速4. 理解时应应掌握以下几个特性。
(1) 矢量性F=ma是一个矢量方程,公式不但表示了大小关系,还表示了方向关系。
(2) 瞬时性a与F同时产生、同时变化、同时消失。
作用力突变,a的大小方向随着改变,是瞬时的对应关系。
(3) 独立性(力的独立作用原理) F合产生a合;Fx合产生ax合;Fy合产生ay合当物体受到几个力作用时,每个力各自独立地使物体产生一个加速度,就象其它力不存在一样,这个性质叫力的独立作用原理。
因此物体受到几个力作用,就产生几个加速度,物体实际的加速度就是这几个加速度的矢量和。
(4) 同体性F=ma中F、m、a各量必须对应同一个物体(5)局限性适用于惯性参考系(即所选参照物必须是静止或匀速直线运动的,一般取地面为参考系);只适用于宏观、低速运动情况,不适用于微观、高速情况。
牛顿运动定律的应用1.应用牛顿运动定律解题的一般步骤:(1) 选取研究对象(2) 分析所选对象在某状态(或某过程中)的受力情况、运动情况(3) 建立直角坐标:其中之一坐标轴沿的方向然后各力沿两轴方向正交分解(4) 列出运动学方程或第二定律方程F合=a合;Fx合=ax合;Fy合=ay合用a这个物理量把运动特点和受力特点联系起来(5) 在求解的过程中,注意解题过程和最后结果的检验,必要时对结果进行讨论.2.物理解题的一般步骤:(1) 审题:解题的关键,明确己知和侍求,特别是语言文字中隐着的条件(如:光滑、匀速、恰好追上、距离最大、共同速度等),看懂文句、及题述的物理现象、状态、过程。
高一物理章节内容课件 第二章质点动力学

地面的加速度是多少?(以竖直向上为
正)
解:以绳为参照系,设绳对地 的加速度为 a绳对地
T '
T a绳对地
人 T mg (ma绳对地) ma0 物 Mg T (Ma绳对地) M 0
Mg ♕ mg
▲ 注意:ห้องสมุดไป่ตู้于滑轮这种左右两边的情形, 左右两边的正方向应相反
3 a绳对地 g a0 方向:右向上,左向下
★ 作用于桌面的压力
N1 N m已落下部分g , 3gm已落下的部分
4. 质点系的动量定理 任意一段时间间隔内质点系所受合外力 的冲量等于在同一时间间隔内质点系内 所有质点的动量矢量和的增量。
5.动量守恒定律(Law of Conservation of Momentum) (1)※
度,是Vx
N mg CyVx2
N
CxVx2
m
dVx dt
(mg CyVx2 ) CxVx2
m dVx dx
dx dt
dx dt
(mg CyVx ) CxVx m
2
2 dVx dx
条件:Vx V0 90km/ h时,
Vx
N
0
mg
C yV02
解:★ 注意 摩此擦M力分r布F在整个圆盘上,因
第一步:在距轴为 r 处取质量元 dm ,它受到
的摩擦力为 df
df kdm g
方向:
df
r
第二步:求 df 产生的摩擦力矩 dM 大小、方向
dM rdf sin rkdm g 方向:沿轴
dm
m
R2
二体问题微分形式

二体问题微分形式二体问题是经典力学中的一个重要问题,研究的是两个质点之间的相互作用。
在这个问题中,我们假设两个质点的质量相互之间不可忽略,而其他外界因素对其运动没有影响。
这个问题可以通过微分形式来描述和求解。
在二体问题中,我们考虑两个质点的位置和速度随时间的变化关系。
我们可以用向量来表示质点的位置和速度,分别记为r1、r2和v1、v2。
根据牛顿第二定律,质点的加速度等于质点所受合力除以质量,即a1=F1/m1,a2=F2/m2。
这里F1和F2分别是质点1和质点2所受的合力,m1和m2是质点的质量。
在二体问题中,质点1和质点2之间的相互作用力可以由万有引力定律来描述。
根据万有引力定律,两个质点之间的引力大小与它们的质量和距离的平方成反比,方向沿着两个质点之间的连线。
因此,质点1所受的合力F1等于质点2对质点1的引力,质点2所受的合力F2等于质点1对质点2的引力。
根据上述分析,我们可以得到质点1和质点2的运动微分方程。
对于质点1,其位置和速度的变化率满足以下微分方程:dr1/dt = v1dv1/dt = F1/m1其中,dr1/dt表示质点1的位置随时间的变化率,即速度;dv1/dt表示质点1的速度随时间的变化率,即加速度。
同样地,对于质点2,其位置和速度的变化率满足以下微分方程:dr2/dt = v2dv2/dt = F2/m2通过求解上述四个微分方程,我们可以得到质点1和质点2的运动轨迹和速度随时间的变化规律。
在实际问题中,如果我们已知质点1和质点2的初始位置和速度,以及它们的质量,我们可以通过数值方法或解析方法求解这些微分方程,从而获得它们的运动轨迹。
二体问题在许多领域中都有重要的应用,特别是在天体力学中。
例如,太阳系中行星的运动可以看作是一个二体问题,太阳作为一个质点,行星作为另一个质点,它们之间通过万有引力相互作用。
通过研究二体问题,我们可以预测行星的运动轨迹和速度变化,从而更好地理解和解释天体运动的规律。
牛顿第二定律微分方程

牛顿第二定律微分方程全文共四篇示例,供读者参考第一篇示例:牛顿第二定律是经典力学中一个非常重要的定律,它描述了物体运动的动力学规律。
牛顿第二定律的数学表达形式为\[ F = ma \]F代表物体受到的合力,m是物体的质量,a是物体的加速度。
这个定律告诉我们,当一个物体受到一个力作用时,它会加速,而加速度的大小与受力的大小成正比,与物体的质量成反比。
在一些结构复杂的系统中,可能受到多个力的作用,牛顿第二定律的微分形式可以更好地描述这种情况。
使用微分方程描述物体的运动是一种非常重要的方法,通过微分方程可以更加精确地描述物体的加速度随时间的变化。
假设一个物体受到多个力的作用,这些力分别是\[ F_1, F_2,F_3, ..., F_n \],根据牛顿第二定律,物体的加速度可以表示为\[ a = \frac{\sum\limits_{i=1}^n F_i}{m} \]我们可以将受到的各个力拆解成不同的部分,比如重力,摩擦力等,最终得到微分方程的形式。
接下来,我们将对一个简单的例子进行分析,说明如何建立牛顿第二定律微分方程。
假设有一个质量为m的物体在水平面上运动,在受到一个恒定的外力F的作用下。
此时,物体受到的合力可以表示为\[ F_{\text{合}} = F - f \]f代表摩擦力,根据库仑摩擦定律,摩擦力大小正比于物体受力的大小,方向与物体的运动方向相反。
根据牛顿第二定律,物体的加速度可以表示为我们可以将摩擦力拆解成两部分,一部分是静摩擦力\[ f_s \],一部分是动摩擦力\[ f_k \]。
在物体刚开始运动时,摩擦力等于静摩擦力,此时静摩擦力可以表示为\[ \mu_s \]是静摩擦系数,N是物体受到的支持力。
如果外力F小于或等于静摩擦力,物体会保持静止;如果外力大于静摩擦力,物体就会开始运动,此时摩擦力等于动摩擦力。
动摩擦力可以表示为\[ \mu_k \]是动摩擦系数。
在这种情况下,物体的加速度可以表示为根据牛顿第二定律微分方程的形式,我们可以进一步将N表示为物体受到的支持力,支持力可以表示为\[ N = mg \],这里g是重力加速度。
世界10大公式

世界10大公式一、麦克斯韦方程组(电磁学)1. 公式内容。
- 积分形式:- ∮_S →D· d→S=∫_Vρ dV(高斯定律,表示通过任意闭合曲面的电位移通量等于该闭合曲面所包围的自由电荷的代数和)。
- ∮_S →B· d→S = 0(高斯磁定律,表明通过任意闭合曲面的磁通量恒为零,即磁场是无源场)。
- ∮_L→E· d→l=-(d)/(dt)∫_S→B· d→S(法拉第电磁感应定律,感应电动势与磁通量变化率的关系)。
- ∮_L→H· d→l=∫_S(→J+(∂→D)/(∂ t))· d→S(安培 - 麦克斯韦定律,磁场强度沿闭合回路的线积分等于穿过该回路所限定面积的全电流)。
- 微分形式:- ∇·→D=ρ- ∇·→B = 0- ∇×→E=-(∂→B)/(∂ t)- ∇×→H=→J+(∂→D)/(∂ t)2. 意义。
- 它统一了电学和磁学,揭示了电场和磁场之间的相互联系、相互转化的规律。
麦克斯韦方程组的建立是经典电磁学理论的集大成者,并且预言了电磁波的存在,为现代通信、电子技术等众多领域奠定了理论基础。
- 在高中物理选修3 - 4中会初步涉及电磁感应现象(法拉第电磁感应定律部分内容),在大学物理教材(如电磁学部分)会详细讲解麦克斯韦方程组的积分形式和微分形式。
二、欧拉公式(复变函数等多领域)1. 公式内容。
- e^iθ=cosθ + isinθ,当θ=π时,有著名的等式e^iπ+1 = 0。
2. 意义。
- 它将数学中最重要的几个常数e(自然对数的底数)、i(虚数单位)、π(圆周率)、1(自然数的基本单位)和0(代表无或起点等多种数学概念)联系在一起,体现了数学的简洁性和统一性。
在复变函数、信号处理、量子力学等众多领域有着广泛的应用。
3. 在人教版教材中的体现。
- 在高中数学选修2 - 2中会简单介绍复数的概念,在大学的复变函数教材中会深入讲解欧拉公式及其应用。
牛顿第二定律课件

所以,答案应选择B、C、D.
牛顿第二定律
1.在牛顿第二定律F=kma中,有关比例系数k的下列说 法,正确的是: A.在任何情况下k都等于1; B.k的数值是由质量、加速度和力的大小决定的; C.k的数值是由质量、加速度和力的单位决定的; D.在国际单位制中,k=1.
m成反比 牛顿第二定律
1.内容:物体加速度与合外力F合成正比.与质 量m成反比.加速度方向与合外力方向相同.
2.公式: F合=ma
3.注意点:矢量性,瞬时性,同时性和独力性.
∵
a∝
F m
∴ F ma
可写成等式为:F kma
k为比例常数。比例常数k与式中物理量单位的选取有关,
若各量的单位均用国际单位制中的单位,则k=1
(1)1牛顿(N)力的规定:
使质量是1千克的物体产生1米/秒2加速度的力,叫做1牛 顿。即: 1牛顿=1千克·米/秒2
(2)牛顿第二定律数学表达式为: F ma
4.独立性:(X方向的合外力产生X轴方向的加速
度,Y方向的合外产生Y轴方向的加速度, Fx=max Fy=may a2=a2x+a2y
此前我们所讲述的是物体只受到一个力作用的情况,物体受几 个力作用时,牛顿第二定律公式 F = ma 中的 F 表示合力,这样我 们可以把牛顿第二定律进一步表述为:
物体的加速度跟物体所受的合力成正比,跟
和速度均为零
例 题 :一个物体,质量是2 kg,受到互成120o角的两 个力 F1和 F2的作用,这两个力的大小都是10N,这个 物体 产生的加速度是多大? 用牛顿第二定律解题的一般步骤 :
牛顿第二定律与动量定理的专题详解

牛顿第二定律与动量定理刍议广东省佛冈中学周长春在高中《物理》教材中,动量定理F·t=mv2-mv1,是由牛顿第二定律F=ma推导出来的,那么应如何准确地理解动量定理与牛顿第二定律呢本文做一初浅的探讨。
一、动量定理是牛顿第二定律原来采用的形式在牛顿提出运动第二定律之前,伽利略在批判亚里士多德的力与速度的依赖关系的基础上,提出了力与加速度的依赖关系,但是他没有也不可能在当时的条件下发现作用力与加速度之间的定量关系。
在1684年8月之后,牛顿用几何法和极限概念论证了引力平方反比律,在为解决万有引力是否跟质量成正比的问题时,他发现了运动第二定律,具体的记载有两处,一处是在“论物体的运动”一文手稿中写道:“…动力与加速度的力之比等于运动与速度之比。
因为运动的量是由速度乘以物质的量导出的…”。
另一处是在《自然哲学的数学原理》的定义Ⅷ中给出的:“因为运动的量是由速度乘以物质的量求出来的,并且动力是由加速度的力乘以同一物质之量求出来的,物体的几个粒子上的加速的力的作用总和就是整个物体的动力”。
上面两段话中,“加速的力”指的是加速度,“运动”“运动的量”指的是动量,“动力”指的是与加速度对应的作用力,“物体”“物质的量”就是质量。
由此可知,牛顿在《自然哲学的数学原理》一书中已明确提出动量的定义:“运动量是用它的速度和质量一起来量度的”,“并把动量的变化率称之为力”,“他又用动量来表述运动第二定律”。
综上所述,牛顿其实已经提出了运动第二定律的文字表述:作用力与加速度成正比。
但当时牛顿并没有明确地用公式(F=ma)表述出来,牛顿第二定律原来采用的形式是力F、质量m、速度v和时间t这四个物理量,选择适当的单位,可使比例系数k=1,这时,牛顿第二定律可表示为①因此,牛顿第二运动定律的真实表述应该是物体所受外力等于其动量对时间的变化率。
①式也叫做牛顿第二定律的微分形式。
《自然哲学的数学原理》已经提出了作用力与加速度成正比,但当时牛顿并没有将公式①直接用F=ma表述出来,这是为什么呢我国研究牛顿的资深学者阎康年先生在他的专着《牛顿的科学发现与科学思想》中专门研究了牛顿的质量观:“牛顿对质量概念的认识分静质量和动质量两个方面。
牛顿第二定律

4、平面运动刚体的动能 刚体的平面运动可以分解为任选基点的平动和绕该基点的转动, 则以质心C为基点,刚体的平面运动动能就等于随质心C的平动动能 与绕质心C转动的动能之和。
1 1 1 2 2 2 T = MvC + J Cω = J Pω 2 2 2
对整个质点系,有: d Σ 则:
P 为刚体平面运动的 瞬心,JP为刚体对瞬 心轴的转动惯量。
达朗贝尔原理 Alemberte)(动静法 D’Alemberte)(动静法) Alemberte)(动静法)
§1. 质点的达朗贝尔原理 G m 称为惯性力,则有: N F
ma=F+N F+N- ma=0
令
G = - ma F+N+G=0
即为质点的达朗贝尔原理。
上式在形式上是一个平衡方程,G 具有力的量纲,是质量和加 速度的乘积,因此称为惯性力。 惯性力是人为地、假想地加上去的,并不真实的作用在物体上。 达朗贝尔原理从形式上将动力学问题转化为静力学问题,它并不改 变动力学问题的实质,质点实际上也并不平衡。
5、质点系的动能定理 设一质点系由n个质点构成,对第 i个质点有:
dT = Σ δ W
m ivi = Σ δW i 2
2
m ivi d = δW i 2
2
即为质点系动能定理的微分形式。 即为质点系动能定理 的积分形式。
积分上式,有:
T2 − T1 = ΣW
动能定理主要用来求解
v、ω、a、ε,不能求反力!
动力学普遍定理
重点研究刚体在 各种运动形式下的 运动微分方程 动量定理 动量矩定理 动能定理
§1. 质点的动量定理 1.质点的动量: k=mv 矢量, 量纲为:kg ⋅ m/s = kg ⋅ m/s 2 ⋅ s = N ⋅ s 2.力的冲量: S =F t 矢量, 量纲为:N s 前式中, F为常力, 若F为变力, 则为 t1 s = F dt S 元冲量: dS =F d t
理想流体的运动微分方程
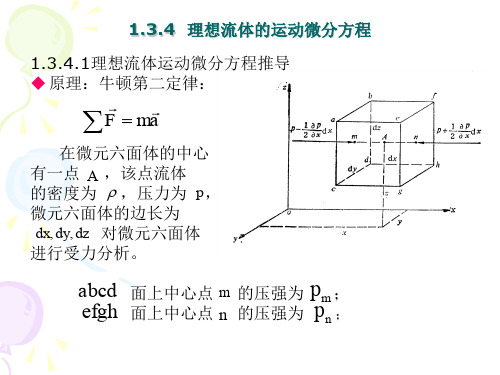
uz x
uy
uz y
uz
uz z
写成矢量表达式为:
F 1 p du
dt
式中哈密顿算子: i j k
x y z
1.3.4.2欧拉运动微分方程的求解
欧拉运动微分方程建立了作用在理想流体上的力与流体运动加速 度之间的关系,它是研究理想流体各种运动规律的基础,对可压缩及不 可压缩理想流体的稳定流动都是适用的。
Y
1
p y
du y dt
u y t
ux
u y x
uy
u y y
uz
u y z
Z
1
p z
duz dz
uz t
ux
uz x
uy
uz y
uz
uz z
因为只考虑稳定流动,所以上式中的p,ux,uy,uz 都只是坐标x,y,z的函数,而与时间无关。
在x轴方向上进行受力分析: (1)表面力:
Fm
(
p
p x
dx )dydz 2
Fn
(p
p x
dx )dydz 2
则 x方向的净表面力
p dx
p dx
p
Fx Fm Fn ( p x
)dydz ( p
2
x
)dydz dxdydz
2
x
(2) 在x轴方向上的质量力为: X dxdydz
x dt
同理在y,z轴方向上也有:
Y 1 p duy 和
y dt
Z 1 p duz
动量守恒专题知识讲座

2.积分形式:
t
t0 F外dt i mivi i mivi0
或: Ii p p0
3.分量式:
i
Iix px p0x
i
Iiy py p0 y i
Iiz pz p0z i
质点系动量定理 :作用于系统旳合外力旳冲量
等于系统总动量旳增量。
讨论:
(1)系统旳内力不能变化系统旳总动量。定理中不出现系 统旳内力,所以研究某些力学问题甚为以便。
物体旳质心一定在物体上吗?
质心与重心是不同旳概念,它们 一定在同一点上吗?
二、质心运动定理
质心旳速度 ( rc 对t 求导)
vc
i
mivi
mi
mivi
i
m
i
质点系旳总动量 p mivi mvc
i
质点系旳总动量旳变化率
dp dt
m d vc
dt
mac
dp dt
m d vc
X
dm v sin dmr v dml v 又:dmr dml dm
联立解得:dmr
1(1 2
sin
)dm,dml
1(1 sin)dm
2
qr
dmr dt
1 2
(q 1
sin
),ql
1 (q 1 sin)
2
3-3 质点系动量守恒定律
对质点系统而言,外力旳矢量和为零时,该系统旳
总动量守恒。
因质点系旳总动量为p 对质心参照系来说 P
mivi mvc
mivi mvC 0
所以,质心参照系是 零动量参照系。
m1v1
m2v20
例. 两质点系统,
在其质心参照系中,m1v10
第二章 牛顿定律

FN
N
θ
R
mg
v mg cosθ − FN = m R vdv mg sin α = m Rdα
2
∵ FN = 0 2 2 θ = arccos 时,小球脱离大球 小球脱离大球. ∴ cosθ = 3 3
1 2 mgR(1 − cos θ ) = mv 2
的液体,上方悬一长为l, 例4 密度为ρ1的液体,上方悬一长为 ,密度为ρ2的 均质细棒AB,棒的B端刚好和液面接触 今剪断绳, 端刚好和液面接触。 均质细棒 ,棒的 端刚好和液面接触。今剪断绳, 并设棒只在重力和浮力作用下下沉, 并设棒只在重力和浮力作用下下沉,求:
棒刚好全部浸入液体时的速度。 棒刚好全部浸入液体时的速度。 A
解 : (1 )
mg − F = ma
B
O
x
dv dv ρ2lsg − ρ1xsg = ρ2sl = ρ2lsv x dt dx ρ1x v x ρ1x vdv = (1− )gdx ∫ vdv = ∫ (1− )gdx 0 0 ρ2l ρ2l
第二章
动力学基本定律
力是维持物体运动的原因。 力是维持物体运动的原因。
力不是维持运动的原因。
牛顿定律
牛顿第一定律(惯性定律)
任何物体都将保持静止或匀速直线运动的 状态直到其他物体所作用的力迫使它改变这种 状态为止。 状态为止。
数学形式: 数学形式:
v = 恒矢量 , F = 0
惯性: 任何物体保持其运动状态不变的性质。 惯性: 任何物体保持其运动状态不变的性质。
f2 = µ2 N2
f1 = µ1N1
由A式: 式
µ1mAg − FT = −mAa 由B式: F − µ1m g − µ2 (m + m )g − F = m a 式 A A B T B
牛顿第二定律及其微分形式(精)

dt
速度远低于光速时,过渡为
F
ma
牛顿第二定律的微分形式是基本的普遍形式, 适用于高速运动情况与变质量问题。
牛顿第二定律及其微分形式
2. 牛顿第二定律的微分形式
牛顿第二定律原文意思:运动的变化与所加的 动力成正比,并且发生在这力所沿直线的方向上。
这牛里顿dp的第p“二m运定Fv动律或”实d指质p物上体是F的: 质d t量和牛二分牛二分牛定速分顿的形顿的形顿 律度形第微式第微式第的矢式二微量的乘积。
§2-3 牛顿第二定律及其微分形式
1. 牛顿第二定律
牛顿第二定律:物体受到外力作用时,它所获
得的加速度的大小与外力的大小成正比,并与物体
的质量成反比,加速度的方向与外力的方向相同。
F
ma
对应单位: N kg m/s 2
牛顿第二定律
讨论:
(1)质量的理解:质量是惯性的量度。不受外力保
持运动状态不变;一定外力作用时,质量越大,加
速度越小,运动状态越难改变;质量越小,加速度
越大,运动状态容易改变。因此,这里的质量叫做
惯性质量。
(2)瞬时性的理解:定律中的力和加速度都是瞬时
的,同时存在,同时消失。
F
md
v
dt
牛顿第二定律
(3)矢量性的理解:矢量表达式,力与加速度 都是矢量,二者方向相同,满足叠加原理。
叠加原理:几个力同时作用在一个物体上,物 体产生的加速度等于每个力单独作用时产生的加 速度的叠加。
m d vz dt
m
d2 dt
z
2
Ft
mat
mdv dt
Fn
man
m
v2
牛顿第二定律及其微分形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
牛顿第二定律
F Fi F1 F2 Fi ma1 ma2 mai
ma
直角坐标系与自然坐标系中的分量形式
d vx d x Fx m m 2 dt dt 2 d vy d y Fy m m 2 dt dt 2 d vz d z Fz m m 2 dt dt
dv F m dt
牛顿第二定律
(3) 矢量性的理解:矢量表达式,力与加速 度都是矢量,二者方向相同,满足叠加原理。 叠加原理:几个力同时作用在一个物体上, 物体产生的加速度等于每个力单独作用时产生的 加速度的叠加。
a F、 力 F1、F2、 、Fi 同时作用在物体上, 、ai 分别 分别表示合力、合加速度, a1、a2、
p mv
牛顿第二定律实质上是:
速度远低于光速时,过渡为 F ma
牛顿第二定律的微分形式是基本的普遍形式, 适用于高速运动情况与变质量问题。
dp F dt
或 d p F dt
牛顿第 二的微 定律的微 二的微 分形式式
1. 牛顿第二定律
牛顿第二定律:物体受到外力作用时,它所
获得的加速度的大小与外力的大小成正比,并与物 体的质量成反比,加速度的方向与外力的方向相同。
F ma
对应单位: N
kg
m/s
2
牛顿第二定律
讨论:
(1)质量的理解:质量是惯性的量度。不受外力 保持运动状态不变;一定外力作用时,质量越大, 加速度越小,运动状态越难改变;质量越小,加速 度越大,运动状态容易改变。因此,这里的质量叫 做惯性质量。 (2)瞬时性的理解:定律中的力和加速度都是瞬 时的,同时存在,同时消失。
速度远低于光速时,过渡为 F ma
牛顿第二定律的微分形式是基本的普遍形式, 适用于高速运动情况与变质量问题。
dp F dt
或 d p F dt
牛顿第 二的微 定律的微 二的微 分形式 分形式 分形式
牛顿第二定律及其微分形式
2. 牛顿第二定律的微分形式
牛顿第二定律原文意思:运动的变化与所加的 动力成正比,并且发生在这力所沿直线的方向上。 这里的“运动”指物体的质量和速度矢量的乘 积。 牛顿第 牛顿第二
2
dv Ft mat m dt
Fn man m v
2
牛顿第二定律及其微分形式
2. 牛顿第二定律的微分形式
牛顿第二定律原文意思:运动的变化与所加的 动力成正比,并且发生在这力所沿直线的方向上。 这里的“运动”指物体的质量和速度矢量的乘 积。 牛顿第 牛顿第二
p mv
牛顿第二定律实质上是:
