苏教版六年级下册《立体图形的表面积和体积》ppt课件
合集下载
六年级下册数学课件《6、立体图形的表面积和体积(1)》苏教版PPT课件

知识梳理
体积
常用的体积单位有哪些?
容积
常用的体积单位 有立方米、立方 分米、立方厘米。
1dm
1cm
六年级下册数学课件《6、立体图形的 表面积 和体积 (1) 》苏教 版PPT课 件
1dm
1立方分米=1升 1立方厘米=1毫升
计量液体的体积 通常用升或毫升 作单位。
六年级下册数学课件《6、立体图形的 表面积 和体积 (1) 》苏教 版PPT课 件
((( )))dcmmcmLm3m333
04.010075..9505dmd4mmLm33=3===((((147509.50400005))))cmdcmLmm3333
六年级下册数学课件《6、立体图形的 表面积 和体积 (1) 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 (1) 》苏教 版PPT课 件
(3)中号陀螺的体积是多少cm3 ?
942+157=1099cm3
六年级下册数学课件《6、立体图形的 表面积 和体积 (1) 》苏教 版PPT课 件
综合运用
中号陀螺
h=6cm
如果做一个长方体纸盒,使中号陀 螺正好能装进去,这个纸盒至少需 要多少平方厘米硬纸?
12cm r=5cmh=18cmFra bibliotek18cm
4 . 初 步 形成 宽容他 人的良 好品质 。 5 . 通 过 具体 事例体 验宽容 对己对 人带来 的慰藉 。 6. 传统的 节日也 应有时 代的价 值,不 符合时 代需要 的,应 该淘汰 。 7. 生活中 ,伴随 着我们 成长有 许多风 俗,其 中不少 体现了 尊老的 传统美 德。
亲爱的同学们,再见!
六年级下册数学课件《6、立体图形的 表面积 和体积 (1) 》苏教 版PPT课 件
六年级数学下册优秀ppt课件立体图形的表面积和体积苏教版6

底面一样 粗细一样
直柱体 V=sh
判断下面哪个图形可以用V=sh来计算。
立体图形的表面积与体积整理
立体图形
表面积
体积
h
a
b
a
a a
r h
S=(ab+ah+bh)×2 S=6a2 S=2兀rh+2兀r2
V= abh
V=a V=sh 3
V=兀r2h
h
s
V=
1 3
sh
一块长方体橡皮泥,长5厘米,宽4厘米, 高3厘米。
(2)切3段一共要切几刀?
(3)每切1刀会增加几个面?
(4)切2刀一共增加了几个面?
d=4厘米 h=3厘米
(1)把圆柱形橡皮泥捏成一个与它等底的圆锥,
圆锥的高为( 9 )厘米。
等体积等底
(2)把圆柱形橡皮泥捏成一个与它等高的圆锥, 圆锥的底面积是圆柱的( 3倍 )。 等体积等高
(3)把圆柱形橡皮泥削成一个最大的圆锥,圆锥
V= abh
V=a 3
V=兀r2h
h
s
V=
1 3
sh
知识回顾
体积 长 第7题:也要提醒学生一般要按照最基本的关系“多的-少的”来列式。
一、图案的欣赏: (2)综合:12×3+15×4
宽高
教学准备:滴管、量桶、水等。
2、让学生学习应用估算的方法判断计算结果的合理性。
1 5 5 1 1 教材简析:这部分内容教学三角形的分类。教材让学生通过对提供得意写三角形的每个内角大小的观察、比较、分类,引出直角三角
5
2 2
3
12 = 3 × 2 × 2
知识回顾
知识回顾
知识回顾
知识回顾
直柱体 V=sh
判断下面哪个图形可以用V=sh来计算。
立体图形的表面积与体积整理
立体图形
表面积
体积
h
a
b
a
a a
r h
S=(ab+ah+bh)×2 S=6a2 S=2兀rh+2兀r2
V= abh
V=a V=sh 3
V=兀r2h
h
s
V=
1 3
sh
一块长方体橡皮泥,长5厘米,宽4厘米, 高3厘米。
(2)切3段一共要切几刀?
(3)每切1刀会增加几个面?
(4)切2刀一共增加了几个面?
d=4厘米 h=3厘米
(1)把圆柱形橡皮泥捏成一个与它等底的圆锥,
圆锥的高为( 9 )厘米。
等体积等底
(2)把圆柱形橡皮泥捏成一个与它等高的圆锥, 圆锥的底面积是圆柱的( 3倍 )。 等体积等高
(3)把圆柱形橡皮泥削成一个最大的圆锥,圆锥
V= abh
V=a 3
V=兀r2h
h
s
V=
1 3
sh
知识回顾
体积 长 第7题:也要提醒学生一般要按照最基本的关系“多的-少的”来列式。
一、图案的欣赏: (2)综合:12×3+15×4
宽高
教学准备:滴管、量桶、水等。
2、让学生学习应用估算的方法判断计算结果的合理性。
1 5 5 1 1 教材简析:这部分内容教学三角形的分类。教材让学生通过对提供得意写三角形的每个内角大小的观察、比较、分类,引出直角三角
5
2 2
3
12 = 3 × 2 × 2
知识回顾
知识回顾
知识回顾
知识回顾
苏教版六年级下册立体图形的表面积和体积课件-PPT课件

4.你能解决下面生活中的问题吗?
1)一个圆柱形水池,直径是20米,深2米。 ①这个水池占地面积是多少? 3.14×(20÷2)
2
②挖成这个水池,共需挖土多少立方米? 3.14×(20÷2) ×2 ③在池内四周和池底抹一层水泥,水泥 面的面积是多少平方米? 3.14×20×2+ 3.14×(20÷2)
苏教版六年级数学下册
教学目标
• 1.使同学们在具体情境中认识正方体、长方 体、圆柱、圆锥等立体图形。 • 2. 通过在具体情境中对图形的观察,促进 同学们的观察、分析、归纳、概括能力的 发展。 • 3. 让同学们充分经历实践、探索、交流, 获得成功的经验。
a
h b
a
2
a a
hrΒιβλιοθήκη 长方体表面积= 正方体表面积=
3.判断
1)一个圆柱形水桶的体积就是它的容积。 …………………………………………(×) 2)正方体的棱长扩大2倍,体积就扩大8 倍。…………………………………(√ ) 1 3)圆锥的体积等于圆柱体积的 ,它们一 3 × 定等底等高。………………………… ( ) 4)圆柱的底面半径扩大2倍,高不变,它的 侧面积扩大4倍,它的体积也扩大4 倍。…………………………………(×)
(1)表示的意义不同 (2)计量的单位不同 (3)计算的方法不同
1.只列式,不计算: 1)一个长方体,它的长是4分米,宽是5分 米,高是2分米,求它的表面积和体积。 2)一个棱长是6分米的正方体,它的表面 积和体积各是多少? 3)一个圆柱的底面半径是3厘米,高12厘 米,求它的表面积和体积。 4)一个圆锥的底面周长是62.8厘米,高 是15厘米,它的体积是多少立方厘米?
(ab+ah+bh) ×2
六年级数学下册课件立体图形的表面积和体积苏教版36(共15张PPT)

(
)
识体系。 4、一个长方体金鱼缸,长40厘米,宽40厘米,高35厘米。
底面半径10cm 高6cm 把一根圆柱形木料削成一个最大的圆锥,削去部分的体积是圆锥体积的(
)。
(1)一间卧室地面的面积是15(
)。
2、什么是物体的体积?什么是容器的容积?常用的体积单位有哪些?相邻单位间的进率各是多少?
5 C. 把一块铁块从这个容器的水中取出后,水面下降2厘米。
学习目标: 棱长是6厘米的正方体,表面积和体积相等。
一个长方体的纸盒,将它展开后,得到什么样的图形?
一个长方体的纸盒,将它展开后,得到什么样的图形?
1、理解并掌握立体图形的 (
)
2、什么是物体的体积?什么是容器的容积?常用的体积单位有哪些?相邻单位间的进率各是多少?
一个圆柱和一个圆锥等底等高,它们的体积相差12立方分米,这个圆柱的体积是( )立方分米,圆锥的体积是( )立方分米。
一个长方体
上
的纸盒,将
它展开后,
得到什么样
的图形?
左
后
右
下 前
底面
底面
底面
底面周长
底面
圆
柱
的
高
表
面
展
开
图
填表
挑战第一关
制作一个圆柱形的油桶,至少需要多 少铁皮,是求圆柱形油桶的( )。
挑战第二关 棱长是6厘米的正方体,表面积
和体积相等。( )
挑战第三关 一个圆柱和一个圆锥等底等高,它 们的体积相差12立方分米,这个圆柱
长4m 宽3m 高2m
棱长是6厘米的正方体,表面积和体积相等。
2、正确、灵活应用公式进
行计算。
小组合作交流: 1、什么是长方体、正方体和圆 柱的表面积?各怎样计算? 2、什么是物体的体积?什么是 容器的容积?常用的体积单位有 哪些?相邻单位间的进率各是多 少?
苏教版六年级下册数学课件 第6课时 立体图形的表面积和体积(1) (共24张PPT)

这个容器的容积。 1立方米=1000立方分米 1立方分米=1000立方厘米
1升=1000毫升
•11、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。 •12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 •13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2021/11/62021/11/6November 6, 2021 •14、孩子在快乐的时候,他学习任何东西都比较容易。 •15、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 •16、一个人所受的教育超过了自己的智力,这样的人才有学问。 •17、好奇是儿童的原始本性,感知会使儿童心灵升华,为其为了探究事物藏下本源。2021年11月2021/11/62021/11/62021/11/611/6/2021 •18、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2021/11/62021/11/6
义务教育苏教版六年级下册
七
总复习
立体图形的表面积和体积(1)
整理反思
什么是长方体、正方体和圆柱的表 面积?各怎样计算?
前
长方体的表面积:
长方体的表面积 =长×宽×2+长×高×2+宽×高×2 =(长×宽+长×高+宽×高)×2
S=2ab+2ah+2bh
右
=(ab+ah+bh)×2
•
整理反思
长方体的体积:
长方体的体积=长×宽×高 V=abh
长方体的体积=底面积×高
整理反思
正方体的体积:
正方体的体积=棱长×棱长×棱长 V=a·a·a 或 V=a3
正方体的体积=底面积×高
整理反思
1升=1000毫升
•11、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。 •12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 •13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2021/11/62021/11/6November 6, 2021 •14、孩子在快乐的时候,他学习任何东西都比较容易。 •15、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 •16、一个人所受的教育超过了自己的智力,这样的人才有学问。 •17、好奇是儿童的原始本性,感知会使儿童心灵升华,为其为了探究事物藏下本源。2021年11月2021/11/62021/11/62021/11/611/6/2021 •18、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2021/11/62021/11/6
义务教育苏教版六年级下册
七
总复习
立体图形的表面积和体积(1)
整理反思
什么是长方体、正方体和圆柱的表 面积?各怎样计算?
前
长方体的表面积:
长方体的表面积 =长×宽×2+长×高×2+宽×高×2 =(长×宽+长×高+宽×高)×2
S=2ab+2ah+2bh
右
=(ab+ah+bh)×2
•
整理反思
长方体的体积:
长方体的体积=长×宽×高 V=abh
长方体的体积=底面积×高
整理反思
正方体的体积:
正方体的体积=棱长×棱长×棱长 V=a·a·a 或 V=a3
正方体的体积=底面积×高
整理反思
六年级数学下册课件7.2.6立体图形的表面积和体积苏教版共16张PPT

1400平方厘米=14平方分米量得酸酸乳饮料的长是7厘米,宽是4 厘米,高是9厘米。
如果这两盒牛奶需要用礼品纸包装,怎样包装用的纸最节省?
把四个棱长是1厘米的正方体木块 拼成一个长方体,这个长方体的表面 积最小是多少平方厘米?
用一根长120厘米的铁丝,做一个 长、宽、高的比是3:4:5的长方 体。这个长方体的长、宽、高分别 是多少?
❖ C、3.14×(2÷2) ×22
3
·
·
常用的体积单位有哪些? 固体:立方米、立方分米、立方厘米 液体: 升,毫升 常用的容积单位有哪些? 立方米,升,毫升 相邻两个体积或容积单位之间的进率 是多少?
平方米 毫升
立方米
×1000
÷1000 ×1000
500 0.06
1040 75
35cm 40cm
40cm
S=bh =40×35 =1400(平方厘米)
❖把一个棱长6厘米的正方体切成棱长2厘米的 小正方体,可以得到( C )个小正方体? ❖ A、6÷2=3 B、6 ×6÷(2 ×2)=9 ❖ C、6×6×6÷(2×2×2)=27
❖如图,把圆柱平均横切成两半,表面积增加 了( B )平方米,平均竖切成两半,2 表面积 增加了( C )平方米。
❖ A、2 ×3 B、2×3×2 2
9、做一个长方体框架需要多少铁丝是求 ( 棱长总和 )
10、圆柱形无盖铁皮水桶是求 ( 侧面积+底面积 ).
什么叫做物体的体积? 物体所占空间的大小叫做物体的体积。 什么叫做容积?
容器所能容纳物体的体积,叫做这 个容器的容积。 物体的体积与容积有什么区别?
所有的物体都有体积,但不一定有容积。 容器的体积一定大于它的容积。
怎样求长方体、正方体、圆柱体的表面积?
六年级数学下册课件立体图形的表面积和体积苏教版59(共30张PPT)
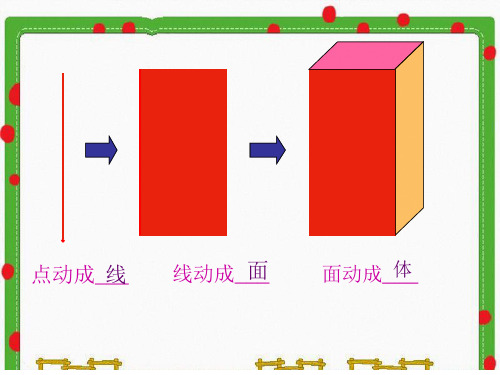
(2)计算的方法不同
(3)计量的单位不同
判断题:
12、 、(一 圆个 锥)长 体方体体积木是箱圆的 柱体 体积 体一 积定 的大1/3于×。它(的容)积√ 。
3、圆柱体的侧面积等于底面积乘高。 ×( )
4、一个正方体的棱长是6厘米,它的表面积和体
积×相等。
()
5、一个圆柱的底面半径扩大3倍,高缩小3倍,它
倍
细心比较
1、一根长方体木料长200厘米,横截面是面
积8平方厘米的正方形,这根木料的体积是多
少立方厘米?
8×200
2、一根长方体木料长200厘米,横截面是
边长8厘米的正方形,这根木料的体积是多
少立方厘米?
8×8×200
3、一根长方体木料长200厘米,横截面是
周长8厘米的正方形,这根木料的体积是
多少立方厘米?
游泳池的占地面积 3、制作圆柱形的水桶用铁皮多少 4、电线杆的占地面积 5、计算通风管材料的面积 6、火柴盒的外盒和内盒
什么是立体图形的体积?
一个立体图形所占空间的 大小叫做它的体积。
什么是容器的容积? 容器所能容纳的物体的体积
叫做它的容积。
a
o·
h
o ·r
h b
h
o ·r
a aa
下面的物体是由几个小正方体摆成的?
22 3 4
你发现什么了规律?
4
4
4
长方体所含小正方体的数量正好等于长 、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
h ab
想一想:正方体的体积怎样计算呢?
正方体的体积=棱长×棱长×棱长
V=a.a.a
a
=a3
aa
你是怎么推导出圆柱的体积公式?
(3)计量的单位不同
判断题:
12、 、(一 圆个 锥)长 体方体体积木是箱圆的 柱体 体积 体一 积定 的大1/3于×。它(的容)积√ 。
3、圆柱体的侧面积等于底面积乘高。 ×( )
4、一个正方体的棱长是6厘米,它的表面积和体
积×相等。
()
5、一个圆柱的底面半径扩大3倍,高缩小3倍,它
倍
细心比较
1、一根长方体木料长200厘米,横截面是面
积8平方厘米的正方形,这根木料的体积是多
少立方厘米?
8×200
2、一根长方体木料长200厘米,横截面是
边长8厘米的正方形,这根木料的体积是多
少立方厘米?
8×8×200
3、一根长方体木料长200厘米,横截面是
周长8厘米的正方形,这根木料的体积是
多少立方厘米?
游泳池的占地面积 3、制作圆柱形的水桶用铁皮多少 4、电线杆的占地面积 5、计算通风管材料的面积 6、火柴盒的外盒和内盒
什么是立体图形的体积?
一个立体图形所占空间的 大小叫做它的体积。
什么是容器的容积? 容器所能容纳的物体的体积
叫做它的容积。
a
o·
h
o ·r
h b
h
o ·r
a aa
下面的物体是由几个小正方体摆成的?
22 3 4
你发现什么了规律?
4
4
4
长方体所含小正方体的数量正好等于长 、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
h ab
想一想:正方体的体积怎样计算呢?
正方体的体积=棱长×棱长×棱长
V=a.a.a
a
=a3
aa
你是怎么推导出圆柱的体积公式?
苏教版六年级下册数学课件 《6、立体图形的表面积和体积》 (共13张PPT)

(3)用一张长40 cm,宽20 cm的长方形铁皮,做 一个深5 cm的无盖的长方体容器(焊接处和铁皮 厚度不计)。怎样焊接才能使容积最大?容积最 大是多少?(画图分一分,再算一算)
20×20×5=2000(cm3) 答:容积最大是2000cm3。
提升练习
易错辨析
4.一个长方体的棱长总和是96 cm,它的长、宽、
是体的一角挖去一个棱长为3
厘米的小正方体,那么剩下部分的体积与原来正方体
的体积相比变小了,表面积也变小了。
( ×)
巩固练习
3.解决实际问题。 (1)建一个长50米,宽25米,深2米的长方体游泳池,在游
泳池的四壁和底面抹水泥,每平方米需用水泥4千克, 5吨水泥够不够?
巩固练习
(3)一个长方体的棱长总和是48厘米,并且它的 长、宽、高是三个连续的自然数,这个长方 体的表面积是( 94 )平方厘米,体积是 ( 60 )立方厘米。
巩固练习
2.判断。
(1)正方体的棱长扩大到原来的3倍,它的体积就扩大到
原来的27倍。
(√)
(2)把一个正方体一刀切成完全相同的两部分,切面一定
(1)正方体的棱长总和=棱长×12,C=12a 正方体 (2)正方体的表面积=棱长×棱长×6,S=6a2
(3)正方体的体积=棱长×棱长×棱长,V=( a3 )
巩固练习
小试牛刀
1.填空。 (1)一个长方体的长、宽、高分别是7 cm、6 cm和5 cm,它
的棱长总和是( 72 )cm。做出这样一个无盖的长方体盒 子,至少需要( 172 ) cm2材料。 (2)棱长为2分米的正方体,它的表面积是( 24 )平方分米。 用3个这样的正方体拼成一个长方体,拼成的长方体的表 面积是( 56 )平方分米。
苏教版六年级下册数学《立体图形的表面积和体积》课件

这个容器的容积。 1立方米=1000立方分米 1立方分米=1000立方厘米
1升=1000毫升
整理反思
长方体的体积:
长方体的体积=长×宽×高 V=abh
长方体的体积=底面积×高
整理反思
正方体的体积:
正方体的体积=棱长×棱长×棱长 V=a·a·a 或 V=a3
正方体的体积=底面积×高
整理反思
圆柱的体积:
圆柱的体积= 底面积 × 高
V= S × h
整理反思
圆锥的体积:
圆柱的体积=
1 3
×底面积 × 高
V=
1 3
sh
整理反思 回忆各立体图形体积公式的推导过程,想一想它们 之间的联系,完成下面的填空,与同学交流。
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
•
14、抱最大的希望,作最大的努力。2020年8月4日 星期二 上午10时36分26秒10:36:2620.8.4
•
15、一个人炫耀什么,说明他内心缺 少什么 。。2020年8月 上午10时36分 20.8.410:36August 4, 2020
•
16、业余生活要有意义,不要越轨。2020年8月4日 星期二10时36分26秒10:36:264 August 2020
练习实践
练习实践
练习实践
课堂小结
通过这节课的学习活动,你有什么收获?
•
9、 人的价值,在招收诱惑的一瞬间被决定 。20.8.420.8.4T uesday, August 04, 2020
•
10、低头要有勇气,抬头要有低气。10:36:2610:36:2610:368/4/2020 10:36:26 AM
1升=1000毫升
整理反思
长方体的体积:
长方体的体积=长×宽×高 V=abh
长方体的体积=底面积×高
整理反思
正方体的体积:
正方体的体积=棱长×棱长×棱长 V=a·a·a 或 V=a3
正方体的体积=底面积×高
整理反思
圆柱的体积:
圆柱的体积= 底面积 × 高
V= S × h
整理反思
圆锥的体积:
圆柱的体积=
1 3
×底面积 × 高
V=
1 3
sh
整理反思 回忆各立体图形体积公式的推导过程,想一想它们 之间的联系,完成下面的填空,与同学交流。
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
练习实践
•
14、抱最大的希望,作最大的努力。2020年8月4日 星期二 上午10时36分26秒10:36:2620.8.4
•
15、一个人炫耀什么,说明他内心缺 少什么 。。2020年8月 上午10时36分 20.8.410:36August 4, 2020
•
16、业余生活要有意义,不要越轨。2020年8月4日 星期二10时36分26秒10:36:264 August 2020
练习实践
练习实践
练习实践
课堂小结
通过这节课的学习活动,你有什么收获?
•
9、 人的价值,在招收诱惑的一瞬间被决定 。20.8.420.8.4T uesday, August 04, 2020
•
10、低头要有勇气,抬头要有低气。10:36:2610:36:2610:368/4/2020 10:36:26 AM
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(ab+ah+bh) ×2
圆柱侧面积= 圆柱表面积=
6a 2лrh 2лrh+ 2лr
2
h h a h b s s a a a 1 3 V= abh V= a V= sh V=相似的地方呢?
?
你能推想一下下面的立体 图形的体积可以怎样计算吗?
立体图形的表面积和体积有什么 区别?
2
2
2)一个圆锥形黄沙堆,底面周长18.84米, 高2米,把这些沙在5米宽的公路上铺2厘 米厚,够铺200米长的路吗?
1 〔(18.84÷3.14÷2)×3.14×2× 〕÷(5×0.02) 3
2
2厘米=0.02米
=18.84÷0.1 =188.4(米) 200米>188.4米 答:够铺200米长的路。
2.填空:
(1)把一个圆柱削成一个最大的圆锥,圆柱体积 1 是圆锥体积的( 3倍 ),圆锥体积是圆柱体积的 ( 3 )。 (2)一个圆锥和一个圆柱的体积相等,底面积也 相等。这个圆锥的高是圆柱的高的( 3 )倍。 (3)一个正方体的棱长5厘米,这个正方体的棱长 总和是( 60 )厘米。
(4)把一段长3米的长方体木料平均截成3 段,表 面积增加8平方厘米,原来这段木料的体积是 (600 )立方厘米。
4.你能解决下面生活中的问题吗?
1)一个圆柱形水池,直径是20米,深2米。 ①这个水池占地面积是多少? 3.14×(20÷2)
2
②挖成这个水池,共需挖土多少立方米? 3.14×(20÷2) ×2 ③在池内四周和池底抹一层水泥,水泥 面的面积是多少平方米? 3.14×20×2+ 3.14×(20÷2)
苏教版六年级数学下册
教学目标
• 1.使同学们在具体情境中认识正方体、长方 体、圆柱、圆锥等立体图形。 • 2. 通过在具体情境中对图形的观察,促进 同学们的观察、分析、归纳、概括能力的 发展。 • 3. 让同学们充分经历实践、探索、交流, 获得成功的经验。
a
h b
a
2
a a
h
r
长方体表面积= 正方体表面积=
3.判断
1)一个圆柱形水桶的体积就是它的容积。 …………………………………………(×) 2)正方体的棱长扩大2倍,体积就扩大8 倍。…………………………………(√ ) 1 3)圆锥的体积等于圆柱体积的 ,它们一 3 × 定等底等高。………………………… ( ) 4)圆柱的底面半径扩大2倍,高不变,它的 侧面积扩大4倍,它的体积也扩大4 倍。…………………………………(×)
怎样测量一块石头的体积
广 告
华联超市想给每份250克的白糖设 计漂亮的外包装,请有兴趣的顾客参与 此项活动,到时将设立一定的奖项。
(1)表示的意义不同 (2)计量的单位不同 (3)计算的方法不同
1.只列式,不计算: 1)一个长方体,它的长是4分米,宽是5分 米,高是2分米,求它的表面积和体积。 2)一个棱长是6分米的正方体,它的表面 积和体积各是多少? 3)一个圆柱的底面半径是3厘米,高12厘 米,求它的表面积和体积。 4)一个圆锥的底面周长是62.8厘米,高 是15厘米,它的体积是多少立方厘米?
