一元二次方程根与系数关系培优强化

合集下载

根与系数的关系及判别式综合问题大题培优强化11题

根与系数的关系及判别式综合问题培优强化30题1．已知关于x的一元二次方程kx2+（k﹣2）x﹣2＝0（k≠0）．（1）求证：不论k为何值，这个方程都有两个实数根；（2）若此方程的两根均整数，求整数k的值．2．已知关于x的一元二次方程x2+（k+2）x+2k＝0．（1）求证：方程总有两个实数根；（2）若该方程有一个根是正数，求k的取值范围．3．已知关于x的方程x2﹣（k+2）x+2k＝0．（1）求证：无论k为何值，方程总有实数根；（2）若等腰三角形一腰长为5，另外两边长度为该方程的两根，求等腰三角形的周长．4．已知关于x的一元二次方程x（x﹣2）＝k．（1）若k＝3，求此方程的解；（2）当k≥﹣1时，试判断方程的根的情况．5．已知：关于x的一元二次方程x2﹣（2k+3）x+k2+3k+2＝0．（1）证明无论k取何值时方程总有两个实数根．（2）△ABC中，BC＝5，AB、AC的长是这个方程的两个实数根，求k为何值时，△ABC是等腰三角形？6．如图，菱形ABCD中，m、n、t分别是菱形ABCD的两条对角线和边长，这时我们把关于x 的形如mx2+2√2tx+n＝0的一元二次方程称为“菱系一元二次方程”．请解决下列问题：（1）填空：①当m＝2，n＝4时，t＝；②用含m、n的代数式表示t2＝；（2）求证：关于x的“菱系一元二次方程”mx2+2tx+12n＝0必有实数根．7．关于x的一元二次方程ax2+6x﹣5a＝0…①和3x2﹣ax+a＝0…②．（1）若a＞0，且方程①有两实根x1，x2，方程②有两实根x3，x4，求代数式x1x2+x1x3+x1x4+x2x3+x2x4+x3x4的最小值；（2）是否存在实数a，使得方程①和②恰有一个公共的实数根？若存在，请求出实数a的值；若不存在请说明理由．8．阅读材料，解答问题：材料1为了解方程（x2）2﹣13x2+36＝0，如果我们把x2看作一个整体，然后设y＝x2，则原方程可化为y2﹣13y+36＝0，经过运算，原方程的解为x1，2＝±2，x3，4＝±3．我们把以上这种解决问题的方法通常叫做换元法．材料2已知实数m，n满足m2﹣m﹣1＝0，n2﹣n﹣1＝0，且m≠n，显然m，n是方程x2﹣x﹣1＝0的两个不相等的实数根，由韦达定理可知m+n＝1，mn＝﹣1．根据上述材料，解决以下问题：（1）直接应用：方程x4﹣5x2+6＝0的解为；（2）间接应用：已知实数a，b满足：2a4﹣7a2+1＝0，2b4﹣7b2+1＝0且a≠b，求a4+b4的值；（3）拓展应用：已知实数m，n满足：1m4+1m2=7，n2﹣n＝7且n＞0，求1m4+n2的值．9．若α=1+√52为一元二次方程x2﹣x+t＝0的根；（1）则方程的另外一个根β＝，t＝；（2）求（α3﹣α2+1）（β3﹣β2+1）的值．10．如果关于x的一元二次方程ax2+bx+c＝0（a≠0）有两个实数根，且其中一个根为另一个根的2倍，那么称这样的方程为“倍根方程”．例如，一元二次方程x2﹣9x+18＝0的两个根是3和6，则方程x2﹣9x+18＝0就是“倍根方程”．（1）若一元二次方程x2﹣6x+k＝0是“倍根方程”，则k＝；（2）若一元二次方程nx2﹣（2n+m）x+2m＝0（n≠0）是“倍根方程”，求m+n2m−n的值；11．已知关于x的方程ax2+2x﹣3＝0有两个不相等的实数根．（1）求a的取值范围；（2）若此方程的一个实数根为2，求a的值；（3）直接写出所有不大于5的正整数a的值，使原方程的两个根均为有理数．。

一元二次方程根与系数的关系同步培优题典(解析版)

专题1.6一元二次方程根与系数的关系姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020•遵化市模拟）关于x的一元二次方程x2﹣2x＝0的两个实数根，下列结论错误的是（）A．x1≠x2B．x1x2＝2C．x1+x2＝2D．x12﹣2x1＝0【分析】根据方程的系数结合根的判别式可得出△＝4＞0，进而可得出x1≠x2，结论A正确；利用一元二次方程的解及根与系数的关系可得出x12﹣2x1＝0，x1•x2＝0，x1+x2＝2，即结论C，D正确，结论B 错误，此题得解．【解析】∵△＝（﹣2）2﹣4×1×0＝4＞0，∴关于x的一元二次方程x2﹣2x＝0有两个不相等的实数根，∴x1≠x2，结论A正确；∵x1，x2是一元二次方程x2﹣2x＝0的两个实数根，∴x12﹣2x1＝0，x1•x2＝0，x1+x2＝2，∴结论C，D正确，结论B错误．故选：B．2．（2020•天心区校级模拟）已知m，n是方程x2+2x﹣1＝0的两个实数根，则m2﹣2n+2015的值是（）A．2021B．2020C．2019D．2018【分析】根据一元二次方程的解及根与系数的关系可得出m2+2m＝1，m+n＝﹣2，将其代入m2﹣2n+2015＝（m2+2m）﹣2（m+n）+2015中即可求出结论．【解析】∵m，n是方程x2+2x﹣1＝0的两个实数根，∴m2+2m＝1，m+n＝﹣2，∴m2﹣2n+2015＝（m2+2m）﹣2（m+n）+2015＝1+4+2015＝2020．故选：B．3．（2019秋•中山市校级期末）关于x的方程x2﹣mx﹣3＝0的一个根是x1＝3，则它的另一个根x2是（）A．0B．1C．﹣1D．2【分析】根据根与系数的关系即可求出答案．【解析】由根与系数的关系可知：3x2＝﹣3，解得x2＝﹣1．故选：C．4．（2019秋•新会区期末）关于x的方程x2﹣mx+6＝0有一根是﹣3，那么这个方程的另一个根是（）A．﹣5B．5C．﹣2D．2【分析】根据两根之积可得答案．【解析】设方程的另一个根为a，∵关于x的方程x2﹣mx+6＝0有一根是﹣3，∴﹣3a＝6，解得a＝﹣2，故选：C．5．（2020春•西湖区期末）关于x的方程k2x2+（2k﹣1）x+1＝0有实数根，则下列结论正确的是（）A．当k=12时，方程的两根互为相反数B．当k＝0时，方程的根是x＝﹣1C．若方程有实数根，则k≠0且k≤1 4D．若方程有实数根，则k≤1 4【分析】因为已知没有明确此方程是否是一个一元二次方程，所以方程有两种情况，既可以是一元一次方程，也可以一元二次方程，所以分两种情况分别去求k的取值范围，然后结合选项判断选择什么．【解析】若k＝0，则此方程为﹣x+1＝0，所以方程有实数根为x＝1，则B错误；若k≠0，则此方程是一元二次方程，由于方程有实数根，∴△＝（2k﹣1）2﹣4k2＝﹣4k+1≥0，∴k≤14且k≠0；综上所述k的取值范围是k≤1 4．故A错误，C错误，D正确．故选：D．6．（2020•红桥区模拟）一元二次方程x2﹣4x+2＝0根的情况是（）A．无实数根B．有一个正根，一个负根C．有两个正根，且都小于3D．有两个正根，且有一根大于3【分析】判断上述方程的根的情况，只要看根的判别式△＝b2﹣4ac的值的符号、以及两根的和，两根的积就可以了．【解析】∵a＝1，b＝﹣4，c＝2，∴△＝b2﹣4ac＝（﹣4）2﹣4×1×2＝8＞0，∴方程有两个不相等的实数根，∵两根的和为4，两根的积为2，∴有两个正根，且有一根大于3．故选：D．7．（2020•湖北）关于x的方程x2+2（m﹣1）x+m2﹣m＝0有两个实数根α，β，且α2+β2＝12，那么m的值为（）A．﹣1B．﹣4C．﹣4或1D．﹣1或4【分析】根据方程的根的判别式，得出m的取值范围，然后根据根与系数的关系可得α+β＝﹣2（m﹣1），α•β＝m2﹣m，结合α2+β2＝12即可得出关于m的一元二次方程，解之即可得出结论．【解析】∵关于x的方程x2﹣2（m﹣1）x+m2＝0有两个实数根，∴△＝[2（m﹣1）]2﹣4×1×（m2﹣m）＝﹣4m+4≥0，解得：m≤1．∵关于x的方程x2+2（m﹣1）x+m2﹣m＝0有两个实数根α，β，∴α+β＝﹣2（m﹣1），α•β＝m2﹣m，∴α2+β2＝（α+β）2﹣2α•β＝[﹣2（m﹣1）]2﹣2（m2﹣m）＝12，即m2﹣3m﹣4＝0，解得：m＝﹣1或m＝4（舍去）．故选：A．8．（2020•南京）关于x的方程（x﹣1）（x+2）＝p2（p为常数）的根的情况，下列结论中正确的是（）A．两个正根B．两个负根C．一个正根，一个负根D．无实数根【分析】先把方程（x﹣1）（x+2）＝p2化为x2+x﹣2﹣p2＝0，再根据方程有两个不相等的实数根可得△＝1+8+4p2＞0，由﹣2﹣p2＞0即可得出结论．【解析】∵关于x的方程（x﹣1）（x+2）＝p2（p为常数），∴x2+x﹣2﹣p2＝0，∴△＝1+8+4p2＝9+4p2＞0，∴方程有两个不相等的实数根，根据根与系数的关系，方程的两个根的积为﹣2﹣p2＜0，∴一个正根，一个负根，故选：C．9．（2020•日照一模）已知m，n（m≠n）满足方程x2﹣5x﹣1＝0，则m2﹣mn+5n＝（）A．﹣23B．27C．﹣25D．25【分析】由根与系数的关系可得出m+n＝5、mn＝﹣1，m2﹣5m＝1，将m2﹣mn+5n变形为m2﹣5m﹣mn+5（m+n），代入数据即可得出结论．【解析】∵m，n（m≠n）满足方程x2﹣5x﹣1＝0，∴m+n＝5，mn＝﹣1，m2﹣5m＝1，∴m2﹣mn+5n＝m2﹣5m﹣mn+5（m+n）＝1+1+25＝27．故选：B．10．（2020•文登区模拟）已知a，b是方程x2+3x﹣5＝0的两个实数根，则a2﹣3b+2020的值是（）A．2016B．2020C．2025D．2034【分析】利用根与系数的关系，求出a2+3a＝5，a+b＝﹣3，再代入计算即可求解．【解析】∵a，b是方程x2+3x﹣5＝0的两个实数根，∴a2+3a＝5，a+b＝﹣3，则a2﹣3b+2020＝a2+3a﹣3（a+b）+2020＝5+9+2020＝2034．故选：D．二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2020•泰州）方程x2+2x﹣3＝0的两根为x1、x2，则x1•x2的值为﹣3．【分析】根据方程的系数结合根与系数的关系，即可得出x1•x2的值．【解析】∵方程x2+2x﹣3＝0的两根为x1、x2，∴x1•x2=ca=−3．故答案为：﹣3．12．（2020•南昌一模）已知α、β是方程x2﹣2x﹣3＝0的两个实数根，则α2﹣3α﹣αβ的值为3或7．【分析】由一元二次方程的解及根与系数的关系可得出α2﹣2α＝3，αβ＝﹣3，将其代入α2﹣3α﹣αβ中可得出α2﹣3α﹣αβ＝6﹣α，利用因式分解法解一元二次方程可求出α的值，再将其代入6﹣α中即可求出结论．【解析】∵α、β是方程x2﹣2x﹣3＝0的两个实数根，∴α2﹣2α＝3，αβ＝﹣3，∴α2﹣3α﹣αβ＝α2﹣2α﹣α﹣αβ＝3﹣α﹣（﹣3）＝6﹣α．∵x2﹣2x﹣3＝0，即（x+1）（x﹣3）＝0，解得：x1＝﹣1，x2＝3，∴α＝3或﹣1，∴6﹣α＝3或7．故答案为：3或7．13．（2020•泉州模拟）已知m，n是方程x2+2x﹣1＝0的两个根，则m2n+mn2＝2．【分析】先根据根与系数的关系得到m+n＝﹣2，mn＝﹣1，再利用因式分解法得到m2n+mn2＝mn（m+n），然后利用整体代入的方法计算．【解析】根据题意得m+n＝﹣2，mn＝﹣1，所以m2n+mn2＝mn（m+n）＝﹣1×（﹣2）＝2．故答案为2．14．（2020•青海）在解一元二次方程x2+bx+c＝0时，小明看错了一次项系数b，得到的解为x1＝2，x2＝3；小刚看错了常数项c，得到的解为x1＝1，x2＝5．请你写出正确的一元二次方程x2﹣6x+6＝0．【分析】利用根与系数的关系得到2×3＝c，1+5＝﹣b，然后求出b、c即可．【解析】根据题意得2×3＝c，1+5＝﹣b，解得b＝﹣6，c＝6，所以正确的一元二次方程为x2﹣6x+6＝0．故答案为x2﹣6x+6＝0．15．（2020•太仓市模拟）已知a，b是一元二次方程x2﹣2x﹣2020＝0的两个根，则a2+2b﹣3的值等于2021．【分析】根据根与系数的关系以及方程的解的定义即可求出答案．【解析】由题意可知：a2﹣2a＝2020，由根与系数的关系可知：a+b＝2，∴原式＝a2﹣2a+2a+2b﹣3，＝2020+2（a+b）﹣3＝2020+2×2﹣3＝2021，故答案为：2021．16．（2020•南昌县模拟）若方程x2﹣4x+2＝0的两个根为x1，x2，则x1（1+x2）+x2的值为6．【分析】欲求x1（1+x2）+x2＝x1+x2+x1•x2的值，根据一元二次方程根与系数的关系，求得两根的和与积，代入数值计算即可．【解析】根据题意x1+x2＝4，x1•x2＝2，∴x1（1+x2）+x2＝x1+x2+x1•x2＝4+2＝6．故答案为：6．17．（2020•荆门）已知关于x的一元二次方程x2﹣4mx+3m2＝0（m＞0）的一个根比另一个根大2，则m的值为1．【分析】设方程的两根分别为t，t+2，利用根与系数的关系得到t+t+2＝4m，t（t+2）＝3m2，利用代入消元法得到（2m﹣1）（2m+1）＝3m2，然后解关于m的方程得到满足条件的m的值．【解析】设方程的两根分别为t，t+2，根据题意得t+t+2＝4m，t（t+2）＝3m2，把t＝2m﹣1代入t（t+2）＝3m2得（2m﹣1）（2m+1）＝3m2，整理得m2﹣1＝0，解得m＝1或m＝﹣1（舍去），所以m的值为1．故答案为1．18．（2020•内江）已知关于x的一元二次方程（m﹣1）2x2+3mx+3＝0有一实数根为﹣1，则该方程的另一个实数根为−13．【分析】把x＝﹣1代入原方程求出m的值，进而确定关于x的一元二次方程，根据根与系数的关系可求出方程的另一个根．【解析】把x＝﹣1代入原方程得，（m﹣1）2﹣3m+3＝0，即：m2﹣5m+4＝0，解得，m＝4，m＝1（不合题意舍去），当m＝4时，原方程变为：9x2+12x+3＝0，即，3x2+4x+1＝0，由根与系数的关系得：x1•x2=13，又x1＝﹣1，∴x2=−1 3故答案为：−1 3．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2019秋•孝南区期末）关于x的方程x2﹣2x+2m﹣1＝0有实根．（1）求m的取值范围；（2）设方程的两实根分别为x1，x2且x1﹣x2＝﹣2，求m的值．【分析】（1）根据判别式的意义得到△＝（﹣2）2﹣4（2m﹣1）≥0，然后就解关于m的不等式；（2）利用根与系数的关系得到x1+x2＝2，x1•x2＝2m﹣1，而x1﹣x2＝﹣2，则可先求出x1、x2的值，然后计算m的值．【解析】（1）根据题意得△＝（﹣2）2﹣4（2m﹣1）≥0，解得m≤1；（2）由根与系数的关系可得x1+x2＝2，x1•x2＝2m﹣1，∵x1﹣x2＝﹣2，∴x1＝0，x2＝2，∴2m﹣1＝0，解得m=1 2．20．（2019秋•鞍山期末）已知关于x的一元二次方程x2+（2k+1）x+k2＝0有实数根．（1）求k的取值范围．（2）设方程的两个实数根分别为x1、x2，若2x1x2﹣x1﹣x2＝1，求k的值．【分析】（1）由△≥0，求出k的范围；（2）由根与系数的关系可知：x1+x2＝﹣2k﹣1，x1x2＝k2，代入等式求解即可．【解析】（1）∵一元二次方程x2+（2k+1）x+k2＝0有实数根，∴△＝（2k+1）2﹣4k2≥0，∴k≥−1 4；（2）由根与系数的关系可知：x1+x2＝﹣2k﹣1，x1x2＝k2，∴2x1x2﹣x1﹣x2＝2k2+2k+1＝1，∴k＝0或k＝﹣1，∵k≥−1 4；∴k＝0．21．（2020•玉林）已知关于x的一元二次方程x2+2x﹣k＝0有两个不相等的实数根．（1）求k的取值范围；（2）若方程的两个不相等的实数根是a，b，求aa+1−1b+1的值．【分析】（1）根据方程有两个不相等的实数根可得△＝4+4k＞0，解不等式求出k的取值范围；（2）由根与系数的关系可得a+b＝﹣2，a•b＝﹣k，代入整理后的代数式，计算即可．【解析】（1）∵方程有两个不相等的实数根，∴△＝b2﹣4ac＝4+4k＞0，解得k＞﹣1．∴k的取值范围为k＞﹣1；（2）由根与系数关系得a+b＝﹣2，a•b＝﹣k，a a+1−1b+1=ab−1ab+a+b+1=−k−1−k−2+1=1．22．（2020•黄石）已知：关于x的一元二次方程x2+√m x﹣2＝0有两个实数根．（1）求m的取值范围；（2）设方程的两根为x1、x2，且满足（x1﹣x2）2﹣17＝0，求m的值．【分析】（1）根据方程的系数结合根的判别式，即可得出△＝m+8≥0，根据二次根式的意义即可得出m ≥0，从而得出m的取值范围；（2）根据根与系数的关系可得x1+x2=−√m，x1•x2＝﹣2，结合（x1﹣x2）2﹣17＝0即可得出关于m的一元一次方程，解之即可得出结论．【解析】（1）∵关于x的一元二次方程x2+√m x﹣2＝0有两个实数根，∴△＝[√m]2﹣4×1×（﹣2）＝m+8≥0，且m≥0，解得：m≥0．（2）∵关于x的一元二次方程x2+√m x﹣2＝0有两个实数根x1、x2，∴x1+x2=−√m，x1•x2＝﹣2，∴（x1﹣x2）2﹣17＝（x1+x2）2﹣4x1•x2﹣17＝0，即m+8﹣17＝0，解得：m＝9．23．（2019秋•南充期末）已知关于x的方程ax2+（3﹣2a）x+a﹣3＝0．（1）求证：无论a为何实数，方程总有实数根．（2）如果方程有两个实数根x1，x2，当|x1﹣x2|=32时，求出a的值．【分析】（1）证明一元二次方程根的判别式恒大于等于0，即可解答；（2）根据一元二次方程根与系数的关系x1+x2=2a−3a，以及x1•x2=a−3a，由|x1﹣x2|=32即可求得a的值．【解答】（1）证明：①当a＝0时，方程为3x﹣3＝0，是一元一次方程，有实数根；②当a≠0时，方程是一元二次方程，∵关于x的方程ax2+（3﹣2a）x+a﹣3＝0中，△＝（3﹣2a）2﹣4a（a﹣3）＝9＞0，∴无论a为何实数，方程总有实数根．（2）解：如果方程的两个实数根x1，x2，则x1+x2=2a−3a，x1•x2=a−3a，∵|x1﹣x2|=3 2，∴√(2a−3a)2−4×a−3a=32，解得a＝±2．故a的值是﹣2或2．24．（2020•广东）已知关于x，y的方程组{ax+2√3y=−10√3，x+y=4与{x−y=2，x+by=15的解相同．（1）求a，b的值；（2）若一个三角形的一条边的长为2√6，另外两条边的长是关于x的方程x2+ax+b＝0的解．试判断该三角形的形状，并说明理由．【分析】（1）关于x ，y 的方程组{ax +2√3y =−10√3，x +y =4与{x −y =2，x +by =15的解相同．实际就是方程组{x +y =4x −y =2的解，可求出方程组的解，进而确定a 、b 的值；（2）将a 、b 的值代入关于x 的方程x 2+ax +b ＝0，求出方程的解，再根据方程的两个解与2√6为边长，判断三角形的形状．【解析】（1）由题意得，关于x ，y 的方程组的相同解，就是方程组{x +y =4x −y =2的解，解得，{x =3y =1，代入原方程组得，a ＝﹣4√3，b ＝12；（2）当a ＝﹣4√3，b ＝12时，关于x 的方程x 2+ax +b ＝0就变为x 2﹣4√3x +12＝0，解得，x 1＝x 2＝2√3，又∵（2√3）2+（2√3）2＝（2√6）2，∴以2√3、2√3、2√6为边的三角形是等腰直角三角形．。

华师版数学九年级上册强化专训-一元二次方程的根与系数的关系(1)

华师版数学九年级上册阶段强化专训一元二次方程的根与系数的关系【知识与技能】1.引导学生在已有的一元二次方程解法的基础上，探索出一元二次方程根与系数的关系，及其关系的运用.2.通过观察、实践、讨论等活动，经历从观察判断到发现关系的过程.【过程与方法】通过探究一元二次方程的根与系数的关系，培养学生观察分析和综合判断的能力，激发学生发现规律的积极性，鼓励学生勇于探索的精神.【情感态度】在积极参与数学活动的同时，初步体验发现问题，总结规律的态度及养成质疑和独立思考的习惯.【教学重点】一元二次方程根与系数之间的关系的运用.【教学难点】一元二次方程根与系数之间的关系的运用.一、情境导入，初步认识1.完成下列表格问题你发现了什么规律？①用语言叙述你发现的规律：（两根之和为一次项系数的相反数；两根之积为常数项）②设方程x2+px+q=0的两根为x1,x2，用式子表示你发现的规律.（x1+x2=-p,x1·x2=q）2.完成下列表格问题上面发现的结论在这里成立吗？（不成立）请完善规律：①用语言叙述发现的规律：（两根之和为一次项系数与二次项系数之比的相反数，两根之积为常数项与二次项系数之比）②设方程ax 2+bx+c=0的两根为x 1,x 2，用式子表示你发现的规律.（x 1+x 2=-a b ,x 1·x 2=ac ）二、思考探究，获取新知通过以上活动你发现了什么规律？对一般的一元二次方程ax 2+bx+c=0（a ≠0）这一规律是否成立？试通过求根公式加以说明.ax 2+bx+c=0的两根a ac b b x 2421-+-=,a ac b b x 2422---=,x1+x2=-a b , x 1·x 2=ac . 【教学说明】教师可引导学生根据求根公式推导出根与系数之间的关系，体会知识形成的过程，加深对知识的理解.例1 不解方程，求下列方程的两根之和与两根之积：（1）x 2-6x-15=0;（2）3x 2+7x-9=0;（3）5x-1=4x 2.解：（1）x1+x2=6,x1·x2=-15;（2）x1+x2=-37,x1·x2=-3；（3）x1+x2=45,x1·x2=41. 【教学说明】先将方程化为一般形式，找出对应的系数.例2 已知方程2x 2+kx-9=0的一个根是-3，求另一根及k 的值. 解：另一根为23，k=3. 【教学说明】本题有两种解法，一种是根据根的定义，将x=-3代入方程先求k ，再求另一个根；一种是利用根与系数的关系解答.。

《一元二次方程的根与系数的关系》解答题专题培优提升训练(附答案)

2021-2022学年北师大版九年级数学上册《2.5一元二次方程的根与系数的关系》解答题专题培优提升训练（附答案）1．已知关于x的方程2mx2﹣（5m﹣1）x+3m﹣1＝0．（1）求证：无论m为任意实数，方程总有实数根．（2）如果这个方程的根的判别式的值等于1，求m的值．2．关于x的一元二次方程x2﹣2x+3m﹣2＝0有实数根．（1）求m的取值范围；（2）若m为正整数，求出此时方程的根．3．已知x1，x2是关于x的一元二次方程x2﹣2（m+1）x+m2+5＝0的两个实数根，求m的取值范围．4．已知关于x的一元二次方程x2﹣3x+a﹣1＝0有实数根．（1）求a的取值范围；（2）当a为符合条件的最大整数时，求此时方程的解．5．已知y1＝x2﹣2x+3．y2＝x+m．（1）若m＝1，当x取何值时y1＝y2？（2）若y1＝2y2，当m为何范围时，存在两个不同的x值？6．已知关于x的一元二次方程|x2﹣1|＝（x﹣1）（kx﹣2）：（1）若k＝3，求方程的解；（2）若方程恰有两个不同解，求实数k的取值范围．7．已知关于x的一元二次方程x2+（2k﹣1）x+k2﹣3＝0有实数根．（ⅰ）求实数k的取值范围；（ⅱ）当k＝2时，方程的根为x1，x2，求代数式（x12+2x1﹣1）（x22+4x2+3）的值．8．已知关于x的一元二次方程：x2﹣（2k+1）x+4（k﹣）＝0．（1）求证：这个方程总有两个实数根；（2）若等腰△ABC的一边长a＝4，另两边长b、c，恰好是这个方程的两个实数根，求△ABC的周长．（3）若方程的两个实数根之差等于3，求k的值．9．已知关于x的一元二次方程x2﹣（2m+4）x+m2+4m＝0．（1）求证：无论m取何值，此方程总有两个不相等的实数根．（2）设方程的两个实数根分别为x1，x2；①求代数式﹣4x1x2的最大值；②若方程的一个根是6，x1和x2是一个等腰三角形的两条边，求等腰三角形的周长．10．关于x的一元二次方程x2+2（k﹣1）x+k2﹣1＝0有实数根．（1）求k的取值范围；（2）若方程的两根x1，x2满足（x1﹣1）（x2﹣1）＝6，求k的值．11．已知关于x的一元二次方程x2+2x+k﹣1＝0有两个不相等的实数根．（1）求k的取值范围；（2）设两个实数根是x1和x2，且x1+x2﹣2x1x2＝2，则k的值为．12．关于x的一元二次方程x2+2mx+m2+m＝0有两个不相等的实数根．（1）求m的取值范围．（2）设出x1、x2是方程的两根，且x12+x22＝12，求m的值．13．已知关于x的一元二次方程（m﹣2）x2+（2m+1）x+m＝0有两个实数根x1，x2．（1）求m的取值范围．（2）若|x1|＝|x2|，求m的值及方程的根．14．关于x的一元二次方程x2﹣4x+k﹣3＝0的两个实数根是x1、x2．（1）已知k＝2，求x1+x2+x1x2．（2）若x1＝3x2，试求k值．15．已知关于x的一元二次方程x2﹣6x﹣k2＝0（k为常数）．（1）求证：方程有两个不相等的实数根；（2）设x1，x2为方程的两个实数根，且x1+2x2＝14，试求出方程的两个实数根和k的值．16．已知m为实数，关于x的方程为mx2+（m﹣2）x﹣1＝0．（1）求证：不论m为何实数，方程总有实数根．（2）若方程有两实根x1，x2，当x1x2﹣2x1﹣2x2＝3时，求m的值．17．已知关于x的一元二次方程x2﹣（2k+1）x+k2+2k＝0（1）若该方程有两个实数根，求k的最大整数值．（2）若该方程的两个实数根为x1，x2，是否存在实数k，使得x1x2﹣x12﹣x22＝﹣16成立？若存在，请求出k的值；若不存在，请说明理由．18．关于x的一元二次方程x2+（2m﹣3）x+m2＝0有两个不相等的实数根．（1）求m的取值范围；（2）若x1、x2是方程的两根，且+＝1，求m的值．19．若x1，x2与是方程x2+x﹣3＝0的两个实数根，求x13﹣4x22+22的值．20．已知关于x的方程（k﹣1）x2+2kx+2＝0．（1）求证：无论k为何值，方程总有实数根．（2）若方程的两个根为x1，x2，且＝0，求k的值．21．已知关于x的一元二次方程x2﹣（2k+1）x+k2﹣2＝0．（1）求证：无论k为何实数，方程总有两个不相等的实数根；（2）若方程的两个实数根x1，x2满足x1﹣x2＝3，求k的值．参考答案1．解：（1）①当m＝0时，该方程是关于x的一元一次方程，符合题意；②关于x的一元二次方程2mx2﹣（5m﹣1）x+3m﹣1＝0．∵△＝（5m﹣1）2﹣8m（3m﹣1）＝（m﹣1）2≥0，∴无论m为任何实数，方程总有实根．（2）由题意得，△＝（m﹣1）2＝1，解得m1＝0，m2＝2，而m≠0，∴m＝2．2．解：（1）∵方程有实数根，∴（﹣2）2﹣4×1×（3m﹣2）≥0，∴m≤1；（2）∵m为正整数，∴m＝1，∴方程为：x2﹣2x+1＝0，∴x1＝x2＝1．3．解：∵关于x的一元二次方程x2﹣2（m+1）x+m2+5＝0有两个实数根，∴△＝[﹣2（m+1）]2﹣4（m2+5）＝8m﹣16≥0，∴m≥2．4．解：（1）∵关于x的一元二次方程x2﹣3x+a﹣1＝0有实数根，∴△＝（﹣3）2﹣4（a﹣1）＝﹣4a+13≥0，解得：a≤，即a的取值范围是a≤；（2）∵a的取值范围是a≤，∴整数a的最大值是3，把a＝3代入方程x2﹣3x+a﹣1＝0得：x2﹣3x+2＝0，解得：x1＝1，x2＝2．5．解：（1）当m＝1时，根据题意，得x2﹣2x+3＝x+1，整理，得（x﹣1）（x﹣2）＝0．所以x﹣1＝0或x﹣2＝0．解得x1＝1，x2＝2；（2）根据题意，得x2﹣2x+3＝2x+2m，整理，得x2﹣4x+3﹣2m＝0，所以△＝（﹣4）2﹣4×1×（3﹣2m）＞0．解得m＞﹣．所以当m＞﹣时，存在两个不同的x值．6．解：（1）把k＝3代入|x2﹣1|＝（x﹣1）（kx﹣2）中，得|x2﹣1|＝（x﹣1）（3x﹣2），当x2＞1，即x＞1或x＜﹣1时，原方程可化为：x2﹣1＝（x﹣1）（3x﹣2），解得，x＝1（舍），或x＝；当x2≤1，即﹣1≤x≤1时，原方程可化为：1﹣x2＝（x﹣1）（3x﹣2），解得，x＝1，或x＝；综上，方程的解为x1＝，x2＝1，x3＝；（2）∵x＝1恒为方程|x2﹣1|＝（x﹣1）（kx﹣2）的解，∴当x≠1时，方程两边都同时除以x﹣1得，，要使此方程只有一个解，只需函数y＝与函数y＝kx﹣2的图象只有一个交点．∵函数：，作出函数图象，由图象可知，当k＜0时，直线y＝kx﹣2与函数y＝图象只有一个交点；当k＝0时，直线y＝kx﹣2＝﹣2与函数y＝图象只有一个交点；当k＝1时，y＝kx﹣2＝x﹣2与y＝x+1平行，则与函数y＝图象只有一个交点；∵当直线y＝kx﹣2过（1，2）点时，2＝k﹣2，则k＝4，∴函数图象可知，当k≥4时，直线y＝kx﹣2与函数y＝图象也只有一个交点，∴要使函数图象与y＝kx﹣2图象有且只有一个交点，则实数k的取值范围是k≤0或k＝1或k≥4．综上，实数k的取值范围：k≤0或k＝1或k≥4．7．解：（i）∵方程有实数根，∴△＝（2k﹣1）2﹣4（k2﹣3）≥0，解得：k≤；（ii）当k＝2时，方程化为x2+3x+1＝0，∴x1+x2＝﹣3，x1x2＝1，∵x1，x2是方程的解，∴x12+3x1+1＝0，x22+3x2+1＝0，∴x12+3x1＝﹣1，x22+3x2＝﹣1，∴原式＝（﹣1﹣x1﹣1）（﹣1+x2+3）＝﹣（x1+2）（x2+2）＝﹣[x1x2+2（x1+x2）+4]＝﹣（1﹣6+4）＝1．8．解：（1）△＝（2k+1）2﹣4×1×4（k﹣）＝4k2﹣12k+9＝（2k﹣3）2，∵无论k取何值，（2k﹣3）2≥0，故这个方程总有两个实数根；（2）由求根公式得x＝，∴x1＝2k﹣1，x2＝2．∵另两边长b、c，恰好是这个方程的两个实数根，设b＝2k﹣1，c＝2，当a，b为腰时，则a＝b＝4，即2k﹣1＝4，计算得出k＝，此时三角形周长为4+4+2＝10；当b，c为腰时，b＝c＝2，此时b+c＝a，构不成三角形，故此种情况不存在．综上所述，△ABC周长为10．（3）∵方程的两个实数根之差等于3，∴，解得：k＝0或3．9．解：（1）△＝（2m+4）2﹣4（m2+4m）＝16，16＞0，∴此方程总有两个不相等的实数根．（2）①﹣4x1x2＝（x1+x2）2﹣6x1x2，∵x1+x2＝＝2m+4，x1x2＝m2+4m，∴（x1+x2）2﹣6x1x2＝（2m+4）2﹣6（m2+4m）＝﹣2m2﹣8m+16＝﹣2（m+2）2+24，∴当m＝﹣2时﹣4x1x2的最大值为24．②把x＝6代入原方程可得m2﹣8m+12＝0，解得m＝2或m＝6，当m＝2时，原方程化简为x2﹣8x+12＝0，解得x＝2或x＝6，三角形三边长为6，6，2时三角形周长为14，三角形边长为2，2，6时不存在．当m＝6时，原方程化简为x2﹣16x+60，解得x＝6或x＝10．三角形三边长为6，6，10时三角形周长为22，三角形三边长为10，10，6时，三角形周长为26．∴等腰三角形周长为14或22或26．10．解：（1）∵关于x的一元二次方程x2+2（k﹣1）x+k2﹣1＝0有实数根，∴△＝[2（k﹣1）]2﹣4（k2﹣1）＝﹣8k+8≥0，解得：k≤1．∴k的取值范围为：k≤1．（2）由根与系数关系得：x1+x2＝﹣2（k﹣1），x1x2＝k2﹣1，所以（x1﹣1）（x2﹣1）＝x1x2﹣（x1+x2）+1＝k2﹣1+2（k﹣1）+1＝6．解得k＝2（舍去）或k＝﹣4．故k的值是﹣4．11．解：（1）∵一元二次方程x2+2x+k﹣1＝0有两个不相等的实数根，∴△＝b2﹣4ac＝22﹣4（k﹣1）＞0，解得k＜2，即k的取值范围是k＜2；（2）∵一元二次方程x2+2x+k﹣1＝0的两个实数根是x1和x2，∴x1+x2＝﹣2，x1x2＝k﹣1，∵x1+x2﹣2x1x2＝2，∴﹣2﹣2（k﹣1）＝2，∴k＝﹣1，故答案为：﹣1．12．解：（1）根据题意得：△＝（2m）2﹣4（m2+m）＞0，解得：m＜0．∴m的取值范围是m＜0．（2）根据题意得：x1+x2＝﹣2m，x1x2＝m2+m，∵x12+x22＝12，∴﹣2x1x2＝12，∴（﹣2m）2﹣2（m2+m）＝12，∴解得：m1＝﹣2，m2＝3（不合题意，舍去），∴m的值是﹣2．13．解：（1）由题意得：△≥0且m﹣2≠0，∴（2m+1）2﹣4m（m﹣2）≥0解得m≥﹣且m≠2（2）由题意得有两种情况：①当x1＝x2，则△＝0，所以m＝﹣，x1＝x2＝﹣×＝．②当x1＝﹣x2时，则x1+x2＝0．，所以m＝﹣，因为m≥﹣且m≠2，所以此时方程无解．综上所述，m＝﹣，x1＝x2＝．14．解：（1）∵方程x2﹣4x+k﹣3＝0的两个实数根是x1、x2，k＝2，∴x1+x2＝4，x1x2＝k﹣3＝﹣1，∴x1+x2+x1x2＝4﹣1＝3．（2）∵x1+x2＝4，x1＝3x2，∴x1＝3，x2＝1，∴k＝x1x2+3＝6．15．解：（1）证明：∵在方程x2﹣6x﹣k2＝0中，△＝（﹣6）2﹣4×1×（﹣k2）＝36+4k2≥36，∴方程有两个不相等的实数根．（2）∵x1，x2为方程x2﹣6x﹣k2＝0的两个实数根，∴x1+x2＝6，∵x1+2x2＝14，∴x2＝8，x1＝﹣2．将x＝8代入x2﹣6x﹣k2＝0中，得：64﹣48﹣k2＝0，解得：k＝±4．答：方程的两个实数根为﹣2和8，k的值为±4．16．（1）证明：当m＝0时，已经方程为﹣2x﹣1＝0，有实数根；当m≠0时，已经方程是一元二次方程，△＝（m﹣2）2﹣4m×（﹣1）＝m2+4＞0，该方程有两个不等实根；综上，不论m为何实数，方程总有实数根；（2）由根与系数的关系可得，，，∵x1x2﹣2x1﹣2x2＝3，∴x1x2﹣2（x1+x2）＝3，∴，解得m＝﹣5，经检验，m＝﹣5是原分式方程的解，即m的值是﹣5．17．解：（1）由题意得：此方程的根的判别式△＝[﹣（2k+1）]2﹣4（k2+2k）≥0，整理得：﹣4k+1≥0，解得，则k的最大整数值是0；（2）存在，由根与系数的关系得：x1+x2＝2k+1，x1x2＝k2+2k，∵＝，∴﹣（2k+1）2+3（k2+2k）＝﹣16，整理得：k2﹣2k﹣15＝0，解得k＝﹣3或k＝5，由（1）可知，，则k＝﹣3．18．解：（1）根据题意，知（2m﹣3）2﹣4m2＞0，解得m＜；（2）由题意知x1+x2＝﹣（2m﹣3）＝3﹣2m，x1•x2＝m2，由+＝1，即＝1可得＝1，解得：m＝1（舍去）或m＝﹣3，所以m的值是﹣3．19．解：∵x1是方程x2+x﹣3＝0的实数根，∴x12+x1﹣3＝0，∴x12＝﹣x1+3，x1＝﹣x12+3，∴x13＝﹣x12+3x1，∴x13﹣4x22+22＝﹣x12+3x1﹣4x22+22＝﹣4x12+9﹣4x22+22＝﹣4（x1+x2）2+8x1•x2+31，∵x1、x2是方程x2+x﹣3＝0的两个实数根，∴x1+x2＝﹣1，x1•x2＝﹣3，∴原式＝﹣4×（﹣1）2+8×（﹣3）+31＝3．20．（1）证明：①当k＝1时，该方程有一个实数根，符合题意．②当k≠1时，∵△＝（2k）2﹣4（k﹣1）×2＝4（k﹣1）2+4＞0，∴当k≠1时，方程总有实数根．综上所述，无论k取任何值，方程总有实数根．（2）∵x1、x2是方程的两个根，∴x1+x2＝，x1•x2＝，∴＝+x1x2＝+＝0．解得k＝2或k＝﹣1．经检验，k＝2或k＝﹣1都符合题意．所以k＝2或k＝﹣1．21．解：（1）∵△＝[﹣（2k+1）]2﹣4×1×（k2﹣2）＝4k2+4k+1﹣2k2+8＝2k2+4k+9＝2（k+1）2+7＞0，∵无论k为何实数，2（k+1）2≥0，∴2（k+1）2+7＞0，∴无论k为何实数，方程总有两个不相等的实数根；（2）由根与系数的关系得出x1+x2＝2k+1，x1x2＝k2﹣2，∵x1﹣x2＝3，∴（x1﹣x2）2＝9，∴（x1+x2）2﹣4x1x2＝9，∴（2k+1）2﹣4×（k2﹣2）＝9，化简得k2+2k＝0，解得k＝0或k＝﹣2．。

一元二次方程根与系数的关系(韦达定理) 浙教版八年级下册培优讲义(含解析)

第2讲韦达定理命题点一：利用判别式求值例1若关于x 的方程ax 2＋2(a ＋2)x ＋a ＝0有实数解，则实数a 的取值范围是 a ≥－1 .例2(1)如果关于x 的一元二次方程kx 2－2k ＋1x ＋1＝0有两个不相等的实数根，那么k 的取值范围是( D ) A ．k ＜12 B ．k ＜12且k ≠0 C ．－12≤k ＜12 D ．－12≤k ＜12且k ≠0 (2)若关于x 的一元二次方程12x 2－2mx －4m ＋1＝0有两个相等的实数根，则(m －2)2－2m (m －1)的值为 72．命题点二：巧用韦达定理妙解代数式例3若m ，n 是方程x 2＋x －1＝0的两个实数根，则m 2＋2m ＋n 的值为 0 .例4(1)已知α，β是方程x 2－x －1＝0的两个实数根，则代数式α2＋α(β2－2)的值为 0 ．(2)若关于x 的一元二次方程2x 2－2x ＋3m －1＝0的两个实数根为x 1，x 2，且x 1x 2>x 1＋x 2－4，则实数m 的取值范围是( D )A ．m >－53B ．m ≤12C ．m ＜－53D ．－53＜m ≤12命题点三：根据根的范围求值例5已知关于x 的方程ax 2＋(a ＋1)x ＋6a ＝0有两个不相等的实数根x 1，x 2(x 1＜1＜x 2)，则实数a 的取值范围是( C )A ．－1＜a ＜0B ．a ＜－1C ．－18＜a ＜0D ．a ＜－18例6已知关于x 的方程x 2＋2px ＋1＝0的两个实数根一个大于1，另一个小于1，则实数p 的取值范围是 p ＜－1 ．命题点四：解绝对值方程例7设方程||x 2＋ax ＝4只有3个不相等的实数根，求a 的值和相应的3个根．解：方程等价于如下两个方程：x 2＋ax －4＝0，① x 2＋ax ＋4＝0. ②∵原方程只有3个不相等的实根，又∵两个方程不可能有公共根，∴必有且只有方程①或②有重根，Δ1＝a 2＋16≥0，Δ2＝a 2－16≥0.由于Δ1>Δ2，故只可能是Δ2＝0，即a ＝±4.∴当a ＝4时，相应的根为－2，－2±22；∴当a ＝－4时，相应的根为2，2±2 2.例8若关于x 的方程x 2－(m ＋5)||x ＋4＝m 恰好有3个实数解，则实数m ＝ 4 .命题点五：构造方程求值例9已知m 2－2m －1＝0，n 2＋2n －1＝0且mn ≠1，则mn ＋n ＋1n 的值为 3 ．例10已知mn ≠1，且5m 2＋2 018m ＋9＝0，9n 2＋2 018n ＋5＝0，则m n值为( B ) A.59 B.95 C.6703D ．－402 命题点六：三角形边的问题例11如果方程(x －1)(x 2－2x ＋m )＝0的三个根可以作为一个三角形的三边之长，那么实数m 的取值范围是( C ) A ．0≤m ≤1 B ．m ≥34 C.34＜m ≤1 D.34≤m ≤1 例12△ABC 的一边长为5，另外两边长恰为方程2x 2－12x ＋m ＝0的两个根，则m 的取值范围是112<m ≤18 ．命题点七：整数根问题例13已知整数p ，q 满足p ＋q ＝2 010，且关于x 的一元二次方程67x 2＋px ＋q ＝0的两个根均为正整数，则p ＝－2278 ．例14求满足如下条件的所有k 的值：使关于x 的方程kx 2＋(k ＋1)x ＋(k －1)＝0的根都是整数．解：分k ＝0和k ≠0两种情况讨论．当k ＝0时，所给方程为x －1＝0，有整数根x ＝1.当k ≠0时，所给方程为二次方程．设两个整数根为x 1和x 2，则x 1＋x 2＝－k ＋1k ＝－1－1k ，① x 1·x 2＝k －1k ＝1－1k .② 由①－②，得x 1＋x 2－x 1·x 2＝－2，整理，得(x 1－1)(x 2－1)＝3.∵方程的根都是整数，∴(x 1－1)(x 2－1)＝3＝1×3＝(－1)×(－3)．有x 1－1＝1，x 2－1＝3或x 1－1＝－1，x 2－1＝－3.故x 1＋x 2＝6或x 1＋x 2＝－2，即－1－1k＝6或－1－1k ＝－2，解得k ＝－17或k ＝1. 又∵Δ＝(k ＋1)2－4k (k －1)＝－3k 2＋6k ＋1，当k ＝－17或k ＝1时，都有Δ＞0.∴满足要求的k 值为0，－17，1. 课后练习1．已知关于x 的一元二次方程mx 2－(m ＋2)x ＋m 4＝0有两个不相等的实数根x 1，x 2，若1x 1＋1x 2＝4m ，则m 的值为( A )A ．2B ．－1C ．2或－1D ．不存在2．已知关于x 的方程x 2－(a 2－2a －15)x ＋a －1＝0的两个根互为相反数，则a 的值是( B )A ．5B ．－3C ．5或－3D ．13．已知四个互不相等的正实数a ，b ，c ，d 满足(a 2012－c 2012)(a 2012－d 2012)＝2 012，(b 2012－c 2012)(b 2012－d 2012)＝2 012，则(ab )2012－(cd )2012的值为( A )A ．－2 012B ．－2 011C ．2 012D ．2 0114．若实数a ，b 满足12a －ab ＋b 2＋2＝0，则实数a 的取值范围是( C ) A ．a ≤－2 B ．a ≥4 C ．a ≤－2或a ≥4 D ．－2≤a ≤45．已知关于x 的方程x 2＋(k －2)x ＋5－k ＝0有两个大于2的实数根，则k 的取值范围是( A )A ．－5＜k ≤－4B ．k >－5C ．k ≤－4D ．－4≤k ＜－26．关于x 的一元二次方程x 2－2kx ＋k 2－k ＝0的两个实数根分别是x 1，x 2，且x 21＋x 22＝4，则x 21－x 1x 2＋x 22的值为 4 ．7．如果m ，n 是两个不相等的实数，且满足m 2－m ＝3，n 2－n ＝3，那么代数式2n 2－mn ＋2m ＋2 015＝ 2026 .8．设a ，b 是一元二次方程x 2－x －1＝0的两个根，则3a 3＋4b ＋2a 2的值为 11 ． 9．若方程||x 2－5x ＝a 有且只有相异的两个实数根，则a 的取值范围是 a ＝0或a >254． 10．若p ＋q ＝198，则方程x 2＋px ＋q ＝0的最大整数解为 200 ．11．关于x 的一元二次方程x 2－mx ＋2m －1＝0的两个实数根分别是x 1，x 2，且x 21＋x 22＝7，求下列代数式的值：(1)(x 1－x 2)2. (2)x 2x 1＋2＋x 1x 2. 解：由根与系数的关系，得x 1＋x 2＝m ，x 1·x 2＝2m －1.∵x 21＋x 22＝(x 1＋x 2)2－2x 1x 2＝m 2－2×(2m －1)＝7， ∴m 2－4m －5＝0.∴m 1＝5，m 2＝－1.当m 1＝5时，Δ＝m 2－4(2m －1)＝25－36＝－9＜0(不合题意，舍去)；当m 2＝－1时，Δ＝1－(－12)＝13>0.∴m ＝－1.∴x 1＋x 2＝－1，x 1x 2＝－3.∴(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2＝13，x 2x 1＋2＋x 1x 2＝(x 1＋x 2)2x 1·x 2＝－13.12．已知方程x 2＋px ＋q ＝0的两个根是x 1，x 2，那么x 1＋x 2＝－p ，x 1x 2＝q .请根据以上结论，解决下列问题：(1)已知a ，b 满足a 2－15a －5＝0，b 2－15b －5＝0，求a b ＋b a的值． (2)已知a ，b ，c 均为实数，且a ＋b ＋c ＝0，abc ＝16，求正数c 的最小值．解：(1)当a ≠b 时，则a ，b 为方程x 2－15x －5＝0的两个根，∴a ＋b ＝15，ab ＝－5.∴原式＝a 2＋b 2ab ＝(a ＋b )2－2ab ab ＝152－2×(－5)－5＝－47. 当a ＝b 时，原式＝2.综上所述，a b ＋b a的值为－47或2. (2)由条件，得a ＋b ＝－c ，ab ＝16c ，则a ，b 为方程x 2＋cx ＋16c＝0的两个实数根， ∴Δ＝c 2－4×16c≥0，c 3≥64，即c ≥4. 故正数c 的最小值为4.13．(自主招生模拟题)已知x 1，x 2，x 3(x 1＜x 2＜x 3)为关于x 的方程x 3－3x 2＋(a ＋2)x －a ＝0的三个实数根，则4x 1－x 21＋x 22＋x 23的值为( A )A ．5B ．6C ．7 D.814．(自主招生模拟题)设a ，b ，c ，d 为四个不同的实数，若a ，b 为方程x 2－10cx －11d ＝0的根，c ，d 为方程x 2－10ax －11b ＝0的根，则a ＋b ＋c ＋d ＝ 1210 ．15．(自主招生真题)设x 为正数，求分式x (x ＋1)2的最大值．解：设k ＝x (x ＋1)2. 整理，得kx 2＋(2k －1)x ＋k ＝0.由Δ＝(2k －1)2－4k 2≥0，得k ≤14，即分式x (x ＋1)2的最大值为14.。

中考数学根与系数关系培优练习含答案

中考数学根与系数关系培优练习阅读与思考根与系数的关系称为韦达定理，其逆定理也成立，是由16世纪的法国数学家韦达所发现的．韦达定理形式简单而内涵丰富，在数学解题中有着广泛的应用，主要体现在： 1．求方程中字母系数的值或取值范围； 2．求代数式的值；3．结合根的判别式，判断根的符号特征； 4．构造一元二次方程； 5．证明代数等式、不等式．当所要求的或所要证明的代数式中的字母是某个一元二次方程的根时，可先利用根与系数的关系找到这些字母间的关系，然后再结合已知条件进行求解或求证，这是利用根与系数的关系解题的基本思路，需要注意的是，应用根与系数的关系的前提条件是一元二次方程有两个实数根，所以，应用根与系数的关系解题时，必须满足判别式△≥0．例题与求解【例1】设关于x 的二次方程22(4)(21)10m x m x -+-+=(其中m 为实数)的两个实数根的倒数和为s ，则s 的取值范围是_________.【例2】如果方程2(1)(2)0x x x m --+=的三个根可以作为一个三角形的三边长，那么，实数m 的取值范围是_________.A ．01m ≤≤B ．34m ≥C ．314m <≤D ．314m ≤≤【例3】已知α，β是方程2780x x -+=的两根，且αβ>．不解方程，求223βα+的值．【例4】设实数,s t 分别满足22199910,99190s s t t ++=++=并且1st ≠，求41st s t++的值．【例5】（1）若实数,a b 满足258a a +=，258b b +=，求代数式1111b a a b --+--的值；（2）关于,,x y z 的方程组32236x y z axy yz zx ++=⎧⎨++=⎩有实数解(,,)x y z ，求正实数a 的最小值；（3）已知,x y 均为实数，且满足17xy x y ++=，2266x y xy +=，求432234x x y x y xy y ++++的值．【例6】 ,,a b c 为实数，0ac <，且2350a b c ++=，证明一元二次方程20ax bx c ++=有大于35而小于1的根．能力训练A 级1．已知m ，n 为有理数，且方程20x mx n ++=有一个根是52-，那么m n += ． 2．已知关于x 的方程230x x m -+=的一个根是另一个根的2倍，则m 的值为． 3．当m = 时，关于x 的方程228(26)210x m m x m -+-+-=的两根互为相反数；当时，关于x 的方程22240x mx m -+-=的两根都是正数；当时，关于m的方程23280x x m ++-=有两个大于2-的根．4．对于一切不小于2的自然数n ．关于x 的一元二次方程22(2)20x n x n -+-=的两根记为,n n a b (2)n ≥则223320072007111(2)(2)(2)(2)(2)(2)a b a b a b +++=------ ．5．设12,x x 是方程222(1)(2)0x k x k -+++=的两个实根，且12(1)(1)8x x ++=，则k 的值为（）A ．31-或B ．3-C ．1D ．12k ≥的一切实数 6．设12,x x 是关于x 的一元二次方程22x x n mx ++-=的两个实数根，且1210,30x x x <-<，则（）A ．12m n >⎧⎨>⎩B ．12m n >⎧⎨<⎩C ．12m n <⎧⎨>⎩D ．12m n <⎧⎨<⎩7．设12,x x 是方程220x x k +-=的两个不等的实数根，则22122x x +-是（） A ．正数 B ．零 C ．负数 D ．不大于零的数8．如图，菱形ABCD 的边长是5，两对角线交于O 点，且AO ，BO 的长分别是关于x 的方程22(21)30x m x m +-++=的根，那么m 的值是（）A ．3-B ．5C ．53-或D ．53-或9．已知关于x 的方程：22(2)04m x m x --=．（1）求证：无论m 取什么实数值，方程总有两个不相等的实数根；（2）若这个方程的两个根是12,x x ，且满足212,x x =+求m 的值及相应的12,x x ．10．已知12,x x 是关于x 的一元二次方程2430kx x +-=的两个不相等的实数根．（1）求k 的取值范围；（2）是否存在这样的实数k ，使12123222x x x x +-=成立？若存在，求k 的值；若不存在，说明理由．11．如图，已知在△ABC 中，∠ACB ＝90°，过C 点作CD ⊥AB 于D ，设AD ＝m ，BD ＝n ，且AC 2：BC 2＝2：1；又关于x 的方程012)1(24122=-+--m x n x 两实数根的差的平方小于192，求整数m 、n 的值．DBAC12．已知,m n 是正整数，关于x 的方程2()0x mnx m n -++=有正整数解，求,m n 的值．B 级1．设1x ，2x 是二次方程032=-+x x 的两根，则3212419x x -+= ．2．已知1ab ≠，且有25199580a a ++=及28199550b b ++=则ab= ． 3．已知关于x 的一元二次方程2610x x k -++=的两个实数根是12,x x ，且221224x x +=，则k = ．4．已知12,x x 是关于x 的一元二次方程22x ax a ++=的两个实数根，则1221(2)(2)x x x x --的最大值为．5．如果方程210x px ++=（p ＞0）的两根之差为1，那么p 等于（）A ．2B ．4C ．3D ．56．已知关于x 的一元二次方程2210x mx m -+-=的两个实数根分别是12,x x ，且22127x x +=，则212()x x -的值是 ( )A ．1B ．12C ．13D ．257．在Rt △ABC 中，∠C ＝90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，a 、b 是关于x 的方程0772=++-c x x 的两根，那么AB 边上的中线长是 ( ) A ．23 B ．25C ．5D ．2 8．设213a a +=，213b b +=且a b ≠，则代数式2211a b+的值为（） A ．5 B ．7 C ．9 D ．119．已知,a b 为整数，a b >，且方程233()40x a b x ab +++=的两个根,αβ满足关系式(1)(1)(1)(1)ααββαβ+++=++．试求所有整数点对(,)a b ．10．若方程2310x x ++=的两根,αβ也是方程620x px q -+=的两根，其中,p q 均为整数，求,p q 的值．11.设,a b 是方程2310x x -+=的两根，c ，d 是方程2420x x -+=的两根，已知a b c dM b c d c d a d a b a b c+++=++++++++．求证：（1）222277a b c d M b c d c d a d a b a b c +++=-++++++++；（2）33334968a b c d M b c d c d a d a b a b c+++=-++++++++．12．设m 是不小于1-的实数，使得关于x 的一元二次方程222(2)310x m x m m +-+-+=有两个不相等实数根12,x x ．（1）若22126x x +=，求m 的值；（2）求22121211mx mx x x +--的最大值．13．已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1，求a b c ++的值．根与系数的关系例1. 152s ≥-且3,5s s ≠-≠ 例2. C 提示: 设三根为121,,x x ,则121x x -< 例 3. 设223,A βα=+223,B αβ=+ 31004A B += ① 85174A B -=- ② 解由① ②联立的方程组得 1(4038517)8A =-例 4. 0,s ≠故第一个等式可变形为211()99()190,s s ++= 又11,,st t s≠∴是一元二次方程299190x x ++=的两个不同实根, 则1199,19,t t s s+=-=即199,19.st s t s +=-=故41994519st s s st s++-+==- 例5. (1) 当a b =时, 原式=2; 当a b ≠时, 原式=-20, 故原式的值为2或-20 (2) 由方程组得232,326(6),x y a z x y z az +=-=-+易知3,2x y 是一元二次方程22()6(6)0t a z t z az --+-+=的两个实数根,0∴∆≥, 即2223221440z az a -+-≤,由z 为实数知,22'(22)423(144)0,a a ∆=--⨯⨯-≥ 解得23,a ≥故正实数a 的最小值为23(3) xy 与x y +是方程217660m m -+=的两个实根,解得11,6x y xy +=⎧⎨=⎩或6,()xy 11.x y +=⎧⎨=⎩舍原式=()()222222212499x y x y xy x y +-++=．例6 解法一：∵ac ＜0，2=40b ac ∆-＞，∴原方程有两个异号实根，不妨设两个根为x 1，x 2，且x 1<0<x 2，由韦达定理得x 1+ x 2=b a -，12c x x a =，由2350b b c ++=，得2+350b ca a ⨯+⨯=，即()12122350x x x x -++=，解得1213253x x x -=-，假设235x ≤，则11323553x x --≤，由10x ＜推得103--≥不成立，故235x ＞；假设21x ≥，则1132153x x --≥，由10x ＜推得132053x --≥＞，矛盾．故21x ＜，综上所述2315x ＜＜．解法二：设()2f x ax bx c =++，由条件得()1253b ac =-+，得()3333131025555555f a b c a a c c a ⎛⎫-=++=-++=⎪ ⎪⎝⎭， ()()()1132533f a b c a a c ⎡⎤=++=----⎣⎦．若a ＞0，0c ＜，则305f ⎛⎫⎪ ⎪⎝⎭＜，()10f ＞；若a ＜0，0c ＞，则305f ⎛⎫⎪⎪⎝⎭＞，()10f ＜．∴0ac ＜时，总有()3105f f ⎛⎫ ⎪ ⎪⎝⎭.＜，故原方程必有一根介于35与1之间．A 级 1．3 2．2 3．-2 m ＞2 0＜m ≤183提示：12x -＞，22x -＞与124x x +-＞，124x x ⋅＞不等价．4．100134016- 提示：由条件得2n n a b n +=+，22n n a b n ⋅=-，则()()()2221n n a b n n --=-+，则()()211112221n a b n n ⎛⎫=-- ⎪--+⎝⎭．5．C 6．C 7．A 8．A 9．提示：（1）()2=2120m ∆-+＞（2）2124m x x =-≤0，m =4或m =0． 10．（1）43k -＞且0k ≠ （2）存在k =4 11．由题意得2m n =，224840n m n --+＜．当n =1时，m =2；当n =2时，m =4． 12．设方程两根为1x ，2x ，则1212,.x x mn x x m n +=⎧⎨=+⎩∵m ，n ，1x ，2x 均为正整数，设121x x ≥≥，1m n ≥≥，则()1212x x x x mn m n +-=-+，即有()()()()1211112x x m n --+--=，则()()()()12112,1,0,110,1,2.x x m n ⎧--=⎪⎨--=⎪⎩∴123,2,5,2,2,1,5,2,3,1,2,2.x x m n =⎧⎪=⎪⎨=⎪⎪=⎩故5,2,3,1;2; 2.m m m n n n ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩ B 级 1．0 提示：由条件得21130x x +-=，22230x x +-=，∴2113x x =-，2223x x =-，∴()3211111111333343x x x x x x x x =-=-+=-+=-，∴原式=()()121212434319431241944x x x x x x ---+=--++=++．又∵121x x +=-,∴原式=0． 2．853．5 4．638- 提示：()2=240a ∆-+＞，原式=2963632488a ⎛⎫----⎪⎝⎭≤． 5．D 6．C 7．B 8．B 9．()231αβαβ+-=，由根与系数关系得()241a b ab +-=，即()21a b -=，a -b =1．又由0∆≥得()2316a b ab +≥，从而()24a b +≤．由a -b =1，()24a b +≤，得满足条件的整数点对（a ，b ）是（1,0）或（0，-1）． 104447αβ+=，662248p αβαβ-==-，()2244227q αβαβαβ-==-． 11．a +b =3,c +d =4,ab =1,cd =2,a +b +c +d =7,222219a b c d +++=．(1)原式=()()()()7a a b c d a b c d d a b c d d a b c aa b c d a b c b c d +++-+++++-+++=-++++++…+ 77777.b c db c d M c d a d a b a b c+-+-+-=-++++++（2）原式=()()()()2222a a b c d a b c d d a b c d d a b c b c da b c+++-+++++-+++=++++…+()()22227774968M a b c d M --+++=-．12．（1）5172m -=．（2）原式=()()()22212121221212352312122m x x x x x x m m m x x x x ⎡⎤+-+⎛⎫⎣⎦=-+=-- ⎪-++⎝⎭．∵11m -≤≤,∴当m =-1时，22121211mx mx x x +--的最大值为10． 13．设20x ax b ++=的两根分别为,αβ（其中,αβ为整数且αβ≤），则方程20x cx a ++=的两根分别为1,1αβ++，又∵,(1)(1)a a αβαβ+=-++=，两式相加，得2210αβαβ+++=，即(2)(2)3αβ++=，从而2123αβ+=⎧⎨+=⎩，或2321αβ+=-⎧⎨+=-⎩，解得12αβ=-⎧⎨=⎩，或53αβ=-⎧⎨=-⎩，∴012a b c =⎧⎪=-⎨⎪=-⎩，或8156a b c =⎧⎪=⎨⎪=⎩，∴3a b c ++=-或29．。

苏科版九年级数学上册一元二次方程的根与系数的关系- 专题培优训练【含答案】

苏科版九年级数学上册一元二次方程的根与系数的关系- 专题培优训练一、选择题1、若x 1，x 2是一元二次方程x 2+10x +16=0的两个根，则x 1+x 2的值是（）A ．﹣10B ．10C ．﹣16D ．162、一元二次方程x 2+4x ﹣3=0的两根为x 1、x 2，则x 1•x 2的值是（）A ．4B ．﹣4C ．3D ．﹣33、已知x 1，x 2是一元二次方程2x 2﹣3x +1＝0的两个根，下列结论正确的是（）A ．x 1+x 2=-23B ．x 1•x 2＝1C ．x 1，x 2都是有理数D ．x 1，x 2都是无理数4、已知关于x 的一元二次方程x 2+mx +n=0的两个实数根分别为x 1=﹣2，x 2=4，则m +n 的值是（）A ．﹣10B ．10C ．﹣6D ．2 5、若关于x 的方程x 2+3x +a=0有一个根为﹣1，则另一个根为（）A ．﹣2B ．2C ．4D ．﹣36、已知实数x 1，x 2满足x 1+x 2=7，x 1x 2=12，则以x 1，x 2为根的一元二次方程是（）A ．x 2﹣7x +12=0B ．x 2+7x +12=0C ．x 2+7x ﹣12=0D ．x 2﹣7x ﹣12=07、若一元二次方程x 2﹣x ﹣2＝0的两根为x 1，x 2，则（1+x 1）+x 2（1﹣x 1）的值是（）A ．4B ．2C ．1D ．﹣28、若方程x 2﹣2x ﹣4＝0的两个实数根为α，β，则α2+β2的值为（）A ．12B ．10C ．4D ．﹣4 9、若α，β是关于x 的一元二次方程x 2﹣2x +m ＝0的两实根，且βα11+＝﹣32，则m 等于（） A ．﹣2 B ．﹣3 C ．2 D ．310、关于x 的一元二次方程x 2+2mx +2n=0有两个整数根且乘积为正，关于y 的一元二次方程y 2+2ny +2m=0同样也有两个整数根且乘积为正，给出三个结论：①这两个方程的根都负根； ②（m ﹣1）2+（n ﹣1）2≥2； ③﹣1≤2m ﹣2n ≤1，其中正确结论的个数是（） A ．0个 B ．1个 C ．2个 D ．3个二、填空题11、若方程x 2﹣3x +2＝0的两根是α、β，则α+αβ+β＝．12、若方程240x x c -+=的一个根为23+，则方程的另一个根为，c = ．13、设1x 、2x 是方程()222120x k x k -+++=的两个不同的实根，且()()12118x x ++=，则k 的值是．14、已知关于x 的方程x 2+（a ﹣2）x +a +1＝0的两实根x 1、x 2满足42221=+x x ，则实数a ＝． 15、已知x 1，x 2是关于x 的一元二次方程x 2+2x +k ﹣1＝0的两个实数根，且x 12+x 22﹣x 1x 2＝13，则k 的值为．16、已知关于x 的一元二次方程x 2﹣4x +m ﹣1＝0的实数根x 1，x 2，满足3x 1x 2﹣x 1﹣x 2＞2，则m 的取值范围是．17、已知α，β是关于x 的一元二次方程（m ﹣1）x 2﹣x +1＝0两个实根，且满足（α+1）（β+1）＝m +1，则m 的值为．18、关于x 的方程（a ﹣1）x 2+2x ﹣a ﹣1＝0的根都是整数，则整数a ＝．19、已知x 1，x 2是关于x 的方程x 2+（3k +1）x +2k 2+1＝0的两个不相等实数根，且满足（x 1﹣1）（x 2﹣1）＝8k 2，则k 的值为．20、已知a ，b 是一元二次方程x 2+x ﹣1＝0的两根，则3a 2﹣b 22a +的值是．三、解答题21、已知于x 的元二次方程x 2﹣6x +2a +5＝0有两个不相等的实数根x 1，x 2．（1）求a 的取值范围；（2）若x 12+x 22﹣x 1x 2≤30，且a 为整数，求a 的值．22、已知关于x 的方程222(2)50x m x m +++-=有两个实数根，并且这两个根的平方和比这两个根的积大16，求m 的值．23、已知关于x 的一元二次方程x 2﹣6x +（4m +1）＝0有实数根．（1）求m 的取值范围；（2）若该方程的两个实数根为x 1、x 2，且|x 1﹣x 2|＝4，求m 的值．24、已知关于x 的方程24280x x m --+=的一个根大于1，另一个根小于1，求m 的取值范围．25、已知关于x 的方程kx 2﹣3x +1＝0有实数根．（1）求k 的取值范围；（2）若该方程有两个实数根，分别为x 1和x 2，当x 1+x 2+x 1x 2＝4时，求k 的值．26、如果实数,a b 分别满足222a a +=，222b b +=，求11a b+的值一、选择题1、若x 1，x 2是一元二次方程x 2+10x +16=0的两个根，则x 1+x 2的值是（）A ．﹣10B ．10C ．﹣16D ．16【分析】根据一元二次方程的根与系数的关系得到两根之和即可．解：∵x 1，x 2一元二次方程x 2+10x +16=0两个根，∴x 1+x 2=﹣10．故选：A ．2、一元二次方程x 2+4x ﹣3=0的两根为x 1、x 2，则x 1•x 2的值是（）A ．4B ．﹣4C ．3D ．﹣3【分析】根据根与系数的关系求解．解：x 1•x 2=﹣3．故选D ．3、已知x 1，x 2是一元二次方程2x 2﹣3x +1＝0的两个根，下列结论正确的是（）A ．x 1+x 2=-23B ．x 1•x 2＝1C ．x 1，x 2都是有理数D ．x 1，x 2都是无理数【分析】利用根与系数的关系对A 、B 进行判断；根据根的判别式对C 、D 进行判断． x 1+x 2=23，x 1x 2=21，所以A 、B 选项错误，因为△＝（﹣3）2﹣4×2×1＝1，所以x1，x2都是有理数，则C选项正确，D选项错误．故选：C．4、已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=﹣2，x2=4，则m+n的值是（）A．﹣10 B．10 C．﹣6 D．2【分析】根据根与系数的关系得出﹣2+4=﹣m，﹣2×4=n，求出即可．解：∵关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=﹣2，x2=4，∴﹣2+4=﹣m，﹣2×4=n，解得：m=﹣2，n=﹣8，∴m+n=﹣10，故选A．5、若关于x的方程x2+3x+a=0有一个根为﹣1，则另一个根为（）A．﹣2 B．2 C．4 D．﹣3【分析】根据一元二次方程根与系数的关系，利用两根和，两根积，即可求出a的值和另一根．解：设一元二次方程的另一根为x1，则根据一元二次方程根与系数的关系，得﹣1+x1=﹣3，解得：x1=﹣2．故选A．6、已知实数x1，x2满足x1+x2=7，x1x2=12，则以x1，x2为根的一元二次方程是（）A．x2﹣7x+12=0 B．x2+7x+12=0 C．x2+7x﹣12=0 D．x2﹣7x﹣12=0【分析】根据以x1，x2为根的一元二次方程是x2﹣（x1+x2）x+x1，x2=0，列出方程进行判断即可．解：以x1，x2为根的一元二次方程x2﹣7x+12=0，故选：A．7、若一元二次方程x2﹣x﹣2＝0的两根为x1，x2，则（1+x1）+x2（1﹣x1）的值是（）A．4 B．2 C．1 D．﹣2A解：根据题意得x1+x2＝1，x1x2＝﹣2，所以（1+x1）+x2（1﹣x1）＝1+x1+x2﹣x1x2＝1+1﹣（﹣2）＝4．故选：A．8、若方程x2﹣2x﹣4＝0的两个实数根为α，β，则α2+β2的值为（）A．12 B．10 C．4 D．﹣4A解：∵方程x2﹣2x﹣4＝0的两个实数根为α，β，∴α+β＝2，αβ＝﹣4，∴α2+β2＝（α+β）2﹣2αβ＝4+8＝12；故选：A ．9、若α，β是关于x 的一元二次方程x 2﹣2x +m ＝0的两实根，且βα11+＝﹣32，则m 等于（） A ．﹣2 B ．﹣3 C ．2 D ．3B解：α，β是关于x 的一元二次方程x 2﹣2x +m ＝0的两实根，∴α+β＝2，αβ＝m ，∵+＝＝＝﹣，∴m ＝﹣3；故选：B ．10、关于x 的一元二次方程x 2+2mx +2n=0有两个整数根且乘积为正，关于y 的一元二次方程y 2+2ny +2m=0同样也有两个整数根且乘积为正，给出三个结论：①这两个方程的根都负根；②（m ﹣1）2+（n ﹣1）2≥2； ③﹣1≤2m ﹣2n ≤1，其中正确结论的个数是（） A ．0个 B ．1个 C ．2个 D ．3个【考点】根与系数的关系；根的判别式．【分析】①根据题意，以及根与系数的关系，可知两个整数根都是负数；②根据根的判别式，以及题意可以得出m2﹣2n≥0以及n2﹣2m≥0，进而得解；③可以采用根与系数关系进行解答，据此即可得解．解：①两个整数根且乘积为正，两个根同号，由韦达定理有，x1•x2=2n＞0，y1•y2=2m＞0，y1+y2=﹣2n＜0，x1+x2=﹣2m＜0，这两个方程的根都为负根，①正确；②由根判别式有：△=b2﹣4ac=4m2﹣8n≥0，△=b2﹣4ac=4n2﹣8m≥0，∵4m2﹣8n≥0，4n2﹣8m≥0，∴m2﹣2n≥0，n2﹣2m≥0，m2﹣2n+n2﹣2m+2=m2﹣2m+1+n2﹣2n+1≥2，（m﹣1）2+（n﹣1）2≥2，②正确；③由根与系数关系可得2m﹣2n=y1y2+y1+y2=（y1+1）（y2+1）﹣1，由y1、y2均为负整数，故（y1+1）•（y2+1）≥0，故2m﹣2n≥﹣1，同理可得：2n﹣2m=x1x2+x1+x2=（x1+1）（x2+1）﹣1，得2n﹣2m≥﹣1，即2m﹣2n≤1，故③正确．故选：D．二、填空题11、若方程x2﹣3x+2＝0的两根是α、β，则α+αβ+β＝．【分析】利用根与系数的关系可得出α+β＝3，αβ＝2，将其代入α+αβ+β中即可求出结论．∵方程x2﹣3x+2＝0的两根是α、β，∴α+β＝3，αβ＝2，∴α+αβ+β＝α+β+αβ＝3+2＝5．故5．12、若方程240x x c -+=的一个根为2+，则方程的另一个根为，c = ．2-1c =根据韦达定理，124x x +=，因为12x =+22x =-所以(12221c x x =⋅==13、设1x 、2x 是方程()222120x k x k -+++=的两个不同的实根，且()()12118x x ++=，则k 的值是．1k =由根与系数的关系得()1221x x k +=+，2122x x k ⋅=+．且有()()224142840k k k ∆=+-+=->，即12k >．所以()()12118x x ++=．从而2230k k +-=，解之得3k =-或1k =．又12k >，所以1k =．14、已知关于x 的方程x 2+（a ﹣2）x +a +1＝0的两实根x 1、x 2满足42221=+x x ，则实数a ＝． 3﹣11解：∵关于x的方程x2+（a﹣2）x+a+1＝0的两实根为x1、x2，∴△＝（a﹣2）2﹣4（a+1）≥0，即a（a﹣8）≥0，∴当a≥0时，a﹣8≥0，即a≥8；当a＜0时，a﹣8＜0，即a＜8，所以a＜0．∴a≥8或a＜0，∴x1+x2＝2﹣a，x1•x2＝a+1，∵x12+x22＝4，（x1+x2）2﹣2x1•x2＝（2﹣a）2﹣2（a+1）＝4，∴（x1+x2）2﹣2x1•x2＝（2﹣a）2﹣2（a+1）＝4，解得a＝3±11．∵3＜11＜4，∴6＜3+＜7（不合题意舍去），3﹣＜0；∴a＝3﹣．故a＝3﹣11．15、已知x1，x2是关于x的一元二次方程x2+2x+k﹣1＝0的两个实数根，且x12+x22﹣x1x2＝13，则k的值为．—2解：根据题意得：x1+x2＝﹣2，x1x2＝k﹣1，x12+x22﹣x1x2＝13＝﹣3x1x2＝4﹣3（k﹣1）＝13，k＝﹣2，故﹣2．16、已知关于x的一元二次方程x2﹣4x+m﹣1＝0的实数根x1，x2，满足3x1x2﹣x1﹣x2＞2，则m的取值范围是．3＜m≤5解：依题意得：，解得3＜m≤5．故答案是：3＜m≤5．17、已知α，β是关于x的一元二次方程（m﹣1）x2﹣x+1＝0两个实根，且满足（α+1）（β+1）＝m+1，则m的值为．—1解：根据题意可得α+β＝﹣＝﹣＝，αβ＝＝，∴（α+1）（β+1）＝αβ+α+β+1＝++1＝m+1，即m2﹣m﹣2＝0，解得m＝﹣1或m＝2，∵m﹣1≠0，∴m≠1，当m＝2时，△＝b2﹣4ac＝﹣3＜0，无实数根，故m≠2，当m＝﹣1时，△＝b2﹣4ac＝9＞0，有实数根，故m＝﹣1．故答案是﹣1．18、关于x 的方程（a ﹣1）x 2+2x ﹣a ﹣1＝0的根都是整数，则整数a ＝．【分析】分两种情况讨论：当a ＝1时，x ＝1；当a ≠1时，△＝4a 2≥0，x 1+x 2=a -12，再由已知，可得1﹣a ＝±1，1﹣a ＝±2，求出a 的值即可．当a ＝1时，2x ﹣2＝0，解得x ＝1；当a ≠1时，（a ﹣1）x 2+2x ﹣a ﹣1＝0，△＝4a 2≥0，x 1+x 2=a -12，x 1•x 2=a a -+11=－112--a ， ∵根都是整数，∴1﹣a ＝±1，1﹣a ＝±2，∴a ＝0或a ＝2或a ＝﹣1或a ＝3，故答案为0或1或﹣1或2或3．19、已知x 1，x 2是关于x 的方程x 2+（3k +1）x +2k 2+1＝0的两个不相等实数根，且满足（x 1﹣1）（x 2﹣1）＝8k 2，则k 的值为．1解：∵x 1，x 2是关于x 的方程x 2+（3k +1）x +2k 2+1＝0的两个实数根，∴x 1+x 2＝﹣（3k +1），x 1x 2＝2k 2+1．∵（x 1﹣1）（x 2﹣1）＝8k 2，即x 1x 2﹣（x 1+x 2）+1＝8k 2，∴2k 2+1+3k +1+1＝8k 2，整理，得：2k 2﹣k ﹣1＝0，解得：k 1＝﹣，k 2＝1．∵关于x 的方程x 2+（3k +1）x +2k 2+1＝0的两个不相等实数根，∴△＝（3k +1）2﹣4×1×（2k 2+1）＞0，解得：k ＜﹣3﹣2或k ＞﹣3+2， ∴k ＝1．故1．20、已知a ，b 是一元二次方程x 2+x ﹣1＝0的两根，则3a 2﹣b 22a +的值是．【分析】根据根与系数的关系即可求出答案．由题意可知：a +b ＝﹣1，ab ＝﹣1， a 2＝1-a ，∴原式＝3（1﹣a ）﹣b +a -12＝3﹣3a ﹣b+a -12＝3﹣2a ﹣（a +b ）+a-12 ＝3﹣2a +1+a -12＝4﹣2a+a-12＝4+a a a -+-12222 ＝4+aa a -+--122)1(2＝4+4＝8，故8．三、解答题21、已知于x 的元二次方程x 2﹣6x +2a +5＝0有两个不相等的实数根x 1，x 2．（1）求a 的取值范围；（2）若x 12+x 22﹣x 1x 2≤30，且a 为整数，求a 的值．（1）a ＜2（2）a 的值为﹣1，0，1解：（1）∵关于x 的一元二次方程x 2﹣6x +2a +5＝0有两个不相等的实数根x 1，x 2，∴△＞0，即（﹣6）2﹣4（2a +5）＞0，解得a ＜2；（2）由根与系数的关系知：x 1+x 2＝6，x 1x 2＝2a +5，∵x 1，x 2满足x 12+x 22﹣x 1x 2≤30，∴（x 1+x 2）2﹣3x 1x 2≤30，∴36﹣3（2a +5）≤30，∴a ≥﹣，∵a 为整数，∴a 的值为﹣1，0，1．22、已知关于x 的方程222(2)50x m x m +++-=有两个实数根，并且这两个根的平方和比这两个根的积大16，求m 的值．-1有实数根，则△≥0，且22121216x x x x +=+，联立解得m 的值．依题意有：12212221212222(2)5164(2)4(5)0x x m x x m x x x x m m +=-+⎧⎪=-⎪⎨+=+⎪⎪∆=+--≥⎩由①②③解得：1m =-或15m =-，又由④可知m ≥94- ∴15m =-舍去，故1m =-23、已知关于x 的一元二次方程x 2﹣6x +（4m +1）＝0有实数根．（1）求m 的取值范围；（2）若该方程的两个实数根为x 1、x 2，且|x 1﹣x 2|＝4，求m 的值．（1）m ≤2 （2）m=1解：（1）∵关于x 的一元二次方程x 2﹣6x +（4m +1）＝0有实数根，∴△＝（﹣6）2﹣4×1×（4m +1）≥0，解得：m ≤2．（2）∵方程x 2﹣6x +（4m +1）＝0的两个实数根为x 1、x 2，∴x 1+x 2＝6，x 1x 2＝4m +1，∴（x 1﹣x 2）2＝（x 1+x 2）2﹣4x 1x 2＝42，即32﹣16m ＝16，解得：m ＝1．24、已知关于x 的方程24280x x m --+=的一个根大于1，另一个根小于1，求m 的取值范围．52m > 设1x ，2x 是方程的两根，且11x >，21x <，即110x ->，210x -<，因此1212121212(1)(1)()10284164(28)0x x x x x x x x m x x m --=-++<⎧⎪=-+⎪⎨+=⎪⎪∆=+->⎩，解得52m >．25、已知关于x 的方程kx 2﹣3x +1＝0有实数根．（1）求k 的取值范围；（2）若该方程有两个实数根，分别为x 1和x 2，当x 1+x 2+x 1x 2＝4时，求k 的值．（1）k ≤49 ；（2）k=1 解：（1）当k ＝0时，原方程为﹣3x +1＝0，解得：x ＝，∴k ＝0符合题意；当k ≠0时，原方程为一元二次方程，∵该一元二次方程有实数根，∴△＝（﹣3）2﹣4×k ×1≥0，解得：k ≤49．综上所述，k 的取值范围为k ≤．（2）∵x 1和x 2是方程kx 2﹣3x +1＝0的两个根，∴x 1+x 2＝，x 1x 2＝．∵x 1+x 2+x 1x 2＝4，∴+＝4，解得：k ＝1，经检验，k ＝1是分式方程的解，且符合题意．∴k 的值为1．26、如果实数,a b 分别满足222a a +=，222b b +=，求11a b+的值当a b ≠时，111a b +=；当a b =时，当13a b ==-+1131a b +，当13a b ==-1113a b+= 由题意知：,a b 为方程2220x x +-=的两个根，且0,0a b ≠≠，解方程2220x x +-=得：11x =-+21x =--⑴当a b ≠时，有2a b +=-，2ab =-，11212a b a b ab +-∴+===-；⑵当a b =时，方程的根为11x =-+21x =--当1a b ==-+1121a b a ∴+===+；当1a b ==--1121a b a ∴+==-。

九年级培优专题二一元二次方程的根与系数的关系课件

A．1
B．2
C．－2
D．－1
1
2
2．方程 6x2 －3x＋2＝0 的两根之和是__________，两根
1
3
之积是__________．
3、如果2是方程 x
2
6x m 0
4
8
的一个根，则另一个根是___ｍ=____。
4、已知关于x的方程 x (m 1) x 2m 1 0
又∵x1＋x2＝m－1，x1x2＝－m，且 m≠0，
1 1
2
x1＋x2＝－3.
x1＋x2
2
∴ x x ＝－3.
1 2
m－1
2
∴
＝－3.
－m
∴3m－3＝2m.
∴m＝3.
【跟踪训练】
7．已知关于 x 的一元二次方程 x2－6x＋k＋1＝0 的两个实
数根是 x1，x2，且 x21＋x22＝24，则 k 的值是( D )
∵x1＋x2＝－3，
13
∴3×(－3)－4x2＝4，x2＝－ 4 .
13
将 x2＝－ 4 代入原方程，得
13
13
13
2
－＋3×－＋m＝0，m＝－ .
4
4
16

2
x
9、已知方程 kx k 2 0 的两个实数根
是
x1, x且
2
x x 4求k的值。
∴可设所求作的方程为
y2－(2x1＋2x2)y＋2x1·2x2＝0.
即 y2＋6y－8＝0.
【跟踪训练】
5．请写出一个两实数根符号相反的一元二次方程
x2－x－6＝0(答案不唯一)
_____________________________．

《一元二次方程根的判别式、根与系数的关系》培优

一元二次方程根的判别式及根与系数的关系【一元二次方程根的判别式】对于一元二次方程()200ax bx c a ++=≠的求根公式x =242b b ac a -±-，我们称24b ac -叫根的判别式，通常用字母 “△” 表示，即△=ac b 42-。

（1）当240b ac ->时，方程根；（2）当240b ac -=时，方程根；（3）当240b ac -<时，方程根。

特别提醒：若一元二次方程02=++c bx ax 有实数根，则ac b 42- 0。

在使用根的判别式解决问题时，如果二次项系数中含有字母，别忘了要加上二次项系数不为零这个限制条件.练习：1、已知方程230x x k -+=有两个不相等的实数根，则k 。

2、关于x 的一元二次方程2210kx x +-=两个不相等的实数根，则k 的取值范围是。

3、在下列方程中，有实数根的是（）（A ）2310x x ++= （B ）411x +=- （C ）2230x x ++= （D ）111x x x =-- 4、当m 满足何条件时，方程()01122=-+--m x m mx 有两个不相等实根？有两个相等实根？有实根？5、关于x 的方程()05222=+++-m x m mx 无实根，试解关于x 的方程()()02252=++--m x m x m 。

6、已知关于x 的一元二次方程()241210x m x m +++-=，求证：不论m 为任何实数，方程总有两个不相等的实数根。

【一元二次方程根与系数的关系】如果一元二次方程()200ax bx c a ++=≠存在实数根，由求根公式得x 1=a ac b b 242-+-，x 2=aac b b 242---，因此有两根之和=+21x x _________，两根之积=⋅21x x __________.这就是一元二次方程的根与系数的关系，又称为韦达定理。

《一元二次方程根与系数的关系》培优资料

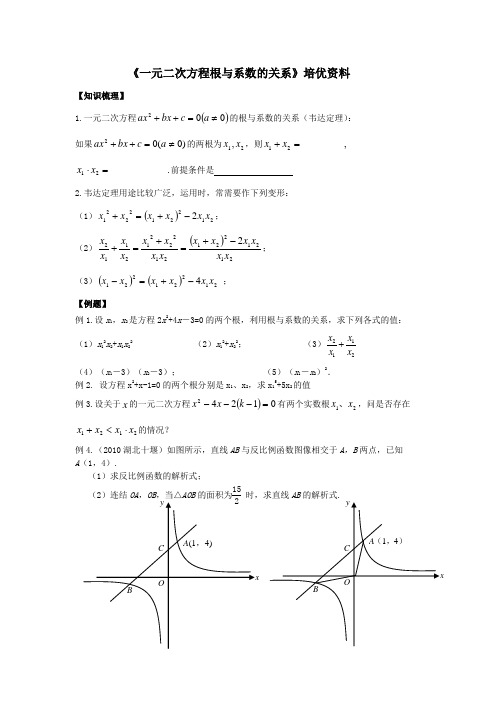
《一元二次方程根与系数的关系》培优资料【知识梳理】1.一元二次方程()002≠=++a c bx ax 的根与系数的关系（韦达定理）：如果)0(02≠=++a c bx ax 的两根为21,x x ，则________,21=+x x .___________21=⋅x x 前提条件是2.韦达定理用途比较广泛，运用时，常需要作下列变形：（1）()2122122212x x x x x x -+=+；（2）()212122121222121122x x x x x x x x x x x x x x -+=+=+；（3）()()212212214x x x x x x -+=- ；【例题】例1.设x 1，x 2是方程2x 2+4x －3=0的两个根，利用根与系数的关系，求下列各式的值：（1）x 12x 2+x 1x 22 （2）x 12+x 22；（3）2112x x x x + （4）（x 1－3）（x 2－3）；（5）（x 1－x 2）2．例2. 设方程x 2+x-1=0的两个根分别是x 1、x 2，求x 15+5x 2的值例3.设关于x 的一元二次方程()01242=---k x x 有两个实数根21x x 、，问是否存在 2121x x x x ⋅<+的情况？例4.（2010湖北十堰）如图所示，直线AB 与反比例函数图像相交于A ，B 两点，已知 A （1，4）.（1）求反比例函数的解析式；（2）连结OA ，OB ，当△AOB 的面积为15时，求直线AB 的解析式.【作业】1.已知：方程3x 2+5x+1=0的两根为x 1、x 2，不解方程.求下列代数式的值.① 11x +21x ②x 21+x 22 ③x 21x 2+x 1 x 22 ④（x 1-3）(x 2-3) ⑤|x 1-x 2 | ⑥21x x +12x x 2.（2013• 济南）函数y =与y=x －2图象交点的横坐标分别为a ，b ，则的值为______． 3.在反比例函数xk y =的图象上有一点P ，它的横坐标m 与纵坐标n 是方程t 2-4t-2=0 的两个根.（1）求k 的值；（2）求点P 与原点O 的距离.4. 已知关于x 的方程042=++a x x 有两个实数根，且7221=-x x ，则=a ____。

苏科版九年级上册知识强化练习：1.3 一元二次方程的根与系数的关系含答案

2020年秋季苏科版九年级上册知识强化练习1.3 一元二次方程的根与系数的关系一．选择题1．设方程x2﹣3x+2＝0的两根分别是x1，x2，则x1+x2的值为（）A．3B．﹣C．D．﹣22．已知关于x的一元二次方程x2﹣3x+k+1＝0，它的两根之积为﹣4．则k的值为（）A．﹣1B．4C．﹣4D．﹣53．若x1、x2是方程x2﹣5x+6＝0的两个解，则代数式（x1+1）（x2+1）的值为（）A．8B．10C．12D．144．设m是整数，关于x的方程mx2﹣（m﹣1）x+1＝0有有理根，则方程的根为（）A．B．x＝﹣1C．D．有无数个根5．关于x的一元二次方程x2+2x+k+1＝0的两根x1，x2，满足x1+x2﹣x1x2＜﹣1，则k的取值范围是（）A．k＞﹣2B．k＞2C．﹣2＜k≤0D．0≤k＜26．已知关于x的方程（m2﹣3m+2）x2+（1﹣2m）x﹣m（m+1）＝0的根是整数，其中m是实数，则m可取的值有（）A．3个B．4个C．5个D．6个7．关于x的方程x2+2（m﹣1）x+m2﹣m＝0有两个实数根α，β，且α2+β2＝12，那么m的值为（）A．﹣1B．﹣4C．﹣4或1D．﹣1或4 8．m、n是方程x2﹣2019x+2020＝0的两根，（m2﹣2020m+2020）•（n2﹣2020n+2020）的值是（）A．2017B．2018C．2019D．2020二．填空题9．已知m，n是方程x2+2x﹣1＝0的两个实数根，则式子3m2+6m﹣mn的值为．10．若方程x2﹣3x﹣4＝0的两个根分别为x1和x2，则＝．11．已知a，b是方程x2+3x﹣1＝0的两根，则a2b+ab2的值是．12．若关于x的方程x2﹣34x+34k﹣1＝0至少有一个正整数根，求满足条件的正整数k的值．13．已知关于x的方程（a﹣1）x2+2x﹣a﹣1＝0的根都是一整数，那么符合条件的整数a 有个．14．设整数a使得关于x的一元二次方程5x2﹣5ax+26a﹣143＝0的两个根都是整数，则a 的值是．三．解答题15．已知x1，x2是一元二次方程2x2﹣2x+m+1＝0的两个实数根．（1）求实数m的取值范围；（2）如果x1，x2满足不等式4+4x1x2＞x12+x22，且m为整数，求m的值．16．已知关于x的一元二次方程x2﹣2mx+（m2+m）＝0有两个实数根．（1）求m的取值范围；（2）如果方程的两个实数根为x1，x2，且x1+x2+x1•x2＝4，求m的值．17．已知关于x的一元二次方程x2﹣4x﹣2k+8＝0有两个实数根x1，x2．（1）求k的取值范围；（2）若x13x2+x1x23＝24，求k的值．18．试求出所有的正整数a，使得关于x的二次方程ax2+（4a﹣1）x+2（2a﹣3）＝0至少有一个整数根．参考答案一．选择题1．解：由x2﹣3x+2＝0可知，其二次项系数a＝1，一次项系数b＝﹣3，由根与系数的关系：x1+x2＝，故选：A．2．解：∵关于x的一元二次方程x2﹣3x+k+1＝0，它的两根之积为﹣4，∴k+1＝﹣4，∴k＝﹣5．故选：D．3．解：根据题意得x1+x2＝5，x1x2＝6，所以（x1+1）（x2+1）＝x1x2+x1+x2+1＝6+5+1＝12．故选：C．4．解：（1）当m＝0，原方程变为：x+1＝0，解得x＝﹣1，为有理根；（2）当m≠0，原方程为一元二次方程，∵方程mx2﹣（m﹣1）x+1＝0有有理根，∴△＝b2﹣4ac为完全平方数，即△＝（m﹣1）2﹣4m＝（m﹣3）2﹣8为完全平方数，而m是整数，∴设（m﹣3）2﹣8＝n2，即（m﹣3）2＝8+n2，∴完全平方数的末位数只能为1，4，5，6，9．∴n2的末位数只能为1，6，而大于10的两个完全平方数相差大于8，∴n＝1，∴m﹣3＝3，即m＝6，所以方程为：6x2﹣5x+1＝0，（2x﹣1）（3x﹣1）＝0，∴x1＝，x2＝，故选：C．5．解：由题意可知：x1+x2＝﹣2，x1x2＝k+1，∵x1+x2﹣x1x2＜﹣1，∴﹣2﹣k﹣1＜﹣1，∴k＞﹣2，∵△＝4﹣4（k+1）≥0，∴k≤0，∴﹣2＜k≤0，故选：C．6．解：①当m2﹣3m+2≠0时，即m≠1和m≠2时，由原方程，得[（m﹣1）x+m][（m﹣2）x﹣（m+1）]＝0解得，x＝﹣1﹣或x＝1+，∵关于x的方程（m2﹣3m+2）x2+（1﹣2m）x﹣m（m+1）＝0的根是整数，∴m＝0.5，m＝1.5，m＝1.25；②当m2﹣3m+2＝0时，m＝1，m＝2，分别可得x＝0，x＝2，因此m＝1，m＝2也可以；综上所述，满足条件的m值共有5个．故选：C．7．解：∵关于x的方程x2﹣2（m﹣1）x+m2＝0有两个实数根，∴△＝[2（m﹣1）]2﹣4×1×（m2﹣m）＝﹣4m+4≥0，解得：m≤1．∵关于x的方程x2+2（m﹣1）x+m2﹣m＝0有两个实数根α，β，∴α+β＝﹣2（m﹣1），α•β＝m2﹣m，∴α2+β2＝（α+β）2﹣2α•β＝[﹣2（m﹣1）]2﹣2（m2﹣m）＝12，即m2﹣3m﹣4＝0，解得：m＝﹣1或m＝4（舍去）．故选：A．8．解：∵m，n是方程x2﹣2019x+2020＝0的两根，∴m2﹣2019m+2020＝0，n2﹣2019n+2020＝0，mn＝2020，∴（m2﹣2020m+2020）•（n2﹣2020n+2020）＝（﹣m）（﹣n）＝mn＝2020．故选：D．二．填空题9．解：∵m是方程x2+2x﹣1＝0的根，∴m2+2m﹣1＝0，∴m2+2m＝1，∴3m2+6m﹣mn＝2（m2+2m）﹣mn＝2×1﹣mn＝2﹣mn，∵m，n是方程x2+2x﹣1＝0的两个实数根，∴mn＝﹣1，∴3m2+6m﹣mn＝2﹣2×（﹣1）＝4．故答案为4．10．解：根据题意得x1+x2＝3，x1x2＝﹣4，所以+＝＝＝﹣．故答案为﹣．11．解：∵a，b是方程x2+3x﹣1＝0的两根，∴根据根与系数的关系得：a+b＝﹣3，ab＝﹣1，∴a2b+ab2＝ab（a+b）＝（﹣1）×（﹣3）＝3，故答案为：3．12．解：∵方程x2﹣34x+34k﹣1＝0至少有1个正整数根，∴△＝342﹣4（34k﹣1）＝1160﹣136k≥0，正整数k可能取值为1，2，3，4，5，6，7，8，∵只有当k＝1时，x1＝1，x2＝33，∴正整数k的值是1．故答案为：1．13．解：①当a＝1时，x＝1；②当a≠1时，原式可以整理为：[（a﹣1）x+a+1]（x﹣1）＝0，易知x＝1是方程的一个整数根，再由1+x＝且x是整数，知1﹣a＝±1或±2，∴a＝﹣1，0，2，3；由①、②得符合条件的整数a有5个．故答案为：5．14．解：∵5x2﹣5ax+26a﹣143＝0⇒25x2﹣25ax+（130a﹣262）﹣39＝0，即（5x﹣26）（5x﹣5a+26）＝39，∵x，a都是整数，故（5x﹣26）、（5x﹣5a+26）都分别为整数，而只存在39＝1×39或39×1或3×13或13×3或四种情况，①当5x﹣26＝1、5x﹣5a+26＝39联立解得a＝2.8不符合，②当5x﹣26＝39、5x﹣5a+26＝1联立解得a＝18，③当5x﹣26＝3、5x﹣5a+26＝13联立解得a＝8.4不符合，④当5x﹣26＝13、5x﹣5a+26＝3联立解得a＝12.4不符合，∴当a＝18时，方程为5x2﹣90x+325＝0两根为13、﹣5．故答案为：18．三．解答题15．解：（1）根据题意得△＝（﹣2）2﹣4×2（m+1）≥0，解得m≤﹣．故实数m的取值范围是m≤﹣；（2）根据题意得x1+x2＝1，x1x2＝，∵4+4x1x2＞x12+x22，∴4+4x1x2＞（x1+x2）2﹣2x1x2，即4+6x1x2＞（x1+x2）2，∴4+6×＞1，解得m＞﹣2，∴﹣2＜m≤﹣，∴整数m的值为﹣1．16．解：（1）根据题意得△＝4m2﹣4（m2+m）≥0，解得m≤0；（2）根据题意得x1+x2＝2m，x1x2＝m2+m，∵x1+x2+x1•x2＝4，∴2m+m2+m＝4，整理得m2+3m﹣4＝0，解得m1＝﹣4，m2＝1，∵m≤0，∴m的值为﹣4．17．解：（1）由题意可知，△＝（﹣4）2﹣4×1×（﹣2k+8）≥0，整理得：16+8k﹣32≥0，解得：k≥2，∴k的取值范围是：k≥2．故答案为：k≥2．（2）由题意得：，由韦达定理可知：x1+x2＝4，x1x2＝﹣2k+8，故有：（﹣2k+8）[42﹣2（﹣2k+8）]＝24，整理得：k2﹣4k+3＝0，解得：k1＝3，k2＝1，又由（1）中可知k≥2，∴k的值为k＝3．故答案为：k＝3．18．解：ax2+（4a﹣1）x+2（2a﹣3）＝0，ax2+4ax+4a＝x+6，a（x+2）2＝x+6，当x＝﹣2时，a不存在，所以x≠﹣2，∵a是正整数，∴a＝≥1，由（x+2）2＞0得（x+2）2≤x+6，整理得x2+3x﹣2≤0．解得：≤x≤，所以x可取﹣3、﹣2（舍去）、﹣1、0，依次代入a＝得到：x＝﹣3，a＝3；x＝﹣1，a＝5；x＝0，a＝1.5（舍去）．∴满足条件的正整数a的值是3和5．。

一元二次方程根与系数的关系—巩固练习(提高)含答案

a a ，（2一元二次方程根与系数的关系—巩固练习（提高）【巩固练习】一、选择题1. 关于 x 的方程 mx 22x 1 0 无实数根，则 m 的取值范围为( )．A ．m≠0B ．m ＞1C ．m ＜1 且 m≠0D ．m ＞-12．已知 a 、b 、c 是△ABC 的三条边，且方程cx 2 2bx a bx 22ax b 有两个相等的实数根，那么这个三角形是（） A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰直角三角形3．（2016曲靖一模）已知一元二次方程 x 2﹣3x ﹣3=0 的两根为 α 与 β，则A ．﹣1B ．1C ．﹣2D ．2的值为（）4．设 a ，b 是方程 x 2x 2013 0 的两个实数根，则 a 2 2a b 的值为（）．A ．2010B ．2011C ．2012D ．20135．若 ab≠1，且有 5a 22012a 9 0 ，及 9b 2a 2012b 5 0 ，则的值是（）．bA ． 9 5 2012 2012B ．C ．D ．5 9 5 96.（2015芦溪县模拟）设 x 1，x 2 是方程 2x 2﹣6x+3=0 的两根，则 x 12+x 22 的值是（）A ．15B ．12C ．6D ．3二、填空题7．已知关于 x 的方程 1 4x 2(m 3)x m 2 0 有两个不相等的实数根，那么 m 的最大整数值是________．n m8．（2015凉山州）已知实数 m ，n 满足 3m 2+6m ﹣5=0，3n 2+6n ﹣5=0，且 m≠n ，则 = ．m n9．（2016濮阳校级自主招生）求一个一元二次方程，使它的两根分别是方程 x 2﹣7x﹣1=0 各根的倒数．10．在 Rt △ABC 中，∠C=900，、b 、c 分别是∠A 、∠B 、∠C 的对边，、b 是关于 x 的方程的两根，那么 AB 边上的中线长是 . 11．已知方程 2(k+1)x 2+4kx+3k-2=0 （1）当 k 为时，两根互为相反数；）当 k 为时，有一根为零，另一根不为零.12．（2015仁寿县一模）关于 x 的一元二次方程 x 2﹣mx+2m ﹣1=0 的两个实数根分别是 x 、x ，且 x 2+x 2=7，1212则 m 的值是．三、解答题13. 已知关于 x 的方程 2x 2mx 2m 1 0 的两根的平方和等于29 4，求 m 的值．△214．已知关于 x 的方程 kx 2-2 (k +1) x +k -1=0 有两个不相等的实数根，(1) 求 k 的取值范围；(2) 是否存在实数 k ，使此方程的两个实数根的倒数和等于 0 ？若存在，求出 k 的值；若不存在，说明理由.15．（2016 春杭州校级期中）如果方程 x 2+px+q=0 的两个根是 x 1，x 2，那么 x 1+x 2=﹣p ，x 1x2=q ，请根据以上结论，解决下列问题：（1）若 p=﹣4，q=3，求方程 x 2+px+q=0 的两根．（2）已知实数 a 、b 满足 a 2﹣15a ﹣5=0，b 2﹣15b ﹣5=0，求 + 的值；（3）已知关于 x 的方程 x 2+mx+n=0，（n≠0），求出一个一元二次方程，使它的两个根分别是已知方程两根的倒数．【答案与解析】一、选择题 1．【答案】B ；【解析】当 m ＝0 时，原方程的解是 x1 2；当 m≠0 时，由题意知＝2△2-4·m×1＜0，所以 m ＞1．2．【答案】A ；【解析】方程化为(c-b)x 2+2(b-a)x+(a-b)＝0，∴＝4(b-a)-4(c-b)(a-b)＝0 即 4(a-b)(a-c)＝0，∴ a ＝b 或 a ＝c ， ∴ △ABC 为等腰三角形．3．【答案】A ；【解析】解：根据题意得 α+β=3，αβ=﹣3，所以故选 A ．4.【答案】C ；【解析】依题意有 a 25．【答案】A ；= = =﹣1．a 2013 ，ab 1 ，∴ a 2 2a b (a 2 a) (a b) 2013 1 2012 ．【解析】因为 5a 22012a 9 0 及 9b 2 2012b 5 0 ，于是有 5a 2 1 2012a 9 0 及 5( )2 2012b1b9 0 ，又因为 ab 1 ，所以 a 1 1，故 a 和可看成方程 5x 2 b b2012x 9 0 的两根，1 9 a 9再运用根与系数的关系得 a ，即．b 5 b 56．【答案】C ；【解析】解：∵x 1，x 2 是方程 2x 2﹣6x+3=0 的两根，∴x 1+x 2=3，x 1x 2= ，2∴x 12+x 22=（x 1+x 2）2﹣2x 1x 2=32﹣2× =6．故选：C ．二、填空题 7．【答案】1；【解析】由题意知△＝[ (m3)]4 1 3m 2 0 ，所以 m ，因此 m 的最大整数值是 1．4 28．【答案】﹣；【解析】解：∵m≠n 时，则 m ，n 是方程 3x 2+6x ﹣5=0 的两个不相等的根，∴m+n=﹣2，mn=﹣ ．∴原式== = =﹣ ，故答案为：﹣．9．【答案】x 2+7x ﹣1=0；【解析】解：设方程 x 2﹣7x ﹣1=0 的两根为 α、β，则有：α+β=7，α β=﹣1．∴= =﹣7， =﹣1，∴以、为根的方程为 x 2+7x ﹣1=0．故答案为：x 2+7x ﹣1=0．10．【答案】；【解析】因直角三角形两直角边 a 、b 是方程的二根，∴有 a+b=7①a·b=c+7②，由勾股定理知 c 2=a 2+b 2③，联立①②③组成方程组求得 c=5，∴斜边上的中线为斜边的一半，故答案为.11．【答案】（1）k=0；（2）k=.【解析】解：设方程的两根为 x 1, x 2，则 x 1+x 2=-=- ；x 1x 2= .1 2 ．2 2 2 ，1 2 ，（1）要使方程两根互为相反数，必须两根的和是零，即 x 1+x 2=-=0，∴k=0，当 k=0 时， =(4k)△2-4×2(k+1)(3k-2)=16>0∴当 k=0 时，方程两根互为相反数.（2）要使方程只有一个根为零，必须二根的积为零，且二根的和不是零，即 x 1x 2==0，解得 k= .又当 k=当 k= 时，x 1+x 2=- ≠0，时， =(4k)△2-4×2(k+1)(3k-2)=>0，∴k= 时，原方程有一根是零，另一根不是零.12.【答案】-1.【解析】解：根据题意得 x 1+x 2=m ，x 1x 2=2m ﹣1，∵x 12+x 22=7，∴（x 1+x 2）2﹣2x 1x 2=7，∴m 2﹣2（2m ﹣1）=7，解得 m 1=﹣1，m 2=5，当 m=﹣1 时，原方程变形为 x △2+x ﹣3=0， =1﹣4×（﹣3）＞0，方程有两个不等实数根；当 m=5 时，原方程变形为 x △2﹣5x+9=0， =25﹣4×9＜0，方程没有实数根；∴m 的值为﹣1．故答案为﹣1．三、解答题13. 【答案与解析】设方程的两根为 x 1、x 2，则由根与系数关系，m1 2m得 xx， x x 1 2由题意，得x 21x 229429即 (xx )22x x4122m1 2m 292，∴224整理，得 m 2 8m 33 0 ．解得 m13 ， m211 ．当 m ＝3 时，△＝ m 2当 m ＝-11 时，△＝ m 28(2m1)490；8(2m1)630，方程无实数根．∴m＝-11不合题意，应舍去．解得 k >- 1 1 1k 1k1x2 k∴ m 的值为 3．14. 【答案与解析】(1) ∵方程有两个不相等的实数根，∴Δ=[-2(k ＋1)]2－4k (k -1)>0，且 k ≠0，1，且 k ≠0 .即 k 的取值范围是 k >- ，且 k ≠0 .3 3(2) 假设存在实数 k ，使得方程的两个实数根 x 1 , x 2 的倒数和为 0.2(k 1)则 x 1 ，x 2 不为 0，且而 k =-1 与方程有两个不相等实根的条件 k >- 13，且 k ≠0 矛盾，故使方程的两个实数根的倒数和为 0 的实数 k 不存在 .15.【答案与解析】解：（1）当 p=﹣4，q=3，则方程为 x 2﹣4x+3=0，解得：x 1=3，x 2=1．（2）∵a 、b 满足 a 2﹣15a ﹣5=0，b 2﹣15b ﹣5=0，∴a 、b 是 x 2﹣15x ﹣5=0 的解，当 a≠b 时，a+b=15，a ﹣b=﹣5，+ == = =﹣47；当 a=b 时，原式=2．（3）设方程 x 2+mx+n=0，（n≠0），的两个根分别是 x 1，x 2，则+ = =﹣ ， = = ，则方程 x 2+ x+ =0 的两个根分别是已知方程两根的倒数．。

第05讲一元二次方程根与系数的关系-2024年新九年级数学暑假提升讲义(人教版学习新知)

第05讲一元二次方程根与系数的关系（5个考点+易错分析）模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1.了解一元二次方程的根与系数的关系,能运用根与系数的关系求一元二次方程的两根之和、两根之积及与两根有关的代数式的值2.能运用根与系数的关系由已知一元二次方程的一个根求出另一个根或由一元二次方程的根确定一元二次方程知识点：一元二次方程根与系数的关系1.一元二次方程根与系数的关系如果方程20(0)ax bx c a -+=≠有两个实数根12x x ，，那么1212b cx x x x a a+=-⋅=，2.有关根与系数的关系的两个重要推论（1）以12x x ，为实数根的一元二次方程(二次项系数为1)是()212120;x x x x x x -++=（2）如果方程20;x mx n ++=的两个实数根是12x x ，，那么1212x x m x x n+=-⋅=，考点1：利用一元二次方程根与系数的关系求关于方程根的代数式的值【例1】已知m 、n 是方程2x 2－x －2＝0的两实数根，则1m ＋1n 的值为()A．－1B.12C．－12D．1考点2：根据方程的根确定一元二次方程【例2】已知一元二次方程的两根分别是4和－5，则这个一元二次方程是()A．x 2－6x ＋8＝0B．x 2＋9x －1＝0C．x 2－x －6＝0D．x 2＋x －20＝0【变式2-1】（23-24九年级上·福建泉州·期末）以2和5-为根的一元二次方程是（）A ．23100x x -+=B ．23100x x ++=C ．23100x x +-=D ．23100x x --=【变式2-2】（23-24九年级上·江西南昌·阶段练习）下列一元二次方程中，有两个符号相反的解的是（）A ．220x x -=B ．210x +=C ．2320x x -+=D ．2510x x +-=【变式2-3】（22-23九年级上·湖南衡阳·阶段练习）解某个一元二次方程时，甲看错了方程的常数项，因而得出两根为8和2；乙看错了方程的一次项的系数，因而得出两根为9-或1-，那么正确的方程为（）A ．21090x x -+=B ．21090x x ++=C ．21090x x --=D ．21090x x +-=考点3：根据根与系数的关系确定方程的解【例3】已知x ＝4是一元二次方程x 2－3x ＋c ＝0的一个根，则另一个根为________．【变式3-1】若方程：2980kx x -+=的一个根为1x =，则k =________；另一个根为________．【变式3-2】已知1x =是方程220x bx +-=的一个根，则方程的另一个根是_____．【变式3-3】（23-24九年级上·湖南长沙·期末）已知关于x 的一元二次方程22210x x a -+-=有一个根是0x =，则另外一个根是．考点4：利用一元二次方程根与系数的关系确定字母系数【例4】关于x 的方程x 2－ax ＋2a ＝0的两根的平方和是5，则a 的值是()A．－1或5B．1C．5D．－1【例5】已知x 1、x 2是一元二次方程(a －6)x 2＋2ax ＋a ＝0的两个实数根．(1)是否存在实数a ，使－x 1＋x 1x 2＝4＋x 2成立？若存在，求出a 的值；若不存在，请你说明理由；(2)求使(x 1＋1)(x 2＋1)为负整数的实数a 的整数值．【变式5-1】已知一个直角三角形的两个直角边的长恰好是方程：22870x x -+=两个根，求这个直角三角形的周长．易错点：没有判断一元二次方程根的情况，直接用一元二次方程的根与系数的关系。

华师版数学九年级上册强化专训-一元二次方程的根与系数的关系

华师版数学九年级上册阶段强化专训一元二次方程的根与系数的关系说课稿教材地位分析：一元二次方程根与系数的关系是在学习了一元二次方程的解法和根的判别式之后引入的。

它深化了两根与系数之间的关系，是我们今后继续研究一元二次方程根的情况的主要工具，是方程理论的重要组成部分。

一元二次方程的根与系数的关系，在中考中多以填空，选择，解答题的形式出现，考查的频率较高，也常与几何、二次函数等问题结合考查，是考试的热点。

教材的处理：一、教学目标：1、掌握一元二次方程的根与系数的关系的关系并会初步应用。

2、提高学生分析、观察、归纳的能力和推理论证的能力。

3、渗透由特殊到一般，再由一般到特殊的认识事物的规律。

4、通过学生探索一元二次方程的根与系数的关系，培养学生观察分析和综合、判断的能力。

激发学生发现规律的积极性，鼓励学生勇于探索的精神。

二、教学重点难点及难点的突破重点：根与系数的关系。

难点：对根与系数的关系的理解和推导。

难点的突破方法：由已知两根构造新方程入手，由学生观察并发现一元二次方程根与系数的关系，用求根公式再严格加以证明，证明的过程是一个再熟悉和再理解的过程。

三、教学构想：在构思这节课时，感到教材中所提供的方法固然能更加直接的引出根与系数的关系，但忽略了定理最初形成的过程（即：为何要检验两根之和，两根之积？）。

因此我根据前面所学内容，从已知两根求作方程入手，引导学生观察并发现根与系数的关系。

此时所得出的恰好是二次项系数为1的方程，这种特殊的方程有这种规律，是不是对二次项系数不为1的方程也同样有这种规律呢？于是引出下文，并推及到韦达定理的出现与证明。

然后加入对数学家韦达的介绍，及我国古代数学家在根与系数关系上的贡献，激发学生的爱科学，用科学的情感，提高学生对学习的兴趣。

最后，再由学生自主小结，谈体会，给整节课画上圆满的句号。

四、教法、学法：为了体现二期课改中“以学生为主体”的教育理念，在课程的引入和新授中充分地考虑在学生已有知识与新知识间架起一座桥梁，通过创设一定的问题情境，注重由学生自己探索，让学生参与韦达定理的发现、不完全归纳验证以及演绎证明等整个数学思维过程。

数学九年级下册考点强化专训一元二次方程的根与系数的关系

数学九年级下册解码专训一元二次方程根与系数的关系学习目标一、1.掌握一元二次方程根与系数的关系，运用根与系数的关系解决相关待定系数的值。

2.通过对一元二次方程根与系数关系的探讨，经历和体验数学的发现过程，提高探究性学习的能力。

二、学习重点重点：运用根与系数的关系求相关待定系数的值。

难点：运用根与系数的关系解题必须是在b 2-4ac 不小于0的情况下。

自主预习三、解下列方程，将得到的根填入下面的表格中，观察表格中两个根的和与积，它们和原来的方程的系数有什么？（1）2x －2x ＝0；（2）2x ＋3x －4＝0；（3）22x －5x-7＝0．方程1x 2x 21x x 21x x 2x －2x ＝02x ＋3x －4＝022x －5x-7＝0请根据以上表格中的观察、发现进一步猜想：若方程ax 2＋bx ＋c ＝0(a ≠0)的根是1x 、2x ，则21x x = ，21x x = ，并加以证明。

因为一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的求根公式x=a acb b 242 ，所以21x x = =21x x = =合作探究四、 1.已知关于x 的方程（k-1）2x +(2k-3)x+k+1=0有两个不相等的实数根1x 、2x .求k 的取值范围；（1）是否存在实数k ，使方程的两个实数根互为相反数？如果存在求出k 的值；如果不（2）存在，请说明理由。

巩固反馈五、1.已知1x 、2x 是方程2x -x-3=0的两个实数根，则21x x = , 21x x = 。

2.若方程x 2+px+2=0的一个根是2，则另一个根是，p= 。

5.下列方程两根的和与两根的积各是多少？①2y -3y+1=0 ② 32x -2x=2③22x +3x=0 ④4p(p-1)=36.已知，是方程2x ＋2x -5＝0的实数根，求 22 的值。

一元二次方程的根与系数关系(能力提升)(原卷版)

专题2.5 一元二次方程的根与系数关系（能力提升）（原卷版）一、选择题。

1．（2022•盘龙区一模）关于x的一元二次方程x2+mx﹣1＝0的根的情况为（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．不能确定2．（2022春•定远县校级月考）以和为根的一元二次方程是（）A．x2﹣10x﹣1＝0B．x2+10x﹣1＝0C．x2+10x+1＝0D．x2﹣10x+1＝0 3．（2022•宁波模拟）已知实数a≠b，且满足（a+1）2＝3﹣3（a+1），3（b+1）＝3﹣（b+1）2，则的值为（）A．23B．﹣23C．﹣2D．﹣13 4．（2021秋•姜堰区期末）方程x2﹣4x+3＝0的两根为x1、x2，则x1+x2等于（）A．4B．﹣4C．3D．﹣3 5．（2022•运城二模）已知关于x的一元二次方程ax2﹣4x﹣2＝0有实数根，则a的取值范围是（）A．a≥﹣2B．a＞﹣2C．a≥﹣2且a≠0D．a＞﹣2且a≠0 6．（2021秋•汉阳区期中）设x1，x2是一元二次方程x2+x﹣3＝0的两根，则x13﹣4x22+20等于（）A．1B．5C．11D．137．（2021春•岳西县期末）已知关于x的方程x2﹣3x+m＝0的一个根是2．则此方程的另一个根为（）A．0B．1C．2D．3 8．（2021•泰安）已知关于x的一元二次方程kx2﹣（2k﹣1）x+k﹣2＝0有两个不相等的实数根，则实数k的取值范围是（）A．k＞﹣B．k＜C．k＞﹣且k≠0D．k＜且k≠0 9．（2021秋•新城区期中）关于x的一元二次方程ax2+bx+c＝0的两根分别为，，下列判断一定正确的是（）A．a＝﹣1B．c＝1C．ac＝﹣1D．10．（2021•商河县校级模拟）已知y＝kx+k﹣1的图象如图所示，则关于x的一元二次方程x2﹣x﹣k2﹣k＝0的根的情况是（）A．无实数根B．有两个相等或不相等的实数根C．有两个不相等的实数根D．有两个相等的实数根二、填空题。

【教育资料】人教版九年级数学上册一元二次方程根与系数的关系课堂培优卷(含答案)学习专用

2019年九年级数学上册一元二次方程根与系数的关系课堂培优卷一、选择题：1、下列一元二次方程中，两实根之和为1的是（）A.x2—x＋1=0B.x2＋x—3=0C.2 x2－x－1=0D.x2－x－5=02、关于x的一元二次方程x2+2x+1=0的根的判断说法正确的是（）A.有两个不等的实根B.有两个相等的实数根C.方程没有实数根D.无法判断3、已知x1、x2是一元二次方程x2－4x＋1=0的两个根，则x1·x2等于（）A.－4B.－1C.1D.44、已知关于x的一元二次方程（a－1）x2－2x＋1=0有两个不相等的实数根，则a的取值范围是（）A.a＞2B.a＜2C.a＜2且a≠1D.a＜－25、关于x的一元二次方程x2+8x+q=0有两个不相等的实数根，则q的取值范围是（）A.q＜16B.q＞16C.q≤4D.q≥46、已知α、β满足α＋β=5，αβ=6，则以α、β为根的一元二次方程（）A.x2＋5x＋6=0B.x2－5x＋6=0C.x2－5x－6=0D.x2＋5x－6=07、已知x1,x2为方程x2+3x+1=0的两实根，则x12-3x2+20的值为（）A. B.－28 C.20 D.288、设x1、x2是方程x2+3x﹣3=0的两个实数根，则的值为（）A.5B.﹣5C.1D.﹣19、已知实数a，b分别满足a2﹣6a+4=0，b2﹣6b+4=0，且a≠b，则a2+b2的值为（）A.36B.50C.28D.2510、若实数a，b（a≠b）分别满足方程a2﹣7a+2=0，b2﹣7b+2=0，则的值为（）A. B. C.或2 D.或211、已知α、β是方程x2﹣2x﹣4=0的两个实数根，则α3+8β+6的值为（）A.﹣1B.2C.22D.3012、一元二次方程x2﹣2x+m=0总有实数根，则m应满足的条件是（）A.m=1B.m≥1C.m＜1D.m≤1二、填空题:13、若是方程x2－2mx＋m2－m－1=0的两个根，且x1＋x2=1－x1x2，则m的值为___________14、如果关于x的方程有两个相等的实数根，那么实数的值是.15、已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=﹣2，x2=4，则m+n= .16、若关于x的一元二次方程（1﹣k）x2+2kx﹣k+1=0有实数根，则实数k的取值范围是.17、已知x1、x2是方程x2﹣5x﹣6=0的两个根，则x12+5x2﹣6= .18、已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2，则（x1﹣1）2+（x2﹣1）2的最小值是三、解答题：19、解方程：x(2x - 6)=x-3 20、解方程：﹣3x2+4x+1=0（用配方法）21、已知关于x的方程x2+ax+a﹣2=0.（1）若该方程的一个根为1，求a的值；（2）求证：不论a取何实数，该方程都有两个不相等的实数根.22、关于x的一元二次方程x2﹣x﹣（m+1）=0有两个不相等的实数根.（1）求m的取值范围；（2）若m为符合条件的最小整数，求此方程的根.23、已知：关于x的方程x2﹣（2m+1）x+2m=0（1）求证：方程一定有两个实数根；（2）若方程的两根为x1，x2，且|x1|=|x2|，求m的值.24、已知：关于x的一元二次方程x2﹣（2m+3）x+m2+3m+2=0.（1）已知x=2是方程的一个根，求m的值；（2）以这个方程的两个实数根作为△ABC中AB、AC（AB＜AC）的边长，当BC=时，△ABC是等腰三角形，求此时m的值.25、如果方程的两个根是，，那么，，请根据以上结论，解决下列问题：（1）若，，求方程的两根。