三年级奥数学练习试卷思维培训资料数阵图 (3)

合集下载

三年级奥数之数阵图习题

数阵图
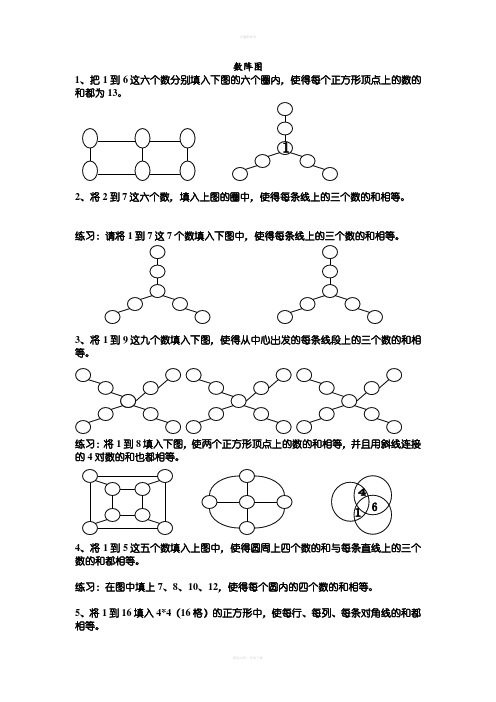
1、把1到6这六个数分别填入下图的六个圈内，使得每个正方形顶点上的数的和都为13。

2、将2到7这六个数，填入上图的圈中，使得每条线上的三个数的和相等。

练习：请将1到7这7个数填入下图中，使得每条线上的三个数的和相等。

3、将1到9这九个数填入下图，使得从中心出发的每条线段上的三个数的和相等。

练习：将1到8填入下图，使两个正方形顶点上的数的和相等，并且用斜线连接的4对数的和也都相等。

4、将1到5这五个数填入上图中，使得圆周上四个数的和与每条直线上的三个数的和都相等。

练习：在图中填上7、8、10、12，使得每个圆内的四个数的和相等。

5、将1到16填入4*4（16格）的正方形中，使每行、每列、每条对角线的和都相等。

数阵图练习
1、将6到10这五个数填入下图，使得每条边上的三个数的和相等。

2、将2到11填入下图，使得每条线段上的三个数之和相等。

3、将2到10填入下图，使得每条线上的四个数的和相等。

. .
.。

小学三年级奥数第39讲：数阵图

【例4】(★★★★★) 将1~7七个数字填入下图的七个○内，使每个圆周和每条直线上的三个数之和都相等。
【例5】(★★★★) 将1~6这六个数字分别填入下图的六个○内，使得三条直线上的数字之和都相等。
【例6】(★★★★★) 如图所示，大三角形被分成了9个小三角形。试将1，2，3，4，5，6， 7，8，9分别填入这9个小三角形内，每个小三角形内填一个数，要求靠近大三角形3条边的每5个数相加的和相等，问这5个数的和最大可能是多少？
数阵图
数阵图：将一些数字按照一定的要求排列而成的某些图形。
数阵图的分类：
辐射型
பைடு நூலகம்封闭型
复合型
【例1】(★★) 将1～7这七个数字，分别填入图中各个○内，使每条线段上的三个○内数的和都等于14。
【例2】(★★★) 将1~11填入下图的各个圆圈内，使每条线段上三个圆圈内的数之和相等。
1
【例3】(★★★) 你能把1～6六个数字分别填入下图的六个圆圈中，使每一边三个数相加的和都等于11吗？
2
【本讲总结】数阵图一、分类
辐射型
封闭型
复合型
二、基本关系各数之和＋重叠数×重叠次数＝线和×线数
三、辐射型数阵图窍门：掐头、去尾、取中间
四、注意事项 (a)关键点：特殊位置 (b)(b) 复合型:在调整的时候，不能改变原有边和
3

三年级数阵图

word格式-可编辑-感谢下载支持
1.将1~7这七个数分别填入左下图中的○里，使每条直线上的三个数之和都等于12。

如果每条直线上的三个数之和等于10，那么又该如何填？
9
（第1题）（第2题）
2.将1~9这九个数分别填入右上图中的○里（其中9已填好），使每条直线上的三个数之和都相等。

如果中心数是5，那么又该如何填？
3将1~9这九个数分别填入右图中的小方格里，
使横行和竖列上五个数之和相等。

（至少找出两
种本质上不同的填法）
4.将3~9这七个数分别填入左下图的○里，使（第3题）
每条直线上的三个数之和等于20。

（第4题）（第5题）
5.将1~11这十一个数分别填入右上图的○里，使每条直线上的三个数之和相等，并且尽可能大。

6.将1~7这七个数分别填入右图的○里，
使得每条直线上三个数之和与每个圆圈
上的三个数之和都相等。

小学奥数5-1-3-3 数阵图(三).专项练习

则从这个圆圈开始顺时针走n步进入另一个圆圈．依此下去，走7次恰好不重复地进入每个圆圈，最后进入的一个圆圈中写8．请给出两种填法．【例 4】在圆的5条直径的两端分别写着1～10（如图）。

现在请你调整一部分数的位置，但保留1、10、5、6不动，使任何两个相邻的数之和都等于直径另一端的相邻两数之和（画在另一个圆上）。

【例 5】图中是一个边长为1的正六边形，它被分成六个小三角形．将4、6、8、10、12、14、16各一个填入7个圆圈之中．相邻的两个小正三角形可以组成6个菱形，把每个菱形的四个顶点上的数相加，填在菱形的中心A、B、C、D、E、F位置上（例如：a b g f A+++=）．已知A、B、C、D、E、F依次分别能被2、3、4、5、6、7整除，那么a g d⨯⨯=___________．【例 6】在如图所示的圆圈中各填入一个自然数，使每条线段两端的两个数的差都不能被3整除。

小学奥数：数阵图(三).专项练习及答案解析

1.了解数阵图的种类2.学会一些解决数阵图的解题方法3.能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1.定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．数阵图与数论【例 1】把0—9这十个数字填到右图的圆圈内，使得五条线上的数字和构成一个等差数列，而且这个等差数列的各项之和为55，那么这个等差数列的公差有种可能的取值．【考点】数阵图与数论【难度】3星【题型】填空【关键词】迎春杯，三年级，初赛，第8题【解析】设顶点分别为A、B、C 、D、E，有45+A+B+C+D+E=55，所以A+B+C+D+E=10，所以A、B、C、D、E分别只能是0-4中的一个数字.则除之外的另外5个数（即边上的）为45-10=35.设所形成的等差数列的首项为a1，公差为d.利用求和公式5（a1＋a1+4d）2=55，得a1+2d=11，故大于等于0+1+5=6，且为奇数，只能取7、9或11，而对应的公差d分别为2、1和0.经试验都能填出来所以共有3中情况，公差分别为2、1、0.例题精讲知识点拨教学目标5-1-3-3.数阵图【答案】2种可能【例 2】将1~9填入下图的○中，使得任意两个相邻的数之和都不是3，5，7的倍数．【考点】数阵图与数论【难度】4星【题型】填空【解析】根据题意可知1的两边只能是3与7；2的两边只能是6与9；3的两边只能是1、5或8；4的两边只能是7与9．可以先将3—1—7--写出来，接下来7的后面只能是4，4的后面只能是9，9的后面只能是2，2的后面只能是6，可得：3—1—7—4—9—2—6--，还剩下5和8两个数．由于6814+=是7的倍数，所以接下来应该是5，这样可得：3—1—7—4—9—2—6—5—8—3．检验可知这样的填法符合题意．【答案】3—1—7—4—9—2—6—5—8—3【例 3】在下面8个圆圈中分别填数字l，2，3，4，5，6，7，8(1已填出)．从1开始顺时针走1步进入下一个圆圈，这个圆圈中若填n(n≤8)。

2020~2021学年三年级奥数思维能力训练：数阵图初步

9．在图中的A、B、C三个圆圈内填入三个不同的自然数，使得三角形每条边上的三个数之和都等于12，那么圆圈B中应填的数是多少？
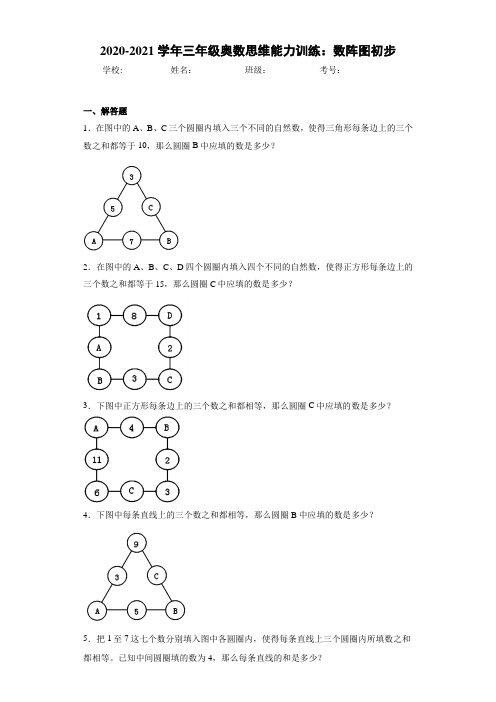
10．在图中的A、B、C三个圆圈内填入三个不同的自然数，使得正方形每条边上的三个数之和都相等，那么圆圈A中应填的数是多少？
参考答案
1．1
【解析】
【分析】
封闭型数阵图，线和是10，先求A，再求B，再求C。
【解析】
【分析】
辐射型数阵图问题，中间数是4，重复了2次，可利用数和、线和及中间数的关系进行求解。
【详解】
先求数和，，中间数重复了2次，再求线和，，所以每条直线的和是12，根据“4+1+7=12”，“4+2+6=12”，“4+3+5=12”，进行合理构造，完成数阵图。
【点睛】
辐射型数阵图，注意中间数的填法，考虑中间数除了4，还可以填多少。
【详解】
A=
B=
【点睛】
本题较为简单，根据数阵图的基本要求直接求解即可。
2．7
【解析】
【分析】
封闭型数阵图，1，B，C，D重复了1次，线和已知，按照D，C，B，A的顺序依次求解。
【详解】
D=
C=
【点睛】
本题较为简单，线和已经给出，按照线和相等这一基本原则，直接计算即可。
3．9
【解析】
【分析】
封闭型数阵图，根据线和相等，先求出B，然后求出线和，再求A和C。
8．
【解析】
【分析】
复合型数阵图问题，每块区域的数都重复了一次，利用数和、线和的关系进行求解。
【详解】
如图，
令；
已知a，b，c，d，e，f，g，h各自用了两次，计算数和，；

(完整版)小学三年级奥数--数阵图

数阵图(一)在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。

它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。

那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。

右上图就更有意思了，1～9 九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。

上面两个图就是数阵图。

准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。

要排出这样巧妙的数阵图，可不是一件容易的事情。

我们还是先从几个简单的例子开始。

例1 把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。

同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。

下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。

分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3 。

重叠数求出来了，其余各数就好填了（见右上图）。

试一试：练习与思考第1 题。

例2 把1～5 这五个数填入下页左上图中的○里（已填入5），使两条直线上的三个数之和相等。

分析与解：与例1 不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。

所以，必须先求出这个“和”。

根据例1 的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[（1+2+3+4+5）+5] ÷2=10。

三年级思维拓展- 数阵图

（1）8个数的和：1+2+3+4+5+6+7+8=36
（2）要使每个五边形上的5个数和为20，那么2个五边形上的数的总和是：20×2=40.
（3）2个五边形上的数的总和比8个数的和多了：40-36=4
（4）多的6就是五边形交叉点重复计算了2次，即多算了1次。在1--8这8个数中有：1+3=4，所以中间位置填1和3.
思路点拨：观察发现中间的圆重复了3次，题目要求3条线上的和相等，那么，每条线上只要有两个数加起来和都相等，中间重复加任何一个数和也都相等。因为1+7=8,2+6=8,3+5=8，所以将4填在中间，再将分好的数填进圆内即可。
活学巧用：
1.，使每条边上的3个数之和都等于10。
活学巧用：
1.将2﹑3﹑4﹑5﹑6﹑7这6个数填在下面的圆圈里，使每条边上3个数的和等于15。
2.把数字1、2、3、4、5、6分别填入下图的圆圈内，使3条边上3个数字之和等于11。
3.将1——9这九个数填入下图中，使三角形每条边上四个数的和等于19
【例3】：将1--7这7个数填入○中，使每条线上三个数的和都相等。
2.计算出所给数的总和。
3.再计算出各个部分的总和。
4.两和之间找出“重复计算的数的和”，填出关键位置的数，再根据要求尝试，调整，填出其他位置上的数。
精选例题：
【例1】：将1、3、5、7、9这5个数分别填入□中，使每条线上的三个数的和都相等。
思路点拨：因为1、3、5、7、9中，一头一尾组合结果都为10，题目只要求每条线上三个数的和相等，那么，只要每条线上的两个数的和相等了，中间重复计算的数填任何一个，这两条线上的和也就相等了。
（5）先填被重复计算的数字，在通过计算填出其余的数字：2+6+8=16,4+5+7=16.

三年级下册数学试题-思维训练：数阵图与数字谜(含部分答案)全国通用

数阵图与数字谜知识要点1．有一种数阵图，它们的特点是从一个中心出发，向外作了一些射线，我们把这种数阵图叫做辐射型数阵图。

填辐射型数阵图的关键是确定中心数以及每条线段上的几个数的和，然后通过对各数的分析，进行试验填数求解。

2．有一种数阵图，它的各边之间相互连接，形成封闭图形，我们称它们为封闭型数阵图。

填这样的图形，主要是顶点数字，抓住条件提供的关系式，进行分析，用试验的方法确定顶点数以及各边上的数字之和，最后填出数阵图。

3．有的数阵图既有辐射型数阵图的特点，又有封闭型数阵图的要求，所以叫做“复合型数阵图”。

我们在思考数阵图问题时，首先要确定所求的和与关键数间的关系，再用试验的方法，找到相等的和与关键数字。

数阵图的解题关键是找”重复数”。

通常的步骤为：⑴观察图表共有几个和⑵找和，思考每个数被加过几个⑶利用整除求重复数例1把1～6这6个数填入下图的○内，使每条直线上3个数的和为9，怎样填？【拓展】如图“好、朋、友、伙、伴、帮、手”这7个汉字分别代表1～7这7个数字。

已知条直线上的3个数相加、2个圆周上的3个数相加，所得的5个和相同。

那么，“好”字代表多少？将1，4，7，10，13，16，19，22，25这9个数分别填入下图的9个○中，使三条边上○中的四个数的和都相等，每条边上四个数的和最大是_____。

弄清楚加减法各部分之间的数量关系是学习数字谜的基础。

1．审题，审题就是找出算式中数字之间的关系和特征，挖掘题目中的隐含条件，它是确定各空格内应该填什么数字的主要依据。

2．选择解题突破口：在审题的基础上，认真思考找出算式中容易填出或关键性的空格，做为解题的突破口，这一步是填空格的关键。

3．确定各空格填什么数字：从突破口开始，依据竖式的已知条件，逐个填出各空格中的数字。

突破口：⑴首位、末分析法；⑵进位、退位分析法；⑶奇偶性分析法；⑷数位分析法；⑸整除。

下式中，不同的字母表示不同的数字，那么ABC表示的三位数是() 例3例2知识要点左式中，不同的符号表示不同的数字，那么◎＋△＋◇＝_____在下面的竖式的各个方框中填上适当的数字，使竖式成立。

三年级奥数学练习试卷思维培训资料数阵图 (2)

讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组第六讲数字谜（二）—数阵图教学目标本讲通过对简单数阵的学习，让学生在数与数之间的变化中，感受到数字的奇妙，体会到数学思维的乐趣.知识点：1．封闭型数阵图；2．辐射型数阵图；3．复合型数阵图．想挑将1、2、3、4、5、6 这六个数填在图中的空灯里，使每个大圆上的四盏灯里的数相加都等于14．战吗？分析：将三个大圆上的所有数字相加，中间三个灯笼上的数字被加了2 遍，其余三个灯笼上的数字只加了一遍，所以，中间三个数的和为（1＋2＋3＋4＋5＋6）－14＝7，三个数相加等于7 的情况只有1＋2＋4，所以中间的三个灯笼上的数为 1，2，4，这 6 个数中四个数相加等于 14 的组合有(6521)(6431)(5432)，就可以填出：在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷．它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留恋其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣．到底什么是数阵呢？下面我们一起来研究吧．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 47讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组专题精讲到底什么是数阵呢？我们先观察右面两个图：左图中有3 个大圆，每个圆周上都有四个数字，有意思的是，7每个圆周上的四个数字之和都等于13．右图就更有意思了，1～9 九个数字被排成三行三列，每行的三个数字之和与每列的三个数字213831567之和，以及每条对角线上的三个数字之和都等于15．上面两个图就645492是数阵图．准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵．（一）辐射型数阵图有一种数阵图，它们的特点是从一个中心出发，向外作了一些射线，我们把这种数阵图叫做辐射型数阵图．填辐射型数阵图的关键是确定中心数以及每条线段上的几个数的和，然后通过对各数的分析，进行试验填数求解．例1 （学而思题库）把1～5 这五个数填入右图中的○里，使每条直线上的三个数之和相等．分析：在图中我们可以看出，中间圆圈里的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”．也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次．我们可以得出：(1＋2＋3＋4＋5)＋重叠数＝每条直线上三数之和×2，所以，每条直线上三数之和等于(15＋重叠数)÷2．因为每条直线上的三数之和是整数，所以重叠数只可能是1，3 或5．若“重叠数”＝1，则两条直线上三数之和为(15＋1)÷2＝8．填法见左下图；若“重叠数”＝3，则两条直线上三数之和为 (15＋3)÷2＝9．填法见下中图；若“重叠数”＝5，则两条直线上三数之和为 (15＋5)÷2＝10．填法见右下图．12 23341544121553[前铺]把1～5 这五个数填入下图中的○里(已填入5)，使两条直线上的三个数之和相等．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 48讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组15 5234分析：与例1不同之处是已知“重叠数”为5，不知道两条直线上的三个数之和都等于什么数．所以，必须先求出这个“和”．两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于 [(1＋2＋3＋4＋5)＋5]÷2＝10．因此，两条直线上另两个数(非“重叠数”)的和等于10－5＝5．在剩下的四个数1，2，3，4 中，只有1＋4＝2＋3＝5．故有右上图的填法．[注意] 求数阵问题的关键是找到关键数，也就是重复数，教会学生学会找关键数的方法是最重要的．例2 （学而思题库）把1～7 这七个数分别填入下图的○内，使每条线段上三个○内数的和相等．263634417275456573211（1）（2）（3）分析：解这道题的关键是首先求出中心数．1～7 七个数的和是28，而计算三条线段中数的和时，中心圆的数要多加两次．因此可得如下关系式：28＋(中心数)×2＝每条线段上三个数的和×3．即：(28＋中心数×2)÷3＝每条线段上三个数的和．用试验的方法，将1～7 这七个数作中心数分别代入上述关系式中．可求出中心数及每条直线上三个数的和．经试验，若中心数取2、3、5、6，此题无解；中心数取1、4、7 时该题数阵图成立．（1）(28＋1×2)÷2＝10，中间圆圈内填1，各线段其它两数和为10－1＝9．（2）(28＋4×2)÷3＝12，中间圆圈内填4，各线段其它两数和为12－4＝8．（3）(28＋7×2)÷3＝14，中间圆圈内填7，各线段其它两数和为14—7＝7．三种基本解法详见右上图的(1)、(2)、(3)．例3 (1993 年武汉市小学数学竞赛试题)把10～20 这11 个数分别填入下图的圆圈内，使每条线段上三个圆圈内的数的和都相等．请你把各种填法都写出来(中心圆圈内的数相同就视为一种填法)．分析：审题可知中心处的数是五条线段的端点，求和时用了5 次，因此，确定中心圆圈里的数是关键（方法一）①列出中心数与每条线段上三数和的关系式：学而思教育08 年寒假三年级竞赛班第六讲教师版Page 49讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组(165＋中心数×4)÷5＝每条线段上三数和②用试验方法求出中心数及每条线段上三数和．中心数分别为10、15、20．每条线段上三数和分别为4l、45、49．分别以10、15、20 为中心数的数阵图，相对应的每条线段上两数和分别为：3l、30、29．和为29 的两数可有：10＋19、1118、12＋17、13＋16、14＋15；和为30 的两数可有：10＋20、11＋19、12＋18、13＋17、14＋16；和为31 的两数可有：11＋20、12＋19、13＋18、14＋17、15＋16．③填图．如下图的(1)、(2)、(3)．201919201211131018161410191018151114111520141513121312171718161617（方法二）设中心的圆圈内的数字是a，每条线段的圆圈内的三个数字和是k，则：10＋11＋12＋13＋14＋15＋16＋17＋18＋19＋20＋4×a＝5k，即165＋4×a＝5k．推出中心处的a 等于10，15，20，k 分别等于41，45，49．当 a＝10 时，k＝41，每条线段上另外两个圆圈内的两数之和是 31，即 11＋20，12＋19，13＋18，14 ＋17，15＋16，从而填出数阵图．当 a＝15 时，k＝45，每条线段上另外两个圆圈内的两数之和是 30，即 10＋20、11＋19、12＋18、13 ＋17、14＋16，从而填出数阵图．当 a＝20 时，k＝49，每条线段上另外两个圆圈内的两数之和是 29，即 10＋19、11＋18、12＋17、13 ＋16、14＋15，从而填出数阵图．[前铺]将 10～20 填入左下图的○内，其中15 已填好，使得每条边上的三个数字之和都相等．201516141015111913121718分析：中间○内的15 是重叠数，并且重叠了四次，所以每条边上的三个数字之和等于 [(10＋11＋…＋20)＋15×4]÷5＝45．剩下的十个数中，两两之和等于(45－15＝)30的有10，20；11，19；12，18；13，17；14，16．于是得到右上图的填法．[小结]以上例题中数阵图都是辐射型数阵图．一般地，有m条边，每边有n个数的形如下图的图形称为辐射型m－n 图．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 50讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组辐射型数阵图只有一个重叠数，重叠次数是“直线条数”－1，即m－1．对于辐射型数阵图，有：已知各数之和＋重叠数×重叠次数＝直线上各数之和×直线条数．由此得到：(1)若已知每条直线上各数之和，则重叠数等于 (直线上各数之和×直线条数－已知各数之和)÷重叠次数．(2)若已知重叠数，则直线上各数之和等于(已知各数之和＋重叠数×重叠次数)÷直线条数．(3)若重叠数与每条直线上的各数之和都不知道，则要从重叠数的可能取值分析讨论．（二）封闭型数阵图有一种数阵图，它的各边之间相互连接，形成封闭图形，我们称它们为“封闭型数阵图”．填这样的图形，主要是顶点数字，抓住条件提供的关系式，进行分析，用试验的方法确定顶点数以及各边上的数字之和，最后填出数阵图．例4（学而思题库）将1～6 这六个自然数分别填入右图的六个○中，使得三角形每条边上的三个数之和都相等．分析：我们不知道每边的三数之和等于几．因为三个重叠数都重叠了一次，由(1＋2＋…＋6)＋重叠数之和＝每边三数之和×3，得到每边的三数之和等于[(1＋2＋…＋6)＋重叠数之和]÷3＝(21＋重叠数之和)÷3＝7＋重叠数之和÷3．因为每边的三数之和是整数，所以重叠数之和应是3 的倍数．考虑到重叠数是1～6 中的数，所以三个重叠数之和只能是6，9，12 或15，对应的每条边上的三数之和就是9，10，11 或12．可得下图的四种填法：112464655332 433254216516每边三数之和＝9 每边三数之和＝10 每边三数之和＝11 每边三数之和＝12[小结]像例题中这样各条边是互相连接的数阵图，叫做封闭型数阵图．思考这类问题，主要是要弄清关键数字．抓住关系式，进行分析，确定顶点上的数以及每条边上的数的和，再用试验的方法，求出解．例5 （学而思题库）将2～9 这八个数分别填入下图的○里，使每条边上的三个数之和都等于18．分析：四个角上的数是重叠数，重叠次数都是1 次．所以四个重叠数之和等于学而思教育08 年寒假三年级竞赛班第六讲教师版Page 51讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组18×4－(2＋3＋…＋9)＝28．而在已知的八个数中，四数之和为28 的只有：4＋7＋8＋9＝28 或5＋6＋8＋9＝28．又由于18－9－8＝1，1 不是已知的八个数之一，所以，8 和9 只能填对角处．由此得到左下图所示的重叠数的两种填法：4594599628786837“试填”的结果，只有右上图的填法符合题意．[巩固]把1～8 这八个数分别填入下图中的八个○内，使每条边上三个○内数的和都相等．15684372分析：这道题的关键是确定正方形四个顶点上的数及正方形每边上数的和．1～8 的和是36，36 加上四个顶点上的数的和是4的倍数．36 是4的倍数，只要考虑从1～8 里选4个数，使其和是4的倍数，可得四个不同的和12、16、20、24．再求出每边四个数的和分别是：(36＋12)÷4＝12 (36＋16)÷4＝13(36＋20)÷4＝14 (36＋24)÷4＝15又因为 1＋2＋3＋6＝12，1＋2＋4＋5＝12．经试验，四个顶点数只能填 l、2、3、6．然后用凑数法使每边和是12．采用同样的方法，可填出每边和是13、14、15 的情况．下面给出一种解法，如右上图．其他解法请同学们自己完成．例6 （学而思题库）用1～9 这九个数字填入下图中，使得每条边上的四个数的和都等于A，问A 可以等于哪些数?给出你的填法．分析：解这道题的关键是确定三边之和与三顶点之和的关系，再运用试验法求解．因为每条边上的四数之和都等于A，则三边之和为3×A．因1 到9 这九个数的和是45，而在3×A 中，三个顶点上的数都被计算了两次，于是顶点上的数之和应为3×A－45．这个和是 3 的倍数，它最小是1＋2＋3＝6，最大是7＋8＋9＝24，从而A 可以取17、18、19、20、21、22、23．但是，当A 为18 或22 时，都得不出一个合乎题目要求的解答，所以A 只能为17、19、20、23 这五个数．图(1)、(2)、(3)、(4)、(5)给出了这五种填法．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 52讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组1A=191A=20 1A=178987 89643626275345375429（1）（2）（3）3A=217A=237856531164294298（4）（5）例7 （学而思题库）将1～8 这八个数分别填入下图的○中，使两个大圆上的五个数之和都等于21．分析：中间两个数是重叠数，重叠次数都是1 次，所以两个重叠数之和为21×2－(1＋2＋…＋8)＝6．在已知的八个数中，两个数之和为6 的只有1 与5，2 与4．每个大圆上另外三个数之和为21－6＝15．如果两个重叠数为1 与5，那么剩下的六个数2，3，4，6，7，8 平分为两组，每组三数之和为15 的只有2＋6＋7＝15 和3＋4＋8＝15，故有左下图的填法．1233216 5645 47887如果两个重叠数为2 与4，那么同理可得右上图的填法．[小结]刚刚学习的这几个数阵图都是封闭型数阵图．一般地，在m边形中，每条边上有n个数的形如下图的图形称为封闭型m－n 图．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 53讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组与“辐射型m－n 图只有一个重叠数，重叠次数是m－1”不同的是，封闭型m－n 图有m个重叠数，重叠次数都是1次．对于封闭型数阵图，因为重叠数只重叠一次，所以：已知各数之和＋重叠数之和＝每边各数之和×边数．由这个关系式，就可以分析解决封闭型数阵图的问题．（三）复合型数阵有的数阵图既有辐射型数阵图的特点，又有封闭型数阵图的要求，所以叫做“复合型数阵图”．我们在思考数阵图问题时，首先要确定所求的和与关键数间的关系，再用试验的方法，找到相等的和与关键数字．例8 （学而思题库）如图“好、助、手、伙、伴、参、谋”这7 个汉字分别代表1 至7 这7 个数字．已知3 条直线上的3 个数相加、2 个圆周上的3 个数相加，所得的5 个和相同．那么，“好”字代表多少?谋伴参伙好助手分析：通过读题可以知道三条直线的三个数之和相等，两个圆圈的三个数之和相等，而且五个和都相等．所以计算5 个和的和，这个和一定是5 的倍数，其中“好”字计算了三遍，其它数只是被计算了2 遍，因此这个和等于（1＋2＋3＋4＋5＋6＋7）×2＋“好”＝56＋“好”，我们这个“好”只能是4 才能保证这个和是5 的倍数．所以“好”＝4．例9 （学而思题库）请问如何才能将26，27，28，36，37，38，46，47，48 这九个数分别填入图中的圆圈中，使得通过中心圆圈的每条直线上的三个数之和都是111．分析：我们已知九个数的和是26＋27＋28＋36＋37＋38＋46＋47＋48＝333．题中要使每条线上三个数的和是 111，那么四条线上数的总和是l11×4＝444．四条线上数的总和比九个数的和多 444—333＝111．中心圆圈里的这个数是重叠数，重叠了四次，即多算了3 次，即重叠数×3＝111．因为只有37×3＝111，所以中心圆圈里填37．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 54讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组先填上中心圆圈里的数37，再通过计算分别填人其余各数：111－37＝74，26＋48＝74，27＋47＝74，28＋46＝74，36＋38＝74．填法如图：262836273747384648例10 （学而思题库）将1～10 这lO 个数分别填入下图中的圆圈内，使每条线段上四个圆内的数的和相等，每个三角形三个顶点的圆圈内数的和也相等．分析：从图中观察可以看出，此题的特点是封闭型数阵图与辐射型数阵图的结合．根据这一特点，可分两步解决这个问题．首先按辐射型数阵图去填数，然后再调整各线段上的数，使每个三角形三个顶点上圆圈内的数的和相等．（1）填辐射型数阵图：按填辐射型数阵图的基本方法即可得到四个基本解．如图 (1)、(2)、(3)、(4)．1010109665521111471043333222 5757464 699988887（1）（2）（3）（4）（2）调整各线段上的数，使每个三角形三个顶点上圆圈内数的和相等．图(1)中，中心数用掉了1，十个数还有2，3，4…10九个数．这九个数都分布在三个三角形的顶点上，因此每个三角形三个顶点的数的和为：(1＋3＋4＋…＋10)÷3＝18．求出了每个三角形三个顶点上的和，再把每条线段上的数，在本线段上进行合理的调整，使每个三角形三个顶点上的和等于18．调整可采用先固定其中的一条线段上的数不动．把其余两条线段上的数进行调整，便可得到此题的一个基本解．如下图(1)．采用同样的方法，从上图的(2)、(3)、(4)中又可得到三个基本解．所以本题共有四个基本解，如图(1)、(2)、(3)、(4)．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 55讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组1 1 11010 10 966 5 521（1）783 9534（2）8247937（3）826 84310（4）7 92 46 5专题展望数阵图是一类非常有趣的数学问题，同学们，你们在这座数学迷宫中感受到它的奇妙了吗？在春季我们还会有类似问题的学习哦，敬请期待吧！练习六1. 将1～7 这七个自然数填入下图的七个○内，使得每条边上的三个数之和都等于10．7214 35 6分析：知道每条边上的三数之和，但不知道重叠数．因为有3 条边，所以中间的重叠数重叠了两次．于是得到 (1＋2＋…＋7)＋重叠数×2＝10×3．由此得出重叠数为[10×3－(1＋2＋…＋7)]÷2＝1．剩下的六个数中，两两之和等于9 的有2，7；3，6；4，5．可得右上图的填法．2. 把1、2、3、4、5、6 六个数字分别填入下图的六个圆圈中，使每一边三个数相加的和都等于9．16 52 4 3分析：根据题意，要求每边三个数的和都是9，那么三边的和应为9×3＝27．但是1～6 六个数的和等于21，三行数的和比题中六个数的和多27—21＝6，原因在于三个顶点的数字都要用2 次，说明三个顶点数之和是6．哪三个数的和是6 呢?只有1、2、3，所以把1、2、3 分别填入三个顶点中，再根据每行和都等于9 的要求填上其他各数．如右上图．学而思教育08 年寒假三年级竞赛班第六讲教师版Page 56讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组3. 请分别将1，2，4，6 这4 个数填在下图的各空白区域内，使得每个圆圈里4 个数的和都等于15．2577516433分析：5＋7＝12，3＋7＝10，3＋5＝8，三个圆中已有数的和与15 的差分别是3、5、7，只有1 能和其他三个数的和分别是3、5、7，所以中间数一定是1，由和为15，其它三个数即可得，见右上图．4. 将l、2、3、4、5、6 六个数字填入图2—1 中的小圆圈内，使每个大圆上四个数字的和都是l6．2513 6 4分析：观察发现，中间的两个圆圈最特殊，它们同时在两个圆上，我们要以此入手，填出这个数阵．这六个数的和是1＋2＋3＋4＋5＋6＝21．题中要使每个大圆上的数字和是16，那么两个大圆上的数字总和是16×2＝32，两个大圆圈上数字的总和比六个数的和多32－21＝11，怎么会多11 呢？因为两个大圆上有两个数被算了两次，也就是多算了一次，即（）＋（）＝11，所以，被算了两次的数是5 和6．先填上被多算的数5 和6，再通过计算填入其余各数：16－5－6＝5，2＋3＝5，1＋4＝5，填法如下：5. 将自然数l～7 填入右图的七个O 中，使得横、竖、斜的每条直线上的三个数之和都相等．47 2 31 6 5分析：三角形顶上的数重叠3 次，其他数都重叠2 次．(1＋2＋…＋7)×2＋顶上的数＝每条线上的三个数之和×5，56＋顶上的数＝每条线上的三个数之和×5．由上式等号左端是5 的倍数，推知“顶上的数”：4．所以每条线上的三个数之和为(56＋4)÷5：12．经试验可得如下填法(填法不惟一)：学而思教育08 年寒假三年级竞赛班第六讲教师版Page 57讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组推理小故事图像从不闪动一个星期日的中午，绿庄公寓里008 号房间的单身职员，到距离很近的售货摊上买东西，只离开房间五六分钟，没有锁门，5万元现金被盗．报案后，刑警问他:“公寓里有谁知道你出去买东西?”“10号房间的北村知道，我出去时他还托我买呢．”刑警马上到10 号房间查看．一进门，就见北村一边在吃方便面一边看漫画．“8号房间的失盗者出去买东西时，你在哪儿?干什么了?”“我一直在看漫画呀．”“你没听见那个房间里有异常动静吗?”“没有，那时正好一架直升飞机在这座公寓的上空盘旋，噪音很大，一点点动静也觉察不到．”据公寓管理人员说，中午并没有外人进公寓．肯定是内部人员干的．“别的房间里有人在吗?”“今天星期日，别人出去玩了，只6 号房间里一个叫寺内的青年人在．”刑警又来到6 号房间，见寺内正穿一身睡衣躺在床上，边吃花生米边看电视．那是台新型彩电．“哎呀，好漂亮的彩电啊!图像一点不闪动吗?”“从来没有过，这是我三天前才买来的新产品．”“听到8 号房间里有可疑动静吗?”“没有，一点没察觉到，因电视里有我喜欢的歌手在演唱，我看得入了迷，再加上那架讨厌的直升飞机在盘旋……”“你说谎．直升飞机盘旋时你并没看电视，而是溜进8 号房间找钱吧．”刑警凭什么识破了寺内的手段呢?答案见第七讲．第五讲“巧断小偷”答案：小偷在甲、乙、丙、丁四人中，并且只有一人说的话是真话，其余三人说的是假话．也就是“一真三假”，这也是我们判断是非的准则．假如乙是小偷，那么其余三人均不是小偷．而甲说乙是小偷，所以甲讲了真话；既然乙是小偷，那么丁就不是小偷，可见丁说：“反正我没偷．”这句也是真话．于是，便有甲、乙两人说了真话，这与“一真三假”的准则相矛盾，所以乙不是小偷．同理可推斯出甲、丙都不是小偷，小偷自然就是丁了．不过，我们还可验证一下．当丁是小偷时，甲、乙、丙三人便不是小偷．丁说：“反正我没偷．”这便是一句假话；乙不是小偷，故甲说：“手表是乙偷的．”也是假话；丙不是小偷，则乙说：“手表是丙偷的．”还是假话；既然乙说的是假话，所以丙说：“乙在撒谎．”就是真话，这不是正符合“一真三假”的准则吗?同学们，你答对了吗？学而思教育08 年寒假三年级竞赛班第六讲教师版Page 58。

三年级奥数学练习试卷思维培训资料数阵图

第六讲数字谜（二）—数阵图教学目标本讲通过对简单数阵的学习，让学生在数与数之间的变化中，感受到数字的奇妙，体会到数学思维的乐趣．知识点：1．封闭型数阵图；2．辐射型数阵图；3．复合型数阵图．几个小朋友玩布阵游戏，他们要用36 名士兵守卫一座城池（见下图，图中间表示城区，四周表示城墙，方格中的数表示兵力分布），要求四个角的兵力相同．现在的兵力分布恰好每边有10 名士兵，如果想使每边有15名士兵，那么兵力应该怎样分布呢？18188181分析：题目要求四个角的兵力相同，而且每边有15 名士兵，那么四条边上的所有士兵数量相加，四个角上的士兵数都加了两遍，也就是15×463363－4×四个角上的士兵数＝36，所以四个角上的士兵数为 6，所以兵力分布如图：636在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷．它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留恋其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣．到底什么是数阵呢？下面我们一起来研究吧．学而思教育08 年寒假三年级提高班第六讲教师版Page 48专题精讲到底什么是数阵呢？我们先观察右面两个图：左图中有3 个大圆，每个圆周上都有四个数字，有意思的是，7每个圆周上的四个数字之和都等于13．右图就更有意思了，1～9 九个数字被排成三行三列，每行的三个数字之和与每列的三个数字213831567之和，以及每条对角线上的三个数字之和都等于15．上面两个图就是数阵图．准确地说，数阵图是将一些数按照一定要求排列而成的645492某种图形，有时简称数阵．有一种数阵图，它们的特点是从一个中心出发，向外作了一些射线，我们把这种数阵图叫做辐射型数阵图．填辐射型数阵图的关键是确定中心数以及每条线段上的几个数的和，然后通过对各数的分析，进行试验填数求解．例1 （学而思题库）小猴丁丁和当当一起玩数阵游戏，他们在地上画了个如右图所示的数阵，丁丁出题，它在最中间的圆圈中写了数5 字5，要求当当把1～4 这四个数填入剩下的四个○里，使两条直线上的三个数之和相等．你能帮当当解决这道题吗？分析：在图中我们可以看出，中间圆圈里的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”．我们知道重叠数，就可以求出每条直线上三个数的“和”．两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于 [(1＋2 ＋3＋4＋5)＋5]÷2＝10．1因此，两条直线上另两个数(非“重叠数”)的和等于10－5＝5．非“重叠数”的和也可以这样求，因为1～4 的和我们可以求，每条直线上两端的数253的和是：（1＋2＋3＋4）÷2＝5．4在剩下的四个数1，2，3，4 中，只有1＋4＝2＋3＝5．所以有右图的填法．[拓展]把1～5 这五个数填入右图中的○里，使每条直线上的三个数之和相等．分析：例题是知道重叠数，不知道两条直线上的三个数之和；这道题是重叠数与三个数的和都不知道．但由例题的分析知道，(1＋2＋3＋4＋5)＋重叠数＝每条直线上三数之和×2，所以，每条直线上三数之和等于(15＋重叠数)÷2．因为每条直线上的三数之和是整数，所以重叠数只可能是1，3 或5．若“重叠数”＝1，则两条直线上三数之和为(15＋1)÷2＝8．填法见左下图；若“重叠数”＝3，则两条直线上三数之和为 (15＋3)÷2＝9．填法见下中图；若“重叠数”＝5，则两条直线上三数之和为 (15＋5)÷2＝10．填法见右下图．学而思教育08 年寒假三年级提高班第六讲教师版Page 49讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组12 223431 4 154553[注意] 求数阵问题的关键是找到关键数，也就是重复数，教会学生学会找关键数的方法是最重要的．例2 （学而思题库）将1～7 这七个自然数填入下图的七个○内，使得每条边上的三个数之和都等于10．你能做到吗？分析：知道每条边上的三数之和，但不知道重叠数．因为有3 条边，所以中间的重7叠数重叠了两次．于是得到 (1＋2＋…＋7)＋重叠数×2＝10×3．2由此得出重叠数为 [10×3－(1＋2＋…＋7)]÷2＝1．1剩下的六个数中，两两之和等于9 的有2，7；3，6；4，5．可得右图的填法．4356 [拓展]把1～7 这七个数分别填入下图的○内，使每条线段上三个○内数的和相等263634417275456573211分析：解这道题的关键是首先求出中心数．1～7 七个数的和是 28，而计算三条线段中数的和时，中心圆的数要多加两次．因此可得如下关系式：28＋(中心数)×2＝每条线段上三个数的和×3．即：(28＋中心数×2)÷3＝每条线段上三个数的和．用试验的方法，将 1～7 这七个数作中心数分别代人上述关系式中．可求出中心数及每条直线上三个数的和．经试验，若中心数取2、3、5、6，此题无解；中心数取1、4、7 时该题数阵图成立．（1）(28＋1×2)÷2＝10，中间圆圈内填1，各线段其他两数和为10－1＝9．（2）(28＋4×2)÷3＝12，中间圆圈内填4，各线段其他两数和为12－4＝8．（3）(28＋7×2)÷3＝14，中间圆圈内填7，各线段其他两数和为14—7＝7．三种基本解法详见右上图的(1)、(2)、(3)．学而思教育08 年寒假三年级提高班第六讲教师版Page 50讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组例3 （学而思题库）数学王国的大门有一把密码锁，它的形状如下，只有将 10～20 填入其中的○内，其中15 已填好，使得每条边上的三个数字之和都相等才能把这把锁打开，顺利的进入数学王国，你也试试吧．1520分析：中间○内的15 是重叠数，并且重叠了四次，所以每条边上的三个数字之和等于[(10＋11＋…＋20)＋15×4]÷5＝45．1614101519111312剩下的十个数中，两两之和等于(45－15＝)30 的有10，20；11，19；12，1718 18；13，17；14，16．于是得到右图的填法．也可以这样求：五条边上两个数的和都是相等的，（10＋11＋…＋20）÷5＝30，所以两两之和等于30．[拓展]把10～20 这11 个数分别填入右图的圆圈内，使每条线段上三个圆圈内的数的和都相等．请你把各种填法都写出来(中心圆圈内的数相同就视为一种填法)．(1993 年武汉市小学数学竞赛试题)分析：审题可知中心处的数是五条线段的端点，求和时用了5 次，因此，确定中心圆圈里的数是关键（方法一）①用例3方法列出中心数与每条线段上三数和的关系式：(165＋中心数×4)÷5②用试验方法求出中心数及每条线段上三数和．中心数分别为10、15、20．每条线段上三数和分别为4l、45、49．分别以10、15、20 为中心数的数阵图，相对应的每条线段上两数和分别为：3l、30、29．和为29 的两数可有：10＋19、1118、12＋17、13＋16、14＋15；和为30 的两数可有：10＋20、11＋19、12＋18、13＋17、14＋16；和为31 的两数可有：11＋20、12＋19、13＋18、14＋17、15＋16．③填图．如下图的(1)、(2)、(3)．1920 19201211131018161410101819151114111520141512131312171718161617（方法二）设中心的圆圈内的数字是 a，每条线段的圆圈内的三个数字和是 k，则：10＋11＋12＋13＋14＋15＋16＋17＋18＋19＋20＋4×a＝5k，即165＋4×a＝5k．推出中心处的a等于10，15，20，k 分别等于41，45，49．当a＝10 时，k＝41，每条线段上另外两个圆圈内的两数之和是31，即11＋20，12＋19，13＋18，14＋17，15＋16，从而填出数阵图当a＝15 时，k＝45，每条线段上另外两个圆圈内的两数之和是30，即10＋20、11＋19、学而思教育08 年寒假三年级提高班第六讲教师版Page 51讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！ ——学而思小学奥数讲义组12＋18、13＋17、14＋16，从而填出数阵图当 a ＝20 时，k ＝49，每条线段上另外两个圆圈内的两数之和是 29，即 10＋19、11＋18、12＋17、13＋ 16、14＋15，从而填出数阵图[小结]以上例题中数阵图都是辐射型数阵图．一般地，有 m 条边，每边有 n 个数的形如下图的图形称为辐射型 m －n 图．辐射型数阵图只有一个重叠数，重叠次数是“直线条数”－1，即m －1．对于辐射型数阵图，有：已知各数之和＋重叠数×重叠次数＝直线上各数之和×直线条数．由此得到：(1)若已知每条直线上各数之和，则重叠数等于 (直线上各数之和×直线条数－已知各数之和)÷重叠次数．(2)若已知重叠数，则直线上各数之和等于(已知各数之和＋重叠数×重叠次数)÷直线条数．(3)若重叠数与每条直线上的各数之和都不知道，则要从重叠数的可能取值分析讨论．有一种数阵图，它的各边之间相互连接，形成封闭图形，我们称它们为“封闭型数阵图”．填这样的图形，主要是顶点数字，抓住条件提供的关系式，进行分析，用试验的方法确定顶点数以及各边上的数字之和，最后填出数阵图．例4 （学而思题库）周末小猪熊去小猴家里玩，过桥的时候遇到了狐狸，狐狸有意刁难它，就挡住了小猪熊的去路，狐狸狡猾的对它说：“只要你能把 1、2、3、4、5、6 六个数字分别填入下图的六个圆圈中，使每一边三个数相加的和都等于 11．我就让你过桥．”小猪熊想了一下，不慌不忙的填了出来，你知道聪明的小猪熊是怎么解答的吗？25 3分析：因为每条边上的和都为 11，那么三条边上的数字之和为 11×3＝33，而 1＋2 ＋…＋5＋6＝21，所以三个角的三个数之和等于 33－21＝12，在 1～6 中选 3 个和为 12 的数，且其中任意两个的和不等于 11，这样的组合有：12＝2＋4＋6＝3＋4＋5，经试验，填法见右图． 41 6 亮点设计：(1)求数阵问题的关键是找到关键数，也就是重复数，教会学生学会找关键数的方法是最重要的．学而思教育08 年寒假三年级提高班第六讲教师版Page 52讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组（2）设计问题：三角形每条边之和是 11，11×3＝33，但是所有数的和是：1＋2＋…＋5＋6＝21，为什么会出现结果不同的问题呢？仔细观察这个数阵，三条边上所有数相加的过程中三个角上的数都被重复加了一次，也就是说三个角上的数是重复数，33－21＝12即为这三个重复数的和．（3）强调分组法与试验法：知道了三个数的和之后，下一步就要先确定这三个数，采用分组法和试验法．分组法是将这个和根据要求拆成三个数，例如本题中如果两个数的和为 11，那么将无法填第三个数，所以，1、5、6 这一组就不符合，所以12＝2＋4＋6＝3＋4＋5，除此之外还需要采用试验法，将它们一一进行试验．（4）小结：对于封闭型的数阵，重复数基本上都是两条线相交的点．[拓展]将1～6 这六个自然数分别填入右图的六个○中，使得三角形每条边上的三个数之和都相等．分析：与例题不同的是不知道每边的三数之和等于几．因为三个重叠数都重叠了一次，由(1＋2＋…＋6)＋重叠数之和＝每边三数之和×3，得到每边的三数之和等于[(1＋2＋…＋6)＋重叠数之和]÷3＝(21＋重叠数之和)÷3＝7＋重叠数之和÷3．因为每边的三数之和是整数，所以重叠数之和应是3的倍数．考虑到重叠数是1～6 中的数，所以三个重叠数之和只能是6，9，12 或15，对应的每条边上的三数之和就是9，10，11 或12．与例题的方法类似，可得下图的四种填法：112465645332 243325416516每边三数之和＝9 每边三数之和＝10 每边三数之和＝11 每边三数之和＝12[小结]像例题中这样各条边是互相连接的数阵图，叫做封闭型数阵图．思考这类问题，主要是要弄清关键数字．抓住关系式，进行分析，确定顶点上的数以及每条边上的数的和，再用试验的方法，求出解．例5 （学而思题库）大脸猫觉得自己比蓝皮鼠聪明，蓝皮鼠不服气，于是他们决定做同一道题目，看谁先做出来，就承认谁比较聪明，可是它们都没做出来，请你试一试吧．题目是：把2～9 这八个数分别填入下图中的八个○内，使每条边上三个○内数的和都等于18．分析：四个角上的数是重叠数，重叠次数都是1 次．所以四个重叠数之和等于18×4－(2＋3＋…＋9)＝28．而在已知的八个数中，四数之和为28 的只有：4＋7＋8＋9＝28 或5＋6＋8＋9＝28．又由于18－9－8＝1，1 不是已知的八个数之一，所以，8 和9 只能填对角处．由此得到左下图所示的重叠数的两种填法：学而思教育08 年寒假三年级提高班第六讲教师版Page 53讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组4594599628683787“试填”的结果，只有右上图的填法符合题意．[巩固]把1～8 这八个数分别填入下图中的八个○内，使每条边上三个○内数的和都相等．15684372分析：这道题的关键是确定正方形四个顶点上的数及正方形每边上数的和．1～8 的和是36，36 加上四个顶点上的数其和是4的倍数．36 是4的倍数，只要考虑从1～8 里选4个数，使其和是4的倍数，可得四个不同的和12、16、20、24．再求出每边四个数的和分别是：(36＋12)÷4＝12 (36＋16)÷4＝13(36＋20)÷4＝14 (36＋24)÷4＝15又因为 1＋2＋3＋6＝12，1＋2＋4＋5＝12．经试验，四个顶点数只能填 l、2、3、6．然后用凑数法使每边和是12．采用同样的方法，可填出每边和是13、14、15 的情况．下面给出一种解法，如右上图．其他解法请同学们自己完成．例6 （学而思题库）用1～9 这九个数字填入下图中，使得每条边上的四个数的和都等于A，问A 可以等于哪些数?给出你的填法．分析：解这道题的关键是确定三边之和与三顶点之和的关系，再运用试验法求解．因为每条边上的四数之和都等于A，则三边之和为3×A．因1 到9 这九个数的和是45，而在3×A 中，三个顶点上的数都被计算了两次，于是顶点上的数之和应为3×A－45．这个和是 3 的倍数，它最小是1＋2＋3＝6，最大是7＋8＋9＝24，从而A 可以取17、18、19、20、21、22、23．但是，当A 为18 或22 时，都得不出一个合乎题目要求的解答，所以A 只能为17、19、20、21、23 这五个数．图(1)、(2)、(3)、(4)、(5)给出了这五种填法．学而思教育08 年寒假三年级提高班第六讲教师版Page 54讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组1A=191A=20 1A=178987 89643626275345375429（1）（2）（3）3A=217A=237856531164294298（4）（5）例7 （学而思题库）小老鼠打洞，撞到一面墙上有一个奇怪的问题挡住了它的去路，问题是这样的：请分别将1，2，4，6 这4 个数填在下图的各空白区域内，使得每个圆圈里4 个数的和都等于15．快点帮帮小老鼠吧．573分析：5＋7＝12，3＋7＝10，3＋5＝8，三个圆中已有数的和与 15 的差分别2是3、5、7，只有1 能和其他三个数的和分别是3、5、7，所以中间数一定是571，由和为15，其它三个数即可得，见右图．1643例8 （学而思题库）唐僧师徒西天取经路过数字山，山中住着一个数学大王告诉他们，只有他们能把l、2、3、4、5、6 六个数字填入下图中的小圆圈内，使每个大圆上四个数字的和都是l6 才允许他们通过，这可急坏了师徒四人，你能解决这个问题吗？分析：观察发现，中间的两个圆圈最特殊，它们同时在两个圆上，我们要以此入手，填出这个数阵．这六个数的和是1＋2＋3＋4＋5＋6＝21．题中要使每个大圆上的数字和是16，那么两个大圆上的数字总和是16×2＝32，两个大圆圈上数字的总和比六个数的和多32－21＝11，怎么会多11呢？因为两个大圆上有两个数被算了两次，也就是多算了一次，即（）＋（）＝11，所学而思教育08 年寒假三年级提高班第六讲教师版Page 55讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组以，被算了两次的数是5 和6．先填上被多算的数5 和6，再通过计算填入其余各数：16－5－6＝5，2＋3＝5，251 1＋4＝5，填法如右图：364 [小结]刚刚学习的这几个数阵图都是封闭型数阵图．一般地，在m边形中，每条边上有n个数的形如下图的图形称为封闭型m－n 图．与“辐射型m－n 图只有一个重叠数，重叠次数是m－1”不同的是，封闭型m－n 图有m个重叠数，重叠次数都是1次．对于封闭型数阵图，因为重叠数只重叠一次，所以：已知各数之和＋重叠数之和＝每边各数之和×边数．由这个关系式，就可以分析解决封闭型数阵图的问题．有的数阵图既有辐射型数阵图的特点，又有封闭型数阵图的要求，所以叫做“复合型数阵图”．我们在思考数阵图问题时，首先要确定所求的和与关键数间的关系，再用试验的方法，找到相等的和与关键数字．例9 （学而思题库）班上进行民主选举，谁能在图中 x，y，z 三个小圆圈内各填上一个数，使得每条直线上三个数的和都等于大三角形三个顶点上三个数的和，谁就是数学课代表，你也来试一试吧．x5416z y分析：如图，我们把三条直线上的三个和相加，相当于把4 算了三遍，1，5，6 算了一遍，三个顶点上的数各算了一遍．根据题意，这三个和应该是相等的，并且和三个顶点上的和也相等．那么4×3＋1＋5＋6＋三个顶点和＝三个顶点和×3，很明显，这个4×3＋1＋5＋6 就是我们最关心的这个和的两倍(加上一倍后等于三倍)．那么这个和是(4×3＋1＋5＋6)÷2＝12．所以，图中x 处的数是l2－4－5＝3；图中y 处的数是l2－4－1＝7；图中z 处的数是l2－4－6＝2．学而思教育08 年寒假三年级提高班第六讲教师版Page 56讲义是乐谱，学生是听众，老师是指挥家，每节课都是一篇乐章，老师您辛苦了！——学而思小学奥数讲义组例10 （学而思题库）如图“好、助、手、伙、伴、参、谋”这7 个汉字分别代表1 至7 这7 个数字．已知3 条直线上的3 个数相加、2 个圆周上的3 个数相加，所得的5 个和相同．那么，“好”字代表多少?谋伴参好伙助手分析：通过读题可以知道三条直线的三个数之和相等，两个圆圈的三个数之和相等，而且五个和都相等．所以计算5 个和的和，这个和一定是5 的倍数，其中“好”字计算了三遍，其它数只是被计算了2 遍，因此这个和等于（1＋2＋3＋4＋5＋6＋7）×2＋“好”＝56＋“好”，我们这个“好”只能是4 才能保证这个和是5 的倍数．所以“好”＝4．专题展望数阵图是一类非常有趣的数学问题，同学们，你们在这座数学迷宫中感受到它的奇妙了吗？在春季我们还会有类似问题的学习哦，敬请期待吧！练习六1. 把1～5 这五个数分别填在下图中的方格中，使得横行三数之和与竖列三数之和都等于9．21 3 54分析：(1＋2＋3＋4＋5)＋重叠数＝9＋9，重叠数＝(9＋9)－(1＋2＋3＋4＋5)＝3．重叠数求出来了，其余各数就好填了(见右上图)．2. 将1～7 这七个数分别填入下图中的○里，使每条直线上的三个数之和都等于12．32 741 65分析：1+2+3+4+5+6+7+2×中间数＝28+2×中间数＝12×3，中间数为4，填法如右上图．学而思教育08 年寒假三年级提高班第六讲教师版Page 573. 把1、2、3、4、5、6 六个数字分别填入下图的六个圆圈中，使每一边三个数相加的和都等于9．16 52 4 3分析：根据题意，要求每边三个数的和都是9，那么三边的和应为9×3＝27．但是1～6 六个数的和等于21，三行数的和比题中六个数的和多27-21＝6，原因在于三个顶点的数字都要用2 次，说明三个顶点数之和是6． 1+2+3=6，所以把1、2、3 分别填入三个顶点中，再根据每行和都等于9 的要求填上其他各数．如右上图．4. 将1～8 填入右图的八个○中，使得每条边上的三个数之和都等于15．分析：四个顶点数之和为15×4－(1＋2＋…＋8)＝24，四个顶点数有3，6，7，8和4，5，7，8 两种可能．经试验只有下图一个解．3 4 85 17 2 65. 将1～7 七个数字填入左下图的七个○内，使每个圆周和每条直线上的三个数之和都相等．1743 25 6分析：设中心数为a，各条直线和各个圆周上的三数之和均为k．因为a 属于三条直线公有，其余数各属于一条直线和一个圆周，于是得到2×（1＋2＋…＋7）＋a＝5k，化简为a＋56＝5k．因为1≤a≤7，a＋56 又是5 的倍数，所以a＝4，k＝12．填数方法见右上图．学而思教育08 年寒假三年级提高班第六讲教师版Page 58推理小故事图像从不闪动一个星期日的中午，绿庄公寓里008 号房间的单身职员，到距离很近的售货摊上买东西，只离开房间五六分钟，没有锁门，5万元现金被盗．报案后，刑警问他:“公寓里有谁知道你出去买东西?”“10号房间的北村知道，我出去时他还托我买呢．”刑警马上到10 号房间查看．一进门，就见北村一边在吃方便面一边看漫画．“8号房间的失盗者出去买东西时，你在哪儿?干什么了?”“我一直在看漫画呀．”“你没听见那个房间里有异常动静吗?”“没有，那时正好一架直升飞机在这座公寓的上空盘旋，噪音很大，一点点动静也觉察不到．”据公寓管理人员说，中午并没有外人进公寓．肯定是内部人员干的．“别的房间里有人在吗?”“今天星期日，别人出去玩了，只6 号房间里一个叫寺内的青年人在．”刑警又来到6 号房间，见寺内正穿一身睡衣躺在床上，边吃花生米边看电视．那是台新型彩电．“哎呀，好漂亮的彩电啊!图像一点不闪动吗?”“从来没有过，这是我三天前才买来的新产品．”“听到8 号房间里有可疑动静吗?”“没有，一点没察觉到，因电视里有我喜欢的歌手在演唱，我看得入了迷，再加上那架讨厌的直升飞机在盘旋……”“你说谎．直升飞机盘旋时你并没看电视，而是溜进8 号房间找钱吧．”刑警凭什么识破了寺内的手段呢?答案见第七讲．第五讲“巧断小偷”答案：小偷在甲、乙、丙、丁四人中，并且只有一人说的话是真话，其余三人说的是假话．也就是“一真三假”，这也是我们判断是非的准则．假如乙是小偷，那么其余三人均不是小偷．而甲说乙是小偷，所以甲讲了真话；既然乙是小偷，那么丁就不是小偷，可见丁说：“反正我没偷．”这句也是真话．于是，便有甲、乙两人说了真话，这与“一真三假”的准则相矛盾，所以乙不是小偷．同理可推斯出甲、丙都不是小偷，小偷自然就是丁了．不过，我们还可验证一下．当丁是小偷时，甲、乙、丙三人便不是小偷．丁说：“反正我没偷．”这便是一句假话；乙不是小偷，故甲说：“手表是乙偷的．”也是假话；丙不是小偷，则乙说：“手表是丙偷的．”还是假话；既然乙说的是假话，所以丙说：“乙在撒谎．”就是真话，这不是正符合“一真三假”的准则吗?同学们，你答对了吗？学而思教育08 年寒假三年级提高班第六讲教师版Page 59。

三年级奥数之数阵图习题

数阵图
1、把1到6这六个数分别填入下图的六个圈内，使得每个正方形顶点上的数的和都为13。

2、将2到7这六个数，填入上图的圈中，使得每条线上的三个数的和相等。

练习：请将1到7这7个数填入下图中，使得每条线上的三个数的和相等。

3、将1到9这九个数填入下图，使得从中心出发的每条线段上的三个数的和相等。

练习：将1到8填入下图，使两个正方形顶点上的数的和相等，并且用斜线连接的4对数的和也都相等。

4、将1到5这五个数填入上图中，使得圆周上四个数的和与每条直线上的三个数的和都相等。

练习：在图中填上7、8、10、12，使得每个圆内的四个数的和相等。

5、将1到16填入4*4（16格）的正方形中，使每行、每列、每条对角线的和都相等。

数阵图练习
1、将6到10这五个数填入下图，使得每条边上的三个数的和相等。

2、将2到11填入下图，使得每条线段上的三个数之和相等。

3、将2到10填入下图，使得每条线上的四个数的和相等。

三年级奥数之数阵图习题

数阵图之欧侯瑞魂创作
1、把1到6这六个数分别填入下图的六个圈内, 使得每个正方形极点上的数的和都为13.
2、将2到7这六个数, 填入上图的圈中, 使得每条线上的三个数的和相等.
练习：请将1到7这7个数填入下图中, 使得每条线上的三个数的和相等.
3、将1到9这九个数填入下图, 使得从中心动身的每条线段上的三个数的和相等.
练习：将1到8填入下图, 使两个正方形极点上的数的和相等, 而且用斜线连接的4对数的和也都相等.
4、将1到5这五个数填入上图中, 使得圆周上四个数的和与每条直线上的三个数的和都相等.
练习：在图中填上7、8、10、12, 使得每个圆内的四个数的和相等.
5、将1到16填入4*4（16格）的正方形中, 使每行、每列、每条对角线的和都相等.
数阵图练习
1、将6到10这五个数填入下图, 使得每条边上的三个数的和相等.
2、将2到11填入下图, 使得每条线段上的三个数之和相等.
3、将2到10填入下图, 使得每条线上的四个数的和相等.。

三年级奥数数阵图

合用标准文案数阵图（一）在奇异的数学王国中，有一类特别幽默的数学问题，它变化多端，令人入迷，巧妙无量。

它就是数阵，一座真切的数字迷宫，它对喜欢研究数字规律的人有着极大的吸引力，致使有些人流连其中，用一世的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。

那么，终究什么是数阵呢？我们先观察下面两个图：左上图中有 3 个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于 13。

右上图就更有意思了， 1～9 九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于 15，不信你就算算。

上面两个图就是数阵图。

正确地说，数阵图是将一些数依照必然要求排列而成的某种图形，有时简称数阵。

要排出这样巧妙的数阵图，可不是一件简单的事情。

我们还是先从几个简单的例子开始。

例 1 把 1～ 5 这五个数分别填在左以下图中的方格中，使得横行三数之和与竖列三数之和都等于 9。

同学们可能会感觉这道题太简单了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。

下面我们就一起来解析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。

解析与解：中间方格中的数很特别，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其他各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于 9，因此(1+2+3+4+5)+重叠数 =9+9，重叠数 =(9+9)-(1+2+3+4+5)=3 。

重叠数求出来了，其他各数就好填了(见右上图 )。

试一试：练习与思虑第 1 题。

例 2 把 1～5 这五个数填入下页左上图中的○里 ( 已填入 5) ，使两条直线上的三个数之和相等。

解析与解：与例 1 不同样之处是已知“重叠数”为 5，而不知道两条直线上的三个数之和都等于什么数。

三年级奥数之数阵图习题

数阵图【2 】
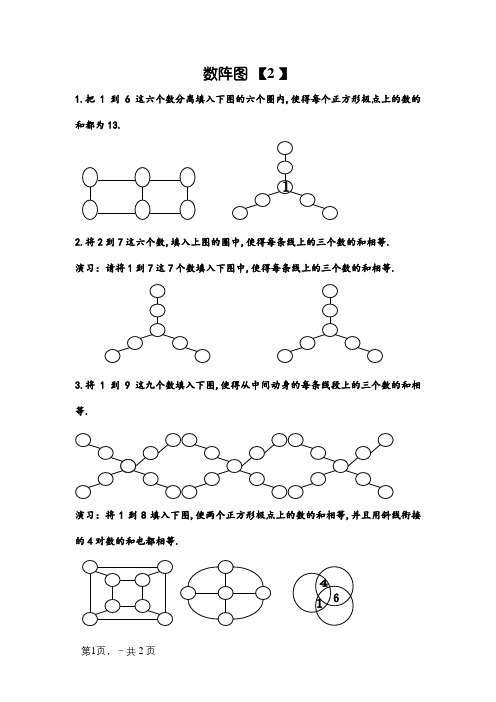
1.把1到6这六个数分离填入下图的六个圈内,使得每个正方形极点上的数的和都为13.
2.将2到7这六个数,填入上图的圈中,使得每条线上的三个数的和相等.
演习：请将1到7这7个数填入下图中,使得每条线上的三个数的和相等.
3.将1到9这九个数填入下图,使得从中间动身的每条线段上的三个数的和相等.
演习：将1到8填入下图,使两个正方形极点上的数的和相等,并且用斜线衔接的4对数的和也都相等.
4.将1到5这五个数填入上图中,使得圆周上四个数的和与每条直线上的三个数的和都相等.
演习：在图中填上7.8.10.12,使得每个圆内的四个数的和相等.
5.将1到16填入4*4（16格）的正方形中,使每行.每列.每条对角线的和都相等.
数阵图演习
1、将6到10这五个数填入下图,使得每条边上的三个数的和相等.
2、将2到11填入下图,使得每条线段上的三个数之和相等.
3、将2到10填入下图,使得每条线上的四个数的和相等.。

三年级奥数之数阵图习题

数阵图
1、把1到6这六个数分别填入下图的六个圈内，使得每个正方形顶点上的数的和都为13。

2、将2到7这六个数，填入上图的圈中，使得每条线上的三个数的和相等。

练习：请将1到7这7个数填入下图中，使得每条线上的三个数的和相等。

3、将1到9这九个数填入下图，使得从中心出发的每条线段上的三个数的和相等。

练习：将1到8填入下图，使两个正方形顶点上的数的和相等，并且用斜线连接的4对数的和也都相等。

4、将1到5这五个数填入上图中，使得圆周上四个数的和与每条直线上的三个数的和都相等。

练习：在图中填上7、8、10、12，使得每个圆内的四个数的和相等。

5、将1到16填入4*4（16格）的正方形中，使每行、每列、每条对角线的和都相等。

数阵图练习
1、将6到10这五个数填入下图，使得每条边上的三个数的和相等。

2、将2到11填入下图，使得每条线段上的三个数之和相等。

3、将2到10填入下图，使得每条线上的四个数的和相等。

三年级奥数学练习试卷思维培训资料数阵图 (3)

三年级奥数之数阵图习题

小学三年级奥数 第39讲：数阵图

三年级数阵图

小学奥数5-1-3-3 数阵图(三).专项练习

小学奥数：数阵图(三).专项练习及答案解析

2020~2021学年三年级奥数思维能力训练：数阵图初步

(完整版)小学三年级奥数--数阵图

三年级思维拓展- 数阵图

三年级下册数学试题-思维训练：数阵图与数字谜(含部分答案)全国通用

三年级奥数学练习试卷思维培训资料数阵图 (2)

三年级奥数学练习试卷思维培训资料数阵图

三年级奥数之数阵图习题

三年级奥数之数阵图习题

三年级奥数数阵图

三年级奥数之数阵图习题

三年级奥数之数阵图习题

小学三年级奥数第39讲：数阵图