北京理工大学2012-2013学年第一学期工科数学分析期末试题(A卷)试题2012-2(A)

合集下载

北京理工大学数学专业应用随机过程期末试题(MTH17096)

北京理工大学2012-2013学年第一学期2010级《应用随机过程》期末试题A 卷一、（15分）设随机过程()X t Yt Z =+，其中Y ,Z 是相互独立的()0,1N 随机变量，求()X t 的数学期望，协方差函数和一维概率密度函数。

二、（15分）设在(]0,t 内到达某商店的顾客数()X t 是具有强度（每分钟）为λ的泊松过程，求：（1）5分钟内来到的顾客数为2人的概率；（2）5分钟内到来的平均顾客数；（3）设T 为首位顾客到达的时间，计算概率()5P T >。

三、（15分）设质点在线段[]1,5的整数点上作随机游动，n X 表示质点在时刻n 所处的位置，其一步转移概率矩阵为：11000221100022100001110033301000P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦。

（1）若初始分布为11,,0,0,022⎛⎫ ⎪⎝⎭，求质点在时刻n=1的概率分布；（2）试讨论该Markov 链的状态分类及其各常返闭集的平稳分布。

四、（10分）设Markov 链的状态空间{}0,1,2,I = ，转移概率,10,111,i i i i p p a ---==，1001,1,2,,1i i i a i a ∞-=<<==∑ 。

（1）试证明该Markov 链是不可约常返链；（2）试给出此链正常返的充要条件，并求出状态0的平均返回时间。

五、（15分）某实验室有两台机器，每台机器发生故障的概率为μ，发生故障后立即修理，且在h 时间内机器从故障到正常的概率为()h o h λ+。

令()X t 表示t 时刻正常工作的机器数，则()X t 是一生灭过程。

（1）写出()X t 的Q 矩阵；（2）写出转移概率所满足的Kolmogorov 向前、向后方程；（3）求平稳分布。

六、（15分）设()()cos X t V at =+Θ，其中()0,2,0,1U EV DV πΘ== ，且,V Θ相互独立。

北京理工大学2010-2011学年第一学期工科数学分析期末试题(A卷)答案

代入方程得解得
6 A 1 ， 2 A 3 B 1
………………..(9 分) ………………..(10 分)
A
1 4 ， B 6 9 x2 4 x )e x 6 9 x2 4 x )e x 6 9
y* (
通解为
y C1e x C 2 e 2 x (
……………..(11 分)
四.
1
………………….(3 分) …………………..(4 分)
dy 1 dx 1 sin y
dy d y dx dx 2 (1 sin y ) 2
2
cos y
……………(6 分)
cos y
1 cos y 1 sin y 2 (1 sin y ) (1 sin y ) 3
0 x
……(6 分)
…………………….(7 分)
令 t u ，得
F ( x) ( x 2t ) f (t )dt
0
x
…………………….(8 分)
( x 2t ) f (t )dt
0
x
( x 2u ) f (u )du F ( x)
v x 0 2 vdv sin xdx
1 2 v cos x C 2
由初值得
C 1
信息与电子学部学生会学习部整理
v 2 2(cos x 1)
…………………….(8 分)
十．
设
f ( x) ln x f ( x) 1 1 x e
x 1 x2 e dx e 0
…………………….(1 分) …………………….(2 分)
令
f ( x) 0 ，得

北京理工大学数学专业复变函数期末试题(MTH17061)

北京理工大学2011-2012学年第一学期2009级复变函数试题A 卷一、（10分）设12,z z ∈，求证：()2221212122Re z z z z z z +=++。

二、（10分）设函数()()()2222f z x axy by i cx dxy y =+++++，试确定常数,,,a b c d 的值使()f z 在复平面上处处解析。

三、（10分）求下列积分，积分路径均为逆时针方向。

1.3z z z dz e =⎰；2.3z z e dz z =⎰；3.1Re z zdz =⎰。

四、（10分）求函数()22sin 41zz z +在1z <内的孤立奇点，说明这些奇点的类型，并求出在这些点处的留数。

五、（10分）1.求()2cos f z z =在0z =处的Taylor 展式；2.求()()()112f z z z =--在环域12z <<和2z <<+∞上的Laurent 展式。

六、（10分）求下列积分。

1.20sin d a πθθ+⎰，其中1a >为常数；2.2cos 1xdx x+∞+⎰。

七、（10分）求方程4510z z -+=在1z <内根的个数。

八、（10分）求一单叶解析函数，使其将带状区域0Im z π<<映射成w 平面的单位圆盘1w <。

九、（10分）设()f z 在00z z r ->上解析，且()lim z zf z A →∞=，求证：对于任何正数0r r >，()f z 在圆C ：0z z r -=上的积分()2Cf z dz iA π=⎰。

十、（10分）设二元实函数(),u x y 在区域D 上有定义，且在D 上有22220u u u x y∂∂∆=+=∂∂，则称(),u x y 是区域D 上的调和函数。

求证：1.解析函数的实部和虚部均为调和函数； 2.设(),u x y 是单连通区域D 上的调和函数，则存在区域D 上的调和函数(),v x y ，使得()(),,u x y iv x y +在区域D 上解析；3. 设(),u x y 是区域D 上的调和函数，且不恒为常数，则(),u x y 不可能在D 的内点达到最大值或最小值。

2012-2013_1_期末试卷A答案(出自17系)

2012 —2013 学年第一学期
部试题答案
习学本答案由 1517 周俊孚同学领仪光学习部编写，不一定是标准答案，
仅供参考，如有问题请立刻询问老师，谢谢
光考试课程复变函数与积分变换 A
仪班级姓名
学号成绩
2017 年 1 月
1
一、选择题(每题 3 分，共 24 分) 1．下列方程所表示的平面点集中，为有界区域的是（D）
6．级数 +
1 3n zn
+
1 32 z2
+
1 3z
+1+
z 2
+
z2 22
++
zn 2n
+ 的收敛域是 1 3
<|
z |<
2
学 7.
函数 F (ω )
=
sin t0ω
的傅立叶逆变换为 δ (t + t0 ) − δ (t 2i
− t0)
8．函数 f (t ) = sin(t − π )u(t − π ) 的 Laplace 变换为
（A）不可导
（B）不解析
（C）不连续
（D）以上答案都不对
解：奇点的定义见课本第 17 页
∫ 3．设 C 为椭圆 x 2 + y 2 = 2 正向，则积分 1 d z = （A）
2
C z−i
部
（A） 2πi
（B） π
（C） 0
dz
∫ 4. 设 c 为正向圆周 z = 2 ，则
=（B）
Cz
习（D）− 2πi
（B） 1 e 2iω F (ω )
2
2
（D） 1 e −2iω F (ω )

北京理工大学《高等数学》历年期末考试试题及答案解析(精编版)

x = (t − 1)et 八. 设曲线 C 的方程为 y = 1 − t4
求
dy dx
,
d2y dx2
及曲线
C
在参数
t
=
0
对应点处
–2/48–
第 1 部分北京理工大学试题集
的曲率半径.
九. 设 f ′(x).
f (x)
=
1 x
−
ex
1 −
1,
x
<
0
1
−
1 c2os x
x
,
, x
x= >0
等于
mg k
.
∫1
十一. 设 f (x) 在 [0, 1] 上连续, 在 (0, 1) 内可导, 且满足 f (1) = 2 2 xe1−x f (x)dx, 证明:
0
至少存在一点 ξ, 使得 f ′(ξ) = (1 − ξ−1) f (ξ).
1.2 2011 级秋季学期期末试卷
一. 填空题
1. 极限 lim
x→0
x
− ln(1 x2
+
x)
=
2. 设 y
=
x2 + ln x, 则
dx dy
=
dy =
∫∞
3. 广义积分
e
dx x ln2
x
=
4.
微分方程
y′′
=
1
1 + x2
的通解为
; lim
1
∫
x
(1
+
sin
2t)
1 t
dt
=
.
x→0 x 0
√ ; 设 f 可导,y = f (tan x) + 1 − x2, 则

工科数学分析上学期AB卷期末考试题及答案2套

,考试作弊将带来严重后果！期末考试《工科数学分析》试卷A1. 考前请将密封线内各项信息填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：闭卷；5分，共10分）（1）)(lim 22x x x x x --++∞→ （2）xx x ln 1)(cot lim +→（10分）设1lim )(2212+++=-∞→n n n x bxax x x f 为连续函数, 试确定常数a 和b .（10分）设参数方程⎩⎨⎧=+=ty t x arctan )1ln(2确定了函数0)(>=x f y , 求x yd d 与22d d xy, 并判定函数)(x f 的单调性及凸性. （10分）造一个容积为V 的圆柱形无盖水池, 问高h 及底半径r为多少时, 可使其表面积最小? （10分）设0>x 时, 方程112=+xkx 有且仅有一个解, 求k 的取值范围.（10分）计算下列积分（每小题5分，共10分）（1）⎰+x x x )1(d 3 （2）⎰-+226d )cos (sin ππx x x x七．（10分）设⎰+∞-=0d e x x I x n n (n 为正整数), 试建立数列}{n I 的递推公式, 并求n I 的值.八．（10分）求抛物线px y 22=在点),2(p p 处法线与抛物线围成的图形的面积.九.（10分）设函数)(x f 在),(+∞-∞上有二阶导数且0)(≥''x f , 如果A xx f x =→)(lim, 试证明对任意),(+∞-∞∈x , 有Ax x f ≥)(. 十．（10分）设01>x , )(211nn n x ax x +=+, 证明数列}{n x 收敛并求其极限.《工科数学分析》试卷A 答案一. （1）解：12lim)(lim 2222=-++=--++∞→+∞→xx x x xx x x x x x（2）解：)1)1sin (cot 1lim exp()ln cot ln lim exp()(cot lim 200ln 10xx x xx x x x x x -==+++→→→ e1)1exp()cos sin lim exp(0=-=-=+→x x x x二. 解: ⎪⎪⎩⎪⎪⎨⎧>-=-+-=++<+=1|| ,/11 ,2/)1(1,2/)1(1|| ,)(2x x x b a x b a x bx ax x f , 由于)(x f 为连续函数, 故)1()1()1(f f f ==+-, )1()1()1(-=-=-+-f f f即1=+b a , 1-=-b a解之得.1 ,0==b a三. 解: t t t t x y 21)1/(2)1/(1d d 22=++=, 32222241)1/(2/121d d tt t t t x y +-=+-=. 因0)(>x f , 故0>t , 从而0d d >xy, 0d d 22<x y . 因此, 方程确定的函数)(x f y =单调增加且上凸.四. 解: 表面积2222r r V r rh S πππ+=+=, 令0222=+-='r rVS π, 得32/πV r =, 此时3/4πV h =. 因S 有唯一驻点, 由实际问题可知必有最小表面积, 故当32/πV r =, 3/4πV h =时, 表面积最小. 五. 解: 令11)(2-+=x kx x f , 则32)(xk x f -='. 0≤k 时, )(x f 在),0(+∞单调下降. 又+∞=+→)(lim 0x f x , -∞=+∞→)(lim x f x (0<k ), 1)(lim -=+∞→x f x (0=k )因此, 当0≤k 时, )(x f 在),0(+∞只有一个零点, 即原方程在),0(+∞内只有一个解. 当0>k 时, )(x f 有唯一驻点30/2k x =, 且)(x f 在),(0+∞x 与),0(0x 内分别单调增加和单调减少. 注意到此时+∞=+→)(lim 0x f x , +∞=+∞→)(lim x f x故当且仅当0)(0=x f 即392=k 时, 函数有且仅有一个零点, 即原方程在),0(+∞内有且仅有一个解. 六. 解: (1) 令6x t =, 于是Cx x C t t dt t dt t t t t dt t x x x +-=+-=+-=+=+=+⎰⎰⎰⎰)arctan (6 )arctan (6)111(616)1(6)1(d 662223253(2)⎰⎰⎰⎰-===+--202022226dcos 2d sin 2d sin d )cos (sin ππππππx x x x x x x x x x x x.2d cos 2cos 2202/0=+-=⎰ππx x x x 七. 因为101010d e 0d e |e d e -+∞--+∞--∞+-+∞-=+=+-==⎰⎰⎰n x n xn x n x n n nI x x n x nx x x x I于是容易知道1!I n I n =. 又因为1|e 0d e |e d e 001=-=+-==∞+-+∞-∞+-+∞-⎰⎰x x x xx x x x I , 故有!.n I n =八. 因p y y 22=', 故1|2=='=y py p x , 从而可知抛物线在点),2(p p 的法线方程为)2(p x p y --=-或y px -=23.除去切点外抛物线与法线的另一个交点坐标为)3,29(p p -, 所以所求图形的面积232316d )223(p y p y y p A pp =--=⎰-九. 0)(lim)(lim )0(0===→→x xx f x f f x x , A xx f x f x f f x x ==-='→→)(lim )0()(lim)0(00. 由泰勒公式, ),(+∞-∞∈∀x , 0≠x , 有Ax x f x f x f f x f ='≥''+'+=)0(!2)()0()0()(2ξ上式当0=x 时显然成立. 证毕.十. 单调增加（减少）有上界（下界）的数列必收敛. 下面我们证明数列}{n x 是单调减少有下界的数列. 由于a x ax x nn n =⋅≥+1 故数列}{n x 有下界. 此外, 因为1)11(21)1(2121=+≤+=+n n n x a x x 故数列}{n x 单调减少. 因此, 数列}{n x 收敛, 设其极限为A , 于是AaA x a x x A n n n n n +=+==∞→+∞→)(21limlim 1 解之得a A =（由极限保号性负根舍去）.,考试作弊将带来严重后果！期末考试《工科数学分析》试卷B1. 考前请将密封线内各项信息填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：闭卷；5分，共10分）（1）)2(lim 2x x x x -++∞→ （2）x x x +→0lim二．（10分）设⎪⎩⎪⎨⎧≤+>=0 ,e 0,1sin )(x x xx x f x βα, 试根据α和β的值, 讨论)(x f 在0=x 处的连续性(包括左连续、右连续及间断点的类型).三．（10分）设方程22ln arctan y x x y +=确定函数)(x f y =, 求22d d x y .四．（10分）试确定数列}{n n 中的最大项.五．（10分）设0>a , 试讨论方程ax x =ln 实根的个数. 六．计算下列积分（每小题5分，共10分）（1）⎰+xx e1d （2）⎰-+22d )e (sin 4ππx x x x七．（10分）设⎰+∞-=0d e x x I x n n (n 为正整数), 试建立数列}{n I 的递推公式, 并求n I 的值.八．（10分）求抛物线x y 22=与直线21=x 所围成的图形绕直线1-=y 旋转而成的立体的体积.九.（10分）设函数)(x f 在]1,0[上二阶可导, a x f ≤|)(|, b x f ≤''|)(|,)1,0(∈c , 试证明22|)(|b a c f +≤'. 十．（10分）已知0>a , a x =1, n n x a x +=+1, 证明数列}{n x 收敛并求其极限.《工科数学分析》试卷B 答案一. （1）解：122lim)2(lim 22=++=-++∞→+∞→xx x x x x x x x（2）解：1)/1/1lim exp()/1ln lim exp()ln lim exp(lim 20000=-===++++→→→→xx x x x x x x x x x x 二. 解: )0(1)0(f f =+=-β. 当0>α时, 0)0(=+f ; 当0≤α时, )0(+f 不存在. 因此, 当0>α且1-=β时, 函数在0=x 处连续; 当0>α且1-≠β时, 函数在0=x 处左连续但又不连续, 0=x 为第一类间断点; 当0≤α时, 函数在0=x 处左连续, 0=x 为第二类间断点.三. 解: 方程两边关于x 求导得22222221)/(11yx y y x x y y x x y +'+=-'+ 整理得 yx yx x y -+=d d 于是, 322222)()(2)()1)(())(1(d d y x y x y x y y x y x y x y -+=-'-+--'+=. 四. 解: 令x x x f /1)(=, 0>x . 令0ln 1)(2/1=-='xxx x f x , 得e /1=x . 则在)/1,0(e 与),/1(+∞e 上)(x f 分别单调增加和单调减少. 从而33)/1(2<<e e因此,33为最大项.五. 解: 令ax x x f -=ln )(, 0>x . 解01)(=-='a xx f 得唯一驻点ax 1=. )(x f 在)/1,0(a 与),/1(+∞a 内分别单调增加和单调减少. 又由于-∞=+→)(lim 0x f x , -∞=+∞→)(lim x f x , 所以有如下结论:(1) 当e a /1>时, 0)/1(<a f , 原方程没有根; (2) 当e a /1=时, 0)/1(=a f , 原方程有一个根; (3) 当e a /1<时, 0)/1(>a f , 原方程有两个根六. (1)令1+=x e t , 则)1ln(2-=t x , 于是Cx e C e e C t t dt t t dt t t t e dxx x x x+--+=+++-+=++-=+--=-=+⎰⎰⎰)11ln(21111ln 11ln )1111(12112(2) ⎰⎰⎰⎰-===+--20202222dcos 2d sin 2d sin d )e (sin 4ππππππx x x x x x x x x x x x.2d cos 2cos 2202/0=+-=⎰ππx x x x 七. 因为1010100d e 0d e |e d e -+∞--+∞--∞+-+∞-=+=+-==⎰⎰⎰n x n xn x n x n n nI x x n x nx x x x I于是容易知道1!I n I n =. 又因为1|e 0d e |e d e 001=-=+-==∞+-+∞-∞+-+∞-⎰⎰x x x xx x x x I , 故有!.n I n = 八. 体积元素x x x dV πππ24)12()12(22=+--+=, 因此所求体积ππ342421==⎰dx x V九. 由泰勒公式21)0)((21)0)(()()0(c f c c f c f f -''+-'+=ξ, ),0(1c ∈ξ 22)1)((21)1)(()()1(c f c c f c f f -''+-'+=ξ, )1,(2c ∈ξ 两式相减得2122)(21)1)((21)()1()0(c f c f c f f f ξξ''--''+'=- 因此22])1[(212 |)(|21)1(|)(|21|)1(||)0(||)(|222122b a c c b a c f c f f f c f +≤+-+≤''+-''++≤'ξξ十. 单调增加（减少）有上界（下界）的数列必收敛. 下面我们证明数列}{n x 是单调增加有上界的数列. 显然, 12x x >, 假设1->n n x x , 则n n n n x x a x a x =+>+=-+11故数列}{n x 单调增加. 此外, 显然, 11+<a x , 假设1+<a x n , 则111+<++<+=+a a a x a x n n故数列}{n x 有上界. 因此, 数列}{n x 收敛, 设其极限为A , 于是A a x a x A n n n n +=+==∞→+∞→lim lim 1解之得2411aA ++-=（由极限保号性负根舍去）.。

北京理工大学2012级线性代数(A)A卷及答案

课程编号：A073122 北京理工大学2012-2013学年第一学期线性代数A 试题 A 卷班级 ________ 学号 _________ 姓名 __________ 成绩 ___________一、（10分）已知3阶方阵123035002A ⎛⎫⎪= ⎪ ⎪⎝⎭，计算行列式*123A I+。

二、（10分）设423110, 2123A AX A X ⎛⎫ ⎪⎪==+ ⎪ ⎪-⎝⎭, 求X 。

三、（10分）已知线性空间4][x F 的自然基为231,,,x x x 。

(1) 证明：2231,12,123,1234x x x x x x ++++++为4][x F 的一个基；(2) 求自然基231,,,x x x 到基2231,12,123,1234x x x x x x ++++++的过渡矩阵，以及23()1h x x x x =--+在后一个基下的坐标。

四、（10分）已知123(1,0,1), (2,2,0), (0,1,1)TTTααα=-==。

(1) 求向量组123,,ααα的一个极大无关组；(2) 求生成子空间123(,,)L ααα的一个标准正交基。

五、（10分）设A 是5阶方阵，且已知存在5阶可逆矩阵P ，使得111112P AP --⎛⎫ ⎪- ⎪= ⎪ ⎪-⎝⎭试写出A 的初等因子，同时判断P 的哪几列是A 的特征向量。

六、（10分）在多项式空间4[]R x 中定义变换σ：233012330201()()a a x a x a x a a a x a a x σ+++=-+++（1）证明：σ是4[]R x 上的线性变换；（2）求σ在4[]R x 的自然基231,,,x x x 下的矩阵，并判断σ是否可逆。

七、（10分）假设A 是m n ⨯的实矩阵，证明：()()TA A A =秩秩八 (10分）已知(1,1,1)T ξ=-是矩阵2125312A a b -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦的一个特征向量，（1）确定参数a , b 及特征向量ξ所对应的特征值；（2）判断A 是否可以相似对角化，说明理由。

高数期末试题

2 1
f ( x)dx 1 , 证明在(0,3)内存在
, 使 f ( ) f ( ) 0.
九 . (8 分) 设 f ( x) 有连续导数 , 且 lim
x 0
f ( x) f ( x) 2, ex 1
f (0) 0, 证明 x 0 是 f ( x) 的
x 0
____________ .
2.
I1
ln 2 x dx 与 I 2 x
dx 中收敛的为 _____________, 其值等于 x ln 3 x
___________. 3.

1
1
3 1 x 2 dx _____________,

1
1
x 1 x 2 dx _____________ .
2x 1 x2
( x 1) 是否恒为常数.
y 1 dy d 2 y 2 2 六. (9 分) 设 arctan ln( x y ) 确定函数 y y ( x) , 求 , 2 . x 2 dx dx
信息与电子二学部学生会学习部整理
七. (10 分) 求下列反常积分. (1)
1
二. (9 分) 求极限 lim(cos x x sin x) .
x2 x 0
三. (9 分) 求不定积分 ( x arctan x
1 x e )dx . x2
1
四. (9 分) 求 f ( x) 3 ( x 2 2 x) 2 在区间 [1,3] 上的最大值和最小值.
五. (8 分) 判断 f ( x) arctan x arcsin
0
x
是 f ( x) 的极值点, 并判断 f (0) 是极大值还是极小值.

工科数学分析2012试题A

.
（D）对于的任意分割， .
2．下列广义积分发散的是（）
（A） ;（B） ;（C） ;（D） .
3．若在区间上，，下列说法正确的是（）
（A）由于函数区间上有原函数，故在区间上可积；
（B）区间上未必连续，但不可能有跳跃间断点；
（C）区间上为连续函数；（D）区间为有界函数.
三、多项选择题：（每题4分）
一、填空题：（每题4分）
1.函数的阶泰勒公式中项的系数是________；
2.由曲线以及直线与轴围成的平面图形绕轴旋转一周产生旋转体的体积为；
3. ，则 =__________________；
4.要使及点分别为曲线的极值与拐点，则 =___________, =____________, =__________ , =_________；
1．定义在上，下列哪些为在上可积的充分条件（）
（A）在上有界；（B）在上连续；
（C）在上单调；（D）在上一致连续.
2．下列哪些为在点可导的充分必要条件（）
（A）存在常数使得；
（B）存在常数使得；
（C）存在；（D）连续且存在.
3．设函数 ,则下述正确的是（）
（A）在上连续；（B）在上可导；
5.若收敛,且极限存在，则，若收敛，则
的取值范围为_____________；
6．用定积分表示 .
二、单项选择题：（每题3分）
1．定义在上，对于的任意分割，分别记，，，，则在上可积的充分必要条件是（）
（A）对于的任意分割，存在；
（B）对于的任意分割，存在；
（C）对于的任意分割，存在；

北理工数值分析考试卷-2013级数值分析考试习题

2013——2014年《数值分析》考试习题一、（15分）设2101202a a ⎡⎤⎢⎥A =⎢⎥⎢⎥⎣⎦ ，123x x x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ ，331b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（1）求出当a 满足何条件时可以对A 进行cholesky 分解（即T LL 分解，L 为非奇异下三角矩阵）（2）若a=1时利用T LL 分解对方程组Ax=b 进行求解（保留两位小数）二、（10分）求证：111a a a a a a ⎡⎤⎢⎥A =⎢⎥⎢⎥⎣⎦，只有当1122a -<< 时用Jacobi 迭代法求解方程组Ax=b 才收敛三、（15分）（1）已知i x1 3 4 6 ()i f x-75814对其进行3次插值，并求出()2f 的值（2）给定函数组i x0 1 2 ()i f x 1 4 15 ()'i f x6对其进行3次Hermite 插值多项式3H 并求出余项()()f x H x - 的表达式四、（15分）利用最小二乘法，求形如2y a bx =+ 的拟合i x 1 2 3 4 5 i y0.12.98.114.924.1五、（15分）（1）选择合适的数值积分方法，对210x e dx ⎰ 进行积分，使其具有2位有效数字（2）根据（1）中选取的数值积分方法，编写Matlab 源程序代码六、（15分）（1）构造迭代格式求解40x x e --= 的根，使其具有4位有效数字（2）从理论上证明你所构造的迭代格式是收敛的七、（15分）对常微分方程初值问题()()'00,y f x y y x y ⎧=⎪⎨=⎪⎩ ，证明其二步公式111(58)12n n n n n hy y f f f ++-=++- 是三阶精度的迭代公式，并求出该二步公式的局部截断误差主项。

(完整word版)北京理工大学数学专业高等代数Ⅱ期末试题(MTH17063)

课程编号：MTH17063 北京理工大学2010—2011学年第一学期2009级数学类高等代数期末考试试题A 卷班级学号姓名成绩一、(25分)设()n n M F ⨯表示域F 上的所有n 阶矩阵构成的F 上的线性空间.取定()n n A M F ⨯∈，对于任意的()n n X M F ⨯∈,定义()X AX XA σ=-. （1)证明：σ为()n n M F ⨯上的一个线性变换.（2）证明:对于任意的,()n n X Y M F ⨯∈都有()()()XY X Y X Y σσσ=+。

（3)当a b A c d ⎡⎤=⎢⎥⎣⎦时，求σ在给定基 1112212201101111,,,11110110F F F F ⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦下的矩阵表示。

（4）当1402A -⎡⎤=⎢⎥⎣⎦时，求()Ker σ的一组基与维数. 二、（15分）设数域K 上3维线性空间V 的线性变换A 在V 的一个基123,,ααα下的矩阵为010440212A ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦.求线性变换A 的Jordan 标准形。

三、（20分）设A 是域F 上n 维线性空间V 上的一个线性变换，证明：（1）如果W 是A 的一维不变子空间，那么W 中任何一个非零向量都是A 的特征向量；反之，如果ξ是A 的一个特征向量,那么ξ生成的子空间ξ<>是A 的一维不变子空间。

（2）A 可以对角化的充分必要条件是V 可以分解成A 的一维不变子空间的直和. 四、(20分）设22()V M F ⨯=，在V 中取一个基11122122,,,E E E E . （1）求它的对偶基11122122,,,f f f f ，要求写出ij f 的表达式. （2)求V 上任意一个线性函数f 的表达式.五、（20分)证明：n 维酉空间V 上的线性变换A 是Hermite 变换A 当且仅当在V 的任意一个标准正交基下的矩阵是Hermite 矩阵。

2012-2013第一学期线性代数A(A卷)

北京信息科技大学2012 ~2013 学年第一学期《线性代数A 》课程期末考试试卷A课程所在学院：理学院适用专业班级：工科48学时考试形式：(闭卷)一、完成下列各题（本题满分48分，共含8道小题，每题6分）1、求排列3154726的逆序数,并判断奇偶性。

2、设101310124D -=-，D 的（i,j ）元的代数余子式A ,ij 求313233A A A ++。

3、计算行列式1234111100,0,1,2,3,4100100i a a D a i a a =≠=其中。

4、设111123111,124111051A B ⎛⎫⎛⎫ ⎪ ⎪=-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,求2T A B A -。

5、120213,121A ⎛⎫ ⎪= ⎪ ⎪⎝⎭求：12+3A E -。

6、设1121212==+r r βαβααβααα=+++，，且向量组12,,,r ααα线性无关，证明：向量组12,,,r βββ组线性无关。

7、若12,t β⎛⎫ ⎪= ⎪ ⎪⎝⎭可由1232211,2,1174ααα-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭线性表出，求t 的值 8、判断二次型12222312133924f x x x x x x x =++-+的正定性。

二、计算题（本题满分40分，共含5道小题，每题8分）1、设110011,2,101A AX X A X -⎛⎫ ⎪=-=+ ⎪ ⎪-⎝⎭求。

2、求非齐次线性方程组的通解。

3、设11021α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭，21201α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭，32514α⎛⎫ ⎪ ⎪= ⎪- ⎪⎝⎭，41131α⎛⎫ ⎪- ⎪= ⎪ ⎪-⎝⎭，（1）求向量组4321,,,αααα的秩；（2）求该向量组的一个最大线性无关组；（3）将其余向量用最大无关组表示。

4、已知向量1111a ⎛⎫ ⎪= ⎪ ⎪⎝⎭，求一组非零向量23,,a a 使得123,,a a a 两两正交。

2012-2013学年度高一第一学期期末考试试卷以及答案

2012-2013学年度期末考试试卷高一数学第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分，每题只有一个正确答案，请把你认为正确的答案填在答题卡上．．．．．．．．，答在试卷上的一律无效．．．．．．．．．．。

）1．若{}9,6,3,1=P {}8,6,4,2,1=Q ，那么=⋂Q P （ C ）A.{1}B.{6}C. {1，6}D. 1，62．下列函数中哪个与函数y x =是同一个函数（ B ）A.2)(x y =B. 33x y = C. xx y 2=D.2x y =3．图（1）是由哪个平面图形旋转得到的（ A ）图（1） A B C D4．下列函数中有两个不同零点的是（ D ）A ．lg y x =B ．2x y =C ．2y x =D ．1y x =-5．函数()12f x x=-的定义域是（ A ） A ．[)()+∞⋃-,22,1 B ．[)+∞-,1 C ．()()+∞⋃∞-,22,D ． 1 22 -⋃+∞(，)(，)6．已知直线m ⊥平面α，直线n ⊂平面β，下面有三个命题：①//m n αβ⇒⊥；②//m n αβ⊥⇒；③//m n αβ⇒⊥；则真命题的个数为（ B ） A ．0 B ．1 C ．2 D ．37．若10x -<<，那么下列各不等式成立的是（ D ）A ．220.2x x x -<<B ．20.22x x x -<<C ．0.222x x x -<<D ．220.2x x x -<<8. 过2 3A -(，) ，2 1B (，) 两点的直线的斜率是（ C ） A ．12B ．12-C ．2-D ．29. 已知函数)31(12)(≤≤+=x x x f ，则（ B ） A ．)1(-x f =)20(22≤≤+x x B ． )1(-x f =)42(12≤≤-x x C ． )1(-x f =)20(22≤≤-x x D ． )1(-x f =)42(12≤≤+-x x10．．已知)(x f 是偶函数，当0<x 时，)1()(+=x x x f ，则当0>x 时，()f x 的值为（ A ） A ．)1(-x x B ．)1(--x x C ．)1(+x x D ．)1(+-x x第Ⅱ卷（非选择题共100分）二、填空题（本大题共4小题，每小题5分，共20分. 请把你认为正确的答案填在答题卡上．．．．．．．．，答在试卷上的一律无效．．．．．．．．．．。

北京理工大学2011-2012学年第一学期工科数学分析期末试题

e4 1 4
二.
1 1 x2 3x 2
2
lim
x 0
x arcsin x e
x3
1
lim
x 0
x arcsin x x3
…………………
1 lim
x 0
……………………
1 ( x 2 ) 1 x 1 lim lim 2 2 2 x0 x0 3x 1 x 3x 2 1 x 2 1 6
0 x 4 x
3 ( x, y )
y
dW xgy 2 dx gx (3 W gx (3
0 4

4 0
9 g (16 x 8 x 2 x 3 )dx 16
3 2 x) dx 4
3 2 x) dx ……………(4 分) 4
……பைடு நூலகம்…………..(6 分)
12g 12000g (J)
令 f ( x) 0 得 x
2 2 f ( x) 在 (0, ) , ( , ) , ( , ) 内单调 3 3 3 3
f ( 0) a 0 f ( ) a 0 f( 2 3 3 ) a 0 3 16
3
x
2 3
3 3 f( ) a 3 16
…………………..(7 分)
10
2 (1
3 e) 5
x 0
………………….(11 分) …………………….(2 分)
十.
令xt u

x 0
g ( x t )dt g (u )du
9
f ( x) 2 x 2 g (u )du
0
x
f ( x) 4 x g ( x)

北京理工数学分析分析试题2012-4(A)

课程编号：MTH17004北京理工大学2012-2013学年第二学期工科数学分析期末试题(A 卷)班级_______________ 学号_________________ 姓名__________________一. 填空题（每小题2分, 共10分）1. 直线241132--=+=-z y x 与平面062=-++z y x 的夹角=ϕ___________________. 2. 设221:x y L = ),10(≤≤x 则=⎰L xdl ________________________.3. 设),(y x f 具有连续偏导数, 曲线0),(=y x f 在其上点),(00y x 处的切线斜率,2=dxdy又,3),(00='y x f y 则='),(00y x f x ________________.4. 函数1)(-=x x f )0(π≤≤x 的以π2为周期的余弦级数的系数=5a ________________.5. 设+S 是曲面1)1(222=-++z y x )1(≥z 的上侧, L 是S 的边界曲线, 从z 轴正向看去L 是逆时针方向, 则⎰⎰⎰+=++S Ldz y xydy ydx x 22_______________________________.二. (8分)设方程组⎩⎨⎧=+=-10xv yu yv xu , 求.,y ux u ∂∂∂∂三. (9分) 将⎰⎰-+=22221x x xdy y x dx I 化成极坐标系中的累次积分, 并计算积分的值.四. (10分) 求函数x xy x z 12323-+=的极值点和极值.五. (9分) 求正数λ的值, 使得曲面λ=xyz 与曲面1222222=++cz b y a x 在某一点相切.六. (9分) 设V 是曲面221y x z --=与22y x z +=所围成的立体, 其上任一点的密度等于此点到原点的距离, 求V 关于z 轴的转动惯量.七. (9分) 求幂级数∑∞=-+-12112)1(n nn n x 的收敛域及和函数.八. (10分) 已知j x f y y x x i x f y y x y A )()8()()6(33322+++=是某二元函数),(y x u 的梯度, 其中)(x f 有连续导数, 且,1)1(=f 求)(x f , 并求).,(y x u九. (9分) 把231)(2++=x x x f 展成1-x 的幂级数, 并指出收敛域.十. (9分) 设S 是曲线)20(022≤≤⎩⎨⎧==z x zy 绕z 轴旋转一周而成的曲面的上侧. (1)求S 的方程; (2) 利用高斯公式计算曲面积分.)1(22⎰⎰-++=Sdxdy z ydzdx x dydz xy I十一. (8分) 设函数)(x f 在]1,1[-有定义, 在0=x 处可导, 且级数∑∞=1)1(n n f 收敛, 证明0)0(='f .。

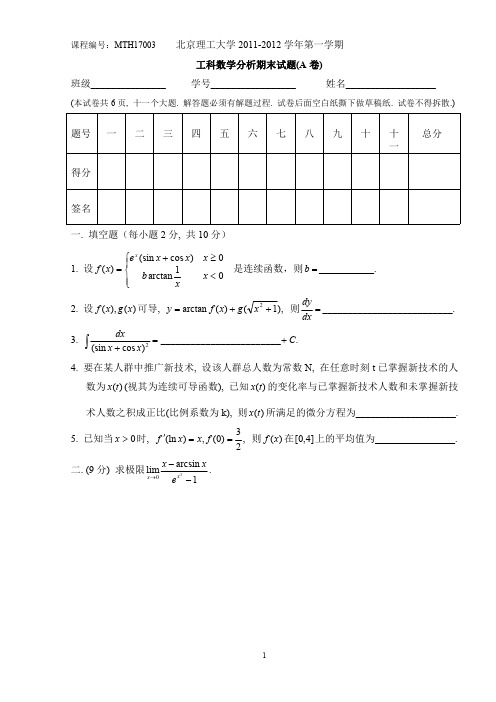
北京理工大学2013-2014学年第一学期《数学分析》期末测试卷(A卷)(附参考答案)

课程编号：MTH17003 北京理工大学2013-2014学年第一学期工科数学分析期末试题(A 卷)班级_______________ 学号_________________ 姓名__________________(本试卷共6页, 十一个大题. 解答题必须有解题过程. 试卷后面空白纸撕下做草稿纸. 试卷不得拆散.)一. 填空题（每小题2分, 共10分）1. 设)(x p 是多项式, 且,2)(lim 23=-∞→x x x p x ,3)(lim 0=→xx p x ，则=)(x p ____________________.2. 曲线θρcos 1-=在4πθ=处的切线斜率等于__________________.3. 已知点)3,1(为曲线23bx ax y +=的拐点, 则_,__________=a .______________=b4. 设⎰⋅+-=102)(arctan 1)(dt t f x x x f , 则=)(x f _________________________________.5. 质量为m 的降落伞从跳伞塔下落, 所受空气阻力与速度成正比(比例系数为0>k ), 则降落伞的位移)(t y 所满足的微分方程为___________________________________. 二. (8分) 求极限 .1)1ln(lim2tan 0--+→xx ex x三. (8分) 设e xy e y=-确定函数)(x y y =, 求22,dxyd dx dy .四. (9分) 设⎰+∞∞→=⎪⎭⎫⎝⎛-+082lim dx e x a x a x x xx ),0(≠a 求常数a 的值.五. (9分) 求微分方程4yx ydx dy +=的通解.六. (9分) 已知x x a x f 3sin 31cos )(-=在3π=x 处取得极值, 求a 的值, 并判断)3(πf 是极大值还是极小值.七. (9分) 求曲线x y =2与直线2-=x y 所围成平面图形的面积A, 以及此平面图形绕y 轴旋转一周所得旋转体的体积V .八. (9分) 求不定积分.11⎰+dx xxx九. (9分) 一圆锥形贮水池, 深3m, 直径4m, 池中盛满了水, 如果将水抽空, 求所作的功. (要求画出带有坐标系的图形)十. (12分) 设0)()()(0=-++⎰-xx dt t f x t e x f , 其中)(x f 是连续函数, 求)(x f 的表达式.十一. (8分) 设)(x f 在]1,0[上非负连续, 试证存在)1,0(∈ξ, 使得区间]1,[ξ上以)(ξf 为高的矩形面积等于区间],0[ξ上以)(x f y =为曲边的曲边梯形的面积.(2013-2014)工科数学分析第一学期期末试题(A 卷)解答（2014.1）一．1. x x x 3223++2.12+3． ,23- 294. x x arctan 2ln 2412+-+-ππ5． dt dyk mg dt y d m -=22二. 原式 x x x x 20tan )1ln(lim-+=→20)1ln(lim xx x x -+=→ ……………..(2分) x x x 2111lim 0--+=→ ……………..(6分) )1(21lim0x x --=→ ……………..(7分)21-= ……………..(8分)三. 0=--dx dy x y dx dy e y……………..(3分) x e ydx dy y-= ……………..(4分) 222)()1()(x e dx dy e y x e dx dy dx y d y y y ----⋅= ……………..(6分) 2)()1()(x e x e y e y x e x e y y yyy y -----⋅-= ……………..(7分) 32)(22x e e y ye xy y yy --+-= ……………..(8分)四. x x a x a x ⎪⎭⎫⎝⎛-+∞→2lim a x axa a x x a x a --∞→-+=33])31[(lim ……………..(2分) a e 3= ……………..(3分)⎰+∞08dx ex x ⎰+∞-=08dx xe x ⎰+∞--=08xxde ……………..(4分) ⎰+∞-∞+-+-=088dx e xe x x ……………..(6分)880=-=+∞-xe ……………..(8分)83=a e 2ln =a ……………..(9分)五.31y x y dy dx += 31y x ydy dx =- ……………..(2分) )(131⎰⎰+⎰=---dy ey C ex dyy dyy……………..(4分))(ln 3ln ⎰-+=dy e y C e y y ……………..(6分) )1(3⎰+=dy yy C y ……………..(8分) 431y Cy += ……………..(9分) 六. x x a x f 3cos sin )(--=' ……………..(3分)由 0123)3(=+-='a f π 得 32=a ……………..(5分)x x a x f 3s i n 3c o s )(+-='' ……………..(7分)因为031)3(<-=''πf 故 )3(πf 是极大值 ……………..(9分)七.抛物线与直线的交点为)2,4(),1,1(- ……………..(1分)⎰--+=212])2[(dy y y A ……………..(3分)29)322(2132=-+=-y y y ……………..(5分)⎰--+=2142])2([dy y y V ππ ……………..(7分)ππ572]51)2(31[2153=-+=-y y ……………..(9分)八. 令 x x t +=1 即 112-=t x ……………..(2分) ⎰--=dt t t I 1222……………..(3分)⎰-+-=dt t )111(22 ……………..(4分) ⎰+--+-=dt t t )1211211(2 ……………..(6分)C t t t +--++-=1ln 1ln 2 ……………..(8分) C xx xx xx +-+-++++-=11ln11ln12 ……………..(9分)九. dx x gx dx x gx dx y g x dW 222)3(94)31(4-=-⋅=⋅=πμπμπμ ……..(3分)⎰-=302)3(94dx x gx w πμ ……………..(5分)⎰+-=3032)69(94dx x x x g πμ30432)41229(94x x x g +-=πμ ……………..(8分)g g ππμ30003==(J) ……………..(9分)十. ⎰⎰-+-=-xxx dt t tf dt t f x e x f 0)()()( ……………..(1分)⎰+='-xx dt t f e x f 0)()( ……………..(2分))()(x f e x f x +-=''- x e x f x f --=-'')()( ……………..(3分) 1)0(-=f 1)0(='f ……………..(5分) 012=-r 1±=r ……………..(6分) x x e C e C x f -+=21)( ……………..(7分)设 xA x e x f -=)(* ……………..(8分)代入微分方程得 1=A x xe x f -=1)(* ……………..(9分)通解为 xx x xe e C e C x f --++=21)(21 ……………..(10分) 由初值得 411-=C 432-=Cx x x xe e e x f --+--=214341)( ……………..(12分)十一. 令 ⎰-=tdx x f t t F 0)()1()( ……………..(2分)则)(t F 在]1,0[连续, 在)1,0(可导, 又 0)1()0(==F F由罗尔定理, )1,0(∈∃ξ, 使 0)(='ξF ……………..(6分)0)()1()(0=-+⎰ξξξf dx x f ……………..(7分)即 ⎰=-ξξξ0)()()1(dx x f f 得证 ……………..(8分)。

2012-2013学年第一学期高数试卷A参考答案

2012-2013学年第一学期《高等数学》期末考试试卷A 参考答案适用专业：生物技术、社会工作、社会保障2012年级各1班本试卷共六大题， 100分一、填空题（每题3分，共15分）1.积分⎰-=⎪⎭⎫ ⎝⎛+-++1122111sin dx x x x x 2 2. 设函数22xy y x z +=，则=∂∂)1,1(x z 3 ，=∂∂)1,1(xz 3 . 3. 设参数方程⎩⎨⎧-=-=)cos 1()sin 1(t t y t t x 确定的函数)(x f y =.则==0t dx dy 0 . 4. 极限=⎪⎭⎫ ⎝⎛+∞→n n n 21lim 2e 5. 函数)1ln(112-+-=x x y 的定义域为 x > 1二、选择题（每题3分，共15分）1. 关于函数6323+-=x x y 的极值点和极值的结论下面正确的是（ C ）A. 0极小值点，极小值为3B. 2是极大值点，极大值为2C. 0极大值点，极大值为6D. 2是极小值点，极小值为62. 设R x x x x f ∈+-=),1)(2()('则在区间()2,0内函数)(x f 是（ D ）A. 先增后减，拐点的横坐标为1B. 先增后减，拐点的横坐标为1.5C. 先减后增，拐点的横坐标为2D. 先减后增，拐点的横坐标为2.53. 由曲线2x y =与x y =所围成的图形的面积为（ C ） A 2 B 1 C 31 D 32 4.函数()x f 在点0x 处有定义，是()x f 在该点处连续的（ A ）。

A. 必要条件B.充分条件C.充要条件D.无关的条件5. 若()()11-=-x x x f ，则()=x f （B ）A.()1+x xB.)2)(1(--x xC.()1-x xD.()12-x x三、计算题（共6小题，每题8分，）1若函数()⎪⎩⎪⎨⎧=≠=⎰020sin 1)(023x x dt mt x x f x 在0=x 连续，求 m 的值.解： 22002303sin lim sin 1lim x mx dt mt x x xx →→=⎰ ………………………………………….….4分 3m =…………………………………………………………………………………….…...6分由连续，则2)0(3==f m …………………………………………………………………7分则6=m ………………………………………………………………………………………8分2.计算定积分：I=x x x d ln 51e 1⎰+. 解：I=x x x d ln 51e 1⎰+ )(ln d )ln 51(e 1x x ⎰+=................................................................2分 )ln 51(d )ln 51(51e 1x x ++=⎰.....................................................4分 []e x 1ln 512151+⨯=......................................................................6分21= ....................................................................8分3. 计算广义积分：I=⎰+∞∞-++26102x x dx 解：原积分=⎰+∞∞-++1)5(2xdx ………………………………………………………………………3分 []+∞∞-+=)5arctan(x ………………………………………………………………………4分)5arctan(lim )5arctan(lim +-+=-∞→+∞→x x x x ……………………………………………6分 πππ=--=)2(2…………………………………………………………………………8分4.计算二重积分：I=⎰⎰D dxdy y x 22 ，其中D 是由曲线2,2==x x y 所围成的闭区域.解：积分区域D ：x y x ≤≤≤≤0,20……………………………………………………………2分⎰⎰D dxdy y x22⎰⎰=x dy y x dx 02220………………………………………………………………4分 ⎰⎥⎦⎤⎢⎣⎡=2003231dx y x x ………………………………………………………………5分 ⎰⎥⎦⎤⎢⎣⎡=202731dx x ………………………………………………………………6分 20299231⎥⎦⎤⎢⎣⎡=x ……………………………………………………………………7分 22732=……………………………………………………………………………8分5.已知)(x f 的一个原函数为x x sin ，计算I=⎰'dx x f x )(解：x x x x x x f cos sin )sin ()(+='=，…………………………………………………2分⎰⎰=')()(x xdf dx x f x ……………………………………………………………..5分⎰-=dx x f x xf )()(………………………………………………………………..7分C x x +=cos 2……………………………………………………………………….8分6.设方程0=+-yx e e xy 所确定的隐函数为)(x f y =，求其在当0=x 时的切线方程.解两边同时对x 求导，注意y 是x 的函数，所以y e 是x 的复合函数，可得 0=+-+dxdy e e dx dy xy y x …………………………………………3分解得 yx e x y e dx dy +-=. ………………………………………5分当0=x 时，0=y ………………………………………6分10==x dxdy………………………………………7分则切线方程为y = x ………………………………………8分五、证明不等式：（本题7分）0>x 时， x e x +>1.证明：令)1()(x e x f x+-=，则0)0(=f …………………………………………2分当0>x 时，01)(>-='xe xf …………………………………………………………………4分则在区间),0[+∞，上)(x f 单调递增，所以0)0()(=>f x f ，…………………………………6分即 x e x+>1 ………………………………………………………………………………7分六、应用题（本题15分）某化肥厂生产某类化肥，假设生产的产品都能销售出去，其总成本函数为 23()1000600.30.001C x x x x =+-+ (元)销售该产品的需求函数为 x =p 320800-(吨), p 为价格，x 为销售量，问销售量为多少时, 可获最大利润, 此时的价格为多少?解：设利润函数为)(x C xp y -=，203120x p -=………………………………………3分则)0(100060203001.0)001.03.0601000()203120()(2332>-++-=+-+--=-=x x x x x x x x x x C xp y …………………………8分令0='y ，即060103003.02=++-='x x y ………………………………………………12分解得200=x 为唯一驻点，由题意即为最大值点………………………………………………14分此时，价格90=p ………………………………………………15分。

2012-2013学年北京市某校高一(上)期末数学试卷(A)(附答案解析)

2012-2013学年北京市某校高一（上）期末数学试卷（A ）一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1. 在0到2π范围内，与角−π3终边相同的角是（） A.π3 B.2π3C.4π3D.5π32. α是一个任意角，则α的终边与α+3π的终边（） A.关于坐标原点对称 B.关于x 轴对称C.关于y 轴对称D.关于直线y =x 对称3. 已知向量a →=(−1, 2)，b →=(1, 0)，那么向量3b →−a →的坐标是（） A.(−4, 2) B.(−4, −2) C.(4, 2) D.(4, −2)4. 若向量a →=(1, 3)与向量b →=(−1, λ)共线，则λ的值为（） A.−3 B.3C.−13D.135. 函数f(x)的图象是中心对称图形，如果它的一个对称中心是(π2，0)，那么f(x)的解析式可以是（） A.sin x B.cos x C.sin x +1 D.cos x +16. 已知向量a →=(1,√3)，b →=(−2,2√3)，则a →、b →的夹角是（） A.π6 B.π4C.π3D.π27. 为了得到函数y =cos (2x −π3)的图象，只需将函数y =cos 2x 的图象（） A.向左平移π6个单位长度 B.向右平移π6个单位长度 C.向左平移π3个单位长度D.向右平移π3个单位长度8. 函数y =1−2cos 2x 的最小正周期是（） A.π4 B.π2C.πD.2π9. 设角θ的终边经过点(3, −4)，则cos (θ+π4)的值等于（） A.√210B.−√210C.7√210D.−7√21010. 在矩形ABCD 中，AB =√3，BC =1，E 是CD 上一点，且AE →⋅AB →=1，则AE →⋅AC →的值为（）A.3B.2C.√32D.√33二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上. sin 4π3=________．若cos α=−12，α∈(0,π)，则α=________．已知向量a →=(−1, 3)，b →=(−3, x)，且a →⊥b →，则x =________．已知sin α−cos α=√2，则sin 2α=________．函数y =2cos x 在区间[−π3，2π3]上的最大值为________，最小值为________．已知函数f(x)=x sin x ，对于[−π2，π2]上的任意x 1，x 2，有如下条件：①x 12>x 22；②x 1>x 2；③x 1>x 2，且x 1+x 22>0．其中能使f(x 1)>f(x 2)恒成立的条件序号是________．（写出所有满足条件的序号）三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤.已知π2<α<π，cos α=−45．（1）求tan α的值；（2）求sin 2α+cos 2α的值．已知函数f(x)=2√3sin 2x2+sin x −√3+1．（1）求f(π3)的值；（2）求f(x)的单调递增区间；（3）作出f(x)在一个周期内的图象．如图，点P 是以AB 为直径的圆O 上动点，P ′是点P 关于AB 的对称点，AB =2a(a >0)．（1）当点P 是弧AB̂上靠近B 的三等分点时，求AP →⋅AB →的值；（2）求AP →⋅OP′→的最大值和最小值．一、填空题：本大题共5小题，每小题4分，共20分.把答案填在题中横线上.已知集合P ={x|−1<x <1}，M ={a}．若M ⊆P ，则a 的取值范围是________．lg 2+lg 5−lg √10=________．满足不等式2x >12的x 的取值范围是________．设f(x)是定义在R 上的奇函数，若f(x)在(0, +∞)上是减函数，且2是函数f(x)的一个零点，则满足xf(x)>0的x 的取值范围是________．已知集合U ={1, 2, ..., n}，n ∈N ∗．设集合A 同时满足下列三个条件： ①A ⊆U ；②若x ∈A ，则2x ∉A ；③若x ∈∁U A ，则2x ∉∁U A ．(1)当n =4时，一个满足条件的集合A 是________；（写出一个即可）(2)当n =7时，满足条件的集合A 的个数为________．二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤.已知函数f(x)=1−1x 2．（1）证明函数f(x)为偶函数；（2）用函数的单调性定义证明f(x)在(0, +∞)上为增函数．设函数f(x)={(2−x)(x +4)x ≤2(2−x)(x −a)x >2．（1）求函数f(x)在区间[−2, 2]上的最大值和最小值；（2）设函数f(x)在区间[−4, 6]上的最大值为g(a)，试求g(a)的表达式．已知函数g(x)=log a x ，其中a >1．（1）当x ∈[0, 1]时，g(a x +2)>1恒成立，求a 的取值范围；（2）设m(x)是定义在[s, t]上的函数，在(s, t)内任取n −1个数x 1，x 2，…，x n−2，x n−1，设x 1<x 2<...<x n−2<x n−1，令s =x 0，t =x n ，如果存在一个常数M >0，使得∑|n i=1m(x i )−m(x i−1)|≤M 恒成立，则称函数m(x)在区间[s, t]上的具有性质P ．试判断函数f(x)=|g(x)|在区间[1a ，a 2]上是否具有性质P ？若具有性质P ，请求出M 的最小值；若不具有性质P ，请说明理由．（注：∑|n i=1m(x i )−m(x i−1)|=|m(x 1)−m(x 0)|+|m(x 2)−m(x 1)|+⋯+|m(x n )−m(x n−1)|）参考答案与试题解析2012-2013学年北京市某校高一（上）期末数学试卷（A ）一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的. 1.【答案】 D【考点】终边相同的角【解析】利用终边相同的角的集合定理即可得出．【解答】解：∵ −π3=−2π+5π3，∴ 在0到2π范围内，与角−π3终边相同的角是5π3．故选：D ． 2.【答案】 A【考点】终边相同的角【解析】直接利用角的终边所在位置关系，判断α的终边与α+3π的终边的对称关系即可．【解答】解：因为α是一个任意角，则α的终边与α+3π的终边相差3π，所以α的终边与α+3π的终边关于坐标原点对称．故选A ． 3.【答案】 D【考点】平面向量的坐标运算【解析】由已知中向量a →=(−1, 2)，b →=(1, 0)，根据数乘向量坐标运算公式及向量减法坐标运算公式，可求出向量3b →−a →的坐标．【解答】解：∵ a →=(−1, 2)，b →=(1, 0)，∴ 向量3b →−a →=3(1, 0)−(−1, 2)=(4, −2). 故选D ． 4.【答案】 A【考点】平行向量的性质平面向量的坐标运算【解析】由向量共线可得1×λ−3×(−1)=0，解之即可．【解答】解：∵ 向量a →=(1, 3)与向量b →=(−1, λ)共线， ∴ 1×λ−3×(−1)=0，解得λ=−3 故选A 5.【答案】 B【考点】函数解析式的求解及常用方法【解析】根据正余弦函数图象利用排除法解答．【解答】解：A 选项：中心对称点是(kπ, 0)，k ∈Z ，故排除．B 选项：中心对称点是(π2+kπ, 0)，k ∈Z ，k =0时，即为(π2，0)，B 为正确答案．C 选项：可以将图象看做正弦函数图象向上平移1个单位，所以中心对称点是(kπ, 1)，k ∈Z ，故排除．D 选项：可以将图象看做余弦函数图象向上平移1个单位，所以中心对称点是(π2+kπ, 1)，k ∈Z ，故排除．故选B ． 6.【答案】 C【考点】数量积表示两个向量的夹角【解析】根据向量a →、b →的坐标，分别算出向量a →、b →的模和a →⋅b →，再用向量的夹角公式算出夹角余弦之值，结合向量夹角的取值范围和特殊角的余弦，即可得到本题答案．【解答】解：∵ 向量a →=(1,√3)，b →=(−2,2√3)， ∴ a →⋅b →=1×(−2)+√3×2√3=4 由此可得向量a →、b →的夹角θ满足：cos θ=|a →|⋅|b →|˙=4√12+(√3)2⋅√(−2)2+(2√3)2=12∵ θ∈[0, π]，∴ θ=π3 故选：C7. 【答案】 B【考点】函数y=Asin （ωx+φ）的图象变换【解析】由条件利用函数y =A sin (ωx +φ)的图象变换规率可得结论．【解答】解：函数y =cos (2x −π3)=cos 2(x −π6)，故把函数y =cos 2x 的图象向右平移π6个单位长度，可得函数y =cos (2x −π3)的图象，故选B ． 8.【答案】 C【考点】求二倍角的余弦三角函数的周期性及其求法【解析】利用倍角的余弦公式化简三角函数解析式，可求得函数的最小正周期．【解答】解：函数y =1−2cos 2x =−cos 2x ， ∴ 函数的最小正周期为π，故答案是π． 9. 【答案】 C【考点】两角和与差的余弦公式三角函数【解析】依题意，利用三角函数的概念可求得sin θ与cos θ，从而可求得cos (θ+π4)．【解答】解：∵ 角θ的终边经过点(3, −4)，∴ sin θ=22=−45，cos θ=35， ∴ cos (θ+π4) =cos θcos π4−sin θsin π4=35×√22−(−45)×√22=7√210．故选C ． 10.【答案】 B【考点】平面向量数量积的运算【解析】设DE →=λAB →，可得AE →=AD →+λAB →，代入AE →⋅AB →=1算出λ=13，从而得到AE →关于AD →、AB →表示式，再由AC →=AD →+AB →，代入AE →⋅AC →结合题中数据即可算出AE →⋅AC →的值．【解答】解：设DE →=λDC →，即DE →=λAB →∵ AE →=AD →+DE →=AD →+λAB →∴ AE →⋅AB →=1即(AD →+λAB →)AB →=1 ∵ AD 、AB 互相垂直，可得AD →⋅AB →=0∴ (AD →+λAB →)AB →=λAB →2=3λ=1，解之得λ=13由此可得DE →=13AB →，AE →=AD →+13AB →∵ AC →=AD →+AB →∴ AE →⋅AC →=(AD →+13AB →)(AD →+AB →)=AD →2+43AD →⋅AB →+13AB →2=12+13×(√3)2=2故选：B二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上. 【答案】−√32【考点】运用诱导公式化简求值【解析】原式中的角度变形后，利用诱导公式及特殊角的三角函数值化简，即可得到结果．【解答】解：sin4π3=sin (π+π3)=−sin π3=−√32．故答案为：−√32【答案】2π3【考点】余弦函数的图象【解析】根据余弦函数的性质可求．【解答】解：∵ y =cos x 在(0, π)上单调递减，且cos 2π3=−12，∴ α=2π3，故答案为：2π3；【答案】 −1【考点】平面向量数量积的运算【解析】根据两个向量垂直的坐标表示建立关于x 的方程，解之即可得到实数x 的值．【解答】解：∵ a →=(−1, 3)，b →=(−3, x)，且a →⊥b →，∴ −1×(−3)+3x =0，解之得x =−1．故答案为：−1 【答案】 −1【考点】求二倍角的正弦【解析】将已知等式两边平方，利用完全平方公式及同角三角函数间的基本关系化简，再利用二倍角的正弦函数公式化简即可求出sin 2α的值．【解答】解：将sin α−cos α=√2两边平方得：(sin α−cos α)2=sin 2α−2sin αcos α+cos 2α=1−sin 2α=2， ∴ sin 2α=−1．故答案为：−1 【答案】 2,−1【考点】三角函数的最值余弦函数的单调性【解析】利用余弦函数的性质，即可求得函数的最值．【解答】解：∵ x ∈[−π3，2π3]∴ cos x ∈[−12, 1]∴ x =0时，函数y =2cos x 取得最大值2；x =2π3时，函数y =2cos x 取得最小值−1故答案为：2，−1；【答案】 ①③ 【考点】函数单调性的性质【解析】先判断函数的奇偶性，易知是偶函数，同时再判断单调性，根据函数性质作出草图，即可得到结论．【解答】解：由已知得f(x)是偶函数，且在区间[−π2, 0]上递减，在[0, π2]上递增，作出函数的草图，如图所示：由图象可知，f(x 1)>f(x 2)⇔|x 1|>|x 2|，即x 12>x 22．故①符合，②不符合；由x 1>x 2，且x 1+x 22>0，知x 1>0，若x 2>0，则显然f(x 1)>f(x 2)成立；若x 2<0，由x 1+x 2>0，得x 1>−x 2，即|x 1|>|x 2|，有f(x 1)>f(x 2)成立，故③符合；故答案为：①③．三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤.【答案】解：（1）因为cos α=−45，π2<α<π，所以sin α=35，… 所以tan α=sin αcos α=−34．…（2）因为sin 2α=2sin αcos α=−2425，… cos 2α=2cos 2α−1=725，…所以sin2α+cos2α=−2425+725=−1725．…【考点】求二倍角的正弦同角三角函数间的基本关系求二倍角的余弦【解析】（1）由已知可先求sinα，然后利用tanα=sinαcosα即可求解（2）由二倍角公式可先求sin2α，cos2α，进而可求【解答】解：（1）因为cosα=−45，π2<α<π，所以sinα=35，…所以tanα=sinαcosα=−34．…（2）因为sin2α=2sinαcosα=−2425，…cos2α=2cos2α−1=725，…所以sin2α+cos2α=−2425+725=−1725．…【答案】解：（1）由已知f(π3)=2√3sin2π6+sinπ3−√3+1…=√32+√32−√3+1=1．…（2）∵f(x)=√3(1−cos x)+sin x−√3+1…=sin x−√3cos x+1=2sin(x−π3)+1．…∵函数y=sin x的单调递增区间为[2kπ−π2，2kπ+π2](k∈Z)，…由2kπ−π2≤x−π3≤2kπ+π2，得2kπ−π6≤x≤2kπ+5π6．所以f(x)的单调递增区间为[2kπ−π6，2kπ+5π6](k∈Z)．…（3）列表：作出f(x)在一个周期[π3，7π3]上的图象如图所示．…【考点】五点法作函数y=Asin（ωx+φ）的图象函数的求值正弦函数的单调性【解析】（1）把x=π3直接代入函数的解析式，求得函数的值．（2）利用两角和差的正弦公式化简函数的解析式，再利用正弦函数的单调性求出它的增区间．（3）用五点法作函数y=A sin(ωx+⌀)在一个周期上的简图．【解答】解：（1）由已知f(π3)=2√3sin2π6+sinπ3−√3+1…=√32+√32−√3+1=1．…（2）∵f(x)=√3(1−cos x)+sin x−√3+1…=sin x−√3cos x+1=2sin(x−π3)+1．…∵函数y=sin x的单调递增区间为[2kπ−π2，2kπ+π2](k∈Z)，…由2kπ−π2≤x−π3≤2kπ+π2，得2kπ−π6≤x≤2kπ+5π6．所以f(x)的单调递增区间为[2kπ−π6，2kπ+5π6](k∈Z)．…（3）列表：作出f(x)在一个周期[π3，7π3]上的图象如图所示．…【答案】解：（1）以直径AB 所在直线为x 轴，以O 为坐标原点建立平面直角坐标系． ∵ P 是弧AB 靠近点B 的三等分点，连接OP ，则∠BOP=π3，点P 坐标为(12a ，√32a)．又点A 坐标是(−a, 0)，点B 坐标是(a, 0)， ∴ AP →=(32a,√32a)，AB →=(2a,0)，∴ AP →⋅AB →=3a 2．（2）设∠POB =θ，θ∈[0, 2π)，则P(a cos θ, a sin θ)， P ′(a cos θ, −a sin θ)，∴ AP →=(a cos θ+a,a sin θ)，OP′→=(a cos θ,−a sin θ)．∴ AP →⋅OP′→=a 2cos 2θ+a 2cos θ−a 2sin 2θ=a 2(2cos 2θ+cos θ−1) =2a 2(cos 2θ+12cos θ+116)−98a 2=2a 2(cos θ+14)2−98a 2．当cos θ=−14时，AP →⋅OP′→有最小值−98a 2，当cos θ=1时，AP →⋅OP′→有最大值2a 2．【考点】平面向量数量积的运算圆的参数方程【解析】（1）由已知先求出点P 的坐标，再利用数量积即可求出；（2）设∠POB =θ，θ∈[0, 2π)，写出点p 与P′的坐标，求出AP →⋅AP ′→的表达式，再利用二次函数和余弦函数的单调性即可求出其最值．【解答】解：（1）以直径AB 所在直线为x 轴，以O 为坐标原点建立平面直角坐标系． ∵ P 是弧AB 靠近点B 的三等分点，连接OP ，则∠BOP =π3，点P 坐标为(12a ，√32a)．又点A 坐标是(−a, 0)，点B 坐标是(a, 0)， ∴ AP →=(32a,√32a)，AB →=(2a,0)，∴ AP →⋅AB →=3a 2．（2）设∠POB =θ，θ∈[0, 2π)，则P(a cos θ, a sin θ)， P ′(a cos θ, −a sin θ)，∴ AP →=(a cos θ+a,a sin θ)，OP′→=(a cos θ,−a sin θ)．∴ AP →⋅OP′→=a 2cos 2θ+a 2cos θ−a 2sin 2θ=a 2(2cos 2θ+cos θ−1) =2a 2(cos 2θ+12cos θ+116)−98a 2=2a 2(cos θ+14)2−98a 2．当cos θ=−14时，AP →⋅OP′→有最小值−98a 2，当cos θ=1时，AP →⋅OP′→有最大值2a 2．一、填空题：本大题共5小题，每小题4分，共20分.把答案填在题中横线上. 【答案】{a|−1<a <1} 【考点】集合的包含关系判断及应用【解析】M是P的子集，元素a∈P，∴−1<a<1【解答】解：∵M⊆P，∴−1<a<1，故答案为{a|−1<a<1}；【答案】12【考点】对数的运算性质【解析】利用对数的运算法则即可得出．【解答】解：原式=√10=lg√10=12lg10=12．故答案为：12．【答案】{x|x>−1}【考点】指数函数的单调性与特殊点【解析】利用指数函数y=2x在R是单调递增即可求出．【解答】解：不等式2x>12可化为2x>2−1，根据指数函数y=2x在R是单调递增，∴x>−1．因此x的取值范围是{x|x>−1}．故答案为{x|x>−1}．【答案】(−2, 0)∪(0, 2)【考点】函数的零点奇偶性与单调性的综合【解析】利用已知函数当x>0时的单调性和奇函数的对称性画出图象即可解出．【解答】解：由f(x)在(0, +∞)上是减函数，且2是函数f(x)的一个零点，可以画出图象，已知f(x)是定义在R上的奇函数，因此其图象关于原点对称，且f(0)=0，据此画出图象．①当x>0时，∵xf(x)>0，∴f(x)>0，因此0<x<2；②当x<0时，∵xf(x)>0，∴f(x)<0，因此−2<x<0．综上可知：满足xf(x)>0的x的取值范围是(−2, 0)∪(0, 2)．故答案为(−2, 0)∪(0, 2)．【答案】{2}，或{1, 4}，或{2, 3}，或{1, 3, 4}；16.【考点】补集及其运算【解析】（1）n=4时，集合U={1, 2, 3, 4}，1，4必须同属于A，此时2属于A的补集；或1，4必须同属于A的补集，此时2属于A；而对元素3与集合A的关系没有限制，此时满足条件的集合有22=4个，列举可得答案．（2）n=7时，集合U={1, 2, 3, 4, 5, 6, 7}，1，4必须同属于A，此时2属于A的补集；或1，4必须同属于A 的补集，此时2属于A；3属于A时，6属于A的补集；3属于A的补集时，6属于A；而元素5，7没有限制．此时满足条件的集合有24=16个．【解答】解：（1）n=4时，集合U={1, 2, 3, 4}，由①A⊆U；②若x∈A，则2x∉A；③若x∈C U A，则2x∉C U A．当1∈A，则2∉A，即2∈C U A，则4∉C U A，即4∈A，但元素3与集合A的关系不确定,故A={1, 4}，或A={1, 3, 4},当2∈A，则4∉A，1∉A，但元素3与集合A的关系不确定,故A={2}，或A={2, 3}.（2）n=7时，集合U={1, 2, 3, 4, 5, 6, 7}，由①A⊆U；②若x∈A，则2x∉A；③若x∈C U A，则2x∉C U A．1，4必须同属于A，此时2属于A的补集；或1，4必须同属于A的补集，此时2属于A；3属于A时，6属于A的补集；3属于A的补集时，6属于A；而元素5，7没有限制,故满足条件的集合A共有：24=16个.二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤.【答案】证明：（1）由已知，函数f(x)的定义域为D={x∈R|x≠0}．设x∈D，则−x∈D，f(−x)=1−1(−x)2=1−1x2=f(x)．所以函数f(x)为偶函数．（2）设x1，x2是(0, +∞)上的两个任意实数，且x1<x2，则△x=x2−x1>0，△y=f(x2)−f(x1)=1−1x22−(1−1x12)=1x12−1x22=x22−x12x12x22=(x2−x1)(x2+x1)x12x22．因为0<x1<x2，所以x2+x1>0，x2−x1>0，所以△y>0，所以f(x)在(0, +∞)上是增函数．【考点】函数单调性的判断与证明函数奇偶性的判断【解析】（1）利用偶函数的定义即可证明；（2）设0<x1<x2，根据增函数的定义只需通过作差证明f(x2)>f(x1)；【解答】证明：（1）由已知，函数f(x)的定义域为D={x∈R|x≠0}．设x∈D，则−x∈D，f(−x)=1−1(−x)2=1−1x2=f(x)．所以函数f(x)为偶函数．（2）设x1，x2是(0, +∞)上的两个任意实数，且x1<x2，则△x=x2−x1>0，△y=f(x2)−f(x1)=1−1x22−(1−1x12)=1x12−1x22=x22−x12x12x22=(x2−x1)(x2+x1)x12x22．因为0<x1<x2，所以x2+x1>0，x2−x1>0，所以△y>0，所以f(x)在(0, +∞)上是增函数．【答案】解：（1）在区间[−2, 2]上，f(x)=(2−x)(x+4)=−x2−2x+8．其对称轴为x=−1，且开口向下，如图，所以f(x)在区间[−2, −1]上单调递增，在区间[−1, 2]上单调递减，所以f(x)在区间[−2, 2]上的最大值为f(−1)=−(−1)2−2×(−1)+8=9，最小值为f(2)=−22−2×2+8=0．（2）当x>2时，f(x)=(2−x)(x−a)=−x2+(a+2)x−2a函数的对称轴为x=a+22，且横过定点(2, 0)．当a≤2时，f(x)在[−4, −1]上单调递增，在[−1, 6]上单调递减，所以f(x)的最大值为f(−1)=9．当2<a≤8时，f(x)在[−4, −1]上单调递增，在[−1, 2]上单调递减，在[2,a+22]单调递增，在[a+22，6]上单调递减，此时f(−1)=9，f(a+22)=(a−22)2≤9，所以f(x)的最大值为9．当8<a≤10时，f(x)在[−4, −1]上单调递增，在[−1, 2]上单调递减，在[2,a+22]单调递增，在[a+22，6]上单调递减．此时f(a+22)=(a−22)2>f(−1)，所以f(x)的最大值为(a−2)24．当a>10时，f(x)在[−4, −1]上单调递增，在[−1, 2]上单调递减，在[2, 6]单调递增，此时f(6)=4(a−6)>f(−1)，所以f(x)的最大值为4(a−6)．综上，g(a)={9a≤8(a−2)248<a≤104(a−6)a>10.【考点】二次函数在闭区间上的最值函数解析式的求解及常用方法【解析】（1）函数在区间[−2, 2]上的解析式一定，找出函数的对称轴，由对称轴把区间[−2, 2]分段，判出函数在两个区间上的单调性，则最大值和最小值可求；（2）函数f(x)=(2−x)(x−a)=−x2+(a+2)x−2a横过定点(2, 0)，根据a的不同取值范围对函数的对称轴所在的位置讨论，结合函数f(x)=(2−x)(x+4)=−x2−2x+8得到函数f(x)在区间[−4, 6]上的单调性．最后通过比较极值与端点处的函数值得到函数在[−4, 6]上的最大值．【解答】解：（1）在区间[−2, 2]上，f(x)=(2−x)(x+4)=−x2−2x+8．其对称轴为x=−1，且开口向下，如图，第21页共22页 ◎ 第22页共22页所以f(x)在区间[−2, −1]上单调递增，在区间[−1, 2]上单调递减，所以f(x)在区间[−2, 2]上的最大值为f(−1)=−(−1)2−2×(−1)+8=9，最小值为f(2)=−22−2×2+8=0．（2）当x >2时，f(x)=(2−x)(x −a)=−x 2+(a +2)x −2a 函数的对称轴为x =a+22，且横过定点(2, 0)．当a ≤2时，f(x)在[−4, −1]上单调递增，在[−1, 6]上单调递减，所以f(x)的最大值为f(−1)=9．当2<a ≤8时，f(x)在[−4, −1]上单调递增，在[−1, 2]上单调递减，在[2,a+22]单调递增，在[a+22，6]上单调递减，此时f(−1)=9，f(a+22)=(a−22)2≤9，所以f(x)的最大值为9．当8<a ≤10时，f(x)在[−4, −1]上单调递增，在[−1, 2]上单调递减，在[2,a+22]单调递增，在[a+22，6]上单调递减．此时f(a+22)=(a−22)2>f(−1)，所以f(x)的最大值为(a−2)24．当a >10时，f(x)在[−4, −1]上单调递增，在[−1, 2]上单调递减，在[2, 6]单调递增，此时f(6)=4(a −6)>f(−1)，所以f(x)的最大值为4(a −6)．综上，g(a)={9a ≤8(a−2)248<a ≤104(a −6)a >10.【答案】解：（1）当x ∈[0, 1]时，g(a x +2)>1恒成立，即x ∈[0, 1]时，log a (a x +2)>1恒成立，因为a >1，所以a x +2>a 恒成立，即a −2<a x 在区间[0, 1]上恒成立，所以a −2<1，即a <3，所以1<a <3．即a 的取值范围是(1, 3)．（2）由已知f(x)=|log a x|，可知f(x)在[1, a 2]上单调递增，在[1a ，1]上单调递减，对于(1a ，a 2)内的任意一个取数方法1a =x 0<x 1<x 2<⋯<x n−1<x n =a 2，当存在某一个整数k ∈{1, 2, 3, ..., n −1}，使得x k =1时， ∑|n i=1f(x i )−f(x i−1)|=[f(x 0)−f(x 1)]+[f(x 1)−f(x 2)]+⋯+[f(x k−1)−f(x k )]+[f(x k+1)−f(x k )]+[f(x k+2)−f(x k+1)]+...+[f(x n )−f(x n−1)]=f(1a )−f(1)+f(a 2)−f(1)=1+2=3．当对于任意的k ∈{0, 1, 2, 3, ..., n −1}，x k ≠1时，则存在一个实数k 使得x k <1<x k+1，此时∑|n i=1f(x i )−f(x i−1)|=[f(x 0)−f(x 1)]+[f(x 1)−f(x 2)]+⋯+[f(x k−1)−f(x k )]+|f(x k+1)−f(x k )|+[f(x k+2)−f(x k+1)]+...+[f(x n )−f(x n−1)]=f(x 0)−f(x k )+|f(x k )−f(x k+1)|+f(x n )−f(x k+1)，(∗) 当f(x k )>f(x k+1)时，(∗)式=f(x n )+f(x 0)−2f(x k+1)<3，当f(x k )<f(x k+1)时，(∗)式=f(x n )+f(x 0)−2f(x k )<3，当f(x k )=f(x k+1)时，(∗)式=f(x n )+f(x 0)−f(x k )−f(x k+1)<3．综上，对于(1a ，a 2)内的任意一个取数方法1a =x 0<x 1<x 2<⋯<x n−1<x n =a 2，均有∑|n i=1f(x i )−f(x i−1)|≤3．所以存在常数M ≥3，使∑|n i=1f(x i )−f(x i−1)|≤M 恒成立，所以函数f(x)在区间[1a ，a 2]上具有性质P ．此时M 的最小值为3．【考点】函数恒成立问题函数与方程的综合运用【解析】（1）当x ∈[0, 1]时，g(a x +2)>1恒成立，可转化为a x +2>a 恒成立，进而转化为函数最值问题解决；（2）先研究函数f(x)在区间[1a ，a 2]上的单调性，然后对(1a ，a 2)内的任意一个取数方法1a =x 0<x 1<x 2<⋯<x n−1<x n =a 2，根据性质P 的定义分两种情况讨论即可：①存在某一个整数k ∈{1, 2, 3, ..., n −1}，使得x k =1时，②当对于任意的k ∈{0, 1, 2, 3, ..., n −1}，x k ≠1时；【解答】解：（1）当x ∈[0, 1]时，g(a x +2)>1恒成立，即x ∈[0, 1]时，log a (a x +2)>1恒成立，因为a >1，所以a x +2>a 恒成立，即a −2<a x 在区间[0, 1]上恒成立，所以a −2<1，即a <3，所以1<a <3．即a 的取值范围是(1, 3)．（2）由已知f(x)=|log a x|，可知f(x)在[1, a 2]上单调递增，在[1a，1]上单调递减，对于(1a ，a 2)内的任意一个取数方法1a =x 0<x 1<x 2<⋯<x n−1<x n =a 2，当存在某一个整数k ∈{1, 2, 3, ..., n −1}，使得x k =1时， ∑|n i=1f(x i )−f(x i−1)|=[f(x 0)−f(x 1)]+[f(x 1)−f(x 2)]+⋯+[f(x k−1)−f(x k )]+[f(x k+1)−f(x k )]+[f(x k+2)−f(x k+1)]+...+[f(x n )−f(x n−1)]=f(1a )−f(1)+f(a 2)−f(1)=1+2=3．当对于任意的k ∈{0, 1, 2, 3, ..., n −1}，x k ≠1时，则存在一个实数k 使得x k <1<x k+1，此时∑|n i=1f(x i )−f(x i−1)|=[f(x 0)−f(x 1)]+[f(x 1)−f(x 2)]+⋯+[f(x k−1)−f(x k )]+|f(x k+1)−f(x k )|+[f(x k+2)−f(x k+1)]+...+[f(x n )−f(x n−1)]=f(x 0)−f(x k )+|f(x k )−f(x k+1)|+f(x n )−f(x k+1)，(∗) 当f(x k )>f(x k+1)时，(∗)式=f(x n )+f(x 0)−2f(x k+1)<3，当f(x k )<f(x k+1)时，(∗)式=f(x n )+f(x 0)−2f(x k )<3，当f(x k )=f(x k+1)时，(∗)式=f(x n )+f(x 0)−f(x k )−f(x k+1)<3．综上，对于(1a，a 2)内的任意一个取数方法1a=x 0<x 1<x 2<⋯<x n−1<x n =a 2，均有∑|n i=1f(x i )−f(x i−1)|≤3．所以存在常数M ≥3，使∑|n i=1f(x i )−f(x i−1)|≤M 恒成立，所以函数f(x)在区间[1a ，a 2]上具有性质P ．此时M 的最小值为3．。

(完整word版)组合数学北京理工期末真题2013答案

课程编号：MTH07065 北京理工大学2012 – 2013学年第二学期计算机科学与技术专业组合数学试题 A 卷班级学号姓名成绩一. (10分) 从数集{1,2,…,15}中取3个数的子集，要求子集中没有相邻数，有多少种取法。

解法一：任选3个数有C(15,3)种方案。

两数相邻另一个分离：1,2和14,15这两个相邻数对，各对应另一不相邻数有12种选择；2,3到13,14共12种相邻数对，各对应另一不相邻数有11种选择。

三数相邻有13种选择。

286131112122315=-⨯-⨯-⎪⎭⎫⎝⎛解法二：任选3个数有C(15,3)种方案。

取两个相邻数有14种选择，另一个与已取出两数不同有13种选择。

每三个相邻的数在前一步被计数了两次，需要补回一次。

286131314315=+⨯-⎪⎭⎫⎝⎛解法三：先放12个0排成一排。

再在13 个空挡中放3个1，有C(13,3)种方法。

在12个0和3个1形成的排列中，数1所在的位置abc ，即得到3个不相邻的1到15中的数。

286313=⎪⎭⎫⎝⎛解法四：令3个数从小到大排列为a,b,d ，满足a+1<b ，b+1<d 。

令B=b-1,D=d-1，则a<B<D 为从1到13中的数，且无不相邻限制。

286313=⎪⎭⎫⎝⎛二. (10分) (1) 求7阶反射Gray 码1010111的前驱和后继。

(2) 在7阶反射Gray 码中，序号是1和2的码是0000000和0000001，求1010111的序号。

(1) 1010111的前驱是1010110，后继是1010101。

(2) 令b=1100101，则1010111的序号是(b)2+1=102三. (10分) 设有4堆硬币，各堆的硬币数分别是17,25,37,50。

游戏人I 和II 轮流取硬币，游戏人I 先取。

每次取硬币任选一堆，至少从该取一枚硬币，至多取走该堆的所有硬币。

当各堆硬币都取完后游戏结束，最后取硬币的人胜。