Mathematics - Complex Algebra 2001
数学复数第一章的知识点总结

数学复数第一章的知识点总结Complex numbers are a fundamental concept in mathematics, extending the idea of real numbers to include imaginary numbers. These numbers are expressed in the form a + bi, where a is the real part and bi is the imaginary part. Complex numbers are crucial in many areas of mathematics, including algebra, calculus, and differential equations. They also have practical applications in physics, engineering, and computer science.复数是数学中的一个基本概念,将实数的概念扩展到包括虚数。
这些数字以a+bi的形式表示,其中a是实部,bi是虚部。
复数在数学的许多领域中至关重要,包括代数、微积分和微分方程。
它们在物理学、工程学和计算机科学中也具有实际应用。
One key property of complex numbers is the ability to represent them geometrically. The complex plane, also known as the Argand diagram, is a two-dimensional plane where the x-axis represents the real part of a complex number and the y-axis represents the imaginary part. Each complex number can be plotted as a point onthe complex plane, allowing for visual representation and understanding of complex numbers and operations.复数的一个关键特性是能够几何表示它们。
上海交大通信培养计划

电子信息工程专业培养计划说明一、指导思想1、体现“教学面向现代化、面向世界、面向未来”的时代精神,全面贯彻落实党的教育方针。
2、为适应我国发展的需要,应加强基础,拓宽专业,在基础上要体现宽、厚、实,专业上突出宽、新、强,即培养科学基础厚,专业口径宽,综合能力强,整体素质高的复合型人才。
3、反映我校的教学水平和优势,体现高起点、严要求、少学时、多自学、重实践的特点。
4、以整体优化为主旨,优化课程体系,加强创新能力培养,重视综合素质提高。
二、学制四年。
三、培养目标培养学生成为基础扎实、知识面宽、实践能力强、综合素质高、适应21世纪信息高速公路建设需要的德智体全面发展的高层次、高质量、高水平的人才。
四、基本要求1、热爱祖国,拥护中国共产党领导,认真学习和基本掌握马列主义、毛泽东思想和邓小平理论,树立科学的世界观、人生观,具有良好的思想品德、道德修养和敬业爱岗、艰苦奋斗、热爱劳动、团队协作精神。
2、具有刻苦学习、善于钻研、锲而不舍的精神,掌握一定的人文社会科学、自然科学基本理论和知识以及经济管理知识,掌握本专业的基本理论、基本技能与方法及相关专业的基础知识,具有合理的知识结构和宽厚的知识面。
3、具有综合应用的能力和创新精神,分析问题、解决问题的能力和竞争意识,获取信息和处理的能力,一定的社会活动能力。
4、有良好的身体素质和心理素质,了解军事理论和体育运动的基本知识,掌握军事、体育的基本技能,养成良好的锻炼和卫生习惯。
五、课程体系及构成:1、教学计划课程安排总学时为2511.5学时(162.5学分,含上机),分四个模块。
(1)公共基础课:13门(包括指定选修课),990学时(61.5学分,含上机),占总学时数的39.5%。
(2)人文、社科、经济、管理类课程:354学时(26学分,含课外),占总学时数的14.1%,其中思想道德修养、毛泽东思想概论、马克思主义政治经济学原理、邓小平理论概论、马克思主义哲学原理、法律基础、军事理论和管理科学基础等8门课程为必修课,计246学时,其余为选修课,课程目录参见上海交通大学人文科学、社会科学、技术经济和管理科学选修课一览。
数学天地的英文

数学天地的英文Mathematical WorldMathematics, often referred to as the language of the universe, encompasses a vast and fascinating world. The study of numbers, shapes, patterns, and relationships not only helps us understand the world around us but also forms the foundation of many scientific and technological advancements. In this article, we will delve into the English vocabulary related to mathematics and explore the various branches and applications of this intriguing field.1. Numbers and OperationsNumbers are the building blocks of mathematics. From the basic integers to the complex realm of imaginary numbers, each numerical concept holds its own significance. Addition, subtraction, multiplication, and division are the fundamental operations that manipulate numbers and create mathematical expressions. Furthermore, concepts such as fractions, decimals, and percentages expand our understanding of numerical values and their representation in everyday life.2. Geometry and ShapesGeometry deals with the study of shapes and their properties. Euclidean geometry, named after the ancient Greek mathematician Euclid, is the most widely recognized branch. It explores the properties of lines, angles, curves, polygons, and three-dimensional figures. Geometric concepts, like symmetry and congruence, play essential roles in architectural design, art, and navigation systems.3. Algebra and EquationsAlgebra introduces variables and symbols into mathematical expressions and equations. By using algebraic techniques, we can solve equations, simplify expressions, and analyze patterns and relationships between variables. Algebraic concepts find applications in fields such as physics, engineering, and economics, providing tools to model and solve real-world problems.4. Calculus and AnalysisCalculus is a branch of mathematics that studies change and motion. It comprises differential calculus, which examines the rate of change, and integral calculus, which analyzes accumulation. Calculus has revolutionized the fields of physics and engineering, enabling the understanding of complex phenomena such as motion, acceleration, and rates of growth.5. Statistics and ProbabilityStatistics deals with data collection, analysis, interpretation, and presentation. It provides methods to make inferences, draw conclusions, and make informed decisions based on available information. Probability, a fundamental concept in statistics, quantifies the likelihood of events occurring. Statistics and probability are widely used in scientific research, social sciences, and business analytics.6. Applied MathematicsApplied mathematics bridges the gap between theory and real-world applications. This interdisciplinary field combines mathematical techniques with other areas like physics, computer science, and finance to solvepractical problems. Examples include mathematical modeling of climate patterns, optimization algorithms, cryptography, and financial forecasting.ConclusionMathematics is a universal language that transcends cultural and linguistic boundaries. Its concepts, vocabulary, and applications are valuable tools in many aspects of life. From counting and measuring to predicting and analyzing, mathematics permeates our everyday experiences. Embracing the beauty and power of mathematics opens doors to endless possibilities and deepens our understanding of the world we live in.Note: The word count of this article is 618 words. If you require additional content, please let me know.。
Algebra1中英版对照目录

分步和混合运算解一元一次方程 P92—P99 2—4:Solving Equations with Variables on Both Sides
变量在两边的一元一次方程的解法 P100—P106 2—5:Solving for a Variable 求变量的值(一元一次)P107—P113
指数幂的乘法运算(同底数幂相乘和积的乘方运算)P460—P466 7—4:Division Properties of Exponents 指数幂的除法 P467—P474 Quiz for Lessons 7-1 through 7-4 第七章 1—4 课小测试 P474—P475 7—5:Polynomials 多项式 P476—P483 7—6:Adding and Subtracting Polynomials 多项式的加减运算 P484—P491 7—7:Multiplying Polynomials 多项式的乘法(单项式与多项式相乘、多项
Algebra 1 与中文数学课本内容在顺序上的对照
Algebra 1
中教数学
CHAPTER 0---- To The Student 0—1:Geometry Formulas
几何公式(s quare,rec tangle,triangle,c irc le)Z3— Z4 0—2:Tree Diagrams 树状图 Z4—Z6 0—3:The Coordinate Plane 直角坐标系 Z7—Z8 0—4:Rounding and Estimating 四舍五入 Z9—Z11 0—5:Adding and Subtracting Decimals 小数的加减运算 Z12—Z13 0—6:Multiplying and Dividing Decimals 小数的乘除运算 Z14—Z16 0—7:Prime and Composite Numbers 素数与合数 Z17—Z18 0—8:Factoring 因数 Z19—Z20 0—9:GCF and LCM 最大公约数和最小公倍数 Z21—Z22
themathematicssubjectclassification

themathematicssubjectclassificationThe Mathematics Subject Classification(2000 Revision)00 GENERAL 一般问题01 HISTORY AND BIOGRAPHY 历史和传记03 MATHEMATICAL LOGIC AND FOUNDATIONS 数理逻辑和数学基础05 COMBINATORICS 组合06 ORDER, LATTICES, ORDERED ALGEBRAIC STRUCTURES 序、格、有序代数结构08 GENERAL ALGEBRAIC SYSTEMS 一般代数系统11 NUMBER THEORY 数论12 FIELD THEORY AND POLYNOMIALS 域论和多项式13 COMMUTATIVE RINGS AND ALGEBRAS 交换环和交换代数14 ALGEBRAIC GEOMETRY 代数几何15 LINEAR AND MULTILINEARALGEBRA;MATRIX THEORY 线性代数和多重线性代数;矩阵论16 ASSOCIATIVE RINGS AND ALGEBRAS 结合环与结合代数17 NONASSOCIATIVE RINGS AND ALGEBRAS非结合环与非结合代数18 CATEGORY THEORY; HOMOLOGICAL ALGEBRA 范畴论;同调代数19 K-THEORY K-理论20 GROUP THEORY AND GENERALIZATIONS群论及其推广22 TOPOLOGICAL GROUPS, LIE GROUPS拓扑群,李群26 REAL FUNCTIONS 实函数28 MEASURE AND INTEGRATION 测度和积分30 FUNCTIONS OF A COMPLEX VARIABLE单复变量函数31 POTENTIAL THEORY 位势理论32 SEVERAL COMPLEX VARIABLES ANDANALYTIC SPACES 多复变量和解析空间33 SPECIAL FUNCTIONS 特殊函数34 ORDINARY DIFFERENTIAL EQUATIONS常微分方程35 PARTIAL DIFFERENTIAL EQUATIONS偏微分方程37 DYNAMICAL SYSTEMS AND ERGODICTHEORY 动力系统和遍历理论39 DIFFERENCE AND FUNCTIONALEQUATIONS 差分方程和泛函方程40 SEQUENCES, SERIES, SUMMABILITY序列,级数,可和性41 APPROXIMATIONS AND EXPANSIONS逼近和展开42 FOURIER ANALYSIS 傅里叶分析43 ABSTRACT HARMONIC ANALYSIS抽象调和分析44 INTEGRAL TRANSFORMS, OPERATIONALCALCULUS 积分变换,算子微积分45 INTEGRAL EQUATIONS 积分方程46 FUNCTIONAL ANALYSIS 泛函方程47 OPERATOR THEORY 算子理论49 CALCULUS OF VARIATIONS AND OPTIMAL CONTROL; OPTIMIZATION变分法与最优控制,最优化51 GEOMETRY 几何52 CONVEX AND DISCRETE GEOMETRY凸几何与离散几何53 DIFFERENTIAL GEOMETRY 微分几何54 GENERAL TOPOLOGY 一般拓扑55 ALGEBRAIC TOPOLOGY 代数拓朴57 MANIFOLDS AND CELL COMPLEXES流形和胞腔复形58 GLOBAL ANALYSIS, ANALYSIS ON MANIFOLDS 大范围分析,流形上的分析60 PROBABILITY THEORY AND STOCHASTIC PROCESSES 概率论和随机过程62 STATISTICS 统计学65 NUMERICAL ANALYSIS 数值分析68 COMPUTER SCIENCE 计算机科学70 MECHANICS OF PARTICLES AND SYSTEMS 质点力学和系统力学74 MECHANICS OF DEFORMABLE SOLIDS 可形变固体力学76 FLUID MECHANICS 流体力学78 OPTICS, ELECTROMAGNETIC THEORY光学,电磁学80 CLASSICAL THERMODYNAMICS, HEAT TRANSFER 经典热力学,热传导81 QUANTUM THEORY 量子理论82 STATISTICAL MECHANICS, STRUCTUREOF MATTER 统计物理,物质结构83 RELATIVITY AND GRAVITATIONALTHEORY 相对论和重力理论85 ASTRONOMY AND ASTROPHYSICS 天文学和天体物理86 GEOPHYSICS 地球物理90 OPERATIONS RESEARCH,MATHEMATICAL PROGRAMMING运筹学,数学规划91 GAME THEORY, ECONOMICS, SOCIALAND BEHAVIORAL SCIENCES博弈论,经济学,社会与行为科学92 BIOLOGY AND OTHER NATURALSCIENCES 生物和其他自然科学93 SYSTEMS THEORY; CONTROL系统理论,控制94 INFORMATION AND COMMUNICATION,CIRCUITS 信息与通讯,电路97 MATHEMATICS EDUCATION 数学教育学科名称Accounts 会计aerospace 太空Aesthetics 美学algebra (alg) 代数学anatomy (anat) 解剖学(解剖) architecture (archit) 建筑学arithmetic (arith) 算术art 艺术astronomy (astron) 天文学biology (biol) 生物学biochemistry 生物化学biocybernetics 生物控制论bio-statistics 生物统计学botany (bot) 植物学business 贸易celestial mechanics 天体力学chemistry (chem) 化学chronology 年代学crystallography 结晶学ecology 生态学economics 经济学embryology 胎生学electrochemistry 电化学engineering (eng) 工程学electricity (electr) 电学finance (fin) 财政学fluid mechanics 流体力学geology (geol) 地质学geography 地理学geometry (geom) 几何学genetics 遗传学journalism新闻学linguistics (ling) 语言学macroscopic mechanics 宏观力学management sciences 管理科学mathematics (maths) 数学mechanics (mech) 机械学medical (med) 医学meteorology (met) 气象学military (mil) 军事molecular biology 分子生物学morphology 形态学music音乐mythology (myth) 神话nautical (naut) 航海pathology (path) 病理学pedagogics 教育学phenomenology 现象学philosophy (phil) 哲学phonetics (phon) 语言学photography (photo) 摄影术physics (phys) 物理学physiology (physiol)生理学politics (pol) 政治学psychology (psych) 心理学semantics 语义学sensory physiology 感觉生理学social sciences 社会科学sociology 社会学structural mechanics 结构力学strigonometry (trig)三角学theology 神学thermodynamics 热动力学theory of Relativity 相对论zoology (zool) 动物学。
代数方程 英语

代数方程英语Algebra EquationsAlgebra is a fundamental branch of mathematics that deals with the study of mathematical expressions and their manipulation. It is a powerful tool that allows us to solve complex problems by representing them in a symbolic form. Algebra equations are the foundation of this branch of mathematics, and they play a crucial role in various fields, including science, engineering, and finance.One of the primary purposes of algebra equations is to represent relationships between variables and constants. These variables can be represented by letters, such as x, y, or z, and they can be manipulated using various operations, such as addition, subtraction, multiplication, and division. Algebra equations can be used to solve for unknown values, to model real-world situations, and to make predictions based on the relationships between the variables.Algebra equations can take many different forms, ranging from simple linear equations to more complex quadratic, polynomial, and exponential equations. Linear equations are the simplest form of algebra equations, and they involve a single variable and a constantterm. These equations can be solved using basic algebraic techniques, such as isolating the variable and performing inverse operations.Quadratic equations, on the other hand, involve a variable raised to the power of two. These equations can be more challenging to solve, but there are various methods available, such as factoring, completing the square, and using the quadratic formula. Polynomial equations involve variables raised to higher powers, and they can be used to model more complex relationships. Exponential equations involve variables with exponents, and they can be used to model growth and decay processes.One of the key advantages of algebra equations is their flexibility and versatility. They can be used to represent a wide range of mathematical relationships, from simple linear functions to more complex nonlinear functions. Additionally, algebra equations can be used to solve a variety of problems, from finding the unknown value in an equation to optimizing the performance of a system.Another important aspect of algebra equations is their role in the development of mathematical thinking and problem-solving skills. By working with algebra equations, students can develop their ability to think logically, analyze problems, and apply mathematical concepts to real-world situations. This can be particularly valuable in fieldssuch as science, engineering, and finance, where the ability to solve complex problems is essential.In conclusion, algebra equations are a fundamental component of mathematics and play a crucial role in various fields. They allow us to represent and manipulate mathematical relationships, solve complex problems, and develop essential problem-solving skills. As technology continues to advance, the importance of algebra equations is likely to grow, as they will be increasingly used to model and analyze complex systems and to make informed decisions in a wide range of applications.。
代数方法 英语

代数方法英语Algebraic MethodsMathematics is a vast and multifaceted field, encompassing a wide range of concepts and techniques. Among the various branches of mathematics, algebra stands out as a fundamental and remarkably powerful tool. Algebraic methods have revolutionized the way we approach and solve complex problems, enabling us to uncover patterns, make predictions, and unlock the secrets of the physical world.At the core of algebraic methods lies the use of variables, symbols, and equations to represent and manipulate quantitative relationships. This abstraction allows us to generalize patterns and apply them to a wide range of scenarios, from everyday life to cutting-edge scientific research. By using the language of algebra, we can transcend the limitations of specific numerical values and instead focus on the underlying structures and relationships that govern these values.One of the primary strengths of algebraic methods is their ability to simplify and streamline complex problems. Through the use of variables and equations, we can break down intricate situations intotheir fundamental components, allowing us to analyze and solve them more efficiently. This approach is particularly useful in fields such as physics, engineering, and economics, where the interplay of various factors can quickly become overwhelming without the aid of algebraic techniques.Moreover, algebraic methods enable us to make predictions and draw conclusions based on the relationships we observe. By manipulating equations and exploring the consequences of changes in one variable or parameter, we can anticipate the outcomes of various scenarios and make informed decisions. This predictive power is invaluable in areas like financial modeling, weather forecasting, and even medical diagnosis, where the ability to foresee potential outcomes can have significant real-world implications.Beyond their practical applications, algebraic methods also serve as a powerful tool for exploring the realms of pure mathematics. Mathematicians often use algebraic techniques to uncover and investigate intricate patterns, relationships, and structures that govern the abstract world of numbers and their interactions. This pursuit of mathematical knowledge not only advances our understanding of the universe but also often leads to unexpected discoveries with far-reaching implications.One such example is the development of abstract algebra, a fieldthat extends the principles of algebra beyond the traditional realm of real numbers. By introducing concepts like groups, rings, and fields, abstract algebra has opened up new avenues for mathematical exploration, allowing us to delve into the deeper complexities of mathematical structures and their applications.The versatility of algebraic methods is further exemplified in their ability to bridge the gap between different branches of mathematics. Algebra serves as a unifying language that enables mathematicians to collaborate and share insights across various disciplines, from geometry and topology to combinatorics and number theory. This interconnectedness not only strengthens our overall mathematical understanding but also fosters the emergence of novel and interdisciplinary approaches to problem-solving.In conclusion, the power of algebraic methods lies in their ability to simplify, generalize, and uncover the underlying patterns and relationships that govern the world around us. Whether we are tackling practical problems or delving into the realms of pure mathematics, the systematic and logical nature of algebra provides us with a powerful toolkit for exploring, understanding, and shaping the world we live in. As we continue to push the boundaries of knowledge, the significance of algebraic methods will undoubtedly grow, serving as a cornerstone of our quest for deeper insights and innovative solutions.。
数学de一些英文名称
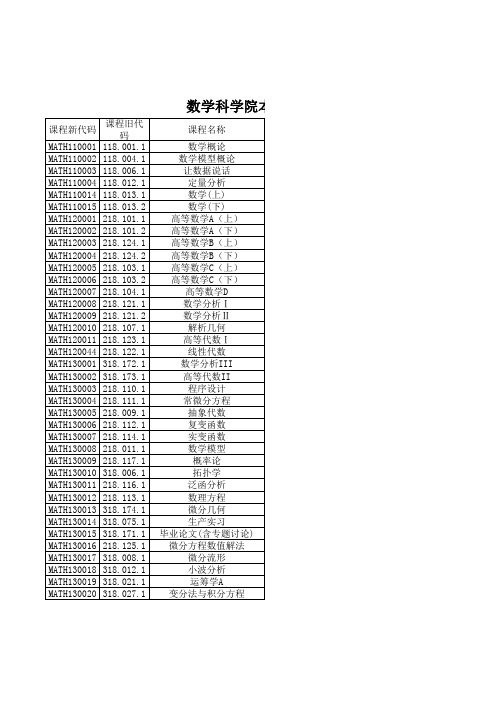
Applied Partial Differential Equations Computer Graphics Computer Aided Geometric Design Selections from System Modeling Biology Mathematics Mathematical Finance Multimedia Techniques Applied Geometry Principle of Computer Network Dynamical Systems The Theory of Interest Actuarial Mathematics Coding Theory Numerical Analysis(Computing Method) Nonlinear Programming Combinatorial Optimization Optimal Control Theory Fractal Geometry Functions of Several Complex Variables Theory of Integral Equations and Its Applications Elementary Number Theory Stochastic Processes Applied software of Mathematics and Practice Introduction to Actuarial Science Advanced course on Mathematical Physics Mathematics of Demography Financial Economics Combinational Analysis Life Insurance Fourier Analysis Introduction to Insurance Introduction to Insurance and Actuarial Science Nonlife Actuarial Mathematics Complex Analysis Introduction to Control Theory Life Actuarial Mathematics Data Structures Statistics Digital Signal Processing Linear Programming Basic Information Theory Element of Database System
数学专业学那些课程

数学专业学那些课程数学与应用数学专业主要课程简介(一)供外系学生修读的课程高等数学A(Higher Mathematics)课程类别:专业必修总学时:160-180总学分:10考核方式:闭卷课程编号:Z1101111高等数学A(一),学时:80-90学分:5考核方式:闭卷课程编号:Z1101112高等数学A(二),学时:80-90学分:5考核方式:闭卷课程目的:通过本课程的学习,使计算机科学与应用、物理学、应用电子、教育技术专业的相关专业的学生熟练掌握高等数学的基础理论,能运用各种基本理论解决实际工作中的专业问题。
课程内容:本课程分二学期讲授,第一学期主要讲授:函数、极限与连续、导数与微分、微分中值定理与导数的应用、不定积分、定积分、定积分的应用。
第二学期主要讲授:空间解析几何与向量代数、多元函数微分法及其应用、重积分、曲线积与曲面积分、无穷级数、微分方程等。
教材:同济大学数学教研室.《高等数学》(上、下册),第六版.北京:高等教育出版社,2002年.高等数学B(Higher Mathematics)课程类别:专业必修学时:142-147学分:8考核方式:闭卷课程编号:Z1101113高等数学B(一),学时:75学分:4考核方式:闭卷课程编号:Z1101114高等数学B(二),学时:72学分:4考核方式:闭卷课程目的:通过本课程的学习,使理工类相关专业专科学生全面掌握高等数学的基础理论,能利用微积分的理论解决实际问题。
课程内容:本课程分二学期讲授,第一学期主要讲授,函数、极限与连续、导数与微分、微分中值定理与导数的应用、不定积分、定积分。
第二学期主要讲授无穷级数、空间解析几何、多元函数微分法及其应用、定积分及其应用、曲线积分与曲面积分、常微分方程等。
教材:陈誌敏.《高等数学》(上、下册),上海:复旦大学出版社,第二版,2005年.课程编号:Z1101115高等数学C(Higher Mathematics)课程类别:专业必修总学时:90总学分:5考核方式:闭卷课程目的:通过本课程的学习,使化学、生物、农、林等相关专业学生掌握高等数学的基础知识,运用基本理论解决一些实际问题。
数学相关英语单词
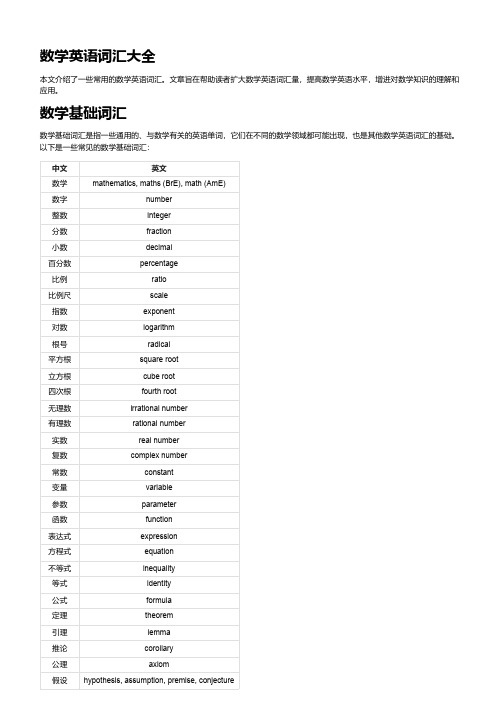
数学英语词汇大全本文介绍了一些常用的数学英语词汇。
文章旨在帮助读者扩大数学英语词汇量,提高数学英语水平,增进对数学知识的理解和应用。
数学基础词汇数学基础词汇是指一些通用的、与数学有关的英语单词,它们在不同的数学领域都可能出现,也是其他数学英语词汇的基础。
以下是一些常见的数学基础词汇:中文英文数学mathematics, maths (BrE), math (AmE)数字number整数integer分数fraction小数decimal百分数percentage比例ratio比例尺scale指数exponent对数logarithm根号radical平方根square root立方根cube root四次根fourth root无理数irrational number有理数rational number实数real number复数complex number常数constant变量variable参数parameter函数function表达式expression方程式equation不等式inequality等式identity公式formula定理theorem引理lemma推论corollary公理axiom假设hypothesis, assumption, premise, conjecture中文英文结论conclusion, result, outcome, consequence证明proof, demonstration, verification反证法proof by contradiction, reductio ad absurdum数值计算numerical computation, numerical analysis符号计算symbolic computation, computer algebra计算器calculator数量和运算数量和运算是指与数字的大小、顺序、关系、组合、变化等有关的英语单词,它们是最基本的数学概念,也是其他数学知识的基础。
高中数学资料书排行榜

高中数学资料书排行榜
由于每个国家和地区高中数学教材和课程标准都不尽相同,因此无法提供全球高中数学资料书的排行榜,以下是部分国家和地区高中数学资料书的推荐:
1. 美国:《高中数学教材》(Holt McDougal),《凯悦代数一》(Glencoe Algebra 1),《凯悦几何》(Glencoe Geometry)
2. 英国:《GCSE 数学教科书》(CGP),《高中数学教科书》(Pearson)
3. 加拿大:《McGraw-Hill Ryerson 数学 11》、《McGraw-Hill Ryerson 数学 12》
4. 澳大利亚:《Cambridge Senior Mathematics: Mathematical Methods》和《Cambridge Senior Mathematics: Specialist Mathematics》
5. 新加坡:《A-Math Topical Revision Guide》、《New Syllabus Mathematics》
6. 中国:《人民教育出版社高中数学教材》、《岛国数学一年级全集》、《岛国数学二年级全集》
7. 日本:《高校数学一年生》、《高校数学二年生》、《高校数学三年生》
这里所列出的书籍和教材只是简单的参考,对于每个学生来说,应该选择适合自己的教材和资料来学习数学。
经典的数学书籍英语

经典的数学书籍英语
经典的数学书籍英语指的是被广泛认可并被广泛引用的数学书籍。
这些书籍内容深入,思维严谨,具有很高的教育和研究价值。
以下是几本经典的数学书籍英语:
1. 《数学原理》(Principia Mathematica):由Bertrand Russell 和Alfred North Whitehead合著,是20世纪最具影响力的数学著作之一。
该书中详细阐述了数学的基础原理和逻辑。
2. 《数学分析基础》(Foundations of Mathematical Analysis):由Richard Courant和Fritz John合著,是一本经典的数学分析教材。
该书中介绍了实数、连续函数、微积分等数学基础概念。
3. 《代数学基础》(Algebraic Foundations of Mathematics):由André Weil合著,该书是20世纪代数学的经典作品之一。
该书中介绍了代数学的基本概念和理论,并对代数学的发展做出了重要贡献。
4. 《微分几何与广义相对论》(Differential Geometry and Relativity Theory):由Yvonne Choquet-Bruhat合著,该书是微分几何和广义相对论领域的一本重要参考书。
该书中介绍了微分几何和广义相对论的基本概念和理论。
5. 《代数拓扑》(Algebraic Topology):由Edwin Spanier合著,该书是代数拓扑领域的重要著作之一。
该书中介绍了代数拓扑的基本概念和理论,并对代数拓扑的发展做出了贡献。
- 1 -。
多圆盘上的Hilbert模

35.J Conway A course in operator theory 1999
36.R Curto Fredholm and invertible n-tuple of operators.the deformation problem 1981
53.R Douglas.K Yan A multi-variable Berger-Shaw theorem 1992(01)
54.R Douglas.K Yan On the rigidity of Hardy submodules 1990
55.D Eisenbud Commgebraic geometry 1999
modules.Systems,approximation,singular integral operatos,and related topics(Bordeaus,2000) 2001
44.R G Douglas.G Misra.C Varughese On quotient modules,the case of arbitrary multiplicity 2000(01)
27.E Brieskorn Beispiele zur Differentialtopogie von ? 1966
28.X Chen.R Douglas Localization of Hilbert modules 1992
29.X Chen.R Douglas Rigidity of Hardy submodules on the unit ball 1992
32.R Curto.P Muhly.K Yan The C~*-algebra of an homogeneous ideal in two variables is type I 1991
最难的是数学作文英语

最难的是数学作文英语下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copyexcerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!Mathematics is undoubtedly one of the most challenging subjects for many students. It requires logical thinking, problem-solving skills, and a deep understanding of various concepts. Writing about mathematics in English can be even more difficult as it requires not only a strong command of the language but also the ability to explain complex ideas in a concise and clear manner.In mathematics, numbers are like the building blocks of the universe. They have a language of their own, a language that transcends borders and cultures. From simple addition and subtraction to complex calculus and algebra, numbers are the tools we use to make sense of the world around us.But mathematics is not just about numbers. It is about patterns, shapes, and relationships. It is about finding the beauty in symmetry and the elegance in simplicity. Mathematics is a language that allows us to describe the world in precise terms, to make predictions, and to solveproblems.One of the most fascinating aspects of mathematics is its universality. The laws of mathematics are the same no matter where you are in the world. Whether you are in China or Brazil, the Pythagorean theorem will always hold true, and the laws of probability will always govern the outcome of a dice roll.Mathematics is also a subject that constantly evolves. New theories are developed, old ones are refined, and new applications are discovered. From the ancient Greeks to the modern-day mathematicians, people have been pushing the boundaries of what is known and exploring the unknown.Despite its challenges, mathematics is also a subject that can be incredibly rewarding. The feeling of solving a difficult problem or discovering a new theorem is like no other. It is a sense of accomplishment and a realization that the human mind is capable of great things.In conclusion, mathematics is a complex and fascinatingsubject that requires both logical thinking and a deep understanding of various concepts. Writing about mathematics in English can be a daunting task, but it is also an opportunity to explore the beauty and universality of this discipline. So let's embrace the challenge and dive into the world of numbers, patterns, and equations.。
数学定理 英文表述

数学定理英文表述Mathematics, often referred to as the "queen of sciences," is a vast field that encompasses various branches, including algebra, geometry, calculus, and more. Central to this discipline are mathematical theorems, which are statements that can be proven true based on a set of axioms or previously established theorems. The elegance and precision of mathematical theorems are often reflected in their English formulations, which strike a balance between brevity and clarity.One such theorem is the Pythagorean Theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Mathematically, this can be expressed as "In a right triangle with legs a and b and hypotenuse c, a² +b² = c²." This theorem, although simple in its statement, has profound implications in geometry and trigonometry.Another notable theorem is the Fundamental Theorem of Algebra, which asserts that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This theorem is fundamental to the studyof polynomials and their properties, and its proof involves concepts such as complex analysis and field theory.The Cauchy-Schwarz Inequality is another essential theorem in mathematics. It states that for any vectors aand b in an inner product space, the absolute value of the inner product of a and b is less than or equal to the product of the norms of a and b. Mathematically, this canbe expressed as "|〈a, b〉| ≤ ||a|| ||b||," where ||a||and ||b|| represent the norms of vectors a and b, respectively. This inequality finds applications in various fields, including linear algebra, functional analysis, and probability theory.These theorems, among many others, form the backbone of mathematics and underlie much of its subsequent development. The precision and clarity of their English formulationsallow mathematicians from different cultures and backgrounds to communicate ideas and concepts effectively. Furthermore, the process of proving these theorems often leads to new insights and discoveries,推进了数学和其他相关领域的发展。
数学在哪里精彩摘抄

数学在哪里精彩摘抄Mathematics is a fascinating subject that can be found everywhere in our daily lives. From calculating the tip at a restaurant to understanding the concepts of probability in gambling, math plays a crucial role in various aspects of our world. Its presence is not only limited to the confines of a classroom but is prevalent in nature, art, music, and even sports. 数学是一个迷人的主题,可以在我们日常生活的各个方面找到。
从在餐厅计算小费到理解赌博中的概率概念,数学在我们世界的各个方面起着至关重要的作用。
它的存在不仅仅局限于教室,而是普遍存在于自然、艺术、音乐,甚至体育中。
One of the most awe-inspiring aspects of mathematics is its ability to describe the world around us with precision. Through the use of equations, formulas, and theorems, mathematicians can provide explanations for natural phenomena that would otherwise seem inexplicable. The elegance and beauty of mathematical concepts often lie in their simplicity and universality, allowing us to understand complex phenomena in a structured and logical manner. 数学最令人敬畏的一个方面是它能够精确描述我们周围的世界。
关于数学名词的英文

关于数学名词的英文Mathematics is a language of its own, with a rich vocabulary that is essential for understanding its concepts. From the basic "addition" and "subtraction" to the more complex "algebra" and "geometry," each term builds the foundation of mathematical thought.At the heart of math lies the "number," which can be "integer," "fraction," or "decimal." These are the building blocks for more advanced concepts like "variables" in algebra, which represent unknown quantities."Equations" are statements that assert the equality oftwo expressions, often involving variables. Solving them is a fundamental skill, leading to the discovery of unknown values that satisfy the equation.Geometry introduces terms like "angle," "triangle," and "circle," which describe shapes and their properties. Understanding these shapes is crucial for spatial reasoning and problem-solving."Pi" is a constant that represents the ratio of acircle's circumference to its diameter. It's an example of a mathematical constant that has specific applications invarious fields."Calculus" is the study of change and motion, involvingconcepts like "derivatives" and "integrals." It's a powerful tool for predicting the future based on the present.Finally, "statistics" is the science of collecting, analyzing, and presenting data. It helps us understand patterns and make informed decisions based on numerical evidence.In essence, the vocabulary of mathematics is a key to unlocking the world of numbers, shapes, and patterns, allowing us to solve problems and make sense of the world around us.。
外国数学教材

外国数学教材以下是一些外国数学教材的推荐:《I. M. Gelfand - Lectures on Linear Algebra》:这是一本线性代数的教材,作者是I. M. Gelfand。
《Michael Artin - Algebra 2e》:这是代数课程的教材,作者是Michael Artin。
《Michael Atiyah, Ian G. Macdonald - Introduction To Commutative Algebra》:这是交换代数的教材,作者是Michael Atiyah和Ian G. Macdonald。
《Ernst Kunz - Introduction to Commutative Algebra and Algebraic Geometry》:这是交换代数和代数几何的教材,作者是Ernst Kunz。
《John B. Conway - Functions of One Complex Variable I》:这是一本复变函数的教材,作者是John B. Conway。
《John B. Conway - Functions of One Complex Variable II Graduate Texts in Mathematics》:这是另一本复变函数的教材,作者是John B. Conway。
此外,还有《Envision Florida Mathematics》数学教材,从G1-G8,外加代数1、代数2、几何三本;美国国家地理和CENGAGE联合出版的最新版 Math BEST MATH教材;哈卡特集团出版的GO MATH G6-G8教材;新加坡和美国合作的Math In Focus MIF GK-G5 MIF G6-G8教材等。
这些教材在各自的领域内都是非常经典和权威的,对于想要深入学习数学的人来说是非常有价值的资源。
数学的英文单词。

数学的英文单词。
English:Mathematics is an academic discipline that involves the study of numbers, quantities, shapes, and patterns. It encompasses a wide range of topics including arithmetic, algebra, geometry, calculus, and statistics. Mathematics is essential in understanding and solving complex problems in various fields such as science, engineering, economics, and finance. It provides a universal language for expressing and analyzing relationships and patterns in the world around us. The fundamental concepts of mathematics, such as addition, subtraction, multiplication, and division, are used in everyday life for tasks such as managing finances, measuring ingredients, and calculating distances. The importance of mathematics in both theoretical and practical applications cannot be overstated, and it continues to play a crucial role in advancing human knowledge and technology.中文翻译:数学是一门学科,涉及数字、数量、形状和模式的研究。
数学名词英文

数学mathematics, maths(BrE),math(AmE) 公理axiom 定理theorem 计算calculati on 运算operati on 证明prove 假设hypothesis, hypotheses(pL) 命题propositi on 算术arithmetic力卩plus(prep.), add(v.), additi on(n.)被加数auge nd, summa nd 加数adde nd 和sum减minu s(prep.), subtract(v.), subtracti on(n.) 被减数minuend 减数subtrahe nd 差rema in der乘times(prep.), multiply(v.), multiplicati on(n.) 被乘数multiplica nd, faciend 乘数multiplicator积product除divided by(prep.), divide(v.), division(n.) 被除数divide nd 除数divisor 商quotie nt等于equals, is equal to, is equivale nt to 大于is greater tha n 小于is lesser tha n大于等于is equal or greater than 小于等于is equal or lesser than 运算符operator 平均数mean算术平均数arithmatic mean 几何平均数geometric mean n个数之积的n次方根倒数(reciprocal )x的倒数为1/x 有理数rational nu mber 无理数irrati onal nu mber 实数real nu mber 虚数imag inary nu mber 数字digit 数nu mber自然数n atural nu mber 整数in teger 小数decimal 小数点decimal point 分数fracti on 分子nu merator 分母denomin ator 比ratio 正positive 负n egative 零n ull, zero, no ught, nil 十进希9 decimal system 二进希9 binary system 十六进希9 hexadecimal system 权weight, sig nifica nee 进位carry 截尾trun catio n四舍五入round 下舍入round dow n 上舍入round up 有效数字sig nifica nt digit 无效数字in sig nifica nt digit 代数algebra 公式formula, formulae(pl.) 单项式mono mial 多项式polyno mial, multi no mial 系数coefficie nt 未知数unknown, x-factor, y-factor, z-factor 等式,方程式equation 一次方程simple equati on 二次方程quadratic equati on 三次方程cubic equati on 四次方程quartic equati on 不等式in equati on 阶乘factorial 对数logarithm 指数,幕exp onent 乘方power二次方,平方square 三次方,立方cube 四次方the power of four, the fourth powern 次方the power of n, the nth power 开方evoluti on, extract ion 二次方根,平方根square root 三次方根,立方根cube root 四次方根the root of four, the fourth rootn 次方根the root of n, the nth rootsqrt(2)=1.414 sqrt(3)=1.732 sqrt(5)=2.236 常量con sta nt 变量variable 坐标系coord in ates 坐标轴x-axis, y-axis, z-axis 横坐标x-coordi nate 纵坐标y-coordi nate 原点orig in 象限quadra nt 截距(有正负之分)intercede (方程的)解solution 几何geometry 点poi nt 线line 面pla ne 体solid 线段segme nt 射线radial 平行parallel 相交in tersect 角an gle 角度degree 弧度radia n 锐角acute an gle 直角right an gle 钝角obtuse an gle 平角straight an gle 周角perig on 底base 边side 高height 三角形tria ngle锐角三角形acute triangle 直角三角形right triangle 直角边leg 斜边hypote nuse 勾股定理Pythagorea n theorem钝角三角形obtuse triangle 不等边三角形scalene triangle 等腰三角形isosceles triangle 等边三角形equilateral triangle 四边形quadrilateral 平行四边形parallelogram 矩形recta ngle 长len gth 宽width 周长perimeter 面积area 相似similar 全等con grue nt 三角trig ono metry 正弦si ne 余弦cos ine 正切tangent 余切cota ngent 正割seca nt 余割coseca nt 反正弦arc si ne反余弦arc cos ine 反正切arc tangent 反余切arc cota ngent 反正割arc seca nt 反余割arc coseca nt 集合aggregate 元素eleme nt 空集void 子集subset 交集in tersect ion 并集union 补集compleme nt 映射mappi ng 函数fun cti on定义域domain, field of definition 值域range单调性mono to ni city 奇偶性parity周期性periodicity 图象image 数列,级数series 微积分calculus 微分differe ntial 导数derivative 极限limit 无穷大infin ite(a.) infin ity (n.) 无穷小infini tesimal 积分in tegral 定积分defi nite in tegral 不定积分indefinite integral 复数complex nu mber 矩阵matrix 行列式determ inant 圆circle 圆心centre(BrE), cen ter(AmE) 半径radius 直径diameter 圆周率pi 弧arc 半圆semicircle 扇形sector 环ring 椭圆ellipse 圆周circumfere nee 轨迹locus, loca(pl.) 平行六面体parallelepiped 立方体cube七面体heptahedr on 八面体octahedro n 九面体enn eahedro n 十面体decahedr on 十面体hendecahedron 十二面体dodecahedron 二十面体icosahedron 多面体polyhedro n 旋转rotati on 轴axis 球sphere 半球hemisphere 底面un dersurface 表面积surface area 体积volume空间space 双曲线hyperbola 抛物线parabola 四面体tetrahedro n 五面体pen tahedr on 六面体hexahedr on 菱形rhomb, rhombus, rhombi(pl.), diam ond 正方形square 梯形trapezoid 直角梯形right trapezoid 等腰梯形isosceles trapezoid 五边形pen tag on 六边形hexag on 七边形heptag on 八边形octag on 九边形enn eag on 十边形decag on 十边形hen decago n 十二边形dodecagon 多边形polyg on 正多边形equilateral polygon 相位phase 周期period 振幅amplitude 内心incentre(BrE), i ncen ter(AmE) 夕卜心exce ntre(BrE), exce nter(AmE) 旁心esce ntre(BrE), esce nter(AmE) 垂心orthoce ntre(BrE),orthoce nter(AmE)重心baryce ntre(BrE), baryce nter(AmE)内切圆in scribed circle 夕卜切圆circumcircle 统计statistics 平均数average 力卩权平均数weighted average 方差varia nee标准差root-mea n-square deviatio n, sta ndard deviati on 比例propoti on 百分比perce nt 百分点perce ntage 百分位数perce ntile排列permutati on 组合comb in ati on 概率,或然率probability 分布distributio n 正态分布normal distribution 非正态分布abnormal distribution 图表graph 条形统计图bar graph 柱形统计图histogram 折线统计图broken line graph 曲线统计图curve diagram代数ALGEBRA1. 数论n atural nu mber 自然数positivenu mber 正数n egative nu mber 负数odd in teger, odd nu mber 奇数eve n in teger, eve n nu mber 偶数in teger, whole number 整数positive whole nu mber 正整数n egative whole number 负整数consecutive number 连续整数real number, rational number 实数,有理数irrational(number)无理数inverse 倒数composite number 合数e.g.4.6.8.9.10.12.14.15 …prime nu mber 质数e.g.2.3.5.7.11.13.15 …reciprocal 倒数com mon divisor 公约数multiple 倍数(minimum) commormultiple (最小)公倍数(prime) factor( 质)因子com mon factor 公因子ordinary scale, decimal scale 十进制nonnegative 非负的tens 十位units 个位mode众数mean平均数media n 中值com mon ratio 公比2. 基本数学概念arithmetic mea n 算术平均值weighted average 力卩权平均值geometric mean 几何平均数exponent 指数,幕base 乘幕的底数, 底边cube 立方数,立方体square root 平方根cube root 立方根commonogarithm 常用对数digit 数字con sta nt 常数variable 变量inv erse fun cti on 反函数compleme ntary fun cti on 余函数lin ear 一次的,线性的factorization 因式分解absolute value 绝对值,e.g. | -32 | =32 round off四舍五入数学3. 基本运算add, plus 力卩subtract 减differe nee 差multiply, times 乘product 积divide 除divisible 可被整除的divided evenly被整除divide nd 被除数,红利divisor 因子,除数,公约数quotient 商rema in der 余数factorial 阶乘power 乘方radical sign, root sign 根号round to 四舍五入to the nearest 四舍五入4. 代数式,方程,不等式algebraic term 代数项like terms, similar terms 同类项nu merical coefficient 数字系数literal coefficie nt 字母系数in equality 不等式tria ngle in equality 三角不等式range 值域original equation 原方程equivale nt equati on 同解方程,等价方程linear equation 线性方程(e.g.5x+6=22) 5. 分数,小数proper fractio n 真分数improper fraction假分数mixed number 带分数vulgar fracti on ,com monfracti on 普通分数simple fractio n简分数complex fractio n 繁分数numerator 分子denominator 分母(least)com mon denomin ator (最小)公分母quarter 四分之一decimal fracti on 纯小数infinite decimal无穷小数recurri ng decimal 循环小数ten ths unit 十分位6. 集合、、union 并集proper subset 真子集soluti on set 解集7. 数列arithmetic progressi on( seque nee)等差数歹U geometric progressi on( seque nee)等比数歹U8. 其它approximate 近似(anti)eloekwise (逆)顺时针方向eardinal 基数ordinal 序数direet proportio n 正比disti net 不同的estimati on 估计,近似parentheses 括号proporti on比例permutatio n 排列eomb in ati on 组合table 表格trigono metric fun etio n 三角函数unit 单位,位几何GEOMETRY1. 角alter nate an gle 内错角eorresp onding an gle 同位角vertieal angle 对顶角eentralangle 圆心角interior angle 内角exterior an gle 夕卜角suppleme ntaryangles 补角eomplementary angle 余角adjaeent angle 令B角aeute angle 锐角obtuse angle 钝角right angle 直角round an gle 周角straight an gle 平角in eluded an gle 夹角2. 三角形equilateral tria ngle 等边三角形seale ne tria ngle 不等边三角形soseeles tria ngle 等腰三角形right triangle 直角三角形oblique 斜三角形inseribed triangle 内接三角形3. 收敛的平面图形,除三角形外semieirele 半圆concen trie eireles 同心圆quadrilateral 四边形pen tag on 五边形hexag on 六边形heptagon 七边形oetagon 八边形nonagon九边形deeagon十边形polygon 多边形parallelogram 平行四边形equilateral 等边形plane 平面square 正方形,平方recta ngle 长方形regular polyg on 正多边形rhombus菱形trapezoid 梯形4. 其它平面图形are 弧line, straight line 直线line segme nt 线段parallel li nes平行线segme nt of a circle 弧形5. 立体图形cube立方体,立方数rectangular solid 长方体regular olid/regularpolyhedro n正多面体circular eylinder 圆柱体cone 圆锥sphere 球体solid 立体的6. 图形的附属概念pla ne geometry 平面几何trigo no metry 三角学bisect 平分ireumseribe 夕卜切in scribe 内切in terseet 相交perpe ndicular 垂直Pythagorea n theorem 勾股定理(毕达哥拉斯定理)eongruent全等的multilateral 多边的altitude 高depth深度side 边长eireumfere nee, perimeter 周长adian 弧度surface area 表面积volume体积arm直角三角形的股cross section 横截面een ter of a circle 圆心chord 弦diameter 直径radius 半径an gle bisector 角平分线diagonal 对角线edge 棱face of a solid 立体的面hypotenuse 斜边in eluded side 夹边leg 三角形的直角边median (三角形的)中线base 底边,底数(e.g. 2的5次方,2就是底数)opposite 直角三角形中的对边midpoint 中点endpoint 端点vertex (复数形式vertices)顶点tangent 切线的transversal 截线in tercept 截距7. 坐标coordi nate system 坐标系rectan gular coordi nate 直角坐标系origi n 原点abscissa 横坐标ordi nate纵坐标nu mber line 数轴quadra nt 象限slope 斜率complex plane复平面8. 计量单位cent 美分penny —美分硬币nickel 5 美分硬币dime 一角硬币dozen 打(12 个)score 廿(20 个) Cen tigrade 摄氏Fahre nheit 华氏quart 夸脱gall on 力口仑(1 gall on =4 quart) yard 码meter 米micron 微米inch 英寸foot 英尺mi nute 分(角度的度量单位,60分=1 度)square measure 平方单位希9 cubic meter 立方米pi nt 品脱(干量或液量的单位)基本规律1所有的质数(2除外)都是奇数,但奇数不一定是质数2 若b>a,则b/a > (b+1)/(a+1);若 b < a>其它1. 单位类cent 美分penny —美分硬币nickel 5 美分硬币dime 一角硬币dozen 打(12 个)score 廿(20 个) Cen tigrade 摄氏Fahre nheit 华氏quart 夸脱gall on 力口仑(1 gall on =4 quart) yard 码meter 米micron 微米inch 英寸foot 英尺mi nute 分(角度的度量单位,60分=1度) square measure 平方单位希9 cubic meter立方米pint 品脱(干量或液量的单位)2. 有关文字叙述题,主要是有关商业in tercalary year(leap year)闰年(366 天)common year 平年(365 天) depreciation 折旧down payment 直接付款discount 打折margin 利润profit 禾U润in terest 禾U息simple in terest 单禾U compo un ded in terest复禾U divide nd 红禾U decrease to 减少至U decrease by 减少了in crease to 增加到in crease by 增加了denote 表示list price 标价markup 丫张价per capita 每人ratio 比率retail price 零售价tie 打。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The plane is named for Jean Robert Argand, a Swiss mathematician who proposed the representation of complex numbers in 1806.
Furthermore, another possible representation of the complex number z in this plane is as a vector OP . We display z = a + ib as a directed line that begins at the origin and terminates at the point P(a , b). Hence the modulus of z, that is z , is the distance of z = P(a , b) from the origin. However, there are simple geometrical relationships between the vectors for z = a + ib , the negative of z; − z and the conjugate of z; z in the Argand plane. The vector − z is vector for z reflected through the origin, whereas z is the vector z reflected about the real axis. The addition and subtraction of complex numbers can be interpreted as vector addition which is given by the parallelogram law. The ‘triangle inequality’ is derivable from this geometric complex plane. The length of the vector z1 + z 2 is z1 + z 2 , which must be less than or equal to the combined lengths z1 + z 2 . Thus z1 + z 2 ≤ z1 + z 2 .
Complex Conjugate and Their Properties
Definition: Let z = a + ib ∈ C , a, b ∈ R. The complex conjugate, or briefly conjugate, of z is defined by z = a − ib. For any complex numbers z , z1 , z 2 ∈ C , we have the following algebraic properties of the conjugate operation: (i). (ii). z1 + z 2 = z1 + z 2 , z1 − z 2 = z1 − z 2 ,
(iii). z1 z 2 = z1 ⋅ z 2 ,
z1 z1 (iv). = , provided z 2 ≠ 0, z2 z2 (v). (vi). z n = (z ) , for all n ∈ Z , (vii). z = z if and only if Im z = 0, (viii). z = − z if and only if Rez = 0, (ix). z + z = 2 Re z , (x). z − z = i (2 Im z ),
n
z = z,
(xi). zz = ( Re z ) + ( Im z ) .
2 2
Modulus and Their Properties
Definition: The modulus or absolute value of a complex number z = a + ib, a , b ∈ R is defined as z = a 2 + b2 . That is the positive square root of the sums of the squares of its real and imaginary parts. For any complex numbers z , z1 , z 2 ∈ C , we have the following algebraic properties of modulus: (i). z ≥ 0; and z = 0 if and only if z = 0, (ii). (iii). z1 z 2 = z1 z 2 , z1 z1 = , provided z 2 ≠ 0, z2 z2 (iv). z = z = − z , (v). z = zz , (vi). z z ≥ Im z , (viii). z1 + z 2 ≤ z1 + z 2 , (triangle inequality) (ix). z1 − z 2 ≤ z1 + z 2 .
The Geometric Representation of Complex Numbers
In analytic geometry, any complex number z = a + ib, a , b ∈ R can be represented by a point z = P(a , b) in xy-plane or Cartesian plane. When the xy-plane is used in this way to plot or represent complex numbers, it is called the Argand plane1 or the complex plane. Under these circumstances, the x- or horizontal axis is called the axis of real number or simply, real axis whereas the y- or vertical axis is called the axis of imaginary numbers or simply, imaginary axis.
The Complex Number System
Definition: A complex number z is a number of the form z = a + ib, where the symbol i = − 1 is called imaginary unit and a , b ∈ R. a is called the real part and b the imaginary part of z, written a = Re z and b = Im z. With this notation, we have z = Re z + i Im z. The set of all complex numbers is denoted by C = { a + ib a , b ∈ R }. If b = 0, then z = a + i 0 = a , is a real number. Also if a = 0, then z = 0 + ib = ib, is a imaginary number; in this case, z is called pure imaginary number. Let a + ib and c + id be complex numbers, with a , b, c, d ∈ R. 1. Equality a + ib = c + id if and only if a = c and b = d . Note: In particular, we have z = a + ib = 0 if and only if a = 0 and b = 0. 2. Fundamental Algebraic Properties of Complex Numbers (i). Addition (a + ib) + (c + id ) = (a + c) + i (b + d ). (ii). Subtraction (a + ib) − (c + id ) = (a − c) + i (b − d ). (iii). Multiplication (a + ib)( c + id ) = (ac − bd ) + i (ad + bc). Remark (a). By using the multiplication formula, one defines the nonnegative integral power of a complex number z as z 1 = z , z 2 = zz , z 3 = z 2 z , ! , z n = z n −1 z. Further for z ≠ 0, we define the zero power of z is 1; that is, z 0 = 1. (b). By definition, we have i 2 = −1, i 3 = −i , i 4 = 1. (iv). Division If c + id ≠ 0 , then
Complex Numbers and Functions
______________________________________________________________________________________________ Natural is the most fertile source of Mathematical Discoveries - Jean Baptiste Joseph Fourier
