河北武邑中学高三周日考试(.1.17)
高三语文一轮复习重难点辨析并修改病句(上)第三章成分残缺(含解析)

高三语文一轮复习重难点辨析并修改病句(上)第三章成分残缺(含解析)重点列表重点、难点类型重要指数重点1 成分赘余☆☆☆☆☆重点2 主语残缺☆☆☆☆☆重点3 中心语残缺☆☆☆☆☆重点1:成分赘余【要点说明】成分赘余一般在句子中都会出现语意重复的地方,注意查找。
辨析方法:分析中心词,对照修饰语,注意近义词,看句子中是否有表意重复的地方,查找重复赘余。
【典例分析】指出下列句子中的语病。
1.三年来的“旅游兴市”竟成为今天发展核电的障碍,这可能是地方政府当初始料未及的。
2.奥运圣火登顶珠峰的瞬间,无论是参与登顶的勇士,还是全世界观看这一壮举的人们,无不毫无例外地感受到了心灵的震撼。
3.90个有特殊编号的“奥运缶”在北京结束了网络竞价,以总价1283.65万元成交,每个缶的均价都超过了14万元。
【名师点睛】分析中心词,对照修饰语,注意近义词,看句子中是否有表意重复的地方,查找重复赘余。
【典例拓展】1.下列各句中没有语病的一句是()A.在国际间文化交流日趋频繁、不同民族文化相互交融和碰撞的今天,更应重视继承和发扬传统节日文化。
B.参加这次探险活动前他已写下遗嘱,万一若在探险中遇到不测,四个子女都能从他的巨额遗产中按月领取固定数额的生活费。
C.初涉文坛,她的第一部处女作就是这样一部意味深长的巨著,不能不令人刮目相看。
D.国产轿车的价格低,适于百姓接受,像“都市贝贝”市场统一售价才6.08万元,“英格尔”是6.88万元,新款“桑塔纳”也不过十几万元。
2.下列各句中没有语病的一句是()A.《语文大辞典》编委会,为了使辞典有较高的质量,在躬耕修典三个春秋的编纂。
B.地震发生之后,当地政府及解放军部队全力救助,目前灾区群众已住进了临时帐篷,防止余震再次发生。
C.随着通讯日渐发达,手机几乎成为大家的必需品,但使用量增加之后,关于手机质量的投诉也越来越多。
D.不少学生偏食、挑食、导致蛋白质的摄入量偏低,钙、锌、铁等营养素明显不足,营养状况不容令人乐观。
河北省武邑中学2022届高三上学期第二次调研化学试题 Word版含答案

可能用到的相对原子质量:H 1 D 2 C l2 N 14 O 16 Na 23 Al 27 S 32 Fe 56第I卷(选择题)(50分)选择题(每小题只有一个选项符合题意,每小题2分)1.唐代中药学著作《新修本草》中,有关于“青矾”的记录为“原来绿色,新出窟未见风者,正如琉璃,……,烧之赤色”。
据此推想,“青矾”的主要成分为A. CuSO4·5H2OB. FeSO4·7H2OC. KAl(SO4)2·12H2OD.ZnSO4·7H2O2.下列物质的成分与“H2O”无关的是A.水晶B.水玻璃C.氯水D.王水3.用浓硫酸、无水氯化钙,碱石灰均可以干燥的气体是A. NH3B.SO2 C.CH4 D. Cl24.下列过程中都涉及到饱和食盐水,其中氯离子被氧化的是A.氯碱工业B.侯氏制碱C.制取乙炔D.除去Cl2中的HCl5.如图所示,两个连通容器用活塞分开,标准状况下,左右两室(体积相同)各充入肯定量气体,打开活塞,充分混合后,恢复到标准状况,容器内气体质量不变的是A. SO2和H2S B.SO2和NO2 C. O2和SO2 D. HCl和NH36.常温下,下列物质能与水反应生成气体,且该气体是电解质的是A.NaH B. Mg3N2 C. Al2S3 D. CaC27.下列各组溶液,只用试管和胶头滴管不能区分开来的是A.氯化铝溶液和盐酸B.纯破溶液和稀硫酸C.硝酸银溶液和氨水D.偏铝酸钠溶液和硝酸8.下列物质中,不符合“既能与某种酸反应,又能与某种碱反应”的是A.BeO B. SiO2 C. FeCl3 D. NaI9.单质X与浓H2SO4共热,反应中X与浓H2SO4的物质的量之比为1:2,则X元素在生成物中的化合价可能为①+l ②+2 ③+3 ④+4A.②④ B.③④ C.①② D. ①③10.如图W、X、Y、Z为四种物质.若箭头表示能一步转化的常见反应,其中常温下能实现图示转化关系的是选项W X Y ZA S SO2 SO3 H2SO4B Na Na2O2 NaOH NaClC Fe FeCl3 Fe(OH)2 FeCl2D Al AlCl3 NaAlO2 Al2(SO4)311.设NA为阿伏伽德罗常数的数值,下列各项叙述中正确的是A. pH=1的HNO3溶液中,含有0.1NA个H+B.在Na2O2与CO2的反应中.每转移NA个电子时,标准状况下消耗11.2L 的CO2C. 1 L1mol/LFeBr2溶液与1mol氯气反应时转移的电子数为3NAD. 239 Na与O2充分反应生成Na2O和Na2O2的混合物,消耗O2的分子数在0.25NA和0.5NA之间12.下列反应的离子方程式正确的是A. 磁性氧化铁(Fe3O4)溶于氢碘酸:Fe3O4+8H+=Fe2++2Fe3++4H2OB.向CuSO4溶液中通入过量的H2S气体:Cu2++H2S=CuS↓+2H+C.向NaHSO4溶液中滴加Ba(OH)2溶液至不再产生沉淀:Ba2++2OH-+2H++SO42-=BaSO4+2H2OD.向KMnO4溶液中通入过量的SO2气体:5SO2+2MnO4-+4H+=2Mn2++5SO42-+2H2O13.如图,在一个容积固定的恒温容器中,有两个可左右滑动的密封隔板,在A、B、C内分别充入等质量的X、H2、Y三种气体,当隔板静止时,A、C内的气体密度相等。
2024届河北省衡水市部分高中高三一模数学试题(解析版)

2024年普通高等学校招生全国统一考试模拟试题数学(一)(考试时间:120分钟,满分:150分)注意事项:1.答题前,先将自己的姓名、准考证号等填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用签字笔直接写在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试题卷和答题卡一并上交.一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集{}0,1,2,3,4,5U =,集合{}1,3,4M =,{}0,3,5N =,则N ()U M = ð()A.{}0,5B.{}1,2,3,4C.{}1,2,3,4,5 D.U【答案】B 【解析】【分析】根据集合并补运算即可求得.【详解】{}0,1,2,3,4,5U =,{}0,3,5N =,所以{}1,2,4U N =ð,所以(){}1,2,3,4U M N = ð,故选:B.2.已知复数z 满足(43i)i z +=-,则z 的虚部为()A.425-B.425 C.4i 25-D.4i 25【答案】A 【解析】【分析】由复数除法运算法则直接计算,结合复数的虚部的概念即可求解.【详解】因为(43i)i z +=-,所以()()()i 43i i 34i 43i 43i 43i 2525z ---===--++-,所以z 的虚部为425-.故选:A.3.将函数()sin 2f x x =的图象向左平移ϕ个单位后得到函数()g x 的图象,若函数()()y f x g x =+的最大值为a ,则a 的值不可能为()A.1B.1C.2D.1【答案】D 【解析】【分析】根据图象的平移变换得到()()sin 22g x x ϕ=+,然后根据和差公式和辅助角公式整理得到()()()2y f x g x x α=+=+,最后根据三角函数的性质求a 的范围即可.【详解】由题意得()()sin 22g x x ϕ=+,则()()()sin 2sin 22y f x g x x x ϕ=+=++sin 2cos 2sin 2sin 2cos 2x x xϕϕ=++()1cos 2sin 2sin 2cos 2x x ϕϕ=++()2x α=+()2x α=+,sin 2tan 1cos 2ϕαϕ=+,因为[]cos 21,1ϕ∈-[]0,2,所以[]0,2a ∈.故选:D.4.在等比数列{}n a 中,若1512a a a ⋅⋅为一确定的常数,记数列{}n a 的前n 项积为n T .则下列各数为常数的是()A.7TB.8T C.10T D.11T 【答案】D 【解析】【分析】根据已知条件判断出6a 为确定常数,再由此确定正确答案.【详解】设等比数列{}n a 的公比为q ,依题意,()3411511111512a a q a a a a q q a =⋅⋅=⋅⋅为确定常数,即6a 为确定常数.7712674T a a a a a == 不符合题意;()48127845T a a a a a a == 不符合题意;()5101291056T a a a a a a == 不符合题意;11111210116T a a a a a == 为确定常数,符合题意.故选:D 5.关于函数4125x y x -=-,N x ∈,N 为自然数集,下列说法正确的是()A.函数只有最大值没有最小值B.函数只有最小值没有最大值C.函数没有最大值也没有最小值D.函数有最小值也有最大值【答案】D 【解析】【分析】先对函数整理化简,根据反比例函数的性质,结合复合函数单调性的“同增异减”,即可求出函数的最小值与最大值.【详解】()22594192252525x x y x x x -+-===+---,52x ¹,由反比例函数的性质得:y 在5,2⎛⎫+∞ ⎪⎝⎭上单调递减,此时2y >,y 在5,2⎛⎫-∞ ⎪⎝⎭上单调递减,此时2y <,又因为N x ∈,N 为自然数集,所以min y 在5,2⎛⎫-∞ ⎪⎝⎭上取到,2x =时,min 7y =-,同理max y 在5,2⎛⎫+∞⎪⎝⎭上取到,3x =时,max 11y =,所以当N x ∈,N 为自然数集时,函数有最小值也有最大值.故选:D .6.已知函数()πcos 12f x x ⎛⎫=-⎪⎝⎭,()πsin 46g x x ⎛⎫=+ ⎪⎝⎭,则“曲线()y f x =关于直线x m =对称”是“曲线()y g x =关于直线x m =对称”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】分别求出两个函数的对称轴的集合,利用两个集合的关系即可判断.【详解】令()11ππ12m k k -=∈Z ,得()11ππ12m k k =+∈Z ,所以曲线()y f x =关于直线()11ππ12x k k =+∈Z 对称.令()22ππ4π62m k k +=+∈Z ,得()22ππ124k m k =+∈Z ,所以曲线()y g x =关于直线()22ππ124k x k =+∈Z 对称.因为()11π{|π}12m m k k =+∈Z ()22ππ{|}124k m m k =+∈Z 所以“曲线()y f x =关于直线x m =对称”是“曲线()y g x =关于直线x m =对称”的充分不必要条件.故选:A.7.O 为坐标原点,F 为抛物线2:8C y x =的焦点,M 为C 上一点,若||6=MF ,则MOF △的面积为()A. B. C. D.8【答案】C 【解析】【分析】首先根据焦半径公式求点M 的坐标,再代入面积公式,即可求解.【详解】设点()00,Mxy ,()2,0F ,所以026MF x =+=,得04x =,0y =±,所以MOF △的面积011222S OF y =⨯=⨯⨯故选:C8.,,a b c 为三个互异的正数,满足2ln 0,31ba cc a a-=>=+,则下列说法正确的是()A.2c a b ->-B.2c b a -≤-C.2c a b +<+D.2c a b+≤+【答案】A 【解析】【分析】对于2ln 0cc a a-=>可构造函数()2ln f x x x =-,利用导函数可求出其单调性,利用数形结合可得02a c <<<,对于31ba =+,可在同一坐标系下画出函数x y =及31x y =+的图象,可得02a b <<<,再由不等式性质可知A 正确.【详解】由2ln0cc a a-=>得2ln 2ln c c a a -=-且c a >,构造函数()2ln f x x x =-,所以()21f x x'=-,易得()f x 在()0,2上单调递减,在()2,+∞上单调递增,其函数图象如下图所示:由图可得02a c <<<,易知函数x y =及31x y =+交于点()2,10,作出函数x y =及31x y =+的图象如下图所示:由图知02a b <<<所以02a b c <<<<,即,2a b c <<,由此可得2a b c +<+,即2c a b ->-.故选:A【点睛】方法点睛:在求解不等式比较大小问题时,经常利用同构函数进行构造后通过函数单调单调性比较出大小,画出函数图象直接由图象观察得出结论.二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有两个或两个以上选项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分)9.已知10个数据的第75百分位数是31,则下列说法正确的是()A.这10个数据中至少有8个数小于或等于31B.把这10个数据从小到大排列后,第8个数据是31C.把这10个数据从小到大排列后,第7个与第8个数据的平均数是31D.把这10个数据从小到大排列后,第6个与第7个数据的平均数是31【答案】AB 【解析】【分析】由百分位数的概念可判断.【详解】因为这10个数据的第75百分位数是31,由100.757.5⨯=,可知把这10个数据从小到大排列后,第8个数为31,可知,选项A ,B 正确,C ,D 错误.故选:AB .10.函数()2,3,x D x x ∈⎧=⎨∉⎩QQ ,则下列结论正确的是()A.()()3.14D D π>B.()D x 的值域为[]2,3C.()()D D x 是偶函数 D.a ∀∈R ,()()D x a D a x +=-【答案】AC 【解析】【分析】根据函数解析式,结合分段函数的性质,逐项判断即可.【详解】()3D π=,()3.142D =,()()3.14D D π>,A 正确;()2,3,x D x x ∈⎧=⎨∉⎩QQ,则()D x 的值域为{}2,3,B 错误;x ∈Q 时,x -∈Q ,()()()22D D x D ==,()()()22D D x D -==,所以()()()()D D x D D x =-,x ∉Q 时,x -∉Q ,()()()32D D x D ==,()()()32D D x D -==,()()()()D D x D D x =-,所以()()D D x 为偶函数,C正确;x =时,取1a =()()12D x a D +==,()(13D a x D -=-=,则()()D x a D a x +≠-,D 错误.故选:AC11.某班级到一工厂参加社会实践劳动,加工出如图所示的圆台12O O ,轴截面ABCD 为等腰梯形,且满足2224cm CD AB AD BC ====.下列说法正确的是()A.该圆台轴截面ABCD 的面积为2B.该圆台的表面积为211πcmC.该圆台的体积为3cmD.【答案】AB 【解析】【分析】求出圆台的高12O O 可判断A ;由圆台的表面积和体积公式可判断B ,C ;由内切圆的性质以及切线长定理易知轴截面ABCD 不存在内切圆可判断D .【详解】对于A ,由2224cm CD AB AD BC ====,可得高12O O ==则圆台轴截面ABCD 的面积为()214m 22⨯+=,故A 正确;对于B ,圆台的侧面积为()()2π1226πcm S =⋅+⨯=侧,又()22ππm1c S =⨯=上,()22π24πcm S=⋅=下,所以()26ππ41cm π1πS =++=表,故B 正确;对于C ,圆台的体积为()()3173π142πcm 33V =++=,故C 错误;对于D ,若圆台存在内切球,则必有轴截面ABCD 存在内切圆,由内切圆的性质以及切线长定理易知轴截面ABCD 不存在内切圆,故D 错误,故选:AB.三、填空题(本题共3小题,每小题5分,共15分)12.已知()12f x x=在点()()1,1f 处的切线为直线20x y t -+=,则=a __________.【答案】12-##-0.5【解析】【分析】结合题目条件,列出方程求解,即可得到本题答案.【详解】因为()12f xx =-,所以21()f x x'=+,因为()f x 在点()()1,1f 处的切线为直线20x y t -+=,所以1(1)12f a '=+=,解得12a =-.故答案为:12-13.已知力123,,F F F ,满足1231N ===F F F ,且123++=F F F 0,则12-=F F ________N.【解析】【分析】将123++=F F F 0变形后平方得到相应结论,然后将12-F F 平方即可计算对应的值.【详解】由123++=F F F 0,可得123+=-F F F ,所以()()22312-=+F F F ,化简可得222312122F =++⋅F F F F ,因为1231===F F F ,所以1221⋅=-F F ,所以12-====F F【点睛】本题考查向量中的力的计算,难度较易.本题除了可以用直接分析计算的方式完成求解,还可以利用图示法去求解.14.已知双曲线C :()222210,0x y a b a b -=>>的左右焦点分别为1F ,2F ,过1F 作x 轴的垂线交C 于点P﹒2OM PF ⊥于点M (其中O 为坐标原点),且有223PF MF =,则C 的离心率为______.【答案】622【解析】【分析】由向量垂直的坐标表示得出关于,,a b c 的齐次式后可得离心率.【详解】如图,易得2(,)b P c a -,2(,0)F c ,22(2,b PF c a=- ,设(,)M x y ,2(,)MF c x y =-- ,由223PF MF = 得2(2,3(,)b c c x y a-=--,223()3c c x b y a =-⎧⎪⎨-=-⎪⎩,解得2133x c b y a ⎧=⎪⎪⎨⎪=⎪⎩,即21(,)33b M c a ,21(,33b OM c a = ,又2OM PF ⊥,∴42222033b OM PF c a⋅=-= ,c e a =,222b c a =-代入得2222(1)0e e --=,因为1e >故解得622e +=,故答案为:2+.四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)15.在ABC 中,内角,,A B C 所对的边分别是,,a b c ,三角形面积为S ,若D 为AC 边上一点,满足,2AB BD BD ⊥=,且223cos 3a S ab C =-+.(1)求角B ;(2)求21AD CD+的取值范围.【答案】(1)2π3(2)3,12⎛⎤ ⎥⎝⎦【解析】【分析】(1)结合面积公式、正弦定理及两角和的正弦公式化简可得tan B =,进而求解即可;(2)在BCD △中由正弦定理可得1sin DC C=,在Rt △ABD 中,可得2sin AD A =,进而得到21sin sin A C AD CD +=+,结合三角恒等变化公式化简可得21πsin 3C AD CD ⎛⎫+=+ ⎪⎝⎭,进而结合正弦函数的图象及性质求解即可.【小问1详解】2cos 3a S ab C =-+ ,23sin cos 3a ab C ab C ∴=-+,即sin cos 3a b C b C =-+,由正弦定理得,3sin sin sin sin cos 3A B C B C =-+,()3sin sin sin sin cos 3B C B C B C ∴+=-+,cos sin sin sin 3B C B C ∴=-,sin 0C ≠,tan B ∴=由0πB <<,得2π3B =.【小问2详解】由(1)知,2π3B =,因为AB BD ⊥,所以π2ABD ∠=,π6DBC ∠=,在BCD △中,由正弦定理得sin sin DC BDDBC C=∠,即π2sin16sin sin DC C C==,在Rt △ABD 中,2sin sin AD A BD A==,sin sin 21sin si 22n 11A CC CA A D D∴++=+=,2π3ABC ∠=,π3A C ∴+=,21ππππsin sin sin sin sin cos cos sin sin sin 3333A C C C C C C C AD CD ⎛⎫⎛⎫∴+=+=-+=-+=+ ⎪ ⎪⎝⎭⎝⎭,π03C << ,ππ2π,333C ⎛⎫∴+∈ ⎪⎝⎭,πsin ,132C ⎛⎤⎛⎫∴+∈ ⎥ ⎪ ⎝⎭⎝⎦,所以21AD CD +的取值范围为3,12⎛⎤ ⎥ ⎝⎦.16.已知数列{}n a 的前n 项和为,0n n S a >,且2241n n n a a S +=-.(1)求{}n a 的通项公式;(2)设1n n n n S b a a +=的前n 项和为n T ,求n T .【答案】(1)21n a n =-(2)242n n n T n +=+【解析】【分析】(1)先用()1n +替换原式中的n ,然后两式作差,结合n a 与n S 的关系,即可得到{}n a 为等差数列,从而得到其通项.(2)由(1)的结论,求得n S 及1n a +,代入1n n n n S b a a +=化简,得到n T 的式子,裂项相消即可.【小问1详解】2241n n n a a S +=-Q ,2111241n n n a a S ++++=-,两式作差得:()()1120n n n n a a a a +++--=,102n n n a a a +>∴-=Q ,{}n a ∴成等差数列,又当1n =时,()2110a -=,所以11a =即()11221n a n n =+-⨯=-【小问2详解】由(1)知21n a n =-,则()()1212122n n n a a n n S n ++-===,即()()()()21111212142121n n n n S n b a a n n n n +⎡⎤===+⎢⎥-+-+⎢⎥⎣⎦1111482121n n ⎛⎫=+- ⎪-+⎝⎭,故1111111483352121n n T n n ⎛⎫=+-+-++- -+⎝⎭L 2111482148442n n n n n n n n +⎛⎫=+-=+= ⎪+++⎝⎭.17.已知椭圆2222:1(0)x y C a b a b +=>>过31,2⎛⎫ ⎪⎝⎭和62⎫⎪⎪⎭两点.12,F F 分别为椭圆的左、右焦点,P 为椭圆上的点(P 不在x 轴上),过椭圆右焦点2F 的直线l 与椭圆交于A B 、两点.(1)求椭圆的标准方程;(2)求AB 的范围.【答案】(1)22143x y +=(2)[]3,4【解析】【分析】(1)将点3(1,2代入椭圆方程,即可求出椭圆C 的标准方程;(2)分类讨论直线斜率是否为0,从而假设直线方程,与椭圆方程联立,利用韦达定理与弦长公式得到关于m 的关系式,再分析即可得解;【小问1详解】由题意可知,将点3(1,2代入椭圆方程,得222291416241a ba b⎧⎪+=⎪⎪⎨⎪⎪+=⎪⎩,解得224,3a b==,所以椭圆的标准方程为22143x y+=.【小问2详解】由(1)知()11,0F-,()21,0F,当直线l的斜率为0时,24AB a==,当直线l的斜率不为0时,设直线l的方程为1x my=+,()11,A x y,()22,B x y,联立221431x yx my⎧+=⎪⎨⎪=+⎩,消去x,得22(34)690m y my++-=,易得()22Δ636(34)0m m=++>,则12122269,3434my y y ym m--+==++,所以AB==2221212443434mm m+===-++,因为20m≥,所以2344m+≥,所以240134m<≤+,所以34AB≤<,综上,34AB≤≤,即AB的范围是[]3,4.18.《中国制造2025》提出“节能与新能源汽车”作为重点发展领域,明确了“继续支持电动汽车、燃料电池汽车发展,掌握汽车低碳化、信息化、智能化核心技术,提升动力电池、驱动电机、高效内燃机、先进变速器、轻量化材料、智能控制等核心技术的工程化和产业化能力,形成从关键零部件到整车的完成工业体系和创新体系,推动自主品牌节能与新能源汽车与国际先进水平接轨的发展战略,为我国节能与新能源汽车产业发展指明了方向.某新能源汽车制造企业为了提升产品质量,对现有的一条新能源零部件产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的新能源零部件产品中随机抽取了1000件,检测产品的某项质量指标值,根据检测数据整理得到频率直方图(如图):(1)从质量指标值在[)55,75的两组检测产品中,采用分层抽样的方法再抽取5件.现从这5件中随机抽取2件作为样品展示,求抽取的2件产品恰好都在同一组的概率.(2)经估计知这组样本的平均数为61x =,方差为2241s =.检验标准中55n x ns a ⎧⎫-=⨯⎨⎬⎩⎭,55n x ns b ⎡⎤+=⨯⎢⎥⎣⎦,N n *∈,其中[]x 表示不大于x 的最大整数,{}x 表示不小于x 的最小整数,s 值四舍五入精确到个位.根据检验标准,技术升级改造后,若质量指标值有65%落在[]11,a b 内,则可以判断技术改造后的产品质量初级稳定,但需要进一步改造技术;若有95%落在[]22,a b 内,则可以判断技术改造后的产品质量稳定,认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造成功?【答案】(1)25;(2)详见解析;【解析】【分析】(1)根据分层抽样确定抽取比例,然后运用组合求解即可;(2)根据题中公式,计算出区间并判段数据落在该区间的概率,然后与题中条件比较即可得出结论.【小问1详解】由题意可知[)[)55,6565,750.330.22P P ==,所以抽取的2件产品恰好都在同一组的概率为:223225C C 42C 105P +===;【小问2详解】因为2241s =,知16s ,则11611661165455755 5a b -+⎧⎫⎡⎤=⨯==⨯=⎨⎬⎢⎥⎩⎭⎣⎦,,该抽样数据落在[]45,75内的频率约为0.160.30.266%65%++=>,又22612166121653059055a b -⨯+⨯⎧⎫⎡⎤=⨯==⨯=⎨⎬⎢⎥⎩⎭⎣⎦,,该抽样数据落在[]30,90内的频率约为10.030.040.9393%95%--==<,,所以可以判断技术改造后的产品质量初级稳定,但不能判定生产线技术改造成功.19.如图,//AD BC ,且AD =2BC ,AD ⊥CD ,//EG AD 且EG =AD ,//CD FG 且CD =2FG ,DG ⊥平面ABCD ,DA =DC =DG =2.(1)若M 为CF 的中点,N 为EG 的中点,求证:MN //平面CDE ;(2)求平面EBC 和平面BCF 所夹角的正弦值;【答案】(1)证明见解析(2)1010【解析】【分析】(1)以D 为坐标原点,分别以DA 、DC 、DG 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,根据空间向量可证MN //平面CDE ;(2)利用平面的法向量可求出结果.【小问1详解】证明:依题意,以D 为坐标原点,分别以DA 、DC 、DG 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,如图:可得D (0,0,0),A (2,0,0),B (1,2,0),C (0,2,0),E (2,0,2),F (0,1,2),G (0,0,2),3(0,,1)2M ,N (1,0,2).依题意,DC =(0,2,0),DE =(2,0,2).设0n =(x ,y ,z )为平面CDE 的法向量,则0020220n DC y n DE x z ⎧⋅==⎪⎨⋅=+=⎪⎩ ,得0y =,令z =-1,得1x =,则0(1,0,1)n =- ,又3(1,,1)2MN =- ,可得00MN n ⋅= ,直线MN ⊄平面CDE ,所以MN //平面CDE .【小问2详解】依题意,可得(1,0,0)BC =- ,(1,2,2)BE =- ,(0,1,2)CF =- ,设111(,,)n x y z = 为平面BCE 的法向量,则11110220n BC x n BE x y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ ,得10x =,令11z =,得11y =,则(0,1,1)n =,设222(,,)m x y z = 为平面BCF 的法向量,则222020m BC x m CF y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ ,得20x =,令21z =,得22y =,则(0,2,1)m =,因此有cos ,||||m n m n m n ⋅<>=⋅ 2152=⨯31010=.于是10sin ,10m n <>= .所以平面EBC 和平面BCF 所夹角的正弦值为1010.。
2021新教材人教版高中物理必修第三册对应练习--5 带电粒子在电场中的运动

5带电粒子在电场中的运动基础过关练题组一带电粒子在电场中的加速1.如图所示,两平行金属板相距为d,电势差为U,一电子质量为m,电荷量为e,从O 点沿垂直于极板的方向射出,最远到达A点,然后返回,OA=h,此电子具有的初动能是()A.edℎUhC.eUdℎD.eUℎd2.(2020江西宜丰中学高二上月考)如图所示,在P板附近有一电子由静止开始向Q 板运动,则关于电子到达Q时的速率与哪些因素有关的下列解释中正确的是()A.两极板间的距离越大,加速的时间就越长,则电子获得的速率越大B.两极板间的距离越小,加速的时间就越短,则电子获得的速率越小C.两极板间的距离越小,加速度就越大,则电子获得的速率越大D.与两板间的距离无关,仅与加速电压U有关3.(2020福建师大附中高二上期末)在显像管的电子枪中,从炽热的金属丝不断放出的电子进入电压为U的加速电场,设其初速度为零,经加速后形成横截面积为S、电流为I的电子束。
已知电子的电荷量为e、质量为m,则在刚射出加速电场时,一小段长为Δl的电子束内的电子个数是()A.IΔleS √m2eUB.ISΔle√m2eUC.IeS √m2eUD.IΔle√m2eU题组二带电粒子在电场中的偏转4.如图所示,两金属板与电源相连接,电子从负极板边缘垂直电场方向射入匀强电场,且恰好从正极板边缘飞出。
现在使电子入射速度变为原来的两倍,而电子仍从原位置射入,且仍从正极板边缘飞出,则两极板长度应变为原来的()A.2倍B.4倍C.12D.145.(2020河北衡水高二上期中)如图所示,平行板电容器上极板带正电,从上极板的端点A释放一个带电荷量为+Q(Q>0)的粒子,粒子重力不计,以水平初速度v0向右射出,当它的水平速度与竖直速度的大小之比为1∶2时,恰好从下极板的端点B射出,则d与L之比为()A.1∶1B.2∶1C.1∶2D.1∶36.如图所示,有一电子(电荷量为e)经电压U0加速后,进入两块间距为d、电压为U 的平行金属板间。
(精)河北省武邑中学2018届高三下学期期中考试数学(理)试卷(含答案)

河北省武邑中学2018届高三下学期期中考试数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合},06|{2N x x x x A ∈>++-=,}2,1,0,1{-=B ,则=B A ( ) A .}2,1{ B .}2,1,0{ C .}1,0{ D .}2,1,0,1{- 2.已知实数n m ,满足53)24)((+=-+i i ni m ,则=+n m ( ) A .59 B .511 C .49 D .4113.给出下列命题:①已知R b a ∈,,“1>a 且1>b ”是“1>ab ”的充分条件;②已知平面向量,,“1||,1||>>”是“1||>+”的必要不充分条件; ③已知R b a ∈,,“122≥+b a ”是“1||||≥+b a ”的充分不必要条件; ④命题p :“R x ∈∃0,使100+≥x ex 且1ln 00-≤x x ”的否定为p ⌝:“R x ∈∀,都有1+<x e x 且1ln ->x ”.其中正确命题的个数是( ) A .0 B .1 C .2 D .34.若定义在R 上的偶函数)(x f 满足)()2(x f x f =+,且当]1,0[∈x 时,x x f =)(,则函数||log )(3x x f y -=的零点个数是( )A .6个B .4个C .3个D .2个 5.设函数)3cos()(ϕ+=x x f ,其中常数ϕ满足0<<-ϕπ.若函数)(')()(x f x f x g +=(其中)('x f 是函数)(x f 的导数)是偶函数,则ϕ等于( ) A .3π-B .65π-C .6π-D .32π- 6.执行如图的程序框图,如果输入的k b a ,,分别为3,2,1,输出的815=M ,那么判断框中应填入的条件为( )A .k n <B .k n ≥C .1+<k nD .1+≥k n 7.总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体编号为A .08B .07C .02D .018.已知R k ∈,点),(b a P 是直线k y x 2=+与圆32222+-=+k k y x 的公共点,则ab 的最大值为( ) A.15B.9C.1D. 35-9.若不等式组⎪⎩⎪⎨⎧≤-+≤+-≥+-08010502y x y x y x 所表示的平面区域存在点),(00y x ,使0200≤++ay x 成立,则实数a 的取值范围是( )A .1-≤aB .1-<aC .1>aD .1≥a10.北京某大学为第十八届四中全会招募了30名志愿者(编号分别是1,2,…,30号),现从中任意选取6人按编号大小分成两组分配到江西厅、广电厅工作,其中三个编号较小的人在一组,三个编号较大的在另一组,那么确保6号、15号与24号同时入选并被分配到同一厅的选取种数是( ) A .25 B .32 C .60 D .10011.已知在ABC Rt ∆中,两直角边1=AB ,2=AC ,D 是ABC ∆内一点,且060=∠DAB ,设),(R ∈+=μλμλ,则=μλ( ) A .332 B .33C .3D .32 12.已知函数)(x f 的定义域为D ,若对于)(),(),(,,c f b f a f D b a ∈∀分别为某个三角形的边长,则称)(x f 为“三角形函数”.给出下列四个函数:①)(ln )(32e x e x xf ≤≤=;②x x f cos 4)(-=;③)41()(21<<=x x x f ;④1)(+=x xe e xf .其中为“三角形函数”的个数是( )A .1B .2C .3D .4二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若y x ,满足约束条件⎪⎩⎪⎨⎧≤+≥+≥32320y x y x x ,则y x z -=的最小值是 .14.若5)1(-ax 的展开式中3x 的系数是80,则实数a 的值是 .15.已知几何体的三视图如图所示,其中俯视图为一正方形,则该几何体的表面积为 .16.若函数)(x f 的图象上存在不同的两点),(11y x A ,),(22y x B ,其中2211,,,y x y x 使得222221212121||y x y x y y x x +⋅+-+的最大值为0,则称函数)(x f 是“柯西函数”. 给出下列函数:①)30(ln )(<<=x x x f ;②)0(1)(>+=x xx x f ;③82)(2+=x x f ;④82)(2-=x x f .其中是“柯西函数”的为 .三、解答题 (本大题共6题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知数列}{n a 的前n 项和为n S ,且满足*),1(34N n a S n n ∈-=. (1)求数列}{n a 的通项公式; (2)令n n a b 2log =,记数列})1)(1(1{+-n n b b 的前n 项和为n T ,证明:2131<≤n T . 18.高二某班共有20名男生,在一次体检中这20名男生被平均分成两个小组,第一组和第二组男生的身高(单位:cm )的茎叶图如下:(1)根据茎叶图,分别写出两组学生身高的中位数;(2)从该班身高超过180cm 的7名男生中随机选出2名男生参加篮球队集训,求这2名男生至少有1人来自第二组的概率;(3)在两组身高位于)180,170[(单位:cm )的男生中各随机选出2人,设这4人中身高位于)180,175[(单位:cm )的人数为X ,求随机变量X 的分布列和数学期望.19.菱形ABCD 的对角线AC 与BD 交于点O ,6,2==AC AB ,点F E ,分别在CD AD ,上,45==CF AE ,EF 交BD 于点H ,将D E F ∆沿EF 折到EF D '∆位置,10'=OD .(1)证明:⊥H D '平面ABCD ; (2)求二面角C A D B --'的正弦值.20.设抛物线)0(42>=m mx y 的准线与x 轴交于1F ,抛物线的焦点2F ,以21,F F 为焦点,离心率21=e 的椭圆与抛物线的一个交点为)362,32(E ;自1F 引直线交抛物线于Q P ,两个不同的点,设F F 11λ=. (1)求抛物线的方程椭圆的方程; (2)若)1,21[∈λ,求||PQ 的取值范围. 21.已知函数21)ln(21)(2+--=ax a x x a x f . (1)设xx f x g 1)()(+=,求函数)(x g 的单调区间; (2)若0>a ,设))(,()),(,(2211x f x B x f x A 为函数)(x f 图象上不同的两点,且满足1)()(21=+x f x f ,设线段AB 中点的横坐标为0x ,证明:10>ax . 请考生在22、23二题中任选一题作答,如果都做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程已知直线l 的参数方程为⎩⎨⎧=+=ααsin cos t y t m x (t 为参数,πα<≤0),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 4=,射线)44(πϕπϕθ<<-=,4πϕθ+=,4πϕθ-=分别与曲线C交于C B A ,,三点(不包括极点O ). (1)求证:||2||||OA OC OB =+;(2)当12πϕ=时,若C B ,两点在直线l 上,求m 与α的值.23.选修4-5:不等式选讲已知函数|12|||)(-++=x m x x f . (1)当1=m ,解不等式3)(≥x f ; (2)若41<m ,且当]2,[m m x ∈时,不等式|1|)(21+≤x x f 恒成立,求实数m 的取值范围.数 学(理科)参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共4小题,每小题5分,共20分. 把答案填在答题卡中对应题号后的横线上.13.3- 14.2 15.23224++ 16.①④三、解答题:本大题共70分,解答应写出文字说明、证明过程或演算步骤. 17.解:(1)当1=n 时,有)1(34111-==a S a ,解得41=a , 当2≥n 时,有)1(3411-=--n n a S ,则 )1(34)1(3411---=-=--n n n n n a a S S a 整理得41=-n na a ∴数列}{n a 是以4=q 为公比,以41=a 为首项的等比数列∴)(444*1N n a n n n ∈=⨯=-. (2)由(1)有n a b nn n 24log log 22===,则)12(1121(21)12)(12(1)1)(1(1+--=-+=-+n n n n b b n n∴)12)(12(1531311+-++⨯+⨯=n n T n )121121()5131()311[(21+--++-+-=n n )1211(21+-=n 易知数列}{n T 为递增数列,∴211<≤n T T ,即2131<≤n T .18.(1) 第一组学生身高的中位数为1742176172=+, 第二组学生身高的中位数为5.1742175174=+; (2)记“这2名男生至少有1人来自第二组”为事件A ,761)(2723=-=C C A P ,∴这2名男生至少有1人来自第二组的概率为76; (3)X 的所有可能取值是0,1,2,3101)0(23252223===C C C C X P ,52)1(23251223221213=+==C C C C C C C X P ,3013)2(23251213122222=+==C C C C C C C X P ,151)3(23251222===C C C C X P X 的分布列为15153302521)(=⨯+⨯+⨯=X E . 19.解:(1)∵45==CF AE , ∴CDCFAD AE =,∴AC EF //, ∵四边形ABCD 为菱形, ∴BD AC ⊥,∴BD EF ⊥,∴DH EF ⊥,∴H D EF '⊥ ∵6=AC ,∴3=AO ;又5=AB ,OB AO ⊥,∴4=OB ,∴1=⋅=OD AOAEOH ,∴3'==H D DH , ∴222|'||||'|H D OH OD +=,∴H D OH '⊥,又∵H EF OH = , ∴⊥H D '平面ABCD .(Ⅱ)建立如图所示的空间直角坐标系:)0,3,1(),3,0,0('),0,3,1(),0,0,5(-A D C B ,)0,6,0(),3,3,1('),0,3,4(=-==AC AD AB ,设平面'ABD 的一个法向量为),,(1z y x n =,由⎪⎩⎪⎨⎧=⋅=⋅0011n AB n 得⎩⎨⎧=++-=+033034z y x y x ,取⎪⎩⎪⎨⎧=-==543z y x , ∴)5,4,3(1-=n ,同理可得平面C AD '的法向量为)1,0,3(2=n ,∴25571025|59||||||cos |2121=⨯+==n n θ,∴25952sin =θ. 20.解:(1)设椭圆的标准方程为)0(12222>>=+b a by ax ,由题意得⎪⎪⎩⎪⎪⎨⎧=-==+211924942222a b a a c b a ,解得⎪⎩⎪⎨⎧==3422b a∴椭圆的方程为13422=+y x ∴点2F 的坐标为)0,1(,∴1=m ,∴抛物线的方程是x y 42=(2)由题意得直线PQ 的斜率存在,设其方程为)0)(1(≠+=k x k y ,由⎩⎨⎧=+=xy x k y 4)1(2消去x 整理得0442=+-k y ky () ∵直线PQ 与抛物线交于两点, ∴016162>-∆k ,设),(),,(2211y x Q y x P ,则421=y y ①,ky y 421=+②, ∵F F 11λ=,)0,1(1-F ∴),1(),1(2211y x y x +=+λ ∴21y y λ=,③由①②③消去21,y y 得22)1(4+=λλk . ∴||PQ 22221221222121616)11(4))[(11())(11(k k ky y y y ky y k-+=-++=-+=441616k k -=,即=2||PQ 441616k k -,将22)1(4+=λλk 代入上式得, =2||PQ 16)21(16)12(16)4(222224-++=-++=-+λλλλλλλ,∵λλλ1)(+=f 在)1,21[∈λ上单调递减,∴)21()()1(f f f ≤<λ,即2512≤+<λλ, ∴<041716)21(2≤-++λλ, ∴217||0≤<PQ ,即||PQ 的取值范围为]217,0(. 21.解:(1) 21)ln(2)(2+-=ax a x a x g ,xax a x a a x g )2(2)('2-=-= ①0>a 时, )(x g 定义域为),0(+∞当)2,0(a x ∈时,0)('<x g ,故)(x g 在)2,0(a上单调递减; 当),2(+∞∈a x 时,0)('>x g ,故)(x g 在),2(+∞a上单调递增; ②0<a 时,)(x g 定义域为)0,(-∞当)2,(a x -∞∈时,0)('>x g ,故)(x g 在)2,(a-∞上单调递增; 当)0,2(a x ∈时,0)('<x g ,故)(x g 在)0,2(a上单调递减. (2)10>ax 2121212x ax a x x ->⇔>+⇔0)1(21)('222≥-=-+=a xx ax a x f ,故)(x f 在定义域),0(+∞上单调递增, 只需证:1)()1(2=+x f x f ,21)1(=af , 不妨设2110x ax <<< axa x x a ax x ax a a x f x a f x F ln 21)2ln(221)2(1)()2()(22--+-----=-+-=则0)2()1(4222)2(1)('2232222≤---=-+---=ax x ax ax a x a ax a x x F ax 1≥∀, 从而)(x F 在),1[+∞a上单调递减,故0)1()(2=<aF x F ,即()式. 22.解:(1)证明:依题意,ϕcos 4||=OA ,)4cos(4||πϕ+=OB ,)4cos(4||πϕ-=OC ,则=+||||OC OB ++)4cos(4πϕ||2cos 24)4cos(4OA ==-ϕπϕ(2)当12πϕ=时,C B ,两点的极坐标分别为)6,32(),3,2(ππ-,化为直角坐标)3,1(B ,)3,3(-C , 经过点C B ,的直线方程为)2(3--=x y , 又直线l 经过点)0,(m ,倾斜角为α,故2=m ,32πα=. 23.解:(1) 当1=m 时,|12||1|)(-++=x x x f ,则⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤---<-=)21(3)211(2)1(3)(x x x x x x x f由3)(≥x f 解得1-≤x 或1≥x ,即原不等式的解集为),1[]1,(+∞--∞ . (2)|1|)(21+≤x x f ,即|1||12|21||21+≤-++x x m x ,又]2,[m m x ∈且41<m 所以410<<m ,且0>x 所以|12|21|1|221--+≤+x x m x 即|12|2--+≤x x m令|12|2)(--+=x x x t ,则⎪⎪⎩⎪⎪⎨⎧≥-<<+=)21(3)210(13)(x x x x x t , 所以]2,[m m x ∈时, 13)()(min +==m m t x t , 所以13+≤m m ,解得21-≥m , 所以实数m 的取值范围是)41,0(.欢迎访问“高中试卷网”——。
2023版高考化学微专题小练习专练43难溶电解质的沉淀溶解平衡(含答案)
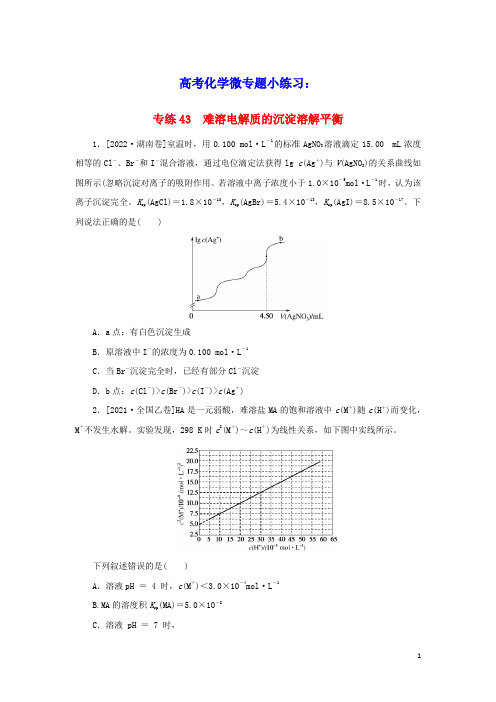
高考化学微专题小练习:专练43 难溶电解质的沉淀溶解平衡1.[2022·湖南卷]室温时,用0.100 mol·L-1的标准AgNO3溶液滴定15.00 mL浓度相等的Cl-、Br-和I-混合溶液,通过电位滴定法获得lg c(Ag+)与V(AgNO3)的关系曲线如图所示(忽略沉淀对离子的吸附作用。
若溶液中离子浓度小于1.0×10-5mol·L-1时,认为该离子沉淀完全。
K sp(AgCl)=1.8×10-10,K sp(AgBr)=5.4×10-13,K sp(AgI)=8.5×10-17。
下列说法正确的是( )A.a点:有白色沉淀生成B.原溶液中I-的浓度为0.100 mol·L-1C.当Br-沉淀完全时,已经有部分Cl-沉淀D.b点:c(Cl-)>c(Br-)>c(I-)>c(Ag+)2.[2021·全国乙卷]HA是一元弱酸,难溶盐MA的饱和溶液中c(M+)随c(H+)而变化,M+不发生水解。
实验发现,298 K时c2(M+)~c(H+)为线性关系,如下图中实线所示。
下列叙述错误的是( )A.溶液pH = 4 时,c(M+)<3.0×10-4mol·L-1B.MA的溶度积K sp(MA)=5.0×10-8C.溶液 pH = 7 时,c (M +)+c (H +)=c (A -)+c (OH -)D .HA 的电离常数K a (HA)≈2.0×10-43.[2021·全国甲卷]已知相同温度下,K sp (BaSO 4)<K sp (BaCO 3)。
某温度下,饱和溶液中-lg[c (SO 2-4 )]、-lg[c (CO 2-3 )]与-lg[c (Ba 2+)]的关系如图所示。
下列说法正确的是( )A .曲线①代表BaCO 3的沉淀溶解曲线B .该温度下BaSO 4的K sp (BaSO 4)值为1.0×10-10C .加适量BaCl 2固体可使溶液由a 点变到b 点D .c (Ba 2+)=10-5.1时两溶液中c (SO 2-4 )c (CO 2-3 )=10y 2−y 1 4.[2022·河北武邑中学高三月考]某温度下,向10 mL 0.1 mol ·L -1CuCl 2溶液中滴加0.1 mol ·L -1的Na 2S 溶液,滴加过程中溶液中-lg c (Cu 2+)与Na 2S 溶液体积(V )的关系如图所示,下列有关说法正确的是( )已知:lg 2=0.3,K sp (ZnS)=3×10-25mol 2·L -2。
河北省衡水市武邑中学2024届中考押题数学预测卷含解析

河北省衡水市武邑中学2024届中考押题数学预测卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(共10小题,每小题3分,共30分)1.某校体育节有13名同学参加女子百米赛跑,它们预赛的成绩各不相同,取前6名参加决赛.小颖已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的()A.方差B.极差C.中位数D.平均数2.如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,CD=3,BD=4,则⊙O的直径等于()A.5B.C.D.73.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC、∠BCD,则∠P的度数是( )A.60°B.65°C.55°D.50°4.已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是()A.方程有两个相等的实数根B.方程有两个不相等的实数根C.没有实数根D.无法确定5.超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程()A.0.8x﹣10=90 B.0.08x﹣10=90 C.90﹣0.8x=10 D.x﹣0.8x﹣10=906.如图1,在△ABC中,D、E分别是AB、AC的中点,将△ADE沿线段DE向下折叠,得到图1.下列关于图1的四个结论中,不一定成立的是()A.点A落在BC边的中点B.∠B+∠1+∠C=180°C.△DBA是等腰三角形D.DE∥BC7.如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()A.(3,1)B.(-4,1)C.(1,-1)D.(-3,1)8.正方形ABCD在直角坐标系中的位置如图所示,将正方形ABCD绕点A按顺时针方向旋转180°后,C点的坐标是( )A.(2,0) B.(3,0) C.(2,-1) D.(2,1)9.如图,在△ABC中,∠ABC=90°,AB=8,BC=1.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM 的平分线于点F,则线段DF的长为()A .7B .8C .9D .1010.半径为R 的正六边形的边心距和面积分别是( )A .32R ,2332RB .12R ,2332RC .32R ,234RD .12R ,234R 二、填空题(本大题共6个小题,每小题3分,共18分)11.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等”这一推论,如图所示,若S EBMF =1,则S FGDN =_____.12.如果正比例函数3)y k x =-(的图像经过第一、三象限,那么k 的取值范围是 __. 13.一个正多边形的一个外角为30°,则它的内角和为_____.14.分解因式2x 2+4x +2=__________.15.使得分式值242x x -+为零的x 的值是_________; 16.现有八个大小相同的矩形,可拼成如图1、2所示的图形,在拼图2时,中间留下了一个边长为2的小正方形,则每个小矩形的面积是_____.三、解答题(共8题,共72分)17.(8分)已知:如图,在矩形纸片ABCD 中,AB 4=,BC 3=,翻折矩形纸片,使点A 落在对角线DB 上的点F 处,折痕为DE ,打开矩形纸片,并连接EF .()1BD 的长为多少;()2求AE 的长;()3在BE 上是否存在点P ,使得PF PC +的值最小?若存在,请你画出点P 的位置,并求出这个最小值;若不存在,请说明理由.18.(8分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC 的顶点A 、C 的坐标分别为()4,5-,(1,3)-.请在如图所示的网格平面内作出平面直角坐标系;请作出ABC ∆关于y 轴对称的'''A B C ∆;点'B 的坐标为 .ABC ∆的面积为 .19.(8分)如图,已知点D 在反比例函数y=m x的图象上,过点D 作x 轴的平行线交y 轴于点B (0,3).过点A (5,0)的直线y=kx+b 与y 轴于点C ,且BD=OC ,tan ∠OAC=25. (1)求反比例函数y=m x和直线y=kx+b 的解析式; (2)连接CD ,试判断线段AC 与线段CD 的关系,并说明理由;(3)点E 为x 轴上点A 右侧的一点,且AE=OC ,连接BE 交直线CA 与点M ,求∠BMC 的度数.20.(8分)如图,已知反比例函数y=kx的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).求n和b的值;求△OAB的面积;直接写出一次函数值大于反比例函数值的自变量x的取值范围.21.(8分)如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°,从楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度(结果保留根号).22.(10分)某公司投入研发费用80万元(80万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为6元/件.此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y=﹣x+1.求这种产品第一年的利润W1(万元)与售价x(元/件)满足的函数关系式;该产品第一年的利润为20万元,那么该产品第一年的售价是多少?第二年,该公司将第一年的利润20万元(20万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润W2至少为多少万元.23.(12分)如图,四边形AOBC 是正方形,点C 的坐标是(42,0).正方形AOBC 的边长为 ,点A 的坐标是 .将正方形AOBC 绕点O 顺时针旋转45°,点A ,B ,C 旋转后的对应点为A′,B′,C′,求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积;动点P 从点O 出发,沿折线OACB 方向以1个单位/秒的速度匀速运动,同时,另一动点Q 从点O 出发,沿折线OBCA 方向以2个单位/秒的速度匀速运动,运动时间为t 秒,当它们相遇时同时停止运动,当△OPQ 为等腰三角形时,求出t 的值(直接写出结果即可).24.如图,已知一次函数1y k x b =+的图象与反比例函数2k y x =的图象交于点()4,A m -,且与y 轴交于点B ;点C 在反比例函数2k y x=的图象上,以点C 为圆心,半径为2的作圆C 与x 轴,y 轴分别相切于点D 、B .(1)求反比例函数和一次函数的解析式;(2)请连结OA ,并求出AOB ∆的面积;(3)直接写出当0x <时,210k k x b x+->的解集.参考答案一、选择题(共10小题,每小题3分,共30分)1、C【解题分析】13个不同的分数按从小到大排序后,中位数及中位数之后的共有7个数,故只要知道自己的分数和中位数就可以知道是否获奖了.故选C.2、A【解题分析】连接AO并延长到E,连接BE.设AE=2R,则∠ABE=90°,∠AEB=∠ACB,∠ADC=90°,利用勾股定理求得AD=,,再证明Rt△ABE∽Rt△ADC,得到,即2R==.【题目详解】解:如图,连接AO并延长到E,连接BE.设AE=2R,则∠ABE=90°,∠AEB=∠ACB;∵AD⊥BC于D点,AC=5,DC=3,∴∠ADC=90°,∴AD=,∴在Rt△ABE与Rt△ADC中,∠ABE=∠ADC=90°,∠AEB=∠ACB,∴Rt△ABE∽Rt△ADC,∴,即2R==;∴⊙O的直径等于.故答案选:A.【题目点拨】本题主要考查了圆周角定理、勾股定理,解题的关键是掌握辅助线的作法.3、A【解题分析】试题分析:根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,∴∠BCD+∠CDE=540°﹣300°=240°,∵∠BCD、∠CDE的平分线在五边形内相交于点O,∴∠PDC+∠PCD=(∠BCD+∠CDE)=120°,∴∠P=180°﹣120°=60°.故选A.考点:多边形内角与外角;三角形内角和定理.4、B【解题分析】试题分析:先求出△=42﹣4×3×(﹣5)=76>0,即可判定方程有两个不相等的实数根.故答案选B.考点:一元二次方程根的判别式.5、A【解题分析】试题分析:设某种书包原价每个x元,根据题意列出方程解答即可.设某种书包原价每个x元,可得:0.8x﹣10=90考点:由实际问题抽象出一元一次方程.6、A【解题分析】根据折叠的性质明确对应关系,易得∠A=∠1,DE是△ABC的中位线,所以易得B、D答案正确,D是AB中点,所以DB=DA,故C正确.【题目详解】根据题意可知DE是三角形ABC的中位线,所以DE∥BC;∠B+∠1+∠C=180°;∵BD=AD,∴△DBA是等腰三角形.故只有A错,BA≠CA.故选A.【题目点拨】主要考查了三角形的内角和外角之间的关系以及等腰三角形的性质.还涉及到翻折变换以及中位线定理的运用.(1)三角形的外角等于与它不相邻的两个内角和.(1)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.通过折叠变换考查正多边形的有关知识,及学生的逻辑思维能力.解答此类题最好动手操作.7、B【解题分析】作出图形,结合图形进行分析可得.【题目详解】如图所示:①以AC为对角线,可以画出▱AFCB,F(-3,1);②以AB为对角线,可以画出▱ACBE,E(1,-1);③以BC为对角线,可以画出▱ACDB,D(3,1),故选B.8、B【解题分析】试题分析:正方形ABCD绕点A顺时针方向旋转180°后,C点的对应点与C一定关于A对称,A是对称点连线的中点,据此即可求解.试题解析:AC=2,则正方形ABCD绕点A顺时针方向旋转180°后C的对应点设是C′,则AC′=AC=2,则OC′=3,故C′的坐标是(3,0).故选B.考点:坐标与图形变化-旋转.9、B【解题分析】根据三角形中位线定理求出DE,得到DF∥BM,再证明EC=EF=12AC,由此即可解决问题.【题目详解】在RT△ABC中,∵∠ABC=90°,AB=2,BC=1,∴AC=22AB BC +=2286+=10,∵DE 是△ABC 的中位线,∴DF ∥BM ,DE=12BC=3, ∴∠EFC=∠FCM , ∵∠FCE=∠FCM ,∴∠EFC=∠ECF ,∴EC=EF=12AC=5, ∴DF=DE+EF=3+5=2.故选B .10、A【解题分析】首先根据题意画出图形,易得△OBC 是等边三角形,继而可得正六边形的边长为R ,然后利用解直角三角形求得边心距,又由S 正六边形=6OBC S求得正六边形的面积.【题目详解】解:如图,O 为正六边形外接圆的圆心,连接OB ,OC ,过点O 作OH ⊥BC 于H ,∵六边形ABCDEF 是正六边形,半径为R ,∴∠BOC =3600166⨯︒=︒, ∵OB=OC=R ,∴△OBC 是等边三角形,∴BC=OB=OC =R ,60OBC ∠=︒∵OH ⊥BC ,∴在Rt OBH 中,sin sin 60∠=︒=OH OBH OB,即=OH R∴=OH R R ;∵2112224=⋅=⋅=OBC S BC OH R R R ,∴S 正六边形=226642=⨯=OBCSR R , 故选:A . 【题目点拨】本题考查了正多边形和圆的知识;求得正六边形的中心角为60°,得到等边三角形是正确解答本题的关键.二、填空题(本大题共6个小题,每小题3分,共18分)11、1【解题分析】根据从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等得S EBMF=S FGDN ,得S FGDN.【题目详解】∵S EBMF=S FGDN ,S EBMF =1,∴S FGDN =1.【题目点拨】本题考查面积的求解,解题的关键是读懂题意.12、k>1【解题分析】根据正比例函数y=(k-1)x 的图象经过第一、三象限得出k 的取值范围即可.【题目详解】因为正比例函数y=(k-1)x 的图象经过第一、三象限,所以k-1>0,解得:k >1,故答案为:k >1.【题目点拨】此题考查一次函数问题,关键是根据正比例函数y=(k-1)x 的图象经过第一、三象限解答.13、1800°【解题分析】 试题分析:这个正多边形的边数为=12,所以这个正多边形的内角和为(12﹣2)×180°=1800°.故答案为1800°.考点:多边形内角与外角.14、2(x+1)2。
河北省武邑中学2019届高三下学期第三次(三模)质检考试物理物理试题(答案+解析)

河北武邑中学2018-2019学年高三年级第三次质检考试理科综合能力测试1.下列说法正确的是A. 温度升高时放射性元素的半衰期变长B. β 衰变所释放的电子是原子核外的最外层电子C. α、β 和γ 三种射线中,γ 射线的穿透能力最强D. 某放射性元素的原子核有80 个,经过2 个半衰期后一定只剩20 个【答案】C【解析】【详解】放射性元素的半衰期与外界因素无关,选项A错误;β衰变所释放的电子是原子核内的中子转化为质子时放出的电子,选项B错误;α、β和γ三种射线中,γ射线的穿透能力最强,选项C正确;半衰期是大量原子核衰变的统计规律,对少量原子核的衰变不适用,选项D错误;故选C.2.个如图所示,质量为4kg的物体A静止在竖直的轻弹簧上面。
质量为1kg的物体B用细线悬挂起来,A、B紧挨在一起但A、B之间无压力。
某时刻将细线剪断,则细线剪断瞬间,B对A的压力大小为(g取l0m/s2)的()A. 0B. 50NC. 10ND. 8N【答案】D【解析】【详解】剪断细线前,A、B间无压力,则弹簧的弹力F=m A g=40N,剪断细线的瞬间,对整体分析,整体加速度:,隔离对B分析,m B g-N=m B a,解得:N=m B g-m B a=10-1×2N=8N.故D正确,ABC错误。
故选D。
3.如图所示,水平面上固定有一个斜面,从斜面顶端向右平抛一个小球,当初速度为v0时,小球恰好落到斜面底端,平抛后飞行的时间为t0。
现用不同的初速度v从该斜面顶端向右平抛这个小球,则下列图象中能正确表示平抛后飞行的时间t随v变化的函数关系的是()A. B.C. D.【答案】C【解析】试题分析:当小球落在斜面上时,有:,解得,与速度v成正比.当小球落在地面上,根据h=gt2得,,知运动时间不变.可知t与v的关系图线先是过原点的一条倾斜直线,然后是平行于横轴的直线.故C正确,ABD错误.故选C。
考点:平抛运动【名师点睛】此题是对平抛运动规律的考查,解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解。
高三化学一轮复习+微专题小练习 难溶电解质的沉淀溶解平衡原理及应用

专练47 难溶电解质的沉淀溶解平衡原理及应用1.[2024·湖北卷]CO2气氛下,Pb(ClO4)2溶液中含铅物种的分布如图。
纵坐标(δ)为组分中铅占总铅的质量分数。
已知c0(Pb2+)=2.0×10-5mol·L-1,p K a1(H2CO3)=6.4、p K a2(H2CO3)=10.3,p K sp(PbCO3)=12.1。
下列说法错误的是( )A.pH=6.5时,溶液中c(CO2-3 )<c(Pb2+)B.δ(Pb2+)=δ(PbCO3)时,c(Pb2+)<1.0×10-5mol·L-1C.pH=7时,2c(Pb2+)+c[Pb(OH)+]<2c(CO2-3 )+c(HCO-3 )+c(ClO-4 )D.pH=8时,溶液中加入少量NaHCO3(s),PbCO3会溶解2.[2024·吉林卷]25 ℃下,AgCl、AgBr和Ag2CrO4的沉淀溶解平衡曲线如图所示。
某实验小组以K2CrO4为指示剂,用AgNO3标准溶液分别滴定含Cl-水样、含Br-水样。
已知:①Ag2CrO4为砖红色沉淀;②相同条件下AgCl溶解度大于AgBr;③25 ℃时,p K a1(H2CrO4)=0.7,p K a2(H2CrO4)=6.5。
下列说法错误的是( )A.曲线②为AgCl沉淀溶解平衡曲线B.反应Ag2CrO4+H+⇌2Ag++HCrO-4的平衡常数K=10-5.2C.滴定Cl-时,理论上混合液中指示剂浓度不宜超过10-2.0mol·L-1D.滴定Br-达终点时,溶液中c(Br-)c(CrO2-4)=10-0.53.[2023·全国乙卷]一定温度下,AgCl和Ag2CrO4的沉淀溶解平衡曲线如图所示。
下列说法正确的是( )A.a 点条件下能生成Ag 2CrO 4沉淀,也能生成AgCl 沉淀B.b 点时,c (Cl -)=c (CrO 2-4 ),K sp (AgCl)=K sp (Ag 2CrO 4)C.Ag 2CrO 4+2Cl -⇌2AgCl +CrO 2-4 的平衡常数K =107.9D.向NaCl 、Na 2CrO 4均为0.1 mol·L -1的混合溶液中滴加AgNO 3溶液,先产生Ag 2CrO 4沉淀4.[2024·全国甲卷]将0.10 mmol Ag 2CrO 4配制成1.0 mL 悬浊液,向其中滴加0.10 mol·L -1的NaCl 溶液。
2023-2024学年河北省衡水市武邑中学高三(上)期中数学试卷【答案版】

2023-2024学年河北省衡水市武邑中学高三(上)期中数学试卷一、单选题.本题共8小题,每小题5分,共40分,将答案填涂在答题卡上相应位置. 1.设集合A ={x |x 2﹣1<0},B ={y |y =2x ,x ∈A },则A ∩B =( ) A .(0,1)B .(﹣1,2)C .(﹣1,+∞)D .(12,1)2.O 是正方形ABCD 的中心.若DO →=λAB →+μAC →,其中λ,μ∈R ,则λμ=( )A .﹣2B .−12C .−√2D .√23.若复数z =1﹣i +i 2﹣i 3+…+i 2022﹣i 2023,则复数z 的虚部为( ) A .0B .﹣1C .1D .i4.正项等比数列{a n }中的a 1,a 4031是函数f(x)=13x 3−4x 2+6x −3的极值点,则log √6a 2016=( )A .1B .2C .√2D .﹣15.已知公比不为1的等比数列{a n }的前n 项和为S n ,且满足a 2,2a 5,3a 8成等差数列,则3S 3S 6=( )A .134B .1312 C .94D .11126.已知正四面体A ﹣BCD 的内切球的表面积为36π,过该四面体的一条棱以及球心的平面截正四面体A ﹣BCD ,则所得截面的面积为( ) A .27√2B .27√3C .54√2D .54√37.已知x =tan1.04,a =log 3x ,b =2a ,c =sinb ,则a ,b ,c 的大小关系为( ) A .a <b <cB .a <c <bC .c <a <bD .c <b <a8.已知f (x )=2cos (2ωx −π6)+b sin2ωx +cos (2ωx +π2)(b >0,ω>0)又g (x )=f (x )﹣2√3,对任意的x 1,x 2均有g (x 1)+g (x 2)≤0成立,且存在x 1,x 2使g (x 1)+g (x 2)=0,方程f (x )+√3=0在(0,π)上存在唯一实数解,则实数ω的取值范围是( ) A .12<ω≤56B .12≤ω<56C .512<ω<34D .512<ω≤34二、多选题:本题共4小题,全部选对得5分,部分选对得2分,多选或错选均不得分,共计20分,将答案填涂在答题卡上相应位置.9.著名的“河内塔”问题中,地面直立着三根柱子,在1号柱上从上至下、从小到大套着n 个中心带孔的圆盘.将一个柱子最上方的一个圆盘移动到另一个柱子,且保持每个柱子上较大的圆盘总在较小的圆盘下面,视为一次操作.设将n 个圆盘全部从1号柱子移动到3号柱子的最少操作数为a n ,则( )A .a 2=3B .a 3=8C .a n +1=2a n +nD .a n =2n −110.折扇又名“纸扇”是一种用竹木或象牙做扇骨,㓞纸或者绫绢做扇面的能折叠的扇子.如图1,其平面图是如图2的扇形AOB ,其中∠AOB =150°,OA =2OC =2OD =2,点F 在弧AB 上,且∠BOF =120°,点E 在弧CD 上运动(包括端点),则下列结论正确的有( )A .OF →在OA →方向上的投影向量为√32OA →B .若OE →=λOC →+μOD →,则λ+μ∈[1,√6+√2] C .OD →⋅DA →=1−√3D .EF →⋅EB →的最小值是﹣311.已知复数z 1=cos α+i sin α,z 2=cos β+i sin β,z 3=cos γ+i sin γ,O 为坐标原点,z 1,z 2,z 3对应的向量分别为OZ 1→,OZ 2→,OZ 3→,则以下结论正确的有( ) A .|z 1•z 2|=|z 1|•|z 2|B .若z 1•z 2=z 1•z 3,则z 2=z 3C .若OZ 1→+OZ 2→=OZ 3→,则OZ 1→与OZ 2→的夹角为π3D .若OZ 1→+OZ 2→+OZ 3→=0→,则△Z 1Z 2Z 3为正三角形 12.已知函数f(x)=lnx −a(x+1)x−1(a ∈R),则下列说法正确的是( ) A .当a >0时,f (x )在(1,+∞)上单调递增B .若f (x )的图象在x =2处的切线与直线x +2y ﹣5=0垂直,则实数a =34C .当﹣1<a <0时,f (x )不存在极值D .当a >0时,f (x )有且仅有两个零点x 1,x 2,且x 1x 2=1 三、填空题:(本大题共4小题,每小题5分,共20分)13.已知函数f(x)={|log 3(x −1)|,1<x ≤4x 2−10x +25,x >4,若方程f (x )=n 有4个解分别为x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则(1x 1+1x 2)(x 3+x 4)= . 14.函数f(x)=ln(2x1+x+a)为奇函数,则实数a = . 15.在平行六面体ABCD ﹣A 1B 1C 1D 1中,以顶点A 为端点的三条棱AB ,AD ,AA 1两两夹角都为60°,且AB =2,AD =1,AA 1=3,M ,N 分别为BB 1,B 1C 1的中点,则MN 与AC 所成角的余弦值为 . 16.各项均为正数的等比数列{a n }的前n 项和为S n ,若a 2a 6=4,a 3=1,则(S n +94)22a n的最小值为 .四、解答题:(本大题满分70分,每题要求写出详细的解答过程否则扣分)17.(10分)函数f (x )=sin (ωx +φ)(ω>0,|φ|<π)的部分图象如图所示,其中MN ∥x 轴. (1)求函数y =f (x )的解析式;(2)将y =f (x )的图像向右平移π4个单位,再向上平移2个单位得到y =g (x )的图像,求g(π8)的值.18.(12分)在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且(a +b )(sin A ﹣sin B )=(c ﹣b )sin C . (1)求角A 的大小; (2)若sin B 是方程x 2−2x +99100=0的一个根,求cos C 的值. 19.(12分)函数y =2sin x ﹣1在(0,+∞)上的零点从小到大排列后构成数列{a n }. (1)求{a n }的通项公式;(2)设b n =a 2n ﹣1+a 2n ,求数列{b n }的前n 项和S n .20.(12分)如图1,在边长为4的菱形ABCD 中,∠DAB =60°,点M ,N 分别是边BC ,CD 的中点,AC ∩BD =O 1,AC ∩MN =G .沿MN 将△CMN 翻折到△PMN 的位置,连接P A ,PB ,PD ,得到如图2所示的五棱锥P ﹣ABMND .(1)在翻折过程中是否总有平面PBD ⊥平面P AG ?证明你的结论; (2)当四棱锥P ﹣MNDB 体积最大时,求点B 到面PDG 的距离;(3)在(2)的条件下,在线段P A 上是否存在一点Q ,使得平面QDN 与平面PMN 所成角的余弦值为√2929若存在,试确定点Q 的位置;若不存在,请说明理由. 21.(12分)已知数列{a n }的前n 项和为S n ,且S n +a n =3. (1)求{a n }的通项公式; (2)数列{b n }满足b 1=1,b n+1b n=n+22(n+1),设数列{b n }的前n 项和为T n ,证明:T n +a n ≥52.22.(12分)已知函数h (x )=ln (2ex ﹣e ),g (x )=2ax ﹣2a ,a ∈R .(1)若曲线f (x )=h (x )﹣g (x )在(1,f (1))处的切线与直线x ﹣y +1=0平行,求函数f (x )的极值;(2)已知f (x )=h (x )﹣g (x ),若f (x )<1+a 恒成立.求证:对任意正整数n >1,都有∑ln 2n k=1k 54<n(n +1).2023-2024学年河北省衡水市武邑中学高三(上)期中数学试卷参考答案与试题解析一、单选题.本题共8小题,每小题5分,共40分,将答案填涂在答题卡上相应位置. 1.设集合A ={x |x 2﹣1<0},B ={y |y =2x ,x ∈A },则A ∩B =( ) A .(0,1)B .(﹣1,2)C .(﹣1,+∞)D .(12,1)解:A ={x |x 2﹣1<0}=(﹣1,1),B ={y |y =2x ,x ∈A }=(12,2),则A ∩B =(12,1),故选:D .2.O 是正方形ABCD 的中心.若DO →=λAB →+μAC →,其中λ,μ∈R ,则λμ=( )A .﹣2B .−12C .−√2D .√2解:因为O 是正方形ABCD 的中心,所以O 为AC 的中点,所以DO →=DC →+CO →=AB →+12CA →=AB →−12AC →,因为DO →=λAB →+μAC →, 所以λ=1,μ=−12,所以λμ=1−12=−2.故选:A .3.若复数z =1﹣i +i 2﹣i 3+…+i 2022﹣i 2023,则复数z 的虚部为( ) A .0B .﹣1C .1D .i解:z =1−i +i 2−i 3+⋯+i 2022−i2023=1×(1−(−i)2024)1−(−i)=1×(1−1)1+i=0,所以复数z 的虚部为0. 故选:A .4.正项等比数列{a n }中的a 1,a 4031是函数f(x)=13x 3−4x 2+6x −3的极值点,则log √6a 2016=( )A .1B .2C .√2D .﹣1解:根据f(x)=13x 3−4x 2+6x −3,可得f ′(x )=x 2﹣8x +6,因为a 1,a 4031是函数f(x)=13x 3−4x 2+6x −3的极值点,所以a 1,a 4031是方程f ′(x )=x 2﹣8x +6=0的两个实数根,所以a 1a 4031=6,又因为数列{a n }为正项等比数列,所以a 1a 4031=a 20162=6,所以a 2016=√6,log √6a 2016=log √6√6=1. 故选:A .5.已知公比不为1的等比数列{a n }的前n 项和为S n ,且满足a 2,2a 5,3a 8成等差数列,则3S 3S 6=( )A .134B .1312 C .94D .1112解:公比q 不为1的等比数列{a n }的前n 项和为S n , a 2,2a 5,3a 8成等差数列, 可得4a 5=a 2+3a 8, 即为4a 1q 4=a 1q +3a 1q 7,即3q 6﹣4q 3+1=0,解得q 3=13(1舍去),则3S 3S 6=3•a 1(1−q 3)1−q •1−q a 1(1−q 6)=3•1−q 31−q 6=3•11+q 3=3•11+13=94, 故选:C .6.已知正四面体A ﹣BCD 的内切球的表面积为36π,过该四面体的一条棱以及球心的平面截正四面体A ﹣BCD ,则所得截面的面积为( ) A .27√2B .27√3C .54√2D .54√3解:设内切球半径为r ,由题意得4πr 2=36π, 设正四面体棱长为a ,由三角形的性质得BE =√32a ,BO ′=23BE =23×√32a =√33a , ∴在△ABO ′中,AO ′′=√AB 2−BO′2=√63a ,又AOOO′=31, ∴OO ′=14AO′=14×√63a =√612a ,∵OO ′=3,∴√612a =3,解得a =6√6.∴BE =√32a =9√2,AO ′=√63a =12,在△ABE 中,S =12×|BE|×|AO′|=12×12×9√2=54√2. 过该四面体的一条棱以及球心的平面截正四面体A ﹣BCD ,所得截面的面积为54√2. 故选:C .7.已知x =tan1.04,a =log 3x ,b =2a ,c =sinb ,则a ,b ,c 的大小关系为( ) A .a <b <cB .a <c <bC .c <a <bD .c <b <a解:因为π4<1.04<π3,x =tan1.04<tan π3=√3,且x =tan1.04>tan π4=1,则1<x <√3,0<a =log 3x <log 3√3=12,即0<a <12;所以1<b =2a <√2,即1<b <√2,所以12=sin π6<sin1<c =sinb <1,即12<c <1.所以a <c <b . 故选:B .8.已知f (x )=2cos (2ωx −π6)+b sin2ωx +cos (2ωx +π2)(b >0,ω>0)又g (x )=f (x )﹣2√3,对任意的x 1,x 2均有g (x 1)+g (x 2)≤0成立,且存在x 1,x 2使g (x 1)+g (x 2)=0,方程f (x )+√3=0在(0,π)上存在唯一实数解,则实数ω的取值范围是( ) A .12<ω≤56B .12≤ω<56C .512<ω<34D .512<ω≤34解:因为f(x)=2cos(2ωx −π6)+bsin2ωx +cos(2ωx +π2)=2sin(2ωx +π3)+(b −1)sin2ωx=bsin2ωx +√3cos2ωx =√b 2+3sin(2ωx +θ), 其中θ满足tanθ=√3b,又由任意的x1,x2均有g(x1)+g(x2)≤0成立,即任意的x1,x2均有f(x1)+f(x2)≤4√3成立,且存在x1,x2使g(x1)+g(x2)=0,可知f(x)最大值为2√3,所以√b2+3=2√3,又b>0,所以b=3,所以f(x)=2√3sin(2ωx+π6 ),当0<x<π时,π6<2ωx+π6≤2ωπ+π6,又f(x)在(0,π)上存在唯一实数x0使f(x0)=−√3,即sin(2ωx0+π6)=−12,所以7π6<2ωπ+π6≤11π6,所以12<ω≤56.故选:A.二、多选题:本题共4小题,全部选对得5分,部分选对得2分,多选或错选均不得分,共计20分,将答案填涂在答题卡上相应位置.9.著名的“河内塔”问题中,地面直立着三根柱子,在1号柱上从上至下、从小到大套着n个中心带孔的圆盘.将一个柱子最上方的一个圆盘移动到另一个柱子,且保持每个柱子上较大的圆盘总在较小的圆盘下面,视为一次操作.设将n个圆盘全部从1号柱子移动到3号柱子的最少操作数为a n,则()A.a2=3B.a3=8C.a n+1=2a n+n D.a n=2n−1解:将圆盘从小到大编为1,2,3,…号圆盘,则将第n+1号圆盘移动到3号柱时,需先将第1~n号圆盘移动到2号柱,需a n次操作;将第n+1号圆盘移动到3号柱需1次操作;再将1~n 号圆需移动到3号柱需a n 次操作,故a n +1=2a n +1,故C 错误; 由此递推关系及a 1=1可求得通项为a n =2n −1,故D 正确; 则a 2=3,a 3=7,故A 正确,B 错误. 故选:AD .10.折扇又名“纸扇”是一种用竹木或象牙做扇骨,㓞纸或者绫绢做扇面的能折叠的扇子.如图1,其平面图是如图2的扇形AOB ,其中∠AOB =150°,OA =2OC =2OD =2,点F 在弧AB 上,且∠BOF =120°,点E 在弧CD 上运动(包括端点),则下列结论正确的有( )A .OF →在OA →方向上的投影向量为√32OA →B .若OE →=λOC →+μOD →,则λ+μ∈[1,√6+√2] C .OD →⋅DA →=1−√3D .EF →⋅EB →的最小值是﹣3解:对于A 选项,由题意可知∠AOF =30°, 所以OF →在OA →方向上的投影向量为|OF →|cos30°⋅OA →|OA →|=√32OA →,即A 选项正确;对于B 选项,以点O 为坐标原点,OD 所在直线为x 轴建立如图所示的平面直角坐标系, 则D (1,0)、C(−√32,12),设点E (cos θ,sin θ),其中0≤θ≤5π6, 由OE →=λOC →+μOD →可得(cosθ,sinθ)=λ(−√32,12)+μ(1,0),所以{−√32λ+μ=cosθ12λ=sinθ,即{λ=2sinθμ=√3sinθ+cosθ,所以λ+μ=(2+√3)sinθ+cosθ=(√6+√2)sin(θ+π12), 又因为0≤θ≤5π6,则π12≤θ+π12≤11π12,所以√6−√24≤sin(θ+π12)≤1, 所以λ+μ=(√6+√2)sin(θ+π12)∈[1,√6+√2], 即B 选项正确;对于C 选项,DA →=OA →−OD →,所以OD →⋅DA →=OD →⋅(OA →−OD →)=OA →⋅OD →−OD →2=2×1×cos150°−12=−√3−1, 即选项C 错误;对于D 选项,E (cos θ,sin θ),其中0≤θ≤5π6,B (2,0)、F(−1,√3), 则EB →=(2−cosθ,−sinθ),EF →=(−1−cosθ,√3−sinθ),所以EB →⋅EF →=(2−cosθ)(−1−cosθ)−sinθ(√3−sinθ)=−2sin(θ+π6)−1,因为0≤θ≤5π6,则π6≤θ+π6≤π, 故当θ+π6=π2时,即θ=π3时,EF →⋅EB →取最小值为﹣2﹣1=﹣3,即D 选项正确.故选:ABD .11.已知复数z 1=cos α+i sin α,z 2=cos β+i sin β,z 3=cos γ+i sin γ,O 为坐标原点,z 1,z 2,z 3对应的向量分别为OZ 1→,OZ 2→,OZ 3→,则以下结论正确的有( ) A .|z 1•z 2|=|z 1|•|z 2|B .若z 1•z 2=z 1•z 3,则z 2=z 3C .若OZ 1→+OZ 2→=OZ 3→,则OZ 1→与OZ 2→的夹角为π3D .若OZ 1→+OZ 2→+OZ 3→=0→,则△Z 1Z 2Z 3为正三角形 解:因为z 1=cos α+i sin α,z 2=cos β+i sin β,z 3=cos γ+i sin γ, 所以|z 1|=|z 2|=|z 3|=1,则|OZ 1→|=|OZ 2→|=|OZ 3→|=1,对于A ,z 1•z 2=cos αcos β﹣sin αsin β+(cos αsin β+sin αcos β)i , 故|z 1•z 2|2=(cos αcos β﹣sin αsin β)2+(cos αsin β+sin αcos β)2=cos 2α•cos 2β﹣2cos α•cos β•sin α•sin β+sin 2α•sin 2β+cos 2α•sin 2β+2sin α•cos β•cos α•sin β+sin 2αcos 2β =cos 2α(cos 2β+sin 2β)+sin 2α(sin 2β+cos 2β), =cos 2α+sin 2α =1,|z 1|•|z 2|=1,所以|z 1•z 2|=|z 1|•|z 2|,故A 正确; 对于B ,若z 1•z 2=z 1•z 3,则z 2=z 1⋅z 3z 1=z 3,故B 正确; 对于C ,设OZ 1→与OZ 2→的夹角为θ,θ∈[0,π], 若OZ 1→+OZ 2→=OZ 3→,则(OZ 1→+OZ 2→)2=(OZ 3→)2, 即OZ 1→2+OZ 2→2=1,即1+1+2cos θ=1,所以cos θ=−12,所以θ=2π3,即OZ 1→与OZ 2→的夹角为2π3,故C 错误;对于D ,若OZ 1→+OZ 2→+OZ 3→=0→,则﹣(OZ 1→+OZ 2→)=OZ 3→, 则[﹣(OZ 1→+OZ 2→)]2=OZ 3→2,即(OZ 1→+OZ 2→)2=OZ 3→2,由C 选项可知OZ 1→与OZ 2→的夹角为2π3,同理OZ 2→与OZ 3→的夹角为2π3,OZ 1→与OZ 3→的夹角为2π3, 又|OZ 1→|=|OZ 2→|=|OZ 3→|=1,所以∠Z 1Z 2Z 3=∠Z 1Z 3Z 2=∠Z 2Z 1Z 3=π3,故D 正确.故选:ABD .12.已知函数f(x)=lnx −a(x+1)x−1(a ∈R),则下列说法正确的是( )A .当a >0时,f (x )在(1,+∞)上单调递增B .若f (x )的图象在x =2处的切线与直线x +2y ﹣5=0垂直,则实数a =34C .当﹣1<a <0时,f (x )不存在极值D .当a >0时,f (x )有且仅有两个零点x 1,x 2,且x 1x 2=1 解:因为f(x)=lnx −a(x+1)x−1(a ∈R),x >0且x ≠1, 所以f ′(x )=1x +2a (x−1)2, 对于A ,当a >0时,f ′(x )>0,所以f (x )在(0,1)和(1,+∞)上单调递增,故正确; 对于B ,因为直线x +2y ﹣5=0的斜率为−12,又因为f (x )的图象在x =2处的切线与直线x +2y ﹣5=0垂直, 令f ′(2)=12+2a =2,解得a =34,故正确; 对于C ,当﹣1<a <0时,不妨取a =−12,则f ′(x )=1x −1(x−1)2=x 2−3x+1x(x−1)2, 令f ′(x )=0,则有x 2﹣3x +1=0,解得x 1=32−√52,x 2=32+√52, 当x ∈(0,32−√52)时,f ′(x )>0,f (x )单调递增;当x ∈(32−√52,32+√52)时,f ′(x )<0,f(x )单调递减;所以此时函数有极值,故错误;对于D ,由A 可知,当a >0时,f (x )在(0,1)和(1,+∞)上单调递增, 当x >1时,f (e a )=a ﹣a (1+2e a −1)=−2ae a −1<0, f (e 3a +1)=3a +1﹣a (1+2e 3a+1−1)=(3a+1)(e 3a+1−1)−a(e 3a+1+1)e 3a+1−1>3a(e 3a+1−1)−a(e 3a+1+1)e 3a+1−1=2a(e 3a+1−2)e 3a+1−1>0,所以f (x )在(1,+∞)上有一个零点, 又因为当0<x <1时,f (e ﹣a )=﹣a ﹣a (1+2e −a −1)=2ae a −1>0,f (e﹣3a ﹣1)=﹣3a ﹣1﹣a (1+2e −3a−1−1)=﹣3a ﹣1﹣a (1+2e 3a+11−e 3a+1)=﹣3a ﹣1﹣a •1+e 3a+11−e 3a+1=− [(3a +1)+a •e 3a+1+11−e 3a+1 ]=−(3a+1)(1−e 3a+1)+a(e 3a+1+1)1−e 3a+1=−3a(1−e 3a+1)+a(e 3a+1+1)1−e 3a+1=−4a−2ae 3a+11−e 3a+1=2a(2−e 3a+1)e 3a+1−1<0,所以f (x )在(0,1)上有一个零点;所以f (x )有两个零点,分别位于(0,1)和(1,+∞); 设0<x 1<1<x 2, 令f (x )=0,则有lnx −a(x+1)x−1=0, 所以ln 1x−a(1x +1)1x−1=−lnx −a⋅x+1x1−x x=−lnx −a(x+1)1−x =−lnx +a(x+1)x−1=−(lnx −a(x+1)x−1)=0, 所以f (x )=0的两根互为倒数, 所以x 1x 2=1,故D 正确. 故选:ABD .三、填空题:(本大题共4小题,每小题5分,共20分)13.已知函数f(x)={|log 3(x −1)|,1<x ≤4x 2−10x +25,x >4,若方程f (x )=n 有4个解分别为x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则(1x 1+1x 2)(x 3+x 4)= 10 . 解:作出函数f (x )的大致图象,如下:可知,0<n <1且当1<x ≤4时,|log 3(x ﹣1)|=n 有2个解x 1,x 2; log 3(x 1﹣1)=﹣n ,log 3(x 2﹣1)=n , 得x 1=3−n+1,x 2=3n+1,∴1x 1+1x 2=13−n +1+13n +1=13n +1+3n 1+3n=1;当x >4时,由x 2﹣10x +21=n 有2个解x 3,x 4,根据图象的对称性,得x 3+x 4=10. ∴(1x 1+1x 2)(x 3+x 4)=1×10=10. 故答案为:10. 14.函数f(x)=ln(2x1+x+a)为奇函数,则实数a = ﹣1 . 解:根据题意,函数f(x)=ln(2x1+x+a)为奇函数,则f (x )+f (﹣x )=0, 即ln (2x 1+x +a )+ln (−2x1−x+a )=0,变形可得:a 2−(a+2)x 21−x 2=1,必有a =﹣1;故答案为:﹣1.15.在平行六面体ABCD ﹣A 1B 1C 1D 1中,以顶点A 为端点的三条棱AB ,AD ,AA 1两两夹角都为60°,且AB =2,AD =1,AA 1=3,M ,N 分别为BB 1,B 1C 1的中点,则MN 与AC 所成角的余弦值为 √9114. 解:∵M ,N 分别为BB 1,B 1C 1的中点,∴MN →=12BC 1→=12AD →+12AA 1→,AC →=AB →+AD →,∴MN →2=14AD →2+14AA 1→2+12AD →⋅AA 1→=14+94+12×1×3×cos60°=134,AC →2=AB →2+AD →2+2AB →⋅AD →=4+1+2×2×1×cos60°=7,MN →⋅AC →=(12AD →+12AA 1→)•(AB →+AD →)=12AD →2+12AB →⋅AD →+12AA 1→⋅AB →+12AA 1→⋅AD →=134,∴cos <MN →,AC →>=MN →⋅AC →|MN →||AC →|=134√132×7=√9114.∴直线MN 与AC 所成角的余弦值为√9114. 故答案为:√911416.各项均为正数的等比数列{a n }的前n 项和为S n ,若a 2a 6=4,a 3=1,则(S n +94)22a n的最小值为 8 .解:各项均为正数的等比数列{a n },由a 2a 6=4=a 42,即a 4=2, ∵a 3=1, ∴q =2,a 1=14,∴a n =14×2n ﹣1=2n ﹣3,S n =14(1−2n)1−2=2n ﹣2−14,∴(S n +94)2=(2n ﹣2+2)2=22(n ﹣2)+4×2n ﹣2+4,∴(S n +94)22a n=22(n−2)+4×2n−2+42n−2=2n ﹣2+42n−2+4≥2√2n−2⋅42n−2+4=4+4=8,当且仅当n =3时取等号,故答案为:8.四、解答题:(本大题满分70分,每题要求写出详细的解答过程否则扣分)17.(10分)函数f (x )=sin (ωx +φ)(ω>0,|φ|<π)的部分图象如图所示,其中MN ∥x 轴. (1)求函数y =f (x )的解析式;(2)将y =f (x )的图像向右平移π4个单位,再向上平移2个单位得到y =g (x )的图像,求g(π8)的值.解:(1)根据函数f (x )=sin (ωx +φ)(ω>0,|φ|<π)的部分图象,可得函数的图象关于直线x =−π2−π62=−π3对称,5π12+π3=34×2πω,∴ω=2.再根据五点法作图,可得2×5π12+φ=0,求得φ=−5π6, 故函数f (x )=sin (2x −5π6). (2)将y =f (x )的图像向右平移π4个单位,可得y =sin (2x −π2−5π6)=sin (2x −4π3)=sin (2x +2π3)的图象;再向上平移2个单位得到y =g (x )=sin (2x +2π3)+2的图像. 故g(π8)=sin 11π12+2=sin π12+2=sin (π3−π4)+2=(sin π3cos π4−cos π3sin π4)+2=(√32×√22−12×√22)+2=√6−√24+2.18.(12分)在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且(a +b )(sin A ﹣sin B )=(c ﹣b )sin C . (1)求角A 的大小; (2)若sin B 是方程x 2−2x +99100=0的一个根,求cos C 的值. 解:(1)∵(a +b )(sin A ﹣sin B )=(c ﹣b )sin C ,∴利用正弦定理化简得:(a +b )(a ﹣b )=c (c ﹣b ),即b 2+c 2﹣a 2=bc , ∴cos A =b 2+c 2−a 22bc =12,∵A ∈(0,π),∴A =π3.(2)∵x 2−2x +99100=0,解得:x 1=910,x 2=1110, ∵由sin B ≤1,得到sin B =910,可得cos B =±√1−sin 2B =±√1910, ∴cos C =﹣cos (A +B )=sin A sin B ﹣cos A cos B =√32×910−12×(±√1910)=9√3±√1920. 19.(12分)函数y =2sin x ﹣1在(0,+∞)上的零点从小到大排列后构成数列{a n }. (1)求{a n }的通项公式;(2)设b n =a 2n ﹣1+a 2n ,求数列{b n }的前n 项和S n . 解:(1)函数y =2sin x ﹣1的最小正周期为2π, 函数y =2sin x ﹣1在(0,2π)上的零点分别为π6,5π6,数列{a 2n ﹣1} 是以π6为首项,2π为公差的等差数列,即当n 为奇数时,a n =π6+n−12d =nπ−5π6; 数列{a 2n } 是以5π6为首项,2π为公差的等差数列,即当n 为偶数时,a n =5π6+n−22d =nπ−7π6. 综上a n ={nπ−5π6,n 为奇数nπ−7π6,n 为偶数;(2)b n =a 2n ﹣1+a 2n =4n π﹣3π, S n =(b 1+b n )n2=n(2n −1)π. 20.(12分)如图1,在边长为4的菱形ABCD 中,∠DAB =60°,点M ,N 分别是边BC ,CD 的中点,AC ∩BD =O 1,AC ∩MN =G .沿MN 将△CMN 翻折到△PMN 的位置,连接P A ,PB ,PD ,得到如图2所示的五棱锥P ﹣ABMND .(1)在翻折过程中是否总有平面PBD⊥平面P AG?证明你的结论;(2)当四棱锥P﹣MNDB体积最大时,求点B到面PDG的距离;(3)在(2)的条件下,在线段P A上是否存在一点Q,使得平面QDN与平面PMN所成角的余弦值为√2929若存在,试确定点Q的位置;若不存在,请说明理由.解:(1)在翻折过程中总有平面PBD⊥平面P AG,证明:折叠前,因为四边形ABCD是菱形,所以AC⊥BD,由于M,N分别是边BC,CD的中点,所以MN∥BD,所以MN⊥AC,折叠过程中,MN⊥GP,MN⊥GA,GP∩GA=G,GP,GA⊂平面P AG,所以MN⊥平面P AG,所以BD⊥平面P AG,由于BD⊂平面PBD,所以平面PBD⊥平面P AG.(2)当平面PMN⊥平面MNDB时,四棱锥P﹣MNDB体积最大,由于平面PMN∩平面MNDB=MN,GP⊂平面PMN,GP⊥MN,所以GP⊥平面MNDB,由于AG⊂平面MNDB,所以GP⊥AG,菱形ABCD边长为4,且∠DAB=60°,所以BD=4,AC=2√3,PG=CG=√3,在Rt△O1DG中,DG=√22+(√3)2=√7,所以S△PGD=12×√7×√3=√212,S△BDG=12×4×√3=2√3,设点B到面PDG的距离为h,则由等体积法有V B﹣PDG=V P﹣BDG,即13S△PDG×ℎ=13S△BDG×PG,即√212ℎ=2√3×√3,所以ℎ=4√21 7,所以点B到面PDG的距离为4√21 7.(3)存在,理由如下:在点G处有GA,GM,GP两两互相垂直,则以G为坐标原点建立如图所示空间直角坐标系,依题意可知P(0,0,√3),D(√3,−2,0),B(√3,2,0),N(0,−1,0),A(3√3,0,0),PA →=(3√3,0,−√3),设PQ =λP A (0≤λ≤1),则GQ →=GP →+PQ →=GP →+λPA →=(0,0,√3)+(3√3λ,0,−√3λ)=(3√3λ,0,√3−√3λ),平面PMN 的法向量为n 1→=(1,0,0),DQ →=(3√3λ−√3,2,√3−√3λ),DN →=(−√3,1,0), 设平面QDN 的法向量为n 2→=(x ,y ,z), 则{n 2→⋅DQ →=(3√3λ−√3)x +2y +(√3−√3λ)z =0n 2→⋅DN →=−√3x +y =0,故可设n 2→=(λ−1,√3λ−√3,3λ+1), 设平面QDN 与平面PMN 所成角为θ, 由于平面QDN 与平面PMN 所成角的余弦值为√2929, 所以cosθ=|n 1→⋅n 2→|n 1→|⋅|n 2→||=|λ−1|√(λ−1)+(√3λ−√3)2+(3λ+1)=√2929,解得λ=12或λ=3(舍去),所以当Q 是P A 的中点时,平面QDN 与平面PMN 所成角的余弦值为√2929.21.(12分)已知数列{a n }的前n 项和为S n ,且S n +a n =3. (1)求{a n }的通项公式; (2)数列{b n }满足b 1=1,b n+1b n=n+22(n+1),设数列{b n }的前n 项和为T n ,证明:T n +a n ≥52.解:(1)由S n +a n =3,当n =1时,S 1+a 1=3,解得a 1=32;当n ≥2时,S n ﹣1+a n ﹣1=3,相减得a n +a n ﹣a n ﹣1=0,即a n a n−1=12,∴数列{a n }是以32为首项,12为公比的等比数列,故a n =32n ,验证n =1时成立, 故a n =32n ; (2)b 1=1,b n+1b n=n+22(n+1),故b n =b n b n−1⋅b n−1b n−2⋅⋯⋅b 2b 1⋅b 1=(12)n−1(n+1n ⋅n n−1⋅n−1n−2⋅⋯⋅32)×1=n+12n (n ≥2), b 1=1适合上式,则b n =n+12n . ∴T n =22+322+423+⋯+n+12n , 12T n =222+323+424+⋯+n+12n+1,两式相减可得: 12T n =1+122+123+124+⋯+12n−n+12n+1=1+122(1−12n−1)1−12−n+12n+1=32−n+32n+1,∴T n =3−n+32n ,T n +a n =3−n 2n . 令c n =n 2n ,c n+1−c n =n+12n+1−n 2n =−n+12n+1,n ∈N *, 故c 1=c 2,且c n+1−c n =−n+12n+1<0,n ≥2,n ∈N *, c n 是从第二项开始单调递减数列,得(c n )max =c 1=c 2=12.故T n +a n =3−n 2n ≥3−12=52. 22.(12分)已知函数h (x )=ln (2ex ﹣e ),g (x )=2ax ﹣2a ,a ∈R .(1)若曲线f (x )=h (x )﹣g (x )在(1,f (1))处的切线与直线x ﹣y +1=0平行,求函数f (x )的极值;(2)已知f (x )=h (x )﹣g (x ),若f (x )<1+a 恒成立.求证:对任意正整数n >1,都有∑ln 2n k=1k 54<n(n +1).解:(1)由f (x )=ln (2ex ﹣e )﹣2ax +2a ,可得f ′(x)=22x−1−2a , 由条件可得f ′(1)=2﹣2a =1,即a =12,则f(x)=ln(2x −1)−x +2,f ′(x)=22x−1−1=−(2x−3)2x−1(x >12),令f′(x)=0可得x=3 2,当x>32时,f′(x)<0,当12<x<32时,f′(x)>0.所以f(x)在(32,+∞)上单调递减,在(12,32)上单调递增,所以f(x)的极大值为f(32)=ln2−32+2=ln2+12,无极小值.(2)证明:f(x)<1+a,即ln(2x﹣1)﹣a(2x﹣1)<0对任意的x>12恒成立,即a(2x﹣1)>ln(2x﹣1),其中x>1 2,令t=2x﹣1>0,则at>lnt,即at>lnt⇒a>lnt t,构造函数g(t)=lntt,则g′(t)=1−lnt2,令g′(t)=0,得t=e,列表如下:所以函数y=g(t)的单调递增区间为(0,e),单调递减区间为(e,+∞),所以g(t)max=g(e)=1 e ,所以a>1 e ,即a>1e时,ln(2x﹣1)<a(2x﹣1)恒成立,取a=25,则ln(2x−1)<2(2x−1)5对任意的x>12恒成立,令k=2x﹣1(k∈N*),则lnk<2k 5,所以ln1+ln2+ln3+⋯+ln(2n)<25(1+2+3+⋯+2n)=2n(1+2n)5<4n(n+1)5,所以∑2n k=154lnk<n(n+1),即∑ln2nk=1k54<n(n+1).。
河北省武邑中学2013届高三上学期期末考试化学试题

河北武邑中学2012~2013学年高三年级期末考试化学试题命题人:李红申审阅修改:张宏志2013-1-25说明:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
考试时间80分钟,总分100分。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
第II卷用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
3.考试结束,只交答题卷。
可能用到的数据:H:1 O:16 F:19 Cl:35.5 Na:23 Ca:40 Cu:64 Fe:56第I卷(选择题)(40分)选择题(每小题只有一个选项符合题意,共20×2分)1.化学与人们的生活密切相关,下列说法中不正确的是( )A.明矾常用做自来水的杀菌消毒剂B.服用铬含量超标的药用胶囊会对人对健康造成危害C.“血液透析”利用了胶体的性质D.钢铁在海水中比在河水中更易生锈2.下列选项中正确的是( )A.甲苯和二氯乙烯分子中所有原子共平面B.1—丁烯既能发生取代反应,又能发生加成反应,但不能被氧化C.由甲苯制三硝基甲苯和苯甲酸都属于取代反应D.分子式为C3H6Cl2的同分异构体有4种3.元素在周期表中的位置,反映了元素的原子结构和元素的性质,下列说法正确的是( ) A.同一元素不可能既表现金属性,又表现非金属性B.第三周期元素的最高正化合价等于它所处的主族序数C.短周期元素形成离子后,最外层电子都达到8电子稳定结构D.同一主族的元素的原子,最外层电子数相同,化学性质完全相同4.三氟化氮(NF3)是无色无味气体,它可由氨气和氟气反应制得:4NH3+3F2=NF3+3NH4F。
下列说法正确的是()A.NH4F的还原性比NH3强B.NF3的氧化性比F2强C .该反应中被氧化和被还原物质的物质的量之比为4∶3D .该反应中得到1 mol NF 3时,转移6 mol 电子 5.下列关于各实验装置图的叙述中正确的是( )A .装置①:常用于分离互不相溶的液体混合物B .装置②:可用于吸收NO 2或HCl 气体,并防止倒吸C .装置③:先从b 口进气集满CO 2,再从a 口进气,可收集NOD .装置④:可用来证明碳的非金属性比硅强 6.在密闭容器中进行反应:A(g)+3B(g)2C(g),有关下列图像的说法不正确...的是( )A .依据图a可判断正反应为放热反应b 中,虚线可表示使用了催化剂C .若正反应的△H <0,图cD .由图d 7.下列离子方程式正确的是( )A .向Ba(OH)2溶液中滴加NH 4HSO 4溶液至刚好沉淀完全:Ba 2+ + SO 42- = BaSO 4↓B .碳酸钡中加入稀硫酸:BaCO 3 + 2H + = Ba 2+ + H 2O + CO 2↑C .铜片插入硝酸银溶液:Cu + Ag + = Cu 2++ AgD .醋酸钠溶液中加入稀盐酸:CH 3COO - + H + = CH 3COOH 8.某温度下,水的离子积约为10-12,将V a L pH =2的硫酸溶液与V b L pH =11的NaOH溶液混合,若混合溶液的pH =10,体积是(V a +V b ) L ,则V a ∶V b 为( ) A .2∶11 B .11∶2 C .9∶2 D .2∶99.相对分子质量为128的有机物A 完全燃烧后只生成二氧化碳和水,若A 含有一个六元碳环且能与NaHCO 3溶液反应生成二氧化碳,则其环上的一溴代物有( )MTabM dMcA .5种B .4种C .3种D .2种10.下列溶液中,一定能大量共存的微粒组是( ) A .室温下,pH =1的溶液中:Na +、Fe 2+、NO 3-、SO 42-B .由水电离的c(H +)=1×10-13mol/L 的溶液中:Ca 2+、K +、Cl -、HCO 3-C .含有大量Fe 3+的溶液中:Al 3+、Cu 2+、Cl -、SO 42- D .c(Fe 3+) =0.1 mol/L 的溶液中:K +、ClO -、SO 42-、SCN -11.X 、Y 、Z 是位于不同周期的三种短周期元素,且原子序数逐渐增大,X 、Z 属于同一主族,三种元素可以形成原子个数比为1∶1∶1的化合物W 。
河北省武邑中学2025届高三语文专题复习作文积累2024

作文积累【文题设计】阅读下面的材料,依据自己的感悟和联想,写一篇不少于800字的文章。
(60分)某书店开启24小时经营模式。
两年来,每到深夜,当大部分顾客离去,有一些人却走进书店。
他们中有喜爱夜读的市民,有自习的高校生,有外来务工人员,也有流浪者和拾荒者。
书店从来不驱逐任何人,工作人员说:“有些人常常看着看着就睡着了,但他们只要来看书,哪怕只看一眼,只看一行,都是我们的读者;甚至有的人只是进来休息,我们也觉得自己的工作是有意义的。
”要求:①选好角度,自拟立意;②自拟题目;③除诗歌外,问题不限;④问题特征明显。
【材料背景】24小时书店不驱逐任何人,拾荒者也可在此过夜。
这两天,合肥新华书店三孝口店因善意地接纳而爆红网络,被网友们称为“暖心书店”。
12月22日,在接受记者采访时,合肥新华书店三孝口店副店长毕升思说,来店里的拾荒、流浪人员也会看书,也会常常看着看着书就入睡了,“只要他们来看书,哪怕只看一页、只看一行,我们都觉得自己的工作有意义。
”毕升思今年26岁,戴着黑框眼镜,说起话来很温柔,2012年高校毕业不久,她就来到三孝口店工作,见证了书店的转型发展。
“暖心书店”的夜晚片段,通过照片在网上爆红,但在她看来,那只是她跟同事700多天坚守中的一般一晚。
作为安徽新华发行集团旗下首家“实体书店提升转型”的示范,合肥新华书店三孝口店于2013年6月重装开业,力图打造城市文化生活科技体验中心。
2014年10月31日,书店起先24小时运营,成为中部地区第一家全天候书店。
“24小时书店,作为一座城市的精神文化地标,是深夜里城市的一盏明灯”,这个理念如今已经深化书店50多名员工的心中。
对员工们而言,这盏“明灯”对全部人发光,不管你是衣着光鲜,还是衣衫褴褛。
毕升思说,在书店转型为24小时书店时,他们就曾预判会有拾荒、流浪人员过来,当时他们的选择就是接纳。
两年多来,每晚到店里来过夜的拾荒、流浪人员有三四十人,比较固定的有一半,另一半多是临时在这里过夜。
名句默写和文学常识带答案

名句默写和文学常识带答案 名句默写和文学常识 1. (2016 届河北省武邑中学高三上学期周考)补写出下列句子中的空缺 部分。
①杜甫在《望岳》中,借齐鲁大地烘托泰山拔地而起,参天耸立形象的语句 是: ,。
②《师说》中以为子择师和自己不从师作对比,韩愈直接点明自己的态度, 认为这样做,最终导致的结果是: , 。
③《登高》中道出诗人心中的自身之苦和国运之恨,无限悲凉难以排遣的句 子是: ,。
2. (2016 届江西省高安中学、玉山县第一中学、临川区第一中学等九校 2016 届高三下学期联考)补写出下列句子的空缺部分。
(6 分) ⑴《离骚》中用“ ,”两句来直接表白自己宁死也不与小人们同流 合污的 心志。
⑵ 《赤壁赋》 中描写诗人泛舟江上随意飘荡自由来去的情景的两句是: “, 。
” ⑶《渔家傲?秋思》中用“ , ”两句,点出了“塞下”的地域性的特点, 并以“异”字领起全篇,为下片怀乡思归之情埋下了伏线。
3. (2016 届海南省海口市湖南师大附中海口中学高三第一次模拟)补写 出下列句子中的空缺部分。
(6 分) (1)《生于忧患,死于安乐》中“ , ”两句,大意是:心意困苦,思绪 阻塞,然后才能有所行为;看到他的脸色,听到他的声音,然后人们才了解他。
(2)《氓》中“ , ”两句,以河流有岸、湿地有边比喻凡事都有底线, 暗示女主人公对负心男子的忍耐已经到了极限。
(3)《师说》中“三人行,则必有我师”语见《论语·述而》,原文为: “三人行, 。
择其善者而从之, 。
” 4. (2016 届山东省枣庄第八中学南校区高三 1 月月考)补写出下列句子 中的空缺部分。
(6 分) (1)在《永遇乐·京口北固亭怀古》感叹东吴那个强盛的局面,孙权那个 英雄、风流余韵,都经历了无数的风雨,一去不返了的句子是: _________ , ________。
(2) 《蜀道难》 中写水石相激、 山谷轰鸣的惊险情景的句子是: _________, ________。
河北省武邑中学2025届高三语文课外文言文复习习题23

课外文言文复习一、阅读下面的文言文,完成1~4题。
(19分)完颜昌,本名挞懒,穆宗①子。
宗翰袭辽主于鸳鸯泺,辽都统马哥奔捣里,挞懒收其群牧。
宗翰使挞懒追击之,不及,获辽枢密使...得里底及其子以还。
诏增赐银牌十。
又降遥辇二部,破兴中兵,降建州官属,得山砦二十,村堡五百八十。
挞懒请以遥辇九营为九猛安②。
上以夺邻有功,使领四猛安,五猛安之都帅,命挞懒择人授之。
挞懒与刘彦宗举萧公翊为兴中尹,郡府各以契丹、汉官摄治,上皆从之。
及宗翰、宗望伐宋,挞懒为六部路都统。
宗望已受宋盟,军还,挞懒乃归中京。
天会四年八月,挞懒、阿里刮破宋兵二万于杞,覆其三营,获京东路.都总管胡直孺及其二子与南路都统制隋师元及其三将,遂克拱州,降宁陵,破睢阳。
宋兵来复睢阳又击走之擒其将宋二帝已降大军北还挞懒为元帅左监军徇地山东取密州天会十五年为左副元帅,封鲁国王。
明年,挞懒朝京师,倡议以废齐旧地与宋,熙宗命群臣议,会东京留守宗隽来朝,与挞懒合力,宗干等争之不能得。
宗隽曰:我以地与宋,宋必德我。
”宗干折之曰:“我俘宋人父兄,怨非一日。
若复资以土地,是助仇也,何德之有。
勿与便。
”挞懒弟勖亦以为不行。
既退,挞懒责勖曰:“他人尚有从我者,汝乃异议乎。
”勖曰:“苟利囯家,岂敢私邪。
”是时,太宗长子宗磐为宰相,位在宗干上,挞懒、宗隽附之,竟执议以河南、陕西地与宋。
久之,宗磐跋扈尤甚,宗隽亦为丞相,挞懒持兵柄,谋反有状。
宗磐、宗隽皆伏诛,诏以挞懒属尊,有大功,因释不问,出为行台..慰遣。
..尚书左丞相,手诏节选自《金史·完颜昌传》)【注】①穆宗:金太祖完颜旻的叔父盈哥。
②猛安:金时一种军政合一的社会基层编制单位1.下列对文中画波浪线部分的断句,正确的一项是(3分)A. 宋兵来复睢阳/又击走之/擒其将/宋二帝已降/大军北还/挞懒为元帅左监军/徇地山东/取密州B. 宋兵来复/睢阳又击走之/擒其将/宋二帝已降/大军北还/挞懒为元帅/左监军徇地山东/取密州C. 宋兵来复睢阳/又击走之/擒其将/宋二帝已降大军/北还/挞懒为元帅左监军/徇地山东/取密州D. 宋兵来复/睢阳又击走之/擒其将宋二帝/已降大军/北还/挞懒为元帅左监军/徇地山东/取密州2.下列对文中加点词语的相关内容的解说,不正确的一项是(3分)A. 枢密使,中国古代官名,负责统帅全国军政,辽时为最高朝官。
河北武邑中学2025届化学高三上期末复习检测试题含解析

河北武邑中学2025届化学高三上期末复习检测试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(共包括22个小题。
每小题均只有一个符合题意的选项)1、给定条件下,下列选项中所示的物质间转化均能一步实现的是()A.S SO2BaSO4B.SiO2H2SiO3Na2SiO3(aq)C.MgCl2•6H2O MgCl2MgD.N2NO2HNO32、下列有关物质的性质与用途具有对应关系的是A.NH4Cl溶液呈酸性,可用于去除铁锈B.SO2具有还原性,可用于漂白纸张C.Al2O3是两性氧化物,可用作耐高温材料D.Na2SiO3溶液呈碱性,可用作木材防火剂3、下列垃圾或废弃物的处理不符合...环保节约理念的是()A.废纸、塑料瓶、废铁回收再利用B.厨余垃圾采用生化处理或堆肥C.稻草、农膜和一次性餐具露天焚烧D.废电池等有毒有害垃圾分类回收4、阿斯巴甜(Aspartame,结构简式如图)具有清爽的甜味,甜度约为蔗糖的200倍.下列关于阿斯巴甜的错误说法是A.在一定条件下能发生取代反应、加成反应B.酸性条件下的水解产物中有两种氨基酸C.一定条件下既能与酸反应、又能与碱反应D.分子式为C14H18N2O3,属于蛋白质5、天然气是一种重要的化工原料和燃料,常含有少量H2S。
一种在酸性介质中进行天然气脱硫的原理示意图如图所示。
下列说法正确的是A.脱硫过程中Fe2(SO4)3溶液的pH逐渐减小B.CH4是天然气脱硫过程的催化剂C.脱硫过程需不断补充FeSO4D.整个脱硫过程中参加反应的n(H2S):n(O2)=2:16、现有短周期主族元素X、Y、Z、R、T。
R原子最外层电子数是电子层数的2倍;Y与Z能形成Z2Y、Z2Y2型离子化合物,Z与T形成的Z2T 化合物能破坏水的电离平衡,五种元素的原子半径与原子序数的关系如图所示,下列推断正确的是A.原子半径和离子半径均满足:Y<ZB.Y的单质易与R、T的氢化物反应C.最高价氧化物对应的水化物的酸性:T<RD.由X、R、Y、Z四种元素组成的化合物水溶液一定显碱性7、单质铁不同于铝的性质是A.遇冷的浓硫酸钝化B.能与氢氧化钠反应C.能与盐酸反应D.能在氧气中燃烧8、常温下,下列有关溶液中微粒的物质的量浓度关系错误的是()A.pH为5的NaHSO3溶液中:c(HSO3-)>c(H2SO3)>c(SO32-)B.向NH4Cl溶液中加入NaOH固体至pH=7:c(Cl-)>c(NH4+)>c(Na+)=c(NH3·H2O)>c(OH-)=c(H+)C.将等体积、等物质的量浓度的CH3COONH4与NaCl溶液混合,pH=7:c(CH3COO-)+c(Na+)=c(Cl-)+c(NH4+) D.20mL0.1mol/LNH4HSO4溶液与30mL0.1mol/LNaOH溶液混合,测得pH>7:c(NH4+)>c(NH3·H2O)>c(OH-)>c(H+) 9、短周期元素W、Ⅹ、Y、Z的原子序数依次增大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北武邑中学2015-2016学年高三周日考试(2016.1.17)数学试题满分150分本试卷分为第I卷(选择题)和第II卷(非选择题)两部分.满分150分,考试用时120分钟.答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在答题卡和答题纸规定的地方.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z满足z=(i为虚数单位),则z的共轭复数的虚部是()A.B.-C.12 D.12-2. 以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于()A .π2B .πC .2D .13.在等差数列{}n a 中,,3321=++a a a 165302928=++a a a ,则此数列前30项和等于( )A .810B .840C .870D .9004.设:12,:21xp x q <<>,则p 是q 成立的(A )充分不必要条件(B )必要不充分条件 (C )充分必要条件(D )既不充分也不必要条件5.设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=()(A )3(B )6(C )9(D )12 6.将函数x y sin =的图像左移2π个单位,得到函数)(x f y =的图像,则下列说法正确的是() A .)(x f y =是奇函数B .)(x f y =的周期是π C .)(x f y =的图像关于直线2π=x 对称D .)(x f y =的图像关于)0,2(π-对称A .2或32-B .32C .-2或32D .27-7..若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A .10cm 3B .20cm 3C .30cm 3D .40cm 38.下列命题中正确的个数是()①过异面直线a,b 外一点P 有且只有一个平面与a,b 都平行;②异面直线a,b 在平面α内的射影相互垂直则a ⊥b ;③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥; ④直线a,b 分别在平面α,β内,且a ⊥b 则α⊥β; A .0B .1C .2D .39.等比数列{}n a 的各项均为正数,且299a a ⋅=,则3132310log log log a a a +++L =( ) A .12 B .10 C .8 D .2+3log 510.设函数f (x )=12x 2-9ln x 在区间[a -1,a +1]上单调递减,则实数a 的取值范围是( )A .1<a ≤2B .a ≥4C .a ≤2D .0<a ≤3第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.请把将答案填在答题卡的相应的横线上.11.已知数列{}n a 的前n 项和2133n n S a =+,则{}n a 的通项公式n a =________. 12.已知1tan 2,tan()7ααβ=-+=,则tan β的值为________.13.菱形ABCD 的边长为2,60A ∠=︒,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM AN ⋅u u u u r u u u r的最大值为____________.14.若集合},4,3,2,1{},,,{=d c b a 且下列四个关系:①1=a ;②1≠b ;③2=c ;④4≠d 有且只有一个是正确的,则符合条件的有序数组),,,(d c b a 的个数是_______.15.已知函数()1ax f x e x =--,(0≠a ).若对一切0)(,≥∈x f R x 恒成立,则a 的取值集合为 .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知f(x)=3sin ωx -2sin2ωx2(ω>0)的最小正周期为3π.(1)当x ∈[π2,3π4]时,求函数f(x)的最小值;(2)在△ABC 中,若f(C)=1,且2sin2B =cosB +cos(A -C),求sinA 的值.17.(本小题满分12分)已知函数2()sin(2)4sin 2(0)6f x x x πωωω=--+>,其图象与x 轴相邻两个交点的距离为2π. (1)求函数()f x 的解析式;(2)若将()f x 的图象向左平移(0)m m >个长度单位得函数()g x 的图象恰好经过点(,0)3π-,求当m 取得最小值时,()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调增区间.18.已知函数()2cos sin 3f x x x x π⎛⎫=⋅+-+ ⎪⎝⎭x R ∈.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在闭区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.19.(本小题满分12分)如图,在四棱柱1111ABCD A B C D -中,侧面11ADD A ⊥底面ABCD ,11D A D D ==ABCD 为直角梯形,其中// , BC AD AB AD ⊥,222AD AB BC ===,为AD 中点.ODCBAD 1C 1B 1A 1(1)求证:1//AO 平面1AB C;(2)求锐二面角C D C A --11的余弦值.20.(本小题满分12分)已知数列{}n a 满足:*121113,,2(2,)44n n n a a a a a n n N +-===+≥∈,数列{}nb 满足:10b <,*13(2,)n n b b n n n N --=≥∈,数列{}n b 的前n 项和为nS .(1)求证:数列}{n n a b -为等比数列;(2)求证:数列}{n b 为递增数列;(3)若当且仅当3n =时,nS 取得最小值,求1b 的取值范围.21.(本小题满分14分)已知函数2()ln f x x ax =- (1)求()f x 的单调区间;(2)设()()1(0)g x f x x a =-+≥,l 是曲线()y g x =的一条切线,证明()y g x =上的任意一点都不能在直线l 的上方;(3)当1a =时,方程[]22()(12)m x f x m x +=-有唯一实数解,求正数m 的值.河北武邑中学2015-2016学年高三周日考试(1.17)数学试题答案1. D2.A3.B4.A5.C6.D7.B8.A9.B 10.A 11.1(2)n -- 12.313.13. 914. 615.{}116..解∵f(x)=3sin(ωx)-2·1-cos ωx 2=3sin(ωx)+cos(ωx)-1=2sin(ωx +π6)-1,由2πω=3π得ω=23,∴f(x)=2sin(23x +π6)-1. (1)由π2≤x ≤3π4得π2≤23x +π6≤2π3,∴当sin(23x +π6)=32时,f(x)min =2×32-1=3-1.…………6分(2)由f(C)=2sin(23C +π6)-1及f(C)=1,得sin(23C +π6)=1,而π6≤23C +π6≤5π6,所以23C +π6=π2,解得C =π2. 在Rt △ABC 中,∵A +B =π2,2sin2B =cosB +cos(A -C),∴2cos2A -sinA -sinA =0,∴sin2A +sinA -1=0,解得sinA =-1±52.∵0<sinA<1,∴sinA =5-12.…………12分17.17.解:(1)函数231()sin(2)4sin 2(0)2cos 2621cos 23342sin 2cos 23)2223f x x x x xx x x x πωωωωωωπωωω=-+>=--+=+=+g g g ,..........4分根据图象与x 轴相邻两个交点的距离为2π,可得函数的最小周期为2222ππω⨯=,求得1ω=,故函A 1B 1C 1D 1ABCDO数()3sin(2)3f x x π=+...................6分 (2)将()f x 的图象向左平移(0)m m >个长度单位得到函数()3sin 2()3sin(22)33g x x m x m ππ⎡⎤=++=++⎢⎥⎣⎦的图象,...............7分再根据()g x 的图象恰好经过点(,0)3π-,可得sin(2)03m π=g ,故2,()3sin(2)63m g x x ππ==+,.................................8分再结合7,612x ππ⎡⎤∈-⎢⎥⎣⎦,可得增区间为,612ππ⎡⎤--⎢⎥⎣⎦、57,1212ππ⎡⎤⎢⎥⎣⎦......................12分 18.18.(1)π=T (2)2141—,最小值最大值是 19.(1)证明:如图,连接 , CO AC ,则四边形ABCO 为正方形,所以11OC AB A B ==,且11////OC AB A B ,………2分故四边形11A B CO为平行四边形,所以11//A O B C.又1AO ⊄平面1AB C ,1B C ⊂平面1AB C,所以1//A O 平面1AB C.……………5分 (2)因为11 , D A D D O =为AD 的中点,所以1 D O AD⊥,又侧面11ADD A ⊥底面ABCD ,交线为AD ,故1D O ⊥底面ABCD 。
…………6分zyxO DC BAD 1C 1B 1A 1以O 为原点,所1, , OC OD OD 在直线分别为x 轴,y 轴,z 轴建立如图所示的坐标系,则()()1,0,0 , 0,1,0 , C D ()()10,0,1 , 0,1,0D A -,()()11,1,0 , 0,1,1 , DC DD ∴--u u u r u u u u u r ()()1110,1,1 , 1,1,0D A DC DC --==-u u u u r u u u u r u u u r,设(),,m x y z =u r为平面11CDD C 的一个法向量,由1 , m DC m DD ⊥⊥u r u u u r u r u u u u r,得00x y y z -=⎧⎨-+=⎩, 令1z =,则()1, 1 , 1,1,1y x m ==∴=u r.又设()111,,n x y z =r为平面11AC D 的一个法向量,由111 , n D A n DC ⊥⊥r u u u u r r u u u u r ,得111100y z x y --=⎧⎨-=⎩,令11z =,则()111, 1 , 1,1,1y x n =-=-∴=--r,…………9分则1cos ,3m n <>==-u r r , 故所求锐二面角C D C A --11的余弦值为13.…………12分注:第2问用几何法做的酌情给分. 20.解:(Ⅰ)),2(2*11N n n a a a n n n ∈≥+=-+Θ.}{n a ∴是等差数列.又43,4121==a a Θ41221)1(41-=⋅-+=∴n n a n ………………2分),2(331*1N n n nb b n n ∈≥+=-Θ)412(31121231412313111--=--=+-++=-∴++n b n b n n b a b n n n n n)(31n n a b -=.又041111≠-=-b a b Θ41}{1--∴b a b n n 是为首项,以31为公比的等比数列.………………5分(Ⅱ)412,)31()41(11-=⋅-=--n a b a b n n n n Θ.412)31()41(11-+⋅-=∴-n b b n n .当211)31)(41(3221,2----=-≥n n n b b b n 时.又01<b , 01>-∴-n n b b .}{n b ∴是单调递增数列.………………8分(Ⅲ)3=n 当且仅当Θ时,取最小值n S .⎩⎨⎧><∴0043b b ,即2131511()()0443711()()0443b b ⎧+-<⎪⎪⎨⎪+->⎪⎩,)11,47(1--∈∴b .………………12分21.解:(I )()f x 的定义域为3121(0,),()2,(0,)ax f x x x x x-+'+∞=-=∈+∞,..............1分①当0a ≤时,()0f x '>恒成立,()f x 为增函数,增区间是(0,)+∞.......................2分②当0a >时,令()0f x '=得:12x x ==(舍去)x ∈时,()0f x '>,()f x 为增函数)x ∈+∞时,()0f x '<,()f x 为减函数.....................................3分 综上所述:当0a ≤时,增区间是(0,)+∞当0a >时,增区间是,减区间是)+∞....................................4分(II )2()ln 1(0)g x x ax x a =--+≥, 设0(,())M x g x 是曲线()g x 上的一点,则()y g x =在点M 处的切线方程为000()()()y g x g x x x '-=-, 即00001(21)()()y ax x x g x x =---+,................................5分令00001()()(21)()()h x g x ax x x g x x ⎡⎤=----+⎢⎥⎣⎦则0011()21(21)h x ax ax x x '=-----,................................6分 显然()h x '在(0,)+∞上是增函数,又∵()0h x '=∴0(0,)x x ∈时,0()()0,()h x h x h x ''≥=为增函数0()x x ∈+∞时,0()()0,()h x h x h x ''≤=为减函数................................7分 ∴()h x 在0x x =处取得最大值0()0h x =,即()0h x ≤恒成立,......................8分 故曲线()y g x =上的任意一点都不能在直线l 的上方..............................9分 (III )∵方程[]22()(12)m x f x m x +=-有唯一实数解 ∴22ln 20x m x mx --=有唯一解........................................10分 设2()2ln 2g x x m x mx =-- 则2222()x mx m g x x--'= 令2()0,0g x x mx m '=--=∵0,0m x >>∴12m x =(舍),22m x += 2(0,)x x ∈时,()0g x '<∴()g x 在2(,)x +∞上单调递增∴当2x x =时,2()0,()g x g x '=有最小值2()g x ...............................12分 ∵方程有唯一解则22()0()0g x g x =⎧⎨'=⎩ 即22222222ln 200x m x mx x mx m ⎧--=⎨--=⎩∴222ln 0m x mx m +-=.....................................13分 ∵0m >∴222ln 10x x +-=设()2ln 1h x x x =+-,当0x >时,()h x 是增函数∴()h x 至多有一解∵(1)0h =∴方程222ln 10x x +-=的解是21x =,1= ∴12m =...........................................14分。
