平行四边形基础练习题(二)

合集下载

上海曲阳第二中学八年级数学下册第十八章《平行四边形》基础练习(答案解析)

一、选择题1．如图，在平行四边形ABCD 中，DE 平分,6,2ADC AD BE ∠==，则平行四边形ABCD 的周长是（）A ．16B ．18C ．20D ．242．如图，在等腰直角ABC 中，AB BC =，点D 是ABC 内部一点， DE BC ⊥，DF AB ⊥，垂足分别为E ，F ，若3CE DE =， 53DF AF =， 2.5DE =，则AF =（）A ．8B ．10C ．12.5D ．15 3．已知正方形ABCD 中，对角线4AC =，这个正方形的面积是（） A ．8 B ．16 C ．82 D ．162 4．如图，将菱形纸片ABCD 折叠，使点A 恰好落在菱形的对称中心O 处，折痕为EF ．若菱形ABCD 的边长为4，120B ∠=︒，则EF 的值是（）A ．3B ．2C ．23D ．45．如图，在ABC 中，点D 在边BC 上，过点D 作//DE AC ，//DF AB ，分别交AB ，AC 于E ，F 两点．则下列命题是假命题的是（）A ．四边形AEDF 是平行四边形B ．若90BC ∠+∠=︒，则四边形AEDF 是矩形C ．若BD CD =，则四边形AEDF 是菱形D ．若AD BD =，则四边形AEDF 是矩形6．已知四边形ABCD 是平行四边形，下列结论中不正确的是（）A ．当AB BC =时，四边形ABCD 是菱形B ．当AC BD ⊥时，四边形ABCD 是菱形C ．当90ABC ∠=时，四边形ABCD 是矩形D ．当AC BD =时，四边形ABCD 是正方形7．下列条件中不能判定一定是平行四边形的有（）A ．一组对角相等，一组邻角互补B ．一组对边平行，另一组对边相等C ．两组对边相等D ．一组对边平行，且另一组对边也平行8．如果平行四边形ABCD 的对角线相交于点O ，那么在下列条件中，能判断平行四边形ABCD 为菱形的是（）A ．OAB OBA ∠=∠；B ．OAB OBC ∠=∠； C ．OAB OCD ∠=∠；D ．OAB OAD ∠=∠． 9．四边形ABCD 中，对角线AC BD 、交于点O ．给出下列四组条件：①AB ∥CD ，AD ∥BC ；②AB CD =，AD BC =；③AO CO =，BO DO =；④AB ∥CD ，AD BC =．其中一定能判定这个四边形是平行四边形的条件共有（）A ．1组；B ．2组；C ．3组；D ．4组． 10．如图，己知四边形ABCD 是平行四边形，下列说法正确．．的是（）A ．若AB AD =，则平行四边形ABCD 是矩形B ．若AB AD =，则平行四边形ABCD 是正方形C ．若AB BC ⊥，则平行四边形ABCD 是矩形D ．若AC BD ⊥，则平行四边形ABCD 是正方形11．如图，以平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边，分别向外侧作等腰直角三角形，直角顶点分别为E 、F 、G 、H ，顺次连结这四个点，得四边形EFGH ，当()090ADC αα∠=︒<<︒时，有以下结论：①180GCF α∠=︒-；②90HAE α∠=︒+；③HE HG =；④ EH GH ⊥；⑤四边形EFGH 是平行四边形．则结论正确的是（）A ．①③④B ．②③⑤C ．①③④⑤D ．②③④⑤ 12．如图，在平行四边形ABCD 中，DE 平分∠ADC ，AD ＝6，BE ＝2，则平行四边形ABCD的周长是（）A ．60B ．30C ．20D ．16 13．如图，直线L 上有三个正方形,,a b c ，若,a c 的边长分别为1和3，则b 的面积为（）A ．8B ．9C ．10D ．11 14．如图，将矩形ABCD 折叠，使点C 和点A 重合，折痕为EF ．若5AF =，3BE =，则EF 的长为（）A ．23B ．17C ．25D ．3515．如图，已知平行四边形ABCD 中，4B A ∠=∠，则C ∠=（）A ．18°B ．36°C ．72°D ．144°二、填空题16．如图，四边形ABCD 为菱形，以AD 为斜边的Rt AED △的面积为3，2DE =，点E ，C 在BD 的同侧，点P 是BD 上的一动点，则PE PC +的最小值是_____________．17．如图，在平行四边形ABCD 中，10,AB BAD =∠的平分线与BC 的延长线交于点E ､与DC 交于点F ，且点F 为边DC 的中点，ADC ∠的平分线交AB 于点M ，交AE 于点N ，连接DE ．若6DM =，则DE 的长为_______．18．如图，在平行四边形ABCD 中，2AD CD =，F 是AD 的中点，CE AB ⊥，垂足E 在线段AB 上．下列结论①DCF ECF ∠=∠；②EF CF =；③3DFE AEF ∠=∠；④2BEC CEF S S <中，一定成立的是_________．（请填序号）19．如图，在矩形ABCD 中，连接AC ，按以下步骤作图：分别以点A ，C 为圆心，以大于12AC 的长为半径作弧，两弧分别相交于点M ，N ，作直线MN 交BC 于点E ，连接AE ．若AB ＝1，BC ＝2，则BE ＝_____．20．我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理，如图所示的图形就用了这种分割方法若5AE =，正方形ODCE 的边长为1，则BD 等于___________．21．如图，在四边形ABCD 中，AC a =，BD b =，且AC BD ⊥顺次连接四边形ABCD 各边的中点，得到四边形1111D C B A ，再顺次连接四边形1111D C B A 各边中点，得到四边形2222A B C D …如此进行下去，得到四边形n n n n A B C D ，下列结论正确的有__________．①四边形2222A B C D 是矩形；②四边形4444A B C D 是菱形；③四边形5555A B C D 的周长是4a b +．22．如图，在ABC ∆中，点,D E 分别在边,AB AC 上，且BD CE =，连接,CD DE ，点,,M N P 分别是,,DE BC CD 的中点，34PMN ∠=，则MPN ∠的度数是_______．23．如图，正方形ABCD 中，5AD =，点E 、F 是正方形ABCD 内的两点，且4AE FC ==，3BE DF ==，则EF 的平方为________．24．如图，在ABCD 中，AC 与BD 相交于点O ，（1）若18cm,24cm AC BD ==，则AO =_______，BO =_______．又若13AB =厘米，则COD △的周长为________．（2）若AOB 的周长为30cm ，12cm AB =，则对角线AC 与BD 的和是________． 25．如图，B ，E ，F ，D 四点在一条直线上，菱形ABCD 的面积为2120cm ，正方形AECF 的面积为250cm ，则菱形的边长为___cm ．26．如图，在Rt △ABC 中，∠ACB ＝90°，D 是斜边AB 中点，若∠B ＝30°，AC ＝2，则CD ＝_____．三、解答题27．如图，平行四边形ABCD 中，,AP BP 分别平分DAB ∠和CBA ∠，交于DC 边上点P ， 2.5AD =．（1）求线段AB 的长．（2）若3BP =，求ABP △的面积．28．已知：AB ⊥CD 于点O ，AB=AC=CD ，点I 是∠BAC ，∠ACD 的平分线的交点，连接IB ，ID（1）求证：IA ID =且IA ID ⊥；（2）填空：①∠AIC+∠BID=_________度；②S IBD ∆______S AIC ∆(填“﹥”“﹤”“=”)（3）将（2）小题中的第②结论加以证明．29．如图，在△ABC 中，AB =AC ，DE 垂直平分AC ，CE ⊥AB ，AF ⊥BC ，（1）求证：CF =EF ；（2）求∠EFB 的度数．30．如图，点E 在正方形ABCD 的边AB 上，点F 在边BC 的延长线上，且90EDF ∠=︒．求证：DE DF =．。

(完整版)平行四边形的性质判定练习题

第一部分平行四边形的性质练习题例题1、平行四边形得周长为50cm ，两邻边之差为5cm,求各边长。

变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形，∠BAC=90°,AB=3,AC=4,求AD 的长。

例题2.平行四边形ABCD 中，∠A-∠B=20°,求平行四边形各内角的度数。

变题3.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图，在平行四边形ABCD 中，∠BAC=34°, ∠ACB=26°，求∠DAC 与∠D 的度数。

例题3.如图，在平行四边形ABCD 中，CE ⊥AD,CF ⊥BA 交BA 的延长线于F ，∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。

变题5.如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

1、如图，四边形ABCD 是平行四边形，AB=6cm,BC=8cm ，∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________.3、平行四边形得周长为50cm ，两邻边之差为5cm,则长边是________ ，短边是__________.4、平行四边形ABCD 中，∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中，∠A+∠C=200°.则：∠A= _______，∠B= _________ .7、如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

平行四边形知识点总结及分类练习题

平行四边形知识点总结及分类练习题一、知识点总结平行四边形是几何学中一个重要的概念，其性质和判定方法对于理解几何学中的其他问题有着至关重要的作用。

以下是对平行四边形知识点的总结：1、定义：平行四边形是一个四边形，其中相对的两边平行且相等。

可以用符号“▭”表示。

2、性质：1)对边平行：平行四边形的对边平行且相等。

2)对角相等：平行四边形的对角相等，邻角互补。

3)平行四边形的面积等于其底乘高。

3.判定方法：1)两组对边分别平行的四边形是平行四边形。

2)两组对边分别相等的四边形是平行四边形。

3)一组对边平行且相等的四边形是平行四边形。

4)对角线互相平分的四边形是平行四边形。

5)邻角互补的四边形是平行四边形。

4.特殊平行四边形：矩形、菱形和正方形都是特殊的平行四边形，它们分别具有以下性质：1)矩形：对角线相等，四个角都是直角。

2)菱形：对角线垂直且平分，四边相等。

3)正方形：对角线垂直且相等，四个角都是直角。

二、分类练习题1、选择题：1)下列哪个条件可以判定一个四边形为平行四边形？A.一组对边相等，一组对角相等B.一组对边平行，另一组对边相等C.一组对角相等，另一组对边平行D.一组对角相等，一组邻角互补答案：(C)一组对角相等，另一组对边平行。

因为一组对角相等，另一组对边平行的四边形可以由一组对边平行，另一组对边相等的四边形经过平移得到，因此选项C正确。

其他选项都不满足平行四边形的定义或判定方法。

2)下列哪个条件可以判定一个四边形为矩形？A.三个内角都是直角B.对角线相等且互相平分C.对角线互相垂直且平分D.一组对边平行且相等，一组邻角互补答案：(B)对角线相等且互相平分的四边形是矩形。

因为矩形的定义是对角线相等的平行四边形，而对角线相等且互相平分的四边形是平行四边形，因此选项B正确。

其他选项分别是矩形的定义或判定方法的一部分，但不足以单独判定一个四边形为矩形。

特殊平行四边形知识点总结及题型一、平行四边形的性质：1、平行四边形的对边平行且相等；2、平行四边形的对角相等；3、平行四边形的对角线互相平分。

北京版-数学-五年级上册-【原创】《平行四边形》测评练习二

《平行四边形》测评练习二
掌握平行四边形面积的计算公式，能利用公式正确计算平行四边形的面积，并能解决实际问题。

基础知识
一、计算下面平行四边形的面积。

（单位：厘米）
二、画出平行四边形底边上的高，并量出所需要的数据，求平行四边形的面积。

三、下面两个平行四边形的面积相等吗？每个平行四边形的面积是多少？
能力提高
四、选择（把正确答案的序号填在括号里）。

1．下面各图中( )的面积最大。

A B C
2．如果两个正方形的周长相等，那么它们的面积( )。

A.一定相等B．一定不相等
C．可能相等，也可能不相等
3．如果两个平行四边形的周长相等，那么它们的面积( )。

A.一定相等B．一-定不相等C．可能相等，也可能不相等4．平行四边形有( )条高。

A.2 B．4 C．无数
五、填表。

1．有一个平行四边形，底长6.8米，高是底的一半，求这个平行四边形的面积。

2．一个平行四边形的面积是64平方米，它的底和高可能是多少米？（底和高均为整数）
3．有一块平行四边形的钢板，底8米、高3.5米，它的面积是多少？如果1平方米的这种钢板重40千克，这块钢板共重多少千克？
4．有一块平行四边形的地，高15米，底比高多4米，这块地的面积是多少平方米？
拓展延伸
七、试一试。

1．下图中给出了平行四边形的一个底和两条高的长度，如果用铁丝围这样一个平行四边形，至少要用多长的铁丝？
2．平行四边形甲的底边长是平行四边形乙底边长的3倍，乙的高是甲的2倍，则甲的面积是乙的多少倍？。

(完整)小学二年级平行四边形的初步认识练习题(2)

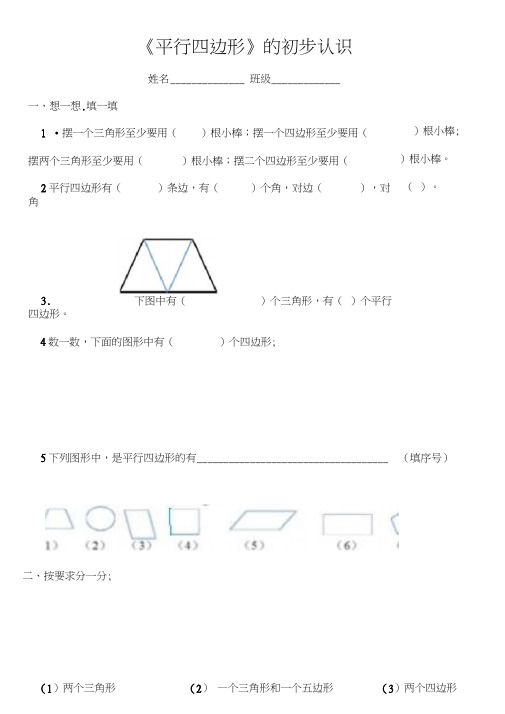
《平行四边形》的初步认识姓名______________ 班级_____________ 一、想一想.填一填1 •摆一个三角形至少要用（）根小棒；摆一个四边形至少要用（摆两个三角形至少要用（）根小棒；摆二个四边形至少要用（2平行四边形有（）条边，有（）个角，对边（），对角3.下图中有（）个三角形，有（）个平行四边形。

4数一数，下面的图形中有（）个四边形;二、按要求分一分;）根小棒; ）根小棒。

（）。

5下列图形中，是平行四边形的有____________________________________ （填序号）（1）两个三角形（2）—个三角形和一个五边形（3）两个四边形1.按要求在每个图形上画一条线，把它分成两个指定的图形3•把下面的图形分成两个四边形4.把下面的图形分成一个三角形、一个四边形三、在下面的点子图上画一个平行四边形和一个正方形。

四、判断题1.平行四边形的对边相等。

（）2.平行四边形的对角相等。

（）3.由四条边围成的图形是平行四边形。

（）4.长方形是特殊的平行四边形，正方形又是特殊的长方形。

（）5.两个完全一样的梯形可以拼成一个平行四边形6.用两根8厘米和两根6厘米的小棒，一定能摆成一个平行四边形五、数一数，下图中有（）个长方形；（）个正方形；（形。

六、选择（将正确答案的序号填在括号里）木头椅子摇晃了，常常在椅子下边斜着钉木条，这是运用了（形是（）①平行四边形②正方形③菱形④长方形）个平行四边1.2.3. 4.①三角形的稳定性能F面的四边形中，（平行四边形的（①四个角②平行四边形容易变形的特性）不是平行四边形相等。

②四条边对边当一个四边形的两组对边分别平行，四条边都相等, 四个角都相等时, 这个四边①②七、数一数，分一分;四边形有（）个，五边形有（）个，六边形有（）个。

平行四边形练习题及答案

20.1 平行四边形的判定一、选择题1．四边形ABCD，从（1）AB∥CD；（2）AB=CD；（3）BC∥AD；（4）BC=AD这四个条件中任选两个，其中能使四边形ABCD是平行四边形的选法有（）A．3种 B．4种 C．5种 D．6种2．四边形的四条边长分别是a，b，c，d，其中a，b为一组对边边长，c，d•为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd，则这个四边形是（）A．任意四边形 B．平行四边形C．对角线相等的四边形 D．对角线垂直的四边形3．下列说法正确的是（）A．若一个四边形的一条对角线平分另一条对角线，则这个四边形是平行四边形B．对角线互相平分的四边形一定是平行四边形C．一组对边相等的四边形是平行四边形D．有两个角相等的四边形是平行四边形二、填空题4．在□ABCD中，点E，F分别是线段AD，BC上的两动点，点E从点A向D运动，点F 从C•向B运动，点E的速度m与点F的速度n满足_______关系时，四边形BFDE为平行四边形．5．如图1所示，平行四边形ABCD中，E，F分别为AD，BC边上的一点，连结EF，若再增加一个条件_______，就可以推出BE=DF．图1 图26．如图2所示，AO=OC，BD=16cm，则当OB=_____cm时，四边形ABCD是平行四边形．三、解答题7．如图所示，四边形ABCD中，对角线BD=4，一边长AB=5，其余各边长用含有未知数x的代数式表示，且AD⊥BD于点D，BD⊥BC于点B．问：四边形ABCD•是平行四边形吗？为什么？四、思考题8．如图所示，在□ABCD中，E，F是对角线AC上的两点，且AF=CE，•则线段DE•与BF的长度相等吗？参考答案一、1．B 点拨：可选择条件（1）（3）或（2）（4）或（1）（2）或（3）（4）．故有4种选法．2．B 点拨：a2+b2+c2+d2=2ab+2cd即（a-b）2+（c-d）2=0，即（a-b）2=0且（c-d）2=0．所以a=b，c=d，即两组对边分别相等，所以四边形为平行四边形．3．B 点拨：熟练掌握平行四边形的判定定理是解答这类题目的关键．二、4．相等点拨：利用“一组对边平行且相等的四边形是平行四边形”来确定． 5．AE=CF 点拨：本题答案不惟一，只要增加的条件能使四边形EBFD•是平行四边形即可．6．8 点拨：根据对角线互相平分的四边形为平行四边形来进行判别．三、7．解：如图所示，四边形ABCD是平行四边形．理由如下：在Rt △BCD中，根据勾股定理，得BC2+BD2=DC2，即（x-5）2+42=（x-3）2，解得x=8．所以AD=11-8=3，BC=x-5=3，DC=x-3=8-3=5，所以AD=BC，AB=DC．所以四边形ABCD是平行四边形．点拨：本题主要告诉的是线段的长度，故只要说明AD=BC，AB=DC即可，本题也可在Rt△ABD中求x的值．四、8．解：线段DE与BF的长度相等；连结BD交AC于O点，连结DF，BE，如图所示．在ABCD中，DO=OB，AO=OC，又因为AF=EC，所以AF-AO=CE-OC，即OF=OE，所以四边形DEBF是平行四边形，所以DE=BF．D A CF O E B点拨：本题若用三角形全等，也可以解答，但过程复杂，学了平行四边形性质后，要学会应用．20.2 矩形的判定一、选择题1．矩形具有而一般平行四边形不具有的性质是（）A ．对角相等B ．对边相等C ．对角线相等D ．对角线互相垂直2．下列叙述中能判定四边形是矩形的个数是（）①对角线互相平分的四边形；②对角线相等的四边形；③对角线相等的平行四边形；④对角线互相平分且相等的四边形．A ．1B ．2C ．3D ．43．下列命题中，正确的是（）A ．有一个角是直角的四边形是矩形B ．三个角是直角的多边形是矩形C ．两条对角线互相垂直且相等的四边形是矩形D ．有三个角是直角的四边形是矩形二、填空题4．如图1所示，矩形ABCD 中的两条对角线相交于点O ，∠AOD=120°，AB=4cm ，则矩形的对角线的长为_____．图1 图25．若四边形ABCD 的对角线AC ，BD 相等，且互相平分于点O ，则四边形ABCD•是_____形，若∠AOB=60°，那么AB ：AC=______．6．如图2所示，已知矩形ABCD 周长为24cm ，对角线交于点O ，OE⊥DC 于点E ， OF⊥AD 于点F ，OF-OE=2cm ，则AB=______，BC=______．三、解答题7．如图所示，□ABCD的四个内角的平分线分别相交于E，F，G，H两点，试说明四边形EFGH是矩形．四、思考题8．如图所示，△ABC中，CE，CF分别平分∠ACB和它的邻补角∠ACD．AE ⊥CE于E，AF⊥CF于F，直线EF分别交AB，AC于M，N两点，则四边形AECF是矩形吗？为什么？参考答案一、1．C 点拨：A与B都是平行四边形的性质，而D是一般矩形与平行四边形都不具有的性质．2．B 点拨：③是矩形的判定定理；④中对角线互相平分的四边形是平行四边形，对角线相等的平行四边形是矩形，故④能判定矩形，应选B．3．D 点拨：选项D是矩形的判定定理．二、4．8cm5．矩；1：2 点拨：利用对角线互相平分来判定此四边形是平行四边形，再根据对角线相等来判定此平行四边形是矩形．由矩形的对角线相等且互相平分，•可知△AOB是等腰三角形，又因为∠AOB=60°，所以AB=AO=12 AC．6．8cm；4cm三、7．解：在□ABCD中，因为AD∥BC，所以∠DAB+∠CBA=180°，又因为∠HAB=12∠DAB，∠HBA=12∠CBA．所以∠HAB+∠HBA=90°，所以∠H=90°．同理可求得∠HEF= ∠F= ∠FGH=90°，所以四边形EFGH是矩形．点拨：由于“两直线平行，同旁内角的平分线互相垂直”，所以很容易求出四边形EFGH 的四个角都是直角，从而求得四边形EFGH是矩形．四、8．解：四边形AECF是矩形．理由：因为CE平分∠ACB，•CF•平分∠ACD，•所以∠ACE=12∠ACB，∠ACF=12∠ACD．所以∠ECF=12（∠ACB+∠ACD）=90°．又因为AE⊥CE，AF⊥CF，•所以∠AEC=∠AFC=90°，所以四边形AECF是矩形．点拨：•本题是通过证四边形中三个角为直角得出结论．还可以通过证其为平行四边形，再证有一个角为直角得出结论．20.3 菱形的判定一、选择题1．下列四边形中不一定为菱形的是（）A．对角线相等的平行四边形 B．每条对角线平分一组对角的四边形C．对角线互相垂直的平行四边形 D．用两个全等的等边三角形拼成的四边形2．四个点A，B，C，D在同一平面内，从①AB∥CD；②AB=CD；③AC⊥BD；④AD= BC；⑤AD∥BC．这5个条件中任选三个，能使四边形ABCD是菱形的选法有（）．A．1种 B．2种 C．3种 D．4种3．菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（）A．8cm和43cm B．4cm和83cm C．8cm和83cm D．4cm和43cm二、填空题4．如图1所示，已知□ABCD，AC，BD相交于点O，•添加一个条件使平行四边形为菱形，添加的条件为________．（只写出符合要求的一个即可）图1 图25．如图2所示，D ，E ，F 分别是△ABC 的边BC ，CA ，AB 上的点，且DE∥AB，DF∥CA，要使四边形AFDE 是菱形，则要增加的条件是________．（只写出符合要求的一个即可）6．菱形ABCD 的周长为48cm ，∠BAD： ∠ABC= 1：•2，•则BD=•_____，•菱形的面积是______．7．在菱形ABCD 中，AB=4，AB 边上的高DE 垂直平分边AB ，则BD=_____，AC=_____．三、解答题8．如图所示，在四边形ABCD 中，AB∥CD，AB=CD=BC ，四边形ABCD 是菱形吗？•说明理由．四、思考题9．如图，矩形ABCD 的对角线相交于点O ，PD∥AC，PC∥BD，PD ，PC 相交于点P ，四边形PCOD 是菱形吗？试说明理由．参考答案一、1．A 点拨：本题用排除法作答．2．D 点拨：根据菱形的判定方法判断，注意不要漏解．3．C 点拨：如图所示，若∠ABC=60°，则△ABC 为等边三角形，•所以AC=AB=14×32=8（cm ），AO=12AC=4cm ．因为AC⊥BD，在Rt△AOB 中，由勾股定理，得OB=222284AB OA -=-=43（cm ），• 所以BD=2OB=83cm ．二、4．AB=BC 点拨：还可添加AC⊥BD 或∠ABD=∠CBD 等．5．点D 在∠BAC 的平分线上（或AE=AF ）6．12cm ；723cm 2点拨：如图所示，过D 作DE⊥AB 于E ，因为AD∥BC，•所以∠BAD+∠ABC=180°．又因为∠BAD：∠ABC=1：2，所以∠BAD=60°，因为AB=AD ，所以△ABD 是等边三角形，所以BD=AD=12cm ．所以AE=6cm ．在Rt △AED 中，由勾股定理，得AE 2+ED 2=AD 2，62+ED 2=122，所以ED 2=108，所以ED=63cm ，所以S 菱形ABCD =12×63=723（cm 2）．7．4；43 点拨：如图所示，因为DE 垂直平分AB ，又因为DA=AB ，所以DA=DB=4．所以△ABD 是等边三角形，所以∠BAD=60°，由已知可得AE=2．在Rt△AED 中，•AE 2+DE 2=AD 2，即22+DE 2=42，所以DE 2=12，所以DE=23，因为12AC ·BD=AB ·DE ，即12AC ·4=4×23，所以AC=43．三、8．解：四边形ABCD 是菱形，因为四边形ABCD 中，AB∥CD，且AB=CD ，所以四边形ABCD 是平行四边形，又因为AB=BC ，所以ABCD 是菱形．点拨：根据已知条件，不难得出四边形ABCD 为平行四边形，又AB=BC ，即一组邻边相等，由菱形的定义可以判别该四边形为菱形．四、9．解：四边形PCOD是菱形．理由如下：因为PD∥OC，PC∥OD，•所以四边形PCOD是平行四边形．又因为四边形ABCD是矩形，所以OC=OD，所以平行四边形PCOD是菱形．20.4 正方形的判定一、选择题1．下列命题正确的是（）A．两条对角线互相平分且相等的四边形是菱形B．两条对角线互相平分且垂直的四边形是矩形C．两条对角线互相垂直，平分且相等的四边形是正方形D．一组邻边相等的平行四边形是正方形2．矩形四条内角平分线能围成一个（）A．平行四边形 B．矩形 C．菱形 D．正方形二、填空题3．已知点D，E，F分别是△ABC的边AB，BC，CA的中点，连结DE，EF，•要使四边形ADEF是正方形，还需要添加条件_______．4．如图1所示，直线L过正方形ABCD的顶点B，点A，C到直线L•的距离分别是1和2，则正方形ABCD的边长是_______．图1 图2 图3D AC F E B5．如图2所示，四边形ABCD 是正方形，点E 在BC 的延长线上，BE=BD 且AB=2cm ，则∠E 的度数是______，BE 的长度为____．6．如图3所示，正方形ABCD 的边长为4，E 为BC 上一点，BE=1，F•为AB•上一点，AF=2，P 为AC 上一动点，则当PF+PE 取最小值时，PF+PE=______．三、解答题7．如图所示，在Rt△ABC 中，CF 为∠ACB 的平分线，FD⊥AC 于D ，FE⊥BC 于点E ，试说明四边形CDFE 是正方形．四、思考题 8．已知如图所示，在正方形ABCD 中，E ，F 分别是AB ，BC 边上的点，且AE=BF ，•请问：（1）AF 与DE 相等吗？为什么？（2）AF 与DE 是否垂直？说明你的理由．参考答案一、1．C 点拨：对角线互相平分的四边形是平行四边形，•对角线互相垂直的平行四边形是菱形，对角线相等的平行四边形是矩形，既是菱形又是矩形的四边形一定是正方形，故选C ．2．D 点拨：由题意画出图形后，利用“一组邻边相等的矩形是正方形”来判定．二、3．△ABC 是等腰直角三角形且∠BAC=90°点拨：还可添加△ABC 是等腰三角形且四边形ADEF 是矩形或∠BAC=90°且四边形ADEF 是菱形等条件．4．5 点拨：观察图形易得两直角三角形全等，由全等三角形的性质和勾股定理得正方形的边长为2221+=5．5．67.5°；22cm点拨：因为BD 是正方形ABCD 的对角线，所以∠DBC=45°，AD=•AB=2cm ．在Rt△BAD 中，由勾股定理得AD 2+AB 2=BD 2，即22+22=BD 2，所以BD=22cm ，所以BE=BD=22（cm ），又因为BE=BD ，所以∠E=∠EDB=12（180°-45°）=67.5°． 6．17 点拨：如图所示，作F 关于AC 的对称点G ．连结EG 交AC 于P ，则PF+•PE=PG+PE=GE 为最短．过E 作EH⊥AD．在Rt △GHE 中，HE=4，HG=AG-AH=AF-BE=1，所以GE=2241+=17，•即PF+PE=17．三、7．解：因为∠FDC=∠FEC=∠BCD=90°，所以四边形CDFE 是矩形，因为CF•平分∠ACB，FE⊥BC，FD⊥AC，所以FE=FD ，所以矩形CDFE 是正方形．点拨：本题先说明四边形是矩形，再求出有一组邻边相等，•还可以先说明其为菱形，再求其一个内角为90°．四、8．解：（1）相等．理由：在△ADE 与△BAF 中，AD=AB ，∠DAE=∠ABF=90°，AE=BF ，所以△ADE≌△BAF（S ．A ．S ．），所以DE=AF ．（2）AF 与DE 垂直．理由：如图，设DE 与AF 相交于点O ．因为△ADE≌△BAF，•所以∠AED=∠BFA．又因为∠BFA+∠EAF=90°，所以∠AEO+∠EAO=90°，所以∠EOA= 90°，所以DE⊥AF．20.5 等腰梯形的判定一、选择题1．下列结论中，正确的是（）A．等腰梯形的两个底角相等 B．两个底角相等的梯形是等腰梯形C．一组对边平行的四边形是梯形 D．两条腰相等的梯形是等腰梯形2．如图所示，等腰梯形ABCD的对角线AC，BD相交于点O，则图中全等三角形有（）A．2对 B．3对 C．4对 D．5对3．课外活动课上，•老师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝，其面积为450cm，则两条对角线所用的竹条长度之和至少为（）A．302cm B．30cm C．60cm D．602cm二、填空题4．等腰梯形上底，下底和腰分别为4，•10，•5，•则梯形的高为_____，•对角线为______． 5．一个等腰梯形的上底长为5cm，下底长为12cm，一个底角为60°，则它的腰长为____cm，周长为______cm．6．在四边形ABCD中，AD∥BC，但AD≠BC，若使它成为等腰梯形，则需要添加的条件是__________（填一个正确的条件即可）．三、解答题7．如图所示，AD是∠BAC的平分线，DE∥AB，DE=AC，AD≠EC．求证：•四边形ADCE是等腰梯形．四、思考题8．如图所示，四边形ABCD中，有AB=DC，∠B=∠C，且AD<BC，四边形ABCD是等腰梯形吗？为什么？参考答案一、1．D 点拨：梯形的底角分为上底上的角和下底上的角，•因此在等腰梯形的性质和判别方法中必须强调同一底上的两个内角（•指上底上的两个内角或下底上的两个内角），否则就会出现错误，因此A，B选项都不正确，而C选项中漏掉了限制条件另外一组对边不平行，若平行该四边形就形成了平行四边形了，因此应选D．2．B 点拨：因为△ABC≌△DCB，△BAD≌△CDA，△AOB≌△DOC，所以共有3对全等的三角形．3．C 点拨：设该等腰梯形对角线长为Lcm，因为两条对角线互相垂直，•所以梯形面积为12L2=450，解得L=30，所以所用竹条长度之和至少为2L=2×30=60（cm）．二、4．4：65点拨：如图所示，连结BD，过A，D分别作AE⊥BC，DF⊥BC，垂足分别为E，F．易知△BAE≌△CDF，在四边形AEFD为矩形，所以BE=CF=3，AD=EF=4．在Rt△CDF中，FC2+DF2=CD2，即32+DF2=52，所以DF=4，在Rt△BFD中，BF2+DF2=BD2，即72+42=BD2，所以BD=65．5．7；31点拨：如图所示，过点D作DE∥AB交BC于E．因为AD∥BC，AB ∥DE，所以四边形ABED是平行四边形．所以BE=AD=5（cm），AB=DE．又因为AB=CD，所以DE=•DC，又因为∠C=60°，所以△DEC是等边三角形，所以DE=DC=EC=7（cm），所以周长为5+•12+7+7=31（cm）．6．AB=CD（或∠A=∠D，或∠B=∠C，或AC=BD，或∠A+∠C=180°，或∠B+∠D=180°）三、7．证明：因为AB∥ED，所以∠BAD=∠ADE．又因为AD是∠BAC的平分线，所以∠BAD=∠CAD，所以∠CAD=∠ADE，所以OA=OD．又因为AC=DE，所以AC-OA=DE-OD即OC=OE，•所以∠OCE=∠OEC，又因为∠AOD=∠COE，所以∠CAD=∠OCE．所以AD∥CE，而AD≠CE，故四边形ADCE是梯形．又因为∠CAD=∠ADE，AD=DA，AC=DE，所以△DAC≌△ADE，所以DC=•AE，所以四边形ADCE是等腰梯形．点拨：证明一个四边形是等腰梯形时，应先证其是梯形而后再证两腰相等或同一底上的FBE D CA HF ED CBA两个角相等．四、8．解：四边形ABCD 是等腰梯形．理由：延长BA ，CD ，相交于点E ，如图所示，由∠B=∠C，可得EB=EC ．又AB=DC ，所以EB-AB=EC-DC ，即AE=DE ，所以∠EAD= ∠EDA．因为∠E+∠EAD+∠EDA=180°，∠E+∠B+∠C=180°，所以∠EAD=∠B．故AD∥BC．•又AD<BC ，所以四边形ABCD 是梯形．又AB=DC ，所以四边形ABCD 是等腰梯形．点拨：由题意可知，只要推出AD∥BC，再由AD<BC 就可知四边形ABCD 为梯形，再由AB=DC ，即可求得此四边形是等腰梯形，由∠B=∠C 联想到延长BA ，CD ，即可得到等腰三角形，从而使AD∥BC．华东师大版数学八年级（下）第20章平行四边形的判定测试（答卷时间：90分钟，全卷满分：100分）姓名得分____________一、认认真真选，沉着应战！（每小题3分，共30分） 1. 正方形具有菱形不一定具有的性质是 ( )（A ）对角线互相垂直（B ）对角线互相平分（C ）对角线相等（D ）对角线平分一组对角2. 如图(1)，EF 过矩形ABCD 对角线的交点O ，且分别交AB 、CD 于E 、F ，那么阴影部分的面积是矩形ABCD 的面积的（）（A ）51 （B ）41 （C ）31 （D ）103）1CBA(1) (2) (3) 3．在梯形ABCD 中，AD ∥BC ，那么:::A B C D ∠∠∠∠可以等于（）（A ）4：5：6：3 （B ）6：5：4：3 （C ）6：4：5：3 （D ）3：4：5：6 4．如图(2)，平行四边形ABCD 中，DE ⊥AB 于E ，DF ⊥BC 于F ，若A B C D 的周长为48，DE ＝5，DF ＝10，则ABCD 的面积等于( )（A ）87.5 （B ）80 （C ）75 （D ）72.55． A 、B 、C 、D 在同一平面内，从①AB ∥CD; ②AB=CD; ③BC ∥AD; ④BC=AD 这四个条件中任选两个，能使四边形ABCD 是平行四边形的选法有（）（A ）3种（B ）4种（C ）5种（D ）6种6．如图(3)，D 、E 、F 分别是ABC 各边的中点，AH 是高，如果5ED cm =，那么HF 的长为（）（A ）5cm （B ）6cm （C ）4cm （D ）不能确定 7. 如图（4）：E 是边长为1的正方形ABCD 的对角线BD 上一点，且BE ＝BC ，P 为CE 上任意一点，PQ ⊥BC 于点Q ，PR ⊥BE 于点R ，则PQ ＋PR 的值是（）（A ）22 （B ）21 （C ）32 （D ）238．如图（5），在梯形ABCD 中，AD ∥BC ，AB CD =，60C ∠=︒，BD 平分ABC ∠，如果这个梯形的周长为30，则AB 的长（）（A ）4 （B ）5 （C ）6 （D ）79．右图是一个利用四边形的不稳定性制作的菱形晾衣架．已知其中每个菱形的边长为20cm ，墙上悬挂晾衣架的两个铁钉A 、B 之间的距离为203cm ，则∠1等于( )（A ）90° （Ｂ）60° （Ｃ）45° （Ｄ）30° 10．某校数学课外活动探究小组，在老师的引导下进一步研究了完全平方公式．结合实数的性质发现以下规律：对于任意正数a 、b ，都有a+b ≥2ab 成立．某同学在做一个面积为3 600cm 2，对角线相互垂直的四边形风筝时，运用上述规律，求得用来做对角线用的竹条至少需要准备x cm ．则x 的值是（）(A) 1202 (B) 602 (C) 120 (D) 60ED CB A R QP（4） DCB A （5）A B C Dl N M D C BA 二、仔仔细细填，记录自信！(每小题2分，共20分)11．一个四边形四条边顺次是a 、b 、c 、d ，且bd ac d c b a 222222+=+++，则这个四边形是_______________．12．在四边形ABCD 中，对角线AC 、BD 交于点O ，从（1）AB CD =；（2）AB CD ∥；（3）OA OC =；（4）OB OD =；（5）AC BD ⊥；（6）AC 平分BAD ∠这六个条件中，选取三个推出四边形ABCD 是菱形．如（1）（2）（5）⇒ABCD 是菱形，再写出符合要求的两个： ⇒A B C D 是菱形； ⇒A B C D是菱形． 13. 如图，已知直线l 把ABCD 分成两部分，要使这两部分的面积相等，直线l 所在位置需满足的条件是____________________.（只需填上一个你认为合适的条件）(第13题) (第16题)14. 梯形的上底长为6cm ，过上底的一顶点引一腰的平行线，与下底相交，所构成的三角形周长为21cm ，那么梯形的周长为_________cm 。

《平行四边形》专题练习(含答案)

平行四边形专题练习一、选择题1. (2018·宜宾)在ABCD 中，若BAD ∠与CDA ∠的平分线交于点E ，则AED ∠的形状是( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定 2. (2018·黔西南州)如图，在ABCD 中，4AC =cm.若ACD ∆的周长为13 cm ，则ABCD 的周长为( )A. 26 cmB. 24 cmC. 20 cmD. 18 cm3. (2018·海南)如图ABCD 的周长为36，对角线,AC BD 相交于点O ，E 是CD 的中点，12BD =，则DOE ∆的周长为( )A.15B. 18C. 21D. 24 4. ( 2018·台州)如图，在ABCD 中，2,3AB BC ==.以点C 为圆心，适当长为半径画弧，交BC 于点P ，交CD 于点Q ，再分别以点,P Q 为圆心，大于12PQ 的长为半径画弧，两弧相交于点N ，射线CN 交BA 的延长线于点E ，则AE 的长是( ) A.12 B. 1 C. 65 D. 325. (2018·东营)如图，在四边形ABCD 中，E 是BC 边的中点，连接DE 并延长，交AB 的延长线于点F ，AB BF =.添加一个条件使四边形ABCD 是平行四边形，你认为下列四个条件中可选择的是( )A. AD BC =B. CD BF =C. A C ∠=∠D. F CDF ∠=∠ 6. (2018·安徽)在ABCD 中，,E F 是对角线BD 上不同的两点.下列条件中，不能得出四边形AECF 一定为平行四边形的是( )A. BE DF =B. AE CF =C. //AF CED. BAE DCF ∠=∠7. (2018·玉林)在四边形ABCD 中:①//AB CD ;②//AD BC ;③AB CD =;④AD BC =，从以上选择两个条件使四边形ABCD 为平行四边形的选法共有( ) A. 3种 B. 4种 C. 5种 D. 6种8. (2018·呼和浩特)顺次连接平面上,,,A B C D 四点得到一个四边形，从①//AB CD ;②BC AD =;③A C ∠=∠;④B D ∠=∠四个条件中任取其中两个，可以得出‘“四边形ABCD 是平行四边形”这一结论的情况共有( )A. 5种B. 4种C. 3种D. 1种 9. (2018·眉山)如图，在ABCD 中，2CD AD =，BE AD ⊥于点E ，F 为DC 的中点，连接,EF BF ，下列结论:①2ABC ABF ∠=∠;②EF BF =;③2EFB DEBC S S ∆=四边形;④3CFE DEF ∠=∠.其中正确的结论共有( )A.1个B. 2个C. 3个D. 4个10. (2018·通辽)如图，ABCD 的对角线,AC BD 交于点O ，DE 平分ADC ∠交AB 于点E ，60BCD ∠=︒，12AD AB =，连接OE .下列结论:①ABCDS AD BD =; ②DB平分CDE ∠; ③AO DE =;④5ADE OFE S S ∆∆=.其中正确的有( ) A. 1个 B. 2个 C. 3个 D. 4个二、填空题11. (2018·常州)如图，在ABCD 中，70A ∠=︒，DC DB =，则CDB ∠= .12. (2018·十堰)如图，ABCD 的对角线,AC BD 相交于点O ，且8AC =，10BD =，5AB =，则OCD ∆的周长为 .13. (2018·泰州)如图，在ABCD 中，,AC BD 相交于点O .若6,16AD AC BD =+=，则BOC ∆的周长为 .14. (2018·衡阳)如图，ABCD 的对角线相交于点O ，且AD CD ≠，过点O 作OM AC ⊥，交AD 于点M .如果CDM ∆的周长为8，那么ABCD 的周长是 .15.(2018·临沂)如图，在ABCD 中，10,6AB AD ==，AC BC ⊥，则BD 的长为 .16. (2018·东营)如图，(3,3)B -，(5,0)C ，以,OC CB 为边作OABC ，则经过点A 的反比例函数的解析式为 . 17. (2018·株洲)如图，在ABCD 中，连接BD ，且BD CD =，过点A 作AM BD ⊥于点M ，过点D 作DN AB ⊥于点N ，且DN =，在DB 的延长线上取一点P ，满足ABD MAP PAB ∠=∠+∠，则AP 的长为 .18.(导学号78816053)(2018·无锡)如图，60XOY ∠=︒，点A 在边OX 上，2OA =.过点A作AC OY ⊥于点C ，以AC 为一边在XOY ∠内作等边三角形ABC ，P 是ABC ∆围成的区域(包括各边)内的一点，过点P 作//PD OY 交OX 于点D ，作//PE OX 交OY于点E .设,OD a OE b ==，则2a b +的取值范围是 . 三、解答题19. (2018·无锡)如图，在ABCD 中，,E F 分别是边,BC AD 的中点.求证:ABF CDE ∠=∠.20. (2018·衢州)如图，在ABCD 中，AC 是对角线，BE AC ⊥，DF AC ⊥，垂足分别为E ，F .求证:AE CF =.21. (2018·大连)如图，ABCD 的对角线,AC BD 相交于点O ，点,E F 在AC 上，且AF CE =.求证:BE DF =.22. (2018·福建)如图，ABCD 的对角线,AC BD 相交于点O ，EF 过点O 且与,AD BC分别相交于点,E F .求证:OE OF =.23. (2018·宿迁)如图，在ABCD 中，点,E F 分别在边,CB AD 的延长线上，且BE DF =，EF 分别与,AB CD 交于点,G H .求证:AG CH =.24. (2018·曲靖)如图，在ABCD 的边,AB CD 上截取,AF CE ，使得AF CE =，连接,,EF M N 是线段EF 上两点，且EM FN =，连接,AN CM .(1)求证: AFN CEM ∆≅∆;(2)若107CMF ∠=︒，72CEM ∠=︒，求NAF ∠的度数.25. (2018·岳阳)如图，在ABCD 中，AE CF =.求证:四边形BFDE 是平行四边形.26. (2018·孝感)如图，,,,B E C F 在一条直线上，已知//,//,AB DE AC DF BE CF =，连接AD .求证:四边形ABED 是平行四边形.27. (2018·陕西)如图，//AB CD ，,E F 分别为,AB CD 上的点，且//EC BF ，连接AD ，分别与,EC BF 相交于点,G H ，若AB CD =，求证:AG DH =.28. (2018·巴中)如图，在ABCD 中，过点B 作BM AC ⊥于点E ，交CD 于点M ，过点D 作DN AC ⊥于点F ，交AB 于点N . (1)求证:四边形BMDN 是平行四边形; (2)已知12,5AF EM ==，求AN 的长.29. (2018·江西)如图，在四边形ABCD 中，//AB CD ，2AB CD =，E 为AB 的中点，请仅用无刻度的直尺分别按下面的要求画图.(保留画图痕迹) (1)在图①中，画出ABD ∆的BD 边上的中线;(2)在图②中，若BA BD =，画出ABD ∆的AD 边上的高.30. (2018·黄冈)如图，在ABCD 中，分别以边,BC CD 作等腰三角形BCF 、等腰三角形CDE ，使,BC BF CD DE ==，CBF CDE ∠=∠，连接,AF AE . (1)求证: ABF EDA ∆≅∆;(2)延长AB 与CF ，相交于点G ，若AF AE ⊥，求证: BF BC ⊥.31. (2018·永州)如图，在ABC ∆中，90ACB ∠=︒，30CAB ∠=︒，以线段AB 为边向外作等边三角形ABD ，E 是线段AB 的中点，连接CE 并延长交线段AD 于点F . (1)求证:四边形BCFD 为平行四边形; (2)若6AB =，求BCFD 的面积.32. (2018·重庆)如图，在ABCD 中，O是对角线AC 的中点，E 是BC 上一点，且AB AE =，连接EO 并延长交AD 于点F .过点B 作AE 的垂线，垂足为H ，交AC 于点G .(1)若3,1AH HE ==，求ABE ∆的面积;(2)若45ACB ∠=︒，求证:DF =.参考答案一、1. B 2. D 3. A 4. B 5. D 6. B 7. B 8. C 9. D 10. B 二、填空题11. 40︒ 12. 14 13. 14 14. 1615. 16. 6y x= 17. 618. 225a b ≤+≤ 三、19. 点拨：证明()ABF CDE SAS ∆≅∆，即可得ABF CDE ∠=∠. 20. 点拨：证明()ABE CDF AAS ∆≅∆，即可得AE CF =. 21. 点拨：证明()BEO DFO SAS ∆≅∆，即可得BE DF =. 22. 点拨：证明()AOE COF ASA ∆≅∆，即可得OE OF =. 23. 点拨：证明()AGF CHE ASA ∆≅∆，即可得AG CH =.24. (1)点拨：由FN EM AFN CEM AF CE =⎧⎪∠=∠⎨⎪=⎩，得到AFN CEM ∆≅∆(2) 35NAF ∠=︒25. 点拨：由//BF DEBF DF ⎧⎨=⎩，得到四边形BFDE 是平行四边形26. 点拨：证明()ABC DEF ASA ∆≅∆，得到AB DE =，又∵//AB DE ，∴四边形ABED 是平行四边形.27. 点拨：证明()AEG DFH ASA ∆≅∆，得到AG DH =.28. (1) 点拨：由////CD ABDN BM⎧⎨⎩，得到四边形BMDN 是平行四边形;(2)13AN =29. (1)如图①，连接CE ，交BD 于点F ，连接AF ，线段AF 即为所求 (2)如图②，连接CE ，交BD 于点F ，连接AF ，DE 交于点G ，连接BG ，并延长BG ，交AD 于点H ，线段BH 即为所求30. (1) 点拨：由BF DA ABF EDA AB DE =⎧⎪∠=∠⎨⎪=⎩，得到ABF EDA ∆≅∆(2) 点拨：由90CBF EAF ∠=∠=︒，得到BF BC ⊥ 31. (1) 点拨：由////BC DFCF BD⎧⎨⎩，得到四边形BCFD 为平行四边形;(2) BCFDS=32. (1) ABE S ∆= (2) 点拨：AOF COE ∆≅∆，得到AF CE =， ∵AD BC =， ∴DF BE =.AME BNG ∆≅∆，得到ME NG =， ∴22BE ME NG ==在Rt GNC ∆中，45GCN ∠=︒，∴CG =，2NG =，∴DF =。

(完整)二年级数学-平行四边形的认识练习题

(完整)二年级数学-平行四边形的认识练习
题
二年级数学-平行四边形的认识练题
1. 已知一组平行线段的长度分别为8cm和12cm，它们之间的距离为6cm，求两条平行线段的夹角大小。

2. 一张平行四边形的底边长为10cm，高为4cm，求该平行四边形的面积。

3. 已知平行四边形的底边长为6cm，高为3cm，求该平行四边形的周长。

4. 一条边长为8cm的正方形上，以边长为4cm的正方形为边从外部剪掉一个正方形，剩下的图形是什么形状？
5. 在一个平行四边形中，两对相对边分别为7cm和9cm，求这个平行四边形的面积。

6. 已知一个平行四边形的周长为24cm，其中一条边长为6cm，求这个平行四边形的高和底边长。

7. 一个平行四边形的一条边长为8cm，高为5cm，求该平行四
边形的面积。

8. 如果一张长方形是一个平行四边形，那么这个长方形的两组
对边是否相等？
9. 在一个平行四边形中，两组对边分别为6cm和8cm，求这个平行四边形的周长。

10. 如果一个四边形的对边互相平行并且长度相等，那么这个
四边形一定是什么几何图形？
以上是二年级数学的平行四边形的认识练习题，希望能够帮助
你加深对平行四边形的理解和掌握。

数学人教版八下《平行四边形性质与判定》同步基础练习卷(含答案)(2022年最新)

7.如图，在▱ABCD中，AD=16，点E，F分别是BD，CD的中点，则EF等于( )
A.10B.8C.6D.4
8.如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1，S2，S3，S4，则一定成立的是（）
A.S1+S2=S3+S4B.S1+S2＞S3+S4C.S1+S3=S2+S4D.S1+S2＜S3+S4
17.如图，E，F是▱ABCD对角线BD上的两点，请你添加一个适当的条件：，使四边形AECF是平行四边形.
18.一个四边形四条边顺次是a、b、c、d，且a2+b2+c2+d2=2ac+2bd，则这个四边形是_______
三、解答题
19.如图，已知△ABC中，D为AB的中点.
（1）请用尺规作图法作边AC的中点E，并连结DE（保留作图痕迹，不要求写作法）；
∵EF=BF，BF=DC，∴EF=DC，
∴四边形EFCD是平行四边形。
23.证明：连接AE、DB、BE，BE交AD于点O，
∵AB DE，∴四边形ABDE是平行四边形，∴OB=OE，OA=OD，
∵AF=DC，∴OF=OC，∴四边形BCEF是平行四边形．
24.解：（1）DE+DF=AB．理由如下：
如图1．∵DE∥AB，DF∥AC，∴四边形AEDF是平行四边形，∴DE=AF．
14.如图，加一个条件与∠A+∠B=180°能使四边形ABCD成为平行四边形.
15.E为□ABCD边AD上一点，将ABE沿BE翻折得到FBE，点F在BD上,且EF=DF．若∠C=52°，则∠ABE=______
16.如图，□ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24厘米，△OAB的周长是18厘米，则EF=厘米．

北师大版八年级数学下册第六章 6.2.2平行四边形的判定(二) 同步练习题

2020-2021学年北师大版八年级数学下册第六章 6.2.2平行四边形的判定(二) 同步练习题A组(基础题)一、填空题1．如图，在▱ABCD中，AC，BD相交于点O，E，F分别为OB，OD上的点，且OE＝OF，再由OC＝OA，即可得到四边形AECF是平行四边形，理由是________________________．2．如图，AC，BD是相交的两条线段，点O为它们的中点．当BD绕点O旋转时，连接AB，BC，CD，DA，所得到的四边形ABCD始终为______．3．在四边形ABCD中，对角线AC，BD相交于点O，下列条件中能判定这个四边形是平行四边形的是______．(填序号)①AB＝CD，AD＝BC；②AB＝CD，AD∥BC；③AB＝CD，AB∥CD；④AD∥BC，AB∥CD.4．如图，在▱ABCD中，E、F是对角线AC上的两点，且AE＝CF，有以下结论：①BE＝DF；②BE∥DF；③AB＝DE；④四边形EBFD为平行四边形；⑤S△ADE＝S△ABE.这些结论中正确的是______．(填序号)二、选择题5．如图，a∥b，AB∥CD，CE⊥b，FG⊥b，E，G为垂足，则下列说法不正确的是( ) A．AB＝CDB．EC＝GFC．A，B两点的距离就是线段AB的长度D．a与b的距离就是线段CD的长度6．如图，四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定这个四边形是平行四边形的是( )A．AB∥DC，AD∥BC B．AB＝DC，AD＝BC C．AO＝CO，BO＝DOD．AB＝DC，AD∥BC7．根据下列条件，能作出平行四边形的是( )A．两组对边的长分别是3和5B．相邻两边的长分别是3和5，且一条对角线长为9C．一边的长为7，两条对角线的长分别为6和8D．一边的长为7，两条对角线的长分别为6和58．如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD＝90°，BC＝4，BE＝ED＝3，AC＝10，则四边形ABCD的面积为( )A．6 B．12 C．20 D．24三、解答题9．(1)如图，▱ABCD的对角线AC，BD相交于点O，过点O的直线EF分别交AB，CD于点E，F，连接DE，BF.求证：四边形DEBF是平行四边形．(2)如图，四边形ABCD的对角线AC，BD相交于点O，AO＝CO，EF过点O且与AD，BC 分别相交于点E，F，OE＝OF.求证：四边形ABCD是平行四边形．10．(1)如图，H，G是▱ABCD对角线上的点，且AG＝CH，E，F分别是AB，CD的中点．求证：四边形EHFG是平行四边形．(2)如图，在四边形ABCD中，BC∥AD，∠ABC＝90°，AD＝5，BC＝13，E是边CD的中点，连接BE并延长与AD的延长线相交于点F.①求证：四边形BDFC是平行四边形；②若BD＝BC，求四边形BDFC的面积．B组(中档题)一、填空题11．在如图所示的▱ABCD中，AB＝2，AD＝3，将△ACD沿对角线AC折叠，点D落在△ABC 所在平面内的点E处，且AE过BC的中点O.则△ADE的周长等于______．12．如图，在4×4的正方形网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，点A，B(均在格点上)的位置如图所示．若以A，B为顶点画面积为2的格点平行四边形，则符合条件的平行四边形的个数有______个．13．如图，Rt△OAB的两直角边OA，OB分别在x轴和y轴上，A(－2，0)，B(0，4)，将△OAB绕点O顺时针旋转90°得到△OCD，直线AC，BD交于点E.点M为直线BD上的动点，点N为x轴上的点．若以A，C，M，N四点为顶点的四边形是平行四边形，则符合条件的点M的坐标为______．二、解答题14．如图，已知AC是▱ABCD的对角线，△ACP和△ACQ都是等边三角形．求证：四边形BPDQ是平行四边形．C组(综合题)15．如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BE＝BF.(1)求证：四边形BDEF为平行四边形；(2)当∠C＝45°，BD＝4时，连接DF，求线段DF的长．参考答案2020-2021学年北师大版八年级数学下册第六章 6.2.2平行四边形的判定(二) 同步练习题A组(基础题)一、填空题1．如图，在▱ABCD中，AC，BD相交于点O，E，F分别为OB，OD上的点，且OE＝OF，再由OC＝OA，即可得到四边形AECF是平行四边形，理由是对角线互相平分的四边形是平行四边形．2．如图，AC，BD是相交的两条线段，点O为它们的中点．当BD绕点O旋转时，连接AB，BC，CD，DA，所得到的四边形ABCD始终为平行四边形．3．在四边形ABCD中，对角线AC，BD相交于点O，下列条件中能判定这个四边形是平行四边形的是①③④．(填序号)①AB＝CD，AD＝BC；②AB＝CD，AD∥BC；③AB＝CD，AB∥CD；④AD∥BC，AB∥CD.4．如图，在▱ABCD中，E、F是对角线AC上的两点，且AE＝CF，有以下结论：①BE＝DF；②BE∥DF；③AB＝DE；④四边形EBFD为平行四边形；⑤S△ADE＝S△ABE.这些结论中正确的是①②④⑤．(填序号)二、选择题5．如图，a∥b，AB∥CD，CE⊥b，FG⊥b，E，G为垂足，则下列说法不正确的是(D) A．AB＝CDB．EC＝GFC．A，B两点的距离就是线段AB的长度D．a与b的距离就是线段CD的长度6．如图，四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定这个四边形是平行四边形的是(D)A．AB∥DC，AD∥BC B．AB＝DC，AD＝BC C．AO＝CO，BO＝DOD．AB＝DC，AD∥BC7．根据下列条件，能作出平行四边形的是(A)A．两组对边的长分别是3和5B ．相邻两边的长分别是3和5，且一条对角线长为9C ．一边的长为7，两条对角线的长分别为6和8D ．一边的长为7，两条对角线的长分别为6和58．如图，在四边形ABCD 中，对角线AC ，BD 相交于点E ，∠CBD ＝90°，BC ＝4，BE ＝ED ＝3，AC ＝10，则四边形ABCD 的面积为(D)A ．6B ．12C ．20D ．24三、解答题9．(1)如图，▱ABCD 的对角线AC ，BD 相交于点O ，过点O 的直线EF 分别交AB ，CD 于点E ，F ，连接DE ，BF.求证：四边形DEBF 是平行四边形．证明：∵四边形ABCD 是平行四边形， ∴AB ∥CD ，OD ＝OB ， AO ＝OC.∴∠DCO ＝∠BAO.在△AEO 和△CFO 中，⎩⎪⎨⎪⎧∠FCO ＝∠EAO ，CO ＝AO ，∠COF ＝∠AOE ，∴△AEO ≌△CFO(ASA)．∴OE ＝OF.∵OD ＝OB ，∴四边形DEBF 是平行四边形．(2)如图，四边形ABCD 的对角线AC ，BD 相交于点O ，AO ＝CO ，EF 过点O 且与AD ，BC 分别相交于点E ，F ，OE ＝OF.求证：四边形ABCD 是平行四边形．证明：∵AO ＝CO ，OE ＝OF ，∠AOE ＝∠COF ， ∴△AOE ≌△COF(SAS)． ∴∠OAE ＝∠OCF.∴AD ∥BC. ∴∠EDO ＝∠FBO.又∵OE ＝OF ，∠EOD ＝∠FOB ， ∴△EOD ≌△FOB(AAS)． ∴OB ＝OD.又∵OA ＝OC ，∴四边形ABCD 是平行四边形．10．(1)如图，H ，G 是▱ABCD 对角线上的点，且AG ＝CH ，E ，F 分别是AB ，CD 的中点．求证：四边形EHFG 是平行四边形．证明：连接CE ，AF ，EF ，EF 与AC 交于点O. ∵四边形ABCD 是平行四边形， ∴AB ∥CD ，AB ＝CD.∵E ，F 分别是AB ，CD 的中点， ∴AE ＝CF ，AE ∥CF.∴四边形AECF 是平行四边形． ∴OA ＝OC ，OE ＝OF. ∵AG ＝CH ，∴OG ＝OH.∴四边形EHFG 是平行四边形．(2)如图，在四边形ABCD 中，BC ∥AD ，∠ABC ＝90°，AD ＝5，BC ＝13，E 是边CD 的中点，连接BE 并延长与AD 的延长线相交于点F.①求证：四边形BDFC 是平行四边形； ②若BD ＝BC ，求四边形BDFC 的面积．解：①证明：∵BC ∥AF ， ∴∠CBE ＝∠DFE.∵E 是边CD 的中点，∴CE ＝DE. 在△BEC 和△FED 中， ⎩⎪⎨⎪⎧∠CBE ＝∠DFE ，∠BEC ＝∠FED ，CE ＝DE ，∴△BEC ≌△FED(AAS)．∴BE ＝FE. ∴四边形BDFC 是平行四边形．②由(1)得：△BEC ≌△FED ，∴DF ＝BC ＝13.∵BC ∥AF ，∠ABC ＝90°，∴∠BAD ＋∠ABC ＝180°. ∴∠BAD ＝90°.∵BD ＝BC ＝13，AD ＝5，∴AB ＝BD 2－AD 2＝132－52＝12. ∴S 四边形BDFC ＝DF ·AB ＝13×12＝156.B 组(中档题)一、填空题 11．在如图所示的▱ABCD 中，AB ＝2，AD ＝3，将△ACD 沿对角线AC 折叠，点D 落在△ABC 所在平面内的点E 处，且AE 过BC 的中点O.则△ADE 的周长等于10．12．如图，在4×4的正方形网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，点A，B(均在格点上)的位置如图所示．若以A，B为顶点画面积为2的格点平行四边形，则符合条件的平行四边形的个数有11个．13．如图，Rt△OAB的两直角边OA，OB分别在x轴和y轴上，A(－2，0)，B(0，4)，将△OAB绕点O顺时针旋转90°得到△OCD，直线AC，BD交于点E.点M为直线BD上的动点，点N为x轴上的点．若以A，C，M，N四点为顶点的四边形是平行四边形，则符合条件的点M的坐标为(2，2)或(6，－2)．二、解答题14．如图，已知AC是▱ABCD的对角线，△ACP和△ACQ都是等边三角形．求证：四边形BPDQ是平行四边形．证明：方法一：(利用全等得两组对边相等)∵AC是▱ABCD的对角线，∴∠DAC＝∠BCA.∵∠ACP＝∠CAQ＝60°，∴∠DAQ＝∠BCP.又∵AD＝CB，AQ＝CP，∴△ADQ≌△CBP.∴DQ＝BP.同理可证△ABQ≌△CDP.∴BQ＝DP.∴四边形BPDQ是平行四边形．方法二：(利用对角线互相平分证明结论)连接BD交AC于点O，连接PO，QO.利用△ACP和△ACQ是全等等边三角形可得P，O，Q三点共线，且PO＝QO.又∵BO＝DO，∴四边形BPDQ是平行四边形．C组(综合题)15．如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BE＝BF.(1)求证：四边形BDEF为平行四边形；(2)当∠C＝45°，BD＝4时，连接DF，求线段DF的长．解：(1)证明：∵△ABC是等腰三角形，∴∠ABC＝∠C.∵EG∥BC，DE∥AC，∴∠AEG＝∠ABC＝∠C，四边形CDEG是平行四边形．∴∠DEG＝∠C.∵BE＝BF，∴∠BFE＝∠BEF＝∠AEG＝∠ABC.∴∠F＝∠DEG.∴BF∥DE.又∵EF∥BD，∴四边形BDEF为平行四边形．(2)作FM⊥BD于点M，连接DF.∵∠C＝45°，∴∠ABC＝∠BFE＝∠BEF＝45°.∴△BDE，△BEF是等腰直角三角形．∴BF＝BE＝22BD＝2 2.易得△BFM是等腰直角三角形．∴FM＝BM＝22BF＝2.∴DM＝6.在Rt△DFM中，DF＝FM2＋DM2＝22＋62＝210.。

平行四边形的判定基础练习

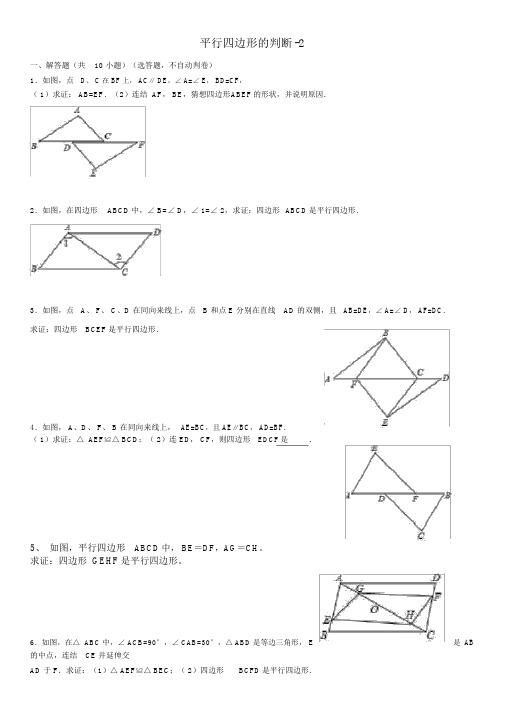
平行四边形的判断 -2一、解答题（共10 小题）（选答题，不自动判卷）1．如图，点D、 C 在 BF 上， AC∥ DE，∠ A=∠ E， BD=CF，（ 1）求证： AB=EF．（2）连结 AF， BE，猜想四边形A BEF的形状，并说明原因．2．如图，在四边形ABCD中，∠ B=∠ D，∠ 1=∠ 2，求证：四边形ABCD是平行四边形．3．如图，点A、 F、 C、D 在同向来线上，点 B 和点 E 分别在直线AD 的双侧，且AB=DE，∠ A=∠ D， AF=DC．求证：四边形BCEF是平行四边形．4．如图， A、D、 F、 B 在同向来线上，AE=BC，且 AE∥BC， AD=BF．（ 1）求证：△ AEF≌△ BCD；（ 2）连 ED， CF，则四边形EDCF是．5、如图，平行四边形ABCD中， BE＝DF，AG＝CH。

求证：四边形 GEHF是平行四边形。

6．如图，在△ ABC 中，∠ ACB=90°，∠ CAB=30°，△ ABD 是等边三角形，E是AB 的中点，连结CE并延伸交AD 于 F．求证：（1）△ AEF≌△ BEC；（ 2）四边形BCFD是平行四边形．7．已知：如图，在四边形ABCD中， AB∥ CD，E， F 为对角线AC 上两点，且AE=CF， DF∥ BE．求证：四边形ABCD为平行四边形．8．如图， AB∥ CD， AB=CD，点 E、F 在 BC 上，且 BE=CF．（ 1）求证：△ ABE≌△ DCF；（ 2）试证明：以A、F、 D、 E 为极点的四边形是平行四边形．9．如图，已知BE∥ DF，∠ ADF=∠ CBE， AF=CE，求证：四边形DEBF是平行四边形．10．如图，已知： AB∥CD， BE⊥ AD，垂足为点 E， CF⊥AD，垂足为点 F，而且 AE=DF．求证：四边形 BECF是平行四边形．【考点训练】平行四边形的判断-2参照答案与试题分析一、解答题（共10 小题）（选答题，不自动判卷）1．如图，点D、 C 在 BF 上， AC∥ DE，∠ A=∠ E， BD=CF，（1）求证： AB=EF．（2）连结 AF， BE，猜想四边形 ABEF的形状，并说明原因．【剖析】（1）利用AAS证明△ ABC≌△ EFD，再依据全等三角形的性质可得AB=EF；（ 2）第一依据全等三角形的性质可得∠B=∠ F，再依据内错角相等两直线平行可获得AB∥ EF，又AB=EF，可证出四边形 ABEF为平行四边形．【解答】（1）证明：∵ AC∥DE，∴∠ ACD=∠EDF，∵BD=CF，∴BD+DC=CF+DC，即BC=DF，又∵∠ A=∠E，∴△ ABC≌△ EFD（AAS），∴ AB=EF；（2）猜想：四边形 ABEF为平行四边形，原因以下：由（ 1）知△ ABC≌△ EFD，∴∠ B=∠ F，∴ AB∥ EF，又∵ AB=EF，∴四边形 ABEF为平行四边形．【评论】本题主要考察了全等三角形的判断与性质，平行四边形的判断，解决问题的重点是证明△ ABC ≌△ EFD．2．如图，在四边形ABCD中，∠ B=∠D，∠ 1=∠2，求证：四边形 ABCD是平行四边形．【剖析】依据三角形内角和定理求出∠ DAC=∠ACB，依据平行线的判断推出 AD∥ BC，AB∥CD，依据平行四边形的判断推出即可．【解答】证明：∵∠ 1+∠B+∠ACB=180°，∠ 2+∠D+∠ CAD=180°，∠ B=∠D，∠1=∠ 2，∴∠ DAC=∠ACB，∴AD∥ BC，∵∠ 1=∠ 2，∴AB∥ CD，∴四边形 ABCD是平行四边形．【评论】本题考察了平行线的判断和平行四边形的判断的应用，主要考察学生的推理能力．3．如图，点 A、F、C、D 在同向来线上，点 B 和点 E 分别在直线 AD 的双侧，且 AB=DE，∠ A=∠D，AF=DC．求证：四边形 BCEF是平行四边形．【剖析】第一证明△ AFB≌△ DCE（SAS），从而得出 FB=CE，FB∥CE，从而得出答案．【解答】证明：在△ AFB和△ DCE中，，∴△ AFB≌△ DCE（SAS），∴FB=CE，∴∠ AFB=∠DCE，∴FB∥CE，∴四边形 BCEF是平行四边形．【评论】本题主要考察了平行四边形的判断以及全等三角形的判断与性质，得出△ AFB≌△ DCE 是解题重点．4．如图， A、D、F、B 在同向来线上， AE=BC，且 AE∥ BC， AD=BF．（1）求证：△ AEF≌△ BCD；（2）连 ED，CF，则四边形 EDCF是．（从平行四边形，矩形，菱形，正方形中选填）．【剖析】（1）依据 AE∥BC 可得∠ A=∠ B，再由 AD=BF可得 AF=BD，再加上条件 AE=CB，可依据SAS 定理证明△ AEF≌△ BCD；（2）依据△ AEF≌△ BCD，可得 EF=CD，∠ EFA=∠ CDB，从而证明出 EF∥ DC，再依据一组对边平行且相等的四边形 EDCF是平行四边形．【解答】解：（1）证明：∵AE∥BC，∴∠ A=∠ B，∵AD=BF，∴AF=DB，∵ AE=BC，在△ AEF和△ BCD中，∴△ AEF≌△ BCD（SAS）；（2）平行四边形．∵△AEF≌△BCD，∴ EF=CD，∠ EFA=∠CDB，∴ EF∥DC，∴四边形 EDCF是平行四边形．【评论】本题主要考察了全等三角形的判断与性质，以及平行四边形的判断，重点是掌握一组对边平行且相等的四边形是平行四边形．5．如图，在 ABCD中， AC 交 BD 于点 O，点 E，点 F 分别是 OA， OC的中点，请判断线段BE，DF 的地点关系和数目关系，并说明你的结论．【剖析】依据平行四边形的性质对角线相互均分得出OA=OC，OB=OD，利用中点的意义得出OE=OF，从而利用平行四边形的判断定理“对角线相互均分的四边形是平行四边形”判断BFDE是平行四边形，从而得出 BE=DF， BE∥DF．【解答】解： BE=DF，BE∥ DF由于 ABCD是平行四边形，因此OA=OC，OB=OD，由于 E，F 分别是 OA，OC的中点，因此OE=OF，因此 BFDE是平行四边形，因此BE=DF，BE∥DF【评论】主要考察了平行四边形的基天性质和判断定理的运用．性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线相互均分．判断：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线相互均分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形．6．如图，在△ ABC中，∠ ACB=90°，∠ CAB=30°，△ ABD 是等边三角形， E 是 AB 的中点，连结CE并延伸交 AD 于 F．求证：（1）△ AEF≌△ BEC；（2）四边形 BCFD是平行四边形．【剖析】（1）利用等边三角形的性质得出∠DAB=60°，即可得出∠ ABC=60°，从而求出△ AEF≌△ BEC （ASA）；（2）利用平行线的判断方法以及直角三角形的性质得出 CF∥BD，从而求出答案．【解答】证明（1）∵ E 是 AB 中点，∴ AE=BE，∵△ABD 是等边三角形，∴∠ DAB=60°，∵∠CAB=30°，∠ACB=90°，∴∠ ABC=60°，在△ AEF和△ BEC中，∴△ AEF≌△ BEC（ASA）；（2）∵∠ DAC=∠DAB+∠ BAC，∠ DAB=60°，∠ CAB=30°，∴∠ DAC=90°，∴AD∥ BC，∵E 是 AB 的中点，∠ACB=90°，∴ EC=AE=BE，∴∠ ECA=30°，∠ FEA=60°，∴∠ EFA=∠BDA=60°，∴CF∥BD，∴四边形 BCFD是平行四边形．【评论】本题主要考察了平行四边形的判断以及全等三角形的判断方法，得出∠ ABC=60°是解题重点．7．已知：如图，在四边形ABCD中， AB∥ CD，E，F 为对角线 AC上两点，且 AE=CF，DF∥BE．求证：四边形 ABCD为平行四边形．【剖析】第一证明△ AEB≌△ CFD可得 AB=CD，再由条件 AB∥CD 可利用一组对边平行且相等的四边形是平行四边形证明四边形 ABCD为平行四边形．【解答】证明：∵ AB∥ CD，∴∠ DCA=∠BAC，∵DF∥BE，∴∠DFA=∠BEC，∴∠AEB=∠DFC，在△ AEB和△ CFD中，∴△ AEB≌△ CFD（ASA），∴AB=CD，∵ AB∥ CD，∴四边形 ABCD为平行四边形．【评论】本题主要考察了平行四边形的判断，重点是掌握一组对边平行且相等的四边形是平行四边形．8．如图， AB∥CD，AB=CD，点 E、F 在 BC上，且 BE=CF．（1）求证：△ ABE≌△ DCF；（2）试证明：以 A、 F、 D、 E 为极点的四边形是平行四边形．【剖析】（1）由全等三角形的判断定理SAS证得△ ABE≌△ DCF；（ 2）利用（ 1）中的全等三角形的对应角相等证得∠AEB=∠DFC，则∠ AEF=∠DFE，因此依据平行线的判断能够证得AE∥ DF．由全等三角形的对应边相等证得AE=DF，则易证得结论．【解答】证明：（1）如图，∵ AB∥CD，∴∠ B=∠ C．∵在△ ABE与△ DCF中，，∴△ ABE≌△ DCF（SAS）；（2）如图，连结 AF、DE．由（ 1）知，△ ABE≌△ DCF，∴ AE=DF，∠ AEB=∠DFC，∴∠ AEF=∠DFE，∴ AE∥DF，∴以 A、F、D、E 为极点的四边形是平行四边形．【评论】本题考察了平行四边形的判断、全等三角形的判断与性质．在证明（2）题时，利用了“一组对边平行且相等的四边形是平行四边形”的判断定理．9．如图，已知 BE∥DF，∠ ADF=∠CBE，AF=CE，求证：四边形D EBF是平行四边形．【剖析】第一依据平行线的性质可得∠ BEC=∠ DFA，再加上条件∠ ADF=∠CBE，AF=CE，可证明△ADF ≌△ CBE，再依据全等三角形的性质可得 BE=DF，依据一组对边平行且相等的四边形是平行四边形进行判断即可．【解答】证明：∵ BE∥ DF，∴∠ BEC=∠DFA，在△ ADF和△ CBE中，∴△ ADF≌△ CBE（AAS），∴BE=DF，又∵ BE∥ DF，∴四边形 DEBF是平行四边形．【评论】本题主要考察了平行四边形的判断，重点是掌握一组对边平行且相等的四边形是平行四边形．10．如图，已知： AB∥ CD， BE⊥AD，垂足为点 E， CF⊥AD，垂足为点 F，而且 AE=DF．求证：四边形 BECF是平行四边形．【剖析】经过全等三角形（△ AEB≌△ DFC）的对应边相等证得 BE=CF，由“在同一平面内，同垂直于同一条直线的两条直线相互平行”证得 BE∥CF．则四边形 BECF是平行四边形．【解答】证明：∵BE⊥ AD，CF⊥AD，∴∠ AEB=∠DFC=90°，∵AB∥ CD，∴∠ A=∠ D，在△ AEB与△ DFC中，，∴△ AEB≌△ DFC（ASA），∴BE=CF．∵BE⊥AD，CF⊥AD，∴ BE∥CF．∴四边形 BECF是平行四边形．【评论】本题考察了平行四边形的判断、全等三角形的判断与性质．一组对边平行且相等的四边形是平行四边形．。

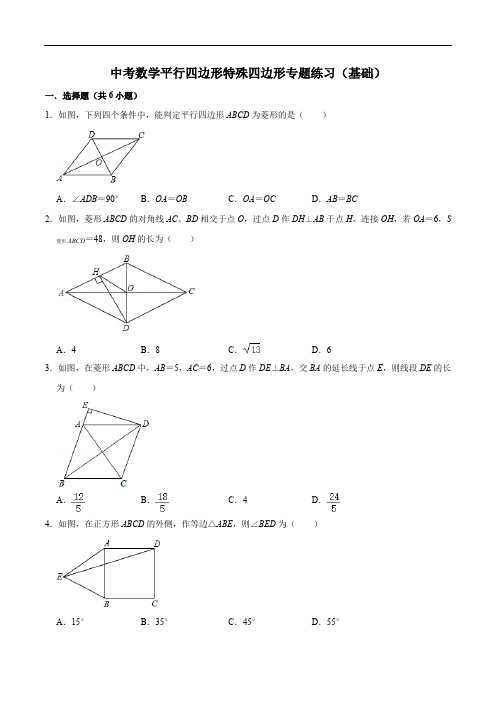
中考数学平行四边形特殊四边形专题练习(基础)

中考数学平行四边形特殊四边形专题练习（基础）一．选择题（共6小题）1．如图，下列四个条件中，能判定平行四边形ABCD为菱形的是（）A．∠ADB＝90°B．OA＝OB C．OA＝OC D．AB＝BC2．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，S＝48，则OH的长为（）菱形ABCDA．4B．8C．D．63．如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（）A．B．C．4D．4．如图，在正方形ABCD的外侧，作等边△ABE，则∠BED为（）A．15°B．35°C．45°D．55°5．如图，在矩形ABCD中，AB＝6，BC＝8，过对角线交点O作EF⊥AC交AD于点E，交BC于点F，则DE的长是（）A．1B．C．2D．6．如图，在平面直角坐标系中，四边形OABC为菱形，O（0，0），A（4，0），∠AOC＝60°，则对角线交点E的坐标为（）A．（2，）B．（，2）C．（，3）D．（3，）二．填空题（共24小题）7．如图，正方形ABCD的边长为2，点P为对角线AC上任意一点．PE⊥AD，PF⊥CD，垂足分别是E，F．则PE+PF＝．8．如图，菱形ABCD中，对角线AC与BD相交于点O，点E是BC的中点，若AC＝10cm，BD＝24cm，则OE的长为cm．9．如图，四边形ABCD是菱形，AC＝24，BD＝10，DH⊥AB于点H，则线段DH的长为．10．如图，在菱形ABCD中，点E是对角线BD上一点，且BE＝CD，连接CE，若AB＝3，BD＝4，则CE 的长为．11．如图，菱形ABCD的两条对角线AC、BD相交于点O，若AC＝4cm，BD＝6cm，则菱形ABCD的面积是．12．如图，在菱形ABCD中，对角线AC、BD交于点O，点E、F分别是边AB、BC的中点，若AB＝5，BD＝8，则△OEF的周长等于．13．如图，已知菱形ABCD中，∠BAD＝120°，对角线AC与BD相交于点O，且AC＝2，则对角线BD的长为．14．如图，正方形ABCD的边长为，O是对角线BD上一动点（点O与端点B，D不重合），OM⊥AD 于点M，ON⊥AB于点N，连接MN，则MN长的最小值为．15．如图，直线l过正方形的顶点B，点A、C到l的距离分别是2和1，则正方形的边长是．16．如图已知P是正方形ABCD对角线BD上一点，且BP＝BC，则的值为．17．如图，矩形OABC的顶点B的坐标为（3，2），则对角线AC＝．18．如图，菱形ABCD的对角线AC与BD相交于点O，点E是DC边上的中点，连接OE，若OE＝5，BD＝12，则菱形ABCD的面积为．19．如图，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点E的坐标为（1，3），则点F的坐标为．20．如图，在边长为1的正方形ABCD中，E，F分别为线段BC，CD上的点，且△AEF为正三角形，则BE的长为．21．如图，矩形ABCD中，对角线AC与BD相交于点O，过点C作CE⊥BD，垂足为点E．若OE＝1，BD ＝2．则CE＝．22．如图，在平面直角坐标系中，菱形ABCD的顶点A，C在x轴上，顶点B的坐标为（2，3），那么顶点D的坐标是．23．如图，正方形ABCD的边长是3，BP＝CQ＝1，连接AQ、DP交于点O，AQ交CD与点F，DP交BC 于点E，则线段OE的长为．24．如图，若菱形ABCD的顶点A，B的坐标分别为（6，0），（﹣4，0），点D在y轴上，则点C的坐标是．25．如图，菱形ABCD的周长为，对角线AC和BD相交于点O，AC：BD＝1：2，则AO：BO＝，菱形ABCD的面积S＝．26．如图，矩形ABCD中，AB＝5，BC＝3，E、F分别在AB、CD上，且EF垂直平分AC，则AE的长为．27．如图，在平面直角坐标系中，矩形ABCO的边CO、OA分别在x轴、y轴上，点E在边BC上，将该矩形沿AE折叠，点B恰好落在边OC上的F处．若OA＝6，AB＝10，则点E的坐标是．28．如图，在Rt△ABC中，∠A＝90°，AB＝6，BC＝10，P是BC边上的一点，作PE垂直AB，PF垂直AC，垂足分别为E、F，求EF的最小值是．29．如图，已知正方形ABCD，E是AD上一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H．BE＝6，则GH＝．30．如图，矩形ABCD的对角线AC，BD交于点O，∠AOD＝120°，AC＝8，则AB＝．三．解答题（共10小题）31．基础探究：如图①，在正方形ABCD中，点E为AD上一点，DF⊥CE交AB于F，垂足为点O．求证：CE＝DF．应用拓展：如图②，在正方形ABCD中，点E为AD上一点，FG⊥CE分别交AB、CD于F、G，垂足为点O．若正方形ABCD的边长为12，DE＝5，则四边形EFCG的面积为．32．如图，在菱形ABCD中，对角线AC、BD相交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF，已知BF＝8，DF＝4，求CD的长．33．如图，四边形ABCD是正方形，G是BC上任意一点，DE⊥AG于点E，BF∥DE，且交AG于点F．（1）求证：△ADE≌△BAF；（2）求证：DE﹣BF＝EF；（3）若AB＝2，BG＝1，求线段EF的长．34．如图所示，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．（1）证明不论E、F在BC、CD上如何滑动，总有BE＝CF；（2）当点E、F在BC、CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．35．如图1，在正方形ABCD中，点E在边CD上（不与点C，D重合），AE交对角线BD于点G，GF⊥AE交BC于点F．（1）求证：AG＝FG．（2）若AB＝10，BF＝4，求BG的长．（3）如图2，连接AF，EF，若AF＝AE，求正方形ABCD与△CEF的面积之比．36．如图，在矩形ABCD中，对角线BD的垂直平分线MN分别与AD、BC相交于点M、N，与BD相交于点O，连结BM，DN．（1）求证：四边形BMDN是菱形；（2）若MD＝2AM，BD＝8，求矩形ABCD的周长．37．如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF ＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）若AC＝10，∠ABC＝60°，则矩形AEFD的面积是．38．如图菱形ABCD的一个内角∠B＝60°，E为BC的中点，F为CD的中点，连结AF、EF．（1）△AEF的形状如何？试证明；（2）若E为BC上的任意一点，F为CD上的点，且∠EAF＝60°，△AEF的形状如何？试证明．39．如图，正方形ABCD中，E，F分别为AB，BC中点，CE，DF交于M，CE与DA的延长线相交于点P，求证：（1）△EBC≌△FCD；（2）CP⊥DF；（3）AM＝AD，40．如图，已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE，连接BG，DE．（1）求证：BG＝DE；（2）连接BD，若CG∥BD，BG＝BD，求∠BDE的度数．参考答案一．选择题（共6小题）1．D；2．A；3．D；4．C；5．B；6．D；二．填空题（共24小题）7．2；8．6.5；9．；10．；11．12cm 2；12．8；13．6；14．1；15．；16．；17．；18．96；19．（﹣2，4）；20．2﹣；21．1；22．（2，﹣3）；23．；24．（﹣10，8）；25．1：2；4；26．3.4；27．（10，）；28．4.8；29．6；30．4；三．解答题（共10小题）31．；32．；33．；34．；35．；36．；37．25；38．；39．；40．；。

(完整版)平行四边形专项练习题

平行四边形专项练习题一．选择题（共12小题）1．在下列条件中，能够判定一个四边形是平行四边形的是（）A．一组对边平行，另一组对边相等B．一组对边相等，一组对角相等C．一组对边平行，一条对角线平分另一条对角线D．一组对边相等，一条对角线平分另一条对角线2．设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（）A．a＞b B．a=b C．a＜b D．b=a+180°3．如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（）A．4S1B．4S2C．4S2+S3D．3S1+4S34．在▱ABCD中，AB=3，BC=4，当▱ABCD的面积最大时，下列结论正确的有（）①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．A．①②③B．①②④C．②③④D．①③④5．如图，在▱ABCD中，AB=6，BC=8，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（）A．2 B．3 C．4 D．66．如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（）A．8 B．10 C．12 D．147．如图，在▱ABCD中，AB=12，AD=8，∠ABC的平分线交CD于点F，交AD的延长线于点E，CG⊥BE，垂足为G，若EF=2，则线段CG的长为（）A．B．4C．2D．8．如图，在▱ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（）A．AG平分∠DAB B．AD=DH C．DH=BC D．CH=DH 9．如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B 为（）A．66°B．104°C．114°D．124°10．如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO 的周长是（）A．10 B．14 C．20 D．2211．四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD从中任选两个条件，能使四边形ABCD为平行四边形的选法有（）A．3种 B．4种C．5种D．6种12．如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④ D．④⑤二．填空题（共6小题）13．如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D1，折痕为EF，若∠BAE=55°，则∠D1AD=．14．如图，在▱ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是．15．如图所示，四边形ABCD的对角线相交于点O，若AB∥CD，请添加一个条件（写一个即可），使四边形ABCD是平行四边形．16．如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为．17．如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=BD，连接DM、DN、MN．若AB=6，则DN=．18．如图，在△ABC中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于cm．三．解答题（共8小题）19．如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F．（1）求证：△ADE≌△FCE．（2）若∠BAF=90°，BC=5，EF=3，求CD的长．20．如图，在▱ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．（1）求证：AB=CF；（2）连接DE，若AD=2AB，求证：DE⊥AF．21．已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．22．如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC 上（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．23．如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．（1）求证：四边形DEFG是平行四边形；（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．24．如图，▱ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N．（1）求证：四边形CMAN是平行四边形．（2）已知DE=4，FN=3，求BN的长．25．如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：（1）DE=BF；（2）四边形DEBF是平行四边形．26．如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=BC，连接CD和EF．（1）求证：DE=CF；（2）求EF的长．参考答案与解析一．选择题1．【分析】根据平行四边形的判定方法以及全等三角形的判定方法一一判断即可．解：A、错误．这个四边形有可能是等腰梯形．B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．故选C．2．【分析】根据多边形的内角和定理与多边形外角的关系即可得出结论．解：∵四边形的内角和等于a，∴a=（4﹣2）•180°=360°．∵五边形的外角和等于b，∴b=360°，∴a=b．故选B．3．【分析】设等腰直角三角形的直角边为a，正方形边长为c，求出S2（用a、c表示），得出S1，S2，S3之间的关系，由此即可解决问题．解：设等腰直角三角形的直角边为a，正方形边长为c，则S2=（a+c）（a﹣c）=a2﹣c2，∴S2=S1﹣S3，∴S3=2S1﹣2S2，∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1．故选A．4．【分析】当▱ABCD的面积最大时，四边形ABCD为矩形，得出∠A=∠B=∠C=∠D=90°，AC=BD，根据勾股定理求出AC，即可得出结论．解：根据题意得：当▱ABCD的面积最大时，四边形ABCD为矩形，∴∠A=∠B=∠C=∠D=90°，AC=BD，∴AC==5，①正确，②正确，④正确；③不正确；故选：B．5．【分析】由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．解：∵四边形ABCD是平行四边形，∴AB∥CD，AD=BC=8，CD=AB=6，∴∠F=∠DCF，∵CF平分∠BCD，∴∠FCB=∠DCF，∴∠F=∠FCB，∴BF=BC=8，同理：DE=CD=6，∴AF=BF﹣AB=2，AE=AD﹣DE=2，∴AE+AF=4；故选：C．6．【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB，得出AF=AB=6，同理可证DE=DC=6，再由EF的长，即可求出BC的长．解：∵四边形ABCD是平行四边形，∴AD∥BC，DC=AB=6，AD=BC，∴∠AFB=∠FBC，∵BF平分∠ABC，∴∠ABF=∠FBC，则∠ABF=∠AFB，∴AF=AB=6，同理可证：DE=DC=6，∵EF=AF+DE﹣AD=2，即6+6﹣AD=2，解得：AD=10；故选：B．7．【分析】先由平行四边形的性质和角平分线的定义，判断出∠CBE=∠CFB=∠ABE=∠E，从而得到CF=BC=8，AE=AB=12，再用平行线分线段成比例定理求出BE，然后用等腰三角形的三线合一求出BG，最后用勾股定理即可．解：∵∠ABC的平分线交CD于点F，∴∠ABE=∠CBE，∵四边形ABCD是平行四边形，∴DC∥AB，∴∠CBE=∠CFB=∠ABE=∠E，∴CF=BC=AD=8，AE=AB=12，∵AD=8，∴DE=4，∵DC∥AB，∴，∴，∴EB=6，∵CF=CB，CG⊥BF，∴BG=BF=2，在Rt△BCG中，BC=8，BG=2，根据勾股定理得，CG===2，故选：C．8．【分析】根据作图过程可得得AG平分∠DAB，再根据角平分线的性质和平行四边形的性质可证明∠DAH=∠DHA，进而得到AD=DH，解：根据作图的方法可得AG平分∠DAB，∵AG平分∠DAB，∴∠DAH=∠BAH，∵CD∥AB，∴∠DHA=∠BAH，∴∠DAH=∠DHA，∴AD=DH，∴BC=DH，故选D．9．【分析】由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC，由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=∠1=22°，再由三角形内角和定理求出∠B 即可．解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠ACD=∠BAC，由折叠的性质得：∠BAC=∠B′AC，∴∠BAC=∠ACD=∠B′AC=∠1=22°，∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°；故选：C．10．【分析】直接利用平行四边形的性质得出AO=CO，BO=DO，DC=AB=6，再利用已知求出AO+BO的长，进而得出答案．解：∵四边形ABCD是平行四边形，∴AO=CO，BO=DO，DC=AB=6，∵AC+BD=16，∴AO+BO=8，∴△ABO的周长是：14．故选：B．11．【分析】根据题目所给条件，利用平行四边形的判定方法分别进行分析即可．解：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD 为平行四边形；③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；①③可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；①④可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；∴有4种可能使四边形ABCD为平行四边形．故选：B．12．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AB，从而判断出①不变；再根据三角形的周长的定义判断出②是变化的；确定出点P到MN 的距离不变，然后根据等底等高的三角形的面积相等确定出③不变；根据平行线间的距离相等判断出④不变；根据角的定义判断出⑤变化．解：∵点A，B为定点，点M，N分别为PA，PB的中点，∴MN是△PAB的中位线，∴MN=AB，即线段MN的长度不变，故①错误；PA、PB的长度随点P的移动而变化，所以，△PAB的周长会随点P的移动而变化，故②正确；∵MN的长度不变，点P到MN的距离等于l与AB的距离的一半，∴△PMN的面积不变，故③错误；直线MN，AB之间的距离不随点P的移动而变化，故④错误；∠APB的大小点P的移动而变化，故⑤正确．综上所述，会随点P的移动而变化的是②⑤．故选：B．二．填空题13．【分析】由平行四边形的性质和折叠的性质得出∠D1AE=∠BAD，得出∠D1AD=∠BAE=55°即可．解：∵四边形ABCD是平行四边形，∴∠BAD=∠C，由折叠的性质得：∠D1AE=∠C，∴∠D1AE=∠BAD，∴∠D1AD=∠BAE=55°；故答案为：55°．14．【分析】根据平行四边形性质得出AD∥CB，AB∥CD，推出∠DAB+∠CBA=180°，求出∠PAB+∠PBA=90°，在△APB中求出∠APB=90°，由勾股定理求出BP，证出AD=DP=5，BC=PC=5，得出DC=10=AB，即可求出答案．解：∵四边形ABCD是平行四边形，∴AD∥CB，AB∥CD，∴∠DAB+∠CBA=180°，又∵AP和BP分别平分∠DAB和∠CBA，∴∠PAB+∠PBA=（∠DAB+∠CBA）=90°，在△APB中，∠APB=180°﹣（∠PAB+∠PBA）=90°；∵AP平分∠DAB，∴∠DAP=∠PAB，∵AB∥CD，∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP是等腰三角形，∴AD=DP=5，同理：PC=CB=5，即AB=DC=DP+PC=10，在Rt△APB中，AB=10，AP=8，∴BP==6，∴△APB的周长=6+8+10=24；故答案为：24．15．【分析】根据平行四边形的定义或判定定理即可解答．解：可以添加：AD∥BC（答案不唯一）．故答案是：AD∥BC．16．【分析】结合题意，总结可知，每个图中三角形个数比图形的编号的4倍少3个三角形，即可得出结果．解：第①是1个三角形，1=4×1﹣3；第②是5个三角形，5=4×2﹣3；第③是9个三角形，9=4×3﹣3；∴第n个图形中共有三角形的个数是4n﹣3；故答案为：4n﹣3．17．【分析】连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，证明四边形DCMN是平行四边形，得到DN=CM，根据直角三角形的性质得到CM=AB=3，等量代换即可．解：连接CM，∵M、N分别是AB、AC的中点，∴NM=CB，MN∥BC，又CD=BD，∴MN=CD，又MN∥BC，∴四边形DCMN是平行四边形，∴DN=CM，∵∠ACB=90°，M是AB的中点，∴CM=AB=3，∴DN=3，故答案为：3．18．【分析】首先证明四边形ADEF是平行四边形，根据三角形中位线定理求出DE、EF即可解决问题．解：∵BD=AD，BE=EC，∴DE=AC=4cm，DE∥AC，∵CF=FA，CE=BE，∴EF=AB=3cm，EF∥AB，∴四边形ADEF是平行四边形，∴四边形ADEF的周长=2（DE+EF）=14cm．故答案为14．三．解答题19．【分析】（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAE=∠F，∠D=∠ECF，∵E是▱ABCD的边CD的中点，∴DE=CE，在△ADE和△FCE中，，∴△ADE≌△FCE（AAS）；（2）解：∵ADE≌△FCE，∴AE=EF=3，∵AB∥CD，∴∠AED=∠BAF=90°，在▱ABCD中，AD=BC=5，∴DE===4，∴CD=2DE=8．20．【分析】（1）由在▱ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．证明：（1）∵四边形ABCD是平行四边形，∴AB∥DF，∴∠ABE=∠FCE，∵E为BC中点，∴BE=CE，在△ABE与△FCE中，，∴△ABE≌△FCE（ASA），∴AB=FC；（2）∵AD=2AB，AB=FC=CD，∴AD=DF，∵△ABE≌△FCE，∴AE=EF，∴DE⊥AF．21．【分析】利用平行线的性质得出∠BAE=∠CFE，由AAS得出△ABE≌△FCE，得出对应边相等AE=EF，再利用平行四边形的判定得出即可．解：四边形ABFC是平行四边形；理由如下：∵AB∥CD，∴∠BAE=∠CFE，∵E是BC的中点，∴BE=CE，在△ABE和△FCE中，，∴△ABE≌△FCE（AAS）；∴AE=EF，又∵BE=CE∴四边形ABFC是平行四边形．22．【分析】（1）选取①②，利用ASA判定△BEO≌△DFO即可；（2）根据△BEO≌△DFO可得EO=FO，BO=DO，再根据等式的性质可得AO=CO，根据两条对角线互相平分的四边形是平行四边形可得结论．证明：（1）选取①②，∵在△BEO和△DFO中，∴△BEO≌△DFO（ASA）；（2）由（1）得：△BEO≌△DFO，∴EO=FO，BO=DO，∵AE=CF，∴AO=CO，∴四边形ABCD是平行四边形．23．【分析】（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF 即可．解：（1）∵D、G分别是AB、AC的中点，∴DG∥BC，DG=BC，∵E、F分别是OB、OC的中点，∴EF∥BC，EF=BC，∴DG=EF，DG∥EF，∴四边形DEFG是平行四边形；（2）∵∠OBC和∠OCB互余，∴∠OBC+∠OCB=90°，∴∠BOC=90°，∵M为EF的中点，OM=3，∴EF=2OM=6．由（1）有四边形DEFG是平行四边形，∴DG=EF=6．24．【分析】（1）只要证明CM∥AN，AM∥CN即可．（2）先证明△DEM≌△BFN得BN=DM，再在RT△DEM中，利用勾股定理即可解决问题．（1）证明：∵四边形ABCD是平行四边形，∴CD∥AB，∵AM⊥BD，CN⊥BD，∴AM∥CN，∴CM∥AN，AM∥CN，∴四边形AMCN是平行四边形．（2）∵四边形AMCN是平行四边形，∴CM=AN，∵四边形ABCD是平行四边形，∴CD=AB，CD∥AB，∴DM=BN，∠MDE=∠NBF，在△MDE和△NBF中，，∴△MDE≌△NBF，∴ME=NF=3，在Rt△DME中，∵∠DEM=90°，DE=4，ME=3，∴DM===5，∴BN=DM=5．25．【分析】（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．证明：（1）∵四边形ABCD是平行四边形，∴AD∥CB，AD=CB，∴∠DAE=∠BCF，在△ADE和△CBF中，∴△ADE≌△CBF，∴DE=BF．（2）由（1），可得△ADE≌△CBF，∴∠ADE=∠CBF，∵∠DEF=∠DAE+∠ADE，∠BFE=∠BCF+∠CBF，∴∠DEF=∠BFE，∴DE∥BF，又∵DE=BF，∴四边形DEBF是平行四边形．26．【分析】（1）直接利用三角形中位线定理得出DE BC，进而得出DE=FC；（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长．（1）证明：∵D、E分别为AB、AC的中点，∴DE为△ABC的中位线，∴DE BC，∵延长BC至点F，使CF=BC，∴DE=FC；（2）解：∵DE FC，∴四边形DEFC是平行四边形，∴DC=EF，∵D为AB的中点，等边△ABC的边长是2，∴AD=BD=1，CD⊥AB，BC=2，∴DC=EF=．。

三角形、平行四边形、梯形的面积综合练习题 (2)

梯形的面积练习题：一、求下面梯形的面积：上底2米下底3米高5米上底4分米下底5分米高2分米上底48米，下底56米，高35米。

上底124米，下底76米，高82米。

上底80米，下底50米，高60米。

上底15分米，下底9分米，高比下底长1分米。

下底24厘米，上底是下底的一半，高1分米。

上底5厘米，下底8厘米，高6厘米上底2.4分米，下底7.6分米，高8分米二、填空：1、两个完全一样的梯形可以拼成一个（）形，这个拼成的图形的底等于梯形的（）与（）的和，高等于梯形的（），每个梯形的面积等于拼成的平行四边形面积的（）。

2、梯形的上底是a，下底是b,高是c,则它的面积＝（）3、一个梯形上底与下底的和是15米，高是4米，面积是（）平方米。

4、一个梯形的面积是8平方厘米，如果它的上底、下底和高各扩大2倍，它的面积是（）平方厘米。

5、用两个完全一样的梯形拼成一个平行四边形，已知每个梯形的面积是24平方分米，拼成的平行四边形的面积是多少平方分米？三、判断：1、梯形的面积等于平行四边形的面积的一半。

（）2、两个完全相同的直角梯形，可以拼成一个长方形。

（）3、一个上底是5厘米，下底是8厘米，高是3厘米的梯形，它的面积是12平方厘米。

（）4、一个梯形的上底是３分米，下底是５分米，高是４分米，面积就是32平方分米。

（）四、应用题1、一座小型拦河坝，横截面的上底5米，下底131米，高21米。

这座拦河坝的横截面积是多少？2、一块梯形稻田，上底长8米，下底比上底长1.2米，高是上底的2倍。

这块稻田的面积是多少平方米？3、一块梯形草坪的面积是90平方米，上底是6米，下底是12米，高是多少米？4、一块梯形的果园，它的上底是160米，下底是120米，高30米。

如果每棵果树占地10平方米，这个果园共有树多少棵？5、用65米长的篱笆沿墙边围一个直角梯形的鸡舍，梯形的直角边是15米，你能计算出围成的鸡舍的面积吗？6、一块三角形地，底长38米，高是27米，如果每平方米收小麦0.7千克，这块地可以收小麦多少千克？1、有一块梯形地，上底长64米，比下底短16米，高50米。

人教版数学八年级下册：第18章《平行四边形》同步练习含答案

F E D C B A O ED C B A D C B A O D C B A 第十八章平行四边形单元练习题一、选择题（每小题5分，共30分）1.如图，下列四组条件中，不能判定四边形ABCD 是平行四边形的是（）A.AB=DC ，AD=BCB.AB ∥DC ，AD ∥BCC.AB ∥DC ，AD=BCD.AB ∥DC ，AB=DC（第1题）（第2题）2.如图，在菱形ABCD 中，对角线AC ，BD 相交于点O ，下列结论中不一定成立的是（）A.AB ∥DCB.AC=BDC.AC ⊥BDD.OA=OC3.顺次连接矩形四边中点得到的四边形一定是（）A.正方形B.矩形C.菱形D.等腰梯形4.如图，矩形ABCD 的对角线AC ，BD 相交于点O ，CE ∥BD ，DE ∥AC.若AC=4，则四边形OCED 的周长为（）A.4B.6C.8D.105.如图，将一个边长分别为4,8的矩形纸片ABCD 折叠，使点C 与点A 重合，则折痕EF 的长为（）6.如图，正方形ABCD 的边长为8，点M 在DC 上，且DM=2，N 是AC 上一动点，则DN+MN 的最小值为（）（第4题）（第5题）（第6题）二、填空题（每小题6分，共24分）7.如图，在四边形ABCD 中，AB ∥CD ，AD ∥BC ，AC ，BD 相交于点O ，若AC=6，则AO 的长度等于________________.8.如图，若将四根木条钉成的矩形木框变形为□ABCD 的形状，并使其面积变为O F E D C B A D CB A DC B A 矩形面积的一半，则□ABCD 的最小内角的大小为______________.（第7题）（第8题）9.如图，将两条宽度都为3的纸片重叠在一起，使∠ABC=600，则四边形ABCD 的面积为__________10.如图，设四边形ABCD 是边长为1的正方形，以对角线AC 为边作第二个正方形ACEF ，再以对角线AE 为边作第三个正方形AEGH ，如此下去.则第n 个正方形的边长为________.（第9题）（第10题）三、解答题（第11题14分，第12,13题各16分，共46分）11.如图，在四边形ABCD 中，AB=CD ，BE=DF ；AE ⊥BD ，CF ⊥BD ，垂足分别为E ，F.（1）求证：△ABE ≌△CDF ；（第11题）（2）若AC 与BD 交于点O ，求证：AO=CO.O D C B AF E D C B A12.如图，在△ABC 中，∠CAB=900，DE ，DF 是△ABC 的中位线，连结EF ，AD.求证：EF=AD.（第12题）∵AE⊥BD,CF ⊥BD,∴∠AEB=∠CFD=90°∵AB =CD,BE=DF ∴ABE≌CDF参考答案：1.C.2.B.3.C.4.C.5.D.6.D7.3. 8.300. 11.（1）证明：（2）提示：证明四边形ABCD 是平行四边形由（1）△ABE ≌△CDF ，可得∠ABE=∠CDF ，AB ∥CD ，可得四边形ABCD 是平行四边形，于是AO=CO.12.提示：由DE ，DF 是△ABC 的中位线，可得四边形EAFD 是平行四边形，又∠CAB=900.可知□EAFD 是矩形，根据矩形对角线相等即可得证.13.提示：（1）证明△AOF ≌△BOE ；（2）结论仍然成立，证明△AOF ≌△BOE.。

二年级上册数学同步练习-2.2 初步认识平行四边形苏教版(含答案)

第二单元：平行四边形的初步认识第2课时：初步认识平行四边形班级：姓名: 等级:【基础训练】一、计算题。

1．直接写得数。

25-6= 61-8= 14+9= 42-8=53-7= 43+7= 30+62= 44-30=24-10+45= 49-40+6= 39+20+11=二、选择题。

2．两个完全一样的锐角三角形可以拼成一个（）。

A．长方形B．正方形C．平行四边形D．梯形3．用同样长的小棒摆一个平行四边形至少要( )根。

A．4 B．6 C．84．用不能拼成的图形是（）。

A．长方形B．正方形C．三角形5．平行四边形的（）一定相等。

A．四个角B．对边C．四条边6．沿下面图形中的虚线剪一剪,拼一拼,不可以拼成平行四边形的是( )号图形。

A．B．C．三、填空题。

7．平行四边形的对边________，对角________．8．数一数，填一填。

有_____个平行四边形有_____个平行四边形9．上图中有______个四边形，有______个平行四边形。

10．数一数，图中有___个三角形，___个平行四边形．11．请你做一个平行四边形框架并拉一拉，说说你发现了什么. 平行四边形具有________性，即________变形.四、作图题12．找一找、涂一涂（找出平行四边形涂上你喜欢的颜色）13．在下面的点子图上画两个不同的平行四边形。

14．在图上画一条线，把它变成两个平行四边形．【拓展运用】15．摆一摆，填一填。

用12根同样长的小棒摆成一个平行四边形，你能摆出几种不同的平行四边形呢？试试看！根数长边短边16．画一画：在下面的平行四边形内画一条线，将这个平行四边形分成两部分。

想一想：上面的平行四边形被分成了（）形和（）形。

（填图形名称）17．把下面的平行四边形剪成大小、形状完全一样的4块,可以怎样剪?画一画。

参考答案1．19、53、23、3446、50、92、1459、15、702．C3．A4．B5．B6．B7．相等相等8．5 69．4 210．5 311．不稳定易12．13．14．或15．根数长边 5 4 3短边 1 2 316．；三角形；三角形17．(答案不唯一)。

平行四边形知识点与经典例题2

平⾏四边形知识点与经典例题2平⾏四边形⼀、基础知识平⾏四边形2、由矩形的性质得到直⾓三⾓形的⼀个性质：直⾓三⾓形斜边上的中线等于斜边的⼀半。

三、例题例1、如图1，平⾏四边形ABCD 中，AE⊥BD，CF⊥BD，垂⾜分别为E 、F. 求证：∠BAE =∠DCF.例2、如图2，矩形ABCD 中，AC 与BD 交于O 点，BE⊥AC 于E ，CF⊥BD 于F.求证：BE = CF.例3、已知：如图3，在梯形ABCD 中，AD∥BC，AB = DC ，点E 、F 分别在AB 、CD 上，且BE = 2EA ，CF = 2FD. 求证：∠BEC =∠CFB.例4、如图6，E 、F 分别是平⾏四边形ABCD 的AD 、BC 边上的点，且AE = CF.（1）求证：△ABE≌△CDF；（2）若 M 、N 分别是BE 、DF 的中点，连结MF 、EN ，试判断四边形MFNE 是怎（图1） BA DBCE F(图6)M NOABCDE F （图2）样的四边形，并证明你的结论.例5、如图7 ABCD的对⾓线AC的垂直平分线与边AD，BC分别相交于点E，F.，求证：四边形AFCE是菱形.例6、如图8，四边形ABCD是平⾏四边形，O是它的中⼼，E、F是对⾓线AC上的点.（1）如果，则△DEC≌△BFA（请你填上⼀个能使结论成⽴的⼀个条件）；（2）证明你的结论.例7、如图9，已知在梯形ABCD中，AD∥BC，AB = DC，对⾓线AC和BD相交于点O，E是BC边上⼀个动点（点E不与B、C 两点重合），EF∥BD交AC于点F，EG∥AC交BD于点C.（1）求证：四边形EFOG的周长等于2OB；（2）请你将上述题⽬的条件“梯形ABCD中，AD∥BC，AB = DC”改为另⼀种四边形，其他条件不变，使得结论，“四边形EFOG的周长等于2OB”仍成⽴，并将改编后的题⽬画出图形，写出已知、求证、不必证明.例8、有⼀块梯形形状的⼟地，现要平均分给两个农户种植（即将梯形的⾯积两等分），试设计两种⽅案（平分⽅案画在备⽤图13(1)、(2)上），并给予合理的解释.备⽤图（1）备⽤图（2）图13B图8CRPDCBAEF 第12题图四、练习⼀、选择题1.下列命题正确的是（）(A)、⼀组对边相等，另⼀组对边平⾏的四边形⼀定是平⾏四边形 (B)、对⾓线相等的四边形⼀定是矩形(C)、两条对⾓线互相垂直的四边形⼀定是菱形 (D)、在两条对⾓线相等且互相垂直平分的四边形⼀定是正⽅形 2. 已知平⾏四边形ABCD 的周长32, 5AB=3BC,则AC 的取值围为( ) A. 64．延长平形四边形ABCD 的⼀边AB 到E ，使BE ＝BD ，连结DE 交BC 于F ，若∠DAB ＝120°,∠CFE ＝135°，AB ＝1，则AC 的长为（）（A ）1 （B ）1.2 （C ）32（D ）1.5 5．若菱形ABCD 中，AE 垂直平分BC 于E ，AE ＝1cm ，则BD 的长是（）（A ）1cm （B ）2cm （C ）3cm （D ）4cm 6.若顺次连结⼀个四边形各边中点所得的图形是矩形，那么这个四边形的对⾓线( ) （A ）互相垂直（B ）相等（C ）互相平分（D ）互相垂直且相等7. 如图，等腰△ABC 中，D 是BC 边上的⼀点，DE ∥AC ，DF ∥AB ，AB=5那么四边形AFDE 的周长是（）（A ）5 （B ）10 （C ）15 （D ）20(第7题）（第8题）（第9题）（第10题）8.如图，将边长为8cm 的正⽅形纸⽚ABCD 折叠，使点D 落在BC 边中点E 处，点A 落在点F 处，折痕为MN ，则线段CN 的长是（）．（A ）3cm （B ）4cm （C ）5cm （D ）6cm9. 如图，在直⾓梯形ABCD 中，AD∥BC，∠B=90°，AC 将梯形分成两个三⾓形，其中△ACD 是周长为18 cm 的等边三⾓形，则该梯形的中位线的长是( )． (A)9 cm (B)12cm (c)29cm (D)18 cm 10.如图，在周长为20cm 的□ABCD中，AB≠AD，AC 、BD 相交于点O ，OE ⊥BD 交AD 于E ，则△ABE 的周长为（） (A)4cm (B)6cm (C)8cm (D)10cm11. 如图2，四边形ABCD 为矩形纸⽚．把纸⽚ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若CD ＝6，则AF 等于（）（A ）34 （B ）33 （C ）24（D ）８12.如图，已知四边形ABCD 中，R 、P 分别是BC 、CD 上的点，E 、F 分别是 AP 、RP 的中点，当点P 在CD 上从C 向D 移动⽽点R 不动时，那么下列结论成⽴的是（ )A 、线段EF 的长逐渐增⼤B 、线段EF 的长逐渐减⼩C 、线段EF 的长不变D 、线段EF 的长与点P 13. 在梯形ABCD 中，AD//BC ，对⾓线AC ⊥BD ，且cm AC 5 ，BD=12c m ，则梯形中位线的长等于（）ABCDEF 图 2ABCDE O第10题图DABCPMN （1）（2）图9A B CDE F O 图A. 7.5cmB. 7cmC. 6.5cmD. 6cm14. 国家级历史⽂化名城——，风光秀丽，花⽊葱茏．某⼴场上⼀个形状是平⾏四边形的花坛（如图），分别种有红、黄、蓝、绿、橙、紫6种颜⾊的花．如果有AB EF DC ∥∥，BC GH AD ∥∥，那么下列说法中错误的是（）A ．红花、绿花种植⾯积⼀定相等B ．紫花、橙花种植⾯积⼀定相等C ．红花、蓝花种植⾯积⼀定相等D ．蓝花、黄花种植⾯积⼀定相等⼆、填空题1.如果四边形四个⾓之⽐1：2：3：4，则这四边形为＿＿＿＿形。

数学四年级上册《平行四边形的认识》练习题(含答案)

第五单元《平行四边形和梯形》第2课时《平行四边形的认识》一．选择题1．（2018秋•黄埔区期末）只有一组对边平行的四边形是（）A ．长方形B ．平行四边形C ．梯形2．（2016春•宝安区校级月考）两组对边分别平行的四边形是（）A ．梯形B ．平行四边形C ．长方形D ．正方形3．（2014秋•凤阳县期末）平行四边形有（）条高．A ．1B ．2C ．无数条4．（2018秋•昆明期末）从平行四边形的一条边上的一点到对边可以引（）垂线．A ．一条B ．两条C ．无数条5．（2015•谢家集区模拟）平行四边形四个角的和是（）A ．180度B ．360度C ．540度二．填空题6．平行四边形的周长是38厘米,其中一条边长是10厘米,与它相邻的一条边长是厘米．7．（2019秋•孝昌县期末）平行四边形的互相平行；对角．8．（2018•吉水县）平行四边形的对边,对角．9．平行四边形四个内角和为,对角．三．判断题10．（2018秋•玉泉区期末）平行四边形的所有高都相等．．（判断对错）11．（2016秋•仙桃期末）平行四边形四条边的长度确定了,它的形状就确定了．．（判断对错）12．平行四边形中不可能有直角．（判断对错）13．（2018秋•长阳县期末）长方形和正方形也具有不稳定性．．（判断对错）四．操作题14．（2012•永春县校级自主招生）（1）以如图线段A B 为底,虚线线段C D 为高,画一个平行四边形．（2）如果A 、B 、C 看作三个点,那么A 点在C 点的方向上；C 点在B 点的方向上．15．在右边画一个同样的平行四边形．16．在如图中画出一个平行四边形：17．（2011秋•路南区期末）请将下面的图形改成平行四边形．18．量出平行四边形四条边的长度,并填在横线上．A B ＝,B C ＝,C D ＝,D A ＝．通过测量边长可以知道：．19．画一个一组邻边分别是3厘米和2厘米、两边夹角是60度的平行四边形．20．画一画,利用下面三角形画一个平行四边形21．（2015秋•遵义期末）画一个高为3厘米的平行四边形,并标出高．五．解答题22．（2017•云阳县）做一做．（请你在方格图上画一个平行四边形）23．（2014秋•历城区校级期末）画一个底边是4厘米的平行四边形．24．（2013秋•万安县期末）在下面的平行四边形中,已知∠B ＝55°,请写出其他三个角的度数．∠A ＝；∠C ＝；∠D ＝．25．（2015秋•仪陇县月考）一个平行四边形的一条边长12厘米,比邻边少2厘米,这个平行四边形的周长是多少厘米？26．小明用一根50厘米长的铁丝围出了一个平行四边形,其中一条边长18厘米,另外三条边长分别是多少厘米？27．平行四边形的周长是56厘米,其中一条边长是10厘米．平行四边形另外三条边分别是多少厘米？28．（2012秋•赣州期末）在右边画出一个同样的平行四边形．29．（2009秋•富宁县期末）在下面的方格纸上画一个平行四边形．你画的平行四边形的边长分别是、、、；周长是．参考答案第五单元《平行四边形和梯形》第2课时《平行四边形的认识》一．选择题1．（2018秋•黄埔区期末）只有一组对边平行的四边形是（）A ．长方形B ．平行四边形C ．梯形【解答】解：只有一组对边平行的四边形是梯形；故选：C ．2．（2016春•宝安区校级月考）两组对边分别平行的四边形是（）A ．梯形B ．平行四边形C ．长方形D ．正方形【解答】解：两组对边分别平行的四边形是平行四边形；故选：B ．3．（2014秋•凤阳县期末）平行四边形有（）条高．A ．1B ．2C ．无数条【解答】解：由分析可知,平行四边形有无数条高,故选：C ．4．（2018秋•昆明期末）从平行四边形的一条边上的一点到对边可以引（）垂线．A ．一条B ．两条C ．无数条【解答】解：由分析得出：从平行四边形的一条边上的一点到对边可以引一条垂线．故选：A ．5．（2015•谢家集区模拟）平行四边形四个角的和是（）A ．180度B ．360度C ．540度【解答】解：连接平行四边形的一条对角线,把这个平行四边形分成了两个相等的三角形, 则平行四边形的四个内角的度数之和,正好等于这两个三角形的内角和之和,因为三角形的内角和是180度,180°×2＝360°．所以平行四边形的内角和是360度．故选：B ．二．填空题6．平行四边形的周长是38厘米,其中一条边长是10厘米,与它相邻的一条边长是9厘米．【解答】解：38÷2﹣10＝19﹣10＝9（厘米）答：与它相邻的一条边长是9厘米．故答案为：9.7．（2019秋•孝昌县期末）平行四边形的对边互相平行；对角相等．【解答】解：由分析可知：平行四边形的对边互相平行；对角相等．故答案为：对边、相等．8．（2018•吉水县）平行四边形的对边相等,对角相等．【解答】解：平行四边形的对边相等,对角相等．故答案为：相等,相等．9．平行四边形四个内角和为360°,对角相等．【解答】解：平行四边形四个内角和为360°,对角相等．故答案为：360°,相等．三．判断题10．（2018秋•玉泉区期末）平行四边形的所有高都相等．×．（判断对错）【解答】解：平行四边形的高为两组,所以平行四边形有两组高,每组的高都相等且有无数条,但每个平行四边形的所有高的长度都相等,说法是错误的；故答案为：×．11．（2016秋•仙桃期末）平行四边形四条边的长度确定了,它的形状就确定了．×．（判断对错）【解答】解：因为平行四边形具有不稳定性,所以所以即使平行四边形四条边的长度确定了,它的形状依然不能确定．所以原题的说法错误．故答案为：×．12．平行四边形中不可能有直角．×（判断对错）【解答】解：长方形、正方形是特殊的平行四边形,四个角都是直角．所以平行四边形中不可能有直角说法错误．故答案为：×．13．（2018秋•长阳县期末）长方形和正方形也具有不稳定性．√．（判断对错）【解答】解：长方形和正方形也具有不稳定性；故答案为：√．四．操作题14．（2012•永春县校级自主招生）（1）以如图线段A B 为底,虚线线段C D 为高,画一个平行四边形．（2）如果A 、B 、C 看作三个点,那么A 点在C 点的西南方向上；C 点在B 点的西北方向上．【解答】解：（1）画图如下：（2）那么A 点在C 点的西南方向上；C 点在B 点的西北方向上；故答案为：西南,西北．15．在右边画一个同样的平行四边形．【解答】解：如图：16．在如图中画出一个平行四边形：【解答】解：根据平行四边形的定义,可以画出图形如下：17．（2011秋•路南区期末）请将下面的图形改成平行四边形．【解答】解：作图如下：18．量出平行四边形四条边的长度,并填在横线上．A B ＝ 2.1C m,B C ＝ 4.3C m,C D ＝ 2.1C m,D A ＝ 4.3C m．通过测量边长可以知道：平行四边形的对边相等．【解答】解：量出平行四边形四条边的长度如下：A B ＝2.1C m,B C ＝4.3C m,C D ＝2.1C m,D A ＝4.3C m通过测量边长可以知道：平行四边形的对边相等．故答案为：2.1C m,4.3C m,2.1C m,4.3C m；平行四边形的对边相等．19．画一个一组邻边分别是3厘米和2厘米、两边夹角是60度的平行四边形．【解答】解：20．画一画,利用下面三角形画一个平行四边形【解答】解：21．（2015秋•遵义期末）画一个高为3厘米的平行四边形,并标出高．【解答】解：作平行四边形及高如下,该平行四边形即高为3厘米的平行四边形：五．解答题22．（2017•云阳县）做一做．（请你在方格图上画一个平行四边形）【解答】解：画图如下：23．（2014秋•历城区校级期末）画一个底边是4厘米的平行四边形．【解答】解：作图如下：24．（2013秋•万安县期末）在下面的平行四边形中,已知∠B ＝55°,请写出其他三个角的度数．∠A ＝125°；∠C ＝125°；∠D ＝55°．【解答】解：因为平行四边形A B C D 中,∠B ＝55°,则∠A ＝∠C ＝180°﹣55°＝125°,∠B 与∠D 为平行四边形的对角,所以∠B ＝∠D ,即∠D ＝55°．故答案为：125°、125°、55°．25．（2015秋•仪陇县月考）一个平行四边形的一条边长12厘米,比邻边少2厘米,这个平行四边形的周长是多少厘米？【解答】解：12+2＝14（厘米）（12+14）×2＝26×2＝52（厘米）答：这个平行四边形的周长是52厘米．26．小明用一根50厘米长的铁丝围出了一个平行四边形,其中一条边长18厘米,另外三条边长分别是多少厘米？【解答】解：A B +A D ＝50÷2＝25厘米假设A B ＝18厘米,所以A D ＝25﹣18＝7（厘米）由于平行四边形的对边相等则所以C D ＝A B ＝18厘米,B C ＝A D ＝7厘米．答：平行四边形另外三条边分别是18厘米、7厘米、7厘米．27．平行四边形的周长是56厘米,其中一条边长是10厘米．平行四边形另外三条边分别是多少厘米？【解答】解：A B +A D ＝56÷2＝28厘米,假设A B ＝10厘米,所以A D ＝28﹣10＝18厘米,由于平行四边形的对边相等则,所以C D ＝A B ＝10厘米,B C ＝A D ＝18厘米．答：平行四边形另外三条边分别是10厘米、18厘米、18厘米．28．（2012秋•赣州期末）在右边画出一个同样的平行四边形．【解答】解：平行四边形的底是3.3厘米,高是2厘米,则：29．（2009秋•富宁县期末）在下面的方格纸上画一个平行四边形．你画的平行四边形的边长分别是6厘米、5厘米、6厘米、5厘米；周长是22厘米．【解答】解：（1）如图所示：；画的平行四边形的边长分别是6厘米、5厘米、6厘米、5厘米；（2）周长是：6+5+6+5＝22（厘米）．答：周长是22厘米．故答案为：6厘米、5厘米、6厘米、5厘米；22厘米．。

平行四边形基础题练习

平行四边形基础题练习1的周长为40cmABC 的周长为25cm ，则AC 得长为（）A ．5cmB ．6cmC ．15cmD ．16cm2、平行四边形不具有的性质是（）A ．对角线互相垂直B ．对边平行且相等C ．对角线互相平分D ．对角相等3、在中，AC=10，BD=6，则边长AB ，AD 的可能取值为（）．A. AB=4，AD=4B. AB=4，AD=7C. AB=9，AD=2D. AB=6，AD=24、平行四边形一边长为12cm ，那么它的两条对角线的长度可能是（）．A.8cm 和14cmB.10cm 和14cmC.18cm 和20cmD.10cm 和34cm5、平行四边形ABCD 的周长32, 5AB=3BC,则对角线AC 的取值范围为( )A. 6<AC<10B. 6<AC<16C. 10<AC<16D. 4<AC<166、如图，在中，∠B=110°，延长AD 至F ，延长CD 至E ，连接EF ，∠E+∠F 等于（）A ．110°B ．30°C ．50°D ．70° 7、如图，在□ABCD 中，已知AD ＝8㎝， AB ＝6㎝， DE 平分∠ADC 交BC 边于点E ，则BE 等于（） A ．2cm B ．4cm C ．6cm D ．8cm8、在平行四边形ABCD 中，AC ⊥AB ，且∠ABC ：∠BCA ＝2：1，则∠ABC 与∠BCD 之比为（）A B CD EA DOB E CA. 1：1B. 1：2C. 1：3D. 1：49、如图所示，在平行四边形ABCD 中，DB ＝DC ，∠C ＝70°，AE ⊥BD 于E ，则∠DAE 等于（）A. 20°B. 25°C. 30°D. 35° 10、如图所示，平行四边形ABCD 的对角线相交于O 点，且AB ≠BC ，过O 点作OE ⊥AC ，交BC 于E ，如果△ABE 的周长为b ，则平行四边形ABCD 的周长是（） A. b B. 1.5b C. 2b D. 3b11、下列条件中能判定一个四边形是平行四边形的是（）A. 一组对边相等B. 一组对边平行C. 两条对角线相等D. 两组对角分别相等12、平行四边形ABCD 中，AB ＝2，BC ＝3，∠B 、∠C 的平分线分别交AD 于E 、F ，则EF ＝__________。