高考复习第1章第1节集合
人教版高中化学必修一第一章第一节高考复习知识梳理及经典考题
第一章从实验学化学第一节化学实验基本方法一、知识点梳理二、知识点填空1、给烧瓶、烧杯等加热时要;在试管中加热固体时,管口。
酒精及其他易燃有机物小面积失火,立即用;钠、磷等失火应#。
2、少量酸(或碱)滴到桌子上应;较多量酸(或碱)流到桌上应;酸沾到皮肤或衣物上应;碱点到皮肤上应。
3、误食重金属应。
4、汞滴落在桌上或地上应。
5、物质提纯时要注意的三个事项:。
6、过滤操作应注意的事项有:)。
7、蒸馏适用的对象是:。
8、蒸馏操作应注意的事项有:。
9、萃取是指:;萃取常用的仪器是:。
10、萃取剂的选择:。
三、典型例题$【例1】进行化学实验,必须注意安全,下列说法正确的是(填写标号)_______。
A.不慎将酸溅到眼中,应立即用水冲洗,边洗边眨眼睛B.不慎将浓碱溶液沾到皮肤上,要立即用大量水冲洗,然后涂上硼酸溶液C.如果浓H2SO4沾到皮肤上,可立即用大量水冲洗D.如果少量酒精失火燃烧,可用湿抹布盖灭火焰E.如果皮肤小面积烫伤,第一件要做的事是拨120或110求助【例2】根据从草木灰(主要成分是K2CO3、KCl和K2SO4)中提取钾盐实验,填写下列空白:(1)此实验操作顺序如下:①称量样品:②溶解沉降;③_____;④___;⑤冷却结晶。
{(2)用托盘天平称量样品时,若指针偏向右边,则表示()A.左盘重,样品轻 B.左盘轻,砝码重C.右盘重,砝码轻 D.右盘轻,样品重(3)在进行第③步操作时,有时可能要重复进行,这是因为____________。
(4)在进行第④步操作时,要用玻璃棒不断地搅动液体,目的是防止________。
【例3】球洗气管是一种多用途仪器,常用于去除杂质、气体干燥、气体吸收(能防止倒吸)等实验操作。
右图是用水吸收下列某气体时的情形,根据下面附表判断由左方进入的被吸收气体的是A.Cl2 B.HCl C.H2S D.CO2:气体Cl2HCI H2S CO21体积的水能吸收气体的体积数 2 ¥5002.6 1【例4】纯碱纯度的测定[案例展示] 纯碱中常含有少量氯化钠,请设计实验测定纯碱中Na2CO3的质量分数。
2021届高考数学热点题型训练:第1章 第1节 集合 Word版含解析

第一节 集 合考点一集合的基本概念[例1] (1)(2021·山东高考)已知集合A ={0,1,2},则集合B ={x -y |x ∈A, y ∈A }中元素的个数是( )A .1B .3C .5D .9(2)已知A ={a +2,(a +1)2,a 2+3a +3},若1∈A ,则实数a 构成的集合B 的元素个数是( ) A .0 B .1 C .2 D .3[自主解答] (1)①当x =0时,y =0,1,2,此时x -y 的值分别为0,-1,-2;②当x =1时,y =0,1,2,此时x -y 的值分别为1,0,-1;③当x =2时,y =0,1,2,此时x -y 的值分别为2,1,0.综上可知,x -y 的可能取值为-2,-1,0,1,2,共5个.(2)①当a +2=1时,a =-1,此时A ={1,0,1},不合题意,故a ≠-1;②当(a +1)2=1时,a =0或a =-2.若a =0,则A ={2,1,3},符合题意;若a =-2,则A ={0,1,1},不符合题意;③当a 2+3a +3=1时,(a +1)(a +2)=0,即a =-1或a =-2.由①②知,不符合题意.综上可知a =0,即实数a 构成的集合B 只有1个元素. [答案] (1)C (2)B 【互动探究】若将本例(1)中的集合B 更换为B ={(x ,y )|x ∈A ,y ∈A ,x -y ∈A },则集合B 中有多少个元素? 解:当x =0时,y =0;当x =1时,y =0或y =1;当x =2时,y =0,1,2.故集合B ={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)},即集合B 中有6个元素. 【方法规律】解决集合的概念问题应关注两点(1)争辩一个集合,首先要看集合中的代表元素,然后再看元素的限制条件,当集合用描述法表示时,留意弄清其元素表示的意义是什么.如本例(1)中集合B 中的元素为实数x -y ,在“互动探究”中,集合B 中的元素为点(x ,y ).(2)对于含有字母的集合,在求出字母的值后,要留意检验集合是否满足互异性.1.(2022·宁波模拟)已知集合M ={1,m },N ={n ,log 2n },若M =N ,则(m -n )2 015=________.解析:由于M =N ,所以⎩⎪⎨⎪⎧n =1,log 2n =m 或⎩⎪⎨⎪⎧n =m ,log 2n =1,即⎩⎪⎨⎪⎧n =1,m =0或⎩⎪⎨⎪⎧n =2,m =2.故(m -n )2 015=-1或0.答案:-1或02.已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ax -1x -a <0,且2∈A,3∉A ,则实数a 的取值范围是________________. 解析:由于2∈A ,所以2a -12-a <0,即(2a -1)(a -2)>0,解得a >2或a <12.①若3∈A ,则3a -13-a <0,即(3a -1)(a -3)>0,解得a >3或a <13,所以3∉A 时,13≤a ≤3.②由①②可知,实数a 的取值范围为⎣⎢⎡⎭⎪⎫13,12∪(2,3].答案:⎣⎢⎡⎭⎪⎫13,12∪(2,3] 考点二集合间的基本关系[例2] (1)(2022·西城模拟)已知M ={x |x -a =0},N ={x |ax -1=0},若M ∩N =N ,则实数a 的值为( )A .1B .-1C .1或-1D .0或1或-1(2)已知集合A ={x |x <-1或x >4},B ={x |2a ≤x ≤a +3},若B ⊆A ,则实数a 的取值范围为________. [自主解答] (1)由于M ∩N =N ,所以N ⊆M .当a =0时,N =∅,M ={0},满足M ∩N =N ;当a ≠0时,M ={a },N =⎩⎨⎧⎭⎬⎫1a ,所以1a=a ,即a =±1.故实数a 的值为0,±1.(2)当B =∅时,只需2a >a +3,即a >3;当B ≠∅时,依据题意作出如图所示的数轴,可得⎩⎪⎨⎪⎧a +3≥2a ,a +3<-1或⎩⎪⎨⎪⎧a +3≥2a ,2a >4,解得a <-4或2<a ≤3.图1图2综上可得,实数a 的取值范围为(-∞,-4)∪(2,+∞). [答案] (1)D (2)(-∞,-4)∪(2,+∞) 【方法规律】。
【步步高】高考语文 古诗文阅读 第一章 第1节讲义课件

例 1 ①蚓无爪牙之利。“爪牙”在本句中是基本义。 ②祈父,予王之爪牙。“爪牙”在本句中是比 喻义,比喻得力的帮手和武士。 ③被发行吟泽畔。“畔”在本句中是引申义, “旁边”。 ④亲戚畔之。“畔”通“叛”,假借义,“背 叛”。
例 2 下列句子中对“逐”的解释,不正确的一 项是 ( C ) A.秦失其鹿,天下共逐 (驱逐)之。 . B.齐师败绩,逐 (追击)之。 . C.非秦者去,为客者逐 (放逐)。 . D.一兔走,百人逐 (追赶)之,非一兔也。 .
古汉语以单音节词语为主,有时两个单音节词语恰好 在相邻的位置, 看起来与现代汉语的一个双音节词语相同, 实际上,这些词形同实异,按照句子结构,它们要拆成两 个词。如“众谓予一行为可以救国”(《指南录后序》 ), “行”“为”相邻,貌似现代汉语的“行为”,其实, “行”是“出行”“行动”,“为”是“是”。再如“妻 子”“地方”“可以”“因为”“祖父”“不行”“突 出”“前进”“不过”“十一”等,课本内外,比比皆是。
3.命题规律 文言实词的考查特点具有以下几个方面: (1)考查以单音节词为主。这与文言文的特点是一致的, 文言文中的词语也是以单音节词为主。 (2)考查的对象为常见常用词。高考考查的文言实词都 是常见常用的,这就提醒我们在学习古文时,要注意出现频 率较高的实词。 (3)一词多义、词类活用和古今异义都有涉及。实词的 考查,一般以考查一词多义为主,同时涉及对词类活用、古 今异义、通假字的考查。 (4)考查形式依然以选择题为主,在翻译题目中也会涉 及到对实词的考查。
例 1
①天下云 集响 应,赢粮而景 从 . . . 彩、回声、影子一样
云、响、景:像云
②人皆得以隶 使之 隶:像奴仆那样 . ③余自齐安舟 行适临汝 舟:乘船 . ④东 割膏腴之地,北 收要害之郡 . . 在北边 东、北:在东边、
高三理科数学第一轮复习§1.1: 集合

解析
解析
第一章:集合与常用逻辑用语
第1节: 集合
解析
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
ቤተ መጻሕፍቲ ባይዱ
解析
第一章:集合与常用逻辑用语
第1节: 集合
解析
第一章:集合与常用逻辑用语
第1节: 集合
解析
第一章:集合与常用逻辑用语
第1节: 集合
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
第一章:集合与常用逻辑用语
第1节: 集合
解析
第一章:集合与常用逻辑用语
第1节: 集合
解析
第一章:集合与常用逻辑用语
第1节: 集合
解析
人教A版高考总复习文科数学精品课件 第1章集合与常用逻辑用语 第3节 命题及其关系、充要条件 (2)

(2)本例3条件不变,问是否存在实数m,使x∈P是x∈S的充要条件?如果存在,
求出m的值,如果不存在,请说明理由.
解:(1)由例题知P={x|-2≤x≤10}.
∵x∈P是x∈S的充分不必要条件,∴P⇒S且S
P.
∴[-2,10]⫋[1-m,1+m].
1- < -2,
1-
≤
-2,
∴
或
1 + ≥ 10,
1 + > 10
∴m≥9,则m的取值范围是[9,+∞).
(2)不存在.理由如下:由例题知P={x|-2≤x≤10}.若x∈P是x∈S的充要条件,
则P=S,
= 3,
1- = -2,
∴
∴
这样的 m 不存在.
1 + = 10, = 9,
去判断.
常用结论
1.充分条件与必要条件的两个特征
(1)对称性:若p是q的充分条件,则q是p的必要条件,即“p⇒q”⇔“q⇐p”.
(2)传递性:若p是q的充分(必要)条件,q是r的充分(必要)条件,则p是r的充分
(必要)条件,即“p⇒q且q⇒r”⇒“p⇒r”(“p⇐q且q⇐r”⇒“p⇐r”).
2.若条件p,q以集合的形式出现,即A={x|p(x)},B={x|q(x)},则
第一章
第三节 命题及其关系、充要条件
内
容
索
引
01
强基础 增分策略
02
增素能 精准突破
课标解读
1.理解命题的概念.
2.了解“若p,则q”形式的命题及
其逆命题、否命题与逆否命题,
会分析四种命题的相互关系.
高中数学 第一节 集合 教案

第一章集合与常用逻辑用语、不等式第一节集合核心素养立意下的命题导向1.与方程、函数、不等式等相结合考查集合元素的性质,凸显数学抽象的核心素养.2.与不等式相结合考查集合的基本关系,凸显数学运算、逻辑推理的核心素养.3.与不等式、数轴、Venn图等相结合考查集合的运算,凸显数学运算、直观想象的核心素养.[理清主干知识]1.集合的有关概念(1)集合元素的特性:确定性、互异性、无序性.(2)集合与元素的关系:若a属于集合A,记作a∈A;若b不属于集合A,记作b∉A.(3)集合的表示方法:列举法、描述法、图示法.(4)五个特定的集合:集合自然数集正整数集整数集有理数集实数集符号N N*或N+Z Q R2.集合间的基本关系表示关系文字语言记法集合间的基本关系子集集合A中任意一个元素都是集合B中的元素A⊆B或B⊇A真子集集合A是集合B的子集,并且B中至少有一个元素不属于AA B或B A相等集合A中的每一个元素都是集合B中的元素,集合B中的每一个元素也都是集合A中的元素A⊆B且B⊆A⇔A=B空集空集是任何集合的子集∅⊆A空集是任何非空集合的真子集∅B且B≠∅设集合A是有n(n∈N*)个元素的有限集,即card(A)=n.(1)A的子集个数是2n;(2)A的真子集个数是2n-1;(3)A的非空子集个数是2n-1;(4)A的非空真子集个数是2n-2.4.集合的三种基本运算符号表示图形表示符号语言集合的并集A∪BA∪B={x|x∈A,或x∈B}集合的交集A∩BA∩B={x|x∈A,且x∈B}集合的补集若全集为U,则集合A的补集为∁U A∁U A={x|x∈U,且x∉A}5.(1)A∩A=A,A∩∅=∅.(2)A∪A=A,A∪∅=A.(3)A∩∁U A=∅,A∪∁U A=U,∁U(∁U A)=A.(4)A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B⇔A∩(∁U B)=∅.[澄清盲点误点]一、关键点练明1.(集合的表示)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为() A.9B.8C.5 D.4答案:A2.(并集与交集的运算)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=()A.{2} B.{2,3}C.{-1,2,3} D.{1,2,3,4}答案:D3.(全集与补集的运算)设全集为R,集合A={x|0<x<2},B={x|x<1},则A∩(∁R B)=() A.{x|0<x≤1} B.{x|0<x<1}C.{x|1≤x<2} D.{x|0<x<2}答案:C4.(相等集合)设集合M={1,x,y},N={x,x2,xy},且M=N,则x2 021+y2 020=________. 答案:-1二、易错点练清1.(忽视元素的互异性)已知集合A ={1,3,m },B ={1,m },若B ⊆A ,则m =( ) A .1 B .0或1或3 C .0或3D .1或3解析:选C 由B ⊆A ,得m =3或m =m , 解m =m ,得m =0或m =1,由集合元素的互异性知m ≠1.∴m =0或3.2.(忽视空集的情形)已知集合M ={x |x -a =0},N ={x |ax -1=0},若M ∩N =N ,则实数a 的值是( ) A .-1 B .1C .-1或1D .0或1或-1 解析:选D 由M ∩N =N ,得N ⊆M ,当N =∅时,a =0;当N ≠∅时,1a =a ,解得a =±1,故a 的值为±1,0.3.(忽视集合运算中端点取值)已知集合A ={x |x ≥3},B ={x |x ≥m },且A ∪B =A ,则实数m 的取值范围是________.解析:因为集合A ={x |x ≥3},B ={x |x ≥m },且A ∪B =A ,所以B ⊆A ,如图所示,所以m ≥3. 答案:[3,+∞)考点一 集合的基本概念[典例] (1)已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( ) A .9 B .8 C .5D .4(2)设A =⎩⎨⎧⎭⎬⎫2,3,a 2-3a ,a +2a +7,B ={|a -2|,3},已知4∈A 且4∉B ,则a 的取值集合为________.[解析] (1)将满足x 2+y 2≤3的整数x ,y 全部列举出来,即(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.故选A. (2)因为4∈A ,即4∈⎩⎨⎧⎭⎬⎫2,3,a 2-3a ,a +2a +7,所以a 2-3a =4或a +2a +7=4. 若a 2-3a =4,则a =-1或a =4;若a +2a +7=4,即a 2+3a +2=0,则a =-1或a =-2.由a 2-3a 与a +2a +7互异,得a ≠-1.故a =-2或a =4.又4∉B ,即4∉{|a -2|,3}, 所以|a -2|≠4,解得a ≠-2且a ≠6. 综上所述,a 的取值集合为{4}. [答案] (1)A (2){4} [方法技巧]与集合元素有关问题的解题策略(1)研究集合问题时,首先要明确构成集合的元素是什么,即弄清该集合是数集、点集,还是其他集合;然后再看集合的构成元素满足的限制条件是什么,从而准确把握集合的含义. (2)利用集合元素的限制条件求参数的值或确定集合中元素的个数时,要注意检验集合是否满足元素的互异性. [针对训练]1.(多选)实数1是下面哪个集合中的元素( ) A .整数集Z B.{}x |x =|x |C.{}x ∈N |-1<x <1D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪x -1x +1≤0解析:选ABD 对于A ,∵1是整数,∴1∈Z ,故A 正确. 对于B ,∵x =|x |,∴x ≥0,∵1>0,∴B 正确.对于C ,∵{}x ∈N |-1<x <1={}0,1不在集合中,∴C 不正确.对于D ,∵⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪x -1x +1≤0={}x ∈R |-1<x ≤1,1是集合中的元素,∴D 正确.故选A 、B 、D.2.已知集合A ={1,x 2}.若x 2∈{1,3,9,x },则x =________.解析:由题意知,x 2≠1,∴x ≠±1.∵x 2∈{1,3,9,x },∴若x 2=3,则x =±3,经检验可知符合题意;若x 2=9,则x =±3,经检验,x =3不满足集合元素的互异性,舍去;若x 2=x ,则x =0或x =1,经检验,x =1不满足集合元素的互异性,舍去.综上可知x =3或-3或-3或0.答案:3或-3或-3或03.设集合A ={-4,2a -1,a 2},B ={9,a -5,1-a },且A ,B 中有唯一的公共元素9,则实数a 的值为________.解析:因为集合A ,B 中有唯一的公共元素9,所以9∈A .若2a -1=9,即a =5,此时A ={-4,9,25},B ={9,0,-4},则集合A ,B 中有两个公共元素-4,9,与已知矛盾,舍去.若a 2=9,则a =±3,当a =3时,A ={-4,5,9},B ={9,-2,-2},B 中有两个元素均为-2,与集合中元素的互异性矛盾,应舍去;当a =-3时,A ={-4,-7,9},B ={9,-8,4},符合题意.综上所述,a =-3. 答案:-3考点二 集合间的基本关系[典例] (1)已知集合A ={x |x 2-2x -3≤0,x ∈N *},则集合A 的真子集的个数为( ) A .7 B .8 C .15D .16(2)已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},若B ⊆A ,则实数m 的取值范围为________.[解析] (1)法一:A ={x |-1≤x ≤3,x ∈N *}={1,2,3},其真子集有:∅,{1},{2},{3},{1,2},{1,3},{2,3},共7个.法二:因为集合A 中有3个元素,所以其真子集的个数为23-1=7(个).(2)因为B ⊆A ,所以,①若B =∅,则2m -1<m +1,此时m <2.②若B ≠∅,则⎩⎪⎨⎪⎧2m -1≥m +1,m +1≥-2,2m -1≤5.解得2≤m ≤3.由①、②可得,符合题意的实数m 的取值范围为(-∞,3].[答案] (1)A (2)(-∞,3][方法技巧] 解决有关集合间的基本关系问题的策略(1)一般利用数轴法、Venn 图法以及结构法判断两集合间的关系,如果集合中含有参数,需要对式子进行变形,有时需要进一步对参数分类讨论.(2)确定非空集合A 的子集的个数,需先确定集合A 中的元素的个数. [提醒] 不能忽略任何非空集合是它自身的子集.(3)根据集合间的关系求参数值(或取值范围)的关键是将条件转化为元素满足的式子或区间端点间的关系,常用数轴法、Venn 图法. [针对训练]1.已知集合M ={x |y =1-x 2,x ∈R },N ={x |x =m 2,m ∈M },则集合M ,N 的关系是( ) A .M N B .NMC .M ⊆∁R ND .N ⊆∁R M解析:选B 依题意知,M ={x |y =1-x 2,x ∈R }={x |-1≤x ≤1},N ={x |x =m 2,m ∈M }={x |0≤x ≤1},所以N M .故选B.2.已知集合A ={x |x 2-3x +2=0,x ∈R },B ={x |0<x <5,x ∈N },则满足条件A ⊆C ⊆B 的集合C 的个数为( ) A .1 B .2 C .3D .4解析:选D 求解一元二次方程,得A ={x |x 2-3x +2=0,x ∈R }={x |(x -1)(x -2)=0,x ∈R }={1,2},易知B ={x |0<x <5,x ∈N }={1,2,3,4}.因为A ⊆C ⊆B ,所以根据子集的定义,集合C 必须含有元素1,2,且可能含有元素3,4,原题即求集合{3,4}的子集个数,即有22=4个,故选D.考点三 集合的基本运算考法(一) 集合间的交、并、补运算[例1] (1)(多选)(2021·山东滨州期末)设全集U ={}0,1,2,3,4,集合A ={}0,1,4,B ={}0,1,3,则( ) A .A ∩B ={}0,1 B .∁U B ={}4C .A ∪B ={}0,1,3,4D .集合A 的真子集个数为8(2)(2021年1月新高考八省联考卷)已知M ,N 均为R 的子集,且∁R M ⊆N ,则M ∪(∁R N )=( )A .∅B .MC .ND .R[解析] (1)∵全集U ={}0,1,2,3,4,A ={}0,1,4,B ={}0,1,3,∴A ∩B ={}0,1,∁U B ={2,4},A ∪B ={0,1,3,4},集合A 的真子集个数为23-1=7,故选A 、C. (2)如图所示,易知答案为B.[答案] (1)AC (2)B[方法技巧] 解决集合运算问题3个技巧考法(二) 利用集合的运算求参数[例2] (1)(2020·全国卷Ⅰ)设集合A ={x |x 2-4≤0},B ={x |2x +a ≤0},且A ∩B ={x |-2≤x ≤1},则a =( ) A .-4 B .-2 C .2D .4(2)集合A ={0,2,a },B ={1,a 2},若A ∪B ={0,1,2,4,16},则a 的值为________.[解析] (1)易知A ={x |-2≤x ≤2},B =⎩⎨⎧⎭⎬⎫x ⎪⎪x ≤-a 2,因为A ∩B ={x |-2≤x ≤1},所以-a2=1,解得a =-2.故选B. (2)根据并集的概念,可知{a ,a 2}={4,16},只能是a =4. [答案] (1)B (2)4 [方法技巧]利用集合的运算求参数的值或取值范围的方法(1)与不等式有关的集合,一般利用数轴解决,要注意端点值能否取到.(2)若集合能一一列举,则一般先用观察法得到不同集合中元素之间的关系,再列方程(组)求解.[提醒] 在求出参数后,注意结果的验证(满足互异性).[针对训练]1.(2020·新高考全国卷Ⅰ)设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =( ) A .{x |2<x ≤3} B .{x |2≤x ≤3} C .{x |1≤x <4}D .{x |1<x <4}解析:选C 因为A ={x |1≤x ≤3},B ={x |2<x <4}, 所以A ∪B ={x |1≤x <4}.2.已知集合A ={x |-1<x <1},B ={x |x 2-x -2<0},则(∁R A )∩B =( )A.(-1,0] B.[-1,2)C.[1,2) D.(1,2]解析:选C∵A={x|-1<x<1},B={x|x2-x-2<0}={x|-1<x<2},∁R A={x|x≤-1或x≥1},则(∁R A)∩B={x|1≤x<2},故选C.3.已知集合A={x|x<3},B={x|x>a},若A∩B≠∅,则实数a的取值范围为() A.[3,+∞) B.(3,+∞)C.(-∞,3) D.(-∞,3]解析:选C因为A∩B≠∅,所以结合数轴可知实数a的取值范围是a<3,故选C.一、创新命题视角——学通学活巧迁移集合中的新定义问题类型(一)定义新运算[例1]定义集合A与B的运算“*”为:A*B={x|x∈A或x∈B,但x∉(A∩B)}.设X是非负偶数集,Y={1,2,3,4,5},则(X*Y)*Y=()A.X B.YC.X∩Y D.X∪Y[解析]由题意可知,X∩Y={2,4},X∪Y={0,1,2,3,4,5,6,8,10,…},∴X*Y={0,1,3,5,6,8,10,…}.∴(X*Y)∩Y={1,3,5},(X*Y)∪Y={0,1,2,3,4,5,6,8,10,…}.∴(X*Y)*Y={0,2,4,6,8,10,…}=X.故选A.[答案] A[名师微点]正确分析新运算法则,把新运算法则所表达的数学本质弄清楚,进而转化成熟悉的数学情境.注意结合集合的基础知识解答.类型(二)定义新概念[例2]已知集合A0={x|0<x<1}.给定一个函数y=f(x),定义集合A n={y|y=f(x),x∈A n-1},若A n∩A n-1=∅对任意的x∈N*成立,则称该函数具有性质“∅”.(1)具有性质“∅”的一个一次函数的解析式可以是________.(2)给出下列函数:①y=1x;②y=x2+1;③y=cosπ2x+2.其中具有性质“∅”的函数的序号是________.[解析](1)答案不唯一,合理即可.示例:对于解析式y=x+1,因为A0={x|0<x<1},所以A1={x|1<x<2},A2={x|2<x<3},…,显然符合A n∩A n-1=∅.故具有性质“∅”的一个一次函数的解析式可以是y=x+1.(2)对于①,A0={x|0<x<1},A1={x|x>1},A2={x|0<x<1},…,依次循环下去,符合A n∩A n-1=∅.对于②,A0={x|0<x<1},A1={x|1<x<2},A2={x|2<x<5},A3={x|5<x<26},…,根据函数y =x2+1的单调性得相邻两个集合不会有交集,符合A n∩A n-1=∅.对于③,A0={x|0<x<1},A1={x|2<x<3},A2={x|1<x<2},A3={x|1<x<2},不符合A n∩A n-1=∅.所以具有性质“∅”的函数的序号是①②.[答案](1)y=x+1(2)①②[名师微点]解决集合创新型问题的方法紧扣新定义首先分析新定义的特点,把新定义所叙述的问题本质弄清楚,并能够应用到具体的解题过程之中,这是解决新定义型问题的关键所在用好集合的性质集合的性质(概念、元素的性质、运算性质等)是解决新定义集合问题的基础,也是突破口,在解题时要善于从试题中发现可以使用集合性质的一些信息,在关键之处用好集合的性质二、创新考查方式——领悟高考新动向1.现有100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么对既带感冒药又带胃药的人数统计中,下列说法正确的是()A.最多人数是55B.最少人数是55C.最少人数是75 D.最多人数是80解析:选B设100名携带药品出国的旅游者组成全集I,其中带感冒药的人组成集合A,带胃药的人组成集合B.设所携带药品既非感冒药又非胃药的人数为x,则0≤x≤20.设以上两种药都带的人数为y.由图可知,x+card(A)+card(B)-y=100.∴x+75+80-y=100,∴y=55+x.∵0≤x≤20,∴55≤y≤75,故最少人数是55.2.中国古代重要的数学著作《孙子算经》下卷有题:今有物,不知其数.三三数之,剩二;五五数之,剩三;七七数之,剩二.问:物几何?现有如下表示:已知A={x|x=3n+2,n∈N *},B ={x |x =5n +3,n ∈N *},C ={x |x =7n +2,n ∈N *},若x ∈(A ∩B ∩C ),则整数x 的最小值为( ) A .128 B .127 C .37D .23解析:选D ∵求整数的最小值,∴先将23代入检验,满足A ,B ,C 三个集合,故选D. 3.若集合{a ,b ,c ,d }={1,2,3,4},且下列四个关系:①a =1;②b ≠1;③c =2;④d ≠4有且只有一个是正确的.请写出满足上述条件的一个有序数组(a ,b ,c ,d )=________,符合条件的全部有序数组(a ,b ,c ,d )的个数是________. 解析:显然①不可能正确,否则①②都正确;若②正确,则⎩⎪⎨⎪⎧ a =2,b =3,c =1,d =4或⎩⎪⎨⎪⎧ a =3,b =2,c =1,d =4.若③正确,则⎩⎪⎨⎪⎧ a =3,b =1,c =2,d =4.若④正确,则⎩⎪⎨⎪⎧ a =2,b =1,c =4,d =3或⎩⎪⎨⎪⎧ a =3,b =1,c =4,d =2或⎩⎪⎨⎪⎧a =4,b =1,c =3,d =2.所以符合条件的数组共6个. 答案:(3,2,1,4)(填一个正确的即可) 64.已知U ={a 1,a 2,a 3,a 4},集合A 是集合U 中的两个元素所组成的集合,且同时满足下列三个条件:①若a 1∈A ,则a 2∈A ;②若a 3∉A ,则a 2∉A ;③若a 3∈A ,则a 4∉A .求集合A .解:假设a 1∈A ,则a 2∈A .又若a 3∉A ,则a 2∉A ,∴a 3∈A ,与集合A 中有且仅有两个元素不符,∴假设不成立,∴a 1∉A .假设a 4∈A ,则a 3∉A ,则a 2∉A ,且a 1∉A ,与集合A 中有且仅有两个元素不符,∴假设不成立,∴a 4∉A . 故集合A ={a 2,a 3},经检验知符合题意.[课时跟踪检测] 1.(多选)若集合M ⊆N ,则下列结论正确的是( ) A .M ∩N =M B .M ∪N =N C .M ⊆(M ∩N )D .(M ∪N )⊆N解析:选ABCD 由于M ⊆N ,即M 是N 的子集,故M ∩N =M ,M ∪N =N ,从而M ⊆(M ∩N ),(M ∪N )⊆N .2.(2020·天津高考)设全集U ={-3,-2,-1,0,1,2,3},集合A ={-1,0,1,2},B = {-3,0,2,3},则A ∩(∁U B )=( )A.{-3,3} B.{0,2}C.{-1,1} D.{-3,-2,-1,1,3}解析:选C法一:由题知∁U B={-2,-1,1},所以A∩(∁U B)={-1,1},故选C.法二:易知A∩(∁U B)中的元素不在集合B中,则排除选项A、B、D,故选C. 3.(2019·北京高考)已知集合A={x|-1<x<2},B={x|x>1},则A∪B=()A.(-1,1) B.(1,2)C.(-1,+∞) D.(1,+∞)解析:选C将集合A,B在数轴上表示出来,如图所示.由图可得A∪B={x|x>-1}.4.已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为() A.3 B.2C.1 D.0解析:选B因为A表示圆x2+y2=1上的点的集合,B表示直线y=x上的点的集合,直线y=x与圆x2+y2=1有两个交点,所以A∩B中元素的个数为2.5.设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=()A.{1,-3} B.{1,0}C.{1,3} D.{1,5}解析:选C因为A∩B={1},所以1∈B,所以1是方程x2-4x+m=0的根,所以1-4+m=0,m=3,方程为x2-4x+3=0,解得x=1或x=3,所以B={1,3}.6.集合A={3,2a},B={a,b}.若A∩B={4},则A∪B=()A.{2,3,4} B.{1,3,4}C.{0,1,2,3} D.{1,2,3,4}解析:选A∵A∩B={4},∴2a=4,则a=2,b=4.∴A∪B={2,3,4}.7.已知全集U={x|-1<x<9},A={x|1<x<a},A是U的子集,若A≠∅,则a的取值范围是()A.{a|a<9} B.{a|a≤9}C.{a|a≥9} D.{a|1<a≤9}解析:选D由题意知,集合A≠∅,所以a>1,又因为A是U的子集,故需a≤9,所以a 的取值范围是{a|1<a≤9}.8.已知集合A={-1,0,1},B={x|x2-3x+m=0},若A∩B={0},则B的子集有() A.2个B.4个C.8个D.16个解析:选B∵A∩B={0},∴0∈B,∴m=0,∴B={x|x2-3x=0}={0,3}.∴B 的子集有22=4个.故选B.9.(多选)已知全集U =R ,函数y =ln(x -2)的定义域为M ,集合N ={}x |x 2-2x >0,则下列结论正确的是( ) A .M ∩N =M B .M ∩(∁U N )=∅ C .M ∪N =UD .M =∁U N解析:选AB 由x -2>0得x >2,所以M =(2,+∞).由x 2-2x >0得x <0或x >2,所以N =(-∞,0)∪(2,+∞),∁U N =[0,2],所以M ∩(∁U N )=∅,M ∩N =M ,M ∪N =N ≠U ,M ≠∁U N .故选A 、B.10.设集合A ={x |y =lg(-x 2+x +2)},B ={x |x -a >0},若A ⊆B ,则实数a 的取值范围是( ) A .(-∞,-1) B .(-∞,-1] C .(-∞,-2)D .(-∞,-2]解析:选B 集合A ={x |y =lg(-x 2+x +2)}={x |-1<x <2},B ={x |x >a },因为A ⊆B ,所以a ≤-1.11.如图,已知I 是全集,A ,B ,C 是它的子集,则阴影部分所表示的集合是( ) A .[(∁I A )∩B ]∩C B .[(∁I B )∪A ]∩C C .(A ∩B )∩(∁I C ) D .[A ∩(∁I B )]∩C解析:选D 由图知阴影部分中的元素属于A ,不属于B ,属于C .则阴影部分表示的集合是[A ∩(∁I B )]∩C .12.(2021·湖北八校联考)已知集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪ x =k +16,k ∈N ,B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =m 2-13,m ∈N ,C =⎩⎨⎧⎭⎬⎫x ⎪⎪x =n 2+16,n ∈N ,则集合A ,B ,C 的关系是( ) A .A C B B .C A B C .A B =CD .A B C解析:选A ∵集合C =⎩⎨⎧⎭⎬⎫x | x =n 2+16,n ∈N ,∴当n =2a (a ∈N )时,x =2a 2+16=a +16,此时C =A ,∴A C .当n =b -1(b ∈N *)时,x =b -12+16=b 2-12+16=b 2-13(b ∈N *).而集合B =⎩⎨⎧⎭⎬⎫x | x =m 2-13,m ∈N ,当m =0时,-13∈B ,但-13∉C ,∴集合C B .综上,A C B ,故选A.13.已知集合P ={y |y 2-y -2>0},Q ={x |x 2+ax +b ≤0},若P ∪Q =R ,P ∩Q =(2,3],则a +b =________.解析:P ={y |y 2-y -2>0}={y |y >2或y <-1}, ∵P ∪Q =R ,P ∩Q =(2,3],∴Q ={x |-1≤x ≤3}, ∴-1,3是方程x 2+ax +b =0的两根,由根与系数的关系得⎩⎪⎨⎪⎧-1+3=-a ,(-1)×3=b ,∴⎩⎪⎨⎪⎧a =-2,b =-3,∴a +b =-5. 答案:-514.若集合{x |x 2+2kx +1=0}中有且仅有一个元素,则满足条件的实数k 的取值集合是________.解析:由题意知,方程x 2+2kx +1=0有两个相等实根, ∴Δ=4k 2-4=0,解得k =±1,∴满足条件的实数k 的取值集合是{1,-1}. 答案:{1,-1}15.对于任意两集合A ,B ,定义A -B ={x |x ∈A 且x ∉B },A *B =(A -B )∪(B -A ),记A ={y |y ≥0},B ={x |-3≤x ≤3},则A *B =________________.解析:由题意知A -B ={x |x >3},B -A ={x |-3≤x <0},所以A *B =[-3,0)∪(3,+∞). 答案:[-3,0)∪(3,+∞)16.设集合A ={x |x +m ≥0},B ={x |-2<x <4},全集U =R ,且(∁U A )∩B =∅,则实数m 的取值范围为________.解析:由已知A ={x |x ≥-m },∴∁U A ={x |x <-m }. ∵B ={x |-2<x <4},(∁U A )∩B =∅,∴-m ≤-2,即m ≥2.∴m 的取值范围为[2,+∞). 答案:[2,+∞)。
2015届高三数学(理)湘教版一轮复习配套课件:第1章 第1节 集合

-1,0,1,2.共5个.
答案:C
2.已知集合 M={1,m},N={n,log2n},若 M=N,则(m- n)2 013=________.
解析:由 M=N 知
n=1, log2n=m
或nlo=g2mn=,1,
∴mn==10, 或mn==22., 答案:-1 或 0
3.已知集合 A={m+2,2m2+m},若 3∈A,则 m 的值为________. 解析:因为 3∈A,所以 m+2=3 或 2m2+m=3.
[针对训练] 1.(2013·福建高考)已知集合 A={1,a},B={1,2,3},则“a=3”
是“A⊆B”的
()
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
解析:因为A={1,a},B={1,2,3},若a=3,则A={1,3},所
图形表 示
意义
_{x_|_x_∈__A_,__或__x_∈__B_} _{x_|_x_∈__A_,__且__x_∈__B_}_ {x|x∈U,且x∉A}
___________________
_________
_______
1.认清集合元素的属性(是点集、数集或其他情形)和化简集 合是正确求解的两个先决条件.
即 A={x|0<x≤4},而 B=(-∞,a),
由于 A⊆B,如图所示,则 a>4,即 c=4. [答案] 4
[类题通法] 1.已知两集合的关系求参数时,关键是将两集合的关系转化 为元素间的关系,进而转化为参数满足的关系,解决这类问题常 常要合理利用数轴、Venn 图帮助分析.
2.当题目中有条件 B⊆A 时,不要忽略 B=∅的情况.
中专 技校 职高单招 对口升学数学总复习 第一章 集合与逻辑用语

充要条件的含义
✔
考试层次要求
理解
掌握
✔
✔
✔
✔
✔
第一节 集合
知识清单
考点一 集合的概念与表示法 考点二 集合间的关系 考点三 集合的运算
考点一 集合的概念与表示法
1
集合
把具有某种属性的一些确定的对象看成一个整体, 便形成一个集合, 常
用大写的拉丁字母A , B , C 等表示。
2
元素 集合中的每一个确定的对象叫作这个集合的元素, 常用小写字母a,b,c 等
本题主要考查集合的运算以及充要条件的判断,运用不等式之间 的关系是解题的关键.
技巧点播
考点二 集合间的关系
3.集合相等
一般地,对于两个集合A 与B,如果集合A 中的任何一个元素都是 集合B 的元素,同时集合B 的任何一个元素都是集合A 的元素,我们 就说集合A 等于集合B,记作A=B(A,B 的所有元素相等)。
注意
(1)若两个集合相等,则两个集合所ห้องสมุดไป่ตู้元素完全相同, 反之亦然.
(2)要判断两个集合是否相等,对于元素较少的有限 集,主要看它们的元素是否完全相同;若是无限集,则从 “互为子集”入手进行判断.
知识清单
考点一 集合的概念与表示法 考点二 集合间的关系 考点三 集合的运算
考点三 集合的运算
1.交集
一般地,由既属于集合A又属于 集合B的所有元素组成的集合,
称为集合A与集合B的交集,
作A∩B
即A∩B={x|x∈A 且x∈B}.
性质
考点三 集合的运算
2.并集
一般地,由所有属于集合A 或属于 集合B 的元素组成的集合,称为集 合A 与集合B 的并集。
集合的基本运算说课稿

《集合的基本运算》说课稿一、说教材1、教材的地位和作用集合的基本运算是高中新课标A版实验教材第一册第一章第一节第三课时的内容,在此之前,学生已学习了集合的概念和基本关系,这为过渡到本节的学习起着铺垫的作用,本节内容在近年的高考中主要考核集合的基本运算,在整个教材中存在着基础的地位,为今后学习函数及不等式的解集奠定了基础,数形结合的思想方法对学生今后的学习中有着铺垫的作用。
此部分主要介绍集合的两类基本运算—-并集和交集,是对集合基本知识的深入研究.在此,通过适当的问题情境,使学生感受、认识并掌握集合的两种基本运算.集合作为现代数学的基本语言,它可以简洁、准确地表达数学内容,因而只有掌握和理解了集合的基本知识,学会用集合语言表示有关数学对象,才能进一步刻画函数概念.可见,此部分的学习是以后研究函数的必然要求.2、教学目标及确立依据根据教材结构及内容以及教材地位和作用,考虑到学生已有的认知结构和心理特征,依据新课标制定以下教学目标:(1)知识与技能目标:根据集合的图形表示,理解并集与交集的概念,掌握并集和交集的表示法以及求解两个集合并集与交集的方法。
(2)过程与方法目标:通过复习旧知,引入并集与交集的概念,培养学生观察、比较、分析、概括的能力,使学生的认知由具体到抽象的过程.(3)情感态度与价值观:积极引导学生主动参与学习的过程,激发他们用数学解决实际问题的兴趣,形成主动学习的态度,培养学生自主探究的数学精神以及合作交流的意识。
教学目标确立的依据:(1)由高中数学大纲所确定的。
即进一步培养学生的思维能力、解决实际问题的能力,进一步培养学生的良好的个性品质和辨证唯物主义观点。
(2)由学生的基础和生理、心理特征确定的。
高中阶段的教学,应以提高学生数学素养、培养学生思维能力及创新意识为重。
3、教学重点与难点根据上述地位与作用的分析及教学目标,我确定了本节课的教学重点及难点。
重点:并集与交集的概念的理解,以及并集与交集的求解。
必修一人教A版第一章第一单元第1节集合的含义与表示

分别用列举法和描述法表示下列集合:
1、方程x-4=0的所有实数根组成的集合 列举法:{-2、2} 描述法:{X︱x2-4=0}
2
2、由大于5小于12的所有整数组成的集合
列举法:{6、7、8、9、10、11、} 描述法:{X︱5<X<12,X∈Z}
•
抛物线y=x上的点集
2
描述法: {(x,y)︱y=x2,X∈R,y∈R}
8、方程
9、集合{
3 的解集中含有_________ 个元素。 }用列举法表示为 {0,1,2,3} _________________
•
10、设集合A={(x,y)|x+y=6, }, 使用列举法表示集合A。 集合A中的元素是点, 点的横坐标,纵坐标都是自然数, 且满足条件x+y=6。 所以用列举法表示为: A={(0,6),(1,5),(2,4),(3,3),(4,2),(5,1),(6,0)}。 11、已知集合A={x| }只有一个元素, 试求实数k的值,并用列举法表示集合A。 当k=0时,原方程变为-8x+16=0,x=2, 此时集合A={2} 当k≠0时, 要使一元二次方程有一个实根,需 即k=1。此时方程的解为 。集合A={4}
问题情境
问题:像“家庭”、“班级”等,有什么 共同特征?
同一类对象的汇集
•
(一)集合的有关概念:
1、集合的含义 (1)集合:一定范围内某些指定对象的 全体构成一个集合。 (2)元素: 集合中的每一个对象叫做该集合 的元素或简称元。
理解定义:1、元素必需具有一定的属性。
2、集合必需是一定属性的元素的总体。
∈
(5)Q(6)R 2 3∈
•
∈ 2 3 ∈
练习 1.若M={1,3},则下列表示方法 正确的是() C A.3MB .1M C.1MD .1M且3M
2020版创新设计高考总复习高三理科数学人教A版第一章第1节

第1节集合最新考纲 1.了解集合的含义,体会元素与集合的属于关系;能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题;2.理解集合之间包含与相等的含义,能识别给定集合的子集;在具体情境中了解全集与空集的含义;3.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;理解在给定集合中一个子集的补集的含义,会求给定子集的补集;能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算.知识梳理1.元素与集合(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于,表示符号分别为∈和∉.(3)集合的三种表示方法:列举法、描述法、图示法.2.集合间的基本关系(1)子集:若对任意x∈A,都有x∈B,则A⊆B或B⊇A.(2)真子集:若A⊆B,且集合B中至少有一个元素不属于集合A,则A B或B A.(3)相等:若A⊆B,且B⊆A,则A=B.(4)空集的性质:∅是任何集合的子集,是任何非空集合的真子集.3.集合的基本运算4.(1)A∩A=A,A∩∅=∅,A∩B=B∩A.(2)A∪A=A,A∪∅=A,A∪B=B∪A.(3)A∩(∁U A)=∅,A∪(∁U A)=U,∁U(∁U A)=A.[微点提醒]1.若有限集A中有n个元素,则A的子集有2n个,真子集有2n-1个.2.子集的传递性:A⊆B,B⊆C⇒A⊆C.3.A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B.4.∁U(A∩B)=(∁U A)∪(∁U B),∁U(A∪B)=(∁U A)∩(∁U B).基础自测1.判断下列结论正误(在括号内打“√”或“×”)(1){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.()(2)若{x2,1}={0,1},则x=0,1.()(3)对于任意两个集合A,B,关系(A∩B)⊆(A∪B)恒成立.()(4)含有n个元素的集合有2n个真子集.()解析(1)错误.{x|y=x2+1}=R,{y|y=x2+1}=[1,+∞),{(x,y)|y=x2+1}是抛物线y =x2+1上的点集.(2)错误.当x=1时,不满足集合中元素的互异性.(4)错误.含有n个元素的集合有2n-1个真子集.【参考答案】(1)×(2)×(3)√(4)×2.(必修1P12A5改编)若集合P={x∈N|x≤ 2 019},a=22,则()A.a∈PB.{a}∈PC.{a}⊆PD.a∉P解析因为a=22不是自然数,而集合P是不大于 2 019的自然数构成的集合,所以a∉P,只有D正确.【参考答案】D3.(必修1P12B1改编)已知集合M={0,1,2,3,4},N={1,3,5},则集合M∪N的子集的个数为________.解析由已知得M∪N={0,1,2,3,4,5},所以M∪N的子集有26=64(个).【参考答案】644.(2018·全国Ⅰ卷)已知集合A={x|x2-x-2>0},则∁R A=()A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}解析法一A={x|x2-x-2>0}={x|(x-2)(x+1)>0}={x|x<-1或x>2},所以∁R A ={x|-1≤x≤2}.法二因为A={x|x2-x-2>0},所以∁R A={x|x2-x-2≤0}={x|-1≤x≤2}.【参考答案】B5.(2019·南昌模拟)已知集合P={x|x2≤1},M={a}.若P∪M=P,则实数a的取值范围为()A.[-1,1]B.[1,+∞)C.(-∞,-1]D.(-∞,-1]∪[1,+∞)解析∵P={x|-1≤x≤1},且P∪M=P,∴M⊆P,∴a∈P,因此-1≤a≤1.【参考答案】A6.(2017·全国Ⅲ卷改编)已知集合A={(x,y)|x2+y2=1},B={(x,y)|x,y∈R,且y=x},则A∩B中元素的个数为________.解析集合A表示圆心在原点的单位圆上所有点的集合,集合B表示直线y=x上所有点的集合,易知直线y=x和圆x2+y2=1相交,且有2个交点,故A∩B中有2个元素.【参考答案】2考点一 集合的基本概念【例1】 (1)(2019·湖北四地七校联考)若集合M ={x ||x |≤1},N ={y |y =x 2,|x |≤1},则( ) A.M =N B.M ⊆N C.M ∩N =∅D.N ⊆M(2)若x ∈A ,则1x ∈A ,就称A 是伙伴关系集合,集合M =⎩⎨⎧⎭⎬⎫-1,0,12,2,3的所有非空子集中具有伙伴关系的集合的个数是()A.1B.3C.7D.31解析 (1)易知M ={x |-1≤x ≤1},N ={y |y =x 2,|x |≤1}={y |0≤y ≤1},∴N ⊆M . (2)具有伙伴关系的元素组是-1,12,2,所以具有伙伴关系的集合有3个:{-1},⎩⎨⎧⎭⎬⎫12,2,⎩⎨⎧⎭⎬⎫-1,12,2. 【参考答案】(1)D (2)B规律方法 1.研究集合问题时,首先要明确构成集合的元素是什么,即弄清该集合是数集、点集,还是其他集合;然后再看集合的构成元素满足的限制条件是什么,从而准确把握集合的含义.2.利用集合元素的限制条件求参数的值或确定集合中元素的个数时,要注意检验集合中的元素是否满足互异性.【训练1】 (1)(2018·全国Ⅱ卷)已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( ) A.9B.8C.5D.4(2)设集合A ={x |(x -a )2<1},且2∈A ,3∉A ,则实数a 的取值范围为________. 解析 (1)由题意知A ={(-1,0),(0,0),(1,0),(0,-1),(0,1),(-1,-1),(-1,1),(1,-1),(1,1)},故集合A 中共有9个元素.(2)由题意得⎩⎨⎧(2-a )2<1,(3-a )2≥1,解得⎩⎨⎧1<a <3,a ≤2或a ≥4.所以1<a ≤2.【参考答案】(1)A (2)(1,2]考点二 集合间的基本关系【例2】 (1)已知集合A ={x |y =1-x 2,x ∈R },B ={x |x =m 2,m ∈A },则( ) A.ABB.BAC.A ⊆BD.B =A(2)(2019·郑州调研)已知集合A ={x |x 2-5x -14≤0},集合B ={x |m +1<x <2m -1},若B ⊆A ,则实数m 的取值范围为________. 解析 (1)易知A ={x |-1≤x ≤1}, 所以B ={x |x =m 2,m ∈A }={x |0≤x ≤1}. 因此BA .(2)A ={x |x 2-5x -14≤0}={x |-2≤x ≤7}. 当B =∅时,有m +1≥2m -1,则m ≤2. 当B ≠∅时,若B ⊆A ,如图.则⎩⎨⎧m +1≥-2,2m -1≤7,m +1<2m -1,解得2<m ≤4.综上,m 的取值范围为(-∞,4]. 【参考答案】(1)B (2)(-∞,4]规律方法 1.若B ⊆A ,应分B =∅和B ≠∅两种情况讨论.2.已知两个集合间的关系求参数时,关键是将两个集合间的关系转化为元素或区间端点间的关系,进而转化为参数满足的关系.解决这类问题常常要合理利用数轴、Venn 图,化抽象为直观进行求解.【训练2】 (1)(2018·唐山模拟)设集合M ={x |x 2-x >0},N =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1x <1,则( )A.M NB.N MC.M =ND.M ∪N =R(2)若将本例(2)的集合A 改为A ={x |x 2-5x -14>0}.其它条件不变,则m 的取值范围是________.解析 (1)集合M ={x |x 2-x >0}={x |x >1或x <0},N =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1x <1={x |x >1或x <0},所以M =N .(2)A ={x |x 2-5x -14>0}={x |x <-2或x >7}. 当B =∅时,有m +1≥2m -1,则m ≤2. 当B ≠∅时,若B ⊆A ,则⎩⎨⎧m +1<2m -1,m +1≥7或⎩⎨⎧m +1<2m -1,2m -1≤-2. 解之得m ≥6.综上可知,实数m 的取值范围是(-∞,2]∪[6,+∞). 【参考答案】(1)C (2)(-∞,2]∪[6,+∞) 考点三 集合的运算 多维探究角度1 集合的基本运算【例3-1】 (1)(2017·全国Ⅰ卷)已知集合A ={x |x <2},B ={x |3-2x >0},则( )A.A ∩B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32B.A ∩B =∅C.A ∪B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32D.A ∪B =R(2)(2018·天津卷)设全集为R ,集合A ={x |0<x <2},B ={x |x ≥1},则A ∩(∁R B )=( ) A.{x |0<x ≤1} B.{x |0<x <1} C.{x |1≤x <2}D.{x |0<x <2}解析 (1)因为B ={x |3-2x >0}=⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32,A ={x |x <2},所以A ∩B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <32,A ∪B ={x |x <2}.(2)因为B ={x |x ≥1},所以∁R B ={x |x <1},因为A ={x |0<x <2},所以A ∩(∁R B )={x |0<x <1}.【参考答案】(1)A (2)B 角度2 抽象集合的运算【例3-2】 设U 为全集,A ,B 是其两个子集,则“存在集合C ,使得A ⊆C ,B ⊆∁U C ”是“A ∩B =∅”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析由图可知,若“存在集合C,使得A⊆C,B⊆∁U C”,则一定有“A∩B=∅”;反过来,若“A∩B=∅”,则一定能找到集合C,使A⊆C且B⊆∁U C.【参考答案】C规律方法 1.进行集合运算时,首先看集合能否化简,能化简的先化简,再研究其关系并进行运算.2.注意数形结合思想的应用.(1)离散型数集或抽象集合间的运算,常借助Venn图求解;(2)连续型数集的运算,常借助数轴求解,运用数轴时要特别注意端点是实心还是空心.【训练3】(1)(2019·延安模拟)若全集U={-2,-1,0,1,2},A={-2,2},B={x|x2-1=0},则图中阴影部分所表示的集合为()A.{-1,0,1}B.{-1,0}C.{-1,1}D.{0}(2)(2019·新乡模拟)已知集合A={x|x2-x≤0},B={x|a-1≤x<a},若A∩B只有一个元素,则a=()A.0B.1C.2D.1或2解析(1)B={x|x2-1=0}={-1,1},阴影部分所表示的集合为∁U(A∪B).A∪B={-2,-1,1,2},全集U={-2,-1,0,1,2},所以∁U(A∪B)={0}. (2)易知A=[0,1],因为A∩B只有一个元素,所以a-1=1,解得a=2.【参考答案】(1)D(2)C[思维升华]1.在解题时经常用到集合元素的互异性,一方面利用集合元素的互异性能顺利找到解题的切入点;另一方面,在解答完毕之时,注意检验集合的元素是否满足互异性以确保答案正确.2.对连续数集间的运算,借助数轴的直观性,进行合理转化;对已知连续数集间的关系,求其中参数的取值范围时,要注意单独考察等号能否取到.3.对离散的数集间的运算,或抽象集合间的运算,可借助Venn图.这是数形结合思想的又一体现.[易错防范]1.集合问题解题中要认清集合中元素的属性(是数集、点集还是其他类型集合),要对集合进行化简.2.空集是任何集合的子集,是任何非空集合的真子集,时刻关注对空集的讨论,防止漏解.3.解题时注意区分两大关系:一是元素与集合的从属关系;二是集合与集合的包含关系.4.Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用数轴图示法时要特别注意端点是实心还是空心.基础巩固题组(建议用时:30分钟)一、选择题1.(2018·全国Ⅲ卷)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=()A.{0}B.{1}C.{1,2}D.{0,1,2}解析由题意知,A={x|x≥1},则A∩B={1,2}.【参考答案】C2.设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M中元素的个数为()A.3B.4C.5D.6解析因为A={1,2,3},B={4,5},又M={x|x=a+b,a∈A,b∈B},∴M={5,6,7,8},即M中有4个元素.【参考答案】B3.(2019·佛山质检)已知全集U={0,1,2,3,4},若A={0,2,3},B={2,3,4},则(∁U A)∩(∁B)=()UA.∅B.{1}C.{0,2}D.{1,4}解析因为全集U={0,1,2,3,4},A={0,2,3},B={2,3,4},所以∁U A={1,4},∁U B={0,1},因此(∁U A)∩(∁U B)={1}.【参考答案】B4.(2018·石家庄质检)设集合A={x|-1<x≤2},B={x|x<0},则下列结论正确的是()A.(∁R A)∩B={x|x<-1}B.A∩B={x|-1<x<0}C.A∪(∁R B)={x|x≥0}D.A∪B={x|x<0}解析易求∁R A={x|x≤-1或x>2},∁R B={x|x≥0},∴(∁R A)∩B={x|x≤-1},A项不正确.A∩B={x|-1<x<0},B项正确,检验C、D错误.【参考答案】B5.已知集合A={x∈N|x2-2x-8≤0},B={x|2x≥8},则集合A∩B的子集的个数为()A.1B.2C.3D.4解析因为A={x∈N|x2-2x-8≤0}={0,1,2,3,4},B={x|x≥3},所以A∩B={3,4},所以集合A∩B的子集个数为4.【参考答案】D6.(2019·豫北名校联考)已知集合M={x|y=x-1},N={x|y=log2(2-x)},则∁R(M∩N)=()A.[1,2)B.(-∞,1)∪[2,+∞)C.[0,1]D.(-∞,0)∪[2,+∞)解析由题意可得M={x|x≥1},N={x|x<2},∴M∩N={x|1≤x<2},∴∁R(M∩N)={x|x<1或x≥2}.【参考答案】B7.设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则满足M⊆(A∩B)的集合M的个数是()A.0B.1C.2D.3解析 由⎩⎨⎧x +y =1,x -y =3,得⎩⎨⎧x =2,y =-1,∴A ∩B ={(2,-1)}.由M ⊆(A ∩B ),知M =∅或M ={(2,-1)}. 【参考答案】C8.(一题多解)(2018·中原名校联考)已知集合A ={x |y =lg(x -x 2)},B ={x |x 2-cx <0,c >0},若A ⊆B ,则实数c 的取值范围为( ) A.(0,1] B.[1,+∞) C.(0,1)D.(1,+∞)解析 法一 由题意知,A ={x |y =lg(x -x 2)}={x |x -x 2>0}={x |0<x <1},B ={x |x 2-cx <0,c >0}={x |0<x <c }.由A ⊆B ,画出数轴,如图所示,得c ≥1.法二 A ={x |y =lg(x -x 2)={x |x -x 2>0}={x |0<x <1},结合选项,取c =1,得B ={x |0<x <1},则A ⊆B 成立,可排除C 、D ;取c =2,得B ={x |0<x <2},则A ⊆B 成立,排除A.【参考答案】B 二、填空题9.(2016·全国Ⅲ卷改编)设集合S ={x |(x -2)(x -3)≥0},T ={x |x >0},则(∁R S )∩T =________.解析 易知S ={x |x ≤2或x ≥3}, ∴∁R S ={x |2<x <3}, 因此(∁R S )∩T ={x |2<x <3}. 【参考答案】{x |2<x <3}10.已知集合A ={1,2},B ={a ,a 2+3},若A ∩B ={1},则实数a 的值为________. 解析 由A ∩B ={1}知,1∈B ,又a 2+3≥3,则a =1. 【参考答案】111.(2019·福州质检)已知集合A ={1,3,4,7},B ={x |x =2k +1,k ∈A },则集合A ∪B 中元素的个数为________.解析 ∵A ={1,3,4,7},B ={x |x =2k +1,k ∈A },∴B ={3,7,9,15},∴A ∪B ={1,3,4,7,9,15},∴集合A ∪B 中元素的个数为6.【参考答案】612.集合A ={x |x <0},B ={x |y =lg[x (x +1)]},若A -B ={x |x ∈A ,且x ∉B },则A -B =________.解析 由题意知,B ={x |y =lg[x (x +1)]}={x |x (x +1)>0}={x |x <-1或x >0},则A -B ={x |-1≤x <0}.【参考答案】{x |-1≤x <0}能力提升题组(建议用时:10分钟)13.(2018·河南百校联盟联考)若集合A ={x |y =lg(3x -x 2)},B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪y =1+4x +1,x ∈A ,则A ∩(∁R B )等于( )A.(0,2]B.(2,3)C.(3,5)D.(-2,-1) 解析 由3x -x 2>0,得0<x <3,则A =(0,3),∴B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪y =1+4x +1,x ∈A =(2,5), 则∁R B =(-∞,2]∪[5,+∞),故A ∩(∁R B )=(0,2].【参考答案】A14.已知集合A ={x |y =4-x 2},B ={x |a ≤x ≤a +1},若A ∪B =A ,则实数a 的取值范围为( )A.(-∞,-3]∪[2,+∞)B.[-1,2]C.[-2,1]D.[2,+∞)解析 集合A ={x |y =4-x 2}={x |-2≤x ≤2},因A ∪B =A ,则B ⊆A ,又B ≠∅,所以有⎩⎨⎧a ≥-2,a +1≤2,所以-2≤a ≤1. 【参考答案】C15.(2019·皖南八校联考改编)已知集合A ={(x ,y )|x 2=4y },B ={(x ,y )|y =x },则A ∩B 的真子集个数是________.解析 由⎩⎨⎧x 2=4y ,y =x 得⎩⎨⎧x =0,y =0或⎩⎨⎧x =4,y =4,即A ∩B ={(0,0),(4,4)},∴A ∩B 的真子集个数为22-1=3.【参考答案】316.集合U =R ,A ={x |x 2-x -2<0},B ={x |y =ln(1-x )},则图中阴影部分所表示的集合是________.解析 易知A =(-1,2),B =(-∞,1),∴∁U B =[1,+∞),A ∩(∁U B )=[1,2).因此阴影部分表示的集合为A ∩(∁U B )={x |1≤x <2}.【参考答案】[1,2)。
高考新课标数学(理)大一轮复习讲义课件第1章集合与常用逻辑用语-第2节命题及其关系、充分条件与必要条件p

4.(2015·重庆卷)“x=1”是“x2-2x+1=0”的( ) A.充要条件 B.充分而不必要条件 C.必要而不充分条件 D.既不充分也不必要条件 解析:若 x=1,则 x2-2x+1=0;若 x2-2x+1=0,即 (x-1)2=0,则 x=1.故选 A.
答案:A
5.设 x∈R,则 x>2 的一个必要不充分条件是( )
2.(2015·山东卷)设 m∈R,命题“若 m>0,则方程 x2 +x-m=0 有实根”的逆否命题是( )
A.若方程 x2+x-m=0 有实根,则 m>0 B.若方程 x2+x-m=0 有实根,则 m≤0 C.若方程 x2+x-m=0 没有实根,则 m>0 D.若方程 x2+x-m=0 没有实根,则 m≤0
A.m<4
B.m>4
C.0<m<4
D.0≤m<4
【解析】 (1)因为函数 f(x)过点(1,0),所以函数 f(x) 有且只有一个零点⇔函数 y=-2x+a(x≤0)没有零点⇔函数 y=2x(x≤0)与直线 y=a 无公共点.由数形结合,可得 a≤0 或 a>1.
观察选项,根据集合间关系{a|a<0} {a|a≤0 或 a>1},
答案:(3,+∞)
1.对于命题正误的判断是高考的热点 之一,理应引起大家的关注,命题正误的 判断可涉及各章节的内容,覆盖面宽,也 是学生的易失分点.命题正误的判断的原 则是:正确的命题要有依据或者给以论证; 不一定正确的命题要举出反例,绝对不要主观臆断,这也是 最基本的数学逻辑思维方式.
解析:依题意,P={x|f(x+t)+1<3}={x|f(x+t)<2}= {x|f(x+t)<f(2)},Q={x|f(x)<-4}={x|f(x)<f(-1)}.
北师版高考总复习一轮文科数学精品课件 第1章 集合与常用逻辑用语 第1节 集合的概念与运算

)
B.[8,+∞)
C.(16,+∞) D.[16,+∞)
(2)(2022山东济南二模)已知集合A={1,2},B={2,4},C={z|z=xy,x∈A,y∈B},
则C中元素的个数为(
A.1
B.2
C.3
D.4
)
答案:(1)C (2)C
解析:(1)因为集合A中至少有3个元素,所以log2k>4,所以k>24=16,故选C.
A.{2,4}
B.{2,4,6}
C.{2,4,6,8}
D.{2,4,6,8,10}
(3)(2022北京,1)已知全集U={x|-3<x<3},集合A={x|-2<x≤1},则∁UA=(
A.(-2,1]
B.(-3,-2)∪[1,3)
C.[-2,1)
D.(-3,-2]∪(1,3)
)
)
答案:(1)A (2)A
则m的取值范围为(
)
A.(-6,+∞)
B.[-6,+∞)
C.(-∞,-6)
D.(-∞,-6]
答案:(1)C (2)A
解析:(1)由题意知A={y|-2≤y≤2},要满足B⫋A,即B⫋[-2,2],结合选项可知B=[-
1,1].故选C.
(2)因为 A={x|3≤x≤4},B= >
2
,A⊆B,所以- <3,解得
C.-2
)
D.-4
(3)(2022江苏南京第一中学三模)非空集合A={x∈N|0<x<3},B={y∈N|y2my+1<0,m∈R},A∩B=A∪B,则实数m的取值范围为(
A.
2023年高考数学总复习第一章 集合与常用逻辑用语 第1节:集合(教师版)

2023年高考数学总复习第一章集合与常用逻辑用语第1节集合考试要求1.了解集合的含义,体会元素与集合的属于关系;能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题;2.理解集合之间包含与相等的含义,能识别给定集合的子集;在具体情境中了解全集与空集的含义;3.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;4.理解在给定集合中一个子集的补集的含义,会求给定子集的补集;5.能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算.1.元素与集合(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于,表示符号分别为∈和∉.(3)集合的三种表示方法:列举法、描述法、图示法.2.集合间的基本关系表示关系文字语言符号语言集合间的基本关系相等集合A 与集合B 中的所有元素都相同A =B 子集A 中任意一个元素均为B 中的元素A ⊆B 真子集A 中任意一个元素均为B 中的元素,且B 中至少有一个元素不是A 中的元素A B空集空集是任何集合的子集,是任何非空集合的真子集3.集合的基本运算集合的并集集合的交集集合的补集符号表示A ∪BA ∩B若全集为U ,则集合A 的补集为∁U A图形表示集合{x|x∈A,或x∈B}{x|x∈A,且x∈B}{x|x∈U,且x∉A}表示4.集合的运算性质(1)A∩A=A,A∩=,A∩B=B∩A.(2)A∪A=A,A∪=A,A∪B=B∪A.(3)A∩(∁U A)=,A∪(∁U A)=U,∁U(∁U A)=A.1.若有限集A中有n个元素,则A的子集有2n个,真子集有2n-1个,非空子集有2n-1个,非空真子集有2n-2个.2.注意空集:空集是任何集合的子集,是非空集合的真子集.3.A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B.4.∁U(A∩B)=(∁U A)∪(∁U B),∁U(A∪B)=(∁U A)∩(∁U B).1.思考辨析(在括号内打“√”或“×”)(1)任何一个集合都至少有两个子集.()(2){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.()(3)若{x2,1}={0,1},则x=0,1.()(4)对于任意两个集合A,B,(A∩B)⊆(A∪B)恒成立.()答案(1)×(2)×(3)×(4)√解析(1)错误.空集只有一个子集.(2)错误.{x|y=x2+1}=R,{y|y=x2+1}=[1,+∞),{(x,y)|y=x2+1}是抛物线y =x2+1上的点集.(3)错误.当x=1时,不满足集合中元素的互异性.2.若集合P={x∈N|x≤2023},a=22,则()A.a∈PB.{a}∈PC.{a}⊆PD.a∉P答案D解析因为a=22不是自然数,而集合P是不大于2023的自然数构成的集合,所以a∉P,只有D正确.3.(2021·新高考Ⅰ卷)设集合A={x|-2<x<4},B={2,3,4,5},则A∩B=()A.{2}B.{2,3}C.{3,4}D.{2,3,4}答案B解析因为A={x|-2<x<4},B={2,3,4,5},所以A∩B={2,3}.4.(易错题)(2021·南昌调研)集合A={-1,2},B={x|ax-2=0},若B⊆A,则由实数a的取值组成的集合为()A.{-2}B.{1}C.{-2,1}D.{-2,1,0}答案D解析对于集合B,当a=0时,B=,满足B⊆A;当a≠0时,B又B⊆A,所以2a=-1或2a=2,解得a=-2或a=1.5.(2021·西安五校联考)设全集U=R,A={x|y=2x-x2},B={y|y=2x,x∈R},则(∁U A)∩B=()A.{x|x<0}B.{x|0<x≤1}C.{x|1<x≤2}D.{x|x>2}答案D解析易知A={x|0≤x≤2},B={y|y>0}.∴∁U A={x|x<0或x>2},故(∁U A)∩B={x|x>2}.6.(2021·全国乙卷)设集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T =()A. B.S C.T D.Z答案C解析法一在集合T中,令n=k(k∈Z),则t=4n+1=2(2k)+1(k∈Z),而集合S中,s=2n+1(n∈Z),所以必有T⊆S,所以S∩T=T.法二S={…,-3,-1,1,3,5,…},T={…,-3,1,5,…},观察可知,T⊆S,所以S∩T=T.考点一集合的基本概念1.已知集合U={(x,y)|x2+y2≤1,x∈Z,y∈Z},则集合U中元素的个数为()A.3B.4C.5D.6答案C解析当x=-1时,y=0;当x=0时,y=-1,0,1;当x=1时,y=0.所以U={(-1,0),(0,-1),(0,0),(0,1),(1,0)},共有5个元素.2.若集合A={a-3,2a-1,a2-4},且-3∈A,则实数a=________.答案0或1解析①当a-3=-3,即a=0时,此时A={-3,-1,-4},②当2a-1=-3,即a=-1时,此时A={-4,-3,-3}舍,③当a2-4=-3,即a=±1时,由②可知a=-1舍,则a=1时,A={-2,1,-3},综上,a=0或1.3.(2022·武汉调研)用列举法表示集合A={x|x∈Z且86-x∈N}=________.答案{-2,2,4,5}解析由题意x可取-2,2,4,5,故答案为{-2,2,4,5}.4.设A是整数集的一个非空子集,对于k∈A,如果k-1∉A,且k+1∉A,那么称k是A的一个“孤立元”.给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.答案6解析依题意可知,由S的3个元素构成的所有集合中,不含“孤立元”时,这三个元素一定是连续的三个整数.∴所求的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},共6个.感悟提升 1.研究集合问题时,首先要明确构成集合的元素是什么,即弄清该集合是数集、点集,还是其他集合;然后再看集合的构成元素满足的限制条件是什么,从而准确把握集合的含义.2.利用集合元素的限制条件求参数的值或确定集合中元素的个数时,要注意检验集合中的元素是否满足互异性.考点二集合间的基本关系例1(1)已知集合A={-1,1},B={x|ax+1=0}.若B⊆A,则实数a的所有可能取值的集合为()A.{-1}B.{1}C.{-1,1}D.{-1,0,1}(2)已知集合A={x|-3≤x≤4},B={x|2m-1≤x≤m+1},且B⊆A,则实数m的取值范围是________.答案(1)D(2)[-1,+∞)解析(1)当B=时,a=0,此时,B⊆A.当B≠时,则a≠0,∴B x|x=-1a又B⊆A,∴-1a∈A,∴a=±1.综上可知,实数a所有取值的集合为{-1,0,1}.(2)∵B⊆A,①当B=时,2m-1>m+1,解得m>2,②当B≠2m-1≤m+1,2m-1≥-3,m+1≤4,解得-1≤m≤2,综上,实数m的取值范围[-1,+∞).感悟提升 1.若B⊆A,应分B=和B≠两种情况讨论.2.已知两个集合间的关系求参数时,关键是将两个集合间的关系转化为元素或区间端点间的关系,进而转化为参数满足的关系.合理利用数轴、Venn图帮助分析及对参数进行讨论.确定参数所满足的条件时,一定要把端点值代入进行验证,否则易增解或漏解.训练1(1)(2022·大连模拟)设集合A={1,a,b},B={a,a2,ab},若A=B,则a2022+b2023的值为()A.0B.1C.-2D.0或-1(2)已知集合A={x|log2(x-1)<1},B={x||x-a|<2},若A⊆B,则实数a的取值范围为()A.(1,3)B.[1,3]C.[1,+∞)D.(-∞,3]答案(1)B(2)B解析(1)集合A={1,a,b},B={a,a2,ab},若A=B,则a2=1或ab=1.由集合互异性知a≠1,当a=-1时,A={1,a,b}={1,-1,b},B={a,a2,ab}={-1,1,-b},有b=-b,得b=0.∴a2022+b2023=(-1)2022+02023=1.当ab=1时,集合A={1,a,b},B={a,a2,ab}={a,a2,1},有b=a2.又b=1a,∴a2=1a,得a=1,不满足题意.综上,a2022+b2023=1,故选B. (2)由log2(x-1)<1,得0<x-1<2,所以A=(1,3).由|x-a|<2得a-2<x<a+2,所以B=(a-2,a+2).因为A⊆B a-2≤1,a+2≥3,解得1≤a≤3.所以实数a的取值范围为[1,3].考点三集合的运算角度1集合的基本运算例2(1)(2021·全国乙卷)已知全集U={1,2,3,4,5},集合M={1,2},N={3,4},则∁U(M∪N)=()A.{5}B.{1,2}C.{3,4}D.{1,2,3,4}(2)(2021·西安测试)设全集U=R,M={x|y=ln(1-x)},N={x|2x(x-2)<1},那么图中阴影部分表示的集合为()A.{x|x≥1}B.{x|1≤x<2}C.{x|0<x≤1}D.{x|x≤1}答案(1)A(2)B解析(1)法一因为集合M={1,2},N={3,4},所以M∪N={1,2,3,4}.又全集U={1,2,3,4,5},所以∁U(M∪N)={5}.故选A.法二因为∁U(M∪N)=(∁U M)∩(∁U N),∁U M={3,4,5},∁U N={1,2,5},所以∁U(M∪N)={3,4,5}∩{1,2,5}={5}.故选A.(2)题图中阴影表示的集合为(∁U M)∩N.易知M={x|x<1},N={x|0<x<2},∴(∁U M)∩N={x|1≤x<2}.角度2利用集合的运算求参数例3(1)(2021·日照检测)已知集合A={x∈Z|x2-4x-5<0},B={x|4x>2m},若A∩B 中有三个元素,则实数m的取值范围是()A.[3,6)B.[1,2)C.[2,4)D.(2,4](2)已知集合A={x|x2-4≤0},B={x|2x+a≤0},若A∪B=B,则实数a的取值范围是()A.a<-2B.a≤-2C.a>-4D.a≤-4答案(1)C(2)D解析(1)因为x2-4x-5<0,解得-1<x<5,则集合A={x∈Z|x2-4x-5<0}={0,|x1,2,3,4},易知集合B又因为A∩B中有三个元素,所以1≤m2<2,解之得2≤m <4.故实数m 的取值范围是[2,4).(2)集合A ={x |-2≤x ≤2},B |x ≤由A ∪B =B 可得A ⊆B ,作出数轴如图.可知-a2≥2,即a ≤-4.感悟提升1.进行集合运算时,首先看集合能否化简,能化简的先化简,再研究其关系并进行运算.2.数形结合思想的应用:(1)离散型数集或抽象集合间的运算,常借助Venn 图求解;(2)连续型数集的运算,常借助数轴求解,运用数轴时要特别注意端点是实心还是空心.训练2(1)(2021·全国甲卷改编)设集合M ={x |0<x <4},N |13≤x <M ∩N =N ,则a 的取值范围为()A.a ≤13B.a >4C.a ≤4D.a >13(2)集合M ={x |2x 2-x -1<0},N ={x |2x +a >0},U =R .若M ∩(∁U N )=∅,则a 的取值范围是()A.(1,+∞)B.[1,+∞)C.(-∞,1)D.(-∞,1]答案(1)C(2)B 解析(1)由M ∩N =N ,∴M ⊇N .当N =∅时,即a ≤13成立;当N ≠∅时,借助数轴易知13<a ≤4.综上,a ≤4.(2)易得M ={x |2x 2-x -1<0}x |-12<x <1∵N ={x |2x +a >0}x |x >-a2∴∁U N x|x ≤-a 2由M ∩(∁U N )=,则-a 2≤-12,得a ≥1.Venn 图的应用用平面上封闭图形的内部代表集合,这种图称为Venn 图.集合中图形语言具有直观形象的特点,将集合问题图形化.利用Venn 图的直观性,可以深刻理解集合的有关概念,快速进行集合的运算.例1设全集U ={x |0<x <10,x ∈N +},若A ∩B ={3},A ∩(∁U B )={1,5,7},(∁U A )∩(∁U B )={9},则A =________,B =________.答案{1,3,5,7}{2,3,4,6,8}解析由题知U ={1,2,3,…,9},根据题意,画出Venn 图如图所示,由Venn图易得A ={1,3,5,7},B ={2,3,4,6,8}.例2(2020·新高考海南卷)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是()A.62%B.56%C.46%D.42%答案C解析如图,用Venn 图表示该中学喜欢足球和游泳的学生所占的比例之间的关系,设既喜欢足球又喜欢游泳的学生占该中学学生总数的比例为x ,则(60%-x )+(82%-x )+x =96%,解得x =46%.故选C.例3向100名学生调查对A,B两件事的看法,得到如下结果:赞成A的人数是全体的35,其余不赞成;赞成B的人数比赞成A的人数多3人,其余不赞成.另外,对A,B都不赞成的人数比对A,B都赞成的学生人数的13多1人,则对A,B都赞成的学生人数为________,对A,B都不赞成的学生人数为________.答案3613解析由题意知赞成A的人数为100×3560,赞成B的人数为60+3=63.如图,记100名学生组成的集合为U,赞成A的学生的全体记为集合A,赞成B的学生的全体记为集合B,并设对A,B都赞成的学生数为x,则对A,B都不赞成的人数为x3+1,由题意,知(60-x)+(63-x)+x+x3+1=100,解得x=36.所以对A,B都赞成的学生人数为36人,对A,B都不赞成的学生人数为13人.1.(2021·新高考Ⅱ卷)设集合U={1,2,3,4,5,6},A={1,3,6},B={2,3,4},则A∩(∁U B)=()A.{3}B.{1,6}C.{5,6}D.{1,3}答案B解析由题设可得∁U B={1,5,6},故A∩(∁U B)={1,6}.2.(2021·郑州模拟)设集合A={x|3x-1<m},若1∈A且2∉A,则实数m的取值范围是()A.(2,5)B.[2,5)C.(2,5]D.[2,5]答案C解析∵A={x|3x-1<m},1∈A且2∉A,∴3×1-1<m且3×2-1≥m,解得2<m≤5.3.(2021·浙江卷)设集合A={x|x≥1},B={x|-1<x<2},则A∩B=()A.{x|x>-1}B.{x|x≥1}C.{x|-1<x<1}D.{x|1≤x<2}答案D解析因为集合A={x|x≥1},B={x|-1<x<2},所以A∩B={x|1≤x<2}.故选D.4.(2022·河南名校联考)已知集合A={a,a2,0},B={1,2},若A∩B={1},则实数a的值为()A.-1B.0C.1D.±1答案A解析由题意a=1或a2=1,当a=1,此时A={1,1,0}与元素互异性矛盾,∴a=-1,故选A.5.已知集合A={x∈Z|y=log5(x+1)},B={x∈Z|x2-x-2<0},则()A.A∩B=AB.A∪B=BC.B AD.A B答案C解析由x+1>0,得x>-1,∴A={x∈Z|x>-1}={0,1,2,3,…}.由x2-x-2<0,得-1<x<2,∴B={0,1},∴A∩B=B,A∪B=A,B A.6.设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则满足M⊆(A∩B)的集合M 的个数是()A.0B.1C.2D.3答案C解析+y =1,-y =3=2,=-1,∴A ∩B ={(2,-1)}.由M ⊆(A ∩B ),知M =或M ={(2,-1)}.7.(2022·太原模拟)已知集合M ={x |(x -2)2≤1},N ={y |y =x 2-1},则(∁R M )∩N =()A.[-1,+∞)B.[-1,1]∪[3,+∞)C.[-1,1)∪(3,+∞)D.[-1,1]∪(3,+∞)答案C解析由已知可得M ={x |-1≤x -2≤1}={x |1≤x ≤3},N ={y |y ≥-1},∴∁R M ={x |x <1或x >3},∴(∁R M )∩N ={x |-1≤x <1或x >3}.8.设集合A ={x |(x +2)(x -3)≤0},B ={a },若A ∪B =A ,则a 的最大值为()A.-2B.2C.3D.4答案C解析因为A ={x |(x +2)(x -3)≤0},所以A ={x |-2≤x ≤3}.又因为B ={a },且A ∪B =A ,所以B ⊆A ,所以a 的最大值为3.9.(2021·合肥模拟)已知集合A ={-2,-1,0,1,2},集合B ={x ||x -1|≤2},则A ∩B =________.答案{-1,0,1,2}解析B ={x |-2≤x -1≤2}={x |-1≤x ≤3},又A ={-2,-1,0,1,2},∴A ∩B ={-1,0,1,2}.10.(2021·湖南雅礼中学检测)设集合A ={x |y =x -3},B ={x |1<x ≤9},则(∁R A )∩B =________.答案(1,3)解析因为A ={x |y =x -3},所以A ={x |x ≥3},所以∁R A ={x |x <3}.又B ={x |1<x ≤9},所以(∁R A )∩B =(1,3).11.已知集合A ={x |y =lg(x -x 2)},B ={x |x 2-cx <0,c >0},若A ⊆B ,则实数c 的取值范围是________.答案[1,+∞)解析由题意知,A ={x |y =lg(x -x 2)}={x |x -x 2>0}=(0,1),B ={x |x 2-cx <0,c >0}=(0,c ).由A ⊆B ,画出数轴,如图所示,得c ≥1.12.已知集合A ={a ,b ,2},B ={2,b 2,2a },若A =B ,则a +b =________.答案34或1解析由A =B=2a ,=b 2=b 2,=2a .=2a ,=b 2,=0,=0=0,=1,=b 2,=2a ,=0,=0=14,=12,又由集合中元素的互异性,=0,=1=14,=12,所以a +b =1或a +b =34.13.若全集U ={-2,-1,0,1,2},A ={-2,2},B ={x |x 2-1=0},则图中阴影部分所表示的集合为()A.{-1,0,1}B.{-1,0}C.{-1,1}D.{0}答案D解析B={x|x2-1=0}={-1,1},阴影部分所表示的集合为∁U(A∪B).又A∪B ={-2,-1,1,2},全集U={-2,-1,0,1,2},所以∁U(A∪B)={0}. 14.(2020·浙江卷)设集合S,T,S⊆N+,T⊆N+,S,T中至少有2个元素,且S,T 满足:①对于任意的x,y∈S,若x≠y,则xy∈T;②对于任意的x,y∈T,若x<y,则yx∈S.下列命题正确的是()A.若S有4个元素,则S∪T有7个元素B.若S有4个元素,则S∪T有6个元素C.若S有3个元素,则S∪T有5个元素D.若S有3个元素,则S∪T有4个元素答案A解析由题意,①令S={1,2,4},则T={2,4,8},此时,S∪T={1,2,4,8},有4个元素;②令S={2,4,8},则T={8,16,32},此时,S∪T={2,4,8,16,32},有5个元素;③令S={2,4,8,16},则T={8,16,32,64,128},此时,S∪T={2,4,8,16,32,64,128},有7个元素.综合①②,S有3个元素时,S∪T可能有4个元素,也可能有5个元素,可排除C,D;由③可知A正确.15.已知集合A={x∈R||x+2|<3},集合B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m=________,n=________.答案-11解析A={x∈R||x+2|<3}={x∈R|-5<x<1},由A∩B=(-1,n),可知m<1,则B={x|m<x<2},画出数轴,可得m=-1,n=1.16.当两个集合有公共元素,且互不为对方的子集时,我们称这两个集合“相交”.对于集合M={x|ax2-1=0,a>0},N={-12,12,1},若M与N“相交”,则a=________.答案1解析M 1a,,由1a=12,得a=4,由1a=1,得a=1.当a=4时,M 12,M⊆N,不合题意;当a=1时,M={-1,1},满足题意.。
2013高考总复习化学:第一章第1节

栏目 导引
第一章
认识化学科学
制造 2.化学的特征是认识分子和_____分
子,它是一门具有创造性和实用性的
科学,化学家们已能在微观层面上操 纵分子和原子。
栏目 导引
第一章
认识化学科学
3.1861年英国科学家波义耳提出
化学元素 ______________的概念,1871年,英
国化学家拉瓦锡建立燃烧现象的氧化 学说,1803年,英国化学家道尔顿提 原子学说 出了____________,1869年,俄国科 门捷列夫 学家__________发现了元素周期律。
栏目 导引
第一章
认识化学科学
思考感悟 1.化学变化中的最小微粒和保持物质
化学性质的最小微粒分别是什么?
【提示】 原子、分子。
栏目 导引
第一章
认识化学科学
二、钠的性质和研究物质性质的基本方法 1.研究物质性质的基本方法为观察、实
分类 验、____、比较,此外还有假说、模型。
2.钠的物理性质
颜色状 态 银白色 ______ 固体
在反应②中,过氧化钠增重的质量实际上相 当于与 CO2 等物质的量的 CO 的质量,其结 果可看做:
CO 相当于CO+O 2 Na2O2 ――――→ Na2CO3+O。
栏目 导引
第一章
认识化学科学
①终态法的思想在过氧化钠计算中的应 用 。 例 如 : Na2O2 + H2===2NaOH 、 Na2O2 +CO===Na2CO3 、2Na2O2 +CO +H2===Na2CO3 +2NaOH(实际上述反 应均不能发生)。
栏目 导引
用途
第一章
认识化学科学
考点串讲深度剖析
钠的性质
新高考高三化学一轮复习 第1章 第1节 物质的量 气体摩尔体积

(4)同温同压同体积的气体的分子数相等,但原子数不一定相等。 (5)阿伏加德罗定律既适用于单一气体也适用于混合气体。 (6)在同温同压条件下,可利用气体的相对分子质量大小判断气 体密度的大小。
[基础判断] (1)标准状况下,1 mol H2 与 1 mol N2、H2 混合气体体积均约为 22.4 L。( ) (2)同温同压下,等体积的两种单质气体一定具有相同的原子数。
(4)摩尔质量、相对分子质量、质量是三个不同的物理量,具有 不同的单位。如 H2O 的摩尔质量为 18 g·mol-1,H2O 的相对分子质 量为 18,1 mol H2O 的质量为 18 g。但若不指明各单位,数值也不一 定相等。如 H2O 的摩尔质量也可以是 0.018 kg·mol-1。
(5)摩尔质量与温度、压强、物质的量多少无关。
D.(2015·全国卷Ⅱ)钠在空气中燃烧可生成多种氧化物。23 g 钠 充分燃烧时转移电子数为 1NA
E.惰性电极电解饱和食盐水时,阴极上生成 2.24 L(标准状况 下)气体时,电路中通过的电子数为 0.2NA
F.向 1 L 0.1 mol·L-1 的 FeBr2 溶液中通入足量 Cl2 充分反应, 转移电子数为 0.1NA
[答案] 0.3 mol 40 1∶3
命题点 1 气体摩尔体积的概念及有关计算 1.一定温度和压强下,30 L 某种气态纯净物中含有 6.02×1023 个分子,这些分子由 1.204×1024 个原子构成,下列有关说法中不正 确的是( ) A.该温度和压强可能是标准状况 B.标准状况下,该纯净物若为气态,其体积约是 22.4 L
[知识应用] (1)由阿伏加德罗常数(NA)和一个水分子的质量(m 水)、一个水分 子的体积(V 水)不能确定的物理量是________。 ①1 摩尔水的质量 ②1 摩尔水蒸气的质量 ③1 摩尔水蒸气的 体积 [答案] ③
2025年高考数学总复习优化设计一轮 第一章-第一节-集合【课件】

7 5 3 1 1
3 1 1 1 1 3
M={…,-4,-4,-4,-4 , 4,…},N={…,-4,-2,-4,0,4 , 2 , 4,…},则
的元素都是N的元素,反之不然,所以M⊆N,故选A.
M中
(2)(2024·福建漳州模拟)已知U是全集,集合A,B满足(∁UA)∩B=∁UA,则下列
重点涉及充分、必要条件的判断,试题难度取决于结合的知识的难度.
复习策略:
1.明晰重要概念:子集、真子集、交集、并集、补集、充分、必要条件
等概念是解题的基础,应明晰这些概念.
2.注意数学思想方法的合理运用:分类讨论、数形结合、等价转化等数
学思想方法在解题中应用广泛.
3.善于列举反例:涉及充分、必要条件以及命题真假的判断等问题,要善
7.(2023·新高考Ⅱ,2)设集合A={0,-a},B={1,a-2,2a-2},若A⊆B,则a=( B )
2
A.2
B.1
C.
D.-1
3
解析 ∵A⊆B,∴a-2=0或2a-2=0.若a-2=0,则a=2,A={0,-2},B={1,0,2},显然
A⊈B;若2a-2=0,则a=1,A={0,-1},B={1,-1,0},A⊆B成立.故选B.
A.( ,+∞)
2
5 10
B.( , ]
2 3
5 10
C.[ , )
2 3
10
D.(-∞, ]
3
解析 由题意可得,2 -2a+1<0 且 3
2
5
10
-3a+1≥0,解得2<a≤ 3 ,故选
2
B.
考点二集合间的基本关系
2022版新高考数学一轮复习教学案:第1章 第1节 集合 (含解析)
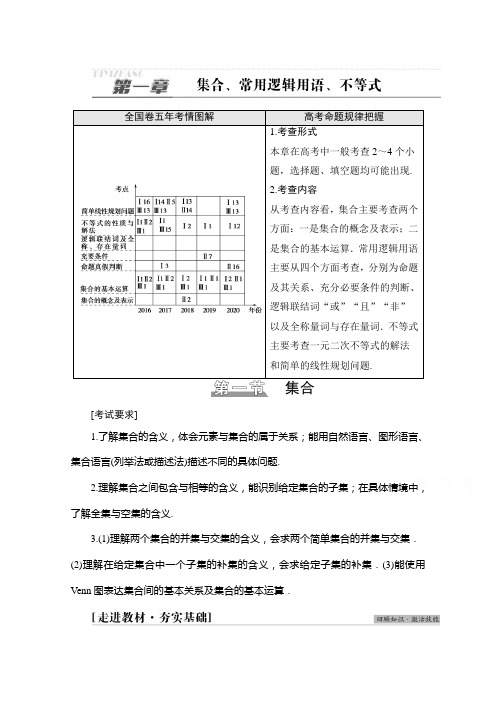
全国卷五年考情图解高考命题规律把握1.考查形式本章在高考中一般考查2~4个小题,选择题、填空题均可能出现.2.考查内容从考查内容看,集合主要考查两个方面:一是集合的概念及表示;二是集合的基本运算.常用逻辑用语主要从四个方面考查,分别为命题及其关系、充分必要条件的判断、逻辑联结词“或”“且”“非”以及全称量词与存在量词.不等式主要考查一元二次不等式的解法和简单的线性规划问题.集合[考试要求]1.了解集合的含义,体会元素与集合的属于关系;能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.理解集合之间包含与相等的含义,能识别给定集合的子集;在具体情境中,了解全集与空集的含义.3.(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.(3)能使用Venn图表达集合间的基本关系及集合的基本运算.1.集合与元素(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于,用符号∈和∉表示.(3)集合的表示方法:列举法、描述法、Venn图法.(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N*(或N+)Z Q R提醒:根据元素的互异性可判断所求参数的值是否符合要求.2.集合间的基本关系关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A,则x∈B)A⊆B或B⊇A真子集集合A是集合B的子集,且集合B中至少有一个元素不在集合A中A B或B A集合相等集合A,B中的元素相同或集合A,B互为子集A=B提醒:∅是任何集合的子集,是任何非空集合的真子集.3.集合的基本运算运算自然语言符号语言Venn图交集由属于集合A且属于集合B的所有元素组成的集合A∩B={x|x∈A且x∈B}并集由所有属于集合A或属于集合B的元素组成的集合A∪B={x|x∈A或x∈B}补集由全集U中不属于集合A∁U A=的所有元素组成的集合{x|x∈U且x∉A}1.对于有限集合A,其元素个数为n,则集合A的子集个数为2n,真子集个数为2n-1,非空真子集个数为2n-2.2.A∪B=A⇔B⊆A,A∩B=A⇔A⊆B.一、易错易误辨析(正确的打“√”,错误的打“×”)(1)任何一个集合都至少有两个子集.()(2){x|y=x2}={y|y=x2}={(x,y)|y=x2}.()(3)若{x2,1}={0,1},则x=0,1.()(4)直线y=x+3与y=-2x+6的交点组成的集合是{1,4}.()[答案](1)×(2)×(3)×(4)×二、教材习题衍生1.若集合A={x∈N|x≤ 2 021},a=22,则下列结论正确的是()A.{a}⊆A B.a⊆AC.{a}∈A D.a∉AD[a=22∉N,则a∉A,故选D.]2.已知集合A={x|-2<x<3},集合B={x|x-1<0},则A∩B=________,A∪B=________.(-2,1)(-∞,3)[∵A={x|-2<x<3},B={x|x-1<0}={x|x<1},∴A∩B={x|-2<x<1},A∪B={x|x<3}.]3.已知U={α|0°<α<180°},A={x|x是锐角},B={x|x是钝角},则∁U(A∪B)=________.[答案]{x|x是直角}4.已知集合M={0,1,2,3,4},N={1,3,5},则集合M∪N的子集的个数为________.64[∵M={0,1,2,3,4},N={1,3,5},∴M ∪N ={0,1,2,3,4,5}, ∴M ∪N 的子集有26=64个.]考点一 集合的含义与表示解决与集合中的元素有关问题的一般思路1.(2018·全国卷Ⅱ)已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( )A .9B .8C .5D .4A [由x 2+y 2≤3知,-3≤x ≤3,-3≤y ≤ 3.又x ∈Z ,y ∈Z ,所以x ∈{-1,0,1},y ∈{-1,0,1},所以A 中元素的个数为C 13C 13=9,故选A.]2.已知a ,b ∈R ,若⎩⎨⎧⎭⎬⎫a ,ba ,1={a 2,a +b,0},则a 2 021+b 2 021=________.-1 [由已知得a ≠0, 则ba =0,所以b =0,于是a 2=1,即a =1或a =-1,又根据集合中元素的互异性可知a =1应舍去,因此a =-1,故a 2 021+b 2 021=(-1)2 021+02 021=-1.]3.(2020·北京人大附中期中)设A 是整数集的一个非空子集,对于k ∈A ,若k -1∉A ,且k +1∉A ,则称k 是A 的一个“孤立元”.集合T ={1,2,3,5},T 的“孤立元”是________;对给定集合S ={1,2,3,4,5,6},由S 中的3个元素构成的所有集合中,含“孤立元”的集合有________个.516[(1)依次判断每个元素是否为“孤立元”:对于1,2∈T,不是“孤立元”;对于2,1∈T,3∈T,不是“孤立元”;对于3,2∈T,不是“孤立元”;对于5,4∉T,6∉T,是“孤立元”.故T中的“孤立元”是5.(2)由S中的3个元素构成的所有集合有C36=20(个),不含“孤立元”的集合有{1,2,3},{2,3,4},{3,4,5},{4,5,6},共4个,故含“孤立元”的集合有16个.] 考点二集合间的基本关系判断集合关系的三种方法[典例1](1)(多选)(2020·辽宁葫芦岛月考)已知集合A={x|x2-2x=0}, 则有() A.∅⊆A B.-2∈AC.{0,2}⊆A D.A⊆{y|y<3}(2)(2020·武汉模拟)集合{x|-1<x<3,x∈N*}的非空子集个数为()A.3B.4C.7D.8(3)已知集合A={x|x2-2x-3<0},B={x|2-a<x<1+a},若B⊆A,则实数a的取值范围为________.(1)ACD(2)A(3)(-∞,2][(1)由题意得,集合A={0,2},由于空集是任何集合的子集,故A正确;因为A={0,2},所以C,D正确,B错误.故选ACD.(2){x|-1<x<3,x∈N*}={1,2},其非空子集个数为3,故选A.(3)A={x|-1<x<3}.①若B=∅,满足B⊆A,此时2-a≥1+a,即a≤12.②若B ≠∅,由B ⊆A 得⎩⎪⎨⎪⎧2-a <1+a 2-a ≥-11+a ≤3,解得12<a ≤2.由①②知a 的取值范围为(-∞,2].]点评:(1)已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn 图等来直观解决这类问题.(2)空集是任何集合的子集,当题目条件中有B ⊆A 时,应分B =∅和B ≠∅两种情况讨论,确定参数所满足的条件时,一定要把端点值代入验证,否则易增解或漏解.[跟进训练]1.(2020·北京模拟)已知集合M ={x ∈R |x ≥0},N ⊆M ,则在下列集合中符合条件的集合N 可能是( )A .{0,1}B .{x |x 2=1}C .{x |x 2>0}D .RA [因为0∈M,1∈M ,所以{0,1}⊆M ,故选A.]2.若集合A ={1,m },B ={m 2,m +1},且A =B ,则m =( ) A .0 B .1 C .±1D .0或1A [由题意知⎩⎪⎨⎪⎧m +1=1m 2=m ,解得m =0,故选A.]考点三 集合的基本运算集合运算三步骤集合的交、并、补运算[典例2-1](1)(2020·全国卷Ⅲ)已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素的个数为()A.2 B.3C.4 D.6(2)(多选)(2020·河北邯郸市第一中学一模)已知全集U=R,集合M={x|2x<1},N={x|log2x>1},则下列结论正确的是()A.M∩N=M B.M∪N=NC.M∩(∁U N)=M D.(∁U M)∩N=N(1)C(2)CD[(1)由题意得,A∩B={(1,7),(2,6),(3,5),(4,4)},所以A∩B 中元素的个数为4,选C.(2)由2x<1,得x<0,则M={x|x<0}.由log2x>1,得x>2,则N={x|x>2}.所以M∩N=∅,故A不正确;M∪N={x|x<0或x>2},故B不正确;M∩(∁N)={x|x<0}∩{x|x≤2}=M,故C正确;(∁U M)∩N={x|x≥0}∩{x|x>2}=N,故UD正确.]点评:解决集合中的运算问题,一般要先研究集合中元素的构成,能化简的要先化简,同时注意数形结合.若集合中的元素是离散的,常用Venn图求解;若集合中的元素是连续的,则用数轴表示,此时要注意端点是实心还是空心.根据集合的运算结果求参数[典例2-2](1)(2020·全国卷Ⅰ)设集合A={x|x2-4≤0},B={x|2x+a≤0},且A ∩B ={x |-2≤x ≤1},则a =( )A .-4B .-2C .2D .4(2)(2020·秦皇岛模拟)若集合A ={x |x ≥3-2a },B ={x |(x -a +1)(x -a )≥0},A ∪B =R ,则实数a 的取值范围为( )A .[2,+∞)B .⎝ ⎛⎦⎥⎤-∞,43 C .⎣⎢⎡⎭⎪⎫43,+∞D .(-∞,2](1)B (2)C [(1)易知A ={x |-2≤x ≤2},B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≤-a2,因为A ∩B ={x |-2≤x ≤1},所以-a2=1,解得a =-2.故选B.(2)B ={x |x ≥a 或x ≤a -1},由A ∪B =R 得3-2a ≤a -1,解得a ≥43,故选C.][跟进训练]1.(2019·天津高考)设集合A ={-1,1,2,3,5},B ={2,3,4},C ={x ∈R |1≤x <3},则(A ∩C )∪B =( )A .{2}B .{2,3}C .{-1,2,3}D .{1,2,3,4}D [由题意可知A ∩C ={1,2},则(A ∩C )∪B ={1,2,3,4},故选D.]2.(2021·全国统一考试模拟演练)已知M ,N 均为R 的子集,且∁R M ⊆N ,则M ∪(∁R N )=( )A .∅B .MC .ND .RB [画韦恩图即可,注意最后求并集.]3.已知集合A =[1,+∞),B =[0,3a -1],若A ∩B ≠∅,则实数a 的取值范围是( )A .[1,+∞)B .⎣⎢⎡⎦⎥⎤12,1C .⎣⎢⎡⎭⎪⎫23,+∞D .(1,+∞)C [由A ∩B ≠∅得3a -1≥1,解得a ≥23,故选C.]。
