自适应课件(北航)5(2)
合集下载
自适应课件(北航)
T (k ) [ y (k 1), y (k 2), , y (k na ), u (k d ), u (k d 1), , u (k d nb )]
T [a1, a2 , , an , b0 , b1, , bn ]
a b
则前式可表为
模 型 检 验
合 格 ?
完
Y
成
1
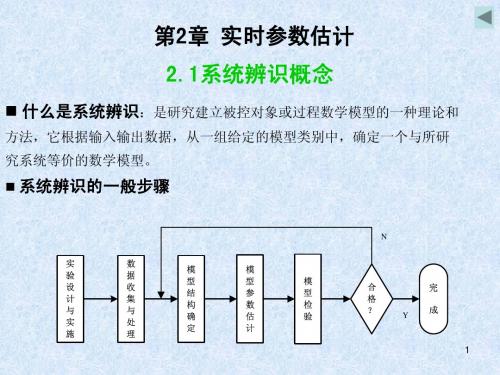
• 实验设计与实施:根据建模目的,确定模型类型、精度和方法,设计
获取系统输入输出信息的具体方案。
• 数据收集与处理:从实验中获得数据,并进行技术处理。
• 确定模型结构:利用先验知识和经验,假定模型的结构形式。
• 估计模型参数:对所假定模型结构形式下的相应参数进行估计。
E LS LS
„ E ( )( )
T T
即最小二乘估计是最小方差估计,也就是参数估计 ˆLS 离参数真值 证明: 由于 ˆ 为 的任一线性无偏差估计,所以 ˆ 可表示为:
最近。
11
ˆ PY
式中, P R ( n n 1) N ,并且
5
C( z ) 1 c1z c2 z cnc z
1
1
2
nc
(k ) 为白噪声序列。
自回归积分滑动平均模型
A( z 1 ) y(k ) B( z 1 )u(k 1) C( z 1 ) (k )
其中, 1 z 1 , 其它含义与式(2-4)相同,且这里 d = 1,当d>1时,
z d B( z 1 ) C0 ( zI A0 )1 B0 D0 A( z 1 )
随机性离散系统
自回归滑动平均模型
matlab自适应控制课件-北航版第5章 模型参考自适应控制5 (6)
e1
k0 yr c1v1 d0 yp d1v2
r1
2 1
r2
2 2
r3
2 3
r4
2 4
e1
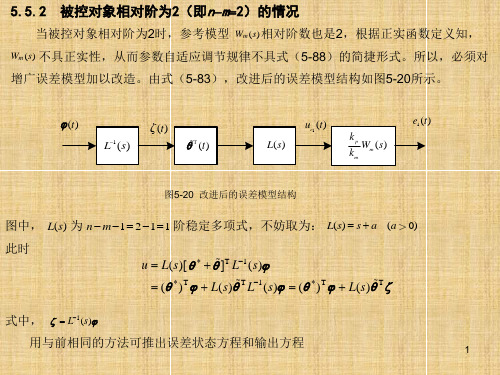
设零初始值,取 r1 r2 r3 r4 150,积分步长 h 0.1,给出 yr ,用数值积分法仿真。 (1) yr (t) 为阶跃输入的仿真:yr (t) 1 , e1(t) 的变化曲线如图5-21所示, ym 和 yp
(5-96)
再考虑式(5-95),则有式(5-96)。
设计步骤:
1)设计参考模型 Wm (s) ,使其与对象具相同阶及相对阶,且 Wm (s) 分子分母是稳定的
多项式,并具理想的动态性能;
2)选择 L(s) s a ,使 L(s)Wm (s) 为正实函数;
3
3)选择滤波器 F(s) Nm (s)L(s),构造辅助信号状态方程
式中, L1(s) 用与前相同的方法可推出误差状态方程和输出方程
1
相应的传递函数为:
e Ace L(s)bc[ T ]
e1 hcTe
We
(s)
hcT
(sI
Ac
) 1 bc
L(s)
kp km
Wm
(s)L(s)
由于We (s) 和 Wm (s)L(s) 为正实函数,根据定理5-3-7知,存在正定对称矩阵P和半正定
L1(s)
s
1 Βιβλιοθήκη 5(yrv1
yp
v2 )T
则
1 5 0 0 0 ζ1 yr
2
3 4
0 0 0
5 0 0 5
0 0
ζ2
ζ3
v1 yp
0
0
5
ζ4
v2
自适应控制 ppt课件

(2.3)
根据广义误差信号,按照一定的自适应规律产生的
对于离散模型参考自适应控制系统
参考模型
xm (k 1) Am xm (k) Bmu(k), xm (0) xm0
可调系统的参数自适应方案的系统模型
x(k 1) A(e,k) x(k) B(e, k)u(k) x(0) x0 , A(0) A0 , B(0) B0
(2.22) (2.23) (2.24)
(2.25) (2.26) (2.27)
式中, v ,De矩阵 称为D线性补偿ppt器课件,它的作用是为了满足系统稳定性所需15 附加的补偿条件。
2.2.1 模型参考自适应控制的数学描述
2.2.1.3 模型参考自适应系统的等价误差系统
模型参考自适应控制系统的设计目标是使得广义误差向量 (广义输出误差)逐渐趋 向零值。
前馈自适应控制系统的
应用就会受到严重的限
r(k)
制。
自适应机构
u(k)
y(k)
可调控制器
被控对象
ppt课件
3
前馈自适应控制结构图
2.1 自适应控制概述
2.1.2 自适应控制系统的分类
(2)反馈自适应控制
除原有的反馈回路之外,反馈自适应控制系统中新增加的自适应机构形成了另一 个反馈回路.
根据系统内部可测信息的变化,来改变控制器的结构或参数,以达到提高控制 质量的目的.
信号综合自适应方案的系统模型
x(k 1) Ax(k) Bu(k) ua (e,k) x(0) x0 ,pupat课(0件) ua0
(2.4) (2.5) (2.160)
2.2.1.1 并联模型参考自适应系统的数学模型 二、用输入-输出方程描述的模型参考自适应系统
自适应学习技术 ppt课件

•做中学。即通过解决具体的问题进行学习。在这种学习方式中,提供 的学习材料是一系列的问题,学习者的任务是利用已经学会的知识解决 这些问题,从而学会解决其他类似问题。
自适应学习的应用
• 适应的对象(改变什么):适应性教学可以调整的对象包括三个方面,关注点是 系统中哪些内容可以调整。首先是改变内容或者题目,如可以通过区分任务或项 目的难度水平改变内容。其次是改变学习内容的表征形式和路径选择,如隐藏或 突出显示链接。再次是通过间接指导调整教学水平和可用的支持。
自适应学习系统的平台(案例)
承儒教育文化发展(深圳)有 限公司成立于2016年,是一家服务 于基础教育的互联网高科技企业, 致力于通过“互联网+教育”的方式, 一站式解决中小学生“学习难”的 问题。 公司提出并倡导“诊断式自 适应学习”,创造性应用国际上先 进的自适应诊断技术,打造了国内 一个“将学业精准诊断和教育资源 智能推送相结合”的中小学生自适 应学习平台——诊学网。 通过此平 台,可以从根本上颠覆传统的教学 模式,变盲目学习为有针对性的学 习,为学习减负,让学习更轻松、 更精准、更高效。
自适应学习技术
目录 1. 自适应学习的概念
2. 自适应学习的应用 3. 自适应学习系统 4. 自适应学习系统在教学中的应用 5. 自适应学习系统的平台(案例) 6. 自适应学习的发展和未来
自适应学习的概念
自适应学习是指根据学习内 容和学习方式的不同,可以将人 的学习分为三种不同的类型,它 们是机械的学习、示教的学习以 及自适应的学习。
通过网络学习与现实学习的结合,实现或者说达到“因材施教”, 这是在线教育的终极目标。
自适应学习系统的平台
自适应学习平台会引导学生进行最适合他自己的下一步学习 内容和活动,并当学生在学习中遇到困难时,课程的难度会自动 降低。老师也可以使用它的实时预测技术来监测每个学生的知识 空白,即时调整,为每个学生提供个性化教学。
自适应学习的应用
• 适应的对象(改变什么):适应性教学可以调整的对象包括三个方面,关注点是 系统中哪些内容可以调整。首先是改变内容或者题目,如可以通过区分任务或项 目的难度水平改变内容。其次是改变学习内容的表征形式和路径选择,如隐藏或 突出显示链接。再次是通过间接指导调整教学水平和可用的支持。
自适应学习系统的平台(案例)
承儒教育文化发展(深圳)有 限公司成立于2016年,是一家服务 于基础教育的互联网高科技企业, 致力于通过“互联网+教育”的方式, 一站式解决中小学生“学习难”的 问题。 公司提出并倡导“诊断式自 适应学习”,创造性应用国际上先 进的自适应诊断技术,打造了国内 一个“将学业精准诊断和教育资源 智能推送相结合”的中小学生自适 应学习平台——诊学网。 通过此平 台,可以从根本上颠覆传统的教学 模式,变盲目学习为有针对性的学 习,为学习减负,让学习更轻松、 更精准、更高效。
自适应学习技术
目录 1. 自适应学习的概念
2. 自适应学习的应用 3. 自适应学习系统 4. 自适应学习系统在教学中的应用 5. 自适应学习系统的平台(案例) 6. 自适应学习的发展和未来
自适应学习的概念
自适应学习是指根据学习内 容和学习方式的不同,可以将人 的学习分为三种不同的类型,它 们是机械的学习、示教的学习以 及自适应的学习。
通过网络学习与现实学习的结合,实现或者说达到“因材施教”, 这是在线教育的终极目标。
自适应学习系统的平台
自适应学习平台会引导学生进行最适合他自己的下一步学习 内容和活动,并当学生在学习中遇到困难时,课程的难度会自动 降低。老师也可以使用它的实时预测技术来监测每个学生的知识 空白,即时调整,为每个学生提供个性化教学。
北航uml课件05

面向对象技术
Object-Oriented Techniques
谭火彬 thbin@ 82339316-806
第 5 章用例分析技术
Use-Case Analysis
Review: Use-Case Modeling
基于用例的需求获取过程
1. 获取原始需求 2. 开发一个可以理解的需求
-16-
OOA目标
开发一系列模型,以描述计算机软件, 从而满足客户定义的需求:分析模型
包括两种图,描述对象及其交互 这些图按照用例模型来组织,每个用例图都 会产生数张图
类图(class diagram):描述了构成一类对象 特征的状态和行为(描述软件架构) 交互图(interaction diagram):描述对象之 间的交互行为(演示用例实现)(描述系统行为)
相对来说,策划一系列的小胜利和接受一些小的 失误总要好一点。策划一个巨大的胜利经常会导 致灾难性的失败!
-23-
用例图:考勤卡系统
Export Time Entries Billing System Change Password <<include>>
Administrativ e User
Login
Login Login
Employee Employee
Record Time Record Time Create Charge Code Create Employee
-29-
内容安排
面向对象分析设计过程 面向对象分析基础 面向对象分析原则 开始分析之前 用例分析技术
-30-
分析的基本原则
Object-Oriented Techniques
谭火彬 thbin@ 82339316-806
第 5 章用例分析技术
Use-Case Analysis
Review: Use-Case Modeling
基于用例的需求获取过程
1. 获取原始需求 2. 开发一个可以理解的需求
-16-
OOA目标
开发一系列模型,以描述计算机软件, 从而满足客户定义的需求:分析模型
包括两种图,描述对象及其交互 这些图按照用例模型来组织,每个用例图都 会产生数张图
类图(class diagram):描述了构成一类对象 特征的状态和行为(描述软件架构) 交互图(interaction diagram):描述对象之 间的交互行为(演示用例实现)(描述系统行为)
相对来说,策划一系列的小胜利和接受一些小的 失误总要好一点。策划一个巨大的胜利经常会导 致灾难性的失败!
-23-
用例图:考勤卡系统
Export Time Entries Billing System Change Password <<include>>
Administrativ e User
Login
Login Login
Employee Employee
Record Time Record Time Create Charge Code Create Employee
-29-
内容安排
面向对象分析设计过程 面向对象分析基础 面向对象分析原则 开始分析之前 用例分析技术
-30-
分析的基本原则
2021-北京大学-人工智能-自适应学习系统-Adaptive-Learing教程

人工智能自适应教育的价值-对教师
• 拥有一个教学助手:减少作业批改、错题统计等重复劳动,减轻 负担;系统协助授课,提高上课效率
• 拥有一个教学伙伴:借助人工智能自适应学习系统,准确知道学 生的薄弱知识点、不同学生在学习行为上的差异,增进对学生的 了解
三 案例分析
模式、技术等因素融合而成的一种经济现象。
自适应学习(Adaptive Learning)
始于1970年,在国内引起广泛关注是在2015年,彼时在线教育正野蛮生长,一小批人注意 到在线教育完课率极低,这是因为在传统学习模式下: 1)不同学习内容之间的跳转逻辑是线性单一的,学生即使已经掌握了某一块内容,还是需要 花费时间去学习; 2)学生有问题也不能得到即时的反馈和帮助。 对此,自适应学习致力于通过计算机手段检测学生当前的学习水平和状态,并相应地调整后 面的学习内容和路径,帮助学生提升学习效率。
• 典型产品——松鼠AI
案例分析——松鼠AI智适应学习系统
测:准确测评,先行测试报告 学:边学边练,视频讲义 练:边学边练,练习题
测:综合测试,综合测试报告
1)哪里不会学哪里
2)追根溯源,找到知识漏洞 3)根据目标战略性放弃 4)动态规划学习路径 5)难度实时调控
辅:智能辅导,系统针对性辅导
教育循环
待解决的问题
• 给定的教学/能力大纲和学习目标,如何在有限的时间内,掌握 大纲中的内容并且通过目标考试?
自适应(Adaptive)学习的概念
• 顾名思义是自我调节和匹配,具体含义是指根据数据的特征自动调整处理方 法、顺序、参数和条件, 以取得最佳处理效果。
• 它不是指某项具体技术,而是多种知识和技术融合达成的一个结果。 • 这个概念类似于“共享经济”,它不是指某个经济领域,而是新场景、商业
船舶运动自适应滑模控制(沈智鹏著)PPT模板

4.2基于强化学习的欠驱动船舶 轨迹跟踪自适应迭代滑模控制
4.3基于混沌粒子群算法的欠驱 动船舶自动靠泊迭代滑模控制
参考文献
第4章基于强化学 习的欠驱动船舶 运动自适应迭代 滑模控制
4.1基于强化学习的欠驱动船 舶路径跟踪自适应迭代滑模 控制
4.1.2船舶路 径跟踪控制 器设计
4.1.1问题 描述
船舶运动自适 应滑模控制 (沈智鹏著)
演讲人 2 0 2 X - 11 - 11
目 录
0 1 前言
0 2 第1章绪论
0 3 第2章全驱动船舶轨迹跟踪的自适应滑模控制
0 4 第3章欠驱动船舶轨迹跟踪的自适应滑模控制
05
第4章基于强化学习的欠驱动船舶运动自适应迭代滑模控制
06
第5章基于Lyapunov稳定性的欠驱动船舶运动自适应迭代滑 模控制
01
前言
前言
02
第1章绪论
第1章绪论
1.1自适应滑模控制概述 1.2船舶运动控制概述 参考文献
第1章绪论
1.1自适应滑模控制概述
A
1.1.1滑模 控制简介
B
1.1.2经典 自适应与 滑模控制
C
1.1.3反演 自适应与 滑模控制
D
1.1.4智能 自适应与 滑模控制
第1章绪论
1.2船舶运动控制概述
第3章欠驱动船 舶轨迹跟踪的自 适应滑模控制
3.3基于神经网络和动态面的 欠驱动船舶轨迹跟踪自适应 滑模控制
01
3.3.1基于神经网络 的欠驱动船舶轨迹 跟踪自适应滑模控
制
02
3.3.2基于动态面和 最小参数法的欠驱 动船舶轨迹跟踪自
适应滑模控制
第3章欠驱动船舶轨迹跟踪 的自适应滑模控制
4.3基于混沌粒子群算法的欠驱 动船舶自动靠泊迭代滑模控制
参考文献
第4章基于强化学 习的欠驱动船舶 运动自适应迭代 滑模控制
4.1基于强化学习的欠驱动船 舶路径跟踪自适应迭代滑模 控制
4.1.2船舶路 径跟踪控制 器设计
4.1.1问题 描述
船舶运动自适 应滑模控制 (沈智鹏著)
演讲人 2 0 2 X - 11 - 11
目 录
0 1 前言
0 2 第1章绪论
0 3 第2章全驱动船舶轨迹跟踪的自适应滑模控制
0 4 第3章欠驱动船舶轨迹跟踪的自适应滑模控制
05
第4章基于强化学习的欠驱动船舶运动自适应迭代滑模控制
06
第5章基于Lyapunov稳定性的欠驱动船舶运动自适应迭代滑 模控制
01
前言
前言
02
第1章绪论
第1章绪论
1.1自适应滑模控制概述 1.2船舶运动控制概述 参考文献
第1章绪论
1.1自适应滑模控制概述
A
1.1.1滑模 控制简介
B
1.1.2经典 自适应与 滑模控制
C
1.1.3反演 自适应与 滑模控制
D
1.1.4智能 自适应与 滑模控制
第1章绪论
1.2船舶运动控制概述
第3章欠驱动船 舶轨迹跟踪的自 适应滑模控制
3.3基于神经网络和动态面的 欠驱动船舶轨迹跟踪自适应 滑模控制
01
3.3.1基于神经网络 的欠驱动船舶轨迹 跟踪自适应滑模控
制
02
3.3.2基于动态面和 最小参数法的欠驱 动船舶轨迹跟踪自
适应滑模控制
第3章欠驱动船舶轨迹跟踪 的自适应滑模控制
《自适应学习技术》课件

挑战与机遇
自适应学习技术面临着技术发展、教育政策和数据 隐私等方面的挑战,但也带来了个性化教育和教学 创新方面的机遇。
总结
自适应学习技术在教育领域中具有重要的意义,通过个性化教学和智能化技 术的结合,可以为学生提供更有效和高效的学习体验。
了解自适应学习技术的定义、特点和应用领域,以及其基础理论和分类方法, 有助于我们更好地应用自适应学习技术。
特点
自适应学习技术的特点包括 个性化、灵活性高、提高学 习效果、节省教学资源等。
应用领域
自适应学习技术被广泛应用 于在线课堂、远程教育、学 校教育和企业培训等各个教 育领域。
自适应学习技术的基础
1
个性化教育理论
个性化教育理论为自适应学习技术的发展提供了指导和基础。
2
认知心理学
认知心理学研究为了解学生的学习行为和需要提供了理论支持。
自适应学习技术在未来将继续发展,结合新技术和挑战,为教育领域带来更 多的创新和改进。
5 基于评测反馈
根据学生的评测结果提供相应的个性化教学 建议。
自适应学习技术的应用
在线课堂
自适应学习技术可以根据学生的学习情况调整 在线课堂的教学内容和难度。
学校教育
自适应学习技术可以在学校教育术为远程教育提供了个性化的学 习体验和教学支持。
企业培训
《自适应学习技术》PPT 课件
自适应学习技术是一种个性化的教育方法,能够根据学生的需求和学习风格 自动调整教学内容和速度。本课件将介绍自适应学习技术的定义、特点和应 用领域。
什么是自适应学习技术?
定义
自适应学习技术是一种个性 化的教育方法,通过利用智 能计算机技术,根据学生的 需求和学习风格个性化地调 整教学内容和难度。
自适应信号处理讲义之三 北京航空航天大学

自适应信号处理-自适应滤波算法
在物理上,输入信号向量中的 M+1 个元素可以是从 L+1 个不同信 源到达的瞬时输入 x k x0 k 适应天线阵), 也可以是从一个信源得到的 L+1 个序贯样本x k xk ——对应于单输入情况(如自适应均衡器)。 对于单输入情况,自适应处理器可以用自适应线性组合器和单位 延迟单元来实现,如下图所示,被称为自适应横向滤波器,它是非递 归自适应滤波器的时间形式。
SD 实际上是个误差校正系统-任何反馈系统都存在稳定性问题。 稳定性的定义是滤波器不发散-是滤波器权误差随时间增长趋于零。滤波稳定性研究的是当 时间充分长以后,初值的影响是否可忽略-是否无论怎样选取滤波初值,只要时间充分长,就能 保证滤波值与最优估计值任意接近。
自适应信号处理-自适应滤波算法
考虑滤波器权误差矢量:
c ( n 1) h ( n 1) h o h ( n ) h o p Rh ( n )
h ( n ) h o p R h ( n ) h o Rh o
c(n) p Rc(n) p
I R c(n) 滤波器稳定条件
考虑一个线性最优滤波器:
自适应信号处理-自适应滤波算法
H 误差 e ( n ) x ( n ) h ( n )z ( n )
x(n) hk (n) z (n k )
k 0
m 1
代价函数或均方误差为:
J ( n ) E e( n )e ( n )
2 x h H ( n )p p H h ( n ) h H ( n ) R h ( n )
在 k 时刻的输入信号和权向量。
自适应第四讲

自适应控制
第四讲 模型参考自适应控制系统MRACS
§4.1 基本概念
1.MRACS组成
参考模型
r+
前置控制器
+e _ u 受控过程 y
可调系统
反馈控制器 自适应机构
§4.1 基本概念
①参考模型(R.model) 用一个model体现对控制系统之要求,即model的输出为理想的 响应(对可调系统的工程要求,如超调量、过渡时间、阻尼等可 由R.model直接规定,无需进行性能指标的变换)。 ②可调系统
Monopoli 增广误差信号设计法 Narendra 稳定自适应控制设计法
1.设计思想:
1°引入一个辅助误差信号z,由它与e共同组成增广误差信号ε;
2°利用正实引理综合出一个不含e导数的自适应律,使ε→0, z→0,从而使e→0。
§4.4 增广误差信号设计法(Monopoli,1974)
参考模型
2. 具有可调增益的MIT律的设计
被控对象 Gp(s)KvG(s)
参考模型 G m(s)K m G (s)
§4.2 MRACS局部参数最优化设计方法(MIT律)
MIT方案
r
KmG(s)
Kc
KvG(s)
ym
+ e
_ yp
自适应机构
G(s) N(s) D(s)
K v 未知、漂移(符号已知); K c 可调增益。K m 给定。
只要e不为零,自适应机构就按减少偏差的方向修正或更
新控制u。
实施方案: a. 修正前置/反馈控制器参数,参数自适应方案; b. 直接改变加到输入端的信号,信号综合自适应方案。
§4.1 基本概念
3.模型参考辨识
被辨识过程
第四讲 模型参考自适应控制系统MRACS
§4.1 基本概念
1.MRACS组成
参考模型
r+
前置控制器
+e _ u 受控过程 y
可调系统
反馈控制器 自适应机构
§4.1 基本概念
①参考模型(R.model) 用一个model体现对控制系统之要求,即model的输出为理想的 响应(对可调系统的工程要求,如超调量、过渡时间、阻尼等可 由R.model直接规定,无需进行性能指标的变换)。 ②可调系统
Monopoli 增广误差信号设计法 Narendra 稳定自适应控制设计法
1.设计思想:
1°引入一个辅助误差信号z,由它与e共同组成增广误差信号ε;
2°利用正实引理综合出一个不含e导数的自适应律,使ε→0, z→0,从而使e→0。
§4.4 增广误差信号设计法(Monopoli,1974)
参考模型
2. 具有可调增益的MIT律的设计
被控对象 Gp(s)KvG(s)
参考模型 G m(s)K m G (s)
§4.2 MRACS局部参数最优化设计方法(MIT律)
MIT方案
r
KmG(s)
Kc
KvG(s)
ym
+ e
_ yp
自适应机构
G(s) N(s) D(s)
K v 未知、漂移(符号已知); K c 可调增益。K m 给定。
只要e不为零,自适应机构就按减少偏差的方向修正或更
新控制u。
实施方案: a. 修正前置/反馈控制器参数,参数自适应方案; b. 直接改变加到输入端的信号,信号综合自适应方案。
§4.1 基本概念
3.模型参考辨识
被辨识过程
自适应学习系统根据学生需求和能力制定个性化学习计划培训课件(2)

自适应学习系统根据
学生需求和能力制定
个性化学习计划培训
汇报人:
课件2023-12-29
目录
• 引言 • 学生需求与能力分析 • 自适应学习系统核心功能 • 个性化学习计划实施策略 • 自适应学习系统优势与挑战 • 案例分享与经验总结
01
引言
背景与意义
01 现代教育需求
随着教育技术的发展,学生个性化学习需求日益 凸显,传统教育模式已无法满足所有学生的需求 。
针对不同需求制定多样化课程
需求分析
通过对学生学习背景、目标、兴 趣等方面的了解,识别学生的个
性化需求。
课程定制
基于需求分析结果,为学生定制符 合其需求的课程,包括课程内容、 教学方式、学习资源等。
多样化课程形式
提供多种课程形式,如录播课、直 播课、实践课等,以满足学生不同 学习偏好。
灵活调整学习进度与难度
• 成果:经过一个学期的使用,该系统的学生英语成绩平均提高了8分以上,同时学生的英语应用能力和跨文化交际能力 也得到了显著提升。
经验教训总结
个性化学习计划的制定需要充分了解学生的需求 01 和能力水平,只有这样才能为学生提供真正适合
他们的学习资源和学习计划。
自适应学习系统需要不断地更新和优化学习资源 02 和学习计划,以适应学生不断变化的学习需求和
能力水平。
在实施自适应学习系统的过程中,需要注重学生 03 的反馈和意见,及时调整系统的功能和性能,以
提高学生的学习效果和满意度。
对未来工作的启示和建议
未来可以进一步探索自适应学习系统在其他学科和领域的应用,为学生提供更加全 面和个性化的学习资源和学习计划。
可以进一步研究和开发自适应学习系统的智能化功能,如自动推荐学习资源、智能 评估学习效果等,以提高系统的自适应能力和智能化水平。
学生需求和能力制定
个性化学习计划培训
汇报人:
课件2023-12-29
目录
• 引言 • 学生需求与能力分析 • 自适应学习系统核心功能 • 个性化学习计划实施策略 • 自适应学习系统优势与挑战 • 案例分享与经验总结
01
引言
背景与意义
01 现代教育需求
随着教育技术的发展,学生个性化学习需求日益 凸显,传统教育模式已无法满足所有学生的需求 。
针对不同需求制定多样化课程
需求分析
通过对学生学习背景、目标、兴 趣等方面的了解,识别学生的个
性化需求。
课程定制
基于需求分析结果,为学生定制符 合其需求的课程,包括课程内容、 教学方式、学习资源等。
多样化课程形式
提供多种课程形式,如录播课、直 播课、实践课等,以满足学生不同 学习偏好。
灵活调整学习进度与难度
• 成果:经过一个学期的使用,该系统的学生英语成绩平均提高了8分以上,同时学生的英语应用能力和跨文化交际能力 也得到了显著提升。
经验教训总结
个性化学习计划的制定需要充分了解学生的需求 01 和能力水平,只有这样才能为学生提供真正适合
他们的学习资源和学习计划。
自适应学习系统需要不断地更新和优化学习资源 02 和学习计划,以适应学生不断变化的学习需求和
能力水平。
在实施自适应学习系统的过程中,需要注重学生 03 的反馈和意见,及时调整系统的功能和性能,以
提高学生的学习效果和满意度。
对未来工作的启示和建议
未来可以进一步探索自适应学习系统在其他学科和领域的应用,为学生提供更加全 面和个性化的学习资源和学习计划。
可以进一步研究和开发自适应学习系统的智能化功能,如自动推荐学习资源、智能 评估学习效果等,以提高系统的自适应能力和智能化水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ym
yr
k mG ( s )
e
kc
k pG ( s )
yp
s
图5-3 自适应控制系统结构图
从式(5-25)可以看出, 中的
和 k m 设定后, 将为一常数,当输入 yr
为恒值时, y m 的稳定值也为恒值,所以 kc (t ) 将根据 e(t ) 的变化而产生调整作 用,作用方向是使 e(t ) 变小,直至为零。 以上参数控制规律的推演过程并没有考虑系统的稳定性问题,由于设计人员 5
将式(5-25)代入,有
a2 a1e e kp kmr 2e 0 e
由Hurwits稳定判据知,当 a1 / a2 > kp km r 2 时,系统才是稳定的。若r 过大, 或 选得过大,均容易使上述不等式不成立,从而导致系统不能稳定工作。
5.2.2 MIT的规范化算法
当参考模型与可调系统完全匹配时,有 y p y m ,并且
k m k p kc
式中, kc 为匹配时 k c 的取值。现在的稳态是如何确定 kc (t )的调节规律。
定义输出误差:
e(t ) ym yp
取性能指标函数为
(5-20)
1 J (kc ) e 2 (t ) 2
kc (t ) 的变化方向应使J在参数空间下降最快的方向,即负梯度方向。
整个系统工作不稳定。
例5.2.2 已知
G(s) 1 s 2 a1s a2
将其代入式(5-27)有:
s 3 a1s 2 a2 s Байду номын сангаас 0
如果
ym0 yr0 kp < a1a2
9
所有的根将在s平面左半部分。 从式(5-28)看, 和 yr0 均与 有关,所以 的选择不仅要以式(527)为基础,而且要考虑输入幅值的大小。 当 选定以后,对某些幅值较小的输入 yr0 ,系统工作可能是稳定的,但对 某些幅值较大的输入 yr0 ,系统工作可能不稳定。对较小幅值的 yr0 ,系统响应 速度可能较慢;对较大幅值的 yr0 ,响应可能较快。 这些清楚地表明:自适应增益的选择,依赖于输入信号的幅度;输入信号的
3
响应的时域表达式为
e(t ) (k m kc k p )G( p) yr (t )
式中, p
d dt
(5-22)
。下面求敏感导数。由于
ym kmG( p) yr (t )
yp kc k pG ( p) y r (t )
(5-23)
两式相比,得
yp kp kc ym k m
幅度影响着系统的特性。为了改变这一现象,我们对MIT控制规律做如下的修
改:
dkc 将 dt eym
修改为
dk c dt
ey m
kp 2 ym km
2
(5-29)
式中, > 0,它是为避免 (k p ym / k m ) 较小时出现上式右端过大而引入的。
5.2 用梯度法设计自适应控制系统
模型参考自适应控制系统的设计关键是可调参数的自适应规律。如前所
述,设计这种自适应规律的方法一般有梯度法和稳定理论法,本节讨论梯度法。 梯度法属于一种局部参数最优化方法,类似的方法还有牛顿-拉夫逊法、共轭梯
度法、变尺度法等,由于梯度法算法简捷,实践中用得最多。
最早用该方法设计并后来被大量使用的自适应控制规律是MIT规律,因该规 律首先在美国麻省理工学院(Massachusetts Institute of Technology,MIT), 的一个仪表实验室产生而得名。
为了清楚地掌握 kc (t ) 的动态特性,我们不妨假设: kc (t ) 开始是一个常数,
自适应机构不与控制器相连,施加恒定的输入信号 yr 。当系统进入稳态之后, 再接入自适应机构,于是控制参数的特性由下列方程描述:
dkc 2 ym0 yr0 [ kpG( p)]kc ym0 dt
ym (s)
稳态输出为
km r a 2 s 2 a1s 1 s
ym (t ) k m r
由式(5-22),输出误差微分方程为
a2 e a1e e [ k m k p kc (t )] r
6
两边对 t 求导,有
a2 a1e e kp rkc (t ) e
从上面的例子可以看出,过大的输入幅度和过大的自适应增益均可能使系统 不稳定,所以有必要对这个问题做进一步的研究。
由式(5-25)知,kc (t ) 与 e(t ) 联系密切,又由式(5-20)知 e(t ) 与 yp (t ) 直接有
关,所以对kc (t ) 特性的研究是间接地对
y p (t )进行研究。
的随意性和控制要求及输入信号的多样性,设计出来的自适应控制系统必须进行
稳定性校验。
例5.2.1 设有稳定的被控对象
k p G(s)
kp a2 s 2 a1s 1
式中, kp未知,输入为阶跃信号,幅度为r,即 y r r ,试研究采用MIT控制规律 后,系统的稳定情况。 解:根据被控对象,参考模型的输出为
y p y p J J e dk k c c e(t )( ) e(t ) dt k c e k c k c k c
y p 式中, > 0 为调整步长, k c 为敏感导数。
(5-21)
关于输出误差,我们有
E(s) (km kc kp )G(s) yr (s)
将式(5-20)代入式(5-25),并考虑式(5-23),有:
7
dkc 2 ym [kpG( p) yr ]kc ym dt
式中 p d / dt
(5-26)
式(5-26)描述了控制器参数的变化规律。其中 y m 可看做是已知的时间 函数,如果 G(s) 是一个有理函数,式(5-26)是一个线性时变的微分方程。我们 很难获得控制参数随时间变化的解析解,更不用说知道自适应增益如何影响参数 特性。
11
k mG(s)
式中, k m 是使模型输出达到期望状态的增益。 控制器的设计根据被控对象与参考模型结构相匹配的原则进行,设计为一个 可调增益 kc (t ) ,整个系统的结构图如图5-2所示。
ym
km G ( s )
yr
u
e
kc
k p G(s)
yp
?
图5-2 系统结构框图
2
图中, y m 和 yp 分别为参考模型输出和对象输出。“ ?”为待定的符号。
式中, y m 0 是模型稳态输出, yr0 是恒值输入信号的幅值。
8
这是一个线性时不变系统,微分方程的系数是恒定的,其稳定性可由下列代 数方程来确定:
s G(s) 0
式中
(5-27)
ym0 yr0 kp
画出零点随 变化的轨迹来。
(5-28)
由于 G(s) 原来设定是稳定的,所以 k c 的特性由 来确定。我们甚至可以 如果方程式(5-27)有零点在s平面右半部,控制器工作将会不稳定,从而
kp yp kc ym km
y p k p ym k c k m
kp dk kc c e y m ey m dt km
(5-25) 4
于是有
(5-24)
两边对 k c 求偏导,得
将此式代入式(5-21),有
式中, kp / km 为自适应增益。
式(5-25)称MIT控制规律,其自适应控制系统结构图如图5-3所示。
10 式(5-29)称为MIT的规范化算法。根据式(5-29),用同样的分析,式
(5-27)将变为
s
y m 0 y r0
kp ym0 km
2
k pG(s) 0
从上式知,由于 y m 0 正比于 yr0 ,所以方程的根不会因输入幅度变化而改变许多。 MIT控制原理明了,结构简单,工程上易于实现,因此近期仍有应用。但 是,它也存在一些问题:设计出的自适应控制系统不能保证其闭环系统的稳定 性,需要进行稳定性检验。此外,仅调整增益只能在较小范围内改变系统的动态 性能,如果需要对系统进行较大的校正,一般难以实现,所以该设计方法的应用 范围有限。
5.2.1 MIT控制规律
设有被控对象或过程
k p G( s)
式中, kp 为增益,未知或慢时变,G(s) 为已知的传递函数,且稳定。 现在的任务有两条:一是根据参考输入和控制要求,选取一个参考模型,并 1
使其输出达到期望的特性;二是设计一个控制器调节规律,使它与被控对象构成
的可调系统,能使其输出接近并最终达到参考模型的输出。 显然,参考模型可取
yr
k mG ( s )
e
kc
k pG ( s )
yp
s
图5-3 自适应控制系统结构图
从式(5-25)可以看出, 中的
和 k m 设定后, 将为一常数,当输入 yr
为恒值时, y m 的稳定值也为恒值,所以 kc (t ) 将根据 e(t ) 的变化而产生调整作 用,作用方向是使 e(t ) 变小,直至为零。 以上参数控制规律的推演过程并没有考虑系统的稳定性问题,由于设计人员 5
将式(5-25)代入,有
a2 a1e e kp kmr 2e 0 e
由Hurwits稳定判据知,当 a1 / a2 > kp km r 2 时,系统才是稳定的。若r 过大, 或 选得过大,均容易使上述不等式不成立,从而导致系统不能稳定工作。
5.2.2 MIT的规范化算法
当参考模型与可调系统完全匹配时,有 y p y m ,并且
k m k p kc
式中, kc 为匹配时 k c 的取值。现在的稳态是如何确定 kc (t )的调节规律。
定义输出误差:
e(t ) ym yp
取性能指标函数为
(5-20)
1 J (kc ) e 2 (t ) 2
kc (t ) 的变化方向应使J在参数空间下降最快的方向,即负梯度方向。
整个系统工作不稳定。
例5.2.2 已知
G(s) 1 s 2 a1s a2
将其代入式(5-27)有:
s 3 a1s 2 a2 s Байду номын сангаас 0
如果
ym0 yr0 kp < a1a2
9
所有的根将在s平面左半部分。 从式(5-28)看, 和 yr0 均与 有关,所以 的选择不仅要以式(527)为基础,而且要考虑输入幅值的大小。 当 选定以后,对某些幅值较小的输入 yr0 ,系统工作可能是稳定的,但对 某些幅值较大的输入 yr0 ,系统工作可能不稳定。对较小幅值的 yr0 ,系统响应 速度可能较慢;对较大幅值的 yr0 ,响应可能较快。 这些清楚地表明:自适应增益的选择,依赖于输入信号的幅度;输入信号的
3
响应的时域表达式为
e(t ) (k m kc k p )G( p) yr (t )
式中, p
d dt
(5-22)
。下面求敏感导数。由于
ym kmG( p) yr (t )
yp kc k pG ( p) y r (t )
(5-23)
两式相比,得
yp kp kc ym k m
幅度影响着系统的特性。为了改变这一现象,我们对MIT控制规律做如下的修
改:
dkc 将 dt eym
修改为
dk c dt
ey m
kp 2 ym km
2
(5-29)
式中, > 0,它是为避免 (k p ym / k m ) 较小时出现上式右端过大而引入的。
5.2 用梯度法设计自适应控制系统
模型参考自适应控制系统的设计关键是可调参数的自适应规律。如前所
述,设计这种自适应规律的方法一般有梯度法和稳定理论法,本节讨论梯度法。 梯度法属于一种局部参数最优化方法,类似的方法还有牛顿-拉夫逊法、共轭梯
度法、变尺度法等,由于梯度法算法简捷,实践中用得最多。
最早用该方法设计并后来被大量使用的自适应控制规律是MIT规律,因该规 律首先在美国麻省理工学院(Massachusetts Institute of Technology,MIT), 的一个仪表实验室产生而得名。
为了清楚地掌握 kc (t ) 的动态特性,我们不妨假设: kc (t ) 开始是一个常数,
自适应机构不与控制器相连,施加恒定的输入信号 yr 。当系统进入稳态之后, 再接入自适应机构,于是控制参数的特性由下列方程描述:
dkc 2 ym0 yr0 [ kpG( p)]kc ym0 dt
ym (s)
稳态输出为
km r a 2 s 2 a1s 1 s
ym (t ) k m r
由式(5-22),输出误差微分方程为
a2 e a1e e [ k m k p kc (t )] r
6
两边对 t 求导,有
a2 a1e e kp rkc (t ) e
从上面的例子可以看出,过大的输入幅度和过大的自适应增益均可能使系统 不稳定,所以有必要对这个问题做进一步的研究。
由式(5-25)知,kc (t ) 与 e(t ) 联系密切,又由式(5-20)知 e(t ) 与 yp (t ) 直接有
关,所以对kc (t ) 特性的研究是间接地对
y p (t )进行研究。
的随意性和控制要求及输入信号的多样性,设计出来的自适应控制系统必须进行
稳定性校验。
例5.2.1 设有稳定的被控对象
k p G(s)
kp a2 s 2 a1s 1
式中, kp未知,输入为阶跃信号,幅度为r,即 y r r ,试研究采用MIT控制规律 后,系统的稳定情况。 解:根据被控对象,参考模型的输出为
y p y p J J e dk k c c e(t )( ) e(t ) dt k c e k c k c k c
y p 式中, > 0 为调整步长, k c 为敏感导数。
(5-21)
关于输出误差,我们有
E(s) (km kc kp )G(s) yr (s)
将式(5-20)代入式(5-25),并考虑式(5-23),有:
7
dkc 2 ym [kpG( p) yr ]kc ym dt
式中 p d / dt
(5-26)
式(5-26)描述了控制器参数的变化规律。其中 y m 可看做是已知的时间 函数,如果 G(s) 是一个有理函数,式(5-26)是一个线性时变的微分方程。我们 很难获得控制参数随时间变化的解析解,更不用说知道自适应增益如何影响参数 特性。
11
k mG(s)
式中, k m 是使模型输出达到期望状态的增益。 控制器的设计根据被控对象与参考模型结构相匹配的原则进行,设计为一个 可调增益 kc (t ) ,整个系统的结构图如图5-2所示。
ym
km G ( s )
yr
u
e
kc
k p G(s)
yp
?
图5-2 系统结构框图
2
图中, y m 和 yp 分别为参考模型输出和对象输出。“ ?”为待定的符号。
式中, y m 0 是模型稳态输出, yr0 是恒值输入信号的幅值。
8
这是一个线性时不变系统,微分方程的系数是恒定的,其稳定性可由下列代 数方程来确定:
s G(s) 0
式中
(5-27)
ym0 yr0 kp
画出零点随 变化的轨迹来。
(5-28)
由于 G(s) 原来设定是稳定的,所以 k c 的特性由 来确定。我们甚至可以 如果方程式(5-27)有零点在s平面右半部,控制器工作将会不稳定,从而
kp yp kc ym km
y p k p ym k c k m
kp dk kc c e y m ey m dt km
(5-25) 4
于是有
(5-24)
两边对 k c 求偏导,得
将此式代入式(5-21),有
式中, kp / km 为自适应增益。
式(5-25)称MIT控制规律,其自适应控制系统结构图如图5-3所示。
10 式(5-29)称为MIT的规范化算法。根据式(5-29),用同样的分析,式
(5-27)将变为
s
y m 0 y r0
kp ym0 km
2
k pG(s) 0
从上式知,由于 y m 0 正比于 yr0 ,所以方程的根不会因输入幅度变化而改变许多。 MIT控制原理明了,结构简单,工程上易于实现,因此近期仍有应用。但 是,它也存在一些问题:设计出的自适应控制系统不能保证其闭环系统的稳定 性,需要进行稳定性检验。此外,仅调整增益只能在较小范围内改变系统的动态 性能,如果需要对系统进行较大的校正,一般难以实现,所以该设计方法的应用 范围有限。
5.2.1 MIT控制规律
设有被控对象或过程
k p G( s)
式中, kp 为增益,未知或慢时变,G(s) 为已知的传递函数,且稳定。 现在的任务有两条:一是根据参考输入和控制要求,选取一个参考模型,并 1
使其输出达到期望的特性;二是设计一个控制器调节规律,使它与被控对象构成
的可调系统,能使其输出接近并最终达到参考模型的输出。 显然,参考模型可取
