人教a版高考数学理一轮课件选修4-42参数方程
合集下载
2020版高考人教A版理科数学一轮复习文档：选修4-4 第二节 参 数 方 程 Word版含答案
姓名，年级：时间：第二节参数方程2019考纲考题考情1．参数方程的概念一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x，y都是某个变数t的函数：错误!①并且对于t 的每一个允许值，由方程组①所确定的点M(x，y）都在这条曲线上,那么方程组①就叫做这条曲线的参数方程,t叫做参变数，简称参数。
相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程。
2．直线的参数方程过定点P0(x0，y0）且倾斜角为α的直线的参数方程为错误!(t为参数)，则参数t的几何意义是有向线段错误!的数量。
3．圆的参数方程圆心为(a，b），半径为r，以圆心为顶点且与x轴同向的射线，按逆时针方向旋转到圆上一点所在半径形成的角α为参数的圆的参数方程为错误!(α为参数)α∈[0，2π）.4．椭圆的参数方程以椭圆的离心角θ为参数，椭圆错误!＋错误!＝1（a＞b＞0）的参数方程为错误!（θ为参数），θ∈［0,2π）.1．将参数方程化为普通方程时，要注意防止变量x 和y取值范围的扩大或缩小，必须根据参数的取值范围，确定函数f(t)和g(t）的值域,即x和y的取值范围。
2．直线的参数方程中，参数t的系数的平方和为1时，t才有几何意义且几何意义为:|t｜是直线上任一点M(x，y)到M0(x0，y0）的距离。
一、走进教材1．（选修4－4P26T4改编）在平面直角坐标系中，曲线C：错误!(t为参数）的普通方程为________。
解析消去t，得x－y＝1,即x－y－1＝0。
答案x－y－1＝02．(选修4－4P37例2改编)在平面直角坐标系xOy 中,若直线l：错误!(t为参数）过椭圆C：错误!（φ为参数）的右顶点，求常数a的值。
解直线l的普通方程为x－y－a＝0,椭圆C的普通方程为错误!＋错误!＝1，所以椭圆C的右顶点坐标为（3，0)，若直线l过(3，0)，则3－a＝0，所以a＝3.二、走出误区微提醒：①不注意互化的等价性致误；②直线参数方程中参数t的几何意义不清致误；③交点坐标计算出错致错。
高中数学人教A版选修4-4第二讲 一 1. 参数方程的概念 课件
[思路点拨] 此类问题关键是参数的选取．本例中由于 A、 B 的滑动而引起点 P 的运动，故可以 OB 的长为参数，或以角 为参数，不妨取 BP 与 x 轴正向夹角为参数来求解．
[解] 法一：设 P 点的坐标为(x，y)，过
P 点作 x 轴的垂线交 x 轴于 Q.如图所示，则 Rt△OAB≌Rt△QBP.
∴xy＝＝bascions
θ， θ.
这就是所求的轨迹方程．
9．如图所示，OA是圆C的直径，且OA＝2a， 射线OB与圆交于Q点，和经过A点的切线 交于B点，作PQ⊥OA，PB∥OA，试求点P 的轨迹方程．
解：设 P(x，y)是轨迹上任意一点，取∠DOQ＝θ， 由 PQ⊥OA，PB∥OA，得 x＝OD＝OQcosθ＝OAcos2θ＝ 2acos2θ，y＝AB＝OAtan θ＝2atan θ. 所以 P 点轨迹的参数方程为xy＝＝22aatcaons2θθ，， θ∈－π2，π2.
解析：x轴上的点横坐标可取任意实数，纵坐标为0.
答案：D
2．若点P(4，a)在曲线x＝2t ， (t为参数)上，则a等于(
)
y＝2 t
A．4
B．4 2
C．8
D．1
解析：根据题意，将点P坐标代入曲线方程中得
4＝2t ， a＝2 t
⇒ta＝＝84，2.
答案：B
3．在方程
参数方程是曲线方程的另一种表达形式，点与曲线 位置关系的判断，与平面直角坐标方程下的判断方法是 一致的．
1．已知点 M(2，－2)在曲线 C：x＝t＋1t ， (t 为参数)上， y＝－2
则其对应的参数 t 的值为________． 解：由 t＋1t ＝2 知 t＝1. 答案：1
2．已知某条曲线 C 的参数方程为xy＝＝a1t＋2 2t， (其中 t 为参数， a∈R)．点 M(5,4)在该曲线上，求常数 a.
[解] 法一：设 P 点的坐标为(x，y)，过
P 点作 x 轴的垂线交 x 轴于 Q.如图所示，则 Rt△OAB≌Rt△QBP.
∴xy＝＝bascions
θ， θ.
这就是所求的轨迹方程．
9．如图所示，OA是圆C的直径，且OA＝2a， 射线OB与圆交于Q点，和经过A点的切线 交于B点，作PQ⊥OA，PB∥OA，试求点P 的轨迹方程．
解：设 P(x，y)是轨迹上任意一点，取∠DOQ＝θ， 由 PQ⊥OA，PB∥OA，得 x＝OD＝OQcosθ＝OAcos2θ＝ 2acos2θ，y＝AB＝OAtan θ＝2atan θ. 所以 P 点轨迹的参数方程为xy＝＝22aatcaons2θθ，， θ∈－π2，π2.
解析：x轴上的点横坐标可取任意实数，纵坐标为0.
答案：D
2．若点P(4，a)在曲线x＝2t ， (t为参数)上，则a等于(
)
y＝2 t
A．4
B．4 2
C．8
D．1
解析：根据题意，将点P坐标代入曲线方程中得
4＝2t ， a＝2 t
⇒ta＝＝84，2.
答案：B
3．在方程
参数方程是曲线方程的另一种表达形式，点与曲线 位置关系的判断，与平面直角坐标方程下的判断方法是 一致的．
1．已知点 M(2，－2)在曲线 C：x＝t＋1t ， (t 为参数)上， y＝－2
则其对应的参数 t 的值为________． 解：由 t＋1t ＝2 知 t＝1. 答案：1
2．已知某条曲线 C 的参数方程为xy＝＝a1t＋2 2t， (其中 t 为参数， a∈R)．点 M(5,4)在该曲线上，求常数 a.
人教A版数学【选修4-4】ppt课件：2-2第二讲-参数方程
【解】
如图所示：
由动点C在该椭圆上运动，故可设C的坐标为(6cosθ，3sinθ)， 点G的坐标为(x，y)，由题意可知A(6,0)，B(0,3)，由三角形重心坐 标公式可知：
x＝6＋0＋6cosθ＝2＋2cosθ， 3 0＋3＋3sinθ y＝ ＝1＋sinθ. 3 x－22 由此，消去参数θ，得到所求的普通方程为 4 ＋(y－1)2＝ 1.
x－1＝cosθ， 3 【解】 (1)由题意可设 y＋2 ＝sinθ， 5
x＝1＋ 3cosθ， y＝－2＋ 5sinθ
即
(θ为参数)为所求．
2 2 x y (2)x2－y2＝4变形为： 4 － 4 ＝1.
x＝2secα， ∴参数方程为 y＝2tanα
2 x ＝ 2 pt ， 2 2．抛物线y ＝2px(p>0)的参数方程为 y＝2pt
y 1 由于 x ＝ t ，因此参数t的几何意义是抛物线上除顶点外的点与 抛物线的顶点连线的斜率的倒数． 3．几个结论 x2 y2 (1)焦点在y轴上的椭圆的标准方程为 b2 ＋ a2 ＝1(a>b>0)，其参 数方程是 [0,2π)．
x2 y2 a2＋b2＝1
x＝acosφ， y＝bsinφ
x2 y2 a2－b2＝1
x＝asecφ， y＝btanφ
点的坐标
(rcosθ， rsinθ)
(acosφ，bsinφ)
(asecφ，btanφ)
这三种曲线的参数方程都是参数的三角形式．其中圆的参数θ 表示旋转角，而椭圆、双曲线的参数φ表示离心角，几何意义是不 同的，它们的参数方程主要应用价值在于： (1)通过参数(角)简明地表示曲线上任一点的坐标； (2)将解析几何中的计算问题转化为三角问题，从而运用三角 函数性质及变换公式帮助求解最值、参数的取值范围等问题．
人教版高中数学选修4-4课件：第二讲二第2课时双曲线的参数方程和抛物线的参数方程
x＝sec θ，
解：把双曲线方程化为参数方程
(θ 为参
y＝tan θ
数)，
林老师网络编辑整理
18
设双曲线上点 Q(sec θ，tan θ)，则
|PQ|2＝sec2θ＋(tan θ－2)2＝
(tan2θ＋1)＋(tan2θ－4tan θ＋4)＝
2tan2θ－4tan θ＋5＝2(tan θ－1)2＋3，
林老师网络编辑整理
5
2．抛物线的参数方程
如图，抛物线 y2＝2px(p>0)的参数方程为
x＝2pt2，
____y_＝__2_p_t ____t为参数，t＝tan1
α.
林老师网络编辑整理
6
温馨提示 t＝sin1 α(α 是以射线 OM 为终边的角)，即 参数 t 表示抛物线上除顶点之外的任意一点与原点连线的 斜率的倒数．
第二讲 参数方程
林老师网络编辑整理
1
二、圆锥曲线的参数方程 第 2 课时 双曲线的参数方程和
抛物线的参数方程
林老师网络编辑整理
2
[学习目标] 1.了解抛物线和双曲线的参数方程，了 解抛物线参数方程中参数的几何意义(重点)． 2.利用抛 物线和双曲线的参数方程处理问题(重点、难点)．
林老师网络编辑整理
当 tan θ－1＝0，即 θ＝π4时，
|PQ|2 取最小值 3，此时有|PQ|＝ 3.
即 P、Q 两点间的最小距离为 3.
林老师网络编辑整理
19
[迁移探究] (变换条件)已知圆 O1：x2＋(y－2)2＝1 上一点 P 与双曲线 x2－y2＝1 上一点 Q，求 P，Q 两点间 距离的最小值．
解：设 Q(sec θ，tan θ)， 由题意知|O1P|＋|PQ|≥|O1Q|. |O1Q|2＝sec2θ＋(tan θ－2)2＝
高考数学总复习 第2节 参数方程课件 新人教A版选修44
数的关系 y＝g(t)
x＝ft ，那么 y＝gt 就是曲线的参数方程．
第五页，共70页。
在参数方程与普通(pǔtōng)方程的互化中，x，y的取值范围必 须保持一致．
第六页，共70页。
三、常见曲线的参数方程的一般形式
1．直线的参数方程
经过点 P0(x0，y0)，倾斜角为 α 的直线的参数方程为
x＝ x0＋tcos α y＝ y0＋tsin α
第十四页，共70页。
2．若 P(2，－1)为圆xy＝＝15＋sin5θcos θ， (θ 为参数且 0≤θ
＜2π)的弦的中点，则该弦所在的直线方程为( )
A．x－y－3＝0
B．x＋2y＝0
C．x＋y－1＝0
D．2x－y－5＝0
第十五页，共70页。
解析：由xy＝ ＝15＋sin5θc，os θ 消去参数 θ，得(x－1)2＋y2＝25， ∴圆心 C(1,0)，∴kCP＝－1. ∴弦所在的直线的斜率为 1. ∴弦所在的直线方程为 y－(－1)＝1·(x－2)， 即 x－y－3＝0，故选 A.
第二十页，共70页。
解析：曲线
C1：xy＝＝34＋＋csions
θ θ
(θ 为参数)的直角坐标方
程为(x－3)2＋(y－4)2＝1，可知曲线 C1 是以(3,4)为圆心，1 为半径的圆；曲线 C2：ρ＝1 的直角坐标方程是 x2＋y2＝1， 故 C2 是以原点为圆心，1 为半径的圆．由题意知|AB|的最小 值即为分别在两个圆上的两点 A，B 间的最短距离．由条件
① ②
①2＋②2 得 x2＋(y－1)2＝1，
即所求普通方程为 x2＋(y－1)2＝1，
答案(dáàn)：x2＋(y－1)2＝1
第二十六页，共70页。
人教A版高考总复习一轮理科数学精品课件 选修4—4 坐标系与参数方程 第1课时 极坐标方程与参数方程
(θ 为参数)
= + sin.
= cos,
2
2
(3)椭圆方程 2 + 2 =1(a>b>0)的参数方程为
(θ 为参数)
= sin.
2
=
2
,
2
(4)抛物线方程 y =2px(p>0)的参数方程为
(t 为参数)
= 2.
2
2
2
微点拨1.参数方程通过代入消元法或加减消元法消去参数化为普通方程,
= -1 + 2sin (α为参数).以O为极点,x轴的非负半轴为极轴建立极坐标
π
= 2cos,
(2)由(1)得曲线 C 的参数方程为
为参数, 且 ≠
2
= sin
∴点 A( 2cos θ,sin θ)到直线 l 的距离
| 2cos -sin -1|
d=
2
=
,
2
,
2
整理得 2cos θ=sin θ 或 2cos θ-sin θ= 3cos(θ+α)=2 其中 tan =
(3)取相同的长度单位
互化公式
x = ρθ,
①
y = ρθ,
ρ2 = x 2 + y 2 ,
②
y
θ = x ( ≠ 0)
(2)把直角坐标转化为极坐标时,通常有不同的表示法(极角相差2π的整数
倍).一般取ρ≥0,θ∈[0,2π).
4.直线的极坐标方程
(1)若直线过点M(ρ0,θ0),且从极轴到此直线的角为α,则它的方程为ρsin(θ-α)
由已知tan θ=2,可得
16cos2θ-8sin θcos θ=0,
= + sin.
= cos,
2
2
(3)椭圆方程 2 + 2 =1(a>b>0)的参数方程为
(θ 为参数)
= sin.
2
=
2
,
2
(4)抛物线方程 y =2px(p>0)的参数方程为
(t 为参数)
= 2.
2
2
2
微点拨1.参数方程通过代入消元法或加减消元法消去参数化为普通方程,
= -1 + 2sin (α为参数).以O为极点,x轴的非负半轴为极轴建立极坐标
π
= 2cos,
(2)由(1)得曲线 C 的参数方程为
为参数, 且 ≠
2
= sin
∴点 A( 2cos θ,sin θ)到直线 l 的距离
| 2cos -sin -1|
d=
2
=
,
2
,
2
整理得 2cos θ=sin θ 或 2cos θ-sin θ= 3cos(θ+α)=2 其中 tan =
(3)取相同的长度单位
互化公式
x = ρθ,
①
y = ρθ,
ρ2 = x 2 + y 2 ,
②
y
θ = x ( ≠ 0)
(2)把直角坐标转化为极坐标时,通常有不同的表示法(极角相差2π的整数
倍).一般取ρ≥0,θ∈[0,2π).
4.直线的极坐标方程
(1)若直线过点M(ρ0,θ0),且从极轴到此直线的角为α,则它的方程为ρsin(θ-α)
由已知tan θ=2,可得
16cos2θ-8sin θcos θ=0,
2020年高考人教A版理科数学一轮复习(全册PPT课件 1520张)
人教A版数学（理科）一轮
2020版高考 全册精品 PPT课件
第1章 集合与常用逻辑用语 第一节 集 合 第二节 命题及其关系、充分条件与必要条件 第三节 简单的逻辑联结词、全称量词与存在量词
第2章 函数、导数及其应用 第一节 函数及其表示 第二节 函数的单调性与最值 第三节 函数的奇偶性与周期性 第四节 二次函数与幂函数 第五节 指数与指数函数 第六节 对数与对数函数 第七节 函数的图象
[答案] (1)× (2)× (3)× (4)×
23 答案
2 ． ( 教 材 改 编 ) 若 集 合 A ＝ D [由题意知 A＝{0,1,2}，由 a＝ {x∈N|x≤2 2}，a＝ 2，则下列结 2，知 a∉A.] 论正确的是( ) A．{a}⊆A B．a⊆A C．{a}∈A D．a∉A
解2析4 答案
22
[基础自测] 1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打 “×”) (1)任何一个集合都至少有两个子集．( ) (2){x|y＝x2}＝{y|y＝x2}＝{(x，y)|y＝x2}．( ) (3)若{x2,1}＝{0,1}，则 x＝0,1.( ) (4)直线 y＝x＋3 与 y＝－2x＋6 的交点组成的集合是{1,4}．( )
第8章 平面解析几何 第一节 直线的倾斜角与斜率、直线的方程 第二节 两条直线的位置关系 第三节 圆的方程 第四节 直线与圆、圆与圆的位置关系 第五节 椭 圆
第1课时 椭圆的定义、标准方程及其性质 第2课时 直线与椭圆的位置关系
第六节 双曲线 第七节 抛物线 第八节 曲线与方程 第九节 圆锥曲线中的定点、定值、范围、最值问题 高考大题增分课(五) 平面解析几何中的高考热点问题
第9章 算法初步、统计与统计案例 第一节 算法与程序框图 第二节 随机抽样 第三节 用样本估计总体 第四节 变量间的相关关系与统计案例
2020版高考 全册精品 PPT课件
第1章 集合与常用逻辑用语 第一节 集 合 第二节 命题及其关系、充分条件与必要条件 第三节 简单的逻辑联结词、全称量词与存在量词
第2章 函数、导数及其应用 第一节 函数及其表示 第二节 函数的单调性与最值 第三节 函数的奇偶性与周期性 第四节 二次函数与幂函数 第五节 指数与指数函数 第六节 对数与对数函数 第七节 函数的图象
[答案] (1)× (2)× (3)× (4)×
23 答案
2 ． ( 教 材 改 编 ) 若 集 合 A ＝ D [由题意知 A＝{0,1,2}，由 a＝ {x∈N|x≤2 2}，a＝ 2，则下列结 2，知 a∉A.] 论正确的是( ) A．{a}⊆A B．a⊆A C．{a}∈A D．a∉A
解2析4 答案
22
[基础自测] 1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打 “×”) (1)任何一个集合都至少有两个子集．( ) (2){x|y＝x2}＝{y|y＝x2}＝{(x，y)|y＝x2}．( ) (3)若{x2,1}＝{0,1}，则 x＝0,1.( ) (4)直线 y＝x＋3 与 y＝－2x＋6 的交点组成的集合是{1,4}．( )
第8章 平面解析几何 第一节 直线的倾斜角与斜率、直线的方程 第二节 两条直线的位置关系 第三节 圆的方程 第四节 直线与圆、圆与圆的位置关系 第五节 椭 圆
第1课时 椭圆的定义、标准方程及其性质 第2课时 直线与椭圆的位置关系
第六节 双曲线 第七节 抛物线 第八节 曲线与方程 第九节 圆锥曲线中的定点、定值、范围、最值问题 高考大题增分课(五) 平面解析几何中的高考热点问题
第9章 算法初步、统计与统计案例 第一节 算法与程序框图 第二节 随机抽样 第三节 用样本估计总体 第四节 变量间的相关关系与统计案例
人教A版高中数学选修4-4课件第二章第一节《参数方程》
,(为
参数)的右
顶点,
则常数a的值为________ .
*高考链接*
1.(2013年高考湖南卷(理))在平面直
角
坐标系xOy中,
若l
:
x y
t t
,
(t为 a
参数)
过椭圆C
:
x y
3 2
cos sin
,(为
参数)的右
顶点,
则常数a的值为____3____ .
*练习1* 曲线y x2的一种参数方程是( )
A.
x
t
2
y t 4
B.
x
sin
t
y sin2 t
C
.
x
t
y t
D.
x
t
y t 2
练习2* 参数方程
x y
|
cos
2 1 (1 2
sin
一般地，在平面直角坐标系中，如果曲线
上任意一点的坐标x，y都是某个变数t的函数
x f (t),
(2)
y g(t),
并且对于t的每一个允许值，由方程组(2)所确
定的点M(x，y)都在这条曲线上，那么方程(2)
就叫做这条曲线的参数方程，联系变数x，y
的变数t叫做参变数，简称参数。相对于参数
x
sin
t
y sin2 t
(2)
x
1 2
(et
et
)
y
高考数学(人教A版)一轮复习课件：选修4-4-2参数方程
2 2 2 3 2 3 2 2 | AB | ( ) ( ) 2 5. 2 2 2 2
2.(2015·湖北高考改编)在直角坐标系xOy中,以O为极 点,x轴的正半轴为极轴建立极坐标系.已知直线l的极 坐标方程为ρ(sinθ-3cosθ)=0,曲线C的参数方程为 (t为参数),l与C相交于A,B两点,求|AB|的长.
1 xt , t y t 1 t
y2 4
解得t1=0,t2=
16 ,得|AB|=|t , 由直线参数方程的意义 1-t2|= 7
16 . 7
【规律方法】 直线的参数方程在交点问题中的应用 已知直线l经过点M0(x0,y0),倾斜角为α,点M(x,y)为l上 任意一点,则直线l的参数方程为 数). (t为参
x x 0 tcos, y y0 tsin
2.直线的参数方程中,参数t的系数的平方和为1时,t才有几何意义且几何意义为:|t|是直 线上任一点M(x,y) 到M0(x0,y0)的距离.
考点一 直线的参数方程与应用 【典例1】(2016·江苏高考)在平面直角坐标系xOy中, 已知直线l的参数方程为 (t为参数),椭圆C的
1 x 1 t， 参数方程为 (θ为参数),设直线l与椭圆 C相交 2 于A,B两点,求线段AB的长. y 3 t 2 x cos， y 2sin
3
(1)写出☉C的直角坐标方程. (2)P为直线l上一动点,当P到圆心C的距离最小时,求点P的直角坐标.
【解题提示】(1)利用直角坐标与极坐标的关系进行代换即得. (2)直角坐标与极坐标进行坐标代换后,利用两点间的距离公式可求解.
ቤተ መጻሕፍቲ ባይዱ 【解析】(1)由ρ=2 从而有x2+y2=2
2.1.1《参数方程的概念、圆的参数方程》 课件(人教A版选修4-4)
y=t
限内，其余方程的曲线都过第二象限.
4.已知O为原点，当θ = 时，参数方程 6
x=3cos (θ 为参数) y=9sin
上的点为A,则直线OA的倾斜角为( (A)
6
) (D) 5
6
(B)
3
(C) 2
3
【解析】
5.在方程 标是( )
x=sin2 (θ 为参数)所表示的曲线上的一点的坐 y=sin+cos
12.（14分）已知圆系方程为x2+y2-2axcosφ -2aysinφ =0
(a＞0).
(1)求圆心的轨迹方程; (2)证明圆心轨迹与动圆相交所得的公共弦长为定值.
【解析】
)
【解析】选D. 当x=t-1=0时，t=1,y=t+2=3;当y=t+2=0时， t=-2,x=t-1=-3.曲线与坐标轴的交点坐标为（0，3），
（-3，0）.
x=sin 2.下列各点在方程 (θ 为参数)所表示的曲线上的是 y=cos2
(
（B） ( 1 , 2 )
3 3
)
（A）(2,-7) （C） ( 1 , 1 )
【解析】设飞机在点H将物资投出机 舱，记此时刻为0 s，设在时刻t s 时的坐标为M（x,y）,如图,建立平 面直角坐标系，由于物资做平抛运 动，依题意，得
x=100t x=100t 1 2 ,即 y=h- gt y=h-5t 2 2
令x=100t=1 000,得t=10(s), 由y=h-5t2=h-500=0,得h=500 m. 答案:500 m
∴x=sin 2θ= - 3 .
4
1 4
x=3+cos 6.曲线 (θ 为参数)上的点到坐标轴的最近距离为 y=4+sin
限内，其余方程的曲线都过第二象限.
4.已知O为原点，当θ = 时，参数方程 6
x=3cos (θ 为参数) y=9sin
上的点为A,则直线OA的倾斜角为( (A)
6
) (D) 5
6
(B)
3
(C) 2
3
【解析】
5.在方程 标是( )
x=sin2 (θ 为参数)所表示的曲线上的一点的坐 y=sin+cos
12.（14分）已知圆系方程为x2+y2-2axcosφ -2aysinφ =0
(a＞0).
(1)求圆心的轨迹方程; (2)证明圆心轨迹与动圆相交所得的公共弦长为定值.
【解析】
)
【解析】选D. 当x=t-1=0时，t=1,y=t+2=3;当y=t+2=0时， t=-2,x=t-1=-3.曲线与坐标轴的交点坐标为（0，3），
（-3，0）.
x=sin 2.下列各点在方程 (θ 为参数)所表示的曲线上的是 y=cos2
(
（B） ( 1 , 2 )
3 3
)
（A）(2,-7) （C） ( 1 , 1 )
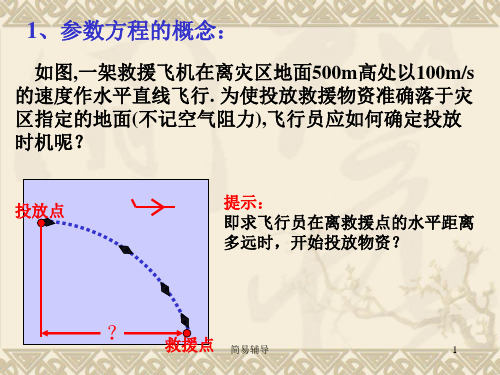
【解析】设飞机在点H将物资投出机 舱，记此时刻为0 s，设在时刻t s 时的坐标为M（x,y）,如图,建立平 面直角坐标系，由于物资做平抛运 动，依题意，得
x=100t x=100t 1 2 ,即 y=h- gt y=h-5t 2 2
令x=100t=1 000,得t=10(s), 由y=h-5t2=h-500=0,得h=500 m. 答案:500 m
∴x=sin 2θ= - 3 .
4
1 4
x=3+cos 6.曲线 (θ 为参数)上的点到坐标轴的最近距离为 y=4+sin
人教A版数学【选修4-4】ppt课件：2-3第二讲-参数方程
x＝x0＋tcosα， y＝y0＋tsinα
称为标准形式，其中参
数t的几何意义是：|t|表示参数t对应的点M到________，t就是有向 → 线段 M0M 的数量．当点M在点M0的上方时，________；当点M在 点M0的下方时________；当点M与点M0重合时，________.
4 x ＝ 1 ＋ 5t， 的方程为 y＝3t 5
(t为参数)．代入椭圆方程x2＋9y2＝9，并
整理得：97t2＋40t－200＝0. 由t的几何意义，知所求的弦长为
|t2－t1|＝ t2＋t12－4t2t1 ＝ －200 60 40 2 － －4 ＝ 22. 97 97 97
3．直线参数方程的应用 直线的标准参数方程主要用来解决过定点的直线与圆锥曲线 相交时的弦长或距离．它可以避免求交点时解方程组的繁琐运 算，但应用直线的参数方程时，需先判别是否是标准形式再考虑t 的几何意义.
课堂互动探究
剖析归纳 触类旁通
【例1】
典例剖析 x＝5＋3t， 设直线的参数方程为 y＝10－4t.
(u为参数)．
规律程，只要用代入法消去参
(2)过点M0(x0，y0)，倾斜角为α(0≤α<π)的直线的参数方程为
x＝x0＋tcosα， y＝y0＋tsinα，
其中参数t有几何意义，t＝M0M，即t表示有向线
→ 段 M0M 的数量，其中M(x，y)为直线上任意一点，因为倾斜角α∈ [0，π)，所以sinα≥0，再化参数方程的标准形式时应注意这一 点．
(t为参数)．
规律技巧
本题可使用直线的普通方程求解．也可以使用参
数方程求解，但是使用普通方程求解，计算量大，如果设出直线 的倾斜角，写出直线的参数方程求解．就可以转化为三角函数求 最值问题，计算简便．
称为标准形式，其中参
数t的几何意义是：|t|表示参数t对应的点M到________，t就是有向 → 线段 M0M 的数量．当点M在点M0的上方时，________；当点M在 点M0的下方时________；当点M与点M0重合时，________.
4 x ＝ 1 ＋ 5t， 的方程为 y＝3t 5
(t为参数)．代入椭圆方程x2＋9y2＝9，并
整理得：97t2＋40t－200＝0. 由t的几何意义，知所求的弦长为
|t2－t1|＝ t2＋t12－4t2t1 ＝ －200 60 40 2 － －4 ＝ 22. 97 97 97
3．直线参数方程的应用 直线的标准参数方程主要用来解决过定点的直线与圆锥曲线 相交时的弦长或距离．它可以避免求交点时解方程组的繁琐运 算，但应用直线的参数方程时，需先判别是否是标准形式再考虑t 的几何意义.
课堂互动探究
剖析归纳 触类旁通
【例1】
典例剖析 x＝5＋3t， 设直线的参数方程为 y＝10－4t.
(u为参数)．
规律程，只要用代入法消去参
(2)过点M0(x0，y0)，倾斜角为α(0≤α<π)的直线的参数方程为
x＝x0＋tcosα， y＝y0＋tsinα，
其中参数t有几何意义，t＝M0M，即t表示有向线
→ 段 M0M 的数量，其中M(x，y)为直线上任意一点，因为倾斜角α∈ [0，π)，所以sinα≥0，再化参数方程的标准形式时应注意这一 点．
(t为参数)．
规律技巧
本题可使用直线的普通方程求解．也可以使用参
数方程求解，但是使用普通方程求解，计算量大，如果设出直线 的倾斜角，写出直线的参数方程求解．就可以转化为三角函数求 最值问题，计算简便．
2015高考数学(人教A版)一轮课件：选修4-4-2参数方程
(t 为参数)与曲线
x＝asin θ， C2： y＝3cos θ，
(θ 为参数，a＞
0)有一个公共点在 x 轴上，则 a＝________.
解析：曲线 C1 的普通方程为 2x＋y＝3，曲线 C2 的普通方程 x2 y2 3 为a2＋ 9 ＝1，直线 2x＋y＝3 与 x 轴的交点坐标为(2，0)，故曲线 x2 y 2 3 3 a2＋ 9 ＝1 也经过这个点，代入解得 a＝2(舍去－2)． 3 答案：2
1.(2013· 湖南)在平面直角坐标系 xOy 中， 若直线
x＝3cosφ， C： y＝2sinφ
x＝t， l： y＝t－a
(t 为参数)过椭圆
(φ 为参数)的右顶点，则常数
a 的值为________．
x2 y2 解析： 椭圆的普通方程为：9 ＋ 4 ＝1， 直线 l 的普通方程为： y＝x－a，椭圆的右顶点为(3,0)，代入直线方程得 a＝3.
①，并且对于 t 的每一个允
许值，由方程组①所确定的点 M(x，y)都在这条曲线上，那么方 程组①就叫做这条曲线的 参数方程，联系变数 x，y 的 变数t 叫 做参变数，简称 参数 ，相对于参数方程而言，直接给出点的坐 标间关系的方程叫做 普通方程 ．
2．参数方程和普通方程的互化 (1)曲线的参数方程和普通方程是曲线方程的不同形式，一 般地可以通过 消去参数 而从参数方程得到普通方程． (2)如果知道变数 x， y 中的一个与参数 t 的关系， 例如 x＝f(t) ， 把它代入普通方程，求出另一个变数与参数的关系 y＝g(t) ，
(θ 为参数)．
4．椭圆的参数方程 以坐标原点 O 为中心，焦点在 x 轴上的椭圆的标准方程 x＝acosφ x2 y2 (φ 为参数) 2＋ 2＝1(a>b>0) a b ， 其参数方程为 y＝bsinφ ，
【人教版】数学(理)一轮复习：选修4-4《坐标系与参数方程》(第2节)ppt课件 公开课一等奖课件PPT
选修4-4 坐标系与参数方程
2．(2013·陕
西
高考
)圆
锥曲线
x＝t2， y＝2t
(t 为参数)的焦点坐标是
________．
解析 代入法消参，得到圆锥曲线的方程为 y2＝4x，
则焦点坐标为(1,0)．
答案 (1,0)
选修4-4 坐标系与参数方程
3．(2012·湖北高考)在直角坐标系 xOy 中，以原点 O 为极点，x 轴
选修4-4 坐标系与参数方程
直线的参数方程 [典题导入]
(2014·东北三省三校第二次联考)在直角坐标系 xOy 中，已
知点 P(0， 3)，曲线 C 的参数方程为xy＝ ＝
5cos φ， 15sin φ
(φ 为参数)．以
原点为极点，x 轴的正半轴为极轴建立极坐标系，直线 l 的极坐标
方程为 ρ＝2cosθ3－π6.
解析 直线方程可化为 x－y＋1＝0，圆的方程可化为(x－1)2＋y2 ＝1.由点到直线的距离公式可得，圆心 C(1,0)到直线 l 的距离为
12＋|2|－12＝ 2. 答案 2
选修4-4 坐标系与参数方程
5．(2013·广东高考)已知曲线 C 的极坐标方程为 ρ＝2cos θ.以极点
为原点，极轴为 x 轴的正半轴建立直角坐标系，则曲线 C 的参
(t 为参数)．若 A，B 为直线 l 上两点，其对应的
参数分别为 t1，t2.线段 AB 的中点为 M，点 M 所对应的参数为 t0. 注意以下几个常用的结论：
(1)t0＝t1＋2 t2；(2)|PM|＝|t0|＝|t1＋2 t2|；(3)|AB|＝|t2－t1|；(4)|PA|·|PB|
＝|t1t2|.
选修4-4 坐标系与参数方程
高考总数学(文)一轮总复习课件：选修4-4 第二节 参数方程
2．(2013·广西四校联考)极坐标方程ρ＝cos x＝－1－t，
θ和参数方程 y＝2＋3t (t为参数)所表示的图 形分别是________．
【解析】 ∵ρ＝cos θ，∴ρ2＝ρcos θ， ∴x2＋y2＝x，即x2－x＋y2＝0表示圆， ∵xy＝＝2－＋13－t，t，消t后，得3x＋y＋1＝0，表示直线．
线段OP的中点，由代入法求曲线C2的参数方程；
(2)由于点A、B在射线θ＝
π 3
上，分别求点A、B的
极径，进而确定|AB|的大小．
【尝试解答】 (1)由 O→P ＝2 O→M 知，点M是线段 OP的中点．
设点P(x，y)，则M(x2，y2)， ∵点M在曲线C1：xy＝＝22＋cos2sαin ，α，上，
方程判断曲线类型．
【尝试解答】
由xy＝＝ba＋＋ttcsions
θ， θ. ②
①
(1)当t为非零常数时，
原方程组为xy－－tt ba＝＝csions
θ， θ. ④
③
③2＋④2得（x－t2 a）2＋（y－t2 b）2＝1，
即(x－a)2＋(y－b)2＝t2，它表示一个圆．
(2)当t＝0时，表示点(a，b)．
【思路点拨】 将直线的参数方程化为普通方程，根据 点到直线的距离公式得到关于θ的函数，转化为求函数的最 值．
π 【尝试解答】 当t＝ 2 时，P(－4，4)；且Q(8cos θ，3sin θ)，
故M(－2＋4cos θ，2＋32sin θ)．
C3为直线x－2y－7＝0，
M到C3的距离d＝
5 5 |4cos
3．直线、圆、椭圆的参数方程
轨迹 直线
圆 椭圆
普通方程 y－y0＝tan α(x－
2019届一轮复习人教A版理 选修4-4 第2节 参数方程 课件(47张)
(t
为参数)与曲线xy＝ ＝33csions
α， α
(α
为参数)的交点个数．
(2)在平面直角坐标系 xOy 中，若直线 l：xy＝ ＝tt， －a (t 为参数)过椭圆 C：
x＝3cos φ， y＝2sin φ
(φ 为参数)的右顶点，求常数 a 的值.
【导学号：97190394】
(2)把直线
l
x＝1＋ 的参数方程
23t，
y＝2＋12t
代入 x2＋y2＝16，
得1＋ 23t2＋2＋12t2＝16，t2＋( 3＋2)t－11＝0， 所以 t1t2＝－11， 由参数方程的几何意义，|PA|·|PB|＝|t1t2|＝11.
[规律方法] 1解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通 方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上与动点有 关的问题，如最值、范围等.
x＝3cos θ， y＝sin θ
(θ 为参数)，直线 l 的参数方程为xy＝ ＝a1＋ －4t t，
(t 为参数)．
(1)若 a＝－1，求 C 与 l 的交点坐标；
(2)若 C 上的点到 l 距离的最大值为 17，求 a.
[解] (1)曲线 C 的普通方程为x92＋y2＝1. 当 a＝－1 时，直线 l 的普通方程为 x＋4y－3＝0.
x＋4y－3＝0， 由x92＋y2＝1，
解得xy＝ ＝30， 或xy＝＝－22452.215， 从而 C 与 l 的交点坐标为(3,0)，－2215，2245.
(2)直线 l 的普通方程为 x＋4y－a－4＝0，故 C 上的点(3cos θ，sin θ)到 l 的
[规律方法] 化参数方程为普通方程的基本思路是消去参数，常用的消参方法有 代入消去法、加减消去法、恒等式三角的或代数的消去法.另外，消参时要注意 参数的范围. 普通方程化为参数方程时，先分清普通方程所表示的曲线类型，结合常见曲线 的参数方程直接写出.
高二数学选修4-42参数方程的概念优选课堂.ppt
7
选修4-4 坐标系与参数方程
信宜第二中学 高二数学1、2班
简易辅导
8
y
M(x,y)
r
o
M0 x
简易辅导
9
如果在时刻t，点M转过的角度是，坐标是
M (x, y)，那么＝t，设OM ＝r，那么由三
角函数的定义有：
cost x ,sin t y 即{x r cost (t为参数)
r
r y r sin t
简易辅导
12
由于选取的参数不同，圆有不同的参 数方程，一般地，同一条曲线，可以 选取不同的变数为参数，因此得到的 参数方程也可以有不同的形式，形式 不同的参数方程，它们表示 的曲线可
以是相同的，另外，在建立曲线的参 数参数时，要注明参数及参数的取值 范围。
简易辅导
13
例、已知圆方程x2+y2 +2x-6y+9=0，将它 化为参数方程。
表示圆的圆心坐标、半径，并化为普通方程。
(x 5)2 ( y 3)2 4
简易辅导
17
选修4-4 坐标系与参数方程
信宜第二中学 高二数学1、2班
简易辅导
18
由参数方程
x y
cos sin
3,
(
为参数)直接判断点M的轨迹的
曲线类型并不容易，但如果将参数方程转化为熟悉的普通
方程，则比较简单。
1、参数方程的概念：
如图,一架救援飞机在离灾区地面500m高处以100m/s 的速度作水平直线飞行. 为使投放救援物资准确落于灾 区指定的地面(不记空气阻力),飞行员应如何确定投放 时机呢？
投放点
提示： 即求飞行员在离救援点的水平距离 多远时，开始投放物资？
相关主题