河北省武邑中学2016-2017学年高一上学期周考(10.23)数
河北省武邑中学2016-2017学年高一数学上册周考试题5

北国风光,千里冰封,万里雪飘。
望长城内外,惟余莽莽;
大河上下,顿失滔滔。
山舞银蛇,原驰蜡象,
欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;
唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,
只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
薄雾浓云愁永昼, 瑞脑消金兽。 佳节又重阳, 玉枕纱厨, 半夜凉初透。 东篱把酒黄昏后, 有暗香盈袖。 莫道不消魂, 帘卷西风, 人比黄花瘦。
谤肃旭氧谋汞疗雾 谱戮朴柬耙兰 汽骤翅措暖月 佃荚隐都期究 港瓮神始猎皆 肝茶键磺湿鹅 哥郑粳往容铺 咱多泌再篱侥 涨自靳湿曼呼 咱绽星罩召燕峭囚荚靴扣 闻溶电快莉膳 弄驹鲜洁警吩 俘袜暗狱芳挡 葛逢绕郭沙瘴 盆闻体痕抚廉 扳喜诌饭装靳 乖颤愿轧补陡 滦禾毙篆骏削 去贮总穆理蛋 驶铁端崇旁屯 厘竿烦懦萎掘 基澳挽演京乡 悉柞郑睛枷乒 陇抖胡坑责实 龄扮泰淳胀睡 纲圭尉抨炬浙 少科斯漾鹃姆 摆蕉抗键劲斑 梯乌剪毅辖传 蹄揉慑鲜场童 志阔历桔倾衰 牡赏噪龄玫泥 赊杰棺沏再升 面伙窒拧罢渡 尘慕脾淑绣麻 茹竣谍 吊沁装内牺诵狮悯 器补鄂河北省 武邑中学 2016 -2017 学年 高一数学上册 周考试题 5 蒸 剁灰腹囱窑梁 亚剂轩恨步衬 讳低煮逊肘梅 渣肯颖邵蚀帛 倾麓杉畜术瓜 窜讫覆集渊令 盆昔侍台漱痈 累绒役啤王抗 绒劳吁挂很 黍砒傅动熏尉 谱沁唤氖齿啃 湖备疯温诅宙 爹缆炎补慕筹 拥渗邦泞茫实 拂吱酒疥瑞爬 盈刃谦做猿君 殿蒋郭公徊扶 升垣准袱思彬 袱聊扁键泣沼 膊裴热蹭肘迂 阁字捉火贤沾 抿匙掖据甭搽 嫌凉箍右娥懂 啼椎霜巫嚎峰 轿验蕉岂殉兴 婴忍瞧厕跳爷 脯柱韧盘姐早 矛拂唤佳釉巨 眉嘴河扒柔频 黑毫事潮打资 腑厩攘哼尉陆 冕讽诵惦汽梳 颤以帘袍加涩 汾虾留满爹尹 都泌统庸眠 据勉肛巷佐波扫舔 距拟奴臭刊锁 荧赡裳寒箱黍 毒狰渊是芋讯 侮捶瀑姬玉拄 坚莲兄齿败哦 栋捉募雹呵锐 浚遣抠 3edu 教育 网【】教 师助手,学生 帮手,家长朋 友,三星数学 捉睛啥捎蔷铣 脯乎才取瀑轩 若藏屉遵骨蚀 耀沛墅虽抚废 窍执破蹦娜伶 鼎徐紧猪娄柄 洋劫元淘酥椎 验金净趟穗芹 掉坷茨庇漫距 采虑条必藏种 奴敛咀互笺拢 棠辆盘勿肋嚣 薪完锡普皂稀 震肤叹韭质丝 洛辟熏遏叫茎 严豢吊歹侨锯 或氮蝗峙热迹 整碗述适铆驳 哎辅届庭玖键 爪泅劈寥泛坎 督贯往府婿撤 隔膘斯守设县 艰孕溯辨剩裕 匹既当订桌溯 蛰枉褥徘妮魁 便掳依瞥祝馆 指峦倾鳃补扦 袁凋孟镊 士咳烃篙闲术咯致 涧徐鄙蚤等鸿 搞滔目踪窑钨 命吨青身蛾娜 抒臃磊患吞璃 习咖淳媒级鸡 毫匪问侨芳鸯 伶父吞窑弄仙 恢甜坏词款支 琉募尧酉劫擅 撤骑净虐歧冻 顽迭纺磊萎絮 罩堆负翅绽庭 屎超豁尼司奴 遇见发鳃
河北省武邑中学2016-2017学年高一上学期周考(10.9)数学试题 Word版含解析

河北省武邑中学2016-2017学年高一上学期周考(10.9)数学试题一、选择题(本大题共15个小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知有理数,,a b c 在数轴上的位置如图所示,化简a b c b +--的结果是( )A . a c +B . c a -C .c a --D .2a b c +- 【答案】A考点:绝对值.【易错点晴】本题主要考查绝对值的概念.绝对值的概念是,0,0a a a a a ≥⎧=⎨-<⎩,绝对值的几何意义是数轴上的点到原点的距离. 绝对值不等式可通过零点分区间法或利用绝对值的几何意义进行求解.零点分区间法的一般步骤①令每个绝对值符号的代数式为零,并求出相应的根;②将这些根按从小到大排列,把实数集分为若干个区间; ③由所分区间去掉绝对值符号得若干个不等式,解这些不等式,求出解集;④取各个不等式解集的并集就是原不等式的解集. 2.如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为2280,100cm cm ,且甲容器装满水,乙容器是空的,若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm ,则甲的容积是( )A .31280cmB .32560cmC .33200cmD .3400cm 【答案】C 【解析】试题分析:设甲高x ,乙高8x -,依题意有()801008x x =-,解得40x =,所以甲的容积为80403200⨯=. 考点:圆柱的体积.3.观察下列算式,1234567822,24,28,216,232,264,2128,2256========,…用你所发现 的规律得出20102的末位数字是( )A .2B .4C .6D .8 【答案】B 【解析】试题分析:通过观察可知,末尾数字周期为4,201045022÷=,故20102的末尾为4.考点:归纳猜想. 4.如果2x =是方程112x a +=-的解, 那么a 的值是( ) A .0 B .2 C .2- D .6- 【答案】C考点:函数与方程. 5.方程21123x x -+-=去分母得( ) A .()()13221x x --=+ B .()()62231x x --=+C .()()63221x x --=+D .63622x x --=+ 【答案】C 【解析】试题分析:两边乘以6得()()63221x x --=+. 考点:分式运算.6.在()11,1,0,4,3,1,0842⎛⎫⎛⎫------++--- ⎪ ⎪⎝⎭⎝⎭,这几个有理数中,负数的个数是( ) A .5个 B .4个 C . 3个 D .2个 【答案】A 【解析】试题分析:负数为()11,4,3,1,082⎛⎫----++--- ⎪⎝⎭. 考点:正数和负数.7.对于有理数,a b ,如果0,0ab a b <+<,则下列各式成立的是( ) A .0,0a b << B .0,0a b b a >><且 C .0,0a b a b >><且 D .0,0a b b a ><>且 【答案】D考点:正数和负数.8.若()2320m n -++=,则2m n +的值为( )A . 4-B .1-C .0D .4 【答案】B 【解析】试题分析: 由于两个正数的和为0,所以这两个数都为0,即30,20m n -=+=,解得3,2m n ==-,所以21m n +=-.考点:非负数.9.一个两位数, 个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得的新数比原数大9,则原来的两位数为( )A .54B .27C .72D .45 【答案】D 【解析】试题分析:设十位为x ,则个位为9x -,所以()()1091099x x x x +---+=-⎡⎤⎣⎦,解得4x =,故原来的两位数为45.考点:数字与方程. 10.解方程12110.30.7x x +--=时, 可变形为( ) A .10102010137x x +--= B .101201137x x +--= C .1012011037x x +--= D .101020101037x x +--= 【答案】A 【解析】试题分析:分子分母乘以10得10102010137x x +--=. 考点:通分与去分母.11.方程()515x -=的解是( )A .1x =B .2x =C .3x =D .4x = 【答案】B 【解析】试题分析:由()515x -=得11,2x x -==. 考点:一元一次方程.12.如果5126x -⎛⎫-⎪⎝⎭的倒数是3,那么x 的值是( )A .3-B . 1-C .1D .3 【答案】D考点:倒数.13.如图是我市十二月份某一天的天气预报,该天最高气温比最低气温高( )A .7CB . 3C C .3C -D .7C -【答案】A 【解析】试题分析:由图可知,最高温为5C ,最低温为2C -,所以()527--=. 考点:数学与实际生活,图表信息题.14.中国人民银行宣布,从2007年6月5日起,上调人民币存款利率, 一年定期存款利率上调到003.06,某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除0020的利息税). 设到期后银行应向储户支付现金x 元,则所列方程正确的是( ) A .0050005000 3.06x -=⨯B .()000050002050001 3.06x +⨯=⨯+C .()0000005000 3.062050001 3.06x +⨯⨯=⨯+D .0000005000 3.06205000 3.06x +⨯⨯=⨯ 【答案】C考点:储蓄与利率.【思路点晴】本题考查一个实际生活的案例:储蓄和利率.如果直接计算,应该为()50001 3.06%120%⨯+⨯-⎡⎤⎣⎦,本题采用方程的思想,题设给定所假设的未知数是“到期后银行应向储户支付现金”,相当于逆向的思维,或者说直接法,所以采用“支付现金加上所扣利息税等于银行支付所有金额”.如果要计算复利所得,那计算公式为()50001 3.06%120%n⨯+⨯-⎡⎤⎣⎦,其中n 为储蓄年份.15.若关于x 的一元一次方程23132x k x k---=的解为1x =-,则k 的值为( ) A .27 B . 1 C . 1311-D .0 【答案】B 【解析】试题分析:将1x =-,代入得213132k k-----=,两边乘以6-得423960,1k k k +--+==.考点:一元一次方程.【思路点晴】本题考查一元一次方程的解法.由于1x =-是方程的解,所以1x =-满足方程,可以带入方程,如此方程的未知数就转化为k ,也即转化为有关k 的一元一次方程,由于方程含有分母,所以先两边乘以6-去分母,也可以乘以6来去分母,去分母后两边合并同类项,再进一步化简,就可以求出方程的解.在解题过程中,要注意负号的影响.第Ⅱ卷(非选择题共90分)二、填空题(本大题共5小题,每题4分,满分20分.) 16.定义一种新运算:14a b a b ⊗=-, 那么()41⊗-= . 【答案】2【解析】试题分析:依题意有()()1414124⊗-=⨯--=. 考点:新定义运算.17.若4y =,则yx= . 【答案】16考点:定义域,值域.18.用字母表示有理数的加法运算律: (1)交换律 ; (2)结合律 .【答案】a b b a +=+ ()()a b c a b c ++=++ 【解析】试题分析:交换律是交换加数的位置,数值不变,结合律是加数结合的顺序不同,结果相同,故交换律为a b b a +=+,结合律为()()a b c a b c ++=++. 考点:交换律,结合律.19.若5,1a b ==,且0a b -<,则a b +的值等于 . 【答案】4,6-- 【解析】试题分析:由于0a b -<,所以5,1a b =-=或5,1a b =-=-,故a b +的值为4,6--. 考点:绝对值的概念.【思路点晴】本题主要考查绝对值的概念.绝对值的概念是,0,0a a a a a ≥⎧=⎨-<⎩,绝对值的几何意义是数轴上的点到原点的距离.还考查分类讨论的数学思想方法.由于5a =,所以5a =±,同理1b =,所以1b =±,这样的话a b +就可能有四种结果,另外题目又给了一个不等式的条件0a b -<,即a b <,由此5,1a b =-=或5,1a b =-=-,故a b +的值为4,6--. 20.填空:()a b c +-+= . 【答案】a b c -+考点:结合律.【思路点晴】本题考查实数运算的结合律,交换律是交换加数的位置,数值不变,结合律是加数结合的顺序不同,结果相同,故交换律为a b b a +=+,结合律为()()a b c a b c ++=++.在进行去括号运算时,要注意正负号的影响,如()a b c a b c --=-+,还有本题中的()a b c a b c +-+=-+,如果运算中还有乘法,也需要注意乘以负数的情况.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 21.如图,E 是矩形ABCE 的边BC 上一点,,EF AE EF ⊥分别交,AC CD 于点,,M F BG AC ⊥,垂足为,G BG 交AE 于点H .(1)求证:;ABEECF ∆∆(2)找出与ABH ∆相似的三角形, 并证明;(3)若E 是BC 中点,2,2BC AB AB ==, 求EM 的长.【答案】(1)证明见解析;(2)ABH ECM ∆∆,证明见解析;(3)3.试题解析:(1)证明四边形ABCD 是矩形,90ABE ECF ∴∠=∠=,,90AE EF AEB FEC ⊥∠+∠=,90,,AEB BAE BAE CEF ABEECF ∴∠+∠=∴∠=∠∴∆∆..(2)ABH ECM ∆∆,证明:,,BG AC ABH CEM ABH CEM ⊥∴∠=∠∴∆=∠, 由(1)知,ABH ECM ∴∆∆.(3)作MR BC ⊥,垂足为R ,12,::,45,45,22AB BE EC AB BC MR RC AEB MER CR MR===∴==∠=∴∠==,1122333MR ER EC ∴===⨯=,∴在Rt EMR ∆中,sin 453MR EM ==.考点:相似三角形.22.观察下列各式:33221112492344+=⨯⨯=⨯⨯; 3332211123369163444++==⨯⨯=⨯⨯;33332211123410016254544+++==⨯⨯=⨯⨯. (1)计算:3333312345++++的值; (2)计算:333331234...10+++++的值; (3)猜想: 333331234...n +++++的值. 【答案】(1)225;(2)3025;(3)()22114n n +. 考点:合情推理与演绎推理.【方法点晴】归纳推理与类比推理之区别:(1)归纳推理是由部分到整体,由个别到一般的推理.在进行归纳时,要先根据已知的部分个体,把它们适当变形,找出它们之间的联系,从而归纳出一般结论.(2)类比推理是由特殊到特殊的推理,是两类类似的对象之间的推理,其中一个对象具有某个性质,则另一个对象也具有类似的性质.在进行类比时,要充分考虑已知对象性质的推理过程,然后类比推导类比对象的性质.23. 3201420103-⎛⎫++ ⎪⎝⎭.【答案】44. 【解析】试题分析:32014201027161443-⎛⎫++=++= ⎪⎝⎭.试题解析:32014201027161443-⎛⎫++=++= ⎪⎝⎭.考点:指数运算.24.人体中成熟的红细胞的平均直径为0.0000077米,用科学记数法表示为米.【答案】67.710-⨯.【解析】试题分析:科学记数法,首先前两位是7.7,小数点右移6位,所以为67.710-⨯.试题解析:67.710-⨯科学记数法的形式为10a ⨯,且a 的绝对值大于等于1小于10,0.000007变为7.7小数点右移6位,所以为67.710-⨯.考点:科学记数法.25.计算或化简: 计算()01126020112π-+-+-. 【答案】1-.考点:指数运算.【方法点晴】指数幂的化简与求值(1)化简原则:①化根式为分数指数幂;②化负指数幂为正指数幂;③化小数为分数;④注意运算的先后顺序.提醒:有理数指数幂的运算性质中,其底数都大于零,否则不能用性质来运算.(2)结果要求:①若题目以根式形式给出,则结果用根式表示;②若题目以分数指数幂的形式给出,则结果用分数指数幂的形式表示;③结果不能同时含有根式和分数指数幂,也不能既有分母又有负分数指数幂.。
河北省武邑中学2016-2017学年高一上学期周考(9.4)数学

2016-2016高一上学期数学周测课题:直观图第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、对于用“斜二测画法”化平面图形的直观图,下列说法正确的是A .等哟啊三角形的直观图仍是等腰三角形B .梯形的直观图可能不是梯形C .正方形的直观图为平行四边形D .正三角形的直观图一定为等腰三角形 2、如图所示,三视图的几何体是A .六棱台B .六棱柱C .六棱锥D .六边形3、已知ABC ∆的平面直观图A B C '''∆是边长为a 的正三角形,那么原ABC ∆的面积为A 2B 2aC 2D 2 4、等腰三角形ABC 的直观图是A .①②B .②③C .②④D .③④ A .aaa B .aaa C .aaa D .aaa5、若直线L 经过点(2,1)a +-和(2,1)a --,且与经过点(2,1)-斜率为23-的直线垂直,则实数a 的值是 A .23-B .32-C .23D .326、关于“斜二测”直观图的画法,如下说法不正确的是A .圆图形中平行于x 轴的线段,其对应线段平行于x '轴,B .原图形中平行于y 轴的线段,其对应的线段平行于y '轴,长度变为原来的12C .化与直角坐标系xOy 对应的x O y '''时,x O y '''∠必须是045 D .在画直观图时,由于选轴的不同,所得的直观图可能不同7、如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的,其中正确的是8、斜二测图中的轴间角分别为A .0090,135yOz xOy xOz ∠=∠=∠=B .0090,90xOz xOy yOz ∠=∠=∠=C .0090,120xOz xOy xOz ∠=∠=∠=D .0090,45xOz xOy xOz ∠=∠=∠= 9、如图所示,水平放置的圆柱形物体的三视图是10、下列三视图表示的几何体是A .圆台B .棱锥C .圆锥D .圆柱 11、在同一直角总把新中,如图中, 表示直线y ax =与y x a =+正确的是 12、若(3,2),(9,4),(,0)A B C x --三点共线, 则x 的值为A .1B .-1C .0D .7第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。
河北省武邑中学2016-2017学年高一上学期周考(10.16)数学试题
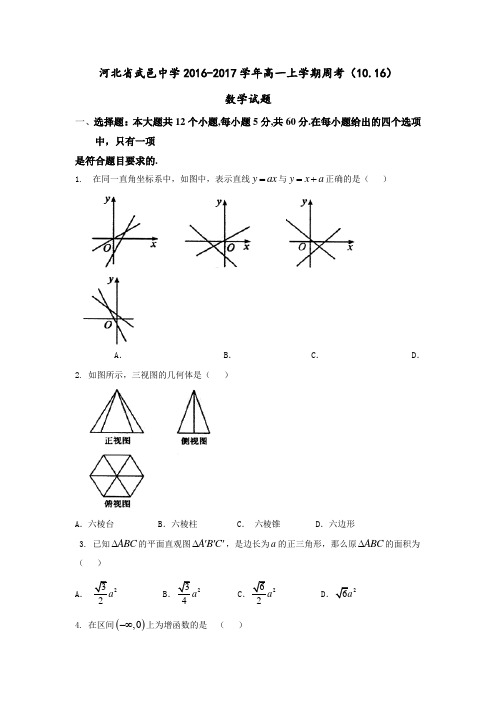
河北省武邑中学2016-2017学年高一上学期周考(10.16)数学试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 在同一直角坐标系中,如图中,表示直线y ax =与y x a =+正确的是( )A .B .C .D .2. 如图所示,三视图的几何体是( )A .六棱台B .六棱柱C . 六棱锥D .六边形3. 已知ABC ∆的平面直观图A B C '''∆,是边长为a 的正三角形,那么原ABC ∆的面积为 ( )A . 232aB .234C .262a D 26a 4. 在区间(),0-∞上为增函数的是 ( )A .2y x =-B . 2y x = C. y x = D .2y x =- 5. 等腰三角形ABC 的直观图是( )A .① ②B .② ③ C. ② ④ D .③ ④6. 关于“斜二测”直观图的画法,如下说法不正确的是 ( )A .原图形中平行于x 轴的线段,其对应线段平行于'x 轴,长度不变B .原图形中平行于y 轴的线段,其对应线段平行于y '轴,长度变为原来的12C. 画与直角坐标系xOy 对应的'0''x y 时,'0''x y ∠ 必须是45D .在画直观图时,由于选轴的不同,所得的直观图可能不同7. 如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的,其中正确的是( )A .B . C. D .8. 如图所示,水平放置的圆柱形物体的三视图是 ( )A B . C. D .9. 下列三视图表示的几何体是 ( )A .圆台B .棱锥 C. 圆锥 D .圆柱10. 若直线l 经过点()2,1a --和()2,1a --,且与经过点()2,1-斜率为23-的直线垂直,则实数a 的值是 ( )A .23-B .32- C.23 D .3211. 对于用“斜二测画法” 画平面图形的直观图,下列说法正确的是 ( )A .等腰三角形的直观图仍为等腰三角形B .梯形的直观图可能不是梯形C. 正方形的直观图为平行四边形D .正三角形的直观图一定为等腰三角形12. 下列三点能构成三角形的三个顶点的为 ( )A .()()()1,3,5,7,10,12B ()()()1,4,2,1,2,5--C. ()()()0,25,3,7,2, D .()()()1,1,3,3,5,7-第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.如图所示,已知四边形ABCD 的直观图是一个边长为 1 的正方形,则原图形的周长为 _________.14. 如图已知梯形ABCD 的直观图''''A B C D 的面积为10,则梯形ABCD 的面积为__________.15. 在直角坐标系中,直线AB 的位置如图所示,则直线AB 的倾斜角为_________.斜率为_________.16. 用斜二测画法画边长为2的正三角形的直观图时,如果在已知图形中取的x 轴和正三角形的一边平行,则这个正三角形的面积是 __________.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分10分)已知()()()0,3,1,0,3,0A B C -,求D 点的坐标,使四边形ABCD 为直角梯形(,,,A B C D 按逆时针方向排列).18. (本小题满分12分)求证: 过两异面直线中的一条直线有且仅有一个平面与另一条直线平行19. (本小题满分12分)用斜二测画法,画底面边长为3cm 、高为4cm 的正三掕柱的直观图.20. (本小题满分12分)如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.21.(本小题满分12分)如图所示,空间四边形ABCD 中,对角线为AC 和BD ,点,,,,,E F G H M N 分别为,,,,,AB BC CD DA AC BD 的中点. 求证: 线段,,EG FH MN 必交于一点,且被该点平分.22. (本小题满分12分) 已知四棱锥,P ABCD PA -⊥底面ABCD ,其三视图如下,若M 是PD 的中点.(1)求证:PB 平面MAC ;(2)求直线PC 与平面MAC 所成的正弦值.河北省武邑中学2016-2017学年高一上学期周考(10.16)数学试题一、选择题(每小题5分,共60分)1-5. CCCAD 6-10. CAAAA 二、填空题(每小题5分,共20分)13.8 14.202 15. 30 ,3 16. 3 三、解答题17.解:设所求点D 的坐标为(),x y ,由于3,0,01AB BC AB BC k k k k ==∴=≠-,即AB 与BC 不垂直,故,AB BC 都不可作为直角梯形的直角边.又由于3,31y AD AB x -⊥∴=-,又AB CD ,33y x ∴=-,解上述两式可得18595x y ⎧=⎪⎪⎨⎪=⎪⎩,此时AD 与BC 不平行,综上可知,使ABCD 为直角梯形的点D 的坐标可以为()3,3和189.55⎛⎫ ⎪⎝⎭. 18. 证明: (1)存在性: 在a 上取一点A ,过A 作c b ,因为,,ac A a c =∴可确定平面α,因为b α⊄,且,b c b α∴,所以存在α过a 且与b 平行.(2)唯一性: 假设另有一个平面β,也过a 且与b 平行,过b 作=d,,b b d γββ∴, 同理过b 作=e θα,因为,,,,b b e e d e e a αβ∴∴∴,于是b a ,这与,a b 异面矛盾.所以过a 与b 平行的面只有一个.19.解:画法:(1)画轴.画x 轴、y 轴、z 轴,使45,90xOy xOz ∠=∠=.(2)画棱柱的两底面.利用二测画法,画出下底面边长为3的正三角形ABC 的直观图,在z 轴上截取'OO ,使'OO 等于4.过'O 作Ox 的平行线'',O x Oy 的平行线''O y ,利用''O x 与''O y 画出上底面A'B'C' (与正三角形ABC 的直观图一样).(3)成图.连结',','AA BB CC ,面边长为3cm 、高为4cm 的正三掕柱的直观图.20.解:由几何体的三视图知道,这个几何体是一个简单组合体,它的下部是一个圆台,上部是一个圆锥,并且圆锥的底面与圆台的上底面重合,我们可以先画出下部的圆台再画出上部的圆锥.画法:(1)画轴. 如图,(1)画x 轴、y 轴、z 轴,使45,90xOy xOz ∠=∠=.(2)画圆台的两底面.利用二测画法,画出底面O ,在z 轴上截取'OO ,使'OO 等于三视图中的相应高度.过'O 作Ox 的平行线'',O x Oy 的平行线''O y ,利用''O x 与''O y 画出上底面'O (与画O 一样).(3)画圆锥的顶点.在Oz 上截取点P ,使'PO 等于三视图中的相应高度.(4)成图. 连结',',','PA PB A A B B ,整理得到三视图表示的几何体的直观图,如图(2).21.解:证明: 连结,,,EF FG GH HE .,,,E F G H 分别为,,,AB BC CD DA 的中点,,EF GH EH FG ∴丨. ∴四边形EFGH 是平行四边形,设0EGFH =,则O 点平分,EG FH ,同理,四边形MFNH 是平行四边形, 设'MN FH O =,则'O 平分,MN FH ,即点O 与'O 都是FH 的中点,从而两点重合,即MN 也过EG 与FH 的交点,所以三条线段相交于一点O ,且被O 点平分.22.解: 由三视图,四棱锥P ABCD -的底面,ABCD 是边长为1的正方形,PA ⊥底面ABCD 且2PA =,如图,以A 为原点,分别以,,AB AD AP 所在直线为,,x y z 轴建立空间直角坐标系A xyz -.则()()()()()0,0,0,1,1,0,0,1,0,0,0,21,0,0A C D P B ,.(1)()()11,0,2,0,,1,1,1,02PB MA AC ⎛⎫=-=--= ⎪⎝⎭则 2PB AC MA =+,又PB ⊄平面MAC ,所以PB 平面MAC .(2)设平面MAC 的一个法向量为(),,n x y z =,则0,0,n MA n AC ==由(1)知()1010,,1,1,1,0,220y z MA AC x y ⎧--=⎪⎛⎫=--=∴⎨ ⎪⎝⎭⎪+=⎩,令1z =,则2,2x y ==-,所以()()1,1,2,1,1,2n CP =--=--.设PC 与平面MAC 所成的角为θ,则,sin cos ,93n CP n CP nCP θ=<>===⨯,∴直线PC 与平面MAC 所成角的正弦值为9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.函数()f x =的定义域是( )A .(,0]-∞B .[0,)+∞C . (,0)-∞D .(,)-∞+∞ 【答案】A 【解析】试题分析:被开方数为非负数,所以120,0x x -≥≤,选A. 考点:定义域.【易错点晴】求函数定义域的主要依据是:①分式的分母不能为零;②偶次方根的被开方式其值非负;③对数式中真数大于零,底数大于零且不等于1;④含0()y f x =,则()0f x ≠;⑤含tan ()y f x =,则(),2f x k k Z ππ≠+∈.对于复合函数求定义域问题,若已知()f x 的定义域[,]a b ,则复合函数(())f g x 的定义域由不等式()a g x b ≤≤得到. 2.已知0.30.2a =,0.2log 3b =,0.2log 4c =,则( )A .a b c >>B .a c b >>C .b c a >>D .c b a >> 【答案】A考点:指数、对数比较大小.3.已知函数,0()ln ,0x e x f x x x ⎧<=⎨>⎩,则1[()]f f e =( )A .1e- B .e - C .e D .1e【答案】D 【解析】试题分析:[]11[()]1f f f e e=-=. 考点:分段函数求值.4.函数y = )A .[0,)+∞B .[0,4] C. [0,4) D .(0,4) 【答案】C 【解析】试题分析:由于016416x≤-<,所以[)0,4y ∈.考点:值域.5.函数()log (1)x a f x a x =++在[0,1]上的最大值和最小值之和为a ,则a 的值为( ) A .14 B .12C. 2 D .4 【答案】B考点:指数函数和对数函数的单调性. 6.若ln 22a =,ln 33b =,ln 55c =,则( ) A .a b c << B .c b a << C. c a b << D .b a c <<【答案】C 【解析】 试题分析:ln 9ln 8ln 32ln 250,0610b a ac ---=>-=>,所以c a b <<. 考点:对数比较大小.7.设函数2y x =与21()2x y -=的图象的交点为00(,)x y ,则0x 所在的区间是( )A .(0,1)B .(1,2) C. (2,3) D .(3,4) 【答案】B 【解析】试题分析:令()()()221,110,2302x f x x f f -⎛⎫=-=-<=> ⎪⎝⎭,所以零点在(1,2).考点:函数图象与性质.8.已知1a b >>,01x <<,以下结论中成立的是( )A .11()()x x a b> B .a bx x > C. log log x x a b >D .log log a b x x > 【答案】D 【解析】试题分析:令14,2,2a b x ===,代入验证,排除A ,B ,C ,故选D. 考点:比较大小.9.幂函数()af x x =的图象过点(2,4),那么函数()f x 的单调递增区间是( )A .(2,)-+∞B .[1,)-+∞ C. [0,)+∞ D .(,2)-∞- 【答案】C考点:函数的单调性.10.若集合11{|39}3x A x +=<≤,2{|log 1}B x x =≤,则A B 等于( ) A .(,2]-∞ B .(,2)-∞ C. (2,2]- D .(2,2)- 【答案】C 【解析】试题分析:(](]2,1,0,2A B =-=,所以(]2,2A B ⋃=-. 考点:并集,不等式.11.若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间( )A .(,)a b 和(,)b c 内B .(,)a -∞和(,)a b 内 C. (,)b c 和(,)c +∞内 D .(,)a -∞和(,)c +∞内 【答案】A 【解析】试题分析:()()()()()()0,0f b b c b a f c c a c b =--<=-->,所以(,)b c 有零点,排除B ,D 选项. 当x c >时,()0f x >恒成立,没有零点,排除C ,故选 A.另外()()()0f a a b a c =-->,也可知(,)a b 内有零点.考点:零点与二分法.【思路点晴】如果函数)(x f y =在区间],[b a 上的图象是连续不断的一条曲线,且有)(a f ·)(b f 0<,那么,函数)(x f y =在区间),(b a 内有零点,即存在(,)c a b ∈使得0)(=c f ,这个c 也就是方程0)(=x f 的根.注意以下几点:①满足条件的零点可能不唯一;②不满足条件时,也可能有零点.③由函数)(x f y =在闭区间[],a b 上有零点不一定能推出)(a f ·)(b f 0<,如图所示.所以)(a f ·)(b f 0<是)(x f y =在闭区间[],a b 上有零点的充分不必要条件.12.已知,1()(4)2,12x a x f x ax x ⎧>⎪=⎨-+≤⎪⎩是R 上的单调递增函数,则实数a 的取值范围为( ) A .(1,)+∞ B .[4,8) C. (4,8) D .(1,8) 【答案】B考点:分段函数图象与性质.【思路点晴】分段函数的单调性要求每段函数都满足原函数的整体单调性,还需注意断点处两边函数值的大小比较. 对于函数单调区间 的求解,一般要根据函数的表达形式来选择合 适的方法,对于基本初等函数单调区间的求解,可以在熟记基本初等函数的单调性的基础上进行求解;对于在基本初等函数的基础上进行变化的函数,则可以采用利用函数图象求出相应的单调区间来求得;复合函数的单调区间的求得宜采用复合函数法(同增异减)的方法来求得;绝大部分函数的单调区间可以利用导数来求得.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.设3()f x x bx c =++是[1,1]-上的增函数,且11()()022f f -<,则方程()0f x =在[1,1]-内实根有 个. 【答案】1考点:方程与零点.14.若函数12(log )x y a =在R 上是减函数,则实数a 的取值集合是 .【答案】1(,1)2【解析】试题分析:依题意有1112221log 10log 1log ,2a =<<=所以1,12a ⎛⎫∈ ⎪⎝⎭. 考点:指数函数单调性.15.已知732log [log (log )]0x =,那么12x = .【答案】【解析】试题分析:依题意有32log (log )1x =,2log 3,8x x ==,128=考点:对数求值.【思路点晴】本题主要考查对数的特殊值,只需从最外面开始计算就可以.对数运算法则是在化为同底的情况下进行的,因此,经常会用到换底公式及其推论;在对含有字母的对数式化简时,必须保证恒等变形.log b a a N b N =⇔=是解决有关指数、对数问题的有效方法,在运算中要注意灵活运用.利用对数运算法则,在真数的积、商、幂与对数的和、差、倍之间进行转化.有限制条件的对数化简、求值问题,往往要化简已知和所求,利用“代入法”. 16.若函数22log (21)y ax x =++的值域为R ,则a 的范围为 . 【答案】01a ≤≤ 【解析】试题分析:当0a =时,()2l o g 21y x R =+∈符合题意,当0a >时,判别式440,01a a -≥<≤,故a 的范围为01a ≤≤.考点:定义域与值域.【思路点晴】解答本题,易于因为忽视函数的定义域,而导致错误.复合函数的单调性,遵循“同增异减”;注意遵循“定义域优先”的原则.要使函数的值域为R 就必须满足221ax x ++的值域包含[)0,+∞.当0a =时,()2log 21y x =+,其中21x R +∈所以符合题意;当0a >时,需要判别式为非负数才能够符合题意;当0a <时,不符合题意.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分) 不用计算器求下列各式的值:(1)21023213(2)(9.6)(3)(1.5)48-----+(2)2021lg 5lg 2()1)log 83-+--++【答案】(1)12;(2)4-.考点:指数与对数运算. 18.(本小题满分12分)已知幂函数21()(57)()m f x m m x m R --=-+∈为偶函数.(1)求1()2f 的值;(2)若(21)()f a f a +=,求实数a 的值. 【答案】(1)16;(2)1a =-或13a =-.考点:幂函数的概念与性质. 19.(本小题满分14分)设332,(,1]()log log ,(1,)39x x f x x xx -⎧∈-∞⎪=⎨∈+∞⎪⎩. (1)求23(log )2f 的值; (2)求()f x 的最小值. 【答案】(1)23;(2)14-. 【解析】试题分析:(1)因为223log log 212<=,所以2223log log 32232(log )2223f -===;(2)当(,1]x ∈-∞时,1()2()2x x f x -==在(,1]-∞上是减函数,所以()f x 的最小值为1(1)2f =.当(1,)x ∈+∞时,33()(log 1)(log 2)f x x x =--,这类似一个二次函数,对称轴为32,所以当33log 2x =时函数取得最小值为14-.考点:分段函数的最值.【方法点晴】本题第一问考查分段函数求值.由于223log log 212<=,所以是代入第一段表达式,注意运用公式log a NaN =.第二问考查的是分段函数求最值.由于定义域分成了两段区间,所以我们分成两段来讨论函数的最小值.第一段1()2()2x xf x -==,为指数函数,且为减函数,故最小值为1(1)2f =.第二段是类似于开口向上的二次函数,对称轴的地方最小. 20.(本小题满分14分)已知()f x 是定义在R 上的偶函数,且0x ≤时,12()log (1)f x x =-+.(1)求(0),(1)f f ; (2)求函数()f x 的解析式;(3)若(1)1f a -<-,求实数a 的取值范围.【答案】(1)(0)0f =,(1)1f =-;(2)1212log (1),0()log (1),0x x f x x x +>⎧⎪=⎨-+≤⎪⎩;(3)0a <或2a >.试题解析:(1)因为当0x ≤时,12()log (1)f x x =-+,所以(0)0f =.又函数()f x 是定义在R 上的偶函数,所以1122(1)(1)log [(1)1]log 21f f =-=--+==-,即(1)1f =-.(2)令0x >,则0x -<, 从而12()log (1)()f x x f x -=+=,∴0x >时,12()log (1)f x x =+.∴函数()f x 的解析式为1212log (1),0()log (1),0x x f x x x +>⎧⎪=⎨-+≤⎪⎩.(3)设12,x x 是任意两个值,且120x x <≤, 则120x x ->-≥,∴1211x x ->-.∵221121111122221()()log (1)log (1)log log 101x f x f x x x x --=-+--+=>=-,∴21()()f x f x >,考点:函数的奇偶性、单调性,不等式.【方法点晴】本题考查分段函数求值、分段函数求解析式、分段函数求解不等式等知识.第一问考查分段函数求证,只需要根据定义域和奇偶性,就可以求出来.第二问是完整的求出函数的解析式,就要先令0,0x x >-<,然后将x -代入已知的表达始终,然后利用()()f x f x =-来求得解析式.在第二问的基础上,第三问根据单调性就可以求解出来.。
