定比分点公式
线段中点坐标公式和定比分点坐标公式
(2)定比分点坐标公式
设定比分点C的坐标为(x, y),由 AC
( x x1 , y y1 ) ( x2 x,
x x1 ( x2 x)
即
λ CB
得
由此得出
{
{
所以
y y1 ( y2 y) x1 x2 y1 y2 x , y ( 1) 1 1
评注:1、点C在线段AB上,则定比 此时称分点C是内分点
0
y
,
B C .
A
e2
o
e1
x
2、线段的定比分点坐标公式
x1 x2 y1 y2 x , y ( 1) 1 1
评注:1、点C在线段AB上,则定比 此时称分点C是内分点
0
C.
y
,
B
A
.
e2
o
e1
ቤተ መጻሕፍቲ ባይዱ
x
2、点C在线段BA(或AB)的延长线上, 则定比
y 3 1 4 2 1 1 2
x1 x2 y1 y2 x , y ( 1) 1 1
64 2 2 1 3
1 2 (- , ) 因此分点C的坐标为 3 3
2、线段的定比分点坐标公式
x1 x2 y1 y2 x , y ( 1) 1 1
.
e2
o
e1
x
思考:
如图,已知线段AB的两个端点A,B的坐标 分别为, ( x1 , y1 ) ( x2 , y2 ) ,设C是线段AB上的一点, 使得 | AC | 1 | CB | 试问:点C的坐标是多少? 2 y .B A
C.
.
定比分点的坐标计算方法

定比分点的坐标计算方法在数学中,当我们需要将一条线段分成若干个等比或不等比的部分时,我们可以使用定比分点的坐标计算方法。
这种方法通过使用比例关系,根据已知条件计算出各个分点的坐标。
本文将介绍定比分点的坐标计算方法及其应用场景。
一、等比分点的坐标计算方法等比分点是指将一条线段按照等比的比例划分为若干个部分。
设有一条线段AB,需要将其分成n段,并且每一段的长度与前一段长度的比例都相等。
设线段AB的起点坐标为(Ax, Ay),终点坐标为(Bx, By)。
假设第一个分点的坐标为P1(x1, y1),则P1与A的距离为d1,与B 的距离为d2。
根据等比关系,我们可以得到以下比例公式:d1 / d2 = (P1A / AP2) * (P2B / BP1) * ... * (Pn-1B / BPn) = k^n其中,k表示公比。
根据已知条件,我们可以推导出以下计算公式:d1 = (k / (k+1)) * ABd2 = AB - d1x1 = Ax + (d1 / AB) * (Bx - Ax)y1 = Ay + (d1 / AB) * (By - Ay)根据上述公式,我们可以递归地计算出其他分点的坐标。
二、不等比分点的坐标计算方法不等比分点是指将一条线段按照不等比的比例划分为若干个部分。
设有一条线段AB,需要将其分成n段,并且每一段的长度与前一段长度的比例都不相等。
同样地,设线段AB的起点坐标为(Ax, Ay),终点坐标为(Bx, By)。
对于不等比分点,我们无法使用上述的等比分点的坐标计算方法。
在这种情况下,我们可以将线段AB按照比例分成若干段,然后使用线性插值的方法计算出分点的坐标。
设第一个分点的坐标为P1(x1, y1),其与A的距离为d1,与B的距离为d2。
根据已知条件,可以计算出每一段的长度dl:dl = (C1 * d2 + C2 * d1) / (C1 + C2)其中,C1和C2分别表示前一段和后一段的比例(C1 + C2 = 1)。
定比分点公式

定比分点公式
定比分点坐标介绍
定比分点坐标公式是数学中一种重要的工具,如果应用得当,常常可以巧妙地解决函数、等差数列、解析几何和不等式中的一些数学难题。
和两点间的中点公式一样,定比分点公式是一种给出中点坐标的公式。
定比分点应该理解为:“固定比例分割点的坐标公式”,中点公式是他的一种特殊情况。
我们可以用它寻找三角形的内心、质心和外心。
他是在一个线段中按照固定比例将线段分为两部分。
定比分点坐标公式是:
x=(x1+kx2)/(1+k)
设x轴上点A(x1),B(x2),坐标分别为x1,x2,点M(x)分AB为定比k:AM:MB=K
则(x-x1):(x2-x)=k
去分母得:x-x1=kx2-kx
所以x(1+k)=x1+kx2
所以x=(x1+kx2)/(1+k)
这就是定比分点的坐标公式
类似的方法可以推导平面上的定比分点的坐标公式
设A(X1,Y1),B(X2,Y2),点M(X,Y)分AB为定比k:AM:MB=K
则有公式x=(x1+kx2)/(1+k) , y=(y1+ky2)/(1+k)。
定比分点公式的运用及类比推理

1 x2 P2 ( 2
+0) ,且
P1 P PP2
,
则 f(x)=
第2页共5页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
定比分点公式参数_妙用

aq a +λ = ap+q= p ∴ 1+λ
即 ap+q=0。
q 1p
=0,
三、 求函数解析式 例3 已知二次函数 f 满足条件 : ( x)
(1)f ( -1) =0,
2
(2)对一切 x∈R ,恒有 x≤f ( x) ≤ 1+x 。
2
求f 的解析式。 ( x)
2 2
2 2 %& 上三点P1,P,P2的横坐标。 ,由定比分点公式可知 P分 P1P2所成比为 λ
2
解
由 x∈R 及 x≤f , 1+x 分别对应 x轴 ( x) ( x) ≤ 1+x ,可设数 x,f
x+λ1+x 2 。 f ( x) = 1+λ
2
-1) -1+λ1+( 2 。 f ( -1) = ∴ 1+λ ∵ f ( -1) =0,
52
解题技巧
伴你走进课堂
1+1 -1+λ 2 ∴ =0,λ =1。 1+λ
又 c=t a+( 1-t ) b, d=( 1-t ) a+t b, 比较可知 t =
1+2λ , 2( 1+λ ) 1+2λ 满足题设和结论。 2( 1+λ )
即存在实数 t ,且 t =
又 Q 在线段 M P上 (不包括 M 、 >0。 P),则 λ 由t =
2t -1 2t -1 1+2λ ,得 λ ,即 >0。 = ) ) ) 2( 1+λ 2( 1-t 2( 1-t 1 <t <1。 ’ 2
2
x+ 1+x 1 1 1 2 ∴ f ( x) = = x2+ x+ , 1+1 4 2 4
定比分点的向量公式及应用

定比分点的向量公式及应用向量是在数学中广泛应用的一种重要概念。
在向量中,可以定义加法、减法和数量乘法等运算,这些运算规则以及向量的模、方向等性质,使得向量在数学、物理和工程等领域的应用中具有重要的意义。
在计算机科学和计算机图形学中,向量被广泛用于表示三维空间中的点、方向和位移等概念。
这些向量通常表示为[x,y,z],其中x、y和z分别表示在三个坐标轴上的分量。
定比分点的向量公式可以用于计算两个点之间的中点、分点以及线段的长度。
假设有两个点A和B,它们的坐标分别为A(x1,y1,z1)和B(x2,y2,z2),我们可以使用如下的公式来计算两个点之间的中点:M=(A+B)/2其中M是点A和点B之间的中点,"+"表示向量的加法运算,"/"表示向量与标量的除法运算。
通过这个公式,我们可以计算出两个点之间的中点的坐标。
在计算两个点之间的分点时,可以使用类似的方法。
假设有一个分点P,它位于点A和点B之间的t比例处,我们可以使用如下的公式来计算分点的坐标:P=A+t*(B-A)其中t是一个介于0和1之间的比例值。
当t等于0时,分点P的坐标就是点A的坐标;当t等于1时,分点P的坐标就是点B的坐标。
通过改变t的值,我们可以在点A和点B之间找到任意位置的分点。
除了计算中点和分点之外,向量的长度也是一个重要的概念。
在三维空间中,向量的长度可以通过计算其模来获得。
一个向量的模定义为其各个分量的平方和的平方根。
对于一个三维向量V=[x,y,z],其模的计算公式如下:V, = sqrt(x^2 + y^2 + z^2)通过计算向量的模,我们可以获得向量的长度信息。
定比分点的向量公式在计算机图形学中有许多应用。
例如,在三维建模中,我们经常需要计算物体的表面上的点的位置和属性。
通过定比分点的向量公式,我们可以在物体的两个顶点之间找到任意位置的点,从而进行物体的细分或者其他形变操作。
此外,向量的线性插值也是一个重要的应用。
高三数学线段的定比分点

高三备课组
一、基础知识
1、 线段的定比分点
(1)定义
设P1,P2是直线L上的两点,点P是L上不同 于P1,P2的任意一点,则存在一个实数 , P 使p1 p pp , 所 2 叫做点P分有向线段 1P 2 成的比。
0 ;当点P在线 当点P在线段 P 上时, 1P 2 <0 段 P1 P2 或 P2 P1 的延长线上时,
(2)定比分点的向量表达式:
点P分有向线段 P 所成的比是 ,则 1P 2 1 OP OP1 OP2 1 1 (O为平面内任意点)
(3)定比分点的坐标形式
x1 x 2 x 1 y y 2 y 1 1
,
(4)中点坐标公式
当 =1时,分点P为线段的中点,即有
练习:
若直线x+2y+m=0,按向量a 1,2平移后与圆C:
x 2 y 2 2x 4 y 0
相切
则实数m的值等于
例5.是否存在这样的平移,使抛物线: y x 2 平移后 过原点,且平移后的抛物线的顶点和它与 x 轴的两个 交点构成的三角形面积为 1 ,若不存在,说明理由;若 存在,求出函数的解析式。 例4.设函数
x1 x y y 1 x2 2 y2 2
ABC 的重心坐标公式: (5)
x A x B xC x 3 y A y B yC y 3
2、平移
(1)图形平移的定义
设F是坐标平面内的一个图形,将图上的所有 点按照同一方向移动同样长度,得到图形 F’ , 我们把这一过程叫做图形的平移。
A(4,1), B(3,4), C (1,2) , BD 是角 ABC 的平分 线,求点D的坐标及BD的长。
定比分点

[编辑本段]定比分点定义对于轴上两个已给的点P,O,它们的坐标分别为X1,X2,在轴上有一点L,可以使PL/LO等于已知常数λ。
即PL/LO=λ,我们就把L叫做有向线段PO的定比分点。
若设L的坐标为X,则X=(X1+λX2)/(1+λ),Y=(Y1+λY 2)/(1+λ)[编辑本段]定比分点相关概念1.线段的定比分点及λ:P1,P2是直线L上的两点,P是L上不同于P1,P2的任一点,存在实数λ,使向量P1P=λ向量PP2,λ叫做点P分P1P2所成的比。
P点位置与λ的关系以P1P2中点为原点,x轴表示P相对P1 P2的位置,y轴表示λ的取值根据右图,从左往右看,λ 的取值有以下五种情况①P在P1左边(P在向量P1P2反向延长线上),λ∈(-1,0)②P与P1重合,λ=0③P在P1与P2之间(P在向量P1P2上),λ∈(0,+∞)*i. P在P1与原点之间,即P1P<PP2,λ∈(0,1)*ii. P与原点重合,即P1P=PP2,λ=1*iii. P在原点与P2之间,即P1P>PP2,λ∈(1,+∞)④P与P2重合,λ∈Φ⑤P在P2右边(P在向量P1P2正向延长线上),λ∈(-∞,-1)2 定比分点公式:若设点P1(x1,y1),P2(x2,y2),λ为实数,且向量P1P=λ向量PP2即P1P=λPP2由向量的坐标运算,得P1P=(x-x1,y-y1),PP2=(x2-x, y2-y)∴(x-x1,y-y1)=λ(x2-x, y2-y)∴定比分点公式为,λ=(x-x1)/(x2-x)λ=(y-y1)/(y2-y)3.定比分点坐标公式:∴λ=(x-x1)/(x2-x)∴λx2-λx=x-x1λx2+x1=λx+x得,x=(λx2+x1)/(λ+1)同理,y=(λy2+y1)/(λ+1)注:当λ=1时,即中点坐标公式。
定比分点定理目录[隐藏]证明定比分点补充公式补充公式证明已知线段PQ上有一点T,且PT/PQ=a,AB是与PQ无交点的一条线段,则S(AT B)=a*S(ABQ)+(1-a)*S(ABP)其中S(AQB)表示AQB的面积,以此类推。
高三数学线段的定比分点

《我爱这土地》中写“为什么我的眼里常含泪水”,上文结尾也写到了“流泪”,简要分析“眼泪”背后两位作者思想感情的异同。 3、文中的语言富有表现力,请结合句中加点的词语作简要分析。 一阵沙尘扑面而来,豆大的雨点砸了下来,劈头劈脸,欢笑的人群直往外冲。 ? 4、文
章第④段的“对我来说,去圆明园是一种凭吊,一种拜谒,甚至是一种提醒。”简要说说作者要“凭吊、拜谒”什么? “提醒”什么呢? 5、简要分析第⑤段中划线句在文中有什么作用? ? 6、请你为圆明园遗址准备一条宣传语,要能揭示遗址给人的警示。(不超过20字,至少用一种
修辞手法) ? 参考答案: 1、A 理由:用拟人手法,容易引起读者的注意;更能表达作者对造成这种现象的悲痛心情(主题)。 2、相同点:都有对祖国的深切的爱。 不同点:艾青是目睹山河破碎、人民涂炭的现实,心中的痛苦。 本文作者是因为部分国人不知铭记历史而十分伤心、
难过。 3、“扑”表现风来得猛,“砸”表现雨下得大,这样写更能突出作者对人们不理解废墟价值的一种愤怒与悲哀。(言之有理,可酌情给分) 4、凭吊、拜谒无数在此长眠的死难者(中华民族屈辱的历史) 提醒自己不忘历史的耻辱,不能让悲剧重演。(意同即可) 5、一方面突
(5)ABC 的重心坐标公式:
x
y
xA yA
xB
3 yB
xC yC
3
2、平移
(1)图形平移的定义
设F是坐标平面内的一个图形,将图上的所有 点按照同一方向移动同样长度,得到图形F’, 我们把这一过程叫做图形的平移。
(2)平移公式
设P(x,y)是图形F上任意一点,它在平移后图形上的
起来,用极低的声音问:“老师,我可以带馒头吗?”一阵其实并没有恶意的笑声刺激着女孩,她的脸通红通红的,低着头默默地坐下,眼泪沿着脸颊流了下来。李老师走过去,抚摸着她的头说:“你放心,可以带馒头的。” ③出发的前一天,女孩子拿着饭票在学校食堂买了六个馒头,
向量专题整理

1向量专题一、定比分点的向量形式及运用定理:(定比分点公式的向量形式)设点P 分21P P 的比为l (即21PP P P l =,1-¹l ),Q 为平面上的任意一点,则.11121QP QP QP ll l +++=证明:,21PP P P l = (),21QP QP QP QP -=-\l即(),121QP QP QP l l +=+即.11121QP QP QP l l l+++=推论1:设点P 为OAB D 的边AB 上的点,且,,n PB m AP ==则.OB nm m OA nm n OP +++=推论2:设点P 为OAB D 的边AB 的中点,则().21OB OA OP +=推论3:OAB D 中,点P 在直线AB 上的充要条件是:存在实数t ,使()OB t OA t OP -+=1成立。
推论4: (定比分点公式)在直角坐标平面中,设()()(),,,,,,222111y x P y x P y x P 且点P 分21P P 的比为l (其中1-¹l ),则.1,11121ll l l ++=++=y y y xx x例1 如图,在ABC D 中,E D ,是BC 边的三等分点,D 在B 和E 之间,F 是AC 的中点,G 是AB 的中点,设H 是线段DF 与EG 的交点,求比值.:HG EH例2 如图所示,已知ABC D 的面积为E D cm ,,142分别是边BC AB ,上的点,且,1:2::==EC BE DB AD 求PAC D 的面积。
例3 已知G 是ABC D 的重心,过点G 任作一条直线l ,分别交边AC AB ,于点,,E D 若.,AC y AE AB x AD ==求证:yx 11+为定值。
二、奔驰定理与三角形五心的向量表达 【奔驰定理】设P 是ABC D 内一点,记三角形PBA PCA PBC ,,面积分别为,C B A S S S ,,则.0=++PC S PB S PA S C B A延长AP 至点D ,则BCPCD ACD PBD ABD PCD PBD ACD ABD S S S S S S S S S S CD BD =--===D D D D D D D D 用同样方法可得ACB S S S PD PA+=由以上两式结合定比分点坐标公式分别可得PB S S S PB S S S PD C B C C B B+++=(1)PA S S S PD CB A+-= (2)()()21-化简即得.0=++PC S PB S PA S C B A奔驰定理:点O 为ABC D 内任意一点,求证:.00=+×+×D D D OC SOB SOA S BA AOCBOC证明:考虑到存在R Îg m l 、、, 使得0=×+×+×OC OB OA g m l (1)如图:设,OC OF OB OE OA OD ×=×=×=g m l ,, 0=++\DF DEOD\点O 为DEF D 的重心。
5-4线段的定比分点与平移
答案:A
)
首页Βιβλιοθήκη 上页下页末页
第五章
平面向量
4.(教材P1352题改编)将点A(-4,3)按向量a=(5,-2)
平移后的坐标是 ( A.(9,-5) C.(1,1) B.(-9,5) D.(-8,1) )
《 走 向 高 考 》 高 考 总 复 习 · ( 数 学 配 统 编 教 材 版
解析:按向量平移公式计算得知应选C.
为________.
答案:y=log2(x+6)+4
)
首页
上页
下页
末页
第五章
平面向量
5.将函数 y=2sin2x 的图象按向量 a 的方向平移,得到 π 函数 y=2sin(2x+ )+1 的图象,则向量 a 的坐标为( 3 π A.(-3,1) π B.(-6,1) )
《 走 向 高 考 》 高 考 总 复 习 · 数 学 配 统 编 教 材 版
《 走 向 高 考 》 高 考 总 复 习 · ( ) 数 学 配 统 编 教 材 版
首页
上页
下页
末页
第五章
平面向量
2.平移公式 设 P(x,y)为图形 F 上任一点,它按向量 a=(h,k)平移 后的图形 F′上对应点为
x′=x+h P′(x′, y′), 则有 y′=y+k
,
《 走 向 高 考 》 高 考 总 复 习 · ( 数 学 配 统 编 教 材 版
首页
上页
下页
末页
第五章
平面向量
《 走 向 高 考 》 高 考 总 复 习 · ( ) 数 学 配 统 编 教 材 版
首页
上页
下页
末页
第五章
平面向量
该类问题要正确地选取线段的起点与终点,应用定比
7.8中点坐标公式与定比分点坐标公式
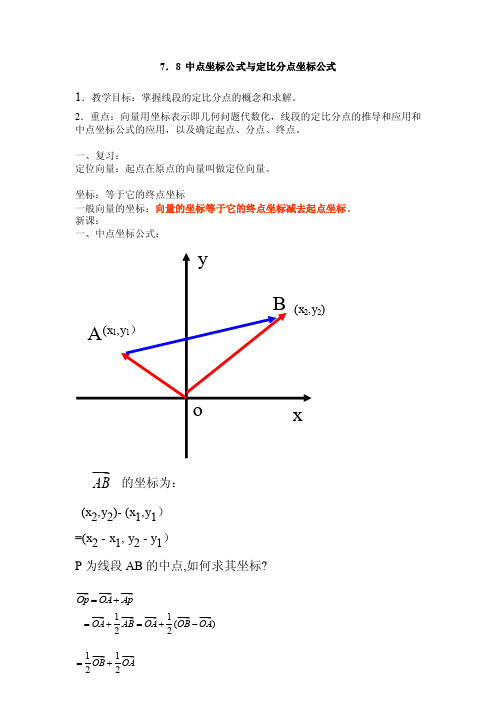
7.8 中点坐标公式与定比分点坐标公式1.教学目标:掌握线段的定比分点的概念和求解。
2.重点:向量用坐标表示即几何问题代数化,线段的定比分点的推导和应用和中点坐标公式的应用,以及确定起点、分点、终点。
一、复习:定位向量:起点在原点的向量叫做定位向量。
坐标:等于它的终点坐标一般向量的坐标:向量的坐标等于它的终点坐标减去起点坐标。
新课:一、中点坐标公式:(x 2,y 2)- (x 1,y 1) =(x 2 - x 1, y 2 - y 1)P 为线段AB 的中点,如何求其坐标?AB的坐标为:yoxAB (x 1,y 1) (x 2,y 2)OpOA Ap =+ 12OA AB =+ 1()2OA OB OA =+- 1122OB OA =+从而 Op 的坐标为: 则AB 中点p 的坐标为: 例2、已知线段AB 的中点M 的坐标为 , 端点A 的坐标为(4,2),求端点B 的坐标。
解:设点B 的坐标为 ,则由中点坐标公式可得:因此点B 的坐标为(2,-1)。
二、定比分点坐标公式:定义:设P 1、P 2是直线l 上的两点,点P 是l 上不同于P 1、P 2的任意一点,则存在一个实数λ,使−→−−→−=21pp p p λ,λ叫做点P 分有向线段−→−21P P 所成的比.方法二:设−→−−→−=21p p p p λ,且点P 1、P 、P 2的坐标分别为(x 1,y 1)、(x ,y )、(x 2,y 2),()()y y x x y y x x --=--2211,,λ()()⎩⎨⎧-=--=-y y y y x x x x 2121λλ 则 λλ++=121x x x (※)λλ++=121y y y说明:(1)在运用线段的定比分点坐标公式时,要注意(x1,y1)是起点坐标,(x2,y2)是终点坐标,(x ,y )是分点坐标.在每个等式中都涉及四个不同的量,只要知道其中的任意的三个量,便可求出第四个量.(2) 在实际的解题过程中,可以根据需要选取起点、终点、分点,但一定要注意此时λ值是不同的.11221[(,)(,)]2x y x y +1212(,)22x x y y ++=1212(,)22x x y y++⎛⎫⎪⎝⎭13,2++==222413,222y x ()22,x y ==-222,1x y例:(1)若A(x,-1),B(1,3),C(2,5)三点共线,求x (2)求证:A(-1,-1),B(1,3),C(2,5)三点共线3. 已知P 2(4, -3),P 2(-2, 6),点P 在P 1P 2的延长线上,若pp p p 212=, 求点P 的坐标.解: ∵点P 在P 1P 2的延长线上,且pp p p 212=∴221==pp p p λ,又因为在P 1P 2的延长线上,所以为-2,设点P(x, y), 则x=821224-=-+--+)())((,y=1521623=-+⨯-+-)()(∴点P 的坐标为(-8,15).总结:。
定比分点公式的向量形式及应用

定比分点公式的向量形式及应用马洪炎 吴文尧(宁波市北仑中学,浙江 315800) 众所周知,向量法是解决平面几何问题的重要方法,而定比分点公式是解析几何中应用非常广泛的重要公式.本文介绍定比分点公式的向量形式及其在解决平面几何问题中的应用,供大家参考.1 定理及其推论定理 (定比分点公式的向量形式)设点P 分P 1P 2的比为λ(即P 1P =λPP 2,λ≠-1),Q 为平面上的任意一点,则QP =11+λQP 1+λ1+λQP 2.证明 ∵P 1P =λP P 2,∴QP -QP 1=λ(QP 2-QP ),即(1+λ)QP =QP 1+λQP 2,即QP =11+λQP 1+λ1+λQP 2.推论1 设点P 为■O AB 的边AB 上的点,且AP =m ,P B =n ,则OP =n m +n OA +mm +nOB .推论2 设点P 为■O AB 的边AB 的中点,则OP =12(OA +OB ).推论3 ■OAB 中,点P 在直线AB 上的充要条件是:存在实数t ,使OP =t OA +(1-t )OB 成立.推论4 (定比分点公式)在直角坐标平面中,设P 1(x 1,y 1),P 2(x 2,y 2),P (x ,y ),且点P 分P 1P 2的比为λ(其中λ≠-1),则x =x 1+λx 21+λ,y =y 1+λy 21+λ.2 应用举例2.1证明比例线段关系例1 如图1,在■ABC 中,D ,E 是BC 边的三等分点,D 在B 和E 之间,F 是AC的中点,G 是AB 的中点,设H 是线段D F与EG 的交点,求比值E H ∶HG .分析 要求比值E H ∶HG 的大小,只须得到向量E H 与向量EG 之间的线性关系,由平面向量基本定理可知,可选择一组合适的基底使向量E H 、向量EG 都可用这组基底的线性组合表示,一旦表示成功,则结论也唾手可得了.图1 例1图解 设CB =a ,CA =b ,连结CG ,EF ,由于BE =2EC ,由推论1可知:GE =23GC +13GB=23GC +13(CB -CG )=13CB -CG =13CB -12(CB +CA )=-16a -12b ,即EG =16a +12b ;∵D ,H ,F 三点共线,∴E H =t ED +(1-t )EF=t ED +(1-t )(CF -CE )=t 3a +(1-t )(12b -13a )=2t -13a +1-t 2b .∵EG 与E H 是共线向量,∴16·1-t 2-12·2t -13=0,即t =35,40数学通讯 2007年第24期故E H =25(16a +12b )=25E G ,∴E H ∶H G =2∶3.评注 ①由于本题的相关点均“生长”在■ABC 的三边上,所以选择以向量CB =a ,CA =b 作为基底比较合理.②在向量运算过程中,通过合理的运用上述定理的推论,可简化运算过程,甚至可直奔结论.例2 (第23届IMO 试题)已知AC ,CE 是正六边形ABCD EF 的两条对角线,点M ,N 分别内分AC ,CE ,使得AM ∶AC =CN ∶CE =r ,如果B ,M ,N 三点共线,求r 的值.分析 ①要求出r 的值,只须得到关于r 的一个方程,故解决问题的关键是如何结合其它已知条件,把条件“B ,M ,N 三点共线”翻译成关于r 的一个方程.②由于B ,M ,N 三点所在直线过顶点B ,因此选择向量B A 、BC 作为基底比较合理,再把向量B M ,B N 用基底表示之,则不难得到关于r 的方程.图2 例2图解 ∵AM ∶AC =CN ∶CE =r ,∴AM ∶MC =CN ∶N E =r ∶(1-r ).由推论1可知BM =r BC +(1-r )B A ,B N =r BE +(1-r )BC .∵ABCDEF 是正六边形,∴B E =2(B A +BC ),∴B N =2r (B A +B C )+(1-r )BC=(1+r )B C +2r B A .∵B ,M ,N 共线,∴r ·2r -(1-r )(1+r )=0,解得r =33.评注 由于本题的“情景”与推论1的使用条件非常吻合,因此上述解法通过推论1的应用使运算过程显得非常简捷,极大地缩短了解题的长度.2.2 证明三角形的面积关系例3 如图3所示,已知■AB C 的面积为14cm 2,D ,E 分别是边AB ,BC 上的点,且AD ∶DB =B E ∶EC =2∶1,求■P AC 的面积.分析 由于已知■AB C 的面积,因此要计算■P AC 的面积,只须求这两个三角形的面积比,注意到■ABC 与■P AC 是同底三角形,设直线BP 与AC 交于点Q ,则只须求出点P 分BQ 的比,若选择以向量B A =a ,BC =c 为基底,再把向量BQ ,B P 用基底表示之,则就大功告成了.图3 例3图解 连结BP 并延长交AC 于Q ,设B A=a ,BC =c .∵C ,P ,D 三点共线,∴B P =t BD +(1-t )BC ,又∵BD =13B A =13a ,∴B P =t 3a +(1-t )c .∵A ,P ,E 三点共线,∴B P =λB A +(1-λ)B E ,即B P =λa +2(1-λ)3c .由平面向量基本定理可知t3=λ且1-t =2(1-λ)3,解得λ=17,∴B P =17a +47c .设BQ =μBP =μ7a +4μ7c ,因为A ,Q ,C三点共线,所以μ7+4μ7=1,即μ=75,∴B P =57BQ ,PQ =27BQ ,S ■PAC =27S ■BAC =4cm 2.评注 在用向量方法解决平面几何问题时,除注意基底的合理选择外,还需注意方程412007年第24期 数学通讯思想的应用,虽然上述解法操作过程有一定的技巧性,但若在操作过程中始终以方程思想为指导,则思路还是比较自然.2.3证明三点共线问题例4 (2004年斯洛文尼亚数学奥林匹克试题)设O,P是平面上的两个不同的点,四边形AB CD是平行四边形,两条对角线相交于点O,点P不在直线AB关于直线CD 对称的图形上,M,N分别是线段P A,PB的中点,Q是直线MC与直线ND的交点.证明:P,Q,O三点共线,且点Q的位置与平行四边形ABCD的选择无关.分析 要证明P,Q,O三点共线,只须证明PO=λPQ,注意到O是AC的中点,即有PO=12(P A+P C)成立,故可选择向量P A,PC为基底,再设法把向量PQ也用基底表示之即可.图4 例4图证明 ∵M,N分别是线段PA,PB的中点,∴MN瓛12AB.∵ABCD是平行四边形,∴AB瓛C D,即MN瓛12CD,∴Q C=2MQ,由推论1可知PQ=23PM+13PC=13P A+13P C.又因为O是线段AC的中点,由推论2可知PO=12(P A+PC),所以PQ=23PO,即PQ,PO共线,且PQ=23PO,即P,Q,O三点共线,且点Q的位置与平行四边形ABCD 的选择无关.评注 证明三点共线是平面几何中的难点之一,利用平面向量方法证明之的思路自然且易于操作.2.4证明平面几何中的定值问题例5 已知G是■ABC的重心,过点G 任作一条直线l,分别交边AB,AC于点D, E,若AD=x AB,AE=y AC.求证:1x+1y为定值.分析 当点D与点B重合,即x=1时,且E为AC之中点,即y=12,此时1x+1y=3,因此只须证明1x+1y=3即可.所以只须得到关于x,y应满足的方程即可,注意到D,G,E三点共线及G是■ABC的重心,因此可选择以向量AB,AC为基底,由向量AG 的两种不同的表示方法得到此方程.图5 例5图证明 ∵D,G,E三点共线,∴AG=λAD+(1-λ)AE=λx AB+(1-λ)y AC,又∵G是■ABC的重心,所以AG=23AF=13AB+13AC,由平面向量基本定理可知λx=13,且(1-λ)y=13,∴1x+1y=3λ+3(1-λ)=3(定值).通过以上各例的解法不难发现,用定比分点公式的向量形式及其推论解决平面几何问题的解题程序如下:1)把平面几何问题转化为平面向量问题;2)合理选择一组基底;3)把问题涉及的向量用基底表示之;4)得到需要的结论并回归到平面几何问题.(收稿日期:2007-09-04)42数学通讯 2007年第24期。
有向线段的中点坐标公式和定比分点坐标公式

课题:有向线段的中点坐标公式和定比分点坐标公式知识目标1.理解点C分有向线段所成的比λ的含义;2.掌握有向线段的定比分点坐标公式和线段的中点坐标公式,并能应用这两个公式进行解题.能力目标能应用有向线段的定比分点坐标公式和线段的中点坐标公式解题。
重点难点1.重点:线段的定比分点坐标公式和中点坐标公式的应用;2.难点:用线段的定比分点坐标公式解题。
时量90分钟教学方式设计1.课前复习(10分钟)2.线段的中点坐标公式(30分钟);3.线段的定比分点坐标公式(35分钟);4.课堂练习及布置作业(15分钟)。
教学过程一、中点坐标公式如图,已知线段AB的两个端点A,B的坐标分别为,1122(,),(,)x y x y,线段AB的中点M的坐标是多少?分析:由于点M是线段AB的中点,因此11111()()22222OM OA AM OA AB OA OB OA OA OB OA OB→→→→→→→→→→→→=+=+=+-=+=+从而OM→的坐标为121211221[(,)(,)](,)222x x y yx y x y+++=因此点M的坐标为1212(,)22x x y y++即线段的中点坐标等于它的两个端点坐标和的一半。
若点111222(,),(,),(,)P x y P x y P x y ,λ为实数,且12PP PP λ=,由向量的坐标等于终点坐标减去起点坐标,我们有:111(,)PP x x y y =--,222(,)PP x x y y =-- 12PP PP λ=1122(,)(,)x x y y x x y y λ∴--=--1212()()x x x x y y y y λλ-=-⎧∴⎨-=-⎩由此可得 若点111222(,),(,),(,)P x y P x y P x y ,λ为实数,且12PP PP λ=,则点P 的坐标(,)x y 满足:121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩我们把上式叫做有向线段12PP 的定比分点坐标公式。
平面向量定比分点公式

平面向量定比分点公式
平面向量定比分点公式是数学中常用的一个公式,用来求解平面向量在一定的比例下分点的坐标。
如果有两个点 A(x1, y1) 和 B(x2, y2),以及一定比例的数 m:n,则该公式可以求出以 A 点为起点,以B 点为终点的向量中点 P 的坐标。
具体来说,设 P 的坐标为 (x, y),则有以下公式:
x = (mx2 + nx1) / (m + n)
y = (my2 + ny1) / (m + n)
其中,m:n 表示向量 AP:PB 的比例,x1、y1 分别表示点 A 的横纵坐标,x2、y2 分别表示点 B 的横纵坐标,m 和 n 是任意实数,但不同时为 0。
需要注意的是,如果 m + n = 0,则公式无法计算,因为此时分点 P 会落在无穷远处。
因此,在应用该公式时,需要确保 m + n 不为 0,或者特别处理这种情况。
定比定比分点公式

定比定比分点公式定比是指两个比例的比值在一定条件下保持不变的关系。
定比分点公式则是用来求解定比的分点的公式。
下面我们将详细讲解定比和定比分点公式。
【定比的定义】定比是指两个比例的比值在一定条件下保持不变的关系。
设a:b=c:d,其中a、b、c、d都是实数,且b、d不为零。
若a、b、c、d之间满足这一条件,我们称之为定比关系,记作a:b∷c:d。
在定比关系中,a和b称为第一个比例的两个比例项,c和d称为第二个比例的两个比例项。
【定比的性质】1.定比关系的比例项间的乘积相等,即a×b=c×d。
证明:设 a : b = c : d,则根据比例的定义,有 a/b = c/d。
两边同乘以bd,得到 ad = bc。
所以 ab = cd。
因此,定比关系的比例项间的乘积相等。
2.定比关系的两个比例可以用一个比值来表示。
证明:设 a : b = c : d,则根据性质 1,有 a/b = c/d。
两边交叉相乘,得到 ad = bc。
所以,比值 a/b 或 c/d 可以表示定比关系的两个比例。
在定比关系a:b∷c:d中,如果要求确定定比关系的分点e,也就是要求找到一个数x,使得a:b=x:e和c:d=x:(1-e),则可以使用定比分点公式进行计算。
定比分点公式如下:e=[a/(a+b)]×(1-d/c)【定比分点公式的证明】设x=a/(a+b),则1-x=1-a/(a+b)=b/(a+b)。
根据定比分点公式的条件,我们有:x:e=a:b带入x=a/(a+b),得到:a/(a+b):e=a:b两边交叉相乘,得到:ae = ab同理,带入1-x=b/(a+b),有:c/(c+d):(1-e)=c:d交叉相乘,得到:ce = cd由定比的性质可知,ab = cd,所以 ae = ab = cd = ce。
所以我们可以得出:ae = ce移项化简,得到:ae - ce = 0根据因式提取法,可将上式化简为:e(a-c)=0由于e≠0,所以我们可以得到a-c=0,即a=c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们能否解决下面的问题?
(1) 已知λ及P1(x1, y1)、P2(x2, y2),求P 点的坐标(x,y);
(2) 已知P1(x1, y1)、P2(x2, y2)及P(x, y), 求λ的值.
2、定比分点P 的坐标
y
如图,P1P PP2
P1 ( x1 , y1 ) P(x , y )
uPu1uPr ( x x1, y y1)
P2
( 0)
P1
P2
P
( 1)
PP2 ( x2 x, y2 y),
P2 ( x2 , y2 )
o
x
( x x1, y y1 )
( x2
x x1 y y1
x, y2 ( x2 ( y2
y),
x) ,
解得:
y)
x y
x1 x2 1
y1 y2
.
1
x
x1 x2 1
y
y1 y2 1
的 实 数1
1
.
2、如果是点 P 分有向线段P1P2 的
比,它的值能是 1吗? 若 1,则 P1P (1)PP2 ,
可 得 :P1P PP2
P12
P
P
PP12
答:不可 能(如果P1P (1)PP2 ,则
点P1、P2一 定 重 合 )
例1 已 知P1P2 2,点P在 P1P2 的 延 长 线 上 , 且PP2 1,
求 点P分P1P2所 成 的 比.
P1
P2
P
只需寻求使P1P PP2的实数.
解:
P1P 3
PP2 1
P1P 3 PP2 3
例2 已 知 点P分 P1P2 所 成 的 比 是- 2, 求 点P1分
有 向 线 段P2P 所 成 的 比.
只需寻求使P2P1 P1P 的实数.
解:Leabharlann P1P2P
y
B
A D
G
C
o
x
坐标公式得点G的坐标为G( x1 x2 x3 , y1 y2 y3 )
x
x3 2
x1 x2 2
3
x1 x2 x3 ,
3
1 2
3
y
y3
2
y1 y2 2
y1 y2 y3 .
1 2
3
小结:
1、点P分有向线段P1P2 所成的比 (这里P1P PP2 )
P1 P
P1P 2 PP2
P1 P 2
PP2
P2 P1 1 P1 P 2
1 P2 P1 2 P1P,
1 .
2
问题2:
已知线段P1P2的两个端点P1(x1, y1)、
P2(x2, 一点,
由y2)共, P线(x向, y量)为知线识段, 必P1有P2所uPu1在uPr 直 线 uP上uPu任r2 ,
P2 ( x2 , y2 )
坐标公式与 (1) 相同吗?
o
x
此 时 点P 分 有 向线 段P2 P1 的 比是 1 , 代入定比分点坐标公式:
P2 P
1
PP1
x
x2
1
x1
1 1
x1 x2 , 1
同理
y
y1 y2 1
那么点P 分有向线段P2P1 的定比分点坐标公式
与 (1)相同.
例3
已 知 两 点P1(3,2),
所 成 的 比.
P1 P
P2
( 0)
P1
P2
P
( 1)
P
P1
P2
(1 0)
}P1P PP2 起分 分终 点点 点点
P1 P
P2
( 0)
P1
P2
P
( 1)
}P1P PP2
P
P1
P2
(1 0)
1、在上面的图中,点P 分有向线段P2P1 的比是什么?
答:点P 分有向线段P2P1 的比是使P2P 1 PP1
杨浦高级中学 江海涛
向量共线的充要条件是什么?
a // b(b 0) a b
(其中 0时,a 与b同向,反之也成立, 0时,a 与b 反向,反之也成立)
a // b(b 0) x1 y2 x2 y1 0
r
r
(a ( x1, y1), b x2, y2 )
问题1:
已 知P是 直 线P1P2上 一 点, 且 P1P PP2 , ( R, 1)设O是 平 面 上 任 意 一 点,
(2)点C坐 标 已 知 ,D坐 标 可 求 , 且
点G分 有 向 线 段CD 的 比 已 知 是2, 根 据 定 比 分 点 坐 标 公 式 可求 出G的 坐 标.
解: D是AB的中点,点D的坐标为
D( x1 x2 , y1 y2 )
CG
2 uuur 2 uuur
2 GD
CG 2GD
设G( x, y), 由定比分点
(1)
该公式叫做有向线段P1P2 的定比分点 坐 标 公 式(公 式 (1) ).
(其中,P1P PP2 ), P1( x1, y1), P2( x2 y2 ))
用向量表示就是:OuuPur
1
1
uuur OP1
1
uuur OP2 .
当 1时 ,点P是 线 段P1P2 的 中 点 , 得
到有 向 线 段P1P2 的 中 点 坐 标公 式(公 式 (2) ).
例4 如 图 ,ABC三 个 顶 点 的 坐 标 分 别 为A( x1 , y1 ),
B( x2 , y2 ), C( x3 , y3 ), D是AB的 中 点 ,G是CD上 一 点 ,
且 CG 2,求 点G的 坐 标. GD
y
A
D
B
G
(1) A、B坐 标 已 知 ,D为 中 点 ,
C
o
x
可 用 中 点 坐 标 公 式 求 出D的 坐 标 ;
P2
(8,3),
求
点P
(
1 2
,
y )分 P1 P2
所 成 的比及y的 值.
解:把
x1
3,
x2
8,
x
1 2
代入定比分点
坐 标 公 式得 :
1 3 (8) , 解得 5
2 1
17
把
y
5 17
,y1
2 5 3 17
1 5 17
2, 49
22
y2
3代入定比分点坐标公式
5
17
y 49 22
求
证:
OP
1
1
OP1
1
OP2
思考: 1,P点位置如何? P1 P
1 OP 2 (OP1 OP2 )
P2 O
1、点 P分有向线段 P1P2 所成的比
设 P1、P2 是直线 l 上的两点,点P 是l上
不 同 于P1、P2的 任 意 一 点 , 则 存 在 一个 实 数,
使P1P PP2 , 叫做点P分有向线段 P1P2
(其中,P1P PP2 ), P1( x1, y1), P2( x2 y2 ))
x
x1 2
x2
y
y1 y2 2
(2)
用向量表示就是:
uuur 1 uuur uuur OP 2 (OP1 OP2 ).
y
如图,若
P1 P
PP , 那 么 P1( x1, y1)
2
P(x , y )
点 P 分有向线段P2P1 的定比分点
