理想别墅的数学
理想别墅的数学

【译者案:昨日,差不多快翻译完毕笛卡尔与佩劳之后,就想起了科林、罗得这篇《理想别墅得数学》名文了。
先说科林、罗,她就是维特考尔得学生,维特考尔就是沃尔夫林得学生。
那我们就知道科林罗得建筑分析跟沃尔夫林就是很有渊源得。
而埃森曼,又就是科林罗得学生,也就就是说,在这位解构主义建筑师得骨子里,一直就就是建筑得形式分析得行家里手。
那么,什么就是建筑案例得形式分析呢?肯定,这就涉及到了建筑得比例分析,几何解析,以及平立剖得构成要素得句法分析。
这些东西,肯定肯定肯定,不就是工匠与结构师要学得。
却就是西方建筑师以及艺术史学家们一样要做得功课。
即使今日,您要欧美得本科生得艺术史与建筑史得课堂上去,对于古典建筑得形式分析仍然就是考试得一个要点。
至于中国各个建筑院校里,本科或就是硕士做不做这样得功课,我不清楚;但就是,我得建筑史就是这么学出来得。
从宗教、文学、人类学、艺术史得角度,正如科林罗所言,这种功课得神圣性肯定已经消失了。
但就是,这种分析却部分地还原了文艺复兴建筑师得创作历程与心态;也解释了很多不然无法瞧懂得柯布得设计条件。
她要呼应什么?反对什么?消解什么?形式分析当然不就是建筑设计得全部。
就像句法分析不就是文学得全部一样。
然而,如果没有读过这篇文章得同学,记住了,一定一定要补上这一课。
否则,您得建筑史永远就是瘸腿得建筑史。
另:我知道王群老师在翻译科林罗得这本书。
可就是,一直不见全书汉译出版,我就把我十多年前得译稿贴出来。
算就是替王群老师补白。
等王老师得译文出来,可以把我得删掉。
】Colin Rowe, “The Mathematics of the Ideal Villa” in“The Mathematics of t he Ideal Villa and Other Essays”, Cambridge: t he MIT Press c、1976理想别墅得数学科林、罗,原美国哈佛大学建筑系历史教授“美有两种起因:天然性与习惯性。
解读埃森曼建筑形式自治的历史传承

解读埃森曼建筑形式自治的历史传承【摘要】该文章对建筑大师埃森曼的历史传承性进行了分析,从埃森曼对特拉尼和柯布西耶的学习解读方面进行了论证,探寻到埃森曼设计语言和手法的来源,为埃森曼的作品思想研究以及对当代的启示提供了思路。
【关键词】形式自治交叠分解深层结构多米诺体系自指涉系统【正文】1.从特拉尼到二号住宅1.1 意大利理性主义作为埃森曼早期的研究学习对象,居塞皮·特拉尼(Giuseppe Terragni)是意大利20世纪20年代的理性主义的代表者,埃森曼在评价他的建筑时将他与柯布西耶进行对比。
柯布西耶的白色形式是现代性的语言象征,它们属于“表层结构”。
而特拉尼的形式是以最客观的方式表现“深层结构”的语法象征。
特拉尼把墙体非物质化了,使它成为介于平与凹,实与虚之间的辩证指示物。
面对历史的元素,特拉尼转换为了现代语言,其建筑的结构形式既满足现代的技术与功能理性,又不失历史语法与传统秩序。
1.2.1 法西斯宫的理性法西斯宫是献给法西斯领袖的伟大作品, 在设计之初就包含了特拉尼“法西斯是人人可达的玻璃房子”的墨索里尼理想。
从中我们可以看出, 政治、社会等方面对于建筑的要求。
建筑采用了传统的意大利宫廷建筑模式, 平面围绕一个开敞庭院而展开。
透过混凝土屋面的玻璃顶采光,四周围绕着长廊、办公室和会议室。
四周的分层立面都是为了保证外部对于内部中庭感知的透明度。
底层庭院与室外广场就能够实现一体化, 允许人流从街道、广场向室内不断流动。
1.2.2 法西斯宫的“转换”埃森曼把建筑的构造元素梁、柱、墙,也就是形式上的线、面、体元素看成是句法中的单元通过组合转换分解等手段形成新的“句子和文本”。
在他看来,法西斯宫立面的实现是一个包含了对称与非对称(Symmetry and Asymmetry )、稳定与旋转(Stasis and Rotation )及网格与实体(Grid and Solid )的交叠过程(图1)。
表皮的透明性_对斯坦因别墅的另一种解读

关于真理,黑格尔在《精神现象学》的序言中有这 么一句话,由于他极少用比喻,所以这句话很显眼:
“真理,就是所有参加者都为之酩酊大醉的一席豪 饮,而因为每个参与者离开酒席就立即陷于瓦解,所以 整个这场豪饮也就同样是一个透明的、单纯的静止”。[7]
“这种一再需要重新建立的和谐似乎受到方盒子内部 这种人为的空虚的影响,它们在这里找到自身的位置, 当感官面对这些从表面上看来任性而为的一切时,理智 却因直觉而更为确信,与表面所见恰恰相反,在此,问 题被认识并得到解答,在此存在一个合理的秩序”。[4]
注意到这里强调“一再需要重新建立的”和谐,而 且认为确信来自“直觉”,从对建筑的体验看来,这是符 合人的生理和心理特征的。而且,通过对感官和理智的 关系作更为清晰的描述,这段话暗示了在建筑中体验到 的这种模棱两可的特征究竟指什么。也许,创作者本人 的话更有助于我们对“透明性”的理解。在全集的第一 卷中的前言部分,柯布写道:
注意到在这段文字中,黑格尔用了“透明”来形容 真理的某一特征。这提醒了我们:“透明性”这一概念使 人容易从静止和孤立的角度看建筑,而不能从联系和运 动的角度看建筑。它使建筑成为一个概念,一种知识,它 剥夺了人的感知在建筑体验中的重要地位。正是从柯 林·罗开始,出现了一种将建筑形式作为概念的认识论
2004/ 8 总第 1 1 0 期
ARCHITECT 21
22
A R C H I T E CT
2004/ 8 总第 110 期
倾向,而他的学生埃森曼,则将这种形式主义的认识论 推向了极致,他认为建筑作为一种知识形式,它排斥主 体认识上的差异,而且建筑形式具有自主性,建筑创作 可以按照某种程式自动生成而不需要作者。以《反功能 主义》一书,他第一个宣布抛弃建筑的功能和社会属性。 然而这种建筑创作和建筑体验的主体的缺席,使他的建 筑成了虚无主义者的概念游戏,让人感到新奇,迷惑,却 无法使人感动,也无法获得明确的认识。他打破了前人 的形式对建筑师的束缚,就此而言他是积极的。他的思 想极大地影响了今日的先锋派,而他本人正是先锋派的 一员。[8]
十大建筑中的数学美

十大建筑中的数学美体现在以下几个方面:
1.黄金分割:许多建筑都采用了黄金分割的比例,这种比例在视
觉上具有美感,也符合人们的审美习惯。
例如,上海东方明珠
电视塔的设计就运用了黄金分割的比例,使其更加协调美观。
2.斐波那契数列:斐波那契数列在建筑设计中也经常被运用,这
种数列的特性使其在建筑设计中具有很强的视觉冲击力。
3.对称与平衡:许多建筑都采用了对称的设计,这种对称不仅使
建筑更加稳定,也增加了建筑的视觉美感。
4.几何形状:建筑中的几何形状也是数学美的重要体现。
例如,
埃及的金字塔就是由几何形状构成的,其线条简洁明了,具有
很强的视觉冲击力。
总的来说,十大建筑中的数学美主要体现在黄金分割、斐波那契数列、对称与平衡以及几何形状等方面。
这些数学元素在建筑设计中被巧妙运用,不仅增加了建筑的视觉美感,也体现了建筑师对数学美的追求和运用。
3布扎和西扎:写给大二的建筑学同学们(城市笔记人)

布扎与西扎:写给大二的建筑学同学们2010-09-09 10:33:02西扎(Alvaro Siza)爷爷病了,东南大学的讲座就泡了汤;阮昕叔叔身体很好,华南理工的讲座就如约进行。
这俩人绝对没有预谋,他们的讲座也不存在任何直接的关系,却因为我很想听到他们的讲座,被我组织到同一篇文章里来了。
阮昕老师在华南的一个讲座,就是有关巴黎美院建筑设计的那套设计方法,叫做parti et poche。
西扎的讲座——因为被短期或是无限期推迟——估计讲的也是他的那套设计方法。
就思想的先后而言,西扎肯定是熟悉并了解巴黎美院的那套体系的,他读书时,他的老师Tavaro也会教给他——万一没教,西扎这么痴迷柯布,他也可以从柯布早期的小房子里悟到这套基本的设计手法。
什么是parti et poche?懂法语或者懂得查法语字典的同学很快就知道,parti是“决定、境遇、政党”。
这个词,就类似英语的part,这个英语和法语的part都来自拉丁文里的partire,就是去“分割”,以及“分割出来的局部”;而poche就是一个衣袋,一种口袋,倒是英语的pocket享有了法语poche的这个词根。
这是一般通用语中的解释,显然,你用“政党或是局部”以及“口袋”,去套用建筑设计,还是找不到北。
那么,在建筑设计中,法国人当初用parti et poche指得到底是什么呢?最近,一本专讲布扎(the Ecole des Beaux Arts)教育体系的专著John F. Harbeson的《建筑设计研究》(The Study of Architectural Design)再版,在该书第75页,Harbeson用Paul Crete(梁思成的老师)1921年的话,做了一个生动的解释,“Parti——就是party,就是决策,就是途径,就是方式,。
就是方法。
Paul Crete教授在回答这个问题时提出,‘Parti一词意味着party【分立】,就像有共和党,又有民主党一样;大选时,每个选民都得挑选一个party,尽管选民并不知道哪个party会获胜,可见,对于一个设计的问题,去选择某个parti,就意味着对设计问题,采纳了某种态度,希望此后的建筑沿着这一态度所期待的路线发展,并因而抵达了对于问题的最佳方案’”。
理想别墅的数学

【译者案:昨日,差不多快翻译完毕笛卡尔和佩劳之后,就想起了科林.罗的这篇《理想别墅的数学》名文了。
先说科林.罗,他是维特考尔的学生,维特考尔是沃尔夫林的学生。
那我们就知道科林罗的建筑分析跟沃尔夫林是很有渊源的。
而埃森曼,又是科林罗的学生,也就是说,在这位解构主义建筑师的骨子里,一直就是建筑的形式分析的行家里手。
那么,什么是建筑案例的形式分析呢?肯定,这就涉及到了建筑的比例分析,几何解析,以及平立剖的构成要素的句法分析。
这些东西,肯定肯定肯定,不是工匠和结构师要学的。
却是西方建筑师以及艺术史学家们一样要做的功课。
即使今日,你要欧美的本科生的艺术史和建筑史的课堂上去,对于古典建筑的形式分析仍然是考试的一个要点。
至于中国各个建筑院校里,本科或是硕士做不做这样的功课,我不清楚;但是,我的建筑史是这么学出来的。
从宗教、文学、人类学、艺术史的角度,正如科林罗所言,这种功课的神圣性肯定已经消失了。
但是,这种分析却部分地还原了文艺复兴建筑师的创作历程和心态;也解释了很多不然无法看懂的柯布的设计条件。
他要呼应什么?反对什么?消解什么?形式分析当然不是建筑设计的全部。
就像句法分析不是文学的全部一样。
然而,如果没有读过这篇文章的同学,记住了,一定一定要补上这一课。
否则,你的建筑史永远是瘸腿的建筑史。
另:我知道王群老师在翻译科林罗的这本书。
可是,一直不见全书汉译出版,我就把我十多年前的译稿贴出来。
算是替王群老师补白。
等王老师的译文出来,可以把我的删掉。
】Colin Rowe, “The Mathematics of the Ideal Villa” in“The Mathematics of t he Ideal Villa and Other Essays”, Cambridge: the MIT Press c.1976理想别墅的数学科林.罗,原美国哈佛大学建筑系历史教授“美有两种起因:天然性和习惯性。
自然美来自构成统一性的几何,即均衡与比例。
现代建筑的写作者们(一)

现代建筑的写作者们(一) (2009-12-16 22:11:46)转载标签:现代建筑现代主义历史现代建筑的第一代理论家中最有影响力的是吉迪恩(Sigfried Giedion1888-1968)。
他的《空间、时间与建筑》出版于1940年,是对现代建筑实践的总结,对现代建筑思想的传播起到了很大推动作用,被认为是里程碑式的著作。
这本书先后增补和修订了五次,仅到60年代初就再版13次。
在那时很多建筑院校把《空间、时间与建筑》当做现代建筑史的教材。
吉迪恩先是学习工程学后研究艺术史,在三十五岁才对现代建筑发生兴趣。
他的艺术史研究方向是巴洛克建筑。
巴洛克建筑的基本特征是空间的复杂性,因此吉迪恩对现代建筑的总结也是从空间入手。
吉迪恩相信在剧烈变化和混乱无序的现实世界以及纷繁复杂的当代文化和艺术潮流中蕴含着一种时代精神,建筑师的任务就是揭示这种一致性和时代施加于所有人的共同的感受,这是他写《空间、时间与建筑》的出发点。
这一点显然来自于启蒙运动的进步的历史观和黑格尔关于时代精神的论断。
吉迪恩认为现代建筑区别于以往建筑的基本特征是空间的通透性(interpenetration),这个特征同时表现在十九世纪的工程技术和新结构形式之中。
他把现代建筑的空间观与爱因斯坦的相对论联系起来,把现代建筑的基本特征归纳为三维空间加上时间向量构成的所谓“四维”空间。
在吉迪恩看来这是现代建筑有别于其他时代的根本特性。
吉迪恩的这个观点应该说相当地牵强附会,受到很多人质疑。
彼得·柯林斯(Peter Collins )在《现代建筑设计思想的演变》一书中对此做出了颇有说服力的剖析。
吉迪恩只比柯布西耶小一岁,但他是柯布忠实的追随者。
据说他转向现代建筑理论的研究和结识柯布有直接的关系。
在他的《时间、空间与建筑》中吉迪恩有意识地排除了与柯布西耶持不同见解的德国表现主义建筑师如门德尔松等的作品。
吉迪恩后来成为现代建筑国际会议(CIAM)的主要发言人,他和柯布一起把像雨果·哈林(Hugo Haring)这样的持北欧浪漫主义立场的建筑师排斥在外,这也是现代建筑会议中的一桩公案。
中班数学三只小猪造高楼

中班数学三只小猪造高楼从前有三只聪明的小猪,名字分别叫小红、小黄和小蓝。
他们定居在一个美丽的森林中,每天都在一起生活、玩耍和学习。
有一天,小猪们想造一个高楼,但是他们不知道该从何处开始。
小红提议:“我们可以首先画出建筑设计图,这样我们就能够有一个清楚的指导。
”小黄和小蓝都觉得这个主意很好,于是他们开始了建筑设计。
小猪们很用心地制作建筑设计图。
小红负责绘制建筑的轮廓图和立体图,小黄负责测量地基的大小和深度,小蓝负责计算所需的材料和设备。
他们每天都在一起讨论和完善设计,直到最终完成了一份完美的建筑设计图。
接下来,小红、小黄和小蓝开始着手建造高楼。
小蓝负责购买材料,小黄负责挖掘地基,小红负责监督工地的施工。
他们相互协作,分工合作,非常有条不紊地进行着工作。
随着时间的推移,高楼的轮廓渐渐显现出来。
小猪们非常高兴,他们看见了自己辛勤劳动的成果。
然而,他们也遇到了一些困难。
小红发现建筑的预算已经超出了原计划,小黄则发现地基处有一些问题需要修复,小蓝则发现材料不够了。
面对这些困难,小猪们并没有放弃,相反,他们更加努力地面对挑战。
小红提议:“我们可以重新评估预算,寻找更便宜的材料。
”小黄建议:“我们可以修复地基并加强其稳定性。
”小蓝提议:“我们可以寻找其他供应商购买所需材料。
”小猪们一致认为这些建议都非常好,并迅速采取行动。
通过小猪们的共同努力,困难都逐渐被解决。
高楼的建设也取得了进展,直到最终完成。
小红、小黄和小蓝非常骄傲地站在高楼的顶端,欣赏着他们的杰作。
这个故事告诉我们,只要我们有明确的目标,通过合作和努力,我们就能克服困难,实现自己的梦想。
小红、小黄和小蓝就是一个例子,他们通过互相帮助,相互支持,最终成功地建造起了高楼。
他们也教会了我们如何面对困难,如何解决问题,如何努力奋斗。
最后,小红、小黄和小蓝决定将高楼作为他们学习和成长的地方。
他们将高楼内部设计成了一个图书馆,里面摆满了各种书籍和学习材料。
小猪们每天都会来这里学习知识、交流经验和分享快乐。
十大建筑中的数学之美(一)2024

十大建筑中的数学之美(一)引言概述:数学与建筑是两个 seemingly unrelated 领域,然而在深入研究后,我们发现数学在建筑设计中发挥着重要的作用。
本文将带领读者一起探索十大建筑中的数学之美。
通过探讨每个建筑中数学的应用,我们将更好地理解数学对建筑设计的重要性,并欣赏到数学的美妙之处。
正文:I. 黄金分割的应用1. 如何使用黄金分割来设计建筑外观,比如矩形长宽比例、窗户的位置等。
2. 黄金比例如何帮助我们创造出更和谐、美观的建筑。
II. 对数螺旋与建筑的契合1. 对数螺旋在建筑中的应用,例如螺旋楼梯或杆塔的设计。
2. 对数螺旋如何帮助我们实现更稳定、优雅的建筑结构。
III. 对称性与建筑的平衡1. 不同类型的对称性在建筑设计中如何运用,如轴对称、中心对称等。
2. 如何利用对称性来达到建筑的视觉平衡与美感。
IV. 曲线与建筑设计的无限可能1. 弧线的运用及其在拱门、拱顶等建筑元素中的作用。
2. 曲线的灵活性如何帮助我们设计出独特、富有创意的建筑结构。
V. 三角函数在建筑设计中的应用1. 正弦函数与波浪形设计的关系,如波浪形屋顶的设计。
2. 余弦函数在设计弧形建筑中的使用。
总结:通过探索十大建筑中的数学之美,我们发现数学在建筑设计中的广泛应用。
黄金分割、对数螺旋、对称性、曲线和三角函数等都为建筑设计提供了新的可能性和灵感。
同时,数学帮助我们创造出更稳定、美观和创造性的建筑结构。
它们的结合共同构建了让人惊叹的建筑作品,展示了数学的美妙之处。
通过更深入地研究数学与建筑之间的关系,我们能够更好地欣赏这些建筑作品,并为今后的设计工作提供启示和灵感。
建筑中用到的数学知识

建筑中用到的数学知识一、平行和垂直在建筑中,平行和垂直是非常重要的概念。
平行线是指在同一平面上永不相交的直线,而垂直线是指与另一条线段或平面成直角的线段或平面。
在建筑中,我们常常需要使用平行和垂直来确定墙壁、地板和天花板的位置和方向。
二、比例和尺寸比例和尺寸是建筑设计中必不可少的数学概念。
在设计建筑物时,我们需要考虑到不同元素之间的比例关系,以及它们与整体建筑的尺寸比例。
比例和尺寸的准确性对于建筑的美观和功能性至关重要。
三、三角形和直角三角形三角形是建筑中常见的形状之一。
我们可以利用三角形的性质来确定建筑物的角度和边长。
特别是直角三角形,它们的边长关系和角度关系可以帮助我们计算出建筑物的高度、宽度、斜度等重要参数。
四、多边形和对称性建筑中常常使用多边形来构建墙壁、屋顶等结构。
多边形的对称性对于保持建筑物的平衡和美观非常重要。
通过对多边形的对称性进行分析和计算,我们可以确保建筑物的各个部分相互匹配,整体呈现出良好的对称性。
五、曲线和弧线曲线和弧线是建筑中常见的元素,它们赋予建筑物以流动和柔和的感觉。
在设计和建造弧线时,我们需要使用曲线的数学知识,如曲线的方程、曲率等。
这些知识帮助我们确定弧线的形状和尺寸,使建筑物呈现出独特的美感。
六、体积和表面积体积和表面积是建筑物的重要参数,它们直接影响建筑物的使用功能和造价。
通过计算建筑物的体积和表面积,我们可以确定建筑物所需的材料和成本,并确保建筑物满足使用要求。
七、力学和结构建筑物需要承受外部荷载和内部力的作用,因此需要使用力学和结构学的知识来设计和构建稳定的建筑物。
通过计算和分析力的大小和方向,我们可以确定建筑物的结构形式,以确保其安全性和稳定性。
八、光线和阴影光线和阴影是建筑中不可忽视的要素。
通过数学计算和分析,我们可以确定建筑物在不同时间和位置的光照条件,以及产生的阴影的位置和形状。
这些信息对于建筑物的照明设计和室内舒适性至关重要。
九、统计和概率在建筑设计和规划中,统计和概率是用来分析和预测建筑物的使用情况和性能的重要工具。
古希腊帕特农神庙中的柱子是黄金分割法则的写照

古希腊帕特农神庙中的柱子是黄金分割法则的写照
黄金比又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1∶0.618,即长段为全段的0.618。
0.618被公认为最具有审美意义的比例数字。
上述比例是最能引起人的美感的比例,因此被称为黄金分割。
黄金分割被认为是建筑和艺术中最理想的比例。
建筑师们对数字0.618特别偏爱,无论是古埃及的金字塔,还是巴黎的圣母院,或者是近世纪的法国埃菲尔铁塔,都有与0.618有关的数据。
黄金分割与大多数门窗的宽长之比也是0.618;还有,在古希腊神庙的设计中就用到了黄金分割。
古希腊巴特农神庙是举世闻名的完美建筑,它的高和宽的比是0.618。
建筑师们发现,按这样的比例来设计殿堂,殿堂更加雄伟、美丽;去设计别墅,别墅将更加舒适、漂亮。
连一扇门窗若设计为黄金矩形都会显得更加协调和令人赏心悦目。
至今这还是世界最美丽的建筑之一,这神庙建筑于古希腊数学繁荣的年代,并且它的美丽就是建立在严格的数学法则上的。
如果我们在巴特农神庙周围描一个矩形,那么发现,它的长是宽的大约1.6倍,这种矩形称为黄
金矩形。
它的边组成黄金分割,数学家给出了黄金分割的精确定义。
吴景祥的学术与建筑教育思想

吴景祥的学术与建筑教育思想王凯【摘要】吴景祥是中国近现代著名建筑师、教育家。
他早年留法,1949年以前任海关总署建筑师,1949年后历任同济大学建筑系主任、同济大学建筑设计院院长、第五届上海建筑学会理事长等职。
他是同济大学建筑教育和同济大学建筑设计院的开创者之一,是今日同济建筑精神中不可或缺的重要组成部分。
本文通过论述吴景祥成长、求学、工作、研究的历程,分析研究吴景祥的超越\"学院派\"与\"现代派\"的学术主张、服务国家和人民的实践特色,以及解决问题与面向实践的教学理念,归纳提炼出吴景祥与同济诸位先生共同开创的\"理性务实、注重实践和职业技能的培养、服务社会\"的精神。
【期刊名称】《中国艺术》【年(卷),期】2019(000)002【总页数】10页(P34-43)【关键词】吴景祥;同济大学;现代建筑;建筑教育【作者】王凯【作者单位】[1]同济大学建筑与城市规划学院;【正文语种】中文【中图分类】G40-0920世纪30年代的吴景祥吴景祥(190 5—1999),字白桦,广东中山人,中国近现代著名建筑师、教育家,同济大学建筑系的创立者之一。
一、学术人生19 0 5年,吴景祥生于广东。
他的父亲吴天赐年轻时曾追随孙中山参加同盟会。
辛亥革命以后,吴老先生一直在邮政界任职,最终任北平邮电总局次长。
吴老先生育有四儿五女,吴景祥是家里的长子,他们从小跟着父亲到北方任职,并在北方长大。
年少时的吴景祥“长得浓眉大眼,聪明伶俐,人也规矩听话,颇受父亲宠爱。
”[1]1. 负笈法国1925年,吴景祥考入刚建立的清华大学土木工程系[2],正式揭开奉献给工程和建筑学术事业的人生序幕。
1929年,他以优异的成绩毕业后,获得官费留学资助,踏上了出国深造的旅程。
据其回忆,“毕业后本来想去美国再求深造,后来想想美国的历史较浅,一切的文化都是由欧洲传去,不如直接去欧洲,遂去法国再学建筑”。
萨伏伊别墅the Villa Savoye
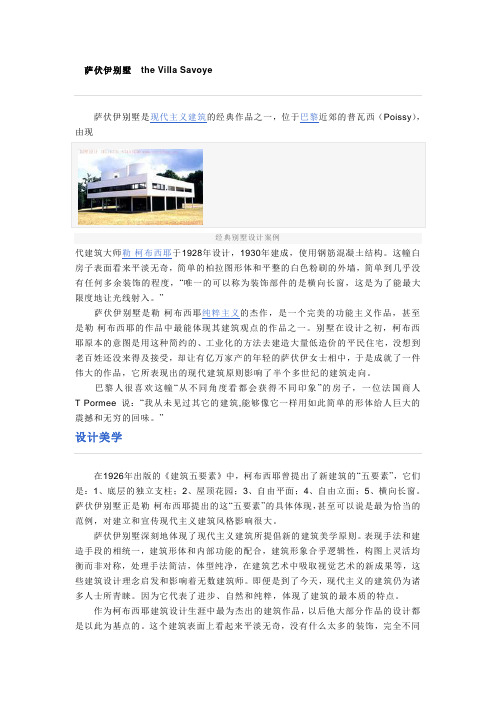
萨伏伊别墅the Villa Savoye萨伏伊别墅是现代主义建筑的经典作品之一,位于巴黎近郊的普瓦西(Poissy),由现经典别墅设计案例代建筑大师勒·柯布西耶于1928年设计,1930年建成,使用钢筋混凝土结构。
这幢白房子表面看来平淡无奇,简单的柏拉图形体和平整的白色粉刷的外墙,简单到几乎没有任何多余装饰的程度,“唯一的可以称为装饰部件的是横向长窗,这是为了能最大限度地让光线射入。
”萨伏伊别墅是勒·柯布西耶纯粹主义的杰作,是一个完美的功能主义作品,甚至是勒·柯布西耶的作品中最能体现其建筑观点的作品之一。
别墅在设计之初,柯布西耶原本的意图是用这种简约的、工业化的方法去建造大量低造价的平民住宅,没想到老百姓还没来得及接受,却让有亿万家产的年轻的萨伏伊女士相中,于是成就了一件伟大的作品,它所表现出的现代建筑原则影响了半个多世纪的建筑走向。
巴黎人很喜欢这幢“从不同角度看都会获得不同印象”的房子,一位法国商人T·Pormee说:“我从未见过其它的建筑,能够像它一样用如此简单的形体给人巨大的震撼和无穷的回味。
”设计美学在1926年出版的《建筑五要素》中,柯布西耶曾提出了新建筑的“五要素”,它们是:1、底层的独立支柱;2、屋顶花园;3、自由平面;4、自由立面;5、横向长窗。
萨伏伊别墅正是勒·柯布西耶提出的这“五要素”的具体体现,甚至可以说是最为恰当的范例,对建立和宣传现代主义建筑风格影响很大。
萨伏伊别墅深刻地体现了现代主义建筑所提倡新的建筑美学原则。
表现手法和建造手段的相统一,建筑形体和内部功能的配合,建筑形象合乎逻辑性,构图上灵活均衡而非对称,处理手法简洁,体型纯净,在建筑艺术中吸取视觉艺术的新成果等,这些建筑设计理念启发和影响着无数建筑师。
即便是到了今天,现代主义的建筑仍为诸多人士所青睐。
因为它代表了进步、自然和纯粹,体现了建筑的最本质的特点。
作为柯布西耶建筑设计生涯中最为杰出的建筑作品,以后他大部分作品的设计都是以此为基点的。
房屋设计中的数学原理

房屋设计中的数学原理
房屋设计中涉及许多数学原理,以下列举一些常见的:
1. 几何学原理:包括平面几何、立体几何以及曲线几何。
房屋设计中需要考虑空间布局、建筑平面布置、空间体积计算等问题,这些都涉及到几何学原理的应用。
2. 比例原理:房屋设计中需要考虑各个空间和物体之间的比例关系,以确保整体的协调和美观。
比例原理也适用于门窗的大小、家具的布置等方面。
3. 数量测量原理:在房屋设计中需要进行测量工作,以确定房间的尺寸、家具的尺寸等。
准确的数学测量原理是保证设计准确性的基础。
4. 结构力学原理:在房屋设计中需要考虑建筑物的结构强度和稳定性。
结构力学原理涉及到材料强度、力的平衡、结构设计等问题。
5. 热传导原理:房屋设计中需要考虑房间的保温和冷却效果。
热传导原理用于计算热量的传递和保温材料的选择。
6. 建筑设计原理:房屋设计需要遵循建筑设计原理,包括权衡各种因素(如功能性、审美性、空间布局等),根据建筑物的用途和预算制定设计方案。
这些数学原理的应用保证了房屋设计的精确性、稳定性和可行性。
房屋设计师需要熟练掌握数学知识,并在设计中灵活运用。
理想别墅的数学——柯林罗

Colin Rowe, “The Mathematics of the Ideal Villa” in“The Mathematics of the Ideal Villa and Other Essays”, Cambridge: the MIT Press c.1976理想别墅的数学科林.罗,原美国哈佛大学建筑系历史教授“美有两种起因:天然性和习惯性。
自然美来自构成统一性的几何,即均衡与比例。
习惯美来自使用,因为熟悉会使人生发对事物原本没有的爱。
后者出错的机会较大。
真正的标准应该是自然或几何美。
几何图形天生地比不规则图形更美:方与圆为最,其次是平行四边形和椭圆。
直线有两种状态最美:水平状态与垂直状态;因为这种美来自大自然,而且来自需要,没有状态会比挺拔更加结实”。
克里斯朵夫.华伦爵士(Sir Christopher Wren),《根源》(Parentalia)***********************************************************************************作为集中式建筑的理想类型,帕拉蒂奥(Palladio)设计的圆厅别墅(Villa Capra-Rontonda)(图1)可能会比任何其它同类建筑更会令人印象深刻。
它的构成很数学化、抽象、四四方方,从外貌看不出功能,非常容易记住。
它的翻版也遍及四海。
即便帕拉蒂奥自己提到它,也会充满深情。
“基地环境极尽愉悦和优美,因为基地就在小山上,出入方便。
基地一侧濒临可以行船的巴奇里奥河;另一边面对着最赏心悦目的山坡,象个巨大的剧场,到处长满最优质的水果和最鲜美的葡萄。
因此,从基地的每一处望去,全是美景,有些是掩映的,有些是舒展的,有些绵延到天际,因此,房子在四个立面上都设计了前厅”。
既然我们的心灵能够接受这样抒情的描写,不妨再多读一段。
柯布西耶(Le Corbusier)在其《论精确》中的一段就很象是帕拉蒂奥的回声。
理想别墅的数学

理想别墅的数学当我们畅想拥有一座理想的别墅时,可能首先浮现在脑海中的是其奢华的装饰、优美的环境和舒适的空间。
然而,在这看似梦幻的背后,数学其实扮演着至关重要的角色。
从建筑设计的比例到空间的布局规划,从材料的成本计算到能源的高效利用,数学的原理和规律无处不在。
让我们先从别墅的建筑设计说起。
一个美观且舒适的别墅,其外观的比例和尺寸往往遵循着一定的数学规律。
黄金分割比例,这个在美学中被广泛应用的数学概念,也在别墅设计中发挥着重要作用。
比如,窗户的高度与宽度之比、阳台的长度与房屋整体长度之比,如果能接近黄金分割比例,就能给人带来视觉上的和谐与美感。
再看看别墅的空间布局。
数学帮助我们精确计算每个房间的面积和尺寸,以确保功能的实用性和空间的高效利用。
客厅的面积需要足够宽敞,以容纳家人和客人的活动,但又不能过大而显得空旷。
卧室的尺寸则要根据床的大小、衣柜的摆放以及通行的便利来合理规划。
通过数学计算,我们可以确定最合适的长宽比例,使得空间既舒适又不浪费。
不仅如此,数学在建筑结构的稳定性方面也起着关键作用。
建筑师需要运用力学和数学原理来计算房屋的承重能力,确保柱子、梁和墙体能够承受房屋的重量和外部的压力。
比如,在计算柱子的直径和间距时,需要考虑到材料的强度和房屋的总重量,运用数学公式进行精确计算,以保障别墅的安全性。
在预算方面,数学更是不可或缺。
从购买土地到建筑材料的采购,再到施工人员的费用,每一项都需要进行详细的成本计算。
通过数学运算,我们可以制定合理的预算,并在各个环节进行成本控制,避免超支。
以建筑材料为例,我们需要根据别墅的面积和设计要求,计算所需的砖块、木材、钢材等材料的数量。
同时,还需要考虑到材料的价格波动,运用数学模型进行预测和分析,以便在合适的时机采购,节省成本。
能源利用也是理想别墅设计中的一个重要考量因素,而这同样离不开数学。
例如,太阳能板的安装角度和面积需要通过数学计算来确定,以最大程度地吸收太阳能。
数学与建筑如何利用数学设计美丽的建筑物

数学与建筑如何利用数学设计美丽的建筑物数学与建筑:创造美丽的建筑艺术现代建筑艺术充满了创意和惊艳,但是很少有人知道,数学是建筑物背后的关键。
数学在建筑设计中发挥着重要的作用,它能够帮助设计师创造出美丽、稳定和功能完善的建筑物。
通过运用数学的原理和技巧,建筑师能够实现更大胆和复杂的设计理念,为人们提供众多令人惊叹的建筑奇观。
一、黄金比例与建筑设计黄金比例是指两个数中较大数与较小数之比等于两数之和与较大数之比,即 (a+b)/a = a/b,这个比例被广泛应用在建筑设计中。
建筑师会通过运用黄金比例,使建筑物的形状和比例更加和谐美观。
黄金比例可以帮助建筑师在大厦的高度、宽度和其他尺寸上作出明智的决策。
例如,某座建筑的高度与宽度比例符合黄金比例,会给人一种宜人的视觉感受。
二、对称与平衡性对称性在建筑设计中起着重要作用。
数学中的几何原理可以帮助建筑师在平面、立面和结构设计上实现对称。
对称的建筑物给人一种稳定和平衡的感觉,符合人们的审美。
某些建筑中使用了轴对称,比如佛罗伦萨大教堂,有多个相互对称的门和窗户,使建筑物看起来更加宏伟和壮观。
三、曲线与曲面数学中的曲线和曲面可以帮助建筑师创造出具有流线型和优雅形状的建筑物。
通过使用曲线和曲面,建筑师可以打破传统的直线和平面设计,创造出令人惊叹的建筑形象。
例如,法国著名建筑师勒·柯布西耶设计的罗纳河艺术中心,通过运用曲面结构,创造出独特的外观和观感。
四、结构稳定性与力学原理建筑物的稳定性是建筑设计的基础,而数学的力学原理则是保证这一点的关键。
数学可以帮助建筑师计算出建筑物的荷载、承重和应力分布情况,从而设计出稳定可靠的结构。
比如,在建造大型桥梁时,数学和力学原理可以帮助工程师计算出桥梁所需的材料和结构尺寸,确保其能够承受车辆和自然力的负荷。
五、光与影的运用数学中的光学原理对于建筑师来说也是非常重要的。
建筑物的照明设计需要考虑到自然光线的角度和强度变化。
通过使用数学模型,建筑师可以确定什么样的设计会产生特定的光与影效果。
柯林·罗的形式分析与德州教改——以《理想别墅的数学》与《手法主义与现代建筑》为例

筑》 ③为中心,通过总结柯林 罗视觉研究的特点与主要方法,尝试在德州教改的背景下解读柯林 • 罗的现代主义建筑观。本文
讨论的两篇文章均发表于 20 世纪 50 年代之前,为柯林 • 罗早期最重要的作品,文章都以现代主义建筑为讨论对象,一经发表即
在美国和欧洲学术界产生了深刻影响并引起广泛讨论,这两篇文章对于了解柯林 • 罗的现代主义建筑的观点及理解同时代的建
萨伏伊之所以呈现出与圆厅别墅不同的内部空间组 织方式,更多的原因在于现代的田园风光与传统的使用功 能之间的强烈反差。如果进一步分析作者挑选案例的原 则,可以发现,除了两个建筑在各自时代的代表性和彼此 间的相似性之外,两位建筑师本身诗情画意的文字描述上 同样表现出极大的相似性(自豪感),而罗认为这种诗情画 意和建筑本身集中式形制之间同样存在矛盾性。另外,罗 认为二者之间存在差异性,圆厅别墅构筑的是一个美好生 活的舞台,而萨伏伊则无疑是一种高度抒情生活的背景, 但这一点并不妨碍罗从视觉感受的角度将二者进行比较。 更为重要的是,柯林 • 罗同期的人们普遍认为,萨伏伊别 墅是一个居住机器,一种体量与空间的穿插组合,一种时 空的流溢,这种对于现代主义建筑描绘的术语表现出人们 的普遍观念,即将现代主义建筑视为与古典建筑割裂的新
Liang Jing (School of Architecture, Southeast University, Nanjing Jiangsu 210096, China)
Abstract: This paper is centered on two typical articles of Colin Rowe selected from The Mathematics of the Ideal Villa and Other Essays——The Mathematics of the Ideal Villa and Mannerism and Modern Architecture. The author tries to interpret Colin Rowe’s view of modernist architecture in the context of education reform in Texas by summarizing the characteristics and main methods of his visual research. The two articles were both published in 1950s and were the most important works of Colin Rowe that discussed modernist architecture. Upon publishing, both of the two typical articles has caused extensive discussion and profound influence in the academic circles of the United States and Europe. These two articles are extremely important for us to understand Colin Rowe’s view of modernist architecture and to understand the contemporary architectural theory, and to learn the clues of the later educational reform in Texas. Key words: modernism; formal analysis; mannerism; transformation view; educational reform in Texas
空间构成训练--香港中文大学基础设计课程

空间构成训练--香港中文大学基础设计课程徐亮【摘要】本文通过介绍一组抽象空间练习,系统回顾了香港中文大学建筑学院基础设计课程”建筑入门”的教学情况。
这些练习根据不同的问题重心分成了五个循序渐进的训练组群:技巧、形式、构成、系统与体验。
在介绍课程内容之余,通过探讨其教学法基础以期建立起关于该课程的全面认识。
【期刊名称】《世界建筑导报》【年(卷),期】2016(031)006【总页数】2页(P40-41)【作者】徐亮【作者单位】香港中文大学建筑系【正文语种】中文“建筑入门”(Introduction to Architecture)是香港中文大学建筑学院2015-16年度开设的一年级基础通识课,该课程的前身为2014-15学年的“活在建筑:理解空间”(Living Architecture: understanding space)。
课程共计十三周,以空间认知与操作为核心,由讲座与设计练习两部分组成,分别安排在周二与周五下午,每周共计五课时。
该课程的主讲教师为布鲁斯·朗曼(Bruce Lonnman)先生,在教学中负责整体统筹与讲座授课。
笔者作为该课程的教学助理,负责设计练习部分的教学协调,与吴佳维女士和毛家谦先生分组进行设计指导。
本文将从设计练习的角度重点介绍该教学体系,辅以讨论其教学法背景,以期为读者提供清晰、系统的教学参考。
为配合该课程的进一步发展[1],我们对原先的“三步走”训练体系(建筑图学、基础空间练习与网格的空间组织)重新梳理,根据主题分为五个练习组群(技巧、形式、构成、系统与体验,详见表1),并安排与之配合的讲座。
五个组群的训练依次由简单到复杂,教师可根据实际需要从各组群中选择练习进行搭配。
(1)技巧 | 绘图第一组群旨在培养学生的基础绘图能力,围绕“徒手线条”与“物件绘图”展开。
“徒手线条”训练学生于对于线型与线宽的认识,强调线条绘制过程中手眼脑之间的控制。
其后,通过在网格纸上使用徒手线条快速记录一组具有模数关系的组合物件(图1),包括各正投形图及轴测投影(plan oblique),以快速掌握建筑图学的基本原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【译者案:昨日,差不多快翻译完毕笛卡尔和佩劳之后,就想起了科林.罗的这篇《理想别墅的数学》名文了。
先说科林.罗,他是维特考尔的学生,维特考尔是沃尔夫林的学生。
那我们就知道科林罗的建筑分析跟沃尔夫林是很有渊源的。
而埃森曼,又是科林罗的学生,也就是说,在这位解构主义建筑师的骨子里,一直就是建筑的形式分析的行家里手。
那么,什么是建筑案例的形式分析呢?肯定,这就涉及到了建筑的比例分析,几何解析,以及平立剖的构成要素的句法分析。
这些东西,肯定肯定肯定,不是工匠和结构师要学的。
却是西方建筑师以及艺术史学家们一样要做的功课。
即使今日,你要欧美的本科生的艺术史和建筑史的课堂上去,对于古典建筑的形式分析仍然是考试的一个要点。
至于中国各个建筑院校里,本科或是硕士做不做这样的功课,我不清楚;但是,我的建筑史是这么学出来的。
从宗教、文学、人类学、艺术史的角度,正如科林罗所言,这种功课的神圣性肯定已经消失了。
但是,这种分析却部分地还原了文艺复兴建筑师的创作历程和心态;也解释了很多不然无法看懂的柯布的设计条件。
他要呼应什么?反对什么?消解什么?形式分析当然不是建筑设计的全部。
就像句法分析不是文学的全部一样。
然而,如果没有读过这篇文章的同学,记住了,一定一定要补上这一课。
否则,你的建筑史永远是瘸腿的建筑史。
另:我知道王群老师在翻译科林罗的这本书。
可是,一直不见全书汉译出版,我就把我十多年前的译稿贴出来。
算是替王群老师补白。
等王老师的译文出来,可以把我的删掉。
】Colin Rowe, “The Mathematics of the Ideal Villa” in“The Mathematics of t he Ideal Villa and Other Essays”, Cambridge: the MIT Press c.1976理想别墅的数学科林.罗,原美国哈佛大学建筑系历史教授“美有两种起因:天然性和习惯性。
自然美来自构成统一性的几何,即均衡与比例。
习惯美来自使用,因为熟悉会使人生发对事物原本没有的爱。
后者出错的机会较大。
真正的标准应该是自然或几何美。
几何图形天生地比不规则图形更美:方与圆为最,其次是平行四边形和椭圆。
直线有两种状态最美:水平状态与垂直状态;因为这种美来自大自然,而且来自需要,没有状态会比挺拔更加结实”。
克里斯朵夫.华伦爵士(Sir Christopher Wren),《根源》(Parentalia)***********************************************************************************作为集中式建筑的理想类型,帕拉蒂奥(Palladio)设计的圆厅别墅(Villa Cap ra-Rontonda)(图1)可能会比任何其它同类建筑更会令人印象深刻。
它的构成很数学化、抽象、四四方方,从外貌看不出功能,非常容易记住。
它的翻版也遍及四海。
即便帕拉蒂奥自己提到它,也会充满深情。
“基地环境极尽愉悦和优美,因为基地就在小山上,出入方便。
基地一侧濒临可以行船的巴奇里奥河;另一边面对着最赏心悦目的山坡,象个巨大的剧场,到处长满最优质的水果和最鲜美的葡萄。
因此,从基地的每一处望去,全是美景,有些是掩映的,有些是舒展的,有些绵延到天际,因此,房子在四个立面上都设计了前厅”。
既然我们的心灵能够接受这样抒情的描写,不妨再多读一段。
柯布西耶(Le Co rbusier)在其《论精确》中的一段就很象是帕拉蒂奥的回声。
柯布西耶的那段文字同样抒情,且更具爆发力。
他是这么描写普瓦西萨沃依别墅(Savoye House at Poissy)的基地的(图2)。
“基地:一片辽阔的草坪缓缓涌向平整的高地。
房子象是浮在空中的盒子。
果园统领着四周的草场。
平面是纯净的。
建筑在普瓦西乡村的景色中找到自己的位置。
正是这儿美丽的乡村景色和农村生活吸引了房子的主人,他们将透过四面长窗、从高地上望出去,在此安坐、静思。
他们的日常起居活动将延伸到建筑里,成为维吉尔之梦”。
对萨沃依别墅人们有着多种解读:它可能只是个“居住的机器”,也可以是空间与体量的相互穿插的布局,或是一次“时-空”的解放;但是柯布西耶在文中提到了“维吉尔之梦”(dreams of Virgil),这使人不得不联想到帕拉蒂奥对圆厅别墅的记述。
只是帕拉蒂奥笔下的风景更乡村化、田园化,他所呼唤倒未必是野性的牧场,他的尺度更大。
不过,这两段二人的文字效果确实很像。
在别处,帕拉蒂奥详述了别墅应有的理想生活。
从一个创造出来的秩序的一隅,别墅的主人将看护着自己家业的成熟,体味田地与花园之间反差的生动;反思更迭,年复一年地冥思古人简朴人生的美德、自己生命的和谐组织,这样,他的居所就类似于天堂。
“古时,先贤通常会归隐的地方当有房舍、花园、喷泉等美景,以便招待到访的贤朋圣亲。
在上追求品质,在下极尽快乐”。
或许,这就是古罗马诗人的“维吉尔之梦”。
随着岁月的流逝,这个梦想被恣意诠释,贴上了古罗马的美德、优秀、帝国辉煌、奢靡,这些人们在想象中虚构了古代世界的东西。
或许,在画家普桑(Poussin)泛着古风魅影的风景画中才能让帕拉蒂奥找到家的感觉;或许,正是这种地景的基本要素,就是孑然的方盒子与如画场所之间、在几何化体量与纯真自然面貌之间对比的那种强烈,才是柯布西耶的文章中古罗马暗喻的真正原因。
如果说圆厅别墅的建筑构成了美好生活的布景,在波塞,建筑则是要为抒情的高效生活,提供舞台背景;虽说这一当代的田园已不再拘于传统的使用方式,显然,维吉尔式的怀旧还可以在萨沃依别墅那里看得出来。
从卫浴齐备的卧房出来,停个片刻,沿坡道向上走去,维吉尔《农事诗集》(memory of the Georgics)的记忆就会在这个片刻自己冒出来;或许,从车库里把车倒出来、准备开往巴黎的时候,对于《农事诗集》的历史援引还会增加一点刺激。
*******************************************************************************然而,这里更具具体可比性的案例倒是帕拉蒂奥建在马康坦塔的佛斯卡里别墅(Villa Foscari in Malcontenta)(1550-60期间)(图3图4)与柯布西耶1 927年在加尔什设计的斯坦因别墅(house of Mr. and Mrs. Michael Stein at Garches)(图5图6)。
从表面上看,这两个房子无论从形象到意象都相去甚远,把它们扯到一起显得小题大做。
但是,如果说帕拉蒂奥的马康坦塔之作(即佛卡里别墅)所具有的令人痴迷的心理和身体引力,柯布的那栋房子很难出其左右,但是柯布之作时而象是条船、时而象个体操房的情绪上的变化倒是值得我们去注意。
首先,马康坦塔与加尔什的共同之处在于二者都是单一的体块(single block)(图7图8);尽管二者屋面的处理方式不同,我们还是会注意到,二者在体量上有相似性,每个的长、宽、高都是8、5.5、5个基本模数单元。
此外,二者都有相似的开间(bay)结构。
从左到右,这两个建筑展示出来的(或暗藏的)交替性节奏,2、1、2、1、2。
从前到后,二者的比例都是三段式(图1)。
但在这个阶段,我们最好使用“差不多”这个字眼。
因为两个建筑在水平座标上的比例相同,却在平行于前后立面的那些结构线的分布上,二者之间存在着细微却重要的差别。
加尔什从前到后的结构支撑间隔比例为0.5、1.5、1.5、1.5、0. 5。
马康坦塔为2、2、1.5。
换言之,柯布西耶通过把斯坦因别墅前后悬挑了0. 5单元,实现了对于中间一跨的压缩,并把人们的关注点从中间一跨转移到了别处。
而帕拉蒂奥则通过导向前厅的递进,突出其中央区间,保证它成为左右、前后这两个区域里的关注点。
因此,一个设计(柯布的)是潜在地分散式的、可能还是平权式的;而另一个设计(帕拉蒂奥的)则属集中式的、明确等级化的。
但是,即便有着这些看上去的差异,我们还可以加上一点,在这两个建筑身上,都有一个突出出来的要素——要么是突出出来的平台要么是贴上去的前厅——深度均为1.5单元。
当然,在结构上,二者没有可比性。
在某种程度上,两位建筑师都把结构视为构成建筑布局的依据。
帕拉蒂奥用的是实体承重墙,对此,他这样写到:“应该看到,这里左右房间的配置是对称的,左右两侧的肌理相同可以均摊房顶的重量。
假如左右跨度一大一小,当然是小跨的那部分更结实,更能承载,而大跨的那一部分是脆弱的,随着时间的推移将带来许多麻烦,甚至毁了整个建筑”。
帕拉蒂奥所言的是那种已经被程式化了的母题的逻辑处置,但是他试图用结构原因去解释自己平面设计上的格局对称。
而柯布西耶则一直想证明结构可以被用作组织设计的形式要素的基础,他用新的体系去跟旧的体系做对比,所以比帕拉蒂奥显得更有些道理。
“我想请您注意钢和混凝土建筑的特点并由此带来的建筑‘平面的解放’。
自由平面自由立面独立的框架结构全部玻璃的水平长窗桩柱屋顶花园具有储藏功能的内墙隔断取代零乱笨重的家具”帕拉蒂奥的墙体结构体系使得他不得不在不同楼层使用相同的平面,柯布西耶的框架结构当然更适于平面的灵活布置。
但是,两位建筑师的说法都让他们所倡导的理由冒进了一些。
帕拉蒂奥说,实墙结构需要绝对的对称;柯布宣称,框架结构需要自由式空间分割。
但这一定,起码部分地,来自他们二人对高级风格上不同个人诠释,因为使用传统结构的不对称建筑一样可以站得住;使用框架结构的建筑也可以使用传统平面,并且很成功。
两栋建筑里都有一个上去一层的夹层,这个夹层都通过平台或前厅以及一跑(或多跑)楼梯,联到户外花园。
在马康坦塔,主层有一个十字厅,布局对称,两边各有三间房、两部楼梯。
加尔什的平面布局没有这么容易辨认,主层也有一个中厅、也有两部楼梯,但是其中一部楼梯跟马康坦塔的排置方式相同,另一部则转了九十度角。
另外,从门厅这一层开始,我们就能在楼板不对称切口那里可以看到楼上。
位于加尔什的斯坦因别墅的屋顶平台(对应着马康坦塔的前厅)通过结构上减了一排柱子,形成了一块部分凹陷的体量,【这种凹陷的半户外空间】,跟主体室内空间形成了肯定不那么容易感受到的关系。
这样,在加尔什这栋房子里,十字厅的形状仅留下一点痕迹(大概,餐厅处半拱空间可以被看成是对十字厅的一点儿痕迹?)因此,与帕拉蒂奥主体空间的中心性相反,加尔什的主层空间是平衡的Z字型结构,为此,柯布西耶在主卧那一层扔进去了一间书房,就是为了平衡这个Z字结构。
最后,在马康坦塔,存在着明显的十字轴线,在加尔什,这种移动流线上的彼此切割,只是在靠边墙的那些向心的虚空处透露了(i ntimated by the central voids)一点点,只被允许隐含地发展了一下,而且还是片段式的。
