16年上海初三上复旦实验中学期中试卷参考答案
上海市复旦实验中学2016届九年级化学上学期期中试题(含解析)沪教版

2015-2016学年上海市复旦实验中学九年级(上)期中化学试卷一、选择题:(每小题1分,共20分,下列各题均只有一个正确选项)1.下列变化中属于化学变化的是( )A.自制冰块 B.葡萄榨汁 C.车胎爆炸 D.燃放烟花2.下列属于物质的化学性质的是( )A.溶解性B.助燃性C.颜色 D.熔点3.生活中食用的“加碘食盐”中的碘是指( )A.碘元素B.碘分子C.碘单质D.碘原子4.我们的生活中常用到下列物质,其中属于纯净物的是( )A.红酒 B.18K金项链C.冰水混合物D.可乐5.下列物质属于氧化物的是( )A.O2B.H2O C.NaOH D.H2SO46.三氧化二铬(Cr2O3)可用作油漆颜料,Cr2O3中Cr的化合价是( )A.﹣3 B.﹣2 C.+2 D.+37.地壳中含量最多的金属元素是( )A.Al B.Fe C.Ca D.O8.不属于空气质量日报主要污染物的是( )A.二氧化碳 B.二氧化硫 C.可吸入颗粒D.氮氧化物9.下列物质中只存在游离态氧元素的是( )A.液氧 B.空气 C.双氧水D.自来水10.如图所示化学实验操作错误的是( )A.液体的倾倒 B.液体的量取C.点燃酒精灯 D.滴加液体11.如图所示实验主要说明( )A.分子很小 B.分子间有间隔C.分子不断运动 D.分子可以分成原子12.天然气的主要成分是甲烷(CH4),下列有关化学式CH4的表示意义,错误的是( ) A.表示甲烷这种物质B.表示甲烷由碳、氢两种元素组成C.表示一个甲烷分子D.表示甲烷由1个碳原子和4个氢原子构成13.下列化学方程式书写正确的是( )A.S+O2SO2↑ B.CuSO4+2NaOH→Na2SO4+Cu(OH)2C.3Fe+2O2Fe3O4D.2P+O5P2O514.关于氧气的叙述错误的是( )A.氧气具有可燃性B.氧气能提供动植物呼吸C.氧气能支持燃烧D.过度吸氧不利于健康15.有关物质的量,说法错误的是( )A.物质的量是联系宏观世界和微观粒子的桥梁B.物质的摩尔质量在数值上等于式量或相对原子质量C.摩尔是国际单位制中七个基本物理量之一D.1mol任何物质都含有约6.02×1023个微粒16.实验现象描述正确的是( )A.磷在空气中燃烧,产生大量的白色烟雾B.铁丝在空气中燃烧,火星四射,生成黑色固体C.硫粉在空气中燃烧,观察到微弱的淡蓝色火焰,并产生二氧化硫D.双氧水加入二氧化锰后,产生大量气泡17.关于原子,分子叙述错误的是( )A.原子和分子都在不停的运动B.原子和分子在化学变化中都能够再分C.分子是原子构成D.原子和分子都是构成物质的微粒18.用如图所示装置测定空气中氧气的含量,实验前在集气瓶内加入少量水,并做上记号.下列说法中错误的是( )A.实验前一定要检验装置的气密性B.实验时红磷一定要过量C.红磷点燃后要迅速伸入瓶中,并盖紧瓶塞D.把红磷改成铁丝,也能得到正确的实验结论19.如图所示图象能正确反映对应变化关系的是( )A.加热一定质量的高锰酸钾B.在密闭的容器中点燃一定质量的镁条C.用等质量、等浓度的双氧水分别制取氧气D.将水电解一段时间:无论任何时刻,氧气的质量:氢气的质量=8:120.在一定条件下,甲、乙、丙、丁在某密闭容器中发生反应,测得反应前后各物质的质量分数如图所示,正确的说法是( )A.该反应是分解反应B.若消耗3g乙,则生成17g丙C.丁一定是该反应的催化剂D.甲、乙的质量之和一定等于生成丙的质量二、填空题:(共19分)请根据要求在答题纸相应的位置作答21.用化学用语填空:(1)2个氢分子__________,硫酸根__________.(2)在空气中:占空气体积78%的是__________;引起温室效应的是__________;可用于制成霓虹灯电光源的是__________;久置空气中使饼干变软的是__________.22.淀粉是植物体中贮存的养分,淀粉在动物和人类肠胃的消化过程中,可以分解成葡萄糖(C6H12O6),试回答以下问题:(1)C6H12O6是由__________种元素组成的,其摩尔质量是__________.(2)C6H12O6中氢、氧原子的物质的量比是__________,碳元素的质量分数是__________.(3)0.5mol C6H12O6中,约含有__________ 个C6H12O6分子,约含有__________mol碳原子.23.如图所示的示意图形象的表示一定条件下发生化学变化的过程,其中表示硫原子,表示氧原子.(1)该反应的化学方程式是__________;反应基本类型是__________(1)从该示意图说明化学变化的实质是__________.24.粗盐中除氯化钠外还含有可溶性的氯化钙、氯化镁以及泥沙等杂质.初步提纯粗盐的实验流程如图所示:(1)“滤渣”是粗盐中含有的__________,(2)实验过程中多次用到玻璃棒,过滤时玻璃棒的作用是__________.(3)提纯过程中蒸馏水的用量过多,造成的后果是__________.(3)实验小组通过正确的计算发现,回收得到的精盐的质量比实际偏低,可能的原因之一是__________.三.简答题(共21分)请根据要求在答题纸相应的位置作答25.实验小组用氯酸钾和二氧化锰的混合物制取氧气,反应过程中混合物的质量变化如图所示.完全反应后最终收集到0.3mol氧气.(1)求原混合物中含氯酸钾的质量.(根据化学方程式列式计算)__________(2)图中P点处试管内的固体物质有__________.26.实验是化学学习的基础,某小组同学利用如图所示装置进行了有关氧气的实验(1)图中标有 I、Ⅱ的仪器名称:I__________;Ⅱ__________.(2)使用C装置收集氧气的依据是__________,证明氧气集满的方法是__________.(3)用装置B制取氧气,反应的化学方程式是__________.通过仪器 I向锥形瓶添加液体时,液面应__________(填“高”或“低”)于仪器 I的末端.利用此装置制取时,发现气泡喷射出来,并带出反应液,不利于气体的收集.为使气体平稳产生,请对该装置进行改进并简述操作要点__________.(4)F、G是两瓶收集好的氧气,进行铁丝与氧气的反应,应选择集气瓶__________(填“F”或“G”),观察到的现象是__________.将点燃的木炭伸入另一集气瓶中完全反应,该反应的化学方程式是__________.若要证明生成物,方法是__________ (简述操作步骤、现象、结论)(5)若要测定一定量的氯酸钾生成氧气的体积,可以将D中的集气瓶改成量筒,把气体收集在量筒中,正确的实验步骤是:__________a.检查装置气密性→装药品→把导气管伸入装满水的量筒中→加热b.检查装置气密性→装药品→加热→待有连续均匀气泡产生时,把导气管伸入装满水的量筒中c.装药品→检查装置气密性→加热→把导气管伸入装满水的量筒中d.装药品→检查装置气密性→加热→待有连续均匀气泡产生时,把导气管伸入装满水的量筒中.27.甲乙两位同学以“化学反应中反应物和生成物之间的质量关系”为课题进行探究.他们设计的实验装置和选用药品如图A、B所示,在反应前后进行了规范的操作、准确的称量和你认为__________(“甲”还是“乙”)的结论正确,导致另一种结论错误的原因是__________.【结论分析】研究“化学反应中反应物和生成物之间的质量关系”,获得正确结论的原因是:化学反应前后,__________(填序号)一定不变.a.原子种类 b.原子数目 c.分子种类 d.分子数目e.元素种类f.物质种类.2015-2016学年上海市复旦实验中学九年级(上)期中化学试卷一、选择题:(每小题1分,共20分,下列各题均只有一个正确选项)1.下列变化中属于化学变化的是( )A.自制冰块 B.葡萄榨汁 C.车胎爆炸 D.燃放烟花【考点】化学变化和物理变化的判别.【专题】结合课本知识的信息;物质的变化与性质.【分析】化学变化过程中有新物质生成,物理变化过程中没有新物质生成,是否生成新物质是判断化学变化的依据.【解答】解:A、自制冰块过程中,只是水的状态发生改变,没有生成新物质,属于物理变化;B、葡萄榨汁,只是把汁液榨取出来,没有生成新物质,属于物理变化;C、车胎爆炸过程中,是因为气体压强过大造成的,没有生成新物质,属于物理变化;D、燃放烟花过程中生成二氧化碳等物质,属于化学变化.故选:D.【点评】搞清楚物理变化和化学变化的本质区别是解答本类习题的关键,判断的标准是看在变化中有没有生成其它物质,一般地,物理变化有物质的固、液、气三态变化和物质形状的变化,而化学变化中有新物质生成.2.下列属于物质的化学性质的是( )A.溶解性B.助燃性C.颜色 D.熔点【考点】化学性质与物理性质的差别及应用.【专题】元素位置、结构与性质;物质的变化与性质.【分析】物质的化学性质是需要通过化学变化才能表现出来的性质,物理性质是不需要发生化学变化就能表现出来的性质,包括物质的颜色、状态、气味、熔点、沸点、密度、溶解性等,化学性质一般包括可燃性、氧化性、稳定性、还原性等.【解答】解:A、溶解性,不需要通过化学变化就能表现出来,属于物理性质,故选项错误.B、助燃性,需要通过化学反应才能表现出来,属于化学性质,故选项正确.C、颜色,不需要通过化学变化就能表现出来,属于物理性质,故选项错误.D、熔点,不需要通过化学变化就能表现出来,属于物理性质,故选项错误.故选B.【点评】本题难度不大,区分物质的性质属于物理性质还是化学性质,关键是看这条性质是否需要通过化学变化表现出来.3.生活中食用的“加碘食盐”中的碘是指( )A.碘元素B.碘分子C.碘单质D.碘原子【考点】元素的概念.【专题】元素位置、结构与性质;物质的微观构成与物质的宏观组成.【分析】加碘食盐的“碘”不能以单质、分子、原子形式存在,一般以无机盐类物质存在,指的是元素.【解答】解:食品、药品、营养品、矿泉水等物质中的“碘、氟、钙、铁、锌”等不能以单质、分子、原子形式存在,而是指元素.故加碘食盐中的“碘”是指元素.故选A.【点评】本题考查物质中的元素,解答本题要求学生理解生活中的各种物质都是由元素组成的.4.我们的生活中常用到下列物质,其中属于纯净物的是( )A.红酒 B.18K金项链C.冰水混合物D.可乐【考点】纯净物和混合物的判别.【专题】物质的分类.【分析】纯净物是由一种物质组成的物质,混合物是由多种物质组成的物质.据此逐项分析即可.【解答】解:A、红酒中有水和酒精,属于混合物,故选项错误;B、18K金项链通常还含有银、铜等其它金属,属于混合物,故选项错误;C、冰水混合物的成分只有水一种,属于纯净物,故选项正确;D、可乐里面有水和二氧化碳等物质,属于混合物,故选项错误;故选C.【点评】解答本题要充分理解纯净物和混合物的区别,要分析物质是由几种物质组成的,如果只有一种物质组成就属于纯净物,如果有多种物质就属于混合物.5.下列物质属于氧化物的是( )A.O2B.H2O C.NaOH D.H2SO4【考点】从组成上识别氧化物.【专题】物质的分类.【分析】氧化物是由两种元素组成,并且一种元素是氧元素的化合物.可以根据物质的组成元素进行分析、判断.【解答】解:A、氧气属于单质,不是氧化物.B、水是由两种元素组成,并且一种元素是氧元素的化合物,属于氧化物.C、氢氧化钠是由三种元素组成的化合物,不属于氧化物.D、硫酸是由三种元素组成的纯净物,不属于氧化物.故选:B.【点评】本题主要考查了氧化物的概念及如何判断一种物质是否属于氧化物的问题,可以依据物质的组成以及氧化物的概念进行.6.三氧化二铬(Cr2O3)可用作油漆颜料,Cr2O3中Cr的化合价是( )A.﹣3 B.﹣2 C.+2 D.+3【考点】有关元素化合价的计算.【专题】化学式的计算.【分析】根据在化合物中正负化合价代数和为零,结合三氧化二铬的化学式进行解答即可.【解答】解:氧元素显﹣2价,设铬元素的化合价是x,根据在化合物中正负化合价代数和为零,可得:2x+(﹣2)×3=0,则x=+3价.故选:D.【点评】本题难度不大,掌握利用化合价的原则(化合物中正负化合价代数和为零)计算指定元素的化合价的方法即可正确解答此类题.7.地壳中含量最多的金属元素是( )A.Al B.Fe C.Ca D.O【考点】地壳中元素的分布与含量.【专题】物质的微观构成与物质的宏观组成.【分析】根据地壳中含量最多的前五种元素和金属元素的判断方法考虑.【解答】解:地壳中含量最多的前五种元素:氧、硅、铝、铁、钙,汉字中带钅字旁(汞和金除外)的属于金属元素,所以地壳中含量最多的金属元素是铝.故选:A.【点评】解答本题关键是要知道金属元素的判断方法,掌握地壳中含量最多的前五种元素.8.不属于空气质量日报主要污染物的是( )A.二氧化碳 B.二氧化硫 C.可吸入颗粒D.氮氧化物【考点】空气的污染及其危害.【专题】课本知识同类信息;空气与水.【分析】本题考查学生对空气污染知识的理解,主要的污染物有可吸入粉尘、一氧化碳、二氧化硫、氮的氧化物等.要在学习有关空气污染物知识的基础上回忆.【解答】解:对空气能造成污染的物质有100多种,但主要的污染物有可吸入粉尘、一氧化碳、二氧化硫、氮的氧化物等,必须在空气质量日报中体现出来,让人们及时了解空气质量.A、二氧化碳不属于空气质量日报范围,不是污染物;B、二氧化硫,是空气的主要污染物之一;C、可吸入颗粒物,是空气的主要污染物之一;C、氮氧化物是空气的主要污染物之一;故选:A.【点评】本题较简单,要熟悉空气的污染物和空气质量日报的知识.9.下列物质中只存在游离态氧元素的是( )A.液氧 B.空气 C.双氧水D.自来水【考点】单质和化合物的判别.【专题】物质的分类.【分析】元素有游离态和化合态两种存在形态,区分这两种形态的方法是:在单质中,元素以游离态存在;在化合物中,元素以化合态存在.【解答】解:A、液氧是氧气的液态,属于单质,所以只存在游离态氧元素,故A正确;B、空气中含有氧气、二氧化碳等物质,氧气是单质,含有游离态的氧元素,二氧化碳属于化合物,以化合态存在.故B错;C、双氧水是化合物,只有化合态的氧元素,故C错;D、自来水中含有水属于化合物,以化合态存在,还含有溶解进去的氧气,以游离态存在.故D错.故选A.【点评】本题借助元素的游离态和化合态,实际考查的是单质和化合物的概念,单质是由一种元素组成的纯净物,而化合物是由不同种元素组成的纯净物.只要能正确区分单质和化合物,此题就会迎刃而解.10.如图所示化学实验操作错误的是( )A.液体的倾倒 B.液体的量取C.点燃酒精灯 D.滴加液体【考点】液体药品的取用;测量容器-量筒;加热器皿-酒精灯.【专题】实验操作型;化学学习中的实验思想;常见仪器及化学实验基本操作.【分析】A、根据向试管中倾倒液体药品的方法进行分析判断.B、根据量筒读数时视线要与凹液面的最低处保持水平进行分析判断.C、使用酒精灯时要注意“两查、两禁、一不可”.D、根据使用胶头滴管滴加少量液体的方法进行分析判断.【解答】解:A、向试管中倾倒液体药品时,瓶塞要倒放,标签要对准手心,瓶口紧挨,图中所示操作正确.B、量筒读数时视线要与量筒内液体的凹液面的最低处保持水平,图中所示操作正确.C、使用酒精灯时要注意“两查、两禁、一不可”,应用火柴点燃酒精灯,图中所示操作正确.D、用胶头滴管滴加少量液体的操作,注意胶头滴管不能伸入到试管内或接触试管内壁,应垂直悬空在试管口上方滴加液体,防止污染胶头滴管,图中所示操作错误.故选:D.【点评】本题难度不大,熟悉各种仪器的用途及使用注意事项、常见化学实验基本操作的注意事项是解答此类试题的关键.11.如图所示实验主要说明( )A.分子很小 B.分子间有间隔C.分子不断运动 D.分子可以分成原子【考点】利用分子与原子的性质分析和解决问题.【专题】实验性简答题.【分析】该演示实验中通过把水和酒精混合后液面会下降来说明构成物质的微粒存在间隔的.【解答】解:水和酒精都是由分子构成的物质,由于分子之间存在间隔,当把二者混合以后分子之间相互穿插渗透,导致混合后的液体总体积小于二者体积之和,说明了分子间有间隔.故选B.【点评】该实验很好地验证了分子间存在间隔.12.天然气的主要成分是甲烷(CH4),下列有关化学式CH4的表示意义,错误的是( ) A.表示甲烷这种物质B.表示甲烷由碳、氢两种元素组成C.表示一个甲烷分子D.表示甲烷由1个碳原子和4个氢原子构成【考点】化学式的书写及意义.【专题】化学用语和质量守恒定律.【分析】根据化学式的意义进行分析:①宏观意义:a.表示一种物质; b.表示该物质的元素组成;②微观意义:a.表示该物质的一个分子; b.表示该物质的分子构成;进行分析判断.【解答】解:A、CH4宏观上可表示甲烷这种物质,故选项说法正确.B、CH4宏观上可表示甲烷由碳、氢两种元素组成,故选项说法正确.C、CH4微观上可表示一个甲烷分子,故选项说法正确.D、甲烷是由甲烷分子构成的,CH4微观上可表示1个甲烷分子是由1个碳原子和4个氢原子构成,故选项说法错误.故选:D.【点评】本题难度不大,掌握化学式的宏观与微观意义并能灵活运用是正确解答本题的关键.13.下列化学方程式书写正确的是( )A.S+O2SO2↑ B.CuSO4+2NaOH→Na2SO4+Cu(OH)2C.3Fe+2O2Fe3O4D.2P+O5P2O5【考点】书写化学方程式、文字表达式、电离方程式.【专题】元素与化合物;化学用语和质量守恒定律.【分析】根据化学方程式判断正误的方法需考虑:应用的原理是否正确;化学式书写是否正确;是否配平;反应条件是否正确;↑和↓的标注是否正确.【解答】解:A、该化学方程式反应物中氧气是气体,二氧化硫的后面不需要标注↑,正确的化学方程式应为S+O2SO2.B、该化学方程式氢氧化铜后面没有标注↓,正确的化学方程式应为CuSO4+2NaOH→Na2SO4+Cu (OH)2↓.C、该化学方程式书写完全正确.D、该化学方程式氧气的化学式书写错误,正确的化学方程式应为4P+5O22P2O5.故选:C.【点评】本题难度不大,在解此类题时,首先分析应用的原理是否正确,然后再根据方程式的书写规则进行判断;化学方程式正误判断方法是:先看化学式是否正确,再看配平,再看反应条件,再看气体和沉淀.14.关于氧气的叙述错误的是( )A.氧气具有可燃性B.氧气能提供动植物呼吸C.氧气能支持燃烧D.过度吸氧不利于健康【考点】氧气的化学性质;氧气的用途.【专题】氧气、氢气的性质与用途.【分析】氧气是人类生产活动的重要资源,氧气是无色无味的气体,不易溶于水等;能支持燃烧,具有氧化性;氧气能供给生物呼吸,氧气还可以支持燃烧,可用于气焊,火箭推动剂等.据此进行分析判断.【解答】解:A、氧气具有助燃性,不具有可燃性,故A错误;B、氧气能提供动植物呼吸,故B正确;C、氧气能支持燃烧,故C正确;D、短时间内吸氧有助于缓解疲劳、增强血液循环,但是长时间、过度吸氧能引起氧中毒,不利于健康,故D正确.故选A.【点评】本题难度不大,考查氧气的物理性质、化学性质及其用途,掌握氧气的性质与用途是正确解答本题的关键.15.有关物质的量,说法错误的是( )A.物质的量是联系宏观世界和微观粒子的桥梁B.物质的摩尔质量在数值上等于式量或相对原子质量C.摩尔是国际单位制中七个基本物理量之一D.1mol任何物质都含有约6.02×1023个微粒【考点】有关化学式的计算和推断.【专题】化学式的计算;有关化学式的计算.【分析】A、根据物质的量表示物质所含微粒数(N)(如:分子,原子等)与阿伏伽德罗常数(N A)之比,进行分析判断.B、摩尔质量是指单位物质的量的物质所具有的质量,据此进行分析判断.C、根据国际单位制中七个基本物理量,进行分析判断.D、根据1mol任何物质都含有约6.02×1023个微粒,进行分析判断.【解答】解:A、物质的量表示物质所含微粒数(N)(如:分子,原子等)与阿伏伽德罗常数(N A)之比,是联系宏观世界和微观粒子的桥梁,故选项说法正确.B、摩尔质量是指单位物质的量的物质所具有的质量,摩尔质量的单位为g/mol,在数值上等于该物质的相对原子质量或相对分子质量,故选项说法正确.C、物质的量是国际单位制中七个基本物理量之一,摩尔是物质的量的单位,故选项说法错误.D、1mol任何物质都含有约6.02×1023个微粒,故选项说法正确.故选:C.【点评】本题难度不大,了解物质的量的概念、单位、摩尔质量、1mol任何物质都含有约6.02×1023个微粒等是正确解答本题的关键.16.实验现象描述正确的是( )A.磷在空气中燃烧,产生大量的白色烟雾B.铁丝在空气中燃烧,火星四射,生成黑色固体C.硫粉在空气中燃烧,观察到微弱的淡蓝色火焰,并产生二氧化硫D.双氧水加入二氧化锰后,产生大量气泡【考点】氧气与碳、磷、硫、铁等物质的反应现象;催化剂的特点与催化作用.【专题】实验现象的观察和记录.【分析】A、根据红磷在空气中燃烧的现象进行分析判断.B、根据铁丝在空气中燃烧的现象进行分析判断.C、根据硫在空气中燃烧的现象进行分析判断.D、根据双氧水加入二氧化锰可产生氧气进行分析判断.【解答】解:A、红磷在空气中燃烧,产生大量的白烟,而不是白雾,故选项说法错误.B、铁丝在氧气中剧烈燃烧,火星四射,生成一种黑色固体,在空气中不能燃烧,氧气的浓度不够,故选项说法错误.C、硫在空气中燃烧,发出淡蓝色火焰,生成有刺激性气味的气体,生成二氧化硫是实验结论而不是实验现象,故选项说法错误.C、红磷在氧气中燃烧,产生大量的白烟,而不是白雾,故选项说法错误.D、双氧水在二氧化锰的催化作用下可迅速产生大量气泡,故选项说法正确.故选:D.【点评】本题难度不大,掌握常见物质燃烧的现象、物质的性质即可正确解答;在描述物质燃烧的现象时,需要注意烟和雾、实验结论和实验现象的区别.17.关于原子,分子叙述错误的是( )A.原子和分子都在不停的运动B.原子和分子在化学变化中都能够再分C.分子是原子构成D.原子和分子都是构成物质的微粒【考点】分子和原子的区别和联系.【专题】物质的微观构成与物质的宏观组成.【分析】根据分子、原子的特性进行分析解答.【解答】解:A、分子、原子都在不断运动,说法正确;B、分子在化学变化中可分解成原子,而原子在化学变化中不可分,说法错误;C、分子是原子构成,说法正确;D、分子和原子都是构成物质的微粒,说法正确;故选B.【点评】分子和原子都是构成物质的微粒,都很小,都在不停的运动,都有间隔;区别是分子在化学变化中可分而原子不可分.18.用如图所示装置测定空气中氧气的含量,实验前在集气瓶内加入少量水,并做上记号.下列说法中错误的是( )A.实验前一定要检验装置的气密性B.实验时红磷一定要过量C.红磷点燃后要迅速伸入瓶中,并盖紧瓶塞D.把红磷改成铁丝,也能得到正确的实验结论【考点】空气组成的测定.【专题】结合课本知识的信息;空气与水.【分析】凡是有气体参加或产生的实验,实验前一定要检查装置的气密性,以防装置漏气影响实验结果;为了使集气瓶中的氧气完全反应,红磷应该足量;为了防止集气瓶中的空气受热膨胀逸出,红磷点燃后要迅速伸入瓶中,并盖紧瓶塞;铁不能在空气中燃烧.【解答】解:A、实验前一定要检验装置的气密性,该选项说法正确;B、为了使集气瓶中的氧气完全反应,红磷应该足量,该选项说法正确;C、为了防止集气瓶中的空气受热膨胀逸出,红磷点燃后要迅速伸入瓶中,并盖紧瓶塞,该选项说法正确;D、因为铁不能在空气中燃烧,把红磷改成铁丝,不能得出正确的结论,该选项说法不正确.故选:D.【点评】合理设计实验,科学地进行实验、分析实验,是得出正确实验结论的前提,因此要学会设计实验、进行实验、分析实验,为学好化学知识奠定基础.19.如图所示图象能正确反映对应变化关系的是( )A.加热一定质量的高锰酸钾B.在密闭的容器中点燃一定质量的镁条。
上海市上海市杨浦区复旦大学附属中学2024-2025学年九年级上学期9月月考物理试题(含答案)

2024~2025学年上海市复旦大学附属中学九年级上学期9月月考卷物理试卷 9.24(考试时间60分钟满分70分)考生注意:1.带2B铅笔、黑色签字笔、橡皮擦等参加考试,考试中途不得传借文具2.不携带具有传送功能的通讯设备,一经发现视为作弊。
与考试无关的所有物品放置在考场外。
3.考试期间严格遵守考试纪律,听从监考员指挥,杜绝作弊,违者由教导处进行处分。
4.答题卡务必保持干净整洁,答题卡客观题建议检查好后再填涂。
若因填涂模糊导致无法识别的后果自负。
一.选择题(共6题,12分)1.现在许多房门设有声音锁,“芝麻开门”成为现实,声音锁辨别屋主身份利用的声音特征是()A.音色B.音调C.响度D.声速2. 第一次测出大气压强值的物理学家是()A.卢瑟福B.阿基米德C.帕斯卡D.托里拆利3.“长征五号B”运载火箭首次采用了我国最新研制的大推力液氧煤油发动机。
火箭升空时发动机向下喷出高温气体,使火箭获得上升的推力。
下列物体的上升原理与火箭升空原理相同的是()A.升空的喷水火箭B.升空的热气球C.向上升的电梯D.向上抛出后的篮球4.将一副眼镜放在太阳底下,使镜片正对太阳光,在地面上观察到如图所示的现象,则下列判断正确的是()A.它是近视眼镜,对光线有会聚作用B.它是远视眼镜,对光线有发散作用C.它是老花眼镜,对光线有会聚作用D.它是近视眼镜,对光线有发散作用5.某容器中水的体积随温度变化的规律如图所示,下列说法正确的是( )二.填空题(共6题,24分)7.手电筒的电键与灯泡是__________(串联/并联)连接的。
手电筒发出的光从空气斜射到水面上会发生_____和折射现象,这时折射角______入射角(选填:“大于”“小于”“等于”)8.随着我国科技进步,已多次成功发射载人飞船进入太空。
某物体搭载飞船进入太空,该物体的质量_______(选填“变大”、“变小”或“不变”),地面指挥中心通过________把信息传输到飞船上(选填“无线电波”、“光波”或“声波”)。
2016学年上海第一学期九年级数学期中试卷及答案

2016学年上海第一学期九年级数学学科期中考试卷(时间:100分钟 总分:150分)一、选择题:(本大题共6题,每题4分,满分24分)1.已知25=b a ,那么下列等式中,不一定正确的是………………………………………( ) (A )b a 52=; (B )25b a =; (C )7=+b a ; (D )27=+b b a . 2.如果点G 是ABC ∆的重心,联结AG 并延长,交对边BC 于点D ,那么AD AG :是( ) (A )3:2; (B )2:1; (C )3:1; (D )4:3.3.已知点D 、E 分别在ABC ∆的边AB 、AC 上,下列给出的条件中,不能判定BCDE //的是…………………………………………………………………………………………( ) (A )AC CE AB BD ::=; (B )AD AB BC DE ::=; (C )AE AD AC AB ::=; (D )EC AE DB AD ::=.4.如图,在四边形ABCD 中,BC AD //,如果添加一个条件,不能使ABC ∆∽DCA ∆成立的是………………………………………………………………………………………( ) (A )ADC BAC ∠=∠; (B )ACD B ∠=∠; (C )BC AD AC ⋅=2; (D )BCABAC DC =. 5.如果二次函数c bx ax y ++=2的图像如图所示,那么下列判断正确的是………( ) (A )0>b ,0>c ; (B )0>b ,0<c ; (C )0<b ,0>c ; (D )0<b ,0<c .6.将抛物线22x y -=向右平移1个单位,再向上平移2个单位后,抛物线的表达式为( ) (A )2)1(22+--=x y ; (B )2)1(22---=x y ; (C )2)1(22++-=x y ; (D )2)1(22-+-=x y .BCDA第4题第5题二、填空题:(本大题共12题,每题4分,满分48分)7.已知线段cm a 4=,cm b 9=,那么线段a 、b 的比例中项等于 cm .8.如图,在ABC ∆中,BC DE //,8:5:=BC DE ,那么=EC AE : . 9.已知点P 是线段AB 的黄金分割点(BP AP >),如果2=AP ,那么线段=AB ____.10.如图,321////l l l ,2=AB ,3=BC ,那么DFDE的值是 . 11.如图,四边形ABCD 、CDEF 、EFGH 都是正方形,则=∠+∠21 度.12.如图,在ABC ∆中,BC DE //,2:3:=DB AD ,则=∆B D E C A D E S S 梯形: .第8、12题 第10题 第11题13.如果抛物线5)3(2-+=x a y 图像开口向下,那么a 的取值范围是 . 14.已知二次函数722-+=x x y 的一个函数值是8,那么对应自变量的值是 . 15.如果抛物线2)1(212+--+=m x m x y 的对称轴是y 轴,那么m 的值是 . 16.若点A (3-,1y )、B (0,2y )是二次函数1)1(22--=x y 图像上的两点,那么1y 与2y 的大小关系是 (填21y y >,21y y =或21y y <).17.如图,有一座抛物线形拱桥,其最大高度为16m ,跨度为40m ,现把它的示意图放在平面直角坐标系中,则抛物线的解析式为 .18.如图,在ABC ∆中,BC AD ⊥,5=BC ,3=AD ,矩形EFGH 的顶点F 、G 在边BC 上,顶点E 、H 分别在边AB 和AC 上,如果设边EF 的长为x (30<<x ),矩形EFGH 的面积为y ,那么y 关于x 的解析式为 .第17题第18题 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)已知抛物线经过(1-,0),(3,0),(1,2)三点,求抛物线的解析式.BAE D C BA21HGF E D C B A DE CF B A l 3l 2l 120.(本题满分10分,第(1)题4分,第(2)题6分) 已知二次函数27212+--=x x y . (1)用配方法把该二次函数的解析式化为k m x a y ++=2)(的形式;(2)指出该二次函数的开口方向、顶点坐标和对称轴.21.(本题满分10分,每小题5分)如图,ABC ∆中,PC 平分ACB ∠,PC PB =, (1)求证:APC ∆∽ACB ∆;(2)若2=AP ,6=PC ,求AC 的长.第21题22.(本题满分10分)如图,在ABC △中,D 是BC 的中点,E 是AC 上一点,2:1:=EC AE ,BE 交AD 于点F ,求FDAF的值.第22题CB P AFED CBA23.(本题满分12分,每小题6分) 已知:如图,在梯形ABCD 中,BC AD //,︒=∠90BCD ,对角线AC 、BD 相交于点E ,且BD AC ⊥.(1)求证:AD BC CD ⋅=2;(2)点F 是边BC 上一点,联结AF ,与BD 相交于点G ,如果DBF BAF ∠=∠,求证:BDBGAD AG =22. 第23题FDCB24.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,已知抛物线2y ax bx c =++与x 轴交于A 、B 两点,与y 轴交于点C ,D 为OC 的中点,直线AD 交抛物线于点(2,6)E ,且ABE ∆与ABC ∆的面积之比为3:2. (1)求直线AD 和抛物线的解析式;(2)抛物线的对称轴与x 轴相交于点F ,点Q 为直线AD 上一点,且ABQ ∆与ADF ∆相似,求点Q 的坐标.备用图25.(本题满分14分,第(1)小题4分,第(2)小题第一问5分,第(2)小题第二问5分)直角三角形ABC 中,30A ∠=︒,1BC =,将其绕直角顶点C 逆时针旋转一个角α(0120α︒<<︒且90α≠︒),得到'''C B A Rt ∆.(1)如图1,当''A B 边经过点B 时,求旋转角α的度数; (2)在三角形旋转过程中,边'A C 与AB 所在直线交于点D ,过点D 作//''DE A B 交'CB 边于点E ,联结BE .①当090α︒<<︒时,设AD x =,BE y =,求y 与x 之间的函数解析式及定义域; ②当ABC BDE S S ∆∆=31时,求AD 的长.第25题 备用图 备用图A B'ABA B2015学年第一学期九年级数学期中试卷答案一.选择题:(本大题共6题,满分24分)1. C ; 2.A ; 3.B; 4.D; 5.B; 6.A . 二.填空题:(本大题共12题,满分48分) 7.6; 8.3:5(或35); 9.15+; 10.52; 11.︒45; 12.16:9(或169); 13.3-<a ; 14.3和5-; 15.1; 16.>;17.x x y 582512+-=; 18.x x y 5352+-=.三.解答题:(本大题共7题,满分78分)19. 解:(1)设二次函数解析式为c bx ax y ++=2(0≠a ),………………………(1分) 所以二次函数解析式为23212++-=x x y .……………………………………………(1分)20..解:(1)27)2(212++-=x x y …………………………………………………(2分) 4)1(212++-=x ……………………………………………………(2分)(2)开口向下,…………………………………………………………………………(2分) 顶点坐标(1-,4),……………………………………………………………………(2分) 对称轴:直线1-=x (不写直线得1分).……………………………………………(2分)21.解:(1)∵PC 平分ACB ∠,∴BCP ACP ∠=∠,………………………………………………………………………(1分) ∵PC PB =,∴BCP B ∠=∠,…………………………………………………………………………(1分) ∴B ACP ∠=∠,…………………………………………………………………………(1分) 在APC ∆与ACB ∆中A A ∠=∠B ACP ∠=∠……………………………………………………………………………(1分)∴APC ∆∽ACB ∆.………………………………………………………………………(1分) (2)∵PC BP =,6=PC ,2=AP ,∴8=AB ,…………………………………………………………………………………(1分) ∵APC ∆∽ACB ∆,∴ABACAC AP =,……………………………………………………………………………(2分) ∴162=⋅=AB AP AC ,…………………………………………………………………(1分) ∴4=AC 或4-=AC (舍). …………………………………………………………(1分)22.解:过点D 作AC DG //,交BE 于点G ,………………………………………(2分) ∵D 是BC 中点,∴CD BD =,………………………………………………………………………………(2分) ∵AC DG //, ∴21==C E DG BC BD ,………………………………………………………………………(2分)∵21=EC AE , ∴1=DGAE,………………………………………………………………………………(2分) ∵AC DG //, ∴1==DGAEFD AF .…………………………………………………………………………(2分)23.证明:(1)∵BC AD //,︒=∠90BCD , ∴︒=∠=∠90BCD ADC ,………………………………………………………………(1分) ∵BD AC ⊥, ∴︒=∠90BEC ,∴︒=∠+∠90BCE CBE ,………………………………………………………………(1分) ∵︒=∠+∠90BCE ACD , ∴ACD CBE ∠=∠,………………………………………………………………………(1分) 在ACD ∆与DBC ∆中 D C B A D C ∠=∠ D B C A C D ∠=∠ ∴ACD ∆∽DBC ∆,………………………………………………………………………(1分) ∴BCCDCD AD =,……………………………………………………………………………(1分) ∴AD BC CD ⋅=2.………………………………………………………………………(1分) (2)∵BC AD //, ∴DBF ADB ∠=∠, ∵DBF BAF ∠=∠, ∴ADB BAF ∠=∠, 在BAG ∆与BDA ∆中 D B A ABG ∠=∠ B D A BAG ∠=∠∴BAG ∆∽BDA ∆,………………………………………………………………………(1分)∴DBA ABG S S ADAG ∆∆=22,…………………………………………………………………………(2分) ∵BDBGS S DBA ABG =∆∆,……………………………………………………………………………(2分) ∴BDBGAD AG =22.……………………………………………………………………………(1分)24.解:∵2:3:=∆∆ABC ABE S S ,E (2,6),∴C (0,4),………………………………………………………………………………(1分) ∵D 是OC 中点, ∴D (0,2),………………………………………………………………………………(1分) 求出AD 的解析式:22+=x y ,…………………………………………………………(1分) ∴A (1-,0),……………………………………………………………………………(1分) 求出抛物线解析式:432++-=x x y ……………………………………………………(2分) (2)由题意可得:B (4,0),F (23,0),…………………………………………(1分) 当点Q 在x 轴下方的直线AD 上时,ABQ ∆是钝角三角形,不可能与ADF ∆相似,因此点Q 一定在x 轴上方.此时ABQ ∆与ADF ∆有一个公共的A ∠,两个三角形相似存在两种情况:①当ADAFAQ AB =时,由于F 是AB 的中点,所以此时D 是AQ 的中点,即点Q 与点A 关于点D 对称,所以点Q 的坐标为(1,4). ………………………………………………(1分)②当AF AD AQ AB =时,2555=AQ ,解得255=AQ . 过点Q 作x QH ⊥轴,垂足为点H . ∵QH DO //,∴AQADHQ OD AH AO ==,即255521==HQ AH , 解得25=AH ,………………………………………………………………………………(1分) 5=HQ ,……………………………………………………………………………………(1分) ∴点Q 坐标为(23,5),…………………………………………………………………(1分) 综上所述,Q 点的坐标为(1,4)或(23,5)…………………………………………(1分)25.解:(1)在ABC Rt ∆中,∵︒=∠30A ,∴︒=∠60ABC .………………………(1分) 旋转过程中,对应边'CB CB =,对应角︒=∠=∠60'ABC B ,旋转角'BCB ∠=α.(1分) 当''B A 边经过点B 时,'BCB ∆是等边三角形,…………………………………………(1分) 此时旋转角︒=60α.………………………………………………………………………(1分) (2)①当︒<<︒900α时,点D 在AB 上.∵''//B A DE ,∴''CB CECA CD =. 在旋转过程中,对应边'CA CA =,'CB CB =,对应角'BCB ACD ∠=∠. ∴CB CECA CD =,∴CA D ∆∽CBE ∆,……………………………………………………(1分) ∴ACBCAD BE =.…………………………………………………………………(1分) 在ABC Rt ∆中,︒=∠30A ,1=BC ,所以3=AC ,可得33=AC BC ,…………(1分) 因此33=x y ,所以y 与x 之间的函数解析式为x y 33=,…………………………(1分) 定义域为20<<x .………………………………………………………………………(1分) ②23=∆ABC S , )(I 当︒<<︒900α时,CAD ∆∽CBE ∆,CBE A ∠=∠,所以BDE ∆是直角三角形.因此)2(63)2(2121x x x y BD BE S BDE -=-=⋅=∆.…………………………………(1分) 当ABC BDE S S ∆∆=31时,解方程63)2(63=-x x ,解得1=x .………………………(1分)11 )(II 当︒<<︒12090α时,同理可证CAD ∆∽CBE ∆,AD BE 33=,所以BDE ∆是直角三角形. 此时)2(63)2(332121-=-⨯=⋅=∆AD AD AD AD BD BE S BDE ,………………(1分) 当ABC BDE S S ∆∆=31时,解方程63)2(63=-AD AD ,解得21+=AD 或21-(舍)…………………………………………………………………………………………(1分) 综上所述,当ABC BDE S S ∆∆=31时,1=AD 或21+=AD .…………………………(1分)。
2016上海复旦大学附中届高三上期中理科数学试卷【含答案及解析】(1)

数列f中,若
,: ■-
(■ ■_
■-),则
+门、十L+和、1)二.
n-^cE1丿■
11.甲、乙两人参加法律知识竞赛,共有10道不同的题目,其中选择题有6道,判
断题4道,甲、乙两人依次各抽一题(不能抽同一题).则甲、乙中至少有一人抽
到选择题的概率等于.(用数字作答)
12.已知等差数列满足:工町:且它的前.项和有最大值,则当
试题分析;-4=(x| Vs^2r>0.x£iE}=(2,+co)U(-oc.O)={x11x+11<2hreJ!}=(-3J),
川I^=(-3.0)
第2题【答案】
[工8
【解析】
试题分析:函数/M= 1十log;心七4)的反函数厂的走义M是函翳[/仗]=1十log. v(y> 4)值虬即卩宀眄
第3题【答案】
,那么称这两个集合“保序同构”.以下集合对不是“保序同构”的是()
A、•.B、
/i
C、应=£坨|卩吒匕忙弘、厘■二我D、眉=飯兰=厂:
三、解答题
19.(本题满分12分;第1小题6分,第2小题6分)
已知函数-.■I|-. . - ■':-二.■|■.I
(1)若:,求•的取值范围;
(2)求i.「I■'的最大值.
16.已知数列「前-项和满足丸-•化、八二;,—P!,则
()
B、:::一IC、#D、-
17.若对任意,.,都有「•,那么」 在;上
( )
A、一定单调递增B、一定没有单调减区间
C、可能没有单调增区间D、一定没有单调增区间
18.设集合’ 是匸的两个非空子集,如果存在一个从> 到 的函数1厂汇
上海复旦实验中学数学九年级上册期末试卷(含答案)

上海复旦实验中学数学九年级上册期末试卷(含答案)一、选择题1.如图,已知一组平行线a ∥b ∥c ,被直线m 、n 所截,交点分别为A 、B 、C 和D 、E 、F ,且AB =1.5,BC =2,DE =1.8,则EF =( )A .4.4B .4C .3.4D .2.4 2.两个相似三角形的面积比是9:16,则这两个三角形的相似比是( ) A .9︰16 B .3︰4 C .9︰4 D .3︰16 3.若直线l 与半径为5的O 相离,则圆心O 与直线l 的距离d 为( )A .5d <B .5d >C .5d =D .5d ≤ 4.下列方程有两个相等的实数根是( )A .x 2﹣x +3=0B .x 2﹣3x +2=0C .x 2﹣2x +1=0D .x 2﹣4=05.已知2x =3y (x ≠0,y ≠0),则下面结论成立的是( ) A .23x y =B .32=y xC .23x y =D .23=y x6.如图,在Rt ABC ∆中,90C CD AB ∠=︒⊥,,垂足为点D ,一直角三角板的直角顶点与点D 重合,这块三角板饶点D 旋转,两条直角边始终与AC BC 、边分别相交于G H 、,则在运动过程中,ADG ∆与CDH ∆的关系是( )A .一定相似B .一定全等C .不一定相似D .无法判断7.如图,ABC △内接于⊙O ,30BAC ∠=︒,8BC = ,则⊙O 半径为( )A .4B .6C .8D .128.如图,在圆内接四边形ABCD 中,∠A :∠C =1:2,则∠A 的度数等于( )A .30°B .45°C .60°D .80°9.如图,O 的直径AB 垂直于弦CD ,垂足是点E ,22.5CAO ∠=,6OC =,则CD 的长为( )A .62B .32C .6D .1210.把函数212y x =-的图象,经过怎样的平移变换以后,可以得到函数()21112y x =--+的图象( ) A .向左平移1个单位,再向下平移1个单位 B .向左平移1个单位,再向上平移1个单位 C .向右平移1个单位,再向上平移1个单位 D .向右平移1个单位,再向下平移1个单位 11.如图,∠1=∠2,要使△ABC ∽△ADE ,只需要添加一个条件即可,这个条件不可能是( )A .∠B =∠D B .∠C =∠E C .AD ABAE AC= D .AC BCAE DE= 12.如图,AC 是⊙O 的内接正四边形的一边,点B 在弧AC 上,且BC 是⊙O 的内接正六边形的一边.若AB 是⊙O 的内接正n 边形的一边,则n 的值为( )A .6B .8C .10D .1213.如图,A 、B 、C 、D 是⊙O 上的四点,BD 为⊙O 的直径,若四边形ABCO 是平行四边形,则∠ADB 的大小为( )A .30°B .45°C .60°D .75°14.如图,点A 、B 、C 在⊙O 上,∠ACB =130°,则∠AOB 的度数为( )A .50°B .80°C .100°D .110°15.如图,△ABC 中AB 两个顶点在x 轴的上方,点C 的坐标是(﹣1,0),以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A′B′C′,且△A′B′C′与△ABC 的位似比为2:1.设点B 的对应点B′的横坐标是a ,则点B 的横坐标是( )A .12a -B .1(1)2a -+ C .1(1)2a -- D .1(3)2a -+ 二、填空题16.平面直角坐标系内的三个点A (1,-3)、B (0,-3)、C (2,-3),___ 确定一个圆.(填“能”或“不能”)17.抛物线y =3(x+2)2+5的顶点坐标是_____. 18.如图,在ABCD 中,13BE DF BC ==,若1BEG S ∆=,则ABF S ∆=__________.19.已知圆锥的侧面积为20πcm 2,母线长为5cm ,则圆锥底面半径为______cm . 20.如图,P 为O 外一点,PA 切O 于点A ,若3PA =,45APO ∠=︒,则O 的半径是______.21.某电视台招聘一名记者,甲应聘参加了采访写作、计算机操作和创意设计的三项素质测试得分分别为70、60、90,三项成绩依次按照5:2:3计算出最后成绩,那么甲的成绩为__.22.如图,O半径为2,正方形ABCD内接于O,点E在ADC上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为________.23.甲、乙两同学近期6次数学单元测试成绩的平均分相同,甲同学成绩的方差S甲2=6.5分2,乙同学成绩的方差S乙2=3.1分2,则他们的数学测试成绩较稳定的是____(填“甲”或“乙”).24.若点 M(-1, y1),N(1, y2),P(72, y3 )都在抛物线 y=-mx2 +4mx+m2 +1(m>0)上,则y1、y2、y3大小关系为_____(用“>”连接).25.如图,在边长为 6 的等边△ABC 中,D 为 AC 上一点,AD=2,P 为 BD 上一点,连接CP,以 CP 为边,在 PC 的右侧作等边△CPQ,连接 AQ 交 BD 延长线于 E,当△CPQ 面积最小时,QE=____________.26.某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这m n个数据的平均数等于______.27.设二次函数y=x2﹣2x﹣3与x轴的交点为A,B,其顶点坐标为C,则△ABC的面积为_____.28.有4根细木棒,它们的长度分别是2cm、4cm、6cm、8cm.从中任取3根恰好能搭成一个三角形的概率是_____.29.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式21220h t t =-++,则火箭升空的最大高度是___m30.如图,AE 、BE 是△ABC 的两个内角的平分线,过点A 作AD ⊥AE .交BE 的延长线于点D .若AD =AB ,BE :ED =1:2,则cos ∠ABC =_____.三、解答题31.如图,已知抛物线经过原点O ,顶点为A(1,1),且与直线-2y x =交于B ,C 两点. (1)求抛物线的解析式及点C 的坐标; (2)求△ABC 的面积;(3)若点N 为x 轴上的一个动点,过点N 作MN ⊥x 轴与抛物线交于点M ,则是否存在以O ,M ,N 为顶点的三角形与△ABC 相似?若存在,请求出点N 的坐标;若不存在,请说明理由.32.市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y (千克)是销售单价x (元)的一次函数,且当x =45时,y =10;x =55时,y =90.在销售过程中,每天还要支付其他费用500元.(1)求出y 与x 的函数关系式,并写出自变量x 的取值范围;(2)求该公司销售该原料日获利w (元)与销售单价x (元)之间的函数关系式; (3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?33.如图,在矩形 ABCD 中,CE ⊥BD ,AB=4,BC=3,P 为 BD 上一个动点,以 P 为圆心,PB 长半径作⊙P ,⊙P 交 CE 、BD 、BC 交于 F 、G 、H (任意两点不重合), (1)半径 BP 的长度范围为 ;(2)连接 BF 并延长交 CD 于 K ,若 tan ∠KFC = 3 ,求 BP ; (3)连接 GH ,将劣弧 HG 沿着 HG 翻折交 BD 于点 M ,试探究PMBP是否为定值,若是求出该值,若不是,请说明理由.34.如图,二次函数22y ax ax c =-+ (a < 0) 与 x 轴交于 A 、C 两点,与 y 轴交于点 B ,P 为 抛物线的顶点,连接 AB ,已知 OA :OC=1:3. (1)求 A 、C 两点坐标;(2)过点 B 作 BD ∥x 轴交抛物线于 D ,过点 P 作 PE ∥AB 交 x 轴于 E ,连接 DE , ①求 E 坐标; ②若 tan ∠BPM=25,求抛物线的解析式.35.如图,已知一次函数3y x =-+分别交x 、y 轴于A 、B 两点,抛物线2y x bx c =-++经过A 、B 两点,与x 轴的另一交点为C .(1)求b 、c 的值及点C 的坐标;(2)动点P 从点O 出发,以每秒1个单位长度的速度向点A 运动,过P 作x 轴的垂线交抛物线于点D ,交线段AB 于点E .设运动时间为(0)t t >秒. ①当t 为何值时,线段DE 长度最大,最大值是多少?(如图1)②过点D 作DF AB ⊥,垂足为F ,连结BD ,若BOC 与BDF 相似,求t 的值(如图2)四、压轴题36.已知:如图1,在O 中,弦2AB =,1CD =,AD BD ⊥.直线,AD BC 相交于点E .(1)求E ∠的度数;(2)如果点,C D 在O 上运动,且保持弦CD 的长度不变,那么,直线,AD BC 相交所成锐角的大小是否改变?试就以下三种情况进行探究,并说明理由(图形未画完整,请你根据需要补全).①如图2,弦AB 与弦CD 交于点F ; ②如图3,弦AB 与弦CD 不相交: ③如图4,点B 与点C 重合.37.如图,在Rt △ABC 中,∠A=90°,0是BC 边上一点,以O 为圆心的半圆与AB 边相切于点D ,与BC 边交于点E 、F ,连接OD ,已知BD=3,tan ∠BOD=34,CF=83.(1)求⊙O 的半径OD ; (2)求证:AC 是⊙O 的切线; (3)求图中两阴影部分面积的和.38.MN 是O 上的一条不经过圆心的弦,4MN =,在劣弧MN 和优弧MN 上分别有点A,B (不与M,N 重合),且AN BN =,连接,AM BM .(1)如图1,AB 是直径,AB 交MN 于点C ,30ABM ︒∠=,求CMO ∠的度数; (2)如图2,连接,OM AB ,过点O 作//OD AB 交MN 于点D ,求证:290MOD DMO ︒∠+∠=;(3)如图3,连接,AN BN ,试猜想AM MB AN NB ⋅+⋅的值是否为定值,若是,请求出这个值;若不是,请说明理由.39.已知点(4,0)、(2,3)-为二次函数图像抛物线上两点,且抛物线的对称轴为直线2x =.(1)求抛物线的解析式;(2)将抛物线平移,使顶点与原点重合,已知点(,1)M m -,点A 、B 为抛物线上不重合的两点(B 在A 的左侧),且直线MA 与抛物线仅有一个公共点.①如图1,当点M 在y 轴上时,过点A 、B 分别作AP y ⊥轴于点P ,BQ x ⊥轴于点Q .若APM △与BQO △ 相似, 求直线AB 的解析式;②如图2,当直线MB 与抛物线也只有一个公共点时,记A 、B 两点的横坐标分别为a 、b .当点M 在y 轴上时,直接写出m am b--的值为 ;当点M 不在y 轴上时,求证:m am b--为一个定值,并求出这个值.40.对于线段外一点和这条线段两个端点连线所构成的角叫做这个点关于这条线段的视角.如图1,对于线段AB 及线段AB 外一点C ,我们称∠ACB 为点C 关于线段AB 的视角. 如图2,点Q 在直线l 上运动,当点Q 关于线段AB 的视角最大时,则称这个最大的“视角”为直线l 关于线段AB 的“视角”.(1)如图3,在平面直角坐标系中,A (0,4),B (2,2),点C 坐标为(﹣2,2),点C 关于线段AB 的视角为 度,x 轴关于线段AB 的视角为 度;(2)如图4,点M 是在x 轴上,坐标为(2,0),过点M 作线段EF ⊥x 轴,且EM =MF =1,当直线y =kx (k ≠0)关于线段EF 的视角为90°,求k 的值;(3)如图5,在平面直角坐标系中,P 3,2),Q 3,1),直线y =ax +b (a >0)与x 轴的夹角为60°,且关于线段PQ 的视角为45°,求这条直线的解析式.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】直接利用平行线分线段成比例定理对各选项进行判断即可.【详解】解:∵a∥b∥c,∴AB DE BC EF=,∵AB=1.5,BC=2,DE=1.8,∴1.5 1.82EF= , ∴EF=2.4故选:D.【点睛】本题考查了平行线分线段成比例,掌握三条平行线截两条直线,所得的对应线段成比例是关键.2.B解析:B【解析】试题分析:根据相似三角形中,面积比等于相似比的平方,即可得到结果.因为面积比是9:16,则相似比是3︰4,故选B.考点:本题主要考查了相似三角形的性质点评:解答本题的关键是掌握相似三角形面积的比等于相似比的平方3.B解析:B【解析】【分析】直线与圆相离等价于圆心到直线的距离大于半径,据此解答即可.【详解】解:∵直线l与半径为5的O相离,∴圆心O与直线l的距离d满足:5d>.故选:B.【点睛】本题考查了直线与圆的位置关系,属于应知应会题型,若圆心到直线的距离为d,圆的半径为r,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交. 4.C解析:C【分析】先根据方程求出△的值,再根据根的判别式的意义判断即可.【详解】A 、x 2﹣x+3=0,△=(﹣1)2﹣4×1×3=﹣11<0,所以方程没有实数根,故本选项不符合题意;B 、x 2﹣3x+2=0,△=(﹣3)2﹣4×1×2=1>0,所以方程有两个不相等的实数根,故本选项不符合题意;C 、x 2﹣2x+1=0,△=(﹣2)2﹣4×1×1=0,所以方程有两个相等的实数根,故本选项符合题意;D 、x 2﹣4=0,△=02﹣4×1×(﹣4)=16>0,所以方程有两个不相等的实数根,故本选项不符合题意;故选:C .【点睛】本题考查了根的判别式,能熟记根的判别式的意义是解此题的关键.5.D解析:D【解析】【分析】根据比例的性质,把等积式写成比例式即可得出结论.【详解】A.由内项之积等于外项之积,得x :3=y :2,即32x y =,故该选项不符合题意, B.由内项之积等于外项之积,得x :3=y :2,即32x y =,故该选项不符合题意, C.由内项之积等于外项之积,得x :y =3:2,即32x y =,故该选项不符合题意, D.由内项之积等于外项之积,得2:y =3:x ,即23=y x,故D 符合题意; 故选:D .【点睛】 本题考查比例的性质,熟练掌握比例内项之积等于外项之积的性质是解题关键.6.A解析:A【解析】根据已知条件可得出A DCB ∠∠=,ADG CDH ∠∠=,再结合三角形的内角和定理可得出AGD CHD ∠∠=,从而可判定两三角形一定相似.【详解】解:由已知条件可得,ADC EDF CDB C 90∠∠∠∠====︒,∵A ACD ACD DCH 90∠∠∠∠+=+=︒,∴A DCH ∠∠=,∵ADG EDC EDC CDH 90∠∠∠∠+=+=︒,∴ADG CDH ∠∠=,继而可得出AGD CHD ∠∠=,∴ADG ~CDH .故选:A .【点睛】本题考查的知识点是相似三角形的判定定理,灵活利用三角形内角和定理以及余角定理是解此题的关键.7.C解析:C【解析】【分析】连接OB ,OC ,根据圆周角定理求出∠BOC 的度数,再由OB =OC 判断出△OBC 是等边三角形,由此可得出结论.【详解】解:连接OB ,OC ,∵∠BAC =30°,∴∠BOC =60°.∵OB =OC ,BC =8,∴△OBC 是等边三角形,∴OB =BC =8.故选:C.【点睛】本题考查的是圆周角定理以及等边三角形的判定和性质,根据题意作出辅助线,构造出等边三角形是解答此题的关键.8.C解析:C【分析】设∠A 、∠C 分别为x 、2x ,然后根据圆的内接四边形的性质列出方程即可求出结论.【详解】解:设∠A 、∠C 分别为x 、2x ,∵四边形ABCD 是圆内接四边形,∴x +2x =180°,解得,x =60°,即∠A =60°,故选:C .【点睛】此题考查的是圆的内接四边形的性质,掌握圆的内接四边形的性质是解决此题的关键.9.A解析:A【解析】【分析】先根据垂径定理得到CE DE =,再根据圆周角定理得到245BOC A ∠=∠=,可得OCE ∆为等腰直角三角形,所以CE ==CD 的长. 【详解】∵CD AB ⊥,AB 为直径,∴CE DE =, ∵∠BOC 和∠A 分别为BC 所对的圆心角和圆周角,∠A=22.5°,∴2222.545BOC A ∠=∠=⨯=,∴OCE ∆为等腰直角三角形,∵OC=6,∴622CE ===∴2CD CE ==故选A .【点睛】本题考查了垂径定理及圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;垂直于弦的直径,平分这条弦且平分这条弦所对的两条弧.10.C解析:C【解析】【分析】根据抛物线顶点的变换规律作出正确的选项.抛物线212y x =-的顶点坐标是00(,),抛物线线()21112y x =--+的顶点坐标是11(,), 所以将顶点00(,)向右平移1个单位,再向上平移1个单位得到顶点11(,), 即将函数212y x =-的图象向右平移1个单位,再向上平移1个单位得到函数()21112y x =--+的图象. 故选:C .【点睛】 主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.11.D解析:D【解析】【分析】先求出∠DAE =∠BAC ,再根据相似三角形的判定方法分析判断即可.【详解】∵∠1=∠2,∴∠1+∠BAE =∠2+∠BAE ,∴∠DAE =∠BAC ,A 、添加∠B =∠D 可利用两角法:有两组角对应相等的两个三角形相似可得△ABC ∽△ADE ,故此选项不合题意;B 、添加∠C =∠E 可利用两角法:有两组角对应相等的两个三角形相似可得△ABC ∽△ADE ,故此选项不合题意;C 、添加AD AB AE AC=可利用两边及其夹角法:两组边对应成比例且夹角相等的两个三角形相似,故此选项不合题意; D 、添加AC BC AE DE=不能证明△ABC ∽△ADE ,故此选项符合题意; 故选:D .【点睛】本题考查相似三角形的判定,解题的关键是掌握相似三角形判定方法:两角法、两边及其夹角法、三边法、平行线法.12.D解析:D【解析】【分析】连接AO 、BO 、CO ,根据中心角度数=360°÷边数n ,分别计算出∠AOC 、∠BOC 的度数,根据角的和差则有∠AOB=30°,根据边数n=360°÷中心角度数即可求解.【详解】连接AO、BO、CO,∵AC是⊙O内接正四边形的一边,∴∠AOC=360°÷4=90°,∵BC是⊙O内接正六边形的一边,∴∠BOC=360°÷6=60°,∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°,∴n=360°÷30°=12;故选:D.【点睛】本题考查正多边形和圆,解题的关键是根据正方形的性质、正六边形的性质求出中心角的度数.13.A解析:A【解析】【详解】解:∵四边形ABCO是平行四边形,且OA=OC,∴四边形ABCO是菱形,∴AB=OA=OB,∴△OAB是等边三角形,∴∠AOB=60°,∵BD是⊙O的直径,∴点B、D、O在同一直线上,∠AOB=30°∴∠ADB=12故选A.14.C解析:C【解析】【分析】根据圆内接四边形的性质和圆周角定理即可得到结论.【详解】在优弧AB上任意找一点D,连接AD,BD.∵∠D=180°﹣∠ACB=50°,∴∠AOB=2∠D=100°,故选:C.【点睛】本题考查了圆周角定理,圆内接四边形的性质,正确的作出辅助线是解题的关键.15.D解析:D【解析】【分析】设点B的横坐标为x,然后表示出BC、B′C的横坐标的距离,再根据位似变换的概念列式计算.【详解】设点B的横坐标为x,则B、C间的横坐标的长度为﹣1﹣x,B′、C间的横坐标的长度为a+1,∵△ABC放大到原来的2倍得到△A′B′C,∴2(﹣1﹣x)=a+1,解得x=﹣12(a+3),故选:D.【点睛】本题考查了位似变换,坐标与图形的性质,根据位似变换的定义,利用两点间的横坐标的距离等于对应边的比列出方程是解题的关键.二、填空题16.不能【解析】【分析】根据三个点的坐标特征得到它们共线,于是根据确定圆的条件可判断它们不能确定一个圆.【详解】解:∵B(0,-3)、C(2,-3),∴BC∥x轴,而点A(1,-3)与C、解析:不能【解析】【分析】根据三个点的坐标特征得到它们共线,于是根据确定圆的条件可判断它们不能确定一个圆.【详解】解:∵B(0,-3)、C(2,-3),∴BC∥x轴,而点A(1,-3)与C、B共线,∴点A、B、C共线,∴三个点A(1,-3)、B(0,-3)、C(2,-3)不能确定一个圆.故答案为:不能.【点睛】本题考查了确定圆的条件:不在同一直线上的三点确定一个圆.17.(﹣2,5)【解析】【分析】已知抛物线的顶点式,可直接写出顶点坐标.【详解】解:由y=3(x+2)2+5,根据顶点式的坐标特点可知,顶点坐标为(﹣2,5).故答案为:(﹣2,5).【点解析:(﹣2,5)【解析】【分析】已知抛物线的顶点式,可直接写出顶点坐标.【详解】解:由y=3(x+2)2+5,根据顶点式的坐标特点可知,顶点坐标为(﹣2,5).故答案为:(﹣2,5).【点睛】本题考查二次函数的性质,熟知二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.18.6【解析】先根据平行四边形的性质证得△BEG∽△FAG,从而可得相似比,然后根据同高的两个三角形的面积等于底边之比可求得,根据相似三角形的性质可求得,进而可得答案.【详解】解:∵四解析:6【解析】【分析】先根据平行四边形的性质证得△BEG ∽△FAG ,从而可得相似比,然后根据同高的两个三角形的面积等于底边之比可求得ABG S ∆,根据相似三角形的性质可求得AFG S ∆,进而可得答案.【详解】解:∵四边形ABCD 是平行四边形,∴AD=BC ,AD ∥BC ,∴△BEG ∽△FAG , ∵13BE DF BC ==, ∴12EG BE AG AF ==, ∴211,24BEG BEG ABG AFG S S EG BE S AG S AF ∆∆∆∆⎛⎫==== ⎪⎝⎭, ∵1BEG S ∆=,∴2ABG S ∆=,4AFG S ∆=,∴6ABF ABG AFG S S S ∆∆∆=+=.故答案为:6.【点睛】本题考查了平行四边形的性质、相似三角形的判定和性质以及三角形的面积等知识,属于常考题型,熟练掌握平行四边形的性质和相似三角形的判定与性质是解答的关键. 19.4【解析】【分析】由圆锥的母线长是5cm ,侧面积是20πcm2,求圆锥侧面展开扇形的弧长,然后再根据锥的侧面展开扇形的弧长等于圆锥的底面周长求解.【详解】解:由圆锥的母线长是5cm ,侧面积解析:4【解析】由圆锥的母线长是5cm,侧面积是20πcm2,求圆锥侧面展开扇形的弧长,然后再根据锥的侧面展开扇形的弧长等于圆锥的底面周长求解.【详解】解:由圆锥的母线长是5cm,侧面积是20πcm2,根据圆锥的侧面展开扇形的弧长为:2405Slrπ===8π,再根据锥的侧面展开扇形的弧长等于圆锥的底面周长,可得822lrπππ===4cm.故答案为:4.【点睛】本题考查圆锥的计算,掌握公式正确计算是解题关键.20.3【解析】【分析】由题意连接OA,根据切线的性质得出OA⊥PA,由已知条件可得△OAP是等腰直角三角形,进而可求出OA的长,即可求解.【详解】解:连接OA,∵PA切⊙O于点A,∴OA解析:3【解析】【分析】由题意连接OA,根据切线的性质得出OA⊥PA,由已知条件可得△OAP是等腰直角三角形,进而可求出OA的长,即可求解.【详解】解:连接OA,∵PA切⊙O于点A,∴OA⊥PA,∴∠OAP=90°,∵∠APO=45°,∴OA=PA=3,故答案为:3.【点睛】本题考查切线的性质即圆的切线垂直于经过切点的半径.若出现圆的切线,连接过切点的半径,构造定理图,得出垂直关系.21.74【解析】【分析】利用加权平均数公式计算.【详解】甲的成绩=,故答案为:74.【点睛】此题考查加权平均数,正确理解各数所占的权重是解题的关键.解析:74【解析】【分析】利用加权平均数公式计算.【详解】甲的成绩=70560290374523,故答案为:74.【点睛】此题考查加权平均数,正确理解各数所占的权重是解题的关键.22.【解析】【分析】先求得正方形的边长,取AB的中点G,连接GF,CG,当点C、F、G在同一直线上时,根据两点之间线段最短,则CF有最小值,此时即可求得这个值. 【详解】如图,连接OA、OD,取1【解析】【分析】先求得正方形的边长,取AB的中点G,连接GF,CG,当点C、F、G在同一直线上时,根据两点之间线段最短,则CF有最小值,此时即可求得这个值.【详解】如图,连接OA 、OD ,取AB 的中点G ,连接GF ,CG ,∵ABCD 是圆内接正方形,2OA OD ==, ∴90AOD ∠=︒,∴()222222AD OA OD =+==, ∵AF ⊥BE ,∴90AFB ∠=︒,∴112GF AB ==, 2222125CG BG BC =+=+=,当点C 、F 、G 在同一直线上时,CF 有最小值,如下图:51,51.【点睛】本题主要考查了正方形的性质,勾股定理,直角三角形斜边上的中线的性质,根据两点之间线段最短确定CF 的最小值是解决本题的关键.23.乙【解析】【分析】根据方差越小数据越稳定即可求解.【详解】解:因为甲、乙两同学近期6次数学单元测试成绩的平均分相同且S 甲2 >S 乙2,所以乙的成绩数学测试成绩较稳定.故答案为:乙.【解析:乙【解析】【分析】根据方差越小数据越稳定即可求解.【详解】解:因为甲、乙两同学近期6次数学单元测试成绩的平均分相同且S甲2>S乙2,所以乙的成绩数学测试成绩较稳定.故答案为:乙.【点睛】本题考查方差的性质,方差越小数据越稳定.24.y1<y3<y2【解析】【分析】利用图像法即可解决问题.【详解】y=mx2 +4mx+m2 +1(m>0),对称轴为x=,观察二次函数的图象可知:y1<y3<y2.故答案为:y解析:y1<y3<y2【解析】【分析】利用图像法即可解决问题.【详解】y=-mx2 +4mx+m2 +1(m>0),对称轴为x=422mm-=-,观察二次函数的图象可知:y1<y3<y2.故答案为:y1<y3<y2.【点睛】本题考查二次函数图象上的点的特征,解题的关键是学会利用图象法比较函数值的大小.25.【解析】【分析】如图,过点D作DF⊥BC于F,由“SAS”可证△ACQ≌△BCP,可得AQ=BP,∠CAQ=∠CBP,由直角三角形的性质和勾股定理可求BD的长,由锐角三角函数可求BP的长,由相解析:67 7【解析】【分析】如图,过点D作DF⊥BC于F,由“SAS”可证△ACQ≌△BCP,可得AQ=BP,∠CAQ=∠CBP,由直角三角形的性质和勾股定理可求BD的长,由锐角三角函数可求BP的长,由相似三角形的性质可求AE的长,即可求解.【详解】如图,过点D作DF⊥BC于F,∵△ABC,△PQC是等边三角形,∴BC=AC,PC=CQ,∠BCA=∠PCQ=60°,∴∠BCP=∠ACQ,且AC=BC,CQ=PC,∴△ACQ≌△BCP(SAS)∴AQ=BP,∠CAQ=∠CBP,∵AC=6,AD=2,∴CD=4,∵∠ACB=60°,DF⊥BC,∴∠CDF =30°,∴CF =12CD =2,DF =CF ÷tan30°= ∴BF =4,∴BD ,∵△CPQ 是等边三角形,∴S △CPQ 2, ∴当CP ⊥BD 时,△CPQ 面积最小,∴cos ∠CBD =BP BF BC BD =, ∴6BP =,∴BP =7,∴AQ =BP , ∵∠CAQ =∠CBP ,∠ADE =∠BDC ,∴△ADE ∽△BDC , ∴AE AD BC BD=, ∴6AE =,∴AE =7,∴QE =AQ−AE .. 【点睛】 本题考查了全等三角形的判定和性质,等边三角形的性质,锐角三角函数,相似三角形的判定和性质,直角三角形的性质,勾股定理等知识,求出BP 的长是本题的关键.26..【解析】【分析】根据加权平均数的基本求法,平均数等于总和除以个数,即可得到答案.【详解】平均数等于总和除以个数,所以平均数.【点睛】本题考查求加权平均数,解题的关键是掌握加权平均数的解析:mx ny m n++.【解析】【分析】根据加权平均数的基本求法,平均数等于总和除以个数,即可得到答案.【详解】平均数等于总和除以个数,所以平均数mx nym n+=+.【点睛】本题考查求加权平均数,解题的关键是掌握加权平均数的基本求法.27.8【解析】【分析】首先求出A、B的坐标,然后根据坐标求出AB、CD的长,再根据三角形面积公式计算即可.【详解】解:∵y=x2﹣2x﹣3,设y=0,∴0=x2﹣2x﹣3,解得:x1=3,解析:8【解析】【分析】首先求出A、B的坐标,然后根据坐标求出AB、CD的长,再根据三角形面积公式计算即可.【详解】解:∵y=x2﹣2x﹣3,设y=0,∴0=x2﹣2x﹣3,解得:x1=3,x2=﹣1,即A点的坐标是(﹣1,0),B点的坐标是(3,0),∵y=x2﹣2x﹣3,=(x﹣1)2﹣4,∴顶点C的坐标是(1,﹣4),∴△ABC的面积=12×4×4=8,故答案为8.【点睛】本题考查了抛物线与x轴的交点,二次函数的性质,二次函数的三种形式的应用,主要考查学生运用性质进行计算的能力,题目比较典型,难度适中.28.【解析】【分析】根据题意列举出所有4种等可能的结果数,再根据题意得出能够构成三角形的结果数,最后根据概率公式即可求解.【详解】从中任取3根共有4种等可能的结果数,它们为2、4、6;2、4、解析:1 4【解析】【分析】根据题意列举出所有4种等可能的结果数,再根据题意得出能够构成三角形的结果数,最后根据概率公式即可求解.【详解】从中任取3根共有4种等可能的结果数,它们为2、4、6;2、4、8;2、6、8;、4、6、8,其中恰好能搭成一个三角形为4、6、8,所以恰好能搭成一个三角形的概率=14.故答案为14.【点睛】本题考查列表法或树状图法和三角形三边关系,解题的关键是通过列表法或树状图法展示出所有等可能的结果数及求出构成三角形的结果数.29.56【解析】【分析】将函数解析式配方,写成顶点式,按照二次函数的性质可得答案.【详解】解:∵==,∵,∴抛物线开口向下,当x=6时,h取得最大值,火箭能达到最大高度为56m.故解析:56【解析】【分析】将函数解析式配方,写成顶点式,按照二次函数的性质可得答案.【详解】解:∵21220h t t =-++=2(23636)120t t -+-+-=2(6)56t --+,∵10a =-<,∴抛物线开口向下,当x=6时,h 取得最大值,火箭能达到最大高度为56m .故答案为:56.【点睛】本题考查了二次函数的应用,熟练掌握配方法及二次函数的性质,是解题的关键.30.【解析】【分析】取DE 的中点F ,连接AF ,根据直角三角形斜边中点的性质得出AF =EF ,然后证得△BAF≌△DAE,得出AE =AF ,从而证得△AEF 是等边三角形,进一步证得∠ABC=60°,即可解析:32【解析】【分析】取DE 的中点F ,连接AF ,根据直角三角形斜边中点的性质得出AF =EF ,然后证得△BAF ≌△DAE ,得出AE =AF ,从而证得△AEF 是等边三角形,进一步证得∠ABC =60°,即可求得结论.【详解】取DE 的中点F ,连接AF ,∴EF =DF ,∵BE :ED =1:2,∴BE =EF =DF ,∴BF =DE ,∵AB =AD ,∴∠ABD =∠D ,∵AD ⊥AE ,EF =DF ,∴AF =EF ,在△BAF 和△DAE 中AB AD ABF D BF DE =⎧⎪∠=∠⎨⎪=⎩∴△BAF ≌△DAE (SAS ),∴AE =AF ,∴△AEF 是等边三角形,∴∠AED =60°,∴∠D =30°,∵∠ABC =2∠ABD ,∠ABD =∠D ,∴∠ABC =60°,∴cos ∠ABC =cos60°【点睛】 本题考查了全等三角形的判定和性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.三、解答题31.(1)y=﹣(x ﹣1)2+1,C(﹣1,﹣3);(2)3;(3)存在满足条件的N 点,其坐标为(53,0)或(73,0)或(﹣1,0)或(5,0) 【解析】【分析】 (1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C 点坐标;(2)设直线AC 的解析式为y =kx +b ,与x 轴交于D ,得到y =2x−1,求得BD 于是得到结论;(3)设出N 点坐标,可表示出M 点坐标,从而可表示出MN 、ON 的长度,当△MON 和△ABC 相似时,利用三角形相似的性质可得MN ON AB BC =或MN ON BC AB=,可求得N 点的坐标.【详解】(1)∵顶点坐标为(1,1),∴设抛物线解析式为y=a (x ﹣1)2+1,又抛物线过原点,∴0=a (0﹣1)2+1,解得a=﹣1,∴抛物线解析式为y=﹣(x ﹣1)2+1,即y=﹣x 2+2x ,联立抛物线和直线解析式可得22-2y x x y x ⎧=+⎨=⎩﹣, 解得20x y =⎧⎨=⎩或13x y =-⎧⎨=-⎩,∴B (2,0),C (﹣1,﹣3); (2)设直线AC 的解析式为y=kx+b ,与x 轴交于D , 把A (1,1),C (﹣1,﹣3)的坐标代入得13k b k b =+⎧⎨-=-+⎩, 解得:21k b =⎧⎨=-⎩, ∴y=2x ﹣1,当y=0,即2x ﹣1=0,解得:x=12,∴D (12,0), ∴BD=2﹣12=32, ∴△ABC 的面积=S △ABD +S △BCD =12×32×1+12×32×3=3; (3)假设存在满足条件的点N ,设N (x ,0),则M (x ,﹣x 2+2x ),∴ON=|x|,MN=|﹣x 2+2x|,由(2)知,,,∵MN ⊥x 轴于点N ,∴∠ABC=∠MNO=90°,∴当△ABC 和△MNO 相似时,有MN ON AB BC =或MN ON BC AB=, ①当MN ON AB BC =时,∴=|x||﹣x+2|=13|x|, ∵当x=0时M 、O 、N 不能构成三角形,∴x≠0,∴|﹣x+2|=13,∴﹣x+2=±13,解得x=53或x=73,此时N 点坐标为(53,0)或(73,0); ②当或MN ON BC AB =时,∴=,即|x||﹣x+2|=3|x|, ∴|﹣x+2|=3,∴﹣x+2=±3,解得x=5或x=﹣1,此时N 点坐标为(﹣1,0)或(5,0),综上可知存在满足条件的N 点,其坐标为(53,0)或(73,0)或(﹣1,0)或(5,0).【点睛】。
上海民办兰生复旦中学化学初三化学上册期中化学试卷

上海民办兰生复旦中学化学上册期中化学试卷一、选择题(培优题较难)1.逻辑推理是一种重要的化学思维方法,下列推理合理的是()A.在同一化合物中,金属元素显正价,则非金属元素一定显负价B.化学变化伴随着能量变化则有能量变化的一定是化学变化C.单质含有一种元素,则含有一种元素的纯净物一定是单质D.催化剂的质量在反应前后不变,则在反应前后质量不变的物质一定是该反应的催化剂2.下列有关水的说法中正确的是()A.水与冰块混合得到混合物B.水的蒸发和水通电分解都属于物理变化C.硬水是指含有较多可溶性钙、镁化合物的水D.水沸腾时可冲起壶盖,说明温度升高分子会变大3.某反应的微观示意图如下,其中“”和“”表示不同元素的原子,下列说法不正确的是( )A.反应物有4种分子B.反应前后原子个数不变C.反应前后元素种类不变D.化学变化中的最小粒子是原子4.最近,我国科学家成功合成新型催化剂,将CO2高效转化为甲醇(CH3OH)。
这不仅可以缓解碳排放引起的温室效应,还将成为理想的能源补充形式。
该化学反应的微观过程如下图所示。
下列说法正确的是A.该反应中四种物质均为化合物B.反应前后H元素的化合价不变C.参加反应的甲、乙分子个数比为1:3D.反应前后原子数目发生改变5.实验室常用加热高锰酸钾固体制取氧气,化学方程式为2KMnO4K2MnO4+MnO2+O2↑,现对一定量的高锰酸钾固体进行加热,加热过程中涉及的相关量随时间变化的图象正确的是A.B.C.D.6.下列有关氧气的说法,错误的是()A.氧气能支持燃烧B.细铁丝在氧气中燃烧,生成氧化铁C.在通常状况下,氧气的密度比空气大D.氧气的化学性质比较活泼,能跟许多物质发生反应7.下列图示中的“错误实验操作”与图下面对应的“可能产生的后果”不一致的是()A.液体喷出B.污染试剂C.酒精溅出D.读数偏大8.下列滴管使用图示正确的是()A.取液时挤入空气B.代替玻璃棒进行搅拌C.向试管中滴加液体D.将残留溶液的滴管倒持9.硼是作物生长必需的微量营养元素,硼元素的相关信息如图所示。
上海市黄浦区2016届九年级上期中数学试卷(含答案)

2015-2016学年上海市黄浦区九年级(上)期中数学试卷一、选择题:(本大题共6题,每题4分,满分24分)1.若ac=bd(ac≠0),则下列比例式中不成立的是()A.B.C.D.2.已知:Rt△ABC中,∠C=90°,sinB=,则tanA等于()A.B.C.D.3.如果点D、E分别在△ABC的两边AB、AC上,下列条件中可以推出DE∥BC的是()A.=,=B.=,=C.=,=D.=,=4.已知小丽同学身高1.5米,经太阳光照射,在地面的影长为2米,她此时测得一建筑物在同一地面的影长为40米,那么这个建筑物的高为()A.20米B.30米C.40米D.50米5.把△ABC的各边长都增加两倍,则锐角A的正弦值()A.增加2倍B.增加4倍C.不变D.不能确定6.如图,∠ABC=∠CDB=90°,BC=3,AC=5,如果△ABC与△CDB相似,那么BD的长()A.B.C.D.或二、填空题:(本大题共12题,每题4分,满分48分)7.如果a:b=2:3,那么(a+b):b=__________.8.在Rt△ABC中,∠A=90°,BC=10,cosB=,AC=__________.9.已知,AB=4,P是AB黄金分割点,PA>PB,则PA的长为__________.10.两个相似三角形对应高的比为5:2,那么这两个相似三角形的面积比是__________.11.如图,l1∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.12.如图,DE∥BC,DF=2,FC=4,那么=__________.13.计算:=__________.14.若斜坡的坡度1:3,沿坡面前进10米,升高__________米.15.如图,若点G是△ABC的重心,GD∥BC,则=__________.16.如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是__________.17.如图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=,则△ABC的边长为__________.。
2016-2017年上海市黄浦区九年级(上)期中数学试卷和答案(五四学制)

2016-2017学年上海市黄浦区九年级(上)期中数学试卷(五四学制)一、单项选择题(本大题共6小题,每小题4分,满分24分)1.(4分)下列各组线段中,能组成比例线段的是()A.0.1,0.2,0.3,0.4 B.0.2,0.8,12,30C.1,3,4,6 D.12,16,45,602.(4分)如图,在△ABC中,点D、E分别在边AB、AC上,下列比例式不能判定DE∥BC的是()A.=B.=C.=D.=3.(4分)已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是()A.sinB=B.cosB=C.tanB=D.cotB=4.(4分)甲、乙两地的实际距离是40千米,在比例尺为1:500000的地图上,甲乙两地的距离是()A.0.8cm B.8cm C.80cm D.800cm5.(4分)下列判断不正确的是()A.B.如果,那么C.如果(k≠0),那么D.6.(4分)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是()A.B.C.D.二、填空题(本大题共12题,每小题4分,满分48分)7.(4分)若,则=.8.(4分)如图,DE∥BC,DE:BC=4:5,则EA:AC=.9.(4分)已知点P是线段AB的黄金分割点,PA>PB,且AB=8,则PA=.10.(4分)如图,已知直线l1∥l2∥l3,AB=4,DF=6,BC=4,则EF=.11.(4分)如图,在△ABC中,AD是中线,G是重心,过点G作EF∥BC,分别交AB、AC于点E、F,若AC=18,则AF=.12.(4分)已知Rt△ABC∽Rt△A1B1C1且相似比为3:4,若Rt△ABC的最长边长为12cm,则Rt△A1B1C1最长边的中线长为cm.13.(4分)化简:3(+2)﹣2(+)=.14.(4分)在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD=.15.(4分)已知梯形的上下两底长度为4和6,将两腰延长交于一点,这个交点到两底边的距离之比是.16.(4分)如图,5个同样大小的正方形拼成一个长方形,则∠ABC+∠ADC+∠ACB=.17.(4分)如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN 的长度为.18.(4分)如图,在△ABC中,AB=AC=12,BC=24,如果将△ABC沿直线l 翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为.三、解答题(本大题共7题,满分78分)19.(10分)计算:cos245°﹣+cot230°.20.(10分)如图,在锐角△ABC中,AB=AC,BC=10,sinA=,(1)求tanB的值;(2)求AB的长.21.(10分)如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,交BD于点G,AE:AB=1:3,设=,=.(1)用向量、分别表示下列向量:=,=,=;(2)在图中求作向量分别在、方向上的分向量.(不写作法,但要写出画图结果)22.(10分)如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EFA;(2)若AB=12,BM=5,求DE的长.23.(12分)在矩形ABCD中,点E是AD的中点,BE垂直AC交AC于点F,求证:(1)=;(2)∠EFD=∠DBC.24.(12分)如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E 在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.(1)求证:AC=CG;(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.25.(14分)如图,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°.(1)若BE=,求CF长.(2)设BE=x,△PEF的面积为y,求y关于x的函数解析式,并写出x的取值范围.(3)当E、F在运动过程中,∠EFP是否可能等于75°?若可能求出x的值,若不可能请说明理由.2016-2017学年上海市黄浦区九年级(上)期中数学试卷(五四学制)参考答案与试题解析一、单项选择题(本大题共6小题,每小题4分,满分24分)1.(4分)下列各组线段中,能组成比例线段的是()A.0.1,0.2,0.3,0.4 B.0.2,0.8,12,30C.1,3,4,6 D.12,16,45,60【解答】解:A、0.1,0.2,0.3,0.4不是成比例线段,故本选项错误;B、0.2,0.8,12,30不是成比例线段,故本选项错误;C、1,3,4,6不是成比例线段,故本选项错误;D、根据12:16=45:60,可得12,16,45,60是成比例线段,故D选项正确.故选:D.2.(4分)如图,在△ABC中,点D、E分别在边AB、AC上,下列比例式不能判定DE∥BC的是()A.=B.=C.=D.=【解答】解:如图,∵当时,△ADE与△ABC不一定相似,∴∠ADE不一定等于∠B,∴不能判定DE∥BC,故选:C.3.(4分)已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是()A.sinB=B.cosB=C.tanB=D.cotB=【解答】解:由勾股定理知,AB===.∴sinB=,cosB=,cotB=.故选:C.4.(4分)甲、乙两地的实际距离是40千米,在比例尺为1:500000的地图上,甲乙两地的距离是()A.0.8cm B.8cm C.80cm D.800cm【解答】解:40千米=4000000厘米,4000000×=8(cm).故选:B.5.(4分)下列判断不正确的是()A.B.如果,那么C.如果(k≠0),那么D.【解答】解:A、﹣=,故本选项正确;B、如果,那么≠;但是如果,那么;故本选项错误;C、如果(k≠0),那么;故本选项正确;D、+=+;故本选项正确.故选:B.6.(4分)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是()A.B.C.D.【解答】解:∵AD⊥BC,DE⊥AB,∴∠ADC=∠AED=90°,∵∠BAC=90°,∴∠DAE=∠C,∴Rt△ACD∽Rt△DAE,∴=,∵AD=3,DE=2,∴=,∴AC=,在Rt△ACD中,CD2+AD2=AC2,∴CD==,故选:D.二、填空题(本大题共12题,每小题4分,满分48分)7.(4分)若,则=.【解答】解:根据题意,设x=2k,y=3k,z=4k,则=,故答案为:.8.(4分)如图,DE∥BC,DE:BC=4:5,则EA:AC=4:5.【解答】解:如图,∵DE∥BC,∴△ADE∽△ABC,∴,故答案为4:5.9.(4分)已知点P是线段AB的黄金分割点,PA>PB,且AB=8,则PA=.【解答】解:∵P是线段AB的黄金分割点,AP>BP,∴PA=AB,而AB=8,∴PA=8×=4﹣4.故答案是:4﹣4.10.(4分)如图,已知直线l1∥l2∥l3,AB=4,DF=6,BC=4,则EF=3.【解答】解:如图,∵l1∥l2∥l3,∴,即,解得:EF=3.故答案为3.11.(4分)如图,在△ABC中,AD是中线,G是重心,过点G作EF∥BC,分别交AB、AC于点E、F,若AC=18,则AF=12.【解答】解:∵G是△ABC的重心,∴AG=2DG,AD=3DG;∵EF∥BC,∴,∵AC=18,∴AF=12.故答案为12.12.(4分)已知Rt△ABC∽Rt△A1B1C1且相似比为3:4,若Rt△ABC的最长边长为12cm,则Rt△A1B1C1最长边的中线长为8cm.【解答】解:设Rt△A1B1C1最长边为xcm,∵Rt△ABC∽Rt△A1B1C1且相似比为3:4,∴12:x=3:4,解得,x=16,则Rt△A1B1C1最长边的中线长为8cm,故答案为:8.13.(4分)化简:3(+2)﹣2(+)=+4.【解答】解:3(+2)﹣2(+),=3+6﹣2﹣2,=+4.故答案为:+4.14.(4分)在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD=.【解答】解:在直角△ABC中,根据勾股定理可得:AB===3.∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,∴∠B=∠ACD.∴sin∠ACD=sin∠B==.15.(4分)已知梯形的上下两底长度为4和6,将两腰延长交于一点,这个交点到两底边的距离之比是2:3.【解答】解:如图,梯形ABCD中,AD∥BC,AD=4,BC=6,∴△EAD∽△EBC,∵EN⊥BC,∴EN⊥AD,∴EM:EN=AD:BC=4:6=2:3,即这个交点到两底边的距离之比是:2:3.故答案为:2:3.16.(4分)如图,5个同样大小的正方形拼成一个长方形,则∠ABC+∠ADC+∠ACB=90°.【解答】解:设每个小正方形的边长为1,由勾股定理得:AC=,AD=,AB=,又∵DC=1,BD=5,∴,=,=,∴,∴△ADC∽△BDA,∴∠DAC=∠ABD,∵∠ACB=45°,∴∠ACB=∠DAC+∠ADB=45°,∴∠ABC+∠ADC+∠ACB=90°;故答案为:90°.17.(4分)如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为.【解答】解:∵四边形DEFG是正方形,∴DE∥BC,GF∥BN,且DE=GF=EF=1,∴△ADE∽△ACB,△AGF∽△ANB,∴=①,=②,由①可得,=,解得:AE=,将AE=代入②,得:=,解得:BN=,故答案为:.18.(4分)如图,在△ABC中,AB=AC=12,BC=24,如果将△ABC沿直线l 翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.【解答】解:过点A作AG⊥BC于点G,∵AB=AC=12,BC=24,∴GC=BG=12,∴AG=24,∵将△ABC沿直线l翻折后,点B落在边AC的中点处,过E点作EF⊥BC于点F,∴EF=AG=12,∴FC=GC=6,设BD=x,则DE=x,∴DF=24﹣x﹣6=18﹣x,∴x2=(18﹣x)2+122,解得:x=13,则BD=13.故答案为:13.三、解答题(本大题共7题,满分78分)19.(10分)计算:cos245°﹣+cot230°.【解答】解:原式=()2﹣+()2=﹣+3=.20.(10分)如图,在锐角△ABC中,AB=AC,BC=10,sinA=,(1)求tanB的值;(2)求AB的长.【解答】解:(1)过点C作CD⊥AB,垂足为D,(1分)在Rt△ACD中,,(1分)设CD=3k,则AB=AC=5k,(1分)∴.(1分)在△BCD中,∵BD=AB﹣AD=5k﹣4k=k.(1分)∴.(1分)(2)在Rt△BCD中,,(1分)∵BC=10,∴.(1分)∴.(1分)∴AB=.(1分)21.(10分)如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,交BD于点G,AE:AB=1:3,设=,=.(1)用向量、分别表示下列向量:=,=﹣,=﹣;(2)在图中求作向量分别在、方向上的分向量.(不写作法,但要写出画图结果)【解答】解:(1)∵=,AE=BA ,∴=,∵=+,EB=﹣,=,∴=﹣, ∵CD ∥EB ,∴EG :CG=EB :CD=4:3,∴EG :EC=4:7,∴=﹣,故答案分别为,﹣,﹣.(2)点G 作GM ∥AB 交BC 于M ,NN ∥BC 交AB 于N ,则向量、是向量分别在、方向上的分向量.22.(10分)如图,正方形ABCD 中,M 为BC 上一点,F 是AM 的中点,EF ⊥AM ,垂足为F ,交AD 的延长线于点E ,交DC 于点N .(1)求证:△ABM∽△EFA;(2)若AB=12,BM=5,求DE的长.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=90°,AD∥BC,∴∠AMB=∠EAF,又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EFA;(2)解:∵∠B=90°,AB=12,BM=5,∴AM==13,AD=12,∵F是AM的中点,∴AF=AM=6.5,∵△ABM∽△EFA,∴,即,∴AE=16.9,∴DE=AE﹣AD=4.9.23.(12分)在矩形ABCD中,点E是AD的中点,BE垂直AC交AC于点F,求证:(1)=;(2)∠EFD=∠DBC.【解答】证明:(1)∵AC⊥BE,∴∠AFB=∠AFE=90°,∵四边形ABCD是矩形,∴∠BAE=90°,∴∠AFE=∠BAE,又∵∠AEF=∠BEA,∴△AEF∽△BEA,∴=;(2)∵点E是AD的中点,∴AE=ED,∴,又∵∠FED=∠DEB,∴△DEF∽△EBD,∴∠EFD=∠EDB,∵AD∥BC,∴∠DBC=∠EDB,∴∠EFD=∠DBC.24.(12分)如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E 在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.(1)求证:AC=CG;(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.【解答】证明:∵BF∥DE,∴=,∵AD=BD,∴AC=CG.(2)解:当PB=5或时,△BCP与△BCD相似;在△ABC和△GBC中:,∴△ABC≌△GBC(SAS),∴AB=BG∴∠DBC=∠CBP,∵AC=6,BC=8,∴AB=10,∴CD=5,∵∠DBC=∠CBP,第一种情况:若∠DCB=∠BCP,如图1:在△BCP与△BCD中∠DCB=∠BCP,BC=BC,∠DBC=∠CBP,∴△BCP≌△BCD(ASA),∴BP=CD=5;第二种情况:若∠PCB=∠DCB,如图2:∵∠CBD=∠CBP,∴△BPC∽△BCD,∴,∴BP=,综上所述:当PB=5或时,△BCP与△BCD相似.25.(14分)如图,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°.(1)若BE=,求CF长.(2)设BE=x,△PEF的面积为y,求y关于x的函数解析式,并写出x的取值范围.(3)当E、F在运动过程中,∠EFP是否可能等于75°?若可能求出x的值,若不可能请说明理由.【解答】解:(1)如图1,∵在△ABC中,AB=AC=2,∠A=90°,∴∠B=∠C=45°.BC=,又∵∠1=180°﹣∠EPF﹣∠3,∠EPF=45°,∠C+∠2+∠3=180°,∴∠1=135°﹣∠3,∠2=135°﹣∠3,∴∠1=∠2,∴△BPE∽△CFP.∴∵P为BC的中点.∴BP=CP=,∴,∴CF=,(2)∵在△ABC中,AB=AC=2,∠A=90°,P为BC的中点∴BP=CP=.由(1)知△BPE∽△CFP,则=,即,解得,CF=.=S△ABC﹣S△BPE﹣S△PFC﹣S△AEF则S△PEF=2﹣×x×﹣×××﹣×(2﹣x)×(2﹣)=﹣1++,即y=﹣1++(1≤x≤2);(3)当E、F在运动过程中,∠EFP可能等于75°.理由如下:如图2,过点F作FM⊥EP于点M.设EM=a.在Rt△EMF中,FM=a.在Rt△FMP中,得到PM=a,FP=a,则==,∵△BPE∽△CFP,∴∴=,∴x=,∵1≤x≤2,∴x=符合题意,∴当E、F在运动过程中,∠EFP可能等于75°.。
上海复旦实验中学初三化学上册期中试卷(含答案)

上海复旦实验中学化学上册期中试卷(含答案)一、选择题(培优题较难)1.仪器的用途及使用注意事项都正确的是( )加热:使用后吹灭,并盖上灯帽吸取液体:滴管口向上防止液体流出测量液体体积:不能被加热称量药品:药品直接放置在天平上A B C DA.A B.B C.C D.D2.某反应的微观示意图如下,其中“”和“”表示不同元素的原子,下列说法不正确的是( )A.反应物有4种分子B.反应前后原子个数不变C.反应前后元素种类不变D.化学变化中的最小粒子是原子3.宏观辨识和微观剖析是化学核心素养之一。
下列说法正确的是 ( )A.反应前后元素的种类及化合价均未发生改变B.参加反应的和的微粒个数比是4:3C.反应涉及到的物质中,是由原子构成的单质,只有属于氧化物D.该反应生成的单质和化合物的质量比时3:204.某工地发生多人食物中毒,经化验为误食工业用盐亚硝酸钠(NaNO2)所致。
NaNO2中氮元素的化合价是()A.+4B.+3C.+2D.+55.实验室常用加热高锰酸钾固体制取氧气,化学方程式为2KMnO4K2MnO4+MnO2+O2↑,现对一定量的高锰酸钾固体进行加热,加热过程中涉及的相关量随时间变化的图象正确的是A.B.C.D.6.用下图装置进行实验。
下列现象能证明空气中O2的含量的是()A.红磷燃烧,产生白烟B.瓶中液面先下降,后上升C.瓶中液面最终上升至1处D.水槽中液面下降7.质量守恒定律是自然界基本的规律之一。
下列装置及实验(天平未画出)能用来验证质量守恒定律的是()A.B.C.D.8.以下是四种微粒的结构示意图,下列有关各微粒的说法中,错误的是A.①的化学性质比较稳定B.③④属于同种元素C.④是一种阴离子D.②容易得到电子9.实验室测定蜡烛在盛有一定体积空气的密闭容器内燃烧至熄灭过程中,O2和CO含量随时间变化曲线如图,通过分析该图可推理出的结论是A.曲线①表示CO含量的变化B.蜡烛发生了不完全燃烧C.蜡烛由碳、氢元素组成D.蜡烛熄灭时,容器内氧气耗尽10.一定条件下,密闭容器内发生的某化学反应,测得t1和t2时各物质的质量见下表,下列说法正确的是( )物质M N P Qt1时的质量/g519317t2时的质量/g233x51A.x的值小于3 B.Q可能是单质C.该反应一定是分解反应D.M与N的质量变化比为14:311.下列有关二氧化碳的检验、制备和用途能达到目的的是( )A.干冰用于人工降雨B.二氧化碳气体通入紫色石蕊试液中,溶液变为蓝色C.用块状石灰石和稀硫酸迅速制备大量二氧化碳D.将燃着的木条伸入集气瓶,火焰立即熄灭,证明瓶内原有气体就是二氧化碳12.某高性能锂电池,其反应原理可表示为: Li+MnO2= LiMnO2,已知锂元素在化合物中显+1价,下列说法正确的是A.LiMnO2是氧化物 B.该反应是化合反应C.此反应中,二氧化锰是催化剂 D.LiMnO2中锰元素的化合价显+2价13.如图为电解水的实验装置图,下列说法正确的是()A.在水中加入少量硫酸钠以增强水的导电性B.与负极相连的玻璃管内得到的气体能使带火星的木条复燃C.该实验中所得氢气和氧气的质量比约为2:1D.该实验说明水是由氢气和氧气组成的14.下图是“尾气催化转换器”将汽车尾气中有毒气体转变为无毒气体的微观示意图,其中不同的圆球代表不同原子。
上海复旦实验中学初三化学上册期中试卷(含答案)
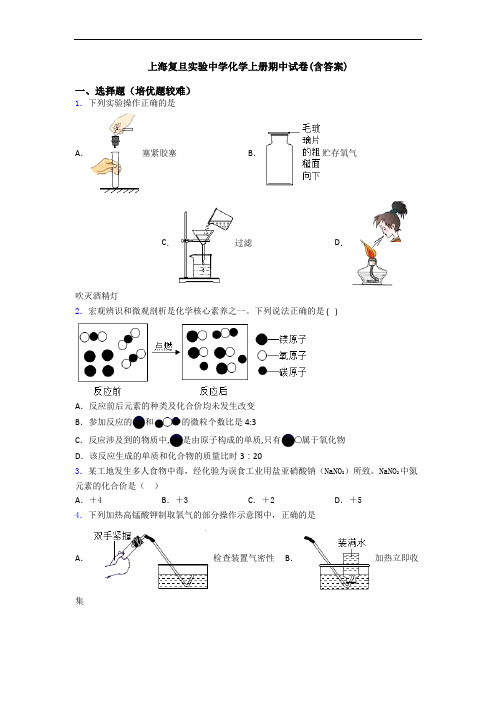
上海复旦实验中学化学上册期中试卷(含答案)一、选择题(培优题较难)1.下列实验操作正确的是A.塞紧胶塞B.贮存氧气C.过滤D.吹灭酒精灯2.宏观辨识和微观剖析是化学核心素养之一。
下列说法正确的是 ( )A.反应前后元素的种类及化合价均未发生改变B.参加反应的和的微粒个数比是4:3C.反应涉及到的物质中,是由原子构成的单质,只有属于氧化物D.该反应生成的单质和化合物的质量比时3:203.某工地发生多人食物中毒,经化验为误食工业用盐亚硝酸钠(NaNO2)所致。
NaNO2中氮元素的化合价是()A.+4B.+3C.+2D.+54.下列加热高锰酸钾制取氧气的部分操作示意图中,正确的是A.检查装置气密性B.加热立即收集C.收满后移出集气瓶 D.结束时停止加热5.下列关于CO2的实验室制法及性质实验的说法不正确的是()A、制CO2的药品B、发生装置C、收集装置D、比较CO2与空气的密度A.A B.B C.C D.D6.实验室用装有等质量的两份氯酸钾的试管a和b分别加热制取氧气过程中,某同学误把少量高锰酸钾当成二氧化锰加入b试管,下面是试管a、b中产生氧气的质量随时间变化的图象,其中正确的是()A.B.C.D.7.下列鉴别两种不同物质的方法,不正确的是()序号待鉴别的物质鉴别方法A CO2与O2燃着的木条,观察燃着的情况B酒精与白醋闻气味C CaCO3与NaCl加水,观察是否溶解D NaOH与Na2CO3滴加酚酞溶液,观察溶液颜色的变化A.A B.B C.C D.D8.某高性能锂电池,其反应原理可表示为: Li+MnO2= LiMnO2,已知锂元素在化合物中显+1价,下列说法正确的是A.LiMnO2是氧化物 B.该反应是化合反应C.此反应中,二氧化锰是催化剂 D.LiMnO2中锰元素的化合价显+2价9.如图所示有关二氧化碳的实验中,只与二氧化碳物理性质有关的实验是()A. B. C. D.10.科学理论在传承中不断发展,科学家们传承前人的正确观点,纠正错误观点,形成科学理论,关于原子结构的学说有:①在球体内充斥正电荷,电子镶嵌其中②原子是可分的③原子呈球形④原子中有带负电的电子⑤原子中有带正电的原子核⑥原子核很小,但集中了原子的大部分质量其中经过卢瑟福传承和发展后形成的观点是()A.②③④⑤⑥B.①②③④C.④⑤⑥D.⑤⑥11.甲、乙、丙、丁四种物质在反应前后的质量关系如图所示,下列有关说法错误的是A.参加反应的甲和乙质量比为2:7 B.丙可能是该反应的催化剂C.丁一定是化合物D.x的值是712.科学家研制出一种新型催化剂,可用于去除装修残留的甲醛(化学式为 CH2O),该反应过程的微观示意图如下。
上海市复旦大学附中2016年10月2016~2017学年度高一第一学期期中考试数学试卷及参考答案教师专用

2016年10月2016~2017学年度上海市复旦大学附中高一上学期期中数学试卷一.填空题1.集合{1,2,3,…,2015,2016}的子集个数为.2.已知全集U=R,集合A={x|x≤1},集合B={x|x≥2},则∁U(A∪B)=.3.已知集合A={x|1≤x≤2},集合B={x|x≤a},若A∩B≠∅,则实数a的取值范围是.4.己知集合U={a,b,c,d,e,f},集合A={a,b,c,d},A∩B={b},∁U(A∪B)={f},求集合B.5.已知a2>a1>0,b2>b1>0,且a1+a2=b1+b2=1,记A=a1b1+a2b2,B=a1b2+a2b1,C=,则按A、B、C从小到大的顺序排列是.6.已知Rt△ABC的周长为定值2,则它的面积最大值为.7.我们将b﹣a称为集合M={x|a≤x≤b}的“长度”,若集合M={x|m≤x≤m+},N={x|n﹣0.5≤x≤n},且集合M和集合N都是集合{x|0≤x≤1}的子集,则集合M∩N的“长度”的最小值是.8.已知A={x|>x},B={x|x(x﹣3)(x+3)>0},则A∩B=.9.对于任意集合X与Y,定义:①X﹣Y={x|x∈X且x∉Y},②X△Y=(X﹣Y)∪(Y﹣X),已知A ={y|y=x2,x∈R},B={y|﹣2≤y≤2},则A△B=.10.已知常数a是正整数,集合A={x||x﹣a|<a+,x∈Z},B={x||x|<2a,x∈Z},则集合A∪B中所有元素之和为.11.非空集合G关于运算⊕满足:(1)对任意a,b∈G,都有a+b∈G;(2)存在e∈G使得对于一切a∈G都有a⊕e=e⊕a=a,则称G是关于运算⊕的融洽集,现有下列集合与运算:①G是非负整数集,⊕:实数的加法;②G是偶数集,⊕:实数的乘法;③G是所有二次三项式构成的集合,⊕:多项式的乘法;④G={x|x=a+b,a,b∈Q},⊕:实数的乘法;其中属于融洽集的是(请填写编号)12.集合A={(x,y)|y=a|x|,x∈R},B={(x,y)|y=x+a,x∈R},已知集合A∩B中有且仅有一个元素,则常数a的取值范围是.二.选择题13.已知集合A={1,2,3,…,2105,2016},集合B={x|x=3k+1,k∈Z},则A∩B中的最大元素是()A.2014B.2015C.2016D.以上答案都不对14.已知全集U=A∪B中有m个元素,(∁U A)∪(∁U B)中有n个元素.若A∩B非空,则A∩B的元素个数为()A.mnB.m+nC.n﹣mD.m﹣n15.命题“已知x,y∈R,如果x2+y2=0,那么x=0且y=0”的逆否命题是()A.已知x,y∈R,如果x2+y2≠0,那么x≠0且y≠0B.已知x,y∈R,如果x2+y2≠0,那么x≠0或y≠0C.已知x,y∈R,如果x≠0或y≠0,那么x2+y2≠0D.已知x,y∈R,如果x≠0且y≠0,那么x2+y2≠016.对任意实数a,b,c,给出下列命题:①“a=b”是“ac=bc”的充要条件;②“a+5是无理数”是“a是无理数”的充要条件;③“a>b”是“a2>b2”的充分条件;④“a<4”是“a<3”的必要条件;其中真命题的个数是()A.1个B.2个C.3个D.4个三.解答题17.已知集合A={1,2,3},B={x|x2﹣(a+1)x+a=0,x∈R},若A∪B=A,求实数a.18.已知a,b,c∈R+,求证:2(a3+b3+c3)≥ab2+a2b+bc2+b2c+ac2+a2c.19.设正有理数a1是的一个近似值,令a2=1+,求证:(1)介于a1与a2之间;(2)a2比a1更接近于.20.已知对任意实数x,不等式mx2﹣(3﹣m)x+1>0成立或不等式mx>0成立,求实数m的取值范围.21.已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R;(1)试求不等式的解集A;(2)对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B为有限集,求实数k的取值范围,使得集合B中元素个数最少,并用列举法表示集合B.2016年10月2016~2017学年度上海市复旦大学附中高一(上)期中数学试卷参考答案与试题解析一.填空题1.(2016秋•杨浦区校级期中)集合{1,2,3,…,2015,2016}的子集个数为22016.【知识考查点】子集与真子集.【专题】集合思想;集合.【试题分析】对于有限集合,我们有以下结论:若一个集合中有n个元素,则它有2n个子集. 【试题解答】解:∵集合{1,2,3,…,2015,2016}中有2016个元素,∴集合M{1,2,3,…,2015,2016}的子集的个数为22016;故答案为:22016.【点评】本题考查了集合的子集个数,若一个集合中有n个元素,则它有2n个子集,有(2n﹣1)个真子集,属于基础题.2.(2016秋•杨浦区校级期中)已知全集U=R,集合A={x|x≤1},集合B={x|x≥2},则∁U(A∪B)={x|1<x<2} .【知识考查点】交、并、补集的混合运算.【专题】集合思想;定义法;集合.【试题分析】根据并集与补集的定义,进行计算即可.【试题解答】解:全集U=R,集合A={x|x≤1},集合B={x|x≥2},所以A∪B={x|x≤1或x≥2},所以∁U(A∪B)={x|1<x<2}.故答案为:{x|1<x<2}.【点评】本题考查了并集与补集的定义与应用问题,是基础题目.3.(2016秋•杨浦区校级期中)已知集合A={x|1≤x≤2},集合B={x|x≤a},若A∩B≠∅,则实数a的取值范围是[1,+∞).【知识考查点】交集及其运算.【专题】计算题;集合思想;定义法;集合.【试题分析】题中条件:“A∩B≠∅,”表示两个集合的交集的结果不是空集,即可求解实数a的取值范围.【试题解答】解:集合A={x|1≤x≤2},集合B={x|x≤a},因为A∩B≠∅,所以a≥1故答案为:[1,+∞)【点评】本题考查集合的关系、一元二次不等式的解法,考查运算能力,是基础题.4.(2016秋•杨浦区校级期中)己知集合U={a,b,c,d,e,f},集合A={a,b,c,d},A∩B={b},∁U(A∪B)={f},求集合B.【知识考查点】交、并、补集的混合运算.【专题】集合思想;综合法;集合.【试题分析】根据全集U,以及A与B并集的补集确定出A与B的并集,再根据A与B的交集及A,确定出B即可.【试题解答】解:∵U={a,b,c,d,e,f},∁U(A∪B)={f},∴A∪B={a,b,c,d,e},∵A∩B={b};A={a,b,c,d},∴b∈B,e∈B,b∉B,c∉B,d∉B,∴B={b,e}.【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.5.(2016秋•杨浦区校级期中)已知a2>a1>0,b2>b1>0,且a1+a2=b1+b2=1,记A=a1b1+a2b2,B=a1b2+a2b1,C=,则按A、B、C从小到大的顺序排列是B<C<A.【知识考查点】不等式比较大小.【专题】计算题;转化思想;转化法;不等式.【试题分析】不妨令a1=,a2=,b1=,b2=,分别求出A,B,比较即可【试题解答】解:∵a2>a1>0,b2>b1>0,且a1+a2=b1+b2=1,不妨令a1=,a2=,b1=,b2=,A=a1b1+a2b2=+=,B=a1b2+a2b1=+=,∵C==∴B<C<A故答案为:B<C<A.【点评】本题主要考查不等式与不等关系,利用特殊值代入法比较几个式子在限定条件下的大小关系,是一种简单有效的方法,属于基础题.6.(2016秋•杨浦区校级期中)已知Rt△ABC的周长为定值2,则它的面积最大值为3﹣2.【知识考查点】正弦定理.【专题】计算题;转化思想;综合法;解三角形;不等式的解法及应用.【试题分析】设直角边长为a,b,则斜边长为,利用直角三角形ABC的三边之和为2,可得a+b+=2,利用基本不等式,即可求△ABC的面积的最大值.【试题解答】解:设直角边长为a,b,则斜边长为,∵直角三角形ABC的三边之和为2,∴a+b+=2,∴2≥2+,∴≤=2﹣,∴ab≤6﹣4,∴S=ba≤3﹣2,∴△ABC的面积的最大值为3﹣2.故答案为:3﹣2.【点评】本题考查基本不等式的运用,考查学生的计算能力,正确运用基本不等式是关键,属于中档题.7.(2016秋•杨浦区校级期中)我们将b﹣a称为集合M={x|a≤x≤b}的“长度”,若集合M={x|m≤x≤m+},N={x|n﹣0.5≤x≤n},且集合M和集合N都是集合{x|0≤x≤1}的子集,则集合M∩N的“长度”的最小值是.【知识考查点】交集及其运算.【专题】计算题;新定义;转化思想;转化法;集合.【试题分析】当集合M∩N的长度的最小值时,M与N应分别在区间[0,1]的左右两端,由此能求出M∩N的长度的最小值.【试题解答】解:根据题意,M的长度为,N的长度为,当集合M∩N的长度的最小值时,M与N应分别在区间[0,1]的左右两端,故M∩N的长度的最小值是=.故答案为:.【点评】本题考查交集的“长度”的最小值的求法,是基础题,解题时要认真审题,注意新定义的合理运用.8.(2016秋•杨浦区校级期中)已知A={x|>x},B={x|x(x﹣3)(x+3)>0},则A∩B={x|﹣3<x<0} .【知识考查点】交集及其运算.【专题】计算题;方程思想;定义法;集合.【试题分析】先利用不等式的性质分别求出集合A和B,由此利用交集的性质能求出A∩B. 【试题解答】解:∵A={x|>x}={x|﹣2≤x≤1,或x<0},B={x|x(x﹣3)(x+3)>0}={x|﹣3<x<0或x>3},∴A∩B={x|﹣3<x<0}.故答案为:{x|﹣3<x<0}.【点评】本题考查交集的求法,是中档题,解题时要认真审题,注意无理不等式和高次不等式性质的合理运用.9.(2016秋•杨浦区校级期中)对于任意集合X与Y,定义:①X﹣Y={x|x∈X且x∉Y},②X△Y =(X﹣Y)∪(Y﹣X),已知A={y|y=x2,x∈R},B={y|﹣2≤y≤2},则A△B=[﹣3,0)∪(3,+∞).【知识考查点】子集与交集、并集运算的转换.【专题】综合题;方程思想;演绎法;集合.【试题分析】由A={y|y=x2,x∈R}={y|y≥0},B={y|﹣2≤y≤2},先求出A﹣B={y|y>2},B﹣A={y|﹣2≤y<0},再求A△B的值.【试题解答】解:∵A={y|y=x2,x∈R}={y|y≥0},B={y|﹣2≤y≤2},∴A﹣B={y|y>2},B﹣A={y|﹣2≤y<0},∴A△B={y|y>2}∪{y|﹣2≤y<0},故答案为:[﹣3,0)∪(3,+∞).【点评】本题考查集合的交、并、补集的运算,解题时要认真审题,仔细解答,注意正确理解X ﹣Y={x|x∈X且x∉Y}、X△Y=(X﹣Y)∪(Y﹣X).10.(2016秋•杨浦区校级期中)已知常数a是正整数,集合A={x||x﹣a|<a+,x∈Z},B={x||x|<2a,x∈Z},则集合A∪B中所有元素之和为2a.【知识考查点】并集及其运算.【专题】集合思想;转化法;集合.【试题分析】分别求出集合A、B中的元素,从而求出A、B的并集,求和即可.【试题解答】解:A={x||x﹣a|<a+,x∈Z}={0,a,2a},B={x||x|<2a,x∈Z}={﹣a,0,a},则集合A∪B={﹣a,0,a,2a},故集合A∪B中所有元素之和是2a,故答案为:2a.【点评】本题考查了集合的运算,考查解绝对值不等式问题,是一道基础题.11.(2016秋•杨浦区校级期中)非空集合G关于运算⊕满足:(1)对任意a,b∈G,都有a+b∈G;(2)存在e∈G使得对于一切a∈G都有a⊕e=e⊕a=a,则称G是关于运算⊕的融洽集,现有下列集合与运算:①G是非负整数集,⊕:实数的加法;②G是偶数集,⊕:实数的乘法;③G是所有二次三项式构成的集合,⊕:多项式的乘法;④G={x|x=a+b,a,b∈Q},⊕:实数的乘法;其中属于融洽集的是①④(请填写编号)【知识考查点】元素与集合关系的判断.【专题】新定义;集合思想;集合.【试题分析】逐一验证几个选项是否分别满足“融洽集”的两个条件,若两个条件都满足,是“融洽集”,有一个不满足,则不是“融洽集”.【试题解答】解:①对于任意非负整数a,b知道:a+b仍为非负整数,所以a⊕b∈G;取e=0,及任意非负整数a,则a+0=0+a=a,因此G对于⊕为整数的加法运算来说是“融洽集”;②对于任意偶数a,b知道:a+b仍为偶数,故有a+b∈G;但是不存在e∈G,使对一切a∈G都有a⊕e=e⊕a=a,故②的G不是“融洽集”.③对于G={二次三项式},若a、b∈G时,a,b的两个同类项系数,则其积不再为二次三项式,故G不是和谐集,故③不正确;④G={x|x=a+b,a,b∈Q},设x1=a+b,x2=c+d,则设x1+x2=(a+c)+(b+d),属于集合G,取e=1,a×1=1×a=a,因此G对于⊕实数的乘法运算来说是“融洽集”,故④中的G是“融洽集”.故答案为①④.【点评】本题考查了对新定义“融洽集”理解能力,及对有关知识的掌握情况.关键是看所给的数集是否满足“融洽集”的两个条件.12.(2016秋•杨浦区校级期中)集合A={(x,y)|y=a|x|,x∈R},B={(x,y)|y=x+a,x∈R},已知集合A∩B中有且仅有一个元素,则常数a的取值范围是[﹣1,1] .【知识考查点】交集及其运算.【专题】计算题;转化思想;转化法;集合.【试题分析】由已知得a|x|=x+a有1个解,由此能求出常数a的取值范围.【试题解答】解:∵集合A={(x,y)|y=a|x|,x∈R},B={(x,y)|y=x+a,x∈R},集合A∩B中有且仅有一个元素,∴a|x|=x+a有1个解,若x≥0,ax=x+a,x=,若x<0,﹣ax=x+a,x=﹣,由已知得或或或,解得﹣1≤a≤1.∴常数a的取值范围是[﹣1,1].故答案为:[﹣1,1].【点评】本题考查常数的取值范围的求法,是基础题,解题时要认真审题,是基础题,解题时要认真审题,注意交集性质的合理运用.二.选择题13.(2016秋•杨浦区校级期中)已知集合A={1,2,3,…,2105,2016},集合B={x|x=3k+1,k∈Z},则A∩B中的最大元素是()A.2014B.2015C.2016D.以上答案都不对【知识考查点】交集及其运算.【专题】计算题;集合思想;定义法;集合.【试题分析】由题意求出A与B的交集,即可作出判断.【试题解答】解:∵A={1,2,3,…,2105,2016},集合B={x|x=3k+1,k∈Z}∴则A∩B中的最大元素是2014.故选:A.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.14.(2009•江西)已知全集U=A∪B中有m个元素,(∁U A)∪(∁U B)中有n个元素.若A∩B非空,则A∩B的元素个数为()A.mnB.m+nC.n﹣mD.m﹣n【知识考查点】Venn图表达集合的关系及运算.【专题】数形结合.【试题分析】要求A∩B的元素个数,可以根据已知绘制出满足条件的韦恩图,根据图来分析(如解法一),也可以利用德摩根定理解决(如解法二).【试题解答】解法一:∵(C U A)∪(C U B)中有n个元素,如图所示阴影部分,又∵U=A∪B中有m个元素,故A∩B中有m﹣n个元素.解法二:∵(C U A)∪(C U B)=C U(A∩B)有n个元素,又∵全集U=A∪B中有m个元素,由card(A)+card(C U A)=card(U)得,card(A∩B)+card(C U(A∩B))=card(U)得,card(A∩B)=m﹣n,故选D.【点评】解答此类型题目时,要求对集合的性质及运算非常熟悉,除教材上的定义,性质,运算律外,还应熟练掌握:①(C U A)∪(C U B)=C U(A∩B)②(C U A)∩(C U B)=C U(A∪B)③card(A∪B)=card(A)+card(B)﹣card(A∩B)等.15.(2016秋•杨浦区校级期中)命题“已知x,y∈R,如果x2+y2=0,那么x=0且y=0”的逆否命题是()A.已知x,y∈R,如果x2+y2≠0,那么x≠0且y≠0B.已知x,y∈R,如果x2+y2≠0,那么x≠0或y≠0C.已知x,y∈R,如果x≠0或y≠0,那么x2+y2≠0D.已知x,y∈R,如果x≠0且y≠0,那么x2+y2≠0【知识考查点】四种命题间的逆否关系.【专题】定义法;简易逻辑.【试题分析】根据已知中原命题,写出逆否命题,可得答案.【试题解答】解:命题“已知x,y∈R,如果x2+y2=0,那么x=0且y=0”的逆否命题是“已知x,y∈R,如果x≠0或y≠0,那么x2+y2≠0”故选:C【点评】本题考查的知识点是四种命题,难度不大,属于基础题.16.(2016秋•杨浦区校级期中)对任意实数a,b,c,给出下列命题:①“a=b”是“ac=bc”的充要条件;②“a+5是无理数”是“a是无理数”的充要条件;③“a>b”是“a2>b2”的充分条件;④“a<4”是“a<3”的必要条件;其中真命题的个数是()A.1个B.2个C.3个D.4个【知识考查点】命题的真假判断与应用;必要条件、充分条件与充要条件的判断.【专题】综合法;简易逻辑.【试题分析】逐项判断即可.①由ac=bc不能推出a=b;②由5是有理数易判断;③根据不等式的性质可得;④根据充分必要条件的定义易得.【试题解答】解:①由“a=b“可得ac=bc,但当ac=bc时,不能得到a=b,故“a=b”是“ac=bc”的充分不必要条件,故①错误;②因为5是有理数,所以当a+5是无理数时,a必为无理数,反之也成立,故②正确;③取a=1,b=﹣2,此时a2<b2,故③错误;④当a<4时,不能推出a<3;当a<3时,有a<4成立,故“a<4”是“a<3”的必要不充分条件,故④正确.综上可得正确的命题有2个.故选:B.【点评】本题考查充分必要条件的判断,掌握充分必要条件的定义是关键.属于基础题.三.解答题17.(2016秋•杨浦区校级期中)已知集合A={1,2,3},B={x|x2﹣(a+1)x+a=0,x∈R},若A∪B =A,求实数a.【知识考查点】并集及其运算.【专题】计算题;分类讨论;集合.【试题分析】根据A∪B=A,得到B⊆A,然后分B为空集和不是空集讨论,A为空集时,只要二次方程的判别式小于0即可,不是空集时,分别把1和2代入二次方程求解a的范围,注意求出a后需要验证.【试题解答】解:由A∪B=A,得B⊆A.①若B=∅,则△=(a+1)2﹣4a<0,解得:a∈∅;②若1∈B,△=(a+1)2﹣4a=0,此时a=1,满足12﹣a﹣1+a=0,此时B={1},符合题意;③若2∈B,则22﹣2a﹣2+a=0,解得:a=2,此时A={2,1},满足题意.④若3∈B,则32﹣3a﹣3+a=0,解得:a=3,此时A={3,1},满足题意.综上所述,实数a的值为:1,2,3.【点评】本题考查了并集及其运算,考查了分类讨论的数学思想,求出a值后的验证是解答此题的关键,是基础题.18.(2016秋•杨浦区校级期中)已知a,b,c∈R+,求证:2(a3+b3+c3)≥ab2+a2b+bc2+b2c+ac2+a2c.【知识考查点】不等式的证明.【专题】证明题;转化思想;演绎法;不等式的解法及应用.【试题分析】作差,因式分解,即可得到结论.【试题解答】证明:(a3+b3)﹣(a2b+ab2)=a2(a﹣b)+b2(b﹣a)=(a﹣b)(a2﹣b2)=(a﹣b)2(a+b)∵a>0,b>0,∴(a3+b3)﹣(a2b+ab2)≥0∴a3+b3≥a2b+ab2.同理b3+c3≥bc2+b2c,a3+c3≥ac2+a2c,三式相加,可得2(a3+b3+c3)≥ab2+a2b+bc2+b2c+ac2+a2c.【点评】本题考查不等式的证明,考查作差法的运用,考查学生分析解决问题的能力,属于中档题.19.(2016秋•杨浦区校级期中)设正有理数a1是的一个近似值,令a2=1+,求证:(1)介于a1与a2之间;(2)a2比a1更接近于.【知识考查点】二分法求方程的近似解.【专题】证明题;转化思想;作差法;不等式.【试题分析】(1)利用作差法,再因式分解,确定其符号,即可得到结论;(2)利用作差法,判断|a2﹣|﹣|a1﹣|<0,即可得到结论【试题解答】证明:(1)a2﹣=1+﹣=,∵若a1>,∴a1﹣>0,而1﹣<0,∴a2<∵若a1<,∴a1﹣<0,而1﹣<0,∴a2>,故介于a1与a2之间;(2)|a2﹣|﹣|a1﹣|=﹣|a1﹣|=|a1﹣|×,∵a1>0,﹣2<0,|a1﹣|>0,∴|a2﹣|﹣|a1﹣|<0∴|a2﹣|<|a1﹣|∴a2比a1更接近于.【点评】本题考查不等式的证明,考查作差法的运用,确定差的符号是关键.20.(2016秋•杨浦区校级期中)已知对任意实数x,不等式mx2﹣(3﹣m)x+1>0成立或不等式mx>0成立,求实数m的取值范围.【知识考查点】一元二次不等式的解法.【专题】分类讨论;转化思想;不等式的解法及应用.【试题分析】①对任意实数x,不等式mx2﹣(3﹣m)x+1>0成立,对m分类讨论,m=0时,易判断出.m≠0时,,解出即可得出.②对任意实数x,不等式mx>0成立,m∈∅.【试题解答】解:①对任意实数x,不等式mx2﹣(3﹣m)x+1>0成立,m=0时化为:﹣3x+1>0,不成立,舍去.m≠0时,,解得.②对任意实数x,不等式mx>0成立,m∈∅.综上可得:.∴实数m的取值范围是.【点评】本题考查了一元二次不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于中档题.21.(2016秋•杨浦区校级期中)已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R;(1)试求不等式的解集A;(2)对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B为有限集,求实数k的取值范围,使得集合B中元素个数最少,并用列举法表示集合B.【知识考查点】一元二次不等式的解法.【专题】分类讨论;不等式的解法及应用;不等式.【试题分析】(1)对k分类讨论,利用一元二次不等式的解法即可得出.(2)根据B=A∩Z(其中Z为整数集),集合B为有限集,即可得出.【试题解答】解:(1)①当k<0,A={x|};②当k=0,A={x|x};③当0<k<1或k>9,A={x|x,或x>};④当1≤k≤9,A={x|x<,或x>};(2)B=A∩Z(其中Z为整数集),集合B为有限集,只有k<0,B={2,3,4,5}.【点评】本题考查了一元二次不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于中档题.11。
2020-2021上海复旦实验中学九年级数学上期中试题(含答案)

2020-2021上海复旦实验中学九年级数学上期中试题(含答案)一、选择题1.方程x 2+x-12=0的两个根为( ) A .x 1=-2,x 2=6B .x 1=-6,x 2=2C .x 1=-3,x 2=4D .x 1=-4,x 2=32.方程2(2)9x -=的解是( ) A .1251x x ==-,B .1251x x =-=,C .12117x x ==-, D .12117x x =-=,3.用配方法解方程2410x x -+=,配方后的方程是 ( )A .2(2)3x +=B .2(2)3x -=C .2(2)5x -=D .2(2)5x +=4.抛物线y=﹣(x +2)2﹣3向右平移了3个单位,那么平移后抛物线的顶点坐标是( )A .(﹣5,﹣3)B .(﹣2,0)C .(﹣1,﹣3)D .(1,﹣3) 5.下列事件中,属于必然事件的是( ) A .三角形的外心到三边的距离相等 B .某射击运动员射击一次,命中靶心 C .任意画一个三角形,其内角和是 180° D .抛一枚硬币,落地后正面朝上6.下列交通标志是中心对称图形的为( ) A .B .C .D .7.如图,AD 、BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O→C→D→O 的路线匀速运动.设∠APB=y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关系图是( )A .AB .BC .CD .D8.若α,β是一元二次方程x 2﹣x ﹣2018=0的两个实数根,则α2﹣3α﹣2β+3的值为( ) A .2020 B .2019 C .2018 D .2017 9.若2245a a x -+-=,则不论取何值,一定有( )A .5x >B .5x <-C .3x ≥-D .3x ≤-10.如图,是两条互相垂直的街道,且A 到B ,C 的距离都是7 km ,现甲从B 地走向A 地,乙从A 地走向C 地,若两人同时出发且速度都是4km /h ,则两人之间的距离为5km时,是甲出发后( )A .1hB .0.75hC .1.2h 或0.75hD .1h 或0.75h11.如图,△ABC 绕点A 旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )A .DE=3B .AE=4C .∠ACB 是旋转角D .∠CAE 是旋转角12.如图,已知二次函数2y ax bx c =++(0a ≠)的图象与x 轴交于点A (﹣1,0),对称轴为直线x=1,与y 轴的交点B 在(0,2)和(0,3)之间(包括这两点),下列结论:①当x >3时,y <0; ②3a+b <0; ③213a -≤≤-; ④248ac b a ->; 其中正确的结论是( )A .①③④B .①②③C .①②④D .①②③④二、填空题13.已知x 1,x 2是一元二次方程x 2+2(m +1)x +m 2﹣1=0的两实数根,且满足(x 1﹣x 2)2=16﹣x 1x 2,实数m 的值为________.14.如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC 与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M ,绕中点M 转动上面的三角尺ABC ,使其直角顶点C 恰好落在三角尺A′B′C′的斜边A′B′上.当∠A =30°,AC =10时,两直角顶点C ,C′间的距离是_____.15.新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.16.如图,从一个直径为1m 的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为_____m .17.如图,把正方形铁片OABC 置于平面直角坐标系中,顶点A 的坐标为(3,0),点P (1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P 的坐标为____________________.18.小蕾有某文学名著上、中、下各1册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率是____________.19.如图,O e 的半径为2,切线AB 的长为23,点P 是O e 上的动点,则AP 的长的取值范围是_________.20.两个全等的三角尺重叠放在△ACB 的位置,将其中一个三角尺绕着点C 按逆时针方向旋转至△DCE 的位置,使点A 恰好落在边DE 上,AB 与CE 相交于点F .已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm ,则CF=______cm .三、解答题21.若关于x 的一元二次方程x 2﹣3x +a ﹣2=0有实数根. (1)求a 的取值范围;(2)当a 为符合条件的最大整数,求此时方程的解.22.如图,已知△ABC 中,AB =AC ,把△ABC 绕A 点沿顺时针方向旋转得到△ADE ,连接BD ,CE 交于点F .(1)求证:△AEC ≌△ADB ;(2)若AB =2,∠BAC =45°,当四边形ADFC 是菱形时,求BF 的长.23.如图,已知抛物线y=﹣x 2+bx +c 与x 轴交于点A (﹣1,0)和点B (3,0),与y 轴交于点C ,连接BC 交抛物线的对称轴于点E ,D 是抛物线的顶点. (1)求此抛物线的解析式; (2)求点C 和点D 的坐标;(3)若点P 在第一象限内的抛物线上,且S △ABP =4S △COE ,求P 点坐标.24.已知关于x 的一元二次方程225x x m --=()() (1)求证:对于任意实数m ,方程总有两个不相等的实数根;(2)若此方程的两实数根12,x x 满足221233x x +=,求实数m 的值.25.已知抛物线y=-x 2-2x+c 与x 轴的一个交点是(1,0). (1)C 的值为_______;(2)选取适当的数据补填下表,并在平面直角坐标系内描点画出该抛物线的图像;x•••1-1•••y•••0•••(3)根据所画图像,写出y>0时x的取值范围是_____.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】试题分析:将x2+x﹣12分解因式成(x+4)(x﹣3),解x+4=0或x﹣3=0即可得出结论.x2+x﹣12=(x+4)(x﹣3)=0,则x+4=0,或x﹣3=0,解得:x1=﹣4,x2=3.考点:解一元二次方程-因式分解法2.A解析:A【解析】【分析】此方程已经配方,根据解一元二次方程的步骤解方程即可.【详解】()229x-=,故x-2=3或x-2=-3,解得:x1=5,x2=-1,故答案选A.【点睛】本题主要考查了解一元二次方程的基本解法,这是很简单的解方程,难度不大.3.B解析:B【解析】【分析】根据配方法可以解答本题.【详解】x2−4x+1=0,(x−2)2−4+1=0,(x−2)2=3,故选:B.【点睛】本题考查解一元二次方程−配方法,解答本题的关键是解一元二次方程的方法.4.D解析:D【解析】试题分析:原抛物线的顶点坐标为(-2,-3),向右平移三个单位后顶点纵坐标不变,横坐标加3,所以平移后抛物线的顶点坐标是(1,-3)。
上海复旦实验中学化学上册期中试卷(含答案)

上海复旦实验中学化学上册期中试卷(含答案)一、选择题(培优题较难)1.下列实验基本操作错误的A.B.C.D.2.元素周期表是学习和研究化学的重要工具,如图是元素周期表的一部分,其中X、Y、Z 代表三种不同的元素。
下列说法中正确的是()A.原子序数:X>Y B.核外电子数:X=ZC.Y和Z处于同一周期D.X和Z的电子层数相同3.在一密闭的容器中,一定质量的碳粉与过量的氧气在点燃的条件下充分反应,容器内各相关量与时间(从反应开始计时)的对应关系正确的是( )A.B.C.D.4.实验室常用加热高锰酸钾固体制取氧气,化学方程式为2KMnO4K2MnO4+MnO2+O2↑,现对一定量的高锰酸钾固体进行加热,加热过程中涉及的相关量随时间变化的图象正确的是A.B.C.D.5.丙烷(C3H8)是液化石油气的主要成分之一,燃烧前后分子种类变化的微观示意图如下。
下列说法正确的是()A.甲中碳、氢元素质量比为3:8 B.乙和丙的元素组成相同C.44g甲完全燃烧至少需160g乙D.生成的丙与丁的分子个数比为1:16.鉴别二氧化碳、氧气、空气三种气体,可选用的最佳方法是( )A.将气体分别通入水中B.将燃着的木条分别伸入气体中C.将带火星的木条分别伸入气体中D.将气体分别通入澄清石灰水中7.下列图示中的“错误实验操作”与图下面对应的“可能产生的后果”不一致的是()A.液体喷出B.污染试剂C.酒精溅出D.读数偏大8.下列事实不能作为相应观点的证据的是( )A.尘土飞扬,说明分子是运动的B.电解水得到氢气和氧气,说明分子是可分的C.气体被压缩后体积发生了较大变化,说明气体分子间距较大D.将两个干净平整的铅柱紧压在一起会结合起来,说明分子间存在引力9.硼是作物生长必需的微量营养元素,硼元素的相关信息如图所示。
下列有关硼的说法正确的是A.相对原子质量为10.81g B.属于金属元素C.原子的核电荷数为5D.原子核外有6个电子10.如图为电解水的实验装置图,下列说法正确的是()A.在水中加入少量硫酸钠以增强水的导电性B.与负极相连的玻璃管内得到的气体能使带火星的木条复燃C.该实验中所得氢气和氧气的质量比约为2:1D.该实验说明水是由氢气和氧气组成的11.图中“”和“”分别表示不同的原子,下列判断不正确的是( )A.①可能是氧化物B.②可能是金属C.③一定是混合物D.④包含组成元素相同的不同物质12.下列关于燃烧现象的解释或分析正确的是()A.图a中将煤球变成蜂窝煤后再燃烧,其目的是延长煤燃烧的时间B.图b中火柴头斜向下时更容易燃烧,是因为降低了火柴梗的着火点C.图c中蜡烛火焰很快熄灭,是因为金属丝阻碍空气的流动D.由图d中的现象可知,金属镁燃烧的火灾不能用二氧化碳灭火13.科学家研制出一种新型催化剂,可用于去除装修残留的甲醛(化学式为 CH2O),该反应过程的微观示意图如下。
上海复旦实验中学九年级上册期中试卷检测题

上海复旦实验中学九年级上册期中试卷检测题一、初三数学一元二次方程易错题压轴题(难)1.(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发时,点P和点Q之间的距离是10cm;(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q 两点的距离为多少?(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?【答案】(1)85s或245s(2)62cm;213cm(3)4s或6s【解析】【分析】(1)过点P作PE⊥BC于E,得到AP=3t,CQ=2t,PE=6,EQ=16﹣3t﹣2t=16﹣5t,利用勾股定理得到方程,故可求解;(2)根据运动时间求出EQ、PE,利用勾股定理即可求解;(3) 分当点P在AO上时,当点P在OC上时和当点P在CB上时,根据三角形的面积公式列出方程即可求解.【详解】解:(1)设运动时间为t秒时,如图,过点P作PE⊥BC于E,由运动知,AP=3t,CQ=2t,PE=6,EQ=16﹣3t﹣2t=16﹣5t,∵点P和点Q之间的距离是10 cm,∴62+(16﹣5t)2=100,解得t1=85,t2=245,∴t=85s或245s.故答案为85s或245s(2)t=2时,由运动知AP =3×2=6 cm ,CQ =2×2=4 cm ,∴四边形APEB 是矩形,∴PE =AB =6,BE =6,∴EQ =BC ﹣BE ﹣CQ =16﹣6﹣4=6,根据勾股定理得PQ=2262PE EQ +=,∴当t =2 s 时,P ,Q 两点的距离为62 cm ;当t =4 s 时,由运动知AP =3×4=12 cm ,CQ =2×4=8cm ,∴四边形APEB 是矩形,∴PE =AB =6,BQ =8,CE=OP=4∴EQ =BC ﹣CE ﹣BQ =16﹣4﹣8=4,根据勾股定理得PQ=22213PE EQ +=,P ,Q 两点的距离为213cm .(3)点Q 从C 点移动到B 点所花的时间为16÷2=8s ,当点P 在AO 上时,S △POQ =2PO CO ⋅=(163)62t -⋅=12, 解得t =4.当点P 在OC 上时,S △POQ =2PO CQ ⋅=(316)22t t -⋅=12, 解得t =6或﹣23(舍弃). 当点P 在CB 上时,S △POQ =2PQ CO ⋅=(2223)62t t +-⨯=12, 解得t =18>8(不符合题意舍弃),综上所述,经过4 s 或6 s 时,△POQ 的面积为12 cm 2.【点睛】此题主要考查勾股定理的应用、一元二次方程与动点问题,解题的关键是熟知勾股定理的应用,根据三角形的面积公式找到等量关系列出方程求解.2.已知关于x 的一元二次方程kx 2﹣2(k +1)x +k ﹣1=0有两个不相等的实数根x 1,x 2. (1)求k 的取值范围;(2)是否存在实数k ,使1211x x -=1成立?若存在,请求出k 的值;若不存在,请说明理由.【答案】(1)k >﹣13且k ≠0;(2)存在,7k =±详见解析 【解析】【分析】(1)根据一元二次方程的根的判别式,建立关于k 的不等式,求得k 的取值范围.(2)利用根与系数的关系,根据21121211,x x x x x x --=即可求出k 的值,看是否满足(1)中k 的取值范围,从而确定k 的值是否存在.【详解】解:(1)由题意知,k ≠0且△=b 2﹣4ac >0∴b 2﹣4ac =[﹣2(k +1)]2﹣4k (k ﹣1)>0,即4k 2+8k +4﹣4k 2+4k >0,∴12k >﹣4解得:k >13-且k ≠0(2)存在,且7k =±理由如下: ∵12122(1)1,,k k x x x x k k+-+== 又有211212111,x x x x x x --== 2112,x x x x ∴-=22222121122,x x x x x x ∴-+=22121212()4(),x x x x x x ∴+-=2222441()(),k k k k k k+--∴-= 22(22)(44)(1),k k k k ∴+--=-21430,k k ∴--=1,14,3,a b c ==-=-24208,b ac ∴∆=-=1472k ±∴==± k >13-且k ≠0, 172130.21,3-≈--> 17.3+-∴满足条件的k 值存在,且7k =± .【点睛】本题考查的是一元二次方程根的判别式,一元二次方程根与系数的关系,掌握以上知识是解题的关键.3.已知关于x 的一元二次方程()221210m x m x +-+=有两个不相等的实数根. (1)求实数m 的取值范围; (2)若原方程的两个实数根分别为1x ,2x ,且满足1212215x x x x +=-,求m 的值.【答案】(1)14m <且0m ≠;(2)15m =- 【解析】【分析】(1)根据一元二次方程的定义和判别式的意义得到:()22140m m ∴∆=-->且20m ≠,然后求出两个不等式解集的公共部分即可.(2)利用根与系数的关系得到12221m x x m -+=, 1221x x m =,加上14m <且0m ≠,则可判断10x <,20x <,所以1212215x x x x --=-,2221215m m m--=-,然后解方程求出m 即可得到满足条件的m 的值.【详解】(1)因为方程()221210m x m x +-+=有两个不相等的实数根, ()221240m m ∴∆=-->,解得14m <; 又因为是一元二次方程,所以20m ≠,0m ∴≠.m ∴的取值范围是14m <且0m ≠. (2)1x ,2x 为原方程的两个实数根,12221m x x m -∴+=,1221x x m = 14m <且0m ≠,122210m x x m -∴+=<,12210x x m =>,10x ∴<,20x <.1212215x x x x +=-,1212215x x x x --=-,2221215m m m -∴-=-,215210m m ∴--=,解得113m =,215m =-, 14m <且0m ≠,113m ∴=不合题意,舍去,15m ∴=-. 【点睛】 此题主要考查一元一次方程的定义和判别式的意义,正确理解概念和熟练运用根的判别式是解题的关键.4.阅读下列材料计算:(1﹣﹣)×(+)﹣(1﹣﹣)(+),令+=t ,则:原式=(1﹣t )(t +)﹣(1﹣t ﹣)t =t +﹣t 2﹣+t 2= 在上面的问题中,用一个字母代表式子中的某一部分,能达到简化计算的目的,这种思想方法叫做“换元法”,请用“换元法”解决下列问题:(1)计算:(1﹣﹣)×(+)﹣(1﹣﹣)×(+) (2)因式分解:(a 2﹣5a +3)(a 2﹣5a +7)+4(3)解方程:(x 2+4x +1)(x 2+4x +3)=3【答案】(1);(2)(a 2﹣5a +5)2;(3)x 1=0,x 2=﹣4,x 3=x 4=﹣2【解析】【分析】(1)仿照材料内容,令+=t 代入原式计算. (2)观察式子找相同部分进行换元,令a 2﹣5a =t 代入原式进行因式分解,最后要记得把t 换为a .(3)观察式子找相同部分进行换元,令x 2+4x =t 代入原方程,即得到关于t 的一元二次方程,得到t 的两个解后要代回去求出4个x 的解.【详解】(1)令+=t ,则: 原式=(1﹣t )(t +)﹣(1﹣t ﹣)t =t +﹣t 2﹣﹣t +t 2+= (2)令a 2﹣5a =t ,则:原式=(t +3)(t +7)+4=t 2+7t +3t +21+4=t 2+10t +25=(t +5)2=(a 2﹣5a +5)2(3)令x2+4x=t,则原方程转化为:(t+1)(t+3)=3t2+4t+3=3t(t+4)=0∴t1=0,t2=﹣4当x2+4x=0时,x(x+4)=0解得:x1=0,x2=﹣4当x2+4x=﹣4时,x2+4x+4=0(x+2)2=0解得:x3=x4=﹣2【点睛】本题考查用换元法进行整式的运算,因式分解,解一元二次方程.利用换元法一般可达到降次效果,从而简便运算.5.计算题(1)先化简,再求值:21xx-÷(1+211x-),其中x=2017.(2)已知方程x2﹣2x+m﹣3=0有两个相等的实数根,求m的值.【答案】(1)2018;(2)m=4【解析】分析:(1)根据分式的运算法则和运算顺序,先算括号里面的,再算除法,注意因式分解的作用;(2)根据一元二次方程的根的判别式求解即可.详解:(1)21xx-÷(1+211x-)=22211 11 x xx x-+÷--=()() 2211 1x xxx x+-⋅-=x+1,当x=2017时,原式=2017+1=2018(2)解:∵方程x2﹣2x+m﹣3=0有两个相等的实数根,∴△=(﹣2)2﹣4×1×(m﹣3)=0,解得,m=4点睛:此题主要考查了分式的混合运算和一元二次方程的根的判别式,关键是熟记分式方程的运算顺序和法则,注意通分约分的作用.二、初三数学 二次函数易错题压轴题(难)6.在平面直角坐标系中,O 为坐标原点,抛物线L :y =ax 2﹣4ax (a >0)与x 轴正半轴交于点A .抛物线L 的顶点为M ,对称轴与x 轴交于点D .(1)求抛物线L 的对称轴.(2)抛物线L :y =ax 2﹣4ax 关于x 轴对称的抛物线记为L ',抛物线L '的顶点为M ',若以O 、M 、A 、M '为顶点的四边形是正方形,求L '的表达式.(3)在(2)的条件下,点P 在抛物线L 上,且位于第四象限,点Q 在抛物线L '上,是否存在点P 、点Q 使得以O 、D 、P 、Q 为顶点的四边形是平行四边形,若存在,求出点P 坐标,若不存在,请说明理由.【答案】(1)2x =;(2)2122y x x =-+ ;(3)存在,P 点的坐标为(33,3或(33,3-或(13,3或(13,3+-或31,2⎛⎫- ⎪⎝⎭ 【解析】【分析】(1)根据抛物线的对称轴公式计算即可.(2)利用正方形的性质求出点M ,M ′的坐标即可解决问题.(3)分OD 是平行四边形的边或对角线两种情形求解即可.【详解】解:(1)∵抛物线L :y =ax 2﹣4ax (a >0),∴抛物线的对称轴x =﹣42a a-=2. (2)如图1中,对于抛物线y=ax2﹣4ax,令y=0,得到ax2﹣4ax=0,解得x=0或4,∴A(4,0),∵四边形OMAM′是正方形,∴OD=DA=DM=DM′=2,∴M((2,﹣2),M′(2,2)把M(2,﹣2)代入y=ax2﹣4ax,可得﹣2=4a﹣8a,∴a=12,∴抛物线L′的解析式为y=﹣12(x﹣2)2+2=﹣12x2+2x.(3)如图3中,由题意OD=2.当OD为平行四边形的边时,PQ=OD=2,设P(m,12m2﹣2m),则Q[m﹣2,﹣12(m﹣2)2+2(m﹣2)]或[m+2,﹣12(m+2)2+2(m+2)],∵PQ∥OD,∴12m2﹣2m=﹣12(m﹣2)2+2(m﹣2)或12m2﹣2m=﹣12(m+2)2+2(m+2),解得m =3±3或1±3, ∴P (3+3,3)或(3﹣3,﹣3)或(1﹣3,3)和(1+3,﹣3),当OD 是平行四边形的对角线时,点P 的横坐标为1,此时P (1,﹣32), 综上所述,满足条件的点P 的坐标为(3+3,3)或(3﹣3,﹣3)或(1﹣3,3)和(1+3,﹣3)或(1,﹣32). 【点睛】本题属于二次函数综合题,考查了二次函数的性质,正方形的性质,平行四边形的判定和性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题7.二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ,顶点为P ,直线PA 与x 轴交于点B .(1)当m =1时,求顶点P 的坐标;(2)若点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上,且0b m ->,试求a 的取值范围;(3)在第一象限内,以AB 为边作正方形ABCD .①求点D 的坐标(用含m 的代数式表示);②若该二次函数的图象与正方形ABCD 的边CD 有公共点,请直接写出符合条件的整数m 的值.【答案】(1)P (2,13);(2)a 的取值范围为:a <0或a >4;(3)①D (m ,m +3); ②2,3,4.【解析】【分析】(1)把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中,进而求顶点P 的坐标即可; (2)把点Q (a ,b )代入二次函数22(0)63m m y x x m m =-+>解析式中,根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组,解出a 的取值范围即可; (3)①过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,求出二次函数与y 轴的交点A 的坐标,得到OA 的长,再根据待定系数法求出直线AP 的解析式,进而求出与x 轴的交点B 的坐标,得到OB 的长;通过证明△ADF ≌△ABO ,得到AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,求出点D 的坐标;②因为二次函数的图象与正方形ABCD 的边CD 有公共点,由①同理可得:C (m+3,3),分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况,进行讨论m 可能取的整数值即可.【详解】解:(1)当m =1时,二次函数为212163y x x =-+, ∴顶点P 的坐标为(2,13); (2)∵点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上, ∴2263m m b a a m =-+, 即:2263m m b m a a -=- ∵0b m ->, ∴2263m m a a ->0, ∵m >0, ∴2263a a ->0, 解得:a <0或a >4,∴a 的取值范围为:a <0或a >4;(3)①如下图,过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,∵二次函数的解析式为2263m m y x x m =-+, ∴顶点P (2,3m ), 当x=0时,y=m ,∴点A (0,m ),∴OA=m ;设直线AP 的解析式为y=kx+b(k≠0),把点A (0,m ),点P (2,3m )代入,得: 23m b m k b =⎧⎪⎨=+⎪⎩, 解得:3m k b m⎧=-⎪⎨⎪=⎩,∴直线AP 的解析式为y=3m -x+m , 当y=0时,x=3,∴点B (3,0);∴OB=3;∵四边形ABCD 是正方形,∴AD=AB ,∠DAF+∠FAB=90°,且∠OAB+∠FAB =90°,∴∠DAF=∠OAB ,在△ADF 和△ABO 中, DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△ABO (AAS ),∴AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,∴点D 的坐标为:(m ,m+3);②由①同理可得:C (m+3,3),∵二次函数的图象与正方形ABCD 的边CD 有公共点,∴当x =m 时,3y m ≤+,可得322363m m m m -+≤+,化简得:32418m m -≤. ∵0m >,∴2184m m m -≤,∴218(2)4m m--≤, 显然:m =1,2,3,4是上述不等式的解,当5m ≥时,2(2)45m --≥,18 3.6m ≤,此时,218(2)4m m-->, ∴符合条件的正整数m =1,2,3,4; 当x = m +3时,y ≥3,可得2(3)2(3)363m m m m m ++-+≥, ∵0m >,∴21823m m m ++≥,即218(1)2m m++≥, 显然:m =1不是上述不等式的解,当2m ≥时,2(1)211m ++≥,189m ≤,此时,218(1)2m m++>恒成立, ∴符合条件的正整数m =2,3,4;综上:符合条件的整数m 的值为2,3,4.【点睛】本题考查二次函数与几何问题的综合运用,熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键.8.如图,在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠交x 轴于点(2,0),(3,0)A B -,交y 轴于点C ,且经过点(6,6)D --,连接,AD BD .(1)求该抛物线的函数关系式;(2)△ANM 与ABD ∆是否相似?若相似,请求出此时点M 、点N 的坐标;若不存在,请说明理由;(3)若点P 是直线AD 上方的抛物线上一动点(不与点,A D 重合),过P 作//PQ y 轴交直线AD 于点Q ,以PQ 为直径作⊙E ,则⊙E 在直线AD 上所截得的线段长度的最大值等于 .(直接写出答案)【答案】(1)2113442y x x =--+;(2)点M (0,32)、点N (34,0)或点M (0,32),N (-3,0)或点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32);(3)QH 有最大值,当x=2-时,其最大值为125. 【解析】【分析】(1)用交点式函数表达式得:y=a (x-2)(x+3),将点D 坐标代入上式即可求解; (2)分∠MAB=∠BAD 、∠MAB=∠BDA ,两种大情况、四种小情况,分别求解即可; (3)根据题意,利用二次函数的性质和三角函数,QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+=23392055x x --+,即可求解. 【详解】解:(1)用交点式函数表达式得:y=a (x-2)(x+3),将点D 坐标代入上式并解得:14a =-, 故函数的表达式为:2113442y x x =--+…①, 则点C (0,32); (2)由题意得:AB=5,AD=10,BD=35,①∠MAN=∠ABD 时,(Ⅰ)当△ANM ∽△ABD 时,直线AD 所在直线的k 值为34,则直线AM 表达式中的k 值为34-, 则直线AM 的表达式为:3(2)4y x =--,故点M (0,32), AD AB AM AN =,则AN=54,则点N (34,0); (Ⅱ)当△AMN ∽△ABD 时,同理可得:点N (-3,0),点M (0,32), 故点M (0,32)、点N (34,0)或点M (0,32),N (-3,0); ②∠MAN=∠BDA 时,(Ⅰ)△ABD ∽△NMA 时, ∵AD ∥MN ,则tan ∠MAN=tan ∠BDA=12, AM :y=12-(x-2),则点M (-1,32)、点N (-3,0); (Ⅱ)当△ABD ∽△MNA 时,AD BD AM AN =,即3535AN =, 解得:AN=94, 故点N (14-,0)、M (-1,32); 故:点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32); 综上,点M (0,32)、点N (34,0)或点M (0,32),N (-3,0)或点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32); (3)如图所示,连接PH ,由题意得:tan ∠PQH=43,则cos ∠PQH=35, 则直线AD 的表达式为:y=3342x -, 设点P (x ,2113442x x --+),则点Q (x ,3342x -),则QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+ =23392055x x --+ =2312(2)205x -++, ∵3020-<, 故QH 有最大值,当x=2-时,其最大值为125. 【点睛】本题考查的是二次函数综合应用,涉及到一次函数、圆的基本知识,解直角三角形,相似三角形的判定和性质,其中(2)需要分类求解共四种情况,避免遗漏.9.如图,已知二次函数1L :()22311y mx mx m m =+-+≥和二次函数2L :()2341y m x m =--+-()1m ≥图象的顶点分别为M 、N ,与x 轴分别相交于A 、B 两点(点A 在点B 的左边)和C 、D 两点(点C 在点D 的左边),(1)函数()22311y mx mx m m =+-+≥的顶点坐标为______;当二次函数1L ,2L 的y 值同时随着x 的增大而增大时,则x 的取值范围是_______;(2)判断四边形AMDN 的形状(直接写出,不必证明);(3)抛物线1L ,2L 均会分别经过某些定点;①求所有定点的坐标;②若抛物线1L 位置固定不变,通过平移抛物线2L 的位置使这些定点组成的图形为菱形,则抛物线2L 应平移的距离是多少?【答案】(1)()1,41m --+,13x ;(2)四边形AMDN 是矩形;(3)①所有定点的坐标,1L 经过定点()3,1-或()1,1,2L 经过定点()5,1-或()1,1-;②抛物线2L 应平移的距离是423+423-.【解析】【分析】(1)将已知抛物线解析式转化为顶点式,直接得到点M 的坐标;结合函数图象填空; (2)利用抛物线解析式与一元二次方程的关系求得点A 、D 、M 、N 的横坐标,可得AD 的中点为(1,0),MN 的中点为(1,0),则AD 与MN 互相平分,可证四边形AMDN 是矩形; (3)①分别将二次函数的表达式变形为1:(3)(1)1L y m x x =+-+和2:(1)(5)1L y m x x =----,通过表达式即可得出所过定点;②根据菱形的性质可得EH 1=EF=4即可,设平移的距离为x ,根据平移后图形为菱形,由勾股定理可得方程即可求解.【详解】解:(1)12b x a=-=-,顶点坐标M 为(1,41)m --+, 由图象得:当13x 时,二次函数1L ,2L 的y 值同时随着x 的增大而增大. 故答案为:(1,41)m --+;13x ;(2)结论:四边形AMDN 是矩形.由二次函数21:231(1)L y mx mx m m =+-+和二次函数22:(3)41(1)L y m x m m =--+-解析式可得:A 点坐标为41(1m m ---,0),D 点坐标为41(3m m -+,0), 顶点M 坐标为(1,41)m --+,顶点N 坐标为(3,41)m -,AD ∴的中点为(1,0),MN 的中点为(1,0),AD ∴与MN 互相平分,∴四边形AMDN 是平行四边形,又AD MN =,∴□AMDN 是矩形;(3)①二次函数21:231(3)(1)1L y mx mx m m x x =+-+=+-+,故当3x =-或1x =时1y =,即二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点,二次函数22:(3)41(1)(5)1L y m x m m x x =--+-=----,故当1x =或5x =时1y =-,即二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点,②二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点,二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点,如图:四个定点分别为(3,1)E -、(1,1)F ,(1,1)H -、(5,1)G -,则组成四边形EFGH 为平行四边形,∴FH ⊥HG ,FH=2,HM=4-x ,设平移的距离为x ,根据平移后图形为菱形,则EH 1=EF=H 1M=4,由勾股定理可得:FH 2+HM 2=FM 2,即22242(4)x =+-,解得:423x =±,抛物线1L 位置固定不变,通过左右平移抛物线2L 的位置使这些定点组成的图形为菱形,则抛物线2L 应平移的距离是423+或423-.【点睛】本题考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.10.如图,已知二次函数22(0)y ax ax c a 的图象与x 轴负半轴交于点A (-1,0),与y 轴正半轴交与点B ,顶点为P ,且OB=3OA ,一次函数y=kx+b 的图象经过A 、B .(1) 求一次函数解析式;(2)求顶点P 的坐标;(3)平移直线AB 使其过点P ,如果点M在平移后的直线上,且3tan 2OAM ∠=,求点M 坐标;(4)设抛物线的对称轴交x 轴与点E ,联结AP 交y 轴与点D ,若点Q 、N 分别为两线段PE 、PD 上的动点,联结QD 、QN ,请直接写出QD+QN 的最小值.【答案】(1) 一次函数的解析式为:y=3x+3(2)顶点P 的坐标为(1,4)(3) M 点的坐标为:15,2(,39⎛⎫- ⎪⎝⎭或 23-)(4【解析】【分析】(1)根据抛物线的解析式即可得出B (0,3),根据OB=3OA ,可求出OA 的长,也就得出了A 点的坐标,然后将A 、B 的坐标代入直线AB 的解析式中,即可得出所求;(2)将(1)得出的A 点坐标代入抛物线的解析式中,可求出a 的值,也就确定了抛物线的解析式进而可求出P 点的坐标;(3)易求出平移后的直线的解析式,可根据此解析式设出M 点坐标(设横坐标,根据直线的解析式表示出纵坐标).然后过M 作x 轴的垂线设垂足为E ,在构建的直角三角形AME 中,可用M 点的坐标表示出ME 和AE 的长,然后根据∠OAM 的正切值求出M 的坐标.(本题要分M 在x 轴上方和x 轴下方两种情况求解.方法一样.)(4)作点D 关于直线x=1的对称点D′,过点D′作D′N ⊥PD 于点N ,根据垂线段最短求出QD+QN 的最小值.【详解】(1)∵A (-1,0),∴OA=1∵OB=3OA ,∴B (0,3)∴图象过A 、B 两点的一次函数的解析式为:y=3x+3(2)∵二次函数22(0)y ax ax c a =-+<的图象与x 轴负半轴交与点A (-1,0),与y 轴正半轴交与点B (0,3),∴c=3,a=-1∴二次函数的解析式为:223y x x =-++∴抛物线223y x x =-++的顶点P (1,4)(3)设平移后的直线的解析式为:3y x b =+∵直线3y x b =+过P (1,4)∴b=1∴平移后的直线为31y x =+∵M 在直线31y x =+,且3tan 2OAM ∠=设M (x,3x+1)① 当点M 在x 轴上方时,有31312x x +=+,∴13x = ∴11,23M ⎛⎫ ⎪⎝⎭②当点M 在x 轴下方时,有31312x x +-=+,∴59x =- ∴25(,9M - 23-) (4)作点D 关于直线x=1的对称点D’,过点D’作D’N ⊥PD 于点N当-x 2+2x+3=0时,解得,x=-1或x=3,∴A (-1,0),P 点坐标为(1,4),则可得PD 解析式为:y=2x+2,令x=0,可得y=2,∴D (0,2),∵D 与D′关于直线x=1对称,∴D′(2,2).根据ND′⊥PD ,设ND′解析式为y=kx+b ,则k=-12,即y=-12x+b , 将D′(2,2)代入,得2=-12×2+b ,解得b=3, 可得函数解析式为y=-12x+3, 将两函数解析式组成方程组得:13222y x y x ⎧=-+⎪⎨⎪=+⎩, 解得25145x y ⎧=⎪⎪⎨⎪=⎪⎩, 故N (214 ,)55, 由两点间的距离公式:5=,∴所求最小值为455【点睛】本题主要考查了一次函数解析式的确定、二次函数解析式的确定、函数图象的平移等知识点.同时考查了应用轴对称和垂线段最短解决线段和的最小值问题.三、初三数学旋转易错题压轴题(难)11.如图,在矩形ABCD中,6AB cm=,8AD cm=,连接BD,将ABD△绕B点作顺时针方向旋转得到A B D'''△(B′与B重合),且点D'刚好落在BC的延长上,A D''与CD相交于点E.(1)求矩形ABCD与A B D'''△重叠部分(如图1中阴影部分A B CE'')的面积;(2)将A B D'''△以每秒2cm的速度沿直线BC向右平移,如图2,当B′移动到C点时停止移动.设矩形ABCD与A B D'''△重叠部分的面积为y,移动的时间为x,请你直接写出y关于x的函数关系式,并指出自变量x的取值范围;(3)在(2)的平移过程中,是否存在这样的时间x,使得AA B''△成为等腰三角形?若存在,请你直接写出对应的x的值,若不存在,请你说明理由.【答案】(1)2452cm;(2)22331624(0)22588020016(4)3335x x xyx x x⎧--+≤<⎪⎪=⎨⎪-+≤≤⎪⎩;(3)存在,使得AA B''△成为等腰三角形的x的值有:0秒、32秒、695.【解析】【分析】(1)先用勾股定理求出BD的长,再根据旋转的性质得出10B D BD cm''==,2CD B D BC cm '=''-=,利用B D A ∠'''的正切值求出CE 的值,利用三角形的面积差即可求阴影部分的面积;(2)分类讨论,当1605x ≤<时和当1645x ≤≤时,分别列出函数表达式; (3)分类讨论,当AB A B '=''时;当AA A B '=''时;当AB AA '='时,根据勾股定理列方程即可.【详解】解:(1)6AB cm =,8AD cm =,10BD cm ∴=,根据旋转的性质可知10B D BD cm ''==,2CD B D BC cm '=''-=,tan A B CE B D A A D CD '''''∠==''', 682CE ∴=, 32CE cm ∴=, ()28634522222A B CE A B D CED S S S cm ''''''⨯∴==-⨯÷=-; (2)①当1605x ≤<时,22CD x '=+,32CE x =, 233+22CD E S x x '∴=△, 22133368242222y x x x ∴=⨯⨯-=--+; ②当1645x ≤≤时,102BC x =-,()41023CE x =- ()221488020010223333y x x x ∴=⨯-=-+. (3)①如图1,当AB A B '=''时,0x =秒;②如图2,当AA A B '=''时,1825A N BM BB B M x '=='+'=+,245A M NB '==, 2236AN A N +'=,222418623655x ⎛⎫⎛⎫∴-++= ⎪ ⎪⎝⎭⎝⎭,解得:x =秒,(x =舍去); ③如图2,当AB AA '='时,1825A N BM BB B M x '=='+'=+,245A M NB '==, 2222AB BB AN A N +'=+'22224183646255x x ⎛⎫⎛⎫∴+=-++ ⎪ ⎪⎝⎭⎝⎭ 解得:32x =秒. 综上所述:使得AA B ''△成为等腰三角形的x 的值有:0秒、32秒、6695-.【点睛】本题主要考查了图形的平移变换和旋转变换,能够数形结合,运用分类讨论的思想方法全面的分析问题,思考问题是解决问题的关键.12.两块等腰直角三角形纸片AOB 和COD 按图1所示放置,直角顶点重合在点O 处,25AB =,17CD =.保持纸片AOB 不动,将纸片COD 绕点O 逆时针旋转(090)αα<<角度,如图2所示.()1利用图2证明AC BD =且AC BD ⊥;()2当BD 与CD 在同一直线上(如图3)时,求AC 的长和α的正弦值.【答案】(1)详见解析;(2)7,725. 【解析】【分析】 (1)图形经过旋转以后明确没有变化的边长,证明AOC BOD ≅,得出AC=BD , 延长BD 交AC 于E ,证明∠AEB=90︒,从而得到BD AC ⊥.(2) 如图3中,设AC=x ,在Rt △ABC 中,利用勾股定理求出x ,再根据sinα=sin ∠ABC=AC AB即可解决问题【详解】 ()1证明:如图2中,延长BD 交OA 于G ,交AC 于E .∵90AOB COD ∠=∠=,∴AOC DOB ∠=∠, 在AOC 和BOD 中,OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩,∴AOC BOD ≅,∴AC BD =,CAO DBO ∠=∠,∵90DBO GOB ∠+∠=,∵OGB AGE ∠=∠,∴90CAO AGE ∠+∠=,∴90AEG ∠=,∴BD AC ⊥.()2解:如图3中,设AC x=,∵BD 、CD 在同一直线上,BD AC ⊥, ∴ABC 是直角三角形,∴222AC BC AB +=,∴222(17)25x x ++=,解得7x =,∵45ODC DBO α∠=∠+∠=,45ABC DBO ∠+∠=,∴ABC α∠=∠, ∴7sin sin 25AC ABC AB α=∠==. 【点睛】本题考查旋转的性质、全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,第二个问题的关键是利用(1)的结论解决问题,属于中考常考题型.13.如图,在直角坐标系中,已知点A (-1,0)、B (0,2),将线段AB 绕点A 按逆时针方向旋转90°至AC.(1)点C的坐标为(,);(2)若二次函数的图象经过点C.①求二次函数的关系式;②当-1≤x≤4时,直接写出函数值y对应的取值范围;Z_X_X_K]③在此二次函数的图象上是否存在点P(点C除外),使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.【答案】(1) ∴点C的坐标为(-3,1) .(2)①∵二次函数的图象经过点C(-3,1),∴.解得∴二次函数的关系式为②当-1≤x≤4时,≤y≤8;③过点C作CD⊥x轴,垂足为D,i) 当A为直角顶点时,延长CA至点,使,则△是以AB为直角边的等腰直角三角形,过点作⊥轴,∵=,∠=∠,∠=∠=90°,∴△≌△,∴AE=AD=2,=CD=1,∴可求得的坐标为(1,-1),经检验点在二次函数的图象上;ii)当B点为直角顶点时,过点B作直线L⊥BA,在直线L上分别取,得到以AB为直角边的等腰直角△和等腰直角△,作⊥y轴,同理可证△≌△∴BF=OA=1,可得点的坐标为(2, 1),经检验点在二次函数的图象上.同理可得点的坐标为(-2, 3),经检验点不在二次函数的图象上综上:二次函数的图象上存在点(1,-1),(2,1)两点,使得△和△是以AB为直角边的等腰直角三角形.【解析】(1)根据旋转的性质得出C点坐标;(2)①把C点代入求得二次函数的解析式;②利用二次函数的图象得出y的取值范围;③分二种情况进行讨论.14.如图,△ABC和△DEC都是等腰三角形,点C为它们的公共直角顶点,连接AD、BE,F 为线段AD的中点,连接CF.(1)如图1,当D点在BC上时,BE与CF的数量关系是__________;(2)如图2,把△DEC绕C点顺时针旋转90°,其他条件不变,问(1)中的关系是否仍然成立?请说明理由;(3)如图3,把△DEC绕C点顺时针旋转一个钝角,其他条件不变,问(1)中的关系是否仍然成立?如成立,请证明;如果不成立,请写出相应的正确的结论并加以证明.【答案】(1)BE=2CF;(2)(1)中的关系是仍然成立,理由见解析;(3)(1)中的关系是仍然成立,理由见解析.【解析】试题分析:(1)根据“SAS”证明△ACD≌△BCE,可得AD=BE,又因为AD=2CF,从而BE=2CF;(2)由点F是AD中点,可得AD=2DF,从而AC= 2DF+CD,又由△ABC和△CDE是等腰直角三角形,可知BC=2DF+CE,所以BE= 2(DF+CE),CF= DF+CD,从而BE=2CF;(3)延长CF至G使FG=CF,即:CG=2CF,可证△CDF≌△GAF,再证明△BCE≌△ACG,从而BE=CG=2CF成立.解:(1)∵△ABC是等腰直角三角形,∴AC=BC,∵△CDE是等腰直角三角形,∴CD=CE,在△ACD和△BCE中,,∴△ACD≌△BCE,∴AD=BE,在Rt△ACD中,点F是AD中点,∴AD=2CF,∴BE=2CF,故答案为BE=2CF;(2)(1)中的关系是仍然成立,理由:∵点F是AD中点,∴AD=2DF,∴AC=AD+CD=2DF+CD,∵△ABC和△CDE是等腰直角三角形,∴AC=BC,CD=CE,∴BC=2DF+CE,∴BE=BC+CE=2DF+CE+CE=2(DF+CE),∵CF=DF+CD=DF+CD,∴BE=2CF;(3)(1)中的关系是仍然成立,理由:如图3,延长CF至G使FG=CF,即:CG=2CF,∵点F是AD中点,∴AF=DF,在△CDF和△GAF中,,∴△CDF≌△GAF,∴AG=CD=CE,∠CDF=∠GAF,∴∠CAG=∠CAD+∠GAF=∠CAD+∠ADC=180°﹣∠ACD,∵∠ACB=∠DCE=90°,∴∠BCE=360°﹣∠ACB﹣∠DCE﹣∠ACD=180°﹣∠ACD,∴∠CAG=∠BCE,连接BE,在△BCE和△ACG中,,∴△BCE≌△ACG,∴BE=CG=2CF,即:BE=2CF.点睛:本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质和旋转的性质,考查了学生综合运用知识的能力,熟练掌握旋转的性质、全等三角形的判定与性质是解答本题的关键.15.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)连接AE,求证:△AEF是等腰三角形;猜想与发现:(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.结论1:DM、MN的数量关系是;结论2:DM、MN的位置关系是;拓展与探究:(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【答案】(1)证明参见解析;(2)相等,垂直;(3)成立,理由参见解析.【解析】试题分析:(1)根据正方形的性质以及等腰直角三角形的知识证明出CE=CF,继而证明出△ABE≌△ADF,得到AE=AF,从而证明出△AEF是等腰三角形;(2)DM、MN的数量关系是相等,利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直,利用三角形外角性质和等腰三角形两个底角相等性质,及全等三角形对应角相等即可得出结论;(3)成立,连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=12AE,利用三角形全等证出AE=AF,而DM=12AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.试题解析:(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF 是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形;(2)DM、MN的数量关系是相等,DM、MN的位置关系是垂直;∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN 是△AEF的中位线,∴AE=2MN,∵AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°,∴DM⊥MN;(3)(2)中的两个结论还成立,连接AE,交MD于点G,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=12AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=12AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性质.四、初三数学圆易错题压轴题(难)16.在圆O中,C是弦AB上的一点,联结OC并延长,交劣弧AB于点D,联结AO、BO、AD、BD.已知圆O的半径长为5,弦AB的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长;(2)如图2,设AC=x ,ACO OBD S S =y ,求y 关于x 的函数解析式并写出定义域;(3)若四边形AOBD 是梯形,求AD 的长.【答案】(1)2;(2)2825x x x -+(0<x <8);(3)AD=145或6. 【解析】【分析】(1)根据垂径定理和勾股定理可求出OC 的长.(2)分别作OH ⊥AB ,DG ⊥AB ,用含x 的代数式表示△ACO 和△BOD 的面积,便可得出函数解析式.(3)分OB ∥AD 和OA ∥BD 两种情况讨论.【详解】解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB=8,∴OD ⊥AB ,AC=12AB=4, 在Rt △AOC 中,∵∠ACO=90°,AO=5,∴22AO AC -,∴OD=5,∴CD=OD ﹣OC=2;(2)如图2,过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH=4,OH=3,∵AC=x ,∴CH=|x ﹣4|,在Rt △HOC 中,∵∠CHO=90°,AO=5,∴22HO HC +223|x 4|+-2825x x -+∴CD=OD ﹣OC=52825x x -+过点DG ⊥AB 于G ,∵OH ⊥AB ,∴DG ∥OH ,∴△OCH ∽△DCG ,∴OH OC DG CD=, ∴DG=OH CD OC ⋅35, ∴S △ACO =12AC ×OH=12x ×3=32x , S △BOD =12BC (OH +DG )=12(8﹣x )×(335)=32(8﹣x ) ∴y=ACO OBD S S=()323582x x -=()58x -(0<x <8) (3)①当OB ∥AD 时,如图3,过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F ,则OF=AE ,∴S=12AB•OH=12OB•AE , AE=AB OH OB ⋅=245=OF , 在Rt △AOF 中,∠AFO=90°,AO=5,∴75∵OF 过圆心,OF ⊥AD , ∴AD=2AF=145. ②当OA ∥BD 时,如图4,过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G ,则由①的方法可得DG=BM=245, 在Rt △GOD 中,∠DGO=90°,DO=5,∴75,AG=AO ﹣GO=185, 在Rt △GAD 中,∠DGA=90°, ∴综上得AD=145或6.故答案为(1)2;(2)y=()282558x x x x -+-(0<x <8);(3)AD=145或6. 【点睛】本题是考查圆、三角形、梯形相关知识,难度大,综合性很强.17.已知:四边形ABCD 内接于⊙O ,∠ADC =90°,DE ⊥AB ,垂足为点E ,DE 的锯长线交⊙O 于点F ,DC 的延长线与FB 的延长线交于点G .(1)如图1,求证:GD =GF ;(2)如图2,过点B 作BH ⊥AD ,垂足为点M ,B 交DF 于点P ,连接OG ,若点P 在线段OG 上,且PB =PH ,求∠ADF 的大小;(3)如图3,在(2)的条件下,点M 是PH 的中点,点K 在BC 上,连接DK ,PC ,D 交PC 点N ,连接MN ,若AB =122,HM +CN =MN ,求DK 的长.【答案】(1)见解析;(2)∠ADF =45°;(3)1810. 【解析】【分析】 (1)利用“同圆中,同弧所对的圆周角相等”可得∠A =∠GFD ,由“等角的余角相等”可得∠A =∠GDF ,等量代换得∠GDF =∠GFD ,根据“三角形中,等角对等边”得GD =GF ; (2)连接OD 、OF ,由△DPH ≌△FPB 可得:∠GBH =90°,由四边形内角和为360°可得:∠G =90°,即可得:∠ADF =45°;(3)由等腰直角三角形可得AH =BH =12,DF =AB =12,由四边形ABCD 内接于⊙O ,可得:∠BCG =45°=∠CBG ,GC =GB ,可证四边形CDHP 是矩形,令CN =m ,利用勾股定。
上海复旦初级中学初三初三化学上册期中试题及答案

上海复旦初级中学初三化学上册期中试题及答案一、选择题(培优题较难)1.现有 18.6g NaOH 和 Na2CO3固体混合物,已知钠元素与碳元素的质量比 23:3,则原混合固体中含有钠元素的质量为()A.9.2 g B.6.9 g C.4.6 g D.2.3 g2.豆腐是人们喜爱的食物,营养丰富,能为人体提供所需的多种氨基酸,其中含量最多的是亮氨酸(C6H13NO2),关于亮氨酸的说法正确的是()A.亮氨酸是氧化物B.亮氨酸中碳元素的质量分数为27.3%C.一个亮氨酸分子由22个原子构成D.亮氨酸中碳、氢、氮、氧四种元素的质量比为6:13:1:23.下列对实验现象的描述或实验操作正确的是A.红磷在空气中燃烧,产生大量白雾B.点燃或加热可燃性气体前,先检验其纯度C.10mL酒精与10mL蒸馏水混合,溶液的体积为20mLD.用高锰酸钾制取O2后,应先熄灭酒精灯再从水中取出导气管4.如图所示有关二氧化碳的实验中,只与二氧化碳物理性质有关的实验是()A. B. C. D.5.碳12是指含6个中子的碳原子。
下列对氧16和氧18两种氧原子的说法正确的是A.质子数相同B.质量相同C.电子数不相同D.16和18表示原子个数6.宏观辨识和微观剖析是化学核心素养之一。
下列说法正确的是 ( )A.反应前后元素的种类及化合价均未发生改变B.参加反应的和的微粒个数比是4:3C.反应涉及到的物质中,是由原子构成的单质,只有属于氧化物D.该反应生成的单质和化合物的质量比时3:207.碳酸乙烯酯(C3H4O3)可用作锂电池电解液,下列有关碳酸乙烯酯的说法正确的是A.碳酸乙烯酯的相对分子质量为(12×3+1×4+16×3)gB.碳酸乙烯酯中C、H、O三种元素的质量比为12:1:16C.碳酸乙烯酯中C、H、O三种原子的个数比为3:4:3D.碳酸乙烯酯中碳元素的质量分数= ×100%8.下列物质含有氢分子的是()A.H2B.H2O2C.H2CO3D.H2O9.如图所示,甲是溴(Br)的原子结构示意图,乙摘自元素周期表。
上海复旦实验中学化学上册期中试题和答案

上海复旦实验中学化学上册期中试题和答案一、选择题(培优题较难)1.在一密闭容器中放入X、Y、Z、Q四种物质,在一定条件下发生化学反应,一段时间后,测得有关数据如下表,则关于此反应的认识正确的是()物质X Y Z Q反应前质量/g202137反应后质量/g15321未知A.物质Y一定是单质B.反应后物质Q的质量为12gC.反应过程中X、Q的质量比为9:4D.物质Z一定的该反应的催化剂2.实验室常用加热高锰酸钾固体制取氧气,化学方程式为2KMnO4K2MnO4+MnO2+O2↑,现对一定量的高锰酸钾固体进行加热,加热过程中涉及的相关量随时间变化的图象正确的是A.B.C.D.3.“” “”表示两种不同元素的原子,下图表示化合物的是A.B.C.D.4.以下是实验室制取、收集、干燥、存放气体的装置图,有关说法错误的是A.实验室用双氧水制取氧气,用石灰石和稀盐酸制取二氧化碳均可使用装置②B.实验室收集氧气和二氧化碳均可使用装置③,气体从导管b进入C.实验室干燥氧气和二氧化碳均可使用装置④,气体从导管a进入D.实验室收集的氧气和二氧化碳,均可如图⑤临时存放5.下图表示某化学反应的微观示意图,依据图分析判断,下列说法正确的是A.甲物质由5个原子构成B.化学变化的后硅元素的化合价不变C.参加反应的乙的质量和生成的丁中氢元素的质量相等D.参加反应的甲、乙两种物质的分子个数比为l:16.如图,将充满CO2的试管倒扣在滴有紫色石蕊的蒸馏水中,一段时间后,下列实验现象描述正确的是①试管内液面上升②试管内溶液变红③试管内液面不上升④试管内溶液变蓝⑤试管内溶液不变色A.①②B.①④C.②③D.③⑤7.逻辑推理是一种重要的化学思维方法,下列推理合理的是()A.在同一化合物中,金属元素显正价,则非金属元素一定显负价B.化学变化伴随着能量变化则有能量变化的一定是化学变化C.单质含有一种元素,则含有一种元素的纯净物一定是单质D.催化剂的质量在反应前后不变,则在反应前后质量不变的物质一定是该反应的催化剂8.某元素R的化合价是奇数(不变化合价),已知其氧化物的相对分子质量为m,其氯化物的相对分子质量为n,则R的化合价为()A.2()55m n-B.2()55n m-C.255m n-D.255n m-9.宏观辨识和微观剖析是化学核心素养之一。
上海复旦实验中学化学上册期中试题和答案

上海复旦实验中学化学上册期中试题和答案一、选择题(培优题较难)1.运用推理、归纳、类比、对比的方法得出下列结论,其中合理的是()A.因为化学变化都遵循质量守恒定律,所以质量不发生改变的变化一定是化学变化B.水和过氧化氢的组成元素相同,则两者的化学性质相同C.Na+、Mg2+、Cl-的最外层电子数均为8,由此得出离子的最外层电子数均为8D.过氧化氢溶液加催化剂的反应速率快,说明催化剂可以改变反应速率2.下列实验操作正确的是A.塞紧橡皮塞B.加热液体C.取用液体D.读出液体的体积3.最近,我国科学家成功合成新型催化剂,将CO2高效转化为甲醇(CH3OH)。
这不仅可以缓解碳排放引起的温室效应,还将成为理想的能源补充形式。
该化学反应的微观过程如下图所示。
下列说法正确的是A.该反应中四种物质均为化合物B.反应前后H元素的化合价不变C.参加反应的甲、乙分子个数比为1:3D.反应前后原子数目发生改变4.下列滴管使用图示正确的是()A.取液时挤入空气B.代替玻璃棒进行搅拌C.向试管中滴加液体D.将残留溶液的滴管倒持5.电解水实验装置如图所示,下列说法正确的是A.电解前后元素种类不变B.实验说明水由H2和O2组成C.反应的化学方程式为2H2O=2H2↑+O2↑D.a管收集的气体能使燃着的木条燃烧更旺6.如图是四种粒子的结构示意图,下列有关说法正确的是()A.④表示的粒子属于金属元素B.①表示的粒子在化学反应中易失电子C.①②③④表示四种不同元素D.②④所表示的粒子化学性质相似7.实验室里制取氧气大致可分为下列步骤:①点燃酒灯,加热试管;②检查装置的气密性;③将药品装入试管,用带导管的塞子塞紧试管并固定在铁架台上;④用排水法收集氧气;⑤连接好装置;⑥熄灭酒精灯;⑦将导管从水槽中取出。
正确的操作顺序是()A.⑤②③①④⑦⑥B.③④⑤⑥⑦①②C.②③⑤①④⑦⑥D.②④③⑤①⑥⑦8.在下列四种含有氯元素的物质中,氯元素化合价最低的是()A.Cl2 B.NaCl C.HClO D.KClO39.如图所示有关二氧化碳的实验中,只与二氧化碳物理性质有关的实验是()A. B. C. D.10.在进行“氧气的实验室制取与性质”实验时,某同学制得的氧气不纯。
上海复旦实验中学初中物理九年级全册第十六章《电压电阻》检测题(答案解析)

一、选择题1.下列所提供的数据中符合实际情况的是()A.一节干电池电压15VB.中考跳绳合格,考生的跳绳功率约1500WC.家用电冰箱的工作电流约1AD.小明将一个鸡蛋从地上拿起并缓慢举过头顶,对鸡蛋做功约10J2.如图所示电路,电源电压为3V,当开关S闭合后,两盏灯都不发光且电压表的示数为3V,产生这一现象的原因可能是()A.灯泡L2处短路B.灯泡L1处短路C.灯泡L1处断路D.灯泡L2处断路3.两只小灯泡L1和L2连接在同一电路中,以下哪个特点可以确认两灯一定是并联的()A.两灯亮度不同B.两盏灯可以同时亮,同时灭C.两灯两端的电压相同D.通过两灯的电流不相等4.下列关于电压的说法正确的是()A.只要有电压就一定能形成电流B.电压是使自由电荷发生定向移动形成电流的原因C.对人体的安全电压为36V D.一节干电池的电压为2V5.一位同学设计了一个风力测定仪,如图所示,O是转动轴,OC是金属杆,下面连接着一块受风板。
无风时OC是竖直的,风越强,OC杆偏转的角度越大。
AB是一段圆弧形电阻,P点是金属杆与弧形电阻相接触的点,电路中接有一个小灯泡,开关闭合时,关于该装置的使用,下列说法错误的是()A.风力越大,接入电路中的电阻越小B.可以通过灯泡的亮度粗略反映风力的大小,灯泡越暗,说明风力越小C.金属杆OC与弧形电阻AB组合在一起相当于一个滑动变阻器,有风时,P A部分连入电路D.若要提高该装置反映风力大小的性能,可以在电路中串联一个电流表6.小明同学在学习过程中整理了如下学习笔记,其中正确的是()A.验电器是根据异种电荷相互排斥的原理制成的B.物理学中把正电荷定向移动的方向规定为电流方向C.并联电路中的总电压等于各支路电路两端的电压之和D.两个小灯泡串联在电路中,发光越亮的灯泡通过的电流越大7.如图所示的电路,开关S闭合后,两灯均发光,下列说法中正确的是()A.电压表测的是灯L1两端的电压B.开关断开时电流表无示数但电压表有示数C.电压表测的是灯L2两端的电压D.电压表测的是电源两端的电压8.小文同学利用家中的电位器、直流稳压电源、导线、开关和小灯泡,组装了一个调光台灯,电路如图所示。
【物理】上海复旦实验中学九年级上册期中精选试卷检测题

【物理】上海复旦实验中学九年级上册期中精选试卷检测题一、初三物理电流和电路易错压轴题(难)1.小敏和小英通过实验探究“并联电路中干路电流与各支路电流的关系”.她们连接的电路如图所示.(1)当小敏用开关“试触”时,发现电流表A1无示数、电流表A2的指针快速右偏,两灯均不发光.由此可知,她们连接的电路发生了________故障;若闭合开关S,可能造成的后果是________.(2)小英只改接了电路中的一根导线,电路便连接正确了,请你在图中画出她的改法.(在错接的导线上画×,然后画出正确的接线)(___________)(3)她们利用改正后的电路进行实验:闭合开关S后,读出两块电流表的示数,得出的初步结论是:________.【答案】短路电流表A2被烧坏在并联电路中,干路电流大于支路电流【解析】【分析】【详解】(1)电流表A1无示数、电流表A2的指针快速右偏,两灯均不发光,由此可知电路发生了短路故障,若闭合开关S,由于电路发生短路,电路中电流过大,可能造成的后果是电流表A2被烧坏.(2)改正电路如图:(3)利用改正后的电路进行实验,闭合开关S后,读出两块电流表的示数,得出的初步结论是:在并联电路中,干路电流大于支路电流.【点睛】电路中发生短路的危害,可能烧毁电流表或电源,为避免短路发生,可采用试触法.2.在“测量小电灯的功率”的实验中,电源电压为4.5V,小灯泡额定电压为2.5V、电阻约为10Ω.滑动变阻器标有“30Ω 1A”字样(1)连接电流表时应选用________________的量程.(2)请你用笔画线代替导线,将图甲中的实物电路连接完整__________.(3)乙同学连完电路并闭合开关后,发现小灯泡不发光且电压表示数为零,电流表示数为0.15A,产生这一现象的原因是 ____________________________________________.(4)故障排除后,移动滑动变阻器的滑片,使小灯泡正常发光时,电流的示数如乙图所示,请读出电流表的示数,并填入表格中_______________ .(5)实验中,同学们记录了多组小灯泡两端的电压及对应通过小灯泡的电流值,但表格的设计仍有不完整的地方,请将所缺内容填写完整____________.(6)小组同学们分析了实验数据得出:小灯泡的发光亮度是由灯泡的______决定的,且_______,灯泡发光越亮.【答案】0—0.6A 灯泡短路 0.24 W 2.5 0.24 0.6 实际功率实际功率越大【解析】试题分析:测灯泡的功率的测量原理是P=UI,即测出灯泡两端的电压和流过小灯泡的电流,算出灯泡的功率.根据题意,灯泡的额定电压为2.5V,所以电压表的量程选0-3V,灯的电阻约为10Ω,根据欧姆定律可以算出灯正常发光时的电流约为0.25A,小于0.6A,所以电流表应选0-0.6A的量程.闭合开关后,灯不亮,电流表有示数,说明电路中的故障是短路,电压表的示数是零,说明灯两端没有电压,所以灯被短路.在实验数据记录表格中,除了要记下需要测的物理,还要写清物理量的单位,灯正常发光时的电压为2.5V,电流表读数是0.24A,算出灯的额定功率为0.6W.根据表格中灯的实际功率与灯的亮暗可以得出灯的亮度与实际功率的关系,灯泡的实际功率越大,灯的亮度越高.考点:测小灯泡的功率3.在用电压表、电流表测量小灯泡电功率的实验中,灯泡上标有“2.5V”的字样.(1)测量小灯泡电功率的实验的原理是______________;小张根据电路图连接如图甲所示的实验电路,小王检查后发现有一根导线连接有错误,请你在这根导线上打“×”,并用笔画线代表导线,画出正确的连线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 2
+5
2015学年第一学期九年级化学期中考试卷参考答案
一、选择题(20分,每题1分)
二、填空题:(17分,除指定分值外,其他均为1分)
21、 (1)2He ; (2)3SO 2;(3);AgNO 3(4)Al 2O 3。
(5)NaCl 、 (6)CuSO 4。
(7)2C 2H 2+5O 2 −−→−点燃
4C O 2+2H 2O 。
(11)6.02×1024。
23、(12)CO (13)B 。
(14)分子,(15)甲、丙(2分,少写一个扣1分,多写或错写不得分)。
(16)化学反应前后原子的种类和数目均没有发生改变。
(合理即给分)
三、简答题:(共23分,除指定分值外,其他均为1分,文字描述题回答合理即给分)
24、(17)水槽。
(18)2H 2O 2−−
→−2
MnO
2H 2O+O 2↑ (19)B 。
(20)控制反应速率,使反应能平稳进行。
(21)集气瓶内未装满水就收集或未等气泡密集就收集。
(22)c 导管下端加长至靠近集气瓶底部(如图)
b c
水
F
2 / 2
2 3
加热 (23)解:设需要氯酸钾固体X 摩尔。
n(O 2)=
)()(22O M O m = 32
6
.9=0.3mol
2KClO 3−−
→−2MnO
2KCl+3O 2↑(1分)
x 2=3
.03(1分) x=0.2 mol (1分) 答:需要氯酸钾固体0.2摩尔。
25、(24)4P+5O 2 −−→−点燃
2P 2O 5 (25)大量白烟产生,放出热量。
(26)烧杯内的水进入约集气瓶容积的1/5。
(27)木炭燃烧生成了CO 2气体,瓶内气压基本不变,水不会倒流。
(28)CO 2+Ca(OH)2→CaCO 3↓+H 2O (29)D 。
(30)污染小或装置始终密闭,减少误差或装置简单,操作方便。
(合理即给分) (31)A 、D(2分,漏选一个扣1分,多选或错选不得分)。
26、 (32)探究Fe 2O 3能否作过氧化氢分解的催化剂。
(33)在装有过氧化氢溶液的试管中伸入带火星的木条。
(34)Fe 2O 3能加快过氧化氢分解的速度。
(35)与实验二作对比,检验加入Fe 2O 3后过氧化氢分解的速率是否发生变化。
(36)Fe 2O 3在反应前后的质量变化或在反应前后的化学性质是否改变。
(写一条即可)
x 0.3。
