数据结构10.3.B+树
数据结构之B树和B树B树和B树的特性应用场景和性能优势

数据结构之B树和B树B树和B树的特性应用场景和性能优势B树和B+树:特性、应用场景和性能优势在计算机科学中,数据结构是指组织和存储数据的方式,而B树(B-Tree)和B+树(B+ Tree)是常用的数据结构之一。
本文将重点介绍B树和B+树的特性、应用场景和性能优势。
一、B树和B+树的特性1. B树特性B树是一种多叉树,它的每个节点可以拥有多个子节点。
B树的特点如下:- 根节点至少有两个子节点,除非它是叶子节点。
- 所有叶子节点在同一层级上,也就是说,B树是平衡的。
- 节点中的键值按照升序排列。
- 节点的子节点数可以超过2。
2. B+树特性B+树是B树的一种变体,相比B树,B+树的特点更适合数据库索引的实现。
B+树的特点如下:- 非叶子节点只存储键值信息,数据只存储在叶子节点。
- 所有叶子节点通过链表连接在一起,方便范围查询。
- 叶子节点之间通过指针相互连接,提高查找效率。
二、B树和B+树的应用场景1. B树应用场景- 文件系统:B树可用于文件系统的索引结构,方便文件的快速定位和存取。
- 数据库:B树可以作为数据库索引的存储结构,加快数据库查询的速度。
- 图书馆管理系统:B树可用于图书馆系统中书籍索引的实现,便于查找和管理。
2. B+树应用场景- 数据库:B+树是关系型数据库中常用的索引结构,能够提高查找效率和范围查询的性能。
- 文件系统:B+树可以作为文件系统的块索引结构,方便大规模文件的管理与存取。
- 排序算法:B+树可以用于外部排序的算法实现,提高排序的效率。
三、B树和B+树的性能优势1. B树的性能优势- 查询性能好:B树的节点可以存储多个键值,使得在查找过程中减少IO操作,提高查询效率。
- 范围查询性能优越:B树是平衡的,叶子节点之间通过指针相互连接,可方便实现范围查询。
2. B+树的性能优势- 更高的存储密度:B+树的非叶子节点只存储键值信息,不存储数据,因此可以存储更多的键值,提高存储密度。
btree原理

btree原理
B树(B-tree)是一种多路平衡查找树,它允许在一颗树中有多于2个子节点。
B树最开始是由Rudolf Bayer和Edward McCreight在1972年所发明的。
它被广泛应用于文件系统及数据库中,具有高效的插入、删除、查找等操作。
B树的原理可以简单概括如下:
1.节点结构
B树中的每个节点就像一个文件夹,里面存放着多个键值对,这些键值对通常是关键字和数据。
2.排序
B树中的关键字需要进行排序,保证查找时可以尽快找到目标。
3.最大度数
B树的最大度数通常为256、512、1024等,这意味着每个节点最多可以存储256个键值对。
4.平衡
B树需要保持平衡,也就是每条从根到叶子的路径长度相同,这样可以保证查找的效率。
5.叶子节点
B树的叶子节点并不是真正的叶子节点,而是带有数据的末尾节点。
6.B+树
B+树是B树的一种扩展,它将所有的数据都存放在叶子节点中,而将非叶子节点作为索引节点,这样可以提高查找效率。
7.插入
当插入新的节点时,如果节点已满,就需要将节点分裂成两个节点,然后把中间的节点插入到父节点中,以保持树的平衡。
8.删除
当删除节点时,如果删除后节点过小,就需要将其他兄弟节点进
行合并,以保持树的平衡。
总之,B树作为一种高效的查找数据结构,广泛应用于文件系统和数据库中。
对于大量数据存储和索引,B树可以通过平衡的方式保证高效的查询和修改速度。
在实际应用中,B树的形态、操作方式等都会针对具体情况进行调整,以获得最佳性能。
树的表示法 字典解释

树的表示法字典解释
树是一种数据结构,它由若干个节点组成,这些节点通过边相连。
树的表示法有多种,其中比较常见的包括以下几种:
1. 儿子-兄弟表示法(孩子兄弟表示法),这种表示法通过每
个节点的指针来表示树的结构。
每个节点有两个指针,一个指向它
的第一个孩子节点,另一个指向它的下一个兄弟节点。
这种表示法
适合于一般的树,但不适合于二叉树。
2. 层次遍历表示法,这种表示法是按照树的层次结构来表示的,通常使用数组或者队列来表示。
从根节点开始,按照层次顺序依次
存储每个节点的数值,空节点用特定的符号表示。
这种表示法适合
于完全二叉树。
3. 括号表示法,这种表示法是通过括号和逗号来表示树的结构。
具体来说,可以使用前序遍历的方式,通过括号表示节点的嵌套关系。
例如,树 (A(B(C))(D)) 可以表示为 A(B(C))(D)。
树的表示法可以根据具体的应用场景和需要选择合适的方式。
每种表示法都有其适用的范围和特点,需要根据实际情况进行选择。
希望这些信息能够帮助你更好地理解树的表示法。
《刘大有数据结构》 chapter 10 查找

10. 1 线性表查找 10. 2 二叉查找(搜索)树 10. 3 数字查找树
10. 4 杂凑
10. 5 (a,b)-树、B树和B+树
查找(又称检索),简单地说就是查表. 一个查找过程, 就是对于给定的变元K,去找出表中哪个记录的关键词域 之值等于K;待查找完成后有两种可能,或者查找成功, 已确定一个其关键词域之值等于K的记录之所在,或者查 找失败,即已确定关键词为K的记录不在表中. 在查找失 败之后,有时还希望把一个关键词域之值为K的新记录插 入到表中,这样的过程称为查找与插入操作. 决定查找操作的是关键词,查找是许多重要计算机程序 中最耗费时间的部分,查找算法的优劣密切关系到查找操 作的速度,从而对包含查找算法的程序的效率影响极大, 因此对查找算法应着重加以研究.
10. 2 二叉查找(搜索)树
前一节我们假定表的逻辑结构是线性结构并给出了几种 查找算法 ,数据存储在数组中;本节我们介绍二叉查找树, 该结构非常适合线性表的链接结构。 定义10.1 一棵二叉查找树(或称为二叉搜索树)是一棵可 能为空的二叉树形,一棵非空的二叉查找树中的所有结点 在中根次序下按其关键词由小到大排序,并且关键词各不 相同.
m阶Fibonacci树形,则Tm的递归定义如下: (1) 当m=0,1时,Tm为空树; (2) 当m>1时,二叉判定树的根结点是有序表中序号为Fm的 记录,根结点的左子树是与有序表R1,R2,… , RFm-1相对 应 的 二 叉 判 定 树 , 根 结 点 的 右 子 树 是 与 有 序 表 RFm+1 , RFm+2,… ,RFm+1 -1相对应的二叉判定树.
这是一个递归构造的过程,例如,T(1,10)如下图所示.
5 2
B树、B-树、B+树、B树都是什么
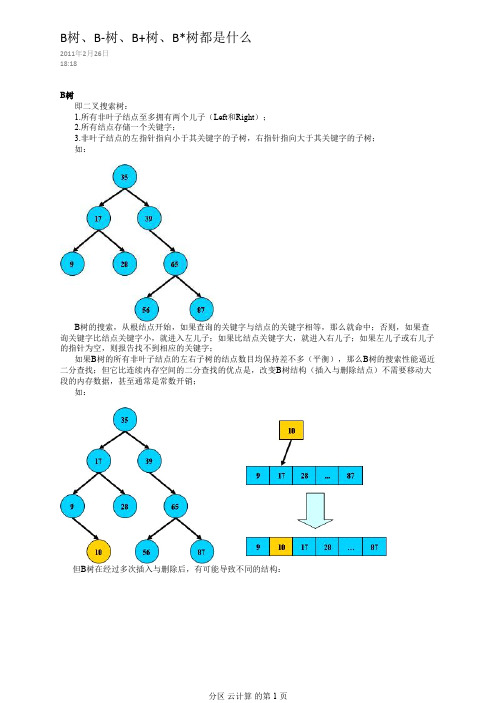
B树、B-树、B+树、B*树都是什么2011年2月26日18:18B树即二叉搜索树:1.所有非叶子结点至多拥有两个儿子(Left和Right);2.所有结点存储一个关键字;3.非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树;如:B树的搜索,从根结点开始,如果查询的关键字与结点的关键字相等,那么就命中;否则,如果查询关键字比结点关键字小,就进入左儿子;如果比结点关键字大,就进入右儿子;如果左儿子或右儿子的指针为空,则报告找不到相应的关键字;如果B树的所有非叶子结点的左右子树的结点数目均保持差不多(平衡),那么B树的搜索性能逼近二分查找;但它比连续内存空间的二分查找的优点是,改变B树结构(插入与删除结点)不需要移动大段的内存数据,甚至通常是常数开销;如:但B树在经过多次插入与删除后,有可能导致不同的结构:但B树在经过多次插入与删除后,有可能导致不同的结构:右边也是一个B 树,但它的搜索性能已经是线性的了;同样的关键字集合有可能导致不同的树结构索引;所以,使用B 树还要考虑尽可能让B 树保持左图的结构,和避免右图的结构,也就是所谓的“平衡”问题;实际使用的B 树都是在原B 树的基础上加上平衡算法,即“平衡二叉树”;如何保持B 树结点分布均匀的平衡算法是平衡二叉树的关键;平衡算法是一种在B 树中插入和删除结点的策略;B-树是一种多路搜索树(并不是二叉的):1.定义任意非叶子结点最多只有M 个儿子;且M>2;2.根结点的儿子数为[2, M];3.除根结点以外的非叶子结点的儿子数为[M/2, M];4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)5.非叶子结点的关键字个数=指向儿子的指针个数-1;6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;8.所有叶子结点位于同一层;如:(M=3)B-树的特性:B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;1.关键字集合分布在整颗树中;2.任何一个关键字出现且只出现在一个结点中;3.搜索有可能在非叶子结点结束;4.其搜索性能等价于在关键字全集内做一次二分查找;5.自动层次控制;由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少利用率,其最低搜索性能为:搜索性能为:其中,M为设定的非叶子啊结点最多子树个数,N为关键字总数;所以B-树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并;B+树B+树是B-树的变体,也是一种多路搜索树:1.其定义基本与B-树同,除了:2.非叶子结点的子树指针与关键字个数相同;3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);5.为所有叶子结点增加一个链指针;6.所有关键字都在叶子结点出现;如:(M=3)B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;B+的特性:1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;2.不可能在非叶子结点命中;3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;4.更适合文件索引系统;B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2); B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;所以,B*树分配新结点的概率比B+树要低,空间使用率更高;小结B树:二叉树,每个结点只存储一个关键字,等于则命中,小于走左结点,大于走右结点;B-树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3;源文档</manesking/archive/2007/02/09/1505979.aspx>。
算法与数据结构第三版

算法与数据结构第三版算法与数据结构——第三版前言本书是一本介绍算法和数据结构的入门书籍。
它适用于计算机科学、软件工程以及其他相关领域的本科生和研究生。
书中涵盖了各种算法和数据结构,如排序、搜索、图算法、哈希表、堆、树、链表等等。
本书旨在帮助读者理解这些算法和数据结构的基本原理,并且能够将其运用于实际问题中。
本书分为三部分。
第一部分为基础知识,介绍了算法分析和大O表示法,以及一些重要的数据结构,例如数组、链表和栈。
第二部分为排序和搜索算法,包括冒泡排序、选择排序、插入排序、快速排序、归并排序、二分搜索和哈希表。
第三部分为高级主题,包括图算法、堆、树和字符串匹配等。
本书内容丰富、通俗易懂,希望能够给读者带来实际帮助。
第一部分基础知识第1章算法分析1.1 算法复杂度1.2 大O表示法1.3 最坏情况与平均情况1.4 最好情况1.5 算法稳定性1.6 实例分析第2章基本数据结构2.1 数组2.2 链表2.3 堆栈2.4 队列第二部分排序和搜索算法第3章冒泡排序和选择排序3.1 冒泡排序3.2 选择排序第4章插入排序和快速排序4.1 插入排序4.2 快速排序第5章归并排序5.1 归并排序5.2 自然归并排序第6章基数排序和桶排序6.1 基数排序6.2 桶排序第7章二分搜索和哈希表7.1 二分搜索7.2 哈希表第三部分高级主题第8章图算法8.1 图的表示8.2 深度优先搜索8.3 广度优先搜索8.4 最短路径算法8.5 最小生成树算法第9章堆和优先队列9.1 堆和堆排序9.2 优先队列第10章树和树算法10.1 树的基本概念10.2 二叉查找树10.3 平衡树10.4 完全二叉树和堆10.5 伸展树第11章字符串匹配11.1 基本思想11.2 暴力匹配算法11.3 KMP匹配算法11.4 Boyer-Moore匹配算法后记本书所介绍的算法和数据结构是计算机科学中的基本知识,并且在实际工程中应用广泛。
它们是计算机科学学习的基石,也是计算机程序员必须掌握的技能。
数据结构树的应用

数据结构树的应用数据结构树的应用数据结构是计算机科学中重要的一个分支,而树是其中一种重要且实用的数据结构之一。
树是由一个根节点和若干子节点组成的一种非线性数据结构,被广泛应用于计算机领域中,特别是在算法设计和数据处理方面。
下面我们将详细介绍树的应用领域。
1. 数据库在数据库管理系统中,树被广泛应用于索引结构。
数据库中的查找过程可以转化为在树中查找某个节点的过程。
常用的树结构包括B-树、B+树和红黑树,这些结构可以高效的处理大量数据,支持高效的检索和排序。
2. 文件系统操作系统中的文件系统其实就是一种树形结构。
目录和文件被视为节点,而目录之间的关系和文件之间的关系则是树的关系。
基于树形结构的文件系统使得我们可以很方便地在系统中查找和管理文件。
3. 编程语言树形结构被广泛运用于编程语言中。
AST(抽象语法树)就是一种常见的语法分析树,它将程序中的语句和表达式抽象成一个树形结构,在编译器中被广泛使用,可以很方便地实现代码的词法分析、语义分析和优化。
此外,树也可以用于构建运行时数据结构,如二叉搜索树、Trie树、AVL树等等。
4. 网络在计算机网络中,树的结构被广泛应用于路由器和交换机中。
这些设备需要通过识别和分析网络中的数据包,将它们分配到不同的路由或交换机上进行处理。
树的结构使得这些设备可以很方便地对不同的数据包进行分类、处理和转发。
5. 人工智能在人工智能中,树也是非常重要的一种数据结构。
决策树是常用的机器学习算法之一,它通过一系列的二叉树形结构对数据进行分类和判断。
在处理自然语言、语音识别和图像处理等领域中,树结构也被广泛应用。
总之,数据结构树在计算机领域中有着非常广泛的应用,可以用于解决各种问题。
从数据库、文件系统到编程语言、网络和人工智能等领域,都需要树这种数据结构来达到高效、快速、准确处理数据的目的。
因此,学习并掌握树这种数据结构非常重要,可以帮助我们更好地理解计算机领域内的各种问题和算法。
数据结构排序PPT课件

注:外部排序时,要将数据分批调入内存来 排序,中间结果还要及时放入外存,显然外 部排序要复杂得多。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
5.待排序记录在内存中怎样存储和处理?
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Void BInsertSort (SqList &L) // 折半插入排序
{ for ( i=2;i<=L.length;++i )
{ L.r[0] = L.r[ i ]; // 将L.r [i] 暂存到L.r[0]
处理方式: ① 顺序排序 —— 数据间的逻辑顺序关系通过其物理
存储位置的相邻来体现,排序时直接移动记录; 适合数据较少的情况!
② 链表排序 ——数据间的逻辑顺序关系通过结点中 的指针体现,排序时只修改指针,不移动数据;
③ 地址排序 —— 数据存储在一段连续地址的空间, 构造一个辅助表保持各数据的存放地址(指针),排 序时先修改辅助表中的地址,最后再移动记录。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
4. 什么叫内部排序?什么叫外部排序? —— 若待排序记录都在内存中,称为内部排序;
内部排序基本操作有两种: ◆ 比较两个关键字的大小;(比不可少的操作) ◆ 存储位置的移动。
i=8
0
1
2
3
4
B树的结构详细讲解

B树的结构详细讲解B树(B-tree)是一种非常常用的数据结构,被广泛应用于文件系统和数据库中用于存储和管理大量数据的索引结构。
B树在磁盘和其他外部存储设备中高效地存储和访问数据,具有快速的插入和删除操作,并且可以高效地支持区间查询。
本文将详细介绍B树的结构和特点。
一、B树的定义B树是一种平衡的m叉树(m-way search tree),特点是每个节点最多含有m个孩子和m-1个关键字。
B树的定义还规定:1.根节点至少有两个孩子,除非它是叶节点;2.所有叶节点都在同一层次上,也就是说它们具有相同的深度。
二、B树的特点B树有以下几个特点:1.B树是一种多路树,每个节点可以拥有多个孩子,普通的二叉树只有两个孩子;2.所有节点的孩子数量是相同的,对于非叶节点,关键字数量比孩子数少一个;3.B树的高度非常低,这是因为每个节点存储多个关键字,减少了树的高度,加快了和插入操作的速度;4. B树的、插入和删除操作的时间复杂度都是O(log n),其中n是数据的规模。
三、B树的结构示意图下面是一个B树的结构示意图:```CG/,\ABDF```在这个示意图中,根节点有三个孩子,图中的关键字为C和G。
A和B是C的两个孩子,D和F是G的两个孩子。
四、B树的操作B树的操作与二叉树的操作类似,只是多了一层循环。
操作从根节点开始,将目标关键字与节点中的关键字进行比较:1.如果目标关键字小于节点中的最小关键字,则进入左子树进行下一轮;2.如果目标关键字大于等于节点中的最小关键字,并且小于等于节点中的最大关键字,则说明已经找到目标关键字;3.如果目标关键字大于节点中的最大关键字,则进入右子树进行下一轮;4.如果节点中没有更多的孩子,则说明目标关键字不存在于B树中。
五、B树的插入操作B树的插入操作有以下几个步骤:1.从根节点开始,按照操作找到关键字应该插入的位置,即找到关键字所在的叶节点。
2.在叶节点中插入关键字。
如果叶节点未满,则直接插入;如果叶节点已满,则需要进行分裂操作。
数据结构 第9章 查找3-B树

插入关键字 = 60, 90, 30
2、B-树的删除
在深度为(h+l)的m阶B-树中删除一个键值k,首先要查 到键值k所在的结点及在结点中的位置。若k在非终端 节点中,则把该结点的右边(或左边)指针所指子树中 的最小(或最大)键值与k对调,使k移到终端节点。 在终端节点中删除一个键值后,使得该结点的值个数n 减1,此时应分以下三种情况进行处理: – (1)若删除后结点中键值数目n≥ ┌m/2┐-1,在该结点 中删去键值k连同右边的指针。 – (2)若删除后结点中键值数目n< ┌m/2┐ -1,且左(或 右)兄弟结点的关键字数目> ┌m/2┐-1,则把左(或 右)兄弟结点中最大(或最小)键值移到父结点中,再 把父结点大于(或小于)上移键值的键值下移到被删 关键字所在结点中。
(3)若删除后结点中键值数目n< ┌m/2┐ -1,及 其左、右兄弟结点的键值数目都等于┌m/2┐ -1,则就必须进行结点的“合并”,即把应删 的键值删去后,将该结点中的剩余键值和指针 连同父结点中指向该结点指针的左边(或右边) 一个键值ki一起合并到左兄弟(或右兄弟)结点 中,将ki从父结点中删去。如果因此使父结点 中关键字数目< ┌m/2┐-1,则对此父结点做同 样处理,以致于可能直到对根结点做这样的处 理而使整个树减少一层。
2.查找性能的分析
在B-树中进行查找时,其查找时间 主要花费在搜索结点(访问外存)上, 即主要取决于B-树的深度 树的深度。 树的深度
问:含 N 个关键字的 m 阶 B-树可 能达到的最大深度 H 为多少?
反过来问: 深度为H的B-树中, 至少含有多少个结点? 先推导每一层所含最少结点数: 第1层 第2层 第3层 第4层 … … 第 H+1 层 1个 2个 2×m/2 个 × 2×(m/2)2 个 × 2×(m/2) H-1 个 ×
数据结构 B树

动态查找结构
动态的m路查找树
现在我们所讨论的m路查找树多为可以动态调 整的多路查找树,它的一般定义为: 一棵m路查找树, 它或者是一棵空树, 或者是满 足如下性质的树:
根最多有 m 棵子树, 并具有如下的结构:
n, A0, ( K1, A1 ), ( K2, A2 ), ……, ( Kn, An ) 其中,Ai 是指向子树的指针,0 i n < m; Ki 是关键码,1 i n < m。 Ki < Ki+1, 1 i < n。
B-树的插入
B-树是从空树起,逐个插入关键码而生成的。
在B-树,除根节点外每个非失败结点的关键码
个数都在
[ m/2 -1, m-1] 之间。
插入在某个最底层非终端节点开始。如果在关 键码插入后结点中的关键码个数超出了上界 m-1,则结点需要“分裂”,否则可以直接插入。
实现结点“分裂”的原则是:
设结点 A 已有 m-1 个关键码,当再插入一个 关键码,结点从中间位置K m/2分裂,左半部 留在A中,右半部分离成一新节点Q, K m/2 升至父节点中,并把其右指针指向新节点Q
(等比级数前 h 项求和)
h mi
1
m h1 1
i 0
m 1
每个结点中最多有 m-1 个关键码,在一棵高 度为 h 的 m 路查找树中关键码的最大个数为 mh+1-1。
对于高度 h=2 的二叉树,关键码最大个数为 7;
对于高度 h=3 的3路查找树,关键码最大个 数为 34-1 = 80。
h-1 log m / 2 ( (N +1) / 2 ) 示例:若B-树的阶数 m = 199,关键码总数 N = 1999999,则B-树的高度 h 不超过
数据结构中各种树
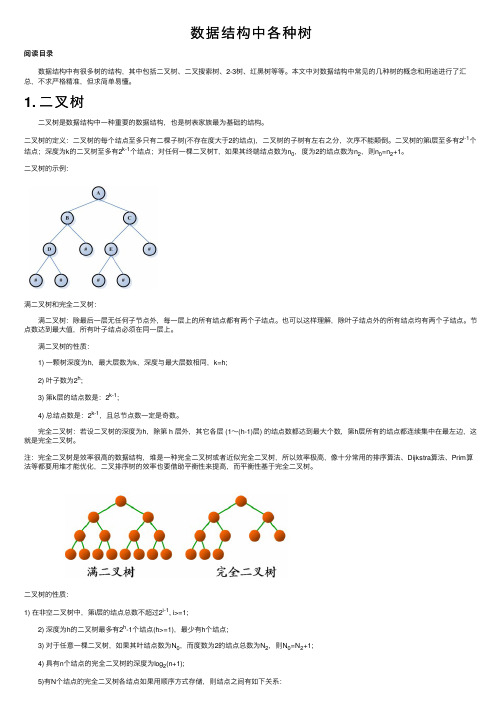
数据结构中各种树阅读⽬录 数据结构中有很多树的结构,其中包括⼆叉树、⼆叉搜索树、2-3树、红⿊树等等。
本⽂中对数据结构中常见的⼏种树的概念和⽤途进⾏了汇总,不求严格精准,但求简单易懂。
1. ⼆叉树 ⼆叉树是数据结构中⼀种重要的数据结构,也是树表家族最为基础的结构。
⼆叉树的定义:⼆叉树的每个结点⾄多只有⼆棵⼦树(不存在度⼤于2的结点),⼆叉树的⼦树有左右之分,次序不能颠倒。
⼆叉树的第i层⾄多有2i-1个结点;深度为k的⼆叉树⾄多有2k-1个结点;对任何⼀棵⼆叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
⼆叉树的⽰例:满⼆叉树和完全⼆叉树: 满⼆叉树:除最后⼀层⽆任何⼦节点外,每⼀层上的所有结点都有两个⼦结点。
也可以这样理解,除叶⼦结点外的所有结点均有两个⼦结点。
节点数达到最⼤值,所有叶⼦结点必须在同⼀层上。
满⼆叉树的性质: 1) ⼀颗树深度为h,最⼤层数为k,深度与最⼤层数相同,k=h; 2) 叶⼦数为2h; 3) 第k层的结点数是:2k-1; 4) 总结点数是:2k-1,且总节点数⼀定是奇数。
完全⼆叉树:若设⼆叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最⼤个数,第h层所有的结点都连续集中在最左边,这就是完全⼆叉树。
注:完全⼆叉树是效率很⾼的数据结构,堆是⼀种完全⼆叉树或者近似完全⼆叉树,所以效率极⾼,像⼗分常⽤的排序算法、Dijkstra算法、Prim算法等都要⽤堆才能优化,⼆叉排序树的效率也要借助平衡性来提⾼,⽽平衡性基于完全⼆叉树。
⼆叉树的性质:1) 在⾮空⼆叉树中,第i层的结点总数不超过2i-1, i>=1; 2) 深度为h的⼆叉树最多有2h-1个结点(h>=1),最少有h个结点; 3) 对于任意⼀棵⼆叉树,如果其叶结点数为N0,⽽度数为2的结点总数为N2,则N0=N2+1; 4) 具有n个结点的完全⼆叉树的深度为log2(n+1); 5)有N个结点的完全⼆叉树各结点如果⽤顺序⽅式存储,则结点之间有如下关系: 若I为结点编号则如果I>1,则其⽗结点的编号为I/2; 如果2I<=N,则其左⼉⼦(即左⼦树的根结点)的编号为2I;若2I>N,则⽆左⼉⼦; 如果2I+1<=N,则其右⼉⼦的结点编号为2I+1;若2I+1>N,则⽆右⼉⼦。
数据结构课程教案

数据结构课程教案一、课程简介1. 课程背景数据结构是计算机科学与技术的基石,广泛应用于各类软件开发和算法设计中。
本课程旨在培养学生掌握基本数据结构及其算法,提高解决问题的能力。
2. 课程目标了解数据结构的基本概念、原理和常用算法。
培养学生使用数据结构解决实际问题的能力。
熟悉常用的数据结构(如数组、链表、栈、队列、树、图等)及其应用场景。
3. 教学方法采用讲授、案例分析、实验和实践相结合的方式进行教学。
通过课堂讲解、小组讨论、编程练习等环节,使学生掌握数据结构的知识和技能。
二、教学内容1. 第四章:线性表4.1 线性表的概念及其基本操作4.2 顺序存储结构及其实现4.3 链式存储结构及其实现4.4 线性表的应用实例2. 第五章:栈和队列5.1 栈的概念及其基本操作5.2 顺序栈及其实现5.3 链栈及其实现5.4 队列的概念及其基本操作5.5 顺序队列及其实现5.6 链队列及其实现5.7 栈和队列的应用实例3. 第六章:串6.1 串的概念及其基本操作6.2 串的顺序存储结构及其实现6.3 串的链式存储结构及其实现6.4 串的应用实例4. 第七章:数组和广义表7.1 数组的概念及其基本操作7.2 multidimensional 数组及其实现7.3 广义表的概念及其基本操作7.4 广义表的实现及其应用实例5. 第八章:树和图8.1 树的概念及其基本操作8.2 二叉树及其实现8.3 树的遍历及其应用实例8.4 图的概念及其基本操作8.5 邻接表及其实现8.6 邻接矩阵及其实现8.7 图的遍历及其应用实例三、教学安排1. 第四章:线性表理论讲解:2课时编程练习:2课时小组讨论:1课时2. 第五章:栈和队列理论讲解:2课时编程练习:2课时小组讨论:1课时3. 第六章:串理论讲解:2课时编程练习:2课时小组讨论:1课时4. 第七章:数组和广义表理论讲解:2课时编程练习:2课时小组讨论:1课时5. 第八章:树和图理论讲解:2课时编程练习:2课时小组讨论:1课时四、教学评价1. 平时成绩:30%课堂表现:10%小组讨论:10%课后作业:10%2. 考试成绩:70%期末考试:50%实验报告:20%五、教学资源1. 教材:《数据结构(C语言版)》2. 辅助资料:PPT课件、编程实例、实验指导书等3. 编程环境:Visual Studio、Code::Blocks等4. 在线资源:相关教程、视频讲座、在线编程练习等六、第九章:排序算法1. 9.1 排序概述了解排序的定义和目的掌握排序算法的分类2. 9.2 插入排序插入排序的基本思想实现插入排序的算法步骤插入排序的时间复杂度分析3. 9.3 冒泡排序冒泡排序的基本思想实现冒泡排序的算法步骤冒泡排序的时间复杂度分析4. 9.4 选择排序选择排序的基本思想实现选择排序的算法步骤选择排序的时间复杂度分析5. 9.5 快速排序快速排序的基本思想实现快速排序的算法步骤快速排序的时间复杂度分析6. 9.6 其他排序算法希尔排序堆排序归并排序7. 9.7 排序算法的应用实例对数组进行排序在文件管理中对文件进行排序六、教学安排1. 理论讲解:2课时2. 编程练习:2课时3. 小组讨论:1课时七、第十章:查找算法1. 10.1 查找概述查找的定义和目的掌握查找算法的分类2. 10.2 顺序查找顺序查找的基本思想实现顺序查找的算法步骤顺序查找的时间复杂度分析3. 10.3 二分查找二分查找的基本思想实现二分查找的算法步骤二分查找的时间复杂度分析4. 10.4 哈希查找哈希查找的基本思想了解哈希函数的设计与实现实现哈希查找的算法步骤5. 10.5 其他查找算法树表查找图查找6. 10.6 查找算法的应用实例在数据库中查找特定记录在字符串中查找特定子串七、教学安排1. 理论讲解:2课时2. 编程练习:2课时3. 小组讨论:1课时八、第十一章:算法设计与分析1. 11.1 算法设计概述算法设计的目的是什么掌握算法设计的方法2. 11.2 贪心算法贪心算法的基本思想贪心算法的应用实例3. 11.3 分治算法分治算法的基本思想分治算法的应用实例4. 11.4 动态规划算法动态规划算法的基本思想动态规划算法的应用实例5. 11.5 回溯算法回溯算法的基本思想回溯算法的应用实例6. 11.6 算法分析的方法渐进估计法比较分析法1. 理论讲解:2课时2. 编程练习:2课时3. 小组讨论:1课时九、第十二章:实践项目1. 12.1 实践项目概述实践项目的要求和目标掌握实践项目的设计与实现2. 12.2 实践项目案例分析分析实践项目的需求设计实践项目的数据结构实现实践项目的算法3. 12.3 实践项目汇报与讨论学生汇报实践项目成果小组讨论实践项目中的问题和解决方案4. 12.4 实践项目的评价与反馈教师对实践项目进行评价学生根据反馈进行改进九、教学安排1. 实践项目指导:2课时2. 实践项目汇报与讨论:2课时3. 实践项目评价与反馈:1课时1. 教材:《数据结构(C语言版)》2. 辅助资料:PPT课件、编程实例、实验指导书等3. 编程环境:Visual Studio、Code::Blocks等4. 在线重点解析1. 基本数据结构的概念、原理和常用算法。
严蔚敏版《数据结构(C语言版)》-内部排序-第10章

high=mid-1 ; else low=mid+1 ;
}
/* 查找插入位置 */
for (j=i-1; j>=high+1; j--)
L->R[j+1]=L->R[j];
L->R[high+1]=L->R[0]; /* 插入到相
应位置 */
}
}
从时间上比较,折半插入排序仅仅减少了关键字的 比较次数,却没有减少记录的移动次数,故时间复杂度 仍然为O(n2) 。
待排序的记录类型的定义如下:
#define MAX_SIZE 100
Typedef int KeyType ;
typedef struct RecType
{ KeyType key ;
/* 关键字码 */
infoType otherinfo ; /* 其他域 */
}RecType ;
typedef struct Sqlist
③ 记录存储在一组连续地址的存储空间:构造另一 个辅助表来保存各个记录的存放地址(指针) :排序 过程不需要移动记录,而仅需修改辅助表中的指针, 排序后视具体情况决定是否调整记录的存储位置。
①比较适合记录数较少的情况;而②、③则适合 记录数较少的情况。
为讨论方便,假设待排序的记录是以①的情况存 储,且设排序是按升序排列的;关键字是一些可直接用 比较运算符进行比较的类型。
(n-1)(n+1)
2
移动次数:∑n (i+1)=
i=2
(n-1)(n+4)
2
一般地,认为待排序的记录可能出现的各种排列的
概率相同,则取以上两种情况的平均值,作为排序的关
数据结构第十章 排序

10.2 插入排序 插入排序
直接插入排序 折半插入排序 2-路插入排序 表插入排序 希尔排序
10.2.1 直接插入排序
基本操作:将一个记录插入到已排好序的有序表中, 从而得到一个新的、记录数增1的有序表。
例:有一组待排序的记录的关键字初始序列如下:
(49,38,65,97,76,13,27,49`)
(4)归并排序 (5)基数排序
按内排过程中所需的工作量分类:
(1)简单的排序方法,其时间复杂度为O(n×n)
(2)先进的排序方法,其时间复杂度为O(nlogn);
(3)基数排序,其时间复杂度为O(d(n+rd))
排序算法的两种基本操作:
(1)比较两个关键字的大小; (2)将记录从一个位置移至另一个位置;
算法实现的关键设计:
将d看成是一个循环数组,并设两个指针first和final分别指示排序过 程中得到的有序序列中的第一个记录和最后一个记录在d中的位置.
例:有一组待排序的记录的关键字初始排列如下:
(49,38,65,97,76,13,27,49`) 16
[初始关键字] 49 38 65 97 76 13 27 49`
18
10.2.3 希尔排序 从直接插入排序
待排序序列基本有序可提高效率 回顾 待排序序列的记录数n很小时可提高效率
希尔排序的基本思想:
先将整个待排记录序列分割成为若干子序列分别进行
直接插入排序,待整个序列中的记录“基本有序”时,再对 全
体记例录:有进一行组一待次排直序接的插记入录排的序关. 键字初始排列如下: (49,38,65,97,76,13,27,49`)
} 12
直接插入排序的性能分析: 10. 3
(1)空间:只需一个记录的辅助空间r[0].
数据结构--树 ppt课件

A BC D
树的度::=
madxeg (nro)ed ee
no tdreee
例如, degree of this tree = 3.
父节点(Parent) ::= 有子树的节点是 其子树根节点的父节点。
E F G HI J
KL
M
子节点(Child) ::= 若A节点是B节点的父节点,则B节点是A节点 的子节点,也叫孩子节点。
A BC D E F G HI J
KL
M
B
E
F
A
C
G
H
D
I
J
§1 预备知识
因此,每个节点的大小取决于 子树数目。噢,这样并不太好! K L M
§1 预备知识
❖ 儿子-兄弟表示法
Element FirstChild NextSibling
A BC D E F G HI JFra bibliotekKLM
A
N
B
C
D
N
E
F G HI J
第四章 树
§1 预备知识
客观世界中许多事物存在层次关系 ◦ 人类社会家谱 ◦ 社会组织结构 ◦ 图书信息管理
图书
哲
学
…
宗
教
文 学
医 药 卫
农 业 科
工 业 技
生学术
综
…
合
哲 学 理
世
欧
界 哲
…
洲 哲
宗 教
论学
学
电 工 技 术
计 算… 机
建 筑 科 学
水 利 工 程
宗 教 分 析 研 究
宗 教… 理 论 与 概 况
} }
T ( N ) = O( N )
B树的原理及应用场景

B树的原理及应用场景B树是一种自平衡的树数据结构,通常用于数据库和文件系统中,能够高效地支持插入、删除和查找操作。
B树的原理和应用场景是数据库系统和文件系统设计中的重要内容,下面将详细介绍B树的原理及其应用场景。
一、B树的原理1. 结构特点B树是一种多路搜索树,每个节点可以包含多个子节点。
B树的特点包括:- 根节点至少有两个子节点。
- 每个非叶子节点有m个子节点,其中[m/2]到m个子节点非空。
- 每个节点中的关键字按递增顺序排列。
- 位于节点n的关键字同时也是节点n的子树的分界线。
2. 插入操作在B树中插入一个新的关键字时,首先找到合适的叶子节点,如果该节点未满,则直接插入;如果该节点已满,则进行节点分裂操作,将中间的关键字上移,并将左右子树分别作为新的子树。
3. 删除操作在B树中删除一个关键字时,首先找到包含该关键字的叶子节点,如果该节点关键字个数大于等于[m/2],则直接删除;如果小于[m/2],则进行节点合并操作,将该关键字从父节点中删除,并将左右子树合并为一个新的子树。
二、应用场景1. 数据库系统B树广泛应用于数据库系统中的索引结构,如MySQL、Oracle等数据库管理系统。
在数据库中,B树可以加快数据的查找速度,提高数据库的性能。
通过B树索引,可以快速定位到需要查询的数据,减少磁盘IO 操作,提高查询效率。
2. 文件系统B树也常用于文件系统中的索引结构,如NTFS、EXT4等文件系统。
在文件系统中,B树可以加快文件的查找速度,提高文件系统的性能。
通过B树索引,可以快速定位到需要访问的文件或目录,减少磁盘IO操作,提高文件读写效率。
3. 搜索引擎搜索引擎中的倒排索引通常采用B树结构,用于存储关键字与文档之间的映射关系。
通过B树索引,搜索引擎可以快速定位到包含查询关键字的文档,提高搜索结果的准确性和响应速度。
4. 文件压缩在文件压缩算法中,B树也有一定的应用场景。
通过B树索引,可以快速定位到需要压缩或解压缩的数据块,提高文件的压缩效率和解压速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• Same structure as B-trees. • Dictionary pairs are in leaves only. Leaves form a doubly-linked list. • Remaining nodes have following structure:
Delete
9 3 5
16 30 5 6 9 17 30 40
ቤተ መጻሕፍቲ ባይዱ
2
3
• Delete pair with key = 2. • Merge with sibling, delete in-between key in parent.
Delete
9 5
16 30
3
5 6
9
17
30 40
• Delete pair with key = 3.
123
• Split into two nodes.
1
23
• Insert smallest key in new node and pointer to this new node into parent.
2 1 23
Insert
9 5 2 2 3 1 5 6 9
16 30
16 17 30 40
Delete
9 6 30 6 17 30 40
5
Delete
9 6
16 30 6 9 17 30 40
5
• Delete pair with key = 6.
• Merge with sibling, delete in-between key in parent.
Delete
9
16 30
5
9
1
2 3
• Now, insert a pair with key = 18.
• Insert an index entry17 plus a pointer into parent.
Insert
9 2 5 16 5 6 9 16 17 30 17 18 30 40
1
2 3
• Now, insert a pair with key = 18.
Delete
16
30
5
17
30 40
•Index node becomes deficient. • Merge with sibling and in-between key in parent.
Delete
16 30
5
17
30 40
•Index node becomes deficient. • It’s the root; discard.
1
2 3
16 17 30 40
• Delete pair with key = 16. • Note: delete pair is always in a leaf.
Delete
9 2 5
16 30 5 6 9 17 30 40
1
2 3
• Delete pair with key = 16. • Note: delete pair is always in a leaf.
•Get >= 1 from sibling and update parent key.
Delete
9 6
16 30 6 9 17 30 40
5
• Delete pair with key = 9.
• Merge with sibling, delete in-between key in parent.
9
5
16 30 5 6 9 16 17 30 40
1 3
index node leaf/data node
B+-tree—Search
9
5
16 30 5 6 9 16 17 30 40
1 3
key = 5 6 <= key <= 20
B+-tree—Insert
9
5
16 30 5 6 9 16 17 30 40
• Insert an index entry17 plus a pointer into parent.
Insert
9 17 2 5 16 5 6 9 16 30 17 18 30 40
1
2 3
• Now, insert a pair with key = 7.
Delete
9 2 5
16 30 5 6 9
17
30 40
• Index node becomes deficient.
•Get >= 1 from sibling, move last one to parent, get parent key.
Delete
16 9
30
5
9
17
30 40
• Delete 9.
• Merge with sibling, delete in-between key in parent.
• Insert an index entry 2 plus a pointer into parent.
Insert
9 2 5
16 30 5 6 9
1
2 3
16 17 30 40
• Now, insert a pair with key = 18.
Insert
9 17 2 5 16 30 5 6 9 16 17 18 30 40
j a0 k 1 a1 k2 a2 … k j aj
• j = number of keys in node. • ai is a pointer to a subtree. • ki <= smallest key in subtree ai and > largest in ai-1.
Example B+-tree
Delete
9 2 5
16 30 5 6 9 17 30 40
1
2 3
• Delete pair with key = 1. • Get >= 1 from sibling and update parent key.
Delete
9 3 5
16 30 5 6 9 17 30 40
2
3
• Delete pair with key = 1. • Get >= 1 from sibling and update parent key.
1
Insert 10
Insert
9 5
16 30
5 6 9 16 17 30 40
1 3
• Insert a pair with key = 2. • New pair goes into a 3-node.
Insert Into A 3-node
• Insert new pair so that the keys are in ascending order.
