勾股定理拔高竞赛题
勾股定理拔高训练
1。
构造几何图形解决问题 (1)求25)8(1x 22+-++x 最小值 (2)求9)12(4x 22+-++x 的最小值2。
某人从A 点观察某高处B 点的仰角为30度, 沿水平方向走80米的C 点观察B 点的仰角为45度, 求AB 、CB 的距离是多少3、已知:2323-+=a ,2323+-=b ,求代数式223b ab a +-的值。
4。
公路MN 和公路PQ 在P 点处交汇,点A 处有一所中学, AP=160米,点A 到公路MN 的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉 机在公路MN 上沿PN 方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度 是18千米/小时,那么学校受到影响的时间为多少5。
ΔABC 中,AB=AC=20,BC=32,∠DAC=90。
,求BD6。
长为4m 的梯子搭在墙上与地面成45°角, 作业时调整成60°角(如图所示), 则梯子的顶端沿墙面升高了 ______m7。
在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C 地南偏西30°方向,则A、C两地的距离为8。
如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为9。
如图,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1km,B村到公路l的距离BD=2km,B村在A村的南偏东45°方向上.(1)求出A,B两村之间的距离;(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置(保留清晰的作图痕迹,并简要写明作法)10。
小明要测量河内小岛B到河边公路l的距离,在A点测得仰角30°,在C点测得仰角60°,又测得AC =米,则小岛B到公路l的距离为()米11。
勾股定理怎么算_勾股定理常用11个公式_勾股定理拓展提高之动态几何(勾股定理)拔高练习

八年级数学勾股定理拓展提高之动态几何(勾股定理)拔高练习一. 计算题(本大题共8小题,共40分)1.(本小题5分)如图,某人在B处通过平面镜看见在B正上方3米处的A物体,已知物体A到平面镜的距离为2米,问B点到物体A的像A′的距离是多少?核心考点:勾股定理则 =_____.核心考点:勾股定理3.(本小题5分)如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?核心考点:勾股定理轴对称的性质的最小值是?核心考点:勾股定理轴对称的性质5.(本小题5分)如图:正方形ABCD中有一点P,且PA=1,PB=2,PC=3,求∠APB的度数.核心考点:勾股定理旋转的性质梯形ABCD的面积.核心考点:勾股定理旋转的性质7.(本小题5分)如图,P是等边三角形ABC内一点,AP=3,BP=4,CP=5,求∠APB的度数.核心考点:勾股定理旋转的性质CE=4 ,求DE 的长.(2)若P是BC边上任意一点,上面的结论还成立吗?若成立请证明,若不成立请说明理由;(3)若P是BC边延长线上一点,线段AB、AP、BP、CP之间有什么样的关系?请证明你的结论.核心考点:等腰三角形的性质勾股定理线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM. (1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为时,求正方形的边长核心考点:三角形三边关系勾股定理11.(本小题10分)如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,若∠EAF=45°,试推断BE、CF、EF之间的数量关系,并说明理由.核心考点:勾股定理旋转的性质12.(本小题10分)如图,在Rt13.(本小题10分)(2008天津)已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.(1)当扇形CEF绕点C在∠ACE的内部旋转时,如图①,求证:MN²=AM²+BN²(2)当扇形CEF绕点C旋转至图②的位置时,关系式MN²=AM²+BN²是否仍然成立?若成立,请证明;若不成立,请说明理由核心考点:旋转的性质运动变化型问题2AD=BD+CD核心考点:勾股定理旋转的性质勾股定理试题一.选择题(共10小题)1.(2016•淄博)如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为()A.B.2C.D.10﹣52.(2016•台州)如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是()A.B.C.D.3.(2016•株洲)如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有()A.1 B.2 C.3 D.44.(2016•南京)下列长度的三条线段能组成钝角三角形的是()A.3,4,4 B.3,4,5C.3,4,6 D.3,4,75.(2016•达州)如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为()A.B.C.D.6.(2016•哈尔滨)如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为()A.60海里B.45海里C.20海里D.30海里7.(2015•大连)如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为()A.﹣1 B.+1 C.﹣1 D.+18.(2015•淄博)如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=8,AD=4,则图中长为4的线段有()A.4条B.3条C.2条D.1条9.(2015•黑龙江)△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是()A.4.8 B.4.8或3.8 C.3.8 D.510.(2015•毕节市)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是()A.,,B.1,,C.6,7,8 D.2,3,4参考答案与试题解析一.选择题(共10小题)1.(2016•淄博)如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为()A.B.2C.D.10﹣5【分析】延长BG交CH于点E,根据正方形的性质证明△ABG≌△CDH≌△BCE,可得GE=BE﹣BG=2、HE=CH﹣CE=2、∠HEG=90°,由勾股定理可得GH的长【解答】解:如图,延长BG交CH于点E在△ABG和△CDH中∴△ABG≌△CDH(SSS)AG2+BG2=AB2∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°∴∠1+∠2=90°,∠5+∠6=90°又∵∠2+∠3=90°,∠4+∠5=90°∴∠1=∠3=∠5,∠2=∠4=∠6在△ABG和△BCE中∴△ABG≌△BCE(ASA)∴BE=AG=8,CE=BG=6,∠BEC=∠AGB=90°∴GE=BE﹣BG=8﹣6=2同理可得HE=2在RT△GHE中,GH===2故选:B【点评】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用,通过证三角形全等得出△GHE为等腰直角三角形是解题的关键。
勾股定理拔高题

1、如图①,美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全图②等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积()
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=6,AB=10,则CE的长为()
3、如图,有四个三角形,各有一边长为6,一边长为8,若第三边分别为6,8,10,12,则面积最大的三角形是()
A.B. C.D.4.如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC的高是()
5.如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上,AB边如图所示,则使△ABC 是直角三角形的点C有()
6.把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB=2,则CD=.。
八年级数学勾股定理拓展提高(勾股定理)拔高练习

八年级数学勾股定理拓展提高(勾股定理)拔高练习一、填空题(共5道,每道4分)1.教材1题:△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是_______.2.教材3题:在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.3题图5题图3.教材4题:△ABC周长是24,M是AB的中点,MC=MA=5,则△ABC的面积是_____.4.教材5题:将一根长24 cm的筷子,置于底面直径为5cm、高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是_____.5.教材10题:矩形ABCD中,BC=4,DC=3,将该矩形沿对角线BD折叠,使点C落在点F处,求EF的长_____.二、解答题(共5道,每道10分)1.教材9题:如图,有一个直角三角形纸片,两直角边AC=8cm,BC=6cm,现将直角边BC沿直线BD折叠,使它落在斜边AB上的点C′处,求CD的长以及折痕BD的平方1题图2题图2.教材8题:如图,已知DE=m,BC=n,∠EBC与∠DCB互余,求+的值.3.教材12题:如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B´处,点A对应点为A´,且B´C=3,求CN和AM的长.3题图4题图5题图4.教材14题:如图,某隧道的截面是一个半径为米的半圆形,一辆高米,宽3米的卡车能通过该隧道吗?5.教材16题:如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动,已知城市A到BC的距离AD=90km(1)台风中心经过多长时间从B点移到D点(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,游人必顺在接到台风警报后的几小时内撤离(撤离速度为6km/h)三、证明题(共3道,每道10分)1.教材2题:如图,在正方形ABCD中,E是DC的中点,F为BC上的一点且BC=4CF,试说明△AEF是直角三角形.1题图2题图3题图2.作业1题:如图,已知P是矩形ABCD内任一点,求证:PA2+PC2=PB2+PD23.教材6题:如图所示.已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.。
第一章勾股定理拔高题

第一章勾股定理拔高题1如图,一只蜘蛛沿长方体表面从长方体的一个端点A爬到另一个端点C1,已知长方体的长、宽、高分别是AB=4cm、BC=3cm、CC1=5cm,求蜘蛛爬行的最短距离_________________2如图,有一圆柱,其高为8cm,它的底面周长为16cm,在圆柱外侧距下底1cm的A处有一只蚂蚁,它想得到距上底1cm 的B处的食物,则蚂蚁经过的最短距离为___________________3为筹备迎春晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠上红色油纸,如图所示,已知圆筒高为108cm,其横截面周长为36cm,如果在表面缠上4圈油纸,最少应裁剪_______________长的油纸(油纸宽度忽略不计)4如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为cm.5如图,在正方形ABCD中,AB边上有一点E,AE=3,EB=1,在AC上有一点P,使EP+BP 最短,求EP+BP的最短长度_______________________6在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺。
突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,请问水深______________7如图是一个直角三角形纸片,∠C=90°,两直角边长分别是3cm,4cm.现要给它再拼接一个完全一样直角三角形纸片,两纸片不重叠且无缝隙,使得拼成的图形形状是等腰三角形,则拼成的等腰三角形的周长为________________.8在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是.9如图,长方形纸片ABCD沿对角线AC折叠,设点D落在点D′处,BC交AD′于点E,AB=6cm,BC=8cm,则S阴影=__________________.10一辆装满货物的卡车高2.5米,宽1.6米,要开进厂门,如图所示,厂门的顶部呈半圆(AB为直径),下部呈长方形,问这辆卡车能否顺利通过厂门?为什么?11如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求EC的长.12如图所示的一块地,已知AD=4cm,CD=3cm ,AD⊥DC,AB=13cm,BC=12cm求这块地的面积?13如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C 处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.14如图,E、F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.15如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是300m和500m,两村庄之间的距离AB为d(已知d2=400000m2),现要在河边l上建造一水厂,向A、B两村送水,铺设水管的工程费用为每米200元,修建该工程政府出资8万元,问两个村庄村民自筹资金至少多少元?16如图所示一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用_______________秒17如图,在△ABC中,∠C=90°,AC=2,BC=1,点A,C分别在x轴、y轴上,当点A在x 轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为___________________.18将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是_____________________19长为25m的云梯AB斜靠墙上(墙与地面垂直)。
word完整版勾股定理拔高竞赛题
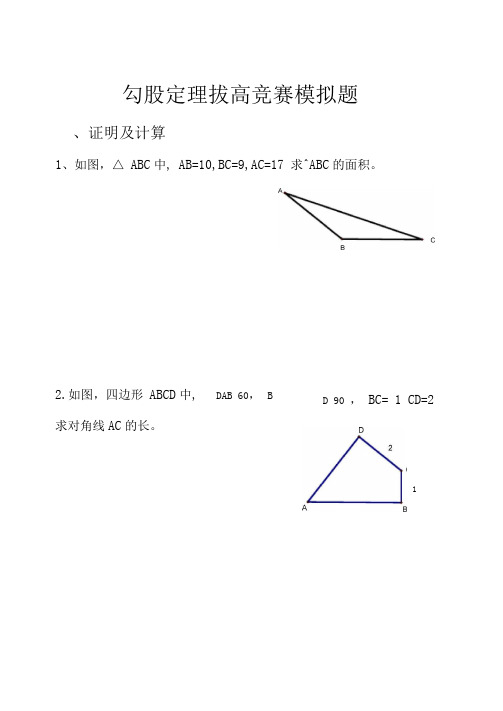
勾股定理拔高竞赛模拟题、证明及计算1、如图,△ ABC中, AB=10,BC=9,AC=17 求^ABC的面积。
2.如图,四边形ABCD中, DAB 60, B求对角线AC的长。
D 90 ,BC= 1 CD=213、如图,在△ ABC中,/ ACB=90,CD 丄AB于点D,若AD=8,BD=2 求CD的长度。
4.如图,P是等边三角形ABC内的一点,连结PA PB PC以BP为边作/ PBQ=60 且BQ=BP 连结CQ PQ 若PA:PB:PC=3:4:5,试判断△ PQC勺形状。
C5.如图,ADC和BCE都是等边三角形,ABC 30,试说明:2 2 2BD2 AB2 BC26.在等腰直角三角形中,AB=AC点D是斜边BC的中点,点E、F 分别为ABAC边上的点,且DE1 DF(1)说明:BE2 CF2 EF2⑵ 若BE=12,CF=5试求DEF的面积。
、勾股定理的应用1.图示是一种“羊头”形图案,其作法是,从正方形 1开始,以 它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边, 分别向外作正方形2,和2’,…,依次类推,若正方形 7的边长 为1cm 则正方形1的边长为置的三个正方形的面积分别为1, 1.21 ,1.44,正放置的四个正 方形的面积为 S 、S 、S3、S,贝J s+s+s+s=(A 3.65B 2.42C 2.44D 2.652、已知数3、6,请再写出一个数,使这三个数中的一个数的平方cm.【变式】:如图,在直线I 上依次摆放着七个正方形,已知斜是另外两个数的积,这个数是3、直角三角形的三边为a-b , a, a+b且a、b都为正整数,则三角形其中一边长可能为(A 61B 、71C 、81D 、914、在^ ABC 中, AB 边上的中线 CD=3 AB=6 BC+AC=8 则^ ABC 勺 面积为已知|x 12 |x y 25与z 2 10z 25互为相反数,变式】:若 ABC 的三边长a b 、c 满足b 2c 2 338 10a 24b 26c ,试判断 ABC 的形状。
勾股定理竞赛试题

勾股定理一、选择题(共5小题,每小题3分,满分15分)1.(3分)△ABC 周长是24,M 是AB 的中点,MC=MA=5,则△ABC 的面积是( )2.(3分)如图,在正方形ABCD 中,N 是DC 上的点,且=,M 是AD 上异于D 的点,且∠NMB=∠MBC,则=( )..CD3.(3分)如图,已知O 是矩形ABCD 内一点,且OA=1,OB=3,OC=4,那么OD 的长为( )224.(3分)如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,那么,正方形ABCD 的面积是( )150+105.(3分)如图,矩形ABCD 中,AB=20,BC=10,若在AB 、AC 上各取一点N 、M ,使得BM+MN 的值最小,这个最小值为( )二、填空题(共5小题,每小题4分,满分20分)6.(4分)如图,△ABC 中,AB=AC=2,BC 边上有10个不同的点P 1,P 2,…P 10,记M i =AP i 2+P i B•P i C (i=1,2,…,10),那么,M 1+M 2+…+M 10= _________ .7.(4分)如图,设∠MON=20°,A 为OM 上一点,OA=4,D 为ON 上一点,OD=8,C 为AM 上任一点,B 是OD 上任意一点,那么折线ABCD 的长最小为 _________ .8.(4分)如图,四边形ABCD是直角梯形,且AB=BC=2AD,PA=1,PB=2,PC=3,那么梯形ABCD的面积= _________ .9.(4分)若x+y=12,求的最小值_________ .10.(4分)已知一个直角三角形的边长都是整数,且周长的数值等于面积的数值,那么这个三角形的三边长分别为_________ .三、解答题(共5小题,满分65分)11.(13分)如图△ABC三边长分别是BC=17,CA=18,AB=19,过△ABC内的点P向△ABC三边分别作垂线PD,PE,PF,且BD+CE+AF=27,求BD+BF的长度.12.(13分)如图,在△ABC中,AB=2,AC=,∠A=∠BCD=45°,求BC的长及△BDC的面积.13.(13分)设a,b,c,d都是正数.求证:+>.14.(13分)(2012•大兴区一模)如图,四边形ABCD中,∠ABC=135°,∠BCD=120°,AB=,BC=5﹣,CD=6,求AD.15.(13分)如图,正方形ABCD内一点E,E到A、B、C 三点的距离之和的最小值为,求此正方形的边长.。
(完整版)勾股定理拔高题

勾股定理拔高题一.选择题1.已知两边的长分别为8,15,若要组成一个直角三角形,则第三边应该为()A.不能确定 B.C.17 D.17或2.一个等腰三角形的腰长为5,底边上的高为4,这个等腰三角形的周长是()A.12 B.13 C.16 D.183.Rt△ABC中∠A=90°,∠A,∠B,∠C的对边分别为a,b,c,则()A.a2+b2=c2B.b2+c2=a2C.a2+c2=b2D.无法确定4.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若∠A:∠B:∠C=1:2:3.则a:b:c=()A.1::2 B.:1:2 C.1:1:2 D.1:2:35.同一平面内有A、B、C三点,A、B两点相距5cm,点C到直线AB的距离为2cm,且△ABC为直角三角形,则满足上述条件的点C有()A.2个B.4个C.6个D.8个6.在四边形ABCD中,AB=1,BC=,CD=,DA=2,S△ABD=1,S△BCD=,则∠ABC+∠CDA等于()A.150°B.180°C.200°D.210°7.已知△ABC中,∠A=60°,BC=a,AC=b,AB=c,AP是BC边上的中线,则AP的长是()A.B.C.D.8.在△ABC中,AB=15,AC=13,BC上的高AD长为12,则△ABC的面积为()A.84 B.24 C.24或84 D.42或849.如图,在△ABC中,D、E分别是BC、AC的中点.已知∠ACB=90°,BE=4,AD=7,则AB的长为()A.10 B.5 C.2D.210.如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=,BC=,CD=,则AD边的长为()A.B.C.D.二.填空题11.如图,△ABC中,CB=CA,∠A﹣∠B=90°,则∠C=.12.如图,矩形ABCD中,AB=4,BC=7,过顶点A作∠BAD的平分线交BC于E,过E作EF⊥ED交AB于F,则EF的长等于.13.在△ABC中,a、b、c分别是∠A、∠B、∠C所对的边长.如果∠A=105°,∠B=45°,,那么c=.14.如图,在△ABC中,AB=AC=5,P是BC边上除点B、C外的任意一点,则AP2+PB•PC=.15.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为.16.如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD=9,AE⊥BC于E,AE=8,则CD的长为.17.如图,已知四边形ABCD中,AC和BD相交于点O,且∠AOD=90°,若BC=2AD,AB=12,CD=9,四边形ABCD的周长是.18.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是.19.如图,AC⊥CE,AD=BE=13,BC=5,DE=7,则AC=.20.如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积.21.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.三.解答题22.已知,如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.(1)求证:GE=GF;(2)若BD=1,求DF的长.23.小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长.24.细心观察下图,认真分析各式,然后解答问题.()2+1=2,S1=()2+1=3,S2=()2+1=4,S 3=(1)请用含n (n 是正整数)的等式表示上述变化规律;(2)推算出OA 10的长;(3)求出S 12+S 22+S 22+…+S 102的值.25.长方形纸片ABCD 中,AD=4cm ,AB=10cm ,按如图方式折叠,使点B 与点D 重合,折痕为EF ,求DE 的长.27.如图,ADC ∆和BCE ∆都是等边ο30=∠ABC ,试说明:222BC AB BD +=D C BA。
八年级数学勾股定理拓展提高(勾股定理) 拔高练习(含答案)
八年级数学勾股定理拓展提高(勾股定理)拔高练
习
试卷简介:本试卷为卢老师八年级线下班第一讲的测试卷,在看卢老师的课程之前,先用这套试卷来检验一下自己,共一道题,为常考题型:拱桥问题,这里的易错点有两个,一是拱桥半径找错;二是不知如何比较
学习建议:先回顾一下教材中勾股定理这一章节的知识
一、解答题(共1道,每道100分)
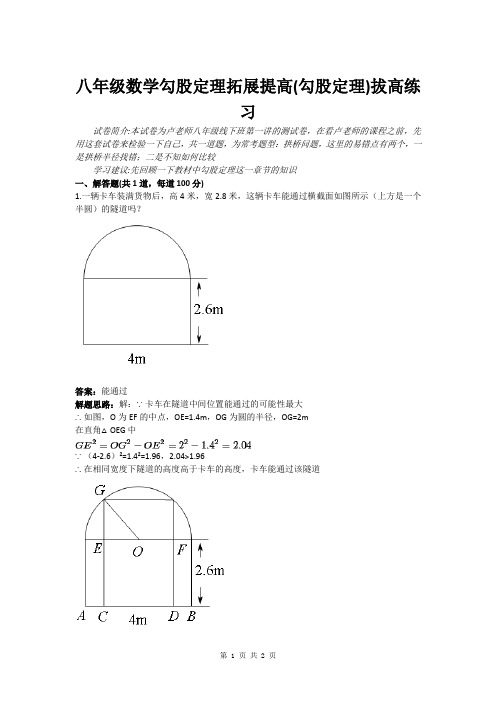
1.一辆卡车装满货物后,高4米,宽
2.8米,这辆卡车能通过横截面如图所示(上方是一个半圆)的隧道吗?
答案:能通过
解题思路:解:∵卡车在隧道中间位置能通过的可能性最大
∴如图,O为EF的中点,OE=1.4m,OG为圆的半径,OG=2m
在直角△OEG中
∵(4-2.6)²=1.4²=1.96,2.04>1.96
∴在相同宽度下隧道的高度高于卡车的高度,卡车能通过该隧道
易错点:一、半径找错;二、比较完,下结论的时候出错试题难度:三颗星知识点:勾股定理的应用。
勾股定理竞赛试卷(含解答)

八年级数学《勾股定理》竞赛试卷(时间:120分钟,总分:120分)一、选择题(每小题5分,共25分)1、△A BC 周长是24,M 是AB 的中点MC =M A=5,则△ABC 的面积是( )A .12; B.16; C .24; D.302、如图,在正方形A BCD 中,N 是CD 的中点,M是A D上异于D 的点,且∠NMB=∠MBC,则AM:AB=( ) A.31; B.33; C.21; D .63第(1)题图 第(2)题图 第(3)题图3、如图,已知O 是矩形ABCD 内一点,且OA =1,OB=3,O C=4,那么OD 的长为( )A.2; B.22; C.23; D.34、如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到C D边的距离也等于10,那么,正方形ABCD 的面积是( )A.200; B.225; C.256; D.150+1025、如图,矩形A BC D中,AB=20,BC=10,若在AB 、AC 上各取一点N、M ,使得BM+M N的值最小,这个最小值为( )A .12;B .102;C .16; D.20二、填空题(每小题5分,共25分) 第(5)题图6、如图,△AB C中,AB=AC=2,BC 边上有10个不同的点1021,,P P P ,记 C P B P AP M i i i i ⋅+=2(i = 1,2,……,10),那么,1021M M M +++ =_________。
第(6)题图7、 如图,设∠MPN =20°,A为O M上一点,OA =43,D 为ON 上一点,OD=83,C 为AM 上任一点,B 是OD 上任意一点,那么折线ABC D的长最小为__________。
第(7)题图 第(8)题图8、如图,四边形A BC D是直角梯形,且AB =BC=2AB ,PA=1,PB=2,PC=3,那么梯形ABC D的面积=__________。
勾股定理竞赛试卷(含解答)

八年级数学《勾股定理》竞赛试卷(时间:120分钟,总分:120分)一、选择题(每小题5分,共25分)1、△ABC 周长是24,M 是AB 的中点MC=MA=5,则△ABC 的面积是(,,) A .12;,B .16;,C .24;,D .302、如图,在正方形ABCD 中,N 是CD 的中点,M 是AD 上异于D 的点,且∠NMB=∠MBC ,则AM :AB=(,,)A .31;B .33; C .21;,D .63第(1)题图,,,,,,,,,, 第(2)题图,,,,,,,, 第(3)题图 3、如图,已知O 是矩形ABCD 内一点,且OA=1,OB=3,OC=4,那么OD 的长为( )A.2;,B.22;,C.23;,D.34、如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,那么,正方形ABCD 的面积是(,,)A .200;,B .225;,C .256;,D .150+1025、如图,矩形ABCD 中,AB=20,BC=10,若在AB 、AC 上各取一点N 、M ,使得BM+MN 的值最小,这个最小值为(,,)A .12;,B .102;,C .16;,D .20,,,,,,,,,,,,,二、填空题(每小题5分,共25分),,,,,,,,,,,,,,,,第(5)题图6、如图,△ABC 中,AB=AC=2,BC 边上有10个不同的点1021,,P P P ,记C P B P AP M i i i i ⋅+=2(i = 1,2,……,10),那么,,1021M M M +++ =_________。
第(6)题图,7、 如图,设∠MPN=20°,A 为OM 上一点,OA=43,D 为ON 上一点,OD=83,C 为AM 上任一点,B 是OD 上任意一点,那么折线ABCD 的长最小为__________。
,,,,,, 第(7)题图,,,,,,,,,,,,,,,,, 第(8)题图8、如图,四边形ABCD 是直角梯形,且AB=BC=2AB ,PA=1,PB=2,PC=3,那么梯形ABCD 的面积=__________。
《勾股定理》拔高题

1《勾股定理》 --- ①1.满足a 2+ b 2= c 2的三个 ,称为勾股数。
注意:①勾股数必须是正整数②一组勾股数扩大相同的正整数倍后,仍是勾股数。
2.填写常见勾股数:(3,4, )(5, ,13 ) ( 6,8, ) ( 7,24, ) ( 8,15, )(9,12, )3.下列各组数据中的三个数,可构成直角三角形的是( )A. 4,5,6B. 2,3,4C. 11,12,13D. 8,15,174.若线段a ,b ,c 组成直角三角形,则它们的比可能是( )A.2∶3∶4B.3∶4∶6C.5∶12∶13D.4∶6∶7 5.下面的三角形中:①△ABC 中,∠C=∠A -∠B ;②△ABC 中,∠A :∠B :∠C=1:1:2; ③△ABC 中,三边长a :b :c=1:1:2; ④△ABC 中,三边长分别为8,15,17.⑤若三角形的一个内角等于另外两个内角之差,那么这个三角形是直角三角形。
其中是直角三角形的个数有( ).A .1个B .2个C .3个D .4个 6.在Rt △ABC 中,∠C=90°①若a=5,b=12,则c=___________; ②若a=15,c=25,则b=___________; ③若c=61,b=60,则a=__________; ④若a ∶b=3∶4,c=10则S △ABC =________。
7.在直角三角形中,若两直角边的长分别为1cm ,2cm ,则斜边长为 .8.变式:已知直角三角形的两边长为3、2,则另一条边长是9.已知直角三角形两直角边长分别为5和12, 斜边上的高是 .10. 以Rt △ABC 的三边为直径分别向外作三个半圆,三个半圆的面积分别是S1、S2中、S3之间的关系是11.四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD 的面积。
《勾股定理》 --- ①1.满足a 2+ b 2= c 2的三个 ,称为勾股数。
勾股定理竞赛试卷(含解答)

八年级数学《勾股定理》竞赛试卷(时间:120分钟,总分:120分)一、选择题(每小题5分,共25分)1、△ABC 周长是24,M 是AB 的中点MC=MA=5,则△ABC 的面积是( )A .12;B .16;C .24;D .302、如图,在正方形ABCD 中,N 是CD 的中点,M 是AD 上异于D 的点,且∠NMB=∠MBC ,则AM :AB=( )A .31; B .33; C .21; D .63第(1)题图 第(2)题图 第(3)题图3、如图,已知O 是矩形ABCD 内一点,且OA=1,OB=3,OC=4,那么OD 的长为( ) A.2; B.22; C.23; D.34、如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,那么,正方形ABCD 的面积是( )A .200;B .225;C .256;D .150+1025、如图,矩形ABCD 中,AB=20,BC=10,若在AB 、AC 上各取一点N 、M ,使得BM+MN 的值最小,这个最小值为( )A .12;B .102;C .16;D .20二、填空题(每小题5分,共25分) 第(5)题图6、如图,△ABC 中,AB=AC=2,BC 边上有10个不同的点1021,,P P P ,记C P B P AP M i i i i ⋅+=2(i = 1,2,……,10),那么, 1021M M M +++ =_________。
第(6)题图7、 如图,设∠MPN=20°,A 为OM 上一点,OA=43,D 为ON 上一点,OD=83,C 为AM 上任一点,B 是OD 上任意一点,那么折线ABCD 的长最小为__________。
第(7)题图 第(8)题图8、如图,四边形ABCD 是直角梯形,且AB=BC=2AB ,PA=1,PB=2,PC=3,那么梯形ABCD 的面积=__________。
初中数学勾股定理拔高综合训练(含答案解析)

初中数学勾股定理拔高综合训练一.选择题(共15小题)1.如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出()A.2个B.3个C.4个D.6个2.如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有()A.1 B.2 C.3 D.43.如图是由5个正方形和5个等腰直角三角形组成的图形,已知③号正方形的面积是1,那么①号正方形的面积是()A.4 B.8 C.16 D.324.分别以下列四组数为一个三角形的边长①6,8,10②5,12,13 ③8,15,16④4,5,6,其中能构成直角三角形的有()A.①④B.②③C.①②D.②④5.如图,是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果正方形的面积是13,小正方形的面积是1,直角三角形的两条边是分别是a,b,则a+b和的平方的值()A.13 B.19 C.25 D.1696.如图,一架25米的梯子AB靠在一座建筑物AO上,梯子的底部B距离建筑物,则梯子底部B AO的底部O有7米(即BO=7米),如果梯子顶部A下滑4米至A1是()滑开的距离BB1A.4米B.大于4米C.小于4米D.无法计算7.工人师傅从一根长90cm的钢条上截取一段后恰好与两根长分别为60cm、100cm 的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为()A.80cm B.C.80cm或D.60cm8.如图,A、B是4×5网格中的格点,网格中的每个小正方形的边长都是1,图中使以A、B、C为顶点的三角形是等腰三角形的格点C有()A.2个B.3个C.4个D.5个9.如图所示:数轴上点A所表示的数为a,则a的值是()A.+1 B.﹣1 C.﹣+1 D.﹣﹣110.如图,在2×2的网格中,有一个格点三角形△ABC,若每个小正方形的边长为1,则△ABC的边长BC边上的高为()A.B.2C.D.211.下列说法中正确的是()A.已知a、b、c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以AB2+AC2=BC2D.在Rt△ABC中,∠C=90°,所以AC2+BC2=AB212.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是()A.0 B.1 C.D.13.如图:一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为()A.11cm B.12cm C.13cm D.14cm14.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,…,依此类推,若正方形①的面积为64,则正方形⑤的面积为()A.2 B.4 C.8 D.1615.请你在如图所示的12×12的网格图形中,到A点的距离为5的格点的个数是()A.4 B.8 C.12 D.16二.解答题(共8小题)16.超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)17.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.18.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t 秒.(1)当t=2秒时,求PQ的长;(2)求出发时间为几秒时,△PQB是等腰三角形?(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.19.如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,(1)试说明△ABC是等腰三角形;=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA (2)已知S△ABC向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),①若△DMN的边与BC平行,求t的值;②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.20.如图,有两只猴子在一棵树CD高5m的点B处,它们都要到A处的池塘去喝水,其中一只猴子沿树爬下走到离树10m处的池塘A处,另一只猴子爬到树顶D 后直线越向池塘的A处.如果两只猴子所经过的路程相等,这棵树高有多少米?21.如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;(1)求证:B′E=BF;(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.22.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?23.如图,D、E分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等.设BC=a,AC=b,AB=c.(1)求AE和BD的长;(2)若∠BAC=90°,△ABC的面积为S,求证:S=AE•BD.初中数学勾股定理拔高综合训练参考答案一.选择题(共15小题)1.D;2.D;3.C;4.C;5.C;6.B;7.A;8.B;9.B;10.C;11.D;12.C;13.C;14.B;15.C;二.解答题(共8小题)16.;17.;18.;19.;20.;21.;22.;23.;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理拔高竞赛模拟题
一、证明及计算
1、如图,△ABC 中,AB=10,BC=9,AC=17,求△ABC 的面积。
2.如图,四边形ABCD 中,︒=∠60DAB ,︒=∠=∠90D B ,BC=1,CD=2,求对角线AC 的长。
C
B
1
C
3、如图,在△ABC 中,∠ACB=90O ,CD ⊥AB 于点D ,若AD=8,BD=2,求CD 的长度。
4.如图,P 是等边三角形ABC 内的一点,连结PA 、PB 、PC ,以BP 为边作∠PBQ=60O ,且BQ=BP ,连结CQ 、PQ ,若PA:PB:PC=3:4:5,试判断△PQC 的形状。
A
C
B
5.如图,ADC ∆和BCE ∆都是等边三角形, 30=∠ABC ,试说明:
222BC AB BD +=
D
6.在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F 分别为AB、AC边上的点,且DE⊥DF。
2
2EF
+
CF
BE=
(2)若BE=12,CF=5,试求DEF
∆的面
积。
二、勾股定理的应用
1.图示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,和2′,…,依次类推,若正方形7的边长为1cm,则正方形1的边长为__________cm.
【变式】:如图,在直线l上依次摆放着七个正方形,已知斜放
置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正
方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4=()
A 3.65
B 2.42
C 2.44
D 2.65
2、已知数
3、6,请再写出一个数,使这三个数中的一个数的平方是另外两个数的积,这个数是.
3、直角三角形的三边为a-b,a,a+b且a、b都为正整数,则三角形其中一边长可能为()
A、61
B、71
C、81
D、91
4、在△ABC 中,AB 边上的中线CD=3,AB=6,BC+AC=8,则△ABC 的面积为_____________.
5、已知2512-++-y x x 与25102+-z z 互为相反数,则以
z y x 、、为三边的三角形是 三角形。
【变式】:若ABC ∆的三边长c b a 、、满足条件
c b a c b a 262410338222++=+++,试判断ABC ∆的形状。
6、已知,如图:在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A 、C 的坐标分别为A (10,0)、C (0,4),点D 是OA 的中点,点P 在BC 边上运动,当△ODP 是腰长为5的等腰三角形时,点P 的坐标为 ____________.
7、如图,EF 为正方形ABCD 的对角线,将∠A 沿DK 折叠,使它的顶点A 落在EF 上的G 点,则∠DKG=_______.
8、以边长为2厘米的正三角形的高为边长作第二个正三角形,以第二个正三角形的高为边长作第三个正三角形,以此类推,则第十个正三角形的边长是( ) A 、2×(22)10厘米 B 、2×(21
)9厘米 C 、2×(
23)10厘米 D 、2×(2
3
)9厘米 9、在△ABC 中,AB 边上的中线CD=3,AB=6,BC+AC=8,则△ABC 的面积为_____________.
10、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm ,正方形A1的边长为6cm ,正方形B 的边长为5cm ,正方形C 的边长为5cm ,则正方形D 的面积是_______cm 2.
11、如图,直线l 上有三个正方形a ,b ,c ,若a ,c 的面积分别为5和11,则b 的面积为___________.
12、如图所示,在边长为2的正三角形ABC 中,已知点P 是三角形内任意一点,则点P 到三角形的三边距离之和PD+PE+PF 等于( ) A 、3 B 、32 C 、34 D 、无法确定
13、如图Rt △ABC 中,AB=BC=4,D 为BC 的中点,在AC 边上存在一点E ,连接ED ,EB ,则△BDE 周长的最小值为( )
A 、25
B 、23
C 、25+2
D 、23+2 14、已知:正方形ABCD 的边长为1,正方形EFGH 内接于ABCD ,AE=a,AF=b,且3
2
=EFGH
S 正方形。
求:a b -的值。
H
G
F
E
C
B。
