有限元网格划分的基本原则
有限元分析网格划分

4.2.4壳单元
壳单元可以模拟平板和曲壳一类结构。壳单元比梁 单元和实体单元要复杂的多,因此,壳类单元中各种 单元的选项很多,如节点与自由度、材料、特性、退 化、协调与非协调,完全积分与减缩积分、面内刚度 选择、剪切变形、节点偏置等,应详细了解各种单元 的使用说明。
2020/10/8
2020/10/8
3.定义材料特性 定义材料特性的命令及其对应的菜单操作如下: 命令:MP、TB
GUI:Main Menu>Preprocessor>Material
Props>Material Models
4.建立梁截面 建立梁截面的命令及其对应菜单操作如下: 命令:ECTYPE、SECDATA
2020/10/8
2020/10/8
Thanks
2020/10/8
粱单元分为多种单元,分别具有不同的特性,是一 类轴向拉压、弯曲、扭转的3D单元。
2020/10/8
4.2.3二维实体单元
2D实体单元是一类平面单元,可用于平面应力、 平面应变的分析,此类单元均位于XY平面内。单元 由不同的节点组成,但每个节点的自由度均为2个(谐 结构实体单元除外),即Ux和Uy。
4.2.5三维实体单元
3D实体单元用于模拟三维实体结构,此类单元每 个节点均具有三个自由度,即Ux,Uy,Uz三个平动 自由度。
2020/10/8
目 录
4.1 网格划分的概述 4.2 单元类型 4.3 网格划分流程
4.3.1单元划分基本过程
1.选择单元类型 选择单元类型的命令及其对应的菜单操作如下: 命令:ET GUI:Main Menu>Preprocessor>Element Type>Add/Edit/Delete 用户可在单元属性数据库中选择所需的单元。 2.定义实常数组 定义实常数组的命令及其对应菜单操作如下: 命令:R GUI:Main Menu>Preprocessor>Real Constants>Add/Edit/Delete 实常数组不是必须的,其定义与否与选用的单元有关该类单 元只承受杆轴向的拉压,不承受弯矩,节点只有平动 自由度。不同的单元具有弹性、塑性、蠕变、膨胀、 大转动、大挠度(也称大变形)、大应变(也称有限 应变),应力刚化(也称几何刚度、初始应力刚度) 等功能。
ANSYS有限元网格划分原则

ANSYS有限元网格划分原则有限元分析中的网格划分好坏直接关系到模型计算的准确性。
本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
作者: 张洪才关键字: CAE ANSYS 网格划分有限元1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
第07讲-有限元网格划分的基本原则及技巧

7-6
网格疏密
• • 网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分 布特点。 在计算数据变化梯度较大的部位(如应力集中处、几何形状、材料、厚度变化的 位置),为了较好地反映数据变化规律,需要采用比较密集的网格。而在计算数 据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。这样,整 个结构便表现出疏密不同的网格划分形式。—— 网格数量应增加在结构的关键 部位,在次要部位增加网格是不必要的,也是不经济的。 边界上最好要在8个单元以上,至少不少于4个; 分析结果完成后,需要检查以下各项,误差较大的位置要进行细分: 单元应力的连续性,比较相邻单元应力值的差值; 应力偏差:结点上的单元结点应力和结点平均应力的差值的较大值; 当以上差值与其中的最大应力的比值较大时,该位置的网格需要细分。
精度 计算时间 精确解 1 2 O
7-4
•
•
P
网格数量
网格数量(续)
在决定网格数量时应考虑分析数据的类型。 实体单元:
• •
1、在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。如 果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。 2、在响应计算中,计算应力响应所取的网格数应比计算位移响应多。 3、在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较 少的网格,如果计算的模态阶次较高,则应选择较多的网格。
左图中(a)、(b)改 变了结构质量的对称分 布,应避免。 (c)是 比较理想的结果。
(a)
7-8
(b)
(c)
单元的形状及评价
• 形状比(长边与短边距离之比) 一般实体单元的长宽比越大,分析误差也越大。 对于板壳单元,评价应力为主时不宜超过1:3,评价位移为主时不宜超过1:5; 对于块体单元,评价应力为主时不宜超过1:2,评价位移为主时不宜超过1:3; 在应力分布几乎没有变化的区域里使用的单元,适当放大也没问题。 倾角(表示单元偏离直角四边形的程度(Angular Deviation)) 四边形的内倾角最好是在45度~135度之间,不要超过15度~165度。 锥度(限于四边形) 用几何偏离(Geometric Deviation)表示四边形单元的变形程度。
Deform网格划分原则及方法

[原]Deform网格划分原则及方法2009-04-04 23:48引言:划分网格是建立有限元模型的一个重要环节,它要求考虑的问题较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、合理的有限元模型,这里介绍网格划分时的一些基本原则及方法。
关键词:Deform 网格局部细化一、网格划分的原则1 网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线,曲线2代表计算时间随网格数量的变化。
可以看出,网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
图1 位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2 网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
图2是中心带圆孔方板的四分之一模型,其网格反映了疏密不同的划分原则。
小圆孔附近存在应力集中,采用了比较密的网格。
板的四周应力梯度较小,网格分得较稀。
有限元分析网格划分的关键技巧

网格规模和分辨率的选择是有限元分析网格划分中的重要环节。以下是选择 合理的网格规模和分辨率时需要考虑的几个因素:
1、分析精度:网格规模和分辨率越大,分析精度越高,但同时也会增加计 算成本。因此,需要在精度和成本之间找到平衡点。
2、计算资源:网格规模和分辨率越大,需要的计算资源越多,需要考虑计 算机硬件的性能和应用场景的需求。
4、三角形单元:适用于不规则区域和复杂结构的模拟,如表面模型等。
5、四边形单元:适用于规则区域和简单结构的模拟,如立方体、圆柱等。
6、高阶单元:高阶单元具有更高的计算精度,但同时也需要更多的计算资 源。
在选择合适的单元类型和阶次时,需要考虑以下因素:
1、分析精度:根据分析目标和实际需求,选择能够满足精度要求的单元类 型和阶次。
4、施加边界条件和载荷:对计算域的边界和加载条件进行定义,以模拟实 际工况。
5、进行有限元分析和求解:利用有限元分析软件进行计算,得到各节点处 的响应和位移等结果。
6、结果后处理:对分析结果进行可视化处理,如云图、动画等,以便更好 地理解和评估仿真结果。
技巧2:如何选择合适的单元类 型和阶次
5、经验准则:根据类似问题的经验和网格划分准则,可以指导网格规模和 分辨率的选择。例如,对于结构分析,通常建议最大单元尺寸不大于最小特征尺 寸的1/10。
技巧4:如何使用有限元分析软件自动划分网格
随着有限元分析软件的发展,越来越多的软件提供了自动划分网格的功能。 使用这些功能可以大大简化网格划分的过程,提高分析效率。下面介绍两种常见 的自动划分网格方法:
2、计算效率:在保证精度的前提下,尽量选择计算效率较高的单元类型和 阶次。
3、单元特性:了解各种单元类型的适用范围和局限性,以便在分析过程中 更好地满足实际需求。
有限元的网格划分技术

有限元的网格划分技术对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
网格化有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
定义网格的属性主要是定义单元的外形、大小。
单元大小基本上在线段上定义,可以用线段数目或长度大小来划分,可以在线段建立后立即声明,或整个实体模型完成后逐一声明。
采纳BottOm-UP方式建立模型时,采纳线段建立后立即声明比较便利且不易出错。
例如声明线段数目和大小后,叁制对象时其属性将会一•起夏制,完成上述操作后便可进行网格化命令。
网格化过程也可以逐步进行,即实体模型对象完成到某个阶段就进行网格话,如所得结果满足,则连续建立其他对象并网格化。
网格的划分可以分为自由网格(free meshing)、映射网格(mapped meshing)和扫略网格(SWeeP meshing)等。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上可以自动生成三角形或四边形网格,在体上自动生成四周体网格。
通常状况下,可采用ANSYS的智能尺寸掌握技术(SMARTSIZE命令)来自动掌握网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并掌握疏密分布以及选择分网算法等( MOPT 命令)。
对于简单几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维简单模型只能生成四周体单元,为了获得较好的计算精度,建议采纳二次四周体单元(92号单元)。
假如选用的是六面体单元,则此方法自动将六面体单元退化为阶次全都的四周体单元,因此,最好不要选用线性(•阶次)的六面体单元(没有中间节点,比如45号单元),由于该单元退化后为线性的四周体单元,具有过大的刚度,计算精度较差;假如选用二次的六面体单元(比如95 号单元),由于其是退化形式,节点数与其六面体原型单元全都,只是有多个节点在同一位置而己,因此,可以采用TCHG命令将模型中的退化形式的四周体单元变化为非退化的四周体单元(如92号单元),削减每个单元的节点数量,提高求解效率。
有限元网格划分

有限元网格划分摘要:总结近十年有限元网格划分技术发展状况。
首先,研究和分析有限元网格划分的基本原则;其次,对当前典型网格划分方法进行科学地分类,结合实例,系统地分析各种网格划分方法的机理、特点及其适用范围,如映射法、基于栅格法、节点连元法、拓扑分解法、几何分解法和扫描法等;再次,阐述当前网格划分的研究热点,综述六面体网格和曲面网格划分技术;最后,展望有限元网格划分的发展趋势。
关键词:有限元网格划分;映射法;节点连元法;拓扑分解法;几何分解法;扫描法;六面体网格1 引言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
2 有限元网格划分的基本原则有限元方法的基本思想是将结构离散化,即对连续体进行离散化,利用简化几何单元来近似逼近连续体,然后根据变形协调条件综合求解。
所以有限元网格的划分一方面要考虑对各物体几何形状的准确描述,另一方面也要考虑变形梯度的准确描述。
为正确、合理地建立有限元模型,这里介绍划分网格时应考虑的一些基本原则。
2.1 网格数量网格数量直接影响计算精度和计算时耗,网格数量增加会提高计算精度,但同时计算时耗也会增加。
当网格数量较少时增加网格,计算精度可明显提高,但计算时耗不会有明显增加;当网格数量增加到一定程度后,再继续增加网格时精度提高就很小,而计算时耗却大幅度增加。
所以在确定网格数量时应权衡这两个因素综合考虑。
2.2 网格密度为了适应应力等计算数据的分布特点,在结构不同部位需要采用大小不同的网格。
在孔的附近有集中应力,因此网格需要加密;周边应力梯度相对较小,网格划分较稀。
机械设计中有限元分析的几个关键问题

机械设计中有限元分析的几个关键问题在机械设计中,有限元分析是一种常用的工具和方法。
它可以帮助工程师们对机械结构进行仿真和分析,评估其性能和可靠性,优化设计方案,减少试验成本和开发周期。
在进行有限元分析时,也存在一些关键问题需要注意和解决。
下面将介绍几个常见的有限元分析的关键问题。
1. 网格划分:网格划分是有限元分析的第一步,也是最关键的一步。
合理的网格划分对于结果的准确性和计算效率至关重要。
过于粗糙的网格会导致计算结果不精确,而过于细密的网格则会增加计算量。
需要根据设计要求和边界条件合理划分网格,尽量在重要的应力集中区域和位移较大的区域细化网格,以获得更准确的结果。
2. 材料本构模型:材料本构模型是用来描述材料力学性质的数学模型,对有限元分析结果的准确性和可靠性有重要影响。
选择合适的本构模型需要考虑材料的性质、应变应力关系和加载条件等因素。
常用的本构模型有弹性模型、塑性模型、粘弹性模型等。
在选择本构模型时,需要根据具体应用场景和加载条件进行合理选择,并进行验证和校准。
3. 边界条件:边界条件是有限元分析中非常重要的一个因素。
它直接影响着模型的应力分布和位移结果。
在设置边界条件时,需要根据实际问题的要求进行准确的设置。
一般包括固支边界、强制位移边界、加载边界等。
在实际应用中,边界条件的设置需要考虑结构的约束和外部加载的作用,并进行合理的假设和简化。
4. 模型验证:模型验证是确保有限元分析结果准确性和可靠性的关键环节。
在进行有限元分析前,可以进行一些简化模型或者理论计算,对部分区域或者特定加载情况进行验证。
验证的方法可以包括理论计算、试验验证、实际工程应用等。
验证的目的是检验有限元模型的准确性和可靠性,进一步提高分析结果的精确性。
5. 结果后处理:有限元分析的结果后处理是对分析结果进行展示和进一步分析的过程。
合适的结果后处理可以帮助工程师们更好地理解分析结果,发现问题和优化设计。
常用的结果后处理方法包括应力和位移的分布图、应变云图、动态变化曲线等。
网格划分基本原则

有限元网格划分的基本原则杜平安 《机械设计与制造》划分网格是建立有限元模型的一个重要环节,它要求考虑的问题较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、合理的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线,曲线2代表计算时间随网格数量的变化。
可以看出,网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
图1位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
图2是中心带圆孔方板的四分之一模型,其网格反映了疏密不同的划分原则。
ANSYS有限元分析中的网格划分

ANSYS有限元分析中的网格划分有限元分析中的网格划分好坏直接关系到模型计算的准确性。
本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
作者: 张洪才关键字: CAE ANSYS 网格划分有限元1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
有限元网格划分

本文讨论了有限元网格的重要概念,包括单元的分类、有限元误差的分类与影响因素;并讨论分析结果的收敛性控制方法,并由实例说明了网格质量及收敛性对取得准确分析结果的重要性。
同时讨论了一些重要网格控制的建议及其他网格设定的说明。
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。
单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
3.按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸。
这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示。
在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
网格划分的方法
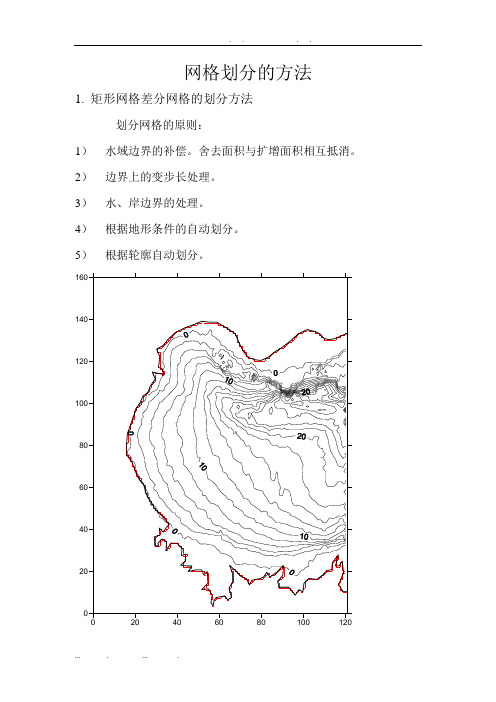
网格划分的方法1.矩形网格差分网格的划分方法划分网格的原则:1)水域边界的补偿。
舍去面积与扩增面积相互抵消。
2)边界上的变步长处理。
3)水、岸边界的处理。
4)根据地形条件的自动划分。
5)根据轮廓自动划分。
2.有限元三角网格的划分方法1)最近点和稳定结构原则。
2)均布结点的网格自动划分。
3)逐渐加密方法。
353025201510505101520253035距离(m)距离(m)3. 有限体积网格的划分方法 1) 突变原则。
2) 主要通道边界。
3) 区域逐步加密。
距离(100m)离距(100m)距离(100m)离距(100m )4. 边界拟合网格的划分方法1) 变换函数:在区域渐变,满足拉普拉斯方程的边值问题。
),(ηξξξP yy xx =+),(ηξηηQ yy xx =+2) 导数变化原则。
⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂=⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂-ηξ1J y x ,⎪⎪⎭⎫ ⎝⎛=ηηξξy x y x J 为雅可比矩阵,⎪⎪⎭⎫⎝⎛--=-ηηξξy x y xJ J 11, ξηηξy x y x J -=)22(1222233ηηξηξηηξηξξηηηηηξξηηξξξηξy y x y y y x y y x x y y x y y x y Jxx +-+-+-=同理可得yy ξ,xx η,yy η。
变换方程为20222=+++-=+++-)()(ηξηηξηξξηξηηξηξξγβαγβαQy Py J y y y Qx Px J x x x其中2222,,ξξηξξηηηγβαy x y y x x y x +=+=+=。
网格划分方法

Total number of elements:197
电子科技大第7学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
电子科技大第8学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
有限元分析与建模 Finite Element Analysis and Modeling
第16章 网 格 划 分 方 法
第一节 网格划分原则
划分什么样的网格?
第二节 网格划分方法
怎样划分网格?
电子科技大第1学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
二、网格疏密 ( relative density)
(a) 一阶振型
(b) 二阶振型
电子科(c) 三技阶振第型大1学5页机/共械48电页(d)子四阶工振型程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling
电子科技大第3学页机/共械48电页 子工程学院
2013,10
有限元分析与建模 Finite Element Analysis and Modeling 在相同网格数量下,位移计算精度高于应力计算精度
电子科技大第4学页机/共械48电页 子工程学院
2013,10
有限元分析与建模
有限元计算单元网格划分

有限元语言及编译器(Finite Element Language And it’s Compiler,以下简称FELAC) 是中国科学院数学与系统科学研究院梁国平研究院于1983年开始研发的通用有限元软件平 台,是具有国际独创性的有限元计算软件,是PFEPG系列软件三十年成果(1983年—2013 年)的总结与提升,有限元语言语法比PFEPG更加简练,更加灵活,功能更加强大。目前 已发展到2.0版本。其核心采用元件化思想来实现有限元计算的基本工序,采用有限元语 言来书写程序的代码,为各领域,各类型的有限元问题求解提供了一个极其有力的工具。 FELAC可以在数天甚至数小时内完成通常需要一个月甚至数月才能完成的编程面或体单元过渡
1)从小单元到大单元过渡时,应使同一节点所连接的单元不致相差太大,避免突然过渡现象。 通常用计算结果调整,保证同一节点所连接的单元精度值至少在0.1以下。单元精度值根据单元内节 点应力与节点平均应力的误差计算。
2)难于过度处最好使用过渡单元,过渡单元的使用要比用同一单元勉强过渡的计算结果要好。 例如:对于复杂体结构间的过渡,最好使用“金子塔”单元过渡。 (5)面或体转接部位的单元 几何模型圆角过渡处的单元划分,根据弧长对应的圆心角和半径确定,对于半径为3mm左右、 圆心角大于90度的转接弧长,通常至少要划分3~4个单元。 (6)高应力区的单元 对高应力区,要进行网格细分应力稳定性计算。即采用多次局部网格细分并进行计算,当前、 后两次计算结果满足所需的精度要求时(通常要求小于0.03)确定网格。 总之,几何模型网格划分时,要在单元类型、单元形态、单元大小、单元过渡和局部应力稳定 等方面下功夫,才能满足工程上的精度要求,达到预期的结果。
网格划分原则

有限元分析中的网格划分好坏直接关系到模型计算的准确性。
本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则。
有限元法基本原理

有限元法基本原理
有限元法是解决偏微分方程数值分析问题的重要方法,它根据力
学原理将构件表示成一系列有限个拉普拉斯单元,采用有限个有限量
节点在某种元素的基质上建立的模型来近似求解构件的本构关系。
它
将复杂的本构关系准确地还原为有限数量的有限单元,以此分析不同
物理状态下物体受力和变形机制,可用于弹性、非线性动力学分析及
多物理场耦合场景等复杂问题的分析。
有限元法由三部分组成:网格划分、体积单元的本构建立及节点
的采样,它将整个物体划分成几种封闭的体积单元,选取合适的节点
对每一种单元进行采样,并为各种单元类型形成有适用的本构关系方程,以串联每个构件的局部分析结果。
首先,在网格划分方面,有限元法可以通过不同的体积单元划分、节点采样及本构关系来处理复杂的问题,如曲面、孔洞等,形成封闭
的有限元网格,随后,对复杂的本构关系准确地还原为有限个有限单元,即针对每一种单元类型的形变量,采取合适的节点、布点一系列
的坐标。
最后,有限元法利用耦合方程作为求解强度和变形问题的基础,
在此基础上,有限元法可以应用于多物理场、非线性动力学分析及其
他复杂的物理状态场景。
另外,它还可以帮助测量构件受力和变形机制,使得构件能正确适应环境变化。
由于有限元法处理方法较为简单,而且力学原理深入,因此,它已在工程计算中得到广泛的应用,有效
提高了模型的准确性和精确度,为进一步探索物理现象带来了巨大的
方便。
有限元网格划分的基本原则

有限元网格划分的基本原则划分网格是建立有限元模型的一个重要环节,它要求考虑的题目较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、公道的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1网格数目。
网格数目的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数目增加,计算精度会有所进步,但同时计算规模也会增加,所以在确定网格数目时应权衡两个因数综合考虑。
2网格疏密。
网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
3单元阶次很多单元都具有线性、二次和三次等形式,其中二次和三次形式的单元称为高阶单元。
选用高阶单元可进步计算精度,由于高阶单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且高次插值函数可更高精度地逼近复杂场函数,所以当结构外形不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数目相同的情况下由高阶单元组成的模型规模要大得多,因此在使用时应权衡考虑计算精度和时间。
4网格质量网格质量是指网格几何外形的公道性。
质量好坏将影响计算精度。
质量太差的网格甚至会中止计算。
直观上看,网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等份点四周的网格质量较好。
网格质量可用细长比、锥度比、内角、翘曲量、拉伸值、边节点位置偏差等指标度量。
划分网格时一般要求网格质量能达到某些指标要求。
在重点研究的结构关键部位,应保证划分高质量网格,即使是个别质量很差的网格也会引起很大的局部误差。
而在结构次要部位,网格质量可适当降低。
5网格分界面和分界点结构中的一些特殊界面和特殊点应分为网格边界或节点以便定义材料特性、物理特性、载荷和位移约束条件。
ANSYS网格划分总结大全

有限元分析中的网格划分好坏直接关系到模型计算的准确性.本文简述了网格划分应用的基本理论,并以ANSYS限元分析中的网格划分为实例对象,详细讲述了网格划分基本理论及其在工程中的实际应用,具有一定的指导意义。
1 引言ANSYS有限元网格划分是进行数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素.从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的.同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分.辛普生积分点的间隔是一定的,沿厚度分成奇数积分点.由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
2 ANSYS网格划分的指导思想ANSYS网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。
在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。
为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。
利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率,例如,轴对称场合多采用柱坐标系。
有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。
在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则.在选用单元时要注意剪力自锁、沙漏和网格扭曲、不可压缩材料的体积自锁等问题ANSYS软件平台提供了网格映射划分和自由适应划分的策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元网格划分的基本原则划分网格是建立有限元模型的一个重要环节,它要求考虑的问题较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、合理的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1 网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线,曲线2代表计算时间随网格数量的变化。
可以看出,网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
图1 位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2 网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
图2是中心带圆孔方板的四分之一模型,其网格反映了疏密不同的划分原则。
小圆孔附近存在应力集中,采用了比较密的网格。
板的四周应力梯度较小,网格分得较稀。
其中图b中网格疏密相差更大,它比图a中的网格少48个,但计算出的孔缘最大应力相差1%,而计算时间却减小了36%。
由此可见,采用疏密不同的网格划分,既可以保持相当的计算精度,又可使网格数量减小。
因此,网格数量应增加到结构的关键部位,在次要部位增加网格是不必要的,也是不经济的。
1图2 带孔方板的四分之一模型划分疏密不同的网格主要用于应力分析(包括静应力和动应力),而计算固有特性时则趋于采用较均匀的钢格形式。
这是因为固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
同样,在结构温度场计算中也趋于采用均匀网格。
3 单元阶次许多单元都具有线性、二次和三次等形式,其中二次和三次形式的单元称为高阶单元。
选用高阶单元可提高计算精度,因为高阶单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且高次插值函数可更高精度地逼近复杂场函数,所以当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数量相同的情况下由高阶单元组成的模型规模要大得多,因此在使用时应权衡考虑计算精度和时间。
图3是一悬臂梁分别用线性和二次三角形单元离散时,其顶端位移随网格数量的收敛情况。
可以看出,但网格数量较少时,两种单元的计算精度相差很大,这时采用低阶单元是不合适的。
当网格数量较多时,两种单元的精度相差并不很大,这时采用高阶单元并不经济。
例如在离散细节时,由于细节尺寸限制,要求细节附近的网格划分很密,这时采用线性单元更合适。
图3 不同阶次单元的收敛情况增加网格数量和单元阶次都可以提高计算精度。
因此在精度一定的情况下,用高阶单元离散结构时应选择适当的网格数量,太多的网格并不能明显提高计算精度,反而会使计算时间大大增加。
为了兼顾计算精度和计算量,同一结构可以采用不同阶次的单元,即精度要求高的重要部位用高阶单元,精度要求低的次要部位用低阶单元。
不同阶次单元之间或采用特殊的过渡单元连接,或采用多点约束等式连接。
4 网格质量网格质量是指网格几何形状的合理性。
质量好坏将影响计算精度。
质量太差的网格甚至会中止计算。
直观上看,网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等份点附近的网格质量较好。
网格质量可用细长比、锥度比、内角、翘曲量、拉伸值、边节点位置偏差等指标度量。
划分网格时一般要求网格质量能达到某些指标要求。
在重点研究的结构关键部位,应保证划分高质量网格,即2使是个别质量很差的网格也会引起很大的局部误差。
而在结构次要部位,网格质量可适当降低。
当模型中存在质量很差的网格(称为畸形网格)时,计算过程将无法进行。
图4是三种常见的畸形网格,其中a单元的节点交叉编号,b单元的内角大于180°,c单元的两对节点重合,网格面积为零。
图4 几种常见的畸形网格5 网格分界面和分界点结构中的一些特殊界面和特殊点应分为网格边界或节点以便定义材料特性、物理特性、载荷和位移约束条件。
即应使网格形式满足边界条件特点,而不应让边界条件来适应网格。
常见的特殊界面和特殊点有材料分界面、几何尺寸突变面、分布载荷分界线(点)、集中载荷作用点和位移约束作用点等。
图5是具有上述几种界面的结构及其网格划分形式。
图5 特殊界面和特殊点网格划分6 位移协调性位移协调是指单元上的力和力矩能够通过节点传递相邻单元。
为保证位移协调,一个单元的节点必须同时也是相邻单元的节点,而不应是内点或边界点。
相邻单元的共有节点具有相同的自由度性质。
否则,单元之间须用多点约束等式或约束单元进行约束处理。
图6是两种位移不协调的网格划分,图a中的节点1仅属于一个单元,变形后会产生材料裂缝或重叠。
图b中的平面单元和梁单元节点的自由度性质不同,粱单元的力矩无法传递到平面单元。
图6 位移不协调的网格划分 37 网格布局当结构形状对称时,其网格也应划分对称网格,以使模型表现出相应的对称特性(如集中质矩阵对称)。
不对称布局会引起一定误差,如在图7中,悬臂粱截面相对y轴对称,在对称载荷作用下,自由端两对称节点1、2的挠度值本应相等。
但若分图b所示的不对称网格,计算出的y1=0.0346,y2=0.0350。
若改用图c所示的网格,则y1和y2完全相同。
图7 网格布局对计算结果的影响8 节点和单元编号节点和单元的编号影响结构总刚矩阵的带宽和波前数,因而影响计算时间和存储容量的大小,因此合理的编号有利于提高计算速度。
但对复杂模型和自动分网而言,人为确定合理的编号很困难,目前许多有限元分析软件自带有优化器,网格划分后可进行带宽和波前优化,从而减轻人的劳动强度。
45、分析完之后想查看之前的加载情况:PlotCtrl>Symbol,在其中选择要选择选择要显示的项目即可46、catia装配图导入ansys之前,先通过Tools>Generate CATPart from Product 将Product转化为Part,如果将Part导入ansys后丢失元素则需在Part中进行一下布尔相加运算再往ansys里导入,此外在装配图转零件图之前应对实体进行一下修改如去掉一些小孔、倒角或圆角,以便于ansys中进合理的网格划分提高分析精度;装配体导入ansys后(多个体)划分网格有三种方式:a、先GLUE,之后对每个体划分网格,粘接导致不能划分网格的利用连接(Concatenate)命令后再划分,此法粘接后对体映射或扫略划分网格有时不是很理想,对于各个体自由划分的装配体此法还是比较方便的;b、先add将所有体合为一体,再切割或不切割以实现映射划分网格;c、先对每个体单独进行网格划分(映射、扫略或自由都可以),之后利用约束耦合将各个体约束耦合在一起,常用到CEINTF命令,此约束命令比较方便,比较常用,应熟练掌握。
47、对复杂形状的体由面分割为几个立方体进行映射(mapped)网格划分时,注意可能会出现立方体不能映射划分的情况,原因应该是四方体的某些面上不具有相同的性质,可能四方体一个面由于和多个分体接触其实已被分割成个多个面,虽是四方体但并不是面对面而是面对多面,所以映射不了;其中一个比较麻烦的解决方法是把立方体切成很多小块,每块都满足映射网格划分的条件;如果不宜进行Bool“加”运算而有元素丢失的话,可以自己补上丢失的元素,另外转化为了零件但各个体是分离的,可以进行“粘接(Glue)“运算再划分网格;装配图转零件之后(不进行Bool“加”运算)有时会多出很多线(多余的线),如一个立方体6个面,每个面都会有4条边,本应12条边变成24条多出了12条,可以通过Delete>Lines Only(选择Pick All)删除多余的边,另外其它一些重叠元素还可以用Numbering>Merge Numbering进行合并编号;48、保存的文件路径不能有中文,否则之后用ANSYS打不开;确定某元素的编号时可以利用PlotCtrls>Numbering,也可以先利用某种操作如delete等选中在选取对话框中会显示编号记住然后取消“删除”操作;49、将catia文件导入ansys中后,会出现工作平面和实体平面(或直线)不重合或不垂直的情况,怎么让工作平面和实体平面重合?利用Align WPWith>Plane Normal to Line将工作平面垂直于实体某条边,这样在实体上画实体时才不会错;50、体扫略时可以通过MeshTool--Globe设定尺寸并可以通过layer来定扫描层数;体扫略和面网格拉伸为体网格的区别:面网格拉伸时体是不存在的,体扫描时体是存在的;网格划分在有限元分析中很重要,注意网格划分的一些基本操作方法、技巧和他人的经验;ansys网格划分:;话费、QQ币、游戏点卡充值:51、在对课题支架装配体体扫略划分网格时出现很多问题:a、设计时注意干涉问题,在导入ansys之前要注意检查一下可能的问题;b、装配体分析目前知道的方法有先粘接(Glue)再划分网格和先划网格再耦合或约束;c、先粘接再划分网格出现的问题是有的零件不能按自己想要的尺寸体扫略,有的总是扫略不了但有的却可以扫略;d、粘接后粘接处变为公共面这样较大面的体就会多一个面,较小面的体不变,所以出现大体不能体扫略而小体却能体扫略,将面合并后虽能划分网格但对粘接会不会有影响呢?;e、以后再遇到不能划分网格的情况时,先检查仔细检查体是否满足条件,如可通过List或Select检查体的面素组成;f、先粘接再划分网格和add整体后divide许多块后划分网格也有一些限制,就是必须在变截面处切割或粘接时在大截面处会多出一个切割面或粘接面,这时无法划分网格;52、在从catia的model文件往ANSYS导之前,要仔细检查model文件模型的细节是否有问题,这样在ansys分析中会避免很多麻烦;catia的model文件导入ansys之后也要检查模型,必要的合并图元及其编号;ansys改文件名不能像大多数软件那样直接在关闭软件情况下直接给文件重命名,只能通过软件中的Jobname对文件名进行修改;53、还是要注意一下ansys的单位统一问题;在ANSYS单位统一变换时,要将单位转换到量纲上,也就是将单位用kg——m——s表示)!!!!!!国际单位制中常用的单位名称长度力时间质量压力(压强)速度加速度密度Stress 杨氏模量单位m N s kg Pa m/s m/s^2 kg/m^3 Pa Pa 量纲m kgm/s^2 s kg kg/ms^2 m/s m/s^2 kg/m^3 kg/ms^2kg/ms^2注意尽量将尺寸转化为国际单位制下的尺寸,即使尺寸量是kg、m、s单位的尺寸量,这样弹性模量、密度等不用转化,而需转化的可能是模型的尺寸,利用放大和缩小即可(在Modeling>Operate>Scale下,并将原实体设置为Moved),最好在把几何模型建好后再利用scale否则对图元旋转和缩放操作时很麻烦;54、ansys求解时软件自动关闭解决:a、求解前点select>everything;b、查看一下.err文件,针对具体问题解决;c、求解空间和存储空间不足,扩充scrach space和database space,scrach space和database space的差值越大越好,点击ANSYS Product Launcher进入设置工作路径与工作名的界面,选择Customization(用户设置)标签,就可以看到这两个设置了;55、allocate:分配;Abridged Menu:缩减的菜单;stiffness:刚度,硬度;angular velocity:角速度;angular acceleration:角加速度;elastic:弹性的;plastic:可塑的;Rate Independent Plasticity:塑性与材料的应变率无关;Initial Condition:初始条件;gravity:万有引力,重力;spectrum:光谱、波谱;excitation:激励;seismic:地震的;Significant Threshold:有效阀值;coupled set:耦合集;adjacent region:邻近区域;stress-strain:应力-应变;56、ansys分析中最好先把角度单位改为“degree”;57、自由网格划分采用六面体单元时,六面体单元会自动退化为同阶次的四面体单元;混合网格划分时最好采用能形成金字塔过渡单元的六面体单元类型(而且能退化为四面体单元),这种单元类型有:结构单元solid95、solid186、visco89,热单元solid90,多物理场单元solid62、117、122;在张洪信的《有限元基础理论与ANSYS应用》的轮子受力分析实例中采用了混合网格划分方法:创建了两种单元类型:45号线性六面体单元和95号二次六面体单元,先映射网格划分部分选用45号单元,之后自由网格划分部分选用95号单元,此时六面体单元自动退化为四面体单元并在与映射网格接触处自动形成金字塔过度单元,之后利用“Modify Mesh”-“Change Tets”-“95 to 92”将退化的95号六面体单元转化为非退化的92号四面体单元,这样45号六面体单元和92号四面体单元通过“金字塔过度单元”协调的结合在了一起;58、映射网格划分要求有“规则的”形状:面有3或4条边,体有4,5或6个面;很多情况下模型的几何形状上有多于4条边的面,有多于6个面的体,为了将它们转换成规则的形状,可以进行如下一项或两项操作:a、把面或体切割成小的、简单的形状(可通过布尔减运算实现);b、连接两条或多条线或面以减少总的边数或面数,其实是把俩或三面当成一个面来看(通过Meshing-Concatenate-Lines或Areas实现);面映射网格时也可以拾取面上的3个或4个角点来暗示一个连接:在MeshTool上将3/4 sided变为Pick corners,按mesh键,拾取面,然后拾取3或4个角点形成一规则的形状;59、扫略网格划分两种方式:在已有体的三维模型上进行扫略,条件是三维模型上有完全一样的平行相对面;另一种方式是由面网格与拖拉成体网格,体网格建立后不要忘了将面网格删除掉;60、装配体分析划分网格方法:切割后两实体之间的关系和粘接两实体之间的关系对划分网格来讲是一样的:切割后一个实体变成两个实体,两个实体之间在切割处形成两个面分别为两个实体所有,注意切割后形成一个大件和一个小件时的情况和一个大件一个小件相粘接的情况一样;装配体分析时可以将各个零件粘接后划分网格,粘接后两实体的情况和切割后形成两个实体的情况一样,注意当一个大件和一个小件粘接在一起时在大件上会多生成一个面,如果两个件都是六面体,此时大件实际是7个面已不满足映射的条件可以自由划分网格,而小件仍满足故可以映射划分网格;另外多个复杂零件装配到一起后在ansys里可以先粘接,之后可对各个零件分别自由划分网格;如果想对其中的各个零件进行映射划分,可以先将各个零件粘接后再对各个零件进行切割直至满足映射条件,也可以先对各个零件切割最后在再粘接,不过明显前者更方便和效率更高,所以在对装配体进行网格划分时应先将各个零件粘接在一起,之后对各个零件进行网格划分或切割后再网格划分;一般情况下一直切割各个零件最后会满足映射条件;这样对各个小体切割且满足映射划分网格后,整个装配体就可以进行映射划分网格了;真是有些小体不满足映射条件时装配体划分网格就属于混合划分网格了,此时注意六面体过渡单元的选择并将退化的六面体单元转化为非退化的四面体单元(通过ModifyMesh”-“Change Tets”)以使分析精度更高!!精度要球不高时也可以先切割再粘接,切割之后将所有小体全部粘接在一起;粘接后划分网格和切割后划分网格实质是一样的,且最后整体划分网格后在接触处和粘接处不会破坏网格之间的协调性;粘接划分网格和切割后划分网格不同之处是:粘接不用考虑过渡单元的问题(无论什么类型的单元切割后粘接处总满足协调性),切割零件进行混合网格划分时需要考虑过渡单元问题;装配体粘接后一个体一个体的切割,对于每个体看哪部份不满足映射条件对哪部份在进行切割!!对于很复杂的模型切割时是有技巧的,从整体角度看看往往需要从一个面将能切到的所有实体切开,如果一点一点的切到后面可能会导致前面改切的没有切,所以最好利用Select--Entities选择好需要切的实体后进行“一刀切”;61、按上述方法粘接切割后如果外观上满足映射或扫掠的条件而不可以划分网格的话,就对细节进行检查,检查体的各个面及面上的线甚至点,查出问题后进行布尔操作修改,还不行的话将小块删除重新对小块建模;特别是CATIA或PROE模型导入ANSYS的情况会产生不少碎线或碎面(本来一条线或一个面被分割成几部分),此时将碎线或碎面add合并之后一般就可以划分网格了;62、用两个正方体100×100×100和50×50×50做了以下试验并得一些结论,小正方体放在大正方体上面的中间位置,在大立方体的底面加约束小立方体的顶面加均压力值取200:(可用此试验和72的试验比较)a、两个正方体不粘接放在一起可以各自映射划分网格,但求解时无法求解;所以需要粘接;(后面学了耦合和约束方程之后也可以通过节点耦合或约束来实现)b、两个立方体各自映射划分网格后可以粘接在一起,但求解释时出现错误,无法完成求解;所以需要先粘接再划分网格;c、两个立方体先粘接在一起,之后划分网格时小立方体可以映射划分网格,大立方体不能映射划分网格只能自由划分,原因明显是粘接后大立方体由7个面组成已不满足映射划分网格的条件,大立方体自由划分之后可以求解,结果最大变形DMX=0.881E-7;粘接后将大立方体的那两个面布尔add为一个面后可以进行映射网格划分但还是求解不了,因为实际上两面布尔相加后相当于取消了刚才的粘接;d、粘接后将下面的大立方体进行切割,之后可以对所有体(用pick all)进行整体映射划分网格,并且可以求解,求解结果最大变形DMX=0.870E-7;如果在切割之前加载,切割后被切割到的载荷会消失,所以只能在切割之后加载;整体映射网格划分后求解速度明显比前面非全部映射网格划分时的快很多;从求解结果看两种情况下的求解结果偏差很小;e、粘接后将下面的大立方体进行切割,之后将所有体glue粘接在一起,之后整体映射划分网格加载,最后的求解结果和d中的求解结果完全一样;f、对小立方体切割后,再沿着立方体两平行侧面的对称面将大小立方体整体切开,这样两立方体的粘接面就被切成两部分,之后整体映射划分网格并加载,最终求解结果最大变形DMX=0.871E-7;可见粘接面被切割开不会影响求解,对求解结果影响也很小;63、《ANSYS工程分析软件应用实例》,史亚杰,清华大学出版社.这本书讲的比较细!!在“有预应力作用结构的模态分析实例”中轮盘的盘心轴向和周向约束而径向放开,这种约束条件在直角坐标系下无法定义,而柱坐标下可以方便的定义;根据ANSYS软件中坐标系的定义规则,需要将柱坐标系的Z轴和旋转轴重合,Y轴表示转角(周向),X轴表示径向,ANSYS软件提供的全局坐标系不满足要求。
