2018版高中数学第一章立体几何初步1.1.3圆柱圆锥圆台和球课件新人教B版必修2
高中数学第一章立体几何1.1.3圆柱、圆锥、圆台和球课件新人教B版必修2

探究一
探究二
探究三
探究四
探究五
思维辨析
概念辨析题 【例1】 下列说法正确的是( ) A.圆台是直角梯形绕其一边旋转而成的 B.圆锥是直角三角形绕其一边旋转而成的 C.圆柱不是旋转体 D.圆台可以看作是由平行于圆锥底面的平面截圆锥得到的 解析:根据旋转体的定义及圆锥与圆台的内在联系易知D正确. 答案:D 反思感悟对于旋转体,必须清楚直角梯形必须绕其垂直于底边的 腰所在直线旋转才能形成圆台;直角三角形必须绕直角边所在直线 旋转才能形成圆锥;圆柱是由矩形绕其一边所在直线旋转形成的几 何体.类比棱台的定义,圆台也可以看作是圆锥被平行于底面的平 面所截得的.
一
二
三
3.填空:(1)概念:一个半圆绕着它的直径所在的直线旋转一周所 形成的曲面叫做球面,球面围成的几何体叫做球.形成球的半圆的 圆心叫球心;连接球面上一点和球心的线段叫球的半径;连接球面 上两点且通过球心的线段叫球的直径. (2)表示:用表示球心的字母来表示. (3)球面也可以看作空间中到一个定点的距离等于定长的点的集 合.球面被经过球心的平面截得的圆叫做球的大圆,被不经过球心 的平面截得的圆叫做球的小圆. (4)在球面上,两点之间的最短距离就是经过这两点的大圆在这两 点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离.
一
二
三
一、圆柱、圆锥、圆台 【问题思考】 1.圆柱、圆锥和圆台这三类几何体能通过平面图形形成吗? 提示:能.这三类几何体都是旋转体,可以分别通过矩形,直角三角 形,直角梯形绕一特定轴旋转形成. 2.将圆柱、圆锥和圆台的侧面沿它们的一条母线剪开,在平面上 展开得到它们的侧面展开图分别是什么图形?请画出来. 提示:将圆柱、圆锥和圆台的侧面沿它们的一条母线剪开,然后 在平面上展开,侧面展开图分别是矩形、扇形和扇环,如图所示.
2019_2020学年高中数学第一章立体几何初步1.1.3圆柱、圆锥、圆台和球课件新人教B版必修2

A.1
B.2
C.3
D.4
【解析】 圆锥是以直角三角形的一条直角边所在直线为旋 转轴的,如果以斜边所在直线为旋转轴旋转,那就变成一个 组合体了,故①错误;圆台是以直角梯形与底边垂直的腰所 在直线为旋转轴的,故②错误;圆柱、圆锥、圆台的底面都 为圆面,故③错误;根据圆柱的定义可知,无论以矩形的哪 条边所在直线为旋转轴,旋转所得的曲面围成的几何体都是 圆柱,但它们并不一定是相同的圆柱,故④正确,因此正确 的命题有 1 个. 【答案】 A
与球有关的计算问题 棱长为 2 的正四面体的四个顶点都在同 一个球面上,若过该球球心的一个截面如图所 示,求图中三角形(正四面体的截面)的面积.
【解】 如图,△ABE 为题中三角形, 由已知得 AB=2,BE=2× 23= 3,
BF=23BE=2 3 3,
所以 AF= AB2-BF2= 所以△ABE 的面积为
1.下列判断正确的是( ) A.平行于圆锥某一母线的截面是等腰三角形 B.平行于圆台某一母线的截面是等腰梯形 C.过圆锥顶点的截面是等腰三角形 D.过圆台上底面中心的截面是等腰梯形 答案:C
2.给出以下说法: ①球的半径是球面上任意一点与球心所连线段的长; ②球的直径是球面上任意两点间所连线段的长; ③用一个平面截一个球,得到的截面可以是一个正方形; ④过圆柱轴的平面截圆柱所得截面形状是矩形. 其中正确说法的序号是________. 解析:根据球的定义知,①正确;②不正确,因为球的直径 必过球心;③不正确,因为球的任何截面都是圆面;④正确. 答案:①④
本题是考查圆柱、圆锥、圆台概念的理解问题.对几何体的 概念理解要到位,稍有疏忽都会造成错误的判断,做题时要 注意以哪条边所在直线为旋转轴,必须清楚地认识到:以直 角三角形的一条直角边所在直线为旋转轴旋转得圆锥,以斜 边为旋转轴旋转就是两个圆锥的组合体;以直角梯形垂直于 底的腰所在直线为旋转轴旋转得圆台,以斜腰所在直线为旋 转轴把直角梯形旋转一周得两个圆锥和一个圆台的组合体.
人教版高一数学必修2(B版)全册完整课件

1.1.6 棱柱、棱锥、棱台和球的表面积
实习作业
1.2.2 空间中的平行关系
本章小结
ห้องสมุดไป่ตู้
第二章 平面解析几何初步
2.1.2 平面直角坐标系中的基本公式
2.2.2 直线方程的几种形式
2.2.4 点到直线的距离
2.3.2 圆的一般方程
2.3.4 圆与圆的位置关系
2.4.2 空间两点的距离公式
阅读与欣赏
笛卡儿
人教版高一数学必修2(B版)全册完 整课件
1.1.6 棱柱、棱锥、棱台和球 的表面积
人教版高一数学必修2(B版)全册完 整课件
1.1.7 柱、锥、台和球的体积
人教版高一数学必修2(B版)全册完 整课件
后记
第一章 立体几何初步
人教版高一数学必修2(B版)全册完 整课件
1.1 空间几何体
1.1.1
构成空间几何体的基本元素
人教版高一数学必修2(B版)全册完 整课件
1.1.2 棱柱、棱锥和棱台的结 构特征
人教版高一数学必修2(B版)全册完 整课件
人教版高一数学必修2(B版)全册 完整课件目录
0002页 0040页 0102页 0185页 0223页 0295页 0343页 0365页 0411页 0460页 0490页 0520页 0548页 0570页 0601页 0603页
第一章 立体几何初步
1.1.2 棱柱、棱锥和棱台的结构特征
1.1.4 投影与直观图
1.1.3 圆柱、圆锥、圆台和球
人教版高一数学必修2(B版)全册完 整课件
1.1.4 投影与直观图
人教版高一数学必修2(B版)全册完 整课件
1.1.5 三视图
[配套K12]2018版高中数学 第一章 立体几何初步 1.1.3 圆柱、圆锥、圆台和球学案(含解析)新人教B版必修2
![[配套K12]2018版高中数学 第一章 立体几何初步 1.1.3 圆柱、圆锥、圆台和球学案(含解析)新人教B版必修2](https://img.taocdn.com/s3/m/83c72ce60029bd64783e2c5c.png)
1.1.3 圆柱、圆锥、圆台和球1.了解圆柱、圆锥、圆台、球的定义.(重点)2.掌握圆柱、圆锥、圆台、球的结构特征.(重点)3.能够根据圆柱、圆锥、圆台、球的结构特征识别和区分几何体.(难点))4.会作旋转体的轴截面,并利用轴截面解决问题.(难点[基础·初探]教材整理1 圆柱、圆锥、圆台、球的结构特征阅读教材P11~P14“例2”以上内容,完成下列问题.判断(正确的打“√”,错误的打“×”)(1)矩形绕其一边所在直线旋转一周而形成的曲面所围成的几何体是圆柱.( ) (2)以直角梯形的一腰为轴旋转所得的旋转体是圆台.( )(3)用一个平面去截圆锥,得到一个圆锥和一个圆台.( ) (4)用任意平面截球所得截面均为圆.( )【解析】 (1)正确;(2)错误.应以直角梯形的垂直于底边的腰为轴;(3)错误,应是平面与圆锥底面平行时;(4)错误,平面截球所得截面是圆面,而不是圆.【答案】 (1)√ (2)× (3)× (4)× 教材整理2 简单组合体的结构特征 阅读教材P 15内容,完成下列问题. 1.简单组合体的概念由简单几何体组合而成的几何体叫做简单组合体. 2.简单组合体的构成形式有两种基本形式:一种是由简单几何体拼接而成的;另一种是由简单几何体截去或挖去一部分而成的.如图1134所示的组合体的结构特征是( )图1134A.一个棱柱中截去一个棱柱B.一个棱柱中截去一个圆柱C.一个棱柱中截去一个棱锥D.一个棱柱中截去一个棱台【解析】由简单组合体的基本形式可知,该组合体是一个棱柱中截去一个棱锥.【答案】 C[小组合作型]【导学号:45722011】A.直角三角形绕一条边所在直线旋转得到的旋转体是圆锥B.夹在圆柱的两个平行截面间的几何体还是一个旋转体C.圆锥截去一个小圆锥后剩余部分是圆台D.通过圆台侧面上一点,有无数条母线【精彩点拨】根据圆柱、圆锥、圆台的定义及结构特征进行判断.【自主解答】A错误,应为直角三角形绕其一条直角边所在直线旋转得到的旋转体是圆锥;若绕其斜边所在直线旋转得到的是两个圆锥构成的一个组合体.B错误,没有说明这两个平行截面与底面的位置关系,当这两个平行截面与底面平行时正确,其他情况则是错误的.D错误,通过圆台侧面上一点,只有一条母线.故选C.【答案】 C1.圆柱、圆锥、圆台和球都是一个平面图形绕其特定边(弦)旋转而成的几何体,必须准确认识各旋转体对旋转轴的具体要求.2.只有理解了各旋转体的生成过程,才能明确由此产生的母线、轴、底面等概念,进而判断与这些概念有关的命题的正误.[再练一题]1.给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥的顶点与底面圆周上的任意点的连线是圆锥的母线;③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是( )A.①②B.②③C.①③D.②④【解析】根据圆柱、圆锥、圆台的定义和性质可知,只有②④两个命题是正确的,①③可能是弦,所以选D.【答案】 D如图ABCD绕AD 所在直线旋转一周时,其他各边旋转围成一个几何体,试描述该几何体的结构特征.图1135【精彩点拨】关键是弄清简单组合体是由哪几部分组成.【自主解答】如图所示,旋转所得的几何体是由一个圆柱挖去两个圆锥后剩余部分而成的组合体.本题是不规则图形的旋转问题.对于不规则平面图形绕轴旋转问题,首先要对原平面图形作适当的分割,一般分割成矩形、梯形、三角形或圆半圆或四分之一圆等基本图形,然后结合圆柱、圆锥、圆台、球的形成过程进行分析.[再练一题]2.描述下列几何体的结构特征.图1136【解】图①所示的几何体是由两个圆台拼接而成的组合体;图②所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图③所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.[探究共研型]探究1 【提示】 圆面.探究2 圆柱、圆锥、圆台过轴的截面是什么样的图形? 【提示】 分别为矩形、等腰三角形、等腰梯形.探究3 经过圆台的任意两条母线作截面,截面是什么图形?【提示】 因为圆台可以看成是圆锥被平行于底面的平面所截得到的几何体,所以任意两条母线长度均相等,且延长后相交,故经过这两条母线的截面是以这两条母线为腰的等腰梯形.如图1137所示,用一个平行于圆锥SO 底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm ,求圆台O ′O 的母线长.图1137【精彩点拨】 过圆锥的轴作截面,利用三角形相似来解决.【自主解答】 设圆台的母线长为l ,由截得圆台上、下底面面积之比为1∶16,可设截得圆台的上、下底面的半径分别为r,4r .过轴SO 作截面,如图所示.则△SO ′A ′∽△SOA ,SA ′=3 cm. ∴SA ′SA =O ′A ′OA ,∴33+l =r 4r =14. 解得l =9(cm), 即圆台的母线长为9 cm.用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质与底面全等或相似,同时结合旋转体中的经过旋转轴的截面轴截面的性质,利用相似三角形中的相似比,构设相关几何变量的方程组而得解.[再练一题]3.一个圆锥的高为2 cm ,母线与轴的夹角为30°,求圆锥的母线长及圆锥的轴截面的面积.【导学号:45722012】【解】 如图,设圆锥SO 的底面直径为AB ,SO 为高,SA 为母线,则∠ASO =30°.在Rt△SOA 中,AO =SO ·tan 30°=233(cm). SA =SOcos 30°=232=433(cm).∴S △ASB =12SO ·2AO =433(cm 2).∴圆锥的母线长为433 cm ,圆锥的轴截面的面积为433cm 2.1.正方形绕其一条对角线所在直线旋转一周,所得几何体是( ) A.圆柱 B.圆锥 C.圆台D.两个圆锥【解析】 连接正方形的两条对角线知对角线互相垂直,故绕对角线旋转一周形成两个圆锥.【答案】 D2.下列说法不正确的是( ) A.圆柱的平行于轴的截面是矩形 B.圆锥的过轴的截面是等边三角形 C.圆台的平行于底面的截面是圆面 D.球的任意截面都是圆面【解析】 圆锥的过轴的截面是等腰三角形,B 错. 【答案】 B3.如图1138所示的几何体是由简单几何体________构成的.图1138【答案】 四棱台和球4.如图1139所示,下列几何体中,图①是圆柱,图②是圆锥,图③是圆台,图1139上述说法正确的个数有________个.【解析】 图(1)不是圆柱,因为从其轴截面可以看出,该几何体不是由矩形绕其一边所在直线旋转一周得到的;图(2)不是圆锥,因为该几何体不是由直角三角形绕其直角边所在直线旋转一周得到的; 图(3)不是圆台,因为该几何体的上、下底面所在的平面不平行,不是由平行于圆锥底面的平面截得的.【答案】 05.已知一个圆柱的轴截面是一个正方形且其面积是Q ,求此圆柱的底面半径. 【解】 设圆柱底面半径为r ,母线为l ,则由题意得⎩⎪⎨⎪⎧2r =l ,2r ·l =Q ,解得r =Q2.所以此圆柱的底面半径为Q2.。
高中数学人教B版必修2第一章立体几何初步1.1.3圆柱、圆锥、圆台课件

为
r,则由已知可得6-x= r,所以
r=6-
x .
62
3
所以轴截面面积 S=2×6-x·x=-2x2+4x,
3
3
(0<x<6).
(2)由(1)可得,S=-2(x-3)2+6,x∈(0,6), 3
所以当 x=3 时,S 最大.
【点评】 轴截面是旋转体中一类重要的截面, 它是把立体几何问题向平面几何问题转化的重要 桥梁.圆柱、圆锥的轴截面有无数个,作图时要 注意已知量与未知量的联系,即将未知量和有用 的已知量充分显示在轴截面图形中,从而有利于 问题的解决. 跟踪训练2 设圆锥的高为h,底面圆的半径为r, 把它的侧面沿一条母线切开展平成一个扇形,求 扇形的圆心角.
解 :过内接 正方体的 一组对 棱作圆锥 的轴截面 ,如 图所示. 设圆锥内接正方体的棱长为 x,则在轴截面中,正方 体的对角面 A1ACC1的一组邻边的长分别为 x和 2x.
∵△ VA1 C1 ∽△ VMN, ∴ 2x=h-x,
2r h
∴ 2hx=2rh-2rx,
∴x= 2rh . 2r+ 2h
【解】 设圆台的上底面半径为 r,则下底面 半径为 2r. 将圆台还原成圆锥,作轴截面如图所示,则 ∠ASO=30°. 在 Rt△SA′O′中,SA′= r =2r,
sin 30°
在 Rt△SAO 中,SA=sin23r 0°=4r,
∴AA′=SA-SA′=2r, 即 2r=8,∴r=4. ∴S = 上底 πr2=16π,S 下底=π·(2r)2=64π.
即圆锥内接正方体的棱长为 2rh 2r+
. 2h
课堂小结
1.对于圆柱的性质,要注意以下两点:一是连心 线垂直于底面;二是三个截面的性质——平行于底 面的截面与底面全等,轴截面是一个由上、下底面 圆的直径和母线所组成的矩形,平行于轴线的截面 是一个以上、下底面圆的弦和母线组成的矩形. 2.对于圆锥的性质,要注意以下两点:一是两类 截面——平行于底面的截面是与底面类似的圆面, 圆锥的过顶点且与底面相交的截面是一个由两条母 线和底面圆的弦组成的等腰三角形;
数学:1.1.3《圆柱、圆锥、圆台和球》课件(新人教B版必修2)

你能从旋转体的概念说说它们是由什么图形旋转而成的吗?
旋转体
你能想象这条曲线绕轴旋转而成的几何图形吗?
O
球心
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
知识小结
简单几何体的结构特征
柱体
棱柱 圆柱
锥体 棱锥 圆锥
台体 棱台 圆台
球
日常生活中我们常用到的日用品,比如:消毒液、 暖瓶、洗洁精等的主要几何结构特征是什么? 由柱、锥、台、球组成了一些简单的组合体.认 识它们的结构特征要注意整体与部分的关系.
圆柱 圆台
S
顶点
(1)底面是圆 (2)侧面展开图是以母线长为半径的扇形 母 (3)母线相交于顶点
轴 侧 面
(4)平行于底面的截面是与底 面平行且半径不相等的圆
(5)轴截面是等腰三角 形.
A
线
O B
底面
前面提到的四种几何体:棱柱、棱锥、圆柱、圆 锥,可以怎样分类?
几何体的分类
柱体
锥体
棱台与圆台的结构特征 下图中的物体具有什么样的共同的结构特征?有 什么不同的结构特征?
有一个面是多边形,其余 各面都是有一个公共顶点的三 角形所围成的几何体叫棱锥.
S
顶点
(1)底面是多边形 (2)侧面都是三角形. (3)侧棱相交于一点.
侧棱
侧面
D
C 底面
B
A
圆柱的结构特征
如何描述下图的几何结构特征?
A′ O′
A
O
圆柱的结构特征
如何描述下图的几何结构特征?
圆柱
底面 以矩形的一边所在直线为 旋转轴,其余边旋转形成的曲 面所围成的几何体叫做圆柱.
简单组合体
2018版高中数学第一章立体几何初步1.1.3圆柱圆锥圆台和球学业分层测评新人教B版

1.1.3 圆柱、圆锥、圆台和球学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.下列命题中,真命题的个数是( )①圆锥的轴截面是所有过顶点的截面中面积最大的一个;②圆柱的所有平行于底面的截面都是圆面;③圆台的两个底面可以不平行.A.0B.1C.2D.3【解析】①中当圆锥过顶点的轴截面顶角大于90°时,其面积不是最大的;③圆台的两个底面一定平行,故①③错误.【答案】 B2.以钝角三角形的较小边所在的直线为轴,其他两边旋转一周所得到的几何体是( )A.两个圆锥拼接而成的组合体B.一个圆台C.一个圆锥D.一个圆锥挖去一个同底的小圆锥【解析】如图,以AB为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥.【答案】 D3.用一个平面去截一个几何体,得到的截面是圆面,这个几何体不可能是( )A.圆锥B.圆柱C.球D.棱柱【解析】用一个平面去截圆锥、圆柱、球均可以得到圆面,但截棱柱一定不会产生圆面.【答案】 D4.在日常生活中,常用到的螺母可以看成一个组合体(如图1140所示),其结构特征是( )图1140A.一个棱柱中挖去一个棱柱B.一个棱柱中挖去一个圆柱C.一个圆柱中挖去一个棱锥D.一个棱台中挖去一个圆柱【解析】一个六棱柱挖去一个等高的圆柱,选B.【答案】 B5.一个正方体内接于一个球,过球心作一截面,如图1141所示,则截面可能的图形是( )图1141A.①③B.②④C.①②③D.②③④【解析】当截面平行于正方体的一个侧面时得③,当截面过正方体的体对角线时得②,当截面不平行于任何侧面也不过对角线时得①,但无论如何都不能截出④.【答案】 C二、填空题6.如图1142是一个几何体的表面展开图形,则这个几何体是________.图1142【解析】一个长方形和两个圆折叠后,能围成的几何体是圆柱.【答案】圆柱7.直角梯形绕其较长底边所在直线旋转一周,所得旋转体的结构特征是________________.【解析】由旋转体的定义知,该几何体为一个圆锥和一个圆柱拼接成的组合体.【答案】一个圆锥和一个圆柱拼接成的组合体8.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为________cm.【解析】如图是圆锥的轴截面,则SA=20 cm,∠ASO=30°,∴AO=10 cm,SO=10 3 cm.【答案】 10 3 三、解答题9.指出如图1143①②所示的图形是由哪些简单几何体构成的.图1143【解】 图①是由一个三棱柱和一个四棱柱拼接而成的简单组合体. 图②是由一个圆锥和一个四棱柱拼接而成的简单组合体.10.一个圆台的母线长为12 cm ,两底面面积分别为4π cm 2和25π cm 2.求: (1)圆台的高;(2)截得此圆台的圆锥的母线长.【解】 (1)圆台的轴截面是等腰梯形ABCD (如图所示).由已知可得上底半径O 1A =2(cm),下底半径OB =5(cm),又因为腰长为12 cm , 所以高AM =122--2=315(cm).(2)如图所示,延长BA ,OO 1,CD ,交于点S ,设截得此圆台的圆锥的母线长为l ,则由△SAO 1∽△SBO 可得l -12l =25,解得l =20(cm),即截得此圆台的圆锥的母线长为20 cm. [能力提升]1.下列判断中正确的个数是( )①圆柱的任意两条母线所在的直线是平行的; ②球面和球是同一个概念;③经过球面上不同的两点只能作一个球大圆. A.1 B.2 C.3D.0【解析】 ①正确;球面和球是两个不同的概念,②错误;若球面上不同的两点恰好为球的直径的端点,则过此两点的球大圆有无数个,故③错误.【答案】 A2.已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且距离为1,那么这个球的半径是( )A.4B.3C.2D.0.5【解析】 如图所示,∵两个平行截面的面积分别为5π、8π,∴两个截面圆的半径分别为r 1=5,r 2=2 2.∵球心到两个截面的距离d 1=R 2-r 21,d 2=R 2-r 22, ∴d 1-d 2=R 2-5-R 2-8=1,∴R 2=9,∴R =3. 【答案】 B3.在如图1144所示的斜截圆柱中,已知圆柱底面的直径为40 cm ,母线长最短50 cm 、最长80 cm ,则斜截圆柱侧面面积S =________cm 2.图1144【解析】 将侧面展开可得S =12(50+80)×40π=2 600π(cm 2).【答案】 2 600π4.一个圆锥的底面半径为2 cm ,高为6 cm ,在圆锥内部有一个高为x cm 的内接圆柱. (1)用x 表示圆柱的轴截面面积S ; (2)当x 为何值时,S 最大?【解】 (1)如图,设圆柱的底面半径为r cm ,则由r 2=6-x 6,得r =6-x3,∴S =-23x 2+4x (0<x <6).(2)由S =-23x 2+4x =-23(x -3)2+6,∴当x =3时,S max =6 cm 2.。
高中数 圆柱圆锥圆台和球课件 新人教B必修

1.圆柱、圆锥、圆台可以分别看作以______矩__形__的__一_、边 _直__角__三__角__形__的__一__条__直__角__边__、_直__角__梯__形__中__垂__直__于__底__边__的__腰__所在 的直线为旋转轴,将其分别旋转一周而形成的曲面所围成的几 何体,旋转轴叫做所围成几何体的_____轴___;在轴上的这条边( 或它的长度),叫做这个几何体的_____高___;垂直于轴的边旋转 而成的圆面叫做这个几何体的____底__面__;不垂直于轴的边旋转 而成的曲面叫做这个几何体的_____侧__面_,无论旋转到什么位置 ,这条边都叫做___侧__面__的__母__线_.
2.(1)球可看作一个___半__圆___绕着它的__直__径__所__在__直__线__旋
转一周所形成的曲面围成的几何体,形成的曲面叫做________
,球形面成球的半圆的圆心叫做________;连球接心球面上一点和球心
的线段叫做球的________;连半接径球面上两点且经过球心的线段
叫做球的________;球面直所径围成的几何体叫做________.
小圆
(5)在球面上两点之间的最短距离就是___经__过__这__两__点__的__大__圆 _在__这__两__点__间__的__一__段__劣__弧__的__长__度___,这个弧长叫做球面距离.
(6)球小圆的圆心O′,球心O,|OO′|=d,球小圆半径r,球 半径为R,则d2=R2-r2.
3.圆柱、圆锥、圆台和球等几何体都是由一个平面图形 绕着一条直线旋转产生的曲面所围成的几何体,这类几何体叫 做__旋__转__体__,这条直线叫做旋转体的___轴_____.
思想方法技巧
球的结构特征及计算
半径是13 cm的球面上有A、B、C三点,并且 AB=BC=CA=12 cm,试求圆心到经过这三点的截面的距离.
高中数学 第一章 1.1.3圆柱、圆锥、圆台和球课件 新人

1.1.3
问题 5 用一个平面去截一个球,如何说明截面是圆面?
答 如图所示,设 OO′=d,对于平面 α 与球面的交线上 任意一点 P,O′P= R2-d2,是一个定值.
1.1.3
探究点一 圆柱、圆锥、圆台的结构特征 导引 观察下面的几何体,你可能会判定它们分别是圆柱、
圆锥、圆台.为什么你会判定它们分别是圆柱、圆锥、圆 台呢?
研一研·问题探究、课堂更高效
1.1.3
问题 1 圆柱、圆锥、圆台分别具有哪些性质?哪些性质可 以分别作为圆柱、圆锥和圆台集合的特征性质? 答 通过观察可以看出,圆柱、圆锥和圆台可以分别看作以 矩形的一边、直角三角形的一直角边、直角梯形中垂直于底 边的腰所在的直线为旋转轴,将矩形、直角三角形、直角梯 形分别旋转一周而形成的曲面所围成的几何体(如图).
研一研·问题探究、课堂更高效
1.1.3
解 设圆台的母线长为 y,截得的圆锥底面与原圆 锥底面半径分别是 x,4x, 根据相似三角形的性质得3+3 y=4xx, 解此方程得 y=9.
因此,圆台的母线长为 9 cm.
小结 处理旋转体的有关问题一般要作出其轴截面,在轴截面 中去寻找各元素的关系.
研一研·问题探究、课堂更高效
研一研·问题探究、课堂更高效
1.1.3
问题 5 圆柱、圆锥、圆台都是旋转体,它们在结构上有哪 些相同点和不同点?三者的关系如何?当底面发生变化
时,它们能否互相转化? 答 它们的相同点是:它们都是由平面图形旋转得到的;
不同点是:圆柱和圆台有两个底面,圆锥只有一个底面,圆 柱的两个底面是半径相等的圆,圆台的两个底面是半径不等
如图中点 O 为球心,OA 为球的半径,AB 为球 O 的直径.
研一研·问题探究、课堂更高效
人教B版必修21.1.3圆柱圆锥圆台和球课件
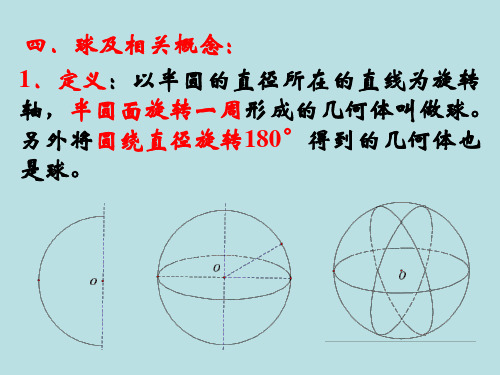
5.球面距离:在球面 上,两点之间的最短距 离就是经过两点的大圆 在这两点间的一段劣弧 的长度。这个弧长叫做 两点的球面距离。
球面距离
• 在球面上两点之间的 最段距离,就是经过
这两点的大圆在这两
点间的劣弧的长 度————这个弧长
叫两点的球面距离
P O
Q
我国首都北京 靠近北纬40 度,球北纬 40度纬线的 长度(地球 半径约是
本 初 子 午
线
C 地
D
北京
40 P
轴
O 纬度40
经度116
A
B
赤
道
五.旋转体的概念
由一个平面图形绕着一条直线旋转产生的 曲面所围成的几何体叫做旋转体,这条直线 叫做旋转体的轴。比如常见的旋转体有圆柱、 圆锥、圆台和球.
六.组合体 由柱、锥、台、球等基本几何体组合而 成的几何体称为组合体。组合体可以通过 把它们分解为一些基本几何体来研究
(1)设球的半径为R,则过球面上任意
两点的截面圆中,最大面积是 πR2 。
(2)过球的半径的中点,作一个垂直于
这条半径的截面,则这个截面圆的半径
是球半径的
3R 。
2
(3)在半径为R的球面上有A、B两点,
半径OA、OB的夹角是60°,则A、B两 点的球面距离是 1 R 。
3
拓展 在一个侧置的正三棱锥容器内放入一个钢球,钢球恰与 棱锥的四个面都接触,过棱锥的一条侧棱和高作截面,正确的 截面图形是( B )
例1 .用一个平行于圆锥底面的平面截这 个圆锥,截得圆台上下底面半径的比是 1 :4,截去的圆锥的母线长是3cm,求 圆台的母线长.
解:设圆台的母线为l,截得的圆锥底面
高中数学 1.1.3 圆柱、圆锥、圆台和球课件 新人教B版

【课标要求】 1.通过观察实物和几何模型,总结出圆柱、圆锥、圆台和球 的结构特征. 2.能根据圆柱、圆锥、圆台和球的定义和结构特征,掌握它 们的相关概念、分类和表示方法. 【核心扫描】 1.通过实例了解组合体的概念. 2.理解圆柱、圆锥、圆台及球的有关概念及其结构特征.(重 点) 3.理解球面距离的概念并能灵活应用.(难点)
提示 对于圆锥,平行于底面的截面是与底面相似的圆面;过 圆锥的顶点且与底面相交的截面是一个由两条母线和底面圆的 弦组成的等腰三角形;圆锥的轴截面是由两条母线和底面圆直 径组成的等腰三角形;圆锥的母线l、高h和底面圆的半径R组成 一个直角三角形,关系式为l2=h2+R2.
2.球 (1) 一个半圆 绕着它的直径所在的直线旋转一周所形成的 曲面叫球面;球面围成的几何体,叫做 球 . (2)球面被经过球心的平面截得的圆叫做球的 大圆 ;被不经 过球心的平面截得的圆叫做球的 小圆 . (3)球的截面的性质:①球的截面是一个 圆 ;②球心与截面 圆心的连线 垂直 于截面;③球半径 R、截面圆半径 r,则球心
5.几种常见的组合体
(1)多面体与多面体的组合体:即由两个或两个以上的多面体组 合而成的几何体.
(2)多面体与旋转体的组合体:即由一个或一个以上的多面体与 一个或一个以上的旋转体组合而成的几何体.
(3)旋转体与旋转体的组合体:即由两个或两个以上的旋转体组 合而成的几何体.
6.地球上的经纬线
当把地球看作一个球时,经线是球面上从北极到南极的半个大 圆.赤道是一个大圆,其余纬线都是小圆.下面用图示说明地 球上的经度、纬度(如图所示):0°经线也叫本初子午线,东经 180°和西经180°同在一条经线上,那就是180°经线.
将圆柱、圆锥和圆台的侧面沿它们的一条母线剪开,然后放在 平面上展开,它们分别是一个矩形、扇形和扇环,如图.
辽宁省北票市高中数学第一章立体几何初步1.1.3圆柱、圆锥、圆台课件新人教B版

圆柱、圆锥、圆台和球
情境引入 一个形的世界,我处处离不开你.
情境引入
我们周围有各种各样的物体,它们都有 怎样的结构特征?
情境引入
情境引入
情境引入
学生活动 问题:观察这些几何体,它们有什 么共同特点或生成规律?
建构数学
矩形
直角三角形
直角梯形
半圆
圆柱
圆锥
圆台
球
建构数学
分别以矩形、直角三角形的直角边、直角梯形垂直
【点评】 轴截面是旋转体中一类重要的截面, 它是把立体几何问题向平面几何问题转化的重要 桥梁.圆柱、圆锥的轴截面有无数个,作图时要 注意已知量与未知量的联系,即将未知量和有用 的已知量充分显示在轴截面图形中,从而有利于 问题的解决. 跟踪训练2 设圆锥的高为h,底面圆的半径为r, 把它的侧面沿一条母线切开展平成一个扇形,求 扇形的圆心角.
圆锥、圆台中各量的计算 圆台也可以看成是圆锥用平行于底面的截面
截得的.
例3 已知圆台的母线长为 8,母线与轴的夹角为
30°,下底面半径是上底面半径的 2 倍,求两底 面面积和轴截面面积.
【分析】
可考虑将圆台还原为圆锥,再作出其
轴截面,在截面中根据条件列式求解,即将空间
问题转化为平面问题求解.
【解】 设圆台的上底面半径为 r, 则下底面 半径为 2r. 将圆台还原成圆锥,作轴截面如图所示,则 ∠ ASO= 30° . r 在 Rt△ SA′ O′中, SA′= = 2r, sin 30° 2r 在 Rt△ SAO 中, SA= = 4r, sin 30°
∴ AA′= SA- SA′= 2r, 即 2r= 8,∴ r= 4. ∴S 上底= πr2= 16π,S 下 底= π·(2r)2 = 64π. 3 在 Rt△ AA′ C 中, A′ C= A′ Acos30° = 8× = 2 4 3, 1 1 ∴ S 轴 截 面 = (2r + 4r)× A′ C = × 24× 4 3 = 2 2 48 3. 因此,圆台的上底面面积为 16π,下底面面积为 64π,轴截面面积为 48 3.
