佛山一中2012-2013学年高二下学期期末数学理试题
广东佛山一中12-13学年高二下期末考试考试-化学要点

佛山一中2012-2013学年高二下学期期末考试化学试题第Ⅰ卷(选择题共40分)一.单项选择题(本题包括10小题,每小题2分,共20分。
每小题给出的四个选项中,只有一个选项符合题目要求,选对得2分,选错或者不答的得0分)1.下列说法正确的是A.蔗糖和麦芽糖、淀粉和纤维素分别属于同分异构体B.煤经干馏、气化和液化三个物理变化过程,可变为清洁能源C.可通过丁达尔效应来鉴别蛋白质溶液和葡萄糖溶液D.加热杀死流感H7N9病毒是因为其蛋白质受热发生盐析2.下列相关化学术语正确的是A.乙烯分子的结构简式:CH2CH2B.中子数为18的氯原子:Cl3517C.HCl的电子式:D.的系统命名为:3—甲基—2—乙基戊烷3.N A为阿伏加德罗常数的数值,下列说法中正确的是A.常温常压下,11.2L CH4含有C—H键数目为2N AB.足量的Fe与1molCl2反应电子转移数为3N AC.32g O2和O3所含的O原子数目均为2N A【M(O)=16g/mol】D.标准状况下,22.4L的己烯中含有的分子数为N A4.下列条件变化会使H2O的电离平衡向电离方向移动,且pH<7的是A.常温下,向水中加少量稀盐酸B.将纯水加热到100℃C.常温下,向水中加少量Na D.常温下,向水中加少量Na2CO3固体5.下列各组中两个变化所发生的反应,属于同一类型的是A.由苯制硝基苯、由乙醇制取乙酸乙酯B.乙烯使溴的CCl4溶液褪色、甲苯使酸性高锰酸钾水溶液褪色C.由HO-CH2-COOH制、由氯乙烯制聚氯乙烯D.由氯乙烷制乙烯、由溴乙烷制乙醇6.常温下,下列说法正确的是A.醋酸钠水解反应的离子方程式为:CH3COO-+H2O = CH3COOH+OH—B.某无色透明溶液中:Na+、MnO4-、SO42-、CO32-能大量共存Cl溶液中:c(H+) + c(NH4+) >c(Cl-) + c(OH-)C.在pH = 4的NHD.等pH等体积的醋酸和盐酸分别与足量的锌反应,前者产生的H2多7.利用右图装置能制取并收集到相应气体的是A.浓氨水与固体CaO制氨气B.浓盐酸与KClO3固体制氯气C.稀硝酸与铜片制NOD.饱和食盐水与电石制乙炔8.已知:乙醇可被强氧化剂氧化为乙酸。
2013年佛山市普通高中高二教学质量检测

D1 A1 D B1
C1 M C
以D为坐标原点建立 如图所示坐标系。
则A(1, 0, 0), B(1,1, 0), 1 D1 (0, 0,1), M (0,1, ) 2
A
x
1 BD1 ( 1, 1,1), AM ( 1,1, ) 2 B 1 1 1 BD1 AM 3 2 cos 3 9 BD1 AM 3 2
(1)因为动圆C 过定点F (1, 0), 且与定直线x 1相切, 所以圆心C 到定点F (1, 0)的距离与到定直线x 1的距离 相等,由抛物线的定义可知, C的轨迹T 是以F (1, 0)为焦点, 直线x 1为准线的抛物线, 所以动员圆心C的轨迹方程 为y 4 x .
2
(Ⅱ)若轨迹T上有两个定点A、B分别在其对称轴的上、 下两侧,且|FA|=2,|FB|=5,在轨迹T位于A、B两点间的曲线 段上求一点P,使P到直线AB的距离最大,并求距离的最大值.
(1)取PA的中点E , 连接ME , BE ,
1 因为M 是PD的中点, 所以EM / / AD , 2 1 又BC / / AD, 所以EM / / BC , 2 所以四边形BCME为平行四边形 ,
P M
E A
所以CM / / BE , 所以四变成BCME D 为平行四边形, 所以CM / / BE , B C 又BE 平面PAB, CM 平面PAB, 所以CM //平面PAB.
(2) OA//BC , kBC kOA
所以直线BC的方程为 3 y2 3 x 2 , 3 即x 3 y 8 0
3 , 3
y C B
A O x
16.如图,在四棱锥P-ABCD中,四边形ABCD是直角梯 形,AD//BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=2, AB=BC=1,M为PD的中点. (1)求证:CM//平面PAB;(2)求证:CD⊥平面PAC。
新课标2012-2013学年高二下学期期末考试数学(理)

2012-2013学年度下学期期末考试高二数学(理)试题【新课标】时量:110分钟 满分:150分一、选择题(本题8个小题,共40分)1.“2320x x -+=”是“1x =” 的( )条件. A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要2.已知命题:,sin 1,p x R x ∀∈≤则p ⌝是 ( ). A .,sin 1x R x ∃∈≥ B .,sin 1x R x ∀∈≥ C .,sin 1x R x ∃∈> D .,sin 1x R x ∀∈>3.若函数32()21f x x x =+-,则'(1)f -=( )。
A .7- B .1- C .1 D .7 4.已知向量)5,3,2(-=与),,4(y x b =平行,则x,y 的值为( ) A. 6和-10 B. –6和10 C. –6和-10 D. 6和105.已知曲线C 的方程为210x x y ++-=,则下列各点中在曲线C 上的点是( ) A .(0,1) B .(-1,3) C .(1,1) D .(-1,2)6、已知P 在椭圆2213x y +=上,1F ,2F 是椭圆的焦点,则12||||PF PF +=( )A .6B .3CD . 7、双曲线22149x y -=的渐近线方程是 ( )A .32y x =±B .23y x =± C.94y x =± D .49y x =± 8. 设A(x 1,y 1),B(x 2,y 2)是抛物线y 2=2px(p>0)上的两点,并且满足OA ⊥OB. 则y 1y 2等于( )A – 4p 2B 4p 2C – 2p 2D 2p 2 二、填空题:(本题共有7小题,共35分) 9.已知(3,2,5),(1,5,1),a b =-=-则2a b -= .10.函数y xInx =在1x =处的切线方程为 . 11.异面直线m 与n 上的单位向量分别为a ,b , 且12a b ∙=, 则两异面直线m 与n 所成角的大小为________.12.抛物线的标准方程为24y x =,则它的准线方程为 。
佛山一中2012届高二下学期期末考试(文数)

佛山一中2012届高二下学期期末考试文数一、选择题:(本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}{}2(4)(1)0,20A x x x B x x x =+-<=-=,则A B = ( )A .{}0B .{}2C .{}0,2D .{}014≠<<-x x x 且 2. 如图,一颗豆子随机扔到桌面上,假设豆子不落在线上,则它落在阴影区域的概率为( )A91 B 61 C 32 D 313.已知复数z 满足i z i 34)4-3(+=,则z 的虚部是 ( )A .i -B . 1C .iD .725-4 已知函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f ,其部分图象如图所示,则函数)(x f 的解析式为 ( )A .)421sin(2)(π+=x x fB .)421sin(4)(π+=x x fC )4321sin(2)(π+=x x f D .)4321sin(4)(π+=x x f5设0x 是方程ln 4x x +=的解,则0x 属于区间( )A. (0,1)B. (1,2)C.(3,4)D. (2, 3) 6 下列有关命题的说法正确的是 ( ).A .命题“若21x =,则1=x ”的否命题为:“若21x =,则1x ≠”.B .“2560x x --=”的必要不充分条件是“1x =-”. C ..命题“若x y =,则sin sin x y =”的逆否命题为真命题D .命题“x R ∃∈,使得210x x ++<”的否定是:“x R ∀∈, 均有210x x ++<”. 7.设,m n 是两条不同的直线,βα,是两个不重合的平面,给定下列四个命题,其中为真图2命题的是( )①m n m n αα⊥⎫⇒⊥⎬⊂⎭ ②a a ααββ⊥⎫⇒⊥⎬⊂⎭ ③//m m n n αα⊥⎫⇒⎬⊥⎭④ ////m n m n αβαβ⊂⎫⎪⊂⇒⎬⎪⎭A. ①和②B. ②和③C. ③和④D. ①和④ 8.阅读如图2所示的程序框图,若输出y 的值为0, 则输入x 的值 为( )A .0B .2C .0 或 2D .1或4 9. 已知定点A (3,1),O 是坐标原点,点(),P x y 满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+008282y x y x y x ,则目标函数z ∙=的最大值为( ) (A)332(B)12 (C)8 (D)24 10已知函数2()f x x bx =+的图像在点(1,(1))A f 处切线的斜率为3,数列1{}的前n 项和为n S ,则2009S 的值为( ) A.20102009 B.20092008 C.20072008 D.20112010二、填空题:(本大题共4小题,每小题5分,共20分) (一)必做题:第11、12、13题为必做题. 11.已知0,0>>b a 且131=+ba ,则b a 2+的最小值为 12.已知向量a 、b 满足:|a|=3,|b|=4,a 、b 的夹角是120°,则|a+2b|=___________. 13 抛物线的顶点在坐标原点,焦点是双曲线222=-y x 的右焦点,抛物线上一点P 到其焦点的距离等于4,则此P 点的坐标是(二)选做题:第14、15题为选做题,考生只能从中选做一题.14. 已知⊙O 的割线PAB 交⊙O 于A,B 两点,割线PCD 经过圆心,若PA=3,AB=1,PO=4,则⊙O 的半径为______________14.已知曲线12C C ,的极坐标方程分别为cos 3ρθ=,π4cos 002ρθρθ⎛⎫=< ⎪⎝⎭,≥≤,则曲线1C 与2C 交点的一个极坐标...为 . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16(本小题共12分)已知ABC △中,内角C B A ,,的对边分别为c b a ,,,且552c os =A , 10103cos =B . (Ⅰ)求C cos 的值;(Ⅱ)设10=a ,求ABC △的面积. 17. (本小题满分12分)某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.(Ⅰ)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试? (Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生接受A 考官进行面试,求:第4组至少有一名学生被考官A 面试的概率?18(本小题满分14分).如上图,边长为a 的正方形11A ABB 所在的平面与正三角形ABC 所在平面垂直,D 是BC 的中点,(Ⅰ)求证:AD A BD 1面⊥ (Ⅱ)求证:A 1C//平面AB 1D ; (Ⅲ)求D AB -A 11三棱锥的体积19已知数列{}n b 的前n 项和12n -+=n n S ,数列{}n a 中,11-=a ,以1,n n a a -为系数的二次方程:21n n a x a x --10+=都有实根,αβ,且满足12)(31=-+αββα(Ⅰ)求数列{}n a 、{}n b 的通项 (Ⅱ)求数列{}n n a b ⋅的前n 项和nW 的20(本小题满分14分)已知直线l :2y kx =+(k 为常数)过椭圆22221x y a b+=(0ab >>)的上顶点B 和左焦点F,直线l 被圆224xy +=截得的弦长为d(Ⅰ)若d =(Ⅱ)若d ≥e 的取值范围.21(本题满分14分)已知函数()2()1e xf x ax =-⋅,a ∈R .(Ⅰ)若函数()f x 在1x =时取得极值,求a 的值; (Ⅱ)当0a ≤时,求函数()f x 的单调区间.。
广东省佛山一中2012-2013学年高一下学期期末数学试卷

2012学年度下学期期末考试高一级数学科试题参考公式: 回归直线方程a bx y +=中,2121121)())((-=--==-=----=---=∑∑∑∑xn xy x n yx x xy y x xb ni ini ii ni ini i i,---=x b y a ;21(1)(21)6ni n n n i =++=∑ .一、选择题.本大题共10小题,每小题5分,共50 分,在每小题给出的四个选项中,只有一项是符合 题目要求的,请把正确填涂在答题卡上.1.如图所示程序框图,能判断任意输入的数x 的奇 偶性.其中判断框内的条件是 ( ) A . 0m = B. 0x = C. 1x = D.1m =2. 设,ab c d >>,则下列不等式中一定成立的是( )A .a c b d ->-B .ac bd >C .a c b d +>+D .a c b d ÷>÷3. △ABC 中,若B a ccos 2=,则△ABC 的形状为 ( )A .直角三角形B .等腰三角形C .等边三角形D .不等边三角形 4. 在等差数列}{n a 中,若前5项和205=S ,则3a 等于 ( )A 4B -4C 2D -25.下列关于数列的命题中,正确的是 ( )A .若数列{}n a 是等差数列,且p q r +=(,,p q r *N ∈),则p q r a a a += B .若数列{}n a 满足n n a a 21=+,则{}n a 是公比为2的等比数列 C . -2和-8的等比中项为±4D . 已知等差数列{}n a 的通项公式为()n a f n =,则()f n 是关于n 的一次函数 6.在△ABC 中,根据下列条件解三角形,其中有两个解的是 ( )(第1题图)A .b = 10,A = 45°,B = 70° B .a = 60,c = 48,B = 100°C .a = 7,b = 5,A = 80°D .a = 14,b = 16,A = 45° 7.已知,x y满足约束条件11y xx y y ≤⎧⎪+≤⎨⎪≥-⎩,则2z x y =+的最大值为 ( )A .32B .52C .3D .58. 某程序框图如图所示, 该程序运行后 输出的S 的值为 ( ) A.63 B.100 C. 127 D.1289.设{}n a 是等比数列,n S 为其前n 项和, (*N n ∈), 下列语句中, 错误..的是 ( ) A .数列1n a ⎧⎫⎨⎬⎩⎭是等比数列 B .数列{}2n a 是等比数列C .数列{}na lg 是等差数列D .n S ,2n n S S -,32n n S S -是等比数列10. 有下列四句话: ① 如果21,x x 是方程02=++c bx ax 的两个实根, 且12x x <,那么不等式20ax bx c ++<的解集为{}21x x x x <<;② 当Δ=240b ac -<时,关于x 的二次不等式20ax bx c ++>的解集为φ;③ 不等式0x ax b-≤-与不等式()()0x a x b --≤的解集相同; ④ 不等式0))((<--b x a x 的解集为{}b x a x <<. 其中可以判断为正确的语句的个数..是 ( ) A .3 B .2 C .1 D .0二、填空题.本大题共4小题,每小题5分,共20分.请把答案填写在答卷(第8题图)B相应的横线上.11. 某公司有1000名员工,其中, 高层管理人员占5%,中层管理人员占15%,一般员工占80%,为了了解该公司的某种情况,现用分层抽样的方法抽取120人进行调查,则一般员工应抽取 人. 12.若06x << ,则(6)x x -的最大值为 。
广东省佛山市2012-2013学年高二期末教学质量检测数学理试题Word版含答案

2013年佛山市普通高中高二教学质量检测数 学 (理科) 2013.1本试卷共4页,20小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生要务必填写答题卷上的有关项目.2.选择题每小题选出答案后,用2B 铅笔把答案涂在答题卡的相应位置上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回. 参考公式:球的表面积公式24S R π=,其中R 为球的半径. 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知点(1,2),(3,6)A B -,则过,A B 两点的直线斜率为A.1-B.12C. D. 22. 若直线1l :410ax y -+=,2l :10ax y ++=,且12l l ⊥,则实数a 的值为A.2B.2±C.4D. 4±3. 若命题p :0x ∃>,2320x x -+>,则命题p ⌝为A. 0x ∃>,2320x x -+≤B. 0x ∃≤,2320x x -+≤C. 0x ∀>,2320x x -+≤D. 0x ∀≤,2320x x -+≤4.如图所示的几何体为正方体的一部份,则它的侧视图可能是A B C D5.若空间三条直线c b a 、、满足b a ⊥,c b //,则直线a 与cA. 一定平行B. 一定垂直C. 一定是异面直线D. 一定相交 6.若集合{}0,A m =,{}1,2B =,则“1m =”是“{}0,1,2AB =”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7.过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是 A. 34150x y +-= B. 34150x y --=第4题图C. 43200x y -+=D. 43200x y --=8.已知命题p :sin y x =,R x ∈是奇函数;命题q :已知,a b 为实数,若22a b =,则a b =.则下列判断正确的是A. p q ∧为真命题B. ()p q ⌝∨为真命题C. ()p q ∧⌝为真命题D. ()()p q ⌝∨⌝为假命题 9.点(1,3)P -到直线:(2)l y k x =-的距离的最大值等于A . 2 B. 3 C.D. 10. 点P 到图形E 上每一个点的距离的最小值称为点P 到图形E 的距离.已知点(1,0)A ,圆C :2220x x y ++=,那么平面内到圆C 的距离与到点A 的距离之差为的点的轨迹是A. 双曲线的一支B. 椭圆C. 抛物线D. 射线二、填空题:本大题共4小题 ,每小题5分,满分20分. 11.棱长为的正方体的外接球的表面积是 .12.若直线210x y -+=平分圆01222=+-++my x y x13.如图所示,在正方体1111ABCD A B C D -中,M 为棱1CC 的中点,则异面直线1BD 与AM 所成角的余弦值为 .14.探照灯反射镜的纵断面是抛物线的一部分,光源在抛物线的焦点,已知灯口直径是60cm ,灯深40cm ,则光源到反射镜顶点的距离是____________cm .A 1第13题图三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 15.(本小题满分12分)如图,已知四边形OABC 是矩形,O 是坐标原点,OA 的坐标是),4AB =.(Ⅰ) 求点C 的坐标; (Ⅱ)求BC 所在直线的方程.16.(本小题满分13分)如图,在四棱锥P ABCD -中,四边形ABCD 为直角梯形,//AD BC ,90BAD ∠=︒, PA ⊥底面ABCD ,且2PA AD ==,1AB BC ==,M 为PD 的中点. (Ⅰ) 求证://CM 平面PAB ; (Ⅱ)求证:CD ⊥平面PAC .17.(本小题满分13分)已知圆C 经过点(0,3)A 和(3,2)B ,且圆心C 在直线y x =上. (Ⅰ) 求圆C 的方程;(Ⅱ)若直线2y x m =+被圆C 所截得的弦长为4,求实数m 的值.第16题图PBAMDC第15题图18.(本小题满分14分)已知动圆C 过定点()1,0F ,且与定直线1x =-相切. (Ⅰ) 求动圆圆心C 的轨迹T 的方程;(Ⅱ)若轨迹T 上有两个定点A 、B 分别在其对称轴的上、下两侧,且||2FA =,||5FB =,在轨迹T 位于A 、B 两点间的曲线段上求一点P ,使P 到直线AB 的距离最大,并求距离的最大值.19.(本小题满分14分)如图,在底面为平行四边形的四棱柱1111ABCD A B C D -中,1D D ⊥底面ABCD ,1AD =,2CD =,60DCB ∠=︒.(Ⅰ) 求证:平面11A BCD ⊥平面1BDD ;(Ⅱ)若二面角1D BC D --的大小为45︒, 求直线CD 与平面11A BCD 所成的角的正弦值.20.(本小题满分14分)已知椭圆C 的中心在原点,焦点在坐标轴上,短轴的一个端点为()0,4B ,离心率35e =. (Ⅰ) 求椭圆C 的方程;(Ⅱ)若()0,0O 、()2,2P ,试探究在椭圆C 内部是否存在整点Q (平面内横、纵坐标均为整数的点称为整点),使得OPQ ∆的面积4OPQ S ∆=?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).2013年佛山市普通高中高二教学质量检测数学试题(理科)参考答案和评分标准一、选择题:本大题共10小题,每小题5分,共50分.第19题图BD CAA 1B 1C 1D 1二、填空题:本大题共4小题 ,每小题5分,满分20分. 11.3π 12.2-1314.458三、解答题:本大题共6小题,满分80分,15.(本小题满分12分)如图,已知四边形OABC 是矩形,O 是坐标原点, O 、A 、B 、C 按逆时针排列,A 的坐标是),4AB =.(Ⅰ) 求点C 的坐标; (Ⅱ)求BC 所在直线的方程. 解: (Ⅰ)因为四边形OABC 是矩形,OA 所在直线的斜率OA k =…2分 所以OC 的斜率为3-,OC 所在的直线方程为y =,…4分 因为4OC AB ==,设(),C x ,则24OC x ===, ……………………6分所以2x =-或2x =(舍去),所以点C的坐标为(2,-.…………………………………………8分(Ⅱ)因为OA 与BC, 所以BC所在直线的斜率BC OA k k ==10分 所以BC所在直线的方程为()23332+=-x y ,即80x -+=.…………………………12分给分说明:第 (Ⅱ)问中的直线若正确地写成一般式或斜截式均给满分.16.(本小题满分13分)如图,在四棱锥P ABCD -中,四边形ABCD 为直角梯形,//AD BC ,90BAD ∠=︒,PA ⊥ 底面ABCD ,且2PA AD ==,1AB BC ==,M 为PD 的中点. (Ⅰ) 求证://CM 平面PAB ; (Ⅱ)求证:CD ⊥平面PAC . 解:(Ⅰ) 取PA 的中点E ,连结,ME BE ,…………1分因为M 为PD 的中点,所以1//2EM AD ,又1//2BC AD …………3分所以//EM BC ,所以四边形BCME 为平行四边形,所以//CM BE ,………………………………………5分 又BE ⊂平面PAB ,CM ⊄平面PAB ,所以//CM 平面PAB .………………………………6分 (Ⅱ)在直角梯形ABCD 中,//AD BC ,90BAD ∠=︒,1AB BC ==,2AD =,过C 作CH AD ⊥于H ,由平几知识易得AC =CD =第16题图P BA MD第16题答案图EPBA MDCH所以222AC CD AD +=,所以AC CD ⊥……………………9分 又PA ⊥ 底面ABCD ,CD ⊂底面ABCD , 所以PA CD ⊥…………………11分 又PAAC A =,所以CD ⊥平面PAC .…………………13分17.(本小题满分13分)已知圆C 经过点(0,3)A 和(3,2)B ,且圆心C 在直线y x =上. (Ⅰ) 求圆C 的方程; (Ⅱ)若直线2y x m =+被圆C 所截得的弦长为4,求实数m 的值.解:(Ⅰ)解法一:设圆心(,)C a a ,因为AC BC =,所以=解得1a =……………………………………………………………………………………………………4分 所以圆心(1,1)C ,半径r AC == ……………………………………………………………………6分所以圆C的方程为22(1)(1)5x y -+-= ………………………………………………………………7分解法二:设圆C的方程为()()()2220x a y a r r -+-=>, ……………………………………………2分依题意得()()()222222332a a r a a r⎧+-=⎪⎨-+-=⎪⎩,………………………………………………………………………5分 解得21,5a r ==,所以圆C的方程为22(1)(1)5x y -+-= ………………………………………7分解法三:依题意易得线段AB 的中垂线方程为32y x =-,……………………………………………2分联立方程组32y x y x =⎧⎨=-⎩,解得11x y =⎧⎨=⎩,所以圆心(1,1)C ,……………5分 下同解法一.(Ⅱ)因为直线2y x m =+被圆C 所截得的弦长为4, 所以圆心(1,1)C 到直线2y x m =+的距离1d == ……………………………10分∴1,解得1m =-± ……………………………………………………………………13分18.(本小题满分14分)已知动圆C 过定点()1,0F ,且与定直线1x =-相切. (Ⅰ) 求动圆圆心C 的轨迹T 的方程;(Ⅱ) 若轨迹T 上有两个定点A 、B 分别在其对称轴的上、下两侧,并且||2FA =,||5FB =,在轨迹T 位于A 、B 两点间的曲线段上求一点P ,使P 到直线AB 的距离最大,并求距离的最大值.解:(Ⅰ) 因为动圆C 过定点()1,0F ,且与定直线1x =-相切,所以圆心C 到定点()1,0F 的距离与到定直线1x =-的距离相等, …………………………………2分由抛物线定义可知,C 的轨迹T 是以()1,0F 为焦点,直线1x =-为准线的抛物线,…………………4分 所以动圆圆心C的轨迹T 的方程为24y x =.……………………………………………………………5分(Ⅱ)由已知得)0,1(F ,设A ),(11y x (其中10y >), 由2=FA 得1,2111==+x x ,所以()1,2A …………………………………………………………7分同理可得()4,4B -,所以直线AB 的方程为042=-+y x . …………………………………………9分解法一:设抛物线曲线段AOB 上任一点),(00y x P ,其中2004y x =,24,4100≤≤-≤≤y x ,则点P 到直线AB 的距离d 12分所以时点P 的坐标为1,14⎛⎫- ⎪⎝⎭. ………………………14分 解法二:设与AB平行的直线()204x y m m ++=≠-,…………………………………10分当与抛物线相切时,切点到AB 的距离最大. 由方程组2204x y m y x++=⎧⎨=⎩消元得()224440x m x m +-+=(*)由()2244160m m ∆=--=得12m =………………………12分 此时(*)式的解为14x =,切点1,14P ⎛⎫- ⎪⎝⎭,距离最大值为1059.…14分19.(本小题满分14分)如图,在底面为平行四边形的四棱柱1111ABCD A B C D -中,1D D ⊥底面ABCD ,1AD =,2CD =,60DCB ∠=︒.(Ⅰ) 求证:平面11A BCD ⊥平面1BDD ;(Ⅱ)若二面角1D BC D --的大小为45︒,求直线CD 与平面11A BCD 所成的角的正弦值.解:(Ⅰ) 在ABD ∆中,由余弦定理得BD == 所以222AD BD AB +=,所以90ADB ∠=︒,即AD BD ⊥ 又四边形ABCD 为平行四边形,所以BC BD ⊥……………2分 又1D D ⊥底面ABCD ,BC ⊂底面ABCD ,所以1D D BC ⊥…4分又1D D BD D =,所以BC ⊥平面1BDD ,…………5分 又BC ⊂平面11A BCD ,所以平面11A BCD ⊥平面1BDD .……6分 (Ⅱ)由(Ⅰ)知BC ⊥平面1BDD ,所以1,D B BC DB BC ⊥⊥ 所以1D BD ∠为二面角1D BC D --的平面角, 所以145D BD ∠=︒,所以1DD BD ==.…………8分解法一:取1BD 的中点M ,连结,DM CM ,则1DM BD ⊥ 又平面11A BCD ⊥平面1BDD ,平面11A BCD 平面1BDD 1BD =,所以DM ⊥平面11A BCD所以DCM ∠为直线CD 与平面11A BCD 所成的角, …………………………10分 在Rt CDM ∆中,112DM BD ==2CD =,所以sin DCM ∠= 所以直线CD 与平面11A BCD ………14解法二: 以D 为原点,建立空间直角坐标系D xyz -如图所示,则(1D ,()C -,()B ,所以()DC =-,()1,0,0BC =-,(11,CD =…10 设平面11A BCD 的法向量为(),,n x y z =,则100n BC n CD ⎧⋅=⎪⎨⋅=⎪⎩,即00x x -=⎧⎪⎨+=⎪⎩,令1z =,得()0,1,1n =,……12分设直线CD 与平面11A BCD 所成的角为θ,则3sin 2n DC n DCθ⋅===⋅第19题图BD CAA 1B 1C 1D 1 第19题解法一图BD C AA 1B 1C 1D 1M1所以直线CD 与平面11A BCD………………………14分 说明:第(Ⅱ)问可不写出C 点的坐标,而直接通过DC AB =,BC AD =,11CD BA =得到所需向量.20.(本小题满分14分)已知椭圆C 的中心在原点,焦点在坐标轴上,短轴的一个端点为()0,4B ,离心率35e =.(Ⅰ) 求椭圆C 的方程;(Ⅱ)若()0,0O 、()2,2P ,试探究在椭圆C 内部是否存在整点Q (平面内横、纵坐标均为整数的点称为整点),使得OPQ ∆的面积4OPQ S ∆=?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).解:(Ⅰ) 设椭圆C 的方程为()222210x y a b a b+=>>,依题意得34,5c b a ==,又222a b c =+,…………………………………………3分 所以5,4,3a b c ===, 所以椭圆C 的方程为2212516x y +=.…………………5分(Ⅱ)依题意OP =,直线OP 的方程为y x =,因为4OPQ S ∆=,所以Q 到直线OP 的距离为, 所以点Q 在与直线OP 平行且距离为, 设:l y x m =+, 解得4m =±………………9分当4m =时,由22412516y x x y =+⎧⎪⎨+<⎪⎩,消元得2412000x x +<,即200041x -<<又x Z ∈,所以4,3,2,1x =----,相应的y 也是整数,此时满足条件的点Q 有4个.…………12分当4m =-时,由对称性,同理也得满足条件的点Q 有4个.综上,存在满足条件的点Q ,这样的点有8个. …………………………………14分。
2012佛山市高二教学质量检测理科数学试题

2012年佛山市普通高中高二教学质量检测数 学 (理科) 2012.1本试卷共4页,20小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生要务必填写答题卷上的有关项目.2.选择题每小题选出答案后,用2B 铅笔把答案涂在答题卡的相应位置上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回. 参考公式:圆台的侧面积公式()S r r l π'=+(其中r 、r '分别为底面半径,l 为母线长).台体的体积公式)下下上上S S S S h V +⋅+=(31(其中h 是台体的高). 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.与直线230x y --=相交的直线的方程是A .4260x y --=B .2y x =C .25y x =+D .23y x =-+2.“ln 1x >”是“2x >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 3.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的 侧视图可以为A .B .C .D . 4.命题“若a b >,则1a b +>”的逆否命题是A .若1a b +≤,则a b >B .若1a b +<,则a b >C .若1a b +≤,则a b ≤D .若1a b +<,则a b <5.已知圆的方程为086222=++-+y x y x ,那么下列直线中经过圆心的直线方程为A .012=+-y xB .012=++y xC .012=--y xD .012=-+y x正视图俯视图6.正方体1111ABCD A BC D -中,E 、F 分别是1DD 、BD 的中点,则直线1AD 与EF 所成的角余弦值是A .12 B.2CD7.若过椭圆22221(0)x y a b a b+=>>的焦点且垂直于x 轴的直线被椭圆截得的弦长为12a ,则该椭圆的离心率为AB .34C .12 D .148.如图,在正方体1111ABCD A BC D -中,,M N 分别是11,BC CD 的中点,则下列说法错误的是A .MN 与1CC 垂直B .MN 与AC 垂直 C .MN 与BD 平行 D .MN 与11A B 平行9.设l ,m 是不同的直线,α,β,γ是不同的平面,则下列命题正确的是A .若l m ⊥,m α⊥,则l α⊥或//l αB .若l γ⊥,αγ⊥,则//l α或l α⊂C .若//l α,//m α,则//l m 或 l 与m 相交D .若//l α,αβ⊥,则l β⊥或l β⊂10.已知圆的方程2225x y +=,过(4,3)M -作直线,MA MB 与圆交于点,A B ,且,MA MB 关于直线3y =对称,则直线AB 的斜率等于A .43- B. 34- C.54- D.45-C 1D 1 B 1 A 1NM B CD AC 1D 1B 1A 1E FBCD A二、填空题:本大共4小题 ,每小题5分,满分20分)11.已知命题:(1,)p x ∀∈+∞,2log 0x >,则p ⌝为 .12.已知直线1l :310ax y ++=,2l :2(1)10x a y +++=,若12//l l ,则实数a 的值 是 .13.已知向量(1, 2)=a,(, 1)x =--b ,若(2)+⊥a b b ,则x = . 14.在正方体的顶点中任意选择4个顶点,对于由这4个顶点构成的四面体的以下判断中,所有正确的结论是 (写出所有正确结论的编号)① 能构成每个面都是等边三角形的四面体; ② 能构成每个面都是直角三角形的四面体;③ 能构成三个面为全等的等腰直角三角形,一个面为等边三角形的四面体; ④ 能构成三个面为不都全等的直角三角形,一个面为等边三角形的四面体. 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 15.(本题满分12分).若一个圆台的的正(主)视图如右图所示.(1)求该圆台的侧面积; (2)求该圆台的体积. 16.(本题满分12分)在平面直角坐标系xOy 中,以(1,2)C -为圆心的圆与直线10x y ++=相切.(1)求圆C 的方程;(2)求过点(3,4)且截圆C所得的弦长为 17.(本题满分14分)如图,在三棱柱111BCD B C D -与四棱锥11A BB D D -的组合体中,已知1BB ⊥平面BCD ,四边形ABCD 是平行四边形,120ABC ∠= ,2AB =,4AD =,11BB =.设O 是线段BD 的中点.(1)求证:1//C O 平面11AB D ; (2)证明:平面⊥11D AB 平面1ADD ;第15题B 1DABC C 1D 1O18.(本题满分14分)已知直线1l 经过两点(3,4)A ,(0,5)B -.(1)求直线1l 关于直线0:l y x =对称的直线2l 方程;(2)直线2l 上是否存在点P ,使点P 到点(1,0)F 的距离等于到直线:1l x =-的距离,如果存在求出P 点坐标,如果不存在说明理由. 19.(本题满分14分)如图,三角ABC 是边长为4正三角形,PA ⊥底面ABC,PA =点D 是BC 的中点,点E 在AC 上,且DE AC ⊥.(1)证明:DE ⊥平面PAC ;(2)求直线AD 和平面PDE 所成角的正弦值. 20.(本题满分14分)已知动点P 到点(1,0)F 的距离与它到直线4x =的距离之比为12. (1)求动点P 的轨迹方程;(2)若点M 是圆22:(3)1C x y +-=上的动点,求||||PM PF +的最大值及此时的P 点坐标.PABCE2012年佛山市普通高中高二教学质量检测数学试题(理科)参考答案和评分标准一、选择题:(每题5分,共40分)二、填空题(每题5分,共30分)11.(1,)x ∃∈+∞,2log 0x ≤. 12.3- 13.1或3- 14.①②③④ 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 15.(本题满分12分) 解析:(1)由图可知,圆台的上底面半径为1,下底面半径为2,圆台的母线长为所以圆台的侧面积为()(12)S r r l ππ'=+=+=. -------------------6分(2)圆台的体积为1114()(4)2333V S S h πππ'=+=⨯=. -------------------12分16.(本题满分12分) 解析:(1)设圆的方程是22(1)(2)x yr -++=, -------------------1分依题意得,所求圆的半径,3r ==,-------------------3分 ∴所求的圆方程是22(1)(2)9x y -++=. -------------------4分(2)∵圆方程是22(1)(2)9x y -++=,当斜率存在时,设直线的斜率为k ,则直线方程为4(3)y k x -=-, -------------------5分即430kx y k -+-=,由圆心(1,C -到直线的距离2d ==,-------------------6分即1=,解得43k =,-------------------8分∴直线方程为44(3)3y x -=-,即43x y -=,-------------------9分∴当斜率不存在时,也符合题意,即所求的直线方程是3x =. -------------------11分∴所求的直线方程为3x =和430x y -=. -------------------12分17.(本题满分14分)(1)证明:取11B D 的中点E ,连结1C E ,OA ,则,,A O C 共线,且1C E OA =, -------------------1分∵111BCD B C D -为三棱柱, ∴平面//BCD 平面111B C D , 故1//C E OA,-------------------3分∴1C EAO 为平行四边形, 从而1//C O EA . -------------------5分又∵1C O ⊄平面11AB D ,EA ⊂平面11AB D , ∴1//C O 平面11AB D . -------------------7分(2)证明:∵120ABC ∠=,4=AB ,2=AD ,则3260cos 4221640=⨯⨯-+=BD ,B 1DAB CC 1D 1(第19题)OE则22216BD AD AB +==,2π=∠ADB ,即AD BD ⊥, -------------------10分又1BB ⊥平面BCD ,⊂BD 平面BCD ,BD BB ⊥1, 在三棱柱111BCD B C D -中,11//DD BB ,则1DD BD ⊥, 而DAD DD = 1,∴⊥BD 平面1AD D ,-------------------12分又11//D B BD ,得⊥11D B 平面1ADD , 而⊂11D B 平面11D AB , ∴平面⊥11D AB 平面1AD D .-------------------14分18.(本题满分14分) 解析:(1)直线1l 的斜率为45330k +==-, 由点斜式得直线1l 的方程为53y x +=,即350x y --=.∴直线1l 关于直线0:l y x =对称的直线2l 方程方程为350x y -+=. ------------------6分 (2)假设存在符合条件的点P ,因为点P 到点(1,0)F 的距离等于到直线:1l x =-的距离,所有由抛物线的定义可知,点P 在抛物线24y x =上, ------------------8分又∵点P在直线2l 上,∴由23504x y y x-+=⎧⎨=⎩,------------------10分消去x得,212200y y -+=,解得12y =,210y =,------------------12分则11x =,225x =,∴存在符合条件的点P,其坐标分别为(1,P 或(25,10). ------------------14分19.(本题满分14分)解析:(1)∵PA ⊥底面ABC ,DE ⊂底面ABC ,∴PA DE ⊥, -------------------2分 又DE AC ⊥,PA AC A = , ∴DE ⊥平面PAC . ------------------4分(2)方法一:由(1)知,DE ⊥平面PAC ,又DE ⊂平面PDE ,∴平面PDE ⊥平面PAC .过点A 作AF PE ⊥,连结DF .-------------------6分∵平面PDE ⊥平面PAC ,平面PDE 平面PAC PE =,AF ⊂平面PAC , ∴AF ⊥平面P,-------------------8分∴ADF∠为直线AD和平面P D E 所成角的平面角. -------------------10分∵ABC ∆是边长为4的正三角形,∴AD =14432AE CE CD =-=-=. 又∵PA =,所以4PE ===,AE PA AF PE ⋅==,∴sin AF ADF AD ∠== -------------------13分 即直线AD和平面PDE所成角的正弦值为8. -------------------14分 方法二:如图所示,以点A 为坐标原点,AD 所在直线为x 轴建立如图空间直角坐标PABEF系.-----2分∵在正三角形ABC ∆中,DE AC ⊥,∴AD =3AE =, ∴(0,0,0)A,(0,0 ,P,(0,0)D,3(,0)2E . --------------------6分 易知(,0,)PD =,3(,,)2PE =,(0,0)AD =. ---------------8分设 (,,)x y z =n 是平面PDE 的一个法向量,则03022PD PE x y ⎧⋅==⎪⎨⋅=+-=⎪⎩n n 解得6x z =,6y z =. 故可取,6)=n .-------------------11分于是cos ,||||ADAD AD ⋅<>=⋅n n n=8=.------13分 由此即知,直线AD 和平面P D E 所成角8. -------------------14分 20.(本题满分14分)解析:(1)设(,)P x y 142x -. 椭圆E的方程为22143x y +=;-------------------5分B(2)∵点M 是圆22:(3)1C x y +-=上的动点,∴||||1PM PC ≤+, -------------------6分设椭圆的左焦点为1(1,0)F -,依据椭圆的定义知,1||4||PF PF =-, -------------------7分∴111||||||14||||||5||5PM PF PC PF PC PF CF +≤++-=-+≤+,当点P 是1CF 延长线与椭圆的交点时,1||||PC PF -取得最大值1||CF , ∴||||PM PF +的最大值为5,-------------------10分此时直线1CF 的方程是33+=x y ,点P 的坐标是方程组⎪⎩⎪⎨⎧=++=1343322y x x y 的解,消去y 得,0824132=++x x , -------------------11分解得1310212±-=x ,根据图形可知1310212--=p x ,131063-=p y ,-------------------13分此时的P点坐标为(1310212--,131063-). -------------------14分。
广东省佛山市2012-2013学年高二期末教学质量检测数学理试题

2013年佛山市普通高中高二教学质量检测数 学 (理科) 2013.1本试卷共4页,20小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生要务必填写答题卷上的有关项目.2.选择题每小题选出答案后,用2B 铅笔把答案涂在答题卡的相应位置上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回. 参考公式:球的表面积公式24S R π=,其中R 为球的半径. 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知点(1,2),(3,6)A B -,则过,A B 两点的直线斜率为A.1-B.12C. D. 22. 若直线1l :410ax y -+=,2l :10ax y ++=,且12l l ⊥,则实数a 的值为A.2B.2±C.4D. 4±3. 若命题p :0x ∃>,2320x x -+>,则命题p ⌝为A. 0x ∃>,2320x x -+≤B. 0x ∃≤,2320x x -+≤C. 0x ∀>,2320x x -+≤D. 0x ∀≤,2320x x -+≤4.如图所示的几何体为正方体的一部份,则它的侧视图可能是A B C D5.若空间三条直线c b a 、、满足b a ⊥,c b //,则直线a 与cA. 一定平行B. 一定垂直C. 一定是异面直线D. 一定相交 6.若集合{}0,A m =,{}1,2B =,则“1m =”是“{}0,1,2A B =U ”的 A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7.过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是第4题图A. 34150x y +-=B. 34150x y --=C. 43200x y -+=D. 43200x y --=8.已知命题p :sin y x =,R x ∈是奇函数;命题q :已知,a b 为实数,若22a b =,则a b =.则下列判断正确的是A. p q ∧为真命题B. ()p q ⌝∨为真命题C. ()p q ∧⌝为真命题D. ()()p q ⌝∨⌝为假命题 9.点(1,3)P -到直线:(2)l y k x =-的距离的最大值等于A . 2 B. 3 C. 32 D . 23 10. 点P 到图形E 上每一个点的距离的最小值称为点P 到图形E 的距离.已知点(1,0)A ,圆C :2220x x y ++=,那么平面内到圆C 的距离与到点A 的距离之差为的点的轨迹是A. 双曲线的一支B. 椭圆C. 抛物线D. 射线二、填空题:本大题共4小题 ,每小题5分,满分20分. 11.棱长为的正方体的外接球的表面积是 .12.若直线210x y -+=平分圆01222=+-++my x y x 的面积,则m = .13.如图所示,在正方体1111ABCD A B C D -中,M 为棱1CC 的中点,则异面直线1BD 与AM 所成角的余弦值为 .14.探照灯反射镜的纵断面是抛物线的一部分,光源在抛物线的焦点,已知灯口直径是60cm ,灯深40cm ,则光源到反射镜顶点的距离是____________cm .ABCD A 1B 1C 1D 1 M第13题图三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 15.(本小题满分12分)如图,已知四边形OABC 是矩形,O 是坐标原点,O 、A 、B 、C 按逆时针排列,A 的坐标是()3,1,4AB =.(Ⅰ) 求点C 的坐标; (Ⅱ)求BC 所在直线的方程.16.(本小题满分13分)如图,在四棱锥P ABCD -中,四边形ABCD 为直角梯形,//AD BC ,90BAD ∠=︒, PA ⊥底面ABCD ,且2PA AD ==,1AB BC ==,M 为PD 的中点. (Ⅰ) 求证://CM 平面PAB ; (Ⅱ)求证:CD ⊥平面PAC .17.(本小题满分13分)已知圆C 经过点(0,3)A 和(3,2)B ,且圆心C 在直线y x =上. (Ⅰ) 求圆C 的方程;(Ⅱ)若直线2y x m =+被圆C 所截得的弦长为4,求实数m 的值.第16题图PBAMDCOxAB Cy第15题图18.(本小题满分14分)已知动圆C 过定点()1,0F ,且与定直线1x =-相切. (Ⅰ) 求动圆圆心C 的轨迹T 的方程;(Ⅱ)若轨迹T 上有两个定点A 、B 分别在其对称轴的上、下两侧,且||2FA =,||5FB =,在轨迹T 位于A 、B 两点间的曲线段上求一点P ,使P 到直线AB 的距离最大,并求距离的最大值.19.(本小题满分14分)如图,在底面为平行四边形的四棱柱1111ABCD A B C D -中,1D D ⊥底面ABCD ,1AD =,2CD =,60DCB ∠=︒.(Ⅰ) 求证:平面11A BCD ⊥平面1BDD ;(Ⅱ)若二面角1D BC D --的大小为45︒, 求直线CD 与平面11A BCD 所成的角的正弦值.20.(本小题满分14分)已知椭圆C 的中心在原点,焦点在坐标轴上,短轴的一个端点为()0,4B ,离心率35e =. (Ⅰ) 求椭圆C 的方程;(Ⅱ)若()0,0O 、()2,2P ,试探究在椭圆C 内部是否存在整点Q (平面内横、纵坐标均第19题图BD CAA 1B 1C 1D 1为整数的点称为整点),使得OPQ ∆的面积4OPQ S ∆=?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).2013年佛山市普通高中高二教学质量检测数学试题(理科)参考答案和评分标准一、选择题:本大题共10小题,每小题5分,共50分. 题号 1 2 3 4 5 6 7 8 9 10 答案ABCDBADCCD二、填空题:本大题共4小题 ,每小题5分,满分20分. 11.3π 12.2- 13.39 14.458三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤.15.(本小题满分12分)如图,已知四边形OABC 是矩形,O 是坐标原点,O 、A 、B 、C 按逆时针排列,A 的坐标是()3,1,4AB =.(Ⅰ) 求点C 的坐标; (Ⅱ)求BC 所在直线的方程. 解: (Ⅰ)因为四边形OABC 是矩形,OA 所在直线的斜率33OAk =…2分 所以OC 的斜率为3-,OC 所在的直线方程为3y x =-,…4分 因为4OC AB ==,设(),3C x x-,则()22324OC x xx =+-==, ……………………6分所以2x =-或2x =(舍去),所以点C的坐标为()2,23-.…………………………………………8分(Ⅱ)因为OA 与BC, 所以BC所在直线的斜率33BC OA k k ==…………………………………10分 所以BC所在直线的方程为()23332+=-x y ,即380x y -+=.…………………………12分给分说明:第 (Ⅱ)问中的直线若正确地写成一般式或斜截式均给满分.16.(本小题满分13分)如图,在四棱锥P ABCD -中,四边形ABCD 为直角梯形,//AD BC ,90BAD ∠=︒,PA ⊥ 底面ABCD ,且2PA AD ==,1AB BC ==,M 为PD 的中点. (Ⅰ) 求证://CM 平面PAB ; (Ⅱ)求证:CD ⊥平面PAC .解:(Ⅰ) 取PA 的中点E ,连结,ME BE ,…………1分第16题P BAMDCOxAB Cy因为M 为PD 的中点,所以1//2EM AD ,又1//2BC AD …………3分 所以//EM BC ,所以四边形BCME 为平行四边形,所以//CM BE ,………………………………………5分 又BE ⊂平面PAB ,CM ⊄平面PAB ,所以//CM 平面PAB .………………………………6分 (Ⅱ)在直角梯形ABCD 中,//AD BC ,90BAD ∠=︒,1AB BC ==,2AD =,过C 作CH AD ⊥于H ,由平几知识易得AC =2CD =,所以222AC CD AD +=,所以AC CD ⊥……………………9分 又PA ⊥ 底面ABCD ,CD ⊂底面ABCD , 所以PA CD ⊥…………………11分又PA AC A =I ,所以CD ⊥平面PAC .…………………13分17.(本小题满分13分)已知圆C 经过点(0,3)A 和(3,2)B ,且圆心C 在直线y x =上. (Ⅰ) 求圆C 的方程; (Ⅱ)若直线2y x m =+被圆C 所截得的弦长为4,求实数m 的值.解:(Ⅰ)解法一:设圆心(,)C a a ,因为AC BC=,所以2222(3)(3)(2)a a a a +-=-+-,解得1a =……………………………………………………………………………………………………4分 所以圆心(1,1)C ,半径5r AC == ……………………………………………………………………6分所以圆C的方程为22(1)(1)5x y -+-= ………………………………………………………………7分解法二:设圆C的方程为()()()2220x a y a r r -+-=>, ……………………………………………2分依题意得()()()222222332a a r a a r⎧+-=⎪⎨-+-=⎪⎩,………………………………………………………………………5分 解得21,5a r ==,所以圆C的方程为22(1)(1)5x y -+-= ………………………………………7分解法三:依题意易得线段AB的中垂线方程为32y x =-,……………………………………………2分第16题答案图EPBA MDCH联立方程组32y x y x =⎧⎨=-⎩,解得11x y =⎧⎨=⎩,所以圆心(1,1)C ,……………5分 下同解法一.(Ⅱ)因为直线2y x m =+被圆C 所截得的弦长为4, 所以圆心(1,1)C 到直线2y x m =+的距离22(5)21d =-= ……………………………10分∴115m +=,解得15m =-± ……………………………………………………………………13分18.(本小题满分14分)已知动圆C 过定点()1,0F ,且与定直线1x =-相切. (Ⅰ) 求动圆圆心C 的轨迹T 的方程;(Ⅱ) 若轨迹T 上有两个定点A 、B 分别在其对称轴的上、下两侧,并且||2FA =,||5FB =,在轨迹T 位于A 、B 两点间的曲线段上求一点P ,使P 到直线AB 的距离最大,并求距离的最大值.解:(Ⅰ) 因为动圆C 过定点()1,0F ,且与定直线1x =-相切,所以圆心C 到定点()1,0F 的距离与到定直线1x =-的距离相等, …………………………………2分由抛物线定义可知,C 的轨迹T 是以()1,0F 为焦点,直线1x =-为准线的抛物线,…………………4分 所以动圆圆心C的轨迹T 的方程为24y x =.……………………………………………………………5分(Ⅱ)由已知得)0,1(F ,设A ),(11y x (其中10y >), 由2=FA 得1,2111==+x x ,所以()1,2A …………………………………………………………7分同理可得()4,4B -,所以直线AB 的方程为042=-+y x . …………………………………………9分解法一:设抛物线曲线段AOB 上任一点),(00y x P ,其中2004y x =,24,4100≤≤-≤≤y x ,则点P 到直线AB 的距离2200001924(1)244221455y y y x y d ⨯+-+-+-===+ ………………12分所以当10-=y 时,距离d 取得最大值1059,此时点P 的坐标为1,14⎛⎫- ⎪⎝⎭. ………………………14分 解法二:设与AB平行的直线的方程为()204x y m m ++=≠-,…………………………………10分当与抛物线相切时,切点到AB 的距离最大. 由方程组2204x y m y x++=⎧⎨=⎩消元得()224440x m x m +-+=(*)由()2244160m m ∆=--=得12m =………………………12分 此时(*)式的解为14x =,切点1,14P ⎛⎫- ⎪⎝⎭,距离最大值为1059.…14分19.(本小题满分14分)如图,在底面为平行四边形的四棱柱1111ABCD A B C D -中,1D D ⊥底面ABCD ,1AD =,2CD =,60DCB ∠=︒.(Ⅰ) 求证:平面11A BCD ⊥平面1BDD ;(Ⅱ)若二面角1D BC D --的大小为45︒,求直线CD 与平面11A BCD 所成的角的正弦值.解:(Ⅰ) 在ABD ∆中,由余弦定理得 222cos 3BD AD AB AD AB DCB =+-⋅∠=所以222AD BD AB +=,所以90ADB ∠=︒,即AD BD ⊥ 又四边形ABCD 为平行四边形,所以BC BD ⊥……………2分 又1D D ⊥底面ABCD ,BC ⊂底面ABCD ,所以1D D BC ⊥…4分又1D D BD D =I ,所以BC ⊥平面1BDD ,…………5分 又BC ⊂平面11A BCD ,所以平面11A BCD ⊥平面1BDD .……6分 (Ⅱ)由(Ⅰ)知BC ⊥平面1BDD ,所以1,D B BC DB BC ⊥⊥ 所以1D BD ∠为二面角1D BC D --的平面角, 所以145D BD ∠=︒,所以13DD BD ==.…………8分解法一:取1BD 的中点M ,连结,DM CM ,则1DM BD ⊥又平面11A BCD ⊥平面1BDD ,平面11A BCD I 平面1BDD 1BD =,所以DM ⊥平面11A BCD所以DCM ∠为直线CD 与平面11A BCD 所成的角, …………………………10分 在Rt CDM ∆中,11622DM BD ==,2CD =,所以6sin 4DM DCM CD ∠==, 第19题BD C AA 1B 1C 1D 1 第19题解法一图BD C AA 1B 1C 1D 1MD CAA 1B 1C 1D 1z . xyOF. A .PB所以直线CD 与平面11A BCD 所成的角的正弦值为64.………14分 解法二: 以D 为原点,建立空间直角坐标系D xyz -如图所示, 则()10,0,3D ,()1,3,0C -,()0,3,0B ,所以()1,3,0DC =-u u u r ,()1,0,0BC =-u u u r ,()11,3,3CD =-u u u u r…10分设平面11A BCD 的法向量为(),,n x y z =r,则100n BC n CD ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u u r,即0330x x y z -=⎧⎪⎨-+=⎪⎩,令1z =,得()0,1,1n =r ,……12分 设直线CD 与平面11A BCD 所成的角为θ,则36sin 422n DC n DCθ⋅===⋅⋅r u u u r r u u u r , 所以直线CD 与平面11A BCD 所成的角的正弦值为64.………………………14分 说明:第(Ⅱ)问可不写出C 点的坐标,而直接通过DC AB =u u u r u u u r ,BC AD =u u u r u u u r ,11CD BA =u u u ur u u u r 得到所需向量.20.(本小题满分14分)已知椭圆C 的中心在原点,焦点在坐标轴上,短轴的一个端点为()0,4B ,离心率35e =.(Ⅰ) 求椭圆C 的方程;(Ⅱ)若()0,0O 、()2,2P ,试探究在椭圆C 内部是否存在整点Q (平面内横、纵坐标均为整数的点称为整点),使得OPQ ∆的面积4OPQ S ∆=?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).解:(Ⅰ) 设椭圆C 的方程为()222210x y a b a b+=>>,依题意得34,5c b a ==,又222a b c =+,…………………………………………3分 所以5,4,3a b c ===, 所以椭圆C 的方程为2212516x y +=.…………………5分 (Ⅱ)依题意22OP =,直线OP 的方程为y x =,…………………………7分 因为4OPQ S ∆=,所以Q 到直线OP 的距离为22, 所以点Q 在与直线OP 平行且距离为22的直线上,xy O5-Pl 1 l 2B.5设:l y x m =+, 则222m =,解得4m =±………………9分当4m =时,由22412516y x x y =+⎧⎪⎨+<⎪⎩,消元得2412000x x +<,即200041x -<<又x Z ∈,所以4,3,2,1x =----,相应的y 也是整数,此时满足条件的点Q 有4个.…………12分当4m =-时,由对称性,同理也得满足条件的点Q 有4个.综上,存在满足条件的点Q ,这样的点有8个. …………………………………14分。
广东省佛山市高二下学期数学期末统考试卷

广东省佛山市高二下学期数学期末统考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共4题;共8分)1. (2分)如图,△ABC中,若,则=()A . 2B . 4C . 6D . 82. (2分)已知正方体,点分别是线段和上的动点,观察直线与,与.给出下列结论:①对于任意给定的点,存在点,使得;②对于任意给定的点,存在点,使得;③对于任意给定的点,存在点,使得;④对于任意给定的点,存在点,使得.其中正确结论的个数是()A . 1个B . 2个C . 3个D . 4个3. (2分) (2016高二上·湖州期中) 已知直三棱柱ABC﹣A1B1C1的各棱长均为1,棱BB1所在直线上的动点M满足,AM与侧面BB1C1C所成的角为θ,若λ∈[ ],则θ的取值范围是()A . [ , ]B . [ ]C . [ , ]D . [ , ]4. (2分)已知等差数列{an}中,a7+a9=10,则S15的值是()A . 60B . 75C . 80D . 70二、填空题 (共12题;共12分)5. (1分) (2019高三上·建平期中) 若复数,满足,(是虚数单位),则________6. (1分)已知k∈R,则两条动直线kx﹣y+2(k+1)=0与x+ky+2(k﹣1)=0的交点P的轨迹方程为________.7. (1分)把直径分别为的三个铁球熔成一个大铁球,则这个大铁球的半径为________.8. (1分)已知直线的参数方程为,点是曲线上的任一点,则点到直线距离的最小值为________.9. (1分)(2017·嘉兴模拟) 若复数,其中是虚数单位,则 ________; ________.10. (1分)(2018·延安模拟) 已知抛物线上一点到其焦点的距离为5,则该抛物线的准线方程为________.11. (1分) (2016高一下·高淳期中) 设Sn是等比数列{an}的前n项和,若S1 , 2S2 , 3S3成等差数列,则公比q等于________.12. (1分)若矩阵A=,矩阵B=,则矩阵A和B的乘积AB=________ .13. (1分)已知圆C:(x+3)2+y2=4及点A(3,0),Q为圆周上一点,AQ的垂直平分线交直线CQ于点M,则动点M的轨迹方程为________14. (1分) (2016高一下·延川期中) 点P(1,﹣1)到直线x﹣y+1=0的距离是________.15. (1分) (2017高二上·西华期中) 数列{an}的首项a1=2,an=2an﹣1﹣3(n≥2),则a7=________.16. (1分)已知向量,满足( +2 )•(﹣)=﹣6且| |=1,| |=2,则与的夹角为________.三、解答题 (共5题;共60分)17. (10分) (2018高二上·北京月考) 如图,在三棱锥中,分别是的中点,(1)求证:平面;(2)求异面直线与所成角的余弦值;(3)求点到平面的距离。
2012年佛山市普通高中高二教学质量检测(理科数学)

2. “lnx 1”是“x 2”的( A ) A.充分不必要条件 B.必要不充分条件 C .充要条件 D.既不充分也不必要条件
ln x 1 x e, e 2.72
3.在一个几何体的三视图中,正视图和俯视图如图所示, 则相应的侧视图可以为( )D
正视图
A
B
俯视图 C D
4.命题“若a b, 则a 1 b”的逆否命题是( C ) A.a 1 b, 则a b B.若a 1 b, 则a b C .若a 1 b, 则a b D.若a 1 b, 则a b
4k 2 6k 4 3 k 2 8 k 3 将上式中k 换为 k , 得 : C , 2 2 k 1 k 1 3k 2 8k 3 3 k 2 8 k 3 2 2 4 k 1 k 1 k BC 2 2 4k 6k 4 4k 6k 4 3 2 k 1 k2 1
二、填空题: (本大共4小题 ,每小题5分,满分20分)
11.已知命题p : x (1, ),log2 x 0, 则p为
.
x (1, ),log2 x 0
12.已知直线l1:ax 3 y 1 0, l2: 2 x (a 1) y 1 0, 若l1 //l2 , 则实数a的值是
2a b (2 x , 0, 3), (2a b) b, ( x 3)( x 1) 0, 解得 : x 3或1
(2a b) b (2 x ) x 3 0, 即x 2 2 x 3 0,
14.在正方体的顶点中任意选择4个顶点,对于由这4个顶 点构成的四面体的以下判断中,所有正确的结论是 ①②③④ (写出所有正确结论的编号) ① 能构成每个面都是等边三角形的四面体; ② 能构成每个面都是直角三角形的四面体; ③ 能构成三个面为全等的等腰直角三角形,一个面为等 边三角形的四面体; ④ 能构成三个面为不都全等的直角三角形,一个面为等 边三角形的四面体.
广东省佛山一中2012-2013学年高二下学期期末数学理试题 含答案

2012-2013学年第二学期 期末考试高二年级数学(理科)试题考试时间:120分钟 满分150分一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
把正确答案的对应符号填涂在答题卡上. 1。
设是虚数单位,复数为纯虚数,则实数a 为A .2B .C . D. -22.若实数a 满足|2a —1|〈 3,那么a 的取值范围是ks5uA. 0〈a<2B. 〈a 〈2 C 。
-1<a<2 D. -2〈a 〈33. 某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x 小时,原油温度(单位:℃)为),50(831)(23≤≤+-=x x xx f ,那么原油温度在第3小时度的瞬时变化率为A .0B .3C . 8D . 11 4.设随机变量ξ服从正态分布N(0,1),若P(ξ>1)= p ,则P(—1<ξ<0)=A .p +21B .p -21C .1—pD .1-2p 5。
类比平面正三角形的“三边相等,三内角相等”的性质,可知正四面体的下列哪些性质,你认为比较恰当的是( 注:正四面体是侧① 各棱长相等,同一顶点上的任两条棱的夹角都相等; ②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等.A .①②③B .①②C .①D .③6。
一工厂生产的100个产品中有90个一等品,10个二等品,现从这批产品中抽取4个,则其中恰好有一个二等品的概率为ks5uA .41004901C C -B .4100390110490010C C C C C + C .4100110C C D .4100390110C C C7.已知R 上的可导函数的图象如图所示,函数的两个零点分别为—2和2,两个极值点分别为-1和1,若为函数的导函数,则不等式的解集为A 。
B.C 。
广东省佛山一中2012-2013学年高二下学期期末物理试题.pdf

2012学年度下学期期末考试高二级物理科试题 一、单项选择题(每小题只有一个答案正确,共8题,每题3分,共24分)1. 首先发现原子核内部有复杂结构的实验是A.原子光谱 B.光电效应C.α粒子散射现象D.天然放射现象2.如图所示,是密闭的气缸,外力推动活塞P压缩气体,对缸内气体做功80 J,同时气体向外界放热0 J,缸内气体的A温度升高,内能增加0J B温度升高,内能减少0J C温度降低,内能增加0J D温度降低,内能减少20J 下列说法正确的是 A液体中悬浮微粒的无规则运动称为布朗运动B液体分子的无规则运动称为布朗运动 C物体从外界吸收热量,其内能一定增加D物体对外界做功,其内能一定减少 AHe+N→O+H B CU+n→Ba+Kr+3n DH+H→He+n 5. 不同频率的紫外光分别照射钨和锌的表面而产生光电效应,可得到光电子的最大初动能Ek随入射光频率v变化的Ek—v图象.已知钨的逸出功是3.28eV,锌的逸出功是3.34eV,若将二者的图线画在同一个坐标中,以实线表示钨、虚线表示锌,能正确反映这一过程的选项是 6.如图所示,倾斜导轨宽为L与水平面成α角,方向竖直向上磁感应强度为B匀强磁场,金属杆ab水平放在导轨上.回路电流强度为I,金属杆ab所受安培力FA.方向沿斜面向上 B.方向水平向右 C. D. 关于变压器下列说法正确的是 A.变压器的工作原理是利用电磁感应现象 B.变压器的铁芯是闭合的, 闭合是为了让电流从原线圈经铁芯流向副线圈 C.变压器不仅可以变压, 也可以改变交流电的频率 D.升压变压器副线圈所用的导线比原线圈所用的导线粗 如图所示,弹簧的一端固定在竖直墙上,质量为m的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量也为m的小球从槽高h处开始自由下滑,则A.在以后的运动过程中,小球和槽的动量始终守恒B.在下滑过程中小球和槽之间的相互作用力始终不做功C.被弹簧反弹后,小球和槽都做匀速直线运动D.被弹簧反弹后,小球和槽的机械能守恒,小球能回到槽高h处 将闭合多匝线圈置于仅随时间变化的磁场中,线圈平面与磁场方向垂直,关于线圈中产生的感应电动势和感应电流,下列表述正确的是 A、感应电动势的大小与线圈的匝数无关 B、当穿过线圈的磁通量为零时,感应电动势可能不为零 C、当穿过线圈的磁通量变化越快时,感应电动势越大 D、感应电流产生的磁场方向与原磁场方向始终相反 如图所示,是某种正弦式交变电压的波形图,由图可确定该电压的A.周期是0.01s B.最大值是311V C.有效值是V D.表达式为U=sin100πt(V) 13. 设氢原子由n=3的状态向n=2的状态跃迁时放出能量为E、频率为ν的光子.则氢原子 A.跃迁时可以放出或吸收能量为任意值的光子 B.由n=2的状态向n=1的状态跃迁时放出光子的能量大于E C.由n=2的状态向n=3的状态跃迁时吸收光子的能量等于E D.由n=4的状态向n=3的状态跃迁时放出光子的频率大于ν 14. .如图所示,理想变压器原、副线圈匝数比n1:n2=2:1, 伏特表和安培表均为理想电表,灯泡电阻R1=6Ω,AB端电压U1=12sin100πt(V).下列说法正确的是 A.电流频率为50HZ B.伏特表的读数为24V C.安培表的读数为0.5A D.变压器输入功率为6W 15. 在如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压和输电线的电阻均不变,随着发电厂输出功率的增大,下列说法中正确的有 A.升压变压器的输出电压增大 B.降压变压器的输出电压增大 C.输电线上损耗的功率增大 D.输电线上损耗的功率占总功率的比例增大 A.充气后,密封气体压强增加 B.充气后,密封气体的分子平均动能增加 C.打开阀门后,密封气体对外界做正功 D.打开阀门后,不再充气也能把水喷光 三、实验题(共2题,每题7分, 前一空3分, 后一空4分, 两题共14分) 17. 在“用单分子油膜估测单分子的大小”的实验中,按照酒精与油酸体积比为m:n配制油酸酒精溶液,现用滴管滴取油酸酒精溶液,N滴溶液的总体积为V.(1)用滴管将一滴油酸酒精溶液滴入浅盘,待稳定后将油酸薄膜轮廓描绘在坐标纸上,如图所示.已知坐标纸上每个小方格面积为S,则油膜面积为(2)估算油酸分子直径的表达式为 .(用题目中物理量的字母表示) 某同学用如图所示的装置通过半径相同的A、B两球的碰撞来碰撞中的守恒,实验时先使A球从斜槽上某一固定位置由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹,重复上述操作10次,得到10个落点痕迹,再把B球放在水平槽上靠近槽末端的,让A球仍从位置G由静止开始滚下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹,重复这种操作10次,图中O点是水平槽末端在记录纸上的垂直投影点,B球落点痕迹如图,其中米尺水平放置,米尺的零点与O点对齐(1)从图可以测出碰撞后B球的水平射程应取为(2)A球和B球的质量 球的直径碰撞中的守恒 四、计算题(共3小题,共36分) 在答卷上 2012学年度下学期期末考试高二级物理科试题答卷 座位号: 三、实验题(共2题,共14分) 17.(1) (2) ----------------- -------------------- 18. (1) (2) --------------- ---------------------- 四、计算题(共3小题,共36分) 19(8分)如图所示,小球1沿半径为R1/4光滑圆弧从A点由静止运动到最低点B时,与小球m2碰撞并粘在一起沿光滑圆弧末端水平飞,最终落至C点。
广东省佛山一中2010-2011学年高二下学期期末考试(数学理)试题
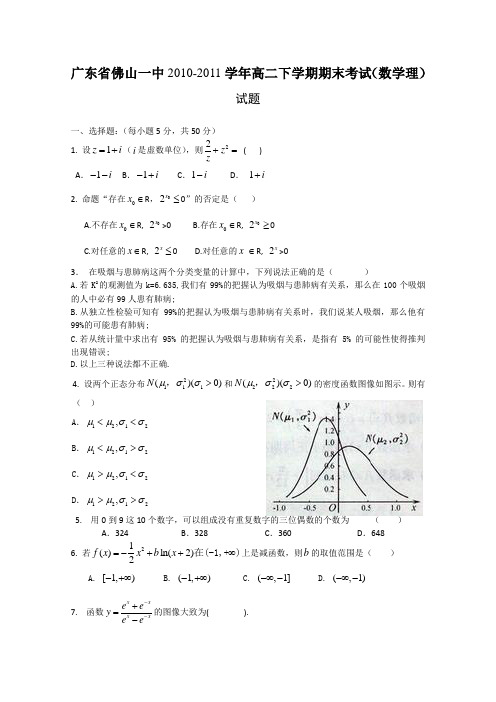
广东省佛山一中2010-2011学年高二下学期期末考试(数学理)试题一、选择题:(每小题5分,共50分) 1. 设1z i =+(i 是虚数单位),则22z z+= ( ) A .1i -- B .1i -+ C .1i - D . 1i +2. 命题“存在0x ∈R ,02x ≤0”的否定是( )A.不存在0x ∈R, 02x>0 B.存在0x ∈R, 02x ≥0C.对任意的x ∈R, 2x ≤0D.对任意的x ∈R, 2x>03. 在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )A.若K 2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误;D.以上三种说法都不正确.4. 设两个正态分布2111()(0)N μσσ>,和2222()(0)N μσσ>,的密度函数图像如图示。
则有( )A .1212,μμσσ<<B .1212,μμσσ<>C .1212,μμσσ><D .1212,μμσσ>>5. 用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为 ( ) A .324 B .328 C .360 D .6486. 若21()ln(2)2f x x b x =-++∞在(-1,+)上是减函数,则b 的取值范围是( )A. [1,)-+∞B. (1,)-+∞C. (,1]-∞-D. (,1)-∞-7. 函数x xx xe e y e e --+=-的图像大致为( ).8.设1122(,),(,)x y x y ,…,),n n y x (是变量x 和y 的n 个样本点,直线l 是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( ) (A )x 和y 的相关系数为直线l 的斜率 (B )x 和y 的相关系数在0到1之间(C )当n 为偶数时,分布在l 两侧的样本点的个数一定相同 (D )直线l 过点(,)x y9. 设0,0.a b >>若1133aba b+与的等比中项,则的最小值为( ) A 8 B 4 C 1 D1410. (1)nax by ++展开式中不含x 的项的系数绝对值的和为243,不含y 的项的系数绝对值的和为32,则,,a b n 的值可能为 ( )A .2,1,5a b n ==-=B .2,1,6a b n =-=-=C .1,2,6a b n =-==D .1,2,5a b n ===二、填空题:(每小题5分,共20分)11.设⎪⎩⎪⎨⎧+=⎰adt t x x x f 023lg )( 00≤>x x ,若((1))1f f =,则a = . 12.已知离散型随机变量X 的分布列如右表.若0EX =,1DX =,则a = __,b = .ACD13. 已知两曲线参数方程分别为(0)sin x y θθπθ⎧=⎪⎨=⎪⎩≤<和25()4x t t R y t⎧=⎪∈⎨⎪=⎩,它们的交点坐标为 ____ .14. 设函数()(0)2xf x x x =>+,观察: 1()(),2x f x f x x ==+ 21()(()),34xf x f f x x ==+32()(()),78xf x f f x x ==+43()(()),1516xf x f f x x ==+…根据以上事实,由归纳推理可得:当n N +∈且2n ≥时,1()(())n n f x f f x -== . 三、解答题:(共80分)15.(12分)已知复数i z 311+=,ααsin cos 32i z +=,求复数21z z z ⋅=实部的最值.16.(12分)如图,已知正三棱柱111ABC A B C -的底面正三角形的边长是2,D 是1CC 的中点,直线AD与侧面11BB C C 所成的角是45. (Ⅰ)求二面角A BD C --的正切值; (Ⅱ)求点C 到平面ABD 的距离.17.(14分)今有甲、乙两个篮球队进行比赛,比赛采用7局4胜制.假设甲、乙两队在每场比赛中获胜的概率都是21.并记需要比赛的场数为ξ.(Ⅰ)求ξ大于5的概率;(Ⅱ)求ξ的分布列与数学期望.B1C18.(14分)在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为sin()42πρθ+=. 圆O的参数方程为cos 2sin 2x r y r θθ⎧=-+⎪⎪⎨⎪=-+⎪⎩,(θ为参数,0r >) (1)求圆心的极坐标;(2)当r 为何值时,圆O 上的点到直线l 的最大距离为3.19.(14分)已知数列{}n a 满足135a =,121n n n a a a +=+ , (Ⅰ)计算出2a 、3a 、4a ;(Ⅱ)猜想数列{}n a 通项公式n a ,并用数学归纳法进行证明.20.(14分)已知函数()ln a xf x x x-=+,其中a 为大于零的常数. (Ⅰ)若曲线()y f x =在点(1,(1)f )处的切线与直线12y x =-平行,求a 的值;(Ⅱ)求函数()f x 在区间[1,2]上的最小值.广东省佛山一中2010-2011学年高二下学期期末考试(数学理)试题答卷座位号:二、填空题:(每小题5分,共20分)11.__ _________________________ 12.___________ ;___________13._____________________________ 14.__________________________ 三、解答题:(共80分) 15.(12分)16.(12分)B1C17.(14分)18.(14分)19.(14分)20.(14分)广东省佛山一中2010-2011学年高二下学期期末考试(数学理)试题答案一、选择题:(5×10=50)DDCAB CADBD 二、填空题:(5×4=20)(11)1 (12)125;41 (13) ⎪⎭⎫⎝⎛552,1 (14) nn x x 2)12(+- 15. 已知复数i z 311+=,ααsin cos 32i z +=,求复数21z z z ⋅=实部的最值.解:由已知得ααααααsin 3cos 33sin cos 3)sin cos 3)(31(21-++=++=⋅=i i i i z z z……….2分)cos 33(sin )sin 3cos 3(αααα++-=i ……….4分的实部为z ∴ααs in 3c o s 3t -=………..6分⎪⎭⎫⎝⎛-=απ6sin 32 ………10分 32max =∴t , 32m in -=t …………12分16.解:解法一(1)设侧棱长为x ,取BC 中点E ,则AE ⊥面11BB C C ,∴45ADE ∠=︒∴tan 45AEED︒==x =分过E 作EF BD ⊥于F ,连AF ,则AF BD ⊥,AFE ∠为二面角A BD C --的平面角∵sin EF BE EBF =∠=,AE =tan 3AE AFE EF∠==………… 6分(2)由(1)知BD ⊥面AEF ,∴面AEF ⊥面ABD过E 作EG AF ⊥于G ,则EG ⊥面ABD ∴30AE EF EG AF ==∴C到面ABD 的距离为2EG = ………… 12分解法二:(1)求侧棱长x = ……………3分 取BC 中点E , 如图建立空间直角坐标系E xyz -, zAA 1AB CDA 1B 1C 1F G E则(0,A,(1,0,0)B-,(1,0,0)C,0) D设(,,)n x y z=是平面ABD的一个法向量,则由0 n ABn AD⎧=⎪⎨=⎪⎩得(3,1) n=--而(0,EA=是面BCD的一个法向量∴10cos10EA nEA nEA n<>==-.而所求二面角为锐角,3,tan>=<∴……6分(2)∵(1,CA=-∴点C到面ABD 的距离为30CA ndn==…… 12分17.解:(Ⅰ)依题意可知,ξ的可能取值最小为4.当ξ=4时,整个比赛只需比赛4场即结束,这意味着甲连胜4场,或乙连胜4场,于是,由互斥事件的概率计算公式,可得P(ξ=4)=240441122C⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=18.……………..2分当ξ=5时,需要比赛5场整个比赛结束,意味着甲在第5场获胜,前4场中有3场获胜,或者乙在第5场获胜,前4场中有3场获胜.显然这两种情况是互斥的,于是,P(ξ=5)=234334111222C-⎡⎤⎛⎫⎛⎫⋅⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦=14,…………….4分∴P(ξ>5)=1-[P(ξ=4)+P(ξ=5)]=1-[18+14]=58.…………….6分即ξ>5的概率为58.(Ⅱ)∵ξ的可能取值为4,5,6,7,仿照(Ⅰ),可得P(ξ=6)=235335111222C-⎡⎤⎛⎫⎛⎫⋅⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦=516,………………..8分P(ξ=7)=236336111222C-⎡⎤⎛⎫⎛⎫⋅⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦=516,………………..10分∴ξ的分布列为:E………..12分ξ的数学期望为:E ξ=4·18+5·14+6·516+7·516=9316.……………14分 18.解:(1)圆心坐标为)22,22(--------2分 设圆心的极坐标为),(θρ则1)22()22(22=-+-=ρ----4分 所以圆心的极坐标为)45,1(π------ 6分(2)直线l 的极坐标方程为22)cos 22sin 22(=+θθρ ∴直线l 的普通方程为01=-+y x ----8分∴圆上的点到直线l 的距离2|1sin 22cos 22|-+-+-=θθr r d ……10分即2|1)4sin(22|-++-=πθr d -----11分∴圆上的点到直线l 的最大距离为32122=++r -----13分∴ 224-=r ---- 14分19.(Ⅰ)11,215n n n a a a a +==+12133532111215a a a ∴===+⨯+3317a = 4323a =-------------------------3分;(Ⅱ)由⑴知分子是3,分母是以首项为5公差为6的等差数列∴猜想数列{}n a 通项公式:361n a n =----------------------6分 用数学归纳法证明如下:① 当1n =时,由题意可知135a =,命题成立. ② 假设当n k =(1,)k k N ≥∈时命题成立,即361k a k =-,----8分 那么,当1n k =+时,133361321656(1)12161k k k a k a a k k k +-====+++-⨯-- 也就说,当1n k =+时命题也成立----------------------------------------------13分综上所述,数列{}n a 的通项公式为361n a n =----------------------------14分 20.解:2221()1'()x a x a x af x x x x x x ----=+=-=(0x >) ………… 2分 (I )因为曲线()y f x =在点(1,(1)f )处的切线与直线12y x =-平行,所以'(1)-2f =,即12, 3.a a -=-=解得…………………4分(II)当01a <≤时,'()0f x >在(1,2)上恒成立, 这时()f x 在[1,2]上为增函数min ()(1)1f x f a ∴==-. ………………………6分当12a <<时,由'()0f x =得,(1,2)x a =∈对于(1,)x a ∈有'()0,f x <()f x 在[1,a]上为减函数,对于(,2)x a ∈有'()0,f x >()f x 在[a ,2]上为增函数,min ()()ln f x f a a∴==. …………………………………10分当2a ≥时,'()0f x <在(1,2)上恒成立,这时()f x 在[1,2]上为减函数,min ()(2)ln 212af x f ∴==+-. ……………………………12分综上,()f x 在[1,2]上的最小值为①当01a <≤时,min ()1f x a =-,②当12a <<时,min ()ln f x a=,③当2a ≥时,min ()ln 212a f x =+-. ………………14分。
(整理)佛山一中届高二下学期期末考试(化学)【含答案与评分标准】

佛山一中2012届高二下学期期末考试化学试卷第一部分选择题(共44分)一、单选题(本题包括10小题,每小题2分,共20分,每小题只有1个选项符合题意。
)1.下列装置或操作能达到实验目的的是()2.下列是摘取学生实验报告单中的语句,其中说法正确的是( )A.日常生活中不能用粥汤检验碘盐中是否含有KIO3B.将铁屑、浓溴水、苯混合可制得溴苯C.用蒸馏方法除去乙醇中的水D.洗涤沉淀时,应用玻璃棒轻轻搅拌,使得沉淀表面上的杂质溶于水中3.下列各有机物的名称错误的是()A.3-甲基-1-戊炔B.3-甲基-2-丁烯C.2,2—二甲基丙烷D.3-甲基-1-丁烯4.下面四个化学反应中,有一个化学反应与其他三个类型不同的是:()A.CH3CH2OH + CH3COOH CH3COOCH2CH3 + H2OB.CH3CH2OH 浓硫酸170℃CH2=CH2↑+H2OC.2CH3CH2OH 浓硫酸140℃CH3CH2OCH2CH3 + H2OD.CH3CH2OH + HBr CH3CH2Br + H2O5.为检验某卤代烃(R—X)中的X元素,有下列实验操作:①加热;②加入AgNO3溶液;③取少量卤代烃;④加入稀硝酸酸化;⑤加入NaOH溶液;⑥冷却。
正确操作的先后顺序是()A.③①⑤⑥②④B.③②①⑥④⑤C.③⑤①⑥④②D.③⑤①⑥②④6.等物质的量的下列各组物质完全燃烧,消耗等量氧气的是()A.乙醇和乙醛 B.乙醇和乙烯 C.乙烯和乙醛 D.乙醇和乙烷浓H2SO47.由2-氯丙烷为主要原料制取1,2-丙二醇CH3CH(OH)CH2OH时,经过的反应为()[来A.加成—消去—取代B.消去—加成—取代C.取代—消去—加成D.取代—加成—消去8.下列涉及有机物的性质或应用的说法不正确的是()A.干馏煤可以得到甲烷、苯和氨等重要化工原料B.用于奥运“祥云”火炬的丙烷是一种清洁燃料C.用大米酿的酒在一定条件下密封保存,时间越长越香醇D.纤维素、蔗糖、葡萄糖和脂肪在一定条件下都可发生水解反应9.下列除去杂质的方法正确的是()① 除去乙烷中少量的乙烯:光照条件下通入Cl2,气液分离;② 除去乙酸乙酯中少量的乙酸:用饱和碳酸钠溶液洗涤,分液、干燥、蒸馏;③ 除去CO2中少量的SO2:气体通过盛饱和碳酸钠溶液的洗气瓶;④ 除去乙醇中少量的乙酸:加足量生石灰,蒸馏。
广东省佛山市高二数学下学期期末考试试卷 理(扫描版)(1)

广东省佛山市2014-2015学年高二数学下学期期末考试试卷理(扫描版)2013-2014学年第二学期理科数学参考答案一、 选择题:二、填空题:11、30 12、95% 13 14、(0,1) 三、解答题:15.解(1) 略 (3分)(2)x =46543+++=4.5 y =45.4435.2+++=3.5 866543222212=+++=∑=n i i x (6分) 266.54 4.5 3.566.563ˆ0.7864 4.58681b-⨯⨯-===-⨯- (8分) ˆˆ 3.50.7 4.50.35=-=-⨯=ay bx (10分) 故线性回归方程为0.70.35=+y x (11分)(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7⨯100+0.35=70.35故耗能减少了90-70.35=19.65(吨) (14分)16.解(1)14402266=A A (3分)(2)1444433=A A (6分)(3) 2520277=A 或252057=A (10分) (4)372055666677=+--A A A A 或37205516551515=+A A A A A (14分) 17.证明:(1)当n =1时,左边=1,右边=22124⨯=1, ∴等式成立. (2分)(2)假设当n =k 时,等式成立,即13+23+33+……+k 3=22(1)4k k +. (4分)那么,当n =k +1时,有13+23+33+……+k 3+(k +1)3=22(1)4k k ++(k +1)3. (6分) =(k +1)2(24k +k +1)=(k +1)22444k k ++=22(1)(2)4k k ++ =2(1)[(1)1]4k k +++. (9分) 这就是说,当n =k +1时,等式也成立. (10分) 根据(1)和(2),可知对n ∈N *等式成立. (12分)18.解:根据月工资的分布列,可得EX 1=1200×0.4+1400×0.3+1600×0.2+1800×0.1=1400. (2分)DX 1=(1200-1400)2×0.4+(1400-1400)2×0.3+(1600-1400)2×0.2+(1800-1400)2×0.1=40000 (4分)EX 2=1000×0.4+1400×0.3+1800×0.2+2200×0.1=1400 (6分)DX 2=(1000-1400)2×0.4+(1400-1400)2×0.3+(1800-1400) 2×0.2+(2200-1400)2×0.1=112000 (8分)因为EX 1=EX 2,DX 1<DX 2.所以两家单位的月工资均值相等,但甲单位不同职位的工资相对集中,乙单位不同职位的工资相对分散. (12分) 这样,如果你希望不同职位的工资差距小一些,就选择甲单位;如果你希望不同职位的工资差距大一些,就选择乙单位. (14分) 注:最后一步言之有理就给2分.19.证明:(用反证法) 假设这三条抛物线没有一条与x 轴有两个交点, (1分) 则方程022=++a cx bx ,022=++c bx ax ,022=++b ax cx均无解或者只有两个相等的解 (4分)则21440∆=-≤b ac ,22440∆=-≤c ab ,23440∆=-≤a bc (7分) 所以222(44)(44)(44)0-+-+-≤b ac c ab a bc即2222222220++-+-+-≤a b c ac ab bc即222()()()0-+-+-≤a b b c a c ......... ① (9分) 因为,,a b c 是互不相等的实数,所以222()()()0-+-+->a b b c a c ......... ② (10分)①式 ②式矛盾,故假设不成立,所以原命题成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012-2013学年第二学期 期末考试高二年级数学(理科)试题考试时间:120分钟 满分150分一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.把正确答案的对应符号填涂在答题卡上. 1. 设是虚数单位,复数为纯虚数,则实数a 为A .2B .C . D. -22.若实数a 满足|2a-1|< 3,那么a 的取值范围是ks5uA. 0<a<2B. <a<2C. -1<a<2D. -2<a<33. 某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x 小时,原油温度(单位:℃)为),50(831)(23≤≤+-=x x x x f ,那么原油温度在第3小时度的瞬时变化率为 A .0 B .3 C . 8 D . 11 4.设随机变量ξ服从正态分布N(0,1),若P(ξ>1)= p ,则P(-1<ξ<0)=A .p +21B .p -21 C .1-p D .1-2p5.类比平面正三角形的“三边相等,三内角相等”的性质,可知正四面体的下列哪些性质,你认为比较恰当的是( 注:正四面体是侧面与底面为全等的正三角形的三棱锥 )① 各棱长相等,同一顶点上的任两条棱的夹角都相等;② 各个面都是全等的正三角形,相邻两个面所成的二面角都相等; ③ 各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等。
A .①②③ B .①② C .① D .③6. 一工厂生产的100个产品中有90个一等品,10个二等品,现从这批产品中抽取4个,则其中恰好有一个二等品的概率为ks5uA .41004901C C -B .4100390110490010C C C C C + C .4100110C C D .4100390110C C C7.已知R 上的可导函数的图象如图所示,函数的两个零点分别为-2和2,两个极值点分别为-1和1,若为函数的导函数,则不等式的解集为A.B.C. D.8.数组(x,y,z ),其中,且x<y ≤z,如(0,1,1),(1,2,3),(8,9,9),这样的数组共有A.45个B.120个C.165个D.576 二、填空题:本大题共6小题,每小题5分,满分30分。
9. 已知X 的分布列为设Y=2X+3. 则ks5u 10. 二项式展开式中的项的系数为________ .(用数字作答)11.在平面直角坐标系xoy 中,直线l 的参数方程是(其中t 为参数),以Ox 为极值的极坐标系中,圆C 的极坐标方程为,则圆心到直线的距离为___________.12.如图,直线2x+y-3=0与抛物线围成的平面区域面积为____________.13.2013年是6月11日17时38分“神十”飞天, 在“神十”飞天确定航天员时,后期有6名航天员(5男1女)入围,其中第一次飞行的女航天员王亚平必选,其它5名男天员中有2位老航天员和3名新航天员,航天员继续沿用“以老带新和两男一女”模式选定,即要求至少1名老航天员入选,问本次从6名航天员中选3名航天员的方法有____________种方法?第12题图第7题图14.点P ()是曲线上的一个动点,曲线C 在点P 处的切线与x,y 轴分别交于A,B 两点,点O 是坐标原点,有下列三个命题① PA=PB;② △OAB 的面积是定值;③ 曲线C 上存在两点M ,N ,使得△OMN 为等腰直角三角形。
其中真命题的个数是______(填写命题的代号)三、解答题:本大题共6小题,满分80分。
解答须写出文字说明、证明过程和演算步骤. 15.(本题满分12分) (1),求证:; (2)求证:16.(本题满分12分)蓝球运动员比赛投篮,命中得1分,不中得0分,已知运动员甲投篮命中率的概率为P .(1)若投篮1次得分记为ξ,求方差D ξ的最大值;(2)当(1)中D ξ取最大值 时,求运动员甲投5次篮得分为4分的概率.17.(本题满分14分)为提高广东中小学生的健康素质和体能水平,广东省教育厅要求广东各级各类中小学每年都要在体育教学中实施“体能素质测试”,测试总成绩满分为100分.根据广东省标准,体能素质测试成绩在[85,100]之间为优秀;在[75,85)之间为良好;在[)75,60之间为合格;在(0,60)之间,体能素质为不合格.现从佛山市某校高一年级的900名学生中随机抽取30名学生的测试成绩如下:(1)在答题卷上完成频率分布表和频率分布直方图,并估计该校高一年级体能素质为优秀的学生人数;(2)在上述抽取的30名学生中任取2名,设ξ为体能素质为优秀的学生人数,求ξ的分布列和数学期望(结果用分数表示);65,84,76,70,56,81,87,83,91,75,81,88,80,82,93, 85,90,77,86,81,83,82,82,64,79,86,68,71,89,96.18.(本题满分14分) 已知函数(1)若曲线y=f(x)在点(a,f(a))处与直线y=b 相切,求a 与b 的值; (2)若曲线y=f(x)与直线y=b 有两个不同交点,求b 的取值范围。
19.(本题满分14分)如图,),(111y x P 、),(222y x P 、…、),(n n n y x P)0(21n y y y <<<< 是曲线C :)0(32≥=y x y 上的n 个点,点)0,(i i a A (n i 3,2,1=)在x 轴的正半轴上,且ii i P A A 1-∆是正三角形(0A 是坐标原点). (1)求1a 、2a 、3a 的值; (2)求出点(n *∈N )的横坐标和点横坐标的关系式;(3)根据(1)的结论猜想关于n 的表达式,并用数学归纳法证明.20.(本题满分14分)已知函数)2()2()1ln()(2≤-++=m xm x x f(1)若)(x f 在0=x 处取得极值,求m 的值; (2)讨论)(x f 的单调性; (3))311ln(2n n a +=记,且数列}{n a 前n 项和为n s ,求证:21s <n 2012-2013年度第二学期期末考试高二级数学(理科)试卷一、 选择题:本大题共8小题,每小题5分,满分40分.第17题图第19题图二、填空题:本大题共6小题,每小题5分,满分30分。
9.___________; 10. ____________; 11.______________;12.___________; 13. ____________; 14.______________;三.解答题:本大题共6小题,满分80分。
解答须写出文字说明、证明过程和演算步骤.15.(本题满分12分)(1)(2)16.(本题满分12分)17.(本题满分14分)18.(本题满分14分)19.(本题满分14分)2 2 4 1020.(本题满分14分)2012-2013学年第二学期期末考试数学(理科)试题答案一、选择题:本大题共8小题,每小题5分,满分40分。
ACBB ADDC8.C提示:由题意可知,三个数互不相同的数组共有个,当y=z时,故数组共有120+45=165个二、填空题:本大题共6小题,每小题5分,满分30分。
9.; 10. -160;11. 1 ; 12.15; 13.7; 14.①②14.解析:,故切线斜率为,点P ()处的切线方程为即+y-=0 ∴A(2 ,B(0,),P ()∴PA=PB= 故①正确ks5u△OMN 的面积S=2=2 故②正确;曲线C 上不存在两点M,N 使△OMN 为等腰直角三角形,所以③不正确。
三、解答题15(12分).(1)证明:(综合法)∵……3分把上式相加,并整理得222a b c ab bc ca ++≥++. ……4分 当且仅当a b c ==时等号成立. ……5分 故222a b c ab bc ca ++≥++ ……6分 (2)分析法:要证:就要证:……7分即证: ……9分即证:2ks5u即证:即证: ……10分因为 成立 ……11分故 ……12分16(12分). 解:(1)依题意,ξ的分布列为 ∴……1分=……4分∴ 当时,取最大值,且最大值为 ……6分(2)由(1)可知P=,投5次蓝得分为,则 ……8分那么P( 11分则运动员甲投5次篮得分为4分概率为。
……12分 17.(14分)解:评分说明:正确填表2分;正确完成频率分布直方图2分. 说明:频率分布表对1个、2个、3个给1分;对4个给2分.频率分布直方图对一个给1分;对2个给2分.根据抽样,估计该校高一学生中体能素质为优秀的有1090030030⨯=人 ………6分ks5u(2) ξ的可能取值为0,1,2. ………7分211220*********30303038409(0),(1),(2).878787C C C C P P P C C C ξξξ⋅========= ……8分 (上述3个对一个给1分)∴ξ分布列为:所以,数学期望38409582()012878787873E ξ=⨯+⨯+⨯==. (14)分18.(14分)解析:由f(x)= 得2分 (1)因为曲线y=f(x)在点(a,f(a))处一直线为y=b,因此, f(a)=b 于是= a (2+cosa)=0 ……3分 且 ……4分ks5u解得 a=0且b=1 ……6分(2)由(1), 于是当x>0时,, f(x)在(0,+∞)单调递增, ……7分 当x<0时, f(x)在(-∞,0)上为单调递减 ……8分当x=0时f(x)取得极小值页是最小值为1 ……9分当1b ≤时,曲线()y f x =与直线y b =最多只有一个交点; ……10分当1b >时,2(2)(2)421f b f b b b -=≥-->421b b b -->, (0)1f b =<, 所以存在1(2,0)x b ∈-,2(0,2)x b ∈,使得12()()f x f x b ==. ……12分由于函数()f x 在区间(,0)-∞和(0,)+∞上均单调,所以当1b >时曲线()y f x =与直线y b =有且只有两个不同交点. ……13分综上可知, b 的取值范围是(1,)+∞. ……14分19.解:(Ⅰ)依题意,O 直线方程为与曲线方程联立 解得点的横坐标为,由中点坐标公式得 ……2分 同理:直线方程为代入求得 ……3分 再由中点坐标公式得直线方程为代入求得再由中点坐标公式得 ……4分(2)依题意,得 ① ……5分 直线的方程为坐标满足方程,则有 ② ……6分把①代入②式得 即 ③ 7分 因为 ④ ……8分把③式代入④得)(23)23(121--+=-⋅n n n n a a a a ,即)(2)(121n n n n a a a a +=---. ……9分(3)由(Ⅰ)可猜想:)(),1(*∈+=N n n n a n . 10分下面用数学归纳法予以证明:(1)当1n =时,命题显然成立; (2)假定当n k =时命题成立,即有(1)n a k k =+, ……11分则当1n k =+时,由归纳假设及211()2()k k k k a a a a ++-=+得211[(1)]2[(1)]k k a k k k k a ++-+=++,即2211()2(1)[(1)][(1)(2)]0k k a k k a k k k k ++-+++-⋅++=,解之得:1(1)(2)k a k k +=++ (1(1)k k a k k a +=-<不合题意,舍去),即当1n k =+时,命题成立. ……13分由(1)、(2)知:命题成立. ……14分20.(本题满分14分)ks5u(1)0x 212)(2/=-++= ,m xx x f 是)(x f 的一个极值点,则 2m =∴,验证知m=2符合条件 …… 4分(2)22/1)2(22)-m )(x m x x x f +-++=( …… 5分 1)若m=2时,()+∞∴,0)(在x f 单调递增,在()0,∞-单调递减;2)若 ⎩⎨⎧≤∆<02m 时,当0)(1/≤≤x f m 时,∴f(x)在R 上单调递减 ……7分3)若 234123410)(2122/--+-----+-+-=<<m m m m m m x f m 、有两根为时, )2341,2341()(22--+-+---+---∴m m m m m m x f 在上单调减),2341(),2341,-()(22+∞--+-+---+---∞m m m m m m x f 在上单调增 …… 9分综上所述,若时,1≤m ∴f(x)在R 上单调递减,若m=2时, ()+∞∴,0)(在x f 单调递增,在()0,∞-单调递减; 若时,21<<m)2341,2341()(22--+-+---+---m m m m m m x f 在上单调减 ),2341(),2341,-()(22+∞--+-+---+---∞m m m m m m x f 在上单调增 ………………………………………………………………10分(3)由(2)知,时,1=m ∴f(x)在R 上单调递减,当()0)0()(,0=<+∞∈f x f x 时,由∴……11分 ∴…………13分=……14分 ks5u。
