重庆大学-数学实验-3微分方程
数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年

数学实验_重庆大学中国大学mooc课后章节答案期末考试题库2023年1.无向图中边的端点地位是平等的、边是无序点对。
而有向图中边的端点的地位不平等,边是有序点对,不可以交换。
参考答案:正确2.人口数量与下列因素都有关,人口基数、出生率、死亡率、年龄结构、性别比例、医疗水平、工农业生产水平、环境、生育政策等等。
参考答案:正确3.一元5次代数方程在复数范围内有多少个根?参考答案:54.任何贪心算法都能求出最优解。
参考答案:错误5.二维插值函数z=interp2(x0,y0,z0,x,y,’method’)中,method的缺省值是()参考答案:linear6.在当前文件夹和搜索路径中都有文件ex1.m,在命令行窗口输入ex1时,则执行的文件是当前文件夹中的ex1.m参考答案:正确7.下列关于Dijkstra算法的哪些说法正确参考答案:Dijkstra算法是求加权图G中从某固定起点到其余各点最短路径的有效算法;_Dijkstra算法的时间复杂度为O(n2),其中n为顶点数;_Dijkstra算法可用于求解无向图、有向图和混合图的最短路径问题;8.如果x=1: 2 : 10,则x(1)和x(5)分别是( )参考答案:1,99.人口是按指数规律无限增长的。
参考答案:错误10.在包汤圆问题的整个建模过程,包括了如下几个步骤(1)找出问题涉及的主要因素(变量),重新梳理问题使之更明确(2)作出简化、合理的假设(3)用数学的语言来描述问题(4)用几何的知识解决问题(5)模型应用参考答案:正确11.下面程序所解的微分方程组,对应的方程和初始条件为:(1)函数M文件weif.m:function xdot=weif(t, x)xdot=[3*x(1)+x(3);2*x(1)+6;-3*x(2)^2+2*x(3)];(2)脚本M文件main.m:x0=[1,2,3] ;[t,x]=ode23(‘weif’,[0,1],x0),plot(t,x’),figure(2),plot3(x( :,1),x( :,2),x( :,3)参考答案:___12.某公司投资2000万元建成一条生产线。
常微分方程实验报告

常微分方程实验报告一、实验目的常微分方程是数学分析和实际应用中非常重要的一部分,本次实验的主要目的是通过实际操作和计算,深入理解常微分方程的概念、性质和求解方法,并能够将其应用到实际问题中,提高我们解决数学问题和实际应用问题的能力。
二、实验原理常微分方程是指含有一个自变量和一个未知函数及其导数的等式。
求解常微分方程的方法有很多,常见的有变量分离法、一阶线性方程的求解方法(如常数变易法)、恰当方程的求解方法(通过积分因子)等。
对于一阶常微分方程,形如\(y' + p(x)y = q(x)\)的方程,可以使用积分因子\(e^{\int p(x)dx}\)来求解。
对于可分离变量的方程,形如\(g(y)dy = f(x)dx\),可以通过分别积分求解。
三、实验内容(一)一阶常微分方程的求解1、求解方程\(y' + 2xy = 2x\)首先,计算积分因子\(e^{\int 2xdx} = e^{x^2}\),然后将方程两边乘以积分因子得到:\((ye^{x^2})'= 2xe^{x^2}\)两边积分可得\(ye^{x^2} = e^{x^2} + C\),解得\(y =1 + Ce^{x^2}\)2、求解方程\(xy' y = x^2\)将方程化为\(y' \frac{y}{x} = x\),这里\(p(x) =\frac{1}{x}\),积分因子为\(e^{\int \frac{1}{x}dx} =\frac{1}{x}\)。
方程两边乘以积分因子得到\((\frac{y}{x})'= 1\),积分可得\(\frac{y}{x} = x + C\),即\(y = x^2 + Cx\)(二)二阶常微分方程的求解1、求解方程\(y'' 2y' + y = 0\)特征方程为\(r^2 2r + 1 = 0\),解得\(r = 1\)(二重根),所以通解为\(y =(C_1 + C_2x)e^x\)2、求解方程\(y''+ 4y = 0\)特征方程为\(r^2 + 4 = 0\),解得\(r =\pm 2i\),所以通解为\(y = C_1\cos(2x) + C_2\sin(2x)\)(三)应用常微分方程解决实际问题1、考虑一个物体在受到与速度成正比的阻力作用下的运动,其运动方程为\(m\frac{dv}{dt} = kv\)(其中\(m\)为物体质量,\(k\)为阻力系数),求解速度\(v\)随时间\(t\)的变化。
重庆大学--数学模型--数学实验作业四
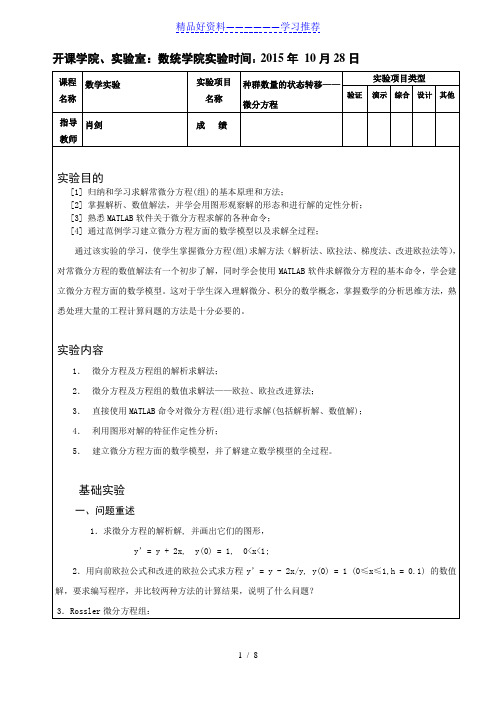
开课学院、实验室:数统学院实验时间:2015年10月28日当固定参数b=2, c=4时,试讨论随参数a 由小到大变化(如a ∈(0,0.65))而方程解的变化情况,并且画出空间曲线图形,观察空间曲线是否形成混沌状?4.Apollo 卫星的运动轨迹的绘制二、实验过程1.编辑程序代码Untitle1:s=dsolve('Dy=y+2*x','y(0)=1','x')ezplot(s,[0,1])运行结果如下:s =3*exp(x) - 2*x – 2图形为:1133121331212222121()()2,2,1/82.45,1,(),()(0) 1.2,(0)0,(0)0,(0) 1.04935751x x x y x r r y y y x y r r r x y r x y x x y y μμμμμμμμμμμ+-=+--=-+--==-=++=-+====-⎪⎩⎪⎨⎧-+=+=--=)('''c x z b z ayx y z y x2.编写程序代码Untitle2:clcy=dsolve('Dy=y-2*x/y','y(0)=1','x')ezplot(y,[0,1])hold onx=[];x(1)=0;y1(1)=1;y2(1)=1;for n=1:10x(n+1)=x(n)+0.1;y1(n+1)=1.1*y1(n)-0.2*x(n)/y1(n);k1=y2(n)-2*x(n)/y2(n);k2=y2(n)+0.1*k1-2*x(n)/(y2(n)+0.1*k1);y2(n+1)=y2(n)+0.05*(k1+k2);endplot(x,y1,'k:',x,y2,'k-.')运行得到y =(2*x + 1)^(1/2),这是解析解。
2024年考研数学偏微分方程题目详解与答案

2024年考研数学偏微分方程题目详解与答案在2024年的考研数学试卷中,偏微分方程题目一直是考生们关注和备考的重点。
本文将详细解析2024年考研数学偏微分方程题目,并提供详细的解答和答案。
一、第一题题目描述:给定二阶常系数线性偏微分方程 $\frac{{\delta^2u}}{{\delta x^2}} + c\frac{{\delta u}}{{\delta t}} + ku = f(x, t)$,其中 $u = u(x, t)$ 为未知函数,$c, k$ 为常数,$f(x, t)$ 为已知连续函数。
要求求解此偏微分方程。
解析:根据题目所给的偏微分方程可知,我们需要求解二阶常系数线性偏微分方程。
此类方程的典型特点是对时间 $t$ 的导数项和对空间$x$ 的二阶导数项。
我们可以采用特征线法来求解此类方程。
首先,我们设方程的通解形式为 $u(x, t) = X(x)T(t)$,其中$X(x)$ 和 $T(t)$ 分别是 $x$ 和 $t$ 的函数。
将通解带入方程中得到:$\frac{{X''}}{{X}} + c\frac{{T'}}{{T}} + k = \frac{{f(x, t)}}{{XT}}$由于方程的左侧只与 $x$ 有关,右侧只与 $t$ 有关,故两侧等于某个常数 $-\lambda$。
得到两个常微分方程:$X'' + \lambda X = 0$ 和 $T' + \left(c -\lambda\right) T = 0$对于方程 $X'' + \lambda X = 0$,根据 $\lambda$ 的值分为三种情况讨论:1. 当 $\lambda > 0$ 时,方程的通解为 $X(x) = A\cos(\sqrt{\lambda}x) + B\sin(\sqrt{\lambda}x)$。
2. 当 $\lambda = 0$ 时,方程的通解为 $X(x) = Ax + B$。
重庆大学出版社高等数学题库参考答案

第五章不定积分1(直接积分法、换元积分法)一、单选题1.设)(x f 是可导函数,则⎰'))((dx x f 为(A ).A.)(x fB.C x f +)(C.)(x f 'D.C x f +')(2.函数)(x f 的(B )原函数,称为)(x f 的不定积分.A.任意一个B.所有C.唯一D.某一个3.⎰=+=)(,2cos )(x f C x e dx x f x则(A ).A.)2sin 22(cos x x e x -B.C x x e x +-)2sin 22(cosC.x e x 2cosD.x e x2sin4.函数x e x f =)(的不定积分是(B ). A.x e B.c e x + C.x ln D.c x +ln5.函数x x f cos )(=的原函数是(A ). A.c x +sin B.x cos C.x sin - D.c x +-cos6.函数211)(x x f -=的原函数是(A ).A.c x x ++1 B.x x 1- C.32x D.c xx ++12 7.设x 2是)(x f 的一个原函数,则[]='⎰dx x f )((B )A.x 2B.2C.2x D.-28.若ce dx e xx +=⎰,则⎰xd e x22=(A )A.c ex+2 B.c e x + C.c e x +-2 D.c e x +-29.函数x x f sin )(=的原函数是(D ) A.c x +sin B.x cos C.x sin - D.c x +-cos10.若)()()()()(x G x F x f x G x F '-'的原函数,则均为、=(B )A.)(x fB.0C.)(x FD.)(x f ' 11.函数211)(xx f +=的原函数是(A ) A.c xx +-1B.x x 1-C.32xD.c x x ++1212.函数211)(x x f -=的原函数是(A ) A.c xx ++1 B.x x 1- C.32x D.c x x ++1213.若函数)(x f 、)(x g 在区间),(b a 内可导,且)()(x g x f '=',则(B ) A.)()(x g x f = B.C x g x f +=)()(C.)()(x g x f ≠D.不能确定)(x f 与)(x g 之间的关系 14.若)()(x f x F =',则下列等式成立的是(B ). A.C x f dx x F +='⎰)()( B.⎰+=C x F dx x f )()(C.⎰+=C x f dx x F )()(D.C x F dx x f +='⎰)()(15.经过点)1,0(-,且切线斜率为x 2的曲线方程是(D ). A.2x y = B.2x y -= C.12+=x y D.12-=x y 二.填空题 1.)25ln(2125x d x dx --=-.2.)1(212x d xdx --=.3.C aa dx a xx +=⎰ln .4.设)(x f 是连续函数,则dxx f dx x f d )()(=⎰.5.xx cos 2+的原函数是x x sin 2+.6.]4)3[(21)3(2---=-x d dx x .7.C x xdx +=⎰7sin 717cos .8.)1(ln 3133-=x x a d adx a .9.)3(cos 313sin x d xdx -=.10.C x dx x x +=⎰2ln 21ln .11.C x dx x +=⎰4341.12.)C 41(2222+-=--x x e ddx xe .13.C x xdx x +=⋅⎰2sin 21sin cos .14.C x dx x +=+⎰3arctan 319112. 15.C x x dx x +-=⎰)sin (212sin 2.16.⎰+='C x f dx x f )2(21)2(.17.设⎰+=.)()(C x F dx x f ,若积分曲线通过原点,则常数)0(F C -=.18.)3(arctan 31912x d x dx=+. 19.)(2122x x e d dx xe =.20.已知xx f C x dx x f 2sin )(,sin )(2=+=⎰则.21.设)()()(21x f x F x F 是、的两个不同的原函数,且=-≠)()(,0)(21x F x F x f 则有 C.22.C x x dx x x +-=+-⎰222111 23.Ce dx e xxx +-=⎰1121.24.)1ln(21122-=-x d dx x x .25.若x x f sin )(的导函数是,则)(x f 的原函数为Cx +-sin .26.设)(3x f x 为的一个原函数,则dxx x df 23)(=.27.)2cos 41(812sin x d xdx -=28.x x sin 2+的一个原函数是x x cos 313-.29.)3(cos 33sin x d dx x -=.30.Cx xdx +-=⎰cos ln tan .31.()C x dx x +--=-⎰)21sin(2121cos .32.Cx xdx +=⎰tan sec 2. 33.C x x dx +-=⎰3cot 313sin 2.34.设x 2是)(x f 的一个原函数,则⎰='])([dx x f 2.三.判断题 1.⎰+=cx xdx cos sin (×)2.x x e dx e =⎰(×)3.⎰-=.cos sin x xdx (×)4.⎰+-=cx xdx cos sin (√)5.)21sin()]21[sin(x dx x -=-⎰(×)6.⎰+-=c x xdx sin cos (×)四.计算题1.求不定积分dx x x ⎰+21.解:原式=C x x d x ++=++⎰23222)1(31)1(1212.求不定积分dx x ⎰-31.解:原式=C x +--3ln3.求不定积分⎰+dx e e xx 1.解:原式=C e e d e x x x ++=++⎰)1ln()1(11 4.求不定积分⎰+-dx x x x )3sin 21(.解:原式=C x x x +++ln 3cos 225.求不定积分⎰-dx xe x 2.解:原式=C e x +--221 6.求不定积分dx x x⎰+12.解:原式=C x ++)1ln(2127.求不定积分dx x x ⎰+2)72(.解:原式=C xx x ++⋅+7ln 24914ln 1422ln 24 8.求不定积分⎰+dx x 10)12(.解:原式=C x ++11)12(2219.求不定积分⎰+-dx xx x )1)(1(.解:原式=C x x x x x +-+-221522210.求不定积分⎰xdx 2sin .解:原式=C x x +-2sin 4121 11.求不定积分⎰dx xx 22cos sin1.解:原式=C x x +-cot tan 12.求不定积分dx x ⎰+321.解:原式=C x ++32ln 2113.求不定积分xdx x arctan 112⎰+.解:原式=C x +2)(arctan 21 14.求不定积分⎰-dx x x 4313.解:原式=C x +--41ln 43 15.求不定积分⎰+dx x 2411.解:原式=C x +2arctan 21 16.求不定积分⎰+dx x x)5(3.解:原式=C x x++5ln 5414 17.求不定积分⎰-dx e x5.解:原式=C e x +--551五.应用题1.设一质点作直线运动,已知其加速度为t t a sin 3122-=,如果0=t 时3,500-==s v , 求(1)t v 与的函数关系;(2)t s 与的函数关系.解:32sin 3)(2sin 3)2cos 34()(2cos 34)(cos 34)sin 312()(43,04335,032-++=−−−→−+++=++=++=−−→−++=-=-====⎰⎰t t t t s c t t t dt t t t s t t t v C t t dt t t t v s t v t2.求经过点(0,0),且切线斜率为x 2的曲线方程. 解:20,022x y C x xdx y y x =−−−→−+====⎰3.一物体由静止开始运动,t 秒末的速度是23t (米/秒),问(1)在3秒末物体与出发点之间的距离是多少?(2)物体走完360米需多长时间? 解:设运动方程为:30,032)(3)(t t S C t dt t t S S s t =−−→−+=====⎰(1)当3=t时,27)3(=S (米)(2)当.360360)(33秒=⇒==t t t S4.一曲线过原点且在曲线上每一点),(y x 处的切线斜率等于3x ,求这曲线的方程. 解:40,0434141x y C x dx x y y x =−−−→−+====⎰ 5.已知物体由静止开始作直线运动,经过t 秒时的速度为180360-t (米/秒),求3秒末物体离开出发点的距离. 解:t t t S C t tdt t S s t 180180)(180180180)-60t 3()(20,02-=−−→−+-====⎰.当3=t时,1080)3(=S (米).6.求经过点)1,(e ,且切线斜率为x 1的曲线方程.解:x y C x dx xy y e x ln ln 11,=−−→−+====⎰.7.求经过点(0,0),且切线斜率为211x+的曲线方程.解:x y C x dx x y y x arctan arctan 110,02=−−−→−+=+===⎰.第五章不定积分2一.单选题1.下列分部积分法中,dv u ,选择正确的是(A ).A.⎰==xdxdv x u xdx x 2sin 2sin ,, B.xdxdv u xdx ln ,1,ln ==⎰C.dxx dv e u dx e x x x22,,==--⎰D.xdx dv e u dx xe xx==⎰,,2.⎰⎰-=)(2arctan d 2arctan Axd x x x x .A.x arctan2B.x arctan4C.x arctan2-D.x arctan4-3.=⎰2-4d x x (A).A.C x +2arcsinB.C x +arcsinC.Cx +2arccos D.C x +arccos二.判断题1.分部积分法u v uv v u d d ⎰-=⎰的关键是恰当的选择u 和v d ,使u v d ⎰应比v u d ⎰容易积分.(√)2.若被积函数中含有22a x ±,则可利用三角函数代换法化原积分为三角函数的积分.(√)三.填空题 1.Cx dx x ++=+⎰1211.2.设)(x f 有一原函数⎰+-='Cx dx x f x x x cos )(,sin 则.3.C x x x xdx x +-=⎰2241ln 21ln .4.)3(arcsin 31912x d xdx =-.5.Cx x e dx e x x x ++-=⎰)22(22.6.⎰++-=C x x x xdx x 3sin 913cos 313sin .四.计算题1.求不定积分⎰-dx x x232.解:原式=Cx x d x +--=---⎰2223231)32(321612.求不定积分⎰dxx ex22.解:原式=C x x e x ++-)21(2122 3.求不定积分⎰++dxx x 11.解:C x x C t t dt t t t x +--+=+-=-=+⎰1)1(3232)22(132232原式4.求不定积分⎰+)1(x x dx.解:cx C t dt t t x +=+=+=⎰arctan 2arctan 21222原式5.求不定积分⎰xdxx 2sin .解:原式=C x x x ++-2sin 412cos 21 6.求不定积分⎰+dx e x x 5)2(.解:原式=C x e x ++)59(515 7.求不定积分dxxex⎰-4.解:原式C x e x ++-=-)16141(48.求不定积分⎰++dxx 111.解:原式[]C x x +++-+=)11ln(129.求不定积分⎰+-dxx 1211.解:原式[]C x x +-+++=112ln12-10.求不定积分dxex⎰+11.解:原式=C e e xx +++-+1111ln11.求不定积分⎰xdxxln 2.解:原式C x x +-=)31(ln 313 12.求不定积分dx x x ⎰-1.解:原式C x x +---=)1arctan 1(213.求不定积分⎰---dxx x 22112.解:原式C x x +-=)(arcsin 214.求不定积分⎰dx a x x 2)1,0(≠>a a .解:原式C aa x a x a x++-=)ln 2ln 2ln (32215.求不定积分dxx⎰-2941.解:原式C x +=23arcsin 31 16.求不定积分dxx ⎰sin .解:原式C x x x ++=sin 2cos -217.求不定积分⎰xdx x 3cos .解:原式C x x x ++=3cos 913sin 31 18.求不定积分dxx x ⎰+2.解:原式C x x ++-+=2123)2(4)2(32五.应用题(增加题)第六章定积分一.单选题 1.)(240Ddx x =-⎰A.⎰⎰-+-4220)2()2(dxx dx x B.⎰⎰-+-422)2()2(dxx dx x C.⎰⎰-+-422)2()2(dxx dx x D.⎰⎰-+-422)2()2(dxx dx x2.=⎰a adx x f )((C)A.大于0B.小于0C.等于0D.不能确定 3.⎰⎰--=+1111)()(dx x f dx x f (C)A.大于0B.小于0C.等于0D.不能确定 4.定积分⎰badxx f )(是(D )A.一个原函数B.()x f 的一个原函数C.一个函数族D.一个常数 5.定积分⎰badxx f )(的值的大小取决于(C)A.)(x fB.区间[]b a ,C.)(x f 和[]b a ,D.都不正确 6.定积分⎰badxx f )(的值的大小取决于(C)A.)(x fB.区间[]b a ,C.)(x f 和[]b a , D.无法确定 7.⎰⎰=-3234)()(dx x f dx x f (A)A.⎰42)(dxx f B.⎰24)(dxx f C.⎰43)(dxx f D.⎰32)(dxx f8.下列命题中正确的是(C )(其中)(),(x g x f 均为连续函数) A.在[]b a ,上若)()(x g x f ≠则dxx g dx x f ba ba⎰⎰≠)()( B.⎰⎰≠babadtt f dx x f )()(C.若)()(x g x f ≠,则⎰⎰≠dxx g dx x f )()( D.⎰=badxx f dx x f d )()(9.=⎰dx x f dxd ba )((B) A.)(x f B.0 C.)(x f ' D.)(x F 10.若1)(=x f ,则⎰=badx x f )((C)A.1B.b a -C.a b -D.0 11.定积分⎰badxx f )(是(B )A.任意的常数B.确定的常数C.)(x f 的一个原函数D.)(x f 的全体原函数 12.若⎰=+12)2(dx k x ,则=k (B)A.-1B.1C.1/2D.0 13.=-⎰dx x 5042(C)A.11B.12C.13D.14 二.判断题1.函数在某区间上连续是该函数在该区间上可定积分的必要条件.(×)2.a b dx ba -=⎰0.(×)3.⎰='badx x f 0))((.(×)4.x xdx dx d ba sin sin ⎰=.(×)三.填空题1.设)(x f '在[]b a ,上连续,则)()()(a f b f dx x f b a-='⎰.2.C dx xxx +=⋅⎰6ln 6321. 3.4111022π-=+⎰dx x x .4.ee dx x e x-=⎰2121.5.设⎰⎰==52515)(,3)(dx x f dx x f ,则2)(21-=⎰dx x f .6..0113=⎰-dx x .7.若)(x f 在[]b a ,上连续,且⎰=ba dx x f 0)(,则[]a b dx x f ba-=+⎰1)(.8.由曲线22+=x y ,直线3,1=-=x x 及x 轴围成曲边梯形的面积352)2(312=+=⎰-dx x A . 9..0sin 12=⎰dx x dx d .10.11ln4141=+-⎰-dx xx.11.1)1sin(212=⎰dx xx ππ. 12.32112=⎰-dx x .13.0cos 11⎰-=xdx x .14.利用定积分的几何意义填写定积分的值π41112=-⎰dx x . 15.22sin sin x dt t dx d x⎰=.16..0sin 222=⎰-xdx x .17..0113=⎰-dx x .18. 的值为积分.21ln 1⎰edx x x 19.2)253(22224⎰⎰=++-dx dx x x .20.11-=⎰e dx e x . 21.431=⎰-dx .22.⎰1212ln xdxx 的值的符号为负.四.计算题 1.求定积分.⎰+411xdx 解:原式)32ln 1(2+=2.求定积分⎰-124x dx.解:原式6arcsin 10π==x3.求定积分⎰-+-01)32)(1(dxx x .解:原式21-=4.求定积分dxx⎰--2121211解:原式3arcsin 2121π==-x5.求定积分⎰-+12511x dx 解:原式=2ln 54)511ln(5112=⎥⎦⎤⎢⎣⎡+-x6.求定积分dx x ⎰+9411解:原式[])2ln 1(2)1ln(232+-=-+-=t t7.求定积分dxex⎰-1.解:原式eex1101-=-=- 8.求定积分dxx ⎰212解:原式3712313==x 9.求定积分θθπd ⎰402tan 解:原式[]4104tan ππθθ-=-=10.求定积分.dx xx ⎰+402sin 12sin π解:原式232ln 04)sin 1ln(=+=πx 11.求定积分dxx x ⎰-ππ23sin .解:原式=012.求定积分()dxxx ⎰--2121221arcsin .解:原式=324)(arcsin 31321213π=-x 13.求定积分dxx x ⎰+911.解:原式2ln 213)1ln(2=+=x14.求定积分dxex x⎰12.解:原式201)22(2-=+-=e x x ex15.求定积分⎰+104)1(x dx 解:原式24701)1(31-3=+=-x 16.求定积分dxxe x ⎰2.解:原式102)1(2+=-=e x ex17.求定积分⎰-1dxxe x .解:原式e x ex2101)1(--=+=-18.求定积分dx x ⎰⎪⎭⎫⎝⎛+πππ33sin .解:原式0)3cos(3=+-=πππx19.已知⎩⎨⎧≤<-≤≤=31,210,)(2x x x x x f ,计算⎰20)(dx x f .解:原式⎰⎰-=-+=2110261)2(dx x dx x 20.求定积分()dx x x +⎰194.解:原式627149)2132(223=+=x x21.求定积分⎰1arctan xdxx .解:原式=214)arctan arctan (21102-=⎥⎦⎤⎢⎣⎡+-πx x x x22.求定积分⎰1arcsin xdx .解:原式1201)1arcsin (2-=-+=πx x x23.求定积分⎰262cos ππudu.解:原式836)2sin 21(2162-=+=πππu u 24.求定积分()dx x x x ⎰+2sin π.解:原式18sin cos 2122+=⎥⎦⎤⎢⎣⎡+-=ππx x x x25.求定积分dx x x ⎰-121221.解:原式[]41cot sin 24πππ-=--=t t t x26.求定积分dx x x 1sin 1212⎰ππ.解:原式11cos12==ππx27.求定积分dx x ⎰+11210.解:原式10ln 4950110ln 21012==+x 28.求定积分xdxx ⎰23cos sin π解:原式410cos 41-24==πx29.求定积分⎰124dx x x .解:原式10ln 710ln 810=⎥⎦⎤⎢⎣⎡=x 30.求定积分dx x x e⎰-1ln 1.解:原式21ln 21ln 12=⎥⎦⎤⎢⎣⎡-=ex x31.求定积分dxx x ⎰+31)1(1.解:原式[]6arctan 2312π==t t x32.求定积分xdxx cos sin 23⎰π.解:原式410sin 4124==πx33.求定积分⎰--1321dx x .解:原式[]5ln 2ln -13=-=-x34.求定积分dx x x x ⎰++21222)1(12解:原式4212arctan 1arctan 21π-+=⎥⎦⎤⎢⎣⎡-=x x 35.求定积分⎰+21ln 1e x x dx.解:原式[])13(2ln 1221-=+=e x36.求定积分dxe x x ⎰22.解:原式)1(21214202-=⎥⎦⎤⎢⎣⎡=e e x37.求定积分dxx ⎰20sin π.解:原式10cos 2=-=πx38.求定积分⎰++10)32)(1(dx x x .解:原式2112521032=⎥⎦⎤⎢⎣⎡++=x x x39.求定积分dttet ⎰-1022.解:原式212112---=⎥⎥⎦⎤⎢⎢⎣⎡-=e e t 40.求定积分dx x x ⎰+102212.解:原式[]22)arctan (210π-=-=x x41.求定积分⎰πsin xdxx .解:原式[]ππ=+-=0sin cos xx x42.求定积分dx x xe⎰12ln .解:原式311ln 313==e x43.求定积分⎰2cos sin 3πxdxx .解:原式230sin 2322==πx44.求定积分()⎰ωπωω20sin 为常数tdt t 解:原式2022sin 1cos 12ωπωωωωωω-=⎥⎦⎤⎢⎣⎡+-=t t t45.求定积分dxx ⎰230cos π.解:原式[][]3sin sin 23220=-=πππx x46.求定积分dxx ⎰--2221.解:原式43131231213113123=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=---x x x x x x47.求定积分⎰+331211dx x .解:原式[]6arctan 331π==x48.求定积分⎰+161 4x x dx .解:原式23ln 2)1ln(2142124+=⎥⎦⎤⎢⎣⎡++-=t t t t x五.应用题1.已知生产某产品x (百台)时,总收入R 的变化率x R -='8(万元/百台),求产量从从1(百台)增加到3(百台)时,总收入的增加量.解:由已知x R -='8得总收入的增加量为:12218)8(R3131312=⎥⎦⎤⎢⎣⎡-=-='=⎰⎰x x dx x dx R2.试描画出定积分⎰ππ2cos xdx所表示的图形面积,并计算其面积.解:[]1sin cos 22=-=-=⎰ππππx xdx S .(图形略)3.试描画出定积分⎰ππ2sin xdx 所表示的面积图形,并计算其面积.解:[]1cos sin 22=-==⎰ππππx xdx S .(图形略)4.计算曲线3x y =,直线3,2=-=x x 及x 轴所围成的曲边梯形面积.解:49741413402433023=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=+-=--⎰⎰x x dx x dx x S.(图形略) 5.计算抛物线24x y -=与x 轴所围成的图形面积. 解:24x y -=与x 轴的交点为(-2,0),(2,0)6.已知生产某产品x (百台)时,总成本C 的变化率为x C +='2(万元/百台),求产量从1(百台)增加到3(百台)时总成本的增加量.解:.8212)2(31312=⎥⎦⎤⎢⎣⎡+=+=⎰x x dx x C7.计算函数x y sin 2=在⎥⎦⎤⎢⎣⎡2,0π上的平均值.解:[]πππππ4cos 222sin 22020=-==⎰x xdxy8.计算函数x y cos 2=在⎥⎦⎤⎢⎣⎡2,0π上的平均值.解:[]πππππ4sin 222cos 2202===⎰x xdxy第七章定积分的应用一.单选题1.变力使)(x f 物体由],[b a 内的任一闭区间]d ,[x x x +的左端点x 到右端点x x d +所做功的近似值为(C).A.)(x df -B.)(dx fC.dx x f )(D.dx x f )(- 2.一物体受连续的变力)(x F 作用,沿力的方向作直线运动,则物体从a x =运动到b x =,变力所做的功为(A).A.⎰b a x x F d )( B.⎰ab x x F d )( C.⎰-ab x x F d )( D.⎰-ba x x F d )(3.将曲线2x y =与x 轴和直线2=x 所围成的平面图形绕y 轴旋转所得的旋转体的体积可表示为=y V (C ).A.dxx ⎰24π B.⎰4ydyπ C.()dyy ⎰-44π D.()dyy ⎰+44π二.判断题 1.定积分⎰badxx f )(反映在几何意义上是一块[a,b]上的面积.(╳)2.已知边际利润求总利润函数可用定积分方法.(√) 三.填空题 1.计算曲线x y sin =与曲线2π=x 及0=y 所围成的平面图形的面积可用定积分表示为⎰=2sin πdxA .2.抛物线3x y =与x 轴和直线2=x 围成的图形面积为⎰23dxx .3.由曲线2x y =与直线1=x 及x 轴所围成的平面图形,绕x 轴旋转所的旋转体的体积可用定积分表示为⎰=14dxx V x π.四.计算题1.求抛物线3x y =与x 轴和直线3=x 围成的图形面积.2.把抛物线ax y 42=及直线)0(>=b b x 所围成的图形绕x 轴旋转,计算所得旋转体的体积.3.一边长为a m 的正方形薄板垂直放入水中,使该薄板的上边距水面1m ,试求该薄板的一侧所受的水的压力(水的密度为33kg/m 10,g 取2m/s 10).4.计算抛物线2x y =与直线轴和x x x 3,1=-=所围成的平面图形绕x 轴旋转所得到的旋转体体积.5.由22x y x y ==和所围成的图形绕x 轴旋转而成的旋转体体积.6.求由曲线x y 1=与直线x y =及2=x 所围成的图形的面积.7.用定积分求由0,1,0,12===+=x x y x y 所围平面图形绕x 轴旋转一周所得旋转体的体积.8.求曲线22)2(,-==x y x y 与x 轴围成的平面图形的面积.9.用定积分求底圆半径为r ,高为h 的圆锥体的体积.10.计算曲线3x y =和x y =所围成的图形面积.11.计算抛物线24x y -=与x 轴所围成的图形面积.12.求曲线2x y =与x y =所围成的图形的面积。
实验2--微分方程(基础实验)

实验2--微分方程(基础实验)119 项目四 无穷级数与微分方程实验2 微分方程(基础实验)实验目的 理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用Mathematica 求微分方程及方程组解的常用命令和方法.基本命令1. 求微分方程的解的命令DSolve对于可以用积分方法求解的微分方程和微分方程组,可用Dsolve 命令来求其通解或特解.例如,求方程023=+'+''y y y 的通解, 输入DSolve[y ''[x]+3y '[x]+2y[x]==0,y[x],x]则输出含有两个任意常数C[1]和C[2]的通解:{}{}]2[C e ]1[C e ]x [y x x 2--+→注:在上述命令中,一阶导数符号 ' 是通过键盘上的单引号 ' 输入的,二阶导数符号 '' 要输入两个单引号,而不能输入一个双引号.又如,求解微分方程的初值问题:,10,6,03400='==+'+''==x x y y y y y输入Dsolve[{y''[x]+4 y'[x]+3y[x]==0,y[0]==6, y'[0]==10},y[x],x](*大括号把方程和初始条件放在一起*)则输出{}{}x 2x 3e 148(e ]x [y +-→-2. 求微分方程的数值解的命令NDSolve对于不可以用积分方法求解的微分方程初值问题,可以用NDSolve 命令来求其特解.例如要求方程5.0,032=+='=x y x y y的近似解)5.10(≤≤x , 输入NDSolve[{y'[x]==y[x]^2+x^3,y[0]==0.5},y[x],{x,0,1.5}](*命令中的{x,0,1.5}表示相应的区间*)则输出{{y->InterpolatingFunction[{{0.,1.5}},< >]}}注:因为NDSolve 命令得到的输出是解)(x y y =的近似值. 首先在区间[0,1.5]内插入一系 列点n x x x ,,,21Λ, 计算出在这些点上函数的近似值n y y y ,,,21Λ, 再通过插值方法得到 )(x y y =在区间上的近似解.3. 一阶微分方程的方向场一般地,我们可把一阶微分方程写为),(y x f y ='的形式,其中),(y x f 是已知函数. 上述微分方程表明:未知函数y 在点x 处的斜率等于函数120f 在点),(y x 处的函数值. 因此,可在Oxy 平面上的每一点, 作出过该点的以),(y x f 为斜率 的一条很短的直线(即是未知函数y 的切线). 这样得到的一个图形就是微分方程),(y x f y ='的方向场. 为了便于观察, 实际上只要在Oxy 平面上取适当多的点,作出在这些点的函数的 切线. 顺着斜率的走向画出符合初始条件的解,就可以得到方程),(y x f y ='的近似的积分曲 线.例如, 画出0)0(,12=-=y y dxdy 的方向场. 输入<<Graphics`PlotField`g1=PlotVectorField[{1,1-y^2},{x,-3,3},{y,-2,2}, Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25}];则输出方向场的图形(图2.1), 从图中可以观察到, 当初始条件为2/10=y 时, 这个微分方程的解介于1-和1之间, 且当x 趋向于-∞或∞时, )(x y 分别趋向于1-与1.-3-2-10123-2-1012 -3-2-10123-2-112下面求解这个微分方程, 并在同一坐标系中画出方程的解与方向场的图解. 输入sol=DSolve[{y'[x]==1-y[x]^2,y[0]==0},y[x],x];g2=Plot[sol[[1,1,2]],{x,-3,3},PlotStyle->{Hue[0.1],Thickness[0.005]}];Show[g2,g1,Axes->None,Frame->True];则输出微分方程的解xxe e x y 2211)(++-=,以及解曲线与方向场的图形(图2.2). 从图中可以看到, 微分方程的解与方向场的箭头方向相吻合.实验内容用Dsolve 命令求解微分方程例2.1 (教材 例2.1) 求微分方程 22x xe xy y -=+'的通解.输入Clear[x,y];DSolve[y '[x]+2x*y[x]==x*Exp[-x^2],y[x],x]或DSolve[D[y[x],x]+2x*y[x]==x*Exp[-x^2],y[x],x]则输出微分方程的通解:121 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+→--]1[C e x e 21]x [y 22x 2x 其中C[1]是任意常数.例2.2 (教材 例2.2) 求微分方程0=-+'x e y y x 在初始条件e y x 21==下的特解. 输入Clear[x,y];DSolve[{x*y ' [x]+y[x]-Exp[x]==0,y[1]==2 E},y[x],x]则输出所求特解:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+→x e e ]x [y x 例2.3 (教材 例2.3) 求微分方程x e y y y x 2cos 52=+'-''的通解.输入DSolve[y ''[x]-2y '[x]+5y[x]==Exp[x]*Cos[2 x],y[x],x]//Simplify则输出所求通解:⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧-++→])x 2[Sin ])1[c 4x (2]x 2[Cos ])2[c 81((e 81]x [y x 例2.4 (教材 例2.4) 求解微分方程x e x y +=''2, 并作出其积分曲线.输入g1=Table[Plot[E^x+x^3/3+c1+x*c2,{x,-5,5},DisplayFunction->Identity],{c1,-10,10,5},{c2,-5,5,5}];Show[g1,DisplayFunction->$DisplayFunction]; -4-224-40-20204060图2.3例2.5 (教材 例2.5) 求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dx t 在初始条件0,100====t t y x 下的特解.输入122Clear[x,y,t];DSolve[{x' [t]+x[t]+2 y[t]==Exp[t], y'[t] -x[t]- y[t]==0,x[0]==1,y[0]==0},{x[t],y[t]},t]则输出所求特解:⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+-→→])t [Sin ]t [Cos e (21]t [y ],t [Cos ]t [x t例2.6 验证c y y x =+--)3305(15152是微分方程2)(42-='y x x y 的通解. 输入命令<<Graphics`PlotField`<<Graphics`ImplicitPlot`sol=(-5x^3-30y+3y^5)/15==C;g1=ImplicitPlot[sol/.Table[{C->n},{n,-3,3}],{x,-3,3}];g2=PlotVectorField[{1,x^2/(y^4-2)},{x,-3,3},{y,-3,3},Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25}];g=Show[g2,g1,Axes->None,Frame->True];Show[GraphicsArray[{g1,g2,g}]];则分别输出积分曲线如图 2.4(a), 微分方程的方向场如图 2.4(b). 以及在同一坐标系中画出积分曲线和方向场的图形如下图2.4 (c).-3-2-1123-2-112-3-2-10123-3-2-10123-3-2-10123-3-2-10123图2.4从图 2.4(c)中可以看出微分方程的积分曲线与方向场的箭头方向吻合, 且当∞→x 时, 无论初始条件是什么, 所有的解都趋向于一条直线方程.例2.7 (教材 例2.6) 求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 输入<<Graphics`PlotField`DSolve[y' [x]-2y[x]/(x+1)==(x+1)^(5/2),y[x],x]则输出所给积分方程的解为 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+++→]1[C )x 1()x 1(32]x [y 22/7123 下面在同一坐标系中作出这个微分方程的方向场和积分曲线(设),3,2,1,0,1,2,3---=C 输入t=Table[2(1+x)^(7/2)/3+(1+x)^2c,{c,-1,1}];g1=Plot[Evaluate[t],{x,-1,1},PlotRange->{{-1,1},{-2,2}},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];g2=PlotVectorField[{1,-2y/(x+1)+(x+1)^(5/2)},{x,-0.999,1},{y,-4,4},Frame->True,ScaleFunction->(1&), ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25},DisplayFunction->Identity];Show[g1,g2,Axes->None,Frame->True,DisplayFunction->$DisplayFunction];则输出积分曲线的图形(图2.5).-0.75-0.5-0.2500.250.50.751-1.5-1-0.50.511.52图2.5例2.8 求解微分方程,2)21(22-+='-y x y xy 并作出其积分曲线.输入命令<<Graphics`PlotField`DSolve[1-2*x*y[x]*y' [x]==x^2+(y[x])^2-2,y[x],x]则得到微分方程的解为.)2(323C y x x y ++-+= 我们在33≤≤-C 时作出积分曲线, 输入命令t1=Table[(3+Sqrt[3])Sqrt[3+24x^2-4x^4-4*c*x]/(6*x),{c,-3,3}];t2=Table[(3-Sqrt[3])Sqrt[3+24x^2-4x^4-4*c*x]/(6*x),{c,-3,3}];gg1=Plot[Evaluate[t1],{x,-3,3},PlotRange->{{-3,3},{-3,3}},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];124gg2=Plot[Evaluate[t2],{x,-3,3},PlotRange->{{-3,3},{-3,3}},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];g1=ContourPlot[y-x^3/3-x*(-2+y^2),{x,-3,3},{y,-3,3},PlotRange->{-3,3},Contours->7,ContourShading->False,PlotPoints->50,DisplayFunction->Identity];g2=PlotVectorField[{1,(x^2+y^2-2)/(1-2*x*y)},{x,-3,3},{y,-3,3},Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25},DisplayFunction->Identity];Show[g1,g2,Axes->None,Frame->True,DisplayFunction->$DisplayFunction];Show[gg1,gg2,g2,Axes->None,Frame->True,DisplayFunction->$DisplayFunction];则输出微分方程的向量场与积分曲线, 并输出等值线的图2.6.-3-2-10123-2-10123-2-10123-2-1123图2.6用NDSolve 命令求微积分方程的近似解例2.9 (教材 例2.7) 求初值问题:1,0)1()1(2.1=='-++=x y y xy y xy 在区间[1.2,4]上的近似解并作图.输入fl=NDSolve[{(1+x*y[x])*y[x]+(1-x*y[x])*y'[x]==0,y[1.2]==1},y,{x,1.2,4}]则输出为数值近似解(插值函数)的形式:{{y->InterpolatingFunction[{{1.2,4.}},< >]}}用Plot 命令可以把它的图形画出来.不过还需要先使用强制求值命令Evalu-ate, 输入 Plot[Evaluate[y[x]/.fl],{x,1.2,4}]则输出近似解的图形(图2.7).125 1.5 2.53 3.5410203040图2.7如果要求区间[1.2,4]内某一点的函数的近似值, 例如8.1=x y ,只要输入y[1.8]/.fl则输出所求结果{3.8341}例2.10 (教材 例2.8) 求范德波尔(Van der Pel)方程5.0,0,0)1(002-='==+'-+''==x x y y y y y y在区间[0,20]上的近似解.输入 Clear[x,y];NDSolve[{y''[x]+(y[x]^2-1)*y'[x]+y[x]==0,y[0]==0,y'[0]==-0.5},y,{x,0,20}];Plot[Evaluate[y[x]/.%],{x,0,20}]可以观察到近似解的图形(图2.8).5101520-2-112图2.8126 ⎪⎩⎪⎨⎧==+-'1)1(01sin 2y x y x y x 的数值解, 并作出数值解的图形.输入命令<<Graphics`PlotField`sol=NDSolve[{x*y'[x]-x^2*y[x]*Sin[x]+1==0,y[1]==1},y[x],{x,1,4}];f[x_]=Evaluate[y[x]/.sol];g1=Plot[f[x],{x,1,4},PlotRange->All,DisplayFunction->Identity];g2=PlotVectorField[{1,(x^2*y*Sin[x]-1)/x},{x,1,4},{y,-2,9},Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25},DisplayFunction->Identity];g=Show[g1,g2,Axes->None,Frame->True];Show[GraphicsArray[{g1,g}],DisplayFunction->$DisplayFunction];则输出所给微分方程的数值解及数值解的图2.9.1.522.533.544681 1.52 2.53 3.54-22468例2.11 (教材 例2.9) 求出初值问题⎪⎩⎪⎨⎧='==+'+''0)0(,1)0(cos sin 22y y xy x y y的数值解, 并作出数值解的图形.输入NDSolve[{y''[x]+Sin[x]^2*y'[x]+y[x]==Cos[x]^2,y[0]==1,y'[0]==0},y[x],{x,0,10}]127 Plot[Evaluate[y[x]/.%],{x,0,10}];则输出所求微分方程的数值解及数值解的图形(图2.10).2468100.20.40.60.8图2.10例2.12 (教材 例2.10) 洛伦兹(Lorenz)方程组是由三个一阶微分方程组成的方程组.这三个方程看似简单, 也没有包含复杂的函数, 但它的解却很有趣和耐人寻味. 试求解洛伦兹方程组,0)0(,4)0(,12)0()(4)()()()()(45)()()()(16)(16)(⎪⎪⎩⎪⎪⎨⎧===-='-+-='-='z y x t z t y t x t z t y t x t z t x t y t x t y t x 并画出解曲线的图形.输入Clear[eq,x,y,z]eq=Sequence[x'[t]==16*y[t]-16*x[t],y'[t]==-x[t]*z[t]-y[t]+45x[t],z'[t]==x[t]*y[t]-4z[t]];sol1=NDSolve[{eq,x[0]==12,y[0]==4,z[0]==0},{x[t],y[t],z[t]},{t,0,16},MaxSteps->10000];g1=ParametricPlot3D[Evaluate[{x[t],y[t],z[t]}/.sol1],{t,0,16},PlotPoints->14400,Boxed->False,Axes->None];则输出所求数值解的图形(图2.11(a)). 从图中可以看出洛伦兹微分方程组具有一个奇异吸引子, 这个吸引子紧紧地把解的图形“吸”在一起. 有趣的是, 无论把解的曲线画得多长, 这些曲线也不相交.128图2.11改变初值为,10)0(,10)0(,6)0(=-==z y x 输入sol2=NDSolve[{eq,x[0]==6,y[0]==-10,z[0]==10}, {x[t],y[t],z[t]},{t,0,24},MaxSteps->10000];g2=ParametricPlot3D[Evaluate[{x[t],y[t],z[t]}/.sol2],{t,0,24},PlotPoints->14400,Boxed->False,Axes->None];Show[GraphicsArray[{g1,g2}]];则输出所求数值解的图形(图2.11(b)). 从图中可以看出奇异吸引子又出现了, 它把解“吸”在某个区域内, 使得所有的解好象是有规则地依某种模式缠绕.实验习题1. 求下列微分方程的通解:(1) ;0136=+'+''y y y(2) ();024=+''+y y y(3) ;2sin 52x e y y y x =+'-''(4) .)1(963x e x y y y +=+'-''2. 求下列微分方程的特解:(1) ;15,0,029400='==+'+''==x x y y y y y(2) .1,1,02sin ='==++''==ππx x y yx y y 3. 求微分方程0cos 2)1(2=-+'-x xy y x 在初始条件10==x y 下的特解.分别求精确解和数值解)10(≤≤x 并作图.4. 求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++t t e y x dt dy e y x dt dx 235的通解.129 5. 求微分方程组⎪⎪⎩⎪⎨⎧==+-==-+==4,081,0300t t y y x dt dyxy x dt dx 的特解. 6. 求欧拉方程组324x y y x y x =-'+''的通解.7. 求方程5,0,011='==+'+''==x x y y y y x y 在区间[0,4]上的近似解.。
重庆大学高等数学教材答案

重庆大学高等数学教材答案在此提供《重庆大学高等数学教材答案》的文章。
重庆大学高等数学教材答案第一章:函数与极限1.1 函数与映射函数是数学中的重要概念之一。
在高等数学教材中,函数被定义为一个一一对应的关系,其中每个自变量对应唯一的一个因变量。
映射是函数的另一个称呼,用来描述函数的输入和输出之间的对应关系。
通过函数和映射的理论,我们可以深入理解数学中的变化规律和性质。
1.2 极限的概念极限是高等数学中的基础概念之一。
在定义中,我们说函数f当自变量趋于某个特定值时,对应的函数值趋于一个确定的常数L,则称函数f在该自变量趋于特定值的情况下有极限L。
通过研究函数的极限,我们可以了解函数的收敛性、趋势以及它们的性质。
第二章:导数与微分2.1 导数的定义与性质导数是函数在某一点上的局部变化率,通过导数可以研究函数的变化趋势以及各点上的斜率。
在高等数学教材中,我们学习了导数的定义以及导数的一些性质,如导数与函数的连续性、导数的四则运算等。
2.2 微分的概念与应用微分是导数的一种形式,通过微分我们可以研究函数的变化率和函数在某一点上的线性逼近。
微分在实际问题中的应用非常广泛,例如在物理学中,通过微分可以描述物体的运动轨迹和速度变化。
第三章:定积分与不定积分3.1 定积分的概念与性质定积分是高等数学中的重要内容之一,它是对函数在一定区间上面积的度量。
通过定义和性质,我们可以计算函数在给定区间上的定积分,并将其应用于求解几何问题、物理问题等。
3.2 不定积分的计算与应用不定积分是定积分的一种逆运算,通过不定积分我们可以找到函数的原函数。
通过学习不定积分的计算方法,我们可以应用于求解一些特定问题,例如计算曲线的长度、求解微分方程等。
第四章:级数4.1 数列极限的概念与性质数列极限是研究函数序列收敛性的一个重要概念。
通过掌握数列极限的定义和性质,我们可以判断函数序列是否收敛,并了解函数序列的收敛趋势。
4.2 级数的概念与性质级数是数列的和的概念,通过级数我们可以了解数列的求和情况。
常微分方程的数值解法及其应用

引 言自然界中很多事物的运动规律可用微分方程来刻画。
常微分方程是研究自然科学和社会科学中的事物、物体和现象运动、演化和变化规律的最为基本的数学理论和方法。
物理、化学、生物、工程、航空航天、医学、经济和金融领域中的许多原理和规律都可以描述成适当的常微分方程,如牛顿的运动定律、万有引力定律、机械能守恒定律,能量守恒定律、人口发展规律、生态种群竞争、疾病传染、遗传基因变异、股票的涨幅趋势、利率的浮动、市场均衡价格的变化等,对这些规律的描述、认识和分析就归结为对相应的常微分方程描述的数学模型的研究。
因此,常微分方程的理论和方法不仅广泛应用于自然科学,而且越来越多的应用于社会科学的各个领域。
它的学术价值是无价的,应用价值是立竿见影的。
求一阶常微分方程的解是数学工作者的一项基本的且重要的工作。
由于国内外众多数学家的努力,使此学科基本上形成了一套完美的学科体系;由于该问题比较复杂且涉及的面广,使得有些问题的解析解很难求出,而对于一些典型的微分方程(如线性方程、某些特殊的一阶非线性方程等)可以运用基本方法求出其解析解,并在理论上可以根据初值问题的条件把其中的任意常数完全确定下来。
然而,在生产实际和科学研究中所遇到的微分方程往往很复杂,在很多情况下都不可能给出解的解析表达式,有时即使能求出形式的解,也往往因计算量太大而不实用,而且高次代数方程求根也并不容易,所以用求解析解的方法来计算微分方程的数值解往往是不适宜的。
实际上,对于解微分方程初值问题,一般只要求得到解在若干个点上的近似解或者解的便于计算的近似表达式(只要满足规定的精度就行)。
所以,研究数学建模中常微分方程模型理论性数值解法迫在眉睫。
本文研究的数值解法主要是针对常微分方程初值问题多种数值解法精度比较而言。
从而得到更常用的数值解法在微分方程模型中的应用。
在自然科学和经济的许多领域中。
常常会遇到一阶常微分方程的初值问题b x a y x y y x f dx dy ≤≤⎪⎩⎪⎨⎧==.)(),,(00 这里),(y x f 是充分光滑,即关于x 或y 满足李普希茨条件的二元函数,0y 是给定的初始值,00)(y x y =称为初始条件。
微分方程数值解法实验报告

微分方程数值解法实验报告姓名: 班级: 学号:一:问题描述求解边值问题:()2(sin cos cos sin (0,1)(0,1)0,(,)x y u e x y x y G u x y G ππππππ+⎧⎫∆=+⎪⎪∈=⨯⎨⎬⎪⎪=∈∂⎩⎭(x,y) 其精确解为)sin()sin(),()(y x e y x u y x πππ+=问题一:取步长h=k=1/64,1/128,作五点差分格式,用Jacobi 迭代法,Gauss_Seidel 迭代法,SOR 迭代法(w=1.45)。
求解差分方程,以前后两次重合到小数点后四位的迭代值作为解的近似值,比较三种解法的迭代次数以及差分解)128/1,64/1)(,(=h y x u h 与精确解的精度。
问题二:取步长h=k=1/64,1/128,作五点差分格式,用单参数和双参数PR 法解差分方程,近似到小数点后四位。
与SOR 法比较精度和迭代步数。
问题三:取步长h=k=1/64,1/128,作五点差分格式,用共轭梯度法和预处理共轭梯度法解差分方程,近似到小数点后四位。
与SOR法与PR 法比较精度和迭代步数。
二.实验目的:分别使用五点差分法(Jacobi 迭代,Gauss_Seidel 迭代,SOR迭代),PR 交替隐式差分法(单参数,双参数),共轭梯度法,预共轭梯度法分别求椭圆方程的数值解。
三.实验原理:(1) Jacobi 迭代法设线性方程组(1)的系数矩阵A 可逆且主对角元素均不为零,令 并将A 分解成(2) 从而(1)可写成令其中. (3) 以为迭代矩阵的迭代法(公式)(4)称为雅可比(Jacobi)迭代法(公式),用向量的分量来表示,(4)为(5) 其中为初始向量. (2) Guass-Seidel 迭代法由雅可比迭代公式可知,在迭代的每一步计算过程中是用的全部分量来计算的所有分量,显然在计算第i 个分量时,已经b Ax =nn a ,...,a ,a 2211()nn a ,...,a ,a diag D 2211=()D D A A +-=()b x A D Dx +-=11f x B x +=b D f ,A D I B 1111--=-=1B ()()111f x B x k k +=+⎩⎨⎧[],...,,k ,n ,...,i x a b a x n ij j )k (j j i i ii )k (i 21021111==∑-=≠=+()()()()()Tn x ,...x ,x x 002010=()k x ()1+k x ()1+k i x计算出的最新分量没有被利用,从直观上看,最新计算出的分量可能比旧的分量要好些.因此,对这些最新计算出来的第次近似的分量加以利用,就得到所谓解方程组的高斯—塞德(Gauss-Seidel )迭代法.把矩阵A 分解成(6)其中,分别为的主对角元除外的下三角和上三角部分,于是,方程组(1)便可以写成 即其中(7)以为迭代矩阵构成的迭代法(公式)(8)称为高斯—塞德尔迭代法(公式),用 量表示的形式为(3) SOR 迭代(4) 交替方向迭代法(PR 法)迭代格式为:()()1111+-+k i k x ,...,x 1+k ()1+k x ()1+k j x U L D A --=()nn a ,...,a ,a diag D 2211=U ,L --A ()b Ux x L D +=-22f x B x +=()()b L D f ,U L D B 1212---=-=2B ()()221f x B x k k +=+⎩⎨⎧[],...,,k ,n ,,i x a x a b a x i j n i j )k (j ij )k (j ij i ii )k (i 21021111111==∑∑--=-=+=++Λ))1(()(1D R L D T ωωω-+-=-b )(1--=L D d ωωhu πμωcos )11/(22opt =-+=2121,,1,1,1,,122L L L L u u u L u u u j i j i j i j i j i j i +==+-=+-+-+-对于单参数PR 法,对于多参数,(5) 共轭梯度法 算法步骤如下: [预置步]任意,计算,并令取:指定算法终止常数,置,进入主步;[主步] (1)如果,终止算法,输出;否则下行;(2)计算:(3)计算:(4)置,转入(1).(6) 预共轭梯度法b uL I uL I b u L I uL I k k k k k k k k k k ττττττ+-=++-=++++211122211)()()()(hh optπτsin 22=2sin a ....2,1)11(421k 221h k a h k πρρτ==+-=--其中[预置步]任意,计算,并令取:指定算法终止常数,置,进入主步;[主步](1)计算:,(2)如果,转入(3).否则,终止算法,输出计算结果(3)计算:(4)置,转入(1)注:在算法[主步]中,引入变量,及,可以简化计算。
重庆大学数学实验课程实验1下

分析:
先用x=linspace(x1,x2)函数确定图像所画的范围,本次实验范围采用[-5,5]即x=linspace(-5,5);再分别用四个函数y1,y2,y3,y4分别表示所需要做图的函数,用plot(x,y,s)函数将四个函数表示在一起,为更好区分不同函数的图像,s分别区实线(‘-’)、点线(‘.’)、虚线(‘:’)、o线(‘o’)做图,最后用legend()函数将全部函数进行标注、区分,做出的图像如图二
由图像可知y1=e^x的图像在x取值越大的时候变化越快;y3=1+x+(1/2)x^2恒大于0;y2=1+x,'y4=1+x+(1/2)x^2+(1/6)x^3都是有正有负
使用subplot()函数将屏幕分成四块,并在每一个块中分别使用plot()函数绘制函数图像,使用title()函数为每一个块赋一个标题即函数解析式,做出的图像如图三
6.作出下列曲面的3维图形,
7.作出函数y=x4-4x3+3x+5(x[0,6])的图形,找出其在[0,6]之间的最小值点。
二、实验过程(一般应包括实验原理或问题分析,变量说明、程序、调试情况记录、图表等,实验结果及分析)
4:
程序:
functionf = sq(x)
a=x;
x=1;
y=(x+a/x)/2;
重庆大学
学生实验报告
实验课程名称数学实验
开课实验室
学院计算机年级2015专业班计科6
学生姓名王博韬学号********
2 实验指导书(2010.4)
页眉内容《数学实验》实验指导书龚劬重庆大学数学实验教学示范中心目录预备实验——桥梁分析.............................................................. 错误!未定义书签。
实验1 MATLAB软件入门.......................................................... 错误!未定义书签。
实验2 方程模型及其求解算法............................................... 错误!未定义书签。
实验3 收敛与混沌——迭代................................................... 错误!未定义书签。
实验4 微分方程模型、求解及稳定性分析........................... 错误!未定义书签。
实验5 插值方法....................................................................... 错误!未定义书签。
实验6 数据拟合及参数辨识方法........................................... 错误!未定义书签。
实验7 回归分析模型、求解及检验....................................... 错误!未定义书签。
实验8 连续系统与离散系统的计算机模拟........................... 错误!未定义书签。
实验9 线性规划模型、求解及灵敏度分析........................... 错误!未定义书签。
实验10 非线性规划与多目标规划模型及其求解................. 错误!未定义书签。
实验11 如何表示二元关系—图的模型及矩阵表示............. 错误!未定义书签。
微分方程(differential equations)

1、definition: general form as
(2-5.1) 2、solution (2-5.1): (a) if g(y)=0, then (b)
(2-5.2)
Notice: (1)
may be included in the general solution. (2) C must make the solution meaningful.
2、 nonlinear differential equations:不是线性的
方程
e.g:
13
1-5 Solution of Differential Equations 1、general solution and specific solution
注:(1)n阶方程通常必含有n个任意常数 (2)通解并不是方程的所有解或一切解,特解 未必包含在通解中(e.g: singular solution奇解)
(3) initial-value problem :即求方程(1.1)满足
初值条件的解称为初值问题,又称Cauchy problem. example: 注意:n阶的方程就有n个初值条件
(4)boundary-value problem
15
16
3、explicit and implicit solution (显式和隐式解)
example 1: example 2: example 3:
26
3、solution (2-5.2): (1) separation of variables (2) Notice: (1)
(2) test the specific solution are included in the general solution
重庆大学数学实验实验报告(参考)

( x) x ( x) 1 ( x)
2 x 5x
4 x 2 x 5 x 3 1 5 2 15 x 2 5 ,算法设计为: 4 1 3 2 1 2 x 5 x 1 5 2 15 x 5 3
1 5
1
x1=0; x2=((2*x1-5*x1^3-1)^(1/5)-1/5*(2*x1-5*x1^3-1)^(-4/5)*(2*x1-15*x1^3))/(1-1/5*(2*x1-5*x1^3-1)^(4/5)*(2-15*x1^2)); for k=1:100 x1=x2; x2=((2*x1-5*x1^3-1)^(1/5)-1/5*(2*x1-5*x1^3-1)^(-4/5)*(2*x1-15*x1^3))/(1-1/5*(2*x1-5*x1^31)^(-4/5)*(2-15*x1^2)); end x1 输出结果为: x1 = -0.1483 + 0.7585i
2 2 1 2 3 2 2 x x 2 3 3 x ( x) x ( x) x x x x ,算法设计为: x h( x ) 2 1 ( x) 2 5 2 3 3x 2 x x
1
2
x1=0; x2=((0.4*x1-0.2*x1^5-0.2)^(1/3)-1/15*(0.4*x1-0.2*x1^5-0.2)^(-2/3)*(2*x1-5*x1^5))/(1-(1/15*(0.4*x 1-0.2*x1^5-0.2)^(-2/3)*(2-5*x1^4))); while abs(x1-x2)>10^(-5) x1=x2; x2=((0.4*x1-0.2*x1^5-0.2)^(1/3)-1/15*(0.4*x1-0.2*x1^5-0.2)^(-2/3)*(2*x1-5*x1^5))/(1-(1/15*(0 .4*x1-0.2*x1^5-0.2)^(-2/3)*(2-5*x1^4))); end x1 输出结果为: x1 = 0.4004 + 0.2860i ③迭代函数为 ( x)
重庆大学数学
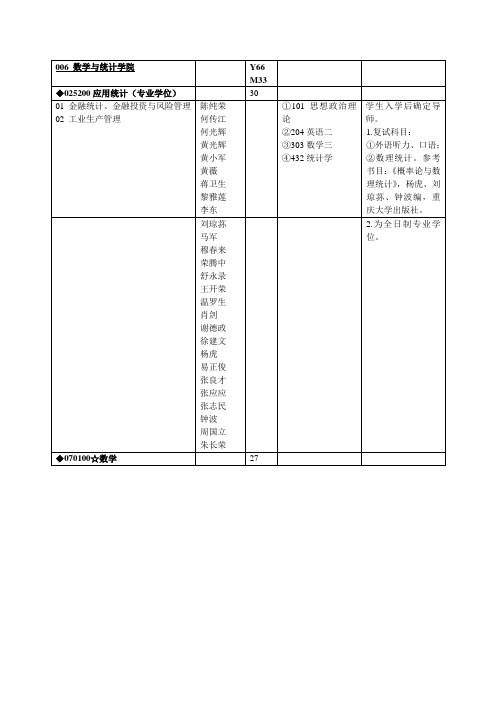
Y66 M33
◆025200应用统计(专业学位)
30
01金融统计、金融投资与风险管理
02工业生产管理
陈纯荣
何传江
何光辉
黄光辉
黄小军
黄薇
蒋卫生
黎雅莲
李东
①101思想政治理论
②204英语二
③303数学三
④432统计学
学生入学后确定导师。
1.复试科目:
①外语听力、口语;②数理统计。参考书目:《概率论与数理统计》,杨虎、刘琼荪、钟波编,重庆大学出版社。
参考书目:《常微分方程教程(第二版)》,丁同仁等编,高等教育出版社;《复变函数教程》,方企勤编,北京大学出版社;《实变函数论与泛函分析(第二版)》,夏道行编,高等教育出版社
王坤
王显金
温罗生
吴德垠
伍俊良
肖剑
谢德政
徐立伟
杨丹
叶仲泉
易正俊
曾理
张良才
张忠
郑德超
周云华
朱长荣
◆071400☆统计学
9
01金融统计
刘琼荪
马军
穆春来
荣腾中
舒永录
王开荣
温罗生
肖剑
谢德政
徐建文
杨虎
易正俊
张良才
张应应
张志民
钟波
周国立
朱长荣
2.为全日制专业学位。
◆070100☆数学
27
01代数学
02泛函分析
03动力系统
04函数论
05组合数学
06偏微分方程数值解
07遍历理论
08智能计算和仿真应用
09数值代数
10密码学
11偏微分方程
12金融数学
常微分方程和偏微分方程举例

常微分方程和偏微分方程举例1. 什么是常微分方程?常微分方程听起来就像是数学界的高大上名词,但其实它就是一个用来描述变化规律的方程。
就好比你想知道一个小球从楼上滚下来,它的速度是怎么变化的,常微分方程就可以帮你搞清楚。
这类方程里,只涉及到一个自变量,也就是我们说的“时间”或“位置”。
举个例子,想象一下你每天的体重变化。
你可能觉得自己最近重了,那就可以用常微分方程来建模,看看这段时间的变化规律。
比如说,体重的变化可以表示为一个方程:dW/dt = rW,其中W是体重,r是增长率,t是时间。
简单地说,就是你体重的变化速度和你的体重本身有关。
这种方程就像是告诉你体重变化的“配方”,看了它,你就能大致知道接下来你的体重会如何“表演”。
1.1 常微分方程的实际应用这些方程在实际生活中大有用场。
比如说,医生用它来研究药物在体内的浓度变化,工程师用它来预测机器的磨损情况,甚至在金融市场中,这类方程也能用来预测股票价格的波动。
比如,咱们就拿药物的浓度来举例,医生会通过常微分方程来计算药物在体内的消失速度,确保药效在合理范围内。
这就像是你在看菜谱一样,知道每一步的量和时间,才能做出美味的菜肴。
1.2 常微分方程的解法要想解决常微分方程,咱们得用点数学小窍门,比如分离变量法、积分因子法等。
别担心,这些名字听上去复杂,其实就像是解谜游戏中的小提示。
你只需要按照这些方法一步步“破解”,就能找到方程的解。
好比是你在解数独一样,找到正确的填入方式,问题就能迎刃而解。
2. 什么是偏微分方程?偏微分方程则稍微复杂一点,因为它涉及到两个或更多的自变量。
比如说,你想了解一个房间的温度分布情况,不光要考虑时间,还要考虑房间的不同位置。
这里就涉及到两个自变量:时间和位置。
这种方程可以描述复杂的现象,比如气温变化、流体的运动等。
想象一下,你在厨房里煮汤,锅底和汤面上的温度肯定不同,偏微分方程就能帮你搞清楚每个点的温度到底是怎么变化的。
2.1 偏微分方程的实际应用在实际应用中,偏微分方程的身影无处不在。
重庆大学高等数学教材

重庆大学高等数学教材重庆大学高等数学教材自出版以来,一直备受学生和教师们的喜爱和青睐。
本教材以系统、全面地介绍高等数学的基本理论和重要应用为主要目标,涵盖了高等数学各个分支的内容,内容全面、深入,旨在培养学生的数学思维和分析问题的能力。
本文将就重庆大学高等数学教材的特点和优势进行介绍和评述。
一、教材内容重庆大学高等数学教材内容全面、深入。
从基础的数列级数到多元函数、微分方程等高级数学领域,每个章节都覆盖了该领域的基本理论和重要应用。
教材注重理论与实践的结合,通过大量的例题和习题,帮助学生理解和掌握数学概念与方法,并培养学生的解决实际问题的能力。
二、教材结构重庆大学高等数学教材结构合理、清晰。
教材按照数学领域的相关性,将内容分为若干个模块,每个模块内部又进行了逻辑的分章节。
这种结构设置,有利于学生系统地学习高等数学知识,同时也方便了教师教学和备课。
教材内的内容层次分明、组织清晰,学生能够轻松地找到所需知识点,帮助提高学习效率。
三、教材语言重庆大学高等数学教材语言简明、通俗易懂。
教材作者运用简练的语言,避免冗长的叙述,使得抽象的数学概念变得易于理解。
作者注重用通俗的例子和生动的形象化描述,帮助学生建立直观的数学感受,并以此为基础进一步深入理解抽象的数学理论。
四、例题和习题重庆大学高等数学教材的例题和习题设计科学、充实。
教材的每个章节都配有丰富的例题和习题,这些例题和习题涵盖了知识点的各个方面,既能帮助学生巩固所学知识,又能提高学生的解题能力和运用能力。
其中,习题的难度逐渐递增,适合不同层次的学生进行巩固和拓展。
五、应用拓展重庆大学高等数学教材注重数学知识的应用拓展。
在教材中,融入了大量的实际问题和案例,使学生可以将所学的数学知识实际运用于解决实际问题。
这种应用拓展的设计,既提高了学生对数学知识的兴趣和学习动力,又培养了学生的实际问题分析与解决能力。
总结起来,重庆大学高等数学教材在内容、结构、语言、例题和习题以及应用拓展等方面具有独特的优势。
高等数学重庆大学版教材答案

高等数学重庆大学版教材答案第一章:极限与连续1.1 极限的概念与性质1.2 极限存在准则及常用极限第二章:函数与导数2.1 函数的概念与性质2.2 一次函数与多项式函数2.3 指数函数与对数函数2.4 三角函数与反三角函数2.5 导数的概念及其几何意义第三章:微分学应用3.1 微分学中的中值定理3.2 泰勒公式与函数的凹凸性3.3 曲线的渐近线与曲率第四章:不定积分与定积分4.1 不定积分的概念与性质4.2 基本积分公式及其应用4.3 定积分的概念与性质4.4 定积分的计算方法第五章:常微分方程5.1 常微分方程的基本概念与解法5.2 一阶线性常微分方程5.3 高阶常系数线性微分方程第六章:多元函数微分学6.1 多元函数的概念与性质6.2 多元函数的偏导数6.3 多元函数的全微分与全导数第七章:多元函数积分学7.1 二重积分及其计算方法7.2 三重积分及其计算方法7.3 曲线与曲面的面积与曲线积分第八章:无穷级数与幂级数8.1 数项级数的概念与性质8.2 收敛级数判别法8.3 幂级数及其收敛半径第九章:向量代数与空间解析几何9.1 向量的概念与性质9.2 空间几何与平面方程第十章:连续性与一元函数微积分应用10.1 函数连续性与间断点10.2 一元函数微积分应用第十一章:二重积分与曲线积分应用11.1 二重积分应用11.2 曲线积分应用第十二章:无穷级数与多元函数微积分应用12.1 数项级数的应用12.2 多元函数微积分的应用总结:以上为高等数学重庆大学版教材的答案提纲。
希望这个提纲能够帮助你更好地学习和理解高等数学的知识。
在实际讲授过程中,还请参考教材详细内容和课堂教学,确保准确性和全面性。
祝你学习进步!。
重庆大学---高等数学总复习总结资料

高等数学常用公式导数公式:基本积分表:axxaaactgxxxtgxxxxctgxxtgxaxxln1)(logln)(csc)(cscsec)(seccsc)(sec)(22='='⋅-='⋅='-='='222211)(11)(11)(arccos11)(arcsinxarcctgxxarctgxxxxx+-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==CaxxaxdxCshxchxdxCchxshxdxCaadxaCxctgxdxxCxdxtgxxCctgxxdxxdxCtgxxdxxdxxx)ln(lncsccscsecseccscsinseccos22222222CaxxadxCxaxaaxadxCaxaxaaxdxCaxarctgaxadxCctgxxxdxCtgxxxdxCxctgxdxCxtgxdx+=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsinln21ln211csclncscseclnsecsinlncosln22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-CaxaxaxdxxaCaxxaaxxdxaxCaxxaaxxdxaxInnxdxxdxInnnnarcsin22ln22)ln(221cossin2222222222222222222222ππ三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , 一些初等函数: 两个重要极限:三角函数公式:和差角公式: 和差化积公式:倍角公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx xx xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x αααααααααα23333133cos 3cos 43cos sin 4sin 33sin tg tg tg tg --=-=-=αααααααααααααα222222122212sin cos sin 211cos 22cos cos sin 22sin tg tg tg ctg ctg ctg -=-=-=-=-==半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg 反三角函数性质: arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
三阶微分方程的多区域谱方法的开题报告

三阶微分方程的多区域谱方法的开题报告一、选题背景微分方程是科学与工程中最基本的数学工具之一,在科学和工程领域中有着广泛的应用。
随着科学技术的不断发展,人们对于微分方程计算方法的要求也越来越高。
多区域谱方法是一种解决微分方程的数值计算方法,由于其高效性和精度较高,得到了广泛应用。
尤其对于高阶微分方程,多区域谱方法是一种非常适用的解决方法。
本篇开题报告将讨论三阶微分方程的多区域谱方法,研究其相关理论和实现方法,并探讨其应用于不同领域的有效性与局限性。
二、选题意义多区域谱方法是解决微分方程的一种较为高效的方法,其在高精度、高效率的数值计算方面表现优秀。
然而,目前研究领域主要集中在低阶微分方程的解决上,对于高阶微分方程的相关研究还存在很多问题和挑战。
本研究旨在研究三阶微分方程的多区域谱方法,以期提高其对高阶微分方程的适应性和泛用性,加强其在相关领域的应用。
三、研究目标1. 深入了解多区域谱方法的基本理论和算法原理。
2. 研究三阶微分方程的多区域谱方法,探究其数值计算稳定性和精度。
3. 针对实际问题,探讨三阶微分方程的多区域谱方法在某些特定领域中的应用,比如材料工程或者化学反应动力学等。
4. 分析三阶微分方程的多区域谱方法的优点和不足之处,探讨其进一步改进的可能性。
四、研究内容1. 多区域谱方法的基本理论和算法原理。
本文将介绍多区域谱方法的基本原理和算法步骤,探讨方法的数值计算精度和稳定性,特别是在高阶微分方程求解中的可行性,同时对方法的算法评价和改进方向进行讨论。
2. 三阶微分方程的多区域谱方法本文将详细阐述三阶微分方程的多区域谱方法,探究其求解稳定性和精度,从理论上证明方法的正确性和可行性,同时在实际问题中应用方法,比较结果与其他求解方法的异同点,证明方法的可靠性和优越性。
3. 方法的应用本文将探讨三阶微分方程的多区域谱方法在实际问题中的应用,比如在材料工程和化学反应动力学等领域,通过实例分析,比较方法与其他求解方法的优劣,证明其在实际问题中的适用性和有效性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆大学
学生实验报告
实验课程名称数学实验
开课实验室DS1422
学院
学生姓名
开课时间
总成绩
教师签名
数理学院制
开课学院、实验室:ds1422实验时间:
课程名称数学实验实验项目
名称
微分方程
实验项目类型
验证演示综合设计其他
指导
教师
成绩
一、实验目的及意义
[1] 归纳和学习求解常微分方程(组)的基本原理和方法;
[2] 掌握解析、数值解法,并学会用图形观察解的形态和进行解的定性分析;
[3] 熟悉MATLAB软件关于微分方程求解的各种命令;
[4] 通过范例学习建立微分方程方面的数学模型以及求解全过程;
通过该实验的学习,使学生掌握微分方程(组)求解方法(解析法、欧拉法、梯度法、改进欧拉法等),对常微分方程的数值解法有一个初步了解,同时学会使用MATLAB软件求解微分方程的基本命令,学会建立微分方程方面的数学模型。
这对于学生深入理解微分、积分的数学概念,掌握数学的分析思维方法,熟悉处理大量的工程计算问题的方法是十分必要的。
二、实验内容
1.微分方程及方程组的解析求解法;
2.微分方程及方程组的数值求解法——欧拉、欧拉改进算法;
3.直接使用MATLAB命令对微分方程(组)进行求解(包括解析解、数值解);
4.利用图形对解的特征作定性分析;
5.建立微分方程方面的数学模型,并了解建立数学模型的全过程。
三、实验步骤
1.开启软件平台——MATLAB,开启MATLAB编辑窗口;
2.根据微分方程求解步骤编写M文件
3.保存文件并运行;
4.观察运行结果(数值或图形);
5.根据观察到的结果和体会写出实验报告。
四、实验要求与任务
根据实验内容和步骤,完成以下实验,要求写出实验报告(实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论)
基础实验
1.求微分方程的解析解, 并画出它们的图形,
(1)y’= y + 2x, y(0) = 1, 0<x<1;
程序如下:
y1=dsolve('Dy=y+2*x','y(0)=1','x')
结果:
y1 = -2*x-2+3*exp(x)
画图的程序:
x=0:0.01:1 ;
y= -2*x-2+3*exp(x);
plot(x,y)
图形为:
y’’ +y cos(x) = 0, y(0)=1, y’(0)=0;建立M文件:
function f=eqs2(x,y)
f=[y(2);,-y(1)*cos(x)]
输入M文件:
[x,y]=ode23('eqs2',[0,1],[1,0])
plot(x,y(:,1),x,y(:,2),'r')
xlabel('x');gtext('y1'),gtext('y2')
运行结果
f = 0 -1
f = -0.0000 -1.0000
f = -0.0001 -1.0000
f = -0.0001 -1.0000
f = -0.0003 -1.0000
f = -0.0004 -1.0000
f = -0.0005 -1.0000
f = -0.0015 -1.0000
f = -0.0020 -1.0000
f = -0.0025 -1.0000
f = -0.0075 -1.0000
f = -0.0100 -0.9999
f = -0.0125 -0.9998
f = -0.0375 -0.9989
f = -0.0499 -0.9973
f = -0.0624 -0.9961
f = -0.1080 -0.9894
f = -0.1304 -0.9821。
