运筹学大作业
运筹学作业(一)

《运筹学》作业(一)题1.某货轮分前、中、后三个舱位,结构参数见表1。
拟装运三种货物,性能参数见表2。
为了航运安全,要求舱位之间载重比例的偏差不超过10%,以保持船体的平衡。
问应如何制订货物的装运方案可使此运输的收益达到最大?建立该问题的LP 模型。
提示:用x ij 表示装运在第i 个舱位中的第j 种货物的重量,其中:i = 前, 中, 后; j = A, B, C ;故一共有9个变量。
目标是使总运费达到最大。
约束条件分为四组:每个舱位中货物的体积限制,重量限制,每种货物的数量限制,和舱位之间载重比例的偏差限制,故一共有12个约束条件。
题2.确定下列约束条件构成的可行域(1) ⎪⎩⎪⎨⎧≥≤+无约束 2121042x x x x (2)⎪⎩⎪⎨⎧≥-无约束无约束 21210x x x x (3) ⎪⎩⎪⎨⎧≥=≤+-05222121 x x x x (4) ⎪⎩⎪⎨⎧=≥≤+21422121 x x x x 题3.已知LP 问题: 0,,,844344243214213214321≥=++=++-++=x x x x x x x x x x x x x x Z s.t.max试确定⎪⎪⎭⎫ ⎝⎛-==-4/114/10,),(132B x x x B T 是否为最优解。
如果是,给出最优目标值;否则,确定新一轮的进、出变量。
提示 检验数 j j B j c p B c -=-1λ,j = 1, 4。
如果检验数的值大于或等于零,则为最优解;否则,令绝对值最大的负检验数对应的非基本变量进入,而令最小正比值对应的基本变量退出。
题4.给定LP 问题: 0,,42044602343025233212131321321≥≤+≤+≤++++=x x x x x x x x x x x x x Z s.t .m a x已知其最优解为:⎪⎪⎪⎭⎫ ⎝⎛--===-11202/1004/12/1,)20,230,100(),,(1632B x x x x T B T。
运筹学大作业

运筹学课程上机实践要求及内容(2)一、实验教学的目的和要求目的:借助运筹学软件的强大功能,通过小组的充分讨论,对管理实践中的实际问题进行建模、求解,并对求解结果进行分析(特别是敏感性分析),进而激发学生的学习兴趣和热情,克服对课程学习的“恐惧感”。
要求:熟练掌握LINGO、WinQSB等软件的基本功能和基本语法结构,能用软件对运筹学问题进行求解和分析。
二、请于第1次-第6次上机时间及平时完成。
三、作业务请写清学号、姓名、专业、班级,上机作业格式请用老师提供的模版。
四、编写的代码请用记事本单独保存。
五、要求所有题目用LINGO和教材自带的求解软件各做一遍。
并分析解释求解的结果。
六、各题目中的A,B,C,D,E,F为参数,除特别规定外,请自行设定,各个同学参数值不能相同,若发现完全一致的,作业以零分计。
A=1,B=2,C=2,D=4,E=4,F=1第1题(线性规划)(1)介绍单纯型算法及其处理人工变量的两阶段法;(2)建立下列问题的数学模型并求解,讨论资源的影子价格;某造纸厂拟生产漂白松木浆、包装纸(水泥、松木包装纸、松木本色纸)、漂白桦木纸和胶版纸等四种产品,单位产品所需资源情况见表1,市场上胶版纸的需求量不超过6000吨。
(a)制订该造纸厂的生产计划;(b)若电的资源可用量下降10%,重新制订该造纸厂的生产计划。
(3)结合本题,谈谈你对线性规划的认识。
Hint: 若参数为5,5,5,5,5,5,则最优目标函数值为(a)167236800;(b)167236800。
解:(1)单纯形法是求解线性规划问题的通用方法。
单纯形法的基本思想是:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。
因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。
如果问题无最优解也可用此法判别。
两阶段单纯形法也是一种人工变量法,它的算法可分为两个阶段:第一阶段,引入人工变量,构造一个具有标准基的新线性规划,求解这个新线性规划,其结果有两种可能:或者将原问题的约束方程组化成具有标准基的形式,或者提供信息,表明原问题没有可行解。
华农14工业工程运筹学大作业

综合性实验报告实验名称:运筹学与系统分析模型在生产决策优化中的应用姓名:学号:姓名:学号:姓名:学号:班级14级工业工程专业(2班)完成时间:2016年12月指导教师:杨振刚老师一、实验目的1.运用运筹学与系统分析的方法来对实际问题进行建模和求解。
2.掌握课程知识的综合应用。
二、实验内容1.运用一个或多个课程模型,针对实际案例问题进行简化和建模。
2.对于所建模型应用计算机软件进行求解,并对求解结果进行分析。
三、实验案例时代服装公司生产一款新的时装,据预测今后6个月的需求量如表7-3所示。
每件时装用工2h和10元原材料,售价40元。
该公司1月初有4名工人,每人每月可工作200h,月薪2000元。
该公司可于任一个月初新雇工人,但每雇1人需一次性额外支出1500元,也可辞退1人,但每辞退1人需补偿1000元。
如当月生产数超过需求,可留到后面月份销售,但需付库存费用每件每月5元,当供不应求时,短缺数不需补上。
试帮助该公司决策,如何使6个月的总利润最大。
表7-3 单位:件四、建模与分析最大收益问题如表1-1所示,本模型分为四个部分————①问题描述②建立模型③决策变量④约束条件①问题描述表1-1中上半部分是问题描述。
该部分描述了(预计每月订货数量)、(每件时装的加工成本,加工时间,售价,每月每件库存价格)、(起始员工数量,每个员工每月工作时间,工作工资,增减员工的花费)列出题目中所有已知信息。
②建立模型根据①问题描述中的已知信息和所要解决的问题建立模型,引入每月工作人数,每月生产量,每月销售量(除去上月库存),每月库存,每月收益等描述模型的概念。
每月工作人数:每月工作人数=上个月的实际人数+当月人数变动在单元格C10中键入:=B10+C16得到1月实际工人数(为方便拖动,引入0月,人数为4),拖动C10到H10,获得其他5个月的工作人数每月生产量:每月生产量=当月员工数*每个员工的每月工作时间/单位时装工时在单元格C11中键入:=C10*$F$5/$C$3得到一月的生产量,拖动C11到H11,获得其他5个月的月生产量。
运筹学作业(5)
运筹学作业(5)
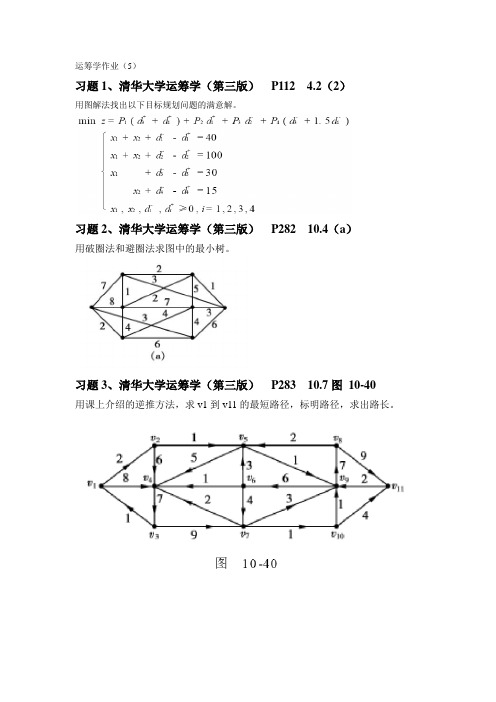
习题1、清华大学运筹学(第三版)P112 4.2(2)
用图解法找出以下目标规划问题的满意解。
习题2、清华大学运筹学(第三版)P282 10.4(a)
用破圈法和避圈法求图中的最小树。
习题3、清华大学运筹学(第三版)P283 10.7图10-40
用课上介绍的逆推方法,求v1到v11的最短路径,标明路径,求出路长。
习题4:已知条件如表所示
p1:每周总利润不得低于10000元;
p2:因合同要求,A型机每周至少生产10台,B型机每周至少生产15台;
p3:希望工序Ⅰ的每周生产时间正好为150小时,工序Ⅱ的生产时间最好用足,甚至可适当加班。
试建立这个问题的目标规划模型并求解(可利用EXCEL求)。
思考题:在上题中,如果工序Ⅱ在加班时间内生产出来的产品,每台A型机减
少利润10元,每台B型机减少利润25元,并且工序Ⅱ的加班时间每周最多不超过30小时,这是p4级目标,试建立这个问题的目标规划模型并求解。
(此题下周四前会给出参考答案)。
运筹学 大作业

运筹学请在以下五组题目中任选一组作答,满分100分。
第一组:计算题(每小题25分,共100分)1.福安商场是个中型的百货商场,它对售货人员的需求经过统计分析如下表所示,为了保证售货人员充分休息,售货人员每周工作五天,休息两天,并要求休息的两天是连续的,问该如何安排售货人员的休息,既满足了工作需要,又使配备的售货人员的人数最少,请列出此问题的数学模型。
2.A、B两人分别有10分(1角)、5分、1分的硬币各一枚,双方都不知道的情况下各出一枚,规定和为偶数,A赢得8所出硬币,和为奇数,8赢得A所出硬币,试据此列出二人零和对策模型,并说明此游戏对双方是否公平。
3、某厂生产甲、乙两种产品,这两种产品均需在A、B、C三种不同的设备上加工,每种产品在不同设备上加工所需的工时不同,这些产品销售后所能获得利润以及这三种加工设备问:该厂应如何组织生产,即生产多少甲、乙产品使得该厂的总利润为最大?4、用图解法求解 max z = 6x1+4x2 s.t.第二组:计算题(每小题25分,共100分)1、用图解法求解min z =-3x1+x2 s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤+≥+≤≤08212523421212121x x x x x x x x ,2、用单纯形法求解 max z =70x1+30x2 s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+072039450555409321212121x x x x x x x x ,3、用单纯形法求解 max z =7x1+12x2 s.t.⑵ ⑶ ⑷ ⑸、⑹1212212210870x x x x x x x +≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩, ⑴ ⑵ ⑶ ⑷ ⑸⑹、⑺⑴⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200543604921212121x x x x x x x x ,4.某企业要用三种原材料A 、B 、C 生产出出三种不同规格的产品甲、乙、丙。
已知产品的规格要求,产品单价,每天能供应的原材料数量及原材料单价,分别见表1和表2。
运筹学大作业

运筹学大作业红牌罐头食品制造商一1、管理部门的目标是什么?在我们看来企业当以有限资源之最小获取利益之最大,也就是将“利润最大化”作为企业的管理目标。
利润代表了企业新创造的财富,利润越多,则说明企业的财富增加得越多,越接近企业的目标。
厂商从事生产或出售商品不仅要求获取利润,而且要求获取最大利润,厂商利润最大化原则就是产量的边际收益等于边际成本的原则。
2、管理部门需要知道什么?我们认为管理部门需要知道市场对我们产品的需求量、产品原料供应量及其他资源等对生产的限制、各个产品的售价、单位产品的人工成本、原料成本和净利润,以及该如何生产才能使利润达到最大。
我们需要知道公司本年度的工作计划,即产品的生产量(销售量)。
3、约束条件有哪些?在这个题目中我们所了解的约束条件主要有三个:一是番茄的数量的限制,总数是300万磅,而其中A级番茄是600000磅,B级番茄是2400000磅,我们在计算产品组合及数量的时候绝对不能超过这个量;二是需求的限制,题中明显给出了需求预测,所以这是生产时的上限,否则生产过多将会供过于求;三是产品质量的限制,题目中明确规定了罐装整番茄的最低输入质量要求为每磅8点,番茄汁为每磅6点,而番茄酱则为每磅5点,所以可完全用B级番茄来制作。
4、你认为红牌罐头食品制造商应生产什么?我们认为红牌罐头食品厂制造商应生产26667箱番茄汁、80000箱番茄酱,才能使利润最大化。
二1、整番茄、番茄酱和番茄汁各应生产多少?设整番茄,番茄汁和番茄酱所使用的A级番茄分别为X1,X2,X3磅,下面计算原料成本。
我们跟迈尔的想法一样,我们认为番茄成本应以质和量两种基础来确定,而不是仅仅依赖于量。
设:Z=每磅A级番茄的成本/美分Y=每磅B级番茄的成本/美分由题可知(600000磅*Z)+(2400000磅*Y)=(3000000磅*6)Z/9=Y/5解得:Z=9.32 Y=5.18所以A级番茄的成本为9.32美分每磅,B级番茄的成本为5.18美分每磅。
运筹学学生(大型作业1学分)(上海电力学院)任务书资料

上海电力学院课程设计(大型作业)任务书(2012/2013 学年第1学期)课题名称运筹学大型作业课题代码141303501,141303513院(系)经济与管理学院专业信息管理与信息系统2011级班级2011131学生时间2013.1.14-18老师签名:赵文会,曹金龙教研室主任(系主任)签名:《运筹学》大型作业任务书一、内容1、基础训练——熟悉计算机软件Winqsb的子菜单和Lindo软件求解线性规划问题。
能用Winqsb软件求解运筹学中的常见数学模型。
完成以下内容:2、综合训练:劳动力资源分配问题的见面。
(见附录1)二、目的通过大型作业教学,培养学生利用所学的运筹学知识,根据具体的问题,进行综合分析、计算、评价的能力,以全面理解运筹学的思想和方法并能用于实际工作。
三、要求:1、总体要求全面结合运筹学的内容,根据自己对问题的理解,通过分析,建立合理的运筹学模型,能利用计算机软件Winqsb求出最优解,并能根据自己的理解给出合理分析。
2、形式要求所用的运筹学内容应先有简明阐述,再与具体问题相结合的结论。
整个作业力求全面、丰富,应用资料注明来源。
打印成稿。
四、组织形式基础训练单独完成;每人交一份打印稿作业(正反打印)。
综合训练分组进行,每小组4人(含4人),小组完成时必须有明确的分工,必须有总负责人(总负责人也必须有自己的局部内容)。
综合训练部分小组提交一份打印稿作业。
任务书与大作业封面要在综合训练部分作业中。
注:小组完成的,应根据各人完成的具体工作,在大型作业的成品上注明,并按顺序排名。
五、考核形式大型作业的所有内容在1月18日结束之前交稿,教师可根据评阅情况的需要,指定部分作品进行答辩质疑与交流。
六、成绩评定1、大作业的总评成绩由三部分组成:基础训练+综合训练报告质量+平时表现(出席和答辩表现),具体比例为:40:30:30成绩由任课老师根据完成质量进行评定,以优\良\中\及格\不及格计分。
2.答辩表述要求答辩,如果由个人完成时由个人全面阐述,小组完成时应由一人总述(总述人也应有自己的局部内容),各成员陈述自己完成部分。
运筹学大作业(选修班)
运筹学大作业(选修)
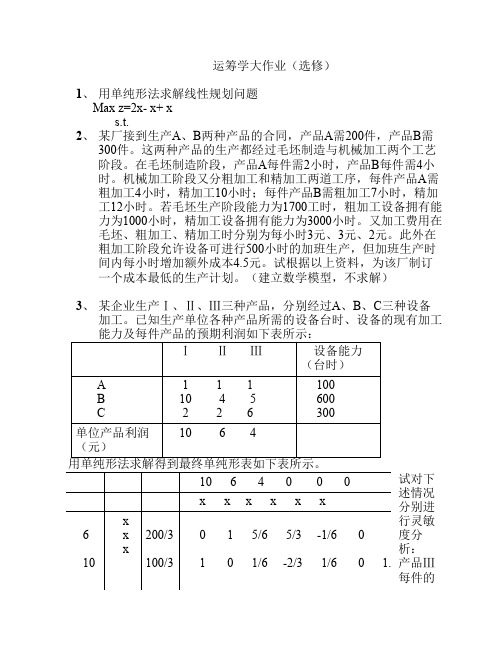
1、 用单纯形法求解线性规划问题 Max z=2x- x+ x s.t.
2、 某厂接到生产A、B两种产品的合同,产品A需200件,产品B需 300件。这两种产品的生产都经过毛坯制造与机械加工两个工艺 阶段。在毛坯制造阶段,产品A每件需2小时,产品B每件需4小 时。机械加工阶段又分粗加工和精加工两道工序,每件产品A需 粗加工4小时,精加工10小时;每件产品B需粗加工7小时,精加 工12小时。若毛坯生产阶段能力为1700工时,粗加工设备拥有能 力为1000小时,精加工设备拥有能力为3000小时。又加工费用在 毛坯、粗加工、精加工时分别为每小时3元、3元、2元。此外在 粗加工阶段允许设备可进行500小时的加班生产,但加班生产时 间内每小时增加额外成本4.5元。试根据以上资料,为该厂制订 一个成本最低的生产计划。(建立数学模型,不求解)
3、 某企业生产Ⅰ、Ⅱ、Ⅲ三种产品,分别经过A、B、C三种设备 加工。已知生产单位各种产品所需的设备台时、设备的现有加工 能力及每件产品的预期利润如下表所示:
Ⅰ ⅡⅢ
设备能力 (台时)
A
1 11
100
B
10 4 5
600
C
2 26
300
单位产品利润 (元)
10 6 4
用单纯形法求解得到最终单纯形表如下表所示。
值得安排生产?如产品Ⅲ每件利润增加到50/6元,求最优计划
的变化;
2. 如有一种新产品,加工一件需设备A、B、C的台时各为1、4、
3小时,预期每件的利润为8元,是否值得安排生产;
3. 如合同规定该企业至少生产10件产品Ⅲ,试确定最优计划的变
化。
4、 某地区有三个化肥厂,除供应外地区需要外,估计每年可供应本
运筹学课堂大作业

课堂作业报告运 筹 学报告题目:货物配送问题(图论、整数规划) 专业班级: 报告人:货物配送问题(图论、整数规划)一、 问题重述1.1 背景知识本文研究的内容是以梦想连锁是一家主营鲜猪肉的肉类食品加工与销售公 司为背景而提出的。
针对该公司的具体情况,按照问题的要求,本文进行了以下 研究。
公司在全省县级及以上城镇设立销售连锁店。
全省县级及以上城镇地理位 置及道路连接见数据文件 1:全省交通网络数据.xlsx1.2 1.2.1 问题一要解决的问题目前公司现有 2 个生产基地、23 家销售连锁店,生产基地设在 120 号和 63 号城镇,为 23 家连锁店提供鲜猪肉,连锁店的日销售量见附录 1。
若运输成本 为 0.45 元/吨公里,请你为公司设计生产与配送方案,使运输成本最低。
1.2.2 问题二公司收集了近 5 年全省各城镇的鲜猪肉月度需求数据(文件 2:各城镇月度 需求数据.txt)请你分析各城镇需求特征,并预测未来数年,何时全省鲜猪肉需 求达到峰值,达到峰值时需求达到前 5 位和后 5 位的城镇是那些?1.2.3 问题三通过广告宣传等手段,未来几年公司在全省的市场占有率可增至 3 成左右 (各城镇对公司产品每日需求预测数据见文件 3:公司未来各城镇每日需求预测 数据.txt) ,调查还发现,公司产品的需求量与销售量并不完全一致,若在当地 (同一城镇)购买,则这一部分需求量与销售量相同,若在不足 10 公里的其他 城镇的销售连锁店购买, 则这一部分需求量只能实现一半 (成为公司产品销售量, 由于距离的原因,另一半需求转向购买其他公司或个体工商户的产品) ,而在超 过 10 公里的其他城镇的销售连锁店购买,销售量只能达到需求量的三成。
于是, 公司决定在各城镇增设销售连锁店,基于现有条件、成本等的考虑,原有的 23 家销售连锁店销售能力可在现有销售量的基础上上浮 20%,增设的销售连锁店销 售能力控制在每日 20 吨至 40 吨内, 并且要求增设的销售连锁店的销售量必须达 到销售能力的下限。
运筹学大作业

运筹大作业
文件说明
rosenbrock.m:函数的matlab符号函数实现。
naive_opt.m:负梯度法
F_R.m:Fletcher-Reeves共轭梯度法
P_R.m:Polak-Ribiere共轭梯度法
B_S.m:Beale-Sorenson共轭梯度法
程序说明
四个程序遵循相同的架构。
对于符号函数,matlab有gradient函数可以求符号函数的梯度,norm函数可以求符号函数的范数。
使用sub可以将符号函数转为数值函数。
之后严格遵循算法流程代入值求解即可。
调用方法
四个程序都不带参数。
直接调用即可获得图像,返回值为double的数值解。
求解结果
负梯度法
共迭代377次,最后结果为(0.999999999906938, 0.999999999790556)(数值解)
Fletcher-Reeves共轭梯度法
(第三个点因为其log为-inf因此无法被画出)
共迭代2次,最后结果为(1.000000000000001, 1.000000000000001)
Polak-Ribiere共轭梯度法
(第三个点因为其log为-inf因此无法被画出)
共迭代2次,最后结果为(1.000000000000001, 1.000000000000001)
Beale-Sorenson共轭梯度法
(第三个点因为其log为-inf因此无法被画出)
共迭代2次,最后结果为(1.000000000000001, 1.000000000000001)。
运筹学大作业(线性规划问题)

线性规划法在救援物资调运问题中的应用【摘要】线性规划法是物资调运问题中最常用的一种方法,本文通过建立线性规划模型,用LINGO数学软件求出了最优解,得到了一个最佳的物资调运方案。
【关键词】:线性规划法;LINGO;调运一、引言由于近几年来地壳运动剧烈,各种自然灾害频频发生,其中各地的地震灾害尤其严重。
汶川地震发生后,为了尽可能的减小国家和人民的损失,各级政府对灾区进行物资救助。
为了解决大规模物资调运的实际问题(通常要处理的实际问题都是大规模的物资调运问题)以及物流管理中的类似问题,我们必须先建立这类问题的数学模型,而后选择合适的计算方法并利用计算机工具求解。
这种数学模型称为规划问题,规划问题中涉及的线性函数关系,我们就称为线性规划问题。
本文将在物资调运中的实际问题建立数学模型,用LINGO数学软件求出物资调用的最优方案。
一下是LINGO软件的简介。
LINGO是LINGO是Linear Interactive and General Optimizer的缩写,即“交互式的线性和通用优化求解器”,由美国LINDO系统公司(Lindo System Inc.)推出的,可以用于求解非线性规划,也可以用于一些线性和非线性方程组的求解等,功能十分强大,是求解优化模型的最佳选择。
其特色在于内置建模语言几个内部函数,可以允许决策变量是整数(即整数规划,包括 0-1 整数规划),方便灵活,而且执行速度非常快。
能方便与EXCEL,数据库等其他软件交换数据。
二、一个物资调运问题现有三家企业捐献物资调运到四个受灾点。
企业A,B,C捐赠物资量分别为100吨、60吨、90吨四个受灾点I, Il,III,Ⅳ,需求量分别为60吨、70吨、50吨、70吨。
企业A往受灾点I,II,III,Ⅳ每吨的运价分别为l0元、15元、20元、25元;企业 B到受灾点I,II,III,Ⅳ每吨的运价分别为2O元、10元、l5元、15元:企业 C 到受灾点I,II,III,Ⅳ每吨的运价分别为25元、30元、20元、25元。
运筹学大作业二

北京科技大学远程教育学院第二学期 《运筹学(36)》大作业模拟题二专业 班级 学号姓名_ _____1.在下面的数学模型中,属于线性规划模型的为( )⎪⎩⎪⎨⎧≥≤+=0Y ,X 3XY .t .s Y X 4S max .A ⎪⎩⎪⎨⎧≥-≥-+=0Y ,X 1Y X 2.t .s YX 3S min .B ⎪⎩⎪⎨⎧≥≤-+=0Y ,X 2Y X .t .s Y X S max .C 22 ⎪⎩⎪⎨⎧≥≥+=0Y ,X 3Y X .t .s XY 2S min .D2.若线性规划问题的最优解同时在可行解域的两个顶点处达到,那么该线性规划问题最优解为( ) A.两个 B.零个 C.无穷多个 D.有限多个3..求运输问题的解就是求满足要求的( ) A.各供应点到各需求点的运费 B.总运费 C.各供应点到各需求点的运量D.总运量4.关于运输问题的说法中错误..的是( ) A.最优运输方案未必唯一 B.必有最优运输方案C.运输方案的任何调整必会引起总运费的下降D.V ogel 法是一种比较简单的计算方法5.考虑某运输问题,其需求量和供应量相等,且供应点的个数为m ,需求点的个数是n 。
若以西北角法求得其初始运输方案,则该方案中数字格的数目应为( )A.(m+n)个B.(m+n-1)个C.(m-n)个D.(m-n+1)个6.考虑某运输问题,设其总需求量为Q,总供应量为G,且Q<G。
欲将其化为供需平衡的运输问题,则应()A.使诸供应点的供应总量减少G-QB.使诸需求点的需求总量增加G-QC.虚设一个需求量为G-Q的需求点,且任一供应点到该虚设需求点的单位运费为充分大D.虚设一个需求量为G-Q的需求点,且任一供应点到该虚设需求点的单位运费为07.关于线性规划模型的可行解区,叙述正确的为()A.可行解区必有界B.可行解区必然包括原点C.可行解区必是凸的D.可行解区内必有无穷多个点8.关于线性规划问题,叙述正确的为()A.其可行解一定存在B.其最优解一定存在C.其可行解必是最优解D.其最优解若存在,在可行解中必有最优解9.在运输问题中如果总需求量小于总供应量,则求解时应()A.虚设一些供应量B.虚设一个供应点C.根据需求短缺量,虚设多个需求点D.虚设一个需求点10.在线性规划中,设约束方程的个数为m,变量个数为n,m<n时,可以把变量分为基变量和非基变量两部分,基变量的个数为m个,非基变量的个数为( )A.m个 B.n个C.n-m个D.0个二、填空题1..求解运输问题时出现的退化现象是指__ __ 。
高级运筹学大作业

课程案例分析
题目:《最速下降法、牛顿法和共轭梯度法的应用》
授课老师:
上海理工大学管理学院
小组成员:
学号 姓名 专业 管理科学与工程 管理科学与工程 管理科学与工程 管理科学与工程 管理科学与工程 管理科学与工程 组长 备注说明
目录
前言 ......................................... - 1 一、作业背景 ................................................ - 1 二、选题说明 ................................................ - 1 三、工作业绩 ................................................ - 2 -
第4章
总结 ................................ - 15 -
4.1. 算法的案例结果分析.............................................................................. - 15 4.2. 算法特征及优劣比较.............................................................................. - 15 4.3. 结后语...................................................................................................... - 16 -
2.2. 算法基本步骤
贡献
% % % % % %
运筹学大作业 哈工大

课程名称:对偶单纯形法1、教学目标在对偶单纯形法的学习过程中,理解和掌握对偶问题;综合运用线性规划和对偶原理知识对对偶单纯形法与单纯形法进行对比分析,了解单纯形法和对偶单纯形法的相同点和不同点,总结出各自的适用范围;掌握对偶单纯形法的求解过程;并能运用对偶单纯形法独立解决一些运筹学问题。
2、 教学内容1) 对偶单纯形法的思想来源(5min)2) 对偶单纯形法原理(5min)3) 总结对偶单纯形法的优点及适用情况(5min)4) 对偶单纯形法的求解过程(10min)5) 对偶单纯形法例题(15min)6) 对比分析单纯形法和对偶单纯形法(10min)3、 教学进程:1)讲述对偶单纯形法思想的来源:1954年美国数学家C.莱姆基提出对偶单纯形法(Dual Simplex Method)。
单纯形法是从原始问题的一个可行解通过迭代转到另一个可行解,直到检验数满足最优性条件为止。
对偶单纯形法则是从满足对偶可行性条件出发通过迭代逐步搜索原始问题的最优解。
在迭代过程中始终保持基解的对偶可行性,而使不可行性逐步消失。
因此在保持对偶可行性的前提下,一当基解成为可行解时,便也就是最优解。
2)讲述对偶单纯形法的原理A.对偶问题的基本性质依照书第58页,我们先介绍一下对偶问题的六个基本性质:性质一:弱对偶性性质二:最优性。
如果(j=1...n)原问题的可行解,是其对偶问题可行解,且有=,则是原问题的最优解,是其对偶问题的最优解。
性质三:无界性。
如果原问题(对偶问题)具有无界解,则其对偶问题(原问题)无可行解。
性质四:强对偶性。
如果原问题有最优解,则其对偶问题也一定有最优解。
性质五:互补松弛型。
在线性规划问题的最优解中,如果对应某一约束条件的对偶变量值为零,则该约束条件取严格等式;反之如果约束条件取严格不等式,则其对应的对偶变量一定为零。
性质六:线性规划的原问题及其对偶问题之间存在一对互补的基解,其中原问题的松弛变量对应对偶问题的变量,对偶问题的剩余变量对应原问题的变量;这些互相对应的变量如果在一个问题的解中是基变量,则在另一问题的解中是非基变量;将这对互补的基解分别代入原问题和对偶问题的目标函数有z=w.B.对偶单纯形法(参考书p64页)设某标准形式的线性规划问题,对偶单纯形表中必须有-≤0(j=1...n),但(i=1...m)的值不一定为正,当对i=1...m,都有≥0时,表中原问题和对偶问题均为最优解,否则通过变换一个基变量,找出原问题的一个目标函数值较小的相邻的基解。
2023年运筹学大作业单纯性法与对偶单纯性法的比较

2023年运筹学大作业单纯性法与对偶单纯性法的比较目前,运筹学领域中的单纯性法和对偶单纯性法是两种最为常用的线性规划求解方法。
随着科技和工业的不断发展,未来的运筹学研究也将越来越受到人们的关注。
因此,在未来的2023年中,我们不仅需要掌握这两种方法的基本概念和原理,还需要深入的了解它们的比较和应用。
第一章单纯性法的基本原理单纯性法是一种常用的线性规划求解方法,其基本流程可以归纳为以下几个步骤:1. 确定一个基本可行解;2. 判断该基本可行解是否是最优解;3. 如果不是最优解,则选择一个入基变量和一个出基变量;4. 对出基变量进行互换,更新基本可行解;5. 重复执行步骤2至步骤4,直至得到最优解。
单纯性法的优点在于可快速地求得最优解,特别是在少数变量和简单约束的情况下,可以快速解决线性规划问题。
但是,当规模较大或者约束条件复杂时,单纯性法很可能会陷入循环,导致计算时间过长。
第二章对偶单纯性法的基本原理对偶单纯性法是单纯性法的一种扩展,其实质是对线性规划模型的对偶模型进行求解。
其基本流程可以归纳为以下几个步骤:1. 确定一个对偶基本可行解;2. 判断该对偶基本可行解是否是最优解;3. 如果不是最优解,则选择一个入基变量和一个出基变量;4. 对出基变量进行互换,更新对偶基本可行解;5. 重复执行步骤2至步骤4,直至得到最优解。
对偶单纯性法的优点在于可以避免陷入循环的情况,同时,还可以通过求解对偶问题来产生原问题的最优解。
第三章两种方法的比较从计算复杂度的角度来比较单纯性法和对偶单纯性法,很明显对偶单纯性法更加高效。
因为对偶单纯性法的目标函数和限制条件比原问题要少,因此需要的计算步骤相对更少。
但是,在实际操作中,对偶单纯性法的计算结果通常需要进行一次转换才能得到原问题的最优解。
从求解结果的角度来比较单纯性法和对偶单纯性法,也可以发现它们的区别。
在某些情况下,单纯性法得出的最优解不一定是方案的唯一最优解,而对偶单纯性法则可以直接得到原问题的唯一最优解。
大学运筹学大作业【精选】

我们的购买价格 上限是8.22美分/ 磅,所以若有可 供应的A级番茄, 红牌罐头食品制 造商愿以每磅价
格小于或等于 8.22美分/磅的价
格买下它;
同时我们也可以 回答2.5,我们 已经计算出可以 接受的购买价格 即价格上限,根 据上面的式子我 们可以判定,我 们不应该购买。
问题2.7的分析及结果
1.3约束条件有哪些?
在这个题目中我们所了解的约束条件主要有三个: 一是番茄的数量的限制,总数是300万磅,而其中A级番茄,即平均质量达到9点指 标的番茄是60万磅,B级番茄,即平均质量达到5点指标的番茄是240万磅,我们在 计算产品组合及数量的时候绝对不能超过这个量;即:X1+X2+X3≤6000000; X4+X5+X6≤2400000; 二是需求的限制,没有需求生产再多的产品都没用,而题中明显给出了需求预测, 所以这是生产时的上限,否则生产再多也是做无用功;即:X1+X4≤800000*18, X2+X5≤50000*20,X3+X6≤80000*25; 三是产品质量的限制,题目中也明确规定了罐装整番茄的最低输入质量要求为每 磅8点,番茄汁为每磅6点,而番茄酱则可完全用B级番茄来制作,不做约束。 即:X1-3X4≥0 3X2-X5≥0,
下它? 4 总收益是多少? 5 红牌罐头食品制造商是否应以0.085美元的价格购买那80000磅
的A级番茄? 6 使用库伯的收益图与迈尔的利润图计算的解与你得到的解有何
不同?为什么会有不同? 7 连锁超市的采购者要以3.6美元/箱的价格买下所有的整番茄
产品,条件是允许红牌罐头食品制造商以最低极限质量点(7点) 的水平进行生产,是否接受? 8 假设可以无限量收购0.085美元/磅的A级番茄,红牌罐头食品 制造商应购进多少?生产将如何组合?
《运筹学》期末大作业2011A

《运筹学》期末大作业一、建立线性规划模型。
(30分)某公司生产I、II两种产品,市场对I、II两种产品的需求量为:产品I在1—4月每月需10000件,5—9月每月30000件,10—12月每月100000件;产品II在3—9月每月15000件,其他月每月50000件。
该公司生产这两种产品成本为:产品I在1—5月内生产每件5元,6—12月内生产每件4.5元;产品II在1—5月内生产每件8元,6—12月内生产每件7元。
该公司每月生产这两种产品的能力总和不超过120000件。
产品I容积每件0.2立方米,产品II每件0.4立方米,该公司仓库容量为15000立方米,占用公司仓库每月每立方米库容需1元;如该公司仓库不足时,可从外面租借,租用外面仓库每月每立方米库容需1.5元。
试问在满足市场需求的情况下,该厂应如何安排生产,使总的生产加库存费用为最少?二、建立运输问题的表格模型。
(25分)某北方研究院有一、二、三三个区。
每年分别需要用煤3000、3000、2000吨,由河北临城、山西盂县两处煤矿负责供应,价格、质量相同。
供应能力分别为3500、4000吨,运价如下表:由于需大于供,经院研究决定一区供应量可减少0--400吨,二区必须满足需求量,三区供应量不少于1600吨,试求总费用为最低的调运方案。
三、建立线性多目标规划模型。
(25分)一个投资者决定在三个项目中投资,投资总额为100000元,这三个项目是储蓄、债券和股票。
预计每个投资项目的年均收益分别是4%、8%、16%。
投资者希望的目标是,第一优先级目标:至少得到9000元的年均收益;第二优先级目标:股票投资不少于债券和储蓄投资的总和;第三优先级目标:股票投资最少为20000元;第四优先级目标:储蓄投资应在15000元到20000元之间。
试问投资总额应如何分配?四、建立线性整数规划模型。
(20分)某汽车生产厂生产A1、A2、A3三种型号的汽车,已知各生产一台时的钢材、劳动力消耗和利润值,每月可供使用的钢材及劳动小时数如下表所示。
运筹学大作业20130904

《运筹学》部分上机大作业
2013-9-4
一.作业题目
1.教材P61案例1、案例2,要求分析问题,设计参数,建立模型,并用计算机求解,且对求解结果进行一定程度的分析。
求解软件可用教材自带的,也可以用Lingo 9.0等。
2.教材P61案例3、4、5自己阅读。
3.教材P156案例6、案例7,要求分析问题,设计参数,建立模型,并用计算机求解,且对求解结果进行一定程度的分析。
案例8用计算机求解,且对求解结果进行一定程度的分析。
求解软件可用教材自带的,也可以用Lingo 9.0等。
4.教材P404阅读案例19并写出你的观点;案例20在三个方案中作出决策。
二.相关要求
5.课程结束前2周提交:
1)打印稿以班级为单位由各班学习委员收齐后交任课老师;
任课老师办公室:C3-411
2)电子版以班级为单位由各班学习委员收齐后发送至老师的邮箱:wlustbshao@
6.请各位务必写清楚你的学号、姓名、班级。
三.该部分成绩
7.上机大作业将以较大的平时成绩权重计入期末总成绩。
运筹学大作业

中石油管道输气运输成本问题一、背景简介:中国石油天然气集团公司(简称中国石油集团,英文缩写:CNPC)是由中央直接管理的国有特大型央企,根据国务院机构改革方案,于1998年7月在原中国石油天然气总公司的基础上组建的特大型石油石化企业集团,系国家授权投资的机构和国家控股公司,是实行上下游、内外贸、产销一体化、按照现代企业制度运作,跨地区、跨行业、跨国经营的综合性石油公司。
2004年国内生产原油11176.1万吨,生产天然气286.6亿立方米,加工原油11077.5万吨;同时在海外获取权益原油产量1642.3万吨、天燃气产量25.9亿立方米。
全年实现销售收入5707亿元,实现利润1289亿元,实现利润在国内企业中位居榜首。
作为中国境内最大的原油、天然气生产、供应商,中国石油集团业务涉及石油天然气勘探开发、炼油化工、管道运输、油气炼化产品销售、石油工程技术服务、石油机械加工制造、石油贸易等各个领域,在中国石油、天然气生产、加工和市场中占据主导地位。
2008年,中国石油在美国《石油情报周刊》世界50家大石油公司综合排名中,位居第5位,在美国《财富》杂志2011年世界500强公司排名中居第6位,在《巴菲特杂志》2009年中国上市公司百强评选中,荣获“中国25家最受尊敬上市公司全明星奖”第一名。
在“2011中国企业500强”中,以营业收入14654.15亿元人民币列第2位。
在2013年荣获中国品牌价值研究院、中央国情调查委员会、焦点中国网联合发布的2013年度中国品牌500强。
进入新世纪新阶段,中国石油集团在国家大公司、大集团战略和有关政策的指导、支持下,正在实施一整套新的发展战略,瞄准国际石油同行业先进水平,加快建设主业突出、核心竞争力强的大型跨国石油企业集团,继续保持排名前列世界大石油公司地位。
二、运输问题成本实例分析1、问题提出中国天然气产业的快速发展仅是一个新阶段的开始。
从整个天然气上下游一体化的系统工程来看,中国天然气产业依然年轻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大连科技学院运筹学(Z)大作业LINGO软件在函数最大值中的运用
学院名称
专业班级
学生组号
学生姓名
指导教师
二〇一八年五月
实验LINGO软件在函数最大值中的运用
大作业目的
掌握LINGO软件求解函数最大值的基本步骤,了解LINGO软件解决函数最大值的基本原理,熟悉常用的函数最大值计算代码,理解函数最大值的迭代关系。
仪器、设备或软件
电脑,LINGO软件
大作业内容
1.LINGO软件求解函数最大值的基本原理;
2.编写并调试LINGO软件求解函数最大值的计算代码;
实施步骤
1.使用LINGO计算并求解函数最大值问题;
2.写出实验报告,并浅谈学习心得体会(选址问题的基本求解思路与方法及求解过程中出现的问题及解决方法)。
实施过程
有一艘货轮,分为前、中、后三个舱位,它们的容积与允许载重量如下表所示。
现有三种商品待运,已知有关数据列于下表中。
又为了航运安全,要求前、中、后舱在实际载重量上大体保持各舱最大允许载重量的比例关系。
具体要求前、后舱分别与中舱之间的载重量比例偏差不超过15%,前、后舱之间不超过10%。
问货轮应装载A、B、C各多少件,运费收入为最大?试建立这个问题的线性规
首先分析问题,建立数学模型:
确定决策变量
假设i=1,2,3分别代表商品A、B、C,8用j=1,2,3分别代表前、中、后舱,设决策变量x ij为装于j舱位的第i种商品的数量(件)。
确定目标函数
商品A 的件数为: 商品B 的件数为: 商品A 的件数为: 为使运费最高,目标函数为:
确定约束条件
前、中、后舱位载重限制为:
前、中、后舱位体积限制为:
A 、
B 、
C 三种商品数量的限制条件:
各舱最大允许载重量的比例关系构成的约束条件:
且决策变量要求非负,即x ij ≥0,i=1,2,3;j=1,2,3。
综上所述,此问题的线性规划数学模型为:
111213x x x ++212223x x x ++313233x x x ++()()()111213212223313233 1000700600Max Z x x x x x x x x x =++++++++112131122232132333865200086530008651500
x x x x x x x x x ++≤++≤++≤112131122232132333105740001057540010571500
x x x x x x x x x ++≤++≤++≤1112132122233132336001000800
x x x x x x x x x ++≤++≤++≤1121311222321323331222321121311323338x 6x 5x 2
2(10.15)(1+0.15)38x 6x 5x 3
8x 6x 5x 11(10.15)(1+0.15)28x 6x 5x 2
8x 6x 5x 4
4(10.10)(1+0.10)38x 6x 5x 3++-≤≤++++-≤≤++++-≤≤++()()()
111213212223313233112131122232132333112131122232132333 1000700600865200086530008651500105740001057540010571500
Max Z x x x x x x x x x x x x x x x x x x x x x x x x x x x =++++++++++≤++≤++≤++≤++≤++≤
x ij ≥0,i=1,2,3;j=1,2,3。
把数学模型编写成代码写入LINGO 程序
编入如下代码:
!设前舱运A 为x11,运B :x12,运C :x13; !设中舱运A 为x21,运B :x22,运C :x23;
!设后舱运A 为x31,运B :x32,运C :x33;!单位:件; !目标函数;
max=1000*(x11+x12+x13)+700*(x21+x22+x23)+600*(x31+x32+x33); !数量约束;
x11+x12+x13<=600; x21+x22+x23<=1000; x31+x32+x33<=800; !容量约束;
x11*10+x21*5+x31*7<=4000; x12*10+x22*5+x32*7<=5400; x13*10+x23*5+x33*7<=1500; !重量约束;
x11*8+x21*6+x31*5<=2000; x12*8+x22*6+x32*5<=3000; x13*8+x23*6+x33*5<=1500; !平衡约束;
(2/3)*(1-0.15)<=(x11*8+x21*6+x31*5)/(x12*8+x22*6+x32*5); (1/2)*(1-0.15)<=(x13*8+x23*6+x33*5)/(x12*8+x22*6+x32*5); (4/3)*(1-0.10)<=(x11*8+x21*6+x31*5)/(x13*8+x23*6+x33*5); (x11*8+x21*6+x31*5)/(x12*8+x22*6+x32*5)<=(2/3)*(1+0.15); (x13*8+x23*6+x33*5)/(x12*8+x22*6+x32*5)<=(1/2)*(1+0.15); (x11*8+x21*6+x31*5)/(x13*8+x23*6+x33*5)<=(4/3)*(1+0.10); !整数约束;
@gin(x11);@gin(x12);@gin(x13); @gin(x21);@gin(x22);@gin(x23); @gin(x31);@gin(x32);@gin(x33); 如下图所示:
1112132122233132336001000800
x x x x x x x x x ++≤++≤++≤1121311222321323331222321121311323338x 6x 5x 2
2(10.15)(1+0.15)38x 6x 5x 38x 6x 5x 1
1(10.15)(1+0.15)28x 6x 5x 28x 6x 5x 4
4(10.10)(1+0.10)38x 6x 5x 3
++-≤≤++++-≤≤++++-≤≤++
然后运行得出结果:
Local optimal solution found.
Objective value: 801000.0
Extended solver steps: 0
Total solver iterations: 4
Variable Value Reduced Cost X11 150.0000 -1000.000 X12 375.0000 -1000.000 X13 75.00000 -1000.000 X21 0.000000 -700.0000 X22 0.000000 -700.0000 X23 150.0000 -700.0000 X31 160.0000 -600.0000 X32 0.000000 -600.0000 X33 0.000000 -600.0000
Row Slack or Surplus Dual Price
1 801000.0 1.000000
2 0.000000 0.000000
3 850.0000 0.000000
4 640.0000 0.000000
5 1380.000 0.000000
6 1650.000 0.000000
7 0.000000 0.000000
8 0.000000 0.000000
9 0.000000 0.000000
10 0.000000 0.000000
11 0.1000000 0.000000
12 0.7500000E-01 0.000000
13 0.1333333 0.000000
14 0.1000000 0.000000
15 0.7500000E-01 0.000000
16 0.1333333 0.000000
由运行结果可以得知:
前舱运输A 150件,B 375件,C 75件;
中舱运输A 0件,B 0件,C 150件;
后舱运输A 160件,B 0件,C 0件;
的总利润最大为801000.0元。
心得体会
运筹学是近几十年发展起来的一门新兴学科。
它的目的是为管理人员在做决议是提供科学的依据,它是实现现代化管理的有力工具。
应用运筹学处理问题是,有两个重要特点:一是从全局观点出发;二是通过建模,对于要求解的问题得到最合理的决策。
我国拥有的资源量,从人均来看,是一个资源相对贫乏的国家。
因此,如何合理、有效、经济的利用资源,是相当重要的。
提高管理工作的效能和效益,是人尽其才,物尽其用,将运筹的方法应用于实践,运筹学拥有广阔的前景。
管理工作者、科学工作者和从事工程科学管理的人们都需要学习和掌握这门科学。
在运筹学上机实验中我自学了应用LINGO软件来实现用计算机的建模和对规划问题的求解。
通过学习,我学会了使用软件对线性规划等运筹学问题。
总之我感觉运筹学是一门很神奇的学科,他对我们有很大的帮助。
