电路的s域模型

4.5 电路的S域模型

4.5 电路的S 域模型利用S 域模型分析具体电路时，不必列写微分方程，而直接写出S 域代数方程，使得分析过程变得更加简单。

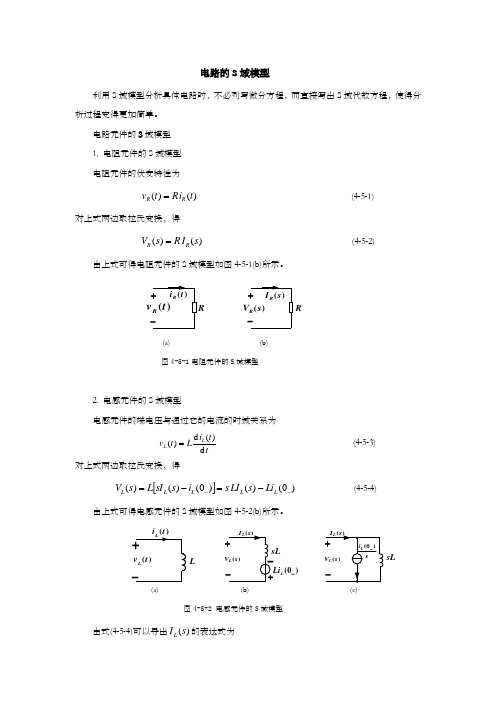
4.5.1电路元件的S 域模型 1. 电阻元件的S 域模型电阻元件的伏安特性为)()(t i R t v R R = (4-5-1)对上式两边取拉氏变换，得)()(s I R s V R R = (4-5-2)由上式可得电阻元件的S 域模型如图4-5-1(b)所示。

(a) (b)图4-5-1电阻元件的S 域模型2. 电感元件的S 域模型电感元件的端电压与通过它的电流的时域关系为tt i Lt v L L d )(d )(= (4-5-3) 对上式两边取拉氏变换，得[])0()()0()()(---=-=L L L L L Li s LI s i s sI L s V (4-5-4)由上式可得电感元件的S 域模型如图4-5-2(b)所示。

(a) (b) (c)图4-5-2 电感元件的S 域模型由式(4-5-4)可以导出)(s I L 的表达式为RRL)0(-LLi sL)0(1)()(-+=L L L i sL s s V s I (4-5-5) 所以电感元件的电流源形式S 域模型如图4-5-2(c)所示。

3. 电容元件的S 域模型电容元件的端电压与通过它的电流的时域关系为⎰∞-=tc C i Ct v ττd )(1)( (4-5-6) 对上式两边取拉氏变换，得s i C sC s I s i s s I C s V C C C C C )0(1)()0()(1)()1()1(----+=⎥⎦⎤⎢⎣⎡+= 式中 )0()(1)0(10)1(-∞---==⎰-C C C v d i Ci C ττ, 所以 )0(1)(1)(-+=C C C v ss I sC s V (4-5-7)由上式可得电容元件的S 域模型如图4-5-3(b)所示。

(a)(b) (c)图4-5-3 电容元件的S 域模型由式(4-5-7)可以导出)(s I C 的表达式为)0()()(--=C C C v C s CV s s I (4-5-8)所以电容元件的电流源形式S 域模型如图4-5-3(c)所示。

用laplace变换法分析电路

(1) H (s) h(t )
先求出H(s)
V0 ( s) 1 H ( s) 2 E ( s) r sl 1 s 2s 1 sc 1 1 1 t h(t ) L [ H ( s)] L [ ] te 2 ( s 1) 参见p181表4-1中9号公式
1 1 20t 20t h( )d [ (t ) 10e ]dt e u (t ) 0 0 2 2 t 1 1 20t t 1 20t 20t 0 2e d 40 e |0 40 (1 e )u(t )
t t
V2 (t ) e(t ) h(t ) e (t ) h( )d
用拉氏变换分析电路的步骤如下： A.将已知的电动势、恒定电流进行拉氏变换。 B.根据原电路图画出运算等效电路图。 C.用计算线性系统或电路稳定状态的任何方法解运算电路，求出待求量的象函数。 D.将求得的象函数变换为原函数。
*.电路如图所示：求：
e(t )
2
1H
1F
v0 (t )
1.冲激响应h(t)=?
2.求系统的起始状态 iL (0 ), u c (0 ) 使得在z.I.r=h(t).
3.求系统的起始状态,使系统对u(t)的激励时的完全响应仍为u(t).
解:
用冲激平衡法求解h(t ) d 2 vc (t ) dvc (t ) LC RC vc (t ) (t )(第二章内容) 2 dt dt
20T
if . f (T ) 0, then, T 0
'
极大值点
T 0, f (T ) 400Te
'
20T
0
所以v2 (t)在t=T时为负值.

“用拉普拉斯变换法分析电路、s域元件模型”的课堂教学设计

“用拉普拉斯变换法分析电路、s域元件模型”的课堂教学设计作者：葛颖来源：《教育教学论坛》2014年第10期摘要：信号与系统是电气类专业的一门专业基础课程，拉普拉斯变换是求解连续时间系统响应的重要方法之一，在变换域分析中有非常重要的作用。

本文从教材分析、教学方法、教学过程和教学反思四个方面讨论了该堂课的教学设计过程，实践证明得到了很好的教学效果。

关键词：拉普拉斯变换；教材分析；教学设计；教学反思中图分类号：G642.3 文献标志码：A 文章编号：1674-9324（2014）10-0234-02用拉普拉斯变换法分析电路、s域元件模型是高等教育出版社《信号与系统》第四章第五节的内容，是第四章拉普拉斯变换、连续时间系统的s域分析中的重要内容。

它解决了通过变换域方法求解连续时间系统响应的问题，是求解微分方程的重要方法之一。

这一节与前面两节拉普拉斯变换的性质和拉普拉斯逆变换紧密相连，由这一节的讨论又引出了下一节系统函数的问题，在本章中占有非常重要的地位。

一、教材分析本次教学内容是用拉普拉斯变换的方法求解连续时间系统响应，主要应用了两种方法得到系统的s域数学模型，一是对微分方程进行拉普拉斯变换，另外一种是采用s域元件模型分析电路直接得到s域的代数方程。

教学目标是让学生掌握连续时间系统的复频域分析法，能通过元件的s域模型得到系统的s域代数方程。

教学重点是对微分方程进行拉普拉斯变换和用s域元件模型简化微分方程。

教学难点是拉普拉斯变换微分性质的应用。

对于教材中本节的例题，选择其中的例4-13和例4-15来进行讲解。

例4-13采用拉氏变换的方法分析电路，例4-15采用的是s域元件模型的分析方法，是比较有代表性的两个例题，涵盖了本节的重要知识点。

另外把第二章的课后作业2-6作为一个补充例题，因为教材中的例题只解决了求解系统完全响应的问题，而没有涉及到用拉氏变换的方法对零输入和零状态的求解。

这个例题很好地体现了系统初始条件和激励与零输入响应和零状态响应之间的关系，通过这道例题可以达到让学生对拉氏变换灵活运用的目的。

信号与系统第四章3郑君里

SL
当初始状态为零时
说明:串、并联形式的S模型之间可进行等效变换
并联形式的S模型
3
3 RLC系统的S域模型及分析方法 us(t) US (S) 对电路的S域模型进行分析时， is(t) IS(S) 可仿照正弦稳态电路的相量分析 u(t) U(S) 法（分压、分流、等效变换、节 i(t) I(S) 点法、网孔法、等效电路）求出待求变量的象函数。时域模型 S域模型
15
pi 、zj 的可能形式
A 一阶实极(零)点 ~ 位于S 平面的实轴上 B 一阶共轭虚极(零)点 ~ 位于S 平面的虚轴上，且对称于实轴 C 一阶共轭复极(零)点 ~ 在S 平面上对称于实轴 D r 阶极(零)点(实、共轭复数)
说明：
1）只研究n m的情况
16
零、极点分布图
´ j2
j
´´
解:
9
二、系统函数H(S)的原函数
L[h(t)]= H(s)
10
解：
11
三、
系统的S域模型
由系统的时域模型根据拉氏变换的性质可得系统的S域模型
a）数乘器
b）加法器
c）积分器
e(t)为因果信号
12
时域框图
S域框图
13
例6
已知图所示系统求H(s)
14
第七节系统函数与系统特性
一、系统函数H(s) 的零点与极点
22
极点分布与h(t)关系
h(t) h(t)
´
0
´
t
´
0
h(t) t
0
t
h(t)
´
t
´ ´ ´
h(t)
0
´
h(t) t t

连续系统的S域分析法

s
s
s2 8s 16
1s 2s
3
1
即 Y s 4.5 4 + 2
s 1 s 2 s 3
反变换， y t 4.5et 4e2t 1 e3t t 0
2
已知微分方程的s域分析
例3 描述某LTI系统的微分方程为： y(t) 5y(t) 6y(t) f (t)
且 y(0-)=1，y’(0-)=-1，f(t)=5cost (t)，求系统的全响应y(t)
解对微分方程取拉氏变换得：
s2Y (s) sy(0 ) y(0) 5 s Y ( s ) y ( 0 ) 6Y(s) 2F (s)
(s2 5s 6)Y(s) 2 F ( s ) sy ( 0 ) y ( 0 ) 5 y ( 0 )
2F (s) Y(s) s 2 5 s 6
1 s
I ( s )
u(0 ) 1 I(s)
s
Cs
+ u(t)
-
Cs
i(t)
+
I(s)
C
1 Cs
U(s)
-
+
U (s)
C u (0-)
-
I(s)
1 Cs +
u(0 )
-s
1 复频域容抗
Cs
u(
0 ) 、 Cu(0
s 内部电源
)
:
电容并联模型（宜于节点分析）电容串联模型（宜于回路分析）
3) 电感
zi
已知微分方程的s域分析
例2 设有方程y(t) 3y(t) 2 y(t) e3t (t)
y ( 0 ) 1, y(0 ) 2, 求 y(t)。
解对方程取拉氏变换，得
[s 2Y (s) sy(0 ) y(0 )] 3[sY (s) y(0 )] 2Y (s)

期末考试《信号与系统课程要点(吴大正)》

信号与线性系统复习提纲第一章信号与系统1．信号、系统的基本概念2．信号的分类，表示方法（表达式或波形）连续与离散；周期与非周期；实与复信号；能量信号与功率信号3．信号的基本运算：加、乘、反转和平移、尺度变换.图解时应注意仅对变量t作变换，且结果可由值域的非零区间验证。

4．阶跃函数和冲激函数极限形式的定义；关系；冲激的Dirac定义阶跃函数和冲激函数的微积分关系冲激函数的取样性质（注意积分区间）；;5．系统的描述方法数学模型的建立:微分或差分方程系统的时域框图，基本单元：乘法器，加法器，积分器（连)，延时单元(离）由时域框图列方程的步骤。

6．系统的性质线性：齐次性和可加性；分解特性、零状态线性、零输入线性.时不变性：常参量LTI系统的数学模型:线性常系数微分(差分）方程（以后都针对LTI系统）LTI系统零状态响应的微积分特性因果性、稳定性（可结合第7章极点分布判定）第二章连续系统的时域分析1．微分方程的经典解法：齐次解+特解(代入初始条件求系数）自由响应、强迫响应、瞬态响应、稳态响应的概念0—～0+初值（由初始状态求初始条件）：目的，方法（冲激函数系数平衡法)全响应=零输入响应+零状态响应；注意应用LTI系统零状态响应的微积分特性特别说明：特解由激励在t>0时或t〉=0+的形式确定2．冲激响应定义，求解(经典法），注意应用LTI系统零状态响应的微积分特性阶跃响应与的关系3．卷积积分定义及物理意义激励、零状态响应、冲激响应之间关系卷积的图示解法(了解）函数与冲激函数的卷积（与乘积不同）；卷积的微分与积分复合系统冲激响应的求解（了解)第三章离散系统的时域分析1．离散系统的响应差分方程的迭代法求解差分方程的经典法求解：齐次解+特解（代入初始条件求系数）全响应=零输入响应+ 零状态响应初始状态(是），而初始条件（指的是）2．单位序列响应的定义，的定义,求解（经典法)；若方程右侧是激励及其移位序列时,注意应用线性时不变性质求解阶跃响应与的关系3．卷积和定义及物理意义激励、零状态响应、冲激响应之间关系卷积和的作图解与的卷积和；结合前面卷积积分和卷积和，知道零状态响应除经典解法外的另一方法。

电路的S 域模型利用S 域模型分析具体电路时，不必列写微分方程，而直接写出S 域代数方程，使得分析过程变得更加简单。

电路元件的S 域模型 1. 电阻元件的S 域模型电阻元件的伏安特性为)()(t i R t v R R = (4-5-1)对上式两边取拉氏变换，得)()(s I R s V R R = (4-5-2)由上式可得电阻元件的S 域模型如图4-5-1(b)所示。

(a) (b)图4-5-1电阻元件的S 域模型2. 电感元件的S 域模型电感元件的端电压与通过它的电流的时域关系为tt i Lt v L L d )(d )(= (4-5-3) 对上式两边取拉氏变换，得[])0()()0()()(---=-=L L L L L Li s LI s i s sI L s V (4-5-4)由上式可得电感元件的S 域模型如图4-5-2(b)所示。

(a) (b) (c)图4-5-2 电感元件的S 域模型由式(4-5-4)可以导出)(s I L 的表达式为)0(1)()(-+=L L L i sL s s V s I (4-5-5) 所以电感元件的电流源形式S 域模型如图4-5-2(c)所示。

3. 电容元件的S 域模型电容元件的端电压与通过它的电流的时域关系为⎰∞-=tc C i Ct v ττd )(1)( (4-5-6) 对上式两边取拉氏变换，得式中 )0()(1)0(10)1(-∞---==⎰-C C C v d i C i C ττ, 所以)0(1)(1)(-+=C C C v ss I sC s V (4-5-7)由上式可得电容元件的S 域模型如图4-5-3(b)所示。

(a) (b) (c)图4-5-3 电容元件的S 域模型由式(4-5-7)可以导出)(s I C 的表达式为)0()()(--=C C C v C s CV s s I (4-5-8)所以电容元件的电流源形式S 域模型如图4-5-3(c)所示。

麻省理工电子与电路学演示——S,SR,SCS模型

6.002 演示#06 (下载安装 Demo#06.set)
S/SR/SCS 模型 Agarwal 2000秋
第6讲（和第8讲）
目的：
本演示研究了MOS管的各种状态模型, 即S, SR, 和SCS 模型。

用正弦电压信号驱动MOS 管V S时，在示波器上显示电流i D(用电阻上的电压间接得到)和对应的电压v DS的关系曲线而不是简单的点。

S和SR模型的演示通过控制v GS高于（导通状态）或低于（关断状态）MOS管门限电压来实现。

SCS模型以同样的方式演示, 即增加v GS使之从小于v T增加到大于v T的某一数值上。

这表明当v GS很大时，MOS管的饱和区域(当前电源电压下)不明显。

步骤：
1.开关模演示型,v IN加一个大的电压, 并且时断时续。

从示波器上观察到的漏源极间的i-v
特性如下所示。

曲线看起来像开路(水平线)和短路(垂直线)。

2.开关电阻器模型, v IN加一个很小的电压, 并且时断时续。

从示波器上观察到的漏源极间的i-v特性如下所示。

曲线看起来象开路(水平线)和电阻器特性(倾斜的线) 。

3.源极控制开关模型, v IN开始设置为小于v T，然后逐渐增加, 得到一组曲线。

注意按钮按下的顺序：>
>0
>
0.4v
v
< 高阻
> 50Ω
*微机面板上的插脚#号和BNC插接元件
（） Pins。

s域和z域分析

VC (s)

1 sC
IC (s)

1 s
vC
(0 )
用于回路分析
R,L,C并联形式的s域模型
VR (s) RIR (s)
VL (s) sLIL (s) LiL (0 )
1
1
VC (s) sC IC (s) s vC (0 )
对电流解出得：
IR (s)

1 R
VR
(s)
I L (s)
(五) z变换与拉普拉斯的关系
(一)从s平面到z平面的映射
z esT
s 1 ln z T
s

2
T
s j
z rej
z e( j )T eT e jT
2
r eT e s
T 2 S
s平面到z平面有如下映射关系：
(1)s平面上的虚轴( 0, s j)映射到z平面是单位圆,其
H (s) LT[r(t)] R(s) LT[e(t)] E(s) h(t) ILT[H (s)]
r(t) e(t) h(t) R(s) E(s)H (s)
r(t) 1 j R(s)estds
2 j j
(八)零极点与系统的时域特性
etu(t)
1
ZT[cos(0n)u(n)]

z(z cos0 ) z2 2z cos0 1
(二)几类序列的收敛域：
(1)有限序列：在有限区间内，有非零的有限值的序列
n2
X (z) x(n)zn
n1 n n2
nn1
除n1 0时，z 和n2 0时z 0外，所有z值都收敛

电路的S域模型

电路的S 域模型利用S 域模型分析具体电路时，不必列写微分方程，而直接写出S 域代数方程，使得分析过程变得更加简单。

电路元件的S 域模型 1. 电阻元件的S 域模型电阻元件的伏安特性为)()(t i R t v R R = (4-5-1)对上式两边取拉氏变换，得)()(s I R s V R R = (4-5-2)由上式可得电阻元件的S 域模型如图4-5-1(b)所示。

(a) (b)图4-5-1电阻元件的S 域模型2. 电感元件的S 域模型电感元件的端电压与通过它的电流的时域关系为tt i Lt v L L d )(d )(= (4-5-3) 对上式两边取拉氏变换，得[])0()()0()()(---=-=L L L L L Li s LI s i s sI L s V (4-5-4)由上式可得电感元件的S 域模型如图4-5-2(b)所示。

(a) (b) (c)图4-5-2 电感元件的S 域模型RRL)0(-LLi sL由式(4-5-4)可以导出)(s I L 的表达式为)0(1)()(-+=L L L i sL s s V s I (4-5-5) 所以电感元件的电流源形式S 域模型如图4-5-2(c)所示。

3. 电容元件的S 域模型电容元件的端电压与通过它的电流的时域关系为⎰∞-=tc C i Ct v ττd )(1)( (4-5-6) 对上式两边取拉氏变换，得s i C sC s I s i s s I C s V C C C C C )0(1)()0()(1)()1()1(----+=⎥⎦⎤⎢⎣⎡+= 式中)0()(1)0(10)1(-∞---==⎰-C C C v d i C i C ττ, 所以 )0(1)(1)(-+=C C C v ss I sC s V (4-5-7)由上式可得电容元件的S 域模型如图4-5-3(b)所示。

(a)(b) (c)图4-5-3 电容元件的S 域模型由式(4-5-7)可以导出)(s I C 的表达式为)0()()(--=C C C v C s CV s s I (4-5-8)所以电容元件的电流源形式S 域模型如图4-5-3(c)所示。

四、电路的s域模型：

Y s

Y s
uc 0
s

0
R sL
R
1
sc
Y s iL 0 s 3uc 0 us s
s2 4s 4
s2 4s 4
y s y s.
x
f
Y xs
6s 20
s2 2
8
6

s2 2 s 2
+
复频域：U(s)=RI(s) I(s)
<2>电感：L.
时域：u(t)=Ldi(t)/dt i(t)
+
s域：U(s)=sLI(s)-LiL(0_)
RR
UL(t) 串联 I(s)
U(s) Ls Li(t)
• 2.元件模型：
<3>电容：c
I(s)= U(s)/sL+ iL(0_) /s 并联 I(s)
时域：u(t)=
开路阻抗z0 s
sL
sL
R

sc 1
sc
u2s
z
0
R
s

R
U
oc
s

u1s 2 s3 2s2 2s 1

H (s)

u2 s u1s

2(s
1
1)(s2

s
1)
,又 t
1 s
Y f s Gs H st
-
s
Y(s)
1 sc
R3 -
例10：电路如图，输入u1t,输出u2 t；
为使电路输出不失真，各元件应满足什么条件。
解：电路中个初始值[uc 0 ，iL 0 ]等均为零。

§ 4.5 用拉普拉斯变换法分析电路、s域元件模型

1 VR (s) + sVR (s) − 2E = 0 RC
三．利用元件的s域模型分析电路
1.电路元件的s域模型 2.电路定理的推广 KCL : ∑i(t ) = 0 → ∑I(s) = 0 i(t ) ↔ I (s),
v(t ) ↔V (s)
KVL : ∑v(t ) = 0 → ∑V(s) = 0
我们采用0 系统求解瞬态电路，简便起见，瞬态电路我们采用 -系统求解瞬态电路，简便起见，只要知起始状态，就可以利用元件值和元件的起始状态，道起始状态，就可以利用元件值和元件的起始状态，求出元件的s域模型域模型。求出元件的域模型。
例4-5-1
− E t < 0 已知 e(t ) = E t >0 求vC (t ), vR (t )。
2
2
逆变换
E i(t ) = e p1t − e p2t L( p1 − p2 )
(
)
设则
R 1 α＝ ,ω = 0 2L LC
第一种情况： α LC (无损耗的回路) 第一种情况： = 0， ω α Q 第二种情况：较小， Q 回路，第二种情况： < ω 即R较小，高的LC回路， = 0 0 2α α 第三种情况 = ω 0
vC (t )
E
E • vC (t )从0−的− E充电到 ;
t
O
• 在求vC (t )时，其 0− 和0+ 符合换路定则，均可。换路定则，采用 0− 和0+ 均可。
−E
求 v (t ) = ? R
1 （）vR (0− ) = 0, vR (0+ ) = 2E (2)以vR (t )为变量列微分方程

李瀚荪《电路分析基础》(第4版)课后习题详解-第12章拉普拉斯变换在电路分析中的应用【圣才出品】

第12章　拉普拉斯变换在电路分析中的应用
§12-1　拉普拉斯变换及其几个基本性质
12-1　RC 串联电路t ＝0时与10 V 电压源接通，已知R ＝2MΩ、C ＝1μF，试用拉氏变换法求电流i （t ）和电容电压M 。

（t ）， t≥0。

已知u C （0－）＝0。

解：电路如图
12-1（a ）所示，画出电路的
s 域模型如图
12-1（b
）所示，可得（s ）的反变换为
比较系数得
解得
所以
U （s ）的反变换为
图12-1
12-2　RL 并联电路如图
12-2所示，已知
试用拉氏变换法求u （t ），
t≥0。

图
12-2
图12-3
解：画出电路的s 域模型如图12-3所示。

列出方程
反变换得。

12-3　t≥0
时电路如图12-4所示，已知，试求
图
12-4
图12-5
解：方法一：画出电路的s域模型如图12-5所示。

列出方程
所以
解得反变换得
方法二：用戴维南定理。

在图12-5中，断开电容支路，得接上电容支路，得以下与方法一相同。

12-4　电路如图12-6所示，
t ＝0时开关打开，求。

图12-6
图12-7
解：画出电路的s 域模型如图12-7所示。

可列出方程
反变换得
§12-2　反拉普拉斯变换
——赫维赛德展开定理
12-5　求若F （s ）为：
解：
所以
F （s ）为假分式，不能直接使用赫维赛德定理。

用长除法，得对真分式部分有
所以。

5.4系统的S域分析

8 5t i (t ) e sin15t 15 (t 0)
上式的反变换为
由此可以看出，用拉氏变换求解电路，电路的起始状态自动地包含在s域的代数方程中，从而一次确定电路的全响应，比时域法简便。如将电流响应的象函数表达式分开两项列写，即
uc (0 ) Li (0 ) s I ( s) 1 1 R sL R sL sC sC 10 s
信号与系统
5.4-1
5.4

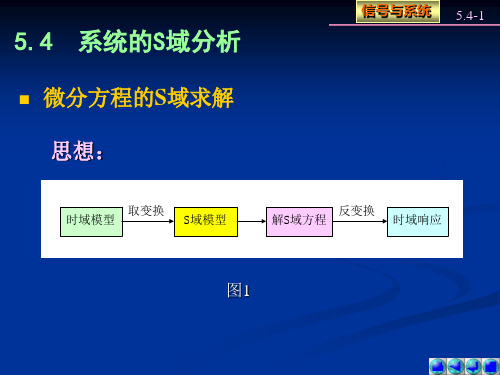
系统的S域分析
微分方程的S域求解思想：
时域模型取变换 S域模型解S域方程
用拉氏变换法分析LTI常系数微分方程时，其特点是：
(1)通过拉氏变换可将时域中的微分方程变换为复频域中的代数方程，使求解化简。
(2)系统的起始状态(条件)可以自动地包含到象函数中，从而可一举求得方程的完全解。
Z ( s)
i (t )
u (t )
I ( s)
I ( s)
U ( s)
U ( s)
RCL串联电路
RCL串联电路对应的s域模型
s 域阻抗电路
信号与系统
由右图可列出KVL方程
1 R sL I ( s) U ( s) sC
I ( s)
5.4-14
即
1 RI ( s ) sLI ( s) I ( s) U ( s) sC
uL max 12000V
小结
F s f t e s td t

信号与系统
5.4-20
1. 拉普拉斯变换是一种线性积分变换，是求解线性常系数微分方程的有力工具，应用非常普遍。函数f (t)的(单边)拉氏变换为 2. 拉氏变换的主要性质如下：

电路的s域模型

电路的S 域模型利用S 域模型分析具体电路时，不必列写微分方程，而直接写出S 域代数方程，使得分析过程变得更加简单。

电路元件的S 域模型 1. 电阻元件的S 域模型电阻元件的伏安特性为)()(t i R t v R R = (4-5-1)对上式两边取拉氏变换，得)()(s I R s V R R = (4-5-2)由上式可得电阻元件的S 域模型如图4-5-1(b)所示。

(a) (b)图4-5-1电阻元件的S 域模型2. 电感元件的S 域模型电感元件的端电压与通过它的电流的时域关系为tt i Lt v L L d )(d )(= (4-5-3) 对上式两边取拉氏变换，得[])0()()0()()(---=-=L L L L L Li s LI s i s sI L s V (4-5-4)由上式可得电感元件的S 域模型如图4-5-2(b)所示。

(a) (b) (c)图4-5-2 电感元件的S 域模型由式(4-5-4)可以导出)(s I L 的表达式为RRL)0(-LLi sL)0(1)()(-+=L L L i sL s s V s I (4-5-5) 所以电感元件的电流源形式S 域模型如图4-5-2(c)所示。

3. 电容元件的S 域模型电容元件的端电压与通过它的电流的时域关系为⎰∞-=tc C i C t v ττd )(1)( (4-5-6)对上式两边取拉氏变换，得s i C sC s I s i s s I C s V C C C C C )0(1)()0()(1)()1()1(----+=⎥⎦⎤⎢⎣⎡+= 式中 )0()(1)0(10)1(-∞---==⎰-C C C v d i C i C ττ, 所以)0(1)(1)(-+=C C C v ss I sC s V (4-5-7)由上式可得电容元件的S 域模型如图4-5-3(b)所示。

(a)(b) (c)图4-5-3 电容元件的S 域模型由式(4-5-7)可以导出)(s I C 的表达式为)0()()(--=C C C v C s CV s s I (4-5-8)所以电容元件的电流源形式S 域模型如图4-5-3(c)所示。

5.4系统的S域分析解析

信号与系统
5.4-4
解得
K1 4.5，K2 4，K3 0.5
故有
4.5 4 0.5 Y ( s) s 1 s 2 s 3
取反变换，得完全响应 y(t) = L1[Y(s)]=4.5et 4e2t + 0.5e3t (t0)
信号与系统

5.4-5
例5-14 设有二阶LTI系统方程
y(t ) 3 y(t ) 2 y (t ) f (t ) 4 f (t )
系统初始状态 y(0 ) 1, y(0 ) 2 ，输入 f (t ) (t ) ，试求零输入响应、零状态响应和全响应。
解
对方程取拉氏变换，得
[ s 2Y ( s) sy (0 ) y(0 )] 3[ sY ( s) y (0 )] 2Y ( s) ( s 4) F ( s)
L
解因换路前电路已达稳态，
故可得 i(0_)=0 uc(0_)=2V 换路后(t >0)，其KVL方程为
图2
di (t ) 1 t Ri (t ) L uc (0 ) i ( )d 10 dt C 0
令 i( t ) I( s )， u( t ) U( s )，则方程的拉氏变换为
由例5-14可知，在s域中求零输入响应、零状态响应可以用代数的方法简单求解，若只求全响应，可不必分出Yzi(t)和Yzs(t)，通过Y(s)一举反变换求得y(t)。
信号与系统
5.4-7
例5-15 对于图2所示电路，原已处于稳态，开关于t=0时
由1端转向2端。已知R = 10Ω，L = 1H，C = 0.004F，求换路后的电流i ( t )。
整理得

用LT法分析电路S域模型教学课件

25 3
e 3t u (t )
*方法二：s域模型
R, L, C元件的时域关系：
(1)vR (t) RiR (t)
(2)vL (t)
L
ห้องสมุดไป่ตู้
diL (t) dt
(3)vC
(t )
1 C
t
iC
(
)d
s域模型一：
(1)VR (s) RIR (s)
(2)VL (s) L[sI L (s) iL (0 )]
(s
j ) R(s)
s j0
Em H 0e j0 2j
k j0
(s
j ) R(s)
s j0
Em H 0e j0 2j
稳态响应rss
(s)
Em H 0 2j
e e j(0t0 )
j (0t 0 )
EmH0 sin(0t 0 )
对比e(t) Em sin 0t 幅度改变相位偏移
H (0 ) H0e j0
H(s)的极点
暂态响应
j轴或右半平面--自由响应
属于稳态响应左半平面----强迫响应属于
E(s)的极点
暂态响应
j轴或右半平面--强迫响应
属于稳态响应
4.8 由系统函数零极点分布决定频响特性
什么是系统频响特性？不同频率的正弦激励下系统的稳态响应.一般为复数，可表示为：
H () H () e j()
转移导纳转移电压比
电流
电流
转移电流比
*冲激响应与系统函数：
H (s) h(t )est dt
0
h(t )
1
j
H (s)est ds
2j j
h(t ) H (s)

电路的s域模型

电路的S 域模型利用S 域模型分析具体电路时，不必列写微分方程，而直接写出代数方程，使得分析过程变得更加简单。

电路元件的S 域模型I. 电阻元件的s 域模型电阻元件的伏安特性为VR (t) RiR (t)(4-5-1)对上式两边取拉氏变换，得V R (S ) RI R (S )(4一5-2)由上式可得电阻元件的S 域模型如图4-5-1⑹所示(a) (b)图4-5-1电阻元件的s 域模型2. 电感元件的S 域模型电感元件的端电压与通过它的电流的时域关系为(4一5-3)I R (S)IRV R (S ) D RVL (t)LdL(t)dt对上式两边取拉氏变换，得由上式可得电感元件的S域模型如图4-5-2⑹ 所示。

所以电感元件的电流源形式S域模型如图4-5-2 (c)所示3.电容元件的S域模型电容元件的端电压与通过它的电流的时域关系为对上式两边取拉氏变换，得由上式可得电容元件的S域模型如图4-5-3(b)所示Vc(s) Ic(s) (1)ic (0 ) lc(s)or r(1)1 ic (0 )式中肖Ao )c° icOdVc(s)1Ic(S)SCVc(0),所以1-y(0)S(4一5-7)ic(t). Vc(t)丰 cIc(S)Vc(s)J_丄~r scv(0 )slc(S)(c)OLi L(0 )(b)由式(4-5-4)可以导岀图4-5-2电感元件的S域模型I L(S)的表达式为I L(S)V L(S)sL -iL(O )(4一5-5)1 Vc(t) ©tic( )d (4一5-6)I L(S)------------- A'L(0)图4-5-3电容元件的S 域模型由式(4-5-7)可以导岀lc(s)的表达式为lc(s) sCVc(s) Cvc(O )所以电容元件的电流源形式S 域模型如图4-5-3 (c)所示利用S 域模型求电路的响应利用S 域模型求解电路响应的一般步骤如下：⑴求起始状态(0-状态)；⑵画s 域模型图；⑶列s 域方程(代数方程)；⑷解s 域方程，求岀响应的拉氏变换V(s)或I (s);⑸利用拉氏逆变换求v(t)或i(t)⑵画出电路的S 域模型图如图4-5-4⑹所示。

电路的s域模型

4.5 电路的S域模型

用laplace变换法分析电路

“用拉普拉斯变换法分析电路、s域元件模型”的课堂教学设计

信号与系统第四章3郑君里

连续系统的S域分析法

期末考试《信号与系统课程要点(吴大正)》

电路的s域模型

麻省理工电子与电路学演示——S,SR,SCS模型

s域和z域分析

电路的S域模型

四、电路的s域模型：

§ 4.5 用拉普拉斯变换法分析电路、s域元件模型

李瀚荪《电路分析基础》(第4版)课后习题详解-第12章 拉普拉斯变换在电路分析中的应用【圣才出品】

5.4系统的S域分析

电路的s域模型

5.4系统的S域分析解析

用LT法分析电路S域模型教学课件

电路的s域模型

李瀚荪《电路分析基础》(第4版)课后习题详解-第12章拉普拉斯变换在电路分析中的应用【圣才出品】