比的意义和比的基本性质练习题

化简比和求比值练习题及答案

化简比和求比值练习题及答案一、知识要点：1、比的意义：2、比的基本性质：3、求比值：用比的前项除以后项4、化简比：化简比就是把一个比变成前项和后项都是整数的，并且前项和后项的公因数只有1。

5、化简比的结果二、求比值：1、整数比整数36：1824：30 15：101：635：1202、小数比小数 0.6：0.240.36：0.0953、分数比分数3：2：9918104、小数比分数0.3:0.45: 1 1:0.75:0.7544416三、化简比：1、整数比整数32：18196:4162：842、小数比小数0.125：0.2.8：3.90.1：0.04213、分数比分数3：：：223749424、整数比小数10：0.81：0.9.1：18265、分数比小数3：2.50.125：： 1.6486、整数比分数9：274：162：1 101547、单位比.5千克：400克400厘米：6米 00毫升：1升20千克：1吨0分钟：2小时 08立方厘米：2立方分米1003求比值和化简比练习一、填空1、 10：36=，读作。

2、/=÷12=9：3、一个正方形的边长为a，边长与周长的比是：，边长与面积的比是：。

4、 A是8.4，B比A少3.6，A：B=：，比值是。

5、：5=9=27÷ 1546、：2=11=：=/12=10从甲地到乙地，小李用了4小时，小张用了3小时。

小李和小张所用的时间的比是：，他们的速度比是：。

7、一块铁与锌的合金，铁占合金的2，那么铁与锌的质量之比：；9合金的质量是锌的质量的倍。

8、甲数除以乙数的商是2，那么甲数与乙数的最简整数比是：。

9、甲、乙两篮各盛有35个鸡蛋。

如果从甲篮取出5个鸡蛋放入乙篮，那么乙篮与甲篮的鸡蛋个数的比是：.10、40克盐放入 2.5千?a href=“http:///fanwen/shuoshuodaquan/”target=“_blank” class=“keylink”>说乃 ?盐与水的质量比是：,盐与盐水的质量比是：.11 、某班女生比男生多1,则女生比男生多的人数与男生人数的比是：,4男生人数与女生人数比是：;女生人数与全班人数的比是：.12、化简比的依据是1、两个正方形的边长比是2：3,它们的周长比是：,面积比是：两个正方体的棱长比是3：2,它们的表面积比是：,体积比是：.14、甲数是乙数的3，乙数与甲数的比是，比值是15、把10克糖溶入100克水中，糖和水的比是：，糖和糖水的比是：，水和糖水的比是：16、把0.85吨：170千克化成最简整数比是6317、：=12： =：10=0.8：=2二、选择题比的前项和后项A.都不能为0B.都可以为0C.前项可以为0D.后项可以为0 ：0.2化成最简整数比是.A.1 ：3B.：1C.3如果5：12的前项加上5，要使比值不变，则后项应加上.A.B.C.10 D.12三、判断题1、甲：乙=3：4，则甲数是3，乙数是4。

化简比练习题分数

化简比练习题分数一、知识要点：1、比的意义：2、比的基本性质：3、求比值：用比的前项除以后项4、化简比：化简比就是把一个比变成前项和后项都是整数的，并且前项和后项的公因数只有1。

5、化简比的结果二、求比值：1、整数比整数36：1824：30 15：101：635：1202、小数比小数 0.6：0.240.36：0.0953、分数比分数3：2：9918104、小数比分数0.3:0.45: 1 1:0.75:0.7544416三、化简比：1、整数比整数32：18196:4162：842、小数比小数0.125：0.2.8：3.90.1：0.04213、分数比分数3：：：223749424、整数比小数10：0.81：0.9.1：18265、分数比小数3：2.50.125：： 1.6486、整数比分数9：274：162：1 101547、单位比.5千克：400克400厘米：6米 00毫升：1升20千克：1吨0分钟：2小时 08立方厘米：2立方分米1003求比值和化简比练习一、知识要点：1、比的意义：2、比的基本性质：3、求比值：用比的前项除以后项4、化简比：化简比就是把一个比变成前项和后项都是整数的，并且前项和后项的公因数只有1。

5、化简比的结果二、求比值：1、整数比整数36：1824：30 15：101：635：1202、小数比小数 0.6：0.240.36：0.0953、分数比分数3：2：9918104、小数比分数0.3:0.45: 1 1:0.75:0.7544416三、化简比：1、整数比整数32：18196:4162：842、小数比小数0.125：0.2.8：3.90.1：0.04213、分数比分数3：：：223749424、整数比小数10：0.81：0.9.1：18265、分数比小数3：2.50.125：： 1.6486、整数比分数9：274：162：1 101547、单位比.5千克：400克400厘米：6米 00毫升：1升20千克：1吨0分钟：2小时 08立方厘米：2立方分米1003求比值和化简比练习一、填空1、 10：36=，读作。

小学六年级数学上册练习题第四单元-比

小学六年级数学上册练习题第四单元-比第一课时比的意义班级：姓名：巩固达标一、填空。

(1)在4:7=中,( )是比的前项,( )是比的后项，比值是( )。

(2)43＝( )÷（ ) ＝( ):( )(3)人体血液中，红细胞的平均寿命是120天，血小板的平均寿命是10天。

红细胞与血小板的寿命的比是( ）。

(4)--辆“复兴号”高铁3小时行驶了1050km,这列高铁行驶的路程和时间的比是( ) :( )，比值是( )，比值表示( ）。

(5)一条公路已修了全长的125，已修的和未修的比是( ),未修的和全长的比是（）。

(6)比与分数、除法的联系。

（）(7) 甲数是乙数的4倍，甲、乙两数的比是（），乙数与两数和的比是（）。

(8)在100克水中加入10克盐，盐和盐水的比是（）。

二、判断。

(对的画“√”，错的画“X”)(1)在今年一场足球比赛中，法国1:0战胜比利时，所以比的后项为0。

( )(2) 小明的身高125cm,弟弟的身高是1m,小明和弟弟身高的比是125:1。

( )三、求下面各比的比值。

0.36 : 0.45 1.5t:400kg 32：9420分: 0.25时能力拓展应用题。

1、小明体重40千克，相当于小军的910，小华的体重是小军的65。

小华体重多少千克？2、修一条工路，第一天修了全长的，第二天修的比第一天的少50米，两周共修了160米，这条路一共有多长？3、学校有彩色粉笔48盒，比白粉笔的少3盒，学校有白粉笔多少盒？4、一满杯糖水正好是200 g,其中含糖20g 。

从杯中倒出20g 糖水后,再往杯里加满水,这时杯子里的糖与水的质量比是多少?第二课时比的基本性质班级：姓名：巩固达标 1、填空（1）.填表后再说一说比与分数、除法有怎样的关系。

(2)如果把3: 7的前项加上12,要使比值不变，后项应加上( ）。

(3)12:16=( ):4=18÷( ）=( ):0.8=32(4)甲数的43等于乙数的32，那么甲、乙两数的最简整数比是( ):( )。

比的意义及比的基本性质

2、比与除法、分数又有什么不同？
比和除法、分数的联系和区别
联
比
系（相
当
于）
区别
一种关系
一种运算一种数
比的前项：比号比的后项比值 ÷除号
—分数线
除法被除数
分数分子
除数
商
分母分数值
比的后项可以是0吗？
• 做一做： • 1、小敏和小亮在文具店买同样的本子。小敏买了6本，花了1.8元。小亮买了8本，花了2.4元。小敏和小亮买的练习本之比是 • （）：（），比值是（），花钱数之比是（）：（），比值是（）。
• （）：（）
• 0.75：2 =(0.75×100): (2×100) • =75:200=( ): ( )
• 例如：15

﹕
3 10 = 15÷10= 2

• 前项比号后项比值 • 根据分数与除法的关系，两个数的比也可以写成分数形式。例如：15：10也可以写成 15 • 仍读作“15 比10”。 10
比值通常用分数表示，能除尽时也可以用小数表示，能整除时就用整数表示。
想一想：
1、比的前项、后项和比值分别相当于除法算式和分数中的什么？
• 6 :8= (6×2) • 6 :8 = (6÷2)

: (8×2) =12 : 16 : (8÷2) = 3 : 4

• 6÷8 = (6÷2) : (8÷2) =3 ÷4 • 你能根据比和分数的关系研究比的规律吗？

比的前项和后项同时乘或除以相同的数（0除外）比值不变。
• 这叫做比的基本性质 • 根据比的基本性质，可以把比化成最简单的整数比。

比的意义和基本性质

比的意义和基本性质比的意义和基本性质1.比的意义：两个数的比表示两个数相除。

2.比的各部分名称。

（1）比号：“:”叫做比号，读作：“比”。

（2）比的前项和后项：在两个数的比中，比号前面的数叫做比的前项，比号后面的数叫做比的后项。

（3）比值：比的前项除以后项所得的商，叫做比值。

3.比和比值的关系：2既可以表示2:3，又可以表示联系：比和比值都可以用分数形式表示，如32:3的比值。

区别：比表示两个数量的倍数关系；比值是一个具体的数，可以是分数，也可以是小数或整数。

温馨提示：当比的后项为1时，1不能省略不写。

如2:1不能写成2，写成2就是2:1的比值。

4.比与分数、除法的关系。

（1）联系：比的前项相当于分数的分子、除法中的被除数；比号相当于分数的分数线、除法中的除号；比的后项相当于分数的分母、除法中的除数；比值相当于分数的分数值、除法中的商。

（2）区别：比表示两个数量的倍数关系，分数是一个数，除法是一种运算。

5.比的基本性质：比的前项和后项同时乘或除以相同的数（0除外），比值不变。

6.化简比：把两个数的比化成最简单的整数比。

（1）整数比的化简方法：比的前项和后项同时除以它们的最大公因数。

（2）分数比的化简方法：比的前项和后项同时乘它们分母的最小公倍数，先转化成整数比，再进行化简；也可以利用求比值的方法化简。

（3）小数比的化简方法：先用恰当的方法转化成整数比，再进行化简。

【诊断自测】1.填空。

（1）甲是乙的23，甲和乙的比是（），乙和甲的比是（）。

（2）5÷8=（）:（）=()()（3）比的后项不能为（）。

（4）把43:1.125化成最简单的整数比是（），比值是（）。

（5）把25克糖放入100克水中，糖和糖水的质量比为（）。

2.求比值。

53:411.2:3.61.5t:240kg 12:1513.求下列各比中的未知数。

113:x=3x:0.6=1099:x=434.化简下面各比。

9:126.5:1.354:1580.3:920.75:2【考点突破】类型一：已知一个数的几分之几等于另一个数的几分之几，求这两个数的比。

六年级比的意义和基本性质练习题

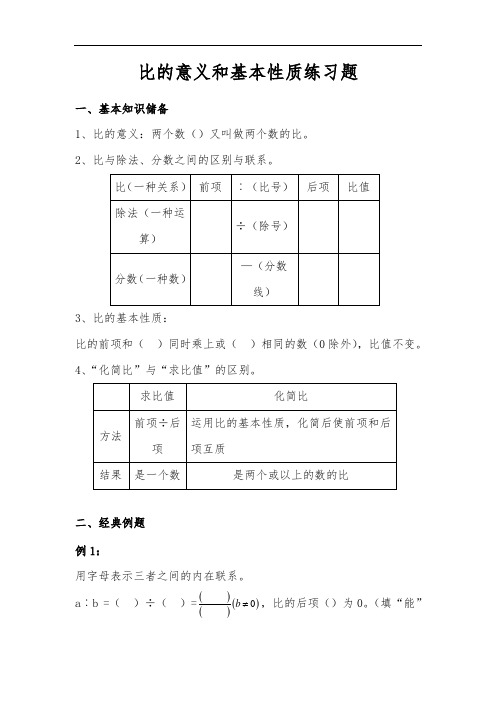
比的意义和基本性质练习题一、基本知识储备1、比的意义：两个数（）又叫做两个数的比。

2、比与除法、分数之间的区别与联系。

3、比的基本性质：比的前项和（）同时乘上或（）相同的数（0除外），比值不变。

4、“化简比”与“求比值”的区别。

二、经典例题例1：用字母表示三者之间的内在联系。

a ︰b =（）÷（）=()()()0b ≠，比的后项（）为0。

（填“能”或“不能”）举一反三1：一袋洗衣粉重320克，一块香皂重80克。

洗衣粉与香皂的重量比是（），比值是（）；香皂与洗衣粉的重量比是（），比值是（）。

例2：盐与水的比是1︰10，则盐︰盐水=（︰），水︰盐=（︰），盐水︰水=（︰）。

举一反三2：两个正方形边长比是1︰3，这两个正方形的周长比是（︰）面积比是（︰）。

例3：男生与女生的人数比是3︰4，男生比女生少() ()。

举一反三3：1、某班有男生20人，女生30人，男生与全班人数的比是（），女生比男生多() ()。

2、甲数除以乙数的商是43，甲数与乙数的比是（）。

例4：易错题分析1、在4︰9中，如果比的前项加上8，要使比值不变，后项应加上（）。

易错题分析2、A ︰B=2︰3，B ︰C=4︰5，那么A ︰B ︰C=（︰︰）。

易错题分析3、一项工程，甲单独完成需要6小时完成，乙单独完成需要5小时完成，甲、乙工作效率之比是（︰）。

举一反三4：1、在3︰8中，如果比的前项加上15，要使比值不变，后项应加上（）。

2、A ︰B=3︰4，B ︰C=5︰6，那么A ︰B ︰C =（︰︰）。

3、一辆汽车从甲地开往乙地，3小时到达，返回时4小时到达，前往速度与返回速度的比是（︰）。

三、迁移拓展例1、如果532CB A ==（其中A 、B 、C 都不等于0），那么A ︰B ︰C=（︰︰）。

举一反三7：如果2A=3B=4C （其中A 、B 、C 都不等于0），那么A ︰B ︰C=（︰︰）。

例2、有两个重叠的正方形，大正方形的边长是5厘米，小正方形的边长是4厘米，重叠部分的面积是9平方厘米，求阴影部分面积。

(完整版)比的意义和基本性质练习题

比的意义一、细心填写:1.两个数相除又叫做这两个数的（）。

比前项除以后项所得的商叫（）。

2、甲数是12, 乙数是18.(1）甲与乙的比是（）∶( ）。

（2)乙与甲的比是（ )∶（）。

（3）甲与甲乙两数和的比是（）∶( ）。

(4)乙与甲乙两数和的比是（）∶（）。

（5）甲乙两数差与甲乙两数和的比是（）∶（）。

3.小明3分钟走了240米, 小杰5分钟走了350米。

(1)小明与小杰行走时间的比是（）, 比值是( ）。

（2）小明与小杰行走路程的比是( ), 比值是（）。

（3）小明路程与时间的比是（）, 比值是（）, 比值表示( ）。

（4)小杰路程与时间的比是（ ),比值是（）, 比值表示（）.（5）小明行走速度与小杰行走速度的比是（ ).4.某校六年级一班男生人数是女生人数的。

男生人数与女生人数的比是（）。

女生人数与全班人数的比是( ）。

全班人数与女生人数的比是（）.5.苹果比梨多, 苹果与梨的比是（ ), 梨与苹果和梨和的比是( ）.5.甲数是乙数的3倍,乙数和甲数的比是（）。

6、一段路,甲走完全程用7小时, 乙走完全程用6小时, 甲、乙的时间比是（）,甲与乙的速度比是（）。

7、两个正方形的边长的比是1∶3, 它们的周长比是（）。

8、2∶13=（ )÷（）=()()95=( ）∶（）=（）÷（）9、将5克糖放入20克水中, 糖与糖水的比是( ).三、求比值。

12: 8 0。

4:0。

12 :5: 41 4.5:0.9 0.75:4130分钟∶41时 0.75吨∶250千克 400厘米∶0.8米比的基本性质一、细心填写1.（）,叫做比的基本性质.2.16:20＝32: ( ）＝（）÷10 ＝＝ ( ）: 0.2（）: 16＝＝＝( )÷24＝3: ( )＝（）÷20＝0.250.8÷1.2=4÷（）=8: （）==（ ): 27=28÷( ）=（）: （ )=0.625=15÷( ）= =20: （）3.火车4小时行驶了600千米,路程和时间的最简整数比是（）, 比值是（）。

求比值和化简比练习(一)

求比值和化简比练习（一）
一、知识要点：
1、比的意义
：
2、比的基本性质：
3、求比值：
用比的前项除以后项（比值通常用
不能除尽就用最简分数表示。

）
4、化简比：化简比就是把一个比变成前项和后项都是整数的，并且前项和后项的公因数只有1。

5、化简比的结果用
二、求比值：
1、整数比整数36：18 24：30 15：105 21：63 35：120
2、小数比小数 0.6：0.24 0.36：0.095
3、分数比分数 83：92 185 ：10
9
4、小数比分数 0.3: 43 0.45: 41 41:0.75 16
5:0.75
三、化简比：（化简比的结果用比的形式或分数两种表示）
1、整数比整数 32：18 196:48 162：84
2、小数比小数 0.125：0.25
7.8：3.9 0.1：0.04
3、分数比分数 43：2
7 21 ：32 75 ：4925
4、整数比小数 10：0.8
1：0.5 9.1：182
5、分数比小数 4
3：2.5 0.125：87 266： 1.5
6、整数比分数 10
9：27 154：16 2：41
7、单位比 2.5千克：400克
400厘米：6米
500毫升：1升
20千克：1001吨 30分钟：3
2小时 308立方厘米：2立方分米。

新人教版六年级数学上册：练习十一

自学星
交流星
展示星
结论： (1)由于没有告知3CM长的线段是长或宽,画法有两种。（2）把重叠部分的面积当作“1”,则大长方形面积含8个重叠部分,小长方形面积含5 个重叠部分,所以面积比是8∶5。（3）题目的条件虽然有变化,但本质不变, 即“形变而神不变”,所以结果不变。
自学星
交流星
展示星
人教版六年级数学上册
比的意义、比的基本性质的应用练习练习十一
一、出示学习目标(学生齐读)：
1、我能理解比的意义。 2、我能运用比的基本性质解题。
自学星
交流星
展示星
二、复习旧知,引入课题
1、什么是“比”？ 2、比的基本性质是什么？
（比的前项和后项同时乘或除以相同的数 (0除外),比值不变。）
自学星
交流星
展示星
三、自主学习,探究新知
导学提示：问题：甲数和乙数的比是2∶3,乙数和丙数的比是3∶4。甲数和丙数的比是多少？交流：把自学的成果在小组内交流。展示：交流气氛热烈的小组进行展示。评价：自学深入,交流有序,展示全面。展示：由于,甲数∶乙数＝2∶3, 乙数∶丙数＝3∶4 两个式子中,乙数都3份,所以,甲星
• 变式： • 甲数和乙数的比是2∶3,乙数和丙数的比是4∶5,甲数和丙数的比是多少？
展示：甲数∶乙数＝2∶3＝8∶12 乙数∶丙数＝4∶5＝12∶15 所以,甲数∶丙数＝8∶15
自学星
交流星
展示星
四、课堂练习,当堂反馈。
学生完成教科书第52、53面作业。
自学星
交流星
展示星
五、梳理小结
• 通过本节课的学习,你有什么收获？
自学星
交流星
展示星

比和比的应用习题精选及答案

车站家教中心比和比的应用基本知识： 1、比的意义，2比与分数、除法之间的关系，3比的基本性质一、把下面各比化成最简单的整数比、求比值。

18：1672：18 0.12：0.06 ：：0.125：二、填空：1．完成一项工程，甲8天完成，乙12天完成，甲乙两人工作时间的比是（）：（）。

2．如果a：b=c，那么a是比的（），b是比的（），c是比的（）。

3．两个相同的瓶子都装满了酒精溶液，一个瓶中酒精与水的体积比是3 ：1，另一个瓶中酒精与水的体积比是4 ：1。

如果把这两个瓶中酒精溶液混合，混合溶液中酒精和水的比是（）：（）。

4．五角人民币与贰角人民币的张数比为12 ：35，那么伍角与贰角的总钱数比为（）：（）。

5．甲、乙、丙三个数的平均数是60。

甲、乙、丙三个数的比是3 ：2 ：1。

甲、乙、丙三个数分别是（）、（）、（）。

6．一个直角三角形的两个锐角度数的比是2 ：1，这两个锐角分别是（）度、（）度。

7．一个长方形长是9分米，宽是6分米，长和宽的比是（）：（），比值是（）。

8．一个直角三角形的三条边总和是60厘米，已知三条边的比是3 ：4 ：5。

这个直角三角形的面积是（）平方厘米？9．甲、乙两包糖果的重量的比是4 ：1，如果从甲包取出13克放入乙包后，甲、乙两包糖果重量的比变为7 ：5。

两包糖果重量的总和（）克。

10．某小学男、女生人数之比是16 ：13，后来有（）位女生转学到这所学校，男、女生人数之比变成为6 ：5，这时全体学生共有880人。

三、解决问题1．大、小两瓶油共重2.7千克，大瓶的油用去0.2千克后，剩下的油与小瓶内油的重量比是3 ：2。

求大、小瓶里各装油多少千克？2．甲、乙、丙三位同学共有图书108本，乙比甲多18本，乙与丙的图书数之比是5 ：4，求甲、乙、丙三人各有图书多少本？3．一瓶盐水，盐和水的重量比是1 ：24，如果再放入75克水，这时盐与水的重量比是1 ：27，原来瓶内盐水重多少千克？4．盒子里有三种颜色的球，黄球个数与红球个数的比是2 ：3，红球个数与白球个数的比是4 ：5。

第十讲比的意义及比的基本性质

BD=10×
【典型例题 2】 1 1 已知 :x= 3 ，求 x. 4 2 1 1 1 1 解析：因为 :x= 3 ；所以 ÷x= 3 ； 4 2 4 2 1 1 1 2 由 x= ÷ 3 ；可得 x= × ； 4 2 4 7 1 所以 x= . 14 点评：要求正确理解分数、除法、比的关系和区别，从而求出所求的未知数。【知识点】分数、除法、比三者之间的关系，如表所示：定义字母关系 a 分数 =c 分子 =分数值 b 分母除法比被除数÷除数=商前项:后项=比值 a÷b=c a:b=c
1 化简后的比是 1；（ 4 7 （4）35 厘米和 25 米的比值是厘米；（ 5 1 1 （5）3: : 可以化简为 3: 5:4. （ 4 5 【解】 ×、×、×、×、×. 1 2. 把 0.3: 化成后项是 100 的比，正确的是：（） 3 100 A、 90 : 100 B、 C、 30 : 100 D、 30 : 33 90
前项（或 =比值）后项
（或
a =c） b
a = a÷b= a:b（b≠0） b 比的前项相当于除法中的被除数和分数中的分子，比的后项相当于除法中的除数和分数中的分母，比值相当于除法中的商和分数中的分数值，比号相当于除法中的除号和分数中的分数线. 但比、除法、和分数三者之间有本质区别的，比是指两个量（或数）的倍数关系，除法是一种运算，分数是一个数.
A、1 B、
6 49
）
1 6
C、6
D、 8
【解】D 【拓展题 1】小丽看一本书，第一天看了全书的
1 3 ，第二天看了全书的，求前两天看的 4 5
书与剩下的书之比，并求出比值. 1 3 1 3 17 3 【解析】( + ) ﹕(1－－ )= ﹕ 4 5 4 5 20 20 17 3 17 3 2 ﹕ = ÷ =5 20 20 20 20 3

比和比例知识点归纳完整版

比和比例知识点归纳标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]比和比例知识点归纳1、比的意义和性质比的意义：两个数相除又叫做两个数的比。

例如：9 : 6 = 1.5前比后比项号项值比的基本性质：比的前项和后项都乘以或除以相同的数（零除外），比值不变。

应用比的基本性质可以化简比。

习题：一、判断。

1、比的前项和后项同时乘一个相同的数，比值不变。

（）2、比的基本性质和商的基本性质是一致的。

（）3、10克盐溶解在100克水中，这时盐和盐水的比是1:10. （）4、比的前项乘5，后项除以1／5，比值不变。

（）5、男生比女生多2／5，男生人数与女生人数的比是7:5. （）6、“宽是长的几分之几”与“宽与长的比”，意义相同，结果表达不同。

（）7、2／5既可以看做分数，也可以看做是比。

（）二、应用题。

1.一项工程，甲单独做20天完成，乙单独做30天完成。

（1）写出甲、乙两队完成这项工程所用的时间比，并化简。

（2）写出甲、乙两队工作效率比，并化简。

2.育才小学参加运动会的男生人数和女生人数的比是5∶3，其中女生72人。

那么男生比女生多多少人3.食品店有白糖和红糖共360千克，红糖的质量是白糖的。

红糖和白糖各有多少千克4.甲、乙两个车间的平均人数是162人，两车间的人数比是5∶7。

甲、乙两车间各有多少人？5.有一块长方形地，周长100米，它的长与宽的比是3∶2。

这块地有多少平方米？6.建筑用混凝土是由水泥、沙、石子按5∶4∶3搅拌而成，某公司建住宅楼需混凝土2400吨，需水泥、沙、石子各多少吨？外项2、比例的意义和性质：比例的意义：表示两个比相等的式子叫做比例。

例如：9 ：6 = 3 ： 2内项比例的基本性质：在比例中两个内项的积等于两个外项的积。

应用比例的基本性质可以解比例。

3、比和分数、除法的关系：习题：一、填空（1）两个数相除又叫做两个数的（）。

（2）在5:4中，比的前项是（），后项是（），比值是（）（3）8:9读作：（），这个比还可以写成（）。

《比的意义和基本性质》练习题

比的意义和基本性质（一）一、细心填写：1、鸡有80只，鸭有100只，鸡和鸭只数的比是（），比值是（）。

2、长方形长3分米，宽12厘米，长与宽的比是（），比值是（）。

3、小李5小时加工60个零件，加工个数与时间的比是（），比值是（）。

4、一本书读了55页，45页没有读，已读与总数的比是（），比值是（）。

5、甲数相当于乙数的92，甲数与乙数的比是（），乙数与甲数的比是（）。

6、三好学生占全班人数的81，三好学生与全班人数的比是（）。

7、白兔只数的31与黑兔相等。

白兔与黑兔的比是（），白兔与黑兔的比是（） 8、若A ÷B ＝5（A 、B 都不等于0）则A ：B ＝( ):( )若A ＝B （A 、B 都不等于0）则A ：B ＝( ):( )9、填写比、除法和分数的关系。

比比的前项除法除数分数 --- 分数线分数值10、（）又叫做两个数的比。

（）叫做比值。

11、43＝( ):( ) ＝( )÷（ )12、在100克水中加入10克盐，盐和盐水的比是（）。

13、男工人数是女工人数的52，男、女工人数的比是（）。

14、甲数是乙数的4倍，甲、乙两数的比是（），乙数与两数和的比是（）。

15、甲数比乙数多41，甲数与乙数的比是（），比值是（）。

16、（），叫做比的基本性质。

17、16：20＝32:( ) ＝( )÷10 ＝()4＝()80＝1.6( ) ＝( ):0.218、火车4小时行驶了600千米，路程和时间的最简整数比是（），比值是（）。

19、甲数是乙数的3倍乙数与甲数的比是（），比值是（）。

20、601班男生与女生人数的比是2：3，女生占全班的（），男生占全班的（）。

21、甲数是乙数的32，乙数与甲数的比是（），甲数与乙数的比是（）。

二、求比值：12：8 0.4:0.12 5: 41 4.5:0.9 31:65 32:910 0.75:41 4: 41 35：45 360：450 0.3:0.15 18: 32 6:0.36 203:54 0.6:52 32:6 三、化简比：35：45 360：450 0.3:0.15 18: 32 6:0.36 203:54 0.6:52 32:683:21 0.75: 43 24: 31 6.4:0.16 2.25:9 815:32 54：83 31：41四、判断是否：1、54可以读作“6比7”。

六年级上数学比的意义和比的基本性质练习题

六年级上数学比的意义和比的基本性质练习题学习是劳动，是充满思想的劳动。

查字典数学网为大伙儿整理了比的意义和比的差不多性质练习题，让我们一起学习，一起进步吧!填空:1,一车水果重1.8吨,按2:3:5的比例分配给甲,乙,丙三个水果店,乙水果店分得这批水果的().2,甲数比乙数多,甲数与乙数的比是().3,甲,乙,丙三个数的平均数是15,甲,乙,丙三个数的比是2:3:4,甲数是().4、东风小学六年级人数是五年级人数的,五年级与六年级人数的比是().5,把3克盐放入12克水中,盐与盐水重量的最简整数比是().6,把(5平方米):(50平方分米)化成最简整数比是( ),它们的比值是( ).7,甲数除以乙数的商是1.5,甲数与乙数的最简整数比是( ).8,写同样多的作业,李莉用12分钟,王祥用15分钟,李莉与王祥的最简单的速度比是( ).9,把1与它的倒数的比化成最简整数比是( ),比值是( ).10,4分:时的比值是( ),最简整数比是( ).11,把:0.75化成最简单的整数比是( ),比值是( ).我国古代的读书人,从上学之日起,就日诵不辍,一样在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。

什么缘故在现代化教学的今天,我们念了十几年书的高中毕业生甚至大学生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在19 78年就尖锐地提出:“中小学语文教学成效差,中学语文毕业生语文水平低,……十几年上课总时数是9160课时,语文是2749课时,恰好是30%,十年的时刻,二千七百多课时,用来学本国语文,却是大多数只是关,岂非咄咄怪事!”寻根究底,其要紧缘故确实是腹中无物。

专门是写议论文,初中水平以上的学生都明白议论文的“三要素”是论点、论据、论证,也通晓议论文的差不多结构:提出问题――分析问题――解决问题,但真正动起笔来就犯难了。

明白“是如此”,确实是讲不出“什么缘故”。

人教版册数学比的意义和基本性质》练习题

人教版册数学《比的意义和基本性质》练习题 The document was prepared on January 2, 202139、比的意义和基本性质（一）一、细心填写：1、鸡有80只，鸭有100只，鸡和鸭只数的比是（），比值是（）。

2、长方形长3分米，宽12厘米，长与宽的比是（），比值是（）。

3、小李5小时加工60个零件，加工个数与时间的比是（），比值是（）。

4、一本书读了55页，45页没有读，已读与总数的比是（），比值是（）。

5、甲数相当于乙数的92，甲数与乙数的比是（），乙数与甲数的比是（）。

6、三好学生占全班人数的81，三好学生与全班人数的比是（）。

7、白兔只数的31与黑兔相等。

白兔与黑兔的比是（），白兔与黑兔的比是（）8、若A ÷B ＝5（A 、B 都不等于0）则A ：B ＝( ):( )若A ＝B （A 、B 都不等于0）则A ：B ＝( ):( )二、求比值：32：94 : 3321:113 : 48:36 : 52 7: 3: 116 1: 9072 三、解决问题：1、一辆汽车从甲地到乙地，每小时行80千米，用了43小时，返回时只用了85小时。

返回时每小时行多少千米2、商店售出2筐橙子，每筐24千克。

售出的橙子占水果总数的116，售出的香蕉占水果总数的41。

售出香蕉多少千克40、比的意义和基本性质（二）一、细心填写：12）叫做比值。

3、43＝( ):( ) ＝( )÷（ ) 4、在100克水中加入10克盐，盐和盐水的比是（）。

5、男工人数是女工人数的52，男、女工人数的比是（）。

6、甲数是乙数的4倍，甲、乙两数的比是（），乙数与两数和的比是（）。

7、甲数比乙数多41，甲数与乙数的比是（），比值是（）。

二、求比值：12：8 :5: 41 : 31:65 32:910 :41 4: 41 三、解决问题：1、小明体重40千克，相当于小军的910，小华的体重是小军的65。