2014新人教版初二数学上册期中卷

合集下载

人教版八年级数学上册期中考试.docx

初中数学试卷桑水出品2014年秋季八年级期中考试数学试题考试时间120分钟总分150分第I 卷（选择题48分）一、选择题（每小题4分，共48分）1.、161的平方根是（） A 、41 B 、41- C 、41± D 、4± 2.下列命题中，真命题是（）A.、相等的角是直角B.、不相交的两条线段平行C.、两直线平行，同位角互补 D 、.经过两点有且只有一条直线3、如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是根据三角形的全等判定（）A 、SAS 带③B 、SSS 带③C 、ASA 带③D 、AAS 带③4. 在实数020.20200200843.143073，，，，，，，π－…中，无理数的个数是（）A 、1B 、2C 、3D 、45.在△ABC 和△A B C '''中,AB =A B '',∠B =∠B ',补充条件后仍不一定能保证△ABC ≌△A B C ''',则补充的这个条件是( )A ．BC =BC '' B ．∠A =∠A ' C ．AC =A C ''D ．∠C =∠C '6.下列运算中，正确的是（）A.B. C. D.7.已知实数x ，y 满足，则以x ，y 的值为两边长的等腰三角形的周长是（）A ． 20或16B ． 20C ． 16D ．以上答案均不对8.．下列从左边到右边的变形，属于因式分解的是（）A 、 1)1)(1(2-=-+x x xB 、1)2(122+-=+-x x x xC 、)4)(4(422y x y x y x -+=-D 、)3)(2(62-+=--x x x x9.设一个正方形的边长为错误！未找到引用源。

，若边长增加3cm ，则新正方形的面积增加了（）A.错误！未找到引用源。

人教版八年级数学上册第一学期期中考试题卷.docx

第7题图A初中数学试卷桑水出品2014—2015学年度第一学期期中考试题卷八年级数学一、选择题（每小题3分，共30分）1.下列图案是我国几家银行的标志，其中不是．．轴对称图形的是（）A. B. C. D.2.下面各组线段中，能组成三角形的是（）A ．5，11，6B ．8，8，16C ．10，5，4D ．6，9，14 3.下列运算正确的是（）A.22a a a =+B. 222a a a =⋅ C.2224)2(a a =- D.222)(b a ab =-4.如果一个三角形两边上的高的交点在三角形的内部，那么这个三角形是（）A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形5.若平面直角坐标系中，△ABO 是关于x 轴对称的轴对称图形，点A 的坐标为（1，-2），则点B 的坐标为（） A ．（-1，2） B ．（-1，-2）C ．（1，2）D ．（-2，1）6.如果等腰三角形的两边长分别是4和5，则它的周长是（）A ．13B ．14C ．13或14D ．无法确定7.如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段PA=5，则线段PB 的长度为（）A.6B.5C.4D.38.一个多边形的内角和是外角和的2倍，则这个多边形的边数为（） A.4 B.5 C.6 D.7 9.如图：将一副三角板按如图所示摆放，图中∠α的度数是（）A ．75°B ．90°C ．105°D ．120° 10.已知9749,27,81===c b a ，则a .b .c 的大小关系是（） A ．a ＞b ＞c B ．a ＞c ＞b C ．a ＜b ＜c D ．b ＞c ＞a第9题图α⌒D CBA第15题图二、填空题（每小题4分，共24分）11.点M（1，2）关于y轴对称的点的坐标为________.12.计算：20142014)2(21(-⨯ =_________.13.如图，AB=AC=12,BC=7,AB的垂直平分线交AB于点E,交AC于点D，则△BCD的周长是________.14.若等腰三角形一个角是100°，则它的底角度数是_____.15.如图，△ABC中，AB=AD=DC,∠BAD=32°,则∠C＝______°.16.已知5,3==nm aa，则=+nma2__________.三、解答题（一）（每小题6分，共18分）17.计算：233232)3()(xxxxx-+-⋅⋅18.如图，在平面直角坐标系xoy中，(15)A-，，(10)B-，，(43)C-，．（1）在图中画出ABC△关于y轴的对称图形111A B C△（2）写出点Ａ1，Ｂ1，Ｃ1的坐标19.如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．四、解答题（二）（每小题7分，共21分）20.如图，△ABC中，∠C＝90°，∠A=60°.(1)作△ABC的角平分线AD(保留作图痕迹);xyABCO 5246-5-2CDBE D C B A (2）画DE ⊥AB,垂足为E;(3)若BC=12㎝,则点D 到边AB 的距离是______.21.如图，在△ABC 和△DEF 中，B.E.C.F 在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的一个作为结论，写出一个正确的命题，并加以证明.①AB=DE ， ②AC=DF ， ③∠ABC=∠DEF ， ④BE=CF. 解：我写的真命题是：在△ABC 和△DEF 中，已知：，求证： .（不能只填序号）证明如下：22. 已知：如图，AC 、BD 相交于点E ，且AC=BD,AB=DC. 求证：BE=CE五.解答题（三）（每小题9分，共27分）23. 如图：在△ABC 中，BE.CF 分别是AC.AB 两边上的高，在BE 上截取BD=AC ，在CF 的延长线上截取CG=AB ，连结AD.AG.求证：（1）AD=AG ，（2）AD 与AG 的位置关系如何.24. 已知：如图， AD ∥BC ，∠ABC ＝90°．点E 是DC 的中点，过点E 作DC 的垂线交AB 于点P ，交CB 的延长线于点M ．点F 在线段ME 上，且满足CF ＝AD ，MF ＝MA ．（1）若∠MFC ＝120°，求证：AM ＝2MB ；（2）求证：∠MPB ＝90°－ 12∠FCM ．G HFEDCB ADC BAD25.如图，△ABC 是等边三角形，D 是三角形外一动点，满足∠ADB=600，（1）当D 点在AC 的垂直平分线上时，求证： DA+DC=DB（2）当D 点不在AC 的垂直平分线上时，（1）中的结论是否仍然成立？请说明理由（3）当D 点在如图的位置时，直接写出DA ，DC ，DB 的数量关系，不必证明参考答案和评分标准一、B D D A B C C B C B 二、11.（－1，2）；12. 1；13.19；14.40；15.37；16.45. 三、17.解：原式＝6669x x x +-………………5分（1+2+2）＝69x ………………6分18.解：（1）如图所示，△A 1B 1C 1为所求………………3分（2）A 1（1，5）；B 1（1，0）；C 1（4，3）………………6分 19.解：∵AD 平分∠BAC ∴∠CAD=21∠BAC=21×60°=30°………………2分 ∵CE 是△ABC 的高∴∠ACE=90°-∠BAC=90°-60°=30°………………4分 ∴∠ACD ＝∠ACE+∠BCE=30°+40°=70°………………5分 ∴∠ADB=∠ACD+∠CAD=70°+30°=100°………………6分四、20解：（1）图略…………3分（2）图略…………5分（3）4㎝…………7分 21.解：已知：_________求证：________………………3分证明：略………………………………7分 22.证明：在△ABC 和△DCB 中⎪⎩⎪⎨⎧===CB BC DC AB BD AC∴△ABC ≌△DCB(SSS)……………………3分 ∴∠ACB=∠DBC ……………………………5分 ∴BE=CE ……………………………7分五、23.证明：（1）∵BE.CF 分别是AC.AB 两边上的高∴∠ACG+∠BAC=90°,∠ABD+∠BAC=90° …………2分 ∴∠ACG=∠ABD ……………………………………3分在△ABD 和△GCA 中GHFE DA⎪⎩⎪⎨⎧=∠=∠=CA BD ACG ABD CG AB∴△ABD ≌△GCA(SAS) ……………………4分 ∴AD=AG ………………………………5分 (2) AD ⊥AG ………………………………6分证明：∵△ABD ≌△GCA∴∠BAD=∠CGA ………………………………7分 ∵∠CGA ＋∠GAF=90°∴∠BAD ＋∠GAF=90° ………………………………8分 ∴∠DAG=90°∴AD⊥AG………………………………9分24. 证明：（1）连结MD ………………………… 1分∵点E 是DC 的中点，ME ⊥DC ，∴MD=MC ………………………… 2分又∵AD=CF ，MF=MA ，∴△AMD ≌△FMC ……………………… 3分 ∴∠MAD=∠MFC=120° ∵AD ∥BC ，∠ABC=90°∴∠BAD=90°，∴∠MAB=30°…………………… 4分在Rt △AMB 中，∠MAB=30°，∴BM=21AM ，即AM=2BM …………………… 5分（2）∵△AMD ≌△FMC ，∴∠ADM=∠FCM ……………………6分 ∵AD ∥BC ，∴∠ADM=∠CMD∴∠CMD=∠FCM …………………… 7分∵MD=MC ，ME ⊥DC ，∴∠DME=∠CME=21∠CMD ……………………8分 ∴∠CME=21∠FCM 在Rt △MBP 中，∠MPB=90°-∠CME=90°-21∠FCM ……………………9分 25.（1）证明：在等边△ABC 中，AB=CB ,∠BAC=60°……………………1分 ∵D 点在AC 的垂直平分线上 ∴AD=CD, ……………………2分 ∴∠DAC=∠DCA= =30°∴∠BAD=90°……………………3分 ∴AD=21BD,即BD=2AD BE∴AD+CD=BD……………………4分(2)解：(1)中的结论仍然成立.……………………5分证明：延长DA到E，使ED=BD，∵∠ADB=60°∴△EBD是等边三角形，∴BE=ED=BD，∠EBD=60°……………………6分又∵△ABC是等边三角形，∴AB=BC，∠ABC=60°，∴∠EBA=∠DBC，，∴△ABE≌△CBD（SAS），……………………7分∴EA=DC，∴AD+CD=AD+AE=ED=BD.……………………8分(3)AD+DB>DC……………………9分。

人教版2014-2015学年八年级数学上期中考试试题

2014-2015学年上学期八年级数学期中测试题满分：120分；时间100分钟；一、选择题（本大题共12题，每小题3分，共36分）1、小明从镜子里看到镜子对面电子钟的像如图所示，实际时间是（）．A 、21：10B 、10：21C 、10：51D 、12：01 2、点M （1，2）关于x 轴对称点的坐标为（）．A 、（－1，－2）B 、（－1，2）C 、（1，－2）D 、（2，－1） 3、如图△ABC 中，AB=AC ，∠B =30°，AB⊥AD，AD=4cm ，则BC 的长为（）． A 、8m B 、4m C 、12m D 、6m4、若等腰三角形的周长为26cm ，一边为6cm ，则腰长为（）． A 、6cm B 、10cm C 、6cm 或10cm D 、以上都不对5、等腰三角形一腰上的高与另一要的夹角为300，则顶角度数为（） A 、300B 、600C 、900D 、1200或6006、如图,∠BAC=110°若MP 和NQ 分别垂直平分AB 和AC,则∠PAQ 的度数是( ) A 、70° B 、 40° C 、50° D 、 60°7、下面是某同学在一次测验中的计算摘录①325a b ab +=； ②33345m n mn m n -=-； ③5236)2(3x x x -=-⋅；④324(2)2a b a b a ÷-=-； ⑤()235a a =；⑥()()32a a a -÷-=-．其中正确的个数有( )A 、1个B 、2个C 、3个D 、4个 8、下列各式是完全平方式的是( )．A 、x 2－x ＋14B 、1＋x 2C 、x ＋xy ＋1D 、x 2＋2x －19、如(x ＋m )与(x ＋3)的乘积中不含x 的一次项，则m 的值为( )．A 、－3B 、3C 、0D 、110、44221625)(______)45(b a b a -=+-括号内应填（）A 、2245b a + B 、2245b a + C 、2245b a +- D 、2245b a --第1题图11、下列分解因式正确的是( )A 、32(1)x x x x -=-．B 、2(3)(3)9a a a +-=-C 、29(3)(3)a a a -=+-.D 、22()()x y x y x y +=+-. 12、下列各式从左到右的变形，正确的是( )．A 、()x y x y --=--B 、22)()(y x x y -=-C 、22)()(y x y x +-=+D 、33)()(a b b a -=-二、填空题（每小题4分，共24分）13、等腰三角形的一内角等于50°，则其它两个内角各为．14、计算2221(3)()3x y xy -＝__________ ；2007200831()(1)43⨯-=15、若310x=,35y =，则23x y-= .16、已知249x mx ++是完全平方式，则m =_________；17、如图：点P 为∠AOB 内一点，分别作出P 点关于OA 、OB 的对称点1P ，2P ，连接12PP 交OA 于M ，交OB 于N ，PMN ∆的周长为15cm , 12PP = ．18、220141(1)(1)......(1)a a a a a a a ++++++++= ．三、解答题：（60分）19、（6分）如图：某地有两所大学和两条相交叉的公路，（点M ，N 表示大学，AO ，BO 表示公路）.现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等。

2014—2015学年度第一学期期中测试初二数学试卷(1)(新人教版)

2014—2015学年度第一学期期中测试初二数学试卷（100分钟）试卷满分：第Ⅰ卷30分第Ⅱ卷70分共100分第Ⅰ卷（机读卷选择题30分）一、选择题（每题3分，共30分）1．多项式b a c ab 33812-的公因式是（） A ． 24ab B ．abc 4- C ．24ab - D ．ab 42．如图，将两根钢条AA′，BB′ 的中点O 钉在一起，使AA′，BB′ 能绕点O 自由转动，就做成一个测量工具，测A′B′ 的长即等于内槽宽AB ，那么判定△OAB ≌△OA′B′的理由是（）．A ．边角边B ．角边角C ．边边边D ．斜边直角边3．若3x =-是分式方程312axx=-的解，则a 的值为（） A. 95- B. 95 C. 59 D. 59-4. 如图，△ABC≌△CDA，∠BAC＝85°，∠B＝65°，则∠CAD 度数为（）A. 30°B. 65°C. 40°D. 85°5．解分式方程12133x x x+-=，去分母后所得的方程是（） A. 13(21)3x -+= B. 13(21)3x x -+= C. 13(21)9x x -+= D. 1639x x -+= 6．下列变形正确的是（） A ．11a ab b+=+B ．11a ab b--=--C ．221a b a b a b-=--D ．()()221a b a b --=-+7. 如图，已知△ABC 的六个元素，则下列甲、乙、丙三个三角形中和△ABC 全等的图形是( )A ．甲B ．乙与丙C ．丙D ．乙ＤＣＡＢE DCBA 8．下列分解因式错误．．的是（） A ．222)(2y x y xy x -=+- B.322()x x x x x x -+=- C ．)(22y x xy xy y x -=- D.))((22y x y x y x +-=- 9．某饭馆用320元钱到商场去购买“白猫”洗洁精，经过还价，每瓶便宜0.5元，结果比用原价买多买了20瓶，求原价每瓶多少元？设原价每瓶x 元，则可列出方程为（）A. 320320200.5x x -=-B. 3203200.520x x -=- C.320320200.5x x -=- D. 3203200.520x x -=- 10. 在数学活动课上，小明提出这样一个问题：如右图, ∠B =∠C = 90︒, E 是BC 的中点, DE 平分∠ADC, ∠CED = 35︒, 则∠EAB 的度数是 ( ) A ．65︒ B ．55︒ C ．45︒ D ．35︒第Ⅱ卷（非机读卷共70分）二、填空题（每小题2分，8个小题，共16分）11.自从扫描隧道显微镜发明后，世界上便诞生了一门新学科，这就是“纳米技术”，已知52个纳米的长度为0.000000052米,用科学记数法表示这个数为__ 米 12.计算:=÷-----322324)()2(b a c b a13.能使分式122--x x x 的值为零的所有x 的值是14. 如图，已知AB ⊥BD , AB ∥ED ，AB =ED ，要证明ΔABC ≌ΔEDC ，若以“SAS”为依据，还要添加的条件为_________；若添加条件AC =EC ，则可以用______方法判定全等. 15.关于x 的方程211x a x +=-的解是正数，则a 的取值范围是16.根据下列已知条件，能确定△ABC 的大小和形状的是 ①AB ＝3，BC ＝4，AC ＝5 ②AB ＝4，BC ＝3，∠A ＝30º ③∠A ＝60º，∠B ＝45º，AB ＝4 ④∠C ＝90º，AB ＝6，AC =5 17. 当n=_ ___ 时，x 2＋(n+3)x ＋25是完全平方式 18．在平面直角坐标系中，已知点A （1，2），B （6，5）， C （5，2），存在点E ，使△ACE 和△ACB 全等，写出所有满足条件的E 点的坐标E D CBA三、计算题（其中19题，每小题4分；20、21题每题5分，共18分） 19．分解因式：（1）92-x （2）y xy y x 442+-20．先化简再求值：xx x x x x x 1)121(22÷+---+，其中3x =．21．解方程： 512552x x x+=--四、列方程解应用题（本题5分）22．八年级学生去距学校10km 的博物馆参观，一部分学生骑自行车先走，过了20min 后，其余学生乘汽车出发，结果他们同时到达。

【中学教材全解】2014年秋八年级数学上学期期中检测题 (新版)新人教版

八年级数学上学期期中检测题班级：姓名：座号：成绩：（本检测题满分：150分，时间：90分钟）一、选择题（每小题4分,共40分） 1．下列图形中，不是．．轴对称图形的是（）A B C D 2.如图，∠BAC =90°，AD ⊥BC ，则图中互余的角有( )A.2对B.3对C.4对D.5对 3.下列各组长度的线段能构成三角形的是（）A.1.5 cm ，3.9 cm ，2.3 cmB.3.5 cm ，7.1 cm ，3.6 cmC.6 cm ，1 cm ，6 cmD.4 cm ，10 cm ，4 c m 4．如图，AC 与BD 相交于点O ，已知AB =CD ，AD =BC ，则图中全等的三角形有（）A. 1对B. 2对C. 3对D. 4对5.如图，AD 是△ABC 中∠BAC 的角平分线，DE ⊥AB 于点E ，ABC S △ =7，DE =2，AB =4，则AC 的长是（）A.3B.4C.6D.56.如图，三条直线表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( )A. 一处B. 两处C. 三处D. 四处7. 如图，∠1=∠2，∠C =∠B ，下列结论中不正确的是（）A. △DAB ≌△DACB. △DEA ≌△DFAC. CD =DED. ∠AED =∠AFD8.如图，A，B，C，D，E，F是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F的度数是（）A.180°B.360°C.540°D.720°9.下列说法中，正确的个数为（）①角是轴对称图形，对称轴是角的平分线；②等腰三角形至少有1条对称轴，至多有3条对称轴；③关于某条直线对称的两个三角形一定是全等三角形；④两图形关于某条直线对称，对称点一定在直线的两旁．A.1B.2C.3D.410．如图，点D、E分别在AC、AB上，已知AB=AC，添加下列条件，不能说明△ABD≌△ACE的是（）A.∠B=∠CB.AD=AEC.∠BDC=∠CEBD.BD=CE二、填空题（每小题4分,共32分）11.（2014·湖南常德中考）如图，已知△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，AD=AO，若∠BAC=80°，则∠BCA的度数为 .12.甲、乙两位同学用围棋子做游戏.如图所示，现轮到黑棋下子，黑棋下一子后白棋再下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也成轴对称图形，则下列下子方法不正确的是 .［说明：棋子的位置用数对表示，如A点在（6，3）］①黑（3，7）；白（5，3）；②黑（4，7）；白（6，2）；③黑（2，7）；白（5，3）；④黑（3，7）；白（2，6）.13.(2013·山东烟台中考)如图，在△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为度.14.已知在△中，垂直平分，与边交于点，与边交于点，∠15°，∠60°，则△是________三角形．15.（2013·四川资阳)如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处.若点P是直线AD上的动点，则△PEB的周长的最小值是 .16.如图，在矩形ABCD中(AD>AB)，M为CD上一点，若沿着AM折叠，点Ｄ恰落在BC上的点Ｎ处，则∠ANB+∠MNC=____________.17.若点为△的边上一点，且，，则∠____________．18.如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是____________.三、解答题（共78分） 19.（9分）如图，已知为△的高，∠∠，试用轴对称的知识说明：．20．（9分）如图，在△ABC 中，∠B =42o，∠C =72 o，AD 是△ABC 的角平分线，（1）∠BAC 等于多少度？简要说明理由.（2）∠ADC 等于多少度？简要说明理由. 21．（10分）（2014•四川宜宾中考）如图，已知：在△AFD 和△CEB 中，点A 、E 、F 、C 在同一直线上，AE =CF ，∠B =∠D ，AD ∥BC ．求证：AD =BC ．22．（10分）如图，△ABC 的两条高AD 、BE 相交于点H ，且AD =BD ，试说明下列结论成立的理由.（1）∠DBH =∠DAC ；（2）△BDH ≌△ADC . 23.（10分）如图，在△中，，边的垂直平分线交于点，交于点，，△的周长为，求的长．A BCDNM第16题图第23题图ACE24.（10分）如图,AD ⊥BD ,AE 平分∠BAC , ∠B =30°,∠ACD =70°,求∠AED 的度数.25.（10分）如图，点E 在△ABC 外部，点D 在BC 边上，DE 交AC 于点F ，若∠1=∠2=∠3，AC =AE ，试说明：△ABC ≌△ADE .26.（10分）某产品的商标如图所示，O 是线段AC 、DB 的交点，且AC =BD ，AB =DC ，小林认为图中的两个三角形全等，他的思考过程是： ∵ AC =DB ，∠AOB =∠DOC ，AB =AC ， ∴ △ABO ≌△DCO.你认为小林的思考过程对吗？如果正确，指出他用的是哪个判别三角形全等的方法；如果不正确，写出你的思考过程.第25题图八年级数学（上）期中检测题参考答案一、选择题：1.A2.C3.C4.D5. A6.D7.C8.B9.B 10.D二、填空题： 11. 60° 解析：由已知可得△DCO ≌△BCO ，∴ ∠ADO =∠CBO =∠ABO .∵ AD =AO ，∴ ∠AOD =∠ADO .∵ △ABC 三个内角的平分线交于点O ，∴ ∠BOC =∠COD =90°＋12∠BAC =130°,∴ ∠BOD =360°－(∠BOC ＋∠COD)=100°. ∵∠BOD ＋∠AOD ＋∠ABO ＋∠BAO =180°,即100°＋∠ABO ＋∠ABO ＋40°=180°,∴ ∠ABO =20°，∴ ∠ABC =2∠ABO =40°，∴ ∠ACB =180°－(∠BAC ＋∠ABC )=60°. 12. ③ 解析:根据轴对称图形的特征，观察发现选项①②④都正确，选项③下子方法不正确. 13. 108 解析：本题考查了线段的垂直平分线的性质、等腰三角形的性质及判定、三角形的内角和、角平分线的定义.如图，连接OB ，OC ，易证△AOB ≌△AOC .又∵ OD 是AB 的垂直平分线，∴ AO ＝BO ＝CO ，∴ 点A ，B ，C 在以点O 为圆心，以AO 为半径的圆上， ∴ ∠BOC =2∠BAC =108°，∠BAO =∠ABO =∠CAO =∠ACO =27°. 又∵ EO =EC ，∴ ∠OBC =∠OCB =∠COE =36°，∴ ∠OEC =180°－∠COE －∠OCB =180°－36°－36°=108°. 14.直角解析：如图，∵ 垂直平分，∴ . 又∠15°，∴ ∠∠15°，∠∠∠30°.又∠60°，∴ ∠∠90°，∴ ∠90°，即△是直角三角形.解析：要使△PEB 的周长最小，需PB +PE 最小.根据“轴对称的性质以及两点之间线段最短”可知当点P 与点D 重合时，PB +PE 最小.如图，在Rt△PEB中，∠B =60°，PE =CD =1，可求出BE =3，PB =3，所以△PEB 的周长的最小值=BE +PB +PE 点拨：在直线同侧有两个点M ，N 时，只要作出点M 关于直线的对称点M ′，连接M ′N 交直线于点P ，则直线上的点中，点P 到M ,N 的距离之和最小，即PM +PN 的值最小.16.90° 解析：∠ANB +∠MNC =180°－∠D =180°－90°=90°. 17. 108° 解析：如图，∵ 在△中，，∴ ∠=∠.∵ ，∴ ∠∠∠1.∵ ∠4是△的外角，∴ ∠∠∠2∠.∵ ，∴ ∠∠∠. 在△中，∠∠∠180°，即5∠180°， ∴ ∠36°，∴ ∠∠∠2∠°°，即∠108°．18.40° 解析：∵∠B =46°，∠C =54°，∴ ∠BAC =180°－∠B －∠C =180°－46°－54°=80°.∵ AD 平分∠BAC ，∴ ∠BAD =12∠BAC =12×80°=40°.∵ DE ∥AB ， ∴ ∠ADE =∠BAD =40°．三、解答题： 19.分析：作出线段，使与关于对称，借助轴对称的性质，得到，借助∠∠，得到．根据题意有，将等量关系代入可得．解：如图，在上取一点，使，连接．可知与关于对称，且，∠∠. 因为∠∠∠，∠∠，所以∠∠2∠，所以∠∠，所以.又，由等量代换可得．20.解：（1）∠BAC =180°－42°－72°=66°（三角形的内角和为180°）.(2) ∠ADC =∠B +∠BAD (三角形的一个外角等于和它不相邻的两内角之和).∵ AD 是角平分线，∴ ∠BAD =∠CAD =12∠BAC =33°（角平分线的定义），∴ ∠ADC =42°+33°=75°.21.证明：∵ AD ∥BC ，∴ ∠A =∠C.∵ AE =CF ，∴ AE +EF =CF +EF ，即AF =CE .∵ 在△AD F 和△CBE 中，,,,B D A C AF CE =⎧⎪=⎨⎪=⎩∠∠∠∠∴ △ADF ≌△CBE （AAS ），∴ AD =BC ． 22.解：（1）∵ AD ⊥BC ，∴ ∠ADC =∠ADB =90°.∵ BE ⊥AC ，∴ ∠BEA =∠BEC =90°. ∴ ∠DBH +∠C=90°，∠DAC +∠C =90°，∴ ∠DBH =∠DAC . (2)∵ ∠DBH =∠DAC （已证），∠BDH =∠CDA =90°（已证），AD =BD （已知），∴ △BDH ≌△ADC （ASA ）. 23.解：因为DE 垂直平分BC ，所以BE =EC . 因为AC =8，所以BE ＋AE =EC ＋AE =8. 因为△ABE 的周长为，所以AB ＋BE ＋AE =14.故AB =14－BE －AE =14－8=6.24. 解：∵ AD ⊥DB ，∴ ∠ADB =90°. ∵ ∠ACD =70°，∴ ∠DAC =20°. ∵ ∠B =30°，∴ ∠DAB =60°，∴ ∠CAB =40°.∵ AE 平分∠CAB ，∴ ∠BAE =20°，∴ ∠AED =50°.25. 解：∵ ∠1=∠2，∴ ∠BAC =∠DAE .∵ )(,32对顶角相等DFC AFE ∠=∠∠=∠，∴ E C ∠=∠. 又∵ AC =AE ，∴ △ABC ≌△ADE （ASA ）. 26.解：小林的思考过程不正确.过程如下：连接BC ，∵ AB =DC ，AC =DB ，BC =BC ，∴ △ABC ≌△DCB （SSS ），∴ ∠A =∠D （全等三角形的对应角相等）.又∵ ∠AOB =∠DOC （对顶角相等），AB =DC （已知）， ∴ △ABO ≌△DCO （AAS ）.。

2014年人教版八年级上期中考试数学试卷

由；（2）若点 Q 的运动速度与点 P 的运动速度不相等，则当 t 为何值时，能够使△BPE 与△CQP 全等；此时点 Q 的运动速度为多少．
25 、（10 分）如图 1，在△ABC 中，∠ACB 为锐角，点 D 为射线 BC 上一动点，连接 AD，以 AD 为直角边且在 AD 的上方作等腰直角三角形 ADF．（1）若 AB=AC，∠BAC=90°． ①当点 D 在线段 BC 上时（与点 B 不重合），试探讨 CF 与 BD 的数量关系和位置关系； ②当点 D 在线段 BC 的延长线上时，①中的结论是否仍然成立，请在图 2 中画出相应图形并说明理由；（2）如图 3，若 AB≠AC，∠BAC≠90°，∠BCA=45°，点 D 在线段 BC 上运动，试探究 CF 与 BC
B.60°
C.80°
D.90°
（）8、用直尺和圆规作一个角等于已知角，其正确的依据是（）
A．AAS
B．SSS
C．SAS
D．ASA
（）9、如果正多边形的一个内角是 144°，则这个多边形是（）.
A.正十边形
B.正九边形
C.正八边形
D.正七边形
（）10、BD、CE 分别是△ABC 中∠ABC、∠ACB 的平分线，且交于点 O，若 O
研究（1）：如果沿直线 DE 折叠，使 A 点落在 CE 上，则∠BDA′与∠A 的数量关系是
研究（2）：如果折成图②的形状，猜想∠BDA′、∠CEA′和∠A 的数量关系是
研究（3）：如果折成图③的形状，猜想∠BDA′、∠CEA′和∠A 的数量关系，并说明理由．
猜想:
。理由
问题 2
研究（4）：将问题 1 推广，如图④，将四边形 ABCD 纸片沿 EF 折叠，使点 A、B 落在四边形 EFCD

2014-2015学年人教版八年级上数学期中试卷

1 / 22014-2015学年上学期期中（全卷满分100分，考试时间120分钟）一、选择题（本大题共8个小题，每小题只有一个正确选项，每小题3分，共24分）1若等腰三角形的一边长等于5，另一边长等于3，则它的周长等于（）．A ．10B ．11C ．13D ．11或132一个三角形的三边长都是整数，并且最长边是5，满足这些条件的三角形有A 5 B7 C9． D113AD 是△ABC 的角平分线，过点D 作DE ⊥AB 于E ，DF ⊥AC 于F•,则下列结论不一定正确的是（）A ．DE=DFB ．BD=CDC ．AE=AFD ．∠ADE=∠ADF4在三角形ABC 中，角ABC 等于90度，AB=6,BC=8,AC=10,BD 平分角 ABC,求CD 长A20/7 B30/7 C40/7 D 无法确定5如图，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（） A ．线段CD 的中点 B ．OA 与OB 的中垂线的交点 C ．OA 与CD 的中垂线的交点 D ．CD 与∠AOB 的平分线的交点第5题图第6题图第7题图 6如图所示，△ABD ≌△CDB ，下面四个结论中，不正确的是（） A ．△ABD 和△CDB 的面积相等 B ．△ABD 和△CDB 的周长相等 C ．∠A +∠ABD ＝∠C +∠CBD D ．AD ∥BC ，且AD ＝BC7一个正方形和两个等边三角形∠3=50度求∠1+∠2多少度（）A90 B100 C130 D1809如图，已知AB ＝DC ，AD ＝BC ，E ，F 在DB 上两点且BF ＝DE ，若∠AEB ＝120°，∠ADB ＝30°，则∠BCF ＝（） A ．150° B ．40° C ．80° D ．90°10．小芳有两根长度为4cm 和9cm 的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（）的木条． A ．5cm B ．3 cm C ．17cm D ．12 cm二、填空题（每题3分，共30分）11．若将十五边形变成十六边形,则他的内角和的度数的变化情况--------12．在△ABC 中，∠C=90°，BC=16cm ，∠BAC 的平分线交BC 于D ，且BD ︰DC=5︰3，则D 到AB 的距离为_____________.13．若正n 边形的每个内角都等于150°，则n= ，其内角和为。

2014学年第一学期八年级数学期中阶段性测试试卷

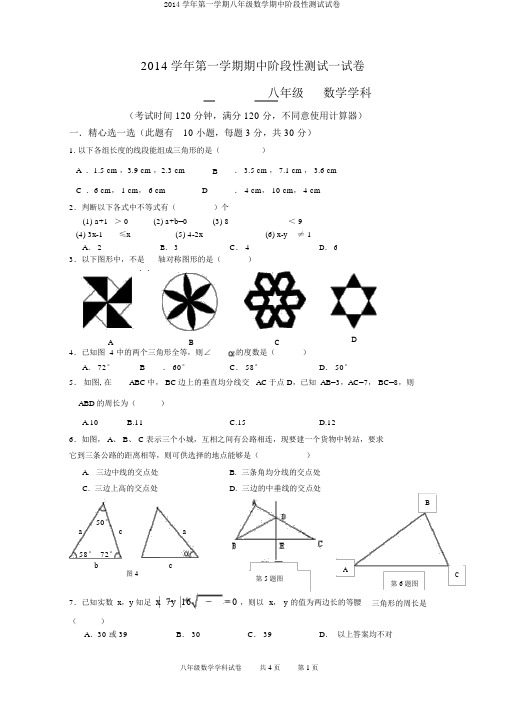
2014学年第一学期期中阶段性测试一试卷八年级数学学科（考试时间 120 分钟，满分 120 分，不同意使用计算器）一．精心选一选（此题有10 小题，每题 3 分，共 30 分）1. 以下各组长度的线段能组成三角形的是（）A ．1.5 cm ，3.9 cm ，2.3 cm B． 3.5 cm ， 7.1 cm ， 3.6 cmC ．6 cm， 1 cm， 6 cm D． 4 cm， 10 cm， 4 cm2．判断以下各式中不等式有（）个(1) a+1＞ 0(2) a+b=0(3) 8＜ 9(4) 3x-1≤x(5) 4-2x(6) x-y≠ 1A． 2B． 3C． 4D． 63．以下图形中，不是轴对称图形的是（）．．A B C D4．已知图 4 中的两个三角形全等，则∠的度数是（）A． 72°B． 60°C． 58°D． 50°5．如图, 在ABC中， BC边上的垂直均分线交 AC于点 D，已知 AB=3，AC=7， BC=8，则ABD的周长为（）A.10B.11C.15D.126．如图， A、 B、 C 表示三个小城，互相之间有公路相连，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地点能够是（）A.三边中线的交点处B. 三条角均分线的交点处C. 三边上高的交点处D. 三边的中垂线的交点处Ba 50°c a58° 72°c b图 4A第 5题图C第 6题图7．已知实数 x，y 知足x 7y 160 ，则以x，y的值为两边长的等腰三角形的周长是（）A．30 或 39B． 30C． 39D．以上答案均不对110 x8、不等式组2的整数解有（）111x2A、5个B、6 个C、7 个D、8 个9．如图， A，B，C，D，E，F 是平面上的 6 个点，则∠ A+∠B+∠C+∠D+∠E+∠F的度数是（）A. 180 °B.360°C.540°D.720°10．已知：如图在△ABC，△ ADE 中，∠ BAC=∠DAE =90°， AB=AC， AD=AE，点 C，D ，E 三点在同一条直线上，连接 BD，BE．以下四个结论：① BD=CE；② BD ⊥ CE；③∠ ACE +∠ DBC =45°；④∠ ACE=∠ DBC 此中结论正确的个数有（）A． 4 B. 3 C. 2 D. 1第9题图第 10题图二．仔细填一填（此题有10 小题，每题 4 分，共 24 分）11．若1B1________三角形 . ABC的三个内角知足A C ，则这个三角形是2312．写出定理“直角三角形斜边上的中线是斜边一半”的抗命题：13．直角三角形的两条边长分别是4 和 9，则此三角形的面积为 ____________.14. 在ABC中， AB=13， AC=12， BC=5，则∠ C= ___________度15．如下图的一块地，∠ ADC ＝ 90°， AD ＝ 12ｍ， CD ＝ 9ｍ， AB ＝ 39ｍ， BC ＝ 36ｍ，则这块地的面积为 ___________ m2．16．如图，在 Rt△ ABC中，∠ C=90°，∠ A=30 ° ,AB=8cm，按图中所示方法将△BCD沿 BD 折叠，使点 C 落在 AB 边的 C′点，那么 AD的长是cm．三．耐心做一做（此题有8 小题，此中 17 题 10 分，（1）题 4 分， (2) 题 6 分， 18、19、 20 题各 6 分， 21、22 题各 8 分， 23 题 10 分，24 题 12 分，共 66 分）17. 解不等式和不等式组B（ 1）不等式x2( x1)121 1 xN2 x4M（ 2）不等式组22并把解集表示在数轴上A C 3 x1x第18题图2218．如图，两个班的学生疏别在M、 N两处参加植树劳动，现要在道路AB、 AC的交错地区内设一个茶水供给点P，使 P 到两条道路的距离相等，且使PM=PN，请你经过尺规作图找出这一P 点，（不写作法，保存作图印迹） .19．假如一个长为 10m 的梯子 AB ，斜靠在墙上，梯子的顶端距地面的垂直距离AC 为 8m．如果梯子的顶端 A 下滑1m 到 A 1，请猜想梯子底端 B 滑动的距离能否也会是1m，若不是，请求出滑动的距离．AA1108B1C第 19题B 20．如图，在△ ABC 中，BD=DC ，∠ ADB= ∠ADC ，求证： AD ⊥BC．ADB第20题图C 21．某产品的商标如下图，O是线段 AC、DB的交点，且AC=BD，AB=DC，小林以为图中的两个三角形全等，他的思虑过程是：∵AC=DB，∠ AOB=∠DOC，AB=DC，∴ △ABO≌△ DCO.你以为小林的思虑过程对吗？假如正确，指出他用的是鉴别三角形全等的哪个方法；假如不正确，写出你的证明过程。

2013-2014学年人教版八年级上期中考试数学试卷

1C A BD 汕头市聿怀初级中学2013－2014学年度第一学期八年级数学科期中考试试卷命题人：林少锐一、精心选一选，相信自己的判断！（每题3分，共30分）1. 如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是（ ▲ ）. A ．2 B ．3 C ．4 D ．82. 若△ABC ≌△DEF,且△ABC 的周长是100 cm ，AB ＝30 cm ，DF ＝25cm ，那么BC 的长是（ ▲ ）. A ．45cm ， B ．55cm C ．30cm D ．25cm 3．将下列命题的题设与结论互换，得到的命题仍是真命题的是（ ▲ ）. A.对顶角相等 B.全等三角形的对应角相等 C.直角三角形两锐角互余 D.如果a >b ，b >c ，那么a >c 4. 下列图形中不．是．轴对称图形的是（ ▲ ）.5. 等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（ ▲ ）. A ．16 B ．20 C ．18 D ．16或206. 在直角坐标系中，点M(-3，4)关于x 轴的对称点 M /的坐标为（ ▲ ）. A ．（-3，-4） B. (3，4) C. (3，-4) D. (3，0) 7. 下列说法中，错误．．的是（ ▲ ）. A.两个全等三角形的对应高相等 B. 一条直角边和斜边对应相等的两个直角三角形全等 C.顶角和一腰对应相等的两个等腰三角形全等 D. 三个角对应相等的两个三角形全等 8．已知等腰三角形的周长为20，腰长为x ，则x 的取值范围是（ ▲ ）.A. x ＜10B. x ＜5C.5＜x ＜10D.0＜x ＜109. 如图，在△ABC 中，点O 是∠ABC 的平分线与线段BC 的垂直平分线的交点，则下列结论不．一定．．成立的是（ ▲ ）.A.OB ＝OCB.OD ＝OFC. BD ＝DCD. OA ＝OB ＝OC10.如图，动点P 从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射11. 一个多边形的每个外角都为30°，则这个多边形的边数为 ▲ ． 12. 等边三角形的两条中线相交所成的钝角的度数是 ▲ .13. 如果三角形的一个角等于其它两个角的差，则这个三角形是 ▲ 三角形． 14. 等腰三角形的一个角为30，则顶角的度数是 ▲ .15. 如图，AB=AC ，要使△ABE ≌△ACD ，应添加的条件是 ▲ （添加一个条件即可）．16. 如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1，5，12，22…为五边形数，则第7个五边形数是 ▲ ．三、用心做一做，显显你的能力！（每题5分，共15分）17. 如图，在△ABC中， 57=∠B ,23=∠C ,AD 是△ABC 的角平分线，求CAD ∠的度数.18. 已知：如图，AB=AE ，∠1＝∠2，∠B=∠E.求证：BC=ED.19. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC 的顶点均在格点上，建立平面直角坐标系后，点A 的坐标为（-4,1），点B 的坐标为（-1,1）.试在图中画出Rt△ABC 关于y 轴对称的图形Rt △A 1B 1C 1，并写出A 1、C 1的坐标.谢第3页共4页第4页共 4页四、仔细观察，耐心研究，展示你的水平！（每题8分，共24分）20. 一个零件的形状如图，按规定∠A=90º ，∠ C=30º，∠B=30º，检验已量得∠BCD=160º，就判断这个零件不合格，运用三角形的有关知识说明零件不合格的理由.21. 如图，在△ABC 中，AB=AC ，AD 是高，AM 是△ABC 外角∠CAE 的平分线. （1）用尺规作图方法，作∠ADC 的平分线DN ；（保留作图痕迹，不写作法和证明）（2）设DN 与AM 交于点F ，判断△ADF 的形状.(只写结果)22. 如图，在△ABC 中，∠C=90°，AD 平分∠CAB ，交CB 于点D ，过点D 作DE ⊥AB 于点E ．（1）求证：△ACD ≌△AED ；（2）若∠B=30°，CD=2，求BD 的长．五、综合实践应用.（每题9分，共27分）23. 如图1，在△ABC 中，AB=AC ，点D 是BC 的中点，点E 在AD 上． (1) 求证：BE=CE ；(2) 如图2，若BE 的延长线交AC 于点F ，且BF ⊥AC ，垂足为F ，∠BAC=45°，原题设其它条件不变．求证：△AEF ≌△BCF ．24.某同学在完成作业时遇到这样一道题：如图1，直线a ，你有什么办法量出这两条直线所成的角的度数？该同学的做法是：如图2，画PC ∥a ，量出直线b 与PC（1）请写出这种做法的理由；（2）这位同学在此基础上又进行了如下操作和探究（如图3 半径画圆弧，分别交直线b ，PC 于点A ，D ；②连结AD 出图3中所有与∠PAB 相等的角，并说明理由；（3）请在图3画板内作出“直线a ，b 部分），只要求作出图形，并保留作图痕迹．25. (1)如图(1)，已知：在△ABC 中，∠BAC ＝90°,AB =AC CE ⊥直线m ,垂足分别为点D 、E .证明:DE =BD +CE .(2) 如图(2)，将(1)中的条件改为：在△ABC 中，AB =AC ，D 有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.如成立,请你给出证明;若不成立,请说明理由.(3) 拓展与应用：如图(3)，D 、E 是D 、A 、E 三点所在直线m 不重合）,点F 为∠BAC 平分线上的一点,且△ABF 和△CE ,若∠BDA =∠AEC =∠BAC ，试判断△DEF 的形状.A C D BABCE D m （图1）（图2）mABCDE 第13题图D。

人教版八年级数学上度第一学期期中考试.docx

初中数学试卷桑水出品2014-2015学年度第一学期期中考试八年级数学试卷一、选择题（每小题3分，共30分）1.下列各数中，最小的实数是（ A ） A.－ 3 B.－1 C.0 D. 32.在实数3.14159，227，5，－0.3·1·中，无理数有（ D ）个A. 4B. 3C. 2D. 13.若3－x 有意义，则x 的取值范围是（ B ） A. x ≥3 B. x ≤3 C. x ≥－3 D. x ≤－34.已知△ABC ≌△DEF ，且∠A ＝600，∠E ＝500，则∠F 等于（ C ） A. 500B. 600C. 700D. 8005.如图，已知CD ⊥AB 于点D ，BE ⊥AC 于点E ，BE 、CD 相交于点O ，且∠BAO ＝∠CAO ，则图中全等三角形共有（ D ） A. 1对 B. 2对 C. 3对 D. 4对6.如图，已知AB ＝DE ，BE ＝CF ，添加下列中一个条件还不能使△ABC ≌△DEF 的是（ D ） A. AC ＝DF B. ∠B ＝∠DEF C. ∠A ＝∠D ＝900D. ∠ACB ＝∠F7.下列交通标志中，不是轴对称图形的是（ C ）A B C D8.到三角形三个顶点的距离相等的点一定是三角形（ B ）的交点 A.三条角平分线 B.三条边的垂直平分线 C. 三条高 D.三条中线9.已知a ，b ，c 是△ABC 的三边长，且满足｜a －b ｜＋c －b ＝0，则是（ B ） A.等腰三角形 B.等边三角形 C.直角三角形 D.不能确定 10.等腰三角形的两边长分别是7 cm 和3 cm ，则它的周长是（ A ） A.17cm B. 13cm C. 17cm 和13cm D. 10cm 二、填空题（每小题3分，共18分）11.已知点P （2,－5），则点P 关于y 轴对称的点P ’的坐标为（－2,－5） . 12. 4的平方根是 ± 2 .13.已知△ABC 中，∠ABC 和∠ACB 的平分线交于点D ，且∠BAC ＝700，则∠BAD ＝ 1250.14.如图，点D 在△ABC 的边BC 上，点E 在△ABC 的外部，且∠1＝∠2＝∠3，要使△ABC ≌△ADE ，还应添加的条件是如：AB ＝AD 等，答案不唯一（写一种即可）15.在平面直角坐标系中，已知点A （0,2），点B （3,1），点C 在x 轴上.当AC ＋BC 最短时，点C 的坐标为（2,0） .16.如图，已知点A 、B 、C 在同一直线上，△ABD 和△BCE 都是等边三角形. 则在下列结论中：①AP ＝DQ ，②EP ＝EC ，③PQ ＝PB ，④∠AOB ＝∠BOC ＝∠COE. 正确的结论是 ①③④ （填写序号）.三、解答题（共72分，17、18、19题各6分，20、21题各8分，22、23题各9分，24、25题各10分）132CA OQP D A17.计算：－31 8×16÷(－2)2－3－27 解：原式＝－ 12×4÷2－（－3）＝－1＋3 ＝218.如图已知AB ＝AC ，BD ＝CD ，AD 与BC 交于点E. 请写出三个不同类型．．．．的正确结论.（不添加字母和辅助线，不要求证明）解：BE ＝CE ； AD 垂直平分BC ；△ABD ≌△ACD ；该图形是轴对称图形等，答案不唯一.19.如图，△ABC 中，AB ＝AC ，∠A ＝500，AB 的垂直平分线DE 分别交AC 、AB 于点D 、E. 求∠CBD 的度数. 解：∵AB ＝AC ，∠A ＝500， ∴∠ABC ＝∠C ＝650， ∵DE 垂直平分AB ， ∴AD ＝BD ，∴∠ABD ＝∠A ＝500，∴∠CBD ＝∠ABC －∠ABD ＝650－500＝150.20.如图，已知在△ABC 中，点D 、E 分别是AB 、AC 上一点，且AD ＝AE ，∠ABE ＝∠ACD ，BE 与CD 相交于点F.试判断△BCF 的形状，并说明理由.解：△BCF 为等腰三角形. 理由如下：在△ABE 和△ACD 中，∠A＝∠A ，DD B∠ABE ＝∠ACD ， AE ＝AD∴△ABE ≌△ACD （AAS ） ∴AB ＝AC ，∠ACB ＝∠ABC ，∴∠ACB －∠ACD ＝∠ABC －∠ABE ，即∠FCB ＝∠FBC. ∴FB ＝FC ，故△BCF 为等腰三角形.21.如图，已知∠BAC ＝∠DAE ＝900，AB ＝AC ，AD ＝AE ，点B 、C 、E 在同一条直线上，求证：DC ⊥BE. 解：∵∠BAC ＝900，AB ＝AC ，∴△ABC 为等腰直角三角形，∠ABC ＝∠ACB ＝450， ∵∠BAC ＝∠DAE ＝900，∴∠BAC ＋∠CAE ＝∠DAE ＋∠CAE ，即∠BAE ＝∠CAD ，在△BAE 和△CAD 中AB ＝AC ， ∠BAE ＝∠CAD ，AD ＝AE ， ∴△BAE ≌△CAD （SAS ） ∴∠ACD ＝∠ABC ＝450，∴∠ACB ＋∠ACD ＝900. 即DC ⊥BE.22.如图所示，△ABC 中，∠ABC ＝600，∠BAC ＝750，AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E ，AD 与CE 相交于点P ，∠ABC 的平分线BF 分别交AD 、CE 、AC 于点M 、N 、F. （1）试写出图中所有的等腰三角形，不要求证明；（2）若DM ＝2cm ，求DC 的长.解：（1）△ABM ，△ACD ，△BCN ，△MNP 都为等腰三角形；（2）∵∠ABC ＝600，AD ⊥BC ，BCB∴∠BAD＝300，∵BF平分∠ABC∴∠ABM＝∠DBM＝300，∴∠ABM＝∠BAD＝300，∴AM＝AM＝2DM＝4cm，∴AD＝AM＋DM＝4＋2＝6cm，∵∠BAC＝750，∴∠DAC＝∠BAC－∠BAD＝750－300＝450，△ACD为等腰直角三角形，∴DC＝AD＝6cm.23.已知如图，△ABC中，∠ACB＝900，AC＝BC，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC，交DE的延长线于点F，连接CF交AD于点G. 试猜想AD和CF有什么关系？并证明你的猜想.解： AD＝CF，AD⊥CF.证明：∵∠ACB＝900，AC＝BC，∴∠CAB＝∠CBA＝450，∵DE⊥AB，∴∠BDE＝∠CBA＝450，∵BF∥AC，∴∠DBF＝1800－900＝900，∴△DBF为等腰直角三角形，BF＝BD，∵D为BC的中点，∴BF＝BD＝CD.在△ACD和△CBD中AC＝CB，∠ACD＝∠CBF，CD＝BF，∴△ACD≌△CBD（SAS）∴AD＝CF，∴∠CAD＝∠BCF，∵∠ACD＝900，即∠ACG＋∠BCF＝900，∴∠ACG＋∠CAG＝900，∴∠AGC＝900，∴AD⊥CF.24.如图，△ABC中，AB＝AC＝12cm，BC＝8cm，点D为AB的中点. 如果点P在BC上以2cm/s的速度由B →C运动，同时，点Q在AC上以相同的速度由C→A运动，当点P到达点C或点Q到达点A时运动停止.（1）经过1s后，△BPD与以点C、P、Q为顶点的三角形是否全等？为什么？（2）如果点Q的速度与点P（2cm/s）不等，（1）中的两个三角形是否全等？若能，求出此时点Q的速度和运动时间；若不能，请说明理由.解：（1）当t=1时，BP=2cm CP=6cm CQ=2cm，∵D是AB中点，∴BD=AD=6cm，∵∠B=∠C，BP= CQ=2cm ，BD=CP=6cm.∴△DBP≌△PCQ（SAS），∴DP=PQ（2）设点Q速度为x，则t秒后CQ长度为x cm，因为P的速度为2cm每秒，所以t秒后BP长度为2t cm CP=8-2t（cm）。

2014年人教版八年级上期中考试数学试卷.doc

2014年秋季期中考试八年级数学试卷命题人：杨本强一、选择题（每题3分，计45分）（）1、下列计算错误的是 ( )A ．2m + 3n=5mnB ．(ab 2)3=a 3b 6C ．(x 2)3=x 6D ．a •a 2=a 3（）2、计算232(3)x x ⋅-的结果是（）A. 56x B. 62x C.62x - D. 56x -（）3．已知(1＋x)(2x 2＋ax ＋1)的结果中x 2项的系数为－2，则a 的值为 ( ) A ．－2 B ．1 C ．－4 D ．以上都不对（）4、如图，阴影部分的面积是( )A ．3.5xyB ．4.5xyC ．4xyD ．2xy （ )5、等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（）度 A.60° B.120° C.60°或 120° D.30°（）6、等腰三角形的周长是18cm ，其中一边长为4cm ，其它两边长分别为（）.A ．4cm ，10cmB ．7cm ，7cmC ．4cm ，10cm 或7cm ，7cmD ．无法确定（）7、已知 △ABC 中，∠B 是∠A 的2倍，∠C 比∠A 大20°，则∠C 等于（）.A.40°B.60°C.80°D.90°（）8、用直尺和圆规作一个角等于已知角，其正确的依据是（）A ．AASB ．SSSC ．SASD ．ASA（）9、如果正多边形的一个内角是144°，则这个多边形是（）.A.正十边形B.正九边形C.正八边形D.正七边形（）10、BD 、CE 分别是△ABC 中∠ABC 、∠ACB 的平分线，且交于点O ，若O到AB 的距离为1，BC =3,则BOC S ∆=（） A.12 B. 1 C.32D. 3 （）11、如图，CD 是的中线，AC =9cm ，BC =3cm ， △ACD 和△BCD 的周长的差是（）. A ．3 cm B ．6cm C ．（）12、已知△ABC 与△DEF 全等,BC=EF=4cm,△ABC 的面积是12cm 2,则EF 边上的高是( ) .A ．3cm B ．4cm C ．6cm D ．无法确定（）13、．若M ＝(a ＋3)(a －4)，N ＝(a ＋2)(2a －5)，其中a 为有理数，则M 与N 的大小关系为( )A ．M>NB ．M<NC ．M ＝ND ．无法确定（）14. 下列各组图形中，是全等形的是（）A 、两个含60°角的直角三角形；B 、腰对应相等的两个等腰直角三角形；C 、边长为3和5的两个等腰三角形；D 、一个钝角相等的两个等腰三角形（）15.如图，已知P A ⊥OA 于A ，PB ⊥OM 于B ，且P A =PB , ∠MON =50°，∠OPC =30°，则∠PCA =（）A.45° B.55° C.65° D.75°二、解答题16、计算：(3x6=18分) (1) ()62)()(a a a -⋅-⋅- (2) (－3x 2y )·(213xy )（3）3223)()(x x -⋅- （4）34223()()a b ab ÷（5）))(()(2y x y x y x -+-+ (6)xy xy y x y x 2)232(2223÷+--17、（4分）先化简，再求值：(a 2b-2ab 2-b 3)÷b-(a+b)(a-b)，其中．18、（4分）已知x m =3,x n =2,求3x m+2n 的值 19、（5分）如图AB=a ，P 是线段AB 上的一点，分别以AP 、BP 为边作正方形，（1）设AP=x ，求两个正方形的面积之和S （用含x 的代数式表示，并注意化简）（2）设当x= a 时，两个正方形面积的和为S 1；当x= a 时，两个正方形的面积的和为S 2，试比较S 1与S 2的大小．EDOCBAADCB第11题图N MPA BOC 第15图20、（5分）（1）如图是用4个全等的长方形拼成的一个“回形”正方形，将图中阴影部分面积用2种方法表示可得一个等式，这个等式为。

2013-2014学年新人教版数学八年级上期中模拟AB卷(详细解析+考点分析+名师点评)-3.doc

新世纪教育网精品资料版权所有@新世纪教育网2013-2014学年新人教版八年级（上）期中数学试卷（A）一、选择题（每小题3分，共30分）1．（3分）在△ABC和△DEF中，①AB=DE，②BC=EF，③AC=DF，④∠A=∠D，⑤∠B=∠E，⑥∠C=∠F，2．（3分）如图，AD平分∠BAC，AB=AC，连接BD，CD并延长交AC，AB于E，F点，则此图中全等三角形共有（）3．（3分）在Rt△ABC中，∠C=90°，BD是∠ABC的平分线，交AC于点D，若CD=n，AB=m，则△ABD的面mn Cmn4．（3分）如图所示，△ABC为等边三角形，AD⊥BC，AE=AD，则∠ADE的度数为（）6．（3分）已知点A的坐标为（2，﹣3），点A关于y轴的对称点为点A1，A1关于x轴的对称点A2，则点A2的坐9．（3分）如图，△ABC中，∠BAC=100°，DF，EG分别是AB，AC的垂直平分线，则∠DAE等于（）10．（3分）如图所示，把直角三角形纸片沿过顶点B的直线（BE交CA于E）折叠，直角顶点C落在斜边AB上，如果折叠后得等腰△EBA，那么结论中：①∠A=30°；②点C与AB的中点重合；③点E到AB的距离等于CE的长，正确的个数是（）二、填空题（每题3分，共30分）11．（3分）已知△ABC≌△FED，若△ABC的周长为32，AB=8，BC=12，则FD的长为_________．12．（3分）如图，∠1=∠2．（1）当BC=BD时，△ABC≌△ABD的依据是_________；（2）当∠3=∠4时，△ABC≌△ABD的依据是_________．13．（3分）如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“HL”判定，还需要加条件_________，若加条件∠B=∠C，则可用_________判定．14．（3分）如图所示，∠A=90°，BD是△ABC的角平分线，AC=8cm，DC：AD=3：1，则点D到BC的距离为_________．15．（3分）已知点A（a，﹣2）和B（3，b），当满足条件_________时，点A和点B关于y轴对称．16．（3分）等腰三角形底边长为5cm，一腰上的中线把其周长分为两部分的差为3cm，则腰长为_________．17．（3分）如图，在△ABC中，AB=AC，CD平分∠ACB交AB于D点，AE∥DC交BC的延长线于点E，已知∠E=36°，则∠B=_________度．18．（3分）如图，Rt△ABC中，CD，CE分别是斜边AB上的高和中线，如果∠A=30°，BD=1cm，那么∠BCD= _________度，BC=_________cm，AD=_________cm．19．（3分）如图，∠A=15°，AB=BC=CD=DE=EF，则∠MEF=_________．20．（3分）已知点P关于x轴的对称点P′的坐标是（2，3），那么P关于y轴对称点P″的坐标是_________．三、解答题：（每小题10分，共60分）21．（10分）如图，在平面直角坐标系xoy中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．（1）求出△ABC的面积．（2）在图中作出△ABC关于y轴的对称图形△A1B1C1．（3）写出点A1，B1，C1的坐标．22．（10分）已知：如图，OP是∠AOC和∠BOD的平分线，OA=OC，OB=OD．求证：AB=CD．23．（10分）如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB=DE，BF=CE．求证：（1）△ABC≌△DEF；（2）GF=GC．24．（10分）如图，点P在∠AOB内，点M，N分别是点P关于AO，BO的对称点，若△PEF的周长是30cm，求MN的长．25．（10分）如图，在△ABC中，∠ACB=120°，CD平分∠ACB，AE∥DC，交BC的延长线于点E，试说明△ACE 是等边三角形．26．（10分）如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，①求证：△BCE≌△ACD；②求证：CF=CH；③判断△CFH的形状并说明理由．。

2014-2015八年级第一学期期中试卷(含答案)

ACB D E 人教版2014-2015学年度第一学期八年级数学期中考试试卷（含参考答案）一、选择题：（本题满分24分，每小题3分）在下列各题的四个备选答案中，只有一个是正确的，请把你认为正确的答案的字母代号填在题后的括号内。

．．．．．．．．． 1．下列各组线段能组成一个三角形的是( )．(A)5cm ，8cm ，12cm (B)2cm ，3cm ，6cm (C)3cm ，3cm ，6cm (D)4cm ，7cm ，11cm 2.下列图案是轴对称图形的有（）。

A.（1）（2）B.（1）（3）C.（1）（4）D.（2）（3）(1) (2) (3) (4)3.下列几种说法：①全等三角形的对应边相等；②面积相等的两个三角形全等；③周长相等的两个三角形全等；④全等的两个三角形一定重合。

其中正确的是（）。

A. ①② B. ②③ C. ③④ D. ①④ 4．已知直角三角形中30°角所对的直角边为2㎝，则斜边的长为（）。

A. 2 ㎝B. 4 ㎝C. 6 ㎝D. 8㎝ 5．点M （1，2）关于y 轴对称的点的坐标为（）。

A.（—1，2）B.（－1，－2）C. （1，－2）D. （2，－1） 6．如图，∠B=∠D=90°，CB=CD ，∠1=40°，则∠2=（）。

A ．40° B. 45° C. 60° D. 50°7. 如图所示,在△ABC 中,已知点D,E,F 分别为边BC,AD,CE 的中点,且S △ABC=4cm 2,则阴影部分的面积等于( )A.2cm 2B.1cm 2C.12cm 2D.1 4 cm 28.已知等腰三角形一个内角是70°，则另外两个内角的度数是（）A.55°， 55°B.70°， 40°C.55°， 55°或70°， 40°D.以上都不对二、填空题：（本题满分24分，每小题3分）9．一扇窗户打开后，用窗钩可将其固定，这里运用的几何原理为。

2014-2015学年新人教版八年级上期中数学试卷及答案解析

2014-2015学年八年级（上）期中数学试卷一、选择题（本大题共12个小题，每小题3分，共36分.）1．下列交通标志是轴对称图形的是( )A．B．C． D．2．三角形的一个外角小于和它相邻的内角，这个三角形为( )A．锐角三角形B．直角三角形C．钝角三角形D．以上三种都有可能3．已知图中的两个三角形全等，则∠1等于( )A．72°B．60°C．50°D．58°4．已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是( )A．13cm B．6cm C．5cm D．4cm5．下列等式成立的是( )A．（﹣3）﹣2=﹣9 B．m•m﹣2•m3=m5C．（﹣a﹣1b﹣3）﹣2=﹣a2b6D．（﹣2m）2÷2m3=6．若b为常数，要使16x2+bx+1成为完全平方式，那么b的值是( )A．4 B．8 C．±4 D．±87．若分式的值为零，则x的值为( )A．0 B．﹣3 C．3 D．3或﹣38．已知，△ABC和△ADC关于直线AC轴对称，如果∠BAD+∠BCD=160°，那么△ABC 是( )A．直角三角形B．等腰三角形C．钝角三角形D．锐角三角形9．如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，线段DE=1cm，则BD 的长为( )A．6cm B．8cm C．3cm D．4cm10．随着生活水平的提高，小林家购置了私家车，这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟，现已知小林家距学校8千米，乘私家车平均速度是乘公交车平均速度的2.5倍，若设乘公交车平均每小时走x千米，根据题意可列方程为( )A．B．C．D．11．如图，设k=（a＞b＞0），则有( )A．k＞2 B．1＜k＜2 C．D．12．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为( )A．B．3 C．4 D．二、填空题（本大题共5小题，每小题3分，共18分）13．一生物教师在显微镜下发现某种植物的细胞直径约为0.000000102mm，用科学记数法表示这个数为__________．14．分解因式：ab2﹣4ab+4a=__________．15．若3x=4，9y=7，则3x﹣2y的值为__________．16．在△ABC中，AB=AC，AB的中垂线与AC所在直线相交所得的锐角为50°，则底角∠B=__________．17．如图，在长方形ABCD中，AB＞BC，BE⊥AC，垂足为E，延长BE交CD于F，S表示面积，则给出的下列命题：①Rt△ABC≌Rt△CDA；②S△AEF＜S△BCE；③∠DAE+∠DFE=180°；④∠AFB＞∠ACB 其中正确命题的代号是__________．三、解答题：（本大题共6小题，共46分）18．（1）解不等式：（2x﹣5）2+（3x+1）2＞13（x2﹣10）（2）解分式方程：．19．先化简：÷（a+），当b=﹣1时，请你为a任选一个适当的数代入求值．20．如图，∠1=∠2，∠3=∠4，求证：AC=AD．21．如图，已知△ABC，P为内角平分线AD，BE，CF的交点，过点P作PG⊥BC于G，试说明∠BPD与∠CPG的大小关系，并说明理由．22．用电脑程序控制小型赛车进行50m比赛，“畅想号”和“和谐号”两辆赛车进入了决赛．比赛前的练习中，两辆车从起点同时出发，“畅想号”到达终点时，“和谐号”离终点还差3m．已知“畅想号”的平均速度为2.5m/s．（1）求“和谐号”的平均速度；（2）如果两车重新开始比赛，“畅想号”从起点向后退3m，两车同时出发，两车能否同时到达终点？若能，求出两车到达终点的时间；若不能，请重新调整一辆车的平均速度，使两车能同时到达终点．23．如图③，点E，D分别是正三角形ABC，正四边形ABCM，正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能相互重合，DB的延长线交AE于点F．（1）在图①中，求∠AFB的度数；（2）在图②中，∠AFB的度数为__________，图③中，∠AFB的度数为__________；（3）继续探索，可将本题推广到一般的正n边形情况，用含n的式子表示∠AFB的度数．2014-2015学年四川省绵阳中学八年级（上）期中数学试卷一、选择题（本大题共12个小题，每小题3分，共36分.）1．下列交通标志是轴对称图形的是( )A．B．C． D．【考点】轴对称图形．【分析】根据轴对称图形的概念求解．【解答】解：A、不是轴对称图形，故错误；B、不是轴对称图形，故错误；C、是轴对称图形，故正确；D、不是轴对称图形，故错误．故选C．【点评】本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．2．三角形的一个外角小于和它相邻的内角，这个三角形为( )A．锐角三角形B．直角三角形C．钝角三角形D．以上三种都有可能【考点】三角形的外角性质．【分析】此题依据三角形的外角性质，即三角形的外角与它相邻的内角互为邻补角，可判断出此三角形有一内角为钝角，从而得出这个三角形是钝角三角形的结论．【解答】解：∵三角形的一个外角与它相邻的内角和为180°，而题中说这个外角小于它相邻的内角，∴与它相邻的这个内角是一个大于90°的角即钝角，∴这个三角形就是一个钝角三角形．故选C．【点评】本题考查的是三角形的外角性质，解题的关键是熟练掌握三角形的外角与它相邻的内角互为邻补角．3．已知图中的两个三角形全等，则∠1等于( )A．72°B．60°C．50°D．58°【考点】全等三角形的性质．【分析】根据三角形内角和定理求得∠2=58°；然后由全等三角形是性质得到∠1=∠2=58°．【解答】解：如图，由三角形内角和定理得到：∠2=180°﹣50°﹣72°=58°．∵图中的两个三角形全等，∴∠1=∠2=58°．故选：D．【点评】本题考查了全等三角形的性质，解题的关键是找准对应角．4．已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是( )A．13cm B．6cm C．5cm D．4cm【考点】三角形三边关系．【分析】此题首先根据三角形的三边关系，求得第三边的取值范围，再进一步找到符合条件的数值．【解答】解：根据三角形的三边关系，得：第三边应大于两边之差，且小于两边之和，即9﹣4=5，9+4=13．∴第三边取值范围应该为：5＜第三边长度＜13，故只有B选项符合条件．故选：B．【点评】本题考查了三角形三边关系，一定要注意构成三角形的条件：两边之和＞第三边，两边之差＜第三边．5．下列等式成立的是( )A．（﹣3）﹣2=﹣9 B．m•m﹣2•m3=m5C．（﹣a﹣1b﹣3）﹣2=﹣a2b6D．（﹣2m）2÷2m3=【考点】负整数指数幂；整式的除法．【分析】根据负整数指数幂、同底数幂的乘法以及整式的除法运算法则进行计算．【解答】解：A、原式=9，故本选项错误；B、原式=m（1﹣2+3）=m2，故本选项错误；C、原式=（﹣1）﹣2•a﹣1×（﹣2）•b（﹣3）×（﹣2）=a2b6，故本选项错误；D、原式==，故本选项正确．‘故选：D．【点评】本题考查了负整数指数幂、整式的除法．掌握运算法则的解题的关键．6．若b为常数，要使16x2+bx+1成为完全平方式，那么b的值是( )A．4 B．8 C．±4 D．±8【考点】完全平方式．【专题】常规题型．【分析】先根据两平方项确定出这两个数，再根据完全平方公式的乘积二倍项即可确定b的值．【解答】解：16x2+bx+1=（4x）2+bx+1，∴bx=±2×4x×1，解得b=±8．故选D．【点评】本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．7．若分式的值为零，则x的值为( )A．0 B．﹣3 C．3 D．3或﹣3【考点】分式的值为零的条件．【专题】计算题．【分析】根据分式的值为零的条件得到当x2﹣9=0且x+3≠0时，分式的值为零，然后解方程和不等式即可得到x的值．【解答】解：∵分式的值为零，∴x2﹣9=0且x+3≠0，∴x=3．故选C．【点评】本题考查了分式的值为零的条件：分式的分子为零且分母不为零时，分式的值为零．也考查了解方程与不等式．8．已知，△ABC和△ADC关于直线AC轴对称，如果∠BAD+∠BCD=160°，那么△ABC 是( )A．直角三角形B．等腰三角形C．钝角三角形D．锐角三角形【考点】轴对称的性质．【分析】作出图形，根据轴对称的性质可得∠BAC=∠DAC，∠ACB=∠ACD，然后求出∠BAC+∠ACB，再根据三角形的内角和定理求出∠B，然后判断三角形的形状即可．【解答】解：如图，∵△ABC和△ADC关于直线AC轴对称，∴∠BAC=∠DAC，∠ACB=∠ACD，∴∠BAC+∠ACB=（∠BAD+∠BCD）=×160°=80°，在△ABC中，∠B=180°﹣（∠BAC+∠ACB）=180°﹣80°=100°，∴△ABC是钝角三角形．故选C．【点评】本题考查了轴对称的性质，根据成轴对称的两个图形能够完全重合得到相等的角是解题的关键，作出图形更形象直观．9．如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，线段DE=1cm，则BD 的长为( )A．6cm B．8cm C．3cm D．4cm【考点】线段垂直平分线的性质；含30度角的直角三角形；三角形中位线定理．【专题】计算题．【分析】过A作AF∥DE交BD于F，则DE是△CAF的中位线，根据线段垂直平分线的性质，即可解答．【解答】解：过A作AF∥DE交BD于F，则DE是△CAF的中位线，∴AF=2DE=2，又∵DE⊥AC，∠C=30°，∴FD=CD=2DE=2，在△AFB中，∠1=∠B=30°，∴BF=AF=2，∴BD=4．故选D．【点评】此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段两个端点的距离相等．10．随着生活水平的提高，小林家购置了私家车，这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟，现已知小林家距学校8千米，乘私家车平均速度是乘公交车平均速度的2.5倍，若设乘公交车平均每小时走x千米，根据题意可列方程为( )A．B．C．D．【考点】由实际问题抽象出分式方程．【分析】根据乘私家车平均速度是乘公交车平均速度的2.5倍，乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟，利用时间得出等式方程即可．【解答】解：设乘公交车平均每小时走x千米，根据题意可列方程为：=+，故选：D．【点评】此题主要考查了由实际问题抽象出分式方程，解题关键是正确找出题目中的相等关系，用代数式表示出相等关系中的各个部分，把列方程的问题转化为列代数式的问题．11．如图，设k=（a＞b＞0），则有( )A．k＞2 B．1＜k＜2 C．D．【考点】分式的乘除法．【专题】计算题．【分析】分别计算出甲图中阴影部分面积及乙图中阴影部分面积，然后计算比值即可．【解答】解：甲图中阴影部分面积为a2﹣b2，乙图中阴影部分面积为a（a﹣b），则k====1+，∵a＞b＞0，∴0＜＜1，∴1＜+1＜2，∴1＜k＜2故选B．【点评】本题考查了分式的乘除法，会计算矩形的面积及熟悉分式的运算是解题的关键．12．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为( )A．B．3 C．4 D．【考点】轴对称-最短路线问题；正方形的性质．【分析】由于点B与D关于AC对称，所以连接BE，与AC的交点即为P点．此时PD+PE=BE 最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的面积为16，可求出AB的长，从而得出结果．【解答】解：设BE与AC交于点P'，连接BD．∵点B与D关于AC对称，∴P'D=P'B，∴P'D+P'E=P'B+P'E=BE最小．∵正方形ABCD的面积为16，∴AB=4，又∵△ABE是等边三角形，∴BE=AB=4．故选C．【点评】本题考查的是正方形的性质和轴对称﹣最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．二、填空题（本大题共5小题，每小题3分，共18分）13．一生物教师在显微镜下发现某种植物的细胞直径约为0.000000102mm，用科学记数法表示这个数为1.02×10﹣7．【考点】科学记数法—表示较小的数．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.000000102=1.02×10﹣7．故答案为：1.02×10﹣7．【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．14．分解因式：ab2﹣4ab+4a=a（b﹣2）2．【考点】提公因式法与公式法的综合运用．【专题】因式分解．【分析】先提取公因式a，再根据完全平方公式进行二次分解．完全平方公式：a2﹣2ab+b2=（a﹣b）2．【解答】解：ab2﹣4ab+4a=a（b2﹣4b+4）﹣﹣（提取公因式）=a（b﹣2）2．﹣﹣（完全平方公式）故答案为：a（b﹣2）2．【点评】本题考查了提公因式法，公式法分解因式，提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．15．若3x=4，9y=7，则3x﹣2y的值为．【考点】同底数幂的除法；幂的乘方与积的乘方．【分析】根据3x﹣2y=3x÷32y=3x÷9 y即可代入求解．【解答】解：3x﹣2y=3x÷32y=3x÷9 y=．故答案是：．【点评】本题考查了同底数的幂的除法运算，正确理解3x﹣2y=3x÷32y=3x÷9 y是关键．16．在△ABC中，AB=AC，AB的中垂线与AC所在直线相交所得的锐角为50°，则底角∠B=70°或20°．【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】由于△ABC的形状不能确定，故应分△ABC是锐角三角形与钝角三角形两种情况进行讨论．【解答】解：如图①，当AB的中垂线与线段AC相交时，则可得∠ADE=50°，∵∠AED=90°，∴∠A=90°﹣50°=40°，∵AB=AC，∴∠B=∠C==70°；如图②，当AB的中垂线与线段CA的延长线相交时，则可得∠ADE=50°，∵∠AED=90°，∴∠DAE=90°﹣50°=40°，∴∠BAC=140°，∵AB=AC，∴∠B=∠C==20°．∴底角B为70°或20°．故答案为：70°或20°．【点评】本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．17．如图，在长方形ABCD中，AB＞BC，BE⊥AC，垂足为E，延长BE交CD于F，S表示面积，则给出的下列命题：①Rt△ABC≌Rt△CDA；②S△AEF＜S△BCE；③∠DAE+∠DFE=180°；④∠AFB＞∠ACB 其中正确命题的代号是①③④．【考点】矩形的性质；全等三角形的判定与性质．【分析】由矩形的性质得出∠ABC=∠D=∠BCD=∠BAD=90°，BC=DA，AB=CD，由SAS 证明△ABC≌△CDA，①正确；由△ABF的面积=△ABC的面积，得出△AEF的面积=△BCE的面积，②不正确；证明A、E、F、D四点共圆，得出∠DAE+∠DFE=180°，③正确；延长AF交矩形ABCD的外接圆于G，连接BG，由圆周角定理得出∠AGB=∠ACB，由三角形的外角性质得出∠AFB＞∠AGB，得出∠AFB＞∠ACB，④正确；即可得出结论．【解答】解：∵四边形ABCD是矩形，∴∠ABC=∠D=∠BCD=∠BAD=90°，BC=DA，AB=CD，在△ABC和△CDA中，，∴△ABC≌△CDA（SAS），∴①正确；∵△ABF的面积=△ABC的面积=AB•BC，∴△AEF的面积=△BCE的面积，∴②不正确；∵BE⊥AC，∴∠AEF=90°，∴∠AEF+∠D=180°，∴A、E、F、D四点共圆，∴∠DAE+∠DFE=180°，∴③正确；∵A、B、C、D四点共圆，如图所示：延长AF交矩形ABCD的外接圆于G，连接BG，则∠AGB=∠ACB，∵∠AFB＞∠AGB，∴∠AFB＞∠ACB，∴④正确；正确的代号是①③④；故答案为：①③④．【点评】本题考查了矩形的性质、全等三角形的判定与性质、四点共圆、圆周角定理、圆内接四边形的性质；熟练掌握矩形的性质，并能进行推理论证是解决问题的关键．三、解答题：（本大题共6小题，共46分）18．（1）解不等式：（2x﹣5）2+（3x+1）2＞13（x2﹣10）（2）解分式方程：．【考点】整式的混合运算；解分式方程；解一元一次不等式．【分析】（1）直接利用完全平方公式化简求出即可；（2）首先去分母进而合并同类项求出即可．【解答】解：（1）（2x﹣5）2+（3x+1）2＞13（x2﹣10）去括号得：4x2+25﹣20x+9x2+1+6x＞13x2﹣130整理得：﹣14x＞﹣156解得：x＜11；（2）去分母得：x（x+2）﹣（x﹣1）（x+2）=3（x﹣1），x2+2x﹣（x2+2x﹣x﹣2）=3x﹣3，则﹣2x=﹣5，解得：x=，检验：当x=时，（x﹣1）（x+2）≠0，则x=是原方程的根．【点评】此题主要考查了整式的混合运算以及分式方程的解法，正确利用乘法公式是解题关键．19．先化简：÷（a+），当b=﹣1时，请你为a任选一个适当的数代入求值．【考点】分式的化简求值．【专题】开放型．【分析】主要考查了分式的化简求值，其关键步骤是分式的化简．要熟悉混合运算的顺序，正确解题．注意化简后，代入的数不能使分母的值为0．【解答】解：原式=÷==，∵a≠0、a≠±1，∴答案不唯一．当a=2时，原式=1．【点评】本题主要考查分式的化简求值，式子化到最简是解题的关键．20．如图，∠1=∠2，∠3=∠4，求证：AC=AD．【考点】全等三角形的判定与性质．【专题】证明题．【分析】先证出∠ABC=∠ABD，再由ASA证明△ABC≌△ABD，得出对应边相等即可．【解答】证明：∵∠3=∠4，∴∠ABC=∠ABD，在△ABC和△ABD中，，∴△ABC≌△ABD（ASA），∴AC=AD．【点评】本题考查了全等三角形的判定与性质；熟练掌握全等三角形的判定方法，证明三角形全等是解决问题的关键．21．如图，已知△ABC，P为内角平分线AD，BE，CF的交点，过点P作PG⊥BC于G，试说明∠BPD与∠CPG的大小关系，并说明理由．【考点】三角形内角和定理．【分析】利用AD平分∠BAC，BE平分∠ABC，CF平分∠ACB，得出∠BAD=∠BAC，∠ABE=∠ABC，∠BCF=∠ACB，再利用三角形的外角意义得出∠BPD=∠BAD+∠ABE 等量代换得出∠BPD=90°﹣∠ACB；再利用PG⊥BC，得出三角形CPG是直角三角形，利用三角形的内角和表示出∠CPG=90°﹣∠ACB，证明结论成立．【解答】∠BPD=∠CPG证明：∵AD平分∠BAC，BE平分∠ABC，CF平分∠ACB，∴∠BAD=∠BAC，∠ABE=∠ABC，∠BCF=∠ACB，∴∠BPD=∠BAD+∠ABE=（∠BAC+∠ABC），∵∠BAC+∠ABC=180﹣∠ACB，∴∠BPD=（180﹣∠ACB）=90°﹣∠ACB；∵PG⊥BC，∴∠PGC=90°，∴∠BCP+∠CPG=180°﹣∠PGC=90°，∴∠CPG=90°﹣∠BCP=90°﹣∠ACB，∴∠BPD=∠CPG．【点评】此题考查角平分线的性质，三角形内角和定理，三角形外角的意义，垂直的性质等知识点．22．用电脑程序控制小型赛车进行50m比赛，“畅想号”和“和谐号”两辆赛车进入了决赛．比赛前的练习中，两辆车从起点同时出发，“畅想号”到达终点时，“和谐号”离终点还差3m．已知“畅想号”的平均速度为2.5m/s．（1）求“和谐号”的平均速度；（2）如果两车重新开始比赛，“畅想号”从起点向后退3m，两车同时出发，两车能否同时到达终点？若能，求出两车到达终点的时间；若不能，请重新调整一辆车的平均速度，使两车能同时到达终点．【考点】分式方程的应用．【分析】（1）设“和谐号”的平均速度为x，根据，“畅想号”运动50m与“和谐号”运动47m所用时间相等，可得方程，解出即可．（2）不能同时到达，设调整后“和谐号”的平均速度为y，根据时间相等，得出方程求解即可．【解答】解：（1）设“和谐号”的平均速度为x，由题意得，=，解得：x=2.35，经检验x=2.35是原方程的解．答：“和谐号”的平均速度2.35m/s．（2）不能同时到达．设调整后“和谐号”的平均速度为y，=，解得：y=．答：调整“畅想号”的车速为m/s可使两车能同时到达终点．【点评】本题考查了分式方程的应用，解答本题的关键是仔细审题，找到等量关系，建立方程，难度一般．23．如图③，点E，D分别是正三角形ABC，正四边形ABCM，正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能相互重合，DB 的延长线交AE于点F．（1）在图①中，求∠AFB的度数；（2）在图②中，∠AFB的度数为90°，图③中，∠AFB的度数为108°；（3）继续探索，可将本题推广到一般的正n边形情况，用含n的式子表示∠AFB的度数．【考点】正多边形和圆；全等三角形的判定与性质；相似三角形的判定与性质．【分析】（1）先根据等边三角形的性质得出∠AC=60°，再由补角的定义可得出∠ABE与∠BCD的度数，根据△ABE与△BCD能相互重合可得出∠E=∠D，∠DBC=∠BAE，由三角形外角的性质可得出结论；（2）根据（1）中的方法可得出△BEF∽△BDC，进而可得出结论；（3）根据（1）（2）的结论找出规律即可．【解答】解：（1）∵△ABC是等边三角形，∴AB=BC，∠ABC=∠ACB=60°，∴∠ABE=∠BCD=120°．∵△ABE与△BCD能相互重合，∴∠E=∠D，∠DBC=∠BAE．∵∠FBE=∠CBD，∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°；（2）图②中，∵△ABE与△BCD能相互重合，∴∠E=∠D．∵∠FBE=∠CBD，∠D+∠CBD=90°，∴∠AFB=∠E+∠FBE=∠D+∠CBD=90°；同理可得，图③中∠AFB=108°．故答案为：90°，108°；（3）由（1）（2）可知，在正n边形中，∠AFB=．【点评】本题考查的是正多边形和圆，在解答此题时要注意正三角形、正四边形及正五边形的性质的应用，根据题意找出规律是解答此题的关键．。

2013-2014人教版八年级上数学期中考试

ABCD2013-2014年八年级（上）数学期中考试卷学校：班级：姓名：考号：一、选择题（3′×10）答案写在下面题卡上题号 12345678910答案1、下列平面图形中，不是轴对称图形的是（）2、在△ABC 中，∠A=2（∠B+∠C ），则∠A 的度数为（） A 、100° B 、120° C 、140° D 、160°3、如图1，把△ABC 纸片沿DE 折叠，当点A 落在四边形BCDE 内部时，则∠A 与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（• ） A ．∠A=∠1+∠2 B ．2∠A=∠1+∠2C ．3∠A=2∠1+∠2D ．3∠A=2（∠1+∠2）图1 4、已知三角形的一个内角是另一个内角的32,是第三个内角的54,则这个三角形各内角的度数分别为( )A.60°,90°,75°B.48°,72°,60°C.48°,32°,38°D.40°,50°,90° 5、如图2，△ACD 中，AB ⊥CD 且BD ＞CB ，△BCE 和△ABD 都是等腰Rt △，下列结论① △ABC ≌△DBE ；② △ACB ≌△ABD ；③ △CBE ≌△BED ； ④ △ACE ≌△ADE ；正确的是（）A. ①②③B. ①C. ①③④D. ②③④6、下列命题正确的是（）图2 A. 两个直角三角形全等 B. 两个等腰三角形全等OBAEFG HC. 两个等边三角形全等D. 两条直角边对应相等的两个Rt △全等7、等腰三角形的底边长为8 cm ，则腰长的范围是( )A ．大于4 cm 且小于8 cmB ．大于4 cm 且小于16 cmC ．大于8 cm 且小于16 cmD ．大于4 cm8、如图3所示的4×4正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7=（）图3A 、330°B 、315°C 、310°D 、320°9、在△ABC 内部取一点P 使得点P 到△ABC 的三边距离相等，则点P 应是△ABC 的哪三条线交点.（）（A ）高（B ）角平分线（C ）中线（D ）垂直平分线 10、如图4,是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC 、DE 垂直于横梁AC,AB=10m, ∠A=30°,则DE 等于 ( )(A)1m (B) 2m (C)2.5m (D) 3.5m二、填空题（3′×10）图4 11、若n 边形的每个内角都是150°，则n= 。