《直角三角形斜边上的中线等于斜边的一半》的专题训练
直角三角形斜边上的中线等于斜边的一半例题

直角三角形斜边上的中线等于斜边的一半例题全文共四篇示例,供读者参考第一篇示例:在中学数学课堂上,直角三角形是一个非常常见的几何形状。
直角三角形的特点是其中一个角为直角(90度),而其他两个角则为锐角和钝角,另外两条边分别为斜边和两条直角边。
直角三角形的性质十分有趣,其中有一条性质是斜边上的中线等于斜边的一半。
这个性质看似简单,但需要一些几何知识和推理来证明。
让我们来了解一下中线是什么。
在一个三角形中,中线是连接一个角的顶点和对边中点的线段。
对于直角三角形来说,如果我们将斜边一分为二,使之成为等分线,那么这条等分的线段就是斜边上的中线。
接下来,让我们来证明斜边上的中线等于斜边的一半。
假设我们有一个直角三角形ABC,其中角A为直角,AB和AC分别为直角边,BC为斜边。
我们需要证明BD(BC的中线)等于BC的一半。
我们可以得出直角三角形ABC中的角B和角C分别为锐角和钝角。
根据直角三角形的性质,角B和角C的和为90度,即B+C=90度。
又因为直角三角形中,直角边的对边相等,所以AB=AC。
我们可以得出结论:斜边上的中线等于斜边的一半。
在这个例子中,BD等于BC的一半,也就是说斜边BC的中线等于一半的斜边BC。
这个性质在几何学中有许多应用,特别是在解题时。
通过掌握这个性质,我们可以更快地解决直角三角形的问题,提高我们的数学能力和解题速度。
直角三角形斜边上的中线等于斜边的一半是一个十分有趣的几何性质。
通过几何推理和证明,我们可以更深入地理解这个性质,并在实际问题中灵活运用。
希望同学们在学习数学的过程中,能够多多探索,多多实践,不断提升自己的数学水平。
【2000字】第二篇示例:直角三角形是三角形中特殊的一种,其中一个角是直角(即90度角)。
在直角三角形中,斜边是最长的一条边,其余两边分别称为直角边。
而直角三角形斜边上的中线等于斜边的一半,这是一个非常有趣且有趣的几何性质。
考虑一个直角三角形ABC,其中∠C是直角,AB为斜边,AC和BC为直角边。
直角三角形斜边上的中点是斜边的一半题

直角三角形斜边上的中点是斜边的一半题大家好,我是一名行业专家,今天我要和大家探讨一个非常有趣的问题:直角三角形斜边上的中点是斜边的一半吗?这个问题看似简单,但实际上涉及到很多理论知识。
在开始之前,我想先问大家一个问题:你们觉得这个问题的答案是什么呢?这个问题的答案并不是那么容易回答的。
因为我们要从不同的角度来看待这个问题。
我们要明确什么是直角三角形,什么是斜边,什么是中点。
然后,我们还要分析各种情况下,中点是否真的是斜边的一半。
接下来,我将从三个方面来展开我的论述:一是直角三角形的定义和性质;二是斜边的定义和性质;三是中点的定义和性质。
我将结合这三个方面的知识,给出我对于这个问题的解答。
我们来看一下直角三角形的定义和性质。
直角三角形是指有一个角为90度的三角形。
在直角三角形中,我们把那个90度的角叫做直角。
而另外两个角分别叫做锐角和钝角。
根据三角形的三边关系,我们知道直角三角形的三条边满足勾股定理:直角边的平方和等于斜边的平方。
也就是说,在一个直角三角形中,如果两条直角边的长度分别为a和b,那么斜边的长度c满足a^2 + b^2 = c^2。
接下来,我们来看一下斜边的定义和性质。
斜边是指在一个直角三角形中,连接直角顶点和对边中点的线段。
在直角三角形中,斜边是最长的边。
根据三角形的三边关系,我们知道斜边的平方大于等于其他两边的平方和。
也就是说,在一个直角三角形中,如果两条直角边的长度分别为a和b,那么斜边的长度c满足a^2 + b^2 ≤ c^2。
我们来看一下中点的定义和性质。
在直角三角形中,如果我们取一条直角边的中点作为中点,那么这个中点就是斜边的一半。
也就是说,在一个直角三角形中,如果两条直角边的长度分别为a和b,那么斜边的一半的长度d满足d = c/2。
现在我们已经知道了直角三角形、斜边和中点的定义和性质,下面我们来分析各种情况下,中点是否真的是斜边的一半。
我们来看一下当直角三角形是一个等腰直角三角形时。
直角三角形斜边上的中线性质练习
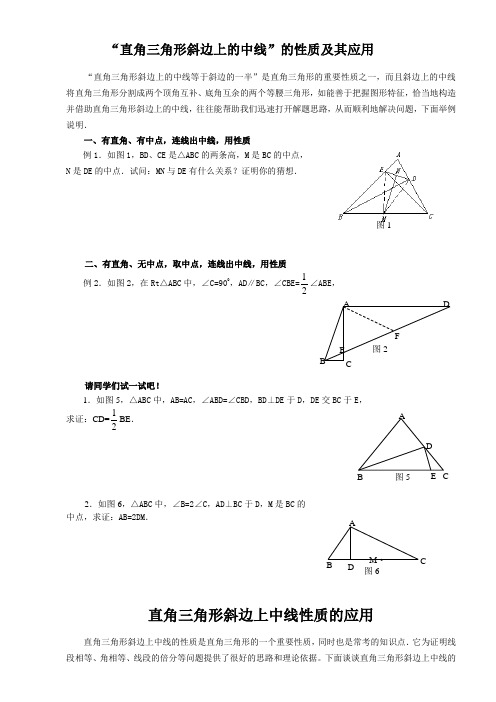
“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,连线出中线,用性质例1.如图1,BD 、CE 是△ABC 的两条高,M 是BC 的中点, N 是DE 的中点.试问:MN 与DE 有什么关系?证明你的猜想.二、有直角、无中点,取中点,连线出中线,用性质 例2.如图2,在Rt △ABC 中,∠C=900,AD ∥BC ,∠CBE=12∠ABE ,请同学们试一试吧!1.如图5,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E , 求证:CD=12BE .2.如图6,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的 中点,求证:AB=2DM .直角三角形斜边上中线性质的应用直角三角形斜边上中线的性质是直角三角形的一个重要性质,同时也是常考的知识点.它为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。
下面谈谈直角三角形斜边上中线的图1BADCEF图2B图5ACBD M · 图6性质及应用。
一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt △BAC 中,∠BAC=︒90,D 为BC 的中点,则BC 21AD =。
2、性质的拓展:如图1:因为D 为BC 中点,所以BC 21DC BD ==,所以AD=BD=DC=BC21,所以∠1=∠2,∠3=∠4, 因此∠ADB=2∠3=2∠4, ∠ADC=2∠1=2∠2。
因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍. 二、性质的应用 1、求值例1、(2004年江苏省苏州市中考)如图2,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、(2004年上海市中考)如图4,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点。
9.21 直角三角形斜边上的中线专项练习20202021学年八年级数学下册基础知识专项讲练苏科版

专题9.21 直角三角形斜边上的中线(专项练习)一、单选题1.(2021·盐城市初级中学九年级月考)如图,在Rt △ABC 中,∠BAC =90°,∠B =35°,AD 是斜边BC 上的中线,将△ACD 沿AD 对折,使点C 落在点F 处,线段DF 与AB 相交于点E ,则∠FAE 等于 ( )A .105°B .75°C .40°D .20°2.(2020·哈尔滨市第四十七中学八年级月考)如图,在Rt △ABC 中,∠BAC =90°,点D 在BC 上,过D 作DF ⊥BC 交BA 的延长线于F ,连接AD ,CF ,若∠CFE =32°,∠ADB =45°,则∠B 的大小是( )A .32°B .64°C .77°D .87°3.(2020·哈尔滨市第四十七中学八年级月考)如图,在Rt △ABC 中,∠B =90°,BC =12,AB =5,则斜边上的中线BO 长是( )A .2.5B .4C .6D .6.54.(2020·浙江杭州市·八年级期中)如图,公路,AC BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得 1.2km AC =, 1.6km BC =,则M ,C 两点间的距离为( )A .2.0kmB .1.2kmC .1.0kmD .0.5km5.(2020·浙江杭州市·学军中学附属文渊中学八年级期末)如图,在ABC V 中,AB AC =,90BAC Ð=°,直角EPF Ð的顶点P 是BC 的中点,两边PE ,PF 分别交AB ,AC 于点E ,F .现给出以下四个结论:①AE CF =;②EPF V 是等腰直角三角形;③EF AP =;④12ABC AEPF S S =四边形△.当EPF Ð在ABC V 内绕顶点P 旋转时(点E 不与点A ,B 重合),上述结论中始终正确的是( )A .①②③B .①②④C .②③④D .①③④6.(2021·上海浦东新区·七年级期末)下列命题中,真命题是( )A .在角平分线上的任意一点到这个角的两边的距离相等B .在三角形中,如果一条边等于另一条边的一半,那么这条边所对的角是30°C .直角三角形斜边上的中线等于直角边的一半D .到角的两边距离相等的点,在这个角的平分线上7.(2020·鞍山市第五十一中学九年级月考)如图,在Rt △ABC 中,∠ACB =90°,将△ABC 绕顶点C 逆时针旋转得到△A 'B 'C ,M 是BC 的中点,N 是A 'B '的中点,连接MN ,若BC =4,∠ABC =60°,则线段MN 的最大值为( )A .4B .8C .D .68.(2020·石家庄市第四十一中学八年级期中)如图,把菱形ABCD 向右平移至DCEF 的位置,作EG ⊥AB ,垂足为G ,EG 与CD 相交于点K ,GD 的延长线交EF 于点H ,连接DE ,则下列结论:①BG =AB +HF ;②DG =DE ;③∠DHE =12∠BAD ;④∠B =∠DEF ,其中正确结论的个数是( )A .1个B .2个C .3个D .4个9.(2021·武汉二中广雅中学九年级期末)如图,正方形ABCD 和正方形CEFG ,点G 在CD 上,AB =5,CE =2,T 为AF 的中点,则CT 的长是( )A .72B .4C D 二、填空题10.(2020·江苏扬州市·八年级月考)如图,Rt △ABC 中,∠ACB =90°,点D 为斜边AB 的中点,CD =6cm ,则AB 的长为_____cm .11.(2020·哈尔滨市第四十七中学八年级月考)在矩形ABCD 中,点E 、F 分别在AB 、AD 上,CD =9,CE =20,∠EFB =2∠AFE =2∠BCE ,则线段AF 的长为_____.12.(2019·云南玉溪市·八年级期中)如图,在四边形ABCD 中,∠BAD=∠ADC=90°,且AD ∥BC ;AC 的长为16,则DO 的长为___.13.(2021·河北廊坊市·八年级期末)如图,在ABC V 中,90C Ð=°,60B Ð=°,AD ,CE 都是ABC V 的中线,点M 是CE 的中点,若1CM =,则CD =______.14.(2018·苏州市吴江区青云中学八年级月考)在Rt ABC V 中,CD 是斜边A B 上的中线,若CD 的长为4,则AB 的长为_______.15.(2020·江苏苏州市·八年级月考)如图,在ABC V 中,90A Ð=°,AB AC =,O 是BC 的中点,如果在AB 和AC 上分别有一个动点M 、N 在移动,且在移动时保持AN BM =.若BC =.则MN 的最小值为_________.16.(2020·江苏苏州市·八年级月考)如图,在四边形ABCD 中,90ABC ADC Ð=Ð=°,点E 是AC 的中点.若45BAD Ð=°,2BD =,则AC =_________.17.(2020·武冈市第二中学八年级开学考试)如图,在Rt △ABC 中,CD 是斜边AB 上的中线,∠A =20°,则∠BCD =________.三、解答题18.(2020·广东惠州市·八年级期末)如图,在矩形ABCD 中,点O 为对角线AC 的中点,过点O 作EF AC ^交BC 于点E ,交AD 于点F ,连接AE ,CF .(1)求证:四边形AECF 是菱形;(2)连接OB ,若4AB =,5AF =,求OB 的长.19.(2019·云南玉溪市·八年级期中)如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,DH ⊥AB 于H ,连接OH ,∠DHO=20°,求∠CAD 的度数.20.(2021·陕西西安市·西北工业大学附属中学九年级一模)如图,在Rt △ABC 中,∠C =90°,请利用尺规在AB 边上求作一点D ,使得CD =12AB .(要求:不写作法,保留作图痕迹)21.(2018·苏州市吴江区青云中学八年级月考)如图(1),ABC V 中,CD 、BE 分别是高,M 、N 分别是线段BC 、DE 的中点.(1)求证:MN DE ^;(2)若A a Ð=,求DME Ð的度数(用含a 的式子表示).(3)如图(2),若将锐角ABC V 变为钝角ABC V ,直接写出DME Ð与BAC Ð的数量关系.22.(2019·苏州市吴江区青云中学八年级月考)如图,在四边形ABCD 中,90ABC ADC Ð=Ð=°,M 、N 分别是AC 、BD 的中点.(1)求证:BM DM =;(2)求证:MN BD ^.23.(2021·上海浦东新区·七年级期末)已知:如图,AD ⊥CD ,BC ⊥CD ,D 、C 分别为垂足,AB 的垂直平分线EF 交AB 于点E ,交CD 于点F ,BC =DF .求证:(1)∠DAF =∠CFB ;(2)EF =12AB .24.(2021·陕西九年级专题练习)如图,△ABC中,∠ACB=90°,AC=2,BC=1.点A、C分别在x轴和y轴的正半轴上,当点A在x轴上运动时,点C也随之在y轴上运动.在整个运动过程中,求点B到原点的最大距离.25.(2020·沙坪坝区·重庆南开中学八年级月考)如图,在四边形ABCD中,AD∥BC,BC=2AD,∠BAC=90°,点E为BC的中点.求证:四边形AECD是菱形.26.(2021·武汉二中广雅中学九年级期末)等腰Rt△ABC,CA=CB,D在AB上,CD=CE,CD⊥CE.(1)如图1,连接BE,探究线段AD与线段BE的关系并证明;(2)如图2,连接AE,CF⊥AE交AB于F,T为垂足,①求证:FD=FB;②如图3,若AE交BC于N,O为AB中点,连接OC,交AN于M,连FM、FN,当S△FMN=,则OF2+BF2的最小值为 .参考答案1.D【分析】根据三角形内角和定理求出∠C=90°-∠B=55°.由直角三角形斜边上的中线的性质得出AD=BD=CD,利用等腰三角形的性质求出∠BAD=∠B=35°,∠DAC=∠C=55°,再根据折叠的性质得出∠DAF=∠DAC=55°,然后计算∠FAE即可.【详解】解:解:∵在Rt△ABC中,∠BAC=90°,∠B=35°,∴∠C=90°-∠B=55°.∵AD是斜边BC上的中线,∴AD=BD=CD,∴∠BAD=∠B=35°,∠DAC=∠C=55°,∵将△ACD沿AD对折,使点C落在点F处,∴∠DAF=∠DAC=55°,∴∠FAE=∠DAF-∠BAD=20°.故选:D【点拨】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了直角三角形斜边上的中线的性质、等腰三角形的性质、三角形内角和定理.2.C【分析】取CF的中点T,连接DT,AT.证明∠TDA=∠TAD,∠TDC=∠TCD,进而证明CT=TF,得到∠AFC=45°,∠BFD=13°,最后求出∠B=77°.【详解】解:如图,取CF的中点T,连接DT,AT.∵∠BAC=90°,FD⊥BC,∴∠CAF=∠CDF=90°,∴AT=DT=12 CF,∴TD =TC =TA ,∴∠TDA =∠TAD ,∠TDC =∠TCD ,∵∠ADB =45°,∴∠ADT +∠TDC =135°,∴∠ATC =360°﹣2×135°=90°,∴AT ⊥CF ,∵CT =TF ,∴AC =AF ,∴∠AFC =45°,∴∠BFD =45°﹣32°=13°,∵∠BDF =90°,∴∠B =90°﹣∠BFD =77°.故选:C【点拨】本题考查了直角三角形斜边上的直线等于斜边一半、等腰三角形的性质、三角形的角的计算等知识,根据题意添加辅助线,构造等腰三角形是解题关键.3.D【分析】先利用勾股定理求解AC 的长,再利用直角三角形斜边上的中线等于斜边的一半,从而可得答案.【详解】解:∵在Rt △ABC 中,∠B =90°,BC =12,AB =5,∴13,AC ===∴斜边上的中线BO =12AC =6.5.故选:D .【点拨】本题考查的是直角三角形斜边上的中线等于斜边的一半,掌握直角三角形斜边上的中线的性质是解题的关键.4.C【分析】首先根据勾股定理求得AB 的长度,然后利用直角三角形斜边上的中线等于斜边一半的性质即可求解.【详解】解:如图,在直角△ABC 中,∠ACB =90°,AC =1.2km ,BC =1.6km ,由勾股定理得到:AB (km ).∵点M 是AB 的中点,∴MC =12AB =1km .故选:C .【点拨】本题主要考查了勾股定理的应用,直角三角形斜边上的中线的性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.5.B【分析】根据等腰直角三角形的性质得出∠B =∠C =∠BAP =∠CAP =45°,AP =PC =PB ,∠APC =∠EPF =90°,求出∠APE =∠CPF ,证△APE ≌△CPF ,推出AE =CF ,EP =PF ,推出S APE =S △CPF ,求出S 四边形AEPF =S △APC =12S △ABC ,EF 不是△ABC 的中位线,故EF ≠AP ,即可得出答案.【详解】解:∵△ABC 中,AB =AC ,∠BAC =90°,P 是BC 中点,∴∠B =∠C =∠BAP =∠CAP =45°,AP =PC =PB ,∠APC =∠EPF =90°,∴∠EPF -∠APF =∠APC -∠APF ,∴∠APE =∠CPF ,在△APE 和△CPF 中45EAP C AP APAPE CPF ÐаìïíïÐÐî====,∴△APE ≌△CPF (ASA ),∴AE =CF ,EP =PF ,∴△EPF 是等腰直角三角形,∴①正确;②正确;∵△ABC 是等腰直角三角形,P 是BC 的中点,∴AP =12BC ,∵EF 不是△ABC 的中位线,∴EF ≠AP ,故③错误;∵△APE ≌△CPF∴S APE =S △CPF ,∴S 四边形AEPF =S △AEP +S △APF =S △CPF +S △APF =S △APC =12S △ABC ,∴④正确;∴正确的有①②④,故选:B .【点拨】本题考查了等腰三角形性质,直角三角形斜边上中线性质,三角形三边关系定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.6.A【分析】根据直角三角形的性质、角平分线的性质进行判断即可.【详解】解:A 、在角平分线上的任意一点到这个角的两边的距离相等,是真命题;B 、在直角三角形中,如果一条直角边等于斜边的一半,那么这条边所对的角是30°,原命题是假命题;C 、直角三角形斜边上的中线等于斜边的一半,原命题是假命题;D 、在角的内部,到角的两边距离相等的点,在这个角的平分线上,原命题是假命题;故选:A.【点拨】本题考查的是命题的真假判断,角平分线的性质,直角三角形的性质,熟悉相关的性质定理是解题的关键.7.D【分析】连接CN,根据直角三角形斜边中线的性质求出CN=12A′B′=4,利用三角形的三边关系即可得出结果.【详解】连接CN,如图所示:在Rt△ABC中,∠ACB=90°,BC=4,∠B=60°,∴∠A=30°,∴AB=A′B′=2BC=8,∵NB′=NA′,∴CN=12A′B′=4,∵CM=BM=2,∴MN≤CN+CM=6,∴MN的最大值为6,故选:D.【点拨】本题考查旋转的性质、含30°角直角三角形的性质、直角三角形斜边中线的性质、三角形的三边关系等知识;解题的关键是灵活运用三角形的三边关系.8.C【分析】首先证明△ADG≌△FDH,再利用菱形的性质、直角三角形斜边中线的性质即可一一判断.【详解】解:∵菱形ABCD向右平移至DCEF的位置,∴AB∥CD∥EF,AD=CD=DF,∴∠GAD=∠F,∵∠ADG=∠FDH,∴△ADG≌△FDH,∴DG=DH,AG=FH,∴BG =AB+AG=AB+HF,故①正确,∵EG⊥AB,∴∠BGE=∠GEF=90°,又∵DG=DH,∴DE=DG=DH,故②正确,∴∠DHE=∠DEH,∵∠DEH=12∠CEF,∠CEF=∠CDF=∠BAD,∴∠DHE=12∠BAD,故③正确,∵∠B=∠DCE,∠CED=∠CDE=∠DEF=∠DHE,∴∠DCE=∠EDH,∴∠B=∠EDH,若∠B=∠DEF,则∠EDH=∠DEF=∠DHE,那么∆ DHE是等边三角形,但题目中没有明确∆ DHE是等边三角形,故④错误.故选:C.【点拨】本题考查菱形的性质、平移变换、全等三角形的判定和性质、直角三角形斜边中线的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.D【分析】据正方形的性质得到AB=BC=5,CG=CE=2,连接AC 、CF ,求出∠ACF =90°,得到CT=12AF ,根据勾股定理求出AF 的长度即可得到答案.【详解】解:连接AC 、CF ,如图,∵四边形ABCD 和四边形CEFG 都是正方形,AB=BC=5,CG=CE=2,∴AC AB = ,CF CE = ,∠ACD =45°,∠GCF =45°,∴∠ACF =45°+45°=90°,在Rt △ACF 中,AF =,∵T 为AF 的中点,∴CT =12 AF .故选:D .【点拨】此题考查了正方形的性质,勾股定理,直角三角形斜边上的中线等于斜边一半的性质,正确引出辅助线得到∠ACF =90°是解题的关键.10.12【分析】根据直角三角形斜边上的中线等于斜边的一半解答即可.【详解】∵在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,∴线段CD 是斜边AB 上的中线;又∵CD =6cm ,∴AB =2CD =12cm .故答案为:12【点拨】本题考查直角三角形斜边上的中线的性质.掌握直角三角形斜边上的中线等于斜边的一半是解答本题的关键.11【分析】设BF与CE的交点为G,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠BCE=2a,由矩形的性质及直角三角形的斜边中线性质得出BH=CH=EH=10,∠HBC=∠HCB=a,再判定EF∥BH、△EFG和△BGH均为等腰三角形,最后由勾股定理求得AF即可.【详解】解:设BF与CE的交点为G,取CE的中点H,连接BH,如图所示:设∠EFB=2∠AFE=2∠BCE=2α,则∠AFB=3α,在矩形ABCD中有AD∥BC,∠A=∠ABC=90°,∴△BCE为直角三角形,∵点H为斜边CE的中点,CE=20,∴BH=CH=EH=10,∴∠HBC=∠HCB=α,∵AD∥BC,∴∠AFB=∠FBC=3α,∴∠GHB=3α﹣α=2α=∠EFB,∴EF∥BH,∴∠FEG=∠GHB=∠HBC+∠HCB=2α=∠EFB=∠GBH,∴△EFG和△BGH均为等腰三角形,∴BF=EH=10,在矩形ABCD中,AB=CD=9,由勾股定理得:AF,【点拨】本题考查了矩形的性质、直角三角形的斜边中线性质、等腰三角形的判定与性质及勾股定理等知识点,数形结合并熟练掌握相关性质及定理是解题的关键.12.8【分析】由题意可以得到四边形ABCD为矩形,再根据矩形和直角三角形的性质求解.【详解】解:∵∠BAD=∠ADC=90°,∴∠BAD+∠ADC=180°,∴AB∥DC,∵AD∥BC,∴四边形ABCD为矩形,∴O为AC中点,∵∠ADC=90°,∴OD=182AC=,故答案为8.【点拨】本题考查矩形与直角三角形的综合应用,熟练掌握矩形的判定与性质、直角三角形的性质是解题关键.13.1【分析】证明△BCE是等边三角形,求出BE=CE=BC=2,由D是BC的中点可得结论.解:在ABC V 中,90C Ð=°,∵CE 是ABC V 的中线,∴12==CE BE AB ∵60B Ð=°,∴BCE D 是等边三角形∴BC CE =∵点M 是CE 的中点,且1CM =,∴22CE CM BC ===∵AD 是BC 边上的中线,∴112122CD BC ==´= 故答案为:1.【点拨】此题主要考查了等边三角形的判定和三角形中线的性质,证明BCE D 是等边三角形是解答此题的关键.14.8.【分析】根据斜边中线等于斜边的一半,直接计算即可.【详解】解:在Rt ABC V 中,CD 是斜边A B 上的中线, CD 的长为4,AB =2CD =8;故答案为:8.【点拨】本题考查了直角三角形中,斜边上的中线等于斜边一半的性质,解题关键是熟记本知识点,准确应用.15.【分析】连接OA ,取MN 的中点D ,连接OD ,AD ,证明△OAN ≌△OBM ,可得MN =OD +AD ,而OD +AD ≥OA ,即OA 就是MN 的最小值.解:连接OA ,取MN 的中点D ,连接OD ,AD ,∵在△ABC 中,∠A =90°,AB =AC ,O 是BC 的中点,∴AO =BO =CO ,∠B =∠C =45°;在△OAN 和OBM 中,AO BO NAO B AN BM =ìïÐ=Ðíï=î,∴△OAN ≌△OBM (SAS ),∴ON =OM ,∠AON =∠BOM ;又∵∠BOM +∠AOM =90°,∴∠NOM =∠AON +∠AOM =90°,∴△OMN 是等腰直角三角形,∴∠MON =∠NAM =90°,∴OD =AD =12MN ,∴MN =OD +AD ,∵OD +AD ≥AO ,∴MN ≥AO ,∴MN 的最小值为AO ,∵BC=,∴AO=∴MN的最小值为故答案为:本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质、直角三角形斜边中线定理、三角形三边关系等知识点,难度适中.“中点”是本题的题眼,在初中阶段,与“中点”的几何知识并不多,同学们可自行总结一下“中点”有几种用法,今后再遇到与“中点”有关的几何题目,就会反应迅速,作出辅助线也就很容易.16.【分析】根据中点的性质、直角三角形的性质求出DE=BE,从而可得AC.【详解】解:∵∠ABC=∠ADC=90°,E是对角线AC的中点,∴BE=DE=AE=EC=12 AC,∴∠ABE=∠BAE,∠ADE=∠DAE,∵∠BEC=∠ABE+∠BAE,∠DEC=∠ADE+∠DAE,∠BED=∠BEC+∠DEC,∠BAE+∠DAE=∠BAD=45°,∴∠BED=2∠BAE+2∠DAE=2∠BAD,∵∠BAD=45°,∴∠BED=90°,∵BD=2,∴BE=DE,∴AC=2BE=,故答案为:【点拨】此题考查了直角三角形的性质,等腰直角三角形的判定和性质,勾股定理,关键是根据中点的性质、直角三角形的性质得出BE=DE=AE=EC=12 AC.17.70°【分析】根据直角三角形两锐角互余求得∠B=70°,然后根据直角三角形斜边上中线定理得出CD =BD ,求出∠BCD =∠B 即可.【详解】解:在Rt △ABC 中,∵∠A =20°,∴∠B =90°-∠A =70°,∵CD 是斜边AB 上的中线,∴BD =CD ,∴∠BCD =∠B =70°,故答案为70°.【点拨】本题考查了直角三角形斜边上的中线性质,等腰三角形性质等知识点的理解和运用,能求出BD =CD =AD 和∠B 的度数是解此题的关键.18.(1)证明见解析,(2)【分析】(1)根据线段垂直平分线的性质,可得AF =CF ,AE =CE ,OA =OC ,然后由四边形ABCD 是矩形,易证得△AOF ≌△COE ,则可得AF =CE ,继而证得结论;(2)连接BO ,由勾股定理可求BE ,AC 的长,由直角三角形的性质可求解.【详解】证明:(1)∵O 是AC 的中点,且EF ⊥AC ,∴AF =CF ,AE =CE ,OA =OC ,∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AFO =∠CEO ,在△AOF 和△COE 中,AFO CEO AOF COE OA OC Ð=ÐìïÐ=Ðíï=î,∴△AOF ≌△COE (AAS ),∴AF =CE ,∴AF =CF =CE =AE ,∴四边形AECF 是菱形;(2)如图,连接BO ,∵AB =4,AF =AE =EC =5,∴BE 3==,∴BC =8,∴AC ==,∵AO =CO ,∠ABC =90°,∴BO =12AC =.【点拨】本题考查了矩形的性质,全等三角形的判定和性质,菱形的判定,证得△AOF ≌△COE 是关键.19.∠CAD=20°【分析】由四边形ABCD 是菱形,可得OB=OD ,AC ⊥BD ,又由DH ⊥AB ,∠DHO=20°,可求得∠OHB的度数,然后由直角三角形斜边上的中线等于斜边的一半,证得△OBH 是等腰三角形,继而求得∠ABD 的度数,然后求得∠CAD 的度数.【详解】解:∵四边形ABCD 是菱形,∴OB=OD ,AC ⊥BD ,∵DH ⊥AB ,∴OH=OB=12BD ,∵∠DHO=20°,∴∠OHB=90°-∠DHO=70°,∴∠ABD=∠OHB=70°,∴∠CAD=∠CAB=90°-∠ABD=20°.本题考查了菱形的性质、直角三角形的性质以及等腰三角形的判定与性质.注意证得△OBH 是等腰三角形是关键.20.见详解【分析】作线段AB的垂直平分线EF交AB于D,连接CD,线段CD即为所求作.【详解】解:如图,线段CD即为所求作.【点拨】本题考查作图——复杂作图,直角三角形斜边的中线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.21.(1)证明见解析;(2)∠DME=180°-2α;(3)∠DME=2∠BAC-180°.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可知DM=ME,再根据N为DE的中点,利用垂直平分线的判定定理即可证明;(2)根据三角形内角和定理和等腰三角形两底角相等可得∠ABC+∠ACB=180°-∠A和∠BMD+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解;(3)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,再根据等腰三角形两底角相等和三角形的一个外角等于与它不相邻的两个内角的和表示出∠BME+∠CMD,然后根据平角等于180°表示出∠DME,整理即可得解.【详解】解:(1)如图(1)∵CD、BE分别是AB、AC边上的高,M是BC的中点,∴11,22DM BC ME BC==,∴DM=ME又∵N为DE中点,∴MN ⊥DE ;(2)在△ABC 中,∠ABC +∠ACB =180°-∠A ,∵CD 、BE 分别是AB 、AC 边上的高,M 是BC 的中点,∴DM =ME =BM =MC ,∴∠ABC =∠BDM ,∠ACB =∠MEC ,∴∠BMD +∠CME =(180°-2∠ABC )+(180°-2∠ACB ),=360°-2(∠ABC +∠ACB ),=360°-2(180°-∠A ),=2∠A ,∴∠DME =180°-2∠A =180°-2α;(3)∠DME =2∠BAC -180°,理由如下:在△ABC 中,∠ABC +∠ACB =180°-∠BAC ,由(2)得DM =ME =BM =MC ,∴∠ABC =∠BDM ,∠ACB =∠MEC ,∴∠BME +∠CMD =2∠ACB +2∠ABC =2(180°-∠BAC )=360°-2∠BAC ,∴∠DME =180°-(360°-2∠BAC )=2∠BAC -180°.【点拨】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,三角形的内角和定理,整体思想的利用是解题的关键.22.(1)见解析;(2)见解析.【分析】(1)连接BM 、DM ,根据直角三角形斜边上的中线等于斜边的一半可得12BM DM AC ==,即可证得结论;(2)根据等腰三角形三线合一的性质证明即可.【详解】证明:(1)如图,连接BM 、DM ,∵90ABC ADC Ð=Ð=°,M 是AC 的中点,∴12BM AC =,12DM AC =,∴BM DM =;(2)∵BM DM =,点N 是BD 的中点,∴MN BD ^.【点拨】本题考查了直角三角形与等腰三角形的性质,熟记性质并作出相应的辅助线是解题的关键.23.(1)见解析;(2)见解析.【分析】(1)由垂直平分线的性质得出AF =BF ,证明△ADF ≌△FCB 就可以得出∠DAF =∠CFB ;(2)根据∠DAF+DFA =90°可以得出∠AFB =90°,就可以得出△AFB 是等腰直角三角形,由AE =BE 就可以得出EF =12AB .【详解】解:(1)EF 垂直平分AB ,∴AF =BF ,AE =BE ,∵AD ⊥CD ,BC ⊥CD ,∴∠D =∠C =90°,在Rt △ADF 和Rt △FCB 中AF FB DF CB =ìí=î,∴△ADF ≌△FCB (HL ),∴∠DAF =∠CFB ;(2)∵∠D =90°,∴∠DAF+∠DFA =90°,∴∠CFB+∠DFA =90°,∴∠AFB =90°,∴△AFB 是等腰直角三角形,∵AE =BE ,∴EF =12AB .【点拨】本题考查了直角三角形的性质的运用,垂直平分线的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.241【分析】取AC 的中点D ,连接BD 、OD ,可知第三边OB 的最大值就是另两边的和.【详解】解:如图7-2,取AC 的中点D ,∵∠ACB =90°,AC =2,BC =1,∴OD =12AC =1,BD =在△OBD 中,总是有OB <OD +BD .如图7-3,当点D 落在OB 上时,OB 1.【点拨】本题考查了最短路径问题和斜边中线的性质,解题关键是恰当的作辅助线,构造三角形,利用三边关系解决问题.25.见解析【分析】由BC =2AD ,E 为BC 的中点,则12EC BC AD ==,再由//AD BC 即知四边形AECD 是平行四边形;又90BAC Ð=°,由直角三角形斜边上的中线的性质,得AE=EC ,从而四边形AECD 是菱形.【详解】∵E 为BC 的中点,90BAC Ð=°∴AE 为Rt ABC V 的斜边BC 上的中线∴AE=EC=BE =12BC ∵BC =2AD ∴12AD BC = ∴EC AD=∵//AD BC∴四边形AECD 是平行四边形∵AE=EC∴四边形AECD 是菱形【点拨】本题考查了菱形的判定、直角三角形斜边上中线的性质.本题也可以用菱形的定义来证明,为此只要证AEC ADC @V V 即可.26.(1)AD ⊥BE ,AD =BE ,证明见解析;(2)①证明见解析,②【分析】(1)利用SAS 证明△ACD ≌△BCE ,从而利用全等三角形的性质即可得出结论;(2)①过点D 作DH ⊥CF 于H ,过点B 作BG ⊥CF ,交CF 的延长线于G ,首先证明△ACT ≌△BCG 及△DCH ≌△ECT ,得到CT =BG ,CT =DH ,通过等量代换得出DH =BG ,再证明△DHF ≌△BGF ,则可证明结论;②首先利用等腰三角形的性质和ASA 证明△AOM ≌△COF ,则有OM =OF ,然后利用等腰直角三角形的性质得出FKBF ,然后利用三角形的面积得出OF×BF =,最后利用平方的非负性和完全平方公式求解即可.【详解】证明:(1)AD ⊥BE ,AD =BE ,理由如下:∵CD ⊥CE ,∴∠ACB =∠DCE =90°,∴∠ACD =∠BCE ,在△ACD 和△BCE 中,AC BC ACD BCE CD CE =ìïÐ=Ðíï=î,∴△ACD ≌△BCE (SAS ),∴∠A =∠CBE =45°,AD =BE ,∴∠CBE +∠ABC =90°=∠ABE ,∴AD ⊥BE ;(2)①如图2,过点D 作DH ⊥CF 于H ,过点B 作BG ⊥CF ,交CF 的延长线于G ,∵CF ⊥AE ,∴∠ACT +∠CAT =90°,又∵∠ACT +∠BCG =90°,∴∠CAT =∠BCG ,在△ACT 和△BCG中,90AC BC ATC BGC °ï=íïÐ=Ð=î,∴△ACT ≌△BCG (ASA ),∴CT =BG ,同理可证△DCH ≌△ECT ,∴CT =DH ,∴DH =BG ,在△DHF 和△BGF 中,DFH BFG DHF BGF DH BG Ð=ÐìïÐ=Ðíï=î,∴△DHF ≌△BGF (AAS ),∴DF =BF ;②如图3,过点F 作FK ⊥BC 于K ,∵等腰Rt △ABC ,CA =CB ,点O 是AB 的中点,∴AO =CO =BO ,CO ⊥AB ,∠ABC =45°,∴∠OCF +∠OFC =90°,∵AT ⊥CF ,∴∠OFC +∠FAT =90°,∴∠FAT =∠OCF ,在△AOM 和△COF中,90OA OCAOM COF ï=íïÐ=Ð=°î,∴△AOM ≌△COF (ASA ),∴OM =OF ,又∵CO ⊥AO ,∴MFOF ,∠OFM =∠OMF =45°,∴∠OFM =∠ABC ,∴MF //BC ,∵∠ABC =45°,FK ⊥BC ,∴∠ABC =∠BFK =45°,∴FK =BK ,∴FKBF ,∵S △FMN =,∴12×MF ×FK =,OFBF =,∴OF ×BF =,∵(BF ﹣OF )2≥0,∴BF 2+OF 2﹣2BF ×OF ≥0,∴BF 2+OF 2=,∴BF 2+OF 2的最小值为,故答案为:.【点拨】本题主要考查全等三角形的判定及性质,掌握等腰三角形的性质和全等三角形的判定方法及性质是解题的关键.。
矩形--直角三角形斜边上的中线等于斜边的一半

18.2.1(2.1)矩形--直角三角形斜边上的中线等于斜边的一半一.【知识要点】1.直角三角形的性质:直角三角形斜边上的中线等于斜边的一半。
二.【经典例题】1.如图,平行四边形ABCD 的周长是26cm ,对角线AC 与BD 交于点O ,AC ⊥AB ,E 是BC 中点,△AOD 的周长比△AOB 的周长多3cm ,求AE 的长.2. 如图,在△ABE 中,AE ⊥BE,AE=BE,AD ⊥BC 于D,BC 平分∠ABE. (1)求证:BC=2AD; (2)求∠ADE 的度数.3.如图,在△ABC 中,BD ⊥AC 于点D ,CE ⊥AB 于点E ,点M,N 分别是BC,DE 的中点, (1)求证:MN ⊥DE; (2)若∠A=60°,求MNDE的值.4.如图,在△ABC 中,AB=BC ,∠ABC=90°,点E ,F 分别在AB ,AC 上,且AE=EF ,点O ,M分别为 AF ,CE 的中点.求证:(1)12OM CE =;(2)OB =5.如图,△CDE中,∠CDE=135°,CB⊥DE于点B,EA⊥CD于点A,求证:CE .6.如图,∠ACB=∠ADB=90°,AD与BC交于点M,∠AMB=105°,点O为AB的中点连CO,OD,求∠COD的度数.7.如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.三.【题库】 【A 】【B 】1. 如图 ,在ABC Rt ∆,︒=∠90ACB ,D 、E 、 F 分别是AB 、BC 、CA 的中点,若CD=5,则EF=__________2.如图,在∆ABC 中,∠C=90°,AC=BC,D 点为AB 的中点,PE ⊥AC 于点E ,PF ⊥BC 于点F ,连接DE ,DF ,求证:DE=DF (10分)【C 】1.(本小题共8分)如图,在四边形ABCD 中,∠ABC=∠ADC=90°,M 、N 分别是AC 、BD 的中点 (1)求证:MN ⊥BD.(2)若AC=10 ,BD=8.求MN 的长.2.如图,在RtΔABC中,∠ACB=900,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,①CF=DE吗?请说明理由.②若AC=6cm,AB=10cm,求四边形DCFE的面积.3. 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为.4.如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于点A,∠BAC=120°,求证:DE=OE.【D】1. 如图,平行四边形ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.(1)若AE平分∠BAF,求证:BE=GE;(2)若点E是BC边上的中点,求证:∠AEF=2∠EFC.2.如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )①2∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.A. ①②③④B. ①②④C. ①②D. ②③3.(16分)已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系式;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.。
动点问题,直角三角形斜边上的中线等于斜边的一半

《直角三角形斜边上的中线等于斜边的一半》的专题训练1、如图,在锐角三角形ABC 中,AD ⊥BC 于D,E 、F 、G 分别是AC 、AB 、BC 的中点。
求证:(1)E F ‖BC ;(2)FG=DE 。
FEG D CBA2、如图所示,BD 、CE 是三角形ABC 的两条高,M 、N 分别是BC 、DE 的中点 求证:MN ⊥DENME DCBA3、如图,在四边形ABCD 中,BD ⊥CD,AC ⊥AB,E 为BC 的中点,∠EDA=60°,求证:AD=DE4.如图,在△ABC 中,AD ⊥CB 、BE ⊥AC ,且相交于O 点,N 、M 是 CO 、AB 的中点,连接MN 、ED ,求证:MN 是ED 的中垂线5、已知在四边形ABCD 中AD ‖B C ,∠B+∠C =90o ,EF 是两底中点的连线,试说明BC -AD=2EFFEDCBA6、如图,四边形ABCD 中,∠DAB=∠DCB=90o ,点M 、N 分别是BD 、AC 的中点。
MN 、AC的位置关系如何?证明你的猜想。
NMCB7、过矩形ABCD 对对角线AC 的中点O 作EF ⊥AC 分别交AB 、DC 于E 、F ,点G 为AE 的中点,若∠AOG =30o 求证:3OG=DCGODA8、如图所示;过矩形ABCD 的顶点A 作一直线,交BC 的延长线于点E ,F 是AE 的中点,连接FC 、FD 。
求证:∠FDA=∠FCBFDA动点问题专题训练1、已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作AB 边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒. (1)、线段MN 在运动的过程中,t 为何值时,四边形MNQP 恰为矩形?并求出该矩形的面积;(2)线段MN 在运动的过程中,四边形MNQP 的面积为S ,运动的时间为t .求四边形MNQP 的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围.2、如图,在四边形ABCD中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.(1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △为等腰三角形.6、如图1,在平面直角坐标系中,已知点(0A ,点B 在x 正半轴上,且30ABO =∠.动点P 在线段AB 上从点A 向点B个单位的速度运动,设运动时间为t 秒.在x 轴上取两点M N ,作等边PMN △. (1)求直线AB 的解析式;(2)求等边PMN △的边长(用t 的代数式表示),并求出当等边PMN △的顶点M 运动到与原点O 重合时t 的值;(3)如果取OB 的中点D ,以OD 为边在Rt AOB △内部作如图2所示的矩形ODCE ,点C 在线段AB 上.设等边PMN △和矩形ODCE 重叠部分的面积为S ,请求出当02t ≤≤秒时S 与t 的函数关系式,并求出S 的最大值.10、已知:如图,△ABC 是边长3cm 的等边三角形,动点 P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 方向匀速移 动,它们的速度都是1cm/s ,当点P 到达点B 时,P 、Q 两 点停止运动.设点P 的运动时间为t (s ),解答下列问题:(1)当t 为何值时,△PBQ 是直角三角形?(2)设四边形APQC 的面积为y (cm 2),求y 与t 的关系式;是否存在某一时刻t ,使四边形APQC 的面积是△ABC 面积的三分之二?如果存在,求出相应的t 值;不存在,说明理由;CPQ B A MNC(图1) (图2)。
直角三角形斜边上的中线等于斜边的一半----经常练(1)

直角三角形斜边上的中线等于斜边的一半----经常练(1)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(直角三角形斜边上的中线等于斜边的一半----经常练(1))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为直角三角形斜边上的中线等于斜边的一半----经常练(1)的全部内容。
1.如图,△ABC中,AB=AC,AD是角平分线,E为AC的中点.(1)若DE=5cm,则AB= cm;(2)若∠CDE=70º,则∠B=2.如图,∠BAC=∠BDC=90º,E为BC的中点,AE=5cm,则BC= cm,DE=cm.3。
如图,Rt△ABC中,CD是斜边AB上的中线,CE⊥AB,垂足为E,CE=5cm,CD=6cm,则AB=cm,△ABC的面积为4.如图,在四边形ABCD中,∠ABC=∠ADC=90º,M、N分别是AC、BD的中点,证明:(1)MD=MB;(2)MN⊥BD.1.如图,在△ABC中,BE和CF是高,M为BC中点,连接ME和MF,EF=5cm,BC=12cm,则△EFM的周长为 cm.2。
如图,△ABC中,BD,CE是高,G、F分别是线段BC,DE的中点,连接FG.求证:FG⊥ED.3.如图,在梯形ABCD中,AD∥BC,∠BAC=90º,AB=AC,AD=2,BC=8,求梯形ABCD的面积.4。
证明:直角三角形斜边上的中线等于斜边的一半。
1。
如图,在△ABC中,AB=AC ,BD平分∠ABC,BD与AC交于点D,DE⊥BD,DE与BC交于点E,DC=5cm,那么BE= cm.2。
如图,AE、BD相交于点C,AC=AD,BC=BE,M、N、P分别是DC、CE、AB的中点,AB=10 cm,那么PM= cm,PN= cm.3。
专题13 斜边上的中线问题(解析版)-2021年中考数学二轮复习经典问题专题训练

专题13 斜边上的中线问题【规律总结】直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”【典例分析】例1.(2021·上海九年级专题练习)一副三角板如图摆放,点F 是45角三角板ABC 的斜边的中点,4AC .当30角三角DEF 的直角顶点绕着点F 旋转时,直角边DF EF ,分别与,AC BC 相交于点.M N ,则CMFN 的面积为____________.【答案】4【分析】连结CF ,证明CFM BFN =,根据12BFC ACB CMFN S SS ==四边形即可求解. 【详解】解:连结CF ,如图,点F 是45角三角板ABC 的斜边的中点,CF BF CF ∴=,平分,,45ACB CF AB B ∠⊥∠=︒,45,2345ACF ∴∠=︒∠+∠=︒1290∠+∠=︒,13∴∠=∠,在CFM △和BFN 中,13MCF B CF BF∠=∠⎧⎪=⎨⎪∠=∠⎩()CFM BFN ASA ∴=,CFM BFNS S ∴=,111444222BFC ACB CMFN S SS ∴===⨯⨯⨯=四边形. 【点睛】 此题考查的知识点有等腰直角三角形,全等三角形的判定与性质等知识点,综合性强,难度较大,是一道难题.例2.(2020·湖北恩施土家族苗族自治州·九年级期中)如图,在等腰直角三角形ABC 中,90C ∠=︒,AC a =,点E 为边AC 上任意一点,点D 为AB 的中点,过点D 作DF DE ⊥交BC 于点F .求证:CE CF +为定值.【答案】证明见解析【分析】连接CD ,证明△CDE△△BDF ,得CE=BF ,进一步证明CE+CF=BC=AC a =,从而得到结论.【详解】 证明:连接CD ,如图,△△ABC 是等腰直角三角形,且D 为AB 的中点,△CD△AB ,CD 平分△ACB ,AD=BD=CD△△DCA=△DCB=△DBC=45°又DE△DF△△EDC+△FDC=90°而△FDC+△FDB=90°△△EDC=△FDB在△CDE 和△BDF 中,DCE DBF CD CDEDC BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩△△CDE△△BDF△CE=BF△BC=AC=a△CE+CF=BE+CF=BC=AC=a ,故:CE CF +为定值.【点睛】此题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,证明CE=BF 是解答此题的关键.【真题演练】一、填空题1.(2020·哈尔滨市萧红中学八年级月考)如图,在ABC 中,∠B=60°,CD 为AB 边上的高,E 为AC 边的中点,点 F 在BC 边上,∠EDF=60°,若 BF=3,CF=5,则AC 边的长为 .【答案】【分析】如图(见解析),先根据直角三角形的性质、勾股定理得出,4D B F D ==,再根据等边三角形的判定与性质得出4,60DH BDH =∠=︒,然后根据三角形的中位线定理、平行线的性质得出60EHD BDH ∠=∠=︒,从而可得EHD B ∠=∠,BDF HDE ∠=∠,最后根据三角形全等的判定定理与性质得出DE DF ==据此根据直角三角形斜边上的中线等于斜边的一半即可得.【详解】如图,过点D 作DG BC ⊥于点G3,5BF CF ==8BC BF CF ∴=+=在Rt BCD 中,60B ∠=︒,9030BCD B ∠=︒-∠=︒142BD BC ∴== 在Rt BDG 中,60B ∠=︒,9030BDG B ∠=︒-∠=︒12,2BG BD DG ∴====1GF BF BG ∴=-=,DF =取BC 的中点H ,连接DH 、EH142DH BH BC BD ∴==== BDH ∴是等边三角形60BDH ∴∠=︒点E 是AC 边的中点∴EH 是ABC 的中位线//EH AB ∴60EHD BDH ∴∠=∠=︒60EHD B ∴∠=∠=︒又60BDF FDH BDH ∠+∠=∠=︒,60HDE FDH EDF ∠+∠=∠=︒BDF HDE ∴∠=∠在HDE 和BDF 中,EHD B DH DBHDE BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩()HDE BDF ASA ∴≅DE DF ∴==则在Rt ACD △中,12DE AC =,即2AC DE ==故答案为:【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质、三角形的中位线定理等知识点,通过作辅助线,构造等边三角形和全等三角形是解题关键.二、解答题2.(2020·庆云县第二中学八年级期中)已知:在ABC 中,AC=BC ,∠ACB=90°,点D 是AB 的中点,点E 是AB 边上一点.(1)直线BF 垂直于CE 于点F ,交CD 于点G (如图1),求证:AE=CG ;(2)直线AH 垂直于CE ,垂足为H ,交CD 的延长线于点M (如图2),求证:BCE CAM ≌.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)运用等腰直角三角形性质,三线合一,可以得到△AEC 和△CGB 一组对应边、一组对应角相等,AC BC =,CAE BCG ∠=∠;然后利用同角的余角相等,证得ACE CBG ∠=∠;两角及其夹边对应相等()ASA 则两三角形全等.(2)运用等腰直角三角形性质,三线合一,可以得到△BCE 和△CAM 一组对应边、一组对应角相等,AC BC =,ACM CBE ∠=∠;然后利用同角的余角相等,证得BEC CMA ∠=∠;两角及其中一角的对边对应相等()AAS 则两三角形全等.【详解】(1)证明:△点D 是AB 中点,AC=BC ,△ACB=90°,△CD△AB ,△ACD=△BCD=45°,△△CAD=△CBD=45°,△△CAE=△BCG ,又△BF△CE ,△△CBG+△BCF=90°,又△△ACE+△BCF=90°,△△ACE=△CBG ,在△AEC 和△CGB 中,CAE BCG AC BCACE CBG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△AEC△△CGB (ASA ),△AE=CG ,(2)证明:△CH△HM ,CD△ED ,△△CMA+△MCH=90°,△BEC+△MCH=90°,△△CMA=△BEC ,又△△ACM=△CBE=45°,在△BCE 和△CAM 中,BEC CMA ACM CBE BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△BCE△△CAM (AAS ).【点睛】本题考查全等三角形判定定理,从题中找到对应边、角的信息,灵活运用三角形判定定理是解题关键.3.(2020·张家港市梁丰初级中学八年级期中)已知,∠ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是线段CA上任意一点,DF∠DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.(1)试说明:①AE=CF;②CG=GD;(2)若AE=6,CH=10,求边AC的长.【答案】(1)理由见详解;(2)AC=14【分析】(1)①由题意易得AD=DC=DB,△A=△B=45°,CD△AB,进而可证△ADE△△CDF,然后根据全等三角形的性质可得;②由直角三角形斜边中线定理可得11,22CG EF DG EF==,进而问题得证;(2)由(1)可得AE=CF=6,由题意易得12DG CH=,则有EF=CH=10,然后根据勾股定理可求解.【详解】解:(1)①AE=CF,理由如下:△AC=BC,△ACB=90°,CD为边AB上的中线,△AD=DC=DB,△A=△B=45°,CD△AB,△△A=△BCD=45°,△DF△DE,△△EDC+△CDF=90°,又△△ADE+△EDC=90°,△△ADE=△CDF,△△ADE△△CDF(ASA),△AE=CF,②CG=GD,理由如下:△△ACB=90°,△EDF=90°,EG=GF,△11,22CG EF DG EF==,△CG=GD;(2)由(1)得:AE=CF=6,CG=GD,12DG EF=,△△GCD=△GDC,△△GCD+△CHD=90°,△GDC+△GDH=90°,△△CHD=△GDH,△GH=GD,△12DG CH=,△CH=10,△CH=EF=10,在Rt△CEF 中,222+=CF CE EF ,即222610CE +=,解得:CE=8,△AC=AE+CE=14.【点睛】本题主要考查等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理,熟练掌握等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理是解题的关键.4.(2019·陇东学院附属中学八年级期末)如图在Rt ABC △中,AB AC =,90BAC ∠=︒,O 为BC 的中点.(1)写出点O 到ABC 的三个顶点A 、B 、C 的距离的大小关系.(2)如果点M 、N 分别在线段AB 、AC 上移动,移动中保持AN BM =,请判断OMN 的形状,并证明你的结论.(3)当点M 、N 分别在AB 、AC 上运动时,四边形AMON 的面积是否发生变化?说明理由.【答案】(1)OA OB OC ==;(2)OMN 是等腰直角三角形,证明见解析;(3)四边形AMON 的面积不变,理由见解析【分析】(1)连接OA ,由O 为BC 的中点可得OC OB =,由直角三角形斜边上的中线的性质可得12OA BC =,即可得OA OB OC ==. (2)由(1)不难证明45CAO B ∠=∠=︒,结合已知条件进而证明OAN △OBM ,即可得OM ON =,NOA MOB ∠=∠,即90NOM AOB ∠=∠=︒,所以OMN 是等腰直角三角形.(3)由(2)可得OAN S =OBM S ,进而将四边形AMON 的面积转化为AOB 的面积,AOB 的面积保持不变,故四边形AMON 的面积保持不变.【详解】(1)连接OA ,Rt ABC △中,O 为BC 的中点,∴12OA BC =,OC OB =, ∴122OA OB OB =⨯⨯=, ∴OA OB OC ==.(2)OMN 是等腰直角三角形,证明如下:AB AC =,O 为BC 的中点,∴AO BC ⊥,∴90AOB ∠=︒,OA OB OC ==,∴45CAO B ∠=∠=︒,在OAN 与OBM 中,OA OB CAO B AN BM =⎧⎪∠=∠⎨⎪=⎩,∴OAN △OBM ,∴OM ON =,NOA MOB ∠=∠,∴90NOM AOB ∠=∠=︒,∴OMN 是等腰直角三角形.(3)四边形AMON 的面积保持不变,理由如下:由(2)可得: OAN S =OBM S , ∴OAN AOM OBM AOM AOB AMON S S S S S S =+=+=四边形. AOB 的面积保持不变∴四边形AMON 的面积保持不变.【点睛】本题主要考查直接三角形斜边上中线的性质以及全等三角形的判定与性质,掌握全等三角形的判定与性质定理并灵活运用是解题关键.5.(2020·乌兰察布市·内蒙古凉城县宏远中学八年级月考)已知:三角形ABC 中,∠A =90°,AB =AC ,D 为BC 边的中点,(1)如图①,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:∠DEF 为等腰直角三角形.(2)如图②,若E ,F 分别为AB ,CA 延长线上的点,仍有BE =AF ,其他条件不变,那么,∠DEF 是否仍为等腰直角三角形?证明你的结论.【答案】(1)见解析;(2)△DEF为等腰直角三角,证明见解析【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有△CAD=△BAD=45°,AD=BD=CD,而△B=△C=45°,所以△B=△DAF,再加上BE=AF,AD=BD,可证出:△BED△△AFD,从而得出DE=DF,△BDE=△ADF,从而得出△EDF=90°,即△DEF是等腰直角三角形;(2)还是证明:△BED△△AFD,主要证△DAF=△DBE(△DBE=180°-45°=135°,△DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.【详解】(1)证明:连接AD,△AB=AC,△BAC=90°,D为BC的中点,△AD△BC,BD=AD.△△B=△DAC=45° 又BE=AF,△△BDE△△ADF(SAS).△ED=FD,△BDE=△ADF.△△EDF=△EDA+△ADF=△EDA+△BDE=△BDA=90°.△△DEF为等腰直角三角形.(2)△DEF为等腰直角三角形.证明:若E,F分别是AB,CA延长线上的点,如图所示:连接AD,△AB=AC,△△ABC为等腰三角形,△△BAC=90°,D为BC的中点,△AD=BD,AD△BC(三线合一),△△DAC=△ABD=45°.△△DAF=△DBE=135°.又AF=BE,△△DAF△△DBE(SAS).△FD=ED,△FDA=△EDB.△△EDF=△EDB+△FDB=△FDA+△FDB=△ADB=90°.△△DEF仍为等腰直角三角形.【点睛】本题利用了等腰直角三角形底边上的中线平分顶角,并且等于底边的一半,还利用了全等三角形的判定和性质,及等腰直角三角形的判定.6.(2019·全国九年级专题练习)如图所示,E,F分别是正方形ABCD的边AD,CD上AB=,连DH.求线段DH长度的最小的两个动点,且AE DF=,BE交AF于点H,2值.【答案】DH1【解析】【分析】根据正方形性质可得AB=DA ,△BAD=△ADF=90°,又根据AE=DF ,利用SAS 可证得△ABE△△DAF ,于是△ABE=△DAF ;由于△DAF+△BAH=△ABE+△BAH=90°,从而△AHB=90°,取AB 的中点O ,连接OH 、OD ,则OH=12AB=1,在Rt△AOD 中,根据勾股定理计算出OD 的值;根据三角形的三边关系,可得OH+DH >OD ,于是当O 、D 、H 三点共线时,DH 的长度最小为OD -OH ,据此解答.【详解】解:△四边形ABCD 是正方形,△AB=DA ,△BAD=△ADF=90°,又△AE=DF ,△△ABE△△DAF ,△△ABE=△DAF.△△DAF+△BAH=△ABE+△BAH=90°,△△AHB=90°,取AB 的中点O ,连OH 、OD ,△112OH AB ==,OD ==OHD ∆中有DH OD OH >-,即1DH >.故O、H、D三点共线时DH最小,△DH1.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边的中线等于斜边的一半,勾股定理及三角形三条边的关系,确定出点H的位置是解答本题的关键.。
