新人教版八年级三角形全等证明基础证明题

合集下载

(完整版)人教版八年级数学上册第12章全等三角形证明50题(含答案),推荐文档

D1. 已知：AB=4，AC=2，D 是 BC 中点，111749AD 是整数，求 ADAB CD 解：延长 AD 到 E,使 AD=DE∵D 是 BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即 4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是 AB 中点，∠ACB=90°，求证： CD 1AB 2AC B延长 CD 与 P ，使 D 为 CP 中点。

连接 AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形 ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是 CD 中点，求证：∠1=∠2A 12BE CF D证明：连接BF 和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED。

∴ ∠ABE=∠AEB。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2) 。

4.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD➴△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC 为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD 平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB 取点E，使AE＝AC，连接DE∵AD 平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC 平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC 平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE7.已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求ADAB CD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCDBD=DC∴△ACD ➴△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=28. 已知：D 是 AB 中点，∠ACB=90°，求证： CD 1AB 2AC B解：延长 AD 到 E,使 AD=DE∵D 是 BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ➴△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=29. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是 CD 中点，求证：∠1=∠2A12B EC F D证明：连接BF 和EF。

八年级数学上册第12章全等三角形证明经典50题(含答案)

八年级数学上册第12章全等三角形证明经典50题1.已知：AB=4，AC=2，D 是BC 中点，111749AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=2AD B C1. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB2. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)AB C D EF 2 1 DAB C∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

3. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DCB ACDF21 E∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC4.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中 AD=DE∠BDE=∠ADC BD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=2AD B C7. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=2DA B C8. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

人教版八年级数学上册全等三角形的证明习题(大题)

全等三角形的证明1、如图，AB ＝AD ，∠BAD ＝∠CAE ，AC=AE ，求证：BC=DE2、如图，AF=DB ，BC=EF ，AC=DE ，求证：BC∠EF 。

3、已知：如图，∠ABC ＝∠DCB ，BD 、CA 分别是∠ABC 、∠DCB 的平分线．求证：AB ＝DC ．4、如图，∠DCE ＝90°，CD ＝CE ，AD∠AC ，BE∠AC ，垂足分别为A 、B ．求证：AD ＋AB ＝BE ．ABCDE5、已知，AC∠CE ，AC=CE ， ∠ABC=∠EDC=900，证明：BD=AB+ED 。

6、如图，在∠ABC 中，D 为BC 边的中点，过D 点分别作DE ∠AB 交AC 于点E ， DF ∠AC 交AB 于点F .求证：BF=DE 。

7、如图，点E 在AB 上，AC=AD ，请你添加一个条件，使图中存在全等三角形，并给予证明。

所添条件为，你得到的一对全等三角形是∆ ∆≅ .证明：ABCDE8、如图，AD 平分∠BAC ，DE∠AB 于E ，DF∠AC 于F ，且DB=DC ，求证：EB=FC.9、如图，AE 是∠BAC 的平分线，AB=AC 。

若点D 是AE 上任意一点，请证明：∠ABD∠∠ACD ；10、（1）把一大一小两个等腰直角三角板（即EC=CD,AC=BC ）如图1放置，点D 在BC上，连结BE ，AD ，AD 的延长线交BE 于点F ．求证：（1）ΔACD∠ΔBCE （2）AF∠BE ．FE D CB AECDBABACDEFB DE A（2）把左边的小三角板逆时针旋转一定的角度如图2放置，问AF与BE是否垂直？并说明理由．图2。

八年级全等三角形证明经典50题(供参考)

全等三角形证明经典50题1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CADBCBA CDF2 1 ECA6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD8. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2A CDEF 21 ADBCDAB10.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC11.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠C12.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE12. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

求证：BC=AB+DC。

13.已知：AB//ED，∠EAB=∠BDE，AF=CD，EF=BC，求证：∠F=∠CBACDF21ECDBDCBAFEA14.已知：AB=CD，∠A=∠D，求证：∠B=∠C15.P是∠BAC平分线AD上一点，AC>AB，求证：PC-PB<AC-AB16.已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证：AC-AB=2BE17.已知，E是AB中点，AF=BD，BD=5，AC=7，求DC18．（5分）如图，在△ABC中，BD=DC，∠1=∠2，求证：AD⊥BC．19．（5分）如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBAAB CDP DACBFAEDCB20．（5分）如图，已知AD∥BC，∠P AB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．21．（6分）如图，△ABC中，AD是∠CAB的平分线，且AB=AC+CD，求证：∠C=2∠B22．（6分）如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．23．（7分）已知：如图，DC∥AB，且DC=AE，E为AB的中点，（1）求证：△AED≌△EBC．（2）观看图前，在不添辅助线的情况下，除△EBC外，请再写出两个与△AED的面积相等的三角形．（直接写出结果，不要求证明）：24．（7分）如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C 点的直线于E，直线CE交BA的延长线于F．求证：BD=2CE．PEDCBAOEDCBAFEADCBA25、（10分）如图：DF=CE ，AD=BC ，∠D=∠C 。

八年级全等三角形简单证明题及答案(15道)

2
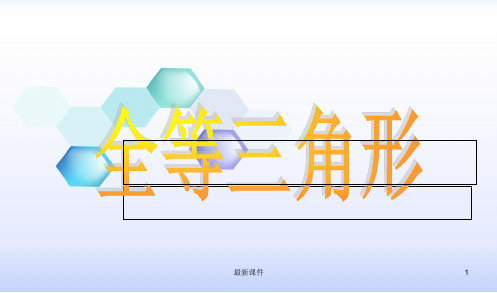
2.如图，在△ABC中，∠C=90°，点D是AB边上的一点，DM⊥AB，
且DM=AC，过点M作ME∥BC交AB于点E．求证：△ABC≌△MED。
证明：∵MD⊥AB， ∴∠MDE=∠C=90°， ∵ME∥BC， ∴∠B=∠MED，在△ABC与△MED中， ∠B=∠MED ∠C=∠EDM DM=AC ，
最新课件
16
全等三角形的判定与性质．
最新课件
10
11.在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．求证： Rt△ABE≌Rt△CBF；
（1）证明：∵∠ABC=90°， ∴∠CBF=∠ABE=90°，在Rt△ABE和Rt△CBF中， AE=CF AB=BC ， ∴Rt△ABE≌Rt△CBF（HL）；
全等三角形的判定与性质．
最新课件
13
如图，△ABC中，AB=AC，过点A作GE∥BC，角平
分线BD、CF相交于点H，它们的延长线分别交GE
于点E、G．试在图中找出3对全等三角形，并对其
中一对全等三角形给出证明．
：△BCF≌△CBD．
△BHF≌△CHD．
△BDA≌△CFA．
证明：在△BCF与△CBD中，
AE=CF ∠AED=∠CFB DE=BF ， ∴△ADE≌△CBF（SAS）．
全等三角形的判定．
最新课件
4
5.如图，在△ABC中，AB=AC，AD平分∠BAC．求证：∠DBC=∠DCB．
解：∵AD平分∠BAC， ∴∠BAD=∠CAD． ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD AD=AD ， ∴△ACD≌△ABD， ∴BD=CD， ∴∠DBC=∠DCB．
全等三角形最新课的件判定；平行线的性质． 9

人教版数学八年级上册第十二章《全等三角形》证明练习题(含答案)

人教版数学八年级上《全等三角形》经典习题集锦1.如图所示，△ABC≌△ADE，BC的延长线过点E，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，求∠DEF的度数。

2.如图，△AOB中，∠B=30°，将△AOB绕点O顺时针旋转52°，得到△A′OB′，边A′B′与边OB交于点C（A′不在OB上），则∠A′CO的度数为多少？3.如图所示，在△ABC中，∠A=90°，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是多少？4.如图所示，把△ABC绕点C顺时针旋转35°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A= .5.已知，如图所示，AB=AC，AD⊥BC于D，且AB+AC+BC=50cm,而AB+BD+AD=40cm，则AD是多少？6.如图，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B、C作过点A的垂线BC、CE，垂足分别为D、E，若BD=3，CE=2，则DE= .7.如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E、F，连接EF，交AD于G，AD与EF垂直吗？证明你的结论。

8.如图所示，在△ABC中，AD为∠BAC的角平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是28cm2,AB=20cm，AC=8cm，求DE的长。

9.已知，如图：AB=AE，∠B=∠E，∠BAC=∠EAD，∠CAF=∠DAF，求证：AF⊥CD10.如图，AD=BD，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点H，则BH与AC相等吗？为什么？11.如图所示，已知，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD，求证：BE⊥AC12.△DAC、△EBC均是等边三角形，AF、BD分别与CD、CE交于点M、N，求证：（1）AE=BD （2）CM=CN （3）△CMN为等边三角形（4）MN∥BC13.已知：如图1，点C为线段AB上一点，△ACM、△CBN都是等边三角形，AN交MC于点E，BM交CN于点F（1）求证：AN=BM（2）求证：△CEF为等边三角形14.如图所示，已知△ABC和△BDE都是等边三角形，下列结论：①AE=CD；②BF=BG；③BH平分∠AHD；④∠AHC=60°；⑤△BFG是等边三角形；⑥FG∥AD，其中正确的有（）A．3个 B. 4个 C. 5个 D. 6个15.已知：BD、CE是△ABC的高，点F在BD上，BF=AC，点G在CE的延长线上，CG=AB，求证：AG⊥AF16.如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG求证：（1）AD=AG（2）AD与AG的位置关系如何17．如图，已知E是正方形ABCD的边CD的中点，点F在BC上，且∠DAE=∠FAE求证：AF=AD-CF18．如图所示，已知△ABC中，AB=AC，D是CB延长线上一点，∠ADB=60°，E是AD上一点，且DE=DB，求证：AE=BE+BC19．如图所示，已知在△AEC中，∠E=90°，AD平分∠EAC，DF⊥AC，垂足为F，DB=DC，求证：BE=CF20．已知如图：AB=DE，直线AE、BD相交于C，∠B+∠D=180°，AF∥DE，交BD于F，求证：CF=CD21．如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于D，PE⊥OB于E，F是OC上一点，连接DF和EF，求证：DF=EF22．已知：如图，BF⊥AC于点F，CE⊥AB于点E，且BD=CD，求证：（1）△BDE≌△CDF （2）点D在∠A的平分线上23．如图，已知AB∥CD，O是∠ACD与∠BAC的平分线的交点，OE⊥AC于E，且OE=2，则AB与CD之间的距离是多少？24．如图，过线段AB的两个端点作射线AM、BN，使AM∥BN，按下列要求画图并回答：画∠MAB、∠NBA的平分线交于E（1）∠AEB是什么角？（2）过点E作一直线交AM于D，交BN于C，观察线段DE、CE，你有何发现？（3）无论DC的两端点在AM、BN如何移动，只要DC经过点E，①AD+BC=AB；②AD+BC=CD谁成立？并说明理由。

人教版八年级数学上册全等三角形的证明(含答案)

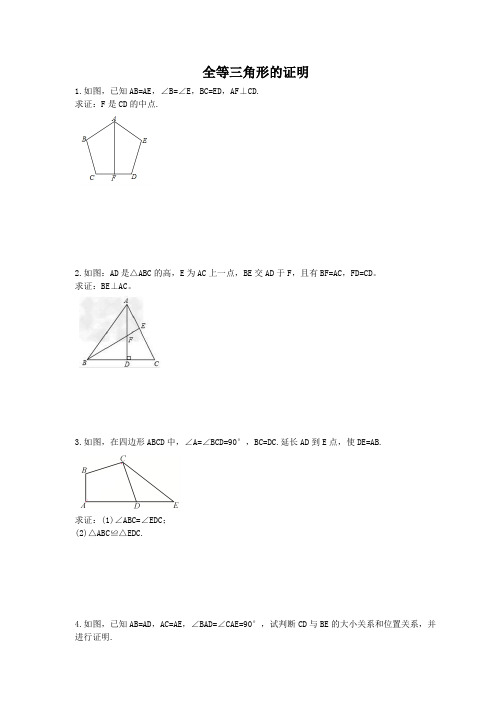
全等三角形的证明1.如图，已知AB=AE，∠B=∠E，BC=ED，AF⊥CD.求证：F是CD的中点.2.如图：AD是△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD。

求证：BE⊥AC。

3.如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC.延长AD到E点，使DE=AB.求证：(1)∠ABC=∠EDC；(2)△ABC≌△EDC.4.如图，已知AB=AD，AC=AE，∠BAD=∠CAE=90°，试判断CD与BE的大小关系和位置关系，并5.如图，已知∠B+∠CDE=180°，AC=CE．求证：AB=DE．6.如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD.(1)求证：△BCE≌△DCF；(2)求证：AB+AD=2AE.7.如图，AD平分∠BAC，EF垂直平分AD交BC的延长线于F，连接AF．求证：∠B=∠CAF．8.如图,在△ABC中,AD平分∠BAC．（1）求证：S△ABD：S△ACD=AB：AC；（2）若AB=4，AC=5，BC=6，求BD的长．9.（1）如图（1）在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：DE=BD+CE；（2）如图（2）将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请给出证明；若不成立，请说明理由．10.如图,在△ABC中,∠ABC=60゜,AD、CE分别平分∠BAC、∠ACB，AD、CE交于O．（1）求∠AOC的度数；（2）求证：AC=AE+CD．参考答案1.证明：连接AC ，AD.在△ABC 和△AED 中，⎩⎪⎨⎪⎧AB ＝AE ，∠B ＝∠E ，BC ＝ED ，∴△ABC ≌△AED(SAS).∴AC=AD.在Rt △ACF 和Rt △ADF 中，⎩⎪⎨⎪⎧AC ＝AD ，AF ＝AF ， ∴Rt △ACF ≌Rt △ADF(HL).∴CF=DF ，即F 为CD 的中点.2.证明：(1) AD 为△ABC 上的高，∴BDA=ADC =90.∵BF=AC,FD=CD.∴Rt △BDF ≌Rt △ADC.(2)由①知∠C=∠BFD ，∠CAD=∠DBF.∠BFD= ∠AFE ，又∠CBE=∠CAD ，∴∠AEF=∠BDF.∠BDF= 90，∴BE ⊥AC.3.证明：(1)在四边形ABCD 中，∵∠BAD=∠BCD=90°，∴∠B ＋∠ADC=180°.又∵∠CDE ＋∠ADC=180°.∴∠ABC=∠EDC.(2)连接AC.⎩⎪⎨⎪⎧AB ＝ED ，∠ABC ＝∠EDC ，CB ＝CD ，∴△ABC ≌△EDC(SAS).4.证明：CD=BE ，CD ⊥BE ，理由如下：因为∠BAD=∠CAE=90°，所以∠BAD+∠DAE=∠CAE+∠DAE ，即∠BAE=∠DAC. 因为，所以△BAE ≌△DAC(SAS).所以BE=DC ，∠BEA=∠DCA.如图，设AE 与CD 相交于点F ，因为∠ACF+∠AFC=90°，∠AFC=∠DFE ，所以∠BEA+∠DFE=90°.即CD ⊥BE.5.证明：如图，过E 点作EH ∥AB 交BD 的延长线于H ，故∠A=∠CEH ，在△ABC 与△EHC 中，∴△ABC ≌△EHC （ASA ），∴AB=HE ，∵∠B+∠CDE=180°，∠HDE+∠CDE=180°∴∠HDE=∠B=∠H ，∴DE=HE ．∵AB=HE ，∴AB=DE ．6. (1)证明：∵AC 是角平分线，CE ⊥AB 于E ，CF ⊥AD 于F ， ∴CE=CF ，∠F=∠CEB=90°，在Rt △BCE 和Rt △DCF 中，(2)解：∵CE⊥AB于E，CF⊥AD于F，∴∠F=∠CEA=90°，在Rt△FAC和Rt△EAC中，，∴Rt△FAC≌Rt△EAC，∴AF=AE，∵△BCE≌△DCF，∴BE=DF，∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.7.证明：∵EF垂直平分AD，∴AF=DF，∠ADF=∠DAF，∵∠ADF=∠B+∠BAD，∠DAF=∠CAF+∠CAD，又∵AD平分∠BAC，∴∠BAD=∠CAD，∴∠B=∠CAF．8.（1）证明：过D作DE⊥AB于E，DF⊥AC于F，∵AD平分∠BAC，∴DE=DF，∵S△ABD=0.5AB•DE，S△ACD=0.5AC•DF，∴S△ABD：S△ACD=（0.5AB•DE）：（0.5AC•DF）=AB：AC；（2）解：∵AD平分∠BAC，∴=0.8，∴BD=0.8CD，∵BC=6，∴BD=．9.证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA=∠CEA=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°，∴∠CAE=∠ABD，∵在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE=BD，AD=CE，∴DE=AE+AD=BD+CE；∴∠CAE=∠ABD，∵在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE=BD，AD=CE，∴DE=AE+AD=BD+CE．10.解：如图，在AC上截取AF=AE，连接OF∵AD平分∠BAC，∴∠BAD=∠CAD，在△AOE和△AOF中∴△AOE≌△AOF（SAS），∴∠AOE=∠AOF，∵∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，∴∠AOC=120°；（2）∵∠AOC=120°，∴∠AOE=60°，∴∠AOF=∠COD=60°=∠COF，在△COF和△COD中，∴△COF≌△COD（ASA）∴CF=CD，∴AC=AF+CF=AE+CD．。

人教版八年级数学上册第12章全等三角形证明50题(含答案)

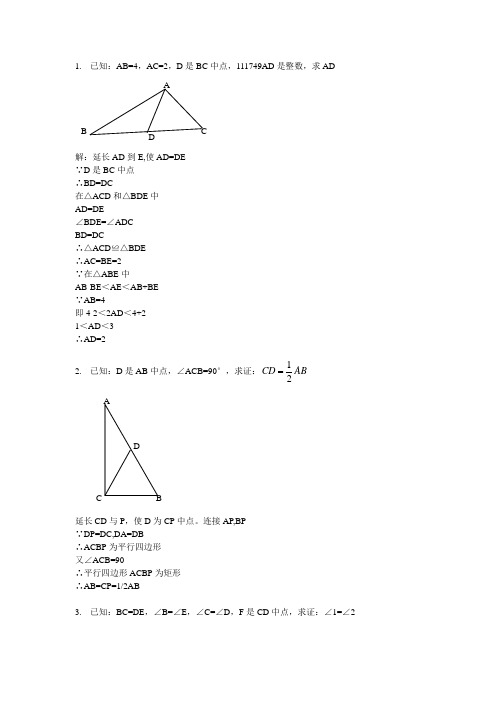
1. 已知：AB=4，AC=2，D 是BC 中点，111749AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。

∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。

∴∠BAF=∠EAF (∠1=∠2)。

4.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC过C作CG∥EF交AD的延长线于点GCG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF 和EF 。

(完整word版)八年级全等三角形证明经典50题(含答案).doc

1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求ADA 解：延长AD 至IJE,使AD=DE・・・D 是BC 中点BD=DC在厶ACD 和厶BDE 中AD=DEZBDE= ZADC BD=DCAA ACD A BDE•*. AC=BE=2・・•在△ ABE 中AB-BE < AE<AB+BE・・・AB=4即 4・2 <2AD < 4+21 < AD < 3・・・AD=2延长CD 与P,使D 为CP 中点。

连接VDP=DC,DA=DBA AC BP 为平行四边形又 Z ACB=90・・・平行四边形ACBP 为矩形AAB=CP=1/2AB 2.已知：D 是AB 中点，Z ACB=90 0,求证：CD [AB 2AAP,BP3.已知：BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点，求证：Z 1= Z2证明：连接BF和EF・・・ BC=ED,CF=DF, Z BCF= Z EDF・・・三角形BCF全等于三角形EDF（边角边）・・・ BF=EF, ZCBF=Z DEF连接BE在三角形BEF中,BF=EF/. Z EBF=Z BEFo・・・ Z ABC= Z AED o・・・ Z ABE= Z AEBo/. AB=AE o在三角形ABF和三角形AEF屮AB=AE,BF=EF,ZABF= Z ABE+ Z EBF= ZAEB+ Z BEF= Z AEF・・・三角形ABF和三角形AEF全等。

・・・ Z BAF= Z EAF（Z 1= Z 2）o4. 己知：Z 1= Z 2 , CD=DE , EF//AB ,求证：EF=AC过C作CG〃EF交AD的延长线于点GCG// EF,可得，Z EFD= CGDDE= DCZFDE= Z GDC （对顶角）AA EFD^A CGDEF= CGZCGD = Z EFD又，EF// AB・・・，Z EFD= Z 1Z1= Z 2・・・Z CGD= Z 2・・・△ AGC为等腰三角形,AC= CG又EF=CG・・・EF= AC5.已知：AD 平分Z BAC, AC=AB+BD ,求证：Z B=2 Z C证明：延长AB取点E,使AE=AC,连接DEVAD 平分Z BACAZ EAD=Z CAD・・・AE=AC, AD = ADA A AED^A ACD ( SAS)AZ E=Z CVAC = AB+BD・・・AE= AB+BD・・・AE= AB+BEABD = BE・・・Z BDE=Z EVZ ABC=Z E+ Z BDEAZ ABC = 2 ZEAZ ABC = 2 ZC6.己知：AC 平分Z BAD , CE丄AB , Z B+ Z D=180 ° ,求证：AE=AD+BE・・・CE丄AB ・・・Z CEB=Z CEF= 90° ・・・EB=EF, CE = CE, AACEB^ACEF ・・・Z B=Z CFEVZ B+Z D= 180 ° , ZCFE+Z CFA= 180 0AZ D = Z CFAVAC 平分Z BAD・・・Z DAC = Z FACVAC = AC・・・△ ADC 竺△ AFC ( SAS)/.AD = AF ・・・AE= AF+ FE= AD + BE解：延长AD至IJE,使AD=DE・・・D是BC中点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DC7.已知：AB=4 , AC=2 , D是BC屮点, AD是整数，求ADA 证明:在AE上取F,使EF= EB,连接CFAAACD^ABDE•*. AC=BE=2・・•在△ ABE中AB-BE < AE<AB+BE・・・AB=4即4・2 < 2AD < 4+21 < AD < 3・・・AD=218.已知：D 是AB 中点，Z ACB=90 0,求证：CD -AB2解：延长AD到E,使AD=DE・・・D是BC屮点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DCAA ACD A BDE•*. AC=BE=2•・•在A ABE中9.已知：BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点，求证：Z 1= Z2A证明：连接BF和EF。

人教版八年级上册数学专题复习证明三角形全等的常见题型

证明三角形全等的常见题型全等三角形是初中几何的重要内容之一，全等三角形的学习是几何入门最关键的一步，这部分内容学习的好坏直接影响着今后的学习。

而一些初学的同学，虽然学习了几种判定三角形全等的公理和推论，但往往仍不知如何根据已知条件证明两个三角形全等。

在辅导时可以抓住以下几种证明三角形全等的常见题型，进行分析。

一、已知一边与其一邻角对应相等1．证已知角的另一边对应相等，再用SAS证全等。

例1已知：如图1，点E、F在BC上，BE=CF，AB=DC，∠B=∠C .求证：AF=DE。

证明∵BE=CF（已知），∴BE+ EF=CF+EF，即 BF=CE。

在△ABF和△DCE中，∴△ABF≌△DCE（SAS）。

∴ AF=DE（全等三角形对应边相等）。

2．证已知边的另一邻角对应相等，再用ASA证全等。

例2已知：如图2，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB。

求证：AE=CE。

证明∵ FC∥AB（已知），∴∠ADE=∠CFE（两直线平行，内错角相等）。

在△ADE和△CFE中，∴△ADE≌△CFE（ASA）.∴ AE=CE（全等三角形对应边相等）3．证已知边的对角对应相等，再用AAS证全等。

例3（同例2）.证明∵ FC∥AB（已知），∴∠A=∠ECF（两直线平行，内错角相等）.在△ADE和△CFE中，∴△ADE≌△CFE（AAS）.∴ AE=CE（全等三角形对应边相等）。

二、已知两边对应相等1．证两已知边的夹角对应相等，再用SAS证等。

例4已知：如图3，AD=AE，点D、E在BCBD=CE，∠1=∠2。

求证：△ABD≌△ACE.证明∵∠1=∠2（已知），∠ADB=180°-∠1，∠AEC=180°-∠2（邻补角定义），∴∠ADB = ∠AEC，在△ABD和△ACE中，∴△ABD≌△ACE（SAS）.2．证第三边对应相等，再用SSS证全等。

例5已知：如图4，点A、C、B、D在同一直线AC=BD，AM=CN， BM=DN。

人教版八年级数学上册《全等三角形证明》专项练习题-附含答案

人教版八年级数学上册《全等三角形证明》专项练习题-附含答案专题简介：本份资料包含《全等三角形》这一章的六种主流中档证明题所选题目源自各名校期中、期末试题中的典型考题具体包含的题型有：重叠边技巧、重叠角技巧、等角的余角相等技巧、证两次全等的证明题、手拉手模型、角平分线的性质与判定的中档题。

适合于公立学校老师和培训机构的老师给学生作全等三角形证明题专项复习时使用或者学生考前刷题时使用。

题型1：重叠边技巧①短边相等＋重叠边=长边相等②长边相等－重叠边=短边相等1．（2019·广东）如图点A 、C 、F 、D 在同一直线上 AF=DC AB=DE BC=EF 求证：AB ∥DE ．【详解】∵AF=DC ∴AF ﹣FC=DC ﹣CF 即AC=DF ．在△ACB 和△DFE 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩∴△ACB ≌△DFE （SSS ） ∴∠A=∠D ∴AB ∥DE ．2．（2021·重庆）已知点A 、E 、F 、C 在同一直线上已知AD BC ∥ AD BC = AE CF = 试说明BE 与DF 的关系．【详解】解：数量关系BE DF = 位置关系BE DF ∥．理由：∵AD BC ∥ ∴∠A =∠C又AE CF = ∴AE +EF =CF +EF 即AF =CE 在ADF 和CBE △中 AD BC A C AF CE =⎧⎪∠=∠⎨⎪=⎩ ADF ∴≌()CBE SAS △∴BE =DF ∠BEF =∠DFE ∴BE DF ∥．3．（2021·湖北荆门）如图点E、F在BC上BE＝CF AB＝DC∠B＝∠C．求证：∠A＝∠D．【详解】解∵BE＝CF∴BE+EF＝CF+EF即BF＝CE．在△ABF和△DCE中AB DCB C BF CE=⎧⎪∠=∠⎨⎪=⎩∴△ABF≌△DCE∴∠A＝∠D．4．（2021·甘肃）如图AB∥CD BN∥MD点M、N在AC上且AM=CN求证：BN=DM．【详解】解：∵AB∥CD BN∥MD ∴∠A=∠C∠CMD=∠ANB ∵AM=CN∴AM+MN=MN+CN即AN=MC 在△ANB和△CMD中∠A=∠C AN=MC∠ANB=∠CMF ∴△ANB≌△CMD（ASA）∴BN=MD．5．（2021·新疆）如图点A、F、C、D在同一直线上点B和点E分别在直线AD的两侧且AB＝DE∠A ＝∠D AF＝DC．求证：(1)△ABC≌△DEF；(2)BC∥EF．【详解】(1)证明：∵AF＝DC∴AF+CF＝DC+CF∴AC＝DF∵在△ABC和△DEF中AB DEA DAC DF=⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△DEF（SAS）；(2)证明：由（1）知△ABC≌△DEF∴∠BCA＝∠EFD∴BC∥EF．题型2：重叠角技巧重叠角技巧：①小角相等+重叠角=大角相等②大角相等-重叠角=小角相等6．（2022·福建·福州）如图AC＝AE∠1＝∠2 AB＝AD．求证：△ABC≌△ADE．【详解】证明：∵∠1=∠2 12EAB EAB∴∠+∠=∠+∠即CAB EAD∠=∠在ABC和ADE中{AC AECAB EAD AB AD=∠=∠=() ABC ADE SAS∴≅．7．（2022·四川资阳）如图在△ABC和△ADE中AB=AD∠B=∠D∠1=∠2．求证：BC=DE．【详解】证明：∵∠1=∠2 ∵∠DAC+∠1=∠2+∠DAC∴∠BAC=∠DAE在△ABC和△ADE中B DAB ADBAC DAE∠∠⎧⎪⎨⎪∠∠⎩＝＝＝∴△ADE≌△ABC（ASA）∴BC=DE8.如图AB＝AD∠C＝∠E∠1＝∠2 求证：△ABC≌△ADE．【解答】证明：∵∠1＝∠2 ∴∠1+∠EAC＝∠2+∠EAC即∠BAC＝∠DAE在△ABC和△ADE中BAC DAE C E AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE （AAS ）． 9．(雅礼)如图 △ABC 和△ADE 都是等腰三角形且∠BAC ＝90° ∠DAE ＝90° B C D 在同一条直线上．求证：BD ＝CE ．【解答】证明：∵△ABC 和△ADE 都是等腰直角三角形 ∴AD ＝AE AB ＝AC 又∵∠EAC ＝90°+∠CAD ∠DAB ＝90°+∠CAD ∴∠DAB ＝∠EAC∵在△ADB 和△AEC 中 ∴△ADB ≌△AEC （SAS ） ∴BD ＝CE ．10．（2020·四川达州）已知△ABN 和△ACM 位置如图所示 AB =AC AD =AE ∠1=∠2．（1）求证：BD =CE ；（2）求证：∠M=∠N ．【详解】（1）证明：在△ABD 和△ACE 中 12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ACE （SAS ） ∴BD =CE ；（2）证明：∵∠1=∠2 ∴∠1+∠DAE =∠2+∠DAE 即∠BAN =∠CAM 由（1）知：△ABD ≌△ACE∴∠B =∠C 在△ACM 和△ABN 中 C B AC AB CAM BAN ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACM ≌△ABN （ASA ） ∴∠M =∠N ．题型3：等角的余角相等技巧：∠1+∠2=90 ∠2+∠3=90 ∴∠1=∠3技巧：把全等三角形中一个三角形的两个锐角分别随意标上∠1、∠2 再从第二个三角形的两个锐角中挑一个和∠1或∠2互余的角标上∠3。

八年级全等三角形简单证明题及解答(5道)

八年级全等三角形简单证明题及解答(5道)
汇报人：XX
目录
• 题目一：基本的全等三角形证明 • 题目二：利用角平分线性质证明 • 题目三：通过边边边条件证明 • 题目四：结合中线性质进行证明 • 题目五：综合应用多种性质证明 • 总结与拓展
01
题目一：基本的全等三角形证明
题目描述
• 已知三角形$ABC$和三角形$DEF$，其中$AB = DE$，$AC = DF$，$\angle BAC = \angle EDF$。求证：$\triangle ABC \cong \triangle DEF$。
由第二步可知，△BDE∽△CFD。
详细解答
4. 第四步，根据相似三角形的性质，对应边成比例，所以BD/CF=DE/DF。
5. 第五步，因为BD=AD（已知），所以AD/CF=DE/DF。又因为AE/EC=DE/EF（已知），所以AD/CF=AE/EC。
6. 第六步，交叉相乘得AD*EC=AE*CF，即AE/AD=EC/CF。又因为∠A=∠ACF（对顶角相等），所以△ADE∽△ACF。
第三步，根据相似三角形的性质，有 AB/AC = BD/DC。
综上，我们证明了 AB/AC = BD/DC。
03
题目三：通过边边边条件证明
题目描述
已知
△ABC和△DEF中，AB = DE，BC = EF，AC = DF。
求证
△ABC ≌ △DEF。
题目描述
【分析】
本题主要考察全等三角形的判定方法——边边边条件。根据已知条件，我们可以直接应用边边边定理来证明两个三角形全等。
题目描述
01
【解答】
02
证明
03
04
∵ 在△ABC和△DEF中，AB = DE，BC = EF，AC = DF（已

人教版八年级上册数学第十二章全等三角形证明题训练

人教版八年级上册数学第十二章全等三角形证明题训练1．如图，已知：AB =AD ，BC =DE ，AC =AE ，试说明：∠1=∠2．2．如图，∠B =∠C =90°，E 是BC 的中点，DE 平分∠ADC ．求证：AE 是∠DAB 的平分线．3．如图：A 、B 、C 、D 四点在同一直线上，AC=DB ，BE ∥CF ，AE ∥DF ．求证：∠ABE ∠∠DCF ．4．已知，在∠ABC 中，∠ACB =2∠B ．当AD 为∠BAC 的角平分线时，求证：AB =AC +CD5．如图，点D ，E 分别在OA ，OB 上，点P 在OC 上，且PD PE =．若180ODP OEP ∠+∠=︒，求证：OC 平分AOB ∠．6．已知：如图，AD 、BF 相交于O 点，OA OD =，AB DF ∥，点E 、C 在BF 上，BE CF =．(1)求证：ABO ∠DFO ；(2)判断线段AC 、DE 的关系，并说明理由．7．如图，在ABC 中，D 是BC 边上的一点，AB DB =，BE 平分ABC ∠交AC 边于点E ，连接DE ．(1)A ∠与BDE ∠相等吗？为什么？(2)若100A ∠=︒，50C ∠=︒，求AEB ∠的度数．8．如图，∠ABC 的两条高BE 、CD 相交于点O ，BD ＝CE ．(1)求证：BE ＝CD ；(2)判断点O 是否在∠BAC 的平分线上，并说明理由．9．如图，A 、B 、C 、D 在同一直线上，且∠ABF ∠△DCE ，求证：(1)AF DE ∥、BF ∠CE ；(2)AC =BD10．如图，∠ABC 中，点D 在边BC 延长线上，100ACB ∠=︒，∠ABC 的平分线交AD 于点E ，过点E 作EH ∠BD ，垂足为H ，且50CEH ∠=︒．(1)求∠ACE 的度数；(2)求证：AE 平分∠CAF ；(3)若AC+CD ＝14，AB ＝8.5，且21ACD S =，求∠ABE 的面积．11．如图，DE ∠AB 于E ，DF ∠AC 于F ，若BD ＝CD 、BE ＝CF ．(1)求证：∠BDE ∠△CDF(2)求证：AD 平分∠BAC ；(3)直接写出AB＋AC与AE之间的等量关系．12．已知如图，B是CE的中点，AD＝BC，AB＝DC．DE交AB于F点．求证：(1)AD BC∥(2)AF＝BF．13．如图，已知点B，E，C，F在一条直线上，BE＝CF，AC DE∥，A D∠=∠．(1)求证：∠ABC ∠∠DFE；(2)若BF＝12，EC＝4，求BC的长．14．如图所示，E、F分别为线段AC上的两个点，且DE∠AC于点E，BF∠AC于点F，若AB=CD，AE=CF，BD交AC于点M．(1)试猜想DE与BF的关系，并证明你的结论；(2)求证：MB=MD．15．如图，已知点C，F在直线AD上，且有BC=EF，AB=DE，CD=AF．求证：∆ABC∠∆DEF．16．如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF∠AE，垂足为F，过B作BD∠BC交CF的延长线于D．(1)求证：AE＝CD；(2)若AC＝12cm，求BD的长17．如图，在∠ABC中，AB=AC，BD∠AC于D，CE∠AB于E，BD、CE相交于F．求证：(1)∠ABD∠∠ACE；(2)AF平分∠BAC．18．如图，在△ABC中，∠ACB=90°，AC=BC，点D在AC上，点E在BC的延长线上，CE=CD，BD的延长线交AE于点F．(1)求证：△ACE∠∠BCD；(2)求证：BF∠AE；(3)若BD=8，DF=2，直接写出△ABE的面积．19．已知：如图，AB＝AD，∠C＝∠E，∠1＝∠2，求证：BC＝DE．20．如图，A、E、F、C在一条直线上，AF＝CE，过E、F分别作DE∠AC，BF∠AC，AB＝CD，求证：(1)∠ABF∠∠CDE(2)BG＝DG。