广东省深圳市龙岗区布吉中学2020年中考复习冲刺试卷一含答案
2020年深圳市数学中考基础冲刺训练卷(含答案)

2020年深圳市数学中考基础冲刺训练卷一.选择题1.﹣3的绝对值是()A.﹣3 B.3 C.D.2.下列图形中,不是轴对称图形的是()A.B.C.D.3.据报道,2020年某市户籍人口中,60岁以上的老人有1230000人,预计未来五年该市人口“老龄化”还将提速.将1230000用科学记数法表示为()A.12.3×105B.1.23×105C.0.12×106D.1.23×1064.如图,将正方体的表面展开,得到的平面图形可能是()A.B.C.D.5.已知一组数据:66,66,62,67,63,这组数据的众数和中位数分别是()A.66,62 B.66,66 C.67,62 D.67,666.下列运算不正确的是()A.a2•a3=a5B.(y3)4=y12C.(﹣2x)3=﹣8x3D.x3+x3=2x67.如图,是一张长方形纸片(其中AB∥CD),点E,F分别在边AB,AD上.把这张长方形纸片沿着EF 折叠,点A落在点G处,EG交CD于点H.若∠BEH=4∠AEF,则∠CHG的度数为()A.108°B.120°C.136°D.144°8.如图,在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于线段BC长度一半的长为半径画圆弧.两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED.一定正确的是()A.①②③B.①②C.①③D.②③9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax﹣2b(a≠0)与反比例函数y=(c≠0)在同一平面直角坐标系中的图象大致是()\A.B.C.D.10.下列命题正确是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.有两条边对应相等的两个直角三角形全等C.16的平方根是4D.对角线相等的平行四边形是矩形11.定义一种新运算n•x n﹣1dx=a n﹣b n,例如2xdx=k2﹣n2,若﹣x﹣2dx=﹣2,则m=()A.﹣2 B.﹣C.2 D.12.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB 方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为()A.1s B.s C.s D.2s二.填空题13.分解因式:m2(x﹣2)+(2﹣x)=.14.一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球10个.现在往袋中放入m 个白球和4个黑球,使得摸到白球的概率为,则m=.15.如图,正方形纸片ABCD沿直线BE折叠,点C恰好落在点G处,连接BG并延长,交CD于点H,延长EG交AD于点F,连接FH.若AF=FD=6cm,则FH的长为cm.16.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD 的边分别平行于x轴、y轴若双曲线y=与正方形ABCD有公共点,则k的取值范围为.三.解答题17.计算:2﹣1﹣2cos30°+|﹣|+(3.14﹣π)0.18.先化简,再求值:+,其中a=.19.某中学体育老师统计了本校九年一班学生参加体育达标测试的报名情况,并把统计的数据绘制成如图所示的不完整的条形统计图和扇形统计图,根据图中提供的信息回答下列问题:(1)九年一班参加体育达标测试的学生有多少人?(2)通过计算补全条形统计图;(3)若该年级有600名学生,估计该年级参加仰卧起坐达标测试的学生有多少人.20.某兴趣小组借无人机航拍测量湖AB的宽度,如图,当无人机位于C处时,从湖边A处测得C处的仰角∠CAB=60°,当无人机沿水平方向飞行至D处时,从湖边A处测得D处的仰角∠DAB=30°,从湖边B处测得D处的仰角∠DBA=45°,且CD=60m.(1)求这架无人机的飞行高度;(结果保留根号)(2)求湖的宽度AB.(结果保留根号)21.我县第一届运动会需购买A,B两种奖品,若购买A种奖品4件和B种奖品3件,共需85元;若购买A种奖品3件和B种奖品1件,共需45元.(1)求A、B两种奖品的单价各是多少元?(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买总费用W元,写出W(元)与m(件)之间的函数关系式,求出自变量m的取值范围,并设计出购买总费用最少的方案.22.如图,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A,B两点,其中A(m,0),B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.(1)求m,n的值及该抛物线的解析式;(2)如图2,若点P为线段AD上的一动点(不与A,D重合),分别以AP,DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标.23.已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(﹣3,0),B(0,3).(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;(2)如图2,已知直线l2:y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2为半径画圆.①当点Q与点C重合时,求证:直线l1与⊙Q相切;②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.2020年深圳市数学中考基础冲刺训练卷参考答案一.选择题1.解:|﹣3|=3.故﹣3的绝对值是3.故选:B.2.解:A、是轴对称图形,故本选项不符合题意;B、是轴对称图形,故本选项不符合题意;C、是轴对称图形,故本选项不符合题意;D、不是轴对称图形,故本选项符合题意.故选:D.3.解:将1230000用科学记数法表示为1.23×106.故选:D.4.解:A.平面图形有凹字形,不能围成正方体,故本选项不合题意;B.平面图形能围成正方体,故本选项符合题意;C.平面图形不能围成正方体,故本选项不合题意;D..平面图形不能围成正方体,故本选项不合题意;故选:B.5.解:把这组数据按照从小到大的顺序排列为:62,63,66,66,67,第3个数是66,所以中位数是66,在这组数据中出现次数最多的是66,即众数是66,故选:B.6.解:A.a2•a3=a2+3=a5,故本选项不合题意;B.(y3)4=y3×4=y12,故本选项不合题意;C.(﹣2x)3=(﹣2)3x3=﹣8x3,故本选项不合题意;D.x3+x3=2x3,故本选项符合题意.故选:D.7.解:由折叠的性质,可知:∠AEF=∠FEH.∵∠BEH=4∠AEF,∠AEF+∠FEH+∠BEH=180°,∴∠AEF=×180°=30°,∠BEH=4∠AEF=120°.∵AB∥CD,∴∠DHE=∠BEH=120°,∴∠CHG=∠DHE=120°.故选:B.8.解:作法得DE⊥BC,而D为BC的中点,所以DE垂直平分BC,则EB=EC,所以∠EBC=∠C,而∠ABC=90°,所以∠A=∠EBA,所以①②正确.故选:B.9.解:∵二次函数的图象开口向上,对称轴在y轴的左侧,函数图象交于y轴的负半轴∴a>0,b>0,c<0,∴反比例函数y=的图象必在二、四象限;一次函数y=ax﹣2b一定经过一三四象限,∵对称轴为直线x=﹣1,且与x轴的交点为(﹣3,0),∴另一个交点为(1,0),∴﹣=﹣1,∴b=2a,把(﹣3,0)代入y=ax2+2ax+c得,9a﹣6a+c=0,∴c=﹣3a,方程ax﹣2b=整理得ax2﹣2bx﹣c=0,即ax2﹣4a+3a=0,∴x2﹣4x+3=0,∵(﹣4)2﹣4×3=4>0,∴一次函数y=ax﹣2b(a≠0)与反比例函数y=(c≠0)的图象有两个交点,故选:D.10.解:A、一组对边平行,另一组对边等的四边形可能是等腰梯形,故原命题错误;B、两条边分别相等的两个直角三角形不一定全等,故原命题错误;C、16的平方根是±4,故原命题错误;D、对角线相等的平行四边形是矩形,正确,故选:D.11.解:由题意得:m﹣1﹣(5m)﹣1=﹣2,﹣=﹣2,5﹣1=﹣10m,m=﹣,经检验:m=﹣是方程﹣=﹣2的解;故选:B.12.解:连接BD,∵四边形ABCD是菱形,∴AB=AD,∠ADB=∠ADC=60°,∴△ABD是等边三角形,又∵△DEF是等边三角形,∴∠EDF=∠DEF=60°,又∵∠ADB=60°,∴∠ADE=∠BDF,在△ADE和△BDF中,,∴△ADE≌△BDF(AAS),∴AE=BF,∵AE=t,CF=2t,∴BF=BC﹣CF=4﹣2t,∴t=4﹣2t∴t=,故选:C.二.填空题13.解:原式=m2(x﹣2)﹣(x﹣2)=(x﹣2)(m2﹣1)=(x﹣2)(m+1)(m﹣1),故答案为:(x﹣2)(m+1)(m﹣1)14.解:由题意得,,解得m=5,经检验,m=5是原分式方程的根,故答案为5.15.解:如图,连接BF.∵四边形ABCD是正方形,∴∠A=∠C=90°,AB=BC=AF+FD=12cm.由折叠可知,BG=BC=12cm,∠BGE=∠BCE=90°.在Rt△ABF和Rt△GBF中BF=BF,AB=GB∴Rt△ABF≌Rt△GBF(HL).∴∠AFB=∠GFB,FA=FG,又∵AF=FD,∴FG=FD.同理可证Rt△FGH≌Rt△FDH,∴∠GFH=∠DFH,∴∠BFH=∠BFG+∠GFH=180°=90°,∴∠AFB+∠DFH=90°.又∵∠AFB+∠ABF=90°,∴∠ABF=∠DFH.又∵∠A=∠D=90°,∴△ABF∽△DFH,∴,在Rt△ABF中,由勾股定理,得BF=,∴,∴FH=.故答案为3.16.解:∵点A在直线y=x上,点A的横坐标为1,∴A(1,1),∵边长为3的正方形ABCD的边分别平行于x轴、y轴,∴C点坐标为(4,4),当双曲线y=经过A点时,k的值最小,此时k=1×1=1;当双曲线y=经过C点时,k的值最大,此时k=4×4=16;∴k的取值范围为1≤k≤16.故答案为1≤k≤16.三.解答题17.解:原式==18.解:原式=﹣=﹣=,当a=时,原式=,19.解:(1)(25+20)÷(1﹣10%)=50(人),答:九年级一班参加体育达标的有50人.(2)50﹣25﹣20=5(人),补全条形统计图如图所示:(3)600×=240(人),答:估计该年级参加仰卧起坐达标测试的学生有240人.20.解:(1)作CE⊥AB于E,DF⊥AB于F,如图,∴CE=DF,EF=CD=60,∵CD∥AB,∴∠CDA=∠DAB=30°,∵∠CAD=∠CAB﹣∠DAB=60°﹣30°=30°,∴CA=CD=60,在Rt△ACE中,AE=AC=30,CE=AE=30,答:这架无人机的飞行高度为30米;(2)易得四边形CDFE为矩形,则EF=CD=60,DF=CE=30,在Rt△BDF中,∵∠DBA=45°,∴BF=DF=30,∴AB=AE+EF+BF=30+60+30=(90+30)米.答:湖的宽度AB为(90+30)米.21.解:(1)设A奖品的单价是x元/件,B奖品的单价是y元/件,根据题意,得:,解得:.答:A奖品的单价是10元/件,B奖品的单价是15元/件.(2)设购买A种奖品m件,购买总费用W元,则购买B种奖品(100﹣m)件,根据题意,得:W=10m+15(100﹣m)=﹣5m+1500.∵购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,∴,解得:70≤m≤75,∴W=﹣5m+1500(70≤m≤75).∵k=﹣5<0,∴W随m的增大而减小,∴当m=75时,W取最小值,最小值=﹣5×75+1500=1125,此时100﹣m=100﹣75=25.答:购买总费用最少的方案是购买A奖品75件、B奖品25件.22.解:(1)把点A(m,0)、点B(4,n)代入y=x﹣1中,得m=1,n=3.∴A(1,0),B(4,3)∵y=﹣x2﹣bx+c过点A、点B,所以解得,∴y=﹣x2+6x﹣5.(2)如图2,∵△APM和△DPN为等腰直角三角形,∴∠APM=∠DPN=45°,∴∠MPN=90°,∴△MPN为直角三角形.令﹣x2+6x﹣5=0,解得x=1或5,∴D(5,0),AD=4.设AP=m,则DP=4﹣m,∴PM=m,PN=(4﹣m),∴S=×PM×PN=m×(4﹣m)△MPN=﹣(m﹣2)2+1.∴当m=2,即AP=2时,△MPN的面积最大,此时OP=3,∴P(3,0).23.解:(1)如图1,连接BC,∵∠BOC=90°,∴点P在BC上,∵⊙P与直线l1相切于点B,∴∠ABC=90°,而OA=OB,∴△ABC为等腰直角三角形,则⊙P的直径长=BC=AB=3;(2)过点作CM⊥AB,由直线l2:y=3x﹣3得:点C(1,0),则CM=AC sin45°=4×=2=圆的半径,故点M是圆与直线l1的切点,即:直线l1与⊙Q相切;(3)如图3,①当点M、N在两条直线交点的下方时,由题意得:MQ=NQ,∠MQN=90°,设点Q的坐标为(m,3m﹣3),则点N(m,m+3),则NQ=m+3﹣3m+3=2,解得:m=3﹣;②当点M、N在两条直线交点的上方时,同理可得:m=3;故点Q的坐标为(3﹣,6﹣3)或(3+,6+3).。
2020年广东中考英语冲刺训练(一)(含答案)

2020年广东中考英语冲刺训练(一)笔试部分二、语法选择(本大题有10小题,每小题1分,共10分)When we think of the Arctic (北极), some people may imagine an icy land of pure white snow, ____31____ imagine it as the last really clean place left on Earth. We have polluted the ____31____ ocean with plastic trash, and now, CNN says, “It's the Arctic's turn.”Recently, German scientists ____33____ microplastics (微塑料) in Arctic snow. Microplastics are pieces of plastic smaller than 5 millimeters. ____34____, the scientists found 1,800 pieces of microplastic per liter of snow.How is plastic pollution reaching the Arctic? According to scientists, “It's apparent (显然的) that most of them come from the air.” They ____35____ by the wind, just like dust. They ____36____ ice in the air and fall to the ground as snow.Are they bad ____37____ us? Scientists cannot answer this question for now. We do know that our bodies cannot take in “large” pieces of microplastics. However, if the plastics are ____38____, they can find ways into our bodies and stay there for a long time, which can be bad for our ____39____.Microplastics have also been found in rivers and oceans around the world. They start in our wastewater, then flow into rivers and out to sea, where they are eaten by sea animals. ____40____ people eat these animals, it means that we're eating the plastic as well.()31. A. other B. others C. another D. the other()32. A. deep B. deeper C. deepest D. most deep()33. A. find B. found C. has found D. have found()34. A. SadlyB. Luckily C. Excitedly D. Happily()35. A. moveB. movesC. are moving D. are moved()36. A. come up with B. mix with C. deal with D. go along with()37. A. to B. for C. with D. at()38. A. small enough B. enough small C. big enough D. enough big()39. A. healthB. healthy C. unhealthy D. healthily()40. A. Although B. If C. Unless D. Because三、完形填空(本大题有10小题,每小题1分,共10分)One day, a young man Gary asked his father why he wasn't able to reach all of his goals. With a smile, his father li stened ____41____ Gary's story and told him, “Come to help me boil a kettle(水壶)of water!”Gary saw a big kettle ____42____ next to small stove(火炉). He ____43____ the kettle with water andstarted with a fire. The kettle was too ____44____ when the wood burned up, the water did not boil. He ran out to get ____45____wood.When he returned, the water had ____46____ turned cold. “How can I boil the water?” He asked himself. Then he learned his____47____ and prepared more wood in advance(预先). Then the water boiled quickly.“If there is not enough wood, ____48____ would you boil the water?” his father asked. Gary thought for a moment, but shook his head.“Well, then just pour out some water!” his father said. Gary ____49____thoughtfully.“At first, you set too many goals,” said his father. “It's just like the large kettle full of water. You didn't have enough wood, ____50____ you couldn't boil the water. If you want to make the water boil, then you will have to either pour some out or prepare more wood!”()41. A. on B. for C. with D. to()42. A. falling B. standing C. burning D. climbing()43. A. took B. connectedC. failed D. protected()44. A. heavy B. large C. long D. thick()45. A. more B. less C. easier D. better()46. A. ever B. never C. only D. almost()47. A. lesson B. problem C. difficulty D. goal()48. A. how B. what C. why D. where()49. A. received B. asked C. nodded D. spoke()50. A. and B. or C. but D. so四、阅读理解(本大题有15小题,每小题2分,共30分)APeople know the dangers of fires. It's good for a family to learn how to prepare for a fire. Here are suggestions:Put a smoke alarm (烟雾警报器) in the house. Smoke from a fire causes the alarm to go off. The alarm makes a loud sound. The sound tells everyone to leave the house at once.Make escape plans. They should know all the ways out of the house. If there is a fire, everyone follows the plan to get out. Part of the plan is to check all the windows to make sure they can be opened easily.Buy fire extinguishers (灭火器) in the house. Everyone in the family should know how to use them.Practice for a fire. They do fire practice because they teach children about fire safety. Everyone in the family should know the following fire rules:★ Don't open a hot door! The fire can grow more quickly if you open the door.★ Stay close to the floor! Smoke can be more dangerous than fire. The best air is near the floor because smoke rises.★ What will you do if your hair or clothes start to burn? First, stop! Don't run! The fire burns faster because of more air. Drop! Fall to the floor. Then roll (滚动)! Turning over and over will make the fire go out. Put a blanket around you to keep air away from the fire that may still be on you.There are many possible causes for fires. A wise family is ready all the time. If there is a fire, don't forget to call 119 for help.()51. What does it mean when a smoke alarm rings at home?A. You have to get up.B. Something is burning.C. Water is running to the floor.D. Someone breaks your window.()52. The writer advises people to do the following to prepare for a fire EXCEPT that ________.A. they practice for a fireB. they make escape plansC. they use electrical cookersD. they buy fire extinguishers()53. When a fire happens, ________if you open the hot door.A. the house will fall downB. the electricity will be cut offC. the door will soon be on fireD. the fire will grow more quickly()54. What are the right steps you should take when your hair or clothes catch fire?A. Stop, drop, roll.B. Stop, run, roll.C. Run, drop, roll.D. Roll, drop, stop.()55. What is the best title for this passage?A. The Dangers of a FireB. Be Ready for a FireC. The Causes of a FireD. Learn to Use a Fire ExtinguisherBHow quickly can you count from one to ten? Do you use ten different words to do it? Can you do it in English or do you have to use your first language? Do you count on your fingers? Many people think that numbers and math are the same all over the world. But scientists have discovered that it is not true.People in different parts of the world use different ways to count on their fingers. In the United States, people begin counting with their first finger which they extend or stick out. They then extend the rest of their fingers and finally the thumb to count to five. Then they repeat this with the other hand to get to ten. In China, people countby using different finger positions. In this way, a Chinese person can easily count to ten on only one hand.Besides ways of finger counting, scientists have found that cultures and languages are also different when it comes to numbers. Some languages have only a few words for numbers and others have no words for numbers. A group of scientists studied aboriginal(土著的)people in Australia. These people don't have hand movements to stand for numbers. They don't even have words for numbers. However, they are still able to understand different ideas about numbers.In a similar study, researchers from the Massachusetts Institute of Technology discovered that people of the Piraha tribe(部落)in northwestern Brazil don't have words for numbers, such as “one” or “three”. They are not able to say “five trees” or “ten trees”, but can say “some trees”, “more trees” or “many trees”. Professor Edward Gibson said that most people believe that everyone knows how to count, “But here is a group that does not count. They could learn, but it's not useful in their culture, so they've never picked it up. ”Although all humans are able to understand quantities(数量), not all languages have numbers and not all people use counting. Number words in a certain language are a result of people needing numbers in their daily lives. Now we know that people have different ideas about numbers and math, too.()56. The writer begins with the four questions in order to ________.A. make a surveyB. interest readersC. tell a storyD. solve math problems()57. What do we learn from the difference in finger counting between the U. S. and China?A. People from China count much faster than people from the U. S.B. People from China need two hands to count from one to ten.C. People from the U. S. count to ten with two hands.D. People of different cultures use the same way of finger counting.()58. Which of the following is TRUE about aboriginal Australians?A. They have only a few words for numbers.B. They have hand movements to stand for numbers.C. They can only count to five on their fingers.D. They can understand different ideas about numbers.()59. What is the meaning of underlined (划线) phrases “picked up”?A. 捡起来B. 使用C. 学习D. 交流()60. What's the main idea of the passage?A. People from different cultures have different ideas about numbers and math.B. Chinese people can count more easily on their fingers than Americans.C. In some aboriginal cultures, people don't even know how to count.D. Some languages don't have number words because people don't need numbers.C配对阅读。
2020年广东省深圳市龙岗区中考数学复习试卷(9)

中考数学复习试卷题号一二三总分得分一、选择题(本大题共12小题,共36.0分)1.的立方根是()A. -4B. ±4C. ±2D. -22.国务院总理李克强在《2017年国务院政府工作报告》中提到,2016年新增第四代移动通信用户3.4亿,数据“3.4亿”用科学记数法表示为()A. 3.4×106B. 3.4×108C. 34×107D. 3.4×1093.如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数,则该几何体的左视图是()A. B. C. D.4.关于x的一元二次方程kx2-4x+1=0有两个不相等的实数根,则k的取值范围是()A. k>4B. k<4C. k<4且k≠0D. k≤4且k≠05.成绩/m 1.50 1.60 1.65 1.70 1.75 1.80人数232341则这些运动员成绩的中位数、众数分别为()A. 1.65、1.70B. 1.65、1.75C. 1.70、1.75D. 1.70、1.706.平面直角坐标系中,已知A(1,2)、B(3,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是()A. 5B. 6C. 7D. 87.某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是()A. -=4B. -=4C. -=4D. -=48.如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则+++…+的值为()A. B. C. D.9.如图,AB∥CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=()A. 30°B. 40°C. 50°D. 60°10.如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:①2b-c=2;②a=;③ac=b-1;④>0其中正确的个数有()A. 1个B. 2个C. 3个D. 4个11.如图,将正方形ABCD折叠,使点A与CD边上的点H重合(H不与C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD周长为m,△CHG周长为n,则为()A.B. 2C.D.12.如图,点A、B在双曲线(x<0)上,连接OA、AB,以OA、AB为边作▱OABC.若点C恰落在双曲线(x>0)上,此时▱OABC的面积为()A.B.C.D. 4二、填空题(本大题共4小题,共12.0分)13.因式分解:-2x2+4xy+30y2=______.14.若关于x的分式方程=的解为非负数,则a的取值范围是______.15.如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为______.16.如图,菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为______.三、解答题(本大题共7小题,共52.0分)17.计算:18.先化简,再求值:(x-1+)÷,其中x的值从不等式组的整数解中选取.19.重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.(1)扇形统计图中九年级参赛作文篇数对应的圆心角是______度,并补全条形统计图;(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.20.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?21.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.22.如图1,在直角坐标系中,直线l与x、y轴分别交于点A(2,0)、B(0,)两点,∠BAO的角平分线交y轴于点D.点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.(1)求出⊙G的半径r,并直接写出点C的坐标;(2)如图2,若点F为⊙G上的一点,连接AF,且满足∠FEA=45°,请求出EF的长?23.已知,抛物线y=ax2+bx+3(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=.(1)求抛物线的解析式及顶点D的坐标;(2)求证:直线DE是△ACD外接圆的切线;(3)在直线AC上方的抛物线上找一点P,使S△ACP=S△ACD,求点P的坐标;(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.答案和解析1.【答案】D【解析】解:∵=-8∴-8的立方根是-2,∴的立方根是-2.故选:D.首先根据立方根的定义计算出的结果,然后利用立方根的定义求解即可.此题主要考查了立方根定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.2.【答案】B【解析】解:3.4亿=3.4×108.故选:B.用科学记数法表示较大的数时,一般形式为a×10-n,其中1≤|a|<10,n为整数,n的值取决于原数变成a时,小数点移动的位数,n的绝对值与小数点移动的位数相同.当原数绝对值大于1时,n是正数;当原数的绝对值小于1时,n是负数.此题主要考查了用科学记数法表示较大的数,一般形式为a×10-n,其中1≤|a|<10,确定a与n的值是解题的关键.3.【答案】D【解析】解:该几何体的左视图是:.故选:D.根据俯视图中每列正方形的个数,再画出从正面,左面看得到的图形即可.此题主要考查了画几何体的三视图;用到的知识点为:主视图,左视图分别是从物体的正面,左面看得到的图形;看到的正方体的个数为该方向最多的正方体的个数.4.【答案】C【解析】解:∵kx2-4x+1=0有两个不相等的实数根,∴△=16-4k>0,且k≠0,解得,k<4且k≠0.故选:C.根据一元二次方程kx2-4x+1=0有两个不相等的实数根,知△=b2-4ac>0,然后据此列出关于k的不等式,解不等式即可.本题主要考查了一元二次方程的根的判别式.解题时,注意一元二次方程的“二次项系数不为0”这一条件.5.【答案】C【解析】解:共15名学生,中位数落在第8名学生处,第8名学生的跳高成绩为1.70m,故中位数为1.70;跳高成绩为1.75m的人数最多,故跳高成绩的众数为1.75;故选:C.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.本题为统计题,考查众数与中位数的意义.众数是一组数据中出现次数最多的数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.6.【答案】C【解析】解:∵点A、B的坐标分别为(1,2)、B(3,0).∴AB=2,①若AC=AB,以A为圆心,AB为半径画弧与坐标轴有3个交点(B点除外),即(-1,0)、(2+,0)、(0,2-),即满足△ABC是等腰三角形的C点有3个;②若BC=AB,以B为圆心,BA为半径画弧与坐标轴有2个交点,即满足△ABC是等腰三角形的C点有2个;③若CA=CB,作AB的垂直平分线与坐标轴有2个交点,即满足△ABC是等腰三角形的C点有2个.综上所述:点C在坐标轴上,△ABC是等腰三角形,符合条件的点C共有7个.故选:C.由点A、B的坐标可得到AB=2,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.本题主考查了等腰三角形的判定以及分类讨论思想的运用,分三种情况分别讨论,注意等腰三角形顶角的顶点在底边的垂直平分线上.7.【答案】D【解析】解:设他上月买了x本笔记本,则这次买了(x+20)本,根据题意得:-=4.故选:D.由设第一次买了x本资料,则设第二次买了(x+20)本资料,由等量关系:第二次比第一次每本优惠4元,即可得到方程.此题考查了由实际问题抽象出分式方程.找到关键描述语,找到合适的等量关系是解决问题的关键.8.【答案】A【解析】解:观察图形,可知:a1=2+1=3=1×3,a2=2+3+2+1=8=2×4,a3=2+3+4+3+2+1=15=3×5,a4=2+3+4+5+4+3+2+1=24=4×6,…,∴a n=n(n+2),∴+++…+=+++…+,=×(1-+-+-+…+-),=×(1+--),=×,=.故选:A.观察图形,根据各图形中“●”个数的变化可找出变化规律“a n=n(n+2)”,再将其代入(+++…+)中即可求出结论.本题考查了规律型:图形的变化类,根据各图形中“●”个数的变化,找出变化规律“a n=n(n+2)”是解题的关键.9.【答案】D【解析】解:∵EC=EA.∠CAE=30°,∴∠C=30°,∴∠AED=30°+30°=60°.∵AB∥CD,∴∠BAF=∠AED=60°.故选:D.先根据EC=EA.∠CAE=30°得出∠C=30°,再由三角形外角的性质得出∠AED的度数,利用平行线的性质即可得出结论.本题考查的是平行线的性质,熟知两直线平行,同位角相等是解答此题的关键.10.【答案】C【解析】解:据图象可知a>0,c<0,b>0,∴<0,故④错误;∵OB=OC,∴OB=-c,∴点B坐标为(-c,0),∴ac2-bc+c=0,∴ac-b+1=0,∴ac=b-1,故③正确;∵A(-2,0),B(-c,0),抛物线线y=ax2+bx+c与x轴交于A(-2,0)和B(-c,0)两点,∴2c=,∴2=,∴a=,故②正确;∵ac-b+1=0,∴b=ac+1,a=,∴b=c+1∴2b-c=2,故①正确;故选:C.根据抛物线的开口方向,对称轴公式以及二次函数图象上点的坐标特征来判断a、b、c 的符号以及它们之间的数量关系,即可得出结论.本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.11.【答案】B【解析】解:连接AH、AG,作AM⊥HG于M.∵四边形ABCD是正方形,∴AD=AB.∴AM=AB.∵EA=EH,∴∠1=∠2,∵∠EAB=∠EHG=90°,∴∠HAB=∠AHG,∵DH∥AB,∴∠DHA=∠HAB=∠AHM,在△AHD和△AHM中,∴△AHD≌△AHM(AAS),∴DH=HM,AD=AM,在Rt△AGM和Rt△AGB中,,∴Rt△AGM≌Rt△AGB(HL),∴GM=GB,∴△GCH的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC,∵四边形ABCD的周长=m=4BC,∴=2;故选:B.连接AH、AG,作AM⊥HG于M.证明△AHD≌△AHM(AAS),得出DH=HM,AD=AM,证明Rt△AGM≌Rt△AGB(HL),得出GM=GB,求出△GCH的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC,由四边形ABCD的周长=m=4BC,即可得出答案.本题考查翻折变换及正方形的性质,全等三角形的判定与性质等知识;证明三角形全等是解题的关键.12.【答案】B【解析】解:如图,连接AC,过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,则△ABF≌△COE,设A(a,-),C(b,),则OE=BF=b,CE=AF=,∴B(a+b,-+),又∵点B在双曲线y=-(x<0)上,∴(a+b)(-+)=-3,∴-=2,设=x,则方程-=2可化为3x-=2,解得x=或x=(舍去),∴=,=,∴平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC-S△AOD-S△COE)=2[(-+)(b-a)-×|-3|-×|2|]=-+3+2--5=-3×-2×(-)=2.故选:B.先过A作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,设A(a,-),C (b,),依据△ABF≌△COE,可得B(a+b,-+),根据点B在双曲线y=-(x<0)上,可得B(a+b)(-+)=-3,设=x,则方程-=2可化为3x-=2,进而得到=,=,最后根据平行四边形OABC的面积=2×S△OAC=2(S梯形ADEC-S△AOD-S△COE),进行计算即可.本题考查了反比例函数比例系数k的几何意义以及反比例函数图象上点的坐标特征,解题时注意:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.解决问题的关键是换元思想以及数形结合思想的运用.13.【答案】-2(x+3y)(x-5y)【解析】解:原式=-2(x2-2xy-15y2)=-2(x+3y)(x-5y).故答案为:-2(x+3y)(x-5y).先提公因式,再利用十字相乘法分解即可.此题考查了提公因式法与十字相乘法的综合运用,熟练掌握因式分解的方法是解本题的关键.14.【答案】a>1,且a≠4【解析】解:两边同时乘以2(x-2),得:4x-2a=x-2,解得x=,由题意可知,x≥0,且x≠2,∴,解得:a≥1,且a≠4,故答案为:a≥1,且a≠4.在方程的两边同时乘以2(x-2),解方程,用含a的式子表示出x的值,再根据x≥0,且x≠2,解不等于组即可.本题主要考查分式方程的解,解决此类问题时,通常先用含a的式子表示出x的值,再根据x的取值范围即可求出a的取值范围,但要注意分式的最简公分母不等于0.15.【答案】(,)【解析】解:如图,过点D作DM⊥x轴于点M,∵四边形AOBC是矩形,∠ABO=30°,点B的坐标为(0,3),∴AC=OB=3,∠CAB=30°,∴BC=AC•tan30°=3×=,∵将△ABC沿AB所在直线对折后,点C落在点D处,∴∠BAD=30°,AD=3,∵∠CAB=∠BAD=30°,∴∠DAM=30°,∴DM=AD=,∴AM=3×cos30°=,∴MO=-=,∴点D的坐标为(,).故答案为:(,).根据翻折变换的性质结合锐角三角函数关系得出对应线段长,进而得出D点坐标.此题主要考查了翻折变换以及矩形的性质和锐角三角函数关系,正确得出∠DAM=30°是解题关键.16.【答案】2【解析】解:如图,∵AB=4,∠A=120°,∴点P′到CD的距离为4×=2,∴PK+QK的最小值为2.故答案为:2.根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连接P′Q与BD的交点即为所求的点K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值,然后求解即可.本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.17.【答案】解:原式=2×-3+1-9=1-3+1-9=-10.【解析】直接利用特殊角的三角函数值以及负整数指数幂的性质和零指数幂的性质分别化简得出答案.此题主要考查了实数运算,正确化简各数是解题关键.18.【答案】解:原式=(+)÷=•=•=,解不等式组得:-1≤x<,∴不等式组的整数解有-1、0、1、2,∵分式有意义时x≠±1、0,∴x=2,则原式=0.【解析】本题主要考查分式的化简求值及解一元一次不等式组的能力,熟练掌握分式的混合运算顺序和法则及解不等式组的能力、分式有意义的条件是解题的关键.先根据分式的混合运算顺序和法则化简原式,再求出不等式组的整数解,由分式有意义得出符合条件的x的值,代入求解可得.19.【答案】(1)126;(2)假设4篇荣获特等奖的作文分别为A、B、C、D,共有12种可能性结果,它们发生的可能性相等,其中七年级特等奖作文被选登在校刊上的可能性有6种,∴P(七年级特等奖作文被选登在校刊上)==.【解析】解:(1)20÷20%=100,九年级参赛作文篇数对应的圆心角=360°×=126°;故答案为:126;100-20-35=45,补全条形统计图如图所示:(2)见答案.(1)求出总的作文篇数,即可得出九年级参赛作文篇数对应的圆心角的度数;求出八年级的作文篇数,补全条形统计图即可:(2)假设4篇荣获特等奖的作文分别为A、B、C、D,其中A代表七年级获奖的特等奖作文.树状图即可得出答案.此题考查了扇形统计图和条形统计图、列表法与树状图法的应用;从统计图中、扇形图中获取信息、画出树状图是解决问题的关键.20.【答案】解:(1)当x=20时,y=-10x+500=-10×20+500=300,300×(12-10)=300×2=600元,即政府这个月为他承担的总差价为600元.(2)由题意得,w=(x-10)(-10x+500)=-10x2+600x-5000=-10(x-30)2+4000∵a=-10<0,∴当x=30时,w有最大值4000元.即当销售单价定为30元时,每月可获得最大利润4000元.(3)由题意得:-10x2+600x-5000=3000,解得:x1=20,x2=40.∵a=-10<0,抛物线开口向下,∴结合图象可知:当20≤x≤40时,4000>w≥3000.又∵x≤25,∴当20≤x≤25时,w≥3000.设政府每个月为他承担的总差价为p元,∴p=(12-10)×(-10x+500)=-20x+1000.∵k=-20<0.∴p随x的增大而减小,∴当x=25时,p有最小值500元.即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.【解析】(1)把x=20代入y=-10x+500求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;(2)由总利润=销售量•每件纯赚利润,得w=(x-10)(-10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;(3)令-10x2+600x-5000=3000,求出x的值,结合图象求出利润的范围,然后设政府每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解,此题难度不大.21.【答案】解:(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°,∵∠EAF=∠GAC,∴∠AED=∠ACB,∵∠EAD=∠BAC,∴△ADE∽△ABC,(2)由(1)可知:△ADE∽△ABC,∴=由(1)可知:∠AFE=∠AGC=90°,∴∠EAF=∠GAC,∴△EAF∽△CAG,∴,∴=.【解析】本题考查相似三角形的判定与性质,解题的关键是熟练运用相似三角形的判定,本题属于中等题型.(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;(2)△ADE∽△ABC,,又易证△EAF∽△CAG,所以,从而可知.22.【答案】解:(1)连接GD,EC.∵∠OAB的角平分线交y轴于点D,∴∠GAD=∠DAO,∵GD=GA,∴∠GDA=∠GAD,∴∠GDA=∠DAO,∴GD∥OA,∴∠BDG=∠BOA=90°,∵GD为半径,∴y轴是⊙G的切线;∵A(2,0),B(0,),∴OA=2,OB=,在Rt△AOB中,由勾股定理可得:AB===设半径GD=r,则BG=-r,∵GD∥OA,∴△BDG∽△BOA,∴=,∴r=2(-r),∴r=,∵AC是直径,∴∠AEC=∠AOB=90°,∴EC∥OB,∴==,∴==,∴EC=2,AE=,∴OE=2-=,∴C的坐标为(,2);(2)过点A作AH⊥EF于H,连接CE、CF,∵AC是直径,∴AC=2×=∴∠AEC=∠AFC=90°∵∠FEA=45°∴∠FCA=45°∴在Rt△AEH中,由勾股定理可知:AF=CF=,设OE=a∴AE=2-a∵CE∥OB∴△ACE∽△ABO∴=,∴CE=,∵CE2+AE2=AC2,∴(2-a)2+(2-a)2=∴a=或a=(不合题意,舍去)∴AE=∴在Rt△AEH中,由勾股定理可得,AH=EH=,∴在Rt△AEH中,由勾股定理可知:FH2=AF2-AH2=()2-()2=2,∴FH=,∴EF=EH+FH=.【解析】(1)要证明y轴是⊙G的切线,只需要连接GD后证明GD⊥OB即可,推出GD∥OA,则△BDG∽△BOA,设半径为r后,利用对应边的比相等列方程即可求出半径r的值.(2)由于∠FEA=45°,所以可以连接CE、CF构造直角三角形.由于要求的EF是弦,所以过点A作AH⊥EF,然后利用垂径定理即可求出EF的长度.此题属于圆的综合题,涉及了切线的判定、相似三角形的判定与性质、勾股定理的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来,灵活运用.23.【答案】解:(1)∵抛物线的对称轴是直线x=1,点A(3,0),∴根据抛物线的对称性知点B的坐标为(-1,0),OA=3,将A(3,0),B(-1,0)代入抛物线解析式中得:,解得:,∴抛物线解析式为y=-x2+2x+3;当x=1时,y=4,∴顶点D(1,4).(2)当x=0时,∴点C的坐标为(0,3),∴AC==3,CD==,AD==2,∴AC2+CD2=AD2,∴△ACD为直角三角形,∠ACD=90°.∴AD为△ACD外接圆的直径,∵点E在轴C点的上方,且CE=.∴E(0,)∴AE==DE==,∴DE2+AD2=AE2,∴△AED为直角三角形,∠ADE=90°.∴AD⊥DE,又∵AD为△ACD外接圆的直径,∴DE是△ACD外接圆的切线;(3)设直线AC的解析式为y=kx+b,根据题意得:,解得:,∴直线AC的解析式为y=-x+3,∵A(3,0),D(1,4),∴线段AD的中点N的坐标为(2,2),过点N作NP∥AC,交抛物线于点P,设直线NP的解析式为y=-x+c,则-2+c=2,解得:c=4,∴直线NP的解析式为y=-x+4,由y=-x+4,y=-x2+2x+3联立得:-x2+2x+3=-x+4,解得:x=或x=,∴y=,或y=∴P(,)或(,);(4)分三种情况:①M恰好为原点,满足△CMB∽△ACD,M(0,0);②M在x轴正半轴上,△MCB∽△ACD,此时M(9,0);③M在y轴负半轴上,△CBM∽△ACD,此时M(0,-);综上所述,点M的坐标为(0,0)或(9,0)或(0,-).【解析】(1)由对称轴求出B的坐标,由待定系数法求出抛物线解析式,即可得出顶点D的坐标;(2)由勾股定理和勾股定理的逆定理证出△ACD为直角三角形,∠ACD=90°.得出AD 为△ACD外接圆的直径,再证明△AED为直角三角形,∠ADE=90°.得出AD⊥DE,即可得出结论;(3)求出直线AC的解析式,再求出线段AD的中点N的坐标,过点N作NP∥AC,交抛物线于点P,求出直线NP的解析式,与抛物线联立,即可得出答案;(4)由相似三角形的性质和直角三角形的性质即可得出答案.本题是二次函数综合题目,考查了待定系数法求二次函数和一次函数的解析式、勾股定理、勾股定理的逆定理、切线的判定、相似三角形的性质等知识;本题综合性强,有一定难度.。
2020年广东省深圳市龙岗中考数学模拟试卷含解析

2020年广东省深圳市龙岗区布吉中学中考数学复习试卷一、选择题(3*12=36)1.(3分)计算﹣32的结果是()A.9B.﹣9C.6D.﹣62.(3分)太阳的半径约为696000km,把696000这个数用科学记数法表示为()A.6.96×103B.69.6×105C.6.96×105D.6.96×1063.(3分)如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°4.(3分)下列计算正确的是()A.a3÷a2=a3•a﹣2B.C.2a2+a2=3a4D.(a﹣b)2=a2﹣b25.(3分)为了考察某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:cm)为:169141112101681719则这组数据的中位数和极差分别是()A.13,16B.14,11C.12,11D.13,116.(3分)下列说法正确的是()A.平分弦的直径垂直于弦B.半圆(或直径)所对的圆周角是直角C.相等的圆心角所对的弧相等D.若两个圆有公共点,则这两个圆相交7.(3分)地球正面临第六次生物大灭绝,据科学家预测,到2050年,目前的四分之一到一半的物种将会灭绝或濒临灭绝,2012年底,长江江豚数量仅剩约1000头,其数量年平均下降的百分率在13%~15%范围内,由此预测,2013年底剩下江豚的数量可能为()头.A.970B.860C.750D.7208.(3分)式子2cos30°﹣tan45°﹣的值是()A.2﹣2B.0C.2D.29.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为()A.B.C.D.10.(3分)如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是()A.8B.9C.16D.1711.(3分)张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是()A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25B.途中加油21升C.汽车加油后还可行驶4小时D.汽车到达乙地时油箱中还余油6升12.(3分)如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x >﹣1时,y>0,其中正确结论的个数是()A.5个B.4个C.3个D.2个二、填空题(3*4=12)13.(3分)用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为cm.14.(3分)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米.15.(3分)如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是,破译“正做数学”的真实意思是.16.(3分)著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为cm.三、解答题(总共52分)17.(5分)先化简,再求值:,其中,a=1+,b=1﹣.18.(5分)直线y=2x+b经过点(3,5),求关于x的不等式2x+b≥0的解集.19.(6分)如图,暑假快要到了,某市准备组织同学们分别到A,B,C,D四个地方进行夏令营活动,前往四个地方的人数.(1)去B地参加夏令营活动人数占总人数的40%,根据统计图求去B地的人数?(2)若一对姐弟中只能有一人参加夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.用列表法或树形图分析这种方法对姐弟俩是否公平?20.(7分)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:DP∥AB;(2)试猜想线段AE,EF,BF之间有何数量关系,并加以证明;(3)若AC=6,BC=8,求线段PD的长.21.(8分)为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.人均住房面积(平方米)单价(万元/平方米)不超过30(平方米)0.3超过30平方米不超过m(平方米)部分(45≤m≤60)0.5超过m平方米部分0.7根据这个购房方案:(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.22.(9分)如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(2)如图2,若点E在线段BC上滑动(不与点B,C重合).①AE=EF是否总成立?请给出证明;②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=﹣x2+x+1上,求此时点F的坐标.23.(12分)如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.(1)求抛物线与x轴的另一个交点B的坐标;(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.①当t为秒时,△P AD的周长最小?当t为秒时,△P AD是以AD为腰的等腰三角形?(结果保留根号)②点P在运动过程中,是否存在一点P,使△P AD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.2020年广东省深圳市龙岗区布吉中学中考数学复习试卷参考答案与试题解析一、选择题(3*12=36)1.(3分)计算﹣32的结果是()A.9B.﹣9C.6D.﹣6【分析】根据有理数的乘方的定义解答.【解答】解:﹣32=﹣9.故选:B.2.(3分)太阳的半径约为696000km,把696000这个数用科学记数法表示为()A.6.96×103B.69.6×105C.6.96×105D.6.96×106【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将696000用科学记数法表示为6.96×105.故选:C.3.(3分)如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°【分析】首先根据同位角相等,两直线平行可得a∥b,再根据平行线的性质可得∠3=∠5,再根据邻补角互补可得∠4的度数.【解答】解:∵∠1=∠2,∴a∥b,∴∠3=∠5,∵∠3=40°,∴∠5=40°,∴∠4=180°﹣40°=140°,故选:C.4.(3分)下列计算正确的是()A.a3÷a2=a3•a﹣2B.C.2a2+a2=3a4D.(a﹣b)2=a2﹣b2【分析】根据合并同类项的法则、同底数幂的乘除法则及幂的乘方法则,结合各选项进行判断即可.【解答】解:A、a3÷a2=a3•a﹣2,计算正确,故本选项正确;B、=|a|,计算错误,故本选项错误;C、2a2+a2=3a2,计算错误,故本选项错误;D、(a﹣b)2=a2﹣2ab+b2,计算错误,故本选项错误;故选:A.5.(3分)为了考察某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:cm)为:169141112101681719则这组数据的中位数和极差分别是()A.13,16B.14,11C.12,11D.13,11【分析】根据中位数及极差的定义,结合所给数据即可作出判断.【解答】解:将数据从小到大排列为:8,9,10,11,12,14,16,16,17,19,中位数为:13;极差=19﹣8=11.故选:D.6.(3分)下列说法正确的是()A.平分弦的直径垂直于弦B.半圆(或直径)所对的圆周角是直角C.相等的圆心角所对的弧相等D.若两个圆有公共点,则这两个圆相交【分析】利用圆与圆的位置关系、垂径定理、圆周角定理等有关圆的知识进行判断即可【解答】解:A、平分弦(不是直径)的直径垂直于弦,故本选项错误;B、半圆或直径所对的圆周角是直角,故本选项正确;C、同圆或等圆中,相等的圆心角所对的弧相等,故本选项错误;D、两圆有两个公共点,两圆相交,故本选项错误,故选:B.7.(3分)地球正面临第六次生物大灭绝,据科学家预测,到2050年,目前的四分之一到一半的物种将会灭绝或濒临灭绝,2012年底,长江江豚数量仅剩约1000头,其数量年平均下降的百分率在13%~15%范围内,由此预测,2013年底剩下江豚的数量可能为()头.A.970B.860C.750D.720【分析】根据2012年底,长江江豚数量仅剩约1000头,其数量年平均下降的百分率在13%~15%范围内,得出2013年底剩下江豚的数量的取值范围.【解答】解:设2013年底剩下江豚的数量为x头,∵2012年底,长江江豚数量仅剩约1000头,其数量年平均下降的百分率在13%~15%范围内,∴2013年底剩下江豚的数量可能为,解得:850<x<870,∴2013年底剩下江豚的数量可能为860头;故选:B.8.(3分)式子2cos30°﹣tan45°﹣的值是()A.2﹣2B.0C.2D.2【分析】将特殊角的三角函数值代入求解.【解答】解:原式=2×﹣1﹣|﹣1|=﹣1﹣(﹣1)=0.故选:B.9.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为()A.B.C.D.【分析】先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.【解答】解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB===5,过C作CM⊥AB,交AB于点M,如图所示,∵CM⊥AB,∴M为AD的中点,∵S△ABC=AC•BC=AB•CM,且AC=3,BC=4,AB=5,∴CM=,在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+()2,解得:AM=,∴AD=2AM=.故选:C.10.(3分)如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是()A.8B.9C.16D.17【分析】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,进而得出即可.【解答】解:由图可知:第一个图案有三角形1个.第二图案有三角形1+3=4个.第三个图案有三角形1+3+4=8个,第四个图案有三角形1+3+4+4=12第五个图案有三角形1+3+4+4+4=16故选:C.11.(3分)张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是()A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25 B.途中加油21升C.汽车加油后还可行驶4小时D.汽车到达乙地时油箱中还余油6升【分析】A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y =kt+b,将(0,25),(2,9)代入,运用待定系数法求解后即可判断;B、由题中图象即可看出,途中加油量为30﹣9=21升;C、先求出每小时的用油量,再求出汽车加油后行驶的路程,然后与4比较即可判断;D、先求出汽车从甲地到达乙地需要的时间,进而得到需要的油量;然后用汽车油箱中原有的油量加上途中的加油量,再减去汽车行驶500千米需要的油量,得出汽车到达乙地时油箱中的余油量即可判断.【解答】解:A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b.将(0,25),(2,9)代入,得,解得,所以y=﹣8t+25,故A选项正确,但不符合题意;B、由图象可知,途中加油:30﹣9=21(升),故B选项正确,但不符合题意;C、由图可知汽车每小时用油(25﹣9)÷2=8(升),所以汽车加油后还可行驶:30÷8=3<4(小时),故C选项错误,但符合题意;D、∵汽车从甲地到达乙地,所需时间为:500÷100=5(小时),∴5小时耗油量为:8×5=40(升),又∵汽车出发前油箱有油25升,途中加油21升,∴汽车到达乙地时油箱中还余油:25+21﹣40=6(升),故D选项正确,但不符合题意.故选:C.12.(3分)如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x >﹣1时,y>0,其中正确结论的个数是()A.5个B.4个C.3个D.2个【分析】由抛物线的对称轴在y轴右侧,可以判定a、b异号,由此确定①正确;由抛物线与x轴有两个交点得到b2﹣4ac>0,又抛物线过点(0,1),得出c=1,由此判定②正确;由抛物线过点(﹣1,0),得出a﹣b+c=0,即a=b﹣1,由a<0得出b<1;由a<0,及ab<0,得出b>0,由此判定④正确;由a﹣b+c=0,及b>0得出a+b+c=2b>0;由b<1,c=1,a<0,得出a+b+c<a+1+1<2,由此判定③正确;由图象可知,当自变量x的取值范围在一元二次方程ax2+bx+c=0的两个根之间时,函数值y>0,由此判定⑤错误.【解答】解:∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(﹣1,0),∴c=1,a﹣b+c=0.①∵抛物线的对称轴在y轴右侧,∴x=﹣>0,∴a与b异号,∴ab<0,正确;②∵抛物线与x轴有两个不同的交点,∴b2﹣4ac>0,∵c=1,∴b2﹣4a>0,b2>4a,正确;④∵抛物线开口向下,∴a<0,∵ab<0,∴b>0.∵a﹣b+c=0,c=1,∴a=b﹣1,∵a<0,∴b﹣1<0,b<1,∴0<b<1,正确;③∵a﹣b+c=0,∴a+c=b,∴a+b+c=2b>0.∵b<1,c=1,a<0,∴a+b+c=a+b+1<a+1+1=a+2<0+2=2,∴0<a+b+c<2,正确;⑤抛物线y=ax2+bx+c与x轴的一个交点为(﹣1,0),设另一个交点为(x0,0),则x0>0,由图可知,当x0>x>﹣1时,y>0,错误;综上所述,正确的结论有①②③④.故选:B.二、填空题(3*4=12)13.(3分)用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为8cm.【分析】根据圆的周长公式和扇形的弧长公式解答.【解答】解:如图:圆的周长即为扇形的弧长,列出关系式解答:=2πx,又∵n=216,r=10,∴(216×π×10)÷180=2πx,解得x=6,h==8.故答案为:8cm.14.(3分)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为750米.【分析】作AD⊥BC于D,根据速度和时间先求得AC的长,在Rt△ACD中,求得∠ACD 的度数,再求得AD的长度,然后根据∠B=30°求出AB的长.【解答】解:如图,过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75°﹣30°=45°,AC=30×25=750(米),∴AD=AC•sin45°=375(米).在Rt△ABD中,∵∠B=30°,∴AB=2AD=750(米).故答案为:750.15.(3分)如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是x+1,y+2,破译“正做数学”的真实意思是祝你成功.【分析】根据坐标中文字位置得出“今”所处的位置为(x,y),则对应文字位置是:(x+1,y+2),进而得出密码钥匙,即可得出“正做数学”的真实意思.【解答】解:∵已破译出“今天考试”的真实意思是“努力发挥”.“今”所处的位置为(x,y),则对应文字位置是:(x+1,y+2),∴找到的密码钥匙是:对应文字横坐标加1,纵坐标加2,∴“正”的位置为(4,2)对应字母位置是(5,4)即为“祝”,“做”的位置为(5,6)对应字母位置是(6,8)即为“你”,“数”的位置为(7,2)对应字母位置是(8,4)即为“成”,“学”的位置为(2,4)对应字母位置是(3,6)即为“功”,∴“正做数学”的真实意思是:祝你成功.故答案为:x+1,y+2;祝你成功.16.(3分)著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为10cm.【分析】连接OP,根据直角三角形斜边上的中线等于斜边的一半可得OP的长,画出的圆的半径就是OP长.【解答】解:连接OP,∵△AOB是直角三角形,P为斜边AB的中点,∴OP=AB,∵AB=20cm,∴OP=10cm,故答案为:10.三、解答题(总共52分)17.(5分)先化简,再求值:,其中,a=1+,b=1﹣.【分析】先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可【解答】解:原式=÷=÷=×=﹣,当a=1+,b=1﹣时,原式=﹣=﹣=﹣.18.(5分)直线y=2x+b经过点(3,5),求关于x的不等式2x+b≥0的解集.【分析】先把点(3,5)代入直线y=2x+b,求出b的值,再根据2x+b≥0即可得出x 的取值范围.【解答】解:∵直线y=2x+b经过点(3,5),∴5=2×3+b,解得b=﹣1,∵2x+b≥0,∴2x﹣1≥0,解得x≥.19.(6分)如图,暑假快要到了,某市准备组织同学们分别到A,B,C,D四个地方进行夏令营活动,前往四个地方的人数.(1)去B地参加夏令营活动人数占总人数的40%,根据统计图求去B地的人数?(2)若一对姐弟中只能有一人参加夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.用列表法或树形图分析这种方法对姐弟俩是否公平?【分析】(1)假设出去B地的人数为x,根据去B地参加夏令营活动人数占总人数的40%,进而得出方程求出即可;(2)根据已知列表得出所有可能,进而利用概率公式求出即可.【解答】解:(1)设去B地的人数为x,则由题意有:;解得:x=40.∴去B地的人数为40人.(2)列表:4(1,4)(2,4)(3,4)(4,4)3(1,3)(2,3)(3,3)(4,3)2(1,2)(2,2)(3,2)(4,2)1(1,1)(2,1)(3,1)(4,1)1234∴姐姐能参加的概率,弟弟能参加的概率为,∵<,∴不公平.20.(7分)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:DP∥AB;(2)试猜想线段AE,EF,BF之间有何数量关系,并加以证明;(3)若AC=6,BC=8,求线段PD的长.【分析】(1)连结OD,由AB为⊙O的直径,根据圆周角定理得AB为⊙O的直径得∠ACB=90°,再由ACD=∠BCD=45°,则∠DAB=∠ABD=45°,所以△DAB为等腰直角三角形,所以DO⊥AB,根据切线的性质得OD⊥PD,于是可得到DP∥AB;(2)根据圆周角定理易得∠ADE+∠BDF=90°=∠FBD+∠BDF=90°,从而得到∠FBD=∠ADE,易得AD=BD,从而得出△ADE≌△DBF,得到BF=DE,AE=DF,从而得出结论BF﹣AE=EF.(3)先根据勾股定理计算出AB=10,由于△DAB为等腰直角三角形,可得到AD==5;由△ACE为等腰直角三角形,得到AE=CE==3,在Rt△AED中利用勾股定理计算出DE=4,则CD=7,易证得∴△PDA∽△PCD,得到===,所以P A=PD,PC=PD,然后利用PC=P A+AC可计算出PD.【解答】(1)证明:连结OD,如图,∵AB为⊙O的直径,∴∠ACB=90°,∵∠ACB的平分线交⊙O于点D,∴∠ACD=∠BCD=45°,∴∠DAB=∠ABD=45°,∴△DAB为等腰直角三角形,∴DO⊥AB,∵PD为⊙O的切线,∴OD⊥PD,∴DP∥AB;(2)答:BF﹣AE=EF,证明如下:∵AB是⊙O的直径,∴∠ADB=∠ADE+∠BDF=90°,∵AE⊥CD,BF⊥CD,∴∠AED=∠BFD=90°,∴∠FBD+∠BDF=90°,∴∠FBD=∠ADE,∵∠AOD=∠BOD,∴AD=BD,在△ADE和△DBF中∴△ADE≌△DBF(AAS),∴BF=DE,AE=DF,∴BF﹣AE=DE﹣DF,即BF﹣AE=EF.[问题二法2:∠ACD=∠CAE=45°,所以AE=CE,∠DCB=∠FBC=45°,所以BF =CF,CF=CE+EF=AE+EF所以AE+FE=BF](3)解:在Rt△ACB中,AB==10,∵△DAB为等腰直角三角形,∴AD===5,∵AE⊥CD,∴△ACE为等腰直角三角形,∴AE=CE===3,在Rt△AED中,DE===4,∴CD=CE+DE=3+4=7,∵∠PDA=∠PCD,∠P=∠P,∴△PDA∽△PCD,∴===,∴P A=PD,PC=PD,而PC=P A+AC,∴PD+6=PD,∴PD=.21.(8分)为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.人均住房面积(平方米)单价(万元/平方米)不超过30(平方米)0.3超过30平方米不超过m(平方米)部分(45≤m≤60)0.5超过m平方米部分0.7根据这个购房方案:(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.【分析】(1)根据房款=房屋单价×购房面积就可以表示出应缴房款;(2)由分段函数当0≤x≤30,当30<x≤m时,当x>m时,分别求出y与x之间的表达式即可;(3)当50≤m≤60和当45≤m<50时,分别讨论建立不等式组就可以求出结论.【解答】解:(1)由题意,得三口之家应缴购房款为:0.3×90+0.5×30=42(万元).(2)由题意,得①当0≤x≤30时,y=0.3×3x=0.9x;②当30<x≤m时,y=0.3×3×30+0.5×3×(x﹣30)=1.5x﹣18;③当x>m时,y=0.3×3×30+0.5×3(m﹣30)+0.7×3×(x﹣m)=2.1x﹣0.6m﹣18.∴y=;(3)由题意,得①当50≤m≤60时,则人均面积为50平方米没有超过m,所以应缴纳的房款:y=1.5x﹣18=1.5×50﹣18=57(万元);②当45≤m<50时,则人均面积为50平方米超过m,则y=2.1x﹣0.6m﹣18=2.1×50﹣0.6m﹣18=87﹣0.6m,∵57<y≤60,∴57<87﹣0.6m≤60解得45≤m<50.综上,45≤m<50.22.(9分)如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(2)如图2,若点E在线段BC上滑动(不与点B,C重合).①AE=EF是否总成立?请给出证明;②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=﹣x2+x+1上,求此时点F的坐标.【分析】(1)取AB的中点G,连接EG,利用ASA能得到△AGE与△ECF全等;(2)①在AB上截取AM=EC,证得△AME≌△ECF即可证得AE=EF;②过点F作FH⊥x轴于H,根据FH=BE=CH设BH=a,则FH=a﹣1,然后表示出点F的坐标,根据点F恰好落在抛物线y=﹣x2+x+1上得到有关a的方程求得a值即可求得点F的坐标;【解答】(1)解:如图1,取AB的中点G,连接EG.△AGE与△ECF全等.(2)①若点E在线段BC上滑动时AE=EF总成立.证明:如图2,在AB上截取AM=EC.∵AB=BC,∴BM=BE,∴△MBE是等腰直角三角形,∴∠AME=180°﹣45°=135°,又∵CF平分正方形的外角,∴∠ECF=135°,∴∠AME=∠ECF.而∠BAE+∠AEB=∠CEF+∠AEB=90°,∴∠BAE=∠CEF,∴△AME≌△ECF.∴AE=EF.②过点F作FH⊥x轴于H,由①知,FH=BE=CH,设BH=a,则FH=a﹣1,∴点F的坐标为F(a,a﹣1)∵点F恰好落在抛物线y=﹣x2+x+1上,∴a﹣1=﹣a2+a+1,∴a2=2,a=±(负值不合题意,舍去),∴.∴点F的坐标为.23.(12分)如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.(1)求抛物线与x轴的另一个交点B的坐标;(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.①当t为2秒时,△P AD的周长最小?当t为4或4﹣或4+秒时,△P AD是以AD为腰的等腰三角形?(结果保留根号)②点P在运动过程中,是否存在一点P,使△P AD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)根据抛物线的轴对称性可得抛物线与x轴的另一个交点B的坐标;(2)先根据梯形ABCD的面积为9,可求c的值,再运用待定系数法可求抛物线的解析式,转化为顶点式可求顶点E的坐标;(3)①根据轴对称﹣最短路线问题的求法可得△P AD的周长最小时t的值;根据等腰三角形的性质可分三种情况求得△P AD是以AD为腰的等腰三角形时t的值;②先证明△APN∽△PDM,根据相似三角形的性质求得PN的值,从而得到点P的坐标.【解答】解:(1)由抛物线的轴对称性及A(﹣1,0),可得B(﹣3,0).(2)设抛物线的对称轴交CD于点M,交AB于点N,由题意可知AB∥CD,由抛物线的轴对称性可得CD=2DM.∵MN∥y轴,AB∥CD,∴四边形ODMN是平行四边形∵∠DON=90°∴平行四边形ODMN是矩形.∴DM=ON=2,∴CD=2×2=4.∵A(﹣1,0),B(﹣3,0),∴AB=2,∵梯形ABCD的面积=(AB+CD)•OD=9,∴OD=3,即c=3.∴把A(﹣1,0),B(﹣3,0)代入y=ax2+bx+3得,解得.∴y=x2+4x+3.将y=x2+4x+3化为顶点式为y=(x+2)2﹣1,得E(﹣2,﹣1).(3)①当t为2秒时,△P AD的周长最小;当t为4或4﹣或4+秒时,△P AD是以AD为腰的等腰三角形.故答案为:2;4或4﹣或4+.②存在.设CD交抛物线对称轴于M,AB交抛物线对称轴于N,∵∠APD=90°,∠PMD=∠PNA=90°,∴∠DPM+∠APN=90°,∠DPM+∠PDM=90°,∴∠PDM=∠APN,∵∠PMD=∠ANP,∴△APN∽△PDM,∴=,∴=,∴PN2﹣3PN+2=0,∴PN=1或PN=2.∴P(﹣2,1)或(﹣2,2).。
广东省深圳市龙岗区布吉中学2019-2020年年下九年级数学总复习试卷14(含答案)
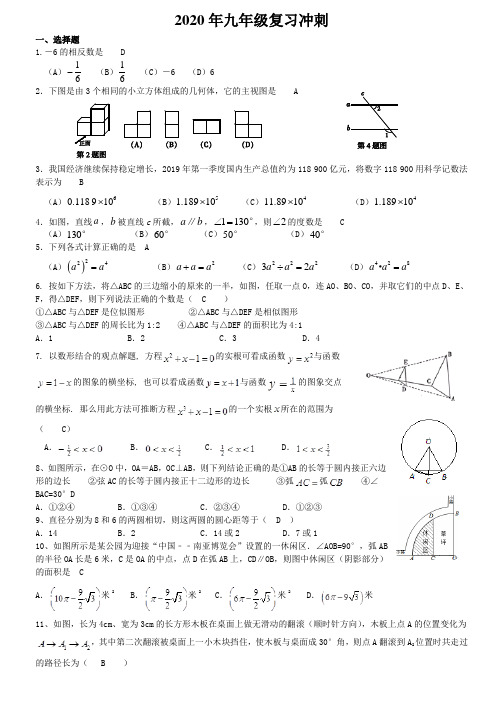
2020年九年级复习冲刺一、选择题1.-6的相反数是 D (A )16-(B )16 (C )-6 (D )62.下图是由3个相同的小立方体组成的几何体,它的主视图是 A3.我国经济继续保持稳定增长,2019年第一季度国内生产总值约为118 900亿元,将数字118 900用科学记数法表示为 B(A )60.118910⨯ (B )51.18910⨯ (C )411.8910⨯ (D )41.18910⨯ 4.如图,直线a ,b 被直线c 所截,a b ∥,1130∠=°,则2∠的度数是 C (A )130° (B )60° (C )50° (D )40° 5.下列各式计算正确的是 A (A )()224aa = (B )2a a a += (C )22232a a a ÷= (D )428a a a =·6. 按如下方法,将△ABC 的三边缩小的原来的一半,如图,任取一点O ,连AO 、BO 、CO ,并取它们的中点D 、E 、F ,得△DEF ,则下列说法正确的个数是( C )①△ABC 与△DEF 是位似图形 ②△ABC 与△DEF 是相似图形 ③△ABC 与△DEF 的周长比为1:2 ④△ABC 与△DEF 的面积比为4:1 A .1 B .2 C .3 D .4 7. 以数形结合的观点解题, 方程的实根可看成函数与函数的图象的横坐标, 也可以看成函数与函数的图象交点的横坐标. 那么用此方法可推断方程的一个实根所在的范围为( C ) A .B .C .D .8、如图所示,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论正确的是①AB 的长等于圆内接正六边形的边长 ②弦AC 的长等于圆内接正十二边形的边长 ③弧弧 ④∠BAC=30°D A .①②④ B .①③④ C .②③④ D .①②③ 9、直径分别为8和6的两圆相切,则这两圆的圆心距等于( D ) A .14 B .2 C .14或2 D .7或110、如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是 C A .米2B .米2C .米2D .米11、如图,长为4cm 、宽为3cm 的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A 的位置变化为,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A 翻滚到A 2位置时共走过的路径长为( B )A .10B .C .D . 12、如图,在直角坐标系中,正方形OABC 的顶点O 与原点重合,顶点A 。
深圳布吉时代学校2020年化学中考试卷及答案

深圳布吉时代学校2020年化学中考试卷及答案一、选择题(培优题较难)1.已知A、B、C、D、E是初中化学中常见的五种物质,均含有同一种元素。
其中,A为单质, B和C含有相同的元素。
它们在一定条件下的转化关系如图所示(“→”表示物质间的转化关系,反应条件和部分反应物、生成物已省略),根据初中所学知识判断下列说法正确的是()A.A→B的反应一定是化合反应B.D和E的物质类别可以相同,也可以不同C.若D是一种白色固体,则B→D的反应属于复分解反应D.若C为单质, A和B含有相同的元素,其他条件不变。
则D→B的反应一定是分解反应【答案】B【解析】【详解】A、A为单质, B和C含有相同的元素,A能生成B和C,故A→B的反应可能是化合反应,也可能是置换反应,如A是碳,B是二氧化碳,C是一氧化碳,故A选项错误;B、当A为碳,B为二氧化碳、C为一氧化碳时,D、E分别可以是碳酸钠和碳酸钙,都属于盐;D、E分别也可以是碳酸钙和碳酸,属于不同类物质,故B选项正确;C、当D为碳酸钙,B为二氧化碳时,B→D的反应不属于复分解反应,故C错误;D、若C为单质, A和B含有相同的元素,则C可能是氧气,A可能是过氧化氢,B可能是水,则D可能是氢氧化钙,氢氧化钙生成水的反应不一定是分解反应,故D选项错误。
故选B。
2.有一包固体粉末,可能含碳、铝、铜、氧化铝、氧化铜中的一种或几种。
为探究该固体粉末的组成,某化学兴趣小组进行了如下图所示实验。
下列结论正确的个数是①固体B中的物质为碳②蓝色溶液乙为硝酸铜溶液③原固体样品中一定含有的物质是碳、铝、铜④蓝色溶液丙中一定含有的溶质是硝酸铝、硝酸铜、硝酸A.1个B.2个C.3个D.4个【答案】B【解析】【详解】①固体B在氧气中充分灼烧,生成能使澄清石灰水变浑浊的二氧化碳气体(说明原固体有碳),可能还含有铜,故该说法不正确;②无色溶液甲与蓝色溶液乙反应生成白色固体,说明蓝色溶液乙中含有硝酸银,故该说法不正确;③向样品中加入过量稀盐酸有气体生成,根据金属活动性顺序可知,是铝与盐酸反应,生成的气体是氢气;固体A与硝酸银反应有蓝色溶液生成,说明固体A中含有铜,铜与硝酸Cu+2AgNO=2Ag+Cu(NO);铜与硝酸银反应生成银和硝酸铜,反应的化学方程式为332银反应生成银;固体B在氧气中充分灼烧,生成能使澄清石灰水变浑浊的气体,该气体是二氧化碳。
深圳布吉布吉中学中考化学模拟试卷

深圳布吉布吉中学中考化学模拟试卷一、选择题1.下列有关实验的分析中,合理的是A.测碱溶液的pH结果偏小——直接把试纸伸入待测液中B.用KMnO4制氧气时试管炸裂——在试管口没有放一团棉花C.粗盐提纯实验后所得产率偏低——蒸发时有一些液体、固体溅出D.用6%NaCl溶液加水配制3%NaCl溶液结果偏小——量筒量取水的体积时俯视读数2.下列依据实验目的所设计的实验方案中,正确的是( )选项实验目的实验方案A除去NaCl溶液中的Na2CO3加适量稀硫酸B除去CaO中的CaCO3加水溶解,过滤C除去CO2中的HCl气体将混合气体通入NaOH溶液D除去KNO3溶液中的KCl加适量的AgNO3溶液,过滤A.A B.B C.C D.D3.相同质量的M、N两种金属,分别与相同质量分数的足量稀盐酸反应(M、N在生成物中均为+2价),生成H2质量和反应时间的关系如图所示.下列有关叙述正确的是A.金属活动性:N>M B.生成H2的质量相等C.相对原子质量:N>M D.消耗盐酸的质量相等4.t℃时,Na2CO3溶解度为Ag,现有饱和Na2CO3溶液(100+A)g,溶质质量分数为a%,向该溶液中投入无水碳酸钠Ag,静置后析出碳酸钠晶体(Na2CO3·10H2O)Bg,加水使晶体全部溶解,所得溶液质量分数为a%,则加入水的质量为( )A.(100+A)g B.100gC.100180286Ag D.(10 -A·a%)g5.除去下列物质中所含杂质(括号内为杂质),所选用试剂及操作方法均正确的一组是选项物质选用的试剂操作方法A.A B.B C.C D.D6.下列鉴别两种不同物质的方法,不正确的是()A.A B.B C.C D.D7.化学趣味小组在学习了金属的化学性质后,对金属R的活动性进行探究发现:将金属R 放入稀盐酸中,观察到有气泡产生(该反应的化学方程式可表示为:R+2HCl2=RCl2+H2↑),将R放入ZnSO4溶液中无任何变化。
深圳布吉布吉中学中考化学模拟试卷

深圳布吉布吉中学中考化学模拟试卷一、选择题1.下列是四种实验操作中各量变化关系的图像,能正确反映其对应操作的图像有①电解水②向一定量pH=3的盐酸溶液中不断加水稀释③向等质量的镁和锌中分别加入溶质质量分数相同的稀盐酸至过量④向盐酸和氯化铜的混合溶液中不断滴加氢氧化钾溶液A.4个B.3个C.2个D.1个2.t℃时,Na2CO3溶解度为Ag,现有饱和Na2CO3溶液(100+A)g,溶质质量分数为a%,向该溶液中投入无水碳酸钠Ag,静置后析出碳酸钠晶体(Na2CO3·10H2O)Bg,加水使晶体全部溶解,所得溶液质量分数为a%,则加入水的质量为( )A.(100+A)g B.100gC.100180286Ag D.(10 -A·a%)g3.将一定量铝粉和氧化铜混合加热,反应的化学方程式为3CuO+2Al3Cu+A12O3.反应结束后,为了检验氧化铜是否完全反应,取少量反应后的固体,加入足量稀硫酸,充分反应后,将铁片插入溶液中.下列叙述的现象中,能够说明氧化铜没有完全反应的是①加入稀硫酸后,有气泡生成②加入稀硫酸后,没有气泡生成③加入稀硫酸后,溶液中有红色不溶物质④插入溶液中的铁片表面有红色物质析出.A.只有④B.②③C.③④D.①③④4.下列各组转化中,一定条件下均能一步实现的组合是A.①②B.①③C.②③D.①②③5.为了达到实验目的,下列方案或结论正确的是选项实验目的实验方案或结论A鉴别碳粉、铁粉和氧化铜粉末取样后,分别加入稀盐酸B除去KCl固体中的K2CO3取样、溶解、加入足量的稀硫酸,蒸发C除去CO2中混有少量HCl气体通入装有足量NaOH溶液的洗气瓶D鉴别某溶液中是否含有SO2-4取少量溶液与试管中,滴加BaCl2溶液,有白色沉淀生成,则该溶液中一定含有SO2-4A.A B.B C.C D.D6.某实验小组将Ba(OH)2溶液逐滴滴入硫酸溶液中,溶质的质量与加入的Ba(OH)2溶液的质量关系如图所示。
广东省深圳市龙岗区2020年中考数学复习练习试卷(含答案)

广东省深圳市龙岗区2020年中考数学复习练习试卷一.选择题(每题3分,满分36分)1.2020的相反数是()A.2020 B.﹣2020 C.D.2.壮丽七十载,奋进新时代.2019年10月1日上午庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行,超20万军民以盛大的阅兵仪式和群众游行欢庆共和国70华诞,其中20万用科学记数法表示为()A.20×104B.2×105C.2×104D.0.2×1063.从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是()A.圆柱B.圆锥C.棱锥D.球4.下列事件中,属于必然事件的是()A.三角形的外心到三边的距离相等B.某射击运动员射击一次,命中靶心C.任意画一个三角形,其内角和是180°D.抛一枚硬币,落地后正面朝上5.如图,已知AB∥CD,直线AB,CD被B C所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=()A.65°B.70°C.75°D.80°6.下列运算正确的是()A.5a2﹣2a2=3 B.a2÷a=a2C.a2•a3=a6D.(﹣ab)2=a2b27.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是()A.8 B.9 C.10 D.128.不等式组的解集在数轴上表示正确的是()A.B.C.D.9.如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于()A.33°B.57°C.67°D.66°10.10年前,小明妈妈的年龄是小明的6倍,10年后,小明妈妈的年龄是小明的2倍,小明和他妈妈现在的年龄分别是多少岁?若设小明和他妈妈现在分别是x岁和y岁,根据题意可列方程组为()A.B.C.D.11.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于()A.1﹣B.1﹣C.D.12.二次函数y=ax2+b与反比例函数y=在同一平面直角坐标系中的图象可能是()A.B.C.D.二.填空题(满分12分,每小题3分)13.若多项式x2+mx+4能用完全平方公式分解因式,则m的值是.14.如图,将△ABC沿着CE翻折,使点A落在点D处,CD与AB交于点F,恰好有CE=CF,若DF=6,AF=14,则tan∠CEF=.15.如图,在平面直角坐标系中,点M的坐标为(3,0),⊙M的半径为2,AB为⊙M的直径,其中点A在第一象限,当OA=AB时,点A的坐标为.16.如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=(x<0)的图象上,则k的值为.三.解答题17.计算: +|1﹣|﹣2cos45°+.18.先化简,再求值:,从﹣1,1,2,3中选择一个合适的数代入并求值.19.广东省新高考模式确定为“3+1+2”,也就是语、数、英3科为必考科目,再从物、历2科中选1科作为选考科目,从生、化、地、政4科中选2科作为选考科目.某校对九年级学生对“高考新模式”的知晓率进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如下统计图,请根据提供的信息回答:(1)本次参与问卷调查的学生有人;扇形统计图中“基本了解”部分所对应的扇形圆心角是度;(2)请补全条形图;(3)某同学对生、化、地、政四科同样感兴趣,想从中随机选择两科,请你用列表或树状图的方法求出刚好选到生、化两科的概率.20.如图,将边长为的正方形ABCD绕点A逆时针方向旋转30o后得到正方形AB′C′D′,求图中阴影部分的面积为多少平方单位?21.某市农机公司筹集到资金130万元,用于一次性购进AB两种型号的收割机共30台,根据市场需求,这些收割机可以全部销售,全部销售后利润不少于15万元,其中,收割机的进价和售价见下表:A型收割机B型收割机进价(万元/台) 5.3 3.6售价(万元/台) 6 4设计公司计划购进A型收割机x台,收割机全部销售后公司获得的利润为y万元.(1)试列出关于字母x、y的二元一次方程;(2)市农机公司有哪几种购进收割机的方案可供选择?22.如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点E,且l∥BC.(1)求证:AE平分∠B AC;(2)作∠ABC的平分线BF交AE于点F,求证:BE=EF.23.如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).(1)求抛物线的函数表达式;(2)若点M 在抛物线上,且S △AOM =2S △BOC ,求点M 的坐标;(3)如图2,设点N 是线段AC 上的一动点,作DN ⊥x 轴,交抛物线于点D ,求线段DN 长度的最大值.参考答案一.选择题1.解:2020的相反数是:﹣2020.故选:B.2.解:20万=200000=2×105.故选:B.3.解:∵主视图和左视图都是长方形,∴此几何体为柱体,∵俯视图是一个圆,∴此几何体为圆柱.故选:A.4.解:A、三角形的外心到三角形的三个顶点的距离相等,三角形的内心到三边的距离相等,只有三角形是等边三角形时才符合,故本选项不符合题意;B、某射击运动员射击一次,命中靶心是随机事件,故本选项不符合题意;C、三角形的内角和是180°,是必然事件,故本选项符合题意;D、抛一枚硬币,落地后正面朝上,是随机事件,故本选项不符合题意;故选:C.5.解:∵AB∥CD,∴∠C=∠1=45°,∵∠3是△CDE的一个外角,∴∠3=∠C+∠2=45°+35°=80°,故选:D.6.解:∵5a2﹣2a2=3a2,故选项A错误;∵a2÷a=a,故选项B错误;∵a2•a3=a5,故选项C错误;∵(﹣ab)2=a2b2,故选项D正确;故选:D.7.解:设这个多边形的外角为x°,则内角为3x°,由题意得:x+3x=180,解得x=45,这个多边形的边数:360°÷45°=8,故选:A.8.解:解不等式x﹣1<1,得:x<2,解不等式x+1≥0,得:x≥﹣1,则不等式组的解集为﹣1≤x<2,故选:A.9.解:连结CD,如图,∵BD是⊙O的直径,∴∠BCD=90°,而∠DBC=33°,∴∠D=90°﹣33°=57°,∴∠A=∠D=57°.故选:B.10.解:设小明和他妈妈现在分别是x岁和y岁.由题意得,,故选:B.11.解:设CD与B′C′相交于点O,连接OA.根据旋转的性质,得∠BAB′=30°,则∠DAB′=60°.在Rt△ADO和Rt△AB′O中,AD=AB′,AO=AO,∴Rt△ADO≌Rt△AB′O.∴∠OAD=∠OAB′=30°.又∵AD=1,∴OD=AD•tan∠OAD=.∴公共部分的面积=2×××1=1×=.故选:D.12.解:A、根据抛物线开口向上,与y轴交于正半轴可得a>0,b>0,即ab>0,所以双曲线在第一、三象限,故A选项错误;B、根据抛物线开口向上,与y轴交于正半轴可得a>0,b>0,即ab>0,所以双曲线在第一、三象限,故B选项正确;C、根据抛物线开口向下,与y轴交于正半轴可得a<0,b>0,即ab<0,所以双曲线在第二、四象限,故C选项错误;D、根据抛物线开口向上,与y轴交于负半轴可得a>0,b<0,即ab<0,所以双曲线在第二、四象限,故D选项错误.故选:B.二.填空13.解:∵x2+mx+4=(x±2)2,即x2+mx+4=x2±4x+4,∴m=±4.故答案为:±4.14.解:如图,作CH⊥AB于H.设CF=EC=x.∵CF=CE,CH⊥EF,∴FH=EH,设FH=EH=y,则有x2﹣y2=(x+6)2﹣(14﹣y)2,整理得3x+7y=40 ①,∵∠CFE=∠CEF,∠CFE=∠D+∠FED,∠CE F=∠A+∠ECA,∠A=∠D,∴∠FED=∠ECA,∴△EFD∽△CEA,∴=,∴=,整理得3x=14y﹣2y2②,由①②可得x=,y=,∴CH==5,∴tan∠CEF==2,故答案为2.15.解:过A作AC⊥OM于C,∴∠ACO=∠ACM=90°,∵点M的坐标为(3,0),∴OM=3,∵⊙M的半径为2,∴AM=2,OA=AB=4,∵OA2﹣OC2=AM2﹣CM2,∴42﹣OC2=22﹣(3﹣OC)2,解得:OC=,∴AC===,∴点A的坐标为(,),故答案为:(,).16.解:连接AC,交y轴于点D,∵四边形ABCO为菱形,∴AC⊥OB,且CD=AD,BD=OD,∵菱形OABC的面积为12,∴△CDO的面积为3,∴|k|=6,∵反比例函数图象位于第二象限,∴k<0,则k=﹣6.故答案为:﹣6.三.解答17.解:原式=1+﹣1﹣2×+4=4.18.解:原式==.∵x2﹣1≠0,x﹣2≠0,∴取x=3,原式==4.19.解(1)本次参与问卷调查的学生有80÷20%=400(人),扇形统计图中“基本了解”部分所对应的扇形圆心角是360°×=144°,故答案为:400、144;(2)补全频数分布直方图如图:(3)依题意列表得:生化地政生(生,化)(生,地)(生,政)化(化,生)(化,地)(化,政)地(地,生)(地,化)(地,政)政(政,生)(政,化)(政,地)由上表可得,共有12种结果,其中选到生与化的共有两种(生,化)、(化,生),因此,刚好选到生、化两科的概率为.20.解:如图,设B′C′和CD的交点是O,连接OA,∵在Rt△ADO和Rt△AB′O中,,∴AD=AB′,∴Rt△ADO≌Rt△AB′O,∴∠OAD=∠OAB′=30°,∵AD=,tan∠OAD=,∴OD=OB′=1,S四边形AB′OD =2S△AOD=2×××1=,∴S阴影部分=S正方形﹣S四边形AB′OD=3﹣.21.解:(1)y=(6﹣5.3)x+(4﹣3.6)×(30﹣x)=0.7x+12﹣0.4x=0.3x+12;(2)由题意得,解得10≤x≤12∴x可取10,11,12三种方案.答:可购进A10台,B20台;A11台,B19台;A12台,B18台.22.证明:(1)连接OE.∵直线l与⊙O相切于E,∴OE⊥l.∵l∥BC,∴OE⊥BC,∴=,∴∠BAE=∠CAE.∴AE平分∠BAC;(2)∵BF平分∠ABC,∴∠ABF=∠CBF.又∵=,∴∠BAE=∠CBE,∴∠CBE+∠CBF=∠BAE+∠ABF.又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB,∴BE=EF.23.解:(1)A (﹣2,0),C (0,2)代入抛物线的解析式y =﹣x 2+mx +n , 得,解得,∴抛物线的解析式为y =﹣x 2﹣x +2.(2)由(1)知,该抛物线的解析式为y =﹣x 2﹣x +2,则易得B (1,0),设M (m ,n )然后依据S △AOM =2S △BOC 列方程可得:•AO ×|n |=2××OB ×OC , ∴×2×|﹣m 2﹣m +2|=2,∴m 2+m =0或m 2+m ﹣4=0,解得x =0或﹣1或,∴符合条件的点M 的坐标为:(0,2)或(﹣1,2)或(,﹣2)或(,﹣2).(3)设直线AC 的解析式为y =kx +b ,将A (﹣2,0),C (0,2)代入 得到,解得,∴直线AC 的解析式为y =x +2,设N (x ,x +2)(﹣2≤x ≤0),则D (x ,﹣x 2﹣x +2),ND =(﹣x 2﹣x +2)﹣(x +2)=﹣x 2﹣2x =﹣(x +1)2+1,∵﹣1<0,∴x =﹣1时,N D 有最大值1.∴ND 的最大值为1.。
广东省深圳市龙岗区布吉中学2020年中考数学复习考试试卷(6) 解析版

2020年广东省深圳市龙岗区布吉中学中考数学复习试卷(6)一.选择题(共12小题)1.﹣5的绝对值是()A.5 B.﹣5 C.D.﹣2.我国平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧130000吨煤所产生的能量.130000用科学记数法表示为()A.13×104B.1.3×105C.0.13×106D.1.3×1083.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β﹣∠γ的值等于()A.45°B.60°C.90°D.180°4.下列运算正确的是()A.3a3•2a2=6a6B.4a2÷2a2=2aC.3=2D.5.几个棱长为1的正方体组成的几何体的三视图如图所示,则这个几何体的体积是()A.4 B.5 C.6 D.76.下列事件中,属于随机事件的是()A.通常水加热到100℃时沸腾B.测量孝感某天的最低气温,结果为﹣150℃C.一个袋中装有5个黑球,从中摸出一个是黑球D.篮球队员在罚球线上投篮一次,未投中7.如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为()A.50米B.100米C.米D.米8.若关于x的一元一次不等式组无解,则a的取值范围是()A.a≥1 B.a>1 C.a≤﹣1 D.a<﹣19.已知关于x的方程(x+1)2+(x﹣b)2=2有唯一的实数解,且反比例函数的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为()A.B.C.D.10.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为()A.B.C.D.11.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD 的长是()A.B.C.﹣1 D.+112.如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=AB2其中正确的结论有()A.1个B.2个C.3个D.4个二.填空题(共4小题)13.计算:cos245°+tan30°•sin60°=.14.如果关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,那么k的取值范围是.15.把如图所示的长方体材料切割成一个体积最大的圆柱,则这个圆柱的体积为cm3(结果不作近似计算).16.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中正确的是(把正确的序号都填上).三.解答题(共7小题)17.先化简,再求值,其中a=,b=.18.解不等式组:.19.某超市销售多种颜色的运动服装,其中平均每天销售红、黄、蓝、白四种颜色运动服的数量如表,由此绘制的不完整的扇形统计图如图:四种颜色服装销量统计表服装颜色红黄蓝白合计数量(件) 20 n 40 1.5n m所对扇形的圆心角α 90° 360°(1)求表中m,n,α的值,并将扇形统计图补充完整;表中m=,n=,α=;(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券.求顾客每转动一次转盘获得购物券金额的平均数.20.如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;(2)若AD=4,BC=9,求⊙O的半径R.21.荆门市是著名的“鱼米之乡”.某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼(俗称黑鱼)共75千克,且乌鱼的进货量大于40千克.已知草鱼的批发单价为8元/千克,乌鱼的批发单价与进货量的函数关系如图所示.(1)请直接写出批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式;(2)若经销商将购进的这批鱼当日零售,草鱼和乌鱼分别可卖出89%、95%,要使总零售量不低于进货量的93%,问该经销商应怎样安排进货,才能使进货费用最低?最低费用是多少?22.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.(1)点E可以是AD的中点吗?为什么?(2)求证:△ABG∽△BFE;(3)设AD=a,AB=b,BC=c①当四边形EFCD为平行四边形时,求a,b,c应满足的关系;②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.23.如图,在平面直角坐标系中,直线y=x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M 与x轴、直线AB都相切,其半径为3(1﹣)a.(1)求点A的坐标和∠ABO的度数;(2)当点C与点A重合时,求a的值;(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?参考答案与试题解析一.选择题(共12小题)1.﹣5的绝对值是()A.5 B.﹣5 C.D.﹣【分析】根据绝对值的性质求解.【解答】解:根据负数的绝对值等于它的相反数,得|﹣5|=5.故选:A.2.我国平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧130000吨煤所产生的能量.130000用科学记数法表示为()A.13×104B.1.3×105C.0.13×106D.1.3×108【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:130000=1.3×105,故选:B.3.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β﹣∠γ的值等于()A.45°B.60°C.90°D.180°【分析】根据互余两角之和为90°,互补两角之和为180°,结合题意即可得出答案.【解答】解:由题意得,∠α+∠β=180°,∠α+∠γ=90°,两式相减可得:∠β﹣∠γ=90°.故选:C.4.下列运算正确的是()A.3a3•2a2=6a6B.4a2÷2a2=2aC.3=2D.【分析】分别根据同底数幂的乘法,除法及二次根式的加减进行各选项的运算,然后即可作出判断.【解答】解:A、3a3•2a2=6a5,故本选项错误;B、4a2÷2a2=2,故本选项错误;C、3=2,故本选项正确;D、+≠,故本选项错误;故选:C.5.几个棱长为1的正方体组成的几何体的三视图如图所示,则这个几何体的体积是()A.4 B.5 C.6 D.7【分析】根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两行三列,故可得出该几何体的小正方体的个数,即可得出这个几何体的体积.【解答】解:综合三视图可知,这个几何体的底层应该有3+1=4个小正方体,第二层应该有1个小正方体,因此搭成这个几何体所用小正方体的个数是4+1=5个,所以这个几何体的体积是5.故选:B.6.下列事件中,属于随机事件的是()A.通常水加热到100℃时沸腾B.测量孝感某天的最低气温,结果为﹣150℃C.一个袋中装有5个黑球,从中摸出一个是黑球D.篮球队员在罚球线上投篮一次,未投中【分析】随机事件就是可能发生也可能不发生的事件,依据定义即可求解.【解答】解:A、C一定正确,是必然事件;B是不可能事件,D、篮球队员在罚球线上投篮未中属于随机事件.故选:D.7.如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为()A.50米B.100米C.米D.米【分析】首先根据题意分析图形;本题涉及到两个直角三角形,设AB=x(米),再利用CD=BC﹣BD=100的关系,进而可解即可求出答案.【解答】解:在Rt△ABD中,∵∠ADB=45°,∴BD=AB.在Rt△ABC中,∵∠ACB=30°,∴=tan30°=,∴BC=AB.设AB=x(米),∵CD=100,∴BC=x+100.∴x+100=x∴x=米.故选:D.8.若关于x的一元一次不等式组无解,则a的取值范围是()A.a≥1 B.a>1 C.a≤﹣1 D.a<﹣1【分析】首先解出两个不等式,再根据“大大小小找不到”的原则解答即可.【解答】解:,由①得:x>a,由②得:x<1,∵不等式组无解,∴a≥1,故选:A.9.已知关于x的方程(x+1)2+(x﹣b)2=2有唯一的实数解,且反比例函数的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为()A.B.C.D.【分析】关于x的方程(x+1)2+(x﹣b)2=2有唯一的实数解,则判别式等于0,据此即可求得b的值,然后根据反比例函数的图象在每个象限内y随x的增大而增大,则比例系数1+b<0,则b的值可以确定,从而确定函数的解析式.【解答】解:关于x的方程(x+1)2+(x﹣b)2=2化成一般形式是:2x2+(2﹣2b)x+(b2﹣1)=0,△=(2﹣2b)2﹣8(b2﹣1)=﹣4(b+3)(b﹣1)=0,解得:b=﹣3或1.∵反比例函数的图象在每个象限内y随x的增大而增大,∴1+b<0∴b<﹣1,∴b=﹣3.则反比例函数的解析式是:y=,即y=﹣.故选:D.10.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为()A.B.C.D.【分析】由于六边形ABCDEF是正六边形,所以∠AOB=60°,故△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,OG=OA•sin60°,再根据S阴影=S△OAB﹣S扇形OMN,进而可得出结论.【解答】解:∵六边形ABCDEF是正六边形,∴∠AOB=60°,∴△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,∴OG=OA•sin60°=2×=,∴S阴影=S△OAB﹣S扇形OMN=×2×﹣=﹣.故选:A.11.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD 的长是()A.B.C.﹣1 D.+1【分析】根据两角对应相等,判定两个三角形相似.再用相似三角形对应边的比相等进行计算求出BD的长.【解答】解:∵∠A=∠DBC=36°,∠C公共,∴△ABC∽△BDC,且AD=BD=BC.设BD=x,则BC=x,CD=2﹣x.由于=,∴=.整理得:x2+2x﹣4=0,解方程得:x=﹣1±,∵x为正数,∴x=﹣1+.故选:C.12.如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=AB2其中正确的结论有()A.1个B.2个C.3个D.4个【分析】先判断出△ABD、BDC是等边三角形,然后根据等边三角形的三心(重心、内心、垂心)合一的性质,结合菱形对角线平分一组对角,三角形的判定定理可分别进行各项的判断.【解答】解:①由菱形的性质可得△ABD、BDC是等边三角形,∠DGB=∠GBE+∠GEB=30°+90°=120°,故①正确;②∵∠DCG=∠BCG=30°,DE⊥AB,∴可得DG=CG(30°角所对直角边等于斜边一半)、BG=CG,故可得出BG+DG=CG,即②也正确;③首先可得对应边BG≠FD,因为BG=DG,DG>FD,故可得△BDF不全等△CGB,即③错误;④S△ABD=AB•DE=AB•BE=AB•AB=AB2,即④正确.综上可得①②④正确,共3个.故选:C.二.填空题(共4小题)13.计算:cos245°+tan30°•sin60°= 1 .【分析】将cos45°=,tan30°=,sin60°=代入即可得出答案.【解答】解:cos245°+tan30°•sin60°=+×==1.故答案为:1.14.如果关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,那么k的取值范围是﹣≤k<且k≠0 .【分析】根据方程有两个不相等的实数根,则△>0,由此建立关于k的不等式,然后就可以求出k的取值范围.【解答】解:∵关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,∴k≠0,△=(﹣)2﹣4k>0,∴k<且k≠0,∵2k+1≥0,∴k≥﹣,∴k的取值范围是﹣≤k<且k≠0,故答案为:﹣≤k<且k≠0.15.把如图所示的长方体材料切割成一个体积最大的圆柱,则这个圆柱的体积为3000πcm3(结果不作近似计算).【分析】首先求得其底面内切圆的半径,然后计算其面积,利用底面积乘以高等于体积计算体积即可.【解答】解:∵底面是边长为20cm的圆,∴其内切圆的半径为10cm,∴其底面积为100πcm2,∴其体积为100π×30=3000π(cm3).故答案为3000π.16.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中正确的是①②③(把正确的序号都填上).【分析】首先根据二次函数图象开口方向可得a<0,根据图象与y轴交点可得c>0,再根据二次函数的对称轴x=﹣=1,结合a的取值可判定出b>0,根据a、b、c的正负即可判断出①的正误;把x=﹣1代入函数关系式y=ax2+bx+c中得y=a﹣b+c,再结合图象判断出②的正误;把b=﹣2a代入a﹣b+c中即可判断出③的正误;利用图象可以直接看出④的正误.【解答】解:根据图象可得:a<0,c>0,对称轴:x=﹣=1,=﹣1,b=﹣2a,∵a<0,∴b>0,∴abc<0,故①正确;把x=﹣1代入函数关系式y=ax2+bx+c中得:y=a﹣b+c,由图象可以看出当x=﹣1时,y<0,∴a﹣b+c<0,故②正确;∵b=﹣2a,∴a﹣(﹣2a)+c<0,即:3a+c<0,故③正确;由图形可以直接看出④错误.故答案为:①②③.三.解答题(共7小题)17.先化简,再求值,其中a=,b=.【分析】先算括号里面的,再算除法,分式化为最简根式后,把a、b的值代入进行计算即可.【解答】解:原式=÷=•=,当a=+1,b=﹣1时,原式==.18.解不等式组:.【分析】先求出两个不等式的解集,再求其公共解.【解答】解:,解不等式①得,x<,解不等式②得,x≥﹣2,所以,不等式组的解集是﹣2≤x<.19.某超市销售多种颜色的运动服装,其中平均每天销售红、黄、蓝、白四种颜色运动服的数量如表,由此绘制的不完整的扇形统计图如图:四种颜色服装销量统计表服装颜色红黄蓝白合计数量(件) 20 n 40 1.5n m所对扇形的圆心角α 90° 360°(1)求表中m,n,α的值,并将扇形统计图补充完整;表中m=160 ,n=40 ,α=90°;(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券.求顾客每转动一次转盘获得购物券金额的平均数.【分析】(1)根据扇形图可知蓝色服装占总数的25%,由统计表可知蓝色服装有40件,总数m=蓝色服装的件数÷蓝色服装所占百分比;把红、黄、蓝、白四种颜色的服装加起来=总数,即可算出n的值;利用黄色衣服的件数÷总数×100%可得黄色衣服所占百分比,再用百分比×360°即可算出α的值;(2)分别计算出红色衣服与蓝色衣服概率,再算出平均数即可.【解答】解:(1)m=40÷25%=160,20+n+40+1.5n=160,解得:n=40,α=40÷160×100%×360°=90°,扇形统计图如图所示:(2)P(红)=20÷160=,P(黄)=40÷160=,每转动一次转盘获得购物券金额的平均数是:60×(元).答:顾客每转动一次转盘获得购物券金额的平均数是12.5元.20.如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;(2)若AD=4,BC=9,求⊙O的半径R.【分析】(1)过O点作OE⊥CD于点E,通过角平分线的性质得出OE=OA即可证得结论.(2)过点D作DF⊥BC于点F,根据切线的性质可得出DC的长度,继而在Rt△DFC中利用勾股定理可得出DF的长,继而可得出半径.【解答】(1)证明:过O点作OE⊥CD于点E,∵AM切⊙O于点A,∴OA⊥AD,又∵DO平分∠ADC,∴OE=OA,∵OA为⊙O的半径,∴OE是⊙O的半径,且OE⊥DC,∴CD是⊙O的切线.(2)解:过点D作DF⊥BC于点F,∵AM,BN分别切⊙O于点A,B,∴AB⊥AD,AB⊥BC,∴四边形ABFD是矩形,∴AD=BF,AB=DF,又∵AD=4,BC=9,∴FC=9﹣4=5,∵AM,BN,DC分别切⊙O于点A,B,E,∴DA=DE,CB=CE,∴DC=AD+BC=4+9=13,在Rt△DFC中,DC2=DF2+FC2,∴DF==12,∴AB=12,∴⊙O的半径R是6.21.荆门市是著名的“鱼米之乡”.某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼(俗称黑鱼)共75千克,且乌鱼的进货量大于40千克.已知草鱼的批发单价为8元/千克,乌鱼的批发单价与进货量的函数关系如图所示.(1)请直接写出批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式;(2)若经销商将购进的这批鱼当日零售,草鱼和乌鱼分别可卖出89%、95%,要使总零售量不低于进货量的93%,问该经销商应怎样安排进货,才能使进货费用最低?最低费用是多少?【分析】(1)根据所需总金额y(元)是进货量x与进价的乘积,即可写出函数解析式;(2)根据总零售量不低于进货量的93%这个不等关系即可得到关于进价x的不等式,解不等式即可求得x的范围.费用可以表示成x的函数,根据函数的增减性,即可确定费用的最小值.【解答】解:(1)批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式y=24x;(2)设该经销商购进乌鱼x千克,则购进草鱼(75﹣x)千克,所需进货费用为w元.由题意得:解得x≥50.由题意得w=8(75﹣x)+24x=16x+600.∵16>0,∴w的值随x的增大而增大.∴当x=50时,75﹣x=25,W最小=1400(元).答:该经销商应购进草鱼25千克,乌鱼50千克,才能使进货费用最低,最低费用为1400元.22.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.(1)点E可以是AD的中点吗?为什么?(2)求证:△ABG∽△BFE;(3)设AD=a,AB=b,BC=c①当四边形EFCD为平行四边形时,求a,b,c应满足的关系;②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.【分析】(1)根据折叠的性质可得AE=GE,∠EGB=∠EAB=90°,再根据直角三角形斜边大于直角边可得DE>EG,从而判断点E不可能是AD的中点;(2)方法一:根据两直线平行,内错角相等可得∠AEB=∠EBF,再根据折叠的性质可以判定出∠AEB=∠BEG,然后得到∠EBF=∠BEF,从而判断出△FEB为等腰三角形,再根据等角的余角相等求出∠ABG=∠EFB,然后根据等腰三角形的两个底角相等求出∠BAG =∠FBE,然后根据两角对应相等,两三角形相似即可证明;方法二:与方法一相同求出∠ABG=∠EFB后,根据等腰三角形的两腰相等,然后根据两边对应成比例且夹角相等判断出两个三角形相似;(3)①方法一:根据勾股定理求出BD的长度,再利用两角对应相等,两三角形相似得到△ABD和△DCB相似,然后根据相似三角形对应边成比例列式计算即可得解;方法二:过点D作DH⊥BC于点H,然后求出∠C=∠ABD,再根据直角相等,判断出△ABD 和△HCD相似,根据相似三角形对应边成比例列式计算即可得解;方法三:先求出△ABD和△GFB相似,根据相似三角形对应边成比例列式求出BF的长度,再求出△EDG和△FBG相似,根据平行四边形的对边相等表示出ED,再表示出DG,然后根据相似三角形对应边成比例列式整理即可得证;②方法一:把b=2代入a、b、c的关系式,利用求根公式求出a的两个根,再根据a 是唯一的,可以判定△=c2﹣16=0,然后求出c=4,再代入根求出a=2,然后判断出H 是BC的中点,利用解直角三角形求出∠C=45°;方法二:把b=2代入a、b、c的关系式,利用根与系数的关系判断出关于a的方程的解是正数,再根据a是唯一的,可以判定△=c2﹣16=0,然后求出c=4,再代入根与系数的关系求出a=2,然后判断出H是BC的中点,利用解直角三角形求出∠C=45°.【解答】解:(1)不可以.据题意得:AE=GE,∠EGB=∠EAB=90°,∴Rt△EGD中,GE<ED,∴AE<ED,故,点E不可以是AD的中点;(2)方法一:证明:∵AD∥BC,∴∠AEB=∠EBF,∵△EAB≌△EGB,∴∠AEB=∠BEG,∴∠EBF=∠BEF,∴FE=FB,∴△FEB为等腰三角形.∵∠ABG+∠GBF=90°,∠GBF+∠EFB=90°,∴∠ABG=∠EFB,在等腰△ABG和△FEB中,∠BAG=(180°﹣∠ABG)÷2,∠FBE=(180°﹣∠EFB)÷2,∴∠BAG=∠FBE,∴△ABG∽△BFE,方法二:∠ABG=∠EFB(见方法一),证得两边对应成比例:,由此可得出结论.(3)①方法一:∵四边形EFCD为平行四边形,∴EF∥DC,证明两个角相等,得△ABD∽△DCB,∴,即,∴a2+b2=ac;方法二:如图,过点D作DH⊥BC,∵四边形EFCD为平行四边形∴EF∥DC,∴∠C=∠EFB,∵△ABG∽△BFE,∴∠EFB=∠GBA,∴∠C=∠ABG,∵∠DAB=∠DHC=90°,∴△ABD∽△HCD,∴,∴,∴a2+b2=ac;方法三:证明△ABD∽△GFB,则有,∴,则有BF=,∵四边形EFCD为平行四边形,∴FC=ED=c﹣,∵ED∥BC,∴△EDG∽△FBG,∴,∴,∴a2+b2=ac;②方法一:解关于a的一元二次方程a2﹣ac+22=0,得:a1=,a2=…9分由题意,△=0,即c2﹣16=0,∵c>0,∴c=4,∴a=2,∴H为BC的中点,且ABHD为正方形,DH=HC,∠C=45°;方法二:设关于a的一元二次方程a2﹣ac+22=0两根为a1,a2,a1+a2=c>0,a1•a2=4>0,∴a1>0,a2>0,由题意,△=0,即c2﹣16=0,∵c>0,∴c=4,∴a=2,∴H为BC的中点,且ABHD为正方形,DH=HC,∠C=45°.23.如图,在平面直角坐标系中,直线y=x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M 与x轴、直线AB都相切,其半径为3(1﹣)a.(1)求点A的坐标和∠ABO的度数;(2)当点C与点A重合时,求a的值;(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?【分析】(1)已知直线AB的解析式,令解析式的x=0,能得到A点坐标;令y=0,能得到B点坐标;在Rt△OAB中,知道OA、OB的长,用正切函数即可得到∠ABO的读数.(2)当C、A重合时,就告诉了点C的坐标,然后结合OC的长以及等边三角形的特性求出OD、OE的长,即可得到D、E的坐标,利用待定系数即可确定a的值.(3)此题需要结合图形来解,首先画出第一次相切时的示意图(详见解答图);已知的条件只有圆的半径,那么先连接圆心与三个切点以及点E,首先能判断出四边形CPMN是正方形,那么CP与⊙M的半径相等,只要再求出PE就能进一步求得C点坐标;那么可以从PE=EQ,即Rt△MEP入手,首先∠CED=60°,而∠MEP=∠MEQ,易求得这两个角的度数,通过解直角三角形不难得到PE的长,即可求出PE及点C、E的坐标.然后利用C、E的坐标确定a的值,进而可求出AC的长,由此得解.【解答】解:(1)当x=0时,y=1;当y=0时,x=﹣,∴OA=1,OB=,∴=∴A的坐标是(0,1)∠ABO=30°.(2)∵△CDE为等边△,点A(0,1),∴tan30°=,∴,∴D的坐标是(﹣,0),E的坐标是(,0),把点A(0,1),D(﹣,0),E(,0)代入y=a(x﹣m)2+n,解得:a=﹣3.(3)如图,设切点分别是Q,N,P,连接MQ,MN,MP,ME,过点C作CH⊥x轴,H为垂足,过A作AF⊥CH,F为垂足.∵△CDE是等边三角形,∠ABO=30°∴∠BCE=90°,∠ECN=90°∵CE,直线AB分别与⊙M相切,∴∠MPC=∠CNM=90°,∴四边形MPCN为矩形,∵MP=MN∴四边形MPCN为正方形∴MP=MN=CP=CN=3(1﹣)a(a<0).∵EC和x轴都与⊙M相切,∴EP=EQ.∵∠NBQ+∠NMQ=180°,∴∠PMQ=60°∴∠EMQ=30°,∴在Rt△MEP中,tan30°=,∴PE=(﹣3)a∴CE=CP+PE=3(1﹣)a+(﹣3)a=﹣2a∴DH=HE=﹣a,CH=﹣3a,BH=﹣3a,∴OH=﹣3a﹣,OE=﹣4a﹣∴E(﹣4a﹣,0)∴C(﹣3a﹣,﹣3a)设二次函数的解析式为:y=a(x+3a+)2﹣3a∵E在该抛物线上∴a(﹣4a﹣+3a+)2﹣3a=0得:a2=1,解之得a1=1,a2=﹣1∵a<0,∴a=﹣1∴AF=2,CF=2,∴AC=4∴点C移动到4秒时,等边△CDE的边CE第一次与⊙M相切.。
2020届中考模拟广东省深圳市中考冲刺模拟英语试题(一)(含参考答案)

中考冲刺模拟试题(一)第一卷选择题(60分)I.词汇测试(15分)( )1. — With the help of my friends, I finally made it! —Congratulations! You’re really amazing.A. failedB. succeededC. developed( )2. — Why did the cat jump suddenly?—Oh, it saw a mouse.A. excitedly and loudlyB. quickly and quietlyC. quickly and unexpectedly( )3. — Do you think he can deal with the difficult problem? —Yes, I am sure he will find a good method to solve it.A.ideaB. opinionC. way( )4. — Remember to switch off the TV before you go to sleep. — OK, I will.A.turn offB. open upC. take off( )5. — The old photos remind me of my best friends. —Then, who are they?A. make me worry aboutB. make me look atC. make me think of( )6. — What is your secret to success?—Keep my dream all the time and never give it up.A. at the same timeB. in a wayC. all the way( )7. — Do you have classes the whole morning?—No, we will have a break from 9:40 a.m. to 10:10 a.m.A. have a restB. have a walkC. have a picnic( )8. — The new iPhone 6S looks so nice. Do you plan to buy one?—I can’t afford to buy it because it is so expensive.A.am not willing toB. am forced toC. don’t have enough money toii.根据句子意思,从下面每小题的A、B、C三个选项中选出恰当的词语完成句子。
广东省深圳市龙岗区布吉中学2020年中考数学复习试卷(1) 解析版

2020年广东省深圳市龙岗区布吉中学中考数学复习试卷(1)一.选择题(共12小题)1.下列运算正确的是()A.2ab+3ab=5a2b2B.a2•a3=a6C.a﹣2=(a≠0)D.2.如图,点A在数轴上表示的实数为a,则|a﹣2|等于()A.a﹣2 B.a+2 C.﹣a﹣2 D.﹣a+23.甲、乙两名运动员在10次的百米跑练习中,平均成绩分别为=10.7秒,=10.7秒,方差分别为S甲2=0.054,S乙2=0.103,那么在这次百米跑练习中,甲、乙两名运动员成绩较为稳定的是()A.甲运动员B.乙运动员C.甲、乙两人一样稳定D.无法确定4.如图,A,B,C,D是直线L上顺次四点,M,N分别是AB,CD的中点,且MN=6cm,BC =1cm,则AD的长等于()A.10cm B.11cm C.12cm D.13cm5.已知等腰三角形的一个外角等于140°,则这个三角形的三个内角的度数分别是()A.20°、20°、140°B.40°、40°、100°C.70°、70°、40°D.40°、40°、100°或70°、70°、40°6.如图,点A在函数(x<0)的图象上,过点A作AE垂直x轴,垂足为E,过点A 作AF垂直y轴,垂足为F,则矩形AEOF的面积是()A.2 B.3 C.6 D.不能确定7.用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为()A.22个B.19个C.16个D.13个8.用半径为6cm、圆心角为120°的扇形做成一个圆锥的侧面,则这个圆锥的底面半径是()A.2cm B.3cm C.4cm D.6cm9.若n为整数,则能使也为整数的n的个数有()A.1个B.2个C.3个D.4个10.已知a为实数,则代数式的最小值为()A.0 B.3 C.D.911.如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于()A.B.C.D.12.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是()A.(,3)、(﹣,4)B.(,3)、(﹣,4)C.(,)、(﹣,4)D.(,)、(﹣,4)二.填空题(共4小题)13.函数y=中自变量x的取值范围是.14.分解因式:﹣3x3y+27xy=.15.已知:3a2﹣6a﹣11=0,3b2﹣6b﹣11=0,且a≠b,则a4﹣b4=.16.如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN =60°,则AB的长是.三.解答题(共7小题)17.计算:(﹣2)0﹣3tan30°﹣||.18.先化简,再求值:÷,其中.19.将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.20.如下图,正方形ABCD,G是CD边上的一个动点(G不与C、D重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE、BG,并延长BG交DE于点H.(1)点G运动到何处时,四边形DGEF是平行四边形,并加以证明;(2)判断BG、DE的位置关系和大小关系;(3)当BH=13,DH=5时,求AH的长.21.某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示.(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;(2)当10<n≤30时,求z与n之间的函数关系式;(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.22.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP是平行四边形时,试求动点P的坐标.23.如图,AB是⊙O的直径,过点B作⊙O的切线BM,点P在右半圆上移动(点P与点A,B不重合),过点P作PC⊥AB,垂足为C;点Q在射线BM上移动(点M在点B的右边),且在移动过程中保持OQ∥AP.(1)若PC,QO的延长线相交于点E,判断是否存在点P,使得点E恰好在⊙O上?若存在,求出∠APC的大小;若不存在,请说明理由;(2)连接AQ交PC于点F,设,试问:k的值是否随点P的移动而变化?证明你的结论.参考答案与试题解析一.选择题(共12小题)1.下列运算正确的是()A.2ab+3ab=5a2b2B.a2•a3=a6C.a﹣2=(a≠0)D.【分析】结合二次根式的加减法、同底数幂的乘法和负整数指数幂的概念和运算法则进行求解即可.【解答】解:A、2ab+3ab=5ab≠5a2b2,本选项错误;B、a2•a3=a5≠a6,本选项错误;C、a﹣2=(a≠0),本选项正确;D、≠+,本选项错误.故选:C.2.如图,点A在数轴上表示的实数为a,则|a﹣2|等于()A.a﹣2 B.a+2 C.﹣a﹣2 D.﹣a+2【分析】首先能够结合数轴得到a的取值范围,从而判断a﹣2的符号,最后根据绝对值的性质进行化简.【解答】解:根据数轴,可知2<a<3,所以a﹣2>0,则|a﹣2|=a﹣2.故选:A.3.甲、乙两名运动员在10次的百米跑练习中,平均成绩分别为=10.7秒,=10.7秒,方差分别为S甲2=0.054,S乙2=0.103,那么在这次百米跑练习中,甲、乙两名运动员成绩较为稳定的是()A.甲运动员B.乙运动员C.甲、乙两人一样稳定D.无法确定【分析】根据方差的定义,方差越小数据越稳定.【解答】解:因为S甲2=0.054,S乙2=0.103,方差小的为甲,所以本题中成绩比较稳定的是甲.故选:A.4.如图,A,B,C,D是直线L上顺次四点,M,N分别是AB,CD的中点,且MN=6cm,BC =1cm,则AD的长等于()A.10cm B.11cm C.12cm D.13cm【分析】由已知条件知MB+CN=MN﹣BC,MB+CN=(AB+CD),故AD=AB+BC+CD可求.【解答】解:∵MN=6cm∴MB+CN=6﹣1=5cm,AB+CD=10cm∴AD=11cm.故选:B.5.已知等腰三角形的一个外角等于140°,则这个三角形的三个内角的度数分别是()A.20°、20°、140°B.40°、40°、100°C.70°、70°、40°D.40°、40°、100°或70°、70°、40°【分析】由于140°的外角不明确等腰三角形顶角和底角的外角,故应分两种情况讨论.【解答】解:(1)当40°角是顶角时,另两个底角度数为70°,70°;(2)当40°角是底角时,另两个底角度数为40°,100°.故选:D.6.如图,点A在函数(x<0)的图象上,过点A作AE垂直x轴,垂足为E,过点A 作AF垂直y轴,垂足为F,则矩形AEOF的面积是()A.2 B.3 C.6 D.不能确定【分析】过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的矩形面积S是个定值|k|.【解答】解:因为过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值,即S=|k|,所以矩形AEOF的面积是6.故选:C.7.用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为()A.22个B.19个C.16个D.13个【分析】主视图、俯视图是分别从物体正面、上面看,所得到的图形.【解答】解:综合主视图和俯视图,这个几何体的底层最少有3+3+1=7个小正方体,第二层最少有3个,第三层最少有2个,第四层最少有1个,因此搭成这样的一个几何体至少需要小正方体木块的个数为:7+3+2+1=13个.故选:D.8.用半径为6cm、圆心角为120°的扇形做成一个圆锥的侧面,则这个圆锥的底面半径是()A.2cm B.3cm C.4cm D.6cm【分析】根据弧长公式计算.【解答】解:设此圆锥的底面半径为r,根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得2πr=,r=2cm.故选:A.9.若n为整数,则能使也为整数的n的个数有()A.1个B.2个C.3个D.4个【分析】原式=1+,则n﹣1的值,一定是±1或±2.就可以求出n的值.【解答】解:原式=1+,当n=0时原式等于﹣1;n=2时原式等于3;n=3时原式等于2;n=﹣1时原式等于0.故选:D.10.已知a为实数,则代数式的最小值为()A.0 B.3 C.D.9【分析】把被开方数用配方法整理,根据非负数的意义求二次根式的最小值.【解答】解:∵原式===∴当(a﹣3)2=0,即a=3时代数式的值最小,为即3故选:B.11.如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于()A.B.C.D.【分析】作出辅助线,构造直角三角形,运用三角形面积相等,求出三角形的高,然后运用sin2α+cos2α=1,根据题中所给的条件,在直角三角形中解题,由角的余弦值与三角形边的关系求解.【解答】解:作AF⊥DB于F,作DE⊥AB于E.设DF=x,则AD=2x,∵∠ADB=60°,∴AF=x,又∵AB:AD=3:2,∴AB=3x,于是BF=x,∴3x•DE=(+1)x•x,DE=x,sin∠A=,cos∠A==.故选:A.12.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是()A.(,3)、(﹣,4)B.(,3)、(﹣,4)C.(,)、(﹣,4)D.(,)、(﹣,4)【分析】首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的对应边成比例,求得答案.【解答】解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,∵四边形AOBC是矩形,∴AC∥OB,AC=OB,∴∠CAF=∠BOE=∠CHO,在△ACF和△OBE中,,∴△CAF≌△BOE(AAS),∴BE=CF=4﹣1=3,∵∠AOD+∠BOE=∠BOE+∠OBE=90°,∴∠AOD=∠OBE,∵∠ADO=∠OEB=90°,∴△AOD∽△OBE,∴,即,∴OE=,即点B(,3),∴AF=OE=,∴点C的横坐标为:﹣(2﹣)=﹣,∴点C(﹣,4).故选:B.二.填空题(共4小题)13.函数y=中自变量x的取值范围是x≥﹣2且x≠1 .【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【解答】解:由题意得,x+2≥0且x﹣1≠0,解得x≥﹣2且x≠1.故答案为:x≥﹣2且x≠1.14.分解因式:﹣3x3y+27xy=﹣3xy(x+3)(x﹣3).【分析】先提取公因式﹣3xy,再对余下的多项式利用平方差公式继续分解.平方差公式:a2﹣b2=(a+b)(a﹣b).【解答】解:﹣3x3y+27xy,=﹣3xy(x2﹣9),﹣﹣(提取公因式)=﹣3xy(x+3)(x﹣3).﹣﹣(平方差公式).15.已知:3a2﹣6a﹣11=0,3b2﹣6b﹣11=0,且a≠b,则a4﹣b4=.【分析】根据根与系数的关系即可求出答案.【解答】解:由题意可知:a、b是方程3x2﹣6x﹣11=0的两解,且a≠b,∴a+b=2,ab=﹣,∴a2+b2=(a+b)2﹣2ab=,(a﹣b)2=(a+b)2﹣4ab=,∴a﹣b=±∴原式=(a+b)(a﹣b)(a2+b2)=±2××=±16.如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN =60°,则AB的长是.【分析】首先延长DC和AM交于E,过点E作EH⊥AN于点H,易证得△ABM≌△ECM,即可得AB=NE,然后由AM=4,AN=3,且∠MAN=60°,求得AH,NH与EH的长,继而求得EN的长,则可求得答案.【解答】解:延长DC和AM交于E,过点E作EH⊥AN于点H,如图.∵四边形ABCD为平行四边形,∴AB∥CE,∴∠BAM=∠CEM,∠B=∠ECM.∵M为BC的中点,∴BM=CM.在△ABM和△ECM中,,∴△ABM≌△ECM(AAS),∴AB=CD=CE,AM=EM=4,∵N为边DC的中点,∴NE=3NC=AB,即AB=NE,∵AN=3,AE=2AM=8,且∠MAN=60°,∴∠AEH=30°,∴AH=AE=4,∴EH==4,∴NH=AH﹣AN=4﹣3=1,∴EN==7,∴AB=×7=.故答案为.三.解答题(共7小题)17.计算:(﹣2)0﹣3tan30°﹣||.【分析】按照实数的运算法则依次计算,注意(﹣2)0=1,|﹣2|=2﹣.【解答】解:原式=1﹣3×﹣(2﹣)=1﹣﹣2+=﹣1.18.先化简,再求值:÷,其中.【分析】先去括号,再把除法统一为乘法把分式化简,再把数代入.【解答】解:原式=(2分)===﹣x﹣4;(4分)当时,原式==.(6分)19.将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.【分析】依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.【解答】解:(1)P偶数==(2)树状图为:或列表法为:第一次1 2 3 4第二次1 ﹣ 21 31 412 12 ﹣ 32 423 13 23 ﹣ 434 14 24 34 ﹣所以P4的倍数=.20.如下图,正方形ABCD,G是CD边上的一个动点(G不与C、D重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE、BG,并延长BG交DE于点H.(1)点G运动到何处时,四边形DGEF是平行四边形,并加以证明;(2)判断BG、DE的位置关系和大小关系;(3)当BH=13,DH=5时,求AH的长.【分析】(1)首先根据题意可得DG∥EF,根据一组对边平行且相等的四边形是平行四边形,可知当DG=EF,即DG=CG时,四边形DGEF是平行四边形;(2)由四边形ABCD和四边形CEFG是正方形,根据正方形的性质,即可得BC=DC,CG =CE,∠BCD=∠ECG=90°,则可根据SAS证得△BCG≌△DCE,进而得出答案;然后根据全等三角形的对应角相等,求得∠CDE+∠DHG=90°,则可得BH⊥DE;(3)连接BD,过点H作HN⊥AB,垂足为N,交DC于点M.先根据AB2+AD2=DH2+BH2求得正方形的边长,设HG=x,由△BCG∽△DHG,可求得HG=,接下来由∠MHG=∠GBC 可求得MG和MH的长,从而可得到AN和HN的长度,最后利用勾股定理即可求得AH的长.【解答】解;(1)当G是CD的中点,即CG=CD时,四边形DGEF是平行四边形.理由:∵G是CD的中点,∴CG=GD.∵四边形ABCD和四边形CEFG是正方形,∴DG∥EF,CG=EF.∴DG=EF.∴四边形DGEF是平行四边形.∴当G是CD的中点,即CG=CD时,四边形DGEF是平行四边形;(2)BG=DE,BG⊥DE.理由:∵四边形ABCD和四边形CEFG是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,在△BCG和△DCE中,,∴△BCG≌△DCE(SAS),∴BG=DE,∵△BCG≌△DCE,∴∠CBG=∠CDE,又∠CBG+∠BGC=90°,∴∠CDE+∠DGH=90°,∴∠DHG=90°,∴BH⊥DE.(3)如图所示:连接BD,过点H作HN⊥AB,垂足为N,交DC于点M.∵在Rt△BDH中,BD2=DH2+BH2=169+25=194,∴BD=.∵在Rt△ADB中,∠ABD=45°,∴AB=BD=.∵∠BGC=∠HGD,∠BCG=∠BHD,∴△BCG∽△DHG.∴.设GH=x,则,整理得:CG=.则DG=.∵△BCG∽△DHG,∴,即.解得:x=.∴GC==.∵∠MHG=∠GBC,∴HM=GH•==,MG===.∴MC=GC+MG=+=,NH==.∴AN=AB﹣BN==.在Rt△ANH中,AH====9.∴AH的长为9.21.某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示.(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是140 元,小张应得的工资总额是2800 元,此时,小李种植水果10 亩,小李应得的报酬是1500 元;(2)当10<n≤30时,求z与n之间的函数关系式;(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.【分析】(1)根据图象数据解答即可;(2)设z=kn+b(k≠0),然后利用待定系数法求一次函数解析式即可;(3)先求出20<m≤30时y与m的函数关系式,再分①10<m≤20时,10<n≤20;②20<m≤30时,0<n≤10两种情况,根据总费用等于两人的费用之和列式整理即可得解.【解答】解:(1)由图可知,如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是(160+120)=140元,小张应得的工资总额是:140×20=2800元,此时,小李种植水果:30﹣20=10亩,小李应得的报酬是1500元;故答案为:140;2800;10;1500;(2)当10<n≤30时,设z=kn+b(k≠0),∵函数图象经过点(10,1500),(30,3900),∴,解得,所以,z=120n+300(10<n≤30);(3)当10<m≤30时,设y=km+b,∵函数图象经过点(10,160),(30,120),∴,解得,∴y=﹣2m+180,∵m+n=30,∴n=30﹣m,∴①当10<m≤20时,10≤n<20,w=m(﹣2m+180)+120n+300,=m(﹣2m+180)+120(30﹣m)+300,=﹣2m2+60m+3900,②当20<m≤30时,0≤n<10,w=m(﹣2m+180)+150n,=m(﹣2m+180)+150(30﹣m),=﹣2m2+30m+4500,所以,w与m之间的函数关系式为w=.22.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP是平行四边形时,试求动点P的坐标.【分析】方法一:(1)由直线y=2x+2可以求出A,B的坐标,由待定系数法就可以求出抛物线的解析式和直线BD的解析式;(2)如图1,2,由(1)的解析式设M(a,﹣a2+a+2),当△BOC∽△MON或△BOC∽△ONM 时,由相似三角形的性质就可以求出结论;(3)设P(b,﹣b2+b+2),H(b,﹣2b+2).由平行四边形的性质建立方程求出b的值就可以求出结论.方法二:(1)利用一次函数求出B点坐标,利用抛物线求出D点坐标,进而求出BD.(2)因为以M、O、N为顶点的三角形与△BOC相似,所以∠OMN=∠OBA或∠OMN=∠OAB,分类讨论MN∥OB或OM⊥BC两种情况,并进行求解.(3)求出PH的参数长度,当PH=BO=2时,求出P点坐标.【解答】方法一:解:(1)∵y=2x+2,∴当x=0时,y=2,∴B(0,2).当y=0时,x=﹣1,∴A(﹣1,0).∵抛物线y=﹣x2+bx+c过点B(0,2),D(3,﹣4),∴解得:,∴y=﹣x2+x+2;设直线BD的解析式为y=kx+b,由题意,得,解得:,∴直线BD的解析式为:y=﹣2x+2;(2)存在.如图1,设M(a,﹣a2+a+2).∵MN垂直于x轴,∴MN=﹣a2+a+2,ON=a.∵y=﹣2x+2,∴y=0时,x=1,∴C(1,0),∴OC=1.∵B(0,2),∴OB=2.当△BOC∽△MNO时,∴,∴,解得:a1=1,a2=﹣2(舍去)∴M(1,2);如图2,当△BOC∽△ONM时,,∴,∴a=或(舍去),∴M(,).∴符合条件的点M的坐标为(1,2),(,);(3)设P(b,﹣b2+b+2),H(b,﹣2b+2).如图3,∵四边形BOHP是平行四边形,∴BO=PH=2.∵PH=﹣b2+b+2+2b﹣2=﹣b2+3b.∴2=﹣b2+3b∴b1=1,b2=2.当b=1时,P(1,2),当b=2时,P(2,0)∴P点的坐标为(1,2)或(2,0).方法二:(1)略.(2)设M(a,﹣a2+a+2),∵MN⊥x轴,∴∠OMN=∠OBA或∠OMN=∠OAB,①当∠OMN=∠OBA时,∵△BOC∽△MON,∴,∴,∴a1=1,a2=﹣2(舍),∴M1(1,2),②当∠OMN=∠OAB时,∵△BOC∽△MON,∴OM⊥BC,∴K OM×K BC=﹣1,∴=﹣1,∴2a2﹣a﹣4=0,∴a1=,a2=(舍),∴M2(,).(3)设P(b,﹣b2+b+2),H(b,﹣2b+2),∵四边形BOHP是平行四边形,∴BO=PH=2,∵PH=﹣b2+b+2+2b﹣2=﹣b2+3b.∴2=﹣b2+3b,∴b1=1,b2=2,当b=1时,P(1,2),当b=2时,P(2,0),∴P点的坐标为(1,2)或(2,0).23.如图,AB是⊙O的直径,过点B作⊙O的切线BM,点P在右半圆上移动(点P与点A,B不重合),过点P作PC⊥AB,垂足为C;点Q在射线BM上移动(点M在点B的右边),且在移动过程中保持OQ∥AP.(1)若PC,QO的延长线相交于点E,判断是否存在点P,使得点E恰好在⊙O上?若存在,求出∠APC的大小;若不存在,请说明理由;(2)连接AQ交PC于点F,设,试问:k的值是否随点P的移动而变化?证明你的结论.【分析】(1)若存在点E在⊙O上时,由已知,根据垂径定理知EC=CP,∠ECO=∠ACP =90°,由两直线平行,内错角相等知,∠E=∠P,由SAS知,△EOC≌△PAC,OC=CA,OE=AP则在Rt△APC中,由正弦的概念知,由特殊角的三角函数值知∠APC=30°;(2)由于P是⊙O右半圆上的任意一点,且AP∥OQ,由两直线平行,同位角相等知,∠PAC=∠QOB由BM是⊙O的切线,由切线的性质知,∠ABQ=90°,已知中有PC⊥AB,即∠ACP=∠ABQ=90°,∴△ACP∽△OBQ得到,,又有∠CAF=∠BAQ,∠ACF=∠ABQ=90°,故由△ACF∽△ABQ可知,又因为AB=2OB,则即得到PC=2CF,即PF=CF,所以有=,即k值不随点P的移动而变化.【解答】解:(1)解法一:当点E在⊙O上时,设OQ与⊙O交于点D,∵AB⊥PC,∴=.∵AP∥OQ,∴∠APE=∠PEQ.∴=.又∠AOE=∠BOD,=,,∴.解法二:设点E在⊙O上时,由已知有EC=CP,∴△EOC≌△PAC.∴OC=CA,OE=AP.在Rt△APC中,,∴∠APC=30°.(2)k值不随点P的移动而变化.理由是:∵P是⊙O右半圆上的任意一点,且AP∥OQ,∴∠PAC=∠QOB.∵BM是⊙O的切线,∴∠ABQ=90°.又∵PC⊥AB,∴∠ACP=90°.∴∠ACP=∠ABQ.∴△ACP∽△OBQ.∴.又∵∠CAF=∠BAQ,∠ACF=∠ABQ=90°,∴△ACF∽△ABQ.∴.又∵AB=2OB,∴即.∴PC=2CF即PF=CF.∴=.即k值不随点P的移动而变化.。
广东省深圳市龙岗区布吉中学2020年中考数学复习试卷(8)解析版

2020年广东省深圳市龙岗区布吉中学中考数学复习试卷(8)一.选择题(共10小题)1.﹣2020的相反数是()A.B.C.2020 D.﹣20202.有理数2.60×104的有效数字有()A.5个B.3个C.2个D.以上都不是3.下列运算正确的是()A.(m﹣n)2=m2﹣n2B.(m2)3=m6C.m2•n2=(mn)4D.m﹣2=﹣m24.下面视图中不是图中物体的视图的是()A.B.C.D.5.下列命题中,正确的是()A.若a•b>0,则a>0,b>0 B.若a•b<0,则a<0,b>0C.若a•b=0,则a=0且b=0 D.若a•b=0,则a=0或b=06.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,3)的点的个数是()A.2 B.1 C.4 D.37.如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足()A.B.R=3r C.R=2r D.8.如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是()A.x2+130x﹣1400=0 B.x2+65x﹣350=0C.x2﹣130x﹣1400=0 D.x2﹣65x﹣350=09.如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是()A.B.C.D.10.如图,直线l与反比例函数y=的图象在第一象限内交于A,B两点,交x轴于点C,若AB:BC=(m﹣1):1(m>1),则△OAB的面积(用m表示)为()A.B.C.D.二.填空题(共6小题)11.若a≤2,化简=.12.在直角梯形ABCD中,AD∥BC,∠C=90°,∠A=2∠B,则∠B=.13.如图(1)的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图(2)为对折后A、B、C、D、E五点均在同一平面上的位置图.若图(2)中,∠AED=15°,则∠BCE的度数为.14.如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是﹣或.其中正确的是.15.如图,已知∠ABC=90°,AB=πr,BC=,半径为r的⊙O从点A出发,沿A→B →C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图;圆心O运动的路程是.16.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是;当点B的横坐标为4n(n为正整数)时,m=(用含n的代数式表示).三.解答题(共7小题)17.计算:+(﹣)﹣1﹣sin45°+(﹣2)0.18.解不等式组:.19.如图,有大小质地相同仅颜色不同的两双拖鞋(分左.右脚)共四只,放置于地板上.【可表示为(A1.A2),(B1.B2)】注:本题采用“长方形”表示拖鞋.(1)若先从两只左脚拖鞋中取一只,再从两只右脚拖鞋中随机取一只,求恰好匹配成一双相同颜色的拖鞋的概率.(2)若从这四只拖鞋中随机取出两只,利用“树形图”或“表格”列举出所有可能出现的情况,并求恰好匹配成一双相同颜色的拖鞋的概率.20.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连接AE,点F是AE的中点,连接BF、DF,求证:BF⊥DF.21.某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.(1)甲、乙工程队每天各能铺设多少米?(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为正整百数).22.如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和B,与y轴交于点C(0,3).(1)求此抛物线的解析式及点B的坐标;(2)设抛物线的顶点为D,连接CD、DB、CB、AC.①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;(3)设Q是抛物线上一点,连接QB、QC,把△QBC沿直线BC翻折得到△Q′BC,若四边形QBQ′C为菱形,求此时点Q的坐标.23.如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,P是线段DF 的中点,连接PG,PC.(1)探究PG与PC的位置关系及的值(写出结论,不需要证明);(2)如图2,将原问题中的正方形ABCD和正方形BEFG换成菱形ABCD和菱形BEFG,且∠ABC=∠BEF=60度.探究PG与PC的位置关系及的值,写出你的猜想并加以证明;(3)如图3,将图2中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的边BG恰好与菱形ABCD的边AB在同一条直线上,问题(2)中的其他条件不变.你在(2)中得到的两个结论是否发生变化?写出你的猜想并加以证明.参考答案与试题解析一.选择题(共10小题)1.﹣2020的相反数是()A.B.C.2020 D.﹣2020【分析】直接利用相反数的定义得出答案.【解答】解:﹣2020的相反数是:2020.故选:C.2.有理数2.60×104的有效数字有()A.5个B.3个C.2个D.以上都不是【分析】科学记数法的表示形式为a×10n的形式(其中1≤|a|<10,n为整数),它的有效数字的个数与a有效数字的个数相同,而与n的大小无关.【解答】解:2.60×104的有效数字有2,6,0,共3个.故选:B.3.下列运算正确的是()A.(m﹣n)2=m2﹣n2B.(m2)3=m6C.m2•n2=(mn)4D.m﹣2=﹣m2【分析】根据完全平方公式对A进行判断;根据幂的乘方对B进行判断;根据积的乘方对C进行判断;根据负整数指数幂的意义对D进行判断.【解答】解:A、(m﹣n)2=m2﹣2mn+n2,所以A选项不正确;B、(m2)3=m6,所以B选项正确;C、m2•n2=(mn)2,所以C选项不正确;D、m﹣2=,所以D选项不正确.故选:B.4.下面视图中不是图中物体的视图的是()A.B.C.D.【分析】根据几何体的三视图,是分别从几何体的正面、左面和上面看物体而得到的图形,对每个选项分别判断、解答.【解答】解:A、是从几何体的上面看所得到的图形,即俯视图;故本选项不符合题意;B、是从几何体的正面看所得到的图形,即主视图;故本选项不符合题意;C、从几何体的正面、左面和上面看都得不出选项C的图形;所以,选项C的图形不是这个立体图形的视图;故本选项符合题意;D、是从几何体的左面看所得到的图形,即左视图;故本选项不符合题意.故选:C.5.下列命题中,正确的是()A.若a•b>0,则a>0,b>0 B.若a•b<0,则a<0,b>0C.若a•b=0,则a=0且b=0 D.若a•b=0,则a=0或b=0【分析】根据不等式的性质,有理数的乘法运算法则对各选项分析判断即可得解.【解答】解:A、若a•b>0,则a>0,b>0或a<0,b<0,所以该命题是假命题,故本选项错误;B、若a•b<0,则a<0,b>0或a>0,b<0,所以该命题是假命题,故本选项错误;C、若a•b=0,则a=0且b=0,错误,所以该命题是假命题,故本选项错误;D、若a•b=0,则a=0或b=0,是真命题,故本选项正确.故选:D.6.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,3)的点的个数是()A.2 B.1 C.4 D.3【分析】画出两条相交直线,到l1的距离为2的直线有2条,到l2的距离为3的直线有2条,看所画的这些直线的交点有几个即为所求的点的个数.【解答】解:如图所示,所求的点有4个,故选:C.7.如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足()A.B.R=3r C.R=2r D.【分析】首先连接OC,根据切线的性质得到OC⊥OB,再根据等腰三角形的性质可得到∠COB=60°,从而进一步求出∠B=30°,再利用直角三角形中30°角所对的边等于斜边的一半,可得到R与r的关系.【解答】解:连接OC,∵C为切点,∴OC⊥AB,∵OA=OB,∴∠COB=∠AOB=60°,∴∠B=30°,∴OC=OB,∴R=2r.故选:C.8.如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是()A.x2+130x﹣1400=0 B.x2+65x﹣350=0C.x2﹣130x﹣1400=0 D.x2﹣65x﹣350=0【分析】根据矩形的面积=长×宽,得出本题的等量关系是:(风景画的长+2个纸边的宽度)×(风景画的宽+2个纸边的宽度)=整个挂图的面积,由此可得出方程.【解答】解:依题意,设金色纸边的宽为xcm,(80+2x)(50+2x)=5400,整理,得x2+65x﹣350=0.故选:B.9.如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是()A.B.C.D.【分析】圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求得圆锥的母线长.根据余弦函数定义求解.【解答】解:设圆锥的母线长为R,由题意得65π=π×5×R,解得R=13,由勾股定理圆锥的高为=12.∴cosθ=,故选:D.10.如图,直线l与反比例函数y=的图象在第一象限内交于A,B两点,交x轴于点C,若AB:BC=(m﹣1):1(m>1),则△OAB的面积(用m表示)为()A.B.C.D.【分析】作AD⊥x轴于点D,BE⊥x轴于点E,根据相似三角形的判定得到△CAD∽△CBE,则CB:CA=BE:AD,而AB:BC=(m﹣1):1(m>1),则有AC:BC=m:1,AD:BE=m:1,若B点坐标为(a,),则A点的纵坐标为,把y=代入得=,易确定A点坐标为(,),然后利用S△OAB=S△AOD+S梯形ADEB﹣S△BOE计算即可.【解答】解:作AD⊥x轴于点D,BE⊥x轴于点E,如图,∵BE∥AD,∴△CAD∽△CBE,∴CB:CA=BE:AD,∵AB:BC=(m﹣1):1(m>1),∴AC:BC=m:1,∴AD:BE=m:1,设B点坐标为(a,),则A点的纵坐标为,∵点A在y=上,把y=代入得=,解得x=,∴A点坐标为(,),S△OAB=S△AOD+S梯形ADEB﹣S△BOE=S梯形ADEB=(+)(a﹣)=(m+1)(1﹣)=.故选:B.二.填空题(共6小题)11.若a≤2,化简=3﹣a.【分析】利用=|a|,进而确定a﹣2的符号,再开平方得出即可.【解答】解:∵a≤2,∴=2﹣a+1=3﹣a.故答案为:3﹣a.12.在直角梯形ABCD中,AD∥BC,∠C=90°,∠A=2∠B,则∠B=60°.【分析】根据两直线平行,同旁内角互补可得∠A+∠B=180°,然后把∠A=2∠B代入进行计算即可得解.【解答】解:∵AD∥BC,∴∠A+∠B=180°,∵∠A=2∠B,∴2∠B+∠B=180°,解得:∠B=60°.故答案为:60°.13.如图(1)的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图(2)为对折后A、B、C、D、E五点均在同一平面上的位置图.若图(2)中,∠AED=15°,则∠BCE的度数为37.5°.【分析】根据直角三角形30°角所对的直角边等于斜边的一半求出∠ABE=30°,再根据直角三角形两锐角互余求出∠AEB=60°,然后求出∠BED的度数,再根据平角等于180°求出∠DED′,然后根据翻折变换的性质求出∠CED′,再根据两直线平行,内错角相等解答.【解答】解:在长方形ABCD中,∠A=90°,AD∥BC,∵BE=2AE,∴∠ABE=30°,∴∠AEB=90°﹣∠ABE=90°﹣30°=60°,∵∠AED=15°,∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°,∴∠DED′=180°﹣60°﹣45°=75°,根据翻折的性质,∠CED′=∠DED′=×75°=37.5°,∴∠BCE=∠CED′=37.5°.故答案为:37.5°.14.如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是﹣或.其中正确的是③④.【分析】当x>0时,一次函数图象位于二次函数上方,可对①做出判断;当x<0,两个函数的函数随着x的增大而增大,故可对②做出判断;y1有最大值2,故可对③做出判断;分别令y1=1,y2=1结合图象可求得x的取值.【解答】解:当x>0时,一次函数图象位于二次函数上方,∴y2>y1故①错误;∵当x<0,两个函数的函数随着x的增大而增大,∴当x越大时,M越大,故②错误;函数y1=﹣2x2+2有最大值,最大值为y1=2,∴不存在使得M大于2的x的值,故③正确;令y1=1,即:﹣2x2+2=1.解得:x1=,x2=﹣不题意舍去)令y2=1,得:2x+2=1,解得:x=﹣.故④正确.故答案为:15.如图,已知∠ABC=90°,AB=πr,BC=,半径为r的⊙O从点A出发,沿A→B →C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图;圆心O运动的路程是2πr.【分析】根据题意画出图形,将运动路径分为三部分:OO1,,O2O3,分别计算出各部分的长再相加即可.【解答】解:圆心O运动路径如图:∵OO1=AB=πr;==πr;O2O3=BC=;∴圆心O运动的路程是πr+πr+=2πr.故答案为:2πr.16.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是3或4 ;当点B的横坐标为4n(n为正整数)时,m=6n﹣3 (用含n的代数式表示).【分析】根据题意画出图形,根据图形可得当点B的横坐标为8时,n=2时,此时△AOB 所在的四边形内部(不包括边界)每一行的整点个数为4×2+1﹣2,共有3行,所以此时△AOB所在的四边形内部(不包括边界)的整点个数为(4×2+1﹣2)×3,因为四边形内部在AB上的点是3个,所以此时△AOB内部(不包括边界)的整点个数为m==9,据此规律即可得出点B的横坐标为4n(n为正整数)时,m的值.【解答】解:如图:当点B在(3,0)点或(4,0)点时,△AOB内部(不包括边界)的整点为(1,1)(1,2)(2,1),共三个点,所以当m=3时,点B的横坐标的所有可能值是3或4;当点B的横坐标为8时,n=2时,△AOB内部(不包括边界)的整点个数m==9,当点B的横坐标为12时,n=3时,△AOB内部(不包括边界)的整点个数m==15,所以当点B的横坐标为4n(n为正整数)时,m==6n﹣3;另解:网格点横向一共3行,竖向一共是4n﹣1列,所以在y轴和4n点形成的矩形内部一共有3(4n﹣1)个网格点,而这条连线为矩形的对角线,与3条横线有3个网格点相交,所以要减掉3点,总的来说就是矩形内部网格点减掉3点的一半,即为[3(4n﹣1)﹣3]÷2=6n﹣3.故答案为:3或4,6n﹣3.三.解答题(共7小题)17.计算:+(﹣)﹣1﹣sin45°+(﹣2)0.【分析】根据零指数幂、乘方、特殊角的三角函数值、算术平方根4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=3﹣2﹣×+1=1﹣1+1=1.18.解不等式组:.【分析】先求出两个不等式的解集,再求其公共解.【解答】解:,解不等式①得,x<,解不等式②得,x≥﹣2,所以,不等式组的解集是﹣2≤x<.19.如图,有大小质地相同仅颜色不同的两双拖鞋(分左.右脚)共四只,放置于地板上.【可表示为(A1.A2),(B1.B2)】注:本题采用“长方形”表示拖鞋.(1)若先从两只左脚拖鞋中取一只,再从两只右脚拖鞋中随机取一只,求恰好匹配成一双相同颜色的拖鞋的概率.(2)若从这四只拖鞋中随机取出两只,利用“树形图”或“表格”列举出所有可能出现的情况,并求恰好匹配成一双相同颜色的拖鞋的概率.【分析】(1)用列表法表示所有可能出现的结果,从中得出配成一双相同颜色的情况,即可求出概率;(2)用列表法列举出所有等可能出现的情况,从中找出符合条件的情况数,进而求出概率.【解答】解:(1)用列表法表示所有可能的情况有:共4种情况,其中配成一双相同颜色的有2种,∴P配成一双相同颜色==;(2)用列表法表示所有可能的情况有:共12种情况,其中配成一双相同颜色的有4种,∴P配成一双相同颜色==.20.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连接AE,点F是AE的中点,连接BF、DF,求证:BF⊥DF.【分析】延长BF,交DA的延长线于点M,连接BD,进而求证△AFM≌△EFB,得AM=BEFB =FM,即可求得BC+BE=AD+AM,进而求得BD=BM,根据等腰三角形三线合一的性质即可求证BF⊥DF.【解答】证明:延长BF,交DA的延长线于点M,连接BD,∵四边形ABCD是矩形,∴MD∥BC,∴∠AMF=∠EBF,∠E=∠MAF,又FA=FE,∴△AFM≌△EFB,∴AM=BE,FB=FM,∵矩形ABCD中,∴AC=BD,AD=BC,∴BC+BE=AD+AM,即CE=MD,∵CE=AC,∴AC=CE=DM,∵FB=FM,∴BF⊥DF.21.某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.(1)甲、乙工程队每天各能铺设多少米?(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为正整百数).【分析】(1)设甲工程队每天能铺设x米.根据甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同,列方程求解;(2)设分配给甲工程队y米,则分配给乙工程队(1000﹣y)米.根据完成该项工程的工期不超过10天,列不等式组进行分析.【解答】解:(1)设甲工程队每天能铺设x米,则乙工程队每天能铺设(x﹣20)米.根据题意得:,即350(x﹣20)=250x,∴7x﹣140=5x解得x=70.经检验,x=70是原分式方程的解,且符合题意,乙工程队每天能铺设:x﹣20=70﹣20=50米.答:甲、乙工程队每天分别能铺设70米和50米.(2)设分配给甲工程队y米,则分配给乙工程队(1000﹣y)米.由题意,得,解得500≤y≤700.所以分配方案有3种:方案一:分配给甲工程队500米,分配给乙工程队500米;方案二:分配给甲工程队600米,分配给乙工程队400米;方案三:分配给甲工程队700米,分配给乙工程队300米.22.如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和B,与y轴交于点C(0,3).(1)求此抛物线的解析式及点B的坐标;(2)设抛物线的顶点为D,连接CD、DB、CB、AC.①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;(3)设Q是抛物线上一点,连接QB、QC,把△QBC沿直线BC翻折得到△Q′BC,若四边形QBQ′C为菱形,求此时点Q的坐标.【分析】(1)因为抛物线经过点A和点C,所以把点A和点C的坐标代入抛物线的解析式中得到关于b和c的方程,联立解出b和c,即可得到抛物线的解析式,又因为点B 是抛物线与x轴的另一交点,令y=0即可求出点B的坐标.(2)①根据(1)中求出的抛物线的解析式求出顶点D的坐标,根据OC与OB相等且互相垂直得到三角形COB为等腰直角三角形,得到角OCB为45°,根据勾股定理分别求出CD和BC的长,求出CD与CB的比值及OA与OC的比值,发现两比值相等,且由角DCy 与角BCO都等于45°,推出角DCB为90°,而角COA也为90°,根据两边对应成比例且夹角相等,得到两三角形相似,得证;②考虑两种情况,当P在x轴上(B的右边),且角ACP为直角时,三角形ACP与三角形DCB,相似比为AC比CD,所以AP比DB也等于相似比即可求出AP的长,进而求出P的坐标;当P在y轴的负半轴上时,角CAP为直角,AC比BC为相似比,斜边CP与DB之比等于相似比即可求出CP的长,进而求出P的坐标;写出P的两种情况的坐标即可;③若四边形QBQ’C为菱形,根据菱形对角线的性质得到QQ′垂直平分BC,得到点Q在线段BC的垂直平分线上,由OB等于OC得到直线QQ′平分角COB,即可求出QQ′的解析式为y=x,将y=x与抛物线的解析式联立即可求出Q的坐标.【解答】解:(1)把A(﹣1,0),C(0,3)代入y=﹣x2+bx+c得:,解得:,∴抛物线的解析式为:y=﹣x2+2x+3,令y=0,即﹣x2+2x+3=0,解得:x1=3,x2=﹣1(舍去),∴点B的坐标是(3,0);(2)①证明:可求得顶点D(1,4);OA=1,OC=OB=3,∠OCB=45°,由勾股定理求得:CD=,BC=.∴,易知:∠DCy=45°,故∠DCB=90°=∠AOC,∴△AOC∽△DCB.②存在符合条件的点P有两个:P1(9,0)或P2(0,);(3)若四边形QBQ′C为菱形,则QQ′垂直平分BC,∴点Q在线段BC的垂直平分线上,∵OC=OB,∴直线QQ’平分∠BOC,即:直线QQ′的解析式为y=x,∵点Q在抛物线y=﹣x2+2x+3上,∴﹣x2+2x+3=x,解得x=,∴Q(,)或(,).23.如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,P是线段DF 的中点,连接PG,PC.(1)探究PG与PC的位置关系及的值(写出结论,不需要证明);(2)如图2,将原问题中的正方形ABCD和正方形BEFG换成菱形ABCD和菱形BEFG,且∠ABC=∠BEF=60度.探究PG与PC的位置关系及的值,写出你的猜想并加以证明;(3)如图3,将图2中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的边BG恰好与菱形ABCD的边AB在同一条直线上,问题(2)中的其他条件不变.你在(2)中得到的两个结论是否发生变化?写出你的猜想并加以证明.【分析】(1)可通过构建全等三角形求解.延长GP交DC于H,可证三角形DHP和PGF 全等,已知的有DC∥GF,根据平行线间的内错角相等可得出两三角形中两组对应的角相等,又有DP=PF,因此构成了全等三角形判定条件中的(AAS),于是两三角形全等,那么HP=PG,DH=GF=BG,那么可得出CH=CG,于是三角形CHG就是等腰三角形且CP是底边上的中线,根据等腰三角形三线合一的特点,即可得出CP=PG=PH,CP⊥PG;(2)方法同(1),只不过三角形CHG是个等腰三角形,且顶角为120°,可根据三角函数来得出PG、CP的比例关系;(3)经过(1)(2)的解题过程,我们要构建出以CP为底边中线的等腰三角形,那么可延长GP到H,使PH=PG,连接CH、DH,那么根据前两问的解题过程,我们要求的是三角形CHG是个等腰三角形,关键是证三角形CDH和CBG全等,已知的只有CD=CB,我们可通过其他的全等三角形来得出三角形CDH和CBG全等的条件.三角形DHP和FGP中,有一组对顶角,DP=PF,HP=PG,那么这两个三角形就全等,可得出DH=GF=BG,∠HDP =∠GFP,根据平行线间的内错角相等可得出∠CDP=∠EFD,那么∠CDH=∠EFG=∠CBG,由此可得出三角形CDH和CBG全等,然后证法同(2).【解答】解:(1)线段PG与PC的位置关系是PG⊥PC;=1;(2)猜想:线段PG与PC的位置关系是PG⊥PC;=.证明:如图2,延长GP交DC于点H,∵P是线段DF的中点,∴FP=DP,由题意可知DC∥GF,∴∠GFP=∠HDP,∵∠GPF=∠HPD,∴△GFP≌△HDP,∴GP=HP,GF=HD,∵四边形ABCD是菱形,∴CD=CB,∴CG=CH,∴△CHG是等腰三角形,∴PG⊥PC,(三线合一)又∵∠ABC=∠BEF=60°,∴∠GCP=60°,∴=;(3)在(2)中得到的两个结论仍成立.证明:如图3,延长GP到H,使PH=PG,连接CH,CG,DH,∵P是线段DF的中点,∴FP=DP,∵∠GPF=∠HPD,∴△GFP≌△HDP,∴GF=HD,∠GFP=∠HDP,∵∠GFP+∠PFE=120°,∠PFE=∠PDC,∴∠CDH=∠HDP+∠PDC=120°,∵四边形ABCD是菱形,∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,∴∠GBC=120°,∵四边形BEFG是菱形,∴GF=GB,∴HD=GB,∴△HDC≌△GBC,∴CH=CG,∠DCH=∠BCG,∴∠DCH+∠HCB=∠BCG+∠HCB=120°,即∠HCG=120°∵CH=CG,PH=PG,∴PG⊥PC,∠GCP=∠HCP=60°,∴=.即PG=PC.。
广东省深圳市2020年九年级数学中考提升冲刺训练一(含答案)

广东省深圳市2020年九年级数学中考提升冲刺训练(一)姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在指定位置上第Ⅰ卷(选择题)一.选择题1.|﹣|的值是()A.2020 B.﹣2020 C.﹣D.2.下列图标,是轴对称图形的是()A.B.C.D.3.5G是第五代移动通信技术,5G网络理论下载速度可以达到每秒1300000KB以上,这意味着下载一部高清电影只需要1秒.将1300000用科学记数法表示应为()A.13×105B.1.3×105C.1.3×106D.1.3×1074.将正方体展开需要剪开的棱数为()A.5条B.6条C.7条D.8条5.数据1,3,6,5,3,6,8,6的中位数、众数分别为()A.5.5,6 B.6,5.5 C.6,3 D.5,66.下列运算,正确的是()A.a3+a3=2a6B.(a2)5=a10C.a2a5=a10D.(3ab)2=3a2b27.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是()A.32°B.68°C.60°D.58°8.如图,在△ABC中,∠C=90°,∠B=15°,AC=1,分别以点A,B为圆心,大于AB 的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则AD的长为()A.1.5 B.C.2 D.9.已知反比例函数y=的图象如图所示,则二次函数y=ax2﹣2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是()A.B.C.D.10.下列命题正确是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.有两条边对应相等的两个直角三角形全等C.16的平方根是4D.对角线相等的平行四边形是正方形11.下列各式:①a0=1;②a2•a3=a5;③2﹣2=﹣;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是()A.①②③B.①③⑤C.②③④D.②④⑤12.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为()A.1s B.s C.s D.2s第Ⅱ卷(非选择题)二.填空题13.因式分解:y3﹣16y=.14.一个不透明的盒子中有4个白球,3个黑球,2个红球,各球的大小与质地都相同,现随机从盒子中摸出一个球,摸到白球的概率是.15.如图,将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH;将AD沿过点G的直线折叠,使点A、点D分别落在边AB、CD上,折痕为EF.则折出的四边形BCEF的长宽之比为.16.如图,正方形ABCD的两个顶点A,B分别在x轴,y轴上,对角线相交于点E,AB=.若反比例函数y=(x>0)的图象经过D,E两点,则k的值是.三.解答题17.计算:|﹣|﹣(4﹣π)0+sin60°+(﹣)﹣2.18.先化简,再求值:,其中19.当前,商丘市正在围绕打响“游商丘古都城,读华夏文明史”文化旅游品牌,加快推进商丘景点保护性修复与宣传工作,以此带动以文化为核心的全域旅游跨越发展,打造华夏历史文明商丘传承创新区.随着社会经济的发展和城市周边交通状况的改善,旅游已成为人们的一种生活时尚,某中学开展以“我最喜欢的商丘风景区”为主题的调查活动,围绕“在森林公园、日月湖、汉梁公园和睢阳古城”四个风景区中,你最喜欢哪一个?(必选且只选一个)”的问题,在全校范围内随机抽取了部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:(1)本次调查共抽取了多少名学生?(2)通过计算补全条形统计图;(3)若该中学共有3000名学生,请你估计最喜欢日月湖风景区的学生有多少名.20.某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼项M的仰角为45°,已知测角仪的高AD为1.5米.请根据他们的测量数据求此楼MF的高.(结果精到0.1m,参考数据:≈1.414,≈1.732,≈2.449)21.某批发市场有考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A,B两种品牌的文具套装共1000套.(1)如果小王按批发价购买这1000套文具花了22000元,那么A,B两种品牌的文具套装各购买了多少套?(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡,并用会员卡购买A,B两种品牌文具套装1000套,共用了y元,设A品牌文具套装买了x套,求出y与x之间的函数关系式;(3)小王用会员卡购买A,B两种品牌文具套装1000套,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本?(运算结果取整数)22.如图,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A,B两点,其中A(m,0),B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.(1)求m,n的值及该抛物线的解析式;(2)如图2,若点P为线段AD上的一动点(不与A,D重合),分别以AP,DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN 面积最大时P点的坐标.23.在平面直角坐标系xOy中,有不重合的两个点Q(x1,y1)与P(x2,y2).若Q,P 为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x轴或y轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“折距”,记做D PQ.特别地,当PQ与某条坐标轴平行(或重合)时,线段PQ的长即点Q与点P 之间的“折距”.例如,在图1中,点P(1,﹣1),点Q(3,﹣2),此时点Q与点P 之间的“折距”D PQ=3.(1)①已知O为坐标原点,点A(3,﹣2),B(﹣1,0),则D AO=,D BO=.②点C在直线y=﹣x+4上,请你求出D CO的最小值.(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=3x+6上以动点.请你直接写出点E与点F之间“折距”D EF的最小值.参考答案一.选择题1.解:,故选:D.2.解:A、不是轴对称图形,故此选项错误;B、不是轴对称图形,故此选项错误;C、不是轴对称图形,故此选项错误;D、是轴对称图形,故此选项正确;故选:D.3.解:将1300000用科学记数法表示为:1.3×106.故选:C.4.解:∵正方体有6个表面,12条棱,要展成一个平面图形必须5条棱连接,∴要剪12﹣5=7条棱,故选:C.5.解:数据1,3,6,5,3,6,8,6按大小排列为:1,3,3,5,6,6,6,8 则最中间是:5和6,故中位数是5.5,6出现次数最多,故众数为6.故选:A.6.解:A.错误,a3+a3=2a3B.正确,因为幂的乘方,底数不变,指数相乘.C.错误,a2a5=a7D.错误,(3ab)2=9a2b2故选:B.7.解:根据题意可知,∠2=∠3,∵∠1+∠2=90°,∴∠2=90°﹣∠1=58°.故选:D.8.解:由作法得MN垂直平分AB,则DA=DB,∴∠DAB=∠B=15°,∴∠ADC=∠DAB+∠B=30°,在Rt△ACD中,AD=2AC=2.故选:C.9.解:∵当x=0时,y=ax2﹣2x=0,即抛物线y=ax2﹣2x经过原点,故A错误;∵反比例函数y=的图象在第一、三象限,∴ab>0,即a、b同号,当a<0时,抛物线y=ax2﹣2x的对称轴x=<0,对称轴在y轴左边,故D错误;当a<0时,b<0,直线y=bx+a经过第二、三、四象限,故B错误,C正确.故选:C.10.解:A、一组对边平行,另一组对边等的四边形可能是等腰梯形,故原命题错误;B、有两条边对应相等的两个直角三角形全等,故正确;C、16的平方根是±4,故原命题错误;D、对角线相等的平行四边形是矩形,故错误,故选:B.11.解:①当a=0时不成立,故本小题错误;②符合同底数幂的乘法法则,故本小题正确;③2﹣2=,根据负整数指数幂的定义a﹣p=(a≠0,p为正整数),故本小题错误;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0符合有理数混合运算的法则,故本小题正确;⑤x2+x2=2x2,符合合并同类项的法则,本小题正确.故选:D.12.解:连接BD,∵四边形ABCD是菱形,∴AB=AD,∠ADB=∠ADC=60°,∴△ABD是等边三角形,∴AD=BD,又∵△DEF是等边三角形,∴∠EDF=∠DEF=60°,又∵∠ADB=60°,∴∠ADE=∠BDF,在△ADE和△BDF中,,∴△ADE≌△BDF(AAS),∴AE=BF,∵AE=t,CF=2t,∴BF=BC﹣CF=4﹣2t,∴t=4﹣2t∴t=,故选:C.二.填空题13.解:原式=y(y+4)(y﹣4),故答案为:y(y+4)(y﹣4)14.解:∵一个不透明的盒子中有4个白球,3个黑球,2个红球,∴随机从盒子中摸出一个球,摸到白球的概率是:.故答案为:.15.解:∵四边形ABCD是正方形∴AD∥BC,AD=BC,∠ABD=45°∵折叠∴BC=BG,∵将AD沿过点G的直线折叠,使点A、点D分别落在边AB、CD上,∴∠AFE=∠EFB=90°,∠DEF=∠FEC,且∠ABC=90°,∴四边形BCEF是矩形,∵∠ABD=45°,∠EFB=90°,∴∠FGB=∠FBG=45°∴FG=BF∴BG=BF,∴BC=BF∴四边形BCEF的长宽之比为16.解:过点D、E分别作DF⊥x轴,EG⊥x轴,垂足为F、G,∵ABCD是正方形,∴易证△AOB≌△DFA,∴OA=DF,OB=FA,又∵E是BD的中点,OB∥EG∥DF,∴OG=FG=,∴EG是梯形OBDF的中位线,∴EG=(OB+DF),设OA=a,OB=b,∴D(a+b,a),E(,)∵点D、E都在反比例函数y=的图象上,∴(a+b)•a=,即:3a2+2ab﹣b2=0,也就是:(a+b)•(3a﹣b)=0,∵a+b≠0,∴3a﹣b=0,即:b=3a,在Rt△AOB中,OA2+OB2=AB2,∴a2+(3a)2=()2,解得:a=,b=,∴D(,),∴k=,故答案为:2.三.解答题17.解:原式=﹣1++16=+15.18.解:原式=÷()=当x=时,==﹣1﹣19.解:(1)10÷20%=50(名),答:本次调查共抽取了50名学生;(2)50﹣10﹣20﹣12=8(名),补全条形统计图如图所示,(3)3000×=1200(名),答:估计最喜欢日月湖风景区的学生有1200名.20.解:设MC=x,∵∠MAC=30°,∴在Rt△MAC中,AC===x.∵∠MBC=45°,∴在Rt△MCB中,MC=BC=x,又∵AB=DE=40,∴AC﹣BC=AB=40,即x﹣x=40,解得:x=20+20≈54.6,∴MF=MC+CF=54.6+1.5=56.1(米),答:楼MF的高56.1米.21.解:(1)设小王够买A品牌文具x套,够买B品牌文具y套,根据题意,得:,解得,答:小王够买A品牌文具600套,够买B品牌文具400套.(2)y=500+0.8[20x+25(1000﹣x)]=500+0.8(25000﹣5x)=500+20000﹣4x=﹣4x+20500,∴y与x之间的函数关系式是:y=﹣4x+20500.(3)根据题意,得:﹣4x+20500=20000,解得:x=125,∴小王够买A品牌文具套装为125套、够买B品牌文具套装为875套,设A品牌文具套装的售价为z元,则B品牌文具套装的售价为(z+5)元,由题意得:125z+875(z+5)≥20000+8×1000,解得:z≥23.625,答:A品牌的文具套装每套定价不低于24元时才不亏本.22.解:(1)把点A(m,0)、点B(4,n)代入y=x﹣1中,得m=1,n=3.∴A(1,0),B(4,3)∵y=﹣x2﹣bx+c过点A、点B,所以解得,∴y=﹣x2+6x﹣5.(2)如图2,∵△APM和△DPN为等腰直角三角形,∴∠APM=∠DPN=45°,∴∠MPN=90°,∴△MPN为直角三角形.令﹣x2+6x﹣5=0,解得x=1或5,∴D(5,0),AD=4.设AP=m,则DP=4﹣m,∴PM=m,PN=(4﹣m),=×PM×PN=m×(4﹣m)∴S△MPN=﹣(m﹣2)2+1.∴当m=2,即AP=2时,△MPN的面积最大,此时OP=3,∴P(3,0).23.解:(1)①D AO=|3﹣0|+|﹣2﹣0|=5,同理D BO=1,故答案为:5,1;②设点C(m,4﹣m),则D CO=|m|+|m﹣4|,当0≤m≤4时,D CO最小,最小值为4;(2)如图2,过点E分别作x、y轴的平行线交直线y=﹣x+4于F1、F2,则EF1是“折距”D EF的最小值,即求EF1的最小值即可,当点E在y轴左侧于平行于直线y=﹣x+4的直线相切时,EF1最小,如图3,将直线y=﹣x+4向右平移与圆相切于点E,平移后的直线与x轴交于点G,连接OE,设原直线与x、y轴交于点M、N,则点M、N的坐标分别为(﹣2,0)、点N(0,6),则MN=2,则△MON∽△GEO,则,即,则GO=,EF1=MG=2﹣=.。
深圳布吉时代学校2020年化学中考试卷及答案

深圳布吉时代学校2020年化学中考试卷及答案一、选择题(培优题较难)1.有部分变质的NaOH 固体18. 6g ,加入100g 的稀硫酸,恰好完全反应,所得溶液的质量是114.2g ,将其蒸干得到固体28.4g ,则原固体混合物中Na 元素与C 元素的质量比为 A .46:3 B .46:11C .23:3D .23:6【答案】C 【解析】 【分析】 【详解】氢氧化钠能与空气中的二氧化碳反应生成碳酸钠和水,从而变质,部分变质的氢氧化钠固体,加入稀硫酸,242422NaOH+H SO =Na SO +2H O ,23242422Na CO +H SO =Na SO +CO +H O ↑,溶液减少的质量,即生成的二氧化碳的质量,生成的二氧化碳的质量为:18.6g+100g-114.2g=4.4g ,由化学方程式可知,原固体混合物中的碳元素全部转化到了二氧化碳中,原固体混合物中的钠元素全部转化到了硫酸钠中,最后蒸干得到的固体即是硫酸钠的质量,故原固体混合物中钠元素的质量为:23228.4g 100%=9.2g 232+32+164⨯⨯⨯⨯⨯,原固体混合物中碳元素的质量为:124.4g 100%=1.2g 12+162⨯⨯⨯,故原固体混合物中Na 元素与C 元素的质量比为:9.2g :1.2g=23:3。
故选C 。
2.往AgNO 3和Cu (NO 3)2的混合溶液中加入一定量的铁粉,充分反应后,有金属析出,过滤、洗涤后往滤渣中加入稀盐酸,有无色气体放出,则滤液中一定存在的物质是 A .Fe (NO 3)2 B .Fe (NO 3)3C .Cu (NO 3)2、Fe (NO 3)2D .AgNO 3、Cu (NO 3)2、Fe (NO 3)2 【答案】A 【解析】根据金属银、铜、铁的活动性由强到弱的顺序铁>铜>银,当把铁粉加入到AgNO 3和Cu (NO 3)2的混合溶液中,首先和硝酸银反应生成银和硝酸亚铁,银被置换完剩余的铁再与硝酸铜反应生成硝酸亚铁和铜;过滤后向滤渣中滴加稀盐酸,有气泡,说明加入的铁有剩余.因此,滤液中只含有Fe (NO 3)2、滤渣中一定含有Ag 、铜、铁的结论.选A 点睛:金属活动顺序表:K Ca Na Mg Al Zn Fe Sn Pb H Cu Hg Ag Pt Au ,在金属活动顺序表中,排在氢前边的金属能和酸发生置换反应生成盐和氢气。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年九年级复习冲刺试卷(一)一、选择题(3×12=36) 1.的相反数是( )A. 22-B. 22C. 2-D. 22. 中国石油天然气集团公司与俄罗斯天然气工业股份公司在上海签署了《中俄东线供气购销合同》,每年的天然气供应量为380亿立方米,380亿立方米用科学记数法表示为( ) A.3.8×1010m 3 B. 38×109m 3 C. 380×108m 3 D. 3.8×1011m 3 3. 二次根式24x -+有意义,则实数x 的取值范围是( )A. x≥-2B. x >-2C. x <2D. x≤24. 一元二次方程01)12()2(22=+++-x m x m 有两个不相等的实数根,则m 的取值范围是( ) A .43>m B .43≥m C .43>m 且2≠m D .43≥m 且2≠m 5. 如果24410x x-+=,那么4x 等于( )A .-2B .2C .4D .-2或46. 如图1所示,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( ) A .6cm B .8cmC .10cmD .12cm7. 为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了10000人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这10000人中,吸烟者患肺癌的人数为x ,不吸烟者患肺癌的人数为y ,根据题意,下面列出的方程组正确的是( ).A.⎩⎨⎧=⨯+⨯=-10000%5.0%5.222y x y xB.⎪⎩⎪⎨⎧=+=-10000%5.0%5.222yx y x C.⎩⎨⎧=⨯-⨯=+22%5.0%5.210000y x y x D.⎪⎩⎪⎨⎧=-=+22%5.0%5.210000yx y x 8.如图2,在四边形ABCD 中,∠A+∠D=α,∠ABC 的平分线与∠BCD 的平分线交于点P ,则∠P=( ) A. 01902α- B. 01902α+ C.12α D. 0360α- 9. 按如图所示的程序计算,若开始输入的n 值为,则最后输出的结果是( )FE DCBAA. 14B. 16C.258+D.214+10. 如图3,Rt △ABC 中,∠ACB=90°,AC=4,BC=6,以斜边AB 上的一点O 为圆心所作的半圆分别与AC 、BC 相切于点D 、E ,则AD 为( )A. 2.5B. 1.6C. 1.5D. 111. 如图4,反比例函数y=(x <0)的图象经过点A (﹣1,1),过点A 作AB ⊥y 轴,垂足为B ,在y 轴的正半轴上取一点P (0,t ),过点P 作直线OA 的垂线l ,以直线l 为对称轴,点B 经轴对称变换得到的点B ′在此反比例函数的图象上,则t 的值是( ) A .B.C.D .12. 如图,在矩形ABCD 中,点E ,F 分别在边AB ,BC 上,且AE =AB ,将矩形沿直线EF 折叠,点B恰好落在AD 边上的点P 处,连接BP 交EF 于点Q ,对于下列结论:①EF =2BE ;②PF =2PE ;③FQ =4EQ ;④△PBF 是等边三角形.其中正确的是( )A . ①②B . ②③C . ①③D . ①④二、填空题(3×4=12)13. 代数式2221x x x ---的值为0,则x 的值为________14. 《庄子。
天下篇》中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图所示:123122121由图易得: 231111 (2222)n ++++=15. 己知实数a 、b 满足 a+b =5,ab =3,则 a-b =______16. 如图,折叠矩形纸片ABCD ,使点B 落在边AD 上,折痕EF 的两端分别在AB 、BC 上(含端点),且AB=6cm,BC=10cm.则折痕EF 的最大值是 cm 三、解答题(5+6+7+8+8+9+9=52)17. (5分)计算:202001)1(12)2(2--+-+-π18. (6分)化简求值:221122(1)21a a a a a a --+÷--+,a 取-1、0、1、2中的一个数19. (7分)四张背面完全相同的纸牌(如图,用①、②、③、④表示)。
正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机抽出一张(不放回),再随机抽出一张。
C(1)写出两次摸牌出现的所有可能的结果(用①、②、③、④表示);(2)以两次摸出的牌面上的结果为条件,求能判断四边形ABCD 为平行四边形的概率。
20. (8分)如图,在△ABC 中,D 是BC 边上的点(不与点B 、C 重合),连结AD . 问题引入:(1)如图①,当点D 是BC 边上的中点时,S △ABD :S △ABC = ;当点D 是BC 边上任意一点时, S △ABD :S △ABC = (用图中已有线段表示). 探索研究:(2)如图②,在△ABC 中,O 点是线段AD 上一点(不与点A 、D 重合),连结BO 、CO ,试猜想S △BOC 与S △ABC 之比应该等于图中哪两条线段之比,并说明理由. 拓展应用:(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想++的值,并说明理由.21. (8分)如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.(1)求一次函数、反比例函数的解析式;(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.22. (9分)△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,(1)求证:△BDF∽△CEF;(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S 取最大值;(3)已知A、D、F、E四点共圆,已知tan∠EDF=,求此圆直径.23. (9分)如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB 平分∠CAO.(1)求抛物线的解析式;(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M 的坐标;如果不存在,说明理由.答案解析一.选择题1.的相反数是()A.﹣B.C.﹣D.【考点】28:实数的性质.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:的相反数是﹣,故选:A.2.中国石油天然气集团公司与俄罗斯天然气工业股份公司在上海签署了《中俄东线供气购销合同》,这份有效期为30年的合同规定,从2018年开始供气,每年的天然气供应量为380亿立方米,380亿立方米用科学记数法表示为()A.3.80×1010m3B.38×109m3C.380×108m3D.3.8×1011m3【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n是负数.【解答】解:将380亿立方米用科学记数法表示为:3.80×1010m3.故选:A.3.二次根式有意义,则实数x的取值范围是()A.x≥﹣2 B.x>﹣2 C.x<2 D.x≤2【考点】72:二次根式有意义的条件.【分析】根据被开方数大于等于0列式计算即可得解.【解答】解:由题意得,﹣2x+4≥0,解得x≤2.故选:D.4.已知关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是()A.m>B.m≥C.m>且m≠2 D.m≥且m≠2【考点】AA:根的判别式.【分析】在与一元二次方程有关的求值问题中,必须满足下列条件:(1)二次项系数不为零;(2)在有不相等的实数根下必须满足△=b2﹣4ac>0.【解答】解:根据题意列出方程组,解之得m>且m≠2.故选:C.5.如果,那么等于()A.﹣2 B.2 C.4 D.﹣2或4【考点】B4:换元法解分式方程.【专题】11:计算题.【分析】此题可利用换元法来解,可设=y,那么原方程可化为关于y的一元二次方程,解方程即可得到y的值,进而可求得的值.【解答】解:设=y,则=y2,那么原方程可化为:y2﹣2y+1=0,解得y=1,则=2y=2,故选:B.6.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cm B.8cm C.10cm D.12cm【考点】KG:线段垂直平分线的性质.【专题】11:计算题.【分析】AC=AE+EC=BE+EC,根据已知条件易求.【解答】解:∵DE是边AB的垂直平分线,∴AE=BE.∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18.又∵BC=8,∴AC=10(cm).故选:C.7.为了研究吸烟是否对肺癌有影响,某研究所随机地抽查了1000人.结果显示:在吸烟者中患肺癌的比例是 2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这1000人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,根据题意,下面列出的方程组正确的是()A.B.C.D.【考点】99:由实际问题抽象出二元一次方程组.【分析】根据题意可以列出相应的方程组,从而可以解答本题.【解答】解:由题意可得,,故选:A.8.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α【考点】K7:三角形内角和定理;L3:多边形内角与外角.【专题】121:几何图形问题.【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.【解答】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.故选:C.9.按如图所示的程序计算,若开始输入的n值为,则最后输出的结果是()A.14 B.16 C.8+5D.14+【考点】79:二次根式的混合运算.【分析】根据给出的运算程序计算即可.【解答】解:当n=时,n(n+1)=2+<15,当n=2+时,n(n+1)=8+5>15,故选:C.10.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为()A.2.5 B.1.6 C.1.5 D.1【考点】MC:切线的性质;S9:相似三角形的判定与性质.【专题】121:几何图形问题.【分析】连接OD、OE,先设AD=x,再证明四边形ODCE是矩形,可得出OD=CE,OE=CD,从而得出CD =CE=4﹣x,BE=6﹣(4﹣x),可证明△AOD∽OBE,再由比例式得出AD的长即可.【解答】解:连接OD、OE,设AD=x,∵半圆分别与AC、BC相切,∴∠CDO=∠CEO=90°,∵∠C=90°,∴四边形ODCE是矩形,∴OD=CE,OE=CD,又∵OD=OE,∴CD=CE=4﹣x,BE=6﹣(4﹣x)=x+2,∵∠AOD+∠A=90°,∠AOD+∠BOE=90°,∴∠A=∠BOE,∴△AOD∽OBE,∴=,∴=,解得x=1.6,故选:B.11.如图,反比例函数y=(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是()A.B.C.D.【考点】GB:反比例函数综合题.【专题】15:综合题;16:压轴题.【分析】根据反比例函数图象上点的坐标特征由A点坐标为(﹣1,1)得到k=﹣1,即反比例函数解析式为y=﹣,且OB=AB=1,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA 可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(﹣,t),于是利用PB=PB′得t﹣1=|﹣|=,然后解方程可得到满足条件的t的值.【解答】解:如图,∵点A坐标为(﹣1,1),∴k=﹣1×1=﹣1,∴反比例函数解析式为y=﹣,∵OB=AB=1,∴△OAB为等腰直角三角形,∴∠AOB=45°,∵PQ⊥OA,∴∠OPQ=45°,∵点B和点B′关于直线l对称,∴PB=PB′,BB′⊥PQ,∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,∴B′P⊥y轴,∴点B′的坐标为(﹣,t),∵PB=PB′,∴t﹣1=|﹣|=,整理得t2﹣t﹣1=0,解得t1=,t2=(不符合题意,舍去),∴t的值为.故选:A.12.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()A.①②B.②③C.①③D.①④【考点】LB:矩形的性质;PB:翻折变换(折叠问题).【专题】121:几何图形问题;16:压轴题.【分析】求出BE=2AE,根据翻折的性质可得PE=BE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠APE=30°,然后求出∠AEP=60°,再根据翻折的性质求出∠BEF=60°,根据直角三角形两锐角互余求出∠EFB=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得EF =2BE,判断出①正确;利用30°角的正切值求出PF=PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③错误;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,判断出④正确.【解答】解:∵AE=AB,∴BE=2AE,由翻折的性质得,PE=BE,∴∠APE=30°,∴∠AEP=90°﹣30°=60°,∴∠BEF=(180°﹣∠AEP)=(180°﹣60°)=60°,∴∠EFB=90°﹣60°=30°,∴EF=2BE,故①正确;∵BE=PE,∴EF=2PE,∵EF>PF,∴PF<2PE,故②错误;由翻折可知EF⊥PB,∴∠EBQ=∠EFB=30°,∴BE=2EQ,EF=2BE,∴FQ=3EQ,故③错误;由翻折的性质,∠EFB=∠EFP=30°,∴∠BFP=30°+30°=60°,∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,∴∠PBF=∠PFB=60°,∴△PBF是等边三角形,故④正确;综上所述,结论正确的是①④.故选:D.二.填空题13.已知代数式=0,则x= 2 .【考点】63:分式的值为零的条件;A8:解一元二次方程﹣因式分解法.【分析】先根据分式的值为0的条件列出关于x的不等式组,求出x的值即可.【解答】解:∵代数式=0,∴,解得x=2.故答案为:2.14.《庄子.天下篇》中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图.由图易得:=1﹣.【考点】38:规律型:图形的变化类.【专题】2A:规律型.【分析】由图可知第一次剩下,截取1﹣;第二次剩下,共截取1﹣;…由此得出第n次剩下,共截取1﹣,得出答案即可.【解答】解:=1﹣故答案为:1﹣.15.已知实数a、b满足a+b=5,ab=3,则a﹣b=±.【考点】4C:完全平方公式.【专题】11:计算题.【分析】将a+b=5两边平方,利用完全平方公式展开,把ab的值代入求出a2+b2的值,再利用完全平方公式即可求出a﹣b的值.【解答】解:将a+b=5两边平方得:(a+b)2=a2+b2+2ab=25,将ab=3代入得:a2+b2=19,∴(a﹣b)2=a2+b2﹣2ab=19﹣6=13,则a﹣b=±.故答案为:±16.如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.则折痕EF的最大值是cm.【考点】PB:翻折变换(折叠问题).【专题】11:计算题.【分析】只有BF大于等于AB时,B′才会落在AD上,判断出点F与点C重合时,折痕EF最大,根据翻折的性质可得BC=B′C,然后利用勾股定理列式求出B′D,从而求出AB′,设BE=x,根据翻折的性质可得B′E=BE,表示出AE,在Rt△AB′E中,利用勾股定理列方程求出x,再利用勾股定理列式计算即可求出EF.【解答】解:如图,点F与点C重合时,折痕EF最大,由翻折的性质得,BC=B′C=10cm,在Rt△B′DC中,B′D===8cm,∴AB′=AD﹣B′D=10﹣8=2cm,设BE=x,则B′E=BE=x,AE=AB﹣BE=6﹣x,在Rt△AB′E中,AE2+AB′2=B′E2,即(6﹣x)2+22=x2,解得x=,在Rt△BEF中,EF===cm.当E与A重合时,EF的最大值为6,6<,∴EF的最大值为,故答案为:.三.解答题17.计算:2﹣1+(π﹣)0+﹣(﹣1)2020【考点】2C:实数的运算;6E:零指数幂;6F:负整数指数幂.【专题】511:实数;66:运算能力.【分析】原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可求出值.【解答】解:原式=+1+2﹣1=+2.18.化简求值:(1+)÷﹣,a取﹣1,0,1,2中的一个数.【考点】6D:分式的化简求值.【专题】11:计算题;513:分式.【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分后计算得到最简结果,把a=2代入计算即可求出值.【解答】解:原式=•﹣=﹣=﹣,则当a=2时,原式有意义,原式=﹣1.19.四张背面完全相同的纸牌(如图,用①、②、③、④表示),正面分别写有四个不同的条件.小明将这4张纸牌背面朝上洗匀后,先随机抽出一张(不放回),再随机抽出一张.(1)写出两次摸牌出现的所有可能的结果(用①、②、③、④表示);(2)以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率.【考点】L6:平行四边形的判定;X6:列表法与树状图法.【分析】(1)利用树状图展示所有等可能的结果数;(2)由于共有12种等可能的结果数,根据平行四边形的判定能判断四边形ABCD为平行四边形有6种,则根据概率公式可得到能判断四边形ABCD为平行四边形的概率=.【解答】解:(1)画树状图为:(2)共有12种等可能的结果数,其中能判断四边形ABCD为平行四边形有6种:①③、①④、②③、③①、③②、④①,所以能判断四边形ABCD为平行四边形的概率==.20.如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.问题引入:(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=1:2 ;当点D是BC边上任意一点时,S△:S△ABC=BD:BC(用图中已有线段表示).ABD探索研究:(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S之比应该等于图中哪两条线段之比,并说明理由.△ABC拓展应用:(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想++的值,并说明理由.【考点】SO:相似形综合题.【专题】152:几何综合题;16:压轴题.【分析】(1)根据三角形的面积公式,两三角形等高时,可得两三角形底与面积的关系,可得答案;(2)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,可得答案;(3)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,再根据分式的加减,可得答案.【解答】解:(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=1:2;当点D是BC边上任意一点时,S△ABD:S△ABC=BD:BC,故答案为:1:2,BD:BC;(2)S△BOC:S△ABC=OD:AD,如图②作OE⊥BC与E,作AF⊥BC与F,∵OE∥AF,∴△OED∽△AFD,.∵,∴;(3)++=1,理由如下:由(2)得,,.∴++=++===1.21.如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.(1)求一次函数、反比例函数的解析式;(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.【考点】GB:反比例函数综合题.【专题】15:综合题.【分析】(1)由AC=BC,且OC⊥AB,利用三线合一得到O为AB中点,求出OB的长,确定出B坐标,从而得到P点坐标,将P与A坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式,将P 坐标代入反比例解析式求出m的值,即可确定出反比例解析式;(2)假设存在这样的D点,使四边形BCPD为菱形,根据菱形的特点得出D点的坐标.【解答】解:(1)∵AC=BC,CO⊥AB,A(﹣4,0),∴O为AB的中点,即OA=OB=4,∴P(4,2),B(4,0),将A(﹣4,0)与P(4,2)代入y=kx+b得:,解得:k=,b=1,∴一次函数解析式为y=x+1,将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y=;(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,连接DC与PB交于E,∵四边形BCPD为菱形,∴CE=DE=4,∴CD=8,将x=8代入反比例函数y=得y=1,∴D点的坐标为(8,1)∴则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).22.△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,(1)求证:△BDF∽△CEF;(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S 取最大值;(3)已知A、D、F、E四点共圆,已知tan∠EDF=,求此圆直径.【考点】H7:二次函数的最值;KK:等边三角形的性质;M5:圆周角定理;SO:相似形综合题;T7:解直角三角形.【专题】15:综合题;2B:探究型.【分析】(1)只需找到两组对应角相等即可.(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,借助三角函数用m表示出AD、DF、AE、EF的长,进而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.(3)易知AF就是圆的直径,利用圆周角定理将∠EDF转化为∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通过解直角三角形就可求出AF长.【解答】解:(1)∵DF⊥AB,EF⊥AC,∴∠BDF=∠CEF=90°.∵△ABC为等边三角形,∴∠B=∠C=60°.∵∠BDF=∠CEF,∠B=∠C,∴△BDF∽△CEF.(2)∵∠BDF=90°,∠B=60°,∴sin60°==,cos60°==.∵BF=m,∴DF=m,BD=.∵AB=4,∴AD=4﹣.∴S△ADF=AD•DF=×(4﹣)×m=﹣m2+m.同理:S△AEF=AE•EF=×(4﹣)×(4﹣m)=﹣m2+2.∴S=S△ADF+S△AEF=﹣m2+m+2=﹣(m2﹣4m﹣8)=﹣(m﹣2)2+3.其中0<m<4.∵﹣<0,0<2<4,∴当m=2时,S取最大值,最大值为3.∴S与m之间的函数关系为:S═﹣(m﹣2)2+3(其中0<m<4).当m=2时,S取到最大值,最大值为3.(3)如图2,∵A、D、F、E四点共圆,∴∠EDF=∠EAF.∵∠ADF=∠AEF=90°,∴AF是此圆的直径.∵tan∠EDF=,∴tan∠EAF=.∴=.∵∠C=60°,∴=tan60°=.设EC=x,则EF=x,EA=2x.∵AC=a,∴2x+x=a.∴x=.∴EF=,AE=.∵∠AEF=90°,∴AF==.∴此圆直径长为.23.如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.(1)求抛物线的解析式;(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M 的坐标;如果不存在,说明理由.【考点】FA:待定系数法求一次函数解析式;H7:二次函数的最值;H8:待定系数法求二次函数解析式;HF:二次函数综合题;JA:平行线的性质;KI:等腰三角形的判定;S9:相似三角形的判定与性质.【专题】16:压轴题;2C:存在型.【分析】(1)如图1,易证BC=AC,从而得到点B的坐标,然后运用待定系数法求出二次函数的解析式.(2)如图2,运用待定系数法求出直线AB的解析式.设点P的横坐标为t,从而可以用t的代数式表示出PQ的长,然后利用二次函数的最值性质就可解决问题.(3)由于AB为直角边,分别以∠BAM=90°(如图3)和∠ABM=90°(如图4)进行讨论,通过三角形相似建立等量关系,就可以求出点M的坐标.【解答】解:(1)如图1,∵A(﹣3,0),C(0,4),∴OA=3,OC=4.∵∠AOC=90°,∴AC=5.∵BC∥AO,AB平分∠CAO,∴∠CBA=∠BAO=∠CAB.∴BC=AC.∴BC=5.∵BC∥AO,BC=5,OC=4,∴点B的坐标为(5,4).∵A(﹣3,0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,∴解得:∴抛物线的解析式为y=﹣x2+x+4.(2)如图2,设直线AB的解析式为y=mx+n,∵A(﹣3,0)、B(5,4)在直线AB上,∴解得:∴直线AB的解析式为y=x+.设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.∴y P=t+,y Q=﹣t2+t+4.∴PQ=y Q﹣y P=﹣t2+t+4﹣(t+)=﹣t2+t+4﹣t﹣=﹣t2++=﹣(t2﹣2t﹣15)=﹣[(t﹣1)2﹣16]=﹣(t﹣1)2+.∵﹣<0,﹣3≤t≤5,∴当t=1时,PQ取到最大值,最大值为.∴线段PQ的最大值为.(3)①当∠BAM=90°时,如图3所示.抛物线的对称轴为x=﹣=﹣=.∴x H=x G=x M=.∴y G=×+=.∴GH=.∵∠GHA=∠GAM=90°,∴∠MAH=90°﹣∠GAH=∠AGM.∵∠AHG=∠MHA=90°,∠MAH=∠AGM,∴△AHG∽△MHA.∴.∴=.解得:MH=11.∴点M的坐标为(,﹣11).②当∠ABM=90°时,如图4所示.∵∠BDG=90°,BD=5﹣=,DG=4﹣=,∴BG===.同理:AG=.∵∠AGH=∠MGB,∠AHG=∠MBG=90°,∴△AGH∽△MGB.∴=.∴=.解得:MG=.∴MH=MG+GH=+=9.∴点M的坐标为(,9).综上所述:符合要求的点M的坐标为(,9)和(,﹣11).。
