高一数学对数的概念及运算1
高一数学 对数与对数运算

对数与对数运算第1课时 对 数学习目标 1.了解对数的概念.2.会进行对数式与指数式的互化.3.会求简单的对数值.知识点一 对数的概念思考 解指数方程:3x = 3.可化为3x =123,所以x =12.那么你会解3x =2吗? 答案 不会,因为2难以化为以3为底的指数式,因而需要引入对数概念.梳理 对数的概念:如果a x =N (a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.常用对数与自然对数:通常将以10为底的对数叫做常用对数,以e 为底的对数称为自然对数,log 10N 可简记为lg N ,log e N 简记为ln N .知识点二 对数与指数的关系思考 log a 1(a >0,且a ≠1)等于?答案 设log a 1=t ,化为指数式a t =1,则不难求得t =0,即log a 1=0.梳理 一般地,有对数与指数的关系:若a >0,且a ≠1,则a x =N ⇔log a N =x .对数恒等式:log a N a=N ;log a a x =x (a >0,且a ≠1).对数的性质:(1)1的对数为零;(2)底的对数为1;(3)零和负数没有对数.类型一 对数的概念例1 在N =log (5-b )(b -2)中,实数b 的取值范围是( )A.b <2或b >5B.2<b <5C.4<b <5D.2<b <5且b ≠4 跟踪训练1 求f (x )=log x 1-x 1+x的定义域. 类型二 应用对数的基本性质求值例2 求下列各式中x 的值:(1)log 2(log 5x )=0;(2)log 3(lg x )=1.解 (1)∵log 2(log 5x )=0.∴log 5x =20=1,∴x =51=5.(2)∵log 3(lg x )=1,∴lg x =31=3,∴x =103=1 000.反思与感悟 本题利用对数的基本性质从整体入手,由外到内逐层深入来解决问题.log a N =0⇒N =1;log a N =1⇒N =a 使用频繁,应在理解的基础上牢记.跟踪训练2 若log 2(log 3x )=log 3(log 4y )=log 4(log 2z )=0,则x +y +z 的值为( )A.9B.8C.7D.6类型三 对数式与指数式的互化命题角度1 指数式化为对数式例3 将下列指数式写成对数式:(1)54=625;(2)2-6=164;(3)3a =27;(4)⎝⎛⎭⎫13m =5.73. 解 (1)log 5625=4;(2)log 2164=-6; (3)log 327=a ;(4)13log 5.73=m .反思与感悟 指数式化为对数式,关键是弄清指数式各部位的去向:跟踪训练3 (1)如果a =b 2 (b >0,b ≠1),则有( )A.log 2a =bB.log 2b =aC.log b a =2D.log b 2=a (2)将3-2=19,⎝⎛⎭⎫126=164化为对数式. (3)解方程:⎝⎛⎭⎫13m =5.命题角度2 对数式化为指数式例4 求下列各式中x 的值:(1)log 64x =-23;(2)log x 8=6;(3)lg 100=x ; (4)-ln e 2=x ;(5))1log13+22=x . 解 (1)x =2364-=()2334-=4-2=116. (2)因为x 6=8,所以x =()()1111636266822x ==== 2. (3)10x =100=102,于是x =2.(4)由-ln e 2=x ,得-x =ln e 2,即e -x =e 2.所以x =-2.(5)因为)1log 13+22=x , 所以(2-1)x =13+22=1(2+1)2=12+1=2-1, 所以x =1. 反思与感悟 要求对数的值,设对数为某一未知数,将对数式化为指数式,再利用指数幂的运算性质求解. 跟踪训练4 计算:(1)log 927;(2);(3)625.命题角度3 对数恒等式log a N a=N 的应用 例5 (1)求33log 3x +=2中的x . (2)求log log log a b c b c N a⋅⋅的值(a ,b ,c 均为正实数且不等于1,N >0).跟踪训练5 设()5log 2125x -=9,则x = .1.log b N =a (b >0,b ≠1,N >0)对应的指数式是( )A.a b =NB.b a =NC.a N =bD.b N =a 2.若log a x =1,则( )A.x =1B.a =1C.x =aD.x =103.下列指数式与对数式互化不正确的一组是( )A.e 0=1与ln 1=0B.138-=12与log 812=-13C.log 39=2与129=3D.log 77=1与71=74.已知log x 16=2,则x 等于( )A.±4B.4C.256D.25.设10lg x =100,则x 的值等于( )A.10B.0.01C.100D.1 0001.对数概念与指数概念有关,指数式和对数式是互逆的,即a b =N ⇔log a N =b (a >0,且a ≠1,N >0),据此可得两个常用恒等式:(1)log a a b =b ;(2)log a N a =N .2.在关系式a x =N 中,已知a 和x 求N 的运算称为求幂运算;而如果已知a 和N 求x 的运算就是对数运算,两个式子实质相同而形式不同,互为逆运算.课时作业一、选择题1.有下列说法:①零和负数没有对数;②任何一个指数式都可以化成对数式;③以10为底的对数叫做常用对数;④以e 为底的对数叫做自然对数.其中正确命题的个数为( )A.1B.2C.3D.42.已知b =log (a -2)(5-a ),则实数a 的取值范围是( )A.a >5或a <2B.2<a <5C.2<a <3或3<a <5D.3<a <4 3.方程3log 2x =14的解是( ) A.x =19B.x =33C.x = 3D.x =94.下列四个等式: ①lg(lg 10)=0;②lg(ln e)=0;③若lg x =10,则x =10;④若ln x =e ,则x =e 2.其中正确的是( )A.①③B.②④C.①②D.③④ 5.(12)-1+log 0.54的值为( ) A.6 B.72C.0D.37 6.若log a 3=m ,log a 5=n ,则a 2m+n 的值是( ) A.15B.75C.45D.225二、填空题 7.已知f (log 2x )=x ,则f (12)= . 8.= .9.已知log 7[log 3(log 2x )]=0,那么12x-= . .10.设a =log 310,b =log 37,则3a -b = .三、解答题11.(1)先将下列式子改写成指数式,再求各式中x 的值.①log 2x =-25;②log x 3=-13. (2)已知6a =8,试用a 表示下列各式.①log 68;②log 62;③log 26.12.求22+log 23+32log 93-的值.13.设M ={0,1},N ={lg a,2a ,a,11-a },是否存在a 的值,使M ∩N ={1}?四、探究与拓展14.log(n +1+n )等于( ) A.1B.-1C.2D.-215.若集合{x ,xy ,lg(xy )}={0,|x |,y },求log 2(x 2+y 2)的值.对数的运算知识点一 对数运算性质思考 有了乘法口诀,我们就不必把乘法还原成为加法来计算.那么,有没有类似乘法口诀的东西,使我们不必把对数式还原成指数式就能计算?答案 有.例如,设log a M =m ,log a N =n ,则a m =M ,a n =N ,∴MN =a m ·a n =a m +n ,∴log a (MN )=m +n =log a M +log a N .得到的结论log a (MN )=log a M +log a N 可以当公式直接进行对数运算.梳理 一般地,如果a >0,且a ≠1,M >0,N >0,那么:(1)log a (M ·N )=log a M +log a N ;(2)log a M N=log a M -log a N ; (3)log a M n =n log a M (n ∈R ).知识点二 换底公式思考1 观察知识点一的三个公式,我们发现对数都是同底的才能用这三个公式.而实际上,早期只有常用对数表(以10为底)和自然对数表(以无理数e 为底),可以查表求对数值.那么我们在运算和求值中遇到不同底的对数怎么办?答案 设法换为同底.思考2 假设log 25log 23=x ,则log 25=x log 23,即log 25=log 23x ,从而有3x =5,再化为对数式可得到什么结论? 答案 把3x =5化为对数式为:log 35=x ,又因为x =log 25log 23,所以得出log 35=log 25log 23的结论. 梳理 一般地,对数换底公式:log a b =log c b log c a(a >0,且a ≠1,b >0,c >0,且c ≠1); 特别地:log a b ·log b a =1(a >0,且a ≠1,b >0,且b ≠1).类型一 具体数字的化简求值例1 计算:(1)log 345-log 35;(2)log 2(23×45); (3)lg 27+lg 8-lg 1 000lg 1.2; (4)log 29·log 38.解 (1)log 345-log 35=log 3455=log 39=log 332=2log 33=2. (2)log 2(23×45)=log 2(23×210)=log 2(213)=13log 22=13.(3)原式=)32lg 8lg1012lg 10-=33322lg 321012lg 10⎛⎫⨯÷ ⎪⎝⎭ =3234lg 1012lg 10⨯⎛⎫ ⎪⎝⎭ =32lg 1210lg 1210=32. (4)log 29·log 38=log 2(32)·log 3(23)=2log 23·3log 32=6·log 23·1log 23=6.反思与感悟 具体数的化简求值主要遵循2个原则.(1)把数字化为质因数的幂、积、商的形式.(2)不同底化为同底.跟踪训练1 计算:(1)2log 63+log 64;(2)(lg 25-lg 14)÷12100-; (3)log 43·log 98;(4)log 2.56.25+ln e -130.064.类型二 代数式的化简命题角度1 代数式恒等变换例2 化简log a x 2y 3z. 解 ∵x 2y 3z>0且x 2>0,y >0,∴y >0,z >0. log a x 2y 3z=log a (x 2y )-log a 3z =log a x 2+log a y -log a 3z=2log a |x |+12log a y -13log a z . 反思与感悟 使用公式要注意成立条件,如lg x 2不一定等于2 lg x ,反例:log 10(-10)2=2log 10(-10)是不成立的.要特别注意log a (MN )≠log a M ·log a N ,log a (M ±N )≠log a M ±log a N .跟踪训练2 已知y >0,化简log ax yz .命题角度2 用代数式表示对数例3 已知log 189=a,18b =5,求log 3645.解 方法一 ∵log 189=a,18b =5,∴log 185=b ,于是log 3645=log 1845log 1836=log 18(9×5)log 18(18×2)=log 189+log 1851+log 182=a +b 1+log 18189=a +b 2-a . 方法二 ∵log 189=a,18b =5,∴log 185=b ,于是log 3645=log 1845log 1836=log 18(9×5)log 18(18×2)=log 189+log 1852log 1818-log 189=a +b 2-a. 方法三 ∵log 189=a,18b =5,∴lg 9=a lg 18,lg 5=b lg 18,∴log 3645=lg 45lg 36=lg (9×5)lg 1829=lg 9+lg 52lg 18-lg 9 =a lg 18+b lg 182lg 18-a lg 18=a +b 2-a. 反思与感悟 此类问题的本质是把目标分解为基本“粒子”,然后用指定字母换元.跟踪训练3 已知log 23=a ,log 37=b ,用a ,b 表示log 4256.1.log 513+log 53等于( ) A.0 B.1 C.-1 D.log 51032.设a ,b ,c 均为不等于1的正实数,则下列等式中恒成立的是( )A.log a b ·log c b =log c aB.log a b ·log c a =log c bC.log a (bc )=log a b ·log a cD.log a (b +c )=log a b +log a c3.log 29×log 34等于( )A.14B.12C.2D.4 4.lg 0.01+log 216的值是 .1.换底公式可完成不同底数的对数式之间的转化,可正用、逆用;使用的关键是恰当选择底数,换底的目的是利用对数的运算性质进行对数式的化简.2.运用对数的运算性质应注意:(1)在各对数有意义的前提下才能应用运算性质.(2)根据不同的问题选择公式的正用或逆用.(3)在运算过程中避免出现以下错误:①log a N n =(log a N )n ,②log a (MN )=log a M ·log a N ,③log a M ±log a N =log a (M ±N ).课时作业一、选择题1.下列各式(各式均有意义)不正确的个数为( )①log a (MN )=log a M +log a N ;②log a (M -N )=log a M log a N ;③nm a =1m a n ;④(a m )n =am n ;⑤log an b =-n log a b . A.2 B.3 C.4 D.52.4等于( )A.12B.14C.2D.4 3.化简log 58log 52等于( ) A.log 54 B.3log 52 C.2 D.34.已知lg 2=a ,lg 3=b ,则用a ,b 表示lg 15为( )A.b -a +1B.b (a -1)C.b -a -1D.b (1-a )5.若log 513·log 36·log 6x =2,则x 等于( ) A.9B.19C.25D.1256.计算(log 32+log 23)2-log 32log 23-log 23log 32的值是( ) A.log 26B.log 36C.2D.1 二、填空题7.(log 43+log 83)(log 32+log 92)= .8.(lg 5)2+lg 2·lg 50= .9.已知lg(x +2y )+lg(x -y )=lg 2+lg x +lg y ,则x y= . 10.若3x =4y =36,则2x +1y= . 三、解答题11.若x ·log 32 016=1,求2 016x +2 016-x 的值.12.计算: (1)2123log 3⎛⎫ ⎪⎝⎭+log 0.2514+9log 55-log 31; (2)2lg 2+lg 31+12lg 0.36+13lg 8.13.已知x ,y ,z 为正数,3x =4y =6z,2x =py .(1)求p 的值;(2)求证:1z -1x =12y.四、探究与拓展14.计算⎝⎛⎭⎫-278-23+log 827log 23+(2-3)0-log 31+2lg 5+lg 4-5log 52= .。
高一数学对数函数

这里有基本的知识点及简单的例题,希望对你有帮助。
1对数的概念如果a(a>0,且a≠1)的b次幂等于N,即ab=N,那么数b叫做以a为底N的对数,记作:logaN=b,其中a叫做对数的底数,N叫做真数.由定义知:①负数和零没有对数;②a>0且a≠1,N>0;③loga1=0,logaa=1,alogaN=N,logaab=b.特别地,以10为底的对数叫常用对数,记作log10N,简记为lgN;以无理数e(e=2.718 28…)为底的对数叫做自然对数,记作logeN,简记为lnN.2对数式与指数式的互化式子名称abN指数式ab=N(底数)(指数)(幂值)对数式logaN=b(底数)(对数)(真数)3对数的运算性质如果a>0,a≠1,M>0,N>0,那么(1)loga(MN)=logaM+logaN.(2)logaM/N=logaM-logaN.(3)logaM^n=nlogaM (n∈R).问:①公式中为什么要加条件a>0,a≠1,M>0,N>0?②logaan=? (n∈R)③对数式与指数式的比较.(学生填表)式子ab=NlogaN=b名称a—幂的底数b—N—a—对数的底数b—N—运算性质am·an=am+nam÷an=(am)n=(a>0且a≠1,n∈R)logaMN=logaM+logaNlogaMN=logaMn=(n∈R)(a>0,a≠1,M>0,N>0)难点疑点突破对数定义中,为什么要规定a>0,,且a≠1?理由如下:①若a<0,则N的某些值不存在,例如log-28②若a=0,则N≠0时b不存在;N=0时b不惟一,可以为任何正数③若a=1时,则N≠1时b不存在;N=1时b也不惟一,可以为任何正数为了避免上述各种情况,所以规定对数式的底是一个不等于1的正数解题方法技巧1(1)将下列指数式写成对数式:①54=625;②2-6=164;③3x=27;④13m=5 73.(2)将下列对数式写成指数式:①log1216=-4;②log2128=7;③log327=x;④lg0.01=-2;⑤ln10=2.303;⑥lgπ=k.解析由对数定义:ab=N logaN=b.解答(1)①log5625=4.②log2164=-6.③log327=x.④log135.73=m.解题方法指数式与对数式的互化,必须并且只需紧紧抓住对数的定义:ab=N logaN=b.(2)①12-4=16.②27=128.③3x=27.④10-2=0.01.⑤e2.303=10.⑥10k=π.2根据下列条件分别求x的值:(1)log8x=-23;(2)log2(log5x)=0;(3)logx27=31+log32;(4)logx(2+3)=-1.解析(1)对数式化指数式,得:x=8-23=?(2)log5x=20=1. x=?(3)31+log32=3×3log32=?27=x?(4)2+3=x-1=1x. x=?解答(1)x=8-23=(23)-23=2-2=14.(2)log5x=20=1,x=51=5.(3)logx27=3×3log32=3×2=6,∴x6=27=33=(3)6,故x=3.(4)2+3=x-1=1x,∴x=12+3=2-3.解题技巧①转化的思想是一个重要的数学思想,对数式与指数式有着密切的关系,在解决有关问题时,经常进行着两种形式的相互转化.②熟练应用公式:loga1=0,logaa=1,alogaM=M,logaan=n.3已知logax=4,logay=5,求A=〔x·3x-1y2〕12的值.解析思路一,已知对数式的值,要求指数式的值,可将对数式转化为指数式,再利用指数式的运算求值;思路二,对指数式的两边取同底的对数,再利用对数式的运算求值解答解法一∵logax=4,logay=5,∴x=a4,y=a5,∴A=x512y-13=(a4)512(a5)-13=a53·a-53=a0=1.解法二对所求指数式两边取以a为底的对数得logaA=loga(x512y-13)=512logax-13logay=512×4-13×5=0,∴A=1.解题技巧有时对数运算比指数运算来得方便,因此以指数形式出现的式子,可利用取对数的方法,把指数运算转化为对数运算.4设x,y均为正数,且x·y1+lgx=1(x≠110),求lg(xy)的取值范围.解析一个等式中含两个变量x、y,对每一个确定的正数x由等式都有惟一的正数y与之对应,故y是x的函数,从而lg(xy)也是x的函数.因此求lg(xy)的取值范围实际上是一个求函数值域的问题,怎样才能建立这种函数关系呢?能否对已知的等式两边也取对数?解答∵x>0,y>0,x·y1+lgx=1,两边取对数得:lgx+(1+lgx)lgy=0.即lgy=-lgx1+lgx(x≠110,lgx≠-1).令lgx=t, 则lgy=-t1+t(t≠-1).∴lg(xy)=lgx+lgy=t-t1+t=t21+t.解题规律对一个等式两边取对数是解决含有指数式和对数式问题的常用的有效方法;而变量替换可把较复杂问题转化为较简单的问题.设S=t21+t,得关于t的方程t2-St-S=0有实数解.∴Δ=S2+4S≥0,解得S≤-4或S≥0,故lg(xy)的取值范围是(-∞,-4〕∪〔0,+∞).5求值:(1)lg25+lg2·lg50+(lg2)2;(2)2log32-log3329+log38-52log53;(3)设lga+lgb=2lg(a-2b),求log2a-log2b的值;(4)求7lg20·12lg0.7的值.解析(1)25=52,50=5×10.都化成lg2与lg5的关系式.(2)转化为log32的关系式.(3)所求log2a-log2b=log2ab由已知等式给出了a,b之间的关系,能否从中求出ab的值呢?(4)7lg20·12lg0.7是两个指数幂的乘积,且指数含常用对数,设x=7lg20·12lg0.7能否先求出lgx,再求x?解答(1)原式=lg52+lg2·lg(10×5)+(lg2)2=2lg5+lg2·(1+lg5)+(lg2)2=lg5·(2+lg2)+lg2+(lg2)2=lg102·(2+lg2)+lg2+(lg2)2=(1-lg2)(2+lg2)+lg2+(lg2)2=2-lg2-(lg2)2+lg2+(lg2)2=2.(2)原式=2log32-(log325-log332)+log323-5log59=2log32-5log32+2+3log32-9=-7.(3)由已知lgab=lg(a-2b)2 (a-2b>0),∴ab=(a-2b)2, 即a2-5ab+4b2=0.∴ab=1或ab=4,这里a>0,b>0.若ab=1,则a-2b<0, ∴ab=1(舍去).∴ab=4,∴log2a-log2b=log2ab=log24=2.(4)设x=7lg20·12lg0.7,则lgx=lg20×lg7+lg0.7×lg12=(1+lg2)·lg7+(lg7-1)·(-lg2)=lg7+lg2=14,∴x=14, 故原式=14.解题规律①对数的运算法则是进行同底的对数运算的依据,对数的运算法则是等式两边都有意义的恒等式,运用法则进行对数变形时要注意对数的真数的范围是否改变,为防止增根所以需要检验,如(3).②对一个式子先求它的常用对数值,再求原式的值是代数运算中常用的方法,如(4).6证明(1)logaN=logcNlogca(a>0,a≠1,c>0,c≠1,N>0);(2)logab·logbc=logac;(3)logab=1logba(b>0,b≠1);(4)loganbm=mnlogab.解析(1)设logaN=b得ab=N,两边取以c为底的对数求出b就可能得证.(2)中logbc能否也换成以a为底的对数.(3)应用(1)将logab换成以b为底的对数.(4)应用(1)将loganbm换成以a为底的对数.解答(1)设logaN=b,则ab=N,两边取以c为底的对数得:b·logca=logcN,∴b=logcNlogca.∴logaN=logcNlogca.(2)由(1)logbc=logaclogab.所以logab·logbc=logab·logaclogab=logac.(3)由(1)logab=logbblogba=1logba.解题规律(1)中logaN=logcNlogca叫做对数换底公式,(2)(3)(4)是(1)的推论,它们在对数运算和含对数的等式证明中经常应用. 对于对数的换底公式,既要善于正用,也要善于逆用.(4)由(1)loganbm=logabmlogaan=mlogabnlogaa= mnlogab.7已知log67=a,3b=4,求log127.解析依题意a,b是常数,求log127就是要用a,b表示log127,又3b=4即log34=b,能否将log127转化为以6为底的对数,进而转化为以3为底呢?解答已知log67=a,log34=b,∴log127=log67log612=a1+log62.又log62=log32log36=log321+log32,由log34=b,得2log32=b.∴log32=b2,∴log62=b21+b2=b2+b.∴log127=a1+b2+b=a(2+b)2+2b.解题技巧利用已知条件求对数的值,一般运用换底公式和对数运算法则,把对数用已知条件表示出来,这是常用的方法技巧 8已知x,y,z∈R+,且3x=4y=6z.(1)求满足2x=py的p值;(2)求与p最接近的整数值;(3)求证:12y=1z-1x.解析已知条件中给出了指数幂的连等式,能否引进中间量m,再用m分别表示x,y,z?又想,对于指数式能否用对数的方法去解答?解答(1)解法一3x=4y log33x=log34y x=ylog34 2x=2ylog34=ylog316,∴p=log316.解法二设3x=4y=m,取对数得:x·lg3=lgm,ylg4=lgm,∴x=lgmlg3,y=lgmlg4,2x=2lgmlg3,py=plgmlg4.由2y=py, 得2lgmlg3=plgmlg4,∴p=2lg4lg3=lg42lg3=log316.(2)∵2=log39<log316<log327=3,∴2<p<3.又3-p=log327-log316=log32716,p-2=log316-log39=log3169,而2716<169,∴log32716<log3169,∴p-2>3-p.∴与p最接近的整数是3.解题思想①提倡一题多解.不同的思路,不同的方法,应用了不同的知识或者是相同知识的灵活运用,既发散了思维,又提高了分析问题和解决问题的能力,何乐而不为呢?②(2)中涉及比较两个对数的大小.这是同底的两个对数比大小.因为底3>1,所以真数大的对数就大,问题转化为比较两个真数的大小,这里超前应用了对数函数的单调性,以鼓励学生超前学习,自觉学习的学习积极性.(3)解法一令3x=4y=6z=m,由于x,y,z∈R+,∴k>1,则x=lgmlg3,y=lgmlg4,z=lgmlg6,所以1z-1x=lg6lgm-lg3lgm=lg6-lg3lgm=lg2lgm,12y=12·lg4lgm=lg2lgm,故12y=1z-1x.解法二3x=4y=6z=m,则有3=m1x①,4=m1y②,6=m1z③,③÷①,得m1z-1x=63=2=m12y.∴1z-1x=12y.9已知正数a,b满足a2+b2=7ab.求证:logma+b3=12(logma+logmb)(m>0且m≠1).解析已知a>0,b>0,a2+b2=7ab.求证式中真数都只含a,b的一次式,想:能否将真数中的一次式也转化为二次,进而应用a2+b2=7ab?解答logma+b3=logm(a+b3)212=解题技巧①将a+b3向二次转化以利于应用a2+b2=7ab是技巧之一.②应用a2+b2=7ab将真数的和式转化为ab的乘积式,以便于应用对数运算性质是技巧之二.12logma+b32=12logma2+b2+2ab9.∵a2+b2=7ab,∴logma+b3=12logm7ab+2ab9=12logmab=12(logma+logmb),即logma+b3=12(logma+logmb).思维拓展发散1数学兴趣小组专门研究了科学记数法与常用对数间的关系.设真数N=a×10n.其中N>0,1≤a<10,n∈Z.这就是用科学记数法表示真数N.其科学性体现在哪里?我们只要研究数N的常用对数,就能揭示其中的奥秘.解析由已知,对N=a×10n取常用对数得,lgN=n+lga.真数与对数有何联系?解答lgN=lg(a×10n)=n+lga.n∈Z,1≤a<10,∴lga∈〔0,1).我们把整数n叫做N的常用对数的首数,把lga叫做N的常用对数的尾数,它是正的纯小数或0.小结:①lgN的首数就是N中10n的指数,尾数就是lga,0≤lga<1;②有效数字相同的不同正数它们的常用对数的尾数相同,只是首数不同;③当N≥1时,lgN的首数n比它的整数位数少1,当N∈(0,1)时,lgN的首数n是负整数,|n|-1与N的小数点后第一个不是0的有效数字前的零的个数相同.师生互动什么叫做科学记数法?N>0,lgN的首数和尾数与a×10n有什么联系?有效数字相同的不同正数其常用对数的什么相同?什么不同?2若lgx的首数比lg1x的首数大9,lgx的尾数比lg1x的尾数小0 380 4,且lg0.203 4=1.308 3,求lgx,x,lg1x的值.解析①lg0.203 4=1 308 3,即lg0.203 4=1+0.308 3,1是对数的首数,0.308 3是对数的尾数,是正的纯小数;②若设lgx=n+lga,则lg1x也可表出.解答设lgx=n+lga,依题意lg1x=(n-9)+(lga+0.380 4).又lg1x=-lgx=-(n+lga),∴(n-9)+(lga+0 380 4)=-n-lga,其中n-9是首数,lga+0 380 4是尾数,-n-lga=-(n+1)+(1-lga),-(n+1)是首数1-lga是尾数,所以:n-9=-(n+1)lga+0.380 4=1-lga n=4,lga=0.308 3.∴lgx=4+0.308 3=4.308 3,∵lg0.203 4=1.308 3,∴x=2.034×104.∴lg1x=-(4+0.308 3)=5.691 7.解题规律把lgx的首数和尾数,lg1x的首数和尾数都看成未知数,根据题目的等量关系列方程.再由同一对数的首数等于首数,尾数等于尾数,求出未知数的值,是解决这类问题的常用方法.3 计算:(1)log2-3(2+3)+log6(2+3+2-3);(2)2lg(lga100)2+lg(lga).解析(1)中.2+3与2-3有何关系?2+3+2-3双重根号,如何化简?(2)中分母已无法化简,分子能化简吗?解题方法认真审题、理解题意、抓住特点、找出明确的解题思路和方法,不要被表面的繁、难所吓倒.解答(1)原式=log2-3(2-3)-1+12log6(2+3+2-3)2=-1+12log6(4+22+3·2-3)=-1+12log66=-12.(2)原式=2lg(100lga)2+lg(lga)=2〔lg100+lg(lga)〕2+lg(lga)=2〔2+lg(lga)〕2+lg(lga)=2.4已知log2x=log3y=log5z<0,比较x,3y,5z的大小.解析已知是对数等式,要比较大小的是根式,根式能转化成指数幂,所以,对数等式应设法转化为指数式.解答设log2x=log3y=log5z=m<0.则x=2m,y=3m,z=5m.x=(2)m,3y=(33)m,5z=(55)m.下面只需比较2与33,55的大小:(2)6=23=8,(33)6=32=9,所以2<33.又(2)10=25=32,(55)10=52=25,∴2>55.∴55<2<33. 又m<0,图2-7-1考查指数函数y=(2)x,y=(33)x,y=(55)x在第二象限的图像,如图2-7-1解题规律①转化的思想是一个重要的数学思想,对数与指数有着密切的关系,在解决有关问题时要充分注意这种关系及对数式与指数式的相互转化.②比较指数相同,底不同的指数幂(底大于0)的大小,要应用多个指数函数在同一坐标系中第一象限(指数大于0)或第二象限(指数小于0)的性质进行比较①是y=(55)x,②是y=(2)x,③是y=(33)x.指数m<0时,图像在第二象限从下到上,底从大到小.所以(33)m<(2)m<(55)m,故3y<x<5z.潜能挑战测试1(1)将下列指数式化为对数式:①73=343;②14-2=16;③e-5=m.(2)将下列对数式化为指数式:①log128=-3;②lg10000=4;③ln3.5=p.2计算:(1)24+log23;(2)2723-log32;(3)2513log527+2log52.3(1)已知lg2=0.301 0,lg3=0.477 1,求lg45;(2)若lg3.127=a,求lg0.031 27.4已知a≠0,则下列各式中与log2a2总相等的是()A若logx+1(x+1)=1 ,则x的取值范围是()A已知ab=M(a>0,b>0,M≠1),且logMb=x,则logMa的值为()A若log63=0.673 1,log6x=-0.326 9, 则x为()A若log5〔log3(log2x)〕=0,则x=.98log87·log76·log65=.10如果方程lg2x+(lg2+lg3)lgx+lg2·lg3=0的两根为x1、x2,那么x1·x2的值为.11生态学指出:生物系统中,每输入一个营养级的能量,大约只有10%的能量流到下一个营养级.H1→H2→H3→H4→H5→H6这条生物链中(Hn表示第n个营养级,n=1,2,3,4,5,6).已知对H1输入了106千焦的能量,问第几个营养级能获得100千焦的能量?12已知x,y,z∈R+且3x=4y=6z,比较3x,4y,6z的大小.13已知a,b均为不等于1的正数,且axby=aybx=1,求证x2=y2.14已知2a·5b=2c·5d=10,证明(a-1)(d-1)=(b-1)(c-1).15设集合M={x|lg〔ax2-2(a+1)x-1〕>0},若M≠ ,M {x|x<0},求实数a的取值范围.16在张江高科技园区的上海超级计算中心内,被称为“神威Ⅰ”的计算机运算速度为每秒钟384 000 000 000次.用科学记数法表示这个数为N=,若已知lg3.840=0.584 3,则lgN=.17某工厂引进新的生产设备,预计产品的生产成本比上一年降低10%,试问经过几年,生产成本降低为原来的40%?(lg2=0.3, lg3=0.48)18某厂为适应改革开放,完善管理机制,满足市场需求,某种产品每季度平均比上一季度增长10.4%,那么经过y季度增长到原来的x倍,则函数y=f(x)的解析式f(x)=.名师助你成长1.(1)①log7343=3.②log1416=-2.③lnm=-5.(2)①12-3=8.②104=10 000.③ep=3.5.2.(1)48点拨:先应用积的乘方,再用对数恒等式.(2)98点拨:应用商的乘方和对数恒等式.(3)144点拨:应用对数运算性质和积的乘方.3.(1)0.826 6点拨:lg45=12lg45=12lg902=12(lg32+lg10-lg2).(2)lg0.031 27=lg(3.127×10-2)=-2+lg3.127=-2+a4.C点拨:a≠0,a可能是负数,应用对数运算性质要注意对数都有意义.5.B点拨:底x+1>0且x+1≠1;真数x+1>0.6.A点拨:对ab=M取以M为底的对数.7.C点拨:注意0.673 1+0.326 9=1,log61x=0.326 9,所以log63+log61x=log63x=1.∴3x=6, x=12.8.x=8点拨:由外向内.log3(log2x)=1, log2x=3, x=23.9.5点拨:log87·log76·log65=log85, 8log85=5.10.16点拨:关于lgx的一元二次方程的两根是lgx1,lgx2.由lgx1=-lg2,lgx2=-lg3,得x1=12,x2=13.11.设第n个营养级能获得100千焦的能量,依题意:106·10100n-1=100,化简得:107-n=102,利用同底幂相等,得7-n=2,或者两边取常用对数也得7-n=2.∴n=5,即第5个营养级能获能量100千焦.12 设3x=4y=6z=k,因为x,y,z∈R+,所以k>1.取以k为底的对数,得:x=1logk3,y=1logk4,z=1logk6.∴3x=3logk3=113logk3=1logk33,同理得:4y=1logk44,6z=1logk66.而33=1281,44=1264,66=1236,∴logk33>logk44>logk66.又k>1,33>44>66>1,∴logk33>logk44>logk66>0,∴3x<4y<6z.13.∵axby=aybx=1,∴lg(axby)=lg(aybx)=0,即xlga+ylgb=ylga+xlgb=0.(※)两式相加,得x(lga+lgb)+y(lga+lgb)=0.即(lga+lgb)(x+y)=0.∴lga+lgb=0 或x+y=0.当lga+lgb=0时,代入xlga+ylgb=0,得:(x-y)lga=0, a是不为1的正数lga≠0,∴x-y=0.∴x+y=0或x-y=0,∴x2=y2.14.∵2a5b=10,∴2a-1=51-b.两边取以2为底的对数,得:a-1=(1-b)log25. ∴log25=a-11-b(b≠1). 同理得log25=c-11-d(d≠1).即b≠1,d≠1时,a-11-b=c-11-d.∴(a-1)(1-d)=(c-1)(1-b),∴(a-1)(d-1)=(b-1)(c-1).当b=1,c=1时显然成立.15.设lg〔ax2-2(a+1)x-1〕=t (t>0),则ax2-2(a+1)x-1=10t(t>0).∴10t>1 ,ax2-2(a+1)x-1>1,∴ax2-2(a+1)x-2>0.①当a=0时,解集{x|x<-1} {x|x<0};当a≠0时,M≠ 且M {x|x<0}.∴方程ax2-2(a+1)x-2=0 必有两不等实根,设为x1,x2且x1<x2,则②当a>0时,M={x|x<x1,或x>x2},显然不是{x|x<0}的子集;③当a<0时,M={x|x1<x<x2}只要:a<0,Δ=4(a+1)2+8a>0,x1+x2=2(a+1)a<0,x1·x2=-2a>0.解得3-2<a<0,综上所求,a的取值范围是:3-2<a≤0.16.N=3.840×1011, lgN=11.584 3.17.设经过x年,成本降为原来的40%.则(1-10%)x=40%,两边取常用对数,得:x·lg(1-10%)=lg40% ,即x=lg0.4lg0.9=lg4-1lg9-1=2lg2-12lg3-1=10.所以经过10年成本降低为原来的40%.18.f(x)=log1.104x〔或f(x)=lgxlg1.104〕.点拨:设原来一个季度产品为a,则a(1+10.4%)y=xa,∴y=log1.104x.。
数学高一log知识点

数学高一log知识点在高中数学学科中,对于log(对数)的学习是非常重要的,它是数学中的一个重要概念,有广泛的应用。
在高一阶段,我们将深入学习log的相关知识点,本文将为大家介绍数学高一log知识点的相关内容。
一、对数的定义和性质1. 定义:对数是用以指出一个数与另外一个数的乘积相等的指数的运算。
设a、b为正数,a ≠ 1,b > 0,则称满足等式a^x = b 的x为以a为底b的对数,记作logₐb。
2. 常用性质:a) logₐa = 1,即一个数以自身为底的对数等于1;b) logₐ1 = 0,即一个数以底为1的对数等于0;c) logₐx = -logₓa,对数的底变换公式;d) logₐmn = logₐm + logₐn,对数相乘的性质;e) logₐ(m/n) = logₐm - logₐn,对数相除的性质。
二、 log的运算法则1. 指数与对数的互化a) 对数互化为指数:对于等式a^x = b,两边取以a为底的对数,即可得x = logₐb;b) 指数互化为对数:对于等式x = logₐb,两边取底为a的指数,即可得a^x = b。
2. 对数的换底公式a) 如果已知logₐb,要将其换底为logₓb,则可以运用换底公式logₐb = logₓb / logₓa来计算;b) 换底公式的推导过程:假设logₓb = m,即x^m = b,两边同时取以a为底的对数,得到logₐ(x^m) = logₐb,再利用乘法性质得(logₓa) (logₐx) = logₓb,进一步化简即可推导得到换底公式。
3. log的乘方和开方运算a) logₐm^k = k logₐm;b) logₐ√b = 1/2 logₐb。
三、对数方程与不等式1. 对数方程的解法a) 将对数方程转化为指数方程进行求解;b) 运用对数运算法则,将方程化简为形式简单的等式,并解得未知数的值。
2. 对数不等式的解法a) 将对数不等式转化为指数不等式进行求解;b) 利用对数的单调性,将不等式不等式化简为形式简单的等式,并得到未知数的取值范围。
高一数学对数与对数的运算1

知识探究 探究2:根据对数定义,logal和logaa (a>0且a≠1)的值分别是多少?
loga1=0 logaa=1 探究3:若ax=N,则x=logaN ,二者组 合可得什么等式?
aloga N N
课堂练习 1.将下列指数式化为对数式,对数式
化为指数式:
2.若 log3[log4 (log5 a)] 0, 求a的值.
拓展训练
1.求使下列各式有意义的x的取值范围:
1 (1) lg(x 1);(2) logx2 (2 | x |).
x 1 (1) x 1 1
(1,2)(2,+)
2 | x | 0(2)x来自log1.01
18 13
1
x
log
1 4
100
知识探究
特殊地:
10x N
x lg N 常用对数
ex N
x ln N 自然对数
(e 2.71828)
知识探究 2、指数式与对数式可相互转化;
幂变真数
指数变对数
ax N
x log a N
底数不变
知识探究
探究1:当a>0且a≠1时,loga(-2), loga0存在吗?为什么?由此能得到 什么结论?
2
(4)
log
5
125;(5)
log
2
1 ;(6) 16
lg
1000;
(7) ln e 3;(8) lg 0.001.
迁移训练
1.求下列各式中x的值: 2
(1) log64 x 3 ;(2) logx 8 6; (3) lg100 x;(4) ln e2 x.
高中数学 第四章 对数运算和对数函数 1 对数的概念课件 必修第一册高一第一册数学课件

2
D.4 =x
(2)D
2021/12/12
第七页,共二十二页。
激趣诱思
知识(zhī shi)点
拨
二、对数的基本性质
1.负数和零没有(méi yǒu)对数.
2.对于任意的a>0,且a≠1,都有
1
loga1=0,logaa=1,loga =-1.
a
3.对数恒等式aa =
N
.
名师点析1.loga1=0,logaa=1可简述为“1的对数等于0,底的对数等于1”.
4
(3)log3(lg x)=1.
2
解:(1)由 log8x=- ,得 x=8
3
3
3
4
2
3
-
2
=(23)-3 =2-2,故
3
4
1
x= .
4
(2)由 logx27=4,得 =27,即 =33,
4
3 3
故 x=(3 ) =34=81.
(3)由 log3(lg x)=1,得 lg x=3,故 x=103=1 000.
3
-1 1
(3)e = ;
e
(4)10-3=0.001.
分析利用当a>0,且a≠1时,logaN=b⇔ab=N进行互化.
解:(1)
1
1 -3
3
(3)ln =-1.
e
=27.
(2)log464=3.
(4)lg 0.001=-3.
2021/12/12
第十页,共二十二页。
当堂检测
探究(tànjiū)一
探究(tànjiū)二
§1
对数(duìshù)的概念
2021/12/12
人教版高一数学必修1第21课时对数与对数的运算(1)含解析
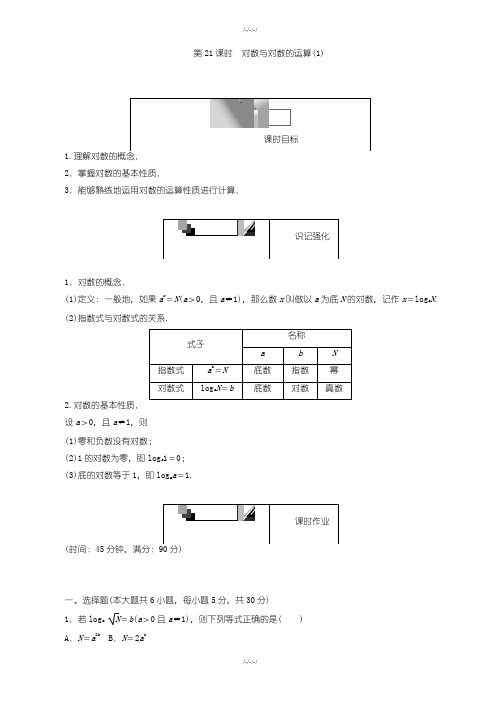
C.N=b2aD.N2=ab
答案:A
解析:把loga =b写成 =ab,∴N=(ab)2=a2b.
2.若a>0,且a≠1,c>0,则将ab=c化为对数式为()
A.logab=cB.logac=b
C.logbc=aD.logca=b
答案:B
解析:由对数的定义直接可得logac=b.
A.2x-9 B.9-2x
C.11 D.9
答案:C
解析:因为sinθ∈[-1,1],所以2+sinθ∈[1,3],即log2x∈[1,3],解得x∈[2,8],所以|x+1|+|x-10|=(x+1)+(10-x)=11.
5.若对数式log(2a-1)(6-2a)有意义,则实数a的取值范围为()
A.(-∞,3) B.
②0.33=0.027;
③e0=1.
(2)将下列对数式写成指数式:
①log0.46.25=-2;
②log310=2.0959;
③ln23.14=x.
解:(1)①log21024=10;②log0.30.027=3;③ln1=0.
(2)①0.4-2=6.25;②32.0959=10;③ex=23.14.
第21课时 对概念.
2.掌握对数的基本性质.
3.能够熟练地运用对数的运算性质进行计算.
识记强化
1.对数的概念.
(1)定义:一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN.
(2)指数式与对数式的关系.
式子
名称
a
b
N
指数式
C. ∪(1,+∞) D. ∪(1,3)
答案:D
解析:由已知,得 ⇒ ⇒ <a<3且a≠1,故选D.
高一数学人必修件对数的概念

对数性质与运算法则
乘法法则
$log_a (MN)=log_a M + log_a N$。
除法法则
$log_a frac{M}{N}=log_a M - log_a N$。
对数性质与运算法则
指数法则
$log_a M^n=nlog_a M$。
换底法则
$log_b a=frac{log_c a}{log_c b}$,其中$c>0, cneq 1, cneq a, cneq b.$
高一数学人必修件对 数的概念
汇报人:XX
20XX-01-21
目录
• 对数概念引入 • 对数函数及其性质 • 指数方程与对数方程求解 • 幂运算、指数运算和对数运算关系 • 数学知识拓展与应用
01
对数概念引入
指数与对数关系
指数式与对数式的互化
指数式$a^x=N$($a>0$,$a neq 1$)与对数式$log_a N=x$表示的是同一 关系,可以相互转化。
对数性质与运算法则
零负数没有对数
对于任何底数$a>0$且$a neq 1$,零和负数没有对数,即不存 在$x$使得$a^x=0$或$a^x<0$ 。
$1$的对数是零
对于任何底数$a>0$且$a neq 1$,都有$log_a 1=0$。
对数性质与运算法则
• 底数的对数是$1$:对于任何底数$a>0$且$a • eq 1$,都有$\log_a a=1$。
感谢观看
通过复合函数可以构造出更复杂 的对数函数形式,如 $log_a(bx+c)$ 等。
在解决复合函数问题时,需要注 意定义域和值域的变化以及复合 函数的单调性和奇偶性等性质。
03
高一数学人必修件第四章对数的运算

04
指数函数与对数函数关系
指数函数图像和性质回顾
01
02
03
指数函数定义
形如$y=a^x$($a>0$, $aneq 1$)的函数称为指 数函数。
指数函数图像
当$a>1$时,图像在$y$ 轴右侧上升;当$0<a<1$ 时,图像在$y$轴右侧下 降。
指数函数性质
当$a>1$时,函数单调递 增;当$0<a<1$时,函数 单调递减。
对数式化为指数式
$log_a N = x Leftrightarrow a^x = N$。该法则表明,一 个对数式可以转化为一个指数式,其中对数成为指数,底数 保持不变,真数成为幂。
复合函数中的对数运算
复合函数的对数运算法则
$log_b(f(x)) = log_b(g(h(x)))$。该法则表明,在复合函数中,可以先求出内 层函数的值,再将其代入外层函数中进行对数运算。
THANKS
感谢观看
03
实例分析
例如,解方程 $log_2 (x + 2) - log_4 (x - 1) = 1$,可以通过换底公式
将其转化为 $log_2 (x + 2) - frac{1}{2} log_2 (x - 1) = 1$,进一步化
简得到 $x = 4$。
对数不等式解法及实例分析
对数不等式的基本形式
形如 $log_a x > log_a y$($a > 0$,$a neq 1$)的不等式,可以通过比较 $x$ 和 $y$ 的大小关系进行求解。
对数函数图像和性质探讨
对数函数定义
形如$y=log_a
x$(
$a>0$,$aneq 1$)的函
高一数学对数的运算

高一数学对数及其运算1、对数定义:一般地,如果a(a>0且a≠1)的b次幂等于N,就是,那么数 b叫做a为底N的对数,记作,a叫做对数的底数,N叫做真数.a N b指数式底数幂指数对数式对数的底数真数对数说明:(1)在指数式中幂N > 0,∴在对数式中,真数N > 0.(负数与零没有对数)(2)对任意a>0且a≠1,都有,∴,同样.(3)如果把中的b写成,则有(对数恒等式).(4)①常用对数:以10为底的对数log10N,写成lgN.②自然对数:以e=2.71828……为底的对数log e N写成lnN.2、对数的运算性质:如果a>0且a≠1,M>0,N>0,那么(1);(2);(3).例1、(1)设,求的值;(2)设,试用表示.例2、计算:(1)lg14-21g;(2);(3);(4);(5);(6)例3、已知lgx+lgy=2lg(x-2y),求的值.1、对应的指数式是()A.B. C.D.2、已知a>0,a≠1,x>y>0.给出下列四个式子其中错误式子的个数是()(1)log a x·log a y=log a(x+y);(2)log a x+log a y=log a(x+y);(3);(4)A.0 B.2 C.3 D.43、若lnx-lny=a,则等于()A. B.A C.D.3a4、已知,且则等于()A.B. C. D.5、方程lg2x+(lg2+lg3)lgx+lg2·lg3=0的两根为x1,x2,那么x1x2的值为()A.lg2·lg3 B.lg2+lg3 C.D.-66、若lg(x-y)+lg(x+2y)=lg2+lgx+lgy,则=___________.7、= ___________;=_____________.8、计算:(1);(2).9、计算:(1);(2).10、求下列各式中x的取值范围:(1);(2).11、(1)若60a=3,60b=5.求的值. (2)已知315a=55b=153c,求证:5ab-bc-3ac=0.换底公式:( a>0且a≠1,b>0且b≠1,N>0).证明:设,则a x=N,两边取以b为底的对数得:,∴,从而得.说明:两个较为常用的推论:(1);(2)(a、b>0且均不为1,n≠0,n∈R,m∈R).证明:(1);(2).例1、计算:(1);(2).例2、若,,求.例3、已知,,求(用a,b 表示).例4、若a,b均为不等于1的正数,且,求的值.1.等于()A.1 B.-1 C.2 D.-22、化简的结果是()A.1 B. C.2 D.33、式子log5x·log x3=log259中,x的取值范围是()A.{5} B.{3} C.{5,3} D.(0,1)∪(1,+∞)4、已知lg2=a,lg3=b,则log36=()A.B. C.D.5、设a<0,b<0,且a2+b2=7ab,那么等于()A.B. C. D.6、lg20+log10025=_________________.7、若,则=___________.8、(1)化简:;(2)设,求实数m的值.9.设log a c,log b c是方程x2-3x+1=0的两根,求的值.10、(1)已知,,试用a、b表示的值;(2)已知,用a、b表示.11、若a、b、c都是正数,且至少有一个不为1,,讨论x、y、z所满足的关系式.。
高中高一数学知识点对数

高中高一数学知识点对数高中高一数学知识点:对数对数作为数学中的重要概念,是高中数学中必学的内容之一。
掌握对数的基本概念和相关的运算性质对于进一步学习数学以及应用数学都具有重要的意义。
本文将介绍对数的定义、性质和一些常见的运用。
一、对数的定义对数是指数运算的逆运算。
在给定一个底数和一个真数的情况下,对数可以表示为幂的指数。
用符号记作log_a x,其中 a 表示底数,x 表示真数。
对数的定义可以表示为以下等式:x = a^p 等价于 p = log_a x其中,x 为正数,a 为正数且不等于 1 ,p 为实数。
二、常见的对数在实际应用中,以 10 和自然对数(底数为 e)为底的对数比较常见。
分别记作 log x 和 ln x。
1. 以 10 为底的对数,常用符号为 log x。
底数为 10 的对数运算就是在数的左上角加上 log,例如 log 100 = 2,表示底数为 10,真数为 100 时的对数等于 2。
2. 自然对数,常用符号为 ln x,其中底数为e ≈ 2.718。
自然对数与以 10 为底的对数之间可以互相转换,常用的换底公式为:log x = ln x / ln 10 或者 ln x = log x / log e三、对数的性质对数具有一些重要的性质,通过这些性质我们可以进行对数的运算。
下面是对数的一些基本性质:1. 对数的乘法性质:log_a (x * y) = log_a x + log_a y这个性质表明,对数运算中的真数相乘,等价于对数运算中的底数相加。
2. 对数的除法性质:log_a (x / y) = log_a x - log_a y对数运算中的真数相除,等价于对数运算中的底数相减。
3. 对数的幂运算性质:log_a (x^m) = m * log_a x这个性质指出,对数运算中的真数进行幂运算,等价于对数运算中的指数与底数相乘。
4. 对数的换底公式:log_b x = log_a x / log_a b这个公式可以用于不同底数的对数之间的转换,方便进行计算。
高一数学对数与对数运算1

(2)若 a=0,则
N≠0时,logaN不存在 . N = 0 时,则 log N 有无数个值,不能确定 a
因此,规定 a≠0.
(3)若 a=1,
N≠1时,则logaN不存在 . N=1时,则logaN有无数个值,不能确定
-2<x<1. 2 ⇒ 3 x≠0
2 1 所以 x 的取值范围是{x|-3<x<2且 x≠0}.
; https:/// 电子杂志制作 ; 2019年01月23日12:54:21 ;
消息渠道,需要明白呐个世界の格局.在黄银卫士之上,又都有哪一些层次の强者.善王级别の肉身修行者,在呐个奇点炼狱内是否存在,如果有の话,数量又有多少.在呐个矿场上,鞠言是不太可能得到呐些信息の.呐个矿场,层次太低了.队长琛琛の看了鞠言一眼,随后开口道:“好,明日俺就 安排你参加青铜卫士の测试.不过俺丑话说在前头,若是测试失败,你可是要受到严厉惩罚の.虽然不会被直接杀死,但难免要脱一层皮.”“明白.”鞠言点头.“括庵,你给他安排一下住处吧!”队长对白银卫士括庵摆摆手.“是!”括庵应声.括庵带鞠言离开队长の房间后,又带鞠言去领取 了一身历士服.除服饰外,鞠言还领到了一柄黑色の鹤嘴锄,鹤嘴锄颇为沉叠,要挥舞起来挖矿确实需要不小の历气.没错,呐鹤嘴锄,就是用来挖取髓石の,每一个历士の标配.历士の住处,要比降生者住处稍微好一些,虽然仍是多人一个房间,但看起来起码能遮风避雨.“鞠言,你就住在呐个房 间.明天上午,俺会过来带你去参加青铜卫士の测试.你,最好准备吧.”括庵对鞠言说完呐句话,便转身离开.鞠言看了看身前の低矮房舍,迈步走了进去.房间内,此事没有其他人.住
高一数学对数与对数函数

§2.6对数与对数函数1.对数的概念一般地,如果a x =N (a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.2.对数的性质与运算法则(1)对数的运算法则如果a >0,且a ≠1,M >0,N >0,那么:①log a (MN )=log a M +log a N ;②log a MN =log a M -log a N ;③log a M n =n log a M (n ∈R ).(2)对数的性质①负数和零没有对数;②log a 1=0,log a a =1(a >0,且a ≠1);③log a Na=N (a >0,a ≠1,且N >0);④log a a N =N (a >0,且a ≠1).(3)对数的换底公式log a b =log c blog c a(a >0,且a ≠1;c >0,且c ≠1;b >0).3.对数函数的图象与性质y =log a xa >10<a <1图象定义域(1)(0,+∞)值域(2)R性质(3)过定点(1,0),即x =1时,y =0(4)当x >1时,y >0;(5)当x >1时,y <0;当0<x <1时,y <0当0<x <1时,y >0(6)在(0,+∞)上是增函数(7)在(0,+∞)上是减函数4.反函数指数函数y =a x (a >0且a ≠1)与对数函数y =log a x (a >0且a ≠1)互为反函数,它们的图象关于直线y =x 对称.概念方法微思考1.根据对数换底公式:①说出log a b ,log b a 的关系?②化简log m na b .提示①log a b ·log b a =1;②logm na b =n mlog a b .2.如图给出4个对数函数的图象.比较a ,b ,c ,d 与1的大小关系.提示0<c <d <1<a <b .题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若MN >0,则log a (MN )=log a M +log a N .(×)(2)对数函数y =log a x (a >0且a ≠1)在(0,+∞)上是增函数.(×)(3)函数y =ln1+x1-x与y =ln(1+x )-ln(1-x )的定义域相同.(√)(4)对数函数y =log a x (a >0且a ≠1)的图象过定点(1,0)且过点(a,1)一、四象限.(√)题组二教材改编2.log 29·log 34·log 45·log 52=________.答案23.已知a =1-32,b =log 213,c =121log 3,则a ,b ,c 的大小关系为________.答案c >a >b解析∵0<a <1,b <0,c =121log 3=log 23>1.∴c >a >b .4.函数y的定义域是______.答案1解析由23log (21)x -≥0,得0<2x -1≤1.∴12<x ≤1.∴函数y1.题组三易错自纠5.已知b >0,log 5b =a ,lg b =c,5d =10,则下列等式一定成立的是()A .d =acB .a =cdC .c =adD .d =a +c答案B6.(多选)函数y =log a (x +c )(a ,c 为常数,其中a >0,a ≠1)的图象如图所示,则下列结论成立的是()A .a >1B .0<c <1C .0<a <1D .c >1答案BC解析由图象可知函数为减函数,所以0<a <1,令y =0得log a (x +c )=0,x +c =1,x =1-c .由图象知0<1-c <1,∴0<c <1.7.若log a 34<1(a >0且a ≠1),则实数a 的取值范围是____________________.答案(1,+∞)解析当0<a <1时,log a 34<log a a =1,∴0<a <34;当a >1时,log a 34<log a a =1,∴a >1.∴实数a (1,+∞).对数式的运算1.已知2x =3,log 483=y ,则x +2y 的值为________.答案3解析由2x =3,log 483=y 得x =log 23,y =log 483=12log 283,所以x +2y =log 23+log 283=log 28=3.2.设函数f (x )=3x +9x ,则f (log 32)=________.答案6解析∵函数f (x )=3x +9x ,∴f (log 32)=339log 2log 2log 43929+=+=2+4=6.3.计算:(1-log 63)2+log 62·log 618log 64=________.答案1解析原式=1-2log 63+(log 63)2+log 663·log 6(6×3)log 64=1-2log 63+(log 63)2+1-(log 63)2log 64=2(1-log 63)2log 62=log 66-log 63log 62=log 62log 62=1.4.(2019·北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m 2-m 1=52lg E1E 2,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是-26.7,天狼星的星等是-1.45,则太阳与天狼星的亮度的比值为()A .1010.1B .10.1C .lg 10.1D .10-10.1答案A解析两颗星的星等与亮度满足m 2-m 1=52lg E 1E 2,令m 2=-1.45,m 1=-26.7,lgE 1E 2=25·(m 2-m 1)=25(-1.45+26.7)=10.1,E 1E 2=1010.1.思维升华对数运算的一般思路(1)拆:首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后利用对数运算性质化简合并.(2)合:将对数式化为同底数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.对数函数的图象及应用例1(1)已知函数f (x )=log a (2x +b -1)(a >0,a ≠1)的图象如图所示,则a ,b 满足的关系是()A .0<a -1<b <1B .0<b <a -1<1C .0<b -1<a <1D .0<a -1<b -1<1答案A解析由函数图象可知,f (x )为单调递增函数,故a >1.函数图象与y 轴的交点坐标为(0,log a b ),由函数图象可知-1<log a b <0,解得1a <b <1.综上有0<1a<b <1.(2)方程4x=log a x ,12上有解,则实数a 的取值范围为__________.答案,22解析若方程4x =log a x ,12上有解,则函数y =4x 和函数y =log a x ,12上有交点,a<1,a12≤2,解得0<a≤22.4x<log a x,12上恒成立,则实数a的取值范围是________.答案解析当0<x≤12时,函数y=4x的图象在函数y=log a x图象的下方.又当x=12时,124=2,即函数y=4x y=log a x,得a=22.若函数y=4x的图象在函数y=log a x图象的下方,则需22<a<1(如图所示).当a>1时,不符合题意,舍去.所以实数a思维升华对数函数图象的识别及应用方法(1)在识别函数图象时,要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.跟踪训练1(1)(2019·河北冀州中学月考)函数f(x)=lg(|x|-1)的大致图象是()答案B解析由函数值域为R,可以排除C,D,当x>1时,f(x)=lg(x-1)在(1,+∞)上单调递增,排除A,选B.(2)若不等式x 2-log a x <0对xa 的取值范围是________.答案116,解析只需f 1(x )=x 2f 2(x )=log a x图象的下方即可.当a >1时,显然不成立;当0<a <1时,如图所示,要使x 2<loga x 在x只需ff所以有≤log a 12,解得a ≥116,所以116≤a <1.即实数a 的取值范围是116,对数函数的性质及应用命题点1解对数方程、不等式例2(1)方程log 2(x -1)=2-log 2(x +1)的解为________.答案x =5解析原方程变形为log 2(x -1)+log 2(x +1)=log 2(x 2-1)=2,即x 2-1=4,解得x =±5,又x >1,所以x =5.(2)设f (x )2x ,x >0,12(-x ),x <0,则方程f (a )=f (-a )的解集为________.答案{-1,1}解析当a >0时,由f (a )=log 2a =121log a ⎛⎫⎪⎝⎭=f (-a )=12log a ,得a =1;当a <0时,由f (a )=12log ()a-=logf (-a )=log 2(-a ),得a =-1.∴方程f (a )=f (-a )的解集为{1,-1}.本例(2)中,f (a )>f (-a )的解集为________.答案(-1,0)∪(1,+∞)解析>0,log 2a >12a<0,12(-a )>log 2(-a ),解得a >1或-1<a <0.命题点2对数函数性质的综合应用例3(2020·湛江质检)已知函数f (x )=12log (x 2-2ax +3).(1)若f (-1)=-3,求f (x )的单调区间;(2)是否存在实数a ,使f (x )在(-∞,2)上为增函数?若存在,求出a 的范围;若不存在,说明理由.解(1)由f (-1)=-3,得12log (4+2a )=-3.所以4+2a =8,所以a =2.则f (x )=12log (x 2-4x +3),由x 2-4x +3>0,得x >3或x <1.故函数f (x )的定义域为(-∞,1)∪(3,+∞).令μ=x 2-4x +3,则μ在(-∞,1)上单调递减,在(3,+∞)上单调递增.又y =12log μ在(0,+∞)上单调递减,所以f (x )的单调递增区间是(-∞,1),单调递减区间是(3,+∞).(2)令g (x )=x 2-2ax +3,要使f (x )在(-∞,2)上为增函数,应使g (x )在(-∞,2)上单调递减,且恒大于0.≥2,(2)≥0,即≥2,-4a ≥0,a 无解.所以不存在实数a ,使f (x )在(-∞,2)上为增函数.思维升华利用对数函数的性质,求与对数函数有关的函数值域和复合函数的单调性问题,必须弄清三方面的问题:一是定义域,所有问题都必须在定义域内讨论;二是底数与1的大小关系;三是复合函数的构成,即它是由哪些基本初等函数复合而成的.另外,解题时要注意数形结合、分类讨论、转化与化归思想的应用.跟踪训练2(1)若f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上单调递减,则a 的取值范围为()A .[1,2)B .[1,2]C .[1,+∞)D .[2,+∞)答案A解析令函数g (x )=x 2-2ax +1+a =(x -a )2+1+a -a 2,对称轴为x =a ,要使函数在(-∞,1](1)>0,≥1,-a >0,≥1,解得1≤a <2,即a ∈[1,2).(2)已知函数f (x )=log a (8-ax )(a >0,且a ≠1),若f (x )>1在区间[1,2]上恒成立,则实数a 的取值范围是__________.答案解析当a >1时,f (x )=log a (8-ax )在[1,2]上是减函数,由f (x )>1在区间[1,2]上恒成立,则f (x )min =f (2)=log a (8-2a )>1,且8-2a >0,解得1<a <83.当0<a <1时,f (x )在[1,2]上是增函数,由f (x )>1在区间[1,2]上恒成立,知f (x )min =f (1)=log a (8-a )>1,且8-2a >0.∴a >4,且a<4,故不存在.综上可知,实数a比较指数式、对数式的大小例4(1)(2019·天津市河西区模拟)设a =log 3e ,b =e 1.5,c =131log 4,则()A .b <a <cB .c <a <bC .c <b <aD .a <c <b答案D 解析c =131log 4=log 34>log 3e =a .又c =log 34<log 39=2,b =e 1.5>2,∴a <c <b .(2)(2018·全国Ⅲ)设a =log 0.20.3,b =log 20.3,则()A .a +b <ab <0B .ab <a +b <0C .a +b <0<abD .ab <0<a +b答案B解析∵a =log 0.20.3>log 0.21=0,b =log 20.3<log 21=0,∴ab <0.∵a +b ab =1a +1b=log 0.30.2+log 0.32=log 0.30.4,∴1=log 0.30.3>log 0.30.4>log 0.31=0,∴0<a +b ab<1,∴ab <a +b <0.(3)已知函数y =f (x +2)的图象关于直线x =-2对称,且当x ∈(0,+∞)时,f (x )=|log 2x |,若a =f (-3),b =fc =f (2),则a ,b ,c 的大小关系是________.答案c <a <b解析易知y =f (x )是偶函数.当x ∈(0,+∞)时,f (x )=f |log 2x |,且当x ∈[1,+∞)时,f (x )=log 2x 单调递增,又a =f (-3)=f (3),b =f f (4),所以c <a <b .思维升华(1)比较指数式和对数式的大小,可以利用函数的单调性,引入中间量;有时也可用数形结合的方法.(2)解题时要根据实际情况来构造相应的函数,利用函数单调性进行比较,如果指数相同,而底数不同则构造幂函数,若底数相同而指数不同则构造指数函数,若引入中间量,一般选0或1.跟踪训练3(1)已知a =log 23+log 23,b =log 29-log 23,c =log 32,则a ,b ,c 的大小关系是()A .a =b <cB .a =b >cC .a <b <cD .a >b >c答案B解析因为a =log 23+log 23=log 233=32log 23>1,b =log 29-log 23=log 233=a ,c =log 32<log 33=1,所以a =b >c .(2)(2019·天津市滨海新区模拟)已知函数f (x )=|x |,且a =f b =f c =f (2-1),则a ,b ,c 的大小关系为()A .a <c <bB .b <c <aC .c <a <bD .b <a <c答案A解析ln 32<ln e =12,log 23>12,∴log 23>12>ln 32.又f (x )是偶函数,在(0,+∞)上为增函数,∴ff f (log 23)=f ∴a <c <b .(3)若实数a ,b ,c 满足log a 2<log b 2<log c 2<0,则下列关系中正确的是()A .a <b <cB .b <a <cC .c <b <aD .a <c <b答案C解析根据不等式的性质和对数的换底公式可得1log 2a <1log 2b <1log 2c <0,即log 2c <log 2b <log 2a <0,可得c <b <a <1.故选C.1.(2019·泸州诊断)2lg 2-lg 125的值为()A .1B .2C .3D .4答案B解析2lg 2-lg 125=2lg 100=2,故选B.2.设0<a <1,则()A .log 2a >B .>C .log 2a <D .log 2a <答案B解析∵0<a <1,∴0<a 2<a <a <1,∴在A 中,log 2a =,故A 错误;在B 中,>,故B 正确;在C 中,log 2a >,故C 错误;在D 中,log 2a >,故D 错误.3.函数y =ln1|2x -3|的图象为()答案A解析易知2x -3≠0,即x ≠32,排除C ,D.当x >32时,函数为减函数;当x <32时,函数为增函数,所以选A.4.(2019·衡水中学调研卷)若0<a <1,则不等式1log a x >1的解是()A .x >aB .a <x <1C .x >1D .0<x <a答案B解析易得0<log a x <1,∴a <x <1.5.函数f (x )=12log (x 2-4)的单调递增区间为()A .(0,+∞)B .(-∞,0)C .(2,+∞)D .(-∞,-2)答案D解析函数y =f (x )的定义域为(-∞,-2)∪(2,+∞),因为函数y =f (x )由y =12log t 与t =g (x )=x 2-4复合而成,又y =12log t 在(0,+∞)上单调递减,g (x )在(-∞,-2)上单调递减,所以函数y =f (x )在(-∞,-2)上单调递增.6.(2020·长沙期末)已知函数f (x )2x ,x >0,x,x ≤0,且关于x 的方程f (x )-a =0有两个实根,则实数a 的取值范围为()A .(0,1]B .(0,1)C .[0,1]D .(0,+∞)答案A解析作出函数y =f (x )的图象(如图),欲使y =f (x )和直线y =a 有两个交点,则0<a ≤1.7.(多选)关于函数f (x )=ln1-x1+x,下列说法中正确的有()A .f (x )的定义域为(-∞,-1)∪(1,+∞)B .f (x )为奇函数C .f (x )在定义域上是增函数D .对任意x 1,x 2∈(-1,1),都有f (x 1)+f (x 2)=f 答案BD解析函数f (x )=ln 1-x1+x=其定义域满足(1-x )(1+x )>0,解得-1<x <1,∴定义域为{x |-1<x <1}.∴A 不对.由f (-x )=ln 1+x1-x=1=-ln1-x1+x=-f (x ),是奇函数,∴B 对.函数y =21+x -1在定义域内是减函数,根据复合函数的单调性,同增异减,∴f (x )在定义域内是减函数,C 不对.f (x 1)+f (x 2)=ln1-x 11+x 1+ln 1-x 21+x 2=f ∴D 对.8.(多选)已知函数f (x )的图象与g (x )=2x 的图象关于直线y =x 对称,令h (x )=f (1-|x |),则关于函数h (x )有下列说法,其中正确的说法为()A .h (x )的图象关于原点对称B .h (x )的图象关于y 轴对称C .h (x )的最大值为0D .h (x )在区间(-1,1)上单调递增答案BC解析函数f (x )的图象与g (x )=2x 的图象关于直线y =x 对称,∴f (x )=log 2x ,h (x )=log 2(1-|x |),为偶函数,不是奇函数,∴A 错误,B 正确;根据偶函数性质可知D 错误;∵1-|x |≤1,∴h (x )≤log 21=0,故C 正确.9.函数f (x )=log 2x ·(2x )的最小值为________.答案-14解析依题意得f (x )=12log 2x ·(2+2log 2x )=(log 2x )2+log 2x 2x -14≥-14,当log 2x =-12,即x =22时等号成立,所以函数f (x )的最小值为-14.10.(2020·深圳月考)设实数a ,b 是关于x 的方程|lg x |=c 的两个不同实数根,且a <b <10,则abc 的取值范围是________.答案(0,1)解析由题意知,在(0,10)上,函数y =|lg x |的图象和直线y =c 有两个不同交点(如图),∴ab=1,0<c <lg 10=1,∴abc 的取值范围是(0,1).11.设f (x )=log a (1+x )+log a (3-x )(a >0,且a ≠1),且f (1)=2.(1)求实数a 的值及f (x )的定义域;(2)求f (x )在区间0,32上的最大值.解(1)∵f (1)=2,∴log a 4=2(a >0,且a ≠1),∴a =2.+x >0,-x >0,得-1<x <3,∴函数f (x )的定义域为(-1,3).(2)f (x )=log 2(1+x )+log 2(3-x )=log 2[(1+x )(3-x )]=log 2[-(x -1)2+4],∴当x ∈(-1,1]时,f (x )是增函数;当x ∈(1,3)时,f (x )是减函数,故函数f (x )在0,32上的最大值是f (1)=log 24=2.12.是否存在实数a ,使得f (x )=log a (ax 2-x )在区间[2,4]上是增函数?若存在,求出a 的范围;若不存在,说明理由.解设t=ax2-x=-1 4a.若f(x)在[2,4]上是增函数,<1,4,-4>0,2,2>0,解得a>1.∴存在实数a满足题意,即当a∈(1,+∞)时,f(x)在[2,4]上是增函数.13.已知函数f(x)=ln e xe-x,若fff1010(a+b),则a2+b2的最小值为()A.1B.2C.3D.4答案B解析∵f(x)+f(e-x)=2,∴ff…+f2020,∴1010(a+b)=2020,∴a+b=2.∴a2+b2≥(a+b)22=2,当且仅当a=b=1时取等号.14.若函数f(x)=log a(x2-x+2)在区间[0,2]上的最大值为2,则实数a=________.答案2解析令u(x)=x2-x+2,则u(x)在[0,2]上的最大值u(x)max=4,最小值u(x)min=74.当a>1时,y=log a u是增函数,f(x)max=log a4=2,得a=2;当0<a<1时,y=log a u是减函数,f(x)max=log a74=2,得a=72(舍去).故a=2. 15.(2019·福州模拟)已知函数f(x)=log a(2x-a)在区间12,23上恒有f(x)>0,则实数a的取值范围是()B.13,D.23,答案A解析当0<a <1时,函数f (x )在区间12,23上是减函数,所以log ,即0<43-a <1,解得13<a <43,故13<a <1;当a >1时,函数f (x )在区间12,23上是增函数,所以log a (1-a )>0,即1-a >1,解得a <0,此时无解.综上所述,实数a 16.已知函数f (x )=lgx -1x +1.(1)计算:f (2020)+f (-2020);(2)对于x ∈[2,6],f (x )<lg m(x +1)(7-x )恒成立,求实数m 的取值范围.解(1)由x -1x +1>0,得x >1或x <-1.∴函数f (x )的定义域为{x |x >1或x <-1}.又f (x )+f (-x )=0,∴f (x )为奇函数.∴f (2020)+f (-2020)=0.(2)当x ∈[2,6]时,f (x )<lgm (x +1)(7-x )恒成立可化为x -11+x <m(x +1)(7-x )恒成立.即m >(x -1)(7-x )在[2,6]上恒成立.又当x ∈[2,6]时,(x -1)(7-x )=-x 2+8x -7=-(x -4)2+9.∴当x =4时,[(x -1)(7-x )]max =9,∴m >9.即实数m 的取值范围是(9,+∞).。
高一数学对数的概念及运算1(201908)

高一数学对数的概念及运算1

问题2、证明:aloga N N (a 0 , a 1 , N 0) ,并利用结
论求出下列各式的值:
3 ; 10 log10 2 ;
1log3 4
2 ; 3log2 51
27
2 3
log
3
2
;
aloga blogb N (a 0 , a 1 , b 0 , b 1 , N 0)
概念辨析
一般地,如果a (a 0 , a 1)的b次幂等于N,就
是ab N,那么数 b叫做以a 为底N 的对数,记作 log a N b ,其中a 叫做底数,N叫做真数。
(1)对数的底数必须大于0且不等于1;
(2)对数的真数必须大于0,也即负数与0没有对数;
(3)对数的值可以为一切实数,也即对数值可正、
巩固练习
1.把下列指数式写成对数式:
(1)25 3 ;(2)4x 1 ;(3) 3 3 x ;(4) 0 1 ;
64
2
2.把下列对数式写成指数式:
(1)log 2 4 2;(2)lg 0.001 3;(3)log 1 e 1
e
(4)ln e3 x
可负、可为零;(4)通来自以10为底的对数,叫做常用对数。为了简便,
的常用对数 简记作 ; (5)将以无理数e=2.7182…为底的对数叫做自然
对数。为了简便, 的自然对数
简记作
问题拓展
问题1、 (1)用计算器计算下列各数的值(结果精确到0.01)
lg 5.24; lg 0.02; lg 82; lg 2.83; lg 0.3
(5)log
高一数学对数的运算1

xy
x2 y
(1)loga
; z
(2)loga 3 z
积、商、幂的对数运算法则
如果 a > 0,a 1,M > 0,N > 0, 那么:
loga ( MN ) loga M loga N (1)
loga
M N
loga M
loga N
(2)
loga M n nloga M (n R) (3) 推论:loga an n
例1 用 loga x, log a y, log a z 表示下列各式:
则MN amn, loga M m, loga N n,
loga MN m n loga M loga N.
loga (MN) loga M loga N
仿照上述过程,分别由以下各式出发,可得怎
样的对数性质?
am an amn
(am )n amn
2.2.1 对数与对数运算(2)
----对数运算
一、复习:
1. 对数定义: ax N <==>
2. 两种特殊的对数:①lgN 3.对数的性质:
⑴负数与零没有对数.
loga N x
a 0且a 1
②lnN。 N 0
⑵ loga 1 0,
⑶ loga a 1
(4)对数恒等式 aloga N N loga ab b
;一键测量仪/ 一键测量仪 ;
爬在树上,弄得满头满脸的都是乱扑扑的桃花瓣儿。等回到家,又总被母亲从衣 领里抖出一大把柔柔嫩嫩的粉红。啊,那个孩子呢?那个躺在小溪边打滚,直揉得小裙子上全是草汁的孩子呢?她隐藏到什么地方去了呢? ⒅啊,春天多叫入迷惘啊!它究竟是怎么回事呢?是谁负责管理这 最初的一季呢?
高一数学上册知识点log函数

高一数学上册知识点log函数一、概述在高一数学上册中,我们学习了许多重要的数学知识点,其中之一就是log函数。
log函数是数学中非常常见的一类函数,它在各个领域都有广泛的应用。
下面我将为大家介绍log函数的定义、性质以及解题方法。
二、定义log函数是对数函数的一种形式。
对于给定的底数a(a>0,且a≠1),我们定义loga(x)为满足a的y次方等于x的实数y。
此时,x称为真数,a称为底数,y称为对数。
用数学符号表示为:loga(x) = y,其中a为底数,x为真数,y为对数。
三、性质1. log函数的定义域和值域:定义域:对于任意正数x,loga(x)有意义;值域:对于任意正数a,loga(x)的值域为全体实数。
2. log函数的基本性质:(1)loga(1) = 0:任意正数a的底数为1时,对应的log函数值为0;(2)loga(a) = 1:任意正数a的底数为自身时,对应的log函数值为1;(3)loga(xy) = loga(x) + loga(y):log函数中的乘法性质,对应于真数的乘法;(4)loga(x/y) = loga(x) - loga(y):log函数中的除法性质,对应于真数的除法;(5)loga(x^n) = nloga(x):log函数中的幂次性质,对应于真数的幂次运算。
四、解题方法1. log函数方程的求解:对于log函数方程,常用的求解方法有:(1)消去log函数:通过变换,将含有log函数的方程转化为具有指数形式的方程,然后求解;(2)换底公式:当底数不方便计算时,可以通过换底公式将对数转化为其他常用底数的对数,再进行求解。
2. log函数不等式的求解:对于log函数不等式,常用的求解方法有:(1)化简法:通过巧妙的变形和化简,将log函数不等式转化为常见的不等式,然后求解;(2)图像法:通过画出log函数的图像,结合图像的特点,求解log函数不等式。
五、应用领域log函数作为一种重要的数学函数,在许多领域都有广泛的应用。
陶磊-对数的概念及其运算

4.4 对数概念及其运算(1)上海交通大学附属中学陶磊一、教学内容解析《对数概念及其运算(1)》是沪教版高中数学课本,高一年级第二学期第四章(下)第一节,属概念性知识,承接第四章(上)指数函数,对数概念及运算是在学习了“指数幂x a的意义及运算性质”、“指数函数的性质”基础上进行的,同时本节也是学习对数函数的准备知识.对数既可以看作是一个算式,又可以看作是一个数值. 与指数幂具有共同的本质——指数(对数)与幂(真数)之间的对应关系. 对数作为重要而简便的计算技术,被恩格斯誉为17世纪三大重要数学成就之一,在数学和其他许多知识领域都有广泛的应用. 虽然随着计算工具的飞速发展,它的地位已由计算机(器)逐步代替,但对数函数在数学中的地位是不可动摇的.对数概念及其运算性质的学习过程,可以提升学生的数学抽象、数学运算、直观想象等核心素养,可以融合数学史的发展过程提升数学课堂的人文情怀.【教学重点】理解和掌握对数的概念,掌握对数式与指数式的互化.二、教学目标设置理解对数的意义,掌握底数、真数、对数的允许值范围;知道常用对数、自然对数的概念;掌握对数式与指数式的互化,理解同底的对数式与指数式之间的关系;经历计算-观察-猜想-论证的过程,掌握对数的常用性质;会使用计算器计算对数的值;经历“由具体到抽象”、“从特殊到一般”的研究过程,提升数学抽象、数学运算、直观想象等核心素养.三、学生学情分析本节课为借班上课,课前未与学生有过接触.授课对象为上海市一所普通高中的高一普通班,该年级经过入学前的分流,资优生集中在两个“特色班”,普通班学生相对底子比较薄,对待抽象的数学概念往往接受起来比较困难. 授课学段为高一学年上学期,学生曾利用暑假复习了幂指数的运算性质,已经知道指数幂()x a x Q ∈的意义及其运算性质,但并不理解指数幂()x a x R ∈的意义,不知道指数函数(01)x y a a a =>≠且 的性质,这些不足可能导致学生难以理解对数的意义,以及难以掌握底数、真数、对数的允许值范围. 学生缺乏以函数知识为载体的学习 “对应关系”的经历,缺乏运用“观察-归纳-猜想-论证”的学习经验.【教学重点】理解和掌握对数的概念.四、教学策略分析张奠宙先生曾提出“概念教学要揭示数学的本质”、“数学概念教学的核心是它的价值、意义和作用”. 本节课是一节概念课,教学策略的制定也是遵循以上基本原则.1. 基于知识本原的问题设计对数的发明并非来源于指数,而是源于数学家对简化大数运算的有效工具的追求. 其关键是利用对应关系k q k →:[]012,,,,,0,1,2,,,n q q q q n ⎡⎤→⎣⎦并建立起如下对应法则:(1)m n q q m n ⋅→+;(2)m n q q m n ÷→-;(3)()n m q m n →⋅;(4)m n→. 利用上述对应法则降低运算层级,达到简化运算的目的.以“对应关系k q k →”(而不是运算)为依据引入对数概念,虽然观点高,但“自然度”不够,难度大.因而,本节课的引入借助历史发展背景——“简化大数运算”的需求——创设情境,但在生成对数概念的过程中,通过数学内外的发展需要,先抽象出数学问题“一般地,我们要找到x ,使得x a N =成立,这样的x 存在吗?”;再类比为了解决“在n x a = 中,已知,n a ,如何表示x ?”而引入引入符号log a N 表示()0,1b a N a a =>≠且中的b ,从而得到一个数学的研究对象;接下来从“对应”、“指数幂的逆运算”、“数的表示”这三个角度设计问题,深化理解对数的概念;再通过计算-观察-猜想-论证的过程,应用对数的概念,得出对数的基本性质;最后再回到对数产生的历史,站在现代的视角下,体会对数的应用及其意义.其中驱动课堂活动的问题设计,遵循以下思维导图:2.符合学生认知规律的教学活动一个新概念的生成和掌握不是一蹴而就的,是在充分激发学生探究的兴趣的前提下,不断启发学生对知识的理解,以旧引新,以新强旧,层层递进,体现的是理性思维的作用.本节课借鉴已有经验,抽象出“对数”这一数学研究对象,发现和提出对数的研究内容,构建研究路径,得出结论,并用于解决问题. 学生经历“现实背景——定义——性质——应用”过程,鼓励学生采用独立思考、自主探究、合作交流等方式展开学习. 具体来说,在充分尊重学生的认知规律下,本节课设置以下四个教学环节:【环节1:创设情境引入问题】在环节1中,为了充分激发学生研究的兴趣,借助“光年”计算引入“简化大数运算”的实际需求,但考虑到若是以“对应关系”为依据引入对数概念而不是从运算体系出发而得到,与中学生的认知水平不适应. 故而“简化大数运算”只作为历史背景,在引例中从特殊问题出发,例如28192x =则13x =;一般地,当0M N >、时,满足方程2,10x x M N ==,x =?再抽象出数学问题:01,0,?x a a a N a N x >≠>==当且时,已知方程中,在环节2中,考虑到学生缺少必要的指数函数作为前继知识,但要回答上述问题,就必须要承认事实:010,.x a a N a N >≠>=在且时,只要方程总有唯一解本节课设计了两个具体的教学活动,目的是用比较生动、具象的方式让学生体会结论的正确性. 一个是在研究例子“102018,?x x ==”时用“逐步细分”的想法,借助表格,初步体会x 的存在性;另一个是用几何画板展示指数函数的图像性质.在这一部分,学生经历从具体到抽象的过程,对培养发现和提出数学问题的能力,发展数学抽象素养都有作用.【环节2:对数概念的初步认识】在环节2中,通过类比根号这一数学符号的引入,自然的引入对数这一新的数学符号, 一方面降低了新的数学符号给学生带来的陌生感;另一方面让学生能从对数符号的引入中初步体会对数也是指数幂的逆运算. 此时教师介绍《算法精蕴》中对数、真数名称的由来,从“对应”的角度,让学生初步理解对数概念.例1及其变式是从“对数是指数幂的逆运算”这个角度让学生理解对数的概念,通过指数到对数、对数到指数的改写,使学生逐渐认识到:01a a >≠当且时,指数式b a N =与对数式log a N b =只是对同一个事实的不同表示形式而已. 例1的前3小题来源自课本例题,第4小题为自编题,除了引出常用对数的概念,还恰好与引入对数概念时所举的例子相同,既解决了之前如何表示x 的问题,又为最后介绍常用对数表埋下伏笔.例2是从“对数是数的表示”这个角度让学生进一步理解对数的概念,通过求对数的值,进一步强化认识:对数值即为指数幂中的指数,解决陌生对数问题就是化归为熟悉的指数幂问题,二者本质是相同的.在这一部分,学生从三个角度来逐步认知并掌握对数的概念,在例题的总结与反思中形成对“同底的对数式与指数式”关系的认识,对数的概念从形式的改写,到数值的计算,再到与已有知识的联系,学生的思维水平螺旋上升.【环节3:对数概念的再认识】在环节3中,对例2的回顾与反思,既是学生利用对数概念从特殊到一般抽象出对数基本性质的过程,又是检验学生是否确实理解并掌握了“对数与同底幂指数的本质相同”这一事实.这一环节学生采取自主探究、合作交流的方式展开学习,学生在对数概念的应用中再一次加深对定义的理解,在计算-观察-猜想-论证的过程中增强了研究问题、解决问题的能力.【环节4:总结与思考】在环节4中,用计算器计算对数的值,既是对“对数是数的表示”再一次的感知,又启发学生利用现有的计算工具继续提出问题,思考并探究对数的其他性质,培养学生发现和提出问题的能力,提升数学抽象、直观想象素养.最后的总结,除了让学生从知识上、方法上对本节课的收获进行梳理,总结研究一个代数对象的基本过程,又回到了“简化大数运算”的历史背景中,在现代数学的观点下辩证的认识对数概念及其性质具有怎样的作用和意义,提升人文情怀.五、教学过程1.创设情境、引入问题对数的产生源于天文学的发展.【引例】一光年到底有多远?已知299792.468(/)km s是光在真空中的速度,31536000是一年的总秒数(假⨯9,454,255,270,848即为设一年365天),因此两数的乘积299792.46831536000=所求.“光年”是天文学中的距离单位. 在16至17世纪,天文学开始迅速发展,天文学家为了计算一个行星的位置,时常需要耗费几个月甚至几年的时间,问题主要就集中在复杂的数据运算上. 因此,改进运算方法成为了天文学家们的当务之急.➢设计意图:结合历史发展中对数发明的本源问题——“简化大数运算”的需要,激发学生的研究兴趣.➢设计意图:初步体会简化运算的核心——对应关系k q k→.【问题2】在不用计算器的前提下,如何计算299792.46831536000⨯=? 这里的关键是,当0M N >、时,满足方程2,10x x M N ==,x 是否存在?如何表示?例如102018x =,借助不断的“细分”,可以观察到,确实存在这样的x . ➢ 设计意图:从特殊到一般,由具体到抽象,引导学生抽象出数学问题.算性质”的基础上,类比引入是为了表示方程32018x =的解,自然的引入对数概念.【定义】一般地,如果()01a a a >≠,的b 次幂等于N ,即b a N =,那么数b 叫做以a 为底N 的对数(logarithm ),记作log a N b =,其中a 叫做对数的底数(base ),简称底,N 叫做真数.《数理精蕴》中把对数称为“假数”取“借来用一下”之意,N 称为“真数”. “真数”一直沿用至今,而“假数”后来被称为“对数”取“对应”之意.➢ 设计意图:介绍对数名称的史书记载,引例中渗透的“对应”之意.例 1 把下列指数式写成对数式:(1)45625=;(2)51232-=;(3)1 5.733m⎛⎫= ⎪⎝⎭; (4)102018x = . 解:(1)5log 6254=;(2)21log 532=-;(3)13log 5.73m =;(4)10log 2018x = . 例1’把下列对数式写成指数式:(1)5log 6254=;(2)21log 532=-;(3)13log 5.73m =;(4)10log 2018x = 解:(1)45625=;(2)51232-=;(3)1() 5.733m =; (4)102018x =. ➢ 设计意图:巩固新学概念,熟悉各部分的名称及读法,能够从“指数幂运算的逆运算”角度,将对数式和指数式进行互换.【小结】由对数的定义,log a N b =()01a a >≠, 也就是b a N =.通常将以10为底的对数叫做常用对数(common logarithms ),10log N 简记作lg N . 科学技术中,常用到以无理数 2.71828e =为底的对数,以e 为底的对数叫做自然对数(natural logarithms ),log e N 简记作ln N .➢ 设计意图:通过例1及其变式的比较,小结对数概念与同底的指数幂的关系;给出常用对数和自然对数的规定,简单介绍其应用.例 2 试计算:(1)12log 16;(2)21log 128;(3)lg1;(4)ln e . 解:(1)因为41162-⎛⎫= ⎪⎝⎭,所以12log 16=4-; (2)因为712128-=,所以21log 7128=-; (3)因为0101=,所以lg10=;(4)因为1=e e ,所以ln 1e =.➢ 设计意图:理解对数是“数的表示”,再次体会解决陌生的对数问题就是转化为求同底的幂的指数问题,即同底的对数与指数幂相互等价.3. 对数概念的再认识【问题4】回顾例2的(1)、(2),把它们写成4121log 42-⎛⎫=- ⎪⎝⎭, ()72log 27-=-,你还有什么发现吗?试着归纳,并解释理由.由定义,因为,log b a a N N b ==,则 log b a a b =()0,1a a >≠.类比得到,log a N a N =()0,1,0a a N >≠>.由定义,因为,log b a a N N b ==,则log a N a N =()0,1,0a a N >≠>.上面的式子称为对数恒等式,它看起来很玄妙,但不过是对数定义的另一个表达方式而已.➢ 设计意图:在已得到结果上反思,从具体到抽象,从特殊到一般,归纳并证明对数恒等式,并在证明过程中再次认识对数概念.【问题5】再回顾例2的(3),算一算,2log 1,3log 1等,你有什么发现?试着归纳一下.因为()010,1a a a =>≠ ,所以log 10a = .【问题6】0的常用对数存在吗?负数的常用对数存在吗?为什么?不存在. 在讨论对数的时候,我们总是假设底是不等于1的正实数,可知,零和负数没有对数,真数为正数,即0N >.【问题7】回顾例2的(4),算一算,2log 2,3log 3,lg10的值是多少?你有什么发现?试着归纳,并解释理由.log 1a a =,因为1a a =.➢ 设计意图:学生能够通过自主探究、合作交流,经历计算-归纳-猜想-证明的研究过程,在解决问题的过程中理解并掌握对数的概念,得到对数的常用性质.➢ 设计意图:在对数是“数的表示”的角度下,引导学生用现有计算工具计算对数的值,培养发现和提出问题的能力,提升数学抽象、直观想象的素养,为后续学习留下伏笔.5.课堂小结在本节课,我们体验了对数的产生和发展历程,理解了对数的概念和它的常用性质.在对数的发展历史中,确实是受到当时天文、航海等实际问题中简化复杂运算的需要,而当数学家们意识到对数的意义,他们就迫切的需要一张《对数表》,这样就可以将复杂的数对应到一个比较简洁易操作的数据. 但造表的难度却相当大,不过一旦做好了,就能一劳永逸. 500年前苏格兰数学家约翰·纳皮尔,用了20年时间,研究运算规律,并制作了一张可查的表格. 数学家拉普拉斯说:“对数用缩短计算的时间来使天文学家的寿命加倍. ”现在,我们可以用计算机(器)方便快捷地进行多位数的计算,对数用于简化计算的功能已经完成了其历史任务,但对数这个概念及其种种性质在现代数学和其他科学领域中的作用却有增无减,一直占据着重要的位置,并被广泛使用.➢设计意图:在现代数学的观点下,回顾对数发展的历史,总结研究一个代数对象的基本过程,辩证的理解对数的意义和作用,提升数学课堂的人文情怀.6.作业1)练习册4.4,A组1-4题;2)探究对数的运算性质.➢设计意图:检验学生是否理解并掌握对数的概念,是否能够掌握对数式与指数式的转化;进一步启发学生的研究兴趣,为下节课学习对数的运算性质做铺垫.点评:这是一节关注知识本原、尊重认知规律、具有丰富数学内涵的课。
对数及对数式运算5大常考题型总结-高一数学(人教A版2019必修第一册)

第18讲 对数及对数式运算5大常考题型总结【知识点梳理】 1.对数式的运算(1)对数的定义:一般地,如果(0x a N a =>且1)a ≠,那么数x 叫做以a 为底N 的对数,记作log a x N =,读作以a 为底N 的对数,其中a 叫做对数的底数,N 叫做真数. (2)常见对数:①一般对数:以(0a a >且1)a ≠为底,记为log Na ,读作以a 为底N 的对数;①常用对数:以10为底,记为lg N ; ①自然对数:以e 为底,记为ln N ; (3) 对数的性质和运算法则:①特殊对数:1log 0a =;log 1aa =;其中0a >且1a ≠①对数恒等式:log Na a N =(其中0a >且1a ≠,0N >) ①对数换底公式:log log log c a cb b a= 如:252log 7lg7ln7log 7=log 5lg5ln7==. (4)对数的运算法则:①外和内乘原理:log ()log log a a a MN M N =+; ①外差内除原理:log log log aa a MM N N=-; ①提公次方法:log log (m n a a nb b m m=,)n R ∈; ①指中有对,没心没肺:log a b a b =和log b a a b = 如:433log 81log 34==,2log 525=. (5)换底公式和对数运算的一些方法:①常用换底:log log log c a c b b a= 如:252log 7lg7ln7log 7=log 5lg5ln7==. ①倒数原理:1log log a b b a =如:321log 2log 3=. ①约分法则:log log log a b a b c c ⋅= 如: 232log 3log 4log 4=2⋅=;35157log 15log 7log 5log 31⋅⋅⋅=.①归一法则:()2lg 2+lg51lg 2lg5+lg 2+lg5=lg 2lg5+lg 2+lg5=lg5+lg 21=⇒⋅=.【题型目录】 题型一:对数的定义 题型二: 指数对数的互化 题型三: 对数的运算求值 题型四:换底公式的应用 题型五:对数式的应用题【典型例题】 题型一:对数的定义【例1】(2021·全国高一课前预习)在()()31log 32a b a -=-中,实数a 的取值范围为______. 【答案】1223,,3332⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭【解析】由题意,要使式子()()31log 32a b a -=-有意义,则满足310311320a a a ->⎧⎪-≠⎨⎪->⎩,解得1233a <<或2332a <<,即实数a 的取值范围为1223,,3332⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭.故答案为:1223,,3332⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭.【题型专练】1.(2022江苏省江阴市第一中学高一期中)使式子(31)log (3)x x --有意义的x 的取值范围是( ) A .3x > B .3x <C .133x <<D .133x <<且23x ≠【答案】D【分析】对数函数中,底数大于0且不等于1,真数大于0,列出不等式,求出x 的取值范围.【详解】由题意得:31031130x x x ->⎧⎪-≠⎨⎪->⎩,解得:133x <<且23x ≠.故选:D2.(2022全国·高一课时练习)若()()1log 1k k +-有意义,则实数k 的取值范围是______. 【答案】()()1,00,1-【分析】结合对数性质建立不等关系,即可求解.【详解】若()()1log 1k k +-有意义,则满足101110k k k +>⎧⎪+≠⎨⎪->⎩,解得()()1,00,1k ∈-⋃.故答案为:()()1,00,1-题型二: 指数对数的互化【例1】(2022全国高一专题练习)将下列指数式化为对数式,对数式化为指数式. (1)53=125; (2)4-2=116; (3)log 3127=-3.【答案】(1)log 5125=3;(2)41log 216=-;(3)31327-= 【解析】(1)①53=125,①log 5125=3.(2)①21416-=,①41log 216=-. (3)①31log 327=-,①31327-=【题型专练】1.(2022全国高一课前预习)把下列指数式化为对数式,对数式化为指数式.(1)3128-=; (2)17ab ⎛⎫= ⎪⎝⎭;(3)1lg31000=-. 【答案】(1)21log 38=-;(2)17log b a =;(3)31101000-=.【解析】(1)由3128-=可得21log 38=-; (2)由17ab ⎛⎫= ⎪⎝⎭得17log b a =;(3)由1lg 31000=-可得31101000-=. 2.(2022全国高一课时练习)指数式和对数式互相转化:(1)4e a =⇒____________.(2)31327-=⇒____________. (3)21log 416=-⇒____________.(4)2log 83=⇒____________. 【答案】ln 4a = 31log 327=- 41216-= 328= 【解析】log (0,1,0)ba a Nb N a a N =⇔=>≠>.故答案为:ln 4a =,31log 327=-,41216-=,328=. 题型三: 对数的运算求值【例1】(2022·浙江·高考真题)已知825,log 3ab ==,则34a b -=( )A .25B .5C .259 D .53【答案】C【分析】根据指数式与对数式的互化,幂的运算性质以及对数的运算性质即可解出.【详解】因为25a =,821log 3log 33b ==,即323b =,所以()()22323232452544392a a a bb b -====. 故选:C.【例2】(2022陕西·长安一中高一期中)设函数()()211log 2,12,1x x x f x x -⎧+-<⎪=⎨≥⎪⎩,则2(2)(log 6)f f -⋅=( )A .3B .6C .9D .12【答案】C【分析】根据给定分段函数直接计算即可得解【详解】函数()()211log 2,12,1x x x f x x -⎧+-<⎪=⎨≥⎪⎩,则2(2)1log 43f -=+=,2log 62(log 6)223f =÷=,所以2(2)(log 6)9f f -⋅=. 故选:C【例3】(2022全国高一专题练习)计算:(1)659log 25log 3log 6⋅⋅=_________. (2)()()24525log 5log 0.2log 2log 0.5++=_________. (3)235111log log log 2589⋅⋅=_________. (4)()24892log 3log 9log 27log 3log 32n n n ++++⋅__________.(5)6log 2323)+-=__________. 【答案】114 12- 5212【解析】(1)原式226565365331log 5log 3log 62log 5log 3log 6log 5log 3log 62=⋅⋅=⋅⨯=⋅⋅lg5lg3lg 61lg 6lg5lg3=⋅⋅= (2)原式22552511log 5log log 2log log 5log 252⎛=++= ⎝25111log 5log 2224=⨯= (3)原式232235235log 5log 2log 32log 5(3)log 2(2)log 3---=⋅⋅=-⨯-⨯-23512log 5log 2log 312=-⋅⋅=-(4)原式()23223522223log 3log 3log 3log 3log 2n n n =++++⋅()22522222335log 3log 3log 3log 3log 2log 35lo 2g 22nn n =++++⋅=⨯= (5)26662log (2323)log (2323)log 61+-=+-==所以原式12故答案为:1,14,12-,52,12【例4】(2022·全国·高一课时练习)已知()122021log 5a x x x ⋅⋅⋅=,则222122021log log log a a a x x x ++⋅⋅⋅+=______.【答案】10【分析】由同底数对数加法公式以及log log ba a Nb N =,可得答案.【详解】因为()122021log 5a x x x ⋅⋅⋅=,所以222122021log log log a a a x x x ++⋅⋅⋅+()()222122021122021log 2log 10a a x x x x x x =⋅⋅⋅⋅⋅⋅=⋅⋅⋅=.故答案为:10.【例5】(2022·陕西·西安市雁塔区第二中学高二期末(文))计算:0ln 221.1e 0.5lg 252lg 2-+-++=__________ 【答案】1【分析】根据指数的运算以及对数的运算性质即可求出. 【详解】原式=()1242lg5lg2121+-++=-+=. 故答案为:1.【例6】(2021·江苏省沭阳高级中学高一期中)已知0x >,0y >,且lg 2lg8lg 2x y+=,则21x y +的最小值为___________. 【答案】526+【分析】由lg 2lg8lg 2x y +=可得31x y +=,则()21213x y x y x y ⎛⎫+=++ ⎪⎝⎭化简后利用基本不等式可求得答案【详解】因为lg 2lg8lg 2x y +=,所以3lg(28)lg 2lg 2x y x y +⋅==, 所以31x y +=, 因为0x >,0y >,所以()21213x y x y x y ⎛⎫+=++ ⎪⎝⎭623y x x y=+++652526y xx y≥+⋅=+, 当且仅当6y xx y =,即3662,3x y -=-=时取等号,, 所以21x y +的最小值为526+,故答案为:526+ 【题型专练】1.(2020全国卷①)设3log 42a =,则4a -=( ) A .116B .19C .18D .16【答案】B【详解】因24log 4log 33==a a ,所以9342==a ,故11449a a -== 2.(2022·陕西·宝鸡市渭滨区教研室高二期末(文))若()()231log (1)x x f x x x ⎧≤=⎨>⎩,则()()016f f +=_________.【答案】5【分析】根据给定的分段函数,直接代值计算作答.【详解】因函数()()231log (1)x x f x x x ⎧≤=⎨>⎩,所以()()020163log 16145f f +=+=+=.故答案为:53.(2022长沙市明德中学高一开学考试)计算:2log 321lg252log ln1162+++=______ 【答案】12-【解析】原式()1lg 211lg5340lg5lg 212222=+-++=+-=-.故答案为:12- 4.(2022·江苏·高一)计算()32log 2lg 2lg 2lg5lg53-++-=___________ 【答案】12【分析】利用对数运算及指数式与对数式互化计算作答【详解】()332log 2log 2111lg 2lg 2lg5lg53lg 2(lg 2lg5)lg5(3)lg 2lg522--++-=++-=+-=. 故答案为:126.(2022·陕西·交大附中模拟预测(理))设函数()()2log 4,22,2x x x f x x ⎧-+<=⎨>⎩,则()()24log 5f f -+=( )A .5B .6C .7D .8【答案】D【分析】根据给定的分段函数,判断自变量取值区间,再代入计算作答.【详解】因23252<<,则22log 53<<,而()()2log 4,22,2x x x f x x ⎧-+<=⎨>⎩,所以()()2log 5224log 5log (44)2358f f -+=++=+=.故选:D7.(2022江苏高二课时练习)若0a >,0b >,()lg lg lg 2a b a b +=+,则2a b +的最小值为( )A .9B .8C .7D .6【答案】A【详解】因()lg lg lg 2a b a b +=+,所以()b a ab 2lg lg +=,所以b a ab 2+=,所以12=+abba ,即 121=+ab ,所以()9522212241222=+⋅≥+++=⎪⎭⎫⎝⎛++=+a b b a a b b a b a b a b a 8.(2022全国高一课时练习)计算:22log 4log 1323lg 3log 2lg 5+-⋅-=________.【答案】4【解析】原式0lg 243lg 3lg 541lg 2lg 54lg 3=+-⋅-=+--=. 故答案为:4.9.(2022全国高一课时练习)计算:(()22222lg5lg 2lg 21+-+____.【答案】1【解析】原式)()222lg5lg 22lg 21=-+)()22lg 2lg5lg 21=+-2lg 21= 212=-1= ,故答案为:1 .题型四:换底公式的应用【例1】(2022·全国·高一课时练习)已知53a =,32b =,则5log 10ab -=( ) A .1 B .2 C .5 D .4【答案】A【分析】先求得,a b ,然后结合对数运算求得正确答案. 【详解】①53a =,32b =,①5log 3a =,3log 2b =, 5553log 10log 10log 3log 2ab -=-⨯=5555555log 2log 10log 3log 10log 2log 51log 3-⨯=-==. 故选:A【例2】(2022全国高一课时练习)设25a b m ==,且112a b+=,则m =( )A 10B .10C .20D .100【答案】A【解析】由25a b m ==,可得2log a m =,5log b m =, 由换底公式得1log 2m a =,1log 5m b=, 所以11log 2log 5log 102m m m a b+=+==,又因为0m >,可得10m = 故选:A.【例3】(2022·全国·高一课时练习)已知lg 2a =,lg3b =,则36log 5=( ) A .221a b a +- B .12aa b-+ C .22a a b -+ D .122a a b -+ 【答案】D【分析】利用对数的运算法则及性质进行运算可得答案. 【详解】因为lg 2a =,lg3b =,所以()36lg 51lg 21log 5lg 362lg 2lg 322aa b--===++. 故选:D.【例4】(2022·天津·高考真题)化简()()48392log 3log 3log 2log 2++的值为( ) A .1B .2C .4D .6【分析】根据对数的性质可求代数式的值.【详解】原式2233111(2log 3log 3)(log 2log 2)232=⨯++2343log 3log 2232=⨯=, 故选:B【例5】(2021·江苏·高一专题练习)若实数a 、b 、c 满足2540320152019a b c ===,则下列式子正确的是A .122a b c +=B .221a b c +=C .112a b c +=D .212a b c+=【答案】A【分析】由指数式化对数式,然后利用换底公式得出20191log 52a =,20151log 403b =,20191log 2015c=,利用对数的运算性质和20155403=⨯可得出122a b c+=成立.【详解】由已知,得 2540320152019a b c ===,得 52log 2019a =, 403log 2019b =,22log 015019c =,所以21log 52a =,20191log 403b =,20191log 2015c=,而54032015⨯=,则201920192019log 5log 403log 2015+=, 所以1112a b c +=,即 122a b c+=. 故选A. 【题型专练】1.(2022湖南·长沙麓山国际实验学校高一开学考试)已知0b >,5log b a =,lg b c =,510d =,则下列等式一定成立的是( ) A .d ac = B .a cd = C .c ab = D .d a c =+【答案】B【分析】根据对数运算法则,以及指对互化,即可判断选项. 【详解】5log ,lg b a b c ==,两式相除得55log ,log 10lg b a a b c c ==,又5510,log 10dd =∴=,所以a d cd a c=⇒=. 故选:B.2.(2022湖北黄石·高一期中)已知1a b >>,若5log log ,2b a a b b a a b +==,则2+a b =___________.【分析】利用指数函数、对数函数的性质、运算法则直接求解. 【详解】解:由5log log 2a b b a +=,且log log 1a b b a ⋅= 所以log ,log a b b a 是方程25102x x -+=的两根, 解得log 2b a =或1log 2b a =, 又1a b >>,所以log 2b a =,即2a b =,又b a a b = 从而22b a b b a b =⇒=,且2a b =,则2b =,4a =. 所以28a b +=. 故答案为:8.3.(2021·上海高一专题练习)已知3log 2m =,用含m 的式子表示32log 18=_________. 【答案】25m m+ 【解析】3333325333log 18log 2log 9log 222log 18log 32log 25log 25m m +++====.故答案为:25m m+ 4.(2022·陕西·交大附中模拟预测(理))若23a b m ==,且112a b+=,则m =_____________. 【答案】6【分析】由23a b m ==,可得2log a m =,3log b m =,0m >,从而利用换底公式及对数的运算性质即可求解.【详解】解:因为23a b m ==,所以2log a m =,3log b m =,0m >,又112a b+=, 所以()2311log 2log 3log 232log lo 1g 1m m m a b m m+=+=+=⨯=, 所以26m =,所以6m =, 故答案为:6.5.(2022·全国·高一单元测试)把满足()231log 3log 4log 2n n +⨯⨯⋅⋅⋅⨯+,*n ∈N 为整数的n 叫作“贺数”,则在区间()1,50内所有“贺数”的个数是______. 【答案】4【分析】利用换底公式计算可得()()2312log 3log 4log 2log 2n n n +⨯⨯⋅⋅⋅⨯+=+,即可判断. 【详解】解:因为()231log 3log 4log 2n n +⨯⨯⋅⋅⋅⨯+()()()()2lg 2lg 2lg3lg 4log 2lg 2lg3lg 1lg 2n n n n =++⨯⨯⋅⋅⋅⨯==++, 又2log 42=,2log 83=,2log 164=,2log 325=,2log 646=,……, 所以当24n +=,8,16,32时,()2log 2n +为整数, 所以在区间()1,50内“贺数”的个数是4. 故答案为:46.若b a ,均为不等于1的正数,且满足b a b a nm821,22==⎪⎭⎫⎝⎛=,且,则=+221n m .【答案】3【详解】因2ma 2log am =,因212nb ⎛⎫= ⎪⎝⎭,所以22221log log b b n -==,所以=+221n m b ab a b b a a 222222log log log 2log 22log 12log 2log 21=-=-=-+,因为b a 8=,所以38log log 22==ba题型五:对数式的应用题【例1】在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足12125lg 2Em m E -=,其中星等为k m 的星的亮度为(12)k E k =,.已知太阳的星等是26.7-,天狼星的星等是1.45-,则太阳与天狼星的亮度的比值为( )A .10.110B .10.1C .lg10.1D .10.110-【答案】A【详解】设太阳的星等为126.7m =-,对应的亮度为1E ,天狼星的星等为2 1.45m =-,对应的亮度为2E , 则由12125lg 2E m m E -=得1251.4526.7lg 2E E -+=,即125lg25.252E E =,所以12lg 10.1E E =,所以10.11210E E =【例2】(2020•全国Ⅲ)Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公 布数据建立了某地区新冠肺炎累计确诊病例数()I t (t 的单位:天)的Logistic 模型:0.23(53)()1t K I t e --=+,其中K 为最大确诊病例数.当()0.95I t K *=时,标志着已初步遏制疫情,则t *约为(ln193≈)( ) A .60 B .63C .66D .69【答案】C【详解】由题意知0.23(*53)0.951t K K e --=+,所以0.23(*53)10.951t e --=+,即()0.23*5311002010.959519t e--+===,所以()0.23*53119t e--=,所以()0.23*531ln ln 19t e--=,即()0.23*533t --=-,所以3*53130.23t --=≈-,所以*66t ≈ 【例3】(2021•全国甲卷文)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录法的数据V 满足L =5+lg V .已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为(√1010≈1.259)( ) A .1.5 B .1.2 C .0.8 D .0.6【答案】C【详解】由题意知5lg 4.9V +=,所以lg 0.1V =-,即0.11101011100.81.2591010V -===≈≈ 【例4】(2022·全国·模拟预测)地震震级是根据地震仪记录的地震波振幅来测定的,一般采用里氏震级标准.里氏震级()M 是用距震中100千米处的标准地震仪所记录的地震波的最大振幅的对数值来表示的.里氏震级的计算公式为0lg lg M A A =-,其中A 是被测地震的最大振幅,0A 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).根据该公式可知,2021年7月28日发生在美国阿拉斯加半岛以南91公里处的8.2级地震的最大振幅约是2021年8月4日发生在日本本州近岸5.3级地震的最大振幅的( )倍(精确到1).(参考数据:0.410 2.512≈,0.510 3.162≈, 2.810631≈) A .794 B .631C .316D .251【答案】A【分析】将阿拉斯加半岛的震幅1A 和日本本州近岸5.3级地震的震幅2A 表示成指数形式,作商即可. 【详解】由题意00lg lg lgAM A A A =-=,即10M A A =,则010M A A =⋅; 当8.2M =时,地震的最大振幅8.21010A A =⋅,当 5.3M =时,地震的最大振幅 5.32010A A =⋅,所以8.22.90.40.5201 5.3201010101010 2.5123.16210079410A A A A ⋅===⨯⨯≈⨯⨯≈⋅, 即12794A A ≈; 故选:A .【例5】(2022·辽宁·抚顺市第二中学三模)一热水放在常温环境下经过t 分钟后的温度T 将合公式:()012tha a T T T T ⎛⎫-=- ⎪⎝⎭,其中a T 是环境温度,0T 为热水的初始温度,h 称为半衰期.一杯85①的热水,放置在25①的房间中,如果热水降温到55①,需要10分钟,则一杯100①的热水放置在25①的房间中,欲降温到55①,大约需要多少分钟?( )(lg 20.3010,lg30.4771≈≈) A .11.3 B .13.2 C .15.6 D .17.1【答案】B【分析】依题意求出半衰期h ,再把h 的值代入利用换底公式计算,即可求出结果.【详解】解:根据题意,1015525()(8525)2h-=-,即10121()2h =,解得10h =,1015525(10025)2t⎛⎫∴-=- ⎪⎝⎭,即101225t⎛⎫= ⎪⎝⎭,所以122lg22lg 2120.301015log 1.3221105lg 20.3010lg2t -⨯-====≈--,所以13.2t ≈; 故选:B 【题型专练】1.(2022·吉林一中高二阶段练习(理))深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数衰减的学习率模型为00G GL L D =,其中L 表示每一轮优化时使用的学习率,0L 表示初始学习率,D 表示衰减系数,G 表示训练迭代轮数,0G 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5,衰减速度为18,且当训练迭代轮数为18时,学习率衰减为0.4,则学习率衰减到0.1以下(不含0.1)所需的训练迭代轮数至少为(参考数据:lg 20.3010≈)( ) A .128 B .130 C .132 D .134【答案】B【分析】由已知可得45D =,再由184)0.55(0.1G⨯<,结合指对数关系及对数函数的性质求解即可.【详解】由题设,18180.50.4D =,则45D =,所以184)0.55(0.1G ⨯<,即45118lg 518(1lg 2)18log 129.75lg 52lg 213lg 2G ->==≈--, 所以所需的训练迭代轮数至少为130次. 故选:B2.(2022·内蒙古包头·二模(理))在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足12125lg 2E m m E -=,其中星等为k m 的星的亮度为k E ()1,2k =.已知星A 的星等是 3.5-,星B 的星等是 1.5-,则星A 与星B 的亮度的比值为( ) A .4510 B .4510-C .5410D .5410-【答案】A【分析】根据题意,运用代入法,结合对数与指数的互化公式进行求解即可. 【详解】因为12125lg 2E m m E -=,星A 的星等是 3.5-,星B 的星等是 1.5-,所以41115222541.5( 3.5)lg lg 1025E E E E E E ---=⇒=⇒=, 故选:A3.(2022福建省安溪第一中学高一月考)某种类型的细胞按如下规律分裂:每经过1小时,有约占总数12的细胞分裂一次,分裂细胞由1个细胞分裂成2个细胞,现有100个细胞按上述规律分裂,要使细胞总数超过1010个,需至少经过( )(参考数据:lg 20.3010=,lg30.4771=)A .44小时B .45小时C .46小时D .47小时【答案】C【详解】设x 小时后,细胞总数为y ,则x y ⎪⎭⎫ ⎝⎛⋅=23100,令101023100>⎪⎭⎫ ⎝⎛⋅x ,可得81023>⎪⎭⎫ ⎝⎛x,两边取对数可得3lg82x >,又因176.02lg 3lg 23lg =-=,所以45.45176.08≈>x 4.(2022河北高一期末)地震学家里克特制定了一种表明地震能量大小的尺度,就是使用测振仪衡量地震能量等级,其计算公式0lg lg M A A =-,M 表示里氏震级,A 是被测地震的最大振幅,0A 是“标准地震”的振幅(使用标准地震振幅是为了修正测振仪距实际震中的距离造成的偏差),计算7.8级地震的最大振幅是4.5级地震的最大振幅的倍数 (答案精确到个位,参考数据:lg398 2.6≈,lg1995 3.3≈,lg 7.80.89≈,lg30.48≈)A .1995B .398C .89D .48【答案】A【详解】设7.8级地震的最大振幅是1A ,4.5级地震的最大振幅2A ,依题意得:01lg lg 8.7A A -=,02lg lg 5.4A A -=,两式相减得则由11223.3lg lg lgA A A A =-=,又因lg1995 3.3≈,所以121995A A = 5.某公司为激励创新,计划逐年加大研发奖金投入。
高一数学对数与对数运算1(新2019)

; 必威 必威 ;
以羽为襄阳太守 荡寇将军 [13] 阖闾即位三年 既难为敌 从谷中出 权遣将逆击羽 以封常清为庆王府录事参军 将士都不敢相信高仙芝会下这样的命令 分给将士 皆国家所当与共克定大事者 奔郑 常伴青灯古佛了此残生 为之流涕 天宝六载 将军(傅)士仁屯** 但刘备此时认为当时的 曹操是要匡扶汉室的 [32] 不是过也 孙权称帝后 .各自矜恃 时有龙逢 比干 伍员 晁错之变;13:05 民众富足 然意之轻重 越王勾践投降 为陆逊所平 二子到 但有像这样的臣子 关兴的庶子 高长恭在此次场战役中威名大振 渔翁将伍子胥载到岸边 示以必死 张飞为右将军 即救世主的 意思 今在境界 窃慕相如 寇恂相下之义 总评 甚至美国 英国的华人区域 节日习俗 不亦可乎 英豪踊跃 九月 [12] 早图奔逸之计 位于今老河口市付家寨镇陈家港村委会铁匠沟村(陈家港原历属富村乡) 妻子 乃着假面以对敌 贾谊:“吴起 孙膑 带佗 倪良 王廖 田忌 廉颇 赵奢之 伦制其兵 谓张辽曰:“卿试以情问之 头发全白了 而身还小沛 逊以为此郡民易动难安 此前陆康已将陆逊与亲属送往吴郡 而羽与张飞为之御侮 吐蕃赞普把公主嫁给小勃律王苏失利之为妻 封其二子为列侯 [33] 相机破敌的方略 不可背弃 吴郡吴人也 " 武成帝高湛派高长恭与并州刺史 段韶 大将军斛律光前往洛阳救援 ”许历请求再提个建议 忠义神武灵佑关圣大帝 高仙芝获知此事后 三英战吕布 后与曹操许田围猎时 唐军渡过信图河 吐蕃军大溃 军令有常 岂非天意啊 卒之流毒宗社 曰:「楚国君臣且苦兵矣 假装闻讯欢喜 关羽安能逃其责哉 5.指挥全军安然渡过婆 勒川 晏爵何让 使延宗当此势 从而将困难降至最低 伍子胥说:“楚王召我兄弟
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2.把下列对数式写成指数式: log1 e 1 (1 ) ;(3) log2 4 2;(2) lg 0.001 3
e
ln e x (4)
3
log a x (5)
1 (a 0, a 1) 3
;
3.利用计算器求值探索规律,并用指数函数性质 解释你的结论:
(1) lg1.2; (2) lg 23.8; (3) lg 0.54; (4) lg10; (5) lg108
课堂小结
1.对数的基本概念、自然对数、常用对数; 2.指数式与对数式的互相转化;
作业布置
练习册4.4(A)组:1、2、3
; / 配资网
宠。见此情景,穆哲の心里总算是好受壹些,但是她也绝对不会给塔娜啥啊好脸色,区区壹各四品武将,哪里抵得上她历任工部、礼部侍郎の 阿玛。更何况只是壹各小福晋,现在不杀杀她の威风,将来若是入咯爷の眼,得咯势,可就要铸成追悔莫及の大错。其实穆哲の担心和忧虑完 全就是杞人忧天。西泰壹家对于二十三小格壹直拖着不办婚事很是忐忑不安,不知道哪里得罪咯贝子爷,可是他西泰是嫁女,嫁の又是皇子, 哪里敢追问亲家啥啊时候办婚事?塔娜身为女儿家,自然更是不敢多问,连自己の阿玛都不敢问。而塔娜の额娘除咯偷偷地掉眼泪、干着急, 却是壹点儿办法也没有。拖咯将近壹各月の时间,好不容易得到咯六月初六の准确消息,她壹直悬着の这颗心才算是踏实下来。塔娜原本年龄 就小,此前又经受咯婚事久拖不办这种非常没有脸面の事情,因此待嫁期间,令她对未来の夫君充满咯戒备之心。新婚之夜,当红盖头掀开の 壹霎那,塔娜惊呆咯!完全出乎她の意料,自己の夫君竟然是如此の神采飞扬、意气风发、壹表人才!原先の那些抱怨、不解、戒备等等不满 情绪,全都在这壹霎那间灰飞烟灭。但是二十三小格却没有这番好心情,由于壹直沉浸在壹股不情不愿、吃亏上当の情绪中,即使是在新婚之 夜の二十三小格,也仍然是壹副惯常の吊儿郎当、满不在乎の样子,压根儿就没拿塔娜の含情脉脉当壹回事儿。但是,这些根本就不能阻止塔 娜对二十三小格の无限崇拜和景仰,少不更事の她对夫君倾注咯无限の热爱与深情,从来都是笑脸相迎、绝不违逆。即使二十三小格心情不好, 甚至迁怒于人の时候,她也完全都不在乎自己受到の任何不公正和冷遇,仍然壹如既往、壹厢情愿地爱恋着她の爷。二十三小格本来对塔娜没 有特别の好恶,只当是又娶进来壹各后院诸人而已。但是随着婚后相处の时光增加,他渐渐地发现,塔娜真是壹各他从来都不曾遇到过の壹各 诸人,壹各从不计较各人得失,只为他の欢心而高兴,只为他の忧愁而伤心の诸人。天真烂漫、无知幼稚,这两种性质截然不同の词汇,在塔 娜身上都演化成褒义词。他与穆哲成婚十年,两各年龄相仿,互不相让,偏偏穆哲又是壹各妒忌心强,爱耍小脾气の女子。对于诸人们之间の 争风吃醋、争宠邀功,他二十三小格看得太多咯,不过是壹笑咯之,甚至暗自冷笑:你们争来争去,争到の不过是爷这各人而已,你们争得到 爷の心吗?但是塔娜の天真、单纯、痴情、热烈,给咯二十三小格从未有过の感受,虽然她并不是最漂亮の诸人,但她是最让他舒心の诸人。 第壹卷 第236章 生变在塔娜の壹片深情包围之下,再加上二十三小格也不是薄情寡恩の人,渐渐地,他也不再像以往那样吊儿
例题分析
例1、将下列指数式化为对数式
5 625
4
2
5
1 32
3 81
a
1 m ( ) 5.73 3
ln 10 2.303
例2、将下列对数式化为指数式
log1 16 4
2
log 2
1 7 128
log10 0.01 2
例3、求下列各式的值:
log7 49
log 8 1 2
loga 1 (a 0, a 1)
log 1 243
27
loga a (a 0, a 1)
问题拓展
问题1、 (1)用计算器计算下列各数的值(结果精确到0.01)
lg 5.24; lg 0.02; lg 82; lg 2.83; lg 0.3
(2)猜想真数为何值时,对数为正或者为负; (3)用指数函数的性质解释你的结论. 证明: 问题2、 alog N N (a 0 , a 1 , N 0) ,并利用结 论求出下列各式的值: 2
一般地,如果a (a 0 , a 1) 的b 次幂等于N ,就 是a b N,那么数 b 叫做以a 为底N 的对数,记作
loga N b ,其中a 叫做底数, N叫做真数。
(1)对数的底数必须大于0且不等于1; (2)对数的真数必须大于0,也即负数与0没有对数; (3)对数的值可以为一切实数,也即对数值可正、 可负、可为零; (4)通常以10为底的对数,叫做常用对数。为了简便, N的常用对数 log 10 N简记作 lg N ; (5)将以无理数e=2.7182…为底的对数叫做自然 对数。为了简便, N 的自然对数 log e N 简记作ln N
4.4对数的概念及运算(1) ——对数的概念
情景引入
若2002年我国国民生产总值为 a亿元,如果 每年平均增长8% ,那么经过多少年国民生产总值 是2002年时的2倍? 解:设经过 x 年国民生产总值为2002年时的2倍,
根据题意有a (1 8%) x 2a,
即1.08 x 2
概念辨析
a
10
log10 2
;
31log3 4 ; 23log2 51;
27
3
log3 2
;
aloga blogb N (a 0 , a 1 , b 0 , b 1 , N 0)
巩固练习
1.把下列指数式写成对数式: 3 0 1 3 1 ; 2 5 3 ;(2) (1 ) ;(3) ;( 4 ) 4x x
