转化单位1
六年级数学重点内容转化单位“1”总复习

六年级重点内容转化单位“1”总复习(一)专题简析:把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化。
如果甲是乙的a b ,乙是丙的c d ,则甲是丙的ac bd ;如果甲是乙的a b ,则乙是甲的b a;如果甲的a b 等于乙的c d ,则甲是乙的c d ÷a b =bc ad ,乙是甲的a b ÷a b =ad bc。
例题1。
乙数是甲数的23 ,丙数是乙数的45,丙数是甲数的几分之几? 23 ×45 =815练习11. 乙数是甲数的34 ,丙数是乙数的35,丙数是甲数的几分之几? 2. 一根管子,第一次截去全长的14 ,第二次截去余下的12,两次共截去全长的几分之几? 3. 一个旅客从甲城坐火车到乙城,火车行了全程的一半时旅客睡着了。
他醒来时,发现剩下的路程是他睡着前所行路程的14。
想一想,剩下的路程是全程的几分之几?他睡着时火车行了全程的几分之几?例题2。
修一条8000米的水渠,第一周修了全长的14 ,第二周修的相当于第一周的45,第二周修了多少米?解一:8000×14 ×45=1600(米) 解二:8000×(14 ×45)=1600(米) 答:第二周修了1600米。
练习2用两种方法解答下面各题:1. 一堆黄沙30吨,第一次用去总数的15 ,第二次用去的是第一次的114倍,第二次用去黄沙多少吨?2. 大象可活80年,马的寿命是大象的12 ,长颈鹿的寿命是马的78,长颈鹿可活多少年? 3. 仓库里有化肥30吨,第一次取出总数的15 ,第二次取出余下的13,第二次取出多少吨?例题3。
晶晶三天看完一本书,第一天看了全书的14 ,第二天看了余下的25,第二天比第一天多看了15页,这本书共有多少页?解: 15÷【(1-14 )×25 - 14】=300(页) 答:这本书有300页。
练习31. 有一批货物,第一天运了这批货物的14 ,第二天运的是第一天的35,还剩90吨没有运。
六年级奥数第6讲 转化单位“1”(一)

第6讲 转化单位“1”(一)一、知识要点把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化.如果甲是乙的b a ,乙是丙的d c ,则甲是丙的bd ac ;如果甲是乙的b a ,则乙是甲的ab;如果甲的b a 等于乙的d c ,则甲是乙的d c ÷b a =ad bc ,乙是甲的b a ÷dc=bc ad .二、精讲精练【例题1】乙数是甲数的32,丙数是乙数的54,丙数是甲数的几分之几? 练习1:1、乙数是甲数的43,丙数是乙数的53,丙数是甲数的几分之几?2、一根管子,第一次截去全长的41,第二次截去余下的21,两次共截去全长的几分之几?3、一个旅客从甲城坐火车到乙城,火车行了全程的一半时旅客睡着了.他醒来时,发现剩下的路程是他睡着前所行路程的41.想一想,剩下的路程是全程的几分之几?他睡着时火车行了全程的几分之几?【例题2】修一条8000米的水渠,第一周修了全长的41,第二周修的相当于第一周的54,第二周修了多少米?练习2:用两种方法解答下面各题:1、一堆黄沙30吨,第一次用去总数的51,第二次用去的是第一次的411倍,第二次用去黄沙多少吨?2、大象可活80年,马的寿命是大象的21,长颈鹿的寿命是马的87,长颈鹿可活多少年?【例题3】晶晶三天看完一本书,第一天看了全书的41,第二天看了余下的52,第二天比第一天多看了15页,这本书共有多少页?练习3:1、有一批货物,第一天运了这批货物的41,第二天运的是第一天的53,还剩90吨没有运.这批货物有多少吨?2、修路队在一条公路上施工.第一天修了这条公路的41,第二天修了余下的32,已知这两天共修路1200米,这条公路全长多少米?【例题4】男生人数是女生人数的54,女生人数是男生人数的几分之几?练习4:1、停车场里有小汽车的辆数是大汽车的43,大汽车的辆数是小汽车的几分之几?2、如果山羊的只数是绵羊的76,那么绵羊的只数是山羊的几分之几?3、如果花布的单价是白布的531倍,则白布的单价是花布的几分之几?【例题5】甲数的31等于乙数的41,甲数是乙数的几分之几,乙数是甲数的几倍?练习5:1、甲数的43于乙数的52,甲数是乙数的几分之几?乙数是甲数的几分之几?2、甲数的321倍等于乙数的65,甲数是乙数的几分之几?乙数是甲乙两数和的几分之几?三、课后作业1、加工一批零件,甲先加工了这批零件的52,接着乙加工了余下的94.已知乙加工的个数比甲少200个,这批零件共有多少个?2、甲数是丙数的43,乙数是丙数的52,甲数是乙数的几分之几?乙数是甲数的几分之几?3、仓库里有化肥30吨,第一次取出总数的51,第二次取出余下的31,第二次取出多少吨?。
六年级奥数专题-转化单位“1”

六年级奥数专题-转化单位“1”转化单位“1”(一)专题简析:把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化。
如果甲是乙的a b ,乙是丙的c d ,则甲是丙的ac bd ;如果甲是乙的a b ,则乙是甲的ba ;如果甲的a b 等于乙的c d ,则甲是乙的c d ÷a b =bc ad ,乙是甲的a b ÷a b =adbc 。
例题1。
乙数是甲数的23 ,丙数是乙数的45 ,丙数是甲数的几分之几?23 ×45 =815练习11. 乙数是甲数的34 ,丙数是乙数的35,丙数是甲数的几分之几?2. 一根管子,第一次截去全长的14 ,第二次截去余下的12 ,两次共截去全长的几分之几?3. 一个旅客从甲城坐火车到乙城,火车行了全程的一半时旅客睡着了。
他醒来时,发现剩下的路程是他睡着前所行路程的14 。
想一想,剩下的路程是全程的几分之几?他睡着时火车行了全程的几分之几?练1 1、 =920 2、 =58 3、 =18 =38例题2。
修一条8000米的水渠,第一周修了全长的14 ,第二周修的相当于第一周的45 ,第二周修了多少米?解一:8000×14 ×45 =1600(米)解二:8000×(14 ×45 )=1600(米)答:第二周修了1600米。
练习2用两种方法解答下面各题:1. 一堆黄沙30吨,第一次用去总数的15 ,第二次用去的是第一次的114倍,第二次用去黄沙多少吨?2. 大象可活80年,马的寿命是大象的12 ,长颈鹿的寿命是马的78,长颈鹿可活多少年?3. 仓库里有化肥30吨,第一次取出总数的15 ,第二次取出余下的13 ,第二次取出多少吨?练2 1、 =7.5(吨) 2、 =35(年) 3、 =8吨例题3。
晶晶三天看完一本书,第一天看了全书的14 ,第二天看了余下的25 ,第二天比第一天多看了15页,这本书共有多少页?解: 15÷【(1-14 )×25 - 14 】=300(页)答:这本书有300页。
第3讲:转化单位”1“(最新数学课件)

文艺书和科技书:1-
1-
4
1 5
文艺书:(1-1
4
-
1)×
5
3
4
4
分量
分率
80÷
[(1-14
-
1)×
5
3
4
4
-
1]
5
=80÷
4 35
=700(本)
答:买回的四种书共有700本。
总结
1. 一般在“是”、“比”、“占”、“相当于”后面的 就是单位“1”。
2. 当题目中存在多个单位“1”时,我们首先要将单位 “1”进行统一,选取其中的一个单位“1”,然后分 别用分数表示出其它量,进而解答。
单位“1”
10 9
10×3
95
“分量”和 “分率”和 500÷(1+10+ 10×3 )=180(千克)
9 95
萝卜:180×10× 3 =120(千克)
95
答:买了120千克萝卜。
例题二
芭啦啦动物园的猴园里,雌性猴子比全部猴子
总数的 3 多6只,雄性猴子是雌性猴子总数的 1 ,这
个猴园共5 有猴子多少只?
3
3 多6只
5
3 5
(
3 5
多6只)×13
1 多2只
5
(6+6×1 )÷(1- 3- 3× 1 )
3
553
=8÷ 1 5
=40(只)
6只 2只 1 5
答:这个猴园共有40只猴子。
练习二
一个小村庄的水田面积占农田总面积的 1 多12亩,
旱田面积是水田面积的 2
2
。这个村庄的农田总面积是
多少亩?
5
水田
2. 当题目中存在多个单位“1”时,我们首 先要将单位“1”进行统一,选取其中的 一个单位“1”,然后分别用分数表示出 其它量,进而解答。
六年级数学上册分数应用题转化单位1的五种解题方法
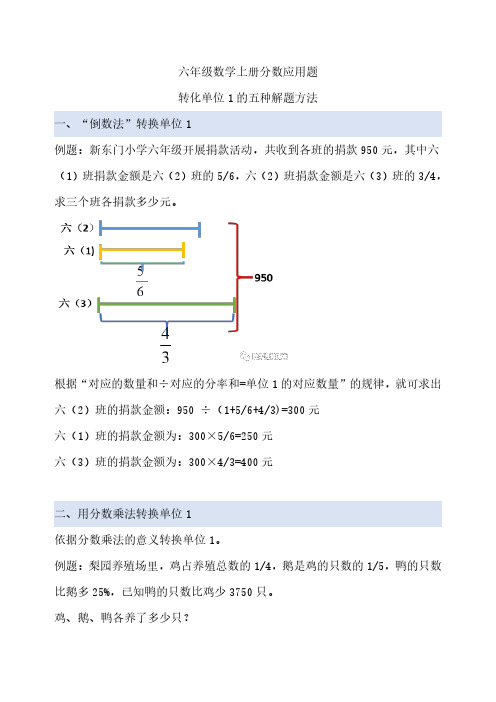
六年级数学上册分数应用题转化单位1的五种解题方法一、“倒数法”转换单位1例题:新东门小学六年级开展捐款活动,共收到各班的捐款950元,其中六(1)班捐款金额是六(2)班的5/6,六(2)班捐款金额是六(3)班的3/4,求三个班各捐款多少元。
根据“对应的数量和÷对应的分率和=单位1的对应数量”的规律,就可求出六(2)班的捐款金额:950÷(1+5/6+4/3)=300元六(1)班的捐款金额为:300×5/6=250元六(3)班的捐款金额为:300×4/3=400元二、用分数乘法转换单位1依据分数乘法的意义转换单位1。
例题:梨园养殖场里,鸡占养殖总数的1/4,鹅是鸡的只数的1/5,鸭的只数比鹅多25%,已知鸭的只数比鸡少3750只。
鸡、鹅、鸭各养了多少只?以养殖总数为单位1,依据分数乘法的意义,鹅占养殖总数的1/4×1/5=1/20,鸭占养殖总数的1/20×(1+25%)=1/16。
鸡、鹅、鸭的分率如下图:这样,鸡与鸭就统一单位1了,都是以养殖总数为单位1的,用鸡与鸭的数量差与分率差相除,就能求出养殖总数了:3750÷(1/4-1/16)=20000只。
鸡的只数:20000×1/4=5000只鹅的只数:20000×1/20=1000只鸭的只数:20000×1/16=1250只三、用份数法转换单位1例题:乌江泥厂有甲、乙、丙、丁四个车间,甲车间人数是其他三个车间的1/4,乙车间人数是其他三个车间的4/11,丙车间人数是其他三个车间的1/2,已知丁车间有60人,该厂有职工多少人?我们可以用全厂职工总数为单位1,用份数法,分别求出甲、乙、丙三车间人数各占全厂职工总数的几分之几,然后,再求出丁车间人数占全厂职工总数的几分之几。
三个车间的分率转换如下:甲车间人数是全厂职工的1÷(1+4)=1/5,乙车间人数占全厂职工的4÷(4+11)=4/15丙车间人数占全厂职工的1÷(1+2)=1/3.现在,本题的数量关系已简化成下图:看图可知,60人的对应分率为1-1/5-4/15-1/3。
分数应用题-转化单位“1”

第九讲 分数应用题--转化单位“1”【知识概述】分数应用题研究的是数与量的对应关系,确定单位“1”是解答分数应用题的关键。
解题时就要注意抓住单位"1"的量,要注意分析题中分率和具体数量的对应关系:如果已知单位"1"的量,求分率对应的具体的数量就用乘法。
如果已知分率对应的具体数量,求单位"1",就要用除法。
温馨提示:对于题中多个单位"1"的量,要注意转化。
【典型例题】 例1 名士小学原有科技书、文艺书共630本,其中科技书占51,后来又买进一些科技书,这时科技书占这两种书的103,又买进科技书多少本? 【名师】根据题意:文艺书的本数是不变的,因此要从这里寻得解题的突破口。
文艺书占原来总本数的54511=-,也就是630 54⨯=504(本),同时也占增加后总本数的1071031=-,说明后来共有504 107÷=720(本),这就说明买进科技书720-630=90(本).解:(1) 文艺书的本数:630=-⨯)511(504(本)(2) 后来共有书的本数为:504÷)1031(-=720(本)(3) 又买进科技书多少本?720-630=90(本) 答:又买进科技书90本。
例2 日立工厂两个车间,甲车间每月的产值比乙车间多16万元,甲车间每月产值的152等于乙车间的32,问两个车间每月产值各是多少万元? 【名师】这一道题中,分数间的关系比较隐蔽,我们不妨先将“甲车间每月产值的152等于乙车间产值的32”这个条件两边同时乘以32的倒数23,我们就可以清楚的看出“甲车间每月的产值的51等于乙车间的产值” ,即把甲车间每月的产值看作单位“1”,乙车间占51,“甲车间每月的产值比乙车间多16万元”,这样可求甲车间每月的产值:16÷(1-51)=20(万元),乙车间每月的产值:20⨯51=4(万元)解:“甲车间每月的152等于乙车间产值的32”可知“甲车间每月的产值的51等于乙车间的产值” 甲车间每月的产值:16÷(1-51)=20(万元)乙车间每月的产值:20⨯51=4(万元)答:甲车间每月的产值20万元,乙车间每月的产值4万元。
转化单位“1”—2022-2023学年六年级数学思维拓展(学生版)

2022-2023学年小学六年级思维拓展专题 转化单位“1”知识精讲把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化。
如果甲是乙的ab,乙是丙的cd,则甲是丙的acbd;如果甲是乙的ab,则乙是甲的ba;如果甲的ab等于乙的cd,则甲是乙的cd÷ab=bcad,乙是甲的ab÷ab=adbc。
我们必须重视转化训练。
通过转化训练,既可理解数量关系的实质,又可拓展我们的解题思路,提高我们的思维能力。
典例分析【典例01】甲数是乙数的23,乙数是丙数的34,甲、乙、丙的和是216,甲、乙、丙各是多少?解法一:把丙数看所单位“1”那么甲数就是丙数的34×23=12,丙:216÷1+34+34×23=96乙:96×34=72甲:72×23=48解法二:可将“乙数是丙数的34”转化成“丙数是乙数的43”,把乙数看作单位“1”。
乙:216÷23+1+43=72甲:72×23=48丙:72÷34=96解法三:将条件“甲数是乙数的23”转化为“乙数是甲数的32”,再将条件“乙数是丙数的34”转化为“丙数是乙数的43”,以甲数为单位“1”。
甲:216÷1+32+32×43=48乙:48×32=72丙:72×43=96答:甲数是48,乙数是72,丙数是96。
【典例02】红、黄、蓝气球共有62只,其中红气球的35等于黄气球的23,蓝气球有24只,红气球和黄气球各有多少只?解法一:将条件“红气球的35等于黄气球的23”转化为“黄气球的只数是红气球的35÷23=910”。
先求红气球的只数,再求出黄气球的只数。
红气球:(62-24)÷1+35÷23=20(只)黄气球:62-24-20=18(只)解法二:将条件“红气球的35等于黄气球的23”转化为“红气球的只数是黄气球的23÷35= 109”。
转化单位“1”

【例题3】已知甲校学生数是乙校学生数的2/5,甲校的 女生数是甲校学生数的3/10,乙校的男生数是乙校学生数 的21/50,那么两校女生总数占两校学生总数的几分之几?
3.一个旅客从甲城坐火车到乙城,火车行了全程的一 半时旅客睡着了。他醒来时,发现剩下的路程是他睡 着前所行路程的1/4。想一想,剩下的路程是全程的几 分之几?他睡着时火车行了全程的几分之几?
【例题2】修一条8000米的水渠,第一周修了全长的1/4, 第二周修的相当于第一周的4/5,第二周修了多少米?
丙:216÷(1+3/4+3/4×2/3)=96 乙:96×3/4=72 甲:72×2/3=48
解法二:可将“乙数是丙数的3/4”转化成“丙数是乙数的4/3”, 把乙数看作单位“1”。
乙:216÷(2/3+1+4/3)=72 甲:72×2/3=48 72÷3/4=96 答:甲数是48,乙数是72,丙数是96。
丙:
1.甲数是乙数的5/6,乙数是丙数的3/4,甲、乙、丙三 个数的和是152,甲、乙、丙三个数各是多少? 2.橘子的千克数是苹果的2/3,香蕉的千克数是橘子的 1/2,香蕉和苹果共有220千克,橘子有多少千克?
3.某中学的初中部三个年级中,初一的学生数是初二学 生数的9/10,初二的学生数是初三学生数的1又1/4倍,这 个学校里初三的学生数占初中部学生数的几分之几?
【例题2】红、黄、蓝气球共有62只,其中红气球的3/5 等于黄气球的2/3,蓝气球有24只,红气球和黄气球各有 多少只?
解法一:将条件“红气球的3/5等于黄气球的2/3”转化为“黄 气球的只数是红气球的(3/5÷2/3)=9/10”。先求红气球的只 数,再求出黄气球的只数。
红气球:(62-24)÷(1+3/5÷2/3)=20(只) 黄气球:62-24-20=18(只)
4第四讲 分数应用题转化单位“1”

第四讲 分数应用题转化单位“1”一、知识梳理分数应用题研究的是数与量的对应关系,确定单位“1”是解答分数应用题的关键。
当问题中有多个分率,且这些分率单位“1”不同时,要分析不变量,将单位“1”进行统一,这种方法叫转化单位“1”二、方法归纳1.总量不变,转化为以总量为单位“1”,一种量不变,以不变的量为单位“1”,差量不变,以差量为单位“1”。
2.在转化的过程中,注意分率与比之间的转化,注意“份数”思想。
三、课堂精讲例1. 修路队修一条公路,第一天修了这条公路的52,第二天修了余下的31,已知这两天共修路120米,这条公路全长多少米?【规律方法】总量不变,以总量(这条公路)为单位“1”。
【搭配课堂训练题】 【难度分级】 A1.小方三天看完一本书,第一天看了全书的31,第二天看了余下的43,第二天比第一天多看了20页,这本书共有多少页?2.运送一堆水泥,第一天运了这堆水泥的41,第二天运的是第一天的32,还剩84吨没有运,这堆水泥有多少吨?例2.(2013天河省实)某校六年级有三个班,在为4.20雅安地震献爱心的活动中,一班的捐款数是二、三班捐款数之和的23,二班的捐款数是一、三班捐款数之和的25,已知三班的捐款数比一班少180元,问三个班共捐款多少元? 【规律方法】三个班捐款总量不变,以总量为单位“1”。
【搭配课堂训练题】 【难度分级】 B3.甲、乙、丙、丁四个筑路队共筑1200米长的一段公路,甲队筑的路是其他三个队的21,乙队筑的路是其他三个队的31,丙队筑的路是其他三个队的41,丁队筑了多少米?例3.兄弟两人各有人民币若干元,其中弟的钱数是兄的54,若弟给兄4元,则弟的钱数是兄的32,求兄弟两人原来各有多少元?【规律方法】在变化过程中,不变的是两人总钱数,以总钱数为单位“1”。
4.小明看一本课外读物,读了几天后,已读的页数是剩下页数的81,后来他又读了20页,这时已读的页数是剩下页数的61,这本课外读物共有多少页?5.王师傅生产一批零件,不合格产品是合格产品的191,后来从合格产品中又发现了2个不合格产品,这时算出产品的合格率是94%。
转化单位1

4.
食堂买来萝卜、青菜和土豆三种熟菜。萝卜的重量占三种蔬菜总重量的 ,青菜的重量比土豆少 ,萝
5 4
2
3
卜比土豆少 360 千克。食数比乙仓少 40%,乙仓存粮的吨数比甲仓多百分之几?
6.
水结成冰体积增加
1
10
,冰化成水体积减少几分之几?
7.
甲、乙两种商品成本共 200 元,甲商品按 30%的利润定价,乙商品按 20%的利润定价,但出售时因商店 “庆元旦促销” ,全部商品按定价的九折销售,结果卖出甲、乙两种商品各可获利 27.7 元。求甲、乙两 种商品的成本各是多少元?
例9、 某厂男工比全厂职工总人数的 多 60 人,女工人数是男工的 ,这个工厂共有职工多少人?
5 3
3
1
例10、 有两筐梨。乙筐是甲筐的 ,从甲筐取出 5 千克梨放入乙筐后,乙筐的梨是甲筐的 。甲、乙两筐梨共
5 9
3
7
重多少千克?
例11、 某学校原有长跳绳的根数占长、短跳绳总数的 。后来又买进 20 根长跳绳,这时长跳绳的根数占长、
2
1
队的3,丙队修的是其他三个队的 ,丁队修了多少米?
4
1
1
24.
书店运来科技书和文艺书共 240 包,科技书占 。后来又运来一批科技书,这时科技书占两种书总和的
6 3 11
1
,现在两种书各有多少包?
25.
把 12 千克盐溶解于 120 千克水中,得到 132 千克盐水,如果要使盐水中含盐 8%,要往盐水中加盐还是 加水?
转化单位“1”
把不同的数量当做单位“1” ,得到的分率可以在一定的条件下转化。如果甲是乙的 ,乙是丙的 ,则甲是
B D A C
动画图解“转化单位1”:单位1就是总体吗?单位1是标准量!

动画图解“转化单位1”:单位1就是总体吗?单位1是标准量!“单位1”⼀定是总体吗?不⼀定哦。
统⼀的尺度作标准来衡量其他数量,在⼀个统⼀的尺度单位1最⼤的特点:标准量标准量。
⽤表⽰“单位1”的量作标准来衡量其他数量,下,使得所有数量可以互相⽐较,这是单位1最⼤的功能。
⽽且选做“单位1”的量相对稳定,不变下,化。
某学校原有长跳绳的根数占长、短跳绳总数的3/8。
后来⼜买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的7/12。
这个学校现有长、短跳绳的总数是多少根?我们先来图解“原有长跳绳的根数占长、短跳绳总数的3/8”:将原话进⾏了简单变形,能看明⽩吧~我们再来图解“后来⼜买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的7/12”:原有跳绳总数加上新购买长跳绳后,⽐例发⽣变化⼤家应该已经发现了:长跳绳总数前后发⽣了变化,长跳绳、短跳绳⼆者总和前后也发⽣了变唯独短跳绳数量没有变化。
所以,我们就可以选择短跳绳数量作为“单位1”,⽤它来衡量长化,唯独短跳绳数量没有变化跳绳数量。
怎么衡量呢?其实两幅图⽚最后⼀句话已经告诉⼤家了。
⼀开始,长跳绳占短跳绳3/5,买来新的长跳绳后,长跳绳占短跳绳7/5;长跳绳占短跳绳的⽐例增加了:7/5-3/5=4/5。
长跳绳占短跳绳的⽐例为什么增加了?因为我们⼜买了20根长跳绳啊,20是分量,4/5是分率,分量÷分率=总量,所以:20÷4/5=25(根),短跳绳⼀共有25根!题⽬问的是“现有长、短跳绳的总数”,应该怎么计算?短跳绳数量除以对应的分率即可:25÷(1-7/12)=60(根)写个⾼⼤上的综合算式: 20÷[7/(12-7)-3/(8-3)]÷(1-7/12)=60(根)你学会了吗?。
第三讲 转化单位“1”

单位“1”是一个标准量,所以我们一般会选择不变量作为单位“1”。
单位“1”已知时可用 单位“1”×对应分率=对应数量
单位“1”未知时可用 对应数量÷对应分率=单位“1”
单位“1”运用方法练习
40的 1 是( ) 5
25是(
)的 5 7
32千米的 1 比56千米的 1 少(
4
4
)
3 吨的1 是( )
我
的
糖
果
是
姐
姐
手
里
的
1 3
,姐姐的糖果是爸爸的
1 3
,我的糖果是爸爸的几分之几?
第二天占余下的 2 ,余下的占全长的(1- 1 ),第二天占全长的 2 3
5
4
54
根据:对应数量÷对应分率=单位“1”
第二天比第一天多读的页数÷第二天比第一天多读的分率=单位“1
15 ÷ 【(1-
1 4
)×
2 5
-
1 】=300(页) 4
24
晶晶三天看完了一本书,第一天看了全书的 1 ,第二天看了
余下的
2
4 ,第二天比第一天多看了15页。这本书共有多少页?
5
第一天的单位“1”是全书,第二天的单位“1”是第一天之后余下的,
12
占4余和下5的是2
单位“1”不同的分率,首先要统一单 转化成第二天占全书的几分之几!
位
“1”
,
将
第二天
5
思考:爸爸手里的糖果是姐姐的3倍,姐姐的是我的3倍,爸爸是我的几倍?
乙数: 10×3=30
甲数: 30×2=60
丙数: 216 (1 3 3 2) 96
乙数:
96 3
4 72
正确找准单位“1”解决难题

转化单位1(一)【例题1】乙数是甲数的2/3,丙数是乙数的4/5,丙数是甲数的几分之几?【解答】(8/15)乙数是甲数的2/3,把甲数看作单位1,乙数就是2/3;丙数是乙数的4/5,也就是说丙数是2/3的4/5,“求一个数的几分之几是多少”用乘法,即2/3×4/5=8/15,丙数是8/15,甲数是1,所以丙数是甲数的8/15。
【练习1】乙数是甲数的3/4,丙数是乙数的6/7,丙数是甲数的几分之几?【解答】(9/14)乙数是甲数的3/4,把甲数看作单位1,乙数就是3/4;丙数是乙数的6/7,也就是说丙数是3/4的6/7,“求一个数的几分之几是多少”用乘法,即3/4×6/7=9/14,丙数是9/14,甲数是1,所以丙数是甲数的9/14。
【例题2】修一条8000米的水渠,第一周修了全长的1/4,第二周修的相当于第一周的4/5,第二周修了多少米?【解答】(1600米)思考一:第一周修了8000×1/4=2000米,第二周修了2000×4/5=1600米。
思考二:第二周占全长的1/4×4/5=1/5,第二周修了8000×1/5=1600米。
【练习2】一堆黄沙30吨,第一次用去总数的1/5,第二次用去的是第一次的2/3,第二次用去黄沙多少吨?【解答】(4吨)思考一:第一次用去30×1/5=6吨,第二次用去6×2/3=4吨。
思考二:第二次用去的占总数的1/5×2/3=2/15,第二次用去30×2/15=4吨。
【例题3】晶晶三天看完一本书,第一天看了全书的1/4,第二天看了余下的2/5,第二天比第一天多看了15页,这本书共有多少页?【解答】(300页)第一天看了后剩下1-1/4=3/4,第二天看的是余下的2/5,第二天看的占总页数的3/4×2/5=3/10,第二天比第一天多的占总页数的3/10-1/4=1/20,即总页数的1/20是15页,所以总页数是15÷1/20=300页。
转化单位1知识点总结

转化单位1知识点总结1.长度单位转换长度是一个物体在空间中占有的位置,是物体大小的一种度量。
在国际单位制中,长度的基本单位是米(m)。
长度单位的换算主要是根据国际单位制与非国际单位制之间的换算,主要包括以下几种单位:1米(m)= 100厘米(cm)1米(m)= 1000毫米(mm)1千米(km)= 1000米(m)1英寸(in)= 2.54厘米(cm)1英尺(ft)= 30.48厘米(cm)1码(yd)= 0.9144米(m)2.时间单位转换时间是物体在运动或变化过程中的持续时间,它是一个物体运动时的参考标准。
在国际单位制中,时间的基本单位是秒(s)。
时间单位的换算主要包括以下几种单位:1分钟(min)= 60秒(s)1小时(h)= 60分钟(min)1天(d)= 24小时(h)1周(week)= 7天(d)1年(year)= 365天(d)3.质量单位转换质量是物体所固有的属性,是物质数量大小的一种度量。
在国际单位制中,质量的基本单位是千克(kg)。
质量单位的换算主要包括以下几种单位:1克(g)= 0.001千克(kg)1千克(kg)= 1000克(g)1吨(t)= 1000千克(kg)1斤= 0.5千克(kg)1磅(lb)= 0.4536千克(kg)4.力单位转换力是物体相互作用的表现,是物体运动状态发生改变的原因。
在国际单位制中,力的基本单位是牛顿(N)。
力单位的换算主要包括以下几种单位:1牛顿(N)= 1千克米/平方秒(kg·m/s²)1千克力(kgf)= 9.8N1磅力(lbf)= 4.448N1千克米/平方秒(kg·m/s²)= 1牛顿(N)5.温度单位转换温度是物体热运动程度的一种度量,是物体热状态的表现。
在国际单位制中,温度的基本单位是摄氏度(℃)。
温度单位的换算主要是根据不同的温标之间的换算,主要包括以下几种单位:摄氏度(℃)= (华氏度(℉)- 32)/1.8摄氏度(℃)= 开尔文度(K)-273.15华氏度(℉)= 摄氏度(℃)*1.8+32开尔文度(K)= 摄氏度(℃)+273.15以上是单位转换的基本知识点以及常用单位的转换公式,通过学习单位转换,可以更好地理解和应用物理学中的相关知识,提高物理学的学习效果。
六年级奥数专题:转化单位“1”

转化单位“1”(一)专题简析:把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化。
如果甲是乙的a b ,乙是丙的c d ,则甲是丙的ac bd ;如果甲是乙的a b ,则乙是甲的b a;如果甲的a b 等于乙的c d ,则甲是乙的c d ÷a b =bc ad ,乙是甲的a b ÷a b =ad bc。
例题1。
乙数是甲数的23 ,丙数是乙数的45,丙数是甲数的几分之几? 23 ×45 =815练习11. 乙数是甲数的34 ,丙数是乙数的35,丙数是甲数的几分之几? 2. 一根管子,第一次截去全长的14 ,第二次截去余下的12,两次共截去全长的几分之几? 3. 一个旅客从甲城坐火车到乙城,火车行了全程的一半时旅客睡着了。
他醒来时,发现剩下的路程是他睡着前所行路程的14。
想一想,剩下的路程是全程的几分之几?他睡着时火车行了全程的几分之几?练1 1、 =920 2、 =58 3、 =18 =38例题2。
修一条8000米的水渠,第一周修了全长的14 ,第二周修的相当于第一周的45,第二周修了多少米?解一:8000×14 ×45=1600(米) 解二:8000×(14 ×45)=1600(米) 答:第二周修了1600米。
练习2用两种方法解答下面各题:1. 一堆黄沙30吨,第一次用去总数的15 ,第二次用去的是第一次的114倍,第二次用去黄沙多少吨?2. 大象可活80年,马的寿命是大象的12 ,长颈鹿的寿命是马的78,长颈鹿可活多少年?3. 仓库里有化肥30吨,第一次取出总数的15 ,第二次取出余下的13,第二次取出多少吨? 练2 1、 =7.5(吨) 2、 =35(年) 3、 =8吨例题3。
晶晶三天看完一本书,第一天看了全书的14 ,第二天看了余下的25,第二天比第一天多看了15页,这本书共有多少页?解: 15÷【(1-14 )×25 - 14】=300(页) 答:这本书有300页。
小升初数学完整版转化单位“1”

转化单位“1”我们是这样定义单位“1”的:单位“1”也称整体“1”。
把一个完整的量(比如一段路程、一项工程、一筐苹果、一本书、一段时间等)或一个数(正数)视为一个整体或一个单位,并赋予自然数1的特性,可记为“1”。
根据这点我们不难总结出寻找单位“1”的方法: 1、提到“谁”的几分之几,“谁”就是单位“1”比如在语句“乙的21”中,分明说“乙”的21,所以乙是单位1。
2、在比较语句中,比“谁”,“谁”是单位“1”比如在语句“甲比乙大21”中,说的是比“乙”,因此“乙”是单位1。
3、一个带单位的分数量,一个单位就是它的单位“1”比如:语句“21千克”中,量21千克的单位是千克,因此1千克就是该量的单位1。
教学目标知识与技能:使学生理解单位1的概念并判断单位1的量,并能正确、灵活地解答分数乘除法应用题;过程与方法:通过对比练习、归类整理、探讨交流,加深学生对分数三类应用题的数量关系和内在联系的认识,提高学生的分析能力和解答应用题的能力;学会用‘转化单位1的方法解答分数应用题。
灵活应用所学的方法解应用题。
情感、态度与价值观:培养学生比较、分析、归纳、转化的逻辑思维能力,感悟数学的知识魅力。
教学重点:理解分数乘除法应用题的异同点,并能正确解答。
教学难点:归纳总结分数三类应用题的解题方法和规律艺海拾贝*同学们已经在知识的海洋里搜集了五颜六色的贝壳,下面老师展示的这些贝壳你拾到了吗?1、如果甲是乙ab,则乙是甲的 。
2、如果甲是乙的a b ,乙是丙的cd,则甲是丙的 。
3、如果甲的a b 等于乙的c d ,则甲是乙的c d ÷a b =bcad ,乙是甲的 。
既然我们已经理解了单位“1”,现在我们就在例题中具体讲述解决这一类问题的有关方法。
一、找准单位“1”正确找准单位“1”,是解答分数(百分数)应用题的关键,每一道分数应用题中总是有关键句(含有分率的句子)。
如何从关键句中找准单位“1”,可以从以下这些方面进行考虑。
分数应用题转化单位一练习题

分数应用题转化单位一练习题分数应用题是数学中的一种重要题型,其中转化单位一的方法是解决这类问题的关键之一。
下面我们通过一些练习题来加深对转化单位一的理解和掌握。
例1:某班有男生20人,女生30人,求女生的数量是男生数量的几倍?这道题中,我们需要将女生数量转化为单位一,然后再计算与男生数量的比值。
由于女生数量为30,比男生数量20大,因此我们需要在女生数量上加上一个分数,使得这个分数与男生数量的比值为1。
根据题意可得:女生数量 = 30男生数量 = 20因此,女生数量是男生数量的1.5倍,即30/20=1.5。
例2:某公司去年销售额为100万元,今年销售额为120万元,求今年销售额是去年销售额的几倍?这道题中,我们需要将去年销售额转化为单位一,然后再计算与今年销售额的比值。
由于今年销售额为120,比去年销售额100大,因此我们需要在去年销售额上加上一个分数,使得这个分数与今年销售额的比值为1。
根据题意可得:去年销售额 = 100万元今年销售额 = 120万元因此,今年销售额是去年销售额的1.2倍,即120/100=1.2。
通过以上两道练习题,我们可以发现转化单位一的方法在分数应用题中的重要性。
在实际解题过程中,我们需要先判断哪个量是单位一,然后根据题目中的条件,将其他量转化为单位一,最后计算比值或者比例关系。
我们还需要注意一些关键词的含义,例如“几倍”、“增加几倍”等,这些关键词往往决定了我们在计算过程中需要使用乘法还是除法。
分数混合运算应用题练习题一分数混合运算应用题练习题一分数混合运算是一种常见的数学问题,它涉及到分数的加减乘除以及各种应用场景。
下面我们通过一道例题来讲解分数混合运算的解题方法和技巧。
例题:某班共有40名学生,其中男生占1/2,女生占1/2。
在一次数学考试中,男生平均分为70分,女生平均分为80分。
请问这个班级的平均分是多少?分析:这个问题涉及到分数的加减乘除,我们可以先计算男女生各自的分数,再根据男女生人数计算班级总分数,最后求得班级平均分。
第9讲 转化单位“1”

姓名一、知识要点在较复杂的分数应用题中,要根据已知条件的分率确定单位“1”,,同时,为了寻求具体数量与分率的对应,常常需要单位“1”的转化,使较隐蔽的数量关系明朗化。
二、典型例题例1 运输队分三次运完一批货物。
第一次运了这批货物的41。
第二次运了余下的52,第三次比第二次多运15吨,这批货物一共有多少吨?例2有两袋大米,第二袋比第一袋重6千克。
已知第一袋大米的重量的31恰好与二袋重量的72相等,问两袋大米各重多少千克?例3有两个粮仓,乙仓的存粮比甲仓少120吨,已知甲仓存粮的41等于乙仓存粮的31,问甲、乙两个仓库各存粮多少吨?例4瓶内原有盐的重量是水的101,加进40克盐后,盐的重量占水的71,瓶内有盐水多少克?十堰市英才培训学校2008秋季六年级奥数精英B 班讲义例5 六(1)班的学生人数比六(2)班的75多3人,如果从六(2)班调两名学生到六(1)班,那么六(1)班的学生人数恰好是六(2)班的87,这两个班原来各有多少人? 三、课外练习 1、运一批水泥,第一天运了这批水泥的41,第二天运了第一天的53,已知第一天比第二天多运20吨,这批水泥有多少吨? 2、某工程对修一条公路,第一天修了全长的52,第二天修了余下部分的103又24米,第三天修的是第一天的43又60米,正好全部修完,这段公路全长多少米? 3、甲乙两个仓库共存粮840吨,已知甲仓存粮的41等于乙仓库存粮的31,问甲乙两个仓库各存粮多少吨?4、某工厂的甲、乙、丙三个车间向灾区捐款,甲车间捐款数是另外两个车间捐款数的32,乙车间捐款数是另外两个车间捐款数的53,已知丙车间捐款1800元,这三个车间共捐款多少元?。
六年级较难分数除法应用题转换单位1

人教版六年级分数除法应用题单位‘1’转化与统一题中若出现多个单位“1”;单位“1”有变化;或较复杂情况时,需要统一单位“1”才能解决问题。
把不同的数量当做单位“1”,得到得的分率可以在一定的条件下转化。
【常见不同单位“1”,分率转化及方法。
】(1) 某班级男生是女生的85,男生占全班人数的几分之几?女生比男生多几分之几?男生比女生少百分之几?(2) 甲比乙少54,甲是乙的几分之几?乙比甲多百分之几?(3) 甲的53等于乙的31,乙比甲是几比几?甲是乙的几分之几?(4) 甲是乙的43,乙是丙的52,甲是丙的?甲、乙、丙三者比为多少?(5) 一推煤,第一天用去72,第二天用去剩下的53,第二天运走的占全部的几分之几?占第一天的几分之几?(6) 某班男生占全班人数的52,男生转走4人后,这是男生占31,问: ① 转走前与转走后男生各占女生的几分之几? ② 转走后男生占原来总人数的几分之几? ③ 转走前总人数与转走后总人数之比是几比几?方法:找不变量,把不变量作单位1,先求其他量是不变量的几分之几,或先求其他量与不变量的比,再求解。
晶晶看完一本书,第一天看了全书的41,第二天看余下的52,第二天比第一天多看了22页,这本书一共有多少页?【题型2】一杯糖水,糖占糖水的10分之1,再加入10g 糖后,糖占水的9分之2,原来有糖水多少克?【题型3】在的田径队男生与女生各队少人?男生的数量是不变【题型4】甲、乙两个粮仓,原来甲粮食吨数是乙的78,现在从甲仓运15吨到乙仓库后,甲仓库粮食吨数是乙仓库的119,甲仓库原来有多少吨粮食?一批货物,第一天运走60吨,第二天运走剩下的31,这是运走的货物质量与没运走的货物质量比为5:4,这批货物一共有几吨?【题型6】一个车间有102人,男员工人数的43与女员工人数的32相等。
该车间男、女员工各有多少人?【题型7】有两支燃烧速度相同的蜡烛,长度之和为56cm ,将它们同时点燃一段时间后,长蜡烛剩余部分与段蜡烛点燃前一样长,且此时短蜡烛长度刚好是剩下长蜡烛的32,点燃前长蜡烛段蜡烛各有多长?1. 小红读一本故事书,第一天读了全书的52,第二天读了余下的41,还剩96页,该故事一共有几页?2. 一根绳子,第一次用去83,第二次用去余下的41,还剩下24m,原来这根绳子有多长?3. 小明三天看一本书,第一天看了全书的 41,第二天看了余下的 52,第二天比第一天多看了 21 页,这本书共多少页?【练习2】4. 有甲、乙两袋大米,如果从甲中拿出51给乙袋,那么两袋大米一样重,原来乙袋大米质量是甲袋的几分之几?若乙袋大米重50kg ,则甲袋重多少千克?5. 六年级(2)班原来的男生人数占总人数的52,后来转进8人后,男生人数占总人数的21,六(2)班原来有多少学生?6. 有一杯糖水,糖的质量占水的51,加入20g 糖后,糖的质量占水的72,这原来杯中的糖水有多少克?7. 某班男生人数占全班的40%,后来又转走10名女生,这时男生人数占全班的50%.这个班有男生多少人?8. 一杯糖水,糖的质量占糖水的101,再加入10g 糖后,这时糖的质量占糖水的112,原来糖水有多少克?【练习3】9. 胜利厂有职工850人,男职工人数的43等于女职工人数的32。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转化单位“1”(一)例题1、晶晶三天看完一本书,第一天看了全书的41,第二天看余下的52,第二天比第一天多看了15页,这本书共有多少页? 举一反三11.有一批货物,第一天运了这批货物的41,第二天运的是第一天的53,还剩90吨没有运,这批货物有多少吨?2.修路队在一条公路上施工。
第一天修了这条公路的41,第二天修了余下的32,已知这两天共修路1200米,这条公路全长多少米? 3.加工一批零件,甲先加工了这批零件的52,接着乙加工了余下的94。
已知乙加工的个数比甲少200个,这批零件共有多少个?例题2、假设2000年我国的国民生产总值为S ,并且以后每年都以8%的幅度递增。
那么,我国的国民生产总值最早在哪一年时可超过4S ? 举一反三21.在例题中,如果每年的增幅都比前一年提高一个百分点,那可以在哪一年,实现国民生产总值翻两倍(达到2S )?2.王先生1998年花3000元购得一种股票,这种股票平均每年可增值50%。
如果王先生一直持有这种股票,最早在哪一年这些股票的总价值会超过30000元?3.电子商场今年销售的某品牌笔记本电脑按台数统计,每月的销售量平均增长20%,今年12月销售了120台,按此速度下去,请你预计什么时候每月的销售量可以突破500台? 例题3、某工厂有三个车间,第一车间的人数占三个车间总人数的25%,第二车间人数是第三车间的43。
已知第一车间比第二车间少40人,三个车间一共有多少人? 举一反三31.某小学五年级三个班植树,一班植树的棵树占三个班总棵树的51,二班与三班植树棵树的比是3:5,二班比三班少植树40棵,这三个班各植树多少棵? 2.图书角有故事书、科技书、文艺书这三种书,故事书的本数占总数的52,科技书的本数是文艺书的43,文艺书比故事书少20本,图书角共有书多少本? 3.食堂买来萝卜、青菜和土豆三种蔬菜。
萝卜的重量占三种蔬菜总重量的52,青菜的重量比土豆少43,萝卜比土豆少360千克。
食堂买来萝卜多少千克? 例题4、牛的头数比羊的头数多25%,羊的头数比牛的头数少百分之几? 举一反三41. 甲仓存粮的吨数比乙仓少40%,乙仓存粮的吨数比甲仓多百分之几? 2.男生比女生少72,女生比男生多几分之几?3.水结成冰体积增加101,冰化成水体积减少几分之几? 例题5、乐乐服装公司进了一批儿童服装,按40%的利润定价,当售出这批服装的90%以后,决定换季减价售出,剩下的儿童服装全部按定价的五折出售,这批儿童服装全部售完后实际可获利百分之几? 举一反三51.甲、乙两种商品成本共200元,甲商品按30%的利润定价,乙商品按20%的利润定价,但出售时因商店“庆元旦大酬宾”,全部商品按定价的“九折”销售,结果卖出甲、乙两种商品各一可获利27.7元。
求甲、乙两种商品的成本各是多少元?2.兰兰把父母给她的压岁钱1500元存入银行。
银行的存款年利率为:三个月0.72%;半年1.7%;一年1.98%;两年2.25%;三年2.52%;五年2.79%。
利息税为20%,请你结合银行的人民币利率及实际情况帮兰兰设计一种存款方案。
如果兰兰五年期的1500元存款,再过3个月才到期,而现在又急用这笔钱,你觉得兰兰怎样做比较合算呢?3.某商店的一种皮衣,销售有一定困难,店老板核算一下:如果按销售价打九折出售,可盈利215元,如果打八折出售就要亏损125元,那么这种皮衣的进价是多少元? 转化单位“1”(二) 例题1、甲数是乙数的32,乙数是丙数的43,甲、乙、丙的和是216,甲、乙、丙各是多少? 举一反三1下面各题怎样计算简便就怎样计算: 1.甲数是乙数的65,乙数是丙数的43,甲、乙、丙三数的和是152,甲、乙、丙三个数各是多少?2.橘子的千克数是苹果的32,香蕉的千克数是橘子的21,香蕉和苹果共有220千克,橘子有多少千克?3.某中学初中部三个年级中,初一的学生数是初二学生数的109,初二学生是初三学生的411倍,这个学校里初三的学生数占初中部学生数的几分之几? 例题2、某班共有学生51人,男生人数的43等于女生人数的32。
这个班男、女生各有多少人?举一反三21.图书馆买来科技书和文艺书共340本,文艺书本数的31等于科技书本数的54。
两种书各买来多少本?2.学校合唱团比舞蹈队多24人,合唱团人数的52等于舞蹈队人数的76。
合唱团和舞蹈队各有多少人?3.粮店里有大米、面粉和玉米共900吨,大米重量的41等于面粉重量的31,玉米重200吨。
大米和面粉的重量各是多少吨? 例题3、已知甲校学生数是乙校学生数的52,甲校的女生数是甲校学生数的103,乙校的男生数是乙校学生数的5021,那么两校女生总数占两校学生总数的几分之几? 举一反三31.在一城市中,中学生数是居民的51,大学生数是中学生数的41,那么占大学生总数的52的理工科大学生是居民数的几分之几? 2.某人在一次选举中,需43的选票才能当选,计算32的选票后,他得到的选票已达到当选票数的65,他还要得到剩下选票的几分之几才能当选? 3.某校有53的学生是男生,男生的201想当医生,全校想当医生的学生的43是男生,那么全校女生的几分之几想当医生?例题4、甲、乙两堆棋子数相等,已知甲堆白子数是乙堆黑子数的51,乙堆白子数是甲堆黑子数的81。
甲堆黑子数是乙堆黑子数的几分之几? 举一反三41.甲乙两班的同学人数相等,各有一些同学参加课外天文小组,甲班参加天文小组的人数恰好是乙班没有参加的人数的31,乙班参加课外天文小组的人数是甲班没有参加的人数的41。
甲班没有参加的人数是乙班没有参加的人数的几分之几? 2.校合唱团和舞蹈队的人数相等,合唱团的男生人数是舞蹈队女生人数的32,舞蹈队男生人数是合唱团女生人数的149。
合唱团的女生人数是舞蹈队女生人数的几分之几? 3.有三堆棋子,每堆棋子一样多,并且都只有黑白两色棋子。
第一堆中的黑子和第二堆中的白子一样多,第三堆中的黑子占全部黑子的52。
把这三堆棋子集中在一起。
白子总数占全部棋子总数的几分之几?例题5、某厂男职工比全厂职工总人数的53多60人,女职工人数是男职工的31,这个厂共有职工多少人? 1.一筐苹果卖掉51后,又卖掉6千克,这时卖出的重量正好是剩下的21。
这筐苹果原来有多少千克?2.甲、乙两车共运一堆煤,运完时,甲车运了总数的157多12吨,比乙车多运21,甲车运了多少吨?3.纺织厂女工人数比全场人数的75%还多100人,男工人数是女工的51,这个纺织厂有男工多少人? 转化单位“1”(三)例题1、有两筐梨。
乙筐是甲筐的53,从甲筐取出5千克梨放入乙筐后,乙筐的梨是甲筐的97。
甲、乙两筐梨共重多少千克? 举一反三11.某小学低年级原有少先队员是非少先队员的31,后来又有39名同学加入了少先队组织。
这样,少先队员的人数是非少先队员的87。
低年级有学生多少人? 2.王师傅生产一批零件,不合格产品是合格产品的191,后来从合格产品中又发现2个不合格产品,这时算出产品合格率是94%。
合格产品共有多少个?3.某校六年级上学期男生占总人数的54%,本学期初转进3名女生,转走3名男生,这时女生占总人数的48%。
现有男生多少人?例题2、某学校原有长跳绳的根数占长、短跳绳总数的83。
后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的127。
这个学校现有长、短跳绳的总数是多少根? 举一反三21.阅览室看书的同学中,女同学占53,从阅览室走出5位女同学后,看书的同学中,女同学占74,原来阅览室里一共有多少名同学在看书? 2.一堆什锦糖,其中奶糖占45%,再放入16千克其他糖后,奶糖只占25%,这堆糖中有奶糖多少千克?3.数学课外兴趣小组,上学期男生占95,这学期增加21名女生后,男生就只占52了,这个小组现有女生多少人?例题3、有两块布,一段布长40米,另一段布长30米,把两段布都用去同样长的一部分后,发现短的一段布剩下的长度是长的一段布所剩长度的53,每段布用去多少米? 举一反三31.有两根塑料绳,一段长80米,另一根长40米,如果从两根绳上各剪去同样长的一段后,短绳剩下的长度是长绳剩下的72,两根绳各剪去多少米? 2.今年父亲40岁,儿子12岁,当儿子的年龄是父亲的125时,儿子多少岁?3.仓库里原来存的大米和面粉袋数相等,运出800袋大米和500袋面粉后,仓库里所剩的大米袋数是面粉的43,仓库里原有大米和面粉各多少袋? 4.甲、乙、丙、丁四个建筑队共筑1200米长的一段公路,甲队筑的路是其他三个队的21,乙队筑的路是其他三个队的31,丙队筑的路是其他三个队的41,丁队筑了多少米?例题4、某商店有黑白彩色电视机共630台,其中黑白电视机占甲队筑的路是其他三个队的51,后来又运进一些黑白电视机。
这时黑白电视机占两种电视机总台数的30%。
问:又运进黑白电视机多少台? 举一反三41.书店运来科技书和文艺书共240包,科技书占61,后来又运来一批科技书,这时科技书占两种书总和的113,现在两种书各有多少包? 2.某市派出60名选手参加田径比赛,其中女选手占41,正式比赛时,有几名女选手因故缺席,这样女选手人数占参赛选手总数的112。
问:正是参赛的女选手有多少人? 3.把12千克盐溶解于120千克水中,得到132千克盐水,如果要使盐水中含盐8%,要往盐水中加盐还是加水?加多少千克?4.东风水果店上午运进梨和苹果共1020千克,其中梨占水果总数的51;下午又运进梨若干千克,这时梨占两种水果总数的52,下午运进梨多少千克? 例题5、甲数是乙数、丙数、丁数之和的21,乙数是甲数、丙数、丁数之和的31,丙数是甲数、乙数、丁数之和的41。
如果丁数是260,求甲、乙、丙、丁四数之和。
举一反三51.甲、乙、丙、丁四个建筑队共筑1200米长的一段公路,甲队筑的路是其他三个队的21,乙队筑的路是其他三个队的31,丙队筑的路是其他三个队的41,丁队筑了多少米? 2.甲、乙、丙三人共同购买一艘游艇,甲支付的钱是其余两人的21,乙支付的钱是其余两人的31,丙支付的钱恰好是5000元。
这艘游艇的单价是多少元?3.学校里买回四种图书,科技书是文艺书的43,连环画是其余三种书的31,史地书是其余三种书的41,史地书比文艺书少80本,买回的两种书共多少本?。
