第二部分专题三第二讲
2022年高考英语二轮专题复习专题三完形填空 第二讲多法并举、瞻前顾后, 稳取句内、句组、语篇层次题

第二讲多法并举、瞻前顾后,稳取句内、句组、语篇层次题一、5 大方法速判句内层次题句内层次题的解题信息分布在本句内,在读懂文意的前提下,利用本句的一些信息凭借语感即可顺利选出答案。
对于此类题目,考生可以边读边填,将原文信息尽量复原。
方法1 利用习惯搭配和固定结构解题[典例][2020·全国卷Ⅱ]It was just after sunrise on a June morning. “Nicolo,” whosereal name cannot be __41__ to the public because of Italy's privacy laws, 42.finished working the whole night at a factory in Turin.41.A.attached B.allocatedC.exposed D.submitted分析:本题可以利用习惯搭配解题。
根据下文的“because of Italy's privacy laws”可知主人公的真名是隐私的、不可透露的。
由此可知正确选项。
自主解答:________方法2 利用生活常识和文化背景解题完形填空的语篇中往往渗透着诸如文化科学、历史地理、风俗民情等方面的知识。
考生在做题时,若能积极地调动自己掌握的文化背景知识和生活常识,巧妙地加以运用,特别是注意中西文化的差异,将会大大简化复杂的分析与判断过程,节省宝贵的时间,从而轻松地做出正确判断。
[典例][2021·全国卷乙]And there you have it. To many people, __59__ lives is part of thejob but styling hair is an extra and should be rewarded.59.A.risking B.changingC.saving D.building分析:第59题考查语境和常识推断。
届数学二轮复习第二部分专题篇素养提升文理专题一三角函数三角恒等变换与解三角形第2讲三角恒等变换与解三

第2讲三角恒等变换与解三角形(文理)JIE TI CE LUE MING FANG XIANG解题策略·明方向⊙︱考情分析︱1.三角恒等变换是高考的热点内容,主要考查利用各种三角函数公式进行求值与化简,其中二倍角公式、辅助角公式是考查的重点,切化弦、角的变换是常考的内容.2.正弦定理、余弦定理以及解三角形问题是高考的必考内容,主要考查:(1)边、角、面积的计算;(2)有关边、角的范围问题;(3)实际应用问题.⊙︱真题分布︱(理科)年份卷别题号考查角度分值202 0Ⅰ卷9、16三角恒等变换和同角间的三角函数关系求值;利用余弦定理解三角形10Ⅱ卷17解三角形求角和周长的12(文科)KAO DIAN FEN LEI XI ZHONG DIAN考点分类·析重点考点一三角恒等变换错误!错误!错误!错误!三角恒等变换与求值1.两角和与差的正弦、余弦、正切公式(1)sin(α±β)=sin αcos β±cos αsin β。
(2)cos(α±β)=cos αcos β∓sin αsin β。
(3)tan(α±β)=错误!。
2.二倍角的正弦、余弦、正切公式(1)sin 2α=2sin αcos α。
(2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.(3)tan 2α=错误!.3.辅助角公式a sin x+b cos x=错误!sin(x+φ)(其中tan φ=错误!)典错误!错误!错误!典例1(1)(2020·全国Ⅱ卷模拟)cos2 40°+2sin 35°sin 55°sin 10°=(A)A.错误!B.错误!C.错误!+错误!D.错误!(2)(2020·宜宾模拟)已知α∈错误!,且3sin2α-5cos2α+sin 2α=0,则sin 2α+cos 2α=(A)A.1B.-错误!C.-错误!或1D.-1(3)已知函数f(x)=错误!cos x cos错误!+sin2错误!-错误!.①求f(x)的单调递增区间;②若x∈错误!,f(x)=错误!,求cos 2x的值.【解析】(1)原式=cos240°+2sin 35°cos 35°sin 10°=cos240°+sin 70°sin 10°=12+12cos 80°+sin 70°sin 10°=错误!+错误!(cos 70°cos 10°-sin 70°sin 10°+2sin 70°sin 10°)=错误!+错误!(cos 70°cos 10°+sin 70°sin 10°)=错误!+错误!cos 60°=34。
高考数学(文)(新课标版)考前冲刺复习讲义:第2部分专题三第2讲 数列求和及其综合应用 Word版含答案

第2讲数列求和及其综合应用错位相减法求和[学生用书P34]共研典例类题通法错位相减法适用于由一个等差数列和一个等比数列对应项的乘积构成的数列的求和,其依据是:c n =a n b n ,其中{a n }是公差为d 的等差数列,{b n }是公比为q (q ≠1)的等比数列,则qc n =qa n b n =a n b n +1,此时c n +1-qc n =(a n +1-a n )·b n +1=db n +1,这样就把对应相减的项变成了一个等比数列,从而达到求和的目的.(2016·高考山东卷)已知数列{a n }的前n 项和S n =3n 2+8n ,{b n }是等差数列,且a n=b n +b n +1.(1)求数列{b n }的通项公式;(2)令c n =(a n +1)n +1(b n +2)n.求数列{c n }的前n 项和T n .【解】(1)由题意知当n ≥2时,a n =S n -S n -1=6n +5, 当n =1时,a 1=S 1=11,符合上式.所以a n =6n +5. 设数列{b n }的公差为d ,由⎩⎪⎨⎪⎧a 1=b 1+b 2,a 2=b 2+b 3,得⎩⎪⎨⎪⎧11=2b 1+d ,17=2b 1+3d ,可解得b 1=4,d =3. 所以b n =3n +1.(2)由(1)知c n =(6n +6)n +1(3n +3)n=3(n +1)·2n +1. 又T n =c 1+c 2+…+c n ,所以T n =3×[2×22+3×23+…+(n +1)×2n +1], 2T n =3×[2×23+3×24+…+(n +1)×2n +2],两式作差,得-T n =3×[2×22+23+24+ (2)+1-(n +1)×2n +2]=3×⎣⎢⎡⎦⎥⎤4+4(1-2n )1-2-(n +1)×2n +2=-3n ·2n +2, 所以T n =3n ·2n +2.应用错位相减法求和需注意的问题(1)错位相减法适用于求数列{a n ·b n }的前n 项和,其中{a n }为等差数列,{b n }为等比数列.(2)所谓“错位”,就是要找“同类项”相减.要注意的是相减后所得部分,求等比数列的和,此时一定要查清其项数.(3)为保证结果正确,可对得到的和取n =1,2进行验证. [跟踪训练](2016·兰州模拟)等差数列{a n }中,已知a n >0,a 1+a 2+a 3=15,且a 1+2,a 2+5,a 3+13构成等比数列{b n }的前三项.(1)求数列{a n },{b n }的通项公式; (2)求数列{a n ·b n }的前n 项和T n .[解] (1)设等差数列{a n }的公差为d ,则由已知得: a 1+a 2+a 3=3a 2=15,即a 2=5. 又(5-d +2)(5+d +13)=100, 解得d =2或d =-13(舍去),所以a 1=a 2-d =3,a n =a 1+(n -1)×d =2n +1. 又b 1=a 1+2=5,b 2=a 2+5=10,所以公比q =2, 所以b n =5×2n -1.(2)因为T n =5[3+5×2+7×22+…+(2n +1)×2n -1], 2T n =5[3×2+5×22+7×23+…+(2n +1)×2n ],两式相减得-T n =5[3+2×2+2×22+…+2×2n -1-(2n +1)×2n ]=5[(1-2n )2n -1], 则T n =5[(2n -1)2n +1].裂项相消法求和[学生用书P35]共研典例类题通法 1.常见的裂项类型 (1)1n (n +1)=1n -1n +1; (2)1n (n +k )=1k ⎝⎛⎭⎫1n -1n +k ;(3)1n 2-1=12⎝⎛⎭⎫1n -1-1n +1;(4)14n 2-1=12⎝⎛⎭⎫12n -1-12n +1;(5)n +1n (n -1)·2n =2n -(n -1)n (n -1)·2n =1(n -1)2n -1-1n ·2n. 2.裂项相消法求和的基本思想是把数列的通项公式a n 分拆成a n =b n +k -b n (k ≥1,k ∈N *)的形式,从而达到在求和时某些项相消的目的,在解题时要善于根据这个基本思想变换数列{a n }的通项公式,使之符合裂项相消的条件.(2016·海口调研测试)在等差数列{a n }中,公差d ≠0,a 1=7,且a 2,a 5,a 10成等比数列.(1)求数列{a n }的通项公式及其前n 项和S n ; (2)若b n =5a n ·a n +1,求数列{b n }的前n 项和T n .【解】(1)因为a 2,a 5,a 10成等比数列, 所以(7+d )(7+9d )=(7+4d )2, 又因为d ≠0,所以d =2,所以a n =2n +5,S n =(7+2n +5)n 2=n 2+6n .(2)由(1)可得b n =5(2n +5)(2n +7)=52⎝ ⎛⎭⎪⎫12n +5-12n +7, 所以T n =52⎝ ⎛⎭⎪⎫17-19+19-111+…+12n +5-12n +7=5n14n +49.裂项相消法的技巧在裂项时要注意把数列的通项分拆成的两项一定是某个数列中的相邻的两项,或者是等距离间隔的两项,只有这样才能实现逐项相消,只剩余有限的几项,从而求出其和.[跟踪训练](2016·石家庄模拟)已知等差数列{a n }中,2a 2+a 3+a 5=20,且前10项和S 10=100.(1)求数列{a n }的通项公式;(2)若b n =1a n a n +1,求数列{b n }的前n 项和.[解] (1)由已知得⎩⎪⎨⎪⎧2a 2+a 3+a 5=4a 1+8d =20,10a 1+10×92d =10a 1+45d =100, 解得⎩⎪⎨⎪⎧a 1=1,d =2.所以{a n }的通项公式为a n =1+2(n -1)=2n -1.(2)由(1)知,b n =1(2n -1)(2n +1)=12×⎝ ⎛⎭⎪⎫12n -1-12n +1,所以数列{b n }的前n 项和T n =12×⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫11-13+⎝⎛⎭⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1 =12×⎝ ⎛⎭⎪⎫1-12n +1=n 2n +1.分组转化求和[学生用书P35]共研典例类题通法 分组转化求和的三种类型分组转化求和是把数列之和分为几组,每组中的各项是可以利用公式(或其他方法)求和的,求出各组之和即得整体之和,这类试题一般有如下三种类型:(1)数列是周期数列,先求出每个周期内的各项之和,然后把整体之和按照周期进行划分,再得出整体之和;(2)奇偶项分别有相同的特征的数列(如奇数项组成等差数列、偶数项组成等比数列),按照奇数项和偶数项分组求和;(3)通项中含有(-1)n 的数列,按照奇数项、偶数项分组,或者按照n 为奇数、偶数分类求和.(2016·呼和浩特模拟)在数列{a n }中,a 1=3,a n =2a n -1+(n -2)(n ≥2,n ∈N *). (1)证明:数列{a n +n }是等比数列,并求{a n }的通项公式; (2)求数列{a n }的前n 项和S n .【解】(1)因为a n +n =2[a n -1+(n -1)],a n +n ≠0, 所以{a n +n }是首项为4,公比为2的等比数列,所以a n +n =4×2n -1=2n +1. 所以a n =2n +1-n .(2)S n =(22+23+24+…+2n +1)-(1+2+3+…+n )=2n +2-n 2+n +82.分组求和的常见方法 (1)根据等差、等比数列分组. (2)根据正号、负号分组.(3)根据数列的周期性分组.[题组通关]1.已知数列{a n }的通项公式是a n =(-1)n -1(n +1),则a 1+a 2+a 3+…+a 2017=( )A .1009B .1010C .-1009D .-1010B [解析] 因为a n =(-1)n -1(n +1),所以a 1+a 2+a 3+…+a 2017=(2-3)+(4-5)+…+(2016-2017)+2018=1008×(-1)+2018=1010.2.设数列{a n }的前n 项和为S n (n ∈N *),数列{a 2n -1}是首项为1的等差数列,数列{a 2n }是首项为2的等比数列,且满足S 3=a 4,a 3+a 5=a 4+2.(1)求数列{a n }的通项公式; (2)求S 2n .[解] (1)设等差数列的公差为d ,等比数列的公比为q ,则a 1=1,a 2=2,a 3=1+d ,a 4=2q ,a 5=1+2d ,所以⎩⎪⎨⎪⎧4+d =2q ,(1+d )+(1+2d )=2+2q ,解得d =2,q =3.所以a n =⎩⎪⎨⎪⎧n ,n =2k -1,2·3n 2-1,n =2k ,(k ∈N *).(2)S 2n =(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n )=(1+3+5+…+2n -1)+(2×30+2×31+…+2×3n -1) =(1+2n -1)n 2+2(1-3n )1-3=n 2-1+3n .等差、等比数列的综合问题[学生用书P36]共研典例类题通法解决等差数列、等比数列的综合问题,要从两个数列的特征入手,理清它们的关系;数列与不等式、函数、方程的交汇问题,可以结合数列的单调性、最值求解.已知数列{a n }满足a 1=12,a n +1a n +1-1-1a n -1=0,n ∈N *.(1)求数列{a n }的通项公式;(2)设b n =a n +1a n -1,数列{b n }的前n 项和为S n ,证明:S n <34.【解】(1)由已知a n +1a n +1-1-1a n -1=0,n ∈N *,得(a n +1-1)+1a n +1-1-1a n -1=0,即1+1a n +1-1-1a n -1=0,亦即1a n +1-1-1a n -1=-1(常数).所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n -1是以1a 1-1=-2为首项, -1为公差的等差数列.可得1a n -1=-2+(n -1)×(-1)=-(n +1),所以a n =nn +1.(2)证明:因为b n =a n +1a n -1=(n +1)2n (n +2)-1=1n (n +2)=12⎝⎛⎭⎪⎫1n -1n +2,所以S n =b 1+b 2+…+b n=12⎝⎛⎭⎫1-13+12⎝⎛⎭⎫12-14+12⎝⎛⎭⎫13-15+…+12⎝ ⎛⎭⎪⎫1n -1-1n +1+12⎝ ⎛⎭⎪⎫1n -1n +2 =12⎝ ⎛⎭⎪⎫1+12-1n +1-1n +2<12×⎝⎛⎭⎫1+12=34.解决数列综合问题的方法(1)等差数列与等比数列交汇的问题,常用“基本量法”求解,但有时灵活地运用性质,可使运算简便.(2)数列的项或前n 项和可以看作关于n 的函数,然后利用函数的性质求解数列问题.(3)数列中的恒成立问题可以通过分离参数,通过求数列的值域求解. [跟踪训练](2016·武汉模拟)已知S n 是公差不为0的等差数列{a n }的前n 项和,S 1,S 2,S 4成等比数列,且a 3=-52.(1)求数列{a n }的通项公式;(2)设b n =1(2n +1)a n ,求数列{b n }的前n 项和T n .[解] (1)设{a n }的公差为d (d ≠0), 因为S 1,S 2,S 4成等比数列,所以S 22=S 1S 4,即(2a 1+d )2=a 1(4a 1+6d ),化简得d 2=2a 1d .因为d ≠0,所以d =2a 1.① 因为a 3=-52,所以a 1+2d =-52.②联立①②,解得⎩⎪⎨⎪⎧a 1=-12d =-1,所以a n =-12+(n -1)×(-1)=-n +12.(2)因为b n =1(2n +1)a n =1(2n +1)⎝⎛⎭⎫-n +12=-2(2n +1)(2n -1)=12n +1-12n -1,所以T n =⎝⎛⎭⎫13-1+⎝⎛⎭⎫15-13+⎝⎛⎭⎫17-15+…+⎝ ⎛⎭⎪⎫12n +1-12n -1=-1+12n +1=-2n 2n +1. 课时作业[学生用书P120(独立成册)]1.设各项均为正数的等差数列{a n }的前n 项和为S n ,且a 4a 8=32,则S 11的最小值为( ) A .22 2B .442C .22D .44B [解析] 因为数列{a n }为各项均为正数的等差数列,所以a 4+a 8≥2a 4a 8=82,S 11=(a 1+a 11)×112=112(a 4+a 8)≥112×82=442,故S 11的最小值为442,当且仅当a 4=a 8=42时取等号.2.已知在数列{a n }中,a 1=-60,a n +1=a n +3,则|a 1|+|a 2|+|a 3|+…+|a 30|等于( ) A .445 B .765 C .1080D .3105B [解析] 因为a n +1=a n +3,所以a n +1-a n =3. 所以{a n }是以-60为首项,3为公差的等差数列. 所以a n =-60+3(n -1)=3n -63. 令a n ≤0,得n ≤21. 所以前20项都为负值. 所以|a 1|+|a 2|+|a 3|+…+|a 30| =-(a 1+a 2+…+a 20)+a 21+…+a 30 =-2S 20+S 30.因为S n =a 1+a n 2n =-123+3n 2×n ,所以|a 1|+|a 2|+|a 3|+…+|a 30|=765.3.已知数列{a n }满足a 1=1,a 2=3,a n +1a n -1=a n (n ≥2),则数列{a n }的前40项和S 40等于( )A .20B .40C .60D .80C [解析] 由a n +1=a na n -1(n ≥2),a 1=1,a 2=3,可得a 3=3,a 4=1,a 5=13,a 6=13,a 7=1,a 8=3,…,这是一个周期为6的数列,一个周期内的6项之和为263,又40=6×6+4,所以S 40=6×263+1+3+3+1=60.4.(2016·郑州模拟)设等比数列{a n }的各项均为正数,且a 1=12,a 24=4a 2a 8,若1b n=log 2a 1+log 2a 2+…+log 2a n ,则数列{b n }的前10项和为( )A .-2011B.2011C .-95D.95A [解析] 设等比数列{a n }的公比为q ,因为a 24=4a 2a 8,所以(a 1q 3)2=4a 1q ·a 1q 7,即4q 2=1,所以q =12或q =-12(舍),所以a n =⎝⎛⎭⎫12n =2-n ,所以log 2a n =log 22-n =-n ,所以1b n =-(1+2+3+…+n )=-n (1+n )2,所以b n =-2n (1+n )=-2⎝ ⎛⎭⎪⎫1n -1n +1,所以数列{b n }的前10项和为-2⎣⎡⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13⎦⎤+…+⎝⎛⎭⎫110-111=-2·⎝⎛⎭⎫1-111=-2011. 5.设b n =a n (a n +1)(a n +1+1)(其中a n =2n -1),数列{b n }的前n 项和为T n ,则T 5=( )A.3133B.3233C.3166D.1633C [解析] 由题意得,b n =2n -1(2n -1+1)(2n +1)=12n -1+1-12n +1,所以T n =⎝ ⎛⎭⎪⎫120+1-121+1+⎝ ⎛⎭⎪⎫121+1-122+1+…+ ⎝ ⎛⎭⎪⎫12n -1+1-12n +1=12-12n +1,所以T 5=12-133=3166.6.已知f (x ),g (x )都是定义在R 上的函数,g (x )≠0,f ′(x )g (x )>f (x )g ′(x ),且f (x )=a x g (x )(a>0,且a ≠1),f (1)g (1)+f (-1)g (-1)=52.若数列⎩⎨⎧⎭⎬⎫f (n )g (n )的前n 项和大于62,则n 的最小值为( )A .8B .7C .6D .9C [解析] 由⎣⎢⎡⎦⎥⎤f (x )g (x )′=f ′(x )g (x )-f (x )g ′(x )g 2(x )>0,知f (x )g (x )在R 上是增函数,即f (x )g (x )=a x 为增函数,所以a >1.又因为a +1a =52,所以a =2或a =12(舍).数列⎩⎨⎧⎭⎬⎫f (n )g (n )的前n 项和S n =21+22+…+2n =2(1-2n)1-2=2n +1-2>62.即2n >32,所以n >5.7.(2016·海口调研测试)设数列{a n }的前n 项和为S n ,且a 1=1,a n +a n +1=12n (n =1,2,3,…),则S 2n +3=________.[解析] 依题意得S 2n +3=a 1+(a 2+a 3)+(a 4+a 5)+…+(a 2n +2+a 2n +3)=1+14+116+…+14n +1=1-14n +21-14=43⎝ ⎛⎭⎪⎫1-14n +2. [答案]43⎝⎛⎭⎫1-14n +28.若等比数列的各项均为正数,前4项的和为9,积为814,则前4项倒数的和为________.[解析] 设等比数列的首项为a 1,公比为q ,则第2,3,4项分别为a 1q ,a 1q 2,a 1q 3,依题意得a 1+a 1q +a 1q 2+a 1q 3=9,a 1·a 1q ·a 1q 2·a 1q 3=814⇒a 21q 3=92,两式相除得a 1+a 1q +a 1q 2+a 1q 3a 21q 3=1a 1+1a 1q +1a 1q 2+1a 1q3=2. [答案]29.数列{a n }满足a n +a n +1=12(n ∈N *),a 2=2,S n 是数列{a n }的前n 项和,则S 2017=________.[解析] 因为a n +a n +1=12(n ∈N *),所以a 1=12-a 2=12-2,a 2=2,a 3=12-2,a 4=2,…,故a 2n =2,a 2n -1=12-2,所以S 2017=1009a 1+1008a 2=1009×⎝⎛⎭⎫12-2+1008×2=10052. [答案]1005210.已知数列{a n }中,a 1=1,a 2=2,设S n 为数列{a n }的前n 项和,对于任意的n >1,n ∈N *,S n +1+S n -1=2(S n +1)都成立,则S 10=________.[解析]因为⎩⎪⎨⎪⎧S n +1+S n -1=2S n +2,S n +2+S n =2S n +1+2,所以a n +2+a n =2a n +1,所以数列{a n }从第二项开始为等差数列,当n =2时,S 3+S 1=2S 2+2,所以a 3=a 2+2=4,所以S 10=1+2+4+6+…+18=1+9(2+18)2=91. [答案]9111.(2016·东北四市联考)已知数列{a n }满足a 1=511,a 6=-12,且数列{a n }的每一项加上1后成为等比数列.(1)求a n ;(2)令b n =|log 2(a n +1)|,求数列{b n }的前n 项和T n .[解] (1)由题意数列{a n +1}是等比数列,设公比为q ,a 1+1=512,a 6+1=12=512×q 5, 解得q =14. 则数列{a n +1}是以512为首项,14为公比的等比数列, 所以a n +1=211-2n ,a n =211-2n -1.(2)由(1)知b n =|11-2n |,当n ≤5时,T n =10n -n 2,当n ≥6时,T n =n 2-10n +50,所以T n =⎩⎪⎨⎪⎧10n -n 2,n ≤5n 2-10n +50,n ≥6. 12.(2016·哈尔滨模拟)已知数列{a n }是等比数列,a 2=4,a 3+2是a 2和a 4的等差中项.(1)求数列{a n }的通项公式;(2)设b n =2log 2a n -1,求数列{a n b n }的前n 项和T n .[解] (1)设数列{a n }的公比为q ,因为a 2=4,所以a 3=4q ,a 4=4q 2.因为a 3+2是a 2和a 4的等差中项,所以2(a 3+2)=a 2+a 4.即2(4q +2)=4+4q 2,化简得q 2-2q =0.因为公比q ≠0,所以q =2.所以a n =a 2q n -2=4×2n -2=2n (n ∈N *).(2)因为a n =2n ,所以b n =2log 2a n -1=2n -1,所以a n b n =(2n -1)2n ,则T n =1×2+3×22+5×23+…+(2n -3)2n -1+(2n -1)2n ,①2T n =1×22+3×23+5×24+…+(2n -3)2n +(2n -1)·2n +1,②由①-②得,-T n =2+2×22+2×23+…+2×2n -(2n -1)2n +1=2+2×4(1-2n -1)1-2-(2n -1)2n +1 =-6-(2n -3)2n +1,所以T n =6+(2n -3)2n +1.13.数列{a n }满足a n +1=a n 2a n +1,a 1=1. (1)证明:数列⎩⎨⎧⎭⎬⎫1a n 是等差数列; (2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n ,并证明1S 1+1S 2+…+1S n >n n +1. [解] (1)证明:因为a n +1=a n 2a n +1,所以1a n +1=2a n +1a n ,化简得1a n +1=2+1a n , 即1a n +1-1a n =2,故数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项,2为公差的等差数列. (2)由(1)知1a n =2n -1,所以S n =n (1+2n -1)2=n 2. 1S 1+1S 2+…+1S n =112+122+…+1n 2>11×2+12×3+…+1n (n +1)=⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=1-1n +1=n n +1. 14.(选做题)已知函数f (x )=2sin(ωx +φ)(ω>0,|φ|<π)的图象经过点⎝⎛⎭⎫π12,-2,⎝⎛⎭⎫7π12,2,且在区间⎝⎛⎭⎫π12,7π12上为单调函数. (1)求ω,φ的值;(2)设a n =nf ⎝⎛⎭⎫n π3(n ∈N *),求数列{a n }的前30项和S 30. [解] (1)由题可得ωπ12+φ=2k π-π2,k ∈Z ,7ωπ12+φ=2k π+π2,k ∈Z , 解得ω=2,φ=2k π-2π3,k ∈Z , 因为|φ|<π,所以φ=-2π3. (2)因为a n =2n sin ⎝ ⎛⎭⎪⎫2n π3-2π3(n ∈N *),数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫2sin ⎝ ⎛⎭⎪⎫2n π3-2π3(n ∈N *)的周期为3,前三项依次为0,3,-3,所以a 3n -2+a 3n -1+a 3n =(3n -2)×0+(3n -1)×3+3n ×(-3)=-3(n ∈N *), 所以S 30=(a 1+a 2+a 3)+…+(a 28+a 29+a 30)=-10 3.。
专题三 第二讲 数列的综合应用

一、选择题1.(2011·安徽高考)若数列{a n }的通项公式是a n =(-1)n ·(3n -2),则a 1+a 2+…+a 10=( )A .15B .12C .-12D .-15解析:a 1+a 2+…+a 10=-1+4-7+10+…+(-1)10·(3×10-2)=(-1+4)+(-7+10)+…+[(-1)9·(3×9-2)+(-1)10·(3×10-2)]=3×5=15.答案:A2.向量v =(a n +1-a n 2,a 2n +12a n),v 是直线y =x 的方向向量,a 1=5,则数列{a n }的前10项和为( )A .50B .100C .150D .200解析:依题意得a 2n +12a n =a n +1-a n 2,化简得a n +1=a n .又a 1=5,所以a n =5,数列{a n }的前10项和为5×10=50.答案:A3.等差数列{a n }中,a 1>0,公差d <0,S n 为其前n 项和,对任意自然数n ,若点(n ,S n )在以下4条曲线中的某一条上,则这条曲线应是( )解析:∵S n =na 1+n (n -1)2d ,∴S n =d 2n 2+(a 1-d 2)n ,又a 1>0,公差d <0,所以点(n ,S n )所在抛物线开口向下,对称轴在y 轴右侧.答案:C4.已知函数f (x )=⎩⎪⎨⎪⎧(1-3a )x +10a ,x ≤6,a x -7, x >6.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递减数列,则实数a 的取值范围是( )A.⎝⎛⎭⎫13,1B.⎝⎛⎭⎫13,12C.⎝⎛⎭⎫13,58D.⎝⎛⎭⎫58,1解析:∵f (n )=⎩⎪⎨⎪⎧(1-3a )n +10a ,n ≤6,a n -7, n >6是递减数列, ∴⎩⎪⎨⎪⎧ 1-3a <0,0<a <1,f (6)>f (7),即⎩⎪⎨⎪⎧ 1-3a <0,0<a <1,6-8a >1,解得13<a <58. 答案:C二、填空题 5.(2011·北京高考)在等比数列{a n }中,若a 1=12,a 4=-4,则公比q =____________;|a 1|+|a 2|+…+|a n |=____________.解析:设等比数列{a n }的公比为q ,则a 4=a 1q 3,代入数据解得q 3=-8,所以q =-2;等比数列{|a n |}的公比为|q |=2,则|a n |= 12×2n -1,所以|a 1|+|a 2|+|a 3|+…+|a n |=12(1+2+22+…+2n -1) =12(2n -1)=2n -1-12. 答案:-2 2n -1-126.设曲线y =x n +1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ,x n =________,令a n =lg x n ,则a 1+a 2+…+a 99的值为________.解析:∵y =x n +1, ∴y ′=(n +1)x n ,它在点(1,1)处的切线方程为y -1=(n +1)(x -1),它与x 轴交点的横坐标为x n =1-1n +1=n n +1. 由a n =lg x n ,得a n =lg n -lg(n +1),于是a 1+a 2+…+a 99=lg1-lg2+lg2-lg3+…+lg99-lg100=lg1-lg100=0-2=-2. 答案:n n +1-2 7.(2011·陕西高考)植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边.使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为________(米).解析:当放在最左侧坑时,路程和为2×(0+10+20+…+190);当放在左侧第2个坑时,路程和为2×(10+0+10+20+…+180)(减少了360米);当放在左侧第3个坑时,路程和为2×(20+10+0+10+20+…+170)(减少了680米);依次进行,显然当放在中间的第10、11个坑时,路程和最小,为2×(90+80+…+0+10+20+…+100)=2 000米.答案:2 000三、解答题8.已知二次函数f (x )=x 2-2(10-3n )x +9n 2-61n +100(n ∈N *).(1)设函数y =f (x )的图像的顶点的横坐标构成数列{a n },求证:数列{a n }是等差数列;(2)在(1)的条件下,若数列{c n }满足c n =1+14n -252+a n (n ∈N *),求数列{c n }中最大的项和最小的项.解:(1)证明:y =f (x )的图像的顶点的横坐标为x =-b 2a =--2(10-3n )2=10-3n ,∴a n =10-3n ,∴a n -a n -1=-3.∴{a n }是等差数列.(2)∵c n =1+14n -252+a n =1+14n -252+10-3n =1+22n -5, 当n ≤2时,22n -5<0,且c 1>c 2, 当n ≥3时,22n -5>0且c n >c n +1. ∴{c n }中最小的项为c 2=-1,最大的项为c 3=3.9.(2011·北京海淀)数列{a n }的前n 项和为S n ,若a 1=2,且S n =S n -1+2n (n ≥2,n ∈N *).(1)求S n ;(2)是否存在等比数列{b n }满足b 1=a 1,b 2=a 3,b 3=a 9?若存在,则求出数列{b n }的通项公式;若不存在,则说明理由.解:(1)因为S n =S n -1+2n ,所以有S n -S n -1=2n 对n ≥2,n ∈N *成立.即a n =2n 对n ≥2成立.又a 1=S 1=2×1,所以a n =2n 对n ∈N *成立.所以a n +1-a n =2对n ∈N *成立.所以{a n }是等差数列. 所以S n =a 1+a n 2·n =n 2+n ,n ∈N *. (2)存在.由(1)知a n =2n 对n ∈N *成立,则a 3=6,a 9=18.又a 1=2,所以由b 1=a 1,b 2=a 3,b 3=a 9,得b 2b 1=b 3b 2=3.即存在以b1=2为首项,公比为3的等比数列{b n},其通项公式为b n=2·3n-1.10.已知数列{a n}满足a1=1,a2=4,a n+2+2a n=3a n+1(n∈N*).(1)求数列{a n}的通项公式;(2)记数列{a n}的前n项和S n,求使得S n>21-2n成立的最小整数n.解:(1)由a n+2+2a n-3a n+1=0得a n+2-a n+1=2(a n+1-a n),∴数列{a n+1-a n}是以a2-a1=3为首项,公比为2的等比数列.∴a n+1-a n=3·2n-1,∴n≥2时,a n-a n-1=3·2n-2,…,a3-a2=3·2,a2-a1=3,累加得a n-a1=3·2n-2+…+3·2+3=3(2n-1-1),∴a n=3·2n-1-2(当n=1时,也满足).(2)由(1)利用分组求和法得S n=3(2n-1+2n-2+…+2+1)-2n=3(2n-1)-2n,S n=3(2n-1)-2n>21-2n得3·2n>24,即2n>8=23,∴n>3,∴使得S n>21-2n成立的最小整数n=4.。
二轮复习专题三第二讲带电粒子在电场磁场中的运动学案

专题三第二讲 带电粒子在电场、磁场中的运动1.(2020·浙江7月选考)如图所示,一质量为m 、电荷量为q (q >0)的粒子以速度v 0从MN 连线上的P 点水平向右射入大小为E 、方向竖直向下的匀强电场中。
已知MN 与水平方向成45°角,粒子的重力可以忽略,则粒子到达MN 连线上的某点时( )A .所用时间为m v 0qEB .速度大小为3v 0C .与P 点的距离为22m v 02qED .速度方向与竖直方向的夹角为30°解析:C 粒子从P 点垂直电场方向出发到达MN 连线上某点时,由几何知识得沿水平方向和竖直方向的位移大小相等,即v 0t =12at 2,其中a =Eq m ,联立解得t =2m v 0qE ,A 项错误;粒子在MN 连线上某点时,粒子沿电场方向的速度v =at =2v 0,所以合速度大小v =(2v 0)2+v 02=5v 0,B 项错误;该点到P 点的距离s =2x =2v 0t =22m v 02qE ,C 项正确;由平行四边形定则可知,在该点速度方向与竖直方向夹角的正切值tan θ=v 02v 0=12,则θ≠30°,D 项错误。
2.(2021·河北高考)如图,距离为d 的两平行金属板P 、Q 之间有一匀强磁场,磁感应强度大小为B 1,一束速度大小为v 的等离子体垂直于磁场喷入板间,相距为L 的两光滑平行金属导轨固定在与导轨平面垂直的匀强磁场中,磁感应强度大小为B 2,导轨平面与水平面夹角为θ,两导轨分别与P 、Q 相连,质量为m 、电阻为R 的金属棒ab 垂直导轨放置,恰好静止,重力加速度为g ,不计导轨电阻、板间电阻和等离子体中的粒子重力,下列说法正确的是( )A .导轨处磁场的方向垂直导轨平面向上,v =mgR sin θB 1B 2Ld B .导轨处磁场的方向垂直导轨平面向下,v =mgR sin θB 1B 2LdC .导轨处磁场的方向垂直导轨平面向上,v =mgR tan θB 1B 2LdD .导轨处磁场的方向垂直导轨平面向下,v =mgR tan θB 1B 2Ld解析:B 等离子体垂直于磁场喷入板间时,根据左手定则可得等离子体中的正离子向金属板Q 偏转,负离子向金属板P 偏转,所以金属板Q 带正电荷,金属板P 带负电荷,则电流方向由金属棒a 端流向b 端。
高三物理二轮复习:专题3 功和能课件 第2讲

专题三
第二讲
走向高考 · 二轮专题复习新课标版 ·物理
拓展提升
一、基础知识要记牢 1.机械能守恒条件 (1)只有重力或系统内弹簧弹力做功。 (2)虽受其他力,但其他力不做功或其他力的总功为零。
2.三种表达式
(1)守恒观点:Ek1+Ep1=Ek2+Ep2 (2)转化观点:ΔEp=-ΔEk (3)转移观点:ΔEA增=ΔEB减
到C过程,由机械能守恒定律:mg(h1+h2)=Ep,C对。
专题三
第二讲
走向高考 · 二轮专题复习新课标版 ·物理
功能关系的应用
(2014· 山东卷)2013 年我国相继完 成“神十”与“天宫”对接、“嫦娥”携“玉 兔”落月两大航天工程。 某航天爱好者提出“玉 兔”回家的设想: 如图, 将携带“玉兔”的返回 系统由月球表面发射到 h 高度的轨道上,与在该轨道绕月球做 圆周运动的飞船对接,然后由飞船送“玉兔”返回地球。设 “玉兔”质量为 m,月球半径为 R,月面的重力加速度为 g 月。
专题三
第二讲
走向高考 · 二轮专题复习新课标版 ·物理
以月面为零势能面,“玉兔”在 h 高度的引力势能可表示 GM+h 为 EP= ,其中 G 为引力常量,M 为月球质量。若忽略 RR+h 月球的自转,从开始发射到对接完成需要对“玉兔”做的功为 ( ) mg月R A. (h+2R) R+h mg月R 2 C. (h+ R) 2 R+h mg月R B. (h+ 2R) R+h mg月R 1 D. (h+ R) 2 R+h
专题三
第二讲
走向高考 · 二轮专题复习新课标版 ·物理
故当 θ3=90° 时,A 的速度最大,设为 vAm,此时 B 下降到 最低点,B 的速度为零,此过程中 B 下降的高度为 h2,则有 1 2 h mgh2= mvAm, 其中 h2= -h, 代入数据解得 vAm=1.63m/s。 2 sinθ1
2020新课标高考物理二轮课件:专题三第2讲 磁场性质及带电粒子在磁场中的运动

角度 2 带电粒子在圆形边界磁场中的运动分析
2.(多选)(2017·高考全国卷Ⅱ)如图,虚线所示的圆形区域内存在一垂直于纸面
的匀强磁场,P 为磁场边界上的一点,大量相同的带电粒子以相同的速率经过 P
点,在纸面内沿不同方向射入磁场.若粒子射入速率为 v1,这些粒子在磁场边界的出射点
分布在六分之一圆周上;若粒子射入速率为 v2,相应的出射点分布在三分之一圆周上.不
带电粒子在匀强磁场中的运动 【高分快攻】
1.“一点、两画、三定、四写”求解粒子在磁场中的圆周运动
(1)一点:在特殊位置或要求粒子到达的位置(如初始位置、要求经过的某一位置等). (2)两画:画出速度 v 和洛伦兹力 F 两个矢量的方向. (3)三定:定圆心、定半径、定圆心角. (4)四写:写出基本方程 qvB=mvR2,半径 R=mqBv,周期 T=2πvR=2qπBm,运动时间 t=vs= 2απT.
2.常见模型的解题思路 (1)解答有关运动电荷在有界匀强磁场中的运动问题时,我们可以先将有界磁场视为无界磁 场,假设粒子能够做完整的圆周运动,确定粒子做圆周运动的圆心,作好辅助线,充分利 用相关几何知识解题. (2)对称规律解题法 ①从直线边界射入的粒子,又从同一边界射出时,速度与边界的夹角相等(如图甲所示).
磁场性质及对电流作用 【高分快攻】 1.磁场性质分析的两点技巧 (1)判断电流磁场要正确应用安培定则,明确大拇指、四指所指的方向及手掌的放法. (2)分析磁场对电流的作用要做到“一明、一转、一析”.即:
2.安培力作用下的平衡与运动问题的求解思路
【典题例析】 (2017·高考全国卷Ⅲ)如图,在磁感应强度大小为 B0 的匀强磁场中,两长直导线 P 和 Q 垂直于纸面固定放置,两者之间的距离为 l.在两导线中均通有方向垂直于纸面向里的电 流 I 时,纸面内与两导线距离均为 l 的 a 点处的磁感应强度为零.如果让 P 中的电流反向、 其他条件不变,则 a 点处磁感应强度的大小为( )
10第一部分 板块二 专题三 立体几何 第2讲 立体几何(大题)

第2讲立体几何(大题)热点一平行、垂直关系的证明高考常考平行、垂直关系的解题策略:(1)证明空间中的平行、垂直关系的常用方法是转化,如证明面面平行时,可转化为证明线面平行,而证明线面平行时,可转化为证明线线平行,但有的时候证明线面平行时,也可先证明面面平行,然后再得出线面平行.(2)在证明时,常通过三角形、平行四边形、矩形等平面图形去寻找平行和垂直的关系.例1(2018·北京)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A⊥PD,P A=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面P AB⊥平面PCD;(3)求证:EF∥平面PCD.跟踪演练1如图,在四棱锥P-ABCD中,∠ADB=90°,CB=CD,点E为棱PB的中点.(1)若PB=PD,求证:PC⊥BD;(2)求证:CE ∥平面P AD .热点二 体积、距离的计算高考常考体积和距离问题的解题策略:(1)求空间几何体的体积的常用方法有换底法,转化法,割补法.换底法的一般思路是找出几何体的底面和高,看底面积和高是否容易计算,若较难计算,则转换顶点和底面,使得底面积和高都比较容易求出;转化法是利用一个几何体与某几何体之间的关系,转化为求该几何体的体积;对于较复杂的几何体,有时也进行分割和补形,间接求得体积.(2)求立体几何中的距离问题时常利用等体积法,即把要求的距离转化成一个几何体的高,利用同一个几何体的体积相等,转换这个几何体的顶点去求解.例2 (2019·东北三省三校模拟)如图,四棱锥P -ABCD 中,底面ABCD 是平行四边形,PG ⊥平面ABCD ,垂足为G ,G 在AD 上,且AG =13GD ,BG ⊥GC ,GB =GC =2,四面体P -BCG的体积为83.(1)求点D 到平面PBG 的距离;(2)若点F 是棱PC 上一点,且DF ⊥GC ,求PFFC 的值.跟踪演练2 (2019·淄博模拟)如图,在四棱锥P -ABCD 中,AB ∥CD ,AB =1,CD =3,AP =2,DP =23,∠P AD =60°,AB ⊥平面P AD ,点M 在棱PC 上.(1)求证:平面P AB⊥平面PCD;(2)若直线P A∥平面MBD,求此时三棱锥P-MBD的体积.热点三翻折与探索性问题高考中翻折与探索性问题的解题策略:(1)翻折问题有一定的难度,在解题时,一定要先弄清楚在翻折过程中哪些量发生了变化,哪些量没有发生变化.一般情况下,长度不发生变化,而位置关系发生变化.再通过连线得到三棱锥、四棱锥等几何体,最后把问题转化到我们较熟悉的几何体中去解决.(2)对于探索性问题,一般根据问题的设问,首先假设其存在,然后在这个假设下进行推理论证,如果通过推理得到了合乎情理的结论就肯定假设,如果得到了矛盾就否定假设.例3如图1,已知菱形AECD的对角线AC,DE交于点F,点E为AB中点.将△ADE沿线段DE折起到△PDE的位置,如图2所示.(1)求证:DE⊥平面PCF;(2)求证:平面PBC⊥平面PCF;(3)在线段PD,BC上是否分别存在点M,N,使得平面CFM∥平面PEN?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.跟踪演练3(2018·全国Ⅲ)如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD 上异于C,D的点.(1)证明:平面AMD⊥平面BMC.(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.真题体验(2019·全国Ⅰ,文,19)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.押题预测如图,在四棱锥P -ABCD 中,平面ABCD ⊥平面P AD ,AD ∥BC ,AB =BC =AP =12AD ,∠ADP=30°,∠BAD =90°.(1)证明:PD ⊥PB ;(2)设点M 在线段PC 上,且PM =13PC ,若△MBC 的面积为273,求四棱锥P -ABCD 的体积.A 组 专题通关1.(2019·全国Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥E -BB 1C 1C 的体积.2.(2019·哈尔滨模拟)如图,多面体ABCDEF 中,底面ABCD 是菱形,∠BCD =π3,四边形BDEF 是正方形,且DE ⊥平面ABCD .(1)求证:CF ∥平面AED ;(2)若AE =2,求多面体ABCDEF 的体积V .3.(2019·长沙模拟)如图,在多边形ABPCD 中(图1),ABCD 为长方形,△BPC 为正三角形,AB =3,BC =32,现以BC 为折痕将△BPC 折起,使点P 在平面ABCD 内的射影恰好在AD 上(图2).(1)证明:PD ⊥平面P AB ;(2)若点E 在线段PB 上,且PE =13PB ,当点Q 在线段AD 上运动时,求三棱锥Q -EBC 的体积.B组能力提高4.(2019·潍坊模拟)如图,三棱柱ABC-A1B1C1中,CA=CB,∠BAA1=45°,平面AA1C1C⊥平面AA1B1B.(1)求证:AA1⊥BC;(2)若BB1=2AB=2,∠A1AC=45°,D为CC1的中点,求三棱锥D-A1B1C1的体积.5.如图,在矩形AB′DE中,AE=6,DE=5,被截去一角(即△BB′C),AB=3,∠ABC=135°,平面P AE⊥平面ABCDE,P A+PE=10.(1)求五棱锥P-ABCDE的体积的最大值;(2)在(1)的情况下,证明:BC⊥PB.。
2025届高三化学一轮专题复习讲义(09)-专题三第二讲 原电池原理及应用

(4)其它介质
如掺杂Y2O3的ZrO3固体作电解质,在高温下能传导正极生成的O2-。根据O2-移向负极,在负极上CH3OH失电子生成CO2气体,而O2在正极上得电子生成O2-。
电极反应:负极:2CH3OH-12e-+6O2-===2CO2↑+4H2O
正极:3O2+12e-===6O2-
6.思维方式:知识迁移
由陌生装置图迁移到课本熟悉的装置图
燃
料
电
池
【体系再构】
【随堂反馈】
基础训练
1.微型银—锌电池可用作电子仪器的电源,其电极分别是Ag/Ag2O和Zn,电解质为KOH溶液,电池总反应为Ag2O+Zn+H2O===2Ag+Zn(OH)2,下列说法正确的是
A.电池工作过程中,KOH溶液浓度降低
D.电池总反应:Zn+4OH-+MnO2+4H+===Zn(OH) +Mn2++2H2O
解析:A项,根据分析,Ⅱ区的K+只能向Ⅰ区移动,错误;B项,根据分析,Ⅰ区的SO 向Ⅱ区移动,B正确;C项,MnO2电极的电极反应式为MnO2+2e-+4H+=Mn2++2H2O,C正确;D项,电池的总反应为Zn+4OH-+MnO2+4H+=Zn(OH) +Mn2++2H2O,正确。
答案:A
例题2.(2022·江苏高考)周期表中ⅣA族元素及其化合物应用广泛,甲烷具有较大的燃烧热(890.3kJ·mol-1),是常见燃料;Si、Ge是重要的半导体材料,硅晶体表面SiO2能与氢氟酸(HF,弱酸)反应生成H2SiF6(H2SiF6在水中完全电离为H+和SiF );1885年德国化学家将硫化锗(GeS2)与H2共热制得了门捷列夫预言的类硅—锗;下列化学反应表示正确的是
20届高考数学(理)二轮复习 第2部分 专题3 第2讲 立体几何(1)

第2讲 立体几何(大题)热点一 平行、垂直关系的证明用向量知识证明立体几何问题,仍然离不开立体几何中的定理.如要证明线面平行,只需要证明平面外的一条直线和平面内的一条直线平行,即化归为证明线线平行,用向量方法证明直线a ∥b ,只需证明向量a =λb (λ∈R )即可.若用直线的方向向量与平面的法向量垂直来证明线面平行,仍需强调直线在平面外.例1 如图,在直三棱柱ADE -BCF 中,平面ABFE 和平面ABCD 都是正方形且互相垂直,点M 为AB 的中点,点O 为DF 的中点.运用向量方法证明:(1)OM ∥平面BCF ; (2)平面MDF ⊥平面EFCD .证明 方法一 (1)由题意,得AB ,AD ,AE 两两垂直,以点A 为原点建立如图所示的空间直角坐标系A -xyz .设正方形边长为1,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0),F (1,0,1),M ⎝⎛⎭⎫12,0,0,O ⎝⎛⎭⎫12,12,12. OM →=⎝⎛⎭⎫0,-12,-12,BA →=(-1,0,0), ∴OM →·BA →=0,∴OM →⊥BA →. ∵棱柱ADE -BCF 是直三棱柱,∴AB ⊥平面BCF ,∴BA →是平面BCF 的一个法向量, 且OM ⊄平面BCF ,∴OM ∥平面BCF . (2)设平面MDF 与平面EFCD 的法向量分别为 n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).∵DF →=(1,-1,1),DM →=⎝⎛⎭⎫12,-1,0,DC →=(1,0,0),CF →=(0,-1,1), 由⎩⎪⎨⎪⎧ n 1·DF →=0,n 1·DM →=0,得⎩⎪⎨⎪⎧x 1-y 1+z 1=0,12x 1-y 1=0,令x 1=1,则n 1=⎝⎛⎭⎫1,12,-12. 同理可得n 2=(0,1,1).∵n 1·n 2=0,∴平面MDF ⊥平面EFCD . 方法二 (1)OM →=OF →+FB →+BM →=12DF →-BF →+12BA →=12(DB →+BF →)-BF →+12BA → =-12BD →-12BF →+12BA →=-12(BC →+BA →)-12BF →+12BA →=-12BC →-12BF →.∴向量OM →与向量BF →,BC →共面, 又BF ,BC ⊂平面BCF ,OM ⊄平面BCF , ∴OM ∥平面BCF .(2)由题意及(1)知,BF ,BC ,BA 两两垂直, ∵CD →=BA →,FC →=BC →-BF →, ∴OM →·CD →=⎝⎛⎭⎫-12BC →-12BF →·BA →=0, OM →·FC →=⎝⎛⎭⎫-12BC →-12BF →·(BC →-BF →) =-12BC →2+12BF →2=0,∴OM →⊥CD →,OM →⊥FC →, 即OM ⊥CD ,OM ⊥FC ,又CD ∩FC =C ,CD ,FC ⊂平面EFCD , ∴OM ⊥平面EFCD .又OM ⊂平面MDF ,∴平面MDF ⊥平面EFCD .跟踪演练1 如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AD ⊥CD ,BC =2,AD =CD =1,M 是PB 的中点.(1)求证:AM ∥平面PCD ; (2)求证:平面ACM ⊥平面P AB .证明 (1)如图,以C 为坐标原点建立空间直角坐标系C -xyz ,则A (1,1,0),B (0,2,0),C (0,0,0),D (1,0,0),P (1,1,a )(a >0),M ⎝⎛⎭⎫12,32,a 2,CP →=(1,1,a ),CD →=(1,0,0),AM →=⎝⎛⎭⎫-12,12,a 2, 设平面PCD 的法向量为n 1=(x 0,y 0,z 0),则⎩⎪⎨⎪⎧x 0+y 0+az 0=0,x 0=0,令y 0=a ,则n 1=(0,a ,-1), 所以AM →·n 1=a 2-a 2=0,又AM ⊄平面PCD , 所以AM ∥平面PCD .(2)由(1)得,CA →=(1,1,0),CM →=⎝⎛⎭⎫12,32,a 2, 设平面ACM 的法向量为n 2=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧x 1+y 1=0,12x 1+32y 1+a2z 1=0, 令x 1=1,则n 2=⎝⎛⎭⎫1,-1,2a , AP →=(0,0,a ),AB →=(-1,1,0),设平面P AB 的法向量为n 3=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧-x 2+y 2=0,az 2=0,令x 2=1,则n 3=(1,1,0), 所以n 2·n 3=1-1=0. 所以平面ACM ⊥平面P AB .热点二 利用空间向量求空间角设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2).平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同). (1)线线夹角设l ,m 的夹角为θ⎝⎛⎭⎫0≤θ≤π2, 则cos θ=|a ·b ||a ||b |=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21 a 22+b 22+c 22. (2)线面夹角设直线l 与平面α的夹角为θ⎝⎛⎭⎫0≤θ≤π2, 则sin θ=|a ·μ||a ||μ|=|cos 〈a ,μ〉|. (3)二面角设α-a -β的平面角为θ(0≤θ≤π), 则|cos θ|=|μ·v ||μ||v |=|cos 〈μ,v 〉|. 例2 (2019·南昌模拟)如图,四棱台ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形,CC 1⊥底面ABCD ,且∠BAD =60°,CD =CC 1=2C 1D 1=4,E 是棱BB 1的中点.(1)求证:AA 1⊥BD ;(2)求二面角E -A 1C 1-C 的余弦值.(1)证明 因为C 1C ⊥底面ABCD ,所以C 1C ⊥BD . 因为底面ABCD 是菱形,所以BD ⊥AC . 又AC ∩CC 1=C ,AC ,CC 1⊂平面ACC 1A 1, 所以BD ⊥平面ACC 1A 1. 又AA 1⊂平面ACC 1A 1, 所以BD ⊥AA 1.(2)解 如图,设AC 交BD 于点O ,依题意,A 1C 1∥OC 且A 1C 1=OC , 所以四边形A 1OCC 1为平行四边形, 所以A 1O ∥CC 1,且A 1O =CC 1. 所以A 1O ⊥底面ABCD .以O 为原点,OA ,OB ,OA 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系. 则A (23,0,0),A 1(0,0,4),C 1(-23,0,4),B (0,2,0), AB →=(-23,2,0).由A 1B 1----→=12AB →,得B 1(-3,1,4).因为E 是棱BB 1的中点, 所以E ⎝⎛⎭⎫-32,32,2, 所以EA 1→=⎝⎛⎭⎫32,-32,2,A 1C 1----→=(-23,0,0).设n =(x ,y ,z )为平面EA 1C 1的法向量,则⎩⎨⎧n ·A 1C 1----→=-23x =0,n ·EA 1→=32x -32y +2z =0,取z =3,得n =(0,4,3),平面A 1C 1C 的法向量m =(0,1,0),又由图可知,二面角E -A 1C 1-C 为锐二面角, 设二面角E -A 1C 1-C 的平面角为θ, 则cos θ=|m ·n ||m ||n |=45,所以二面角E -A 1C 1-C 的余弦值为45.跟踪演练2 (2019·河南名校联盟联考)如图,在四棱锥P -ABCD 中,∠P AB =90°,AB ∥CD ,且PB =BC =BD =6,CD =2AB =22,∠P AD =120°.E 和F 分别是棱CD 和PC 的中点.(1)求证:CD ⊥BF ;(2)求直线PB 与平面PCD 所成的角的正弦值. (1)证明 ∵E 为CD 中点,CD =2AB , ∴AB =DE .又AB∥CD,∴四边形ABED为平行四边形.∵BC=BD,E为CD中点,∴BE⊥CD,∴四边形ABED为矩形,∴AB⊥AD.由∠P AB=90°,得P A⊥AB,又P A∩AD=A,P A,AD⊂平面P AD,∴AB⊥平面P AD.∵AB∥CD,∴CD⊥平面P AD.又PD⊂平面P AD,∴CD⊥PD.∵EF∥PD,∴CD⊥EF.又CD⊥BE,BE∩EF=E,BE,EF⊂平面BEF,∴CD⊥平面BEF.又∵BF⊂平面BEF,∴CD⊥BF.(2)解由(1)知AB⊥平面P AD.以A为原点,AB所在直线为x轴,AD所在直线为y轴,平面P AD内过点A且与AD垂直的线为z轴建立空间直角坐标系A-xyz,如图所示.∵∠P AD=120°,∴∠P Az=30°.又PB=6,AB=2,AB⊥P A,∴P A=2.∴点P到z轴的距离为1.∴P(0,-1,3),同时知A(0,0,0),B(2,0,0).又BC=BD=6,CD=22,∴BE=2.∴C (22,2,0),D (0,2,0).设平面PCD 的一个法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·PD →=(x ,y ,z )·(0,3,-3)=0,n ·CD →=(x ,y ,z )·(-22,0,0)=0,得⎩⎨⎧3y -3z =0,-22x =0.令y =1,则n =(0,1,3). 又PB →=(2,1,-3),设直线PB 与平面PCD 所成的角为θ. 则sin θ=|cos 〈n ,PB →〉|=|n ·PB →||n |·|PB →|=22+1+3×1+3=66.即直线PB 与平面PCD 所成的角的正弦值为66. 热点三 利用空间向量解决探索性问题与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则是:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.例3 (2019·临沂模拟)如图,平面ABCD ⊥平面ABE ,四边形ABCD 是边长为2的正方形,AE =1,F 为CE 上的点,且BF ⊥平面ACE .(1)求证:AE ⊥平面BCE ;(2)线段AD 上是否存在一点M ,使平面ABE 与平面MCE 所成二面角的余弦值为34?若存在,试确定点M 的位置;若不存在,请说明理由. (1)证明 ∵BF ⊥平面ACE ,AE ⊂平面ACE , ∴BF ⊥AE ,∵四边形ABCD 是正方形,∴BC ⊥AB ,又平面ABCD ⊥平面ABE ,平面ABCD ∩平面ABE =AB , ∴CB ⊥平面ABE , ∵AE ⊂平面ABE , ∴CB ⊥AE ,∵BF ∩BC =B ,BF ,BC ⊂平面BCE , ∴AE ⊥平面BCE .(2)解 线段AD 上存在一点M ,当AM =3时,使平面ABE 与平面MCE 所成二面角的余弦值为34. ∵AE ⊥平面BCE ,BE ⊂平面BCE , ∴AE ⊥BE ,在Rt △AEB 中,AB =2,AE =1, ∴∠ABE =30°,∠BAE =60°,以A 为原点,建立空间直角坐标系A -xyz , 设AM =h ,则0≤h ≤2, ∵AE =1,∠BAE =60°, ∴M (0,0,h ),E ⎝⎛⎭⎫32,12,0,B (0,2,0),C (0,2,2),所以ME →=⎝⎛⎭⎫32,12,-h ,CE →=⎝⎛⎭⎫32,-32,-2,设平面MCE 的一个法向量n =(x ,y ,z ), 则⎩⎨⎧n ·ME →=3x 2+12y -hz =0,n ·CE →=3x 2-32y -2z =0,令z =2,解得n =⎝⎛⎭⎫33(2+3h ),h -2,2,平面ABE 的一个法向量m =(0,0,1),由题意可知cos 〈m ,n 〉=m ·n|m ||n |=213(2+3h )2+(h -2)2+4=34, 解得h =3,所以当AM =3时,使平面ABE 与平面MCE 所成二面角的余弦值为34. 跟踪演练3 如图,在直三棱柱ABC -A 1B 1C 1中,AC ⊥BC ,AC =BC =AA 1=2,点P 为棱B 1C 1的中点,点Q 为线段A 1B 上一动点.(1)求证:当点Q 为线段A 1B 的中点时,PQ ⊥平面A 1BC ;(2)设BQ →=λBA 1→,试问:是否存在实数λ,使得平面A 1PQ 与平面B 1PQ 所成锐二面角的余弦值为3010?若存在,求出这个实数λ;若不存在,请说明理由. (1)证明 连接AB 1,AC 1,∵点Q 为线段A 1B 的中点, ∴A ,Q ,B 1三点共线, 且Q 为AB 1的中点, ∵点P 为B 1C 1的中点, ∴PQ ∥AC 1.在直三棱柱ABC -A 1B 1C 1中, AC ⊥BC ,∴BC ⊥平面ACC 1A 1, 又AC 1⊂平面ACC 1A 1, ∴BC ⊥AC 1.∵AC =AA 1,∴四边形ACC 1A 1为正方形, ∴AC 1⊥A 1C ,又A 1C ,BC ⊂平面A 1BC ,A 1C ∩BC =C , ∴AC 1⊥平面A 1BC , 而PQ ∥AC 1, ∴PQ ⊥平面A 1BC .(2)解 由题意可知,CA ,CB ,CC 1两两垂直,以C 为原点,分别以CA ,CB ,CC 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系C -xyz , 连接B 1Q ,PB ,设Q (x ,y ,z ), B (0,2,0),A 1(2,0,2), P (0,1,2),B 1(0,2,2), ∵BQ →=λBA 1→,∴(x ,y -2,z )=λ(2,-2,2), ∴⎩⎪⎨⎪⎧x =2λ,y =2-2λ,z =2λ,∴Q (2λ,2-2λ,2λ). ∵点Q 在线段A 1B 上运动,∴平面A 1PQ 的法向量即为平面A 1PB 的法向量, 设平面A 1PB 的法向量为n 1=(x ,y ,z ), BP →=(0,-1,2),P A 1→=(2,-1,0), 由⎩⎪⎨⎪⎧n 1·BP →=0,n 1·P A 1→=0,得⎩⎪⎨⎪⎧-y +2z =0,2x -y =0,令y =2,得n 1=(1,2,1),设平面B 1PQ 的法向量为n 2=(x ,y ,z ), PB 1→=(0,1,0),B 1Q →=(2λ,-2λ,2λ-2).由⎩⎪⎨⎪⎧n 2·PB 1→=0,n 2·B 1Q →=0,得⎩⎪⎨⎪⎧y =0,2λx -2λy +(2λ-2)z =0,令z =1得n 2=⎝⎛⎭⎫1-λλ,0,1=1λ(1-λ,0,λ), 取n 2=(1-λ,0,λ),由题意得|cos 〈n 1,n 2〉|=|()1,2,1·()1-λ,0,λ|6·(1-λ)2+λ2=16×2λ2-2λ+1=3010,∴9λ2-9λ+2=0, 解得λ=13或λ=23,∴当λ=13或λ=23时,平面A 1PQ 与平面B 1PQ 所成锐二面角的余弦值为3010.真题体验(2019·全国Ⅰ,理,18)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A -MA 1-N 的正弦值.(1)证明 连接B 1C ,ME .因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C .又因为N 为A 1D 的中点,所以ND =12A 1D .由题设知A 1B 1∥DC 且A 1B 1=DC ,可得B 1C ∥A 1D 且B 1C =A 1D ,故ME ∥ND 且ME =ND ,因此四边形MNDE 为平行四边形,MN ∥ED .又MN ⊄平面C 1DE ,ED ⊂平面C 1DE ,所以MN ∥平面C 1DE .(2)解 由已知可得DE ⊥DA ,以D 为坐标原点,DA →的方向为x 轴正方向,建立如图所示的空间直角坐标系D -xyz ,则A (2,0,0),A 1(2,0,4),M (1,3,2),N (1,0,2),A 1A →=(0,0,-4),A 1M →=(-1,3,-2),A 1N →=(-1,0,-2),MN →=(0,-3,0).设m =(x ,y ,z )为平面A 1MA 的一个法向量,则 ⎩⎪⎨⎪⎧m ·A 1M →=0,m ·A 1A →=0,所以⎩⎨⎧-x +3y -2z =0,-4z =0,可得m =(3,1,0).设n =(p ,q ,r )为平面A 1MN 的一个法向量,则 ⎩⎪⎨⎪⎧n ·MN →=0,n ·A 1N →=0,所以⎩⎨⎧-3q =0,-p -2r =0,可取n =(2,0,-1).于是cos 〈m ,n 〉=m ·n |m ||n |=232×5=155,所以二面角A -MA 1-N 的正弦值为105.押题预测如图1,在梯形ABCD 中,AB ∥CD ,过A ,B 分别作AE ⊥CD ,BF ⊥CD ,垂足分别E ,F ,AB =AE =2,CD =5,已知DE =1,将梯形ABCD 沿AE ,BF 同侧折起,得空间几何体ADE -BCF ,如图2.(1)若AF ⊥BD ,证明:DE ⊥平面ABFE ;(2)若DE ∥CF ,CD =3,线段AB 上存在一点P ,满足CP 与平面ACD 所成角的正弦值为520,求AP 的长.(1)证明 由已知得四边形ABFE 是正方形,且边长为2,在图2中,AF ⊥BE , 由已知得AF ⊥BD ,BE ∩BD =B ,BE ,BD ⊂平面BDE , ∴AF ⊥平面BDE ,又DE ⊂平面BDE ,∴AF ⊥DE ,又AE ⊥DE ,AE ∩AF =A ,AE ,AF ⊂平面ABFE , ∴DE ⊥平面ABFE .(2)解 在图2中,AE ⊥DE ,AE ⊥EF ,DE ∩EF =E ,DE ,EF ⊂平面DEFC ,即AE ⊥平面DEFC ,在梯形DEFC 中,过点D 作DM ∥EF 交CF 于点M ,连接CE , 由题意得DM =2,CM =1, 由勾股定理可得DC ⊥CF , 则∠CDM =π6,CE =2,过E 作EG ⊥EF 交DC 于点G , 可知GE ,EA ,EF 两两垂直,以E 为坐标原点,以EA →,EF →,EG →分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系, 则A (2,0,0),B (2,2,0),C (0,1,3),D ⎝⎛⎭⎫0,-12,32,AC →=(-2,1,3),AD →=⎝⎛⎭⎫-2,-12,32.设平面ACD 的一个法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·AC →=0,n ·AD →=0,得⎩⎪⎨⎪⎧-2x +y +3z =0,-2x -12y +32z =0, 取x =1,得n =(1,-1,3), 设AP =m ,则P (2,m ,0),0≤m ≤2, 得CP →=(2,m -1,-3), 设CP 与平面ACD 所成的角为θ, sin θ=|cos 〈CP →,n 〉|=|m |5×7+(m -1)2=520⇒m =23(舍负). 所以AP =23.A 组 专题通关1.(2019·全国Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B -EC -C 1的正弦值.(1)证明 由已知得,B 1C 1⊥平面ABB 1A 1,因为BE ⊂平面ABB 1A 1,故B 1C 1⊥BE . 又BE ⊥EC 1,EC 1∩B 1C 1=C 1, 所以BE ⊥平面EB 1C 1. (2)解 由(1)知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E ,所以∠AEB =45°,故AE =AB ,AA 1=2AB .以D 为坐标原点,DA →的方向为x 轴正方向,|DA →|为单位长,建立如图所示的空间直角坐标系D -xyz ,则C (0,1,0),B (1,1,0),C 1(0,1,2),E (1,0,1),CB →=(1,0,0),CE →=(1,-1,1),CC 1→=(0,0,2). 设平面EBC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧CB →·n =0,CE →·n =0,即⎩⎪⎨⎪⎧x =0,x -y +z =0,所以可取n =(0,-1,-1).设平面ECC 1的法向量为m =(x 1,y 1,z 1),则 ⎩⎪⎨⎪⎧CC 1→·m =0,CE →·m =0,即⎩⎪⎨⎪⎧2z 1=0,x 1-y 1+z 1=0,所以可取m =(1,1,0).于是cos 〈n ,m 〉=n ·m |n ||m |=-12,sin 〈n ,m 〉=1-⎝⎛⎭⎫-122=32, 所以二面角B -EC -C 1的正弦值为32. 2.(2019·全国Ⅲ)图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连接DG ,如图2. (1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B —CG —A 的大小.(1)证明 由已知得AD ∥BE ,CG ∥BE ,所以AD ∥CG , 故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,BE ∩BC =B , BE ,BC ⊂平面BCGE ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)解 作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,平面BCGE ∩平面ABC =BC ,所以EH ⊥平面ABC .由已知,菱形BCGE 的边长为2,∠EBC =60°, 可求得BH =1,EH = 3.以H 为坐标原点,HC →的方向为x 轴的正方向, 建立如图所示的空间直角坐标系H -xyz ,则A (-1,1,0),C (1,0,0),G (2,0,3),CG →=(1,0,3),AC →=(2,-1,0). 设平面ACGD 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧CG →·n =0,AC →·n =0,即⎩⎨⎧x +3z =0,2x -y =0.所以可取n =(3,6,-3).又平面BCGE 的法向量可取为m =(0,1,0), 所以cos 〈n ,m 〉=n ·m |n ||m |=32.因此二面角B -CG -A 的大小为30°.3.(2019·马鞍山模拟)如图,在三棱柱ABC -A 1B 1C 1中,∠ACB =90°,A 1B ⊥AC 1,AC =AA 1=4,BC =2.(1)求证:平面A 1ACC 1⊥平面ABC ;(2)若∠A 1AC =60°,在线段AC 上是否存在一点P ,使二面角B -A 1P -C 的平面角的余弦值为34?若存在,确定点P 的位置;若不存在,请说明理由. (1)证明 如图,∵AC =AA 1, ∴四边形AA 1C 1C 为菱形,连接A 1C ,则A 1C ⊥AC 1,又A 1B ⊥AC 1,且A 1C ∩A 1B =A 1, A 1C ,A 1B ⊂平面A 1CB ,∴AC 1⊥平面A 1CB ,则AC 1⊥BC , 又∠ACB =90°,即BC ⊥AC ,又AC 1∩AC =A ,AC 1,AC ⊂平面A 1ACC 1, ∴BC ⊥平面A 1ACC 1,而BC ⊂平面ABC ,∴平面A 1ACC 1⊥平面ABC .(2)解 在平面ACC 1A 1中,过点C 作CE ⊥AC 交A 1C 1于E , 由(1)知,CE ⊥平面ABC ,以C 为坐标原点,分别以CA ,CB 所在直线为x 轴,y 轴建立如图所示的空间直角坐标系C -xyz ,∵AC =AA 1=4,BC =2,∠A 1AC =60°, ∴C (0,0,0),B (0,2,0),A (4,0,0),A 1(2,0,23).设在线段AC 上存在一点P ,满足AP →=λAC →(0≤λ<1),使得二面角B -A 1P -C 的平面角的余弦值为34. 则AP →=(-4λ,0,0).BP →=BA →+AP →=(4,-2,0)+(-4λ,0,0) =(4-4λ,-2,0),A 1P →=A 1A →+AP →=(2-4λ,0,-23), CA 1→=(2,0,23).设平面BA 1P 的一个法向量为m =(x 1,y 1,z 1), 由⎩⎪⎨⎪⎧m ·BP →=(4-4λ)x 1-2y 1=0,m ·A 1P →=(2-4λ)x 1-23z 1=0,取x 1=1,得m =⎝⎛⎭⎪⎫1,2-2λ,1-2λ3;平面A 1PC 的一个法向量为n =(0,1,0). 由|cos 〈m ,n 〉|=|m ·n ||m ||n |=|2-2λ|1+(2-2λ)2+(1-2λ)23×1=34, 解得λ=43或λ=34,因为0≤λ<1,所以λ=34.故在线段AC 上存在一点P ,满足AP →=34AC →,使二面角B -A 1P -C 的平面角的余弦值为34.B 组 能力提高4.如图所示,在四棱锥P -ABCD 中,P A =PD =AD =2CD =2BC =2,且∠ADC =∠BCD =90°.(1)当PB =2时,证明:平面P AD ⊥平面ABCD ;(2)当四棱锥P -ABCD 的体积为34,且二面角P -AD -B 为钝角时,求直线P A 与平面PCD所成角的正弦值.(1)证明 如图所示,取AD 的中点O ,连接PO ,OB .∵P A =PD ,∴PO ⊥AD . ∵∠ADC =∠BCD =90°, ∴BC ∥AD ,又BC =12AD =1,∴BC =OD ,∴四边形BCDO 为矩形, ∴OB =CD =1.在△POB 中,PO =3,OB =1,PB =2, ∴∠POB =90°,则PO ⊥OB .∵AD ∩OB =O ,∴PO ⊥平面ABCD , 又PO ⊂平面P AD , ∴平面P AD ⊥平面ABCD .(2)解 由(1)知AD ⊥PO ,AD ⊥BO , ∵PO ∩OB =O ,∴AD ⊥平面POB , 又AD ⊂平面ABCD , ∴平面POB ⊥平面ABCD . 过点P 作PE ⊥平面ABCD ,则垂足E 一定落在平面POB 与平面ABCD 的交线OB 上. ∵四棱锥P -ABCD 的体积为34,∴13×PE ×12×(AD +BC )×CD =13×PE ×12×(2+1)×1 =12PE =34, ∴PE =32.∵PO =3,∴OE =PO 2-PE 2=32. 以O 为坐标原点,OA ,OB 所在直线分别为x 轴,y 轴, 在平面POB 内过点O 作垂直于平面AOB 的直线为z 轴, 建立如图所示的空间直角坐标系O -xyz . 由题意可知A (1,0,0),P ⎝⎛⎭⎫0,-32,32,D (-1,0,0),C (-1,1,0), 则DP →=⎝⎛⎭⎫1,-32,32,DC →=(0,1,0),P A →=⎝⎛⎭⎫1,32,-32.设平面PCD 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧ n ·DP →=0,n ·DC →=0,即⎩⎪⎨⎪⎧x -32y +32z =0,y =0,令x =1,则y =0,z =-23,∴n =⎝⎛⎭⎫1,0,-23. 设直线P A 与平面PCD 所成的角为θ,则sin θ=|P A →·n ||P A →||n |=22×133=31313,故直线P A 与平面PCD 所成角的正弦值为31313.5.如图,已知圆锥OO 1和圆柱O 1O 2的组合体(它们的底面重合),圆锥的底面圆O 1的半径为r =5,OA 为圆锥的母线,AB 为圆柱O 1O 2的母线,D ,E 为下底面圆O 2上的两点,且DE =6,AB =6.4,AO =52,AO ⊥AD .(1)求证:平面ABD ⊥平面ODE; (2)求二面角B -AD -O 的正弦值.(1)证明 依题意知,圆锥的高为h =(52)2-52=5,又圆柱的高为AB =6.4,AO ⊥AD ,所以OD 2=OA 2+AD 2, 因为AB ⊥BD , 所以AD 2=AB 2+BD 2,连接OO 1,O 1O 2,DO 2,易知O ,O 1,O 2三点共线,OO 2⊥DO 2,所以OD 2=OO 22+O 2D 2, 所以BD 2=OO 22+O 2D 2-AO 2-AB 2=(6.4+5)2+52-(52)2-6.42=64,解得BD =8,又因为DE =6,圆O 2的直径为10,圆心O 2在∠BDE 内, 所以∠BDE =90°,所以DE ⊥BD .因为AB ⊥平面BDE ,DE ⊂平面BDE ,所以DE ⊥AB , 因为AB ∩BD =B ,AB ,BD ⊂平面ABD , 所以DE ⊥平面ABD . 又因为DE ⊂平面ODE , 所以平面ABD ⊥平面ODE .(2)解 如图,以D 为原点,DB ,DE 所在直线为x ,y 轴,建立空间直角坐标系.则D (0,0,0),A (8,0,6.4),B (8,0,0),O (4,3,11.4).所以DA →=(8,0,6.4),DB →=(8,0,0),DO →=(4,3,11.4), 设平面DAO 的法向量为u =(x ,y ,z ),所以DA →·u =8x +6.4z =0,DO →·u =4x +3y +11.4z =0,令x =12,则u =(12,41,-15).可取平面BDA 的一个法向量为v =(0,1,0),所以cos 〈u ,v 〉=u·v |u||v |=41582=8210, 所以二面角B -AD -O 的正弦值为3210.。
2021年新课标新高考地理复习练习讲义:专题三第二讲 大气环流与气候

第二讲大气环流与气候备考篇提纲挈领【考情探究】课标解读考情分析备考指导内容解读全球性大气环流全球气压带、风带的分布、移动规律及其对气候的影响近5年本讲内容一直是高考考查的重点,是高频考点。
试题多以区域图附加气候要素信息的方式呈现,考查学生获取信息、运用知识分析问题及运用地理原理阐释自然现象的能力。
突出考查区域认知、综合思维和地理实践力的学科素养本讲内容为自然地理的核心知识,是高考知识点中的重点和难点。
备考复习时要突出对基础知识的理解,理顺知识点之间的关系。
多联系生活和生产实际,分析和解决现实生活中的问题是备考的关键气温与降水气候类型全球气候变化全球气候变化对人类活动的影响【真题探秘】基础篇固本夯基【基础集训】知识1全球性大气环流读全球近地面气压带和风带局部示意图,回答下面两题。
1.图中的M气压带为()A.赤道低气压带B.北半球副热带高气压带C.南半球副热带高气压带D.副极地低气压带答案B2.下列关于图中M、N两气压带所反映的时间与季节的叙述,正确的是()A.M表示3月份、春季B.N表示7月份、夏季C.M表示12月份、夏季D.N表示1月份、冬季答案B知识2 气温与降水下图示意某地区年均温的分布。
读下图,完成下面两题。
1.影响该地区年均温分布特征的主要因素是()A.台风B.海陆分布C.地形D.大气环流答案C2.图示①②③④四地中,年降水量最低的是()A.①地B.②地C.③地D.④地答案A知识3气候类型读四城市资料图,完成下面两题。
1.关于四城市气候的分析,正确的是()A.乙地气候海洋性最强B.甲地年降水量最大C.丁地气候一年分干湿两季D.丙地气候类型南北半球都有分布答案D2.关于四城市气候成因的判断,正确的是()A.丁地主要受赤道低气压带的控制B.甲地受气压带和风带的交替控制C.乙地受海陆热力性质差异影响D.丙地终年受西风带的影响答案C知识4全球气候变化2016年上海沿海海平面比常年高102毫米,比2015年高45毫米,预计未来30年,上海沿海海平面将上升65~150毫米,读下图,完成下面两题。
2024浙江地理高考二轮专题复习--专题三第二讲 大气环流与气候

专题三地球上的大气第二讲大气环流与气候五年高考考点1大气环流(2022广东,9,3分)某研究统计了50°N 以北地区1979 —2016年发生的所有气旋,并将中心气压值最低的前5%的气旋定义为超强气旋。
下图示意该地区1979—2016年超强气旋总频数空间分布。
据此完成下题。
频数(次)=20~40 —40~80 —80~120 =120~160 —160~2001.影响图中北大西洋地区超强气旋生成的气压带、风带主要是( )①副极地低气压带②副热带高气压带③极地东风带④盛行西风带⑤东北信风带A.①③④B.①③⑤C.②③④D.②④⑤答案 A(202 1浙江 1 月选考,11—12, 4分)下图为非洲西部局部大气环流示意图。
完成下面两题。
2.图中( ) 蔬甲垂真气流水平气流乙章jmA.甲风带的风向有明显季节变化B.乙气流因受动力因素影响而上升C.丙风向形成受地转偏向力影响D.丁风带为大陆西岸带来充足水汽答案 C3.图示季节,最可能出现的现象有( )A. 北印度洋的洋流呈逆时针流动B.黄河中游含沙量明显增加C. 北半球副极地低气压带被切断D.地中海沿岸地区温和多雨答案 B(2020 浙江1月选考,10,2分)下图为雅鲁藏布江流域示意图。
完成下题。
4.甲山地位于亚热带地区,但其南坡1100米以下分布着热带季雨林,原因是( )A.夏季受印度低压控制B.常年受盛行西风影响C.夏季受西南季风影响D.常年受副热带高压控制答案 C(2020浙江1月选考,25,3分)海陆间常常存在气温差异。
T1、T₂分别为亚欧大陆东、西海岸海陆间平均气温差(T1、T2取绝对值)。
下图分别为1月和7月△T 沿经向分布折线图(图中△T 为T₁与T₂差的绝对值)。
完成下题。
1月5.1 月亚欧大陆45°N 以北,△T 较大的主要原因是①亚洲低压与大洋副热带高压形成热力差异②北大西洋暖流增加西部海岸温度③大陆中部高原的存在缩小了东西沿岸温差④季风影响了东部陆地与海洋间温差A.①②B.①③C.②④D.③④答案 C7月( )(2020 江苏单科,8,2 分)选择大洋航线时,应在确保航行安全的前提下,充分考虑气象、海况条件和岛礁等 因素,尽可能沿地球表面大圆(以地心为圆心过地表两点的圆)航行。
(浙江专用)2013届高考数学 冲刺必备 第二部分 专题三 第二讲 冲刺直击高考

设数列 {an}的公差为d,
则(a2+3d)2=(a2+2d)(a2+6d).
将a2=3代入上式化简整理得d2+2d=0.
又因为d≠0,所以d=-2.
于是an=a2+(n-2)d=-2n+7,即数列{an}的通项公式为an=-2n+7.
(2)假设存在正整数对(n,k),使得nan=kSn,则由(1)知Sn==6n-n2.
(1)求{an}的通项公式;
(2)若bn=an +qan(q>0),求数列{bn}的前n项和Sn.
解:(1)设数列{an}的首项为a1,公差为d,则由a5=9,a2+a6=14,得
解得
所以{an}的通项an=2n-1.
(2)由an=2n-1得bn=2n-1+q2n-1.
当q>0且q≠1时,Sn=[1+3+5+…+(2n-1)]+(q1+q3+q5+…+q2n-1)=n2+;
2013届高考数学(浙江专用)冲刺必备:第二部分专题三第二讲冲刺直击高考
限时:60分钟 满分:84分
1.(满分14分)已知数列{an}的前n项和Sn=-n2+kn(其中k∈N*),且Sn的最大值为8.
(1)确定常数k,并求an;
(2)求数列的前n项和Tn.
解:(1)当n=k∈N+时,Sn=-n2+kn取最大值,
(1)试用an-1,bn-1表示an,bn;
(2)求证:数列{an-bn}是等比数列,数列{an+bn}是常数数列;
(3)求数列{an},{bn}的通项公式.
解:(1)由题意知,
an==an-1+bn-1,
bn==bn-1+an-1.
(2)证明:由(1)知,an-bn=(an-1-bn-1),
高考英语二轮复习专题三阅读理解第二讲主旨意题习

第二讲│ 主旨大意题一、题型解读主旨大意题是高考英语阅读理解中常考的题型之一,主要考查考生把握全文主题和理解中心思想的能力。
通常以概括文章或段落大意以及选择标题等形式出现。
主旨大意题是阅读理解题中的高难度题,能够拉开考生的分数差距,所以此类题目在高考试题中具有很好的选拔作用,属于能力型题目。
主旨大意题一般分为三类:二、设问方式解答主旨大意题时要抓住文章的首尾段和每一段的首尾句,要注意贯穿文章始终的词语。
1.标题归纳类主旨大意题的主要设题形式·What is the best title for this passage?·Which of the following can be the best title for the passage?·The title that best expresses the idea of the passage is ________.·The most suitable title of this passage is ________.·What w ould be the most suitable title for the text?·The suitable title of the passage may be ________.2.文章大意类主旨大意题的主要设题形式·What is the main idea of the passage?·The passage is mainly about ________.·Which of the following can best summarize the passage?·Wha t is the subject discussed in the passage?·What does the passage mainly deal with?3.段落大意类主旨大意题的主要设题形式·The main idea of the second paragraph is probably that ________.·What is the last paragraph chiefly concerned with?·What does the writer try to expre ss in Paragraph 3?·Which of the following can best summarize Paragraph 1?·What is the main idea discussed in Paragraph 2?三、选项特征1.主旨大意题正确选项的特征(1)涵盖性强,覆盖全文或全段。
2020版高三数学二轮复习(全国理)讲义:专题三第二讲三角恒等变换与解三角形

[解析] 由题意S △ABC =12ab sin C =a2+b2-c24.即sin C =a2+b2-c22ab .由余弦定理可知sin C =cos C .即tan C =1.又C ∈(0.π).所以C =π4.3.(20xx·全国Ⅰ卷.11)已知角α的顶点为坐标原点.始边与x 轴的非负半轴重合.终边上有两点A ()1,a .B ()2,b .且cos2α=23.则||a -b =( B )A .15B .55C .255D .1[解析] 由cos2α=2cos 2α-1=23可得cos 2α=56=cos2αsin2α+cos2α=1tan2α+1.化简可得tan α=±55;当tan α=55时.可得a 1=55.b 2=55.即a =55.b =255.此时|a -b |=55;当tan α=-55时.仍有此结果.故|a -b |=55. 4.(20xx·天津卷.6)将函数y =sin ⎝ ⎛⎭⎪⎫2x +π5的图象向右平移π10个单位长度.所得图象对应的函数( A )A .在区间⎣⎢⎡⎦⎥⎤3π4,5π4上单调递增 B .在区间⎣⎢⎡⎦⎥⎤3π4,π上单调递减 C .在区间⎣⎢⎡⎦⎥⎤5π4,3π2上单调递增 D .在区间⎣⎢⎡⎦⎥⎤3π2,2π上单调递减 [解析] 选A .因为将函数y =sin ⎝ ⎛⎭⎪⎫2x +π5的图象向右平移π10个单位长度.得到函数y =sin2x 的图象. 用五点法作出草图.如图:从图中可以看出选项A 正确.其他都不正确.⎝ ⎛4-α=5.sin22+=4.+c=.则△7.(20xx·淮北二模)在△ABC 中.角A .B .C 的对边分别为a .b .c .若a 2=3b 2+3c 2-23bc sin A .则C 等于π6.[解析] 由余弦定理得a 2=b 2+c 2-2bc cos A . 所以b 2+c 2-2bc cos A =3b 2+3c 2-23bc sin A .3sin A -cos A =b2+c2bc .2sin(A -π6)=b2+c2bc ≥2.因此b =c .A -π6=π2⇒A =2π3.所以C =π-2π32=π6. 8.(20xx·长沙三模)在锐角△ABC 中.D 为BC 的中点.满足∠BAD +∠C =90°.则角B .C 的大小关系为B =C .(填“B <C ”“B =C ”或“B >C ”)[解析] 设∠BAD =α.∠CAD =β.因为∠BAD +∠C =90°.所以α=90°-C .β=90°-B . 因为D 为BC 的中点. 所以S △ABD =S △ACD . 所以12c ·AD sin α=12b ·AD sin β.所以c sin α=b sin β.所以c cos C =b cos B . 由正弦定理得.sin C cos C =sin B cos B .即sin2C =sin2B .所以2B =2C 或2B +2C =π. 因为△ABC 为锐角三角形.所以B =C .9.为了竖起一块广告牌.要制造三角形支架.如图.要求∠ACB =60°.BC 的长度大于1米.且AC 比AB 长0.5米.为了稳定广告牌.要求AC 越短越好.则AC 最短为2+3.[解析] 由题意设BC =x (x >1)米. AC =t (t >0)米.依题设AB =AC -0.5 =(t -0.5)米.在△ABC 中.由余弦定理得: AB 2=AC 2+BC 2-2AC ·BC cos60°.所以sin2A =2sin A cos A =1213. cos2A =1-2sin 2A =-513. 所以sin(2A +π4)=sin2A cos π4+cos2A sin π4=7226.B 组1.(20xx·福州三模)已知a .b .c 分别是△ABC 的内角A .B .C 所对的边.点M 为△ABC 的重心.若a MA →+b MB →+33c MC →=0.则C =( D )A .π4B .π2 C .5π6D .2π3[解析] ∵M 为△ABC 的重心.则MA →+MB →+MC →=0. ∴MA →=-MB →-MC →. ∵a MA →+b MB →+33c ·MC →=0.∴a ·(-MB →-MC →)+b MB →+33c ·MC →=0.即(b -a )·MB →+(33c -a )·MC →=0.∵MB →与MC →不共线. ∴b -a =0.32c -a =0.得a b33c =111.令a =1.b =1.c =3.则cos C =a2+b2-c22ab =1+1-32×1×1=-12.∴C =2π3.故选D .2.(20xx·××市一模)若sin(π6-α)=13.则cos(2π3+2α)=( A )。
2020版高三数学二轮复习(全国理)讲义:专题三第二讲三角恒等变换与解三角形

高考考点考点解读[解析] 由题意S △ABC =12ab sin C =a2+b2-c24,即sin C =a2+b2-c22ab ,由余弦定理可知sin C =cos C ,即tan C =1,又C ∈(0,π),所以C =π4.3.(20xx·全国Ⅰ卷,11)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A ()1,a ,B()2,b ,且cos2α=23,则||a -b =( B ) A .15B .55C .255D .1[解析] 由cos2α=2cos 2α-1=23可得cos 2α=56=cos2αsin2α+cos2α=1tan2α+1,化简可得tan α=±55;当tan α=55时,可得a 1=55,b 2=55,即a =55,b =255,此时|a -b |=55;当tan α=-55时,仍有此结果,故|a -b |=55. 4.(20xx·天津卷,6)将函数y =sin ⎝ ⎛⎭⎪⎫2x +π5的图象向右平移π10个单位长度,所得图象对应的函数( A )A .在区间⎣⎢⎡⎦⎥⎤3π4,5π4上单调递增 B .在区间⎣⎢⎡⎦⎥⎤3π4,π上单调递减 C .在区间⎣⎢⎡⎦⎥⎤5π4,3π2上单调递增 D .在区间⎣⎢⎡⎦⎥⎤3π2,2π上单调递减 [解析] 选A .因为将函数y =sin ⎝ ⎛⎭⎪⎫2x +π5的图象向右平移π10个单位长度,得到函数y=sin2x 的图象.用五点法作出草图,如图:从图中可以看出选项A 正确,其他都不正确.⎝ ⎛4-α=5,则sin22 .=4+2c=R,则△9.为了竖起一块广告牌,要制造三角形支架,如图,要求∠ACB =60°,BC 的长度大于1米,且AC 比AB 长0.5米,为了稳定广告牌,要求AC 越短越好,则AC 最短为2+3.[解析] 由题意设BC =x (x >1)米, AC =t (t >0)米,依题设AB =AC -0.5 =(t -0.5)米,在△ABC 中,由余弦定理得: AB 2=AC 2+BC 2-2AC ·BC cos60°, 即(t -0.5)2=t 2+x 2-tx ,化简并整理得: t =x2-0.25x -1(x >1),即t =x -1+0.75x -1+2,因为x >1,故t =x -1+0.75x -1+2≥2+3, 当且仅当x =1+32时取等号,此时取最小值2+3.10.(20xx·全国卷Ⅰ,17)在平面四边形ABCD 中,∠ADC =90°,∠A =45°,AB =2,BD =5.(1)求cos ∠ADB ; (2)若DC =22,求BC .[解析] (1)在△ABD 中,由正弦定理得BD sinA =AB sin ∠ADB. 由题设知,5sin45°=2sin ∠ADB ,所以sin ∠ADB =25. 由题意知,∠ADB <90°, 所以cos ∠ADB =1-225=235.∴a ·(-MB →-MC →)+b MB →+33c ·MC →=0.即(b -a )·MB →+(33c -a )·MC →=0,∵MB →与MC →不共线, ∴b -a =0,32c -a =0. 得a b33c =111,令a =1,b =1,c =3, 则cos C =a2+b2-c22ab =1+1-32×1×1=-12,∴C =2π3,故选D .2.(20xx·××市一模)若sin(π6-α)=13,则cos(2π3+2α)=( A ) A .-79B .79C .-29D .29[解析] ∵cos(2π3+2α)=-cos(π3-2α)=-[1-2sin 2(π6-α)]=-(1-29)=-79.3.(20xx·威海二模)已知等腰△ABC 满足AB =AC ,3BC =2AB ,点D 为BC 边上的一点且AD =BD ,则sin ∠ADB 的值为( C )A .36B .23C .223D .63[解析] 如图,设AB =AC =a ,AD =BD =b ,由3BC =2AB ,。
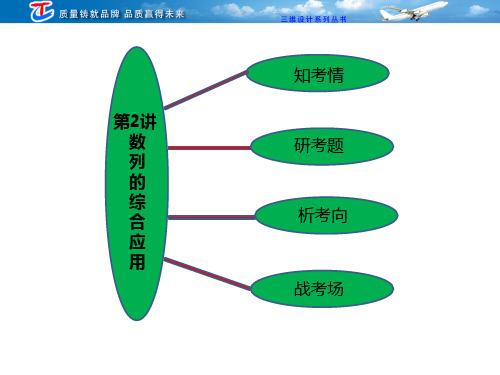
专题三 第二讲 数列的综合应用
解析: 两点坐标代入f(x)得 解析:将A、B两点坐标代入 得 、 两点坐标代入 1 1 =ab2 a= = 2 ,解得 8 , 1=ab3 b=2 = = 1 1 - ∴f(x)= ·2x,∴f(n)= ·2n=2n 3, = = 8 8 ∴an=log2f(n)=n-3. = - , - ≤ , ≤ 令an≤0,即n-3≤0,n≤3. 项小于或等于零, ∴数列前3项小于或等于零,故S3或S2最小. 数列前 项小于或等于零 最小. S3=a1+a2+a3=- +(-1)+0=- =-2+ - + =- =-3.
+
nban-1 an-1+n-1 -
[解] 解
nban-1 (1)∵a1=b>0,an= ∵ > , , an-1+n-1 -
- n 1 1 n-1 ∴ a = b+ b· , an-1 n n 1 1 令cn=a ,则cn=b+bcn-1, n 1 1 ①当b=1时,cn=1+cn-1,且c1=a =b=1 = 时 +
解答题
数列的实际 数列的实际应用问题一般是等差数列或等比 解答题为 应用 数列通项、求和问题,题目难度一般较大 数列通项、求和问题,题目难度一般较大. 主
[联知识 串点成面 联知识 串点成面] 数列求和的方法技巧: 数列求和的方法技巧: (1)转化法: 转化法: 转化法 有些数列,既不是等差数列,也不是等比数列, 有些数列,既不是等差数列,也不是等比数列,若将数 列通项拆开或变形,可转化为几个等差、 列通项拆开或变形,可转化为几个等差、等比数列或常 见的数列,即先分别求和,然后再合并. 见的数列,即先分别求和,然后再合并.
(2)Tn=1×2+4×5+42×8+…+4n-1(3n-1),① × + × + + - ,
-
2023年高考英语二轮复习专题三概要写作第2讲微观把握、突破概要写作技法二变化句式,方法独特

第三部分专题三第2讲技法2(2022·上海市杨浦区高三二模)阅读下面短文,根据其内容写一篇60词左右的内容概要。
A New Wave of MigrationAs the sea extends steadily inland in countries such as Bangladesh and as decreasing rains put already marginal farmland out of play in Ethiopia and other places, a wave of migration caused by the changing climate is taking shape on the horizon.But most “climate migrants” will not be heading abroad to start new lives; instead they will settle elsewhere in their home countries.A report released this week declares that if nothing is done to control global warming and factor migration into development planning, by mid-century this internal population shift could involve more than 140 million people in three regions examined: sub-Saharan Africa, south Asia and Latin America.“Climate change is already a driver of internal migration, and it will become more so in the future,” says John Roome, senior director of Climate change at The World Bank Group.The potential for such an increase in area consisting of 55 percent of the developing worldʼs population raises questions of environmental justice because those who have contributed the least to global warming are forced to shoulder more of the burden.It is necessary for developed countries like the U.S.to step up, says Maria Cristina Garcia, a professor of American Studies at Cornell University.Developed countries can help by both working to limit greenhouse gas emissions and funding efforts to help developing nations plan for climate migration challenges.The study of climate migration is still relatively new, and projections of just how many people might be driven from their homes as the world warms are hard to pin down.Some people will need to migrate despite any measures that might be taken—but “this doesnʼt have to be a crisis” Roome says.Properly managed migration could even bring more economic opportunities to some poor communities.But planning needs to start now.【范文】As the sea extends steadily inland, a wave of migration caused by the changing climate appears.Most “climate migrants” will settle elsewhere in their home countries.Itʼs unfair for the countries who have contributed the least to global warming to shoulder more of the burden.Though the climate migration is still relatively new, planning needs to start now.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.显微镜使用过程中,能调节通光孔大小吗? 显微镜使用过程中,能调节通光孔大小吗? 显微镜使用过程中 不能。通光孔是位于显微镜载物台上的固定孔道。 答案 不能。通光孔是位于显微镜载物台上的固定孔道。 4.由低倍镜换成高倍镜时,需使用粗准焦螺旋吗? 由低倍镜换成高倍镜时,需使用粗准焦螺旋吗? 由低倍镜换成高倍镜时 不是。直接旋转转换器即可换上高倍物镜。 答案 不是。直接旋转转换器即可换上高倍物镜。 5.动物体干重最多的元素是 O 吗? 动物体干重最多的元素是 不是。动物体中蛋白质多,糖类少, 最多, 答案 不是。动物体中蛋白质多,糖类少,故干重中 C 最多, 而植物相反。 而植物相反。 6.碳是生命的核心元素吗? 碳是生命的核心元素吗? 碳是生命的核心元素吗 答案 碳能够通过化学键连接成链或环, 是。碳能够通过化学键连接成链或环,从而形成各种
49.有丝分裂过程中有联会现象吗? 有丝分裂过程中有联会现象吗? 有丝分裂过程中有联会现象吗 没有。联会发生在减数分裂过程中。 答案 没有。联会发生在减数分裂过程中。 50.一个精原细胞只能产生两种配子吗? 一个精原细胞只能产生两种配子吗? 一个精原细胞只能产生两种配子吗 不是。 个精子、 答案 不是。经过交叉互换后就产生 4 个精子、四 种类型。 种类型。 51.两大遗传定律适用于原核生物吗? 两大遗传定律适用于原核生物吗? 两大遗传定律适用于原核生物吗 答案 不适用。 不适用。 两大遗传定律只适用于进行有性生
专题三 教材回扣与考前指导
二、易错易混辨析
1.病毒属于生命系统吗? 病毒属于生命系统吗? 病毒属于生命系统吗 答案 不属于。病毒没有细胞结构, 不属于。病毒没有细胞结构,细胞是生命系统的基本
单位。 单位。 2.病毒是原核生物吗? 病毒是原核生物吗? 病毒是原核生物吗 答案 不是。 病毒没有细胞结构, 主要由蛋白质和核酸构成。 不是。 病毒没有细胞结构, 主要由蛋白质和核酸构成。
间的细胞质构成的。 间的细胞质构成的。 26.核膜是双膜细胞器吗? 核膜是双膜细胞器吗? 核膜是双膜细胞器吗 不是。核膜是双膜细胞结构。 答案 不是。核膜是双膜细胞结构。 27.胞吞、胞吐体现了细胞膜具有选择透过性吗? 胞吞、胞吐体现了细胞膜具有选择透过性吗? 胞吞 答案 没有。胞吞、胞吐体现了细胞膜具有流动性。 没有。胞吞、胞吐体现了细胞膜具有流动性。
生物大分子。 生物大分子。
7.晒干的种子中有水吗? 晒干的种子中有水吗? 晒干的种子中有水吗 晒干的种子中的水少量以自由水存在, 答案 有。晒干的种子中的水少量以自由水存在,大量以结 合水形式存在。 合水形式存在。 8.一条肽链只含一个游离的氨基、一个游离的羧基吗? 一条肽链只含一个游离的氨基、一个游离的羧基吗? 一条肽链只含一个游离的氨基 不一定。 基上可能含有。 答案 不一定。在 R 基上可能含有。一条肽链至少含一个 游离的氨基、一个游离的羧基。 游离的氨基、一个游离的羧基。 9.蛋白质是生命活动的体现者吗? 蛋白质是生命活动的体现者吗? 蛋白质是生命活动的体现者吗 不是。蛋白质是生命活动的承担者,控制者是基因 控制者是基因。 答案 不是。蛋白质是生命活动的承担者 控制者是基因。 10.蛋白质都是由 20 种氨基酸合成的吗? 蛋白质都是由 种氨基酸合成的吗? 不是。蛋白质不同,利用的氨基酸可能不同 利用的氨基酸可能不同。 答案 不是。蛋白质不同 利用的氨基酸可能不同。
质不变。 质不变。 40.NaOH 在琼脂中扩散深度代表物质吸收速率吗? 在琼脂中扩散深度代表物质吸收速率吗? 答案 不是。NaOH 在琼脂块中扩散体积与整个琼脂块 不是。
体积之比代表物质吸收速率。 体积之比代表物质吸收速率。
41.用洋葱鳞片叶表皮细胞能观察到分裂现象吗? 用洋葱鳞片叶表皮细胞能观察到分裂现象吗? 用洋葱鳞片叶表皮细胞能观察到分裂现象吗 不能。洋葱鳞片叶表皮细胞是高度分化细胞, 答案 不能。洋葱鳞片叶表皮细胞是高度分化细胞,不进 行分裂。 行分裂。 42.细胞衰老,个体一定衰老吗? 细胞衰老,个体一定衰老吗? 细胞衰老 不一定。 幼年个体,有细胞的衰老。 答案 不一定。如:幼年个体,有细胞的衰老。 43.狗的长毛和卷毛是相对性状吗? 狗的长毛和卷毛是相对性状吗? 狗的长毛和卷毛是相对性状吗 答案 不是。 不是。 相对性状是指一种生物的同一性状的不同表 现类型。 现类型。 44.AA1、aa′基因型个体是纯合子吗? ′基因型个体是纯合子吗? 不是。 答案 不是。 纯合子是由基因型相同的配子结合成的合子 发育成的个体。 发育成的个体。A 与 A1、a 与 a′基因不同。AA1、aa′ ′基因不同。 ′ 个体是杂合子。 个体是杂合子。
18.观察 DNA 和 RNA 在细胞中的分布实验中,能选植物 观察 在细胞中的分布实验中, 叶肉细胞吗? 叶肉细胞吗? 不能。避免叶绿体中色素的干扰。 答案 不能。避免叶绿体中色素的干扰。 19.双缩脲试剂是直接混合后使用吗? 双缩脲试剂是直接混合后使用吗? 双缩脲试剂是直接混合后使用吗 不是。 答案 不是。先加 A 液再加 B 液。 20.斐林试剂和双缩脲试剂成分相同吗? 斐林试剂和双缩脲试剂成分相同吗? 斐林试剂和双缩脲试剂成分相同吗 答案 相同。都含有 NaOH、CuSO4 两种成分。 相同。 两种成分。 、 21.光学显微镜下,能看见植物细胞的细胞膜吗? 光学显微镜下,能看见植物细胞的细胞膜吗? 光学显微镜下 在植物细胞发生质壁分离时,能看到。 答案 能。在植物细胞发生质壁分离时,能看到。 22.线粒体、叶绿体都是内膜面积大于外膜吗? 线粒体、叶绿体都是内膜面积大于外膜吗? 线粒体 不是。叶绿体的外膜面积大于内膜。 答案 不是。叶绿体的外膜面积大于内膜。 23.植物体都没有中心体吗? 植物体都没有中心体吗? 植物体都没有中心体吗 低等植物有中心体。 答案 不。低等植物有中心体。
45.基因型相同的个体,表现型一定相同吗? 基因型相同的个体,表现型一定相同吗? 基因型相同的个体 一定。 基因表达过程中受环境条件影响。 关系如下: 答案 不一定。 基因表达过程中受环境条件影响。 关系如下: 表现型=基因型+环境条件。 表现型=基因型+环境条件。 46.利用豌豆做自交实验必须套袋吗? 利用豌豆做自交实验必须套袋吗? 利用豌豆做自交实验必须套袋吗 没必要。豌豆是闭花传粉植物。 答案 没必要。豌豆是闭花传粉植物。 47.基因在染色体上成对存在吗? 基因在染色体上成对存在吗? 基因在染色体上成对存在吗 不是。基因在染色体上呈线性排列。 答案 不是。基因在染色体上呈线性排列。 48.遗传定律发生在受精过程中吗? 遗传定律发生在受精过程中吗? 遗传定律发生在受精过程中吗 不是。遗传定律发生在减数分裂产生配子过程中。 答案 不是。遗传定律发生在减数分裂产生配子过程中。
过取决于分子大小与膜上孔径的大小。 过取决于分子大小与膜上孔径的大小。选择透过性膜是 具有生命的生物膜, 具有生命的生物膜,载体蛋白的存在决定物质是否能被 运输。 运输。 30.主动运输中,物质一定是由低浓度一侧向高浓度一侧运 主动运输中, 主动运输中 输吗? 输吗? 不一定。 答案 不一定。 酶在低温下丧失活性吗? 31.酶在低温下丧失活性吗? 酶在低温下丧失活性吗 答案 不。酶在低温下活性降低,但不变性,随温度升 酶在低温下活性降低,但不变性,
A、T、G、C,烟草花叶病毒的遗传物质 、 、 、 ,烟草花叶病毒的遗传物质 病毒的遗传物质(RNA)构成的碱基 构成的碱基 是 A、U、G、C。 、 、 、 。 14.脱氧核糖不含氧元素吗? 脱氧核糖不含氧元素吗? 脱氧核糖不含氧元素吗 答案 素。 含。核糖经脱氧形成脱氧核糖,但脱氧核糖仍含氧元 核糖经脱氧形成脱氧核糖,
37.无氧呼吸产生酒精、CO2 的过程与产生乳酸的过程中, 无氧呼吸产生酒精、 的过程与产生乳酸的过程中, 无氧呼吸产生酒精 同质量的葡萄糖产生的能量相同吗? 同质量的葡萄糖产生的能量相同吗? 答案 不相同。 的过程中产生能量多, 不相同。产生酒精和 CO2 的过程中产生能量多,
量相同。 但两个生理过程产生的 ATP 量相同。 38.细胞分裂过程中,赤道板能用光学显微镜观察到吗? 细胞分裂过程中,赤道板能用光学显微镜观察到吗? 细胞分裂过程中 答案 不能。赤道板不是真实存在的结构。 不能。赤道板不是真实存在的结构。 3Байду номын сангаас.细胞分化过程中,遗传物质改变吗? 细胞分化过程中,遗传物质改变吗? 细胞分化过程中 答案 不改变。细胞分化是基因的选择性表达,遗传物 不改变。细胞分化是基因的选择性表达,
高,酶的活性会恢复。 酶的活性会恢复。
32.酶一定是蛋白质吗? 酶一定是蛋白质吗? 酶一定是蛋白质吗 不一定。 答案 不一定。少量酶的本质是 RNA。 。 33.缺氧状态下,需氧生物一定不产生 ATP 吗? 缺氧状态下, 缺氧状态下 产生。通过无氧呼吸, 答案 产生。通过无氧呼吸,可产生 ATP,但不能满 ,但不能满 足机体需要。 足机体需要。 34.线粒体能氧化分解葡萄糖吗? 线粒体能氧化分解葡萄糖吗? 线粒体能氧化分解葡萄糖吗 答案 不能。线粒体缺乏催化葡萄糖水解的酶。 不能。线粒体缺乏催化葡萄糖水解的酶。 35.人呼出的 CO2 中的氧是吸入的 O2 中的氧吗? 人呼出的 中的氧吗? 不是。 答案 不是。人呼出的 CO2 中的氧来自体内有机物质 和水, 变成了水中的氧。 和水,吸入的 O2 变成了水中的氧。 36.扩散最快的色素在层析液中溶解度最大吗? 扩散最快的色素在层析液中溶解度最大吗? 扩散最快的色素在层析液中溶解度最大吗 在层析液中溶解度最大的色素, 答案 是。在层析液中溶解度最大的色素,在滤纸条 上扩散速率最快。 上扩散速率最快。
24.植物细胞都有叶绿体和液泡吗? 植物细胞都有叶绿体和液泡吗? 植物细胞都有叶绿体和液泡吗 答案 不。植物体不见光部位无叶绿体,分裂活动旺盛部 植物体不见光部位无叶绿体,
位没有液泡(大液泡 。 位没有液泡 大液泡)。 大液泡 25.原生质层包括细胞核吗? 原生质层包括细胞核吗? 原生质层包括细胞核吗 答案 不包括。原生质层是由细胞膜、 不包括。原生质层是由细胞膜、液泡膜以及两者之
