最新六年级正反比例练习题
六年级数学下册正反比例判断练习题(人教版)

正反比例练习题班级:姓名:成绩:一、判断题1.植树的成活率一定,植树的棵树和成活的棵树成正比例。
( )2.圆的面积和半径成正比例。
( )3.正方形的周长和边长成正比例。
( )4.圆柱体的高一定,底面半径与体积成正比例。
( )5.小明的年龄和她的妈妈的年龄成正比例。
( )6.圆锥体的高一定,体积和底面半径的平方成正比例。
( )7.总价一定,单价和数量成反比例。
()8..实际距离一定,图上距离与比例尺成正比例。
()9.正方体体积一定,底面积和高成反比例。
()10.订阅《辽沈晚报》的总钱数和分数成正比例。
()11、方砖的边长一定,要铺地面积和用砖块数成正比例。
()12、用瓷砖铺地,要用的砖数一定,铺地的面积和瓷砖的面积成正比例。
()13、要铺地的总面积一定,每块方砖的边长与需要的块数成正比例。
()16、梯形的面积一定,高和上下底的和成反比例。
()17、圆的半径一定,圆的面积和兀不成比例。
()18、加工时间一定,加工零件个数和加工每个零件所需的时间成反比例。
()19、南京到北京,所行驶的路程和速度不成比例。
()20、出盐率一定,盐的重量和盐水重量成正比例。
()21、正方形的边长和面积成正比例。
()22. y:7=x y和x成()比例。
23.圆柱德高一定,体积和底面积成()关系。
24.圆的周长和直径成()比例。
二、选择题1、因为14 X=2Y,所以X:Y=():(),X和Y成()比例。
2、因为X=2Y,所以X:Y=():(),X和Y成()比例。
3、下列各式中(a、b均不为0),a和b成正比例的是()。
A 、a×8=b×5B 、9a=6bC 、a×13 -1÷b= 0 D、a+710 =b4、下面不成比例的是( )。
A、正方形的周长和边长B、某同学从家到学校的步行速度和所用时间C、圆的体积和表面积5、如果y=15x, x和y成( )比例;如果y=X15, x和y成( )比例6、如果Y = 8X ,X 和Y 成()比例如果Y =X8,X 和Y 成()比例。
小学六年级数学:正反比例练习题

)
四、下列各题中的两种量就是不就是成比例 , 成什么比例 , 并说明理由。
(1) 买相同的电脑 , 购买的电脑台数与总价
(2) 每捆练习本的本数相同 , 练习本的总本数与捆数 (3) 总路程一定 , 已行的路程与未行的路程 (4) 分数值一定 , 分数的分子与分母 (5) 长方形的长一定 , 它的面积与宽 (6) 长方体的体积一定 , 底面积与高 (7) 一本书的总页数一定 , 瞧的天数与平均每天瞧的页数
) 。 A、 成正比例
10 …… …… B、
成反比例
X2 Y (2)X 与 Y(
35
10 ……
4 2、4 12
……
) 。A、 成正比
例
B 、 成反比例
3. 选择填空。
(1) 长方形的 _________________,它的长与
面积成正比例。
A. 周长一定
B、宽一定
C 、面
积一定
(2) 圆柱体体积一定 ,________________与
高成反比例。A 、底面半径B、来自面积C、表面积
六、应用题
(1) 工厂制作一种零件 , 现在每个零件所用的
时间由革新前的 8 分钟减少到 3 分钟 , 原来制
造 60 个的时间现在能生产多少个? ( 用比例方
法解答 )
a÷ b=c, 当 c 一定时 a 与 b( ); 当 a 一定时 b
与 c( ); 当 b 一定时 a 与 c( ) 。A、 成正比
) 。A、成正
(4) 平行四边形的面积不变 , 它的底与高成反
例
B、成反比
比例。 ( )
例
C、不成比例
五、选择题
年龄 2 3 4
5
6 ……
(完整)六年级正反比例实例练习题

(完整)六年级正反比例实例练习题六年级正反比例实例练题
问题一
在某个比例中,正比例常数是4。
如果当x等于6时,y等于8,那么y是多少时,x等于10?
根据正比例的定义,我们可以得到以下比例关系式:
x y
- = -
6 8
再根据比例的性质,我们可以发现两个关键点:(6, 8) 和 (10, y)。
现在我们可以利用已知的关键点来求解未知的值:
6/8 = 10/y
通过交叉相乘的运算,我们可以得到:
6y = 80
最后,我们将上式解为y:
y = 80/6
因此,当x等于10时,y的值为13.33。
问题二
某公司的收入和投资之间存在着正反比例关系。
该公司的收入是100万美元,而投资是200万美元。
如果该公司的收入增加至150万美元,那么投资会减少到多少?
根据正反比例的定义,我们可以得到以下比例关系式:
收入投资
---- = ------
100万 200万
现在我们可以利用已知的比例关系来解决问题。
已知收入增加到150万美元,我们要求投资的值。
150/100 = 200/投资
通过交叉相乘的运算,我们可以得到:
150 * 投资 = 100 * 200
最后,我们将上式解为投资:
投资 = (100 * 200) / 150
因此,当收入增加到150万美元时,投资会减少到133.33万美元。
以上是关于六年级正反比例实例练习题的解答,希望对您有帮助。
如果还有其他问题,请随时提问。
正反比例练习题六年级

正反比例练习题六年级一、判断题1. 如果两个变量的比值一定,那么这两个变量成正比例。
2. 两个量的乘积一定时,这两个量成反比例。
3. 物体行驶的速度与行驶的时间成反比例。
4. 成本和数量成正比例。
5. 一个数与它的倒数的乘积为1,所以一个数与它的倒数成反比例。
二、选择题1. 下列哪个关系成正比例?A. 圆的半径和面积B. 物体的质量和体积C. 路程和时间D. 圆的周长和直径2. 下列哪个关系成反比例?A. 单价和总价B. 速度和时间C. 工作效率和工作量D. 路程和速度三、填空题1. 如果两个变量成正比例,那么它们的比值是______。
2. 如果两个变量成反比例,那么它们的乘积是______。
3. 在平面直角坐标系中,正比例函数的图像是一条经过______的直线。
4. 在平面直角坐标系中,反比例函数的图像是______双曲线。
5. 一个长方形的面积是30平方厘米,如果长和宽成反比例,那么当长为6厘米时,宽为______厘米。
四、应用题1. 某品牌手机充电器输出电压为5V,充电电流为1A。
请问充电器的功率是多少?2. 小明骑自行车去图书馆,路程为8公里,速度为4公里/小时。
请问小明骑车去图书馆需要多长时间?3. 某商品的单价是50元,如果购买5件可以享受8折优惠。
请问购买5件商品的总价是多少?4. 一个水池,每小时进水量为30立方米,出水口每小时出水20立方米。
请问经过5小时,水池中的水增加了多少立方米?5. 某班学生平均分为80分,其中最高分为95分。
如果将最高分改为100分,平均分将变为多少?五、计算题1. 已知正方形的周长是24厘米,求正方形的面积。
2. 一个数的2倍与它的3倍的和是60,求这个数。
3. 某数是它的1/3加上5,求这个数。
4. 一个长方形的长是宽的2倍,如果宽是6厘米,求长方形的面积。
5. 某人用每千克5元的价格购买了若干千克的苹果,总共花费了25元,求购买的苹果重量。
六、作图题1. 在方格纸上画出一个正比例函数的图像,其比例系数为2。
完整版六年级正反比例练习题
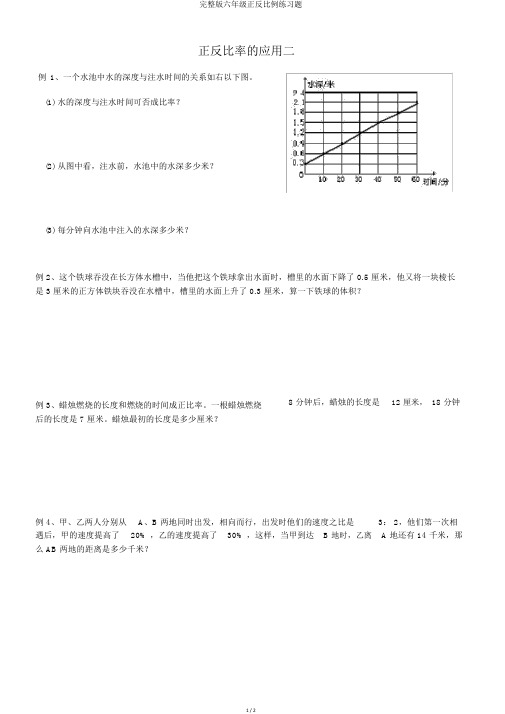
正反比率的应用二例1、一个水池中水的深度与注水时间的关系如右以下图。
(1)水的深度与注水时间可否成比率?(2)从图中看,注水前,水池中的水深多少米?(3)每分钟向水池中注入的水深多少米?例 2、这个铁球吞没在长方体水槽中,当他把这个铁球拿出水面时,槽里的水面下降了 0.5 厘米,他又将一块棱长是 3 厘米的正方体铁块吞没在水槽中,槽里的水面上升了 0.3 厘米,算一下铁球的体积?例 3、蜡烛燃烧的长度和燃烧的时间成正比率。
一根蜡烛燃烧后的长度是 7 厘米。
蜡烛最初的长度是多少厘米?8 分钟后,蜡烛的长度是12 厘米,18 分钟例 4、甲、乙两人分别从A、B 两地同时出发,相向而行,出发时他们的速度之比是遇后,甲的速度提高了20% ,乙的速度提高了30% ,这样,当甲到达 B 地时,乙离3: 2,他们第一次相A 地还有 14 千米,那么 AB 两地的距离是多少千米?看看你会做吗?1、用不相同的杯子装水,水的高度与杯子的底面积的关系如右图。
( 1)从图中看,水的高度与杯子的底面积可否成比率?成什么比率?为什么?( 2)从图中估计,当杯子的底面积是50 平方厘米时,水深多少厘米?当水深25 厘米时,杯子的底面积是多少平方厘米?2、将一个圆柱体完好吞没在一个装满水的水槽中,拿出后水面下降了9 厘米。
尔后放入一个底面积和圆柱体相同,高是圆柱体1的圆锥,这时水面会上升多少厘米?23、蜡烛燃烧的长度和燃烧的时间成正比率。
一根蜡烛燃烧12 分钟后,蜡烛的长度是17 厘米, 18 分钟后的长度是 9 厘米。
蜡烛最初的长度是多少厘米?4、甲、乙两人分别从A、 B 两地同时出发,相向而行,出发时他们的速度之比是后,甲的速度提高了20% ,乙的速度提高了40% ,当甲到达目的地后,乙还有AB 两地的距离是多少千米?4: 3,他们第一次相遇44 千米到达目的地,那么。
六年级正反比例题100道

六年级正反比例题100道正比例题:1. 如果一个苹果的价格是2元,那么5个苹果的价格是多少元。
2. 5本书的价格是20元,那么每本书的价格是多少元。
3. 一个足球的价格是50元,购买3个足球需要多少钱。
4. 如果一辆车每小时行驶60公里,行驶2小时后能行驶多少公里。
5. 4个橙子的总价是16元,1个橙子多少钱。
6. 一条绳子长6米,3条绳子总长多少米。
7. 如果每辆车能载5人,10辆车能载多少人。
8. 一盒巧克力有10块,3盒巧克力有多少块。
9. 每个学生要交100元的学费,10个学生总共交多少钱。
10. 一台电脑的价格是4000元,4台电脑的总价是多少元。
11. 如果1升油的价格是8元,5升油的价格是多少元。
12. 一辆自行车的价格是300元,7辆自行车总共需要多少钱。
13. 1本书的页数是200页,5本书的总页数是多少页。
14. 如果每个学生需要2支铅笔,20个学生需要多少支铅笔。
15. 一棵树的高度是3米,5棵树的总高度是多少米。
16. 1块蛋糕的价格是15元,3块蛋糕总共多少钱。
17. 如果每本杂志售价10元,9本杂志总共多少钱。
18. 一辆车每小时行驶80公里,4小时能行驶多少公里。
19. 如果1公斤米的价格是5元,2公斤米总共多少钱。
20. 每个孩子要喝250毫升的牛奶,8个孩子需要多少牛奶。
21. 一支笔的价格是3元,12支笔总共多少钱。
22. 如果一个篮球的价格是120元,3个篮球的价格是多少元。
23. 一根铅笔的长度是20厘米,4根铅笔的总长度是多少厘米。
24. 如果一个人的工资是3000元,5个人的总工资是多少元。
25. 每条鱼的重量是200克,10条鱼的总重量是多少克。
26. 如果1个西瓜的价格是30元,4个西瓜的价格是多少元。
27. 一辆车的油耗是每公里8升,行驶100公里需要多少升油。
28. 每个学生要用5张纸,25个学生需要多少张纸。
29. 如果一个房间的面积是50平方米,5个这样的房间总面积是多少平方米。
(完整)六年级正反比例练习题

一、判断。
1、一个因数不变,积与另一个因数成正比例。
()2、长方形的长一定,宽和面积成正比例。
()3、圆的半径和周长成正比例。
()4、铺地面积一定,方砖的边长和所需块数成反比例。
()5、铺地面积一定,方砖面积和所需块数成反比例。
()6、圆的面积和圆的半径成正比例。
()7、圆的面积和圆的半径的平方成正比例。
()8、圆的面积和圆的周长的平方成正比例。
()9、正方形的面积和边长成正比例。
()10、正方形的周长和边长成正比例。
()11、长方形的面积一定时,长和宽城反比例。
()12、长方形的周长一定时,长和宽城反比例。
()13、梯形的面积一定时,上底和下底的和与高成反比例。
()下列各题中的两个量是不是成比例?如果成比例,成什么比例?简单说明理由。
1.路程一定,速度和时间。
()2.车轮的直径一定,所行是的路程和车轮的转数。
()3.图上距离一定,实际距离和比例尺。
()4.数A与它的倒数。
()5.收入一定,支出和结余。
()6.除数一定,被除数和商。
()7.5A=3B,A和B。
()8.总价一定,观看同一场电影的票价和人数。
()9.三角形的面积和它的高。
()10.长方形的周长一定,它的长和宽。
()11、年龄和身高。
()12、比例尺一定,图上距离和实际距离。
()13、比的前项一定,比的后项与比值。
()二、应用题。
1、工厂制作一种零件,现在每个零件所用的时间由革新前的8分钟减少到3分钟,原来制造60个的时间现在能生产多少个?(用比例的方法解答)2、一个晒盐场用500千克海水可以晒15千克盐,照这样计算,用100吨海水可以晒多少千克盐?(用比例方法解答)3、印刷厂装订一批图书,原计划每天装订500本,30天完成;实际上只用了25天就完成了任务,实际每天装订多少本?(用比例方法解答)4、修路队修一条长120千米的公路,前4天修了20千米,照这样的速度,修完全路共需要多少天?(用比例方法解答)三、解比例25:7=X:35 X:15=13:56 2.8:0.8=0.7:X四、汽车的速度是火车速度的四分之三,两车从A底同时向B地开出,火车6小时到达,当火车到达B地时,汽车还需要再行多少小时到达?。
人教版六年级下册数学用正反比例解决问题练习题(含答案)

用正反比例解决问题练习题一、填空1.一种盐水,是由盐和水按1:50 配制而成的。
其中,盐的重量占盐水的(),水的重量占盐水的()。
2.一幅地图,图上A、B距离3厘米,地面上A、B距离150千米。
这幅图的比例尺是()。
3.如果x÷y = 11×5,那么x和y成()比例;如果x:4=5:y,那么x和y成()比例。
4.如果甲÷乙=丙,那么,甲一定时,乙和丙成()比例;乙一定时,甲和丙成()比例;丙一定时,甲和乙成()比例。
5.在比例尺为1:8的图纸上,甲、乙两圆的直径比是2:3,那么甲、乙两圆的实际的直径比是()。
二、选择1.如果3x=8y(x、y都不等于0),那么x和y()A、成正比例B、成反比例不成比例 D、以上说法都不对2.如果x3= y8(x、y都不等于0),那么x和y()A、成正比例B、成反比例C、不成比例D、以上说法都不对3.下列表示x和y成反比例的式子是()A、x+3y=12B、y=4xC、y=23x D、y=-32x4.已知kx=y,且x和y都不为0,当k一定时,x和y()A、成正比例B、成反比例C、不成比例D、以上说法都不对5.甲数的34是乙数,那么甲数与乙数()A、成正比例 B、成反比例C 、不成比例D 、以上说法都不对三、判断题1.正方形的边长和周长成正比例。
( )2.正方形的边长和面积成正比例。
( )3.a 是b 的57,数a 和数b 成正比例。
( )4.如果4a=3b,那么a ∶b=3∶4 。
( )5.A8= B ,那么A 和B 成反比例。
( )6.长方体的体积一定,底面积和高成反比例。
( )7.如果x 与y 成反比例,那么3 x 与y 也成反比例。
( )8.圆的面积与半径的平方成正比例。
( )9.圆锥的体积一定,底面积和高成反比例。
( ) 10.全班总人数一定,出勤人数和出勤率成正比例。
( )四、根据比例关系填表1.根据yx=10,填写下表。
(完整)六年级正反比例练习题册子

(完整)六年级正反比例练习题册子---目标本练题册致力于帮助六年级学生掌握正反比例的概念和运用,通过练题的演练,提升学生在解决正反比例问题上的能力。
练题册结构本练题册共分为四个部分,每个部分包含不同难度和类型的正反比例练题,涵盖了六年级正反比例相关的知识点和应用场景。
第一部分: 正比例练题该部分共包含30道正比例练题,题目类型包括选择题、填空题和计算题。
学生需要根据题目所给的条件,判断是否为正比例关系,并进行相关计算。
第二部分: 反比例练题该部分共包含30道反比例练题,题目类型同样包括选择题、填空题和计算题。
学生需要根据题目所给的条件,判断是否为反比例关系,并进行相关计算。
第三部分: 正反比例综合练题该部分共包含20道正反比例综合练题,旨在考察学生对正反比例的综合应用能力。
题目类型包括实际问题的分析和解决,需要学生灵活运用正反比例的概念和计算方法。
第四部分: 挑战题该部分共包含10道挑战题,考验学生在正反比例问题上的思维拓展和创新能力。
题目类型较为复杂,需要学生综合运用正反比例的知识进行解答。
使用方法学生可以根据自己的研究进度选择相应的部分进行练,建议按照顺序进行,逐渐提高难度。
每道题目的答案与解析都提供在练题册的尾页,学生可以通过自行核对答案和阅读解析来巩固所学知识和提高解题能力。
注意事项在完成练题时,请学生注意以下几点:- 仔细阅读题目,理解题意;- 注意题目所给的条件,判断正反比例关系;- 在计算过程中,注意单位的转换和精确度的处理;- 检查答案时,注意是否符合正反比例的要求。
尾声本练题册旨在帮助六年级学生巩固正反比例的知识和运用技巧。
希望学生通过练题的完成,能够对正反比例有更加深入的理解,并能够熟练运用到实际问题的解决中。
祝愿各位同学取得优异成绩!---。
六年级数学正比例和反比例试题答案及解析

六年级数学正比例和反比例试题答案及解析1.把一根木料锯成4段要用12分钟,照这样,如果要锯成6段,一共需要______分钟。
【答案】20【解析】解:设一共需要x分钟,则有12:(4-1)=x:(6-1),3x=12×5,3x=60,x=20;答:一共需要20分钟。
2.把一根木料锯成4段要6分钟,锯成7段要______分钟。
【答案】12【解析】6÷(4-1)×(7-1),=6÷3×6,=2×6,=12(分钟)答:锯成7段要12分钟。
3.学校买来161米塑料绳子,剪下21米,做12根跳绳,照这样计算,剩下的塑料绳还可以剪______根跳绳。
【答案】80【解析】解:设剩下的塑料绳还可以剪x根跳绳,21:12=(161-21):x,21:12=140:x,x=804.正午时小丽量得自己的影子有40cm,同时它量得身旁一棵树的影长是1m,已知小丽的身高是160cm,那么这棵树高______m。
【答案】4【解析】解:设这棵数高xm,160:40=x;1,40x=160×1,x=160÷40,x=4;答:这棵数高4米。
5.张师傅5小时生产了300个零件.照这样计算,生产480个零件需要多少小时?因题中______一定,所以这道题用______解答。
设_________________为X,列式为__________。
【答案】工作效率;正比例;生产480个零件需要的时间;300:5=480:x.【解析】因为题中的工作效率一定,所以这道题用正比例解答,设生产480个零件需要x小时,300:5=480:x,300x=480×5,x=x=86.正午时小丽量得自己的影子有30cm,同时它量得身旁一棵树的影长是1m,已知小强的身高是180cm,那么这棵树高______m。
【答案】6【解析】解:设这棵数高xm,180:30=x;1,30x=180×1,x=180÷30,x=6答:这棵数高6米。
小学六年级数学:正反比例练习题

小学六年级数学:正反比例练习题
在小学六年级数学的研究过程中,正反比例是一个重要的概念。
掌握正反比例的概念和运用,对于学生的数学能力的提升至关重要。
下面是一些正反比例的练题,帮助学生巩固和应用所学知识。
练题一
小明用 2 小时走了 10 公里的路程。
按照这个比例,如果他用 4 小时走,那么他能走多远?
练题二
一辆自行车每小时能骑行 15 公里的路程。
根据这个比例,如
果骑行时间是 5 小时,那么总共能骑行多远?
练题三
小红用 32 分钟做完了 8 道数学题。
如果按照这个比例,她需
要多少时间才能做完 12 道数学题?
练题四
Emma 一分钟能骑行 25 米。
如果她要骑行 5000 米,需要多少时间?
练题五
小杰一共用了 24 张纸来制作纸飞机。
如果他要制作 36 个纸飞机,需要多少张纸?
练题六
一辆汽车每小时耗油 10 升。
如果行驶 200 公里,需要多少升油?
以上是一些关于小学六年级数学正反比例的练题。
希望同学们通过解答这些题目,加深对正反比例的理解,并能正确应用于实际生活中的问题。
不断练和巩固相关知识,将有助于提高数学解题能力,为今后的研究打下坚实的基础。
祝大家学习进步!。
六年级判断正反比例练习题

六年级判断正反比例练习题判断下面每题中的两种量是不是成比例,成什么比例。
(1)一条水渠的长度一定,每天修的米数和共需要的天数。
()(2)一条水渠的长度一定,已修的长度和剩下的长度。
()(3)订阅《小学生研究报》的份数和钱数。
()(4)从甲地到乙地,汽车行驶的速度和所要的时间。
()(5)生产每个零件所用时间一定,工作时间和生产零件个数。
()(6)生产零件的时间一定,生产零件的个数和生产一个零件所用的时间。
()(7)同一时间,同一地点,杆高和影长。
()(8)小明的身高和体重。
()(9)铺地面积一定,每块砖的边长和所需砖的块数。
()(10)铺地面积一定,每块砖的面积和所需砖的块数。
()(11)每块地砖的面积一定,铺地的面积和地砖的块数。
()(12)两个互相咬合的齿轮,齿数与转数。
()(13)直角三角形的两个锐角。
()(14)花生出油率一定,花生和榨出的油。
()(15)圆的半径与面积。
()圆的面积和半径的平方()(16)圆的周长与直径。
()圆的周长与半径()(17)。
(18)圆的直径一定,它的周长和圆周率。
()圆的半径一定,它的周长和圆周率(19)路程肯定,车轮的直径和转数。
()路程一定,车轮的周长和转数(20)正方形的边长和周长。
()(21)正方形的边长和面积。
()正方形的边长的平方和面积()(22)长方形的周长一定,它的长和宽。
()(23)长方形的面积一定,它的长和宽。
()(24)长方形的长一定,它的面积和宽。
()(25)三角形面积一定,它的底和高。
()(26)直角三角形面积一定,它的两条直角边的长度。
()(27)平行四边形的高肯定,它的面积和底。
()(28)长方体的体积一定,底面积和高。
()(29)被除数一定,除数和商。
()(30)比的前项一定,比的后项和比值。
()(31)比值一定,比的前项和后项。
()(32)比例尺一定,图上距离和实际距离。
()(33)实际距离一定,图上距离的比例尺。
()(34)分母一定,分子和分数值。
六年级数学正反比例判断题(附答案)

六年级数学正反比例判断题(附答案)1、速度一定,路程和时间()比例
路程一定,速度和时间()比例
时间一定,路程和速度()比例
2、工作效率一定,工作总量和工作时间()比例
工作时间一定,工作效率和工作总量()比例工作总量一定,工作效率和工作时间()比例3、总价一定,单价和数量()比例
数量一定,单价和总价()比例
单价一定,数量和总价()比例
4、每公顷产量一定,总产量和公顷数()比例
公顷数一定,每公顷产量和总产量()比例
总产量一定,每公顷产量和公顷数()比例5、份数一定,每份数和总数()比例
每份数一定,份数和总数()比例
总数一定,每份数和份数()比例
6、商一定,除数和被除数()比例
除数一定,商和被除数()比例
被除数一定,除数和商()比例
7、积一定,两个因数()比例
一个因数一定,另一个因数和积()比例
8、和一定,两个加数()比例
一个加数一定,另一个加数与和()比例
9、差一定,减数和被减数()比例
减数一定,被减数和差()比例
被减数一定,减数和差()比例10、前项一定,比的后项和比值()比例
比值一定,比的前项和后项()比例后项一定,比的前项和比值()比例答案
1、正反正
2、正正反
3、反正正
4、正正反
5、正正反
6、正正反
7、反正
8、不成不成
9、不成不成不成
10、反正正。
六年级数学正比例和反比例试题

六年级数学正比例和反比例试题1.(1分)在一定时间里,做一个零件所用时间和做这种零件的个数成比例.【答案】反.【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.解:因为:做一个零件所用时间×做这种零件的个数=总时间(一定),即乘积一定,所以做一个零件所用时间和做这种零件的个数成反比例;故答案为:反.点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.2.(3分)两变一不变,一定,成正比例关系,一定,成关系.【答案】比值,乘积,反.【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.解:两变一不变,比值一定,成正比例关系,乘积一定,成反关系.故答案为:比值,乘积,反.点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.3.(3分)A÷C=B,当A一定时,B与C成反比例..【答案】正确【解析】要想判定B和C是不是成反比例关系,必须根据式子,进行推导.再根据正反比例的意义,分析数量关系,找出一定的量A,然后看B与C是比值一定还是乘积一定,从而判定成什么比例关系.解:因为:A÷C=B,所以:B×C=A(一定);可以看出,B和C是两种相关联的量,B随C的变化而变化,A是一定的,也就是B与C相对应数的乘积一定,所以B与C成反比例关系.故答案为:正确.点评:此题重点考查反比例的意义.4.(2分)(2013•芜湖县)圆的面积与它的半径()A.成正比例B.成反比例C.不成比例D.无法判断【答案】C【解析】判断圆的面积与它的半径之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.解:因为圆的面积S=πr2,所以S÷r2=π(一定),是面积与半径的平方的比值一定,所以圆的面积与半径的平方成正比例;但圆的面积与半径不成比例;故选:C.点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.5.(1分)实际距离一定,图上距离和比例尺()A.成正比例B.成反比例C.不成比例【答案】A【解析】判断图上距离和比例尺成什么比例,就看这两种量是相对应的比值一定,还是乘积一定,如果是比值一定,则成正比例;如果是乘积一定,则成反比例.解:图上距离÷比例尺=实际距离(一定),是比值一定,所以图上距离和比例尺成正比例.故选:A.点评:此题属于辨识成正比例的量与成反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做判断.6.(6分)如果a=(c≠0),那么一定时,和成反比例;一定时,和成正比例.【答案】b,a,c ;a,b,c或(c,b,a).【解析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.解:因为a=(c≠0),当b一定时,则有ac=b(一定),是a和c对应的乘积一定,所以a和c成反比例;a一定时,则有=a(一定),是b和c对应的比值一定,所以b和c成正比例;或c一定时,则有=c(一定),是b和a对应的比值一定,所以b和a成正比例;故答案为:b,a,c,a,b,c或(c,b,a).点评:此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.7.(2分)(2008•南海区)时间一定,路程和速度成正比例..(判断对错)【答案】正确【解析】由“速度×时间=路程”可得“(定值)”,从而可以判定路程和速度成正比例.解:因为速度×时间=路程,则(定值),所以说路程和速度成正比例.故答案为:正确.点评:解答此题的主要依据是:若两个量的商一定,则这两个量成正比例关系.8.王老师的钱数一定,购买《好卷》的单价和本数成反比例。
新人教版六年级下册数学正反比例精选练习题..共53页

10
100
12
50
0.25
11.判断下面每题中的两个量是否成反比例,并说明理由。
(1)学校食堂新进一批煤,每天的用煤量与使用天数。
每天的用煤量与使用天数是两种相关联的量,因为每 天用煤量×使用天数=煤的总量(一定),所以每天的用煤 量与使用天数成反比例。
1
●
09
8
7
6
●
5
4
●
3
2
●
1
⑵图1是表示汽车所行路程与相应耗油量关系 的图像,说一说有什么特点。
答:汽车所行路程与相应的耗油量是两种相 关联的量,耗油量随着所行路程和变化而变 化。所行路程增加,耗油量随着增加,所行 路程减少,耗油量也随着减少。 ⑶利用图像估计一下,汽车行驶55㎞的耗油 量是多少?
两种相关联的量,一种量变化,另一种量 也随着变化。
比值(也就是商)一定 y =K(一定)
x
积一定
x×y=k(一定)
例7
数
观察下面的两个表,再回答问题。
学
1、表中各有哪两种相关联的量?
2、在各表的两种相关联的量中,一种量是怎样随着另一 种量的变化而变化的?它们的变化规律各有什么特征?
3、哪个表中的两种量成正比例关系?哪个表中的两种量 成反比例关总价)一定,( 单价)和(数量 )成( 反 )比例
4、判断
数
1)全班的学生人数一定,每组的人数和组数成反比例 (√ )学
2)订阅《小学语文学习》的总份数和总钱数成正比例 (√ ) 3) 和一定,加数和另一个加数成反比例 (×) 4)三角形面积一定,它的底和高不成比例 (×)
●
B
120
●
90
●
60
六年级正反比例奥数题及答案

六年级正反比例奥数题及答案
正反比例奥数题及答案
一、正反比例题
1. 某工厂发出8000瓶汽水,其中百分之八十的汽水放在
2.5升的瓶桶中,尚餘的放在5升的桶中。
则5升的桶发出了多少瓶汽水?
答案:1000瓶。
2. 小明带了500元去旅行,其中百分之三十的钱用来买水,剩余的钱用来买礼物,请问小明可以买多少礼物?
答案:350元。
3. 某学校有650名学生,其中的75%的学生参加思想品德课,其余student参加英语课,问思想品德课一共有多少学生参加?
答案:487.5 名。
4. 李明在拍卖会上以620元买了一台电视,其中百分之50的钱用来买一台操作简单的DVD机,他剩下多少钱?
答案:310 元。
5. 李华有600元购物,其中百分之五十的钱用来买图书,其余的钱用来买衣服,他最多可以买多少件衣服?
答案:300 元。
二、反比例题
1. 某书店有5000本书,其中文学及历史类的书有七成,请问,数学及物理的书有多少本?
答案:2000 本。
2. 小芳有700元要购物,其中百分之25的钱用来买图书,那么剩下的
钱它最多可以买多少件衣服?
答案:525 元。
3. 某公司总收入6500元,其中百分之九十的收入用来购买原料,问剩下的收入可用来购买什么?
答案:650 元。
4. 一个幼儿园有200名小学生,其中百分之八十的小孩参加音乐课,问参加体育课的小孩有多少名?
答案:40 名。
5. 某工厂发出7500瓶汽水,其中6升的桶装的有七成,请问其余放在2.5升的桶中有多少。
答案:1500 瓶。
(完整)六年级正反比例练习题集

(完整)六年级正反比例练习题集六年级正反比例练题集
以下是一些六年级正反比例练题,希望能帮助同学们提高对正
反比例的理解和运用能力。
1. 问题:小明用3个小时做完了30道题目,请问他再用多长
时间能做完90道同样的题目?
答案:小明在相同速度下,需要6个小时才能完成90道题目。
2. 问题:某电影院一天卖出60张票,那么30天能卖出多少张票?
答案:按照正比例计算,电影院在30天内能卖出1800张票。
3. 问题:某奶茶店每天卖出120杯奶茶,如果数量减少了一半,那么卖出60杯奶茶需要多长时间?
答案:奶茶店在相同时间内,需要卖出30杯奶茶才能完成60杯。
4. 问题:某汽车油箱加满油后能行驶500公里,如果行驶距离
减少了三分之一,剩下的油能行驶多长距离?
答案:剩下的油能行驶333.33公里。
5. 问题:某工人每小时生产4个零件,他工作4小时后停工了,他一共生产了多少个零件?
答案:工人在停工前一共生产16个零件。
通过以上的练题,同学们可以更好地理解和运用正反比例的概念。
在解题过程中,要注意理解题意,确定比例关系,并灵活运用
正反比例的求解方法。
祝同学们在研究中取得好成绩!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正反比例的应用二
例1、一个水池中水的深度与注水时间的关系如右下图。
(1)水的深度与注水时间是否成比例?
(2)从图中看,注水前,水池中的水深多少米?
(3)每分钟向水池中注入的水深多少米?
例2、这个铁球浸没在长方体水槽中,当他把这个铁球拿出水面时,槽里的水面下降了0.5厘米,他又将一块棱长是3厘米的正方体铁块浸没在水槽中,槽里的水面上升了0.3厘米,算一下铁球的体积?
例3、蜡烛燃烧的长度和燃烧的时间成正比例。
一根蜡烛燃烧8分钟后,蜡烛的长度是12厘米,18分钟后的长度是7厘米。
蜡烛最初的长度是多少厘米?
例4、甲、乙两人分别从A、B两地同时出发,相向而行,出发时他们的速度之比是3:2,他们第一次相遇后,甲的速度提高了20%,乙的速度提高了30%,这样,当甲到达B地时,乙离A地还有14千米,那么AB两地的距离是多少千米?
看看你会做吗?
1、用不同的杯子装水,水的高度与杯子的底面积的关系
如右图。
(1)从图中看,水的高度与杯子的底面积是否成比例?成什么比例?为什么?
(2)从图中估算,当杯子的底面积是50平方厘米时,水深多少厘米?当水深25厘米时,杯子的底面积是多少平方厘米?
2、将一个圆柱体完全浸没在一个装满水的水槽中,拿出后水面下降了9厘米。
然后放入一个底面积和圆
1的圆锥,这时水面会上升多少厘米?
柱体一样,高是圆柱体
2
3、蜡烛燃烧的长度和燃烧的时间成正比例。
一根蜡烛燃烧12分钟后,蜡烛的长度是17厘米,18分钟后的长度是9厘米。
蜡烛最初的长度是多少厘米?
4、甲、乙两人分别从A、B两地同时出发,相向而行,出发时他们的速度之比是4:3,他们第一次相遇后,甲的速度提高了20%,乙的速度提高了40%,当甲到达目的地后,乙还有44千米到达目的地,那么AB两地的距离是多少千米?。
