中考复习 探究题专题
中考生物专题复习--题型三 探究题

形成对照
【解题思路】 对照实验是在研究一种条件对研究对象的影响时,所进行的除了这种条件不同外,其他条件都相同的实验,这个不同的条件,就是唯一变量。一般对实验变量进行特殊处理的是实验组,不进行特殊处理的是对照组。实验二的目的是探究“空心菜对池塘水体中含氮总量的影响”,实验变量是空心菜,所以,实验二设置“不种植空心菜组”的目的是形成对照。
3.甲醛是无色、有刺激性气味的气体,是室内空气的主要污染物。研究甲醛对果蝇生长发育的影响,可为研究甲醛对人类健康的危害提供基础。某科研小组设计并实施了以下实验:将若干果蝇受精卵均分为三份,分别放入甲醛浓度为0、 、 的三管培养基中,均置于 环境中培养,观察并记录数据如表所示;在果蝇幼虫期和成虫期分别从每管中取10只观察,测量其体重并计算其体重的平均值,结果如图所示。请分析并回答问题。
生物与环境相互影响
【解题思路】 由实验一可知,环境能够影响生物;由实验二可知,生物能够影响环境。综合以上实验,生物与环境的关系是生物与环境相互影响。
2.[2022陕西中考] 洗洁精是被广泛应用的日常生活用品。八年级某班生物学探究小组,通过实验探究某品牌洗洁精废水对小麦种子的萌发是有利还是有害的,进而推测其对农业环境的影响。小组成员将若干粒饱满的小麦种子放在水中浸泡1天,把浸泡后的种子放于已编号的铺有1层滤纸的培养皿中(每3个为一个处理组,编号为甲组和乙组),每个培养皿中平铺50粒小麦种子。每天向甲组和乙组培养皿中分别滴加等量的稀释120倍的洗洁精稀释液和清水(以稀释液和清水不浸没种子为准),其他条件均相同且适宜。第4天记录数据,统计平均发芽率后绘制如下柱状图。
增加
【解题思路】 分析图甲结果,可得出:①四组实验 中,空心菜的植株增长长度随温度升高而增加。②每次数据记录时, 这一组的植株增长长度均最长,说明四组实验中,空心菜植株在 条件下生长最快。
统编版九年级道德与法治中考专题复习:情景探究题

②。
5.【生活在线】
下面是小泰同学的三个生活场景,作为朋友的你,请给他提一些建议:
场景一:我想让他周末陪我到社区参加志愿者活动,进行安全知识宣传,他以没有时间拒绝了。
(1)小泰,你应该:
理由:
场景二:总是沉迷于网络游戏,最近他的学习成绩急剧下降,身心健康也深受影响。
情境一:中考即将来临,莉莉紧张得吃不好,睡不好,总觉得自己还没有做好充足的准备。
(1)莉莉这是的表现。莉莉可以通过途径来缓解。
情境二:莉莉认为,当前疫情全球肆虐,唯有中国疫情得到了很好的控制,可见,经济全球化弊大于利,中国应该拒绝融入经济全球化。
(2)莉莉的看法是的。(填写“正确”或者“错误”)理由:。
(2)我应该告诉小泰:
场景三:期中考试前,偷偷对我说,马上英语考试的时候能不能把答案传给他。
(3)小泰,你应该:
理由:
6.【情境探究】
以下是七年级小文同学日常生活中的三个情境,请你运用所学知识进行探究.
情境一小文进入初中后特别想念自己的老朋友,因为有些人在小学毕业后就再也没有见过面,感情变得越来越淡,小文很失落。
(2)正确做法:。
理由:。
情境三近来,你发现同学们总在你的背后嘀嘀咕咕,表情怪怪的。一打听,原来是小明把你的私人日记上传到了网上。
(3)正确做法:。
理由:。
情境四团委组织同学们参加“认领种植一棵树”活动。
(4)正确做法:。
理由:。
8.【情境探究与法同行】
以下是初中生飞飞同学生活中的三个情境,请你运用所学法律知识,对其进行探究。
15.以下是八年级小明同学生活中的三个情境,请你运用所学知识,对其进行探究并回答有关问题:
中考化学总复习《科学探究》专项试题及答案

中考化学总复习《科学探究》专项试题一、科学探究题1.小竹同学对只含有X、Y、Z、W四种金属单质的混合物进行如下图所示探究。
请根据实验流程回答问题:(1)滤液A中含有_________种溶质。
(2)若测得所得滤液C中含有X(NO3)2,则X、Y、Z、W四种金属的活动性由强到弱的顺序为_________。
(3)往无色W(NO3)2溶液中加入一定量的金属锌和铁的混合固体,充分反应,过滤,得到滤渣和浅绿色滤液。
则滤液中一定含有的溶质有__________________(写化学式)。
2.某班同学为验证碳酸钠的化学性质,向盛有碳酸钠的试管中加入一定量的稀盐酸,迅速用带导气管的橡胶塞塞紧试管口,并将导管另一端通入盛有澄清石灰水的试管中(如图所示)。
请回答下列问题:(1)右侧试管中澄清石灰水变浑浊,写出该反应的化学方程式_____。
(2)实验结束后,将两支试管中的所有物质倒入同一个废液缸中,充分反应后得到澄清溶液。
同学们对废液中溶质的成分进行如下探究(忽略二氧化碳的影响):【提出问题】废液中溶质的成分是什么?【做出猜想】猜想一:CaCl2、NaCl和HCl猜想二:CaCl2、NaCl和Na2CO3猜想三:_____;【进行讨论】经过讨论,同学们一致认为猜想_____是错误的。
【设计实验】请完成实验报告【反思拓展】最终同学们确认了废液中溶质的成分。
若将废液直接排入铸铁管道引起的危害是_____,你认为该废液的处理方法是_____。
3.某研究小组发现,维C泡腾片【保健药品,主要成分维生素C(C6H9O6)、碳酸氢钠( NaHCO3)、柠檬酸(C6H8O7)】溶于水,有许多气泡产生。
该小组同学进行如下探究。
探究:该气体的成分。
【查阅资料】CO是有毒气体,氢气是最清洁的燃料,二氧化碳通常状态下不支持燃烧,所以可用于灭火。
【猜想与假设】小华说:该气体可能是CO2、O2、CO、H2。
小明说:不可能含有H2,因为___________________。
2024年中考数学复习专题课件★★-二次函数综合探究题精选全文

解:(1)∵抛物线与 x 轴交于 A(1,0)和 B(-5,0)两点, ∴抛物线对称轴为直线 x=-52+1=-2,在 y=-3x+3 中,当 x=-2 时,y=9, ∴抛物线顶点 P 的坐标为(-2,9), 设抛物线解析式为 y=a(x+2)2+9, ∴a(1+2)2+9=0,∴a=-1, ∴抛物线解析式为 y=-(x+2)2+9=-x2-4x+5.
(2)①∵抛物线解析式为 y=-x2-4x+5,点 C 是抛物线与 y 轴的交点,
∴C(0,5).设直线 BC 的解析式为 y=kx+b1,∴-b1=5k5+,b1=0,∴kb==15,, ∴直线 BC 的解析式为 y=x+5,
∵直线 x=m(-5<m<0)与抛物线交于点 E,与直线 BC 交于点 F,
解:(1)点 B 在直线 y=x+m 上, 理由:∵直线 y=x+m 经过点 A(1,2), ∴2=1+m,解得 m=1,∴y=x+1, 把 x=2 代入 y=x+1,得 y=3, ∴点 B(2,3)在直线 y=x+m 上. (2)易得直线 y=x+1 与抛物线 y=ax2+bx+1 都经过点(0,1),若抛物 线经过 A,B 两点,则直线与抛物线有三个交点,与实际不符, 又∵B,C 两点的横坐标相同,∴抛物线只能经过 A,C 两点, 把 A(1,2),C(2,1)代入 y=ax2+bx+1,得 a=-1, b=2.
6 2-2).
【教学反思】 教学启发:
教学总结:
类型二:与线段有关的探究 (安徽:2021T22,2019T22)
已知二次函数 y=ax2+2x+c 的图象与 x 轴交于点 A(-1,0),B, 与 y 轴交于点 C(0,3). (1)求该二次函数的解析式和直线 BC 的解析式; (2)如图,过直线 BC 上方的拋物线上一动点 P 作 x 轴的垂线 PH,垂足为 H,线段 PH 交 BC 于点 Q,过点 P 作 PG⊥BC 于点 G,求△PGQ 周长的最大 值.
中考九年级化学二轮系统复习专题七 实验探究题(Ⅰ)

Ⅲ. 将注射器中的稀硫酸平均分5次推入锥形瓶中:
每次推入稀硫酸、待不再产生气泡后,记录收集气体的总体积(忽略其
他因素对测量结果造成的影响),如下表。
次数
第1次 第2次 第3次 第4次 第5次
收集气体的总体积/mL 200 400 515
x
525
(1)上表中的数据x=_5_2_0_。
【评价反思】(1)小组同学一致认为小艳的实验不能证明氢氧化钠溶液与 稀盐酸发生了化学反应,理由是__稀__盐__酸__和__氯__化__钠__都__能__与__硝__酸__银__反__应__生__ _成__氯__化__银__白__色__沉__淀__。 (2)小平的实验中强调“溶液pH≤7”而不是“溶液pH减小”作为判断二 者发生化学反应的理由是_溶__液__p_H__减__小__,__可__能__是__由__于__加__入__稀__盐__酸__后__氢__氧__ _化__钠__溶__液__浓__度__变__小__,__碱__性__减__弱__;__溶__液__p_H_<__7_,__说__明__溶__液__显__酸__性__,__或__溶__液__ _p_H_=__7_,__说__明__溶__液__显__中__性__,__可__证__明__反__应__发__生__,__氢__氧__化__钠__消__失___。
金属的形状
收集50mL氢气 所需时间/s
粉状
60
片状
120
片状
102
片状
110
(1)要比较金属的形状对反应快慢的影响,应选择的实验编号是_①__③____。 (2)通过对比实验②③,可得出的结论是_其__他__条__件__一__定__时__,__镁__与__酸__的__反___ _应__速__率__比__铁__快__。
专题30规律探究问题-备战2023年中考数学必刷真题考点分类专练(全国通用)02【解析版】

备战2023年中考数学必刷真题考点分类专练(全国通用)专题30规律探究问题一.选择题(共10小题)1.(2022•西藏)按一定规律排列的一组数据:,﹣,,﹣,,﹣,….则按此规律排列的第10个数是()A.﹣B.C.﹣D.【分析】把第3个数转化为:,不难看出分子是从1开始的奇数,分母是n2+1,且奇数项是正,偶数项是负,据此即可求解.【解析】原数据可转化为:,﹣,,﹣,,﹣,…,∴=(﹣1)1+1,﹣=(﹣1)2+1,=(﹣1)3+1,...∴第n个数为:(﹣1)n+1,∴第10个数为:(﹣1)10+1=﹣.故选:A.2.(2022•牡丹江)观察下列数据:,﹣,,﹣,,…,则第12个数是()A.B.﹣C.D.﹣【分析】根据给出的数据可以推算出第n个数是×(﹣1)n+1所以第12个数字把n=12代入求值即可.【解析】根据给出的数据特点可知第n个数是×(﹣1)n+1,∴第12个数就是×(﹣1)12+1=﹣.故选:D.3.(2022•云南)按一定规律排列的单项式:x,3x2,5x3,7x4,9x5,……,第n个单项式是()A.(2n﹣1)x n B.(2n+1)x n C.(n﹣1)x n D.(n+1)x n【分析】根据题目中的单项式,可以发现系数是一些连续的奇数,x的指数是一些连续的整数,从而可以写出第n个单项式.【解析】∵单项式:x,3x2,5x3,7x4,9x5,…,∴第n个单项式为(2n﹣1)x n,故选:A.4.(2022•新疆)将全体正偶数排成一个三角形数阵:按照以上排列的规律,第10行第5个数是()A.98B.100C.102D.104【分析】由三角形的数阵知,第n行有n个偶数,则得出前9行有45个偶数,且第45个偶数为90,得出第10行第5个数即可.【解析】由三角形的数阵知,第n行有n个偶数,则得出前9行有1+2+3+4+5+6+7+8+9=45个偶数,∴第9行最后一个数为90,∴第10行第5个数是90+2×5=100,故选:B.5.(2022•广州)如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒,则n的值为()A.252B.253C.336D.337【分析】根据图形特征,第1个图形需要6根小木棒,第2个图形需要6×2+2=14根小木棒,第3个图形需要6×3+2×2=22根小木棒,按此规律,得出第n个图形需要的小木棒根数即可.【解析】由题意知,第1个图形需要6根小木棒,第2个图形需要6×2+2=14根小木棒,第3个图形需要6×3+2×2=22根小木棒,按此规律,第n个图形需要6n+2(n﹣1)=(8n﹣2)个小木棒,当8n﹣2=2022时,解得n=253,故选:B.6.(2022•玉林)如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形ABCDEF的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是()A.4B.2C.2D.0【分析】分别计算红跳棋和黑跳棋过2022秒钟后的位置,红跳棋跳回到A点,黑跳棋跳到F点,可得结论.【解析】∵红跳棋从A点按顺时针方向1秒钟跳1个顶点,∴红跳棋每过6秒返回到A点,2022÷6=337,∴经过2022秒钟后,红跳棋跳回到A点,∵黑跳棋从A点按逆时针方向3秒钟跳1个顶点,∴黑跳棋每过18秒返回到A点,2022÷18=112•••6,∴经过2022秒钟后,黑跳棋跳到E点,连接AE,过点F作FM⊥AE,由题意可得:AF=AE=2,∠AFE=120°,∴∠FAE=30°,在Rt△AFM中,AM=AF=,∴AE=2AM=2,∴经过2022秒钟后,两枚跳棋之间的距离是2.故选:B.7.(2022•江西)将字母“C”,“H”按照如图所示的规律摆放,依次下去,则第4个图形中字母“H”的个数是()A.9B.10C.11D.12【分析】列举每个图形中H的个数,找到规律即可得出答案.【解析】第1个图中H的个数为4,第2个图中H的个数为4+2,第3个图中H的个数为4+2×2,第4个图中H的个数为4+2×3=10,故选:B.8.(2022•重庆)用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为()A.32B.34C.37D.41【分析】根据图形的变化规律得出第n个图形中有4n+1个正方形即可.【解析】由题知,第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,…,第n个图案中有4n+1个正方形,∴第⑨个图案中正方形的个数为4×9+1=37,故选:C.9.(2022•重庆)把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为()A.15B.13C.11D.9【分析】根据前面三个图案中菱形的个数,得出规律,第n个图案中菱形有(2n﹣1)个,从而得出答案.【解析】由图形知,第①个图案中有1个菱形,第②个图案中有3个菱形,即1+2=3,第③个图案中有5个菱形即1+2+2=5,……则第n个图案中菱形有1+2(n﹣1)=(2n﹣1)个,∴第⑥个图案中有2×6﹣1=11个菱形,故选:C.10.(2022•荆州)如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD 各边的中点,得到四边形A1B1C1D1;第二次,顺次连接四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…如此反复操作下去,则第n次操作后,得到四边形A n B n∁n D n的面积是()A.B.C.D.【分析】连接A1C1,D1B1,可知四边形A1B1C1D1的面积为矩形ABCD面积的一半,则S1=ab,再根据三角形中位线定理可得C2D2=C1,A2D2=B1D1,则S2=C1×B1D1=ab,依此可得规律.【解析】如图,连接A1C1,D1B1,∵顺次连接矩形ABCD各边的中点,得到四边形A1B1C1D1,∴四边形A1BCC1是矩形,∴A1C1=BC,A1C1∥BC,同理,B1D1=AB,B1D1∥AB,∴A1C1⊥B1D1,∴S1=ab,∵顺次连接四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2,∴C2D2=C1,A2D2=B1D1,∴S2=C1×B1D1=ab,……依此可得S n=,故选:A.二.填空题(共14小题)11.(2022•恩施州)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为a n,且满足+=.则a4=,a2022=.【分析】由题意可得a n=,即可求解.【解析】由题意可得:a1=2=,a2==,a3=,∵+=,∴2+=7,∴a4==,∵=,∴a5=,同理可求a6==,•••∴a n=,∴a2022=,故答案为:,.12.(2022•宿迁)按规律排列的单项式:x,﹣x3,x5,﹣x7,x9,…,则第20个单项式是﹣x39.【分析】观察指数规律与符号规律,进行解答便可.【解析】根据前几项可以得出规律,奇数项为正,偶数项为负,第n项的数为(﹣1)n+1×x2n﹣1,则第20个单项式是(﹣1)21×x39=﹣x39,故答案为:﹣x39.13.(2022•怀化)正偶数2,4,6,8,10,…,按如下规律排列,则第27行的第21个数是744.【分析】由图可以看出,每行数字的个数与行数是一致的,即第一行有1个数,第二行有2个数,第三行有3个数••••••••第n行有n个数,则前n行共有个数,再根据偶数的特征确定第几行第几个数是几.【解析】由图可知,第一行有1个数,第二行有2个数,第三行有3个数,•••••••第n行有n个数.∴前n行共有个数.∴前27行共有378个数,∴第27行第21个数是一共378个数中的第372个数.∵这些数都是正偶数,∴第372个数为372×2=744.故答案为:744.14.(2022•泰安)将从1开始的连续自然数按以下规律排列:若有序数对(n,m)表示第n行,从左到右第m个数,如(3,2)表示6,则表示99的有序数对是(10,18).【分析】根据第n行的最后一个数是n2,第n行有(2n﹣1)个数即可得出答案.【解析】∵第n行的最后一个数是n2,第n行有(2n﹣1)个数,∴99=102﹣1在第10行倒数第二个,第10行有:2×10﹣1=19个数,∴99的有序数对是(10,18).故答案为:(10,18).15.(2022•青海)木材加工厂将一批木料按如图所示的规律依次摆放,则第n个图中共有木料根.【分析】观察图形可得:第n个图形最底层有n根木料,据此可得答案.【解析】由图可知:第一个图形有木料1根,第二个图形有木料1+2=3(根),第三个图形有木料1+2+3=6(根),第四个图形有木料1+2+3+4=10(根),......第n个图有木料1+2+3+4+......+n=(根),故答案为:.16.(2022•大庆)观察下列“蜂窝图”,按照这样的规律,则第16个图案中的“”的个数是49.【分析】从数字找规律,进行计算即可解答.【解析】由题意得:第一个图案中的“”的个数是:4=4+3×0,第二个图案中的“”的个数是:7=4+3×1,第三个图案中的“”的个数是:10=4+3×2,...∴第16个图案中的“”的个数是:4+3×15=49,故答案为:49.17.(2022•绥化)如图,∠AOB=60°,点P1在射线OA上,且OP1=1,过点P1作P1K1⊥OA交射线OB 于K1,在射线OA上截取P1P2,使P1P2=P1K1;过点P2作P2K2⊥OA交射线OB于K2,在射线OA上截取P2P3,使P2P3=P2K2…按照此规律,线段P2023K2023的长为(1+)2022.【分析】根据题意和题目中的数据,可以写出前几项,然后即可得到P n K n的式子,从而可以写出线段P2023K2023的长.【解析】由题意可得,P1K1=OP1•tan60°=1×=,P2K2=OP2•tan60°=(1+)×=(1+),P3K3=OP3•tan60°=(1+++3)×=(1+)2,P4K4=OP4•tan60°=[(1+++3)+(1+)2]×=(1+)3,…,P n K n=(1+)n﹣1,∴当n =2023时,P 2023K 2023=(1+)2022,故答案为:(1+)2022.18.(2022•聊城)如图,线段AB =2,以AB 为直径画半圆,圆心为A 1,以AA 1为直径画半圆①;取A 1B 的中点A 2,以A 1A 2为直径画半圆②;取A 2B 的中点A 3,以A 2A 3为直径画半圆③…按照这样的规律画下去,大半圆内部依次画出的8个小半圆的弧长之和为π.【分析】由AB =2,可得半圆①弧长为π,半圆②弧长为()2π,半圆③弧长为()3π,......半圆⑧弧长为()8π,即可得8个小半圆的弧长之和为π+()2π+()3π+...+()8π=π.【解析】∵AB =2,∴AA 1=1,半圆①弧长为=π,同理A 1A 2=,半圆②弧长为=()2π,A 2A 3=,半圆③弧长为=()3π,......半圆⑧弧长为=()8π,∴8个小半圆的弧长之和为π+()2π+()3π+...+()8π=π.故答案为:π.19.(2022•十堰)如图,某链条每节长为2.8cm ,每两节链条相连接部分重叠的圆的直径为1cm ,按这种连接方式,50节链条总长度为91cm .【分析】先求出1节链条的长度,2节链条的总长度,3节链条的总长度,然后从数字找规律,进行计算即可解答.【解析】由题意得:1节链条的长度=2.8cm,2节链条的总长度=[2.8+(2.8﹣1)]cm,3节链条的总长度=[2.8+(2.8﹣1)×2]cm,...∴50节链条总长度=[2.8+(2.8﹣1)×49]=91(cm),故答案为:91.20.(2022•常德)剪纸片:有一张长方形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片;从这3张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有4张纸片;…;如此下去,若最后得到10张纸片,其中有1张五边形纸片,3张三角形纸片,5张四边形纸片,则还有一张多边形纸片的边数为6.【分析】根据题意,用剪刀沿不过顶点的直线剪成两部分时,每剪开一次,多边形的边数增加4,如第一次,将其中两个边分成四条边,且剪刀所在那条直线增加两条边,即为2+2×2+1×2=8=4+4×1(边),分成两个图形;第二次,边数为:8﹣2+2×2+2×1=12=4+4×2,分成三个图形;……;当剪第n刀时,边数为4+4n,分成(n+1)个图形;令n=9即可得出结论.【解析】根据题意,用剪刀沿不过顶点的直线剪成两部分时,每剪开一次,多边形的边数增加4,第一次,将其中两个边分成四条边,且剪刀所在那条直线增加两条边,即为2+2×2+1×2=8=4+4×1(边),分成两个图形;第二次,边数为:8﹣2+2×2+2×1=12=4+4×2,分成三个图形;……;当剪第n刀时,边数为4+4n,分成(n+1)个图形;∵最后得到10张纸片,设还有一张多边形纸片的边数为m,∴令n=9,有4+4×9=5+3×3+5×4+m,解得m=6.故答案为:6.21.(2022•德阳)古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下:其中:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是1+2=3,第三个三角形数是1+2+3=6,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是1+3=4,第三个正方形数是1+3+5=9,…………由此类推,图④中第五个正六边形数是45.【分析】根据前三个图形的变化寻找规律,即可解决问题.【解析】图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是1+2=3,第三个三角形数是1+2+3=6,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是1+3=4,第三个正方形数是1+3+5=9,……图③的点数叫做五边形数,从上至下第一个五边形数是1,第二个五边形数是1+4=5,第三个五边形数是1+4+7=12,……由此类推,图④中第五个正六边形数是1+5+9+13+17=45.故答案为:45.22.(2022•遂宁)“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为127.【分析】由已知图形观察规律,即可得到第六代勾股树中正方形的个数.【解析】∵第一代勾股树中正方形有1+2=3(个),第二代勾股树中正方形有1+2+22=7(个),第三代勾股树中正方形有1+2+22+23=15(个),......∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),故答案为:127.23.(2022•黑龙江)如图,下列图形是将正三角形按一定规律排列,则第5个图形中所有正三角形的个数有485.【分析】由图可以看出:第一个图形中5个正三角形,第二个图形中5×3+2=17个正三角形,第三个图形中17×3+2=53个正三角形,由此得出第四个图形中53×3+2=161个正三角形,第五个图形中161×3+2=485个正三角形.【解析】第一个图形正三角形的个数为5,第二个图形正三角形的个数为5×3+2=2×32﹣1=17,第三个图形正三角形的个数为17×3+2=2×33﹣1=53,第四个图形正三角形的个数为53×3+2=2×34﹣1=161,第五个图形正三角形的个数为161×3+2=2×35﹣1=485.如果是第n个图,则有2×3n﹣1个故答案为:485.24.(2022•黑龙江)如图所示,以O为端点画六条射线OA,OB,OC,OD,OE,OF,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线OC上.【分析】根据规律得出每6个数为一周期.用2013除以6,根据余数来决定数2013在哪条射线上.【解析】∵1在射线OA上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OA上,…每六个一循环,2013÷6=335…3,∴所描的第2013个点在射线和3所在射线一样,∴所描的第2013个点在射线OC上.故答案为:OC.三.解答题(共2小题)25.(2022•嘉兴)设是一个两位数,其中a是十位上的数字(1≤a≤9).例如,当a=4时,表示的两位数是45.(1)尝试:①当a=1时,152=225=1×2×100+25;②当a=2时,252=625=2×3×100+25;③当a=3时,352=1225=3×4×100+25;……(2)归纳:与100a(a+1)+25有怎样的大小关系?试说明理由.(3)运用:若与100a的差为2525,求a的值.【分析】(1)根据规律直接得出结论即可;(2)根据=(10a+5)(10a+5)=100a2+100a+25=100a(a+1)+25即可得出结论;(3)根据题意列出方程求解即可.【解析】(1)∵①当a=1时,152=225=1×2×100+25;②当a=2时,252=625=2×3×100+25;∴③当a=3时,352=1225=3×4×100+25,故答案为:3×4×100+25;(2)=100a(a+1)+25,理由如下:=(10a+5)(10a+5)=100a2+100a+25=100a(a+1)+25;(3)由题知,﹣100a=2525,即100a2+100a+25﹣100a=2525,解得a=5或﹣5(舍去),∴a的值为5.26.(2022•安徽)观察以下等式:第1个等式:(2×1+1)2=(2×2+1)2﹣(2×2)2,第2个等式:(2×2+1)2=(3×4+1)2﹣(3×4)2,第3个等式:(2×3+1)2=(4×6+1)2﹣(4×6)2,第4个等式:(2×4+1)2=(5×8+1)2﹣(5×8)2,……按照以上规律,解决下列问题:(1)写出第5个等式:(2×5+1)2=(6×10+1)2﹣(6×10)2;(2)写出你猜想的第n个等式(用含n的式子表示),并证明.【分析】(1)根据题目中等式的特点,可以写出第5个等式;(2)根据题目中等式的特点,可以写出猜想,然后将等式左边和右边展开,看是否相等,即可证明猜想.【解析】(1)因为第1个等式:(2×1+1)2=(2×2+1)2﹣(2×2)2,第2个等式:(2×2+1)2=(3×4+1)2﹣(3×4)2,第3个等式:(2×3+1)2=(4×6+1)2﹣(4×6)2,第4个等式:(2×4+1)2=(5×8+1)2﹣(5×8)2,第5个等式:(2×5+1)2=(6×10+1)2﹣(6×10)2,故答案为:(2×5+1)2=(6×10+1)2﹣(6×10)2;(2)第n个等式:(2n+1)2=[(n+1)×2n+1]2﹣[(n+1)×2n]2,证明:左边=4n2+4n+1,右边=[(n+1)×2n]2+2×(n+1)×2n+12﹣[(n+1)×2n]2=4n2+4n+1,∴左边=右边.∴等式成立.。
2024年中考生物专题复习:实验探究题
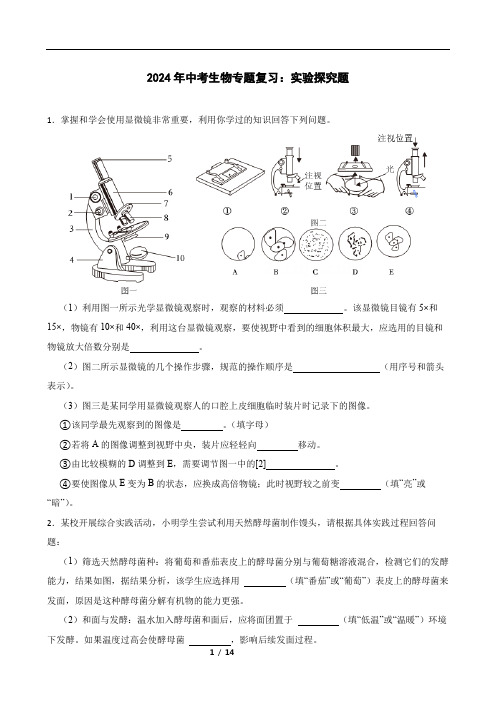
2024年中考生物专题复习:实验探究题1.掌握和学会使用显微镜非常重要,利用你学过的知识回答下列问题。
(1)利用图一所示光学显微镜观察时,观察的材料必须。
该显微镜目镜有5×和15×,物镜有10×和40×,利用这台显微镜观察,要使视野中看到的细胞体积最大,应选用的目镜和物镜放大倍数分别是。
(2)图二所示显微镜的几个操作步骤,规范的操作顺序是(用序号和箭头表示)。
(3)图三是某同学用显微镜观察人的口腔上皮细胞临时装片时记录下的图像。
①该同学最先观察到的图像是。
(填字母)②若将A的图像调整到视野中央,装片应轻轻向移动。
③由比较模糊的D调整到E,需要调节图一中的[2]。
④要使图像从E变为B的状态,应换成高倍物镜;此时视野较之前变(填“亮”或“暗”)。
2.某校开展综合实践活动,小明学生尝试利用天然酵母菌制作馒头,请根据具体实践过程回答问题:(1)筛选天然酵母菌种:将葡萄和番茄表皮上的酵母菌分别与葡萄糖溶液混合,检测它们的发酵能力,结果如图,据结果分析,该学生应选择用(填“番茄”或“葡萄”)表皮上的酵母菌来发面,原因是这种酵母菌分解有机物的能力更强。
(2)和面与发酵:温水加入酵母菌和面后,应将面团置于(填“低温”或“温暖”)环境下发酵。
如果温度过高会使酵母菌,影响后续发面过程。
(3)上锅蒸制:将发酵好的面团做成自己喜欢的小份,上锅蒸制约20分钟后,馒头就做好了。
做出来的馒头松软可口,是因为酵母菌分解有机物,产生气体遇热膨胀所致。
(4)分享成果:该学生把做好的馒头拿给同学们品尝,大家发现馒头越嚼越甜,原因是口腔里的唾液淀粉酶将馒头中的淀粉转化成为的缘故。
(5)优化创新:有了这次成功的经验,该学生决定尝试制作五彩馒头。
他用菠菜和火龙果榨汁作为天然色素,这些色素来自于植物细胞中的。
(填结构名称)3.如下图是用以研究生命起源的化学进化过程的模拟实验装置示意图,请据图回答问题。
2024中考数学复习 重难题型分类练 题型九 几何探究题 (含答案)

2024中考数学复习重难题型分类练题型九几何探究题类型一非动点探究题1.已知四边形ABCD中,BC=CD,连接BD,过点C作BD的垂线交AB于点E,连接DE.(1)如图①,若DE∥BC,求证:四边形BCDE是菱形;(2)如图②,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.(i)求∠CED的大小;(ii)若AF=AE,求证:BE=CF.第1题图2.已知正方形ABCD,E为对角线AC上一点.【建立模型】(1)如图①,连接BE,DE.求证:BE=DE;【模型应用】(2)如图②,F是DE延长线上一点,FB⊥BE,EF交AB于点G.①判断△FBG的形状并说明理由;②若G为AB的中点,且AB=4,求AF的长;【模型迁移】(3)如图③,F是DE延长线上一点,FB⊥BE,EF交AB于点G,BE=BF.求证:GE=(2-1)DE.第2题图3.(1)如图①,在△ABC 中,∠ACB =2∠B ,CD 平分∠ACB ,交AB 于点D ,DE ∥AC ,交BC 于点E .①若DE =1,BD =32,求BC 的长;②试探究AB AD -BE DE是否为定值.如果是,请求出这个定值;如果不是,请说明理由;(2)如图②,∠CBG 和∠BCF 是△ABC 的2个外角,∠BCF =2∠CBG ,CD 平分∠BCF ,交AB 的延长线于点D ,DE ∥AC ,交CB 的延长线于点E .记△ACD 的面积为S 1,△CDE 的面积为S 2,△BDE 的面积为S 3.若S 1·S 3=916S 22,求cos ∠CBD 的值.第3题图类型二动点探究题4.如图,在矩形ABCD 中,点O 是AB 的中点,点M 是射线DC 上动点,点P 在线段AM上(不与点A 重合),OP =12A B.(1)判断△ABP 的形状,并说明理由;(2)当点M 为边DC 中点时,连接CP 并延长交AD 于点N .求证:PN =AN ;(3)点Q 在边AD 上,AB =5,AD =4,DQ =85,当∠CPQ =90°时,求DM 的长.5.如图①,AB为半圆O的直径,C为BA延长线上一点,CD切半圆于点D,BE⊥CD,交CD延长线于点E,交半圆于点F,已知BC=5,BE=3.点P,Q分别在线段AB,BE上(不与端点重合),且满足APBQ=54.设BQ=x,CP=y.(1)求半圆O的半径;(2)求y关于x的函数表达式;(3)如图②,过点P作PR⊥CE于点R,连接PQ,RQ.①当△PQR为直角三角形时,求x的值;②作点F关于QR的对称点F′,当点F′落在BC上时,求CF′BF′的值.第5题图6.在▱ABCD中,∠C=45°,AD=BD,点P为射线CD上的动点(点P不与点D重合),连接AP,过点P作EP⊥AP交直线BD于点E.(1)如图①,当点P为线段CD的中点时,请直接写出PA,PE的数量关系;(2)如图②,当点P在线段CD上时,求证:DA+2DP=DE;(3)点P在射线CD上运动,若AD=32,AP=5,请直接写出线段BE的长.第6题图7.如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D,E分别为BC,PC的中点,连接DE.过点E作BC的垂线,与BC,AC分别交于F,G两点.连接DG,交PC于点H.(1)∠EDC的度数为________°;(2)连接PG,求△APG的面积的最大值;(3)PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)求CHCE的最大值.类型三平移探究题8.已知:在正方形ABCD的边BC上任取一点F,连接AF,一条与AF垂直的直线l(垂足为点P)沿AF方向,从点A开始向下平移,交边AB于点E.(1)当直线l经过正方形ABCD的顶点D时,如图①所示.求证:AE=BF;(2)当直线l经过AF的中点时,与对角线BD交于点Q,连接FQ,如图②所示.求∠AFQ 的度数;(3)直线l继续向下平移,当点P恰好落在对角线BD上时,交边CD于点G,如图③所示.设AB=2,BF=x,DG=y,求y与x之间的关系式.第8题图9.在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图①),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.活动一:将图①中的纸片DEF沿AC方向平移,连接AE,BD(如图②),当点F与点C重合时停止平移.【思考】图②中的四边形ABDE是平行四边形吗?请说明理由;【发现】当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图③),求AF的长;活动二:在图③中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连接OB,OE(如图④).【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.第9题图10.已知:点C ,D 均在直线l 的上方,AC 与BD 都是直线l 的垂线段,且BD 在AC 的右侧,BD =2AC ,AD 与BC 相交于点O .(1)如图①,若连接CD ,则△BCD 的形状为________,AO AD的值为________;(2)若将BD 沿直线l 平移,并以AD 为一边在直线l 的上方作等边△ADE .①如图②,当AE 与AC 重合时,连接OE ,若AC =32,求OE 的长;②如图③,当∠ACB =60°时,连接EC 并延长交直线l 于点F ,连接OF .求证:OF ⊥A B.第10题图类型四旋转探究题11.在Rt△ABC中,AC=BC,将线段CA绕点C旋转α(0°<α<90°),得到线段CD,连接AD,B D.(1)如图①,将线段CA绕点C逆时针旋转α,则∠ADB的度数为________;(2)将线段CA绕点C顺时针旋转α时.①在图②中依题意补全图形,并求∠ADB的度数;②若∠BCD的平分线CE交BD于点F,交DA的延长线于点E,连接BE.用等式表示线段AD,CE,BE之间的数量关系,并证明.第11题图12.在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.(1)如图①,当点A′落在AC的延长线上时,求AA′的长;(2)如图②,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;(3)如图③,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.第12题图13.如图,在△ABC中,AB=AC=25,BC=4,D,E,F分别为AC,AB,BC的中点,连接DE,DF.DE;(1)如图①,求证:DF=52(2)如图②,将∠EDF绕点D顺时针旋转一定角度,得到∠PDQ,当射线DP交AB于点G,射线DQ交BC于点N时,连接FE并延长交射线DP于点M,判断FN与EM的数量关系,并说明理由;(3)如图③,在(2)的条件下,当DP⊥AB时,求DN的长.第13题图14.如图①,四边形ABCD中,AD∥BC,∠ABC=90°,∠C=30°,AD=3,AB=23,DH⊥BC于点H.将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B 在PM上,其中∠Q=90°,∠QPM=30°,PM=43.(1)求证:△PQM≌△CHD;(2)△PQM从图①的位置出发,先沿着BC方向向右平移(图②),当点P到达点D后立刻绕点D逆时针旋转(图③),当边PM旋转50°时停止.①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;②如图②,点K在BH上,且BK=9-43.若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;③如图③,在△PQM旋转过程中,设PQ,PM分别交BC于点E,F,若BE=d,直接..写出CF的长(用含d的式子表示).第14题图类型五折叠探究题15.如图,在△ABC中,∠ABC=30°,AB=AC,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将△ACD沿AD折叠得到△AED,连接BE.(1)当AE⊥BC时,∠AEB=________°;(2)探究∠AEB与∠CAD之间的数量关系,并给出证明;(3)设AC=4,△ACD的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.16.在矩形ABCD中,BC=3CD,点E、F分别是边AD、BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;(2)如图②,当点P在线段CB的延长线上时,GH交AB于点M,求证:点M在线段EF的垂直平分线上;(3)当AB=5时,在点E由点A移动到AD中点的过程中,计算出点G运动的路线长.第16题图17.(1)发现:如图①所示,在正方形ABCD中,E为AD边上一点,将△AEB沿BE翻折到△BEF处,延长EF交CD边于G点,求证:△BFG≌△BCG;(2)探究:如图②,在矩形ABCD中,E为AD边上一点,且AD=8,AB=6.将△AEB沿BE 翻折到△BEF处,延长EF交BC边于G点,延长BF交CD边于点H,且FH=CH,求AE 的长;(3)拓展:如图③,在菱形ABCD中,AB=6,E为CD边上的三等分点,∠D=60°.将△ADE 沿AE翻折得到△AFE,直线EF交BC于点P.求PC的长.第17题图18.如图①,矩形ABCD中,AB=6,AD=8,点P在边BC上,且不与点B,C重合,直线AP与DC的延长线交于点E.(1)当点P是BC的中点时,求证:△ABP≌△ECP;(2)将△APB沿直线AP折叠得到△APB′,点B′落在矩形ABCD的内部,延长PB′交直线AD 于点F.①证明FA=FP,并求出在(1)条件下AF的值;②连接B′C,求△PCB′周长的最小值;③如图②,BB′交AE于点H,点G是AE的中点,当∠EAB′=2∠AEB′时,请判断AB与HG 的数量关系,并说明理由.第18题图19.小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.如图,在▱ABCD中,AN为BC边上的高,ADAN=m,点M在AD边上,且BA=BM.点E是线段AM上任意一点,连接BE,将△ABE沿BE翻折得△FBE.(1)问题解决:如图①,当∠BAD=60°,将△ABE沿BE翻折后,使点F与点M重合,则AMAN=________;(2)问题探究:如图②,当∠BAD=45°,将△ABE沿BE翻折后,使EF∥BM,求∠ABE的度数,并求出此时m的最小值;(3)拓展延伸:当∠BAD=30°,将△ABE沿BE翻折后,若EF⊥AD,且AE=MD,根据题意在备用图中画出图形,并求出m的值.第19题图类型六类比探究题20.已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.(1)如图①,分别以AC,CB为边向形外作正方形ACDE和正方形BGF C.记正方形ACDE的面积为S1,正方形BGFC的面积为S2.①若S1=9,S2=16,求S的值;②延长EA交GB的延长线于点N,连接FN,交BC于点M,交AB于点H.若FH⊥AB(如图②所示),求证:S2-S1=2S;(2)如图③,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1,等边三角形CBE的面积为S2.以AB为边向上作等边三角形ABF(点C 在△ABF内),连接EF,CF.若EF⊥CF,试探索S2-S1与S之间的等量关系,并说明理由.第20题图21.问题提出:如图①,在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究AFAB的值.问题探究:(1)先将问题特殊化,如图②,当∠BAC=60°时,直接写出AFAB的值;(2)再探究一般情形,如图①,证明(1)中的结论仍然成立;问题拓展:如图③,在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,CGBC=1n(n<2),延长BC至点E,使DE=DG,延长ED交AB于点F,直接写出AFAB的值(用含n的式子表示).第21题图22.【问题呈现】如图①,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE;【类比探究】如图②,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出BDCE的值;【拓展提升】如图③,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且ABBC=ADDE=34.连接BD,CE.(1)求BDCE的值;(2)延长CE交BD于点F,交AB于点G,求sin∠BFC的值.图①图②图③第22题图其他类型23.现有若干张相同的半圆形纸片,点O是圆心,直径AB的长是12cm,C是半圆弧上的一点(点C与点A,B不重合),连接AC,B C.(1)沿AC,BC剪下△ABC,则△ABC是________三角形(填“锐角”、“直角”或“钝角”);(2)分别取半圆弧上的点E,F和直径AB上的点G,H.已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);(3)经过数次探索,小明猜想,对于半圆弧上的任意一点C,一定存在线段AC上的点M、线段BC上的点N和直径AB上的点P,Q,使得由这四个点顺次连接构成的四边形是一个边长为4cm的菱形.小明的猜想是否正确?请说明理由.第23题图备用题24.同学们还记得吗?图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形,受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:【问题一】如图①,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,OA1交AB于点E,OC1交BC于点F,则AE与BF的数量关系为________;【问题二】受图①启发,兴趣小组画出了图③;直线m,n经过正方形ABCD的对称中心O,直线m分别与AD,BC交于点E,F,直线n分别与AB,CD交于点G,H,且m⊥n,若正方形ABCD边长为8,求四边形OEAG的面积;【问题三】受图②启发,兴趣小组画出了图④;正方形CEFG的顶点G在正方形ABCD的边CD上,顶点E在BC的延长线上,且BC=6,CE=2.在直线BE上是否存在点P,使△APF 为直角三角形?若存在,求出BP的长度;若不存在,说明理由.第24题图源自人教八下P63实验与探究参考答案与解析1.(1)证明:如解图①,设DB与CE交于点O,第1题解图①∵CD=CB,∴∠CDB=∠CBD,又∵DE∥BC,∴∠EDB=∠CBD,∴∠EDB=∠CDB,∵CE⊥BD,∴∠DOE=∠DOC=90°,又∵DO=DO,∴△EDO≌△CDO(ASA),∴DE=DC,∴DE=BC,∴四边形BCDE为平行四边形,∵CB=CD,∴四边形BCDE为菱形;【一题多解】解法二:如解图①,由(1)得,△EDO≌△CDO,∴EO=CO,∵DC=BC,CE⊥BD,∴DO=BO,∴四边形BCDE是平行四边形,∵CE与BD互相垂直且平分,∴四边形BCDE为菱形.解法三:如解图①,∵BD⊥CE,BC=CD,∴BO=DO,∴CE垂直平分BD,∴EB=ED,由(1)可知△EDO≌△CDO,∴ED=DC,∴ED=EB=CD=BC,∴四边形BCDE为菱形.(2)(ⅰ)解:∵DE垂直平分AC,∴AD=CD,AE=CE,又∵DE=DE,∴△AED≌△CED(SSS),∴∠AED=∠CED,又∵CB=CD,CE⊥BD,∴CE垂直平分BD,同理可证△CBE≌△CDE,∴∠CEB=∠CED,∴∠CEB=∠CED=∠AED,又∵∠CEB+∠CED+∠AED=180°,∴∠CED=60°;(ⅱ)证明:如解图②,第1题解图②设BD与CE相交于点G,AC与DE相交于点H,由(ⅰ)可知∠HAE=30°,∠GBE=30°,∴∠AFB=120°,FA=FB,又∵∠AEC=∠AED+∠CED=120°,∴∠ACE=180°-30°-120°=30°,∴EA=EC,又∵AF=AE,∴AF=AE=EC=FB,∵∠AFB=∠AEC=120°,∴△AFB≌△AEC(SAS),∴AB=AC,∴AB-AE=AC-AF,∴BE=CF.2.(1)证明:∵四边形ABCD为正方形,AC为对角线,∴AB=AD,∠BAE=∠DAE=45°.∵AE=AE,∴△ABE≌△ADE(SAS),∴BE=DE;(2)解:①△FBG为等腰三角形.理由如下:∵四边形ABCD为正方形,∴∠GAD=90°,∴∠AGD+∠ADG=90°.∵FB⊥BE,∴∠FBG+∠EBG=90°,由(1)得∠ADG=∠EBG,∴∠AGD=∠FBG,又∵∠AGD=∠FGB,∴∠FBG=∠FGB,∴△FBG为等腰三角形;②如解图,过点F作FH⊥AB,垂足为H.第2题解图∵四边形ABCD为正方形,点G为AB的中点,AB=4,∴AG=BG=2,AD=4.由①知FG =FB ,∴GH =BH =1,∴AH =AG +GH =3.在Rt △FHG 与Rt △DAG 中,∵∠FGH =∠DGA ,∴tan ∠FGH =tan ∠DGA ,∴FH GH =AD AG =42,∴FH =2.在Rt △AHF 中,AF =AH 2+FH 2=9+4=13;(3)证明:∵FB ⊥BE ,∴∠FBE =90°.在Rt △EBF 中,BE =BF ,∴EF =2BE .由(1)得BE =DE ,由(2)得FG =BF ,∴GE =EF -FG =2BE -BF =2DE -DE =(2-1)DE .3.解:(1)①∵CD 平分∠ACB ,∴∠ACD =∠DCB =12∠ACB .∵∠ACB =2∠B ,∴∠ACD =∠DCB =∠B .∴CD =BD =32.∵DE ∥AC ,∴∠ACD =∠EDC .∴∠EDC =∠DCB =∠B .∴CE =DE =1.∴△CED ∽△CDB .∴CE CD =CD CB.即132=32CB ,解得BC =94;②AB AD -BE DE是定值.∵DE ∥AC ,∴AB AD =BC CE.由①同理可得CE =DE ,∴AB AD =BC DE.∴AB AD -BE DE =BC DE -BE DE =CE DE=1.∴AB AD -BE DE是定值,定值为1;(2)∵DE ∥AC ,∴S 1S 2=AC DE =BC BE.∵S 3S 2=BE CE,∴S 1·S 3S 22=BC CE.又∵S 1·S 3=916S 22,∴BC CE =916.设BC =9x ,则CE =16x .∵CD 平分∠BCF ,∴∠ECD =∠FCD =12∠BCF .∵∠BCF =2∠CBG ,∴∠ECD =∠FCD =∠CBD .∴BD =CD .∵DE ∥AC ,∴∠EDC =∠FCD .∴∠EDC =∠CBD =∠ECD .∴CE =DE .∵∠DCB =∠ECD ,∴△CDB ∽△CED .∴CD CE =CB CD,∴CD 2=CB ·CE =144x 2.∴CD =12x (负值已舍去).如解图,过点D 作DH ⊥BC 于点H .∵BD =CD =12x ,∴BH =12BC =92x ,∴cos ∠CBD =BH BD =92x 12x=38.第3题解图4.(1)解:△ABP 为直角三角形.理由如下:∵O 为AB 的中点,∴OA =OB =12AB .∵OP =12AB ,∴OP =OA =OB ,∴点P 在以AB 为直径的⊙O 上.∴∠APB =90°.故△ABP 为直角三角形;(2)证明:如解图①,连接ON ,连接OC 交PB 于点E .∵M 为DC 的中点,O 为AB 的中点,AB ∥CD ,AB =CD ,∴MC ∥OA 且MC =OA .∴四边形MAOC 为平行四边形.∴OC ∥AM ,∴∠CEP =∠APB =90°,∴OC ⊥PB .∵OP =OB ,∴E 为PB 的中点.∴CP =BC .∴△OPC ≌△OBC ,∴∠CPO =∠CBO =90°.∴∠OPN =∠OAN =90°.又∵OP =OB =OA ,ON =ON ,∴△OPN ≌△OAN .∴PN =AN ;第4题解图(3)解:如解图②,过点P 作GH ∥AB 与AD ,BC 分别交于点G ,H .设AG =BH =x ,则QG =125-x ,CH =4-x .∵∠GPA +∠HPB =∠GPA +∠GAP =90°,∴∠GAP =∠HPB .∵∠AGP =∠PHB =90°,∴△GAP ∽△HPB .∴AG PH =GP HB,∴AG ·HB =PH ·GP .同理可证:QG ·CH =PH ·GP ,∴AG ·HB =QG ·CH .∴x ·x =(125-x )(4-x ),解得x =32.∴AG =BH =32.∵GP ·HP =AG ·HB ,∴GP ·(GH -GP )=94,GP =12或92.∵GP ∥DM .∴GP DM =AG AD,∴DM =GP ·AD AG =43或12.5.解:(1)如解图①,连接OD ,设半圆O 的半径为r ,∵CD 切半圆O 于点D ,∴OD ⊥CD .∵BE ⊥CD ,∴OD ∥BE ,∴△COD ∽△CBE ,∴OD BE =CO CB ,即r 3=5-r 5,∴r =158,即半圆O 的半径是158;第5题解图①(2)由(1)得CA =CB -AB =5-2×158=54,∵AP BQ =54,BQ =x ,∴AP =54x .∵CP =AP +AC ,∴y =54x +54;(3)①显然∠PRQ <90°,∴分两种情况.ⅰ)当∠RPQ =90°时,如解图②.第5题解图②∵PR ⊥CE ,∴∠ERP =90°.∵∠E =90°,∴四边形RPQE 为矩形,∴PR =QE .∵PR =PC ·sin C =35y =34x +34,∴34x +34=3-x ,∴x =97;ⅱ)当∠PQR =90°时,如解图③,过点P 作PH ⊥BE 于点H ,第5题解图③则四边形PHER 是矩形,∴PH =RE ,EH =PR .∵CB =5,BE =3,∴CE =52-32=4.∵CR =CP ·cos C =45y =x +1,∴PH =RE =CE -CR =4-(x +1)=3-x =EQ ,∴∠EQR =∠ERQ =45°,∴∠PQH =45°=∠QPH ,∴HQ =HP =3-x ,由EH =PR 得:(3-x )+(3-x )=34x +34,∴x =2111.综上所述,x 的值是97或2111;②如解图④,连接AF ,QF ′,由对称可知QF =QF ′,第5题解图④由(3)①得,ER =EQ ,∠F ′QR =∠EQR =45°,∴∠BQF ′=90°,∴QF =QF ′=BQ ·tan B =43x .∵AB 是半圆O 的直径,∴∠AFB =90°,∴BF =AB ·cos B =94,∴43x +x =94,∴x =2728,∴CF ′BF ′=BC -BF ′BF ′=BC BF ′-1=3x -1=199.或利用QF ′∥CE 得,CF ′BF ′=EQ QB =3-x x=3x -1=199.6.(1)解:PA =PE ;【解法提示】如解图①,连接PB ,∵四边形ABCD 是平行四边形,∴AD =BC ,∵AD =BD ,∴BD =BC ,∴∠C =∠BDC =45°,∴∠DBC =90°,∵P 是CD 的中点,∴BP =PD =PC ,∴BP ⊥CD ,∠PBD =45°,∴∠PDA =∠PBE =135°,∵EP ⊥AP ,∴∠DPB =∠APE =90°,∴∠DPA =∠BPE ,∴△PAD ≌△PEB ,∴PA =PE .第6题解图①(2)证明:如解图②,过点P作PF⊥CD交DE于点F,∵PF⊥CD,EP⊥AP,∴∠DPF=∠APE=90°,∴∠DPA=∠FPE,∵四边形ABCD是平行四边形,∴∠C=∠DAB=45°,AB∥CD,又∵AD=BD,∴∠DAB=∠DBA=∠C=∠CDB=45°,∴∠ADB=∠DBC=90°,∴∠PFD=45°,∴∠PFD=∠PDF,∴PD=PF,∴∠PDA=∠PFE=135°,∴△ADP≌△EFP,∴AD=EF,在Rt△FDP中,∠PDF=45°,∵cos∠PDF=DP DF,∴DF=DPcos∠PDF =DPcos45°=2DP,∵DE=DF+EF,∴DA+2DP=DE;第6题解图②(3)解:2或72.【解法提示】①当点P在线段CD上时,如解图③,过点A作AM⊥CD延长线于点M,∵四边形ABCD为平行四边形,∴∠MDA=∠C=45°,∴DM=AM=AD·sin∠MDA=32×sin45°=3,∴PM=AP2-AM2=52-32=4,∴DP=PM-DM=4-3=1,由(2)知DE=AD+2DP=32+2×1=42,∵BD=AD=32,∴BE=DE-BD=42-32=2;②当点P在CD的延长线上时,如解图④,过点A作AM⊥CD延长线于点M,过点P作PF⊥CD延长线交DE于点F,∵四边形ABCD为平行四边形,∴∠MDA=∠C=45°,∴DM=AM=AD·sin∠MDA=32×sin45°=3,∴PM=AP2-AM2=52-32=4,∴DP=PM+DM=4+3=7,由(2)知EF=AD,∴DE=DF-EF=2DP-AD=2×7-32=42,∵BD=AD=32,∴BE=DE+BD=42+32=72.综上所述,BE的长为2或72.第6题解图7.解:(1)45;【解法提示】∵AB=AC,∠A=90°,∴∠B=∠ACB=45°.∵D,E分别是BC,PC的中点,∴DE是△BPC的中位线,∴DE∥BP,∴∠EDC=∠B=45°.(2)如解图①,延长DE,交AC于点I,第7题解图①∵DE∥AB,∴∠DIC=∠A=90°.∵GF⊥BC,∴∠GFB=∠GFC=90°.∵∠ACB=45°,∴△GIE ,△DEF ,△CFG 均为等腰直角三角形.∵∠A =∠EIC ,∠ACP =∠ICE ,∴△CAP ∽△CIE .∴IE AP =IC AC =EC PC =12.∵AC =12,∴IC =6.设AP =2x ,则IE =IG =x ,∴AG =AC -GI -IC =6-x .∴S △APG =12AP ·AG =12·2x ·(6-x )=-x 2+6x =-(x -3)2+9.∴当x =3时,△APG 的面积最大,最大值为9;(3)PE ⊥DG ,PE =DG .理由如下:由(2)得△GIE ,△DEF ,△CFG 均为等腰直角三角形,∴DF =EF ,CF =GF ,∠DFG =∠EFC =90°,∴△DFG ≌△EFC (SAS).∴∠DGF =∠ECF ,DG =EC .∵∠ECF +∠CEF =90°,∠CEF =∠GEH ,∴∠DGF +∠GEH =90°,∴∠GHE =90°,即DG ⊥PC .∵D 为BC 的中点,DI ∥AB ,∴I 为AC 的中点,E 为PC 的中点,∴EC =PE ,∵EC =DG ,∴PE ⊥DG ,PE =DG ;(4)如解图②,作△DCG 的外接圆⊙O ,过点O 作OJ ⊥DG 于点J ,连接OG ,OC ,OD .设⊙O 的半径为r ,则OC =OD =OG =r ,DG =2r ,OJ =12DG =22r ,∵△DFG ≌△EFC ,∴DG =CE =2r .∴CH CE =CH DG ≤OC +OJ DG =r +22r 2r=1+22,即CH CE 的最大值为1+22.第7题解图②8.(1)证明:∵四边形ABCD 是正方形,∴AB =AD ,∠B =∠BAD =90°,∵DE ⊥AF ,∴∠APD =90°,∴∠PAD +∠ADE =90°,∠PAD +∠BAF =90°,∴∠BAF =∠ADE ,∴△ABF ≌△DAE (ASA),∴AE =BF ;(2)解:如解图①,连接AQ ,CQ .第8题解图①∵四边形ABCD 是正方形,∴BA =BC ,∠ABQ =∠CBQ =45°,∵BQ =BQ ,∴△ABQ ≌△CBQ (SAS),∴QA =QC ,∠BAQ =∠QCB ,∵EQ 垂直平分线段AF ,∴QA =QF ,∴QC =QF ,∴∠QFC =∠QCF ,∴∠QFC =∠BAQ ,∵∠QFC +∠BFQ =180°,∴∠BAQ +∠BFQ =180°,∴∠AQF +∠ABF =180°,∵∠ABF =90°,∴∠AQF =90°,∴∠AFQ =∠FAQ =45°;(3)解:如解图②,过点E 作ET ⊥CD 于点T ,则四边形BCTE 是矩形.第8题解图②∴ET =BC ,∠BET =∠AET =90°,∵四边形ABCD 是正方形,∴AB =BC =ET ,∠ABC =90°,∵AF ⊥EG ,∴∠APE =90°,∵∠AEP +∠BAF =90°,∠AEP +∠GET =90°,∴∠BAF =∠GET ,∵∠ABF =∠ETG ,AB =ET ,∴△ABF ≌△ETG (ASA),∴BF =GT =x ,∵AD ∥CB ,DG ∥BE ,∴△BEP ∽△DGP ,△BPF ∽△DPA ,∴BE DG =BP DP =BF DA,∴BE y =x 2,∴BE =TC =12xy ,∵GT =CG -CT ,即x =2-y -12xy ,∴y =4-2x x +2(0≤x ≤2).9.解:【思考】四边形ABDE 是平行四边形,理由如下:∵△ABC ≌△DEF ,∴AB =DE ,∠BAC =∠EDF .∴AB ∥DE .∴四边形ABDE 是平行四边形;【发现】如解图①,连接BE 交AD 于点O ,∵四边形ABDE 为矩形,∴OA =OD =OB =OE .设AF =x cm ,则OA =OE =12(x +4).∴OF =OA -AF =2-12x .在Rt △OFE 中,根据勾股定理得(2-12x )2+32=14(x +4)2,解得x =94.∴AF =94cm ;第9题解图【探究】BD =2OF .理由如下:如解图②,延长OF 交AE 于点H .由矩形性质可得∠OAB =∠OBA =∠ODE =∠OED ,OA =OB =OE =OD .∴∠OBD =∠ODB ,∠OAE =∠OEA .∵∠ABD +∠BDE +∠DEA +∠EAB =360°,∴∠ABD +∠BAE =180°,∴AE ∥BD ,∴∠OHE =∠ODB .∵EF 平分∠OEH ,∴∠OEF =∠HEF .∵∠EFO =∠EFH =90°,EF =EF ,∴△EFO ≌△EFH ,∴EO =EH ,FO =FH ,∴∠EHO =∠EOH =∠OBD =∠ODB ,∴△EOH ≌△OBD ,∴BD =OH =2OF .10.(1)解:等腰三角形,13;【解法提示】如解图①,过点C 作CF ⊥BD 于点F ,∵AC ⊥l ,BD ⊥l ,∴∠CAB =∠DBA =∠CFB =90°,∴四边形ABFC 是矩形,∴AC ∥BD ,AC =BF ,∵BD =2AC ,∴BF =DF ,在△BCF 和△DCF =DFBFC =∠DFC ,=CF∴△BCF ≌△DCF (SAS).∴BC =DC ,∴△BCD是等腰三角形.∵AC ∥BD ,∴△AOC ∽△DOB ,∴OD OA =BD CA =2,∴OD =2OA ,∴OA AD=OA OA +OD=OA 3OA =13.第10题解图①(2)①解:如解图②,过点E 作EG ⊥AD 于点G ,第10题解图②∵AC =32,△ADE 是等边三角形,∴BD =2AC =3,∠EAD =60°,∴∠DAB =90°-∠EAD =30°,∴AD =AE =2BD =6,∵AO AD =13,∴AO =13AD =2,∵AG =12AD =3,∴OG =AG -AO =1,∴EG =AE 2-AG 2=62-32=33,∴OE =OG 2+EG 2=12+(33)2=27;②证明:如解图③,连接CD ,第10题解图③由(1)可知△BCD 是等腰三角形,∵∠ACB =60°,∴∠DBC =∠ACB =60°,∴△BCD 是等边三角形,∠ABC =30°,∵∠EDC =∠EDA -∠CDA =60°-∠CDA ,∠ADB =∠CDB -∠CDA =60°-∠CDA ,∴∠EDC =∠ADB .在△ECD 和△ABD 中,=ADEDC =∠ADB =BD,∴△ECD ≌△ABD (SAS),∴∠ECD =∠ABD =90°,∴∠ACF =∠ECD +∠DCB +∠ACB -180°=90°+60°+60°-180°=30°,设AF =x ,则AC =3x ,AB =3AC =3x ,∴AF AB =x 3x =13=AO AD,∵∠OAF =∠DAB ,∴△OAF ∽△DAB ,∴∠OFA =∠DBA =90°,∴OF ⊥AB .11.解:(1)135°;【解法提示】由题意知,AC =CD =BC ,∴∠CAD =∠CDA ,∠DBC =∠BDC ,又∵△ABC 为直角三角形,∴∠ADB =∠CDA +∠BDC ,即∠ADB =12(180°-α)+12[180°-(90°-α)]=135°.(2)①补全图形,如解图①.第11题解图①∵线段CA 绕点C 顺时针旋转α得到线段CD ,∴CD =CA =BC ,∵∠ACB =90°,∠ACD =α,∴∠CDA =∠CAD =90°-α2,∠CDB =∠CBD =45°-α2,∴∠ADB =∠CDA -∠CDB =45°;②2CE =2BE -AD .证明:过点C 作CG ∥BD ,交EB 的延长线于点G ,如解图②,第11题解图②∵BC =CD ,CE 平分∠BCD ,∴CE 垂直平分BD ,∴BE =DE ,∠EFB =90°,由①知,∠ADB =45°.∴∠EBD =∠EDB =45°,∴∠FEB =45°,∵BD ∥CG ,∴∠ECG =∠EFB =90°,∠G =∠EBD =45°,∴EC =CG ,EG =2EC .∵∠ACE =90°-∠ECB ,∠BCG =90°-∠ECB ,∴∠ACE =∠BCG ,∵AC =BC ,∴△ACE ≌△BCG ,∴AE =BG ,∵EG =EB +BG =EB +AE =EB +ED -AD =EB +EB -AD =2EB -AD ,∴2CE =2BE -AD .12.解:(1)由旋转的性质得,BA =BA ′,∵∠ACB =90°,∴CB 垂直平分AA ′,∴AC =CA ′=52-32=4,∴AA ′=AC +CA ′=8;(2)如解图①,过点C 作CH ⊥AB 于点H ,作CF ∥BM 交AB 于点F ,∴∠CFB =∠A ′BC ′,由旋转的性质得,∠ABC =∠A ′BC ′,∴∠CFB =∠ABC ,∴CB =CF =3,FH =BH ,由(1)知AC =4,∵AC 2-AH 2=BC 2-(5-AH )2,解得AH =165,∴BH =FH =95,BF =185,CH =AC 2-AH 2=125,∴C ′F =C ′B +BF =335,∵CF ∥BM ,∴△C ′MB ∽△C ′CF ,∴BM FC =C ′B C ′F ,即BM 3=3335,∴BM =1511;图①图②第12题解图【一题多解】如解图②,过点C 作CH ⊥AB 于点H ,过点M 作MG ⊥BC ′于点G ,由旋转的性质得,∠MBG =∠CBA ,∴tan ∠MBG =MG BG =tan ∠CBA =AC BC =43,设MG =4x ,则BG =3x ,BM =5x ,同理(2)得CH =125,BH =95,∵tan ∠CC ′H =CH C ′H =125245=12,∴MG C ′G =12,∴C ′G =8x ,∵BC ′=3,∴3x +8x =3,解得x =311,∴BM =5x =1511;(3)存在.理由如下:如解图③,连接A ′C ,过点A 作AP ∥A ′C ′交C ′D 的延长线于点P ,则∠A ′C ′D =∠P,第12题解图③由旋转的性质得,BC =BC ′,∴∠BC ′C =∠BCC ′,∵∠BC ′C +∠A ′C ′C =90°,∠BCC ′+∠ACP =90°,∴∠ACP =∠A ′C ′C =∠P ,∴AP =AC =A ′C ′,∵∠ADP =∠A ′DC ′,∴△ADP ≌△A ′DC ′(AAS),∴A ′D =AD ,∵点E 为AC 的中点,∴DE 为△AA ′C 的中位线,∴DE =12A ′C ,∵A ′C ≥A ′B -BC =2,∴DE ≥12(A ′B -BC )=1,∴DE 的最小值为1.13.(1)证明:∵AB =AC =25,BC =4,D ,E ,F 分别为AC ,AB ,BC 的中点,∴DE =12BC =2,∴DF =12AB =5,∴DF =52DE ;(2)解:FN =52EM ,理由如下:∵AB =AC =25,BC =4,D ,E ,F 分别为AC ,AB ,BC 的中点,∴EF =12AC =CD ,EF ∥DC ,∴四边形CDEF 是平行四边形,∴∠DEF =∠C ,由(1)得DF =12AB =12AC =DC ,∴∠DFC =∠C ,∴∠DEF =∠DFC ,∴180°-∠DEF =180°-∠DFC ,∴∠DEM =∠DFN ,∵将∠EDF 绕点D 顺时针旋转一定角度,得到∠PDQ ,∴∠EDF =∠PDQ ,∴∠FDN +∠NDE =∠EDM +∠NDE ,∴∠FDN =∠EDM ,∴△DNF ∽△DME ,∴NF ME =DF DE =52,∴FN =52EM ;(3)解:如解图,连接AF ,过点C 作CH ⊥AB 于点H ,第13题解图在Rt △AFC 中,FC =12BC =2,∴AF =AC 2-FC 2=4,∵S △ABC =12BC ·AF =12AB ·CH ,∴HC =BC ·AF AB =4×425=855,∵DP ⊥AB ,∴∠AGD =∠AHC =90°.又∵∠GAD =∠HAC ,∴△AGD ∽△AHC ,∴GD HC =AD AC =12,∴GD =12HC =455,在Rt △GED 中,GE =ED 2-GD 2=22-(455)2=255,在Rt △AGD 中,AG =AD 2-GD 2=(5)2-(455)2=355,∴tan ∠ADG =AG GD =355455=34,∵EF ∥AD ,∴∠EMG =∠ADG ,∴tan ∠EMG =EG MG =34,∴MG =43GE =43×255=8515,∴MD =MG +GD =8515+455=453,由(2)得△DNF ∽△DME ,∴DN DM =DF DE =52,∴DN =52DM =52×453=103.14.(1)证明:∵AD ∥BC ,∠ABC =90°,∴∠DAB =180°-∠ABC =90°,∵DH ⊥BC ,即∠DHB =90°,∴四边形ABHD 为矩形.∴AB =DH =23,∠DHC =90°,∵∠C =30°,∴CD =2DH =43,在△PQM 和△CHD 中,Q =∠DHCQPM =∠HCD =CD,∴△PQM ≌△CHD (AAS);(2)解:①∵PM =43,∠QPM =30°,∴PQ =PM ·cos ∠QPM =6.如解图①,过点D 作DT ⊥QA ,交QA 的延长线于点T ,∵∠QPM =30°,∠BPD =90°,∴∠TPD =60°,∴DT =AD ·sin ∠TPD =332,∴边PQ 平移扫过的面积为AQ ·DT =6×332=93,∵边PQ 旋转扫过的面积为50π×62360=5π,∴边PQ 扫过的面积为93+5π;图①图②第14题解图②由(1)可得BH =AD =3,∵BK =9-43,∴KH =BH -BK =43-6,如解图②,当点P 平移到与点D 重合时,连接DK ,设DQ 交BC 于点E ,∵∠QPM =∠HPE ,∠PQM =∠PHE ,∴△PHE ∽△PQM ,∴EH QM =PH PQ ,即EH 23=236,∴EH =2,∵EH -KH =8-43>0,∴点K 在△PQM 中,∵△PQM 右移的速度为每秒1个单位长,∴在△PQM 右移的过程中,点K 在△PQM 区域(含边界)内的时长为(43-6)秒;∵CH =6,BH =3,∴BC =9,∵BK =9-43,∴CK =BC -BK =43,∴CD =CK ,∵∠C =30°,∴∠CDK =∠CKD =75°,∴∠KDH =∠KDC -∠HDC =15°,∴∠QPK =∠QPM -∠KDH =15°,∵△PQM 旋转的速度为每秒5°,∴在△PQM 旋转的过程中,点K 在△PQM 区域(含边界)内的时长为15°÷5°=3秒.∴点K 在△PQM 区域(含边界)内的时长为43-6+3=(43-3)秒;③CF 的长为60-12d 9-d.【解法提示】∵BE =d ,∴EH =|3-d |,EC =BH +HC -BE =3+6-d =9-d ,在Rt △DEH 中,DE 2=DH 2+EH 2=(23)2+|3-d |2=d 2-6d +21,∵∠EDF =∠C ,∠DEF =∠CED ,∴△DEF ∽△CED ,∴DE CE =EF ED ,∴EF =DE 2EC =d 2-6d +219-d,∴CF =BC -BE -EF =9-d -d 2-6d +219-d =60-12d 9-d.15.解:(1)60;【解法提示】当AE ⊥BC 时,△ABE 是等边三角形,∴∠AEB =60°.(2)∠AEB -∠CAD =30°;证明:设∠CAD =α,∵AE =AC =AB ,∴∠BAC =180°-2∠ABC =120°,∴∠BAE =120°-2α,∴∠AEB =12(180°-∠BAE )=12[180°-(120°-2α)]=30°+α,∴∠AEB -∠CAD =30°;(3)如解图,连接AO ,∵O 为BC 的中点,AB =AC ,∴AO ⊥BC .在Rt △AOC 中,AC =4,∠ACO =30°,∴AO =2,OC =23,∵S △ACD =12AO ·DC ,即x =12×2·DC ,∴DC =x .在Rt △AOD 中,∵AD 2=AO 2+OD 2,∴y =22+(23-x )2,整理得y =x 2-43x +16.∴y 关于x 的函数解析式为y =x 2-43x +16(0<x <23).第15题解图16.(1)证明:由折叠的性质得∠PEF=∠FED,∵AD∥BC,∴∠FED=∠EFP,∴∠PEF=∠EFP,∴PE=PF;(2)证明:如解图①,连接PM、EM、FM,∵AD=BC,AE=CF,∴ED=BF,∴EH=BF,由(1)可得PE=PF,∴PH=PB,∵∠PHM=∠PBM=90°,PM=PM,∴Rt△PMH≌Rt△PMB(HL),∴HM=BM,∵∠MHE=∠MBF,HE=BF,∴△MHE≌△MBF(SAS),∴ME=MF,∴点M在线段EF的垂直平分线上;第16题解图(3)解:如解图②,连接AC交BD于点O,由题意可得点E由点A移动到AD中点的过程中,BC的长度.点G运动的路线是以点O为圆心,OC长为半径的圆的一部分,即解图中。
中考数学专题复习_几何探究题
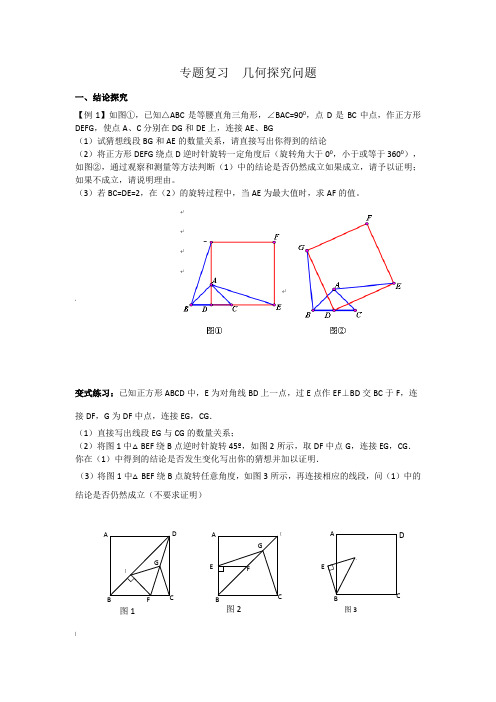
专题复习几何探究问题一、结论探究【例1】如图①,已知△ABC是等腰直角三角形,∠BAC=900,点D是BC中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论(2)将正方形DEFG绕点D逆时针旋转一定角度后(旋转角大于00,小于或等于3600),如图②,通过观察和测量等方法判断(1)中的结论是否仍然成立如果成立,请予以证明;如果不成立,请说明理由。
(3)若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值。
'变式练习:已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)直接写出线段EG与CG的数量关系;(2)将图1中△BEF绕B点逆时针旋转45º,如图2所示,取DF中点G,连接EG,CG.你在(1)中得到的结论是否发生变化写出你的猜想并加以证明.(3)将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立(不要求证明)| A D]G图1FA[EG图2、AE图3DFEC BAB'C'二、条件探究【例2】已知两个全等的直角三角形纸片ABC 、DEF ,如图(1)放置,点B 、D 重合,点F 在BC 上,AB 与EF 交于点G ,∠C=∠EFB=900,∠E=∠ABC=300,AB=DE=4 (1)求证:△EGB 是等腰三角形(2)若纸片DEF 不动,问△ABC 绕点F 旋转最小 度时,四边形ACDE 成为以ED 为底的梯形(如图(2)),求此梯形的高。
,【例3】如图,Rt △AB C 是由Rt △ABC 绕点A 顺时针旋转得到的,连结CC 交斜边于点E ,CC 的延长线交BB 于点F . |(1)证明:△ACE ∽△FBE ;(2)设∠ABC =α,∠CAC =β,试探索α、β满足什么关系时,△ACE 与△FBE 是全等三角形,并说明理由.;E图1A:CD图2三、类比探究 【例4】(1)操作发现:如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE ,且点G 在举行ABCD 内部.小明将BG 延长交DC 于点F ,认为GF =DF ,你同意吗说明理由. (2)问题解决:保持(1)中的条件不变,若DC =2DF ,求ABAD的值; /(3)类比探求:保持(1)中条件不变,若DC =nDF ,求ABAD的值.【例5】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________;((2)如图1,梯形ABCD 中,AB ∥DC ,如果延长DC 到E ,使CE =AB ,连接AE ,那么有S 梯形ABCD=S △ABE .请你给出这个结论成立的理由,并过点A 作出梯形ABCD 的面积等分线(不写作法,保留作图痕迹);(3)如图,四边形ABCD 中,AB 与CD 不平行,S △ADC >S △ABC ,过点A 能否作出四边形ABCD 的面积等分线若能,请画出面积等分线,并给出证明;若不能,说明理由.AB。
中考物理复习命题点 实验探究、综合应用题组限时练(三)

无关
②根据A、C、D图的结果,可得浮力和物体浸入液体的深度______(选填
“有关”或“无关”);根据A、B、C图的结果,可得物体所受浮力大小与
排开液体的体积
________________有关;
③为了研究浮力大小与液体密度的关系,如图C、 E 所示,分别将塑料瓶
浸没在水和盐水中,比较弹簧测力计的示数,可得出结论:物体排开液体
动力做功的功率: =
=
.×
= . × .
21.某学校科技小组为杜绝餐饮浪费的行为,为
学校餐厅设计了如图甲所示的电路,控制电路
的电源电压恒为 6 V , 0 的阻值为 100 Ω ,
1 为压敏电阻,其阻值随压力大小变化的图像
如图乙所示,学生就餐完毕将剩余食物和餐盘
秒表
______.
第17题图
(2)点燃酒精灯时,打开灯帽,可闻到淡淡的酒精味,说明酒精分子在
不停地做无规则运动
____________________.
(3)当乙温度计示数达到 99 ℃ 后保持不变,但试管中的水始终没有沸
试管中的水达到沸点后不能继续吸热
腾,其原因是__________________________________.
由图乙可知,此时压敏电阻受到的压力 = ,因食
物和餐盘对称重盘的压力等于自身的重力,所以,称重
盘中食物和餐盘的总质量的限定值:
=
=
=
/
= . = ;
第21题图
(3)当称重盘中食物和餐盘的总质量为 400 g 时,压敏电阻 1 的电功率
(4)当小李同学在烧杯的水中加入少量的食盐后,发现试
九上科学中考复习试卷——探究题专题50题

九上科学中考复习试卷——探究题专题50题1.在“测定小灯泡的功率”的实验中,小明同学设计的电路如下图所示,他选用的小灯泡的额定电压为2.5V,电阻约为8Ω,电源为两节干电池.(1)请用笔画线代替导线,按照图甲所示的电路图,将图乙中的实物电路连接完整(导线不得交叉).(2)正确连好电路后,闭后开关前应把滑动变阻器滑片调到________ (选填“A”或“B”)端.(3)如果连好电路后,闭合开关S,小明发现灯泡不发光,电流表的示数为零,电压表的示数约为3V,则产生故障的原因可能是_____ .A.小灯泡短路B.小灯泡的灯丝断了C.滑动变阻器滑片接触不良D.电压表的正、负接线柱接反(4)排除故障后,调节滑动变阻器使小灯泡在额定电压下正常发光时,电流表的指针位置如图丙所示,则小灯泡的额定功率为________ W.2.小强同学想知道橡皮泥的密度有多大,他用天平、量筒、水和细线进行如图所示的实验操作。
(1)在调节天平时,小强发现指针偏向分度盘中央刻度线的右侧,为使天平横梁水平平衡,他应将平衡螺母向________ 端调。
(2)在如图所示的实验过程中,合理的操作顺序是(填图中对应序号):________ 。
(3)由图可知,橡皮泥质量m=________ g,通过计算,橡皮泥的密度ρ=________kg/m3 。
3.汽车追尾是高速公路上常发生的交通事故,其重要原因是遇到意外情况时不能立即停车。
研究发现,司机从看到情况到踩刹车需要一段时间,这段时间叫反应时间;在反应时间内汽车要保持原速前进一段距离,这段距离叫反应距离;从踩刹车到车停止,汽车还要前进一段距离,这段距离叫制动距离。
如图所示。
下表是一个机警的司机驾驶一辆保养得很好的汽车.在于燥的水平公路上以不同的速度行驶时。
测得的反应距离和制动距离。
原行驶速度v/km•h-1反应距离s1/m 制动距离s2/m60 11 2080 15 34100 19 54(1)利用上表数据,算出该司机的反应时间大约是________ 秒。
中考化学综合题专题复习【探究题】专题解析及详细答案

一、中考初中化学科学探究题1.生石灰常用作食品干燥剂.久置的生石灰里可能会含有氧化钙、氢氧化钙、碳酸钙三种物质中的一种或几种(假设久制的生石灰中不再含有其它成分).为了探究久置的生石灰的成分,某校化学兴趣小组进行了以下探究活动.(设计实验)取0.94g久置的生石灰样品放入烧杯中,进行了以下探究实验,如图所示:(讨论与分析)(1)生石灰可以做干燥剂的原因是_____________________(用化学方程式表示).(2)向0.2g滤渣A中滴加稀盐酸,有气泡产生,说明久置的生石灰样品中一定含有_______(填写化学式).(3)②中反应过程中的实验现象是_________________________________.(4)将混合物C、D全部倒入一个洁净的烧杯中混合,充分反应后,过滤,得到1g滤渣E 和红色滤液F.向滤液F中滴加CaCl2溶液,有白色沉淀生成,则滤液F的溶质中一定含有__________,还可能含有________.(解释与结论)依据实验现象和测得的数据判断,0.94g久置的生石灰样品的成分是____________.【答案】CaO+H2O=Ca(OH)2 CaCO3溶液先变红色,然后逐渐变成无色 Na2CO3、NaCl;NaOH Ca(OH)2、CaCO3【解析】【分析】【详解】讨论与分析:(1)生石灰可以做干燥剂的原因是氧化钙能和水反应生成氢氧化钙,反应的化学方程式为:CaO+H2O=Ca(OH)2;(2)碳酸钙与盐酸反应生成氯化钙、水和二氧化碳。
向0.2g滤渣A中滴加稀盐酸,有气泡产生,说明久置的生石灰样品中一定含有CaCO3;(3)②中,向氢氧化钙溶液中滴加酚酞试液时,由于氢氧化钙溶液显碱性,能使酚酞试液变红色,氢氧化钙能和稀盐酸反应生成氯化钙和水,氯化钙溶液显中性,不能使酚酞试液变色,因此反应过程中能够观察到溶液先变红色,然后逐渐变成无色;(4)向滤液F中滴加CaCl2溶液,有白色沉淀生成,说明滤液F中含有Na2CO3,同时一定含有碳酸钠和氯化钙反应生成的NaCl;还可能含有①中反应生成的NaOH;解释与结论:样品中含有0.2g碳酸钙,如果除去碳酸钙外全部是氢氧化钙,则氢氧化钙质量为:0.94g-0.2g=0.74g,氢氧化钙中的钙元素经过反应后全部转化到滤渣E中。
中考数学专题复习题型-多条件探究题

1.(成都28)如图,在平面直角坐标系xOy中,抛物线()213y a x=+-与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,83-),顶点为D,对称轴与x轴交于点H.过点H的直线l交抛物线于P,Q两点,点Q在y轴右侧.(1)求a的值及点A、B的坐标;(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN 能否成为菱形?若能,求出点N的坐标;若不能,请说明理由.2.(昆明23).如图,对称轴为直线21=x的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.(1)求抛物线的解析式;(2)若点P为第一象限内抛物线上一点,设四边形COBP的面积为S,求S的最大值;(3)如图①,若M是线段BC上一动点,在x轴上是否存在这样有点Q,使∆MQC为等腰三角形且∆MQB 为直角三角形?若存在,求出Q点坐标;若不存在,请说明理由.1/ 22 / 2(日照22).如图1,抛物线()2325y x n ⎡⎤=--+⎢⎥⎣⎦与x 轴交于点A (m ﹣2,0)和B (2m +3,0)(点A 在点B 的左侧),与y 轴交于点C ,连结BC .(1)求m 、n 的值;(2)如图2,点N 为抛物线上的一动点,且位于直线BC 上方,连接CN 、BN .求△NBC 面积的最大值; (3)如图3,点M 、P 分别为线段BC 和线段OB 上的动点,连接PM 、PC ,是否存在这样的点P ,使△PCM 为等腰三角形,△PMB 为直角三角形同时成立?若存在,求出点P 的坐标;若不存在,请说明理由.。
中考复习-几何探究题(含答案)

几何探究题1题(1)如图1,图2,图3,在ABC △中,分别以AB AC ,为边,向ABC △外作正三角形,正四边形,正五边形,BE CD ,相交于点O .①如图1,求证:ABE ADC △≌△;②探究:如图1,BOC ∠= ;如图2,BOC ∠=; 如图3,BOC ∠= .(2)如图4,已知:AB AD ,是以AB 为边向ABC △外所作正n 边形的一组邻边;AC AE ,是以AC 为边向ABC △外所作正n 边形的一组邻边.BE CD ,的延长相交于点O .①猜想:如图4,BOC ∠= (用含n 的式子表示);②根据图4证明你的猜想.2题.请阅读下列材料: 问题:如图1,在菱形ABCD 和菱形BEFG 中,点A B E ,,在同一条直线上,P 是线段()()a a b a b +-的中点,连结PG PC ,.若60ABC BEF ∠=∠=,探究PG 与PC 的位置关系及PGPC的值. 小聪同学的思路是:延长GP 交DC 于点H ,构造全等三角形,经过推理使问题得到解决.问题:(1)写出上面问题中线段PG 与PC 的位置关系及PGPC的值; (2)将图1中的菱形BEFG 绕点B 顺时针旋转,使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)若图1中2(090)ABC BEF ∠=∠=<<αα,将菱形BEFG 绕点B 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出PGPC的值(用含α的式子表示). D A BE F C P G 图1 D C G PA B F图23题。
如图,等腰梯形ABCD 中,AB =4,CD =9,∠C =60°,动点P 从点C 出发沿CD 方向向点D 运动,动点Q 同时以相同速度从点D 出发沿DA 方向向终点A 运动,其中一个动点到达端点时,另一个动点也随之停止运动. (1)求AD 的长;(2)设CP =x ,问当x 为何值时△PD Q 的面积达到最大,并求出最大值;(3)探究:在BC 边上是否存在点M 使得四边形PD Q M 是菱形?若存在,请找出点M ,并求出BM 的长;不存在,请说明理由.4题已知矩形ABCD 和点P ,当点P 在BC 上任一位置(如图(1)所示)时,易证得结论:2222PA PC PB PD +=+,请你探究:当点P 分别在图(2)、图(3)中的位置时,2222PA PB PC PD 、、和又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.答:对图(2)的探究结论为____________________________________. 对图(3)的探究结论为_____________________________________. 证明:如图(2)(第25题图) (备用图)5题如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.(1)直接写出点E、F的坐标;(2)设顶点为F的抛物线交y轴正半轴...于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.6题如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka,CG=kb(a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结DG、BE,且a=3,b=2,k=12,求22BE DG+的值.7题正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B A 几何探究题讲练专题 例题:
例1:如图,点G 是正方形ABCD 的边CD 上的一点(不包括点C. D ).将△CBG 绕点C 按顺时针方向旋转90∘,请你在图中画出旋转后的图形;
例2:【条件】在正方形ABCD 中,已知E 、F 分别是边BC 、CD 上的点,且满足∠EAF =45°,AE 、AF 分别与对角线BD 交于点M 、N .
【结论】
(1) BE +DF =EF ;(2) S △ABE +S △ADF =S △AEF ;(3) AH =AB ;(4) C △ECF =2AB ;
(5) BM 2+DN 2=MN 2;
B A
B A
B A
B A 【条件】在正方形ABCD 中,已知E 、F 分别是边B
C 、C
D 上的点,且满足∠EAF =45°,A
E 、A
F 分别与对角线BD 交于点M 、N .
(6) △ANM ∽△DNF ∽△BEM ∽△AEF ∽△BNA ∽△DAM ; (由AO :AH =AO :AB =1:2可得到△ANM 和△AEF 的相似比为1:2);
(7) S △AMN =S 四边形MNFE ;(8) △AOM ∽△ADF ,△AON ∽△ABE ;
(9) △AEN 为等腰直角三角形,∠AEN =45°;△AFM 为等腰直角三角形,∠AFM =45°. (1. ∠EAF =45°;2.AE :AN =1:2);
(10)A 、M 、F 、D 四点共圆,A 、B 、E 、N 四点共圆,M 、N 、F 、C 、E 五点共圆.
例3:已知∠MAN=135∘,正方形ABCD绕点A旋转。
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是___;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2) 如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD 交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由。
练习:
1.在矩形ABCD中,已知AD>AB.在边AD上取点E,使AE=AB,连结CE,过点E作EF⊥CE,与边AB或其延长线交于点F.
猜想:如图①,当点F在边AB上时,线段AF与DE的大小关系为___.
探究:如图②,当点F在边AB的延长线上时,EF与边BC交于点G.判断线段AF与DE
的大小关系,并加以证明。
应用:如图②,若AB=2,AD=5,利用探究得到的结论,求线段BG的长。
2.如图1所示,在正方形ABCD和正方形CGEF中,点B. C. G在同一条直线上,M是线段AE 的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程) (1)如图2,当点B. C. F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E. B. C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想。
3.【问题探究】
(1)如图1,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由。
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45∘,求BD的长。
(3) 如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长。
4.(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90∘.求证:
AD⋅BC=AP⋅BP.
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由。
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC 为半径的圆与AB相切,求t的值。
5.已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90∘,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+√3,PA=√2,则:
①线段PB=___,PC=___;
②猜想:PA2,PB2,PQ2三者之间的数量关系为___;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足PA/PB=1/3,求PC/AC的值.(提示:请利用备用图进行探求)
6.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”。
(1)概念理
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”。
请写出你添加的一个条件。
(2)问题探究:
①小红猜想:对角线互相平分的“等邻边四边形”是菱形,她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90∘,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′,小红要使平移后的四边形ABC′A′是“等邻边四边形”,应平移多少距离(即线段BB′的长)?
(3)拓展应用:
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90∘,AC,BD为对角线,AC=√2AB,试探究BC,CD,BD的数量关系。
7.如图,已知AB是O的直径,过点A作O的切线MA,P为直线MA上一动点,以点P为圆心,PA为半径作圆P,交圆O于点C,连接PC、OP、BC.
(1)知识探究(如图1):
①判断直线PC与圆O的位置关系,请证明你的结论;
②判断直线OP与BC的位置关系,请证明你的结论。
(2)知识运用(如图2):
当PA>OA时,直线PC交AB的延长线于点D,若BD=2AB,求tan∠ABC的值。
8.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90∘,若点P是BF的中点,连接PC,PE.
特殊发现:
如图1,若点E,F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).
问题探究:
把图1中的△AEF绕着点A顺时针旋转。
(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)记AC/BC=k,当k为何值时,△CPE总是等边三角形?(请直接写出k的值,不必说明理由)
9.已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点。
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A. B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系:___.
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB 的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由。
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90∘(如图③所示),若两平行线m、n之间的距离为2k.求证:PA⋅PB=k⋅AB.。
