数电3
数电3(1)

EXIT
逻辑代数基础
[例] 将逻辑式
Y ABC AB C D 化为标准与或式。
解:(1) 利用反演律和分配律把逻辑函数式展开为与或式。
Y ABC AB C 如何将逻辑式转化 D ABC AB (C D标准与-或式呢 ? 为 ) ABC ABC ABD
AB ABC ABC BC ABC A BC 应用A+AB=A
A B BC AC
方法二: 应用 AC BC AB AC BC
Z AB BC AC AB BC
AB B C AC AB BC
先扩展
后吸收
A B AC AB BC
化简法 缺点:需技巧,不易判断是否最简式。 卡诺图 化简法
优点:简单、直观,有一定的步骤和方法 易判断结果是否最简。 缺点:适合变量个数较少的情况。 一般用于四变量以下函数的化简。
EXIT
逻辑代数基础
1、逻辑函数的最小项
(1)最小项的定义
n 个变量有 2n 种组合,可对应写出 2n 个乘积
项,这些乘积项均具有下列特点:包含全部变量, 且每个变量在该乘积项中 (以原变量或反变量)只
四、逻辑函数的化简
化 使逻辑式最简,以便设计出最简的逻辑电路, 简 从而节省元器件、优化生产工艺、降低成本和提 意 义 高系统可靠性。 不同形式逻辑式有不同的最简式,一般先求取 最简与 - 或式,然后通过变换得到所需最简式。
EXIT
逻辑代数基础
最简与 - 或式标准
(1)乘积项(即与项)的个数最少 (2)每个乘积项中的变量数最少
B CD
Y A( BC BC ) A( BC BC ) AB C A( B C )
数电-第3章 逻辑代数基础

一般形式 F ( A, B,C) ABC ABC ABC ABC
简写形式 F ( A, B, C) m3m5 m6 m7
F(A, B,C) m(3,5,6,7)
逻辑代数基础
在与或逻辑函数表达式中,若与项不是最小项, 可利用A+/A=1形式补充缺少的变量, 将逻辑函数变换成最小项之和的最小项表达式。
2. 最小项的基本性质
(1) 对任意一最小项,只有一组变量取值使它的值为 1,
而其余各种变量取值均使其值为 0。 (2) 不同的最小项,使其值为 1 的那组变量取值也不同。 (3) 对于变量的任一组取值,任意两个最小项的乘积为 0。 (4) 对于变量的任一组取值,全体最小项的和为 1。
三
AB
C
m0 ABC
逻辑表达式 Y = A + B 开关 A 开关 B 灯 Y
有1出1 全0出0
断 断 合
≥断1 合 断
灭 或门 亮 (OR gate) 亮
合
合亮
3.
非逻辑
决定某一事件的条件满足时,
开关 A 或事B件闭不合发或生两;者反都之闭事合件时发,生灯。Y 才亮。
AY 01 10
Y=A
1开关闭合时非又灯门称灭(“N,反OT相g器at”e) 开关断开时灯亮。
二、复合逻辑
逻辑代数基础
由基本逻辑运算组合而成
与非逻辑(NAND) 先与后非
AB Y
00 01
1 1
若有 0 出 1
1 0 1 若全 1 出 0
11 0
或非逻辑 ( NOR ) 先或后非
AB Y 0 0 1 若有 1 出 0 01 0 1 0 0 若全 0 出 1
数电实验3-译码器及其应用
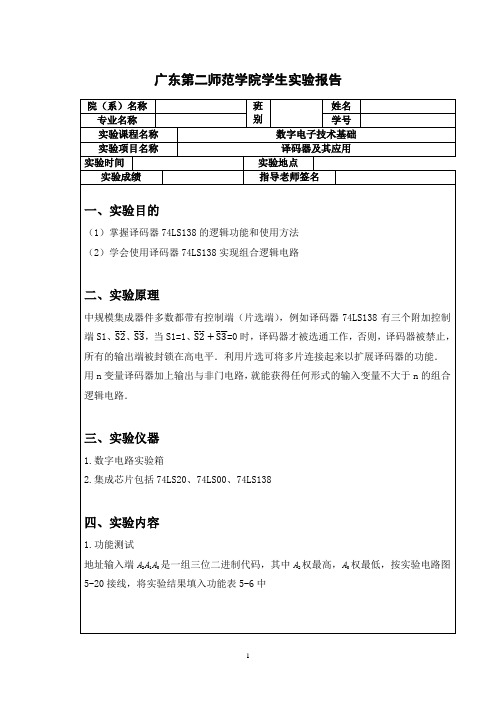
输出
A
B
C
Y
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
(2)写标准与非表达式
又A2=A,A1=B,A0=C
Y=
(3)画连线图
3.用74LS138和门电路设计一个全加器
(1)全加器有3个输入信号Ai、Bi、Ci,两个输出信号Si、Ci-1。
真值表
输入
输出
Ai
Bi
Ci-1
Si
Ci
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
(2)与非表达式
(3)确认表达式
A2=AiA1=BiA0=Ci-1
(4)连线图
五、实验心得
设计这些电路根据题目要先画出真值表,再根据真值表列逻辑表达式,化简成最小项,最后根据38译码器的特点连线就可以了。难度不大,注意三个选通端都接1。
广东第二师范学院学生实验报告
院(系)名称
班别
姓名
专业名称
学号
实验课程名称
数字电子技术基础
实验项目名称
数电实验三
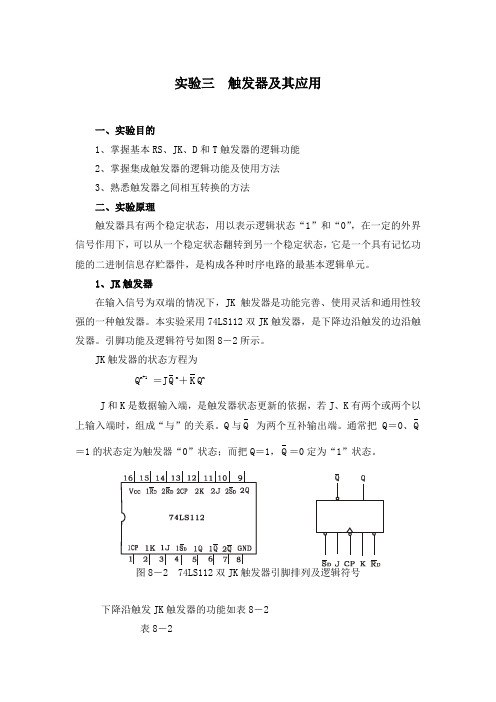
实验三触发器及其应用一、实验目的1、掌握基本RS、JK、D和T触发器的逻辑功能2、掌握集成触发器的逻辑功能及使用方法3、熟悉触发器之间相互转换的方法二、实验原理触发器具有两个稳定状态,用以表示逻辑状态“1”和“0”,在一定的外界信号作用下,可以从一个稳定状态翻转到另一个稳定状态,它是一个具有记忆功能的二进制信息存贮器件,是构成各种时序电路的最基本逻辑单元。
1、JK触发器在输入信号为双端的情况下,JK触发器是功能完善、使用灵活和通用性较强的一种触发器。
本实验采用74LS112双JK触发器,是下降边沿触发的边沿触发器。
引脚功能及逻辑符号如图8-2所示。
JK触发器的状态方程为Q n+1=J Q n+K Q nJ和K是数据输入端,是触发器状态更新的依据,若J、K有两个或两个以上输入端时,组成“与”的关系。
Q与Q为两个互补输出端。
通常把 Q=0、Q =1的状态定为触发器“0”状态;而把Q=1,Q=0定为“1”状态。
图8-2 74LS112双JK触发器引脚排列及逻辑符号下降沿触发JK触发器的功能如表8-2表8-2注:×—任意态↓—高到低电平跳变↑—低到高电平跳变Q n(Q n)—现态 Q n+1(Q n+1 )—次态φ—不定态JK触发器常被用作缓冲存储器,移位寄存器和计数器。
2、D触发器在输入信号为单端的情况下,D触发器用起来最为方便,其状态方程为Q n+1=D n,其输出状态的更新发生在CP脉冲的上升沿,故又称为上升沿触发的边沿触发器,触发器的状态只取决于时钟到来前D端的状态,D触发器的应用很广,可用作数字信号的寄存,移位寄存,分频和波形发生等。
有很多种型号可供各种用途的需要而选用。
如双D 74LS74、四D 74LS175、六D 74LS174等。
图8-3 为双D 74LS74的引脚排列及逻辑符号。
功能如表8-3。
图8-3 74LS74引脚排列及逻辑符号表8-3 D触发器特性表表8-4 T触发器特性表4、触发器之间的相互转换在集成触发器的产品中,每一种触发器都有自己固定的逻辑功能。
数电第三章讲解

(1) 传输门组成的异或门
B=0
A
B
TG1断开, TG2导通
L=A B=1
TG1导通, TG2断开
L=A
TG1
L
TG2
2. 传输门的应用
(2) 传输门组成的数据选择器
C=0
X
TG1导通, TG2断开
L=X
C=1
Y
TG2导通, TG1断开
C
L=Y
VDD TG1 L
TG2
3.3 CMOS逻辑门电路的不同输出结构及参数
3.3.1 CMOS逻辑门电路的保护和缓冲电路 3.3.2 CMOS漏极开路和三态门电路 3.3.3 CMOS逻辑门电路的重要参数
3.3.1 输入保护电路和缓冲电路
采用缓冲电路能统一参数,使不同内部逻辑集成逻辑门电路 具有相同的输入和输出特性。
VDD
vi
基本逻辑
vo
功能电路
输入保护缓冲电路 基本逻辑功能电路 输出缓冲电路
异或门电路324cmos传输门双向模拟开关5v0v电路tg逻辑符号5v0v1传输门的结构及工作原理tp2vttn2v的变化范围为0到5v0v5v0v到5vgsp5v0v到5v5到0v开关断开不能转送信号c00vc15v5v0v5v0v2v5v2v5vgsn5vtg1断开tg2导通tg1导通tg2断开tg1导通tg2断开tg2导通tg1断开tg2tg133cmos逻辑门电路的不同输出结构及参数331cmos逻辑门电路的保护和缓冲电路332cmos漏极开路和三态门电路333cmos逻辑门电路的重要参数331输入保护电路和缓冲电路基本逻辑功能电路基本逻辑功能电路输入保护缓冲电路输出缓冲电路采用缓冲电路能统一参数使不同内部逻辑集成逻辑门电路具有相同的输入和输出特性
数电实验3

深圳大学实验报告课程名称:数字电子技术实验项目名称:实验三三态门实验学院:光电工程专业:光电信息指导教师:报告人:刘恩源学号:2012170042 班级:2 实验时间:实验报告提交时间:一、实验目的与要求:1、掌握三态门逻辑功能和使用方法。
2、掌握三态门构成总线的特点和方法。
3、初步学会用示波器测量简单的数字波形。
二、实验仪器1、四2输入与非门74LS00 1片2、三态输出的四总线缓冲门74LS125 1片3、万用表4、示波器三、实验内容与步骤:1、74LS125三态门的输出负载为74LS00一个与非门输入端。
74LS00同一个与非门的另一个输入端接低电平,测试74LS125三态门三态输出、高电平输出、低电平输出的电压值。
同时测试74LS125三态输出时74LS00输出值。
2、74LS125三态输出负载为74LS00一个与非门输入端。
74LS00同一个与非门的另一个输入端接高电平,测试74LS125三态门三态输出、高电平输出、低电平输出的电压值。
同时测试74LS125三态输出时74LS00输出值。
3、用74LS125两个三态门输出构成一条总线。
使两个控制端一个为低电平,另一个为高电平。
一个三态门的输入接100kH Z信号,另一个三态门的输入接10kH Z信号。
用示波器观察三态门的输出。
PS:1、三态门74LS125的控制端EN为低电平有效。
2、用实验板上的逻辑开关输出作为被测器件作为被测器件的输入。
按入或弹出开关,则改变器件的输入电平。
四、实验接线图和实验结果1、实验内容1和内容2接线图图3.1 实验内容1和内容2接线图图中K1、K2和K3是逻辑开关输出,电压表指示电压测量点。
按入或弹出逻辑开关K3、K2、K1,则改变74LS00一个与非门输入端、74LS125三态门控制端、三态门输入端的电平。
2、当74LS00引脚2为低电平时,测试74LS125引脚3和74LS00引脚3,结果如下:3、当74LS00引脚2为高电平时,测试74LS125引脚3和74LS00引脚3,结果如下:4、用三态门构成总线接线图图3.2 三态门构成总线结果:123UA74LS125456UB74LS125K2K1CP1CP2OUT五、数据处理:1、将实验数据与真值表比较,确认三态门特性功能。
数电第三章门电路

§3.4 TTL门电路
数字集成电路:在一块半导体基片上制作出一个 完整的逻辑电路所需要的全部元件和连线。 使用时接:电源、输入和输出。数字集成电 路具有体积小、可靠性高、速度快、而且价 格便宜的特点。
TTL型电路:输入和输出端结构都采用了半导体晶 体管,称之为: Transistor— Transistor Logic。
输出高电平
UOH (3.4V)
u0(V)
UOH
“1”
输出低电平
u0(V)
UOL
UOL (0.3V)
1
(0.3V)
2 3 ui(V)
1 2 3 ui(V)
阈值UT=1.4V
传输特性曲线
理想的传输特性 28
1、输出高电平UOH、输出低电平UOL UOH2.4V UOL 0.4V 便认为合格。 典型值UOH=3.4V UOL 0.3V 。
uA t
uF
截止区: UBE< 死区电压, IB=0 , IC=ICEO 0 ——C、 E间相当于开关断开。
+ucc
t
4
0.3V
3.2.3MOS管的开关特 恒流区:UGS>>Uth , UDS
性: +VDD
0V ——D、S间相当于 开关闭合。
R
uI
Uo
Ui
NMO S
uO
夹断区: UGS< Uth, ID=0 ——D、S间相当于开关断开。
3.3.4 其它门电路
一、 其它门电路
其它门电路有与非门、或非门、同或门、异或门等等,比如:
二、 门电路的“封锁”和“打开”问题
A B
&
Y
C
当C=1时,Y=AB.1=AB
数电习题3

习题三【试题3-1】 用74LS138设计一个能对32地址译码的译码电路。
【解题方法指导】构成32地址译码系统需要用4片74LS138译码器。
32地址对应5位二进制地址码A 4A 3A 2A 1A 0,低三位地址A 2A 1A 0为每一片译码器提供8个低位地址,高位地址A 4A 3作为译码器的使能信号。
A 4A 3=00时,74138-1译码输出;A 4A 3=01时,74138-2译码输出;A 4A 3=10时,74138-3译码输出;A 4A 3=11时,74138-4译码输出。
A 4A 3可以用2/4线译码器译码,为74138-1~74138-4提供使能信号。
考虑到74138有多个使能端;可利用使能端本身的译码功能。
由于74138只有一个高电平有效的使能端,所以A 4中A 3要有一个反相后接低电平有效的使能端,使A 4A 3=11时,74138-4译码输出。
【解答】能实现32地址译码的译码系统之一如图3-53所示。
图3-53 74138实现32地址译码【试题3-2】用74138和74151组成图3-54所示16通道数据传输系统,可将任一输入通道的输入数据从任一输出通道输出。
图3-54【解题方法指导】本题实质是将8通道数据选择器和8通道数据分配器扩展为16通道。
八选一数选器74151只有一个使能端,所以要用一个反相器使两片74151分别使能。
八通道数据分配器74138有三个使能端,一片74138用高电平使能,另一片74138则用低电平使能,剩余一个低电平使能端作为数据输入端。
因为,低电平使能端作为数据输入端,输入输出数据同相,所以,74151用高电平输出有效的输出端Y 。
Y 24~Y 31 A Y 8~Y 15 A I I 1 I Y 0Y 1Y 1【解答】能实现16通道数据传输系统之逻辑图如图3-55所示。
图3-55【试题3-3】用一片74LS48实现三位十进制数动态扫描显示。
【解题方法指导】图3-18中用三片7448实现三位十进制数动态扫描显示,选通信号ST 作为灭灯输入BI 。
数电 第3章 习题.
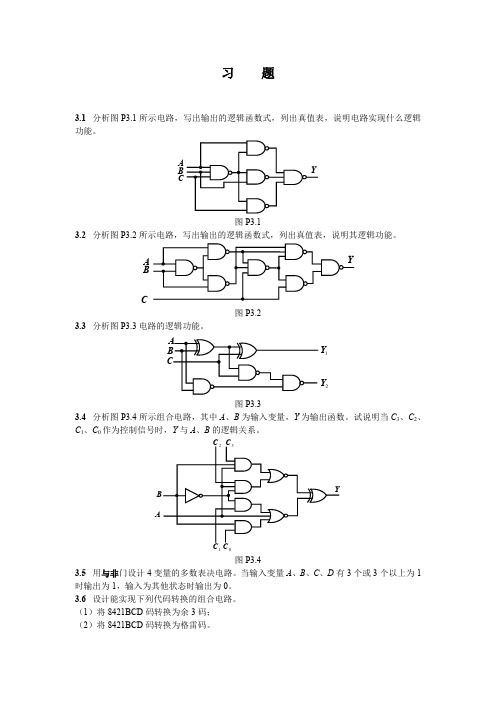
D0
D1
D2
74HC151
D3
D4
Y
Y
D5
D6
D7 A0 A1 A2 S B1
EF A
图 P4.16 3.18 试用双 4 选 1 数据选择器 74HC153 产生逻辑函数
Y ABC AC BC
3.19 试用 8 选 1 数据选择器 74HC151 产生逻辑函数
Y ACD ABCD BC BCD
3.20 用数据选择器实现一个楼道开关控制电路,当上楼时,可用楼下开关开亮楼道灯,上楼
后,可用楼上开关关闭楼道灯;当下楼时,可用楼上开关开辆楼道灯,下楼后,可用楼下开
关关闭楼道灯。
3.21 试用 8 选 1 数据选择器 74HC151 设计一个多功能组合逻辑电路,电路功能表如表题 3.20
所示。
表题 3.20
ห้องสมุดไป่ตู้
电路芯片实现。
(1)门电路(2)3 线-8 线译码器 74HC138 和必要门电路(3)双 4 选 1 数据选择器 74HC153 和必要门电路(4)全加器。 3.23 用 4 位超前进位加法器 74LS283 设计一个将余 3 码转换为 8421BCD 码的电路。 3.24 试用 2 片 4 位超前进位加法器 74LS283 和必要的门电路组成 1 个二-十加法器电路。(提 示:根据 BCD 码中 8421 码的加法运算规则,当两数之和小于、等于 9(1001)时,相加的 结果和按二进制数相加所得的结果一样。当两数之和大于 9 时(即 10~15),则应在按二进 制数相加的结果上加上 6(0110),这样就可以给出进位信号,同时得到一个小于 9 的和。) 3.25 用 两 片 4 位 比 较 器 74LS85 和 必 要 的 门 电 路 实 现 3 个 4 位 二 进 制 数 A=A3A2A1A0 , B=B3B2B1B0,C=C3C2C1C0 的并行比较,要求给出“A 最大”、“A 最小”和“3 个数相等”三 个输出信号。 3.26 判断下列函数对应的组合逻辑电路是否存在竞争-冒险。
3-数电-第三讲

•带符号的二进制数可以用原码、反码、补码三种形式来表示,其中最高位为符号位,其它为数值位。
•一般用0表示正号,用1表示负号。
•二进制正数,原码、反码、补码相同•原码的数值位和二进制负数的绝对值相同•反码的数值位是将二进制负数的绝对值按位取反•补码的数值位是将二进制负数的绝对值按位取反后,在最低位加1•用4位二进制码元来表示1位十进制数符“0~9”的代码,简称BCD码•用BCD 码表示十进制数时,只要把十进制数的每一位数码,分别用BCD码取代即可。
•格雷码:任何相邻的两个码字(包括首、尾两个码字)中,只有一位取值不同。
•奇偶校验码由信息位和校验位两部分组成。
信息位是要传输的原始信息,校验位仅有一位。
•奇校验:使每一个码组中信息位和校验位的“1”的个数之和为奇数。
•偶校验:使每一个码组中信息位和校验位的“1”的个数之和为偶数。
•对各个字母和符号编制的代码叫字符代码。
1.5 逻辑变量及基本逻辑运算一、逻辑变量取值:逻辑0、逻辑1。
逻辑0和逻辑1不代表数值大小,仅表示相互矛盾、相互对立的两种逻辑状态二、基本逻辑运算与运算或运算非运算逻辑表达式F=A B =AB与逻辑真值表与逻辑关系表1.与逻辑开关A 开关B 灯F 断断断合合断合合灭灭灭亮A BF 1 01 10 10 00010只有决定某一事件的所有条件全部具备,这一事件才能发生将开关接通记作1,断开记作0;灯亮记作1,灯灭记作0。
可以作出如下表格来描述与逻辑关系:与逻辑运算符、∩实现“与运算”的电路叫与门,其逻辑符号如图所示,其中图(a)是我国常用的传统符号,图(b )为国外流行符号,图(c )为国家标准符号。
(a)FA B(b )FAB(c )&FA B与门的逻辑符号(a) 常用符号;(b) 国外流行符号;(c) 国标符号逻辑表达式F=A +B或逻辑真值表2.或逻辑只有决定某一事件的条件有一个或一个以上具备,这一事件才能发生A B F 1 01 10 10 01110N 个输入:F= A + B+ ...+ N或逻辑运算符或逻辑关系表+FA BFA B≥1FAB (b )(c )(a )或门的逻辑符号(a) 常用符号;(b) 国外流行符号;(c) 国标符号3.非逻辑当决定某一事件的条件满足时,事件不发生;反之事件发生。
数电项目实验报告(3篇)

第1篇一、实验目的1. 理解数字电路的基本概念和组成原理。
2. 掌握常用数字电路的分析方法。
3. 培养动手能力和实验技能。
4. 提高对数字电路应用的认识。
二、实验器材1. 数字电路实验箱2. 数字信号发生器3. 示波器4. 短路线5. 电阻、电容等元器件6. 连接线三、实验原理数字电路是利用数字信号进行信息处理的电路,主要包括逻辑门、触发器、计数器、寄存器等基本单元。
本实验通过搭建简单的数字电路,验证其功能,并学习数字电路的分析方法。
四、实验内容及步骤1. 逻辑门实验(1)搭建与门、或门、非门等基本逻辑门电路。
(2)使用数字信号发生器产生不同逻辑电平的信号,通过示波器观察输出波形。
(3)分析输出波形,验证逻辑门电路的正确性。
2. 触发器实验(1)搭建D触发器、JK触发器、T触发器等基本触发器电路。
(2)使用数字信号发生器产生时钟信号,通过示波器观察触发器的输出波形。
(3)分析输出波形,验证触发器电路的正确性。
3. 计数器实验(1)搭建异步计数器、同步计数器等基本计数器电路。
(2)使用数字信号发生器产生时钟信号,通过示波器观察计数器的输出波形。
(3)分析输出波形,验证计数器电路的正确性。
4. 寄存器实验(1)搭建移位寄存器、同步寄存器等基本寄存器电路。
(2)使用数字信号发生器产生时钟信号和输入信号,通过示波器观察寄存器的输出波形。
(3)分析输出波形,验证寄存器电路的正确性。
五、实验结果与分析1. 逻辑门实验通过实验,验证了与门、或门、非门等基本逻辑门电路的正确性。
实验结果表明,当输入信号满足逻辑关系时,输出信号符合预期。
2. 触发器实验通过实验,验证了D触发器、JK触发器、T触发器等基本触发器电路的正确性。
实验结果表明,触发器电路能够根据输入信号和时钟信号产生稳定的输出波形。
3. 计数器实验通过实验,验证了异步计数器、同步计数器等基本计数器电路的正确性。
实验结果表明,计数器电路能够根据输入时钟信号进行计数,并输出相应的输出波形。
数电习题3
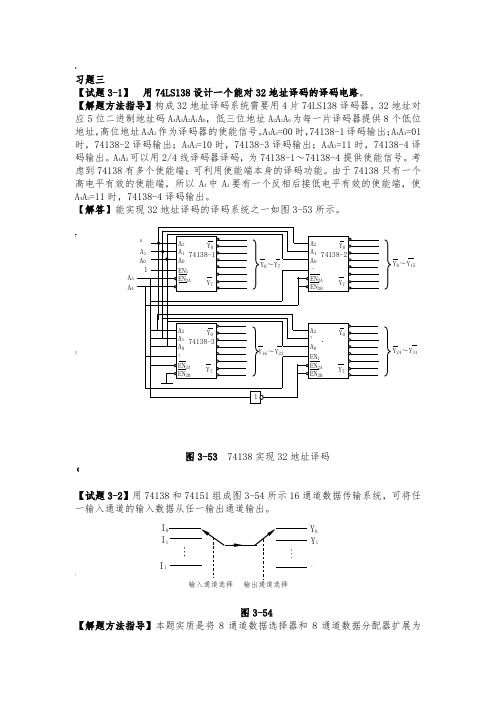
,习题三【试题3-1】 用74LS138设计一个能对32地址译码的译码电路。
【解题方法指导】构成32地址译码系统需要用4片74LS138译码器。
32地址对应5位二进制地址码A 4A 3A 2A 1A 0,低三位地址A 2A 1A 0为每一片译码器提供8个低位地址,高位地址A 4A 3作为译码器的使能信号。
A 4A 3=00时,74138-1译码输出;A 4A 3=01时,74138-2译码输出;A 4A 3=10时,74138-3译码输出;A 4A 3=11时,74138-4译码输出。
A 4A 3可以用2/4线译码器译码,为74138-1~74138-4提供使能信号。
考虑到74138有多个使能端;可利用使能端本身的译码功能。
由于74138只有一个高电平有效的使能端,所以A 4中A 3要有一个反相后接低电平有效的使能端,使A 4A 3=11时,74138-4译码输出。
【解答】能实现32地址译码的译码系统之一如图3-53所示。
》图3-53 74138实现32地址译码《【试题3-2】用74138和74151组成图3-54所示16通道数据传输系统,可将任一输入通道的输入数据从任一输出通道输出。
;图3-54【解题方法指导】本题实质是将8通道数据选择器和8通道数据分配器扩展为Y 24~Y 31A 3Y 8~Y 15A 4I I 1 I Y 0Y 1~Y16通道。
八选一数选器74151只有一个使能端,所以要用一个反相器使两片74151分别使能。
八通道数据分配器74138有三个使能端,一片74138用高电平使能,另一片74138则用低电平使能,剩余一个低电平使能端作为数据输入端。
因为,低电平使能端作为数据输入端,输入输出数据同相,所以,74151用高电平输出有效的输出端Y 。
【解答】能实现16通道数据传输系统之逻辑图如图3-55所示。
\:图3-55【试题3-3】用一片74LS48实现三位十进制数动态扫描显示。
数电第三章门电路知识点总结

数电第三章门电路知识点总结
数电第三章——门电路
1.杂志半导体特点
在杂质半导体中,多数载流子的浓度主要取决于掺入的杂质浓度;而小数载流子的浓度主要取决于温度。
杂质半导体,无论是N型还是P型,从总体上看,仍然保持着电中性。
2.CMOS与非门
P并N串
3.CMOS或非门
P串N并
4.CMOS传输门
5.三态门
三态分别是导通、截止、高阴态。
是有一个控制端,如果控制端设置为某个值(1或0),会让输入端无论输入什么都是不通的(有些情况是通的,就是状态不改变),这就叫高阻态,在图中由一个三角形表示。
6.TTL与CMOS优缺点
TL电路的优点是开关速度较高,抗干扰能力较强,带负载的能力也比较强,缺点是功耗较大。
CMOS电路具有制造工艺简单、功耗小、输入阻抗高、集成度高、电源电压范国宽等优点,其主要缺点是工作速度稍低,但随着集成工艺的不断改进,CMOS电路的工作速度已有了大幅度的提高。
数电实验实验三、四

12.3 数据选择器 2.3.1 实验目的1.测试集成数据选择器74151的逻辑功能。
2.用74151构成大、小月份检查电路。
3.用74151构成比较2个4位二进制数是否相等的电路。
2.3.2 实验设备与器件1.74151型8选1数据选择器1块 2.7404型六反相器1块 2.3.3 实验原理数据选择器从多路输入数据中选择其中的一路数据送到电路的输出端。
数据选择器分为4选1数据选择器和8选1数据选择器。
74151是8选1数据选择器,数据输入端0D ~7D 是8位二进制数,2A 1A 0A 是地址输入端,Y 和Y 是一位互补的数据输出端,S 是控制端。
其管脚如图2-3-1所示,逻辑功能如表2-3-1所示。
74151的逻辑表达式是:)A A A (D )A A A (D )A A A (D )A A A (D Y 0123012201210120+++=)A A A (D )A A A (D )A A A (D )A A A (D 0127012601250124++++图2-3-1 74151管脚图逻辑开关LED图2-3-2 74151逻辑功能测试图D0D1D2D3D4D5D6D7A2A1A0YVCC GNDYS74151432115141312161011798562表2-3-1 74151功能表2.3.4预习要求1. 理解数据选择器的工作原理,掌握四选一数据选择器和八选一数据选择器的逻辑表达式。
2. 查找八选一数据选择器74151的管脚图。
3. 写出大、小月检查电路的设计方法,要求是:用4位二进制数0123A A A A 表示一年中的十二个月,从0000~1100为1月到12月,其余为无关状态;用Y 表示大小月份,Y=0为月小(二月也是小),Y=1为月大(7月和8月都是月大)。
4.用两片74151设计一个判断两个2位二进制数是否相等的电路。
5.根据实验内容的要求,完成有关实验电路的设计,拟好实验步骤。
数电1-3答案

数电1一、填空:(14分)1. 数制转换 (DC)H = ( 220 )D= ( 1101 1100 )B = ( 334 )O。
2. 有一数码10010011,作为自然二进制数时,它相当于十进制数 147 ,作为8421BCD码时,它相当于十进制数 93 。
3. 已知某函数,该函数的反函数 =( ),该函数的对偶函数F '= ( )。
4. 某函数有n个变量,则共有个最小项。
5. 将一个最大幅值为5.1V的模拟信号转换为数字信号,要求模拟信号每变化20mV能使数字信号最低位LSB发生变化,则应选用 8 位 A/D 转换器。
6. 一个1024×8位的ROM,其存储容量为 8k 。
7. 为构成4096×4片RAM,需要 8 片1024×1的RAM。
8. 在TTL门电路的一个输入端与地之间接一个10KW电阻,相当于在该输入端输入高电平;在CMOS门电路的输入端与地之间接一个10KW电阻,相当于在该输入端输入低电平。
四、将题图电路各输出逻辑表达式填入表1栏中;各门电路的名称填入表2栏中;若ABCD = 1001,将各输出值填入表3栏中。
(14分)F1 F2 F3 F4 F5 F6 F712 与非或非同或异或与或非 OC门三态门3 1 0 0 1 0 0 1七、试画出题图电路在时钟脉冲CP、输入信号A作用下,Q1、Q2和X的输出波形,并说明电路的逻辑功能。
设触发器的初始状态均为0。
(10分)解:图中所示电路是一个同步单次脉冲发生电路。
波形如右图所示,在输入信号A上升沿后产生一个与CP 脉冲同步、且宽度等于CP脉冲宽度的时钟单脉冲。
八、中规模四位二进制计数器T214,其功能表和符号图如下所示,其中A,B,C,D是同步预置数端(A为低位,D为高位),是预置数控制端,是异步清零端,P、T是计数允许控制端,进位端OC未标出。
(10分)1. 利用T214的同步预置端构成一个六进制加法计数器。
数电本科总复习3-时序逻辑电路总复习20100527

A.基本触发器 B.边沿触发器
C.同步触发器
D.施密特触发器
13、下表所示为四位二进制计数器T215 的功能表,试分析下图 电路所具有的功能。要求画出状态转换图。
Cr
CP- CP+
A B C D QD QC QB QA
1× × 00 ×
× × × × × 00 0 0 × A B C D ABCD
A.3 B.4 C.6 D.5
32、某计数器的状态转换图如图所示,试问该计数器是一 个 7 进制 减 法计数器,它有 7 个有效状态, 1 个无效状 态,该电路 能 自启动。若用JK触发器组成,至少要 3 个JK触发器。
33、要构成5进制计数器,至少需要 3 个触发器,其无效状态
有 3 个。
34、分析下图所示的时序电路的逻辑功能,写出电路的驱动方 程、状态方程和输出方程,画出电路的状态转换图,并说明该 电路是否能自启动。(15分)
·
·
& “1”CP“1” “1”CP“1” CP“1”
Q3 Q2 Q1 Q0
C 74161
CP
CR LD CTP CTT D3 D2 D1 D0
Q3 Q2 Q1 Q0
CO 74161
CP
CR LD CTP CTT D3 D2 D1 D0
(2)画电路图。
6、分析下图所示序列发生电路,要求写出DSR的逻辑函数 式,列出状态转换表,写出Z的输出序列码。
解:
从图可知,X是控制端,CP是时钟脉冲输入端,该时序电路属于计数器.对
其功能分析如下:
1) 时钟方程CP1=CP2=CP,是同步工作方式.
2) 驱动方程 代入特性方程中得
状态方程
画状态转换图
数电实验实验三 组合逻辑电路

1. 测试用异或门和与非门组成的半加器的逻辑功能
如果不考虑来自低位的进位而能够实现将两个 1 位二进制数相加的电路,称为半加器,
半加器的符号如图 3-2 所示。
半加器的逻辑表达式为:
S = AB + AB = A B CO = AB
12
根据半加器的逻辑表达式可知,半加和 S 是输入 A、B 的异或,而进位 CO 则为输入 A、 B 相与,故半加器可用一个集成异或门和二个与非门组成,电路如图 3-3 所示。 (仿真图,并把仿真结果填入表中)
2. 用卡诺图或代数法化简,求出最简逻辑表达 式。
设计要求 逻辑抽象
真值表
3. 根据简化后的逻辑表达式,画出逻辑电路图。
若已知逻辑电路,欲分析组合电路的逻辑功能, 逻辑表达式
则分析步骤为:
代数法化减
卡诺图 卡诺图法化减
1. 由逻辑电路图写出各输出端的逻辑表达式。
2. 由逻辑表达式列出真值表。
最简逻辑表达式
实验三 组合逻辑电路
姓名: 赖馨兰 班级: 光信 1802 学号:1810830225
一、实验目的
1. 通过简单的组合逻辑电路设计与调试,掌握采用小规模(SSI)集成电路设计组合逻
辑电路的方法。
2. 用实验验证所设计电路的逻辑功能。
3. 熟悉、掌握各种逻辑门的应用。
二、实验原理
组合逻辑电路是最常见的逻辑电路之一,可以用一些常用的门电路来组合成具有其他功
要求:写出详细的设计过程,画出完整的控制电路图,并在实验以上选择相应的器件对 所设计的电路进行实验测试,记录实验结果。 (仿真图)(设计过程) 设计过程: 1.列真值表 设 0 为开关切断,1 为接通。L=0 为灯泡不亮,L=1 为灯泡亮,初始状态为三个开关都为断 开状态,且灯泡不亮。
数电(任务3_表决器电路的设计和逻辑关系)

74LS20D 3 VCC VCC 5V
74LS00D U1C
&
6 R3 1.0k
8 74LS00D R2 1.0k R1 1.0k 0
裁判中的逻辑关系
裁判的裁决
因
逻辑
比赛的成绩
果
举重比赛中的三位裁判员,设为:A、B、C。 裁判的裁决,只有两种可能:成功和不成功。
裁判的成功裁决可以用“1”表示, 不成功裁判用“0”表示。
或门:实现“或”逻辑
“或”逻辑图符号为:
A B
“或”逻辑国际流行图符号为:
A L
L
≥1
L
B
74LS32
四2或门
动脑设计
A B C 8 9
1 2
74ls08 U1A
& 3
74ls32 1
1 1A 2 1B
U2A
>=1 1Y 3
4
1 1A 2 1B
U2C
>=1 1Y 3
6 X1 LED
71
2 1 2
1 1A 2 1B
U2A
>=1 1Y 3
4 1 1A U2C
2 1B >=1
1Y 3
6 X1 LED
U1B
& 3
2
C
9
2 1 2
电平开关
U1C
& 3
5 3
1 1A 2 1B
U2B
>=1 1Y 3
0
LED显示
2 实训内容
模拟裁判的裁决过程。
器件资料
74LS08
四2与门
74LS32
四2或门
U1B
& 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 3 逻辑代数Logic Algebra逻辑代数是由George Boole 在1849年提出的,也被称为Boolean 代数. 逻辑代数是按照逻辑规律运算的代数,是分析和设计数字电路不可缺少的基础数学工具.fz=x),(y输入: x, y,是逻辑变量;输出: z,逻辑变量;逻辑映射关系: f,表示从x y到z的逻辑关系映射逻辑变量由一个符号表示。
任何一个逻辑变量只有0和1两个可能的取值.1逻辑代数不同于算术(arithmetic).算术的基本运算是:加、减、乘、除算术的基本运算是加减乘除‘addition’, ‘subtraction’, ‘multiplication’ and ‘division’.逻辑代数的基本运算是:与、或、非‘AND’, ‘OR’, ‘NOT’.逻辑代数必须按照逻辑代数的基本规律进行运算,比如结合律、交换律、摩根定理等等。
23)3) 对偶规则Duality+用•替换,所有求对偶式的方法,把所有的 用替换, 所有的•用+替换, 所有的1用0替换, 所有的0用1替换.•函数F +新函数F '新函数’F的对偶式如果F 成立,10F 被称为函数F的对偶式. 如果F 成立,则对偶式F ’也成立.求对偶式与求反函数的区别:7反变量与原变量互相替换1例1: 把下列函数转换成标准与或式F(A,B,C) = AB + BC + ACSOP formAB(C C) BC(A A) AC(B B)=AB(C+C)+BC(A+A)+AC(B+B)= ABC + ABC + ABC + ABC= m7+ m6+ m3+ m5∑=)7,6,5,3(m标准与或式注: F(A,B,C)字母必须写全,字母的顺序不能随意改变,涉及最小项编号20字母的顺序不能随意改变,涉及最小项编号举例F(A,B,C) =3m12(,,)∑),,(= ABC + ABC + ABCF(B,A,C) ∑=)3,2,1(m=BAC+BAC+BACBAC + BAC + BAC21从真值表中我们可以发现,当ABC 取某一组值时, 只有个最大项值为0使某一最大项为,ABC 取值的二进制数对应的十进制数一个最大项值为0, 其他都等于1某最大项为0时, ABC 取值的进制数对应的十进制数为此最大项的编号3A B C例:3 变量A, B, C = A+B+C (010 A+B+C = 0)M (使)A+B+C M 4=24变量A,B,C,DA+B+C+D M =A+B+C+D2M 10=24F : SOP form F(A,B,C) = Σm (2,3,6,7) F 1与或式12F : POS form= ΠM (0,1,4,5) F 2或与式2F 1F F =F =F 000A B C F001M M m F = F 1= F 20 0 00 0 101002m 3F 1说明函数何时为10 1 00 1 11001145M M F 2说明函数何时为01 0 01 0 100m 6m 71 1 01 1 11127标准与或式和标准或与式是同一个逻辑关系的两种表达方式§3.3逻辑函数的公式化简个数许种式同一个逻辑函数可以写成许多种不同的形式如比如:XZ是冗余项F = XY + YZ (AND –OR)与或式= ( X + Y )( Y + Z ) (OR –AND)或与式= XY • YZ ( NAND –NAND) 与非-与非式XY YZ= X+Y + Y+Z ( NOR –NOR) –(NO NO)或非或非式=XY + YZ ( AND –OR –NOT) 与或非28§3.4卡诺图(Karnaugh map)化简逻辑函数(Karnaugh map)3.4.1 卡诺图卡诺图类似于真值表,它给出了输入变量的所有可能的组合和相应的函数值。
不同之处在于,真值表中把输入输出变量按照行列排列,而卡诺图把输出划分成若干方格,每个方格对应特定的输出。
卡诺图中,方格的数量等于2n, 这里n是变量的个数.所以每个方格表示一个最小项.n个变量→2n 方格362变量卡诺图F(A,B)()F A 真值表B 0 10ABF(A,B)00F(0,0)F(01)F(0,0)F(1,0)110F(1,0)10F(0,1)F(0,1)F(1,1)卡诺图和真值表有一一对应的关系,11F(1,1)都描述了函数F(A,B)的所有可能情况373变量卡诺图F(A,B,C)卡诺图中单元的排列方式要求:()F AB00011110相邻单元只有一个变量改变C00 01 11 1002640的相邻格:1,2,42的相邻格:0,3,6 013757的相邻格:的相邻格3,6,5 1几何相邻: 位置相邻AB顺序的排列方法逻辑相邻: 只有一个变量变化相邻格卡诺图与真值表的区别卡诺图与真值表的区别:卡诺图:几何相邻的单元逻辑相邻,有利于对函数化简38真值表:没有逻辑相邻,不利于函数化简4变量卡诺图: F(A,B,C,D)F AB 00011110 F CD 00011110CD00 01 11 100004128AB00 01 11 1000013201511390154761110327615141110111012131511141089的相邻格:1,24141510120的相邻格:,,,815的相邻格:7,11,13,14的相邻格:6,5,0,39每个单元有4 个相邻单元5变量卡诺图: F(A,B,C,D,E)532cells=()232 cells F ABC00011111DE00000 001 011 0100481216202428111001110001113579111311517192123252729311026101418222630相邻格包括对称位置146, 15, 10, 12,:8:306,5,0,,12, 9, 24, 0, 10结论:401)每个小格有n 个相邻格2)相邻格与排列方式无关3.4.2 用卡诺图表示逻辑函数 卡诺 表 辑 数 例 1: 1 从真值表到卡诺图A B C0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1F0 0 0 1 0 1 1 1F AB C00 0 0 1 001 0 111 1 110 0 1三人选举的逻辑关系41例 2: 在卡诺图中填标准 SOP 或 POSF(X Y, F(X, Y Z) = ∑ m(0,4,6)F 何时为 1 (最小项) 最小项F XYF(X Y, F(X, Y Z) = ∏ M(1,2,3,5, M(1 2 3 5 7)F 何时为 0 (最大项) 最大项F XY00 Z 0 1 1 001 0 011 1 010 1 0等价00 Z 0 1 1001 0011 1010 1042例 3: 把下列非标准SOP填入卡诺图F(X, Y, Z) = XY + YZ + XZ = XY(Z + Z) + YZ(X + X) + XZ(Y + Y)= XYZ + XYZ + XYZ + XYZ + XYZ + XYZ= ∑ m(0,1,2,5,6,7)直接填写F XY ZXY XY:00 1 101 111 1 110在 XY = 11 的两个格中填10 1F XY Z001 1011111 1431010 113.4.3 使用 K-Map 化简 1. 求最简与或式 方法 : 把相邻格中的1圈在一起, 把相邻格中的1圈在一起 合并最小项 圈1的规则如下: ① 圈出一个矩形,包含2n 个相邻格 ② 尽可能多圈1,使得圈最大 使得圈最大 ③每个圈中至少有一个其它圈未圈过的1, 1可以重复圈, 所有 的1都要圈 ④ 消去圈内变化了的量, 留下不变的变量 留下不变的变量,是 是 1 的写原变量, 是0 的写反变量, 组成“与”项 ⑤ 各圈之间为“或”关系44一句话描述 句话描述尽可能多地把相邻的矩形的 2n 个 1 圈在 圈在一起,消去 起,消去 变化了的n 个变量,留下不变的变量,是 1 写原变量, 是 0 写反变量,组成 “与” 项;每个圈中至少有一个 别的圈没圈过的 1 ,所有的 1 都要圈;1 可以重复圈; 圈之间为 “或” 的关系。
圈 1个1,2个1,4个1,8个1,16个145例1: 使用卡诺图化简下列函数 使 卡诺 简 数:F(A, B) = ∑ (0,1,3)F BA 0 0 1 1 1A1解: ① 填卡诺图 ② 按照规则圈1 ③ 所有的与项逻辑加:1 BF=A+B46例 2: 化简下列函数成最简与或式 简 数 最简 式F AB00 C 0 1 1 10111 110 1 1卡诺图中需要画几个 圈?F = B + ACBAC47例 3:F AB CD0001 111 1 1 110 100 1 01 11 101需要画几个圈?F(A, B, C, D) = D + AB111482. 求最简或与式 求最简或与式与求最简与或式的方法类似尽可能多地把相邻的2n个0 圈在一起, 消去变化了 的 个量 留下不变的变量 (是0 写原变量, 的n个量, 写原变量 是 1 写反 变量)组成或项; 每个圈中至少有 每个圈中至少有一个别的圈没圈过的0 个别的圈没圈过的0, 所有0 都要圈, 0 可重复圈, 圈之间为与关系.49例 1 最简或与式,圈 0:F AB CD需要画几个圈?0001 111 1 1 110 1B+ D00 1 01 11A+D∴ F = (A + D)(B + D)10 1111= AB + DPOS 和 SOP 可以互相转换. 总结:SOP 式 ---- 与或式,圈1 POS 式---- 或与式,圈 或与式 圈050。
