【推荐精选】2018年高三物理一轮总复习 专题13.8 气体的等容变化和等压变化名师伴学
高中物理:气体的等容变化和等压变化详解
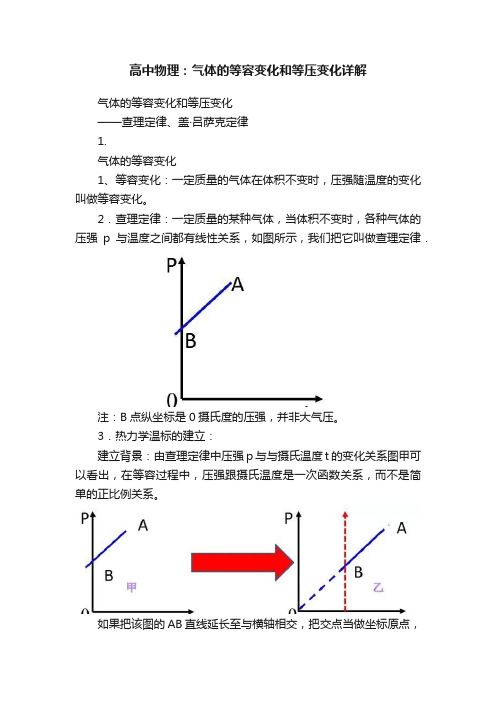
高中物理:气体的等容变化和等压变化详解气体的等容变化和等压变化——查理定律、盖·吕萨克定律1.气体的等容变化1、等容变化:一定质量的气体在体积不变时,压强随温度的变化叫做等容变化。
2.查理定律:一定质量的某种气体,当体积不变时,各种气体的压强p与温度之间都有线性关系,如图所示,我们把它叫做查理定律.注:B点纵坐标是0摄氏度的压强,并非大气压。
3.热力学温标的建立:建立背景:由查理定律中压强p与与摄氏温度t的变化关系图甲可以看出,在等容过程中,压强跟摄氏温度是一次函数关系,而不是简单的正比例关系。
如果把该图的AB直线延长至与横轴相交,把交点当做坐标原点,建立新的坐标系(图乙)此时压强与温度的关系就是正比例关系了。
图乙坐标原点的意义“气体压强为零时其温度为零”,由此可见,为了使一定质量的气体在体积不变的情况下,压强与体积成正比,只需要建立一种新的温标就可以了。
在现实中通过对大量的“压强不太大(相对标准大气压),温度不太低(相对于室温)”的各种不同气体做等容变化的实验数据可以证明“一定质量的气体压在强不太大,温度不太低时,坐标原点代表的温度就是热力学温度的零度,这就是热力学温度零点的物理意义。
由此可见:热力学的零点就规定为气体压强为零的温度。
在建立热力学温标之前,人们已经建立了华氏、摄氏温标,但这些温标都是与测温物质的热学性质有关,当采用不同的测温物质去测量同一温度时会产生一定差异,这种差异是不能克服的。
而由热力学温标的建立可知:热力学温度是在摄氏温度的基础上建立起来的,零点的确定与测温物质无关,因此热力学温标是一种更为简便科学的理论的温标,它的零度不可能达到。
又叫绝对零度。
4、查理定律的热力学温标描述:——查理定律:(1).查理定律:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比。
(2).表达式:注:这里的C和玻意耳定律表达式中的C都泛指比例常数,它们并不相等。
这里的C与气体的种类、质量和压强有关。
气体的等容变化和等压变化 课件

答案:轮胎体积一定,由查理定律知,气体压强与热力学温度成正
比,当轮胎打足气后,温度升高车胎内压强增大,车胎易胀破。
气体的等容变化
问题探究
某登山运动员在一次攀登珠穆朗玛峰的过程中,在接近山顶时他
裸露在手腕上的防水手表的表盘玻璃突然爆裂了,而手表没有受到
度t是一次函数关系,不是简单的正比例关系,如图所示,等容线是一
条延长线通过横轴-273.15 ℃的点的倾斜直线,且斜率越大,体积越
小。图象纵轴的截距p0是气体在0 ℃时的压强。
等容线在p-T图象中是一条经过原点的直线,而在p-t图象中不过
原点,其延长线与横轴的交点为-273.15 ℃。
任何撞击。
(1)表盘没爆裂之前,内部气体的体积是否变化?
(2)攀登珠穆朗玛峰的时候,随着高度的增加,温度怎样变化?压强
怎样变化?
(3)你认为表盘是向内爆裂还是向外爆裂的?理论依据是什么?
要点提示(1)手表表壳可以看成一个密闭容器,出厂时封闭着一定
质量的气体,登山过程中气体体积基本上没有发生变化,可认为是
273.15K+
p0⇒p=
p 0。
27பைடு நூலகம்.15K
273.15K
由此可得 0 =
,即 1 = 2 。
273.15K
273.15K+
1
2
关系式 p-p0=
(在以后计算中,如没特别说明,0 ℃对应的热力学温度一般取273 K)
2.查理定律的适用条件
(1)气体质量一定,体积不变。
(2)(实际)气体的压强不太大(小于几个标准大气压),温度不太低(不
气体的等容变化和等压变化公开课ppt课件

练习1、密闭在容积不变的容器中的气体,当 温度降低时: D A、压强减小,密度减小; B、压强减小,密度增大; C、压强不变,密度减小; D、压强减小,密度不变
练习2、下列关于一定质量的气体的等容变化的说 法中正确的是: D A、气体压强的改变量与摄氏温度成正比; B、气体的压强与摄氏温度成正比; C、气体压强的改变量与热力学温度成正比; D、气体的压强与热力学温度成正比。
体积越大,斜率越小; 体积越小,斜率越大。 V1<V2
例1 一定质量的气体,保持体积不变,温度从1℃
升高到5℃,压强的增量为 2.0×103 Pa,则 [ C]
A.它从5℃升高到10℃,压强增量为2.0×103Pa B.它从15℃升高到20℃,压强增量为2.0×103Pa C.它在0℃时,压强约为1.4×105Pa
查理定律与盖—吕萨克定律的比较
定律 表达
式 成立 条件
查理定律
Tp11=Tp22=恒量 气体的质量一定,体积
不变
盖—吕萨克定律
VT11=VT22=恒量 气体的质量一定,压强不
变
图线 表达
应用
直线的斜率越大,体积 越小,如图V2<V1
直线的斜率越大,压强越 小,如图p2<p1
如图甲所示,为一定质量的气体由状态A经过状态B变为状 态C的V-T图象.已知气体在状态A时的压强是1.5×105 Pa.
一、气体的等容变化
1、等容变化:一定质量气体在体积不变的情 况下,其压强随温度的变化叫做等容变化.
思考:为什么隔夜的水杯( 半杯水 )难以打开?
(压强随着温度的升高而增大,随着温度的降低而 减小,但压强P和温度t不是正比关系。)
2、查理定律:一定质量的某种气体,在体积 不变的情况下,压强p与热力学温度T成正比.
高三物理气体的等压变化和等容变化

T2 8 5 p2 p1 p1 3.2 10 Pa T1 5
p1
p2
12.如图所示,上端开口的光滑圆柱形气缸竖直放置, 截面积为40cm2的活塞将一定质量的气体和一形状不规 则的固体A封闭在气缸内。在气缸内距缸底60cm处设 有a、b两限制装置,使活塞只能向上滑动。开始时活 塞搁在a、b上,缸内气体的压强为p0(p0=1.0×105 Pa 为大气压强),温度为300K。现缓慢加热汽缸内气体, 当温度为330K,活塞恰好离开a、b;当温度为360K时, 活塞上升了4cm。求: (1)活塞的质量 (2)物体A的体积 a b
(C)若把弯管向下移动少许,
右管内的水银柱沿管壁上升
h
(D)若环境温度升高,右管内
的水银柱沿管壁上升 解见下页解析: 封闭气体的压强等于大气压与水银柱产生压强之差, 故左管内外水银面高度差也为h,A对; 弯管上下移动,封闭气体温度和压强不变,体积不变, B错C对; 环境温度升高,封闭气体体积增大, 则右管内的水银柱沿管壁上升,D对。
气体的等容变化
和
等
压
变
化
在物理学中,当需要研究三个物理量之间的关系时, 往往采用“控制变量法”——保持一个量不变,研 究其它两个量之间的关系,然后综合起来得出所要 研究的几个量之间的关系。 一、气体的等容变化:
1、等容变化:当体积(V)保持不变时, 压强(p) 和温度(T)之间的关系。
2、查理定律: 一定质量的气体,在体积不变的情况下,温度每升高 (或降低) 1℃,增加(或减少)的压强等于它0℃时 压强的1/273. 或一定质量的某种气体,在体积保持不变的情况下, 压 强p与热力学温度T成正比. p2 p1 常量 3、公式: T2 T1 4、查理定律的微观解释: 一定质量(m)的气体的总分子数(N)是一定的, 体积(V)保持不变时,其单位体积内的分子数(n) 也保持不变,当温度(T)升高时,其分子运动的平 均速率(v)也增大,则气体压强(p)也增大;反之 当温度(T)降低时,气体压强(p)也减小。
高三物理一轮总复习 专题13.8 气体的等容变化和等压变化名师伴学

专题13.8 气体的等容变化和等压变化课前预习● 自我检测1.有人设计了一种测温装置,其结构如图所示,玻璃泡A内封有一定质量的气体,与A 相连的B管插在水银槽中,管内外水银面的高度差x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出.设B管的体积与A泡的体积相比可略去不计.(1)在1标准大气压下对B管进行温度标刻(1标准大气压相当于76 cmHg的压强).已知当温度t1=27 ℃时,管内水银面的高度为x1=16 cm,此高度即为27 ℃的刻线,问t=0 ℃的刻线在何处?(2)若大气压已变为相当于75 cmHg的压强,利用该测温装置测量温度时所得读数仍为27 ℃,问:此时的实际温度为多少?【答案】(1)21.4 cm (2)22 ℃2.一定质量的理想气体,在压强不变的情况下,温度由5 ℃升高到10 ℃,体积的增量为ΔV1;温度由10 ℃升高到15 ℃,体积的增量为ΔV2,则( )A.ΔV1=ΔV2B.ΔV1>ΔV2C.ΔV1<ΔV2D.无法确定【答案】 A【解析】 由盖—吕萨克定律V 1T 1=V 2T 2可得V 1T 1=ΔV ΔT ,即ΔV =ΔT T 1V 1,所以ΔV 1=5278V 1,ΔV 2=5283V 2(V 1、V 2分别是气体在5 ℃和10 ℃时的体积),而V 1278=V 2283,所以ΔV 1=ΔV 2,A 正确. 3. (多选)如图所示,四支两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态.如果管内两端的空气都升高相同的温度,则水银柱向左移动的是( )【答案】 CD4.如图甲所示是一定质量的气体由状态A 经过状态B 变为状态C 的V -T 图象.已知气体在状态A 时的压强是1.5×105Pa.(1)说出A →B 过程中压强变化的情形,并根据图象提供的信息,计算图中T A 的温度值. (2)请在图乙坐标系中,画出由状态A 经过状态B 变为状态C 的p -T 的图象,并在图线相应位置上标出字母A ,B ,C .如果需要计算才能确定有关坐标值,请写出计算过程.【答案】 (1)200 K (2)见【解析】【解析】 (1)由题图甲可以看出,A 与B 的连线的延长线经过原点O ,所以A →B 是一个等压变化,即p A =p B .根据盖—吕萨克定律可知:V A T A =V B T B ,即T A =V A V B ·T B =0.40.6×300 K=200 K.(2)由题图甲可知,B →C 是等容变化,根据查理定律得:p B T B =p C T C ,即p C =T C T B ·p B =400300·p B=43p B=43p A=43×1.5×105 Pa=2.0×105 Pa.可画出由状态A→B→C的p-T图象如图所示.课堂讲练● 典例分析【要点提炼】一、气体的等容变化1.等容变化:一定质量的某种气体在体积不变时压强随温度的变化规律.2.查理定律(1)内容:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比.(2)表达式:p1T1=p2T2=C(C是比例常数)推论式:pT=ΔpΔT.(3)图象:如图所示:1①p-T图中的等容线是一条过原点的倾斜直线.②p-t图上等容线不过原点,但反向延长交t轴于-273.15_℃.③无论p-T图象还是p-t图象,其斜率都能判断气体体积的大小,斜率越大,体积越小.【典例1】气体温度计结构如图所示.玻璃测温泡A内充有气体,通过细玻璃管B和水银压强计相连.开始时A处于冰水混合物中,左管C中水银面在O点处,右管D中水银面高出O 点h1=14 cm,后将A放入待测恒温槽中,上下移动D,使C中水银面仍在O点处,测得D中水银面高出O点h2=44 cm.求恒温槽的温度(已知外界大气压为1个标准大气压,1标准大气压相当于76 cmHg).【答案】 364 K(或91 ℃)二、气体的等压变化1.等压变化:一定质量的某种气体,在压强不变的情况下,体积V 随热力学温度T 的变化规律.2.盖—吕萨克定律(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V 与热力学温度T 成正比. (2)表达式:V 1T 1=V 2T 2=C (C 是比例常数) 推论式:V T =ΔVΔT. (3)图象:如图所示.①V -T 图中的等压线是一条过原点的倾斜直线.②V -t 图上的等压线不过原点,反向延长线交t 轴于-273.15_℃.③无论V -T 图象还是V -t 图象,其斜率都能判断气体压强的大小,斜率越大,压强越小.(4) p -T 图象与V -T 图象的比较【典例2】(多选)一定质量的某种气体自状态A 经状态C 变化到状态B ,这一过程在V -T 图上的表示如图所示,则( )A .在AC 过程中,气体的压强不断变大B .在CB 过程中,气体的压强不断变小C .在状态A 时,气体的压强最大D .在状态B 时,气体的压强最大 【答案】 AD【反思总结】在V -T 图象中,比较两个状态的压强大小,可以通过这两个状态与原点连线的斜率大小来判断,斜率越大,压强越小;斜率越小,压强越大.一定质量的气体,温度不变,体积越大,压强越小. 三、假设法判断液柱(或活塞)的移动问题此类问题的特点是:当气体的状态参量p 、V 、T 都发生变化时,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解.其一般思路为:(1)假设液柱或活塞不发生移动,两部分气体均做等容变化.(2)对两部分气体分别应用查理定律的分比形式Δp =p TΔT ,求出每部分气体压强的变化量Δp ,并加以比较.【典例3】如图所示,两端封闭、粗细均匀、竖直放置的玻璃管内,有一长为h 的水银柱,将管内气体分为两部分,已知l 2=2l 1.若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)【答案】 水银柱上移假设水银柱不动,两部分气体都做等容变化,分别对两部分气体应用查理定律: 上段:p 2T 2=p 2′T 2′,所以p 2′=T 2′T 2p 2,Δp 2=p 2′-p 2=(T 2′T 2-1)p 2=ΔT 2T 2p 2; 同理下段:Δp 1=ΔT 1T 1p 1.又因为ΔT 2=ΔT 1,T 1=T 2,p 1=p 2+p h >p 2, 所以Δp 1>Δp 2,即水银柱上移. 【反思总结】同一问题可从不同角度考虑,用不同方法求解,培养同学们的发散思维能力.此类问题中,如果是气体温度降低,则ΔT 为负值,Δp 亦为负值,表示气体压强减小,那么降温后水银柱应该向压强减小得多的一方移动.课后巩固 ● 课时作业题组一 查理定律的应用1.民间常用“拔火罐”来治疗某些疾病,方法是将点燃的纸片放入一个小罐内,当纸片燃烧完时,迅速将火罐开口端紧压在皮肤上,火罐就会紧紧地被“吸”在皮肤上.其原因是,当火罐内的气体( )A .温度不变时,体积减小,压强增大B .体积不变时,温度降低,压强减小C .压强不变时,温度降低,体积减小D .质量不变时,压强增大,体积减小 【答案】 B【解析】 体积不变,当温度降低时,由查理定律p T=C 可知,压强减小,故B 项正确. 2.在密封容器中装有某种气体,当温度从50 ℃升高到100 ℃时,气体的压强从p 1变到p 2,则( )A.p 1p 2=12B.p 1p 2=21C.p 1p 2=323373 D .1<p 1p 2<2 【答案】 C【解析】 由于气体做等容变化,所以p 1p 2=T 1T 2=t 1+273 K t 2+273 K =323373,故C 选项正确.3.一定质量的气体,在体积不变的条件下,温度由0 ℃升高到10 ℃时,其压强的增量为Δp 1,当它由100 ℃升高到110 ℃时,其压强的增量为Δp 2,则Δp 1与Δp 2之比是( )A .10∶1B .373∶273C .1∶1D .383∶283 【答案】 C4.一个密闭的钢管内装有空气,在温度为20 ℃时,压强为1 atm ,若温度上升到80 ℃,管内空气的压强约为( )A .4 atm B.14 atmC .1.2 atm D.56atm 【答案】 C【解析】 由查理定律知p 1T 1=p 2T 2,代入数据解得p 2≈1.2 atm,所以C 正确. 题组二 盖-吕萨克定律的应用5.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,改变的量有( )A .活塞高度hB .汽缸高度HC .气体压强pD .弹簧长度L 【答案】 B6.如图所示,上端开口的圆柱形汽缸竖直放置,截面积为5×10-3m 2,一定质量的气体被质量为2 kg 的光滑活塞封闭在汽缸内,其压强为__①__ Pa(大气压强取1.01×105Pa ,g 取10 m/s 2).若从初温27 ℃开始加热气体,使活塞离汽缸底部的高度由0.50 m 缓慢地变为0.51 m ,则此时气体的温度为__②__ ℃.下列选项正确的是( )A .①1.05×105B .①0.04×105C .②33D .②300 【答案】 AC 【解析】 p 1=F S =mg S =2×105×10-3 Pa =0.04×105Pa ,所以p =p 1+p 0=0.04×105 Pa +1.01×105Pa =1.05×105Pa ,由盖—吕萨克定律得V 1T 1=V 2T 2, 即0.5S 273+27=0.51S273+t,所以t =33 ℃.题组三 液柱移动问题的判断7.如图所示,两端开口的直玻璃管A 和B ,竖直插入同一水银槽中,各用一段水银柱封闭着一定质量、同温度的空气,空气柱长度H 1>H 2,水银柱长度h 1>h 2,今使封闭气柱降低相同的温度(大气压保持不变),则两管中气柱上方水银柱的移动情况是( )A .均向下移动,A 管移动较多B .均向上移动,A 管移动较多C .A 管向上移动,B 管向下移动D .无法判断 【答案】 A8.两个容器A 、B ,用截面均匀的水平细玻璃管连通,如图所示,A 、B 所装气体的温度分别为17 ℃和27 ℃,水银柱在管中央平衡,如果两边温度都升高10 ℃,则水银柱将( )A .向右移动B .向左移动C .不动D .条件不足,不能确定 【答案】 A【解析】 假设水银柱不动,A 、B 气体都做等容变化:由Δp =ΔT T p 知 Δp ∝1T,因为T A<T B,所以Δp A>Δp B,所以水银柱向右移动.题组四综合应用9.1697年法国物理学家帕平发明了高压锅,高压锅与普通铝锅不同,锅盖通过几个牙齿似的锅齿与锅体镶嵌旋紧,加上锅盖与锅体之间有橡皮制的密封圈,所以锅盖与锅体之间不会漏气,在锅盖中间有一排气孔,上面再套上类似砝码的限压阀,将排气孔堵住(如图).当加热高压锅,锅内气体压强增加到一定程度时,气体就把限压阀顶起来,这时蒸气就从排气孔向外排出.由于高压锅内的压强大,温度高,食物容易煮烂.若已知排气孔的直径为0.3 cm,外界大气压为1.0×105 Pa,温度为20 ℃,要使高压锅内的温度达到120 ℃,则限压阀的质量应为多少?(g=10 m/s2)【答案】0.024 kg10.如图所示,上端开口的光滑圆柱形汽缸竖直放置,截面积为40 cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60 cm处设有a、b两限制- 11 - 装置,使活塞只能向上滑动.开始时活塞搁在a 、b 上,缸内气体的压强为p 0(p 0=1.0×105Pa 为大气压强),温度为300 K .现缓慢加热汽缸内气体,当温度为330 K 时,活塞恰好离开a 、b ;当温度为360 K 时,活塞上升了4 cm.g 取10 m/s 2求:(1)活塞的质量;(2)物体A 的体积.【答案】 (1)4 kg (2)640 cm 3【解析】 (1)设物体A 的体积为ΔV .T 1=300 K ,p 1=1.0×105Pa ,V 1=60×40-ΔVT 2=330 K ,p 2=⎝ ⎛⎭⎪⎫1.0×105+mg40×10-4Pa ,V 2=V 1(2)由状态2到状态3为等压过程,有V 2T 2=V 3T 3代入数据得ΔV =640 cm 3.。
气体的等容变化和等压变化)

表达式: P P1 C “斜率”
T T1
推论1:一定质量的气体在等容变化时,升高
(或降低)相同的温度,所增加(或减小)的压强
是相同的.
包括摄氏温度
即斜率相等
二、两个推论
如图:一定质量的气体从初状态(V1、 T1)开始,发生一个等压变化过程, 其体积的变化量ΔV与温度变量ΔT间
的关系
V
3、图像的斜率与压强的关系 斜率越小压强越大
1、等容线 2、等压线
V2<V1
一定质量的气体,不同 体积下的图像1、2,等 容线的斜率反映了体积 的大小
P2<P1
一定质量的气体,不同 压强下的图像1、2,等 容线的斜率反映了体积 的大小
基本规律简单应用
例1、一定质量的氢气在0℃时的压强是9×104Pa, 保持氢气的体积不变,它在30℃时的压强是多大?
例3、说出下列图像 的气体状态的变化 过程
例5.如图8-2-7所示,p表示压强,V表示体积,T表 示热力学温度,t表示摄氏温度,各图中正确描述
一定质量理想气体等压变化规律的是( AC )
气体图像及转换
1、说出下例图像中的气体状态过程
2、图像的转换 思考:如果是V—T图呢?
例4.一定质量的理想气体,从图示A状态开始,经历
表达式:T
V1 T1
C
“斜率”
推论2:一定质量的气体在等压时,升高(或降
低)相同的温度,所增加(或减小)的体积是相同
的.
即斜率相等
包括摄氏温度
例1.一定质量的气体,在体积不变时,温度每
升高1℃,它的压强增加量( A )
A.相同
B.逐渐增大
C.逐渐减小
D.成正比例增大
例2.一定质量的气体,体积不变在0℃时的压 强为2.73×104Pa,则温度每变化1℃,气体的 压强变化多大?如果气体的压强变为 2.73×105Pa则此时气体的温度为多少摄氏度。
高中物理:气体的等容变化和等压变化

4.V-T 和 V-t 图象. (1)V-T 图象:一定质量的某种气体,在等压过程中, 气体的体积 V 和热力学温度 T 的图线是过原点的倾斜直 线,如下图左所示,p1<p2,即压强越大,斜率越小.
(2)V-t 图象:一定质量的某种气体,在等压过程中, 体积 V 与摄氏温度 t 是一次性函数,不是简单的正比例关 系,如上图右所示,图象纵轴的截距 V0 是气体在 0 ℃时 的体积,等压线是一条延长线通过横轴上-273.15 ℃的 倾斜直线,且斜率越大表示压强越小.
1.气体的等容变化. 气体的等容变化:气体体积保持不变的情况下所发 生的状态变化叫等容变化. 2.等容变化的规律. (1)实验条件: ①气体质量一定; ②气体体积不变.
(2)实验过程: ①在室温 t1 下将一定质量的气体封闭在烧瓶中,记 下气体的体积 V1 和压强 p1=p. ②把烧瓶放入冰水混合物的容器里,记下这时温度 为 t2=0 ℃,调整压强计保持气体体积不变,记下压强 p2=p-h.如图所示.
知识点一 气体的等容变化
提炼知识 1.等容变化:一定质量的某种气体在体积不变时压 强随温度的变化规律. 2.查理定律: (1)内容:一定质量的某种气体,在体积不变的情况 下,压强 p 与热力学温度 T 成正比.
(2)表达式:p=CT 或_T_p_11=__Tp_22__或pp12=TT12. (3)图象:一定质量的气体,在体积不变的情况下, 压强与热力学温度成正比.在 p-T 图上等压线为过原点 的倾斜直线,在 p-t 图上等容线不过原点,其反向延长 线与时间轴的交点为-273.15℃.
判断正误
1.气体在等容变化时,升高相同的温度所增加的压 强一定相同.(√)
2.由查理定律知,在体积不变的情况下压强与温度 成正比.(×)
高中物理复习 等容变化和等压变化

(4)适用条件:①气体的质量不变.②气体的体积不变.
直线的斜率越大,体积越小,如图V 2<V 1
直线的斜率越大,压强越小,如图p 2<p 1
查理定律的分比形式Δp =p
ΔT 即一定质量气体在体积不变条件下,压强变化量与热力学温度的变化量成正比.图象的比较:
纵坐标
压强p
体积V
(4)适用条件:①气体的 不变.②气体的 不变.
图象的比较:
纵坐标
1.对于一定质量的气体,以下说法正确的是( )
A .气体做等容变化时,气体的压强和温度成正比
基础达标
2.一定质量的某种气体自状态A经状态C变化到状态B,这一过程在V-T图上表示如图所示,则()
A.在过程AC中,气体的压强不断变小
A.如果把烧瓶浸在热水中,应把A向下移
【答案】AD
【答案】D
8.如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以
能力提升
1.如图所示是一定质量的气体从状态A经B到状态C的V-T图象,由图象可知()
T
【答案】B
3.(多选)如右图所示,两端开口的弯管,左管插入水银槽中,右管有一段高为h的水银柱,中间封有一段空4.
如图所示,气缸A中封闭有一定质量的气体,活塞B与A的接触是光滑的且不漏气,B上放一重物C,B与
求重物m下降的高度.
【解析】初末状态,物块静止,分析活塞受力,可知绳中拉力大小相等,气体发生等压变化,由盖-吕萨克。
高中物理(人教版)精品讲义—气体的等压变化和等容变化

高中物理(人教版)精品讲义—气体的等压变化和等容变化知识点01 气体的等压变化和等容变化(一)气体的等压变化1.等压变化:一定质量的某种气体,在压强不变时,体积随温度变化的过程。
2.盖-吕萨克定律(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(2)表达式:V=CT或V1T1=V2T2.(3)适用条件:气体的质量和压强不变。
(4)图像:如图所示:V-T图像中的等压线是一条过原点的直线.(二)气体的等容变化1.等容变化:一定质量的某种气体,在体积不变时,压强随温度变化的过程;2.查理定律(1)内容:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T 成正比;(2)表达式:p=CT或p1T1=p2T2.(3)适用条件:气体的质量和体积不变。
(4)图像:如图所示.①p-T图像中的等容线是一条过原点的直线.②p-t图像中的等容线不过原点,但反向延长线交t轴于-273.15 ℃. 【知识拓展】(一)气体的等压变化1.盖-吕萨克定律及推论表示一定质量的某种气体从初状态(V、T)开始发生等压变化,其体积的变化量ΔV与热力学温度的变化量ΔT成正比.2.V-T图像和V-t图像一定质量的某种气体,在等压变化过程中(1)V-T图像:气体的体积V随热力学温度T变化的图线是过原点的倾斜直线,如图甲所示,且p1<p2,即斜率越小,压强越大.(2)V-t图像:体积V与摄氏温度t是一次函数关系,不是简单的正比例关系,如图乙所示,等压线是一条延长线通过横轴上-273.15 ℃的倾斜直线,且斜率越大,压强越小,图像纵轴的截距V是气体在0 ℃时的体积。
3.应用盖-吕萨克定律解题的一般步骤(1)确定研究对象,即被封闭的一定质量的气体;(2)分析被研究气体在状态变化时是否符合定律的适用条件:质量一定,压强不变;(3)确定初、末两个状态的温度、体积;(4)根据盖-吕萨克定律列式求解;(5)求解结果并分析、检验。
高中物理——气体的等容变化和等压变化

①图线上每一个点表示气体一个确定的状态, 同一条上各状态的压强相同(等压线)
②不同的等压线,斜率越大,压强 越小
(同一温度下,体积大的压强小)如图的气体发生等压变化时,升高(或降低) 相同的温度,增加(或减小)的体积是 相同 的(相同 或不同)。
VT而不于t,但 V t( T)
表达式
或
3.说明: (1)盖·吕萨克定律是实验定律,由法国科学家盖·吕 萨克通过实验发现的。 (2)适用条件:气体质量一定,压强不变。 (3)解题时前后两状态的体积单位要统一。
(4)在 V/T=C 中的C与气体的种类、质量、压强有关。
3.说明:
(5)一定质量气体的V -T图象:
是一条倾斜直线,其延长线经过坐标原点
A
B
C
解(1)气体由状态A 变为状态B 的过程遵从玻意耳定律.
由pAVA= PBVB,
PB=105Pa
(2)气体由状态B变为状态C的过程遵从查理定律.
由 pB pc TB Tc
pc=1.5×105Pa
1.解释视频中现象
2.高压锅(排气阀没开启) 内发生的是什么变化,怎样产 生的高压呢? 3.热气球是怎么飞上天空的?
二、气体的等压变化
1.等压变化:气体在压强不变的情况下发生的状态变 化过程叫做等压过程.
气体的等压变化遵循什么规律?
二、气体的等压变化
1.等压变化:一定质量的某种气体,在压强不变时, 体积随温度的变化叫做等压变化。
2.盖·吕萨克定律:一定质量的某种气体,在压强不
变的情况下,体积V与热力学温度T成正比 ( V T )。
2、图象意义:
(1)物理意义: 反映温度不变时压强随体积的变化关系
(2)某点的意义: 对应着气体的某一状态
气体的等容变化和等压变化精品课件

V V2 1 = T T2 1
或
V =C T
3.说明: 3.说明: 说明
吕萨克定律是实验定律, (1)盖·吕萨克定律是实验定律,由法国科学 家盖·吕萨克通过实验发现的. 家盖·吕萨克通过实验发现的. 适用条件:气体质量一定,压强不变. (2)适用条件:气体质量一定,压强不变. 与气体的种类、质量、 V/ T (3 )在 V/T=C 中的C与气体的种类、质量、 压强有关. 压强有关. 注意: 注意: V正比于T而不正比于t,但 ∆V∝∆t ∆ 一定质量的气体发生等压变化时, ( 4 ) 一定质量的气体发生等压变化时 , 升高 或降低)相同的温度,增加(或减小) ( 或降低 ) 相同的温度 , 增加 ( 或减小 )的体 积是相同的. 积是相同的. 解题时前后两状态的体积单位要统一. (5)解题时前后两状态的体积单位要统一.
二、气体的等压变化
等压过程: 1 . 等压过程 : 气体在压强不变的情况 下发生的状态变化过程叫做等压过 程. 吕萨克定律: 2 . 盖 · 吕萨克定律 : 一定质量的某种 气体, 在压强不变的情况下, 气体 , 在压强不变的情况下 , 体积 V 与热力学温度成正比( V ∝T ). 与热力学温度成正比(
一定质量的气体在等容变化时, 一定质量的气体在等容变化时,遵守 查理定律. 查理定律.
p1 p2 p = =C 可写成 或 T T2 T 1 一定质量的气体在等压变化时, 一定质量的气体在等压变化时,遵守 吕萨克定律. 盖·吕萨克定律.
可写成
V V2 1 = T T2 1
或
பைடு நூலகம்
V =C T
例题:某种气体在状态A时压强2×105Pa,体积为1m3,温度为 例题:某种气体在状态A时压强2 Pa,体积为1m 体积为 200K,(1)它在等温过程中由状态 变为状态B,状态B 它在等温过程中由状态A B,状态 200K,(1)它在等温过程中由状态A变为状态B,状态B 的体积为 求状态B 的压强. 2m3,求状态B 的压强. (2)随后,又由状态B 在等容过程中变为状态C ,状态 状态C (2)随后,又由状态B 在等容过程中变为状态C ,状态C 的温度 随后 300K,求状态 的压强. 求状态C 为300K,求状态C 的压强.
高中物理之气体的等容变化和等压变化知识点

高中物理之气体的等容变化和等压变化知识点气体的等容变化和等压变化——查理定律、盖·吕萨克定律气体的等容变化1、等容变化:一定质量的气体在体积不变时,压强随温度的变化叫做等容变化。
2、查理定律:一定质量的某种气体,当体积不变时,各种气体的压强p与温度之间都有线性关系,如图所示,我们把它叫做查理定律.注:B点纵坐标是0摄氏度的压强,并非大气压。
3、热力学温标的建立:建立背景:由查理定律中压强p与与摄氏温度t的变化关系图甲可以看出,在等容过程中,压强跟摄氏温度是一次函数关系,而不是简单的正比例关系。
如果把该图的AB直线延长至与横轴相交,把交点当做坐标原点,建立新的坐标系(图乙)此时压强与温度的关系就是正比例关系了。
图乙坐标原点的意义“气体压强为零时其温度为零”,由此可见,为了使一定质量的气体在体积不变的情况下,压强与体积成正比,只需要建立一种新的温标就可以了。
在现实中通过对大量的“压强不太大(相对标准大气压),温度不太低(相对于室温)”的各种不同气体做等容变化的实验数据可以证明“一定质量的气体压在强不太大,温度不太低时,坐标原点代表的温度就是热力学温度的零度,这就是热力学温度零点的物理意义。
由此可见:热力学的零点就规定为气体压强为零的温度。
在建立热力学温标之前,人们已经建立了华氏、摄氏温标,但这些温标都是与测温物质的热学性质有关,当采用不同的测温物质去测量同一温度时会产生一定差异,这种差异是不能克服的。
而由热力学温标的建立可知:热力学温度是在摄氏温度的基础上建立起来的,零点的确定与测温物质无关,因此热力学温标是一种更为简便科学的理论的温标,它的零度不可能达到。
又叫绝对零度。
4、查理定律的热力学温标描述:——查理定律:(1)查理定律:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比。
(2)表达式:注:这里的C和玻意耳定律表达式中的C都泛指比例常数,它们并不相等。
这里的C与气体的种类、质量和压强有关。
高中物理气体的等容变化和等压变化教材梳理素材新人教选修

2 气体的等容变化和等压变化庖丁巧解牛知识·巧学一、气体的等容变化——查理定律1.内容:一定质量的气体,在体积不变的情况下,它的压强跟热力学温度成正比.2.公式p∝T(或11T p =22T p ). 3.气体等容变化的图象(p-T 图象)(1)作法:以横轴表示热力学温度T ,纵轴表示压强p ,根据实际数据取单位,定标度,描出表示气体状态的若干个点,用平滑线连接各点便是p-T 图象.(2)特点:①在p-T 直角坐标系中,等容线是一条延长线通过原点的倾斜直线,事实上,在温度很低时,查理定律已不适用了.由查理定律外推得出的结果表明,绝对零度时,气体压强为零,说明分子将停止运动,这是不可能的,所以,绝对零度是低温的极限,只能接近,不能达到.正因为如此,在p-T 直角坐标系中画等容线时,原点附近一小段应画成虚线,表示它仅是外推的结果.②一定质量气体在不同容积的容器中作等容变化时,得到的是通过坐标原点的一簇倾斜直线(见图8-2-2).直线的斜率越大,体积越小.图8-2-2(3)如果以横轴表示摄氏温度,纵轴表示压强,一定质量气体的等容线是一条不过原点的倾斜直线,在纵轴上的截距表示0 ℃时的压强,其斜率tanα=tp p 0 ,与体积有关.一定质量气体保持不同的体积时,可得到一簇倾斜直线.图线越陡,对应的体积越小,在图8-2-3中,V 2<V 1.图8-2-3误区警示 在pt 图中,并非任意一条在p 轴上有截距的直线都是等容线,等容线的延长线与t 轴的交点应为-273 ℃.二、气体的等压变化——盖·吕萨克定律1.内容:一定质量的气体,在压强不变的情况下,它的体积跟热力学温度成正比.2.公式:V∝T(或11T V =22T V ) 3.气体等压变化的图象(V-T 图象)(1)作法:以横轴表示热力学温度T ,纵轴表示体积V ,根据实际数据取单位,定标度,描出表示气体状态的若干个点,用平滑线连接各点便得V-T 图象.(2)特点:①在V-T 直角坐标系中,等压线是一条延长线通过原点的倾斜直线.事实上,在温度很低时,盖·吕萨克定律已不适用了,因此,在V-T 直角坐标系中画等压线时,原点附近一小段应画成虚线.②一定质量气体在不同压强下做等压变化时,得到的是通过坐标原点的一簇倾斜直线(见图8-2-4).直线的斜率越大,压强越小.图8-2-4联想发散 如果以横轴表示摄氏温度,纵轴表示体积,一定质量气体的等压线是一条不过原点的倾斜直线,在纵轴上的截距表示0 ℃时的体积,其斜率tanα=tV V 0 ,与压强有关.一定质量气体保持不同的压强时,可得到一簇倾斜直线.图线越陡,对应的压强越小,在图8-2-5中,p 2<p 1.图8-2-5深化升华 在V-t 图中,并非任意一条在V 轴上有截距的直线都是等压线,等压线的延长线与t 轴的交点应为-273 ℃.典题·热题知识点一 等容变化——查理定律例1 上端开口竖直放置的玻璃管,内横截面积为0.10 cm 2,管中有一段15 cm 长的水银柱将一些空气封闭在管中,如图8-2-6,此时气体的温度为27 ℃.当温度升高到30 ℃时,为了使气体体积不变,需要再注入多少克水银?设大气压强为p 0=75 cmHg 且不变,水银密度ρ=13.6 g/cm 3.图8-2-6解析:由于气温升高,压强不变,体积增大,使管中水银上移,为保持体积不变,应向管中再注入一定量的水银,增加的压强使体积减小与由于温度升高而增加的体积相互抵消,就能保持体积不变.设再注入水银柱长x cm,以封闭在管中的气体为研究对象.初态:p 1=p 0+h=90 cmHg ,T 1=300 K.末态:p 2=(90+x) cmHg ,T 2=303 K.由查理定律:p 2/T 2=p 1/T 1得:(90+x )/303=90/300所以x=0.9 cm则注入水银的质量:m=ρxS=13.6×0.9×0.10 g=1.2 g.方法归纳 使用查理定律解题,仍然是找出气体变化的两个状态参量,对于多段气体,使用方程仍然是对同一气体的两个不同状态.使用查理定律解决等容变化问题的一般程序:(1)选定体积不变一定质量的气体为研究对象;(2)分析初状态的压强和温度;(3)据查理定律列方程;(4)解方程,对结果进行讨论.例2 有人设计了一种测温装置,其结构如图8-2-7所示,玻璃泡A 内封有一定量气体,与A 相连的B 管插在水银槽中,管内水银面的高度x 即可反映泡内气体的温度,即环境温度,并可由B 管上的刻度直接读出.设B 管的体积与A 泡的体积相比可略去不计.在1标准大气压下对B 管进行温度刻度(1标准大气压相当于76 cmHg 的压强).已知当温度t 1=27 ℃时,管内水银面高度x 1=16 cm ,此高度即为27 ℃的刻度线,问t=0 ℃的刻度线在何处?图8-2-7解析:应选玻璃泡A 内的一定量的气体为研究对象,由于B 管的体积略去不计,温度变化时A 内气体经历的是一个等容过程.(1)玻璃泡A 内气体的初始状态:T 1=300 K ,p 1=(76-16) cmHg=60 cmHg末态即t=0 ℃的状态:T 0=273 K ,p=?由查理定律得 p=10T T p 1=300273×60 cmHg=54.6 cmHg 所以t=0 ℃时水银面高度,即刻度线的位置是x 0=(76-54.6) cm=21.4 cm.方法归纳 该题目用到了近似,由于忽略B 管的体积,才可认为泡A 中的气体经历的是等容变化,今后凡是遇到一个大容器与细管相连的模型,一般皆可略去细管的体积.巧妙变式 若大气压已变为相当于75 cmHg 的压强,利用该测温装置测量温度时所得示数仍为27 ℃,问此时实际温度为多少?从该测温装置所得温度示数为27 ℃时,表示水银面高度仍为x 1=16 cm ,所以玻璃泡A 内气体压强为p 2=(75-16)cmHg=59 cmHg同理得此时的实际气温为T 2=12p p T 1=6059×300 K=295 K 即t 2=22 ℃.知识点二 等压变化——盖·吕萨克定律例3 如图8-2-8所示,三支粗细相同的玻璃管,中间都用一段水银柱封住温度相同的空气柱,且V 1=V 2>V 3,h 1<h 2=h 3.若升高相同的温度,则管中水银柱向上移动最多的是( )图8-2-8A.丙管B.甲管和乙管C.乙管和丙管D.三管中水银柱上移一样多解析:温度上升时,三支管中的气体都在等压膨胀,根据盖·吕萨克定律:11T V =22T V =T V ∆∆,即ΔV=T T ∆V ,由此可见,三支管中气体的体积变化的大小取决于原来状态时管中气体体积的大小.开始时甲、乙两管中气体体积一样大且都比丙管中气体体积大,所以升高相同温度后,甲、乙管中的水银柱上移得最多,选项B 正确.答案:B巧妙变式 若改换条件——降低相同温度,则水银柱移动最多的仍是甲、乙两管.例4 体积为V=100 cm 3的空心球带有一根有刻度的均匀长管,管上共有N=101个刻度,设长管与球连接处为第一个刻度,以后顺序往上排列,相邻两刻度间管的容积为0.2 cm 3,水银液滴将球内空气与大气隔开,如图8-2-9所示.当温度t=5 ℃时,水银液滴在刻度为n=21的地方.那么在此大气压下,能否用它测量温度?说明理由,若能,求其测量范围,不计热膨胀.图8-2-9解析:因为管口和大气相通,所以球内气体的体积随温度的升高而膨胀,气体是等压变化,根据盖·吕萨克定律:11T V =22T V =TV ∆∆=恒量. 温度的增加与体积的增加成正比,所以可以用来测量温度.测量温度的范围应该为气体的体积从V 1=100 cm 3,等压变化到V 2=(100+100×0.2) cm 3=120 cm 3这个范围所对应的气体温度T 1—T 2之间.根据题意,当T 0=273+5 K=278 K 时,气体的体积V 0=(100+20×0.2) cm 3=104 cm 3.根据盖·吕萨克定律:00T V =11T V T 1=001V T V =104278100⨯ K=267.3 K 00T V =22T V ,所以T 2=022V T V =104278120⨯ K=320.8 K 267.3 K=-5.7 ℃320.8 K=47.8 ℃能测量温度的范围从-5.7 ℃—47.8 ℃.巧解提示 本题也可用V-T 图象进行计算,先画出图象,然后应用比例法计算很简捷.知识点三 图象分析及应用例5 图8-2-10甲是一定质量的气体由状态A 经过状态B 变为状态C 的V-T 图象,已知气体在状态A 时的压强是1.5×105 Pa.图8-2-10 一定质量气体的状态变化图(1)说出A→B 过程中压强变化的情形,并根据图象提供的信息,计算图中T A 的温度值.(2)请在图乙坐标系中,作出由状态A 经过状态B 变为状态C 的pT 图象,并在图线相应位置上标出字母A 、B 、C.如果需要计算才能确定有关坐标值,请写出计算过程.解析:由图8-2-10甲可以看出,A 与B 的连线的延长线过原点O ,所以A→B 是一个等压变化,即p A =p B .由图8-2-10甲可知,由B→C 是等容变化.(1)根据盖·吕萨克定律可得:A A T V =B B T V 所以T A =A A T V ×T B =6.04.0×300 K=200 K. (2)根据查理定律得:B B T p =C C T p p C =B C T T p B =300400p B =34p B =34p A =34×1.5×105 Pa=2.0×105 Pa 则可画出由状态A→B→C 的p-T 图象如图8-2-11所示.图8-2-11方法归纳 图线的分析方法及应用(1)用图线表示气体状态的变化过程及变化规律,比数学公式更形象、更直观,不仅有助于对气体实验定律的理解,而且为解答问题带来了很大的方便;(2)图线上的一个点表示一定质量气体的一个平衡状态,图线上的某一线段,表示一定质量气体状态变化的一个过程;(3)应用图象解决问题时,要注意数学公式与图象的数图转换,图象与物理过程、物理意义之间的相互关系,对于图线有关问题的分析讨论,常常需要添加辅助线,然后根据有关方程讨论.例6 如图8-2-12所示为某一定质量的气体的压强—温度变化图象,A 、B 是它的两个状态,A 、B 、O 三点共线.则A 、B 两状态的体积关系是( )图8-2-12A.V A <V BB.V A =V BC.V A >V BD.无法确定解析:比较体积,宜用通过A 、B 状态的特殊图线——等容图线,结合玻意耳定律讨论.如图8-2-13所示,分别作出过A 、B 的等容图线,交p 轴于A′、B′,由于V A =V A ′,V B =V B ′,而A′、B′状态下p A ′>P B ′,根据玻意耳定律V B >V A ,此题正确选项是A.图8-2-13答案:A误区警示 该题易错选为B ,其错误原因是不能正确地区别等容变化在p-T 和p-t 图中的图象.一定质量的气体的等容变化在p-T 图上是一条过原点(0,0)的直线,而在p-t 图上是过(-273,0)的直线,要注意区别.知识点四 实验定律和力学综合类问题例7 如图8-2-14所示,圆柱形气缸倒置在水平粗糙地面上,气缸内被活塞封闭有一定质量的空气,气缸质量为M=10 kg ,缸壁厚度不计,活塞质量m=5.0 kg ,其圆面积S=50 cm 2,与缸壁摩擦不计.在缸内气体温度为27 ℃时,活塞刚好与地面接触并对地面无压力.现设法使缸内气体温度升高,问当缸内气体温度升高到多少摄氏度时,气缸对地面恰好无压力?(大气压强p 0=105 Pa ,g 取10 m/s 2)图8-2-14解析:根据已知条件,分别对活塞和气缸作受力分析,列平衡方程,结合查理定律进行计算.当温度T 1=273+27=300 K 时,活塞对地面无压力,列平衡方程:p 1S+mg=p 0S解得p 1=p 0-S mg =105 Pa-3-105105⨯⨯ Pa=0.9×105 Pa 若温度升高,气体压强增大,气缸恰对地面无压力时,列平衡方程:p 2S=Mg+p 0S解得p 2=p 0+S Mg =105 Pa+4-10501010⨯⨯ Pa=1.2×105 Pa 根据查理定律:11T p =22T p 300100.95⨯=t273101.25+⨯ t=127 ℃.问题·探究思想方法探究问题 如图8-2-15所示,粗细均匀、两端封闭的玻璃管中有一段水银,将空气隔成不等长的A 、B 两部分,若使管内两部分气体的温度同时升高相同的温度,则管内水银柱将向哪个方向移动?怎样判断水银柱移动的方向?图8-2-15探究过程:方法一(假设法):假设上下两部分气体体积不变,升温前后的温度为T 、T+ΔT,压强分别为p A 、p A ′,p B 、p B ′.对于A 气体,根据查理定律得:'A A P P =TT T ∆+ 得p A =TT T ∆+p A 所以Δp A =T T T T -+∆p A =TT ∆p A B 气体也可得:Δp B =T T ∆p B 由已知:p A =p B +h>p BΔp A >Δp B水银柱上移.方法二:极限分析法:由于升温前p A >p B ,让p B 趋于零,则温度升高,p A 增大,水银柱上升.方法三:(图象分析法):如图8-2-16所示,在温度为T 时,下端气体A 的压强p A 大于上端气体B 的压强p B ,即p A >p B ;图8-2-16L 1的斜率大于L 2的斜率,当气体升高相同温度时,Δp A >Δp B ,故水银柱上移.探究结论:利用“假设法”“极限分析法”“图象法”判断水银柱移动方向.若玻璃管水平放置,初温不相同,升高或降低相同温度时水银柱也会移动(证明方法同上).由此总结如下规律:玻璃管竖直或倾斜放置时,水银柱升温上移(初始温度相同),降温下移.玻璃管水平放置时,水银柱升温高移(初始温度高的),降温低移(初始温度低的).交流讨论探究问题 如何挖掘热学题中的隐含条件和相关条件.探究过程:周林:例如某些题目中出现“缓慢”“慢慢”二字,就隐含气体状态变化过程中可充分与外界进行热交换,与环境温度时刻相同,过程等温.焦珊:例如,“密封容器内封有一定质量的气体……,”这里“密封”二字隐含气体状态变化过程中质量不变,体积不变.韩腾:例如:“一定质量的气体,密度不变时……”隐含过程体积不变,等容.王培:“两个球形容器用极细的玻璃管连通……”这句话隐含①极细的管——管的体积忽略不计,②“连通”,两部分气体压强总相等.李江:“过程进行得极为迅速……”“迅速”隐含绝热.老师:例如:如图8-2-17,一密闭气缸被活塞分为左右两室,活塞与气缸壁紧密接触且无摩檫,两室内温度相等.现利用右室内的电热丝对右室中气体加热一段时间,达到平衡后,左室体积变为原来的3/4……图8-2-17这里的相关条件有:p左=p右,p左′=p右′;V左+V右=V左′+V右′隐含条件有:活塞无摩擦p左=p右,p左′=p右′;紧密不漏气,左、右气体质量一定.探究结论:(1)隐含条件是指题目中没有明确给出的条件,它往往隐含在某些文字说明中.(2)相关条件是指两个或几个研究对象之间的相互联系、相互制约的关系,常常表现为压强和体积间的关系,在某些问题中,隐含条件和相关条件一致.高考理综物理模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
高中物理:气体的等容变化和等压变化

高中物理:气体的等容变化和等压变化1、对查理定律和盖·吕萨克定律的理解及应用(1)查理定律①可表示为=恒量或.②它的适用范围温度不太低,压强不太大.③应用时注意单位统一.④据等比定理可得.即一定质量的气体,在体积不变时,温度每升高(或降低)l℃,增大(或减小)的压强等于它在0。
C时压强的·(2)盖·吕萨克定律①可写成=恒量或者.②适用范围是温度不太低和压强不太大.③解决实际问题时要单位统一.④运用等比定理可得.即:一定质量的气体,在压强不变时,温度每升高(或降低)l℃,增大(或减小)的体积等于它在0℃时体积的·2、等容线和等压线的分析及应用(1)等容线一定质量的气体,体积不变时,压强与热力学温度成正比,在P—T坐标系中等容线为过原点的直线,图中,A、B两状态体积相等.(2)等压线因m,P一定,V与T成正比,在V-T图中,等压线应为过原点的直线.图中,A、B两状态压强是相同的.例1、如图所示,是伽利略设计的一种测温装置,玻璃泡A内封有一定质量的空气,与A相连的B 管插在水银槽中.制作时,先给球形容器微加热,跑出一些空气,插入水银槽中时,水银能上升到管内某一高度.试证明管内外液面高度差h与温度t成线性函数关系.设B管的体积与A泡的体积相比可略去不计.证明:由于题设B管的体积与A泡的体积相比可略去不计,因此A泡内气体状态变化可认为是等容变化.制作时先给玻璃泡A微微加热,跑出一些空气.设此时温度为t0,管内气体的状态为初状态,则p1=p0,温度为T0=t0+273.把细管插入水银槽中,管内外水银面的高度差为h,此时管内气体的状态为末状态,则,由查理定律得:化简上式得:对上式进行讨论.当外界大气压不变时,上式变为:设,h与t是一次函数,即成线性关系.例2、如图所示,为一定质量的理想气体的三种变化过程,以下四种解释中,哪些是正确的?A. a到d的过程气体体积增加B. a到d的过程气体体积不变C. c到d的过程气体体积增加D. c到d的过程气体体积减小解析:在P-T图线上等容线的延长线是过原点的直线,且体积越大,直线的斜率越小,由此可见,Va<Vb<Vc,所以选项AD是正确的.答案:AD。
2018届高中物理第八章气体第2节气体的等容变化和等压变化课件新人教版

p1 p2 T2 373 解析 根据查理定律 = 得 p2= p1= p ,即 T1 T2 T1 323 1 373 气体的压强是原来的 倍,选项 A、 C 均错误。 323 Δp p1 Δ p Δ p p1 50 由 = = 得 = ,即Δ p= p, T1 Δ T Δ t 273+ 50 50 323 1 50 可见气体的压强比原来增加了 ,选项 D 正确,选项 323 B 错误。
立,即液柱不动;若压强变化不同,进一步判断出液 柱移动方向。
(2)图像法:如图8-2-10甲所示,水银柱处于静
止,当温度变化时,水银柱移动情况的判断可用 p- T
图像法。假设水银柱不动 ,两部分气体都为等容变 化,在同一 p - T坐标系中画出两段气柱的等容线,如
图乙所示,在温度相同时p1>p2,得气柱 l1等容线的斜
(2)塞子塞紧后,选瓶中剩余气体为研究对象: 初态:p1′=1.0×105 Pa,T1′=400 K 末态:p2′=?,T2′=300 K 由查理定律可得
T2′ 300 p2′= p1′= ×1.0×105 Pa=0.75×105 Pa。 400 T1′
答案
(1)1.33×105 Pa
(2)0.75×105 Pa
温度成正比。( × ) p (2)公式 T =C中C与体积有关。( √ ) (3)一定质量的气体在体积不变的情况下,压强p与 摄氏温度t成线性关系。(√ )
二、气体的等压变化 压强 不 1 . 等压变化: 一定质量的某种气体,在 _____ 体积 随_____ 温度 的变化。 变时,_____ 2.盖-吕萨克定律 (1) 内容:一定质量的某种气体,在压强不变的情
3 . ( 多选 ) 一定质量的理想气体经历
如图 8 - 2 - 8 所示的一系列过程, ab 、
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题13.8 气体的等容变化和等压变化课前预习● 自我检测1.有人设计了一种测温装置,其结构如图所示,玻璃泡A内封有一定质量的气体,与A 相连的B管插在水银槽中,管内外水银面的高度差x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出.设B管的体积与A泡的体积相比可略去不计.(1)在1标准大气压下对B管进行温度标刻(1标准大气压相当于76 cmHg的压强).已知当温度t1=27 ℃时,管内水银面的高度为x1=16 cm,此高度即为27 ℃的刻线,问t=0 ℃的刻线在何处?(2)若大气压已变为相当于75 cmHg的压强,利用该测温装置测量温度时所得读数仍为27 ℃,问:此时的实际温度为多少?【答案】(1)21.4 cm (2)22 ℃2.一定质量的理想气体,在压强不变的情况下,温度由5 ℃升高到10 ℃,体积的增量为ΔV1;温度由10 ℃升高到15 ℃,体积的增量为ΔV2,则( )A.ΔV1=ΔV2B.ΔV1>ΔV2C.ΔV1<ΔV2D.无法确定【答案】 A【解析】 由盖—吕萨克定律V 1T 1=V 2T 2可得V 1T 1=ΔV ΔT ,即ΔV =ΔT T 1V 1,所以ΔV 1=5278V 1,ΔV 2=5283V 2(V 1、V 2分别是气体在5 ℃和10 ℃时的体积),而V 1278=V 2283,所以ΔV 1=ΔV 2,A 正确. 3. (多选)如图所示,四支两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态.如果管内两端的空气都升高相同的温度,则水银柱向左移动的是( )【答案】 CD4.如图甲所示是一定质量的气体由状态A 经过状态B 变为状态C 的V -T 图象.已知气体在状态A 时的压强是1.5×105Pa.(1)说出A →B 过程中压强变化的情形,并根据图象提供的信息,计算图中T A 的温度值. (2)请在图乙坐标系中,画出由状态A 经过状态B 变为状态C 的p -T 的图象,并在图线相应位置上标出字母A ,B ,C .如果需要计算才能确定有关坐标值,请写出计算过程.【答案】 (1)200 K (2)见【解析】【解析】 (1)由题图甲可以看出,A 与B 的连线的延长线经过原点O ,所以A →B 是一个等压变化,即p A =p B .根据盖—吕萨克定律可知:V A T A =V B T B ,即T A =V A V B ·T B =0.40.6×300 K=200 K.(2)由题图甲可知,B →C 是等容变化,根据查理定律得:p B T B =p C T C ,即p C =T C T B ·p B =400300·p B=43p B=43p A=43×1.5×105 Pa=2.0×105 Pa.可画出由状态A→B→C的p-T图象如图所示.课堂讲练● 典例分析【要点提炼】一、气体的等容变化1.等容变化:一定质量的某种气体在体积不变时压强随温度的变化规律.2.查理定律(1)内容:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比.(2)表达式:p1T1=p2T2=C(C是比例常数)推论式:pT=ΔpΔT.(3)图象:如图所示:1①p-T图中的等容线是一条过原点的倾斜直线.②p-t图上等容线不过原点,但反向延长交t轴于-273.15_℃.③无论p-T图象还是p-t图象,其斜率都能判断气体体积的大小,斜率越大,体积越小.【典例1】气体温度计结构如图所示.玻璃测温泡A内充有气体,通过细玻璃管B和水银压强计相连.开始时A处于冰水混合物中,左管C中水银面在O点处,右管D中水银面高出O 点h1=14 cm,后将A放入待测恒温槽中,上下移动D,使C中水银面仍在O点处,测得D中水银面高出O点h2=44 cm.求恒温槽的温度(已知外界大气压为1个标准大气压,1标准大气压相当于76 cmHg).【答案】 364 K(或91 ℃)二、气体的等压变化1.等压变化:一定质量的某种气体,在压强不变的情况下,体积V 随热力学温度T 的变化规律.2.盖—吕萨克定律(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V 与热力学温度T 成正比. (2)表达式:V 1T 1=V 2T 2=C (C 是比例常数) 推论式:V T =ΔVΔT. (3)图象:如图所示.①V -T 图中的等压线是一条过原点的倾斜直线.②V -t 图上的等压线不过原点,反向延长线交t 轴于-273.15_℃.③无论V -T 图象还是V -t 图象,其斜率都能判断气体压强的大小,斜率越大,压强越小.(4) p -T 图象与V -T 图象的比较【典例2】(多选)一定质量的某种气体自状态A 经状态C 变化到状态B ,这一过程在V -T 图上的表示如图所示,则( )A .在AC 过程中,气体的压强不断变大B .在CB 过程中,气体的压强不断变小C .在状态A 时,气体的压强最大D .在状态B 时,气体的压强最大 【答案】 AD【反思总结】在V -T 图象中,比较两个状态的压强大小,可以通过这两个状态与原点连线的斜率大小来判断,斜率越大,压强越小;斜率越小,压强越大.一定质量的气体,温度不变,体积越大,压强越小. 三、假设法判断液柱(或活塞)的移动问题此类问题的特点是:当气体的状态参量p 、V 、T 都发生变化时,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解.其一般思路为:(1)假设液柱或活塞不发生移动,两部分气体均做等容变化.(2)对两部分气体分别应用查理定律的分比形式Δp =p TΔT ,求出每部分气体压强的变化量Δp ,并加以比较.【典例3】如图所示,两端封闭、粗细均匀、竖直放置的玻璃管内,有一长为h 的水银柱,将管内气体分为两部分,已知l 2=2l 1.若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)【答案】 水银柱上移假设水银柱不动,两部分气体都做等容变化,分别对两部分气体应用查理定律: 上段:p 2T 2=p 2′T 2′,所以p 2′=T 2′T 2p 2,Δp 2=p 2′-p 2=(T 2′T 2-1)p 2=ΔT 2T 2p 2; 同理下段:Δp 1=ΔT 1T 1p 1.又因为ΔT 2=ΔT 1,T 1=T 2,p 1=p 2+p h >p 2, 所以Δp 1>Δp 2,即水银柱上移. 【反思总结】同一问题可从不同角度考虑,用不同方法求解,培养同学们的发散思维能力.此类问题中,如果是气体温度降低,则ΔT 为负值,Δp 亦为负值,表示气体压强减小,那么降温后水银柱应该向压强减小得多的一方移动.课后巩固 ● 课时作业题组一 查理定律的应用1.民间常用“拔火罐”来治疗某些疾病,方法是将点燃的纸片放入一个小罐内,当纸片燃烧完时,迅速将火罐开口端紧压在皮肤上,火罐就会紧紧地被“吸”在皮肤上.其原因是,当火罐内的气体( )A .温度不变时,体积减小,压强增大B .体积不变时,温度降低,压强减小C .压强不变时,温度降低,体积减小D .质量不变时,压强增大,体积减小 【答案】 B【解析】 体积不变,当温度降低时,由查理定律p T=C 可知,压强减小,故B 项正确. 2.在密封容器中装有某种气体,当温度从50 ℃升高到100 ℃时,气体的压强从p 1变到p 2,则( )A.p 1p 2=12B.p 1p 2=21C.p 1p 2=323373 D .1<p 1p 2<2 【答案】 C【解析】 由于气体做等容变化,所以p 1p 2=T 1T 2=t 1+273 K t 2+273 K =323373,故C 选项正确.3.一定质量的气体,在体积不变的条件下,温度由0 ℃升高到10 ℃时,其压强的增量为Δp 1,当它由100 ℃升高到110 ℃时,其压强的增量为Δp 2,则Δp 1与Δp 2之比是( )A .10∶1B .373∶273C .1∶1D .383∶283 【答案】 C4.一个密闭的钢管内装有空气,在温度为20 ℃时,压强为1 atm ,若温度上升到80 ℃,管内空气的压强约为( )A .4 atm B.14 atmC .1.2 atm D.56atm 【答案】 C【解析】 由查理定律知p 1T 1=p 2T 2,代入数据解得p 2≈1.2 atm,所以C 正确. 题组二 盖-吕萨克定律的应用5.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,改变的量有( )A .活塞高度hB .汽缸高度HC .气体压强pD .弹簧长度L 【答案】 B6.如图所示,上端开口的圆柱形汽缸竖直放置,截面积为5×10-3m 2,一定质量的气体被质量为2 kg 的光滑活塞封闭在汽缸内,其压强为__①__ Pa(大气压强取1.01×105Pa ,g 取10 m/s 2).若从初温27 ℃开始加热气体,使活塞离汽缸底部的高度由0.50 m 缓慢地变为0.51 m ,则此时气体的温度为__②__ ℃.下列选项正确的是( )A .①1.05×105B .①0.04×105C .②33D .②300 【答案】 AC 【解析】 p 1=F S =mg S =2×105×10-3 Pa =0.04×105Pa ,所以p =p 1+p 0=0.04×105Pa +1.01×105Pa =1.05×105Pa ,由盖—吕萨克定律得V 1T 1=V 2T 2, 即0.5S 273+27=0.51S273+t,所以t =33 ℃.题组三 液柱移动问题的判断7.如图所示,两端开口的直玻璃管A 和B ,竖直插入同一水银槽中,各用一段水银柱封闭着一定质量、同温度的空气,空气柱长度H 1>H 2,水银柱长度h 1>h 2,今使封闭气柱降低相同的温度(大气压保持不变),则两管中气柱上方水银柱的移动情况是( )A .均向下移动,A 管移动较多B .均向上移动,A 管移动较多C .A 管向上移动,B 管向下移动D .无法判断 【答案】 A8.两个容器A 、B ,用截面均匀的水平细玻璃管连通,如图所示,A 、B 所装气体的温度分别为17 ℃和27 ℃,水银柱在管中央平衡,如果两边温度都升高10 ℃,则水银柱将( )A .向右移动B .向左移动C .不动D .条件不足,不能确定 【答案】 A【解析】 假设水银柱不动,A 、B 气体都做等容变化:由Δp =ΔT T p 知 Δp ∝1T,因为T A<T B,所以Δp A>Δp B,所以水银柱向右移动.题组四综合应用9.1697年法国物理学家帕平发明了高压锅,高压锅与普通铝锅不同,锅盖通过几个牙齿似的锅齿与锅体镶嵌旋紧,加上锅盖与锅体之间有橡皮制的密封圈,所以锅盖与锅体之间不会漏气,在锅盖中间有一排气孔,上面再套上类似砝码的限压阀,将排气孔堵住(如图).当加热高压锅,锅内气体压强增加到一定程度时,气体就把限压阀顶起来,这时蒸气就从排气孔向外排出.由于高压锅内的压强大,温度高,食物容易煮烂.若已知排气孔的直径为0.3 cm,外界大气压为1.0×105 Pa,温度为20 ℃,要使高压锅内的温度达到120 ℃,则限压阀的质量应为多少?(g=10 m/s2)【答案】0.024 kg10.如图所示,上端开口的光滑圆柱形汽缸竖直放置,截面积为40 cm2的活塞将一定质量的气体和一形状不规则的固体A封闭在汽缸内.在汽缸内距缸底60 cm处设有a、b两限制推荐精选K12资料推荐精选K12资料 装置,使活塞只能向上滑动.开始时活塞搁在a 、b 上,缸内气体的压强为p 0(p 0=1.0×105Pa 为大气压强),温度为300 K .现缓慢加热汽缸内气体,当温度为330 K 时,活塞恰好离开a 、b ;当温度为360 K 时,活塞上升了4 cm.g 取10 m/s 2求:(1)活塞的质量;(2)物体A 的体积.【答案】 (1)4 kg (2)640 cm 3【解析】 (1)设物体A 的体积为ΔV . T 1=300 K ,p 1=1.0×105Pa ,V 1=60×40-ΔVT 2=330 K ,p 2=⎝ ⎛⎭⎪⎫1.0×105+mg40×10-4Pa ,V 2=V 1(2)由状态2到状态3为等压过程,有V 2T 2=V 3T 3代入数据得ΔV =640 cm 3.。
