2010年中考数学试题(150套)分类汇编35 梯形(含答案)
2010年中考数学试题分类汇编(150套)专题二 实数的运算

1.(2010某某某某)20100的值是 A .2010 B .0 C .1 D .-1【答案】C2.(2010某某威海)计算()201020092211-⨯⎪⎭⎫ ⎝⎛-的结果是 A .-2 B .-1 C .2D .3【答案】B3.(2010某某)计算 | -1-(-35) |-| -611-67| 之值为何? (A) -37 (B) -31 (C) 34 (D)311。
【答案】A4.(2010某某)计算106⨯(102)3÷104之值为何?(A) 108 (B) 109 (C) 1010 (D) 1012。
【答案】A5.(2010某某)下列四个选项中的数列,哪一个不是等差数列? (A) 5,5,5,5,5 (B) 1,4,9,16,25(C)5,25,35,45,55 (D) 1,22,33,44,55。
【答案】D6.(2010某某)图(五)数在线的A 、B 、C 三点所表示的数分别为 a 、b 、c 。
根据图中各点位置,判断下列各式何者 正确? (A) (a -1)(b -1)>0 (B) (b -1)(c -1)>0 (C) (a +1)(b +1)<0 (D) (b +1)(c +1)<0 。
【答案】D7.(2010某某某某)计算 (– 1)2 + (– 1)3 =A.– 2B. – 1C. 0D. 2 【答案】C8.(2010 某某义乌)28 cm 接近于( ▲ )A .珠穆朗玛峰的高度B .三层楼的高度C .姚明的身高D .一X 纸的厚度A B CO a bc 0 -11图(五)9.(2010 某某德化)2-的3倍是() A 、6- B 、1 C 、6 D 、5- 【答案】A10.(2010 某某某某)某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高( )A .-10℃B .-6℃C .6℃D .10℃ 【答案】D11.(2010 东某某)下列各式中,运算正确的是()A =B .=C .632a a a ÷=D .325()a a =【答案】A12.(2010某某某某)计算()21-的值等于 (A )-1 (B )1 (C )-2 (D )2 【答案】B13.(2010 某某)计算3×(-2) 的结果是A .5B .-5C .6D .-6【答案】D14.(2010 某某)下列计算中,正确的是A .020=B .2a a a =+C 3±D .623)(a a =【答案】D15.(2010 某某省某某)下列计算正确的是(A)020=(B)331-=-3==【答案】C16.(2010某某宿迁)3)2(-等于A .-6B .6C .-8D .8 【答案】C17.(2010 某某莱芜)如图,数轴上A 、B 两点分别对应实数a 、b ,则下列结论正确的是A .0>abB .0>-b aC .0>+b aD .0||||>-b a【答案】D18.(2010某某) 计算 -2- 6的结果是( )A .-8B . 8C . -4D . 4 【答案】A19.(2010年某某某某)有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为() A .8人 B .9人 C .10人 D .11人【答案】B.20.(2010某某某某)()()2012321-+-+⎪⎭⎫ ⎝⎛--π的值为( )A .-1B .-3C . 1D . 0【答案】C21.(2010 某某某某)3x 表示( )(A )3x (B )x x x ++ (C )x x x ⋅⋅ (D )3x + 【答案】C22.(2010某某荆州)温度从-2°C 上升3°C 后是A .1°CB . -1°C C .3°CD .5°C 【答案】A1 0 -1 a b B A (第5题图)23.(2010某某荆州)下面计算中正确的是 A .532=+ B .()111=--C . ()2010201055=- D . x 32x •=x 6【答案】C24.(2010某某荆州)在电子显微镜下测得一个圆球体细胞的直径是5×105-cm.,3102⨯个这样的细胞排成的细胞链的长是A .cm 210- B .cm 110- C .cm 310- D .cm 410- 【答案】B25.(2010某某省某某)下列运算正确的是 A .263-=- B .24±=C .532a a a =⋅D .3252a a a+= 【答案】C26.(2010某某某某)观察下列各式:()1121230123⨯=⨯⨯-⨯⨯ ()1232341233⨯=⨯⨯-⨯⨯()1343452343⨯=⨯⨯-⨯⨯……计算:3×(1×2+2×3+3×4+…+99×100)=A .97×98×99B .98×99×100C .99×100×101D .100×101×102 【答案】C27.(2010某某某某)下列运算结果等于1的是() A .)3()3(-+-B .)3()3(---C .)3(3-⨯-D .)3()3(-÷-【答案】D28.(2010某某某某)如图,数轴上A 、B 两点对应的实数分别为,a b ,则下列结论不正确的是()A 、0a b +>B 、0ab <C 、0a b -<D 、0a b ->【答案】D29.(2010某某红河哈尼族彝族自治州)下列计算正确的是A .(-1)-1=1 B.(-3)20=1 D.(-2)6÷(-2)3=(-2)2 【答案】C30.(2010某某某某)下列计算正确的是( )A .a 2·a 3=a 6B .6÷2=3C .(21)-2=-2 D . (-a 3)2=-a 6 【答案】B31. (2010某某随州)下列运算正确的是( )A .1331-÷= B 2a a = C .3.14 3.14ππ-=- D .326211()24a b a b =【答案】D32. (2010某某某某)计算(-2)×3的结果是( )(A)-6 (B)6 (C)-5 (D)5 【答案】A33. (2010某某某某)某年某某市一月份的平均气温为-18℃,三月份的平均气温为2℃,则三月份的平均气温比一月份的平均气温高( )(A )16℃(B )20℃(C )-16℃(D ).-20℃【答案】B34. (2010 某某某某)如果□,1)23(=-⨯则□内应填的实数是 ( )A .23-B .32-C .23 D .32 【答案】B35. (2010某某襄樊)某市2010年元旦这天的最高气温是8℃,最低气温是-2℃,则这天的最高气温比最低气温高( ) A .10℃B .-10℃C .6℃D .-6℃【答案】A36. (2010 某某某某)2010)1(-的值是( )A .1B .—1C .2010D .—2010【答案】A37.(2010 某某某某)下列结论中不能由0=+b a 得到的是(A )ab a -=2(B )b a =(C )0=a ,0=b (D )22b a = 【答案】C38.(2010 某某某某)如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为(A )6 (B )3 (C )200623(D )10033231003⨯+【答案】B39.(2010某某某某)的结果是)(计算12010)21(1:.1--- A. 1 B. -1 C.0 D. 2【答案】B40.(2010 某某)()=-21( )A .1B .-1C .2D .-2【答案】A41.(2010 某某荷泽)2010年元月19日,某某省气象局预报我市元月20日的最高气温是4℃,最低气温是-6℃,那么我市元月20日的最大温差是(第11题)A .10℃B .6℃C .4℃D .2℃【答案】A42.(2010某某某某)计算)3(21-⨯--的结果等于A.5B.5-C.7D.7-【答案】A43.(2010某某某某)用0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数(每个数字都只用一次),然后把所得的数相加,它们的和不可能是( ) A .36 B .117 C .115 D .153 【答案】44.(2010某某某某)观察下列算式,用你所发现的规律得出20102的末位数字是( )21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,… A .2 B .4 C .6 D .8 【答案】B45.(2010某某某某)冰箱冷冻室的温度为-6℃,此时房屋内的温度为20℃,则房屋内的温度比冰箱冷冻室的温度高( )。
陕西省2010年中考数学试题(word版附带详细答案)

2010年陕西省初中毕业学业考试一、 选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.13-= A.3 B.3- C.13 D.-132.如图,点O 在直线AB 上,且OC OD ⊥.若36COA ∠=°,则DOB ∠的大小为 A.36° B. 54° C.64° D. 72°3.计算2(2)3a a -·的结果是 A.26a - B.36a - C.312a D.36a 4.如图是由正方形和圆锥组成的几何体,它的俯视图是5.一个正比例函数的图象经过点(2,3-),它的表达式为A.32y x =- B.23y x =C.32y x =D.23y x =-6.中国2010年上海世博会充分体现着“城市,让生活更美好”的主题.据统计:5月1日到5月7日入园人数(单位:万人)分别为20.3,21.5,13.2,14.6,10.9,11.3,13.9.这组数据的中位数和平均数分别为A. 14.6,15.1B. 14.6,15.0C. 13.9,15.1D. 13.9,15.07.不等式组1102321x x ⎧-⎪⎨⎪+>-⎩≥,的解集是A. 12x -<≤B. 21x -<≤C. 12x x <-或≥D. 2x -<≤-18.若一个菱形的边长为2,则这个菱形两条对角线长的平方和为 A. 16 B. 8C. 4D. 19.如图,点A 、B 、P 在O ⊙上,且50APB ∠=°.若点M 是O ⊙上的动点,要使ABM △为等腰三角形,则所有符合条件的点M 有 A. 1个 B. 2个 C. 3个 D. 4个10.已知抛物线2:=+310C y x x -,将抛物线C 平移得到抛物线C '.若两条抛物线C 、C '关于直线1x =对称,则下列平移方法中,正确的是 A.将抛物线C 向右平移52个单位 B.将抛物线C 向右平移3个单位 C.将抛物线C 向右平移5个单位 D.将抛物线C 向右平移6个单位第二部分(非选择题 共90分)二、填空题(共6小题,每小题3分,计18分)11.在1230π--,,,,五个数中,最小的数是_______________. 12.方程240x x -=的解是______________.13.如图,在ABC △中,D 是AB 边上一点,连接CD .要使ADC △与ABC △相似,应添加的条件是______________.(只需写出一个条件即可)14.如图是一条水平铺设的直径为2米的通水管道横截面,其水面宽为1.6米,则这条管道中此时水最深为_________米.15.已知11()A x y ,,22()B x y ,都在反比例函数6y x=的图象上,若123x x =-,则12y y 的值为__________. 16.如图,在梯形ABCD 中,DC AB ∥,90A B ∠+∠=°.若104AB AD ==,, 5DC =,则梯形ABCD 的面积为____________. 三、解答题(共9小题,计72分.解答应写出过程)17.(本题满分5分) 化简:222m n mnm n m n m n-+-+-.18.(本题满分6分)如图,A 、B 、C 三点在同一条直线上,2AB BC =.分别以AB 、BC 为边作正方形ABEF 和正方形BCMN ,连接FN EC ,. 求证:.FN EC =19.(本题满分7分)某县为了了解“五一”期间该县常住居民的出游情况,有关部分随机调查了1 600名常住居民,并根据调查结果绘制了如下统计图: 根据以上信息,解答下列问题:(1)补全条形统计图.在扇形统计图中,直接填入出游主要目的是采集发展信息人数的百分数; (2)若该县常住居民共24万人,请估计该县常住居民中,利用“五一”期间出游采集发展信息的人数;(3)综合上述信息,用一句话谈谈你的感想.20.(本题满分8分)在一次测量活动中,同学们要测量某公园湖的码头A 与它正东方向的亭子B 之间的距离,如图.他们选择了与码头A 、亭子B 在同一水平面上的点P ,在点P 处测得码头A 位于点P 北偏西30°方向,亭子B 位于点P 北偏东43°方向;又测得点P 与码头A 之间的距离为200米.请你运用以上测得的数据求出码头A 与亭子B 之间的距离.(结果精确到1米,参考数据:3 1.732≈,0.933tan 43≈°)21.(本题满分8分)某蒜薹(tái )生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并且按这三种方式销售,计划每吨平均的售价及成本如下表:销售方式 批发 零售 储藏后销售 售价(元/吨) 3 000 4 500 5 500 成本(元/吨) 7001 0001 200若经过一段时间,蒜薹按计划全部售出获得的总利润为y (元),蒜薹零售x (吨),且零售量是批发量的13.(1)求y x 与之间的函数关系式;(2)由于条件上限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.22.(本题满分8分)某班毕业联欢会设计了即兴表演节目的摸球游戏.游戏采用了一个不透明的盒子,里面装有五个分别标有数字1、2、3、4、5的乒乓球.这些球除数字外,其它完全相同.游戏规则是:参加联欢会的50名同学,每人将盒子里的五个乒乓球摇匀后,闭上眼睛从中随机地一次摸出两个球.......(每位同学必须且只能摸一次).若两个球上的数字之和为偶数,就给大家即兴表演一个节目;否则,下一个同学接着做摸球游戏,依次进行.(1)用列表法或画树状图法求参加联欢会的某位同学即兴表演节目的概率; (2)估计本次联欢会上有多少名同学即兴表演节目?23.(本题满分8分)如图,在Rt 90ABC ABC ∠=△中,°,斜边AC 的垂直平分线交BC 于点D ,交AC 于点E ,连接BE . (1)若BE 是DEC △外接圆的切线,求C ∠的大小; (2)当12AB BC ==,时,求DEC △外接圆的半径. 24.(本题满分10分)如图,在平面直角坐标系中,抛物线经过(10)(30)(01)-,,,,,-三点.A B C(1)求该抛物线的表达式;(2)点Q在y轴上,点P在抛物线上,要使以点Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.25.(本题满分12分)问题探究直线,使它将矩形ABCD分成面积相等的两部分;(1)请你在图①中作一条..(2)如图②,点M是矩形ABCD内一定点.请你在图②中过点M作一条直线,使它将矩形ABCD 分成面积相等的两部分.问题解决(3)如图③,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中644∥,,,.开发区综合服务管理委员会(其占地面积不计)设在===DC OB OB BC CD点(42)P,处.为了方便驻区单位,准备过点P修一条笔直的道路(路的宽度不计),并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分.你认为直线l是否存在?若存在,求出直线l的表达式;若不存在,请说明理由.2010年陕西省初中毕业学业考试一、选择题(共10小题,每小题3分,计30分)题号 1 2 3 4 5 6 7 8 9 10 A 卷答案CBBDACAADC二、填空题(共6小题,每小题3分,计18分) 11. 2- 12.04x x ==或 13.()AD ACACD B ADC ACB AC AB∠=∠∠=∠=或之一亦可 14. 0.4 15.12- 16. 18三、解答题(共9小题,计72分)(以下给出了各题的一种解法及评分参考,其它符合题意的解法请参照相应题的解答赋分) 17.解:原式=()()2()()()()()()m m n n m n mnm n m n m n m n m n m n +--+-+-+-+=222()()m mn nm n mnm n m n +-++-+ ············································ (3分)=222()()m mn n m n m n ++-+=2()()()m n m n m n +-+ ························································· (4分)=m nm n+- ···································································· (5分) 18.证明:在正方形ABEF 和正方形BCMN 中,90AB BE EF BC BN FEN EBC ===∠=∠=,,°. ······························ (2分) 2AB BC =,.EN BC ∴= ·············································································· (4分) FEN EBC ∴△≌△. ····································································· (5分) .FN EC ∴= ·············································································· (6分)19.解:(1)如图所示. ······························································· (2分)(2)162420% 1.8.1 600⨯⨯=·························································· (5分) ∴该县常住居民利用“五一”期间出游采集发展信息的人数约为1.8万人. (6分)(3)略.(只要谈出合理、健康、积极的感想即可给分) ················· (7分) 20.解:过点P 作PH AB ⊥,垂足为H .则3043.APH BPH ∠=∠=°,° (1分) 在Rt APH △中,100cos301003AH PH AP ===,·°. ··········· (4分)在Rt PBH △中,BH PH =·tan43?10030.933161.60⨯≈≈. ·········· (6分) 100161.60262AB AH BH ∴=++≈≈.答:码头A 与亭子B 之间的距离约为262米. ·································· (8分) 21.解:(1)由题意,得批发蒜薹3x 吨,储藏后销售(2004x -)吨, ·· (2分) 则3(3 000700)y x =-+·(4 5001 000)(2004)(5 5001 200)x x -+--··= 6 800860 000.x -+ ····························································· (4分) (2)由题意,得2004x -≤80.解之,得30x ≥.································· (6分)6 800860 000 6 8000y x =-+-<,.y ∴的值随x 的值增大而减小.∴当x 30=时,y =最大值 6 80030860 000656 000-⨯+=.∴该生产基地按计划全部售完蒜薹的最大利润为656 000元. ·············· (8分)22.解:(1)游戏所有可能出现的结果如下表:······························································································ (4分) 从上表可以看出,一次游戏共有20种等可能结果,其中两数和为偶数的共有8种.将参 加联欢会的某位同学即兴表演节目记为事件A ,()P A P ∴=(两数和为偶数)=82205=.··········································· (6分) (2)250205⨯=(人). ∴估计本次联欢会上有20名同学即兴表演节目. ······························ (8分)23.解:(1)DE 垂直平分AC , 90DEC ∴∠=°.DC DEC ∴为△外接圆的直径.DC ∴的中点O 即为圆心.····························································· (1分) 连接.OE又知BE O 是⊙的切线,90EBO BOE ∴∠+∠=°. ······························································ (2分) 在Rt ABC △中,E 是斜边AC 的中点, BE EC ∴=. EBC C ∴∠=∠. 又2BOE C ∠=∠,290C C ∴∠+∠=°.30C ∴∠=°. ·············································································· (4分) (2)在Rt ABC △中,225AC AB BC =+=.1522EC AC ∴==. ····································································· (6分)90ABC DEC ∠=∠=°,D C ABCE ∴∽△△.AC BCDC EC∴=.54DC ∴=.DEC ∴△外接圆的半径为58. ··················································· (8分) 24.解:(1)设该抛物线的表达式为2y ax bx c =++.根据题意,得09301a b c a b c c -+=⎧⎪++=⎨⎪=-⎩,,.解之,得13231a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩,,.················································· (2分) ∴所求抛物线的表达式为212133y x x =--.(2)①当AB 为边时,只要PQ AB ∥,且4PQ AB ==即可. 又知点Q 在y 轴上,∴点P 的横坐标为4或4-.这时,符合条件的点P 有两个,分别记为12P P ,. 而当4x =时,53y =;当4x =-时,7y =.此时1543P ⎛⎫⎪⎝⎭,,2(47)P-,. ······························································ (7分) ②当AB 为对角线时,只要线段PQ 与线段AB 互相平分即可.又知点Q 在y 轴上,且线段AB 中点的横坐标为1,∴点P 的横坐标为2.这时,符合条件的点P 只有一个,记为3P .而当2x =时,1y =-.此时3(21)P -,. 综上,满足条件的点P 为1543P ⎛⎫⎪⎝⎭,,23(47)(21)PP -,,,. ······················ (10分) 25.解:(1)如图①,作直线DB ,直线DB 即为所求.(所求直线不唯一,只要过矩形 对称中心的直线均可) ······························································· (2分)11 (2)如图②,连接AC 、DB 交于点P ,则点P 为矩形ABCD 的对称中心.作直线MP , 直线MP 即为所求. ···································································· (5分)(3)如图③,存在符合条件的直线l . ··········································· (6分) 过点D 作DA OB ⊥于点A ,则点(42)P ,为矩形ABCD 的对称中心. ··········································· (6分) ∴过点P 的直线只要平分DOA △的面积即可. 易知,在OD 边上必存在点H ,使得直线PH 将DOA △面积平分. 从而,直线PH 平分梯形OBCD 的面积. 即直线PH 为所求直线l . ····························································· (9分) 设直线PH 的表达式为y kx b =+,且点(42)P ,,24k b ∴=+.即2424b k y kx k =-∴=+-.. 直线OD 的表达式为2y x =.∴242y kx k y x =+-⎧⎨=⎩,.解之,得242482k x k k y k -⎧=⎪⎪-⎨-⎪=⎪-⎩,. ∴点H 的坐标为244822k k k --⎛⎫ ⎪--⎝⎭,. PH 与线段AD 的交点F 的坐标为(222)k -,, 022411k k ∴<-<∴-<<.. ()14222DHF S k ∴=-+△·2411224222k k -⎛⎫-=⨯⨯⨯ ⎪-⎝⎭. 解之,得13313322k k ⎛⎫---== ⎪ ⎪⎝⎭.不合题意,舍去 8213b ∴=-.∴直线l 的表达式为13382132y x -=+-. ··································· (12分)。
浙江省台州市2010年中考数学试题(含答案)

2010年台州市初中学业水平考试数学试题卷亲爱的考生:欢迎参加考试!请你认真审题,仔细答题,发挥最佳水平。
请注意以下几点: 1.全卷共6页,满分150分,考试时间120分钟。
2.答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上无效。
3.答题前,请认真阅读答题纸上的《注意事项》,按规定答题。
本次考试不得使用计算器。
祝你成功!一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)7.梯形ABCD 中,AD ∥BC ,AB=CD=AD =2,∠B =60°,则下底BC 的长是( ) A .3 B .4 C . 23 D .2+23 8.反比例函数xy 6=图象上有三个点)(11y x ,,)(22y x ,,)(33y x ,,其中3210x x x <<<,则1y ,2y ,3y 的大小关系是( )A .321y y y <<B .312y y y <<C .213y y y <<D .123y y y << 9.如图,矩形ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点M ,CN ⊥AN 于点N . 则DM +CN 的值为(用含a 的代数式表示)( ) A .a B .a54 C .a 22 D .a 2310.如图,点A ,B 的坐标分别为(1, 4)和(4, 4),抛物线n m x a y +-=2)(的顶点在线段AB 上运动,与x 轴交于C 、D 两点(C 在D 的左侧),点C 的横坐标最小值为3-,则点D 的横坐标最大值为( )A .-3B .1C .5D .8二、填空题(本题有6小题,每小题5分,共30分)三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)aN MCDA B (第9题)yxO(第10题)D CB (4,4)A (1,4)19.施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离AB =4米,斜面距离BC =4.25米,斜坡总长DE =85米. (1)求坡角∠D 的度数(结果精确到1°);(2)若这段斜坡用厚度为17c m 的长方体台阶来铺,需要铺几级台阶?20.A ,B 两城相距600千米,甲、乙两车同时从A 城出发驶向B 城,甲车到达B 城后立即返回.如图是它们离A 城的距离y (千米)与行驶时间 x (小时)之间的函数图象. (1)求甲车行驶过程中y 与x 之间的函数解析式,并写出自变量x 的取值范围; (2)当它们行驶7了小时时,两车相遇,求乙车速度.21.果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树产量把杨梅树划分成A ,B ,C ,D ,E 五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:17cm(第19题)ABCDE F参考数据 cos20°≈0.94, sin20°≈0.34, sin18°≈0.31, cos18°≈0.95 乙地块杨梅等级分布扇形统计图49.5~59.859.5~69.769.5~79.679.5~89.589.5~99.5甲地块杨梅等级频数分布直方图6 7 频数 E x/小时y /千米600146OFEC D (第20题)(1)补齐直方图,求a的值及相应扇形的圆心角度数;(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果;(3)若在甲地块随机抽查1棵杨梅树,求该杨梅树产量等级是B的概率.22.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(2 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移a个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移b个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为}{}{}{d b c a d c b a ++=+,,,. 解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.(2)①动点P 从坐标原点O 出发,先按照“平移量”{3,1}平移到A ,再按照“平移量”{1,2}平移到B ;若先把动点P 按照“平移量”{1,2}平移到C ,再按照“平移量” {3,1}平移,最后的位置还是点B 吗? 在图1中画出四边形OABC . ②证明四边形OABC 是平行四边形.(3)如图2,一艘船从码头O 出发,先航行到湖心岛码头P (2,3),再从码头P 航行到码头Q (5,5),最后回到出发点O . 请用“平移量”加法算式表示它的航行过程.23.如图1,Rt △ABC ≌Rt △EDF ,∠ACB =∠F =90°,∠A =∠E =30°.△EDF 绕着边AB 的中点D 旋转, DE ,DF 分别交线段..AC 于点M ,K .(1)观察: ①如图2、图3,当∠CDF =0° 或60°时,AM +CK _______MK (填“>”,“<”或“=”).②如图4,当∠CDF =30° 时,AM +CK ___MK (只填“>”或“<”).(第22题)yO图2Q (5, 5)P (2, 3)yO 图111 xx(2)猜想:如图1,当0°<∠CDF <60°时,AM +CK _______MK ,证明你所得到的结论. (3)如果222AMCKMK =+,请直接写出∠CDF 的度数和AMMK 的值.24.如图,Rt △ABC 中,∠C =90°,BC =6,AC =8.点P ,Q 都是斜边AB 上的动点,点P 从B 向A 运动(不与点B 重合),点Q 从A 向B 运动,BP=AQ .点D ,E 分别是点A ,B 以Q ,P 为对称中心的对称点, HQ ⊥AB 于Q ,交AC 于点H .当点E 到达顶点A 时,P ,Q 同时停止运动.设BP 的长为x ,△HDE 的面积为y . (1)求证:△DHQ ∽△ABC ;图1图2图3(第23题)(M )EKDCA BF M EKDCABF MEKD C ABF 图 4LM EDC AB(F ,K )DEB P(2)求y关于x的函数解析式并求y的最大值;(3)当x为何值时,△HDE为等腰三角形?2010年台州市初中学业水平考试数学参考答案和评分细则一、选择题(本题有10小题,每小题4分,共40分)题号 1 2 3 4 5 6 7 8 9 10 答案A B A C A D B B C D二、填空题(本题有6小题,每小题5分,共30分)11.0≠x 12.)4)(4(-+x x 13. 100)1(1202=-x 14.甲2S <乙2S 15.相切(2分),-6π (3分) 16.(83+4)π 三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.(8分)(1)解:原式=2+1+1 …………………………………………………………3分 =4 ………………………………………………………………1分(2)解:x x 233=-3=x . ……………………………………………………………………3分经检验:3=x 是原方程的解.…………………………………………………………1分所以原方程的解是3=x . 18.(8分)⎩⎨⎧+>>-.12,026x x x 解①得,x <3, ……………………………………………………………………2分 解②得,x >1, ………………………………………………………………………2分 ∴不等式组的解集是1<x <3. ……………………………………………………2分 在数轴上表示 ………………………………………………………………………2分 19.(8分)(1) cos ∠D =cos ∠ABC =BCAB =25.44≈0.94, ………………………………… 3分∴∠D ≈20°. ………………………………………………………………………1分 (2)EF =DE sin ∠D =85sin20°≈85×0.34=28.9(米) , ……………………………3分 共需台阶28.9×100÷17=170级. ………………………………………………1分 20.(8分)(1)①当0≤x ≤6时, ………………………………………………………1分x y 100=; ………………………………………………………………………………2分②当6<x ≤14时, ……………………………………………………………………1分 设b kx y +=,∵图象过(6,600),(14,0)两点, ∴⎩⎨⎧=+=+.014,6006b k b k 解得⎩⎨⎧=-=.1050,75b k∴105075+-=x y . ∴⎩⎨⎧≤<+-≤≤=).146(105075)60(100x x x x y …………………………………………………………2分(2)当7=x 时,5251050775=+⨯-=y , ……………………………………1分757525==乙v (千米/小时). ………………………………………………………1分 21.(10分)(1)画直方图 …………………………………………………………………2分a =10, 相应扇形的圆心角为:360°×10%=36°. ………………………………2分①②(2)5.8020155365575685595=⨯+⨯+⨯+⨯+⨯=甲x ,7520255465975285395=⨯+⨯+⨯+⨯+⨯=乙x , …………………………………2分甲x >乙x ,由样本估计总体的思想,说明通过新技术管理甲地块杨梅产量高于乙地块杨梅产量. ……………………………………………………………………………1分 (若没说明“由样本估计总体”不扣分) (3)P =3.0206=. ………………………………………………………………………3分22.(12分)(1){3,1}+{1,2}={4,3}. ……………………………………………2分 {1,2}+{3,1}={4,3}. …………………………………………………………………2分(2)①画图 …………………………………………………2分 最后的位置仍是B .……………………………………1分 ② 证明:由①知,A (3,1),B(4,3),C (1,2) ∴OC=AB =2221+=5,OA=BC =2213+=10,∴四边形OABC 是平行四边形.…………………………3分 (3){2,3}+{3,2}+{-5,-5}={0, 0}.……………………2分23.(12分)(1)① = ………………………………………………………………………2分② > …………………………………………………………………………………2分 (2)>………………………………………………………………………………………2分 证明:作点C 关于FD 的对称点G , 连接GK ,GM ,GD ,则CD =GD ,GK = CK ,∠GDK =∠CDK , ∵D 是AB 的中点,∴AD =CD =GD . ∵=∠A 30°,∴∠CDA =120°,∵∠EDF =60°,∴∠GDM +∠GDK =60°, ∠ADM +∠CDK =60°.∴∠ADM =∠GDM ,………………………………………………………………………3分 ∵DM =DM ,∴△ADM ≌△GDM ,∴GM =AM .∵GM +GK >MK ,∴AM +CK >MK .……………………………………………………1分 (3)∠CDF =15°,23=AMMK.…………………………………………………………2分24.(14分)(1)∵A 、D 关于点Q 成中心对称,HQ ⊥AB ,∴C HQD ∠=∠=90°,HD =HA ,∴A HDQ ∠=∠,…………………………………………………………………………3分 ∴△DHQ ∽△ABC . ……………………………………………………………………1分BPPBGM EKDCABF yO 11 xABC(2)①如图1,当5.20≤<x 时,ED =x 410-,QH =x A AQ 43tan =∠, 此时x x x x y 4152343)410(212+-=⨯-=. …………………………………………3分当45=x 时,最大值3275=y .②如图2,当55.2≤<x 时, ED =104-x ,QH =x A AQ 43tan =∠, 此时x x x x y 4152343)104(212-=⨯-=. …………………………………………2分当5=x 时,最大值475=y .∴y 与x 之间的函数解析式为⎪⎩⎪⎨⎧≤<-≤<+-=).55.2(41523),5.20(4152322x x x x x x yy 的最大值是475.……………………………………………………………………1分(3)①如图1,当5.20≤<x 时,若DE =DH ,∵DH =AH =x AQA 45cos =∠, DE =x 410-,∴x 410-=x 45,2140=x .显然ED =EH ,HD =HE 不可能; ……………………………………………………1分 ②如图2,当55.2≤<x 时, 若DE =DH ,104-x =x 45,1140=x ; …………………………………………1分若HD =HE ,此时点D ,E 分别与点B ,A 重合,5=x ; ………………………1分 若ED =EH ,则△EDH ∽△HDA ,∴ADDH DHED =,xxxx 24545104=-,103320=x . ……………………………………1分 ∴当x 的值为103320,5,1140,2140时,△HDE 是等腰三角形. (其他解法相应给分)。
(免费)2010年部分省市中考数学试题分类汇编 操作探究(含答案)

2010年部分省市中考数学试题分类汇编操作探究(2010年安徽省B 卷)10.在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能...是下列数中的( )A .5【关键词】图形的变换 【答案】D .23(2010年浙江省东阳县)如图,在一块正方形ABCD 木板上要贴三种不同的墙纸,正方形EFCG 部分贴A 型墙纸,△ABE 部分贴B 型墙纸,其余部分贴C 型墙纸。
A 型、B 型、C 型三种墙纸的单价分别为每平方60元、80元、40元。
探究1:如果木板边长为2米,FC =1米,则一块木板用墙纸的费用需 元; 探究2:如果木板边长为1米,求一块木板需用墙纸的最省费用; 探究3:设木板的边长为a (a 为整数),当正方形 EFCG 的边长为多少时?墙纸费用最省;如要用这 样的多块木板贴一堵墙(7×3平方米)进行装饰, 要求每块木板A 型的墙纸不超过1平方米,且尽量 不浪费材料,则需要这样的木板 块。
【关键词】操作探究 【答案】(1)220 (2)y=20x 2—20x+60 当x=21时,y 小=55元。
(3)y=20x 2—20ax+60a 2当x=21a 时,21块23.(2010年山东省青岛市)问题再现现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、四边形、正六边形的镶嵌问题.今天我们把正多边形....的镶嵌作为研究问题的切入点,提出其中几个问题,共同来探究.我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如右图中,用正方形镶嵌平面,可以发现在一个顶点O 周围围绕着4个正方形的内角. 试想:如果用正六边形来镶嵌平面,在一个顶点周围应该围绕着 个 正六边形的内角.问题提出如果我们要同时用两种不同的正多边形镶嵌平面,可能设计出几种不同的组合方案? 问题解决猜想1:是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌?分析:我们可以将此问题转化为数学问题来解决.从平面图形的镶嵌中可以发现,解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点.具体地说,就是在镶嵌平面时,一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角.验证1:在镶嵌平面时,设围绕某一点有x 个正方形和y 个正八边形的内角可以拼成一个周角.根据题意,可得方程:()82180903608x y -⨯+= ,整理得:238x y +=,我们可以找到惟一一组适合方程的正整数解为12x y =⎧⎨=⎩ .结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.验证2:结论2: . 上面,我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其它可能的组合方案.问题拓广O请你仿照上面的研究方式,探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程.猜想3:.验证3:结论3:.【关键词】【答案】解:3个;················ 1分验证2:在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角.根据题意,可得方程:60120360a b+=.整理得:26a b+=,可以找到两组适合方程的正整数解为22ab=⎧⎨=⎩和41ab=⎧⎨=⎩.························· 3分结论2:镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌.5分猜想3:是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌?······························ 6分验证3:在镶嵌平面时,设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角. 根据题意,可得方程:6090120360m n c++=,整理得:23412m n c++=,可以找到惟一一组适合方程的正整数解为121mnc=⎧⎪=⎨⎪=⎩. ······························ 8分结论3:镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌. (说明:本题答案不惟一,符合要求即可.)1.(2010年福建省晋江市)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;...,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( ) .A. 669B. 670C.671D. 672【关键词】正方形、实验操作、规律探索答案:B;22.(2010年北京崇文区) 正方形A B C D 的边长为a ,等腰直角三角形F A E 的斜边A E b = (a b 2<),且边A D 和A E 在同一直线上 .小明发现:当b a =时,如图①,在B A 上选取中点G ,连结F G 和C G ,裁掉F A G ∆和C H D ∆的位置构成正方形F G C H . (1)类比小明的剪拼方法,请你就图②和图③两种情形分别画出剪拼成一个新正方形的示意图.(2)要使(1)中所剪拼的新图形是正方形,须满足=AEBG .【关键词】正方形的剪拼、 【答案】(1)(2)21.(2010年浙江省绍兴市)分别按下列要求解答:(1)在图1中,将△ABC 先向左平移5个单位,再作关于直线AB 的轴对称图形,经两次变换后得到△A 1B 1 C 1.画出△A 1B 1C 1; (2)在图2中,△ABC 经变换得到△A 2B 2C 2.描述变换过程.1211 10 9 8 76 5 4 32 AC2B 2 12 11 10 9 8 7 6 5 4 3 2 C【答案】(1) 如图.(2) 将△ABC先关于点A作中心对称图形,再向左平移2个单位,得到△A2B2C2.(变换过程不唯一)2.(2010年宁德市)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是().A.2+10B.2+210C.12 D.18【答案】B27.(2010江苏泰州,27,12分)如图,二次函数cxy+-=221的图象经过点D⎪⎭⎫⎝⎛-29,3,与x轴交于A、B两点.⑴求c的值;⑵如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;⑶设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由.(图②供选用)第18题图1 第18题图2第18题图②4【答案】⑴ ∵抛物线经过点D (29,3-)∴29)3(212=+-⨯-c∴c=6.⑵过点D 、B 点分别作AC 的垂线,垂足分别为E 、F ,设AC 与BD 交点为M , ∵AC 将四边形ABCD 的面积二等分,即:S △ABC =S △ADC ∴DE =BF 又∵∠DME =∠BMF , ∠DEM =∠BFE ∴△DEM ≌△BFM∴DM =BM 即AC 平分BD ∵c =6. ∵抛物线为6212+-=x y∴A (0,32-)、B (0,32)∵M 是BD 的中点 ∴M (49,23) 设AC 的解析式为y =kx +b ,经过A 、M 点∴⎪⎩⎪⎨⎧=+=+-4923032b k b k 解得⎪⎪⎩⎪⎪⎨⎧==591033b k ∴直线AC 的解析式为591033+=x y.⑶存在.设抛物线顶点为N (0,6),在Rt △AQN 中,易得AN=,于是以A 点为圆心,AB =为半径作圆与抛物线在x 上方一定有交点Q ,连接AQ ,再作∠QAB 平分线AP 交抛物线于P ,连接BP 、PQ ,此时由“边角边”易得△AQP ≌△ABP .【关键词】二次函数、一次函数、解直角三角形及其知识的综合运。
(免费)2010年部分省市中考数学试题分类汇编 综合型问题(含答案)

2010年部分省市中考数学试题分类汇编综合型问题20、(2010年浙江省东阳县)如图,BD 为⊙O 的直径,点A 是弧BC 的中点,AD 交BC 于E 点,AE=2,ED=4.(1)求证: ABE ∆~ABD ∆;(2) 求tan ADB ∠的值; (3)延长BC 至F ,连接FD ,使BDF ∆的面积等于 求EDF ∠的度数.【关键词】圆、相似三角形、三角形函数问题【答案】(1)∵点A 是弧BC 的中点 ∴∠ABC=∠ADB 又∵∠BAE=∠BAE ∴△ABE∽△ABD(2)∵△ABE∽△ABD ∴AB2=2×6=12 ∴AB=23在Rt△ADB中,tan∠ADB=33632=(3)连接CD,可得BF=8,BE=4,则EF=4,△DEF是正三角形, ∠EDF=60°20.(2010年山东省青岛市)某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.(1)求该校八年级学生参加社会实践活动的人数;(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金. 【关键词】不等式与方程问题 【答案】解:(1)设单独租用35座客车需x 辆,由题意得:3555(1)45x x =--,解得:5x =.∴35355175x =⨯=(人).答:该校八年级参加社会实践活动的人数为175人. ········· 3分 (2)设租35座客车y 辆,则租55座客车(4y -)辆,由题意得:3555(4)175320400(4)1500y y y y +-⎧⎨+-⎩≥≤, ······· 6分解这个不等式组,得111244y ≤≤.∵y 取正整数, ∴y = 2.∴4-y = 4-2 = 2.∴320×2+400×2 = 1440(元).所以本次社会实践活动所需车辆的租金为1440元. (2010年安徽省B 卷)23.(本小题满分12分)如图, Rt ABC △内接于O ⊙,AC BC BAC =∠,的平分线AD 与O ⊙交于点D ,与BC 交于点E ,延长BD ,与AC 的延长线交于点F ,连接CD G ,是CD 的中点,连结OG .(1)判断OG 与CD 的位置关系,写出你的结论并证明; (2)求证:AE BF =; (3)若3(2OG DE = ,求O ⊙的面积.【关键词】圆 等腰三角形 三角形全等 三角形相似 勾股定理【答案】(1)猜想:OG CD ⊥. 证明:如图,连结OC 、OD . ∵OC OD =,G 是CD 的中点,∴由等腰三角形的性质,有OG CD ⊥.(2)证明:∵AB 是⊙O 的直径,∴∠ACB =90°. 而∠CAE =∠CBF (同弧所对的圆周角相等). 在Rt △ACE 和Rt △BCF 中, ∵∠ACE =∠BCF =90°,AC =BC ,∠CAE =∠CBF , ∴Rt △ACE ≌Rt △BCF (ASA ) ∴ AE BF =.(3)解:如图,过点O 作BD 的垂线,垂足为H .则H 为BD 的中点.∴OH =12AD ,即AD =2OH . 又∠CAD =∠BAD ⇒CD =BD ,∴OH =OG . 在Rt △BDE 和Rt △ADB 中, ∵∠DBE =∠DAC =∠BAD , ∴Rt △BDE ∽Rt △ADB∴BD DE AD DB=,即2BD AD DE =·AA∴226(2BD AD DE OG DE ===·· 又BD FD =,∴2BF BD =.∴22424(2BF BD == … ① 设AC x =,则BC x =,.∵AD 是∠BAC 的平分线, ∴FAD BAD ∠=∠.在Rt △ABD 和Rt △AFD 中, ∵∠ADB =∠ADF =90°,AD =AD ,∠F AD =∠BAD , ∴Rt △ABD ≌Rt △AFD (ASA ). ∴AF =AB,BD =FD . ∴CF =AF -AC1)x x -= 在Rt △BCF 中,由勾股定理,得2222221)]2(2BF BC CF x x x =+=+= …②由①、②,得22(224(2x =. ∴212x =.解得x =-.∴AB ===∴⊙O∴π6πO S =⋅2⊙=(2010年安徽省B 卷)24.(本小题满分12分)已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.【关键词】二次函数解析式 对称点 相似三角形 三角形面积【答案】(1)由题意得129302b a a bc c ⎧=⎪⎪⎪-+=⎨⎪⎪=-⎪⎩解得23432a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩∴此抛物线的解析式为224233y x x =+- (2)连结AC 、BC .因为BC 的长度一定,所以PBC △周长最小,就是使PC PB +最小.B 点关于对称轴的对称点是A 点,AC 与对称轴1x =-的交点即为所求的点P .设直线AC 的表达式为y kx b =+则302k b b -+=⎧⎨=-⎩,解得232k b ⎧=-⎪⎨⎪=-⎩∴此直线的表达式为223y x =--.把1x =-代入得43y =-∴P 点的坐标为413⎛⎫--⎪⎝⎭, (3)S 存在最大值 理由:∵DE PC ∥,即DE AC ∥. ∴OED OAC △∽△.∴OD OE OC OA =,即223m OE-=. ∴332OE m =-,连结OPOAC OED AEP PCD S S S S S =---△△△△=()1131341323212222232m m m m ⎛⎫⨯⨯-⨯-⨯--⨯⨯-⨯⨯ ⎪⎝⎭ =()22333314244m m m -+=--+ ∵304-<∴当1m =时,34S =最大(2010年福建省晋江市)已知:如图,把矩形OCBA 放置于直角坐标系中,3=OC ,2=BC ,取AB 的中点M ,连结MC ,把MBC ∆沿x 轴的负方向平移OC 的长度后得到DAO ∆.(1)试直接写出点D 的坐标;(2)已知点B 与点D 在经过原点的抛物线上,点P 在第一象限内的该抛物线上移动,过点P 作x PQ ⊥轴于点Q ,连结OP .①若以O 、P 、Q 为顶点的三角形与DAO ∆相似,试求出点P 的坐标;②试问在抛物线的对称轴上是否存在一点T ,使得TB TO -的值最大.【关键词】二次函数、相似三角形、最值问题答案:解:(1)依题意得:⎪⎭⎫ ⎝⎛-2,23D ;(2) ① ∵3=OC ,2=BC , ∴()2,3B .∵抛物线经过原点,∴设抛物线的解析式为bx ax y +=2()0≠a又抛物线经过点()2,3B 与点⎪⎭⎫⎝⎛-2,23D∴⎪⎩⎪⎨⎧=-=+22349,239b a b a 解得:⎪⎪⎩⎪⎪⎨⎧-==32,94b a ∴抛物线的解析式为x x y 32942-=. ∵点P 在抛物线上, ∴设点⎪⎭⎫ ⎝⎛-x x x P 3294,2. 1)若PQO ∆∽DAO ∆,则AO QO DA PQ =, 22332942x xx =-,解得:01=x (舍去)或16512=x ,∴点⎪⎭⎫⎝⎛64153,1651P . 2)若OQP ∆∽DAO ∆,则AO PQ DA OQ =, 23294232xx x -=,解得:01=x (舍去)或292=x ,∴点⎪⎭⎫⎝⎛6,29P . ②存在点T ,使得TO TB -的值最大. 抛物线x x y 32942-=的对称轴为直线43=x ,设抛物线与x 轴的另一个交点为E ,则点⎪⎭⎫⎝⎛0,23E . ∵点O 、点E 关于直线43=x 对称, ∴TE TO =要使得TB TO -的值最大,即是使得TB TE -的值最大,根据三角形两边之差小于第三边可知,当T 、E 、B 三点在同一直线上时,TB TE -的值最大.设过B 、E 两点的直线解析式为b kx y +=()0≠k ,∴⎪⎩⎪⎨⎧=+=+023,23b k b k 解得:⎪⎩⎪⎨⎧-==2,34b k∴直线BE 的解析式为234-=x y . 当43=x 时,124334-=-⨯=y . ∴存在一点⎪⎭⎫⎝⎛-1,43T 使得TO TB -最大.2. (2010年福建省晋江市)如图,在等边ABC ∆中,线段AM 为BC 边上的中线. 动点D 在直线..AM 上时,以CD 为一边且在CD 的下方作等边CDE ∆,连结BE .(1) 填空:______ACB ∠=度;(2) 当点D 在线段..AM 上(点D 不运动到点A )时,试求出BEAD的值; (3)若8=AB ,以点C 为圆心,以5为半径作⊙C 与直线BE 相交于点P 、Q 两点,在点D 运动的过程中(点D 与点A 重合除外),试求PQ 的长.(2)∵ABC ∆与DEC ∆都是等边三角形∴BC AC =,CE CD =,︒=∠=∠60DCE ACB ∴BCE DCB DCB ACD ∠+∠=∠+∠ ∴BCE ACD ∠=∠CAB 备用图(1) AB C备用图(2)∴ACD ∆≌BCE ∆()SAS∴BE AD =,∴1=BEAD. (3)①当点D 在线段AM 上(不与点A 重合)时,由(2)可知ACD ∆≌BCE ∆,则︒=∠=∠30CAD CBE ,作BE CH ⊥于点H ,则HQ PQ 2=,连结CQ ,则5=CQ .在CBH Rt ∆中,︒=∠30CBH ,8==AB BC ,则421830sin =⨯=︒⋅=BC CH . 在CHQ Rt ∆中,由勾股定理得:3452222=-=-=CH CQ HQ ,则②当点D 在线段AM 的延长线上时,∵ABC ∆与DEC ∆都是等边三角形 ∴BC AC =,CE CD =,︒=∠=∠60DCE ACB ∴DCB ACB =∠+∠∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴=∠=∠CAD CBE ③当点D 在线段MA ∵ABC ∆与DEC ∆∴BC AC =,CD =∴=∠+∠ACE ACD ∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴CAD CBE ∠=∠∵︒=∠30CAM∴︒=∠=∠150CAD CBE ∴︒=∠30CBQ . 同理可得:6=PQ . 综上,PQ 的长是6.1.(2010年浙江省东阳市)如图,P 为正方形ABCD 的对称中心,A (0,3),B (1,0),直线OP 交AB 于N ,DC 于M ,点H 从原点O 出发沿x 轴的正半轴方向以1个单位每秒速度运动,同时,点R 从O 出发沿OM 方向以2个单位每秒速度运动,运动时间为t 。
2010年中考数学真题分类汇编(150套)专题十七·反比例函数

35.(2010湖北十堰)(本小题满分8分)如图所示,直线AB与反比例函数图像相交于A,B两点,已知A(1,4).(1)求反比例函数的解析式;(2)连结OA,OB,当△AOB的面积为15y=kx∵点A(1,4)在反比例函数的图象上∴4=1k,∴k=4,∴反比例函数的解析式为y=4x.(2)设直线AB的解析式为y=ax+b(a>0,b>0),则当x=1时,a+b=4即b=4-a.联立4yxy ax b⎧=⎪⎨⎪=+⎩,得ax2 +bx-4=0,即ax2 +(4-a)x-4=0,方法1:(x-1)(ax+4)= 0,解得x1=1或x=-4a,设直线AB交y轴于点C,则C(0,b),即C(0,4-a)由S△AOB=S△AOC+S△BOC=11415(4)1(4)222a aa-⨯+-⨯=,整理得a2+15a-16=0,∴a=1或a=-16(舍去)∴b=4-1=3∴直线AB的解析式为y=x+3方法2:由S△AOB=12|OC|·|x2-x1|=152而|x2-x14||aa+=4(0)aaa+>,|OC|=b=4-a,可得1415(4)()22aaa+-=,解得a=1或a=-16(舍去). 36.(2010 重庆江津)如图,反比例函数kyx=的图像经过点()4,A b,过点A作AB x⊥轴于点B,△AOB的面积为2.(1)求k和b的值;(2)若一次函数3y ax =-的图象经过点A , 求这个一次函数的解析式.【答案】解:(1)(4)AB BO A b ⊥,, 122AOB S AB BO ∴=⋅=△ 即1422b ⋅= 1b ∴=……………………………………………………………4分又 点A 在双曲线ky x=上144k ∴=⨯=……………………………………………………7分(2) 点A ()4,1又在直线3y ax =-上 143a ∴=- 1a ∴=3y x ∴=-……………………………………………………………10分 37.(2010广西梧州)如图,在平面直角坐标系中,点A (10,0),∠OBA =90°,BC ∥OA ,OB =8,点E 从点B 出发,以每秒1个单位长度沿BC 向点C 运动,点F 从点O 出发,以每秒2个单位长度沿OB 向点B 运动,现点E 、F 同时出发,当F 点到达B 点时,E 、F 两点同时停止运动。
2010年中考数学模拟试题分类汇编——反比例函数

A B C D反比例函数一、选择题1.(2010年广州中考数学模拟试题一)若反比例函数k y x=的图象经过点(-1,2),则这个反比例函数的图象一定经过点( )A 、(2,-1)B 、(12-,2) C 、(-2,-1) D 、(12,2)答:A2.( 2010年山东菏泽全真模拟1)正比例函数kx y 2=与反比例函数xk y 1-=在同一坐标系中的图象不可能...是()答案:D3.(2010年河南中考模拟题1)如图,过反比例函数图象上任意两点A 、B分别作x 轴的垂线,垂足分别为C 、D ,连结OA 、OB ,设AC 与OB 的交点为E , 与梯形ECDB 的面积分别为 ,比较它们的大小,可得( )A.B.C.D. 大小关系不能确定答案:B4.(2010年河南中考模拟题6)如图,直线y=mx 与双曲线k y x=交与A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连接BM ,若S △ABM=2,则k 的值是 ( )A 、2B 、m-2C 、mD 、4 答案:A5.(2010天水模拟)在同一直角坐标系中,函数y=kx+k,与y=xk -(k ≠0)的图像大致( )答案:B6.(2010年杭州月考)如图,点A 在双曲线6y x=上,且OA =4,过A 作AC⊥x 轴,垂足为C ,OA 的垂直平分线交OC 于B ,则△ABC 的周长为( )A. B.5 C.答案:C7.(黑龙江一模)在反比例函数xa y =中,当x >0时,y 随x 的增大而减小,则二次函数axaxy -=2的图象大致是下图中的( )答案:A8.(济宁师专附中一模)函数y x m =+与(0)m y m x=≠在同一坐标系内的图象可以是( )xxxx答案:B9.(2010山东新泰)对于函数xy 2=下列说法错误的是( )A .它的图象分布在一、三象限,关于原点中心对称B .它的图象分布在一、三象限,是轴对称图形C .当x >0时,y 的值随x 的增大而增大D .当x <0时,y 的值随x 的增大而减小 答案:C10. (2010三亚市月考).若反比例函数y=k x的图象经过点(-2,1),则此函数的图象一定经过点( )A. (-2,-1)B. (2,-1)C. (12-,2) D. (12,2)答案:B11.(2009年聊城冠县实验中学二模)如下图,是一次函数b kx y +=与反比例函数xy 2=的图像,则关于x 的方程xb kx 2=+的解为( )A .11=x ,22=xB .21-=x ,12-=xC .11=x ,22-=xD .21=x ,12-=x答案:C12.(2010安徽省模拟)函数1k y x-=的图象经过点(1,3)A -,则k 的值为( ) A .4 B .4-C .2D .2-答案:D13.(2010北京市朝阳区模拟)函数6y x =-与函数()40y x x=>的图象交于A 、B 两点,设点A 的坐标为()11,x y ,则边长分别为1x 、1y 的矩形面积和周长分别为( )A. 4,12B. 4,6C. 8,12D. 8,6 答案:A二、填空题1.(2010年广州中考数学模拟试题(四)) 已知点(12)-,在反比例函数k y x=的图象上,则k = .答:-22.(2010年河南省南阳市中考模拟数学试题)如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数k y x=的图象上,若点A 的坐标为(-2,-2),则k 的值为______.答:4 3.(2010年河南中考模拟题6)函数()1240,x x xyy=≥=(x ﹥0),的图像如图所示,则结论:①两函数图像的交点坐标A 的坐标为(2、2);②当x ﹥2时,2y﹥1y;③当x=1时,BC=3;④当x 逐渐增大时,1y 随x 的增大而增大,2y 随x 的增大而减小。
(免费)2010年部分省市中考数学试题分类汇编 圆的有关性质(含答案)

OCBA2010年部分省市中考数学试题分类汇编圆的有关性质1.(2010年山东省青岛市)如图,点A 、B 、C 在⊙O 上,若∠BAC = 24°,则∠BOC = °. 【关键词】圆周角与圆心角的关系【答案】482、(2010年安徽省B 卷)13.如图,一条公路的转弯处是一段圆弧(图中的 AB ),点O 是这段弧的圆心,C 是 AB 上一点,OC ⊥AB ,垂足为D , AB =300m ,CD =50m ,则这段弯路的半径是 m . 【关键词】圆的性质 勾股定理 【答案】2501、(2010福建德化)如图,点B 、C 在⊙O 上,且BO=BC ,则圆周角B A C ∠等于( ) A .60︒ B .50︒ C .40︒ D .30︒ 答案:D11.(2010年北京崇文区) 如图,A B 是O 的直径,C D 是O 的弦,D A B ∠=48︒,则A C D ∠= ︒.【关键词】圆的有关性质 【答案】4210.(2010年门头沟区)如图,C D AB ⊥于E ,若60B ∠=,则A ∠=度.【关键词】圆的有关性质【答案】30OAB C第10题图·1.(2010年台湾省)如图(二),AB 为圆O 的直径,C 、D 两点均在圆上,其中OD 与AC 交于E 点,且OD ⊥AC 。
若OE =4,ED =2,则BC 长度为何? (A) 6 (B) 7 (C) 8 (D) 9 。
【关键词】垂径定理 【答案】C24、(2010年宁波)如图,AB 是⊙O 的直径,弦DE 垂直平分半径OA ,C 为垂足,弦DF 与半径OB 相交于点P ,连结EF 、EO ,若32=DE ,︒=∠45DPA 。
(1)求⊙O 的半径;(2)求图中阴影部分的面积。
24、解:(1)∵直径AB ⊥DE ∴321==DE CE∵DE 平分AO ∴OE AO CO 2121==又∵︒=∠90OCE∴︒=∠30CEO 在Rt △COE 中,223330cos ==︒=CE OE∴⊙O 的半径为2。
2010年部分省市中考数学试题分类汇编 压轴题(五)及答案
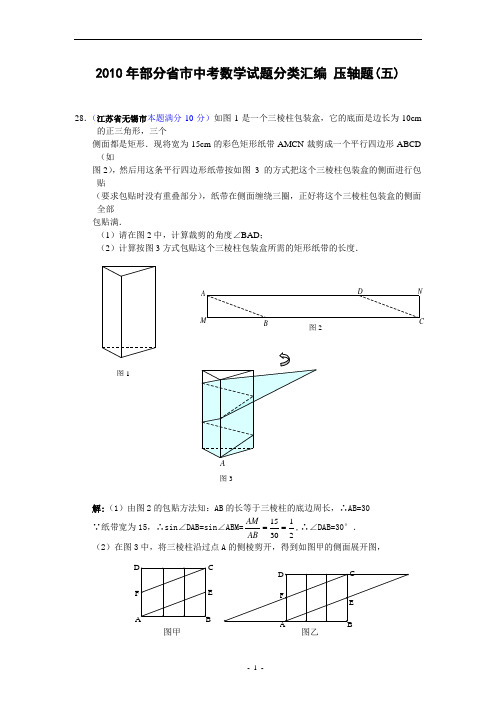
2010年部分省市中考数学试题分类汇编压轴题(五)28.(江苏省无锡市本题满分10分)如图1是一个三棱柱包装盒,它的底面是边长为10cm 的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD (如图2),然后用这条平行四边形纸带按如图3 的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.(1)请在图2中,计算裁剪的角度∠BAD;(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.解:(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30∵纸带宽为15,∴sin∠DAB=sin∠ABM=151302AMAB==,∴∠DAB=30°.(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,C 图甲图1图3A将图甲种的△ABE 向左平移30cm ,△CDF 向右平移30cm ,拼成如图乙中的平行四边形ABCD ,此平行四边形即为图2中的平行四边形ABCD 由题意得,知:BC=BE+CE=2CE=2×cos 30CD =︒∴所需矩形纸带的长为MB+BC=30·cos30°+cm .28.(江苏省宿迁市 本题满分12分)已知抛物线c bx x y ++=2交x 轴于)0,1(A 、)0,3(B ,交y 轴于点C ,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴; (2)连接BC ,过点O 作直线BC OE ⊥交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形; (3)问Q 抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE 的面积的31?若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)求出:4-=b ,3=c ,抛物线的对称轴为:x=2 ……3分(2) 抛物线的解析式为342+-=x x y ,易得C 点坐标为(0,3),D 点坐标为(2,-1) 设抛物线的对称轴DE 交x 轴于点F ,易得F 点坐标为(2,0),连接OD ,DB ,BE ∵∆OBC 是等腰直角三角形,∆DFB 也是等腰直角三角形,E 点坐标为(2,2), ∴∠BOE= ∠OBD=45 ∴OE ∥BD∴四边形ODBE 是梯形 ………………5分在ODF Rt ∆和EBF Rt ∆中,(第28题)(第28题2)OD=5122222=+=+DF OF ,BE=5122222=+=+FB EF∴OD= BE∴四边形ODBE 是等腰梯形 ……………7分(3) 存在, ……8分 由题意得:29332121=⨯⨯=⋅=DE OB S ODBE 四边形 ………………9分 设点Q 坐标为(x ,y ), 由题意得:y y OB S OBQ 2321=⋅=三角形=23293131=⨯=ODBE S 四边形 ∴1±=y当y=1时,即1342=+-x x ,∴ 221+=x , 222-=x ,∴Q 点坐标为(2+2,1)或(2-2,1) …………11分 当y=-1时,即1342-=+-x x , ∴x=2, ∴Q 点坐标为(2,-1)综上所述,抛物线上存在三点Q 1(2+2,1),Q 2 (2-2,1) ,Q 3(2,-1) 使得OBQ S 三角形=ODBE S 四边形31. ………………12分EFQ 1 Q 3Q 226.(湖南省长沙市)如图,在平面直角坐标系中,矩形OABC 的两边分别在x 轴和y轴上,OA =cm , OC=8cm ,现有两动点P 、Q 分别从O 、C 同时出发,P 在线段OA 上沿OAcm 的速度匀速运动,Q 在线段CO 上沿CO 方向以每秒1 cm 的速度匀速运动.设运动时间为t 秒. (1)用t 的式子表示△OPQ 的面积S ;(2)求证:四边形OPBQ 的面积是一个定值,并求出这个定值;(3)当△OPQ 与△P AB 和△QPB 相似时,抛物线214y x bx c =++经过B 、P 两点,过线段BP 上一动点M 作y 轴的平行线交抛物线于N ,当线段MN 的长取最大值时,求直线MN 把四边形OPBQ 分成两部分的面积之比.解:(1) ∵CQ =t ,OPt ,CO =8 ∴OQ =8-t∴S △OPQ=21(8)222t t -=-+(0<t <8) …………………3分 (2) ∵S 四边形OPBQ =S 矩形ABCD -S △PAB -S △CBQ=1188)22⨯⨯-⨯⨯=………… 5分 ∴四边形O PBQ 的面积为一个定值,且等于 …………6分(3)当△OPQ 与△P AB 和△QPB 相似时, △QPB 必须是一个直角三角形,依题意只能是∠QPB =90°又∵BQ 与AO 不平行 ∴∠QPO 不可能等于∠PQB ,∠APB 不可能等于∠PBQ ∴根据相似三角形的对应关系只能是△OPQ ∽△PBQ ∽△ABP ………………7分8=解得:t =4经检验:t =4是方程的解且符合题意(从边长关系和速度) 此时P(0)∵B (8)且抛物线214y x bxc =++经过B 、P 两点, 第26题图∴抛物线是212284y x x =-+,直线BP 是:28y x =- …………………8分 设M (m , 28m -)、N (m ,212284m m -+)∵M 在BP 上运动 ∴4282m ≤≤ ∵2112284y x x =-+与228y x =-交于P 、B 两点且抛物线的顶点是P ∴当4282m ≤≤时,12y y > ………………………………9分 ∴12MN y y =-=21(62)24m --+ ∴当62m =时,MN 有最大值是2 ∴设MN 与BQ 交于H 点则(62,4)M 、(62,7)H ∴S △BHM =13222⨯⨯=32 ∴S △BHM :S 五边形QOPMH =32:(32232)-=3:29 ∴当MN 取最大值时两部分面积之比是3:29. ……10分28.(南京市8分)如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止,连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG 。
2010年各地中考数学试题分类选编(中)

字是 (
)
工A
B
A上
B 海 . C 世 .
D. 博
第2 题图 1
第 1 题 图 5
■, . ● 主视 . ● ●● 2 . 湛 江) 察 下列 几 何 体-t一 图 、 视 2( 观 左
1 . 临 沂 ) 图 , 面 几 何 体 的 俯 视 图 6( 如 下
A B
O / ,
A. - a。 6 ( 一 ) B ( a, 6 1 .- 一 一 ) C. - a, 6 1 ( 一 + ) D. - a, 6 2 ( 一 — )
第 4 图 题
2( . 天津) 列 图形 中 , 可 以看做 是 轴 对 下 既 称 图 形 , 可 以 看 做 是 中 心 对 称 图 形 的 又
l m c
)
第 9 图 题
口
1. 兰州) 察下列 银行标 志 , 0( 观 从 是轴 对称 图形又 是 中心对 称 图形 的有
√2c m
口
第 1 题 图 4
C
第 l 图 O题
试题类编
1. 连 云港 ) 图所 示 的几 何 体 的左 视 图 5( 如
是( )
教
是( )
图和俯 视 图都是矩 形 的是 (
)
田c
③ 。 目匝
第 1 题 图 6
块搭成 的 几 何 体 , 么 这 个 几 何 体 的 左 视 图 那
是( )
则该 几何体
D. 4个 )
1. 昆明) 右 图是 某个 几何体 的三视 图 , 1( 若
邑 口 曲 [ [ 日 日 ]
A
第 6 图 题
△棱 BB .柱 三
的体验 .
2010年全国中考数学试题汇编专题三十五·梯形.doc

15. (2010 四川达州) 如图 4,在一块形状为直角梯形的草坪中,修建了一条由 A→M→N→C 的小路(M 、N 分别是 AB、CD 中点). 极少数同学为了走“捷径” ,沿线段 AC 行走,破坏了草坪, 实际上他们仅少走了图 4 A. 7 米 C. 5 米 B. 6 米 D. 4 米
图4 【答案】B 16. (2010 湖南娄底)下列说法中错误的是( ) A. 平行四边形的对角线互相平分 B. 矩形的对角线互相垂直 C. 菱形的对角线互相垂直平分 D. 等腰梯形的对角线相等 【答案】B 1 二、填空题 1. (2010 甘肃兰州) 如图,直角梯形 ABCD 中,AD∥BC,AB⊥BC,AD = 2,将腰 CD 以 D 为 中心逆时针旋转 90°至 DE, 连接 AE、 CE, △ADE 的面积为 3, 则 BC 的长为 .
A 4cm D
cm.
B
60 ° 6cm E 4cm C
【答案】6 4. (2010 江苏无锡)如图,梯形 ABCD 中, AD∥ BC,EF 是梯形的中位线,对角线 AC 交 EF 于 G,若 BC=10cm,EF=8cm,则 GF 的长等于 ▲ cm.
A E B D F C
G
(第 17 题) 【答案】3 5. (2010 黄冈)如图,在等腰梯形 ABCD 中,AC ⊥BD ,AC =6cm,则等腰梯形 ABCD 的 面积为_____cm 2 .
A E B
D F C
(第 7 题) A.12 cm2 B .18 cm2 C.24 cm2 D.30 cm2 【答案】C 14. (2010 湖北咸宁)如图,菱形 ABCD 由 6 个腰长为 2,且全等的等腰梯形镶嵌而成, 则线段 AC 的长为 A.3 B.6 C. 3 3 D. 6 3
(免费)2010年部分省市中考数学试题分类汇编 点线面角(含答案)

(第3题)2010年部分省市中考数学试题分类汇编点、线、面、角1.(2010年福建晋江) 附加题:若︒=∠35A , 则A ∠的余角等于 度. 答案:552010年广东省广州市)将图1所示的直角梯形绕直线l 旋转一周,得到的立体图开是( )lA .B .C .D . 图1 【关键词】面动成体 【答案】C2.(2010年浙江台州市)如图,△ABC 中,∠C =90°,AC =3,点P 是边BC 上的动点, 则AP 长不可能...是(▲) A .2.5 B .3 C .4 D .5 【关键词】点到直线的距离 【答案】A3.(2010年益阳市)如图3,已知△ABC ,求作一点P ,使P 到∠A 的两边的距离相等,且P A =PB .下列A.P 为∠A 、∠B 两角平分线的交点B.P 为∠A 的角平分线与AB 的垂直平分线的交点 C.P 为AC 、AB 两边上的高的交点 D.P 为AC 、AB 两边的垂直平分线的交点【关键词】角平分线、垂直平分线、三角形的高 【答案】B4.(2010年台湾省)如图(十二),直线CP 是AB 的中垂线且交AB 于P ,其中AP =2CP 。
甲、乙两人想在AB 上取两点D 、E ,使得AD =DC =CE =EB ,其作法如下:(甲) 作∠ACP 、∠BCP 之角平分线,分别交AB 于D 、E , 则D 、E 即为所求(乙) 作AC 、BC 之中垂线,分别交AB 于D 、E ,则D 、 E 即为所求对于甲、乙两人的作法,下列判断何者正确?ABCP 图(十二)AB3图(A) 两人都正确 (B) 两人都错误 (C) 甲正确,乙错误 (D) 甲错误,乙正确。
【关键词】垂线 【答案】D5、(2010年宁波)《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方法的学科,它奠定了现代数学的基础,它是下列哪位数学家的著作( ) A 、欧几里得 B 、杨辉 C 、费马 D 、刘徽 答案:A4. (金华)下图所示几何体的主视图是( ▲ ) A . B . C . D .正面。
2010年部分省市中考数学试题分类汇编 有理数(含答案)

2010年部分省市中考数学试题分类汇编 有理数一 选择题1.(2010重庆市) 3的倒数是()A .13B .— 13C .3D .—3解析:由一个不为0的数a 倒数是a 1知: 3的倒数是— 13 .答案:B.2. (2010重庆市潼南县)2的倒数是( )A .21 B .-2 C . -21D . 2 答案:A3.(2010年四川省眉山市)5-的倒数是A .5B .15C .5-D .15- 【关键词】有理数的倒数的概念和性质 【答案】D4.(2010年福建省晋江市)51-的相反数是( ). A. 51 B. 51- C. 5 D.5-【关键词】倒数的概念与性质 【答案】D5.(2010年浙江省东阳市)73是 ( ) A .无理数B .有理数C .整数D .负数【关键词】有理数的概念 【答案】B6.(2010年浙江省东阳市)73是 ( ) A .无理数B .有理数C .整数D .负数【关键词】有理数的概念 【答案】B7.(2010年四川省眉山市)5-的倒数是A .5B .15 C .5- D .15- 【关键词】有理数的倒数的概念和性质 【答案】D8.(2010年福建省晋江市)51-的相反数是( ). A.51 B. 51- C. 5 D.5- 【关键词】倒数的概念与性质 【答案】D9.(2010重庆市) 3的倒数是()A .13B .— 13C .3D .—3解析:由一个不为0的数a 倒数是a 1知: 3的倒数是— 13 .答案:B.10.(2010江苏宿迁)3)2(-等于( )A .-6B .6C .-8D .8 【关键词】有理数的乘方【答案】C11.(2010江苏宿迁)有理数a 、b 在数轴上的位置如图所示,则b a +的值A .大于0B .小于0C .小于aD .大于b 【关键词】数轴 【答案】A12.(2010江苏宿迁)下列运算中,正确的是( )A .325=-m mB .222)(n m n m +=+C .n m nm =22 D .222)(mn n m =⋅【关键词】有理数的运算【答案】D13.(2010年毕节地区)若23(2)0m n -++=,则2m n +的值为( ) A .4- B .1- C .0 D .4 【关键词】绝对值、代数式的值、两个非负数的和 【答案】B14.(2010年重庆市潼南县)2的倒数是( )A .21 B .-2 C . -21D . 2 【关键词】有理数运算、倒数 【答案】A(第3题)15. (2010年浙江省东阳市)73是 ( ) A .无理数 B .有理数C .整数D .负数【关键词】有理数 【答案】B16. (2010年浙江省东阳市)某电视台报道,截止到2010年5月5日,慈善总会已接受支援玉树地震灾区的捐款15510000元.将15510000用科学记数法表示为 ( )A.8101551.0⨯ B. 4101551⨯ C.710551.1⨯ D.61051.15⨯【关键词】科学记数法 【答案】C17.(2010年安徽中考) 在2,1,0,1-这四个数中,既不是正数也不是负数的是( ) A )1- B )0 C )1 D )2 【关键词】有理数 【答案】B18. (2010年安徽中考) 2010年一季度,全国城镇新增就业人数为289万人,用科学记数法表示289万正确的是…………………………( )A )2.89×107.B )2.89×106 .C )2.89×105.D )2.89×104. 【关键词】科学记数法 【答案】B19. (2010年宁波市)-3的相反数是( ) A 、3 B 、31 C 、-3 D 、31- 【关键词】相反数【答案】A 20、(2010年宁波市)据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( ) A 、111082.0⨯ B 、10102.8⨯ C 、9102.8⨯ D 、81082⨯ 【关键词】科学记数法 【答案】B21.(2010·重庆市潼南县)2的倒数是( )A .21 B .-2 C. -21D. 2 【关键词】倒数的概念 【答案】A22.(2010年山东聊城)据市旅游局统计,今年“五·一”小长假期间,我市旅游市场走势良好,假期旅游总收入达到8.55亿元,用科学记数法可以表示为A .8.55×106B .8.55×107C .8.55×108D .8.55×109 【关键词】科学记数法 【答案】C23.(2010·重庆市潼南县)2的倒数是( )A .21 B .-2 C. -21D. 2 【关键词】倒数的概念 【答案】A24.(2010年辽宁省丹东市)在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材,那么84.610⨯的原数为( )A .4 600 000B .46 000 000C .460 000 000D .4 600 000 000 【关键词】科学计数法 【答案】C 25(2010辽宁省丹东市)1在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材,那么84.610⨯的原数为( )A .4 600 000B .46 000 000C .460 000 000D .4 600 000 000 【关键词】科学记数法 【答案】C 25.(2010年山东聊城)据市旅游局统计,今年“五·一”小长假期间,我市旅游市场走势良好,假期旅游总收入达到8.55亿元,用科学记数法可以表示为A .8.55×106B .8.55×107C .8.55×108D .8.55×109 【关键词】科学记数法 【答案】C 1、(2010年宁波)-3的相反数是( ) A 、3 B 、31 C 、-3 D 、31- 答案:A27、(2010年宁波)据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( ) A 、111082.0⨯ B 、10102.8⨯ C 、9102.8⨯ D 、81082⨯ 答案:B28.(2009年山东省济南市)某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高 ( ) A .-10℃ B .-6℃ C .6℃ D .10℃ 【关键词】有理数 【答案】D29.(2010年台湾省)下列何者是0.000815的科学记号?(A) 8.15⨯10-3 (B) 8.15⨯10-4 (C) 815⨯10-3 (D) 815⨯10-6 。
2010年北京市中考数学试卷(含答案)

2010年北京市高级中等学校招生考试数 学 试 卷学校 姓名 准考证号考生须知 1.本试卷共6页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个‧‧是符合题意的.1.2-的倒数是 A .12- B .12C .2-D .22.2010年6月3日,人类首次模拟火星载人航天飞行试验“火星 — 500”正式启动,包括中国志愿者王跃在内的6名志愿者踏上了为期12 480小时的“火星之旅”. 将12 480用科学记数法表示应为 A .312.4810⨯ B .50.124810⨯ C .41.24810⨯ D .31.24810⨯ 3.如图,在△ABC 中,点D E 、分别在边上,DE ∥BC ,若:3:4AD AB =,6AE =,则AC 等于AB AC 、A. 3B. 4C. 6D. 8 4.若菱形两条对角线的长分别为6和8,则这个菱形的周长为A .20B .16C .12D .105.从 1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是A .15B .310C .13 D .126.将二次函数223y x x =-+化为2()y x h k =-+的形式,结果为A .2(1)4y x =++B .2(1)4y x =-+C .2(1)2y x =++D .2(1)2y x =-+ 7.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm )如下表所示:队员1 队员2 队员3 队员4 队员5 甲队 177 176 175 172 175 乙队170175173174183设两队队员身高的平均数依次为x 甲,x乙,身高的方差依次为2S 甲,2S 乙,则下列关系中完全正确的是 A .x x =甲乙,22S S>乙甲B .x x =甲乙,22S S<乙甲 C.x x >甲乙,22S S >乙甲D .x x <甲乙,22S S<乙甲8.美术课上,老师要求同学们将右图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个‧‧‧‧符合上述要求,那么这个示意图是A BC D 二、填空题(本题共16分,每小题4分)9.若二次根式21x -有意义,则x 的取值范围是 . 10.分解因式:34m m -= .11.如图,AB 为⊙O 的直径,弦CD AB ⊥,垂足为点E ,连结OC ,若5OC =,8CD =,则AE = .12.右图为手的示意图,在各个手指间标记字母 A ,B ,C ,D.请你按图中箭头所指方向(即 A →B →C →D →C→B →A →B →C → … 的方式)从 A 开始数连续的正整数 1,2,3,4,…,当数到 12 时,对应的字母是 ;当字母C 第201次出现时,恰好数到的数是 ;当字母C 第21n +次出现时(n 为正整数),恰好数到的数是 (用含n 的代数式表示).三、解答题(本题共30分,每小题5分) 13.计算:101201043tan 603-⎛⎫-+--︒ ⎪⎝⎭.14.解分式方程 312422x x x -=--.15.已知:如图,点A B C D 、、、在同一条直线上,EA AD ⊥,FD AD ⊥,AE DF =,AB DC =. 求证:ACE DBF ∠=∠.16.已知关于 x 的一元二次方程 2410x x m -+-= 有两个相等的实数根,求m 的值及方程的根.17.列方程或方程组解应用题:2009年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米.18.如图,直线23y x =+与x 轴交于点A ,与y 轴交于点B .(1) 求A ,B 两点的坐标;(2) 过B 点作直线BP 与x 轴交于点P ,且使2OP OA =,求△ABP 的面积.四、解答题(本题共20分,每小题5分)19.已知:如图,在梯形ABCD 中,AD ∥BC ,2AB DC AD ===,4BC =.求B ∠的度数及AC 的长.20.已知:如图,在△ABC 中,D 是AB 边上一点,⊙O 过D B C 、、三点,290DOC ACD ∠=∠=︒.(1)求证:直线AC 是⊙O 的切线;(2)如果75ACB ∠=︒,⊙O 的半径为2,求BD 的长.21.根据北京市统计局公布的2006—2009年空气质量的相关数据,绘制统计图如下: 2006—2009年北京全年市区空气质量达到二级和好于二级的天数统计图由统计图中的信息可知,北京全年市区空气质量达到二级和好于二级的天数与上一年相比,增加最多的是 年,增加了 天;(2) 表1是根据《中国环境发展报告(2010)》公布的数据绘制的2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比的统计表,请将表1中的空缺部分补充完整(精确到1%);表1 2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比统计表城 市北京上海天津昆明 杭州广州南京成都沈阳西宁百分比91% 84% 100% 89% 95% 86% 86% 90% 77%(3) 根据表1中的数据将十个城市划分为三个组,百分比不低于95%的为A 组,不低于85%且低于95%的为B 组,低于85%的为C 组.按此标准,C 组城市 数量在这十个城市中所占的百分比为 %;请你补全右边的 扇形统计图.22.阅读下列材料:小贝遇到一个有趣的问题:在矩形ABCD 中,8AD =cm ,6AB =cm . 现有一动点P 按下列方式在矩形内运动:它从A 点出发,沿着与AB 边夹角为45︒的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45︒的方向作直线运动,并且它一直按照这种 方式不停地运动,即当P 点碰到BC 边,沿与BC 边夹角为45︒的方向作直线运动,当P 点碰到CD 边,再沿着与CD 边夹角为45︒的方向作直线运动,…,如图1所示.问P 点第一次与D 点重合前‧‧‧与边相碰几次,P 点第一次与D 点重‧合时‧‧所经过的路径的总长是多少.小贝的思考是这样开始的 : 如图2,将矩形ABCD 沿直线CD 折叠,得到矩形11A B CD .由轴对称的知识,发现232P P P E =,11P A PE =. 请你参考小贝的思路解决下列问题:(1)P 点第一次与D 点重合前‧‧‧与边相碰 次;P 点从A 点出发到第一次与D 点重合时‧‧‧所经过的路径的总长是 cm ; (2) 进一步探究:改变矩形ABCD 中AD 、AB 的长,且满足AD AB >.动点P 从A 点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD 相邻的两边上. 若P 点第一次与B 点重合前‧‧‧与边相碰7次,则:A B A D 的值为 .2009年十个城市空气质量达到 二级和好于二级的天数占全年天数百分比分组统计图图1图2五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知反比例函数ky x=的图象经过点(31)A -,. (1) 试确定此反比例函数的解析式;(2) 点O 是坐标原点,将线段OA 绕O 点顺时针旋转30°得到线段OB ,判断点B 是否在此反比例函数的图象上,并说明理由;(3) 已知点(36)P m m +, 也在此反比例函数的图象上(其中 0m <),过P 点作x 轴的垂线,交x 轴于点M . 若线段PM 上存在一点Q ,使得△OQM 的面积是12,设Q 点的纵坐标为n ,求2239n n -+的值.24.在平面直角坐标系xOy 中,抛物线22153244m my x x m m -=-++-+与x 轴的交点分别为原点O 和点A ,点(2,)B n 在这条抛物线上.(1) 求B 点的坐标;(2) 点P 在线段 OA 上,从O 点出发向A 点运动,过P 点作x 轴的垂线,与直线 OB 交于点E ,延长PE 到点D ,使得ED PE =,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动).① 当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时,求OP 的长;② 若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动).过Q 点作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM QF =,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点、N 点也随之运动).若P 点运动到 t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t 的值.25.问题:已知△ABC 中,2B A C A C B ∠=∠,点D 是△ABC 内的一点,且AD CD =,BD BA =.探究DBC∠与ABC ∠度数的比值. 请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.(1) 当90BAC ∠=︒时,依问题中的条件补全右图.观察图形,AB 与AC 的数量关系为 ;当推出15DAC ∠=︒时,可进一步可推出DBC ∠的度数为 ;可得到DBC ∠与ABC ∠度数的比值为 .(2) 当90BAC ∠≠︒时,请你画出图形,研究DBC ∠与ABC ∠度数的比值是否与(1)中的结论相同,写出你的猜想并加以证明.2010年北京市高级中等学校招生考试数学试卷答案一、选择题 1.A , 2.C , 3.D , 4.A , 5.B , 6.D , 7.B , 8.B , 二、填空题 9. x ≥21, 10. m (m +2)(m -2), 11. 2, 12. B 、603、6n +3; 三、解答题13. 解:原式=3-1+43-3=2+33。
2010年北京市中考数学试卷-含答案详解

北京市2010年高级中等学校招生考试一、选择题(本大题共8小题,共32.0分。
在每小题列出的选项中,选出符合题目的一项)1.−2的倒数是( )A. −B.C. −2D. 22.2010年6月3日,人类首次模拟火星载人航天飞行试验“火星—500”正式启动,包括中国志愿者王跃在内的6名志愿者踏上了为期12480小时的“火星之旅”.将12480用科学记数法表示应为( )A. 12.48×103B. 0.1248×105C. 1.248×104D. 1.248×1033.如图,在△ABC中,点D,E分别在AB,AC边上,DE//BC,若AD∶AB=3∶4,AE=6,则AC等于( )A. 3B. 4C. 6D. 84.若菱形两条对角线的长分别为6和8,则这个菱形的周长为( )A. 20B. 16C. 12D. 105.从1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是( )A. B. C. D.6.将二次函数y=x 2−2x+3化为y=(x−ℎ)2+k的形式,结果为( )A. y=(x+1)2+4B. y=(x−1)2+4C. y=(x+1)2+2D. y=(x−1)2+27.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:队员1队员2队员3队员4队员5甲队177176175172175乙队170175173174183设两队队员身高的平均数依次为 甲, 乙,身高的方差依次为,,则下列关系中完全正确的是( )A. 甲= 乙,>B. 甲= 乙,<C. 甲> 乙,>D. 甲< 乙,<8.美术课上,老师要求同学们将下图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是( )A. B.C. D.二、填空题(本大题共5小题,共21.0分)9.若二次根式有意义,则x的取值范围是________.10.分解因式:m 3−4m=________.11.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE= ________.12.下图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→⋯的方式)从A开始数连续的正整数1,2,3,4,…,当数到12时,对应的字母是________;当字母C第201次出现时,恰好数到的数是________;当字母C第2n+1次出现时(n为正整数),恰好数到的数是_________(用含n的代数式表示).13.阅读下列材料:小贝遇到一个有趣的问题:在矩形ABCD中,AD=8cm,AB=6cm.现有一动点P按下列方式在矩形内运动:它从A点出发,沿着与AB边夹角为45°的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45°的方向作直线运动,并且它一直按照这种方式不停地运动,即当P点碰到BC边,沿着与BC边夹角为45°的方向作直线运动,当P点碰到CD边,再沿着与CD边夹角为45°的方向作直线运动……如图1所示.问P点第一次与D点重合前与边相碰几次,P点第一次与D点重合时所经过的路径的总长是多少.小贝的思考是这样开始的:如图2,将矩形ABCD沿直线CD折叠,得到矩形A 1B 1CD.由轴对称的知识,发现P 2P 3=P 2E,P 1A=P 1E.请你参考小贝的思路解决下列问题:(1)P点第一次与D点重合前与边相碰________次;P点从A点出发到第一次与D点重合时所经过的路径的总长是________cm;(2)进一步探究:改变矩形ABCD中AD,AB的长,且满足AD>AB.动点P从A点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上.若P点第一次与B点重合前与边相碰7次,则AB∶AD的值为________.三、计算题(本大题共2小题,共10.0分)14.计算:.15.解分式方程四、解答题(本大题共10小题,共57.0分。
2010年中考数学试题分类汇编

2010中考数学试题分类汇编专题——矩形、菱形、正方形(选择题)1.(2010江苏苏州)如图,在菱形ABCD 中,DE ⊥AB ,3cos 5A =,BE=2,则tan ∠DBE 的值是 A .12 B .2 C .52 D .55【答案】B 2.(2010湖南怀化)如图2,在菱形ABCD 中, 对角线AC=4,∠BAD=120°, 则菱形ABCD 的周长为( )A .20B .18C .16D .15 【答案】C 3.(2010安徽芜湖)下列命题中是真命题的是()A .对角线互相垂直且相等的四边形是正方形B .有两边和一角对应相等的两个三角形全等C .两条对角线相等的平行四边形是矩形D .两边相等的平行四边形是菱形 【答案】C4.(2010甘肃兰州)如图所示,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,sin A=53,则下列结论正确的个数有①cm DE 3= ②cm BE 1= ③菱形的面积为215cm ④cm BD 102= A . 1个 B . 2个 C . 3个 D . 4个【答案】C5.(2010江苏南通) 如图,菱形ABCD 中,AB = 5,∠BCD = 120°,则对角线AC 的长是A .20B .15C .10D .5【答案】D6.(2010江苏盐城)如图所示,在菱形ABCD 中,两条对角线AC =6,BD =8,则此菱形 的边长为 A .5B .6C .8D .10【答案】A 7.(2010 浙江省温州)下列命题中,属于假命题的是(▲)A .三角形三个内角的和等于l80°B .两直线平行,同位角相等C .矩形的对角线相等D .相等的角是对顶角. 【答案】D 8.(2010 浙江省温州)如图,AC ;BD 是矩形ABCD 的对角线,过点D 作DE //AC 交BC 的延长线于E ,则图中-与AABC 全等的 三角形共有(.▲) A .1个 B .2个 C .3个 D .4个【答案】D 9.(2010 浙江义乌)下列说法不正确...的是( ▲ ) A .一组邻边相等的矩形是正方形 B .对角线相等的菱形是正方形 C .对角线互相垂直的矩形是正方形 D .有一个角是直角的平行四边形是正方形【答案】DABD(第6题)BACD(第8题)10.(2010 重庆)已知:如图,在正方形ABCD 外取一点E ,连接AE ,BE ,DE .过点A 作AE 的垂线交ED 于点P .若1AE AP ==, 5PB①△APD ≌△AEB ;②点B 到直线AE 2 ③EB ED ⊥;④16APD APB S S ∆∆+=46ABCD S =正方形其中正确结论的序号是( )A .①③④B .①②⑤C .③④⑤D .①③⑤ 【答案】D11.(2010山东聊城)如图,点P 是矩形ABCD 的边AD 的一个动点,矩形的两条边AB 、BC 的长分别为3和4,那么点P 到矩形的两条对角线AC 和BD 的距离之和是( )A .125B .65C .245D .不确定【答案】A12.(2010 福建晋江)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;...,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( ) .10题图A PEDCBA. 669B. 670C.671D. 672【答案】B 13.(2010 山东济南) 如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2010厘米后停下,则这只蚂蚁停在 点.【答案】C14.(2010 江苏连云港)如图,四边形ABCD 的对角线AC 、BD 互相垂直,则下列条件能判定四边形ABCD 为菱形的是( ).BA =BC B .AC 、BD 互相平分 C .AC =BD D .AB ∥CD 【答案】B15.直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ). A .2+10 B .2+210 C .12 D .18 【答案】B16.(2010江西)如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,∠BEG>60°,现沿直线EG 将纸片折叠,使点B 落在纸片上的点H 处,连接AH ,则与∠BEG 相等的角的个数为( )A .4B .3C .2D .1B C D 第7题 CAD G第7题图① ②3 4【答案】B 17.(2010 山东滨州) 如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为( )A.60°B.30°C.45°D.90° 【答案】C 18.(2010山东潍坊)如图,已知矩形ABCD ,一条直线将该矩形ABCD 分割成两个多边形(含三角形),若这两个多边形的内角和分别为M 和N ,则M +N 不可能是( ).【答案】D19.(2010北京) 若菱形两条对角线的长分别为6和8,则这个菱形的周长为( )A .20B .16C .12D . 10【答案】A 20.(2010 浙江省温州)下列命题中,属于假命题的是(▲)A .三角形三个内角的和等于l80°B .两直线平行,同位角相等C .矩形的对角线相等D .相等的角是对顶角. 【答案】D 21.(2010 浙江义乌)下列说法不正确...的是( ▲ ) A .一组邻边相等的矩形是正方形 B .对角线相等的菱形是正方形 C .对角线互相垂直的矩形是正方形D .有一个角是直角的平行四边形是正方形【答案】D 22.(2010陕西西安)若一个菱形的边长为2,则这个菱形两条对角线长的平方和为 A .16 B .8 C .4 D .1B AGCDHE(第8题图)【答案】A23.(2010江西省南昌)如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,︒>∠60BEG ,现沿直线EG 将纸片折叠,使点B 落在约片上的点H 处,连接AH ,则与BEG ∠相等的角的个数为 ( )A.4B. 3C.2D.1(第10题) 【答案】B 24.(2010湖北襄樊)下列命题中,真命题有( ) (1)邻补角的平分线互相垂直 (2)对角线互相垂直平分的四边形是正方形 (3)四边形的外角和等于360° (4)矩形的两条对角线相等A .1个B .2个C .3个D .4个 【答案】C 25.(2010湖北襄樊)菱形的周长为8cm ,高为1cm ,则菱形两邻角度数比为( )A .3:1B .4:1C .5:1D .6:1 【答案】C 26.(2010 四川泸州)如图1,四边形ABCD 是正方形,E 是边CD 上一点,若△AFB 经过逆时针旋转角θ后与△AED 重合,则θ的取值可能为( )A .90°B .60°C .45°D .30° 【答案】A27.(2010 山东淄博)如图所示,把一长方形纸片沿MN 折叠后,点D ,C 分别落在D ′,C ′的位置.若∠AMD ′=36°,则∠NFD ′等于(A )144° (B )126°BCD ′NF (第10题)(C )108° (D )72° 【答案】B28.(2010 天津)下列命题中正确的是(A )对角线相等的四边形是菱形 (B )对角线互相垂直的四边形是菱形 (C )对角线相等的平行四边形是菱形(D )对角线互相垂直的平行四边形是菱形 【答案】D29.(2010 湖南湘潭)下列说法中,你认为正确的是A .四边形具有稳定性B .等边三角形是中心对称图形C .任意多边形的外角和是360oD .矩形的对角线一定互相垂直【答案】C30.(2010 福建泉州南安)已知四边形ABCD 中,90A B C ===∠∠∠,如果添加 一个条件,即可推出该四边形是正方形,那么这个条件可以是( ).A .90D =∠ B .AB CD = C .AD BC = D .BC CD =【答案】D31.(2010 四川自贡)边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB ′C ′D ′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )。
(免费)2010年部分省市中考数学试题分类汇编 整式与因式分解(含答案)

2010年部分省市中考数学试题分类汇编整式与因式分解12. (2010年浙江省东阳县)因式分解:x 3-x=___ ____ 【关键词】因式分解 【答案】x(x+1)(x-1)12. (2010年浙江省东阳县)因式分解:x 3-x=___ ____ 【关键词】因式分解 【答案】x(x+1)(x-1)1、(2010年宁波市)下列运算正确的是( )A 、22x x x =⋅B 、22)(xy xy =C 、632)(x x =D 、422x x x =+ 【关键词】整式运算 【答案】C2(2010年宁波市)、若3=+y x ,1=xy ,则=+22y x ___________。
【关键词】完全平方公式 【答案】71、(2010年宁波市)下列运算正确的是( )A 、22x x x =⋅B 、22)(xy xy =C 、632)(x x =D 、422x x x =+ 【关键词】整式运算 【答案】C2(2010年宁波市)、若3=+y x ,1=xy ,则=+22yx ___________。
【关键词】完全平方公式 【答案】711.(2010浙江省喜嘉兴市)用代数式表示“a 、b 两数的平方和”,结果为_______. 【关键词】代数式 【答案】22b a + 14.(2010浙江省喜嘉兴市)因式分解:2mx 2-4mx +2m = . 【关键词】提公因式、完全平方公式 【答案】2)1(2-x m17、(2010浙江省喜嘉兴市)计算:a (b +c )-ab 【关键词】单项式与多项式的积、整式加减 【答案】ab c b a -+)(ab ac ab -+=ac =.7(2010年浙江省金华). 如果33-=-b a ,那么代数式b a 35+-的值是( ▲ ) A .0 B .2 C .5 D .8 【关键词】整体带入、代数式 【答案】D11(2010年浙江省金华). 分解因式=-92x . 【关键词】分解因式 【答案】(x -3)(x +3);4.(2010年浙江台州市)下列运算正确的是(▲)A .22a a a =⋅B .33)(ab ab =C .632)(a a =D .5210a a a =÷ 【关键词】幂的有关运算 【答案】C12.(2010年浙江台州市)因式分解:162-x = ▲ . 【关键词】因式分解、平方差公式 【答案】)4)(4(-+x x9. (2010年益阳市)若622=-n m ,且3=-n m ,则=+n m . 【关键词】平方差 【答案】215.(2010年益阳市)已知31=-x ,求代数式4)1(4)1(2++-+x x 的值.【关键词】完全平方公式、整式加减【答案】15.解法一:原式=2)21(-+x =2)1(-x 原式= 2)3( =3 解法二:由31=-x 得13+=x化简原式=444122+--++x x x=122+-x x=1)13(2)13(2++-+=12321323+--++ =32. (2010江西) 计算 -(-3a)2的结果是( )A .-6a 2B . -9a 2C . 6a 2D . 9a 2 【关键词】有关幂的运算 【答案】B9.(2010江西) 因式分解:=-822a . 【关键词】因式分解、平方差公式 【答案】)2)(2(2-+a a(2010年广东省广州市)下列运算正确的是( )A .-3(x -1)=-3x -1B .-3(x -1)=-3x +1C .-3(x -1)=-3x -3D .-3(x -1)=-3x +3【关键词】去括号 【答案】D(2010年广东省广州市)因式分解:3ab 2+a 2b =_______.【关键词】提公因式法因式分解【答案】ab (3b +a )(2010年四川省眉山)下列运算中正确的是A .2325a a a +=B .22(2)(2)4a b a b a b +-=-C .23622a a a ⋅=D .222(2)4a b a b +=+ 【关键词】幂的运算 【答案】B(2010年四川省眉山)把代数式269mx mx m -+分解因式,下列结果中正确的是A .2(3)m x +B .(3)(3)m x x +-C .2(4)m x -D .2(3)m x - 【关键词】因式分解 【答案】D第3章 整式与因式分解2.(2010年重庆)计算232x x ⋅的结果是( )A .x 2B .52x C .62x D .5x 【答案】B2.(2010年重庆)计算232x x ⋅的结果是( )A .x 2B .52x C .62x D .5x 【答案】B(2010年广东省广州市)下列运算正确的是( )A .-3(x -1)=-3x -1B .-3(x -1)=-3x +1C .-3(x -1)=-3x -3D .-3(x -1)=-3x +3 【关键词】去括号 【答案】D(2010年广东省广州市)因式分解:3ab 2+a 2b =_______.【关键词】提公因式法因式分解【答案】ab (3b +a )(2010年四川省眉山)下列运算中正确的是A .2325a a a +=B .22(2)(2)4a b a b a b +-=-C .23622a a a ⋅=D .222(2)4a b a b +=+ 【关键词】幂的运算 【答案】B(2010年四川省眉山)把代数式269mx mx m -+分解因式,下列结果中正确的是A .2(3)m x +B .(3)(3)m x x +-C .2(4)m x -D .2(3)m x - 【关键词】因式分解 【答案】D12.(2010年安徽省芜湖市)因式分解:9x 2-y 2-4y -4=__________. 【关键词】分解因式、完全平方公式、平方差公式 【答案】)23)(23(--++y x y x12. (2010年浙江省东阳县)因式分解:x 3-x=___ ____ 【关键词】因式分解 【答案】x(x+1)(x-1)(2010年山东省济宁市)把代数式 322363x x y xy -+分解因式,结果正确的是A .(3)(3)x x y x y +-B .223(2)x x xy y -+ C .2(3)x x y - D .23()x x y - 【关键词】先运用提公因式法再运用完全平方公式 【答案】D12.(2010年山东省济宁市)若代数式26x x b -+可化为2()1x a --,则b a -的值是 .【关键词】配方法的应用 【答案】5(2010年山东省济宁市)把代数式 322363x x y xy -+分解因式,结果正确的是A .(3)(3)x x y x y +-B .223(2)x x xy y -+C .2(3)x x y -D .23()x x y - 【关键词】先运用提公因式法再运用完全平方公式 【答案】D12.(2010年山东省济宁市)若代数式26x x b -+可化为2()1x a --,则b a -的值是 .【关键词】配方法的应用 【答案】5(2010年山东省济宁市)把代数式 322363x x y xy -+分解因式,结果正确的是A .(3)(3)x x y x y +-B .223(2)x x xy y -+C .2(3)x x y -D .23()x x y - 【关键词】先运用提公因式法再运用完全平方公式 【答案】D12.(2010年山东省济宁市)若代数式26x x b -+可化为2()1x a --,则b a -的值是 .【关键词】配方法的应用 【答案】52.(2010重庆市)计算2x 3·x 2的结果是()A .2xB .2x 5C .2x 6D .x 5解析:由单项式乘法法则知, 2x 3·x 2=2x 5 . 答案:B.2.(2010重庆市)计算2x 3·x 2的结果是()A .2xB .2x 5C .2x 6D .x5解析:由单项式乘法法则知, 2x 3·x 2=2x 5 .答案:B. (2010日照市)10.由m (a +b +c )=ma +mb +mc ,可得:(a +b )(a 2-ab +b 2)=a 3-a 2b +ab 2+a 2b-ab 2+b 3=a 3+b 3,即(a +b )(a 2-ab +b 2)=a 3+b 3. ………………………①我们把等式①叫做多项式乘法的立方公式。
2010年中考数学试题分类(精选版):多边形与平行四边形

2010年中考数学试题分类汇编多边形与平行四边形一、选择题1. (2010年四川眉山市).如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ABC 的度数为( )A .90°B .60°C .45°D .30°【答案】C2.(2010福建龙岩)下列图形中,单独选用一种图形不能进行平面镶嵌的图形是( )A. 正三角形B. 正方形C. 正五边形D. 正六边形 【答案】C3.(2010年北京顺义)若一个正多边形的一个内角是120°,则这个正多边形的边数是A .9B .8C .6D .4 【答案】C4. (2010年台湾省) 图(十)为一个平行四边形ABCD ,其中H 、G 两点分别在BC 、 CD 上,AH ⊥BC ,AG ⊥CD ,且AH 、AC 、AG 将∠BAD 分成 ∠1、∠2、∠3、∠4四个角。
若AH =5,AG =6,则下列关系何者 正确? (A) ∠1=∠2 (B) ∠3=∠4 (C) BH =GD (D) HC =CG 【关键词】平行四边形【答案】A二、填空题1.(2010年福建福州)14.如图,在□ABCD 中,对角线AC 、BD 相交于点O ,若AC=14,BD=8,AB=10,则△OAB 的周长为 . 【答案】212.(2010年福建宁德)如图,在□ABCD 中,AE =EB ,AF =2, 则FC 等于_____. 【答案43.(2010年山东滨州)如图,平行四边形ABCD 中, ∠ABC=60°,E 、F 分别在CD、BC 的延长线上,AE ∥BD,EF ⊥BC,DF=2,则EF 的长为ABC EFAB CD G H 12 3 4 图(十)FEDC BA【答案】4.(2010年福建宁德)如图,在△ABC 中,点E 、F 分别为AB 、AC 的中点.若EF 的长为2,则BC 的长为___________. 【答案】4三、解答题1. (2010年福建晋江)如图,请在下列四个关系中,选出两个恰...当.的关系作为条件,推出四边形ABCD 是平行四边形,并予以证明.(写出一种即可)关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B .已知:在四边形ABCD 中, , ; 求证:四边形ABCD 是平行四边形.解:已知:①③,①④,②④,③④均可,其余均不可以. (解法一)已知:在四边形ABCD 中,①AD ∥BC ,③C A ∠=∠.……………………(2分) 求证:四边形ABCD 是平行四边形. 证明:∵ AD ∥BC∴︒=∠+∠180B A ,︒=∠+∠180D C ………………………………………(5分) ∵C A ∠=∠,∴D B ∠=∠∴四边形ABCD 是平行四边形…………………………………………………(8分) (解法二)已知:在四边形ABCD 中,①AD ∥BC ,④︒=∠+∠180C B .………………(2分)AB CD第4题图 F A E BC D求证:四边形ABCD 是平行四边形.证明:∵︒=∠+∠180C B ,∴AB ∥CD ……………………………………………………………………(5分) 又∵AD ∥BC∴四边形ABCD 是平行四边形.…………………………………………………(8分) (解法三)已知:在四边形ABCD 中,②CD AB =,④︒=∠+∠180C B .………………(2分) 求证:四边形ABCD 是平行四边形.证明:∵︒=∠+∠180C B ,∴AB ∥CD ……………………………………………………………………(5分) 又∵CD AB =∴四边形ABCD 是平行四边形.…………………………………………………(8分) (解法四)已知:在四边形ABCD 中,③C A ∠=∠,④︒=∠+∠180C B .………………(2分) 求证:四边形ABCD 是平行四边形.证明:∵︒=∠+∠180C B ,∴AB ∥CD ……………………………………………………………………(4分) ∴︒=∠+∠180D A ………………………………………………………………(6分) 又∵C A ∠=∠ ∴D B ∠=∠∴四边形ABCD 是平行四边形.…………………………………………………(8分)2. (2010年浙江衢州)已知:如图,E ,F 分别是ABCD 的边AD ,BC 的中点.求证:AF =CE .证明:方法1:∵ 四边形ABCD 是平行四边形,且E ,F 分别是AD ,BC 的中点,∴ AE = CF . ……2分又 ∵ 四边形ABCD 是平行四边形,∴ AD ∥BC ,即AE ∥CF .∴ 四边形AFCE 是平行四边形. ……3分 ∴ AF =CE .……1分方法2:∵ 四边形ABCD 是平行四边形,且E ,F 分别是AD ,BC 的中点, ∴ BF =DE . ……2分又 ∵ 四边形ABCD 是平行四边形, ∴ ∠B =∠D ,AB =CD .A D E FB C ADEFBC(第19题)∴ △ABF ≌△CDE .……3分 ∴ AF =CE . ……1分3.(2010浙江省嘉兴)如图,在□ABCD 中,已知点E 在AB 上,点F 在CD 上且AE =CF .(1)求证:DE =BF ;(2)连结BD ,并写出图中所有的全等三角形.(不要求证明) 【关键词】平行四边形的判定与性质、全等三角形 【答案】(1)在□ABCD 中,AB //CD ,AB =CD .∵AE =CF ,∴BE =DF ,且BE //DF . ∴四边形BFDE 是平行四边形. ∴BF DE . …5分 (2)连结BD ,如图, 图中有三对全等三角形: △ADE ≌△CBF , △BDE ≌△DBF ,△ABD ≌△CDB . …3分4. (2010年山东滨州)如图,四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点.(1)请判断四边形EFGH 的形状?并说明为什么.(2)若使四边形EFGH 为正方形,那么四边形ABCD 的对角线应具有怎样的性质?解:(1) 四边形EFGH 为平行四边形,连接AC ∵E 、F 分别是AB 、BC 的中点,EF ∥AC ,EF=21AC. 同理HG ∥AC ,HG=21AC. ∴EF ∥HG, EF=HG.∴四边形EFGH 是平行四边形(2) 四边形ABCD 的对角线垂直且相等.5.(2010年江苏泰州)如图,四边形ABCD 是矩形,∠EDC =∠CAB ,∠DEC =90°.(1)求证:AC ∥DE ;(2)过点B 作BF ⊥AC 于点F ,连结EF ,试判断四边形BCEF 的形状,并说明理由.BE(第3题)AB CD【答案】⑴在矩形ABCD 中,AC ∥DE ,∴∠DCA =∠CAB ,∵∠EDC =∠CAB , ∴∠DCA =∠EDC ,∴AC ∥DE ; ⑵四边形BCEF 是平行四边形.理由:由∠DEC =90°,BF ⊥AC ,可得∠AFB =∠DEC =90°, 又∠EDC =∠CAB ,AB=CD ,∴△DEC ≌△AFB ,∴DE =AF ,由⑴得AC ∥DE , ∴四边形AFED 是平行四边形,∴AD ∥EF 且AD =EF , ∵在矩形ABCD 中,AD ∥BC 且AD =BC , ∴EF ∥BC 且EF =BC ,∴四边形BCEF 是平行四边形.【关键词】矩形的性质 平行四边形的判定 全等三角形的判定6.(2010年福建晋江)如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形ABCD 是平行四边形,并予以证明.(写出一种即可)关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B . 已知:在四边形ABCD 中, , ; 求证:四边形ABCD 是. 【关键词】平行四边形的判定【答案】已知:①③,①④,②④,③④均可,其余均不可以. (解法一)已知:在四边形ABCD 中,①AD ∥BC ,③C A ∠=∠.……………………(2分) 求证:四边形ABCD 是平行四边形. 证明:∵ AD ∥BC∴︒=∠+∠180B A ,︒=∠+∠180D C ∵C A ∠=∠,∴D B ∠=∠ ∴四边形ABCD 是平行四边形 (解法二)已知:在四边形ABCD 中,①AD ∥BC ,④︒=∠+∠180C B . 求证:四边形ABCD 是平行四边形.证明:∵︒=∠+∠180C B , ∴AB ∥CD 又∵AD ∥BC∴四边形ABCD 是平行四边形. (解法三)已知:在四边形ABCD 中,②CD AB =,④︒=∠+∠180C B . 求证:四边形ABCD 是平行四边形. 证明:∵︒=∠+∠180C B , ∴AB ∥CD 又 ∵CD AB =∴四边形ABCD 是平行四边形. (解法四)已知:在四边形ABCD 中,③C A ∠=∠,④︒=∠+∠180C B . 求证:四边形ABCD 是平行四边形.证明:∵︒=∠+∠180C B , ∴AB ∥CD∴︒=∠+∠180D A 又∵C A ∠=∠ ∴D B ∠=∠∴四边形ABCD 是平行四边形. 7.(2010年贵州毕节地区)如图,已知: ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC ∠的平分线BG 交CE 于F ,交AD 于G .求证:AE DG =.【关键词】平行四边形、角平分线【答案】证明:∵ 四边形ABCD 是平行四边形(已知),AD BC ∴∥,AB CD =(平行四边形的对边平行,对边相等)GBC BGA ∴∠=∠,BCE CED ∠=∠(两直线平行,内错角相等) 又∵ BG 平分ABC ∠,CE 平分BCD ∠(已知)ABG GBC ∴∠=∠,BCE ECD ∠=∠(角平分线定义) ABG GBA ∴∠=∠,ECD CED ∠=∠.AB AG ∴=,CE DE =(在同一个三角形中,等角对等边) AG DE ∴=AG EG DE EG ∴-=-,即AE DG =. 分7.(2010年重庆市潼南县)如图,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG ,点E 、F 分别在AG 上,连接BE 、DF ,∠1=∠2 , ∠3=∠4. ABC E FG【关键词】全等三角形【答案】解:(1)∵四边形ABCD 是正方形∴AB=AD在△ABE 和△DAF 中⎪⎩⎪⎨⎧∠=∠=∠=∠3412DA AB∴△ABE ≌△DAF -----------------------4分(2)∵四边形ABCD 是正方形∴∠1+∠4=900∵∠3=∠4∴∠1+∠3=900∴∠AFD=900----------------------------6分 在正方形ABCD 中, AD ∥BC∴∠1=∠AGB=300在Rt △ADF 中,∠AFD=900AD=2∴AF=3 DF =1----------------------------------------8分 由(1)得△ABE ≌△ADF ∴AE=DF=1∴EF=AF-AE=13- -----------------------------------------10分8.(2010年江苏宿迁)如图,在□ABCD 中,点E 、F 是对角线AC 上两点,且AE =CF .求证:∠EBF =∠FDE .【关键词】平行四边形 【答案】证明:连接BD 交AC 于O 点 …… 1分∵四边形ABCD 是平行四边形∴OA=OC ,OB=OD ………………3分 又∵AE=CF ∴OE=OF∴四边形BEDF 是平行四边形 …… 6分 ∴∠EBF=∠EDF …………… 8分9.(2010年浙江宁波)如图1,有一张菱形纸片ABCD ,8=AC ,6=BD .(1)请沿着AC 剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图2中用实数画出你所拼成的平行四边形;若沿着BD 剪开, 请在图3中用实线画出拼成的平行四边形;并直接写出这两个平行四边 形的周长。
2010年中考数学真题分类汇编(150套)专题十七·反比例函数3
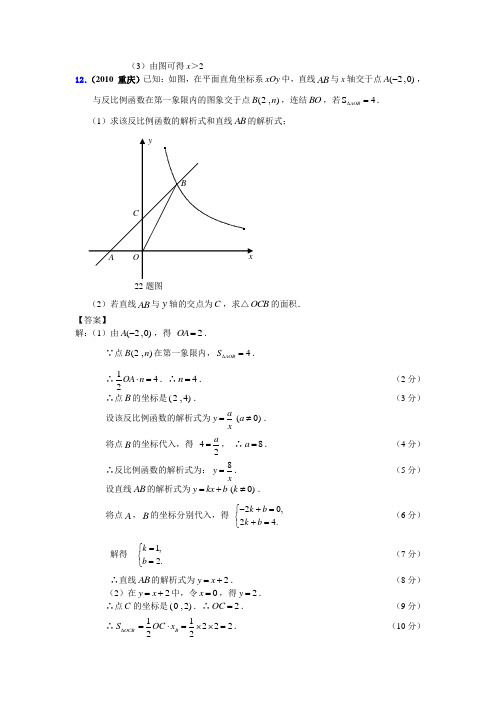
(3)由图可得x >2 12.(2010 重庆)已知:如图,在平面直角坐标系xOy 中,直线AB 与x 轴交于点(2,0)A -,与反比例函数在第一象限内的图象交于点(2,)B n ,连结BO ,若S 4AOB ∆=. (1)求该反比例函数的解析式和直线AB 的解析式;(2)若直线AB 与y 轴的交点为C ,求△OCB 的面积. 【答案】 解:(1)由(2,0)A -,得 2OA =.∵点(2,)B n 在第一象限内,4AOB S ∆=.∴142OA n ⋅=.∴4n =. ··············································································· (2分) ∴点B 的坐标是(2,4). ·················································································· (3分) 设该反比例函数的解析式为(0)ay a x=≠. 将点B 的坐标代入,得 42a=, ∴8a =. ··················································· (4分) ∴反比例函数的解析式为:8y x=. ································································ (5分)设直线AB 的解析式为(0)y kx b k =+≠.将点A ,B 的坐标分别代入,得 20,2 4.k b k b -+=⎧⎨+=⎩ ·············································· (6分)解得 1,2.k b =⎧⎨=⎩·································································································· (7分)∴直线AB 的解析式为2y x =+. ·································································· (8分)(2)在2y x =+中,令0x =,得2y =. ∴点C 的坐标是(0,2).∴2OC =. ····························································· (9分)∴OCB S ∆1122222B OC x =⋅=⨯⨯=. ······························································ (10分)22题图13.(2010重庆市潼南县)(10分)如图, 已知在平面直角坐标系xOy 中,一次函数b kx y +=(k ≠0)的图象与反比例函数xmy =(m ≠0)的图象相交于A 、B 两点,且点B 的纵坐标为21-,过点A 作AC ⊥x 轴于点C , AC =1,OC =2. 求:(1)求反比例函数的解析式;(2)求一次函数的解析式.【答案】解:(1)∵A C ⊥x 轴 AC=1 OC=2∴点A 的坐标为(2,1)------------------------------1分∵反比例函数xmy =的图像经过点A (2,1) ∴ m =2------------------------------------------4分∴反比例函数的解析式为xy 2=---------------------5分 (2)由(1)知,反比例函数的解析式为xy 2=∵反比例函数x y 2=的图像经过点B 且点B 的纵坐标为-21∴点B 的坐标为(-4,-21)---------------------------6分∵一次函数y =kx +b 的图象经过点A (2,1)点B (-4,-21)∴⎪⎩⎪⎨⎧-=+-=+21412b k b k解得:k =41 b =21----------------------------------9分 ∴一次函数的解析式为2141+=x y ----------------------10分14.(2010江苏宿迁)(本题满分10分)如图,已知一次函数2-=x y 与反比例函数xy 3=的图象交于A 、B 两点.(1)求A 、B 两点的坐标;(2)观察图象,可知一次函数值小于反比例函数值的x 的取值范围是 ▲ .(把答案题图23直接写在答题卡相应位置上)【答案】解:(1)由题意得:⎪⎩⎪⎨⎧=-=x y x y 32 ………………………………………2分 解之得: ⎩⎨⎧==1311y x 或⎩⎨⎧-=-=3122y x ………………………………………4分∴A 、B 两点坐标分别为A ()1,3、B ()3,1-- ……………………6分(2)x 的取值范围是:1-<x 或30<<x ……………………………10分15.(2010浙江金华)(本题10分)已知点P 的坐标为(m ,0),在x 轴上存在点Q (不与P 点重合),以PQ 为边作正方形PQMN ,使点M 落在反比例函数y = 2x-的图像上.小明对上述问题进行了探究,发现不论m 取何值,符合上述条件的正方形只有..两个,且一个正方形的顶点M 在第四象限,另一个正方形的顶点M 1在第二象限.(1)如图所示,若反比例函数解析式为y = 2x-,P 点坐标为(1, 0),图中已画出一符合(第23题条件的一个正方形PQMN ,请你在图中画出符合条件的另一个正方形PQ 1M 1N 1,并写出点M 1的坐标; M 1的坐标是 ▲(2) 请你通过改变P 点坐标,对直线M 1 M 的解析式y ﹦kx +b 进行探究可得 k ﹦ ▲ , 若点P 的坐标为(m ,0)时,则b ﹦ ▲ ;(3) 依据(2)的规律,如果点P 的坐标为(6,0),请你求出点M 1和点M 的坐标. 【答案】解:(1)如图;M 1 的坐标为(-1,2)(2)1-=k ,m b =(3)由(2)知,直线M 1 M 的解析式为6+-=x y 则M (x ,y )满足2)6(-=+-⋅x x 解得1131+=x ,1132-=x ∴ 1131-=y ,1132+=y∴M 1,M 的坐标分别为(113-,113+),(113+,113-). 16.(2010 山东济南)如图,已知直线12y x =与双曲线(0)ky k x=>交于A ,B 两点,且点A 的横坐标为4.(1)求k 的值; (2)若双曲线(0)ky k x=>上一点C 的纵坐标为8,求△AOC 的面积; (3)过原点O 的另一条直线l 交双曲线(0)ky k x=>于P ,Q 两点(P 点在第一象限),若由点A ,B ,P ,Q 为顶点组成的四边形面积为24,求点P 的坐标.x【答案】(1)∵点A横坐标为4 ,∴当x = 4时,y = 2∴点A的坐标为(4,2 )…………2’∵点A是直线12y x=与双曲线8yx=(k>0)的交点,∴k = 4×2 = 8 ………….3’(2)解法一:∵点C在双曲线上y = 8时,x = 1∴点C的坐标为(1,8)………..4’过点A、C分别做x轴、y轴的垂线,垂足为M、N,得矩形DMONS矩形ONDM= 32 ,S△ONC = 4 ,S△CDA = 9,S△OAM = 4S△AOC= S矩形ONDM-S△ONC-S△CDA-S△OAM= 32-4-9-4 = 15 ………..6’解法二:过点C、A分别做x轴的垂线,垂足为E、F,∵点C在双曲线8yx=上,当y = 8时,x = 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1.(2010安徽芜湖)如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE
⊥BC,DF⊥BC,垂足分别为E、F,AD=4,BC=8,则AE+EF等于()
A.9 B.10 C.11 D.
12
【答案】B
2.(2010山东日照)已知等腰梯形的底角为45o,高为2,上底为2,则其面积为
(A)2 (B)6 (C)8 (D)12
【答案】C
3.(2010山东烟台)如图,小区的一角有一块形状为等梯形的空地,为了美化小区,社区
居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是
A、等腰梯形
B、矩形
C、菱形
D、正方形
【答案】C
4.(2010山东威海)如图,在梯形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,垂足
为O.若CD=3,AB=5,则AC的长为
O A B
B.4
D.25 A.42 C.33
【答案】A
BC=10,5.(2010台湾)如图(十五)梯形ABCD的两底长为AD=6,中线为EF,且?B=90?,
若P为AB上的一点,且PE将梯形ABCD分成面积相同的两区域,则△EFP与梯形ABCD的面积比为何?
(A) 1:6 (B) 1:10 (C) 1:12 (D) 1:16 。
- 1 -。
