第二十届华罗庚金杯少年数学邀请赛初赛试卷A卷(小学中年级组)
第二十二届华罗庚金杯少年数学邀请赛初赛试卷

第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学中年级组)一、选择题(每小题10分)1、两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由()拼成。
A、两个锐角三角形B、两个直角三角形C、两个钝角三角形D、一个锐角三角形和一个钝角三角形2、从1到10这10个整数中,至少取()个数,才能保证其中有两个数的和等于10.A、4B、5C、6D、73、小明行李箱的密码是由两个数字8与5构成的三位数,某次旅行,小明忘记了密码,他最少要试()次,才能确保打开行李箱。
A、9B、8C、7D、64猎豹跑一步长为2米,狐狸跑一步为1米,猎豹跑2步的时间狐狸跑3步,猎豹距离狐狸30米,则猎豹跑动()米可以追上狐狸。
A、90B、105、C、120D、1355、图中的八边型是将大长方形纸片剪去一个小长方形得到的,则至少需要知道()条线段的长度,才可以计算出这个八边型的周长。
A、4B、3C、5D106、一个数串219,从第4个数开始,每个数字都是前面3个数字和的个位数,下面有4个四位数,1113、2226、2125、2215,其中共有()个不出现在该数串中。
A、1B、2C、3D、4二、填空题(每题10分,共40分)7、计算1000-257-84-43-16=()8、已知动车的时速是普快的两倍,动车的时速提高25%即达到高铁的时速,高铁与普快的平均时速比特快快15千米/小时,动车与普快的平均时速比特快慢10千米/小时,则高铁和普快列车的时速分别是()千米/小时和()千米/小时。
9、《火星救援》中,马克不幸没有跟上其他5名航天员飞回地球,独自留在了火星,马克必须想办法生存,等待救援,马克的居住舱内留有每名航天员5天的食品和50千克的非饮用水,还有一个足够大的菜园,马克计划用来种植土豆,30天后每平方米可以收获2.5千克,但是需要浇灌4千克的水。
马克每天需要吃1.875千克土豆,才可以维持生存,则食品和土豆可供马克最多可以支撑()天。
第二十届华罗庚金杯少年数学邀请赛决赛试题A

第二十届华罗庚金杯少年数学邀请赛决赛试题A答案及评分标准(北京小学中年级组)一、填空(每题10 分, 共80分)所以共有:6×(2+12)=84(本)(5分)答:这批作业有84本。
解(3):设:共改了x小时.6x=6×2+8(x―2―3)(5分)x=14 (5分)6×14=84 (本) (5分)答:这批作业有84本。
解(4):每小时改6本,改1本需 60÷6=10 (分/本) (5分) 每小时改8本,改1本需 60÷6=7.5(分/本) (5分) 180÷(10-7.5)=72(本)72+12=84(本) (5分) 答:这批作业有84本。
注:答案正确,解题过程错误(或只有简单算式,没有说明),只给答案分5分.2. 用五种不同的颜色涂正方体的六个面. 如果相邻的两个面不能涂同种颜色, 则共有多少种不同的涂色方法?(将正方体任意翻转后仍然不同的涂色方法才被认为是不同的)解(1):由题意,涂有相同颜色的2个面相对,总可以将相同颜色的2个面置于上下底面,有5种涂法.(3分)固定1种涂法,即上下底的颜色后,总可以在保持上下底的颜色条件下,通过转动将余下4种颜色中1种固定为正面的涂色. (4分) 余下3种颜色选1种涂后面,共有3种涂法,(3分) 左右侧面经旋转后相同(3分)所以,共有5×3=15(种)(5分)答:共有15种涂法.解(2):枚举法, 正确画出15种涂色方法. (15分)解(3):只用3种颜色的35C =10 (种) (5分) 只用4种颜色的25C ×23C =30 (种) (5分) 用5种颜色的15C ×13C =30 (种)10+30+15=15(种) (5分) 答:共有55种涂法.注:答案正确,解题过程错误(或只有简单算式,没有说明),只给答案分5分.3.如右图所示, 有一个圆圈填了数字1. 请在空白圆圈内填上2, 3, 4, 5, 6中的一个数字, 要求无重复数字, 且相邻圆圈内的数字的差至少为2. 问共有几种不同的填法?解:如图,2只能填在c 或d 中 (2分) (1)如c=2,则a=3,由于5不能和4、6相邻,所以b =5。
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
第二十届华罗庚金杯少年数学邀请赛决赛试题(小学中年级组)

第二十届华罗庚金杯少年数学邀请赛 决赛试题(小学中年级组) (时间:2015年4月11日14:00~15:30) 一、填空题(每小题 10分, 共80分) 1、9.198.287.37 6.46 5.55 4.64 3.73 2.82 1.91________++++++++=。
2、两个个位数字不是0的自然数的积是40000,那么其中较大的数是_________。
3、“九指”先生是一个无可救药的赌徒,他每次都拿出口袋里一半的钱作为赌注。
我们只知道他输赢各10次,那么最后他_________了。
(填“赢”或“输”) 4、机场有一个24时制的电子钟,当棉花糖先生到达机场时,钟表显示为09:39,而他要乘的航班预定09:57起飞。
因天气原因,航班延误,凑巧的是航班实际起飞时间和前两个时间的数字和都为21(0939095721+++=+++=)。
那么棉花糖先生至少等了__________分钟。
5、如图,3个中国人,2个美国人,1个俄罗斯人,1个德国人站成一排。
其中2个美国人站在一起,且不与中国人相邻;俄罗斯人两边都是中国人;E 不是俄罗斯人,G 不是中国人,那么德国人是___________(填字母)。
A B C D E F G 6、下列算式中,不同的字母代表不同的数字,相同的字母代表相同的数字。
71000A A A AB AB AB A BC A A A C C C ⨯⨯+⨯⨯==⨯⨯⨯+⨯⨯ 那么三位数ABC =____________。
7、如右图,圆周上有36个等分点:1236,,,A A A 。
从1A 点开始,顺时针每隔1个点连一条线段,直至回到1A 点结束构成图案1;顺时针每隔2个点连一条线段,直至回到1A 点结束构成图案2;按此规律操作下去,(武汉童老师)可得到很多不一样的图案。
其中可以经过圆周上所有36个点的称为“完美图”。
那么图案1至图案10中,有________个“完美图”。
2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组a卷)

2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组A卷)一、填空题(每小题10分,共80分)1.(10分)4584 1.3751050.91919⨯+⨯.2.(10分)如图是用六个正方形,六个三角形、一个正六边形组成的图案,正方形边长都是2cm,这个图案的周长是cm.3.(10分)某项工程需要100天完成,开始由10个人用30天完成了全部工程的15,随后再增加10个人来完成这项工程,那么能提前天完成任务.4.(10分)王教授早上8点到达车站候车,登上列车时,站台上的时钟的时针和分针恰好左右对称.列车8点35分出发,下午2点15分到达终点站.当王教授走下列车时,站台上时钟的时针和分针恰好上下对称,走出车站时恰好3点整.那么王教授在列车上的时间共计分钟.5.(10分)由四个非零数字组成的没有重复数字的所有四位数的和为73326,则这些四位数中最大的是.6.(10分)如图所示,从长、宽、高分别为15cm,5cm,4cm的长方体中切割走一块长、宽、高分别为ycm,5cm,xcm的长方体(x,y为整数),余下部分的体积为3120cm,那么x y+=.7.(10分)一次数学竞赛有A,B,C三题,参赛的39个人中,每人至少答对了一道题.在答对A的人中,只答对A的比还答对其它题目的多5人;在没答对A的人中,答对B的是答对C的2倍;又知道只答对A的等于只答对B的与只答对C的人数之和.那么答对A的最多有人.8.(10分)甲,乙进行乒乓球比赛,三局两胜制.每局比赛中,先得11分且对方少于10分者胜;10平多得2分者胜.甲、乙二人得分总和都是30分,在不计比分先后顺序时,三局的比分共有种情况.二、解答下列各题(每小题10分,共40分,要求写出简要过程)9.(10分)两个自然数之和为667,它们的最小公倍数除以最大公约数所得的商等于120.求这两个数.10.(10分)酒店有100个标准间,房价为400元/天,但入住率只有50%.若每降低20元的房价,则能增加5间入住.求合适的房价,使酒店收到的房费最高.11.(10分)如图,长方形ABCD的面积是256cm.3=.请你回答:三DF cmBE cm=,2角形AEF的面积是多少?12.(10分)当N取遍1,2,3,⋯,2015中所有的数时,形如3+的数中能够被7整3n n除的有多少个?三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.(15分)如图所示,ABCD是平行四边形,AM MB=,DN CN=,BE EF FC==,四边形EFGH的面积是1,求平行四边形ABCD的面积.14.(15分)“虚有其表”,“表里如一”,“一见如故”,“故弄玄虚”四个成语中每个汉字代表11个非零连续自然数中的一个,相同的汉字代表相同的数,不同的汉字代表不同的数,且“表”>“一”>“故”>“如”>“虚”,且各个成语中四个汉字所代表的数的和都是21.则“弄”可以代表的数最大是多少?2015年第二十届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组A卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)4584 1.3751050.91919⨯+⨯.【解答】解:4584 1.3751050.91919⨯+⨯.160011200091981910=⨯+⨯220018001919=+400019=1021019=故答案为:10 210192.(10分)如图是用六个正方形,六个三角形、一个正六边形组成的图案,正方形边长都是2cm,这个图案的周长是24cm.【解答】解:2626⨯+⨯1212=+24()cm=答:这个图案的周长是24cm.故答案为:24.3.(10分)某项工程需要100天完成,开始由10个人用30天完成了全部工程的15,随后再增加10个人来完成这项工程,那么能提前10天完成任务.【解答】解:1110030(1)[(1030)(1010)]55---÷÷⨯⨯+ 4170575=-÷ 7060=-10=(天)答:能提前10天完成任务.故答案为:10.4.(10分)王教授早上8点到达车站候车,登上列车时,站台上的时钟的时针和分针恰好左右对称.列车8点35分出发,下午2点15分到达终点站.当王教授走下列车时,站台上时钟的时针和分针恰好上下对称,走出车站时恰好3点整.那么王教授在列车上的时间共计 360 分钟.【解答】解:8时整时分针与时针的夹角是120︒,240120(60.5)13÷+=(分),王教授登上车的时间是:8时24013分; 下午2时15分时,分钟与时针的夹角是156(600.515)22.5⨯-+⨯=(度),4522.5(60.5)13÷+=(分),王教授下车的时间是:2时15分4513+分=下午2时24013分; 下午下午2时24013分化成24计时法是14时24013分 14时24013分8-时24013分6=小时 6小时360=分钟.故答案为:360.5.(10分)由四个非零数字组成的没有重复数字的所有四位数的和为73326,则这些四位数中最大的是 5321 .【解答】解:设四个数字分别为a 、b 、c 、d .根据题意可得以a 开头的组合有:abcd ,abdc ,acbd ,acdb ,adbc ,6adcb 个,则这六个四位数分别是:1000100101a b c d ⨯+⨯+⨯+⨯,1000100110a b c d ⨯+⨯+⨯+⨯,1000110100a b c d ⋯⨯+⨯+⨯+⨯,这6个数的和是6000222222222a b c d +++++;同理,以b 开头的6个四位数的和是2226000222222a b c d +++;以c 开头的6个四位数的和是2222226000222a b c d +++;以d 开头的6个四位数的和是2222222226000a b c d +++;则6666()73326a b c d +++=,即11a b c d +++=,分析可得a 、b 、c 、d 是1、2、3、5中的一个数字,所以组成的四位数中最大四位数是5321.故答案为:5321.6.(10分)如图所示,从长、宽、高分别为15cm ,5cm ,4cm 的长方体中切割走一块长、宽、高分别为ycm ,5cm ,xcm 的长方体(x ,y 为整数),余下部分的体积为3120cm ,那么x y += 15cm .【解答】解:1554120⨯⨯-300120=-3180()cm =则5180xy =,即36xy =,因为x ,y 为整数,且04x <<,015y <<,所以x 为3cm ,y 为12cm ,15x y cm +=.故答案为:15.7.(10分)一次数学竞赛有A ,B ,C 三题,参赛的39个人中,每人至少答对了一道题.在答对A 的人中,只答对A 的比还答对其它题目的多5人;在没答对A 的人中,答对B 的是答对C 的2倍;又知道只答对A 的等于只答对B 的与只答对C 的人数之和.那么答对A 的最多有 23 人.【解答】解:只答对A 的人数是3b a +,答对A 还答对其他题目的人数是35b a +-,所以有:3353239b a b a b a +++-++=,化简得:4944a b +=,因为a 、b 都为自然数,所以当2a =时,4b =;当11a =时,0b =,即24a b =⎧⎨=⎩或110a b =⎧⎨=⎩答对A 的人共335625b a b a b a +++-=+-,把a 、b 的最大值代入625b a +-中,最大值是:64225⨯+⨯-2445=+-23=(人)答:答对A 的人最多有23人.故答案为:23.8.(10分)甲,乙进行乒乓球比赛,三局两胜制.每局比赛中,先得11分且对方少于10分者胜;10平多得2分者胜.甲、乙二人得分总和都是30分,在不计比分先后顺序时,三局的比分共有 8 种情况.【解答】解:甲、乙二人得分总和都是30分30311<⨯三局中其中一个人胜了两局,所以至少有两个分数不小于11,甲得分总和是:30:3011910=++乙对应的得分是:3071112:=++对应的比分是11:79:1110:12⎧⎪⎨⎪⎩,之后7、9依次减1,10和12依次加1:11:68;1111:13⎧⎪⎨⎪⎩、11:57:1112:14⎧⎪⎨⎪⎩、11:46:1113:15⎧⎪⎨⎪⎩、11:35:1114:16⎧⎪⎨⎪⎩、11:24:1115:17⎧⎪⎨⎪⎩、11:13:1116:18⎧⎪⎨⎪⎩、11:02:1117:19⎧⎪⎨⎪⎩上面8种都是乙取得了胜利,甲取得胜利对应的也是8种,但考虑不计比分先后顺序,故有8种情况,答:三局的比分共有8种情况.故答案为:8.二、解答下列各题(每小题10分,共40分,要求写出简要过程)9.(10分)两个自然数之和为667,它们的最小公倍数除以最大公约数所得的商等于120.求这两个数.【解答】解:6672329=+,=⨯,由题意,假设23是它们的最大公约数,由于29245⨯=,245120所以两数分别是2423552⨯=;⨯=,523115假设29是它们的最大公约数,由于23158⨯=,⨯=;所以两数分别是1529435=+,158120⨯=;829232答:这两个数是115和552,或者232和435.10.(10分)酒店有100个标准间,房价为400元/天,但入住率只有50%.若每降低20元的房价,则能增加5间入住.求合适的房价,使酒店收到的房费最高.【解答】解:由题意分析得①房价为400元/天,入住房间为10050%50⨯=元;⨯=,所以收到的房费为:4005020000②房价为380元/天,入住房间为50555⨯=元;+=,所以收到的房费为:3805520900③房价为360元/天,入住房间为60,所以收到的房费为:3606021600⨯=元;④房价为340元/天,入住房间为65,所以收到的房费为:3406522100⨯=元;⑤房价为320元/天,入住房间为70,所以收到的房费为:3207022400⨯=元;⑥房价为300元/天,入住房间为75,所以收到的房费为:3007522500⨯=元;⑦房价为280元/天,入住房间为80,所以收到的房费为:2808022400⨯=元;⑧房价为260元/天,入住房间为85,所以收到的房费为:2608522100⨯=元;答:当房价为300元/天时,酒店受到的房费最高.11.(10分)如图,长方形ABCD的面积是256cm.3DF cm=.请你回答:三=,2BE cm角形AEF的面积是多少?【解答】解:据分析可知:四边形AGEF的面积为:56228÷=(平方厘米),则阴影部分的面积为:28232-⨯÷=-283=(平方厘米).25答:三角形AEF的面积是25平方厘米.12.(10分)当N取遍1,2,3,⋯,2015中所有的数时,形如3+的数中能够被7整3n n除的有多少个?【解答】解:如图:3n除以7的余数以6为周期,3、2、6、4、5、1;3N除以除以7的余数以7为周期,1、1、6、1、6、6、0;则总周期为42:2015424741÷=⋯⨯+47662826=+=(个)288答:能够被7整除的有288个.三、解答下列各题(每小题15分,共30分,要求写出详细过程)13.(15分)如图所示,ABCD是平行四边形,AM MB=,DN CN==,四=,BE EF FC边形EFGH的面积是1,求平行四边形ABCD的面积.【解答】解:如图,,作//EQ CD ,//FP CD ,分别交BN 与点Q 、P , 因为13EQ EQ BE BM CN BC ===, 所以13EH OE HM BM ==; 因为BEM ∆的面积占平行四边形ABCD 的面积的:111132212⨯⨯=, 所以HEQ ∆的面积占平行四边形ABCD 的面积的:2131()12313⨯⨯+ 1311249=⨯⨯ 1144= 因为23FP FP ND CN ==, 所以BFP ∆的面积占BCN ∆的面积的:224()39=, 所以四边形EFPQ 的面积占平行四边形ABCD 的面积的:21141()[1()]2292⨯⨯⨯- 143494=⨯⨯ 112= 因为23FP FG ND GD ==, 所以FGP ∆的面积占平行四边形ABCD 的面积的:211312()()323223⨯⨯⨯⨯+13146529=⨯⨯⨯145=所以平行四边形ABCD的面积的:1111()1441245÷++9180=÷889=答:平行四边形ABCD的面积是889.14.(15分)“虚有其表”,“表里如一”,“一见如故”,“故弄玄虚”四个成语中每个汉字代表11个非零连续自然数中的一个,相同的汉字代表相同的数,不同的汉字代表不同的数,且“表”>“一”>“故”>“如”>“虚”,且各个成语中四个汉字所代表的数的和都是21.则“弄”可以代表的数最大是多少?【解答】解:根据分析可知,表、一、故、如、虚”,五个重复数字之和为18,因为所有数是111--,重复数字只有以下几种可能:①1、2、3、4、8;②1、2、3、5、7;③1、2、4、5、6代入发现只有情况③符合情况,每个数都填入后,可得虚1=,故4=,弄、玄只能是9、7,弄最大是9.答:“弄”可以代表的数最大是9.。
小学数学竞赛难题解析试卷(小中组)

第二十二届华罗庚金杯少年数学邀请赛 初赛试卷(小学中年级组) (时间: 2016年12月10日10:00—11:00 ) 一、选择题(每小题10分, 共60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.) 1. 两个小三角形不重叠放置可以拼成一个大三角形, 那么这个大三角形不可能由( )拼成. (A )两个锐角三角形 (B )两个直角三角形 (C )两个钝角三角形 (D )一个锐角三角形和一个钝角三角形 2. 从1至10这10个整数中, 至少取( )个数, 才能保证其中有两个数的和等于10. (A )4 (B )5 (C )6 (D )7 3. 小明行李箱锁的密码是由两个数字8与5构成的三位数. 某次旅行, 小明忘记了密码, 他最少要试( )次, 才能确保打开箱子. (A )9 (B )8 (C )7 (D )6 4. 猎豹跑一步长为2米, 狐狸跑一步长为1米. 猎豹跑2步的时间狐狸跑3步.猎豹距离狐狸30米, 则猎豹跑动( )米可追上狐狸. (A )90 (B )105 (C )120 (D )135 5. 图1中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道( )条线段的长度, 才可以计算出这个八边形的周长. (A )4 (B )3 (C )5 (D )10图1 装订线6.一个数串Λ219, 从第4个数字开始, 每个数字都是前面3个数字和的个位数.下面有4个四位数:1113, 2226, 2125, 2215, 其中共有()个不出现在该数串中.(A)1(B)2(C)3(D)4二、填空题(每小题 10 分, 满分40分.)7.计算=----1643842571000.8.已知动车的时速是普快的两倍, 动车的时速提高%25即达到高铁的时速, 高铁与普快的平均时速比特快快15千米/小时, 动车与普快的平均时速比特快慢10千米/小时, 则高铁和普快列车的时速分别是千米/小时和千米/小时.9.《火星救援》中, 马克不幸没有跟上其他5名航天员飞回地球, 独自留在了火星,马克必须想办法生存, 等待救援. 马克的居住舱内留有每名航天员5天的食品和50千克的非饮用水, 还有一个足够大的菜园, 马克计划用来种植土豆, 30天后每平方米可以收获5.2千克,但是需要灌溉4千克的水.马克每天需要吃875.1千克土豆, 才可以维持生存, 则食品和土豆可供马克最多可以支撑天.10.图2五角星中, 位于顶点处的“华”、“罗”、“庚”、“金”、“杯”5个汉字分别代表1至5的数字, 不同的汉字代表不同的数字.每条线段两端点上的数字和恰为5个连续自然数.如果“杯”代表数字“1”, 则“华”代表的数字是或.图2第二十一届华罗庚金杯少年数学邀请赛 初赛试卷(小学中年级组) (时间: 2015年12月12日10:00—11:00) 一、选择题 (每小题10分, 共60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.) 1. 计算: 124+129+106+141+237-500+113=( ). (A )350 (B )360 (C )370 (D )380 解题分析:(124+106)+(129+141)+(237+113)-500 =(230+270)+350-500 =500-500+350 =350 答案选A 2. 如右图所示, 韩梅家的左右两侧各摆了2盆花. 每次, 韩梅按照以下规则往家中搬一盆花: 先选择左侧还是右侧, 然后搬该侧离家最近的. 要把所有的花搬到家里, 共有( )种不同的搬花顺序. (A )4 (B )6 (C )8 (D )10 解题分析:原则是先选择门口左侧的c 或右侧的b ,从b 点入手 b→a→c→d ;b→c→a→d ;b→c→d→a装订线总分 a b c d左侧c同理:c→d→b→a;c→b→a→d;c→b→d→a共3×2=6种答案选B3.在桌面上, 将一个边长为1的正六边形纸片与一个边长为1的正三角形纸片拼接,要求无重叠, 且拼接的边完全重合, 则得到的新图形的边数为().(A)8 (B)7 (C)6 (D)5解题分析:答案选D4.甲、乙、丙、丁四支足球队进行比赛.懒羊羊说: 甲第一, 丁第四; 喜羊羊说: 丁第二, 丙第三; 沸羊羊说: 丙第二, 乙第一. 每个的预测都只对了一半, 那么, 实际的第一名至第四名的球队依次是().(A)甲乙丁丙(B)甲丁乙丙(C)乙甲丙丁(D)丙甲乙丁解题分析:代入排出法将A代入,懒羊羊说:甲第一, 丁第四;对一半(符合题意)喜羊羊说:丁第二, 丙第三;全错(不符合题意)终止A 将B代入,懒羊羊说:甲第一, 丁第四;对一半(符合题意)喜羊羊说:丁第二, 丙第三;对一半(符合题意)沸羊羊说:丙第二, 乙第一;全错(不符合题意)终止B 将C代入,懒羊羊说:甲第一, 丁第四;对一半(符合题意)喜羊羊说:丁第二, 丙第三;对一半(符合题意)沸羊羊说:丙第二, 乙第一;对一半(符合题意)答案选C5.如右图, 在5×5的空格内填入数字, 使每行、每列及每个粗线框中的数字为1, 2, 3, 4, 5, 且不重复. 那么五角星所在的空格内的数字是().(A)1 (B)2(C)3 (D)4解题分析:根据题意,☆不能为2(列重复)、5(行重复)、3(粗线框内重复)只能为1或4;☆为1答案选A6.在除法算式中, 被除数为2016, 余数为7, 则满足算式的除数共有()个.(A)3 (B)4 (C)5 (D)6解题分析:根据题意2016-7=2009,求2009的因数2009的因数:1,7,41,49,287,20092016÷1=2016(×);2016÷7=288(×);2016÷41=49……7(√);2016÷49=41……7(√);2016÷287=7……7(√);2016÷2009=1……7(√)符合条件的4个答案选B二、填空题(每小题10 分, 共40分)7.动物园里有鸵鸟和梅花鹿若干, 共有腿122条.如果将鸵鸟与梅花鹿的数目互换,则应有腿106条, 那么鸵鸟有只, 梅花鹿有头.解题分析:第一种方法:设鸵鸟有X只,梅花鹿有Y只2X+4Y=122 4X+8Y=244 6Y=244-106=1384X+2Y=106 4X+2Y=106 Y=2323=122 2X=30 X=15第二种方法:设鸵鸟有X只,梅花鹿有(122-2X) ÷4只4X+(122-2X) ÷4×2=106 4X+(122-2X) ÷2=1064X+61-X=106 3X=106-61X=15梅花鹿只数=(122-15×2) ÷4=23(只)答案:鸵鸟15只,梅花鹿23只8.某年, 端午节距离儿童节和父亲节的天数相同, 在月历中与六月最后一天同列, 父亲节是六月的第三个星期日, 则该年的父亲节是六月日.(右图是某个月的月历示意图)解题分析:根据右图28天,可知是二月份的日历,先求出6月1日星期几?3月31天、4月30日、5月31日,6月1日共计31+30+31+1=93天93÷7=13(周) ……2(天) 从3月1日星期四算,第2天是星期五,六月一日为星期五。
第二十届华罗庚金杯少年数学邀请赛 决赛试题C(小学高年级组) 试题及参考答案详细解析

第二十届华罗庚金杯少年数学邀请赛决赛试题C 参考答案 (小学高年级组)一、填空题(每题10分, 共80分)二、解答下列各题(每题10分, 共40分, 要求写出简要过程)9.答案: 336千米解答.设A 和B 两地距离是336千米(1)乙车上午7点从B 出发,10点30分到A 地,说明乙车走完全程需要3小时30分;丙车上午7点从中点C 出发,10点丙车到达A 地,说明丙车走半程需要3小时,走完全程需要6小时,所以, 3.573.5=6 612⨯⨯==丙速乙速丙速,乙速;(2)当甲车和丙车相遇时,乙车恰好走完全程的38,所以,142338+==甲速丙速乙速,结合(1),可知:493=34=-=甲速7乙速1212; (3)当乙车走到A 地时,甲车距离B 地还有84千米,84484336AB AB AB -==⨯=甲的速度,乙的速度(千米).10.答案: 33解答. 注意,可化为有限小数的分数的分母的质因数只能是2和5.2015个分数12,13,14,…,12014,12015,12016中, (1)分母只有质因数2的分数:23101111121024222,,,=,10个;(2)分母只有质因数5的分数:234111115625555,,,=,4个; (3)分母只有质因数2和5的分数:23811111251280252525⨯⨯⨯⨯,,,,=,222326211111160025252525⨯⨯⨯⨯,,,,=,323334311111200025252525⨯⨯⨯⨯,,,=,411125025⨯=,19个. 所以,共有10+4+8+6+4+1=33个有限小数. 11.答案: 9解答. a + b =9.通分,a b a b ++=755735. 由小数点第3位经四舍五入,故有:52.675=..a b ⨯≤+<⨯15053575151535=53.025,既然a ,b 为正整数,a b ≤+≤537553,即:a b +=7553.解出a b ==4,5,故a + b =9. 12.答案: 3015.解答. 四位数abcd 最大值是3015.显然,e d ≠=0,5.并设e f =-10,这里f ≥1,故有:abc aa e =⨯55,abc aa aa f =-⨯5505,所以,bc a aa f =-⨯5505. 上式右端a 50大于aa f ⨯5,所以f =1,50bc a =-55,得到:b =0和a c +=4.所以abcd 最大值是3015.三、解答下列各题(每题15分, 共30分, 要求写出详细过程)13.答案: 35 cm 2.解答.△CDE 的面积是35 cm 2.连接BD ,见图3a ,由共边定理,ABF DBF S S ∆∆==82123. (1)由已知条件ABCD 是平行四边形和三角形面积公式,可知:()ABF DBF ABF S S S ∆∆∆+=+1722,(2) 由(1)和(2),得到,ABF S ∆=18cm 2.所以ABE S 18810∆=-=cm 2.平行四边形ABCD 的面积=(72+18)=90(cm 2),BCE AED ABCD S S S 平行四边形11904522∆∆+=⨯=⨯=,=BCE AED AEF DEF S S S S 45454581225∆∆∆∆=-=--=--.所以,△CDE 的面积=72-25-12=35cm 2.14.答案: 3名解答. 至少有3名学生分到的书的数量相同.如果48名学生分到的书籍的数量不同,则书籍总数是:474801234711282⨯+++++==(本), 1128大于530,显然会有2名以上学生分到的书籍的数量相同.将48名学生分成24组,每组有2名学生,如果允许每组内的两名学生分到相同数量的书籍,但是不同组的学生分到的书籍数量不相同,则书籍的总数是:()20123232324552⨯+++++=⨯=,552仍然大于530,希望最多仅有两名学生分到的书籍的数量相同是做不到的.图3a所以,至少有三名学生分到的书籍的数量相同.现在将530本书分给48名学生,相当于拆分一个自然数530,()530201232224=⨯++++++.上式的含义是有23组共46名学生,同一组内的学生分到相同数量的书籍,但是不同组的的学生分到的书籍数量不同,则一共有()⨯+++++=(本),2012322506余下的24本书分给第24组的2名学生,则至少有一个学生分到的书籍的数量不大于22.所以,一定有3名学生分到相同数量的书籍.。
2015年第二十届华罗庚金杯少年数学邀请赛

第二十届华罗庚金杯少年数学邀请赛初赛A卷(小学高年级组)(总分:100分,时间:60分钟)姓名:一、选择题.(每小题10分,共60分.以下每题的四个选项中,仅有一个是正确,请将表示正确答案的英文字母写在每题的圆括号内.)1.现在从甲、乙、丙、丁四个人中选出两个人参加一项活动。
规定:如果甲去,那么乙也去;如果丙不去,那么乙也不去;如果丙去,那么丁不去.最后去参加活动的两个人是()。
(A)甲、乙(B)乙、丙(C)甲、丙(D)乙、丁2.以平面上任意4个点为顶点的三角形中,钝角三角形最多有()个。
(A)5 (B)2 (C)4 (D)33.桌上有编号1至20的20张卡片,小明每次取出2张卡片,要求一张卡片的编号是另一张卡片的2倍多2,则小明最多取出()张卡片。
(A)12 (B)14 (C)16 (D)184.足球友谊比赛的票价是50元,赛前一小时还有余票,于是决定降价.结果售出的票增加了三分之一,而票房收入增加了四分之一,那么每张票售价降了()元。
(A)10 (B)252(C)503(D)255.一只旧钟的分针和时针每重合一次,需要经过标准时间66分.那么,这只旧钟的24小时比标准时间的24小时()。
(A)快12分(B)快6分(C)慢6分(D)慢12分6.在右图的6×6方格内,每个方格中只能填A,B,C,D,E,F中的某个字母,要求每行、每列、每个标有粗线的2×3长方形的六个字母均不能重复.那么,第四行除了首尾两个方格外,中间四个方格填入的字母从左到右的顺序是().(A)E,C,D,F (B)E,D,C,F(C)D,F,C,E (D)D,C,F,E二、填空题 (每小题10分,共40分)1. 计算48116 +265112 +904120 -1842930 -1604142 -70355562. 过正三角形ABC 内一点P ,向三边作垂线,垂足依次为D E F 连接AP ,BP ,CP ,如果正三角形ABC 的面积是2028平方厘米,三角形PAD 和三角形PBE 的面积都192平方厘米,则三角形 PCF 的面积为________平方厘米。
第10~21届全国华罗庚金杯少年数学邀请赛试题

第十届“华罗庚金杯”少年数学邀请赛初赛试题1、2005年是中国伟大航海家郑和首次下西洋600周年,西班牙伟大航海家歌伦布首次远洋航行是在1492年。
问这两次远洋航行相差多少年?2、从冬至之日起每九天分为一段,依次称之为一九,二九,……,九九,2004年的冬至为12月21日,2005年的立春是2月4日。
问立春之日是几九的第几天?3、右下方是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形。
问这个直三棱柱的体积是多少?4、爸爸、妈妈、客人和我四人围着圆桌喝茶。
若只考虑每人左邻的情况,问共有多少种不同的入座方法?5、在奥运会的铁人三项比赛中,自行车比赛距离是长跑的4倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米。
求三项的总距离。
6、如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形。
其中最小的三角形顶点的个数(重合的顶点只计一次)依次为:3,6,10,15,21,……问这列数中的第9个是多少?7、一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示。
若用甲容器取水来注满乙容器,问:至少要注水多少次?8、100名学生参加社会实践,高年级学生两人一组,低年级学生三人一组,共有41组。
问:高、低年级学生各多少人?9、小鸣用48元钱按零售价买了若干练习本。
如果按批发价购买,每本便宜2元,恰好多买4本。
问:零售价每本多少元?10、不足100名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈。
问最多有多少名同学?11、输液100毫升,每分钟输2.5毫升。
请你观察第12分钟时吊瓶图像中的数据,回答整个吊瓶的容积是多少毫升?12、两条直线相交所成的锐角或直角称为两条直线的“夹角”。
现平面上有若干条直线,它们两两相交,并且“夹角”只能是30°,60°或90°。
小学华杯赛中年级组初赛真题及答案(第十八届-第二十三届)

华罗庚金杯少年数学邀请赛(小学中年级组)初赛试卷及答案(第18届-第23届)共9套(内部资料)第十八届华罗庚金杯少年数学邀请赛初赛试卷A(小学中年级组)(时间:2013年3月23日10:00~11:00)一、选择题(每小题10分,满分60分。
以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1.45与40的积的数字和是()。
(A)9(B)11(C)13(D)152.在下面的阴影三角形中,不能由右图中的阴影三角形经过旋转、平移得到的是图()中的三角形。
3.小东、小西、小南、小北四个小朋友在一起做游戏时,捡到了一条红领巾,交给了老师.老师问是谁捡到的?小东说不是小西;小西说是小南;小南说小东说的不对;小北说小南说的也不对。
他们之中只有一个人说对了,这个人是()。
(A)小东(B)小西(C)小南(D)小北4.2013年的钟声敲响了,小明哥哥感慨地说:这是我有生以来遇到的第一个没有重复数字的年份.己知小明哥哥出生的年份是19的倍数,那么2013年小明哥哥的年龄是()岁。
(A)16(B)18(C)20(D)225.如右图,一张长方形的纸片,长20厘米,宽16厘米,如果从这张纸片上剪下一个长10厘米,宽5厘米的小长方形,而且至少有一条边在原长方形的边上,那么剩下纸片的周长最大是()厘米。
(A)72(B)82(C)92(D)1026.张老师每周的周一,周六和周日都跑步锻炼20分钟,而其余日期每日都跳绳20分钟,某月他总共跑步5小时,那么这个月的第10天是()(A)周日(B)周六(C)周二(D)周一二、填空题(每小题10分,满分40分)7.如右图,一个正方形被分成了4个相同的长方形,每个长方形的周长都是20厘米,则这个正方形的面积是_______平方厘米。
8.九个同样的直角三角形卡片,拼成了如右图所示的平面图形,这种三角形卡片中的两个锐角较大的一个是_______度。
9.幼儿园的老师给班里的小朋友送来55个苹果,114块饼干,83块巧克力,每样都平均分发完毕后,还剩3个苹果,10块饼干,5块巧克力,这个班最多有_______位小朋友。
第二十届华罗庚金杯少年数学邀请赛决赛试题A组(小学中
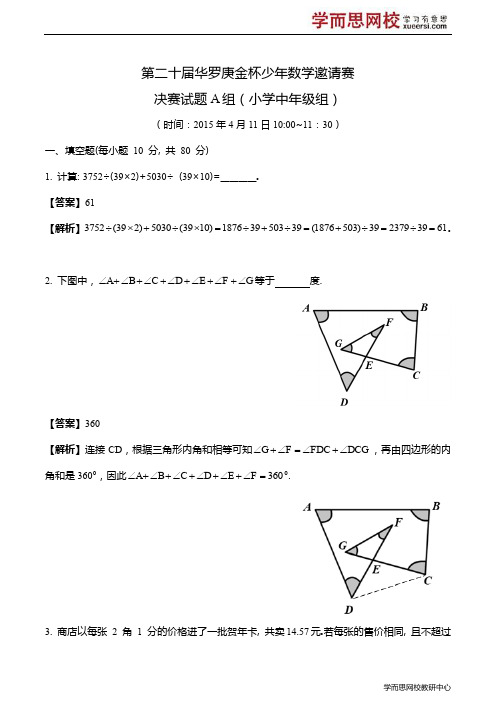
第二十届华罗庚金杯少年数学邀请赛决赛试题A 组(小学中年级组)(时间:2015年4月11日10:00~11:30)一、填空题(每小题 10 分, 共 80 分)1. 计算: 3752÷(39×2)+5030÷ (39×10)=________.【答案】61【解析】3752(392)5030(3910)187********(1876503)3923793961÷⨯+÷⨯=÷+÷=+÷=÷=.2. 下图中,A B C D E F G ∠+∠+∠+∠+∠+∠+∠等于 度.【答案】360【解析】连接CD ,根据三角形内角和相等可知G F FDC DCG ∠+∠=∠+∠,再由四边形的内角和是360°,因此360A B C D E F ∠+∠+∠+∠+∠+∠=°.3. 商店以每张 2 角 1 分的价格进了一批贺年卡, 共卖14.57元.若每张的售价相同, 且不超过买入价格的两倍, 则商店赚了________元.【答案】4.7【解析】由已知得进价为21分,则售价不超过42分,总的销售收入为1457分.由于1457在21到42的约数只有31,可得售价为31分,共有14573147÷=(个)贺年卡,商店共赚了47(3121)470⨯-=(分),即4.7元.4.两个班植树, 一班每人植3棵, 二班每人植5棵, 共植树115棵. 两班人数之和最多为________.【答案】37【解析】设一班有x 人,二班有y 人,列方程35115x y +=,要使()x y +最大,应使x 尽量大,经尝试352x y ==、时两班人数的和最多,即为35237+=(人).5.某商店第一天卖出一些笔, 第二天每支笔降价 1 元后多卖出 100 支, 第三天每支笔比前一天涨价 3 元后比前一天少卖出 200 支.如果这三天每天卖得的钱相同, 那么第一天每支笔售价是________元.【答案】4【解析】方法一:设第一天卖出笔的数量为x 支,单价为y 元,由已知可得(100)(1)(100)(1)(100)(2)xy x y x y x y =+-⎧⎨+-=-+⎩ 即1001003200100y x x y -=⎧⎨-=⎩ 解得3004x y =⎧⎨=⎩则第一天每支笔售价为4元.方法二:设第一天卖出笔的数量为x 支,单价为y 元,根据题意画出左下图,可知①号面积=②号面积,所以(1)100y x -⨯=,所以100100x y =-;同理根据第一天和第三天的关系画出右下图,2(100)100x y -=⋅即2100200x y =+,解得300x =,4y =.则第一天每支笔售价为4元.6.一条河上有A, B两个码头, A在上游, B在下游.甲、乙两人分别从A, B同时出发, 划船相向而行, 4小时后相遇.如果甲、乙两人分别从A, B同时出发, 划船同向而行, 乙16小时后追上甲.已知甲在静水中划船的速度为每小时6千米, 则乙在静水中划船每小时行驶________千米.【答案】10【解析】设乙在静水中速度为每小时x千米,水速为每小时y千米,可得++-=--+,y x y x y y4(6)16(6)x=,即乙在静水中划船每小时行驶10千米.解得107.某个两位数是2的倍数, 加1是3的倍数, 加2是4的倍数, 加3是5的倍数, 那么这个两位数是________.【答案】62【解析】由已知该两位数除以3、4、5均余2,满足条件的两位数只有62,且该数为2的倍数,因此这个两位数是62.8. 在三个词语“尽心尽力”、“力可拔山”和“山穷水尽”中, 每个汉字代表1至8之间的数字, 相同的汉字代表相同的数字, 不同的汉字代表不同的数字.如果每个词语的汉字所代表的数字之和都是 19, 且“尽”>“山”>“力”, 则“水”最大等于________.【答案】7【解析】因为2尽+心+力=19、力+可+拔+山=19、山+穷+水+尽=19,所以力+可+拔+2山+穷+水+尽=38、力+可+拔+山+穷+水+尽+心=36,那么山-心=2,所以山3≥;而2尽+心+力=2尽+山-2+力=19,因此2尽+山+力=21,有尽>山>力,所以山1-≥力、尽2-≥力,那么4尽321-≥,尽6≥.若水=8、尽=6、心=3、力=4、山=5、穷=0,矛盾;若水=8、尽=7、山=3、穷=1、新=1,矛盾;若水=7、尽=6、山=5、力=4、心=3、穷=1、可=2或8、拔=8或2,成立,所以水最大为7.二、简答题(每小题15分,共60分,要求写出简要过程)9. 有一批作业, 王老师原计划每小时批改6本. 批改了2小时后, 他决定每小时批改 8 本, 结果提前 3 小时批改完.那么这批作业有多少本?【答案】84【解析】前2小时批改了6212⨯=(本),因为提前了3小时,那么这3小时按照原计划需要批改3618⨯=(本).根据差倍问题:18(86)9÷-=(小时),因此作业一共有981284⨯+=(本).10. 用五种不同的颜色涂正方体的六个面. 如果相邻的两个面不能涂同种颜色, 则共有多少种不同的涂色方法?(将正方体任意翻转后仍然不同的涂色方法才被认为是不同的)【答案】30种(官网),15种(学而思)【解析】从5种颜色选出一种,另外四种颜色排列有1454430C A ⨯÷=(种)(官网);从5种颜色选出一种,另外四种颜色排列有1454430C A⨯÷=(种),考虑到翻转的情况,最后应该只有30215÷=(种).(学而思提供, 仅供参考)11. 如右图所示, 有一个圆圈填了数字1.请在空白圆圈内填上2, 3, 4, 5, 6中的一个数字, 要求无重复数字, 且相邻圆圈内的数字的差至少为2.问共有几种不同的填法?【答案】3种【解析】如下图,把字母标在空白的圆圈里,那么2不能为A、B、C,只能为D或E,下面分情况讨论:①当D=2时,A、C、E不能为3,所以B=3,由于A和E的差不能为1,所以C=5,A=4,E=6或C=5,A=6,E=4,此时共有2种填法;②当E=2时,A、D不能为3.当B=3时,A、C、D需要取4、5、6,而D与A和C的差均至少为2,故此时无解;当C=3时,A和D的差至少为2,所以B=5,A=4,D=6,此时共有1中填法.综上,共有3种不同的填法.12.边长分别为8cm和6cm的两个正方形ABCD与BEFG如右图并排放在一起.连接DE交BG于P, 则图中阴影部分APEG的面积是多少?【答案】182cm【解析】连接BD ,那么()2224AEP ABP EBP DBP EBP DBE S S S S S S BE AD cm ∆∆∆∆∆∆=+=+==⨯÷=,()2=224422418AGE APE S S S AE BG cm ∆∆-=⨯÷-=-=阴影.。
第二十届华杯初赛小学高级组C卷(含解析)

第二十届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级C 卷)(时间:2014 年 3 月 14 日 10:00〜11:00)一、选择题(每小题10分,满分60分•以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内 )『9 11 13 1517 )1 11120 一30 42 5672 丿 3 43.春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、 下的对话:甲:“丙、丁之中至少有1人捐了款” 乙:“丁、甲之中至多有1人捐了款” 丙:“你们3人中至少有2人捐了款” 丁: “你们3人中至多有2人捐了款” 己知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这 4位同学是()A .甲、乙 B.丙、丁 C.甲、丙D.乙、丁4.六位同学数学考试的平均成绩是 92.5分,他们的成绩是互不相同的整数,最高的那么按分数从高到低居第三位的同学的分数至少是().A. 94 B . 95 C. 96D . 975.如图,BH 是直角梯形ABCD 的高,E 为梯形对角线 AC 上一点;如果 DEH 、•汨EH 、厶BCH 的面积 依次为56、50、40,那么 CEH 的面积是(). A. 32B . 34C. 35D. 366.—个由边长为1的小正方形n n 的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的 4个用上的小正方形不全同色,那么正整数的最大值是(). A . 3 B. 4 C. 5D. 6二、填空题(每小题10分,满分40分.)7.在每个格子中填入1〜6中的一个,使得每行、每列及每个 2 3长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯 是 __________ .&整数n —共有10个约数,这些约数从小到大排列.笫 8个是-.那么整数的最大值是=(20 A. 42B. 43C.2.如图, 有一排间距相同但高度不等的小树,1 2 15— D. 1633这两条直线成45度角.最高的小树高2.8米,最低的小树高1.4米, 那么从左向右数第 4棵树的高度是()米.A . 2.6 B. 2.4 C. 2.2 D. 2.0丙、丁 4位同学有如99分,最低的76分,39.在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是 _____________ 厘米.(二取3.14)10. A 地、B 地、C 地依次分布在同一条公路上,甲、乙、丙三人分别从 A 地、B 地、C 地同时出发,匀 速向D 地行进.当甲在 C 地追上乙时,甲的速度减少 40% ;当甲追上丙时,甲的速度再次减少 40% ;甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少 25% ;如乙追上丙后再行 50米,三人同时到 D地•已知乙出发时的速度是每分钟 60米,那么甲出发时的速度是每分钟 _______ 米,A 、D 两地间的路程是 ___________ 米.第二十届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级C 卷)参考答案参考解析【考点】速算巧算【考点】等差数列 【难度】☆☆ 【答案】C【解析】如右图,AB =2.8-1.4 =1.4 (米),AC =1.4'7 3=0.6 (米)因此,第四高的小树为 2.8-0.6=2.2 (米).3. 春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、下的对话:甲:“丙、丁之中至少有1人捐了款”一、选择题 (每小题10分,满分60分•以下每题的四个选项中,仅有一个是正确的,请将表示正确答案 的英文字母写在每题的圆括号内『9 Il L 131 ———-—20 30 42d 卫56 72120一3 =(A. 42B. 43C.115 3D. 163【答案】Af 1【解析】原式=寸2.如图,有一排间距相同但高度不等的小树,IL 8 9树根成一条直线, 120 3 4 1竺=42 .3树顶也成一条直线.这两条直线成45度角.最高的小树高2.8米,最低的小树高1.4米, 那么从左向右数第 4棵树的高度是()米.A . 2.6B. 2.4C. 2.2D. 2.0丙、丁 4位同学有如乙:“丁、甲之中至多有1人捐了款”丙:“你们3人中至少有2人捐了款”丁:“你们3人中至多有2人捐了款”己知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这4位同学是()•A.甲、乙B.丙、丁C.甲、丙D.乙、丁【考点】逻辑推理【难度】☆☆☆【答案】D【解析】因为恰有2位同学捐了款,据丙所说知甲、乙、丁就至少2人捐款,所以丙没捐款;再据甲所说知丙、丁之中至少有1人捐了款,现在丙没捐款,所以丁一定捐款了;再据乙所说知丁、甲之中至多有1人捐了款,现在丁捐款了,所以甲一定没捐款;恰有2位同学捐了款,即恰有2位同学没捐款,现在甲、丙都没捐款,所以乙、丁都捐款了.4.六位同学数学考试的平均成绩是92.5分,他们的成绩是互不相同的整数,最高的99分,最低的76分,那么按分数从高到低居第三位的同学的分数至少是().A. 94B. 95C. 96D. 97【考点】最值问题【难度】☆☆☆【答案】B【解析】“至少”的含义是:第三位同学的得分若低于这个分数,不论其它同学得多少分,平均分都不会达到92.5分.要想使第三位同学的得分尽可能的少,应使第二位同学的得分尽可能的多;同时,第四位、第五位的同学得分与第4位同学的得分尽可能的接近.由此,可先求出第三位、第四位、第五位同学的平均分,再对三位同学的分数进行调整即可解决问题.由己知,第三、四、五三位同学的平均分是(92.5 6 -99 -76 -98)十3 = 282 “ 3 = 94 (分),故第三位同学的得分至少是94 •仁95 .5.如图,BH是直角梯形ABCD的高,E为梯形对角线AC上一点;如果DEH、•汨EH、厶BCH的面积依次为56、50、40,那么CEH的面积是().A. 32B. 34C. 35D. 36【考点】几何【难度】☆☆☆【答案】B【解析】因为S DEH ' S.AEH =S ABCD ' 2 = S ABC ~ S.BCE ' S AEB 所以S~ S DEH =56 ;所以,S .CEH = S BEH S BCH _ S BCE = 50 40- 56 = 34 .6.—个由边长为1的小正方形n n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个用上的小正方形不全同色,那么正整数的最大值是().A. 3B. 4C. 5D. 6【考点】最值问题【难度】☆☆☆☆【答案】B【解析】假设n =5 ,笫1行中至少有3个格子颜色相同,不妨设前3格为黑色(如图1).在这3个黑格下方可以分割为4个横着的3 1的长方形,若其中有一个中有2个黑格(如图2),则存在巷图中的粗线长方形4个角上的小正方形都是黑格;所以这4个横着的3 1的长方形中,每个至多1个黑格.假设这4个横着的3 1的长方形中,有两个对应格子颜色都一样(如图3),则一样存在图中的粗线长方形4个角上的小正方形都是白格.而3 1的长方形中至多1个黑格的只有如图4的这4种.如果这4种都存在的话(如图5),则同样存在图中的粗线长方形4个角上的小正方形都是白格•矛盾!所以n <5.而图6给出了n =4的一种构造•所以,正整数n的最大值是4 .二、填空题(每小题10分,满分40分.)7•在每个格子中填入1〜6中的一个,使得每行、每列及每个 2 3长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是___________ .【考点】数阵图【难度】☆☆☆☆【答案】4123【解析】如下左图,因为A 3为质数且A =4 ,所以A =2 ;因为“月”1为质数且“月”-2、4 ,所以“月” =6 ;从而C=5 ;因为“杯”4为质数且“杯”-1 ,所以“杯” =3 ;从而C =5 ;因为D 3为合数且D =2或6 ,所以D =6 ;从而“华” =2 ;因为“相”3为质数且“相”-2 ,所以“相” -4 ;因为B 4为合数且D =1或5 ,所以B =5 ;从而“约”=1 ;所以,相约华杯=4123(如下中图)•实际上其它格子中的数也能唯一确定(如下右图)&整数n—共有10个约数,这些约数从小到大排列•笫8个是-•那么整数的最大值是3 ----------【考点】数论【难度】☆☆☆【答案】162【解析】n有10个约数,由于第8个是-,而第10个必然是n ,所以第9个只能是-•所以n有质因子2和3 23 •所以n可能是24 3或者34 2 •而最大是34 2 =162 .9•在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是_ 平方厘米,两块阴影部分的周长差是_____________ 厘米.(二取3.14)【考点】几何基本概念【难度】☆☆☆【答案】①15975 :②485 .【解析】①QS阴影ABE -S l影CDE =S扇形ABD S扇形ABC —SE方形ABCD —S半圆AB②因为ABE为等边三角形,所以∙EAB =. E B A=60 ,从而∙DAE =. CBE=30 ;阴影CDE的周长=弧CE 弧DE CD =2二300^12 2 300 =100二300 ;阴影ABE的周长二弧AE •弧BE •弧AB =2二300-:-6 2 • 300-:-2 = 350二;所以,的周长差=350二_(100二300)=250二_300 : 485 .10. A地、B地、C地依次分布在同一条公路上,甲、乙、丙三人分别从A地、B地、C地同时出发,匀速向D地行进.当甲在C地追上乙时,甲的速度减少40% ;当甲追上丙时,甲的速度再次减少40% ;甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少25% ;如乙追上丙后再行50米,三人同时到D地•已知乙出发时的速度是每分钟60米,那么甲出发时的速度是每分钟________ 米,A、D两地间的路程是 __________ 米.【考点】行程问题【难度】☆☆☆☆【答案】①125 :②1880 .【解析】①因为三人同时到D地,所以甲、乙最后的速度和丙相同;所以丙速为60 (1 -25%)=45(米/分);甲减速一次后的速度为45 “(1 - 40%)=75 (米/分),甲出发时的速度为75 “(1 -40%)=125(米/分).②如下图,设甲在E地追上丙,乙在F地追上丙,因为甲、乙出发时的速度比为125:60 =25:12 , 所以AB:BC =25:12 ;设AC为25份,则BC为12份;因为乙、丙出发时的速度比为60: 45=4:3 ,所以BF :CF =4:3 ,从而CF 为12“(4-3) 3=36 份,AF 为25 *36=61 份.因为甲减速一次后与丙的速度比为75: 45 = 5:3 ,而甲原速行AC这25份时,相当于以75米/分行25 60% =15份;所以CE=15"(5-3) 3=22.5 份,从而EF =36-22.5 =13.5 份;而EF是丙9分钟所行的路程,为45 9 =405(米),所以每份405 "13.5 =30(米),从而AF =30 61 H 1830 (米),所以AD =1830 50 -1880 (米).。
2015年第二十届华罗庚金杯少年数学邀请赛初赛试卷

第二十届华罗庚金杯少年数学邀请赛初赛试卷一、选择题(每小题10分,共60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.森林里举行比赛,要派出狮子、老虎、豹子、大象中的两个动物去参加,如果派狮子去,那么也要派老虎去;如果不派豹子去,那么也不能派老虎去;要是豹子参加的话,大象可不愿意去.那么,最后能去参加比赛的是( ).(A )狮子、老虎 (B)老虎、豹子 (C )狮子、豹子 (D )老虎、大象2.小明有多张面额为1元、2元、5元的人民币,他想用其中不多于10张的人民币购买一只价格为18元的风筝,要求至少用两种面额的人民币,那么不同的付款方式有( )种(A)3 (B) 9 (C)11 (D)83.如下图,在由1x1的正方形组成的网格中写有2015四个数字(阴影部分),其边线要么是水平或竖直的直线段,要么是连接1x1的正方形相邻两边中点的线段,或者是1x1 的正方形的对角线,则图中2015四个数字(阴影部分)的面积是( )。
(A)47 (B)2147 (C) 48 (D)2148 4.新生入校后,合唱队、田径队和舞蹈队共招收学员100人,如果合唱队招收的人数比田径队多一倍,舞蹈队比合唱队多10人,那么舞蹈队招收( )人.(注:每人限加入一个队)(A)30 (B)42(C)46 (D)525、一直旧钟的分针和时针每重合一次,需要经过标准时间66分,那么,这只旧钟的24小时比标准时间的24小时( )。
(A)快12分 (B)快6分 (C)慢6分 (D)慢12分6.一次考试共有6道选择题,评分规则如下:每人先给6分,答对一题加4分。
答错一题减1分,不答得0分。
现有51名同学参加考试,那么,至少有( )人得分相同。
(A)3 (B)4 (C)5 (D)6二、填空题(每小题10分,共40分)7.计算:(1000+15+314)×(201+360+110)+(1000-201-360-110)×(15+314)= .8、角可以用它的两边上的两个大写字母和顶点的字母表示,如右图的∠AOB符号(“∠”表示角)也可以用∠O表示(顶点处只有一个角时).下图的三角形ABC中,∠BAO=∠CAO,∠CBO=∠ABO,∠ACO=∠BCO,∠AOC=110°,则∠CBO= .9.张叔叔和李叔叔两人年龄和是56岁,当张叔叔是李叔叔现在年龄的一半时,李叔叔当时的年龄是张叔叔现在的年龄,那么张叔叔现在有岁。
第二十届华杯初赛小学高年级组C卷含解析

第二十届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级C卷)(时间:2014年3月14日10:00~11:00)一、选择题(每小题10分,满分60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内)1.91113151711120203042567234⎛⎫-+-+⨯-÷=⎪⎝⎭( ).A.42B.43C.1153D.21632.如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线.这两条直线成45度角.最高的小树高2.8米,最低的小树高1.4米,那么从左向右数第4棵树的高度是( )米.A.2.6 B.2.4 C.2.2D.2.03.春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、丙、丁4位同学有如下的对话:甲:“丙、丁之中至少有1人捐了款” 乙:“丁、甲之中至多有1人捐了款” 丙:“你们3人中至少有2人捐了款” 丁:“你们3人中至多有2人捐了款”己知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这4位同学是( ). A .甲、乙B .丙、丁C .甲、丙D .乙、丁4.六位同学数学考试的平均成缋是92.5分,他们的成绩是互不相同的整数,最高的99分,最低的76分,那么按分数从高到低居第三位的同学的分数至少是( ). A .94B . 95C . 96D . 975.如图,BH 是直角梯形ABCD 的高,E 为梯形对角线AC 上一点;如果DEH ∆、BEH ∆、BCH ∆的面积依次为56、50、40,那么CEH ∆的面积是( ).A .32B . 34C . 35D . 366.—个由边长为1的小正方形n n ⨯的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个用上的小正方形不全同色,那么正整数的最大值是( ). A .3B . 4C . 5D . 6二、填空题(每小题10分,满分40分.)7.在每个格子中填入1~6中的一个,使得每行、每列及每个23⨯长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是 .8.整数n 一共有10个约数,这些约数从小到大排列.笫8个是3n .那么整数的最大值是 .9.在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是 平方厘米,两块阴影部分的周长差是 厘米.( 取3.14)A10.A地、B地、C地依次分布在同一条公路上,甲、乙、丙三人分别从A地、B地、C地同时出发,匀速向D地行进.当甲在C地追上乙时,甲的速度减少40%;当甲追上丙时,甲的速度再次减少40%;甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少25%;如乙追上丙后再行50米,三人同时到D地.已知乙出发时的速度是每分钟60米,那么甲出发时的速度是每分钟米,A、D两地间的路程是米.第二十届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级C卷)参考答案参考解析一、选择题(每小题10分,满分60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内)1.91113151711120203042567234⎛⎫-+-+⨯-÷=⎪⎝⎭( ).A.42B.43C.1153D.2163【考点】速算巧算【难度】☆☆【答案】A【解析】原式1111111111412612042 455667788933⎛⎫=+--++--++⨯-==⎪⎝⎭.2.如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线.这两条直线成45度角.最高的小树高2.8米,最低的小树高1.4米,那么从左向右数第4棵树的高度是( )米.A.2.6 B.2.4 C.2.2D.2.0【考点】等差数列【难度】☆☆【答案】C【解析】如右图, 2.8 1.4 1.4AB=-= (米), 1.4730.6AC=÷⨯= (米)因此,第四高的小树为2.80.6 2.2-=(米).3.春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生;事后,甲、乙、丙、丁4位同学有如下的对话:甲:“丙、丁之中至少有1人捐了款”乙:“丁、甲之中至多有1人捐了款”丙:“你们3人中至少有2人捐了款”丁:“你们3人中至多有2人捐了款”己知这4位同学说的都是真话且其中恰有2位同学捐了款,那么这4位同学是( ).A.甲、乙B.丙、丁C.甲、丙D.乙、丁【考点】逻辑推理【难度】☆☆☆【答案】D【解析】因为恰有2位同学捐了款,据丙所说知甲、乙、丁就至少2人捐款,所以丙没捐款;再据甲所说知丙、丁之中至少有1人捐了款,现在丙没捐款,所以丁一定捐款了;再据乙所说知丁、甲之中至多有1人捐了款,现在丁捐款了,所以甲一定没捐款;恰有2位同学捐了款,即恰有2位同学没捐款,现在甲、丙都没捐款,所以乙、丁都捐款了.4.六位同学数学考试的平均成缋是92.5分,他们的成绩是互不相同的整数,最高的99分,最低的76分,那么按分数从高到低居第三位的同学的分数至少是( ). A .94B . 95C . 96D . 97【考点】最值问题 【难度】☆☆☆ 【答案】B【解析】“至少”的含义是:第三位同学的得分若低于这个分数,不论其它同学得多少分,平均分都不会达到92.5分.要想使第三位同学的得分尽可能的少,应使第二位同学的得分尽可能的多;同时,第四位、第五位的同学得分与第4位同学的得分尽可能的接近.由此,可先求出第三位、第四位、第五位同学的平均分,再对三位同学的分数进行调整即可解决问题.由己知,第三、四、五三位同学的平均分是(92.56997698)3282394⨯---÷=÷= (分),故第三位同学的得分至少是941=95+.5.如图,BH 是直角梯形ABCD 的高,E 为梯形对角线AC 上一点;如果DEH ∆、BEH ∆、BCH ∆的面积依次为56、50、40,那么CEH ∆的面积是( ).A .32B . 34C . 35D . 36【考点】几何【难度】☆☆☆ 【答案】B 【解析】因为2DEHAEH ABCD ABC BCE AEB S S S S S S ∆∆∆∆∆+=÷==+W 所以56BCE DEH S S ∆∆==;所以,50405634CEH BEH BCH BCE S S S S ∆∆∆∆=+-=+-=.6.—个由边长为1的小正方形n n ⨯的方格网,用白色或黑色对每个小正方形涂色,要求满 足在任意矩形的4个用上的小正方形不全同色,那么正整数的最大值是( ). A .3B .4C .5D .6【考点】最值问题 【难度】☆☆☆☆ 【答案】B【解析】假设5n=,笫1行中至少有3个格子颜色相同,不妨设前3格为黑色(如图1).在这3个黑格下方可以分割为4个横着的31⨯的长方形,若其中有一个中有2个黑格(如图2),则存在巷图中的粗线长方形4个角上的小正方形都是黑格;所以这4个横着的31⨯的长方形中,每个至多1个黑格.假设这4个横着的31⨯的长方形中,有两个对应格子颜色都一样(如图3),则一样存在图中的粗线长方形4个角上的小正方形都是白格.而31⨯的长方形中至多1个黑格的只有如图4的这4种.如果这4种都存在的话(如图5),则同样存在图中的粗线长方形4个角上的小正方形都是白格.矛盾!所以5n<.而图6给出了4n=的一种构造.所以,正整数n的最大值是4.二、填空题(每小题10分,满分40分.)7.在每个格子中填入1~6中的一个,使得每行、每列及每个23⨯长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是.【考点】数阵图 【难度】☆☆☆☆ 【答案】4123【解析】如下左图,因为3A +为质数且4A ≠,所以2A =;因为“月”1+为质数且“月” 2≠、4,所以“月”6=;从而5C =; 因为“杯”4+为质数且“杯” 1≠,所以“杯”3=;从而5C =; 因为3D +为合数且2D =或6,所以6D =;从而“华”2=; 因为“相”3+为质数且“相” 2≠,所以“相”4=; 因为4B +为合数且1D =或5,所以5B =;从而“约”1=;所以,相约华杯4123=(如下中图).实际上其它格子中的数也能唯一确定(如下右图).8.整数n 一共有10个约数,这些约数从小到大排列.笫8个是3n .那么整数的最大值是 . 【考点】数论 【难度】☆☆☆ 【答案】162【解析】n 有10个约数,由于第8个是3n ,而第10个必然是n ,所以第9个只能是2n .所以n 有质因子2和3.所以n 可能是423⨯或者432⨯.而最大是432162⨯=.9.在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是 平方厘米,两块阴影部分的周长差是 厘米.(π取3.14)【考点】几何基本概念 【难度】☆☆☆【答案】①15975;②485. 【解析】①ABECDE ABCD ABD ABC AB SS S S S S -=--阴影阴影正方形扇形扇形半圆22230042300150233750-9000015975πππ=⨯÷⨯--⨯÷=≈②因为ABE ∆为等边三角形,所以60EAB EBA ∠=∠=︒,从而30DAE CBE ∠=∠=︒; 阴影=2300122300100300CDE CE DE CD ππ++=⨯÷⨯+=+的周长弧弧; 阴影2300623002350ABE AE BE AB ππ=++=⨯÷⨯+÷=的周长弧弧弧; 所以,350(100300)250300485πππ=-+=-≈的周长差.A10.A地、B地、C地依次分布在同一条公路上,甲、乙、丙三人分别从A地、B地、C地同时出发,匀速向D地行进.当甲在C地追上乙时,甲的速度减少40%;当甲追上丙时,甲的速度再次减少40%;甲追上丙后9分钟,乙也追上了丙,这时乙的速度减少25%;如乙追上丙后再行50米,三人同时到D地.已知乙出发时的速度是每分钟60米,那么甲出发时的速度是每分钟米,A、D两地间的路程是米.【考点】行程问题【难度】☆☆☆☆【答案】①125;②1880.【解析】①因为三人同时到D地,所以甲、乙最后的速度和丙相同;⨯-=(米/分);所以丙速为60(125%)45÷-=(米/分),甲减速一次后的速度为45(140%)75÷-=(米/分).甲出发时的速度为75(140%)125②如下图,设甲在E地追上丙,乙在F地追上丙,因为甲、乙出发时的速度比为125:6025:12AB BC=;=,所以:25:12设AC为25份,则BC为12份;因为乙、丙出发时的速度比为60:454:3BF CF=,=,所以:4:3从而CF 为12(43)336÷-⨯=份,AF 为25 3661+=份. 因为甲减速一次后与丙的速度比为75:45 5:3=,而甲原速行AC 这25份时,相当于以75米/分行2560%15⨯=份; 所以15(53)322.5CE =÷-⨯=份,从而36-22.513.5EF ==份; 而EF 是丙9分钟所行的路程,为459405⨯=(米), 所以每份40513.530÷=(米),从而3061 1830 AF =⨯=(米),所以1830501880 AD =+-(米).D。
第二十届华罗庚金杯少年数学邀请赛初赛试卷A卷(小学中年级组)

第二十届华罗庚金杯少年数学邀请赛初赛试卷A卷(小学中年级组)第二十届华罗庚金杯少年数学邀请赛初赛A卷(小学中年级组)(时间: 2021年3月14日10:00―11:00)一、选择题 (每小题10分,共60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 森林里举行比赛,要派出狮子、老虎、豹子和大象中的两个动物去参加.如果派狮子去,那么也要派老虎去;如果不派豹子去,那么也不能派老虎去;要是豹子参加的话,大象可不愿意去.那么,最后能去参加比赛的是().(A)狮子、老虎(B)老虎、豹子(C)狮子、豹子(D)老虎、大象 2. 小明有多张面额为1元、2元和5元的人民币,他想用其中不多于10张的人民币购买一只价格为18元的风筝,要求至少用两种面额的人民币,那么不同的付款方式有()种.(A)3 (B)9 (C)11 (D)8 3. 如右图,在由1?1的正方形组成的网格中,写有2021四个数字(阴影部分).其边线要么是水平或竖直的直线段、要么是连接1?1的正方形相邻两边中点的线段,或者是1?1的正方形的对角线.则图中2021四个数字(阴影部分)的面积是().11(A)47 (B)47 (C)48 (D)48224. 新生入校后,合唱队、田径队和舞蹈队共招收学员100人.如果合唱队招收的人数比田径队多一倍,舞蹈队比合唱队多10人,那么舞蹈队招收()人.(注:每人限加入一个队)(A)30(B)42(C)46(D)525. 一只旧钟的分针和时针每重合一次,需要经过标准时间66分.那么,这只旧钟的24小时比标准时间的24小时().(A)快12分(B)快6分(C)慢6分(D)慢12分6. 一次考试共有6道选择题,评分规则如下:每人先给6分,答对一题加4分,答错一题减1分,不答得0分.现有51名同学参加考试,那么,至少有()人得分相同.(A)3 (B)4 (C)5 (D)6二、填空题(每小题 10 分,共40分)7. 计算: (1000?15?314)?(201?360?110)?(1000?201?360?110)?(15?314)? .8. 角可以用它的两边上的两个大写字母和顶点的字母表示,如右图的?AOB符号(“∠”表示角),也可以用?O表示(顶点处只有一个角时).下图的三角形ABC 中,?BAO??CAO,?CBO??ABO,?ACO??BCO,?AOC?110,O B A 则?CBO? .9. 张叔叔和李叔叔两人年龄和是56岁,当张叔叔是李叔叔现在年龄的一半时,李叔叔当时的年龄是张叔叔现在的年龄.那么张叔叔现在有岁.10. 妈妈决定假期带小花驾车去10个城市旅游,小花查完地图后惊奇地发现:这10个城市的任意三个城市之间或者都开通了高速公路,或者只有两个城市间没有开通高速路.那么这10个城市间至少开通了条高速公路.(注:两个城市间最多只有一条高速公路)感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十届华罗庚金杯少年数学邀请赛初赛
A卷(小学中年级组)
(时间:2015年3月14日10:00—11:00)
一、选择题(每小题10分,共60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)
1.森林里举行比赛,要派出狮子、老虎、豹子和大象中的两个动物去参加.如果派狮
子去,那么也要派老虎去;如果不派豹子去,那么也不能派老虎去;要是豹子参加的话,大象可不愿意去.那么,最后能去参加比赛的是().
(A)狮子、老虎(B)老虎、豹子(C)狮子、豹子(D)老虎、大象
2.小明有多张面额为1元、2元和5元的人民币,他想用其中不多于10张的人民币购
买一只价格为18元的风筝,要求至少用两种面额的人民币,那么不同的付款方式有()种.
(A)3 (B)9 (C)11 (D)8
3.如右图,在由11
⨯的正方形组成的网格中,写有
2015四个数字(阴影部分).其边线要么是水平
或竖直的直线段、要么是连接11
⨯的正方形相邻
两边中点的线段,或者是11
⨯的正方形的对角
线.则图中2015四个数字(阴影部分)的面积是().
(A)47 (B)
1
47
2
(C)48 (D)
1
48
2
4.新生入校后,合唱队、田径队和舞蹈队共招收学员100人.如果合唱队招收的人数
比田径队多一倍,舞蹈队比合唱队多10人,那么舞蹈队招收()人.(注:每人限加入一个队)
(A)30 (B)42 (C)46 (D)52
5. 一只旧钟的分针和时针每重合一次,需要经过标准时间66分.那么,这只旧钟的24
小时比标准时间的24小时( ).
(A )快12分 (B )快6分 (C )慢6分 (D )慢12分
6. 一次考试共有6道选择题,评分规则如下:每人先给6分,答对一题加4分,答错
一题减1分,不答得0分.现有51名同学参加考试,那么,至少有( )人得分相同.
(A )3 (B )4 (C )5 (D )6
二、填空题(每小题 10 分, 共40分)
7. 计算: (100015314)(201360110)(1000201360110)(15314)++⨯+++---⨯+= .
8. 角可以用它的两边上的两个大写字母和顶点的字母表示,如右图
的AOB ∠符号(“∠”表示角),也可以用O ∠表示(顶点处只有一个
角时).下图的三角形ABC 中,BAO CAO ∠=∠, CBO ABO ∠=∠,ACO BCO ∠=∠,110AOC ∠=,
则CBO ∠= .
9. 张叔叔和李叔叔两人年龄和是56岁,当张叔叔是李叔叔现在年龄的一半时,李叔叔
当时的年龄是张叔叔现在的年龄.那么张叔叔现在有 岁.
10. 妈妈决定假期带小花驾车去10个城市旅游,小花查完地图后惊奇地发现:这10个
城市的任意三个城市之间或者都开通了高速公路,或者只有两个城市间没有开通高速路.那么这10个城市间至少开通了 条高速公路.(注:两个城市间最多只有一条高速公路) B A O。
