第三节动点二次函数与等腰三角形存在性问题
二次函数特殊三角形存在性问题(等腰三角形、直角三角形)

特殊图形存在性问题一、等腰三角形1、情景:平面内有点A、B,要找到点P使得△ABP为等腰三角形。
2、思想:分类讨论(1)A为顶点:AB=AP(以A为圆心、AB长为半径画圆)(2)B为顶点:AB=BP(以B为圆心、AB长为半径画圆)(3)P为顶点:PA=PB(AB中垂线)【注】:1.利用两圆一线,找到符合要求的点,如P在抛物线对称轴上,在x轴上等;然后将问题转化为,求线段等长。
2.求线段等长:两点间距离(最笨的方法);向坐标轴做垂线,构造一线三等角例1.如图,抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为______.练习1.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B 两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,−3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.练习2、已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.练习3.如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣x+1与y轴交于点D.(1)求抛物线的解析式;(2)证明:△DBO∽△EBC;(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.练习4.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点,与y轴交于点C(0,−3),其顶点为D.(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x−h)2+k的形式;(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?练习5.如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n (m<n)分别是方程x2﹣2x﹣3=0的两根.(1)求抛物线的解析式;(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E 两点(点D在y轴右侧),连接OD、BD.①当△OPC为等腰三角形时,求点P的坐标;②求△BOD 面积的最大值,并写出此时点D的坐标.25.(10分)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).(Ⅰ)求抛物线的解析式及它的对称轴;(Ⅱ)点P(0,n)在线段OB上,点Q在线段BC上,若OP=2BQ,且P A=QA.求n 的值;(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.19-红桥一模25.(10分)如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.(17河北一模)25(10分)如图,己知抛物线y=x2+bx+c图象经过点A(﹣1,0),B(0,﹣3),抛物线与x轴的另一个交点为C.(1)求这个抛物线的解析式:(2)若抛物线的对称轴上有一动点D,且△BCD为等腰三角形(CB≠CD),试求点D的坐标;二、直角三角形1.情景:平面内有点A、B,要找到点P使得△ABP为直角三角形2.思想:分类讨论(1)A为顶点:∠A(过A做垂线)(2)B为顶点:∠B(过B做垂线)(3)P为顶点:∠C(AB为直径的圆)【注】1.等腰直角三角形,只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A,B与x 轴交于点E,F且B,E两点的坐标分别为B(2,32)E(−1,0)(1)求二次函数的解析式;(2)在抛物线上是否存在点Q,使△QBF为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.练习1.如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=13(1)求抛物线的对称轴和PP的坐标.(2)在抛物线的对称轴上是否存在这样的点D,使△ABD为直角三角形?如果存在,求点D 的坐标;如果不存在,请说明理由.例2.如图,抛物线y=−x2+bx+c与x轴相交于AB两点,与y 轴相交与点C,且点B与点CC 的坐标分别为(3,0),C(0,3),点M是抛物线的顶点.(1)求二次函数的关系式(2)在MB上是否存在点P,过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由练习2.如图,在平面直角坐标系中,直线y=−13x+2交x轴点P,交y轴于点A.抛物线y=x2+bx+c的图象过点E(−1,0),并与直线相交于A、B两点.(1)求抛物线的解析式(关系式);(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;(3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.练习3.如图,抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.(1)求抛物线的解析式;(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.(18东丽-一模)25.如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.(1)直接写出抛物线所对应的函数表达式.(2)当矩形PFOE的面积被抛物线的对称轴平分时,求m的值.(3)当m<2时,求L与m之间的函数关系式.(4)设线段BD与矩形PFOE的边交于点Q,当△FDQ为等腰直角三角形时,直接写出m的取值范围.三、平行四边形存在性问题类型一:1.情景:一直平面内三点A、B、C,求一点P使四边形ABCP为平行四边形2.思想:分类讨论(1)以AC为对角线:ABCP1(2)以AB为对角线:ACBP3(3)以BC为对角线:ACP2B【注】找到P点后,用平行四边形的判定定理,求等长线段,或利用等角度、平行线求坐标即可。
二次函动点问题——等腰三角形存在性问题

二次函动点问题——等腰三角形存在性问题二次函动点问题——等腰三角形都存在性问题1.如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B 两点的抛物线交x轴于另一点C(3,0).(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.2.如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.(1)求此二次函数关系式和点B的坐标;(2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,A、B两点的坐标分别是(0,1)和(1,0),P是线段AB上的一动点(不与A、B重合),坐标为(m,1﹣m)(m为常数).(1)求经过O、P、B三点的抛物线的解析式;(2)当P点在线段AB上移动时,过O、P、B三点的抛物线的对称轴是否会随着P的移动而改变;(3)当P移动到点()时,请你在过O、P、B三点的抛物线上至少找出两点,使每个点都能与P、B两点构成等腰三角形,并求出这两点的坐标.4.图,已知二次函数y=的图象与y轴交于点A,与x轴交于B、C 两点,其对称轴与x轴交于点D,连接AC.(1)点A的坐标为_________,点C的坐标为_________;(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?5.已知抛物线y=+bx+c与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,﹣1).(1)求抛物线的解析式;(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连接DC,当△DCE的面积最大时,求点D的坐标;(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由.6.如图,抛物线y=ax2+2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A(﹣4,0)和B.(1)求该抛物线的解析式;(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CEQ 的面积最大时,求点Q的坐标;(3)平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(﹣2,0).问是否有直线l,使△ODF是等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.。
二次函数与三角形存在性问题

4二次函数与三角形存在性问题(2-3次课)(总17页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--二次函数与三角形存在性问题一、等腰三角形的存在性问题例1、如图,抛物线与x轴交于A、B两点,与y轴交于点C.在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形若存在,请求出符合条件的P点坐标;若不存在,请说明理由。
巩固练习 1、如图,抛物线与轴交于、两点,与轴交于点,已知A(3,0),且M(1,38 )是抛物线上另一点。
连接,设点是轴上任一点,若以、、三点为顶点的三角形是等腰三角形,求点的坐标。
2、如图1,直线与轴、轴分别交于点、点,经过、两点的抛物线与轴的另一个交点为,顶点为。
(1)求该抛物线的解析式。
(2)在该抛物线的对称轴上是否存在点,使以、、为顶点的三角形为等腰三角形若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由。
(3)当<x<3时,在抛物线上求一点,使△CBE的面积有最大值。
(图2、图3供画图探究)二、直角三角形存在性例2、如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)(1)求抛物线的解析式;(2)y轴上是否存在一点N,恰好使得△PNB为直角三角形若存在,直接写出满足条件的所有点N的坐标;若不存在,请说明理由.巩固练习1、如图,抛物线=-x2+2x+3与x轴交于B、E两点,与y轴交于A 点.点P是直线AE上方抛物线上一动点,设点P的横坐标为t,是否存在点P,使△PAE为直角三角形若存在,求出t的值;若不存在,说明理由2、如图,已知直线与抛物线相交于A,B两点,且点为抛物线的顶点,点B在x轴上.若点Q是y轴上一点,且为直角三角形,求点Q的坐标.三、等腰直角三角形存在性例3、在平面直角坐标系中,抛物线3-x与x轴交于A,B两点(A在=x2y2+-B的左侧),与y轴交于点C,顶点为D.(1)请直接写出点A,C,D的坐标;(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;(3)(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形若存在,求出点P的坐标,若不存在,请说明理由.巩固练习1、如图,抛物线bx=2经过A(4,0),B(1,3)两点,点B、C关于抛物线的y+ax对称轴l对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的解析式;(2)若点M在直线BH上运动,点N在x轴上运动,是否存在这样的点M、N,使得以点M为直角顶点△CNM是等腰直角三角形若存在,请求出点M、N的坐标;若不存在,请说明理由.2、如图,已知直线3y与x轴、y轴分别交于A,B两点,抛物=x+-线c-+=2经过A,B两点,点P在线段OA上,从点O出发,向点A以bxxy+每秒1个单位的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B 以每秒2个单位的速度匀速运动,连接PQ,设运动时间为t秒.3、(1)求抛物线的解析式;4、(2)问:当t为何值时,△APQ为等腰直角三角形;四、全等三角形的存在性问题例4、如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)(1)求抛物线的解析式;(2)点M为抛物线上一点,恰使△MOA≌△MOB,求点M的坐标;巩固练习如图,已知直线与抛物线相交于A,B两点,且点为抛物线的顶点,点B在x轴上.(1)求抛物线的解析式;(2)在(1)中抛物线的第二象限图象上是否存在一点P,使与全等若存在,求出点P的坐标;若不存在,请说明理由;五、相似三角形的存在性问题例5、如图,直线与轴、轴分别相交于点、,经过、两点的抛物线与轴的另一个交点为,顶点为,且对称轴为直线2=x 。
二次函数与几何综合专题 等腰直角三角形存在性问题

III、若 是等腰直角三角形,当DM为斜边时,则: ,
即: ,解得 ,
此时: ,
故不存在M坐使 是以DM为斜边的等腰直角三角形;
综上所述:点M坐标为(0,-1).
(3)解:∵ ,
∴ ,
以点P、C、Q为顶点的三角形是等腰直角三角形,有3种情况,
I.当 时,则 ,
∵四边形OHGQ是矩形,
∴ ,
∴ ,
设 ,其中 ,则P点坐标为(x,-x)
∵P在抛物线 上,即 ,解得: (不合题意舍去), ,
故此时P坐标为 ,
综上所述:点P在x轴上方的抛物线上,点Q在y轴正半轴上,当 是以AQ为斜边的等腰直角三角形时,符合条件的点P的坐标 或 .
易得: (AAS)
∴ , ,
∵四边形OHGQ是矩形,
∴ ,
∴ ,
设 ,则P点坐标为(x,x)
∵P在抛物线 上,即 ,解得: , (不合题意舍去),
此时点P坐标为
II、点P在y轴左侧的抛物线上时,如图:
以等腰 构造K字形,过P点作PH⊥x轴,垂足为H,过Q点作QG⊥PH,垂足为G,
易得: (AAS)
∴ , ,
(2)在y轴上是否存在点M,使得 是等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(3)直线AC下方的抛物线上有一动点P,直线AC上有一动点Q,若以点P、C、Q为顶点的三角形是等腰直角三角形,求出点Q的坐标.
(4)点P在x轴上方的抛物线上,点Q在y轴正半轴上,当 是以AQ为斜边的等腰直角三角形时,求出符合条件的点P的坐标.
(2)解:如图,设M点坐标为(0,y)
∵点A坐标为(-3,0),点D坐标为(-1,-4),
二次函数动点与等腰三角形ppt课件

于点D,连接AC、AB.
(1)求该二次函数的表达式;
(2)判断ΔABC的形状,并加以说明;
(3)线段AC上是否存在点E,使得△EDC为等腰三角形?
若存在,直接写出符合条件的点E的坐标;若不存在,请说明理由.
(4)若点P是抛物线上的动点,则能使△PDC称为等腰三角形的点P的个数有____个.
PART 03
方法总结
方法总结
此类代几综合题
通用思路:
几何关系
1、求、设坐标
(定点求出来,动点设出来)
→
代数关系
常用计算工具:
2、分情况讨论表示边长、列方程
(按腰、底边分类,表示长度)
1、勾股定理
3、解方程
2、相似
4、检验
(去掉重合或共线等无法构成三角
形的解)
3、两点距离坐标公式
方法总结
在平面中找点P,使得点P与已知点A、点B构成等腰三角形.
目录
01
考情分析
02
例题讲解
03
方法总结
04
经典例题
PART 01
考情分析
考情分析
1.题目背景:
以二次函数抛物线为载体,探讨是否存在一些点,使其能构成某些特殊的
几何图形,或研究构成几何图形的面积、周长,这是代几综合性问题的一种重
01
要考察形式,也是各地中考中常见的考点,这类问题有以下常见的形式:
第一类点:图1所示,以AB为底,做AB的垂直平分线,则垂直平分线上的点(除
AB中点外都可构成等腰三角形)
第二类点:图2所示,以AB为腰,分别以A、B为圆心,AB的长为半径画圆,则两
二次函数的动点问题(等腰、直角三角形的存在性问题)解析

_ Q_ G_P_ O二次函数中的动点问题 三角形的存在性问题一、技巧提炼1、利用待定系数法求抛物线解析式的常用形式(1)、【一般式】已知抛物线上任意三点时,通常设解析式为 ,然后解三元方程组求解; (2)、【顶点式】已知抛物线的顶点坐标和抛物线上另一点时,通常设解析式为 求解; 2、二次函数y=ax 2+bx+c 与x 轴是否有交点,可以用方程ax 2+bx+c = 0是否有根的情况进行判定;判别式ac b 42-=∆ 二次函数与x 轴的交点情况一元二次方程根的情况△ > 0 与x 轴 交点 方程有 的实数根△ < 0 与x 轴 交点 实数根 △ = 0与x 轴 交点方程有 的实数根3、抛物线上有两个点为A (x 1,y ),B (x 2,y ) (1)对称轴是直线2x 21x x +=(2)两点之间距离公式:已知两点()()2211y ,x Q ,y ,x P , 则由勾股定理可得:221221)()(y y x x PQ -+-=练一练:已知A (0,5)和B (-2,3),则AB = 。
4、 常见考察形式1)已知A (1,0),B (0,2),请在下面的平面直角坐标系 坐标轴上找一点C ,使△ABC 是等腰三角形; 总结:两圆一线方法规律:平面直角坐标系中已知一条线段,构造等腰三角形,用的是“两圆一线”:分别以线段的两个端点为圆心,线段长度为半径作圆,再作线段的垂直平分线;2)已知A (-2,0),B (1,3),请在平面直角坐标系中坐标轴 上找一点C ,使△ABC 是直角三角形;总结: 两线一圆方法规律{平面直角坐标系中已知一条线段,构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆; 5、求三角形的面积:(1)直接用面积公式计算;(2)割补法;(3)铅垂高法; 如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线, 外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的 这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h ). 我们可得出一种计算三角形面积的新方法:S △ABC =12ah ,即三角形面积等于水平宽与铅垂高乘积的一半。
二次函数中等腰三角形的存在问题

零点是函数图像与x轴相交的点,用于解方程 和确定函数的根。
二次函数的最值是函数图像的最高点(最大 值)或最低点(最小值),在寻求极值时非 常重要。Leabharlann II. 等腰三角形的性质定义
等腰三角形是一种具有两条边相等的三角形, 拥有一些特殊的性质和几何关系。
面积
等腰三角形的面积可以通过底边的长度和高度 来计算,其中高度与等边的长度有关。
2. Johnson, L. (2019). "Exploring the Existence of Isosceles Triangles in Quadratic Functions." Geometrical Review, 30(4), 267-286.
3. Wang, Y. (2018). "Applications of Isosceles Triangles in Quadratic Function Analysis." Mathematica, 55(3), 189-205.
二次函数中等腰三角形的 存在问题
本演示将探讨二次函数中等腰三角形的存在问题。我们将介绍二次函数和等 腰三角形的基本概念,并深入研究二次函数中等腰三角形的性质及其应用。
I. 介绍
二次函数
二次函数是一个具有二次方的多项式函数,可呈现多种形态和特征。
等腰三角形
等腰三角形是一种具有两条边相等的三角形,具有一些特殊的几何性质。
周长
等腰三角形的周长可以通过两条等边的长度和 第三条边的长度来计算。
内角
等腰三角形的内角具有特定的测量值,其中包 括基角、等边角和顶角。
IV. 二次函数中等腰三角形的探讨
1
确定三角形三个顶点坐标
专题 二次函数与等腰三角形有关的问题(知识解读)-中考数学(全国通用)

专题06 二次函数与等腰三角形有关的问题(知识解读)【专题说明】二次函数之等腰三角形存在性问题,主要指的是在平面直角坐标系下,已知一条边(或两个顶点)的等腰三角形存在,求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。
【解题思路】等腰三角形的存在性问题【方法1 几何法】“两圆一线”(1)以点A为圆心,AB为半径作圆,与x轴的交点即为满足条件的点C,有AB=AC;(2)以点B为圆心,AB为半径作圆,与x轴的交点即为满足条件的点C,有BA=BC;(3)作AB的垂直平分线,与x轴的交点即为满足条件的点C,有CA=CB.注意:若有重合的情况,则需排除.以点C1 为例,具体求点坐标:过点A作AH⊥x轴交x轴于点H,则AH=1,又32121131311==-=∴=HC AC ,()03211,坐标为故点-C类似可求点 C 2 、C 3、C 4 .关于点 C 5 考虑另一种方法.【方法2 代数法】点-线-方程表示点:设点C 5坐标为(m ,0),又A (1,1)、B (4,3),表示线段:11-m 225+=)(AC 94-m 225+=)(BC 联立方程:914-m 1-m 22+=+)()(,623m =解得:,),坐标为(故点06232C总结:【典例分析】【考点1 等腰角形的存在性】【典例1】(2020•泰安)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A (﹣4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,﹣2),连接AE.(1)求二次函数的表达式;(2)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标,若不存在,请说明理由.【变式11】(2022•澄海区模拟)如图,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,点A的坐标为(﹣1,0),点C坐标为(0,3),对称轴为x=1.点M为线段OB上的一个动点(不与两端点重合),过点M作PM⊥x轴,交抛物线于点P,交BC 于点Q.(1)求抛物线及直线BC的表达式;(2)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.【变式1-2】(2022•荣昌区自主招生)如图,在平面直角坐标系中,抛物线y=ax2+x+c (a≠0)与x轴交于A(﹣1,0),B(4,0),与y轴交于点C.(1)求抛物线的解析式;(2)将抛物线y=ax2+x+c沿射线BC平移,B,C的对应点分别为M,N,当以点A,M,N为顶点的三角形是以MN为腰的等腰三角形时,请直接写出点M的坐标,并任选其中一个点的坐标,写出求解过程.【典例2】(2020•贵港)如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与线段BC 交于点M,连接PC.当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.【变式2-1】(2022•东营)如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C.(1)求抛物线的表达式;(2)在对称轴上找一点Q,使△ACQ的周长最小,求点Q的坐标;(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当△PMB是以PB为腰的等腰直角三角形时,请直接写出所有点M的坐标.【变式2-1】(2021•大渡口区自主招生)如图,若抛物线y=x2+bx+c与x轴相交于A,B 两点,与y轴相交于点C,直线y=x﹣3经过点B,C.(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.专题06 二次函数与等腰三角形有关的问题(知识解读)【专题说明】二次函数之等腰三角形存在性问题,主要指的是在平面直角坐标系下,已知一条边(或两个顶点)的等腰三角形存在,求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。
【中考2021】二次函数与等腰三角形存在性问题

【中考2021】二次函数与等腰三角形存在性问题
写在前面
距离中考的时间只剩不到30天,为了帮助广大初三考生能在未来的中考中取得好成绩,笔者开设了《中考2021》专题突破的系列专栏,结合自身收集的好题与优质公众号的内容,以及笔者的《领跑数学中考二轮专题复习》,对一些热门中考内容作一个整理,今天分享专题——二次函数与等腰三角形存在性问题!
动态几何问题是近年来中考的热点问题,以运动的观点来探究几何图形的变化规律问题,动态问题的解答,一般要将动态问题转化为静态问题,抓住运动过程中的不变量,利用不变的关系和几何性质建立关于方程(组)、函数关系问题,将几何问题转化为代数问题。
在动态问题中,动点形成的等腰三角形问题是常见的一类题型,可以与旋转、平移、对称等几何变化相结合,也可以与一次函数、反比例函数、二次函数的图象相结合,从而产生数与形的完美结合.解决动点产生的等腰三角形问题的重点和难点在于应用分类讨论思想和数形结合思想进行准确的分类.
方法指点
典例精析
01
02
03
04。
专题一:二次函数中等腰三角形存在性问题

专题:二次函数中等腰三角形存在性问题类型一、等腰三角形存在性问题以(,)A A A x y 、(,)B B B x y 为三角形的边,在x 轴上找一点P 使得△PAB 为等腰三角形(二定一动)一.找法:画圆和作垂直平分线①以A 为圆心,线段AB 为半径画圆,与x 轴交点即为1P 、2P 点;(AB=AP )②以B 为圆心,线段AB 为半径画圆,与x 轴交点即为3P 、4P 点;(AB=BP )③作线段AB 的垂直平分线,与x 轴交点即为5P 点;(AP=BP )二、算法:利用两点距离公式进行计算 公式:22()()A B A B AB x x y y =-+- ,设(,)p p P x y ,分三种情况:①AB=AP 时 2222()()()()A B A B A P A P x x y y x x y y -+-=-+-可得1P 、2P ,(特殊情况可能是一个点,例如2P 与B 重合)②AB=BP 时2222()()()()A B A B B P B P x x y y x x y y -+-=-+-可得3P 、4P ,(特殊情况可能是一个点,例如3P 与A 重合)③AP=BP 时2222()()()()A P A P B P B P x x y y x x y y -+-=-+-可得5P 、例题1、如图,已知二次函数2y x bx c =++的图像与x 轴交于点A 、B 两点,其中A 点坐标为(-3,0),与y 轴交于点C ,点D (-2,-3)在抛物线上.(1)求抛物线的表达式;(2)抛物线的对称轴上是否存在动点Q ,使得△BCQ 为等腰三角形?若存在,求出点Q 的坐标;若不存在,说明理由.1、(2021·云南九年级一模)如图所示,抛物线()240y ax bx a =++≠经过点()1,0A -,点()4,0B ,与y 轴交于点C ,连接AC ,BC .点M 是线段OB 上不与点O 、B 重合的点,过点M 作DM x ⊥轴,交抛物线于点D ,交BC 于点E .(1)求抛物线的表达式;(2)过点D 作DF BC ⊥,垂足为点F .设M 点的坐标为(),0M m ,请用含m 的代数式表示线段DF 的长,并求出当m 为何值时DF 有最大值,最大值是多少?(3)试探究是否存在这样的点E ,使得以A ,C ,E 为顶点的三角形是等腰三角形.若存在,请求出此时点E 的坐标;若不存在,请说明理由.2、(八中2020级初三第三次月考)如图在平面直角坐标系中,已知抛物线2(0)y ax bx c a =++≠交x 轴于A (-4,0),B (1,0),交y 轴于C (0,3)(1)求此抛物线解析式;(2)如图1,点P 为直线AC 上方抛物线上一点,过点P 作PQ ⊥x 轴于点Q ,再过点Q 作QR//AC 交y 轴于点R ,求PQ+QR 的最大值及此时点P 的坐标;(3)如图2,点E 在抛物线上,横坐标为-3,连接AE ,将线段AE 沿直线AC 平移,得到线段''A E ,连接'CE ,当△''A E C 为等腰三角形时,只写写出点'A 的坐标。
二次函数动点问题(等腰、直角三角形存在性问题).docx
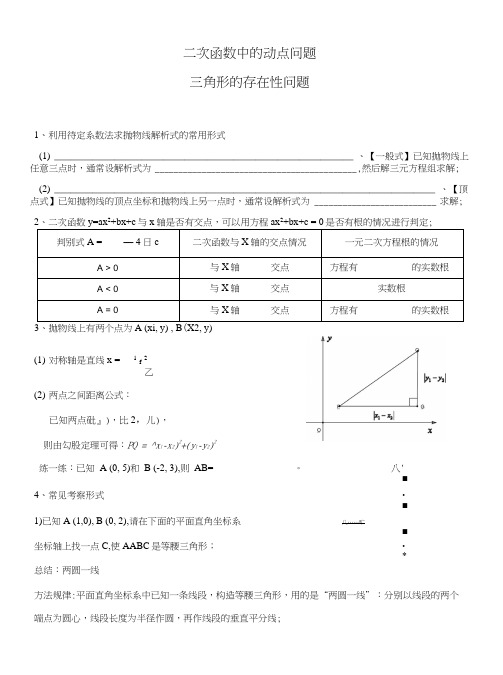
二次函数中的动点问题三角形的存在性问题1、利用待定系数法求抛物线解析式的常用形式(1)_______________________________________________________ 、【一般式】已知抛物线上任意三点时,通常设解析式为___________________________________________ ,然后解三元方程组求解;(2)______________________________________________________________________ 、【顶点式】已知抛物线的顶点坐标和抛物线上另一点时,通常设解析式为 __________________________ 求解;、二次函数2与轴是否有交点,可以用方程2是否有根的情况进行判定;判别式A = — 4日c二次函数与X轴的交点情况一元二次方程根的情况A > 0与X轴交点方程有的实数根A < 0与X轴交点实数根A = 0与X轴交点方程有的实数根3、抛物线上有两个点为A (xi, y) , B(X2, y)(1)对称轴是直线x = 1f2乙(2)两点之间距离公式:已知两点砒』),比2,儿),则由勾股定理可得:PQ = ^x l-x2)2+(y l-y2)2练一练:已知A (0, 5)和B (-2, 3),则AB= _______________ 。
八'■4、常见考察形式•■1)已知A (1,0), B (0, 2),请在下面的平面直角坐标系八……旷■坐标轴上找一点C,使AABC是等腰三角形;•*总结:两圆一线方法规律:平面直角坐标系中已知一条线段,构造等腰三角形,用的是“两圆一线”:分别以线段的两个端点为圆心,线段长度为半径作圆,再作线段的垂直平分线;2)已知A (-2,0), B (1, 3),请在平面直角坐标系中坐标轴上找一点C,使AABC是直角三角形;总结:两线一圆方法规律{平面直角坐标系中已知一条线段,构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆;5、求三角形的面积:(1)直接用面积公式计算;(2)割补法;(3)铅垂高法;如图,过AABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫AABC的“水平宽”(a),中间的这条直线在AABC内部线段的长度叫AABC的“铅垂高” (h).我们可得岀一种计算三角形面积的新方法:SgBC=|ah,即三角形面积等于水平宽与铅垂高乘积的一半。
第三节 动点--二次函数与等腰三角形存在性问题

动点问题—二次函数中等腰三角形存在性问题方法总结:假设结论成立;当所给条件中没有说明哪条边是等腰三角形的底、哪条是腰时,要对其进行分类讨论,假设某两条边相等,等到三种情况;设未知量,求边长,在每种情况下,直接或间接设出所求点的坐标,并用所设点坐标表示出假设相等的两条边的长或第三边的长;④计算求解,根据等腰三角形的性质或利用勾股定理或相似三角形的性质列等量关系式,根据等量关系式求解即可。
典型例题:例1.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点P,使△POC是以OC为底边的等腰三角形若存在,求出P点坐标;若不存在,请说明理由;(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.例2.如图,抛物线y=﹣221x+nmx 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形如果存在,直接写出P 点的坐标;如果不存在,请说明理由;(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大求出四边形CDBF的最大面积及此时E点的坐标.例3.如图,二次函数212y x bx c =-++的图象经过A(2,0),B(0,-6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x 轴交于点C ,连接BA ,BC ,求△ABC 的面积.(3)在x 轴上是否存在一点P ,使△ABP 为等腰三角形,若存在,求出P 的坐标,若不存在,说明理由.例4. (2014•绵阳)如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,),顶点坐标为N(﹣1,),且与x轴交于A、B两点,与y轴交于C点.(1)求抛物线的解析式;(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;(3)在直线AC上是否存在一点Q,使△QBM的周长最小若存在,求出Q点坐标;若不存在,请说明理由.例5. (2014年四川资阳)如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.(1)求抛物线的解析式;(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;例6.如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.(1)求出二次函数的解析式;(2)当点P在直线OA的上方时,用含m的代数式表示线段PC的长,并求线段PC的最大值;(3)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,如果存在,请直接写出所有P的坐标;如果不存在,请说明理由.例8.如图,抛物线2323y x x 63-=与x 轴交于点A ,将线段OA 绕点O 逆时针旋转1200至OB 的位置. (1)点B 在抛物线上;(2)在此抛物线的对称轴上,是否存在点P ,使得以点P 、O 、B 为顶点的三角形是等腰三角形若存在,求点P 的坐标;若不存在,说明理由.例9.如图,在平面直角坐标系中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C (8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.(1)求该二次函数的解析式;(2)如图1,连结BC ,在线段BC 上是否存在点E ,使得△CDE 为等腰三角形若存在,求出所有符合条件的点E 的坐标;若不存在,请说明理由;(3)如图2,若点P (m ,n )是该二次函数图象上的一个动点(其中m >0,n <0),连结PB ,PD ,BD ,求△BDP 面积的最大值及此时点P 的坐标.例10.如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,例11.如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为x 轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.(1)求∠DAB的度数及A、D、C三点的坐标;(2)求过A、D、C三点的抛物线的解析式及其对称轴L.(3)若P是抛物线的对称轴L上的点,那么使 PDB为等腰三角形的点P有几个(不必求点P的坐标,只需说明理由)例12.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形请直接写出相应的t值.。
二次函数的动点问题(等腰、直角三角形的存在性问题)

_ Q_ G_P_ O二次函数中的动点问题 三角形的存在性问题一、技巧提炼1、利用待定系数法求抛物线解析式的常用形式(1)、【一般式】已知抛物线上任意三点时,通常设解析式为 ,然后解三元方程组求解; (2)、【顶点式】已知抛物线的顶点坐标和抛物线上另一点时,通常设解析式为 求解; 2、二次函数y=ax 2+bx+c 与x 轴是否有交点,可以用方程ax 2+bx+c = 0是否有根的情况进行判定;判别式ac b 42-=∆ 二次函数与x 轴的交点情况一元二次方程根的情况△ > 0 与x 轴 交点 方程有 的实数根△ < 0 与x 轴 交点 实数根 △ = 0与x 轴 交点方程有 的实数根3、抛物线上有两个点为A (x 1,y ),B (x 2,y ) (1)对称轴是直线2x 21x x +=(2)两点之间距离公式:已知两点()()2211y ,x Q ,y ,x P , 则由勾股定理可得:221221)()(y y x x PQ -+-=练一练:已知A (0,5)和B (-2,3),则AB = 。
4、 常见考察形式1)已知A (1,0),B (0,2),请在下面的平面直角坐标系 坐标轴上找一点C ,使△ABC 是等腰三角形; 总结:两圆一线方法规律:平面直角坐标系中已知一条线段,构造等腰三角形,用的是“两圆一线”:分别以线段的两个端点为圆心,线段长度为半径作圆,再作线段的垂直平分线;2)已知A (-2,0),B (1,3),请在平面直角坐标系中坐标轴 上找一点C ,使△ABC 是直角三角形;总结: 两线一圆方法规律{平面直角坐标系中已知一条线段,构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆; 5、求三角形的面积:(1)直接用面积公式计算;(2)割补法;(3)铅垂高法; 如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线, 外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的 这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h ). 我们可得出一种计算三角形面积的新方法:S △ABC =12ah ,即三角形面积等于水平宽与铅垂高乘积的一半。
二次函数中存在性问题(等腰三角形存在性问题)

二次函数中的存在性问题 (等腰三角形 )[07 福建龙岩 ]如图,抛物线y ax 2 5ax 4 经过 △ ABC 的三个极点,y已知 BC ∥ x 轴,点 A 在 x 轴上,点 C 在 y 轴上,且 ACBC .CB(1)求抛物线的对称轴;1(2)写出 A , B , C 三点的坐标并求抛物线的分析式;A(3)研究:若点P 是抛物线对称轴上且在x 轴下方的动点,1 x能否存在 △ PAB 是等腰三角形.若存在,求出全部切合条 件的点 P 坐标;不存在,请说明原因.解:( 1)抛物线的对称轴 x 5a 52a2y(2) A( 3,0)B(5,4)C (0,4)CMB把点 A 坐标代入 yax 25ax 4 中,解得 a1A1N6Qx151P 3x 2Kyx 466P 共有 3 个.以下分三类情况研究.P 2(3)存在切合条件的点设抛物线对称轴与 x 轴交于 N ,与 CB 交于 M .P 1过点 B 作 BQx 轴于 Q ,易得 BQ4 , AQ 8 , AN5.5 , BM52① 以 AB 为腰且顶角为角A 的 △ PAB 有 1 个: △ P 1AB .AB 2 AQ 2 BQ 2 82 4280在 Rt △ ANP 中, PNAP 2 AN 2AB 2 AN 280(5.5) 2199 P 1 5 ,199111222② AB 为腰且顶角为角B 的 △PAB 有 1 个: △ P 2 AB .在 Rt △ BMP 2 中, MP 2 22AB22252955 8295BP 2BMBM 802P 2 2 ,42③以 AB 为底,顶角为角P 的 △ PAB 有 1 个,即 △ P 3 AB .画 AB 的垂直均分线交抛物线对称轴于P 3 ,此时均分线必过等腰 △ ABC 的极点 C .过点 3 作P 3 K 垂直y 轴,垂足为 K,明显Rt △ 3∽ Rt △ BAQ .P 3KBQ 1.PPCKCKAQ2Q P 3 KCK 5 于是 OK1P 3, 1)[07 广西河池 ]如图,已知抛物线y 2 x24x 2的图象与 x 轴交于 A,B 两点,与 y 轴交于点 C,抛物33线的对称轴与 x 轴交于点 D.点 M 从 O 点出发,以每秒 1 个单位长度yP的速度向 B 运动,过 M 作 x 轴的垂线,交抛物线于点P,交 BC 于 Q.C(1)求点 B 和点 C 的坐标;Q(2)设当点 M 运动了 x(秒)时,四边形OBPC 的面积为 S,求 S 与 x 的函数关系式,并指出自变量x 的取值范围.B xA(3)在线段 BC 上能否存在点Q,使得△ DBQ 成为以 BQ 为一腰的ODM等腰三角形?若存在,求出点Q 的坐标,若不存在,说明原因.(1)把 x =0 代入y 2 x2 4 x2得点 C 的坐标为 C( 0, 2)33把 y =0 代入y2x24x 2 得点B的坐标为B(3,0)3 3(2)连接 OP,设点 P 的坐标为 P( x, y)四边形 OBPC =S△OPC+S△OPB=12x13y = x3 2 x24x 2= x23x 3S22233∵点 M 运动到 B 点上停止,∴0≤ x ≤ 32∴ S x33( 0≤ x ≤ 3 )24(3)存在. BC= OB2OC2=13①若 BQ = DQ∵ BQ = DQ ,BD = 2∴ BM = 1∴ OM = 3 1 = 2∴ tan OBC QM OC2∴ QM =2因此 Q 的坐标为 Q ( 2,2).BM OB333②若 BQ=BD=2∵ △ BQM ∽△ BCO,∴BQ QM BM==BO BC CO∴2QM∴ QM =4 13 13=213∵ BQ= BM∴2=BM BC OB133∴ BM = 613∴ OM =3613··························11 分1313因此 Q 的坐标为 Q (3613, 4 13)···························12 分1313[07 年云南省 ]已知:如图,抛物线y ax2bx c 经过 A (1, 0) 、 B (5 , 0) 、 C (0 , 5) 三点.(1)求抛物线的函数关系式;y(2)若过点 C 的直线y kx b 与抛物线订交于点E(4,m),C恳求出△ CBE 的面积 S的值;(3)在抛物线上求一点P0使得△ABP0为等腰三角形并1A–O B x 1写出 P0点的坐标;E(4)除( 3)中所求的P0点外,在抛物线上能否还存在其他的点P 使得△ ABP 为等腰三角形?若存在,请求出一共有几个知足条件的点P(要求简要说明原因,但不证明);若不存在这样的点P ,请说明原因.解:( 1)∵抛物线经过点A(1, 0)、 B(5 , 0)∴ y a(x 1)(x5) .又∵抛物线经过点 C(0 , 5)∴ 5a 5 , a 1 .∴抛物线的分析式为y( x1)(x5)x2 6 x 5 .( 2)∵ E 点在抛物线上,∴ m = 42–4× 6+5 = - 3.∵直线 y = kx+b 过点 C(0, 5)、E( 4,–3),∴ b 5,解得 k = - 2,b = 5.4k b 3.设直线 y=- 2x+5 与 x 轴的交点为 D ,当 y=0 时, - 2x+5=0 ,解得 x=5.∴D 点的坐标为(5,0).22∴ S=S BDC + S BDE=1(5515 3 =10.)5+(5)△△2222(3)∵抛物线的极点P0(3 ,4)既在抛物线的对称轴上又在抛物线上,∴点 P0 (3 , 4) 为所求知足条件的点.(4)除P0点外,在抛物线上还存在其他的点P 使得△ ABP 为等腰三角形.原因以下:∵ AP0BP02242254,∴分别以 A 、 B 为圆心半径长为 4 画圆,分别与抛物线交于点 B 、P1、P2、P3、 A 、P4、P5、P6,除掉 B 、 A 两个点外,其他 6 个点为知足条件的点.(说明:只说出P 点个数但未简要说明原因的不给分)[07 山东威海 ]如图①, 在平面直角坐标系中,点 A 的坐标为 (12), ,点 B 的坐标为 (31), ,二次函数yx 2的图象记为抛物线 l 1 .( 1)平移抛物线 l 1 ,使平移后的抛物线过点 A ,但可是点 B ,写出平移后的一个抛物线的函数表达式:(任写一个即可) .(2)平移抛物线 l 1 ,使平移后的抛物线过 A , B 两点,记为抛物线 l 2 ,如图②,求抛物线l 2 的函数表达式.(3)设抛物线l 2 的极点为C , K 为y 轴上一点.若△△ABC ,求点 K 的坐标.S ABK S(4)请在图③上用尺规作图的方式研究抛物线 l 2 上能否存在点 P ,使 △ ABP 为等腰三角形.若存在,请判断点 P 共有几个可能的地点(保存作图印迹);若不存在,请说明原因.yyl 2yl 1l 21AB1 AB AxCx1BxO1OO11图①图②图③解:( 1)有多种答案,切合条件即可.比如 yx 2 1, yx 2x , y ( x 1)22或 y x 22x 3 , y (x2 1)2 , y ( x 12) 2 .yl 2(2)设抛物线 l 2 的函数表达式为 yx 2 bx c ,KQ 点 A(12), , B(31), 在抛物线 l 2 上,GABxCOb 9 ,D F E1 b c,29 11图②2解得2抛物线 l 2 的函数表达式为 y.9 3b c 1 11.xxc222911927, C 点的坐标为9 ,7(3) yx 2 x x .2 2 4164 16过 A , B ,C 三点分别作 x 轴的垂线,垂足分别为 D ,E ,F ,则 AD2 , CF7, BE 1, DE 2 , DF5, FE3 .1644S 梯形S 梯形15延伸 BA 交 y 轴于点 G ,设直线 AB 的函数表达式为ymx n ,Q 点 A(12), , B(31), 在直线 AB 上,2 m, m1 ,1 55 n2直线 AB 的函数表达式为y. G 点的坐标为解得5 .x0, .1 3m n.n2222设 K 点坐标为 (0, h) ,分两种状况:若 K 点位于 G 点的上方,则KG h5.连接 AK , BK .2S △ ABKS △ BKG S △ AKG1 3 h 51 1 h 5h 5 .22222Q S △ ABK15h5 15 ,解得 h55 K 点的坐标为55S △ ABC,2 16. 0,.161616若 K 点位于 G 点的下方,则KG5 h .同理可得,h25 .K 点的坐标为25.216 0,16(4)作图印迹如图③所示.由图③可知,点P 共有 3 个可能的地点.yl 2注:作出线段 AB 的中垂线得1 分,画出此外两段弧得1 分.ABxO图③[07 山东泰安 ]如图,在 △OAB 中, B90o , BOA 30o , OA 4,将 △OAB 绕点 O 按逆时针方向旋转至 △OA B , C 点的坐标为( 0,4).(1)求 A 点的坐标;(2)求过 C , A , A 三点的抛物线 y ax2bx c 的分析式;(3)在( 2)中的抛物线上能否存在点P ,使以 O ,A ,P 为极点的三角形是等腰直角三角形?若存在,求出全部点P 的坐标;若不存在,请说明原因 解:( 1)过点 A 作 A D 垂直于 x 轴,垂足为 D , 则四边形 OB A D 为矩形在 △ A DO 中, A DOA sinA OD 4 sin 60o 2 3yCBABOA xOD A B AB 2 点A 的坐标为 (2,2 3)(2) Q C (0,4) 在抛物线上,c 4yax 2 bx 4Q A(4,0) , A (2,2 3) ,在抛物线 yax 2 bx 4 上16a 4b 4 0,a 1324a 2b42 解之得3b 2 3 3所求分析式为 y3 x 2 (2 3 3) x4 .2(3)①若以点 O 为直角极点,因为 OC OA 4 ,点 C 在抛物线上,则点 C (0,4) 为知足条件的点.②若以点 A 为直角极点,则使△PAO 为等腰直角三角形的点P 的坐标应为 (4,4) 或 (4, 4) ,经计算知;此两点不在抛物线上.③若以点 P 为直角极点,则使△PAO 为等腰直角三角形的点 P 的坐标应为 (2,2) 或 (2, 2) ,经计算知;此两点也不在抛物线上.综上述在抛物线上只有一点P(0,4) 使 △OAP 为等腰直角三角形[08 广东梅州 ]如图 11 所示,在梯形 ABCD 中,已知 AB∥ CD , AD ⊥ DB , AD=DC=CB, AB=4.以 AB 所在直线为x轴,过 D 且垂直于AB 的直线为y 轴成立平面直角坐标系.(1)求∠ DAB 的度数及A、D 、C 三点的坐标;(2)求过 A、 D、 C 三点的抛物线的分析式及其对称轴L .(3)若 P 是抛物线的对称轴L 上的点,那么使PDB 为等腰三角形的点P 有几个 ?(不用求点P 的坐标,只要说明原因)解:(1)DC∥ AB, AD =DC=CB,∠ CDB=∠ CBD=∠ DBA,∠ DAB =∠ CBA ,∠ DAB=2∠ DBA,∠DAB+∠ DBA =90 ,∠DAB =60,∠DBA=30 , AB=4 ,DC =AD=2 ,Rt AOD, OA=1, OD= 3 ,.A( - 1, 0), D (0, 3 ),C(2, 3 ).( 2)依据抛物线和等腰梯形的对称性知,知足条件的抛物线必过点A(- 1,0), B( 3, 0),故可设所求为y = a ( x +1)( x -3)将点 D ( 0, 3 )的坐标代入上式得, a =3.3所求抛物线的分析式为y =3(x1)( x3).·················7分3其对称轴L 为直线x =1.·····································8分( 3)PDB 为等腰三角形,有以下三种状况:①因直线 L 与 DB 不平行, DB 的垂直均分线与L 仅有一个交点 P1,P1D =P1B,P1DB 为等腰三角形;······································9 分②因为以 D 为圆心,DB 为半径的圆与直线L 有两个交点 P232323、P ,DB =DP ,DB =DP ,P DB,P DB 为等腰三角形;③与②同理, L 上也有两个点 P4、 P5,使得 BD=BP4, BD=BP5.··········10 分因为以上各点互不重合,因此在直线L 上,使PDB 为等腰三角形的点P 有 5 个.[08 福建南平 ]如图,平面直角坐标系中有一矩形纸片OABC , O 为原点,点 A ,C 分别在 x 轴, y 轴上,点 B 坐标为 (m , 2) (此中 m0 ),在 BC 边上选用适合的点 E 和点 F ,将 △OCE 沿 OE 翻折,获得△OGE ;再将 △ ABF 沿 AF 翻折,恰巧使点 B 与点 G 重合,获得 △AGF ,且OGA 90o .( 1)求 m 的值;(2)求过点 O ,G ,A 的抛物线的分析式和对称轴; ( 3)在抛物线的对称轴 上能否存在点 P ,使得 △OPG 是...等腰三角形?若不存在,请说明原因;若存在,直接答出....全部知足条件的点 P 的坐标(不要求写出求解过程) .( 1) Q B( m , 2) ,由题意可知 AG AB2 , OG OC2 , OA mQ OGA 90o ,OG 2AG 2OA 22 2m 2 .又 Q m 0 ,m 2(2)过 G 作直线 GH x 轴于 H ,则 OH 1 , HG1,故 G (11), .又由( 1)知 A(2,0) ,设过 O ,G ,A 三点的抛物线分析式为yax 2 bx cQ 抛物线过原点,c 0 .a b 1a 1又Q 抛物线过 G , A 两点, 2b 0解得24ab所求抛物线为 yx 2 2x它的对称轴为 x1 .(3)答:存在 ,知足条件的点 P 有 (10), , (1, 1) , (11,2) , (11, 2) .[08 湖南株洲 ]如 ( 1),在平面直角坐 系中,点A 的坐 ( 1,- 2),点B 的坐 ( 3, - 1),二次函数 yx 2 的 象 l 1 .( 1)平移抛物 l 1 ,使平移后的抛物 点A ,但不 点 B ,写出平移后的抛物 的一个分析式(任写一个即可) .( 2)平移抛物 l 1 ,使平移后的抛物A 、B 两点, 抛物l 2 ,如 ( 2),求抛物 l 2 的函数解析式及 点 C 的坐 .( 3) P y 上一点,且 S ABC S ABP ,求点 P 的坐 .( 4) 在 ( 2)上用尺 作 的方式研究抛物l 2 上能否存在点Q ,使 QAB 等腰三角形 . 若存在,判断点 Q 共有几个可能的地点(保存作 印迹);若不存在, 明原因 .yyoxoxl 1l 2( 1)( 2)(1) yx 2 2 x 3或 yx 24x 5等 ( 足条件即可)⋯⋯ 1 分(2) l 2 的分析式 yx 2bx c , 立方程2 1 b c ,1 9 3bc解得: b9 , c 11, l 2 的分析式 yx 2 9 x 11 ,⋯⋯ 3 分2222点 C 的坐 ( 9,7 ) ⋯⋯ 4 分4 167 ,( 3)如答23- 1, 点 A 、 B 、C 三点分 作 x 的垂 ,垂足分 D 、E 、F , AD2 , CF5,FE3 . 16BE 1, DE2 , DF4415 .得:S ABCS梯形 ABEDS梯形 BCFES梯形ACFD⋯⋯ 5 分16延 BA 交 y 于点 G ,直 AB 的分析式y1 5 , 点 G 的坐 ( 0, 5), 点 P 的坐2x22( 0, h )①当点P 位于点G 的下方,PG 5AP 、 BP,S ABP S BPG S APG5h ,h ,又22S ABC S ABP 15,得h55,点 P 的坐(0,55 ).⋯⋯ 6 分161651625 ).②当点 P 位于点 G 的上方,PG,同理h25,点 P 的坐( 0,h1616 2上所述所求点P 的坐( 0,55)或( 0,25 )⋯⋯ 7 分1616(4)作印迹如答 23-2 所示 .由可知,足条件的点有Q1、 Q2、Q3、 Q4,共 4 个可能的地点.⋯⋯10 分F E答 23-1答 23-211 / 12[08 浙江温州 ]如图,在 Rt △ ABC 中, A 90o , AB 6 , AC 8 , D ,E 分别是边 AB ,AC 的中点,点 P 从点 D 出发沿 DE 方向运动,过点P 作 PQ BC 于 Q ,过点 Q 作 QR ∥ BA 交 AC 于R ,当点 Q 与点 C 重合时,点 P 停止运动.设 BQx , QRy .A(1)求点 D 到 BC 的距离 DH 的长;PR(2)求 y 对于 x 的函数关系式(不要求写出自变量的取值范围) ;D E(3)能否存在点P ,使 △ PQR 为等腰三角形?若存在,BH QC恳求出全部知足要求的 x 的值;若不存在,请说明原因.解:( 1)QARt , AB 6 , AC 8,BC 10 .Q 点 D 为 AB 中点, BD 1 3 .AB2Q DHBA 90o , BB . △BHD ∽△ BAC , DH BD , DHBDgAC3 8 12 .ACBCBC10 5(2) Q QR ∥ AB , QRCA 90o .Q CC , △ RQC ∽△ ABC ,RQ QC,y10 xABBC 610 , A3即 y 对于 x 的函数关系式为:y6 . DP RxE(3)存在,分三种状况:51 MBH Q2C①当 PQ PR 时,过点 P 作 PMQR 于 M ,则 QMRM .Q 1290o , C2 90o ,1C .cos 1cosC8 4 , A10 5QM 41 3 x 6 418 DPE,25,RQP5125x.5BHQC5②当 PQRQ 时,3 x 6 12 , x 6 . A55③当 PRQR 时,则 R 为 PQ 中垂线上的点,于是点R 为 EC 的中点,DE PR 11QR BA2 . Q tanCBHQ CCRCE ACCR,24CA3 x 6 61518 或 6 或 15时, △ PQR 为等腰三角形. 5 , x .综上所述,当 x 为28 2 5 211二次函数中的存在性问题(直角三角形 )[08 辽宁十二市 ]如图 16,在平面直角坐标系中,直线y3x 3 与 x 轴交于点 A ,与 y 轴交于点C,抛物线 y ax22 3x c(a 0) 经过A,B,C三点.3(1)求过A,B,C三点抛物线的分析式并求出极点 F 的坐标;(2)在抛物线上能否存在点P ,使△ ABP 为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明原因;(3)尝试究在直线AC上能否存在一点M,使得△MBF的周长最小,若存在,求出M 点的坐标;若不存在,请说明原因.yxA O BCF图 161212 / 12。
二轮专题:二次函数中动点存在等腰三角形问题

二次函数中动点存在等腰三角形问题【已知等腰三角形的两个顶点寻找第三个顶点的基本模型】问题:一次函数y=43x+3的图像分别与x 轴、y 轴交于A 、B 两点,设坐标轴上有点C,若△ABC 为等腰三角形,求点C 的坐标。
已知两个固定点寻找等腰三角形第三个顶点问题,方法归纳:(1)令固定点A 为等腰三角形的顶点,则以固定点A 为圆心、以AB 为半径画弧,交坐标轴某点,找第三点;(2)令固定点B 为等腰三角形的顶点,以固定点B 为圆心、以AB 为半径画弧,交坐标轴某点,找第三点,;(3)令不确定的点为等腰三角形的顶点,则作两个固定点连线的中垂线,交坐标轴某点,找到这个不确定点作为等腰三角形的顶点。
【典例探究】1.如图,已知抛物线y=ax 2﹣x +c 与x 轴相交于A 、B 两点,与y 轴相交于C 点,已知点A 、B 的坐标分别是A (﹣1,0)、B (4,0).(1)求该抛物线的解析式:y=x 2﹣x ﹣2(2)在x 轴上是否存在一点P ,使△PBC 是以BC 为腰的等腰三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.2.如图,抛物线y=ax2+bx+c与x轴交于点A和B(1,0),与y轴交于点C,抛物线的顶点为D.(1)求抛物线的解析式:y=﹣x2+x﹣2(3)在抛物线的对称轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由.3.如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.(1)求该抛物线的解析式:y=﹣x2﹣2x+3(3)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.4.如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于A、B两点,其中A点的坐标为(﹣4,0).(1)求直线AC和抛物线的解析式;(3)在y轴上是否存在点D,使得△ACD为等腰三角形?若存在,求出点D的坐标;若不存在,请说明理由.5.如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B (﹣3,0),与y轴交于点C.(1)求抛物线的解析式;(2)点D的坐标为(﹣2,0).问:直线AC上是否存在点F,使得△ODF是等腰三角形?若存在,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.6、已知:如图,抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点.(1)求抛物线的函数关系式:2(1)(5)65y x x x x =--=-+(3)在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标;(4)除(3)中所求的0P 点外,在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形?若存在,请求出一共有几个满足条件的点P (要求简要说明理由,但不证明);若不存在这样的点P ,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不积跬步无以至千里
动点问题—二次函数中等腰三角形存在性问题
方法总结:
假设结论成立;
当所给条件中没有说明哪条边是等腰三角形的底、哪条是腰时,要对其进行分类讨论,假
设某两条边相等,等到三种情况;
设未知量,求边长,在每种情况下,直接或间接设出所求点的坐标,并用所设点坐标表示
出假设相等的两条边的长或第三边的长;
④计算求解,根据等腰三角形的性质或利用勾股定理或相似三角形的性质列等量关系式,根据
等量关系式求解即可。
典型例题:
例1.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点 P 是直线 BC下方抛物线上一动点.
( 1)求这个二次函数的解析式;
( 2)是否存在点 P,使△ POC是以 OC为底边的等腰三角形?若存在,求出 P 点坐标;若不存在,请
说明理由;
( 3)动点 P 运动到什么位置时,△ PBC面积最大,求出此时 P 点坐标和△ PBC的最大面积.
不积跬步无以至千里
1 x 2
例 2. 如图,抛物线 y=﹣ 2
+ mx n
与 x 轴交于 A 、 B 两点,与 y 轴交于点 C ,抛物线的对称轴交
x 轴于点 D ,已知 A (﹣ 1,0),C (0,2). ( 1)求抛物线的表达式;
( 2)在抛物线的对称轴上是否存在点 P ,使△ PCD 是以 CD 为腰的等腰三角形?如果存在,直接写出 P 点的坐标;如果不存在,请说明理由;
( 3)点 E 时线段 BC 上的一个动点,过点 E 作 x 轴的垂线与抛物线相交于点 F ,当点 E 运动到什么位置时,四边形 CDBF 的面积最大?求出四边形 CDBF 的最大面积及此时 E 点的坐标.
不积跬步无以至千里
例 3.如图,二次函数y 1 x2bx c 的图象经过A(2,0),B(0,-6)两点.
2
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与 x 轴交于点 C,连接 BA, BC,求△ ABC的面积.
(3)在 x 轴上是否存在一点 P,使△ ABP为等腰三角形,若存在,求出 P 的坐标,若不存在,说明理由 .
例 4. (2014?绵阳)如图,抛物线y=ax2+bx+c(a≠0)的图象过点 M(﹣ 2,),顶点坐标为N(﹣
1,),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点 P 为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P 的坐标;
(3)在直线 AC上是否存在一点 Q,使△ QBM的周长最小?若存在,求出 Q点坐标;若不存在,请说明理由.
例 5. (2014 年四川资阳 ) 如图,已知抛物线 y=ax2+bx+c 与 x 轴的一个交点为 A(3,0),与 y 轴的交点为 B(0,3),其顶点为 C,对称轴为 x=1.
(1)求抛物线的解析式;
(2)已知点 M为 y 轴上的一个动点,当△ ABM为等腰三角形时,求点M的坐标;
例6.如图,已知二次函数的图象经过点 A( 3, 3)、B(4,0)和原点 O.P 为二次函数图象上的一
个动点,过点 P 作 x 轴的垂线,垂足为 D( m, 0),并与直线 OA交于点 C.
(1)求出二次函数的解析式;
(2)当点 P 在直线 OA的上方时,用含 m的代数式表示线段 PC的长,并求线段 PC的最大值;
( 3)当 m>0 时,探索是否存在点 P,使得△ PCO为等腰三角形,如果存在,请直接写出所有 P 的坐标;如果不存在,请说明理由.
例 7.( 2014 年浙江义乌 12 分)如图,直角梯形 ABCO的两边 OA,OC在坐标轴的正半轴上, BC∥ x 轴,OA=OC=4,以直线 x=1 为对称轴的抛物线过 A,B,C 三点 .
( 1)求该抛物线线的函数解析式.
( 2)已知直线 l 的解析式为,它与x轴的交于点G,在梯形ABCO的一边上取点P.
①当 m=0时,如图 1,点 P 是抛物线对称轴与 BC的交点,过点 P作 PH⊥直线 l 于点 H,连结 OP,试求△ OPH的面积 .
②当时,过 P 点分别作 x 轴、直线 l 的垂线,垂足为点E,F. 是否存在这样的点P,使以 P,E,F 为顶点的三角形是等腰三角形?若存在,求出点P 的坐标;若不存在,请说明理由.
例 8.如图,抛物线与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置.
(1)点 B 在抛物线上 ;
(2)在此抛物线的对称轴上,是否存在点 P,使得以点 P、 O、 B 为顶点的三角形是等腰三角形?若
存在,求点 P 的坐标;若不存在,说明理由.
例 9.如图,在平面直角坐标系中,二次函数y=ax2+bx﹣ 4(a≠0)的图象与 x 轴交于 A(﹣ 2,0)、C (8, 0)两点,与 y 轴交于点 B,其对称轴与 x 轴交于点 D.
(1)求该二次函数的解析式;
(2)如图 1,连结 BC,在线段 BC上是否存在点 E,使得△ CDE为等腰三角形?若存在,求出所有符
合条件的点 E 的坐标;若不存在,请说明理由;
( 3)如图 2,若点 P(m,n)是该二次函数图象上的一个动点(其中 m>0,n<0),连结 PB,PD,BD,求△ BDP面积的最大值及此时点 P 的坐标.
例 10. 如图,抛物线 y ax25ax 4 经过△ABC的三个顶点,已知BC ∥ x 轴,
点 A 在x轴上,点C在 y 轴上,且AC BC .
(1)求抛物线的对称轴;
(2)求抛物线的解析式;
(3)探究:若点P是抛物线对称轴上且在x轴下方的动点,是否存在△PAB是等腰三角形.若存在,求出所有符合条件的点 P 坐标;不存在,请说明理由.
y
C B
1
A
0 1
x
不积跬步无以至千里
例11. 如图 11 所示,在梯形 ABCD中,已知 AB∥ CD, AD⊥ DB,AD=DC=CB,AB=4.以 AB所在直线为x 轴,过 D 且垂直于 AB的直线为y轴建立平面直角坐标系.
(1)求∠ DAB的度数及 A、D、C三点的坐标;
(2)求过 A、 D、 C 三点的抛物线的解析式及其对称轴 L.
(3)若 P 是抛物线的对称轴 L 上的点,那么使 PDB为等腰三角形的点 P 有几个 ?(不必求点 P 的坐标,只需说明理由)
不积跬步无以至千里
例 12. 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点 B(,)、C(,)、 D(,)抛
4 08 08 8 .
物线 y=ax2+bx 过 A、C两点 .
(1)直接写出点 A 的坐标,并求出抛物线的解析式;
(2)动点 P 从点 A 出发.沿线段 AB向终点 B 运动,同时点 Q从点 C 出发,沿线段 CD 向终点 D 运动.速度均为每秒1 个单位长度,运动时间为 t 秒. 过点 P 作 PE⊥ AB交 AC于点 E
①过点 E 作 EF⊥ AD于点 F,交抛物线于点 G.当 t 为何值时,线段 EG最长 ?
②连接 EQ.在点 P、 Q运动的过程中,判断有几个时刻使得△ CEQ是等腰三角形 ?
请直接写出相应的 t 值 .。
