一次函数拔高
(完整word版)初二数学一次函数拔高训练题
初二数学一次函数拔高训练题1.若直线y=3x-1与y=x-k 的交点在第四象限,则k 的取值范围是( )A 、k 〈31B 、31 < k 〈1 C 、k>1 D 、k 〉1或k<31 2.一次函数y=ax+b(a 为整数)的图象过点(98,19),交x 轴于(p,0),交y 轴于(0,q ),若p 为质数,q 为正整数,那么满足条件的一次函数的个数为( )A 。
0 B.1 C.2 D.无数3.在直角坐标系中,横,纵坐标都是整数的点称为整点,设k 为整数,当直线y=x -3与y=kx+k 的交点为整点时,k 的值可以取( )(A)2个 (B )4个 (C )6个 (D )8个4.甲、乙二人在如图所示的斜坡AB 上作往返跑训练.已知:甲上山的速度是a 米/分,下山的速度是b 米/分,(a <)b ;乙上山的速度是12a 米/分,下山的速度是2b 米/分.如果甲、乙二人同时从点A 出发,时间为t (分),离开点A 的路程为S (米).那么下面图象中,大致表示甲、乙二人从点A 出发后的时间t (分)与离开点A 的路程S (米)之间的函数关系的是( )5.函数的自变量x 的取值范围是_____。
6.若直线1103457323=+y x 与直线897543177=+y x 的交点坐标是(a ,b ),则222004b a +的值是 7.若一次函数y =kx +b ,当-3≤x ≤1时,对应的y 值为1≤y ≤9,则一次函数的解析式为________________________.8.某矿泉水厂生产一种矿泉水,经测算,用一吨水生产的矿泉水所获利润y (元)与1吨水的价格x(元)的关系如图所示。
(A ) t (分) S (米) (B ) t (分) S (米) (C ) t (分) S (米)(D ) t (分)S (米)(1)求y与x的函数关系式及自变量x的取值范围;(2)为节约用水,特规定:该厂日用水量不超过20水价为每吨4元;日用水量超过20吨时,超过部分按每吨x40元收费。
一次函数拔高题(含答案)

巩固练习一、选择题:1.已知y与x+3成正比例,并且x=1时,y=8,那么y与x之间的函数关系式为()(A)y=8x (B)y=2x+6 (C)y=8x+6 (D)y=5x+32.若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过()(A)一象限(B)二象限(C)三象限(D)四象限3.直线y=-2x+4与两坐标轴围成的三角形的面积是()(A)4 (B)6 (C)8 (D)164.若甲、乙两弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数解析式分别为y=k1x+a1和y=k2x+a2,如图,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为()(A)y1>y2(B)y1=y2(C)y1<y2(D)不能确定5.设b>a,将一次函数y=bx+a与y=ax+b的图象画在同一平面直角坐标系内,•则有一组a,b的取值,使得下列4个图中的一个为正确的是()6.若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过第()象限.(A)一(B)二(C)三(D)四7.一次函数y=kx+2经过点(1,1),那么这个一次函数()(A)y随x的增大而增大(B)y随x的增大而减小(C)图像经过原点(D)图像不经过第二象限8.无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在()(A)第一象限(B)第二象限(C)第三象限(D)第四象限9.要得到y=-32x-4的图像,可把直线y=-32x().(A)向左平移4个单位(B)向右平移4个单位(C)向上平移4个单位(D)向下平移4个单位10.若函数y=(m-5)x+(4m+1)x2(m为常数)中的y与x成正比例,则m的值为()(A)m>-14(B)m>5 (C)m=-14(D)m=511.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是().(A)k<13(B)13<k<1 (C)k>1 (D)k>1或k<1312.过点P(-1,3)直线,使它与两坐标轴围成的三角形面积为5,•这样的直线可以作()(A)4条(B)3条(C)2条(D)1条13.已知abc≠0,而且a b b c c ac a b+++===p,那么直线y=px+p一定通过()(A)第一、二象限(B)第二、三象限(C)第三、四象限(D)第一、四象限14.当-1≤x≤2时,函数y=ax+6满足y<10,则常数a的取值范围是()(A)-4<a<0 (B)0<a<2(C)-4<a<2且a≠0 (D)-4<a<215.在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有()(A)1个(B)2个(C)3个(D)4个16.一次函数y=ax+b(a为整数)的图象过点(98,19),交x轴于(p,0),交y轴于(•0,q),若p为质数,q为正整数,那么满足条件的一次函数的个数为()(A)0 (B)1 (C)2 (D)无数17.在直角坐标系中,横坐标都是整数的点称为整点,设k为整数.当直线y=x-3与y=kx+k 的交点为整点时,k的值可以取()(A)2个(B)4个(C)6个(D)8个18.(2005年全国初中数学联赛初赛试题)在直角坐标系中,横坐标都是整数的点称为整点,设k为整数,当直线y=x-3与y=kx+k的交点为整点时,k的值可以取()(A)2个(B)4个(C)6个(D)8个19.甲、乙二人在如图所示的斜坡AB上作往返跑训练.已知:甲上山的速度是a米/分,下山的速度是b米/分,(a<b);乙上山的速度是12a米/分,下山的速度是2b米/分.如果甲、乙二人同时从点A出发,时间为t(分),离开点A的路程为S(米),•那么下面图象中,大致表示甲、乙二人从点A出发后的时间t(分)与离开点A的路程S(米)•之间的函数关系的是()20.若k、b是一元二次方程x2+px-│q│=0的两个实根(kb≠0),在一次函数y=kx+b中,y随x的增大而减小,则一次函数的图像一定经过()(A)第1、2、4象限(B)第1、2、3象限(C)第2、3、4象限(D)第1、3、4象限二、填空题1.已知一次函数y=-6x+1,当-3≤x≤1时,y的取值范围是________.2.已知一次函数y=(m-2)x+m-3的图像经过第一,第三,第四象限,则m的取值范围是________.3.某一次函数的图像经过点(-1,2),且函数y的值随x的增大而减小,请你写出一个符合上述条件的函数关系式:_________.4.已知直线y=-2x+m不经过第三象限,则m的取值范围是_________.5.函数y=-3x+2的图像上存在点P,使得P•到x•轴的距离等于3,•则点P•的坐标为__________.6.过点P(8,2)且与直线y=x+1平行的一次函数解析式为_________.7.y=23x与y=-2x+3的图像的交点在第_________象限.8.某公司规定一个退休职工每年可获得一份退休金,•金额与他工作的年数的算术平方根成正比例,如果他多工作a年,他的退休金比原有的多p元,如果他多工作b年(b≠a),他的退休金比原来的多q元,那么他每年的退休金是(以a、b、p、•q•)表示______元.9.若一次函数y=kx+b,当-3≤x≤1时,对应的y值为1≤y≤9,•则一次函数的解析式为________.10.(湖州市南浔区2005年初三数学竞赛试)设直线kx+(k+1)y-1=0(为正整数)与两坐标所围成的图形的面积为S k (k=1,2,3,……,2008),那么S 1+S 2+…+S 2008=_______.11.据有关资料统计,两个城市之间每天的电话通话次数T•与这两个城市的人口数m 、n (单位:万人)以及两个城市间的距离d (单位:km )有T=2kmn d的关系(k 为常数).•现测得A 、B 、C 三个城市的人口及它们之间的距离如图所示,且已知A 、B 两个城市间每天的电话通话次数为t ,那么B 、C 两个城市间每天的电话次数为_______次(用t 表示).三、解答题1.已知一次函数y=ax+b 的图象经过点A (2,0)与B (0,4).(1)求一次函数的解析式,并在直角坐标系内画出这个函数的图象;(2)如果(1)中所求的函数y 的值在-4≤y ≤4范围内,求相应的y 的值在什么范围内.2.已知y=p+z ,这里p 是一个常数,z 与x 成正比例,且x=2时,y=1;x=3时,y=-1.(1)写出y 与x 之间的函数关系式;(2)如果x 的取值范围是1≤x ≤4,求y 的取值范围.3.为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.•小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身高调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:第一档 第二档 第三档 第四档凳高x (cm )桌高y (cm )(1)小明经过对数据探究,发现:桌高y 是凳高x 的一次函数,请你求出这个一次函数的关系式;(不要求写出x 的取值范围);(2)小明回家后,•测量了家里的写字台和凳子,写字台的高度为77cm ,凳子的高度为43.5cm ,请你判断它们是否配套?说明理由.4.小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x (小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?(2)求小明出发两个半小时离家多远?(3)•求小明出发多长时间距家12千米?5.已知一次函数的图象,交x轴于A(-6,0),交正比例函数的图象于点B,且点B•在第三象限,它的横坐标为-2,△AOB的面积为6平方单位,•求正比例函数和一次函数的解析式.6.如图,一束光线从y轴上的点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),求光线从A点到B点经过的路线的长.7.由方程│x-1│+│y-1│=1确定的曲线围成的图形是什么图形,其面积是多少?8.在直角坐标系x0y中,一次函数y=23x+2的图象与x轴,y轴,分别交于A、B两点,•点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D•两点的一次函数的解析式.9.已知:如图一次函数y=12x-3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.10.已知直线y=43x+4与x轴、y轴的交点分别为A、B.又P、Q两点的坐标分别为P(•0,-1),Q(0,k),其中0<k<4,再以Q点为圆心,PQ长为半径作圆,则当k取何值时,⊙Q•与直线AB相切?11.(2005年宁波市蛟川杯初二数学竞赛)某租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地收割小麦,其中30•台派往A 地,20台派往B地.两地区与该租赁公司商定的每天的租赁价格如下:甲型收割机的租金乙型收割机的租金A地 1800元/台 1600元/台B地 1600元/台 1200元/台(1)设派往A地x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),请用x表示y,并注明x的范围.(2)若使租赁公司这50台联合收割机一天获得的租金总额不低于79600元,•说明有多少种分派方案,并将各种方案写出.12.已知写文章、出版图书所获得稿费的纳税计算方法是f(x)=(800)20%(130%),400(120%)20%(130%),400x xx x--≤⎧⎨-->⎩其中f(x)表示稿费为x元应缴纳的税额.假如张三取得一笔稿费,缴纳个人所得税后,得到7104元,•问张三的这笔稿费是多少元?13.某中学预计用1500元购买甲商品x个,乙商品y个,不料甲商品每个涨价元,乙商品每个涨价1元,尽管购买甲商品的个数比预定减少10个,总金额多用29元.•又若甲商品每个只涨价1元,并且购买甲商品的数量只比预定数少5个,那么买甲、乙两商品支付的总金额是元.(1)求x、y的关系式;(2)若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205,但小于210,求x,y的值.14.某市为了节约用水,规定:每户每月用水量不超过最低限量am3时,只付基本费8元和定额损耗费c元(c≤5);若用水量超过am3时,除了付同上的基本费和损耗费外,超过部分每1m3付b元的超额费.某市一家庭今年一月份、二月份和三月份的用水量和支付费用如下表所示:用水量(m3) 交水费(元)一月份 9 9二月份 15 19三月 22 33根据上表的表格中的数据,求a、b、c.15.A市、B市和C市有某种机器10台、10台、8台,•现在决定把这些机器支援给D 市18台,E市10.已知:从A市调运一台机器到D市、E市的运费为200元和800元;从B•市调运一台机器到D市、E市的运费为300元和700元;从C市调运一台机器到D市、E 市的运费为400元和500元.(1)设从A市、B市各调x台到D市,当28台机器调运完毕后,求总运费W(元)关于x(台)的函数关系式,并求W的最大值和最小值.(2)设从A市调x台到D市,B市调y台到D市,当28台机器调运完毕后,用x、y 表示总运费W(元),并求W的最大值和最小值.答案:1.B 2.B 3.A 4.A 5.B 6.B 7.B 8.C 9.D 10.C 11.B 12.C 13.B14.D 15.D 16.A 17.C 18.C 19.C 20.A二、1.-5≤y ≤19 2.2<m<3 3.如y=-x+1等.4.m ≥0.提示:应将y=-2x+m 的图像的可能情况考虑周全.5.(13,3)或(53,-3).6.y=x-6. 8.222()aq bp bp aq --. 9.y=2x+7或y=-2x+3 10.1004200911.据题意,有t=25080160⨯k ,∴k=325t . 因此,B 、C 两个城市间每天的电话通话次数为T BC =k ×2801003253205642t t ⨯=⨯=.三、1.(1)由题意得:20244a b a b b +==-⎧⎧⎨⎨==⎩⎩解得 ∴这个一镒函数的解析式为:y=-2x+4(•函数图象略).(2)∵y=-2x+4,-4≤y ≤4,∴-4≤-2x+4≤4,∴0≤x ≤4.2.(1)∵z 与x 成正比例,∴设z=kx (k ≠0)为常数,则y=p+kx .将x=2,y=1;x=3,y=-1分别代入y=p+kx ,得2131k p k p +=⎧⎨+=-⎩ 解得k=-2,p=5,∴y 与x 之间的函数关系是y=-2x+5;(2)∵1≤x ≤4,把x 1=1,x 2=4分别代入y=-2x+5,得y 1=3,y 2=-3.∴当1≤x ≤4时,-3≤y ≤3.另解:∵1≤x ≤4,∴-8≤-2x ≤-2,-3≤-2x+5≤3,即-3≤y ≤3.3.(1)设一次函数为y=kx+b ,将表中的数据任取两取,不防取(,)和(,)代入,得2131k p k p +=⎧⎨+=-⎩ ∴一次函数关系式为y=+.(2)当x=时,y=×+=.∵77≠,∴不配套.4.(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米.(2)设直线CD 的解析式为y=k 1x+b 1,由C (2,15)、D (3,30),代入得:y=15x-15,(2≤x ≤3).当x=时,y=(千米)答:出发两个半小时,小明离家22.5千米.(3)设过E 、F 两点的直线解析式为y=k 2x+b 2,由E (4,30),F (6,0),代入得y=-15x+90,(4≤x ≤6)过A 、B 两点的直线解析式为y=k 3x ,∵B (1,15),∴y=15x .(0≤x ≤1),• 分别令y=12,得x=265(小时),x=45(小时). 答:小明出发小时265或45小时距家12千米. 5.设正比例函数y=kx ,一次函数y=ax+b ,∵点B 在第三象限,横坐标为-2,设B (-2,y B ),其中y B <0,∵S △AOB =6,∴12AO ·│y B │=6, ∴y B =-2,把点B (-2,-2)代入正比例函数y=kx ,•得k=1.把点A (-6,0)、B (-2,-2)代入y=ax+b ,得1062223a b a a b b ⎧=-+=-⎧⎪⎨⎨-=-+⎩⎪=-⎩解得 ∴y=x ,y=-12x-3即所求. 6.延长BC 交x 轴于D ,作DE ⊥y 轴,BE ⊥x 轴,交于E .先证△AOC ≌△DOC , ∴OD=OA=•1,CA=CD ,∴222234DE BE ++= 5.7.当x ≥1,y ≥1时,y=-x+3;当x ≥1,y<1时,y=x-1;当x<1,y ≥1时,y=x+1;当x<•1,y<1时,y=-x+1.2,面积为2.8.∵点A、B分别是直线y=2 3x+2与x轴和y轴交点,∴A(-3,0),B(0,2),∵点C坐标(1,0)由勾股定理得BC=3,AB=11,设点D的坐标为(x,0).(1)当点D在C点右侧,即x>1时,∵∠BCD=∠ABD,∠BDC=∠ADB,∴△BCD∽△ABD,∴BC CDAB BD=,∴23112x=+①∴22321112x xx-+=+,∴8x2-22x+5=0,∴x1=52,x2=14,经检验:x1=52,x2=14,,∵x=14,不合题意,∴舍去,∴x=52,∴D•点坐标为(52,0).设图象过B、D两点的一次函数解析式为y=kx+b,2225522b kk bb⎧⎧==-⎪⎪∴⎨⎨+=⎪⎪=⎩⎩∴所求一次函数为y=-22x+2.(2)若点D在点C左侧则x<1,可证△ABC∽△ADB,∴AD BDAB CB=22113x+=②∴8x2-18x-5=0,∴x1=-14,x2=52,经检验x1=14,x2=52,都是方程②的根.∵x2=52不合题意舍去,∴x1=-14,∴D点坐标为(-14,0),∴图象过B、D(-14,0)两点的一次函数解析式为22,综上所述,满足题意的一次函数为y=-252或22.11.(1)y=200x+74000,10≤x≤30(2)三种方案,依次为x=28,29,30的情况.12.稿费是8000元.13.(1)设预计购买甲、乙商品的单价分别为a元和b元,则原计划是:ax+by=1500,①.由甲商品单价上涨元,乙商品单价上涨1元,并且甲商品减少10个情形,得:(a+)(x-10)+(b+1)y=1529,②再由甲商品单价上涨1单价上涨仍是1元的情形得:(a+1)(x-5)+(b+1)y=1563.5,③.由①,②,③得:1.51044,568.5.x y ax y a+-=⎧⎨+-=⎩④-⑤×2并化简,得x+2y=186.(2)依题意有:205<2x+y<210及x+2y=186,得54<y<5523.由于y是整数,得y=55,从而得x=76.14.设每月用水量为xm3,支付水费为y元.则y=8,08(),c x ab x ac x a+≤≤⎧⎨+-+≥⎩由题意知:0<c≤5,∴0<8+c≤13.从表中可知,第二、三月份的水费均大于13元,故用水量15m3、22m3均大于最低限量am3,将x=15,x=22分别代入②式,得198(15)338(22)b a cb a c=+-+⎧⎨=+-+⎩解得b=2,2a=c+19,⑤.再分析一月份的用水量是否超过最低限量,不妨设9>a,将x=9代入②,得9=8+2(9-a)+c,即2a=c+17,⑥.⑥与⑤矛盾.故9≤a,则一,则8+c=9,∴c=1代入⑤式得,a=10.综上得a=10,b=2,c=1.(18-2x)+800(10-x)+700(10-x)+500(2x-10)=-800x+17200.又010,010, 01828,59, x xx x≤≤≤≤⎧⎧∴⎨⎨≤-≤≤≤⎩⎩∴5≤x≤9,∴W=-800x+17200(5≤x≤9,x是整数).(2)由题设知,A市、B市、C市发往D市的机器台数分别为x,y,18-x-y,发往E市的机器台数分别是10-x,10-y,x+y-10,于是W=200x+800(10-x)+300y+700(10-y)+•400(19-x-y)+500(x+y-10)=-500x-300y-17200.又010,010, 010,010, 0188,1018, x xy yx y x y ≤≤≤≤⎧⎧⎪⎪≤≤∴≤≤⎨⎨⎪⎪≤--≤≤+≤⎩⎩∴W=-500x-300y+17200,且010,010,018.xyx y≤≤⎧⎪≤≤⎨⎪≤+≤⎩(x,y为整数).W=-200x-300(x+y)+17200≥-200×10-300×18+17200=9800.当x=•10,y=8时,W=9800.所以,W的最小值为9800.又W=-200x-300(x+y)+17200≤-200×0-300×10+17200=14200.当x=0,y=10时,W=14200,。
一次函数信息题拔高

一次函数信息题拔高前言题型分类:一般分为行程问题,注水问题,进出货问题三大类。
其中行程问题是出题最多、相对也较难的题型,应重点关注。
注水问题在2022年大连中考中第一次出现,是新出现的题型,体现了一次函数信息题从行程问题向其他生活相关问题思路的转化。
所以,对于一些生产效率、注水、进出货等也可以用一次函数图像解决的题目,也要给与一定的关注。
解题方法与技巧:一次函数信息题,重点是信息二字。
题目含有一部分信息,图像含有一部分信息,重点是信息的解读、结合与运用。
1,一次函数求解析式的方法:待定系数法,在一次函数图像中一般已知两点坐标就可以求出解析式;2,求交点(行程问题中的相遇),一般求解方式是划在同一坐标参照体系内求交点,联立两条直线的解析式,解二元一次方程组;3,行程问题:做题首先要区分坐标系中纵坐标的意义,一般纵坐标可以分为“相对同一出发点的距离”,“相对各自出发点的距离”,“两者之间距离”三种类型,再切换到该种类型下的解题思路;4,注水问题:要注意底面积改变相对应于一次函数图像发生转折。
5,进出货(进出水):注意货物的总量(或水的总量)是总量守恒的。
一、行程问题1,追及问题例1,(2022年大连)甲、乙两人从少年宫出发,沿相同的路线分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆。
图10是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间某(秒)的函数图象。
(1)在跑步的全过程中,甲共跑了___米,甲的速度为___米/秒;(2)乙跑步的速度是多少?乙在途中等候甲用了多长时间?(3)甲出发多长时间第一次与乙相遇?此时乙跑了多少米?练习1,甲,乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC,线段DE分别表示甲,乙两车所行路程y(千米)与某(小时)之间的函数关系对应的图象(线段AB表示甲出发不足2小时因故障停车检修)。
北师大版八年级数学上册第四章一次函数综合练习拔高题(有答案)

一次函数综合应用练习题一.填空题1.已知直线y=﹣x+3与坐标轴相交于A、B两点,动点P从原点O出发,以每秒1个单位长度的速度沿x轴正方向运动,当点P的运动时间是秒时,△P AB是等腰三角形.二.解答题2.如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O →C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.3.如图,在平面直角坐标系xOy中,直线l1:y=kx+b与x轴交于点A(﹣6,0),与y轴交于点B(0,4),与直线l2:y=x相交于点C.(1)求直线l1的函数表达式;(2)求△COB的面积;(3)在x轴上是否存在一点P,使△POC是等腰三角形.若不存在,请说明理由;若存在,请直接写出点P的坐标.4.如图,直线l1的函数关系式为y=﹣x﹣1,且l1与x轴交于点A,直线l2经过点B(2,0),C(﹣1,3),直线l1与l2交于点D.(1)求直线l2的函数关系式;(2)求△ABD的面积;(3)点P是x轴上一动点,问是否存在一点P,恰好使△ADP为直角三角形?若存在,直接写出点P 的坐标;若不存在,请说明理由.5.已知直线y=x+3与x轴相交于点A,与y轴相交于点B,P是直线AB上的一个动点,过P点分别作x轴、y轴的垂线PE,PF,如图所示,(1)若P为线段AB的中点,请求出OP的长度;(2)若四边形PEOF是正方形时,求出P点坐标;(3)P点在AB上运动过程中,EF是否有最小值?若有,请求出这个最小值;若没有请说明理由.6.如图,已知在平面直角坐标系中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是线段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.(1)写出S与x的函数关系式;(2)当△OMB的面积是△OAB面积的时,求点M的坐标;(3)当△OMB是以OB为底的等腰三角形,求它的面积.7.如图,一次函数y=﹣x+6的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合.直线CD与x轴交于点C,与AB交于点D.(1)求点A和点B的坐标.(2)求OC的长度;(3)已知点P从点O出发,以每秒钟2个单位长度沿OB、BA运动到点A停止运动,设运动时间为t,问t为何值时,三角形OAP的面积等于三角形OAB面积的?8.如图,一次函数y=﹣的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合、直线CD与x轴交于点C,与AB交于点D.(1)点A的坐标为,点B的坐标为;(2)求OC的长度;(3)在坐标平面内,是否存在点P(除点O外),使得△ABO与△ABP全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.9.已知:如图1,在平面直角坐标系中,一次函数y=x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.(1)求点A,B的坐标.(2)如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.(3)若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ,若存在,请求出对应的点Q坐标;若不存在,请说明理由.10.已知:如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.(1)求A、B两点的坐标;(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,问:①若△PBO的面积为S,求S关于a的函数关系式;②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.11.已知:如图,一次函数y=x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为;(直接写出结果)(2)在x轴上求一点P使△P AD为等腰三角形,直接写出所有满足条件的点P的坐标.(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.12.如图,已知直线y=﹣x+1与x轴y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt △ABC,∠BAC=90°,点P(x,y)为线段BC上一个动点(点P不与B、C重合),设△OP A的面积为S.(1)求点C的坐标;(2)求S关于x的函数解析式,并写出x的取值范围;(3)△OP A的面积能等于吗?如果能,求出此时点P坐标;如果不能,说明理由.13.如图,在平面直角坐标系中,0为坐标原点,矩形OABC的顶点A(12,0)、C(0,9).(1)求线段OB的长度;(2)若将矩形OABC的一个角沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与x轴交于点D,求线段AD的长度;(3)在(2)的条件下,求直线BD所对应的函数表达式.14.如图,一次函数y=x+2的图象与x,y轴分别交于A,B两点,点C与点A关于y轴对称.动点P,Q分别在线段AC,AB上(点P与点A,C不重合),且满足∠BPQ=∠BAO.(1)点A的坐标为,点B的坐标为,线段BC的长度=;(2)当点P在什么位置时,△APQ≌△CBP?说明理由;(3)当△PQB为等腰三角形时,求点P的坐标.15.如图,在平面直角坐标系中,直线l1的解析式为y=x﹣1,与x轴、y轴分别交于点A、点B,直线l2的解析式为,与x轴、y轴分别交于点C、点D,直线l1与l2交于点E.(1)求点E的坐标;(2)若直线l2上存在点P,使得S△OCP=6,请求出点P的坐标;(3)在y轴右侧、点E左侧有一条平行于y轴的动直线,分别与l1,l2交于点M,N,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请求出满足条件的所有点Q的坐标;若不存在;请说明理由.16.如图1,平面直角坐标系中,直线与x轴、y轴分别交于点A,B,直线y=﹣x+b经过点A,并与y轴交于点C.(1)求A,B两点的坐标及b的值;(2)如图2,动点P从原点O出发,以每秒1个单位长度的速度沿x轴正方向运动.过点P作x轴的垂线,分别交直线AC,AB于点D,E.设点P运动的时间为t.①点D的坐标为.点E的坐标为;(均用含t的式子表示)②请从下面A、B两题中任选一题作答我选择题.A.当点P在线段OA上时,探究是否存在某一时刻,使DE=OB?若存在,求出此时△ADE的面积;若不存在说明理由.B.点Q是线段OA上一点.当点P在射线OA上时,探究是否存在某一时刻使?若存在、求出此时t的值,并直接写出此时△DEQ为等腰三角形时点Q的坐标;若不存在,说明理由.17.已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数的表达式;(2)在x轴上能否找到一点M,使△AOM是等腰三角形?若存在,求点M的坐标;若不存在,请说明理由.18.已知正比例函数y=kx的图象经过点A,点A在第四象限,过A作AH⊥x轴,垂足为H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数y=kx的解析式.(2)点P为x轴上一点,△AOP的面积为4,求直线AP的函数解析式.19.已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)(1)求a、b的值;(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△P AC为等腰三角形时,直接写出t的值.20.阅读下列一段文字,然后回答下列问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;(4)在(3)的条件下,平面直角坐标系中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.21.如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),(1)则n=,k=,b=;(2)函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是(3)求四边形AOCD的面积;(4)在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形?若存在求出点P的坐标;若不存在,请说明理由.22.如图,直线y=﹣x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.(1)求A、B两点的坐标;(2)求直线AM的表达式;(3)在x轴上是否存在点P,使得以点P、M、B′为顶点的三角形是等腰三角形,若存在,请直接写出所有点P的坐标;若不存在,请说明理由.23.如图,在平面直角坐标系中,点A,B,C的坐标分别是(4,0),(0,3),(9,0).过直线AB上的点P作PC的垂线,分别交x,y轴于点E,F.(1)求直线AB的函数表达式.(2)如图,点P在第二象限,且是EF的中点,求点P的横坐标.24.如图,直线y=x+4与x轴相交于点A,与y轴相交于点B.(1)求点A,B的坐标;(2)过点B作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.(3)如果x轴上有一动点M,要使以A、B、M为顶点的三角形构成为等腰三角形,请探究并求出符合条件的所有M点坐标.25.如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B 的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.(1)求点E、F的坐标;(2)求AF所在直线的函数关系式;(3)在x轴上求一点P,使△P AF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.参考答案一.填空题1.解:令x=0,则y=3,故B(0,3).令y=0,则x=4,故A(4,0).所以OB=3,OA=4.在直角△AOB中,由勾股定理知,AB==5.设P(t,0).①当AP=BP时,OB2+OP2=BP2=AP2,即32+t2=(4﹣t)2,解得t=.②当AB=AP=5时,P′(9,0),此时t=9.综上所述,点P的运动时间是或9秒.故答案是:或9.二.解答题2.解:(1)∵点A的坐标为(0,6),∴设直线AB的解析式为y=kx+6,∵点C(2,4)在直线AB上,∴2k+6=4,∴k=﹣1,∴直线AB的解析式为y=﹣x+6;(2)由(1)知,直线AB的解析式为y=﹣x+6,令y=0,∴﹣x+6=0,∴x=6,∴B(6,0),∴S△OBC=OB•y C=12,∵△OPB的面积是△OBC的面积的,∴S△OPB=×12=3,设P的纵坐标为m,∴S△OPB=OB•m=3m=3,∴m=1,∵C(2,4),∴直线OC的解析式为y=2x,当点P在OC上时,x=,∴P(,1),当点P在BC上时,x=6﹣1=5,∴P(5,1),即:点P(,1)或(5,1);(3)∵△OBP是直角三角形,∴∠OPB=90°,当点P在OC上时,由(2)知,直线OC的解析式为y=2x①,∴直线BP的解析式的比例系数为﹣,∵B(6,0),∴直线BP的解析式为y=﹣x+3②,联立①②,解得,∴P(,),当点P在BC上时,由(1)知,直线AB的解析式为y=﹣x+6③,∴直线OP的解析式为y=x④,联立③④解得,,∴P(3,3),即:点P的坐标为(,)或(3,3).3.解:(1)将点A(﹣6,0),B(0,4)代入y=kx+b中,得,∴,∴直线l1的函数表达式为y=x+4;(2)由(1)知,直线l1的函数表达式为y=x+4①,∵直线l2:y=x,联立①②解得,,∴C(6,8),∵B(0,4),∴OB=4,∴S△COB=OB•|x C|=×4×6=12;(3)设P(m,0),∵O(0,0),C(6,8),∴OP=|m|.OC=10,CP=,∵△POC是等腰三角形,①当OP=OC时,∴|m|=10,∴m=±10,∴P(﹣10,0)或(10,0),②当OP=CP时,∴|m|=,∴m=,∴P(,0),③当OC=CP时,∴10=,∴m=0(舍)或m=12,∴P(12,0),即:满足条件的点P的坐标为(﹣10,0)或(10,0)或(12,0)或(,0).4.解:(1)设直线l2的函数关系式为:y=kx+b,∵直线过点B(2,0),C(﹣1,3),∴,解得:,∴直线l2的函数关系式为:y=﹣x+2;(2)∵直线l1与l2交于点D.∴,解得,∴D(6,﹣4)将y=0代入y=﹣x﹣1得x=﹣2,∴点A的坐标是(﹣2,0),∵点B的坐标是(2,0),∴AB=4,∴S△ABC=AB×|y D|=×4×4=8;(3)存在一点P,恰好使△ADP为直角三角形,点P的坐标为(6,0)或(8,0),如图,当∠APD=90°时,DP⊥x轴,由(2)知,D(6,4),∴P点坐标为(6,0),当∠ADP=90°时,设P'(m,0),则PP'=m﹣6,AP'=m+2,∵A(﹣2,0),D(6,4),∴DP=4,AD2=82+42=80,在Rt△ADP'中,DP'2=AP'2﹣AD2=(m+2)2﹣80,在Rt△DPP'中,DP'2=DP2+PP'2=16+(m﹣6)2,∴(m+2)2﹣80=16+(m﹣6)2,解得:m=8,∴P(8,0),即:满足条件的点P的坐标为(6,0)或(8,0).5.解;(1)令x=0得:y=3;令y=0得x=﹣4∴点A的坐标为(﹣4,0),点B的坐标为(0,3).在Rt△ABO中,AB===5,在Rt△ABO中,点P是AB的中点,∴PO=AB=.(2)∵四边形PEOF为正方形,∴PE=PF.∴点P位于一、三象限或二、四象限的角平分线上.设点P的坐标为(a,),则a+=0,或a=,解得a=或a=12∴点P的坐标为(,)或(12,12).(3)如图所示:连接OP.∵∠EOF=∠PEO=∠PFO=90°,∴四边形PEPF为矩形.∴PO=EF.由垂线段最短可知;当OP⊥AB时,OP有最小值.∵,∴.∴OP=.∴EF存在最小值,最小值为.6.解:(1)针对于直线l:y=﹣2x+6,令y=0,则﹣2x+6=0,∴x=3,∴B(3,0),∴OB=3,∵点M在线段AB上,∴M(x,﹣2x+6),∴S=S△OBM=×3×(﹣2x+6)=﹣3x+9(0≤x≤3),(2)针对于直线l:y=﹣2x+6,令x=0,则y=6,∴A(0,6),∴S△AOB=OA•OB=×6×3=9,∵△OMB的面积是△OAB面积的,∴S△OBM=×9=6,由(1)知,S△OBM=﹣3x+9(0≤<3),∴﹣3x+9=6,∴x=1,∴M(1,4);(3)∵△OMB是以OB为底的等腰三角形,∴点M是OB的垂直平分线上,∴点M(,3),∴S△OBM=×3×3=.7.解:(1)对于一次函数y=﹣x+6,令x=0得y=6,令y=0得x=8,∴A(8,0),B(0,6).(2)在Rt△AOB中,∵∠AOB=90°,OA=8,OB=6,∴AB===10,设OC=x,则CB=CA=8﹣x,在Rt△BOC中,∵BC2=OB2+OC2,∴62+x2=(8﹣x)2,∴x=,∴OC=.(3)①当P在OB上时,OP=OB时,三角形OAP的面积等于三角形OAB面积的,∴2t=×6,∴t=2,②当P在AB上时,AP=AB时,三角形OAP的面积等于三角形OAB面积的,∴AP=,BP=10﹣=,∴2t=6+,∴t=,综上所述,t=2s或s时,三角形OAP的面积等于三角形OAB面积的.8.解:(1)令x=0,则y=4,∴B(0,4),令y=0,则0=﹣,∴x=8,∴A(8,0),故答案为:(8,0),(0,4);(2)设OC=a,∴AC=8﹣a,由折叠知,BC=AC=8﹣a,在Rt△BOC中,OB=4,根据勾股定理得,BC2﹣OC2=OB2,∴(8﹣a)2﹣a2=16,∴a=3,即:OC=3,(3)设P(m,n),∵A(8,0),B(0,4),∴AP2=(m﹣8)2+n2,BP2=m2+(n﹣4)2,∵△ABO与△ABP,∴①△ABO≌△ABP,∴AP=OA,BP=OB,∴(m﹣8)2+n2=64,m2+(n﹣4)2=16∴(舍)或,∴P(,);②△ABO≌△BAP,∴BP=OA,AP=OB,∴(m﹣8)2+n2=16,m2+(n﹣4)2=64,∴或,∴P(8,4)或(,﹣),即:满足条件的点P(8,4)或(,)或(,﹣).9.解:(1)令x=0,则y=3,∴B(0,3),令y=0,则x+3=0,∴x=﹣4,∴A(﹣4,0);(2)∵点C是点A关于y轴对称的点,∴C(4,0),∵CD⊥x轴,∴x=4时,y=6,∴D(4,6),∴AC=8,CD=6,AD=10,由折叠知,AC'=AC=8,∴C'D=AD﹣AC'=2,设PC=a,∴PC'=a,DP=6﹣a,在Rt△DC'P中,a2+4=(6﹣a)2,∴a=,∴P(4,);(3)设P(4,m),∴CP=m,DP=|m﹣6|,∵S△CPQ=2S△DPQ,∴CP=2PD,∴2|m﹣6|=m,∴m=4或m=12,∴P(4,4)或P(4,12),∵直线AB的解析式为y=x+3①,当P(4,4)时,直线OP的解析式为y=x②,联立①②解得,x=12,y=12,∴Q(12,12),当P(4,12)时,直线OP解析式为y=3x③,联立①③解得,x=,y=4,∴Q(,4),即:满足条件的点Q(12,12)或(,4).10.解:(1)对于直线AB解析式y=2x+10,令x=0,得到y=10;令y=0,得到x=﹣5,则A(0,10),B(﹣5,0);(2)连接OP,如图所示,①∵P(a,b)在线段AB上,∴b=2a+10,由0≤2a+10≤10,得到﹣5≤a≤0,由(1)得:OB=5,∴S△PBO=OB•(2a+10),则S=(2a+10)=5a+25(﹣5≤a≤0);②存在,理由为:∵∠PFO=∠FOE=∠OEP=90°,∴四边形PFOE为矩形,∴EF=PO,∵O为定点,P在线段AB上运动,∴当OP⊥AB时,OP取得最小值,∵AB•OP=OB•OA,∴•OP=50,∴EF=OP=2,综上,存在点P使得EF的值最小,最小值为2.11.解:(1)将点D的横坐标为4代入一次函数y=x+3表达式,解得:y=6,即点D的坐标为(4,6),将点C、D的坐标代入一次函数表达式y=kx+b得:,解得:,故:答案为:y=3x﹣6;(2)①当P A=PD时,点B是AD的中点,故:过点B且垂直于AD的直线方程为:y=﹣x+3,令y=0,则x=,即点P的坐标为(,0);②当P A=AD时,AD==10,故点P的坐标为(6,0)或(﹣14,0);③当DP=AD时,同理可得:点P的坐标为(12,0);故点P的坐标为(,0)或(6,0)或(﹣14,0)或(12,0);(3)设翻转后点D落在y轴上的点为D′,设点Q的坐标为(x,3x﹣6),则:BD=BD′,DQ=D′Q,BD′=BD==5,故点D′的坐标为(0,﹣2),DQ2=D′Q2,即:x2+(3x﹣6+2)2=(x﹣4)2+(3x﹣6﹣6)2,解得:x=,故点Q的坐标为(,).12.解:(1)当x=0时,y=﹣x+1=1,∴点B的坐标为(0,1);当y=0时,﹣x+1=0,解得:x=3,∴点A的坐标为(3,0).过点C作CE⊥x轴,垂足为点E,如图1所示.∵△ABC为等腰直角三角形,∠BAC=90°,∴∠BAO+∠CAE=90°,AB=CA.又∵∠BAO+∠ABO=90°,∴∠ABO=∠CAE.在△ABO和CAE中,,∴△ABO≌CAE(AAS),∴AE=BO=1,CE=AO=3,∴OE=AO+AE=4,∴点C的坐标为(4,3).(2)过点P作PF⊥x轴,垂足为点F,如图2所示.设直线BC的解析式为y=kx+b(k≠0),将B(0,1),C(4,3)代入y=kx+b,得:,解得:,∴直线BC的解析式为y=x+1.∴S=OA•PF=×3×(x+1)=x+(0<x<4).(3)不能,理由如下:当S=时,x+=,解得:x=4.∵0<x<4,∴△OP A的面积不能等于.13.解:(1)∵A(12,0)、C(0,9).∴OA=12,OC=9,∵四边形OABC为矩形,∴AB=OC=9,∠OAB=90°,在Rt△OAB中,;(2)设AD=x,则OD=OA﹣AD=12﹣x,根据折叠知DE=x,BE=AB=9,又OB=15,∴OE=OB﹣BE=15﹣9=6,在Rt△OED中,OE2+DE2=OD2,即62+x2=(12﹣x)2,解得x=,∴AD=;(3)由(2)得AD=,∴OD=12﹣=,∴点D的坐标为(,0).由题意知点B的坐标为(12,9),设直线BD所对应的函数表达式为y=kx+b(k≠0),把(,0),(12,9)分别代入y=kx+b,得,解得,所以直线BD所对应的函数表达式为y=2x﹣15.14.解:(1)∵y=x+2,∴当x=0时,y=2,当y=0时,x=﹣4,即点A的坐标是(﹣4,0),点B的坐标是(0,2),∵C点与A点关于y轴对称,∴C的坐标是(4,0),∴OA=4,OC=4,OB=2,由勾股定理得:BC==2.故答案为:(﹣4,0),(0,2),2.(2)当P的坐标是(2﹣4,0)时,△APQ≌△CBP,理由是:∵OA=4,P(2﹣4,0),∴AP=4+2﹣4=2=BC,∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,∴∠AQP=∠BPC,∵A和C关于y轴对称,∴∠BAO=∠BCP,在△APQ和△CBP中,,∴△APQ≌△CBP(AAS),∴当P的坐标是(2﹣4,0)时,△APQ≌△CBP;(3)分为三种情况:①当PB=PQ时,由(2)知,△APQ≌△CBP,∴PB=PQ,即此时P的坐标是(2﹣4,0);②当BQ=BP时,则∠BPQ=∠BQP,∵∠BAO=∠BPQ,∴∠BAO=∠BQP,而根据三角形的外角性质得:∠BQP>∠BAO,∴此种情况不存在;③当QB=QP时,则∠BPQ=∠QBP=∠BAO,即BP=AP,设此时P的坐标是(x,0),∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,∴(x+4)2=x2+22,解得:x=﹣,即此时P的坐标是(﹣,0).∴当△PQB为等腰三角形时,点P的坐标是(2﹣4,0)或(﹣,0).15.解:(1)联立y=x﹣1与得,解得,∴;(2)设,对于,令=0,解得x=6,故点C(6,0),即OC=6,则S△OPC=×OC×|y P|,即6=×6×|﹣m+3|,解得:m=2或m=10,故P1(2,2)P2(10,﹣2);(3)存在.理由:设点Q(0,a),①当MQ=MN时,∵MN=MQ,∴,解得:,∴Q(0,);②当MN=NQ时,同理可得:a﹣(5﹣2a)=6﹣2a,解得a=,∴;③当QN=QM时,过Q作QT⊥MN于点T,∵MN=2QT,则﹣a+3﹣(a﹣1)=2a,解得a=,∴,综上满足条件的所有点Q的坐标为,,.16.解:(1)将y=0代入得,解得:x=4,∴点A的坐标为(4,0).将x=0代入,并解得:y=﹣2,∴点B的坐标为(0,﹣2).将A(4,0)代入y=﹣x+b,得0=﹣4+b,解得b=4;(2)①由(1)知,直线的表达式为y=﹣x+4,∵点P(t,0),∴当x=t时,y=﹣x+4=﹣t+4,即D(t,﹣t+4);同理可得:,故答案为(t,﹣t+4)、(t,t﹣2);②A.存在,理由:由①得D(t,﹣t+4),,∵点P在线段OA上,∴,∵B(0,﹣2),∴OB=2.∵DE=OB,∴,解得:.∴,∴;B.存在,理由:由①得D(t,﹣t+4),.∵OP=t,.当点P在线段OA上时,,∴,解得t=3,故点D、E的坐标分别为(3,1)、(3,﹣),设点Q(m,0),则DE2=,DQ2=(m﹣3)2+1,DE2=(m﹣3)2+,当DE=DQ时,即=(m﹣3)2+1,解得m=3±(舍去3+);当DE=QE时,同理可得:m=3(舍去3+);点Q的坐标为或.当点P在线段OA的延长线上时,,∴,解得t=6,同理可得:点Q的坐标为或;综上所述,点Q的坐标为或或或.17.解:(1)∵点A的横坐标为3,△AOH的面积为3,点A在第四象限,∴点A的坐标为(3,﹣2).将A(3,﹣2)代入y=kx,﹣2=3k,解得:k=﹣,∴正比例函数的表达式为y=﹣x.(2)①当OM=OA时,如图1所示,∵点A的坐标为(3,﹣2),∴OH=3,AH=2,OA==,∴点M的坐标为(﹣,0)或(,0);②当AO=AM时,如图2所示,∵点H的坐标为(3,0),∴点M的坐标为(6,0);③当OM=MA时,设OM=x,则MH=3﹣x,∵OM=MA,∴x=,解得:x=,∴点M的坐标为(,0).综上所述:当点M的坐标为(﹣,0)、(,0)、(6,0)或(,0)时,△AOM是等腰三角形.18.解:(1)∵点A的横坐标为3,且△AOH的面积为3,∴•3•AH=3,解得AH=2,∴A(3,﹣2),把A(3,﹣2)代入y=kx得3k=﹣2,解得k=﹣,∴正比例函数解析式为y=﹣x;(2)设P(t,0),∵△AOP的面积为4,∴•|t|•2=4,∴t=4或t=﹣4,∴P点坐标为(4,0)或(﹣4,0),设直线AP的解析式为y=mx+n,把P(4,0),A(3,﹣2)代入得,解得,此时,直线AP的解析式为y=2x﹣8,把P(﹣4,0),A(3,﹣2)代入得,解得.此时,直线AP的解析式为y=﹣x﹣,综上,直线AP的函数解析式为y=2x﹣8或y=﹣x﹣.19.解:(1)∵点C是直线l1:y=x+1与轴的交点,∴C(0,1),∵点C在直线l2上,∴b=1,∴直线l2的解析式为y=ax+1,∵点B在直线l2上,∴2a+1=0,∴a=﹣;(2)由(1)知,l1的解析式为y=x+1,令y=0,∴x=﹣1,由图象知,点Q在点A,B之间,∴﹣1<n<2(3)如图,∵△P AC是等腰三角形,∴①点x轴正半轴上时,当AC=P1C时,∵CO⊥x轴,∴OP1=OA=1,∴BP1=OB﹣OP1=2﹣1=1,∴1÷1=1s,②当P2A=P2C时,易知点P2与O重合,∴BP2=OB=2,∴2÷1=2s,③点P在x轴负半轴时,AP3=AC,∵A(﹣1,0),C(0,1),∴AC=,∴AP3=,∴BP3=OB+OA+AP3=3+或BP3=OB+OA﹣AP3=3﹣,∴(3+)÷1=(3+)s,或(3﹣)÷1=(3﹣)s,即:满足条件的时间t为1s,2s,或(3+)或(3﹣)s.20.解:(1)∵A(2,4)、B(﹣3,﹣8),∴AB==13;(2)∵A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,∴AB=|4﹣(﹣1)|=5;(3)△DEF为等腰三角形,理由为:∵D(1,6)、E(﹣2,2)、F(4,2),∴DE==5,DF==5,EF==6,即DE =DF,则△DEF为等腰三角形;(4)做出F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,设直线DF′解析式为y=kx+b,将D(1,6),F′(4,﹣2)代入得:,解得:,∴直线DF′解析式为y=﹣x+,令y=0,得:x=,即P(,0),∵PF=PF′,∴PD+PF=DP+PF′=DF′==,则PD+PF的长度最短时点P的坐标为(,0),此时PD+PF的最短长度为.21.解:(1)对于直线y=x+1,令x=0,得到y=1,即A(0,1),把B(0,﹣1)代入y=kx+b中,得:b=﹣1,把D(1,n)代入y=x+1得:n=2,即D(1,2),把D坐标代入y=kx﹣1中得:2=k﹣1,即k=3,故答案为:2,3,﹣1;(2)∵一次函数y=x+1与y=3x﹣1交于D(1,2),∴由图象得:函数y=kx+b的函数值大于函数y=x+1的函数值时x的取值范围是x>1;(3)过D作DE⊥x轴,垂足为E,如图1所示,则S四边形AOCD=S梯形AOED﹣S△CDE=(AO+DE)•OE﹣CE•DE=×(1+2)×1﹣××2=﹣=;(4)在x轴上存在点P,使得以点P,C,D为顶点的三角形是直角三角形,理由为:如图2所示,分两种情况考虑:①当P′D⊥DC时,可得k P′D•k DC=﹣1,∵直线DC斜率为3,∴直线P′D斜率为﹣,∵D(1,2),∴直线P′D解析式为y﹣2=﹣(x﹣1),令y=0,得到x=7,即P′(7,0);②当DP⊥CP时,由D横坐标为1,得到P横坐标为1,∵P在x轴上,∴P的坐标为(1,0).22.解:(1)当x=0时,y=8,∴B(0,8),当y=0时,﹣x+8=0,x=6,∴A(6,0);(2)在Rt△AOB中,∠AOB=90°,OA=6,OB=8,∴AB=10,由折叠得:AB=AB'=10,∴OB'=10﹣6=4,设OM=a,则BM=B'M=8﹣a,由勾股定理得:a2+42=(8﹣a)2,a=3,∴M(0,3),设AM:y=kx+b,则,解得:,∴直线AM的解析式为:y=﹣x+3;(3)在x轴上存在点P,使得以点P、M、B′为顶点的三角形是等腰二角形,如图∵M(0,3),B′(﹣4,0),∴B′M=5,当PB′=B′M时,P1(﹣9,0),P2(1,0);当B′M=PM时,P3(4,0),当PB′=PM时,作BM的垂直平分线,交x轴于P4,交B′M与Q,连接MP4,设OP4=m,则P4M=P4B′=4﹣m,∵PM2=OP2+PM2,∴(4﹣m)2=m2+32解得m=,∴P4(﹣,0),综上,P点的坐标为(﹣9,0)或(1,0)或(4,0)或(﹣,0).23.解:(1)∵A(4,0),B(0,3),设直线AB的解析式为:y=kx+b(k≠0),∴,∴,∴直线AB的解析式为:y=﹣x+3;(2)设E(a,0),F(0,b),则CE=9﹣a,CF=,∵P是EF的中点,CP⊥EF,∴CE=CF,即9﹣a=,P(a,b),∵P在直线AB上,∴b=,即b=﹣,把b=﹣代入9﹣a=即﹣18a+a2=b2,得﹣18a+a2=,解得a=24(舍),或a=﹣∴点P的横坐标为﹣;24.解:(1)把x=0代入y=x+4,得y═4,∴B点坐标为(0,4);把y=0代入y=x+4,得0=x+4,解得x=﹣3,∴A点坐标为(﹣3,0);(2)分两种情况:①当点P位于y轴左侧时;∵OP=2OA=2×|﹣3|=6,∴AP=3,则;②当点P位于y轴右侧时;∵OP=2OA=2×|﹣3|=6,∴AP=3+6=9,则,∴△ABP的面积为6或18;(2)∵A(﹣3,0),B(0,4),∴OA=3,OB=4;∴,分三种情况:①当AB=AM时,则AM=5,且M在x轴上,∴M在A点左侧时,OM=3+5=8,∴M(﹣8,0),当M在A点右侧时,OM=5﹣3=2,∴M(2,0),②当BA=BM时,M位于y轴右侧,∵BM=5,∴,∴M(3,0),③当MA=MB时,如图:直线MN为AB的垂直平分线,则MA=MB,在Rt△BOM中,设BM=AM=x,则OM=x﹣3,∴由勾股定理得:OB2+OM2=BM2,∴42+(x﹣3)2=x2,解得:,∴,∴,∴符合条件的所有M点坐标为(﹣8,0)或(2,0)或(3,0)或.25.解:(1)AF=AC=10,0A=8,则OF=6,则点F(6,0)设:CE=x,则BE=8﹣x,在△BEF中,由勾股定理得:x2=16+(8﹣x)2,解得:x=5,故点E(10,3);(2)将点A、F的坐标代入一次函数表达式:y=kx+b并解得:k=﹣,b=8,故直线AF的表达式为:y=﹣x+8;(3)①当点P在x轴负半轴时,AP=AF,则点P(﹣6,0);当AF=PF时,点P(﹣4,0);②当点P′在x轴正半轴时,AF=FP′=10,故点P′(16,0);综上,点P的坐标为:(﹣6,0)或(﹣4,0)或(16,0).。
一次函数的综合拔高题

一次函数的综合题一、在数学试卷中,数学综合题一般以压轴题形式出现。
二、数学综合题大致可分为代数综合题,几何综合题以及代数、几何综合题三类。
三、求解这类数学题的基本原则是:先拆分成几个熟悉的数学小题分别求解,然后再找出它们之间的联系综合解之。
【典型例题】例1. 已知直线符合以下条件时,求m,n的取值范围。
(1)直线过第一、三、四象限;(2)直线与y轴的交点不在x轴的下方,且函数值随x的增大而减小。
答案(1)(2)∴当时,函数的图象满足题设的要求。
例2. 设,其中p为常数,z与x成正比。
当x=2时,y=1;当x=3时,y=-1,若1≤x≤4,求函数值的取值范围。
答案;当时,即时,可解得。
例3. 已知一次函数,当时,,求直线与坐标轴围成的图形面积。
答案例4. 设,其中与x成正比例,与x成正比例,并且当x=1时,,求:(1)该函数的图象与坐标轴所围成的三角形的面积。
(2)当时,求x的取值范围。
答案(1)(2)当时,x的取值范围为:。
例5. 如图,直线PA为,直线PB为,点Q是PA与y轴的交点,且四边形PQOB的面积是,AB=2,求点P的坐标以及直线PA、PB的解析式。
答案:直线PA、PB的解析式分别为【模拟试题】1. 若直线过点P(3,4),则一定过点Q(k,b)的直线为()A. B.C. D.2. 直线关于x轴对称的直线解析式是________,关于y轴对称的直线解析式是________,关于原点对称的直线解析式是________。
3. 已知P(3,2)在直线上,且直线与x轴交于点A,若P、Q两点关于x轴轴对称,求直线AQ的解析式。
4. 若函数是一次函数,求这个函数的图象与坐标轴围成的图形的周长和面积。
5. 已知直线与x、y轴分别交于A、B两点,若△OAB的周长为,求△OAB 的面积。
6. 已知函数的图象与x、y轴分别交于点A、B,问:在x轴上是否存在这样的点P,使得△ABP为等腰三角形?若存在,求点P的坐标;否则,请说明理由。
一次函数历年真题拔高(几何综合+实际应用)

一次函数综合拔高本专题三个部分:1、一次函数几何综合问题;2、一次函数实际应用——图象问题;3、一次函数实际应用——应用题:第一部分:几何综合问题1、(成外)如图,在平面直角坐标系中,点A,B分别在x轴,y轴上,线段OA=6,OB=12,C是线段AB的中点,点D在线段OC上,OD=2CD.(1)C点坐标为______;(2)求直线AD的解析式;(3)直线OC绕点O逆时针旋转90°,求出点D的对应点D′的坐标.2、(武侯)如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a)(1)求a的值及直线DE的函数表达式;(2)现将长方形OABC沿直线DE折叠,使顶点C落在坐标平面内的点'C处,过点'C作y轴的平行线分别交x轴和BC于点F、G①求'C的坐标;②若点P为直线DE上一动点,连接P'C,当D为等腰三角形时,求点P的PC'坐标。
3、如图,平面直角坐标系中,直线AB :b x y +-=31交y 轴于点A (0,1),交x 轴于点B ,直线1=x 交AB 于点D ,交x 轴于点E ,P 是直线1=x 上一动点,且在点D 的上方,设()n P ,1(1)求PD 的长及△ABP 的面积(用含n 的代数式表示)(2)当2=∆ABP S 时,以PB 为边在第一象限做等腰直角三角形BPC ,求出点C 的坐标;(3)当2=∆ABP S 时,在坐标轴上存在点Q ,使得2=∆BPQ S ,请直接写出这些点Q 的坐标(A 除外)4、如图,直线b x y AB --=:分别与x 、y 轴交于()B A ,0,6两点,过点B 的直线交x 轴负半轴于C ,且1:3:=OC OB(1)求直线BC 的函数关系式;(2)如图2,P 为x 轴上A 点右侧的一动点,以P 为直角顶点,BP 为一腰在第一象限内作等腰直角三角形BPQ ,连接QA 并延长交y 轴于点K ,当P 点运动时,K 点的位置是否发生变化?如果不变请求出它的坐标,如果变化,请说明理由;(3)直线EF :y=2x-k (k ≠0)交AB 于E ,交BC 于点F ,交x 轴于点D ,是否存在这样的直线EF ,使得FBD EBD S S ∆∆=?若存在,求出k 的值;若不存在,请说明理由.5、如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q 的位置为B.(1)求点B的坐标;(2)求证:当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值;(3)连接OQ,当OQ∥AB时,求出P的坐标;6、如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0)点P在线段AC上移动。
一次函数几何拔高专题

一次函数几何专题经典例题例1、已知:一次函数y=kx・b的图象经过M (0,2), N(1,3)两点。
(1) 求k,b的值;⑵若一次函数八kx・b的图象与x轴的交点为A(a,0),求a的值。
例2、直线y=kx・b与直线y=5-4x平行,且与直线y二一3(x—6)相交,交点在y 轴上,求此直线的解析式.例3、求直线y=2x ・1向左平移2个单位后的解析式.例4、已知点P(x,y)是第一象限内的点,且x y=8,点A的坐标为(10 , 0), 设厶OAP 的面积为S.(1) 求S关于x的函数解析式,并写出自变量的取值范围;(2) 画出此函数的图象.例5、在直角坐标系中,是否存在x轴上的动点,使得它到定点P(5 , 5)和到Q(0, 1)的距离MP十MQ勺值最小?若存在,求出点M的横坐标x;若不存在,请说明理由例6、已知,如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线i i与经过点A的直线12相交于点B,点B坐标为(18,6).⑴求直线i i、I?的表达式;⑵点C为线段OB上一动点(点C不与点O, B重合),作CD// y轴交直线I?于点D,过点C, D分别向y轴作垂线,垂足分别为F, E,得到矩形CDEF①设点C的纵坐标为a ,求点D的坐标(用含a 代数式表示)②若矩形CDEF的面积为60,请直接写出此时点的坐标.例7、如图,在平面直角坐标系中,直线AB交x轴于点A(a , 0),交y轴于点B(0 , 6),且a,b满足•一了N(b-2)2=0,直线y = x交AB于点M.(I)求直线AB的解析式;⑵过点M作MCL AB交y轴于点C求点C的坐标;(3)在直线上是否存在一点D,使得S A ABD =6?若存在,求出D点的坐标;若不存在,请说明理由.巩固练习1. 如图,在平面直角坐标系中,一条直线1与X轴相交于点A(2 , 0),与正比例函数八kx (k工0,且k为常数) 的图象相交于点P(1 , 1).⑴求k的值;(2) 求厶AOP的面积.2. 如图,直线y = ;x+i交x轴于B,交丫轴于M点A在y轴负半轴上,Sx BAO =2S x BMO(l)求点B、M的坐标;⑵求点A的坐标;(3)在直线BM上是否存在一点画出草图,并求出P的坐标;说明理由.3. 如图,已知直角坐标系中,轴对称,并且MN交x轴于点点A的横坐标是1 .⑴求△ OMN勺面积;(2)试在线段OMk找一点B使得PB = PA,求直线PB的解析式.4. 如图,直线i i的解析表达式为八亠・3,且i i与x轴交于点D,直线12经过点A B,直线i i,i2交于点Co(1)求点D的坐标;(2)求直线12的解析表达式;⑶求厶ADC的面积;(4) 在直线上存在异于点C的另一点ADP与厶ADC的面积相等,请直接写出点5. 如图,直线“2x 3和直线y—2X—1分别交y轴于点A、B,两直线交于点C. 1 2(1)求两直线交点C的坐标;⑵求厶ABC的面积;(3) 在直线上能否找到点P,使得S A APC 乂?若能,请求出点P的坐标;若不能,请说明理由.6. 如图1直线AB:y= -x-b 分别与x、y轴交于A(6, 0)、B两点,过点B的直线交x轴负半轴于C,且OB OC=3 1;(1)求直线BC的解析式;⑵直线EF:y=kx-k ( k z O)交AB于E,交BC于点F,交x轴于D 是否存在这样的直线EF,使得S A EBD =S A FBD ?若存在,求出k的值;若不存在,说明理由.⑶如图2, P为A点右侧x轴上的一动点,以P为直角顶点、BP为腰在第一象限内作等腰直角三角形BPQ连结QA并延长交y轴于点K.当P点运动时,K点的位置是否发生变化?如果不变,请求出它的坐标;如果变化,请说明理由.7. 如图1,在平面直角坐标系中,△ AOB为等腰直角三角形,A(4 , 4).(1) 求B点的坐标;(2) 如图2,若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ ACDZ ACD =90。
(定稿)一次函数应用题拔高训练
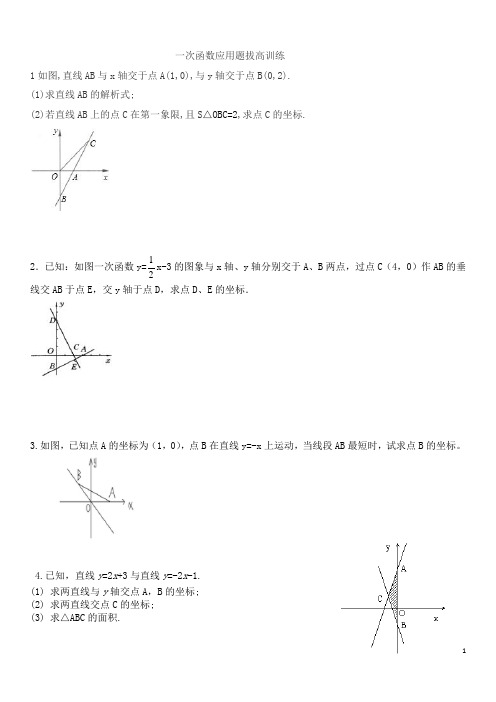
一次函数应用题拔高训练1如图,直线AB 与x 轴交于点A(1,0),与y 轴交于点B(0,2).(1)求直线AB 的解析式;(2)若直线AB 上的点C 在第一象限,且S △OBC=2,求点C 的坐标.2.已知:如图一次函数y=21x-3的图象与x 轴、y 轴分别交于A 、B 两点,过点C (4,0)作AB 的垂线交AB 于点E ,交y 轴于点D ,求点D 、E 的坐标.3.如图,已知点A 的坐标为(1,0),点B 在直线y=-x 上运动,当线段AB 最短时,试求点B 的坐标。
4.已知,直线y =2x +3与直线y =-2x -1.(1) 求两直线与y 轴交点A ,B 的坐标;(2) 求两直线交点C 的坐标;(3) 求△ABC 的面积.5如图,在平面直角坐标系中,一条直线l与x轴相交于点A(2,0),与正比例函数(k为常数)的图象相交于点P(1,1).(1)求k的值;(2)求△AOP的面积.6.某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题;(1)分别求出y甲,y乙与x的函数关系式;(2)现厂家分配该商品800件给甲商场,400件给乙商场,当甲、乙商场售完这批商品,厂家可获得总利润是多少元?7.甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象。
请根据图象所提供的信息,解答问题。
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量的取值范围。
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米。
8.洛阳大剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有名老师与若干名(不少于4人)学生听音乐会。
一次函数拔高题含复习资料

一次函数拔高练习(一)一、选择题:1.已知y与x+3成正比例,并且x=1时,y=8,那么y与x之间的函数关系式为()(A)y=8x (B)y=2x+6 (C)y=8x+6 (D)y=5x+32.若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过()(A)一象限(B)二象限(C)三象限(D)四象限 3.直线y=-2x+4与两坐标轴围成的三角形的面积是()(A)4 (B)6 (C)8 (D)16 4.若甲、乙两弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数解析式分别为y=k1x+a1和y=k2x+a2,如图,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为()(A)y1>y2(B)y1=y2(C)y1<y2(D)不能确定5.设b>a,将一次函数y=bx+a与y=ax+b的图象画在同一平面直角坐标系内,•则有一组a,b的取值,使得下列4个图中的一个为正确的是()6.若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过第()象限(A)一(B)二(C)三(D)四 7.一次函数y=kx+2经过点(1,1),那么这个一次函数()(A)y随x的增大而增大(B)y随x的增大而减小(C)图像经过原点(D)图像不经过第二象限8.无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在()(A)第一象限(B)第二象限(C)第三象限(D)第四象限9.要得到y=-32x-4的图像,可把直线y=-32x().(A)向左平移4个单位(B)向右平移4个单位(C)向上平移4个单位(D)向下平移4个单位 10.若函数y=(m-5)x+(4m+1)x2(m为常数)中的y与x成正比例,则m的值为()(A)m>-14(B)m>5 (C)m=-14(D)m=511.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是().(A)k<13(B)13<k<1 (C)k>1 (D)k>1或k<1312.过点P(-1,3)直线,使它与两坐标轴围成的三角形面积为5,•这样的直线可以作()(A)4条(B)3条(C)2条(D)1条15.在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有()(A)1个(B)2个(C)3个(D)4个19.甲、乙二人在如图所示的斜坡AB上作往返跑训练.已知:甲上山的速度是a米/分,下山的速度是b米/分,(a<b);乙上山的速度是12a米/分,下山的速度是2b米/分.如果甲、乙二人同时从点A出发,时间为t(分),离开点A的路程为S(米),•那么下面图象中,大致表示甲、乙二人从点A出发后的时间t(分)与离开点A的路程S(米)•之间的函数关系的是()二、填空题1.已知一次函数y=-6x+1,当-3≤x≤1时,y的取值范围是________.2.已知一次函数y=(m-2)x+m-3的图像经过第一,第三,第四象限,则m的取值范围是________.3.某一次函数的图像经过点(-1,2),且函数y的值随x的增大而减小,请你写出一个符合上述条件的函数关系式:_________. 4.已知直线y=-2x+m不经过第三象限,则m的取值范围是_________.5.函数y=-3x+2的图像上存在点P,使得P•到x•轴的距离等于3,•则点P•的坐标为__________.6.过点P(8,2)且与直线y=x+1平行的一次函数解析式为_________.7.y=23x与y=-2x+3的图像的交点在第_________象限.9.若一次函数y=kx+b,当-3≤x≤1时,对应的y值为1≤y≤9,•则一次函数的解析式为________.三、解答题2.已知y=p+z,这里p是一个常数,z与x成正比例,且x=2时,y=1;x=3时,y=-1.(1)写出y与x之间的函数关系式;(2)如果x的取值范围是1≤x≤4,求y的取值范围5.已知一次函数的图象,交x轴于A(-6,0),交正比例函数的图象于点B,且点B•在第三象限,它的横坐标为-2,△AOB的面积为6平方单位,•求正比例函数和一次函数的解析式.6.如图,一束光线从y轴上的点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),求光线从A点到B点经过的路线的长.8.已知:如图一次函数y=12x-3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.9、在直角坐标系x0y中,一次函数y=2x+2的图象与x轴,y轴,分别交于A、B两点,•点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D•两点的一次函数的解析式.答案:1.B 2.B 3.A 4.A 5.B 6.B 7.B 8.C 9.D 10.C 11.B 12.C 13.B14.D 15.D 16.A 17.C 18.C 19.C 20.A二、1.-5≤y ≤19 2.2<m<3 3.如y=-x+1等.4.m ≥0.提示:应将y=-2x+m 的图像的可能情况考虑周全.5.(13,3)或(53,-3).6.y=x-6. 8.222()aq bp bp aq --. 9.y=2x+7或y=-2x+3 10.10042009 11.据题意,有t=25080160⨯k ,∴k=325t . 因此,B 、C 两个城市间每天的电话通话次数为T BC =k ×2801003253205642t t ⨯=⨯=.三、1.(1)由题意得:20244a b a b b +==-⎧⎧⎨⎨==⎩⎩解得∴这个一镒函数的解析式为:y=-2x+4(•函数图象略).(2)∵y=-2x+4,-4≤y≤4,∴-4≤-2x+4≤4,∴0≤x≤4.2.(1)∵z与x成正比例,∴设z=kx(k≠0)为常数,则y=p+kx.将x=2,y=1;x=3,y=-1分别代入y=p+kx,得2131k pk p+=⎧⎨+=-⎩解得k=-2,p=5,∴y与x之间的函数关系是y=-2x+5;(2)∵1≤x≤4,把x1=1,x2=4分别代入y=-2x+5,得y1=3,y2=-3.∴当1≤x≤4时,-3≤y≤3.另解:∵1≤x≤4,∴-8≤-2x≤-2,-3≤-2x+5≤3,即-3≤y≤3.3.(1)设一次函数为y=kx+b,将表中的数据任取两取,不防取(37.0,70.0)和(42.0,78.0)代入,得21 31 k pk p+=⎧⎨+=-⎩∴一次函数关系式为y=1.6x+10.8.(2)当x=43.5时,y=1.6×43.5+10.8=80.4.∵77≠80.4,∴不配套.4.(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米.(2)设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),代入得:y=15x-15,(2≤x≤3).当x=2.5时,y=22.5(千米)答:出发两个半小时,小明离家22.5千米.(3)设过E、F两点的直线解析式为y=k2x+b2,由E(4,30),F(6,0),代入得y=-15x+90,(4≤x≤6)过A、B两点的直线解析式为y=k3x,∵B(1,15),∴y=15x.(0≤x≤1),•分别令y=12,得x=265(小时),x=45(小时).答:小明出发小时265或45小时距家12千米.5.设正比例函数y=kx,一次函数y=ax+b,∵点B在第三象限,横坐标为-2,设B(-2,y B),其中y B<0,∵S△AOB=6,∴12AO·│y B│=6,∴y B=-2,把点B(-2,-2)代入正比例函数y=kx,•得k=1.把点A(-6,0)、B(-2,-2)代入y=ax+b,得1 062 223a b aa bb⎧=-+=-⎧⎪⎨⎨-=-+⎩⎪=-⎩解得∴y=x,y=-12x-3即所求.6.延长BC交x轴于D,作DE⊥y轴,BE⊥x轴,交于E.先证△AOC≌△DOC,∴OD=OA=•1,CA=CD,∴= 5.7.当x≥1,y≥1时,y=-x+3;当x≥1,y<1时,y=x-1;当x<1,y≥1时,y=x+1;当x<•1,y<1时,y=-x+1.2.8.∵点A、B分别是直线y=3x轴和y轴交点,∴A(-3,0),B(0,∵点C坐标(1,0)由勾股定理得设点D的坐标为(x,0).(1)当点D在C点右侧,即x>1时,∵∠BCD=∠ABD,∠BDC=∠ADB,∴△BCD∽△ABD,∴BC CDAB BD==①∴22321112x xx-+=+,∴8x2-22x+5=0,∴x1=52,x2=14,经检验:x1=52,x2=14,都是方程①的根,∵x=14,不合题意,∴舍去,∴x=52,∴D•点坐标为(52,0).设图象过B、D两点的一次函数解析式为y=kx+b,5 52b kk bb⎧⎧==-⎪⎪∴⎨⎨+=⎪⎪=⎩⎩∴所求一次函数为(2)若点D在点C左侧则x<1,可证△ABC∽△ADB,∴AD BDAB CB=22113x+=②∴8x2-18x-5=0,∴x1=-14,x2=52,经检验x1=14,x2=52,都是方程②的根.∵x2=52不合题意舍去,∴x1=-14,∴D点坐标为(-14,0),∴图象过B、D(-14,0)两点的一次函数解析式为22综上所述,满足题意的一次函数为2222211.(1)y=200x+74000,10≤x≤30(2)三种方案,依次为x=28,29,30的情况.12.稿费是8000元.13.(1)设预计购买甲、乙商品的单价分别为a元和b元,则原计划是:ax+by=1500,①.由甲商品单价上涨1.5元,乙商品单价上涨1元,并且甲商品减少10个情形,得:(a+1.5)(x-10)+(b+1)y=1529,②再由甲商品单价上涨1元,而数量比预计数少5个,乙商品单价上涨仍是1元的情形得:(a+1)(x-5)+(b+1)y=1563.5,③.由①,②,③得:1.51044,568.5.x y ax y a+-=⎧⎨+-=⎩④-⑤×2并化简,得x+2y=186.(2)依题意有:205<2x+y<210及x+2y=186,得54<y<552 3.由于y是整数,得y=55,从而得x=76.14.设每月用水量为xm3,支付水费为y元.则y=8,08(),c x ab x ac x a+≤≤⎧⎨+-+≥⎩由题意知:0<c≤5,∴0<8+c≤13.从表中可知,第二、三月份的水费均大于13元,故用水量15m3、22m3均大于最低限量am3,将x=15,x=22分别代入②式,得198(15)338(22)b a cb a c=+-+⎧⎨=+-+⎩解得b=2,2a=c+19,⑤.再分析一月份的用水量是否超过最低限量,不妨设9>a,将x=9代入②,得9=8+2(9-a)+c,即2a=c+17,⑥.⑥与⑤矛盾.故9≤a,则一月份的付款方式应选①式,则8+c=9,∴c=1代入⑤式得,a=10.综上得a=10,b=2,c=1. ()15.W=200x+300x+400(18-2x)+800(10-x)+700(10-x)+500(2x-10)=-800x+17200.又010,010, 01828,59, x xx x≤≤≤≤⎧⎧∴⎨⎨≤-≤≤≤⎩⎩∴5≤x≤9,∴W=-800x+17200(5≤x≤9,x是整数).(2)由题设知,A市、B市、C市发往D市的机器台数分别为x,y,18-x-y,发往E市的机器台数分别是10-x,10-y,x+y-10,于是W=200x+800(10-x)+300y+700(10-y)+•400(19-x-y)+500(x+y-10)=-500x-300y-17200.又010,010, 010,010, 0188,1018, x xy yx y x y ≤≤≤≤⎧⎧⎪⎪≤≤∴≤≤⎨⎨⎪⎪≤--≤≤+≤⎩⎩∴W=-500x-300y+17200,且010,010,018.xyx y≤≤⎧⎪≤≤⎨⎪≤+≤⎩(x,y为整数).W=-200x-300(x+y)+17200≥-200×10-300×18+17200=9800.当x=•10,y=8时,W=9800.所以,W的最小值为9800.又W=-200x-300(x+y)+17200≤-200×0-300×10+17200=14200.当x=0,y=10时,W=14200,所以,W的最大值为14200.。
人教版八年级数学下《一次函数》拔高练习
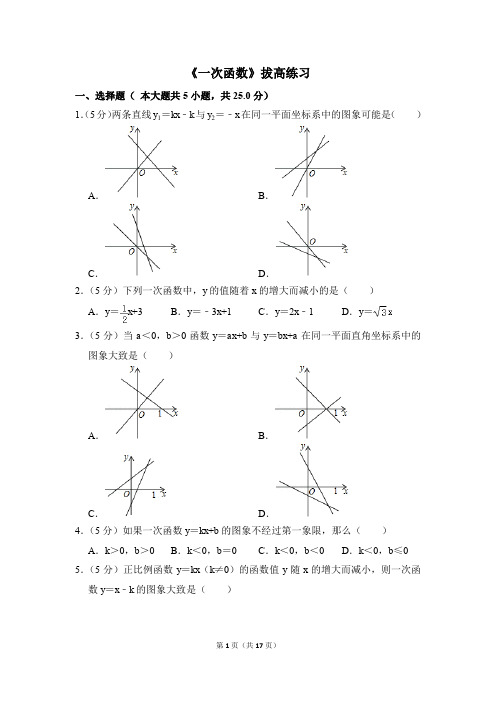
《一次函数》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)两条直线y1=kx﹣k与y2=﹣x在同一平面坐标系中的图象可能是()A.B.C.D.2.(5分)下列一次函数中,y的值随着x的增大而减小的是()A.y=x+3B.y=﹣3x+1C.y=2x﹣1D.y=3.(5分)当a<0,b>0函数y=ax+b与y=bx+a在同一平面直角坐标系中的图象大致是()A.B.C.D.4.(5分)如果一次函数y=kx+b的图象不经过第一象限,那么()A.k>0,b>0B.k<0,b=0C.k<0,b<0D.k<0,b≤0 5.(5分)正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x﹣k的图象大致是()A.B.C.D.二、填空题(本大题共5小题,共25.0分)6.(5分)如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点B n的坐标为.7.(5分)已知点A(x1,y1),点B(x2,y2)在直线y=kx+b(k≠0)上,且x1y1=x2y2=k,若y1y2=﹣9,则k的值等于.8.(5分)设正比例函数y=mx的图象经过点A(m,9),且y的值随x值的增大而增大,则m=.9.(5分)一次函数y=3x+1的图象与y轴相交于点A,一次函数y=2x﹣b的图象与y轴交于点B,且AB=2,则直线y=2x﹣b与x轴的交点坐标为.10.(5分)如图,已知在平面直角坐标系xOy中,O是坐标原点,直线l:y=x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2017的横坐标为.三、解答题(本大题共5小题,共50.0分)11.(10分)函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.12.(10分)如图,在平面直角坐标系xOy中,直线y=﹣x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长;(2)求点C和点D的坐标;(3)y轴上是否存在一点P,使得S△P AB =S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.13.(10分)已知一次函数y=(m﹣2)x+3﹣m的图象不经过第三象限,且m 为正整数.(1)求m的值.(2)在给出的平面直角坐标系中画出该一次函数的图象.(3)当﹣4<y<0时,根据函数图象,求x的取值范围.14.(10分)已知:y与x﹣1成正比例,且当x=2时,y=﹣4.(1)求y与x之间的函数关系式;(2)若点(a,2)在这个函数的图象上,求a的值.15.(10分)如图,已知直线l1经过点A(0,﹣1)与点P(2,3),另一条直线l2经过点P,且与y轴交于点B(0,m).(1)求直线l1的解析式;(2)若△APB的面积为3,求m的值.《一次函数》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)两条直线y1=kx﹣k与y2=﹣x在同一平面坐标系中的图象可能是()A.B.C.D.【分析】根据一次函数图象与一次项,常数项的关系,利用排除法可得答案.【解答】解:∵直线y2=﹣x只经过二,四象限,故A、B选项排除;当k>0时,直线y1=kx﹣k经过一、三、四象限,当k<0时,直线y1=kx﹣k经过一、二、四象限,故D选项排除,故选:C.【点评】本题考查了一次函数图象,解决问题的关键是利用一次函数图象与一次项、常数项的关系.2.(5分)下列一次函数中,y的值随着x的增大而减小的是()A.y=x+3B.y=﹣3x+1C.y=2x﹣1D.y=【分析】由一次函数的性质,在直线y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.【解答】解:∵y=kx+b中,k>0时,y随x的增大而增大;当k<0时,y随x 的增大而减小A项中,k=>0,故y的值随着x值的增大而增大;B项中,k=﹣3<0,y的值随着x值的增大而减小;C项中,k=2>0,y的值随着x值的增大而增大;D项中,k=>0,y的值随着x值的增大而增大;故选:B.【点评】本题考查了一次函数的性质,在直线y=kx+b中,当k>0时,y随x 的增大而增大;当k<0时,y随x的增大而减小.3.(5分)当a<0,b>0函数y=ax+b与y=bx+a在同一平面直角坐标系中的图象大致是()A.B.C.D.【分析】根据a、b的取值范围判定0函数y=ax+b与y=bx+a所经过的象限,从而得到正确的答案.【解答】解:∵a<0,b>0,∴函数y=ax+b的图象经过第一、二、四象限,函数y=bx+a的图象经过第一、三、四象限,观察图象,只有选项B符合题意.故选:B.【点评】此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.4.(5分)如果一次函数y=kx+b的图象不经过第一象限,那么()A.k>0,b>0B.k<0,b=0C.k<0,b<0D.k<0,b≤0【分析】由一次函数图象不经过第一象限可得出该函数图象经过第二、四象限或第二、三、四象限,再利用一次函数图象与系数的关系,即可找出结论.【解答】解:∵一次函数y=kx+b(k、b是常数)的图象不经过第一象限,∴一次函数y=kx+b(k、b是常数)的图象经过第二、四象限或第二、三、四象限.当一次函数y=kx+b(k、b是常数)的图象经过第二、四象限时,k<0,b=0;当一次函数y=kx+b(k、b是常数)的图象经过第二、三、四象限时,k<0,b<0.综上所述:k<0,b≤0.故选:D.【点评】本题考查了一次函数图象与系数的关系,分一次函数图象经过第一、三象限或第一、三、四象限两种情况考虑是解题的关键.5.(5分)正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x﹣k的图象大致是()A.B.C.D.【分析】根据自正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x﹣k的图象经过第一、三象限,且与y轴的正半轴相交.【解答】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,∴k<0,∵一次函数y=x﹣k的一次项系数大于0,常数项大于0,∴一次函数y=x+k的图象经过第一、三象限,且与y轴的正半轴相交.故选:A.【点评】本题考查了一次函数图象:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).二、填空题(本大题共5小题,共25.0分)6.(5分)如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点B n的坐标为(2n﹣1,2n).【分析】先根据题意求出A2点的坐标,再根据A2点的坐标求出B2的坐标,以此类推总结规律便可求出点B n的坐标.【解答】解:∵点A1坐标为(1,0),∴OA1=1,过点A1作x轴的垂线交直线于点B1,可知B1点的坐标为(1,2),∵点A2与点O关于直线A1B1对称,∴OA1=A1A2=1,∴OA2=1+1=2,∴点A2的坐标为(2,0),B2的坐标为(2,4),∵点A3与点O关于直线A2B2对称.故点A3的坐标为(4,0),B3的坐标为(4,8),依此类推便可求出点A n的坐标为(2n﹣1,0),点B n的坐标为(2n﹣1,2n).故答案为:(2n﹣1,2n).【点评】本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式.也考查了轴对称的性质.7.(5分)已知点A(x1,y1),点B(x2,y2)在直线y=kx+b(k≠0)上,且x1y1=x2y2=k,若y1y2=﹣9,则k的值等于3或﹣3.【分析】由x1y1=x2y2=k可得出点A、B在反比例函数y=的图象上,将y=代入y=kx+b中,整理后即可得出关于x的一元二次方程,根据根与系数的关系即可得出x1•x2=﹣1,结合x1y1=x2y2=k、y1y2=﹣9即可得出关于k的一元二次方程,解之即可求出k值,取其负值即可.【解答】解:∵x1y1=x2y2=k,∴点A、B在反比例函数y=的图象上,将y=代入y=kx+b中,整理得:kx2+bx﹣k=0,∴x1、x2为该方程的两个不相等的实数根,∴x1•x2=﹣1.∵x1y1=x2y2=k,y1y2=﹣9,∴y1y2==﹣k2=﹣9,解得:k=﹣3或k=3(舍去).故答案为:3或﹣3.【点评】本题考查了反比例函数与一次函数的交点问题、根与系数的关系以及解一元二次方程,根据点A、B坐标的特征找出点A、B为反比例函数y=与一次函数y=kx+b的交点是解题的关键.8.(5分)设正比例函数y=mx的图象经过点A(m,9),且y的值随x值的增大而增大,则m=3.【分析】直接根据正比例函数的性质和待定系数法求解即可.【解答】解:把x=m,y=9代入y=mx中,可得:m=±3,因为y的值随x值的增大而增大,所以m=3,故答案为:3.【点评】本题考查了正比例函数的性质:正比例函数y=kx(k≠0)的图象为直线,当k>0时,图象经过第一、三象限,y值随x的增大而增大;当k<0时,图象经过第二、四象限,y值随x的增大而减小.也考查了一次函数图象上点的坐标特征.9.(5分)一次函数y=3x+1的图象与y轴相交于点A,一次函数y=2x﹣b的图象与y轴交于点B,且AB=2,则直线y=2x﹣b与x轴的交点坐标为(,0)或(﹣,0).【分析】根据解析式求得A、B的坐标,然后根据题意得到|1+b|=2,求得b的值,然后令y=0即可求得直线y=2x﹣b与x轴的交点坐标.【解答】解:∵一次函数y=3x+1的图象与y轴相交于点A,一次函数y=2x﹣b 的图象与y轴交于点B,∴A(0,1),B(0,﹣b),∵AB=2,∴|1+b|=2,∴b=1或﹣3,∴直线y=2x﹣b为:y=2x﹣1或y=2x+3,令y=0,则,x=或﹣,∴直线y=2x﹣b与x轴的交点坐标为(,0)或(﹣,0),故答案为:(,0)或(﹣,0).【点评】本题考查了一次函数图象上点的坐标特征,属于基础题,关键是掌握用代入法求函数解析式.10.(5分)如图,已知在平面直角坐标系xOy中,O是坐标原点,直线l:y=x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2017的横坐标为.【分析】根据题意求出B1点的坐标,进而找到A2点的坐标,逐个解答便可发现规律,进而求得点A2017的坐标.【解答】解:已知点A1坐标为(4,0),且点B1在直线y=x上,可知B1点坐标为(4,3),由题意可知OB1=OA2,故A2点坐标为(5,0),同理可求的B2点坐标为(5,),故A3点坐标为(,0),按照这种方法逐个求解便可发现规律,A n点坐标为(,0),故点A2017的坐标为(,0).故答案为:.【点评】本题主要考查了一次函数的综合应用,是各地中考的热点,在解题时注意数形结合思想的运用,同学们要加强训练.三、解答题(本大题共5小题,共50.0分)11.(10分)函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.【分析】由正比例函数的定义可求得k的取值,再再利用其增减性进行取舍,代入代数式求值即可.【解答】解:∵y=(k﹣1)x2|k|﹣3是正比例函数,∴2|k|﹣3=1,解得k=2或k=﹣2,∵y随x的增大而减小,∴k﹣1<0,即k<1,∴k=﹣2,∴(k+3)2018=(﹣2+3)2018=1.【点评】本题主要考查正比例函数性质,掌握正比例函数的增减性是解题的关键,即在y=kx中,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.12.(10分)如图,在平面直角坐标系xOy中,直线y=﹣x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长;(2)求点C和点D的坐标;(3)y轴上是否存在一点P,使得S△P AB =S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.【分析】(1)先求得点A和点B的坐标,则可得到OA、OB的长,然后依据勾股定理可求得AB的长,(2)依据翻折的性质可得到AC的长,于是可求得OC的长,从而可得到点C 的坐标;设OD=x,则CD=DB=x+4.,Rt△OCD中,依据勾股定理可求得x的值,从而可得到点D(0,﹣6).(3)先求得S△P AB的值,然后依据三角形的面积公式可求得BP的长,从而可得到点P的坐标.【解答】解:(1)令x=0得:y=4,∴B(0,4).∴OB=4令y=0得:0=﹣x+4,解得:x=3,∴A(3,0).∴OA=3.在Rt△OAB中,AB==5.∴OC=OA+AC=3+5=8,∴C(8,0).设OD=x,则CD=DB=x+4.在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,解得:x=6,∴D(0,﹣6).(3)∵S△P AB =S△OCD,∴S△P AB=××6×8=12.∵点Py轴上,S△P AB=12,∴BP•OA=12,即×3BP=12,解得:BP=8,∴P点的坐标为(0,12)或(0,﹣4).【点评】本题主要考查的是一次函数的综合应用,解答本题主要应用了翻折的性质、勾股定理、待定系数法求函数解析式、三角形的面积公式,依据勾股定理列出关于x的方程是解题的关键.13.(10分)已知一次函数y=(m﹣2)x+3﹣m的图象不经过第三象限,且m 为正整数.(1)求m的值.(2)在给出的平面直角坐标系中画出该一次函数的图象.(3)当﹣4<y<0时,根据函数图象,求x的取值范围.【分析】(1)根据题意和一次函数的性质,可以求得m的值;(2)根据(1)中m的值可以求得该函数的解析式,然后根据两点确定一条直线可以画出该函数的图象;(3)根据(2)中的函数解析式和题意,可以求得当﹣4<y<0时,x的取值范围.【解答】解:(1)∵一次函数y=(m﹣2)x+3﹣m的图象不经过第三象限,∴,得m<2,∵m为正整数,∴m=1,即m的值是1;(2)由(1)知,m=1,∴y=(1﹣2)x+3﹣1=﹣x+2,当x=0时,y=2,当y=0时,x=2,该一次函数的图象如右图所示;(3)当y=﹣4时,﹣4=﹣x+2,得x=6,当y=0时,0=﹣x+2,得x=2,由图象可得,当﹣4<y<0时,x的取值范围是2<x<6.【点评】本题考查一次函数的性质、一次函数的图象,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.14.(10分)已知:y与x﹣1成正比例,且当x=2时,y=﹣4.(1)求y与x之间的函数关系式;(2)若点(a,2)在这个函数的图象上,求a的值.【分析】(1)根据正比例函数的定义可设y=k(x﹣1),然后x=2,y=6代入求出k即可得到y与x之间的函数关系式;(2)把点(a,2)代入(1)中的函数关系式中,解方程即可.【解答】解:(1)设y=k(x﹣1)(k≠0),当x=2,y=﹣4时,则﹣4=k(2﹣1),即k=﹣4,所以y=﹣4(x﹣1)=﹣4x+4;(2)∵点(a,2)在这个函数的图象上,∴2=﹣4a+4,∴a=.【点评】本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.15.(10分)如图,已知直线l1经过点A(0,﹣1)与点P(2,3),另一条直线l2经过点P,且与y轴交于点B(0,m).(1)求直线l1的解析式;(2)若△APB的面积为3,求m的值.【分析】(1)利用待定系数法确定直线l1的函数关系式;(2)过点P作PH⊥y轴于点EH,则PH=2,再由△APB的面积为3,可确定AB的长度,继而可得m的值.【解答】解:(1)设直线l1的表达式为y=kx+b,则,解得:.∴直线l1的函数关系式为:y=2x﹣1.(2)过P作PH⊥y轴于H,则PH=2,=AB•PH=3,∵S△APB∴AB×2=3,∴AB=3,∵A(0,﹣1),∴B(0,2)或(0,﹣4),∴m=2或﹣4.【点评】本题考查了一次函数综合题,涉及了待定系数法求一次函数解析式、平行四边形的性质及三角形的面积,解答本题的关键是数形结合思想及分类讨论思想的运用.。
一次函数全章拔高训练1.16

一次函数训练一、学科内综合题1.下列各图中,是函数图象的是().2.一次函数y=kx+b的图象经过点(m,1)和(-1,m),其中m>1,则k,b应满足条件( •).A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<03.一次函数与直线y=-x+6的交点A的横坐标是4,与直线y=x-1的交点B•的纵坐标是1,求这个一次函数的关系式.24.如图所示,甲、乙两车从A地出发,沿同一条高速公路行驶至距A地400千米的B地,L1、L2分别表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系,•根据图象提供的信息,解答下列问题.(1)求L2的函数表达式(不要求写出x的取值范围);(2)甲、乙两车哪一辆先到达B地?该车比另一辆车早多长时间到达B地?5.已知直线y=2x+1.(1)求已知直线与y轴交点A的坐标;(2)若直线y=kx+b与已知直线关于y轴对称,求k与b的值.6.一梯形的上底长为4,下底长为7,一腰长为12,写出梯形的周长y•与另一腰长x的函数关系式,并写出自变量x的取值范围.7.画出函数y=2x+1的图象,利用图象求:(1)方程2x+1=0的根;(2)不等式2x+1≥0的解;(3)求图象与坐标轴的两个交点之间的距离.8.如图所示,一个正比例函数图象与一个一次函数图象交于点(3,4),且一次函数的图象与y轴相交于点B.(1)求这两个函数的关系式;(2)求△AOB的面积.9.某地区水电资源丰富,并且得到了较好地开发,电力充足,•某供电公司为了鼓励居民用电采用分段收费的方法计算电费,月用电量x(千瓦时)与相应电费y(元)•之间的函数关系的图象如图所示.(1)月用电量为100千瓦时,应交电费______元.(2)当x≥100时,求y与x之间的函数关系式;(3)月用电量为260千瓦时,应交电费多少元?二、学科间综合题10.某礼堂有若干排座位,已知每排的座位数y是这排的排数x的一次函数,第1排有20个座位,第19排有56个座位.(1)写出x、y之间的关系式;(2)第26排有多少个座位?11.甲、乙两辆汽车同时从相距280km的A、B两地相向而行,s(km)•表示汽车与A地的距离,t (min)表示汽车行驶的时间,如图所示,L1,L2分别表示两辆汽车的s与t的关系.(1)L1表示哪辆汽车到A地的距离与行驶时间的关系;(2)汽车乙的速度是多少?(3)1h后,甲、乙两辆汽车相距多少千米?(4)行驶多长时间,甲、乙两辆汽车相遇?三、应用题12.某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q (L)与行驶时间t(h)之间的函数关系如图6-6-6所示,•根据图回答问题:(1)机动车行驶________h后加油;(2)加油前油箱余油量Q与行驶时间t的函数关系式是________;(3)中途加油________L;(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.四、创新题13.某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y(元)是行李质量x(kg)的一次函数,•其图象如图所示,求:(1)y与x之间的函数关系式;(2)旅客可免费携带的行李的质量是多少?五、中考题14.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.。
一次函数的图像与性质拔高讲义

一次函数的图像与性质拔高讲义一、【知识点拨】1、一次函数:形如y=kx+b (k ≠0, k, b 为常数)的函数。
注意:(1)k ≠0,否则自变量x 的最高次项的系数不为1;(2)当b=0时,y=kx ,y 叫x 的正比例函数。
2、图象:一次函数的图象是一条直线,(1)两个常用的特殊点:与y 轴交于(0,b );与x 轴交于(-,0) (2)由图象可以知道,直线y=k x+b 与直线y=k x 平行,例如直线:y=2x+3与直线y=2x-5都与直线y=2x 平行。
3、性质:(1)增减性 k>0时,y 随x 增大而增大 k<0时,y 随x 增大而减小 (2)图象的位置二、【典型例题剖析】例1(1)已知直线y=kx+b 经过点(3,-1)和点(-6,5),则k=_______,b=______.教师寄语:沟潭之水,凝滞沉闷,飞瀑之流,奋迅高亢——同是为水,性却异,前者满足安逸,后者进取不已。
奋斗者的幸福是从痛苦起步的,享乐者的痛苦是从“幸福”开始的。
(2)已知一次函数y=kx+5过点P(-1,2),则k=________. 例2(1)一次函数1-=x y 的图象不经过( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限(2)如图,表示一次函数y =mx+n 与正比例函数y=mnx(m ,n 是常数,且 mn ≠0)图像的是( ).例3.直线y=kx+b 与直线y=5-4x 平行,且与直线y=-3(x-6)相交,交点在y 轴上,求此直线解析式。
例4. 已知函数221(43)3a a y a a x --=-++是一次函数,则a 的值为 ( )例5如图,一次函数y =kx +b (k <0)的图象经过点A .当y <3时,x 的取值范围是 .例6(2011山东省潍坊, 14,3分)一个y 关于x 的函数同时满足两个条件:①图象过(2,1)点;②当0x >时.y 随x 的增大而减小,这个函数解析式为_______________ (写出一个即可)三【知识点分类专练】知识点1:一次函数的定义xy:一次函数通常可以表示 的形式,其中k 、b 是 ,k 0.特别地,当 时,一次函数y =kx (常数k ≠0)也叫 .正比例函数也是一次函数,它是一次函数的特例. 【课堂练习】:1、下列函数:①y=-8x;②y=8x;③y=8x 2;④y=8x+1;⑤y=53++z x .其中是一次函数的有( )A.1个B.2个C.3个D.4个 2、(1)若函数y=(m —2)x+5是一次函数,则m 满足的条件是 。
一次函数拔高题含答案

一次函数拔高题(含答案)一次函数拔高练习(一)一、选择题:1.已知y与x+3成正比例,并且x=1时,y=8,那么y与x之间的函数关系式为()(A)y=8x (B)y=2x+6 (C)y=8x+6 (D)y=5x+32.若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过()(A)一象限(B)二象限(C)三象限(D)四象限3.直线y=-2x+4与两坐标轴围成的三角形的面积是()(A)4 (B)6 (C)8 (D)16 4.若甲、乙两弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数解析式分别为y=k1x+a1和y=k2x+a2,如图,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为()(A)y1>y2(B)y1=y2(C)y1<y2(D)不能确定5.设b>a,将一次函数y=bx+a与y=ax+b的图象画在同一平面直角坐标系内,•则有一组a,b的取值,使得下列4个图中的一个为正确的是()6.若直线y=kx+b经过一、二、四象限,则直线y=bx+k不经过第()象限(A)一(B)二(C)三(D)四 7.一次函数y=kx+2经过点(1,1),那么这个一次函数()(A)y随x的增大而增大(B)y随x的增大而减小(C)图像经过原点(D)图像不经过第二象限8.无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在()(A)第一象限(B)第二象限(C)第三象限(D)第四象限9.要得到y=-32x-4的图像,可把直线y=-32x().(A)向左平移4个单位(B)向右平移4个单位(C)向上平移4个单位(D)向下平移4个单位 10.若函数y=(m-5)x+(4m+1)x2(m为常数)中的y与x成正比例,则m的值为()(A)m>-14(B)m>5 (C)m=-14(D)m=511.若直线y=3x-1与y=x-k的交点在第四象限,则k的取值范围是().(A)k<13(B)13<k<1 (C)k>1 (D)k>1或k<1312.过点P(-1,3)直线,使它与两坐标轴围成的三角形面积为5,•这样的直线可以作()(A)4条(B)3条(C)2条(D)1条15.在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有()(A)1个(B)2个(C)3个(D)4个19.甲、乙二人在如图所示的斜坡AB上作往返跑训练.已知:甲上山的速度是a米/分,下山的速度是b米/分,(a<b);乙上山的速度是12a米/分,下山的速度是2b米/分.如果甲、乙二人同时从点A出发,时间为t(分),离开点A的路程为S(米),•那么下面图象中,大致表示甲、乙二人从点A出发后的时间t(分)与离开点A的路程S(米)•之间的函数关系的是()二、填空题1.已知一次函数y=-6x+1,当-3≤x≤1时,y的取值范围是________.2.已知一次函数y=(m-2)x+m-3的图像经过第一,第三,第四象限,则m的取值范围是________.3.某一次函数的图像经过点(-1,2),且函数y的值随x的增大而减小,请你写出一个符合上述条件的函数关系式:_________. 4.已知直线y=-2x+m不经过第三象限,则m的取值范围是_________.5.函数y=-3x+2的图像上存在点P,使得P•到x•轴的距离等于3,•则点P•的坐标为__________.6.过点P(8,2)且与直线y=x+1平行的一次函数解析式为_________.7.y=23x与y=-2x+3的图像的交点在第_________象限.9.若一次函数y=kx+b,当-3≤x≤1时,对应的y值为1≤y≤9,•则一次函数的解析式为________.三、解答题2.已知y=p+z,这里p是一个常数,z与x成正比例,且x=2时,y=1;x=3时,y=-1.(1)写出y与x之间的函数关系式;(2)如果x的取值范围是1≤x≤4,求y的取值范围5.已知一次函数的图象,交x轴于A(-6,0),交正比例函数的图象于点B,且点B•在第三象限,它的横坐标为-2,△AOB的面积为6平方单位,•求正比例函数和一次函数的解析式.6.如图,一束光线从y轴上的点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),求光线从A点到B点经过的路线的长.8.已知:如图一次函数y=12x-3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.9、在直角坐标系x0y中,一次函数y=2x+2的图象与x轴,y轴,分别交于A、B两点,•点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D•两点的一次函数的解析式.答案:1.B 2.B 3.A 4.A 5.B 6.B 7.B 8.C 9.D 10.C 11.B 12.C 13.B14.D 15.D 16.A 17.C 18.C 19.C 20.A二、1.-5≤y ≤19 2.2<m<3 3.如y=-x+1等.4.m ≥0.提示:应将y=-2x+m 的图像的可能情况考虑周全.5.(13,3)或(53,-3).6.y=x-6. 8.222()aq bp bp aq --. 9.y=2x+7或y=-2x+3 10.10042009 11.据题意,有t=25080160⨯k ,∴k=325t . 因此,B 、C 两个城市间每天的电话通话次数为T BC =k ×2801003253205642t t ⨯=⨯=.三、1.(1)由题意得:202 44a b ab b+==-⎧⎧⎨⎨==⎩⎩解得∴这个一镒函数的解析式为:y=-2x+4(•函数图象略).(2)∵y=-2x+4,-4≤y≤4,∴-4≤-2x+4≤4,∴0≤x≤4.2.(1)∵z与x成正比例,∴设z=kx(k≠0)为常数,则y=p+kx.将x=2,y=1;x=3,y=-1分别代入y=p+kx,得2131k pk p+=⎧⎨+=-⎩解得k=-2,p=5,∴y与x之间的函数关系是y=-2x+5;(2)∵1≤x≤4,把x1=1,x2=4分别代入y=-2x+5,得y1=3,y2=-3.∴当1≤x≤4时,-3≤y≤3.另解:∵1≤x≤4,∴-8≤-2x≤-2,-3≤-2x+5≤3,即-3≤y≤3.3.(1)设一次函数为y=kx+b,将表中的数据任取两取,不防取(37.0,70.0)和(42.0,78.0)代入,得21 31 k pk p+=⎧⎨+=-⎩∴一次函数关系式为y=1.6x+10.8.(2)当x=43.5时,y=1.6×43.5+10.8=80.4.∵77≠80.4,∴不配套.4.(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米.(2)设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),代入得:y=15x-15,(2≤x≤3).当x=2.5时,y=22.5(千米)答:出发两个半小时,小明离家22.5千米.(3)设过E、F两点的直线解析式为y=k2x+b2,由E(4,30),F(6,0),代入得y=-15x+90,(4≤x≤6)过A、B两点的直线解析式为y=k3x,∵B(1,15),∴y=15x.(0≤x≤1),•分别令y=12,得x=265(小时),x=45(小时).答:小明出发小时265或45小时距家12千米.5.设正比例函数y=kx,一次函数y=ax+b,∵点B在第三象限,横坐标为-2,设B(-2,y B),其中y B<0,∵S△AOB=6,∴12AO·│y B│=6,∴y B=-2,把点B(-2,-2)代入正比例函数y=kx,•得k=1.把点A(-6,0)、B(-2,-2)代入y=ax+b,得1 062 223a b aa bb⎧=-+=-⎧⎪⎨⎨-=-+⎩⎪=-⎩解得∴y=x,y=-12x-3即所求.6.延长BC交x轴于D,作DE⊥y轴,BE⊥x轴,交于E.先证△AOC≌△DOC,∴OD=OA=•1,CA=CD,∴.7.当x≥1,y≥1时,y=-x+3;当x≥1,y<1时,y=x-1;当x<1,y≥1时,y=x+1;当x<•1,y<1时,y=-x+1.2.8.∵点A、B分别是直线y=3x轴和y轴交点,∴A(-3,0),B(0,∵点C坐标(1,0)由勾股定理得,设点D的坐标为(x,0).(1)当点D在C点右侧,即x>1时,∵∠BCD=∠ABD,∠BDC=∠ADB,∴△BCD∽△ABD,∴BC CDAB BD==①∴22321112x xx-+=+,∴8x2-22x+5=0,∴x1=52,x2=14,经检验:x1=52,x2=14,都是方程①的根,∵x=14,不合题意,∴舍去,∴x=52,∴D•点坐标为(52,0).设图象过B、D两点的一次函数解析式为y=kx+b,5 52b kk bb⎧⎧==-⎪⎪∴⎨⎨+=⎪⎪=⎩⎩∴所求一次函数为y=-5(2)若点D在点C左侧则x<1,可证△ABC∽△ADB,∴AD BDAB CB=,∴22113x+=②∴8x2-18x-5=0,∴x1=-14,x2=52,经检验x1=14,x2=52,都是方程②的根.∵x2=52不合题意舍去,∴x1=-14,∴D点坐标为(-14,0),∴图象过B、D(-14,0)两点的一次函数解析式为22综上所述,满足题意的一次函数为y=-2522211.(1)y=200x+74000,10≤x≤30(2)三种方案,依次为x=28,29,30的情况.12.稿费是8000元.13.(1)设预计购买甲、乙商品的单价分别为a元和b元,则原计划是:ax+by=1500,①.由甲商品单价上涨1.5元,乙商品单价上涨1元,并且甲商品减少10个情形,得:(a+1.5)(x-10)+(b+1)y=1529,②再由甲商品单价上涨1元,而数量比预计数少5个,乙商品单价上涨仍是1元的情形得:(a+1)(x-5)+(b+1)y=1563.5,③.由①,②,③得:1.51044,568.5.x y ax y a+-=⎧⎨+-=⎩④-⑤×2并化简,得x+2y=186.(2)依题意有:205<2x+y<210及x+2y=186,得54<y<5523.由于y是整数,得y=55,从而得x=76.14.设每月用水量为xm3,支付水费为y元.则y=8,08(),c x ab x ac x a+≤≤⎧⎨+-+≥⎩由题意知:0<c≤5,∴0<8+c≤13.从表中可知,第二、三月份的水费均大于13元,故用水量15m3、22m3均大于最低限量am3,将x=15,x=22分别代入②式,得198(15)338(22)b a cb a c=+-+⎧⎨=+-+⎩解得b=2,2a=c+19,⑤.再分析一月份的用水量是否超过最低限量,不妨设9>a,将x=9代入②,得9=8+2(9-a)+c,即2a=c+17,⑥.⑥与⑤矛盾.故9≤a,则一月份的付款方式应选①式,则8+c=9,∴c=1代入⑤式得,a=10.综上得a=10,b=2,c=1. ()15.W=200x+300x+400(18-2x)+800(10-x)+700(10-x)+500(2x-10)=-800x+17200.又010,010, 01828,59, x xx x≤≤≤≤⎧⎧∴⎨⎨≤-≤≤≤⎩⎩∴5≤x≤9,∴W=-800x+17200(5≤x≤9,x是整数).(2)由题设知,A市、B市、C市发往D市的机器台数分别为x,y,18-x-y,发往E市的机器台数分别是10-x,10-y,x+y-10,于是W=200x+800(10-x)+300y+700(10-y)+•400(19-x-y)+500(x+y-10)=-500x-300y-17200.又010,010, 010,010, 0188,1018, x xy yx y x y ≤≤≤≤⎧⎧⎪⎪≤≤∴≤≤⎨⎨⎪⎪≤--≤≤+≤⎩⎩∴W=-500x-300y+17200,且010,010,018.xyx y≤≤⎧⎪≤≤⎨⎪≤+≤⎩(x,y为整数).W=-200x-300(x+y)+17200≥-200×10-300×18+17200=9800.当x=•10,y=8时,W=9800.所以,W的最小值为9800.又W=-200x-300(x+y)+17200≤-200×0-300×10+17200=14200.当x=0,y=10时,W=14200,所以,W的最大值为14200.。
专题十二 一次函数 拔高题 含解析

专题十二一次函数拔高题满分:100学校 __________ 班级 __________ 学生 __________一、选择题( 本大题共20小题每题1 分)1、如图所示,函数y=k(x-1),与y=k(x2-1)(k≠0)在同一坐标系内的图象大致是()参考答案:C解析:C解析:①当k>0时,y=kx-k经过一、三、四象限,的两个分支分别在第一、三象限内,开口向上且与y轴负半轴相交,没有符合条件的选项;②当k<0时,y=kx-k经过第一、二、四象限,的两个分支分别在第二、四象限内,y=kx2-k开口向下且与y轴的正半轴相交,符合条件的选项为C.2、如图所示,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与这三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是( ).A.12.5 B.25 C.12.5aD.25a参考答案:A解析:A点拨:本题将一次函数与几何图形的面积相结合,结合点非常巧妙.观察图象并计算可知,AC=AD-CD=(a+2)x-(a+1)x=x,CB=CD-BD=(a+1)x-ax =x,所以AC=CB.由此可知OC是△OAB的边AB上的中线,所以△OAC与△OBC 的面积相等.同理可知,直线y=(a+1)x与过点(1,0),(2,0),(3,0)(4,0)且垂直于x轴的直线的交点平分△OAB中的相应线段,根据几何知识知,上下对应的阴影部分与非阴影部分的面积相等,所以图中阴影部分的面积等于△OAB的面积的一半.∵AB=(a+2)×5-a×5=10,OD=5,∴△OAB的面积是.∴图中阴影部分的面积是.3、小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图).若小亮上坡、平路、下坡的速度分别为v1、v2、v3,且v1<v2<v3,则小亮同学骑车上学时,离家的路程s与所用时间t的函数关系图像可能是().参考答案:C解析:C点拨:前段与后段都是平路,速度不变,则这两段的图像的坡度相同,第二段是下坡,速度快,则图像的坡度陡,第三段是上坡,速度慢,则图像坡度缓,所以整个图像的坡度是斜——变陡——变缓——与开始相同,则选C.4、小明从家中出发,到离家1.2千米的早餐店吃早餐,用了一刻钟吃完早餐后,按原路返回到离家1千米的学校上课,在下列图像中,能反映这一过程的大致图象是().参考答案:B解析:B点拨:由吃早餐的过程是离家距离不变的,所以排除A和D,再由吃完早餐后,原路返回去离家1千米的学校上课,排除C.故选B.5、为支援四川灾区,一列满载着2 400多吨“爱心”大米的专列向四川灾区进发.途中除3次因更换车头等原因停车外,一路快速行驶,经过80小时到达成都,描述上述过程的大致图像是图中的().参考答案:D解析:D点拨:火车一开始速度加快,中间一段速度不变.为换车头,速度逐渐变小,直到停止.换车头,速度为零,共四个过程.6、已知直线y=3x+b与两坐标轴围成的三角形的面积是6,则b等于().A.6 B.-6 C.±6D.±3参考答案:C解析:C点拨:直线与两坐标轴的交点为(0,b)与,所以围成的三角形的两条直角边的长为和.因为围成的三角形的面积为6,所以,即b2=36,所以b=±6.7、如图所示,以方程y-2x-2=0的解为坐标的点组成的图像是().参考答案:C解析:C点拨:原方程可化为y=2x+2,此函数的图像与y轴的交点为(0,2),且经过第一、二、三象限,则选C.8、函数y1=|x|,.当y1>y2时,x的范围是().A.x<-1 B.-1<x<2C.x<-1或x>2 D.x>2参考答案:C解析:C点拨:由函数图像可得,两函数的交点分别为(-1,1),(2,2).y1>y2就是函数y1的图像在函数y2的函数图像的上方,观察图像可知,y1>y2的解集是x<-1或x>2.9、小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1,l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪的速度分别是().A.3 km/h和4 km/h B.3 km/h和3 km/hC.4 km/h和4 km/h D.4 km/h和3 km/h参考答案:D解析:D点拨:根据图像不难发现:经过1.6 h,小聪走了4.8 km,则其速度为3 km/h;经过2.8-1.6=1.2(小时),小敏走了4.8 km,则其速度为4 km/h.10、小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图).若小亮上坡、平路、下坡的速度分别为v1、v2、v3,且v1<v2<v3,则小亮同学骑车上学时,离家的路程s与所用时间t的函数关系图像可能是().参考答案:C解析:C点拨:前段与后段都是平路,速度不变,则这两段的图像的坡度相同,第二段是下坡,速度快,则图像的坡度陡,第三段是上坡,速度慢,则图像坡度缓,所以整个图像的坡度是斜——变陡——变缓——与开始相同,则选C.11、小明从家中出发,到离家1.2千米的早餐店吃早餐,用了一刻钟吃完早餐后,按原路返回到离家1千米的学校上课,在下列图像中,能反映这一过程的大致图象是().参考答案:B解析:B点拨:由吃早餐的过程是离家距离不变的,所以排除A和D,再由吃完早餐后,原路返回去离家1千米的学校上课,排除C.故选B.12、为支援四川灾区,一列满载着2 400多吨“爱心”大米的专列向四川灾区进发.途中除3次因更换车头等原因停车外,一路快速行驶,经过80小时到达成都,描述上述过程的大致图像是图中的().参考答案:D解析:D点拨:火车一开始速度加快,中间一段速度不变.为换车头,速度逐渐变小,直到停止.换车头,速度为零,共四个过程.13、已知直线y=3x+b与两坐标轴围成的三角形的面积是6,则b等于().A.6 B.-6 C.±6D.±3参考答案:C解析:C点拨:直线与两坐标轴的交点为(0,b)与,所以围成的三角形的两条直角边的长为和.因为围成的三角形的面积为6,所以,即b2=36,所以b=±6.14、如图所示,以方程y-2x-2=0的解为坐标的点组成的图像是().参考答案:C解析:C点拨:原方程可化为y=2x+2,此函数的图像与y轴的交点为(0,2),且经过第一、二、三象限,则选C.15、函数y1=|x|,.当y1>y2时,x的范围是().A.x<-1 B.-1<x<2C.x<-1或x>2 D.x>2参考答案:C解析:C点拨:由函数图像可得,两函数的交点分别为(-1,1),(2,2).y1>y2就是函数y1的图像在函数y2的函数图像的上方,观察图像可知,y1>y2的解集是x<-1或x>2.16、小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1,l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪的速度分别是().A.3 km/h和4 km/h B.3 km/h和3 km/hC.4 km/h和4 km/h D.4 km/h和3 km/h参考答案:D解析:D点拨:根据图像不难发现:经过1.6 h,小聪走了4.8 km,则其速度为3 km/h;经过2.8-1.6=1.2(小时),小敏走了4.8 km,则其速度为4 km/h.17、如图,小虎在篮球场上玩,从点O出发,沿着O→A→B→O的路径匀速跑动,能近似刻画小虎所在位置距出发点O的距离s与时间t之间的函数关系的大致图象是( )参考答案:B解析:B18、已知一次函数y=2x+b和y=-x+a的图象都经过点A(0,-4),且与x轴分别交于B、C两点,则△ABC的面积应为( )A.13B.14 C .11 D.12参考答案:D解析:解析:因为函数y=2x+b和y=-x+a都经过A(0,-4),代入得a=b=-4,所以B(2,0),C(-4,0).=×4=12.所以S△ABC答案:D19、下列各曲线不能表示y是x的函数的是( )参考答案:C解析:解析:根据函数的定义,在一个变化过程中的两个变量x与y,对于x 的每一个确定的值,y总有唯一确定的值与其对应,那么y是x的函数.当过横轴上任意一点作纵轴的平行线时,如果所作的直线与图象的交点不超过一个(交点数目是1个或0个),此时图象表示的就是函数的关系;若在某一处所作纵轴的平行线与图象的交点有2个或2个以上,这时图象表示的就不是函数关系.其中A、B、D满足函数定义,只有C中对于一个x值,对应的y值的个数不确定,不满足函数关系.答案C20、小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分钟)的函数图象,那么符合这个同学行驶情况的图象大致是( )参考答案:C解析:解析:A表明一开始是匀速行驶,一段时间后随着时间的增加路程并不增加,说明一直在休息,不合题意;B开始是匀速行驶,后加快速度行驶,不合题意;D中间有一段下降的斜线段,说明中途又往回走了一段距离,也不合题意.故应选C,C图中的水平线段正体现了“行至中途自行车出了故障,只好停下来修车”这句话.答案:C二、填空题( 本大题共10小题每题2 分)1、商品的销售量也受销售价格的影响,比如,某衬衣定价为100元时,每月可卖出2 000件,价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)销售之间的函数关系式为______.解析:y=-5x+2 500点拨:根据题意,得每上涨1元,销售量便减少5件,则每月售出的衬衣的总件数等于原可卖出的2 000件减去少卖的件数,即y=2 000-5(x-100),整理,得y=-5x+2 500.2、小红的爸爸为小红存一份教育储蓄,首次存入2万元,以后每个月存入400元,存满4万元为止,则存款的总额y(元)与存入的月数x(月)之间的关系式为______,存满金额需______个月.解析:y=20 000+400x(0≤x≤50)50点拨:总额等于首次存入的金额加上后来存入的金额,即y=20 000+400x,由于存满4万元为止,则x的取值范围为0≤x≤50.把y=40 000代入y=20 000+400x,得x=50.3、如图,正方形ABCD的边长为10,点E在CB的延长线上,EB=10,点P在边CD上运动(C,D两点除外),EP与AB相交于点F,若CP=x,四边形FBCP的面积为y,则y关于x的函数关系式是______.解析:(0<x<10)点拨:由相似或三角形中位线定理,得BF=CP=x.由梯形面积公式,得y =×10×(x+x)=.又因为CP在CD上,所以0<x<10.4、商品的销售量也受销售价格的影响,比如,某衬衣定价为100元时,每月可卖出2 000件,价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)销售之间的函数关系式为______.解析:y=-5x+2 500点拨:根据题意,得每上涨1元,销售量便减少5件,则每月售出的衬衣的总件数等于原可卖出的2 000件减去少卖的件数,即y=2 000-5(x-100),整理,得y=-5x+2 500.5、小红的爸爸为小红存一份教育储蓄,首次存入2万元,以后每个月存入400元,存满4万元为止,则存款的总额y(元)与存入的月数x(月)之间的关系式为______,存满金额需______个月.解析:y=20 000+400x(0≤x≤50)50点拨:总额等于首次存入的金额加上后来存入的金额,即y=20 000+400x,由于存满4万元为止,则x的取值范围为0≤x≤50.把y=40 000代入y=20 000+400x,得x=50.6、育英中学需要添置某种教学仪器,方案1:到商家购买,每件需要8元;方案2:学校自己制作,每件4元,另外需要制作工具租用费120元.设需要仪器x件,方案1与方案2的费用分别为y1,y2(元).(1)写出y1的函数表达式是__________,y2的函数表达式是__________.(2)在下图所示的直角坐标系中,画出两个函数的图象.(3)观察图象发现制作仪器__________件时,两种方案的费用相同;制作仪器__________件时,方案1费用少;制作仪器__________件时,方案2费用少;和你的同学交流,你是怎样发现的.(4)瞬间决策:学校需制作仪器56件,采用方案__________便宜.解析:解:(1)根据题意写出函数解析式为y1=8x,y2=4x+120.(2)在x>0的范围内,画出两个函数图象.(3)观察图象发现:当x=30时,两图象相交,即当x=30时,两方案费用相同;当x<30时,y1=8x的图象低于y2=4x+120的图象,方案1费用低;当x>30时,y1=8x的图象高于y2=4x+120的图象,方案2费用低.(4)因为x=56>30,所以方案2费用低.7、如图中的折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)和行驶时间t(h)之间的函数关系,根据图中提供的信息,回答下列问题:(1)汽车共行驶了__________km;(2)汽车在行驶途中停留了__________h;(3)汽车在整个行驶过程中的平均速度为__________km/h;(4)汽车自出发后3 h至4.5 h之间行驶的方向是__________.解析:解析:图象上的最高点就是汽车离出发点最远的距离.汽车来回一次,共行驶了120×2=240(km),整个过程用时4.5 h,平均速度为240÷4.5=(km/h),行驶途中1.5 h~2 h之间汽车没有行驶.答案:(1)240 (2)0.5 (3) (4)从目的地返回出发点8、如图,直线y=kx+b经过A(-1,1)和两点,则不等式0<kx+x<-x的解集为_______.解析:【解析】本题考查一次函数的图象与性质,难度较大.解题关键是采用图象法求不等式组的解集.在同一直角坐标系中画出y=-x的图象.(如图)直线y=-x过A(-1,1)点.欲求0<kx+b<-x,直线y=kx+b在x轴上方且在直线y=-x的下方.故.9、如图,直线y=kx+b经过A(-1,1)和两点,则不等式0<kx+x<-x的解集为_______.解析:【解析】本题考查一次函数的图象与性质,难度较大.解题关键是采用图象法求不等式组的解集.在同一直角坐标系中画出y=-x的图象.(如图)直线y=-x过A(-1,1)点.欲求0<kx+b<-x,直线y=kx+b在x轴上方且在直线y=-x的下方.故.10、如图,直线y=kx+b经过A(-1,1)和两点,则不等式0<kx+x <-x的解集为_______.解析:【解析】本题考查一次函数的图象与性质,难度较大.解题关键是采用图象法求不等式组的解集.在同一直角坐标系中画出y=-x的图象.(如图)直线y=-x过A(-1,1)点.欲求0<kx+b<-x,直线y=kx+b在x轴上方且在直线y=-x的下方.故.三、解答题( 本大题共30小题每题2 分)1、教室里放有一台饮水机(如图①),饮水机上有两个放水管,课间同学们依次到饮水机前用茶杯接水,假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同,放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着,饮水机的存水量y(L)与放水时间x(min)的函数关系如图②所示:(1)求出饮水机的存水量y(L)与放水时间x(min)(x≥2)的函数关系式;(2)如果打开第一个水管后,2 min时恰好有4个同学接完水,然后打开第二个水管,则前22个同学接完水共需要几分钟?(3)按(2)的放法,求出在课间10 min内班级中最多有多少个同学能及时接完水?解析:解:(1)由图象,可设y=kx+b,将x=2,y=17,x=12,y=8代入,得,,即.(2)前2min只开放一个水管,4人接完水,即每人接水用时0.5 min,开放两个水管后,每分钟可有四人接完水,即每0.5 min两人接完水,故前22人接完水用时2+18÷2×0.5=6.5(min).(3)x=10时,,即10 min内水管里有水.前2 min有四人接完水,后8min每0.5 min有两人接完水,故课间10 min共可使4+32=36(人)接完水.2、一报刊销售亭从报社订购某晚报的价格是每份0.7元,销售价是每份1元,卖不掉的报纸还可以以0.20元的价格退回报社,在一个月内(以30天计算),有20天每天可卖出100份,其余10天每天只能卖出60份,但每天报亭从报社订购的份数必须相同.若以报亭每天从报社订购报纸的份数为自变量x,每月所获得利润为y.(1)写出y与x之间的函数关系式,并指出自变量x的取值范围;(2)报亭应该每天从报社订购多少份报纸,才能使每月获得的利润最大?最大利润是多少?解析:(1)y=0.30(20x+10×60)-0.50×10(x-60)=x+480,60≤x≤100且x为正整数;(2)∵当60≤x≤100时,函数y随x的增大而增大,∴当x=100时,y有最大值,最大值为100+480=580.3、某市20位下岗职工在近邻承包50亩土地办农场,这些地可种蔬菜、烟叶或数值1 100750600请你设计一个种植方案,使每亩地都种上农作物,20位职工都有工作,且使农作物预计总产值最多.解析:解:设种植蔬菜x亩,烟叶y亩,则小麦为(50-x-y)亩,由题意知,即3x+y=90,∴y=90-3x(0≤x≤30),再设预计总产值为M元,则有M=1 100x+750y+600(50-x-y)=500x+150y+30 000.将y=90-3x代入得M=500x+150(90-3x)+30 000,M=50x+43 500,因为50>0,所以M随x的增大而增大,即当x=30时,预计总产值最多,当x=30,y=0,50-x-y=20,此时种蔬菜15人,种小麦5人.答:种蔬菜30亩,小麦20亩,不种烟叶时,所有职工都有工作,且农作物预计总产值最多.4、教室里放有一台饮水机(如图①),饮水机上有两个放水管,课间同学们依次到饮水机前用茶杯接水,假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同,放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着,饮水机的存水量y(L)与放水时间x(min)的函数关系如图②所示:(1)求出饮水机的存水量y(L)与放水时间x(min)(x≥2)的函数关系式;(2)如果打开第一个水管后,2 min时恰好有4个同学接完水,然后打开第二个水管,则前22个同学接完水共需要几分钟?(3)按(2)的放法,求出在课间10 min内班级中最多有多少个同学能及时接完水?解析:解:(1)由图象,可设y=kx+b,将x=2,y=17,x=12,y=8代入,得,,即.(2)前2min只开放一个水管,4人接完水,即每人接水用时0.5 min,开放两个水管后,每分钟可有四人接完水,即每0.5 min两人接完水,故前22人接完水用时2+18÷2×0.5=6.5(min).(3)x=10时,,即10 min内水管里有水.前2 min有四人接完水,后8min每0.5 min有两人接完水,故课间10 min共可使4+32=36(人)接完水.5、在一条直线上依次有A,B,C三个港口,甲,乙两船同时分别从A,B港口出发,沿直线匀速驶向C港,最终达到C港.设甲,乙两船行驶x(h)后,与B港的距离分别为y1,y2(km),y1,y2与x的函数关系如图所示.(1)填空:A,C两港口间的距离为________km,a=________;(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;(3)若两船的距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.解析:解:(1)120 2(2)由点(3,90),求得y2=30x.当x>0.5时,由点(0.5,0),(2,90),求得y1=60x-30.当y1=y2时,60x-30=30x,解得x=1.此时y1=y2=30.所以点P的坐标为(1,30).该点坐标的意义为:两船出发1 h后,甲船追上乙船,此时两船离B港的距离为30 km.(3)①当x≤0.5时,由点(0,30),(0.5,0),求得y1=-60x+30.依题意,由(-60x+30)+30x≤10,解得.不合题意,舍去.②当0.5<x≤1时,依题意,由30x-(60x-30)≤10.解得.所以.③当x>1时,依题意,由(60x-30)-30x≤10.解得.所以.综上所述,当时,甲、乙两船可以相互望见.6、汽车在行驶过程中,速度往往是变化的,下图图像表示的是一辆汽车的速度随时间变化而变化的情况.(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?(3)出发后8分钟到10分钟之间可能发生了什么情况?解析:解:(1)汽车从出发到最后停止共经过了24分钟,它的最高时速为90千米/时;(2)2分钟~6分钟时速度为30千米/时,18分钟~22分钟时速度为90千米/时;(3)修车或堵车等.7、小刚在劳动艺术课中要制作一个周长为80 cm的等腰三角形,请你写出底边长y(cm)与腰长x(cm)的函数关系式,并求出自变量x的取值范围.解析:解:y=80-2x,由两边之和大于第三边,两边之差小于第三边,得0<80-2x<2x,解得20<x<40.即y=80-2x(20<x<40).8、已知y+5与3x+4成正比例,且当x=1时,y=2.(1)求y与x的函数关系式.(2)求当x=-1时的函数值.(3)如果y的取值范围是0≤y≤5,求x的取值范围.解析:解:(1)因为y+5与3x+4成正比例,所以设y+5=k(3x+4).因为当x =1时,y=2,所以k=1,所以y=3x-1.(2)当x=-1时,y=-4.(3)因为0≤y≤5,所以0≤3x-1≤5,所以.9、已知一次函数y=(2m+4)x+(3-n),求:(1)m,n是什么数时,y随x的增大而增大.(2)m,n为何值时,函数的图像与y轴的交点在x轴下方.(3)m,n为何值时,函数的图像经过原点.解析:解:(1)因为y随x的增大而增大,所以2m+4>0,解得m>-2,所以当m>-2,n为任意实数时,y随x的增大而增大.(2)因为图像与y轴的交点在x轴下方,所以解得所以当m≠-2且n>3时,函数的图像与y轴的交点在x轴下方.(3)因为图像经过原点,所以解得所以当m≠-2,n=3时,函数图像经过原点.10、某中学要印制期末考试卷.甲印刷厂提出:每套试卷收0.6元的印刷费,另收400元的制版费;乙印刷厂提出:每套试卷收1元的印刷费,但不再收制版费.(1)分别写出两个厂的收费y(元)与印刷数量x(套)之间的函数关系式;(2)请在直角坐标系中分别作出(1)中两个函数的图像,并根据图像回答:若印800套试卷,则选择哪家印刷厂合算?若学校有学生2 000人,为保证每个学生均有一套试卷,那么学校至少要付印刷费多少元?(3)从图像上你还能获得哪些信息?(写出一条与(2)中不同的信息即可)解析:解:(1)y甲=400+0.6x;y乙=x(x为非负整数).(2)如图所示.由图像知,印800套选择乙厂,印2 000套至少要1 600元.(3)当印1 000套时,不论选哪个印刷厂都是一样的;当超过1 000套时,选择甲厂印刷合算;当小于1 000套时,选择乙厂印刷合算.11、汽车在行驶过程中,速度往往是变化的,下图图像表示的是一辆汽车的速度随时间变化而变化的情况.(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?(3)出发后8分钟到10分钟之间可能发生了什么情况?解析:解:(1)汽车从出发到最后停止共经过了24分钟,它的最高时速为90千米/时;(2)2分钟~6分钟时速度为30千米/时,18分钟~22分钟时速度为90千米/时;(3)修车或堵车等.12、已知y+5与3x+4成正比例,且当x=1时,y=2.(1)求y与x的函数关系式.(2)求当x=-1时的函数值.(3)如果y的取值范围是0≤y≤5,求x的取值范围.解析:解:(1)因为y+5与3x+4成正比例,所以设y+5=k(3x+4).因为当x =1时,y=2,所以k=1,所以y=3x-1.(2)当x=-1时,y=-4.(3)因为0≤y≤5,所以0≤3x-1≤5,所以.13、已知一次函数y=(2m+4)x+(3-n),求:(1)m,n是什么数时,y随x的增大而增大.(2)m,n为何值时,函数的图像与y轴的交点在x轴下方.(3)m,n为何值时,函数的图像经过原点.解析:解:(1)因为y随x的增大而增大,所以2m+4>0,解得m>-2,所以当m>-2,n为任意实数时,y随x的增大而增大.(2)因为图像与y轴的交点在x轴下方,所以解得所以当m≠-2且n>3时,函数的图像与y轴的交点在x轴下方.(3)因为图像经过原点,所以解得所以当m≠-2,n=3时,函数图像经过原点.14、一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61 000元.设购进A型手机x部,B(1)用含x,y的式子表示购进C型手机的部数;(2)求出y与x之间的函数关系式;(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1 500元.①求出预估利润P(元)与x(部)的函数关系式;(注:预估利润P=预售总额-购机款-各种费用)②求出预估利润的最大值,并写出此时购进三款手机各多少部.解析:解:(1)60-x-y.(2)由题意,得900x+1 200y+1 100(60-x-y)=61 000,即y=2x-50.(3)①由题意,得P=1 200x+1 600y+1 300(60-x-y)-61 000-1 500,即P=500x+500.②购进C型手机部数为60-x-y=60-x-(2x-50)=110-3x.根据题意列不等式组,得解得29≤x≤34.∴x的范围为29≤x≤34,且x为整数.∵P是x的一次函数,k=500>0,∴P随x的增大而增大.∴当x取最大值34时,P有最大值,最大值为17 500元.此时购进A型手机34部,B型手机18部,C型手机8部.15、小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程s(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):(1)求点B的坐标;(2)小明能否在比赛开始前到达体育馆?解析:解:(1)从图象可以看出:父子俩从出发到相遇时花费了15分钟.设小明步行的速度为x米/分钟,则小明父亲骑车的速度为3x米/分钟,依题意得15x+45x=3 600.解得x=60.∴两人相遇处离体育馆的距离为60×15=900(米).∴点B的坐标为(15,900).(2)小明取票后,赶往体育馆的时间为=5.小明取票花费的时间为15+5=20分钟.∵20<25,∴小明能在比赛开始前到达体育馆.16、如图,已知一次函数的图象交正比例函数图象于M点,交x轴于点N(-6,0),又知点M位于第二象限,其横坐标为-4,若△MON的面积为15,求正比例函数和一次函数的解析式.解析:分析:要确定一次函数的解析式,必须知道图象的两个已知点的坐标,而要确定正比例函数又必须知道图象上一个点的坐标.已知条件中给出了△MON的面积,而△MON的面积,因底边NO可求得,所以求出高,就求出了M点的纵坐标,问题得到解决.解:过点M作MC⊥ON于点C,=×ON×MC.则S△MON∵点N的坐标为(-6,0),∴|ON|=6.∴×ON×MC=15.∴MC=5.∵点M在第二象限,∴点M的坐标为(-4,5).设一次函数解析式为y=k1x+b,正比例函数解析式为y=k2x.直线y=k1x+b经过点(-6,0)和(-4,5),∴即解得∴一次函数解析式为y=x+15.∵正比例函数y=k2x的图象经过(-4,5)点,∴k2=-.∴正比例函数解析式为y=-x.点拨:确定一次函数(或正比例函数)的解析式,常用待定系数法,其一般过程可简称为“一列二化三解四还原”.一次函数y=kx+b(k≠0)中含有两个待定字母,设法建立含k,b的两个方程,解方程组即可.17、某蔬菜加工厂承担出口蔬菜加工的任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:方案一:从纸箱厂定制购买,每个纸箱价格为4元;方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16 000元,每加工一个纸箱还需成本费2.4元.(1)若需要这种规格的纸箱x个,请分别写出从纸箱厂购买纸箱的费用y1(元)和蔬菜加工厂自己加工制作纸箱的费用y2(元)关于x(个)的函数关系式;(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.解析:解:(1)从纸箱厂定制购买纸箱费用y1=4x;蔬菜加工厂自己加工纸箱费用y2=2.4x+16 000.(2)y2-y1=(2.4x+16 000)-4x=16 000-1.6x,由y1=y2,得16 000-1.6x=0,解得x=10 000.当x<10 000时,y1<y2;当x>10 000时,y1>y2.因此,当纸箱数量小于10 000个时,选择方案一;当纸箱数量大于10 000个时,选择方案二;当纸箱数量等于10 000个时,两种方案都可以选择.18、某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为w(元),求w关于x的函数关系式,并求出x的取值范围;(2)若公司要求总利润不低于17 560元,说明有多少种不同的分配方案,并将各种方案设计出来;(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?。
中考一次函数倒数第三题拔高重难点总结

中考一次函数倒数第三题拔高重难点总结函数的概念及性质,对学生来说并不难。
主要是对它的灵活运用,如判断对错,求值域范围等,而拔高题一般有以下特点:(1)知识点多、跨度大、综合性强;(2)知识点考查由易到难;(3)分数值小,需精准计算;(4)有利于启发联想思维。
但同时又具有“形象直观”和简单明了的特点。
对此类问题进行总结梳理既可拓展知识面,又可提升解决能力。
这里选取中考真题为例,对本节课的重难点作出简要总结。
解析几何题中,三角函数部分考查比较多,占35%左右,其中最常见的就是解直角三角形,因此掌握正弦定理是必须的。
其次还有余弦定理,反三角函数,它们在平面向量中也经常会遇到。
所以掌握好平面向量与三角函数之间的关系是很有必要的。
然后是圆锥曲线中的圆与方程,它们的综合题目较少,且相对独立,但通过研究发现它们之间存在着密切的联系,我们应该将圆锥曲线与方程的综合运用起来,这样才能更快地解答这类问题。
至于函数,则要注意基础知识的积累,尤其是一些基本的公式定理要牢记,否则容易丢分。
- 1 -。
一次函数综合拔高训练(一)

一次函数综合拔高训练(一)试卷副标题考试范围:xxx;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分评卷人得分一.选择题(共4小题)1.如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()A.B.C.D.2.如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为()A.B.C.2D.43.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是()A.y=﹣x+4B.y=x+4C.y=x+8D.y=﹣x+84.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2B.3C.4D.6评卷人得分二.填空题(共2小题)5.如图,已知平面直角坐标系中两定点A(2,﹣1)和B(0,﹣1),P为x轴上一动点,则当P A+PB的值最小时点P的横坐标是,此时P A+PB=.6.如图,直线y=x+1与x轴交于点A,与y轴交于点B,正方形OCDE的顶点D在线段AB上,点C在y轴上,点E在x轴上,则点D的坐标为.评卷人得分三.解答题(共6小题)7.如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②,已知BC=8cm.(1)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;(2)当E点停止后,求△ABE的面积.8.如图,直线y=﹣2x+3与x轴相交于点A,与y轴相交于点B.(1)求A,B两点的坐标;(2)过B点作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.9.如图,已知函数y=mx的图象为直线l1,函数y=kx+b的图象为直线l2,直线l1、l2分别交x轴于点B和点C (3,0),分别交y轴于点D和E,l1和l2相交于点A(2,2).(1)填空:m=;求直线l2的解析式为;(2)若点M是x轴上一点,连接AM,当△ABM的面积是△ACM面积的2倍时,请求出符合条件的点M的坐标;(3)若函数y=nx﹣6的图象是直线l3,且l1、l2、l3不能围成三角形,直接写出n的值.10.如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:(1)求直线AC的表达式;(2)求△OAC的面积;(3)是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.11.如图,A(0,4),B(﹣4,0),D(﹣2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.(1)求直线AB和直线AD的解析式;(2)求点M的坐标;(3)求点E、F的坐标.12.如图,点A的坐标为(4,0).点P是直线y=x+3在第一象限内的点,过P作PM⊥x轴于点M,O是原点.(1)设点P的坐标为(x,y),试用它的纵坐标y表示△OP A的面积S;(2)S与y是怎样的函数关系?它的自变量y的取值范围是什么?(3)如果用P的坐标表示△OP A的面积S,S与x是怎样的函数关系?它的自变量的取值范围是什么?(4)在直线y=x+3上求一点Q,使△QOA是以OA为底的等腰三角形.一次函数综合拔高训练(一)参考答案与试题解析一.选择题(共4小题)1.如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()A.B.C.D.【分析】由题意当0≤x≤3时,y=3,当3<x<5时,y=×3×(5﹣x)=﹣x+.由此即可判断.解:由题意当0≤x≤3时,y=3,当3<x<5时,y=×3×(5﹣x)=﹣x+.故选:D.2.如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为()A.B.C.2D.4【分析】由一次函数解析式分别求出点A和点B的坐标,即可作答.解:一次函数y=2x+1中,当x=0时,y=1;当y=0时,x=﹣0.5;∴A(﹣0.5,0),B(0,1)∴OA=0.5,OB=1∴△AOB的面积=0.5×1÷2=故选:A.3.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是()A.y=﹣x+4B.y=x+4C.y=x+8D.y=﹣x+8【分析】设P点坐标为(x,y),由坐标的意义可知PC=x,PD=y,根据围成的矩形的周长为8,可得到x、y 之间的关系式.解:如图,过P点分别作PD⊥x轴,PC⊥y轴,垂足分别为D、C,设P点坐标为(x,y),∵P点在第一象限,∴PD=y,PC=x,∵矩形PDOC的周长为8,∴2(x+y)=8,∴x+y=4,即该直线的函数表达式是y=﹣x+4,故选:A.4.在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=﹣2x交于点A、B,则△AOB的面积为()A.2B.3C.4D.6【分析】根据方程或方程组得到A(﹣3,0),B(﹣1,2),根据三角形的面积公式即可得到结论.解:在y=x+3中,令y=0,得x=﹣3,解得,,∴A(﹣3,0),B(﹣1,2),∴△AOB的面积=3×2=3,故选:B.二.填空题(共2小题)5.如图,已知平面直角坐标系中两定点A(2,﹣1)和B(0,﹣1),P为x轴上一动点,则当P A+PB的值最小时点P的横坐标是(1,0),此时P A+PB=2.【分析】作点B关于x轴的对称点B′,连接B′A交x轴于点P,则点P即为所求点;求出直线AB′的函数解析式,再把y=0代入即可求得P的坐标,根据勾股定理即可求得线段AB的长,即P A+PB的最小值.解:作点B关于x轴的对称点B′(0,1),连接AB′交x轴于P,∵B的坐标是(0,﹣1),∴B′(0,1),设直线AB′的函数解析式为y=kx+b,∴,解得,,∴直线AB′的函数解析式为y=﹣x+1,令y=0,则0=﹣x+1,解得x=1,∴点P的坐标是(1,0).∵B′(0,1),A(2,﹣1),∴AB′==2;故答案为(1,0)、2.6.如图,直线y=x+1与x轴交于点A,与y轴交于点B,正方形OCDE的顶点D在线段AB上,点C在y轴上,点E在x轴上,则点D的坐标为(﹣,).【分析】可设出点D的坐标,表示出DE和OE,可求得D点的坐标.解:∵四边形OCDE为正方形,∴DE⊥EO,DE=EO,∵D点在y=x+1上,∴可设D点坐标为(x,x+1),∴DE=x+1,EO=﹣x,∴x+1=﹣x,解得x=﹣,∴在点坐标为(﹣,),故答案为:(﹣,).三.解答题(共6小题)7.如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②,已知BC=8cm.(1)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;(2)当E点停止后,求△ABE的面积.【分析】根据三角形的面积公式,可得答案.解:(1)有图2可知E点的速度为3,∴y=×3x×AD=9x,即y=9x(0<x≤2).(2)当E点停止后,BE=6,∴x=,2时,y=9×2=18.∴△ABE的面积是18cm2.8.如图,直线y=﹣2x+3与x轴相交于点A,与y轴相交于点B.(1)求A,B两点的坐标;(2)过B点作直线BP与x轴相交于点P,且使OP=2OA,求△ABP的面积.【分析】(1)先令y=0求出x的值,再令x=0求出y的值即可得出A、B两点的坐标;(2)根据OP=2OA求出P点坐标,再根据三角形的面积公式求解即可.解:(1)∵令y=0,则x=;令x=0,则y=3,∴A(,0),B(0,3);(2)∵OP=2OA,∴P(3,0)或(﹣3,0),∴AP=或,∴S△ABP=AP×OB=××3=,或S△ABP=AP×OB=××3=.故答案为:或.9.如图,已知函数y=mx的图象为直线l1,函数y=kx+b的图象为直线l2,直线l1、l2分别交x轴于点B和点C (3,0),分别交y轴于点D和E,l1和l2相交于点A(2,2).(1)填空:m=;求直线l2的解析式为y=﹣2x+6;(2)若点M是x轴上一点,连接AM,当△ABM的面积是△ACM面积的2倍时,请求出符合条件的点M的坐标;(3)若函数y=nx﹣6的图象是直线l3,且l1、l2、l3不能围成三角形,直接写出n的值.【分析】(1)将点A坐标代入y=mx中,即可得出m的值;将带你A,C坐标代入y=kx+b中,即可根据待定系数法求得解析式;(2)先利用两三角形面积关系判断出CM=2BM,再分两种情况,即可得出结论;(3)分三种情况,利用两直线平行,比例系数相等即可得出结论.解:(1)∵点A(2,2)在函数y=mx的图象上,∴2m+=2,∴m=,∵直线过点C(3,0)、A(2,2),可得方程组为,解得,∴直线l2的解析式为y=﹣2x+6;故答案为:m=;y=﹣2x+6;(2)∵B是l1与x轴的交点,当y=0时,x+=0,∴x=﹣4,B坐标为(﹣4,0),同理可得,C点坐标(3,0),设点A到x轴的距离为h∵S△ABM=BM•h,S△ACM=CM•h,又∵△ABM的面积是△ACM面积的2,∴BM•h=2×CM•h,∴BM=2CM第一种情况,当M在线段BC上时,∵BM+CM=BC=7,∴3CM=7,CM=,∴M1坐标(,0),第二种情况,当M在射线BC上时,∵BC+CM=BM∴CM=BC=7∴M2坐标(10,0),∴M点的坐标为(,0)或(10,0),(3)∵l1、l2、l3不能围成三角形,∴直线l3经过点A或l3∥l1或l3∥l2,①∵直线l3的解析式为y=nx﹣6,A(2,2),∴2n﹣6=2,∴n=4,②当l3∥l1时,则n=,③当l3∥l2时,则n=﹣2,即n的值为4或或﹣2.10.如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:(1)求直线AC的表达式;(2)求△OAC的面积;(3)是否存在点M,使△OMC的面积是△OAC的面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.【分析】(1)利用待定系数法即可求得函数的解析式;(2)求利用三角形的面积公式即可求解;(3)当△OMC的面积是△OAC的面积的时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.解:(1)设直线AC的解析式是y=kx+b,根据题意得:,解得:.则直线的解析式是:y=﹣x+6;(2)S△OAC=×6×4=12;(3)设OA的解析式是y=mx,则4m=2,解得:m=.则直线的解析式是:y=x,∵当△OMC的面积是△OAC的面积的时,∴M到y轴的距离是×4=1,∴点M的横坐标为1或﹣1;当M的横坐标是:1,在y=x中,当x=1时,y=,则M的坐标是(1,);在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).则M的坐标是:M1(1,)或M2(1,5).当M的横坐标是:﹣1,在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7).综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).【点评】本题主要考查了一次函数综合题,用待定系数法求函数的解析式以及三角形面积求法等知识,利用M 点横坐标为±1分别求出是解题关键.11.如图,A(0,4),B(﹣4,0),D(﹣2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.(1)求直线AB和直线AD的解析式;(2)求点M的坐标;(3)求点E、F的坐标.【分析】(1)利用待定系数法求出直线AB、AD的解析式即可;(2)利用全等三角形的判定方法得出△ADO≌△OMB(AAS),求出M点坐标;(3)利用二元一次方程组的解法求出E,F点坐标即可.解:(1)设直线AB的解析式为:y=ax+b,则,解得:,故直线AB的解析式为:y=x+4;设直线AD的解析式为:y=kx+c,则,解得:,故直线AD的解析式为:y=2x+4;(2)∵OE⊥AD,∴∠DOM+∠ODF=90°,∵BM⊥OB,∴∠BOM+∠OMB=90°,∴∠ADO=∠BMO,在△ADO和△OMB中∵,∴△ADO≌△OMB(AAS),∴DO=BM=2,则点M的坐标为:(﹣4,2);(3)设直线MO的解析式为:y=dx,则﹣4d=2,解得:d=﹣,故直线MO的解析式为:y=﹣x,由题意可得:,解得:,故E点坐标为:(﹣,),,解得:,故F点坐标为:(﹣,).12.如图,点A的坐标为(4,0).点P是直线y=x+3在第一象限内的点,过P作PM⊥x轴于点M,O是原点.(1)设点P的坐标为(x,y),试用它的纵坐标y表示△OP A的面积S;(2)S与y是怎样的函数关系?它的自变量y的取值范围是什么?(3)如果用P的坐标表示△OP A的面积S,S与x是怎样的函数关系?它的自变量的取值范围是什么?(4)在直线y=x+3上求一点Q,使△QOA是以OA为底的等腰三角形.【分析】(1)根据直线解析式确定出B坐标,设P(x,y),以OA为底,P的纵坐标为高表示出S与y的关系式即可;(2)判断出S与y的函数关系式,并求出y的范围即可;(3)以OA为底,PM为高列出S与x的函数解析式,求出x的范围即可;(4)△QOA是以OA为底的等腰三角形,可得出点Q在OA的中垂线上,求出Q坐标即可.解:(1)直线y=﹣x+3与y轴的交点为B(0,3),设点P(x,y),∵点P在第一象限,x>0,y>0,∴S=OA•PM=×y×4=2y;(2)S是y的正比例函数,自变量y的取值范围是0<y<3;(3)S=2y=2(﹣x+3)=﹣x+6,S是x的一次函数,自变量的取值范围是0<x<6.(4)∵△QOA是以OA为底的等腰三角形,∴点Q在OA的中垂线上,设Q(x0,y0),则有,解得:,则点Q的坐标为(2,2).。
浙教版数学八年级上册《第五章 一次函数》拔高训练试卷

浙教版数学八年级上册《一次函数》拔高训练试卷(无解析)一.选择题1.函数y=kx与y=﹣kx+k的大致图象是()A.B.C.D.2.如图,一次函数y=(m-2)x-1的图象经过第二、三、四象限,则m的取值范围是( )A.m>0 B.m<0 C.m>2 D.m<23.已知直线y=k1x,y=k2x,y=k3x的图象如图,则k1、k2、k3的大小关系为()A.k1>k2>k3B.k1>k3>k2C.k3>k2>k1D.k2>k1>k34.在同一坐标系中,函数与的图象大致是()A. B. C. D.5.如图,直角梯形OABC的直角顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上,OA∥BC,D 是直线y=x与线段BC的交点,OA=4,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的点,且∠DEF=45°,OE=,则AF的值为()A.1 B.2 C.D.6.如图,一束光线从点A(4,4)出发,经y轴上的点C反射后经过点B(1,0),则点C的坐标是()A.(0,)B.(0,)C.(0,1)D.(0,2)7.在平面直角坐标系内,已知点A 的坐标为(-6,0),直线l:y =kx+b 不经过第四象限,且与x 轴的夹角为30°,点P 为直线l 上的一个动点,若点P 到点A 的最短距离是2,则b 的值为( ) A.332 或3310 B.3310 C.32 D.32或3108.甲、乙两车从A 地出发,匀速驶向B 地,甲车以80km/h 的速度行驶1h 后,乙车才沿相同的路线行驶,乙车先到达B 地并停留1h 后,再以原速按原路返回,直至与甲车相遇,在此过程中,两车的距离y (km )与乙车行驶的时间x (h )之间的函数关系如图所示.下列说法:①乙车的速度为120km/h ;②m =160;③H 点的坐标为(7,80);④n =7.4,其中正确的说法个数为( )A. 1B. 2C. 3D. 49.在同一条道路上,甲车从A 地到B 地,乙车从B 地到A 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离y (千米)与行驶时间x (小时)的函数关系的图象,下列说法错误的是( ) A .甲乙两车出发2小时后相遇 B .甲车速度是40千米/小时 C .乙车到A 地比甲车到B 地早小时D .当甲乙两车相距100千米时,x 的值一定为110.如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y (厘米)与注水时间x (秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是( )A. 8000cm 3B. 10000 cm 3C. 2000πcm 3D. 3000πcm 3二.填空题11.如图,直线y =-43x +8与x 轴、y 轴分别交于点A 和点B ,M 是OB 上的一点,若将△ABM 沿AM 折叠,点B 恰好落在x 轴上的点B ′处,则直线AM 的表达式为_____________.12.如图,一次函数y =kx+b (k<0)的图象经过点A .当y<3时,x 的取值范围是________.13.如图,点、、在一次函数的图象上,它们的横坐标依次为、、,分别过这些点作轴与轴的垂线,则图中阴影部分的面积的和是________.14.如图,直线y=2x+4与x ,y 轴分别交于A ,B 两点,以OB 为边在y 轴右侧作等边三角形OBC ,将点C 向左平移,使其对应点C ′恰好落在直线AB 上,则点C ′的坐标为________.15.如图,放置的△OAB 1,△B 1A 1B 2,△B 2A 2B 3,都是边长为2的等边三角形,边AO 在y 轴上,点B 1、B 2、B 3都在直线y =x 上,则点A 2020的坐标为 .16.如图,在平面直角坐标系中,四边形OA 1B 1C 1,OA 2B 2C 2,OA 3B 3C 3,…都是菱形,点A 1,A 2,A 3……都在x 轴上,点C 1,C 2,C 3,……都在直线y =,且∠C 1OA 1=∠C 2A 1A 2=∠C 3A 2A 3=……=60°,OA 1=1,则点∁n 的坐标是 .17.如图,平面直角坐标系中,, 为 轴正半轴上一点,连接,在第一象限作 ,则直线解析式为________.三.解答题18.如图1,已知平行四边形ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是平行四边形ABCD边上的一个动点.(Ⅰ)若点P在边BC.上,PD=CD,求点P的坐标.(Ⅱ)若点P在AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.(Ⅲ)若点P在CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).19.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车与C地的距离y1(单位:km),y2(单位:km)与甲车行驶时间t(单位:h)之间的函数关系如图.请根据所给图象解答下列问题:(1)求甲、乙两车的行驶速度;(2)求乙车与C地的距离y2与甲车行驶时间t之间的函数关系式;(3)求乙车出发多少小时,两车相遇?20.某甜品店用A ,B 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品x 份,乙款甜品y 份,共用去A 原料2000克. 原料 款式A 原料(克) B 原料(克) 甲款甜品 30 15 乙款甜品1020(1)求y 关于x 的函数表达式.(2)已知每份甲甜品的利润为5元,每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元,则至少要用去B 原料多少克?21.如图,直线24y x =+分别与x 轴,y 轴交于点A ,B ,过点B 的直线y x b =-+交x 轴于点C .D 为OC 的中点,P 为射线BC 上一动点,连结PA ,PD ,过D 作DE AP ⊥于点E .(1)直接写出点A ,D 的坐标:A (______,______),D (______,______). (2)当P 为BC 中点时,求DE 的长.(3)当ABP ∆是以AP 为腰的等腰三角形时,求点P 坐标.(4)当点P 在线段BC (不与B ,C 重合)上运动时,作P 关于DE 的对称点P ',若P '落在x 轴上,则PC 的长为_______.22.如图,直线y =kx +8(k <0)交y 轴于点A ,交x 轴于点B .将△AOB 关于直线AB 翻折得到△APB .过点A 作AC ∥x 轴交线段BP 于点C ,在AC 上取点D ,且点D 在点C 的右侧,连结BD . (1)求证:AC =BC (2)若AC =10.①求直线AB 的表达式.②若△BCD 是以BC 为腰的等腰三角形,求AD 的长.(3)若BD 平分∠OBP 的外角,记△APC 面积为S 1,△BCD 面积为S 2,且3221 S S ,则ADOB 的值为______(直接写出答案)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章(一次函数)评价试题
(时间:45分钟满分:100分)
一、选择题(共6小题,每小题5分,共30分•在四个选项中,只有一项是符合题目
要求的,请把符合要求一项的字母代号填在题后括号内.)
1•经过点(3,2)的一次函数是()
A.y=3x-5
B.y=2x+1
C.y=x-1
D.y=x+1
丄
2. 在函数(1)y= n,⑵y=2x-1,(3)y=x,(4)y=2-1-3x,(5)y=x2-1 中,是一次函数的有()
A.4个
B.3个
C.2个
D.1个
3. —次函数y=2x-1的图象大致是()
/yj
\
//
0/\\0
/0 ---- */0\r
\
k
A E C D
4.2008年5月12日,四川汶川发生8.0级大地震,我解放军某部火速向灾区推
进,最初坐车以某一速度匀速前进,中途由于道路出现泥石流,被阻停下,耽误了一段
时间,为了尽快赶到灾区救援,官兵们下车急行军匀速步行前往,下列是官兵们行进的距离S(千米)与行进时间t(小时)的函数大致图象,你认为正确的是()
1 /,
5•已知点(-4, y i), (2, y2)都在直线y=p x+2上,则y i、y大小关系是( )
A.y i> y2
B.y i=y2
C.y i V y
D.不能比较
6•已知一次函数y=kx+b的图象如图所示,当x v 1时,y的取值范围是()
A.-2 v y v 0
B.-4 v y v 0
C.y v -4
D.y v -2
二、填空题(共10个空,每空3分,共30分.把答案填在题后的横线上.)
7. 已知一个正比例函数的图象经过点(-2, 4),则这个正比例函数的表达式
是_______ .
8. _________________________________ —次函数y=-x-1图象不经过第象限.
9. 如图,点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,
点B的坐标为________
10. __________________ 已知一次函数y=kx-2,要使y随x
的增大而减小,请你写出一个满足条件的k值.
11. __________________________________________ 一次函数y=-2x+4的图象与x轴交点坐标是______________________________________ ,与y轴交点坐标
是_______ .
12. 如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列
问题:
(1) _______________________________ 此蜡烛燃烧1小时后,高度为cm,经过_________________________________________ 小时燃烧完毕;
(2) _____________________________________________________ 这个蜡烛在燃烧过程中高度与时间之间的函数表达式是____________________________
(3)上述函数自变量的取值范围是 _______
三、解答题(共4小题,第13、14小题各8分,第15、16小题各12分,共40 分.解答应写出文字说明,证明过程或演算步骤.)
13. 画出函数y=2x+6的图象,利用图象求方程2x+6=0的解.
14. 已知一次函数y=-2x + 2的图象与x轴交于点A,与y轴交于点B,求△ AOB 面积•
15. 小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢•现在小明让小亮先跑若干米•图中11、|2分别表示两人的路程与小明追赶时间的关系•根据图象回答:
(1) 直线11、12分别表示谁的路程与时间的函数关系?
(2) 小明让小亮先跑了多少米?
(3) 小明与小亮的速度各是多少?
(4) 谁能赢得这场比赛的胜利?
16•已知一次函数图象经过点(0,-1),(3,5)两点.
(1) 求这个一次函数表达式;
(2) 求函数图象和坐标轴交点坐标;
(3) 点(a , 2在图象上,求a的值.
附加题
如图,直线y=kx+6与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点
A的坐标为(-6,0).
(1) 求k的值;
(2) 若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试
写出△ OPA的面积S与x的函数关系式, 范围;
(3) 探究:当点P运动到什么位置时,明理由.
、1.C 2.B 3.B 4.C 5.A 6.D
7.y=-2x 8•—9.(0.5,-0.5) 10.答案不唯一,k v 0 即可11.(2,0) (0,4) B 15
12. (1)7cm,瓦(2)y=-8x+15 (3)0 <x S
13. 图象如图.……4分
x=-3. ....... 8 分
14. 根据题意知点A坐标为(1 , 0),点B坐标为(0, 2),……4分
—y 1 2 = 1
则厶AOB面积为2 .……8分
15. (1)直线11表示小亮的路程与时间的函数关系,12表示小明的路程与时间的函数关系.……3分
(2)小明让小亮先跑了10米……6分
(3) v 35^5 = 7,(40 - 10)吒=6,
二小明的速度是7米/秒,小亮的速度是6米/秒.……9分
100 £0
⑷•.•〒”石,小明赢得这场比赛的胜利.……12分
附加题解:(1)把点(-8,0)的坐标代入y=kx+6,得-8k+6=0,解得3 1 3 ?
- S = + -S + 18
k=4.……3分(2) 2 4 4 (-8 v x v 0).……7分
并写出自变量x的取值
△ OPA的面积
为,
13L3 3 9
⑶当4 £时,解得x=- 2. 把
x=-T
代入y二出x+6,解得y,
广L3厂27
当P点的坐标为1小时,△ OPA的面积
为3.……10分
第三章(位置的确定)评价试题
(时间:45分钟满分:100分)
一、选择题(共5小题,每小题4分,共20分•在四个选项中,只有一项是符合 题目要求的,请把符合要求一项的字母代号填在题后括号内
.)
1•在平面内,确定一个点的位置一般需要的数据个数是
()
3•已知点M 到x 轴的距离为3,到y 轴的距离为2,则M 点的坐标为() A.(3,2) B.(-3, -2) C.(3, -2)
D.(2, 3), (2, -3), (-2, 3), (-2, -3)
4•点P (-1,3)关于原点对称的点的坐标是()
A.(-1,-3)
B.(1,3)
C.(1, -3)
D.(-3,1)
5•平面直角坐标系内有一点 A (a ,b ),若ab=0,则点A 的位置在() A.坐标轴上
B.x 轴上
C.y 轴上
D.原点
二、填空题(共6小题,每小题5分,共30分•把答案填在题中的横线上.) 6•点A (-2,1)在第 _____ 限.
A.1
B.2
C.3
D.4
2•如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数 为()
(1) 实验楼的坐标是3 (2) 实验楼的坐标是(3,3) (3) 实验楼的坐标为(4,4)
(4) 实验楼在校门的东北方向上,距200 米
A.1个
B.2个
C.3个
D.4个
7•在直角坐标系内,将点A (-2.3)向右平移3个单位到B 点,则点B 的坐标是
8•已知点P (-3, 2),点A 与点P 关于y 轴对称,则点A 的坐标是 __________ . 9•在矩形ABCD 中,A 点的坐标为(1,3),B 点坐标为(1,-2), C 点坐标为(-4,-2), 则D 点的坐标是 .
10•—正三角形ABC, A (0,0),B (-4,0),C (-2,卜二|),将三角形ABC 绕原点顺时针旋转
120°得到的三角形的三个顶点坐标分别是 ________ .
11.如图,一个机器人从 O 点出发,向正东方向走 3米到达A 1点,再向正北方 向走6米到达A 2点,再向正西方向走9米到达A 3点,再向正南方向走12米到达 A 4点,再向正东方向走15米到达A 5点•按如此规律走下去, 离O 点的距离是 _________ 米.
三、解答题(共5小题,每小题10分,共50分•解答应写出文 字说明,证明过程或演算步骤.)
12根据图填表:
当机器人走到A 6点时,
F
13. 在直角坐标系中,描出下列各点
(1)(2, 1), (-2, 1);
⑵(-3 ,4), (3, 4);
⑶(5, -4), (-5 , -4).
你能发现上述各对点的位置有何特点吗?它们的坐标有何异同?你能总结出一般的规律吗?
14. 某地为了城市发展,在现有的四个城市
A、B、C、D附近新建机场E.试建
立适当的直角坐标系,写出点A、B、C、D、E的坐标.
15. 对于边长为6的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
16. 在直角坐标系中,描出点(1 , 0), (1, 2), (2, 1), (1 , 1),并用线段依次连
接起来.(1)纵坐标不变,横坐标分别加上2,所得图案与原图相比有什么变化?
(2)横坐标不变,纵坐标分别乘以-1呢?
(3) 横坐标,纵坐标都变成原来的2倍呢?
//r
/
a
D
\£
十。
