4.4 角的比较
4.4角的比较

3、O 是直线 AB 上一点,∠AOC=53°,OD 平分∠BOC,求∠BOD 的度数?
D C B
A
O
五 自我提高 如图,∠AOB=90°,∠BOC=30°,OM 平分∠AOB,ON 平分∠BOC, ⑴求∠MON 的度数, ⑵若∠AOB=∠α ,若∠BOC=∠β (∠β 为锐角)其他条件不变,求∠MON 的度数。 (用含 α 、β 的式子表示) ⑶探究:从⑴⑵中你发现有什么规律?
2、如图,OB 是平角∠AOC 的角平分线,OD 平分∠BOC,求∠AOD 的度数。
B D
A
O
C
六.教学反思:
角的大小比较和角平分线的概念. 角的大小比较和角平分线的概念.
重点 难点
导学过程 一、学前准备: (1)海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗? (2)虎豹园、猴山、大象馆分别在大门的北偏东(或南偏东) 多少度? (3)在图中连接各个景点与大门,并用适当方式表示各角。 (4)上面各个角中,哪些是锐角?哪些是钝角?哪些是直角?并指出它们 的大小关系。 猴山B
大象馆D
练习: 1、根据图形填空: (1) AOB AOC _____ ; (2) AOD AOB ____ ___ COD ; (3) AOC BOD AOB _____ .
B C
D O 第 2题
A
(5)知识目标: 1、理解角的大小比较意义;掌握直角、锐角、钝角的概念;掌握角平分线的概念. 2、会估计一个角的大小;会用叠合法和度量法进行角的大小比较;会区别直角、锐角和 钝角;会运用角平分线的性质解决一些角的计算问题. 德育目标: 体验生活中的几何知识,激发学生对生活的热爱;通过动脑、动手、动口、合作和探究, 启发学生的智慧,感受快乐数学,接受逻辑推理思维的熏陶.
《角的比较》参考课件1

观察与思考:
① 使用叠合法比较角的大小必须注意哪些细节? ②角的大小与两边画出部分的长短是否相关?
【例
1】
根据下图,求解下列问题:
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小,并指出 其中 的锐角、直角、钝角、平角. (2)写出∠AOB、∠AOC、∠BOC、 ∠AOE中某些角之间的两个等量 关系. (3)借助三角尺估测 图中各角的度数. C O D E A B
一个含150角的方法很多。请你画出其中两种不
同构成的示意图,并在图上作出必要的标注,
不写作法。
想一想:
用一副三角板可以画出哪些不同度数的角?
4.4 角的比较
想一想:
► 如何比较两条线段的长短? ► 如何比较两个角的大小呢?
A O B
A
O
B c
c
c
o
D
o
D
D
o
与比较线段的长短类似,如果直接观察难以判断,我们可以 用两种方法对角进行比较: 一种方法是用量角器量出它们的度数,在进行比较; 另一种方法是将两个角的定点及一条边重合,另一边放在重 合的同侧就可比较大小。
在方格纸上有三个角,试确定每个角的大小及各角之
间的等量关系.(直接作在课本上)
闯一闯:
(1) 如图,∠AOC和∠BOD都是直角。
①估测∠COB的度数;
②若∠DOC=28°,说出∠AOB的度数。
D A B O C
试一试:
一副三角板由一个等腰直角三角形和一个含
300角的直角三角形组成。利用这副三角板构成
角平分线
A B
C O D
∠AOE =2∠AOC =2∠COE 1 ∠AOC =∠COE = ∠AOE 2
初一上册第四章--角与角的比较

§4.3角【教学目标】1、使学生通过实际生活中对角的认识,建立起几何中角的概念,并能掌握角的两个定义方法.2、使学生掌握角的各种表示方法,生掌握平角、周角和直角的概念.【教学重难点】重点:角的概念及两个定义和角的表示法.难点:角的概念及两个定义和角的表示法.【教学过程】考点一 角的概念概念:有公共端点的两条射线组成的图形叫做角.两条射线的公共端点是这个角的顶点.平角:一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角.周角:一条射线绕它的端点旋转,当终边和始边重合时,所成的角叫做周角.例1如图1,AOE 是一条直线,图中的角共有________个.图1 图2例2 如图2,图中包含小于平角的角的个数有__________个.考点二 度分秒的换算公式:1°的601为1分,记作1′,即1°=60′1′的601为1秒,记作1″,即1′=60″ 例3:(1)2.42°=_____ °_____ ′_____″(2)20°15′24″×3=(3)48°39′+67°41′=考点三 钟面角例4 早上9点20分,钟表上时针与分针所成的钝角是_______度.考点四 方位角例5:如图,C 岛在A 岛的北偏东54°的方向上,C 岛在B 岛的北偏西36°的方向上,则从C 岛看A ,B 两岛的视角∠C 的度数是( )【探究提高】在一次夏令营活动中,小霞同学从营地A 点出发,要到距离A 点1000m 的C 地去,先沿北偏东70°方向到达B 地,然后再沿北偏西20°方向走了500m 到达目的地C ,此时小霞在营地A 的( )【课后练习】§4.4角的比较【教学目标】1、使学生掌握角的平分线的定义以及数学表达式.2、使学生通过联想线段和、差、倍、分的作法,掌握角的和、差、倍、分的作法和计算.【教学重难点】重点:角的平分线.难点:角的计算.【教学过程】上节课我们已经学习了角的概念,今天我们也要学习如何比较角的大小,以及角的和、差、倍、分的问题.考点一角平分线的定义如图1,我们观察∠AOB,利用量角器测量得出∠AOC=∠BOC,那么就可以说射线OC是∠AOB的角平分线。
北师大版数学七年级上册4.4《角的比较》教案

北师大版数学七年级上册4.4《角的比较》教案一. 教材分析《角的比较》是北师大版数学七年级上册4.4节的内容,主要包括角的概念、分类和度量。
本节课通过引入角的比较,让学生理解角的大小不仅与边的长短有关,还与角的开口大小有关。
教材内容由浅入深,从基本概念到实际应用,使学生能够逐步掌握角的大小比较方法。
二. 学情分析学生在进入七年级前,已经学习了角的基本概念,如锐角、直角、钝角等。
他们对角的大小有一定的认识,但可能仅局限于边的长短。
通过本节课的学习,学生需要理解角的大小不仅与边的长短有关,还与角的开口大小有关。
此外,学生需要学会用量角器测量角的大小,并能进行角的比较。
三. 教学目标1.知识与技能:学生能够理解角的概念,掌握角的大小比较方法,会用量角器测量角的大小。
2.过程与方法:学生通过观察、操作、交流等活动,培养逻辑思维能力和解决问题的能力。
3.情感态度与价值观:学生培养对数学的兴趣,激发探究精神,培养合作意识。
四. 教学重难点1.教学重点:学生能够理解角的大小比较方法,会用量角器测量角的大小。
2.教学难点:学生能够灵活运用角的大小比较方法,解决实际问题。
五. 教学方法1.情境教学法:通过生活实例引入角的概念,激发学生学习兴趣。
2.启发式教学法:引导学生主动探究角的大小比较方法,培养学生的思维能力。
3.合作学习法:学生分组讨论,共同解决问题,培养学生的合作意识。
六. 教学准备1.教具:量角器、直尺、三角板等。
2.教学素材:课件、教学图片等。
七. 教学过程1.导入(5分钟)利用课件展示生活中常见的角,如钟表、自行车等,引导学生关注角的大小。
提问:你们认为角的大小与什么有关?2.呈现(10分钟)介绍角的概念,讲解角的大小比较方法。
通过示例,让学生明白角的大小不仅与边的长短有关,还与角的开口大小有关。
3.操练(10分钟)学生分组进行实践活动,使用量角器测量不同角的大小,并进行比较。
教师巡回指导,解答学生的疑问。
山西出版社精品课件4.4角的比较

O
4.上面各个角中,哪些是锐角?那些是钝 角?那些是直角?并指出他们的大小关系.
议一议
角的大小比较的主要方法:
1.度量法.
2.重叠法.
B(D) O D B (1) ∠AOB=∠COD A(C) O (2) ∠AOB<∠COD A(C)O B D (3) ∠AOB>∠COD A(C)
∠AOD=∠AOB+∠BOD或 ∠AOB=∠AOD-∠BOD ∠BOD=∠AOD-∠AOB
拼一拼
利用一副三角尺可以画哪些度数的角?请 你试一试,并与同伴交流.
小结
1.角的动态定义. 2.角的大小比较的主要方法:度量法、重叠法. 3.角平分线的定义. 4.本节课的学习体会.
O A D
B
2.角平分线的定义:从一个 ∠AOD=∠BOD 角的顶点引出的一条射线, ∠AOB=2∠AOD 把这个角分成两个相等的角, ∠AOB=2∠BOD) (或 1 这条射线叫做这个角的平分 ∠AOD= ∠AOB 2 1 线.
(或∠BOD= 2 ∠AOB)
问题
1.已知,如图∠AOB=130°,∠AOD=30°, ∠BOC=70°.问:OC是∠AOB的平分线吗?OD是 ∠AOC的平分线吗?为什么?
例2 计算: ⑴1.45°等于多少分? 等于多少秒? ⑵1800″等于多少分? 等于多少度?
练一练
1.0.25°等于多少分? 等于多少秒?
解:60′×0.25=15′
60″×15=900″ 即0.25°=15′=900″.
练一练
2. 2700″等于多少分?等于多少度?
1 解: ( ) 2700 45 60 1 ( ) 45 0.75 60 即2700 45 0.75 .
《第四章4角的比较》作业设计方案-初中数学北师大版12七年级上册

《角的比较》作业设计方案(第一课时)一、作业目标通过本节课的作业设计,旨在使学生能够:1. 理解角的概念及其表示方法。
2. 掌握角的大小比较方法。
3. 学会运用角的比较知识解决实际问题。
二、作业内容1. 基础知识练习:(1)掌握并熟练运用“同位角”、“内错角”、“同旁内角”等概念,能够正确判断各类角的名称。
(2)能够根据角的表示方法,正确绘制并标注角的度数。
2. 角的大小比较:(1)通过练习题,掌握比较角大小的基本方法,如利用量角器、三角板等工具进行测量和比较。
(2)通过图形变换,如平移、旋转等,理解角的大小变化规律。
3. 实际应用题:(1)结合实际生活中的场景,设计题目让学生运用角的比较知识解决实际问题,如测量建筑物窗户的角度等。
(2)通过数学游戏或趣味题,激发学生的学习兴趣,巩固角的比较知识。
三、作业要求1. 学生在完成作业时,应先复习本节课所学内容,确保对基础知识有充分的理解和掌握。
2. 作业中应注重思考和探索,不仅仅是机械地完成题目,而是要理解题目的意图和解题思路。
3. 对于应用题部分,学生应结合实际生活场景进行思考,尝试用所学知识解决实际问题。
4. 作业完成后,学生应自行检查答案,确保准确无误。
如有疑问或困难,可向老师或同学请教。
四、作业评价1. 老师将根据学生完成作业的情况,对每位学生的知识掌握程度、解题思路、答案准确性等方面进行评价。
2. 对于表现优秀的学生,老师将给予表扬和鼓励,以激发其学习积极性;对于表现不佳的学生,老师将给予指导和帮助,帮助其改进学习方法和提高学习成绩。
五、作业反馈1. 老师将根据学生的作业情况,对课堂讲解内容进行适当的调整和补充,以确保学生能够更好地掌握所学知识。
2. 对于学生在作业中普遍存在的问题和困难,老师将在课堂上进行讲解和答疑,帮助学生解决疑惑。
3. 老师将定期与学生进行沟通,了解学生的学习情况和需求,以便更好地指导学生的学习。
作业设计方案(第二课时)一、作业目标1. 熟练掌握角的比较基本方法和技巧,如用量角器进行度数比较和角的空间比较等。
角的比较方法

角的比较方法
角的比较可以通过以下几种方式进行:
1. 角的大小比较:可以通过角的度数来比较角的大小。
对于两个角,比较它们的度数大小即可判断它们的大小关系,例如:角A的度数大于角B。
2. 角的类型比较:可以通过角的类型来比较角的大小。
根据角的度数,可以判断角的类型,如锐角、直角、钝角等。
例如:直角大于锐角,锐角大于钝角。
3. 角的位置比较:可以通过角所在的位置来比较角的大小。
如果两个角的边存在重合,可以通过比较这些边的相对位置来判断角的大小关系。
例如:如果角A的边与角B的边重合且位
于角B内部,则角A大于角B。
4. 角的相互关系比较:可以通过角的相互关系来比较角的大小。
例如,如果两个角互为补角,则它们的大小关系是互逆的,即一个角的度数增加,另一个角的度数减少。
需要注意的是,在文中不要使用标题相同的文字,以免造成重复或冗余的表达。
使用上述方法可以清晰地描述角的比较关系。
北师大版七年级数学上册《基本平面图形——角的比较》教学PPT课件(4篇)

角的大小的比较方法: (1)如果已知角是锐角、直角、钝角、平角、周角几类中不同 类的角,就可以直接由它们之间的关系比较出它们的大小; (2)可以通过量角器进行量度来比较角的大小; (3)可以根据各角在同一图中的位置关系比较角的大小.
角的平分线
活动:大家在练习本上画一个角,然后把角的两边 对折,展开以后你会发现折痕把角分成了两个角, 这两个角有什么关系呢,它们又和原来的角有着怎 样的等量关系?
4.4 角的比较
知识回顾 比较两条线段的长短的方法? 1、度量法:用刻度尺测量线段的长度的方法。 2、叠合法:将其中一条线段移到另一条线段 上作比较。
猜想:比较两个角的大小方法?
获取新知
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的 一段对话:
张:我的折扇大一些,所以我的折扇的角也大一些.
2
2
2
(2)结合(1)的结论可求出∠DOE的度数,从而求出∠BOE的度数
解:(1)因为OC平分∠AOD,
1 所以∠DOC= 2 ∠AOD.
因为OE平分∠BOD,
1
所以∠DOE= 2∠BOD.
所以∠COE=∠DOC+∠DOE=
1
(∠AOD+∠BOD)
= 1 ∠AOB= 1 ×130°=65°.
2
2
2
2. 已知,如图,∠AOB = 130°,∠AOD = 30°,∠BOC = 70° ,问:OC 是∠AOB 的平 分线吗?OD 是∠AOC 的平分线吗?
解: OC不是∠AOB 的平分线 OD是∠AOC 的平分线 B
C D
A O
3. 如图,直线 m 外有一定点 O,A 是 m 上的 一个动点,当点 A 从左向右运动时,观察∠α 和 ∠β 是如何变化的,∠α 和 ∠β 之间有关系吗?
第四章基本平面图形4.4角的比较

C
B O A
如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
B C ∠BOD=2∠AOB ∴∠AOB=1/3∠AOD=38° ∵OC平分∠AOD O D ∴∠AOC=1/2∠AOD=57° (角平分线的定义)
数学·课标版(BS)
将一副三角板按图示方法放置(直角顶点重合) 则∠AOB+∠DOC= ____ 180° .
D A
┓
C
O
H
29
已知点O是直线AB上一点 ∠AOC=60°, OM、ON分别平分 ∠AOC、∠BOC, 求∠MON
C M A O B N
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小? 解: C ∵ OE平分 ∠ AOC,OF平分 ∠COB (已知) 1 ∴∠EOC= 2 ∠AOC, (角平分线的定义) ∠COF= 1 ∠COB F
75°、 90° 105°、120°、
135°、150°、 165°、180°
用一副学生用的三角板的内角 (其中一个三角板的内角是45°,45°,90°;另一 个是30°,60°,90°) 可以画出大于0°且小于等于150° 的不同角度的角共有(C )种. A.8 B.9 C.10 D.11
如图,∠AOC和∠BOD都是直角。
①∠COB和∠AOD有何关系?
②若∠DOC=28°,求∠AOB的度数。 ③若∠AOB=150°,求∠COD的度数。 ④图中相等的角是_________
D A B O C
如图,∠AOC和∠BOD都是直角。
(1)若∠DOC=28°,说出∠AOB的度数。 (2)找出图中相等的角。如果∠DOC≠28°,它 们还会相等吗? (3)若∠DOC变化,∠AOB 如何变化?
角的比较教学反思

4.4角的比较教学反思
本节课是教学内容是角的比较,而在这之前学生已经学习了角和比较线段的长短,也对线段的比较的研究有了经验,因此对于即将开始的角的比较,可以与线段的比较进行类比探索学习。
重点研究角的比较的方法,我课前让学生制作两个不同的角,在小组合作时,引导学生类比线段的比较,通过观察、操作、猜测、验证进一步研究角的比较,通过度量从数的方面比较形的大小,通过动手操作,让学生小组内总结,利用叠合法比较大小时的步骤。
通过折叠手中的角,引出角平分线以及角平分线的性质,并类比线段的中点的几何语言,描述角平分线的几何语言,多次让学生体会类比的思想。
初次熟悉课本,我将本节课重点研究两点:角的比较大小的方法与角平分线及其性质,认为两者是独立的,通过反复研读课本,研究教材,认真研究课本P119页做一做,设计的目的,即是对上面角的比较的再次巩固,又是从折叠感受叠合法比较角的大小同时,引出角平分线,让两者融为一体,在磨课中发现,学生对于做一做(3)在操作中可能会存在困难,我采取利用手中的透明袋,制作图形,让学生课堂动手折叠,很直观的观察出它们之间的关系,再利用PPT演示的形式,隐去多余的线段,引出角平分线。
对于如何上好本节课、本节课教学深度的把握,我依然存在疑惑和不足,期待各位评委老师的点拨与指正。
点评:
1.本节课教师语言清晰,表达准确,教态自然,课堂的教学思路清晰,环节过渡自然,重难点突出,过程的安排符合初中学生的认知规律,多媒体的使用充分得当,给学生留下了比较深刻的印象,是一堂清晰实在数
学课。
2.教师充分发挥学生主动学习,引导学生,经历知识的形成过程,学生动手,动脑,动口,学生参与度高,既调动了学生学习的积极性、主动性,又提高了学生合作交流的意识,充分体现了学生的主体地位,教师的主导地位。
(完整版)北师版七年级上数学第四章基本平面图形知识点及练习题

4.1 线段、射线、直线1、线段、射线、直线 线段:绷紧的琴弦,人行横道线都可以近似的看做线段。
线段有两个端点。
射线:将线段向一个方向无限延长就形成了射线。
射线有一个端点。
直线:将线段向两个方向无限延长就形成了直线。
直线没有端点。
2、名称 图形 表示方法 端点 长度直线 直线AB (或BA )直线l 无端点 无法度量 射线射线OM 1个 无法度量 线段线段AB (或BA ) 线段l2个可度量长度3、直线的性质(1)直线公理:经过两个点有且只有一条直线。
(两点确定一条直线。
) (2)过一点的直线有无数条。
(3)直线是是向两方面无限延伸的,无端点,不可度量,不能比较大小。
4、点和直线的位置关系有两种:①点在直线上,或者说直线经过这个点。
②点在直线外,或者说直线不经过这个点。
※课时达标 1.填写下表:2.如图,共有 条线段.3.用两个钉子就可以把木条钉在墙上,其依据是_________ .4.平面上有五条直线,则这五条直线最多有_____交点,最少有_____个交点.5.平面上两条直线的位置关系只有两种,即__________和_________________.6.平面上有四个点,无三点共线,以其中一点为端点,并且经过另一点的射线共有_______条.※课后作业 ★基础巩固1.下列各直线的表示法中,正确的是( ).l BAMOlBA 名称 图例 端点数 延伸方向 有无长度 线段射线直线 A B C DA.直线AB.直线AB C直线ab D.直线Ab2.下列说法不正确的是( ) .A.直线AB与直线BA是同一条直线B.射线AB与射线BA是同一条射线C.线段AB与线段BA是同一条线段D.线段有两个端点,射线有一个端点,直线没有端点3.下列说法正确的是().A.射线比直线短B.两点确定一条直线C.经过三点只能作一条直线D.两条射线的长度的和等于直线的长度4.下列说法正确的是( ).A.过一点P只能作一条直线B.射线AB和射线BA表示同一条射线C.直线AB和直线BA表示同一条直线D.射线a比直线b短5.下列说法正确的是().A.延长射线OAB.延长直线lC.延长线段CDD.反向延长直线l6.平面内的三点可确定直线的条数是().A.3B.1或3C.0或1D.07.已知C,D在直线AB上,那么直线AB上的射线共有().A.6条B.7条C.8条D.9条8.下列说法中,错误的有().①射线是直线的一部分;②画一条射线,使它的长度为5厘米;③线段AB和线段BA是同一条线段;④射线AB和射线BA是同一条射线;⑤直线AB和直线BA是同一条直线.A.1个B.2个C.3个D.4个9.在一条笔直的校园大道两旁种树时,先定下两棵树的位置,然后其它树的位置也就确定下来了,这说明了直线的基本性质:________________________. 10.已知平面内的四个点A,B,C,D,过其中的两个点画直线:(1)若A,B,C,D四个点在同一条直线上,可以画出______条直线;(2)若A,B,C,D四个点有三个在同一条直线上,可以画出______条直线;(3)若A,B,C,D四个点中的任意三个都不在同一条直线上,可以画出_______条直线.11.读下列语句,并画出相应图形.(1)经过点M,N画一条直线;(2)直线ba,相交于点P,点A在直线a上,但不在直线b上;(3)三条直线cb,两两相交于点A,B,C.a,☆能力提高12.读句画图:如图所示,已知平面上四个点(1)画直线AB;(2)画线段AC;(3)画射线AD、DC、CB;(4)如图,指出图中有_____条线段,有___ 条射线并写出其中能用图中字母表示的线段和射线 .13.已知直线l上有n个点,试问:(1)此图形上有多少条射线?(2)此图形上有多少条线段?14.如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6条,如果线段AB上有5个点时,线段总数共有10条,……A C B3=2+1A C D B6=3+2+1A C D E B10=4+3+2+1(1)当线段AB上有6个点时,线段总数共有__________条.(2)当线段AB上有100个点时,线段总数共有多少条?●中考在线15.平面上不重合的两点确定一条直线,不同三点最多可确定3条,若平面上不同的n个点最多可确定21条直线,则n的值为().A.5B.6C.7D.816.同一平面内互不重合的三条直线的公共点的个数是( ).A.可能是0个,1个,2个B.可能是0个,2个,3个C.可能是0个,1个,2个或3个D.可能是1个或3个4.2 比较线段的长短1、线段的性质(1)线段公理:两点之间的所有连线中,线段最短。
初中数学七年级上册《角的比较》

1. 在现实情境中,进一步丰富锐角、钝角、直角及大小的认识; 2. 学会比较角的大小,能估计一个角的大小;3. 在操作活动中认识角平分线,能画出一个角的平分线。
4. 认识度、分、秒,并会进行简单的换算。
【情感态度与价值观】1. 能通过角的测量、折叠等体验数、符号和图形是描述现实世界的重要手段。
2. 通过实际观察、操作体会角的大小,发展几何直觉。
3. 能用符号语言叙述角的大小关系,解决实际问题。
【重点与难点】1、角的大小的比较方法2、从图形中观察角的和、差关系。
【学习过程】一、预习导学1、 请同学们回忆,比较两条线段的大小关系有哪几种方法? (测量法和叠合法---类比联想,探索解决问题的方法)2、引导学生观看P148/图4-15并回答](1)请同学们把图中的五大景点中的任何两个之间都用线段连接。
(2)你能比较出这两个角的大小吗?你是怎样比较的?引导学生探讨出角的大小比较的一种方法———测量法。
3、 引导由学生动手操作探讨出叠合法的比较过程,若两个角能完全重合,说说这两个角的大小有何关系?4、角的分类二、例题讲解:例1 P148. 根据图4-16 ,求解下列问题:(1) 比较∠AOB 、∠AOC 、∠AOD 、∠AOE 的大小,并指出其中的锐角、直角、钝角、平角;(2) 写出∠AOB 、∠AOC 、∠BOC 、∠AOE 中某些角之间的两个等量关系。
例2、下面请大家各自在纸上任意画一个∠BOA ,再完成书上的做一做。
发现了什么?像刚才这条折痕,它是由角的顶点出发,把原来的角分成两个相等的角。
那么这条射线叫做 。
对这个定义的理解要注意以下几点:1.角平分线是一条射线,不是一条直线,也不是一条线段.它是由角的顶点出发的一条射线,这一点也很好理解,因为角的两边都是射线.2.当一个角有角平分线时,可以产生几个数学表达式.可写成 因为 OC 是∠AOB 的角平分线,所以 ∠AOB=2∠AOC=2∠COB , (1)⎪⎪⎪⎩⎪⎪⎪⎨⎧︒=∠︒=∠︒<∠<︒︒=∠︒<∠<︒3601801809090900ααααα周角:平角:钝角:直角:锐角:角的分类∠AOC=∠COB , (2)反过来,只要具备上述(1)、(2)、中的式子之一,就能得到OC 为∠AOB 的角平分线。
4.4角的比较
教案、学案一体化设计
投影显示:两个度数相差1度以内的角,不标明度数,只凭眼观察不能确定两个角的大小.
[板书] 1.4 角的比较
由学生熟知的三角板各角的比较入手,把学生带入比较角的大小的意境.但问题一转,出现了不标度数,观察又不能确定大小的角,当学生束手无策时,教师提出这就是我们要学习的新内容,调动学生的积极性,吸引其注意力.
1.角的比较
(1)叠合法
演示:移动,使其顶点与的顶点重合,一边和
请同学们观察的另一边
①与重合,等于,记作
②落在的内部,小于,记作
③落在的外部,大于,记作
,、.
,,把移到上,使它们的顶点重合,一边重合,会
你如何把移到才能保证
)在,是与的差,记作:
)在,是与的和,记作:
几何语言表示:是的平分线,(或
如何移到
教师根据学生回答小结:量角器可起移角的作用,测量的度数,然后以
边为作作一个角等于。
4.4角的比较

七年级第四章第四节角的比较课型:新授课教学目标:1.经历比较角的大小的研究过程,体会角的比较和线段的比较方法的一致性.2.会比较角的大小,能估计一个角的大小.3.理解角平分线的意义.教法与学法指导:本课利用了东沙河中学“三为主,六环节”课堂教学模式,采用自主探索,启发引导,合作交流展开教学,引导学生主动地进行观察、归纳、猜测和验证.学生已经掌握了线段的比较方法,在此基础上,学生通过类比的方法,探索、归纳角的比较方法,整个过程突出以学生为主体的探索性学习活动.重点:角的比较方法.难点:角平分线的意义及应用.课前准备:教师:多媒体课件,导学案.教学过程:一、创设情境,导入新课师:请大家回忆两个线段是如何比较大小的?生:用度量法和叠合法.师:怎样用叠合法比较线段的大小?生:将两条线段的一个端点重合,另一个端点落在重合端点的同一侧,看另一端点的位置来比较线段的长短.师:同学们说的很好,那对于两个角的大小我们又怎么比较呢,这就是我们今天要探究的内容.(板书:角的比较)设计意图:复习回顾旧知,同时利用线段的比较方法引入角的比较方法,并为角的比较方法做铺垫.二、目标展示师:看一下我们这节课的学习目标(多媒体展示)学习目标:1.会比较角的大小,能估计一个角的大小.2.理解角平分线的意义并会应用.设计意图:让学生了解本节课要学习的内容,激发学生的探究欲望.三、自主学习,合作探究探究活动一:比较角的大小师:如何比较下面两个角的大小呢? 请大家讨论归纳出比较的方法及相关步骤。
(多媒体展示)(学生利用导学案,独立思考6、7分钟之后小组讨论.) 师:哪位同学能说一说你是如何比较这两个角大小的. 生1:我是用量角器量出它们的度数,再比较的. 师:这就是度量法,还有其他方法吗?生2:我是把这两个角减下来,再放在一起比较的. 师:你能给大家演示,并讲解一下吗?生2:(上台演示并讲解)两个角的顶点和一边要重合,另一边要放在重合边的同侧,观察另一边的位置.如果这条边落在角的内部,则它比这个角小;如果落在角的外部,则它比这个角大;如果与另一边重合,则这两个角相等.师:很好,这种方法和我们以前学的那种方法很类似? 生:线段的比较方法中的叠合法. 师:在这里我们也称这种方法为叠合法.下面我就用多媒体演示一下如何用叠合法比较两个角的大小:首先确定∠ABC 的位置,然后使∠DEF 的顶点E 与∠ABC 的顶点BC 重合,边EF 与BC 重合,并使另一边ED 与BA 在重合边的同一侧;(1)如果DE 和AB 重合,那么∠ABC 等于∠DEF ,记作∠DEF =∠ABC . 如图(动画演示):(2)如果ED 落在∠ABC 内部,那么∠DEF 小于∠ABC ,记作∠DEF <∠ABC .如图(动画演示):BACEDFB AC (E )(F )(D )(3)如果ED 落在∠ABC 外部,那么∠DEF 大于∠ABC ,记作∠DEF >∠ABC .如图(动画演示):(教师板书:角的比较方法:1、度量法 2、叠合法 )设计意图:通过复习线段的比较方法,让学生通过类比的方法总结出角的比较方法.探究活动二:角的平分线(多媒体展示)根据图4-19求解下列问题:(1)比较∠AOB ,∠AOC ,∠AOD ,∠AOE 的大小,并指出其中的锐角、直角、钝角、平角.(2)试比较∠BOC 和∠DOE 的大小.(3)小亮通过折叠的方法,使OD 与OC 重合,OE 落在∠BOC 的内部,所以∠BOC 大于∠DOE .你能理解这种方法吗?(4)请在图中画出小亮的折痕OF ,∠DOF 与∠COF 有什么大小关系?(学生分组讨论完成)师:如图4-19,∠AOB ,∠AOC ,∠AOD ,∠AOE 分别是属于什么角,并比较它们的大小.生1:∠AOB 是锐角,∠AOC 是直角,∠AOD 是钝角,∠AOE 是平角,因为锐角<直角<钝角<平角,所以∠AOB <∠AOC <∠AOD <∠AOE .DB AC(E )(F ) (F )B AC DOEDCBA图4-19-1师:很好,哪位同学还有其他的方法比较这几个角的大小吗? 生2:可以用度量法.生3:可以用叠合法,因为这几个角的顶点O 及一边OA 重合,另一边都在重合边OA 的同侧,只需观察另一边的位置就可比较它们的大小。
4.4 角的比较

第四章 基本平面图形4.4 角的比较一、选择题:1.在∠AOB 的内部任取一点C ,作射线OC ,则一定存在( )A .∠AOB >∠AOC B .∠AOC =∠BOCC .∠BOC >∠AOCD .∠AOC >∠BOC2.如图所示,已知O 是直线AB 上一点,∠1=40°,OD 平分∠BOC ,则∠2的度数是( )A .20°B .25°C .30°D .70°3.如图,点B ,O ,D 在同一直线上,若∠1=15°,∠2=105°,则∠AOC 的度数是( )A .75°B .90°C .105°D .125°第2题图 第3题图 第4题图4.如图所示,已知∠AOC =∠COD =∠BOD ,若∠COD =14°34′,则∠AOB 的度数是( ) A .28°68′ B .43°102′ C .43°2′ D .43°42′5.如图,下列条件中不能确定OC 平分∠AOB 的是( )A .∠AOC =∠BOCB .∠AOC =12∠AOB C .∠AOB =2∠BOC D .∠AOC +∠BOC =∠AOB6.如图,OC 是∠AOB 的平分线,∠BOD =14∠DOC ,∠BOD =10°,则∠AOD 的度数为( )A .50°B .60°C .70°D .80°7.如图,射线OB 、OC 将∠AOD 分成三部分,下列判断错误的是( )A .如果∠AOB =∠COD ,那么∠AOC =∠BODB .如果∠AOB >∠COD ,那么∠AOC >∠BODC .如果∠AOB <∠COD ,那么∠AOC <∠BODD .如果∠AOB =∠BOC ,那么∠AOC =∠BOD第5题图 第6题图 第7题图8.已知∠AOB =70°,以O 为端点作射线OC ,使∠AOC =42°,则∠BOC 的度数为( )A .28°B .112°C .28°或112°D .68°二、填空题:9.用“<”“=”或“>”填空:(1)若∠α=∠β,∠β=∠γ,则∠α ∠γ;(2)若∠1+∠2=70°,∠3+∠2=100°,则∠1 ∠3.10.用一副三角板拼角,能拼出的最小角(非0°)的大小是 °,能拼出的最大角(非平角)的大小是 .11.如图,∠AOB =∠COD =90°,∠AOD =140°,则∠BOC = .三、解答题:12.如图,OB是∠AOC的平分线,∠BOC=30°,∠COD=40°,求∠AOD的度数.13.如图,∠AOD=120°,∠2=2∠1=60°,求:(1)∠DOC的度数;(2)∠BOD的度数.14.如图,点O是直线AB上的一点,∠AOC=130°,OB平分∠COD,OE平分∠AOD,求∠AOE的度数.四、选做题:15.如图,∠AOB是直角,∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线.(1)求∠MON的大小;(2)当锐角∠AOC的大小发生改变时,∠MON的大小也会发生改变吗,为什么?。
比较角的大小方法有

比较角的大小方法有
比较角的大小方法主要有以下几种:
1. 角度的度数比较:通过比较两个角的度数大小来判断角的大小关系。
度数大的角一般比度数小的角更大。
2. 角的比较大小:如果两个角具有相同的顶点和一个共同的边,并且一个角的内侧完全包含另一个角的内侧,则前者的度数大于后者。
3. 角的边长比较:若两个角具有相同的顶点和一个共同的边,并且这个共同的边与两个角的另一边分别相交(且都在相交点的同侧),如果一个角的另一边长于另一个角的另一边,则前者的度数小于后者。
4. 角的相对位置:观察两个角的顶点、所在平面和旋转方向。
如果两个角的顶点相同,但一个角旋转方向相较于另一个角是逆时针的,则前者的度数大于后者。
5. 角的三角函数比较:利用正弦、余弦和正切等三角函数的值来比较角的大小。
通过计算角的三角函数值并比较大小可以得出角大小关系。
以上是比较角的大小常用的一些方法,不同方法适用于不同的情况和问题。
在实际应用中,根据问题的具体要求选择合适的方法进行角的比较,并根据比较结果
进行判断和分析。
同时,需要注意在计算和比较角的过程中,要准确理解角的度数和位置关系,以避免错误的结论和误解。
七年级数学上册教学课件《角的比较》

所以∠AOC=2x=2×40°=80°,
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOC+∠AOD=80°+20°=100°.C
所以OC与∠AOB的平分线所成的角的度数为4°或100°.
探究新知 方法点拨
4.4 角的比较
涉及到角度的计算时,除常规的和差倍分计算外, 通常还需运用方程思想和分类讨论思想解决问题.
探究新知
4.4 角的比较
素养考点 3 利用角平分线求角的度数 例3 如图,OB 是∠AOC的平分线,OD是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC, ∠AOC=80°,
E
DC
B
所以∠BOC= 12∠AOC
=
1 2
×80°
O
A
=40°.
探究新知
A
所以∠AOC=2x=2×8°=16°.
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOD-∠AOC=20°-16°=4°.
探究新知
4.4 角的比较
②如图,OC在∠AOB外部,OD平分∠AOB,
B
所以设∠AOC=2x,∠COB=3x,
D
因为∠AOB=40°,
O
A
所以3x-2x=40°,得x=40°,
提示:无图条件下要分情况讨论.
4.4 角的比较
B C
O
A
C
巩固练习
变式训练
4.4 角的比较
如图,借助一副三角尺可以画出15°和75°的角, 你还能画出哪些度数的角?
75°
15°
探究新知
素养考点 2 角的度数的计算
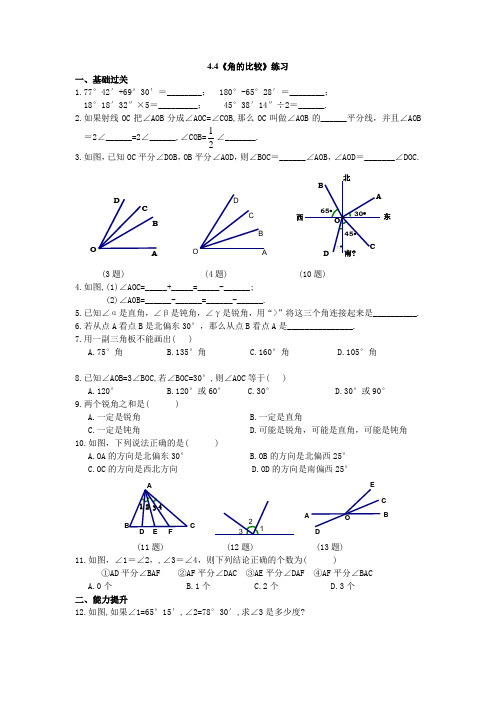
4.4《角的比较》练习
4.4《角的比较》练习一、基础过关1.77°42′+69°30′=________; 180°-65°28′=________; 18°18′32″×5=_________; 45°38′14″÷2=______.2.如果射线OC 把∠AOB 分成∠AOC=∠COB,那么OC 叫做∠AOB 的______平分线,并且∠AOB =2∠______=2∠______,∠COB=21∠_______. 3.如图,已知OC 平分∠DOB ,OB 平分∠AOD ,则∠BOC =______∠AOB ,∠AOD =_______∠DOC.OD C BAODC BA︒北西南东45︒65︒30︒ODCBA(3题) (4题) (10题) 4.如图,(1)∠AOC=_____+_____=_____-______;(2)∠AOB=______-______=______-______.5.已知∠α是直角,∠β是钝角,∠γ是锐角,用“>”将这三个角连接起来是__________.6.若从点A 看点B 是北偏东30°,那么从点B 看点A 是_______________.7.用一副三角板不能画出( )A.75°角B.135°角C.160°角D.105°角8.已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC 等于( )A.120°B.120°或60°C.30°D.30°或90° 9.两个锐角之和是( )A.一定是锐角B.一定是直角C.一定是钝角D.可能是锐角,可能是直角,可能是钝角 10.如图,下列说法正确的是( )A.OA 的方向是北偏东30°B.OB 的方向是北偏西25°C.OC 的方向是西北方向D.OD 的方向是南偏西25°FEDCBA 4321321COEDBA(11题) (12题) (13题)11.如图,∠1=∠2,,∠3=∠4,则下列结论正确的个数为( )①AD 平分∠BAF ②AF 平分∠DAC ③AE 平分∠DAF ④AF 平分∠BAC A.0个 B.1个 C.2个 D.3个 二、能力提升12.如图,如果∠1=65°15′,∠2=78°30′,求∠3是多少度?13.如图,已知直线AB 、CD 相交于O 点,∠AOE =130°,OC 是∠BOE 的平分线,求∠AOD.14.如图,∠AOB 是平角,OD 、OC 、OE 是三条射线,OD 是∠AOC 的平分线, 请你补充一个条件,使∠DOE=90°,并说明你的理由.EODCBA(14题)15.如图,AOB 为直线,OE 、OD 、OC 为射线,OC 平分∠BOD ,∠AOE ∶∠EOD =1∶3,∠AOD ―∠DOB=40°,求∠EOC 的度数.OE DC BA(15题)16.(1)如图,已知∠AOB=90°,∠BOC=30°,OM 平分∠AOC,ON 平分∠BOC, 求∠MON 的度数. (2)如果(1)中的∠AOB=α,其他条件不变,求∠MON 的度数.(3)如果(1)中的∠BOC=β (β为锐角),其他条件不变,求∠MON 的度数. (4)从(1)、(2)、(3)的结果中能得出什么结论?N MOCBA(16题)三、聚沙成塔数学小知识丹顶鹤总是成群结队迁飞,而且排成“人”字形.“人”字形的角度是110度.更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?。
