电磁场2静电场
工程电磁场(清华大学出版社)课后题解

l 2 + 4l 25 a 2 ⎭ ⎭ 2l α 0 ⎝ 0 0 2x0 r 0r 0l 0 第二章 静电场(注意:以下各题中凡是未标明电介质和导体的空间,按真空考虑) 2-1 在边长为a 的正方形四角顶点上放置电荷量为q 的点电荷,在正方形几何中心处放置电荷量为Q 的点电荷。
问Q 为何值时四个顶点上的电荷受力均为零。
解 如图建立坐标系,可得q ⎛ 12 1 ⎫ Q 2 1 E x e x = 4πε + 2 ⨯ 2a 2 ⎪e x + 4πε ⨯ 2 ⨯ a 2 / 2 e x q ⎛ 1 2 1 ⎫ Q 2 1 E y e y =+ 4πε 0 ⎝ 2 ⨯ 2a 2 ⎪e y + 4πε ⨯ 2 ⨯ a 2 / 2 e y ⎛ 2 ⎫ ⎛ 2 ⎫据题设条件,令 q 1 + ⎪ + Q 4 ⎪ = 0 ,2 ⎝ 解得 Q = - q(1 + 2 2)4⎭ ⎝ ⎭2- 有一长为2l ,电荷线密度为τ 的直线电荷。
1) 求直线延长线上到线电荷中心距离为2l 处的电场强度和电位; 2) 求线电荷中垂线上到线电荷中心距离为2l 处的电场强度和电位。
解 1)如图(a )建立坐标系,题设线电荷位于 x 轴上l ~ 3l 之间,则 x 处的电荷微元在坐标原点产生的电场强度和电位分别为d E = τd x (-e ), d ϕ = τd x4πε 0 x 4πε 0 x由此可得线电荷在坐标原点产生的电场强度和电位分别为 E (0) = 3l d E3lτd x(- e ) =τ(- e )⎰l⎰l4πε 0xx6πε lxϕ (0) = ⎰3ld ϕ = ⎰3lτd x =τln 3ll4πε 0 x 4πε 02)如图(b )建立坐标系,题设线电荷位于 y 轴上- l ~ l 之间,则 y 处的电荷微元在点(0,2l ) 处产生的电场强度和电位分别为d E = τd y (-e ), d ϕ = τd y4πε 2r 4πε 0 r 式中, d y = 2l d θ cos 2 θ , r = , sin α = l cos θ = 1 ,分别代入上两式,并考虑 对称性,可知电场强度仅为 x 方向,因此可得所求的电场强度和电位分别为 E (2l ,0) = α = 2eα τd ycos θ = τe x cos θd θ = τe x sin α = τe x 2⎰0 d E x ⎰0 4πε 2 4πε ⎰0 4πε 0l 4 5πε 0l ϕ (2l ,0) = α ϕ = τ α d θ = τ ⎡ ⎛ 1 tan -1 1 + π ⎫⎤ = 0.24τ 2⎰0 d 4πε ⎰0co s θ 2πε ln ⎢tan 2 2 4 ⎪⎥ πε 0 0 ⎣ ⎝ 2-3 半径为a 的圆盘,均匀带电,电荷面密度为σ 。
工程电磁场总结笔记

工程电磁场总结笔记
工程电磁场总结笔记
1. 电磁场的概念:电磁场是指由电荷和电流所引起的物理现象,包括静电场和电流场。
2. 静电场:静电场是指电荷之间由于电荷不平衡而产生的电场。
电荷分为正电荷和负电荷,正电荷之间相互排斥,负电荷之间相互排斥,正负电荷之间相互吸引。
静电场的强弱由电荷量和距离的平方倒数决定。
3. 电流场:电流场是指电流通过导体时所产生的电场。
电流流动时会形成环绕导体的电磁场,根据安培定理,电流越大,产生的磁场越强。
电流场的强弱由电流大小和导线距离的关系决定。
4. 电磁场的相互作用:电磁场中的电荷和电流相互作用,电荷和电流受到力的作用。
根据洛伦兹力公式,电荷在电磁场中受到的力等于电荷电场力和磁场力的矢量和。
电磁场的相互作用是电磁感应和电磁辐射的基础。
5. 电磁感应:当导体中的磁通量发生变化时,会在导体中产生感应电动势,从而产生感应电流。
根据法拉第电磁感应定律,感应电动势的大小与磁通量和时间的变化率成正比。
电磁感应是电动机和发电机的基本原理。
6. 电磁辐射:当电荷加速运动时,会产生电磁辐射,即电磁波。
电磁波具有电场和磁场的振荡,可以在真空中传播。
电磁辐射是无线通信和无线电广播的基础。
7. 电磁场的应用:工程电磁场的应用广泛,包括通信、雷达、无线电、电视、计算机等。
通过电磁场的相互作用,可以实现信息的传输和处理。
工程电磁场学是工程学、物理学和电子学等学科的重要基础。
电磁场理论课件 2-1静电场的标势及其微分方程

(P)
Q
4 0
(1 r
1 r
)
r2 R 2 l 2 2Rl cos
Q
2l
x -Q
求近似值:
r R
1
l2 R2
2l
cos
/
R
R
1 2l cos / R
R(1 1 2l cos ) R l cos
2R
R r
y
(l R)
同理
r R l cos
1 1 r r 2l cos 2l cos
R02 R2
20
ln
R R0
若选P0为参考点,则
(P)
ln R
ER
R
20
,
2 0 R
R0 E EZ 0
解2:
z
电荷源
dq dz z' o
r
场点
p
R
选取柱坐标:源点的坐标为(0, z'),场点的坐标为
(R, 0),考虑到导线是无限长,电场强度显然与z
无关。
这里,先求场强 E
,后求电势
E 0
D
E
这两方程连同介质的 电磁性质方程是解决 静电问题的基础。
静电场的无旋性是它的一个重要特 性,由于无旋性,我们可以引入一 个标势来描述静电场。
无旋性的积分形式是电场 沿任一闭合回路的环量等 于零,即
E dl 0
设C1和C2为P1和P2点的两 条不同路径。C1与C2合成 闭合回路,因此
量与存在着电荷分布的空间有关。真实的静电能量是以
密度 w 1 E D的形式在空间连续分布,场强大的地方 2
能量也大;
(4)W 1 dV中的 是由电荷分布 激发的电势; 2
电磁场与电磁波静电场
q
R0 dl
q
RP dR
A 4 0 R2
4 0 R R2
q
4
0
1 R
1 RP
q
4 0
R
C
若选取无穷远点为参考点,则 C 0 ,于是 (R) q 4 0 R
体电荷、面电荷和线电荷分布的电位函数表达式为:
(r)
1
4 0
r
(r
'
)
r
'
d
'
C
(r )
1
4 0
s
r
s
(r
'
r
) dS
流密度的值为
Js
lim I l0 l
dI dl
图2.1.5 面电流密度与面电流
穿过线段l 的电流为
I J s (r )dl l
3、线电流:
电荷在一根很细的导线中流过,或电荷通过的横截面 积很小时,可将电流视为在一根无限细的线上流动, 这样的电流称为线电流。用电流强度来描述:
线电流I与线电荷密度 l、电荷流动速度 v的关系为:
I lv
2.2 静电场的基本方程
2.2.1库仑定律、电场强度
电荷间的相互作用规律由库仑定
律描述。真空中 静止的电荷 q1 对 q2 的相互作用力F12 为
图2.2.1电荷与电荷的相互作用
F12
1
4 0
q1q2 R2
R0
1
4 0
q1q2 R3
R
若电在荷电q ,场则强度q受为到E的的静空电间力某为点qE 放置点
1
4 0 V
r
r
'
r
r
'
电磁场实验指导书

电磁场实验讲义实验一 二线输电线静电场的造型 一、试验目的:1.学习两维电场模拟的原理与方法。
2.通过测量等位线及绘制电力线,学习电场图形的描绘方法。
二、实验原理(见教材静电模拟一节) 三、实验内容及步骤1、 将方格纸和导电纸的相对位置固定好,定好方格纸的坐标原点及x 轴y 轴。
2、连接线路,调节电源电压为9V ,依次测绘对电源负极电位分别为1V 、2V 、3V 、4V 、4.5V 、5V 、6V 、7V 、8V 时的各等位线。
四 实验原理1. 两导线电轴之间的电场是平行平面场;2. 电力线与等位线正交, 由于两线输电线的等位线方程为22222)12(2)11(-=+-+-K bK y b K K x所以得电力线方程为:2222)(c b c y x +=++3. 利用静电比拟原理, 使用电流线模拟电力线. 五、实验设备1.模拟试验台一套(导电纸半径为90mm ,电极半径为6.5mm ,电极几何中心连线构成的弦对应的圆心角为120)直流稳压电源一台; 数字万用表一只六、总结报告要求1.在实验用的方格纸上描绘等位线。
2.根据实验测得的等位线,描绘电力线,并与理论计算所得的电力线进行比较。
3.根据实验结果,试分析主要是哪些因素影响本实验精度?你认为这些因素是否可以解决。
实验二 接地电阻的研究 一、试验目的:1.学习用模拟实验的方法研究场的问题。
2.研究接地电阻与接地器的形状、大小以及埋入深度的关系。
3.观察接地器周围导电媒质表面上电位的分布。
二、原理与说明1.接地电阻指电流由接地装置流入大地再经大地向远处扩散时所遇到的电阻。
接地电阻主要是接地体到无限远处的大地的电阻,而接地线和接地体本身的电阻一般可以忽略。
对于半球埋地的接地器的电阻,可以用镜像法求解。
对于整个球埋入地下,而地面的影响又不可以忽略时,也可以用镜像法近似求解。
实际工作中,会遇到一些问题,它们既难通过实验获得满意的解答,又不便于实地测量,这类问题可以用“模拟法”研究。
电磁感应与电磁场的知识点总结

电磁感应与电磁场的知识点总结电磁感应是电磁学中的一个重要概念,指的是导体中的电流会受到磁场的影响而产生感应电动势。
而电磁场则是由电荷和电流所产生的物理现象,可以用来描述电磁力的作用。
本文将对电磁感应与电磁场的相关知识点进行总结,帮助读者更好地理解这一领域。
一、电磁感应1. 法拉第电磁感应定律法拉第电磁感应定律是电磁感应研究的基础,它表明当导体中的磁场发生变化时,会产生感应电动势。
具体表达式为:感应电动势等于磁通量变化率的负值乘以线圈的匝数。
这个定律解释了电磁感应现象的产生原理。
2. 楞次定律楞次定律是法拉第电磁感应定律的补充,它描述了感应电流的方向。
根据楞次定律,感应电流的产生会产生磁场,其磁场的方向使得感应电流所产生的磁场与引发感应电流变化的磁场方向相反。
换言之,楞次定律说明了感应电流的方向与磁场变化的关系。
3. 磁通量与磁感应强度磁通量描述的是磁场通过某一平面的程度,与磁场的面积和磁感应强度有关。
磁感应强度表示单位面积上的磁通量,它的方向垂直于磁场线。
通过改变磁通量和磁感应强度,可以实现对电磁感应的控制。
二、电磁场1. 静电场与静电力静电场是由电荷所产生的一种场,它可以通过电场线来表示。
静电力是静电场作用在电荷上的力,根据库仑定律,静电力与电荷之间的距离和大小成反比。
2. 磁场与磁力磁场是由电流所产生的一种场,它可以通过磁感线来表示。
磁力是磁场对电荷和电流所产生的力,它的方向垂直于磁场线和电荷或电流的方向。
3. 电磁场和电磁力电磁场是由电荷和电流共同产生的场,它是电场和磁场的综合体现。
电磁力是电场和磁场对电荷和电流所产生的综合力,它同时包含了静电力和磁力的作用。
4. 麦克斯韦方程组麦克斯韦方程组是描述电磁场性质的基本方程,它由四个方程组成。
其中包括了法拉第电磁感应定律、库仑定律以及电磁场的高斯定律和安培环路定律。
麦克斯韦方程组的推导和理解有助于深入学习电磁场的原理和性质。
总结:电磁感应和电磁场是电磁学中的两个核心概念,通过磁场对导体产生感应电动势,我们可以利用电磁感应现象实现电磁能量的转换和传输。
电磁场与电磁波理论基础 第二章 课后答案

u=0
∂u 1 ∂u ∂u E = −∇u = − e ρ + eϕ + e z ρ ∂ϕ ∂z ∂ρ
得到 题 2-9 图
E = −∇u = 0, ρ ≤ a
a2 a2 E = − A 1 + 2 cos ϕ e ρ + A 1 − 2 sin ϕ eϕ , ρ ≥ a ρ ρ
代入得到
2 2
r1
-2 q
Y
S1 (-a, 0 , 0)
X
S 2 (a, 0, 0)
题 2-7 图
u (r ) =
q 4πε 0
1
( x + a)
2
+ y2 + z2
−
2 2 2 ( x − a) + y + z 2
电位为零,即令
q u (r ) = 4πε 0
∂u2 =0 ∂x
代入,得到
ρ S下 = −ε 0
∂u1 ∂x
=
x =0
ρd ρd ε U ε U x2 − 0 0 + 0 = − 0 0 + 0 2d 6 x =0 6 d d
ρ0
对于上极板,导体中的电位为常数
u1 = U 0
有
∂u1 =0 ∂x
上极板下表面电荷密度为
l
场分布具有柱对称性,电通密度矢量 D 仅有 e ρ 分量,由 高斯定理 题 2-15 图
D ⋅ dS = ρ
(S ) (V )
V
dV
取圆柱面为高斯面,有
2π
Dρ ρ ldϕ = 20 ρ e
0 0 0
电磁场理论-2011-2[1]
![电磁场理论-2011-2[1]](https://img.taocdn.com/s3/m/9b8462c7bb4cf7ec4afed0be.png)
q ne , (n , ,) 1 2
静电场—静电场的基本规律
上式中,基元电荷电量在数值上等于一个电子所带 的电量。即
密立根油滴实验说明:物体所带电量是不连续的, 即自然界中的电荷是量子化的。 现代科学实验证明,任何物体都由大量的原子构 成,而原子则由带正电的原子核和带负电的电子组 成。 通常,同一个原子中正负电量数值相等,因而整 个物体呈现电中性。当它们因为某种原因,例如摩 擦、受热、化学变化等失去一部分电子时,则表现 为正电性;当获得额外电子时,则呈现负电性。
静电场的保守力性质也可以用另一个等价形式表 示,即
上式表明:在静电场中,电场强度沿任意闭合环 路的线积分恒等于零。 通常,将某一个量沿任意闭合环路的线积分称为 该物理量的环流。于是上式又可以表述为:在静电 场中,电场强度的环流为零。这一结论称为静电场 的环路定理,它是静电场的基本规律之一。
静电场—静电场的基本规律
静电场—静电场的基本规律
例题5 半径为a 的球中充满密度为ρ(r)的体分布电 荷,已知
求:电荷密度为ρ(r)。 解:由高斯定理,在球内有
静电场—静电场的基本规律
解得
(r ) 5 0 r 4 0 Ar
2
又考虑在球外,有
0
0
r
2
a r
5
Ar 4 0 Ar
4
即求得电荷密度
(r ) 5 0 r
2
静电场—电势及静电势能
电势
§2.2 电势及静电势能
电势差
静电场环路定理说明:电场力移动电荷所作的功 只与电荷的始末位置有关,而与具体的路径无关。 因此可以用一个位置函数φ(x,y,z)描述电场力电荷 所作的功,即
电磁场与电磁波静电场

电场线与电通量密度
电场线表示电场强度的方向和大小,电通量密度表示电场通 过某一面积的电场强度。
电势与电场力
电势表示电场中某点的电势能,电 场力表示电荷在电场中受到的作用 力。
03
恒定磁场
恒定磁场的定义
01
02
03
04
ห้องสมุดไป่ตู้
恒定磁场
磁场强度不随时间变化的磁场 。
磁力线
描述磁场分布的闭合曲线,磁 力线密集的地方磁场强度大,
递信息。
电磁波在医疗领域的应用,如 微波治疗、放射治疗和核磁共 振成像等,为疾病的诊断和治 疗提供了新的手段。
电磁波在科研领域的应用,如 光谱分析、天文学和量子力学 等,推动了科学技术的进步和 发展。
02
静电场
静电场
由静止电荷产生的电场,不随时间变化。
静电场的性质
具有方向性和矢量性,对电荷产生作用力。
稀疏的地方磁场强度小。
磁感应强度
描述磁场强弱的物理量,单位 是特斯拉(T)。
磁通量密度
描述单位面积内的磁通量,单 位是韦伯/平方米 (Wb/m^2)。
磁感应线与磁通量密度
01
02
03
磁感应线
描述磁场分布的闭合曲线, 磁力线不相交,闭合曲线 表示磁场强度的方向和大 小。
磁通量密度
描述单位面积内的磁通量, 与磁感应强度成正比,与 距离成反比。
磁通量
穿过某一面积的磁力线总 数,单位是韦伯(Wb)。
安培环路定律与奥斯特实验
安培环路定律
表示磁场与电流之间的关系,即 磁场对电流的作用力与电流成正 比,与距离成反比。
奥斯特实验
发现电流周围存在磁场,即电流 的磁效应。
电磁场与电磁波第二章讲义

(r )
第二章 静 电 场
当r<a时,
Er 4r2
0 0
4
3
r3
所以
Er
0r 30
(r )
第二章 静 电 场
例 2 - 3 已知半径为a的球内、 外的电场强度为
E
er E0
a2 r2
(r a)
E
er E0 5
r 2a
3
r3 2a3
(r a)
们的连线, 同号电荷之间是斥力, 异号电荷之间是引力。点电
荷q′受到q的作用力为F′,且F′=-F,可见两点电荷之间的作用力 符合牛顿第三定律。
第二章 静 电 场
库仑定律只能直接用于点电荷。所谓点电荷,是指当带电体 的尺度远小于它们之间的距离时,将其电荷集中于一点的理想化 模型。 对于实际的带电体, 一般应该看成是分布在一定的区域 内,称其为分布电荷。用电荷密度来定量描述电荷的空间分布情 况。电荷体密度的含义是,在电荷分布区域内,取体积元ΔV, 若其中的电量为Δq,则电荷体密度为
(r)
P(r' )V '
4 0
r r' r r' 3
整个极化介质产生的电位是上式的积分:
(r) 1
4 0
V
P(r' ) (r r r' 3
4 0R2
R
q' q
4 0
R R3
式中:R=r-r′表示从r′到r的矢量;R是r′到r的距离;R°是R的单
位矢量;ε0是表征真空电性质的物理量,称为真空的介电常数,
其值为
电磁场与电磁波 第2章静电场

如果是一个闭合路径,则W=0 电场强度的环路线积分恒为零,即
应用斯托克斯定理
因此,静电场的电场强度 可以用一个标量函数 的梯度来表示,即定义
单位正实验电荷在电场中移动电场力做功
两点间的电位差定义为两点间的电压U,即
单位:V
电位函数不唯一确定,取
故可选空间某点Q作为电位参考点,空间任一点P的电位为 通常选取无限远作为电位参考点,则任一P点的电位为
在交界面上不存在 时,E、D满足折射定律。
D 1 n D 2 n 1 E 1 c1 o 2 E s 2 c2 os
E 1 t E 2 t E 1 si1 n E 2 si2n
图2.3.3 分界面上E线的折射
t电位函数 表示分界面上的衔接条件
Ax Ay Az
对应静电场的基本方程 E 0 ,矢量 A 可以表示一个静电场。
能否根据矢量场的散度来判断该矢量场是否是静电场?
2.3.2 分界面上的边界条件
1、 电位移矢量D的衔接条件 以分界面上点P作为观察点,作一
小扁圆柱高斯面( L 0)。
图2.3.1 在电介质分界面上应用高斯定律
根据 DdSq
V ' P d ' V S 'P e n d ' S 0
• 在均匀极化的电介质内,极化电荷体密度 p 0。
• 有电介质存在的场域中,任一点的电位及电场强度表示为
(r) 4 1 0 V '( r f r 'p )d' V S '( r f r 'p )d' S E (r ) 4 1 0 V '( f r p r )'3 r( r ')d' V S '( f r p r ) '3 r( r ')d' S
电磁场与电磁波第二章课后答案

第二章 静电场重点和难点电场强度及电场线等概念容易接受,重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程,即散度方程和旋度方程,并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。
利用亥姆霍兹定理,直接导出真空中电场强度与电荷之间的关系。
通过书中列举的4个例子,总结归纳出根据电荷分布计算电场强度的三种方法。
至于媒质的介电特性,应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。
讲解介质中静电场方程时,应强调电通密度仅与自由电荷有关。
介绍边界条件时,应说明仅可依据积分形式的静电场方程,由于边界上场量不连续,因而微分形式的场方程不成立。
关于静电场的能量与力,应总结出计算能量的三种方法,指出电场能量不符合迭加原理。
介绍利用虚位移的概念计算电场力,常电荷系统和常电位系统,以及广义力和广义坐标等概念。
至于电容和部分电容一节可以从简。
重要公式真空中静电场方程:积分形式:⎰=⋅SS E 0d εq⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E已知电荷分布求解电场强度:1,)()(r r E ϕ-∇=; ⎰''-'=V Vd )(41)(|r r |r r ρπεϕ2,⎰'''-'-'=V V 3d |4))(()(|r r r r r r E περ3,⎰=⋅SS E 0d εq高斯定律介质中静电场方程:积分形式:q S=⋅⎰ d S D⎰=⋅ll E 0d微分形式:ρ=⋅∇D0=⨯∇E线性均匀各向同性介质中静电场方程:积分形式:εqS=⋅⎰ d S E⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E静电场边界条件:1,t t E E 21=。
对于两种各向同性的线性介质,则2211εεttD D =2,s n n D D ρ=-12。
在两种介质形成的边界上,则n n D D 21=对于两种各向同性的线性介质,则n n E E 2211εε=3,介质与导体的边界条件:0=⨯E e n ; S n D e ρ=⋅若导体周围是各向同性的线性介质,则ερS n E =;ερϕS n -=∂∂静电场的能量:孤立带电体的能量:Q C Q W e 21212Φ== 离散带电体的能量:∑==ni i i e Q W 121Φ分布电荷的能量:l S V W l l S S Ve d 21d 21d 21ρϕρϕρϕ⎰⎰⎰===静电场的能量密度:E D ⋅=21e w 对于各向同性的线性介质,则2 21E w e ε=电场力:库仑定律:rrq q e F 2 4πε'=常电荷系统:常数=-=q e lW F d d常电位系统:常数==ϕlW F e d d题 解2-1 若真空中相距为d 的两个电荷q 1及q 2的电量分别为q 及4q ,当点电荷q '位于q 1及q 2的连线上时,系统处于平衡状态,试求q '的大小及位置。
电磁场与电磁波第二章课后答案解析

第二章 静电场重点和难点电场强度及电场线等概念容易接受,重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程,即散度方程和旋度方程,并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。
利用亥姆霍兹定理,直接导出真空中电场强度与电荷之间的关系。
通过书中列举的4个例子,总结归纳出根据电荷分布计算电场强度的三种方法。
至于媒质的介电特性,应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。
讲解介质中静电场方程时,应强调电通密度仅与自由电荷有关。
介绍边界条件时,应说明仅可依据积分形式的静电场方程,由于边界上场量不连续,因而微分形式的场方程不成立。
关于静电场的能量与力,应总结出计算能量的三种方法,指出电场能量不符合迭加原理。
介绍利用虚位移的概念计算电场力,常电荷系统和常电位系统,以及广义力和广义坐标等概念。
至于电容和部分电容一节可以从简。
重要公式真空中静电场方程:积分形式:⎰=⋅SS E 0d εq⎰=⋅ll E 0d微分形式: 0ερ=⋅∇E0=⨯∇E已知电荷分布求解电场强度:1,)()(r r E ϕ-∇=;⎰''-'=V Vd )(41)(|r r |r r ρπεϕ2,⎰'''-'-'=V V 3d |4))(()(|r r r r r r E περ3,⎰=⋅SS E 0d εq高斯定律介质中静电场方程:积分形式:q S=⋅⎰ d S D⎰=⋅ll E 0d微分形式:ρ=⋅∇D0=⨯∇E线性均匀各向同性介质中静电场方程:积分形式:εqS=⋅⎰ d S E⎰=⋅ll E 0d微分形式: ερ=⋅∇E0=⨯∇E静电场边界条件:1,t t E E 21=。
对于两种各向同性的线性介质,则2211εεttD D =2,s n n D D ρ=-12。
在两种介质形成的边界上,则n n D D 21=对于两种各向同性的线性介质,则n n E E 2211εε=3,介质与导体的边界条件:0=⨯E e n ; S n D e ρ=⋅若导体周围是各向同性的线性介质,则ερS n E =;ερϕS n -=∂∂静电场的能量:孤立带电体的能量:Q C Q W e 21212Φ== 离散带电体的能量:∑==ni i i e Q W 121Φ分布电荷的能量:l S V W l l S S Ve d 21d 21d 21ρϕρϕρϕ⎰⎰⎰===静电场的能量密度:E D ⋅=21e w 对于各向同性的线性介质,则2 21E w e ε=电场力:库仑定律:rrq q e F 2 4πε'=常电荷系统:常数=-=q e lW F d d常电位系统:常数==ϕlW F e d d题 解2-1 若真空中相距为d 的两个电荷q 1及q 2的电量分别为q 及4q ,当点电荷位于q 1及q 2的连线上时,系统处于平衡状态,试求的大小及位置。
《电磁场理论》2.2 真空中静电场的基本方程

2)解为球坐标系下的表达形式。
Q ( 4 r 2 er ) (r a) 0 (r a) 0 1 2 Qr E ( Qr e ) (r a) r 2 r (r 4 a3 ) (r a) r 0 3 4 a 0 0 E 3Q 4 a3 0 0
S
E (r ) dS
1
(r )dV
Q
球对称分布:
8
a
ρ0 O
9
轴对称分布
无限大平面电荷
例1 求电荷密度为 S 的无限大面电荷在空间中产生的 电场。 分析:电场方向垂直表面。在 S n 平行电荷面的面上大小相等。 解:取如图所示高斯面。 由高斯定律,有
s S E1 (r ) ez S E2 (r ) (ez ) S 0 s ez ( z 0) s 2 0 E 2 0 E s ez ( z 0) 2 0 10
E (r )
1 4 0
V'
(r ')
R dV ' 3 R
(r ') R E 3 dV ' V ' 4 R 0
R 3 0 R
E 0 ——静电场是无旋场,或保守场。 5
2.静电场的环路定理 对静电场取任意闭合回路L作路径积分: 由Stokes定理得: E d l ( E ) d S 0
对高斯定理的讨论 物理意义:静电场 E 穿过闭合面S的通量只与闭合面内
所围电荷量有关
静电场是有源场,静电荷是其散度源。
4
二、真空中静电场的旋度
1.静电场的旋度:
静电场概念

静电场概念静电场是研究物质之间电力作用而产生的一种电磁场,它是一种由电荷发出的动力,可以在电荷之间引起力。
因此,静电场是由电荷创造的一种力场,它可以产生强烈的电力作用,并在电荷之间传递。
静电场能够影响其它电荷,它可以改变电荷的运动轨迹,从而电荷的运动受到影响。
静电场的力可以从局部地方感受到,甚至从距离上感受到,就像一种虚拟的电力场一样。
在实验中,可以用金属片或棉花等物体可以产生电荷,使它们产生电力作用,这就是静电场。
金属片上电荷发生变化时,静电场也会随之发生变化,从而影响它们之间的电力作用。
认识静电场,首先要了解电荷和静电力。
电荷是指由电离引起的电子团,它是电学体系中最基本的粒子,可以被分为正电荷和负电荷。
静电力是指电荷之间的作用力,它以电磁力的形式存在,会在电荷之间产生强烈的力,这就是静电场。
由于静电场是一种强烈的电力,因此它可以影响某个物体上有电荷的运动轨迹。
当电荷发生变化时,其上的电力也会随之发生变化,它会影响电荷的运动轨迹并做出各种反应。
例如,当电荷在电荷的局部地方发生变化时,静电力的作用也会随之发生变化,它会改变电荷的运动轨迹,从而影响其结果。
当物质的性质发生变化时,静电场也会发生相应的变化。
例如,当物质的电离度发生变化时,其上电荷的作用也会发生变化,这会改变静电场的能量,形成一种新的静电场,它可以影响物质的性质,从而引发各种物理效应。
静电场的作用,不仅仅可以在物质间产生,而且还可以在物质与空气之间产生。
在空气中,由于电荷的不同,静电场就会存在于空气中,它会影响空气中的物质,促使它们沿着特定的路径前进。
例如,当人们在玩吸尘器时,有电荷的尘埃会被静电场吸住,而无电荷的尘埃则不会受到影响。
最后,让我们来看看静电场的实际应用。
由于静电场可以影响电荷的运动轨迹,因此它可以用于物理实验、化学反应和处理生物样本中的电荷及其他物质。
此外,静电场还可以用于空气清洁,例如吸尘器,它可以将有电荷的灰尘物聚集起来,从而使空气清洁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Dz z
q
4
r2
3z2 r5
Dx x
Dy y
Dz z
q
4
3r 2
3(x2 r5
y2
z2)
v D
Dx
Dy
Dz
0
x y z
2.3 静电场的无旋性-环路定理
(1)电位
静电场中某点的电位是指单位正电荷从无穷远处移到静电 场中某点b时,外力克服电场力所做的功。
b
b E dl
体电荷: 1 v dV ' C 面电荷: 1 S dS' C
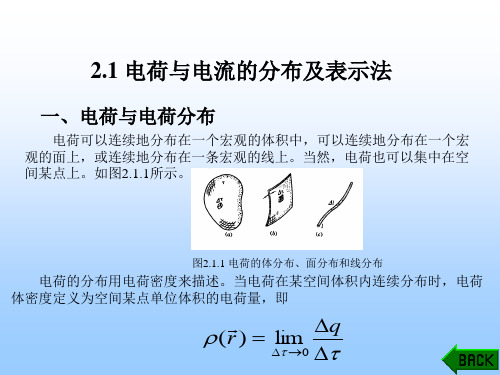
2 静电场
2.1 库仑定律与电场强度 2.2 静电场的有散性-高斯定理 2.3 静电场的无旋性-环路定理 2.4 电偶极子 2.5 静电场中的导体和电介质 2.6 静电场基本方程与边界条件 2.7 边值问题
研究对象
静电场
本章任务
掌握静电场的基本场量;会分析静电场中的导体和电介 质状态;掌握静电场基本方程及边界条件;已知电荷或电 位能对电场进行求解。
克斯定理得:
C E dl S E dS S ( ) dS 0
静电场中,电场强度 E沿任意闭合路径的线积分恒等于零。
(4)电场线与等电位面
电场强度线是一族有方向的线,其上每一点的切线 方向就是该点的电场强度方向。
电场线方程:
设 dl 是电场线上的有向线段,则有:E dl 0
在直角坐标系下可以得出电场线方的微分方程:
S
E
dS
q
0
dS
evn
E
➢ 静电场对任一闭合曲面的通量等于面内电荷与真空介 电常数比值;
➢ 电场是有源场,源为电荷,正电荷是静电场的正源, 负电荷为负源;
➢ 电场的电力线从正电荷出发,终止于负电荷;
➢ 它适用求解对称性很高情况下的静电场。
(3)高斯定理的微分形式 静电场的散度
S
E dS
4 0 R
4 0 R
线电荷: 1 l dl' C
4 0 R
n个点电荷:
1
4 0
n k 1
qk Rk
C
(2)电位与电场强度的关系
微分关系
在静电场中,任意一点的电场强度 E 的方向总是沿
着电位减少的最快方向,其大小等于电位的最大变化
率。
E
积分关系
电位 P数值上等于将单位正电荷从P点移到零电位处
存在于电荷周围的能对其他带电体产生作用力的特 殊物质称为电场。电场对电荷的作用力称为电场力。
静电场
qi
由静止电荷激发的电场称为静电场。
电场力的叠加原理
多个电荷体系中某个电荷受到的作用力是其余电荷
与该电荷单独存在时作用力之矢量和,满足线性叠加
原理。
Fi
1
4 0
k i
qk qi Rki2
eki
场是特殊的物质形式: ①物理量空间分布; ②物理量可以叠加; ③具有质量、能量、动量。
dx dy dz
qx
qy
qz
40r3 40r3 40r3
即
dx x
dy y
dy
dz
y z
对 dx dy 两边积分可得 xy
ln x ln y C eln x eln yeC
y C1x 其中 C1 eC
同理可得 z C2 y
电场强度E的矢量线方程为
y z
C1 C2
x y
1
E
4 0
N k 1
qk r rk
2
r r
rrkk
1
4 0
N k 1
qk Rk 2
ek
c) 连续分布电荷产生的电场强度
线电荷密度:单位长度上的电荷量
l
lim
l 0
q l
面电荷密度:单位面积上的电荷量
S
lim
S 0
q S
体电荷密度:单位体积内的电荷量 V
lim q V 0 V
E
dE
• 达到静电平衡时,导体内部的场是零,导体 是等势体。 ( )
(2)静电场中的电介质
电介质:绝缘,内部电子受原子核很强的束缚
分类:依据正负电荷重心的分布
电子云的等 效“重心”
正电荷的等 效“重心”
p
ql
无极分子:无外场时,分 子内部正负电荷的“重心” 重合,对外不显电。例如氢、 甲烷等
p 0
极性分子:无外场时,分子内部正负电荷的“重心”不重 合,可等效为一个电偶极子,形成电偶极矩,但由于热运动, 每个极性分子的电偶极矩方向随机,从宏观上看不显电性。 如水、有机玻璃等
rv ,求电位移矢
量在空间中任意一点的散度。
解:电位移:
v D
q
4
x (r3
evx
y r3
evy
z r3
evz )
Dxevx
Dyevy
Dzevz
Dx
q
4
x, r3
Dy
q
4
y, r3
Dz
q
4
z r3
其中 r (x2 y2 z2)1/2
Dx x
q
4
r2
3x2 r5
,
Dy y
q
4
r2
3y2 r5
x2 y2
4 o
1 L22 y2
1) L12 y2
Ey
l
L1 4 o (x2 y2 )
y dx l (
x2 y2
4 o
L2 L22 y2
L1 ) L12 y2
x
例2:求均匀带电圆环轴线上的场强。
已知圆环半径为a,电荷线密度为ρl 。
r
解: dq ldl
dE
l dl 4 0R2
对于均匀电介质,电介质内 部仍是电中性的,但在垂直于 电场方向的端面上出现正负电 荷(束缚电荷)。
➢有极分子的取向极化
在外电场作用下,极性分子的等效电偶极子受到一个力矩 作用发生偏转,绝大多数分子电矩的方向都不同程度的指向 外场方向。但是由于分子热运动,不可能使所有分子的电偶 极矩都按电场的方向排列,场强越强,转向效果越显著,排 列就越整齐。在有极分子电介质与外电场垂直的界面上出现 束缚电荷。这种极化机制称为取向极化。
➢ 高斯定理是由库仑定律导出的,它是一个有限范围,
而库仑定律是一个宏观无限小的 (V 0) 此推导是
合理的。
➢ 高 斯 定 理 反 映 了 电 荷 激 发 电 场 通 量 的 基 本 规 律 , ρ是因,E 是果。
(4)电位移矢量
电通密度:单位面积上的电通量 真空中: D 0E
点电荷q产生的电场中,在半径为r处的电位移矢量:
V
EdV
1
0
V
( x)dV
E
0
➢ 说明空间某点的电场强度的散度只与该点电荷体密 度有关,与其它点的无关;
➢ 静电场是有散场(发散场),散度源是电荷;
➢ 仅适用于连续分布的区域,在分界面上,电场强度 一般不连续,因而不能使用;
v
E
0
讨论:
➢ 空间任一点 E 的散度仅仅决定于该点的电荷密度, 因而 E 描述场源的性质(有检源作用)。
因此等电位方程为
(r) q C 4 0 r
q 解得 r
4 0C
点电荷电场线与等势面
上式为以原点为球心的球面方程
例5:点电荷q位于坐标原点,其周围空间为真空, 求电场强度E的矢量线。
解:空间中任一点处的电场强度为
E
q
4 0r3
r
其中
r
xex
yey
zez
为场中任一点的位矢
矢量线所满足的方程为
dx dy dz Ex Ey Ez 其解就是描绘电场强度线的函数关系式。
等电位面 静电场中电位相同的点连成的面。
等位面的性质:( x, y, z ) C
➢在等位面上移动电荷,电场力不做功; ➢等位面与电力线处处正交; ➢电场线指向电位降落的方向。
一个点电荷所产生的电位为
(r) q 4 0 r
E
1
4 0
2al z
z2 a2
3 2
1
4 0
q z2
ez
2.2 静电场的有散性-高斯定理
(1)电通量
表征电场分布情况的物理量; 当一个测试电荷在电场中自由移动时,作用在此电荷上的 力将使它按一定的路线移动,此路线称为电通线或电力线; 一个电荷产生电通线的数量等于用库仑表示的电荷量。
(2)高斯定理的积分形式
电位() 边界条件
2.1 库仑定律与电场强度
(1)库仑定律
F21
k
q1q2 R12 2
R12 R12
F12
R12 R12
:
R12方向的单位矢量
e12
.
F12
q1.
q2
R12
F21
设 q1 和 q2 同号
q1 和 q2异号,上式仍成立。
v F12
1
4 0
q2 q1 R212
ev21
ε0真空介电常数
D
q
4r 2
er
用 D 表示的静电场方程
E
D
0
静电场为发散场,其散度源为电荷。
S
E
dS
q
0
D dS q
S
通过一个封闭面穿出的电通量等于该曲面包围的总电荷。
例其3:中r在是点点电电荷荷qq产到生场的点电M场的中距,离D, evr4是qr从2 e点r 电荷q指向场点
M的单位矢量。设S为以点电荷为中心,R为半径的球面, 求从球内散出S的电通量Φ 。
解: 根据通量的定义可得,电通量为
