(完整版)工程电磁场公式
电磁场公式总结
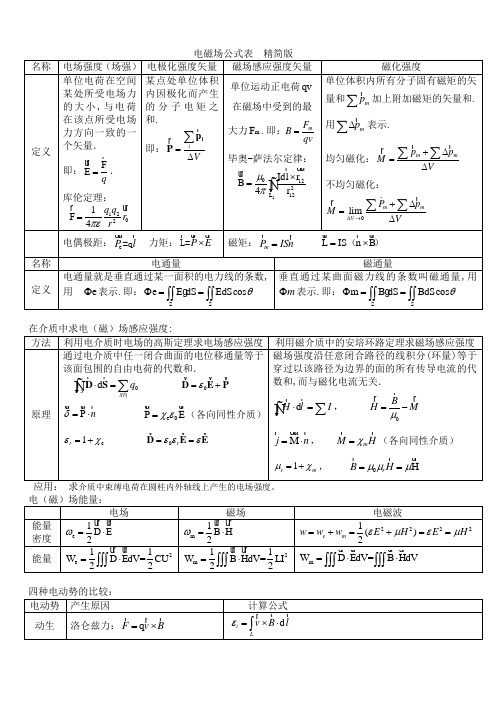
电磁场公式表 精简版 名称 电场强度(场强) 电极化强度矢量 磁场感应强度矢量 磁化强度定义 单位电荷在空间某处所受电场力的大小,与电荷在该点所受电场力方向一致的一个矢量. 即:F E q = . 库伦定理:12021F 4q q r rπε= 某点处单位体积内因极化而产生的分子电矩之和.即:i V =∆∑i p P 单位运动正电荷qv在磁场中受到的最大力m F .即:m F B qv = 毕奥-萨法尔定律: 1012212L Idl r B 4r μπ⨯=⎰ 单位体积内所有分子固有磁矩的矢量和m p ∑ 加上附加磁矩的矢量和.用m p ∆∑ 表示. 均匀磁化:m m p p M V +∆=∆∑∑ 不均匀磁化:0limm m V P p M V ∆→+∆=∆∑∑ 电偶极距:e P l =q 力矩:P E ⨯ L= 磁矩:m P ISn =L IS n B =⨯ () 名称电通量 磁通量定义 电通量就是垂直通过某一面积的电力线的条数,用 e Φ表示.即:SSe E dS EdScos θΦ==⎰⎰⎰⎰垂直通过某曲面磁力线的条数叫磁通量,用m Φ表示.即:SSm B dS BdScos θΦ==⎰⎰⎰⎰在介质中求电(磁)场感应强度:方法 利用电介质时电场的高斯定理求电场感应强度利用磁介质中的安培环路定理求磁场感应强度 原理 通过电介质中任一闭合曲面的电位移通量等于该面包围的自由电荷的代数和.0d SS q ⋅=∑⎰D S 内0ε=+D E PP n δ=⋅e 0P E χε=(各向同性介质)e 1r εχ=+ 0r εεε==D E E磁场强度沿任意闭合路径的线积分(环量)等于穿过以该路径为边界的面的所有传导电流的代数和,而与磁化电流无关.d H l I ⋅=∑⎰, 0B H M μ=-M j n =⋅ , m M H χ=(各向同性介质)1r m μχ=+, 0H r B H μμμ==应用: 求介质中束缚电荷在圆柱内外轴线上产生的电场强度。
电磁场里的公式

下载后可以查看编辑公式1-1库伦定律:F21=−F12 =q1q24πεo R2R21oεo=8.85×10−12F/m坐标原来不在q上时R=r−r′=(x−x′)i+(y−y′)j+(z−z′)k 坐标原来在q上时:R=r=xi+yj+zk电场强度:定义式:E=F q o库仑定律:F=14πq o∙qq or2r o得E=Fq o=qr o4πεo r2=qr4πεo r3大小E=qo2电场叠加原理F=F1+F2+∙∙∙+F nE=Fq o=F1q o+F2q o+∙∙∙+F nq o=E1+E2+∙∙∙+E n电荷的线密度τ=dq dldE=dqr o 4πεo r2E=∫ dEα=14πεo r2∫ατdαr2∙r o电荷分布的面密度σ=dq dsdE=dqr o 4πεo r2E=∫ dE =1 4πεos ∙∬σdsr2∙r os体分布电荷p=dq dvE=∑E=∫dEv =14πεo∙∭pdvr2∙r ov一E=E n∙n o 电偶极子P=ql 极化矢量P=lim∆V→0(∑P)∆VP=xεo E σp=P∙n o p p=−∇∙P∑q p s内=−∮P∙dSs5介质的击穿V MAX=kE MAX一1E=dN dS⊥dN=EdS⊥dS⊥=dS∙cosθ∴dN=EdS⊥=EdS∙cosθ=E∙dS=dψE 电通量dψE=EdSψE=∫dψEs =∫EdSs=N2 (1)E=qr o 4πεo R2ψE=∮EdSs =∮EdS RS R=∮qr o ds R4πεo R2S R==14πεo R2∮dS RS R=q4πεo R2∙4πR2=qεo(2)E=E1+E2+∙∙∙∮EdS s =∮E1dSs+∮E2dSs+∙∙∙+∮E n dSs= =q1εo+q2εo+∙∙∙+q nεo==1εo∑q is内(3)ψE=∮EdSs =1εo∑q is内=1εo∫pdVv二,2∮EdS s =1εo[∑(q i+q p)]s内=1εo[∑q i+∑q ps内s内]∵∑q ps内=−∮PdSs∮(εo E+P)dS s =∑q自s内即D=εo E+P=εo E+xεo E=(1+x)εo E==εrεo E=εEεr=εεoσp=P∙nσp=−∇P三∵∮DdS =∑q自s内s左边=∮DdSs ∙cos0o =∮DdSs=D∮dSs=D∙4πr2右边={0 , r<RQ ,r>R∴D={0,r<RQ4πr2,r>R∵D=εE=εo EE={0,r<RQr o4πεo r2,r>R例2S=S A+S B+S侧,∮DdS s =∑q自s内左边∫D A∙dS SA +∫D B dSSB+∫D侧dSS侧=∫D A∙dS+SA∫D B dSSB+0=2DS右边=σS1∴D右S右=D右S1=∑q自s内=σS1D右=D=σ=εEE=σεi例4∵∮DdSs =∑q自s内=τl左边=∫S上+∫S下+∫S侧=++∫Dds∙cos0oS侧=D∙S侧=D∙2πrl故D=τ2πr=εEE=τR o 2πεr例题5∵∮DdSs =∑q自s内D∙4πr2=43πr3ρ或43πb3(r>b)∴D=ρ3r (r<b) ,b3ρ3r2r (r>b)又∵D=εE得E={ρr3ε,r<bρb3r3εo r3 ,r>bP=(ε−εo)E=(ε−εo)3ερr (r<b)σp=p∙n=ρ|r=b=(ε−εo)3ερbρρ=− ∇p=−(ε−εo)3ερ∇r=(ε−εo)ερ ,(r<b)∴∇∙r=3 ,[∇∙rr3=0]1-2P13电位一w=∮FdL=0l∵E=Fq∴w=q∮EdL=0l即∮EdL=0l微分方程∮EdL= l ∫∇×EdSs=0 ∴∇×E=02.∮EdL=0l令l=l1+l2P13二电位24例3例题4 P17例6P191-5一2二2P20P21P22P23P24P25P26P27P28P29P30 P31P32P33P34P35P36P37P38P39P41P42P43P44P4533P46P47P48P49P50P51P53P55。
工程电磁场 第1章 电磁场的数学基础

《工程电磁场》
第1章 电磁场的数学基础
1
第1章 电磁场的数学基础
1.1 场的概念及其分类
1.2 正交曲面坐标系
1.3 矢量代数
1.4 场的可视化描述
1.5 场的梯度、散度、旋度
1.6 场论分析常用定理
1.7 电磁场麦克斯韦方程组与场论
《工程电磁场》
1.1 场的概念及其分类
《工程电磁场》
《工程电磁场》
标量及其乘积运算
两个标量a与b相乘,标量参数之间可用
“
”号、“ • ” 号或什么符号也不加,
都代表二者之间的倍数关系,即
,
a b a b ab
《工程电磁场》
矢量及其表示方法
《工程电磁场》
一个由大小和方向共同确定的物理量叫做矢量。
=
,
= + + =
ex
ey
ez
A B Ax Ay Az
Bx B y Bz
9. A ( B C ) B (C A) C ( A B )
10. ( A B )C A( B C )
11. A ( B C ) ( A B ) C
Ԧ )
——不随空间变化的时变场 φ(t) , (t
第1章 电磁场的数学基础
1.1 场的概念及其分类
1.2 正交曲面坐标系
1.3 矢量代数1.4 源自的可视化描述1.5 场的梯度、散度、旋度
1.6 场论分析常用定理
1.7 电磁场麦克斯韦方程组与场论
电磁场公式梳理

公式总结注:此文档仅梳理了相关公式,需掌握的概念、知识点请仔细研读课件。
第一章•三种正交坐标系长度元,面积元和体积元表达式•三种正交坐标系坐标单位矢量的转换•标量场图和矢量场图对应的方程•方向导数,梯度•面元矢量:•场量穿过面元的通量:0=⨯r d r A)(le G dldf ⋅=∴zfe yf e x f e f zy x ∂∂+∂∂+∂∂=∇ G f =∇dSeS d n =dSA S d A θcos =⋅AA div ⋅∇=y zx A A A divA A x y z∂∂∂=∇⋅=++∂∂∂⎰⎰⋅∇=⋅VSdVA S d A⎰⎰=⋅CCdlA l d A θcos环量散度高斯散度定理环量面密度n n e A rot A rot ⋅=旋度AA rot ⨯∇=斯托克斯定理Sd A l d A SC⋅⨯∇=⋅⎰⎰)(0=∇⨯∇φ0)(=⨯∇⋅∇AԦe x∂A z ∂y −∂A y ∂z +Ԧe y ∂A x ∂z −∂A z∂x +Ԧe z ∂A y ∂x −∂A x ∂y∇×ԦA =第二章()SI J r dS=⋅⎰v J Vρ=s N lI J e dl=⋅⎰PE D +=0εEP e χε0=0r D E Eεεε===⎰⨯=222C Bl d I F Bv q E q F ⨯+=在线性各向同性介质中在线性各向同性磁介质中m M Hχ=MBH -=μB Hμ=⋅=-=-⎰⎰S V dQ dJ d S dVdtdt ρ∂=+=+∂t d DJ J J J tS d t DJ l d H S l⋅∂∂+=⋅⎰⎰)(Sd B dt d l d E S l ⋅-=⋅⎰⎰0SB d S ⋅=⎰∑⎰⎰==⋅qdV S d D VV Sρt D J H ∂∂+=⨯∇t BE ∂∂-=⨯∇=⋅∇B vD ρ=⋅∇⎪⎪⎩⎪⎪⎨⎧=-=-=-=-ρn n n n t t SN t t D D B B E E J H H 1212121200⎪⎪⎩⎪⎪⎨⎧=-⋅=-⋅=-⨯=-⨯ρ)(0)(0)()(12121212D D e B B e E E e JH H e n n n n第三章22RdS R e S d d R θcos =∙=Ω⎰⋅=PA A ld Eφφ-∇=E⎰∙=-BA B A ld Eφφ⎪⎩⎪⎨⎧==∙∇=⨯∇EDD E ερ0''s n v P e Pρρ⎧=∙⎪⎨=-∇∙⎪⎩束缚面电荷:束缚体电荷:ερφv -=∇212φφ=1212sn nφφεερ∂∂-=∂∂R RV d E v v⎰''=341ρπε⎰=vv Rdvρπεφ041⎩⎨⎧=∙∇=⨯∇00J EJ E=γ1212n nφφγγ∂∂=∂∂12φφ=p J E=∙焦耳定理恒定电场()322121mJ E E D w e ε=∙= ⎰=V e dvW ρφ21⎰=V e dvE W 221ε电场能量密度电场能量H J B ⎧∇⨯=⎨∇⋅=⎩B H μ=B A=∇⨯024RCIdl e B Rμπ⨯=⎰V d RJ A V '=⎰'πμ40Sv n J MJ M e ⎧'=∇⨯⎨'=⨯⎩介质内部束缚体电流密度:介质表面束缚面电流密度:)(H IL 单位:亨ψ=1()2m VW H B dV=∙⎰221Hw m μ=AB⨯∇=φ-∇=∂∂+tA EtA ∂∂-=⋅∇φμε()m e S w w pt∂-∇⋅=++∂⎰⎰⎰++=⋅-V Vm m S pdv dv w w dt dS d S )((,)Re j t E r t E e ω∙⎡⎤=⎢⎥⎣⎦()()()()x xm y ym z zm E r e E r e E r e E r =++复矢量0ωωρH J j DE j B B D ⎧∇⨯=+⎪∇⨯=-⎪⎨∇=⎪⎪∇=⎩1(()())2c S E r H r *=⨯⎪⎪⎪⎩⎪⎪⎪⎨⎧><<<--100101022ωεγωεγωεγ良好导体:有损耗介质:良介质:100()()()()()()c c c j j j γγωγωεεωεωμμωμω'''=-'''=-'''=-()⎪⎪⎪⎩⎪⎪⎪⎨⎧=∙=∙∙-=∙∙+=∙⎰⎰⎰⎰⎰⎰⎰dv S d D S d B Sd B j l d E S d D j J l d H V CSSC SC ρωω 0ρω j J -=∙∇⎰⎰-=∙VSdv j S d J ρω EJ H B E Dγμε===⎥⎦⎤⎢⎣⎡⨯=*)()(Re r H r E S av 21第七章k ωμμηε==1z zH e E E H e ηη=⨯=⨯,k βωμε==22k ππλωμε==1p V fk ωλμε∴===avav e w S v ||=良介质12112,,,p c V j f γμαβωμεεμεμγμληεωεεμε⎧≈≈≈⎪⎪⎨⎛⎫⎪≈=+≈ ⎪⎪⎝⎭⎩良导体222222212,,()p c ff V j f ωμγωωπαβπμγβμγμγππωμλπηβωμγμγγ⎧≈≈==≈=⎪⎪⎨⎪=≈=≈+⎪⎩⎪⎩⎪⎨⎧====⋅-∙⋅-∙∙⋅-∙⋅-∙∙r k j r e jk rk j r e jk e H e H H e E eE E n n 0000沿任意方向传播的均匀平面波c cj K γεεωμεω=-=导电媒质引入复介电常数及复波速E =E 0•e −Γz =E 0•e −αz e −jβzn k e k=波矢量E =ηH ×Ԧe n ,H =1ηԦe n ×E极化的判别方法1、利用E x 和E y 的振幅和相位之间的关系判断x xm x y ym y E e E t kz e E t kz ωϕωϕ=-++-+cos()cos()线极化时,或当→±=-πϕϕ0x y 圆极化时,且当→±=-=2/,πϕϕx y xm xm E E )波传播的波为右旋(左旋,沿若)(z 2/z x y -+-=-πϕϕ椭圆极化其他一般情形,→)波传播的波为左旋(右旋,沿若)(z 2/z x y -++=-πϕϕ)波传播的波为右旋(左旋,沿若)(z z x y -+<-<-0ϕϕπ)波传播的波为左旋(右旋,沿若)(z z x y -+<-<πϕϕ02、利用复数形式判断)()(y x kz j ym y kz j xm x eE e e E e E ϕϕ+-+-∙+= y xj ym y j xm x eE e e E e z E ϕϕ +==∙)0()sin (cos )sin (cos y y ym y x x xm x j E e j E e ϕϕϕϕ+++=)sin sin ()cos cos (y ym y x xm x y ym y x xm x E e E e j E e E e ϕϕϕϕ+++=IR E j E +=线极化或或若:→==00//I R I R E E E E圆极化且若→=⊥||||I R I R E E E EI R I R E E E E 若、与波的传播方向符合右手螺旋关系,则为右旋波;若、与波的传播方向符合左手螺旋关系,则为左旋波。
电磁场力公式

电磁场力公式
电磁场力公式是指描述电磁场中物体所受到的力的数学表达式。
根据经典电动力学理论,电磁场力公式可以分为洛伦兹力公式和库仑力公式。
1. 洛伦兹力公式:
洛伦兹力公式描述了带电粒子在电磁场中受到的力。
该公式为:F = q(E + v × B),其中F为洛伦兹力,q为电荷量,E为电场
强度,v为粒子速度,B为磁感应强度。
该公式说明了当带电
粒子同时存在电场和磁场时,会受到一个相互作用力。
2. 库仑力公式:
库仑力公式描述了两个电荷之间相互作用的力。
该公式为:F = k(q1q2 / r^2),其中F为库仑力,k为库仑常数,q1和q2为
两个电荷的电荷量,r为两者之间的距离。
该公式说明了电荷
之间的相互作用力随着电荷量的增加而增强,距离的增加而减弱。
需要注意的是,电磁场力公式只适用于电磁场中的粒子受力情况,对于电磁场本身的力则需要使用麦克斯韦方程组进行描述。
电磁学常用公式

电磁学常用公式
库仑定律:F=kQq/r²
电场强度:E=F/q
点电荷电场强度:E=kQ/r²
匀强电场:E=U/d
电势能:E₁ =qφ
电势差:U₁₂=φ₁-φ₂
静电力做功:W₁₂=qU₁₂
电容定义式:C=Q/U
电容:C=εS/4πkd
带电粒子在匀强电场中的运动
加速匀强电场:1/2*mv² =qU
v² =2qU/m
偏转匀强电场:
运动时间:t=x/v₀
垂直加速度:a=qU/md
垂直位移:y=1/2*at₂ =1/2*(qU/md)*(x/v₀)²偏转角:θ=v⊥/v₀=qUx/md(v₀)²
微观电流:I=nesv
电源非静电力做功:W=εq
欧姆定律:I=U/R
串联电路
电流:I₁ =I₂ =I₃ = ……
电压:U =U₁ +U₂ +U₃ + ……
并联电路
电压:U₁=U₂=U₃= ……
电流:I =I₁+I₂+I₃+ ……
电阻串联:R =R₁+R₂+R₃+ ……
电阻并联:1/R =1/R₁+1/R₂+1/R₃+ ……
焦耳定律:Q=I² Rt
P=I² R
P=U² /R
电功率:W=UIt
电功:P=UI
电阻定律:R=ρl/S
全电路欧姆定律:ε=I(R+r)
ε=U外+U内
安培力:F=ILBsinθ
磁通量:Φ=BS
电磁感应
感应电动势:E=nΔΦ/Δt
导线切割磁感线:ΔS=lvΔt
E=Blv*sinθ
感生电动势:E=LΔI/Δt。
高中电磁场公式汇总

高中电磁场公式汇总在高中物理中,电磁场是一个重要的概念。
它描述了电荷的运动和相互作用的方式,并且在日常生活中有很多应用。
下面是一些常见的电磁场公式:1.充电粒子的电场强度:E = k * Q / r^2其中,E是电场强度(单位是伏特/米),k是电力常数(9.0 * 10^9 N * m^2 /C^2),Q是充电粒子的电荷(单位是库仑),r是充电粒子到观察点的距离(单位是米)。
2.静电场能量密度:u = 1/2 * ε * E^2其中,u是能量密度(单位是焦耳/平方米),ε是真空介电常数(8.85 * 10^-12F/m),E是电场强度(单位是伏特/米)。
3.电动势:ΔV = E * d其中,ΔV是电动势(单位是伏特),E是电场强度(单位是伏特/米),d是电荷在电场中的位移(单位是米)。
4.电动势能:U = Q * ΔV其中,U是电动势能(单位是焦耳),Q是电荷(单位是库仑),ΔV是电动势(单位是伏特)。
5.电动势功率:P = U / t其中,P是电动势功率(单位是瓦),U是电动势能(单位是焦耳),t是时间(单位是秒)。
6.电容电压:V = Q / C其中,V是电容电压(单位是伏特),Q是电容器内的电荷(单位是库仑),C是电容(单位是库仑/伏特)。
7.电容电流:I = C * dV/dt其中,I是电流(单位是安培),C是电容(单位是库仑/伏特),dV/dt是电容电压的时间导数(单位是伏特/秒)。
8.电感电压:V = L * di/dt其中,V是电感电压(单位是伏特),L是电感(单位是亨利),di/dt是电感电流的时间导数(单位是安培/秒)。
9.电感电流:I = 1/L * ∫V dt其中,I是电流(单位是安培),L是电感(单位是亨利),V是电感电压(单位是伏特),∫V dt是电感电压的时间积分(单位是伏特*秒)。
10.磁场强度:B = μ * I / (2πr)其中,B是磁场强度(单位是牛顿/伏特),μ是真空磁导率(4π * 10^-7 牛顿/伏特),I是电流(单位是安培),r是观察点到电流的距离(单位是米)。
工程电磁场
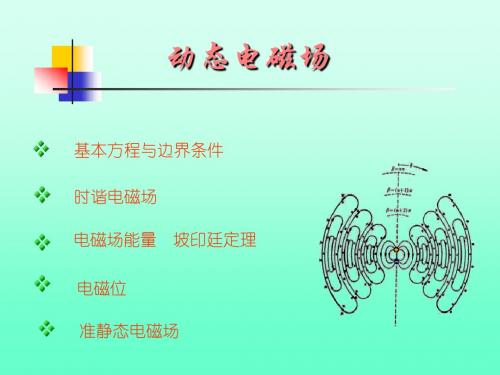
E m j Bm
Bm 0
Dm m
不再含有场量对时间t的偏导数,从而使时谐电磁场的分析得 以简化。
例4-2:写出与时谐电磁场对应的复矢量(有效值)或瞬时矢量,
H x jH 0 sin cos(x cos )e
jz sin
E
U e ln( b / a
U I ez ln( b / a ) 2
同轴电缆中的电磁能流
单位时间内流入内外导体间的横截面A的总能量为 b UI P S dA 2d UI A a 2 2 ln b / a 这表明: • 穿出任一横截面的能量相等,电源提供的能量全部被负载吸收。
时变电磁场中媒质分界面上的衔接条件的推导方式与前三章类同,归纳如下:
e n H 2 H 1 k e n E 2 E1 0
E2t E1t
B1n B2n
D2n D1n
e n B2 B1 0
tan 1 1 tan 2 2
时谐电磁场
4.2.1 时谐电磁场的复数表示
E(r, t ) ex Exm r cost x r e y Eym r cost y r ez Ezm r cost z r
(三要素) 是角频率,Exm、Eym、Ezm及x、y、z 分别是 电场强度在直角坐标系下的三个分量的振幅和初相位。 采用相量表示法,上式可表示为如下复矢量(相量),即
~ j
通常的磁导率
通常的介电常数
表征磁介质中的 磁化损耗
在高频时谐电磁场以上参数通常是频率的函数
当电介质同时存在电极化损耗和欧姆损耗时,其等效复介电 常数可写为 ~ e j 为了表征电介质中损耗的特性,通常采用损耗角的正切
电磁场公式总结
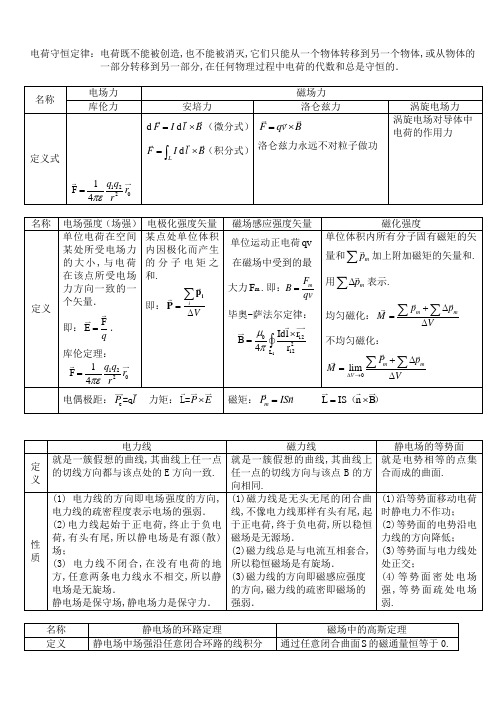
1.磁感应强度是用来表示磁场的强弱和方向的物理量,是矢量,单位T),1T=1N/A•m
2.安培力F=BIL;(注:L⊥B) {B:磁感应强度(T),F:安培力(F),I:电流强度(A),L:导线长度(m)}
3.洛仑兹力f=qVB(注V⊥B);质谱仪〔见第二册P155〕 {f:洛仑兹力(N),q:带电粒子电量(C),V:带电粒子速度(m/s)}
8.电源总动率、电源输出功率、电源效率:P总=IE,P出=IU,η=P出/P总{I:电路总电流(A),E:电源电动势(V),U:路端电压(V),η:电源效率}
9.电路的串/并联 串联电路(P、U与R成正比) 并联电路(P、I与R成反比)
电阻关系(串同并反) R串=R1+R2+R3+…1/R并=1/R1+1/R2+1/R3+…
9.电势能:EA=qUA {EA:带电体在A点的电势能(J),q:电量(C),UA:A点的电势(V)}
10.电势能的变化ΔEAB=EB-EA {带电体在电场中从A位置到B位置时电势能的差值}
11.电场力做功与电势能变化ΔEAB=-WAB=-qUAB (电势能的增量等于电场力做功的负值)
12.电容C=Q/U(定义式,计算式) {C:电容(F),Q:电量(C),U:电压(两极板电势差)(V)}
接入被测电阻Rx后通过电表的电流为
Ix=E/(r+Rg+Ro+Rx)=E/(R中+Rx)
由于Ix与Rx对应,因此可指示被测电阻大小
(3)使用方法:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)}、拨off挡。
(4)注意:测量电阻时,要与原电路断开,选择量程使指针在中央附近,每次换挡要重新短接欧姆调零。
工程电磁场原理实用公式总结

1
1
力������ = q′ ������ =
������������ ������������
=
������������ 2
功率P = γ������ 2
真空高斯定理∮ ������ ∙ ������������ =
∫ ������������������ ������
=
������ ������
∆������→0 ������ ������ ������
媒质构成方程������ = ε������ ������ = μ������ ������ = γ������
������������������ ������������ ∆������→0
散度∇ ∙ ������ = lim ∮ ������ ∙ ������������⁄∆������ = ������
电荷线密度分布τ(������′ ) = lim ∆������(������′)⁄∆������ ′ = ������������(������′)⁄������������ ′ (������/������)
∆������`→0
R = ������������⁄������ ������������ = ������(������������ × ������)
������ ������ 2������������������ ������
������ = tan ������
������ 4������������������������
������������ = sec ������ 2 ������������ dq = ρdv ′ = σds ′ = τdl′
2������2
1 +������2
电磁场公式总结

电场的无旋性
磁场的无源性
∫ 电位差(电压):单位正电荷的电位能差.即:U AB
=
WAB q
=
AAB q
=
B �� � Ed l .
A
磁介质:在磁场中影响原磁场的物质称为磁介质.
名称
电通量
电通量就是垂直通过某一面积的电力线的条数,
定义 用 Φe表示.即: Φe = ∫∫ EidS = ∫∫ EdScosθ
均匀磁化:
� M
=
∑
� pm
+
∑
� ∆pm
∆V
不均匀磁化:
� M
=
lim
�
∑ Pm
�
+ ∑ ∆pm
∆V →0
∆V
��
� ��
L = IS(n × B)
电力线
磁力线
静电场的等势面
就是一簇假想的曲线,其曲线上任一点 就是一簇假想的曲线,其曲线上 就是电势相等的点集 定
的切线方向都与该点处的 E 方向一致. 任一点的切线方向与该点 B 的方 合而成的曲面. 义
ss名称静电感应磁化定义电场对电场中的物质的作用磁场对磁场中的物质的作用利用电介质时电场的高斯定理求电场感应利用磁介质中的安培环路定理求磁场感应强度强度原理通过电介质中任一闭合曲面的电位移通量等于该面包围的自由电荷的代数和
电荷守恒定律:电荷既不能被创造,也不能被消灭,它们只能从一个物体转移到另一个物体,或从物体的 一部分转移到另一部分,在任何物理过程中电荷的代数和总是守恒的.
��
��
高斯面,求出电位移矢量 D .
环路,求出磁场强度 H .
解题 步骤
��
��
��
��
理工科目必备湖北省考研电磁场与微波重要公式速查

理工科目必备湖北省考研电磁场与微波重要公式速查电磁场与微波是理工科目中一门重要的学科,掌握其中的公式是学习和应用的基础。
本文将为大家提供湖北省考研电磁场与微波学科的重要公式速查,供大家参考学习。
1. 电场与静电场公式①库伦定律:F = k * ((q1 * q2) / r^2)该公式用于计算两个点电荷之间的电力,其中 F 为电力大小,k为库伦常数,q1 和 q2 分别为两个点电荷的电荷量,r 为两点电荷之间的距离。
②高斯定律:∮E * dS = (1 / ε0) * ∫ρdV高斯定律用于计算电场强度与电荷分布之间的关系,其中 E 为电场强度,dS 为闭合曲面的面积分,ρ 为电荷密度,ε0 为真空介质的介电常数,V 为闭合曲面包围的体积。
2. 磁场与静磁场公式①洛伦兹力公式:F = q * (v × B)洛伦兹力公式用于计算电荷在磁场中受到的力,其中F 为力大小,q 为电荷量,v 为电荷运动的速度矢量,B 为磁场矢量。
②安培环路定理:∮B * dl = μ0 * I安培环路定理用于计算磁感应强度与电流之间的关系,其中 B 为磁感应强度,dl 为闭合回路的线元,μ0 为真空中的磁导率,I 为通过闭合回路的电流。
3. 电磁感应公式①法拉第电磁感应定律:ε = -dφ / dt法拉第电磁感应定律用于计算感应电动势的大小,其中ε 为感应电动势,dφ / dt 为磁通变化率。
②麦克斯韦-安培定理:∮B * dl = μ0 * (I + εdA / dt)麦克斯韦-安培定理用于计算磁场沿闭合回路的环路积分与闭合回路内的总电流之和的关系,其中 B 为磁场,dl 为闭合回路的线元,μ0为真空中的磁导率,I 为通过闭合回路的电流,εdA/ dt 为感应电动势。
4. 麦克斯韦方程组①高斯定律:∮E * dS = (1 / ε0) * ∫ρdV该公式与电场与静电场公式中的高斯定律相同。
②麦克斯韦方程(法拉第电磁感应定律):∮E * dl = -dφ / dt该公式与电磁感应公式中的法拉第电磁感应定律相同。
电磁场中的电势与电场强度公式整理

电磁场中的电势与电场强度公式整理在电磁学中,电势和电场强度是描述电磁场的重要概念。
它们之间有一定的数学关系,可以通过一些公式来表达和计算。
本文将对电磁场中的电势和电场强度的公式进行整理和介绍。
一、电势公式电势是描述电场中某一点电荷所具有的势能的物理量。
在电磁学中,电势通常用电势差来表示。
电势差是指在电场中从一个点移动到另一个点所需的功与单位正电荷之比。
电势与电场强度之间的关系可以通过以下公式来表示:V = -∫ E · dl其中,V表示电势差,E表示电场强度,dl表示电场线元素的微小位移。
这个公式实际上是电场强度的负梯度形式,它表示了沿着电场线方向的势能变化率。
二、电场强度公式电场强度是描述电场中单位正电荷所受到的力的物理量。
在电磁学中,电场强度通常用矢量形式表示。
电场强度与电势之间的关系可以通过以下公式来表示:E = -∇V其中,E表示电场强度,V表示电势,∇表示梯度运算符。
这个公式表示了电场强度是电势的负梯度,它是一个矢量,指向电势变化最快的方向。
三、电势和电场强度的关系电场强度和电势是描述电磁场的两个重要物理量,它们之间满足一定的数学关系。
根据电场强度和电势的定义以及电势公式和电场强度公式,可以推导出它们之间的关系:E = -∇V这个公式说明了电场强度的方向是电势变化最快的方向,且电场强度的大小与电势的变化率成正比。
换句话说,电场强度在任意点的方向是沿着电势等值面的法线方向,且电场强度的大小与电势在该点的梯度成正比。
四、电磁场中的电势与电场强度公式的应用电势和电场强度是电磁学中的基本概念,它们的公式可以用于解决各种电磁场问题。
通过求解电场强度和电势的公式,可以计算电荷在电场中受到的力、电势差和电势能等物理量。
例如,在求解带电粒子在电场中受力的问题时,可以利用电场强度公式计算电场强度,再通过电势公式计算电势差,然后利用电势差和电荷量的乘积得到该粒子所受的力。
这样,可以有效地分析和解决复杂的电磁场问题。
电磁学公式大全

电磁学公式大全电磁学是物理学的一个重要分支,研究电荷和电流所产生的电场和磁场以及它们之间的相互作用。
电磁学公式是电磁学理论的重要组成部分,它们描述了电磁场的性质和规律。
在电磁学的学习和研究过程中,掌握和运用这些公式是至关重要的。
本文将为您介绍一些常见的电磁学公式,希望能对您的学习和工作有所帮助。
1. 库仑定律。
库仑定律描述了两个电荷之间的电力作用。
如果两个电荷的大小分别为q1和q2,它们之间的距离为r,那么它们之间的电力F可以用以下公式表示:\[ F = k\frac{q_1q_2}{r^2} \]其中,k为库仑常数,其数值为\(8.9875 × 10^9 N·m^2/C^2\)。
2. 电场强度。
电场强度E描述了单位正电荷在电场中所受到的力。
如果一个点电荷q在某一点产生了电场,那么在该点的电场强度可以用以下公式表示:\[ E = \frac{kq}{r^2} \]其中,k为库仑常数,q为点电荷的大小,r为点电荷到该点的距离。
3. 静电势能。
两个电荷之间由于电力作用而具有的势能称为静电势能。
如果两个电荷分别为q1和q2,它们之间的距离为r,那么它们之间的静电势能U可以用以下公式表示:\[ U = \frac{kq_1q_2}{r} \]4. 安培环路定理。
安培环路定理描述了通过任意闭合路径的电流总和等于该路径所围成的面积的变化率。
如果一条闭合路径上的电流总和为I,那么该路径所围成的面积S的变化率可以用以下公式表示:\[ \oint \vec{B} \cdot d\vec{l} = \mu_0 I \]其中,\(\vec{B}\)为磁感应强度,\(\mu_0\)为真空磁导率,d\(\vec{l}\)为路径元素。
5. 洛伦兹力。
洛伦兹力描述了电荷在电场和磁场中所受到的合力。
如果一个电荷q在电场E和磁场B中运动,那么它所受到的洛伦兹力F可以用以下公式表示:\[ \vec{F} = q(\vec{E} + \vec{v} \times \vec{B}) \]其中,\(\vec{E}\)为电场强度,\(\vec{v}\)为电荷的速度,\(\vec{B}\)为磁感应强度。
