电动力学
电动力学与电磁波

电动力学与电磁波电动力学是物理学中的一个重要分支,研究电荷的运动以及与之相关的电场和磁场的性质和相互作用。
电磁波则是电动力学的一个重要应用,是指通过电和磁的相互作用而产生的传播能量的波动。
一、电动力学的基本原理和定律电动力学的基本原理源于库仑定律和法拉第电磁感应定律。
库仑定律表明了电荷之间的相互作用力与它们之间的距离和电荷量的乘积成正比,反比于距离的平方。
法拉第电磁感应定律则说明了通过一个闭合线圈的磁通量变化会在线圈中产生感应电动势。
二、电场和电势电场是由电荷所产生的力场,它描述了电荷在空间中的分布情况。
电场的强度用电场强度表示,它是单位正电荷所受到的电力。
电势则是电场对单位正电荷所做的功,用于描述电荷在电场中的势能。
三、磁场和磁感应强度磁场是由磁荷或电流所产生的力场,它描述了磁荷或电流在空间中的分布情况。
磁感应强度是描述磁场强度的物理量,它定义为单位磁力所施加的力。
四、麦克斯韦方程组麦克斯韦方程组是电动力学的基本方程组,它们由麦克斯韦根据实验结果整理得出。
麦克斯韦方程组包括了电场和磁场的动力学方程以及它们与电荷和电流的关系。
五、电磁波的性质和传播电磁波是在电磁场中传播的能量传递的波动。
它由变化的电场和磁场相互作用而产生,具有电磁场垂直传播、幅度衰减、速度恒定等特点。
电磁波的频率和波长决定了它们的能量和传播特性。
六、应用于现实生活的例子电动力学和电磁波在现实生活中有着广泛的应用。
例如,电动力学理论为电子技术的发展提供了基础,无线电、电视和手机等无线通信技术都是建立在电磁波传播的原理上。
此外,电动力学还解释了静电现象、电磁感应现象和电磁波传播的机制。
总结电动力学和电磁波是现代物理学的重要分支,研究了电荷的运动、电场和磁场的性质以及它们之间的相互作用。
电磁波是电动力学的一个重要应用,通过电和磁的相互作用而产生的传播能量的波动。
电动力学和电磁波的研究不仅有助于我们理解自然界的现象,也广泛应用于现代科技和生活中的各个领域。
电动力学的第一章总结

第一章 电磁现象的普遍规律本章重点:从特殊到一般,由实验定律加假设总结出麦克斯韦方程。
主要内容:讨论几个定律,总结出静电场、静磁场方程;找出问题,提出假设,总结真空中麦氏方程; 讨论介质电磁性质,得出介质中麦氏方程; 给出求解麦氏方程的边值关系;引入电磁场能量,能流并讨论电磁能量的传输。
§1. 电荷和静电场一、 库仑定律和电场强度1. 库仑定律一个静止点电荷Q 对另一静止点电荷Q '的作用力为:34rrQ Q F o πε'=⑴ 静电学的基本实验定律 (2)两种物理解释超距作用: 一个点电荷不需中间媒介直接施力与另一点电荷。
场传递: 相互作用通过场来传递。
对静电情况两者等价。
2. 点电荷电场强度每一电荷周围空间存在电场:即任何电荷都在自己周围空间激发电场。
它的基本性质是:电荷对处在其中的其它电荷具有作用力。
对库仑定律重新解释:描述一个静止点电荷激发的电场对其他任何电荷的电场力。
描述电场的函数——电场强度定义:试探点电荷F ,则30()4F Q rE x Q rπε==' 它与试探点电荷无关,给定Q ,它仅是空间点函数,因而是一个矢量场——静电场。
3.场的叠加原理(实验定律)n 个点电荷在空间某点的场强等于各点电荷单独存在时在该点场强的矢量和,即:3110()4nni ii i i i Q r E x E r πε====∑∑。
4.电荷密度分布体密度: ()0limV Q dQx V dVρ∆→∆'==''∆ 面密度: ()0lim S Q dQx S dS σ∆→∆'==''∆ 线密度 : ()0lim l Q dQx l dl λ∆→∆'==''∆ ()dQ x dV ρ''=()()(),,VSLQ x dV Q x dS Q x dl ρσλ''''''===⎰⎰⎰5.连续分布电荷激发的电场强度()30()4Vx r E x dV r ρπε''=⎰或()30()4S x r E x dS rσπε''=⎰ 或 ()30()4L x rE x dl r λπε''=⎰ 对于场中的一个点电荷,受力F Q E '=仍然成立。
电动力学

英国物理学家和化学家。
最主要贡献:1831年发现了电磁感应现象。 1834年他研究电流通过溶液时产生的化 学变化,提出了法拉第电解定律。这一定 律为发展电结构理论开辟了道路。 1845年9月13日法拉第发现,一束平面偏 振光通过磁场时发生旋转,这种现象被称 为“法拉第效应”。法拉第认为光具有电 磁性质,是光的电磁波理论的先驱 1852年他引进磁力线概念。 他的很多成就不仅非常重要、且是带根 本性的理论。
单位张量与矢量、 张量的点乘
I C C I C I AB AB I AB
I : AB A B
2 B A 1.计算 A B A B 2.证明 M b a c a b c 与矢量 c 垂直,即 M c 0
林斯顿。遵照他的遗嘱,不举行任何丧礼,不筑坟 墓,不立纪念碑,骨灰撒在永远对人保密的地方, 为的是不使任何地方成为圣地。 爱因斯坦的后半生一直从事寻找大统一理论的工作, 不过这项工作没有获得成功,现在大统一理论是理 论物理学研究的中心问题。 爱因斯坦是耶路撒冷希伯来大学的注册商标
§2 矢量代数与张量初步
难点:公式多、数学推导较繁杂;解题难度大、
相对论概念不易理解。
二、电动力学与电磁学的联系与区别
范围
既讨论静场又讨论变化场,外加相对论。
深度
从矢量场论出发,总结电磁现象普遍规律,解题更具一般性。
方法
建立模型、求解方程、注重理论。
数学
矢量分析与场论、线性代数、数理方程、特殊函数 „
三、理论物理的特点
电动力学——精选推荐

电动⼒学电动⼒学第⼀章静电场⼀、考核知识点1、真空与介质中静电场场⽅程,场的性质、物理特征。
2、电场的边值关系、在两种介质分界⾯上电场的跃变性质。
3、由场⽅程、边值关系,通过电荷分布确定场分布及极化电荷的分布。
4、静电场的势描述。
由势分布确定场分布、荷分布;通过静电势的定解问题,确定静电势的分布、场分布及介质极化性质的讨论。
⼆、考核要求(⼀)、场⽅程、场的确定1、场⽅程,场的边值关系,体、⾯极化电荷密度的确定式等规律的推导。
2、识记:(1)、真空与介质静电场⽅程。
(2)、电场的边值关系。
(3)、体、⾯极化电荷密度的确定式。
3、领会与理解:(1)、静电场的物理特征。
12(2)、P D E ,,与电荷的关系,⼒线分布的区别与联系。
(3)、在介质分界⾯上场的跃变性质。
4、应⽤:通过对称性分析,运⽤静电场的⾼斯定理确定场,讨论介质的极化,正确地由电荷分布画出场的⼒线分布。
(⼆)、静电势1、静电势⽅程、边值关系的推导。
2、识记:静电势的积分表述、势⽅程、势的边值关系、势的边界条件、唯⼀性定理。
3、领会与理解:势的边值关系与边界条件,荷、势与场的关系,解的维数的确定,电像法的指导思想与像电荷的确定。
4、应⽤:求解静电势定解问题的⽅法(分离变量法、电像法)的掌握及应⽤,求解的准确性,场的特征分析及由势对介质极化问题的讨论。
第⼆章稳恒磁场⼀、考核知识点1、电荷守恒定律。
2、稳恒磁场场⽅程,场的性质特点。
3、由场⽅程,通过流分布确定场分布与磁化流。
4、磁场的边值关系。
5、稳恒磁场的⽮势。
6、由磁标势法确定场。
3⼆、考试要求1、规律的推导:真空、介质中稳恒磁场场⽅程,电荷守恒定律的微分表述,体、⾯磁化电流密度的确定式,磁场的边值关系,⽮势⽅程及其积分解,磁标势⽅程和边值关系等。
2、识记:电荷守恒定律,稳恒磁场场⽅程,体、⾯磁化电流密度的确定式,⽮势引⼊的定义式,磁标势引⼊条件,磁场的边值关系,0=f α情况磁标势的边值关系。
电动力学公式总结

电动力学公式总结电动力学是物理学中研究电荷间相互作用及其相关现象的分支学科。
电动力学公式是描述电场、电势、电流、电荷等电动力学量之间关系的数学表达式。
本文将总结常见的电动力学公式,并进行简要解释。
1. 库仑定律(Coulomb's Law)库仑定律用于描述两个电荷之间的相互作用力。
假设两个电荷分别为q1和q2,它们之间的作用力F由以下公式给出:F = k * (q1 * q2) / r^2其中,k为库仑常数,r为两个电荷间的距离。
2. 电场强度(Electric Field Strength)电场强度描述在给定点附近单位正电荷所受到的力的大小和方向。
电场强度E由以下公式给出:E =F / q其中,F为单位正电荷所受的力,q为正电荷的大小。
3. 电势差(Electric Potential Difference)电势差描述电场对电荷进行的功所引起的状态变化。
电势差V由以下公式给出:V = W / q其中,W为电场对电荷进行的功,q为电荷的大小。
4. 高斯定理(Gauss's Law)高斯定理是一个描写电场线分布和电荷分布之间关系的重要定理。
它表示电场的流出和流入电荷的总和等于电荷总量除以真空介电常数ε0。
该定理由以下公式给出:∮E · dA = (1 / ε0) * Q_enclosed其中,E为电场强度,dA为微元的面积矢量,Q_enclosed为电荷的总量。
5. 法拉第电磁感应定律(Faraday's Law of Electromagnetic Induction)法拉第电磁感应定律描述通过磁场的变化引起的电场变化。
它由以下公式给出:ε = -dΦ/dt其中,ε代表感应电动势,dΦ/dt为磁通量的变化率。
6. 奥姆定律(Ohm's Law)奥姆定律描述了电流、电压和电阻之间的关系。
根据奥姆定律,电流I等于电压V与电阻R的比值,即:I = V / R其中,I为电流,V为电压,R为电阻。
电动力学(全套课件)ppt课件

电磁波的传播遵循惠更斯原理,即波 面上的每一点都可以看作是新的波源。
电磁波在真空中的传播速度等于光速, 而在介质中的传播速度会发生变化。
电磁波的能量与动量
01
电磁波携带能量和动量,其能量密度和动量密度与 电场和磁场的振幅平方成正比。
02
电磁波的能量传播方向与波的传播方向相同,而动 量传播方向则与波的传播方向相反。
03
电磁波的能量和动量可以通过坡印廷矢量进行描述 和计算。
06
电动力学的应用与发展前 景
电动力学在物理学中的应用
描述电磁现象
电动力学是描述电荷和电流如何 产生电磁场,以及电磁场如何对 电荷和电流产生作用的理论基础。
解释光学现象
光是一种电磁波,电动力学为光 的传播、反射、折射、衍射等现 象提供了理论解释。
麦克斯韦方程组与电磁波
01
麦克斯韦方程组是描述电磁场的基本方程组,包括高斯定律、 高斯磁定律、法拉第电磁感应定律和安培环路定律。
02
电磁波是由变化的电场和磁场相互激发而产生的,其传播速度
等于光速。
麦克斯韦方程组揭示了电磁波的存在和传播规律,为电磁学的
03
发展奠定了基础。
电磁波的性质与传播
电磁波具有横波性质,其电场和磁场 振动方向相互垂直,且都垂直于传播 方向。
电场能量
W=∫wdV,表示整个电场 中的总能量。
功率
P=UI,表示单位时间内电 场中消耗的能量或提供的 能量。
04
恒磁场
磁感应强度与磁场强度
磁感应强度的定义与物理意义 磁感应强度与磁场强度的关系
磁场强度的定义与计算 磁场的叠加原理
安培环路定理与磁通量
01
安培环路定理 的表述与证明
电动力学

4. 磁场的散度
磁场的通量
磁场的散度 S 任意
S B dS 0
S B dS V ( B)dV 0
B 0
恒定磁场的另一基本方程。
B 0J
B 0
结论: 恒定磁场 ——无源,有旋
5. 例题(p.13 例)
电流 I 均匀分布于半径为 a 的无穷长直导线内,求空
间各点磁感应强度,并由此计算磁场的旋度。
1. 介质的概念
介质
分子
原子核:正电荷 电子: 负电荷
电中性 分子电流杂乱
宏观物理量 ← 微观量的平均 (宏观无穷小 内包含 大量的微观粒子)
外场
正负电荷相对位移,极性分子取向 —— 极化
分子电流取向规则化
—— 磁化
束缚电荷(极化电荷)→ 附加电场 E’
诱导电流(磁化电流等)→ 附加磁场 B’
2. 介质的极化
r
dV
'
JdV ' JdSdl Idl
B( x)
0 4
Idl
r
r3
3. 磁场的环量和旋度
安培环路定理:
L B dl 0I 0 S J dS
磁场的旋度
L B dl S ( B) dS
S 任意
B 0J
讨论: (1) 安培环路定理的微分形式,恒定磁场的基本方程 (2) 某点磁场的旋度只与该点的电流密度有关
)
t
(1) 法拉第电磁感应定律的微分形式
(2) 感应电场是有旋场
(3) 感应电场是由变化磁场激发的
2. 位移电流
电荷守恒定律
J
0
非恒定电流
磁场旋度
t
B 0J
矛盾!?
B 0 J 0
电动力学总结

(3)无限大均匀线性介质中点电荷
Q 4 r
点电荷在均匀介质中 的空间电势分布(Q 为自由电荷)
Q 产生的电势 Q P产生的电势
f
Qf
4 0 r
P
QP
4 0 r
(QP
(0
1)Qf
)
( 4) 连续f 分 布P 电 荷Q 4 f 0 (Q r PP ) 4 VQ f4 (rx )d 0 rV
机动 目录 上页 下页 返回 结束
值关系表达式*
nˆ D
nˆ nˆ nˆ
B 0
E H
0α
其它边值关系*
Ñ Ñ sLPM rrddSrLrsVJrMpddVSr nrnrPr2M r2Pr1 M r1prM
r
s Jf
dSr d dt
dVnr
V
rr J2 J1
f
t
7.电磁场的能量和能流 单位体积的能量 --- 能量密度
Ñ r r r r L B • d l0S rJ • d S r
安培环路定律*
旋度方程 B0J
uv
磁场的散度方程 B0
法拉第电磁感应定律
Ñ LiE rird lrdd t Bd dt(S其 B r中 dS r B EriSB rd S Brtr)
Ei 0 感生电场是有旋无源场
rr r
总电场为: ErESEi r B r
)
r
2 2
f (r) 0
g ( ) a 1s in a 2c o s
r r f (r) 有两个线性无关解 、
单值性要求 (0)(2),只能取整数,令 n
( r ,) r n ( A n s in n B n c o s n ) r n ( C n s in n D n c o s n ) n 1
物理学中的电动力学理论

物理学中的电动力学理论
电动力学理论是指描述电荷、电磁波和电场以及它们之间相互
作用的物理学理论。
这个理论在物理学中占据重要地位,被广泛
应用于许多领域,从电子学到材料科学。
电动力学理论的基础是电磁场方程式,这是一个完整描述电荷、电磁场和它们之间相互作用的数学方程组。
这个方程组由四个方
程组成,它们分别描述电荷的产生和消失,以及电场和磁场的行为。
在电荷形成的物理过程中,电磁场的存在是必须的。
通过电磁
场方程式中的第一个方程,可以描述电荷是如何受到电场和磁场
的相互作用的。
电荷的行为和性质与电磁场的行为和性质密切相关。
在电动力学理论中,研究电磁场与物质的相互作用也是非常重
要的。
电磁场可以通过空气、金属、绝缘体和半导体等物质中传播。
这种传播方式与电子和原子结构的行为紧密联系,在物体表
面产生共振现象,导致一些复杂的现象。
电磁场还可以通过电磁波的形式传播。
电磁波是一种用电场和磁场交替振荡的方式在空间中传播的能量。
电磁波分为不同频率的光谱,包括无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线等。
电动力学理论可以用来解释和预测这些事实。
电动力学理论是研究电子学和计算机技术的基础,通过对电荷和磁荷的形成与行为的理解,我们可以开发出更好的计算机芯片和其他电子设备。
此外,电动力学也用于研究天体物理学,如太阳和其他星系中的电磁场和电磁波的行为。
总之,电动力学理论在物理学中扮演着极其重要的角色。
通过深入研究电磁场和电磁波的行为,我们可以更好地理解和应用这个理论,从而推进科学和技术的进步。
论动体的电动力学

论动体的电动力学
1 电动力学:内在的奥秘
电动力学是一门集电动力、机械力和能源学在一起的力学学科,一般用于研究运动物体中所发挥的力和活动时所显示的能量行为。
它也是一门研究系统如何响应外力,释放动能和在运动过程中发挥力的学科,是机械、电、光、声、振动等力学系统的综合研究。
电动力学的研究通常涉及两个主要工作领域:动力学和电磁学。
从动力学的角度研究,主要包括分析力对物体的作用,物体的运动和物体在运动过程中的变形;从电磁学的角度研究,主要包括研究运动物体的电磁特性,如电流回路、电磁电容、静电源和电磁感应等。
在可应用性方面,电动力学发挥了巨大的作用,它可以解释各种物理系统如发动机、飞机涡扇发动机、磁力传动机等。
其中真空电动力学是电动力学的一个重要应用,它研究的实体介质的重要研究,是关于介质的真空电磁性能及真空电气磁学变换的研究,用于分析实体介质在真空条件下的电磁特性。
电动力学也是电工学中重要的一个分支,由电磁感应理论和电磁学变换理论组成,用于解释地球运动、地球潮汐运动等不同运动系统中发生的电磁运动。
它也为量子电动力学提供理论支持,在作用等离子体中,用电磁学变换原理,通过磁场在原子核中加速粒子,产生X 射线。
电动力学的研究和应用已逐渐发展趋向复杂,它不仅在物理和工程中具有强大的启发作用,而且在探索物质本质的深层奥秘中也发挥着重要的作用。
在未来,电动力学的研究将给人们带来更多惊喜,将为更多的实际应用服务,也将深入探索系统复杂性和非线性动力学之间的关系。
电动力学

电动力学(Electrodynamics)一、电动力学——理论物理范畴.理论物理:1、理论力学:对象:机械运动,牛顿力学基础动力学运动学2、热力学与统计物理学热运动第零定律热平衡第一定律能量守恒热力学:热现象的宏观理论基础几个定律第二定律熵增加(....)第三定律绝对零度不能达到统计物理学:热现象的微观理论用概率用统计方法分析系统的宏观性质变化规律3、量子力学微观粒子运动4、电动力学——属于电磁学范畴电磁运动:电磁场的基本属性,运动规律和EmF与带电粒子间相互作用EmF——是一种由带电体产生物理场,属于其中的带电体受电磁力的作用建立M.eq 讨论静电、磁场、电磁波、辐射、狭义相对论二、电磁学发展第一阶段:第一次结合1、BC前6 7世纪磁石吸铁指南磁石指南针应用研究磁现象研究早于电磁现象电——BC前5世纪希腊就有静电现象的研究2、系统研究磁:1600年吉尔伯特《论磁磁体和地球作为一个巨大磁体》——电:1660 盖里克发明了摩擦起电开始系统研究电磁学没有找出合适的产生静电困难如何测量3、定量研究静电力基本特性电现象直到1754年静电学三条基本原理电荷守恒静电感应原理1750年 来切尔 磁极间作用力1785年 库伦 静止 点电荷间作用力 平方反比定律 电磁学研究进入定量化阶段 4、静电 动电 1780 伽伐尼——动物电现象 1800 扶打(Volta ) 发明电堆(把锌块 铜块夹在用水浸湿的低点中,重复叠成一排,形成电源)[把锌块和铜块插入盐水中或稀酸杯中也可以形成电源——扶打电池] 电池堆 静电 动电5、第一结合电、磁结合规律1820年奥斯特(Oersted,丹麦) 电流磁效应 电磁学研究进入新阶段1820年前 研究电磁间相互作用 奥 信奉康德哲学 认为自然界的各种基本力都可相互 想知道 电是否以其隐蔽方式对磁作用第二阶段——M.eq 方程建立1、法拉第电磁感应法拉第 猜 磁 电流1831年ðB ⃑ ðt 电场 法拉第电磁感应定律电磁感应 电荷 磁极周围充满了力线法贡献 创立了力的思想 力线。
电动力学理论在电路设计中的应用

电动力学理论在电路设计中的应用一、电动力学理论概述电动力学是物理学的一个分支,研究电荷在电场和磁场中的运动规律以及它们之间的相互作用。
在电路设计中,电动力学理论提供了重要的基础和指导,为电路的构建和优化提供了理论依据。
二、电场与电势1. 电场概念:电场是由电荷产生的一种物理场,可以用来描述电荷对周围空间的作用。
2. 电势概念:电势是电场的一种性质,用来描述电荷在电场中的能量。
三、电荷分布与电容器设计1. 电容器基本原理:电容器是一种能够存储电荷的装置,由正负两极板和介质组成。
2. 电荷分布对电容器性能的影响:电容器的电容量与电荷分布密切相关,合理设计电荷分布可以提高电容器的性能。
四、电流与电阻器设计1. 电流概念:电流是电荷的流动,是描述电荷在导体中移动的物理量。
2. 电阻器的作用与设计原则:电阻器用来调节电流大小,其设计原则包括选择合适的电阻值、适当的功率承受能力等。
五、电感与电感器设计1. 电感概念:电感是导体中电流变化引起的电磁感应现象,与电流及其变化率有关。
2. 电感器的设计要点:电感器的设计与电感大小、材料选择、线圈的匝数等有关,需要根据具体要求进行合理选择。
六、交流电路与谐振器设计1. 交流电路基本特点:交流电路中电压和电流都随时间变化,具有周期性特点。
2. 谐振器的应用与设计:谐振器是利用电动力学理论中的共振现象,用于增强特定频率的电信号。
七、电磁场与电磁波传播1. 电磁场概念:电磁场是由电荷和电流产生的一种物理场,包括电场和磁场两个部分。
2. 电磁波传播与天线设计:电磁波是由振荡电荷或电流产生的,天线是用于发射和接收电磁波的装置。
八、磁感应与电动机设计1. 磁感应概念:磁感应是磁场的一种性质,用于描述磁场对电荷运动的影响。
2. 电动机的设计与原理:电动机是利用电磁感应原理将电能转换为机械能的装置,需要合理设计磁场、线圈、转子等部分。
结语:电动力学理论作为电路设计的基础,为我们理解和应用电路提供了重要的支持和指导。
电动力学

基地拓展训练子课题
分子反应动力学是在分子和原子的水平上观察和研究化学 反应的最基本过程——分子碰撞;从中揭示出化学反应的 基本规律,使人们能从微观角度直接了解并掌握化学反应 的本质。
准经典轨线法的基本思想是,将A、B、C三个原子都近似 看作是经典力学的质点,通过考察它们的坐标和动量(广义 坐标和广义动量)随时间的变化情况,就能知道原子之间是 否发生了重新组合,即是否发生了化学反应,以及碰撞前 后各原子或分子所处的能量状态。通过计算各种不同碰撞 条件下原子间的组合情况,并对所有结果作统计平均,就 可以获得能够和宏观实验数据相比较的理论动力学参数。
《电动力学》授课计划表
《电动力学》授课计划表
——2015-2016学年第1学期
本学期上课18周(包括国庆节放假1周) 实际讲课17周,共34讲
《电动力学》授课计划表
《电动力学》授课计划表
绪论
《电动力学》课程考试办法:
⑴ 闭卷笔试 ⑵ 课堂学习 ⑶ 课下作业 (4) 小论文
占 70%; 占10%; 占10%; 占 10%。
绪论
小论文要求: (1) 格式正确,具体格式要求同中文核心期刊正式论
文; (2) 内容新颖、充实,经过自己的独立思考; (3) 严禁从网络上直接下载,严禁互相抄袭; (4) 与自然科学密切相关,与物理学相关; (5) 论文书写用时应在10课时以上,字数应在5K+; (6) 若10月10日补课,安排宣讲小论文; (7) 2015年12月31日前网上提交小论文。
基地拓展训练子课题
具体训练内容和计划安排如下:
(1)阅读相关资料,理解势能面的概念;通过分析势能面的结 构形状,理解插入反应和取代反应。
电动力学应用

电动力学应用电动力学是物理学中研究电荷和电场相互作用的分支,它对于理解电磁现象以及应用于实际生活中的各种技术具有重要的意义。
本文将探讨电动力学在不同领域中的应用,包括电力输送、电子设备、磁共振成像以及电磁波传播。
1. 电力输送电动力学在电力输送领域中具有广泛的应用。
当电流通过导线时,会产生磁场,而这个磁场又会影响附近的导线。
根据法拉第电磁感应定律,当磁场发生变化时会产生感应电动势。
这个原理被应用在变压器中,通过变压器将电能从发电站输送到不同的地方,并适当提高或降低电压。
这样的电力输送系统可以高效地将电能输送到远距离,并用于我们的家庭和工业用电。
2. 电子设备电动力学在电子设备中起着重要的作用。
例如,半导体器件,如二极管和晶体管,利用电场对载流子的控制实现电信号的调节和放大。
电动力学的电磁感应原理也被运用于发电机和发电机,将机械能转化为电能供给电子设备使用。
另外,电动力学也用于计算机的运行,通过运用电场对电子的操控来实现信息的存储和处理。
3. 磁共振成像磁共振成像(MRI)是利用核磁共振现象探测人体内部结构的一种影像技术。
电动力学中的磁场和电磁感应原理是MRI实现原理的基础。
在MRI扫描中,人体被放置在一个强磁场中,通过放射射频脉冲诱导样品中的原子核进入共振状态。
利用检测原子核共振时释放出的能量以及不同组织对磁场的响应差异,可以生成高分辨率的人体影像。
MRI在医学诊断中具有广泛的应用,对于发现疾病以及进行脑部和器官的检查非常有帮助。
4. 电磁波传播电动力学中的麦克斯韦方程组描述了电场和磁场的相互关系,它们共同构成了电磁波的传播。
电磁波是一种由电场和磁场交替变化产生的波动现象,包括射频波、微波、可见光、紫外线和X射线等。
电磁波在通信和无线电技术中广泛应用,包括手机通信、卫星通信和电视广播等。
通过电动力学的研究和应用,人们可以更好地理解电磁波的特性以及如何控制和利用它们。
总结:电动力学在电力输送、电子设备、磁共振成像以及电磁波传播等领域具有广泛的应用。
《芝加哥大学物理学讲义:电动力学讲义》笔记

《芝加哥大学物理学讲义:电动力学讲义》阅读札记1. 电动力学概述在电动力学的世界中,物理现象既神秘又充满魅力。
从电荷的运动到电磁波的传播,电动力学为我们揭示了自然界中电与磁的奇妙联系。
本次阅读《芝加哥大学物理学讲义:电动力学讲义》,我深入了解了电动力学的核心概念和原理,对这一领域有了更为深刻的认识。
电动力学作为物理学的一个重要分支,主要研究电荷、电流以及它们产生的电场和磁场之间的关系。
它不仅描述了电场的产生、传播和变化,还涉及了磁场的性质以及电流产生磁场的原因。
在这个过程中,我们探讨了电磁感应、电磁辐射等问题,并学习了麦克斯韦方程组这一电动力学的基石,它统一了电场和磁场的关系,为我们理解电磁现象提供了基本框架。
电动力学还与许多现代技术紧密相关,如无线通信、电磁铁、电动机等。
这些应用不仅展示了电动力学的实用价值,也激发了我们对于探索未知领域的兴趣。
通过学习电动力学,我更加明白理论知识的重要性,以及它在解决实际问题中的巨大作用。
我期待着将所学应用于实践,为科学的发展贡献自己的力量。
1.1 电荷与电场在阅读《芝加哥大学物理学讲义:电动力学讲义》的第一章中,我首先被引导理解电荷这一基础概念。
电荷是物理学中描述物质带电性质的物理量,其载体可以是电子、质子等带电粒子。
理解电荷的关键在于理解其在电动力学中所起的作用以及其带电量的大小。
当电荷聚集在某一空间时,它们会产生电场,这是电动力学研究的核心内容之一。
电场是由于电荷的存在而产生的,每个电荷周围都存在一个电场,它会对放入其中的其他电荷施加力。
电场具有空间性和物质性,电场是存在于一定空间的,并且可以对其他物体产生影响。
电场的强度取决于源电荷的电量和距离,电场还表现出一些独特的性质,如叠加性、保守性等。
这些性质对于理解电动力学中的许多现象至关重要。
电荷是电场的源头,电场的存在和传播是由于电荷的作用。
当电荷产生时,它会在其周围形成电场,这个电场会向周围空间传播。
电场的强度和方向取决于源电荷的电量、距离和方向。
电动力学内容简介
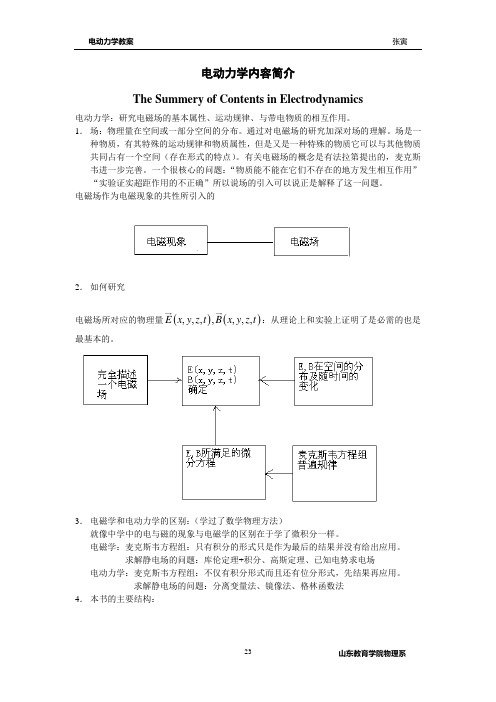
电动力学内容简介The Summery of Contents in Electrodynamics电动力学:研究电磁场的基本属性、运动规律、与带电物质的相互作用。
1. 场:物理量在空间或一部分空间的分布。
通过对电磁场的研究加深对场的理解。
场是一种物质,有其特殊的运动规律和物质属性,但是又是一种特殊的物质它可以与其他物质共同占有一个空间(存在形式的特点)。
有关电磁场的概念是有法拉第提出的,麦克斯韦进一步完善。
一个很核心的问题:“物质能不能在它们不存在的地方发生相互作用” “实验证实超距作用的不正确”所以说场的引入可以说正是解释了这一问题。
电磁场作为电磁现象的共性所引入的2. 如何研究电磁场所对应的物理量()(),,,,,,,E x y z t B x y z t :从理论上和实验上证明了是必需的也是最基本的。
3. 电磁学和电动力学的区别:(学过了数学物理方法)就像中学中的电与磁的现象与电磁学的区别在于学了微积分一样。
电磁学:麦克斯韦方程组:只有积分的形式只是作为最后的结果并没有给出应用。
求解静电场的问题:库伦定理+积分、高斯定理、已知电势求电场电动力学:麦克斯韦方程组:不仅有积分形式而且还有位分形式,先结果再应用。
求解静电场的问题:分离变量法、镜像法、格林函数法4. 本书的主要结构:⎧⎧→⎨⎪⎪⎩→⎨⎧⎪→⎨⎪⎩⎩第二章静电场静第三章静磁场第一章电磁现象的普遍规律第四章电磁场的的传播动第五章电磁场的发射第六章相对论第一章 电磁现象的普遍规律Universal Law of Electromagnetic Phenomenon本章将从基本的电磁实验定律出发建立真空中的Maxwell’s equations 。
并从微观角度论证了存在介质时的Maxwell’s equations 的形式及其电磁性质的本构关系。
继而给出Maxwell’s equat ions 在边界上的形式,及其电磁场的能量和能流,最后讨论Maxwell’s equations 的自洽性和完备性。
电磁学和电动力学

电磁学和电动力学引言电磁学和电动力学是物理学中重要的分支,研究电荷和电流之间相互作用的规律。
本文将全面、详细、完整地探讨电磁学和电动力学的基本概念、主要定律以及其在日常生活和工业应用中的重要性。
电磁学基础电荷与电场1. 电荷电荷是物质所具有的一种基本性质,分为正电荷和负电荷。
相同电荷之间相互排斥,不同电荷之间相互吸引。
2. 电场电场是电荷周围所产生的力场。
一个电荷会在其周围产生电场,其他电荷会受到电场力的作用而发生运动或变形。
电动力学定律1. 库仑定律库仑定律描述了两个电荷之间的电场力的作用关系。
两个电荷之间的作用力与它们的电荷量成正比,与它们之间的距离的平方成反比。
2. 高斯定律高斯定律描述了电场的产生和分布与电荷的分布之间的关系。
电场线从正电荷发出,趋向于负电荷。
3. 法拉第电磁感应定律法拉第电磁感应定律描述了磁场变化时电场的产生。
当磁场穿过一个闭合线圈时,会在线圈中产生感应电动势,并引起电流流动。
4. 电动势和电流电动势是指电源提供给一个电荷单位所做的功。
电流是电荷的流动,单位时间内通过某一截面的电荷量。
5. 安培环路定理安培环路定理描述了磁场和电流之间的关系。
沿着一条闭合回路的磁场强度的总量等于通过该回路的电流的总和乘以真空中的磁导率。
电磁学与现实生活电磁学和电动力学对我们的日常生活产生了极大的影响,并应用于许多领域。
家用电器我们日常使用的家用电器,如电视、冰箱、洗衣机等,都离不开电磁学和电动力学。
电动机的原理使得这些电器可以正常运行,电磁感应定律也是指导电磁炉、电磁炉等发明的基础。
通信技术现代通信技术中的无线电、微波、红外线等也是电磁学和电动力学的应用。
电磁波的传播使得我们可以进行远距离的通信,并广泛应用于手机、电视、无线网络等设备中。
医学影像医学影像技术如X光、CT扫描、MRI等的原理都基于电磁学和电动力学。
将电磁波用于人体成像,可以帮助医生诊断和治疗许多疾病。
可再生能源电磁学和电动力学的研究也对可再生能源的开发和利用具有重要意义。
《论动体的电动力学》

《论动体的电动力学》引言:电动力学是物理学的重要分支之一,研究电荷在电场和磁场中的行为规律。
而动体则指的是具有运动状态的物体。
本文将探讨动体在电动力学中的行为和特性,旨在深入理解动体在电场和磁场中的相互作用。
一、动体在电场中的行为1. 电场的概念电场是由电荷引起的一种物理场,具有方向和大小。
在电场中,电荷会受到电场力的作用,产生运动或受力。
2. 动体的电荷性质动体可以带有正电荷、负电荷或无电荷。
带电的动体在电场中会受到电场力的作用,根据电场力的方向和大小,动体会产生不同的运动状态。
3. 动体的电场力动体在电场中受到的电场力与电荷的大小和电场的强度有关。
当电荷和电场同向时,动体受到电场力的作用会加速;当电荷和电场反向时,动体受到电场力的作用会减速或反向运动。
4. 动体在电场中的运动根据动体的电荷性质和电场力的方向,动体在电场中的运动形式有所不同。
带正电荷的动体会朝着电场力的方向加速运动或保持匀速直线运动;带负电荷的动体会朝着电场力的方向减速或反向运动;无电荷的动体不受电场力的作用,保持匀速直线运动。
二、动体在磁场中的行为1. 磁场的概念磁场是由电流或磁体产生的一种物理场,具有方向和大小。
在磁场中,动体会受到磁场力的作用,产生运动或受力。
2. 动体的磁性质动体可以是磁性物质或非磁性物质。
磁性物质在磁场中会受到磁场力的作用;非磁性物质不会受到磁场力的作用。
3. 动体的磁场力动体在磁场中受到的磁场力与电流的方向和大小有关。
当电流和磁场方向垂直时,动体受到的磁场力的大小与电流和磁场的强度成正比;当电流和磁场方向平行时,动体不受磁场力的作用。
4. 动体在磁场中的运动根据动体的磁性质和磁场力的方向,动体在磁场中的运动形式有所不同。
磁性物质在磁场中会受到磁场力的作用,产生磁场力对磁力矩的转动,使动体发生旋转或转动;非磁性物质不受磁场力的作用,保持原有运动状态。
三、动体在电磁场中的行为1. 电磁场的概念电磁场是由电荷和电流共同产生的一种物理场,包括电场和磁场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 电磁现象的普遍规律3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离,r 的方向规定为从源点指向场点。
(1)证明下列结果,并体会对源变量求微商与对场变量求微商的关系:r r r /'r =-∇=∇ ; 3/)/1(')/1(r r r r -=-∇=∇ ; 0)/(3=⨯∇r r ;0)/(')/(33=⋅-∇=⋅∇r r r r , )0(≠r 。
(2)求r ⋅∇ ,r ⨯∇ ,r a )(∇⋅ ,)(r a ⋅∇ ,)]sin([0r k E ⋅⋅∇及)]sin([0r k E ⋅⨯∇ ,其中a 、k 及0E 均为常向量。
(1)证明:222)'()'()'(z z y y x x r -+-+-=○1 r z z y y x'x r r z y x /])'()'()()[/1(r e e e =-+-+-=∇ r z z y y x'x r r z y x /])'()'()()[/1('r e e e -=------=∇可见 r r '-∇=∇○2 3211d d 1r r r r r r r r -=∇-=∇⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛∇ 32'1'1d d 1'r r r r r r r r =∇-=∇⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛∇可见 ()()r r /1'/1-∇=∇○3 r r r r ⨯∇+⨯∇=⨯∇=⨯∇)/1()/1(])/1[()/(3333r r r r 0301d d 43=⨯-=+⨯∇⎪⎭⎫ ⎝⎛=r rr rr r r r ○4 r r r r ⋅∇+⋅∇=⋅∇=⋅∇33331)/1(])/1[()/(r r r r 03334=+⋅-=rr r r r , )0(≠r(2)解:○13])'()'()'[()(=-+-+-⋅∂∂+∂∂+∂∂=⋅∇z y x z y x z z y y x x z y x e e e e e e r ○2 0'''///=---∂∂∂∂∂∂=⨯∇z z y y x x z y x zy x e e e r ○3 ])'()'()')[(()(z y x z y x z z y y x x za y a x a e e e r a -+-+-∂∂+∂∂+∂∂=∇⋅ a e e e =++=z z y y x x a a a○4 r a r a a r a r r a )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇ 因为,a 为常向量,所以,0=⨯∇a , 0)(=∇⋅a r , 又0=⨯∇r ,a r a r a =∇⋅=⋅∇∴)()(○5 )]sin([)sin()()]sin([000r k E r k E r k E ⋅∇⋅+⋅⋅∇=⋅⋅∇ 0E 为常向量,00=⋅∇E ,而k r k r k r k r k )cos()()cos()sin(⋅=⋅∇⋅=⋅∇,所以 )cos()]sin([00r k E k r k E ⋅⋅=⋅⋅∇○6 )]cos()]sin([)]sin([000r k E k E r k r k E ⋅⨯=⨯⋅∇=⋅⨯∇ 7. 有一内外半径分别为1r 和2r 的空心介质球,介质的电容率为ε,使介质球内均匀带静止自由电荷f ρ,求:(1)空间各点的电场;(2)极化体电荷和极化面电荷分布。
解:(1)设场点到球心距离为r 。
以球心为中心,以r 为半径作一球面作为高斯面。
由对称性可知,电场沿径向分布,且相同r 处场强大小相同。
当1r r <时,01=D , 01=E 。
当21r r r <<时, f r r D r ρππ)(34431322-=231323)(r r r D f ρ-=∴ , 231323)(r r r E fερ-= , 向量式为 r E 331323)(r r r fερ-=当2r r >时, f r r D r ρππ)(344313232-=2313233)(r r r D f ρ-=∴ 20313233)(r r r E fερ-= 向量式为 r E 30313233)(rr r fερ-=(2)当21r r r <<时,)()(202202D D E D P εεερ-⋅-∇=-⋅-∇=⋅-∇=p f ρεεεε)1()1(020--=⋅∇--=D 当1r r =时,0)1()()(12020212=--=-⋅-=-⋅-==r r p D D D n P P n εεεεσ当2r r =时,f r r p r r r ρεεεεσ22313202023)1()1(2--=-=⋅==D P n 8. 内外半径分别为1r 和2r 的无穷长中空导体圆柱,沿轴向流有恒定均匀自由电流f J ,导体的磁导率为μ,求磁感应强度和磁化电流。
解:(1)以圆柱轴线上任一点为圆心,在垂直于轴线平面内作一圆形闭合回路,设其半径为r 。
由对称性可知,磁场在垂直于轴线的平面内,且与圆周相切。
当 1r r < 时,由安培环路定理得:0,011==B H当 21r r r << 时,由环路定理得:)(22122r r J rH f -=ππ 所以 rr r J H f 2)(2122-=, f J r r r B 2)(2122-=μ 向量式为 r J e B ⨯-=-=f f rr r J r r r 221221222)(ˆ2)(μμθ 当 2r r > 时,)(221223r r J rH f -=ππ所以 rr r J H f 2)(21223-=, f J r r r B 2)(212203-=μ向量式为 r J e B ⨯-=-=f f r r r J r r r 2212202122032)(ˆ2)(μμθ (2)当 21r r r << 时,磁化强度为r J H M ⨯--=-=f rr r 22120202)()1()1(μμμμ 所以 f M J H H M J )1()1(])1[(02020-=⨯∇-=-⨯∇=⨯∇=μμμμμμ在 1r r = 处,磁化面电流密度为⎰=⋅=0d 211l M r M πα 在 2r r = 处,磁化面电流密度为⎰---=⋅-=f MJ r r r r 222122022)()1(d 210μμπαl M 向量式为 f M r r r J α22212202)()1(---=μμ第二章 静电场2. 在均匀外电场中置入半径为0R 的导体球,试用分离变量法求下列两种情况的电势:(1)导体球上接有电池,使球与地保持电势差0Φ; (2)导体球上带总电荷Q解:(1)该问题具有轴对称性,对称轴为通过球心沿外电场0E 方向的轴线,取该轴线为极轴,球心为原点建立球坐标系。
当0R R >时,电势ϕ满足拉普拉斯方程,通解为∑++=nn n nn n P R b R a )(cos )(1θϕ 因为无穷远处 0E E →,)(coscos 10000θϕθϕϕRP E R E -=-→ 所以 00ϕ=a ,01E a -=,)2(,0≥=n a n当 0R R →时,0Φ→ϕ 所以 0101000)(cos )(cos Φ=+-∑+nnn nP R b P R E θθϕ 即:002010000/,/R E R b R b =Φ=+ϕ所以 )2(,0,),(30010000≥==-Φ=n b R E b R b n ϕ⎩⎨⎧≤Φ>+-Φ+-=)()(/cos /)(cos 000230000000R R R R R R E R R R E θϕθϕϕ(2)设球体待定电势为0Φ,同理可得⎩⎨⎧≤Φ>+-Φ+-=)()(/cos /)(cos 000230000000R R R R R R E R R R E θϕθϕϕ当 0R R →时,由题意,金属球带电量Qφθθθϕθεϕεd d sin )cos 2cos (d 200000000R E R E S nQ R R ⎰⎰+-Φ+=∂∂-== )(40000ϕπε-Φ=R所以 00004/)(R Q πεϕ=-Φ⎩⎨⎧≤+>++-=)(4/)(cos )/(4/cos 00002300000R R RQ R R R R E R Q R E πεϕθπεθϕϕ 9. 接地的空心导体球的内外半径为1R 和2R ,在球内离球心为a 处(a <1R )置一点电荷Q 。
用镜像法求电势。
导体球上的感应电荷有多少?分布在内表面还是外表面? 解:假设可以用球外一个假想电荷'Q 代替球内表面上感应电荷对空间电场的作用,空心导体球接地,球外表面电量为零,由对称性,'Q 应在球心与Q 的连线上。
考虑球内表面上任一点P ,边界条件要求:0'/'/=+R Q R Q (1)式R 为Q 到P 的距离,R’为'Q 到P 的距离,因此,对球面上任一点,应有=-=Q Q R R /'/'常数 (2)只要选择'Q 的位置,使OPQ P OQ ∆∆~',则==a R R R //'1常数 (3)设'Q 距球心为b ,则a R R b //11=,即a R b /21= (4) 由(2)(3)两式得: a Q R Q /'1-=]/cos 2//cos 2[412124121220aR R a R R a Q R Ra a R Q θθπεϕ-+--+=导体内电场为零,由高斯定理可知球面上的感应电荷为Q -,分布于内表面。
由于外表面没有电荷,且电势为零,所以从球表面到无穷远没有电场,0=外ϕ。
11. 在接地的导体平面上有一半径为a 的半球凸部(如图),半球的球心在导体平面上,点电荷Q 位于系统的对称轴上,并与平面相距为b (b >a ),试用电象法求空间电势。
解:如图,根据一点电荷附近置一无限大接地导体平板和一点电荷附近置一接地导体球两个模型,可确定三个镜像电荷的电量和位置。
Q b aQ -=1,z b a e r 21=;Q b a Q =2,z b a e r 22-=;Q Q -=3,z b e r -=3,所以),20(,]cos 2cos 2cos 21cos 21[42242224222220a R R b a b a R b aR b a b a R b aRb b R Rb b R Q ><≤-+++++++--+=πθθθθθπεϕ'Q θQ b a-Q baQ-RPO第三章 静磁场4. 设x<0半空间充满磁导率为μ的均匀介质,x>0空间为真空,今有线电流I 沿z 轴流动,求磁感应强度和磁化电流分布。
