2019年中考数学复习专题分类练习---二次函数压轴题(20200709225644)
2019-2020年中考数学二次函数压轴题汇总训练(50题含答案和解析)

解答题(共50题)1.如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.【分析】(1)根据待定系数法即可求得;(2)根据抛物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC是直角三角形.(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC 的垂直平分线与x轴交于一个点,即可求得点N的坐标;(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=(n+2),然后根据S=S△ABN﹣S△BMN△AMN得出关于n的二次函数,根据函数解析式求得即可.【解答】解:(1)∵二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x 轴交于点B、C,点C坐标为(8,0),∴,解得.∴抛物线表达式:y=﹣x2+x+4;(2)△ABC是直角三角形.令y=0,则﹣x2+x+4=0,解得x1=8,x2=﹣2,∴点B的坐标为(﹣2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形.(3)∵A(0,4),C(8,0),∴AC==4,①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).(4)如图,AB==2,BC=8﹣(﹣2)=10,AC==4,∴AB2+AC2=BC2,∴∠BAC=90°.∴AC⊥AB.∵AC∥MN,∴MN⊥AB.设点N的坐标为(n,0),则BN=n+2,∵MN∥AC,△BMN∽△BAC∴=,∴=,BM==,MN==,AM=AB﹣BM=2﹣==AM•MN∵S△AMN=××=﹣(n﹣3)2+5,当n=3时,△AMN面积最大是5,∴N点坐标为(3,0).∴当△AMN面积最大时,N点坐标为(3,0).【点评】本题是二次函数的综合题,解(1)的关键是待定系数法求解析式,解(2)的关键是勾股定理和逆定理,解(3)的关键是等腰三角形的性质,解(4)的关键是三角形相似的判定和性质以及函数的最值等.2.对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2).(1)求d(点O,△ABC);(2)记函数y=kx(﹣1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t的取值范围.【分析】(1)根据点A、B、C三点的坐标作出△ABC,利用“闭距离”的定义即可得;(2)由题意知y=kx在﹣1≤x≤1范围内函数图象为过原点的线段,再分别求得经过(1,﹣1)和(﹣1,﹣1)时k的值即可得;(3)分⊙T在△ABC的左侧、内部和右侧三种情况,利用“闭距离”的定义逐一判断即可得.【解答】解:(1)如图所示,点O到△ABC的距离的最小值为2,∴d(点O,△ABC)=2;(2)y=kx(k≠0)经过原点,在﹣1≤x≤1范围内,函数图象为线段,当y=kx(﹣1≤x≤1,k≠0)经过(1,﹣1)时,k=﹣1,此时d(G,△ABC)=1;当y=kx(﹣1≤x≤1,k≠0)经过(﹣1,﹣1)时,k=1,此时d(G,△ABC)=1;∴﹣1≤k≤1,∵k≠0,∴﹣1≤k≤1且k≠0;(3)⊙T与△ABC的位置关系分三种情况:①当⊙T在△ABC的左侧时,由d(⊙T,△ABC)=1知此时t=﹣4;②当⊙T在△ABC内部时,当点T与原点重合时,d(⊙T,△ABC)=1,知此时t=0;当点T位于T3位置时,由d(⊙T,△ABC)=1知T3M=2,∵AB=BC=8、∠ABC=90°,∴∠C=∠T3DM=45°,则T3D===2,∴t=4﹣2,故此时0≤t≤4﹣2;③当⊙T在△ABC右边时,由d(⊙T,△ABC)=1知T4N=2,∵∠T4DC=∠C=45°,∴T4D===2,∴t=4+2;综上,t=﹣4或0≤t≤4﹣2或t=4+2.【点评】本题主要考查圆的综合问题,解题的关键是理解并掌握“闭距离”的定义与直线与圆的位置关系和分类讨论思想的运用.3.如图,在平面直角坐标系中,点A在抛物线y=﹣x2+4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB的长;(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当△PBE的面积最大时,求PH+HF+FO的最小值;(3)在(2)中,PH+HF+FO取得最小值时,将△CFH绕点C顺时针旋转60°后得到△CF′H′,过点F'作CF′的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.【分析】(1)求出A、B两点坐标,即可解决问题;(2)如图1中,设P(m,﹣m2+4m),作PN∥y轴交BE于N.构建二次函数利用二次函数的性质求出满足条件的点P坐标,作直线OG交AB于G,使得∠COG=30°,作HK⊥OG于K交OC于F,因为FK=OF,推出PH+HF+FO=PH+FH+Fk=PH+HK,此时PH+HF+OF的值最小,解直角三角形即可解决问题;(3)分两种情形分别求解即可;【解答】解:(1)由题意A(1,3),B(3,3),∴AB=2.(2)如图1中,设P(m,﹣m2+4m),作PN∥y轴J交BE于N.∵直线BE的解析式为y=x,∴N(m,m),=×2×(﹣m2+3m)=﹣m2+3m,∴S△PEB∴当m=时,△PEB的面积最大,此时P(,),H(,3),∴PH=﹣3=,作直线OG交AB于G,使得∠COG=30°,作HK⊥OG于K交OC于F,∵FK=OF,∴PH+HF+FO=PH+FH+FK=PH+HK,此时PH+HF+OF的值最小,。
2019中考二次函数压轴题专题分类训练(word文档良心出品)

中考二次函数压轴题专题分类训练题型一:面积问题【例1】(2009湖南益阳)如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式; (2)求△CAB 的铅垂高CD 及S △CAB ;(3)设点P 是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.【变式练习】1.(2009广东省深圳市)如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB . (1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由. (4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.图22.(2010绵阳)如图,抛物线y = ax 2+ bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G .(1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)在直线EF 上求一点H ,使△CDH 的周长最小,并求出最小周长; (3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时, △EFK 的面积最大?并求出最大面积.3.(2012铜仁)如图,已知:直线3+-=x y 交x 轴于点A ,交y 轴于点B ,抛物线y=ax 2+bx+c 经过A 、B 、C (1,0)三点.(1)求抛物线的解析式;(2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P,使ΔABO 与ΔADP 相似,求出点P 的坐标;(3)在(2)的条件下,在x 轴下方的抛物线上,是否存在点E ,使ΔADE 的面积等于四边形APCE 的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.C ED GAxy OB F题型二:构造直角三角形【例2】(2010山东聊城)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;(3)设点P 为抛物线的对称轴x=1上的一动点,求使∠PCB=90º的点P的坐标.E【变式练习】1.(2012广州)如图,抛物线y=与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.2.(2009成都)在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且COS∠BCO=10。
2019年中考专题:二次函数压轴题(精编含解析)

1.在平面直角坐标系中,已知抛物线 y=ax2+bx+c(a≠0)经过点 A(1,0)、B(4,0),C(0,2)三 点,直线 y=kx+t 经过 B、C 两点,点 D 是抛物线上一个动点,过点 D 作 y 轴的平行线,与直线 BC 相 交于点 E. (1)求直线和抛物线的解析式; (2)当点 D 在直线 BC 下方的抛物线上运动,使线段 DE 的长度最大时,求点 D 的坐标; (3)点 D 在运动过程中,若使 O、C、D、E 为顶点的四边形为平行四边形时,请直接写出满足条件的 所有点 D 的坐标.
令 m2﹣2m=2,
解得 m=2
,
∴此时 D(2+2 ,3﹣ )或(2﹣2 ,3+ ),
综上所述,点 D 的坐标是(2,﹣1)或(2+2 ,3﹣ )或(2﹣2 ,3+ )时,都可以使 O、C、D、E 为顶点的四边形为平行四边形.
【点评】本题是二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式,二次函数的性质及 平行四边形的判定与性质等知识点.
,利用二次函数的性质,即可求得当△
(3)直角三角形斜边上的中线等于斜边的一半列出关系式 m=(n﹣ )2﹣ ,然后根据 n 的取值得 到最小值.
【解答】解:(1)由题意得:
,
解得: , ∴抛物线解析式为 y=﹣x2+2x+3;
(2)令﹣x2+2x+3=0, ∴x1=﹣1,x2=3, 即 B(3,0), 设直线 BC 的解析式为 y=kx+b′,
∴
,
解得:
,
∴直线 BC 的解析式为 y=﹣x+3,
设 P(a,3﹣a),则 D(a,﹣a2+2a+3),
2019年中考二次函数压轴题整理

2019年中考二次函数压轴题整理1.给定三个点A(-1.a)。
B(3.b)。
C(c。
3),求经过这三个点的抛物线的解析式,以及线段BC上一点M关于抛物线的对称点N到y轴的距离MN的表达式。
进一步地,连接NB、NC,判断是否存在一个点M,使得△BNC的面积最大。
若存在,求出该点的横坐标m,否则说明理由。
2.给定点A、B、C,其中B(4.b)在抛物线y=ax^2+bx+c上,求该抛物线的解析式。
进一步地,探究△ABC的外接圆的圆心位置,求出圆心的坐标。
若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标。
3.给定抛物线y=x+mx+n和点A(3.a)、B(b。
-3),点P是线段AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t。
求出直线AB和抛物线的解析式。
进一步地,当点P在第四象限时,连接AM、BM,求出线段PM最长时△ABM的面积。
然后判断是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形。
若存在,直接给出点P的横坐标;否则说明理由。
4.在平面直角坐标系中放置一直角三角板,其顶点为A(a。
1),B(2.b),O(0.0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O。
给定抛物线经过点A′、B′、B,求该抛物线的解析式。
进一步地,设点P是在第一象限内抛物线上的一动点,判断是否存在点P,使得四边形PB′A′B的面积是△A′B′O面积的4倍。
若存在,求出点P的坐标;否则说明理由。
最后,确定四边形PB′A′B的形状,并给出两条性质。
5.给定抛物线y=x-2x+c的顶点A在直线l:y=x-5上。
求出抛物线顶点A的坐标。
进一步地,设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),判断△ABD的形状。
然后在直线l上判断是否存在一点P,使得以点P、A、B、D为顶点的四边形是平行四边形。
若存在,求出点P的坐标;否则说明理由。
2019年数学中考总复习:压轴题专项训练(二次函数)(含解析答案)

2019年数学中考总复习:压轴题专项训练(二次函数)1.如图,直线AB与x轴,y轴分别交于点A(2,0),点B(0,2),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F(1)求∠OAB度数;(2)当t为何值时,四边形ADEF为菱形,请求出此时二次函数解析式;(3)是否存在实数t,使△AGF为直角三角形?若存在,求t的值;若不存在,请说明理由.2.如图,已知抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,点D是第四象限内该抛物线上一动点,连AC、AD与抛物线对称轴分别交于点M、N,延长DC交抛物线对称轴于点E.(1)直接写出线段AB的长;(2)若∠CAB=∠DAB,求的值;(3)若在第三象限内该抛物线上有一点P,使得以A、B、P为项点的三角形与△ABC相似,求点P的坐标.3.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4ax﹣交x轴正半轴于点A (5,0),交y轴于点B.(1)求抛物线的解析式;(2)如图1,点P为第一象限内抛物线上一点,连接AP,将射线AP绕点A逆时针旋转60°,与过点P且垂直于AP的直线交于点C,设点P横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出t的取值范围);(3)如图2,在(2)的条件下,过点C作直线交x轴于点D,在x轴上取点F,连接FP,点E为AC的中点,连接ED,若F的横坐标为,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.4.如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC 于点D.(1)求抛物线的函数表达式;(2)当AD=2PD时,求点P的坐标;(3)求线段PE的最大值;(4)当线段PE最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.5.如图,在平面直角坐标系中,点A(0,1),点B(﹣9,10),抛物线y=2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)过点A作x轴的平行线,与抛物线交于点C,点P是直线AC下方抛物线上一点,过点P且与y轴平行的直线与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)当点P运动到抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.6.二次函数y=ax2+x+3的图象与x轴分别相交于A、B两点,且A(﹣1,0),与y轴交于点C.(1)如图1,求抛物线解析式(2)如图2,点P是第一象限抛物线上一点,设点P的横坐标为t(t>1),连接PC、PB、BC.设△PBC的面积为s,求s与t的函数关系式.(3)如图3,在(2)的条件下当s=时,点Q为第二象限抛物线上一点,连接PQ交y 轴于点E,延长PQ交x轴于点M,点N在点C上方的y轴上,连接MN,若MP平分∠NMB,MN=5CN,且OM<ON.将线段PQ绕点P逆时针旋转45°得到线段PR,求点R的坐标.7.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(﹣3,4)、B(﹣3,0)、C(﹣1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.(1)求抛物线的解析式;(2)当t为何值时,四边形BDGQ的面积最大?最大值为多少?(3)动点P、Q运动过程中,是否存在某一时刻,使△PQF是等腰三角形?若存在,请求出此时t的值;若不存在,请说明理由.8.已知抛物线经过y=ax2+bx+c点A(﹣4,0)、B(1,0)、C(0,3).(1)求抛物线解析式和直线AC的解析式;(2)若点P是第四象限抛物线上的一点,若S△PAC=10,求点P的坐标;(3)如图2,点M是线段AC上的一个动点(不与A、C重合),经过A、M、O三点的圆与过A且垂直于AC的直线交于点N,求当S△OMN 最小时点M的坐标及S△OMN最小值.9.在平面直角坐标系中,点0为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于点B,C,与y轴交于点A,点A的坐标为(0,),点D为抛物线的顶点.(1)如图1,求拋物线的顶点D的坐标;(2)如图2,点P是第一象限内对称轴右侧拋物线上一点,连接PB,过点D作DQ⊥BP 于点H,交x轴于点Q,设点P的横坐标为m,点Q的横坐标为n,求n与m的函数关系式;(3)如图3,在(2)的条件下,过点C作CE∥y轴交BP的延长线于点E,点F为CE的中点,连接FQ,若∠DQC+∠CQF=135°,求点P的坐标.10.如图,抛物线y =ax 2+bx 的对称轴为y 轴,且经过点(,),P 为抛物线上一点,A(0,).(1)求抛物线解析式;(2)Q 为直线AP 上一点,且满足AQ =2AP .当P 运动时,Q 在某个函数图象上运动,试写出Q 点所在函数的解析式;(3)如图2,以PA 为半径作⊙P 与x 轴分别交于M (x 1,0),N (x 2,0)(x 1<x 2)两点,当△AMN 为等腰三角形时,求点P 的横坐标.11.如图,抛物线y=+bx+c经过△ABC的三个顶点,其中点A(0,﹣1),点B(9,﹣10),AC∥x轴,点P是直线AC上方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.12.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+8与x轴相交于点A(﹣2,0)和点B(4,0),与y轴相交于点C,顶点为点P.点D(0,4)在OC上,联结BC、BD.(1)求抛物线的表达式并直接写出点P的坐标;(2)点E为第一象限内抛物线上一点,如果△COE与△BCD的面积相等,求点E的坐标;(3)点Q在抛物线对称轴上,如果△BCD∽△CPQ,求点Q的坐标.13.如图,抛物线y=ax2+bx+2与直线y=﹣x交第二象限于点E,与x轴交于A(﹣3,0),B两点,与y轴交于点C,EC∥x轴.(1)求抛物线的解析式;(2)点P是直线y=﹣x上方抛物线上的一个动点,过点P作x轴的垂线交直线于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;(3)如果点N是抛物线对称轴上的一个动点,抛物线上存在一动点M,若以M,A,C,N 为顶点的四边形是平行四边形,请直接写出所有满足条件的点M的坐标.14.如图,在平面直角坐标系中,以直线x=1为对称轴的抛物线恰好经过A(0,4),B(4,0)两点,连结AB.(1)求该抛物线的函数解析式.(2)点C为线段AB上一动点,延长OC交抛物线于点D,连结BD.若△AOC与△BCD的面积相等,求点C的坐标.(3)设k=,求k的最大值.15.如图,直线y=﹣x+4与x轴交于点A,与y轴交于点B.抛物线y=﹣x2+bx+c经过A,B两点,与x轴的另外一个交点为C(1)填空:b=,c=,点C的坐标为.(2)如图1,若点P是第一象限抛物线上的点,连接OP交直线AB于点Q,设点P的横坐标为m.PQ与OQ的比值为y,求y与m的数学关系式,并求出PQ与OQ的比值的最大值.(3)如图2,若点P是第四象限的抛物线上的一点.连接PB与AP,当∠PBA+∠CBO=45°时.求△PBA的面积.参考答案1.解:(1)∵直线AB与x轴,y轴分别交于点A(2,0),点B(0,2),∠BOA=90°,∴OA=2,OB=2,∴tan∠OAB=,∴∠OAB=60°;(2)∵AD=t,BE=tm∴,∴DE∥AB,∴∠EDO=∠BAO=60°,∵过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F,∴四边形ADEF为平行四边形,当AD=DE时,四边形ADEF为菱形,∵OD=2﹣t或OD=t﹣2,DE=2OD,∴DE=4﹣2t或DE=2t﹣4,∴t=4﹣2t或t=2t﹣4,解得:t=或t=4,当t=时,点E坐标为(0,),设二次函数解析式为y=a(x﹣2)2,将点E坐标代入,可得a=,∴二次函数解析式为y=(x﹣2)2;当t=4时,点E坐标为(0,),设二次函数解析式为y=a(x﹣2)2,将点E坐标代入,可得a=,∴二次函数解析式为y=(x﹣2)2;(3)∵EG∥OA,∴∠GFA=∠BAO=60°,∵G在二次函数图象上,∴∠FGA≠90°,∴使△AGF为直角三角形,只能是∠FAG=90°,由对称性可得,EG=4,∵四边形ADEF为平行四边形,∴EF=AD=t,AF=DE=2(2﹣t),∵FG=2AF,∴4﹣t=4(2﹣t),解得:t=,∴存在实数t=,使△AGF为直角三角形.2.解:(1)当y=0时,ax2+2ax﹣3a=0,解得:x1=﹣3,x2=1,∴点A的坐标为(﹣3,0),点B的坐标为(1,0),∴AB=1﹣(﹣3)=4.(2)当x=0时,y=ax2+2ax﹣3a=﹣3a,∴点C的坐标为(0,﹣3a).设直线AC的解析式为y=kx+b(k≠0),将A(﹣3,0),C(0,﹣3a)代入y=kx+b,得:,解得:,∴直线AC的解析式为y=﹣ax﹣3a.∵∠CAB=∠DAB,∴直线AD过点(0,3a),同理,可求出直线AD的解析式为y=ax+3a.联立直线AD和抛物线解析式成方程组,得:,解得:,,∴点D的坐标为(2,5a).利用待定系数法,可求出:直线CD 的解析式为y =4ax ﹣3a .∵y =ax 2+2ax ﹣3a =a (x +1)2﹣4a ,∴抛物线的对称轴为直线x =﹣1.当x =﹣1时,y =4ax ﹣3a =﹣7a ,y =﹣ax ﹣3a =﹣2a ,y =ax +3a =2a ,∴点E 的坐标为(﹣1,﹣7a ),点M 的坐标为(﹣1,﹣2a ),点N 的坐标为(﹣1,2a ), ∴EM =﹣5a ,MN =﹣4a ,∴=.(3)∵点P 在第三象限,∴∠BAP >90°,∴只能∠BAP =∠ACB .分两种情况考虑:①当△BAP ∽△ACB 时,∠BAC =∠PBA ,∴BP ∥AC .∵直线AC 的解析式为y =﹣ax ﹣3a ,点B 的坐标为(1,0),∴直线BP 的解析式为y =﹣ax +a .联立直线BP 和抛物线解析式成方程组,得:,解得:,,∴点P 的坐标为(﹣4,5a ).∵点A (﹣3,0),点C (0,﹣3a ),点B (1,0),∴AC =3,BP =5,BC =,∴=,=,∴=,解得:a 1=﹣,a 2=(舍去),∴点P 的坐标为(﹣4,﹣);②当△PAB ∽△ACB 时,∠ABP =∠CBA ,∴直线BP 过点(0,3a ).利用待定系数法,可求出直线BP 的解析式为y =﹣3ax +3a ,联立直线BP 和抛物线解析式成方程组,得:,解得:,,∴点P 的坐标为(﹣6,21a ),∴BP =7,∴===,解得:a 1=﹣,a 2=(舍去),∴点P 的坐标为(﹣6,﹣3).综上所述:点P 的坐标为(﹣4,﹣)或(﹣6,﹣3).3.解:(1)∵抛物线y =ax 2﹣4ax ﹣过点A (5,0),∴25a ﹣20a ﹣=0解得:a =∴抛物线的解析式为y =x 2﹣x ﹣(2)过点P作MN⊥x轴于点N,过点C作CM⊥MN于点M∴∠M=∠ANP=90°∴∠MCP+∠CPM=90°∵CP⊥AP∴∠APC=90°∴∠CPM+∠APN=90°∴∠MCP=∠APN∴△MCP∽△NPA∴∵∠APC=90°,∠PAC=60°∴∠ACP=30°,tan∠PAC=∴,即MC=NP∵x P=t,x C=m∴MC=t﹣m,PN=y P=t2﹣t﹣∴t﹣m=(t2﹣t﹣)整理得:m=t2+t+3(3)过点C作CH⊥x轴于点H,在x轴上取点Q,连接PQ且使PQ=AQ,∴∠CHD=90°,∠PAN=∠PQN∵∠ACP=30°,∠APC=90°,点E是AC中点∴AP=AC=CE=AE∴CE=PQ∵∠FAP+∠ACD=180°,∠FAP+∠PAN=180°∴∠ACD=∠PAN∴∠ACD=∠PQN在△CDE与△QFP中∴△CDE≌△QFP(AAS)∴CD=QF由(1)得,AN=t﹣5,PM=AN=(t﹣5),PN=t2﹣t﹣∴CH=MN=PM+PN=(t﹣5)+t2﹣t﹣=t2+t﹣6∵∠CDH=360°﹣∠CDP﹣∠APC﹣∠FAP=360°﹣(∠ACD+∠FAP)﹣∠ACP﹣∠APC=360°﹣180°﹣30°﹣90°=60°∴sin∠CDH=∴CD=CH=(t2+t﹣6)=t2+t﹣12∵F(﹣,0)∴QF=AF+AQ=AF+2AN=5﹣(﹣)+2(t﹣5)=2t﹣∴t2+t﹣12=2t﹣解得:t1=﹣3,t2=7∵点P在第一象限,t>5∴t=7∴m=t2+t+3=×72+×7+3=4.解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3)(a≠0),则3=a×1×(﹣3),∴a=﹣1,∴抛物线的解析式为:y=﹣(x+1)(x﹣3),即y=﹣x2+2x+3;(2)过A作EF⊥x轴,与BC相交于点F,如图1,设P(t,﹣t2+2t+3),则AF∥PE,设BC的解析式为y=kx+b(k≠0),则,解得,,∴直线BC的解析式为:y=﹣x+3,∴E(t,﹣t+3),F(﹣1,4),∴AF=4,PE=﹣t2+3t,∵AF∥PE,∴△AFD∽△PED,∴,∵AD=2PD,∴,解得,t=1或2,∴P(1,4)或P(2,3);(3)∵PE的解析式为:PE=﹣t2+3t=﹣(t﹣)2+(0<t<3),∴当t=时,PE的值最大为;(4)①当F点在PE的左边时,过点P作PM⊥BC于点M,过E作EN⊥x轴于点N,过点F作FQ⊥x轴于点Q,过点O作OG⊥AC于点G,取AC的中点H,连接OH,由(3)知,当PE取最大值时,P(,),PE=,E(,),∵OB=OC=3,∴∠OBC=∠OCB=45°,∴BE=EM=,∠PEM=45°,∴PM=EM=,∵AC=,∴OH=CH=,OG=,∴HG=,∠OHG=2∠ACO,∵∠EFP=2∠ACO,∴∠EFP=∠OHG,∵∠OGH=∠PMF,∴△OGH∽△PMF,∴,即,∴MF=,∴BF=BE+EM+MF=,∴FQ=BQ=BF=,∴OQ=,∴F(﹣,),②当F点在PE的右边时,此时的F点恰好与(﹣,)关于PM对称,易求此时F(,).故F的坐标为(﹣,)或(,).5.解:(1)将A(0,1),B(﹣9,10)代入y=2+bx+c,得:,解得:,∴抛物线的解析式为y=x2+2x+1.(2)当y=1时, x2+2x+1=1,解得:x1=﹣6,x2=0,∴点C的坐标为(﹣6,1).设直线AB的解析式为y=kx+a(k≠0),将A (0,1),B (﹣9,10)代入y =kx +a ,得:,解得:,∴直线AB 的解析式为y =﹣x +1.设点P 的坐标为(m , m 2+2m +1)(﹣6<m <0),则点E 的坐标为(m ,﹣m +1),点F 的坐标为(m ,1), ∴S 四边形AECP =S △AEC +S △ACP ,=AC •EF +AC •PF ,=×6×(﹣m +1﹣1)+×6×[1﹣(m 2+2m +1)], =﹣m 2﹣9m .∵S 四边形AECP =﹣m 2﹣9m =﹣(m +)2+,﹣1<0,∴当m =﹣时,S 四边形AECP 取得最大值,此时点P 的坐标为(﹣,﹣).(3)∵y =x 2+2x +1=(x +3)2﹣2, ∴点P 的坐标为(﹣3,﹣2).∵A (0,1),B (﹣9,10),C (﹣6,1),P (﹣3,﹣2),∴AB =9,AC =6,CP =3.设直线CP 的解析式为y =nx +d (n ≠0),将C (﹣6,1),P (﹣3,﹣2)代入y =nx +d ,得:,解得:,∴直线CP 的解析式为y =﹣x ﹣5, ∴CP ∥AB , ∴∠PCQ =∠BAC .∵以C 、P 、Q 为顶点的三角形与△ABC 相似,∴=或=,即=或=,∴CQ =9或CQ =2,∴存在,点Q 的坐标为(3,1)或(﹣4,1).6.(1)把(﹣1,0)代入得解得∴(2)令y =0,得解得x 1=﹣1,x 2=4∴B (4,0),A (﹣1,0),C (0,3) 设BC 的解析式为y =kx +b则有解得k=所以BC的解析式为作PG⊥x轴,交BC于点G则G(t,),P(t,﹣\frac{3}{4}{t}^{2}+\frac{9}{4}t+3$)∴$PG=﹣\frac{3}{4}{t}^{2}+3t∴$S=\frac{1}{2}BO•PG=\frac{1}{2}×4×(﹣\frac{3}{4}{t}^{2}+3t)$=$﹣\frac{3}{2}{t}^{2}+6t(3)由$﹣\frac{3}{2}{t}^{2}+6t=\frac{9}{2}$得t=3.所以P(3,3),∴PC∥x轴延长PC交MN于点H∵∠NMP=∠PMB,∠HPM=∠PMB∴∠HMP=∠HPM∴MH=PH设HC=d,CN=m,则MH=HP=d+3,MN=5m∵$\frac{NH}{MH}=\frac{NC}{CO}\frac{5m﹣(d+3)}{d+3}=\frac{m}{3}$ 得d=$\frac{12m﹣9}{m+3}$①又∵HN2=HC2+NC2∴[5m﹣(d+3)]2=d2+m2②将①代入②,得8m3﹣26m2+27m﹣9=0解得${m}_{1}=1,{m}_{2}=\frac{3}{4}(舍去),{m}_{3}=\frac{3}{2}(舍去)$ ∴M(﹣3,0)∴$PM的解析式为y=\frac{1}{2}x+\frac{3}{2}$令$﹣\frac{3}{4}{x}^{2}+\frac{9}{4}x+3=\frac{1}{2}x+\frac{3}{2}$解得${x}_{1}=3,{x}_{2}=﹣\frac{2}{3}$∴Q($﹣\frac{2}{3}\frac{7}{6}$)分别过R,Q作x轴的垂线,交过P于x轴平行的直线于T,K易证△QTP≌△PKR∴PK=QT=3﹣$\frac{7}{6}\frac{11}{6}$∴R的横坐标为$3+\frac{11}{6}=\frac{29}{6}$RK=PT=3﹣$(﹣\frac{2}{3})\frac{11}{3}$∴R的纵坐标为3﹣$\frac{11}{3}﹣\frac{2}{3}$∴R($\frac{29}{6},﹣\frac{2}{3}$)7.解:(1)∵A(﹣3,4)、B(﹣3,0)、C(﹣1,0),∴D(﹣1,4),∴设抛物线的解析式为y=a(x+1)2+4,代入点B,0=a(﹣3+1)2+4,解得a=﹣1,∴抛物线的解析式为y=﹣x2﹣2x+3.(2)由题意可知,DP=BQ=t,∵tan∠BDC=,∴EP=t,∴G的横坐标为﹣1﹣t,∴G(﹣1﹣t,4﹣),∴EG=t﹣,S=(t﹣)••=﹣,△DGESQBEG=(t﹣+t)•(2﹣)•=2t﹣﹣+,∴S=2t﹣=﹣(t﹣2)2+2,∵﹣<0,∴当t=2时,S有最大值为2.(3)∵P(﹣1,4﹣t),Q(﹣3,t),F(﹣1﹣,4),∴PQ=,PF=,QF=,①PQ=PF,=,解得t1=4(舍),t2=;②PQ=QF,=,解得t1=0(舍),t2=;③PF=QF,=,解得t=2.综上所述:t=或或2.8.解:(1)∵抛物线与x轴交于点A(﹣4,0)、B(1,0)∴y=a(x+4)(x﹣1)把点C(0,3)代入得:﹣4a=3∴a=∴抛物线解析式为:y=(x+4)(x﹣1)=设直线AC的解析式为:y=kx+3∴﹣4k+3=0 解得:k=∴直线AC 的解析式为:y =x +3(2)过点P 作PH ⊥x 轴于点H ,设点P (t ,﹣t 2﹣t +3)(t >1)∴PH =|﹣t 2﹣t +3|=t 2+t ﹣3 ∵AB =1﹣(﹣4)=5,OC =3∴S △PAC =S △ABC +S △ABP =AB •OC +AB •PH =AB (OC +PH )=∵S △PAC =10∴=10,即解得:t 1=(舍去),t 2=∴y P =﹣PH =﹣(4﹣3)﹣1∴点P 坐标为(,﹣1)(3)连接MN 、OM 、ON ,取MN 中点Q ,过点M 作ME ⊥y 轴于点E ,过点N 作NF ⊥y 轴于点F∴∠MEO =∠OFN =90° ∴∠MOE +∠OME =90°设M (m ,)(﹣4<m <0),N 的横坐标为n ,∴ME =﹣m ,OE =,NF =﹣n∵AN⊥AM∴∠MAN=90°∴MN为过A、M、O三点的圆的直径∴Q为圆心,∠MON=90°∴∠MOE+∠NOF=90°∴∠OME=∠NOF∴△OME∽△NOF∴=∵圆心Q在AO的⊥平分线上∴x Q=∵Q为MN中点∴m+n=2x Q=﹣4∴﹣n=m+4∴∴ON=OM=OM•ON=OM•OM=OM2===∴S△OMN=∴当m=时,最小值S△OMN∴=∴点M坐标为()时,S最小值为△OMN9.解:(1)将点A (0,)代入抛物线中,﹣3a =,解得a =﹣,∴抛物线的解析式为y =﹣x 2+x +,∵﹣=1,解得y =2,∴D (1,2).(2)如图1所示,过点D 作DH 垂直于x 轴于点H ,过点P 作PN 垂直于x 轴于点N ,∴DH =2,QH =n ﹣1,PN =﹣m 2+m +,BN =m +1,∵△BPN ∽△DHQ ,∴,即,解得n =4﹣m .(3)如图2所示,∵D(1,2),Q(4﹣m,0),C(3,0)B(﹣1,0),∴BN=2,DN=2,NQ=3﹣m,∵∠BNG=∠DNQ,∠NDQ=∠GBN,∴△BGN≌△DNQ(ASA),∴GN=NQ=3﹣m,连接GQ,∴∠GQN=45°,∵∠DQC+∠FQC=135°,∴∠GQD=∠FQC,∵DG=m﹣1,过点P作y轴的平行线PM,过点D作x轴的平行线交MP于点M,连接MG,∴MD=m﹣1,∴MD=DG,∴∠DGM=45°,∵∠NGQ=45°,∴∠MGQ=90°,∴∠MGP=∠GQD=∠FQC,连接GF,GF∥BC,∴∠GFQ=∠FQC=∠MGP,∠FGQ=∠GMP=45°,∴△GMP∽△GQF,∴,∵MP=2﹣(﹣m2+m+)=m2﹣m+,MG=(m﹣1),FG=2,GQ=(3﹣m),解得m 1=1(舍),m 2=,∴m =,∴P (,).10.解:(1)抛物线y =ax 2+bx 的对称轴为y 轴,则b =0,将点(,),代入y =ax 2并解得:a =,故抛物线的表达式为:y =x 2;(2)设点Q 的坐标为(x ,y ),点P (m , m 2),①当点Q 在点P 下方时(点Q 位置),∵AQ =2AP ,∴P 为AP 的中点,由中点公式得:m =x , m 2=,整理得:y =x 2﹣;②当点Q 在点P 上方时(点Q ′位置),同理可得:y =﹣x 2+;Q 点所在函数的解析式为:y =x 2﹣或y =﹣x 2+;(3)过点P 作PH ⊥x 轴于点H ,设点P (m , m 2),则PM =PN =PA ==,MH =NH ===,则MN =3,设点M (m ﹣,0),则N (m +,0),AM 2=(m ﹣)2+,AN 2=(m +)2+,MN 2=9,①当AM =AN 时,AM 2=(m ﹣)2+=(m +)2+,解得:m =0;②当AM =MN 时,同理可得:m =(负值已舍去); ③当AN =MN 时,同理可得:m =(负值已舍去);故点P 的横坐标为:0或或. 11.解:(1)将A (0,﹣1),B (9,﹣10)代入函数解析式,得, 解得,抛物线的解析式y =﹣x 2+2x ﹣1;(2)∵AC ∥x 轴,A (0,﹣1),∴﹣x 2+2x ﹣1=﹣1.解得x 1=6,x 2=0.∴点C 的坐标为(6,﹣1).∵点A (0,﹣1),B (9,﹣10),∴直线AB 的解析式为y =﹣x ﹣1.设点P (m ,﹣m 2+2m ﹣1),∴E (m ,﹣m ﹣1).∴PE =(﹣m 2+2m ﹣1)﹣(﹣m ﹣1)=﹣m 2+3m .∵AC ⊥EP ,AC =6,∴S 四边形AECP =S △AEC +S △APC=AC •PF +AC •FE=AC •(PF +FE )=AC •PE=×6×(﹣m 2+3m )=﹣m 2+9m=﹣(m ﹣)2+.∵0<m <6,∴当m =时,四边形AECP 的面积的最大值是.此时点P (,).(3)∵y =﹣x 2+2x ﹣1=﹣(x ﹣3)2+2,∴P (3,2).∴PF =2﹣(﹣1)=3,CF =6﹣3=3.∴PF =CF .∴∠PCF =45°.同理可得∠EAF =45°.∴∠PCF =∠EAF .分两种情况:①当=时,△CPQ ∽△ABC .∵AB==9,AC=6,CP=3,∴=.解得CQ=2.∴Q(4,﹣1).②当=时,△CQP∽△ABC.即=.解得CQ=9.∴Q(﹣3,﹣1).综合①②得,存在这样的点Q,其坐标是(4,﹣1)或(﹣3,﹣1).12.解:(1)将点A(﹣2,0),B(4,0)代入y=ax2+bx+8,得:,解得:,∴抛物线的表达式为y=﹣x2+2x+8.∵y=﹣x2+2x+8=﹣(x﹣1)2+9,∴点P的坐标为(1,9).(2)当x=0时,y=﹣x2+2x+8=8,∴点C的坐标为(0,8).设点E的坐标为(x,﹣x2+2x+8)(0<x<4),∵S△COE =S△BCD,∴×8•x=×4×4,解得:x=2,∴点E的坐标为(2,8).(3)过点C作CM∥x轴,交抛物线对称轴于点M,如图所示.∵点B(4,0),点D(0,4),∴OB=OD=4,∴∠ODB=45°,BD=4,∴∠BDC=135°.∵点C(0,8),点P(1,9),∴点M的坐标为(1,8),∴CM=PM=1,∴∠CPM=45°,CP=,∴点Q在抛物线对称轴上且在点P的上方,∴∠CPQ=∠CDB=135°.∵△BCD∽△CPQ,∴=或=.①当=时,,解得:PQ=2,∴点Q的坐标为(1,11);②当=时,,解得:PQ=1,∴点Q的坐标为(1,10).综上所述,点Q的坐标为(1,11)或(1,10).13.解:(1)由题意知A(﹣3,0),C(0,2)且EC∥x轴∴点E的纵坐标为2又∵点E在直线y=﹣x上∴x=﹣y=﹣2,∴点E(﹣2,2)∵点A(﹣3,0)、E(﹣2,2)在抛物线y=ax2+bx+2上∴,解得:∴所求抛物线的解析式为:(2)∵PG⊥x轴,PH⊥EO,点G在y=﹣x上,∴△PHG为等腰直角三角形,且G(m,﹣m),设PH的长为l令∴=∴∴所求l与m的函数关系式为:,l的最大值为:(3)点N是抛物线对称轴x=﹣1上的一个动点,抛物线上存在一动点M,若以M,A,C,N为顶点的四边形是平行四边形,则M点的坐标可能是理由如下:①以AC为平行四边形的一边时,则有MN∥AC且MN=AC,如图,过M作对称轴的垂线,垂足为F,设AC交对称轴于点L则∠ALF=∠ACO=∠FNM∴在△MFN与△AOC中,∠MFN=∠AOC,∠FNM=∠ACO,MN=AC∴△MFN≌△AOC∴MF=AO=3∴点M到对称轴x=﹣1的距离为3,设点M(x,y),则|x+1|=3解得x=2或x=﹣4,∴当x=2时,y=,当x=﹣4时,y=∴②当AC为对角线时,高AC的中点为K,∵A(﹣3,0),C(0,2)∴∵点N在对称轴x=﹣1上,∴点N人横坐标为﹣1,设点M的横坐标为x,则有:,解得x=﹣2,此时y=2,∴M(﹣2,2)综上所述,M点的坐标可能是.14.解:(1)设:抛物线的表达式为:y=ax2+bx+c,x=﹣=1,则b=﹣2a,则:y=ax2﹣2ax+4,将点B坐标代入上式并解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+4;(2)△AOC与△BCD,则△AOB与△BOD的面积相等,则y D=y A=4,则点D坐标为(2,4),则直线OD的表达式为:y=2x,同理直线AB的表达式为:y=4﹣x,将上述两个表达式联立并求解得:x=,即点C坐标为(,);(3)设点C(m,4﹣m),点D(n,﹣n2+n+4),设k====﹣1,则直线OC的表达式为:y=x,将点D的坐标代入上式并化简得:=﹣n2+n+1,k=﹣1=﹣n2+n,∵﹣<0,函数k开口向下,∴k有最大值,当n=﹣=2时,k的最大值为:.15.解:(1)∵直线y=﹣x+4与x轴交于点A,与y轴交于点B.∴A(4,0),B(0,4).又∵抛物线过B(0,4)∴c=4.把A(4,0)代入y=﹣x2+bx+4得,0=﹣×42+4b+4,解得,b=1.∴抛物线解析式为,y=﹣x2+x+4.令﹣x2+x+4=0,解得,x=﹣2或x=4.∴C(﹣2,0).(2)如图1,分别过P、Q作PE、QD垂直于x轴交x轴于点E、D.设P(m,﹣m2+m+4),Q(n,﹣n+4),则PE=﹣m2+m+4,QD=﹣n+4.又∵==y.∴n=.又∵=,即=把n═代入上式得,=整理得,4y=﹣m2+2m.∴y=﹣m2+m.y==.max即PQ与OQ的比值的最大值为.(3)如图2,∵∠OBA=∠OBP+∠PBA=45°∠PBA+∠CBO=45°∴∠OBP=∠CBO此时PB过点(2,0).设直线PB解析式为,y=kx+4.把点(2,0)代入上式得,0=2k+4.解得,k=﹣2∴直线PB解析式为,y=﹣2x+4.令﹣2x+4=﹣x2+x+4整理得, x2﹣3x=0.解得,x=0(舍去)或x=6.当x=6时,﹣2x+4=﹣2×6+4=﹣8∴P(6,﹣8).过P作PH⊥y轴于点H.则S四边形OHPA=(OA+PH)•OH=(4+6)×8=40.S△OAB=OA•OB=×4×4=8.S△BHP=PH•BH=×6×12=36.∴S△PBA =S四边形OHPA+S△OAB﹣S△BHP=40+8﹣36=12.。
2019-2020年中考数学二次函数压轴题人教新课标版.docx

2019-2020 年中考数学 二次函数压轴题人教新课标版(26) ( 本小题 10 分 )已知二次函数 y = ax 2+bx + c .(Ⅰ)若 a = 2, c =- 3,且二次函数的图象经过点(- 1,- 2),求 b 的值(Ⅱ)若 a = 2, b +c =- 2, b > c ,且二次函数的图象经过点(p ,- 2),求证: b ≥ 0;(Ⅲ)若 a + b +c = 0, a >b > c ,且二次函数的图象经过点( q ,- a ),试问自变量 x = q + 4 时,二次函数y= ax 2+ bx + c 所对应的函数值 y 是否大于 0?并证明你的结论。
26. 本小题满分 10 分 ( 1)当 a2 , c3 时,二次函数为y2x 2bx3∵ 该函数的图象经过点 ( 1 , 2)∴2 2 ( 1) 2 b ( 1) 3解得 b 1 2分( 2)当 a2 , b c2 时,二次函数为y2x 2 bxb 2∵ 该函数的图象经过点 ( p ,2)∴2 2p2bp b 2 ,即 2 p 2bp b 0于是, p 为方程 2x 2 bx b0 的根∴ 判别式 b 28b b(b 8)又 ∵ b c2 , b c∴ b b 2 ,即 b 1 ,有 b 8 0∴b 05 分( 3)∵ 二次函数yax2bxc的图象经过点(q ,a)∴ aq2bq c a 0∴ q为方程 ax 2bx c a 0 的根 于是,判别式b 2 4a(a c) 0又 ∵ a b c 0∴b 2 4ab b(b 4a)b(3a c) 0又 a b c 0 ,且 a b c ,知 a 0 , c 0∴ 3a c 0∴ b0 ∵ q 为方程 ax 2bx ca0 的根qbb 2 4ab qbb 2 4ab2a2a∴或当xq 4时y a(q 4) 2b( q 4) caq 2 8aq 16abq 4b c(aq 2 bqc a) 8aq 15a 4b8aq 15a 4bqbb 2 4ab2a若y8abb 2 4ab 15a 4b 15a4 b 2 4ab则2a∵ ab 0∴ b 24aba 2 4a a 5a 2 ,b 2 4ab 5a4 b24ab4 5a∴y15a4 5a (15 4 5 )aqbb 2 4ab2a若y8a bb 24ab15a 4b 15a4 24ab 02a b 则∴当x q 4时,二次函数y ax2bx c所对应的函数值y大于0 10分2006 年天津市初中毕业生学业考试数学试卷(26) (本小题10分)已知抛物线y= ax 2+ bx+ c 的定点坐标为(2,4).(Ⅰ)试用含 a 的代数式分别表示b, c;(Ⅱ)若直线y= kx + 4( k≠ 0)与 y 轴及该抛物线的交点依次为D、E、F,且SODE=1,其中 O为坐标原点,SOEF3试用含 a 的代数式表示k;(Ⅲ)在(Ⅱ)的条件下,若线段EF 的长 m满足3 2 m 3 5 ,试确定a的取值范围。
二次函数压轴题专题分类训练(完整资料).doc

【最新整理,下载后即可编辑】中考二次函数压轴题专题分类训练题型一:面积问题【例1】如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式; (2)求△CAB 的铅垂高CD 及S △CAB ;(3)设点P 是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S △PAB =89S △CAB存在,请说明理由.【变式练习】1.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB . (1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由. (4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.图22.如图,抛物线y = ax 2 + bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G .(1)求抛物线的函数解析式,并写出顶点D 的坐标; (2)在直线EF 上求一点H ,使△CDH小周长;(3)若点K 在x 轴上方的抛物线上运动,当K 时,△EFK 的面积最大?并求出最大面积.3.如图,已知:直线3+y交x轴于点A,交y轴于点B,抛=x-物线y=ax2+bx+c经过A、B、C(1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(-1,0),在直线3+y上有一点=x-P,使ΔABO与ΔADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.题型二:构造直角三角形【例2】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90º的点P的坐标.E【变式练习】1.如图,抛物线y=与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.O 11x y2.在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且310。
(完整版)中考二轮二次函数压轴题专题复习20题(含答案)

2019年九年级数学中考二轮二次函数压轴题专题复习1.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,﹣),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=.(1)求抛物线的解析式;(2)动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒.①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由.②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t 的值;若不存在,请说明理由.2.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D 两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.3.如图,二次函数错误!未找到引用源。
的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).(1)b=,点B的坐标是;(2)设直线PB与直线AC相交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在求出点P的横坐标;若不存在,请说明理由;(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.4.综合与探究:如图1所示,直线y=x+c与x轴交于点A(﹣4,0),与y轴交于点C,抛物线y=﹣x2+bx+c 经过点A,C.(1)求抛物线的解析式(2)点E在抛物线的对称轴上,求CE+OE的最小值;(3)如图2所示,M是线段OA上一个动点,过点M垂直于x轴直线与直线AC和抛物线分别交于点P、N.①若以C,P,N为顶点的三角形与△APM相似,则△CPN的面积为;②若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.5.已知抛物线y=0.5x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.(1)求抛物线的解析式;(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.6.如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.(1)当a=﹣1时,抛物线顶点D的坐标为,OE=;(2)OE的长是否与a值有关,说明你的理由;(3)设∠D EO=β,45°≤β≤60°,求a的取值范围;(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m的函数解析式及自变量m的取值范围.7.如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C(1)求抛物线的解析式;(2)点P从点A出发,以每秒错误!未找到引用源。
2019年中考数学专题《二次函数》复习试卷含答案解析.doc

2019年中考数学专题复习卷: 二次函数一、选择题1.若二次函数y=(a-1)x2+3x+a2-1的图象经过原点,则a的值必为()A. 1或-1 B. 1C. -1 D. 02.对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在()A. 第一象限B. 第二象限 C. 第三象限 D. 第四象限3.把抛物线y=- 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为()A. y=-(x-1)2-3B. y=-(x+1)2-3 C. y=-(x-1)2+3 D. y=-(x+1)2+34.已知抛物线(,,为常数,)经过点. ,,其对称轴在轴右侧,有下列结论:①抛物线经过点;②方程有两个不相等的实数根;③.,正确结论的个数为()A. 0B. 1C. 2D. 35.当a≤x≤a+1时,函数y=x2-2x+1的最小值为1,则a的值为()A. -1B. 2C. 0或2 D. -1或26.二次函数的图象如图所示,则反比例函数与一次函数在同一坐标系内的大致图象是()A. B. C. D.7.已知二次函数( 为常数),当自变量的值满足时,与其对应的函数值的最大值为-1,则的值为( )A. 3或6B. 1或6 C. 1或3 D. 4或68.已知抛物线y=x2+bx+c(其中b,c是常数)经过点A(2,6),且抛物线的对称轴与线段BC有交点,其中点B(1,0),点C(3,0),则c的值不可能是()A.4 B.6 C.8 D.109.有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行()A. 2.76米B. 6.76米C. 6米 D. 7米10.已知抛物线y=-x2+mx的对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是()A. t>-5B. -5<t<3 C. 3<t≤4 D. -5<t≤411.如图,已知二次函数图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0;②4a+b=0;③若点A坐标为(−1,0),则线段AB=5;④若点M(x1, y1)、N(x2, y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为()A. ①,②B. ②,③ C. ③,④ D. ②,④12.如图,在中,,,,动点从点开始沿向点以以的速度移动,动点从点开始沿向点以的速度移动.若,两点分别从,两点同时出发,点到达点运动停止,则的面积随出发时间的函数关系图象大致是()A. B. C.D.二、填空题13.抛物线y=2(x+2) +4的顶点坐标为________.14.将二次函数的图像向上平移3个单位长度,得到的图像所对应的函数表达式是________.15.已知二次函数,当时,函数值的最小值为,则的值是________.16.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若p、q(P是关于x的方程2-(x-a)(x-b)=0的两根且a则请用“<”来表示a、b、P、q的大小是________17.如图,抛物线与直线的两个交点坐标分别为,,则方程的解是________.18.已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位,平移后的抛物线于x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为________.19.小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E 到洗手盆内侧的距离EH为________cm.20.如图,在中,,,,点是边上的动点(不与点重合),过作,垂足为,点是的中点,连接,设,的面积为,则与之间的函数关系式为________.三、解答题21.已知:二次函数y=ax 2+bx+c(a≠0)的图象如图所示.请你根据图象提供的信息,求出这条抛物线的表达式.22.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%.经试销发现,销售量P(件)与销售单价x(元)符合一次函数关系,当销售单价为65元时销售量为55件,当销售单价为75元时销售量为45件.(Ⅰ)求P与x的函数关系式;(Ⅱ)若该商场获得利润为y元,试写出利润y与销售单价x之间的关系式;(Ⅲ)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?23.如图,平面直角坐标系xOy中,抛物线y=a(x+1)(x-9)经过A,B两点,四边形OABC矩形,已知点A坐标为(0,6)。
2019中考数学 题型训练- 二次函数综合题压轴

2019中考·数学 ---二次函数综合题压轴题型类型1线段问题1.如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(,)和B(4,c),点P是直线AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,交x轴于点M.(1)求抛物线的解析式;(2)当点P在线段AB上运动时(点P不与点A,B重合),是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)点P在直线AB上自由移动,当点C,P,M中恰有一点是其他两点所连线段的中点时,请直接写出n的值.2.如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x 轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=3EF,求m的值;(3)连接PC,是否存在点P,使△PCE是以PC为腰的等腰三角形?若存在,请直接写出m的值;若不存在,请说明理由.3.[2019原创]如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A,C(1,0),与y轴交于点B(0,-3).(1)求抛物线的解析式;(2)点P是直线AB下方的抛物线上一动点,过点P作x轴的垂线,垂足为点F,交直线AB于点E,作PD⊥AB于点D.①当△PDE的周长最大时,求出点P的坐标;②连接AP,以AP为边在其右侧作正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.则当顶点M或N恰好落在抛物线的对称轴上时,请直接写出点P的坐标.备用图类型2面积问题4.[2018四川绵阳]如图,已知抛物线y=ax2+bx(a≠0)过点A(,-3)和点B(3,0),过点A 作直线AC∥x轴,交y轴于点C.(1)求抛物线的解析式;(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出点P的坐标;(3)抛物线上是否存在点Q,使得S△AOC=S△AOQ?若存在,求出点Q的坐标;若不存在,请说明理由.5.[2018山东东营]如图,抛物线y=a(x-1)(x-3)(a>0)与x轴交于A,B两点,抛物线上另有一点C在x轴下方,且△OCA∽△OBC.(1)求线段OC的长度;(2)设直线BC与y轴交于点M,点C恰为BM的中点,求直线BM和抛物线的解析式;(3)在(2)的条件下,直线BC下方的抛物线上是否存在一点P,使得四边形ABPC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.6.[2017开封二模]如图,已知抛物线y=a(x+1)(x-5)与x轴从左至右交于A,B两点,与y轴交于点C(0,5).(1)求该抛物线的函数解析式;(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD,直线BC能否把△BDF分成面积之比为2∶3的两部分?若能,请求出点D的坐标;若不能,请说明理由;(3)若M为抛物线对称轴上一动点,△MBC为直角三角形,请直接写出点M的坐标.类型3等腰三角形的存在性问题7.[2018山西中考改编]如图,抛物线y=ax2+bx-4与x轴交于点A(-3,0),B(4,0),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.(1)求抛物线的解析式;(2)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值;(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由.8.[2018洛阳二模]如图,二次函数y=x2+bx+c的图象交x轴于A,B两点,交y轴于点C,顶点为点P,经过B,C两点的直线的解析式为y=-x+3. (1)求二次函数的解析式;(2)Q是直线BC下方抛物线上一动点,△QBC的面积是否有最大值?若有,请求出这个最大值和此时点Q的坐标;若无,请说明理由;(3)该抛物线的对称轴上是否存在点M,使以点C,P,M为顶点的三角形是等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由.9.如图,二次函数y=x2+bx-的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)求抛物线的解析式及点B的坐标;(2)当点P在线段AO(点P不与A,O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.备用图类型4直角三角形、等腰直角三角形的存在性问题10.[2018四川眉山中考改编]如图(1),已知抛物线y=ax2+bx+c经过点A(0,3),B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P 是抛物线上一个动点,设其横坐标为m. (1)求抛物线的解析式;(2)若动点P在直线OE下方的抛物线上运动,连接PE,PO,当m为何值时,四边形AOPE的面积最大?并求出其最大值;(3)如图(2),点F是抛物线的对称轴l上的一点,在对称轴左侧、y轴右侧的抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.图(1)图(2)11.[2018辽宁沈阳中考改编]如图,在平面直角坐标系中,抛物线C1:y=ax2+bx-1经过点A(-2,1)和点B(-1,-1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M (1)求抛物线C1的解析式; (2)直接..用含t的代数式表示线段MN的长;(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.备用图12.[2018平顶山二模]如图,已知直线y=x-3与x轴、y轴分别交于点A,B,抛物线y=x2+bx+c经过点A,B,且交x轴于点C. (1)求抛物线的解析式.(2)点P为抛物线上一点,且点P在直线AB的下方,设点P的横坐标为m.①试求当m为何值时,△PAB的面积最大;②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,则在直线PD上是否存在点Q,使△QBC为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.备用图类型5平行四边形的存在性问题13.[2018濮阳一模]如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y 轴交于点C,且OC=3OB. (1)求抛物线的解析式; (2)点D在y轴上,且∠BDO=∠BAC,求点D 的坐标; (3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.14.[2018新乡一模]如图,一次函数y=-x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点. (1)求抛物线的解析式; (2)作垂直于x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t取何值时,MN有最大值,最大值是多少;(3)在(2)的条件下,以A,M,N,D(点D为平面内一点)为顶点作平行四边形,求顶点D的坐标.15.在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a,b,c为常数,a≠0)的“梦想直线”;定义有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.已知抛物线y=-x2-x+2与其“梦想直线”交于A,B两点(点A在点B的左侧),与x 轴负半轴交于点C. (1)填空:该抛物线的“梦想直线”的解析式为,点A的坐标为,点B的坐标为; (2)如图,点M为线段CB上一动点,将△ACM以AM 所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标; (3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A,C,E,F为顶点的四边形为平行四边形?若存在,请直接写出点E,F的坐标;若不存在,请说明理由.备用图类型6矩形、菱形、正方形的存在性问题16.如图,以直线x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A,点B(-1,0),与y 轴交于点C(0,4),作直线AC.(1)求抛物线的解析式;(2)点P在抛物线的对称轴上,且到直线AC和x轴的距离相等.设点P的纵坐标为m,求m的值;(3)点M在y轴上且位于点C上方,点N在直线AC上,点Q为第一象限内抛物线上一点,若以点C,M,N,Q为顶点的四边形是菱形,请直接写出点Q的坐标.备用图17.[2018四川南充]如图,抛物线的顶点为P(1,4),且与y轴交于C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,且△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为点D,E.是否存在点M,N使四边形MNED为正方形?若存在,请直接写出正方形MNED的边长;若不存在,请说明理由.18.如图,在平面直角坐标系中,直线l:y=kx+h与x轴相交于点A(-1,0),与y轴相交于点C,与抛物线y=-x2+bx+3的一交点为点D,抛物线过x轴上的A,B两点,且CD=4AC.(1)求直线l和抛物线的解析式;(2)点E是直线l上方抛物线上的一动点,连接AE,DE,求△ADE面积最大时点E的坐标;(3)设点P是抛物线对称轴上一点,点Q在抛物线上,以A,D,P,Q为顶点的四边形能否为矩形?若能,请直接写出点P的坐标;若不能,请说明理由.备用图类型7相似三角形或全等三角形的存在性问题19.[2018四川达州中考改编]如图,抛物线经过原点O(0,0),A(1,1),B(,0).(1)求抛物线的解析式;(2)连接OA,过点A作AC⊥OA交抛物线于点C,连接OC,求△AOC的面积;(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.备用图20.[2018郑州外国语三模]如图,抛物线y=-x2+(3m+1)x-m(m>,且m为实数)与x轴交于A,B(点B位于点A的右侧,且AB≠OA)两点,与y轴交于点C.(1)填空:点B的坐标为,点C的坐标为(用含m的代数式表示).(2)当m=3时,在直线BC上方的抛物线上有一点M,过点M作x轴的垂线,交直线BC于点N,求线段MN长度的最大值.(3)在第四象限内是否存在点P,使得△PCO,△POA和△PAB中的任意两个三角形都相似(全等是相似的特殊情况)?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.备用图21.[2018山东潍坊]如图(1),抛物线y1=ax2-x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B,且对称轴为直线l的抛物线y2.(1)求抛物线y2的解析式.(2)如图(2),在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出点T的坐标;若不存在,请说明理由.(3)点P为抛物线y1上一动点,过点P作y轴的平行线,交抛物线y2于点Q,点Q关于直线l的对称点为R.若以点P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.图(1)图(2)备用图类型8角度的存在性问题22.[2018广东]如图,已知顶点为C(0,-3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.(1)求m的值;(2)求抛物线y=ax2+b(a≠0)的解析式;(3)抛物线上是否存在点M,使得∠MCB=15°?若存在,请求出点M的坐标;若不存在,请说明理由.23.[2018许昌二模]如图,抛物线y=-x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=-x+2经过点A,C. (1)求抛物线的解析式. (2)点P为直线AC上方抛物线上一动点.①连接PO,交AC于点E,求的最大值.②过点P作PF⊥AC,垂足为点F,连接PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.24.[2018安阳二模]如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与坐标轴交于A,B,C三点,其中点B的坐标为(1,0),点C的坐标为(0,4).已知点D的坐标为(0,2),点P为二次函数图象上的一动点. (1)求二次函数的解析式; (2)当点P位于第二象限内二次函数的图象上时,连接AD,AP,以AD,AP为邻边作平行四边形APED,设平行四边形APED的面积为S,求S 的最大值; (3)点F是y轴上一点,是否存在点F,P,使∠PDF与∠ADO互余?若存在,请直接写出点P的横坐标;若不存在,请说明理由.参考答案1.(1)∵B(4,c)在直线y=x+2上,∴c=6,则B(4,6).∵A(,),B(4,6)在抛物线y=ax2+bx+6上,∴解得故抛物线的解析式为y=2x2-8x+6.(2)存在.易知点P的坐标为(n,n+2)(<n<4),点C的坐标为(n,2n2-8n+6),∴PC=(n+2)-(2n2-8n+6)=-2n2+9n-4=-2(n-)2+.∵-2<0,∴当n=时,线段PC的长取得最大值.(3)n的值为或.2.(1)将A(-1,0),B(3,0)两点的坐标分别代入y=ax2+bx-3中,得解得∴抛物线的解析式为y=x2-2x-3.(2)∵点P的横坐标为m,点P在x轴下方,∴P(m,m2-2m-3),E(m,m-2),F(m,0),且-1<m<3,∴PE=|y E-y P|=|(m-2)-(m2-2m-3)|=|-m2+3m+1|,EF=|y F-y E|=|0-(m-2)|=|-m+2|.∵PE=3EF,∴|-m2+3m+1|=3|-m+2|.①若-m2+3m+1=3(-m+2),整理,得m2-6m+5=0,解得m=1或m=5.∵-1<m<3,∴m=5不合题意,应舍去,∴m=1.②若-m2+3m+1=-3(-m+2),整理,得m2-7=0,解得m=或m=-.∵-1<m<3,∴m=-不合题意,应舍去,∴m=.综上所述,m的值为1或.(3)存在,m的值为1+,1-,或.3.(1)将B(0,-3),C(1,0)分别代入y=x2+bx+c,得解得故抛物线的解析式为y=x2+2x-3.(2)①令y=x2+2x-3=0,得x1=1,x2=-3,∴A(-3,0),∴OA=OB,∴∠BAO=45°,又∵PF⊥AO,∴∠AEF=45°,∴∠PED=45°,∴PD=DE,∴△PDE为等腰直角三角形,△PDE的周长为PE+2×=(1+)PE.设点F的横坐标为m,则PF=-m2-2m+3,FE=AF=m+3,∴PE=PF-FE=-m2-3m=-(m+)2+.∵点P是直线AB下方的抛物线上一动点,∴-3<m<0,∴当m=-时,PE最大,为,此时△PDE的周长最大,点P的坐标为(-,-).②点P的坐标为(,)或(-1-,-2).4.(1)把点A,B的坐标分别代入抛物线的解析式,得解得故抛物线的解析式为y=x2-x.(2)设点P的坐标为(m,n).∵A(,-3),∴C(0,-3),D(m,-3),∴PD=n+3,CO=3,AD=m-,AC=.①当△ADP∽△ACO时,=,即=,∴n=m-6.∵点P在抛物线上,∴n=m2-m,∴m-6=m2-m,解得m1=4,m2=(不合题意,舍去),∴P(4,6).②当△PDA∽△ACO时,=,即=,∴n=m-4.∵点P在抛物线上,∴n=m2-m,∴m-4=m2-m,解得m1=,m2=(不合题意,舍去),∴P(,-).综上所述,点P的坐标为(4,6)或(,-).(3)存在.∵A(,-3),∴AC=,OC=3,∴OA=2.在△AOC中,设边OA上的高为h,则S△AOC=OC·AC=OA·h,即×3×=×2×h,解得h=.∵S△AOC=S△AOQ,∴△AOQ的边OA上的高为.如图,过点O作OR⊥OA,在射线OR上截取OM=,过点M作MN∥OA交y轴于点N,过点M作MH⊥x轴于点H.∵AC=,OA=2,∴∠AOC=30°.∵MN∥OA,∴∠MNO=∠AOC=30°,OM⊥MN,∴ON=2OM=9,∠NOM=60°,∴点N的坐标为(0,9),∠MOB=30°,∴MH=OM=,OH=MH=,∴M(,).设直线MN的解析式为y=kx+c,则解得联立抛物线与直线MN的解析式,得整理,得x2-x-18=0,解得x1=3,x2=-2,故点Q的坐标为(3,0)或(-2,15). 5.(1)由题可知,当y=0时,a(x-1)(x-3)=0,解得x1=1,x2=3,即A(1,0),B(3,0),∴OA=1,OB=3.∵△OCA∽△OBC,∴OC∶OB=OA∶OC,∴OC2=OA·OB=3,则OC=.(2)∵点C是BM的中点,∴点C的横坐标为,又OC=,点C在x轴下方,∴C(,-).设直线BM的解析式为y=kx+b,把点B(3,0),C(,-)分别代入,得解得将C(,-)代入抛物线的解析式,得a=,故抛物线的解析式为y=x2-x+2.(3)存在.设点P的坐标为(m,m2-m+2),过点P作PQ⊥x轴,交直线BM于点Q,则Q(m,m-),∴PQ=m--(m2-m+2)=-m2+3m-3.当△BCP的面积最大时,四边形ABPC的面积最大,S△BCP=PQ·(3-)=PQ=-m2+m-,当m=-=时,S△BCP有最大值,四边形ABPC的面积最大,此时点P的坐标为(,-).6.(1)∵抛物线y=a(x+1)(x-5)经过C(0,5).∴5=a(0+1)(0-5),解得a=-1,∴抛物线的函数关系式为y=-(x+1)(x-5),即y=-x2+4x+5.(2)直线BC能把△BDF分成面积之比为2∶3的两部分.设直线BC的函数关系式为y=kx+b,则解得∴y=-x+5.设D(m,-m2+4m+5),则E(m,-m+5).∴DE=-m2+4m+5+m-5=-m2+5m,EF=-m+5.∵△BDE和△BFE是等高的,∴=.(i)当DE∶EF=2∶3时,即=,解得m1=,m2=5(舍去),此时,D(,).(ii)当DE∶EF=3∶2时,即=,解得m1=,m2=5(舍去),此时,D(,).综上所述,点D的坐标为(,)或(,).(3)点M的坐标为(2,7),(2,-3),(2,6)或(2,-1).7.(1)将点A(-3,0),B(4,0)分别代入y=ax2+bx-4,得解得故抛物线的解析式为y=x2-x-4.(2)如图,过点F作FG⊥PQ于点G,则FG∥x轴.由B(4,0),C(0,-4),得△OBC为等腰直角三角形,∴∠QFG=∠OBC=45°,∴GQ=FG=QF.∵PE∥AC,∴∠1=∠2.∵FG∥x轴,∴∠2=∠3,∴∠1=∠3.又∵∠FGP=∠AOC=90°,∴△FGP∽△AOC,∴=,即=,∴GP=FG=×QF=QF,∴QP=GQ+GP=QF+QF=QF,∴QF=QP.∵PM⊥x轴,点P的横坐标为m,∠MBQ=45°,∴QM=MB=4-m,PM=-m2+m+4,∴QP=PM-QM=-m2+m+4-(4-m)=-m2+m,∴QF=QP=(-m2+m)=-m2+m.∵-<0,∴QF有最大值,∴当m=-=2时,QF有最大值.(3)存在.点Q的坐标为(,-4)或(1,-3).8.(1)∵直线y=-x+3经过B,C两点,∴B(3,0),C(0,3).∵二次函数y=x2+bx+c的图象经过点B,C,∴解得故二次函数的解析式为y=x2-4x+3.(2)有.设点Q的横坐标为m,则点Q的纵坐标为m2-4m+3.如图,过点Q作x轴的垂线交BC于点D,则点D的坐标为(m,-m+3),∴QD=(-m+3)-(m2-4m+3)=-m2+3m,∴S△QBC=S△QDC+S△QDB=m·QD+(3-m)QD=×3×QD=(-m2+3m)=-(m-)2+.故当m=时,△QBC的面积取最大值,为,此时点Q的坐标为(,-).(3)存在.点M的坐标为(2,7),(2,2-1),(2,)或(2,-2-1).9.(1)将点A坐标代入y=x2+bx-,解得b=1,故抛物线的解析式为y=x2+x-.令y=0,得x2+bx-=0,解得x1=1,x2=-3,故点B的坐标为(1,0).(2)由题意知,正方形ABCD的边长为4,OA=3,OB=1.设PA=t,OE=l.由∠DAP=∠POE=∠DPE=90°,易得△DAP∽△POE.∴=,即=.∴l=-t2+t=-(t-)2+,故当t=时,l有最大值,即P为AO的中点时,OE的最大值为.(3)存在.由题意知,若△PED是等腰三角形,则PD=PE.①当点P在y轴左侧时,如图(1),设DE与x轴交于点G.图(1)易知△DAP≌△POE,∴OP=AD=4,OE=AP=4-3=1,∴点P的坐标为(-4,0).∵AD⊥x轴,EO⊥x轴,∴△ADG∽△OEG,∴==,∴AG=4GO=AO=,∴重叠部分的面积为S△ADG=××4=.图(2)②当点P在y轴右侧时,如图(2),设DE与x轴交于点G,DP与BC交于点F.同①可得OP=4,OE=AP=7,∴点P的坐标为(4,0).由△ADG∽△OEG,得AG=OG=OA=.由△DCF∽△PBF,得CF=BF=BC=.∴重叠部分的面积S四边形DGBF=4×4-××4-××4=.10.(1)设抛物线与x轴的另一个交点为D,由抛物线的对称性,得D(3,0),则抛物线的解析式可变形为y=a(x-1)(x-3),把A(0,3)代入,得3=3a,解得a=1,故抛物线的解析式为y=x2-4x+3.(2)易得点P的坐标为(m,m2-4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3).易得直线OE的解析式为y=x,过点P作PG∥y轴,交直线OE于点G,则G(m,m),∴PG=m-(m2-4m+3)=-m2+5m-3,∴S四边形AOPE=+=×3×3+PG·AE=+×3×(-m2+5m-3)=-m2+m=-(m-)2+.∵-<0,∴当m=时,S四边形AOPE有最大值,最大值是.(3)存在.点P的坐标为(,)或(,).11.(1)∵抛物线C1:y=ax2+bx-1经过点A(-2,1)和B(-1,-1),∴解得故抛物线C1的解析式为y=x2+x-1.(2)MN=t2+2.(3)分两种情况讨论.①当∠ANM=90°时,AN=MN,∵AN=t-(-2)=t+2,由(2)得MN=t2+2,∴t+2=t2+2,解得t1=0,t2=1.∵t=0时,∠AMN=90°,不符合题意,舍去,∴t=1.②当∠AMN=90°时,AM=MN,∵AM=t-(-2)=t+2,由(2)得MN=t2+2,∴t+2=t2+2,解得t3=0,t4=1.∵t=1时,∠ANM=90°,不符合题意,舍去,∴t=0.综上所述,t的值为0或1.12.(1)对于直线y=x-3,令x=0,得y=-3,令y=0,得x=6,∴A(6,0),B(0,-3).将点A,B的坐标分别代入y=x2+bx+c,得解得故抛物线的解析式为y=x2-x-3.(2)①由题易知P(m,m2-m-3).如图,过点P作PE⊥x轴,交AB于点E,则E(m,m-3),∴PE=m-3-(m2-m-3)=-m2+2m,∴S△PAB=PE·OA=×(-m2+2m)×6=-(m-3)2+9,∵点P在直线AB下方的抛物线上,∴0<m<6,∴当m=3时,△PAB的面积最大,为9.②存在,点Q的坐标为(3,)或(3,-).13.(1)当x=0时,y=-3,∴C(0,-3).∵OC=3OB,∴OB=1,∴B(-1,0).将A,B两点的坐标代入抛物线的解析式,得解得故抛物线的解析式为y=x2-2x-3.(2)过点B作BF⊥AC,交AC的延长线于点F.易得AF=BF=3,∴∠BAC=45°,∴∠BDO=∠BAC=45°.∵点D在y轴上,∴OB=OD=1,故点D的坐标为(0,1)或(0,-1).(3)存在.如图,当AB为对角线时,易得平行四边形AM1BN1,∴M1(0,-3).当AB为一边时,在▱ABM2N2中,点A的横坐标是2,点N2的横坐标是1,点B的横坐标是-1,由图形平移前后点的坐标关系,得点M2的横坐标是-2,∴点M2的纵坐标为(-2)2-2×(-2)-3=5,∴M2(-2,5).在▱ABN3M3中,点B的横坐标是-1,点N3的横坐标是1,点A的横坐标是2,由图形平移前后点的坐标关系,得点M3的横坐标为4,∴点M3的纵坐标为42-2×4-3=5,∴M3(4,5).14.(1)易知点A,B的坐标分别为(0,2),(4,0).将x=0,y=2代入y=-x2+bx+c,得c=2,将x=4,y=0,c=2代入y=-x2+bx+c,得0=-16+4b+2,解得b=,故抛物线的解析式为y=-x2+x+2.(2)易得M(t,-t+2),N(t,-t2+t+2),则MN=y N-y M=-t2+t+2-(2-t)=-t2+4t=-(t-2)2+4,∴当t=2时,MN有最大值4.(3)易知A(0,2),M(2,1),N(2,5),设D(m,n).当AM是对角线时,AM的中点的坐标为(1,),DN的中点的坐标为(,),∴1=,=,解得m=0,n=-2,此时点D的坐标为(0,-2).当AN是对角线时,AN的中点的坐标为(1,),DM的中点的坐标为(,),∴1=,=,解得m=0,n=6,此时点D的坐标为(0,6).当MN是对角线时,MN的中点的坐标为(2,3),AD的中点的坐标为(,),∴2=,3=,解得m=4,n=4,此时点D的坐标为(4,4).15.(1)y=-x+(-2,2)(1,0)(2)∵抛物线与x轴负半轴交于点C,∴C(-3,0).过点A作AG⊥y轴,垂足为点G.当点N在y轴上时,如图(1),△AMN为抛物线的“梦想三角形”.设N(0,n),∵A(-2,2),C(-3,0),∴AC=,∴AN=AC=.在Rt△AGN中,AG2+GN2=AN2,又AG=2,GN=|n-2|,∴4+(n-2)2=13,解得n=2-3或n=2+3.设M(m,0),当n=2-3时,在Rt△MNO中,ON2+OM2=MN2,即(2-3)2+m2=(m+3)2,解得m=2-2.当n=2+3时,在Rt△MNO中,ON2+OM2=MN2,即(2+3)2+m2=(m+3)2,解得m=2+2.又-3<m≤1,∴m=2+2不合题意,舍去,∴m=2-2,此时n=2-3,∴N(0,2-3).图(1)图(2)当点M在y轴上时,如图(2),△AMN为“梦想三角形”,此时点M与点O重合,在Rt△AGM中,AG=2,GM=2,∴tan∠AMG==,∴∠AMG=30°,∴∠AMC=∠AMN=∠NMB=60°,过点N作NP⊥x轴于点P,在Rt△NMP中,MN=CM=3,∴NP=,OP=,∴N(,).综上所述,点N的坐标为(0,2-3)或(,).(3)E1(-1,-),F1(0,);E2(-1,-),F2(-4,).16.(1)由题意得,c=4,则解得∴抛物线的解析式为y=-x2+x+4.(2)∵抛物线与x轴交于点B(-1,0),对称轴为直线x=1,∴点A的坐标为(3,0).∵直线AC经过点A(3,0),点C(0,4),∴直线AC的解析式为y=-x+4.令对称轴与直线AC交于点D,与x轴交于点E,则DE⊥x轴,点D的坐标为(1,).∴DE=,AE=2,AD=.图(1)①当点P在∠CAB的平分线上时,如图(1),过点P作PH⊥AC于点H,则PH=PE=m,DP=-m.易得△DPH∽△DAE,∴=,即=,解得m=1.图(2)②当点P在∠CAB的邻补角的平分线上时,如图(2),过点P作PG⊥AC于点G,则PG=PE=-m,DP=-m.易得△DPG∽△DAE,∴=,即=,解得m=-4.∴m的值为1或-4.(3)点Q的坐标为(1,)或(,).17.(1)由题可设抛物线的解析式为y=a(x-1)2+4(a≠0),将C(0,3)代入,得a+4=3,∴a=-1,故抛物线的解析式为y=-(x-1)2+4=-x2+2x+3. (2)易得B(3,0),根据待定系数法,易得直线BC的解析式为y=-x+3.分以下两种情况讨论.①当点Q在直线BC上方时,∵S△PBC=S△QBC,∴PQ∥BC.如图(1),过点P作平行于BC的直线,交抛物线于点Q1,∵P(1,4),∴直线PQ的解析式为y=-x+5.联立y=-x+5与y=-x2+2x+3,得解得∴Q1(2,3).②当点Q在直线BC下方时,如图,设抛物线的对称轴交BC于点G,交x轴于点H,则G(1,2),∴PG=GH=2.过点H作平行于BC的直线,交抛物线于点Q2,Q3.易得直线Q2Q3的解析式为y=-x+1,联立y=-x+1与y=-x2+2x+3,得解得∴Q2(,),Q3(,).综上所述,点Q的坐标为(2,3),(,)或(,).(3)存在.正方形MNED的边长为9或.18.(1)将A(-1,0)代入y=-x2+bx+3,得b=2,故抛物线的解析式为y=-x2+2x+3,过点D作DF⊥x轴于点F,易证△AOC∽△AFD,∴=.∵CD=4AC,∴==,∴点D横坐标为4.把x=4代入y=-x2+2x+3,得y=-5,∴D(4,-5).把A(-1,0),D(4,-5)分别代入y=kx+h,解得k=-1,h=-1,故直线l的解析式为y=-x-1.(2)过点E作EM⊥x轴,交AD于点M,设E(m,-m2+2m+3),则M(m,-m-1),∴EM=-m2+2m+3-(-m-1)=-m2+3m+4,∴S△ADE=×5(-m2+3m+4)=-m2+m+10,当m=-=时,△ADE的面积最大,此时,E(,).(3)以A,D,P,Q为顶点的四边形不能为矩形.理由:设P(1,n),AD2=25+25=50.①若AD是一边,则∠QAD=90°.易知x Q-x P=x A-x D,即x Q-1=-1-4,解得x Q=-4,故点Q的坐标为(-4,-21).此时AQ2=32+212=450,DQ2=82+162=320,∴AQ2+AD2≠DQ2,∴∠QAD≠90°,故此时以A,D,P,Q为顶点的四边形不是矩形.②若AD是对角线,则∠AQD=90°.用同样的方法求得Q(2,3),此时QD2=22+82=68,QA2=32+32=18,∴QD2+QA2≠AD2,∴∠AQD≠90°,故此时以A,D,P,Q为顶点的四边形不是矩形.综上所述,以A,D,P,Q为顶点的四边形不能为矩形.19.(1)设抛物线的解析式为y=ax(x-).将点A的坐标代入,得1=a(1-),解得a=-.故抛物线的解析式为y=-x(x-)=-x2+x.(2)如图,过点C作CD⊥x轴于点D,延长CA交y轴于点E,设AC与x轴交于点H.∵A(1,1),∴∠AOE=45°.∵AC⊥OA,∴△AOE为等腰直角三角形.∴OE=2,∴E(0,2).设直线AC的解析式为y=kx+b.根据题意,得解得故直线AC的解析式为y=-x+2.联立抛物线与直线AC的解析式,得解得∴C(5,-3),∴CD=3.易知H(2,0),∴S△AOC=OH·(1+CD)=×2×4=4.(3)存在,点M的坐标为(,),(,-)或(,-54).过点M作MF⊥x轴于点F,则△MNO∽△FMO.①当点M在x轴上方时,由题意得△MNO∽△AOC,设M(m,-m2+m),则OF=m.∴△FMO∽△AOC,∴=.∵A(1,1),∴OA=.∵C(5,-3),∴AC=4,∴=,∴=.∵m>0,∴-m+=,解得m=,当m=时,-m2+m=,∴M(,).②当点M在x轴下方时.(i)若△MNO∽△AOC,同①可得=.∵m>0,∴m-=,解得m=,当m=时,-m2+m=-,∴M(,-).(ii)若△MNO∽△ACO,可得△FMO∽△ACO,∴=,∴=4,∵m>0,∴m-=4,解得m=.当m=时,-m2+m=-54,∴M(,-54).综上,满足条件的点M的坐标为(,),(,-)或(,-54).20.(1)(3m,0)(0,-m)(2)当m=3时,y=-x2+x-3,点B的坐标为(9,0),点C的坐标为(0,-3),易得直线BC的解析式为y=x-3.设M(a,-a2+a-3),则N(a,a-3),∴MN=-a2+a-3-(a-3)=-a2+3a.∵点M在直线BC上方的抛物线上,∴0<a<9,∴当a=-=时,MN的长有最大值,为-×()2+3×=. (3)存在,点P的坐标为(1,-3),(1,-)或(1,).21.(1)将C(0,),B(1,0)分别代入y1=ax2-x+c,得解得故抛物线y1的解析式为y1=-x2-x+.∵抛物线y1平移后得到抛物线y2,且顶点为B(1,0),∴抛物线y2的解析式为y2=-(x-1)2,即y2=-x2+x-.(2)存在.易得抛物线y2的对称轴l为直线x=1,A(-3,0),设T(1,t),过点T作TE⊥y轴于点E,则TC2=TE2+CE2=12+(-t)2, TA2=TB2+AB2=t2+(1+3)2=t2+16,AC2=.分以下三种情况讨论:①当TC=AC时,12+(-t)2=,解得t1=,t2=;②当TA=AC时,t2+16=,此方程无实数解;③当TA=TC时,12+(-t)2=t2+16,解得t3=-.综上可知,在直线l上存在点T,使△TAC是等腰三角形,此时点T的坐标为(1,),(1,)或(1,-).(3)设P(m,-m2-m+),则Q(m,-m2+m-).∵Q,R关于直线x=1对称,∴R(2-m,-m2+m-).分以下两种情况讨论:①当点P在直线l的左侧时,PQ=-m2-m+-(-m2+m-)=1-m,QR=2-2m,a.当△PQR≌△GMA,即PQ=GM,QR=AM时,易得m=0,∴P(0,),即点P与点C重合,∴R(2,-).设直线PR的解析式为y=kx+b,将P(0,),R(2,-)分别代入,得解得故直线PR的解析式为y=-x+.b.当△PQR≌△AMG,即PQ=AM,QR=MG时,这种情况不存在.②当点P在直线l的右侧时,PQ=-m2+m--(-m2-m+)=m-1,RQ=2m-2,同理可得P(2,-),R(0,-),利用待定系数法,可得直线PR的解析式为y=-x-.综上所述,直线PR的解析式为y=-x+或y=-x-.22.(1)将C(0,-3)代入y=x+m,得-3=0+m,解得m=-3.(2)对于y=x-3,令y=0,得x=3,∴B(3,0).将C(0,-3),B(3,0)分别代入y=ax2+b,得解得故抛物线y=ax2+b(a≠0)的解析式为y=x2-3.(3)存在.分以下两种情况讨论.①若点M在BC上方,设MC交x轴于点D,则∠ODC=45°+15°=60°,∴OD==,∴D(,0).设直线DC的解析式为y=kx-3,把D(,0)代入,得k-3=0,解得k=,故直线DC的解析式为y=x-3.联立直线DC和抛物线的解析式,得解得(不合题意,舍去)∴M(3,6).②若点M在BC下方,设MC交x轴于点E,则∠OEC=45°-15°=30°,∴OE==3.设直线EC的解析式为y=mx-3,把E(3,0)代入,得0=3m-3,解得m=,故直线EC的解析式为y=x-3.联立直线EC和抛物线的解析式,得解得(不合题意,舍去)∴M(,-2).综上所述,点M的坐标为(3,6)或(,-2).23.(1)对于y=-x+2,当x=0时,y=2,当y=0时,x=4,∴A(4,0),C(0,2).∵抛物线y=-x2+bx+c经过点A(4,0),C(0,2),∴解得故抛物线的解析式为y=-x2+x+2.(2)如图,过点P作PN⊥x轴于点N,交直线AC于点M,则PN∥y轴,∴∠PME=∠OCE.又∵∠PEM=∠OEC,∴△PEM∽△OEC,∴=.∵C(0,2),∴OC=2.设点P的坐标为(t,-t2+t+2),则点M(t,-t+2),∴PM=-t2+t+2-(-t+2)=-t2+2t,∴=-t2+t=-(t-2)2+1.∵-<0,0<t<4,∴当t=2时,有最大值1.(3)存在.点P的坐标为(2,3)或(,).24.(1)∵二次函数y=-x2+bx+c的图象过点B(1,0),C(0,4),∴解得故二次函数的解析式为y=-x2-3x+4.(2)如图,连接PD,过点P作PM⊥x轴于点M,交AD于点N,令-x2-3x+4=0,解得x1=1,x2=-4,∴A(-4,0).设直线AD的解析式为y=kx+t,将A(-4,0),D(0,2)分别代入,得解得故直线AD的解析式为y=x+2.设P(m,-m2-3m+4),则N(m,m+2),∴PN=-m2-3m+4-(m+2)=-m2-m+2,∴S=2S△APD=2(S△APN+S△PND)=2×(PN·AM+PN·MO)=PN·AO=(-m2-m+2)×4=-4(m+)2+.∵-4<m<0,∴当m=-时,S有最大值,为.(3)存在,点P的横坐标为1,-2,或.。
2019年中考真题数学试题分项汇编--二次函数(解析版)

专题07二次函数1.(2019•重庆)抛物线2362y x x =-++的对称轴是 A .直线2x = B .直线2x =- C .直线1x = D .直线1x =-【答案】C【解析】∵223623(1)5y x x x =-++=--+, ∴抛物线顶点坐标为(1,5),对称轴为1x =. 故选C .【名师点睛】本题考查了二次函数的性质.抛物线2()y a x h k =-+的顶点坐标为(h ,k ),对称轴为x =h .2.(2019•荆门)抛物线244y x x =-+-与坐标轴的交点个数为 A .0 B .1 C .2 D .3【答案】C【解析】当0x =时,2444y x x =-+-=-,则抛物线与y 轴的交点坐标为(0,4)-,当0y =时,2440x x -+-=,解得122x x ==,抛物线与x 轴的交点坐标为(2,0), 所以抛物线与坐标轴有2个交点. 故选C .【名师点睛】本题考查了抛物线与x 轴的交点:把求二次函数2(,,y ax bx c a b c =++是常数,0)a ≠与x 轴的交点坐标问题转化为解关于x 的一元二次方程.3.(2019•咸宁)已知点()()()()1,,1,,2,0A m B m C m n n -->在同一个函数的图象上,这个函数可能是 A .y x = B .2y x=-C .2y x =D .2y x =﹣【答案】D【解析】()()1,,1,A m B m -,∴点A 与点B 关于y 轴对称;由于2y x y x==-,的图象关于原点对称,因此选项A ,B 错误; ∵0n >,∴m n m -<,由()()1,,2,B m C m n -可知,在对称轴的右侧,y 随x 的增大而减小, 对于二次函数只有0a <时,在对称轴的右侧,y 随x 的增大而减小, ∴D 选项正确,故选D .【名师点睛】考查正比例函数、反比例函数、二次函数的图象和性质,可以采用排除法,直接法得出答案.4.(2019 •青岛)已知反比例函数y =ab x的图象如图所示,则二次函数y =ax 2-2x 和一次函数y =bx +a 在同一平面直角坐标系中的图象可能是A. B .C. D .【答案】C【解析】∵当x =0时,y =ax 2–2x =0,即抛物线y =ax 2–2x 经过原点,故A 错误;∵反比例函数y =abx的图象在第一、三象限, ∴ab >0,即a 、b 同号,当a <0时,抛物线y =ax 2–2x 的对称轴x =1a<0,对称轴在y 轴左边,故D 错误; 当a >0时,b >0,直线y =bx +a 经过第一、二、三象限,故B 错误; C 正确.故选C .【名师点睛】本题主要考查了一次函数、反比例函数、二次函数的图象与性质,根据函数图象与系数的关系进行判断是解题的关键,同时考查了数形结合的思想.5.(2019•哈尔滨)将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为A .22(2)3y x =++B .22(2)3y x =-+C .22(2)3y x =--D .22(2)3y x =+-【答案】B【解析】将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为()2223y x =-+, 故选B .【名师点睛】本题考查了二次函数的平移规律,熟练掌握其平移规律是解题的关键.6.(2019•成都)如图,二次函数2y ax bx c =++的图象经过点()1,0A ,()5,0B ,下列说法正确的是A .0c <B .240b ac -<C .0a b c -+<D .图象的对称轴是直线3x =【答案】D【解析】由图象可知图象与y 轴交点位于y 轴正半轴,故c >0,A 选项错误; 函数图象与x 轴有两个交点,所以24b ac ->0,B 选项错误; 观察图象可知x =-1时y =a -b +c >0,所以a -b +c >0,C 选项错误;根据图象与x 轴交点可知,对称轴是(1,0),(5,0)两点的中垂线,1532x +==, 即x =3为函数对称轴,D 选项正确, 故选D .【名师点睛】此题主要考查二次函数的图象与性质,解题的关键是熟知二次函数的图象.7.(2019•雅安)在平面直角坐标系中,对于二次函数22()1y x =-+,下列说法中错误的是 A .y 的最小值为1B .图象顶点坐标为(2,1),对称轴为直线2x =C .当2x <时,y 的值随x 值的增大而增大,当2x ≥时,y 的值随x 值的增大而减小D .它的图象可以由2y x =的图象向右平移2个单位长度,再向上平移1个单位长度得到 【答案】C【解析】二次函数22()1y x =-+,10a =>,∴该函数的图象开口向上,对称轴为直线2x =,顶点为(2,1),当2x =时,y 有最小值1,当2x >时,y 的值随x 值的增大而增大,当2x <时,y 的值随x 值的增大而减小;故选项A 、B 的说法正确,C 的说法错误;根据平移的规律,2y x =的图象向右平移2个单位长度得到2(2)y x =-,再向上平移1个单位长度得到22()1y x =-+,故选项D 的说法正确, 故选C .【名师点睛】本题考查二次函数的性质、二次函数的最值,二次函数图象与几何变换,解答本题的关键是明确题意,利用二次函数的性质解答.8.(2019•岳阳)对于一个函数,自变量x 取a 时,函数值y 也等于a ,我们称a 为这个函数的不动点.如果二次函数y =x 2+2x +c 有两个相异的不动点x 1、x 2,且x 1<1<x 2,则c 的取值范围是A .c <-3B .c <-2C .c <14D .c <1【答案】B【解析】由题意知二次函数y =x 2+2x +c 有两个相异的不动点x 1、x 2, 所以x 1、x 2是方程x 2+2x +c =x 的两个不相等的实数根, 整理,得:x 2+x +c =0,所以∆=1–4c >0,又x 2+x +c =0的两个不相等实数根为x 1、x 2,x 1<1<x 2, 所以函数y =x 2+x +c =0在x =1时,函数值小于0,即1+1+c <0, 综上则140110c c ->⎧⎨++<⎩,解得c <-2, 故选B .【名师点睛】本题考查了二次函数与一元二次方程的关系,正确理解题中的定义,熟练掌握二次函数与一元二次方程的关系是解题的关键.9.(2019•泸州)已知二次函数(1)(1)37y x a x a a =---+-+(其中x 是自变量)的图象与x 轴没有公共点,且当1x <-时,y 随x 的增大而减小,则实数a 的取值范围是 A .2a < B .1a >- C .12a -<≤ D .12a -≤<【答案】D【解析】(1)(1)37y x a x a a =---+-+22236x ax a a =-+-+, ∵抛物线与x 轴没有公共点,∴22(2)4(36)0a a a ∆=---+<,解得2a <, ∵抛物线的对称轴为直线22ax a -=-=,抛物线开口向上, 而当1x <-时,y 随x 的增大而减小, ∴1a ≥-,∴实数a 的取值范围是12a -≤<, 故选D .【名师点睛】本题考查了二次函数图象与x 轴交点问题,抛物线的对称轴,二次函数图象的增减性,熟练掌握和灵活运用相关知识是解题的关键.10.(2019•随州)如图所示,已知二次函数2y ax bx c =++的图象与x 轴交于,A B 两点,与y 轴交于点C ,OA OC =,对称轴为直线1x =,则下列结论:①0abc <;②11024a b c ++=;③10ac b -+=;④2c +是关于x 的一元二次方程20ax bx c ++=的一个根.其中正确的有A .1个B .2个C .3个D .4个【答案】B【解析】∵抛物线开口向下,∴0a <, ∵抛物线的对称轴为直线12bx a=-=,∴20b a =->, ∵抛物线与y 轴的交点在x 轴上方,∴0c >,∴0abc <,所以①正确;∵2b a =-,∴102a b a a +=-=, ∵0c >,∴11024a b c ++>,所以②错误;∵(0,)C c ,OA OC =,∴(,0)A c -,把(,0)A c -代入2y ax bx c =++得20ac bc c -+=,∴10ac b -+=,所以③错误; ∵(,0)A c -,对称轴为直线1x =,∴(2,0)B c +,∴2c +是关于x 的一元二次方程20ax bx c ++=的一个根,所以④正确, 综上正确的有2个, 故选B .【名师点睛】本题考查了抛物线与x 轴交点及与二次函数图象与系数的关系,做好本题要知道以下几点:①当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;②当a 与b 同号时(即ab >0),对称轴在y 轴左;当a 与b 异号时(即ab <0),对称轴在y 轴右.(简称:左同右异);③常数项c 决定抛物线与y 轴交点,抛物线与y 轴交于(0,c ).④抛物线2y ax bx c =++与x 轴交点的横坐标就是一元二次方程20ax bx c ++=的根.注意利用数形结合的思想.11.(2019•南通)如图是王阿姨晚饭后步行的路程s (单位:m )与时间t (单位:min )的函数图象,其中曲线段AB 是以B 为顶点的抛物线一部分,下列说法不正确的是A .25min~50min ,王阿姨步行的路程为800mB .线段CD 的函数解析式为324002550s t t =+≤≤()C .5min~20min ,王阿姨步行速度由慢到快D .曲线段AB 的函数解析式为23(20)1200(520)s t t =--+≤≤ 【答案】C【解析】观察图象可知5min~20min ,王阿姨步行速度由快到慢,25min~50min ,王阿姨步行的路程为2000–1200=800m ,故A 选项正确,C 选项错误;设线段CD 的解析式为s =mt +n ,将点(25,1200)、(50,2000)分别代入得120025200050m n m n =+⎧⎨=+⎩,解得:32400m n =⎧⎨=⎩, 所以线段CD 的函数解析式为32400(2550)s t t =+≤≤,故B 选项正确;由曲线段AB 是以B 为顶点的抛物线一部分,所以设抛物线的解析式为y =a (x –20)2+1200, 把(5,525)代入得:525=a (5–20)2+1200,解得:a =–3,所以曲线段AB 的函数解析式为23(20)1200(520)s t t =--+≤≤,故D 选项正确, 故选C .【名师点睛】本题考查了函数图象问题,涉及了待定系数法求一次函数解析式,求二次函数解析式,读懂图象,正确把握相关知识是解题的关键.12.(2019•嘉兴)小飞研究二次函数y =–(x –m )2–m +1(m 为常数)性质时如下结论:①这个函数图象的顶点始终在直线y =–x +1上;②存在一个m 的值,使得函数图象的顶点与x 轴的两个交点构成等腰直角三角形;③点A (x 1,y 1)与点B (x 2,y 2)在函数图象上,若x 1<x 2,x 1+x 2>2m ,则y 1<y 2;④当–1<x <2时,y 随x 的增大而增大,则m 的取值范围为m ≥2其中错误结论的序号是 A .① B .② C .③D .④【答案】C【解析】把(m ,–m +1)代入y =–x +1,–m +1=–m +1,左=右,故①正确;当–(x –m )2–m +1=0时,x 1=m -x 2=m +若顶点与x 轴的两个交点构成等腰直角三角形,则1–m +(1–m )2+1–m +(1–m )2=4(1–m ),即m 2–m =0,∴m =0或1时,∴存在一个m 的值,使得函数图象的顶点与x 轴的两个交点构成等腰直角三角形;故②正确;当x 1<x 2,且x 1、x 2在对称轴右侧时,∵–1<0,∴在对称轴右侧y 随x 的增大而减小,即y 1>y 2,故③错误; ∵–1<0,∴在对称轴左侧y 随x 的增大而增大, ∴m ≥2,故④正确, 故选C .【名师点睛】本题考查了二次函数的图象与性质,勾股定理,二次函数与坐标轴的交点,熟练掌握二次函数的图象与性质是解答本体的关键.对于二次函数y=a (x –h )2+k (a ,b ,c 为常数,a ≠0),当a >0时,抛物线开口向上,在对称轴的左侧y 随x 的增大而减小,在对称轴的右侧y 随x 的增大而增大;当a <0时,抛物线开口向下,在对称轴的左侧y 随x 的增大而增大,在对称轴的右侧y 随x 的增大而减小.其顶点坐标是(h ,k ),对称轴为x =h .13.(2019•荆州)二次函数2245y x x =--+的最大值是__________.【答案】7【解析】222452(1)7y x x x =--+=-++, 即二次函数245y x x =--+的最大值是7, 故答案为:7.【名师点睛】本题考查的是二次函数的最大值,熟练掌握配方法求二次函数的最值是解题的关键. 14.(2019•株洲)若二次函数2y ax bx =+的图象开口向下,则__________0(填“=”或“>”或“<”).【答案】<【解析】∵二次函数2y ax bx =+的图象开口向下, ∴0a <. 故答案为:<.【名师点睛】考查了二次函数图象与系数的关系.二次项系数a 决定抛物线的开口方向和大小.当0a >时,抛物线向上开口;当0a <时,抛物线向下开口;a 还可以决定开口大小,a 越大开口就越小. 15.(2019•武汉)抛物线2y ax bx c =++经过点(3,0)A -、(4,0)B 两点,则关于x 的一元二次方程2(1)a x c b bx -+=-的解是__________.【答案】12x =-,25x =【解析】依题意,得:9301640a b c a b c -+=⎧⎨++=⎩,解得:12b ac a=-⎧⎨=-⎩,所以,关于x 的一元二次方程a (x -1)2+c =b -bx 为:2(1)12a x a a ax --=-+,即:2(1)121x x --=-+, 化为:23100x x --=, 解得:12x =-,25x =, 故答案为:12x =-,25x =.【名师点睛】本题考查了抛物线上点的坐标特征,解方程组,解一元二次方程等,综合性较强,正确把握抛物线上的点的坐标一定满足抛物线的解析式,得到用含a 的式子表示出b 和c 是解题的关键. 16.(2019•徐州)已知二次函数的图象经过点(2,2)P ,顶点为(0,0)O 将该图象向右平移,当它再次经过点P 时,所得抛物线的函数表达式为__________. 【答案】21(4)2y x =- 【解析】设原来的抛物线解析式为:2y ax =(0)a ≠,把(2,2)P 代入,得24a =, 解得12a =, 故原来的抛物线解析式是:212y x =, 设平移后的抛物线解析式为:21()2y x b =-,把(2,2)P 代入,得212(2)2b =-, 解得0b =(舍去)或4b =, 所以平移后抛物线的解析式是:21(4)2y x =-, 故答案为:21(4)2y x =-. 【名师点睛】本题考查了二次函数图象与几何变换,二次函数的性质,二次函数图象上点的坐标特征.利用待定系数法确定原来函数关系式是解题的关键.17.(2019•天水)二次函数2y ax bx c =++的图象如图所示,若42M a b =+,N a b =-.则M 、N 的大小关系为M __________N .(填“>”、“=”或“<”)【答案】<【解析】当1x =-时,0y a b c =-+>, 当2x =时,420y a b c =++<,()42M N a b a b -=+--()420a b c a b c =++--+<,即M N <, 故答案为:<.【名师点睛】本题考查了二次函数图象上点的坐标特征,作差法比较代数式的大小,熟练掌握二次函数图象上点的坐标满足二次函数解析式是解答本题的关键.18.(2019•襄阳)如图,若被击打的小球飞行高度h (单位:m )与飞行时间t (单位:s )之间具有的关系为2205h t t =-,则小球从飞出到落地所用的时间为__________s .【答案】4【解析】依题意,令0h =得:∴20205t t =-,得:(205)0t t -=,解得:0t =(舍去)或4t =,∴即小球从飞出到落地所用的时间为4s ,故答案为:4.【名师点睛】本题考查了二次函数的性质在实际生活中的应用.此题为数学建模题,关键在于读懂小球从飞出到落地即飞行的高度为0时的情形,借助二次函数解决实际问题.此题较为简单.19.(2019•云南)已知k 是常数,抛物线y =x 2+(k 2+k -6)x +3k 的对称轴是y 轴,并且与x 轴有两个交点.(1)求k 的值:(2)若点P 在抛物线y =x 2+(k 2+k -6)x +3k 上,且P 到y 轴的距离是2,求点P 的坐标.【解析】(1)∵抛物线y =x 2+(k 2+k -6)x +3k 的对称轴是y 轴, ∴26022b k k x a +-=-=-=, 即k 2+k -6=0,解得k =-3或k =2,当k =2时,二次函数解析式为y =x 2+6,它的图象与x 轴无交点,不满足题意,舍去,当k =-3时,二次函数解析式为y =x 2-9,它的图象与x 轴有两个交点,满足题意,∴k =-3.(2)∵P 到y 轴的距离为2,∴点P 的横坐标为-2或2,当x =2时,y =-5;当x =-2时,y =-5,∴点P 的坐标为(2,-5)或(-2,-5).【名师点睛】本题考查了抛物线的对称轴,抛物线与x 轴的交点等知识,熟练掌握相关内容是解题的关键.20.(2019•绍兴)有一块形状如图的五边形余料ABCDE ,6AB AE ==,5BC =,90A B ∠=∠=︒,135C ∠=︒,90E ∠>︒.要在这块余料中截取一块矩形材料,其中一边在AE 上,并使所截矩形的面积尽可能大.(1)若所截矩形材料的一条边是BC 或AE ,求矩形材料的面积;(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.【解析】(1)①若所截矩形材料的一条边是BC,如图1所示,过点C作CF⊥AE于F,S1=AB·BC=6×5=30.②若所截矩形材料的一条边是AE,如图2所示,过点E作EF∥AB交CD于F,FG⊥AB于G,过点C作CH⊥FG于H,则四边形AEFG为矩形,四边形BCHG为矩形,∵∠C=135°,∴∠FCH=45°,∴△CHF为等腰直角三角形,∴AE=FG=6,HG=BC=5,BG=CH=FH,∴BG=CH=FH=FG–HG=6–5=1,∴AG=AB–BG=6–1=5,∴S2=AE·AG=6×5=30.(2)能;理由如下:在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,则四边形ANFM为矩形,四边形BCGM为矩形,∵∠C=135°,∴∠FCG=45°,∴△CGF为等腰直角三角形,∴MG=BC=5,BM=CG,FG=DG,设AM=x,则BM=6–x,∴FM=GM+FG=GM+CG=BC+BM=11–x,∴S=AM×FM=x(11–x)=–x2+11x=–(x–5.5)2+30.25,∴当x=5.5时,S的最大值为30.25.【名师点睛】本题考查了矩形的性质、等腰直角三角形的判定与性质、矩形面积公式以及二次函数的应用等知识;熟练掌握矩形的性质,证明三角形是等腰直角三角形是解题的关键.21.(2019•鄂尔多斯)某工厂制作,A B两种手工艺品,B每天每件获利比A多105元,获利30元的A与获利240元的B数量相等.(1)制作一件A和一件B分别获利多少元?(2)工厂安排65人制作A,B两种手工艺品,每人每天制作2件A或1件B.现在在不增加工人的情况下,增加制作C.已知每人每天可制作1件C(每人每天只能制作一种手工艺品),要求每天制作A,C两种手工艺品的数量相等.设每天安排x人制作B,y人制作A,写出y与x之间的函数关系式.(3)在(1)(2)的条件下,每天制作B不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知C每件获利30元,求每天制作三种手工艺品可获得的总利润W (元)的最大值及相应x 的值.【解析】(1)设制作一件A 获利x 元,则制作一件B 获利(105x +)元,由题意得:30240105x x =+,解得:15x =, 经检验,15x =是原方程的根,当15x =时,105120x +=,答:制作一件A 获利15元,制作一件B 获利120元.(2)设每天安排x 人制作B ,y 人制作A ,则2y 人制作C ,于是有:265y x y ++=, ∴16533y x =-+, 答:y 与x 之间的函数关系式为∴16533y x =-+. (3)由题意得:2152[1202(5)]230213090W y x x y x x y =⨯⨯+--+⨯=-++, 又∵16533y x =-+, ∴222165213090213090()2100195033W x x y x x x x x =-++=-++-+=-++, ∵221001950W x x =-++,对称轴为25x =,而25x =时,y 的值不是整数,根据抛物线的对称性可得:当26x =时,22261002619502198W =-⨯+⨯+=最大元.此时制作A 产品的13人,B 产品的26人,C 产品的26人,获利最大,最大利润为2198元.【名师点睛】考核知识点:分式方程,二次函数应用.根据题意列出方程,把实际问题转化为函数问题是关键.22.(2019•湘潭)某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店,A B 两种湘莲礼盒一个月的销售情况,A 种湘莲礼盒进价72元/盒,售价120元/盒,B 种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.(1)求该店平均每天销售这两种湘莲礼盒各多少盒?(2)小亮调査发现,A 种湘莲礼盒售价每降3元可多卖1盒.若B 种湘莲礼盒的售价和销量不变,当A 种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?【解析】(1)根据题意,可设平均每天销售A 礼盒x 盒,B 种礼盒为y 盒,则有(12072)(8040)1280120802800x y x y -+-=⎧⎨+=⎩,解得1020x y =⎧⎨=⎩, 故该店平均每天销售A 礼盒10盒,B 种礼盒为20盒.(2)设A 种湘莲礼盒降价m 元/盒,利润为W 元,依题意 总利润(12072)(10)8003m W m =--++, 化简得221161280(9)130733W m m m =-++=--+, ∵103a =-<, ∴当9m =时,取得最大值为1307,故当A 种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.【名师点睛】本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案. 23.(2019•辽阳)我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量y (千克)与销售单价x (元)符合一次函数关系,如图所示.(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围;(2)若在销售过程中每天还要支付其他费用450元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?【解析】(1)设一次函数关系式为(0)y kx b k =+≠,由图象可得,当30x =时,140y =;50x =时,100y =,∴1403010050k b k b =+⎧⎨=+⎩,解得2200k b =-⎧⎨=⎩,∴y 与x 之间的关系式为2200(3060)y x x =-+≤≤.(2)设该公司日获利为W 元,由题意得2(30)(2200)4502(65)2000W x x x =--+-=--+,∵20a =-<,∴抛物线开口向下,∵对称轴65x =,∴当65x <时,W 随着x 的增大而增大,∵3060x ≤≤,∴60x =时,W 有最大值,22(6065)200015=90W -⨯-+=最大值.即,销售单价为每千克60元时,日获利最大,最大获利为1950元.【名师点睛】此题主要考查二次函数的应用,解题的关键是熟知一次函数的图象与二次函数的性质.。
2019精选教育年中考数学专题复习分类练习 二次函数压轴题

2019年中考数学复习专题分类练习---二次函数压轴题2 是常数.,其中a1.已知二次函数y=x-(a-1)x+a-2 轴一定有公共点;为何值,该二次函数的图象与x (1)求证:不论a 点,求Cy 轴交于,与x 轴交于B ,D 两点,与(2)当a=4时,该二次函数的图象顶点为A 的面积.四边形ABCD 2如图所示2.已知抛物线y=x+1 ;, ),对称轴是 (1)填空:抛物线的顶点坐标是( .若BP 作PB ⊥x 轴,垂足为2)如图,已知y 轴上一点A (0,),点P 在抛物线上,过点(2 的坐标;△PAB 是等边三角形,求点POACOC 、BC 、PC ,当△,连接3)如图,在第二问的基础上,在抛物线有一点C (x ,y )AC 、( 的面积等于△BCP 的面积时,求C 的横坐标. 22m ?2mx ?y ?2xm ?4)(m 3.已知二次函数.是常数C )(m (1)求该函数图像的顶点的代数式表示的坐标;用含C m 为何值时,函数图像的顶点在第二、四象限的角平分线上?(2)当2Ax )x ?m)m ?a(x ?(y ?a)(0a ?ma ,,轴交于为常数,且4.已知二次函数的图像与DBAByC )( 的左侧.点,与在点,其顶点为轴交于点两点BA 的坐标;,(1)求点OxEDAECBOD )(,试讨论相似与△轴的垂线,垂足为为坐标原点(2)过点.若△作am 与的关系;2)mx ?m)??a(y ??a(x )在同一直角坐标系中,若该二次函数的图像与二次函数3(. 的图像组合成一个新的图像,则这个新图形的对称轴为5.阅读材料,解答问题.2xx -3>0.-2 例 用图像法解一元二次不等式: 2yxxyx 的二次函数.,则 -2是-3 解:设=a =1>0∵,∴抛物线开口向上,22yxxxx =3. 1=-10时,,-2-3=0又∵当 ,解得=2yxx -3的大致图像如图12-2 ∴由此得抛物线所示,=xxy >0.或 >3观察函数图像可知:当 时,<-12xxxx >3. -21-3>0的解集是:或< ∴-2xx -3<0的解集是________ (1)观察图像,直接写出一元二次不等式:.-22x -1>0仿照上例,用图像法解一元二次不等式:. (2)2﹣3ax ﹣4a (a <0)的图象与x 轴交于A 、B 两点(A6.如图①已知抛物线y=ax 在B 的左侧),与y 的正半轴交于点C ,连结BC ,二次函数的对称轴与x轴的交点E.(1)抛物线的对称轴与x轴的交点E坐标为,点A的坐标为;(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;页 1 第(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.xOy??????2和点中,抛物线7.在平面直角坐标系经过点.4,5AB?1,00aax??bx?3y?(1)求该抛物线的表达式;(2)求直线关于轴的对称直线的表达式;ABxll xx PP与该抛物线交于点,作垂直于,(3)点轴的直线是直线轴上的动点,过点MP的横坐标的取值范围.时,求点与直线交于点.当PNN<PMABx P12xy?F(0,上的点到点8.研究发现,抛物线41?y?l.的距离相等:1)的距离与到直线12xy?P上任1如图所示,若点是抛物线4PHPF?HlPH. 意一点,于点⊥,则yx O基于上述发现,对于平面直角坐标系M到到点中的点的距离与点,记点PPM M,dd为点称点的距离之和的最小值为F1122?yy?xx M关于抛物线的关联点时,称点. 为抛物线的关联距离;当4d≤2≤4412,,?4)M(2(40)M(1,2)M,5)M(0xy?)在点(中,抛物线,,,1的关联点是14324;______,(tA?1,3)A1)(t ABCDtC中,点2( ,点,在矩形. (2)如图12xy?dMtMABCD的取值范围;求点上,的关联距离①若=4,点关于抛物线在矩形412x?y tABCD的取值范围是②若矩形上的所有点都是抛物线的关联点,则4__________.CB,3,1)(?A,xOyCB(?1,1)(m,n)A1?n以点其中,,9.,,在平面直角坐标系已知点中,D,,DD. 为顶点的平行四边形有三个,记第四个顶点分别为,如图所示3123n,?m??1DD,D,);()若(1),,则点的坐标分别是()(,321页 2 第CCD,,D,DA,B的坐,使得点)是否存在点在同一条抛物线上?若存在,求出点(2312.标;若不存在,说明理由为边向上作等2m,以OBx点B在轴正半轴上,OB的长度为10.如图1,在平面直角坐标系中,2. O,A,B三点l:y=ax经过点+bx+c边三角形AOB,抛物线 ,a= ;,a= ,当m=3时时(1)当m=2的关系,并证明你的结论;a与m猜想(2)根据(1)中的结果,当2n,的长度为P、Q两点,PQ轴的平行线交抛物线的基础上)如图(32,在图1,作xl于;的关系式为 a= nAPQ△为等腰直角三角形时,a和(4)利用(2)(3)中的结论,求△AOB与△APQ的面积比.页 3 第Byx轴交于点与、两点,与11.轴交于如图,抛物线xD.轴于点,抛物线的对称轴交求抛物线的解析式;求的值;PCD使是以,为腰的等腰三角形?如果存在,在抛物线的对称轴上是否存在点P的坐标;如果不存在,请说明理由;直接写出点EBCExFE运动点作是线段,当点上的一个动点,过点轴的垂线与抛物线相交于点EFE点的坐标.最长?求出此时到什么位置时线段320)?c??ax(ax?y x轴交如图,二次函数的图像与12.2y1,0)?A(CBA,点两点,与,已知点于、轴交于点2)(0,C.; 求抛物线的函数解析式,并求出该抛物线的顶点坐标(1)D若点是抛物线在第一象限的部分上的一动点,(2)OCDBD;的面积最大时,求点①当四边形的坐标BCBEF?ABEFDE为钝角三角形时,②若于点为当的中点,,的延长线交线段yD.请直接写出点的范围的纵坐标20).(﹣1,B两点,与y轴交于C点,且如图,抛物线13.Ay=x 与+bx﹣2x轴交于A,的坐标;1)求抛物线的解析式及顶点D(的形状,证明你的结论;2)判断△ABC(的值.的值最小时,求m0)是x轴上的一个动点,当MC+MD)点(3M(m,).3,,已知直线y=kx与抛物线6Ay=交于点(114.如图的长度;y=kx的解析式和线段OA(1)求直线,O不重合)M(点M、,交为抛物线第一象限内的动点,过点(2)点PP作直线PMx轴于点QN与线段N.试探究:线段QM轴于点的垂线,交作直线,再过点于点交直线OAQQPMy的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;页 4 第(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D (m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?(a≠0)的图象与x轴交于A、B两点,与y轴交于点15.如图,二次函数y=axC,已知点A 2+x+c(﹣1,0),点C(0,2).(1)求抛物线的函数解析式,并求出该抛物线的顶点坐标;(2)若点D是抛物线在第一象限的部分上的一动点,①当四边形OCDB的面积最大时,求点D的坐标;②若E为BC的中点,DE的延长线交线段AB于点F,当△BEF为钝角三角形时,请直接写出点D 的纵坐标y的范围.axOy a?2BA,二次函数的横坐标分别为16.在平面直角坐标系、中,点、2?(m?2)x?y??x2mm2a?m?ddBA为常数(,且).的图像经过点满足、y?kx?b AB两点的图像经过若一次函数. 、 (1)1a?1d??1k的值;①当、时,求yx d的取值范围的增大而减小,求②若随.1x4?2a??d??4a?AB轴的位置关系,并说明理由与且时,判断直线; (2)当、aABBAy 轴分别相交的变化而变化,设点 (3)点、、的位置随着运动的路线与CCDCD D的长;的长度会发生变化吗?如果不变,求出如果变化,于点、,线段请说明理由.页 5 第。
2019年秋人教版九年级《二次函数》压轴大题专项训练题(含答案)

《二次函数》压轴大题专项训练题一.解答题1.如图,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D是抛物线的顶点.(1)求抛物线的解析式.(2)点N是y轴负半轴上的一点,且ON=,点Q在对称轴右侧的抛物线上运动,连接QO,QO与抛物线的对称轴交于点M,连接MN,当MN平分∠OMD时,求点Q的坐标.(3)直线BC交对称轴于点E,P是坐标平面内一点,请直接写出△PCE与△ACD全等时点P的坐标.2.在平面直角坐标系中,如果某点的横坐标与纵坐标的和为10,则称此点为“合适点”例如,点(1,9),(﹣2019,2029)…都是“合适点”.(1)求函数y=2x+1的图象上的“合适点”的坐标;(2)求二次函数y=x2﹣5x﹣2的图象上的两个“合适点”A,B之间线段的长;(3)若二次函数y=ax2+4x+c的图象上有且只有一个合适点”,其坐标为(4,6),求二次函数y=ax2+4x+c的表达式;(4)我们将抛物线y=2(x﹣n)2﹣3在x轴下方的图象记为G1,在x轴及x轴上方图象记为G2,现将G1沿x轴向上翻折得到G3,图象G2和图象G3两部分组成的记为G,当图象G上恰有两个“合适点”时,直接写出n的取值范围.3.若关于x的二次函数y=ax2+bx+c(a,b,c为常数)与x轴交于两个不同的点A(x1,0),B(x2,0)与y轴交于点C,其图象的顶点为点M,O是坐标原点.(1)若A(﹣2,0),B(4,0),C(0,3)求此二次函数的解析式并写出二次函数的对称轴;(2)如图1,若a>0,b>0,△ABC为直角三角形,△ABM是以AB=2的等边三角形,试确定a,b,c的值;(3)设m,n为正整数,且m≠2,a=1,t为任意常数,令b=3﹣mt,c=﹣3mt,如果对于一切实数t,AB≥|2t+n|始终成立,求m、n的值.4.如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.(1)求该抛物线的函数解析式.(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF :S△CDF=4:3时,求点D的坐标.(3)如图2,点E的坐标为(0,﹣2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,将矩形AOCD 中的点D 沿AE 对折,使点D 落在OC 上F 点,已知AO =8.AD =10,G (﹣1,7),已知抛物线过点O ,F ,G .(1)求抛物线的解析式;(2)点M 为抛物线的对称轴上一动点,当|MG ﹣MF |取得最大值时,求点M 的坐标.(3)一条动直线过平面上一点B ,点B 的坐标为(3,﹣8),且该直线与(1)中的抛物线交于P 、Q 两点,请判断;是否为定值,若是定值请求出定值,着不是定值请求出其取值范围.(参考公式:在平面直角坐标系中,若H (x 1,y 1),N (x 2,y 2),则H ,N 两点间的距离为HN =).6.如图,在平面直角坐标系中,抛物线y =﹣x 2+bx +c 与x 轴交于B ,C 两点,与y 轴交于点A ,直线y =﹣x +2经过A ,C 两点,抛物线的对称轴与x 轴交于点D ,直线MN 与对称轴交于点G ,与抛物线交于M ,N 两点(点N 在对称轴右侧),且MN ∥x 轴,MN =7.(1)求此抛物线的解析式.(2)求点N 的坐标.(3)过点A 的直线与抛物线交于点F ,当tan ∠FAC =时,求点F 的坐标.(4)过点D 作直线AC 的垂线,交AC 于点H ,交y 轴于点K ,连接CN ,△AHK 沿射线AC 以每秒1个单位长度的速度移动,移动过程中△AHK 与四边形DGNC 产生重叠,设重叠面积为S ,移动时间为t (0≤t ≤),请直接写出S 与t 的函数关系式.7.如图,抛物线y=ax2﹣2x+c与x轴交于点A,B两点,与y轴交于点C,直线y=x+3经过A,C两点.(1)求抛物线的解析式;(2)点N是x轴上的动点,过点N作x轴的垂线,交抛物线于点M,交直线AC于点H.①点D在线段OC上,连接AD、BD,当AH=BD时,求AD+AH的最小值;②当OC=3OD时将直线AD绕点A旋转45°,使直线AD与y轴交于点P,请直接写出点P的坐标.8.在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(﹣t ,y 1)和(t ,y 2)(其中t 为常数且t >0),将x <﹣t 的部分沿直线y =y 1翻折,翻折后的图象记为G 1;将x >t 的部分沿直线y =y 2翻折,翻折后的图象记为G 2,将G 1和G 2及原函数图象剩余的部分组成新的图象G .例如:如图,当t =1时,原函数y =x ,图象G 所对应的函数关系式为y =.(1)当t =时,原函数为y =x +1,图象G 与坐标轴的交点坐标是 .(2)当t =时,原函数为y =x 2﹣2x①图象G 所对应的函数值y 随x 的增大而减小时,x 的取值范围是 .②图象G 所对应的函数是否有最大值,如果有,请求出最大值;如果没有,请说明理由.(3)对应函数y =x 2﹣2nx +n 2﹣3(n 为常数).①n =﹣1时,若图象G 与直线y =2恰好有两个交点,求t 的取值范围.②当t =2时,若图象G 在n 2﹣2≤x ≤n 2﹣1上的函数值y 随x 的增大而减小,直接写出n 的取值范围.9.如图1,抛物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),与y轴交于点C,顶点为D,直线AD交y轴于点E.(1)求抛物线的解析式.(2)如图2,将△AOE沿直线AD平移得到△NMP.①当点M落在抛物线上时,求点M的坐标.②在△NMP移动过程中,存在点M使△M BD为直角三角形,请直接写出所有符合条件的点M的坐标.10.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点C(0,4),交x轴正半轴于点B,连接AC,点E是线段OB上一动点(不与点O,B重合),以OE为边在x轴上方作正方形OEFG,连接FB,将线段FB绕点F逆时针旋转90°,得到线段FP,过点P作PH∥y轴,PH交抛物线于点H,设点E(a,0).(1)求抛物线的解析式.(2)若△AOC与△FEB相似,求a的值.(3)当PH=2时,求点P的坐标.11.在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.(1)求抛物线的解析式.(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD =2S△APQ时,求点P的坐标.(3)如图2,G是线段OC上一个动点,连接DG,过点G作GM⊥DG交AC于点M,过点M 作射线MN,使∠NMG=60°,交射线GD于点N;过点G作GH⊥MN,垂足为点H,连接BH.请直接写出线段BH的最小值.12.如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C.(1)求这个抛物线的函数表达式.(2)点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP 面积的最大值.(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.13.如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交点C,抛物线y =﹣2x2+bx+c过A,C两点,与x轴交于另一点B.(1)求抛物线的解析式.(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当EF=BF 时,求sin∠EBA的值.(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.14.如图,在平面直角坐标系中,O为坐标原点,抛物线y=x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0).P为该抛物线上一动点,设点P的横坐标为m.(1)求抛物线对应的函数关系式;(2)将该抛物线沿y轴向下平移AB个单位,点P的对应点为P',若OP=OP',求△OPP'的面积;(3)连结AP,BP,设△APB的面积为S,当﹣2≤m≤2时,求S的取值范围;(4)若二次函数的自变量x的取值范围是m≤x≤m+1,且最大值为,直接写出m的值.15.如图,过点A(0,1)作直线PQ,交抛物线y=x2于P,Q两点,点B是点A关于x 轴的对称点.(1)试判断以点P为圆心,PA为半径的圆与直线l:y=﹣1的位置关系;(2)证明:直线BQ和直线BP关于y轴对称;(3)过点P作y轴的平行线交直线l:y=﹣1于H点,连接AH交x轴于E,直线PE与抛物线y=x2是否还有除点P之外别的交点?请说明理由.参考答案一.解答题1.解:(1)∵抛物线y=ax2+bx﹣3经过A(﹣1,0),B(3,0)两点,∴,解得:,∴抛物线的解析式为:y=x2﹣2x﹣3.(2)如图1,设对称轴与x轴交于点H,∵MN平分∠OMD,∴∠OMN=∠DMN,又∵DM∥ON,∴∠DMN=∠MNO,∴∠MNO=∠OMN,∴OM=ON=.在Rt△OHM中,∠OHM=90°,OH=1.∴,∴M1(1,1);M2(1,﹣1).①当M1(1,1)时,直线OM解析式为:y=x,依题意得:x=x2﹣2x﹣3.解得:,,∵点Q在对称轴右侧的抛物线上运动,∴Q点纵坐标y=.∴,②当M2(1,﹣1)时,直线OM解析式为:y=﹣x,同理可求:,综上所述:点Q 的坐标为:,,(3)由题意可知:A (﹣1,0),C (0,﹣3),D (1,﹣4),∴AC =,AD =,CD =,∵直线BC 经过B (3,0),C (0,﹣3), ∴直线BC 解析式为y =x ﹣3,∵抛物线对称轴为x =1,而直线BC 交对称轴于点E , ∴E 坐标为(1,﹣2);∴CE =,设P 点坐标为(x ,y ), 则CP 2=(x ﹣0)2+(y +3)2, 则EP 2=(x ﹣1)2+(y +2)2,∵CE =CD ,若△PCE 与△ACD 全等,有两种情况, Ⅰ.PC =AC ,PE =AD ,即△PCE ≌△ACD .∴,解得:,,即P 点坐标为P 1(﹣3,﹣4),P 2(﹣1,﹣6). Ⅱ.PC =AD ,PE =AC ,即△PCE ≌△ACD .∴,解得:,,即P 点坐标为P 3(2,1),P 4(4,﹣1).故若△PCE 与△ACD 全等,P 点有四个,坐标为P 1(﹣3,﹣4),P 2(﹣1,﹣6),P 3(2,1),P(4,﹣1).42.解:(1)联立x+y=10和y=2x+1并解得:x=3,y=7,故“合适点”的坐标为(3,7);(2)联立x+y=10和y=x2﹣5x﹣2并解得:x=﹣2或6,故点A、B的坐标分别为:(﹣2,12)、(6,4),则AB==8;(3)将点(4,6)代入二次函数表达式得:16a+16+c=6…①,联立y=10﹣x和y=ax2+4x+c并整理得:ax2+5x+(c﹣10)=0,△=25﹣4a(c﹣10)=0…②,联立①②并解得:a=﹣,c=0,故抛物线的表达式为:y=﹣x2+4x;(4)图象G,如下图所示:G 2的顶点坐标为(n,3),则G2的函数表达式为:y=﹣2(x﹣n)2+3,x+y=10,则y=10﹣x,设直线m为:y=10﹣x,①当直线m与图象G2只有一个交点时,直线m与图象G有3个交点,即有3个“合适点”,联立直线m与G2的表达式得:y=﹣2(x﹣n)2+3=10﹣x,整理得:2x2﹣(4n+1)x+(2n2+7)=0,△=b2﹣4ac=8n﹣55=0,解得:n=,故当n<时,图象G恰好有2个“合适点”;②当直线m经过点A、B时,直线m与图象G有3个交点,即有3个“合适点”,则在这两个点之间有2个“合适点”,直线m与x轴的交点为(10,0),将(10,0)代入y=2(x﹣n)2﹣3并解得:n=10,故10﹣<n<10+;综上,n的取值范围为:n<或10﹣<n<10+.3.解:(1)函数的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),则﹣8a=3,解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+3;(2)如图所示,△ABC为直角三角形,则∠ACB=90°,∵△AMB 是等边三角形,则点C 是MB 的中点,则BC =MC =1,则BO =BC =,同理OC =,OA =2﹣=,则点A 、B 、C 的坐标分别为(﹣,0)、(,0),(0,﹣),则函数的表达式为:y =a (x +)(x ﹣)=a (x 2+x ﹣),即﹣a =﹣,解得:a =,则函数表达式为:y =x 2+x ﹣;(3)y =ax 2+bx +c =x 2+(3﹣mt )x ﹣3mt , 则x 1+x 2=mt ﹣3,x 1x 2=﹣3mt ,AB =x 2﹣x 1==|mt +3|≥|2t +n |,对于一切实数t ,上式都成立, 则必然存在|mt +3|=|2t +n |, 即:mt +3=±(2t +n ), ∵m ≠2,则m =﹣2,n =﹣3, 即m =﹣2、n =﹣3. 4.解:(1)∵OB =OC =4, ∴B (4,0),C (0,4),把B (4,0),C (0,4)代入y =ax 2+3x +c ,得,解得∴抛物线的函数解析式为y =﹣x 2+3x +4;(2)如图1,设直线BC解析式为y=kx+b,则,解得∴直线BC解析式为y=﹣x+4,令点D、F的横坐标分别为x D,x F,∵S△COF :S△CDF=4:3,∴S△COF =S△COD,即OC•x F=×OC•x D,∴x D=x F,设点D横坐标为7t,点F横坐标为4t,∵点F在直线BC上,∴F(4t,4﹣4t),设直线OF解析式为y=k′x,则4﹣4t=4tk′,∴k′==,∴直线OF解析式为y=x,∵点D在直线OF上,∴D(7t,7﹣7t),将D(7t,7﹣7t)代入y=﹣x2+3x+4中,得7﹣7t=﹣(7t)2+3×7t+4,解得:t1=,t2=,∴D的坐标为(1,6)或(3,4);(3)①当∠PEB=2∠OBE,且点P在x轴上方时,如图2,作BE的垂直平分线交OB于F,连接EF,在∠BEO内部作射线EP交x轴于G,交抛物线于P,使∠PEB=∠EFO,过点G作GH⊥BE于H,则BF=EF,设BF=EF=m,∴OF=OB﹣BF=4﹣m在Rt△OEF中,∠EOF=90°,∵OE2+OF2=EF2∴22+(4﹣m)2=m2,解得:m=,∴BF=EF=,OF=4﹣=,∴tan∠OBE===,tan∠OFE===,∵BF=EF∴∠BEF=∠OBE∵∠OFE=∠BEF+∠OBE∴∠OFE=2∠OBE∵∠PEB=2∠OBE∴∠PEB=∠OFE∴tan∠PEB==tan∠OFE=,设GH=4a,则EH=3a,∴BE===2,BH=2﹣3a∵=tan∠∠OBE=,∴=,解得:a=,∴GH=,BH=∴BG==∴OG=OB﹣BG=4﹣=∴G(,0),设直线EG解析式为y=k″x+b″,则,解得∴直线EG解析式为y=x﹣2,联立方程组,解得:(舍去),,∴P(,),②当∠PEB=2∠OBE,且点P在x轴下方时,如图3,过点E作EF⊥y轴,作点B关于直线EF的对称点G,连接BG交EF于F,射线EG交抛物线于点P,∵E(0,﹣2),∴直线EF为:y=﹣2∵B(4,0),∴G(4,﹣4)∴直线EG解析式为y=﹣x﹣2,解方程组,得,(不符合题意,舍去),∴P(,);③当∠PBE=2∠OBE,且点P在x轴上方时,如图4,在y轴正半轴上截取OF=OE=2,作射线BF交抛物线于P,在△BOE和△BOF中,∴△BOE≌△BOF(SAS)∴∠PBO=∠OBE∴∠PBE=2∠OBE易求得直线PF解析式为y=﹣x+2,联立方程组,解得(不符合题意,舍去),,∴P(﹣,);④当∠PBE=2∠OBE,且点P在x轴下方时,如图5,过点E作EF⊥BE交直线BP于F,过F作FG⊥y轴于G,由①知:tan∠PBE==,BE=2∴EF=∵∠EGF=∠BOE=∠BEF=90°∴∠BEO+∠FEG=∠BEO+OBE=90°∴∠FEG=∠OBE∴△EFG∽△BEO∴==,即==∴FG=,EG=∴OG=OE+EG=2+=∴F(,﹣)易求得直线BF解析式为y=x﹣22,联立方程组,解得(舍去),∴∴P(﹣,﹣);综上所述,符合条件的点P的坐标为:(,)、(,)、(﹣,)、(﹣,﹣).5.解:(1)∵矩形AOCD中的点D沿AE对折,使点D落在OC上F点,∴AF=AD=10,在Rt△AOF中,OF==6,∴F(6,0),设抛物线解析式为y=ax(x﹣6),把G(﹣1,7)代入得a×(﹣1)×(﹣1﹣6)=7,解得a=1,∴抛物线解析式为y=x(x﹣6),即y=x2﹣6x;(2)∵点M为抛物线的对称轴上一动点,∴MF=MO,∴|MG﹣MF|=|MG﹣MO|≤GO(当且仅当G、O、M共线时,取等号),易得直线OG的解析式为y=﹣7x,当x=3时,y=﹣7x=﹣21,∴当|MG﹣MF|取得最大值时,点M的坐标为(3,﹣21);(3)1<的值≤2.理由如下:设直线PQ的解析式为y=kx+b,把B(3,﹣8)代入得3k+b=﹣8,则b=﹣3k﹣8,∴直线PQ的解析式为y=kx﹣3k﹣8,设P(x1,kx1﹣3k﹣8),Q(x2,kx2﹣3k﹣8),则x 1、x 2为方程x 2﹣6x =kx ﹣3k ﹣8的两根, ∴x 1+x 2=6+k ,x 1x 2=3k +8,∴PQ ==•=•=•=•,PB ==•=•|x 1﹣3|,BQ ==•=•|x 2﹣3|,∴PB •BQ =(1+k 2)|(x 1﹣3)(x 2﹣3)|=(1+k 2)|(x 1x 2﹣3x 1x 2+9|=(1+k 2)|3k +8﹣3(6+k )+9|=1+k 2,∴===∵0<≤3 ∴1<的值≤2.6.解:(1)直线y =﹣x +2经过A ,C 两点,则点A 、C 的坐标分别为(0,2)、(4,0),则c =2,抛物线表达式为:y =﹣x 2+bx +2,将点C 坐标代入上式并解得:b =,故抛物线的表达式为:y =﹣x 2+x +2…①;(2)抛物线的对称轴为:x =,点N 的横坐标为: +=5,故点N的坐标为(5,3);(3)∵tan∠ACO==tan∠FAC=,即∠ACO=∠FAC,①当点F在直线AC下方时,设直线AF交x轴于点R,∵∠ACO=∠FAC,则AR=CR,设点R(r,0),则r2+4=(r﹣4)2,解得:r=,即点R的坐标为:(,0),将点R、A的坐标代入一次函数表达式:y=mx+n得:,解得:,故直线AR的表达式为:y=﹣x+2…②,联立①②并解得:x=,故点F(,﹣);②当点F在直线AC的上方时,∵∠ACO=∠F′AC,∴AF′∥x轴,则点F′(3,2);综上,点F的坐标为:(3,2)或(,﹣);(4)如图2,设∠ACO=α,则tanα==,则sinα=,cosα=;①当0≤t≤时(左侧图),设△AHK移动到△A′H′K′的位置时,直线H′K′分别交x轴于点T、交抛物线对称轴于点S,则∠DST=∠ACO=α,过点T作TL⊥KH,则LT=HH′=t,∠LTD=∠ACO=α,则DT====t,DS=,S=S=DT×DS=t2;△DST②当<t≤时(右侧图),同理可得:S=S=×DG×(GS′+DT′)=3+(+﹣)=t﹣;梯形DGS′T′综上,S=.7.解:(1)直线y=x+3经过A,C两点,则点A、C的坐标分别为(﹣3,0)、(0,3),将点A、C的坐标代入抛物线表达式得:,解得:,故抛物线的表达式为:y=﹣x2﹣2x+3;(2)①令y=﹣x2﹣2x+3=0,则x=﹣3或1,即点B(1,0),当AH=BD时,AD+AH=AD+BD,当A、B、D三点共线时,AD+AH=AD+BD最小,最小值为:AB=1﹣(﹣3)=4,答:AD+AH的最小值为4;②当OC=3OD时,OD=1,AD=,则tan∠ADO=,则sinα=,当点P在y轴上方时,如下图,过点P作△APD的高PH,交AD的延长线与点H,设:PH=m,∵∠PAD=45°,则AH=m,tan∠PDH==tanα=3,解得:m=,PD===5,故点P(0,6);当点P在y轴下方时,如下图所示,同理可得: DP′=故:点P(0,﹣);综上,点P(0,6)或(0,﹣)8.解:(1)当x=时,y=,当x≥时,翻折后函数的表达式为:y=﹣x+b,将点(,)坐标代入上式并解得:翻折后函数的表达式为:y=﹣x+2,当y=0时,x=2,即函数与x轴交点坐标为:(2,0);同理沿x=﹣翻折后函数的表达式为:y=﹣x,函数与x轴交点坐标为:(0,0),故答案为:(2,0)或(0,0);(2)当t=时,由函数为y=x2﹣2x构建的新函数G的图象,如下图所示:点A、B分别是t=﹣、t=的两个翻折点,点C是抛物线原顶点,则点A、B、C的横坐标分别为﹣、1、,①函数值y随x的增大而减小时,﹣≤x≤1或x≥,故答案为:﹣≤x≤1或x≥;②函数在点A处取得最大值,x=﹣,y=(﹣)2﹣2×(﹣)=,答:图象G所对应的函数有最大值为;(3)n=﹣1时,y=x2+2x﹣2,①参考(2)中的图象知:当y=2时,y=x2+2x﹣2=2,解得:x=﹣1±,若图象G与直线y=2恰好有两个交点,则t>﹣1;②函数的对称轴为:x=n,令y=x2﹣2nx+n2﹣3=0,则x=n±,当t=2时,点A、B、C的横坐标分别为:﹣2,n,2,当x=n在y轴左侧时,(n≤0),此时原函数与x轴的交点坐标(n+,0)在x=2的左侧,如下图所示,则函数在AB段和点C右侧,故:﹣2≤x≤n,即:在﹣2≤n2﹣2≤﹣x≤n2﹣1≤n,解得:n≤;当x=n在y轴右侧时,(n≥0),同理可得:n≥;综上:n≤或n≥.9.解:(1)抛物线的表达式为:y=a(x+2)(x﹣6)=a(x2﹣4x﹣12)=ax2﹣4ax﹣12a,即:﹣12a=6,解得:a=﹣,故抛物线的表达式为:y=﹣x2+2x+6,令y=0,解得:x=4或﹣2,故点A(﹣2,0),函数的对称轴为:x=2,故点D(2,8);(2)将点A、D的坐标代入一次函数表达式:y=mx+n得:,解得:,故直线AD的表达式为:y=2x+4,设点N(n,2n+4),∵MN=OA=2,则点M(n+2,2n+4),①将点M的坐标代入抛物线表达式得:2n+4=﹣(n+2)2+2(n+1)+6,解得:n=﹣2±2,故点M的坐标为(2,4)或(﹣2,﹣4);②点M(n+2,2n+4),点B、D的坐标分别为(6,0)、(2,8),则BD2=(6﹣2)2+82,MB2=(n﹣4)2+(2n+4)2,MD2=n2+(2n﹣4)2,当∠BMD为直角时,由勾股定理得:(6﹣2)2+82=(n﹣4)2+(2n+4)2+n2+(2n﹣4)2,解得:n=,当∠MBD为直角时,同理可得:n=﹣4,当∠MDB为直角时,同理可得:n=,故点M的坐标为:(﹣2,﹣4)或(,)或(,)或(,).10.解:(1)点C(0,4),则c=4,二次函数表达式为:y=﹣x2+bx+4,将点A的坐标代入上式得:0=﹣1﹣b+4,解得:b=3,故抛物线的表达式为:y=﹣x2+3x+4;(2)tan∠ACO==,△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,即:tan∠FEB=或4,∵四边形OEFG为正方形,则FE=OE=a,EB=4﹣a,则或,解得:a=或;(3)令y=﹣x2+3x+4=0,解得:x=4或﹣1,故点B(4,0);分别延长CF、HP交于点N,∵∠PFN+∠BFN=90°,∠FPN+∠PFN=90°,∴∠FPN=∠NFB,∵GN∥x轴,∴∠FPN=∠NFB=∠FBE,∵∠PNF=∠BEF=90°,FP=FB,∴△PNF≌△BEF(AAS),∴FN=FE=a,PN=EB=4﹣a,∴点P(2a,4),点H(2a,﹣4a2+6a+4),∵PH=2,即:﹣4a2+6a+4﹣4=|2|,解得:a=1或或或(舍去),故:点P的坐标为(1,4)或(,4)或().11.解:(1)将点A(3,4),B(﹣1,0)代入y=ax2+bx+4,得:,解得,∴y=﹣x2+3x+4;(2)如图1,过点P作PE∥x轴,交AB于点E,∵A (3,4),AD ⊥x 轴,∴D (3,0),∵B (﹣1,0),∴BD =3﹣(﹣1)=4,∵S △AQD =2S △APQ ,△AQD 与△APQ 是等高的两个三角形,∴=,∵PE ∥x 轴,∴△PQE ∽△DQB ,∴==,∴=,∴PE =2,∴可求得直线AB 的解析式为y =x +1,设E (x ,x +1),则P (x ﹣2,x +1),将点P 坐标代入y =﹣x 2+3x +4得﹣(x +2)2+3(x +2)+4=x +1,解得x 1=3+,x 2=3﹣,当x =3+时,x ﹣2=3+﹣2=1+,x +1=3++1=4+,∴点P (1+,4+);当x =3﹣时,x ﹣2=3﹣﹣2=1﹣,x +1=3﹣+1=4﹣,∴P (1﹣,4﹣),∵点P 是直线AB 上方抛物线上的一个动点,∴﹣1<x ﹣2<3,∴点P 的坐标为(1+,4+)或(1﹣,4﹣);(3)由(1)得,抛物线的解析式为y =﹣x 2+3x +4,∴C (0,4),∵A (3,4),∴AC ∥x 轴,∴∠OCA =90°,∴GH ⊥MN ,∴∠GHM=90°,在四边形CGHM中,∠GCM+∠GHM=180°,∴点C、G、H、M共圆,如图2,连接CH,则∠GCH=∠GMH=60°,∴点H在与y轴夹角为60°的定直线上,∴当BH⊥CH时,BH最小,过点H作HP⊥x轴于点P,并延长PH交AC于点Q,∵∠GCH=60°,∴∠HCM=30°,又BH⊥CH,∴∠BHC=90°,∴∠BHP=∠HCM=30°,设OP=a,则CQ=a,∴QH=a,∵B(﹣1,0),∴OB=1,∴BP=1+a,在Rt△BPH中,HP==(a+1),BH==2(1+a),∵QH+HP=AD=4,∴a+(a+1)=4,解得a=,=2(1+a)=.∴BH最小12.解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3)=ax2+2ax﹣3a,即﹣3a=2,解得:a=﹣,故抛物线的表达式为:y=﹣x2﹣x+2,则点C(0,2),函数的对称轴为:x=1;(2)连接OP,设点P(x,﹣x2﹣x+2),则S=S四边形ADCP=S△APO+S△CPO﹣S△ODC=×AO×y P+×OC×|x P|﹣×CO×OD=(﹣x2﹣x+2)×2×(﹣x)﹣=﹣x2﹣3x+2,∵﹣1<0,故S有最大值,当x=﹣时,S的最大值为;(3)存在,理由:△MNO为等腰直角三角形,且∠MNO为直角时,点N的位置如下图所示:①当点N在x轴上方时,点N的位置为N1、N2,N1的情况(△M1N1O):设点N1的坐标为(x,﹣x2﹣x+2),则M1E=x+1,过点N1作x轴的垂线交x轴于点F,过点M1作x轴的平行线交N1F于点E,∵∠FN 1O +∠M 1N 1E =90°,∠M 1N 1E +∠EM 1N 1=90°,∴∠EM 1N 1=∠FN 1O , ∠M 1N 1E =∠N 1OF =90°,ON 1=M 1N 1, ∴△M 1N 1E ≌△N 1OF (AAS ),∴M 1E =N 1F ,即:x +1=﹣x 2﹣x +2,解得:x =(舍去负值),则点N 1(,);N 2的情况(△M 2N 2O ):同理可得:点N 2(,);②当点N 在x 轴下方时,点N 的位置为N 3、N 4,同理可得:点N 3、N 4的坐标分别为:(,)、(,);综上,点N 的坐标为:(,)或(,)或(,)或(,).13.解:(1)在y =2x +6中,当x =0时y =6,当y =0时x =﹣3, ∴C (0,6)、A (﹣3,0),∵抛物线y =﹣2x 2+bx +c 的图象经过A 、C 两点,∴,解得,∴抛物线的解析式为y =﹣2x 2﹣4x +6;(2)令﹣2x 2﹣4x +6=0, 解得x 1=﹣3,x 2=1, ∴B (1,0), ∵点E 的横坐标为t , ∴E (t ,﹣2t 2﹣4t +6),如图,过点E 作EH ⊥x 轴于点H ,过点F 作FG ⊥x 轴于点G ,则EH ∥FG ,∵EF =BF ,∴===,∵BH =1﹣t ,∴BG =BH =﹣t ,∴点F 的横坐标为+t ,∴F (+t , +t ),∴﹣2t 2﹣4t +6=(+t ),∴t 2+3t +2=0,解得t 1=﹣2,t 2=﹣1, 当t =﹣2时,﹣2t 2﹣4t +6=6, 当t =﹣1时,﹣2t 2﹣4t +6=8, ∴E 1(﹣2,6),E 2(﹣1,8),当点E 的坐标为(﹣2,6)时,在Rt △EBH 中,EH =6,BH =3,∴BE ===3,∴sin ∠EBA ===;同理,当点E 的坐标为(﹣1,8)时,sin ∠EBA ==,∴sin ∠EBA 的值为或;(3)∵点N 在对称轴上,∴x N==﹣1,①当EB为平行四边形的边时,分两种情况:(Ⅰ)点M在对称轴右侧时,BN为对角线,∵E(﹣2,6),x N=﹣1,﹣1﹣(﹣2)=1,B(1,0),∴x M=1+1=2,当x=2时,y=﹣2×22﹣4×2+6=﹣10,∴M(2,﹣10);(Ⅱ)点M在对称轴左侧时,BM为对角线,∵x N=﹣1,B(1,0),1﹣(﹣1)=2,E(﹣2,6),∴x M=﹣2﹣2=﹣4,当x=﹣4时,y=﹣2×(﹣4)2﹣4×(﹣4)+6=﹣10,∴M(﹣4,﹣10);②当EB为平行四边形的对角线时,∵B(1,0),E(﹣2,6),x N=﹣1,∴1+(﹣2)=﹣1+x M,∴x M=0,当x=0时,y=6,∴M(0,6);综上所述,M的坐标为(2,﹣10)或(﹣4,﹣10)或(0,6).14.解:(1)由题意,得.解得.则该抛物线解析式为:y=﹣x2+x+;(2)∵抛物线y=x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),∴AB=4.∴抛物线是向下平移了2个单位,∴PP ′=2. ∵OP =OP ',∴当y =1时,﹣x 2+x +=1.∴x 1=1﹣,x 2=1+;∴△OPP '的面积为或;(3)将抛物线:y =﹣x 2+x +配方,得:y =﹣(x ﹣1)2+2. 当m =1时,S =4. 当m =2时,S =3. 当m =﹣2时,S =5.∴当﹣2≤m ≤2时,S 的取值范围为:0<S ≤5;(4)m =2或m =﹣1.解析:抛物线y =﹣(x ﹣1)2+2的对称轴是直线x =1. ①当m +1<1,即m <0时,当x =m +1时,y 取得最大值为,即﹣(m +1﹣1)2+2=, 解得m 1=1,m 2=﹣1(舍去). ∴m =﹣1.②当m +1≥1,且m ≤1,即0≤m ≤1时,当x =1时,y 取得最大值为2≠,即﹣(m +1﹣1)2+2=, 解得m 1=1,m 2=﹣1(舍去). ∴m =﹣1.③当m >1,x =m 时,y 取得最大值为,即﹣(m ﹣1)2+2=,解得m 1=2,m 2=0(舍去). 综上所述,m =2或m =﹣1.15.解:(1)以点P 为圆心,PA 为半径的圆与直线l :y =﹣1的位置关系为相切.设点P (m ,m 2),点P 到直线l :y =﹣1的距离为d =+1,则PA ==+1,d =m 2﹣(﹣1)=+1,∴PA =d∴以点P 为圆心,PA 为半径的圆与直线l :y =﹣1相切;(2)如图,过点P 作PH ⊥直线l 于H ,作PA ⊥y 轴于M ,过点Q 作QG ⊥l 于G ,QN ⊥y 轴于N ,则:∠QGB =∠QNA =∠QNB =∠GBN =∠HBM =∠PMA =∠PHB =90° ∴四边形BGQN 、BHPM 均为矩形, ∴BN =QG ,BM =PH由(1)知:PA =PH ,QA =QG ∴QA =BN ,PA =BM ∵∠PAM =∠QAN ∴△PAM ∽△QAN∴=∴=∵∠BMP =∠BNQ =90° ∴△BMP ∽△BNQ ∴∠PBM =∠QBN∴直线BQ 和直线BP 关于y 轴对称; (3)除点P 之外无别的交点.∵P(m,),H(m,﹣1),A(0,1)设直线AH解析式为y=k′x+b′,则,解得∴直线AH解析式为y=x+1,令y=0,得x=,∴E(,0)设直线PE解析式为y=k″x+b″,则,解得∴直线PE解析式为y=x,联立方程组,得=x,∴x2﹣2mx+m2=0∵△=(﹣2m)2﹣4m2=0∴直线PE与抛物线y=x2有且只有一个交点,即除点P之外无别的交点.。
2019年中考数学专题复习分类练习二次函数压轴题(无答案)
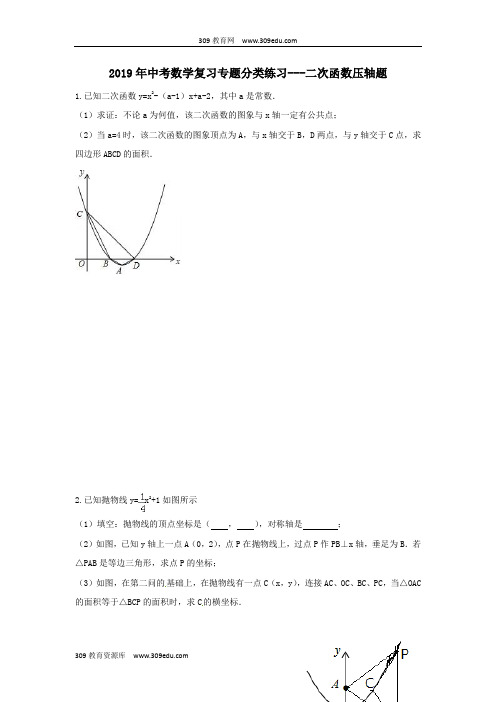
2019年中考数学复习专题分类练习---二次函数压轴题1.已知二次函数y=x2-(a-1)x+a-2,其中a是常数.(1)求证:不论a为何值,该二次函数的图象与x轴一定有公共点;(2)当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积.2.已知抛物线y=x2+1如图所示(1)填空:抛物线的顶点坐标是(,),对称轴是;(2)如图,已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;(3)如图,在第二问的基础上,在抛物线有一点C(x,y),连接AC、OC、BC、PC,当△OAC 的面积等于△BCP的面积时,求C的横坐标.3.已知二次函数22242y x mx m m =-++(m 是常数).(1)求该函数图像的顶点C 的坐标(用含m 的代数式表示);(2)当m 为何值时,函数图像的顶点C 在第二、四象限的角平分线上?4.已知二次函数2()()y a x m a x m =---(a m ,为常数,且0a ≠)的图像与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为D .(1)求点A ,B 的坐标;(2)过点D 作x 轴的垂线,垂足为E .若△CBO 与△DAE 相似(O 为坐标原点),试讨论m 与a 的关系;(3)在同一直角坐标系中,若该二次函数的图像与二次函数2()()y a x m a x m =--+-的图像组合成一个新的图像,则这个新图形的对称轴为 .5.阅读材料,解答问题.例 用图像法解一元二次不等式:x 2-2x -3>0.解:设y =x 2-2x -3,则y 是x 的二次函数.∵a =1>0,∴抛物线开口向上,又∵当y =0时,x 2-2x -3=0,解得x 1=-1,x 2=3.∴由此得抛物线y =x 2-2x -3的大致图像如图12所示,观察函数图像可知:当x <-1或x >3时,y >0.∴x 2-2x -3>0的解集是:x <-1或x >3.。
